Trắc nghiệm số phức có giải chi tiết trong các đề thi thử Toán 2018

Trắc nghiệm số phức có giải chi tiết trong các đề thi thử Toán 2018 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

61 31 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

153 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Câu 1:
(TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018)
Cho hai số thực
x
,
y
thoả mãn phương
trình
2 3 4x i yi
. Khi đó giá trị của
x
và
y
là:
A.
3
x
,
2
y
. B.
3x i
,
1
2
y
. C.
3
x
,
1
2
y
. D.
x
,
1
2
y
.
Lời giải
Chọn C
Từ
2 3 4x i yi
3
2 4
x
y
3
1
2
x
y
.
Vậy
3
x
,
1
3
y
.
Câu 2:
(TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018)
Phần thực và phần ảo của số phức
1 2z i
lần lượt là:
A.
2
và
1
B.
1
và
2i
. C.
1
và
2
. D.
1
và
i
.
Lời giải
Chọn C
Số phức
1 2z i
có phần thực và phần ảo lần lượt là
1
và
2
.
Câu 3:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Cho hai số phức
z a bi
,
z a b i
( , , , )
a b a b
. Tìm phần ảo của số phức
zz
.
A.
ab a b i
. B.
ab a b
. C.
ab a b
. D.
aa bb
.
Lời giải
Chọn B
Ta có:
zz
2
a bi a b i aa ab i a bi bb i
aa bb ab a b i
Vậy phần ảo của số phức
zz
là
ab a b
.
Câu 4:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Tìm tất cả các nghiệm của phương trình
2
2 5 0
z z
trên tập số phức
.
A.
1 2 i
;
1 2 i
. B.
1 i
;
1i
. C.
1 2 i
;
1 2 i
. D.
1 i
;
1 i
.
Lời giải:
Chọn C
2 2
1 5 4 4
i
.
Suy ra phương trình có hai nghiệm phức:
1
2
1 2
1 2
z i
z i
.
Câu 5:
(Đề tham khảo BGD năm 2017-2018)
Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
2z i
. B.
1 2z i
.
C.
2z i
. D.
1 2z i
.
Lời giải
Chọn A
Điểm
2;1
M
biểu diễn số phức
2z i
.
O
x
y
2
1
M
Câu 1:
(THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018)
Điểm nào trong hình vẽ dưới đây là điểm
biểu diễn của số phức
1 2
z i i
?
A.
P
. B.
M
. C.
N
. D.
Q
.
Lời giải
Chọn D
Ta có
1 2
z i i
3z i
. Điểm biểu diễn của số phức
z
là
3;1
Q
.
Câu 2:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Số phức
z
thỏa mãn
5 8z i
có
phần ảo là
A.
8
. B.
8i
. C.
5
. D.
8
.
Lời giải
Chọn D
Ta có
5 8z i
suy ra phần ảo của
z
là
8
.
Câu 3:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Nghiệm phức có phần ảo dương
của phương trình
2
1 0
z z
là:
A.
1 3
2 2
i
. B.
1 3
2 2
i
. C.
1 3
2 2
i
. D.
1 3
2 2
i
.
Lời giải
Chọn A
Ta có:
2
1 4 3 3i
.
Phương trình đã cho có hai nghiệm
1 3
2
i
và
1 3
2
i
.
Vậy nghiệm phức có phần ảo dương là
1 3
2 2
i
.
Câu 4:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Cho hai số phức
1
2 3z i
,
2
4 5z i
. Số
phức
1 2
z z z
là
A.
2 2z i
. B.
2 2z i
. C.
2 2z i
. D.
2 2z i
.
Lời giải
Chọn B
1 2
2 3 4 5 2 2z z z i i i
.
Câu 5:
(THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018)
Tìm giá trị cực tiểu của hàm số
4 2
4 3
y x x
A.
4
CT
y
. B.
6
CT
y
. C.
1
CT
y
. D.
8
CT
y
.
Hướng dẫn giải
Chọn C
Ta có:
3
4 8y x x
.
0
y
3
4 8 0
x x
0 3
2 1
2 1
x y
x y
x y
.
Bảng biến thiên
Vậy giá trị cực tiểu của hàm số là
1
CT
y
tại
2
CT
x
,
2
CT
x
.
Câu 1:
(THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018)
Phần ảo của số phức
2 3z i
là
A.
3i
. B.
3
. C.
3
. D.
3i
.
Lời giải
Chọn C
Phần ảo của số phức
2 3z i
là
3
.
Câu 2:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Cho số phức
2018 2017z i
. Điểm
M
biểu diễn của số phức liên hợp của
z
là
A.
2018;2017
M
. B.
2018; 2017
M
. C.
2018; 2017
M
. D.
2018;2017
M
.
Lời giải
Chọn D
Ta có
2018 2017z i
, nên
2018;2017
M
.
Câu 3:
(THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
1 2z i
. Số phức liên hợp
của
z
là
A.
1 2z i
. B.
1 2z i
. C.
2z i
. D.
1 2z i
.
Lời giải
Chọn D
Số phức liên hợp của
z
là
1 2z i
.
Câu 4:
(THPT Chuyên Tiền Giang-lần 1 năm 2017-2018)
Tìm tọa độ điểm biểu diễn của số phức
2 3 4
3 2
i i
z
i
.
A.
1; 4
. B.
1;4
. C.
1; 4
. D.
1;4
Lời giải
Chọn A
Ta có
2 3 4
3 2
i i
z
i
5 14
3 2
i
i
5 14 3 2
13
i i
13 52
13
i
1 4i
.
Do đó điểm biểu diễn cho số phức
z
có tọa độ
1; 4
.
Câu 5:
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
1
3 2z i
,
2
6 5z i
. Tìm số
phức liên hợp của số phức
1 2
6 5z z z
A.
51 40z i
. B.
51 40z i
. C.
48 37z i
. D.
48 37z i
.
Lời giải
Chọn D
Ta có:
1 2
6 5z z z
6 3 2 5 6 5i i
48 37i
.
Suy ra
48 37z i
.
Câu 6:
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018)
Xác định phần ảo của số phức
18 12z i
.
A.
12
. B.
18
. C.
12
. D.
12i
.
Lời giải
Chọn A
Phần ảo của số phức
18 12z i
là
12
.
Câu 7:
(THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018)
Số phức liên hợp của số phức
1 2z i
là
A.
1 2i
. B.
1 2i
. C.
2 i
. D.
1 2i
.
Lời giải
Chọn A
Số phức liên hợp của số phức
1 2z i
là
1 2z i
.
Câu 8: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Tìm phần ảo của số phức
z
, biết
1 3i z i
.
A.
2
. B.
2
. C.
1
. D.
1
.
Lời giải
Chọn B
Ta có:
1 3i z i
3
1
i
z
i
3 1
1 1
i i
z
i i
1 2z i
.
Vậy phần ảo của số phức
z
bằng
2
.
Câu 9: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Hỏi điểm
3; 1
M
là điểm biểu diễn
số phức nào sau đây?
A.
1 3z i
. B.
1 3z i
. C.
3z i
. D.
3z i
.
Lời giải
Chọn C
Điểm
;M a b
trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số
phức
z a bi
.
Do đó điểm
3; 1
M
là điểm biểu diễn số phức
3z i
.
Câu 10:
(THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018)
Cho số phức
4 5z i
. Biểu
diễn hình học của
z
là điểm có tọa độ
A.
4;5
. B.
4; 5
. C.
4; 5
. D.
4;5
.
Lời giải
Chọn A
Số phức
4 5z i
có phần thực
4
a
; phần ảo
5
b
nên điểm biểu diễn hình học của số
phức
z
là
4;5
.
Câu 11:
(THPT Chuyên Phan Bội Châu-lần 2 năm 2017-2018)
Cho số phức
2 3z i
. Môđun của số
phức
1
w i z
A.
26
w
. B.
37
w
. C.
5
w
. D.
4
w
.
Lời giải
Chọn A
Ta có
1
w i z
1 2 3i i
5 i
,
2
2
5 1 26
w
.
Câu 12:
(THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018)
Trong mặt phẳng
Oxy
, cho
các điểm
A
,
B
như hình vẽ bên. Trung điểm của đoạn thẳng
AB
biểu diễn số phức.
O
x
y
2
1
1
3
B
A
A.
1
2
2
i
. B.
1 2i
. C.
2 i
. D.
1
2
2
i
.
Lời giải
Chọn A
Trung điểm
AB
là
1
;2
2
I
biểu diễn số phức là
1
2
2
z i
.
Câu 13: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Số phức
z
nào sau đây
thỏa
5
z
và
z
là số thuần ảo?
A.
5
z
. B.
2 3z i
. C.
5z i
. D.
5z i
.
Lời giải
Chọn D
Gọi
z bi
, với
0
b
,
b
là số thuần ảo
loại A, B.
Ta có
5
z
5
b
Chọn D
Câu 14: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Cho số phức
z mi
,
( )
m
. Tìm phần ảo của số phức
1
z
?
A.
1
m
. B.
1
m
. C.
1
i
m
. D.
1
i
m
.
Lời giải
Chọn A
1 1
z mi
1
.
i
mi i
1
i
m
.
Câu 15: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Cho số phức
1 4 2i z i
. Tìm môđun của số phức
3w z
.
A.
5
. B.
10
. C.
25
. D.
7
.
Lời giải
Chọn A
Ta có:
4 2
1 3
1
i
z i
i
. Do đó:
3 4 3w z i
.
Vậy
2 2
4 3 5
w
.
Câu 16: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Phần ảo của số phức
5 2z i
bằng
A.
5
. B.
5i
. C.
2
. D.
2i
.
Lời giải
Chọn C
Câu 17:
(SGD Bắc Giang – năm 2017 – 2018)
Cho số phức
1 2z i
. Số phức
z
được biểu
diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ?
A.
1;2
P
. B.
1; 2
N
. C.
1; 2
Q
. D.
1;2
M
.
Lời giải
Chọn C
Ta có
1 2z i
1 2z i
. Suy ra điểm biểu diễn của số phức
z
là
1; 2
Q
.
Câu 18: (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho hai số phức
1
2 3z i
,
2
4 5z i
.
Tính
1 2
z z z
.
A.
2 2z i
. B.
2 2z i
. C.
2 2z i
. D.
2 2z i
.
Lời giải
Chọn A
1 2
z z z
2 3 4 5i i
2 2i
.
Câu 19: Cho số phức
3 2z i
. Tính
z
.
A.
5
z
. B.
13
z
. C.
5
z
. D.
13
z
.
Câu 20:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Cho số phức
3 2z i
. Tính
z
.
A.
5
z
. B.
13
z
. C.
5
z
. D.
13
z
.
Lời giải
Chọn B
Ta có
2 2
3 2 13
z
.
Câu 21: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức
3 4 .z i
Môđun
của
z
là
A.
3
. B.
5
. C.
4
. D.
7
.
Lời giải
Chọn B
Ta có
2
2
3 4 5.
z
Câu 22: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức
z
có biểu diễn
hình học là điểm
M
ở hình vẽ bên. Khẳng định nào sau đây là đúng?
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Lời giải
Chọn D
Điểm biểu diễn của số phức
z a bi
là
;M a b
.
Câu 23: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức
1z i
. Số phức
nghịch đảo của
z
là
A.
1
2
i
. B.
1 i
. C.
1
2
i
. D.
1
2
i
.
Lời giải
Chọn C
Ta có
1 1 1
1
1 2
i
z i
z i
.
O
x
y
M
3
2
Câu 24: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Tìm số phức liên hợp của số phức
z i
.
A.
1
. B.
1
. C.
i
. D.
i
.
Lời giải
Chọn D
Câu 25: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Gọi
A
,
B
lần lượt là các điểm biểu
diễn của các số phức
1
1 2z i
;
2
5z i
. Tính độ dài đoạn thẳng
.AB
A.
5 26
. B.
5
. C.
25
. D.
37
.
Lời giải
Chọn B
Ta có:
1;2
A
,
5; 1
B
5
AB
.
Câu 26: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Cho số phức
7 3z i
. Tính
z
.
A.
5
z
. B.
3
z
. C.
4
z
. D.
4
z
.
Lời giải
Chọn C
Ta có
7 9 4
z
.
Câu 27: (THPT Thuận Thành 2 – Bắc Ninh - Lần 2 năm 2017 – 2018)Mô đun của số phức
7 5z i
bằng
A.
74
. B.
24
. C.
74
. D.
2 6
.
Lời giải
Chọn C
Ta có
2 2
7 5 74
z
.
Câu 28: (THPT Thuận Thành 2 – Bắc Ninh - Lần 2 năm 2017 – 2018)Phần thực của số phức
3 1 4z i i
là
A.
1
. B.
13
. C.
1
. D.
13
.
Lời giải
Chọn A
Ta có:
3 1 4 1 13z i i i
.
Câu 29:
(THPT Chuyên Lương Thế Vinh – Đồng Nai – Lần 2 năm 2017 – 2018)
Cho số phức
z
thỏa mãn
1 3 5z i i
. Tính môđun của
z
.
A.
17
z
. B.
16
z
. C.
17
z
. D.
4
z
.
Lời giải
Chọn A
Ta có:
1 3 5z i i
3 5
1
i
z
i
1 4i
2 2
1 4
z
17
.
Câu 30: (THPT Chuyên Lương Thế Vinh – Đồng Nai – Lần 2 năm 2017 – 2018) Điểm
M
trong
hình vẽ bên là điểm biểu diễn của số phức
z
.
Tìm phần thực và phần ảo cú số phức
z
.
A. Phần thực bằng
4
và phần ảo bằng
3
. B. Phần thực bằng
4
và phần ảo bằng
3i
.
C. Phần thực bằng
3
và phần ảo bằng
4
. D. Phần thực bằng
3
và phần ảo bằng
4i
.
Lời giải
Chọn C
Từ hình vẽ ta có
3;4
M
nên
3 4z i
.
Vậy Phần thực bằng
3
và phần ảo bằng
4
.
Câu 31: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Cho số phức
2z i
. Điểm
nào dưới đây là điểm biểu diễn của số phức
w iz
trên mặt phẳng tọa độ?
A.
2;1
P
. B.
2;1
N
. C.
1;2
Q
. D.
1; 2
M
.
Lời giải
Chọn A
2 1 2w iz i i i
điểm
2;1
P
là điểm biểu diễn của số phức
w iz
trên
mặt phẳng tọa độ.
Câu 32:
(SGD Quảng Nam – năm 2017 – 2018)
Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
2 3z i
. D.
2 3z i
.
Lời giải
Chọn A
3 2z i
.
Câu 33: (ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Cho số phức
1 2z i
thì số phức liên hợp
z
có
A. phần thực bằng
1
và phần ảo bằng
2
. B. phần thực bằng
2
và phần ảo bằng
1
.
C. phần thực bằng
1
và phần ảo bằng
2
. D. phần thực bằng
2
và phần ảo bằng
1
.
Lời giải
Chọn C
1 2z i
. Do đó số phức liên hợp
z
có phần thực bằng
1
và phần ảo bằng
2
.
Câu 34:
(THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018)
Trong hình vẽ bên, điểm
M
biểu diễn số phức
z
. Số phức
z
là
A.
2 i
. B.
1 2i
. C.
1 2i
. D.
2 i
.
Lời giải
Chọn A
Dựa vào hình vẽ ta có
2z i
, suy ra
2z i
.
Câu 35: (SGD Nam Định – năm 2017 – 2018) Trong các mệnh đề sau, mệnh đề nào đúng?
O
x
y
M
3
4
A. Số phức
2 3z i
có phần thực là
2
, phần ảo là
3
.
B. Số phức
2 3z i
có phần thực là
2
, phần ảo là
3i
.
C. Số phức
2 3z i
có phần thực là
2
, phần ảo là
3i
.
D. Số phức
2 3z i
có phần thực là
2
, phần ảo là
3
.
Lời giải
Chọn A
Mỗi số phức
z a bi
có phần thực là
a
, phần ảo là
b
.
Câu 36:
(SGD Nam Định – năm 2017 – 2018)
Cho hai số phức
1
1 2z i
,
2
3z i
. Tìm số
phức
2
1
z
z
z
.
A.
1 7
5 5
z i
. B.
1 7
10 10
z i
. C.
1 7
5 5
z i
. D.
1 7
10 10
z i
.
Lời giải
Chọn C
Ta có
2
1
z
z
z
3
1 2
i
i
1 7
5 5
i
.
Câu 1:
(SGD Thanh Hóa – năm 2017 – 2018)
Tính môđun của số phức
3 4z i
.
A.
3
. B.
5
. C.
7
. D.
7
.
Lời giải
Chọn B
Môđun của số phức
3 4z i
là:
2 2
3 4
z
5
.
Câu 2: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Số phức
liên hợp của số phức
1 2z i i
có điểm biểu diễn là điểm nào dưới đây?
A.
2; 1
E
. B.
1;2
B
. C.
1;2
A
. D.
2;1
F
.
Lời giải
Chọn A
Ta có:
1 2 2 2z i i i z i
nên điểm biểu diễn của số phức
z
là
2; 1
E
.
Câu 3:
(THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018)
Điểm
A
trong hình vẽ bên dưới
biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng?
x
y
3
A
O
2
A. Phần thực là
3
, phần ảo là
2
. B. Phần thực là
3
, phần ảo là
2i
.
C. Phần thực là
3
, phần ảo là
2i
. D. Phần thực là
3
, phần ảo là
2
.
Lời giải
Chọn A
Câu 4:
(THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018)
Cho số phức
1 2z i
. Điểm
nào dưới đây là điểm biểu diễn của số phức
w z i z
trên mặt phẳng toạ độ?
A.
3;3
M
. B.
3;2
Q
. C.
2;3
N
. D.
3;3
P
.
Lời giải
Chọn A
w z iz
1 2 1 2i i i
3 3i
.
Vậy điểm biểu diễn của số phức
w z i z
là
3;3
M
.
Câu 5:
(SGD Hà Tĩnh – Lần 2 năm 2017 – 2018)
Cho hai số phức
1
2 3z i
,
2
1z i
. Giá trị của biểu
thức
1 2
3z z
là
A.
55
. B.
5
. C.
6
. D.
61
.
Hướng dẫn giải
Chọn D
Ta có:
1 2
3 2 3 3 1
z z i i
5 6i
2 2
5 6
61
.
Câu 6:
(SGD Hà Tĩnh – Lần 2 năm 2017 – 2018)
Gọi
0
z
là nghiệm phức có phần ảo dương của phương
trình
2
2 10 0
z z
. Tính
0
iz
.
A.
0
3iz i
. B.
0
3 1iz i
. C.
0
3iz i
. D.
0
3 1iz i
.
Hướng dẫn giải
Chọn C
Ta có:
2
2 10 0
z z
1 3
1 3
z i
z i
0
1 3z i
0
3iz i
.
Câu 7: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Phần thực và phần ảo của số phức liên hợp của số
phức
1z i
là:
A. Phần thực là
1
, phần ảo là
1
. B. Phần thực là
1
, phần ảo là
i
.
C. Phần thực là
1
, phần ảo là
i
. D. Phần thực là
1
, phần ảo là
1
.
Lời giải
Chọn A
Ta có số phức liên hợp của số phức
1z i
là
1z i
, suy ra Phần thực và phần ảo của số
phức liên hợp của số phức
1z i
là và
1
.
Câu 8:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Điểm biểu diễn của số phức
z
là
1;2
M
. Tọa
độ của điểm biểu diễn cho số phức
2w z z
là
A.
2; 3
. B.
2;1
. C.
1;6
. D.
2;3
.
Lời giải
Chọn C
Ta có:
1 2z i
nên
2 1 2 2 1 2 1 6w z z i i i
.
Do đó, số phức
2w z z
có điểm biểu diễn là
1;6
.
Câu 9:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Gọi
1
z
và
2
z
lần lượt là hai nghiệm của
phương trình
2
4 5 0
z z
. Giá trị của biểu thức
1 2 2 1
2 . 4P z z z z
bằng:
A.
10
. B.
10
. C.
5
. D.
15
.
Lời giải
Chọn D
Ta có
2
4 5 0
z z
1
2
2
2
z i
z i
.
Vậy
1 2 2 1
2 . 4P z z z z
2 2 2 . 2 4 2
i i i i
15
.
Câu 10:
(THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018)
Mô đun của số phức
7 3z i
là.
A.
5
z
. B.
10
z
. C.
16
z
. D.
4
z
.
Hướng dẫn giải
Chọn D
Ta có:
7 9 4
z
.
Câu 11:
(THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018)
Cho
1
z
,
2
z
là hai nghiệm
phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương. Số phức liên hợp của số
phức
1 2
2z z
là?
A.
3 2i
. B.
3 2i
. C.
2 i
. D.
2 i
.
Hướng dẫn giải
Chọn A
Ta có:
1
2
2
1 2i
2 5 0
1 2i
z
z z
z
( Vì
1
z
có phần ảo dương)
Suy ra:
1 2
2 1 2i 2 1 2i 3 2i
z z
.
Vậy: Số phức liên hợp của số phức
1 2
2z z
là
3 2i
.
Câu 12:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Cho số phức
2
1 1 2z i i
. Số phức
z
có phần
ảo là:
A.
2
. B.
4
. C.
2
. D.
2i
.
Lời giải
Chọn A
Ta có
2
1 1 2 2 1 2 4 2z i i i i i
. Vậy số phức
z
có phần ảo là
2
.
Câu 13:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Điểm
M
trong hình bên là điểm biểu diễn
cho số phức
A.
4 2z i
. B.
2 4z i
. C.
4 2z i
. D.
2 4z i
.
Lời giải
Chọn B
Điểm
M
biểu diễn cho số phức
2 4z i
.
Câu 14: Cho hai số phức
1
1 2z i
và
2
2 3z i
. Phần ảo của số phức
1 2
3 2w z z
là
A.
1
. B.
11
. C.
12
. D.
12i
.
Câu 15: Cho hai số phức
1
1 2z i
và
2
2 3z i
. Phần ảo của số phức
1 2
3 2w z z
là
A.
1
. B.
11
. C.
12
. D.
12i
.
Lời giải
Chọn C
Ta có
1 2
3 2w z z
3 1 2 2 2 3i i
1 12i
.
Vậy phần ảo của số phức
w
là 12.
Câu 16: Cho số phức
z a bi
,a b
. Khẳng định nào sau đây sai?
A.
2 2
z a b
. B.
z a bi
. C.
2
z
là số thực. D.
.z z
là số thực.
Câu 17: Cho hai số phức
z
và
z
. Trong các mệnh đề sai, mệnh đề nào sai?
A.
z z z z
. B.
. .z z z z
. C.
. .z z z z
. D.
z z z z
.
Câu 18: Cho số phức
z a bi
,a b
. Khẳng định nào sau đây sai?
A.
2 2
z a b
. B.
z a bi
. C.
2
z
là số thực. D.
.z z
là số thực.
Lời giải
Chọn C
Đáp án A và B đúng theo định nghĩa.
Đáp án C: Ta có
2
2 2 2
2
z a bi a bi b
là số phức có phần ảo khác
0
khi
0
b
Sai.
Đáp án D:
2
2 2 2
.
z z a bi a bi a bi a b
là một số thực
Đúng.
Câu 19: Cho hai số phức
z
và
z
. Trong các mệnh đề sai, mệnh đề nào sai?
A.
z z z z
. B.
. .z z z z
. C.
. .z z z z
. D.
z z z z
.
Lời giải
Chọn A
Với hai số phức
z
và
z
, ta có:
z z z z
.
Câu 20: Cho hai số phức
1
3z i
và
2
4z i
. Tính môđun của số phức
2
1 2
z z
.
A.
12
. B.
10
. C.
13
. D.
15
.
Câu 21: Cho hai số phức
1
3z i
và
2
4z i
. Tính môđun của số phức
2
1 2
z z
.
A.
12
. B.
10
. C.
13
. D.
15
.
Lời giải
Chọn C
Ta có:
2
1 2
z z
2
3 4
i i
12 5i
nên
2 2 2
1 2
12 5 13
z z
.
Câu 22: Tìm tọa độ điểm
M
là điểm biểu diễn số phức
3 4z i
.
A.
3; 4
M
. B.
3;4
M
. C.
3; 4
M
. D.
3;4
M
.
Câu 23: Tìm tọa độ điểm
M
là điểm biểu diễn số phức
3 4z i
.
A.
3; 4
M
. B.
3;4
M
. C.
3; 4
M
. D.
3;4
M
.
Lời giải
Chọn A
Ta có điểm
3; 4
M
biểu diễn số phức
3 4z i
.
Câu 24: Số phức
4 2z i
có điểm biểu diễn trên mặt phẳng tọa độ là
M
. Tìm tọa độ điểm
M
A.
4;2
M
. B.
2;4
M
. C.
4; 2
M
. D.
4; 2
M
.
Câu 25: Số phức
4 2z i
có điểm biểu diễn trên mặt phẳng tọa độ là
M
. Tìm tọa độ điểm
M
A.
4;2
M
. B.
2;4
M
. C.
4; 2
M
. D.
4; 2
M
.
Lời giải
Chọn A
Số phức
4 2z i
có điểm biểu diễn trên mặt phẳng tọa độ là
4;2
M
.
Câu 26: Cho số phức
z
thỏa mãn
1 1 5 0z i i
. Số phức
1w z
bằng
A.
1 3i
.
B.
1 3i
. C.
2 3i
. D.
2 3i
.
Câu 27: Cho số phức
z
thỏa mãn
1 1 5 0z i i
. Số phức
1w z
bằng
A.
1 3i
.
B.
1 3i
. C.
2 3i
. D.
2 3i
.
Lời giải
Chọn D
Ta có
1 1 5 0z i i
1 2 3z i
1 3z i
.
Vậy
1w z
1 1 3 2 3i i
.
Câu 28: Gọi
,a b
lần lượt là phần thực và phần ảo của số phức
1 3 1 2 3 4 2 3 .z i i i i
Giá trị của
a b
là
A.
7
. B.
7
. C.
31
. D.
31
.
Câu 29: Gọi
,a b
lần lượt là phần thực và phần ảo của số phức
1 3 1 2 3 4 2 3 .z i i i i
Giá trị của
a b
là
A.
7
. B.
7
. C.
31
. D.
31
.
Lời giải
Chọn B
Ta có:
1 3 1 2 3 4 2 3z i i i i
2 1 2 5 2 3i i
12 19i
Vậy
12 19 7.
a b
Câu 30: Cho số phức
z
có số phức liên hợp
3 2z i
. Tổng phần thực và phần ảo của số phức
z
bằng.
A.
1
. B.
5
. C.
5
. D.
1
.
Câu 31: Cho số phức
z
thỏa mãn
1 2 1 2 2
i z i i
. Mô đun của
z
bằng
A.
2
. B.
1
. C.
2
. D.
10
.
Câu 32: Cho số phức
z
có số phức liên hợp
3 2z i
. Tổng phần thực và phần ảo của số phức
z
bằng.
A.
1
. B.
5
. C.
5
. D.
1
.
Hướng dẫn giải
Chọn C
Ta có:
3 2z i
. Vậy tổng phần thực và phần ảo của số phức
z
bằng
5
.
Câu 33: Cho số phức
z
thỏa mãn
1 2 1 2 2
i z i i
. Mô đun của
z
bằng
A.
2
. B.
1
. C.
2
. D.
10
.
Hướng dẫn giải
Chọn C
3
1 2 1 2 2 1 2 3 1
1 2
i
i z i i i z i z i
i
. Vậy
2
z
.
Câu 34: Cho các số phức
1
2 3z i
,
2
4 5z i
. Số phức liên hợp của số phức
1 2
2
w z z
là
A.
8 10w i
. B.
12 16w i
. C.
12 8w i
. D.
28w i
.
Câu 35: Cho các số phức
1
2 3z i
,
2
4 5z i
. Số phức liên hợp của số phức
1 2
2
w z z
là
A.
8 10w i
. B.
12 16w i
. C.
12 8w i
. D.
28w i
.
Lời giải
Chọn B
Ta có
2 6 8 12 16 12 16w i i w i
.
Câu 36: Cho số phức
z a bi
với
a
,
b
là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
A. Phần ảo của
z
là
bi
. B. Môđun của
2
z
bằng
2 2
a b
.
C.
z z
không phải là số thực. D. Số
z
và
z
có môđun khác nhau.
Câu 37: Cho số phức
z a bi
với
a
,
b
là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
A. Phần ảo của
z
là
bi
. B. Môđun của
2
z
bằng
2 2
a b
.
C.
z z
không phải là số thực. D. Số
z
và
z
có môđun khác nhau.
Lời giải
Chọn B
2
2
2 2 2 2 2
z z a b a b
.
Câu 38: Cho số phức
3z i
. Tính
z
.
A.
2 2
z
. B.
2
z
. C.
4
z
. D.
10
z
.
Câu 39: Điểm M trong hình vẽ dưới đây biểu thị cho số phức
A.
3 2i
. B.
2 3i
.
C.
2 3i
. D.
3 2i
.
Câu 40: Cho
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 1 0
z
(trong đó số phức
1
z
có phần ảo âm). Tính
1 2
3z z
.
A.
1 2
3 2.z z i
. B.
1 2
3 2
z z
. C.
1 2
3 2.z z i
. D.
1 2
3 2
z z
.
Câu 41: Cho số phức
3z i
. Tính
z
.
A.
2 2
z
. B.
2
z
. C.
4
z
. D.
10
z
.
Lời giải
Chọn D
Ta có
2 2
3 1 10
z z
.
Câu 42: Điểm M trong hình vẽ dưới đây biểu thị cho số phức
A.
3 2i
. B.
2 3i
. C.
2 3i
. D.
3 2i
.
Lời giải
Chọn B
Hoành độ, tung độ của điểm
M
là phần thực, phần ảo của số phức
2 3z i
.
Câu 43: Cho
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 1 0
z
(trong đó số phức
1
z
có phần ảo âm). Tính
1 2
3z z
.
O
x
y
M
2
3
O
x
y
M
2
3
A.
1 2
3 2.z z i
. B.
1 2
3 2
z z
. C.
1 2
3 2.z z i
. D.
1 2
3 2
z z
.
Lời giải
Chọn A
Ta có:
2
2 1 0
z
1
2
2
2
2
2
z i
z i
. Khi đó:
1 2
3z z
2 2
3
2 2
i i
2i
.
Câu 44: Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z a bi
(
,a b
,
0
ab
),
M
là điểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng?
A.
M
đối xứng với
M
qua
Oy
.
B.
M
đối xứng với
M
qua
Ox
.
C.
M
đối xứng với
M
qua đường thẳng
y x
.
D.
M
đối xứng với
M
qua
O
.
Câu 45: Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z a bi
(
,a b
,
0
ab
),
M
là điểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng?
A.
M
đối xứng với
M
qua
Oy
.
B.
M
đối xứng với
M
qua
Ox
.
C.
M
đối xứng với
M
qua đường thẳng
y x
.
D.
M
đối xứng với
M
qua
O
.
Lời giải
Chọn B
Ta có
M
là điểm biễu diễn cho số phức
z a bi
;
M a b
nên
M
đối xứng với
M
qua
Ox
.
Câu 46: Gọi
1 2 3
, ,z z z
là ba nghiệm của phương trình
3
1 0
z
. Tính
1 2 3
S z z z
A.
1
S
. B.
4
S
. C.
2
S
. D.
3
S
.
Câu 47: Gọi
1 2 3
, ,z z z
là ba nghiệm của phương trình
3
1 0
z
. Tính
1 2 3
S z z z
A.
1
S
. B.
4
S
. C.
2
S
. D.
3
S
.
Lời giải
Chọn D
Ta có:
3
1
1 3
1 0
2 2
1 3
2 2
z
z z i
z i
. Do đó:
1 3 1 3
1 3
2 2 2 2
S i i
.
Câu 48: Trong mặt phẳng phức, cho số phức
1 2z i
. Điểm biểu diễn cho số phức
z
là điểm nào sau
đây
A.
1; 2
M
. B.
1;2
Q
. C.
1;2
P
. D.
2;1
N
.
Câu 49: Trong mặt phẳng phức, cho số phức
1 2z i
. Điểm biểu diễn cho số phức
z
là điểm nào sau
đây
A.
1; 2
M
. B.
1;2
Q
. C.
1;2
P
. D.
2;1
N
.
Lời giải
Chọn B
Ta có:
1 2z i
1 2z i
nên có điểm biểu diễn là
1;2
.
Câu 50: Trong mặt phẳng
Oxy
, điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Số phức
z
là
A.
2 i
. B.
1 2i
. C.
2 i
. D.
1 2i
.
Câu 51: Trong mặt phẳng
Oxy
, điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Số phức
z
là
A.
2 i
. B.
1 2i
. C.
2 i
. D.
1 2i
.
Hướng dẫn giải
Chọn C
Ta có
2 2z i z i
.
Câu 52: Cho số phức
11z i
. Điểm biểu diễn số phức liên hợp của
z
là điểm nào dưới đây?
A.
11;0
Q
. B.
11;1
M
. C.
11;0
P
. D.
11; 1
N
.
Câu 53: Cho số phức
11z i
. Điểm biểu diễn số phức liên hợp của
z
là điểm nào dưới đây?
A.
11;0
Q
. B.
11;1
M
. C.
11;0
P
. D.
11; 1
N
.
Lời giải
Chọn D
Vì
11z i
nên điểm biểu diễn số phức liên hợp
z
là
11; 1
N
.
Câu 54: Phần thực của số phức
1 2z i
bằng
A.
2
. B.
1
. C.
1
. D.
3
.
Câu 55: Phần thực của số phức
1 2z i
bằng
A.
2
. B.
1
. C.
1
. D.
3
.
Hướng dẫn giải
Chọn C
Phần thực của số phức
1 2z i
bằng
1
.
Câu 56: Cho hai số phức
1
2 3z i
,
2
3 2z i
. Tích
1 2
.z z
bằng:
A.
5i
. B.
6 6i
. C.
5i
. D.
12 5i
.
Câu 57: Số phức nghịch đảo
1
z
của số phức
2 2z i
là
A.
1 1
4 4
i
. B.
1 1
4 4
i
. C.
1 1
4 4
i
. D.
1 1
4 4
i
.
Câu 58: Cho hai số phức
1
2 3z i
,
2
3 2z i
. Tích
1 2
.z z
bằng:
A.
5i
. B.
6 6i
. C.
5i
. D.
12 5i
.
Lời giải
Chọn D
Ta có
1 2
. 2 3 . 3 2 12 5z z i i i
.
Câu 59: Số phức nghịch đảo
1
z
của số phức
2 2z i
là
A.
1 1
4 4
i
. B.
1 1
4 4
i
. C.
1 1
4 4
i
. D.
1 1
4 4
i
.
Lời giải
Chọn C
Ta có
1
z
1
2 2i
2 2
8
i
1 1
4 4
i
.
Câu 60: Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là
A.
2
. B.
4
. C.
2
. D.
2i
.
Câu 61: Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là
A.
2
. B.
4
. C.
2
. D.
2i
.
Lời giải
Chọn A
2
1 1 2z i i
2
1 2 1 2i i i
2 1 2i i
2
2 4i i
2 4i
có phần ảo là
2
.
Câu 62: Số phức
15 3z i
có phần ảo bằng
A.
3
. B.
15
. C.
3i
. D.
3
.
Câu 63: Cho hai số phức
3 5z i
và
1 2w i
. Điểm biểu diễn số phức
.z z w z
trong mặt phẳng
Oxy
có tọa độ là
A.
4; 6
. B.
4; 6
. C.
4; 6
. D.
6; 4
.
Câu 64: Số phức
15 3z i
có phần ảo bằng
A.
3
. B.
15
. C.
3i
. D.
3
.
Lời giải
Chọn A
Câu 65: Cho hai số phức
3 5z i
và
1 2w i
. Điểm biểu diễn số phức
.z z w z
trong mặt phẳng
Oxy
có tọa độ là
A.
4; 6
. B.
4; 6
. C.
4; 6
. D.
6; 4
.
Lời giải
Chọn A
Ta có
.z z w z
3 5 1 2 3 5i i i
3 5 7 11i i
4 6i
.
Câu 66: Tìm phần thực và phần ảo của số phức
3 2 z i
.
A. Phần thực bằng
3
và phần ảo bằng
2 . i
B. Phần thực bằng
3
và phần ảo bằng
2.
C. Phần thực bằng 3 và phần ảo bằng
2 .i
D. Phần thực bằng 3 và phần ảo bằng 2.
Câu 67: Tìm phần thực và phần ảo của số phức
3 2 z i
.
A. Phần thực bằng
3
và phần ảo bằng
2 . i
B. Phần thực bằng
3
và phần ảo bằng
2.
C. Phần thực bằng 3 và phần ảo bằng
2 .i
D. Phần thực bằng 3 và phần ảo bằng 2.
Lời giải
Chọn D
Số phức
3 2 z i
có phần thực bằng 3 và phần ảo bằng 2.
Câu 68: Cho số phức
2 4z i
. Hiệu phần thực và phần ảo của
z
bằng.
A.
2
. B.
2 5
. C.
2
. D.
6
.
Câu 69: Cho số phức
2 4z i
. Hiệu phần thực và phần ảo của
z
bằng.
A.
2
. B.
2 5
. C.
2
. D.
6
.
Hướng dẫn giải
Chọn C
Phần thực và phần ảo lần lượt là
2
và
4
. Vậy hiệu phần thực và phần ảo của
z
bằng
2
.
Câu 70: Điểm
M
trong hình vẽ dưới đây biểu diễn số phức
z
.
x
y
2
3
M
O
1
Số phức
z
bằng
A.
2 3i
. B.
2 3i
. C.
3 2i
. D.
3 2i
.
Câu 71: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 5 0
z z
. Giá trị của biểu thức
2 2
1 2
z z
bằng.
A.
10
. B.
20
. C.
6
. D.
6 8i
.
Câu 72: Điểm
M
trong hình vẽ dưới đây biểu diễn số phức
z
.
x
y
2
3
M
O
1
Số phức
z
bằng
A.
2 3i
. B.
2 3i
. C.
3 2i
. D.
3 2i
.
Lời giải
Chọn A
Theo hình vẽ thì
2 3z i
2 3z i
.
Câu 73: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 5 0
z z
. Giá trị của biểu thức
2 2
1 2
z z
bằng.
A.
10
. B.
20
. C.
6
. D.
6 8i
.
Lời giải
Chọn A
2
4 5 0
z z
1
2
2
2
z i z
z i z
.
2 2
1 2
z z
2 2
1 2
5 5 10
z z
.
Câu 74: Cho số phức
1 2z i
. Điểm biểu diễn của số phức
z
là
A.
1;2
M
. B.
1; 2
M
. C.
1; 2
M
. D.
2;1
M
.
Câu 75: Cho phương trình
2
4 5 0
z z
có hai nghiệm phức
1
z
,
2
z
. Tính
1 2 1 2
A z z z z
.
A.
25 2 5
A . B.
0
A
. C.
5 2 5
A . D.
5 2 5
A .
Câu 76: Cho số phức
1 2z i
. Điểm biểu diễn của số phức
z
là
A.
1;2
M
. B.
1; 2
M
. C.
1; 2
M
. D.
2;1
M
.
Lời giải
Chọn C
Ta có
1 2z i
có điểm biểu diễn là
1; 2
M
.
Câu 77: Cho phương trình
2
4 5 0
z z
có hai nghiệm phức
1
z
,
2
z
. Tính
1 2 1 2
A z z z z
.
A.
25 2 5
A . B.
0
A
. C.
5 2 5
A . D.
5 2 5
A .
Lời giải
Chọn D
2
4 5 0
z z
1
1
2
2
z i
z i
.
Do đó:
1 2 1 2
A z z z z
5 2 5
.
Câu 78: Cho số phức
3 4z i
. Môđun của
z
bằng
A.
25
. B.
7
. C.
1
. D.
5
.
Câu 79: Cho số phức
3 4z i
. Môđun của
z
bằng
A.
25
. B.
7
. C.
1
. D.
5
.
Lời giải
Chọn D
Ta có
2
2
3 4 5
z
.
Câu 80: Số phức nào dưới đây là số thuần ảo?
A.
3 2z i
. B.
2 3z i
. C.
2z i
. D.
2z
.
Câu 81: Trên mặt phẳng tọa độ
Oxy
cho điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức
z
.
x
y
3
-4
M
O 1
Tìm
z
?
A.
4 3z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Câu 82: Số phức nào dưới đây là số thuần ảo?
A.
3 2z i
. B.
2 3z i
. C.
2z i
. D.
2z
.
Hướng dẫn giải
Chọn C
Câu 83: Trên mặt phẳng tọa độ
Oxy
cho điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức
z
.
x
y
3
-4
M
O 1
Tìm
z
?
A.
4 3z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Hướng dẫn giải
Chọn C
Số phức
z
có phần thực
3
a
và phần ảo
4
b
nên
3 4z i
.
Câu 84: Cho số phức
1 4z i
. Tìm phần thực của số phức
z
.
A.
1
. B.
1
. C.
4
. D.
4
.
Câu 85: Tìm các số thực
,x y
thỏa mãn
2 1 1 2 2 3 2x y i x y i
.
A.
3
1;
5
x y
. B.
3
3;
5
x y
. C.
1
3;
5
x y
. D.
1
1;
5
x y
.
Câu 86: Cho số phức
1 4z i
. Tìm phần thực của số phức
z
.
A.
1
. B.
1
. C.
4
. D.
4
.
Lời giải
Chọn A
Ta có
1 4z i
. Vậy phần thực của số phức
z
là
1
.
Câu 87: Tìm các số thực
,x y
thỏa mãn
2 1 1 2 2 3 2x y i x y i
.
A.
3
1;
5
x y
. B.
3
3;
5
x y
. C.
1
3;
5
x y
. D.
1
1;
5
x y
.
Lời giải
Chọn D
2 1 1 2 2 3 2
x y i x y
2 1 2
1 2 3 2
x x
y y
1
1
5
x
y
Câu 88: Trong mặt phẳng tọa độ, điểm
3;2
M
là điểm biểu diễn của số phức nào dưới đây?
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 89: Trong mặt phẳng tọa độ, điểm
3;2
M
là điểm biểu diễn của số phức nào dưới đây?
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Lời giải
Chọn B
Điểm
3;2
M
là điểm biểu diễn của số phức
3 2z i
.
Câu 90: Cho bốn điểm
A
,
B
,
C
,
D
trên hình vẽ biểu diễn 4 số phức
khác nhau. Chọn mệnh đề sai.
A.
B
là biểu diễn số phức
1 2z i
.
B.
D
là biểu diễn số phức
1 2z i
.
C.
C
là biểu diễn số phức
1 2z i
.
D.
A
là biểu diễn số phức
2z i
.
Câu 91: Cho bốn điểm
A
,
B
,
C
,
D
trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai.
A.
B
là biểu diễn số phức
1 2z i
. B.
D
là biểu diễn số phức
1 2z i
.
C.
C
là biểu diễn số phức
1 2z i
. D.
A
là biểu diễn số phức
2z i
.
Lời giải
Chọn B
Theo hình vẽ thì điểm
D
là biểu diễn số phức
2z i
. Suy ra B sai.
Câu 92: Kí hiệu
1
z
,
2
z
là hai nghiệm phức của phương trình
2
1 0
z z
. Giá trị của biểu thức
2 2
1 2 1 2
P z z z z
bằng:
A.
1P
. B.
2P
. C.
1P
. D.
0
P
.
Câu 93: Điểm M trong hình bên là điểm biểu diễn của số phức
z
.
O
x
y
1
1
1
1
2
2
A
D
C
B
O
x
y
1
1
1
1
2
2
A
D
C
B
x
y
O
-4
3
Mệnh đề nào dưới đây đúng?
A. Số phức
z
có phần thực là
3
và phần ảo là
4
.
B. Số phức
z
phần thực là
3
và phần ảo là
4i
.
C. Số phức
z
phần thực là
4
và phần ảo là
3
.
D. Số phức
z
phần thực là
4
và phần ảo là
3i
.
Câu 94: Kí hiệu
1
z
,
2
z
là hai nghiệm phức của phương trình
2
1 0
z z
. Giá trị của biểu thức
2 2
1 2 1 2
P z z z z
bằng:
A.
1P
. B.
2P
. C.
1P
. D.
0
P
.
Lời giải
Chọn D
2
1 0
z z
có
1 2
1
z z
và
1 2
. 1
z z
Khi đó
2 2
1 2 1 2
P z z z z
2
1 2 1 2
.z z z z
0
P
.
Câu 95: Điểm M trong hình bên là điểm biểu diễn của số phức
z
.
x
y
O
-4
3
Mệnh đề nào dưới đây đúng?
A. Số phức
z
có phần thực là
3
và phần ảo là
4
.
B. Số phức
z
phần thực là
3
và phần ảo là
4i
.
C. Số phức
z
phần thực là
4
và phần ảo là
3
.
D. Số phức
z
phần thực là
4
và phần ảo là
3i
.
Lời giải
Chọn A
Điểm
M
biểu diễn cho số phức
3 4z i
.
Câu 96: Điểm
M
trong hình vẽ bên biểu diễn số phức
z
. Số phức
z
bằng
A.
2 3i
. B.
2 3i
. C.
3 2i
. D.
3 2i
.
Câu 97: Điểm
M
trong hình vẽ bên biểu diễn số phức
z
. Số phức
z
bằng
A.
2 3i
. B.
2 3i
. C.
3 2i
. D.
3 2i
.
Lời giải
Chọn B
Ta có
2;3
M
là điểm biểu diễn số phức
2 3z i
.
Do đó
2 3z i
.
Câu 98: Cho hai số phức
1
2 2z i
,
2
3 3z i
. Khi đó số phức
1 2
z z
là
A.
5 5i
. B.
5i
. C.
5 5i
. D.
1 i
.
Câu 99: Cho hai số phức
1
2 2z i
,
2
3 3z i
. Khi đó số phức
1 2
z z
là
A.
5 5i
. B.
5i
. C.
5 5i
. D.
1 i
.
Lời giải
Chọn C
Ta có
1 2
2 2 3 3 5 5z z i i i
.
Câu 100: Tìm tọa độ của điểm biểu diễn hình học của số phức
8 9 z i
.
A.
8;9
. B.
8; 9
. C.
9;8
. D.
8; 9 i
.
Câu 101: Cho số phức
z a bi
, với
,a b
. Tìm mệnh đề đúng trong các mệnh đề sau?
A.
2z z bi
. B.
2z z a
. C.
2 2
.
z z a b
. D.
2
2
z z
.
Câu 102: Tìm tọa độ của điểm biểu diễn hình học của số phức
8 9 z i
.
A.
8;9
. B.
8; 9
. C.
9;8
. D.
8; 9 i
.
Lời giải
Chọn B
Câu 103: Cho số phức
z a bi
, với
,a b
. Tìm mệnh đề đúng trong các mệnh đề sau?
3
2
x
M
y
O
3
2
x
M
y
O
A.
2z z bi
. B.
2z z a
. C.
2 2
.
z z a b
. D.
2
2
z z
.
Lời giải
Chọn D
Câu 104: Số phức nào dưới đây là số thuần ảo ?
A.
2z
. B.
2z i
. C.
2 2z i
. D.
1 2z i
.
Câu 105: Số phức nào dưới đây là số thuần ảo ?
A.
2z
. B.
2z i
. C.
2 2z i
. D.
1 2z i
.
Lời giải
Chọn B
Câu 106: Cho số phức
1
z
,
2
z
thỏa mãn
1
1
z
và
2 2
1 6 2z z i i
là một số thực. Tìm giá trị nhỏ
nhất của biểu thức
2
2 1 2 1 2
P z z z z z
.
A.
18 6 2
. B.
3 2
. C.
18 6 2
. D.
18 9 2
.
Câu 107: Cho số phức
1
z
,
2
z
thỏa mãn
1
1
z
và
2 2
1 6 2z z i i
là một số thực. Tìm giá trị nhỏ
nhất của biểu thức
2
2 1 2 1 2
P z z z z z
.
A.
18 6 2
. B.
3 2
. C.
18 6 2
. D.
18 9 2
.
Hướng dẫn giải
Chọn A
Đặt
2
z x yi
,
,x y
, ta có
2 2
2 2
1 6 2 2 6z z i i x y x y x y i
.
Vì
2 2
1 6 2z z i i
là số thực nên
6 0
x y
.
Ta có
2 2 2 2 2
2 1 2 1 2 1 2
1
P z z z z z z z
.
Gọi
A
là điểm biểu diễn số phức
1
z
, suy ra
A
nằm trên đường tròn
C
tâm
O
bán kính
1r
.
Gọi
B
là điểm biểu diễn số phức
2
z
, suy ra
B
nằm trên đường thẳng
: 6 0
x y
.
Ta có
2
1P AB
.
Mà
0 0 6
; 1 3 2 1
2
AB d O r
.
Nên
2
3 2 1 1 18 6 2
P
.
Dấu “=” xảy ra khi và chỉ khi
B
là hình chiếu vuông góc của
O
trên
và
A
là giao điểm của
đoạn
OB
với đường tròn
C
.
Câu 1:
(THTT Số 1-484 tháng 10 năm 2017-2018)
Kí hiệu
0
z
là nghiệm phức có phần thực âm và phần
ảo dương của phương trình
2
2 10 0
z z
. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm
biểu diễn số phức
2017
0
w i z
?
A.
3; 1
M
. B.
3; 1
M
. C.
3; 1
M
. D.
3; 1
M
.
Lời giải
Chọn D
Ta có:
2
1 3
2 10 0
1 3
z i
z z
z i
. Suy ra
0
1 3z i
.
2017
0
. 1 3 3w i z i i i
.
Suy ra : Điểm
3; 1
M
biểu diễn số phức
w
.
Câu 2:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Cho số phức
z
thỏa mãn:
2 13 1z i i
. Tính mô đun của số phức
z
.
A.
34
z
. B.
34
z
. C.
34
3
z
. D.
5 34
3
z
.
Lời giải
Chọn B
Cách 1: Ta có
2 13 1z i i
1 13
2
i
z
i
1 13
34
2
i
z
i
.
2 2
11 27
5 5
z
850
34
25
z
.
Cách 2: Dùng máy tính Casio bấm
1 13
2
i
z
i
.
Câu 3:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Trong mặt phẳng phức, gọi
M
là điểm biểu diễn cho số phức
2
z z
với
z a bi
, , 0
a b b
. Chọn kết luận
đúng.
A.
M
thuộc tia
Ox
. B.
M
thuộc tia
Oy
.
C.
M
thuộc tia đối của tia
Ox
. D.
M
thuộc tia đối của tia
Oy
.
Lời giải
Chọn C
Gọi
z a bi
2
2
2
4z z a bi a bi b
.
Câu 4:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Tìm số phức
z
thỏa mãn
2
z z
và
1
z z i
là số thực.
A.
1 2 .z i
B.
1 2 .z i
C.
2 .z i
D.
1 2 .z i
Lời giải
Chọn D
Gọi
z x iy
với
,x y
ta có hệ phương trình
2
1
z z
z z i
2
2 2 2
2
1
x y x y
x iy x iy i
2
2 2 2
2
1
x y x y
x iy x iy i
1
1 1 0
x
x y xy
1
2
x
y
Câu 5:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Cho bốn điểm
M
,
N
,
P
,
Q
là các điểm trong
mặt phẳng phức theo thứ tự biểu diễn các số
i
,
2 i
,
5
,
1 4i
. Hỏi, điểm nào là trọng tâm
của tam giác tạo bởi ba điểm còn lại?
A.
M
. B.
N
. C.
P
. D.
Q
.
Lời giải
Chọn B
Tọa độ các điểm:
0; 1
M
,
2;1
N
,
5;0
P
,
1;4
Q
.
Dễ thấy
0 5 1
2
3
1 0 4
1
3
nên
N
là trọng tâm của tam giác
MPQ
.
Câu 6:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Trong các số phức:
3
1
i
,
4
1
i
,
5
1
i
,
6
1
i
số phức nào là số phức thuần ảo?
A.
3
1
i
. B.
4
1
i
. C.
5
1
i
. D.
6
1
i
.
Lời giải
Chọn D
Ta có
2
2
1 1 2 1 2 1 2i i i i i
.
Do đó:
3 2
2
1 1 1 2 1 2 2 2 2i i i i i i i i
.
4 2 2
2
1 1 1 2 .2 4 4
i i i i i i
.
5 4
1 1 1 4 1 4 4i i i i i
.
2
6 3 3
1 1 2 8i i i i
.
Câu 7:
(TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018)
Cho số phức
z
thoả mãn
1 1 3i z i
.
Hỏi điểm biểu diễn của
z
là điểm nào trong các điểm
M
,
N
,
P
,
Q
ở hình dưới đây?
A. Điểm
Q
. B. Điểm
P
. C. Điểm
M
. D. Điểm
N
.
Lời giải
Chọn C
Ta có
1 3
1
i
z
i
1 3 1
2
i i
1 3 3
2
i i
1 2i
. Do đó điểm biểu diễn số phức
z
là điểm
1;2
M
.
Câu 8:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Phần thực và phần ảo của số phức
1 2z i i
lần lượt là
A.
1
và
2
. B.
2
và
1
. C.
1
và
2
. D.
2
và
1
.
Lời giải
Chọn B
Ta có
1 2 2z i i i
. Vậy phần thực của số phức
z
bằng
2
và phần ảo của số phức
z
bằng
1
.
Câu 9:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Gọi
1
z
là nghiệm phức có phần ảo âm của
phương trình
2
2 3 0
z z
. Tọa độ điểm
M
biểu diễn số phức
1
z
là:
A.
1; 2
M
. B.
1;2
M
. C.
1; 2
M
. D.
1; 2M i
.
Lời giải
Chọn A
Ta có:
2
1 3 2 2i
nên phương trình
2
2 3 0
z z
có hai nghiệm phức là
1 2 .z i
Do nghiệm cần tìm có phần ảo âm nên
1
1 2z i
. Vậy
1; 2
M
.
Câu 10:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Điểm biểu diễn của các số phức
7
z bi
với
b
nằm trên đường thẳng có phương trình là:
A.
7
y
. B.
7
x
. C.
7
y x
. D.
y x
.
Lời giải
Chọn B
Điểm biểu diễn của các số phức
7
z bi
với
b
là
7; M b
.
y
O
x
1
1
2
2
N
M
Q
P
Rõ ràng điểm
7; M b
thuộc đường thẳng
7
x
.
Câu 11:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Cho số phức
z
thỏa mãn:
3
1 3
1
i
z
i
.
Tìm môđun của
z iz
.
A.
4 2
. B.
4
. C.
8 2
. D.
8
.
Lời giải
Chọn C
3
1 3
1
i
z
i
4 4z i
4 4z i
4 4 4 4iz i i i
4 4 4 4 8 8z iz i i i
2 2
8 8 8 2
z iz
Câu 12:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Cho số phức
z
thỏa mãn điều kiện
1 2 2i z i z i
. Môđun của số phức
2
2 1z z
w
z
là:
A.
10
. B.
8
. C.
10
. D.
8
.
Lời giải
Chọn A
Ta có
1 2 2 3 1 3
i z i z i i z i z i
.
Suy ra
2 2
2 1 2 1
1 3
z z i i
w i
z i
.
Vậy
10
w
.
Câu 13:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Cho
z
là số phức có mô-đun bằng
2017
và
w
là số phức thỏa mãn
1 1 1
z w z w
. Mô đun của số phức
w
là:
A.
2015
. B.
0
. C.
1
. D.
2017
.
Lời giải.
Chọn D
Ta có
1 1 1
z w z w
2
z w zw
2 2
0
w wz z
3
2
z z i
w
.
Với
3
2
z z i
w
3
2
z z i
w
1 3
.
2
i
z
2017
z
.
Với
3
2
z z i
w
3
2
z z i
w
1 3
.
2
i
z
2017
z
.
Câu 14:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Tính môđun số phức nghịch đảo của số phức
2
1 2
z i
.
A.
1
5
. B.
5
. C.
1
25
. D.
1
5
.
Lời giải
Chọn D
Cách 1:
Ta có
3 4 z i
.
Suy ra
1 1 3 4
3 4 25 25
i
z i
.
Nên
2 2
3 4 1
25 25 5
z
.
Cách 2: Ta có
3 4z i
. Do đó
2 2
1 1 1 1
5
3 4
z z
Câu 15:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Cho số phức
z
thỏa mãn
4 7 7
z z i z
. Khi đó, môđun của
z
bằng bao nhiêu?
A.
5
z
. B.
3
z
. C.
5
z
. D.
3
z
.
Lời giải
Chọn C
Đặt
z a bi
với
a
,
b
. Khi đó
z a bi
.
Ta có
4 7 7 4 7 7
z z i z a bi a bi i a bi
4 4 7 7a bi a bi ai b i
5 3 7 7a b a b i i
5 7 1
3 7 2
a b a
a b b
.
Do đó
1 2z i
. Vậy
5
z
.
Câu 16:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Cho số phức
z
thỏa mãn
1 3 5 7i z i
. Mệnh đề nào sau đây đúng?
A.
13 4
5 5
z i
. B.
13 4
5 5
z i
. C.
13 4
5 5
z i
. D.
13 4
5 5
z i
.
Lời giải
Chọn D
Ta có:
5 7 13 4 13 4
1 3 5 7
1 3 5 5 5 5
i
i z i z i z i
i
.
Câu 17:
(Đề tham khảo BGD năm 2017-2018)
Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
4 4 3 0
z z
. Giá trị của biểu thức
1 2
z z
bằng
A.
3 2
. B.
2 3
. C.
3
. D.
3
.
Lời giải
Chọn D
Ta có:
2
4 4 3 0
z z
1
2
1 2
2 2
1 2
2 2
z i
z i
.
Khi đó:
2 2
2 2
1 2
1 2 1 2
3
2 2 2 2
z z
.
Câu 1:
(THPT Đức Thọ-Hà Tĩnh-lần 1 năm 2017-2018)
Cho
2
1
d
f x x a
. Tính
1
2
0
. 1 dI x f x x
theo
a
.
A.
2I a
. B.
4I a
. C.
2
a
I
. D.
4
a
I
.
Lời giải
Chọn C
Đặt
2
1
t x
d 2 dt x x
d
d
2
t
x x
Đổi cận
0 1x t
và
1 2x t
. Khi đó:
1
2
0
. 1 dI x f x x
2
1
1
dt
2
f t
.
Do tính chất của tích phân là tích phân không phụ thuộc vào biến số tích phân nên
2
1
dtf t
2
1
df x x
a
suy ra
2
a
I
.
Câu 2:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Cho số phức
z a bi
(trong đó
a
,
b
là các số thực thỏa
mãn
3 4 5 17 11z i z i
. Tính
ab
.
A.
6
ab
. B.
3
ab
. C.
3
ab
. D.
6
ab
.
Lời giải
Chọn A
Ta có
z a bi
z a bi
.
Khi đó
3 4 5 17 11 3 4 5 17 11z i z i a bi i a bi i
5 17 2
5 5 7 17 11 2 3
5 7 11 3
a b a
a b a b i i z i
a b b
.
Vậy
6
ab
.
Câu 3:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Tổng các nghiệm phức của phương trình
3 2
2 0
z z
là
A.
1
. B.
1
. C.
1 i
. D.
1 i
.
Lời giải
Chọn B
Ta có
3 2 2
2
2
1
1
2 0 1 2 2 0
1
1 1
z
z
z z z z z
z i
z i
.
Do đó tổng các nghiệm phức của
3 2
2 0
z z
là
1 1 1 1
i i
.
Câu 4:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Trên mặt phẳng phức tập hợp các số phức
z x yi
thỏa
mãn
2 3z i z i
là đường thẳng có phương trình
A.
1y x
. B.
1y x
. C.
1y x
. D.
1y x
.
Lời giải
Chọn D
Từ
.z x yi z x yi
Do đó
2 3 2 1 3x yi i x yi i x y i x y i
2 2 2
2
2 1 3 4 2 5 6 9 1x y x y x y y y x
.
Câu 5:
(THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018)
Tích phân
2
0
2
d
2 1
x
x
bằng.
A.
2ln5
. B.
1
ln5
2
. C.
ln5
. D.
4ln5
.
Lời giải
Chọn C
Ta có
2
2
0
0
2
d ln 2 1 ln5
2 1
x x
x
.
Câu 6:
(THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018)
. Tập hợp tất cả các điểm biểu diễn các số
phức
z
thỏa mãn:
2 4
z i
là đường tròn có tâm
I
và bán kính
R
lần lượt là:
A.
2; 1
I
;
4R
. B.
2; 1
I
;
2R
. C.
2; 1
I
;
4R
. D.
2; 1
I
;
2; 1
I
.
Lời giải
Chọn A
Gọi số phức
,z x iy x y
Ta có:
2 4 2 1 4
z i x y i
2 2
2 1 16
x y
Vậy tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa mãn:
2 4
z i
là đường tròn có
tâm
2; 1
I
và có bán kính
4R
.
Câu 7:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Trong tập số phức
, chọn phát
biểu đúng ?
A.
1 2 1 2
z z z z
. B.
là số thuần ảo.
C.
1 2 1 2
z z z z
. D.
2
2
4z z ab
với
z a bi
.
Lời giải
Chọn A
Xét
1
z x yi
,
2
z m ni
, , , x y m n
.
Ta có
1 2 1 2
1 2
z z x m y n i z z x m y n i
z z x yi m ni x m y n i
A đúng.
2 2
1 2
z z x m y m
và
2 2 2 2
1 2
z z x y m n
nên C sai.
Lại có
2
a bi a bi a
B sai.
2
2
z z
2 2
a bi a bi
2 2 2 2
2 2 4
a b abi a b abi abi
D sai.
Câu 8:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Cho số phức
z
thỏa mãn
3 0z i
. Modun của
z
bằng
A.
10
. B.
10
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta có
2 2
3 0 3 3 3 1 10
z i z i z i z
.
Câu 9:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Kí hiệu
1
z
là nghiệm phức có phần ảo âm của
phương trình
2
4 16 17 0.
z z
Trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số
phức
1
3
1 2
2
w i z i
?
A.
2;1 .
M
B.
3; 2 .
M
C.
3;2 .
M
D.
2;1 .
M
Lời giải
Chọn C
Ta có:
1
2
2
1
2
2
4 16 17 0
1
2
2
z i
z z
z i
.
Khi đó:
1
3
1 2
2
w i z i
1 3
1 2 2
2 2
i i i
3 2i
tọa độ điểm biểu diễn số phức
w
là:
3;2
M
.
Câu 1:
(THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018)
Cho hai số phức
1
1 2z i
,
2
1 2z i
. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
10
. B.
10
. C.
6
. D.
4
.
Lời giải
Chọn B
Ta có
2 2
2 2 2 2 2
2
1 2
1 2 1 2 10
z z
.
Câu 2:
(THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018)
Cho số phức
z a bi
,
,a b
thỏa mãn
1
1
z
z i
và
3
1
z i
z i
. Tính
P a b
.
A.
7
P
. B.
1P
. C.
1P
. D.
2P
.
Lời giải
Chọn D
Ta có
1
1
z
z i
1
z z i
1 1a bi a b i
2 2 0
a b
(1).
3
1
z i
z i
3
z i z i
3 1a b i a b i
1b
(2).
Từ (1) và (2) ta có
1
1
a
b
. Vậy
2P
.
Câu 3:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Cho số phức
z
thỏa mãn:
2
3 2 2 4i z i i
. Hiệu phần thực và phần ảo của số phức
z
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn D
Ta có
2
3 2 2 4i z i i
2
3 2 4 2
i z i i
3 2 1 5i z i
1 5
3 2
i
z
i
1z i
phần thực của số phức
z
là
1
a
, phần ảo của số phức
z
là
1b
.
Vậy
0
a b
.
Câu 4:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
1
1z i
và
2
2 3z i
.
Tìm số phức liên hợp của số phức
1 2
w z z
?
A.
3 2w i
. B.
1 4w i
. C.
1 4w i
. D.
3 2w i
.
Lời giải
Chọn D
Vì:
1
1z i
và
2
2 3z i
nên
1 2
w z z
1 2 1 3 3 2w i i
3 2w i
.
Câu 5:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Gọi
1
z
,
2
z
là các nghiệm của
phương trình
2
2 10 0
z z
trên tập hợp số phức, trong đó
1
z
là nghiệm có
phần ảo dương. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu
diễn số phức
1 3
3 2w z z
.
A.
1;15
M
. B.
15; 2
M
. C.
2;15
M
. D.
15; 1
M
.
Lời giải
Chọn A
2
2 10 0
z z
1
2
1 3
1 3
z i
z i
.
1 3
3 2w z z
3 1 3 2 1 3i i
1 15i
Vậy điểm
1;15
M
biểu diễn số phức
1 3
3 2w z z
.
Câu 6:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Biết
z a bi
,a b
là số phức
thỏa mãn
3 2 2 15 8i z i z i
. Tổng
là
A.
5
a b
.
B.
1
a b
.
C.
9
a b
.
D.
1a b
.
Lời giải
Chọn A
Ta có
z a bi
z a bi
.
Theo đề bài ta có
3 2 2 15 8i z iz i
3 2 2 15 8i a bi i a bi i
3 4 3 15 8a a b i i
3 15
4 3 8
a
a b
5
4
a
b
. Vậy
9
a b
.
Câu 7:
(THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
z
thỏa mãn
2
3 2 2 4i z i i
. Hiệu phần thực và phần ảo của số phức
z
bằng
A.
1
. B.
0
. C.
4
. D.
2
.
Lời giải
Chọn D
2
3 2 2 4i z i i
2
4 2
3 2
i i
z
i
5 1
3 2
i
i
=
1 i
.
Suy ra
1z i
. Vậy hiệu phần thực và ảo của
z
bằng
2
.
Câu 8:
(THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018)
Cho số phức
1 3
2 2
z i
. Tìm số
phức
2
1
w z z
.
A.
2 3i
. B.
1
. C.
0
. D.
1 3
2 2
i
.
Lời giải
Chọn C
2
1 3 1 3
1 0
2 2 2 2
iw i
.
Câu 9: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Tìm phần thực và phần ảo của số phức
2 2
1 2
z z
biết
1
z
,
2
z
là hai nghiệm phức của phương trình:
2
4 5 0
z z
.
A.
4
. B.
6
. C.
8
. D.
5
.
Lời giải
Chọn B
Do
1
z
và
2
z
là nghiệm phương trình nên
1 2
4
z z
và
1 2
5
z z
.
Ta có
2
2 2
1 2 1 2 1 2
2
z z z z z z
2
4 2.5
6
.
Câu 10:
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018)
Tính môđun của số phức
z
thỏa mãn:
3 . 2017 48 2016 .z z z z i
A.
4
z
. B.
2016
z
. C.
2017
z
. D.
2
z
.
Lời giải
Chọn A
Gọi
z x yi
, với
,x y
Ta có
3 . 2017 48 2016z z z z i
2
3 2017 48 2016z x yi x yi i
2
2
16
3 48
1008
2.2017 2016
2017
z
z
y
y
4
z
.
Câu 11: (THTT số 6-489 tháng 3 năm 2018) Cho số phức
z a bi
,a b
thỏa mãn
1 3
1
1 2
i
a b i
i
. Giá trị nào dưới đây là môđun của
z
?
A.
5
. B.
1
. C.
10
. D.
5
.
Lời giải
Chọn D
Xét
1 3
w 1
1 2
i
i
i
mà
1 3
1
1 2
i
a b i
i
1 1a b i i
1
2
a
b
Vậy modun của
z
là
5
z
.
Câu 12:
(THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018)
Gọi
1
z
và
2
z
là hai nghiệm của phương trình
2
2 6 5 0
z z
trong đó
2
z
có phần ảo âm. Phần thực và phần ảo của số phức
1 2
3z z
lần lượt
là
A.
6;1
. B.
1; 6
. C.
6; 1
. D.
6;1
.
Lời giải
Chọn C
Ta có
2
2 6 5 0
z z
1
2
3
2 2
3
2 2
i
z
i
z
. Suy ra
1 2
3 6z z i
Vậy Phần thực và phần ảo của số phức
1 2
3z z
lần lượt là
6; 1
.
Câu 13:
(THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018)
Cho số phức
z
thỏa mãn điều
kiện
1 2 1 5 1
i i z i i i
. Tính môđun của số phức
2
1 2
w z z
.
A.
100
. B.
10
. C.
5
. D.
10
.
Lời giải
Chọn D
Ta có
1 2 1 5 1
i i z i i i
1 3 1 6 4i z i i
1 3 5 5i z i
5 5
1 3
i
z
i
2z i
Suy ra
2
1 2
w z z
8 6i
,
2 2
w 8 6 10
Câu 14:
(THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018)
Cho số phức
,z a bi a b
thỏa mãn
2 5 5
z i
và
. 82
z z
. Tính giá trị của biểu thức
P a b
.
A.
10
. B.
8
. C.
35
. D.
7
.
Lời giải
Chọn B
Theo giả thiết ta có
2 2
2 2
2 2
5 43
1
2 5 5
2
82
82 2
b
a
a b
a b
a b
Thay
1
vào
2
ta được
2
9
29 430 1521 0
169
29
b
b b
b
Vì
b
nên
9 1b a
. Do đó
8
P a b
.
Câu 15:
(THPT Chuyên Phan Bội Châu-lần 2 năm 2017-2018)
Biết phương trình
2
0
z az b
có
một nghiệm
2z i
. Tính
a b
?
A.
9
. B.
1
. C.
4
. D.
1
.
Lời giải
Chọn A
Phương trình
2
0
z az b
có một nghiệm
2z i
nên ta có:
2
2 2 0
i a i b
2 3 4 0a b a i
2 3 4
4 0 5
a b a
a b
.
Vậy
1
a b
.
Câu 16:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Cho
m
là số thực, biết phương trình
2
5 0
z mz
có hai nghiệm phức trong đó có một nghiệm có phần ảo là
1
. Tính tổng môđun
của hai nghiệm.
A.
3
. B.
5
. C.
2 5
. D.
4
.
Lời giải
Chọn C
Cách 1: Phương trình
2
5 0
z mz
có hai nghiệm phức
1
z
,
2
z
thì hai nghiệm phức là hai số
liên hợp của nhau nên
1 2 1
2z z z
.
Gọi
1
z a i
, (
a
) là một nghiệm của phương trình.
Ta có:
2
5 0
a i m a i
2
4 2 0a ma a m i
2
4 0
2 0
a ma
a m
2 2
2 4 0
2
a a
m a
2
4
a
m
hoặc
2
4
a
m
Suy ra
1
2z i
hoặc
1
2z i
. Do đó
1
2z i
.
Vậy
1 2
2 5
z z
.
Cách 2: Ta có
2
20
m
Phương trình có hai nghiệm phức thì
0 2 5 2 5
m
.
Khi đó phương trình có hai nghiệm là
2
1
20
2 2
m m
z i
và
2
2
20
2 2
m m
z i
Theo đề
2
20
1 4
2
m
m
(t/m).
Khi đó phương trình trở thành
1
2
2
2
4 5 0
2
z i
z z
z i
hoặc
1
2
2
2
z i
z i
Vậy
1 2
2 5
z z
.
Câu 17:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Tính
2018 2018
1 3 1 3
P i i
.
A.
2P
. B.
1010
2P
. C.
2019
2P
. D.
4P
.
Lời giải
Chọn C
Ta có
2018 2018
1 3 1 3
P i i
2018 2018
2 2
2 2
1 3 1 3
2018 2018
2 2
2019
2
.
Câu 18:
(THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018)
Gọi
1
z
,
2
z
là các nghiệm
của phương trình
2
8 25 0
z z
. Giá trị
1 2
z z
bằng
A.
8
. B.
5
. C.
6
. D.
3
.
Lời giải
Chọn C
Xét phương trình
2
8 25 0
z z
1
1
4 3
4 3
z i
z i
Vậy
1 2
4 3 4 3z z i i
6i
6
.
Câu 19: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Cho hai số phức
2
z a b a b i
và
1 2w i
. Biết
.z w i
. Tính
S a b
.
A.
7
S
. B.
4
S
. C.
3
S
. D.
7
S
.
Lời giải
Chọn A
Ta có
2
z a b a b i
1 2 .i i
2 i
2 2
1
a b
a b
4
3
a
b
.
Vậy
S a b
7
.
Câu 20: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Gọi
1
z
và
2
z
là hai nghiệm của
phương trình
2
2 3 3 0
z z
. Khi đó, giá trị
2 2
1 2
z z
là
A.
9
4
. B.
9
4
. C.
9
. D.
4
.
Lời giải
Chọn B
Theo định lý Vi-ét, ta có
1 2
3
2
z z
và
1 2
3
.
2
z z
.
2
2 2
1 2 1 2 1 2
2 .z z z z z z
2
3 3
2
2 2
3 9
3
4 4
.
Câu 21: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho
i
là đơn vị ảo. Gọi
S
là tập
hợp các số nguyên dương
n
có
2
chữ số thỏa mãn
n
i
là số nguyên dương. Số phần tử của
S
là
A.
22
. B.
23
. C.
45
. D.
46
.
Lời giải
Chọn A
Ta có
n
i
là số nguyên dương khi
4n k
,
k
. Vì số nguyên dương
n
có
2
chữ số nên
10 4 99 2,5 24,75
k k
k k
suy ra có
24 3 1 22
số.
Câu 22: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Cho số phức
z a bi
khác
0
,a b
. Tìm phần ảo của số phức
1
z
.
A.
2 2
a
a b
. B.
2 2
b
a b
. C.
2 2
bi
a b
. D.
2 2
b
a b
.
Lời giải
Chọn D
Ta có
1
2 2 2 2 2 2
1 1
a bi a b
z i
z a bi a b a b a b
. Vậy phần ảo của
1
z
là
2 2
b
a b
.
Câu 23: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Tập hợp các điểm biểu diễn cho số
phức
z
thỏa mãn
3 4 5
z i
là
A. Một đường tròn. B. Một đường thẳng. C. Một đường parabol. D. Một đường Elip.
Lời giải
Chọn A
Tập hợp điểm biểu diễn cho số phức
z
là đường tròn tâm
3; 4
I
, bán kính
5
R
.
Câu 24: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Gọi
A
,
B
là hai điểm biểu
diễn hai nghiệm phức của phương trình
2
2 5 0
z z
. Tính độ dài đoạn thẳng
AB
:
A.
6
. B.
2
. C.
4
. D.
12
.
Lời giải
Chọn C
Ta có:
2
2 5 0
z z
1 2
1 2
z i
z i
suy ra
1;2
A
và
1; 2
B
. Vậy
4AB
.
Câu 25: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Trong tất cả các số phức
z
thỏa mãn điều kiện sau:
1 3
2
z z
z
, gọi số phức
iz a b
là số phức có môđun nhỏ
nhất. Tính
2
S a b
.
A.
0
. B.
4
. C.
2
. D.
2
Lời giải
Chọn C
Ta có
1 3
2
z z
z
1 i 3
a b a
2 2
2
1 3
a b a
2
4 8
b a
.
Do đó
2
2 2
z a b
2
4 8
a a
2
1 4 4
a
.
min 2
z
khi và chỉ khi
1 4iz
. Suy ra
2 2
S a b
Câu 26:
(SGD Quảng Nam – năm 2017 – 2018)
Cho số phức
z
thoả mãn
3 4 5
z i
. Biết
rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn các số phức
z
là một đường tròn. Tìm toạ
độ tâm
I
và bán kính
R
của đường tròn đó.
A.
3; 4
I
,
5
R
. B.
3;4
I
,
5
R
. C.
3; 4
I
,
5
R
. D.
3;4
I
,
5
R
.
Lời giải
Chọn D
Đặt
z x yi
,x y
. Khi đó
2 2
3 4 5 3 4 25
z i x y
.
Vậy tập điểm biểu diễn số phức
z
là đường tròn tâm
3;4
I
, bán kính
5
R
.
Câu 27:
(SGD Quảng Nam – năm 2017 – 2018)
Tổng phần thực và phần ảo của số phức
z
thoả mãn
1 2iz i z i
bằng
A.
2
. B.
2
. C.
6
. D.
6
.
Lời giải
Chọn C
Đặt
z x yi
,x y
. Khi đó
1 2 1 2iz i z i i x yi i x yi i
2 0 4
2 2
2 2
x y x
x y yi i
y y
, suy ra
6
x y
.
Câu 28:
(ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018)
Kí hiệu
0
z
là nghiệm phức của
phương trình
2
4 4 3 0
z z
sao cho
0
z
có phần ảo là số thực âm. Điểm
M
biểu diễn số phức
0
2w z
thuộc góc phần tư nào trên mặt phẳng phức?
A. Góc phần tư
I
. B. Góc phần tư
II
.
C. Góc phần tư
III
. D. Góc phần tư
IV
.
Lời giải
Chọn B
2
1 2
4 4 3 0
2 2
z z z i
.
Do đó
0
1 2
2 2
z i
0
2 1 2w z i
.
w
có điểm biểu diễn là
1; 2
M
nằm ở góc phần tư thứ
II
.
Câu 29:
(THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018)
Phương trình bậc hai nào
sau đây có nghiệm
1 2i
?
A.
2
2 3 0
z z
. B.
2
2 5 0
z z
. C.
2
2 5 0
z z
. D.
2
2 3 0
z z
.
Lời giải
Chọn C
Vì
1 2i
là nghiệm của phương trình bậc hai
2
0
az bz c
nên
1 2i
cũng là nghiệm của
phương trình bậc hai
2
0
az bz c
.
Ta có
1 2 1 2 5
1 2 1 2 2
i i
i i
suy ra
1 2i
là nghiệm của phương trình bậc hai
2
2 5 0
z z
.
Câu 30:
(THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018)
Có bao nhiêu số phức
z
thỏa mãn
1 2 13 2i z i z i
?
A.
4
. B.
3
. C.
2
. D.
1.
Lời giải
Chọn D
Gọi
z a bi
,
,a b
.
1 2 13 2 1 2 13 2i z i z i i a bi i a bi i
2 2 13 2a b a b i a b b a i i
3 2 13
2
a b
b
3
3 2
2
a
z i
b
.
Vậy có một số phức thỏa mãn yêu cầu bài toán.
Câu 1:
(SGD Thanh Hóa – năm 2017 – 2018)
Gọi
, ,A B C
lần lượt là các điểm biểu diễn của các số phức
1
2
z
,
2
4z i
,
3
2 4z i
trong mặt phẳng tọa độ
.Oxy
Tính diện tích tam giác
.ABC
A.
8
. B.
2
. C.
6
. D.
4
.
Lời giải
Chọn D
Ta có
2;0
A
,
0;4
B
,
2;4
C
suy ra
0;4
AC
;
2;0
BC
. 0
AC BC
.
Do đó tam giác
ABC
là tam giác vuông tại
C
. Suy ra
1
.
2
ABC
S CA CB
1
.4.2 4
2
.
Câu 2:
(Tạp chí THTT – Tháng 4 năm 2017 – 2018)
Cho số phức
z
thỏa mãn
2
z
. Tập hợp điểm biểu
diễn số phức
1 2w i z i
là
A. Một đường tròn. B. Một đường thẳng.
C. Một Elip. D. Một parabol hoặc hyperbol.
Lời giải
Chọn A
Ta có:
1 2w i z i
2 1
w i i z
2 1
w i i z
2 2 2
w i
.
Do đó, tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
0;2
I
và bán kính
2 2
.
Câu 3:
(Tạp chí THTT – Tháng 4 năm 2017 – 2018)
Cho hai số phức
1
z
,
2
z
thỏa mãn
1
1
z
,
2
2
z
và
1 2
3
z z
. Giá trị của
1 2
z z
là
A.
0
. B.
1
. C.
2
. D. một giá trị khác.
Lời giải
Chọn B
Cách 1:
Sử dụng công thức hình bình hành
2 2
2 2
1 2 1 2 1 2
2
z z z z z z
2
1 2 1 2
2 1 4 9 1
z z z z
.
Cách 2:
Giả sử
1 1 1
z a b i
1 1
;a b
,
2 2 2
z a b i
2 2
;a b
.
Theo bài ra ta có:
1
2
1 2
1
2
3
z
z
z z
2 2
1 1
2 2
2 2
2 2
1 2 1 2
1
4
9
a b
a b
a a b b
2 2
1 1
2 2
2 2
1 2 1 2
1
4
2 2 4
a b
a b
a a b b
.
Khi đó, ta có:
2 2
1 2 1 2 1 2
z z a a b b
2 2 2 2
1 1 2 2 1 2 1 2
2 2
a b a b a a b b
1
.
Vậy
1 2
1
z z
.
Câu 4:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình
4 2
6 0
z z
. Tính
1 2 3 4
S z z z z
.
A.
2 3
S . B.
2 2 3
S
. C.
2 2
S
. D.
2 2 3
S
.
Lời giải
Chọn D
Ta có:
4 2
6 0
z z
2
2
2
3
z
z
2
3
z
z i
.
Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình, ta có:
1 2 3 4
S z z z z
2 2 3
.
Câu 5:
(THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018)
Cho số phức
z
thỏa mãn:
1 2 . 15z i z i i
. Tìm modun của số phức
z
?
A.
5
z
. B.
4
z
. C.
2 5
z
. D.
2 3
z
.
Lời giải
Chọn A
Gọi
z x yi
,
,x y
.
Theo đề ra ta có:
1 2 . 15x yi i x yi i i
2 2 15x y yi xi xi y i
3 15x y y x i i
3 15
1
x y
x y
3
4
x
y
3 4 5
z i z
.
Câu 6:
(THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018)
Gọi
1
z
là nghiệm phức có phần
ảo âm của phương trình
2
2 5 0
z z
. Tìm tọa độ điểm biểu diễn số phức
1
7 4i
z
trên mặt
phẳng phức?
A.
3; 2
P
. B.
1; 2
N
. C.
3; 2
Q
. D.
1; 2
M
.
Lời giải
Chọn A
Ta có:
2
2 5 0
z z
1 2 TM
1 2
z i
z i L
Suy ra
1
7 4i
z
7 4
3 2
1 2
i
i
i
.
Điểm biểu diễn là
3; 2
P
.
Câu 7: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Tìm phần ảo của số phức
z
biết
2
3 3
z i i
.
A.
4
. B.
4 3
. C.
4 3
. D.
4
.
Lời giải
Chọn D
Ta có:
2
3 3 4 3 4 4 3 4z i i i z i
.
Vậy phần ảo của số phức
z
là
4
.
Câu 8: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho số phức
3 4z i
.
Mệnh đề nào dưới đây sai?
A. Môđun của số phức
z
bằng
5
.
B. Số phức liên hợp của
z
là
3 4i
.
C. Phần thực và phần ảo của
z
lần lượt là
3
và
4
.
D. Biểu diễn số phức
z
lên mặt phẳng tọa độ là điểm
3; 4
M
.
Lời giải
Chọn C
Số phức liên hợp của
3 4z i
là
3 4z i
. Mệnh đề B sai.
Câu 9: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho số phức
z
thỏa mãn
2 3 1 9z i z i
. Tính tích phần thực và phần ảo của số phức
z
.
A.
1
. B.
2
. C.
1
. D.
2
.
Lời giải
Chọn B
Gọi
iz x y
(với
,x y
), ta có
iz x y
.
Theo giả thiết, ta có
i 2 3 i 1 9x y i x y i
3 3 3 i 1 9i
x y x y
3 1
3 3 9
x y
x y
2
1
x
y
. Vậy
2
xy
.
Câu 10:
(THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018)
Cho số phức
3 5z i
.
Gọi
,w x yi x y
là một căn bậc hai của
z
. Giá trị của biểu thức
4 4
T x y
là
A.
706
T
. B.
17
2
T
. C.
43
2
T
. D.
34
T
.
Lời giải
Chọn C
Ta có
,w x yi x y
là một căn bậc hai của
z
khi và chỉ khi
2
w
z
2
2 2
3 5 2 3 5x yi i x y xyi i
.
2 2
3
2 5
x y
xy
Ta có
2
2
4 4 2 2 2 2 2
5 43
2 3 2.
2 2
T x y x y x y
.
Câu 11:
(THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018)
Tổng phần thực và phần ảo
của số phức
2
1 3 3z i i
là
A.
4
. B.
4
. C.
3 i
. D.
10
.
Lời giải
Chọn B
Ta có
2
1 3 3z i i
2
1 2 3 3i i i
3 i
phần thực
3
a
, phần ảo
1
b
.
Vậy
4
a b
.
Câu 12:
(SGD Hà Tĩnh – Lần 2 năm 2017 – 2018)
Cho số phức
z
thỏa mãn:
1 2 3z z i
. Tập hợp
các điểm biểu diễn số phức
z
là
A. Đường tròn tâm
1;2
I
, bán kính
1R
.
B. Đường thẳng có phương trình
2 6 12 0
x y
.
C. Đường thẳng có phương trình
3 6 0
x y
.
D. Đường thẳng có phương trình
5 6 0
x y
.
Hướng dẫn giải
Chọn C
Gọi
z x yi
; (
x
,
y
).
Ta có:
1 2 3z z i
2 2 2
2
1 2 3
x y x y
3 6 0
x y
.
Vậy tập hợp các điểm biểu diễn số phức
z
là đường thẳng có phương trình
3 6 0
x y
.
Câu 13:
(THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018)
Cho số phức
z
thỏa mãn
2
z z
. Biết rằng phần thực của
z
bằng
a
. Tính
z
theo
a
A.
1
1
z
a
. B.
2
1
2
a a
z
. C.
2
1
2
a a
z
. D.
2
4
2
a a
z
.
Hướng dẫn giải
Chọn D
Đặt
z a bi
,
a
,
b
2 2
z a b
. Theo đề bài ta có
2
z z
2 2
2
a bi a b
2
2 2 2
2
a a b b
2 2 2 2
1 0
a b a a b
2
2 2
2
2 2
4
2
4
/
2
a a
a b loai
a a
a b t m
.
Vậy
2
4
2
a a
z
.
Câu 14:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Gọi
1
z
,
2
z
là nghiệm của phương trình
2
2 4 0
z z
. Tính giá trị của biểu thức
2 2
1 2
2 1
z z
P
z z
A.
4
. B.
4
. C.
8
. D.
11
4
.
Lời giải
Chọn B
Ta có:
2
2 4 0
z z
1
2
1 3
1 3
z i
z i
.
Suy ra:
2 2
2 2
1 2
2 1
1 3 1 3
4
1 3 1 3
i i
z z
P
z z
i i
.
Câu 15:
(Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018)
Tìm tập hợp điểm biểu diễn số phức
z
thoả
1 2 3
z i
.
A. Đường tròn tâm
1;2
I
, bán kính
9
r
. B. Đường tròn tâm
1;2
I
, bán kính
r
.
C. Đường tròn tâm
1; 2
I
, bán kính
3
r
. D. Đường tròn tâm
1;2
I
, bán kính
3
r
.
Hướng dẫn giải
Chọn D
Gọi
z x yi
2
, , 1
x y i
.
Ta có:
1 2 3
z i
2 2
1 2 3
x y
2 2
1 2 9
x y
.
Vậy tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
1;2
I
, bán kính
3
r
.
Câu 16:
(Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018)
Trong
mặt phẳng phức, cho điểm
M
trong hình vẽ bên là điểm biểu diễn số
phức
z
. Trong các mệnh đề sau mệnh đề nào là sai?
A.
6
z z
. B. Số phức
z
có phần ảo bằng
4
.
C.
5
z
. D.
3 4z i
.
Hướng dẫn giải
Chọn A
Ta dễ thấy các mệnh đề B, C, D đúng.
Từ hình vẽ ta có
3 4z i
3 4 3 4 8z z i i i
. Do đó A
sai.
Câu 17:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
, cho số phức
z
thỏa mãn
1 2 3
z i
. Tập hợp các điểm biểu diễn cho số phức
1
w z i
là đường tròn
A. Tâm
3; 1
I
,
3 2
R
. B. Tâm
3;1
I
,
3
R
.
C. Tâm
3;1
I
,
3 2
R
. D. Tâm
3; 1
I
,
3
R
.
Lời giải
Chọn A
Ta có
1 2 3
z i
1 1 2 1 3 1z i i i i
3 3 2
w i
.
Giả sử
w x yi
,x y
3 1 3 2
x y i
2 2
3 1 18
x y
3; 1
I
,
18 3 2
R
.
Câu 18:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Có bao nhiêu số phức
z
thỏa mãn
1
i z z
là số thuần ảo và
2 1z i
A.
2
. B.
1
. C.
0
. D.Vô số.
Lời giải
Chọn A
Đặt
z a bi
với
,a b
ta có :
1
i z z
1
i a bi a bi
2
a b ai
.
Mà
1
i z z
là số thuần ảo nên
2 0
a b
2b a
.
Mặt khác
2 1z i
nên
2
2
2 1
a b
2
2
2 2 1
a a
2
5 8 3 0
a a
1
3
5
a
a
.
Ứng với mỗi
a
ta tìm được một
b
duy nhất, vậy có 2 số phức thỏa mãn yêu cầu bài toán.
Câu 19: Cho hai số thực
x
,
y
thỏa mãn
2 1 1 2 2 2
x y i i yi x
. Khi đó giá trị của
2
3
x xy y
bằng
A.
2
. B.
1
. C.
3
. D.
1
.
Câu 20: Tính tổng
3 6 2016
1 ...
S i i i
.
A.
1
S
. B.
S i
. C.
S i
. D.
1
S
.
Câu 21: Cho hai số thực
x
,
y
thỏa mãn
2 1 1 2 2 2
x y i i yi x
. Khi đó giá trị của
2
3
x xy y
bằng
A.
2
. B.
1
. C.
3
. D.
1
.
Lời giải
Chọn A
Ta có:
2 1 1 2 2 2
x y i i yi x
2 1 1 2 4 2x y i x y i
2 1 4
1 2 2
x x
y y
1
1
x
y
2
3 2
x xy y
.
Câu 22: Tính tổng
3 6 2016
1 ...
S i i i
.
A.
1
S
. B.
S i
. C.
S i
. D.
1
S
.
Lời giải
Chọn A
Áp dụng công thức
1
2
1
1 ...
1
n
n
x
x x x
x
với
3
x i
,
2016
672
3
n
ta được
673
3
3
1
1
i
S
i
673
1
1
i
i
336
2
1
1
i i
i
1
1
i
i
1
.
Câu 23: Gọi
1
z
là nghiệm phức có phần ảo dương của phương trình
2
6 13 0
z z
. Tìm tọa độ điểm
M
biểu diễn số phức
1
1w i z
.
A.
5; 1
M
. B.
5;1
M
. C.
1; 5
M
. D.
1;5
M
.
Câu 24: Gọi
1
z
là nghiệm phức có phần ảo dương của phương trình
2
6 13 0
z z
. Tìm tọa độ điểm
M
biểu diễn số phức
1
1w i z
.
A.
5; 1
M
. B.
5;1
M
. C.
1; 5
M
. D.
1;5
M
.
Lời giải
Chọn A
Ta có
1
2
2
3 2
6 13 0
3 2
z i
z z
z i
. Suy ra
1
1w i z
1 3 2i i
5 i
.
Vậy tọa độ điểm
M
biểu diễn số phức
1
1w i z
là
5; 1
M
.
Câu 25: Tìm phần ảo của số phức
z
, biết
1 3
1
i i
z
i
.
A.
3.
B.
3.
C.
0.
D.
1.
Lời giải
Chọn C
Ta có:
2
2
1 3 1 3
2 .3
3 3.
1 1 2
i i i i
i i
z z
i i
Vậy phần ảo của số phức
z
là
0.
Câu 26: Cho số phức
z
thỏa mãn
1 2 5
z i
và
;M x y
là điểm biểu diễn số phức
z
. Điểm
M
thuộc đường tròn nào sau đây?
A.
2 2
1 2 25
x y
. B.
2 2
1 2 25
x y
.
C.
2 2
1 2 5
x y
. D.
2 2
1 2 5
x y
.
Lời giải
Chọn B
Ta có
1 2 5
z i
1 2 5
x y i
2 2
1 2 25
x y
.
Vậy điểm
M
thuộc đường tròn
2 2
1 2 25
x y
.
Câu 27: Cho số phức
z
thỏa mãn
2 3 4 10
z i
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
z
. Khi đó
M m
bằng
A.
5
. B.
15
. C.
10
. D.
20
.
Câu 28: Cho hàm số
2 2 2 2 2
1 4 9 16
f x x x x x x
. Hỏi phương trình
0
f x
có bao
nhiêu nghiệm?
A.
9
. B.
8
. C.
7
. D.
6
.
Câu 29: Cho số phức
z
thỏa mãn
2 3 4 10
z i
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
z
. Khi đó
M m
bằng
A.
5
. B.
15
. C.
10
. D.
20
.
Lời giải
Chọn C
Đặt
z x yi
.
Ta có:
2 3 4 10
z i
3
2 5
2
z i
2
2
3
2 25
2
x y
.
Tập hợp điểm biểu diễn số phức thỏa đề là đường tròn tâm
3
;2
2
I
, bán kính
5
R
.
Khi đó:
m IO R
M IO R
2 10
M m R
.
Câu 30: Cho hàm số
2 2 2 2 2
1 4 9 16
f x x x x x x
. Hỏi phương trình
0
f x
có bao
nhiêu nghiệm?
A.
9
. B.
8
. C.
7
. D.
6
.
Lời giải
Chọn A
Ta có
0 0; 1; 2; 3; 4
f x x
.
Bảng xét dấu
f x
Từ bảng xét dấu biểu thức
và do tính chất liên tục của hàm số
, suy ra:
0
x
là điểm cực trị của hàm số;
f x
có ít nhất 8 điểm cực trị, khác
0
, lần lượt thuộc mỗi khoảng
4; 3
,
3; 2
,
2; 1 ,
1;0 ,
0;1
,
,
2;3
,
3;4
.
Suy ra hàm số
có ít nhất 9 điểm cực trị.
Do đó, theo điều kiện cần để hàm số có cực trị, ta có phương trình
0
f x
có ít nhất 9
nghiệm.
Mặt khác vì bậc của
là
10
nên bậc của
f x
là
9
phương trình
0
f x
có không
quá 9 nghiệm.
Vậy phương trình
0
f x
có đúng 9 nghiệm.
Câu 31: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 11 0
z z
. Giá trị của biểu thức
1 2
3
z z
bằng
A.
22
. B.
11
. C.
2 11
. D.
11
.
Câu 32: Gọi tam giác cong
( )OAB
là hình phẳng giới hạn bởi đồ thị các hàm số
2
2y x
,
3
y x
,
0
y
(tham khảo hình vẽ bên). Diện tích của
OAB
bằng
A.
8
3
. B.
5
3
. C.
4
3
. D.
10
3
.
Câu 33: Xét các số phức
z a bi
,
,a b
thỏa mãn
2
4 15 1
z z i i z z
. Tính
4F a b
khi
1
3
2
z i
đạt giá trị nhỏ nhất
A.
7
F
. B.
6
F
. C.
5
F
. D.
4F
.
Câu 34: Cho số phức
z ,a bi a b
thỏa mãn
5
z
và
2 1 2z i i
là một số thực. Tính
P a b
A.
5
P
B.
7
P
C.
8
P
D.
4P
Câu 35: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 11 0
z z
. Giá trị của biểu thức
1 2
3
z z
bằng
A.
22
. B.
11
. C.
2 11
. D.
11
.
Lời giải
Chọn C
Ta có
1
z
và
2
z
là hai số phức liên hợp của nhau nên
2 2
1 2 1 2
11
z z z z
1 2
11
z z
.
Do đó:
1 2 1
3 2 2 11
z z z
.
Câu 36: Gọi tam giác cong
( )OAB
là hình phẳng giới hạn bởi đồ thị các hàm số
2
2y x
,
3
y x
,
0
y
(tham khảo hình vẽ bên). Diện tích của
OAB
bằng
A.
8
3
. B.
5
3
. C.
4
3
. D.
10
3
.
Lời giải
Chọn A
Gọi parabol
2
: 2P y x
và đường thẳng
: 3
d y x
.
Ta có phương trình hoành độ giao điểm của
P
và
d
là:
2 2
1
2 3 2 3 0
3
2
x
x x x x
x
Suy ra tọa độ điểm
(1;3)
A
và
( ) (3;0)
d Ox B
.
Khi đó
1 3
2
( ) 1 2
0 1
2 8
2 d (3 )d 2
3 3
OAB
S S S x x x x
.
Câu 37: Xét các số phức
z a bi
,
,a b
thỏa mãn
2
4 15 1
z z i i z z
. Tính
4F a b
khi
1
3
2
z i
đạt giá trị nhỏ nhất
A.
7
F
. B.
6
F
. C.
5
F
. D.
4F
.
Lời giải
Chọn A
Ta có
2
4 15 1
z z i i z z
2
4 15 1
a bi a bi i i a bi a bi
2
8 15 2 1
b a
suy ra
15
8
b
.
2 2
2 2
1 1 1 1
3 2 1 2 6 8 15 4 24 36 4 32 21
2 2 2 2
z i a b b b b b b
Xét hàm số
2
4 32 21
f x x x
với
15
8
x
15
8 32 0,
8
f x x x
suy ra
f x
là hàm số đồng biến trên
15
;
8

nên
15 4353
8 16
f x f
.
Do đó
1
3
2
z i
đạt giá trị nhỏ nhất bằng
1 4353
2 16
khi
15 1
;
8 2
b a
.
Khi đó
4 7
F a b
.
Câu 38: Cho số phức
z ,a bi a b
thỏa mãn
5
z
và
2 1 2z i i
là một số thực. Tính
P a b
A.
5
P
B.
7
P
C.
8
P
D.
4P
Lời giải
Chọn B
2 2
5 25
z a b
1
2 1 2 4 3 4a 3 4 3az i i a bi i b b i
là số thực nên
4 3a 0
b
.
Thay vào
1
ta được
2
2
3
25
4
a a
4 3
a b
7
P
Câu 39: Phương trình
2
5 0
z z
có hai nghiệm
1 2
;z z
trên tập hợp số phức. Tính giá trị của biểu thức
2 2
1 2
P z z
A.
10
P
. B.
9
P
. B.
37
2
P
. D.
11P
.
Câu 40: Phương trình
2
5 0
z z
có hai nghiệm
1 2
;z z
trên tập hợp số phức. Tính giá trị của biểu thức
2 2
1 2
P z z
A.
10
P
. B.
9
P
. B.
37
2
P
. D.
11P
.
Lời giải
Chọn B
2
5 0
z z
1
2
1 19
2 2
1 19
2 2
z i
z i
2 2
1 2
9
P z z
.
Câu 41: Gọi
1
z
,
2
z
,
3
z
là ba nghiệm phức của phương trình
3
8 0
z
. Giá trị của
1 2 3
z z z
bằng
A.
2 2 3
. B.
3
. C.
2 3
. D.
6
.
Câu 42: Gọi
1
z
,
2
z
,
3
z
là ba nghiệm phức của phương trình
3
8 0
z
. Giá trị của
1 2 3
z z z
bằng
A.
2 2 3
. B.
3
. C.
2 3
. D.
6
.
Lời giải
Chọn D
3
8 0
z
1
2
1
2
1 3
1 3
z
z i
z i
1 2 3
6
z z z
.
Câu 43: Cho số phức
z a bi
thỏa mãn
8 6 5 5z i z i i
. Giá trị của
bằng
A.
19
. B.
5
. C.
14
. D.
2
.
Câu 44: Cho số phức
z a bi
thỏa mãn
8 6 5 5z i z i i
. Giá trị của
bằng
A.
19
. B.
5
. C.
14
. D.
2
.
Lời giải
Chọn A
Ta có
8 6 5 5z i z i i
1 5 19i z i
12 7z i
.
Mà
z a bi
nên
12
7
a
b
19
a b
.
Câu 45: Gọi
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 6 5 0
z z
. Số phức
0
iz
bằng
A.
1 3
2 2
i
. B.
1 3
2 2
i
. C.
1 3
2 2
i
. D.
1 3
2 2
i
.
Câu 46: Gọi
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 6 5 0
z z
. Số phức
0
iz
bằng
A.
1 3
2 2
i
. B.
1 3
2 2
i
. C.
1 3
2 2
i
. D.
1 3
2 2
i
.
Lời giải
Chọn B
Ta có
2
2 6 5 0
z z
2
2 2
3
4 12 10 0 2 3 1
2
i
z z z i z
0 0
3 1 1 3
2 2 2 2
z i iz i
.
Câu 47: Cho các số phức
1
3 2z i
,
2
3 2z i
. Phương trình bậc hai có hai nghiệm
1
z
và
2
z
là
A.
2
6 13 0
z z
. B.
2
6 13 0
z z
. C.
2
6 13 0
z z
. D.
2
6 13 0
z z
.
Câu 48: Cho các số phức
1
3 2z i
,
2
3 2z i
. Phương trình bậc hai có hai nghiệm
1
z
và
2
z
là
A.
2
6 13 0
z z
. B.
2
6 13 0
z z
. C.
2
6 13 0
z z
. D.
2
6 13 0
z z
.
Lời giải
Chọn A
Cách 1: Ta có:
1 2
6
S z z
,
2
1 2 1
9 4 13
P z z z
nên
1
z
,
2
z
là hai nghiệm của phương
trình
2
0
z Sz P
2
9 13 0
z z
.
Cách 2: Do
1
3 2z i
,
2
3 2z i
là hai nghiệm của phương trình nên
1 2
0
z z z z
3 2 3 2 0
z i z i
2
3 4 0
z
2
6 13 0
z z
.
Câu 49: Tìm nguyên hàm
F x
của hàm số
sin 2f x x
, biết
0
6
F
.
A.
1
cos 2
2 6
xF x
. B.
2
1
cos
4
F x x
.
C.
2
1
sin
4
F x x
. D.
1
cos2
2
F x
x
.
Câu 50: Có bao nhiêu số phức thỏa mãn
2
3
. 1 0
4
z z i i
?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 51: Tìm nguyên hàm
F x
của hàm số
sin 2f x x
, biết
0
6
F
.
A.
1
cos 2
2 6
xF x
. B.
2
1
cos
4
F x x
.
C.
2
1
sin
4
F x x
. D.
1
cos2
2
F x
x
.
Lời giải
Chọn C
Ta có:
1
sin 2 d cos 2
2
F x x x x C
;
1
0
6 4
F C
.
Vậy
1 1
cos2
2 4
F x x
2
1 1
1 2sin
2 4
x
2
1
sin
4
x
.
Câu 52: Có bao nhiêu số phức thỏa mãn
2
3
. 1 0
4
z z i i
?
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn A
Đặt
z x yi
,x y
thì
2
3
. 1 0
4
z z i i
2 2
3
1 0
4
x yi x y i i
2 2
1 0
3
0
4
x
y x y
1
1
2
x
y
1
1
2
z i
.
Câu 53: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 3 0
z z
. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
3
. B.
3
18
. C.
9
4
. D.
9
8
.
Câu 54: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 3 0
z z
. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
3
. B.
3
18
. C.
9
4
. D.
9
8
.
Lời giải
Chọn C
Ta có
2
2 3 3 0
z z
S a b c
.
Suy ra
2 2
1 2
z z
2 2
3 21 3 21 9
4 4 4 4 4
i i
.
Câu 55: Cho hai số phức
1
4 8z i
và
2
2z i
. Tính
1 2
2 .z z
A.
4 5
. B.
5
. C.
20
. D.
40
.
Câu 56: Cho hai số phức
1
4 8z i
và
2
2z i
. Tính
1 2
2 .z z
A.
4 5
. B.
5
. C.
20
. D.
40
.
Lời giải
Chọn D
Ta có
1 2
2 . 2 4 8 2 40
z z i i
.
Câu 57: Gọi
1
z
,
2
z
là hai nghiệm của phương trình
2
2 1 0
z z
. Tính
1 1 2 2
z z z z
?
A.
2
. B.
2
4
. C.
1
. D.
2
2
.
Câu 58: Gọi
1
z
,
2
z
là hai nghiệm của phương trình
2
2 1 0
z z
. Tính
1 1 2 2
z z z z
?
A.
2
. B.
2
4
. C.
1
. D.
2
2
.
Lời giải
Chọn B
Ta có
2
2 1 0
z z
2
2
1 7
4 16
z i
1
2
1 7
4 4
1 7
4 4
z i
z i
1 2
2
2
z z
.
Vậy
1 1 2 2 1 2
2
2
z z z z z z
2 1 7 1 7
2 4 4 4 4
i i
2
4
.
Câu 59: Phần ảo của số phức
1
1 i
là
A.
1
2
i
. B.
1
2
. C.
1
2
. D.
1
.
Câu 60: Có bao nhiêu số phức
z
thỏa mãn đồng thời hai điều kiện sau:
10 2 2 14z i z i
và
1 10 5
z i
?
A. Hai. B. Không. C. Một. D. Vô số.
Câu 61: Cho số phức
z
thỏa mãn
2 4z z i
. Môđun của
z
là
A.
4
. B.
5
. C.
3
. D.
25
.
Câu 62: Phần ảo của số phức
1
1 i
là
A.
1
2
i
. B.
1
2
. C.
1
2
. D.
1
.
Hướng dẫn giải
Chọn B
Ta có
1 1 1
1 2 2
i
i
nên có phần ảo là
1
2
.
Câu 63: Có bao nhiêu số phức
z
thỏa mãn đồng thời hai điều kiện sau:
10 2 2 14z i z i
và
1 10 5
z i
?
A. Hai. B. Không. C. Một. D. Vô số.
Hướng dẫn giải
Chọn C
Đặt
z a bi
với
, .
a b
Từ giả thiết
10 2 2 14z i z i
2 2 2 2
10 2 2 14
a b a b
24 32 96 0
a b
4
4
3
a b
Ta có:
1 10 5
z i
2 2
1 10 25
a b
2
2
4
5 20 100 25
3
b b b
2
25 100
100 0
9 3
b b
6
b
. Suy ra
4
a
.
Vậy có một số phức thỏa mãn.
Câu 64: Cho số phức
z
thỏa mãn
2 4z z i
. Môđun của
z
là
A.
4
. B.
5
. C.
3
. D.
25
.
Hướng dẫn giải
Chọn B
Đặt
z x iy
,x y
, ta có
2 4z z i
2 2
2 4x iy x y i
2 2
2
4
x x y
y
2
2 16
x x
2 2
2
4 4 16
x
x x x
3
x
.
Vậy
3 4z i
5
z
.
Câu 65: Cho số phức
z
thỏa mãn
2 3 1i z z
. Môđun của
z
bằng
A.
1
10
. B.
1
10
. C.
1
. D.
10
.
Câu 66: Cho số phức
z
thỏa mãn
2 3 1i z z
. Môđun của
z
bằng
A.
1
10
. B.
1
10
. C.
1
. D.
10
.
Lời giải
Chọn A
2 3 1i z z
1 3 1
i z
1
1 3
z
i
1 3
10 10
z i
1 3 1
10 10
10
z i z
.
Câu 67: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 3 0
z z
. Khi đó
1 2
2 1
z z
z z
bằng:
A.
3
2
i
. B.
3 3
2 2
i
. C.
3
2
. D.
3
2
.
Câu 68: Modun của số phức
1 2 2
z i i
là
A.
5
z
. B.
5
z
. C.
10
z
. D.
6
z
.
Câu 69: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 3 0
z z
. Khi đó
1 2
2 1
z z
z z
bằng:
A.
3
2
i
. B.
3 3
2 2
i
. C.
3
2
. D.
3
2
.
Hướng dẫn giải
Chọn D
2
2 3 3 0
z z
có hai nghiệm
1
z
,
2
z
suy ra
1 2
1 2
3
2
3
.
2
z z
z z
.
Ta có
1
2
2 2
2
1 2
1 2
2 1 1 2 1 2
3
3
4
2 2
3
. 2
2
z z
z z
z z
z z z z z z
.
Câu 70: Modun của số phức
1 2 2
z i i
là
A.
5
z
. B.
5
z
. C.
10
z
. D.
6
z
.
Hướng dẫn giải
Chọn A
Ta có
1 2 2
z i i
4 3i
nên
5
z
.
Câu 71: Gọi
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm phân biệt của phương trình
4 2
3 4 0
z z
trên tập số phức.
Tính giá trị của biểu thức
2 2 2 2
1 2 3 4
T z z z z
A.
8
T
. B.
6
T
. C.
4T
. D.
2T
.
Câu 72: Gọi
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm phân biệt của phương trình
4 2
3 4 0
z z
trên tập số phức.
Tính giá trị của biểu thức
2 2 2 2
1 2 3 4
T z z z z
A.
8
T
. B.
6
T
. C.
4T
. D.
2T
.
Lời giải
Chọn A
Ta có
4 2
3 4 0
z z
2
2
3 7
1
2 2
3 7
2
2 2
z i
z i
.
Không mất tính tổng quát giả sử
1
z
,
2
z
là nghiệm của
1
và
3
z
,
4
z
là nghiệm của
2
.
2
2
2 2
1 2
3 7 9 7
2
2 2 4 4
z z
.
Tương tự
2
2
2 2
3 4
3 7 9 7
2
2 2 4 4
z z
.
Vậy
8
T
.
Câu 73: . Cho
1
z
,
2
z
là các số phức khác
0
và
1 2
z z
. Trong các mệnh đề sau, mệnh đề sai?
A.
1 2
z z
. B.
1 2 1 2
z z z z
.
C.
1 1 2 2
z z z z
. D.
1 2
1 2
z z
z z
.
Câu 74: Cho số phức
3 2z i
. Môđun của
2
z
w
z z
bằng
A.
13
6
. B.
15
6
. C.
11
6
. D.
2
.
Câu 75: Cho số
z
thỏa mãn các điều kiện
8 3
z i z i
và
8 7 4
z i z i
. Tìm số phức
7 3w z i
.
A.
3w i
. B.
13 6w i
. C.
1w i
. D.
4 3w i
.
Câu 76: . Cho
1
z
,
2
z
là các số phức khác
0
và
1 2
z z
. Trong các mệnh đề sau, mệnh đề sai?
A.
1 2
z z
. B.
1 2 1 2
z z z z
.
C.
1 1 2 2
z z z z
. D.
1 2
1 2
z z
z z
.
Lời giải
Chọn D
Ta có:
1 2
z z
;
2
1 2 1 2 1 2
z z z z z z
;
2 2
1 1 2 2 1 2
z z z z z z
.
Xét mệnh đề “
1 2
1 2
z z
z z
”: Cho
1
1
z
và
2
z i
thì
1 2
1 2
1
1
z z
i
i i
z z i
, nên
mệnh đề này sai.
Câu 77: Cho số phức
3 2z i
. Môđun của
2
z
w
z z
bằng
A.
13
6
. B.
15
6
. C.
11
6
. D.
2
.
Lời giải
Chọn A
Ta có
2
3 2
5 12
3 2 3 2 6
i
i
w
i i
.
Do đó
5 12 13
6 6
i
w
.
Câu 78: Cho số
z
thỏa mãn các điều kiện
8 3
z i z i
và
8 7 4
z i z i
. Tìm số phức
7 3w z i
.
A.
3w i
. B.
13 6w i
. C.
1w i
. D.
4 3w i
.
Lời giải
Chọn D
Đặt
z x yi
, với
,x y
. Ta có
8 3
z i z i
8 3
x yi i x yi i
8 3 1x y i x y i
2 2 2
2
8 3 1
x y x y
4 18 0
x y
.
8 7 4
z i z i
8 7 4x yi i x yi i
8 7 4 1x y i x y i
2 2 2 2
8 7 4 1
x y x y
2 3 24 0
x y
.
Ta có hệ phương trình:
4 18 0 3
2 3 24 0 6
x y x
x y y
.
Như vậy
3 6z i
7 3w z i
3 6 7 3 4 3i i i
.
Câu 79: Cho số phức
cos .sin
z i
. Tìm môđun của
z
.
A.
cos sin
. B.
1
.
C.
cos sin
i
. D.
cos 2
.
Câu 80: Cho số phức
cos .sin
z i
. Tìm môđun của
z
.
A.
cos sin
. B.
1
.
C.
cos sin
i
. D.
cos 2
.
Lời giải
Chọn B
Ta có:
2 2
cos sin 1
z
.
Câu 81: Cho
1
z
,
2
z
là hai số phức thỏa mãn
2
4 5 0
z z
. Biểu thức
2018 2018
1 2
1 1z zP
có giá
trị bằng
A.
0
. B.
2018
2
. C.
1009
2
. D.
2
.
Câu 82: Cho
1
z
,
2
z
là hai số phức thỏa mãn
2
4 5 0
z z
. Biểu thức
2018 2018
1 2
1 1z zP
có giá
trị bằng
A.
0
. B.
2018
2
. C.
1009
2
. D.
2
.
Lời giải
Chọn A
Biệt số
2
4 5 1
i
.
Do đó phương trình có hai nghiệm phức:
1
2z i
và
2
2z i
.
Suy ra
1009 1009
2018 2018 2 2
1 1 1 1P i i i i
1009 1009
1009 1009
2 2 2 2 0i i i i
.
Câu 83: Biết
z
là một nghiệm của phương trình
1
1
z
z
. Tính giá trị của biểu thức
3
3
1
P z
z
.
A.
2P
. B.
0
P
. C.
4P
. D.
7
4
P
.
Câu 84: Tập hợp điểm biểu diễn số phức
z
thỏa mãn
3
z
z i
là đường nào?
A. Một đường thẳng. B. Một đường parabol. C. Một đường tròn. D. Một đường elip.
Câu 85: Cho số phức
1
1
3
z i
. Tính số phức
3w i z z
.
A.
8
3
w
. B.
8
3
w i
. C.
10
3
w i
. D.
10
3
.
Câu 86: Biết
z
là một nghiệm của phương trình
1
1
z
z
. Tính giá trị của biểu thức
3
3
1
P z
z
.
A.
2P
. B.
0
P
. C.
4P
. D.
7
4
P
.
Lời giải
Chọn A
Ta có
1
1
z
z
2
1 0
z z
, do
1z
nên
3
1 0
z
3
1
z
. Vậy
2P
.
Câu 87: Tập hợp điểm biểu diễn số phức
z
thỏa mãn
3
z
z i
là đường nào?
A. Một đường thẳng. B. Một đường parabol. C. Một đường tròn. D. Một đường elip.
Lời giải
Chọn C
Gọi
z x yi
,
x
,
y
.
3
z
z i
3
z z i
3
x yi x yi i
2
2 2 2
3 1
x y x y
2
2 2 2
9 1
x y x y
2 2
8 8 18 9 0
x y y
2 2
9 9
0
4 8
x y y
.
Vậy tập hợp điểm biểu diễn số phức
z
là một đường tròn.
Câu 88: Cho số phức
1
1
3
z i
. Tính số phức
3w i z z
.
A.
8
3
w
. B.
8
3
w i
. C.
10
3
w i
. D.
10
3
.
Lời giải
Chọn A
1 1 1 8
1 3 1 3
3 3 3 3
w i i i i i
.
Câu 89: Cho biết có hai số phức
z
thỏa mãn
2
119 120z i
, kí hiệu là
1
z
và
2
z
. Tính
2
1 2
z z
.
A.
169
. B.
114244
. C.
338
. D.
676
.
Câu 90: Cho
w
là số phức thay đổi thỏa mãn
2
w
. Trong mặt phẳng phức, các điểm biểu diễn số phức
3 1 2z w i
chạy trên đường nào?
A. Đường tròn tâm
1; 2
I
, bán kính
6
R
.
B. Đường tròn tâm
1;2
I
, bán kính
2R
.
C. Đường tròn tâm
1; 2
I
, bán kính
2R
.
D. Đường tròn tâm
1;2
I
, bán kính
6
R
.
Câu 91: Cho biết có hai số phức
z
thỏa mãn
2
119 120z i
, kí hiệu là
1
z
và
2
z
. Tính
2
1 2
z z
.
A.
169
. B.
114244
. C.
338
. D.
676
.
Hướng dẫn giải
Chọn D
Giả sử:
z a bi
,
,a b
.
Ta có:
2
119 120z i
2 2
2 119 120a b abi i
2 2
119 1
2 120 2
a b
ab
.
Ta có
, 0
a b
.
Từ
60
2 a
b
, thay vào
1
, ta được:
2
2
3600
119
b
b
4 2
119 3600 0
b b
2
2
144
25
b
b
.
*
2
144
b
(vô nghiệm).
*
2
25
b
5 -12
5 12
b a
b a
.
Vậy
1
12 5z i
,
2
12 5z i
.
Suy ra
2
1 2
z z
2
24 10i
676
.
Câu 92: Cho
w
là số phức thay đổi thỏa mãn
2
w
. Trong mặt phẳng phức, các điểm biểu diễn số phức
3 1 2z w i
chạy trên đường nào?
A. Đường tròn tâm
1; 2
I
, bán kính
6
R
.
B. Đường tròn tâm
1;2
I
, bán kính
2R
.
C. Đường tròn tâm
1; 2
I
, bán kính
2R
.
D. Đường tròn tâm
1;2
I
, bán kính
6
R
.
Hướng dẫn giải
Chọn A
Gọi
;M x y
là điểm biểu diễn số phức
z x yi
,x y
.
Ta có
2
w
2 1
2
3
z i
2 1 6
z i
2 2
1 2 36
x y
.
Vậy tập hợp điểm cần tìm là đường tròn tâm
1; 2
I
, bán kính
6
R
.
Câu 93: Xét các số phức
z
thỏa điều kiện
3 2 5
z i
. Trong mặt phẳng tọa độ
Oxy
, tập hợp các
điểm biểu diễn số phức
1w z i
là?
A. Đường tròn tâm
4; 3
I
, bán kính
5
R
.
B. Đường tròn tâm
4;3
I
, bán kính
5
R
.
C. Đường tròn tâm
3; 2
I
, bán kính
5
R
.
D. Đường tròn tâm
2;1
I
, bán kính
5
R
.
Câu 94: Xét các số phức
z
thỏa điều kiện
3 2 5
z i
. Trong mặt phẳng tọa độ
Oxy
, tập hợp các điểm biểu
diễn số phức
1w z i
là?
A. Đường tròn tâm
4; 3
I
, bán kính
5
R
.
B. Đường tròn tâm
4;3
I
, bán kính
5
R
.
C. Đường tròn tâm
3; 2
I
, bán kính
5
R
.
D. Đường tròn tâm
2;1
I
, bán kính
5
R
.
Lời giải
Chọn A
Gọi
;M x y
là điểm biểu diễn số phức
z x yi
,x y
.
Ta có
3 2 5
z i
1 3 2 2
w i i
4 3 6
x yi i
2 2
4 3 25
x y
.
Vậy tập hợp điểm cần tìm là đường tròn tâm
4; 3
I
, bán kính
5
R
.
Câu 95: Số phức
2018
1z i
có phần thực bằng
A.
1
. B.
2019
2
. C.
1009
2
. D.
0
.
Câu 96: Số phức
2018
1z i
có phần thực bằng
A.
1
. B.
2019
2
. C.
1009
2
. D.
0
.
Lời giải
Chọn D
Ta có
1009
504
2018 2 1009
1009 2 1009
1 1 2 2 . . 2 .z i i i i i i
Suy ra
z
có phần thực bằng
0
.
Câu 97: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4 4 37 0
z z
. Trên mặt phẳng
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
w iz
?
A.
2
1
3;
2
M
. B.
3
1
3;
2
M
. C.
3
1
3;
2
M
. D.
1
1
3;
2
M
.
Câu 98: Có bao nhiêu số phức
z
thỏa mãn
2 3 5
z i
và
2
z
z
là số thuần ảo ?
A.
2
. B. vô số. C.
1
. D.
0
.
Câu 99: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4 4 37 0
z z
. Trên mặt phẳng
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
w iz
?
A.
2
1
3;
2
M
. B.
3
1
3;
2
M
. C.
3
1
3;
2
M
. D.
1
1
3;
2
M
.
Lời giải
Chọn D
Ta có
0
1
3
2
z i
nên
0
1
3
2
w iz i
1
1
3;
2
M
.
Câu 100: Có bao nhiêu số phức
z
thỏa mãn
2 3 5
z i
và
2
z
z
là số thuần ảo ?
A.
2
. B. vô số. C.
1
. D.
0
.
Lời giải
Chọn C
Ta gọi
z
a bi
,a b
,
2z
.
Ta có
2 2
2 3 5 2 3 25 1
z i a b
.
Mặt khác
2 2
2 2
2 2
2a 2
2 2
2 2
z a bi a b b
i
z a bi
a b a b
.
2
z
z
là số thuần ảo
2 2
2 0 2
a b a
.
Từ
1
và
2
ta có
2 2
2
2 2
2
2 3 25
3a 2 0
2 0
a b
a b
a
a b a
1
1
2
0
a
b
a
b
.
Vì
2z
nên
1
1 1
1
a
z i
b
.
Câu 101: Gọi
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 6 5 0
z z
. Tìm
0
iz
?
A.
0
1 3
2 2
iz i
. B.
0
1 3
2 2
iz i
. C.
0
1 3
2 2
iz i
. D.
0
1 3
2 2
iz i
.
Câu 102: Cho số phức
z a bi
,
,a b
thỏa mãn
1 3 0z i z i
. Tính
3S a b
.
A.
5
S
. B.
7
3
S
. C.
7
3
S
. D.
5
S
.
Câu 103: Cho
, 0;x y
,
1x y
. Biết
;m a b
thì phương trình
2 2
5 4 5 4 40
x y y x xy m
có nghiệm thực. Tính
25 16T a b
.
A.
829
T
. B.
825
T
. C.
816
T
. D.
820
T
.
Câu 104: Gọi
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 6 5 0
z z
. Tìm
0
iz
?
A.
0
1 3
2 2
iz i
. B.
0
1 3
2 2
iz i
. C.
0
1 3
2 2
iz i
. D.
0
1 3
2 2
iz i
.
Hướng dẫn giải
Chọn B
2
2 6 5 0
z z
0
3 1
2 2
z i
.
Khi đó
0
1 3
2 2
iz i
.
Câu 105: Cho số phức
z a bi
,
,a b
thỏa mãn
1 3 0z i z i
. Tính
3S a b
.
A.
5
S
. B.
7
3
S
. C.
7
3
S
. D.
5
S
.
Hướng dẫn giải
Chọn A
Ta có :
1 3 0z i z i
2 2
1 3 0
a bi i i a b
2 2
1 3 0a b a b i
2 2
1 0
3 0
a
b a b
2
1
1 3
a
b b
2
2
1
3
1 3
a
b
b b
1
4
3
a
b
.
Vậy
3S a b
1 4 5
.
Câu 106: Cho
, 0;x y
,
1x y
. Biết
;m a b
thì phương trình
2 2
5 4 5 4 40
x y y x xy m
có nghiệm thực. Tính
25 16T a b
.
A.
829
T
. B.
825
T
. C.
816
T
. D.
820
T
.
Hướng dẫn giải
Chọn B
Ta có:
2 2 3
3 3
25 20 56 25 20 3 56m xy x y xy xy x y xy x y xy
2
2
25 4 20 25 4 20
xy xy t t
, với
2
1
4 4
x y
t xy
.
Xét hàm số
2
25 4 20
f t t t
trên đoạn
1
0;
4
.
Ta có:
50 4f t t
. Xét
2
0
25
f t t
.
Ta có:
0 20
f
,
2 496
25 25
f
và
1 329
4 16
f
.
Do đó để phương trình có nghiệm thực thì
496 329
;
25 16
m
496 329
,
25 16
a b
suy ra
825
T
.
Câu 107: Gọi
1
z
và
2
4 2z i
là hai nghiệm của phương trình
2
0
az bz c
(
, ,a b c
,
0
a
). Tính
1 2
3T z z
.
A.
6
T
. B.
4 5
T
. C.
2 5
T
. D.
8 5
T
.
Câu 108: Gọi
1
z
và
2
4 2z i
là hai nghiệm của phương trình
2
0
az bz c
(
, ,a b c
,
0
a
). Tính
1 2
3T z z
.
A.
6
T
. B.
4 5
T . C.
2 5
T . D.
8 5
T .
Lời giải
Chọn D
Phương trình bậc hai với hệ số thực có hai nghiệm phức là hai số phức liên hợp.
Do đó
1
4 2z i
. Khi đó
1 2
2 5
z z
1 2
3 8 5
T z z
.
Câu 109: Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
2 3 7 0
z z
. Tính giá trị của biểu thức
1 2
P z z
.
A.
2 3
P
. B.
14P
. C.
7
P
. D.
14
P
.
Câu 110: Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
2 3 7 0
z z
. Tính giá trị của biểu thức
1 2
P z z
.
A.
2 3
P
. B.
14P
. C.
7
P
. D.
14
P
.
Lời giải
Chọn D
Ta có:
2
2 3 7 0
z z
3 47
4 4
3 47
4 4
x i
x i
1 2
14
P z z
.
Câu 111: Gọi
1
z
là nghiệm có phần ảo âm của phương trình
2
4 20 0
z z
. Tìm tọa độ điểm biểu diễn
của
1
z
.
A.
2; 4
M
. B.
4; 2
M
. C.
2; 4
M
. D.
4; 2
M
.
S
A
B
C
D
O
Câu 112: Gọi
1
z
là nghiệm có phần ảo âm của phương trình
2
4 20 0
z z
. Tìm tọa độ điểm biểu diễn
của
1
z
.
A.
2; 4
M
. B.
4; 2
M
. C.
2; 4
M
. D.
4; 2
M
.
Lời giải
Chọn C
Có
2
2 4
4 20 0
2 4
z i
z z
z i
1
2 4z i
.
Vậy điểm biểu diễn của số phức
1
z
là
2; 4
M
.
Câu 113: Định tất cả các số thực
m
để phương trình
2
2 1 0
z z m
có nghiệm phức
z
thỏa mãn
2
z
.
A.
1, 9
m m
. B.
3
m
.
C.
3, 1, 9
m m m
. D.
3, 9
m m
.
Câu 114: Định tất cả các số thực
m
để phương trình
2
2 1 0
z z m
có nghiệm phức
z
thỏa mãn
2
z
.
A.
1, 9
m m
. B.
3
m
.
C.
3, 1, 9
m m m
. D.
3, 9
m m
.
Lời giải
Chọn C
Ta có:
4 4 1 4m m
.
TH1:
0 0
m
. Phương trình có nghiệm là
1
1
z m
z m
.
Nếu
1 2
m
1
m
1
m
.
Nếu
1 2
m
3
1
m
m
9
m
.
TH2:
0 0
m
. Phương trình có nghiệm
1z
không thỏa mãn.
TH3:
0 0
m
. Khi đó nghiệm của phương trình là
1 .
1 .
z m i
z m i
.
Do đó
2 1 4
z m
3
m
.
Câu 115: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 2 0
z z
. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
8
. B.
0
. C.
4
. D.
8i
.
Câu 116: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 2 0
z z
. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
8
. B.
0
. C.
4
. D.
8i
.
Lời giải.
Chọn C
Ta có :
2
2 2 0
z z
1
2
1
1
z i
z i
.
Vậy
2 2
1 2
4
z z
.
Câu 117: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 4 0
z z
. Tính
1 2
1 2
1 1
w iz z
z z
.
A.
3
2
4
w i
. B.
3
2
2
w i
. C.
3
2
2
w i
. D.
3
2
4
w i
.
Câu 118: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 4 0
z z
. Tính
1 2
1 2
1 1
w iz z
z z
.
A.
3
2
4
w i
. B.
3
2
2
w i
. C.
3
2
2
w i
. D.
3
2
4
w i
.
Lời giải
Chọn A
Theo định lý Viét ta có
1 2
3
2
z z
,
1 2
2
z z
.
1 2
1 2
1 1
w iz z
z z
1 2
1 2
1 2
z z
iz z
z z
3
2
4
i
.
Câu 119: Trong mặt phẳng tọa độ
Oxy
, Gọi
A
,
B
,
C
lần lượt là các điểm biểu diễn số phức
1 2i
,
4 4i
,
3i
. Số phức biểu diễn trọng tâm tam giác
ABC
là
A.
1 3i
. B.
1 3i
. C.
3 9i
. D.
3 9i
.
Câu 120: Trong mặt phẳng tọa độ
Oxy
, Gọi
A
,
B
,
C
lần lượt là các điểm biểu diễn số phức
1 2i
,
4 4i
,
3i
. Số phức biểu diễn trọng tâm tam giác
ABC
là
A.
1 3i
. B.
1 3i
. C.
3 9i
. D.
3 9i
.
Lời giải
Chọn B
Ta có
1; 2
A
,
4; 4
B
,
0; 3
C
nên trọng tâm
G
của tam giác ABC có tọa độ là
1; 3
G
. Do đó, số phức biểu diễn điểm
G
là
1 3i
.
Câu 121: Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
z 2 0
z
. Tìm phần ảo của số phức
2018
1 2
w i z i z
.
A.
1009
2
. B.
1009
2
. C.
1008
2
. D.
1008
2
.
Câu 122: Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
z 2 0
z
. Tìm phần ảo của số phức
2018
1 2
w i z i z
.
A.
1009
2
. B.
1009
2
. C.
1008
2
. D.
1008
2
.
Lời giải
Chọn B
Theo định lí Viet ta có:
1 2
1
z z
;
1 2
. 2
z z
.
2018 2018
1 2 1 2 1 2
1w i z i z i z z z z
2018
1 i
.
2018
1 i
1009
2 1009
1009 1008 1009
1 2 2 . . 2 .i i i i i
.
Câu 123: Tìm phần thực, phần ảo của số phức
z
, biết
z
là một căn bậc hai của
221 60w i
và có phần
thực lớn hơn phần ảo.
A. Phần thực bằng
15
, phần ảo bằng
2
. B. Phần thực bằng
2
, phần ảo bằng
15
.
C. Phần thực bằng
15
, phần ảo bằng
2
. D. Phần thực bằng
15
, phần ảo bằng
2
.
Câu 124: Tìm phần thực, phần ảo của số phức
z
, biết
z
là một căn bậc hai của
221 60w i
và có phần
thực lớn hơn phần ảo.
A. Phần thực bằng
15
, phần ảo bằng
2
. B. Phần thực bằng
2
, phần ảo bằng
15
.
C. Phần thực bằng
15
, phần ảo bằng
2
. D. Phần thực bằng
15
, phần ảo bằng
2
.
Lời giải
Chọn D
Gọi
,z a bi a b
. Ta có
2
2 2 2
2
z a bi a b abi
.
Suy ra
2 2
15
2
221
2 60
15
2
a
b
a b
ab
a
b
.
Do phần thực của
z
lớn hơn phần ảo của
z
nên
15 2z i
.
Câu 125: Cho số phức
z
thỏa mãn điều kiện
1 1 3 0i z i
. Tìm phần ảo của số phức
1
w iz z
.
A.
i
. B.
1
. C.
2
. D.
2i
.
Câu 126: Gọi
1 2
,z z
là các nghiệm phức của phương trình
2
4 13 0
z z
. Khi đó
1 2 1
.
z z z
bằng.
A.
26
. B.
13 13
. C.
13
. D.
13 5
.
Câu 127: Có bao nhiêu số phức
z
thỏa mãn
1 3
1?
z z i
z i z i
A.
0
. B.
1
. C.
2
. D.
4
.
Câu 128: Cho số phức
z
thỏa mãn
4 3 10
z i z i
. Giá trị nhỏ nhất của
z
bằng
A.
1
2
. B.
5
7
. C.
3
2
. D.
1
.
Câu 129: Cho số phức
z
thỏa mãn điều kiện
1 1 3 0i z i
. Tìm phần ảo của số phức
1
w iz z
.
A.
i
. B.
1
. C.
2
. D.
2i
.
Lời giải
Chọn B
1 1 3 0i z i
1 3
2
1
i
z i
i
2z i
.
1
w iz z
1 2 2i i i
2 i
.
Vậy phần ảo của
1
w iz z
bằng
1
.
Câu 130: Gọi
1 2
,z z
là các nghiệm phức của phương trình
2
4 13 0
z z
. Khi đó
1 2 1
.
z z z
bằng.
A.
26
. B.
13 13
. C.
13
. D.
13 5
.
Lời giải
Chọn B
2
4 13 0
z z
2 3
2 3
z i
z i
.
Vì
2 3 2 3 13
i i
nên
1 2 1
. 13 13
z z z
.
Câu 131: Có bao nhiêu số phức
z
thỏa mãn
1 3
1?
z z i
z i z i
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn B
Gọi số phức
z a bi
với
,a b
.
Ta có
1
1
z
z i
1
z z i
2 2
2 2
1 1
a b a b
0
a b
3
1
z i
z i
2 2
2 2
3 1
a b a b
1b
Suy ra
1
1
a
b
. Vậy
1z i
Vậy có
1
số phức thỏa mãn yêu cầu bài toán.
Câu 132: Cho số phức
z
thỏa mãn
4 3 10
z i z i
. Giá trị nhỏ nhất của
z
bằng
A.
1
2
. B.
5
7
. C.
3
2
. D.
1
.
Lời giải
Chọn D
Gọi
z a bi
với
,a b
suy ra
2
2 2
z a b
Ta có
2 22
2
1 1 2 1z i a b i z i a b z b
2 22
2
1 1 2 1z i a b i z i a b z b
Theo giả thiết và bất đẳng thức Bnhiacopsky ta có
2 2 2
2 2
10 4 3 4 3 . 5 2 2
z i z i z i z i z
2
1
z
suy ra
min 1
z
.
Câu 133: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 4 3 0
z z
. Giá trị của biểu thức
1 2
2 1
z z
z z
bằng.
A.
3
2
. B.
1
2
. C.
1
3
. D.
2
3
.
Câu 134: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 4 3 0
z z
. Giá trị của biểu thức
1 2
2 1
z z
z z
bằng.
A.
3
2
. B.
1
2
. C.
1
3
. D.
2
3
.
Lời giải
Chọn D
1 2
2 1
z z
z z
2
1 2 1 2
1 2
2
z z z z
z z
2
3
1 2.
4
3
4
2
3
.
Câu 135: Cho số phức
z
thỏa mãn
2
1
z
là số thực. Tập hợp các điểm
M
biểu diễn số phức
z
là?
A. Hai đường thẳng. B. Parabol. C. Đường thẳng. D. Đường tròn.
Câu 136: Cho ba số phức
1
z
,
2
z
,
3
z
thỏa mãn
1 2 3
0
z z z
và
1 2 3
2 2
3
z z z
. Mệnh đề nào
dưới đây đúng?
A.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
. B.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
.
C.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
. D.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
.
Câu 137: Cho số phức
z
thỏa mãn
2
1
z
là số thực. Tập hợp các điểm
M
biểu diễn số phức
z
là?
A. Hai đường thẳng. B. Parabol. C. Đường thẳng. D. Đường tròn.
Hướng dẫn giải
Chọn A
Gọi
z x yi
,x y
. Khi đó, ta có
2 2
1 1
z x yi
2
2
1 2 1x y x yi
.
Do
2
1
z
là số thực nên
2 1 0
x y
0
1 0
y
x
.
Vậy tập hợp các điểm
M
biểu diễn số phức
z
là hai đường thẳng
1 0
x
và
0
y
.
Câu 138: Cho ba số phức
1
z
,
2
z
,
3
z
thỏa mãn
1 2 3
0
z z z
và
1 2 3
2 2
3
z z z
. Mệnh đề nào
dưới đây đúng?
A.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
. B.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
.
C.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
. D.
1 2 3 1 2 2 3 3 1
z z z z z z z z z
.
Hướng dẫn giải
Chọn A
Do
1
z
,
2
z
,
3
z
đều khác
0
nên ta có
1 2 2 3 3 1
1 2 3 1 2 3
1 1 1
z z z z z z
z z z z z z
3
1 2
1 1 2 2 3 3
. . .
z
z z
z z z z z z
1 2 3
8
3
z z z
1
vì
1 1 2 2 3 3
8
. . .
3
z z z z z z
.
Lấy mô đun hai vế của
1
ta có
1 2 3
1 2 2 3 3 1
1 2 3
8
3
z z z
z z z z z z
z z z
1 2 2 3 3 1 1 2 3
2 2
3
z z z z z z z z z
1 2 3
2 2
3
z z z
1 2 3
2 2
0
3
z z z
.
Câu 1:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Cho số phức
z
thỏa mãn
2 4z i z i
và
3 3 1z i
. Giá trị lớn nhất của biểu thức
2
P z
là:
A.
13 1
. B.
10 1
. C.
13
. D.
10
.
Lời giải
Chọn C
Gọi
;M x y
là điểm biểu diễn số phức
z
ta có:
2 4z i z i
2 2
2 2
2 4
x y x y
3
y
;
3 3 1z i
điểm M nằm trên đường tròn tâm
3;3
I
và bán kính bằng 1. Biểu
thức
2
P z AM
trong đó
2;0
A
, theo hình vẽ thì giá trị lớn nhất của
2
P z
đạt
được khi
4;3
M
nên
2 2
max 4 2 3 0 13
P
.
Câu 2:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Trong tập các số phức, cho
phương trình
2
6 0
z z m
,
m
1
. Gọi
0
m
là một giá trị của
m
để phương trình
1
có
hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 1 2 2
. .z z z z
. Hỏi trong khoảng
0;20
có bao nhiêu giá
trị
0
m
?
A.
13
. B.
11
. C.
12
. D.
10
.
Lời giải
Chọn D
Điều kiện để phương trình
1
có hai nghiệm phân biệt là:
9 0 9
m m
.
Phương trình có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 1 2 2
. .z z z z
thì
1
phải có nghiệm
phức. Suy ra
0 9
m
.
Vậy trong khoảng
0;20
có
10
số
0
m
.
Câu 3:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Gọi số phức
z a bi
,
,a b
thỏa mãn
1 1
z
và
1 1
i z
có phần thực bằng
1
đồng thời
z
không là số
thực. Khi đó
.a b
bằng :
A.
. 2
a b
. B.
. 2
a b
. C.
. 1
a b
. D.
. 1
a b
.
Lời giải
Chọn C
Theo giả thiết
1 1
z
thì
2
2
1 1
a b
.
Lại có
1 1
i z
có phần thực bằng
1
nên
2
a b
.
Giải hệ có được từ hai phương trình trên kết hợp điều kiện
z
không là số thực ta được
1
a
,
1b
.
Suy ra
. 1
a b
.
Trình bày lại
Theo giả thiết
1 1
z
thì
2
2
1 1
a b
1
.
Lại có
1 1 1 1i z a b a b i
có phần thực bằng
1
nên
2
0
a b
b
2
.
Giải hệ có được từ hai phương trình trên ta được
1
a
,
1b
.
Suy ra
. 1
a b
.
Câu 4:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Cho số phức
z
thoả
mãn
1 i
z
là số thực và
2
z m
với
m
. Gọi
0
m
là một giá trị của
m
để có đúng một số
phức thoả mãn bài toán. Khi đó:
A.
0
1
0;
2
m
. B.
0
1
;1
2
m
. C.
0
3
;2
2
m
. D.
0
3
1;
2
m
.
Lời giải
Chọn D
Giả sử
,z a bi
,a b
.
Đặt:
1
i
w
z
1
i
a bi
2 2
1
a b a b i
a b
2 2 2 2
a b a b
i
a b a b
.
w
là số thực nên:
1
a b
.
Mặt khác:
2
a bi m
2
2 2
2 2
a b m
.
Thay
1
vào
2
được:
2
2 2
2
a a m
2 2
2 4 4 0 3
a a m
.
Để có đúng một số phức thoả mãn bài toán thì PT
3
phải có nghiệm
a
duy nhất.
0
2
4 2 4 0
m
2
2
m
3
1;
2
2m
(Vì
m
là mô-đun).
Trình bày lại
Giả sử
,z a bi
vì
0
z
nên
2 2
0
a b
*
.
Đặt:
1
i
w
z
1
i
a bi
2 2
1
a b a b i
a b
2 2 2 2
a b a b
i
a b a b
.
w
là số thực nên:
1
a b
.Kết hợp
*
suy ra
0
a b
.
Mặt khác:
2
a bi m
2
2 2
2 2
a b m
.(Vì
m
là mô-đun nên
0
m
).
Thay
1
vào
2
được:
2
2 2
2
a a m
2 2
2 4 4 0
g a a a m
3
.
Để có đúng một số phức thoả mãn bài toán thì PT
3
phải có nghiệm
0
a
duy nhất.
Có các khả năng sau :
KN1 : PT
3
có nghiệm kép
0
a
ĐK:
2
2
0
2 0
2
0 0
4 0
m
m
g
m
.
KN2: PT
3
có hai nghiệm phân biệt trong đó có một nghiệm
0
a
ĐK:
2
2
0
2 0
2
0 0
4 0
m
m
g
m
.
Từ đó suy ra
0
3
2 1;
2
m
.
Câu 5:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Trong tập hợp các số phức,
gọi
1
z
,
2
z
là nghiệm của phương trình
2
2017
0
4
z z
, với
2
z
có thành phần ảo dương. Cho
số phức
z
thoả mãn
1
1
z z
. Giá trị nhỏ nhất của
2
P z z
là
A.
2016 1
. B.
2017 1
2
. C.
2016 1
2
. D.
2017 1
.
Lời giải
Chọn A
Xét phương trình
2
2017
0
4
z z
Ta có:
2016 0
phương trình có hai nghiệm phức
1
2
1 2016
2 2
1 2016
2 2
z i
z i
.
Khi đó:
1 2
2016
z z i
2 1 1 2 1 2 1
2016 1
z z z z z z z z z z P
.
Vậy
min
2016 1
P
.
Câu 6:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Gọi
S
là tập hợp các số
thực
m
sao cho với mỗi
m S
có đúng một số phức thỏa mãn
6
z m
và
4
z
z
là số thuần
ảo. Tính tổng của các phần tử của tập
S
.
A.
10.
B.
0.
C.
16.
D.
8.
Lời giải
Chọn D
Cách 1:
Gọi
z x iy
với
,x y
ta có
2
2 2
2 2
4 4 4
4 4
4 4
x iy x iy x x y iy
z x iy
z x iy
x y x y
là số thuần ảo khi
2
2 2
4 0 2 4
x x y x y
Mà
2
2
6 36
z m x m y
Ta được hệ phương trình
2
2
2
2
2
2
2
2
2
2
2
36
4 2 36
36
4 2
36
4 2
2 4
4 2
4 2
m
x
m x m
x m y
m
m
y x
x y
y
m
Ycbt
2
2
36
4 2 0
4 2
m
m
2
36
2 2
4 2
m
m
hoặc
2
36
2 2
4 2
m
m
10
m
hoặc
2
m
hoặc
6
m
Vậy tổng là
10 2 6 6 8
.
Cách 2:
Để có một số phức thỏa mãn ycbt thì hpt
2
2
2
2
36
2 4
x m y
x y
có đúng một nghiệm
Nghĩa là hai đường tròn
2
2
1
: 36
C x m y
và
2
2
2
: 2 4
C x y
tiếp xúc nhau.
Xét
1
C
có tâm
1
2;0
I
bán kính
1
2
R
,
2
C
có tâm
2
;0
I m
bán kính
2
6
R
Cần có :
1 2 1 2
1 2 1 2
I I R R
I I R R
2 4
2 6
m
m
6;6;10; 2
m
.
Vậy tổng là
10 2 6 6 8
.sss
Câu 7:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Cho hình chóp
.
S ABCD
có
đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
,
N
,
K
lần lượt là trung điểm của
CD
,
CB
,
SA
. Thiết diện của hình chóp cắt bởi mặt phẳng
MNK
là một đa giác
H
. Hãy chọn khẳng
định đúng?
A.
H
là một hình thang. B.
H
là một hình bình hành.
C.
H
là một ngũ giác. D.
H
là một tam giác.
Lời giải
Chọn C Sửa trên hình điểm
P
thành điểm
K
nhé
Gọi
E MN AC
và
F PE SO
. Trong
SBD
qua
F
kẻ đường thẳng song song với
s
MN
và lần lượt cắt
,SB SD
tại
,H G
. Khi đó ta thu được thiết diện là ngũ giác
.MNHKG
Câu 8:
(TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018)
Cho các số phức
z
thỏa mãn
5
z i
.
Biết rằng tập hợp điểm biểu diễn số phức
1w iz i
là đường tròn. Tính bán kính của đường
tròn đó.
A.
22r
. B.
20
r
. C.
4r
. D.
r
.
Lời giải
Chọn D
Gọi
w x yi
,
,x y
.
Ta có:
1w iz i
1x yi iz i
( 1) (1 )z y x i
.
Mà
5
z i
1 5
y xi
2
2 2
1 5
x y
.
Câu 9:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Cho số phức thỏa
3
z
. Biết rằng tập hợp
số phức
w z i
là một đường tròn. Tìm tâm của đường tròn đó.
A.
0;1
I
. B.
0; 1
I
. C.
1;0
I
. D.
1;0
I
.
Lời giải
Chọn A
Đặt
, , .
w x yi x y
Ta có
w z i x yi z i
1z x y i
1
z x y i
.
Mặt khác ta có
3
z
suy ra
2
2
1 9
x y
hay
2
2
1 9
x y
.
Vây tập hợp số phức
w z i
là đường tròn tâm
0;1
I
.
Câu 10:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Đường nào dưới đây là tập hợp các điểm
biểu diễn số phức
z
trong mặt phẳng phức thỏa mãn điều kiện
z i z i
?
A. Một đường thẳng. B. Một đường tròn. C. Một đường elip. D. Một đoạn thẳng.
Lời giải
Chọn A
Gọi
z xi y
, (với
,
x y
) được biểu diễn bởi điểm
;M x y
trong mặt phẳng tọa độ
xoy
.
Ta có
1 1
z i z i x y i x y i
2 2
2 2
1 1
x y x y
0
y
(phương trình một đường thẳng).
Câu 11:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Có bao nhiêu số phức
z
thỏa mãn
1
z z z
?
A.
0
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn C
Giả sử
z x yi
,
x y
2 z x yi z z x
.
Bài ra ta có
2 2
2 2
1
1
1
1
1
2 1
2
x y
z
x y
z z
x
x
Với
2
1 1 3
1
2 4 2
x y y
.
Do đó có 4 số phức thỏa mãn là
1
1 3
2 2
z i
,
2
1 3
2 2
z i
,
3
1 3
2 2
z i
,
4
1 3
2 2
z i
.
Câu 12:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 1 2
z z z
trên mặt phẳng tọa độ là một
A. đường thẳng. B. đường tròn. C. parabol. D. hypebol.
Lời giải
Chọn C
Giả sử
z x yi
,
x y
z x yi
2 z z x
.
Bài ra ta có
2
2
2 1 2 2 2 1 2 2
x yi x x y x
2 2
2 2 2 2 2
1 1 2 1 2 1 4
x y x x x y x x y x
.
Do đó tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 1 2
z z z
trên mặt phẳng tọa
độ là một parabol.
Câu 13:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Tìm giá trị lớn nhất của
2 2
1 P z z z z
với
z
là số phức thỏa mãn
1
z
.
A.
3
. B.
3
. C.
13
4
. D.
5
.
Lời giải
Chọn C
Cách 1: Đặt
,
z a bi a b
. Do
1
z
nên
2 2
1
a b
.
Sử dụng công thức:
.
u v u v
ta có:
2
2 2
1 1 1 2 2
z z z z z a b a
.
2
2 2
2 2 2 2 2
1 1 1 2 1 2
z z a bi a bi a b a ab b i a b a ab b
2
2 2 2
(2 1) 2 1 2 1
a a b a a
(vì
2 2
1
a b
).
Vậy
2 1 2 2 P a a
.
 TH1:
1
2
a
.
Suy ra
2 1 2 2 2 2 2 2 3 4 2 3 3
P a a a a
(vì
0 2 2 2
a
).
 TH2:
1
2
a
.
Suy ra
2
1 1 13
2 1 2 2 2 2 2 2 3 2 2 3
2 4 4
P a a a a a
.
Đẳng thức xảy ra khi
1 7
2 2 0
2 8
a a
.
Cách 2: Đặt
,z a bi a b
. Do
1
z
nên
2 2
1
a b
. Nhận xét:
1;1
a
Lập luận như cách 1 được
1
2
1
2 1 2 2 , 1
2
2 1 2 2
1
2 1 2 2 , 1
2
f a a a a
P a a
f a a a a
Ta có
1 1
2 , 1
2
2 2
1 1
2 , 1
2
2 2
a
a
f a
a
a
. Xét
7
0
8
f a a
Lập bbt xét dấu
f a
ta thấy hàm số đạt giá trị lớn nhất là
13
4
khi
7
8
a
.
Câu 14:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Cho số phức
z
và
w
thỏa
mãn
3 4z w i
và
9
z w
. Tìm giá trị lớn nhất của biểu thức
T z w
.
A.
max 176
T
. B.
max 14
T
. C.
max 4
T
. D.
max 106
T
.
Lời giải
Chọn D
Đặt
,z x yi x y
. Do
3 4z w i
nên
3 4
w x y i
.
Mặt khác
9
z w
nên
2 2
2 2
2 3 2 4 4 4 12 16 25 9
z w x y x y x y
2 2
2 2 6 8 28
x y x y
1
. Suy ra
2 2
2 2
3 4
T z w x y x y
.
Áp dụng bất đẳng thức Bunyakovsky ta có
2 2 2
2 2 2 6 8 25
T x y x y
2
.
Dấu
" "
xảy ra khi
2 2
2 2
3 4
x y x y
.
Từ
1
và
2
ta có
2
2. 28 25 106 106
T T
. Vậy
106
MaxT
.
Câu 15:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Trong mặt phẳng phức,
gọi
A
,
B
,
C
,
D
lần lượt là các điểm biểu diễn số phức
1
1z i
,
2
1 2z i
,
3
2z i
,
4
3z i
. Gọi
S
là diện tích tứ giác
ABCD
. Tính
S
.
A.
17
2
S
. B.
19
2
S
. C.
23
2
S
. D.
21
2
S
.
Lời giải
Chọn A
Ta có
1
1 1;1
z i A
,
2
1 2 1;2
z i B
,
3
2 2; 1
z i C
,
4
3 0; 3
z i D
O
x
y
A
B
C
D
1
2
2
1
3
1
1
3; 2AC
13
AC ,
2;3
n
là véc tơ pháp tuyến của
AC
, phương trình
AC
:
2 1 3 1 0 2 3 1 0
x y x y
.
Khoảng cách từ
B
đến
AC
là:
2 3.2 1
7
;
13 13
d B AC
1 1 7 7
; . . 13.
2 2 2
13
ABC
S d B AC AC
.
Khoảng cách từ
D
đến
AC
là:
0 9 1
10
;
13 13
d D AC
1 1 10
. ; . . . 13 5
2 2
13
ADC
S d D AC AC
.
Vậy
7 17
5
2 2
ABC ADC
S S S
.
Câu 16:
(Đề tham khảo BGD năm 2017-2018)
Cho số phức
z a bi
,a b
thỏa mãn
2 1 0
z i z i
và
1
z
. Tính
P a b
.
A.
1P
. B.
5
P
. C.
3
P
. D.
7
P
.
Lời giải
Chọn D
2 1 0 2 1
z i z i a b i z i z
2 2
2 2
2
2 1
1
1 2
a z a a b
b z
b a b
Lấy
1
trừ
2
theo vế ta được
1 0 1a b b a
. Thay vào
1
ta được
2
2
2
2 1 do 1
2 1 3
2 3 0
a z
a a a a
a a
. Suy ra
4
b
.
Do đó
3 4z i
có
5 1
z
(thỏa điều kiện
1
z
).
Vậy
3 4 7
P a b
.
Câu 1:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Cho số phức
z
thoả mãn
3 4 5
z i
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
2
P z z i
. Tính môđun
của số phức
w M mi
.
A.
1258
w
. B.
1258
w
. C.
2 314
w
. D.
2 309
w
.
Lời giải
Chọn B
Giả sử
z a bi
(
,a b
).
2 2
3 4 5 3 4 5
z i a b
(1).
2 2 2 2
2 2
2 2 1 4 2 3P z z i a b a b a b
(2).
Từ (1) và (2) ta có
2 2
20 64 8 22 137 0
a P a P P
(*).
Phương trình (*) có nghiệm khi
2
4 184 1716 0
P P
13 33 1258
P w
.
Câu 2:
(THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018)
Cho số phức
z
, biết rằng các điểm biểu
diễn hình học của các số phức
z
;
iz
và
z i z
tạo thành một tam giác có diện tích bằng
18
. Mô
đun của số phức
z
bằng
A.
2 3
. B.
3 2
. C.
6
. D.
9
.
Lời giải
Chọn C
Gọi
z a bi
,
,a b
nên
iz ai b
,
z i z
a bi b ai
a b a b i
Ta gọi
,A a b
,
,B b a
,
,
C a b a b
nên
,
AB b a a b
,
,AC b a
1
,
2
S AB AC
2 2
1
2
a b
2 2
1
18
2
a b
2 2
6
a b
.
Câu 3:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Cho số phức
z
thỏa mãn
2
z
.
Biết rằng tập hợp các điểm biểu diễn số phức
3 2 2
w i i z
là một đường tròn. Bán kính
R
của đường tròn đó bằng ?
A.
7
. B.
20
. C.
2 5
. D.
7
.
Lời giải
Chọn C
Ta có
3 2 2
w i i z
3 2
2
w i
z
i
. Đặt
w x yi
,x y
.
Khi đó
3 2
2
x yi i
z
i
.
Ta có
2
z
3 2
2
2
x yi i
i
3 2
2
2
x y i
i
3 2
2
2
x y i
i
3 2 2 2
x y i i
3 2 2 5
x y i
2
2 2
3 2 2 5
x y
.
Vậy tập hợp các điểm biểu diễn số phức
3 2 2
w i i z
là một đường tròn có bán kính
2 5
R
.
Câu 4:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Cho số phức
z
thỏa mãn
4 3 10
z i z i
. Giá trị nhỏ nhất của
z
bằng:
A.
1
2
. B.
5
7
. C.
3
2
. D.
1
.
Lời giải
Chọn D
Gọi
z a bi
,a b
. Khi đó:
4 3
z i z i
2 2
2 2
4 1 3 1
a b a b
2 2
2 2 2 2
4 3 1 1
a b a b
2
2
10 25 2 2
z
1
z
.
Vậy giá trị nhỏ nhất của
z
là 1, đạt khi
24 7
;
25 25
a b
hay
24 7
25 25
z i
.
Câu 5:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
, gọi
M
,
N
,
P
lần lượt là các điểm biểu diễn các số phức
1
1z i
,
2
8z i
,
3
1 3z i
. Khẳng định nào sau
đây đúng?
A. Tam giác
MNP
cân. B. Tam giác
MNP
đều.
C. Tam giác
MNP
vuông. D. Tam giác
MNP
vuông cân.
Lời giải
Chọn C
M
là điểm biểu diễn số phức
1
1z i
nên tọa độ điểm
M
là
1;1
.
N
là điểm biểu diễn số phức
2
8z i
nên tọa độ điểm
N
là
.
P
là điểm biểu diễn số phức
3
1 3z i
nên tọa độ điểm
P
là
1; 3
.
Ta có
7;0
MN
,
0; 4
MP
nên
. 0
MN MP
MN MP
hay tam giác
MNP
vuông tại
M
và
không phải tam giác cân.
Câu 6:
(THTT số 5-488 tháng 2 năm 2018)
Có bao nhiêu số phức
z
thỏa mãn
1 3
1
z z i
z i z i
?
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn B
Gọi
z a bi
,a b
.
Ta có:
1
3
z z i
z i z i
2 2
2 2
2 2
2 2
1 1
3 1
a b a b
a b a b
2 1 2 1
6 9 2 1
a b
b b
1
1
a
b
.
Vậy có một số phức thỏa mãn là
1z i
.
Câu 1:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Số phức
z a bi
( với
a
,
b
là số
nguyên) thỏa mãn
1 3i z
là số thực và
2 5 1z i
. Khi đó
a b
là
A.
9
. B.
8
. C.
6
. D.
7
.
Lời giải
Chọn B
Ta có:
1 3i z
1 3
i a bi
3 3a b b a i
.
Vì
1 3i z
là số thực nên
3 0
b a
3b a
1
.
2 5 1z i
2 5 1a b i
2 2
2 5 1
a b
2
.
Thế
1
vào
2
ta có:
2 2
2 5 3 1
a a
2
10 34 28 0
a a
2 6
7
(
5
a b
a
loaïi)
.
Vậy
2 6 8
a b
.
Câu 2:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2 2
5 5, 1 3 3 6z z i z i
. Giá trị nhỏ nhất của
1 2
z z
là
A.
5
2
. B.
7
2
. C.
1
2
. D.
3
2
.
Lời giải
Chọn A
Giả sử
1 1 1 1 1
,z a b i a b
,
2 2 2 2 2
,z a b i a b
.
Ta có
1
5 5
z
2
2
1 1
5 25
a b
. Do đó, tập hợp các điểm
A
biểu diễn cho số phức
1
z
là
đường tròn
2
2
: 5 25
C x y
có tâm là điểm
5;0
I
và bán kính
5
R
.
2 2
1 3 3 6z i z i
2 2 2 2
2 2 2 2
1 3 3 6
a b a b
2 2
8 6 35 0
a b
. Do đó tập hợp các điểm
B
biểu diễn cho số phức
2
z
là đường thẳng
:8 6 35 0
x y
.
Khi đó, ta có
1 2
z z AB
.
Suy ra
1 2 min
min
z z AB
;
d I R
2 2
8. 5 6.0 35
5
8 6
5
2
.
Vậy giá trị nhỏ nhất của
1 2
z z
là
5
2
.
Câu 3:
(THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
w x yi
,
,x y
thỏa
mãn điều kiện
2
4 2w w
. Đặt
2 2
8 12
P x y
. Khẳng định nào dưới đây đúng?
A.
2
2
2
P w
. B.
2
2
2
P w
. C.
2
4
P w
. D.
2
2
4
P w
.
Đáp án A và B có giá trị như nhau nên em đã sửa đáp án A.
A.
2
2
w 2
P
. B.
2
2
2
P w
. C.
2
4
P w
. D.
2
2
4
P w
.
Lời giải
Chọn B
Ta có
2
4
w
2
4
x yi
2 2
2 4x y xyi
2
2 2 2 2 2
4 4 4
w x y x y
.
Do đó
2
4 2w w
2
2 2 2 2 2 2
4 4 2
x y x y x y
2
2 2 2 2 2 2
4 4 4
x y x y x y
4 4 2 2 2 2 2 2 2 2
2 8 16 4 4
x y x y x y x y x y
4 4 2 2 2 2 2 2
2 4 4 8 12 0
x y x y x y x y
2
2 2 2 2 2 2
4 4 8 12 0
x y x y x y
2
2 2 2 2
2 8 12 0
x y x y
2
2 2 2 2
8 12 2
x y x y
2
2
2
P w
.
Câu 4:
(THPT Chuyên Tiền Giang-lần 1 năm 2017-2018)
Cho số phức
z a bi
, a b
thỏa mãn
1 3 0z i z i
. Tính
3S a b
.
A.
7
3
S
. B.
5
S
. C.
5
S
. D.
7
3
S
.
Lời giải
Chọn B
Ta có
1 3 0z i z i
2 2
1 3 0
a bi i i a b
2 2
1 3 0a b a b i
2 2
1 0
3
a
b a b
2
2
1
3
3 1
a
b
b b
1
4
3
a
b
5
S
.
Câu 5:
(THPT Chuyên Tiền Giang-lần 1 năm 2017-2018)
Biết số phức
z
thỏa mãn
3 4 5
z i
và
biểu thức
2 2
2
T z z i
đạt giá trị lớn nhất. Tính
z
.
A.
33
z
. B.
50
z
. C.
10
z
. D.
5 2
z
.
Lời giải
Chọn D
Đặt
z x yi
, theo giả thiết
2 2
3 4 5 3 4 5
z i x y
.
C
Ngoài ra
2 2
2 4 2 3 0
T z z i x y T
đạt giá trị lớn nhất.
Rõ ràng
C
và
có điểm chung do đó
23
5 13 33
2 5
T
T
.
Vì
T
đạt giá trị lớn nhất nên
33
T
suy ra
4 2 30 0 15 2x y y x
thay vào
C
ta
được
2
5 50 125 0 5
x x x
5
y
. Vậy
5 2
z
.
Câu 6: (THTT số 6-489 tháng 3 năm 2018) Cho hai điểm
A
,
B
là hai điểm biểu diễn hình học số phức
theo thứ tự
0
z
,
1
z
khác
0
và thỏa mãn đẳng thức
2 2
0 1 0 1
z z z z
. Hỏi ba điểm
O
,
A
,
B
tạo
thành tam giác gì? (
O
là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
A. Cân tại
O
. B. Vuông cân tại
O
. C. Đều. D. Vuông tại
O
.
Lời giải
Chọn C
Theo giả thiết suy ra:
0
OA z
,
1
OB z
và
1 0
AB z z
.
Ta có:
2 2
0 1 0 1
z z z z
2 2 2 2
0 0 1 1 0 1 0 0 1 1
0 0
z z z z z z z z z z
.
3 3 3 3
0 1 0 1 0 1
0
z z z z z z OA OB
.
Xét
2
2 2
1 0 0 1 0 1 0 1
2
z z z z z z z z
2
1 0 1 0
.z z z z
2
.
AB OA OB AB OB
.
Vậy
AB OB OA
hay tam giác
là tam giác đều.
Câu 7: (THTT số 6-489 tháng 3 năm 2018) Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của
z i
P
z
, với
z
là số phức khác
0
thỏa mãn
2
z
. Tính
2
M m
.
A.
3
2
2
M m
. B.
5
2
2
M m
. C.
2 10
M m
. D.
2 6
M m
.
Lời giải
Chọn B
z i
P
z
z i z i
z z
1 3
1
2
z
. Dấu bằng xảy ra khi
2z i
. Vậy
3
2
M
.
z i
P
z
z i
z i
z z
z i
z
1 1
1
2
z
. Dấu bằng xảy ra khi
2z i
.
Vậy
1
2
m
.
Vậy
5
2
2
M m
.
Câu 8:
(THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
z a bi
, , 0
a b a
thỏa
mãn
1 2 5
z i
và
. 10
z z
. Tính
P a b
.
A.
4P
. B.
4P
. C.
2P
. D.
2P
.
Lời giải
Chọn A
Từ giả thiết
1 2 5
z i
và
. 10
z z
ta có hệ phương trình
2 2
2 2
1 2 5
10
a b
a b
2 2
2 5
10
a b
a b
2
2
2 5
2 5 10
a b
b b
3
1
a
b
hay
1
3
a
b
(loại). Vậy
4P
.
Câu 9:
(THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018)
Cho số phức
z
thỏa mãn
1 1z i
, số phức
w
thỏa mãn
2 3 2
w i
. Tìm giá trị nhỏ nhất của
z w
.
A.
13 3
. B.
17 3
. C.
17 3
. D.
13 3
.
Lời giải
Chọn B
Gọi
;M x y
biểu diễn số phức
z x iy
thì
M
thuộc đường tròn
1
C
có tâm
1
1;1
I
, bán
kính
1
1
R
.
;N x y
biểu diễn số phức
w x iy
thì
N
thuộc đường tròn
2
C
có tâm
2
2; 3
I
, bán
kính
2
2
R
. Giá trị nhỏ nhất của
z w
chính là giá trị nhỏ nhất của đoạn
MN
.
Ta có
1 2
1; 4
I I
1 2
17
I I
1 2
R R
1
C
và
2
C
ở ngoài nhau.
min
MN
1 2 1 2
I I R R
17 3
Câu 10:
(THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018)
Cho các số phức
1
2z i
,
2
2z i
và số phức
z
thay đổi thỏa mãn
2 2
1 2
16
z z z z
. Gọi
M
và
m
lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của
z
. Giá trị biểu thức
2 2
M m
bằng
A.
15
. B.
7
. C.
11
. D.
8
.
Lời giải
Chọn D
Giả sử
,z x yi x y
.
Ta có:
2 2
1 2
16
z z z z
2 2
2 2 16
x yi i x yi i
2
2
1 4
x y
.
Suy ra tập hợp điểm biểu diễn của số phức
z
là đường tròn tâm số phức
0;1
I
bán kính
2R
.
Do đó
1
m
,
3
M
.
Vậy
2 2
8
M m
.
Câu 11: [2D4 -3]
(THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018)
Cho các số
p
,
q
thỏa
mãn các điều kiện:
1p
,
1
q
,
1 1
1
p q
và các số dương
a
,
b
. Xét hàm số:
1p
y x
0
x
có đồ thị là
C
. Gọi
1
S
là diện tích hình phẳng giới hạn bởi
C
, trục
hoành, đường thẳng
x a
, Gọi
2
S
là diện tích hình phẳng giới hạn bởi
C
, trục tung,
đường thẳng
y b
, Gọi
S
là diện tích hình phẳng giới hạn bởi trục hoành, trục tung và hai
đường thẳng
x a
,
y b
. Khi so sánh
1 2
S S
và
S
ta nhận được bất đẳng thức nào trong các
bất đẳng thức dưới đây?
O
x
y
2
2
1
3
1
I
O
x
y
y b
1p
y x
x a
a
b
2
S
1
S
A.
p q
a b
ab
p q
B.
1 1
1 1
p q
a b
ab
p q
. C.
1 1
1 1
p q
a b
ab
p q
. D.
p q
a b
ab
p q
.
Lời giải
Chọn D
Ta có:
1 2
S S S
.
1
1
0
0
d
a
a
p p
p
x a
S x x
p p
;
1
1
1
1
1
2
0
0
0
d
1
1
1
b
b
b
q q
p
p
y y b
S y y
q q
p
.
Vì:
1 1 1
1
1 1
1 1
1
p
q
p p
p q
.
Vậy
p q
a b
ab
p q
.
Câu 12:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Gọi
H
là tập hợp các điểm biểu diễn số
phức
z
thỏa
1 1 2
z
trong mặt phẳng phức. Tính diện tích hình
H
.
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn B
Đặt
z x yi
,
1 1
z x yi
2
2
1
x y
.
Do đó
1 1 2
z
2
2
1 1 2
x y
2
2
1 1 4
x y
.
Tập hợp các điểm biểu diễn số phức
z
là hình phẳng nằm trong đường tròn tâm
1;0
I
bán
kính
2R
và nằm ngoài đường tròn
1;0
I
bán kính
1r
.
Diện tích hình phẳng
2 2
.2 .1 3
S
.
Câu 13:
(THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018)
Có bao nhiêu số phức
z
thỏa mãn điều
kiện
2
2
z z z
?
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
Đặt
z a bi
,a b
.
Ta có
2
2
z z z
2
2 2
a bi a b a bi
2 2
2
abi b b a bi
2 2
2
ab b
b b a
2
0
1
2
2 0
b
a
b a

0 0
b a
0
z
.

1 1
2 2
a b
1 1
2 2
z i
.
Vậy có
3
số phức thỏa ycbt.
Câu 14: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Cho hai số phức
1
z
,
2
z
có điểm
biểu diễn lần lượt là
1
M
,
2
M
cùng thuộc đường tròn có phương trình
2 2
1
x y
và
1 2
1
z z
. Tính giá trị biểu thức
1 2
P z z
.
A.
3
2
P
. B.
2
P
. C.
2
2
P
. D.
3
P
.
Lời giải
Chọn D
Ta có
1
M
,
2
M
cùng thuộc đường tròn tâm
0;0
O
bán kính
1R
.
Vì
1 2
1
z z
nên suy ra
1 2
1
M M
. Vậy tam giác
1 2
OM M
là tam giác đều cạnh bằng
1
.
Gọi
H
là trung điểm của
1 2
M M
thì
OH
là trung tuyến của tam giác đều
1 2
OM M
có cạnh
bằng
1
. Suy ra
1. 3
2
OH
3
2
.
Ta có
1 2
P z z
1 2
OM OM
 
2
OH
2
OH
3
2.
2
3.
Câu 15: (SGD Bắc Giang – năm 2017 – 2018) Cho
1
2
1
3
d 2
3 9 1
x
x a b
x x
, với
a
,
b
là các số
hữu tỉ. Khi đó, giá trị của
a
là
A.
26
27
. B.
26
27
. C.
27
26
. D.
25
27
.
Lời giải
Chọn B
Ta có:
1
1 1
3
2 3 2
2
2
1
1 1
3
3 3
2 26 32
d 3 9 1 d 9 1 2
27 27 27
3 9 1
x
x x x x x x x
x x
.
Câu 16: (SGD Bắc Giang – năm 2017 – 2018) Cho số phức
z
thỏa mãn
2 7 3
z z i z
. Tính
z
.
A. 3. B.
13
4
. C.
25
4
. D.
5
.
Lời giải
Chọn D
Giả sử
z x yi
,x y
.
Ta có:
2 2
2 7 3 2 2 7 3z z i z x y x yi x y i
2 2
4
2 7
3
2 3
x
x y x x
y
y y
. Vậy
5
z
.
Câu 17: (SGD Bắc Giang – năm 2017 – 2018) Cho hai số phức
z
,
w
thỏa mãn
3 2 1
1 2 2
z i
w i w i
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
P z w
.
A.
min
3 2 2
2
P
. B.
min
2 1
P
. C.
min
5 2 2
2
P
. D.
min
3 2 2
2
P
.
Lời giải
Chọn C
Giả sử
z a bi
;
w x yi
, , ,a b x y
. Ta có
3 2 1z i
2 2
3 2 1
a b
. Suy ra tập hợp điểm
M
biểu diễn số phức
z
là hình
tròn tâm
3;2
I
, bán kính
1R
.
1 2 2w i w i
2 2 2 2
1 2 2 1 0
x y x y x y
. Suy ra tập hợp
điểm
N
biểu diễn số phức
w
là nửa mặt phẳng giới hạn bởi đường thẳng
: 0
x y
(tính cả
bờ đường thẳng) (hình vẽ)
Ta có
5
,
2
d I
. Gọi
H
là hình chiếu của
I
trên
.
Khi đó
5 2
, 1
2
z w MN d I R
. Suy ra
min
5 2
1
2
P
.
Câu 18: (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho hai số phức
1
z
,
2
z
thỏa mãn
1
1 2
z i
và
2 1
z iz
. Tìm giá trị lớn nhất
m
của biểu thức
1 2
z z
A.
2 2 2
m
. B.
2 1
m
. C.
2 2
m
. D.
2
m
.
Lời giải
Chọn A
Gọi
1
z x yi
(
x
,
y
), khi đó theo giả thiết của đề bài ta có
2
z y xi
.
Khi đó
2 2
1
1 2 1 1 4
z i x y
.
Vì vậy tồn tại
t
để
1 2sinx t
và
1 2cosy t
.
Do đó
2
2 2
1 2
z z x y y x
2 2
2
x y
2 6 4 sin cost t
12 8 2 sin
4
t
12 8 2
.
Do đó
12 8 2 2 2 2
m
.
y
x
3
2
I
O
Câu 19: Cho số phức
z a bi
(
a
,
b
là các số thực ) thỏa mãn
2 0z z z i
. Tính giá trị của biểu
thức
2
T a b
.
A.
4 3 2
T
. B.
3 2 2
T
. C.
3 2 2
T
. D.
4 2 3
T .
Câu 20:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Cho số phức
z a bi
(
a
,
b
là các số thực
) thỏa mãn
2 0z z z i
. Tính giá trị của biểu thức
2
T a b
.
A.
4 3 2
T
. B.
3 2 2
T
. C.
3 2 2
T
. D.
4 2 3
T .
Lời giải
Chọn C
Ta có
2 0 2 0z z z i a bi a bi a bi i
2 2 2 2 2 2 2 2
2 2 0 2 2 0a a b a b a b i bi i a a b a b a b i bi i
2 2
2 2 2 2
2 2
2 0
2 2 1 0
2 1 0
a a b a
a a b a b a b b i
b a b b
2
0
0
2 1
2 1 0
a
a
b
b
b b b
b
.
2 1
2 1
1 2
1
0
2
b
b
b
b
b b
b
b
. Suy ra
2
3 2 2
T a b
.
Câu 21: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Có bao nhiêu số phức
z
thỏa mãn
1 3 3 2
z i
và
2
2z i
là số thuần ảo?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Giả sử
z x yi
,x y
. Khi đó
2 2
1 3 3 2 1 3 18 1
z i x y
.
2
2 2
2
2 2 2 2 2z i x y i x y x y i
.
Theo giả thiết ta có
2
2
2
2 0
2
x y
x y
x y
.
Với
2
x y
thay vào
1
ta được phương trình
2
2 0 0 2
y y x
1
2
z
.
Với
2
x y
thay vào
1
ta được phương trình
2
1 5
2 4 8 0
1 5
y
y y
y
2
3
3 5 1 5
3 5 1 5
z i
z i
.
Vậy có
3
số phức thỏa mãn yêu cầu bài toán.
Câu 22: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Giả sử
1 2
,z z
là hai nghiệm
phức của phương trình
2 i 1 2i 1 3i
z z z
và
1 2
1
z z
. Tính
1 2
2 3M z z
.
A.
19
M
. B.
25
M
. C.
5
M
. D.
19
M .
Lời giải
Chọn D
Từ giả thiết, ta có
2 1 2 i . 10
z z z
2 2
2
2 1 2 . 10
z z z
4 2
5 5 10 0
z z
1
z
(vì
0
z
).
Gọi
1 1 1
iz x y
và
2 2 2
iz x y
. Ta có
1 2
1
z z
nên
2 2 2 2
1 1 2 2
1
x y x y
.
Mặt khác,
1 2
1
z z
nên
2 2
1 2 1 2
1
x x y y
. Suy ra
1 2 1 2
1
2
x x y y
.
Khi đó
1 2
2 3M z z
2 2
1 2 1 2
2 3 2 3
x x y y
2 2 2 2
1 1 1 2 1 2 1 2
4 9 12
x y y y x x y y
Vậy
19
M
.
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Cho
1
z
,
2
z
là hai trong các số phức
z
thỏa mãn điều
kiện
5 3 5
z i
, đồng thời
1 2
8
z z
. Tập hợp các điểm biểu diễn của số phức
1 2
w z z
trong mặt phẳng tọa độ
Oxy
là đường tròn có phương trình nào dưới đây?
A.
2 2
5 3 9
2 2 4
x y
. B.
2 2
10 6 36
x y
.
C.
2 2
10 6 16
x y
. D.
2 2
5 3
9
2 2
x y
.
Lời giải
Chọn B
Gọi
A
,
B
,
M
là các điểm biểu diễn của
1
z
,
2
z
,
w
. Khi đó
A
,
B
thuộc đường tròn
2 2
: 5 3 25
C x y
và
1 2
8
AB z z
.
C
có tâm
5;3
I
và bán kính
5
R
, gọi
T
là trung điểm của
AB
khi đó
T
là trung điểm
của
OM
và
2 2
3
IT IA TA
.
Gọi
J
là điểm đối xứng của
O
qua
I
suy ra
10;6
J
và
IT
là đường trung bình của tam giác
OJM
, do đó
2 6
JM IT
.
Vậy
M
thuộc đường tròn tâm
J
bán kính bằng
6
và có phương trình
2 2
10 6 36
x y
.
Câu 2:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Biết số phức
z
có
phần ảo khác
0
và thỏa mãn
2 10
z i
và
. 25
z z
. Điểm nào sau đây biểu diễn số
phức
z
trên?
A.
4; 3
P
. B.
3; 4
N
. C.
3; 4
M
. D.
4; 3
Q
.
Lời giải
Chọn C
Giả sử
z x yi
, , 0
x y y
.
Ta có
2 10
z i
2 10
x yi i
2 1 10
x y i
2 2
2 1 10
x y
2 2
4 2 5
x y x y
.
Lại có
. 25
z z
2 2
25
x y
nên
25 4 2 5
x y
2 10
x y
10 2y x
2
2
10 2 25
x x
2
5 40 75 0
x x
5
3
x
x
.
+ Với
5 0
x y
, không thỏa mãn vì
0
y
.
+ Với
3 4
x y
, thỏa mãn
0
y
3 4z i
.
Do đó điểm
3; 4
M
biểu diễn số phức
z
.
Câu 3:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Cho
A
,
B
là hai
điểm biểu diễn hình học số phức theo thứ tự
0
z
,
1
z
khác
0
và thỏa mãn đẳng thức
2 2
0 1 0 1
z z z z
. Hỏi ba điểm
O
,
A
,
B
tạo thành tam giác gì (
O
là gốc tọa độ) ? Chọn phương
án đúng và đầy đủ nhất.
A. Đều. B. Cân tại
O
. C. Vuông tại
O
. D. Vuông cân tại
O
.
Lời giải
Chọn A
Do
1
0
z
nên chia
2
vế của đẳng thức cho
2
1
z
, ta được:
2
0 0 0
0 1
1 1 1
1 3 1 3
1
2 2 2 2
z z z
i z i z
z z z
.
Đặt
1
z OA a
0 1
1 3
2 2
OB z i z a
.
Lại có
0 1 1 1 1
1 3 1 3
2 2 2 2
z z i z z i z
0 1 1
1 3
2 2
AB z z i z a
.
Vậy
OAB
đều.
Câu 4:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của
z i
P
z
, với
z
là số phức khác
0
và thỏa mãn
2
z
. Tính tỷ số
M
m
.
A.
5
M
m
. B.
3
M
m
. C.
3
4
M
m
. D.
1
3
M
m
.
Lời giải
Chọn B
Gọi
1
z i
T T z i
z
.
Nếu
1
T
Không có số phức nào thoả mãn yêu cầu bài toán.
Nếu
1
1 2 1
1 1 2
i i
T z z T
T T
.
Vậy tập hợp điểm biểu diễn số phức
T
là hình tròn tâm
1;0
I
có bán kính
1
2
R
.
3
2
1
2
M OB OI R
m OA OI R
3
M
m
.
Câu 5: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho số phức
z
thỏa mãn
1 2 1 2 4 2
i z i z
. Gọi
maxm z
,
minn z
và số phức
w m ni
. Tính
2018
w
A.
1009
4
. B.
1009
5
. C.
1009
6
. D.
1009
2
.
Lời giải
Chọn C
Ta có
1 2 1 2 4 2
i z i z
1 1 4
z i z i
.
Gọi
M
là điểm biểu diễn của số phức
z
,
1
1;1
F
là điểm biểu diễn của số phức
1
1z i
và
2
1; 1
F
là điểm biểu diễn của số phức
2
1z i
. Khi đó ta có
1 2
4
MF MF
. Vậy tập hợp
điểm
M
biểu diễn số phức
z
là Elip nhận
1
F
và
2
F
làm hai tiêu điểm.
Ta có
1 2
2 2 2 2 2
F F c c c
.
Mặt khác
2 4 2
a a
suy ra
2 2
4 2 2
b a c
.
Do đó Elip có độ dài trục lớn là
1 2
2 4
A A a
, độ dài trục bé là
1 2
2 2 2
B B b
.
Mặt khác
O
là trung điểm của
AB
nên
m max z
max
OM
1
OA
2
a
và
n min z
min
OM
1
2
OB b
.
Do đó
2 2w i
suy ra
6
w
2018
1009
6
w
.
Câu 6:
(THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Cho số phức
z
thỏa
mãn
2 2 25
z i z i
. Biết tập hợp các điểm
M
biểu diễn số phức
2 2 3w z i
là
đường tròn tâm
;I a b
và bán kính
c
. Giá trị của
a b c
bằng
A.
17
. B.
20
. C.
10
. D.
18
.
Lời giải
Chọn D
Giả sử
z a bi
;a b
và
w x yi
;x y
.
2 2 25 2 1 2 1 25
z i z i a b i a b i
2 2
2 1 25
a b
1
Theo giả thiết:
2 2 3 2 2 3 2 2 3 2w z i x yi a bi i x yi a b i
.
2
2 2
2
3 2 3
2
x
a
x a
y b y
b
2
.
Thay
2
vào
1
ta được:
2 2
2 2
2 3
2 1 25 2 5 100
2 2
x y
x y
.
Suy ra, tập hợp điểm biểu diễn của số phức
w
là đường tròn tâm
2;5
I
và bán kính
10
R
.
Vậy
17
a b c
.
Câu 7: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Biết rằng hai số phức
1
z
,
2
z
thỏa mãn
1
3 4i 1
z
và
2
1
3 4i
2
z
. Số phức
z
có phần thực là
a
và phần ảo là
b
thỏa mãn
3 2 12
a b
. Giá trị nhỏ nhất của
1 2
2 2
P z z z z
bằng:
A.
min
9945
11
P
. B.
min
5 2 3
P
. C.
min
9945
13
P
. D.
min
5 2 5
P
.
Hướng dẫn giải
Chọn C
Gọi
1
M
,
2
M
,
M
lần lượt là điểm biểu diễn cho số phức
1
z
,
2
2z
,
z
trên hệ trục tọa độ
Oxy
.
Khi đó quỹ tích của điểm
1
M
là đường tròn
1
C
tâm
3;4
I
, bán kính
1R
;
quỹ tích của điểm
2
M
là đường
2
C
tròn tâm
6;8
I
, bán kính
1R
;
quỹ tích của điểm
M
là đường thẳng
:3 2 12 0
d x y
.
Bài toán trở thành tìm giá trị nhỏ nhất của
1 2
2
MM MM
.
I
3
I
2
I
1
M
8
6
4
3O
y
x
B
A
Gọi
3
C
có tâm
3
138 64
;
13 13
I
,
1R
là đường tròn đối xứng với
2
C
qua
d
. Khi đó
1 2 1 3
min 2 min 2
MM MM MM MM
với
3 3
M C
.
Gọi
A
,
B
lần lượt là giao điểm của đoạn thẳng
1 3
I I
với
1
C
,
3
C
. Khi đó với mọi điểm
1 1
M C
,
3 3
M C
,
M d
ta có
1 3
2 2
MM MM AB
, dấu "=" xảy ra khi
1 3
,
M A M B
. Do đó
min 1 3
2 2 2
P AB I I
1 3
9945
13
I I
.
Câu 8: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho các số phức
z
thỏa mãn
1 2z i z i
.
Tập hợp các điểm biểu diễn các số phức
2w z i
trên mặt phẳng tọa độ là một đường thẳng.
Phương trình đường thẳng đó là:
A.
4 3 0
x y
. B.
3 4 0
x y
. C.
3 4 0
x y
. D.
3 4 0
x y
.
Lời giải
Chọn D
Giả sử
w x yi
,
,x y
. Khi đó
2 2 2w z i z w i x y i
. Do đó biểu thức
1 2z i z i
trở thành
2 2 1 2x y i i x y i i
3 1
x y i x yi
2 2
2 2
3 1
x y x y
3 4 0
x y
.
Câu 9:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Số phức
2 2018
1 1 ... 1z i i i
có
phần ảo bằng
A.
1009
2 1
. B.
1009
2 1
. C.
1009
1 2
. D.
1009
2 1
.
Lời giải
Chọn B
Có
2018
2 2018 2018
1 1
1 1 ... 1 1 . 1 1 1
i
z i i i i i i
i
Do
1009
504
2018 2 1009
1009 2 1009
1 1 2 2 . . 2
i i i i i i
Suy ra
1009 1009 1009
1 . 2 1 2 1 1 2
z i i i
. Vậy phần ảo của số phức
z
là
1009
2 1
.
Câu 10:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Khai triển của biểu thức
2018
2
1x x được
viết thành
2 4036
0 1 2 4036
...
a a x a x a x
. Tổng
0 2 4 6 4034 4036
...
S a a a a a a
bằng:
A.
1009
2
. B.
0
. C.
1009
2
. D.
1
.
Lời giải
Chọn D
Ta có
2018
2 2 4036
0 1 2 4036
1 ...
x x a a x a x a x
.
Cho
ix
ta được
2018
2
0 1 2 3 4 5 6 4036
1 ...i i i i i
a a a a a a a a
.
Hay
0 2 4 6 4034 4036
...
S a a a a a a
2018
1 1 1
i
.
Câu 11:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Cho các số phức
1
z
,
2
z
,
3
z
thỏa mãn điều
kiện
1
4
z
,
2
3
z
,
3
2
z
và
1 2 2 3 1 3
4 16 9 48
z z z z z z
. Giá trị của biểu thức
1 2 3
P z z z
bằng:
A.
1
. B.
8
. C.
2
. D.
6
.
Lời giải
Chọn C
Ta có
1
4
z
,
2
3
z
,
3
2
z
nên
2
1 1 1
. 16
z z z
,
2
2 2 2
. 9
z z z
,
2
3 3 3
. 4
z z z
.
Khi đó
1 2 2 3 1 3
4 16 9 48
z z z z z z
3 1 2 3 1 1 2 3 2 1 2 3
48
z z z z z z z z z z z z
3 1 2 1 2 3
48
z z z z z z
3 1 2
2
z z z
hay
1 2 3
2
P z z z
.
Câu 12:
(THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018)
Cho số phức
1
z
,
2
z
thỏa
mãn
1
12
z
và
2
3 4i 5
z
. Giá trị nhỏ nhất của
1 2
z z
là:
A.
0
. B.
2
. C.
7
. D.
17
.
Hướng dẫn giải
Chọn B
Gọi
1 1 1
iz x y
và
2 2 2
iz x y
, trong đó
1
x
,
1
y
,
2
x
,
2
y
; đồng thời
1 1 1
;M x y
và
2 2 2
;M x y
lần lượt là điểm biểu diễn các số phức
1
z
,
2
z
.
Theo giả thiết, ta có:
2 2
1 1
2 2
2 2
144
3 4 25
x y
x y
.
Do đó
1
M
thuộc đường tròn
1
C
có tâm
0;0
O
và bán kính
1
12
R
,
2
M
thuộc đường tròn
2
C
có tâm
3;4
I
và bán kính
2
5
R
.
Mặt khác, ta có
2
1 2
5 7
O C
OI R R
nên
2
C
chứa trong
1
C
.
(C
2
)
(C
1
)
M
2
O
M
1
I
Khi đó
1 2
z z
1 2
M M
. Suy ra
1 2 1 2
min
min
z z M M
1 2 1 2
2 2
M M R R
.
Câu 13:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Cho số phức
z
thỏa mãn
2018 2017
11 10 10 11 0.
z iz iz
Mệnh đề nào sau đây đúng?
A.
1 3
;
2 2
z
. B.
1;2
z
. C.
0;1
z
. D.
2;3
z
.
Lời giải
Chọn A
Đặt
z x yi
.
2018 2017
11 10 10 11 0
z iz iz
2017
2017
11 10 11 10
11 10 11 10
iz iz
z z
z i z i
2 2
2017
2 2
100 121 220
121 100 220
x y y
z
x y y
TH1:
2 2
1 1
z x y
2 2 2 2
100 121 220 121 100 220x y y x y y
1 sai
z
TH2:
2 2
1 1
z x y
2 2 2 2
100 121 220 121 100 220x y y x y y
1 sai
z
TH2:
2 2
1 1
z x y
. Thay vào thấy đúng.
Vậy
1
z
.
Câu 14:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Cho số phức
z
thỏa mãn
2 2 5
z z
. Gọi
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
z
. Tính
M m
?
A.
17
2
M m
. B.
8
M m
. C.
1
M m
. D.
4
M m
.
Lời giải
Chọn D
Gọi
;M x y
,
1
2;0
F
,
1
2;0
F
biểu diễn cho số phức
z
,
2
,
2
.
Ta có
1 2
5
MF MF
M
chạy trên Elip có trục lớn
2 5
a
, trục nhỏ
25
2 2 4 3
4
b
.
Mà
z OM
. Do đó giá trị lớn nhất, giá trị nhỏ nhất của
z
là
5
2
M
;
3
2
m
.
Suy ra
4
M m
.
Câu 15:
(Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018)
Cho phương trình
4 3 2
2 6 8 9 0
z z z z
có bốn nghiệm phức phân biệt là
1
z
,
2
z
,
3
z
,
4
z
. Tính giá trị của biểu
thức
2 2 2 2
1 2 3 4
4 4 4 4
T z z z z
.
A.
2T i
. B.
1T
. C.
2T i
. D.
0
T
.
Hướng dẫn giải
Chọn B
Đặt
4 3 2
2 6 8 9 0
f z z z z z f z
.
Ta có
2 2 2
4 4 2 2z z i z i z i
1 2 3 4 1 2 3 4
2 2 2 2 . 2 2 2 2T z i z i z i z i z i z i z i z i
4
2 . 2 1
f i f i
.
Câu 16: Cho
M
là tập hợp các số phức
z
thỏa
2 2
z i iz
. Gọi
1
z
,
2
z
là hai số phức thuộc tập hợp
M
sao
cho
1 2
1
z z
. Tính giá trị của biểu thức
1 2
P z z
.
A.
3
P
. B.
3
2
P
. C.
2
P
. D.
2P
.
Câu 17: Cho
M
là tập hợp các số phức
z
thỏa
2 2
z i iz
. Gọi
1
z
,
2
z
là hai số phức thuộc tập hợp
M
sao
cho
1 2
1
z z
. Tính giá trị của biểu thức
1 2
P z z
.
A.
3
P
. B.
3
2
P
. C.
2
P
. D.
2P
.
Lời giải
Chọn A
Đặt
z x yi
với
x
,
y
.
Ta có:
2 2
2 2 2 2 1 2 1
z i iz x y i y xi x y
.
Suy ra tập hợp các điểm biểu diễn số phức
z
trên mặt phẳng phức là đường tròn
;1
O
1 2
1
z z
.
Ta có:
2 2 2 2
2
1 2 1 2 1 2
2 3 3
z z z z z z P P
.
Câu 18: Tìm môđun của số phức
z
biết
4 1 i 4 3 iz z z
.
A.
1
2
z
. B.
2
z
. C.
4
z
. D.
1
z
.
Câu 19: Cho số phức
z x yi
với
,x y
thỏa mãn
1 1z i
và
3 3 5
z i
. Gọi
,m M
lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
2P x y
. Tính tỉ số
M
m
.
A.
9
4
. B.
7
2
. C.
5
4
. D.
14
5
.
Câu 20: Tìm môđun của số phức
z
biết
4 1 i 4 3 iz z z
.
A.
1
2
z
. B.
2
z
. C.
4
z
. D.
1
z
.
Lời giải
Chọn B
Ta có
4 1 i 4 3 iz z z
1 3i 4 4 i
z z z
Suy ra
1 3i 4 4 i
z z z
2 2
10 4 4
z z z
2 2
2
10 4 4
z z z
2
8 32
z
2
4
z
2
z
.
Câu 21: Cho số phức
z x yi
với
,x y
thỏa mãn
1 1z i
và
3 3 5
z i
. Gọi
,m M
lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
2P x y
. Tính tỉ số
M
m
.
A.
9
4
. B.
7
2
. C.
5
4
. D.
14
5
.
Lời giải
Chọn B
x
1
3
3
J
O
I
1
Gọi
A
là điểm biểu diễn của số phức
z
.
Từ giả thiết
1 1z i
ta có
A
là các điểm nằm bên ngoài hình tròn
1
C
có tâm
1;1
I
bán
kính
1
1
R
.
Mặt khác
3 3 5
z i
ta có
A
là các điểm nằm bên trong hình tròn
2
C
có tâm
3;3
J
bán kính
2
5
R
.
Ta lại có:
2 2 0P x y x y P
. Do đó để tồn tại
,x y
thì
và phần gạch chéo
phải có điểm chung tức là
9
; 5 5
5
P
d J
9 5 4 14
P P
. Suy ra
7
4; 14
2
M
m M
m
.
Câu 22: Cho số phức
z
thỏa mãn
2 3 2 3z i z i
. Biết
1 2 7 4 6 2
z i z i
,
;M x y
là
điểm biểu diễn số phức
z
, khi đó
x
thuộc khoảng
A.
0;2
. B.
1;3
. C.
4;8
. D.
2;4
.
Lời giải
Chọn D
Ta có:
2 3 2 3z i z i
2 2 2 2
2 3 2 3
x y x y
0
y
.
Ta có:
1 2 7 4 6 2
z i z i
2 2
1 4 7 16 6 2
x x
2 2
1 4 6 2 7 16
x x
2
2 28 130 11
x x x
2
2
11
11 2 28 130
x
x x x
2
11
6 9 0
x
x x
3
x
. Thử lại thấy thỏa.
Vậy
3 2;4
x
.
Câu 23: Cho số phức
z
thay đổi thỏa mãn
6
z i z i
. Gọi
S
là đường cong tạo bởi tất cả các điểm
biểu diễn số phức
1
z i i
khi
z
thay đổi. Tính diện tích hình phẳng giới hạn bởi đường
cong
S
.
A.
12
. B.
12 2
. C.
9 2
. D.
BF
.
Câu 24: Cho số phức
z
thay đổi thỏa mãn
6
z i z i
. Gọi
S
là đường cong tạo bởi tất cả các điểm
biểu diễn số phức
1
z i i
khi
z
thay đổi. Tính diện tích hình phẳng giới hạn bởi đường
cong
S
.
A.
12
. B.
12 2
. C.
9 2
. D.
BF
.
Lời giải
Chọn B
Gọi
M
là điểm biểu diễn số phức
1
w z i i
. Suy ra:
1
w
z i
i
.
Viết lại giả thiết:
6 6
1 1
w w
z i z i i i i i
i i
2 2 6 2
w w i
.
1 2
6 2
MF MF
với
1
0;0
F
,
2
2; 2
F
,
1 2
2 2 2
F F c
.
Tập hợp điểm
M
là điểm biểu diễn số phức
w
là elip có độ dài trục lớn
2 6 2
a
,
2 2 2
c
,
2 2
4
b a c
. Diện tích elip là
. . 12 2
S a b
.
Câu 25: Trên tập hợp số phức, cho phương trình
2
0
z bz c
với
,b c
. Biết rằng hai nghiệm của phương
trình có dạng
3
w
và
2 15 9w i
với
w
là một số phức. Tính
2
2S b c
A.
32
S
. B.
1608
S
. C.
1144
S
. D.
64
S
.
Câu 26: Cho hai số phức
1
z
,
2
z
thỏa
1 2
2 5
z z
. Gọi
M
,
N
lần lượt là điểm biểu diễn hai số phức
1
z
,
2
z
trên mặt phẳng tọa độ. Biết
2 2
MN
. Gọi
H
là đỉnh thứ tư của hình bình hành
OMHN
và
K
là
trung điểm của
ON
. Tính
l KH
A.
3 2
l
.
B.
6 2
l
. C.
41
l
. D.
5
l
.
Câu 27: Trên tập hợp số phức, cho phương trình
2
0
z bz c
với
,b c
. Biết rằng hai nghiệm của phương
trình có dạng
3
w
và
2 15 9w i
với
w
là một số phức. Tính
2
2S b c
A.
32
S
. B.
1608
S
. C.
1144
S
. D.
64
S
.
Lời giải
Chọn A
Từ đề bài suy ra
2
2
3 3 0
2 15 9 2 15 9 0
w b w c
w i b w i c
2 15 9 3
2 15 9 3
w i w c
w i w b
Giả sử
w x yi
,
,x y
.
Khi đó
3 3
w x yi
,
2 15 9 2 9 2 15w i x y i
.
Theo đề ta có
2 15 9 3
2 15 9 3
w i w c
w i w b
2 9 2 15 3
2 9 2 15 3
x y i x yi c
x y i x yi b
.
Vì
,b c
nên
3 2 15 2 9 0
6
5
2 15 0
x y y x
x
y
y y
.
Suy ra
6 5w i
, do đó
2 15 9 3
34
6
2 15 9 3
w i w c
c
b
w i w b
.
2
2 32
S b c
Câu 28: Cho hai số phức
1
z
,
2
z
thỏa
1 2
2 5
z z
. Gọi
M
,
N
lần lượt là điểm biểu diễn hai số phức
1
z
,
2
z
trên mặt phẳng tọa độ. Biết
2 2
MN
. Gọi
H
là đỉnh thứ tư của hình bình hành
OMHN
và
K
là
trung điểm của
ON
. Tính
l KH
A.
3 2
l
.
B.
6 2
l
. C.
41
l
. D.
5
l
.
Lời giải
Chọn C
y
x
2 5
2 2
K
H
N
M
O
Xét tam giác
OMN
ta có
2 2 2
4
cos
2 . 5
OM ON MN
MON
OM ON
.
Vì
180
MON ONH
nên
4
cos
5
ONH
.
Xét tam giác
HNK
có
2 2
2 . .cos
HK NH NK NH NK KNH
2
2
1 1
2 . .cos
2 2
OM ON OM ON ONH
41
.
Câu 29: Giá trị của biểu thức
0 2 4 6 98 100
100 100 100 100 100 100
... C
C C C C C
bằng
A.
100
2
. B.
50
2
. C.
100
2
. D.
50
2
.
Câu 30: Giá trị của biểu thức
0 2 4 6 98 100
100 100 100 100 100 100
... C
C C C C C
bằng
A.
100
2
. B.
50
2
. C.
100
2
. D.
50
2
.
Lời giải
Chọn B
Ta có
100
0 1 2 2 100 100
100 100 100 100
1 ...
i C iC i C i C
0 2 4 100 1 3 5 99
100 100 100 100 100 100 100 100
...
C C C C C C C C i
.
Mặt khác
50
100 2
1 1i i
50
2i
50
2
.
Vậy
0 2 4 6 98 100 50
100 100 100 100 100 100
... C 2
C C C C C
.
Câu 31: Cho số phức
z
thỏa mãn
1
z
. Giá trị lớn nhất của biểu thức
1 2 1
P z z
bằng
A.
5
. B.
6 5
. C.
2 5
. D.
4 5
.
Câu 32: Cho số phức
z
thỏa mãn
1
z
. Giá trị lớn nhất của biểu thức
1 2 1
P z z
bằng
A.
5
. B.
6 5
. C.
2 5
. D.
4 5
.
Lời giải
Chọn B
Gọi số phức
iz x y
, với
,x y
.
Theo giả thiết, ta có
1
z
2 2
1
x y
. Suy ra
1 1x
.
Khi đó,
1 2 1
P z z
2 2
2 2
1 2 1
x y x y
2 2 2 2 2x x
.
Suy ra
2 2
1 2 2 2 2 2
P x x
hay
2 5
P
, với mọi
1 1x
.
Vậy
max
2 5
P
khi
2 2 2 2 2x x
3
5
x
,
4
5
y
.
Câu 33: Cho số phức
z
thoả mãn
3 4i 5
z
và biểu thức
2 2
2 i
P z z
đạt giá trị lớn nhất.
Môđun của số phức
z
bằng
A.
10
. B.
5 2
. C.
13
. D.
10
.
Câu 34: Cho số phức
z
thoả mãn
3 4i 5
z
và biểu thức
2 2
2 i
P z z
đạt giá trị lớn nhất.
Môđun của số phức
z
bằng
A.
10
. B.
5 2
. C.
13
. D.
10
.
Hướng dẫn giải
Chọn B
Đặt
iz x y
với
,x y
và gọi
;M x y
là điểm biểu diễn của
z
trên
Oxy
, ta có
3 4 5
z i
2 2
3 4 5
x y
Và
2 2
2
P z z i
2 2
2 2
2 1
x y x y
4 2 3x y
.
Như vậy
4 2 3P x y
4 3 2 4 23
x y
2 2
2 2
4 2 . 3 4 23
x y
33
Dấu “=” xảy ra khi và chỉ khi
3 4
4 2
4 3 2 4 10
x y
t
x y
5
5
0,5
x
y
t
.
Vậy
P
đạt giá trị lớn nhất khi
5 5z i
5 2
z
.
Câu 35: Cho số phức
z
thoả mãn đồng thời hai điều kiện
3 4 5
z i
và biểu thức
2 2
2
M z z i
đạt giá trị lớn nhất. Môđun của số phức
2z i
bằng
A.
5
. B.
9
. C.
25
. D.
5
.
Câu 36: Cho số phức
z
thoả mãn đồng thời hai điều kiện
3 4 5
z i
và biểu thức
2 2
2
M z z i
đạt giá trị lớn nhất. Môđun của số phức
2z i
bằng
A.
5
. B.
9
. C.
25
. D.
5
.
Lời giải
Chọn D
Đặt
, ,z x yi x y
3 4 5
z i
2 2
3 4 5 1
x y
.
Ta có:
2 2
2
M z z i
2 2
2 2
2 1
x y x y
4 2 3x y
4 3 2 4 23
x y
2 2
20 3 4 23 33
x y
.
Dấu
" "
xảy ra khi chỉ khi
3 4
4 2
x
y
kết hợp với
1
suy ra
5 5 5
1, 3 1 3
x y z i
x y z i
Thử lại ta có
max
33
M
5 5z i
2 5
z i
.
Câu 37: Cho số phức
z
. Gọi
A
,
B
lần lượt là các điểm trong mặt phẳng
Oxy
biểu diễn các số phức
z
và
1
i z
. Tính
z
biết diện tích tam giác
bằng
8
.
A.
2 2
z
. B.
4 2
z
. C.
2
z
. D.
4
z
.
Câu 38: Cho số phức
z
. Gọi
A
,
B
lần lượt là các điểm trong mặt phẳng
Oxy
biểu diễn các số phức
z
và
1
i z
. Tính
z
biết diện tích tam giác
bằng
8
.
A.
2 2
z
. B.
4 2
z
. C.
2
z
. D.
4
z
.
Lời giải
Chọn D
Ta có
OA z
,
1 2OB i z z
,
1
AB i z z iz z
.
Suy ra
OAB
vuông cân tại
A
(
OA AB
và
2 2 2
OA AB OB
)
Ta có:
2
1 1
. 8
2 2
OAB
S OA AB z
4
z
.
Câu 39: Cho hàm số
y f x
xác định và liên tục trên
\{0}
thỏa mãn:
2 2
2 1 . 1
x f x x f x x f x
với đồng thời
1 2
f
. Tính
4
1
df x x
.
A.
1
2ln 2
4
. B.
3
2ln 2
4
. C.
3
ln 2
4
. D.
1
ln 2
4
.
Câu 40: Cho hàm số
y f x
xác định và liên tục trên
\{0}
thỏa mãn:
2 2
2 1 . 1
x f x x f x x f x
với đồng thời
1 2
f
. Tính
4
1
df x x
.
A.
1
2ln 2
4
. B.
3
2ln 2
4
. C.
3
ln 2
4
. D.
1
ln 2
4
.
Lời giải
Chọn B
Từ giả thiết ta có:
2
1
xf x f x xf x
.
Đặt
2
2 2
1
. 1 1 dx .
u u
u x f x u u x C x C
u u u
Vậy
1
. 1
x f x
x C
, mà
1 2 0
f C
.
Vậy
4
2
1
1 1 3
d 2ln 2
4
f x f x x
x x
.
Câu 41: Trong các số phức
z
thỏa mãn
2 4 2z i z i
. Số phức
z
có môđun nhỏ nhất là
A.
1z i
. B.
2 2z i
. C.
2 2z i
. D.
3 2z i
.
Câu 42: Trong các số phức
z
thỏa mãn
2 4 2z i z i
. Số phức
z
có môđun nhỏ nhất là
A.
1z i
. B.
2 2z i
. C.
2 2z i
. D.
3 2z i
.
Lời giải
Chọn C
Đặt
z a bi
(
a
,
b
). Khi đó
2 4 2z i z i
2 4 2a b i a b i
2 2 2
2
2 4 2
a b a b
4 4
a b b a
Khi đó:
2 2
2 2 2 2
4 2 8 16 2 2 8 2 2
z a b a a a a a
.
Đẳng thức xảy ra
2
2
a
b
.
Vậy
2 2z i
.
Câu 43: Trong nặt phẳng phức, xét
;M x y
là điểm biểu diễn của số phức
;z x yi x y
thỏa mãn
z i
z i
là số thực. Tập hợp các điểm
M
là
A. Parabol. B. Trục thực.
C. Đường tròn trừ hai điểm trên trục ảo. D. Trục ảo trừ điểm
.
Câu 44: Cho hai số phức
z
,
w
thỏa mãn
3
z
và
1 1 1
z w z w
. Khi đó
w
bằng:
A.
3
.
B.
1
2
. C.
2
. D.
1
3
.
Câu 45: Trong nặt phẳng phức, xét
;M x y
là điểm biểu diễn của số phức
;z x yi x y
thỏa mãn
z i
z i
là số thực. Tập hợp các điểm
M
là
A. Parabol. B. Trục thực.
C. Đường tròn trừ hai điểm trên trục ảo. D. Trục ảo trừ điểm
0;1
.
Lời giải
Chọn D
Ta có
2
2 2
2 2 2 2
2z
z i
z i z i i
z i z i z i
2 2
2 2
1 2
1
x y x yi i
x y
2 2
2 2 2 2
2 1 2
1 1
x y y x
i
x y x y
là
một số thực
0
1
x
y
. Chọn đáp án D.
Câu 46: Cho hai số phức
z
,
w
thỏa mãn
3
z
và
1 1 1
z w z w
. Khi đó
w
bằng:
A.
3
.
B.
1
2
. C.
2
. D.
1
3
.
Lời giải
Chọn A
Ta có:
1 1 1
z w z w
1
0
z w
zw z w
2
0
z w zw
zw z w
2 2
0
z w zw
2
2
1 3
2 4
z w w
2
2
1 3
2 2
i
z w w
1 3
2 2
iz w
1 3
2 2
iz w
z w
.
Vậy
3
w
.
Câu 47: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
4 5 0
z z
. Giá trị của
2018 2018
1 2
( 1) ( 1)
z z
bằng
A.
1010
2
i
. B.
1009
2
i
. C.
0
. D.
2018
2
.
Câu 48: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
4 5 0
z z
. Giá trị của
2018 2018
1 2
( 1) ( 1)
z z
bằng
A.
1010
2
i
. B.
1009
2
i
. C.
0
. D.
2018
2
.
Hướng dẫn giải
Chọn C
1
2
2
2
4 5 0
2
z i z
z z
z i z
.
2018 2018
1 2
1 1z z
2018 2018
1 1i i
1009 1009
2 2
1 2 1 2i i i i
1009 1009
2 2
i i
1009 1009
2 2 0
i i
.
Câu 49: Cho số phức
z
thỏa mãn
2
1
3
z i
z i
. Giá trị nhỏ nhất của
3 2z i
bằng
A.
2 10
5
. B.
2 10
. C.
10
. D.
10
5
.
Câu 50: Cho số phức
2018
3 5z i
. Biết phần ảo của
z
có dạng
3 5 15
a b c d
. Trong các
số
a
,
b
,
c
,
d
có đúng bao nhiêu số bằng
0
?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 51: Cho số phức
z
thỏa mãn
2
1
3
z i
z i
. Giá trị nhỏ nhất của
3 2z i
bằng
A.
2 10
5
. B.
2 10
. C.
10
. D.
10
5
.
Lời giải
Chọn A
Giả sử
,z x yi x y
. Ta có
2
1
3
z i
z i
2 3z i z i
2 2 2
2
2 3 1
x y x y
3 3y x
.
Lại có:
2 2
3 2 3 2
z i x y
2 2
3 3 5
x x
2
10 36 34
x x
2
18 16
10
10
10
x
2 10
5
.
Vậy GTNN của
3 2z i
bằng
2 10
5
.
Câu 52: Cho số phức
2018
3 5z i
. Biết phần ảo của
z
có dạng
3 5 15
a b c d . Trong các
số
a
,
b
,
c
,
d
có đúng bao nhiêu số bằng
0
?
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
Ta có:
2018
2018 2018
2018
0
3 5 3 5
k k
k k
k
z i C i
.
Phần ảo của số phức
z
là
1008
2018 2 1 2 1
2 1
2018
0
3 5 1
m m
m
m
m
C
1008
2 1 1009
2018
0
1 .3 .15 . 15
m
m m
m
C
.
Suy ra
0
a b c
và
0
d
.
Câu 53: Cho số phức
z
thỏa mãn
2
z z
và
2
z z
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của
2T z i
. Tổng
M n
bằng
A.
1 10
. B.
2 10
. C.
4
. D.
1
.
Câu 54: Cho số phức
z
thỏa mãn
1 3 4 10
z z i
. Giá trị nhỏ nhất
min
P
của biểu thức
1 2P z i
bằng?
A.
min
17
P
. B.
min
34
P
. C.
min
2 10
P
. D.
min
34
2
P
.
Câu 55: Cho số phức
z
thỏa mãn
2
z z
và
2
z z
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của
2T z i
. Tổng
M n
bằng
A.
1 10
. B.
2 10
. C.
4
. D.
1
.
Hướng dẫn giải
Chọn A
Gọi
z x yi
,
,x y
.
Ta có
2 2 1
2 2 1
x x
yi y
.
Gọi
;M x y
là điểm biểu diễn số phức
z
trong mặt phẳng tọa độ
Oxy
. Khi đó tập hợp các
điểm
M
là hình vuông
ABCD
(hình vẽ).
-2
1
-1
1
-1
N
O
y
x
D
C
B
A
Điểm
0; 2
N
biểu diễn số phức, khi đó
2
T z i MN
.
Dựa vào hình vẽ ta có
, 1
MN d M AB
nên
min 1
m T
,
10
MN NC nên
max 10
M T
, do đó
1 10
M m
.
Câu 56: Cho số phức
z
thỏa mãn
1 3 4 10
z z i
. Giá trị nhỏ nhất
min
P
của biểu thức
1 2P z i
bằng?
A.
min
17
P
. B.
min
34
P
. C.
min
2 10
P
. D.
min
34
2
P
.
Hướng dẫn giải
Chọn A
Giả sử
,z a bi a b
. Ta có
1 3 4 10
z z i
2 2 2
2
1 3 4 10
a b a b
Gọi
;M a b
là điểm biểu diễn cho số phức
z
. Xét hai điểm
1
1;0
F
,
2
3;4
F
thì tập hợp
điểm
M
là elip
E
có hai tiêu điểm là
1
F
,
2
F
và tâm là điểm
1;2
I
.
Elip
E
này có độ dài trục lớn là
2 10
a
và tiêu cự là
1 2
2 4 2
c F F
. Do đó
5
a
,
2 2
c
2 2 2
17
b a c
.
Lại có:
1 2P z i
2 2
1 2
a b
MI
.
Suy ra
min min
P IM
khi và chỉ khi
IM b
hay
min
17
P
.
Câu 57: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
4 13 0
z z
, với
1
z
có phần ảo dương. Biết
số phức
z
thỏa mãn
1 2
2
z z z z
, phần thực nhỏ nhất của
z
là
A.
6
. B.
2
. C.
1
. D.
9
.
Câu 58: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
4 13 0
z z
, với
1
z
có phần ảo dương. Biết
số phức
z
thỏa mãn
1 2
2
z z z z
, phần thực nhỏ nhất của
z
là
A.
6
. B.
2
. C.
1
. D.
9
.
Lời giải
Chọn B
Ta có
2
4 13 0
z z
1
2 3i
z
hoặc
2
2 3i
z
.
Gọi
iz x y
, với
,x y
.
Theo giả thiết,
1 2
2
z z z z
2 2 2 2
2 2 3 2 3
x y x y
2 2 2 2
4 2 3 2 3
x y x y
2 2
2 5 16
x y
.
Suy ra tập hợp các điểm biểu diễn số phức
z
là miền trong của hình tròn
C
có tâm
2;5
I
,
bán kính
4R
, kể cả hình tròn đó.
Do đó, phần thực nhỏ nhất của
z
là
min
2
x
.
Câu 59: Cho hai số thực
a
và
b
thoả mãn
2
4 3 1
lim 0
2 1
x
x x
ax b
x

. Khi đó
2a b
bằng:
A.
4
. B.
5
. C.
4
. D.
3
.
Câu 60: Cho các số phức
z
,
w
thỏa mãn
5 3 3
z i
,
4 2 2
iw i
. Tìm giá trị lớn nhất của biểu
thức
3 2T iz w
.
A.
554 5
. B.
578 13
. C.
578 5
.
D.
554 13
.
Câu 61: Cho số phức
z
thỏa mãn
1 5
z
. Biết tập hợp các điểm biểu diễn số phức
w
xác định bởi
2 3 3 4w i z i
là một đường tròn bán kính
R
. Tính
R
.
A.
5 17
R . B.
5 10
R . C.
5 5
R . D.
5 13
R .
Câu 62: Cho hai số thực
a
và
b
thoả mãn
2
4 3 1
lim 0
2 1
x
x x
ax b
x

. Khi đó
2a b
bằng:
A.
4
. B.
5
. C.
4
. D.
3
.
Lời giải
Chọn D
Ta có:
2
4 3 1 5 7
lim lim 2
2 1 2 2 2 1
x x
x x
ax b x ax b
x x
 
Mà
2
4 3 1
lim 0
2 1
x
x x
ax b
x

5 7
lim 2 0
2 2 2 1
x
x ax b
x

2 0
5
0
2
a
b
2
5
2
a
b
.
Khi đó:
2 3
a b
.
Câu 63: Cho các số phức
z
,
w
thỏa mãn
5 3 3
z i
,
4 2 2
iw i
. Tìm giá trị lớn nhất của biểu
thức
3 2T iz w
.
A.
554 5
. B.
578 13
. C.
578 5
.
D.
554 13
.
Lời giải
Chọn D
5 3 3 3 15 9 9
z i iz i
là đường tròn có tâm
9;15
I
và
9
R
.
4 2 2 2 8 4 4
iw i w i
là đường tròn có tâm
4; 8
J
và
4R
.
3 2T iz w
đạt giá trị lớn nhất khi
554 13
T IJ R R
.
Câu 64: Cho số phức
z
thỏa mãn
1 5
z
. Biết tập hợp các điểm biểu diễn số phức
w
xác định bởi
2 3 3 4w i z i
là một đường tròn bán kính
R
. Tính
R
.
A.
5 17
R
. B.
5 10
R
. C.
5 5
R
. D.
5 13
R
.
Lời giải
Chọn D
Tập hợp điểm biểu diễn số phức
z
thỏa mãn
1 5
z
là đường tròn
C
tâm
1;0
I
và bán
kính
5
R
. Ta có
C
nhận trục hoành là trục đối xứng nên tọa độ điểm biểu diễn
z
cũng nằm
trên đường tròn này hay
1 5
z
.
Ta có
2 3 3 4w i z i
2 3 1 2 3 3 4w i z i i
5 7 2 3 1
w i i z
5 7 2 3 1
w i i z
5 7 5 13
w i
.
Câu 65: Với mọi số phức
z
thỏa mãn
1 2
z i
, ta luôn có
A.
1 2
z
. B.
2 1 3 2
z i
. C.
2 1 2
z i
. D.
2
z i
.
Câu 66: Xét các số phức
1
3 4z i
và
2
2
z mi
,
m
. Giá trị nhỏ nhất của môđun số phức
2
1
z
z
bằng ?
A.
2
5
. B.
2
. C.
3
. D.
1
5
.
Câu 67: Với mọi số phức
z
thỏa mãn
1 2
z i
, ta luôn có
A.
1 2
z
. B.
2 1 3 2
z i
. C.
2 1 2
z i
. D.
2
z i
.
Lời giải
Chọn B
Ta có
1 1 1 1 2 2
z z i i z i i
.
Vì vậy
2 1 1 1 3 2
z i z i z z i z
.
Câu 68: Xét các số phức
1
3 4z i
và
2
2
z mi
,
m
. Giá trị nhỏ nhất của môđun số phức
2
1
z
z
bằng ?
A.
2
5
. B.
2
. C.
3
. D.
1
5
.
Lời giải
Chọn A
2
1
2 3 4 6 4 3 8
2 6 4 3 8
3 4 3 4 3 4 25 25 25
mi i m m i
z mi m m
i
z i i i
2 2
2
1
6 4 3 8
25 25
z m m
z
2 2
2
2
1
36 48 16 9 48 64
25
z m m m m
z
2 2
2 2
2
1 1
25 100 4 4 2
25 25 25 5
z m z m
z z
.
Hoặc dùng công thức:
2
2
1 1
z
z
z z
.
Câu 69: Trong mặt phẳng tọa độ
Oxy
, gọi
H
là tập hợp điểm biểu diễn số phức
1 3 2w i z
thỏa mãn
1 2
z
. Tính diện tích của hình
H
.
A.
8
. B.
18
. C.
16
. D.
4
.
Câu 70: Trong mặt phẳng tọa độ
Oxy
, gọi
H
là tập hợp điểm biểu diễn số phức
1 3 2w i z
thỏa mãn
1 2
z
. Tính diện tích của hình
H
.
A.
8
. B.
18
. C.
16
. D.
4
.
Lời giải
Chọn C
Ta có
1 3 2w i z
3 3 1 3 1
w i i z
.
3 3 1 3 1 4
w i i z
.
Vậy điểm biểu diễn số phức
w
nằm trên hình tròn có bán kính
4r
.
Diện tích hình
H
là
2
16
S r
.
Câu 71: Cho
1
z
,
2
z
là các số phức thỏa mãn
1 2
1
z z
và
1 2
2 6
z z
. Tính giá trị của biểu thức
1 2
2
P z z
.
A.
2P
. B.
3
P . C.
3
P
. D.
1P
.
Câu 72: Cho
1
z
,
2
z
là các số phức thỏa mãn
1 2
1
z z
và
1 2
2 6
z z
. Tính giá trị của biểu thức
1 2
2
P z z
.
A.
2P
. B.
3
P
. C.
3
P
. D.
1P
.
Lời giải
Chọn A
Đặt
1 1 1
z a b i
,
2 2 2
z a b i
.
Suy ra
2 2 2 2
1 1 2 2
1
a b a b
và
1 2 1 2 1 2
1
2 6 . .
4
z z a a b b
.
Suy ra
1 2
2 2
P z z
.
Câu 73: Cho hình phẳng
H
giới hạn bởi các đường
ln 2 1
y x
,
0
y
,
0
x
,
1x
. Tính thể tích
của khối tròn xoay tạo thành khi quay hình
H
quanh trục
Ox
.
A.
2
ln3 1
3
. B.
ln3
2
. C.
1
ln3 1
2
. D.
3
ln3
2
.
Câu 74: Cho hình phẳng
H
giới hạn bởi các đường
ln 2 1
y x
,
0
y
,
0
x
,
1x
. Tính thể tích
của khối tròn xoay tạo thành khi quay hình
H
quanh trục
Ox
.
A.
2
ln3 1
3
. B.
ln3
2
. C.
1
ln3 1
2
. D.
3
ln3
2
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
ln 2 1
y x
với trục
Ox
:
0
y
ln 2 1 0 0
x x
Thể tích cần tìm:
1
0
ln 2 1 dx
V x
Đặt:
2
ln 2 1 du dx
2 1
dv dx
u x
x
v x
1
1
0
0
2
ln 2 1 dx
2 1
x
V x x
x
1
0
1
ln3 1 dx
2 1x
1
0
1
ln3 ln 2 1
2
x x
1 3
ln 3 1 ln3 ln 3
2 2
Câu 75: Cho ba số phức
1
z
,
2
z
,
3
z
thỏa mãn
1 2 3
2
1 2 3
1 2
1
.
6 2
2
z z z
z z z
z z
. Tính giá trị của biểu thức
2 3 3 1
M z z z z
.
A.
6 2 3
. B.
6 2 3
. C.
6 2 2
2
. D.
6 2 2
2
.
Câu 76: Cho ba số phức
1
z
,
2
z
,
3
z
thỏa mãn
1 2 3
2
1 2 3
1 2
1
.
6 2
2
z z z
z z z
z z
. Tính giá trị của biểu thức
2 3 3 1
M z z z z
.
A.
6 2 3
. B.
6 2 3
. C.
6 2 2
2
. D.
6 2 2
2
.
Hướng dẫn giải
Chọn D
Gọi
M
,
N
,
P
lần lượt là các điểm biểu diễn trong hệ trục tọa độ của các số phức
1
z
,
2
z
,
3
z
.
Suy ra:
M
,
N
,
P
thuộc đường tròn
;1
O
.
1 2
MN z z
6 2
4
6 2
cos
4
OMN
0
15
OMN
0
150
MON
.
Ta có:
3 1 1 3 1
z z z z z
2
3 1 1
z z z
3 1 3 2
z z z z
3 1 2
z z z
6 2
2
.
6 2
2
MN MP
0
150
MOP
0
60
NOP
NOP
đều
1
NP
2 3
1
z z
.
Vậy
6 2 2
2
M
.
Câu 77: Có tất cả bao nhiêu giá trị nguyên của
m
để có đúng hai số phức
z
thỏa mãn
2 1 10
z m i
và
1 2 3z i z i
.
A.
40
. B.
41
. C.
165
. D.
164
.
Câu 78: Có tất cả bao nhiêu giá trị nguyên của
m
để có đúng hai số phức
z
thỏa mãn
2 1 10
z m i
và
1 2 3z i z i
.
A.
40
. B.
41
. C.
165
. D.
164
.
Lời giải
Chọn B
Giả sử
,z x yi x y
,
;M x y
là điểm biểu diễn số phức
z
2 1 10
z m i
2
2 1 100
z m i
2
2
2 1 1 100
x m y
Khi đó tập hợp điểm biểu diễn số phức
z
là đường tròn
C
tâm
2 1;1
I m
,
10
R
1 2 3z i z i
2 2
1 1 2 3
x y i x y i
2 2 2 2
1 1 2 3
x y x y
2 8 11 0
x y
.
Khi đó tập hợp điểm biểu diễn số phức
z
là đường thẳng
: 2 8 11 0
x y
Để có đúng hai số phức
z
thì đường thẳng
cắt đường tròn
C
tại 2 điểm phân biệt
Tức là
, 10
d I
2 2
2 2 1 8 11
10
2 8
m
5 20 7 5 20 7
4 4
m
.
Vậy có
41
giá trị nguyên của
m
để có đúng hai số phức
z
thỏa mãn yêu cầu bài toán.
Câu 79: Cho hai số phức
1
z
,
2
z
thỏa mãn
1
2 3 2
z i
và
2
1 2 1z i
. Tìm giá trị lớn nhất của
1 2
P z z
.
A.
3 34
P
. B.
3 10
P
.
C.
6
P
. D.
3
P
.
Câu 80: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
0
az bz c
,
2
, , , 0, 4 0
a b c a b ac
. Đặt
2 2
1 2 1 2
P z z z z
. Mệnh đề nào sau đây đúng?
A.
2
c
P
a
. B.
c
P
a
. C.
2c
P
a
. D.
4c
P
a
.
Câu 81: Cho hai số phức
1
z
,
2
z
thỏa mãn
1
2 3 2
z i
và
2
1 2 1z i
. Tìm giá trị lớn nhất của
1 2
P z z
.
A.
3 34
P
. B.
3 10
P
. C.
6
P
. D.
3
P
.
Lời giải
Chọn A
Gọi
1 1
;M x y
là điểm biểu diễn số phức
1
z
,
2 2
;N x y
là điểm biểu diễn số phức
2
z
Số phức
1
z
thỏa mãn
1
2 3 2
z i
2 2
1 1
2 3 4
x y
suy ra
1 1
;M x y
nằm trên
đường tròn tâm
2;3
I
và bán kính
1
2
R
.
Số phức
2
z
thỏa mãn
2
1 2 1z i
2 2
2 1
1 2 1
x y
suy ra
2 2
;N x y
nằm trên
đường tròn tâm
1; 2
J
và bán kính
2
1
R
.
Ta có
1 2
z z MN
đạt giá trị lớn nhất bằng
1 2
R IJ R
2 34 1
3 34
.
Câu 82: Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
2
0
az bz c
,
2
, , , 0, 4 0
a b c a b ac
. Đặt
2 2
1 2 1 2
P z z z z
. Mệnh đề nào sau đây đúng?
A.
2
c
P
a
. B.
c
P
a
. C.
2c
P
a
. D.
4c
P
a
.
Lời giải
Chọn D
Ta có
1
z
,
2
z
là các nghiệm phức của phương trình
2
0
az bz c
nên
2
1,2
4
2
b i ac b
z
a
Do đó
1 2
b
z z
a
và
2
1 2
4
i ac b
z z
a
Suy ra
2 2
1 2 1 2
P z z z z
2
2
2
4 4b ac b c
a a a
.
Câu 83: Cho số phức
z
thỏa mãn
1
z
. Tìm giá trị lớn nhất của biểu thức
1 31
P z z
.
A.
2 10
P
. B.
6 5
P
. C.
3 15
P
. D.
2 5
P
.
Câu 84: Cho số phức
z
thỏa mãn
1
z
. Tìm giá trị lớn nhất của biểu thức
1 31
P z z
.
A.
2 10
P
. B.
6 5
P
. C.
3 15
P
. D.
2 5
P
.
Lời giải
Chọn D
Theo bất đẳng thức Bunhiacopxki ta có
1 31
P z z
2 2
2 2
1 3 1 1
z z
2
10 1
z
10 1 1
2 5
.
Vậy
max
2 5
P
.
Câu 85: Cho số phức
z
thỏa mãn
1 3 3 4 10
z i z i
,
1
z
. Tính
z
.
A.
1 65
4
z
. B.
1 65
2
z
. C.
1 65
2
z
. D.
1 65
4
z
.
Câu 86: Cho số phức
z
thỏa mãn
1 3 3 4 10
z i z i
,
1
z
. Tính
z
.
A.
1 65
4
z
. B.
1 65
2
z
. C.
1 65
2
z
. D.
1 65
4
z
.
Lời giải
Chọn C
1 3 3 4 10
z i z i
3 3 1 4 10
z z z i
2 2
3 3 1 4 10
z z z
2 2
2
3 3 1 160
z z z
4 2
10 10 160 0
z z
2
2
1 65
2
1 65
2
z
z
1 65
2
z
( do
1
z
).
Câu 87: Xét các số phức
z a bi
,
,a b
thỏa mãn đồng thời hai điều kiện
4 3z z i
và
1 2 3z i z i
đạt giá trị nhỏ nhất. Giá trị
2P a b
là:
A.
252
50
P
B.
41
5
P
. C.
61
10
P
. D.
18
5
P
.
Câu 88: Xét các số phức
z a bi
,
,a b
thỏa mãn đồng thời hai điều kiện
4 3z z i
và
1 2 3z i z i
đạt giá trị nhỏ nhất. Giá trị
2P a b
là:
A.
252
50
P
B.
41
5
P
. C.
61
10
P
. D.
18
5
P
.
Lời giải
Chọn C
Giả sử
z a bi
được biểu diễn bởi điểm
;M a b
.
Ta có:
4 3z z i
2 2
2 2
4 3
a b a b
8 6 25 0
a b
:8 6 25 0
M x y
.
( , ) 1 2 3f a b z i z i
2 2 2 2
, 1 1 2 3
f a b a b a b
.
Gọi
1;1
A
,
2; 3
B
. Khi đó
,
f a b AM BM
.
Như vậy ta cần tìm
:8 6 25 0
M x y
sao cho
,
f a b AM BM
nhỏ nhất.
M
I
B'
B
A
M
A
và
B
nằm về một phía đối với
nên gọi
B
là điểm đối xứng của
B
qua
.
Khi đó
AM BM AM B M AB
AM BM
nhỏ nhất là
AB
khi
M AB
.
BB
và đi qua
2; 3
B
nên
: 6 8 36 0
BB x y
.
Gọi
I BB
ta có tọa độ của
I
là nghiệm của hệ:
8 6 25 0
6 8 36 0
x y
x y
4
25
219
50
x
y
hay
4 219
;
25 50
I
.
42
2
25
2 144
25
B
B I B
B I B
B
x
x x x
y y y
y
hay
42 144
;
25 25
B
.
17 169 1
; 17;169
25 25 25
AB
. Phương trình
:169 17 186 0
AB x y
.
Tọa độ của
M
là nghiệm của hệ:
67
169 17 186 0
50
8 6 25 0 119
50
x
x y
x y
y
.
Vậy
61
2 2
10
P a b x y
.
Câu 89: Hỏi có bao nhiêu số phức
z
thỏa đồng thời các điều kiện
5
z i
và
2
z
là số thuần ảo?
A.
2
. B.
3
. C.
0
. D.
4
.
Câu 90: Xét số phức
z
thỏa mãn
10
1 2 2i z i
z
. Mệnh đề nào dưới đây là đúng?
A.
1 3
2 2
z
. B.
3
2
2
z
. C.
2
z
. D.
1
2
z
.
Câu 91: Hỏi có bao nhiêu số phức
z
thỏa đồng thời các điều kiện
5
z i
và
2
z
là số thuần ảo?
A.
2
. B.
3
. C.
0
. D.
4
.
Lời giải
Chọn D
Đặt
z x iy
(với
,x y
)
Ta có:
2
2
5 1 25
z i x y
1
Ta có:
2
z
là số thuần ảo
2 2
0
x y
x y
x y
2
Suy ra
2
2
1 25
x x
hay
2
2
1 25
x x
4 3 3 4
x x x x
Vậy có
4
số phức
z
thỏa yêu cầu bài toán.
Câu 92: Xét số phức
z
thỏa mãn
10
1 2 2i z i
z
. Mệnh đề nào dưới đây là đúng?
A.
1 3
2 2
z
. B.
3
2
2
z
. C.
2
z
. D.
1
2
z
.
Lời giải
Chọn A
10
1 2 2i z i
z
10
2 2 1z z i
z
10
2 2 1z z i
z
2 2
10
2 2 1z z
z
2 2
2
10
2 2 1z z
z
4 2
5 5 10 0
z z
1
z
.
Vậy
1 3
2 2
z
.
Câu 93: Trong mặt phẳng tọa độ
Oxy
, biết tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2
2 2
2 2 1 3 2 2018
z i z z i
là một đường tròn. Tìm tâm
I
của đường tròn đó.
A.
4 5
;
3 6
. B.
4 5
;
3 6
. C.
1;1
. D.
4 7
;
3 6
.
Câu 94: Trong mặt phẳng tọa độ
Oxy
, biết tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2
2 2
2 2 1 3 2 2018
z i z z i
là một đường tròn. Tìm tâm
I
của đường tròn đó.
A.
4 5
;
3 6
. B.
4 5
;
3 6
. C.
1;1
. D.
4 7
;
3 6
.
Lời giải
Chọn A
Gọi
;M x y
biểu diễn số phức
z
. Khi đó
2
2 2
2 2 1 3 2 2018
z i z z i
2 2 2 2
2 2
2 2 1 2 3 2 3 1 2018
x y x y x y
2 2
6 6 16 10 1997 0
x y x y
2 2
8 5 1997
0
3 3 6
x y x y
.
Tâm của đường tròn là
4 5
;
3 6
.
Câu 95: Cho số phức
z
thỏa mãn
2 i 1 i 13
z z
. Tìm giá trị nhỏ nhất
m
của biểu thức
2 i
z
.
A.
1
m
. B.
2 13
13
m
. C.
13
13
m
. D.
1
13
m
.
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B D
C A
A
A
B A
C A
B B
D
A
B C C B D
C C B B A
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C A
B A
A
B
A
C A
B A
A
B D
D
B A
D
A
A
B D
A
D
A
HƯỚNG DẪN GIẢI
Câu 96: Cho số phức
z
thỏa mãn
2 i 1 i 13
z z
. Tìm giá trị nhỏ nhất
m
của biểu thức
2 i
z
.
A.
1
m
. B.
2 13
13
m
. C.
13
13
m
. D.
1
13
m
.
Lời giải
Chọn A
Gọi
iz x y
,
,x y
,
2; 1
A
và
1;1
B
. Tọa độ điểm biểu diễn số phức
z
là
;M x y
.
Ta có
13
AB
và
2 i 1 i 13
z z
13
MA MB
. Suy ra
MA MB AB
nên
;M x y
thuộc đoạn thẳng
AB
.
Xét
2 i
P z MC
với
2;1
C
.
x
y
-2
-1
1
2
-1
A
B
C
O
M
Do đó,
min
1
P BC
khi
M B
.
Câu 97: Cho số phức
z
thoả mãn
1
z i
, tìm tập hợp các điểm biểu diễn cho số phức
2 1w iz
trong mặt phẳng
Oxy
.
A. Đường tròn tâm
0; 1
I
,
bán kính
2R
.
B. Đường tròn tâm
1;0
I
,
bán kính
2R
.
C. Đường tròn tâm
1;0
I
,
bán kính
2R
.
D. Đường tròn tâm
0;1
I
,
bán kính
2R
.
Câu 98: Nếu
z
là số phức thỏa mãn
2z z i
thì giá trị nhỏ nhất của
4
z i z
là
A.
4
. B.
2
. C.
3
. D.
5
.
Câu 99: Biết phương trình
4 3 2
3 4 3 1 0
z z z z
có
3
nghiệm phức
1
z
,
2
z
,
3
z
. Tính
1 2 3
T z z z
.
A.
3
T
. B.
4
T
. C.
1T
. D.
2T
.
Câu 100: Cho số phức
z
thoả mãn
1
z i
, tìm tập hợp các điểm biểu diễn cho số phức
2 1w iz
trong mặt phẳng
Oxy
.
A. Đường tròn tâm
0; 1
I
,
bán kính
2R
.
B. Đường tròn tâm
1;0
I
,
bán kính
2R
.
C. Đường tròn tâm
1;0
I
,
bán kính
2R
.
D. Đường tròn tâm
0;1
I
,
bán kính
2R
.
Lời giải
Chọn B
Ta có:
2 1w iz
1
2
w
z
i
.
Đặt
w x yi
,x y
.
Mặt khác:
1
z i
1
1
2
w
i
i
1 2 2
w
1 2
w
2
2
1 4
x y
.
Vậy tập hợp các điểm biểu diễn cho số phức
2 1w iz
trong mặt phẳng
Oxy
là: đường tròn
tâm
1;0
I
,
bán kính
2R
.
Câu 101: Nếu
z
là số phức thỏa mãn
2z z i
thì giá trị nhỏ nhất của
4
z i z
là
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn D
Đặt
z x yi
biểu diễn điểm
;M x y
.
2 1
z z i y
.
4
z i z
nhỏ nhất
MA MB
nhỏ nhất, với
0;1
A
,
4;0
B
.
Gọi
B
đối xứng với
B
qua đường thẳng
1
y
suy ra
4; 2
B
.
Do đó,
5
MA MB MA MB AB
.
Câu 102: Biết phương trình
4 3 2
3 4 3 1 0
z z z z
có
3
nghiệm phức
1
z
,
2
z
,
3
z
. Tính
1 2 3
T z z z
.
A.
3
T
. B.
4
T
. C.
1T
. D.
2T
.
Lời giải
Chọn A
4 3 2
3 4 3 1 0
z z z z
2
2
3 1
3 4 0
z z
z z
2
1 1
2 3 4 0
z z
z z
2
1 1
3 2 0
z z
z z
Đặt
1
t z
z
2
3 2 0
pt t t
1
2
t
t
Ta có:
1
1
z
z
2
1 0
z z
1 3
2 2
z i
1
2
z
z
2
2 1 0
z z
1
z
1 2 3
T z z z
1 3 1 3
1
2 2 2 2
i i
3
.
Câu 103: Có bao nhiêu số phức
z
thoả mãn
3 5
z i
và
4
z
z
là số thuần ảo?
A.
0
. B. vô số. C.
1
. D.
2
.
Câu 104: Có bao nhiêu số phức
z
thoả mãn
3 5
z i
và
4
z
z
là số thuần ảo?
A.
0
. B. vô số. C.
1
. D.
2
.
Lời giải
Chọn D
Giả sử
z x yi
,x y
.
Ta có
2
2
3 5 3 5
z i x y
.
4 4
z x yi
z x yi
2
2
. 4
4
x yi x yi
x y
2 2
2
2
4 4
4
x x y yi
x y
.
4
z
z
là số thuần ảo
2 2
4 0
x x y
.
Ta có hệ:
2
2
2 2
3 5
4 0
x y
x x y
2 2
3 2
1
2
4 0 2
y
x
x x y
.
Thay
1
vào
2
, ta có:
2
2
3 2 3 2
4. 0
2 2
y y
y
2 2
9 12 4 24 16 4 0
y y y y
2
10
13
y
y
.
*
2 2
y x
. Ta có
2 2z i
.
*
10 2
13 13
y x
. Ta có
2 10
13 13
z i
.
Vậy có
2
số phức
z
thỏa yêu cầu bài toán.
Câu 105: Cho số phức
z
. Gọi
,A B
lần lượt là các điểm trong mặt phẳng tọa độ
Oxy
biểu diễn số phức
z
và
1
i z
. Tính mô đun của số phức
z
biết tam giác
có diện tích bằng
32
.
A.
2
z
. B.
8
z
. C.
4
z
. D.
4 2
z
.
Câu 106: Cho số phức
z
. Gọi
,A B
lần lượt là các điểm trong mặt phẳng tọa độ
Oxy
biểu diễn số phức
z
và
1
i z
. Tính mô đun của số phức
z
biết tam giác
có diện tích bằng
32
.
A.
2
z
. B.
8
z
. C.
4
z
. D.
4 2
z
.
Hướng dẫn giải
Chọn B
Gọi
;A a b
biểu diễn
z
và
;
B a b a b
biểu diễn
1
i z
.
Tam giác
có
OA z
,
2
OB z
,
2 2
AB a b z
.
Suy ra tam giác
vuông cân tại
A
.
1
.
2
OAB
S OA AB
2
1
32
2
z
8
z
.
Câu 1:
(THTT Số 1-484 tháng 10 năm 2017-2018)
Cho số phức
z a bi
,a b
. Biết tập hợp các
điểm
A
biểu diễn hình học số phức
z
là đường tròn
C
có tâm
4;3
I
và bán kính
3
R
.
Đặt
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của
4 3 1F a b
. Tính giá trị
M m
.
A.
63
M m
. B.
48
M m
. C.
50
M m
. D.
41
M m
.
Lời giải
Chọn B
Cách 1. Ta có phương trình đường tròn
2 2
: 4 3 9
C x y
.
Do điểm
A
nằm trên đường tròn
C
nên ta có
2 2
4 3 9
a b
.
Mặt khác
4 3 1 4 4 3 3 24
F a b a b
24 4 4 3 3
F a b
.
Ta có
2
2 2
2 2
4 4 3 3 4 3 4 3 25.9 255
a b a b
.
15 4 4 3 3 15
a b
15 24 15
F
9 39
F
.
Khi đó
39
M
,
9
m
.
Vậy
48
M m
.
Cách 2. Ta có
1 3
4 3 1
4
F b
F a b a
2
2 2
2
2 2
1 3
4 3 9 4 6 9 9
4
25 2 3 3 225 0
F b
a b b b
b F b F
2
2
3 3 25 5625
F F
2
0 16 18 5625 0 9 39.
F F F
Câu 2:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Xác định tất cả các số thực
m
để phương trình
2
2 1 0
z z m
có nghiệm phức
z
thỏa mãn
2
z
.
A.
3
m
. B.
3
m
,
9
m
.
C.
1
m
,
9
m
. D.
3
m
,
1
m
,
9
m
.
Lời giải
Chọn D
Ta có:
m
,
1 .P m
Trường hợp
1
:
0 0
m
.
Khi đó, phương trình có hai nghiệm thực:
1
z m
hoặc
1
z m
.
+ Với 1
z m
. Suy ra:
1 2 1
m m
(nhận).
+ Với
1
z m
. Suy ra:
1 2 9
m m
(nhận).
Trường hợp
2
:
0 0.
m
Vì đây là phương trình hệ số thực có
0
nên phương trình có hai nghiệm phức là liên hợp
của nhau. Do đó:
2 . 4 4 1 4 3
z z z P m m
(nhận).
Vậy
3;1;9 .
m
Câu 3:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Cho
z
là số phức thỏa mãn
1
z m z m
và số phức
1z i
. Xác định tham số thực
m
để
z z
nhỏ nhất.
A.
1
2
m
. B.
1
2
m
. C.
1
3
m
. D.
1
m
.
Lời giải
Chọn B
Đặt
z x iy
,x y
.
Ta có:
2 2
2 2
1
1 1 .
2
z m z m x m y x m y x m
2
2
1
1 1 0.
2
z z m y
Đẳng thức xảy ra khi và chỉ khi
1 1
1 0
.
2 2
1 0 1
m m
y y
Vậy
1
2
m
thì
min 0.
z z
Câu 4:
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Xét số phức
z
thỏa mãn
2 2 2
z i
.
Giá trị nhỏ nhất của biểu thức
1 5 2P z i z i
bằng
A.
1 10
. B.
4
. C.
17
D.
5
.
Lời giải
Chọn C
Gọi
;M x y
là điểm biểu diễn số phức
z
. Do
2 2 2
z i
nên tập hợp điểm
M
là đường
tròn
2 2
: 2 2 4
C x y
.
Các điểm
1;1
A
,
5;2
B
là điểm biểu diễn các số phức
1 i
và
5 2i
. Khi đó,
P MA MB
.
Nhận thấy, điểm
A
nằm trong đường tròn
C
còn điểm
B
nằm ngoài đường tròn
C
, mà
17
MA MB AB . Đẳng thức xảy ra khi
M
là giao điểm của đoạn
AB
với
C
.
Ta có, phương trình đường thẳng
: 4 3 0
AB x y
.
Tọa độ giao điểm của đường thẳng
AB
và đường tròn
C
là nghiệm của hệ với
1 5
y
2 2 2 2
2 2 4 4 5 2 4
4 3 0 4 3
x y y y
x y x y
Ta có
2 2
2
22 59
17
4 5 2 4 17 44 25 0
22 59
17
y N
y y y y
y L
Vậy
min 17
P khi
37 4 59 22 59
17 17
z i
Câu 5:
(Đề tham khảo BGD năm 2017-2018)
Xét các số phức
z a bi
,a b
thỏa mãn
4 3 5
z i
. Tính
P a b
khi
1 3 1z i z i
đạt giá trị lớn nhất.
A.
10
P
. B.
4P
. C.
6
P
. D.
8
P
.
Lời giải
Chọn A
Ta có:
4 3 5
z i
2 2
4 3 5
a b
2 2
8 6 20
a b a b
Đặt
1 3 1A z i z i
ta có:
2 2 2 2
1 3 1 1
A a b a b
2 2 2 2
2 2 2
1 1 1 3 1 1
A a b a b
2 2
2 2 4 12
a b b
2 16 8 28
a b
8 4 2 7
a b
1
Mặt khác ta có:
4 2 7 4 4 2 3 15
a b a b
2 2
2 2
4 2 4 3 15 25
a b
2
Từ
1
và
2
ta được:
2
200
A
Để
max
10 2
A
4 2 7 25
4 3
4 2
a b
a b
6
4
a
b
Vậy
10
P a b
.
Câu 1:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Cho hai số phức
1 2
,z z
thỏa mãn
1
1 2
z i
và
2 1
z iz
. Tìm giá trị nhỏ nhất
m
của biểu thức
1 2
z z
?
A.
2 1
m
. B.
2 2
m
. C.
2
m
. D.
2 2 2
m
.
Lời giải
Chọn D
Đặt
1
; ,z a bi a b
2
z b ai
1 2
z z a b b a i
.
Nên
2 2
1 2 1
2.z z a b b a z
Ta lại có
1 1 1
2 1 1 2
z i z i z
1
2 2
z
. Suy ra
1 2 1
2. 2 2 2
z z z
.
Dấu
" "
xảy ra khi
0
1 1
a b
.
Vậy
1 2
min 2 2 2
m z z
.
Câu 2:
(THTT số 5-488 tháng 2 năm 2018)
Cho các số phức
1
z
,
2
z
với
1
0
z
. Tập hợp các điểm biểu
diễn số phức
1 2
.
w z z z
là đường tròn tâm là gốc tọa độ và bán kính bằng
1
. Tập hợp các
điểm biểu diễn số phức
z
là đường nào sau đây?
A. Đường tròn tâm là gốc tọa độ, bán kính bằng
1
z
.
B. Đường tròn tâm là điểm biểu diễn số phức
2
1
z
z
, bán kính bằng
1
1
z
.
C. Đường tròn tâm là gốc tọa độ, bán kính bằng
1
1
z
.
D. Đường tròn tâm là điểm biểu diễn số phức
2
1
z
z
, bán kính bằng
1
1
z
.
Lời giải
Chọn B
1 2
.
w z z z
2
1
1
1
z
z z
z
2
1 1
1
z
z
z z
Nên tập hợp điểm là đường tròn có tâm là điểm biểu diễn số phức
2
1
z
z
, bán kính bằng
1
1
z
.
Câu 1:
(THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018)
Cho số phức
z
thoả mãn
3 4 5
z i
. Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
2
P z z i
. Tính môđun của số phức
.w M mi
A.
2315
w
. B.
1258
w
. C.
3 137
w
. D.
2 309
w
.
Lời giải
Chọn B
Đặt
z x yi
. Ta có
2 2
2 2
2 1 4 2 3
P x y x y x y
.
Mặt khác
2 2
3 4 5 3 4 5
z i x y
.
Đặt
3 5 sinx t
,
4 5 cosy t
Suy ra
4 5 sin 2 5 cos 23
P t t
.
Ta có
10 4 5 sin 2 5 cos 10
t t
.
Do đó
13 33 33
P M
,
2 2
13 33 13 1258
m w
.
Câu 2:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Cho hai số phức
z
,
w
thỏa mãn
2 3
z w
,
2 3 6
z w
và
4 7
z w
. Tính giá trị của biểu thức
. .P z w z w
.
A.
14P i
. B.
28P i
. C.
14P
. D.
28
P
.
Lời giải
Chọn D
Ta có:
2 3
z w
2
2 9
z w
2 . 2 9
z w z w
2 . 2 9
z w z w
. 2 . . 4 . 9
z z z w z w w w
2 2
2 4 9
z P w
1
.
Tương tự:
2 3 6
z w
2
2 3 36
z w
2 3 . 2 3 36
z w z w
2 2
4 6 9 36
z P w
2
.
4 7
z w
4 . 4 49
z w z w
2 2
4 16 49
z P w
3
.
Giải hệ phương trình gồm
1
,
2
,
3
ta có:
2
2
33
28
8
z
P
w
28
P
.
Câu 3: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Cho số phức
z
thỏa mãn
5 1 3 3 1z i z i z i
. Tìm giá trị lớn nhất
M
của
2 3z i
?
A.
10
3
M
. B.
1 13
M
. C.
4 5
M
. D.
9
M
.
Chọn C
Lời giải
Gọi
0;1
A
,
1;3 , 1; 1
B C
. Ta thấy
A
là trung điểm của
BC
2 2 2
2
2 4
MB MC BC
MA
2
2 2 2 2
2 2 10
2
BC
MB MC MA MA
.
Ta lại có:
5 1 3 3 1z i z i z i
2 2
5 3 10.
MA MB MC MB MC
2 2
25 10 2 10
MA MA
2 5
MC
Mà
2 3 2 4z i z i i
2 4z i i
2 5 4 5
z i
.
Dấu
" "
xảy ra khi
2 5
1
2 4
z i
a b
, với
z a bi
;
, a b
2 3
2 5
z i loai
z i
.
Câu 4:
(THPT Chuyên Phan Bội Châu-lần 2 năm 2017-2018)
Với hai số phức
1
z
và
2
z
thỏa mãn
1 2
8 6z z i
và
1 2
2
z z
, tìm giá trị lớn nhất của
1 2
P z z
.
A.
4 6
. B.
2 26
. C.
5 3 5
. D.
34 3 2
.
Lời giải
Chọn B
Cách 1: Ta có:
1 2
8 6 10
z z i
.
Suy ra:
2 2 2 2
1 2 1 2 1 2
2 100 4 104
z z z z z z
.
Ta có:
2 2
1 2 1 2
2 104 2 26
P z z z z
.
Đẳng thức xảy ra khi và chỉ khi
1 2
1 2
1 2
26
8 6
2
z z
z z i
z z
(hệ này có nghiệm)
Vậy
max 2 26
P
.
Cách 2: Gọi
1
, ,z a bi a b
,
2
, ,z c di c d
.
Theo giả thiết ta có
2 2
8 1
6 2
4 3
a c
b d
a c b d
2 2
2 2
100
4
a c b d
a c b d
2 2 2 2
52
a b c d
Ta có
2 2 2 2
1 2
P z z a b c d
.
Áp dụng bất đẳng thức
2
2 2
2
x y x y
ta có:
2 2 2 2 2
2 2 104 2 26
P a b c d P
Vậy giá trị lớn nhất của
P
bằng
2 26
. Dấu bằng sảy ra khi
2 2
2 2 2 2
8
6
4
a c
b d
a c b d
a b c d
2
4
2
2
3
2
2
4
2
2
3
2
a
b
c
d
.
Câu 5:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Cho số phức
z
thõa mãn
1 2
z i
. Tìm giá
trị lớn nhất của biểu thức
2 2
2 2 3P z i z i
.
A.
18
. B.
38 8 10
. C.
18 2 10
. B.
16 2 10
.
Lời giải
Chọn B
Cách 1: Gọi
;M x y
là điểm biểu diễn cho số phức
z
. Gọi
1; 1
I
,
2;1
A
,
2;3
B
lần
lượt là điểm biểu diễn cho các số phức
1 i
;
2 i
;
2 3i
. Khi đó, ta có:
2MI
nghĩa là
M
thuộc đường tròn
C
có tâm
1; 1
I
,
2R
và
2 2
P MA MB
.
Ta có:
2
2 2 2 2
2 2
2
AB
P ME EA EB ME
, với
0;2
E
là trung điểm của
AB
. Do đó
P
có giá trị lớn nhất khi và chỉ khi
ME
có giá trị lớn nhất.
Ta có :
1 9 10
IE R
nên
max
2 10
ME IE R
.
Vậy
2
2 2
max
2 2 10 2 2 10 10 38 8 10
2
AB
P
.
Cách 2: Giả sử
z x yi
(
,x y
).
;M x y
là điểm biểu diễn của
z
.
Suy ra
1
M C
có tâm
1
1; 1
I
và bán kính
1
2
R
.
2 2
1 2 1 1 4
z i x y
1
.
Ta có:
0
P
và
2 2
2 2 2 2
2 2 3 2 1 2 3
P z i z i x y x y
.
Suy ra
2 2 2 2
2 2
1 1 2 10 16 1 5 6
P x y x y x y x y
.
Ta có
2 2
1 5 6 6
x y P
2
nên
2
là phương trình của đường tròn
2
C
có tâm
2
1;5
I
, bán kính
2 1
6
R P R
;
1 2
2 10
I I
.
Để tồn tại
x
,
y
thì
1
C
và
2
C
có điểm chung
1 2
6 2 6 2
P I I P
.
Suy ra :
1 2
6 2
P I I
2
2 2 10 6 38 8 10
P
.
Đẳng thức xảy ra khi và chỉ khi
1
C
và
2
C
tiếp xúc trong.
Vậy
max 38 8 10
P
.
Câu 6:
(THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018)
Giả sử
1
z
,
2
z
là hai trong số
các số phức
z
thỏa mãn
2 1iz i
và
1 2
2
z z
. Giá trị lớn nhất của
1 2
z z
bằng
A.
4
. B.
2 3
. C.
3 2
. D.
3
.
Lời giải
Chọn A
Ta có
2 1 1 2 1
iz i z i
. Gọi
0
1 2z i
có điểm biểu diễn là
1; 2
I
.
Gọi
A
,
B
lần lượt là các điểm biểu diễn của
1
z
,
2
z
.
Vì
1 2
2
z z
nên
I
là trung điểm của
AB
.
Ta có
2 2 2 2
1 2
2 4 16 4
z z OA OB OA OB OI AB
.
1 2
2 2
OA OB z z
.
Vậy giá trị lớn nhất của
1 2
z z
bằng
4
.
Câu 7: ----------HẾT----------(THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Cho số
phức
z
thỏa mãn
1 1
3
2
z
z i
. Tìm giá trị lớn nhất của biểu thức
2 4 7P z i z i
.
A.
8
. B.
20
. C.
2 5
. D.
4 5
.
Lời giải
Chọn B
Gọi
z x yi
với
,x y
, gọi
M
là điểm trong mặt phẳng tọa độ biểu diễn số phức
z
. Ta
có:
1 1
3
2
z
z i
2 1 3z z i
2 1 3x yi x y i
2 2
2 2
2 1 3
x y x y
2 2
2 3 20
x y
.
Như vậy, tập hợp điểm
M
biểu diễn số phức
z
là đường tròn
C
tâm
2;3
I
và bán kính
2 5
R
.
Gọi
0; 1
A
,
4;7
B
lần lượt là các điểm biểu diễn các số phức
1
z i
,
2
4 7z i
. Dễ thấy
,A B
thuộc đường tròn
C
. Vì
4 5 2AB R
nên
AB
là đường kính của đường tròn
C
2 2 2
80
MA MB AB
.
Từ đó:
2 4 7P z i z i
2 4 7z i z i
2 2 2 2
2 1 2 20
MA MB MA MB
.
Dấu
" "
xảy ra khi
2 2
2
4
8
80
MB MA
MA
MB
MA MB
.
Vậy
max 20
P
.
Câu 8: . (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho hai số phức
1 2
,z z
thoả mãn
1 2
2, 3
z z
. Gọi
M
,
N
là các điểm biểu diễn cho
1
z
và
2
iz
. Biết
30
MON
. Tính
2 2
1 2
4S z z
.
A.
5 2
. B.
3 3
. C.
4 7
. D.
5
.
Lời giải
Chọn C
Ta có
2
2 2 2
1 2 1 2 1 2 1 2
4 2 2 . 2S z z z iz z iz z iz
Gọi
P
là điểm biểu diễn của số phức
2
2iz
.
Khi đó ta có
1 2 1 2
2 . 2 .
z iz z iz OM OP OM OP

. 2 2 .PM OI PM OI

.
Do
30
MON
nên áp dụng định lí cosin ta tính được
1
MN
. Khi đó
OMP
có
MN
đồng
thời là đường cao và đường trung tuyến, suy ra
OMP
cân tại
M
2
PM OM
.
Áp dụng định lí đường trung tuyến cho
OMN
ta có:
2 2 2
2
7
2 4
OM OP MP
OI
.
Vậy
2 . 2.2. 7 4 7
S PM OI .
Câu 9: Cho hai số phức
1
z
,
2
z
thỏa mãn
1
3 5 2
z i
và
2
1 2 4
iz i
. Tìm giá trị lớn nhất của biểu
thức
1 2
2 3T iz z
.
A.
313 16
. B.
313
. C.
313 8
. D.
313 2 5
.
Câu 10:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Cho hai số phức
1
z
,
2
z
thỏa mãn
1
3 5 2
z i
và
2
1 2 4
iz i
. Tìm giá trị lớn nhất của biểu thức
1 2
2 3T iz z
.
A.
313 16
. B.
313
. C.
313 8
. D.
313 2 5
.
Lời giải
Chọn A
Ta có
1 1
3 5 2 2 6 10 4
z i iz i
1
;
2 2
1 2 4 3 6 3 12
iz i z i
2
.
Gọi
A
là điểm biểu diễn số phức
1
2iz
,
B
là điểm biểu diễn số phức
2
3z
. Từ
1
và
2
suy
ra điểm
A
nằm trên đường tròn tâm
1
6; 10
I
và bán kính
1
4
R
; điểm
B
nằm trên đường
tròn tâm
2
6;3
I
và bán kính
2
12
R
.
I
2
I
1
B
A
Ta có
2 2
1 2 1 2 1 2
2 3 12 13 4 12 313 16
T iz z AB I I R R
.
Vậy
max 313 16
T
.
Câu 11: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Cho
hàm số
3 2
3
f x x x m
. Hỏi có bao nhiêu giá trị nguyên của tham số
m
2018
m
để với mọi bộ ba số phân biệt
a
,
b
,
1;3
c
thì
f a
,
f b
,
f c
là độ dài ba cạnh của một tam giác.
A.
2011
. B.
2012
. C.
2010
. D.
2018
.
Lời giải
Chọn C
Ta có
f a
,
f b
,
f c
là ba cạnh của một tam giác nên
f a f b f c
3 2 3 2 3 2
3 3 3
a a m b b m c c m
với mọi
a
,
b
,
1;3
c
3 2 3 2 3 2
3 3 3
a a b b c c m
với mọi
a
,
b
,
1;3
c
Do đó
3 2 3 2 3 2
3 3 3min
a a b b c c m
với mọi
a
,
b
,
1;3
c
Ta cần tìm
3 2 3 2
3n 3mi
a a b b
và
3 2
ax
3
m
c c
với mọi
a
,
b
,
1;3
c
Xét hàm
3 2
3f x x x
với
1;3
x
Ta có
2
3 6f x x x
,
2
0
0 3 6 0
2
x
f x x x
x
. Do
1;3
x
nên
2
x
.
Ta có
1 2
f
,
2 4
f
,
3 0
f
.
1;3
max 3 0
f x f
,
1;3
min 2 4
f x f
.
Suy ra
3 2 3 2 3 2
3 3 3 4.2m
8
in a a b b c c
.
Đẳng thức xảy ra khi
2
a b
,
3
c
hoặc
2
a c
,
3
b
hoặc
2
b c
,
a
.
Do đó
8
m
8
m
. Mà
2018
m
và
m
nguyên nên
9;..;2018
m
.
Vậy có
2010
giá trị
m
thỏa mãn.
Câu 12: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Xét các số phức
z a bi
(
,a b
)
thỏa mãn
3 2 2
z i
. Tính
khi
1 2 2 2 5z i z i
đạt giá trị nhỏ nhất.
A.
4 3
. B.
2 3
. C.
3
. D.
4 3
.
Lời giải
Chọn D
Cách 1:
Đặt
3 2
z i w
với
w x yi
,x y
. Theo bài ra ta có
2 2
2 4
w x y
.
Ta có
2 2 2
2
1 2 2 2 5 4 2 1 3 4 2 1 3
P z i z i w w i x y x y
2 2 2 2
20 8 2 1 3 2 5 2 2 1 3
x x y x x y
2 2 2 2 2
2 2 2
2 2 1 1 3 2 1 1 3
x y x x y x y x y
2 3 2 3 6
y y y y
.
2 2
1
1
6 3 0
3
4
x
x
P y y
y
x y
.
Vậy GTNN của
P
là bằng
6
đạt được khi
2 2 3z i
.
Cách 2:
3 2 2
z i
2
MI
;2M I
với
3;2
I
.
1 2 2 2 5 2
P z i z i MA MB
với
1;2
A
,
2;5
B
.
Ta có
2IM
;
4IA
. Chọn
2;2
K
thì
1IK
. Do đó ta có
2
.
IA IK IM
IA IM
IM IK
IAM
và
IMK
đồng dạng với nhau
2
AM IM
MK IK
2
AM MK
.
Từ đó
2P MA MB
2
MK MB
2BK
.
Dấu bằng xảy ra khi và chỉ khi
M
,
K
,
B
thẳng hàng và
M
thuộc đoạn thẳng
BK
.
Từ đó tìm được
2;2 3
M
.
Cách 3:
Gọi
;M a b
là điểm biểu diễn số phức
.z a bi
Đặt
3;2
I
,
1;2
A
và
2;5
B
.
Ta xét bài toán: Tìm điểm M thuộc đường tròn
C
có tâm
I
, bán kính
2R
sao cho biểu
thức
2P MA MB
đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm
;K x y
sao cho
2MA MK
M C
.
Ta có
2 2
2 2
2 4 4
MA MK MA MK MI IA MI IK
2 2 2 2 2 2 2
2 . 4 2 . 2 4 3 4
MI IA MI IA MI IK MI IK MI IA IK R IK IA

*
.
*
luôn đúng
2 2 2
4 0
3 4 0
IA IK
M C
R IK IA
.
4 3 4
2
4 0
2
4 2 0
x
x
IA IK
y
y
.
Thử trực tiếp ta thấy
2;2
K
thỏa mãn
2 2 2
3 4 0
R IK IA
.
Vì
2 2 2 2
1 3 10 4
BI R
nên
B
nằm ngoài
C
.
Vì
2 2
1 4KI R
nên
K
nằm trong
C
.
K
M
0
M
A
B
I
5
2
32
O
-1
x
y
Ta có
2 2 2 2 2
MA MB MK MB MK MB KB
.
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi
M
thuộc đoạn thẳng
BK
.
Do đó
2MA MB
nhỏ nhất khi và chỉ khi M là giao điểm của
C
và đoạn thẳng
.BK
Phương trình đường thẳng
: 2
BK x
.
Phương trình đường tròn
2 2
: 3 2 4
C x y
.
Tọa độ điểm
M
là nghiệm của hệ
2 2
2
2
3 2 4
2 3
x
x
x y
y
hoặc
2
2 3
x
y
.
Thử lại thấy
2;2 3
M
thuộc đoạn
BK
.
Vậy
2
a
,
2 3
b
4 3
a b .
Câu 13:
(SGD Quảng Nam – năm 2017 – 2018)
Cho số phức
z
thỏa mãn
2
z
. Giá trị nhỏ
nhất của biểu thức
2 1 2 1 4P z z z z i
bằng:
A.
4 2 3
. B.
2 3
. C.
14
4
15
. D.
7
2
15
.
Lời giải
Chọn A
Gọi
i, ,z x y x y
. Theo giả thiết, ta có
2 2
2 4
z x y
.
Suy ra
2 , 2
x y
.
Khi đó,
2 1 2 1 4P z z z z i
2 2
2 2
2 1 1 2
x y x y y
2 2
2 2
2 1 1 2
P x y x y y
2
2 2 1 2
y y
.
Dấu “
” xảy ra khi
0
x
.
Xét hàm số
2
2 1 2
f y y y
trên đoạn
2; 2
, ta có:
2
2
1
1
y
f y
y
2
2
2 1
1
y y
y
;
1
0
3
f y y
.
Ta có
1
2 3
3
f
;
2 4 2 5
f
;
2 2 5
f
.
Suy ra
2; 2
min 2 3
f y
khi
1
3
y
.
Do đó
2 2 3 4 2 3
P
. Vậy
min
4 2 3
P
khi
1
i
3
z
.
Câu 14:
----------HẾT----------(ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018)
Nếu
z
là số phức thỏa
2z z i
thì giá trị nhỏ nhất của
4
z i z
là
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn D
Đặt
z x yi
với
x
,
y
theo giả thiết
2i
z z
1
y
.
d
Vậy tập hợp các điểm biểu diễn số phức
z
là đường thẳng
d
.
Gọi
0;1
A
,
4;0
B
suy ra
4
z i z P
là tổng khoảng cách từ điểm
; 1
M x
đến hai
điểm
A
,
B
.
Thấy ngay
0;1
A
và
4;0
B
nằm cùng phía với
d
. Lấy điểm đối xứng với
0;1
A
qua
đường thẳng
d
ta được điểm
0; 3
A
.
Do đó khoảng cách ngắn nhất là
2 2
3 4 5
A B
.
Câu 15:
(THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018)
Trong các số phức
z
thỏa
mãn
2
1 2z z
gọi
1
z
và
2
z
lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Khi đó
môđun của số phức
1 2
w z z
là
A.
2 2
w
. B.
2
w
. C.
2
w
. D.
1 2
w
.
Lời giải
Chọn A
Đặt
z a bi
,a b
thì
2
1 2z z
2
1 2
a bi a bi
2 2
1 2 2
a b abi a bi
2
2 2 2 2 2 2
1 4 4
a b a b a b
4 4 2 2 2 2
1 2 6 2 0
a b a b a b
2
2 2 2
1 4 0
a b b
2 2 2 2
1 2 1 2 0
a b b a b b
2 2
2 2
1 2 0
1 2 0
a b b
a b b
TH1:
2 2
1 2 0
a b b
2
2
1 2
a b
.
Khi đó tập hợp điểm
;M a b
biểu diễn số phức
z
là đường tròn có tâm
1
0;1
I
, bán kính
2
R
, giao điểm của
OI
(trục tung) với đường tròn là
1
0; 2 1
M
và
2
0;1 2
M
2 1 1 2w i i
2w i
2
w
TH2:
2 2
1 2 0
a b b
2
2
1 2
a b
.
Khi đó tập hợp điểm
;M a b
biểu diễn số phức
z
là đường tròn có tâm
2
0; 1
I
, bán kính
2
R
, giao điểm của
OI
(trục tung) với đường tròn là
3
0; 2 1
M
và
4
0; 2 1
M
2 1 1 2w i i
2w i
2
w
.
Với đáp án của trường ĐH Vinh đưa ra là A thì ta chọn số phức
1
M
và
3
M
có
2 2w i
2 2
w
nên đề bài chưa chuẩn, có thể chọn phương án B.
Đáp án ĐH Vinh đưa ra theo mình là chính xác, bởi lẽ trong các số phức z thỏa mãn ta tìm các
số phức gọi
1
z
và
2
z
có môđun nhỏ nhất và lớn nhất nên phải tổng hợp cả hai TH1 và TH2.
Thầy đừng vội tính
w
mà sau cùng hãy tìm
1
z
và
2
z
rồi tính
w
Một vài góp ý thầy xem nhé
Câu 16:
(SGD Nam Định – năm 2017 – 2018)
Trong mặt phẳng tọa độ
Oxy
, gọi
H
là phần
mặt phẳng chứa các điểm biểu diễn các số phức
z
thỏa mãn
16
z
và
16
z
có phần thực và phần
ảo đều thuộc đoạn
0;1
. Tính diện tích
S
của
H
.
A.
32 6S
. B.
16 4S
. C.
256
. D.
64
.
Lời giải
Chọn A
Giả sử
,z x yi x y
.
Ta có:
16 16 16
z x y
i
;
16
z
16
x yi
2 2 2 2
16 16
x y
i
x y x y
.
Vì
16
z
và
16
z
có phần thực và phần ảo đều thuộc đoạn
0;1
nên
2 2
2 2
0 1
16
0 1
16
16
0 1
16
0 1
x
y
x
x y
y
x y
2 2
2 2
0 16
0 16
0 16
0 16
x
y
x x y
y x y
2
2
2
2
0 16
0 16
8 64
8 64
x
y
x y
x y
.
Suy ra
H
là phần mặt phẳng giới hạn bởi hình vuông cạnh
16
và hai hình tròn
1
C
có tâm
1
8;0
I
, bán kính
1
8
R
và
2
C
có tâm
2
0;8
I
, bán kính
2
8
R
.
Gọi
S
là diện tích của đường tròn
2
C
.
Diện tích phần giao nhau của hai đường tròn là:
2
1
1 1 1
2 2 . .8 .8.8
4 4 2
OEJ
S S S
.
Vậy diện tích
S
của hình
H
là:
2 2 2
1 1
16 .8 2. . .8 .8.8
4 2
S
256 64 32 64
192 32
32 6
.
Câu 17:
(SGD Nam Định – năm 2017 – 2018)
.Cho hai số phức
1 2
,z z
thoả mãn
1
6
z
,
2
2
z
. Gọi
M
,
N
là các điểm biểu diễn cho
1
z
và
2
iz
. Biết
60
MON
. Tính
2 2
1 2
9T z z
.
A.
18
T
. B.
24 3
T
. C.
36 2
T
. D.
36 3
T
.
Lời giải
Chọn D
16
16
x
B
C
A
y
O
I
J
E
Ta có
2
2 2 2
1 2 1 2 1 2 1 2
9 3 3 . 3T z z z iz z iz z iz
Gọi
P
là điểm biểu diễn của số phức
2
3iz
.
Khi đó ta có
1 2 1 2
3 . 3 .
z iz z iz OM OP OM OP
. 2 2 .PM OI PM OI
.
Do
60
MON
và
6
OM OP
nên
MOP
đều suy ra
6
PM
và
3
6. 3 3
2
OI
.
Vậy
2 . 2.6.3 3 36 3
T PM OI
.
----------HẾT----------
Câu 1: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Gọi
1
z
,
2
z
là hai
trong các số phức thỏa mãn
1 2 5
z i
và
1 2
8
z z
. Tìm môđun của số phức
1 2
2 4w z z i
.
A.
6
w
. B.
16
w
. C.
10
w
. D.
13
w
.
Lời giải
Chọn A
Gọi
A
là điểm biểu diễn của số phức
1
z
,
B
là điểm biểu diễn của số phức
2
z
.
Theo giả thiết
1
z
,
2
z
là hai trong các số phức thỏa mãn
1 2 5
z i
nên
A
và
B
thuộc
đường tròn tâm
1; 2
I
bán kính
r
.
Mặt khác
1 2
8 8
z z AB
.
Gọi
M
là trung điểm của
AB
suy ra
M
là điểm biểu diễn của số phức
1 2
2
z z
và
3
IM
.
Do đó ta có
1 2
3 1 2
2
z z
IM i
1 2 1 2
1
3 2 4 2 4 6
2
z z i z z i
6
w
.
Câu 2: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho số phức
z
thỏa mãn
1 3 2 8
z i z i
. Giá trị nhỏ nhất
m
của
2 1 2z i
là
A.
4
m
. B.
9
m
. C.
8
m
. D.
39
m
.
Lời giải
Chọn D
Giả sử
;M x y
biểu diễn số phức
z x iy
(
x
,
y
),
1; 3
A
,
2;1
B
,
5
AB
.
1 3 2 8
z i z i
8
AM BM
, tập hợp điểm
M
là Elip có phương trình
2 2
4
1
16 39
x y
. Đặt
2 1 2P z i
1
2
2
P z i
, gọi
I
là trung điểm
AB
thì
1
; 1
2
I
1
2 2
2
P z i IM
IM
.
Ta tìm điểm
M
trên
E
sao cho
IM
có độ dài nhỏ nhất.
IM
nhỏ nhất khi
IM
bằng độ dài nửa trục bé,
39
2
IM
min
39
P
.
Câu 3:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Cho số phức
z
thỏa mãn
2
z z z z z
. Giá trị lớn nhất của biểu thức
5 2P z i
bằng:
A.
2 5 3
. B.
2 3 5
. C.
5 2 3
. D.
5 3 2
.
Lời giải
Chọn B
Gọi
iz x y
(với
x
,
y
). Suy ra
iz x y
và
2 2 2
2 iz x y xy
.
Theo giả thiết, ta có
2
z z z z z
2
2 2 2 2
2 2 4
x y x y x y
2 2
2 2
x y x y
2 2
1 1 2
x y
. Từ đó suy ra tập hợp các điểm biểu diễn số
phức
z
là các đường tròn có tâm
1; 1
I
và bán kính
2
R
.
Khi đó,
5 2P z i
MA
, với
5;2
A
và
;M x y
là tọa độ điểm biểu diễn số phức
z
.
Mặt khác, vì
5;2
A
thuộc góc phần tư thứ nhất nên
MA
lớn nhất
M
thuộc đường tròn
3
C
có tâm
1; 1
I
và bán kính
2
R
.
Câu 4: Vậy
max max
P MA
3 5 2
IA R
. Trong mặt phẳng phức, xét hình bình hành tạo bởi các
điểm
0
,
z
,
1
z
và
1
z
z
. Biết
z
có phần thực dương và diện tích hình bình hành bằng
35
37
. Tìm
giá trị nhỏ nhất của
2
1
z
z
.
A.
53
20
. B.
60
37
. C.
22
9
. D.
50
37
.
Lời giải
Chọn D
Gọi
, , ,O A B C
lần lượt là điểm biểu diễn số phức
1
0, ,z
z
và
1
z
z
.
Khi đó diện tích hình bình hành
OACB
là
. .sin
S OA OB
1 35
. .sin
37
z
z
35
sin
37
.
Suy ra
2
12
cos 1 sin
37
.
Áp dụng định lý cosin trong tam giác
OAC
ta có
2
2 2 2
1
2 . .cos
z OC OA OB OA OB
z
2
2
1 1
2 .cos
z z
z z
2
2
1
2cos
z
z
2
1
z
z
12 50
2 2.
37 37
. Vậy
2
1
z
z
nhỏ nhất bằng
50
37
.
Dấu “
” xảy ra
1
z
và
12
cos
37
.
Chẳng hạn như
1 12 1 12
sin arccos cos arccos
2 37 2 37
z i
.
Câu 5: Vậy
2
1
z
z
nhỏ nhất bằng
50
37
.Biết
0 1 2 3
2 32768
n k k n n
n n n n n n
C iC C iC i C i C i
, với
k
n
C
là các số tổ hợp chập
k
của
n
và
2
1
i
. Đặt
1
k k
k n
T i C
, giá trị của
8
T
bằng
A.
330i
. B.
8i
. C.
36i
. D.
120i
.
Câu 6: Biết
0 1 2 3
2 32768
n k k n n
n n n n n n
C iC C iC i C i C i
, với
k
n
C
là các số tổ hợp chập
k
của
n
và
2
1
i
. Đặt
1
k k
k n
T i C
, giá trị của
8
T
bằng
A.
330i
. B.
8i
. C.
36i
. D.
120i
.
Hướng dẫn giải
Chọn B
Ta có:
0 1 2 3
2 32768
n k k n n
n n n n n n
C iC C iC i C i C i
0 1 2 2 3 3
2 32768
n k k n n
n n n n n n
C iC i C i C i C i C i
15
2 1 2
n
n
i i
*
Ta có
2
1 2i i
nên nếu
2 1n k
,
k
, thì
2 1
1 1 2 1
n k
k k
i i i i
nên không
thỏa mãn
*
.
Xét
2n k
,
k
, thì
2
1 1 2
n k
k k
i i i
, nên:
2 15 3 15
* 2 .2 . 2 2 2
k k k k k
i i i i
5 10
k n
.
Từ đó ta có
7 7
8 8
8T i C i
.
Câu 7: Cho các số phức
w
,
z
thỏa mãn
3 5
5
w i
và
5 2 4
w i z
. Giá trị lớn nhất của biểu
thức
1 2 5 2P z i z i
bằng
A.
6 7
. B.
4 2 13
. C.
2 53
. D.
4 13
.
Câu 8: Cho các số phức
w
,
z
thỏa mãn
3 5
5
w i
và
5 2 4
w i z
. Giá trị lớn nhất của biểu
thức
1 2 5 2P z i z i
bằng
A.
6 7
. B.
4 2 13
. C.
2 53
. D.
4 13
.
Lời giải
Chọn C
Gọi
z x yi
, với
,x y
. Khi đó
;M x y
là điểm biểu diễn cho số phức
z
.
Theo giả thiết,
5 2 4
w i z
5 2 4 5w i i z i
2 3 2i w i z i
3 2 3
z i
. Suy ra
;M x y
thuộc đường tròn
2 2
: 3 2 9
C x y
.
Ta có
1 2 5 2P z i z i
MA MB
, với
1;2
A
và
5;2
B
.
Gọi
H
là trung điểm của
AB
, ta có
3;2
H
và khi đó:
P MA MB
2 2
2
MA MB
hay
2 2
4
P MH AB
.
Mặt khác,
MH KH
với mọi
M C
nên
2 2
4
P KH AB
2
2
4
IH R AB
2 53
.
Vậy
max
2 53
P
khi
M K
MA MB
hay
3 5z i
và
3 11
w i
5 5
.
Câu 9: Cho số phức
1z i
. Biết rằng tồn tại các số phức
1
5z a i
,
2
z b
(trong đó
, , 1
a b b
)
thỏa mãn
1 2 1 2
3 3
z z z z z z
. Tính
b a
.
A.
5 3
b a
. B.
2 3
b a
. C.
4 3
b a
. D.
3 3
b a
.
Câu 10: Cho số phức
1z i
. Biết rằng tồn tại các số phức
1
5z a i
,
2
z b
(trong đó
, , 1
a b b
)
thỏa mãn
1 2 1 2
3 3
z z z z z z
. Tính
b a
.
A.
5 3
b a
. B.
2 3
b a
. C.
4 3
b a
. D.
3 3
b a
.
Lời giải
Chọn D
Ta có:
1 2 1 2
3 3
z z z z z z
2 2
2
2 2
1 4 1 1
*
25 3 1 16
a b
b a a
Cách 1:
*
2 2
2 2 2 2 2
1 1 15
23
1 2 1 1 1 3 1 1 1
15
b a
b b a a a b a
2 2
2 2
1 1 15
8 1 2 1 1 7 1 0
b a
b b a a
2 2
1 1 15
2 3
1
1
3
1 1
3 3
4
7 3
1
7
1 1
3
2
b a
a
b a
b a
b
b a
.
Cách 2: Đặt
1
1
u a
v b
ta có hpt:
2 2
2 2
15
2 23
v u
v uv u
(Hệ đẳng cấp quen thuộc).
Câu 11: Gọi
n
là số các số phức
z
đồng thời thỏa mãn
1 2 3
iz i
và biểu thức
2 5 2 3 3T z i z i
đạt giá trị lớn nhất. Gọi
M
là giá trị lớn nhất của
T
. Giá trị tích của
.M n
là
A.
10 21
. B.
6 13
. C.
5 21
. D.
2 13
.
Câu 12: Gọi
n
là số các số phức
z
đồng thời thỏa mãn
1 2 3
iz i
và biểu thức
2 5 2 3 3T z i z i
đạt giá trị lớn nhất. Gọi
M
là giá trị lớn nhất của
T
. Giá trị tích của
.M n
là
A.
10 21
. B.
6 13
. C.
5 21
. D.
2 13
.
Lời giải
Chọn A
Gọi
iz x y
, với
,x y
. Khi đó
;M x y
là điểm biểu diễn cho số phức
z
.
Theo giả thiết,
1 2 3
iz i
2 3
z i
2 2
2 1 9
x y
.
Ta có
2 5 2 3 3T z i z i
2 3
MA MB
, với
5; 2
A
và
0;3
B
.
Nhận xét rằng
A
,
B
,
I
thẳng hàng và
2 3IA IB
.
Cách 1: Gọi
là đường trung trực của
AB
, ta có
: 5 0
x y
.
2 3
T MA MB
PA PB
. Dấu “
” xảy ra khi
M P
hoặc
M Q
.
Giải hệ
2 2
5 0
2 1 9
x y
x y
8 2 2 2
;
2 2
P
và
8 2 2 2
;
2 2
Q
.
Khi đó
max 5 21
M T
.
Vậy
. 10 21
M n
.
Cách 2: Ta có
A
,
B
,
I
thẳng hàng và
2 3IA IB
nên
2 3 0
IA IB
.
2 2
2 3
MA MB
2 2
2 3
MI IA MI IB
2 2 2
5 2 3MI IA IB
105
.
Do đó
2
2
2. 2 3. 3
T MA MB
2 2
5 2 3
MA MB
525
hay
5 21
T
.
Khi đó
max 5 21
M T
. Dấu “
” xảy ra khi
M P
hoặc
M Q
.
Vậy
. 10 21
M n
.
Cách 3: Gọi
z x yi
, với
,x y
. Khi đó
;M x y
là điểm biểu diễn cho số phức
z
.
Theo giả thiết,
i 1 2i 3
z
2 i 3
z
2 2
2 1 9
x y
.
Đặt
2 3sin
1 3cos
x t
y t
. Khi đó
2 2 2 2
2 3 2 3 3sin 3 3cos 3 2 3sin 2 3cosP MA MB t t t t
2 27 18 sin cos 3 17 12 sin cost t t t
2. 54 36 sin cos 3. 51 36 sin cost t t t
Ta thấy:
2 3 54 36 sin cos 51 36 sin cos 521
P t t t t
.
P
đạt giá trị lớn nhất là
521
khi:
54 36 sin cos 51 36 sin cos
2 3
t t t t
1
sin cos
3
t t
2 0
x y
.
Toại độ điểm
M
thỏa mãn hệ phương trình:
2 2
2 0
2 1 9
x y
x y
Có hai điểm
M
thỏa
mãn. Vậy
. 10 21
M n
.
Câu 13: Cho số phức
0
z
có
0
2018.
z
Diện tích của đa giác có các đỉnh là các điểm biểu diễn của
0
z
và
các nghiệm của phương trình
0 0
1 1 1
z z z z
được viết dạng
3n
,
n
. Chữ số hàng đơn vị
của
n
là
A.
9
. B.
8
. C.
3
. D.
4
.
Câu 14: Cho hàm số
y f x
liên tục và nhận giá trị dương trên đoạn
0;
4
thỏa mãn
tan .
f x x f x
,
0;
4
x
,
0 1
f
. Khi đó
4
0
cos . dx f x x
bằng
A.
1
4
. B.
4
. C.
1
ln
4
. D.
0
.
----------HẾT----------
ĐÁP ÁN THAM KHẢO
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
A
C
B D
D
A
B B B C
A
A
C
D
D
A
A
B C
B A
D
D
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B C
D
D
C
D
C
D
C
C
A
D
B B
A
C
C
B B A
C
D
D
A
B
HƯỚNG DẪN GIẢI
Câu 15: Cho số phức
0
z
có
0
2018.
z
Diện tích của đa giác có các đỉnh là các điểm biểu diễn của
0
z
và
các nghiệm của phương trình
0 0
1 1 1
z z z z
được viết dạng
3n
,
n
. Chữ số hàng đơn vị
của
n
là
A.
9
. B.
8
. C.
3
. D.
4
.
Hướng dẫn giải
Chọn C
Điều kiện:
0
0
0
z
z
Ta có:
0 0
1 1 1
z z z z
0 0 0 0
.z
z z z z z z z
2 2
0 0
z.z 0
z z
2
0 0
1 0
z z
z z
0
1 3
2 2
z
i
z
0 1,2
1 3
2 2
z i z z
Ta có:
1 2 0
1 3
2 2
z z i z
0
2018
z
và
0 1 2
0.
z z z
Do đó
0
z
,
1
z
,
2
z
được biểu diễn bởi ba điểm
0
M
,
1
M
,
2
M
tạo thành một tam giác đều nằm
trên đường tròn tâm
O
bán kính
2018.
R
Tam giác đều này có chiều cao:
3
2
h R
và độ dài cạnh:
2
.
3
a h
2 3
.
2
3
R
3.R
Diện tích tam giác:
1
.
2
S a h
2
3
. 3
4
R
2
3.2018
. 3
4
3054243. 3
.
Vậy
3054243
n
có chữ số hàng đơn vị là 3.
Câu 16: Cho hàm số
y f x
liên tục và nhận giá trị dương trên đoạn
0;
4
thỏa mãn
tan .
f x x f x
,
0;
4
x
,
0 1
f
. Khi đó
4
0
cos . dx f x x
bằng
A.
1
4
. B.
4
. C.
1
ln
4
. D.
0
.
Hướng dẫn giải
Chọn B
Từ
tan .
f x x f x
,
0;
4
x
và
f x
liên tục và nhận giá trị dương trên đoạn
0;
4
,
ta có:
tan
f x
x
f x
,
0;
4
x
d tan d
f x
x x x
f x
,
0;
4
x
sin
d d
cos
f x
x
x x
f x x
,
0;
4
x
ln ln cos
f x x C
,
0;
4
x
.
Mà
0 1
f
nên suy ra
ln 0 ln cos0 0
f C C
.
Như vậy
1
ln ln cos
cos
f x x f x
x
,
0;
4
x
.
Từ đó
4
0
cos . dI x f x x
4
0
1
cos . d
cos
x x
x
4
0
d
4
x
.
----------HẾT----------
Câu 17: Cho số phức
z
thỏa mãn điều kiện
2 2z z i
. Giá trị nhỏ nhất của biểu thức
1 2 3 4 5 6P z i z i z i
được viết dưới dạng
17
2
a b
với
a
,
b
là các số hữu
tỉ. Giá trị của
a b
là
A.
3
. B.
7
. C.
2
. D.
4
.
Câu 18: Cho số phức
z
thỏa mãn điều kiện
2 2z z i
. Giá trị nhỏ nhất của biểu thức
1 2 3 4 5 6P z i z i z i
được viết dưới dạng
17
2
a b
với
a
,
b
là các số hữu
tỉ. Giá trị của
a b
là
A.
3
. B.
7
. C.
2
. D.
4
.
Hướng dẫn giải
Chọn A
Giả sử
z x yi
với
,x y
, ta có
2 2z z i
2 2x yi x yi i
2 2x yi x y i
2 2
2 2
2 2
x y x y
x y
.
Như vậy
z x xi
với
x
. Khi đó ta có
1 2 3 4 5 6P x x i x x i x x i
2 2 2 2 2 2
1 2 3 4 5 6
x x x x x x
2 2 2
2 6 5 2 14 25 2 22 61
x x x x x x
2 2 2 2 2
3 1 11 1 7 1
2. 2
2 2 2 2 2 2
x x x
2 2 2
3 11 1 1 7 1
2. 2
2 2 2 2 2 2
x x x
1 1 2 17
2. 17
2
2
.
Dấu bằng xảy ra khi
3 11
7
2 2
7
2
0
2
x x
x
x
.
Vậy:
1 2 17
min .
2
P
Suy ra
1, 2
a b
nên
3
a b
.
Câu 19: Cho hai số phức
u
,
v
thỏa mãn
3 6 3 1 3 5 10
u i u i
,
1 2
v i v i
. Giá trị nhỏ nhất
của
u v
là:
A.
10
3
. B.
2 10
3
. C.
10
. D.
5 10
3
.
----------HẾT----------
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B
C
D
D
D
A
B
C
B
C
D
B
C
D
C
D
A
C
A
A
D
D
B
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B A
C A
D
A
D
C D
B A
B D
A
C A
B D
C A
A
C A
D
B
HƯỚNG DẪN GIẢI
Câu 20: Cho hai số phức
u
,
v
thỏa mãn
3 6 3 1 3 5 10
u i u i
,
1 2
v i v i
. Giá trị nhỏ nhất
của
u v
là:
A.
10
3
. B.
2 10
3
. C.
10
. D.
5 10
3
.
Lời giải
Chọn B
Ta có:
3 6 3 1 3 5 10
u i u i
5 10
6 1 3
3
u i u i
1 2
5 10
3
MF MF
.
u
có điểm biểu diễn M thuộc elip với hai tiêu điểm
1 2
0;6 , 1;3
F F
, tâm
1 9
;
2 2
I
và độ
dài trục lớn là
5 10
2
3
a
5 10
6
a
.
1 2 1 2
1; 3 :3 6 0
F F F F x y
.
Ta có:
1 2
v i v i v i
NA NB
v
có điểm biểu diễn N thuộc đường thẳng d là trung trực của đoạn AB với
1; 2 , 0;1
A B
.
1;3
AB
,
1 1
;
2 2
K
là trung điểm của AB
: 3 2 0
d x y
.
2
2
1 27
2
3 10
2 2
,
2
1 3
d I d
Dễ thấy
1 2
F F d
2 10
min min ,
3
u v MN d I d a
.
Câu 21: Cho
z x yi
với
x
,
y
là số phức thỏa mãn điều kiện
2 3 2 5
z i z i
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
8 6P x y x y
. Tính
M m
.
A.
156
20 10
5
. B.
60 20 10
. C.
156
20 10
5
. D.
60 2 10
.
Câu 22: Cho
z x yi
với
x
,
y
là số phức thỏa mãn điều kiện
2 3 2 5
z i z i
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
8 6P x y x y
. Tính
M m
.
A.
156
20 10
5
. B.
60 20 10
. C.
156
20 10
5
. D.
60 2 10
.
Lời giải
Chọn B
6
4
2
2
4
6
8
10
10 5 5 10
x
y
-1
A
B
-1
2
J
I
K
- Theo bài ra:
2 3 2 5
z i z i
2 2 2 2
2 3 2 1 5
x y x y
2 2
2 2 0
2 1 25
x y
x y
tập hợp điểm biểu diễn số phức
z
là miền mặt phẳng
T
thỏa mãn
2 2
2 2 0
2 1 25
x y
x y
(là miền tô đậm trên hình vẽ, kể cả biên)
- Gọi
2; 6
A
,
2;2
B
là các giao điểm của đường thẳng
2 2 0
x y
và đường tròn
2 2
: 2 1 25
C x y
.
- Ta có:
2 2
8 6P x y x y
2 2
4 3 25
x y P
.
Gọi
C
là đường tròn tâm
4; 3
J
, bán kính
25
R P
.
- Đường tròn
C
cắt miền
T
khi và chỉ khi
JK R JA
IJ IK R IA
2 10 5 25 3 5
P
40 20 10 20
P
(trong đó
JK
là bán kính đường tròn tâm
J
và tiếp xúc ngoài với đường tròn
C
)
20
M
và
40 20 10
m
.
Vậy
60 20 10
M m
.
Câu 23: Gọi
1
z
,
2
z
là hai trong tất cả các số phức thỏa mãn điều kiện
1 3 3 2
i z i
và
1 2
2.
z z
Gọi
m
,
n
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
1 2
P z z
. Giá trị của
3 3
S m n
bằng
A.
72
. B.
90
. C.
54
. D.
126
.
Câu 24: Gọi
1
z
,
2
z
là hai trong tất cả các số phức thỏa mãn điều kiện
1 3 3 2
i z i
và
1 2
2.
z z
Gọi
m
,
n
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
1 2
P z z
. Giá trị của
3 3
S m n
bằng
A.
72
. B.
90
. C.
54
. D.
126
.
Lời giải
Chọn A
Ta có
1 3 3 2 1 3 2 3 2
i z i i z z
.
Gọi
M
là điểm biểu diễn của
z
ta có
M
nằm trên đường tròn
C
tâm
3;0
I
,
2
R
.
Gọi
A
,
B
lần lượt là điểm biểu diễn cho
1
z
,
2
z
ta có
1 2
2 2
z z AB
.
Gọi
H
là trung điểm
AB
ta có tam giác
IAB
vuông tại
I
(theo định lý Pitago đảo)
2
1
2 2
AB
IH
H
chạy trên đường tròn tâm
I
bán kính
1R
.
2 2 2 2
1 2
1 1
P z z OA OB OA OB
Mặt khác theo công thức độ dài đường trung tuyến ta có
2 2
2 2 2 2 2
2
2 2 2 2
2 2
AB
OA OB OH OH OH
max 3 1 4
P OI R
;
min 3 1 2
P OI R
4
m
,
2
n
64 8 72
S
.
Câu 25: Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2 1 2
0
z z z z
. Tính
4 4
1 2
2 1
z z
A
z z
.
A.
1
. B.
1 i
. C.
1
. D.
1 i
.
Câu 26: Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2 1 2
0
z z z z
. Tính
4 4
1 2
2 1
z z
A
z z
.
A.
1
. B.
1 i
. C.
1
. D.
1 i
.
Lời giải
Chọn C
Đặt
1
z a bi
,
2
z a b i
, với
, , ,a a b b
, ta có:
1 2 1 2
0
z z z z
1 2 1
1 2
z z z
z z
1 2 1 2 1 1
1 1 2 2
z z z z z z
z z z z
1 1 1 2 2 1 2 2 1 1
1 1 2 2
z z z z z z z z z z
z z z z
1 2 2 1 1 1
1 1 2 2
z z z z z z
z z z z
.
Ta có :
2 2 2
1 2 1 2
2 1 2 1
2
z z z z
z z z z
2
1 2 2 1
2 2 1 1
2
z z z z
z z z z
2
1 2 2 1
1 1
2
z z z z
z z
2
1 1
1 1
2 1
z z
z z
.
Từ đó:
4 4
1 2
2 1
z z
A
z z
2
2 2
2
1 2
2 1
2 1 2 1
z z
z z
.
Câu 27: Cho số phức
z a bi
,a b
thỏa
4 4 10
z z
và
6
z
lớn nhất. Tính
S a b
.
A.
3
S
. B.
5
S
. C.
5
S
. D.
11
S
.
Câu 28: Cho số phức
z a bi
,a b
thỏa
4 4 10
z z
và
6
z
lớn nhất. Tính
S a b
.
A.
3
S
. B.
5
S
. C.
5
S
. D.
11
S
.
Lời giải
Chọn C
Gọi
;M a b
là điểm biểu diễn số phức
z a bi
,a b
,
4;0
A
,
4;0
B
,
6;0
C
lần
lượt là điểm biểu diễn số phức
1
4
z
,
2
4
z
,
3
6
z
.
Khi đó ta có
4 4 10
z z
10
MA MB
suy ra tập hợp điểm
M
là
E
nhận
A
,
B
là các tiêu điểm, độ dài trục lớn
2 10 5
a a
, tiêu cự
2 8 4
c c
,
b
E
:
2 2
1
25 9
x y
.
Ta tìm giá trị lớn nhất của
6
z
MC
, khi đó
max
MC
11
EF FC
, khi đó
M E
với
5;0
E
,
5;0
F
5
z
. Vậy
S a b
5
.
Câu 29: Xét các số phức
z a bi
(
a
,
b
) có môđun bằng
2
và phần ảo dương. Tính giá trị biểu
thức
2018
5 2S a b
khi biểu thức
2 3 2
P z z
đạt giá trị lớn nhất.
A.
1
S
. B.
2018
2
S
. C.
1009
2
S
. D.
0
S
.
Câu 30: Xét các số phức
z a bi
(
a
,
b
) có môđun bằng
2
và phần ảo dương. Tính giá trị biểu
thức
2018
5 2S a b
khi biểu thức
2 3 2
P z z
đạt giá trị lớn nhất.
A.
1
S
. B.
2018
2
S
. C.
1009
2
S
. D.
0
S
.
Lời giải
Chọn D
z a bi
;
2
z
2 2
2
a b
2 2
4
a b
.
2 3 2
P z z
2 2
2 2
2 3 2
a b a b
4 8 3 8 4a a
.
4 8 3 8 4a a
2 2
1 3 8 4 8 4a a
4 10
.
Dấu đẳng thức xẩy ra khi
4 8
1
a
8 4
3
a
9 4 8 8 4a a
8
5
a
.
Với
8
5
a
6
5
b
(do
b
).
Vậy
min 4 10
P
8 6
5 5
z i
. Khi đó
2018
8 6
5 2
5 5
S
0
.
Câu 31: Cho số phức
z
thỏa mãn
2 1 2 1 10
z i z i
. Gọi
M
,
m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của
z
. Tính tổng
S M m
.
A.
9
S
. B.
8
S
. C.
2 21
S
. D.
2 21 1
S
.
Câu 32: Cho số phức
z
thỏa mãn
2 1 2 1 10
z i z i
. Gọi
M
,
m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của
z
. Tính tổng
S M m
.
A.
9
S
. B.
8
S
. C.
2 21
S
. D.
2 21 1
S
.
Hướng dẫn giải
Chọn C
Giả sử
z a bi
,
,a b
z a bi
.
Chia hai vế cho
i
ta được:
2 2 10
z i z i
.
Đặt
;M a b
,
;
N a b
,
2;1
A
,
2; 1
B
,
2;1
C
NB MC
.
Ta có:
10
MA MC
2 2
: 1
25 21
X Y
M E
.
Elip này có phương trình chính tắc với hệ trục tọa độ
IXY
,
0;1
I
là trung điểm
AC
.
Áp dụng công thức đổi trục
2
2
1
1
1
25 21
X x
y
x
Y y
.
Đặt
5sin
1 21cos
a t
b t
,
0;2
t
2
2 2 2
z OM a b
2
2
25sin 1 21cost t
2
26 4cos 2 21cost t
.
max
0
1 21 cos 1
1 21
a
z t
b
.
min
0
1 21 cos 1
1 21
a
z t
b
.
2 21
M m
.
Câu 33: Cho hai số phức
,z z
thỏa mãn
5 5
z
và
1 3 3 6z i z i
. Tìm giá trị nhỏ nhất của
z z
.
A.
5
2
. B.
5
4
. C.
10
. D.
3 10
.
Câu 34: Cho hai số phức
,z z
thỏa mãn
5 5
z
và
1 3 3 6z i z i
. Tìm giá trị nhỏ nhất của
z z
.
A.
5
2
. B.
5
4
. C.
10
. D.
3 10
.
Hướng dẫn giải
Chọn A
Gọi
;M x y
là điểm biểu diễn của số phức
z x yi
,
;N x y
là điểm biểu diễn của số
phức
z x y i
.
Ta có
2
2 2
5 5 5 5 5 5
z x yi x y
.
Vậy
M
thuộc đường tròn
2
2 2
: 5 5
C x y
1 3 3 6z i z i
1 3 3 6x y i x y i
2 2 2 2
1 3 3 6 8 6 35
x y x y x y
Vậy
N
thuộc đường thẳng
:8 6 35
x y
Dễ thấy đường thẳng
không cắt
C
và
z z MN
Áp dụng bất đẳng thức tam giác, cho bộ ba điểm
, ,I M N
ta có.
0
MN IN IM IN R IN R
2 2
8. 5 6.0 5
5
, 5
2
8 6
d I R
Dấu bằng đạt tại
0 0
;
M M N N
.
Câu 35: Cho
a
là số thực, phương trình
2
2 2 3 0
z a z a
có
2
nghiệm
1
z
,
2
z
. Gọi
M
,
N
là
điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Biết tam giác
OMN
có một góc bằng
120
,
tính tổng các giá trị của
a
.
A.
6
. B.
6
. C.
4
. D.
4
.
Câu 36: Gọi
1
z
,
2
z
,
3
z
,
4
z
là các nghiệm của phương trình
4 3 2
4 3 3 3 0
z z z z
. Tính
2 2 2 2
1 1 2 2 3 3 4 4
2 2 2 2 2 2 2 2
T z z z z z z z z
.
A.
102
T
. B.
101
T
. C.
99
T
. D.
100
T
.
Câu 37: Cho
a
là số thực, phương trình
2
2 2 3 0
z a z a
có
2
nghiệm
1
z
,
2
z
. Gọi
M
,
N
là
điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Biết tam giác
OMN
có một góc bằng
120
,
tính tổng các giá trị của
a
.
A.
6
. B.
6
. C.
4
. D.
4
.
Lời giải
Chọn B
Vì
O
,
M
,
N
không thẳng hàng nên
1
z
,
2
z
không đồng thời là số thực, cũng không đồng thời
là số thuần ảo
1
z
,
2
z
là hai nghiệm phức, không phải số thực của phương trình
2
2 2 3 0
z a z a
. Do đó, ta phải có:
2
12 16 0
a a
6 2 5; 6 2 5
a
.
Khi đó, ta có:
2
1
2
1
2 12 16
2 2
2 12 16
2 2
a a a
z i
a a a
z i
.
1 2
2 3
OM ON z z a
và
2
1 2
12 16
MN z z a a
.
Tam giác
OMN
cân nên
120
MON
2 2 2
cos120
2 .
OM ON MN
OM ON
2
8 10 1
2 2 3 2
a a
a
2
6 7 0
a a
3 2
a
(thỏa mãn).
Suy ra tổng các giá trị cần tìm của
a
là
6
.
Câu 38: Gọi
1
z
,
2
z
,
3
z
,
4
z
là các nghiệm của phương trình
4 3 2
4 3 3 3 0
z z z z
. Tính
2 2 2 2
1 1 2 2 3 3 4 4
2 2 2 2 2 2 2 2
T z z z z z z z z
.
A.
102
T
. B.
101
T
. C.
99
T
. D.
100
T
.
Lời giải
Chọn B
Đặt
4 3 2
4 3 3 3f z z z z z
1 2 3 4
f z z z z z z z z z
.
Do
2
1 1 1 1
2 2 1 1
z z z i z i
nên
2 2 2 2
1 1 2 2 3 3 4 4
2 2 2 2 2 2 2 2
T z z z z z z z z
1 1
f i f i
10 10
i i
101
.
Câu 39: Tìm số phức
z
thỏa mãn
1 5
z i
và biểu thức
7 9 2 8T z i z i
đạt giá trị nhỏ nhất.
A.
5 2z i
. B.
1 6z i
.
C.
1 6z i
và
5 2z i
. D.
4 5z i
.
----------HẾT----------
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
D
A
C
B
B
C
B
B
C
B
B
B
C
D
A
D
A
C
D
D
D
B
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B A
D
D
A
D
C A
A
A
B A
A
A
D
B C C A
A
C A
D
C B
HƯỚNG DẪN GIẢI
Câu 40: Tìm số phức
z
thỏa mãn
1 5
z i
và biểu thức
7 9 2 8T z i z i
đạt giá trị nhỏ nhất.
A.
5 2z i
. B.
1 6z i
.
C.
1 6z i
và
5 2z i
. D.
4 5z i
.
Lời giải
Chọn B
M
0
K
A
I
M
B
Từ giả thiết
1 5
z i
suy ra tập hợp các điểm
M
biểu diễn số phức
z
là đường tròn (C)
tâm
1;1
I
, bán kính
5
R
.
Xét các điểm
7;9
A
và
0;8
B
. Ta thấy
10 2.IA IM
.
Gọi
K
là điểm trên tia
IA
sao cho
1
4
IK IA
5
;3
2
K
Do
1
2
IM IK
IA IM
, góc
chung
IKM IMA
∽
. .c g c
1
2
MK IK
MA IM
2.MA MK
.
Lại có:
7 9 2 8T z i z i
2.MA MB
2
MK MB
2. 5 5
BK
min
5 5
T
M BK C
,
M
nằm giữa
B
và
K
5
0
2
M
x
.
Ta có: phương trình đường thẳng
BK
là: 2x+y-8=0
Tọa độ điểm
M
là nghiệm của hệ:
2 2
2 8 0
1 1 25
x y
x y
1
6
5
2
x
y
x
y
1;6
M
.
Vậy
1 6z i
là số phức cần tìm.
Câu 41: Cho số thực
1
z
và số phức
2
z
thoả mãn
2
2 1z i
và
2 1
1
z z
i
là số thực. Gọi
, a b
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của
1 2
.z z
Tính
.T a b
A.
4T
. B.
4 2
T
. C.
3 2 1
T
. D.
2 3
T
.
Câu 42: Cho số thực
1
z
và số phức
2
z
thoả mãn
2
2 1z i
và
2 1
1
z z
i
là số thực. Gọi
, a b
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của
1 2
.z z
Tính
.T a b
A.
4T
. B.
4 2
T
. C.
3 2 1
T
. D.
2 3
T
.
Lời giải
Chọn B
Gọi
1
z
m
;
2
z
x yi
;
, ,m x y
. Theo đầu bài ta có
2 1
1
1 2
x m yi i
z z
i
là một số
thực nên ta có
0
x m y m x y
.
Do
2
2
2
2 1 2 1
z i x y
2
2 1 1 3
y y
nên ta có:
2 2
2 2
1 2
2 2 3 2
z z x m y x y x y y
1 2
min 2
a z x
;
1 2
max 3 2
b z x
4 2
T a b
.
Câu 43: Cho
a
,
b
,
c
là các số thực sao cho phương trình
3 2
0
z az bz c
có ba nghiệm phức lần
lượt là
1
3z w i
;
2
9z w i
;
3
2 4
z w
, trong đó
w
là một số phức nào đó. Tính giá trị của
P a b c
.
A.
36
P
. B.
208
P
. C.
136
P
. D.
84
P
.
Câu 44: Cho
a
,
b
,
c
là các số thực sao cho phương trình
3 2
0
z az bz c
có ba nghiệm phức
lần lượt là
1
3z w i
;
2
9z w i
;
3
2 4
z w
, trong đó
w
là một số phức nào đó. Tính
giá trị của
P a b c
.
A.
36
P
. B.
208
P
. C.
136
P
. D.
84
P
.
Hướng dẫn giải
Chọn C
Đặt
w x yi
, với
,x y
.
Ta có
1 2 3
4 4 12 4 4 12 4 0z z z a w i a x a y i
4 4 0 4 4
12 4 0 3
x a x a
y y
.
Từ đó
3w x i
1
z x
;
2
6z x i
;
3
2 4 6z x i
.
Vì phương trình bậc ba
3 2
0
z az bz c
có một nghiệm thực nên hai nghiệm phức còn lại
phải là hai số phức liên hợp, suy ra
2 4 4
x x x
.
Như vậy
1
4
z
;
2
4 6z i
;
3
4 6z i
.
Do đó
1 2 3
1 2 2 3 3 1
1 2 3
12 12
84 84
208 208
z z z a
a a
z z z z z z b b
c c
z z z c
.
Vậy
12 84 208 136
P a b c
.
| 1/153
| | Tải xuống

Có thể bạn quan tâm:

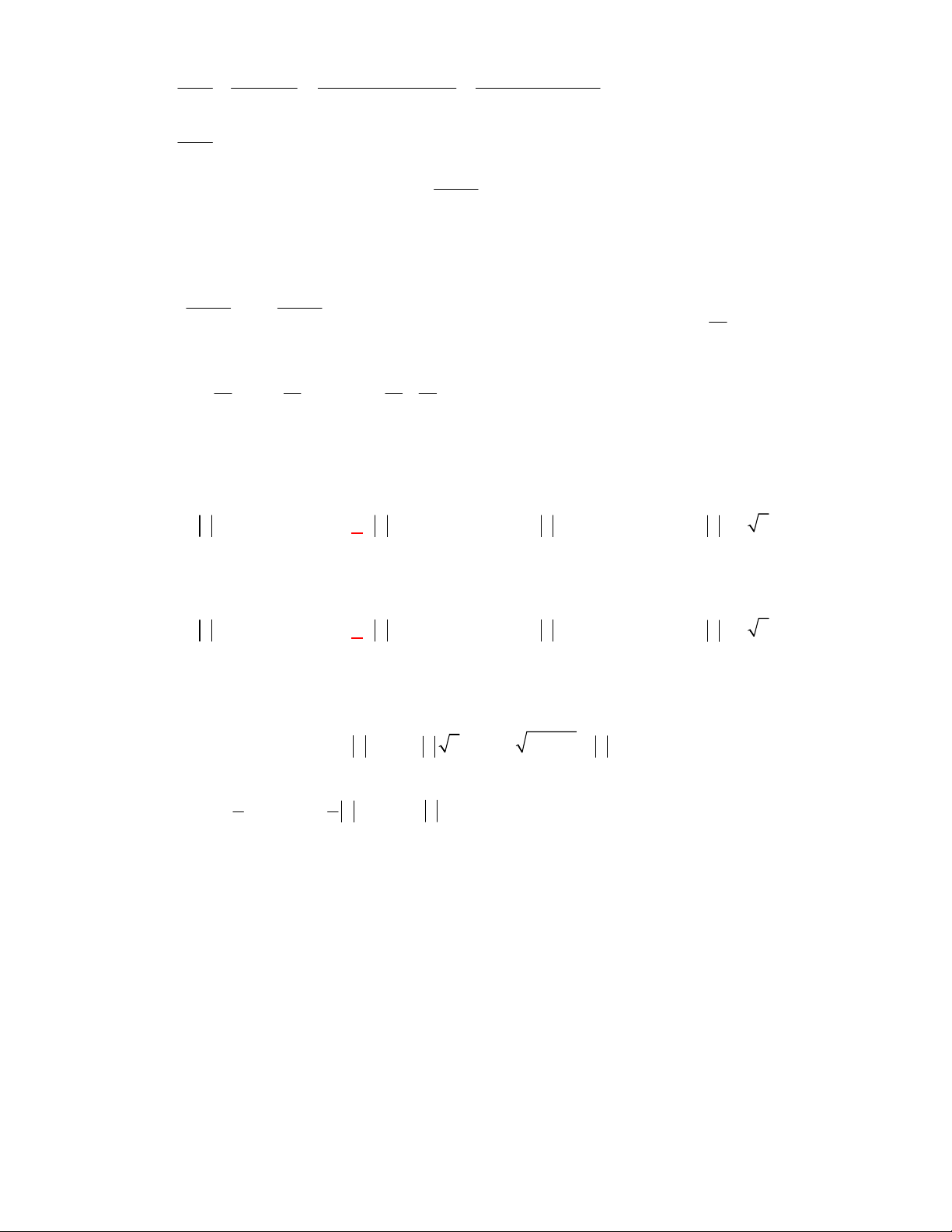
Preview text:

Câu 1: (TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018) Cho hai số thực x , y thoả mãn phương
trình x  2i  3  4 yi . Khi đó giá trị của x và y là: 1 1 1
A. x  3 , y  2 .
B. x  3i , y  .
C. x  3 , y  .
D. x  3 , y   . 2 2 2 Lời giải Chọn Cx  3 x  3 
Từ x  2i  3  4 yi     1 . 2  4 yy    2 1
Vậy x  3 , y  . 3
Câu 2: (TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018) Phần thực và phần ảo của số phức
z  1 2i lần lượt là: A. 2 và 1 B. 1 và 2i . C. 1 và 2 . D. 1 và i . Lời giải Chọn C
Số phức z  1 2i có phần thực và phần ảo lần lượt là 1 và 2 .
Câu 3: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Cho hai số phức z a bi ,
z  a  bi (a,b, a ,  
b  ) . Tìm phần ảo của số phức zz . A.  
ab abi . B.
ab ab . C.
ab ab . D. aa   bb . Lời giải Chọn B
Ta có: zz  a bia b i 2    aa  
ab i abi  
bb i aa   bb   
ab abi
Vậy phần ảo của số phức zz là ab  ab .
Câu 4: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Tìm tất cả các nghiệm của phương trình 2
z  2z  5  0 trên tập số phức  .
A. 1 2i ; 1 2i .
B. 1 i ; 1 i .
C. 1 2i ; 1 2i .
D. 1 i ; 1 i . Lời giải: Chọn C 2 2   1  5  4   4i .
z  1 2i
Suy ra phương trình có hai nghiệm phức: 1  . z  1 2  i 2
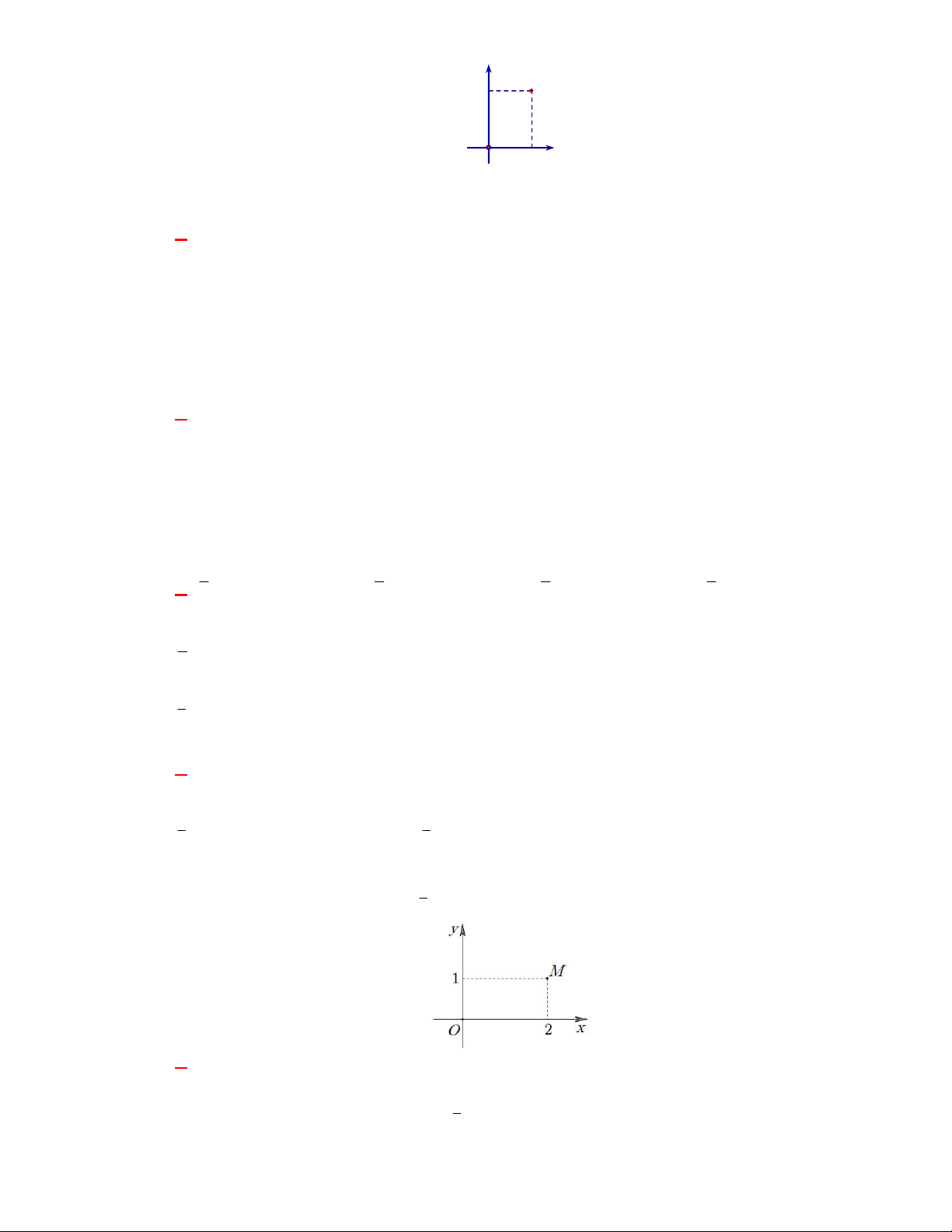
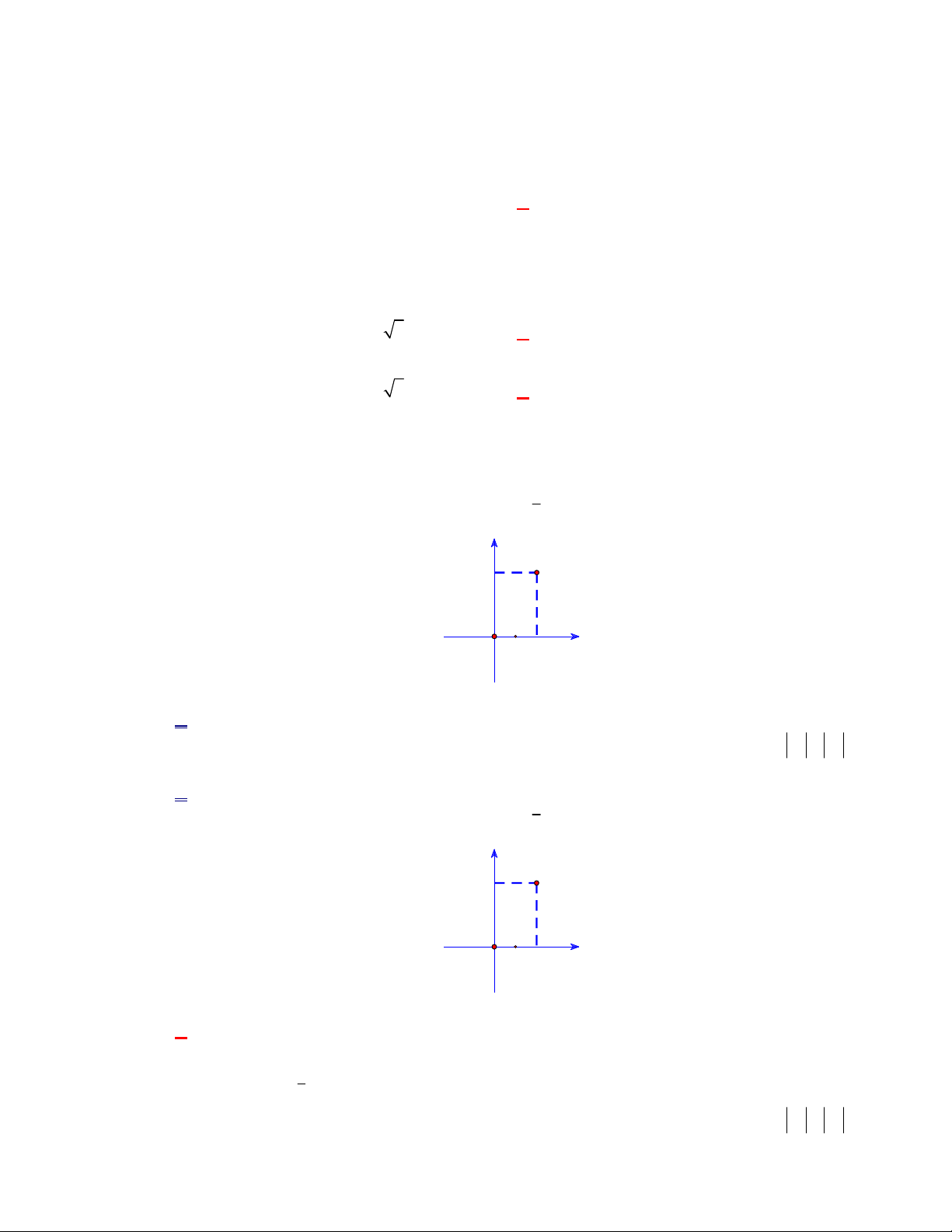
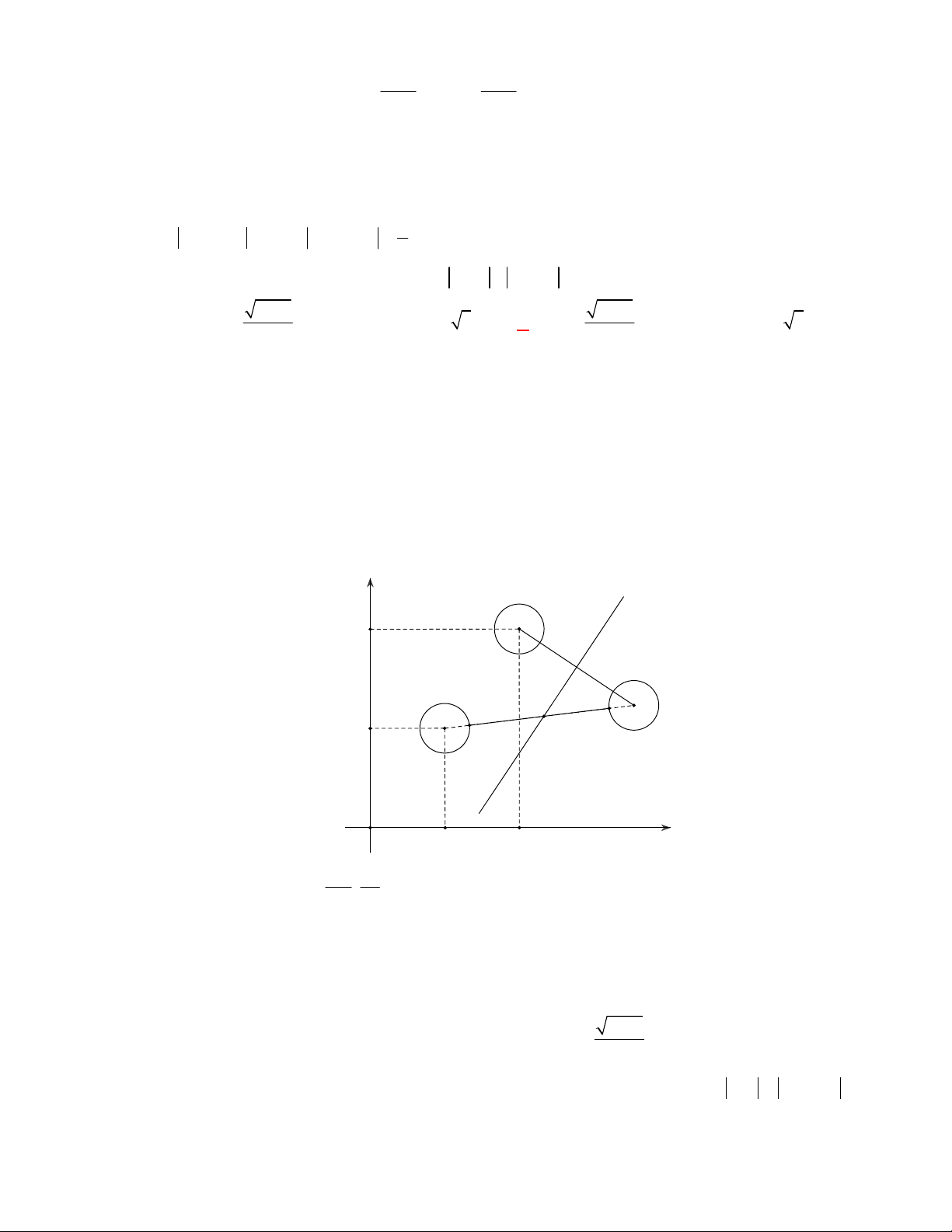
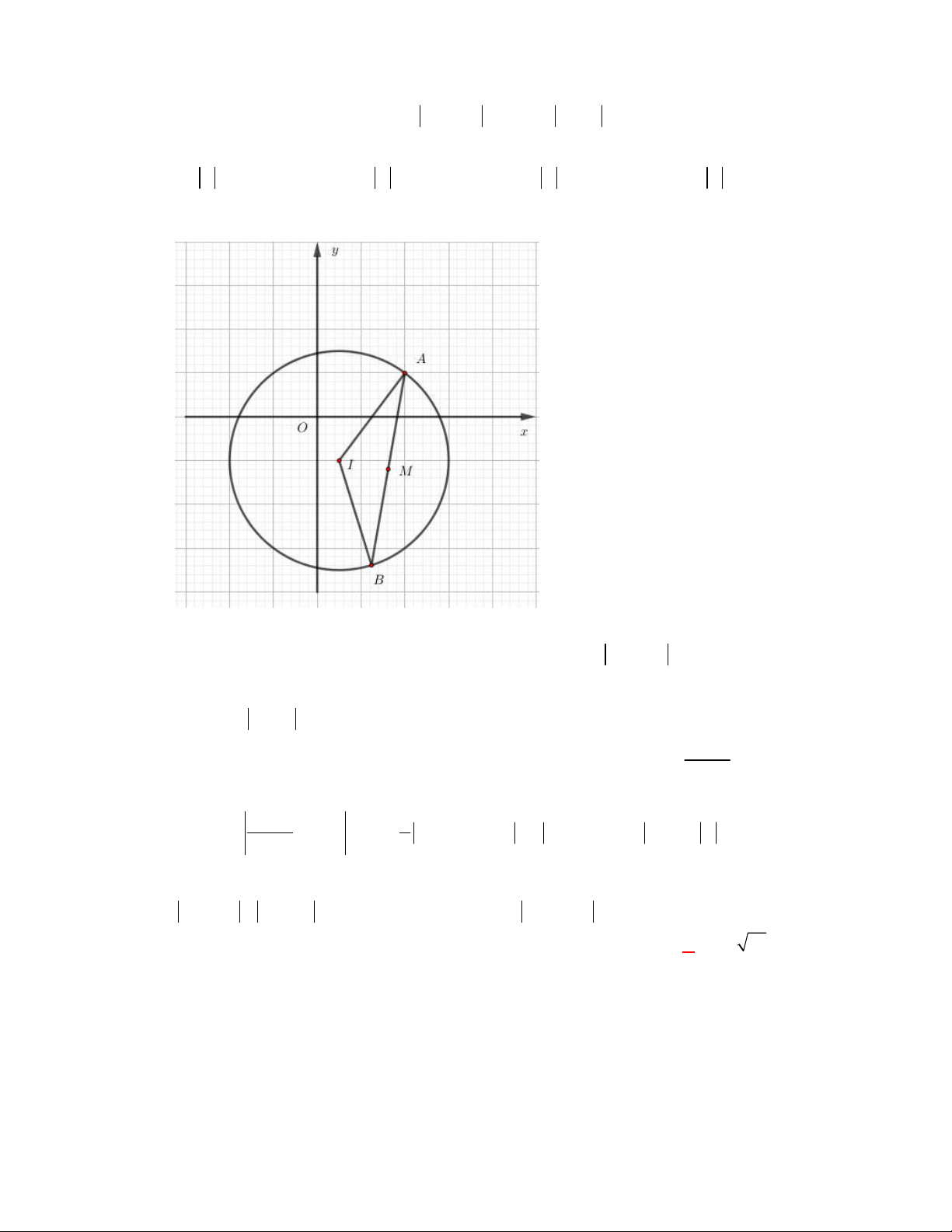
Câu 5: (Đề tham khảo BGD năm 2017-2018) Điểm M trong hình vẽ bên là điểm biểu diễn số phức y A. z  2   i .
B. z  1 2i . M 1
C. z  2  i .
D. z  1 2i . Lời giải Chọn A O 2 x Điểm M 2; 
1 biểu diễn số phức z  2   i .
Câu 1: (THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018) Điểm nào trong hình vẽ dưới đây là điểm
biểu diễn của số phức z  1 i2  i ? A. P . B. M . C. N . D. Q . Lời giải Chọn D
Ta có z  1 i2  i  z  3  i . Điểm biểu diễn của số phức z là Q 3  ;1 .
Câu 2: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Số phức z thỏa mãn z  5  8i có phần ảo là A. 8 . B. 8  i . C. 5 . D. 8  . Lời giải Chọn D
Ta có z  5  8i suy ra phần ảo của z là 8  .
Câu 3: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Nghiệm phức có phần ảo dương của phương trình 2
z z 1  0 là: 1 3 1 3 1 3 1 3 A.i . B.   i . C.i . D.   i . 2 2 2 2 2 2 2 2 Lời giải Chọn A Ta có: 2   1 4  3   3i . 1 3i 1 3i
Phương trình đã cho có hai nghiệm và . 2 2 1 3
Vậy nghiệm phức có phần ảo dương là  i . 2 2
Câu 4: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Cho hai số phức z  2  3i , z  4  5i . Số 1 2
phức z z z là 1 2
A. z  2  2i . B. z  2   2i .
C. z  2  2i . D. z  2   2i . Lời giải
Chọn B
z z z  2  3i  4  5i  2   2i . 1 2
Câu 5: (THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018) Tìm giá trị cực tiểu của hàm số 4 2
y x  4x  3 A. y  4 . B. y  6 . C. y  1. D. y  8 . CT CT CT CT
Hướng dẫn giải Chọn C Ta có: 3
y  4x  8x .
x  0  y  3  y  0 3
 4x  8x  0  x  2  y  1  .
x   2  y  1   Bảng biến thiên
Vậy giá trị cực tiểu của hàm số là y  1 tại x  2 , x   2 . CT CT CT
Câu 1: (THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018) Phần ảo của số phức z  2  3i là A. 3i . B. 3 . C. 3  . D. 3i . Lời giải Chọn C
Phần ảo của số phức z  2  3i là 3  .
Câu 2: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Cho số phức z  2018  2017i . Điểm M
biểu diễn của số phức liên hợp của z là A. M  2  018; 2017 . B. M 2018; 2
 017 . C. M  2  018; 2
 017 . D. M 2018; 2017 . Lời giải Chọn D
Ta có z  2018  2017i , nên M 2018; 2017 .
Câu 3: (THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức z  1 2i . Số phức liên hợp của z là A. z  1   2i . B. z  1   2i .
C. z  2  i .
D. z  1 2i . Lời giải Chọn D
Số phức liên hợp của z là z  1 2i .
Câu 4: (THPT Chuyên Tiền Giang-lần 1 năm 2017-2018) Tìm tọa độ điểm biểu diễn của số phức
2  3i4  iz  . 3  2i A. 1; 4   . B. 1; 4 . C. 1; 4 . D. 1; 4 Lời giải Chọn A
2  3i4  i 5 14i
5 14i3  2i 13  52i Ta có z      1   4i . 3  2i 3  2i 13 13
Do đó điểm biểu diễn cho số phức z có tọa độ 1; 4   .
Câu 5: (THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức z  3  2i , z  6  5i . Tìm số 1 2
phức liên hợp của số phức z  6z  5z 1 2
A. z  51 40i .
B. z  51 40i .
C. z  48  37i .
D. z  48  37i . Lời giải
Chọn D
Ta có: z  6z  5z  63  2i  56  5i  48  37i . 1 2
Suy ra z  48  37i .
Câu 6: (THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Xác định phần ảo của số phức z  18 12i . A. 12 . B. 18 . C. 12 . D. 12  i . Lời giải Chọn A
Phần ảo của số phức z  18 12i là 12 .
Câu 7: (THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018) Số phức liên hợp của số phức z  1 2i là A. 1 2i . B. 1 2i . C. 2  i . D. 1 2i . Lời giải Chọn A
Số phức liên hợp của số phức z  1 2i là z  1 2i .
Câu 8: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Tìm phần ảo của số phức z , biết
1 iz  3  i . A. 2 . B. 2  . C. 1. D. 1  . Lời giải Chọn B 3  i
3  i1 i
Ta có: 1 iz  3  i z   z
z  1 2i . 1 i
1 i1 i
Vậy phần ảo của số phức z bằng 2  .
Câu 9: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Hỏi điểm M 3;   1 là điểm biểu diễn số phức nào sau đây?
A. z  1 3i .
B. z  1 3i .
C. z  3  i . D. z  3   i . Lời giải Chọn C Điểm M  ;
a b trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số
phức z a bi .
Do đó điểm M 3; 
1 là điểm biểu diễn số phức z  3  i .
Câu 10: (THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) Cho số phức z  4   5i . Biểu
diễn hình học của z là điểm có tọa độ A. 4;5 . B. 4;5 . C. 4; 5   . D. 4;5 . Lời giải Chọn A Số phức z  4
  5i có phần thực a  4
 ; phần ảo b  5 nên điểm biểu diễn hình học của số
phức z là 4;5 .
Câu 11: (THPT Chuyên Phan Bội Châu-lần 2 năm 2017-2018) Cho số phức z  2  3i . Môđun của số
phức w  1 iz A. w  26 . B. w  37 . C. w  5 . D. w  4 . Lời giải Chọn A
Ta có w  1 iz  1 i2  3i  5  i , w    2 2 5 1  26 .
Câu 12: (THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018) Trong mặt phẳng Oxy , cho
các điểm A , B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức. y B 3 A 1 2  O 1 x 1 1 A.   2i . B. 1 2i . C. 2  i . D. 2  i . 2 2 Lời giải Chọn A  1  1
Trung điểm AB là I  ; 2 
 biểu diễn số phức là z    2i .  2  2
Câu 13: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Số phức z nào sau đây
thỏa z  5 và z là số thuần ảo? A. z  5 . B. z  2  3i .
C. z  5i .
D. z   5i . Lời giải Chọn D
Gọi z bi , với b  0 , b   là số thuần ảo  loại A, B.
Ta có z  5  b  5  Chọn D
Câu 14: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Cho số phức z mi , 1
(m  ) . Tìm phần ảo của số phức ? z 1 1 1 1 A.  . B. . C.i . D. i . m m m m Lời giải Chọn A 1 1 1 1   i   i . z mi . mi i m
Câu 15: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Cho số phức
1 iz  4  2i . Tìm môđun của số phức w z  3 . A. 5 . B. 10 . C. 25 . D. 7 . Lời giải Chọn A 4  2i Ta có: z
 1 3i . Do đó: w z  3  4  3i . 1 i Vậy 2 2 w  4  3  5 .
Câu 16: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Phần ảo của số phức z  5  2i bằng A. 5 . B. 5i . C. 2 . D. 2i . Lời giải Chọn C
Câu 17: (SGD Bắc Giang – năm 2017 – 2018) Cho số phức z  1 2i . Số phức z được biểu
diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ?
A. P 1;2 .
B. N 1; 2 .
C. Q 1; 2 . D. M  1  ; 2 . Lời giải Chọn C
Ta có z  1 2i z  1
  2i . Suy ra điểm biểu diễn của số phức z là Q 1; 2 .
Câu 18: (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho hai số phức z  2  3i , z  4  5i . 1 2
Tính z z z . 1 2 A. z  2   2i . B. z  2   2i .
C. z  2  2i .
D. z  2  2i . Lời giải Chọn A
z z z  2  3i   4   5i  2   2i . 1 2
Câu 19: Cho số phức z  3  2i . Tính z . A. z  5 . B. z  13 . C. z  5 . D. z  13 .
Câu 20: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức z  3  2i . Tính z . A. z  5 . B. z  13 . C. z  5 . D. z  13 . Lời giải Chọn B Ta có 2 2 z  3  2  13 .
Câu 21: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức z  3   4 . i Môđun của z là A. 3 . B. 5 . C. 4 . D. 7 . Lời giải Chọn B
Ta có z   2 2 3  4  5.
Câu 22: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức z có biểu diễn
hình học là điểm M ở hình vẽ bên. Khẳng định nào sau đây là đúng? y 3 O x 2 M
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  3  2i . Lời giải Chọn D
Điểm biểu diễn của số phức z a bi là M  ; a b .
Câu 23: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức z  1 i . Số phức
nghịch đảo của z là 1  i 1  i 1   i A. . B. 1 i . C. . D. . 2 2 2 Lời giải Chọn C Ta có 1 1 1 i z  1 i    . z 1 i 2
Câu 24: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Tìm số phức liên hợp của số phức z  i . A. 1. B. 1. C.i . D. i . Lời giải
Chọn D
Câu 25: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Gọi A , B lần lượt là các điểm biểu
diễn của các số phức z  1 2i ; z  5  i . Tính độ dài đoạn thẳng A . B 1 2 A. 5  26 . B. 5 . C. 25 . D. 37 . Lời giải
Chọn B
Ta có: A1;2 , B 5;   1  AB  5 .
Câu 26: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Cho số phức z  7  3i . Tính z . A. z  5 . B. z  3 . C. z  4 . D. z  4 . Lời giải
Chọn C
Ta có z  7  9  4 .
Câu 27: (THPT Thuận Thành 2 – Bắc Ninh - Lần 2 năm 2017 – 2018)Mô đun của số phức
z  7  5i bằng A. 74 . B. 24 . C. 74 . D. 2 6 . Lời giải Chọn C Ta có 2 2 z  7  5  74 .
Câu 28: (THPT Thuận Thành 2 – Bắc Ninh - Lần 2 năm 2017 – 2018)Phần thực của số phức
z  3  i1 4i là A. 1. B. 13 . C. 1. D. 1  3 . Lời giải Chọn A
Ta có: z  3  i1 4i  113i .
Câu 29: (THPT Chuyên Lương Thế Vinh – Đồng Nai – Lần 2 năm 2017 – 2018)
Cho số phức z thỏa mãn z 1 i  3  5i . Tính môđun của z . A. z  17 . B. z  16 . C. z  17 . D. z  4 . Lời giải Chọn A 3  5i 2 2
Ta có: z 1 i  3  5i z   1
  4i z    1   4    17 . 1 i
Câu 30: (THPT Chuyên Lương Thế Vinh – Đồng Nai – Lần 2 năm 2017 – 2018) Điểm M trong
hình vẽ bên là điểm biểu diễn của số phức z . y M 4 O 3 x
Tìm phần thực và phần ảo cú số phức z .
A. Phần thực bằng 4 và phần ảo bằng 3 .
B. Phần thực bằng 4 và phần ảo bằng 3i .
C. Phần thực bằng 3 và phần ảo bằng 4 .
D. Phần thực bằng 3 và phần ảo bằng 4i . Lời giải Chọn C
Từ hình vẽ ta có M 3;4 nên z  3  4i .
Vậy Phần thực bằng 3 và phần ảo bằng 4 .
Câu 31: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Cho số phức z  2   i . Điểm
nào dưới đây là điểm biểu diễn của số phức w iz trên mặt phẳng tọa độ? A. P  2   ;1 . B. N 2;  1 .
C. Q 1;2 .
D. M 1;2 . Lời giải
Chọn A
w iz i  2   i  1
  2i  điểm P 2 
;1 là điểm biểu diễn của số phức w iz trên mặt phẳng tọa độ.
Câu 32: (SGD Quảng Nam – năm 2017 – 2018) Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i .
C. z  2  3i .
D. z  2  3i . Lời giải Chọn A
z  3  2i .
Câu 33: (ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Cho số phức z  1 2i thì số phức liên hợp z có
A. phần thực bằng 1 và phần ảo bằng 2  .
B. phần thực bằng 2  và phần ảo bằng 1.
C. phần thực bằng 1 và phần ảo bằng 2 .
D. phần thực bằng 2 và phần ảo bằng 1. Lời giải Chọn C
z  1 2i . Do đó số phức liên hợp z có phần thực bằng 1 và phần ảo bằng 2 .
Câu 34: (THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018) Trong hình vẽ bên, điểm
M biểu diễn số phức z . Số phức z là A. 2  i . B. 1 2i . C. 1 2i . D. 2  i . Lời giải Chọn A
Dựa vào hình vẽ ta có z  2  i , suy ra z  2  i .
Câu 35: (SGD Nam Định – năm 2017 – 2018) Trong các mệnh đề sau, mệnh đề nào đúng?
A. Số phức z  2  3i có phần thực là 2 , phần ảo là 3  .
B. Số phức z  2  3i có phần thực là 2 , phần ảo là 3i .
C. Số phức z  2  3i có phần thực là 2 , phần ảo là 3i .
D. Số phức z  2  3i có phần thực là 2 , phần ảo là 3 . Lời giải Chọn A
Mỗi số phức z a bi có phần thực là a , phần ảo là b .
Câu 36: (SGD Nam Định – năm 2017 – 2018) Cho hai số phức z  1 2i , z  3  i . Tìm số 1 2 z phức 2 z  . z1 1 7 1 7 1 7 1 7 A. z   i . B. z   i . C. z   i . D. z    i . 5 5 10 10 5 5 10 10 Lời giải
Chọn C z 3  i 1 7 Ta có 2 z     i . z 1 2i 5 5 1
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Tính môđun của số phức z  3  4i . A. 3 . B. 5 . C. 7 . D. 7 . Lời giải
Chọn B
Môđun của số phức z  3  4i là: 2 2 z  3  4  5 .
Câu 2: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Số phức
liên hợp của số phức z i 1 2i có điểm biểu diễn là điểm nào dưới đây?
A. E 2;   1 .
B. B 1; 2 .
C. A1; 2 . D. F  2  ;  1 . Lời giải Chọn A
Ta có: z i 1 2i  2  i z  2  i nên điểm biểu diễn của số phức z là E 2;   1 .
Câu 3: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Điểm A trong hình vẽ bên dưới
biểu diễn cho số phức z . Mệnh đề nào sau đây đúng? y A 2 x 3 O
A. Phần thực là 3 , phần ảo là 2 .
B. Phần thực là 3 , phần ảo là 2i . C. Phần thực là 3
 , phần ảo là 2i . D. Phần thực là 3  , phần ảo là 2 . Lời giải
Chọn A
Câu 4: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho số phức z  1  2i . Điểm
nào dưới đây là điểm biểu diễn của số phức w z i z trên mặt phẳng toạ độ?
A. M 3;3 .
B. Q 3; 2 .
C. N 2;3 .
D. P 3;3 . Lời giải Chọn A
w z i z  1  2i i 1 2i  3  3i .
Vậy điểm biểu diễn của số phức w z i z là M 3;3 .
Câu 5: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho hai số phức z  2  3i , z  1 i . Giá trị của biểu 1 2
thức z  3z là 1 2 A. 55 . B. 5 . C. 6 . D. 61 .
Hướng dẫn giải Chọn D
Ta có: z  3z  2  3i  3 1 i  5  6i 2 2  5  6  61 . 1 2  
Câu 6: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Gọi z là nghiệm phức có phần ảo dương của phương 0 trình 2
z  2z 10  0 . Tính iz . 0
A. iz  3  i .
B. iz  3i 1 . C. iz  3   i .
D. iz  3i 1. 0 0 0 0
Hướng dẫn giải Chọn C
z  1 3i Ta có: 2
z  2z 10  0    z  1
  3i iz  3  i . z  1 3i 0 0 
Câu 7: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Phần thực và phần ảo của số phức liên hợp của số
phức z  1 i là:
A. Phần thực là 1, phần ảo là 1  .
B. Phần thực là 1, phần ảo là i  .
C. Phần thực là 1, phần ảo là i .
D. Phần thực là 1, phần ảo là 1. Lời giải Chọn A
Ta có số phức liên hợp của số phức z  1  i là z  1 i , suy ra Phần thực và phần ảo của số
phức liên hợp của số phức z  1 i là và 1  .
Câu 8: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Điểm biểu diễn của số phức z là M 1; 2 . Tọa
độ của điểm biểu diễn cho số phức w z  2z là A. 2; 3   . B. 2;  1 . C.  1  ;6 . D. 2;3 . Lời giải
Chọn C
Ta có: z  1 2i nên w z  2z  1 2i  21 2i  1   6i .
Do đó, số phức w z  2z có điểm biểu diễn là  1  ;6 .
Câu 9: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Gọi z và z lần lượt là hai nghiệm của 1 2 phương trình 2
z  4z  5  0 . Giá trị của biểu thức P   z  2z .z  4z bằng: 1 2  2 1 A. 10 . B. 10 . C. 5  . D. 15 . Lời giải
Chọn D
z  2  i Ta có 2
z  4z  5  0 1   . z  2  i  2
Vậy P   z  2z .z  4z  2  i  22  i.2  i  42  i  15 . 1 2  2 1
Câu 10: (THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018) Mô đun của số phức
z  7  3i là. A. z  5 . B. z  10 . C. z  16 . D. z  4 .
Hướng dẫn giải Chọn D
Ta có: z  7  9  4 .
Câu 11: (THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018) Cho z , z là hai nghiệm 1 2 phức của phương trình 2
z  2z  5  0 , trong đó z có phần ảo dương. Số phức liên hợp của số 1
phức z  2z là? 1 2 A. 3  2i . B. 3  2i . C. 2  i . D. 2  i .
Hướng dẫn giải Chọn A z  1   2i Ta có: 2 1
z  2z  5  0  
( Vì z có phần ảo dương) z  1   2i 1  2
Suy ra: z  2z  1   2i  2 1   2i  3  2i . 1 2  
Vậy: Số phức liên hợp của số phức z  2z là 3  2i . 1 2 2
Câu 12: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Cho số phức z  1  i 1  2i. Số phức z có phần ảo là: A. 2 . B. 4 . C. 2 . D. 2i . Lời giải Chọn A 2
Ta có z  1  i 1  2i  2i 1  2i  4
  2i . Vậy số phức z có phần ảo là 2 .
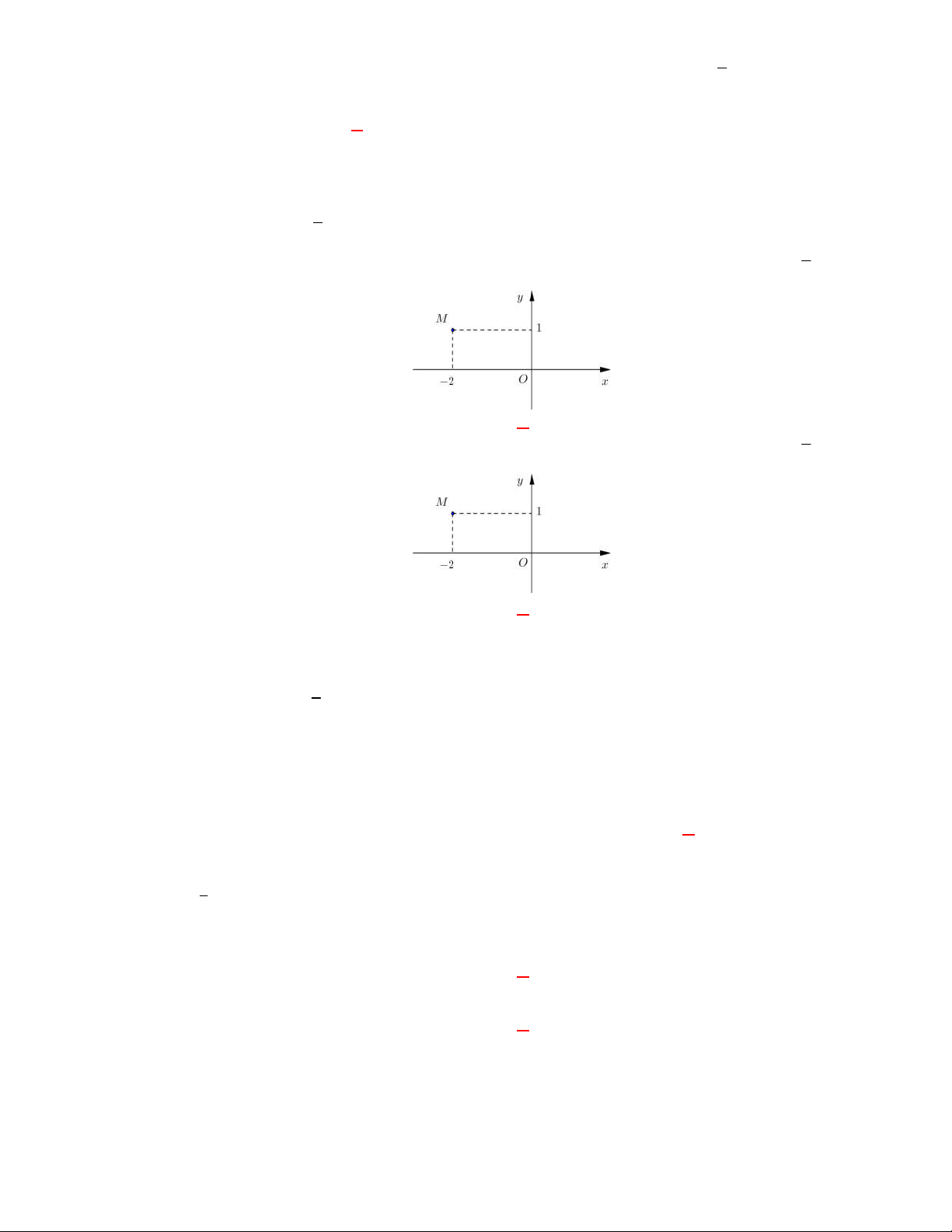
Câu 13: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Điểm M trong hình bên là điểm biểu diễn cho số phức
A. z  4  2i .
B. z  2  4i .
C. z  4  2i .
D. z  2  4i . Lời giải Chọn B
Điểm M biểu diễn cho số phức z  2  4i .
Câu 14: Cho hai số phức z  1 2i và z  2  3i . Phần ảo của số phức w  3z  2z là 1 2 1 2 A. 1. B. 11. C. 12 . D. 12i .
Câu 15: Cho hai số phức z  1 2i và z  2  3i . Phần ảo của số phức w  3z  2z là 1 2 1 2 A. 1. B. 11. C. 12 . D. 12i . Lời giải Chọn C
Ta có w  3z  2z  31 2i  22  3i  1  12i . 1 2
Vậy phần ảo của số phức w là 12.
Câu 16: Cho số phức z a bi a,b   . Khẳng định nào sau đây sai? A. 2 2
z a b .
B. z a bi . C. 2 z là số thực. D. . z z là số thực.
Câu 17: Cho hai số phức z và z . Trong các mệnh đề sai, mệnh đề nào sai?
A. z z  z z . B. .
z z  z . z . C. .
z z  z.z .
D. z z  z z .
Câu 18: Cho số phức z a bi a,b   . Khẳng định nào sau đây sai? A. 2 2
z a b .
B. z a bi . C. 2 z là số thực. D. . z z là số thực. Lời giải Chọn C
Đáp án A và B đúng theo định nghĩa.
Đáp án C: Ta có z  a bi2 2 2 2
a  2bi b là số phức có phần ảo khác 0 khi b  0  Sai. Đáp án D:          2 2 2 2 . z z a bi a bi a bi
a b là một số thực  Đúng.
Câu 19: Cho hai số phức z và z . Trong các mệnh đề sai, mệnh đề nào sai?
A. z z  z z . B. .
z z  z . z . C. .
z z  z.z .
D. z z  z z . Lời giải Chọn A
Với hai số phức z và z , ta có: z z  z z .
Câu 20: Cho hai số phức z  3  i và z  4  i . Tính môđun của số phức 2 z z . 1 2 1 2 A. 12 . B. 10 . C. 13 . D. 15 .
Câu 21: Cho hai số phức z  3  i và z  4  i . Tính môđun của số phức 2 z z . 1 2 1 2 A. 12 . B. 10 . C. 13 . D. 15 . Lời giải Chọn C 2 Ta có: 2
z z  3  i  4  i  12  5i nên 2 2 2
z z  12  5  13 . 1 2 1 2
Câu 22: Tìm tọa độ điểm M là điểm biểu diễn số phức z  3  4i .
A. M 3; 4 .
B. M 3; 4 . C. M 3; 4   .
D. M 3; 4 .
Câu 23: Tìm tọa độ điểm M là điểm biểu diễn số phức z  3  4i .
A. M 3; 4 .
B. M 3; 4 . C. M 3; 4   .
D. M 3; 4 . Lời giải Chọn A
Ta có điểm M 3; 4 biểu diễn số phức z  3  4i .
Câu 24: Số phức z  4  2i có điểm biểu diễn trên mặt phẳng tọa độ là M . Tìm tọa độ điểm M
A. M 4;2 .
B. M 2; 4 . C. M 4; 2   . D. M  4  ; 2   .
Câu 25: Số phức z  4  2i có điểm biểu diễn trên mặt phẳng tọa độ là M . Tìm tọa độ điểm M
A. M 4;2 .
B. M 2; 4 . C. M 4; 2   . D. M  4  ; 2   . Lời giải Chọn A
Số phức z  4  2i có điểm biểu diễn trên mặt phẳng tọa độ là M 4;2 .
Câu 26: Cho số phức z thỏa mãn 1 z1 i  5  i  0 . Số phức w  1 z bằng A. 1 3i . B. 1 3i .
C. 2  3i . D. 2  3i .
Câu 27: Cho số phức z thỏa mãn 1 z1 i  5  i  0 . Số phức w  1 z bằng A. 1 3i . B. 1 3i .
C. 2  3i . D. 2  3i . Lời giải Chọn D
Ta có 1 z1 i  5  i  0  1 z  2  3i z  1 3i .
Vậy w  1 z  11 3i  2  3i .
Câu 28: Gọi a, b lần lượt là phần thực và phần ảo của số phức
z  1 3i 1 2i  3  4i 2  3i. Giá trị của a b là A. 7 . B. 7  . C. 31. D. 31  .
Câu 29: Gọi a, b lần lượt là phần thực và phần ảo của số phức
z  1 3i 1 2i  3  4i 2  3i. Giá trị của a b là A. 7 . B. 7  . C. 31. D. 31  . Lời giải Chọn B
Ta có: z  1 3i 1 2i  3  4i 2  3i  21 2i  52  3i  12 19i
Vậy a b  12 19  7. 
Câu 30: Cho số phức z có số phức liên hợp z  3  2i . Tổng phần thực và phần ảo của số phức z bằng. A. 1. B. 5  . C. 5 . D. 1  .
Câu 31: Cho số phức z thỏa mãn 1 2iz  1 2i  2  i . Mô đun của z bằng A. 2 . B. 1. C. 2 . D. 10 .
Câu 32: Cho số phức z có số phức liên hợp z  3  2i . Tổng phần thực và phần ảo của số phức z bằng. A. 1. B. 5  . C. 5 . D. 1  .
Hướng dẫn giải Chọn C
Ta có: z  3  2i . Vậy tổng phần thực và phần ảo của số phức z bằng 5 .
Câu 33: Cho số phức z thỏa mãn 1 2iz  1 2i  2  i . Mô đun của z bằng A. 2 . B. 1. C. 2 . D. 10 .
Hướng dẫn giải Chọn C 3  i
1 2iz  1 2i   2
  i  1 2iz  3  i z
 1 i . Vậy z  2 . 1 2i
Câu 34: Cho các số phức z  2  3i , z  4  5i . Số phức liên hợp của số phức w  2  z z là 1 2  1 2
A. w  8 10i .
B. w  12 16i .
C. w  12  8i .
D. w  28i .
Câu 35: Cho các số phức z  2  3i , z  4  5i . Số phức liên hợp của số phức w  2  z z là 1 2  1 2
A. w  8 10i .
B. w  12 16i .
C. w  12  8i .
D. w  28i . Lời giải Chọn B
Ta có w  2 6  8i  12 16i w  12 16i .
Câu 36: Cho số phức z a bi với a , b là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
A. Phần ảo của z là bi . B. Môđun của 2 z bằng 2 2 a b .
C. z z không phải là số thực.
D. Số z và z có môđun khác nhau.
Câu 37: Cho số phức z a bi với a , b là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
A. Phần ảo của z là bi . B. Môđun của 2 z bằng 2 2 a b .
C. z z không phải là số thực.
D. Số z và z có môđun khác nhau. Lời giải Chọn B     2 2 2 2 2 2 2 z z a ba b .
Câu 38: Cho số phức z  3  i . Tính z . A. z  2 2 . B. z  2 . C. z  4 . D. z  10 .
Câu 39: Điểm M trong hình vẽ dưới đây biểu thị cho số phức y M 3 A. 3  2i .
B. 2  3i . C. 2  3i . D. 3  2i . 2  O x
Câu 40: Cho z , z là hai nghiệm phức của phương trình 2
2z 1  0 (trong đó số phức 1 2
z có phần ảo âm). Tính z  3z . 1 1 2
A. z  3z  2.i .
B. z  3z   2 .
C. z  3z   2.i .
D. z  3z  2 . 1 2 1 2 1 2 1 2
Câu 41: Cho số phức z  3  i . Tính z . A. z  2 2 . B. z  2 . C. z  4 . D. z  10 . Lời giải Chọn D Ta có 2 2
z z  3 1  10 .
Câu 42: Điểm M trong hình vẽ dưới đây biểu thị cho số phức y M 3 2  O x A. 3  2i .
B. 2  3i . C. 2  3i . D. 3  2i . Lời giải Chọn B
Hoành độ, tung độ của điểm M là phần thực, phần ảo của số phức  z  2  3i .
Câu 43: Cho z , z là hai nghiệm phức của phương trình 2
2z 1  0 (trong đó số phức z có phần ảo âm). Tính 1 2 1 z  3z . 1 2
A. z  3z  2.i .
B. z  3z   2 .
C. z  3z   2.i .
D. z  3z  2 . 1 2 1 2 1 2 1 2 Lời giải Chọn A  2 z   i  1 2 2 2 Ta có: 2 2z 1  0  
. Khi đó: z  3z   i  3 i  2i . 1 2  2 2 2 z i 2  2
Câu 44: Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z a bi ( a, b   , ab  0 ), M
là điểm biểu diễn cho số phức z . Mệnh đề nào sau đây đúng?
A. M  đối xứng với M qua Oy .
B. M  đối xứng với M qua Ox .
C. M  đối xứng với M qua đường thẳng y x .
D. M  đối xứng với M qua O .
Câu 45: Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z a bi ( a, b   , ab  0 ), M
là điểm biểu diễn cho số phức z . Mệnh đề nào sau đây đúng?
A. M  đối xứng với M qua Oy .
B. M  đối xứng với M qua Ox .
C. M  đối xứng với M qua đường thẳng y x .
D. M  đối xứng với M qua O . Lời giải Chọn B
Ta có M  là điểm biễu diễn cho số phức z a bi M  ; a b
  nên M  đối xứng với M qua Ox .
Câu 46: Gọi z , z , z là ba nghiệm của phương trình 3
z 1  0 . Tính S z z z 1 2 3 1 2 3 A. S  1 . B. S  4 . C. S  2 . D. S  3 .
Câu 47: Gọi z , z , z là ba nghiệm của phương trình 3
z 1  0 . Tính S z z z 1 2 3 1 2 3 A. S  1. B. S  4 . C. S  2 . D. S  3. Lời giải Chọn D   z  1   1  3 1 3 1 3 Ta có: 3
z 1  0  z  
i . Do đó: S  1   i   i  3 .  2 2 2 2 2 2   1  3 z   i  2 2
Câu 48: Trong mặt phẳng phức, cho số phức z  1 2i . Điểm biểu diễn cho số phức z là điểm nào sau đây A. M  1  ; 2   .
B. Q 1;2 . C. P  1  ; 2 . D. N  2  ;  1 .
Câu 49: Trong mặt phẳng phức, cho số phức z  1 2i . Điểm biểu diễn cho số phức z là điểm nào sau đây
A. M 1; 2 .
B. Q 1; 2 .
C. P 1; 2 . D. N  2   ;1 . Lời giải Chọn B
Ta có: z  1 2i z  1 2i nên có điểm biểu diễn là 1; 2 .
Câu 50: Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức z là A. 2  i . B. 1 2i . C. 2  i . D. 1 2i .
Câu 51: Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức z là A. 2  i . B. 1 2i . C. 2  i . D. 1 2i .
Hướng dẫn giải Chọn C Ta có z  2
  i z  2  i .
Câu 52: Cho số phức z  11 i . Điểm biểu diễn số phức liên hợp của z là điểm nào dưới đây? A. Q  11  ; 0 . B. M 11;  1 .
C. P 11;0 .
D. N 11;   1 .
Câu 53: Cho số phức z  11 i . Điểm biểu diễn số phức liên hợp của z là điểm nào dưới đây? A. Q  11  ; 0 . B. M 11;  1 .
C. P 11;0 .
D. N 11;   1 . Lời giải Chọn D
Vì z  11 i nên điểm biểu diễn số phức liên hợp z là N 11;  1 .
Câu 54: Phần thực của số phức z  1 2i bằng A. 2  . B. 1. C. 1. D. 3 .
Câu 55: Phần thực của số phức z  1 2i bằng A. 2  . B. 1. C. 1. D. 3 .
Hướng dẫn giải Chọn C
Phần thực của số phức z  1 2i bằng 1.
Câu 56: Cho hai số phức z  2  3i , z  3  2i . Tích z .z bằng: 1 2 1 2 A. 5i . B. 6  6i . C. 5i . D.12  5i .
Câu 57: Số phức nghịch đảo 1
z của số phức z  2  2i là 1 1 1 1 1 1 1 1 A.i . B.   i . C.i . D.   i . 4 4 4 4 4 4 4 4
Câu 58: Cho hai số phức z  2  3i , z  3  2i . Tích z .z bằng: 1 2 1 2 A. 5i . B. 6  6i . C. 5i . D.12  5i . Lời giải Chọn D
Ta có z .z  2  3i . 3  2i  12  5i . 1 2    
Câu 59: Số phức nghịch đảo 1
z của số phức z  2  2i là 1 1 1 1 1 1 1 1 A.i . B.   i . C.i . D.   i . 4 4 4 4 4 4 4 4 Lời giải Chọn C 1 2  2i 1 1 Ta có 1 z     i . 2  2i 8 4 4 2
Câu 60: Cho số phức z  1 i 1 2i . Số phức z có phần ảo là A. 2 . B. 4 . C. 2 . D. 2i . 2
Câu 61: Cho số phức z  1 i 1 2i . Số phức z có phần ảo là A. 2 . B. 4 . C. 2 . D. 2i . Lời giải Chọn A
z    i2 1 1 2i   2
1 2i i 1 2i  2i 1 2i 2
 2i  4i  2i  4 có phần ảo là 2 .
Câu 62: Số phức z  15  3i có phần ảo bằng A. 3  . B. 15 . C. 3i . D. 3 .
Câu 63: Cho hai số phức z  3  5i và w  1
  2i . Điểm biểu diễn số phức z  z  .
w z trong mặt phẳng
Oxy có tọa độ là A.  4  ;  6 . B. 4;  6 . C. 4; 6 . D.  6  ;  4 .
Câu 64: Số phức z  15  3i có phần ảo bằng A. 3  . B. 15 . C. 3i . D. 3 . Lời giải Chọn A
Câu 65: Cho hai số phức z  3  5i và w  1
  2i . Điểm biểu diễn số phức z  z  .
w z trong mặt phẳng
Oxy có tọa độ là A.  4  ;  6 . B. 4;  6 . C. 4; 6 . D. 6;  4 . Lời giải Chọn A
Ta có z  z  .
w z  3  5i  1 2i3  5i  3  5i  7 11i  4   6i .
Câu 66: Tìm phần thực và phần ảo của số phức z  3  2i .
A. Phần thực bằng 3
 và phần ảo bằng 2 . i
B. Phần thực bằng 3  và phần ảo bằng 2. 
C. Phần thực bằng 3 và phần ảo bằng 2 . i
D. Phần thực bằng 3 và phần ảo bằng 2.
Câu 67: Tìm phần thực và phần ảo của số phức z  3  2i .
A. Phần thực bằng 3
 và phần ảo bằng 2 . i
B. Phần thực bằng 3  và phần ảo bằng 2. 
C. Phần thực bằng 3 và phần ảo bằng 2 . i
D. Phần thực bằng 3 và phần ảo bằng 2. Lời giải Chọn D
Số phức z  3  2i có phần thực bằng 3 và phần ảo bằng 2.
Câu 68: Cho số phức z  2  4i . Hiệu phần thực và phần ảo của z bằng. A. 2 . B. 2 5 . C. 2  . D. 6 .
Câu 69: Cho số phức z  2  4i . Hiệu phần thực và phần ảo của z bằng. A. 2 . B. 2 5 . C. 2  . D. 6 .
Hướng dẫn giải Chọn C
Phần thực và phần ảo lần lượt là 2 và 4 . Vậy hiệu phần thực và phần ảo của z bằng 2  .
Câu 70: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . y M 3 O 1 2 x Số phức z bằng A. 2  3i . B. 2  3i . C. 3  2i . D. 3  2i .
Câu 71: Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của biểu thức 2 2 z z 1 2 1 2 bằng. A. 10 . B. 20 . C. 6 .
D. 6  8i .
Câu 72: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . y M 3 O 1 2 x Số phức z bằng A. 2  3i . B. 2  3i . C. 3  2i . D. 3  2i . Lời giải Chọn A
Theo hình vẽ thì z  2  3i z  2  3i .
Câu 73: Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của biểu thức 2 2 z z 1 2 1 2 bằng. A. 10 . B. 20 . C. 6 .
D. 6  8i . Lời giải Chọn A
z  2  i z 2
z  4z  5  0 1   .
z  2  i z  2 2 2 2 2 z zzz  5  5  10 . 1 2 1 2
Câu 74: Cho số phức z  1 2i . Điểm biểu diễn của số phức z là A. M  1  ; 2 . B. M  1  ;  2 .
C. M 1;  2 . D. M 2  ;1 .
Câu 75: Cho phương trình 2
z  4z  5  0 có hai nghiệm phức z , z . Tính A z z z z . 1 2 1 2 1 2
A. A  25  2 5 . B. A  0 .
C. A  5  2 5 .
D. A  5  2 5 .
Câu 76: Cho số phức z  1 2i . Điểm biểu diễn của số phức z là A. M  1  ; 2 . B. M  1  ;  2 .
C. M 1;  2 . D. M 2  ;1 . Lời giải Chọn C
Ta có z  1 2i có điểm biểu diễn là M 1;  2 .
Câu 77: Cho phương trình 2
z  4z  5  0 có hai nghiệm phức z , z . Tính A z z z z . 1 2 1 2 1 2
A. A  25  2 5 . B. A  0 .
C. A  5  2 5 .
D. A  5  2 5 . Lời giải Chọn D z  2  i 2
z  4z  5  0 1   . z  2  i  1
Do đó: A z z z z  5  2 5 . 1 2 1 2
Câu 78: Cho số phức z  3  4i . Môđun của z bằng A. 25 . B. 7 . C. 1. D. 5 .
Câu 79: Cho số phức z  3  4i . Môđun của z bằng A. 25 . B. 7 . C. 1. D. 5 . Lời giải Chọn D Ta có z    2 2 3 4  5 .
Câu 80: Số phức nào dưới đây là số thuần ảo?
A. z  3  2i . B. z  2   3i .
C. z  2i . D. z  2  .
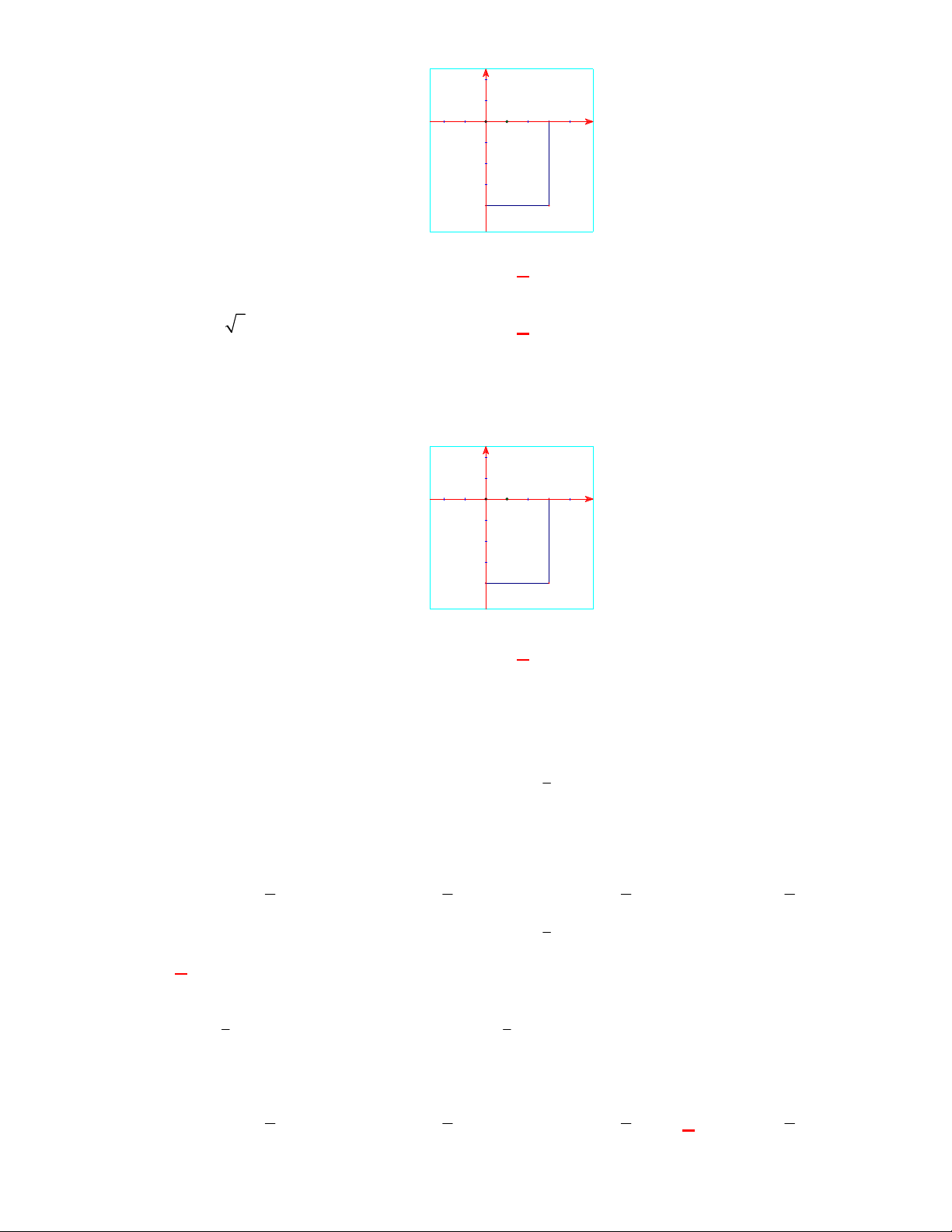
Câu 81: Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . y 3 x O 1 -4 M Tìm z ? A. z  4   3i . B. z  3   4i .
C. z  3  4i .
D. z  3  4i .
Câu 82: Số phức nào dưới đây là số thuần ảo?
A. z  3  2i . B. z  2   3i .
C. z  2i . D. z  2  .
Hướng dẫn giải Chọn C
Câu 83: Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . y 3 x O 1 -4 M Tìm z ? A. z  4   3i . B. z  3   4i .
C. z  3  4i .
D. z  3  4i .
Hướng dẫn giải Chọn C
Số phức z có phần thực a  3 và phần ảo b  4
 nên z  3  4i .
Câu 84: Cho số phức z  1
  4i . Tìm phần thực của số phức z . A. 1. B. 1. C. 4 . D. 4  .
Câu 85: Tìm các số thực x, y thỏa mãn 2x 1 1 2 yi  2  x  3y  2i . 3 3 1 1
A. x  1; y  .
B. x  3; y  .
C. x  3; y   .
D. x  1; y   . 5 5 5 5
Câu 86: Cho số phức z  1
  4i . Tìm phần thực của số phức z . A. 1. B. 1. C. 4 . D. 4  . Lời giải Chọn A Ta có z  1
  4i . Vậy phần thực của số phức z là   1 .
Câu 87: Tìm các số thực x, y thỏa mãn 2x 1 1 2 yi  2  x  3y  2i . 3 3 1 1
A. x  1; y  .
B. x  3; y  .
C. x  3; y   .
D. x  1; y   . 5 5 5 5 Lời giải Chọn Dx  1
2x 1  2  x
2x 1 1 2 yi  2  x  3y  2     1
1 2 y  3y  2  y     5
Câu 88: Trong mặt phẳng tọa độ, điểm M  3
 ; 2 là điểm biểu diễn của số phức nào dưới đây?
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  3  2i .
Câu 89: Trong mặt phẳng tọa độ, điểm M  3
 ; 2 là điểm biểu diễn của số phức nào dưới đây?
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  3  2i . Lời giải Chọn B Điểm M  3
 ; 2 là điểm biểu diễn của số phức z  3   2i .
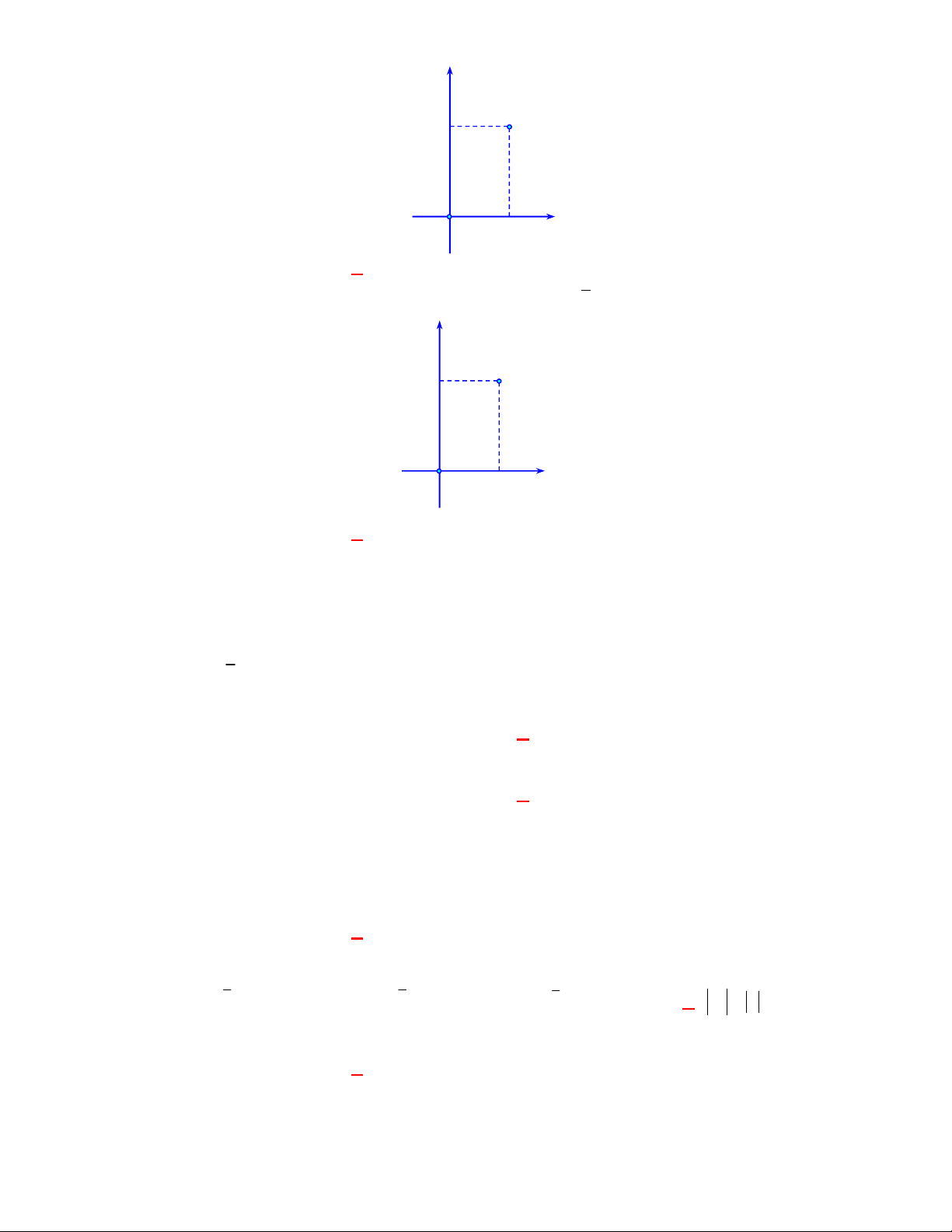
Câu 90: Cho bốn điểm A , B , C , D trên hình vẽ biểu diễn 4 số phức y A
khác nhau. Chọn mệnh đề sai. 1
A. B là biểu diễn số phức z  1 2i . 2  1 1
B. D là biểu diễn số phức z  1   2i . O x
C. C là biểu diễn số phức z  1 2i . 1  D
D. A là biểu diễn số phức z  2   i . C 2  B
Câu 91: Cho bốn điểm A , B , C , D trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai. y A 1 2  1  1 O x 1 D C 2  B
A. B là biểu diễn số phức z  1 2i .
B. D là biểu diễn số phức z  1 2i .
C. C là biểu diễn số phức z  1 2i .
D. A là biểu diễn số phức z  2   i . Lời giải Chọn B
Theo hình vẽ thì điểm D là biểu diễn số phức z  2
  i . Suy ra B sai.
Câu 92: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z z 1  0 . Giá trị của biểu thức 1 2 2 2
P z z z z bằng: 1 2 1 2 A. P  1  .
B. P  2 .
C. P  1 . D. P  0 .
Câu 93: Điểm M trong hình bên là điểm biểu diễn của số phức z . y O 3 x -4
Mệnh đề nào dưới đây đúng?
A. Số phức z có phần thực là 3 và phần ảo là 4  .
B. Số phức z phần thực là 3 và phần ảo là 4i .
C. Số phức z phần thực là 4  và phần ảo là 3 .
D. Số phức z phần thực là 4
 và phần ảo là 3i .
Câu 94: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z z 1  0 . Giá trị của biểu thức 1 2 2 2
P z z z z bằng: 1 2 1 2 A. P  1  .
B. P  2 .
C. P  1 . D. P  0 . Lời giải Chọn D 2
z z 1  0 có z z  1
 và z .z  1 1 2 1 2 Khi đó 2 2
P z z z z   z z
z .z P  0 . 1 2 2 1 2 1 2 1 2
Câu 95: Điểm M trong hình bên là điểm biểu diễn của số phức z . y O 3 x -4
Mệnh đề nào dưới đây đúng?
A. Số phức z có phần thực là 3 và phần ảo là 4  .
B. Số phức z phần thực là 3 và phần ảo là 4i .
C. Số phức z phần thực là 4  và phần ảo là 3 .
D. Số phức z phần thực là 4
 và phần ảo là 3i . Lời giải Chọn A
Điểm M biểu diễn cho số phức z  3  4i .
Câu 96: Điểm M trong hình vẽ bên biểu diễn số phức z . Số phức z bằng y M 3 O 2 x A. 2  3i . B. 2  3i . C. 3  2i . D. 3  2i .
Câu 97: Điểm M trong hình vẽ bên biểu diễn số phức z . Số phức z bằng y M 3 O 2 x A. 2  3i . B. 2  3i . C. 3  2i . D. 3  2i . Lời giải Chọn B
Ta có M 2;3 là điểm biểu diễn số phức z  2  3i .
Do đó z  2  3i .
Câu 98: Cho hai số phức z  2  2i , z  3  3i . Khi đó số phức z z là 1 2 1 2
A. 5  5i .
B. 5i .
C. 5  5i .
D. 1 i .
Câu 99: Cho hai số phức z  2  2i , z  3  3i . Khi đó số phức z z là 1 2 1 2
A. 5  5i .
B. 5i .
C. 5  5i .
D. 1 i . Lời giải Chọn C
Ta có z z  2  2i  3
  3i  5  5i . 1 2    
Câu 100: Tìm tọa độ của điểm biểu diễn hình học của số phức z  8  9i . A. 8;9 . B. 8; 9   . C. 9;8 . D. 8; 9  i .
Câu 101: Cho số phức z a bi , với a, b   . Tìm mệnh đề đúng trong các mệnh đề sau? 2
A. z z  2bi .
B. z z  2a . C. 2 2
z.z a b . D. 2 z z .
Câu 102: Tìm tọa độ của điểm biểu diễn hình học của số phức z  8  9i . A. 8;9 . B. 8; 9   . C. 9;8 . D. 8; 9  i . Lời giải Chọn B
Câu 103: Cho số phức z a bi , với a, b   . Tìm mệnh đề đúng trong các mệnh đề sau? 2
A. z z  2bi .
B. z z  2a . C. 2 2
z.z a b . D. 2 z z . Lời giải Chọn D
Câu 104: Số phức nào dưới đây là số thuần ảo ? A. z  2 . B. z  2  i .
C. z  2  2i . D. z  1   2i .
Câu 105: Số phức nào dưới đây là số thuần ảo ? A. z  2  . B. z  2  i .
C. z  2  2i . D. z  1   2i . Lời giải Chọn B
Câu 106: Cho số phức z , z thỏa mãn z  1 và z
z 1 i  6i  2 là một số thực. Tìm giá trị nhỏ 2  2  1 2 1 2
nhất của biểu thức P zz z z z . 2  1 2 1 2  A. 18  6 2 . B. 3  2 . C. 18  6 2 . D. 18  9 2 .
Câu 107: Cho số phức z , z thỏa mãn z  1 và z
z 1 i  6i  2 là một số thực. Tìm giá trị nhỏ 2  2  1 2 1 2
nhất của biểu thức P zz z z z . 2  1 2 1 2  A. 18  6 2 . B. 3  2 . C. 18  6 2 . D. 18  9 2 .
Hướng dẫn giải Chọn A
Đặt z x yi ,  x, y   , ta có 2
z z 1 i 2 2
 6i  2  x y x y  2  x y  6 i . 2 2   Vì z
z 1 i  6i  2 là số thực nên x y  6  0 . 2  2  Ta có 2 2 2 2 2 P zz zzzz z 1. 2 1 2 1 2 1 2
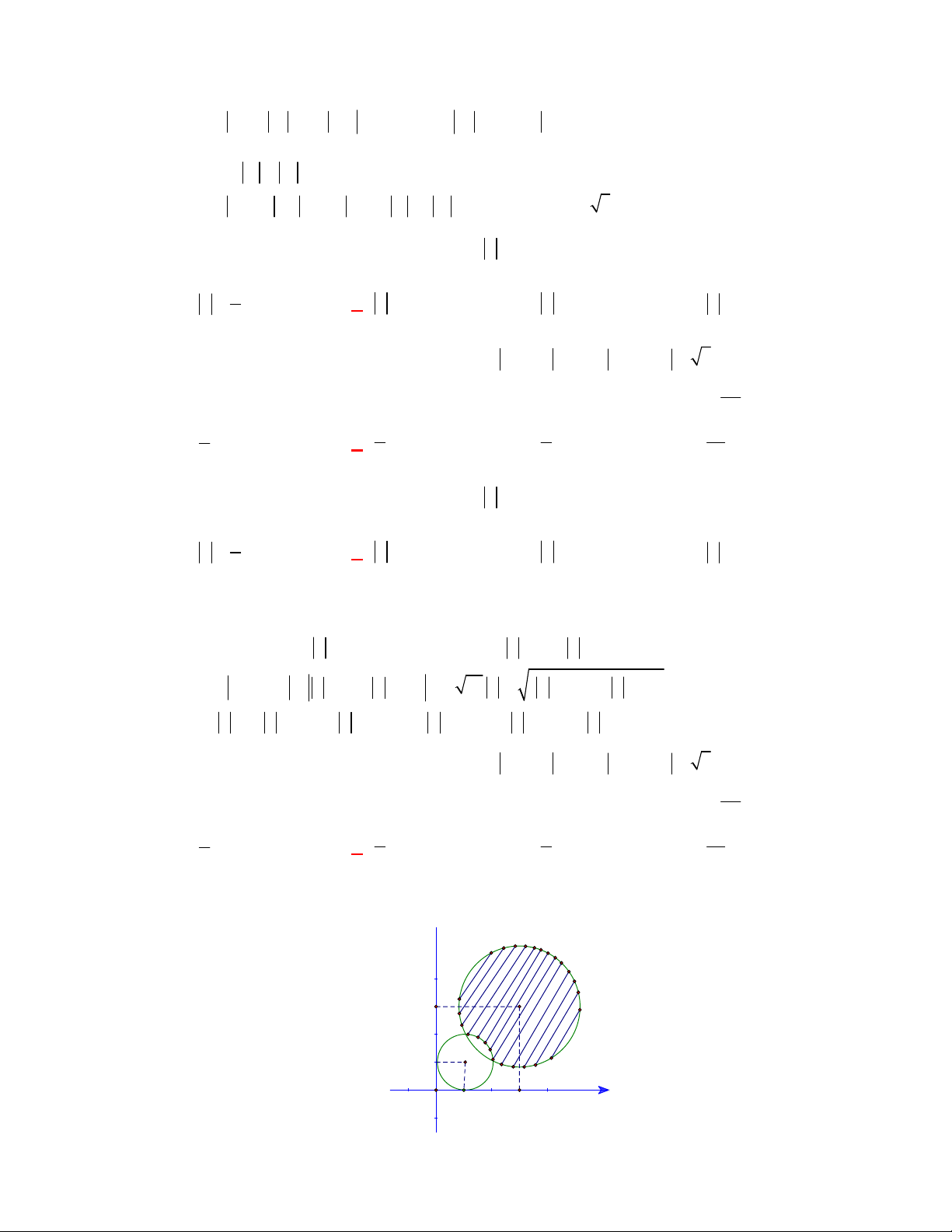
Gọi A là điểm biểu diễn số phức z , suy ra A nằm trên đường tròn C  tâm O bán kính 1 r  1.
Gọi B là điểm biểu diễn số phức z , suy ra B nằm trên đường thẳng  : x y  6  0 . 2 Ta có 2 P AB 1. 0  0  6
Mà AB d  ;
O   r  1  3 2 1. 2 Nên P    2 3 2 1 1  18  6 2 .
Dấu “=” xảy ra khi và chỉ khi B là hình chiếu vuông góc của O trên  và A là giao điểm của
đoạn OB với đường tròn C  .
Câu 1: (THTT Số 1-484 tháng 10 năm 2017-2018) Kí hiệu z là nghiệm phức có phần thực âm và phần 0
ảo dương của phương trình 2
z  2z 10  0 . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức 2017 w i z ? 0
A. M 3;   1 . B. M 3;  1 . C. M  3  ;  1 . D. M  3  ;   1 . Lời giải Chọn Dz  1   3i Ta có: 2
z  2z 10  0   . Suy ra z  1   3i . z  1   3i 0  2017 w i z  .
i 1 3i  3  i . 0  
Suy ra : Điểm M 3;  
1 biểu diễn số phức w .
Câu 2: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Cho số phức z thỏa mãn:
z 2  i 13i  1. Tính mô đun của số phức z . 34 5 34 A. z  34 . B. z  34 . C. z  . D. z  . 3 3 Lời giải
Chọn B 113i 113i
Cách 1: Ta có z 2  i 13i  1  z   z   34 . 2  i 2  i 2 2  11    27  850  z        z   34 .  5   5  25 113i
Cách 2: Dùng máy tính Casio bấm z  . 2  i
Câu 3: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)Trong mặt phẳng phức, gọi
M là điểm biểu diễn cho số phức   2 z z
với z a bi a, b  ,b  0 . Chọn kết luận đúng.
A. M thuộc tia Ox .
B. M thuộc tia Oy .
C. M thuộc tia đối của tia Ox .
D. M thuộc tia đối của tia Oy . Lời giải Chọn C
Gọi z a bi
z z2  a bi a bi2 2  4b .
Câu 4: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)Tìm số phức z thỏa mãn
z  2  z và  z  
1  z i là số thực.
A. z  1 2 . i B. z  1   2 . i C. z  2  . i
D. z  1 2 . i Lời giải
Chọn D
Gọi z x iy với x, y   ta có hệ phương trình
z  2  z 2 2 2 2 2 2 2 2   
x  2  y x y  
x  2  y x y       z  
1  z i     
x 1 iy  x iy i     
x 1 iy  x iy i    x  1  x  1      x    1  y   1  xy  0  y  2  
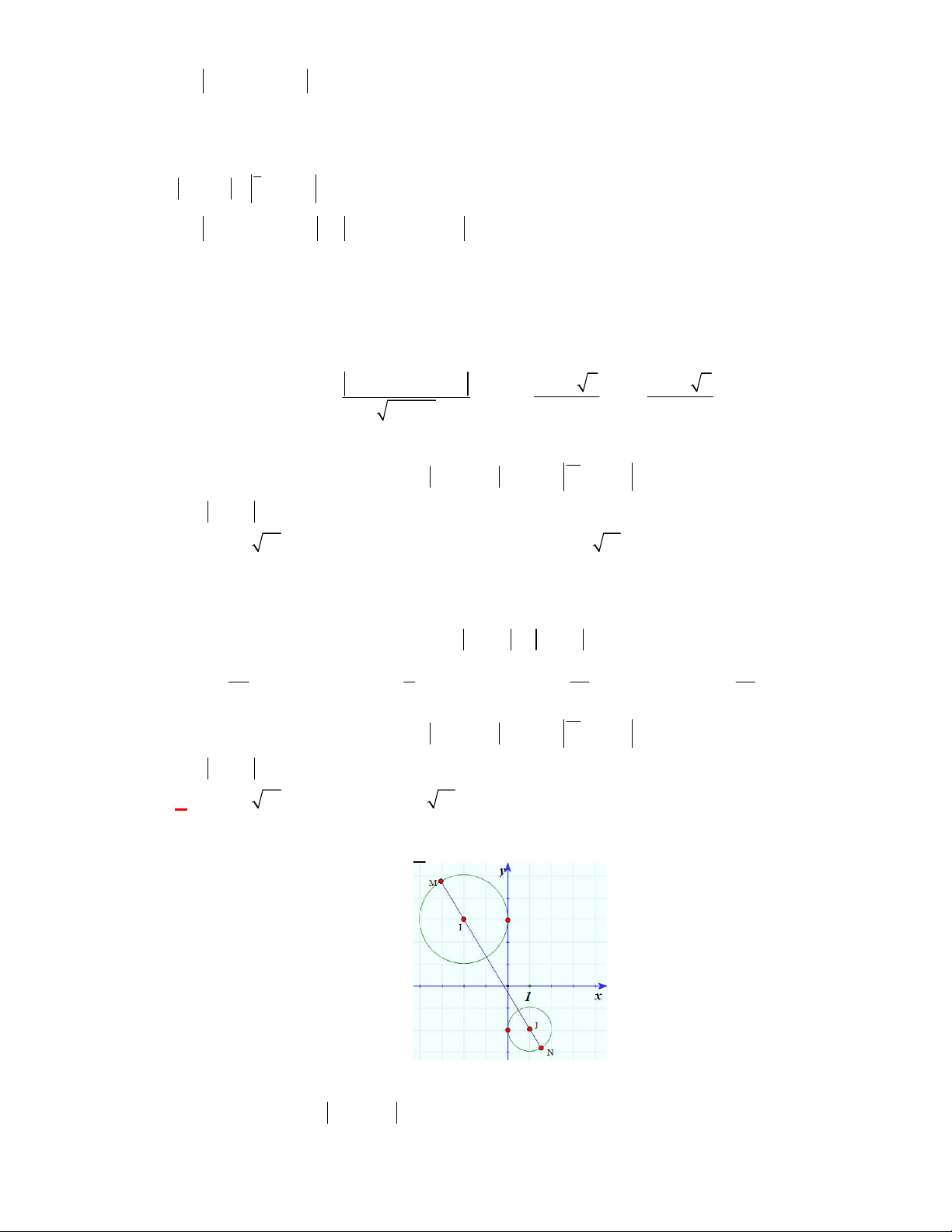
Câu 5: (THTT Số 2-485 tháng 11-năm học 2017-2018) Cho bốn điểm M , N , P , Q là các điểm trong
mặt phẳng phức theo thứ tự biểu diễn các số i
 , 2  i , 5 , 1 4i . Hỏi, điểm nào là trọng tâm
của tam giác tạo bởi ba điểm còn lại? A. M . B. N . C. P . D. Q . Lời giải
Chọn B
Tọa độ các điểm: M 0;   1 , N 2; 
1 , P 5;0 , Q 1;4 . 0  5 1  2   3 Dễ thấy 
nên N là trọng tâm của tam giác MPQ . 1   0  4   1   3
Câu 6: (THTT Số 2-485 tháng 11-năm học 2017-2018) Trong các số phức:   3 1 i ,   4 1 i ,   5 1 i ,   6 1 i
số phức nào là số phức thuần ảo? A.   3 1 i . B.   4 1 i . C.   5 1 i . D.   6 1 i . Lời giải
Chọn D Ta có   i2 2 1
 1 2i i  1 2i 1  2i . Do đó:
   i3    i2   i  i   i 2 1 1 1 2 1
 2i  2i  2  2i .  4 2 2
  i    i   i 2 1 1 1  2 .
i 2i  4i  4  .  5 4
1 i  1 i 1 i  4  1 i  4   4i . 2  6 3 3 1 i 1 i    
 2i  8i .  
Câu 7: (TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018) Cho số phức z thoả mãn 1 iz  1 3i .
Hỏi điểm biểu diễn của z là điểm nào trong các điểm M , N , P , Q ở hình dưới đây? y 2 N M 1 O x 1 P 2 Q A. Điểm Q . B. Điểm P . C. Điểm M . D. Điểm N . Lời giải Chọn C 1 3i  1
  3i 1 i 1
  3  3i i Ta có z   
 1 2i . Do đó điểm biểu diễn số phức z là điểm 1 i 2 2 M 1; 2 .
Câu 8: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Phần thực và phần ảo của số phức
z  1 2ii lần lượt là A. 1 và 2 . B. 2  và 1. C. 1 và 2  . D. 2 và 1. Lời giải Chọn B
Ta có z  1 2ii  2  i . Vậy phần thực của số phức z bằng 2
 và phần ảo của số phức z bằng 1.
Câu 9: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Gọi z là nghiệm phức có phần ảo âm của 1 phương trình 2
z  2z  3  0 . Tọa độ điểm M biểu diễn số phức z là: 1
A. M 1; 2. B. M  1;  2 .
C. M 1; 2 . D. M  1;   2i . Lời giải Chọn A Ta có: 2   1 3  2
  2i nên phương trình 2
z  2z  3  0 có hai nghiệm phức là z  1   2 . i
Do nghiệm cần tìm có phần ảo âm nên z  1
  2i . Vậy M 1; 2. 1
Câu 10: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Điểm biểu diễn của các số phức z  7  bi
với b   nằm trên đường thẳng có phương trình là: A. y  7 . B. x  7 .
C. y x  7 .
D. y x . Lời giải Chọn B
Điểm biểu diễn của các số phức z  7  bi với b   là M 7; b .
Rõ ràng điểm M 7; b thuộc đường thẳng x  7 .   i3 1 3
Câu 11: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Cho số phức z thỏa mãn: z  . 1 i
Tìm môđun của z iz . A. 4 2 . B. 4 . C. 8 2 . D. 8 . Lời giải Chọn C   i3 1 3 z   z  4
  4i z  4   4i 1 i iz i  4   4i   4   4i
z iz  4  4i  4  4i  8   8i
z iz   2   2 8 8  8 2
Câu 12: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Cho số phức z thỏa mãn điều kiện z  2z 1
1 i z i  2z  2i . Môđun của số phức w  là: 2 z A. 10 . B. 8 . C.  10 . D.  8 . Lời giải Chọn A
Ta có 1 i z i  2z  2i  3  iz  1
  3i z i . z  2z 1 i  2i 1 Suy ra w    1   3i . 2 2 z i Vậy w  10 .
Câu 13: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Cho z là số phức có mô-đun bằng 2017 1 1 1
và w là số phức thỏa mãn  
. Mô đun của số phức w là: z w z w
A. 2015 . B. 0 . C. 1. D. 2017 . Lời giải. Chọn D 1 1 1
z z 3i Ta có      2 z wzw 2 2
w wz z  0  w  . z w z w 2
z z 3i
z z 3i 1 i 3 Với w   w   z .  z  2017 . 2 2 2
z z 3i
z z 3i 1 i 3 Với w   w   z .  z  2017 . 2 2 2
Câu 14: (THTT Số 3-486 tháng 12 năm 2017-2018) Tính môđun số phức nghịch đảo của số phức
z    i2 1 2 . 1 1 1 A. . B. 5 . C. . D. . 5 25 5 Lời giải Chọn D Cách 1: Ta có z  3   4i . 1 1 3 4 Suy ra     i . z 3   4i 25 25 2 2  3   4  1 Nên z        .  25   25  5 1 1 1 1
Cách 2: Ta có z  3   4i . Do đó    z z  2   2 5 3 4
Câu 15: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Cho số phức z thỏa mãn
z  4z  7  i z  7 . Khi đó, môđun của z bằng bao nhiêu? A. z  5 . B. z  3 . C. z  5 . D. z  3 . Lời giải Chọn C
Đặt z a bi với a , b   . Khi đó z a bi .
Ta có z  4z  7  i z  7  a bi  4a bi  7  i a bi  7
a bi  4a  4bi  7  ai b  7i  5a b  a  3bi  7  7i 5
a b  7 a  1     . a  3b  7 b  2  
Do đó z  1 2i . Vậy z  5 .
Câu 16: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Cho số phức z thỏa mãn
1 3iz  5  7i . Mệnh đề nào sau đây đúng? 13 4 13 4 13 4 13 4 A. z    i . B. z    i . C. z    i . D. z   i . 5 5 5 5 5 5 5 5 Lời giải Chọn D 5  7i 13 4 13 4
Ta có: 1 3iz  5  7i z    i z   i . 1 3i 5 5 5 5
Câu 17: (Đề tham khảo BGD năm 2017-2018) Gọi z và z là hai nghiệm phức của phương trình 1 2 2
4z  4z  3  0 . Giá trị của biểu thức z z bằng 1 2 A. 3 2 . B. 2 3 . C. 3 . D. 3 . Lời giải Chọn D  1 2 z    i 1 2 2 Ta có: 2
4z  4z  3  0   .  1 2 z   i 2  2 2 2 2 2 2 1  2  1  2     
Khi đó: z z               3 . 1 2 2  2  2  2          2 1
Câu 1: (THPT Đức Thọ-Hà Tĩnh-lần 1 năm 2017-2018) Cho
f x dx a  . Tính I  . x f  2 x    1 dx 1 0 theo a . a a
A. I  2a .
B. I  4a . C. I  . D. I  . 2 4 Lời giải Chọn C dt Đặt 2
t x 1  dt  2 d x x  d x x  2 1 2 1
Đổi cận x  0  t  1 và x  1  t  2 . Khi đó: I  . x f  2 x    1 dx f t  dt  . 2 0 1
Do tính chất của tích phân là tích phân không phụ thuộc vào biến số tích phân nên 2 2 a f t  dt  
f x dx
a suy ra I  . 2 1 1
Câu 2: (THTT Số 4-487 tháng 1 năm 2017-2018) Cho số phức z a bi (trong đó a , b là các số thực thỏa
mãn 3z  4  5iz  17 
11i . Tính ab . A. ab  6 .
B. ab  3 . C. ab  3 .
D. ab  6 . Lời giải
Chọn A
Ta có z a bi z a bi .
Khi đó 3z  4  5iz  17 
11i  3a bi  4  5ia bi  17  11i
a  5b  17  a  2
 a  5b  5a  7bi  17 11i    
z  2  3i . 5
a  7b  11 b  3   Vậy ab  6 .
Câu 3: (THTT Số 4-487 tháng 1 năm 2017-2018) Tổng các nghiệm phức của phương trình 3 2
z z  2  0 là A. 1. B. 1. C. 1 i . D. 1 i . Lời giải
Chọn B z  1  z  1 Ta có 3 2
z z  2  0   z   1  2
z  2z  2  0    .   z  2 2 1  1   i z  1   i  
Do đó tổng các nghiệm phức của 3 2
z z  2  0 là 1 1 i   1   i  1.
Câu 4: (THTT Số 4-487 tháng 1 năm 2017-2018) Trên mặt phẳng phức tập hợp các số phức z x yi thỏa
mãn z  2  i z  3i là đường thẳng có phương trình
A. y x 1.
B. y  x 1.
C. y  x 1.
D. y x 1. Lời giải Chọn D
Từ z x yi z x y . i
Do đó x yi  2  i x yi  3i   x  2   y  
1 i x   y  3i
  x  2   y  2  x   y  2 2 2 1 3
 4x  2 y  5  6 y  9  y x 1. 2 2
Câu 5: (THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018) Tích phân dx  bằng. 2x 1 0 1 A. 2 ln 5 . B. ln 5 . C. ln 5 . D. 4 ln 5 . 2 Lời giải Chọn C 2 2 2 Ta có
dx  ln 2x 1  ln 5  . 0 2x 1 0
Câu 6: (THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018). Tập hợp tất cả các điểm biểu diễn các số
phức z thỏa mãn: z  2  i  4 là đường tròn có tâm I và bán kính R lần lượt là: A. I  2  ;   1 ; R  4 . B. I  2  ;   1 ; R  2 .
C. I 2;   1 ; R  4 .
D. I 2;  1 ; I 2;  1 . Lời giải Chọn A
Gọi số phức z x iy x, y   Ta có: 2 2
z  2  i  4   x  2   y  
1 i  4   x  2   y   1  16
Vậy tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z  2  i  4 là đường tròn có tâm I 2;  
1 và có bán kính R  4 .
Câu 7: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Trong tập số phức  , chọn phát biểu đúng ?
A. z z z z .
B. z z là số thuần ảo. 1 2 1 2
C. z z z z .
D. z   z 2 2
 4ab với z a bi . 1 2 1 2 Lời giải Chọn A
Xét z x yi , z m ni x, y, ,
m n   . 1 2
z z x m y n i z z x m y n i  1 2     1 2   Ta có   A đúng.
z z x yi m ni x m y n i  1 2      
z z   x m2   y m2 và 2 2 2 2 z z
x y m n nên C sai. 1 2 1 2
Lại có z z  a bi  a bi  2a  B sai. 2 2   2 2 z z
 a bi  a bi   2 2
a b abi    2 2 2
a b  2abi  4abi  D sai.
Câu 8: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Cho số phức z thỏa mãn
z  3  i  0 . Modun của z bằng A. 10 . B. 10 . C. 3 . D. 4 . Lời giải Chọn A Ta có 2 2
z  3  i  0  z  3  i z  3  i z  3 1  10 .
Câu 9: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Kí hiệu z là nghiệm phức có phần ảo âm của 1 phương trình 2
4z 16z 17  0. Trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số 3
phức w  1 2iz i ? 1 2 A. M  2   ;1 . B. M 3; 2  .
C. M 3; 2. D. M 2;  1 . Lời giải
Chọn C  1 z  2  i 1  Ta có: 2 2
4z 16z 17  0   . 1
z  2  i 2  2 3  1  3
Khi đó: w  1 2iz i  1 2i 2  i i  3  2i  tọa độ điểm biểu diễn số phức w 1   2  2  2 là: M 3;2 .
Câu 1: (THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018) Cho hai số phức z  1   2i , 1 2 2
z  1 2i . Giá trị của biểu thức zz bằng 2 1 2 A. 10 . B. 10 . C. 6  . D. 4 . Lời giải Chọn B 2 2 2 2 2 2 2 Ta có zz     2 1  2  1  2   10 . 1 2       
Câu 2: (THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018) Cho số phức z a bi , z 1 z  3i
a,b   thỏa mãn  1 và
 1. Tính P a b . z i z i A. P  7 . B. P  1  . C. P  1 . D. P  2 . Lời giải Chọn D z 1 Ta có
 1  z 1  z i a 1 bi a  b  
1 i  2a  2b  0 (1). z i
z  3i 1  z 3i z i a b 3i a b  1i b 1 (2). z ia  1 Từ (1) và (2) ta có  . Vậy P  2 . b  1 
Câu 3: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Cho số phức z thỏa mãn:
  iz    i2 3 2 2
 4  i . Hiệu phần thực và phần ảo của số phức z là A. 3 . B. 2 . C. 1. D. 0 . Lời giải Chọn D
Ta có   iz    i2 3 2 2
 4  i    iz   i    i2 3 2 4 2 1 5i
 3  2iz  1 5i z
z  1 i 3  2i
 phần thực của số phức z là a  1, phần ảo của số phức z là b  1.
Vậy a b  0 .
Câu 4: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức z  1 i và z  2  3i . 1 2
Tìm số phức liên hợp của số phức w z z ? 1 2
A. w  3  2i .
B. w  1 4i . C. w  1   4i .
D. w  3  2i . Lời giải Chọn D
Vì: z  1 i và z  2  3i nên w z z w  1 2  1 3i  3  2i w  3  2i . 1 2 1 2
Câu 5: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Gọi z , z là các nghiệm của 1 2 phương trình 2
z  2z 10  0 trên tập hợp số phức, trong đó z là nghiệm có 1
phần ảo dương. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu
diễn số phức w  3z  2z . 1 3 A. M  1  ;15 .
B. M 15; 2 .
C. M 2;15 .
D. M 15;   1 . Lời giải Chọn Az  1   3i 2
z  2z 10  0 1  
. w  3z  2z  31 3i  2 1   3i  1  15i z  1   3i 1 3  2 Vậy điểm M  1
 ;15 biểu diễn số phức w  3z  2z . 1 3
Câu 6: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Biết z a bi a,b  là số phức
thỏa mãn 3  2iz  2iz  15 8i . Tổng a b là
A. a b  5 .
B. a b  1  .
C. a b  9 .
D. a b  1. Lời giải Chọn A
Ta có z a bi z a bi . Theo đề bài ta có
3  2iz  2iz  15  8i  3  2ia bi  2i a bi 15 8i  3a  4a  3bi  15 8i 3  a  15 a  5    
. Vậy a b  9 . 4a  3b  8  b  4 
Câu 7: (THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức z thỏa mãn
  iz    i2 3 2 2
 4  i . Hiệu phần thực và phần ảo của số phức z bằng A. 1. B. 0 . C. 4 . D. 2 . Lời giải Chọn D
i    i2 4 2 5i 1
  iz    i2 3 2 2
 4  i z   =1 i . 3  2i 3  2i
Suy ra z  1 i . Vậy hiệu phần thực và ảo của z bằng 2 . 1 3
Câu 8: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Cho số phức z    i . Tìm số 2 2 phức 2
w  1 z z . 1 3 A. 2  3i . B. 1. C. 0 . D.   i . 2 2 Lời giải Chọn C 2  1 3   1 3  w  1    i      i   0 .  2 2   2 2     
Câu 9: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Tìm phần thực và phần ảo của số phức 2 2
z z biết z , z là hai nghiệm phức của phương trình: 2
z  4z  5  0 . 1 2 1 2 A. 4 . B. 6 . C. 8 . D. 5 . Lời giải Chọn B
Do z và z là nghiệm phương trình nên z z  4 và z z  5 . 1 2 1 2 1 2
Ta có z z   z z 2 2 2  2z z 2  4  2.5  6 . 1 2 1 2 1 2
Câu 10: (THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Tính môđun của số phức z thỏa mãn: 3 .
z z  2017  z z   48  2016 .i A. z  4 . B. z  2016 . C. z  2017 . D. z  2 . Lời giải
Chọn A
Gọi z x yi , với x, y   2 Ta có 3 .
z z  2017  z z   48  2016i  3 z  2017  x yi   x yi  48  2016i   2  2 z  16 3   z  48      1008  z  4 . 2.2017 y  2016   y    2017
Câu 11: (THTT số 6-489 tháng 3 năm 2018) Cho số phức z a bi a, b   thỏa mãn 1 3i
a  b   1 i
. Giá trị nào dưới đây là môđun của z ? 1 2i A. 5 . B. 1. C. 10 . D. 5 . Lời giải Chọn D 1 3i 1 3ia  1  Xét w   1
  i mà a  b   1 i
a  b  
1 i  1 i   1 2i 1 2i b  2 
Vậy modun của z là z  5 .
Câu 12: (THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018) Gọi z và z là hai nghiệm của phương trình 1 2 2
2z  6z  5  0 trong đó z có phần ảo âm. Phần thực và phần ảo của số phức z  3z lần lượt 2 1 2 là A. 6;1. B. 1  ; 6  . C. 6  ; 1  . D. 6;1 . Lời giải Chọn C  3 i z    1  2 2 Ta có 2
2z  6z  5  0  
. Suy ra z  3z  6   i 3 i 1 2  z    2  2 2
Vậy Phần thực và phần ảo của số phức z  3z lần lượt là 6; 1  . 1 2
Câu 13: (THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) Cho số phức z thỏa mãn điều
kiện 1 i2  iz 1 i  5  i1 i . Tính môđun của số phức 2
w  1 2z z . A. 100 . B. 10 . C. 5 . D. 10 . Lời giải Chọn D Ta có  5  5i
1 i2  iz 1 i  5  i1 i  1 3iz 1 i  6  4i  1 3iz  5  5i z  13i
z  2  i Suy ra 2
w  1 2z z  8  6i , 2 2 w  8  6  10
Câu 14: (THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) Cho số phức
z a bi a,b   thỏa mãn z  2  5i  5 và .
z z  82 . Tính giá trị của biểu thức P a b . A. 10 . B. 8  . C. 3  5 . D. 7  . Lời giải Chọn B  5  b  43 
 a  22  b  52  5 a     1 Theo giả thiết ta có   2  2 2 2 2
a b  82  
a b  82 2  b  9  Thay   1 vào 2 ta được 2 29b 430b 1521 0      169 b   29
Vì b   nên b  9
  a  1. Do đó P a b  8  .
Câu 15: (THPT Chuyên Phan Bội Châu-lần 2 năm 2017-2018) Biết phương trình 2
z az b  0 có một nghiệm z  2
  i . Tính a b ? A. 9 . B. 1. C. 4 . D. 1  . Lời giải Chọn A 2 Phương trình 2
z az b  0 có một nghiệm z  2
  i nên ta có: 2  i  a  2
  i  b  0
2a b  3 a  4
 2a b  3  a  4i  0     . a  4  0 b  5  
Vậy a b  1.
Câu 16: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Cho m là số thực, biết phương trình 2
z mz  5  0 có hai nghiệm phức trong đó có một nghiệm có phần ảo là 1. Tính tổng môđun của hai nghiệm. A. 3 . B. 5 . C. 2 5 . D. 4 . Lời giải Chọn C
Cách 1: Phương trình 2
z mz  5  0 có hai nghiệm phức z , z thì hai nghiệm phức là hai số 1 2
liên hợp của nhau nên z z  2 z . 1 2 1
Gọi z a i , ( a   ) là một nghiệm của phương trình. 1 2
Ta có: a i  m a i  5  0   2
a ma  4  2a mi  0 2
a ma  4  0 2 2
a  2a  4  0 a  2 a  2       hoặc   2a m  0  m  2  am  4   m  4 
Suy ra z  2  i hoặc z  2  i . Do đó z  2  i . 1 1 1
Vậy z z  2 5 . 1 2 Cách 2: Ta có 2   m  20
Phương trình có hai nghiệm phức thì   0  2 5  m  2 5 . 2 m 20  m 2 m 20  m
Khi đó phương trình có hai nghiệm là z    i và z    i 1 2 2 2 2 2 2 20  m Theo đề  1  m  4  (t/m). 2
z  2  iz  2  i
Khi đó phương trình trở thành 2 1
z  4z  5  0   hoặc 1  z  2  iz  2  i 2  2
Vậy z z  2 5 . 1 2 2018 2018
Câu 17: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Tính P  1 3i  1 3i . A. P  2 . B. 1010 P  2 . C. 2019 P  2 . D. P  4 . Lời giải Chọn C Ta có 2018 2018 2018 2018 2 2     P  1 3i  1 3i 2      2 1 3  1     3      2018 2018  2  2 2019  2 .
Câu 18: (THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018) Gọi z , z là các nghiệm 1 2 của phương trình 2
z  8z  25  0 . Giá trị z z bằng 1 2 A. 8 . B. 5 . C. 6 . D. 3 . Lời giải
Chọn C
z  4  3i Xét phương trình 2
z  8z  25  0 1   z  4  3i  1
Vậy z z  4  3i  4  3i  6i  6 . 1 2    
Câu 19: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Cho hai số phức
z  a  2b  a bi và w  1 2i . Biết z  .
w i . Tính S a b . A. S  7  . B. S  4  . C. S  3 . D. S  7 . Lời giải Chọn A
a  2b  2 a  4
Ta có z  a  2b  a bi  1 2i.i  2  i     . a b  1  b  3  
Vậy S a b  7  .
Câu 20: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Gọi z và z là hai nghiệm của 1 2 phương trình 2
2z  3z  3  0 . Khi đó, giá trị 2 2 z z là 1 2 A. 9 . B. 9  . C. 9 . D. 4 . 4 4 Lời giải Chọn B
Theo định lý Vi-ét, ta có 3 3 z z   và z .z  . 1 2 2 1 2 2 2  3  3
z z   z z 2 2 2
 2z .z      2  3 9   3   . 1 2 1 2 1 2  2  2   4 4
Câu 21: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho i là đơn vị ảo. Gọi S là tập
hợp các số nguyên dương n có 2 chữ số thỏa mãn n
i là số nguyên dương. Số phần tử của S là A. 22 . B. 23 . C. 45 . D. 46 . Lời giải Chọn A Ta có n
i là số nguyên dương khi n  4k , k   . Vì số nguyên dương n có 2 10   4k  99 2,5  k  24, 75 chữ số nên   
suy ra có 24  3 1  22 số. k    k     
Câu 22: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Cho số phức z a bi khác 0
a,b   . Tìm phần ảo của số phức 1 z . a bbi bA. . B. . C. . D. . 2 2 a b 2 2 a b 2 2 a b 2 2 a b Lời giải
Chọn D   b  1 1 a bi a b Ta có 1 z     
i . Vậy phần ảo của 1 z là . 2 2 2 2 2 2 z a bi a b a b a b 2 2 a b
Câu 23: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Tập hợp các điểm biểu diễn cho số
phức z thỏa mãn z  3  4i  5 là
A. Một đường tròn.
B. Một đường thẳng. C. Một đường parabol. D. Một đường Elip. Lời giải Chọn A
Tập hợp điểm biểu diễn cho số phức z là đường tròn tâm I 3; 4
  , bán kính R  5.
Câu 24: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Gọi A , B là hai điểm biểu
diễn hai nghiệm phức của phương trình 2
z  2z  5  0 . Tính độ dài đoạn thẳng AB : A. 6 . B. 2 . C. 4 . D.12 . Lời giải Chọn C
z  1 2i Ta có: 2
z  2z  5  0  
suy ra A1; 2 và B 1; 2 . Vậy AB  4 . z  1 2i
Câu 25: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Trong tất cả các số phức z z z
thỏa mãn điều kiện sau: z 1 
 3 , gọi số phức z a  i
b là số phức có môđun nhỏ 2
nhất. Tính S  2a b . A. 0 . B. 4  . C. 2 . D. 2  Lời giải Chọn C z z 2 2 Ta có z 1   3  a   1  i
b a  3  a   2
1  b  a  3 2
b  4a  8 . 2 2 Do đó 2 2
z a b 2
a  4a  8  a  2 1  4  4 .
min z  2 khi và chỉ khi z  1
  4i . Suy ra S  2a b  2
Câu 26: (SGD Quảng Nam – năm 2017 – 2018) Cho số phức z thoả mãn z  3  4i  5 . Biết
rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn các số phức z là một đường tròn. Tìm toạ
độ tâm I và bán kính R của đường tròn đó.
A. I 3; 4 , R  5 . B. I  3
 ; 4 , R  5 . C. I 3;4 , R  5 .
D. I 3; 4 , R  5 . Lời giải Chọn D 2 2
Đặt z x yi x, y   . Khi đó z  3  4i  5   x  3   y  4  25 .
Vậy tập điểm biểu diễn số phức z là đường tròn tâm I 3;4 , bán kính R  5 .
Câu 27: (SGD Quảng Nam – năm 2017 – 2018) Tổng phần thực và phần ảo của số phức z
thoả mãn iz  1 iz  2i bằng A. 2 . B. 2  . C. 6 . D. 6  . Lời giải Chọn C
Đặt z x yi x, y   . Khi đó iz  1 iz  2
i i x yi  1 i x yi  2  i
x  2 y  0 x  4
  x  2 y  yi  2  i    
, suy ra x y  6 . y  2 y  2  
Câu 28: (ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Kí hiệu z là nghiệm phức của 0 phương trình 2
4z  4z  3  0 sao cho z có phần ảo là số thực âm. Điểm M biểu diễn số phức 0
w  2z thuộc góc phần tư nào trên mặt phẳng phức? 0
A. Góc phần tư I .
B. Góc phần tư II .
C. Góc phần tư III .
D. Góc phần tư IV  . Lời giải Chọn B 1 2 2
4z  4z  3  0  z   i . 2 2 1 2 Do đó z   i w  2  z  1   2i . 0 2 2 0
w có điểm biểu diễn là M 1; 2  nằm ở góc phần tư thứ II .
Câu 29: (THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018) Phương trình bậc hai nào
sau đây có nghiệm 1 2i ? A. 2
z  2z  3  0 . B. 2
z  2z  5  0 . C. 2
z  2z  5  0 . D. 2
z  2z  3  0 . Lời giải Chọn C
Vì 1 2i là nghiệm của phương trình bậc hai 2
az bz c  0 nên 1 2i cũng là nghiệm của phương trình bậc hai 2
az bz c  0 . 
 1 2i1 2i  5 Ta có 
suy ra 1 2i là nghiệm của phương trình bậc hai 2
z  2z  5  0 .
1 2i 1 2i  2 
Câu 30: (THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018) Có bao nhiêu số phức z
thỏa mãn 1 iz  2  iz  13  2i ? A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn D
Gọi z a bi , a,b   . 1 iz  2  iz  13  2i  1 ia bi  2  ia bi  13  2i
 a b  a bi  2a b  2b ai  13  2i 3
a  2b  13 a  3    
z  3  2i . b  2  b  2  
Vậy có một số phức thỏa mãn yêu cầu bài toán.
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Gọi ,
A B, C lần lượt là các điểm biểu diễn của các số phức
z  2 , z  4i , z  2  4i trong mặt phẳng tọa độ Ox .
y Tính diện tích tam giác ABC. 1 2 3 A. 8 . B. 2 . C. 6 . D. 4 . Lời giải
Chọn D    
Ta có A2;0 , B 0; 4 , C 2;4 suy ra AC  0; 4 ; BC  2;0  AC.BC  0 . 1 1
Do đó tam giác ABC là tam giác vuông tại C . Suy ra SC . A CB  .4.2  4 . ABC  2 2
Câu 2: (Tạp chí THTT – Tháng 4 năm 2017 – 2018) Cho số phức z thỏa mãn z  2 . Tập hợp điểm biểu
diễn số phức w  1 iz  2i là
A. Một đường tròn.
B. Một đường thẳng. C. Một Elip.
D. Một parabol hoặc hyperbol. Lời giải Chọn A
Ta có: w  1 iz  2i w  2i  1 iz w  2i  1 iz w  2i  2 2 .
Do đó, tập hợp điểm biểu diễn số phức w là đường tròn tâm I 0; 2 và bán kính 2 2 .
Câu 3: (Tạp chí THTT – Tháng 4 năm 2017 – 2018) Cho hai số phức z , z thỏa mãn z  1, z  2 và 1 2 1 2
z z  3 . Giá trị của z z là 1 2 1 2 A. 0 . B. 1. C. 2 .
D. một giá trị khác. Lời giải Chọn B Cách 1:
Sử dụng công thức hình bình hành
2  z z  2 2 2 2  z zz z  2 1 4 2  z z
 9  z z  1. 1 2 1 2 1 2 1 2 1 2 Cách 2:
Giả sử z a b i a ; b   , z a b i a ; b   . 2 2  1 1  1 1 1 2 2 2  z  1 2 2 a b  1 2 2 a b  1 1 1 1 1 1     Theo bài ra ta có: 2 2 2 2  z  2
 a b  4
 a b  4 . 2 2 2 2 2    z z  3 2 2
2a a  2b b  4  1 2 a ab b  9   1 2 1 2 1 2   1 2   Khi đó, ta có:
z z  a a 2  b b 2   2 2
a b    2 2 a b
 2a a  2b b  1. 1 1 2 2   1 2 1 2  1 2 1 2 1 2
Vậy z z  1. 1 2
Câu 4: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Kí hiệu z , z , z , 1 2 3
z là bốn nghiệm của phương trình 4 2
z z  6  0 . Tính S z z z z . 4 1 2 3 4 A. S  2 3 .
B. S  2 2  3 . C. S  2 2 .
D. S  2 2  3 . Lời giải Chọn D 2 z  2  z   2 Ta có: 4 2
z z  6  0     . 2 z  3   z  i 3 
Kí hiệu z , z , z , z là bốn nghiệm của phương trình, ta có: 1 2 3 4
S z z z z  2 2  3 . 1 2 3 4
Câu 5: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho số phức z thỏa mãn:
z 1  2i  z.i  15  i . Tìm modun của số phức z ? A. z  5 . B. z  4 . C. z  2 5 . D. z  2 3 . Lời giải Chọn A
Gọi z x yi , x, y   .
Theo đề ra ta có:  x yi1 2i   x yi.i  15  i
x  2 y yi  2xi xi y  15  i
x  3y   y xi  15  i
x  3y  15 x  3    
z  3  4i z  5. x y  1  y  4 
Câu 6: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Gọi z là nghiệm phức có phần 1 7  4i
ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu diễn số phức trên mặt z1 phẳng phức?
A. P 3; 2 .
B. N 1;  2 .
C. Q 3;2 .
D. M 1; 2 . Lời giải Chọn A Ta có:
z  1  2i TM 2
z  2z  5  0  
z  1  2iL  7  4i 7  4i Suy ra   3  2i . z 1  2i 1
Điểm biểu diễn là P 3; 2 .
Câu 7: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Tìm phần ảo của số phức 2
z biết z   3  i  3  i . A. 4 . B. 4 3 . C. 4 3 . D. 4  . Lời giải Chọn D 2
Ta có: z   3  i  3  i  4 3  4i z  4 3  4i .
Vậy phần ảo của số phức z là 4  .
Câu 8: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho số phức z  3  4i .
Mệnh đề nào dưới đây sai?
A. Môđun của số phức z bằng 5 .
B. Số phức liên hợp của z là 3  4i .
C. Phần thực và phần ảo của z lần lượt là 3 và 4  .
D. Biểu diễn số phức z lên mặt phẳng tọa độ là điểm M 3;  4 . Lời giải Chọn C
Số phức liên hợp của z  3  4i là z  3  4i . Mệnh đề B sai.
Câu 9: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho số phức z thỏa mãn
z  2  3iz  1 9i . Tính tích phần thực và phần ảo của số phức z . A. 1. B. 2  . C. 1. D. 2 . Lời giải Chọn B
Gọi z x  i
y (với x, y ), ta có z x  i y .
Theo giả thiết, ta có x  i
y  2  3i x  i
y   1 9i  x  3y  3x  3yi  1 9i
x  3y  1 x  2     . Vậy xy  2  . 3x  3y  9  y  1  
Câu 10: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Cho số phức z  3  5i .
Gọi w x yix, y   là một căn bậc hai của z . Giá trị của biểu thức 4 4
T x y là 17 43 A. T  706 . B. T  . C. T  . D. T  34 . 2 2 Lời giải Chọn C
Ta có w x yix, y   là một căn bậc hai của z khi và chỉ khi 2 w z 2 2 x y  3
  x yi2 2 2
 3  5i x y  2xyi  3  5i .   2xy  5  2 2  5  43 Ta có 4 4
T x y   2 2 x y  2 2 2  2x y  3  2.    .  2  2
Câu 11: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Tổng phần thực và phần ảo 2
của số phức z  1 i  3  3i là A. 4 . B. 4  . C. 3  i . D. 10 . Lời giải
Chọn B 2
Ta có z  1 i  3  3i 2
 1 2i i  3  3i  3
  i  phần thực a  3
 , phần ảo b  1.
Vậy a b  4  .
Câu 12: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho số phức z thỏa mãn: z 1  z  2  3i . Tập hợp
các điểm biểu diễn số phức z là
A. Đường tròn tâm I 1;2 , bán kính R  1 .
B. Đường thẳng có phương trình 2x  6 y 12  0 .
C. Đường thẳng có phương trình x  3y  6  0 .
D. Đường thẳng có phương trình x  5y  6  0 .
Hướng dẫn giải Chọn C
Gọi z x yi ; ( x , y   ). 2 2 2
Ta có: z 1  z  2  3i   x   2
1  y   x  2   y  3  x  3y  6  0 .
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình x  3y  6  0 .
Câu 13: (THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018) Cho số phức z thỏa mãn z z
2 . Biết rằng phần thực của z bằng a . Tính z theo a 1 2 a a 1 2 a a 1 2 a a  4 A. z  . B. z  . C. z  . D. z  . 1 a 2 2 2
Hướng dẫn giải Chọn D
Đặt z a bi , a , b   2 2  z
a b . Theo đề bài ta có z z  2 2 2
a bi a b
2  a a b 2 2 2 2  b  2 2  a a  4 2 2  a b  loai 2   2 2 a b  2 2
a a b 1  0   .  2 a a  4 2 2  a b  t / m  2 2 a a  4 Vậy z  . 2
Câu 14: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Gọi z , z là nghiệm của phương trình 1 2 2 2 z z 2
z  2z  4  0 . Tính giá trị của biểu thức 1 2 P   z z 2 1 11 A. 4 . B. 4 . C. 8 . D.  . 4 Lời giải
Chọn B
z  1 3i Ta có: 2
z  2z  4  0  1  .
z  1 3i  2
1 3i2 1 3i z z 2 2 2 Suy ra: 1 2 P      4  . z z 1 3i 1 3i 2 1
Câu 15: (Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018) Tìm tập hợp điểm biểu diễn số phức
z thoả z 1 2i  3 .
A. Đường tròn tâm I 1; 2 , bán kính r  9 .
B. Đường tròn tâm I 1; 2 , bán kính r  9 .
C. Đường tròn tâm I 1;  2 , bán kính r  3.
D. Đường tròn tâm I 1; 2 , bán kính r  3.
Hướng dẫn giải Chọn D
Gọi z x yi  2
x, y  , i    1 . 2 2 2 2
Ta có: z 1 2i  3   x  
1   y  2  3   x  
1   y  2  9 .
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm I 1;2 , bán kính r  3.
Câu 16: (Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018) Trong
mặt phẳng phức, cho điểm M trong hình vẽ bên là điểm biểu diễn số
phức z . Trong các mệnh đề sau mệnh đề nào là sai?
A. z z  6 .
B. Số phức z có phần ảo bằng 4 . C. z  5 .
D. z  3  4i .
Hướng dẫn giải Chọn A
Ta dễ thấy các mệnh đề B, C, D đúng.
Từ hình vẽ ta có z  3  4i z z  3  4i  3  4i  8i . Do đó A sai.
Câu 17: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho số phức
z thỏa mãn z 1 2i  3 . Tập hợp các điểm biểu diễn cho số phức w z 1 i là đường tròn
A. Tâm I 3;   1 , R  3 2 . B. Tâm I  3   ;1 , R  3 . C. Tâm I  3   ;1 , R  3 2 .
D. Tâm I 3;   1 , R  3 . Lời giải Chọn A
Ta có z 1 2i  3  z 1 i   1
  2i1 i  3 1 i w  3  i  3 2 .
Giả sử w x yi x, y    x  3   y   1 i  3 2
  x  2   y  2 3 1
 18  I 3;   1 , R  18  3 2 .
Câu 18: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Có bao nhiêu số phức z thỏa mãn
1 iz z là số thuần ảo và z  2i 1 A. 2 . B. 1. C. 0 . D.Vô số. Lời giải Chọn A
Đặt z a bi với a,b   ta có : 1 iz z  1 ia bi  a bi  2a b ai .
Mà 1 iz z là số thuần ảo nên 2a b  0  b  2a . a  1
Mặt khác z  2i  1 nên a  b  2 2 2
 1  a   a  2 2 2 2  1 2
 5a  8a  3  0   3 . a   5
Ứng với mỗi a ta tìm được một b duy nhất, vậy có 2 số phức thỏa mãn yêu cầu bài toán.
Câu 19: Cho hai số thực x , y thỏa mãn 2x 1 1 2 yi  22  i  yi x . Khi đó giá trị của 2
x  3xy y bằng A. 2  . B. 1. C. 3  . D. 1.
Câu 20: Tính tổng 3 6 2016
S  1  i i  ...  i . A. S  1.
B. S i .
C. S i  . D. S  1  .
Câu 21: Cho hai số thực x , y thỏa mãn 2x 1 1 2 yi  22  i  yi x . Khi đó giá trị của 2
x  3xy y bằng A. 2  . B. 1. C. 3  . D. 1. Lời giải Chọn A
Ta có: 2x 1 1 2 yi  22  i  yi x  2x 1 1 2yi  4  x   y  2i
2x 1  4  xx  1  2   
x  3xy y  2 .
1 2 y y  2  y  1 
Câu 22: Tính tổng 3 6 2016
S  1  i i  ...  i . A. S  1.
B. S i .
C. S i  . D. S  1  . Lời giải Chọn A n 1 x   2016 n 1 Áp dụng công thức 2
1 x x  ...  x  với 3
x i , n   672 ta được x 1 3 i 673 3 1  i  673 1  i 336 2 i 1 i  1 S      1 . 3 i 1 i  1 i  1 i  1
Câu 23: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z  13  0 . Tìm tọa độ điểm 1
M biểu diễn số phức w  i   1 z . 1
A. M 5;  1 . B. M 5;  1 .
C. M 1; 5 .
D. M 1;5 .
Câu 24: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z  13  0 . Tìm tọa độ điểm 1
M biểu diễn số phức w  i   1 z . 1
A. M 5;  1 . B. M 5;  1 .
C. M 1; 5 .
D. M 1;5 . Lời giải Chọn Az  3   2i Ta có 2 1
z  6z  13  0  
. Suy ra w  i  
1 z  1 i 3   2i  5   i .
z  3  2i 1  2
Vậy tọa độ điểm M biểu diễn số phức w  i  
1 z là M 5;  1 . 1 1 i3i
Câu 25: Tìm phần ảo của số phức z , biết z  . 1 i A. 3. B. 3. C. 0. D. 1.  Lời giải Chọn C
1 i3i 1 i2 3i 2 .3 i i Ta có: z     3   z  3. 2 1 i 1 i 2
Vậy phần ảo của số phức z là 0.
Câu 26: Cho số phức z thỏa mãn z 1 2i  5 và M  ;
x y là điểm biểu diễn số phức z . Điểm M
thuộc đường tròn nào sau đây? 2 2 2 2 A.  x  
1   y  2  25 . B.x  
1   y  2  25 . 2 2 2 2 C.  x  
1   y  2  5 . D.  x  
1   y  2  5 . Lời giải Chọn B 2 2
Ta có z 1 2i  5  x 1  y  2i  5   x  
1   y  2  25 . 2 2
Vậy điểm M thuộc đường tròn  x  
1   y  2  25 .
Câu 27: Cho số phức z thỏa mãn 2z  3  4i  10 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của z . Khi đó M m bằng A. 5 . B. 15 . C. 10 . D. 20 .
Câu 28: Cho hàm số f x 2  x  2 x   2 x   2 x   2 1 4 9
x 16 . Hỏi phương trình f  x  0 có bao nhiêu nghiệm? A. 9 . B. 8 . C. 7 . D. 6 .
Câu 29: Cho số phức z thỏa mãn 2z  3  4i  10 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của z . Khi đó M m bằng A. 5 . B. 15 . C. 10 . D. 20 . Lời giải Chọn C
Đặt z x yi . 2 3  3  2
Ta có: 2z  3  4i  10  z
 2i  5  x    
y  2  25 . 2  2   3 
Tập hợp điểm biểu diễn số phức thỏa đề là đường tròn tâm I ; 2 
 , bán kính R  5 .  2 
m IO R Khi đó: 
M m  2R  10 .
M IO R
Câu 30: Cho hàm số f x 2  x  2 x   2 x   2 x   2 1 4 9
x 16 . Hỏi phương trình f  x  0 có bao nhiêu nghiệm? A. 9 . B. 8 . C. 7 . D. 6 . Lời giải Chọn A
Ta có f x  0  x 0; 1  ; 2; 3  ;   4 .
Bảng xét dấu f x
Từ bảng xét dấu biểu thức f (x) và do tính chất liên tục của hàm số f (x) , suy ra:
x  0 là điểm cực trị của hàm số;
f x có ít nhất 8 điểm cực trị, khác 0 , lần lượt thuộc mỗi khoảng 4;3 , 3;2 , 2;  1 ,  1  ; 0, 0; 
1 , 1; 2 , 2;3 , 3; 4 .
Suy ra hàm số f (x) có ít nhất 9 điểm cực trị.
Do đó, theo điều kiện cần để hàm số có cực trị, ta có phương trình f  x  0 có ít nhất 9 nghiệm.
Mặt khác vì bậc của f (x) là 10 nên bậc của f  x là 9  phương trình f  x  0 có không quá 9 nghiệm.
Vậy phương trình f  x  0 có đúng 9 nghiệm.
Câu 31: Gọi z và z là hai nghiệm phức của phương trình 2
z  6z 11  0 . Giá trị của biểu thức 1 2
3z z bằng 1 2 A. 22 . B. 11. C. 2 11 . D. 11 .
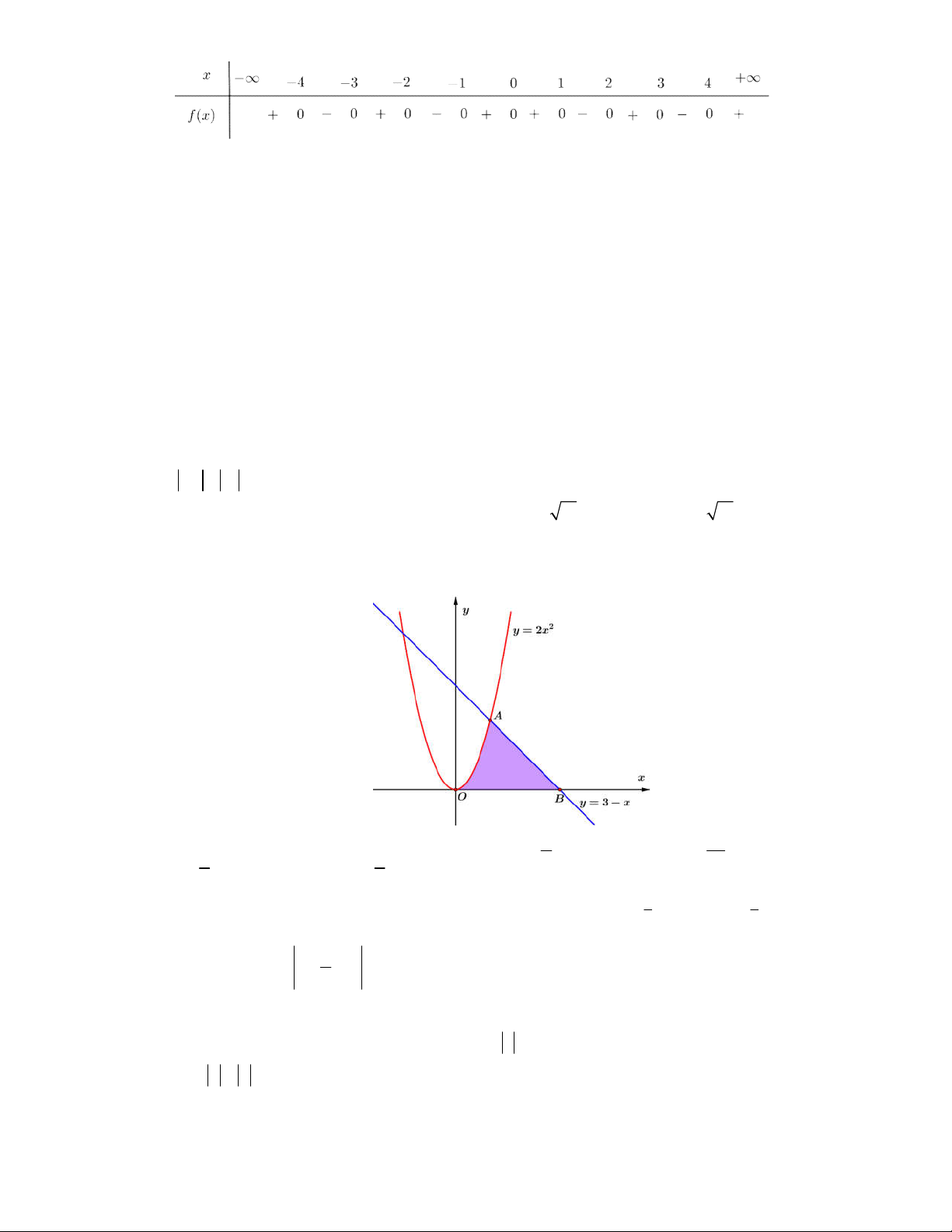
Câu 32: Gọi tam giác cong (OAB) là hình phẳng giới hạn bởi đồ thị các hàm số 2
y  2x , y  3  x ,
y  0 (tham khảo hình vẽ bên). Diện tích của OAB bằng 4 10 8 5 A. . B. . C. 3 . D. 3 . 3 3
Câu 33: Xét các số phức z a bi , a,b   thỏa mãn
z z  i iz z  2 4 15 1 . Tính 1
F  a  4b khi z
 3i đạt giá trị nhỏ nhất 2 A. F  7 . B. F  6 . C. F  5 . D. F  4 .
Câu 34: Cho số phức z  a bi a,b   thỏa mãn z  5 và z 2  i1 2i là một số thực. Tính
P a b
A. P  5
B. P  7
C. P  8 D. P  4
Câu 35: Gọi z và z là hai nghiệm phức của phương trình 2
z  6z 11  0 . Giá trị của biểu thức 1 2
3z z bằng 1 2 A. 22 . B. 11. C. 2 11 . D. 11 . Lời giải Chọn C 2 2
Ta có z và z là hai số phức liên hợp của nhau nên zz
z z  11  z z  11 . 1 2 1 2 1 2 1 2
Do đó: 3z z  2 z  2 11 . 1 2 1
Câu 36: Gọi tam giác cong (OAB) là hình phẳng giới hạn bởi đồ thị các hàm số 2
y  2x , y  3  x ,
y  0 (tham khảo hình vẽ bên). Diện tích của OAB bằng 4 10 8 5 A. . B. . C. 3 . D. 3 . 3 3 Lời giải Chọn A Gọi parabol  P 2
: y  2x và đường thẳng d  : y  3  x .
Ta có phương trình hoành độ giao điểm của  P và d  là: x  1 2 2 2x 3 x 2x x 3 0         3 x    2 Suy ra tọa độ điểm (
A 1; 3) và (d )  Ox B(3; 0) . 1 3 2 8 Khi đó 2 S
S S  2x dx  (3  x)dx   2  (OAB ) 1 2   . 3 3 0 1
Câu 37: Xét các số phức z a bi , a,b   thỏa mãn
z z  i iz z  2 4 15 1 . Tính 1
F  a  4b khi z
 3i đạt giá trị nhỏ nhất 2 A. F  7 . B. F  6 . C. F  5 . D. F  4 . Lời giải Chọn A Ta có
z z  i iz z  2 4 15 1
 a bi a bi  i i a bi a bi  2 4 15 1 15  b    a  2 8 15 2 1 suy ra b  . 8 1 1 1 1 z   3i  2a  2 1  2b  62 2 2 
8b 15  4b  24b  36 
4b  32b  21 2 2 2 2 15
Xét hàm số f x 2
 4x  32x  21 với x  8 15 15 
f  x  8x  32  0, x  
suy ra f x là hàm số đồng biến trên ;    nên 8  8   15  4353
f x  f    .  8  16 1 1 4353 15 1 Do đó z
 3i đạt giá trị nhỏ nhất bằng khi b  ; a  . 2 2 16 8 2
Khi đó F  a  4b  7 .
Câu 38: Cho số phức z  a bi a,b   thỏa mãn z  5 và z 2  i1 2i là một số thực. Tính
P a b
A. P  5
B. P  7
C. P  8 D. P  4 Lời giải Chọn B 2 2
z  5  a b  25   1
z 2  i1 2i  a bi4  3i  4a  3b  4b  3ai là số thực nên 4b  3a  0 . 2  3  Thay vào   1 ta được 2 a a  25  
a  4  b  3  P  7  4 
Câu 39: Phương trình 2
z z  5  0 có hai nghiệm z ; z trên tập hợp số phức. Tính giá trị của biểu thức 1 2 2 2
P z z 1 2 37 A. P  10 . B. P  9 . B. P   . D. P  11 . 2
Câu 40: Phương trình 2
z z  5  0 có hai nghiệm z ; z trên tập hợp số phức. Tính giá trị của biểu thức 1 2 2 2
P z z 1 2 37 A. P  10 . B. P  9 . B. P   . D. P  11 . 2 Lời giải Chọn B  1 19 z    i  1 2 2 2
z z  5  0   2 2
P z z  9  . 1 2  1 19 z    i 2  2 2
Câu 41: Gọi z , z , z là ba nghiệm phức của phương trình 3
z  8  0 . Giá trị của z z z bằng 1 2 3 1 2 3 A. 2  2 3 . B. 3 . C. 2  3 . D. 6 .
Câu 42: Gọi z , z , z là ba nghiệm phức của phương trình 3
z  8  0 . Giá trị của z z z bằng 1 2 3 1 2 3 A. 2  2 3 . B. 3 . C. 2  3 . D. 6 . Lời giải Chọn D z  2  1  3
z  8  0  z  1 3i
z z z  6 . 2 1 2 3 z 1 3i  1
Câu 43: Cho số phức z a bi thỏa mãn  z  8i z  6i  5  5i . Giá trị của a b bằng A. 19 . B. 5 . C. 14 . D. 2 .
Câu 44: Cho số phức z a bi thỏa mãn  z  8i z  6i  5  5i . Giá trị của a b bằng A. 19 . B. 5 . C. 14 . D. 2 . Lời giải Chọn A
Ta có  z  8i z  6i  5  5i  1 iz  5 19i z  12  7i . a  12
Mà z a bi nên 
a b  19 . b  7 
Câu 45: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
2z  6z  5  0 . Số phức iz bằng 0 0 1 3 1 3 1 3 1 3 A.   i . B.i . C.   i . D.i . 2 2 2 2 2 2 2 2
Câu 46: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
2z  6z  5  0 . Số phức iz bằng 0 0 1 3 1 3 1 3 1 3 A.   i . B.i . C.   i . D.i . 2 2 2 2 2 2 2 2 Lời giải Chọn B 3  i Ta có 2
2z  6z  5  0  4z 12z 10  0  2z  32 2 2  1
  i z  2 3 1 1 3  z   i iz   i . 0 0 2 2 2 2
Câu 47: Cho các số phức z  3  2i , z  3  2i . Phương trình bậc hai có hai nghiệm z và z là 1 2 1 2 A. 2
z  6z 13  0 . B. 2
z  6z 13  0 . C. 2
z  6z 13  0 . D. 2
z  6z 13  0 .
Câu 48: Cho các số phức z  3  2i , z  3  2i . Phương trình bậc hai có hai nghiệm z và z là 1 2 1 2 A. 2
z  6z 13  0 . B. 2
z  6z 13  0 . C. 2
z  6z 13  0 . D. 2
z  6z 13  0 . Lời giải Chọn A
Cách 1: Ta có: S z z  6 , 2
P z z z
 9  4  13 nên z , z là hai nghiệm của phương 1 2 1 2 1 1 2 trình 2
z Sz P  0 2
z  9z 13  0 .
Cách 2: Do z  3  2i , z  3  2i là hai nghiệm của phương trình nên 1 2  z z z z
 0   z  3  2i z  3  2i  0   z  2 3  4  0 2
z  6z 13  0 . 1   2    
Câu 49: Tìm nguyên hàm F x của hàm số f x  sin 2x , biết F  0   .  6  1   1
A. F x  cos 2x  .
B. F x 2  cos x  . 2 6 4 1 1 
C. F x 2  sin x  .
D. F x  cos 2x . 4 2 2 3
Câu 50: Có bao nhiêu số phức thỏa mãn z z .i 1 i  0 ? 4 A. 1. B. 3 . C. 2 . D. 0 .   
Câu 51: Tìm nguyên hàm F x của hàm số f x  sin 2x , biết F  0   .  6  1   1
A. F x  cos 2x  .
B. F x 2  cos x  . 2 6 4 1 1 
C. F x 2  sin x  .
D. F x  cos 2x . 4 2 Lời giải Chọn C 1    1
Ta có: F x  sin 2 d
x x   cos 2x C  ; F  0  C    . 2  6  4 1 1 1 1 1
Vậy F x   cos 2x     2 1 2 sin x  2  sin x  . 2 4 2 4 4 2 3
Câu 52: Có bao nhiêu số phức thỏa mãn z z .i 1 i  0 ? 4 A. 1. B. 3 . C. 2 . D. 0 . Lời giải Chọn A 2 3 3
Đặt z x yi  ,
x y   thì z z .i 1 i  0  x yi   2 2
x y i 1 i  0 4 4 x 1  0 x  1   1   3   1  z  1 i . 2 2
y x y   0  y    2  4  2
Câu 53: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Giá trị của biểu thức 1 2 2 2 z z bằng 1 2 3 9  9  A. 3 . B. . C. . D. . 18 4 8
Câu 54: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Giá trị của biểu thức 1 2 2 2 z z bằng 1 2 3 9  9  A. 3 . B. . C. . D. . 18 4 8 Lời giải Chọn C Ta có 2
2z  3z  3  0 S a b c . 2 2  3 21i   3 21i  9 Suy ra 2 2 z z             . 1 2  4 4   4 4  4    
Câu 55: Cho hai số phức z  4  8i và z  2  i . Tính 2z .z 1 2 1 2 A. 4 5 . B. 5 . C. 20 . D. 40 .
Câu 56: Cho hai số phức z  4  8i và z  2  i . Tính 2z .z 1 2 1 2 A. 4 5 . B. 5 . C. 20 . D. 40 . Lời giải Chọn D
Ta có 2z .z  2 4  8i 2  i  40 . 1 2   
Câu 57: Gọi z , z là hai nghiệm của phương trình 2
2z z 1  0 . Tính z z z z ? 1 2 1 1 2 2 2 2 A. 2  . B. . C. 1. D.  . 4 2
Câu 58: Gọi z , z là hai nghiệm của phương trình 2
2z z 1  0 . Tính z z z z ? 1 2 1 1 2 2 2 2 A. 2  . B. . C.1. D.  . 4 2 Lời giải Chọn B  1 7 2 z   i   1  7 1 4 4 2 Ta có 2
2z z 1  0 2  z   i      z z  . 1 2  4  16  1 7 2 z   i 2  4 4 2 2  1 7 1 7  2
Vậy z z z z z z    i   i  . 1 1 2 2  1 2   2 2  4 4 4 4    4 1
Câu 59: Phần ảo của số phức là 1 i 1 1 1 A.i . B.  . C. . D. 1  . 2 2 2
Câu 60: Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: z 10  2i z  2 14i và
z 110i  5 ? A. Hai. B. Không. C. Một. D. Vô số.
Câu 61: Cho số phức z thỏa mãn z z  2  4i . Môđun của z là A. 4 . B. 5 . C. 3 . D. 25 . 1
Câu 62: Phần ảo của số phức là 1 i 1 1 1 A.i . B.  . C. . D. 1  . 2 2 2
Hướng dẫn giải Chọn B 1 1 1 1 Ta có  
i nên có phần ảo là  . 1 i 2 2 2
Câu 63: Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: z 10  2i z  2 14i và
z 110i  5 ? A. Hai. B. Không. C. Một. D. Vô số.
Hướng dẫn giải Chọn C
Đặt z a bi với a,b  .  2 2 2 2
Từ giả thiết z 10  2i z  2 14i  a 10  b  2  a  2  b 14 4
 24a  32b  96  0  a b  4 3 2 2 2  4 
Ta có: z 110i  5  a  
1  b 10  25 2  b  5
b  20b 100  25    3  25 100 2  b
b 100  0  b  6 . Suy ra a  4 . 9 3
Vậy có một số phức thỏa mãn.
Câu 64: Cho số phức z thỏa mãn z z  2  4i . Môđun của z là A. 4 . B. 5 . C. 3 . D. 25 .
Hướng dẫn giải Chọn B
Đặt z x iy  ,
x y   , ta có z z  2  4i 2 2
x iy x y  2   4i 2 2 
x x y  2 x  2  2   x  2  x 16    x  3 . 2 2  y  4  
x  4x  4  x 16 
Vậy z  3  4i z  5 .
Câu 65: Cho số phức z thỏa mãn 2  3iz z 1. Môđun của z bằng 1 1 A. . B. . C. 1. D. 10 . 10 10
Câu 66: Cho số phức z thỏa mãn 2  3iz z 1. Môđun của z bằng 1 1 A. . B. . C. 1. D. 10 . 10 10 Lời giải Chọn A 1  1 3 1 3 1
2  3iz z 1  1 3iz  1  z   z    i z    i z  . 1 3i 10 10 10 10 10 z z
Câu 67: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Khi đó 1 2  bằng: 1 2 z z 2 1 3  3 3  3 3  A. i . B.i . C. . D. . 2 2 2 2 2
Câu 68: Modun của số phức z  1 2i2  i là A. z  5 . B. z  5 . C. z  10 . D. z  6 . z z
Câu 69: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Khi đó 1 2  bằng: 1 2 z z 2 1 3  3 3  3 3  A. i . B.i . C. . D. . 2 2 2 2 2
Hướng dẫn giải Chọn D   3 z z   1 2 2 
2z  3z  3  0 có hai nghiệm z , z suy ra 2 . 1 2  3 z .z  1 2   2 3 2 2 2 z z z z z z 3  1 2 1 2  1 2  Ta có 4     2   2  . z z z .z z z 3 2 2 1 1 2 1 2 2
Câu 70: Modun của số phức z  1 2i2  i là A. z  5 . B. z  5 . C. z  10 . D. z  6 .
Hướng dẫn giải Chọn A
Ta có z  1 2i2  i  4  3i nên z  5 .
Câu 71: Gọi z , z , z , z là bốn nghiệm phân biệt của phương trình 4 2
z  3z  4  0 trên tập số phức. 1 2 3 4 2 2 2 2
Tính giá trị của biểu thức T zzzz 1 2 3 4
A. T  8 .
B. T  6 .
C. T  4 . D. T  2 .
Câu 72: Gọi z , z , z , z là bốn nghiệm phân biệt của phương trình 4 2
z  3z  4  0 trên tập số phức. 1 2 3 4 2 2 2 2
Tính giá trị của biểu thức T zzzz 1 2 3 4
A. T  8 .
B. T  6 .
C. T  4 . D. T  2 . Lời giải Chọn A  3 7 2 z    i    1 2 2 Ta có 4 2
z  3z  4  0    .  3 7 2 z    i 2  2 2
Không mất tính tổng quát giả sử z , z là nghiệm của  
1 và z , z là nghiệm của 2 . 1 2 3 4 2 2   2 2  3  7 9 7 zz            2 . 1 2 2  2    4 4   2 2   2 2  3  7 9 7 Tương tự zz           2 . 3 4 2  2    4 4   Vậy T  8 .
Câu 73: . Cho z , z là các số phức khác 0 và z z . Trong các mệnh đề sau, mệnh đề sai? 1 2 1 2
A. z z   .
B.z z
z z   . 1 2   1 2  1 2  z z
C. z z z z   . D. 1 2   . 1 1 2 2   z z  1 2  2 z
Câu 74: Cho số phức z  3  2i . Môđun của w  bằng z z 13 15 11 A. . B. . C. . D. 2 . 6 6 6
Câu 75: Cho số z thỏa mãn các điều kiện z  8  3i z i và z  8  7i z  4  i . Tìm số phức
w z  7  3i .
A. w  3  i .
B. w  13  6i .
C. w  1 i .
D. w  4  3i .
Câu 76: . Cho z , z là các số phức khác 0 và z z . Trong các mệnh đề sau, mệnh đề sai? 1 2 1 2
A. z z   .
B.z z z z   . 1 2   1 2  1 2  z z
C. z z z z   . D. 1 2   . 1 1 2 2   z z  1 2  Lời giải
Chọn D 2 2
Ta có: z z   ;  z z z zz z
  ; z z z z zz   . 1 2   1 2  2 1 2 1 2 1 1 2 2 1 2  z z   z z   1 i  Xét mệnh đề “ 1 2   
 ”: Cho z  1 và z i thì 1 2   i i        , nên z z 1 2  z z    1 i 1 2  1 2  mệnh đề này sai. 2 z
Câu 77: Cho số phức z  3  2i . Môđun của w  bằng z z 13 15 11 A. . B. . C. . D. 2 . 6 6 6 Lời giải
Chọn A   i2 3 2 5 12i Ta có w   .
3  2i  3  2i 6 5 12i 13 Do đó w   . 6 6
Câu 78: Cho số z thỏa mãn các điều kiện z  8  3i z i và z  8  7i z  4  i . Tìm số phức
w z  7  3i .
A. w  3  i .
B. w  13  6i .
C. w  1 i .
D. w  4  3i . Lời giải Chọn D
Đặt z x yi , với x, y   . Ta có
z  8  3i z i   x yi  8  3i   x yi  i
  x  8   y  3i x   y   1 i
  x  2   y  2  x   y  2 2 8 3 1
 4x y 18  0 .
z  8  7i z  4  i
  x yi  8  7i   x yi  4  i
  x  8   y  7i   x  4   y   1 i
  x  2   y  2   x  2   y  2 8 7 4 1
 2x  3y  24  0 .
4x y 18  0 x  3 
Ta có hệ phương trình:    .
2x  3y  24  0 y  6   Như vậy z  3
  6i w z  7  3i   3
  6i  7  3i  4  3i .
Câu 79: Cho số phức z  cos  .
i sin     . Tìm môđun của z . A. cos  sin . B. 1.
C. cos  i sin . D. cos 2 .
Câu 80: Cho số phức z  cos  .
i sin     . Tìm môđun của z . A. cos  sin . B. 1.
C. cos  i sin . D. cos 2 . Lời giải Chọn B Ta có: 2 2
z  cos   sin   1. 2018 2018
Câu 81: Cho z , z là hai số phức thỏa mãn 2
z  4z  5  0 . Biểu thức P   z 1  z 1 có giá 1   2  1 2 trị bằng A. 0 . B. 2018 2 . C. 1009 2 . D. 2 . 2018 2018
Câu 82: Cho z , z là hai số phức thỏa mãn 2
z  4z  5  0 . Biểu thức P   z 1  z 1 có giá 1   2  1 2 trị bằng A. 0 . B. 2018 2 . C. 1009 2 . D. 2 . Lời giải Chọn A Biệt số 2   4  5  1   i .
Do đó phương trình có hai nghiệm phức: z  2  i và z  2  i . 1 2 1009 1009 2018 2018 2 2
Suy ra P  1 i 1 i 1 i  1 i            
  i1009   i1009 1009 1009 2 2  2  i  2 i  0 . 1 1
Câu 83: Biết z là một nghiệm của phương trình z
 1 . Tính giá trị của biểu thức 3 P z  . z 3 z 7 A. P  2 . B. P  0 . C. P  4 . D. P  . 4 z
Câu 84: Tập hợp điểm biểu diễn số phức z thỏa mãn
 3 là đường nào? z i
A. Một đường thẳng.
B. Một đường parabol. C. Một đường tròn.
D. Một đường elip. 1
Câu 85: Cho số phức z  1 i . Tính số phức w i z  3z . 3 8 8 10 10 A. w  . B. w   i . C. w   i . D. . 3 3 3 3 1 1
Câu 86: Biết z là một nghiệm của phương trình z
 1 . Tính giá trị của biểu thức 3 P z  . z 3 z 7 A. P  2 . B. P  0 . C. P  4 . D. P  . 4 Lời giải Chọn A 1 Ta có z   1 2
z z 1  0 , do z  1 nên 3 z 1  0 3  z  1
 . Vậy P  2 . z z
Câu 87: Tập hợp điểm biểu diễn số phức z thỏa mãn
 3 là đường nào? z i
A. Một đường thẳng.
B. Một đường parabol. C. Một đường tròn.
D. Một đường elip. Lời giải Chọn C
Gọi z x yi , x , y   . z
 3  z  3 z i x yi  3 x yi i x y
x   y  2 2 2 2 3 1 z i 9 9 x yxy 2 2 2 2 9 1       2 2
 8x  8 y 18 y  9  0 2 2  x y y   0 .   4 8
Vậy tập hợp điểm biểu diễn số phức z là một đường tròn. 1
Câu 88: Cho số phức z  1 i . Tính số phức w i z  3z . 3 8 8 10 10 A. w  . B. w   i . C. w   i . D. . 3 3 3 3 Lời giải Chọn A  1   1  1 8
w i 1 i  3 1 i i   3  i      .  3   3  3 3 2
Câu 89: Cho biết có hai số phức z thỏa mãn 2
z  119 120i , kí hiệu là z và z . Tính z z . 1 2 1 2 A. 169 . B. 114244 . C. 338 . D. 676 .
Câu 90: Cho w là số phức thay đổi thỏa mãn w  2 . Trong mặt phẳng phức, các điểm biểu diễn số phức
z  3w 1 2i chạy trên đường nào?
A. Đường tròn tâm I 1; 2 , bán kính R  6 .
B. Đường tròn tâm I 1; 2 , bán kính R  2 .
C. Đường tròn tâm I 1; 2 , bán kính R  2 .
D. Đường tròn tâm I 1; 2 , bán kính R  6 . 2
Câu 91: Cho biết có hai số phức z thỏa mãn 2
z  119 120i , kí hiệu là z và z . Tính z z . 1 2 1 2 A. 169 . B. 114244 . C. 338 . D. 676 .
Hướng dẫn giải Chọn D
Giả sử: z a bi , a,b   . 2 2 
a b  119   1 Ta có: 2
z  119 120i 2 2
a b  2abi  119 120i   . 2ab  120   2 
Ta có a,b  0 . 60
Từ 2  a   , thay vào   1 , ta được: b 3600 2 b  144 2  b  119 4 2
b 119b  3600  0  . 2  b 2 b  25  * 2 b  144  (vô nghiệm).
b  5  a  -12 * 2 b  25   . b  5   a  12  Vậy z  12 
 5i , z  12  5i . 1 2 2 2 Suy ra z z  24  10i  676 . 1 2
Câu 92: Cho w là số phức thay đổi thỏa mãn w  2 . Trong mặt phẳng phức, các điểm biểu diễn số phức
z  3w 1 2i chạy trên đường nào?
A. Đường tròn tâm I 1; 2 , bán kính R  6 .
B. Đường tròn tâm I 1; 2 , bán kính R  2 .
C. Đường tròn tâm I 1; 2 , bán kính R  2 .
D. Đường tròn tâm I 1; 2 , bán kính R  6 .
Hướng dẫn giải Chọn A Gọi M  ;
x y là điểm biểu diễn số phức z x yi x, y   . z  2i 1 2 2 Ta có w  2 
 2  z  2i 1  6   x  
1   y  2  36 . 3
Vậy tập hợp điểm cần tìm là đường tròn tâm I 1; 2 , bán kính R  6 .
Câu 93: Xét các số phức z thỏa điều kiện z  3 2i  5 . Trong mặt phẳng tọa độ Oxy , tập hợp các
điểm biểu diễn số phức w z 1 i là?
A. Đường tròn tâm I 4; 
3 , bán kính R  5 .
B. Đường tròn tâm I  4  ; 
3 , bán kính R  5 .
C. Đường tròn tâm I 3; 2
  , bán kính R  5.
D. Đường tròn tâm I  2  ; 
1 , bán kính R  5 .
Câu 94: Xét các số phức z thỏa điều kiện z  3 2i  5 . Trong mặt phẳng tọa độ Oxy , tập hợp các điểm biểu
diễn số phức w z 1 i là?
A. Đường tròn tâm I 4; 
3 , bán kính R  5 .
B. Đường tròn tâm I  4  ; 
3 , bán kính R  5 .
C. Đường tròn tâm I 3; 2
  , bán kính R  5.
D. Đường tròn tâm I  2  ; 
1 , bán kính R  5 . Lời giải Chọn A Gọi M  ;
x y là điểm biểu diễn số phức z x yi  , x y   . 2 2
Ta có z  3 2i  5  w 1  i  3  2i  2  x yi  4  3i  6   x  4   y  3  25 .
Vậy tập hợp điểm cần tìm là đường tròn tâm I 4; 
3 , bán kính R  5 .
Câu 95: Số phức z    i2018 1
có phần thực bằng A. 1. B. 2019 2 . C. 1009 2  . D. 0 .
Câu 96: Số phức z    i2018 1
có phần thực bằng A. 1. B. 2019 2 . C. 1009 2  . D. 0 . Lời giải Chọn D 1009 504 2018 2 1009 Ta có zi   i        i 1009   i  2 i  1009 1 1 2 2 . .  2 .i  
Suy ra z có phần thực bằng 0 .
Câu 97: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
4z  4z  37  0 . Trên mặt phẳng 0
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0  1   1   1   1  A. M 3; . B. M 3; . C. M 3; . D. M 3; . 2   3   3   1    2   2   2   2  z
Câu 98: Có bao nhiêu số phức z thỏa mãn z  2  3i  5 và là số thuần ảo ? z  2 A. 2 . B. vô số. C. 1. D. 0 .
Câu 99: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
4z  4z  37  0 . Trên mặt phẳng 0
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0  1   1   1   1  A. M 3; . B. M 3; . C. M 3; . D. M 3; . 2   3   3   1    2   2   2   2  Lời giải Chọn D 1 1  1  Ta có z  
 3i nên w iz  3   i M 3  ;  . 0   2 0 2 1  2  z
Câu 100: Có bao nhiêu số phức z thỏa mãn z  2  3i  5 và là số thuần ảo ? z  2 A. 2 . B. vô số. C. 1. D. 0 . Lời giải Chọn C
Ta gọi z  a bi a,b   , z  2 . 2 2
Ta có z  2  3i  5  a  2  b  3  25   1 . 2 2 z a bi a b  2a 2b Mặt khác    i . z  2
a  2  bi a  22  ba  22 2 2  b z là số thuần ảo 2 2
a b  2a  0 2 . z  2 a  1   
a  22  b  32  25 a b  2 b  1  Từ   1 và 2 ta có     . 2 2 2 a  3a  2  0 
a b  2a  0   a  2   b  0  a  1 Vì z  2 nên 
z  11i . b  1 
Câu 101: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
2z  6z  5  0 . Tìm iz ? 0 0 1 3 1 3 1 3 1 3 A. iz    i . B. iz   i . C. iz    i . D. iz   i . 0 2 2 0 2 2 0 2 2 0 2 2
Câu 102: Cho số phức z a bi , a,b   thỏa mãn z 1 3i z i  0 . Tính S a  3b . 7 7 A. S  5 . B. S  . C. S   . D. S  5 . 3 3 Câu 103: Cho
x, y 0;   , x y  1. Biết
m a;b thì phương trình  2 x y 2 5 4
5 y  4x  40xy m có nghiệm thực. Tính T  25a 16b . A. T  829 . B. T  825 . C. T  816 . D. T  820 .
Câu 104: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
2z  6z  5  0 . Tìm iz ? 0 0 1 3 1 3 1 3 1 3 A. iz    i . B. iz   i . C. iz    i . D. iz   i . 0 2 2 0 2 2 0 2 2 0 2 2
Hướng dẫn giải Chọn B 3 1 2
2z  6z  5  0  z   i . 0 2 2 1 3 Khi đó iz   i . 0 2 2
Câu 105: Cho số phức z a bi , a,b   thỏa mãn z 1 3i z i  0 . Tính S a  3b . 7 7 A. S  5 . B. S  . C. S   . D. S  5 . 3 3
Hướng dẫn giải Chọn A
Ta có : z 1 3i z i  0 2 2
a bi 1 3i i a b  0  a    2 2 1
b  3  a b i  0 a  1  a  1  a 1  0  a  1           b   3    4 . 2 2 b
  3  a b  0 2 
 1 b b  3   b    1 b   b  32 2  3 
Vậy S a  3b  1   4  5  . Câu 106: Cho
x, y 0;   , x y  1. Biết
m a;b thì phương trình  2 x y 2 5 4
5 y  4x  40xy m có nghiệm thực. Tính T  25a 16b . A. T  829 . B. T  825 . C. T  816 . D. T  820 .
Hướng dẫn giải Chọn B 2 2 3 Ta có: mxy  3 3 25 20 x
y  56xy 25 xy 20  x y
3xy x y           56xy    x y2 1   xy2 2 25
 4xy  20  25t  4t  20 , với t xy   . 4 4  1 
Xét hàm số f t  2
 25t  4t  20 trên đoạn 0;  . 4    2
Ta có: f t   50t  4 . Xét f t   0  t  . 25  2  496  1  329
Ta có: f 0  20 , f    và f    .  25  25  4  16  496 329  496 329
Do đó để phương trình có nghiệm thực thì m  ;   a  ,b  suy ra 25 16    25 16 T  825 .
Câu 107: Gọi z và z  4  2i là hai nghiệm của phương trình 2
az bz c  0 ( a,b, c   , a  0 ). Tính 1 2
T z  3 z . 1 2 A. T  6 . B. T  4 5 . C. T  2 5 . D. T  8 5 . S
Câu 108: Gọi z và z  4  2i là hai nghiệm của phương trình 2
az bz c  0 ( a,b, c   , a  0 ). Tính 1 2
T z  3 z . 1 2 A A. T  6 . B. T  4 5 . C. T  2 5 . D. T  8 5 . D Lời giải O Chọn D B C
Phương trình bậc hai với hệ số thực có hai nghiệm phức là hai số phức liên hợp.
Do đó z  4  2i . Khi đó z z  2 5  T z  3 z  8 5 . 1 1 2 1 2
Câu 109: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  7  0 . Tính giá trị của biểu thức 1 2
P z z . 1 2 A. P  2 3 . B. P  14 . C. P  7 . D. P  14 .
Câu 110: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  7  0 . Tính giá trị của biểu thức 1 2
P z z . 1 2 A. P  2 3 . B. P  14 . C. P  7 . D. P  14 . Lời giải Chọn D  3 47 x   i  4 4 Ta có: 2
2z  3z  7  0  
P z z  14 . 1 2  3 47 x   i  4 4
Câu 111: Gọi z là nghiệm có phần ảo âm của phương trình 2
z  4z  20  0 . Tìm tọa độ điểm biểu diễn 1 của z . 1 A. M  2  ;  4 . B. M  4  ;  2 .
C. M 2;  4 .
D. M 4;  2 .
Câu 112: Gọi z là nghiệm có phần ảo âm của phương trình 2
z  4z  20  0 . Tìm tọa độ điểm biểu diễn 1 của z . 1 A. M  2  ;  4 . B. M  4  ;  2 .
C. M 2;  4 .
D. M 4;  2 . Lời giải Chọn C
z  2  4i Có 2
z  4z  20  0  
z  2  4i . z  2  4i 1 
Vậy điểm biểu diễn của số phức z là M 2;  4 . 1
Câu 113: Định tất cả các số thực m để phương trình 2
z  2z 1 m  0 có nghiệm phức z thỏa mãn z  2 .
A. m  1,m  9 . B. m  3  . C. m  3
 ,m  1,m  9 .
D. m  3,m  9 .
Câu 114: Định tất cả các số thực m để phương trình 2
z  2z 1 m  0 có nghiệm phức z thỏa mãn z  2 .
A. m  1,m  9 . B. m  3  .
C. m  3,m  1,m  9 .
D. m  3,m  9 . Lời giải Chọn C
Ta có:   4  41 m  4m . z  1 m
TH1:   0  m  0 . Phương trình có nghiệm là  . z  1 m  Nếu 1 m  2 
m  1  m  1.  m  3
Nếu 1 m  2    m  9 .  m  1  
TH2:   0  m  0 . Phương trình có nghiệm z  1 không thỏa mãn.
z  1 m.i
TH3:   0  m  0 . Khi đó nghiệm của phương trình là  .
z  1 m.i
Do đó z  2  1 m  4  m  3  .
Câu 115: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  2  0 . Giá trị của biểu thức 2 2 zz 1 2 1 2 bằng A. 8 . B. 0 . C. 4 . D. 8i .
Câu 116: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  2  0 . Giá trị của biểu thức 2 2 zz 1 2 1 2 bằng A. 8 . B. 0 . C. 4 . D. 8i . Lời giải. Chọn C
z  1  i Ta có : 2
z  2z  2  0 1   . z  1  i  2 Vậy 2 2 zz  4 . 1 2 1 1
Câu 117: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  4  0 . Tính w    iz z . 1 2 1 2 z z 1 2 3 3 3 3 A. w   2i . B. w   2i .
C. w  2  i .
D. w    2i . 4 2 2 4 1 1
Câu 118: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  4  0 . Tính w    iz z . 1 2 1 2 z z 1 2 3 3 3 3 A. w   2i . B. w   2i .
C. w  2  i .
D. w    2i . 4 2 2 4 Lời giải Chọn A 3
Theo định lý Viét ta có z z  , z z  2 . 1 2 2 1 2 1 1 z z 3 w    iz z 1 2   iz z   2i . 1 2 z z 1 2 z z 4 1 2 1 2
Câu 119: Trong mặt phẳng tọa độ Oxy , Gọi A , B , C lần lượt là các điểm biểu diễn số phức 1 2i , 4  4i , 3
i . Số phức biểu diễn trọng tâm tam giác ABC là A. 1 3i . B. 1 3i .
C. 3  9i . D. 3  9i .
Câu 120: Trong mặt phẳng tọa độ Oxy , Gọi A , B , C lần lượt là các điểm biểu diễn số phức 1 2i , 4  4i , 3
i . Số phức biểu diễn trọng tâm tam giác ABC là A. 1 3i . B. 1 3i .
C. 3  9i . D. 3  9i . Lời giải Chọn B Ta có A 1  ; 2   , B 4; 4   , C 0; 3
  nên trọng tâm G của tam giác ABC có tọa độ là
G 1;3 . Do đó, số phức biểu diễn điểm G là 1 3i .
Câu 121: Gọi z , z là hai nghiệm phức của phương trình 2
z  z  2  0 . Tìm phần ảo của số phức 1 2
w  i z i z  2018   1 2  . A. 1009 2 . B. 1009 2  . C. 1008 2 . D. 1008 2  .
Câu 122: Gọi z , z là hai nghiệm phức của phương trình 2
z  z  2  0 . Tìm phần ảo của số phức 1 2
w  i z i z  2018   1 2  . A. 1009 2 . B. 1009 2  . C. 1008 2 . D. 1008 2  . Lời giải Chọn B
Theo định lí Viet ta có: z z  1; z .z  2 . 1 2 1 2
w  i z i z  2018    1
  i z z  2018  z z     1 2   1 2 1 2   2018 1 i . 1009  2 1009  2018 1 i  i      i 1009 1008 1009 1 2  2  .i .i  2  .i   .
Câu 123: Tìm phần thực, phần ảo của số phức z , biết z là một căn bậc hai của w  221  60i và có phần
thực lớn hơn phần ảo.
A. Phần thực bằng 15 , phần ảo bằng 2  .
B. Phần thực bằng 2
 , phần ảo bằng 15 .
C. Phần thực bằng 15 , phần ảo bằng 2  .
D. Phần thực bằng 15 , phần ảo bằng 2 .
Câu 124: Tìm phần thực, phần ảo của số phức z , biết z là một căn bậc hai của w  221 60i và có phần
thực lớn hơn phần ảo.
A. Phần thực bằng 15 , phần ảo bằng 2  .
B. Phần thực bằng 2
 , phần ảo bằng 15 .
C. Phần thực bằng 15 , phần ảo bằng 2  .
D. Phần thực bằng 15 , phần ảo bằng 2 . Lời giải
Chọn D
Gọi z a bi a,b   . Ta có z  a bi2 2 2 2
a b  2abi . a  15  2 2
a b  221 b  2  Suy ra   . 2ab 60    a  15   b  2  
Do phần thực của z lớn hơn phần ảo của z nên z  15  2i .
Câu 125: Cho số phức z thỏa mãn điều kiện 1 iz 1 3i  0 . Tìm phần ảo của số phức w  1 iz z . A.i . B. 1. C. 2 . D. 2  i .
Câu 126: Gọi z , z là các nghiệm phức của phương trình 2
z  4z  13  0 . Khi đó z .z z bằng. 1 2 1 2 1 A. 26 . B. 13  13 . C. 13 . D. 13  5 . z 1 z  3i
Câu 127: Có bao nhiêu số phức z thỏa mãn   1? z i z i A. 0 . B. 1. C. 2 . D. 4 .
Câu 128: Cho số phức z thỏa mãn 4 z i  3 z i  10 . Giá trị nhỏ nhất của z bằng 1 5 3 A. . B. . C. . D. 1. 2 7 2
Câu 129: Cho số phức z thỏa mãn điều kiện 1 iz 1 3i  0 . Tìm phần ảo của số phức w  1 iz z . A.i . B. 1. C. 2 . D. 2  i . Lời giải Chọn B 1 3i
1 iz 1 3i  0  z
 2  i z  2  i . 1 i
w  1 iz z  1 i 2  i  2  i  2  i .
Vậy phần ảo của w  1 iz z bằng 1.
Câu 130: Gọi z , z là các nghiệm phức của phương trình 2
z  4z  13  0 . Khi đó z .z z bằng. 1 2 1 2 1 A. 26 . B. 13  13 . C. 13 . D. 13  5 . Lời giải Chọn B
z  2  3i 2
z  4z  13  0   . z  2  3i
Vì 2  3i  2  3i  13 nên z .z z  13  13 . 1 2 1 z 1 z  3i
Câu 131: Có bao nhiêu số phức z thỏa mãn   1? z i z i A. 0 . B. 1. C. 2 . D. 4 . Lời giải Chọn B
Gọi số phức z a bi với a,b   . z 1 2 2 Ta có
 1  z 1  z i  a   2 2
1  b a  b   1
a b  0 z i z  3i 2 2  1 2
a  b   2 3
a  b   1  b  1 z ia  1 Suy ra 
. Vậy z  1 i b  1 
Vậy có 1 số phức thỏa mãn yêu cầu bài toán.
Câu 132: Cho số phức z thỏa mãn 4 z i  3 z i  10 . Giá trị nhỏ nhất của z bằng 1 5 3 A. . B. . C. . D. 1. 2 7 2 Lời giải Chọn D 2
Gọi z a bi với a,b   suy ra 2 2
z a b 2 2 2
Ta có z i a  b   2
1 i z i a  b   1
z  2b 1
z i a  b   2 2
1 i z i a  b  2 2 1
z  2b 1
Theo giả thiết và bất đẳng thức Bnhiacopsky ta có 2 2 2 2 2
10  4 z i  3 z i  4  3 . z i z i  5 2 z  2 2
z  1 suy ra min z  1. z z
Câu 133: Gọi z , z là hai nghiệm phức của phương trình 2
4z  4z  3  0 . Giá trị của biểu thức 1 2  1 2 z z 2 1 bằng. 3 1 1 2 A. . B.  . C. . D.  . 2 2 3 3 z z
Câu 134: Gọi z , z là hai nghiệm phức của phương trình 2
4z  4z  3  0 . Giá trị của biểu thức 1 2  1 2 z z 2 1 bằng. 3 1 1 2 A. . B.  . C. . D.  . 2 2 3 3 Lời giải
Chọn D 2 3 1  2. z zz z  2z z 2 1 2 2 1 2  1 2  4    . z z z z 3 3 2 1 1 2 4
Câu 135: Cho số phức z thỏa mãn   2 1 z
là số thực. Tập hợp các điểm M biểu diễn số phức z là?
A. Hai đường thẳng. B. Parabol.
C. Đường thẳng.
D. Đường tròn. 2 2
Câu 136: Cho ba số phức z , z , z thỏa mãn z z z  0 và z z z  . Mệnh đề nào 1 2 3 1 2 3 1 2 3 3 dưới đây đúng?
A. z z z z z z z z z .
B. z z z z z z z z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
C. z z z z z z z z z .
D. z z z z z z z z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
Câu 137: Cho số phức z thỏa mãn   2 1 z
là số thực. Tập hợp các điểm M biểu diễn số phức z là?
A. Hai đường thẳng. B. Parabol.
C. Đường thẳng.
D. Đường tròn.
Hướng dẫn giải Chọn A 2 2 2
Gọi z x yi x, y   . Khi đó, ta có 1 z  1 x yi   x   2
1  y  2  x   1 yi .  y  0 Do   2 1 z
là số thực nên 2  x   1 y  0   . x 1  0 
Vậy tập hợp các điểm M biểu diễn số phức z là hai đường thẳng x 1  0 và y  0 . 2 2
Câu 138: Cho ba số phức z , z , z thỏa mãn z z z  0 và z z z  . Mệnh đề nào 1 2 3 1 2 3 1 2 3 3 dưới đây đúng?
A. z z z z z z z z z .
B. z z z z z z z z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
C. z z z z z z z z z .
D. z z z z z z z z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
Hướng dẫn giải Chọn A
Do z , z , z đều khác 0 nên ta có 1 2 3
z z z z z z 1 1 1 z z z
z z z 1 2 2 3 3 1    1 2 3    1 2 3    1 vì z z z z z z z .z z .z z .z 8 1 2 3 1 2 3 1 1 2 2 3 3 3 8
z .z z .z z .z  . 1 1 2 2 3 3 3
Lấy mô đun hai vế của   1 ta có
z z z
z z z z z z 1 2 3 1 2 2 3 3 1  z z z 8 1 2 3 3 2 2 2 2 2 2
z z z z z z
z z z
z z z
z z z  0 . 1 2 2 3 3 1 1 2 3 3 1 2 3 3 1 2 3 3
Câu 1: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Cho số phức z thỏa mãn
z  2i z  4i và z  3  3i  1. Giá trị lớn nhất của biểu thức P z  2 là: A. 13 1 . B. 10 1. C. 13 . D. 10 . Lời giải
Chọn C Gọi M  ;
x y là điểm biểu diễn số phức z ta có: 2 2
z  2i z  4i 2
x   y   2 2
x   y  4
y  3 ; z  3  3i  1  điểm M nằm trên đường tròn tâm I 3;3 và bán kính bằng 1. Biểu
thức P z  2  AM trong đó A2;0 , theo hình vẽ thì giá trị lớn nhất của P z  2 đạt 2 2
được khi M 4;3 nên max P  4  2  3  0  13 .
Câu 2: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Trong tập các số phức, cho phương trình 2
z  6z m  0 , m    
1 . Gọi m là một giá trị của m để phương trình   1 có 0
hai nghiệm phân biệt z , z thỏa mãn z .z z .z . Hỏi trong khoảng 0;20 có bao nhiêu giá 1 2 1 1 2 2
trị m   ? 0 A. 13 . B. 11. C. 12 . D. 10 . Lời giải Chọn D
Điều kiện để phương trình  
1 có hai nghiệm phân biệt là:   9  m  0  m  9 .
Phương trình có hai nghiệm phân biệt z , z thỏa mãn z .z z .z thì   1 phải có nghiệm 1 2 1 1 2 2
phức. Suy ra   0  m  9 .
Vậy trong khoảng 0;20 có 10 số m . 0
Câu 3: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Gọi số phức z a bi ,
a,b  thỏa mãn z 1  1 và 1 iz  
1 có phần thực bằng 1 đồng thời z không là số thực. Khi đó . a b bằng : A. . a b  2  . B. . a b  2 . C. . a b  1 . D. . a b  1  . Lời giải Chọn C
Theo giả thiết z 1  1 thì a  2 2 1  b  1.
Lại có 1 i z  
1 có phần thực bằng 1 nên a b  2 .
Giải hệ có được từ hai phương trình trên kết hợp điều kiện z không là số thực ta được
a  1 , b  1 . Suy ra . a b  1 . Trình bày lại
Theo giả thiết z 1  1 thì a  2 2 1  b  1   1 . a b  2
Lại có 1 i z  
1  a b  
1  a b  
1 i có phần thực bằng 1 nên  2 . b  0 
Giải hệ có được từ hai phương trình trên ta được a  1, b  1 . Suy ra . a b  1 .
Câu 4: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Cho số phức z thoả 1 i mãn
là số thực và z  2  m với m   . Gọi m là một giá trị của m để có đúng một số z 0
phức thoả mãn bài toán. Khi đó:  1   1   3   3  A. m  0; . B. m  ;1 . C. m  ; 2 . D. m  1; . 0   0   0   0    2   2   2   2  Lời giải
Chọn D
Giả sử z a bi, a,b   . 1 i 1 i 1 a b a b Đặt: w   
a b  a bi   i . z a bi 2 2 a b    2 2 2 2 a b a b
w là số thực nên: a b   1 . 2
Mặt khác: a  2  bi m  a   2 2 2
b m 2 . Thay  
1 vào 2 được: a  2 2 2 2  a m 2 2
 2a  4a  4  m  0 3 .
Để có đúng một số phức thoả mãn bài toán thì PT 3 phải có nghiệm a duy nhất.  3     0    2 4 2 4  m   0 2
m  2  m  2  1; 
 (Vì m là mô-đun).  2  Trình bày lại
Giả sử z a bi, vì z  0 nên 2 2
a b  0 * . 1 i 1 i 1 a b a b Đặt: w   
a b a b i   i . 2 2   z a bi a b    2 2 2 2 a b a b
w là số thực nên: a b  
1 .Kết hợp * suy ra a b  0 . 2
Mặt khác: a  2  bi m  a   2 2 2
b m 2 .(Vì m là mô-đun nên m  0 ). Thay  
1 vào 2 được: a  2 2 2 2
a m g a 2 2
 2a  4a  4  m  0 3 .
Để có đúng một số phức thoả mãn bài toán thì PT 3 phải có nghiệm a  0 duy nhất. Có các khả năng sau :
KN1 : PT 3 có nghiệm kép a  0 2   0   m  2  0 ĐK:     m  2 . g  0 2  0  4  m  0 
KN2: PT 3 có hai nghiệm phân biệt trong đó có một nghiệm a  0 2   0   m  2  0 ĐK:     m  2 . g  0 2  0  4  m  0   3  Từ đó suy ra m   2  1; . 0    2 
Câu 5: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Trong tập hợp các số phức, 2017
gọi z , z là nghiệm của phương trình 2 z z
 0 , với z có thành phần ảo dương. Cho 1 2 4 2
số phức z thoả mãn z z  1 . Giá trị nhỏ nhất của P z z là 1 2 2017 1 2016 1 A. 2016 1. B. . C. . D. 2017 1. 2 2 Lời giải
Chọn A 2017 Xét phương trình 2 z z   0 4  1 2016 z   i  1 2 2
Ta có:   2016  0  phương trình có hai nghiệm phức  .  1 2016 z   i 2  2 2
Khi đó: z z i 2016 1 2
z z z z z z
z z z z P  2016 1 . 2  1   1 2  1 2 1 Vậy P  2016 1. min
Câu 6: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Gọi S là tập hợp các số z
thực m sao cho với mỗi m S có đúng một số phức thỏa mãn z m  6 và là số thuần z  4
ảo. Tính tổng của các phần tử của tập S . A. 10. B. 0. C. 16. D. 8. Lời giải Chọn D Cách 1: z x iy
x iy x  4  iyx x  4 2  y  4iy
Gọi z x iy với x, y   ta có    z  4 x  4  iy
x  42  yx  42 2 2  y
là số thuần ảo khi x x    y    x  2 2 2 4 0 2  y  4 Mà z m
  x m2 2 6  y  36
Ta được hệ phương trình 2  36  m x     x m  2 2  y  36   4  2m 2 x  36  m 4  2m        2   x  22 2 2  y  4
y  4   x  22 2  36  m     2 y  4   2    4  2m    2 2  36  m  2 36  m 2 36  m Ycbt  4   2  0    2   2 hoặc 2   2 4  2m   4  2m 4  2m
m  10 hoặc m  2  hoặc m  6 
Vậy tổng là 10  2  6  6  8 . Cách 2:   x m  2 2  y  36
Để có một số phức thỏa mãn ycbt thì hpt  có đúng một nghiệm   x  22 2  y  4 
Nghĩa là hai đường tròn C  :  x m2 2
y  36 và C : x  2  y  4 tiếp xúc nhau. 2   2 2 1
Xét C có tâm I 2;0 bán kính R  2 , C có tâm I ;
m 0 bán kính R  6 2   2  1   1  1 2
I I R Rm  2  4 Cần có : 1 2 1 2     m  6  ; 6;10;   2 .
I I R R   m  2  6 1 2 1 2 
Vậy tổng là 10  2  6  6  8 .sss
Câu 7: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Cho hình chóp S.ABCD có
đáy ABCD là hình bình hành tâm O . Gọi M , N , K lần lượt là trung điểm của CD , CB ,
SA . Thiết diện của hình chóp cắt bởi mặt phẳng  MNK  là một đa giác  H  . Hãy chọn khẳng định đúng?
A.H  là một hình thang.
B.H  là một hình bình hành.
C.H  là một ngũ giác.
D.H  là một tam giác. Lời giải
Chọn C Sửa trên hình điểm P thành điểm K nhé
Gọi E MN AC và F PE SO . Trong  SBD qua F kẻ đường thẳng song song với
s MN và lần lượt cắt SB, SD tại H , G . Khi đó ta thu được thiết diện là ngũ giác MNHK . G
Câu 8: (TT Diệu Hiền-Cần Thơ-tháng 10-năm 2017-2018) Cho các số phức z thỏa mãn z i  5 .
Biết rằng tập hợp điểm biểu diễn số phức w iz 1 i là đường tròn. Tính bán kính của đường tròn đó. A. r  22 . B. r  20 . C. r  4 . D. r  5 . Lời giải Chọn D
Gọi w x yi ,  x, y   .
Ta có: w iz 1 i x yi iz 1 i z  ( y 1)  (1 x)i .
Mà z i  5  y 1 xi  5  x   y  2 2 2 1  5 .
Câu 9: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Cho số phức thỏa z  3 . Biết rằng tập hợp
số phức w z i là một đường tròn. Tìm tâm của đường tròn đó. A. I 0  ;1 .
B. I 0;   1 .
C. I 1;0 .
D. I 1;0 . Lời giải Chọn A
Đặt w x yi, x, y  .
Ta có w z i x yi z i z x   y  
1 i z x  1 yi .
Mặt khác ta có z  3 suy ra x    y2 2 1
 9 hay x   y  2 2 1  9 .
Vây tập hợp số phức w z i là đường tròn tâm I 0  ;1 .
Câu 10: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Đường nào dưới đây là tập hợp các điểm
biểu diễn số phức z trong mặt phẳng phức thỏa mãn điều kiện z i z i ?
A. Một đường thẳng.
B. Một đường tròn.
C. Một đường elip.
D. Một đoạn thẳng. Lời giải Chọn A
Gọi z xi y , (với x, y   ) được biểu diễn bởi điểm M  ;
x y trong mặt phẳng tọa độ  xoy .
Ta có z i z i x   y  
1 i x   y   1 i
x   y  2  x   y  2 2 2 1 1
y  0 (phương trình một đường thẳng).
Câu 11: (THTT Số 3-486 tháng 12 năm 2017-2018) Có bao nhiêu số phức z thỏa mãn z z z  1? A. 0 . B. 1. C. 4 . D. 3 . Lời giải Chọn C
Giả sử z x yi  ,
x y    z x yi z z  2x . 2 2  2 2 x y  1  z  1  
x y  1  Bài ra ta có      1 z z  1    2x  1 x      2 1 1 3 Với 2 x   
y  1  y   . 2 4 2 1 3 1 3 1 3 1 3
Do đó có 4 số phức thỏa mãn là z   i , z   i , z    i , z    i . 1 2 2 2 2 2 3 2 2 4 2 2
Câu 12: (THTT Số 3-486 tháng 12 năm 2017-2018) Tập hợp các điểm biểu diễn số phức z thỏa mãn
2 z 1  z z  2 trên mặt phẳng tọa độ là một A. đường thẳng. B. đường tròn. C. parabol. D. hypebol. Lời giải Chọn C
Giả sử z x yi  ,
x y    z x yi z z  2x . Bài ra ta có x   yi x    x  2 2 2 1 2 2 2
1  y  2x  2
  x  2  y   x  2 2 2 2 2 2 1 1
x  2x 1 y x  2x 1  y  4x .
Do đó tập hợp các điểm biểu diễn số phức z thỏa mãn 2 z 1  z z  2 trên mặt phẳng tọa độ là một parabol.
Câu 13: (THTT Số 3-486 tháng 12 năm 2017-2018) Tìm giá trị lớn nhất của 2 2
P z z z z 1 với
z là số phức thỏa mãn z  1. 13 A. 3 . B. 3 . C. . D. 5 . 4 Lời giải
Chọn C
Cách 1: Đặt z a bi a,b   . Do z  1 nên 2 2 a b  1 . Sử dụng công thức: .
u v u v ta có: z z z z   z   a  2 2 2 1 1
1  b  2  2a . 2
z z   a bi2  a bi   a b a    ab bi  a b a     ab b2 2 2 2 2 2 1 1 1 2 1 2  a a
b a  2 2 2 2 (2 1) 2 1  2a 1 (vì 2 2
a b  1 ).
Vậy P  2a 1  2  2a . 1
 TH1: a   . 2
Suy ra P  2a 1 2  2a  2  2a  2  2a  3  4  2  3  3 (vì 0  2  2a  2 ). 1  TH2: a   . 2 2  1  1 13
Suy ra P  2a 1 2  2a   2  2a  2  2a  3   2  2a   3     .  2  4 4 1 7
Đẳng thức xảy ra khi 2  2a   0  a  . 2 8
Cách 2: Đặt z a bi a,b   . Do z  1 nên 2 2
a b  1 . Nhận xét: a  1  ;  1  1 
f a  2a 1 2  2a ,  a  1 1     2
Lập luận như cách 1 được P  2a 1  2  2a   1   f a  2
a 1 2  2a , 1  a  2     2  1 1 2  ,  a  1   2  2a 2 7
Ta có f a  
. Xét f a  0  a  1 1   8 2   , 1  a    2  2a 2 13 7
Lập bbt xét dấu f a ta thấy hàm số đạt giá trị lớn nhất là khi a  . 4 8
Câu 14: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Cho số phức z và w thỏa
mãn z w  3  4i và z w  9 . Tìm giá trị lớn nhất của biểu thức T z w .
A. max T  176 .
B. max T  14 .
C. max T  4 .
D. max T  106 . Lời giải Chọn D
Đặt z x yi x, y   . Do z w  3  4i nên w  3  x  4  yi . 2 2
Mặt khác z w  9 nên z w   x     y   2 2 2 3 2 4
 4x  4 y 12x 16 y  25  9 2 2  2 2
2x  2 y  6x  8 y  28   1 . Suy ra 2 2
T z w
x y  3  x  4  y .
Áp dụng bất đẳng thức Bunyakovsky ta có 2 T   2 2
2 2x  2 y  6x  8 y  25 2 . 2 2 Dấu "  " xảy ra khi 2 2
x y  3  x  4  y . Từ   1 và 2 ta có 2
T  2.28  25   106  T  106 . Vậy MaxT  106 .
Câu 15: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Trong mặt phẳng phức,
gọi A , B , C , D lần lượt là các điểm biểu diễn số phức z  1
  i , z  1 2i , z  2  i , 1 2 3
z  3i . Gọi S là diện tích tứ giác ABCD . Tính S . 4 17 19 23 21 A. S  . B. S  . C. S  . D. S  . 2 2 2 2 Lời giải Chọn A Ta có z  1
  i A 1;1 , z  1 2i B 1; 2 , z  2  i C 2; 1  , z  3
i D 0; 3 4   3   2   1   y B 2 A 1 1 x 2 1 O 1 C 3  D   AC  3; 2
   AC  13 , n  2;3 là véc tơ pháp tuyến của AC , phương trình AC : 2  x   1  3 y  
1  0  2x  3y 1  0 .
Khoảng cách từ B đến AC là: 2  3.2 1 7 1 1 7 7
d B; AC     Sd B AC AC   . ABC   ; . . 13. 13 13 2 2 13 2 0  9 1 10
Khoảng cách từ D đến AC là: d  ; D AC    13 13 1 1 10  S  .d D AC AC   . ADC   ; . . . 13 5 2 2 13 7 17 Vậy S SS   5  . ABC ADC 2 2
Câu 16: (Đề tham khảo BGD năm 2017-2018) Cho số phức z a bi a,b   thỏa mãn
z  2  i z 1 i  0 và z  1. Tính P a b . A. P  1  . B. P  5 . C. P  3 . D. P  7 . Lời giải Chọn D
z  2  i z 1 i  0  a  2  b  
1 i z i z 2 2 a 2 z    
a  2  a b     1     2 2 b 1  z   b
 1  a b 2  Lấy  
1 trừ 2 theo vế ta được a b 1  0  b a 1. Thay vào   1 ta được a  2  1 do z  1 2 2   
a  2  a  a   1  
a  3 . Suy ra b  4 . 2
a  2a  3  0 
Do đó z  3  4i có z  5  1 (thỏa điều kiện z  1).
Vậy P a b  3  4  7 .
Câu 1: (THTT Số 4-487 tháng 1 năm 2017-2018) Cho số phức z thoả mãn z  3  4i  5 . Gọi M và 2 2
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P z  2  z i . Tính môđun
của số phức w M mi . A. w  1258 . B. w  1258 .
C. w  2 314 .
D. w  2 309 . Lời giải Chọn B
Giả sử z a bi ( a,b   ). z   i
 a  2  b  2 3 4 5 3 4  5 (1). 2 2 P z z ia 2 bab 2 2 2 2 2 1           
 4a  2b  3(2).   Từ (1) và (2) ta có 2 a    P 2 20 64 8
a P  22P 137  0 (*).
Phương trình (*) có nghiệm khi 2   4
P 184P 1716  0
 13  P  33  w  1258 .
Câu 2: (THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018) Cho số phức z , biết rằng các điểm biểu
diễn hình học của các số phức z ; iz và z i z tạo thành một tam giác có diện tích bằng 18 . Mô
đun của số phức z bằng A. 2 3 . B. 3 2 . C. 6 . D. 9 . Lời giải Chọn C
Gọi z a bi , a,b   nên iz ai b , z i z a bi b ai a b  a bi  
Ta gọi Aa,b , B  ,
b a , C a  ,
b a b nên AB b
  a, a b , AC  , b a 1   1 1 S   AB, AC 2 2  a b   2 2
a b   18 2 2  a b  6 . 2   2 2
Câu 3: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Cho số phức z thỏa mãn z  2 .
Biết rằng tập hợp các điểm biểu diễn số phức w  3  2i  2  iz là một đường tròn. Bán kính
R của đường tròn đó bằng ? A. 7 . B. 20 . C. 2 5 . D. 7 . Lời giải Chọn C w  3  2i
Ta có w  3  2i  2  iz z
. Đặt w x yi  , x y   . 2  i
x yi  3  2i Khi đó z  . 2  i
x yi  3  2i
x  3   y  2i
x  3   y  2 i Ta có z  2   2   2   2 2  i 2  i 2  i
x  3   y  2 i  2 2  i x  3   y  2 i  2 5   x     y     2 2 2 3 2 2 5 .
Vậy tập hợp các điểm biểu diễn số phức w  3  2i  2  iz là một đường tròn có bán kính R  2 5 .
Câu 4: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Cho số phức z thỏa mãn
4 z i  3 z i  10 . Giá trị nhỏ nhất của z bằng: 1 5 3 A. . B. . C. . D. 1. 2 7 2 Lời giải Chọn D
Gọi z a bi a,b   . Khi đó: 2 2 2 2
4 z i  3 z i 2 
a  b   2 4 1
 3 a  b   1   2 2   2
a  b   2 4 3
1  a  b   1     2 2 10
25 2 z  2  z 1. 24 7 24 7
Vậy giá trị nhỏ nhất của z là 1, đạt khi a  ; b  hay z   i . 25 25 25 25
Câu 5: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Trong mặt phẳng tọa độ Oxy , gọi M , N , P
lần lượt là các điểm biểu diễn các số phức z  1 i , z  8  i , z  1 3i . Khẳng định nào sau 1 2 3 đây đúng?
A. Tam giác MNP cân.
B. Tam giác MNP đều.
C. Tam giác MNP vuông.
D. Tam giác MNP vuông cân. Lời giải
Chọn C
M là điểm biểu diễn số phức z  1  i nên tọa độ điểm M là 1;  1 . 1
N là điểm biểu diễn số phức z  8  i nên tọa độ điểm N là 8;  1 . 2
P là điểm biểu diễn số phức z  1  3i nên tọa độ điểm P là 1;  3 . 3     MN.MP  0 
Ta có MN  7;0 , MP  0; 4 nên  
 hay tam giác MNP vuông tại M và MN MP   không phải tam giác cân. z 1 z  3i
Câu 6: (THTT số 5-488 tháng 2 năm 2018) Có bao nhiêu số phức z thỏa mãn   1? z i z i A. 0 . B. 1. C. 2 . D. 4 . Lời giải Chọn B
Gọi z a bi a,b   . Ta có: 2 2
z 1  z i 2 2   a  
1  b a  b    1  2  a 1  2  b 1 a  1        .
z  3i z i 2 2  2 2 
a  b  3  a  b   1 6
b  9  2b 1 b  1   
Vậy có một số phức thỏa mãn là z  1 i .
Câu 1: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Số phức z a bi ( với a , b là số
nguyên) thỏa mãn 1 3iz là số thực và z  2  5i  1. Khi đó a b là A. 9 . B. 8 . C. 6 . D. 7 . Lời giải Chọn B
Ta có: 1 3iz  1 3ia bi  a  3b  b  3ai .
Vì 1 3iz là số thực nên b  3a  0  b  3a   1 . 2 2
z  2  5i  1  a  2  5  bi  1  a  2  5  b  1 2 .
a  2  b  6 2 2 Thế  
1 vào 2 ta có: a  2  5  3a  1 2
 10a  34a  28  0   7 . a  (loaïi)  5
Vậy a b  2  6  8 .
Câu 2: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Cho hai số phức z , z thỏa mãn 1 2
z  5  5, z 1 3i z  3  6i . Giá trị nhỏ nhất của z z là 1 2 2 1 2 5 7 1 3 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn A
Giả sử z a b i a , b   , z a b i a ,b   . 2 2 2  2 2  1 1 1  1 1  Ta có
z  5  5  a  5  b  25 . Do đó, tập hợp các điểm A biểu diễn cho số phức z là 1 2 2 1 1 1
đường tròn C   x  2 2 : 5
y  25 có tâm là điểm I  5
 ;0 và bán kính R  5. 2 2 2 2
z 1 3i z  3  6i  a 1  b  3  a  3  b  6 2   2   2   2  2 2
 8a  6b  35  0 . Do đó tập hợp các điểm B biểu diễn cho số phức z là đường thẳng 2 2 2
 : 8x  6 y  35  0 .
Khi đó, ta có z z AB . 1 2 8. 5    6.0  35 5 Suy ra z zAB
d I;   R   5  . 1 2 min min 2 2 8  6 2 5
Vậy giá trị nhỏ nhất của z z là . 1 2 2
Câu 3: (THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức w x yi ,  x , y   thỏa mãn điều kiện 2
w  4  2 w . Đặt P   2 2
8 x y  12 . Khẳng định nào dưới đây đúng?
A. P    w  2 2 2 .
B. P    w  2 2 2 .
C. P    w  2 4 .
D. P    w  2 2 4 .
Đáp án A và B có giá trị như nhau nên em đã sửa đáp án A. A. P     2 2 w 2 .
B. P    w  2 2 2 .
C. P    w  2 4 .
D. P    w  2 2 4 . Lời giải Chọn B Ta có 2
w  4   x yi2  4 2 2
x y  2xyi  4  w
  x y  2 2 2 2 2 2 4 4  4x y . Do đó 2 2
w  4  2 w   x y  2 2 2 2 2 2 2 4
 4x y  2 x y   2 2 x y   2 2  x y   2 2 4 4 4 x y  4 4 2 2
x y x y   2 2 x y  2 2   x y   2 2 2 8 16 4 4 x y  4 4 2 2
x y x y   2 2
x y     2 2 2 4
4 8 x y  12  0 2
  x y 2 2 2   2 2
x y     2 2 4
4 8 x y  12  0   2 2
x y     2 2 2
8 x y  12  0
  x y  
   x y  2 2 2 2 2 8 12 2
P    w  2 2 2 .
Câu 4: (THPT Chuyên Tiền Giang-lần 1 năm 2017-2018) Cho số phức z a bi a, b   thỏa mãn
z 1 3i z i  0 . Tính S a  3b . 7 7 A. S  . B. S  5 . C. S  5 . D. S   . 3 3 Lời giải Chọn B
Ta có z 1 3i z i  0 2 2
a bi 1 3i i a b  0 a 1  0   a    2 2 1
b  3  a b i  0   2 2 b   3  a b  a  1 a  1     b   3    4  S  5  .   b     b  3  2 2  1 b   3
Câu 5: (THPT Chuyên Tiền Giang-lần 1 năm 2017-2018) Biết số phức z thỏa mãn z  3  4i  5 và 2 2
biểu thức T z  2  z i đạt giá trị lớn nhất. Tính z . A. z  33 . B. z  50 . C. z  10 . D. z  5 2 . Lời giải Chọn D 2 2
Đặt z x yi , theo giả thiết z  3  4i  5   x  3   y  4  5 . C  2 2
Ngoài ra T z  2  z i  4x  2 y  3  T  0  đạt giá trị lớn nhất. 23  T
Rõ ràng C  và  có điểm chung do đó
 5  13  T  33. 2 5
Vì T đạt giá trị lớn nhất nên T  33 suy ra 4x  2 y  30  0  y  15  2x thay vào C  ta được 2
5x  50x 125  0  x  5  y  5 . Vậy z  5 2 .
Câu 6: (THTT số 6-489 tháng 3 năm 2018) Cho hai điểm A , B là hai điểm biểu diễn hình học số phức
theo thứ tự z , z khác 0 và thỏa mãn đẳng thức 2 2
z z z z . Hỏi ba điểm O , A , B tạo 0 1 0 1 0 1
thành tam giác gì? ( O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
A. Cân tại O .
B. Vuông cân tại O . C. Đều.
D. Vuông tại O . Lời giải Chọn C
Theo giả thiết suy ra: OA z , OB z và AB z z . 0 1 1 0 Ta có: 2 2
z z z z 2 2
z z z z  0   z z  2 2
z z z z  0 . 0 0 1 1 0 1 0 0 1 1  0 1 0 1 3 3 3 3
z z  0  z  z z z OA OB . 0 1 0 1 0 1 2
Xét  z z 2 2 2
z z  2z z  z z z zz . z 1 0 0 1 0 1 0 1 1 0 1 0 2  AB  .
OA OB AB OB .
Vậy AB OB OA hay tam giác OAB là tam giác đều.
Câu 7: (THTT số 6-489 tháng 3 năm 2018) Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất z i của P
, với z là số phức khác 0 thỏa mãn z  2 . Tính 2M m . z 3 5
A. 2M m  .
B. 2M m  .
C. 2M m  10 .
D. 2M m  6 . 2 2 Lời giải Chọn B z i z i z i 1 3 3 P     1 
. Dấu bằng xảy ra khi z  2i . Vậy M  . z z z z 2 2 z i z i z i z i 1 1 P      1 
. Dấu bằng xảy ra khi z  2  i . z z z z z 2 1 Vậy m  . 2 5
Vậy 2M m  . 2
Câu 8: (THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức z a bi a,b  , a  0 thỏa
mãn z 1 2i  5 và .
z z  10 . Tính P a b . A. P  4 . B. P  4 . C. P  2 . D. P  2 . Lời giải Chọn A    a  2
1  b  22  5
Từ giả thiết z 1 2i  5 và .
z z  10 ta có hệ phương trình  2 2
a b  10 
a  2b  5
a  2b  5  a  3 a  1        hay 
(loại). Vậy P  4 . 2 2 a b  10  2b  5  2 2  b  10  b  1  b  3 
Câu 9: (THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018) Cho số phức z thỏa mãn z 1 i  1, số phức
w thỏa mãn w  2  3i  2 . Tìm giá trị nhỏ nhất của z w . A. 13  3 . B. 17  3. C. 17  3 . D. 13  3 . Lời giải Chọn B Gọi M  ;
x y biểu diễn số phức z x iy thì M thuộc đường tròn C có tâm I 1;1 , bán 1   1  kính R  1. 1
N x ; y biểu diễn số phức w x  iy thì N thuộc đường tròn C có tâm I 2; 3  , bán 2   2 
kính R  2 . Giá trị nhỏ nhất của z w chính là giá trị nhỏ nhất của đoạn MN . 2  Ta có I I  1; 4 
I I  17  R R  C và C ở ngoài nhau. 2  1  1 2   1 2 1 2  MN
I I R R  17  3 min 1 2 1 2
Câu 10: (THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) Cho các số phức z  2   i , 1 2 2
z  2  i và số phức z thay đổi thỏa mãn z zz z
 16 . Gọi M và m lần lượt là giá 2 1 2
trị lớn nhất và giá trị nhỏ nhất của z . Giá trị biểu thức 2 2 M m bằng A. 15 . B. 7 . C. 11. D. 8 . Lời giải Chọn D
Giả sử z x yi x, y   . 2 2 2 2 Ta có: z zz z
 16  x yi  2  i x yi  2  i  16  x   y  2 2 1  4 . 1 2
Suy ra tập hợp điểm biểu diễn của số phức z là đường tròn tâm số phức I 0  ;1 bán kính R  2 . y 3 1 I 2  O 2 x 1
Do đó m  1, M  3 . Vậy 2 2 M m  8 .
Câu 11: [2D4 -3](THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) Cho các số p , q thỏa 1 1
mãn các điều kiện: p  1, q  1, 
 1 và các số dương a , b . Xét hàm số: p q p 1 y x  
x  0 có đồ thị là C . Gọi S là diện tích hình phẳng giới hạn bởi C , trục 1 
hoành, đường thẳng x a , Gọi  S là diện tích hình phẳng giới hạn bởi C  , trục tung, 2 
đường thẳng y b , Gọi  S  là diện tích hình phẳng giới hạn bởi trục hoành, trục tung và hai
đường thẳng x a , y b . Khi so sánh S S và S ta nhận được bất đẳng thức nào trong các 1 2
bất đẳng thức dưới đây? y x a p 1 y x   b y b S2 S1 O a x p q a b p 1  q 1 a b p 1  q 1 a b p q a b A.   ab B.   ab . C.   ab . D.   ab . p q p 1 q 1 p 1 q 1 p q Lời giải Chọn D
Ta có: S S S . 1 2 b  1  a 1  b a p p   b 1    p 1  q q y   y b S    x a p 1 x dx   ; p 1
S   y   dy      . 1       p p 2   1   q q 0       0 0 1 0  p 1     0 1 p 1 1 Vì: 1     q . p 1 p 1 1 1 1 p q p q a b Vậy   ab . p q
Câu 12: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Gọi  H  là tập hợp các điểm biểu diễn số
phức z thỏa 1  z 1  2 trong mặt phẳng phức. Tính diện tích hình  H  . A. 2 . B. 3 . C. 4 . D. 5 . Lời giải Chọn B
Đặt z x yi , z 1  x 1 yi   x  2 2 1  y .
Do đó 1  z 1  2    x  2 2 1
1  y  2    x  2 2 1 1  y  4 .
Tập hợp các điểm biểu diễn số phức z là hình phẳng nằm trong đường tròn tâm I 1;0 bán
kính R  2 và nằm ngoài đường tròn I 1;0 bán kính r  1. Diện tích hình phẳng 2 2
S   .2   .1  3 .
Câu 13: (THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018) Có bao nhiêu số phức z thỏa mãn điều 2 kiện 2
z z z ? A. 1. B. 4 . C. 2 . D. 3 . Lời giải
Chọn D
Đặt z a bi a,b   . 2 Ta có 2
z z z    2 2 2 a bi
a b a bi 2 2
 2abi b b a bi b  0  2ab b    1      a   2 2
b b a   2  2
2b a  0  
b  0  a  0  z  0 . 1 1 1 1  a    b    z    i . 2 2 2 2
Vậy có 3 số phức thỏa ycbt.
Câu 14: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Cho hai số phức z , z có điểm 1 2
biểu diễn lần lượt là M , M cùng thuộc đường tròn có phương trình 2 2
x y  1 và 1 2
z z  1. Tính giá trị biểu thức P z z . 1 2 1 2 3 2 A. P  . B. P  2 . C. P  . D. P  3 . 2 2 Lời giải Chọn D
Ta có M , M cùng thuộc đường tròn tâm O 0;0 bán kính R  1 . 1 2
Vì z z  1 nên suy ra M M  1. Vậy tam giác OM M là tam giác đều cạnh bằng 1. 1 2 1 2 1 2
Gọi H là trung điểm của M M thì OH là trung tuyến của tam giác đều OM M có cạnh 1 2 1 2 1. 3 3 bằng 1. Suy ra OH   . 2 2
   3
Ta có P z zOM OM
 2OH  2OH  2.  3. 1 2 1 2 2 1 x
Câu 15: (SGD Bắc Giang – năm 2017 – 2018) Cho
dx a b 2 
, với a , b là các số 2 1 3x  9x 1 3
hữu tỉ. Khi đó, giá trị của a là 26 26 27 25 A.  . B. . C. . D.  . 27 27 26 27 Lời giải Chọn B 1 1 1 3 x  2  26 32 Ta có: dx x    2
3x  9x 1 3 dx x    2 9x  2 1   2  . 2 27 1 27 27 1 3x  9x 1 1   3 3 3
Câu 16: (SGD Bắc Giang – năm 2017 – 2018) Cho số phức z thỏa mãn z  2z  7  3i z . Tính z . 13 25 A. 3. B. . C. . D. 5 . 4 4 Lời giải Chọn D
Giả sử z x yi x, y   . Ta có: 2 2 z  2z  7
  3i z
x y  2x  2 yi  7
  x   y  3i 2 2 
x y  2x  7  xx  4     . Vậy z  5 .  2 y y  3 y  3  
Câu 17: (SGD Bắc Giang – năm 2017 – 2018) Cho hai số phức z , w thỏa mãn
z  3  2i  1  
. Tìm giá trị nhỏ nhất P
của biểu thức P z w . min
w 1 2i w  2  i   3 2  2 5 2  2 3 2  2 A. P  . B. P  2 1. C. P  . D. P  . min 2 min min 2 min 2 Lời giải Chọn C
Giả sử z a bi ; w x yi a, ,
b x, y   . Ta có 2 2
z  3  2i  1  a  3  b  2  1 . Suy ra tập hợp điểm M biểu diễn số phức z là hình
tròn tâm I 3;2 , bán kính R  1. 2 2 2 2
w 1 2i w  2  i   x  
1   y  2   x  2   y   1
x y  0 . Suy ra tập hợp
điểm N biểu diễn số phức w là nửa mặt phẳng giới hạn bởi đường thẳng  : x y  0 (tính cả
bờ đường thẳng) (hình vẽ) y 2 I O 3 x 5
Ta có d I,  
. Gọi H là hình chiếu của I trên  . 2 5 2 5 2
Khi đó z w MN d I,   R  1. Suy ra P  1 . 2 min 2
Câu 18: (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho hai số phức z , z thỏa mãn 1 2
z 1 i  2 và z iz . Tìm giá trị lớn nhất m của biểu thức z z 1 2 1 1 2
A. m  2 2  2 . B. m  2 1. C. m  2 2 . D. m  2 . Lời giải Chọn A
Gọi z x yi ( x , y   ), khi đó theo giả thiết của đề bài ta có z   y xi . 1 2 2 2
Khi đó z 1 i  2  x 1  y 1  4 . 1    
Vì vậy tồn tại t   để x  1
  2 sin t và y  1 2 cos t . 2 2 2 Do đó z zx yy x   2 2 2 x y  1 2       
 2 6  4 sin t  cos t  
  12  8 2 sin t     12  8 2 .  4 
Do đó m  12  8 2  2 2  2 .
Câu 19: Cho số phức z a bi ( a , b là các số thực ) thỏa mãn z z  2z i  0 . Tính giá trị của biểu thức 2
T a b .
A. T  4 3  2 .
B. T  3  2 2 .
C. T  3  2 2 .
D. T  4  2 3 .
Câu 20: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Cho số phức z a bi ( a , b là các số thực
) thỏa mãn z z  2z i  0 . Tính giá trị của biểu thức 2
T a b .
A. T  4 3  2 .
B. T  3  2 2 .
C. T  3  2 2 .
D. T  4  2 3 . Lời giải Chọn C
Ta có z z  2z i  0  a bia bi  2a bi  i  0 2 2 2 2 2 2 2 2
a a b  2a b a b i  2bi i  0  a a b  2a b a b i  2bi i  0 2 2 
a a b  2a  0 2 2
a a b  2a   2 2
b a b  2b   1 i  0   2 2 b
a b  2b 1  0  a  0 a  0       2b 1 . 2 b
b  2b 1  0 b      b  2b 1 b   2b 1    b b    
b  1 2 . Suy ra 2
T a b  3  2 2 . b 1   b  0   2
Câu 21: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Có bao nhiêu số phức z thỏa mãn
z  1  3i  3 2 và  z i2 2 là số thuần ảo? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C 2 2
Giả sử z x yi  ,
x y   . Khi đó z 1  3i  3 2   x   1
  y  3  18   1 .
z i2  x   y   2
i  x   y  2 2 2 2 2
 2x y  2i   . x y  2 2 Theo giả thiết ta có 2
x   y  2  0   .
x    y  2 
Với x y  2 thay vào   1 ta được phương trình 2
2 y  0  y  0  x  2  z  2 . 1  y 1 5 
Với x   y  2 thay vào   1 ta được phương trình 2
2 y  4 y 8  0    y 1 5 
z  3  5  1 5 i 2     .  z  3   5  1 5 i 3    
Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Câu 22: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Giả sử z , z là hai nghiệm 1 2
phức của phương trình 2  i z z  1 2i z  1 3i và z z  1. Tính M  2z  3z . 1 2 1 2 A. M  19 . B. M  25 . C. M  5 . D. M  19 . Lời giải Chọn D 2 2 2
Từ giả thiết, ta có 2 z  
1   z  2i . z  10 2 z  1  z 2      . z  10   4 2
 5 z  5 z 10  0  z  1 (vì z  0 ).
Gọi z x y i và z x y i . Ta có z z  1 nên 2 2 2 2
x y x y  1. 1 1 1 2 2 2 1 2 1 1 2 2 2 2 1
Mặt khác, z z  1 nên  x xy y
 1. Suy ra x x y y  . 1 2   1 2  1 2 1 2 1 2 2 2 2
Khi đó M  2z  3z  2x  3x  2 y  3y 1 2   1 2  1 2  4  2 2
x y   9 2 2 y y
12 x x y y 1 1 1 2   1 2 1 2  Vậy M  19 .
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Cho z , z là hai trong các số phức z thỏa mãn điều 1 2
kiện z  5  3i  5 , đồng thời z z  8 . Tập hợp các điểm biểu diễn của số phức w z z 1 2 1 2
trong mặt phẳng tọa độ Oxy là đường tròn có phương trình nào dưới đây? 2 2  5   3  9 2 2 A. x   y       .
B.x 10   y  6  36 .  2   2  4 2 2 2 2  5   3 
C.x 10   y  6  16 . D. x   y   9     .  2   2  Lời giải
Chọn B
Gọi A , B , M là các điểm biểu diễn của z , z , w . Khi đó A , B thuộc đường tròn 1 2
C   x  2   y  2 : 5 3
 25 và AB z z  8 . 1 2
C  có tâm I 5;3 và bán kính R  5 , gọi T là trung điểm của AB khi đó T là trung điểm của OM và 2 2 IT
IA TA  3 .
Gọi J là điểm đối xứng của O qua I suy ra J 10;6 và IT là đường trung bình của tam giác
OJM , do đó JM  2IT  6 . Vậy
M thuộc đường tròn tâm
J bán kính bằng 6 và có phương trình
x  2   y  2 10 6  36 .
Câu 2: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Biết số phức z có
phần ảo khác 0 và thỏa mãn z  2  i  10 và .
z z  25 . Điểm nào sau đây biểu diễn số phức z trên?
A. P 4;  3 .
B. N 3;  4 .
C. M 3; 4 .
D. Q 4; 3 . Lời giải Chọn C
Giả sử z x yi x, y  , y  0 .
Ta có z  2  i  10  x yi  2  i  10 2 2
  x  2   y  
1 i  10   x  2   y   1  10 2 2
x y  4x  2 y  5 . Lại có . z z  25 2 2
x y  25 nên 25  4x  2 y  5  2x y  10  y  10  2x x  5  x    x2 2 10 2  25 2
 5x  40x  75  0   . x  3 
+ Với x  5  y  0 , không thỏa mãn vì y  0 .
+ Với x  3  y  4 , thỏa mãn y  0  z  3  4i .
Do đó điểm M 3; 4 biểu diễn số phức z .
Câu 3: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Cho A , B là hai
điểm biểu diễn hình học số phức theo thứ tự z , z khác 0 và thỏa mãn đẳng thức 0 1 2 2
z z z z . Hỏi ba điểm O , A , B tạo thành tam giác gì ( O là gốc tọa độ) ? Chọn phương 0 1 0 1
án đúng và đầy đủ nhất. A. Đều.
B. Cân tại O .
C. Vuông tại O .
D. Vuông cân tại O . Lời giải Chọn A
Do z  0 nên chia 2 vế của đẳng thức cho 2 z , ta được: 1 1 2  z z z 1 3  1 3  0 0 0 1     i z      i z . 0  1 z z z 2 2  2 2   1  1 1   1 3
Đặt z OA a OB z   i z a . 1 0 1 2 2  1 3   1 3  1 3
Lại có z z   
i z z    
i z AB z z    i z a . 0 1 1 1  1  2 2   2 2  0 1 1     2 2 Vậy OAB đều.
Câu 4: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Gọi M và m lần z i
lượt là giá trị lớn nhất và nhỏ nhất của P
, với z là số phức khác 0 và thỏa mãn z M
z  2 . Tính tỷ số . m M M M 3 M 1 A.  5 . B.  3 . C.  . D.  . m m m 4 m 3 Lời giải Chọn B z i Gọi T   T   1 z i . z
Nếu T  1  Không có số phức nào thoả mãn yêu cầu bài toán. i i 1
Nếu T  1  z   z   2  T 1  . T 1 T 1 2 1
Vậy tập hợp điểm biểu diễn số phức T là hình tròn tâm I 1;0 có bán kính R  . 2  3
M OB OI R    2 M     3 . 1  m
m OA OI R    2
Câu 5: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho số phức z thỏa mãn
1 iz  2  1 iz  2  4 2 . Gọi m  max z , n  min z và số phức w m ni . Tính 2018 w A. 1009 4 . B. 1009 5 . C. 1009 6 . D. 1009 2 . Lời giải
Chọn C
Ta có 1  iz  2  1  iz  2  4 2  z  1 i z 1 i  4 .
Gọi M là điểm biểu diễn của số phức z , F 1
 ;1 là điểm biểu diễn của số phức z  1   i và 1   1
F 1;  1 là điểm biểu diễn của số phức z  1  i . Khi đó ta có MF MF  4 . Vậy tập hợp 2   2 1 2
điểm M biểu diễn số phức z là Elip nhận F và F làm hai tiêu điểm. 1 2
Ta có F F  2c  2c  2 2  c  2 . 1 2
Mặt khác 2a  4  a  2 suy ra 2 2 b a c  4  2  2 .
Do đó Elip có độ dài trục lớn là A A  2a  4 , độ dài trục bé là B B  2b  2 2 . 1 2 1 2
Mặt khác O là trung điểm của AB nên m  max z  max OM OA a  2 và 1
n  min z  min OM OB b  2 . 1 2018
Do đó w  2  2i suy ra w  6 1009  w  6 .
Câu 6: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Cho số phức z thỏa
mãn  z  2  i z  2  i  25 . Biết tập hợp các điểm M biểu diễn số phức w  2z  2  3i là
đường tròn tâm I  ;
a b và bán kính c . Giá trị của a b c bằng A. 17 . B. 20 . C. 10 . D. 18 . Lời giải
Chọn D
Giả sử z a bi  ;
a b   và w x yi  ; x y   .
z  2  iz  2  i  25  a  2  b  
1 i a  2  b   1 i  25    
 a  2  b  2 2 1  25   1
Theo giả thiết: w  2z  2  3i x yi  2a bi  2  3i x yi  2a  2  3  2bi .  x  2 a
x  2a  2   2     2 . y  3  2b 3  yb     2 2 2  x  2   3  y  2 2 Thay 2 vào   1 ta được:  2  1  25     
x  2   y  5  100 .  2   2 
Suy ra, tập hợp điểm biểu diễn của số phức w là đường tròn tâm I 2;5 và bán kính R  10 .
Vậy a b c  17 .
Câu 7: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Biết rằng hai số phức z , z thỏa mãn 1 2 1
z  3  4i  1 và z  3  4i 
. Số phức z có phần thực là a và phần ảo là b thỏa mãn 1 2 2
3a  2b  12 . Giá trị nhỏ nhất của P z z z  2z  2 bằng: 1 2 9945 9945 A. P  . B. P  5  2 3 . C. P  . D. P  5  2 5 . min 11 min min 13 min
Hướng dẫn giải Chọn C
Gọi M , M , M lần lượt là điểm biểu diễn cho số phức z , 2z , z trên hệ trục tọa độ Oxy . 1 2 1 2
Khi đó quỹ tích của điểm M là đường tròn C tâm I 3;4 , bán kính R  1 ; 1  1
quỹ tích của điểm M là đường C tròn tâm I 6;8 , bán kính R  1 ; 2  2
quỹ tích của điểm M là đường thẳng d : 3x  2 y 12  0 .
Bài toán trở thành tìm giá trị nhỏ nhất của MM MM  2 . 1 2 y I2 8 I3 B I A 1 M 4 O 3 6 x  138 64 
Gọi C có tâm I ;
, R  1 là đường tròn đối xứng với C qua d . Khi đó 2  3  3    13 13 
min MM MM  2  min MM MM  2 với M C . 3  3  1 2   1 3 
Gọi A , B lần lượt là giao điểm của đoạn thẳng I I với C , C . Khi đó với mọi điểm 3  1  1 3
M C , M C , M d ta có MM MM  2  AB  2 , dấu "=" xảy ra khi 3  3  1  1 1 3 9945 M  ,
A M B . Do đó P
AB  2  I I  2  2  I I  . 1 3 min 1 3 1 3 13
Câu 8: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho các số phức z thỏa mãn z i z 1 2i .
Tập hợp các điểm biểu diễn các số phức w z  2i trên mặt phẳng tọa độ là một đường thẳng.
Phương trình đường thẳng đó là:
A. x  4 y  3  0 .
B. x  3y  4  0 .
C.x  3y  4  0 .
D. x  3y  4  0 . Lời giải Chọn D
Giả sử w x yi ,  ,
x y   . Khi đó w z  2i z w  2i x   y  2i . Do đó biểu thức
z i z 1 2i trở thành x   y  2i i x   y  2i 1 2i x   y  3i   x   1  yi
x   y  2   x  2 2 2 3
1  y x  3y  4  0 . 2 2018
Câu 9: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Số phức z  1 i  1 i  ...  1 i có phần ảo bằng A. 1009 2 1 . B. 1009 2  1. C. 1009 1 2 . D.   1009 2   1 . Lời giải
Chọn B 1 i2018 2 2018 1 2018 Có z
1 i 1 i ... 1 i 1 i.
1 i 1 i 1              i   1009 504 2018 2 1009 Do  i  i        i 1009   2i  1009 1 1 2 2 . .i  2 i  
Suy ra z    i  1009i     1009     1009 1 . 2 1 2 1 1 2
i . Vậy phần ảo của số phức z là 1009 2 1 .
Câu 10: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Khai triển của biểu thức  x x  2018 2 1 được viết thành 2 4036
a a x a x  ...  a x
. Tổng S a a a a  ...  aa bằng: 0 1 2 4036 0 2 4 6 4034 4036 A. 1009 2  . B. 0 . C. 1009 2 . D. 1  . Lời giải
Chọn D
Ta có  x x  2018 2 2 4036 1
a a x a x  ...  a x . 0 1 2 4036
Cho x  i ta được i  i  2018 2 1
a a i  a a i  a a i  a  ...  a . 0 1 2 3 4 5 6 4036
Hay S a a a a  ...  aa    i  2018 1 1  1  . 0 2 4 6 4034 4036
Câu 11: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Cho các số phức z , z , z thỏa mãn điều 1 2 3 kiện z  4 , z  3 ,
z  2 và 4z z 16z z  9z z  48 . Giá trị của biểu thức 1 2 3 1 2 2 3 1 3
P z z z bằng: 1 2 3 A. 1. B. 8 . C. 2 . D. 6 . Lời giải
Chọn C 2 2 2
Ta có z  4 , z  3 , z  2 nên z .z z
 16 , z .z z
 9 , z .z z  4 . 1 2 3 1 1 1 2 2 2 3 3 3
Khi đó 4z z 16z z  9z z  48  z z z z z z z z z z z z  48 1 2 2 3 1 3 3 1 2 3 1 1 2 3 2 1 2 3
  z z z z z z  48  z z z  2 hay P z z z  2 . 3 1 2  1 2 3 3 1 2 1 2 3
Câu 12: (THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018) Cho số phức z , z thỏa 1 2
mãn z  12 và z  3  4i  5 . Giá trị nhỏ nhất của z z là: 1 2 1 2 A. 0 . B. 2 . C. 7 . D. 17 .
Hướng dẫn giải Chọn B
Gọi z x y i và z x y i , trong đó x , y , x , y ; đồng thời M x ; y và 1  1 1  1 1 1 2 2 2 1 1 2 2 M x ; y
lần lượt là điểm biểu diễn các số phức z , z . 2  2 2  1 2 2 2
x y  144  1 1
Theo giả thiết, ta có:  .  x  3 
2   y  42  25  2 2
Do đó M thuộc đường tròn C có tâm O 0;0 và bán kính R  12 , M thuộc đường tròn 1  1 1 2
C có tâm I 3;4 và bán kính R  5. 2  2 O    C2  Mặt khác, ta có 
nên C chứa trong C . 1  2  OI
 5  7  R R  1 2 M1 M (C 2 2) I O (C1)
Khi đó z z M M . Suy ra z zM M
M M R  2R  2 . 1 2  1 2  1 2 1 2 min min 1 2 1 2
Câu 13: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Cho số phức z thỏa mãn 2018 2017 11z 10iz
10iz 11  0. Mệnh đề nào sau đây đúng?  1 3  A. z  ;   . B. z  1; 2 . C. z 0  ;1 . D. z 2;3 .  2 2  Lời giải Chọn A
Đặt z x yi . 2018 2017 11z 10iz 10iz 11  0 1110iz 2017 1110iz 2017  z   z  11z 10i 11z 10i 100  2 2 x y 121 220 y 2017   z  121 2 2
x y  100  220 y TH1: 2 2
z  1  x y  1   2 2 x y    y   2 2 100 121 220
121 x y  100  220y z  1sai TH2: 2 2
z  1  x y  1   2 2 x y    y   2 2 100 121 220
121 x y  100  220y z  1sai TH2: 2 2
z  1  x y  1 . Thay vào thấy đúng. Vậy z  1.
Câu 14: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Cho số phức z thỏa mãn z  2  z  2  5 . Gọi
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của z . Tính M m ? 17 A. M m  .
B. M m  8 .
C. M m  1.
D. M m  4 . 2 Lời giải Chọn D
Gọi M x; y , F 2;0 , F 2;0 biểu diễn cho số phức z , 2 , 2 . 1   1   25
Ta có MF MF  5  M chạy trên Elip có trục lớn 2a  5 , trục nhỏ 2b  2  4  3 . 1 2 4 5 3
Mà z OM . Do đó giá trị lớn nhất, giá trị nhỏ nhất của z là M  ; m  . 2 2
Suy ra M m  4 .
Câu 15: (Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018) Cho phương trình 4 3 2
z  2z  6z  8z  9  0 có bốn nghiệm phức phân biệt là z , z , z , z . Tính giá trị của biểu 1 2 3 4 thức T   2 z  4 2 z  4 2 z  4 2 z  4 . 1 2 3 4 
A. T  2i . B. T  1.
C. T  2i . D. T  0 .
Hướng dẫn giải Chọn B
Đặt f z 4 3 2
z  2z  6z  8z  9  f z  0 . Ta có 2 2 2
z  4  z  4i   z  2i z  2i
T   z  2i z  2i z  2i z  2i . z  2i z  2i z  2i z  2i   1  2  3  4     1  2  3  4 
  f  if i 4 2 . 2   1   .
Câu 16: Cho M là tập hợp các số phức z thỏa 2z i  2  iz . Gọi z , z là hai số phức thuộc tập hợp M sao 1 2
cho z z  1. Tính giá trị của biểu thức P z z . 1 2 1 2 3 A. P  3 . B. P  . C. P  2 . D. P  2 . 2
Câu 17: Cho M là tập hợp các số phức z thỏa 2z i  2  iz . Gọi z , z là hai số phức thuộc tập hợp M sao 1 2
cho z z  1. Tính giá trị của biểu thức P z z . 1 2 1 2 3 A. P  3 . B. P  . C. P  2 . D. P  2 . 2 Lời giải Chọn A
Đặt z x yi với x , y   .
Ta có: z i   iz
x   y   2 2 2 2 2 2
1 i  2  y xi x y  1.
Suy ra tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức là đường tròn  ; O
1  z z  1 . 1 2 2 2 2 2 Ta có: z zz z
 2  z z  2
P  3  P  3 . 1 2 1 2 1 2
Câu 18: Tìm môđun của số phức z biết z  4  1 i z  4  3zi . 1 A. z  . B. z  2 . C. z  4 . D. z  1. 2
Câu 19: Cho số phức z x yi với x, y   thỏa mãn z 1 i 1 và z 3 3i  5 . Gọi m, M lần M
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P x  2 y . Tính tỉ số . m 9 7 5 14 A. . B. . C. . D. . 4 2 4 5
Câu 20: Tìm môđun của số phức z biết z  4  1 i z  4  3zi . 1 A. z  . B. z  2 . C. z  4 . D. z  1. 2 Lời giải Chọn B
Ta có z  4  1 i z  4  3zi  1 3i z z  4   z  4i 2 2
Suy ra 1 3i z z  4   z  4i  10 z   z  4   z  4 2 2 2
 10 z   z  42   z  42  8 z  32  z  4  z  2 .
Câu 21: Cho số phức z x yi với x, y   thỏa mãn z 1 i 1 và z  3 3i  5 . Gọi m, M lần M
lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P x  2 y . Tính tỉ số . m 9 7 5 14 A. . B. . C. . D. . 4 2 4 5 Lời giải Chọn B J 3 I 1 x O 1 3
Gọi A là điểm biểu diễn của số phức z .
Từ giả thiết z 1 i  1 ta có A là các điểm nằm bên ngoài hình tròn C có tâm I 1  ;1 bán 1  kính R  1. 1
Mặt khác z  3  3i  5 ta có A là các điểm nằm bên trong hình tròn C có tâm J 3;3 2  bán kính R  5 . 2
Ta lại có: P x  2 y x  2 y P  0  . Do đó để tồn tại x, y thì  và phần gạch chéo 9  P
phải có điểm chung tức là d J ;   5 
 5  9  P  5  4  P  14 . Suy ra 5 M 7
m  4; M  14   . m 2
Câu 22: Cho số phức z thỏa mãn z  2  3i z  2  3i . Biết z 1 2i z  7  4i  6 2 , M  ; x y là
điểm biểu diễn số phức z , khi đó x thuộc khoảng A. 0; 2 . B. 1;3 . C. 4;8 . D. 2; 4 . Lời giải Chọn D 2 2 2 2
Ta có: z  2  3i z  2  3i x  2   y  3   x  2   y  3  y  0 . 2 2
Ta có: z 1 2i z  7  4i  6 2   x  
1  4   x  7 16  6 2
  x  2     x  2 1 4 6 2 7 16 2 
2x  28x 130  x 11 x  11  x  11    
x  3 . Thử lại thấy thỏa. x  2  2 2 11
 2x  28x 130 
x  6x  9  0 
Vậy x  3 2; 4 .
Câu 23: Cho số phức z thay đổi thỏa mãn z i z i  6 . Gọi S là đường cong tạo bởi tất cả các điểm
biểu diễn số phức  z ii  
1 khi z thay đổi. Tính diện tích hình phẳng giới hạn bởi đường cong S . A. 12 . B. 12 2 . C. 9 2 . D. BF .
Câu 24: Cho số phức z thay đổi thỏa mãn z i z i  6 . Gọi S là đường cong tạo bởi tất cả các điểm
biểu diễn số phức  z ii  
1 khi z thay đổi. Tính diện tích hình phẳng giới hạn bởi đường cong S . A. 12 . B. 12 2 . C. 9 2 . D. BF . Lời giải Chọn B w
Gọi M là điểm biểu diễn số phức w   z i1 i . Suy ra: z   i . 1 i w w
Viết lại giả thiết: z i z i  6   i i
i i  6  w w  2  2i  6 2 . 1 i 1 i
MF MF  6 2 với F 0; 0 , F 2; 2 , F F  2c  2 2 . 2   1   1 2 1 2
Tập hợp điểm M là điểm biểu diễn số phức w là elip có độ dài trục lớn 2a  6 2 , 2c  2 2 , 2 2 b
a c  4 . Diện tích elip là S   . . a b  12 2 .
Câu 25: Trên tập hợp số phức, cho phương trình 2
z bz c  0 với ,
b c   . Biết rằng hai nghiệm của phương
trình có dạng w  3 và 2w 15i  9 với w là một số phức. Tính 2
S b  2c A. S  32  . B. S  1608 . C. S  1144 . D. S  64  .
Câu 26: Cho hai số phức z , z thỏa z z  2 5 . Gọi M , N lần lượt là điểm biểu diễn hai số phức z , z 1 2 1 2 1 2
trên mặt phẳng tọa độ. Biết MN  2 2 . Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là
trung điểm của ON . Tính l KH A. l  3 2 . B. l  6 2 . C. l  41 . D. l  5 .
Câu 27: Trên tập hợp số phức, cho phương trình 2
z bz c  0 với ,
b c   . Biết rằng hai nghiệm của phương
trình có dạng w  3 và 2w 15i  9 với w là một số phức. Tính 2
S b  2c A. S  32  . B. S  1608 . C. S  1144 . D. S  64  . Lời giải Chọn A   w  3 
2  bw  3  c  0  
 2w 15i  9  w  3  c Từ đề bài suy ra    
 2w 15i  92  b  2w 15i  9  c  0
2w 15i  9  w  3  b  
Giả sử w x yi , x, y   .
Khi đó w  3  x  3  yi , 2w 15i  9  2x  9  2y 15 i .  
 2w 15i  9  w  3  c
 2x  9  2 y 15i
 x  3 yi  c Theo đề ta có    .
2w 15i  9  w  3  b  
2x  9  2y 15i   x  3 yi  b     
x  3  2 y 15  y  2x  9  0 x  6
Vì b, c   nên    .
2 y 15  y  0 y  5    
 2w 15i  9  w  3  cc  34 Suy ra w  6
  5i , do đó    .
2w 15i  9  w  3  b b  6   2
S b  2c  32 
Câu 28: Cho hai số phức z , z thỏa z z  2 5 . Gọi M , N lần lượt là điểm biểu diễn hai số phức z , z 1 2 1 2 1 2
trên mặt phẳng tọa độ. Biết MN  2 2 . Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là
trung điểm của ON . Tính l KH A. l  3 2 . B. l  6 2 . C. l  41 . D. l  5 . Lời giải
Chọn C H y M 2 5 2 2 N K O x
OM ON MN
Xét tam giác OMN ta có  2 2 2 4 cos MON   . 2OM .ON 5 Vì  
MON ONH  180 nên  4 cos ONH   . 5
Xét tam giác HNK có 2  1  1 2 2  HK
NH NK  2NH.NK.cos KNH 2   OM ON
 2OM . ON.cos ONH    41 .  2  2
Câu 29: Giá trị của biểu thức 0 2 4 6 98 100 CCCC  ...  C  C bằng 100 100 100 100 100 100 A. 100 2  . B. 50 2 . C. 100 2 . D. 50 2 .
Câu 30: Giá trị của biểu thức 0 2 4 6 98 100 CCCC  ...  C  C bằng 100 100 100 100 100 100 A. 100 2  . B. 50 2 . C. 100 2 . D. 50 2 . Lời giải Chọn B Ta có 1 i100 0 1 2 2 100 100  CiCi C  ...  i C 100 100 100 100   0 2 4 100 CCC  ...  C    1 3 5 99 CCCC i 100 100 100 100 100 100 100 100  . 50  i100  i2 1 1      50 Mặt khác    50 2i  2  . Vậy 0 2 4 6 98 100 50 CCCC  ...  C  C  2 . 100 100 100 100 100 100
Câu 31: Cho số phức z thỏa mãn z  1. Giá trị lớn nhất của biểu thức P  1 z  2 1 z bằng A. 5 . B. 6 5 . C. 2 5 . D. 4 5 .
Câu 32: Cho số phức z thỏa mãn z  1. Giá trị lớn nhất của biểu thức P  1 z  2 1 z bằng A. 5 . B. 6 5 . C. 2 5 . D. 4 5 . Lời giải Chọn B
Gọi số phức z x  i
y , với x, y .
Theo giả thiết, ta có z  1  2 2
x y  1. Suy ra 1   x  1. 2 2
Khi đó, P  1 z  2 1 z   x   2  y   x   2 1 2
1  y  2x  2  2 2  2x . Suy ra P   2 2
1  2  2x  2  2  2x 
 hay P  2 5 , với mọi 1   x  1. 3 4 Vậy P
 2 5 khi 2 2x  2  2  2x x   , y   . max 5 5 2 2
Câu 33: Cho số phức z thoả mãn z  3  4i  5 và biểu thức P z  2  z  i đạt giá trị lớn nhất.
Môđun của số phức z bằng A. 10 . B. 5 2 . C. 13 . D. 10 . 2 2
Câu 34: Cho số phức z thoả mãn z  3  4i  5 và biểu thức P z  2  z  i đạt giá trị lớn nhất.
Môđun của số phức z bằng A. 10 . B. 5 2 . C. 13 . D. 10 .
Hướng dẫn giải Chọn B
Đặt z x  i
y với x, y   và gọi M  ;
x y là điểm biểu diễn của z trên Oxy , ta có 2 2
z  3  4i  5   x  3   y  4  5 2 2 2 2
Và P z  2  z i   x   2 2 2
y x   y   1
 4x  2 y  3 . 2 2
Như vậy P  4x  2 y  3  4  x  3  2 y  4  23 2 2  
 4  2 .  x  3   y  4  23  33  x  3 y  4 x  5   t  
Dấu “=” xảy ra khi và chỉ khi  4 2   y  5 .
4 x  3  2 y  4 10   t  0,5 
Vậy P đạt giá trị lớn nhất khi z  5  5i z  5 2 .
Câu 35: Cho số phức z thoả mãn đồng thời hai điều kiện z  3  4i  5 và biểu thức 2 2
M z  2  z i đạt giá trị lớn nhất. Môđun của số phức z  2  i bằng A. 5 . B. 9 . C. 25 . D. 5 .
Câu 36: Cho số phức z thoả mãn đồng thời hai điều kiện z  3  4i  5 và biểu thức 2 2
M z  2  z i đạt giá trị lớn nhất. Môđun của số phức z  2  i bằng A. 5 . B. 9 . C. 25 . D. 5 . Lời giải Chọn D 2 2
Đặt z x yi ,  ,
x y    z  3  4i  5   x  3   y  4  5   1 . 2 2 2 2
Ta có: M z  2  z i   x   2 2 2
y x   y   1
 4x  2 y  3 2 2
 4 x  3  2 y  4  23  20  x  3   y  4  23  33. x  3 4
x y  5  z  5  5i
Dấu "  " xảy ra khi chỉ khi  kết hợp với   1 suy ra  y  4 2
x  1, y  3  z  1 3i  Thử lại ta có M
 33  z  5  5i z  2  i  5 . max
Câu 37: Cho số phức z . Gọi A , B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z
và 1 iz . Tính z biết diện tích tam giác OAB bằng 8 . A. z  2 2 . B. z  4 2 . C. z  2 . D. z  4 .
Câu 38: Cho số phức z . Gọi A , B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z
và 1 iz . Tính z biết diện tích tam giác OAB bằng 8 . A. z  2 2 . B. z  4 2 . C. z  2 . D. z  4 . Lời giải Chọn D
Ta có OA z , OB  1 iz  2 z , AB  1 iz z iz z . Suy ra OAB
vuông cân tại A ( OA AB và 2 2 2
OA AB OB ) 1 1 2 Ta có: S  . OA AB
z  8  z  4 . OAB 2 2 Câu 39: Cho hàm số
y f x xác định và liên tục trên  \{0} thỏa mãn: 4 2 2
x f x  2x  
1 f x  .
x f  x 1 với đồng thời f   1  2 . Tính
f x dx  . 1 1 3 3 1 A. 2 ln 2  . B. 2 ln 2  . C.  ln 2  . D.  ln 2  . 4 4 4 4 Câu 40: Cho hàm số
y f x xác định và liên tục trên  \{0} thỏa mãn: 4 2 2
x f x  2x  
1 f x  .
x f  x 1 với đồng thời f   1  2 . Tính
f x dx  . 1 1 3 3 1 A. 2 ln 2  . B. 2 ln 2  . C.  ln 2  . D.  ln 2  . 4 4 4 4 Lời giải Chọn B 2
Từ giả thiết ta có:  xf x   1
f x  xf  x . uu 1 Đặt u  . x f x 2
1  u u   1 
dx  x C   x C. 2  2 u u u 1 Vậy . x f x  1 , mà f  
1  2  C  0 . x C 4 1 1 3
Vậy f x    
f x dx  2  ln 2  2  . x x 4 1
Câu 41: Trong các số phức z thỏa mãn z  2  4i z  2i . Số phức z có môđun nhỏ nhất là
A. z  1 i . B. z  2   2i .
C. z  2  2i .
D. z  3  2i .
Câu 42: Trong các số phức z thỏa mãn z  2  4i z  2i . Số phức z có môđun nhỏ nhất là
A. z  1 i . B. z  2   2i .
C. z  2  2i .
D. z  3  2i . Lời giải Chọn C
Đặt z a bi ( a , b   ). Khi đó z  2  4i z  2i 2 2 2
 a  2  b  4i a  b  2i  a    b   2 2 4
a  b  2
a b  4  b  4  a Khi đó:
z a b a    a2  a a   a  2 2 2 2 2 4 2 8 16 2 2  8  2 2 . a  2
Đẳng thức xảy ra   . b  2 
Vậy z  2  2i .
Câu 43: Trong nặt phẳng phức, xét M  ;
x y là điểm biểu diễn của số phức z x yi  ;
x y   thỏa mãn
z i là số thực. Tập hợp các điểm M là z i A. Parabol. B. Trục thực.
C. Đường tròn trừ hai điểm trên trục ảo.
D. Trục ảo trừ điểm 0;  1 . 1 1 1
Câu 44: Cho hai số phức z , w thỏa mãn z  3 và  
. Khi đó w bằng: z w z w 1 1 A. 3 . B. . C. 2 . D. . 2 3
Câu 45: Trong nặt phẳng phức, xét M  ;
x y  là điểm biểu diễn của số phức z x yi  ;
x y   thỏa mãn
z i là số thực. Tập hợp các điểm M là z i A. Parabol. B. Trục thực.
C. Đường tròn trừ hai điểm trên trục ảo.
D. Trục ảo trừ điểm 0;  1 . Lời giải Chọn D z iz i2 2 2
z  2zi i 2 2
x y 1 2  x yii 2 2
x y  2 y 1 2x Ta có      i là 2 2 2 2 z i z i z i 2 2 x y 1 2 2 2 2 x y 1 x y 1 x  0 một số thực   . Chọn đáp án D. y  1  1 1 1
Câu 46: Cho hai số phức z , w thỏa mãn z  3 và  
. Khi đó w bằng: z w z w 1 1 A. 3 . B. . C. 2 . D. . 2 3 Lời giải Chọn A Ta có: 2 1 1 1 z w 1
z w  zw      0   0 2 2
z w zw  0 z w z w zw z w
zwz w 2 2 2  1  3  1   3i   1 3  2  z w   w    z w    
w  z     i  w  2  4 2  2        2 2   1 3  z   
i w z w . 2 2 Vậy w  3 .
Câu 47: Gọi z , z là các nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 1 2 2018 2018 (z 1)  (z 1) bằng 1 2 A. 1010 2 i . B. 1009 2 i . C. 0 . D. 2018 2 .
Câu 48: Gọi z , z là các nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 1 2 2018 2018 (z 1)  (z 1) bằng 1 2 A. 1010 2 i . B. 1009 2 i . C. 0 . D. 2018 2 .
Hướng dẫn giải Chọn C
z  2  i z 2 1
z  4z  5  0   .
z  2  i z  2 1009 1009  2018 2018 z  2018 1   z  2018 1  1 i  1 i   2  i i    2 1 2
1 2i i  1 2 1009 1009
  i1009   i1009 2 2  2i  2i  0 . z  2i
Câu 49: Cho số phức z thỏa mãn
 1 . Giá trị nhỏ nhất của z  3  2i bằng z  3  i 2 10 10 A. . B. 2 10 . C. 10 . D. . 5 5
Câu 50: Cho số phức z    i 2018 3 5
. Biết phần ảo của z có dạng a b 3  c 5  d 15 . Trong các
số a , b , c , d có đúng bao nhiêu số bằng 0 ? A. 2 . B. 1. C. 4 . D. 3 . z  2i
Câu 51: Cho số phức z thỏa mãn
 1 . Giá trị nhỏ nhất của z  3  2i bằng z  3  i 2 10 10 A. . B. 2 10 . C. 10 . D. . 5 5 Lời giải Chọn A
Giả sử z x yi x, y   . Ta có z  2i 2 2 2
 1  z  2i z  3  i 2 
x   y  2   x  3   y   1  y  3  x  3 . z  3  i 2 2 2 2
Lại có: z  3  2i   x  3   y  2   x  3  3x  5 2
 10x  36x  34 2  18  16 2 10  10x      .  10  10 5 2 10
Vậy GTNN của z  3  2i bằng . 5
Câu 52: Cho số phức z    i 2018 3 5
. Biết phần ảo của z có dạng a b 3  c 5  d 15 . Trong các
số a , b , c , d có đúng bao nhiêu số bằng 0 ? A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn D Ta có: 2018  z   k k 3  5i 2018 kC   32018 5 k i . 2018   k 0
Phần ảo của số phức z là 1008    1008 m C    m m m m
3 2018 2 1  52 1 2 1 1 2m 1  C  1  .3 .15 . m 15  . 2018   1009 2018   m0 m0
Suy ra a b c  0 và d  0 .
Câu 53: Cho số phức z thỏa mãn z z  2 và z z  2 . Gọi M , m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của T z  2i . Tổng M n bằng A. 1 10 . B. 2  10 . C. 4 . D. 1.
Câu 54: Cho số phức z thỏa mãn z 1  z  3  4i  10 . Giá trị nhỏ nhất P của biểu thức min
P z 1 2i bằng? 34 A. P  17 . B. P  34 . C. P  2 10 . D. P. min min min min 2
Câu 55: Cho số phức z thỏa mãn z z  2 và z z  2 . Gọi M , m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của T z  2i . Tổng M n bằng A. 1 10 . B. 2  10 . C. 4 . D. 1.
Hướng dẫn giải Chọn A
Gọi z x yi , , x y   .  2x  2  x  1   Ta có    . 2 yi  2 y  1     Gọi M  ;
x y là điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy . Khi đó tập hợp các
điểm M là hình vuông ABCD (hình vẽ). y D 1 C -1 O 1 x -1 A B -2 N Điểm N 0; 2
  biểu diễn số phức, khi đó T z  2i MN .
Dựa vào hình vẽ ta có MN d M , AB  1 nên m  min T  1, MN NC  10 nên
M  max T  10 , do đó M m  1 10 .
Câu 56: Cho số phức z thỏa mãn z 1  z  3  4i  10 . Giá trị nhỏ nhất P của biểu thức min
P z 1 2i bằng? 34 A. P  17 . B. P  34 . C. P  2 10 . D. P. min min min min 2
Hướng dẫn giải Chọn A
Giả sử z a bi a,b   . Ta có 2 2 2
z 1  z  3  4i  10  a   2
1  b  a  3  b  4  10 Gọi M  ;
a b là điểm biểu diễn cho số phức z . Xét hai điểm F 1;0 , F 3;4 thì tập hợp 2   1  
điểm M là elip  E  có hai tiêu điểm là F , F và tâm là điểm I 1;2 . 1 2
Elip  E  này có độ dài trục lớn là 2a  10 và tiêu cự là 2c F F  4 2 . Do đó a  5 , 1 2 c  2 2 2 2 2
b a c  17 . 2 2
Lại có: P z 1 2i  a  
1  b  2  MI . Suy ra PIM
khi và chỉ khi IM b hay P  17 . min min min
Câu 57: Gọi z , z là các nghiệm phức của phương trình 2
z  4z 13  0 , với z có phần ảo dương. Biết 1 2 1
số phức z thỏa mãn 2 z z z z , phần thực nhỏ nhất của z là 1 2 A. 6 . B. 2 . C. 1. D. 9 .
Câu 58: Gọi z , z là các nghiệm phức của phương trình 2
z  4z 13  0 , với z có phần ảo dương. Biết 1 2 1
số phức z thỏa mãn 2 z z z z , phần thực nhỏ nhất của z là 1 2 A. 6 . B. 2 . C. 1. D. 9 . Lời giải Chọn B Ta có 2
z  4z 13  0  z  2  3i hoặc z  2  3i . 1 2
Gọi z x  i
y , với x, y . 2 2 2 2
Theo giả thiết, 2 z z z z
 2  x  2   y  3   x  2   y  3 1 2  2 2 x 2  y 2     
  x  2   y  2 4 2 3 2 3
  x  2   y  5  16 .  
Suy ra tập hợp các điểm biểu diễn số phức z là miền trong của hình tròn C  có tâm I 2;5 ,
bán kính R  4 , kể cả hình tròn đó.
Do đó, phần thực nhỏ nhất của z là x  2 . min 2
 4x  3x  1 
Câu 59: Cho hai số thực a và b thoả mãn lim
ax b  0  
. Khi đó a  2b bằng: x 2x  1   A. 4  . B. 5  . C. 4 . D. 3  .
Câu 60: Cho các số phức z , w thỏa mãn z  5  3i  3, iw  4  2i  2 . Tìm giá trị lớn nhất của biểu
thức T  3iz  2w . A. 554  5 . B. 578  13 . C. 578  5 . D. 554 13.
Câu 61: Cho số phức z thỏa mãn z 1  5 . Biết tập hợp các điểm biểu diễn số phức w xác định bởi
w  2  3iz  3  4i là một đường tròn bán kính R . Tính R . A. R  5 17 . B. R  5 10 . C. R  5 5 . D. R  5 13 . 2
 4x  3x  1 
Câu 62: Cho hai số thực a và b thoả mãn lim
ax b  0  
. Khi đó a  2b bằng: x 2x  1   A. 4  . B. 5  . C. 4 . D. 3  . Lời giải Chọn D 2
 4x  3x  1   5 7  Ta có: lim
ax b  lim    2x  
ax b x 2x 1 x  2 2 2x  1        2  a  0 2
 4x  3x  1   5 7   Mà lim
ax b  0    lim  2x  
ax b   0   5 x 2x  1     x 2 2 2x   1     b  0   2 a  2    5 . b     2
Khi đó: a  2b  3.
Câu 63: Cho các số phức z , w thỏa mãn z  5  3i  3, iw  4  2i  2 . Tìm giá trị lớn nhất của biểu
thức T  3iz  2w . A. 554  5 . B. 578  13 . C. 578  5 . D. 554 13. Lời giải Chọn D
z  5  3i  3  3iz 15i  9  9 là đường tròn có tâm I 9;15 và R  9 .
iw  4  2i  2  2w  8i  4  4 là đường tròn có tâm J 4; 8
  và R  4 .
T  3iz  2w đạt giá trị lớn nhất khi T IJ R R  554  13.
Câu 64: Cho số phức z thỏa mãn z 1  5 . Biết tập hợp các điểm biểu diễn số phức w xác định bởi
w  2  3iz  3  4i là một đường tròn bán kính R . Tính R . A. R  5 17 . B. R  5 10 . C. R  5 5 . D. R  5 13 . Lời giải Chọn D
Tập hợp điểm biểu diễn số phức z thỏa mãn z 1  5 là đường tròn C  tâm I 1;0 và bán
kính R  5 . Ta có C  nhận trục hoành là trục đối xứng nên tọa độ điểm biểu diễn z cũng nằm
trên đường tròn này hay z 1  5 . Ta có
w  2  3iz  3  4i w  2  3i z  
1  2  3i  3  4i w  5  7i  2  3i z   1
w  5  7i  2  3i  z  
1  w  5  7i  5 13 .
Câu 65: Với mọi số phức z thỏa mãn z 1 i  2 , ta luôn có A. z 1  2 .
B. 2z 1 i  3 2 .
C. 2z 1 i  2 .
D. z i  2 . z
Câu 66: Xét các số phức z  3  4i và z  2  mi , m   . Giá trị nhỏ nhất của môđun số phức 2 1 2 z1 bằng ? 2 1 A. . B. 2 . C. 3 . D. . 5 5
Câu 67: Với mọi số phức z thỏa mãn z 1 i  2 , ta luôn có A. z 1  2 .
B. 2z 1 i  3 2 .
C. 2z 1 i  2 .
D. z i  2 . Lời giải
Chọn B
Ta có z z 1 i 1 i z 1 i  1 i  2 2 .
Vì vậy 2z 1 i z 1 i z z 1 i z  3 2 . z
Câu 68: Xét các số phức z  3  4i và z  2  mi , m   . Giá trị nhỏ nhất của môđun số phức 2 1 2 z1 bằng ? 2 1 A. . B. 2 . C. 3 . D. . 5 5 Lời giải
Chọn A z 2  mi
2  mi 3  4i
6  4m  3m  8 i 6  4m 3m  8 2           i z 3  4i
3  4i 3  4i 25 25 25 1    2 2 z  6  4m   3m  8  2 2 z
36  48m 16m  9m  48m  64 2    2       z 2  25   25 z 25 1  1 2 2 z 25m 100 z m  4 4 2 2 2       . 2 z 25 z 25 25 5 1 1 z z Hoặc dùng công thức: 2 2  . z z 1 1
Câu 69: Trong mặt phẳng tọa độ Oxy , gọi  H  là tập hợp điểm biểu diễn số phức w  1 3iz  2
thỏa mãn z 1  2 . Tính diện tích của hình  H  . A. 8 . B. 18 . C. 16 . D. 4 .
Câu 70: Trong mặt phẳng tọa độ Oxy , gọi  H  là tập hợp điểm biểu diễn số phức w  1 3iz  2
thỏa mãn z 1  2 . Tính diện tích của hình  H  . A. 8 . B. 18 . C. 16 . D. 4 . Lời giải Chọn C
Ta có w  1 3iz  2  w  3  3i  1 3iz   1 .
w  3  3i  1  3i z  1  4 .
Vậy điểm biểu diễn số phức w nằm trên hình tròn có bán kính r  4 .
Diện tích hình  H  là 2
S   r  16 .
Câu 71: Cho z , z là các số phức thỏa mãn z z  1 và z  2z  6 . Tính giá trị của biểu thức 1 2 1 2 1 2
P  2z z . 1 2 A. P  2 . B. P  3 . C. P  3 . D. P  1 .
Câu 72: Cho z , z là các số phức thỏa mãn z z  1 và z  2z
6 . Tính giá trị của biểu thức 1 2 1 2 1 2
P  2z z . 1 2 A. P  2 . B. P  3 . C. P  3 . D. P  1 . Lời giải Chọn A
Đặt z a b i , z a b i . 1 1 1 2 2 2 1 Suy ra 2 2 2 2
a b a b  1 và z  2z  6  a .a b .b  . 1 1 2 2 1 2 1 2 1 2 4
Suy ra P  2z z  2 . 1 2
Câu 73: Cho hình phẳng H giới hạn bởi các đường y  ln 2x  
1 , y  0 , x  0 , x  1 . Tính thể tích
của khối tròn xoay tạo thành khi quay hình H quanh trục Ox . 2   1  3 A. ln 3 1 . B. ln 3   . C.   ln 3 1   . D. ln 3  . 3 2  2  2
Câu 74: Cho hình phẳng H giới hạn bởi các đường y  ln 2x  
1 , y  0 , x  0 , x  1 . Tính thể tích
của khối tròn xoay tạo thành khi quay hình H quanh trục Ox . 2   1  3 A. ln 3 1 . B. ln 3   . C.   ln 3 1   . D. ln 3   . 3 2  2  2 Lời giải Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số y  ln 2x  
1 với trục Ox : y  0 ln 2x   1  0  x  0 1
Thể tích cần tìm:V   ln 2x   1 dx  0  2 u
  ln 2x   1  du  dx Đặt:  2x 1
dv  dx  v x  1 1  1 2x   1     1   
V    x ln 2x   1 1  dx      ln 3  1 dx  
    ln 3  x  ln 2x 1    0 2x 1     2x 1   2  0   0  0    1  3   ln 3 1 ln 3  ln 3      2  2 
z z z  1 1 2 3  
Câu 75: Cho ba số phức z , z , z thỏa mãn 2
z z .z
. Tính giá trị của biểu thức 1 2 3 1 2 3  6  2  z z  1 2   2
M z z z z . 2 3 3 1 6  2  2  6  2  2 A.  6  2  3 . B.  6  2  3 . C. . D. . 2 2 
z z z  1 1 2 3  
Câu 76: Cho ba số phức z , z , z thỏa mãn 2
z z .z
. Tính giá trị của biểu thức 1 2 3 1 2 3  6  2  z z  1 2   2
M z z z z . 2 3 3 1 6  2  2  6  2  2 A.  6  2  3 . B.  6  2  3 . C. . D. . 2 2
Hướng dẫn giải Chọn D
Gọi M , N , P lần lượt là các điểm biểu diễn trong hệ trục tọa độ của các số phức z , z , z . 1 2 3
Suy ra: M , N , P thuộc đường tròn   ;1 O . 6  2 
MN z z   6 2  cos OMN   0  OMN  15  0  MON  150 . 1 2 4 4 6  2
Ta có: z z z z z 2  z z z
z z z z z z z  . 3 1 1 3 1 3 1 1 3 1 3 2 3 1 2 2 6  2
MN MP   0  MOP  150 2  0
NOP  60  N
OP đều  NP  1  z z  1. 2 3  6  2  2 Vậy M  . 2
Câu 77: Có tất cả bao nhiêu giá trị nguyên của m để có đúng hai số phức z thỏa mãn
z  2m  
1  i  10 và z 1 i z  2  3i . A. 40 . B. 41 . C. 165 . D. 164 .
Câu 78: Có tất cả bao nhiêu giá trị nguyên của m để có đúng hai số phức z thỏa mãn
z  2m  
1  i  10 và z 1 i z  2  3i . A. 40 . B. 41. C. 165 . D. 164 . Lời giải Chọn B
Giả sử z x yi x, y   , M  ;
x y là điểm biểu diễn số phức z
z  2m   1  i  10
z   m   2 2 1  i  100 2 2
 x  2m   1    y   1  100  
Khi đó tập hợp điểm biểu diễn số phức z là đường tròn C  tâm I 2m 1;  1 , R  10
z 1 i z  2  3i 2 2   x   1   y  
1 i   x  2  3  yi 2 2 2 2   x   1   y   1
  x  2  3  y
 2x  8 y 11  0 .
Khi đó tập hợp điểm biểu diễn số phức z là đường thẳng  : 2x  8 y 11  0
Để có đúng hai số phức z thì đường thẳng  cắt đường tròn C  tại 2 điểm phân biệt 22m   1  8 11 5  20 7 5  20 7
Tức là d I,   10   10   m  . 2 2 2  8 4 4
Vậy có 41 giá trị nguyên của m để có đúng hai số phức z thỏa mãn yêu cầu bài toán.
Câu 79: Cho hai số phức z , z thỏa mãn z  2  3i  2 và z 1 2i  1. Tìm giá trị lớn nhất của 1 2 1 2
P z z . 1 2
A. P  3  34 .
B. P  3  10 . C. P  6 . D. P  3 . Câu 80: Gọi z , z là các nghiệm phức của phương trình 2
az bz c  0 , 1 2  2 2 2 a, ,
b c  , a  0, b  4ac  0 . Đặt P z z z z . Mệnh đề nào sau đây đúng? 1 2 1 2 c c 2c 4c A. P  . B. P  . C. P  . D. P  . 2a a a a
Câu 81: Cho hai số phức z , z thỏa mãn z  2  3i  2 và z 1 2i  1. Tìm giá trị lớn nhất của 1 2 1 2
P z z . 1 2
A. P  3  34 .
B. P  3  10 . C. P  6 . D. P  3 . Lời giải Chọn A
Gọi M x ; y là điểm biểu diễn số phức z , N x ; y là điểm biểu diễn số phức z 2 2  1 1  1 2 2 2
Số phức z thỏa mãn z  2  3i  2   x  2  y  3  4 suy ra M x ; y nằm trên 1 1  1   1  1 1
đường tròn tâm I 2;3 và bán kính R  2 . 1 2 2
Số phức z thỏa mãn z 1 2i  1   x 1  y  2  1 suy ra N x ; y nằm trên 2 2  2   1  2 2
đường tròn tâm J 1; 2
  và bán kính R  1 . 2
Ta có z z MN đạt giá trị lớn nhất bằng R IJ R  2  34 1  3  34 . 1 2 1 2 Câu 82: Gọi z , z là các nghiệm phức của phương trình 2
az bz c  0 , 1 2  2 2 2 a, ,
b c  , a  0, b  4ac  0 . Đặt P z z z z . Mệnh đề nào sau đây đúng? 1 2 1 2 c c 2c 4c A. P  . B. P  . C. P  . D. P  . 2a a a a Lời giải Chọn D 2
b i 4ac b
Ta có z , z là các nghiệm phức của phương trình 2
az bz c  0 nên z  1 2 1,2 2a b 2
i 4ac b
Do đó z z   và z z  1 2 a 1 2 a 2 2 2 2  b   4ac b 4c
Suy ra P z zz z    . 1 2 1 2   2  a a a
Câu 83: Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. P  2 10 . B. P  6 5 . C. P  3 15 . D. P  2 5 .
Câu 84: Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. P  2 10 . B. P  6 5 . C. P  3 15 . D. P  2 5 . Lời giải Chọn D
Theo bất đẳng thức Bunhiacopxki ta có 2 2 2
P  1 z  3 1 z   2 2
1  3  1 z  1 z   101 z   101  1  2 5 . Vậy P  2 5 . max
Câu 85: Cho số phức z thỏa mãn z 1 3iz  3  i  4 10  
, z  1. Tính z . 1 65 1 65 1 65 1 65 A. z  . B. z  . C. z  . D. z  . 4 2 2 4
Câu 86: Cho số phức z thỏa mãn z 1 3iz  3  i  4 10  
, z  1. Tính z . 1 65 1 65 1 65 1 65 A. z  . B. z  . C. z  . D. z  . 4 2 2 4 Lời giải Chọn C
z 1 3iz  3  i  4 10  
z  z  3  3 z   1 i  4 10   2 2 2  z
z  2   z  2 3 3 1  4 10 z  z 3 3 z  1       160    2 1   65 z   4 2 2 1 65
 10 z 10 z 160  0    z  ( do z  1 ).  2 2 1   65  z   2
Câu 87: Xét các số phức z a bi , a,b   thỏa mãn đồng thời hai điều kiện z z  4  3i và
z 1 i z  2  3i đạt giá trị nhỏ nhất. Giá trị P a  2b là: 252 41 61 18 A. P   B. P   . C. P   . D. P   . 50 5 10 5
Câu 88: Xét các số phức z a bi , a,b   thỏa mãn đồng thời hai điều kiện z z  4  3i và
z 1 i z  2  3i đạt giá trị nhỏ nhất. Giá trị P a  2b là: 252 41 61 18 A. P   B. P   . C. P   . D. P   . 50 5 10 5 Lời giải Chọn C
Giả sử z a bi được biểu diễn bởi điểm M  ; a b . 2 2
Ta có: z z  4  3i 2 2
a b  a  4  b  3  8a  6b  25  0
M   : 8x  6 y  25  0 . 2 2 2 2
f (a,b)  z 1 i z  2  3i f a,b  a   1  b   1
 a  2  b  3 . Gọi A 1  
;1 , B 2;3 . Khi đó f a,b  AM BM .
Như vậy ta cần tìm M   : 8x  6 y  25  0 sao cho f a,b  AM BM nhỏ nhất. A B MI M B'
A và B nằm về một phía đối với  nên gọi B là điểm đối xứng của B qua  .
Khi đó AM BM AM B M
AB  AM BM nhỏ nhất là AB khi M AB   .
BB   và đi qua B 2;3 nên BB : 6x  8y  36  0 .  4 x  8
x  6 y  25  0   25
Gọi I BB   ta có tọa độ của I là nghiệm của hệ:   
6x  8 y  36  0  219  y     50  4 219  hay I ;    .  25 50   42 x  x  2 B x x   BI B  25  42  144      hay B ;   .
y  2 y y 144    25 25 BI B   y B   25
  17 169  1 AB   ;   
17;169 . Phương trình AB :169x 17y 186  0 .  25 25  25  67 x  169 
x 17 y 186  0   50
Tọa độ của M là nghiệm của hệ:    .
8x  6 y  25  0 1  19   y    50 61 
Vậy P a  2b x  2 y  . 10
Câu 89: Hỏi có bao nhiêu số phức z thỏa đồng thời các điều kiện z i  5 và 2
z là số thuần ảo? A. 2 . B. 3 . C. 0 . D. 4 . 10
Câu 90: Xét số phức z thỏa mãn 1 2iz
 2  i . Mệnh đề nào dưới đây là đúng? z 1 3 3 1 A.z  . B.z  2 . C. z  2 . D. z  . 2 2 2 2
Câu 91: Hỏi có bao nhiêu số phức z thỏa đồng thời các điều kiện z i  5 và 2
z là số thuần ảo? A. 2 . B. 3 . C. 0 . D. 4 . Lời giải Chọn D
Đặt z x iy (với x, y   )
Ta có: z i   x   y  2 2 5 1  25   1  x y Ta có: 2
z là số thuần ảo 2 2
x y  0   2 x   y
Suy ra x   x  2 2 1
 25 hay x   x  2 2 1
 25  x  4  x  3
  x  3  x  4 
Vậy có 4 số phức z thỏa yêu cầu bài toán. 10
Câu 92: Xét số phức z thỏa mãn 1 2iz
 2  i . Mệnh đề nào dưới đây là đúng? z 1 3 3 1 A.z  . B.z  2 . C. z  2 . D. z  . 2 2 2 2 Lời giải Chọn A 10
1 2iz
 2  i z    z   10 2 2 1 i z z 2 2 10
z    z   10 2 2 1 i
  z  2  2 z   1  z z 4 2
  z  2   z  2 10 2 2 1 
 5 z  5 z 10  0  z  1 . 2 z 1 3 Vậy  z  . 2 2
Câu 93: Trong mặt phẳng tọa độ Oxy , biết tập hợp các điểm biểu diễn số phức z thỏa mãn 2 2 2
z  2i  2 1 z  3 z  2  i  2018 là một đường tròn. Tìm tâm I của đường tròn đó.  4 5   4  5   4 7   A. ;    . B. ;   . C. 1  ;1 . D. ;   .  3 6   3 6   3 6 
Câu 94: Trong mặt phẳng tọa độ Oxy , biết tập hợp các điểm biểu diễn số phức z thỏa mãn 2 2 2
z  2i  2 1 z  3 z  2  i  2018 là một đường tròn. Tìm tâm I của đường tròn đó.  4 5   4  5   4 7   A. ;    . B. ;   . C. 1  ;1 . D. ;   .  3 6   3 6   3 6  Lời giải Chọn A Gọi M  ;
x y biểu diễn số phức z . Khi đó 2 2 2
z  2i  2 1 z  3 z  2  i  2018
x   y  2   x  2  y   x  2   y  2 2 2 2 2 1 2 3 2 3 1  2018 8 5 1997 2 2
 6x  6 y 16x 10 y 1997  0 2 2  x y x y   0 . 3 3 6  4 5 
Tâm của đường tròn là ;    .  3 6 
Câu 95: Cho số phức z thỏa mãn z  2  i  z 1 i  13 . Tìm giá trị nhỏ nhất m của biểu thức z  2  i . 2 13 13 1 A. m  1. B. m  . C. m  . D. m  . 13 13 13
BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B D C A A A B A C A B B D A B C C B D C C B B A A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C A B A A B A C A B A A B D D B A D A A B D A D A
HƯỚNG DẪN GIẢI
Câu 96: Cho số phức z thỏa mãn z  2  i  z 1 i  13 . Tìm giá trị nhỏ nhất m của biểu thức z  2  i . 2 13 13 1 A. m  1. B. m  . C. m  . D. m  . 13 13 13 Lời giải
Chọn A
Gọi z x  i
y ,  x, y   , A2;   1 và B 1; 
1 . Tọa độ điểm biểu diễn số phức z là
M x; y .
Ta có AB  13 và z  2  i  z 1 i  13  MA MB  13 . Suy ra MA MB AB nên
M x; y thuộc đoạn thẳng AB .
Xét P z  2  i  MC với C 2  ;1 . y B C 1 2 x -2 -1 O M -1 A Do đó, P
BC  1 khi M B . min
Câu 97: Cho số phức z thoả mãn z i  1 , tìm tập hợp các điểm biểu diễn cho số phức w  2iz  1
trong mặt phẳng Oxy .
A. Đường tròn tâm I 0;  
1 , bán kính R  2 .
B. Đường tròn tâm I 1;0 , bán kính R  2 .
C. Đường tròn tâm I 1;0 , bán kính R  2 .
D. Đường tròn tâm I 0 
;1 , bán kính R  2 .
Câu 98: Nếu z là số phức thỏa mãn z z  2i thì giá trị nhỏ nhất của z i z  4 là A. 4 . B. 2 . C. 3 . D. 5 .
Câu 99: Biết phương trình 4 3 2
z  3z  4z  3z 1  0 có 3 nghiệm phức z , z , z . Tính 1 2 3
T z z z . 1 2 3 A. T  3 . B. T  4 . C. T  1 . D. T  2 .
Câu 100: Cho số phức z thoả mãn z i  1 , tìm tập hợp các điểm biểu diễn cho số phức w  2iz  1
trong mặt phẳng Oxy .
A. Đường tròn tâm I 0;  
1 , bán kính R  2 .
B. Đường tròn tâm I 1;0 , bán kính R  2 .
C. Đường tròn tâm I 1;0 , bán kính R  2 .
D. Đường tròn tâm I 0 
;1 , bán kính R  2 . Lời giải Chọn B w 1
Ta có: w  2iz  1  z  . 2i
Đặt w x yi  , x y   . w 1
Mặt khác: z i  1 
i  1  w  1  2  2  w  1  2   x  2 2 1  y  4 . 2i
Vậy tập hợp các điểm biểu diễn cho số phức w  2iz  1 trong mặt phẳng Oxy là: đường tròn
tâm I  1;0 , bán kính R  2 .
Câu 101: Nếu z là số phức thỏa mãn z z  2i thì giá trị nhỏ nhất của z i z  4 là A. 4 . B. 2 . C. 3 . D. 5 . Lời giải Chọn D
Đặt z x yi biểu diễn điểm M  ; x y  .
z z  2i y  1  .
z i z  4 nhỏ nhất  MA MB nhỏ nhất, với A0;  1 , B 4;0 .
Gọi B đối xứng với B qua đường thẳng y  1 suy ra B4; 2   .
Do đó, MA MB MA MB  AB  5 .
Câu 102: Biết phương trình 4 3 2
z  3z  4z  3z 1  0 có 3 nghiệm phức z , z , z . Tính 1 2 3
T z z z . 1 2 3 A. T  3 . B. T  4 . C. T  1 . D. T  2 . Lời giải Chọn A 2 3 1 4 3 2  1   1 
z  3z  4z  3z  1  0 2
z  3z  4    0  z   2  3 z   4  0 2     z zz   z  2  1   1  1  z   3 z   2  0    
Đặt t z   z   z zt  1 2
pt t  3t  2  0   t  2  1 1 3 Ta có: z   1 2
z z  1  0  z   i z 2 2 1 z   2 2
z  2z  1  0  z  1 z 1 3 1 3
T z z z   i   i  1  3 . 1 2 3 2 2 2 2 z
Câu 103: Có bao nhiêu số phức z thoả mãn z  3i  5 và
là số thuần ảo? z  4 A. 0 . B. vô số. C. 1. D. 2 . z
Câu 104: Có bao nhiêu số phức z thoả mãn z  3i  5 và
là số thuần ảo? z  4 A. 0 . B. vô số. C. 1. D. 2 . Lời giải Chọn D
Giả sử z x yi  , x y   .
Ta có z i
x   y  2 2 3 5 3  5 . z x yi
x yi. x  4  yi 2 2
x  4x y  4 yi    . z  4 x  4  yi  2 x  42 2  yx  4 2  y z là số thuần ảo 2 2
x  4x y  0 . z  4  3y  2 
x   y  32 2  5  x    1 Ta có hệ:    2 . 2 2
x  4x y  0  2 2
x  4x y  0 2  Thay   1 vào 2 , ta có: 2  y  2  3y  2  3y  2 2  4.  y  0 2 2   
 9 y 12 y  4  24 y 16  4 y  0  10 .  2  2  y   13
* y  2  x  2 . Ta có z  2  2i . 10 2 2 10 * y   x  . Ta có z   i . 13 13 13 13
Vậy có 2 số phức z thỏa yêu cầu bài toán.
Câu 105: Cho số phức z . Gọi ,
A B lần lượt là các điểm trong mặt phẳng tọa độ Oxy biểu diễn số phức
z và 1 iz . Tính mô đun của số phức z biết tam giác OAB có diện tích bằng 32 . A. z  2 . B. z  8 . C. z  4 . D. z  4 2 .
Câu 106: Cho số phức z . Gọi ,
A B lần lượt là các điểm trong mặt phẳng tọa độ Oxy biểu diễn số phức
z và 1 iz . Tính mô đun của số phức z biết tam giác OAB có diện tích bằng 32 . A. z  2 . B. z  8 . C. z  4 . D. z  4 2 .
Hướng dẫn giải Chọn B Gọi A ;
a b biểu diễn z và B a  ;
b a b biểu diễn 1 iz .
Tam giác OAB có OA z , OB z 2 , 2 2
AB a b z .
Suy ra tam giác OAB vuông cân tại A . 1 1 2 S  . OA AB
z  32  z  8 . OAB  2 2
Câu 1: (THTT Số 1-484 tháng 10 năm 2017-2018) Cho số phức z a bi a,b   . Biết tập hợp các
điểm A biểu diễn hình học số phức z là đường tròn C  có tâm I 4;3 và bán kính R  3 .
Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F  4a  3b 1. Tính giá trị M m .
A. M m  63 .
B. M m  48 .
C. M m  50 .
D. M m  41. Lời giải Chọn B 2 2
Cách 1. Ta có phương trình đường tròn C  :  x  4   y  3  9 . 2 2
Do điểm A nằm trên đường tròn C  nên ta có a  4  b  3  9 .
Mặt khác F  4a  3b 1  4 a  4  3b  3  24  F  24  4a  4  3b  3 . 2 2 2 Ta có  a  b     2 2 4 4 3 3 4 3  a 4 b 3           25.9  255 .    15 
 4 a  4  3b  3  15  15 
F  24  15  9  F  39 .
Khi đó M  39 , m  9 .
Vậy M m  48 . F 1 3b
Cách 2. Ta có F  4a  3b 1  a  4 2  F 1 3b  
a  42  b  32 2  9   4
b  6b  9  9    4  2
 25b  2 3F  3 2
b F  225  0
   F  2 2 3 3  25F  5625 2   0  16 
F 18F  5625  0  9  F  39.
Câu 2: (THTT Số 2-485 tháng 11-năm học 2017-2018) Xác định tất cả các số thực m để phương trình 2
z  2z 1 m  0 có nghiệm phức z thỏa mãn z  2 . A. m  3  . B. m  3  , m  9 .
C. m  1, m  9 . D. m  3
 , m  1, m  9 . Lời giải Chọn D
Ta có:   m , P  1 . m
Trường hợp 1:   0  m  0 .
Khi đó, phương trình có hai nghiệm thực: z  1 m hoặc z  1 m .
+ Với z  1 m . Suy ra: 1 m  2  m  1 (nhận).
+ Với z  1 m . Suy ra: 1 m  2  m  9 (nhận).
Trường hợp 2 :   0  m  0.
Vì đây là phương trình hệ số thực có   0 nên phương trình có hai nghiệm phức là liên hợp của nhau. Do đó: z  2  .
z z  4  P  4  1 m  4  m  3  (nhận). Vậy m  3  ;1;  9 .
Câu 3: (THTT Số 2-485 tháng 11-năm học 2017-2018) Cho z là số phức thỏa mãn z m z 1 m
và số phức z  1 i . Xác định tham số thực m để z z nhỏ nhất. 1 1 1 A. m  . B. m   . C. m  . D. m  1. 2 2 3 Lời giải
Chọn B
Đặt z x iy  , x y   . 2 2 1 Ta có:
z m z 1 m   x m 2
y   x 1 m 2  y x   . m 2 2  1  2 z z   m 1     y   1  0.  2  1  1   m 1  0 m  
Đẳng thức xảy ra khi và chỉ khi 2   2 .  y 1 0    y  1   1 Vậy m  
thì min z z  0. 2
Câu 4: (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Xét số phức z thỏa mãn z  2  2i  2 .
Giá trị nhỏ nhất của biểu thức P z 1 i z  5  2i bằng A. 1 10 . B. 4 . C. 17 D. 5 . Lời giải Chọn C Gọi M  ;
x y là điểm biểu diễn số phức z . Do z  2  2i  2 nên tập hợp điểm M là đường 2 2
tròn C  :  x  2   y  2  4 . Các điểm A1; 
1 , B 5; 2 là điểm biểu diễn các số phức 1 i và 5  2i . Khi đó,
P MA MB .
Nhận thấy, điểm A nằm trong đường tròn C  còn điểm B nằm ngoài đường tròn C  , mà
MA MB AB  17 . Đẳng thức xảy ra khi M là giao điểm của đoạn AB với C  .
Ta có, phương trình đường thẳng AB : x  4 y  3  0 .
Tọa độ giao điểm của đường thẳng AB và đường tròn C  là nghiệm của hệ với 1  y  5    x 2  y 2       
y  2   y  2 2 2 4 4 5 2  4   
x  4 y  3  0 
x  4 y  3   22  59  y   N  2 2 17
Ta có 4 y  5   y  2 2
 4  17 y  44 y  25  0    22  59  y  L  17 37  4 59 22  59
Vậy min P  17 khi z   i 17 17
Câu 5: (Đề tham khảo BGD năm 2017-2018) Xét các số phức z a bi a,b   thỏa mãn
z  4  3i  5 . Tính P a b khi z 1 3i z 1 i đạt giá trị lớn nhất. A. P  10 . B. P  4 . C. P  6 .
D. P  8 . Lời giải Chọn A 2 2
Ta có: z  4  3i  5  a  4  b  3  5 2 2
a b  8a  6b  20
Đặt A z 1 3i z 1 i ta có:
A  a  2  b  2  a  2  b  2 1 3 1 1
A    a  2  b  2  a  2  b  2 2 2 2 1 1 1 3 1 1     2 2
2 2 a b   4b 12
 2 16a  8b  28  84a  2b  7   1 Mặt khác ta có: 2 2
4a  2b  7  4 a  4  2b  3 15   2 2
4  2 a  4  b 3  15  25 2 Từ   1 và 2 ta được: 2 A  200
4a  2b  7  25  a  6 Để A  10 2   max  a  4 b  3    b  4   4 2
Vậy P a b  10 .
Câu 1: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Cho hai số phức z , z thỏa mãn z 1 i  2 1 2 1
và z iz . Tìm giá trị nhỏ nhất m của biểu thức z z ? 2 1 1 2 A. m  2 1 . B. m  2 2 . C. m  2 .
D. m  2 2  2 . Lời giải
Chọn D
Đặt z a b ; i ,
a b    z b   ai 1 2
z z a b b a i . 1 2     2 2 Nên z z a bb a  2. z 1 2     1
Ta lại có 2  z 1 i z  1 i z  2 1 1 1
z  2  2 . Suy ra z z  2. z  2 2  2 . 1 1 2 1 a b Dấu "  " xảy ra khi   0 . 1 1 
Vậy m  min z z  2 2  2 . 1 2
Câu 2: (THTT số 5-488 tháng 2 năm 2018) Cho các số phức z , z với z  0 . Tập hợp các điểm biểu 1 2 1
diễn số phức w z .z z là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các 1 2
điểm biểu diễn số phức z là đường nào sau đây?
A. Đường tròn tâm là gốc tọa độ, bán kính bằng z . 1 z 1
B. Đường tròn tâm là điểm biểu diễn số phức 2  , bán kính bằng . z z 1 1 1
C. Đường tròn tâm là gốc tọa độ, bán kính bằng . z1 z 1
D. Đường tròn tâm là điểm biểu diễn số phức 2 , bán kính bằng . z z 1 1 Lời giải Chọn B z z 1
w z .z z 2  1  z z  2  z   1 2 1 z z z 1 1 1 z 1
Nên tập hợp điểm là đường tròn có tâm là điểm biểu diễn số phức 2  , bán kính bằng . z z 1 1
Câu 1: (THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018) Cho số phức z thoả mãn
z  3  4i  5 . Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P z  2  z i . Tính môđun của số phức w M m . i A. w  2315 . B. w  1258 .
C. w  3 137 .
D. w  2 309 . Lời giải Chọn B 2 2
Đặt z x yi . Ta có Px  2 2 2 yxy  1       
 4x  2 y  3 .   2 2
Mặt khác z  3  4i  5   x  3   y  4  5 .
Đặt x  3  5 sin t , y  4  5 cos t
Suy ra P  4 5 sin t  2 5 cos t  23 .
Ta có 10  4 5 sin t  2 5 cos t  10 .
Do đó 13  P  33  M  33 , 2 2
m  13  w  33 13  1258 .
Câu 2: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Cho hai số phức z , w thỏa mãn
z  2w  3 , 2z  3w  6 và z  4w  7 . Tính giá trị của biểu thức P  . z w  . z w. A. P  1  4i . B. P  2  8i .
C. P  14 . D. P  2  8 . Lời giải Chọn D 2
Ta có: z  2w  3  z  2w  9   z  2w. z  2w  9   z  2w. z  2w  9 2 2  .
z z  2  z.w z.w  4 .
w w  9  z  2P  4 w  9   1 . Tương tự: 2 2 2
2z  3w  6  2z  3w  36  2z  3w.2z  3w  36  4 z  6P  9 w  36 2 . 2 2
z  4w  7   z  4w. z  4w  49  z  4P 16 w  49 3 . 2  z  33  
Giải hệ phương trình gồm  
1 , 2 , 3 ta có: P  28  P  28  .  2 w  8  
Câu 3: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Cho số phức z thỏa mãn
5 z i z 1 3i  3 z 1 i . Tìm giá trị lớn nhất M của z  2  3i ? A. 10 M  .
B. M  1 13 . C. M  4 5 . D. M  9 . 3 Chọn C Lời giải Gọi A0  ;1 , B  1
 ;3,C 1;  
1 . Ta thấy A là trung điểm của BC 2 2 2 MB MC BC 2 BC 2  MA   2 2 2 2
MB MC  2MA   2MA 10 . 2 4 2
Ta lại có: 5 z i z 1 3i  3 z 1 i 2 2
 5MA MB  3MC  10. MB MC 2  MA   2 25
10 2MA 10  MC  2 5
Mà z  2  3i   z i   2
  4i   z i  2  4i z i  2 5  4 5 .
z i  2 5 
z  2  3iloai
Dấu "  " xảy ra khi  a
b 1 , với z a bi ; a, b     .  
z  2  5i   2  4
Câu 4: (THPT Chuyên Phan Bội Châu-lần 2 năm 2017-2018) Với hai số phức z và z thỏa mãn 1 2
z z  8  6i và z z  2 , tìm giá trị lớn nhất của P z z . 1 2 1 2 1 2 A. 4 6 . B. 2 26 . C. 5  3 5 . D. 34  3 2 . Lời giải Chọn B
Cách 1: Ta có: z z  8  6i  10 . 1 2 2 2 2 2
Suy ra: 2  z zz zz z  100  4  104 . 1 2  1 2 1 2 2 2
Ta có: P z z  2 zz  104  2 26 . 1 2  1 2 
z z  26 1 2  
Đẳng thức xảy ra khi và chỉ khi z z  8  6i (hệ này có nghiệm) 1 2
z z  2  1 2  Vậy max P  2 26 .
Cách 2: Gọi z a bi, a, b   , z c di, c, d   . 2   1   a c  8   1  
Theo giả thiết ta có b   d  6 2 a c
2  b d 2  4 3    a c
2  b d 2  100  2 2 2 2 
a b c d  52 
a c2  b d 2  4  Ta có 2 2 2 2
P z z a b c d . 1 2 2
Áp dụng bất đẳng thức  x y   2 2
2 x y  ta có: 2 P   2 2
a b    2 2 2
2 c d   104  P  2 26
Vậy giá trị lớn nhất của P bằng 2 26 . Dấu bằng sảy ra khi  2 a  4   2  a c  8  2 b d  6 b   3    2    .
a c2  b d 2  4   2 c  4   2 2 2 2
a b c d   2   2 d  3    2
Câu 5: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Cho số phức z thõa mãn z 1 i  2 . Tìm giá 2 2
trị lớn nhất của biểu thức P z  2  i z  2  3i . A. 18 . B. 38  8 10 . C. 18  2 10 . B. 16  2 10 . Lời giải Chọn B
Cách 1: Gọi M  ;
x y là điểm biểu diễn cho số phức z . Gọi I 1;  1 , A2  ;1 , B 2;3 lần
lượt là điểm biểu diễn cho các số phức 1 i ; 2  i ; 2  3i . Khi đó, ta có:
MI  2 nghĩa là M thuộc đường tròn C  có tâm I 1;  1 , R  2 và 2 2
P MA MB . 2 AB Ta có: 2 2 2 2
P  2ME EA EB  2ME
, với E 0; 2 là trung điểm của AB . Do đó P 2
có giá trị lớn nhất khi và chỉ khi ME có giá trị lớn nhất.
Ta có : IE  1 9  10  R nên  ME
IE R  2  10 . max 2 2 2 AB Vậy P  2 2  10   2 2  10 10  38  8 10 . max     2
Cách 2: Giả sử z x yi ( x, y   ). M  ;
x y là điểm biểu diễn của z .
Suy ra M  C có tâm I 1; 1 và bán kính R  2 . 1   1  1 z   i
  x  2   y  2 1 2 1 1  4   1 . 2 2 2 2 2 2
Ta có: P  0 và P z  2  i z  2  3i   x  2   y  
1   x  2   y  3 . 2 2 2 2
Suy ra P   x     y   2 2 1
1  x y  2x 10 y 16   x  
1   y  5  6 . 2 2 Ta có  x  
1   y  5  P  6  6 2 nên 2 là phương trình của đường tròn C có tâm 2  I 1
 ;5 , bán kính R
P  6  R ; I I  2 10 . 2   2 1 1 2
Để tồn tại x , y thì C và C có điểm chung  P  6  2  I I P  6  2 . 2  1  1 2
Suy ra : P  6  2  I I P    2 2 2 10  6  38  8 10 . 1 2
Đẳng thức xảy ra khi và chỉ khi C và C tiếp xúc trong. 2  1 
Vậy max P  38  8 10 .
Câu 6: (THPT Chuyên ĐH Vinh – lần 1 - năm 2017 – 2018) Giả sử z , z là hai trong số 1 2
các số phức z thỏa mãn iz  2  i  1 và z z  2 . Giá trị lớn nhất của z z bằng 1 2 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3 . Lời giải Chọn A
Ta có iz  2  i  1  z  1 i 2 1. Gọi z 1 i 2 có điểm biểu diễn là I 1; 2 . 0
Gọi A , B lần lượt là các điểm biểu diễn của z , z . 1 2
Vì z z  2 nên I là trung điểm của AB . 1 2
Ta có z z OA OB  2  2 2 OA OB  2 2
 4OI AB  16  4 . 1 2
OA OB  2  z z  2 . 1 2
Vậy giá trị lớn nhất của z z bằng 4 . 1 2
Câu 7: ----------HẾT----------(THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Cho số z 1 1 phức z thỏa mãn 
. Tìm giá trị lớn nhất của biểu thức P z i  2 z  4  7i . z  3i 2 A. 8 . B. 20 . C. 2 5 . D. 4 5 . Lời giải Chọn B
Gọi z x yi với x, y   , gọi M là điểm trong mặt phẳng tọa độ biểu diễn số phức z . Ta z 1 1 có:  
2 z 1  z  3i  2  x  
1  yi x   y  3i z  3i 2 2 2 
x  2  y x   y  2 2 2 2 1 3
  x  2   y  3  20 .
Như vậy, tập hợp điểm M biểu diễn số phức z là đường tròn C  tâm I 2;3 và bán kính R  2 5 . Gọi A0;  
1 , B 4;7 lần lượt là các điểm biểu diễn các số phức z  i , z  4  7i . Dễ thấy 1 2 ,
A B thuộc đường tròn C  . Vì AB  4 5  2R nên AB là đường kính của đường tròn C  2 2 2
MA MB AB  80 . Từ đó:
P z i  2 z  4  7i z i  2 z  4  7i MA MB   2 2   2 2 2 1 2
MA MB   20 . MB  2MAMA  4 Dấu "  " xảy ra khi    . 2 2 MA MB  80 MB  8   Vậy max P  20 .
Câu 8: . (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho hai số phức z , z thoả mãn 1 2
z  2, z  3 . Gọi M , N là các điểm biểu diễn cho z và iz . Biết  MON  30 . Tính 1 2 1 2 2 2
S z  4z . 1 2 A. 5 2 . B. 3 3 . C. 4 7 . D. 5 . Lời giải Chọn C
Ta có S z  4z z  2iz 2 2 2 2
z  2iz . z  2iz 1 2 1 2 1 2 1 2
Gọi P là điểm biểu diễn của số phức 2iz . 2
     
Khi đó ta có z  2iz . z  2iz OM OP . OM OP PM . 2OI  2PM .OI . 1 2 1 2 Do 
MON  30 nên áp dụng định lí cosin ta tính được MN  1. Khi đó OM
P có MN đồng
thời là đường cao và đường trung tuyến, suy ra OMP cân tại M PM OM  2 . 2 2 2 OM OP MP
Áp dụng định lí đường trung tuyến cho OMN ta có: 2 OI    7 . 2 4
Vậy S  2PM .OI  2.2. 7  4 7 .
Câu 9: Cho hai số phức z , z thỏa mãn z  3i  5  2 và iz 1 2i  4 . Tìm giá trị lớn nhất của biểu 1 2 1 2
thức T  2iz  3z . 1 2 A. 313 16 . B. 313 . C. 313  8 . D. 313  2 5 .
Câu 10: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Cho hai số phức z , z thỏa mãn 1 2
z  3i  5  2 và iz 1 2i  4 . Tìm giá trị lớn nhất của biểu thức T  2iz  3z . 1 2 1 2 A. 313 16 . B. 313 . C. 313  8 . D. 313  2 5 . Lời giải Chọn A
Ta có z  3i  5  2  2iz  6 10i  4  
1 ; iz 1 2i  4  3z
 6  3i  12 2 . 2  2  1 1
Gọi A là điểm biểu diễn số phức 2iz , B là điểm biểu diễn số phức 3  z . Từ   1 và 2 suy 1 2
ra điểm A nằm trên đường tròn tâm I 6; 10 và bán kính R  4 ; điểm B nằm trên đường 1   1 tròn tâm I
6;3 và bán kính R  12 . 2   2 B A I I 2 1 Ta có 2 2
T  2iz  3z AB I I R R  12 13  4 12  313 16 . 1 2 1 2 1 2
Vậy max T  313 16 .
Câu 11: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Cho
hàm số f x 3 2
x  3x m . Hỏi có bao nhiêu giá trị nguyên của tham số m
m  2018 để với mọi bộ ba số phân biệt a , b , c 1; 
3 thì f a , f b , f c
là độ dài ba cạnh của một tam giác. A. 2011. B. 2012 . C. 2010 . D. 2018 . Lời giải Chọn C
Ta có f a , f b , f c là ba cạnh của một tam giác nên f a  f b  f c 3 2 3 2 3 2
a  3a m b  3b m c  3c m với mọi a , b , c 1;  3   3 2
a a    3 2
b b    3 2 3 3
c  3c   m với mọi a , b , c 1;  3 Do đó min  3 2
a a    3 2
b b    3 2 3 3
c  3c   m với mọi a , b , c 1;  3   Ta cần tìm min  3 2
a  3a    3 2
b  3b  và m  3 2
ax c  3c  với mọi a , b , c 1;  3  
Xét hàm f x 3 2
x  3x với x 1;  3 x  0
Ta có f  x 2
 3x  6x , f  x 2
 0  3x  6x  0   . Do x 1;  3 nên x  2 . x  2  Ta có f   1  2  , f 2  4
 , f 3  0 .
max f x  f 3  0 , min f x  f 2  4 . 1  ;3   1;3 Suy ra min  3 2
a a    3 2
b b    3 2 3 3
c  3c   4.2   8  .  
Đẳng thức xảy ra khi a b  2 , c  3 hoặc a c  2 , b  3 hoặc b c  2 , a  3 .
Do đó 8  m m  8 . Mà m  2018 và m nguyên nên m  9;..; 201  8 .
Vậy có 2010 giá trị m thỏa mãn.
Câu 12: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Xét các số phức z a bi ( a,b   )
thỏa mãn z  3  2i  2 . Tính a b khi z 1 2i  2 z  2  5i đạt giá trị nhỏ nhất. A. 4  3 . B. 2  3 . C. 3 . D. 4  3 . Lời giải Chọn D Cách 1:
Đặt z  3  2i w với w x yi x, y   . Theo bài ra ta có 2 2
w  2  x y  4 . 2 2 2
Ta có P z   i
z   i w  
w   i   x   2 1 2 2 2 5 4 2 1 3 4
y  2  x   1   y  3   x
x  2   y  2   x
x  2   y  2 20 8 2 1 3 2 5 2 2 1 3 
x y x    x  2   y    2  
x  2  y   x  2   y    2 2 2 2 2 2 1 1 3 2 1 1 3 
 2  y y  3   2 y  3  y  6 . x  1  x  1 
P  6   y 3  y  0   .   y  3  2 2 x y  4 
Vậy GTNN của P là bằng 6 đạt được khi z  2  2  3i . Cách 2: y B 5 M M 0 A I 2 K -1 O 2 3 x
z  3  2i  2  MI  2  M   I;2 với I  3;2 .
P z 1 2i  2 z  2  5i MA  2MB với A  1;2 , B  2;5 . IA IM
Ta có IM  2 ; IA  4 . Chọn K 2; 2 thì IK  1. Do đó ta có 2 . IA IK IM   IM IK AM IMIAM  và IM
K đồng dạng với nhau  
 2  AM  2MK . MK IK
Từ đó P MA  2MB  2 MK MB  2BK .
Dấu bằng xảy ra khi và chỉ khi M , K , B thẳng hàng và M thuộc đoạn thẳng BK .
Từ đó tìm được M  2;2  3. Cách 3: Gọi M  ;
a b là điểm biểu diễn số phức z a  .
bi Đặt I  3; 2 , A1; 2 và B 2;5 .
Ta xét bài toán: Tìm điểm M thuộc đường tròn C  có tâm I , bán kính R  2 sao cho biểu
thức P MA  2MB đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K  ;
x y  sao cho MA  2MK M   C  .     2 2 Ta có 2 2
MA  2MK MA  4MK  MI IA  4MI IK         2 2
MI IA MI IA   2 2
MI IK MI IK   MI IA IK  2 2 2 2 . 4 2 . 2 4
 3R  4IK IA * .    
IA  4IK  0   * luôn đúng M   C    . 2 2 2 3
R  4IK IA  0     4
  x  3  4 x  2
IA  4IK  0     . 4
  y  2  0 y  2  
Thử trực tiếp ta thấy K 2; 2 thỏa mãn 2 2 2
3R  4IK IA  0 . Vì 2 2 2 2
BI  1  3  10  R  4 nên B nằm ngoài C  . Vì 2 2
KI  1  R  4 nên K nằm trong C  .
Ta có MA  2MB  2MK  2MB  2  MK MB  2KB .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK .
Do đó MA  2MB nhỏ nhất khi và chỉ khi M là giao điểm của C  và đoạn thẳng BK.
Phương trình đường thẳng BK : x  2 . 2 2
Phương trình đường tròn C  :  x  3   y  2  4 . x  2 x  2   x  2 
Tọa độ điểm M là nghiệm của hệ    hoặc  .  x  3 
2   y  22  4  y  2  3    y  2  3 
Thử lại thấy M 2;2  3 thuộc đoạn BK .
Vậy a  2 , b  2  3  a b  4  3 .
Câu 13: (SGD Quảng Nam – năm 2017 – 2018) Cho số phức z thỏa mãn z  2 . Giá trị nhỏ
nhất của biểu thức P  2 z 1  2 z 1  z z  4i bằng: 14 7 A. 4  2 3 . B. 2  3 . C. 4  . D. 2  . 15 15 Lời giải Chọn A
Gọi z x yi,  x, y   . Theo giả thiết, ta có 2 2
z  2  x y  4 .
Suy ra 2  x, y  2 . 2 2
Khi đó, P  2 z 1  2 z 1  z z  4i   x   2
y   x    2 2 1
1  y y  2   P
x  2  y    x  2 2 2 2 1 1
y y  2    2
2 2 1 y  2  y.
Dấu “  ” xảy ra khi x  0 .
Xét hàm số f y 2
 2 1 y  2  y trên đoạn 2; 2 , ta có: 2 y 2 2 y  1 y 1
f  y  1 
; f  y  0  y  . 2 1 y 2 1 y 3  1  Ta có f  2  3   ; f  2
   4  2 5 ; f 2  2 5 .  3  1
Suy ra min f y  2  3 khi y  .  2  ; 2 3 1
Do đó P  2 2  3  4  2 3 . Vậy P  4  2 3 khi z  i . min 3
Câu 14: ----------HẾT----------(ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Nếu z
là số phức thỏa z z  2i thì giá trị nhỏ nhất của z i z  4 là A. 2 . B. 3 . C. 4 . D. 5 . Lời giải Chọn D
Đặt z x yi với x , y   theo giả thiết z z  2i  y  1  . d
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng d  . Gọi A0 
;1 , B 4;0 suy ra z i z  4  P là tổng khoảng cách từ điểm M  ; x   1 đến hai điểm A , B . Thấy ngay A0 
;1 và B 4;0 nằm cùng phía với d  . Lấy điểm đối xứng với A0  ;1 qua
đường thẳng d  ta được điểm A0;  3 .
Do đó khoảng cách ngắn nhất là 2 2 A B   3  4  5 .
Câu 15: (THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018) Trong các số phức z thỏa mãn 2
z 1  2 z gọi z và z lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Khi đó 1 2
môđun của số phức w z z là 1 2 A. w  2 2 . B. w  2 . C. w  2 .
D. w  1 2 . Lời giải Chọn A
Đặt z a bi a,b   thì 2
z 1  2 z  a bi2 1  2 a bi 2 2 2
a b 1 2abi  2 a bi   2 2 a b   2 2  a b   2 2 1 4 4 a b  4 4 2 2 2 2
a b 1 2a  6b  2a b  0  a b  2 2 2 2 1  4b  0   2 2
a b   b 2 2 1 2
a b 1 2b  0 2 2
a b 1 2b  0   2 2
a b 1 2b  0  TH1: 2 2
a b 1 2b  0  a  b  2 2 1  2 .
Khi đó tập hợp điểm M  ;
a b biểu diễn số phức z là đường tròn có tâm I 0;1 , bán kính 1  
R  2 , giao điểm của OI (trục tung) với đường tròn là M 0; 2 1 và M 0;1 2 2   1    w   2  
1 i  1 2 i w  2i w  2 TH2: 2 2
a b 1 2b  0  a  b  2 2 1  2 .
Khi đó tập hợp điểm M  ;
a b biểu diễn số phức z là đường tròn có tâm I 0;1 , bán kính 2  
R  2 , giao điểm của OI (trục tung) với đường tròn là M 0; 2 1 và M 0;  2 1 4   3    w   2  
1 i  1 2 i w  2
i w  2 .
Với đáp án của trường ĐH Vinh đưa ra là A thì ta chọn số phức M và M có 1 3
w  2 2i w  2 2 nên đề bài chưa chuẩn, có thể chọn phương án B.
Đáp án ĐH Vinh đưa ra theo mình là chính xác, bởi lẽ trong các số phức z thỏa mãn ta tìm các
số phức gọi z và z có môđun nhỏ nhất và lớn nhất nên phải tổng hợp cả hai TH1 và TH2. 1 2
Thầy đừng vội tính w mà sau cùng hãy tìm z và z rồi tính w 1 2
Một vài góp ý thầy xem nhé
Câu 16: (SGD Nam Định – năm 2017 – 2018) Trong mặt phẳng tọa độ Oxy , gọi  H  là phần z 16
mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn và có phần thực và phần 16 z
ảo đều thuộc đoạn 0 
;1 . Tính diện tích S của  H  .
A. S  32 6    .
B. S  16 4    . C. 256 . D. 64 . Lời giải
Chọn A
Giả sử z x yi x, y   . z x y 16 16 16x 16 y Ta có:   i ;    i . 16 16 16 z x yi 2 2 2 2 x y x y z 16 Vì và có phần thực và phần ảo đều thuộc đoạn 0  ;1 nên 16 zx 0   1  16  0  x  16 y 0  x  16 0   1    0  y  16  16 0  y  16      . 16x  2 2 2   x 8 2  y  64 0   1
0  16x x y   2 2  x y 2 2
0  16y x y
x   y 82 2  64    16 y 0   1 2 2  x yy 16 C B E I 16 O J A x
Suy ra  H  là phần mặt phẳng giới hạn bởi hình vuông cạnh 16 và hai hình tròn C có tâm 1 
I 8; 0 , bán kính R  8 và C có tâm I 0;8 , bán kính R  8 . 2   2  1   1 2
Gọi S là diện tích của đường tròn C . 2   1   1 1 
Diện tích phần giao nhau của hai đường tròn là: 2 S  2 S  S  2 . .8  .8.8 . 1      4 OEJ   4 2 
Vậy diện tích S của hình  H  là:  1 1 2 2 2 
S  16   .8  2. . .8  .8.8 
  256  64  32  64  192  32  326    .  4 2 
Câu 17: (SGD Nam Định – năm 2017 – 2018).Cho hai số phức z , z thoả mãn z  6 , 1 2 1
z  2 . Gọi M , N là các điểm biểu diễn cho z và iz . Biết  MON  60 . Tính 2 2
T z  9z . 2 1 2 1 2 A. T  18 . B. T  24 3 . C. T  36 2 . D. T  36 3 . Lời giải
Chọn D
Ta có T z  9z z  3iz 2 2 2 2
z  3iz . z  3iz 1 2 1 2 1 2 1 2
Gọi P là điểm biểu diễn của số phức 3iz . 2
     
Khi đó ta có z  3iz . z  3iz OM OP . OM OP PM . 2OI  2PM .OI . 1 2 1 2 3 Do 
MON  60 và OM OP  6 nên MO
P đều suy ra PM  6 và OI  6.  3 3 . 2
Vậy T  2PM .OI  2.6.3 3  36 3 .
----------HẾT----------
Câu 1: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Gọi z , z là hai 1 2
trong các số phức thỏa mãn z 1 2i  5 và z z  8 . Tìm môđun của số phức 1 2
w z z  2  4i . 1 2 A. w  6 . B. w  16 . C. w  10 .
D. w  13 . Lời giải
Chọn A
Gọi A là điểm biểu diễn của số phức z , B là điểm biểu diễn của số phức z . 1 2
Theo giả thiết z , z là hai trong các số phức thỏa mãn z 1 2i  5 nên A và B thuộc 1 2
đường tròn tâm I 1; 2
  bán kính r  5 .
Mặt khác z z  8  AB  8 . 1 2 z z
Gọi M là trung điểm của AB suy ra M là điểm biểu diễn của số phức 1 2 và IM  3. 2 Do đó ta có z z 1 1 2 3  IM  1 2i  3 
z z  2  4i z z  2  4i  6  w  6 . 2 1 2 1 2 2
Câu 2: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho số phức z thỏa mãn
z 1 3i z  2  i  8 . Giá trị nhỏ nhất m của 2z 1 2i là A. m  4 . B. m  9 . C. m  8 . D. m  39 . Lời giải Chọn D Giả sử M  ;
x y  biểu diễn số phức z x iy ( x , y   ), A1; 3 , B  2  ;  1 , AB  5 .
z 1 3i z  2  i  8  AM BM  8 , tập hợp điểm M là Elip có phương trình 2 2 x 4 y 1  1  
 1 . Đặt P  2z 1 2i P  2 z
i , gọi I là trung điểm AB thì I  ; 1   16 39 2  2  1
P  2 z
i  2IM IM . 2
Ta tìm điểm M trên  E  sao cho IM có độ dài nhỏ nhất. 39
IM nhỏ nhất khi IM bằng độ dài nửa trục bé, IM   P  39 . 2 min
Câu 3: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Cho số phức z thỏa mãn 2
z z z z z . Giá trị lớn nhất của biểu thức P z  5  2i bằng: A. 2  5 3 . B. 2  3 5 . C. 5  2 3 . D. 5  3 2 . Lời giải Chọn B
Gọi z x  i
y (với x , y ). Suy ra z x  i y và 2 2 2
z x y  2 i xy . Theo giả thiết, ta có 2
z z z z zx
y   x y 2 2 2 2 2 2 2  4x y 2 2  2 2
2 x  2 y x y   x   1   y   1
 2 . Từ đó suy ra tập hợp các điểm biểu diễn số
phức z là các đường tròn có tâm I 1; 
1 và bán kính R  2 .
Khi đó, P z  5  2i MA , với A5; 2 và M  ;
x y là tọa độ điểm biểu diễn số phức z .
Mặt khác, vì A5; 2 thuộc góc phần tư thứ nhất nên MA lớn nhất  M thuộc đường tròn
C có tâm I 1; 
1 và bán kính R  2 . 3 
Câu 4: Vậy PMA
IA R  3 5  2 . Trong mặt phẳng phức, xét hình bình hành tạo bởi các max max 1 1 35 điểm 0 , z , và z
. Biết z có phần thực dương và diện tích hình bình hành bằng . Tìm z z 37 2 1
giá trị nhỏ nhất của z  . z 53 60 22 50 A. . B. . C. . D. . 20 37 9 37 Lời giải Chọn D 1 1 Gọi O, ,
A B,C lần lượt là điểm biểu diễn số phức 0, z, và z  . z z 1 35 35
Khi đó diện tích hình bình hành OACB là S O . A .
OB sin   z . .sin    sin   . z 37 37 12 Suy ra 2
cos   1 sin    . 37
Áp dụng định lý cosin trong tam giác OAC ta có 2 2 1 1 2 2 2 2 1 1 2 z
OC OA OB  2 . OA .
OB cos  z   2 z .cos  z   2 cos z z z 2 z 2 2 1 12 50 1 50  z   2  2.  . Vậy z  nhỏ nhất bằng . z 37 37 z 37 12
Dấu “  ” xảy ra  z  1 và cos  . 37  1 12   1 12 
Chẳng hạn như z  sin arccos  i cos arccos     .  2 37   2 37  2 1 50
Câu 5: Vậy z  nhỏ nhất bằng .Biết n  0 1 2 3 2 k k n n
C iC C iC   i C   i Ci , với n n n n n n  32768 z 37 k
C là các số tổ hợp chập k của n và 2 i  1  . Đặt k k T
i C , giá trị của T bằng n k 1  n 8 A. 33  0i . B. 8i . C. 36i . D. 12  0i .
Câu 6: Biết n  0 1 2 3 2 k k n n
C iC C iC   i C   i Ci , với k
C là các số tổ hợp chập k của n n n n n n  32768 n n và 2 i  1  . Đặt k k T
i C , giá trị của T bằng k 1  n 8 A. 330  i . B. 8i . C. 36i . D. 120  i .
Hướng dẫn giải Chọn B Ta có: n  0 1 2 3 2 k k n n
C iC C iC   i C   i Ci n n n n n n  32768 n   0 1 2 2 3 3 2 k k n n
C iC i C i C   i C   i Ci n n n n n n  32768    in n 15 2 1  2 i * n 2k 1  Ta có   i2 1
 2i nên nếu n  2k 1, k   , thì 1   1   2k k i i
i 1 i nên không thỏa mãn * . n k
Xét n  2k , k   , thì       2 1 1  2k k i i i , nên:   2k k k 15 3k k 15
*  2 .2 .i  2 i  2 i  2 i k  5  n  10 . Từ đó ta có 7 7
T i C  8i . 8 8 3 5
Câu 7: Cho các số phức w , z thỏa mãn w i
và 5w  2  i z  4 . Giá trị lớn nhất của biểu 5
thức P z 1 2i z  5  2i bằng A. 6 7 . B. 4  2 13 . C. 2 53 . D. 4 13 . 3 5
Câu 8: Cho các số phức w , z thỏa mãn w i
và 5w  2  i z  4 . Giá trị lớn nhất của biểu 5
thức P z 1 2i z  5  2i bằng A. 6 7 . B. 4  2 13 . C. 2 53 . D. 4 13 . Lời giải Chọn C
Gọi z x yi , với x, y . Khi đó M  ;
x y là điểm biểu diễn cho số phức z .
Theo giả thiết, 5w  2  i z  4  5w i  2  i z  4  5i  2  i w i  z  3  2i 2 2
z  3  2i  3 . Suy ra M  ;
x y thuộc đường tròn C  :  x  3   y  2  9 .
Ta có P z 1 2i z  5  2i MA MB , với A1; 2 và B 5; 2 .
Gọi H là trung điểm của AB , ta có H 3; 2 và khi đó:
P MA MB   2 2
2 MA MB  hay 2 2 P  4MH AB .
Mặt khác, MH KH với mọi M  C  nên 2 2
P  4KH AB    2 2 4 IH RAB  2 53 . M K 3 11 Vậy P  2 53 khi
hay z  3  5i và w   i . max MA MB  5 5
Câu 9: Cho số phức z  1 i . Biết rằng tồn tại các số phức z a  5i , z b (trong đó a,b  ,b  1 ) 1 2
thỏa mãn 3 z z  3 z z z z . Tính b a . 1 2 1 2
A. b a  5 3 . B. b a  2 3 .
C. b a  4 3 .
D. b a  3 3 .
Câu 10: Cho số phức z  1 i . Biết rằng tồn tại các số phức z a  5i , z b (trong đó a, b  , b  1 ) 1 2
thỏa mãn 3 z z  3 z z z z . Tính b a . 1 2 1 2
A. b a  5 3 . B. b a  2 3 .
C. b a  4 3 .
D. b a  3 3 . Lời giải Chọn D
 1 a2  4  b  2 2 1 1 
Ta có: 3 z z  3 z z z z     * 1 2 1 2
b a2 25 31 a2 16            b  2
1  1 a2  15 
Cách 1: *   23   b 2 1 2 b
1 1 a 1 a2 31 a2 b 2 1 1 a2              15      b   2
1  1 a2  15   8  b  2 1  2 b  
1 1 a  7 1 a2  0  
b  2    a2 1 1  15   2 3 a  1  1    b 1 1 a     3    
b a  3 3 4 .   7 3 7 b  1 b 1 1 a      3   2 u   a 1 2 2 
v u  15
Cách 2: Đặt  ta có hpt: 
(Hệ đẳng cấp quen thuộc). v b 1 2 2 
v  2uv u  23 
Câu 11: Gọi n là số các số phức z đồng thời thỏa mãn iz 1 2i  3 và biểu thức
T  2 z  5  2i  3 z  3i đạt giá trị lớn nhất. Gọi M là giá trị lớn nhất của T . Giá trị tích của M .n là A. 10 21 . B. 6 13 . C. 5 21 . D. 2 13 .
Câu 12: Gọi n là số các số phức z đồng thời thỏa mãn iz 1 2i  3 và biểu thức
T  2 z  5  2i  3 z  3i đạt giá trị lớn nhất. Gọi M là giá trị lớn nhất của T . Giá trị tích của M .n là A. 10 21 . B. 6 13 . C. 5 21 . D. 2 13 . Lời giải Chọn A
Gọi z x  i
y , với x, y . Khi đó M  ;
x y là điểm biểu diễn cho số phức z . 2 2
Theo giả thiết, iz 1 2i  3  z  2  i  3   x  2   y   1  9 .
Ta có T  2 z  5  2i  3 z  3i  2MA  3MB , với A 5  ; 2
  và B 0;3 .
Nhận xét rằng A , B , I thẳng hàng và 2IA  3IB .
Cách 1: Gọi  là đường trung trực của AB , ta có  : x y  5  0 .
T  2MA  3MB PA PB . Dấu “  ” xảy ra khi M P hoặc M Q .
x y  5  0   8   2 2   2   8   2 2  2  Giải hệ   P  ;  và Q  ;   .  x  2      2   y  2 1  9  2 2   2 2  
Khi đó M  max T  5 21 .
Vậy M .n  10 21 .   
Cách 2: Ta có A , B , I thẳng hàng và 2IA  3IB nên 2IA  3IB  0 .     2 2  2 2
2MA  3MB  2MI IA  3MI IB 2 2 2
 5MI  2IA  3IB  105 . Do đó T   MA MB2 2 2. 2 3. 3   2 2
5 2MA  3MB   525 hay T  5 21 .
Khi đó M  max T  5 21 . Dấu “  ” xảy ra khi M P hoặc M Q .
Vậy M .n  10 21 .
Cách 3: Gọi z x yi , với x, y . Khi đó M  ;
x y là điểm biểu diễn cho số phức z . 2 2
Theo giả thiết, iz 1 2i  3  z  2  i  3   x  2   y   1  9 . x  2   3sin t Đặt  . Khi đó
y  1 3cos t
P MA MB    t 2    t 2    t 2    t 2 2 3 2 3 3sin 3 3cos 3 2 3sin 2 3cos
 2 27 18sin t  cos t   3 17 12sin t  cos t
 2. 54  36sin t  cost   3. 51 36sin t  cost
Ta thấy: P  2  3 54  36sin t  cost   51 36sin t  cost   521.
P đạt giá trị lớn nhất là 521 khi:
54  36 sin t  cos t
51 36sin t  cos t  1  
 sin t  cos t
x y  2  0 . 2 3 3
x y  2  0 
Toại độ điểm M thỏa mãn hệ phương trình: 
 Có hai điểm M thỏa  x  2  2   y  2 1  9 
mãn. Vậy M .n  10 21 .
Câu 13: Cho số phức z có z  2018. Diện tích của đa giác có các đỉnh là các điểm biểu diễn của z và 0 0 0 1 1 1
các nghiệm của phương trình  
được viết dạng n 3 , n   . Chữ số hàng đơn vị z z z z 0 0 của n là A. 9 . B. 8 . C. 3 . D. 4 .   
Câu 14: Cho hàm số y f x liên tục và nhận giá trị dương trên đoạn 0;  thỏa mãn 4        4
f  x  tan .
x f x , x   0; 
, f 0  1. Khi đó cos .
x f x dx  bằng 4    0 1   1  A. . B. . C. ln . D. 0 . 4 4 4
----------HẾT----------
ĐÁP ÁN THAM KHẢO 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A C B D D A B B B C A A C D D A A B C B A D D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C D D C D C D C C A D B B A C C B B A C D D A B
HƯỚNG DẪN GIẢI
Câu 15: Cho số phức z có z  2018. Diện tích của đa giác có các đỉnh là các điểm biểu diễn của z và 0 0 0 1 1 1
các nghiệm của phương trình  
được viết dạng n 3 , n   . Chữ số hàng đơn vị z z z z 0 0 của n là A. 9 . B. 8 . C. 3 . D. 4 .
Hướng dẫn giải Chọn C z  0 Điều kiện:  z  0  0 1 1 1 Ta có:    .
z z  z z
z z z z 2 2
z  z.z  z  0 0  0  0  0  z z z z 0 0 0 0 2  z z z 1 3  1 3    1  0      
i z    
i z z z z 0 1,2    z 2 2 2 2 0  0 0   1 3
Ta có: z z   
i z z  2018 và z z z  0. 1 2 0 2 2 0 0 1 2
Do đó z , z , z được biểu diễn bởi ba điểm M , M , M tạo thành một tam giác đều nằm 0 1 2 0 1 2
trên đường tròn tâm O bán kính R  2018. 3 2 2 3
Tam giác đều này có chiều cao: h
R và độ dài cạnh: a  .h  . R  3.R 2 3 3 2 1 2 3R 2 3.2018
Diện tích tam giác: S  . a h  . 3  . 3  3054243. 3 . 2 4 4
Vậy n  3054243 có chữ số hàng đơn vị là 3.   
Câu 16: Cho hàm số y f x liên tục và nhận giá trị dương trên đoạn 0;  thỏa mãn 4        4
f  x  tan .
x f x , x   0; 
, f 0  1. Khi đó cos .
x f x dx  bằng 4    0 1   1  A. . B. . C. ln . D. 0 . 4 4 4
Hướng dẫn giải Chọn B      
Từ f  x  tan .
x f x , x   0; 
và f x liên tục và nhận giá trị dương trên đoạn 0; , 4       4  ta có: f  x     tan x , x   0; f x  4    f  x     dx  tan d x x   , x   0; f x  4    f  x sin x     dx  dx   , x   0; f x cos x  4      
 ln f x   ln cos x  C , x   0;  . 4   
Mà f 0  1 nên suy ra ln f 0   ln cos 0  C C  0 . 1   
Như vậy ln f x   ln cos x  f x  , x   0; . cos x  4       4 4 1 4  Từ đó I  cos .
x f x dx   cos . x dx   dx   . cos x 4 0 0 0
----------HẾT----------
Câu 17: Cho số phức z thỏa mãn điều kiện z  2  z  2i . Giá trị nhỏ nhất của biểu thức a b 17
P z 1 2i z  3  4i z  5  6i được viết dưới dạng
với a , b là các số hữu 2
tỉ. Giá trị của a b là A. 3 . B. 7 . C. 2 . D. 4 .
Câu 18: Cho số phức z thỏa mãn điều kiện z  2  z  2i . Giá trị nhỏ nhất của biểu thức a b 17
P z 1 2i z  3  4i z  5  6i được viết dưới dạng
với a , b là các số hữu 2
tỉ. Giá trị của a b là A. 3 . B. 7 . C. 2 . D. 4 .
Hướng dẫn giải Chọn A
Giả sử z x yi với x, y   , ta có
z  2  z  2i
  x yi  2   x yi  2i
  x  2  yi x   y  2i
  x  2  y x   y  2 2 2 2 2  x y .
Như vậy z x xi với x   . Khi đó ta có
P   x  
1   x  2i   x  3   x  4i   x  5   x  6i
  x  2   x  2   x  2   x  2   x  2   x  2 1 2 3 4 5 6 2 2 2
 2x  6x  5  2x 14x  25  2x  22x  61 2 2 2 2 2  3 1 11 1           7  1  2. x     x    2 x               2   2   2   2    2  2   2 2 2  3 11   1 1   7  1  2. x    x    2 x          2 2   2 2   2  2 1 1 2 17  2. 17   . 2 2  3 11 x    x   2 2 7 Dấu bằng xảy ra khi   x  . 7 2 x   0   2 1 2 17 Vậy: min P
. Suy ra a  1,b  2 nên a b  3 . 2
Câu 19: Cho hai số phức u , v thỏa mãn 3 u  6i  3 u 1 3i  5 10 , v 1 2i v i . Giá trị nhỏ nhất
của u v là: 10 2 10 5 10 A. . B. . C. 10 . D. . 3 3 3
----------HẾT----------
BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B C D D D A B C B C D B C D C D A C A A D D B C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B A C A D A D C D B A B D A C A B D C A A C A D B
HƯỚNG DẪN GIẢI
Câu 20: Cho hai số phức u , v thỏa mãn 3 u  6i  3 u 1 3i  5 10 , v 1 2i v i . Giá trị nhỏ nhất
của u v là: 10 2 10 5 10 A. . B. . C. 10 . D. . 3 3 3 Lời giải Chọn B 5 10 5 10
 Ta có: 3 u  6i  3 u 1 3i  5 10  u  6i u 1 3i
MF MF  . 3 1 2 3  1 9 
u có điểm biểu diễn M thuộc elip với hai tiêu điểm F 0; 6 , F 1;3 , tâm I ; và độ 1   2      2 2  5 10 5 10
dài trục lớn là 2a   a  . 3 6  F F  1; 3 
F F : 3x y  6  0 . 1 2   1 2
 Ta có: v 1 2i v i v i NA NB
v có điểm biểu diễn N thuộc đường thẳng d là trung trực của đoạn AB với A1; 2, B 0  ;1 .   1 1  AB   1  ;3 , K ;  
 là trung điểm của AB d : x  3y  2  0 .  2 2  1 27   2 2 2 3 10
d I, d      2 2 2 1 3 2 10
Dễ thấy F F d  min u v  min MN d I, d   a  . 1 2 3
Câu 21: Cho z x yi với x , y   là số phức thỏa mãn điều kiện z  2  3i z i  2  5 . Gọi M ,
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y  8x  6 y . Tính M m . 156 156 A.  20 10 . B. 60  20 10 . C.  20 10 .
D. 60  2 10 . 5 5
Câu 22: Cho z x yi với x , y   là số phức thỏa mãn điều kiện z  2  3i z i  2  5 . Gọi M ,
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y  8x  6 y . Tính M m . 156 156 A.  20 10 . B. 60  20 10 . C.  20 10 .
D. 60  2 10 . 5 5 Lời giải Chọn B 6 y 4 2 B x 2 10 5 -1 5 10 -1 I 2 K J 4 6 A 8 10 2 2 2 2
- Theo bài ra: z  2  3i z i  2  5   x  2   y  3   x  2   y   1  5
2x y  2  0     x  2  2   y  2 1  25 
 tập hợp điểm biểu diễn số phức z là miền mặt phẳng T  thỏa mãn
2x y  2  0  
(là miền tô đậm trên hình vẽ, kể cả biên)  x  2  2   y  2 1  25  - Gọi A2; 6
  , B 2; 2 là các giao điểm của đường thẳng 2x y  2  0 và đường tròn
C  x  2   y  2 : 2 1  25 . 2 2 - Ta có: 2 2
P x y  8x  6 y   x  4   y  3  P  25 .
Gọi C  là đường tròn tâm J  4  ; 3
  , bán kính R P  25 .
- Đường tròn C  cắt miền T  khi và chỉ khi
JK R JA IJ IK R IA  2 10  5  25  P  3 5  40  20 10  P  20
(trong đó JK là bán kính đường tròn tâm J và tiếp xúc ngoài với đường tròn C )
M  20 và m  40  20 10 .
Vậy M m  60  20 10 .
Câu 23: Gọi z , z là hai trong tất cả các số phức thỏa mãn điều kiện i  
1 z  3i  3  2 và z z  2. 1 2 1 2
Gọi m , n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P z z . Giá trị của 3 3
S m n 1 2 bằng A. 72 . B. 90 . C. 54 . D. 126 .
Câu 24: Gọi z , z là hai trong tất cả các số phức thỏa mãn điều kiện i  
1 z  3i  3  2 và z z  2. 1 2 1 2
Gọi m , n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P z z . Giá trị của 3 3
S m n 1 2 bằng A. 72 . B. 90 . C. 54 . D. 126 . Lời giải Chọn A Ta có i  
1 z  3i  3  2  i  
1  z  3  2  z  3  2 .
Gọi M là điểm biểu diễn của z ta có M nằm trên đường tròn C  tâm I 3;0 , R  2 .
Gọi A , B lần lượt là điểm biểu diễn cho z , z ta có z z  2  AB  2 . 1 2 1 2
Gọi H là trung điểm AB ta có tam giác IAB vuông tại I (theo định lý Pitago đảo) AB 2  IH    1 2 2
H chạy trên đường tròn tâm I bán kính R  1 .
P z z OA OB   2 2 1 1  2 2 OA OB 1 2 
Mặt khác theo công thức độ dài đường trung tuyến ta có 2 2 AB 2 2 2 2 2 2
OA OB  2OH   2OH   2OH  2 2 2
 max POI R  3 1  4 ; min POI R  3 1  2  m  4 , n  2  S  64  8  72 . 4 4  z   z
Câu 25: Cho hai số phức z , z thỏa mãn z z z z  0 . Tính 1 2 A   . 1 2 1 2 1 2     z z  2   1  A. 1. B. 1 i . C. 1. D. 1 i . 4 4  z   z
Câu 26: Cho hai số phức z , z thỏa mãn z z z z  0 . Tính 1 2 A   . 1 2 1 2 1 2     z z  2   1  A. 1. B. 1 i . C. 1. D. 1 i . Lời giải Chọn C
Đặt z a bi , z a  b i
 , với a, a , ,
b b   , ta có: 1 2
z z z  1 2 1
z z z z  0  1 2 1 2  z z   1 2   z z z zz z  
z z z z z z z z z z 1 2   1 2  1 1  1 1 1 2 2 1 2 2 1 1    z z z z  z z z z  1 1 2 2 1 1 2 2 
z z z z z z 1 2 2 1 1 1   . z z z z  1 1 2 2 Ta có : 2 2 2 2  z   z   z z   z z z z  1 2 1 2     2 1 2 2 1            2 z z z zz z z z 2   1   2 1   2 2 1 1  2 2
z z z z   z z  1 2 2 1     2 1 1     2  1  . z zz z 1 1   1 1  Từ đó: 2 4 4 2 2  z   z   z z      1 2 2 A   1 2          2        1  2  1. z z   z z 2   1   2   1    
Câu 27: Cho số phức z a bi a,b   thỏa z  4  z  4  10 và z  6 lớn nhất. Tính S a b . A. S  3  . B. S  5 . C. S  5  . D. S  11.
Câu 28: Cho số phức z a bi a,b   thỏa z  4  z  4  10 và z  6 lớn nhất. Tính S a b . A. S  3  . B. S  5 . C. S  5  . D. S  11. Lời giải Chọn C Gọi M  ;
a b là điểm biểu diễn số phức z a bi a,b   , A 4
 ;0 , B 4;0 , C 6;0 lần
lượt là điểm biểu diễn số phức z  4
 , z  4 , z  6 . 1 2 3
Khi đó ta có z  4  z  4  10  MA MB  10 suy ra tập hợp điểm M là  E  nhận A , B
là các tiêu điểm, độ dài trục lớn 2a  10  a  5 , tiêu cự 2c  8  c  4 , b  3 2 2 x y   E :   1. 25 9
Ta tìm giá trị lớn nhất của z  6  MC , khi đó MC
EF FC  11, khi đó M E với max E  5
 ;0 , F 5;0  z  5
 . Vậy S a b  5 .
Câu 29: Xét các số phức z a bi ( a , b   ) có môđun bằng 2 và phần ảo dương. Tính giá trị biểu
thức S   a b 2018 5  2  
khi biểu thức P  2  z  3 2  z đạt giá trị lớn nhất. A. S  1. B. 2018 S  2 . C. 1009 S  2 . D. S  0 .
Câu 30: Xét các số phức z a bi ( a , b   ) có môđun bằng 2 và phần ảo dương. Tính giá trị biểu
thức S   a b 2018 5  2  
khi biểu thức P  2  z  3 2  z đạt giá trị lớn nhất. A. S  1. B. 2018 S  2 . C. 1009 S  2 . D. S  0 . Lời giải Chọn D
z a bi ; z  2 2 2  a b  2 2 2
a b  4 . 2 2
P  2  z  3 2  z  a   2  b    a 2 2 3 2  b
4a  8  3 8  4a .
4a  8  3 8  4a   2 2
1  3 8  4a  8  4a  4 10 . 4a  8 8  4a 8
Dấu đẳng thức xẩy ra khi 
 9 4a  8  8  4a a   . 1 3 5 8 6 Với a    b  (do b  0 ). 5 5 2018 8 6   8 6  
Vậy min P  4 10  z   
i . Khi đó S  5    2     0 . 5 5    5 5  
Câu 31: Cho số phức z thỏa mãn  z  2i 1   z  2i 1  10 . Gọi M , m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của z . Tính tổng S M m . A. S  9 . B. S  8 . C. S  2 21 .
D. S  2 21 1 .
Câu 32: Cho số phức z thỏa mãn  z  2i 1   z  2i 1  10 . Gọi M , m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của z . Tính tổng S M m . A. S  9 . B. S  8 . C. S  2 21 .
D. S  2 21 1 .
Hướng dẫn giải Chọn C
Giả sử z a bi , a,b    z a bi .
Chia hai vế cho i ta được: z  2  i z  2  i  10 .
Đặt M a;b , N a;  b , A2;  1 , B 2;   1 , C 2 
;1  NB MC . 2 2 X Y
Ta có: MA MC  10  M   E  :   1. 25 21
Elip này có phương trình chính tắc với hệ trục tọa độ IXY , I 0 
;1 là trung điểm AC .  X x xy  2 2 1
Áp dụng công thức đổi trục     1. Y y 1 25 21  a  5sin t  2 Đặt 2 2 2 
, t 0; 2   z OM a b t    t 2 2 25sin 1 21 cos b  1  21 cos t     2 26
4 cos t  2 21 cos t  . a  0  z
 1 21  cos t  1   . max b   1 21  a  0  z
 1 21  cos t  1    . min b   1 21 
M m  2 21 .
Câu 33: Cho hai số phức z, z thỏa mãn z  5  5 và z 1 3i z  3  6i . Tìm giá trị nhỏ nhất của z z . 5 5 A. . B. . C. 10 . D. 3 10 . 2 4
Câu 34: Cho hai số phức z, z thỏa mãn z  5  5 và z 1 3i z  3  6i . Tìm giá trị nhỏ nhất của z z . 5 5 A. . B. . C. 10 . D. 3 10 . 2 4 Hướng dẫn giải Chọn A Gọi M  ;
x y là điểm biểu diễn của số phức z x yi , N x ; y là điểm biểu diễn của số
phức z x  y i  . Ta có z
  x   yi    x  2 2 2 5 5 5 5 5  y  5 .
Vậy M thuộc đường tròn C   x  2 2 2 : 5  y  5
z 1 3i z  3  6i   x  
1   y  3i   x  3   y  6i
  x  2   y  2   x  2   y  2 1 3 3 6
 8x  6 y  35
Vậy N thuộc đường thẳng  : 8x  6 y  35
Dễ thấy đường thẳng  không cắt C  và z z  MN
Áp dụng bất đẳng thức tam giác, cho bộ ba điểm  I, M , N  ta có. 8.5  6.0  5 5
MN IN IM IN R IN R d I,   R   5  0 2 2 2 8  6
Dấu bằng đạt tại M M ; N N . 0 0
Câu 35: Cho a là số thực, phương trình 2
z  a  2 z  2a  3  0 có 2 nghiệm z , z . Gọi M , N là 1 2
điểm biểu diễn của z , z trên mặt phẳng tọa độ. Biết tam giác OMN có một góc bằng 120 , 1 2
tính tổng các giá trị của a . A. 6  . B. 6 . C. 4  . D. 4 .
Câu 36: Gọi z , z , z , z là các nghiệm của phương trình 4 3 2
z  4z  3z  3z  3  0 . Tính 1 2 3 4 T   2
z  2z  2 2
z  2z  2 2
z  2z  2 2
z  2z  2 . 1 1 2 2 3 3 4 4  A. T  102 . B. T  101. C. T  99 . D.T  100 .
Câu 37: Cho a là số thực, phương trình 2
z  a  2 z  2a  3  0 có 2 nghiệm z , z . Gọi M , N là 1 2
điểm biểu diễn của z , z trên mặt phẳng tọa độ. Biết tam giác OMN có một góc bằng 120 , 1 2
tính tổng các giá trị của a . A. 6  . B. 6 . C. 4  . D. 4 . Lời giải
Chọn B
Vì O , M , N không thẳng hàng nên z , z không đồng thời là số thực, cũng không đồng thời 1 2
là số thuần ảo  z , z là hai nghiệm phức, không phải số thực của phương trình 1 2 2
z  a  2 z  2a  3  0 . Do đó, ta phải có: 2
  a 12a 16  0  a  6  2 5; 6  2 5 . 2  2  a
a 12a 16 z   i 1  2 2 Khi đó, ta có:  . 2  2  a
a 12a 16 z   i 1   2 2
OM ON z z  2a  3 và 2
MN z z  a 12a 16 . 1 2 1 2 2 2 2
OM ON MN
Tam giác OMN cân nên  MON  120   cos120 2OM .ON 2 a  8a 10 1    2
a  6a  7  0 a  3  2 (thỏa mãn). 2 2a  3 2
Suy ra tổng các giá trị cần tìm của a là 6 .
Câu 38: Gọi z , z , z , z là các nghiệm của phương trình 4 3 2
z  4z  3z  3z  3  0 . Tính 1 2 3 4 T   2
z  2z  2 2
z  2z  2 2
z  2z  2 2
z  2z  2 . 1 1 2 2 3 3 4 4  A. T  102 . B. T  101. C. T  99 . D.T  100 . Lời giải
Chọn B
Đặt f z 4 3 2
z  4z  3z  3z  3  f z   z z z z z z z z . 1   2   3   4  Do 2
z  2z  2  z  1 i
z  1 i nên 1 1  1  1  T   2
z  2z  2 2
z  2z  2 2
z  2z  2 2
z  2z  2  f 1 if  1   i 1 1 2 2 3 3 4 4 
 10  i10  i  101.
Câu 39: Tìm số phức z thỏa mãn z 1 i  5 và biểu thức T z  7  9i  2 z  8i đạt giá trị nhỏ nhất.
A. z  5  2i .
B. z  1 6i .
C. z  1 6i và z  5  2i .
D. z  4  5i . ----------HẾT----------
BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C D A C B B C B B C B B B C D A D A C D D D B D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B A D D A D C A A A B A A A D B C C A A C A D C B
HƯỚNG DẪN GIẢI
Câu 40: Tìm số phức z thỏa mãn z 1 i  5 và biểu thức T z  7  9i  2 z  8i đạt giá trị nhỏ nhất.
A. z  5  2i .
B. z  1 6i .
C. z  1 6i và z  5  2i .
D. z  4  5i . Lời giải Chọn B M I K A M0 B
Từ giả thiết z 1 i  5 suy ra tập hợp các điểm M biểu diễn số phức z là đường tròn (C) tâm I 1 
;1 , bán kính R  5 .
Xét các điểm A7;9 và B 0;8 . Ta thấy IA  10  2.IM . 1  5 
Gọi K là điểm trên tia IA sao cho IK IA K  ;3   4  2  IM IK 1 Do   , góc 
MIK chung  IKM  ∽ IMA  . c g.cIA IM 2 MK IK 1   
MA  2.MK . MA IM 2
Lại có: T z  7  9i  2 z  8i MA  2.MB  2 MK MB  2.BK  5 5 5  T
 5 5  M BK  C  , M nằm giữa B và K  0  x  . min M 2
Ta có: phương trình đường thẳng BK là: 2x+y-8=0 x  1 
2x y  8  0  y  6 
Tọa độ điểm M là nghiệm của hệ:    M  1;6 .  x    2 1   y  2 1  25  x  5   y  2 
Vậy z  1 6i là số phức cần tìm. z z
Câu 41: Cho số thực z và số phức z thoả mãn z  2i  1 và 2
1 là số thực. Gọi a, b lần lượt là 1 2 2 1 i
giá trị lớn nhất và giá trị nhỏ nhất của z z . Tính T a  . b 1 2 A. T  4 . B. T  4 2 .
C. T  3 2 1.
D. T  2  3. z z
Câu 42: Cho số thực z và số phức z thoả mãn z  2i  1 và 2
1 là số thực. Gọi a, b lần lượt là 1 2 2 1 i
giá trị lớn nhất và giá trị nhỏ nhất của z z . Tính T a  . b 1 2 A. T  4 . B. T  4 2 .
C. T  3 2 1.
D. T  2  3. Lời giải
Chọn B z z
x m yi1 i
Gọi z m ; z x yi ; m, x, y   . Theo đầu bài ta có 2 1  là một số 1 2 1 i 2
thực nên ta có x m y  0  m x y .
Do z  2i  1  x   y  22 2
 1   y  2 2
 1  1  y  3 nên ta có: 2
2  z z   x m2  y   x y x2 2 2
y y 2  3 2 1 2
a  min z x  2 ; b  max z x  3 2  T a b  4 2 . 1 2 1 2
Câu 43: Cho a , b , c là các số thực sao cho phương trình 3 2
z az bz c  0 có ba nghiệm phức lần
lượt là z w  3i ; z w  9i ; z  2w  4 , trong đó w là một số phức nào đó. Tính giá trị của 1 2 3
P a b c . A. P  36 . B. P  208 . C. P  136 . D. P  84 .
Câu 44: Cho a , b , c là các số thực sao cho phương trình 3 2
z az bz c  0 có ba nghiệm phức
lần lượt là z w  3i ; z w  9i ; z  2w  4 , trong đó w là một số phức nào đó. Tính 1 2 3
giá trị của P a b c . A. P  36 . B. P  208 . C. P  136 . D. P  84 .
Hướng dẫn giải Chọn C
Đặt w x yi , với x, y   .
Ta có z z z  a  4w  4 12i  a  4x  4  a  12  4 y i  0 1 2 3    
4x  4  a  0
4x  4  a     . 12  4 y  0 y  3  
Từ đó w x  3i z x ; z x  6i ; z  2x  4  6i . 1 2 3 Vì phương trình bậc ba 3 2
z az bz c  0 có một nghiệm thực nên hai nghiệm phức còn lại
phải là hai số phức liên hợp, suy ra x  2x  4  x  4 .
Như vậy z  4 ; z  4  6i ; z  4  6i . 1 2 3 Do đó
z z z  a 12   aa  12  1 2 3   
z z z z z z    84   bb   84 . 1 2 2 3 3 1 z z z c 208 c    c  208  1 2 3  
Vậy P a b c  12  84   208    136 .
Document Outline

  • Chương 4 - SỐ PHỨC - Mức độ 1 Phần 1
  • Chương 4 - SỐ PHỨC - Mức độ 1 Phần 2
  • Chương 4 - SỐ PHỨC - Mức độ 1 Phần 3
  • Chương 4 - SỐ PHỨC - Mức độ 1 Phần 4
  • Chương 4 - SỐ PHỨC - Mức độ 2 Phần 1
  • Chương 4 - SỐ PHỨC - Mức độ 2 Phần 2
  • Chương 4 - SỐ PHỨC - Mức độ 2 Phần 3
  • Chương 4 - SỐ PHỨC - Mức độ 2 Phần 4
  • Chương 4 - SỐ PHỨC - Mức độ 3 Phần 1
  • Chương 4 - SỐ PHỨC - Mức độ 3 Phần 2
  • Chương 4 - SỐ PHỨC - Mức độ 3 Phần 3
  • Chương 4 - SỐ PHỨC - Mức độ 3 Phần 4
  • Chương 4 - SỐ PHỨC - Mức độ 4 Phần 1
  • Chương 4 - SỐ PHỨC - Mức độ 4 Phần 2
  • Chương 4 - SỐ PHỨC - Mức độ 4 Phần 3
  • Chương 4 - SỐ PHỨC - Mức độ 4 Phần 4