Trọng tâm kiến thức và các dạng đề ôn thi vào lớp 10 môn Toán

TRẦN HỮU THÁP (Chủ biên)

NGUYỄN VĂN CHI - HUỲNH THANH HÙNG

HỒ TẤN YÊN - ĐỊNH VĂN THÂN - ĐOÀN VĂN TRÚC

TRỌNG TÂM KIẾN THỨC

và CÁC DẠNG ĐỀ ÔN THI VO LỚP 10

Môn

TOÁN

NHÀ XUẤT BẢN GIÁO DỤC VIỆT NAM

3

LỜI NÓI ĐẦU

Để đáp ứng nhu cầu của đông đảo thầy cô giáo, các bậc phụ huynh và học

sinh trên địa bàn tỉnh Quảng Ngãi có một tài liệu ôn tập môn Toán cấp Trung học

cơ sở (THCS) nói chung và ôn tập môn Toán lớp 9 nói riêng. Sở Giáo dục và Đào

tạo Quảng Ngãi đã tổ chức biên soạn tài liệu này.

Nội dung của tài liệu này dựa trên chương trình bộ môn Toán cấp THCS

(trọng tâm là lớp 9) hiện hành và hướng dẫn nội dung ôn thi vào lớp 10 năm học

2015 - 2016 của Sở Giáo dục và Đào tạo Quảng Ngãi.

Cấu trúc của tài liệu gồm có bốn phần chính :

− Phần một : Đại số.

− Phần hai : Hình học.

− Phần ba : Số học và toán suy luận lô-gic (dành cho học sinh khá, giỏi).

− Phần tư : Một số đề thi vào lớp 10 THPT và THPT chuyên Lê Khiết.

Trong các phần thứ nhất, thứ hai, thứ ba được phân loại theo từng chủ đề

liên quan mật thiết đến những dạng toán trong cấu trúc của đề thi. Các bạn có

đồng ý với chúng tôi rằng : “Dạy và học phương pháp giải toán vẫn tốt hơn là dạy

và học từng bài toán cụ thể”. Với quan điểm như thế nên trong từng chủ đề chúng

tôi đã cố gắng thể hiện theo trình tự như sau :

− Kiến thức cần sử dụng.

− Các dạng toán thường gặp. Gồm có :

+ Phương pháp giải cho từng dạng cụ thể.

+ Các ví dụ minh hoạ phương pháp giải cho từng dạng toán.

− Bài tập vận dụng (gồm hệ thống bài tập cơ bản, bài tập nâng cao...).

Với hi vọng sẽ giúp bạn đọc trong một thời gian ngắn có thể hệ thống được

toàn bộ những kiến thức cần nhớ trong chương trình môn Toán cấp THCS (trọng

tâm là môn Toán lớp 9), đặc biệt hơn cả là cung cấp cho bạn đọc những phương

pháp giải toán cơ bản để các bạn có nhiều hướng giải quyết trước một vấn đề cụ

thể. Các bài tập tổng hợp nhằm giúp bạn đọc vận dụng linh hoạt những hiểu biết

riêng lẻ từ các ví dụ minh hoạ để giải quyết những vấn đề phức tạp hơn.

4

Phần thứ tư sẽ giới thiệu một số đề thi để bạn đọc làm quen trước khi bước

vào kì thi tuyển sinh vào lớp 10 Trung học phổ thông và Trung học phổ thông

chuyên Lê Khiết năm học 2015 - 2016.

Tài liệu ôn tập này do tập thể các giáo viên có nhiều năm kinh nghiệm trong

giảng dạy bộ môn Toán ở các trường THCS trên địa bàn tỉnh biên soạn.

Chúng tôi hi vọng rằng, tài liệu ôn tập này, không dám nói là cẩm nang, thì

cũng là một trong những tài liệu thật sự bổ ích không những cho học sinh mà còn

là tài liệu tham khảo hết sức cần thiết cho nhiều giáo viên trong việc hướng dẫn

học sinh ôn tập môn Toán lớp 9 và luyện thi vào lớp 10.

Vì khuôn khổ cuốn sách và thời gian biên soạn có hạn nên chúng tôi dù đã

cố gắng rất nhiều nhưng vẫn không thể hiện hết những gì bạn đọc mong muốn.

Mong nhận được những góp ý của bạn đọc để lần tái bản sách sẽ được tốt hơn.

Quảng Ngãi, tháng 03 năm 2015

Tập thể tác giả

5

Phần một.

ĐẠI SỐ

BIẾN ĐỔI BIỂU THỨC ĐẠI SỐ

I. KIẾN THỨC CẦN SỬ DỤNG

1. Đa thức : Khái niệm đa thức ; khái niệm bậc và nghiệm của đa thức ; các

phép toán về đa thức.

2. Phân thức : Khái niệm ; tính chất ; các phép toán về phân thức.

3. Căn thức : Khái niệm căn bậc hai và căn bậc hai số học ; điều kiện tồn tại

căn bậc hai ; các phép tính về căn thức.

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

RÚT GỌN, TÍNH GIÁ TRỊ CỦA BIỂU THỨC

1. PHƯƠNG PHÁP GIẢI

Đối với bài tập rút gọn biểu thức : Biểu thức cần rút gọn thường gồm nhiều

đơn thức, nhị thức chứa luỹ thừa và căn thức, kết hợp với nhau trong một dãy các

phép tính phức tạp, ta có thể tiến hành các bước như sau :

Bước 1 : Nhận xét chung toàn bộ biểu thức để thấy các biểu thức con phức

tạp, cồng kềnh và các biểu thức con tương đối đơn giản hơn. Nhận xét các luỹ

thừa và căn thức có thể liên quan đến các hằng đẳng thức quen thuộc. Tìm điều

kiện xác định.

Bước 2 : Rút gọn từng biểu thức con đã cho ; có thể kí hiệu riêng từng biểu

thức con đó bằng một chữ cái A, B, C,… riêng biệt. Thực hiện đúng thứ tự các

phép tính. Chú ý nhóm các số hạng thích hợp.

Ch

ChCh

Ch 

  

 

1

11

1

6

Bước 3 : Kết hợp các kết quả của bước 2 vào biểu thức để bài đã cho tiếp tục

thực hiện các phép biến đổi.

Chú ý :

- Luôn phải kiểm tra lại các điều kiện thực hiện các biến đổi, các công thức vận

dụng.

- Có thể giải quyết gọn nhờ tiến hành ngay các phép tính giữa các biểu thức

phức tạp của đề bài, không cần rút gọn từng biểu thức con.

- Các bài tập rút gọn có chứa căn thức có thể vận dụng đưa một thừa số ra

hoặc vào dấu căn ; trục căn thức ở mẫu số nếu có.

- Các bài tập có dạng phân thức chú ý đến cách phân tích đa thức thành nhân

tử.

- Bài tập tính giá trị một biểu thức thường rút gọn trước, cũng có thể tính trực

tiếp giá trị từng biểu thức con rồi kết hợp lại.

2. CÁC VÍ DỤ

Ví dụ 1 : Rút gọn rồi tính giá trị của biểu thức

x

3

(x + y) – x

2

(x

2

+ y) + x(xy – y) tại x = 1 và y = 2.

Hướng dẫn giải

x

3

(x + y) – x

2

(x

2

+ y) + x(xy – y) = x

4

+ x

3

y – x

4

– x

2

y + x

2

y – xy

= x

3

y – xy = xy(x

2

– 1).

Thay x = 1 và y = 2 vào biểu thức, ta được 1.2.(1

2

– 1) = 0.

Vậy giá trị của biểu thức đã cho tại x = 1 và y = 2 bằng 0.

Ví dụ 2 : Cho phân thức

2

6 5

( 1)( 3)( 5)

x x

Q

x x x

+ +

=

+ − +

.

a) Rút gọn Q.

b) Tìm giá trị của Q khi x = 2015.

Hướng dẫn giải

a) ĐKXĐ :

1; 3; 5.

≠ − ≠ ≠ −

x x x

7

2

6 5 ( 1)( 5) 1

( 1)( 3)( 5) ( 1)( 3)( 5) 3

+ + + +

= = =

+ − + + − + −

x x x x

Q

x x x x x x x

.

b) Thay x = 2015 vào biểu thức Q ta được

1 1

2015 3 2012

= =

−

Q .

V

ậ

y giá tr

ị

c

ủ

a bi

ể

u th

ứ

c Q t

ạ

i x = 2015 là

1

2012

.

Ví dụ 3 :

Cho bi

ể

u th

ứ

c A =

2

1

−

+

− −

x x x

.

a) Tìm

đ

i

ề

u ki

ệ

n c

ủ

a x

để

A có ngh

ĩ

a.

b) Rút g

ọ

n A.

c) Tính giá tr

ị

c

ủ

a A khi x = 6 + 2

5

.

Hướng dẫn giải

a) A có ngh

ĩ

a

⇔

x > 0 và x

1

≠

.

b) A

2

1

−

= +

− −

x x x

(

)

( )

2 1

1

−

= +

−

x x

x

x x

1 2

1 1

−

= +

− −

x x

2 1

1

− +

=

−

x x

x

(

)

2

1

−

=

−

x

1

= −

x

c) x

(

)

2

6 2 5 5 1

= + = +

Do

đ

ó giá tr

ị

c

ủ

a bi

ể

u th

ứ

c A t

ạ

i

(

)

2

5 1

= +x

là

A

( )

2

5 1 1

= + −

5 1 1

= + −

5

=

8

Dạng 2.

CHỨNG MINH ĐẲNG THỨC

1. PHƯƠNG PHÁP GIẢI

Để chứng minh một đẳng thức A = B ta có thể thực hiện :

− Biển đổi đại số một vế của đẳng thức (A hoặc B) để được kết quả là vế kia.

Thông thường là xuất phát từ một vế phức tạp hơn vế kia. Như vậy, thực chất là

tiến hành một bài tập rút gọn biểu thức đã trình bày ở trên.

− Biến đổi đồng thời cả hai vế để được cùng một kết quả là C.

− Chứng minh hiệu A – B = 0 hoặc B – A = 0.

− Chứng minh bằng phương pháp quy nạp.

− Khi chứng minh đẳng thức có điều kiện, ta sử dụng điều kiện của giả thiết

thay vào biểu thức hoặc bình phương hai vế của đẳng thức cần chứng minh và kết

hợp với điều kiện của giả thiết.

Chú ý :

−

Khác với bài tập rút gọn, bài tập chứng minh đòi hỏi các biến đổi đại số có

định hướng rõ rệt về một dạng định sẵn (vế còn lại hoặc biểu thức C trung

gian).

−

Chứng minh một biểu thức có chứa chữ không phụ thuộc vào biến là chứng

minh biểu thức đó là một hằng số.

2. CÁC VÍ DỤ

Ví dụ 1 : Chứng minh đẳng thức (a

2

+ b

2

)(x

2

+ y

2

) – (ax + by)

2

= (ay – bx)

2

.

Hướng dẫn giải

Ta có VT = (a

2

+ b

2

)(x

2

+ y

2

) – (ax + by)

2

= a

2

x

2

+ a

2

y

2

+ b

2

x

2

+ b

2

y

2

– a

2

x

2

– 2abxy – b

2

y

2

= a

2

y

2

– 2abxy + b

2

x

2

= (ay – bx)

2

= VP.

Đẳng thức được chứng minh.

9

Ví dụ 2 : Chứng minh đẳng thức

3 2 2 3 2 2 8 2 7 8 2 7

+ − − = + − −

.

Hướng dẫn giải

Ta có

VT =

2 2

3 2 2 3 2 2 ( 2 1) ( 2 1)

+ − − = + − −

2 1 2 1 2

= + − − =

(1)

VP =

2 2

8 2 7 8 2 7 ( 7 1) ( 7 1)

+ − − = + − −

7 1 7 1 2

= + − − =

(2)

Từ (1) và (2) suy ra

3 2 2 3 2 2 8 2 7 8 2 7

+ − − = + − −

. Đẳng

thức được chứng minh.

Ví dụ 3 :

1 1

+ −

=

+ −

a a a a

a a

(với a

0 ; 1

≥ ≠

a

).

Hướng dẫn giải

Điều kiện a

0 ; 1

≥ ≠

a

.

Ta có

( 1) (1 )

0.

1 1 (1 ) (1 )

+ − + −

− = − = − =

+ − + −

a a a a a a a a

a a

a a a a

Vậy

1 1

+ −

=

+ −

a a a a

a a

. Đẳng thức được chứng minh.

Ví dụ 4 : Chứng minh rằng với mọi số n nguyên dương ta có

2 2 2 2

( 1)(2 1)

1 2 3 .....

6

+ +

+ + + + =

n n n

n .

Hướng dẫn giải

− Khi n = 1 : V

ế

trái 1

2

= 1 ; V

ế

ph

ả

i

1.2.3

1

6

=

.

Đẳ

ng th

ứ

c

đ

úng.

− Gi

ả

s

ử

đẳ

ng th

ứ

c

đ

úng khi n = k, khi

đ

ó :

2 2 2 2

k(k 1)(2 1)

1 2 3 ..... .

6

+ +

+ + + + =

k

10

− Ta ch

ứ

ng minh

đẳ

ng th

ứ

c

đ

úng khi n = k + 1. Th

ậ

t v

ậ

y :

2

2 2 2 2 2

2 2

( 1)(2k 1) 6( 1)

1 2 3 ..... ( 1)

6 6

( 1)(2 6 6)] ( 1)(2 7 6)

6 6

(k 1)( 2)(2 3) ( 1)[(k+1)+1][2( 1) 1]

.

6 6

k k k

k k

k k k k k k k

k k k k

+ + +

+ + + + + + = +

+ + + + + + +

= =

+ + + + + +

= =

Đẳng thức được chứng minh.

Ví dụ 5 : Cho x, y thoả mãn x + y = 1. Chứng minh x

3

+ y

3

+ 3xy = 1.

Hướng dẫn giải

Ta có x + y = 1

⇒

y = 1 – x.

Do đó : x

3

+ y

3

+ 3xy = x

3

+ (1 – x)

3

+ 3x(1 – x)

= x

3

+ 1 – 3x + 3x

2

– x

3

+ 3x – 3x

2

= 1.

Đẳng thức được chứng minh.

Ví dụ 6 : Cho biểu thức

2 2 2

4

2

2015

− +

= −

−

x x xy y

A

x y

x

(với x ≠ 0 và x ≠ y).

Chứng tỏ giá trị của biểu thức A không phụ thuộc vào hai biến x và y.

Hướng dẫn giải

Với x ≠ 0 và x ≠ y, ta có :

2 2 2

4

2

2015

− +

= −

−

x x xy y

A

x y

x

2

2015 .

−

= −

−

x y

x

x y

x

2015

−

= −

−

x y

.

Khi x

−

y > 0 : A = 2015 – 1 = 2014.

Khi x

−

y < 0 : A = 2015 + 1 = 2016.

Vậy với x ≠ 0 và x ≠ y thì giá trị của biểu thức A không phụ thuộc vào hai biến

x và y.

11

III. BÀI TẬP VẬN DỤNG

1. Bài tập cơ bản

Bài 1. a) Chứng minh rằng a

3

+ b

3

= (a + b)

3

– 3ab(a + b).

b) Cho a + b + c = 0. Chứng minh rằng a

3

+ b

3

+ c

3

= 3abc.

Bài 2. Thực hiện phép tính

2

3

1 : 1 .

1

 

− +

 

−

− 

 

x x

x

Bài 3. Rút gọn biểu thức

3 2 2 3

.

− − +

+ − −

x x y xy y

Bài 4.

Tìm

x

để

phân th

ứ

c

2

3 2

3 4

2 2

− −

=

+ − −

x x

A

x x x

b

ằ

ng 0.

Bài 5.

Th

ự

c hi

ệ

n các phép tính

a)

4 12 3 3

+ +

+ 6 ; b)

(

)

(

)

3 5 10 2 3 5

− − +

;

c)

5 3 5 3 5 1

− + +

+ −

+ − −

;

d)

( )

14 7 15 5 216

7 5 .

1 2 1 3 3 6

 

− −

− + +

 

− −

 

Bài 6.

Rút g

ọ

n các bi

ể

u th

ứ

c

a) A =

2

1

 

+

− +

 

−

+ +

 

x x y y y

xy

x y

x y x y

(

x

> 0 ;

y

> 0 ;

x

≠

y

) ;

b) B =

4

+ −

−

− +

x y x y

y

x y

x y x y

(v

ớ

i

x

> 0 ;

y

> 0 ;

x

≠

y

) ;

c) C =

1 2 2

1

2 1

 

+ + −

−

 

−

+ +

 

x x x

x

x x x

(v

ớ

i

x

> 0 ;

x

≠

1) ;

d) D =

2

2 1 2

1: : 1

1 1

1

 

− −

 

+ −

 

−

 

x x

x

(v

ớ

i

−

1 <

x

< 1) ;

12

e) E =

( )

2

1

:

2

+ + −

−

+

+ +

x y y xy y y xy

x y

x x y y

(v

ớ

i

x

>

y

> 0) ;

g) G =

1 2 2

2 1

− − −

− −

x x

x

(v

ớ

i

x

≥

2 ;

x

≠

3) ;

h) H =

1 1 1

... .

1 2 2 3

2014 2015

+ + +

+ +

+

Bài 7.

Cho bi

ể

u th

ứ

c A =

2 2 1

.

1

2 1

 

+ − +

−

 

−

+ +

 

x x x

x

x x x

a) Rút g

ọ

n A.

b) Tìm giá tr

ị

nguyên c

ủ

a x

để

giá tr

ị

t

ươ

ng

ứ

ng c

ủ

a A là s

ố

nguyên.

Bài 8.

Cho bi

ể

u th

ứ

c B =

( )

2

 

+

 

− +

 

−

− +

−

 

x y xy y

x

x y

x y x y

x y

,

v

ớ

i x > 0 ; y > 0 và x

≠

y. Ch

ứ

ng t

ỏ

r

ằ

ng giá tr

ị

c

ủ

a bi

ể

u th

ứ

c B không

ph

ụ

thu

ộ

c vào 2 bi

ế

n x và y.

Bài 9.

Cho bi

ể

u th

ứ

c : C =

2

.

1

−

+

− −

x x x

a) Tìm

đ

i

ề

u ki

ệ

n c

ủ

a x

để

bi

ể

u th

ứ

c xác

đị

nh.

b) Rút g

ọ

n C.

c) Tính giá tr

ị

c

ủ

a C khi x = 4 +

12

.

Bài 10.

Cho bi

ể

u th

ứ

c E =

2 2

: .

1

2 1 1

 

+ −

−

 

−

+ + +

 

x x x

x

x x x

a) Tìm

đ

i

ề

u ki

ệ

n c

ủ

a x

để

E có ngh

ĩ

a.

b) Rút g

ọ

n E.

c) Tính giá tr

ị

c

ủ

a E khi x =

16 6 7 7.

− +

d) Tìm các giá tr

ị

nguyên c

ủ

a x sao cho giá tr

ị

t

ươ

ng

ứ

ng c

ủ

a E là s

ố

nguyên.

Bài 11.

Tính

3 3

5 2 13 5 2 13.

= + + −A

13

2. BÀI TẬP NÂNG CAO

Bài 1.

Ch

ứ

ng minh r

ằ

ng v

ớ

i m

ọ

i a,b,c ta luôn có :

(a + b)(b + c)(c +a) + abc = (a + b + c)(ab + bc + ca).

Bài 2.

Cho ab = 1. Ch

ứ

ng minh r

ằ

ng a

5

+ b

5

= (a

3

+ b

3

) (a

2

+ b

2

) – (a + b).

Bài 3.

a) Cho a + b + c = 0 và a

2

+ b

2

+ c

2

= 14.

Tính giá tr

ị

c

ủ

a bi

ể

u th

ứ

c A = a

4

+ b

4

+ c

4

.

b) Gi

ả

s

ử

a

3

+ b

3

+ c

3

= 3abc và abc

≠

0.

Tính giá tr

ị

c

ủ

a bi

ể

u th

ứ

c B =

1 1 1

   

+ + +

   

   

a b c

b c a

.

Bài 4.

Rút g

ọ

n bi

ể

u th

ứ

c

3 3 3

2 2 2

3

.

+ + −

=

+ + − − −

x y z xyz

M

x y z xy yz zx

Bài 5.

Cho a, b, c và x, y, z khác nhau và khác 0. Ch

ứ

ng minh r

ằ

ng n

ế

u :

0

+ + =

a b c

x y z

và

1

+ + =

x y z

a b c

thì

2 2 2

1.

+ + =

x y z

a b c

Bài 6.

Cho 0 < x < y và 2x

2

+ 2y

2

= 5xy. Ch

ứ

ng minh r

ằ

ng

3.

+

=

−

x y

Bài 7.

Bi

ế

t xyz = 1. Ch

ứ

ng minh r

ằ

ng

1 1 1

1.

1 1 1

+ + =

+ + + + + +x xy y yz z zx

Bài 8.

Ch

ứ

ng minh r

ằ

ng

S = 1.2.3 + 2.3.4 + 3.4.5 +......+ n(n + 1)(n + 2) =

( 1)( 2)( 3)

.

4

+ + +

n n n n

Bài 9.

Tính giá tr

ị

c

ủ

a bi

ể

u th

ứ

c :

N =

( )

3

2 3

2

1 1 .( (1 ) 1 )

2 1

+ − + − −

+ −

x x x

x

t

ạ

i x =

1

.

5

3. BÀI TẬP TỰ GIẢI

Bài 1.

Cho bi

ể

u th

ứ

c A =

3 2

5 1 1 2 2

.

1

1 1

+ −

− −

−

− + +

x x

x

x x x

14

a) Tìm điều kiện của x để A xác định.

b) Rút gọn A.

c) Tìm giá trị nguyên của x để A nhận giá trị nguyên.

Bài 2. Rút gọn các biểu thức :

a)

2 2

1 2

+

; b)

1

−

a a

a

(với a

0 ; 1

≥ ≠

a

) ;

c)

+

a ab

a b

(với a > 0 ; b > 0) ; d)

x

+

x x y y

y

(với x > 0 ; y > 0).

Bài 3. Tính giá trị của biểu thức :

M =

2 3

2 2

2

+ +

x y xy xy

y

x xy y

tại x = 1 và y = 3.

Bài 4. Tính :

a) P =

2

2014 2014

1 2014

2015

+ + +

; b)

3 3

2 5 2 5.

= + + −Q

PHƯƠNG TRÌNH V HỆ PHƯƠNG TRÌNH

I. KIẾN THỨC CẦN SỬ DỤNG

1. Phương trình : Phương trình bậc nhất ; hệ phương trình bậc nhất hai ẩn ;

phương trình bậc hai ; các phương trình quy về bậc nhất hoặc phương

trình bậc hai (Dạng tổng quát và cách giải từng loại đó, tính chất các

nghiệm).

2. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Ch

ChCh

Ch 

  

 

2

22

2

15

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

GIẢI PHƯƠNG TRÌNH BẬC HAI MỘT ẨN

1. PHƯƠNG PHÁP GIẢI

Bước 1 : Biến đổi phương trình đã cho về dạng tổng quát

2

0

+ + =

ax bx c

.

− Nếu hệ số a có chứa tham số thì xét trường hợp a = 0 sau đó xét trường hợp

a

≠

0.

− Nếu phương trình ban đầu có chứa ẩn ở mẫu thì phải đặt điều kiện cho ẩn từ

điều kiện mẫu khác 0. Tìm mẫu chung để quy đồng mẫu, sau đó khử mẫu bằng

cách nhân cả hai vế của phương trình với mẫu chung.

− Nếu phương trình chứa các hệ số là tham số, khi biến đổi luôn phải chú ý

đặt điều kiện thích hợp cho các tham số đó.

Bước 2 : Xác định các hệ số a ; b ; c và tính biệt số

∆

(hoặc

′

∆

nếu b =

2

b

′

)

sau đ

ó tính

∆

(ho

ặ

c

′

∆

). C

ầ

n chú ý v

ớ

i bi

ể

u th

ứ

c A b

ấ

t kì thì

2

=

A A

.

Ch

ẳ

ng h

ạ

n

2 2

2 1 ( 1) 1

∆ = − + = −

⇒

∆ = −

m m m m

.

B

ướ

c 3 : Tính các nghi

ệ

m s

ố

(n

ế

u có) theo công th

ứ

c :

1,2

2

− ± ∆

=

b

x

a

ho

ặ

c

1, 2

.

b

x

a

′ ′

− ± ∆

=

B

ướ

c 4 :

Đố

i chi

ế

u các

đ

i

ề

u ki

ệ

n

đ

ã

đặ

t ra trong quá trình bi

ế

n

đổ

i,

để

k

ế

t

lu

ậ

n v

ề

nghi

ệ

m c

ủ

a ph

ươ

ng trình.

Chú ý :

- Nên biến đổi phương trình ở dạng tổng quát

ax + bx + c =

2

0

sao cho a >

0

để

các tính toán sau

đ

ó ít b

ị

nh

ầ

m d

ấ

u.

- C

ầ

n nh

ậ

n xét các bi

ể

u th

ứ

c c

ủ

a m

ộ

t ph

ươ

ng trình ph

ứ

c t

ạ

p, tìm ra m

ố

i liên h

ệ

gi

ữ

a các bi

ể

u th

ứ

c con, trên c

ơ

s

ở

đ

ó l

ự

a ch

ọ

n

ẩ

n ph

ụ

thay cho m

ộ

t bi

ể

u th

ứ

c

để

l

ờ

i gi

ả

i

đơ

n gi

ả

n h

ơ

n.

16

2. CÁC VÍ DỤ

Ví dụ 1 : Giải phương trình

1

.

1

− −

=

− −

a x bx

ax b x

Hướng dẫn giải

Đ

i

ề

u ki

ệ

n

1 0

0.

− ≠





− ≠



ax

b x

(1)

V

ớ

i

đ

i

ề

u ki

ệ

n trên ph

ươ

ng trình t

ươ

ng

đươ

ng v

ớ

i

2

(1 ) 1 0

− − + =

ab x ab

2

(1 ) 1

⇔ − = −

ab x ab

(*)

+ N

ế

u 1 – ab = 0 thì m

ọ

i x tho

ả

mãn

đ

i

ề

u ki

ệ

n (1) là nghi

ệ

m c

ủ

a ph

ươ

ng trình.

+ N

ế

u 1 – ab

≠

0 ta có (*)

1

⇔ = ±

x

. Trong tr

ườ

ng h

ợ

p này

đố

i chi

ế

u

đ

i

ề

u

ki

ệ

n (1) ta có n

ế

u

1; 1

≠ ± ≠ ±

a b

thì

1

= ±

x

là nghi

ệ

m.

Ví dụ 2 :

Gi

ả

i ph

ươ

ng trình

2

48 4

10 .

3 3

 

+ = −

 

 

x x

x

Hướng dẫn giải

Đ

i

ề

u ki

ệ

n

0

≠

x

. Ta có :

2 2

4 16 8 4 48

3 8.

3 9 3 3 3

   

− = + − ⇒ − = + −

   

   

x x x x

x x

Đặ

t

4

3

= −

x

y

x

. Ta có ph

ươ

ng trình

2

3 10 8 0

− + =

y y

4

2 ; .

3

⇒

= =

y y

Ti

ế

p t

ụ

c gi

ả

i ph

ươ

ng trình

đố

i v

ớ

i x :

* V

ớ

i y = 2 ta có :

2

4

2 6 12 0

3

− =

⇒

− − =

x

x x

x

1 2

21; 3 21, 3 21.

x x

′

∆ = = + = −

* V

ớ

i y =

4

3

ta có :

2

4 4

4 12 0.

3 3

− =

⇒

− − =

x

x x

x

3 4

16 ; 6, 2.

x x

′

∆ = = = −

V

ậ

y ph

ươ

ng trình

đ

ã cho có 4 nghi

ệ

m

1

3 21,

= +x

2

3 21

= −x ;

3

6,

=

x

4

2.

= −

x

17

Dạng 2.

ĐIỀU KIỆN VỀ NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI MỘT ẨN

1. PHƯƠNG PHÁP GIẢI

Bước 1 : Xác định các hệ số a,b,c của phương trình dạng

2

0

+ + =

ax bx c

đã cho, xác định các giả thiết đã cho về điều kiện các hệ số đó hoặc tìm các

điều kiện đó.

Bước 2 : (Khi

0

≠

a

) L

ậ

p bi

ể

u th

ứ

c bi

ệ

t s

ố

∆

(ho

ặ

c

′

∆

), bi

ế

n

đổ

i bi

ể

u th

ứ

c

này v

ề

d

ạ

ng d

ễ

nh

ậ

n xét d

ấ

u c

ủ

a toàn bi

ể

u th

ứ

c (có th

ể

bi

ế

n

đổ

i v

ề

d

ạ

ng t

ổ

ng bình

ph

ươ

ng các nh

ị

th

ứ

c).

B

ướ

c 3 : Tu

ỳ

theo yêu c

ầ

u c

ủ

a

đề

bài

để

đặ

t

đ

i

ề

u ki

ệ

n cho bi

ể

u th

ứ

c

∆

(ho

ặ

c

′

∆

).

Chú ý :

Việc giải điều kiện của biệt số

∆

có thể dẫn tới việc giải một phương

trình hoặc một bất phương trình.

2. CÁC VÍ DỤ

Ví dụ 1 : Cho phương trình

2

( 2) 2 2 3 0

− − + − =

m x mx m (v

ớ

i

2

≠

m

).

V

ớ

i giá tr

ị

nào c

ủ

a m thì ph

ươ

ng trình có nghi

ệ

m s

ố

kép ? Tìm nghi

ệ

m s

ố

kép

đ

ó.

Hướng dẫn giải

V

ớ

i

2

≠

m

, ph

ươ

ng trình

đ

ã cho là ph

ươ

ng trình b

ậ

c hai. Ph

ươ

ng trình có

nghi

ệ

m s

ố

kép khi

2 2

( 2)(2 3) 0 7 6 0 1

m m m m m m

′

∆ = − − − = ⇔ − + − = ⇔ =

ho

ặ

c

6.

=

m

V

ậ

y v

ớ

i

1

=

m

ho

ặ

c

6

=

m

ph

ươ

ng trình

đ

ã cho có nghi

ệ

m kép.

+ Khi

1

=

m

nghi

ệ

m kép

đ

ó là

1.

( 2)

= = −

−

m

x

m

18

+ Khi

6

=

m

nghi

ệ

m kép

đ

ó là

3

.

2

=

x

Ví dụ 2 :

Ch

ứ

ng minh r

ằ

ng ph

ươ

ng trình

2

( 1) 0

+ + + =

ax ab x b luôn luôn có

nghi

ệ

m v

ớ

i m

ọ

i giá tr

ị

c

ủ

a

và

b

. Tìm

a

và

b

để

ph

ươ

ng trình có m

ộ

t nghi

ệ

m

duy nh

ấ

t

1

.

2

x

=

Hướng dẫn giải

−

N

ế

u

0,

a

=

ph

ươ

ng trình có nghi

ệ

m

.

= −

x b

−

N

ế

u

0,

a

≠

ph

ươ

ng trình

đ

ã cho là ph

ươ

ng trình b

ậ

c hai và có

2

( 1) 4

ab ab

∆ = + −

2 2

( ) 2 1 4 ( 1) 0

ab ab ab ab

= + + − = − ≥

(v

ớ

i m

ọ

i a, b).

V

ậ

y ph

ươ

ng trình luôn có nghi

ệ

m v

ớ

i m

ọ

i giá tr

ị

c

ủ

a

và

b

.

* Khi

0

=

a

ph

ươ

ng trình có nghi

ệ

m duy nh

ấ

t

= −

x b

,

để

ph

ươ

ng trình có

nghi

ệ

m duy nh

ấ

t

1

2

=

x

thì

1

.

2

= −

b

* Khi

0

≠

a

ph

ươ

ng trình có nghi

ệ

m duy nh

ấ

t

1

2

=

x

thì

0

∆ =

và

1

2

nghi

ệ

m

đ

úng ph

ươ

ng trình

đ

ã cho.

Do

đ

ó ta có :

1 0 1

2

( 1) 1 2 1

1

.

2 2 2 2

2

− = =

= −

  

  

⇔ ⇔

− + −

  

= =

= −

  



 

ab ab a

ab

b

a a

V

ậ

y ph

ươ

ng trình có m

ộ

t nghi

ệ

m duy nh

ấ

t

1

2

=

x

khi

0

=

a

và

1

2

= −

b

ho

ặ

c

2

= −

a

và

1

2

= −

b

.

Ví dụ 3 :

Ch

ứ

ng minh r

ằ

ng n

ế

u

+ >

a b c

và

− <

a b c

thì ph

ươ

ng trình

2 2 2 2 2 2

( ) 0

+ + − + =

a x a b c x b

vô nghi

ệ

m.

19

Hướng dẫn giải

N

ế

u

0

=

a

thì không th

ể

có

đồ

ng th

ờ

i

>

b c

và

<

b c

do

đ

ó

0

≠

a

. Ph

ươ

ng

trình

đ

ã cho là ph

ươ

ng trình b

ậ

c hai có :

2 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2

( ) 4 ( 2 )( 2 )

( ) ( )

∆ = + − − = + − − + − +

   

= − − + −

   

b a c a b b a c ab b a c ab

a b c a b c

Theo gi

ả

thi

ế

t

+ >

a b c

và

> −

c a b

nên

2 2

( )

+ >

a b c

và

2 2

( ) .

− <

a b c

V

ậ

y

0

∆ <

và ph

ươ

ng trình

đ

ã cho vô nghi

ệ

m.

Dạng 3.

ỨNG DỤNG ĐỊNH LÍ VI-ÉT

1. PHƯƠNG PHÁP GIẢI

* Biến đổi biểu thức biểu thị quan hệ đại số giữa hai nghiệm số

1 2

,

x x

mà đề

bài đã cho (hoặc thay thế quan hệ đại số được diễn tả bằng lời trong đề bài bằng

biểu thức đại số) để nhận được một biểu thức mới chứa một dãy các phép tính

chứa tổng và tích hai nghiệm số.

* Áp dụng định lí Vi-ét vào dãy các phép tính nói trên.

Chú ý :

- Các quan hệ đại số giữa hai nghiệm thường được cho bởi các biểu thức liên

quan đến các hằng đẳng thức quen thuộc.

- Để lập phương trình bậc hai nhận hai số

α

và

β

làm nghiệm ta cần tính

= α + β

S

và

.

= α β

P

rồi áp dụng định lí Vi-ét. Nếu

,

α β

liên quan đến các

nghiệm của phương trình bậc hai cho trước thì lại áp dụng định lí Vi-ét để biến

đổi.

20

2. CÁC VÍ DỤ

Ví dụ 1 : Cho phương trình

2

1 0.

− + − =

x ax a

a) Chứng tỏ phương trình luôn có hai nghiệm

1 2

,

x x

.

b) Tính giá trị của biểu thức

2 2

1 2

2 2

1 2 2 1

3 3 3

.

+ −

=

+

x x

M

x x x x

c) Tìm m

ộ

t bi

ể

u th

ứ

c liên h

ệ

gi

ữ

a

1 2

;

x x

không ph

ụ

thu

ộ

c vào a.

d) Tìm a

để

t

ổ

ng các bình ph

ươ

ng hai nghi

ệ

m

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t.

Hướng dẫn giải

a)

2 2 2

( ) 4( 1) 4 4 ( 2) 0

∆ = − − − = − + = − ≥

a a a a a nên ph

ươ

ng trình luôn có

nghi

ệ

m

1 2

,

x x

.

b) S

ử

d

ụ

ng

đị

nh lí Vi-ét, ta có :

2

2 2

1 2 1 2

1 2

1 2 1 2 1 2 1 2

3 ( ) 2 1

3( 1)

( ) ( )

x x x x

x x

M

x x x x x x x x

 

+ − −

+ −

 

= =

+ +

2

3 2( 1) 1

3( 1) 3

3 .

( 1)

a a

a

a a a a

 

− − −

−

 

= = = −

−

c) Theo

đị

nh lí Vi-ét ta có :

1 2

(1)

. 1 (2)

x x a

+ =





= −



Tr

ừ

t

ừ

ng v

ế

(1) và (2) ta

đượ

c :

1 2 1 2

1,

x x x x

+ − =

đ

ây là bi

ể

u th

ứ

c liên h

ệ

c

ầ

n

tìm.

d) Ta có

2 2 2 2 2 2

1 2 1 2 1 2

( ) 2 2( 1) 2 2 ( 1) 1 1

+ = + − = − − = − + = − + ≥

x x x x x x a a a a a

(vì

2

( 1) 0

− ≥

a )

2 2

1 2

1

+ =

x x

khi a = 1. V

ậ

y

2 2

1 2

+

x x

nh

ỏ

nh

ấ

t khi a = 1.

21

Ví dụ 2 :

Cho ph

ươ

ng trình

2

3 7 4 0.

x x

+ + =

Không gi

ả

i ph

ươ

ng trình, g

ọ

i

,

α β

là các nghi

ệ

m s

ố

c

ủ

a nó, hãy l

ậ

p m

ộ

t ph

ươ

ng trình b

ậ

c hai có các nghi

ệ

m là

1

α

β −

và

.

1

β

α −

Hướng dẫn giải

Ta có

7 4

; .

3 3

α + β = − α β =

(1) (

Đị

nh lí Vi-ét

đố

i v

ớ

i ph

ươ

ng trình

đ

ã cho).

Ph

ươ

ng trình c

ầ

n tìm có d

ạ

ng

2

0,

y Sy P

− + =

ph

ươ

ng trình có hai nghi

ệ

m là

1

α

β −

và

1

β

α −

nên ta có :

2 2 2

( ) 2 ( )

1 1 ( 1)( 1) ( ) 1

.

1 1 ( ) 1

S

P

α β α − α + β − β α + β − αβ − α + β

= + = =

β − α − β − α − αβ − α + β +

α β αβ

= ⋅ =

β − α − αβ − α + β +

Thay các h

ệ

th

ứ

c

ở

(1) vào

S

và

P

ta

đượ

c

23

21

=S và

6

.

21

P =

V

ậ

y ph

ươ

ng trình c

ầ

n tìm là

2

21 23 6 0.

y y

− + =

Dạng 4.

HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

1. PHƯƠNG PHÁP GIẢI

−

Phương pháp đồ thị (minh hoạ hình học tập nghiệm hệ phương trình bậc

nhất hai ẩn) ;

−

Phương pháp thế ;

−

Phương pháp cộng đại số.

22

Chú ý :

* Mỗi nghiệm của hệ là một cặp giá trị tương ứng của x, y. Cặp

0 0

(x ; y )

là

nghiệ

m c

ủ

a h

ệ

+ =





′ ′ ′

+ =



ax by c

a x b y c

khi và ch

ỉ

khi ta có

+ =





′ ′ ′

+ =



0 0

.

ax by c

a x b y c

* S

ố

nghi

ệ

m c

ủ

a h

ệ

là s

ố

giao

đ

i

ể

m c

ủ

a hai

đườ

ng th

ẳ

ng có ph

ươ

ng trình

t

ươ

ng

ứ

ng v

ớ

i m

ỗ

i ph

ươ

ng trình c

ủ

a h

ệ

.

2. CÁC VÍ DỤ

Ví dụ 1 : a) Với giá trị nào của k thì hệ phương trình

1

2

+ =





+ =



x y

kx y k

có nghiệm duy

nhất ? có vô số nghiệm ?

b) Với giá trị nào của k và m thì hệ

1 0

− + =





+ + =



kx my

mx y

nhận cặp

( 1 ; 0)

x y

= − =

làm nghiệm ?

Hướng dẫn giải

a) Từ phương trình đầu ta có

1

= −

y x

, thay vào phương trình thứ hai ta được

phương trình

( 2) 2.

k x k

− = −

(*)

− Khi k = 2, phương trình (*) có nghiệm vô số nghiệm, do đó hệ đã cho có vô

số nghiệm.

− Khi

2,

k

≠

phương trình (*) có nghiệm duy nhất, do đó hệ có nghiệm duy

nhất.

b)

1, 0

x y

= − =

là nghiệm của hệ đã cho khi và chỉ khi

1 0

k

m

− + =





− + =



1.

k m

⇔ = =

Ví dụ 2 :

Gi

ả

i h

ệ

2

3

1 1

3

1.

1 1

x y



+ =



+ +







+ = −



+ +



23

Hướng dẫn giải

Đ

i

ề

u ki

ệ

n

1 ; 1.

x y

≠ − ≠ −

Đặ

t

;

1 1

x y

u v

x y

= =

+ +

t

ừ

h

ệ

đ

ã cho ta có :

2 3 2 3 5 5 1

.

3 1 2 6 2 2 3 2

u v u v v v

u v u v u v u

+ = + = = − = −

   

⇔ ⇔ ⇔

   

+ = − + = − + = =

   

T

ừ

đ

ó ta có :

2 2

1

= ⇔ = −

+

x

(tho

ả

mãn)

1

1 2

= − ⇔ = −

+

y

(tho

ả

mãn)

V

ậ

y h

ệ

ph

ươ

ng trình có nghi

ệ

m duy nh

ấ

t là

1

( 2 ; ).

2

− −

Dạng 5.

PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI HOẶC

HỆ PHƯƠNG TRÌNH

1. PHƯƠNG PHÁP GIẢI

Biến đổi phương trình hoặc hệ phương trình đã cho và nhóm các biểu thức

thích hợp rồi đặt ẩn phụ.

2. CÁC VÍ DỤ

Ví dụ 1 : Giải phương trình : 4x

4

+ 5x

2

− 9 = 0. (*)

Hướng dẫn giải

Đặt x

2

= t ≥ 0 (*) ⇔ 4t

2

+ 5t − 9 = 0.

Có dạng : a + b + c = 4 + 5 − 9 = 0.

Ta có nghiệm t

1

= 1 (nhận) và t

2

=

9

4

= −

c

a

(lo

ạ

i).

24

Do

đ

ó : x

2

= 1 ⇔

1

.

1

x

= −





=



V

ậ

y t

ậ

p nghi

ệ

m là S = {−1 ; 1}.

Ví dụ 2 :

Gi

ả

i ph

ươ

ng trình :

50 36

1

−

+

x x

= 1. (1)

Hướng dẫn giải

Đ

i

ề

u ki

ệ

n x

≠

0 và x

≠

−1

(1)

⇒

50x − 36(x + 1) = x(x + 1) ⇔ 50x − 36x – 36 = x

2

+ x

⇔ x

2

− 13x + 36 = 0 (*)

∆ = (−13)

2

− 4.36 = 169 – 144 = 25 > 0 ;

∆

= 5.

Ph

ươ

ng trình (*) có hai nghi

ệ

m phân bi

ệ

t : x

1

=

13 5

2

+

= 9 ; x

2

=

13 5

2

−

= 4.

C

ả

hai giá tr

ị

x = 9 và x = 4

đề

u tho

ả

mãn

đ

i

ề

u ki

ệ

n. V

ậ

y ph

ươ

ng trình

đ

ã cho

có hai nghi

ệ

m là : x = 9 và x = 4. T

ậ

p nghi

ệ

m S = {4 ; 9}.

Ví dụ 3 :

Gi

ả

i ph

ươ

ng trình x

3

+ 2x

2

+ 4x = 0.

Hướng dẫn giải

x

3

+ 2x

2

+ 4x = 0

2

( 2 4) 0

⇔ + + =

x x x

2

0

2 4 0.

x

x x

=



⇔



+ + =



Ta có

2

1 1.4 3 0

′

∆ = − = − <

nên ph

ươ

ng trình vô nghi

ệ

m.

V

ậ

y ph

ươ

ng trình

đ

ã cho có m

ộ

t nghi

ệ

m là x = 0. T

ậ

p nghi

ệ

m S =

{

}

0

.

Ví dụ 4 :

Gi

ả

i ph

ươ

ng trình :

4 6 .

x x

− = −

Hướng dẫn giải

Chú ý

0

≥



= ⇔



=



A

A B

4 0 4

4 6 5.

4 6 5

x x

x x x

− ≥ ≥

 

− = − ⇔ ⇔ ⇔ =

 

− = − =

 

V

ậ

y t

ậ

p nghi

ệ

m ph

ươ

ng trình là

{

}

5 .

S =

25

Ví dụ 5 :

Gi

ả

i ph

ươ

ng trình

4 4

( 1) ( 2) 257.

x x+ + − =

Hướng dẫn giải

Đặ

t x +1 = u ; x – 2 = v. (1)

Ta

đượ

c h

ệ

ph

ươ

ng trình

4 4

4

257

1.

3

u

u v

v

u v



=



+ =



⇔

 

=

− =





Thay u và v vào (1) ta

đượ

c x = 3.

V

ậ

y t

ậ

p nghi

ệ

m ph

ươ

ng trình là

{

}

3 .

S =

Ví dụ 6 :

Gi

ả

i ph

ươ

ng trình

5 2 7.

x x

+ + − =

Hướng dẫn giải

Đ

i

ề

u ki

ệ

n

2

≥

x

.

Đặ

t

5 ; 2

u x v x

= + = −

( ; 0).

u v

≥

Ta

đượ

c h

ệ

ph

ươ

ng trình

2 2

7

4

3.

7

u v

u

v

u v

+ =



=





⇔

 

=

− =





Thay u và v vào (1) ta

đượ

c x = 11 (tho

ả

mãn).

V

ậ

y t

ậ

p nghi

ệ

m ph

ươ

ng trình là

{

}

11 .

S =

Dạng 6.

GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH,

HỆ PHƯƠNG TRÌNH

Các bài tập này đề cập đến nhiều đối tượng khác nhau. Sự chuyển động của

động tử, quan hệ giữa các số, sắp xếp chỗ ngồi hoặc phân phối hàng hoá theo quy

định, thực hiện một công việc, các hiện tượng vật lí, hoá học, các bài toán liên

quan đến hình học.

26

1. PHƯƠNG PHÁP GIẢI

Bước 1 : Lập phương trình

* Xét xem bài toán đề cập đến đối tượng nào. Thường bài toán yêu cầu tìm

giá trị của một đại lượng nào đó thì chọn giá trị đó làm ẩn (chiều dài, thời gian,

vận tốc,…). Cần ghi rõ đơn vị của giá trị ẩn số.

Theo đề bài quy định cho giá trị ẩn số mà đặt điều kiện thích hợp. Nếu không

chọn giá trị của đại lượng bài toán yêu cầu làm ẩn số thì phải chọn được một đại

lượng khác mà qua đó có thể tính ngay giá trị đại lượng cần tìm.

* Dùng ẩn số và các số khác đã biết để “phiên dịch” từng câu diễn đạt về quan

hệ trong đề bài thành các biểu thức đại số, qua đó biểu thị các số chưa biết khác.

Ví dụ :

− Bài toán chuyển động phải “phiên dịch”và lập đủ các quan hệ của ba đại

lượng : quãng đường, thời gian, vận tốc chuyển động đều theo công thức S = v.t.

− Bài toán về “vòi nước chảy” hoặc “làm chung công việc” với giả thiết là

trong mỗi đơn vị thời gian, phần công việc hoàn thành như nhau thì tương quan

chung là : Nếu toàn bộ công việc được hoàn thành trong x đơn vị thời gian thì mỗi

đơn vị thời gian làm được

1

x

công việ

c…

* Sau khi

đ

ã “phiên d

ị

ch”

đề

bài thành các bi

ể

u th

ứ

c

đạ

i s

ố

ti

ế

n hành l

ậ

p

ph

ươ

ng trình (bi

ể

u th

ị

b

ằ

ng quan h

ệ

đẳ

ng th

ứ

c gi

ữ

a các bi

ể

u th

ứ

c

đạ

i s

ố

).

B

ướ

c 2 : Gi

ả

i ph

ươ

ng trình.

B

ướ

c 3 : Nh

ậ

n

đị

nh k

ế

t qu

ả

, tr

ả

l

ờ

i.

*

Đố

i chi

ế

u nghi

ệ

m s

ố

tìm

đượ

c v

ớ

i

đ

i

ề

u ki

ệ

n thích h

ợ

p c

ủ

a

ẩ

n s

ố

.

* Bi

ệ

n lu

ậ

n (n

ế

u c

ầ

n).

* Th

ử

l

ạ

i và tr

ả

l

ờ

i theo n

ộ

i dung câu h

ỏ

i c

ủ

a

đề

bài.

2. CÁC VÍ DỤ

Ví dụ 1 :

Hai ng

ườ

i kh

ở

i hành cùng m

ộ

t lúc và

đ

i ng

ượ

c chi

ề

u t

ừ

hai

đầ

u

đ

o

ạ

n

đườ

ng AB dài 18km và g

ặ

p nhau sau 2 gi

ờ

. Ng

ườ

i

đ

i t

ừ

A m

ỗ

i km

đ

i nhanh

h

ơ

n 3 phút so v

ớ

i ng

ườ

i

đ

i t

ừ

B. H

ỏ

i m

ỗ

i ng

ườ

i

đ

i v

ớ

i v

ậ

n t

ố

c là bao nhiêu ?

Hướng dẫn giải

2 gi

ờ

= 120 phút.

27

G

ọ

i x phút là th

ờ

i gian ng

ườ

i A (

đ

i t

ừ

A)

đ

i 1km .

Đ

i

ề

u ki

ệ

n x > 0.

Th

ờ

i gian ng

ườ

i B

đ

i 1km là

( 3)

+

x

phút.

Trong 2 gi

ờ

ng

ườ

i A

đ

i

đượ

c quãng

đườ

ng

120

x

km, ng

ườ

i B

đ

i

đượ

c quãng

đườ

ng

120

3

+

x

km.

Sau 2 gi

ờ

h

ọ

g

ặ

p nhau nên ta có ph

ươ

ng trình :

120 120

18

3

+ =

+

x x

hay

2

3 31 60 0

− − =

x x

Gi

ả

i ph

ươ

ng trình này

đượ

c

1 2

5

12 ; .

3

x x

= = −

Đố

i chi

ế

u

đ

i

ề

u ki

ệ

n ta lo

ạ

i nghi

ệ

m

2

x

.

Trả lời :

Ng

ườ

i A

đ

i 1km h

ế

t 12 phút v

ậ

y trong 1 gi

ờ

(60 phút)

đ

i

đượ

c

60

5

12

=

km.

V

ậ

n t

ố

c c

ủ

a ng

ườ

i A là 5km/h.

Trong 60 phút ng

ườ

i B

đ

i

đượ

c

60

4

12 3

=

+

(km).

V

ậ

n t

ố

c c

ủ

a ng

ườ

i B là 4km/h.

Ví dụ 2 :

Hai ng

ườ

i làm chung m

ộ

t công vi

ệ

c trong 10 ngày s

ẽ

hoàn thành. Sau

khi làm chung

đượ

c 6 ngày thì ng

ườ

i th

ứ

nh

ấ

t ngh

ỉ

, ng

ườ

i th

ứ

hai ti

ế

p t

ụ

c làm

đượ

c 6 ngày. Ph

ầ

n vi

ệ

c còn l

ạ

i ng

ườ

i th

ứ

hai ngh

ỉ

, ng

ườ

i th

ứ

nh

ấ

t làm trong

3 ngày thì xong. H

ỏ

i n

ế

u làm riêng m

ỗ

i ng

ườ

i ph

ả

i làm trong bao nhiêu ngày

để

hoàn thành công vi

ệ

c.

Hướng dẫn giải

G

ọ

i th

ờ

i gian ng

ườ

i th

ứ

nh

ấ

t, ng

ườ

i th

ứ

hai làm m

ộ

t mình hoàn thành công

vi

ệ

c l

ầ

n l

ượ

t là x (ngày) ; y (ngày).

Đ

i

ề

u ki

ệ

n : x ; y > 10.

Trong 1 ngày ng

ườ

i th

ứ

nh

ấ

t làm

đượ

c

1

x

(công vi

ệ

c).

28

Trong 1 ngày ng

ườ

i th

ứ

hai làm

đượ

c

1

y

(công vi

ệ

c).

Ta có ph

ươ

ng trình :

1

x

+

1

y

=

1

.

10

Ng

ườ

i th

ứ

nh

ấ

t làm trong 9 ngày

đượ

c

9

x

(công vi

ệ

c).

Ng

ườ

i th

ứ

hai làm trong 12 ngày

đượ

c

12

y

(công vi

ệ

c).

Ta có ph

ươ

ng trình :

9

x

+

12

y

= 1.

Ta

đượ

c h

ệ

ph

ươ

ng trình :

1 1 1

10

9 12

1.

x y



+ =







+ =





Đặ

t X =

1

x

; Y =

1

.

y

Ta có :

1

10

9 12 1



+ =







+ =



X Y

⇔

9

9 9

10

9 12 1



+ =







+ =



X Y

⇔

1

3

10

1

10



=







= −





Y

X Y

⇔

1

30

1 1 1

10 30 15



=







= − =





Y

X

Do

đ

ó :

1 1

15

1 1

30



=







=





x

y

⇔

15

30

=





=



x

y

(tho

ả

mãn

đ

i

ề

u ki

ệ

n

ẩ

n).

29

V

ậ

y th

ờ

i gian

để

ng

ườ

i th

ứ

nh

ấ

t, ng

ườ

i th

ứ

hai làm riêng hoàn thành công

vi

ệ

c l

ầ

n l

ượ

t là 15 ngày ; 30 ngày.

Ví dụ 3 :

Tìm m

ộ

t s

ố

có hai ch

ữ

s

ố

, bi

ế

t r

ằ

ng s

ố

đ

ó g

ấ

p 7 l

ầ

n ch

ữ

s

ố

hàng

đơ

n v

ị

c

ủ

a nó và n

ế

u

đ

em s

ố

c

ầ

n tìm chia cho t

ổ

ng các ch

ữ

s

ố

c

ủ

a nó thì

đượ

c

th

ươ

ng là 4 và s

ố

d

ư

là 3.

Hướng dẫn giải

G

ọ

i ch

ữ

s

ố

hàng ch

ụ

c là a, ch

ữ

s

ố

hàng

đơ

n v

ị

là b.

Đ

i

ề

u ki

ệ

n : a, b là các s

ố

t

ự

nhiên : 1 ≤ a ≤ 9 ; 0 < b ≤ 9.

Vì s

ố

c

ầ

n tìm g

ấ

p 7 l

ầ

n ch

ữ

s

ố

đơ

n v

ị

c

ủ

a nó, nên ta có ph

ươ

ng trình :

10a + b = 7b ⇔ 10a − 6b = 0 ⇔ 5a − 3b = 0.

S

ố

c

ầ

n tìm chia cho t

ổ

ng các ch

ữ

s

ố

c

ủ

a nó thì

đượ

c th

ươ

ng là 4 và s

ố

d

ư

là 3,

ta có ph

ươ

ng trình :

10a + b = 4(a + b) + 3 ⇔ 6a − 3b = 3 ⇔ 2a − b = 1.

Ta

đượ

c h

ệ

ph

ươ

ng trình :

5 3 0 5 3(2 1) 0

2 1 2 1

− = − − =

 

⇔

 

− = = −

 

a b a a

a b b a

⇔

3

2 1

− = −





= −



a

b a

⇔

3

5

=





=



a

b

(tho

ả

mãn

đ

i

ề

u

ki

ệ

n c

ủ

a

ẩ

n).

V

ậ

y s

ố

có hai ch

ữ

s

ố

c

ầ

n tìm là 35.

Ví dụ 4 :

M

ộ

t m

ả

nh v

ườ

n hình ch

ữ

nh

ậ

t có chi

ề

u dài h

ơ

n chi

ề

u r

ộ

ng là 6m, có

di

ệ

n tích là 280m

2

. Tìm chu vi c

ủ

a m

ả

nh v

ườ

n

đ

ó.

Hướng dẫn giải

G

ọ

i chi

ề

u r

ộ

ng hình ch

ữ

nh

ậ

t là x (m).

Đ

i

ề

u ki

ệ

n : x > 0.

Chi

ề

u dài hình ch

ữ

nh

ậ

t là x + 6 (m).

Theo

đề

bài ta có ph

ươ

ng trình :

x(x + 6) = 280 ⇔ x

2

+ 6x − 280 = 0

∆' = 9 + 280 = 289 > 0 ;

'

∆

= 17

x

1

= −3 + 17 = 14

30

x

2

= −3 − 17 = −20 (lo

ạ

i)

Giá tr

ị

x = 14 tho

ả

mãn

đ

i

ề

u ki

ệ

n

ẩ

n.

Chi

ề

u r

ộ

ng hình ch

ữ

nh

ậ

t là 14m. Chi

ề

u dài hình ch

ữ

nh

ậ

t là 20m.

Chu vi hình ch

ữ

nh

ậ

t là 68m.

III. BÀI TẬP VẬN DỤNG

1. Bài tập cơ bản

Bài 1.

Gi

ả

i các ph

ươ

ng trình :

a) x

2

+ x – 12 = 0 ; b) 9x

2

+ 6x + 2 = 0 ; c) 4x

2

– 12x + 9 = 0.

Bài 2.

Cho ph

ươ

ng trình x

2

+ (m + 1)x + m = 0. Ch

ứ

ng minh ph

ươ

ng trình

đ

ã cho

luôn có nghi

ệ

m v

ớ

i m

ọ

i m.

Bài 3.

Cho ph

ươ

ng trình

ẩ

n x : (2a – 1)x

2

– 2(a + 4)x + 5a + 2 = 0. Tìm a

để

ph

ươ

ng trình có nghi

ệ

m.

Bài 4.

Gi

ả

i các ph

ươ

ng trình :

a ) x

3

– 7x

2

+ 12x = 0 ; b) x

4

– 4x

2

– 5 = 0 ;

c)

1 3

− =

x ; d)

4

+

x = x – 2.

Bài 5.

Cho ph

ươ

ng trình b

ậ

c hai

ẩ

n x : (m + 1)x

2

−

2(m

−

1)x + m

−

3 = 0.

a) Ch

ứ

ng minh r

ằ

ng ph

ươ

ng trình luôn có hai nghi

ệ

m v

ớ

i m

ọ

i m

≠

−

1.

b) Tìm m

để

ph

ươ

ng trình có hai nghi

ệ

m cùng d

ấ

u.

c) Tìm m

để

ph

ươ

ng trình có hai nghi

ệ

m cùng d

ấ

u và nghi

ệ

m này g

ấ

p

đ

ôi

nghi

ệ

m kia.

Bài 6.

Cho ph

ươ

ng trình b

ậ

c hai

ẩ

n x : x

2

−

(2a

−

3)x + a

2

−

3a = 0.

a) Ch

ứ

ng minh r

ằ

ng ph

ươ

ng trình luôn có hai nghi

ệ

m phân bi

ệ

t v

ớ

i m

ọ

i a.

Tìm các nghi

ệ

m

đ

ã cho theo a.

b) Tìm a

để

ph

ươ

ng trình

đ

ã cho có hai nghi

ệ

m trái d

ấ

u.

c) G

ọ

i x

1

; x

2

là hai nghi

ệ

m c

ủ

a ph

ươ

ng trình

đ

ã cho, tìm a sao cho

2 2

1 2

+

x x

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t.

31

Bài 7.

Cho ph

ươ

ng trình b

ậ

c hai

ẩ

n x : kx

2

−

(k

−

1)x

−

1 = 0.

a) Tìm giá tr

ị

c

ủ

a k

để

ph

ươ

ng trình có nghi

ệ

m x =

−

1.

b) Ch

ứ

ng minh r

ằ

ng ph

ươ

ng trình luôn có nghi

ệ

m v

ớ

i m

ọ

i k. Tìm h

ệ

th

ứ

c

độ

c l

ậ

p

đố

i v

ớ

i k gi

ữ

a các nghi

ệ

m x

1

và x

2

c

ủ

a ph

ươ

ng trình.

Bài 8.

Cho ph

ươ

ng trình b

ậ

c hai

ẩ

n x : 2x

2

+(2m

−

1)x + m

−

1 = 0.

a) Ch

ứ

ng t

ỏ

r

ằ

ng ph

ươ

ng trình luôn có nghi

ệ

m.

b) Tìm m

để

hai nghi

ệ

m c

ủ

a ph

ươ

ng trình cùng âm.

c) Tìm m

để

ph

ươ

ng trình có hai nghi

ệ

m x

1

; x

2

tho

ả

mãn

đ

i

ề

u ki

ệ

n

2x

1

−

2x

2

= 15.

Bài 9.

Cho ph

ươ

ng trình b

ậ

c hai

ẩ

n x : 3x

2

−

4x + 2(m

−

1) = 0.

a) Tìm m

để

ph

ươ

ng trình có hai nghi

ệ

m phân bi

ệ

t x

1

và x

2

.

b) Tìm m

để

ph

ươ

ng trình có hai nghi

ệ

m cùng d

ươ

ng.

c)

Đặ

t y =

2 2

1 2

x x

+2x

1

x

2

+ (x

1

+ x

2

).

Tính y theo m. Tìm m

để

y

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t.

Bài 10.

Minh ho

ạ

hình h

ọ

c t

ậ

p nghi

ệ

m c

ủ

a h

ệ

ph

ươ

ng trình

3 5

2 5.

x y

− =





+ =



Bài 11.

Gi

ả

i các h

ệ

ph

ươ

ng trình :

a)

2 3

3 4

− = −





+ =



x y

; b)

2

3

2 2

− =







− =





x y

; c)

2 3

3 2 1



+ =





− =





x y

Bài 12.

Cho h

ệ

ph

ươ

ng trình

2 3

3 4

− = −





+ =



x ay

ax y

. V

ớ

i giá tr

ị

nguyên nào c

ủ

a a thì

nghi

ệ

m c

ủ

a h

ệ

tho

ả

mãn x < 0 và y > 0 ?

Bài 13.

M

ộ

t ng

ườ

i

đ

i b

ộ

đ

o

ạ

n

đườ

ng AB v

ớ

i v

ậ

n t

ố

c 12km/h r

ồ

i

đ

i ti

ế

p

đ

o

ạ

n

đườ

ng BC v

ớ

i v

ậ

n t

ố

c 6km/h h

ế

t c

ả

th

ả

y 1 gi

ờ

15 phút. Lúc v

ề

, ng

ườ

i

đ

ó

đ

i

đ

o

ạ

n

đườ

ng CB v

ớ

i v

ậ

n t

ố

c 8km/h r

ồ

i

đ

i

đ

o

ạ

n

đườ

ng BA v

ớ

i v

ậ

n t

ố

c

4km/h, m

ấ

t th

ờ

i gian khi v

ề

c

ả

th

ả

y là 1 gi

ờ

30 phút. Tính quãng

đườ

ng

AB và BC.

32

Bài 14.

Hai ca nô cùng kh

ở

i hành m

ộ

t lúc t

ừ

hai b

ế

n A và B cách nhau 85km và

đ

i ng

ượ

c chi

ề

u nhau. Sau 1 gi

ờ

40 phút thì hai ca nô g

ặ

p nhau. Tính v

ậ

n

t

ố

c riêng c

ủ

a m

ỗ

i ca nô, bi

ế

t r

ằ

ng v

ậ

n t

ố

c ca nô

đ

i xuôi dòng h

ơ

n v

ậ

n t

ố

c

ca nô

đ

i ng

ượ

c dòng là 9km/h và v

ậ

n t

ố

c dòng n

ướ

c là 3km/h. Cho bi

ế

t ca

nô

đ

i t

ừ

A

đ

i xuôi dòng và ca nô

đ

i t

ừ

B

đ

i ng

ượ

c dòng.

Bài 15.

Hai xe ô tô kh

ở

i hành cùng m

ộ

t lúc t

ừ

Qu

ả

ng Ngãi

đế

n thành ph

ố

Quy Nh

ơ

n

cách nhau 180km. M

ỗ

i gi

ờ

xe th

ứ

nh

ấ

t ch

ạ

y nhanh h

ơ

n xe th

ứ

hai 5km

nên

đ

ã

đế

n thành ph

ố

Quy Nh

ơ

n tr

ướ

c xe th

ứ

hai 24 phút. Tìm v

ậ

n t

ố

c c

ủ

a

m

ỗ

i xe.

Bài 16.

Hai

độ

i cùng làm trong 8 gi

ờ

thì xong m

ộ

t công vi

ệ

c. N

ế

u

để

riêng

độ

i th

ứ

nh

ấ

t làm

1

2

công vi

ệ

c r

ồ

i ngh

ỉ

, và

độ

i th

ứ

hai làm ti

ế

p

đế

n lúc hoàn thành

công vi

ệ

c thì th

ờ

i gian t

ổ

ng c

ộ

ng là 18 gi

ờ

. H

ỏ

i m

ỗ

i

độ

i làm riêng thì xong

công vi

ệ

c trong bao lâu ?

Bài 17.

M

ộ

t nhóm th

ợ

theo k

ế

ho

ạ

ch d

ự

đị

nh s

ả

n xu

ấ

t 1200 s

ả

n ph

ẩ

m. Trong 12 ngày

đầ

u h

ọ

làm theo

đ

úng k

ế

hoach

đề

ra, nh

ữ

ng ngày còn l

ạ

i h

ọ

đ

ã làm v

ượ

t

m

ứ

c m

ỗ

i ngày 10 s

ả

n ph

ẩ

m, nên hoàn thành k

ế

ho

ạ

ch s

ớ

m 2 ngày. H

ỏ

i

theo k

ế

ho

ạ

ch m

ỗ

i ngày nhóm th

ợ

c

ầ

n s

ả

n xu

ấ

t bao nhiêu s

ả

n ph

ẩ

m ?

Bài 18.

M

ộ

t

độ

i xe c

ầ

n chuyên ch

ở

140 t

ấ

n hàng. Hôm làm vi

ệ

c có hai xe ph

ả

i

đ

i

ề

u

đ

i n

ơ

i khác nên m

ỗ

i xe còn l

ạ

i ph

ả

i ch

ở

thêm 8 t

ấ

n. H

ỏ

i

độ

i xe có bao

nhiêu xe ?

Bài 19.

Trong m

ộ

t h

ộ

i tr

ườ

ng có 120 ng

ườ

i d

ự

h

ọ

p,

đượ

c s

ắ

p x

ế

p ng

ồ

i v

ừ

a

đủ

trên các dãy gh

ế

, m

ỗ

i dãy gh

ế

có s

ố

ng

ườ

i ng

ồ

i nh

ư

nhau. N

ế

u b

ớ

t

đ

i 2

dãy gh

ế

thì m

ỗ

i dãy gh

ế

ph

ả

i ng

ồ

i thêm 2 ng

ườ

i n

ữ

a m

ớ

i

đủ

ch

ỗ

. H

ỏ

i lúc

đầ

u trong h

ộ

i tr

ườ

ng có m

ấ

y dãy gh

ế

và m

ỗ

i dãy

đượ

c x

ế

p bao nhiêu

ng

ườ

i ng

ồ

i ?

Bài 20.

Hai công nhân A và B cùng làm chung m

ộ

t công vi

ệ

c thì hoàn thành trong

2 gi

ờ

. N

ế

u làm riêng, công nhân A hoàn thành s

ớ

m h

ơ

n công nhân B là 3

gi

ờ

. Tính th

ờ

i gian

để

công nhân A làm riêng hoàn thành công vi

ệ

c.

Bài 21.

M

ộ

t s

ố

có hai ch

ữ

s

ố

, ch

ữ

s

ố

hàng ch

ụ

c l

ớ

n h

ơ

n ch

ữ

s

ố

hàng

đơ

n v

ị

là 7.

N

ế

u

đổ

i ch

ữ

s

ố

cho nhau thì

đượ

c m

ộ

t s

ố

m

ớ

i b

ằ

ng

2

9

s

ố

ban

đầ

u. Tìm s

ố

ban

đầ

u.

33

Bài 22.

M

ộ

t hình ch

ữ

nh

ậ

t có chu vi 216m. N

ế

u gi

ả

m chi

ề

u dài

đ

i 20%, t

ă

ng

chi

ề

u r

ộ

ng thêm 25% thì chu vi hình ch

ữ

nh

ậ

t không

đổ

i. Tính di

ệ

n tích

hình ch

ữ

nh

ậ

t

đ

ó.

Bài 23.

Có hai lo

ạ

i dung d

ị

ch c

ủ

a m

ộ

t th

ứ

axit ; lo

ạ

i 1 ch

ứ

a 20% axit, lo

ạ

i 2 ch

ứ

a

5% axit. Mu

ố

n có 30 lít lo

ạ

i dung d

ị

ch h

ỗ

n h

ợ

p ch

ứ

a 10% axit thì ph

ả

i

tr

ộ

n bao nhiêu lít m

ỗ

i lo

ạ

i ?

2. Bài tập nâng cao

Bài 1.

Cho ba s

ố

a, b, c

≠

0. Ch

ứ

ng minh r

ằ

ng ba ph

ươ

ng trình sau không th

ể

đồ

ng th

ờ

i vô nghi

ệ

m : ax

2

+ 2bx + c = 0 ; bx

2

+ 2cx + a = 0 ; cx

2

+ 2ax + b = 0.

Bài 2.

Gi

ả

i ph

ươ

ng trình :

a) (x + 1)(x + 2)(x + 3)(x + 4) = 15 ;

b)

2

2 2 4 8 16 2 2

− + − = − + +x x x x .

Bài 3.

Tìm giá tr

ị

nguyên nh

ỏ

nh

ấ

t c

ủ

a k

để

ph

ươ

ng trình :

x

2

−

2(k + 1)x + 3 + k

2

= 0 có hai nghi

ệ

m th

ự

c phân bi

ệ

t.

Bài 4.

Gi

ả

i ph

ươ

ng trình : x

4

+ 4 = 5x(x

2

−

2).

Bài 5.

Xác

đị

nh các s

ố

th

ự

c a và b sao cho hai ph

ươ

ng trình

x

2

+ ax + 1 = 0 và x

2

+ bx + 2 = 0 có nghi

ệ

m chung và

+

a b

nh

ỏ

nh

ấ

t.

Bài 6.

Gi

ả

s

ử

a, b là hai nghi

ệ

m c

ủ

a ph

ươ

ng trình

x

2

+ m

x

+ 1 = 0 và b, c là hai

nghi

ệ

m c

ủ

a ph

ươ

ng trình

x

2

+ n

x

+ 2 = 0.

Ch

ứ

ng minh h

ệ

th

ứ

c : (b − a)(b − c) = m.n

−

6.

Bài 7.

Tìm nghi

ệ

m c

ủ

a ph

ươ

ng trình

x

2

+ p

x

+ q = 0, bi

ế

t r

ằ

ng chúng là nh

ữ

ng s

ố

nguyên và p + q = 18.

Bài 8.

Gi

ả

i các h

ệ

ph

ươ

ng trình : a)

7 12( )

9 20( )

8 15( )

= +





= +





= +



xy x y

yz y z

zx z x

; b)

3

4

5

6

+ + =





+ + =





+ + =



+ + =



x y z

y z t

z t x

t x y

.

34

Bài 9.

Gi

ả

i các h

ệ

ph

ươ

ng trình : a)

2

3

4



+ − =



+ − =





− − = −





x xy xz

y xy yz

z xz yz

; b)

4

5

3

7

4



=



+



=



+



=



+



xyz

x y

xyz

y z

xyz

z x

.

Bài 10. Giải hệ phương trình :

2 2 2

2014 2014 2014 2015

3



+ + = + +





+ + =





x y z xy yz zx

x y z

.

3. Bài tập tự giải

Bài 1. Giải phương trình

2 2

4 4 2.

x x x

− − + =

Bài 2. Cho phương trình : x

2

−

2mx + 4m

−

4 = 0 (m là tham số).

a) Chứng minh phương trình luôn có nghiệm với mọi m.

b) Tìm m để phương trình có nghiêm số kép. Tính nghiệm kép đó.

c) Chứng minh phương trình luôn có nghiệm x = 2.

d) Tìm m để phương trình có hai nghiêm trái dấu.

e) Tìm hệ thức giữa hai nghiệm độc lập với m.

Bài 3. Một ôtô phải đi quãng đường AB dài 60km trong một thời gian nhất định.

Ôtô đi nửa đoạn đường đầu với vận tốc hơn vận tốc dự định 10km/h và đi

nửa đoạn đường sau với vận tốc kém vận tốc dự định 6km/h. Biết ôtô đến

B đúng thời gian quy định. Tính thời gian ôtô dự định đi quãng đường AB.

Bài 4. Một đội xe dự định chở 180 tấn hàng, số hàng chia đều cho mỗi xe, nhưng

khi thực hiện có 3 xe bị hỏng , do đó mỗi xe phải chở thêm 5 tấn hàng nữa

thì mới hết số hàng. Tính số xe ban đầu của đội.

Bài 5. Một hội trường có 360 ghế được xếp thành từng hàng, mỗi hàng có số ghế

bằng nhau. Nhưng để đủ chổ cho 400 người ngồi, phải kê thêm một hàng

và mỗi hàng kê thêm một ghế. Hỏi ban đầu hội trường có mấy hàng ghế,

mỗi hàng có mấy chiếc ghế ?

35

HM SỐ V ĐỒ THỊ

I. KIẾN THỨC CẦN SỬ DỤNG

Khái niệm, tính chất và dạng đồ thị của các hàm số

y = ax + b và y = ax

2

(a

≠

0).

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

XÁC ĐỊNH HÀM SỐ THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC

1. PHƯƠNG PHÁP GIẢI

- Viết công thức tổng quát của hàm số cần tìm.

- Từ các điều kiện đã cho, ta thiết lập được một phương trình (hoặc một hệ)

mà ẩn số là các hệ số, trong công thức tổng quát của hàm số cần tìm. Từ đó tìm

được các hệ số.

2. CÁC VÍ DỤ

Ví dụ 1 : Tìm hàm số bậc nhất biết đồ thị của nó đi qua hai điểm M(1 ;

−

2) và

N(

−

1 ;

−

8).

Hướng dẫn giải

Hàm số cần tìm có dạng : y = ax + b (a ≠ 0).

* Đồ thị hàm số đi qua điểm M(1 ;

−

2) nên

−

2 = a + b. (1)

* Đồ thị hàm số đi qua điểm N(

−

1 ;

−

8) nên

−

8 =

−

a + b. (2)

Ch

ChCh

Ch 

  

 

3

33

3

36

Từ (1) và (2) ta có :

2

8

a b

+ =





− + = −



⇔

2 10

2

= −





+ = −



b

a b

⇔

3

.

5

a

b

=





= −



Hàm số cần tìm là : y = 3x

−

5.

Ví dụ 2 : Cho hàm số (P) :

2

=

y ax

. (1)

Tìm giá trị của

a

để đồ thị hàm số (1) đi qua điểm

(

)

2 ; 1 .

−

Hướng dẫn giải

Đồ

th

ị

hàm s

ố

qua

đ

i

ể

m

(

)

2 ; 1

−

2

1

1 .2 4 1 .

4

a a a

⇔ − = ⇔ = − ⇔ = −

V

ậ

y v

ớ

i

1

4

= −

a thì

đồ

th

ị

hàm s

ố

(1)

đ

i qua

đ

i

ể

m

(

)

2 ; 1 .

−

Dạng 2.

VẼ ĐỒ THỊ CỦA HÀM SỐ

1. PHƯƠNG PHÁP GIẢI

a) Hàm số y = ax + b (a

≠

0).

Cách vẽ đồ thị hàm số y = ax + b (a

≠

0) :

Cách 1 : Xác định toạ độ giao điểm của đồ thị với hai trục toạ độ.

Cách 2 : Xác định hai điểm phân biệt bất kì thuộc đồ thị, rồi vẽ đường thẳng

đi qua hai điểm đó.

b) Hàm số y = ax

2

(a

≠

0).

Cách vẽ đồ thị hàm số y = ax

2

(a

≠

0).

- Lập bảng giá trị tương ứng (x ; f(x)).

- Vẽ tất cả các điểm

(

)

; ( )

x f x

trên mặ

t ph

ẳ

ng to

ạ

độ

Oxy.

37

2. CÁC VÍ DỤ

Ví dụ : Vẽ đồ thị các hàm số a) y = x + 3 (d) ; b) y =

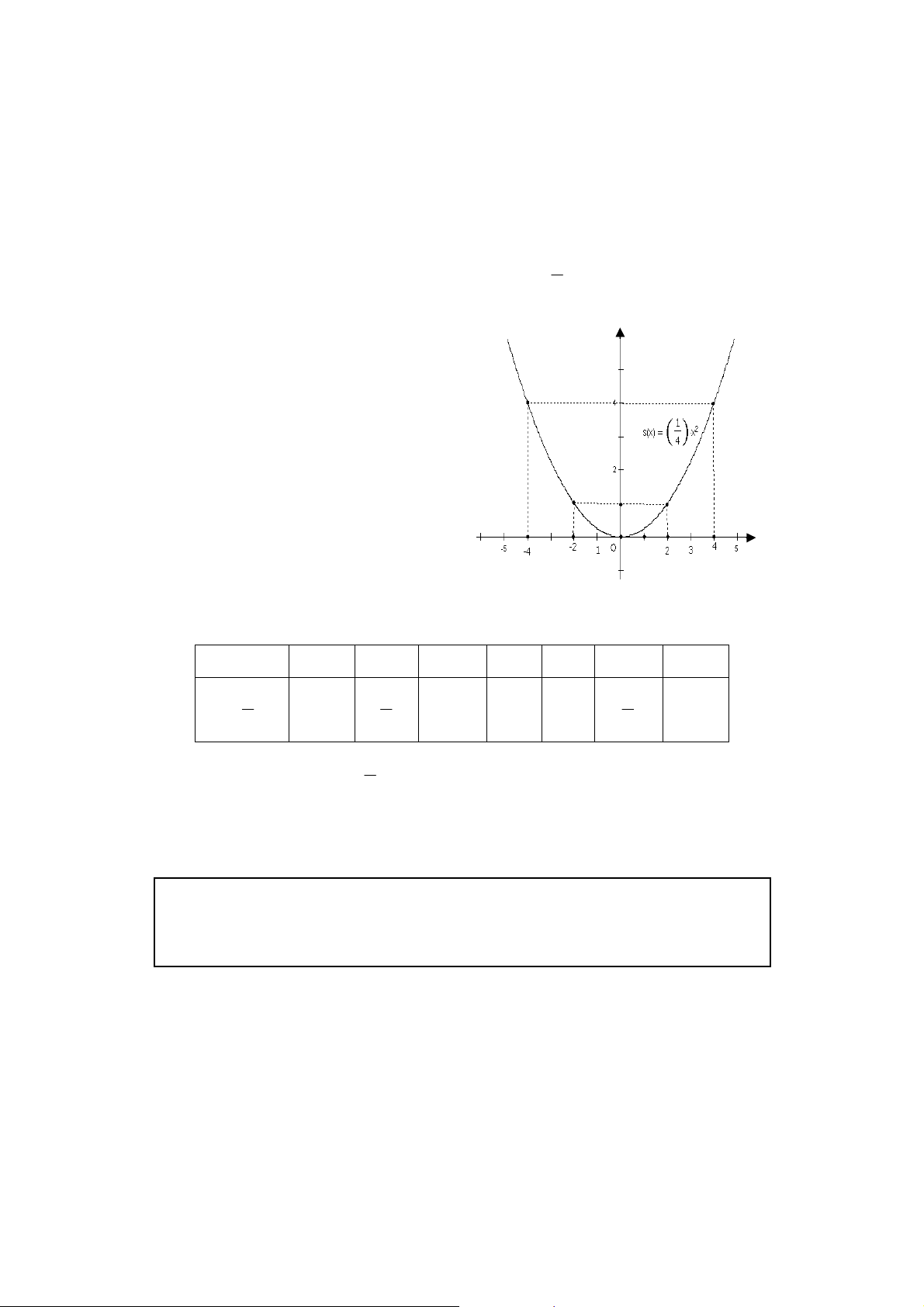
1

4

x

2

(P).

Hướng dẫn giải

a) Cho

x

= 0 thì

y

= 3, ta

đượ

c

đ

i

ể

m

A(0 ; 3).

Cho

y

= 0 thì

x

+ 3 = 0

⇒

x

=

−

3 ta

đượ

c

đ

i

ể

m B(

−

3 ; 0).

Đườ

ng th

ẳ

ng AB

là

đồ

th

ị

c

ủ

a hàm s

ố

y

=

x

+ 3.

b) L

ậ

p b

ả

ng m

ộ

t s

ố

giá tr

ị

t

ươ

ng

ứ

ng c

ủ

a

x

và

y

:

x

−

4

−

3

−

2 0 2 3 4

y =

1

4

x

2

4

9

4

1 0 1

9

4

Đồ

th

ị

c

ủ

a hàm s

ố

y

=

1

4

x

2

là m

ộ

t

đườ

ng parabol n

ằ

m phía trên tr

ụ

c hoành,

nh

ậ

n tr

ụ

c tung làm tr

ụ

c

đố

i

xứ

ng ; nh

ậ

n g

ố

c to

ạ

độ

O(0 ; 0) làm

đỉ

nh.

Dạng 3.

ĐIỀU KIỆN ĐỂ ĐIỂM THUỘC HOẶC KHÔNG THUỘC ĐỒ THỊ

HÀM SỐ ; ĐIỀU KIỆN ĐỂ HÀM SỐ ĐỒNG BIẾN, NGHỊCH BIẾN,

THỎA MÃN TÍNH CHẤT CHO TRƯỚC

1. PHƯƠNG PHÁP GIẢI

− Để xác định điểm thuộc hoặc không thuộc đồ thị ta thay toạ độ điểm đã cho

vào hàm số.

x

y

38

− Hàm số bậc nhất

= +

y ax b

( 0)

≠

a

đồng biến khi a > 0 và nghịch biến khi

a < 0.

− Hàm số y = ax

2

(a

≠

0) :

+ Khi a > 0 : đồng biến khi x > 0 và nghịch biến khi x < 0.

+ Khi a < 0 : đồng biến khi x < 0 và nghịch biến khi x > 0.

2. CÁC VÍ DỤ

Ví dụ 1 : Trong mặt phẳng toạ độ Oxy, cho đường thẳng (d) : y =

−

2x

−

2.

a) Giải thích vì sao điểm A(

−

3 ; 4) nằm trên đường thẳng (d).

b) Tìm m sao cho đường thẳng (d') : y = mx

−

1 cắt (d).

Hướng dẫn giải

a) Thay x = x

A

=

−

3 vào phương trình của (d), ta có :

y =

−

2(

−

3)

−

2 = 6

−

2 = 4 = y

A

.

Do đó A nằm trên (d).

b) Để (d) và (d') : y = mx

−

1 cắt nhau ta phải có m ≠

−

2.

Ví dụ 2 : Tìm m để hàm số y =

2

4

3

 

− −

 

 

m x + 2 là hàm số bậc nhất và đồng biến.

Hướng dẫn giải

Hàm số y =

2

4

3

 

− −

 

 

m x + 2 là hàm số bậc nhất và đồng biến

⇔

2

3

−

m

−

4 > 0

⇔

2 12

3

− −

m

> 0 ⇔ – (2m + 12) > 0

⇔ 2m + 12 < 0 ⇔ 2m < – 12 ⇔ m < – 6.

V

ậ

y v

ớ

i m < –6 thì hàm s

ố

đ

ã cho là hàm s

ố

b

ậ

c nh

ấ

t và

đồ

ng bi

ế

n.

Ví dụ 3 :

Cho hàm s

ố

y = (m

−

3)x

2

. Tìm giá tr

ị

c

ủ

a m

để

:

a) Hàm s

ố

ngh

ị

ch bi

ế

n v

ớ

i x < 0 ;

b) Có giá tr

ị

y = 3 khi x =

−

1.

39

Hướng dẫn giải

a) Hàm s

ố

y = (m

−

3)x

2

ngh

ị

ch bi

ế

n v

ớ

i x < 0 ⇔ m

−

3 > 0 ⇔ m > 3.

b) Vì hàm s

ố

có giá tr

ị

y = 3 khi x =

−

1 nên

3 = (m

−

3).(

−

1)

2

⇔ 3 = m – 3 ⇔ m = 6.

Dạng 4.

SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ

1. PHƯƠNG PHÁP GIẢI

Để xét sự tương giao của hai đồ thị, ta xét số nghiệm của phương trình

f(x) = g(x), với y = f(x) và y = g(x) là hai hàm số đã cho. Do yêu cầu đòi hỏi của

đề bài để lập luận phương trình đó vô nghiệm, có nghiệm kép, hoặc có số nghiệm

cần thiết.

2. CÁC VÍ DỤ

Ví dụ 1. Cho parabol (P) : y = 2x

2

và đường thẳng (d) : y =

−

3x – 4.

Chứng tỏ rằng (P) và (d) không có điểm chung.

Hướng dẫn giải

Phương trình hoành độ giao điểm của (d)

và (P) :

2x

2

=

−

3x – 4 ⇔ 2x

2

+ 3x + 4 = 0

∆ = 9

−

32 =

−

23 < 0.

Vậy (d) và (P) không có điểm chung.

Ví dụ 2. Trên cùng hệ trục toạ độ Oxy :

a) Vẽ đồ thị hàm số (P) : y = x

2

và (d) :

y =

−

x + 2.

b) Tìm toạ độ giao điểm của (P) và (d).

c) Kiểm nghiệm lại toạ độ giao điểm nói trên bằng phép tính.

40

Hướng dẫn giải

a) Bảng giá trị

x ...

−

2

−

1 0 1 2 ...

y 4 1 0 1 4

Đồ thị của hàm số y =

−

x + 2 là một đường thẳng cắt trục hoành tại điểm (2 ; 0)

và cắt trục tung tại điểm (0 ; 2).

b) Trên đồ thị ta thấy (d) cắt P tại hai điểm A(

−

2 ; 4) và B(1 ; 1).

c) Phương trình hoành độ giao điểm của (P) và (d)

x

2

=

−

x + 2 ⇔ x

2

+ x

−

2 = 0

Phương trình có dạng a + b + c = 0 nên có hai nghiệm x

1

= 1 và x

2

=

c

a

=

−

2,

suy ra

y

1

= 1 ;

y

2

= 4. Vậy (d) cắt (P) tại điểm A(

−

2 ; 4) và B(1 ; 1).

Dạng 5.

CHỨNG MINH ĐỒ THỊ ĐI QUA ĐIỂM CỐ ĐỊNH VỚI MỌI GIÁ TRỊ

CỦA THAM SỐ

1. PHƯƠNG PHÁP GIẢI

Có hai cách :

− Chọn

0

=

x x

thích hợp thay vào biểu thức của hàm số, nhận được một giá

trị không phụ thuộc tham số.

− Xem phương trình y = f(x, m) (m là tham số) với ẩn là m và chuyển về dạng :

2

( , ). ( , ). ( , ) 0

+ + =

g x y m h x y m k x y . To

ạ

độ

đ

i

ể

m c

ố

đị

nh mà

đồ

th

ị

luôn

đ

i qua là

nghi

ệ

m c

ủ

a h

ệ

( , ) 0

=





=





=



g x y

h x y

k x y

41

2. CÁC VÍ DỤ

Ví dụ : Chứng minh rằng đường thẳng (d) :

2( 1)

= − +

y mx m

luôn luôn đi qua

một điểm cố định khi m thay đổi.

Hướng dẫn giải

Xét phương trình

2( 1)

= − +

y mx m

( 2) (2 ) 0.

m x y

⇔ − − + =

Nếu

(

)

0 0

;

x y

là

đ

i

ể

m c

ố

đị

nh c

ủ

a

đồ

th

ị

thì

0 0

( 2) (2 ) 0

− − + =

m x y

v

ớ

i m

ọ

i

m

.

Đ

ây là ph

ươ

ng trình b

ậ

c nh

ấ

t

đố

i v

ớ

i

m

. Ph

ươ

ng trình này

đượ

c nghi

ệ

m

đ

úng

v

ớ

i m

ọ

i m nên ph

ả

i có

0 0

2 0 2

− = =

 

⇔

 

+ = = −

 

x x

y y

V

ậ

y

đồ

th

ị

hàm s

ố

luôn

đ

i qua

đ

i

ể

m c

ố

đị

nh

(

)

2 ; 2

−

v

ớ

i m

ọ

i giá tr

ị

c

ủ

a m.

III. BÀI TẬP VẬN DỤNG

1. Bài tập cơ bản

Bài 1.

Xác

đị

nh a và b sao cho

đồ

th

ị

c

ủ

a hàm s

ố

y = ax + b

đ

i qua

đ

i

ể

m P(4 ;

−

3)

và song song v

ớ

i

đườ

ng th

ẳ

ng y =

−

2

3

x

+ 1.

Bài 2.

Tìm to

ạ

độ

giao

đ

i

ể

m c

ủ

a hai

đườ

ng th

ẳ

ng :

y

=

−

3

x

+ 2 và

y

= 4(

x

−

3).

Bài 3.

Tìm hàm s

ố

b

ậ

c nh

ấ

t bi

ế

t h

ệ

s

ố

góc b

ằ

ng

−

2 và

đồ

th

ị

hàm s

ố

đ

i qua

đ

i

ể

m

A(3 ; 2).

Bài 4.

Trên m

ặ

t ph

ẳ

ng to

ạ

độ

O

xy

cho

đườ

ng th

ẳ

ng (d) :

y

=

x

+ 1.

Vi

ế

t ph

ươ

ng trình

đườ

ng th

ẳ

ng (d') song song v

ớ

i

đườ

ng th

ằ

ng (d) c

ắ

t tr

ụ

c

tung t

ạ

i

đ

i

ể

m N có tung

độ

b

ằ

ng

−

4.

Bài 5.

Cho hàm s

ố

y

= (m

2

−

3)

x

2

có

đồ

th

ị

là (P).

a) Tìm giá tr

ị

c

ủ

a m bi

ế

t (P)

đ

i qua

đ

i

ể

m A(1 ; 6).

b) V

ớ

i giá tr

ị

đ

ó c

ủ

a m,

đồ

th

ị

c

ủ

a hàm s

ố

có

đ

i qua

đ

i

ể

m B(

−

1 ;

−

6)

không ?

Bài 6.

Cho hàm s

ố

y

= a

x

2

(a

≠

0) có

đồ

th

ị

(P).

a) Tìm a bi

ế

t

đồ

th

ị

đ

i qua M

1

1 ; .

2

 

−

 

 

b) Tìm m sao cho N(−3 ; m)

∈

(P).

42

Bài 7.

Cho hàm s

ố

y

=

−

x

2

. V

ẽ

đồ

th

ị

c

ủ

a hàm s

ố

.

Bài 8.

Cho

đườ

ng th

ẳ

ng có ph

ươ

ng trình : m

x

+ 3 + (3m

−

1)

y

= 0 (d).

a) Bi

ế

t

đườ

ng th

ẳ

ng

đ

i qua A(1 ;

−

2). Tìm h

ệ

s

ố

góc c

ủ

a

đườ

ng th

ẳ

ng này.

b) Ch

ứ

ng t

ỏ

r

ằ

ng

đườ

ng th

ẳ

ng (d) luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh khi giá tr

ị

c

ủ

a m thay

đổ

i. Tìm to

ạ

độ

đ

i

ể

m c

ố

đị

nh

đ

ó.

2. Bài tập nâng cao

Bài 1.

Tìm a

để

ba

đườ

ng th

ẳ

ng sau

đ

â

y

đồ

ng quy :

y

= 3

x

;

y

=

−

x

+ 4 và

y

= a

x

–

3

.

2

Bài 2.

L

ậ

p ph

ươ

ng trình

đườ

ng th

ẳ

ng (d) qua

đ

i

ể

m A(3 ; 0) và vuông góc v

ớ

i

đườ

ng th

ẳ

ng (d') :

y

= 2

x

+ 1.

Bài 3.

Trên m

ặ

t ph

ẳ

ng to

ạ

độ

O

xy

l

ấ

y

ba

đ

i

ể

m A(1 ; 2) ; B(1 ;

−

1) và C(0 ; 2).

a) Tính

độ

dài các c

ạ

nh c

ủ

a

∆

ABC.

b) Tính di

ệ

n tích

∆

ABC.

c) Vi

ế

t ph

ươ

ng trình

đườ

ng th

ẳ

ng BC.

Bài 4.

Trên cùng h

ệ

tr

ụ

c to

ạ

độ

O

xy

cho parabol (P) :

y

=

−

x

2

và

đườ

ng th

ẳ

ng

(D) :

y

=

−

x

–2. Tìm ph

ươ

ng trình ti

ế

p tu

y

ế

n v

ớ

i (P) song song v

ớ

i (D).

Ch

ỉ

rõ to

ạ

độ

ti

ế

p

đ

i

ể

m.

Bài 5.

Cho hàm s

ố

y

= a

x

2

có

đồ

th

ị

là (P).

a) Xác

đị

nh a bi

ế

t

đồ

th

ị

đ

i qua

đ

i

ể

m A(1 ; 1).

b) G

ọ

i (D) là

đườ

ng th

ẳ

ng

đ

i qua A và c

ắ

t tr

ụ

c hoành t

ạ

i

đ

i

ể

m có hoành

độ

là m (m

≠

1). Vi

ế

t ph

ươ

ng trình

đườ

ng th

ẳ

ng (D).

c) Tìm giá tr

ị

m

để

đườ

ng th

ắ

ng (d) ti

ế

p

x

úc v

ớ

i parabol (P).

Bài 6.

Cho hàm s

ố

y

= (m + 1)

x

+ m + 1.

a) Tìm m

để

hàm s

ố

đ

ã cho

đồ

ng bi

ế

n và

đồ

th

ị

c

ủ

a nó

đ

i qua

đ

i

ể

m (1 ; 2).

b) Tìm m

để

trong cùng m

ộ

t h

ệ

tr

ụ

c to

ạ

độ

đồ

th

ị

c

ủ

a hàm s

ố

đ

ã cho ti

ế

p

xúc v

ớ

i parabol

y

=

−

2

x

2

. Tìm to

ạ

độ

ti

ế

p

đ

i

ể

m.

43

3. Bài tập tự giải

Bài 1.

Cho hàm s

ố

y

= a

x

2

có

đồ

th

ị

(P).

a) Tìm a bi

ế

t (P)

đ

i qua M(

1 1

;

2 12

− ). V

ẽ

(P) v

ớ

i a v

ừ

a tìm

đượ

c.

b) Tìm to

ạ

độ

các

đ

i

ể

m trên (P) có hoành

độ

b

ằ

ng

1

3

−

; có tung

độ

b

ằ

ng 4.

c) Ch

ứ

ng t

ỏ

r

ằ

ng n

ế

u

đ

i

ể

m (a ; b) thu

ộ

c (P) thì

đ

i

ể

m (

−

a ; b) c

ũ

ng thu

ộ

c

(P).

d) Tìm m sao cho C(−3 ; m) thu

ộ

c (P).

e) Tìm nh

ữ

ng

đ

i

ể

m trên thu

ộ

c parabol (P) cách

đề

u hai tr

ụ

c to

ạ

độ

.

Bài 2.

Cho hai hàm s

ố

y

=

x

2

có

đồ

th

ị

(P) và

y

= 2

x

+ 3 có

đồ

th

ị

(D).

a) V

ẽ

(P) và (D) trên cùng h

ệ

tr

ụ

c to

ạ

độ

.

b) Tìm to

ạ

độ

giao

đ

i

ể

m c

ủ

a (P) và (D).

c) Vi

ế

t ph

ươ

ng trình

đườ

ng th

ẳ

ng (d) song song v

ớ

i (D) và ti

ế

p xúc (P).

Xác

đị

nh to

ạ

độ

ti

ế

p

đ

i

ể

m.

BẤT ĐẲNG THỨC − BẤT PHƯƠNG TRÌNH

I. KIẾN THỨC CẦN SỬ DỤNG

1. Định nghĩa và các tính chất của bất đảng thức.

2. Các quy tắc cộng trừ cùng một số vào hai vế của bất đẳng thức, quy tắc

chuyển vế, quy tắc nhân hoặc chia cả hai vế của một bất đẳng thức với

cùng một số dương, với cùng một số âm.

3. Bất đẳng thức Cô-si.

4. Biết cách giải bất phương trình bậc nhất, bậc hai một ẩn.

Ch

ChCh

Ch 

  

 

4

44

4

44

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

CHỨNG MINH BẤT ĐẲNG THỨC

1. PHƯƠNG PHÁP GIẢI

− Dùng định nghĩa bất đẳng thức.

− Biến đổi tương đương (thành tổng các biểu thức có giá trị không âm).

− Áp dụng bất đẳng thức Cô-si.

2. CÁC VÍ DỤ

Ví dụ 1. Chứng minh a

2

+ 4b

2

+ 4c

2

≥

4ab − 4ac + 8bc.

Hướng dẫn giải

Ta có a

2

+ 4b

2

+ 4c

2

−

4ab + 4ac

−

8bc =

( )

2

2 2

+ −

a c b

≥

0 (bất đẳng thức

được chứng minh).

Ví dụ 2. Chứng minh rằng với mọi số thực a, b, c ta luôn có :

2 2 2

.

a b c ab bc ca

+ + ≥ + +

Hướng dẫn giải

Ta có :

2 2 2

+ + ≥ + +

a b c ab bc ca

2 2 2

2( ) 2( ) 0

a b c ab bc ca

⇔ + + − + + ≥

2 2 2 2 2 2

( 2 ) ( 2 ) ( 2 ) 0

a ab b b bc c c ca a

⇔ − + + − + + − + ≥

2 2 2

( ) ( ) ( ) 0.

a b b c c a

⇔ − + − + − ≥

(1)

B

ấ

t

đẳ

ng th

ứ

c (1) luôn

đ

úng nên

2 2 2

.

a b c ab bc ca

+ + ≥ + +

45

Ví dụ 3.

Ch

ứ

ng minh r

ằ

ng :

2 2 2 2

.

a b c d ab ac ad

+ + + ≥ + +

Hướng dẫn giải

Ta có :

2 2

2 2 2 2 2 2

4 4

a a

a b c d ab ac ad ab b ac c

   

+ + + − − − = − + + − + +

   

   

2 2

2

4 4

a a

ad d

 

+ − + +

 

 

2 2 2

2

0

2 2 2 4

     

= − + − + − + ≥

     

     

a a a a

b c d

2 2 2 2

a b c d ab ac ad

⇒

+ + + ≥ + +

(

đ

pcm).

Ví dụ 4.

Ch

ứ

ng minh r

ằ

ng :

2 2 2

4 4 4 4 8 .

a b c ab ac bc

+ + ≥ − +

Hướng dẫn giải

Ta có :

2 2 2 2 2 2

4 4 4 4 8 ( 4 4 ) 4 (4 8 )

+ + − + − = − + + + −

a b c ab ac bc a ab b c ac bc

2 2

( 2 ) 2.( 2 ).2 (2 )

= − + − +

a b a b c c

2

( 2 2 ) 0.

a b c

= − + ≥

⇒

2 2 2

4 4 4 4 8

+ + ≥ − +

a b c ab ac bc

(

đ

pcm).

Ví dụ 5.

Cho

1

+ >

a b

. Ch

ứ

ng minh :

4 4

1

.

8

a b

+ >

Hướng dẫn giải

Ta có :

2

2 2 2

( ) 1

( ) 0

2 2

+

− ≥ ⇒ + ≥ >

a b

a b a b

⇒

2 2 2

4 4

( ) 1

2 8

+

+ ≥ >

a b

(

đ

pcm).

46

Ví dụ 6.

Cho a, b > 0 tho

ả

mãn

đ

i

ề

u ki

ệ

n :

. 1

=

a b

. Ch

ứ

ng minh r

ằ

ng :

2 2

4

( 1)( ) 8.

a b a b

a b

+ + + + ≥

+

Hướng dẫn giải

Áp d

ụ

ng b

ấ

t

đẳ

ng th

ứ

c Cô-si cho hai s

ố

d

ươ

ng

2

a

và

2

b

ta có :

2 2

+ ≥ =

a b ab

⇒

2 2

4 4

( 1)( ) 2( 1)a b a b a b

a b a b

+ + + + ≥ + + +

+ +

4

( ) 2

 

= + + + + +

 

+

 

a b a b

a b

(1)

T

ươ

ng t

ự

: áp d

ụ

ng B

Đ

T Cô-si, ta có :

2 2

4 4

2 ( ). 4

( )

a b ab

a b a b



+ ≥ =





+ + ≥ + =



+ +



⇒

4

( ) 2 2 4 2 8

 

+ + + + + ≥ + + =

 

+

 

a b a b

a b

(2)

T

ừ

(1) và (2)

⇒

2 2

4

( 1)( ) 8

+ + + + ≥

+

a b a b

a b

(

đ

pcm).

Dạng 2.

GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT

1. PHƯƠNG PHÁP GIẢI

Cho biểu thức f(x, y…).

* Ta nói M là giá trị lớn nhất của f(x, y…) kí hiệu maxf(x, y…) = M, nếu hai

điều kiện sau được thoả mãn :

47

− Với mọi x, y… để f(x, y…) xác định thì f(x, y…)

≤

M.

− Tồn tại x

0

, y

0

… sao cho f(x

0

, y

0

…) = M.

* Ta nói m là giá trị nhỏ nhất của f(x, y…) kí hiệu minf(x, y…) = m, nếu hai

điều kiện sau được thoả mãn :

− Với mọi x, y… để f(x, y…) xác định thì f(x, y…)

≥

m.

− Tồn tại x

0

, y

0

… sao cho f(x

0

, y

0

…) = m.

Chú ý :

+ A = k + M

2

≥

k. Giá trị nhỏ nhất của A là k

⇔

M = 0.

+ B = h – N

2

≤

h. Giá trị lớn nhất của B là h

⇔

N = 0.

2. CÁC VÍ DỤ

Ví dụ 1. a) Tìm GTNN của A = 3x

2

– 4x + 1.

b) Tìm GTLN của B = – 5x

2

+ 6x – 2.

Hướng dẫn giải

a) A =

2

2 4 1 2 1 1

3 2. . 3

3 9 3 3 3 3

   

− + − = − − ≥ −

   

   

x x x .

V

ậ

y GTNN c

ủ

a A là

1

3

−

,

đ

i

ề

u này x

ả

y ra khi

2 2

0 .

3 3

x x

− = ⇔ =

b) B =

2

6 9 1 3 1 1

5 5

5 25 5 5 5 5

   

− − + − = − − − ≤ −

   

   

x x x .

V

ậ

y GTLN c

ủ

a B là

1

5

−

,

đ

i

ề

u này x

ả

y ra khi

3 3

0 .

5 5

x x

− = ⇔ =

Ví dụ 2 :

Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a B(x) = x

2

+ 4y

2

– 6x + 12y + 21.

48

Hướng dẫn giải

B(x) = x

2

+ 4y

2

– 6x + 12y + 21

= (x

2

– 6x + 9) + (4y

2

+ 12y + 9) + 3

= (x – 3)

2

+ (2y + 3)

2

+ 3

≥

3.

V

ậ

y giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a B(x) b

ằ

ng 3 khi x = 3 và y =

3

.

2

−

Ví dụ 3 :

Tìm giá tr

ị

l

ớ

n nh

ấ

t c

ủ

a bi

ể

u th

ứ

c E =

3 6 21

.

2 4

x x

− +

Hướng dẫn giải

Đ

i

ề

u ki

ệ

n : x

0

≥

;

E

3 6 21

2 4

− +

=

− +

x x

(

)

3 2 4 9

2 4

− + +

=

− +

x x

9

3

2 4

= +

− +

x x

( )

9

3

2 1 3

= +

− + +

x x

2

9

3

( 1) 3

= +

− +

x

.

Vì

( )

2

9 9

3.

3

1 3x

≤ =

− +

Vậy giá trị lớn nhất của E là 6

1 0

⇔ − =

x

1

⇔ =

x

(thoả điều kiện).

Dạng 3.

BẤT PHƯƠNG TRÌNH

1. PHƯƠNG PHÁP GIẢI

− Vận dụng quy tắc cộng vào hai vế của một bất phương trình một số hoặc

một đa thức chứa ẩn thì được một bất phương trình mới tương đương.

− Vận dụng quy tắc nhân hai vế của một bất phương trình với cùng một số

dương thì được một bất phương trình mới tương đương. Nếu nhân hai vế của một

bất phương trình với cùng một số âm và đổi chiều của bất phương trình thì được

một bất phương trình mới tương đương.

49

2. CÁC VÍ DỤ

Ví dụ 1. Giải các bất phương trình

a)

3(1 ) 1 2

− > +

x x

; b)

( 1)( 3) 1 4 .

x x x

+ + < +

Hướng dẫn giải

a)

3(1 ) 1 2 3 3 1 2

x x x x

− > + ⇔ − > +

2

3 2 1 3 5 2 .

5

x x x x

⇔ − − > − ⇔ − > − ⇔ <

V

ậ

y

2

/ .

5

S x x

 

= <

 

 

b)

2

( 1)( 3) 1 4 4 3 1 4

x x x x x x

+ + < + ⇔ + + < +

2 2

4 4 1 3 2.

⇔ + − < − ⇔ < −

x x x x

Ta nh

ậ

n th

ấ

y v

ớ

i m

ọ

i

2

, 0

x R x

∈ ≥

và v

ế

ph

ả

i là m

ộ

t s

ố

âm.

V

ậ

y không có giá tr

ị

nào c

ủ

a x là nghi

ệ

m c

ủ

a b

ấ

t ph

ươ

ng trình. Do

đ

ó

.

S

= ∅

Ví dụ 2.

Tìm m

để

b

ấ

t ph

ươ

ng trình sau có t

ậ

p nghi

ệ

m là R

2

( 1) 3 1 0.

m x m x

− + − + ≥

Hướng dẫn giải

Ta có

2 2

( 1) 3 1 0 ( 3) 1 0.

m x m x m x m m

− + − + ≥ ⇔ − + − + ≥

Để

m

ọ

i

∈

x R

đề

u là nghi

ệ

m thì ta ph

ả

i có

2 2

3 0 3

3.

1 0 1 0

m m

m

m m m m

− = =

 

 

⇔ ⇔ =

 

− + ≥ − + ≥

 

 

V

ậ

y m = 3 thì b

ấ

t ph

ươ

ng trình

đ

ã cho có t

ậ

p nghi

ệ

m là R.

Ví dụ 3.

Gi

ả

i b

ấ

t ph

ươ

ng trình

( 2)( 3) 0.

x x

− + ≥

Hướng dẫn giải

Ta có

2 0 ; 3 0

( 2)( 3) 0

2 0 ; 3 0

x x

− ≥ + ≥



− + ≥ ⇔



− ≤ + ≤



2 ; 3 2

.

2 ; 3 3

x x x

≥ ≥ − ≥

 

⇔ ⇔

 

≤ ≤ − ≤ −

 

V

ậ

y S = { x/

2

≥

x

ho

ặ

c

3

≤ −

x

}.

50

III. BÀI TẬP VẬN DỤNG

1. Bài tập cơ bản

Bài 1.

Ch

ứ

ng minh r

ằ

ng :

a)

4 4 3 3

2( ) ( )( )

+ ≥ + +

a b a b a b

; (1)

b)

4 4 4 3 3 3

3( ) ( )( ).

a b c a b c a b c

+ + ≥ + + + + (2)

Bài 2.

Gi

ả

s

ử

2014 2016

≤ ≤

x

. Ch

ứ

ng minh

2016 2014 2.

x x

− + − ≤

Bài 3.

Ch

ứ

ng minh b

ấ

t

đẳ

ng th

ứ

c : (ac + bd)

2

≤ (a

2

+ b

2

)(c

2

+ d

2

).

Bài 4.

Ch

ứ

ng minh r

ằ

ng v

ớ

i m

ọ

i x ∈ R :

2

7

3

+

x

≥ 4.

Bài 5.

Cho b

ố

n s

ố

d

ươ

ng a ; b ; c tho

ả

mãn ad − bc = 1.

Ch

ứ

ng minh r

ằ

ng : A = a

2

+ b

2

+ c

2

+ d

2

+ ac + bd ≥

3.

Bài 6.

Cho ba s

ố

a, b, c tho

ả

mãn

đ

i

ề

u ki

ệ

n : a

2

+ b

2

+ c

2

= 1.

Ch

ứ

ng minh r

ằ

ng : 2(1 + a + b + c + ab + bc + ca) + abc

≥

0.

Bài 7.

Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c A =

−

2

x

+ x + 5.

Bài 8.

Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c C =

1

.

2 3

x x

− −

Bài 9.

a) Cho x + y = 1. Tìm giá tr

ị

l

ớ

n nh

ấ

t c

ủ

a P = 3xy – 4.

b) Cho x – 2y = 2. Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a Q = x

2

+ 2y

2

– x + 3y.

Bài 10.

Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c :

M =

3 5 7 3

− + −

x x

v

ớ

i

5 7

3 3

≤ ≤

x .

2. Bài tập nâng cao

Bài 1.

Cho a, b, c > 0.

Ch

ứ

ng minh r

ằ

ng :

2 2 2

( ) ( ) ( ) 3 .

a b c a b c a b c a b c abc

+ − + + − + + − ≤

(1)

Bài 2.

Ch

ứ

ng minh r

ằ

ng :

3 3 3

4( ) ( )

+ ≥ +

a b a b

v

ớ

i

, 0

a b

>

.

51

Bài 3.

Cho a, b, c > 0. Ch

ứ

ng minh r

ằ

ng :

1 1 4

.

a b a b

+ ≥

+

Bài 4.

Cho a, b, c > 0. Ch

ứ

ng minh r

ằ

ng :

2.

a b c

a b b c c a

+ + <

+ + +

Bài 5.

Ch

ứ

ng minh b

ấ

t

đẳ

ng th

ứ

c :

( )

2

.

x y x y

+ ≥ +

Bài 6.

Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a A = (x – 2)

2

+ (x – 3)

2

.

Bài 7.

Tìm c

ặ

p s

ố

(x, y) v

ớ

i y nh

ỏ

nh

ấ

t tho

ả

mãn

đ

i

ề

u ki

ệ

n :

x

2

+ 5y

2

+ 2y – 4xy – 3 = 0.

Bài 8.

Cho x, y liên h

ệ

v

ớ

i nhau b

ở

i h

ệ

th

ứ

c : x

2

+ 2xy + 7(x + y) + 2y

2

+ 10 = 0.

Hãy tìm giá tr

ị

l

ớ

n nh

ấ

t, giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c : S = x + y + 1.

Bài 9.

Gi

ả

i và bi

ệ

n lu

ậ

n b

ấ

t ph

ươ

ng trình

5 3

− > +

x mx x

(m là tham s

ố

).

3. Bài tập tự giải

Bài 1.

Cho a, b, c > 0. Ch

ứ

ng minh :

a)

2

+ ≥

a b

b a

; b)

1 1 1 1 1 1

. . . 6.

a b c

b c c a a b

     

+ + + + + ≥

     

     

Bài 2.

Cho x, y, z là các s

ố

th

ự

c d

ươ

ng tho

ả

mãn : xyz = 1.

Tìm giá tr

ị

l

ớ

n nh

ấ

t c

ủ

a bi

ể

u th

ứ

c :

3 3 3 3 3 3

1 1 1

.

1 1 1

A

x y y z z x

= + +

+ + + + + +

52

GỢI Ý - HƯỚNG DẪN GIẢI PHẦN ĐẠI SỐ

Chủ đề 1. BIẾN ĐỔI BIỂU THỨC ĐẠI SỐ

1. Bài tập cơ bản

Bài 1.

a) (a + b)

3

– 3ab(a + b) = a

3

+ 3a

2

b + 3ab

2

+ b

3

– 3a

2

b – 3ab

2

= a

3

+ b

3

.

b) Vì a + b + c = 0 nên a + b = – c

⇒

(a + b)

3

= – c

3

⇒

a

3

+ b

3

+ 3ab(a + b) = – c

3

⇒

a

3

+ b

3

+ c

3

– 3abc = 0

⇒

a

3

+ b

3

+ c

3

= 3abc.

Bài 2.

2 2 2

2 2

3 1 1 3

1 : 1 :

1 1

x x x x x x

x x

 

− + − +

 

− + =

 

− −

− − 

 

2

2 2

1 1 1

.

1

4 1 4 1

x x

x

x x

− +

= ⋅ =

−

− −

Bài 3.

3 2 2 3 2 2 2 2

( ) ( ) ( )( )

.

( ) ( ) ( )( )

x x y xy y x x y y x y x y x y x y

x y

x x y xy y x x y y x y x y x y

− − + − − − − − −

= = =

+

+ − − + − + + −

Bài 4.

Đ

i

ề

u ki

ệ

n x

3

+ 2x

2

– x – 2

≠

0. Ta có

2

( 2) ( 2) 0 ( 2)( 1)( 1) 0

x x x x x x

+ − + ≠

⇒

+ + − ≠

2 ; 1 ; 1.

x x x

⇒

≠ − ≠ − ≠

2 2

0 3 4 0 4 4 0

( 4) ( 4) 0 ( 4)( 1) 0.

A x x x x x

x x x x x

= ⇒ − − = ⇒ − + − =

⇒ − + − = ⇒ − + =

Suy ra x = 4 (tho

ả

mãn

đ

i

ề

u ki

ệ

n) ; x = −1 (lo

ạ

i).

V

ậ

y A = 0 khi x = 4.

Bài 5.

a)

4 12 3 3 6 4 2 3 3 3 6

+ + + = + + +

=

( )

2

3 1 3 3 6

+ + +

=

3

+ 1 + 3

3

+ 6 = 4

3

+ 7

= (2 +

3

)

2

.

53

b)

(

)

(

)

(

)

(

)

3 5 10 2 3 5 3 5. 2 5 1 3 5

− − + = − − +

=

(

)

(

)

6 2 5 5 1 3 5

− − +

=

( ) ( )( )

2

5 1 5 1 3 5

− − +

=

(

)

(

)

2

5 1 3 5

− +

=

(

)

(

)

6 2 5 3 5

− +

=

(

)

(

)

2 3 5 3 5

− +

= 2(9

−

5) = 8.

c)

(

)

(

)

( )( )

2 2

5 3 5 3

5 3 5 3 5 1 5 1

5 3 5 3

− + +

− + + +

+ − = −

+ − − −

+ −

=

(

)

2

5 1

8 2 15 8 2 15

5 3 5 1

+

− + +

−

− −

=

16 6 2 5

2 4

+

−

= 8

−

3 5

2

+

=

13 5

.

2

−

d)

( )

14 7 15 5 216

7 5

1 2 1 3 3 6

 

− −

− + +

 

− −

 

=

( )

(

)

(

)

7 2 1 5 3 1

7 5 2

1 2 1 3

 

− −

 

− + +

 

− −

 

=

(

)

(

)

7 5 7 5

− − −

+ 2

= −

(

)

(

)

7 5 7 5

− +

+ 2 =

−

2 + 2 = 0.

Bài 6.

a) A =

2

1

.

x x y y y

xy

x y

x y x y

 

+

− +

 

−

+ +

 

(

)

0 ; 0 ;

x y x y

> > ≠

=

( ) ( )

3 3

2

1

.

x y

y

xy

x y

x y x y

 

+

 

− +

 

−

+ +

 

 

54

=

(

)

(

)

2

1

.

x y x xy y

y

xy

x y

x y x y

 

+ − +

 

− +

 

−

+ +

 

=

( )( )

2 2

x xy y y

x y

x y x y

− +

+

+ −

=

2

x y y

x y x y

−

+

+ +

=

1.

x + y

=

b) Với x > 0 ; y > 0 ; x ≠ y, ta có :

B =

4

x y x y

y

x y

x y x y

+ −

−

− +

=

(

)

(

)

2 2

4

x y x y

y

x y x y x y

+ −

− − −

=

2 2 4

x xy y x xy y y

x y

+ + + − + −

−

=

(

)

( )

2

2.

x y

−

=

−

c) Với x > 0 ; x ≠ 1, ta có :

C =

1

1 1

−

− −

m

x

m m

=

( )

( )( )

2

1 2 2

.

1 1

1

x x x

x

x x

x

 

+ + −

 

−

 

+ −

+

 

 

=

1 2 2

1 1

x x

x x x

 

+ −

−

 

+ −

 

=

(

)

(

)

(

)

(

)

2 1 2 1

1

x x x x

x

 

+ − − − +

 

−

 

=

( )

2 2

.

1

x

x x

=

−

d) Với −1 < x < 1, ta có :

D =

2

2 1 2

1: : 1

1 1

1

x x

x

 

− −

 

+ −

 

−

 

55

=

2

2 2

2 2 1

1 :

1

1 1

x

x x

 

−

 

 

− − −

 

+

 

− −

 

=

(

)

2

2 1

:

1

x

− −

+

−

=

(

)

( )

2

2 1

1 . 1

.

1

2 1

x

x x

x

− −

+ −

+

− −

=

1 .

x

−

e) V

ớ

i x > y > 0, ta có :

E =

( )

2

1

. :

2

x y y xy y y xy

x y

x x y y

+ + −

−

+

+ +

=

(

)

(

)

2

1

. :

2

y x y y x y xy

x y

x x y y

+ + −

−

+

+ +

=

( )

2

( )

. .( )

y x y

x y

−

+

−

+

=

(

)

(

)

(

)

( )

.

y x y y x y x y

x y x y

+ − +

− +

=

(

)

( )

y x y x y

x y x y

+ −

− +

= y.

g) V

ớ

i x ≥ 2 ; x

≠

3, ta có :

G =

1 2 2

2 1

x x

x

− − −

− −

=

2 2 2 1

2 1

x x

x

− − − +

− −

=

( )

2

2 1

2 1 2 1

x

x x

− −

=

− − − −

=

1 3

1 2 3

x

>





− ≤ <



h) H =

1 1 1

...

1 2 2 3

2014 2015

+ + +

+ +

+

n

ế

u

n

ế

u

56

=

1 1 1

...

2 1 3 2 2015 2014

+ + +

2 1 3 2 2015 2014

...

1 1 1

− − −

= + + +

2015 1.

= −

Bài 7.

a)

Đ

i

ề

u ki

ệ

n x > 0 và x nguyên, x

≠

1. Ta có :

A =

2 2 1

.

1

2 1

x x x

x

x x x

 

+ − +

−

 

−

+ +

 

=

2

2 2 1

.

( 1)( 1)

( 1)

 

+ − +

−

 

+ −

+

 

x x x

x

=

2 2 1

.

1 1

x x

x x x

 

+ −

−

 

+ −

 

=

2 1 2

. .

1 1

x

x x

x

=

− −

b) A nh

ậ

n giá tr

ị

nguyên

⇔

x – 1

∈

Ư

(2) =

{

}

1 ; 2

± ±

1 1 2

1 1 0

.

1 2 3

1 2 1

x x

− = =

 

 

− = − =

 

⇔ ⇔

 

− = =

 

− = − = −

 

V

ậ

y v

ớ

i x = 2 ho

ặ

c x = 3 thì giá tr

ị

t

ươ

ng

ứ

ng c

ủ

a A nguyên.

Bài 8.

V

ớ

i x > 0 ; y > 0 và x

≠

y, ta có :

B =

( )

2

.

2

x y xy y

x

x y

x y x y

x y

 

+

 

− +

 

−

− +

−

 

=

( )

2

.

2( )

x y

xy y

x

x y x y

 

+

 

− +

 

− −

− +

 

 

=

( )

2

.

2( )

x y

y

x

x y

x y x y

 

−

 

+

 

−

− +

 

 

57

=

(

)

( )( )

2

.x y x

y

x y

x y x y

−

+

+ −

=

y

x

+

x + y x + y

=

1

=

x + y

.

V

ậ

y v

ớ

i x > 0 ; y > 0 và x

≠

y thì giá tr

ị

c

ủ

a bi

ể

u th

ứ

c B không ph

ụ

thu

ộ

c

vào hai bi

ế

n x và y.

Bài 9.

a) C xác

đị

nh ⇔

0

1 0

0

>





− ≠





− ≠



x

x x

⇔ x > 0 ; x

≠

1.

b) C =

2

1

−

+

− −

x x x

=

(

)

( )

2 1

1

−

+

−

x x

x

x x

=

2 1

1 1

−

− −

x x

=

2 1

1

− +

−

x x

x

=

(

)

2

1

−

=

−

x

− 1.

c) x = 4 +

(

)

2

12 4 2 3 3 1 .

= + = +

Do

đ

ó giá tr

ị

c

ủ

a bi

ể

u th

ứ

c C t

ạ

i x =

(

)

2

3 1

+

là

A =

( )

2

3 1

+ − 1 =

3

+ 1 − 1 =

3.

Bài 10.

a) E có ngh

ĩ

a

0

⇔ >

x

và

1

≠

x

.

b) E

( )

( )( )

2

2 2 1

1 1

1

x x x

x

x x

x

 

+ − +

 

= −

 

+ −

+

 

 

2 2 1

1 1

x x

x x x

 

+ −

= −

 

+ −

 

(

)

(

)

(

)

(

)

2 1 2 1

1

.

1

x x x x

x

+ − − − +

=

−

2 1

.

1

x

=

−

2

.

1

x

=

−

58

c) x =

16 6 7 7

− +

( )

2

3 7 7

= − +

3 7 7 3 7 7 3.

= − + = − + =

Do

đ

ó giá tr

ị

c

ủ

a bi

ể

u th

ứ

c A t

ạ

i x = 3 là

2

1.

3 1

A

= =

−

d) E nguyên

1

⇔ −

x

là

ướ

c c

ủ

a 2 (

Ư

(2) =

{ 1 ; 2})

± ±

1 1 2

1 1 0

.

1 2 3

1 2 1

x x

− = =

 

 

− = − =

 

⇔ ⇔

 

− = =

 

− = − = −

 

Theo

đ

i

ề

u ki

ệ

n

ở

câu a) ch

ỉ

có hai giá tr

ị

x = 2 ho

ặ

c x = 3 là tho

ả

mãn.

V

ậ

y v

ớ

i x = 2 ho

ặ

c x = 3 thì E nh

ậ

n giá tr

ị

nguyên.

Bài 11.

3 3 3 3

3 3

5 2 13 5 2 13 ( 5 2 13 5 2 13)

A A= + + −

⇒

= + + −

⇒

3

5 2 13 5 2 13 3 (5 2 13)(5 2 13). 10 9

A A A

= + + − + + − = −

⇒

3 2

9 10 0 ( 1)( 10) 0 1 0

A A A A A A

+ − =

⇒

− + + =

⇒

− =

⇒

A = 1 (Vì

2

10 0

+ + >

A A

v

ớ

i m

ọ

i A).

2. Bài tập nâng cao

Bài 1.

Ta có

* (a + b)(b + c)(c + a) + abc = (ab + ac + b

2

+ bc)(c + a) + abc

= abc + a

2

b + ac

2

+ a

2

c

+b

2

c + b

2

a + bc

2

+ abc + abc

= 3abc + a

2

b + ac

2

+ a

2

c

+ b

2

c + b

2

a + bc

2

(1)

* (a + b + c)(ab + bc + ca)

= a

2

b + abc + a

2

c + ab

2

+ b

2

c + abc + abc + bc

2

+ ac

2

= 3abc + a

2

b + ac

2

+ a

2

c

+ b

2

c + b

2

a + bc

2

(2)

T

ừ

(1) và (2) suy ra (a + b)(b + c)(c +a) + abc = (a + b + c)(ab + bc + ca).

Bài 2.

(a

3

+ b

3

) (a

2

+ b

2

) – (a + b) = a

5

+ b

5

+ a

3

b

2

+ a

2

b

3

– (a + b)

= a

5

+ b

5

+ a

2

b

2

(a + b) – (a + b)

= a

5

+ b

5

+ (a + b) – (a + b) = a

5

+ b

5

(do ab = 1).

59

Bài 3.

a) 14

2

= (a

2

+ b

2

+ c

2

)

2

⇔

4 4 4 2 2 2 2 2 2

196 2 2 2

a b c a b b c c a

= + + + + +

⇔

4 4 4 2 2 2 2 2 2

196 2( )

a b c a b b c c a

+ + = − + +

L

ạ

i có

2

0 ( ) 0

+ + =

⇒

+ + =

a b c a b c

⇒

2 2 2

2 2 2 0

a b c ab bc ca

+ + + + + =

⇒

7

ab bc ca

+ + = −

⇒

2

( ) 49

ab bc ca

+ + =

⇒

2 2 2 2 2 2 2 2 2

2 2 2 49

a b b c c a ab c bc a ca b

+ + + + + =

⇒

2 2 2 2 2 2

2 ( ) 49.

a b b c c a abc b c a+ + + + + =

Do

đ

ó

2 2 2 2 2 2

49

+ + =

a b b c c a

.

Suy ra A =

4 4 4

196 2.49 98.

a b c+ + = − =

b) Ta có a

3

+ b

3

+ c

3

= 3abc

⇔

a

3

+ b

3

+ c

3

– 3abc = 0

Thay a

3

+ b

3

= (a + b)

3

– 3ab(a + b) ta

đượ

c

(a + b)

3

– 3ab(a + b) + c

3

– 3abc = 0

⇔

2 2 2

( )( ) 0

a b c a b c ab bc ca

+ + + + − − − =

⇔

2 2 2

0

0.

a b c

a b c ab bc ca

+ + =





+ + − − − =



* N

ế

u a + b + c = 0 thì

B = 1 1 1

   

+ + +

   

   

a b c

b c a

=

( ) ( ) ( )

1.

b a c b a c c a b

b c a b c a

+ + + − − −

⋅ ⋅ = ⋅ ⋅ = −

* N

ế

u

2 2 2

0

+ + − − − =

a b c ab bc ca

thì

2 2 2

2( ) 0

+ + − − − =

a b c ab bc ca

2 2 2

( ) ( ) ( ) 0 .

a b b c c a a b c

⇔ − + − + − = ⇔ = =

Khi

đ

ó B = 1 1 1

   

+ + +

   

   

a b c

b c a

= (1 + 1)(1 + 1)(1 + 1) = 8.

Bài 4.

x

3

+ y

3

+ z

3

– 3xyz = (x + y)

3

– 3x

2

y – 3xy

2

+ z

3

– 3xyz

= [(x + y)

3

+ z

3

] – 3xy(x + y + z)

60

= (x + y + z)[(x + y)

2

– (x + y)z + z

2

] – 3xy(x + y + z)

= (x + y + z)(x

2

+ y

2

+ z

2

– xy – yz – zx).

3 3 3 2 2 2

2 2 2 2 2 2

3 ( )( )

x y z xyz x y z x y z xy yz zx

M

x y z xy yz zx x y z xy yz zx

+ + − + + + + + + +

= =

+ + − − − + + + + +

= + +

x y z

.

Bài 5.

Ta có :

0

a b c

x y z

+ + =

0 0

ayz bxz cxy

xyz

+ +

⇒

=

⇒

+ + =

2

2 2 2

1 2. 1

x y z x y z x y z ayz bxz cxy

a b c a b c abc

a b c

+ +

 

+ + =

⇒

+ + = + + + =

 

 

2 2 2

1.

x y z

a b c

⇒

+ + =

Bài 6.

2

2 2 2 2

2

2 2 2 2

2 2 2 4

.

2 2 2 4

x y x xy y x y xy

A

x y

x xy y x y xy

 

+ + + + +

= = =

 

−

− + + −

 

Vì 2x

2

+ 2y

2

= 5xy nên

2

5 4 9

9.

5 4

xy xy xy

A

xy xy xy

+

= = =

−

Vì x > y > 0

0 ; 0 0

x y x y > A

⇒ + > − ⇒ >

.

Ta có A

2

= 9 và A > 0

⇒

A = 3.

Bài 7.

Ta có xyz = 1 nên :

A

1 1 1

x xy y yz z zx

= + +

+ + + + + +

2

1

z xz

z zx xyz z zx

xz yxz yxz

= + +

+ + + +

+ +

1

1 1 1

z xz

z zx zx z z zx

= + +

+ + + + + +

1

1.

1

z zx

+ +

= =

+ +

Bài 8.

- Khi n = 1 : V

ế

trái S = 1.2.3 = 6 ; V

ế

ph

ả

i

1.2.3.4

6

4

=

.

Đẳ

ng th

ứ

c

đ

úng.

- Gi

ả

s

ử

đẳ

ng th

ứ

c

đ

úng khi n = k, t

ứ

c là :

61

S = 1.2.3 + 2.3.4 + 3.4.5 +......+ k(k + 1)(k + 2) =

( 1)( 2)( 3)

.

4

k k k k

+ + +

Ta ch

ứ

ng minh

đẳ

ng th

ứ

c

đ

úng khi n = k + 1.

Ta có

S = 1.2.3 + 2.3.4 + 3.4.5 +......+ k(k + 1)(k + 2) + (k + 1)(k + 2)(k +3)

( 1)( 2)( 3)

4

k k k k

k k k

+ + +

= + + + +

( 1)( 2)( 3) 4( 1)( 2)( 3)

4

( 1)( 2)( 3)( 4)

.

4

k k k k k k k

k k k k

+ + + + + + +

=

+ + + +

=

Đẳ

ng th

ứ

c

đượ

c ch

ứ

ng minh.

Bài 9.

Đ

i

ề

u ki

ệ

n : −1

1

≤ ≤

x

.

N =

( ) ( )

3 3

2

1 1 . 1 1

2 1

 

+ − + − −

 

 

+ −

x x x

x

=

2 2

2

1 1 .( 1 1 )(1 1 1 )

2 1

+ − + − − + + − + −

+ −

x x x x x x

x

=

( )

2

1 1 . 1 1

+ − + − −

x x x

(

)

(

)

2 2 2

1 1 1 2 1 1

⇒ = + − + − − + −

N x x x x

=

(

)

(

)

2 2

1 1 2 2 1+ − − −

x x

= 2

(

)

(

)

2 2

1 1 1 1+ − − −

x x

= 2

2

x

.

Do

đ

ó : N =

2

x

=

2.

x

T

ạ

i x =

1

5

, giá tr

ị

c

ủ

a bi

ể

u th

ứ

c N là N =

1 2

2 .

5 5

=

62

Chủ đề 2. PHƯƠNG TRÌNH - HỆ PHƯƠNG TRÌNH

1. Bài tập cơ bản

Bài 1.

a) ∆ = 1

2

−

4.1.(

−

12) = 1 + 48 = 49 > 0 ;

∆

= 7.

Ph

ươ

ng trình có hai nghi

ệ

m phân bi

ệ

t là :

x

1

=

1 7

2

− +

= 3 ; x

2

=

1 7

2

− −

=

−

4.

V

ậ

y S = {3 ;

−

4}.

b) ∆' = 3

2

−

9.2 = 9

−

18 =

−

9 < 0.

Ph

ươ

ng trình

đ

ã cho vô nghi

ệ

m. V

ậ

y S =

∅

.

c) ∆' = (

−

6)

2

−

4.9 = 36

−

36 = 0

Ph

ươ

ng trình có nghi

ệ

m kép : x

1

= x

2

=

6 3

4 2

=

. V

ậ

y S =

3

.

2

 

 

 

Bài 2.

∆ = (m + 1)

2

−

4m = m

2

+ 2m + 1

−

4m

= m

2

−

2m + 1 = (m

−

1)

2

≥ 0 v

ớ

i m

ọ

i m.

V

ậ

y ph

ươ

ng trình

đ

ã cho luôn có nghi

ệ

m v

ớ

i m

ọ

i m.

Bài 3.

* Khi a =

1

2

, ph

ươ

ng trình

đ

ã cho tr

ở

thành

−

9x +

9

2

= 0

9 1

9

2 2

⇔ = ⇔ =

x x (1)

* Khi a

1

2

≠

, ta có

2

( 4) (2 1)(5 2)

a a a

′

∆ = + − − +

2 2 2 2

8 16 10 2 9 9 18 9( 2).

a a a a a a a a

= + + − + + = − + + = − − −

Để

ph

ươ

ng trình có nghi

ệ

m ta ph

ả

i có

2

0 2 0

a a

′

∆ ≥ ⇔ − − ≤

2

2 2 0 ( 1) 2( 1) 0

⇔ + − − ≤ ⇔ + − + ≤

a a a a a a

1 0 ; 2 0

( 1)( 2) 0

1 0 ; 2 0

a a

+ ≥ − ≤



⇔ + − ≤ ⇔



+ ≤ − ≥



63

1 ; 2

1 2.

1 ; 2

a a

a

a a

≥ − ≤



⇔ ⇔ − ≤ ≤



≤ − ≥



(2)

K

ế

t h

ợ

p (1) và (2), suy ra ph

ươ

ng trình có nghi

ệ

m

1 2.

a

⇔ − ≤ ≤

Bài 4.

a) x

3

−

7x

2

+ 12x = 0

⇔ x(x

2

−

7x + 12) = 0 ⇔

2

0

7 12 0

x

x x

=





− + =



⇔

0

3 ; 4.

x

x x

=





= =



Ph

ươ

ng trình

đ

ã cho có ba nghi

ệ

m : x

1

= 0 ; x

2

= 3 và x

3

= 4.

T

ậ

p h

ợ

p nghi

ệ

m S = {0 ; 3 ; 4}.

b) x

4

– 4x

2

−

5 = 0 (1).

Đặ

t X = x

2

(X

≥

0) (1)

⇔

X

2

– 4X

−

5 = 0.

Có d

ạ

ng a – b + c = 1 + 4 – 5 = 0. Suy ra X

1

=

−

1 (lo

ạ

i) ; X

2

= 5 (nh

ậ

n).

Do

đ

ó x

2

= 5 suy ra x

1

=

5

; x

2

=

5

−

. V

ậ

y

{

}

5; 5

= −S

.

c)

Đ

i

ề

u ki

ệ

n : x – 1

≥

0

1

⇔ ≥

x

1 3

− =

x

2 2

( 1) 3

⇔ − =

x

1 9 9 1 10

⇔ − = ⇔ = + ⇔ =

x x x

(tho

ả

mãn

đ

i

ề

u ki

ệ

n).

V

ậ

y t

ậ

p nghi

ệ

m ph

ươ

ng trình là S =

{

}

10 .

d)

2

2 0

4 2

4 ( 2)

− ≥





+ = − ⇔



+ = −





x

x x

⇔

2

4 4 4

≥







+ = − +





x

x x x

⇔

2

5 0

≥







− =





x

x x

⇔

2

( 5) 0

≥





− =



x

x x

⇔

2

0 ; 5

x

x x

≥





= =



⇔ x = 5.

V

ậ

y nghi

ệ

m c

ủ

a ph

ươ

ng trình

đ

ã cho là : x = 5.

Bài 5.

a) V

ớ

i m

≠

–1 ;

∆' = [–(m – 1)]

2

– (m + 1)(m – 3) = m

2

– 2m + 1 – m

2

+ 2m + 3 = 4 > 0.

V

ậ

y ph

ươ

ng trình

đ

ã cho luôn có hai nghi

ệ

m phân bi

ệ

t v

ớ

i m

ọ

i m

≠

–1.

64

b)

Để

ph

ươ

ng trình có hai nghi

ệ

m cùng d

ấ

u ta ph

ả

i có

0

0.

P

∆ ≥





>



Ta có : P = x

1

.x

2

=

3

1

−

+

m

> 0

⇔

3 0 ; 1 0

m m

− > + >





− < + <



⇔

3 ; 1

m m

> > −





< < −



⇔

3

1.

m

>





< −



V

ậ

y v

ớ

i m > 3 ho

ặ

c m <

−

1 thì ph

ươ

ng trình

đ

ã cho có hai nghi

ệ

m cùng

d

ấ

u.

c) Theo câu b) ph

ươ

ng trình có hai nghi

ệ

m cùng d

ấ

u khi m > 3 ho

ặ

c m < –1.

G

ọ

i hai nghi

ệ

m là x

1

và x

2

và gi

ả

s

ử

x

1

= 2x

2

.

Theo

đị

nh lí Vi-ét, ta có :

1 2 2

2

1 2 2

1 2 1 2

2( 1) 2( 1)

3

1 1

3 3

. 2

1 1

2 2

− −

 

+ = =

 

+ +

 

− −

 

= ⇔ =

 

+ +

 

= =

 

 

m m

x x x

m m

x x x

m m

x x x x

⇔

2

2( 1)

3( 1)

3

2( 1)

−



=



+





−



=



+



m

x

m

x

m

.

Do

đ

ó :

2

4( 1) 3

2( 1)

9( 1)

− −

=

+

m m

m

⇔ 8(m – 1)

2

= 9(m – 3)(m + 1) ⇔ m

2

– 2m – 35 = 0

∆' = 1 + 35 = 36 > 0

m

1

= 1 + 6 = 7 ; m

2

= 1 – 6 = –5.

C

ả

hai giá tr

ị

này

đề

u tho

ả

mãn m > 3 ho

ặ

c m < –1.

V

ậ

y ph

ươ

ng trình có hai nghi

ệ

m cùng d

ấ

u và nghi

ệ

m này g

ấ

p

đ

ôi nghi

ệ

m

kia khi m = 7 ho

ặ

c m = –5.

Bài 6.

a) ∆ = (2a – 3)

2

– 4(a

2

– 3a) = 4a

2

– 12a + 9 – 4a

2

+ 12a = 9 > 0.

V

ậ

y ph

ươ

ng trình b

ậ

c hai

đ

ã cho luôn có hai nghi

ệ

m phân bi

ệ

t v

ớ

i m

ọ

i a.

Hai nghi

ệ

m c

ủ

a ph

ươ

ng trình là :

x

1

=

2 3 3

2

− −

a

= a – 3 ; x

2

=

2 3 3

2

− +

a

= a.

65

b)

Để

ph

ươ

ng trình có hai nghi

ệ

m trái d

ấ

u, ta ph

ả

i có :

⇔ x

1

.x

2

< 0 ⇔ a(a − 3) < 0 ⇔

0 ; 3 0

a a

< − >





> − <



⇔

0 ; 3

a a

< >





> <



⇔ 0 < a < 3

c)

2 2

1 2

+

x x

= (x

1

+ x

2

)

2

– 2x

1

x

2

= (2a – 3)

2

– 2(a

2

– 3a)

= 4a

2

– 12a + 9 – 2a

2

+ 6a

= 2a

2

− 6a + 9 = 2

2

9

3

2

 

− +

 

 

a a

= 2

2

3 9 9 9

2 .

2 4 4 2

 

 

− + − +

 

 

 

 

a a

= 2

2

3 9

2 4

 

 

− +

 

 

 

 

 

a = 2

2

3 9 9

.

2 2 2

a

 

− + ≥

 

 

V

ậ

y giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a

2 2

1 2

+

x x

là

9

2

khi và ch

ỉ

khi a –

3

2

= 0 hay a =

3

2

.

Bài 7.

a) Vì x = −1 là nghi

ệ

m c

ủ

a ph

ươ

ng trình nên :

k.(–1)

2

– (k – 1).(–1) – 1 = 0 ⇔ k + k – 1 – 1 = 0 ⇔ 2k = 2 ⇔ k = 1.

V

ậ

y k = 1 thì ph

ươ

ng trình

đ

ã cho có nghi

ệ

m x =

−

1.

b) * Khi k = 0, ph

ươ

ng trình

đ

ã cho tr

ở

thành : x

−

1 = 0 ⇔ x = 1.

* Khi k

≠

0 :

∆ = (k – 1)

2

+ 4k = k

2

– 2k + 1 + 4k = k

2

+ 2k + 1 = (k + 1)

2

≥ 0 v

ớ

i m

ọ

i

k

≠

0.

V

ậ

y ph

ươ

ng trình

đ

ã cho luôn có nghi

ệ

m v

ớ

i m

ọ

i k.

Trong tr

ườ

ng h

ợ

p k

≠

0, g

ọ

i x

1

, x

2

là hai nghi

ệ

m c

ủ

a ph

ươ

ng trình.

Theo

đị

nh lí Vi-ét ta có :

1 2 1 2

1 1

1 (1)

1 1

(2)

k

x x x x

k k

x x x x

k k

−

 

+ = + = −

 

⇔

 

− −

 

= =

 

 

(lo

ạ

i)

66

T

ừ

(1) và (2), ta suy ra : x

1

+ x

2

= 1 + x

1

x

2

,

đ

ây là h

ệ

th

ứ

c

độ

c l

ậ

p gi

ữ

a x

1

và x

2

đố

i v

ớ

i k.

Bài 8.

a) ∆ = (2m – 1)

2

– 8(m – 1) = 4m

2

– 4m + 1 – 8m + 8 = 4m

2

– 12m + 9

= (2m – 3)

2

≥ 0.

V

ậ

y ph

ươ

ng trình luôn có nghi

ệ

m v

ớ

i m

ọ

i m.

b)

Để

ph

ươ

ng trình có hai nghi

ệ

m cùng âm thì

1

0

2

0

(2 1)

0

2

−



∆ ≥



>



 

> ⇔

 

− −

 

<







m

P

m

S

⇔

1

1 0

1

2 1 0

2

>



− >





⇔

 

− >

>







m

⇔ m > 1.

c) Theo Vi-ét và

đề

cho ta có :

1 2

(2 1)

2

1

.

2

2 2 15

− −



+ =



−



=





− =





m

x x

m

x x

⇔

1 2

2 2 1 2 (1)

2 2 15 (2)

1

(3)

2

x x m

x x

m

x x





+ = −



− =





−



=



T

ừ

(1) và (2) : 4x

1

= 16 – 2m ⇔ x

1

= 4 –

8

.

2 2

m m

−

=

Thay vào (2) : 8

−

m

−

2x

2

= 15 ⇔ 2x

2

=

−

7 – m ⇔ x

2

=

7

.

2

m

− −

Thay x

1

và x

2

theo m vào (3) :

8 7 1

.

2 2 2

− − − −

   

=

   

   

m m m

⇔

−

56

−

m + m

2

= 2m – 2 ⇔ m

2

−

3m

−

54 = 0

∆ = 9 + 216 = 225 > 0 ;

∆

= 15

m

1

=

3 15

2

+

= 9 ; m

2

=

3 15

2

−

= –6.

V

ậ

y v

ớ

i m = 9 ho

ặ

c m = –6 thì ph

ươ

ng trình tho

ả

mãn

đ

i

ề

u ki

ệ

n

2x

1

– 2x

2

= 15.

67

Bài 9.

a) ∆' = 4 – 6(m – 1) = 10 – 6m.

Để

ph

ươ

ng trình có hai nghi

ệ

m phân bi

ệ

t ta ph

ả

i có ∆ > 0 ⇔ 10 – 6m > 0

⇔ 6m < 10 ⇔ m <

5

3

.

b)

Để

ph

ươ

ng trình có hai nghi

ệ

m cùng d

ươ

ng thì

5

3

0

4

0 0

3

0

2( 1)

0

3

m

S S

P

m

P



≤



∆ ≥





 

> ⇔ = >

 

 

>



−



= >





⇔

5

3

4 5

0 1 .

3 3

1

m

S m

m



≤



= > ⇔ < ≤





>





V

ậ

y v

ớ

i 1 < m ≤

5

3

thì ph

ươ

ng trình

đ

ã cho có hai nghi

ệ

m cùng d

ươ

ng.

c) y = (x

1

x

2

)

2

+ 2x

1

x

2

+ x

1

+ x

2

=

( )

2

4 4 4

1 ( 1)

9 3 3

− + − +

m m

=

4

9

(m

2

+ m + 1)=

4

9

2

1 1 1

2 . 1

2 4 4

 

 

+ + − +

 

 

 

 

m m

=

4

9

2

1 3

2 4

 

 

+ +

 

 

 

 

 

m =

4

9

2

1 1 1

.

2 3 3

m

 

+ + ≥

 

 

y

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t là

1

3

khi và ch

ỉ

khi m = –

1

.

2

Bài 10.

H

ệ

đ

ã cho t

ươ

ng

đươ

ng v

ớ

i h

ệ

:

3 5 (1)

2 5 (2)

y x

= −





= − +



V

ẽ

đồ

th

ị

hai hàm s

ố

(1) và (2).

Hai

đườ

ng th

ẳ

ng (1) và (2) có

h

ệ

s

ố

góc khác nhau nên trên

m

ặ

t ph

ẳ

ng to

ạ

độ

Oxy chúng

c

ắ

t nhau t

ạ

i m

ộ

t

đ

i

ể

m N có to

ạ

độ

giao

đ

i

ể

m là (x = 2 ; y = 1).

V

ậ

y h

ệ

ph

ươ

ng trình

đ

ã cho có

nghi

ệ

m duy nh

ấ

t là

(2 ; 1).

y

x

68

Bài 11.

a)

2 3 2 3 7 11

3 4 2 6 8 3 4

− = − − = − =

  

⇔ ⇔

  

+ = + = + =

  

x y x y y

x y x y x y

11

7

33 5

4 .

7 7

y

x



=



⇔





= − = −





V

ậ

y h

ệ

ph

ươ

ng trình có nghi

ệ

m duy nh

ấ

t (x =

5

7

−

; y =

11

7

).

b)

2

6

3

2 2

− =



− =





⇔ ⇔

 

− =







x y

(

)

( )

0 0 4 1

6 2

x y

+ = −







− =





Ph

ươ

ng trình (1) c

ủ

a h

ệ

vô nghi

ệ

m nên h

ệ

ph

ươ

ng trình

đ

ã cho vô nghi

ệ

m.

c)

2 3

3 2 1



+ =





− =





x y

⇔

(1 3) 1 3

2 3

x

x y



+ = +





+ =





1

2 3 1

x

y

=





⇔



= −





1

3 1

6 2

.

2 2

x

y

=



 

⇔ ⇔

 

−

=

 



V

ậ

y h

ệ

ph

ươ

ng trình có nghi

ệ

m duy nh

ấ

t là :

6 2

1 ; .

2

 

−

 

 

Bài 12.

Ta có :

2

6 3 9

2 3

ax +3y=4

3 4

− = −



− = −





⇔

 

+ =





x ay

a x ay a

2

( 6) 4 9

ax+3y = 4



+ = −



⇔







a x a

2

4 9

6

(4 9)

. 3 4

6

−



=



+

⇔



−



+ =



+



a

x

a

a y

a

2

4 9

6

3 8

.

6

a

x

a

y

a

−



=



+

⇔



+



=



+



V

ậ

y h

ệ

ph

ươ

ng trình

đ

ã cho luôn có nghi

ệ

m duy nh

ấ

t là :

2 2

4 9 3 8

;

6 6

a a

− +

 

 

+ +

 

.

Để

nghi

ệ

m c

ủ

a h

ệ

tho

ả

mãn x < 0 ; y > 0, ta có :

69

0 4 9 0

0 3 8 0

< − <

 

⇔

 

> + >

 

x a

y a

(Vì a

2

+ 6 > 0)

9

4

8

3



<



⇔





> −





a

⇔

8 9

.

3 4

a

−

< <

Vì a nguyên nên a =

−

2 ; a =

−

1 ; a = 0 ; a = 1 ; a = 2.

Bài 13.

1 gi

ờ

15 phút =

5

4

gi

ờ

; 1 gi

ờ

30 phút =

3

2

gi

ờ

.

G

ọ

i quãng

đườ

ng AB ; quãng

đườ

ng BC l

ầ

n l

ượ

t là x(km) ; y(km).

Đ

i

ề

u

ki

ệ

n : x, y > 0.

Th

ờ

i gian

đ

i quãng

đườ

ng AB là

12

x

(gi

ờ

).

Th

ờ

i gian

đ

i quãng

đườ

ng BC là

6

y

(gi

ờ

).

Ta có ph

ươ

ng trình :

12

x

+

6

y

=

5

4

.

Th

ờ

i gian v

ề

trên quãng

đườ

ng CB là

8

y

(gi

ờ

).

Th

ờ

i gian v

ề

trên quãng

đườ

ng BA là

4

x

(gi

ờ

).

Ta có ph

ươ

ng trình :

8

y

+

4

x

=

3

2

.

Ta

đượ

c h

ệ

ph

ươ

ng trình :

5

2 15

12 6 4

3 2 12

4 8 2

x y

x y x y



+ =



+ =





⇔

 

+ =





+ =





⇔

2 4 30 3 18

2 12 2 12

x y y

x y x y

+ = =

 

⇔

 

+ = + =

 

⇔

6

3

=





=



y

x

(tho

ả

mãn

đ

i

ề

u ki

ệ

n c

ủ

a

ẩ

n).

V

ậ

y quãng

đườ

ng AB dài 3km ; quãng

đườ

ng BC dài 6km.

70

Bài 14.

1 gi

ờ

40 phút =

5

3

(gi

ờ

).

G

ọ

i v

ậ

n t

ố

c riêng c

ủ

a ca nô

đ

i t

ừ

A và ca nô

đ

i t

ừ

B l

ầ

n l

ượ

t là x(km/h) ;

y (km/h).

Đ

i

ề

u ki

ệ

n : x > 0 ; y > 3.

Quãng

đườ

ng ca nô A

đ

i trong

5

3

(gi

ờ

) là :

5

3

(x + 3) (km).

Quãng

đườ

ng ca nô B

đ

i trong

5

3

gi

ờ

là :

5

3

(y

−

3) (km).

Ta có ph

ươ

ng trình :

5

3

(x + 3) +

5

3

(y − 3) = 85.

Vì v

ậ

n t

ố

c ca nô

đ

i xuôi dòng h

ơ

n v

ậ

n t

ố

c ca nô

đ

i ng

ượ

c dòng là 9km/h

nên ta có ph

ươ

ng trình : (x + 3) – (y

−

3) = 9 ⇔ x

−

y = 3.

Ta có h

ệ

ph

ươ

ng trình :

( ) ( )

5 5

3 3 85

3 3

3



+ + − =







− =



x y

⇔

5 5 255 51

3 3

+ = + =

 

⇔

 

− = − =

 

x y x y

⇔

2 54 27

3 24

= =

 

⇔

 

− = =

 

x x

x y y

(tho

ả

mãn

đ

i

ề

u ki

ệ

n c

ủ

a

ẩ

n).

V

ậ

y v

ậ

n t

ố

c riêng c

ủ

a ca nô A là 27km/h, v

ậ

n t

ố

c riêng c

ủ

a ca nô B là

24km/h.

Bài 15.

24 phút =

2

5

(gi

ờ

).

G

ọ

i v

ậ

n t

ố

c xe th

ứ

nh

ấ

t, xe th

ứ

hai l

ầ

n l

ượ

t là x (km/h) ; y (km/h).

Đ

i

ề

u

ki

ệ

n x > y > 0.

Theo

đề

bài ta có ph

ươ

ng trình : x − y = 5.

Th

ờ

i gian xe th

ứ

nh

ấ

t

đ

i t

ừ

Qu

ả

ng Ngãi

đế

n thành ph

ố

Quy Nh

ơ

n là :

180

x

(gi

ờ

).

71

Th

ờ

i gian xe th

ứ

hai

đ

i t

ừ

Qu

ả

ng Ngãi

đế

n thành ph

ố

Quy Nh

ơ

n là :

180

y

(gi

ờ

).

Ta có ph

ươ

ng trình :

180

y

−

180

x

=

2

5

.

Ta

đượ

c h

ệ

ph

ươ

ng trình :

5 (1)

180 180 2

(2)

5

− =







− =





x y

y x

T

ừ

(1) : x = y + 5. (3)

Thay vào (2) :

180

y

−

180

5

+

y

=

2

5

⇔ 900(y + 5)

−

900y = 2y(y + 5)

⇔ 4500 = 2y

2

+ 10y ⇔ y

2

+ 5y – 2250 = 0 ⇔ y

2

−

45y + 50y

−

2250 = 0

⇔ y(y

−

45) + 50(y

−

45) = 0 ⇔ (y

−

45)(y + 50) = 0

⇔

45

50

y

=





= −



Thay y = 45 vào (3) : x = 45 + 5 = 50 (tho

ả

mãn

đ

i

ề

u ki

ệ

n c

ủ

a

ẩ

n).

V

ậ

y v

ậ

n t

ố

c c

ủ

a xe th

ứ

nh

ấ

t là 50km/h, v

ậ

n t

ố

c c

ủ

a xe th

ứ

hai là 45km/h.

Bài 16.

G

ọ

i th

ờ

i gian

độ

i th

ứ

nh

ấ

t làm riêng hoàn thành công vi

ệ

c là x (gi

ờ

).

Đ

i

ề

u ki

ệ

n : 8 < x < 36.

Th

ờ

i gian

độ

i th

ứ

hai làm riêng hoàn thành công vi

ệ

c là y (gi

ờ

).

Đ

i

ề

u ki

ệ

n : 8 < y < 36.

Trong 1 gi

ờ

độ

i th

ứ

nh

ấ

t làm

đượ

c

1

x

(công vi

ệ

c).

Trong 1 gi

ờ

độ

i th

ứ

hai làm

đượ

c

1

y

(công vi

ệ

c).

Ta có ph

ươ

ng trình :

1

x

+

1 1

8

=

y

.

(

tho

ả

mãn

đ

i

ề

u ki

ệ

n

)

(lo

ạ

i)

72

Th

ờ

i gian

độ

i th

ứ

nh

ấ

t làm

1

2

công vi

ệ

c là

2

x

(gi

ờ

).

Th

ờ

i gian

độ

i th

ứ

hai làm

1

2

công vi

ệ

c là

2

y

(gi

ờ

).

Ta có ph

ươ

ng trình :

2

x

+

2

y

= 18.

Ta

đượ

c h

ệ

ph

ươ

ng trình :

1 1 1

8

18

2 2

x y



+ =







+ =





⇔

1 1 1

8

36



+ =







+ =



x y

⇔

1 1 1

(1)

36 8

36 (2)



+ =



−





= −



x x

y x

T

ừ

(1) : 8(36

−

x) + 8x = x(36

−

x) ⇔ 288 =36x

−

x

2

⇔ x

2

−

36x + 288 = 0 ⇔ x

2

−

12x

−

24x + 288 = 0

⇔ x(x

−

12)

−

24(x

−

12) = 0 ⇔ (x

−

12)(x

−

24) = 0

⇔ x

1

= 12 ; x

2

= 24 (tho

ả

mãn

đ

i

ề

u ki

ệ

n

ẩ

n).

Khi x

1

= 12 thì y

1

= 36

−

12 = 24 tho

ả

mãn

đ

i

ề

u ki

ệ

n.

Khi x

2

= 24 thì y

2

= 36

−

24 = 12 tho

ả

mãn

đ

i

ề

u ki

ệ

n

ẩ

n.

V

ậ

y :

Độ

i th

ứ

nh

ấ

t làm riêng thì s

ẽ

hoàn thành công vi

ệ

c trong 12 gi

ờ

và

độ

i th

ứ

hai làm riêng thì s

ẽ

hoàn thành công vi

ệ

c trong 24 gi

ờ

.

Độ

i th

ứ

nh

ấ

t làm riêng thì s

ẽ

hoàn thành công vi

ệ

c trong 24 gi

ờ

thì

độ

i th

ứ

hai làm riêng thì s

ẽ

hoàn thành công vi

ệ

c trong 12 gi

ờ

.

Bài 17.

G

ọ

i s

ố

s

ả

n ph

ẩ

m làm trong m

ộ

t ngày theo d

ự

đị

nh là x (s

ả

n ph

ẩ

m).

Đ

i

ề

u ki

ệ

n : x nguyên d

ươ

ng.

Th

ờ

i gian d

ự

đị

nh là

1200

x

(ngày).

Th

ờ

i gian v

ề

sau k

ể

t

ừ

khi t

ă

ng n

ă

ng su

ấ

t là

1200 1200

12 2 14

− − = −

x x

(ngày).

73

S

ố

s

ả

n ph

ẩ

m làm trong 12 ngày

đầ

u là 12x (s

ả

n ph

ẩ

m).

S

ố

s

ả

n ph

ẩ

m làm sau khi t

ă

ng n

ă

ng su

ấ

t là

1200

( 14)( 10)

− +x

x

(s

ả

n ph

ẩ

m).

Ta có ph

ươ

ng trình :

1200

12x + ( 14)( 10) 1200

x

x− + =

⇒

12000

12 1200 14 140 1200

x x

x

+ + − − =

⇒

12000

2 140 0

x

− + − =

⇒

2

6000

70 0 70 6000 0.

x x x

x

− + = ⇒ + − =

Gi

ả

i ph

ươ

ng trình tìm

đượ

c x = 50 (tho

ả

mãn) ; x = −120 (lo

ạ

i).

V

ậ

y theo k

ế

ho

ạ

ch thì trong m

ộ

t ngày nhóm th

ợ

đ

ó làm 50 s

ả

n ph

ẩ

m.

Bài 18.

G

ọ

i s

ố

xe c

ủ

a

độ

i là x (xe).

Đ

i

ề

u ki

ệ

n : x nguyên ; x > 2.

S

ố

xe v

ề

sau : x

−

2 (xe).

Lúc

đầ

u m

ỗ

i xe ch

ở

140

x

(t

ấ

n). V

ề

sau m

ỗ

i xe ch

ở

140

2

−

x

(t

ấ

n).

Theo

đề

ta có ph

ươ

ng trình :

140

2

−

x

−

140

x

= 8

⇔ 140x

−

140(x

−

2) = 8x(x

−

2) ⇔ 280 = 8x

2

−

16x

⇔ x

2

−

2x

−

35 = 0

∆' = 1 + 35 = 36 > 0 ;

'

∆

= 6

x

1

= 1 + 6 = 7 ; x

2

= 1

−

6 =

−

5 (lo

ạ

i).

Giá tr

ị

x = 7 tho

ả

mãn

đ

i

ề

u ki

ệ

n c

ủ

a

ẩ

n. V

ậ

y s

ố

xe c

ủ

a

độ

i là 7 xe.

Bài 19.

G

ọ

i s

ố

dãy gh

ế

ban

đầ

u trong h

ộ

i tr

ườ

ng là x (dãy).

Đ

i

ề

u ki

ệ

n : x nguyên ;

x > 2.

74

S

ố

dãy gh

ế

còn l

ạ

i sau khi

đ

ã b

ớ

t

đ

i 2 dãy là : x

−

2 (dãy).

S

ố

ng

ườ

i ng

ồ

i trên m

ỗ

i dãy lúc ban

đầ

u là

120

x

(ng

ườ

i).

S

ố

ng

ườ

i ng

ồ

i trên m

ỗ

i dãy v

ề

sau là

120

2

−

x

(ng

ườ

i).

Theo

đề

ta có ph

ươ

ng trình :

120

2

−

x

−

120

x

= 2 ⇔ x

2

−

2x

−

120 = 0

∆' = 1 + 120 = 121 > 0 ;

'

∆

= 11

x

1

= 1 + 11 = 12 ; x

2

= 1

−

11 =

−

10 (lo

ạ

i).

Đố

i chi

ế

u v

ớ

i

đ

i

ề

u ki

ệ

n và th

ử

l

ạ

i ta th

ấ

y x = 12 là thích h

ợ

p.

V

ậ

y s

ố

dãy gh

ế

ban

đầ

u là 12 dãy và m

ỗ

i dãy gh

ế

có :

120

12

= 10 (ng

ườ

i).

Bài 20.

G

ọ

i th

ờ

i gian

để

công nhân A làm riêng xong công vi

ệ

c là x (gi

ờ

).

Đ

i

ề

u

ki

ệ

n x > 2.

Th

ờ

i gian

để

công nhân B làm riêng xong công vi

ệ

c là x + 3 (gi

ờ

).

Trong 1 gi

ờ

công nhân A làm

đượ

c

1

x

(công vi

ệ

c).

Trong 1 gi

ờ

công nhân B làm

đượ

c

1

3

+

x

(công vi

ệ

c).

Theo

đề

ta có ph

ươ

ng trình :

1 1 1

2( 3) 2 ( 3)

3 2

x x x x

x x

+ = ⇔ + + = +

+

2

2 6 2 3

x x x x

⇔ + + = +

2

6 0

x x

⇔ − − =

.

1 24 25 0

∆ = + = >

1 2

1 5 1 5

3 ; 2

2 2

x x

+ −

= = = = −

(lo

ạ

i).

Giá tr

ị

x = 3 tho

ả

mãn

đ

i

ề

u ki

ệ

n.

V

ậ

y th

ờ

i gian

để

công nhân A làm riêng hoàn thành công vi

ệ

c trong 3 gi

ờ

.

75

Bài 21.

G

ọ

i ch

ữ

s

ố

hàng ch

ụ

c là a. Ch

ữ

s

ố

hàng

đơ

n v

ị

là b.

Đ

i

ề

u ki

ệ

n : 7 ≤ a ≤ 9 ; 0 < b < 3 ; a, b nguyên.

Ch

ữ

s

ố

hàng ch

ụ

c l

ớ

n h

ơ

n ch

ữ

s

ố

hàng

đơ

n v

ị

là 7 nên ta có ph

ươ

ng trình :

a

−

b = 7.

Đổ

i ch

ữ

s

ố

cho nhau

đượ

c s

ố

m

ớ

i b

ằ

ng

2

9

s

ố

ban

đầ

u nên ta có ph

ươ

ng

trình :

10b + a =

2

9

(10a + b) ⇔ 90b + 9a = 20a + 2b

⇔ 11a

−

88b = 0 ⇔ a − 8b = 0.

Ta có h

ệ

ph

ươ

ng trình :

7 7

8 0 7 8 0

− = = +

 

⇔

 

− = + − =

 

a b a b

a b b b

⇔

8

1

=





=



a

b

(tho

ả

mãn

đ

i

ề

u ki

ệ

n c

ủ

a

ẩ

n). V

ậ

y s

ố

c

ầ

n tìm là 81.

Bài 22.

20%

1

5

=

; 25%

1

4

=

.

G

ọ

i chi

ề

u dài hình ch

ữ

nh

ậ

t là x (m), chi

ề

u r

ộ

ng hình ch

ữ

nh

ậ

t là y (m).

Đ

i

ề

u ki

ệ

n x > y > 0.

Vì hình ch

ữ

nh

ậ

t có chu vi là 216m nên có ph

ươ

ng trình

x + y = 108.

(1)

Chi

ề

u dài v

ề

sau là

4x

5 5

− =

x

x ; chi

ề

u r

ộ

ng v

ề

sau là

5

.

4 4

y y

y + =

Vì chu vi không

đổ

i nên có ph

ươ

ng trình

4x 5

108

5 4

y

+ =

16 25 2160

x y

⇔ + =

(2)

T

ừ

(1) và (2) ta

đượ

c h

ệ

ph

ươ

ng trình

108

16x + 25y = 2160.

x y+ =







Gi

ả

i h

ệ

ta

đượ

c x = 60 và y = 48 (tho

ả

mãn).

Di

ệ

n tích hình ch

ữ

nh

ậ

t ban

đầ

u là 60 . 48 = 2880 (m

2

).

76

Bài 23.

G

ọ

i l

ượ

ng dung d

ị

ch lo

ạ

i I là x (lít) ; l

ượ

ng dung d

ị

ch lo

ạ

i II là y (lít).

Đ

i

ề

u ki

ệ

n : 0 < x ; y < 30.

Ta có ph

ươ

ng trình : x + y = 30.

L

ượ

ng axit ch

ứ

a trong dung d

ị

ch lo

ạ

i I là

20

100

x.

L

ượ

ng axit ch

ứ

a trong dung d

ị

ch lo

ạ

i II là :

5

.

100

y

Ta có ph

ươ

ng trình :

20 5 10

100 100 100

+ =

x y

(x + y) ⇔ 20x + 5y = 10x + 10y ⇔ 10x

−

5y = 0.

Ta

đượ

c h

ệ

ph

ươ

ng trình :

30 30

10 5 0 2 0

+ = + =

 

⇔

 

− = − =

 

x y x y

⇔

10

20

=





=



x

y

(tho

ả

mãn

đ

i

ề

u ki

ệ

n)

V

ậ

y l

ượ

ng dung d

ị

ch lo

ạ

i I là 10 lít. L

ượ

ng dung d

ị

ch lo

ạ

i II là 20 lít.

2. Bài tập nâng cao

Bài 1.

Ta có : ∆'

1

= b

2

−

ac ; ∆'

2

= c

2

−

ab ; ∆'

3

= a

2

−

bc

∆'

1

+ ∆'

2

+ ∆'

3

= a

2

+ b

2

+ c

2

−

ab

−

bc

−

ca

=

1

2

(2a

2

+ 2b

2

+ 2c

2

−

2ab

−

2bc

−

2ca)

=

1

2

[(a

2

−

2ab + b

2

) + (a

2

−

2ac + c

2

) + (b

2

−

2bc + c

2

)]

=

1

2

[(a

−

b)

2

+ (a

−

c)

2

+ (b

−

c)

2

]

≥

0.

Do

đ

ó t

ồ

n t

ạ

i ít nh

ấ

t m

ộ

t trong ba s

ố

∆'

1

, ∆'

2

, ∆'

3

không âm. V

ậ

y ba

ph

ươ

ng trình

đ

ã cho không th

ể

cùng vô nghi

ệ

m.

Bài 2.

a) Ta có (x + 1)(x + 2)(x + 3)(x + 4) = 15

⇒ (x + 1)(x + 4)(x + 2)(x + 3) = 15

⇒ (x

2

+ 5x + 4)(x

2

+ 5x + 6) = 15 (*)

77

Đặ

t t = x

2

+ 5x + 4 ; (*) ⇒ t(t + 2) = 15 ⇔ t

2

+ 2t

−

15 = 0

∆' = 1 + 15 = 16 > 0 ;

'

∆

= 4

t

1

=

−

1 + 4 = 3 ; t

2

=

−

1

−

4 =

−

5.

* Khi t = 3, ta có :

x

2

+ 5x + 4 = 3 ⇔ x

2

+ 5x + 1 = 0.

∆ = 25

−

4 = 21 > 0

x

1

=

5 21

2

− +

; x

2

=

5 21

.

2

− −

* Khi t =

−

5, ta có :

x

2

+ 5x + 4 =

−

5 ⇔ x

2

+ 5x + 9 = 0

∆ = 25

−

36 =

−

11 < 0 (ph

ươ

ng trình vô nghi

ệ

m).

V

ậ

y ph

ươ

ng trình

đ

ã cho có hai nghi

ệ

m là :

x

1

=

5 21

2

− +

và x

2

=

5 21

.

2

− −

b)

Đ

i

ề

u ki

ệ

n :

2 0

4 0

− ≥





− ≥



x

⇔ 2 ≤ x ≤ 4.

2 2 4

− + −

x x

= x

2

− 8x + 16 + 2

2

⇔ 2 2 4

− + −

x x

= (x − 4)

2

+ 2

2

.

V

ế

trái c

ủ

a ph

ươ

ng trình luôn ≤ 2

2

còn v

ế

ph

ả

i c

ủ

a ph

ươ

ng trình luôn

≥ 2

2

nên

để

ph

ươ

ng trình có nghi

ệ

m thì ph

ả

i có

đồ

ng th

ờ

i hai v

ế

đề

u

b

ằ

ng 2

2

.

2

2 2 4 2 2 (1)

( 4) 2 2 2 2 (2)

x x

x



− + − =





− + =





T

ừ

(2) suy ra : x = 4. Thay x = 4 vào (1) : 2

2

+ 0 = 2

2

tho

ả

mãn.

V

ậ

y nghi

ệ

m c

ủ

a ph

ươ

ng trình là : x = 4.

Bài 3.

Ta có ∆' = (k + 1)

2

−

(3 + k

2

) = k

2

+ 2k + 1

−

3

−

k

2

= 2k

−

2.

78

Để

ph

ươ

ng trình có hai nghi

ệ

m th

ự

c phân bi

ệ

t ⇔ ∆' > 0 ⇔ 2k

−

2 > 0

⇔ 2k > 2 ⇔ k > 1

V

ậ

y k nguyên nh

ỏ

nh

ấ

t là k = 2 thì ph

ươ

ng trình có hai nghi

ệ

m th

ự

c phân

bi

ệ

t.

Bài 4.

Ta có x

4

+ 4 = 5x(x

2

−

2) ⇔ x

4

−

5x

3

+ 10x + 4 = 0.

Vì x = 0 không ph

ả

i là nghi

ệ

m c

ủ

a ph

ươ

ng trình nên chia c

ả

hai v

ế

c

ủ

a

ph

ươ

ng trình cho x

2

ta

đượ

c :

x

2

−

5x +

2

10 4

+

x

= 0 ⇔

2

4 2

5

 

+ − −

 

 

x x

x

= 0 (*)

Đặt t = x

−

2

x

⇔ t

2

+ 4 = x

2

+

2

4

x

phương trình (*) ⇔ t

2

+ 4

−

5t = 0 ⇔

t

2

−

5t + 4 = 0.

Có dạng a + b + c = 0 nên t

1

= 1 và t

2

= 4.

Khi t = 1 : x

−

2

x

= 1 ⇔ x

2

−

x

−

2 = 0. Suy ra x

1

=

−

1 ; x

2

= 2.

Khi t = 4 : x

−

2

x

= 4 ⇔ x

2

−

4x

−

2 = 0. Suy ra x

3

= 2 +

6

; x

4

= 2

−

6.

Vậy phương trình đã cho có bốn nghiệm là : x

1

= 1 ; x

2

= 2 ; x

3

= 2 +

6

;

x

4

= 2

−

6.

Bài 5. Giả sử hai phương trình x

2

+ ax + 1 và x

2

+ bx + 2 = 0 có nghiệm chung là

x

0

.

Lúc đó :

2

0 0

+

x ax

+ 1 = 0

2

0 0

+

x bx

+ 2 = 0

⇒

2

0

x

+ (a + b)x

0

+ 3 = 0

∆ = (a + b)

2

– 24 ≥ 0 ⇔

24

+ ≥a b

⇔

2 6

+ ≥a b

Do

+ ≥ +

a b a b

nên

2 6

+ ≥a b

.

(1) có nghiệm ⇔

2 6.

a b+ ≥

Mặt khác :

+

a b

nhỏ nhất là 2

6.

79

Mà

+

a b

nhỏ nhất ⇔ (1) có nghiệm kép

x

01

= x

02

=

(

)

2 6 6

.

4 4 2

a b− +

±

= = ±

Thay x

0

=

6

2

±

vào hai phương trình đã cho ta tìm được :

5 7

;

6 6

a b

 

= =

 

 

hoặc

5 7

; .

6 6

a b

− −

 

= =

 

 

Bài 6. Vì a và b là hai nghiệm của phương trình x

2

+ mx + 1 = 0 nên theo định lí

Vi-ét ta có :

. 1

+ = −





=



a b m

a b

Vì b và c là hai nghiệm của phương trình x

2

+ nx + 2 = 0 nên theo định lí

Vi-ét ta có :

2

+ = −





=



b c n

bc

Mặt khác : (b – a)(b – c) = b

2

– bc – ab + ac

= b

2

+ ab + bc + ac – 2(ab + bc) = b(a + b) + c(a + b) – 2(ab + bc)

= (a + b)(b + c) – 2(ab + bc) = (–m)(–n) – 2(1 + 2) = mn – 6

Bài 7. Gọi x

1

, x

2

là hai nghiệm của phương trình x

2

+ px + q = 0 (x

1

; x

2

∈



).

Theo Vi-ét, ta có : x

1

+ x

2

=

−

p ; x

1

.x

2

= q.

Do đó : 18 = p + q = –(x

1

+ x

2

) + x

1

.x

2

= –x

1

– x

2

+ x

1

x

2

= (x

1

– 1)(x

2

– 1) – 1

⇔ (x

1

– 1)(x

2

– 1) = 19

Do 19 là số nguyên tố, nên cặp số (x

1

– 1 ; x

2

– 1) hoặc trùng với cặp số

(1 ; 19) hoặc trùng với cặp số (

−

1 ;

−

19).

Vậy nghiệm của phương trình là : (x

1

= 2 ; x

2

= 20) ứng với p =

−

22 ;

q = 40 hoặc (x

1

= 0 ; x

2

=

−

18) ứng với p = 18 ; q = 0.

80

Bài 8. a) (x ; y ; z) = (0 ; 0 ; 0) là một nghiệm của hệ phương trình.

Khi x ≠ 0 ; y ≠ 0 ; z ≠ 0 hệ đã cho tương đương với hệ.

7 1 1 7

12 12

9 1 1 9

.

20 20

8 1 1 8

15 15

x y

xy x y

y z

yz y z

z x

zx z x

+

 

= + =

 

+

 

= ⇔ + =

 

 

+

= + =

 

 

Cộng vế theo vế các phương trình của hệ, ta được

2

1 1 1 47 1 1 1 47

.

30 60

x y z x y z

 

+ + = ⇔ + + =

 

 

* Vì

1 1 7 1 47 7 1

12 60 12 5

+ = ⇒ = − =

x y z

⇒ z = 5.

* Vì

1 1 9 1 47 9 1

20 60 20 3

+ = ⇒ = − =

y z x

⇒ x = 3.

* Vì

1 1 8 1 47 8 1

15 60 15 4

+ = ⇒ = − =

z x y

⇒ y = 4.

Vậy hệ phương trình đã cho có hai bộ nghiệm là : (x ; y ; z) = (0 ; 0 ; 0) và

(x ; y ; z) = (3 ; 4 ; 5).

b) Cộng vế theo vế các phương trình của hệ, ta được :

3(x + y + z + t) = 18 ⇒ x + y + z + t = 6

* Vì x + y + z = 3 nên t = 3.

* Vì y + z + t = 4 nên x = 2.

* Vì z + t + x = 5 nên y = 1.

* Vì t + x + y = 6 nên z = 0.

Vậy hệ phương trình có nghiệm duy nhất là : (x = 2 ; y = 1 ; z = 0 ; t = 3).

Bài 9. a) Cộng từng vế các phương trình của hệ, ta có :

x

2

+ y

2

+ z

2

+ 2xy

−

2yz

−

2xz = 1 ⇔ (x + y

−

z)

2

= 1

⇔ x + y

−

z = 1 hoặc x + y

−

z = 1.

81

Mặt khác hệ phương trình đã cho được viết dưới dạng :

( ) 2

( ) 3

( ) 4

+ − =





+ − =





− − = −



x x y z

y y x z

z z x y

⇔

( ) 2 ( ) 2

( ) 3 ( ) 3

( ) 4 ( ) 4

+ − = + − =

 

 

+ − = ⇔ + − =

 

 

− + − = − + − =

 

x x y z x x y z

y x y z y x y z

z x y z z x y z

* Khi x + y – z = 1 ta được nghiệm của hệ là : (x = 2 ; y = 3 ; z = 4).

* Khi x + y – x =

−

1. Ta có :

.( 1) 2 2

( 1) 3 3.

.( 1) 4 4

x x

y y

z z

− = = −

 

 

− = ⇔ = −

 

 

− = = −

 

Vậy hệ phương trình đã cho có hai nghiệm là : (x = 2 ; y = 3 ; z = 4) và

(x =

−

2 ; y =

−

3 ; z =

−

4).

b) Điều kiện : x ≠ 0 ; y ≠ 0 ; z ≠ 0.

Hệ đã cho viết dưới dạng :

5 1 1 5

24 24

7 1 1 7

24 24

1 1 1 1

4 4

x y

xyz yz zx

y z

xyz zx xy

z x

xyz xy yz

 

+

= + =

 

+

= ⇔ + =

 

 

+

= + =

 

 

(*')

Cộng từng vế các phương trình của hệ, ta được

2

1 1 1 3 1 1 1 3

4 8

 

+ + = ⇔ + + =

 

 

xy yz zx xy yz zx

Kết hợp với hệ (*) ta được :

6

12

8

=





=





=



xy

zy

zx

(*')

Nhân vế theo vế hệ (*') ta được : (xyz)

2

= 576 = (±24)

2

.

Do đó :

* Khi xyz = 24 ta tìm được nghiệm của hệ là : (x = 2 ; y = 3 ; z = 4).

* Khi xyz =

−

24, ta tìm được nghiệm của hệ là : (x =

−

2 ; y =

−

3 ; z =

−

4).

Vậy hệ đã cho có hai nghiệm là : (x = 2 ; y = 3 ; z = 4) và (x =

−

2 ; y =

−

3 ;

z =

−

4).

82

Bài 10. Ta có : x

2

+ y

2

+ z

2

= xy + yz + zx ⇔ 2(x

2

+ y

2

+ z

2

) = 2xy + 2yz + 2zx

⇔ (x − y)

2

+ (y − z)

2

+ (z − x)

2

0 ⇔

0

− =





− =





− =



x y

y z

z x

⇔ x = y = z.

Thay vào phương trình thứ hai của hệ, ta được :

3.x

2014

= 3

2015

⇔ x

2014

= 3

2014

⇔ x = 3

Vậy hệ phương trình đã cho có nghiệm là : x = y = z = 3.

Chủ đề 3 : HÀM SỐ VÀ ĐỒ THỊ

1. Bài tập cơ bản

Bài 1. Vì đường thẳng y = ax + b song song với đường thẳng y =

−

2

3

x + 1 nên

a =

−

2

3

và b ≠ 1. Khi đó : y =

−

2

3

x + b.

Đường thẳng này đi qua điểm P(4 ;

−

3) nên :

−

3 =

−

2

3

4 + b ⇒ b =

−

1

3

(thoả mãn).

Vậy : a =

−

2

3

và b =

−

1

3

.

Bài 2. Phương trình hoành độ giao điểm của hai đường thẳng là :

−

3x + 2 = 4(x

−

3)

⇔

−

3x + 2 = 4x – 12 ⇔ 7x = 14 ⇔ x = 2.

Khi x = 2, giá trị y tương ứng là : y =

−

3.2 + 2 =

−

4.

Vậy toạ độ giao điểm của hai đường thẳng là : (x = 2 ; y =

−

4).

Bài 3. Hàm số cần tìm có dạng : y = ax + b (a ≠ 0).

- Vì hàm số có hệ số góc bằng

−

2 nên : a =

−

2 ⇒ y =

−

2x + b.

- Vì đồ thị của hàm số đi qua A(3 ; 2) nên : 2 =

−

2.3 + b ⇒ b = 8.

83

Hàm số cần tìm là : y =

−

2x + 8.

Bài 4. Phương trình đường thẳng (d') cần lập có dạng : y = ax + b.

* Vì (d') song song với (d) nên a = 1. Lúc đó (d') : y = x + b.

* Vì (d') đi qua điểm N trên trục tung có tung độ là

−

4 hay (d') đi qua

điểm N có toạ độ (0 ;

−

4) nên : y

N

= ax

N

+ b ⇔

−

4 = a.0 + b ⇔ b =

−

4.

Vậy đường thẳng (d') cần lập là : y = x

−

4.

Bài 5. a) Vì đồ thị của (P) : y = (m

2

– 3)x

2

đi qua A(1 ; 6) nên

6 = m

2

−

3 ⇔ m

2

= 9.

⇔ m

2

−

9 = 0 ⇔ (m + 3)(m

−

3) = 0 ⇔

3

.

3

m

= −





=



Vậy với m = 3 hoặc m =

−

3 thì đồ thị của hàm số đi qua điểm A(1 ; 6).

b) Khi m = 3 hoặc m =

−

3 ta được hàm số y = 6x

2

.

Do đó điểm B(

−

1 ;

−

6) không thuộc đồ thị của hàm số.

Bài 6. a) Đồ thị đi qua M

1

1;

2

 

−

 

 

nên :

1

2

= a.(

−

1)

2

⇔ a =

1

2

. Lúc đó : y =

1

2

x

2

.

b) Vì N(

−

3 ; m) ∈ (P) nên : m =

1

2

.(

−

3)

2

=

9

.

2

Bài 7. Lập bảng một số giá trị tương ứng

của x và y.

x

−

3

−

2

−

1

0 1 2 3

y

−

9

−

4

−

1

0

−

1

−

4

−

9

Đồ thị hàm số y =

−

x

2

là một

đường parabol nằm phía dưới trục

hoành nhận trục tung là trục đối

xứng ; nhận gốc toạ độ O(0 ; 0)

làm đỉnh.

y

x

84

Bài 8. a) mx + 3 + (3m

−

1)y = 0 (*)

Vì đường thẳng đi qua A(1 ;

−

2) nên

m.1 + 3 +(3m

−

1)(

−

2) = 0

⇔ m + 3

−

6m + 2 = 0 ⇔

−

5m + 5 = 0 ⇔ 5m = 5 ⇔ m = 1

Khi m = 1 (*) ⇔ x + 3 + 2y = 0 ⇔ 2y =

−

x – 3 ⇔ y =

−

1 3

2 2

−

x

Vậy hệ số góc của đường thẳng là

−

1

.

2

b) Gọi A(x

0

; y

0

) là điểm cố định mà (d) luôn đi qua.

Ta có : mx

0

+ 3 + (3m

−

1)y

0

= 0 (∀m)

⇔ mx

0

+ 3my

0

= y

0

−

3 (∀m)

⇔ m(x

0

+ 3y

0

) = y

0

−

3 (∀m)

⇔

0 0

0

3 0

+ =





− =



x y

y

⇔

0

9

.

3

x

y

= −





=



Vậy (d) luôn đi qua điểm cố định A(−9 ; 3).

2. Bài tập nâng cao

Bài 1. Phương trình hoành độ giao điểm của hai hàm số y = 3x và y =

−

x + 4 là :

3x =

−

x + 4 ⇔ 4x = 4 ⇔ x = 1

Lúc đó giá trị y tương ứng : y = 3.1 = 3.

Toạ độ giao điểm của chúng là : (x = 1 ; y = 3).

Thay toạ độ này vào hàm số : y = ax

−

3

2

, ta có :

3 = a.1

−

3

2

⇒ a = 3 +

3

2

=

9

.

2

Vậy : a =

9

2

thì ba đường thẳng đã cho đồng quy.

85

Bài 2. Phương trình đường thẳng (d) có dạng y = ax + b (a ≠ 0).

Vì (d) vuông góc (d') nên 2a = – 1. Suy ra : a =

−

1

2

.

Khi đó (d) : y =

−

1

2

x + b.

Vì (d) đi qua A(3 ; 0) nên 0 =

−

1

2

.3 + b ⇒ b =

3

.

2

Vậy đường thẳng (d) cần tìm là : y =

−

1

2

x +

3

2

.

Bài 3. a) ∆ABC có AC = 1 ; AB = 3 và

BC =

2 2

AC AB

+

1 9 10

= + =

b) S

ABC

=

. 3.1 3

2 2 2

= =

AB AC

(đvdt).

c) Phương trình đường thẳng BC

có dạng y = ax + b (a ≠ 0)

Vì đường thẳng đi qua B(1 ;

−

1)

nên

−

1 = a + b.

Vì đường thẳng đi qua C(0 ; 2)

nên 2 = a.0 + b ⇒ b = 2.

Do đó : a =

−

b

−

1 =

−

2

−

1 =

−

3.

Vậy phương trình đường thẳng BC là y =

−

3x + 2.

Bài 4. Phương trình tiếp tuyến với (P) có dạng y = ax + b (D')

vì (D') // (D) nên a =

−

1. (D') : y =

−

x + b.

Phương trình hoành độ giao điểm của (P) với (D') :

−

x

2

=

−

x + b ⇔ x

2

−

x + b = 0 (1)

∆ = 1

−

4b

x

y

86

Do (D') và (P) tiếp xúc nên ∆ = 0. Hay 1

−

4b = 0 ⇔ b =

1

.

4

Suy ra (D') : y =

−

x +

1

4

.

Hoành độ tiếp điểm là nghiệm kép của phương trình (1) : x

0

=

1

.

2

Do đó toạ độ tiếp điểm là

1 1

; .

2 4

 

−

 

 

Bài 5. a) Vì đồ thị của hàm số y = ax

2

đi qua A(1 ; 1) nên : 1 = a.1

2

⇔ a = 1.

Lúc đó : y = x

2

.

b) Phương trình đường thẳng (D) cần tìm có dạng : y = ax + b.

Vì (D) đi qua A(1 ; 1) nên : 1 = a + b.

Vì (D) cắt trục hoành tại điểm có hoành độ m (m ≠ 1) nên : 0 = a.m + b.

Ta được hệ phương trình :

1

0

+ =





+ =



a b

ma b

⇔

1

(1 ) 1

1

.

1

a

m a

m

b a m

b

m



=



− =





−

⇔

 

= − −





=



−



Do đó phương trình đường thẳng (D) là : y =

1

1 1

−

− −

m

x

m m

(m ≠ 1).

c) Phương trình hoành độ giao điểm của (P) và (D)

x

2

=

1

1 1

−

− −

m

x

m m

(m ≠ 1) ⇒ (1

−

m)x

2

−

x + m = 0

∆ = 1

−

4m(1

−

m) = 4m

2

−

4m + 1 = (2m

−

1)

2

Để (P) và (D) tiếp xúc ⇔ ∆ = 0 ⇔ 2m

−

1 = 0 ⇔ m =

1

.

2

Vậy với m =

1

2

thì (P) và (D) tiếp xúc.

Bài 6. a) Hàm số y = (m + 1)x + m + 1 đồng biến

87

⇔ m + 1 > 0 ⇔ m >

−

1 (1)

Vì đồ thị của hàm số đi qua điểm (1 ; 2) nên :

2 = m + 1 + m + 1 ⇔ 2m = 0 ⇔ m = 0 (2)

Kết hợp (1) và (2) để hàm số đã cho là đồng biến và đi qua điểm (1 ; 2)

khi m = 0.

b) Phương trình hoành độ giao điểm của đường thẳng và parabol là :

−

2x

2

= (m + 1)x + m + 1 ⇔ 2x

2

+ (m + 1)x + m + 1 = 0 (*)

∆ = (m + 1)

2

−

8(m + 1) = m

2

−

6m

−

7

Để đường thẳng và parabol tiếp xúc ⇔ ∆ = 0 ⇔ m

2

−

6m

−

7 = 0

∆' = 9 + 7 = 16 > 0

m

1

= 3 + 4 = 7 ; m

2

= 3

−

4 =

−

1.

Vậy với m = 7 hoặc m =

−

1 thì đường thẳng và (P) tiếp xúc.

* Khi m =

−

1, đường thẳng trở thành y = 0 và tiếp xúc với (P) tại gốc toạ

độ O(0 ; 0).

* Khi m = 7, phương trình (*) có nghiệm kép :

x

1

= x

2

=

( 1)

4

− +

m

=

−

2, lúc đó : y

1

= y

2

=

−

8.

Vậy toạ độ tiếp điểm là M(

−

2 ;

−

8).

Chủ đề 4 : BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH

1. Bài tập cơ bản

Bài 1. a) Ta có :

(1)

4 4 4 3 3 4 4 3 4 3

2 2 ( ) 0 ( ) ( ) 0

⇔ + − + + + ≥ ⇔ − + − ≥

a b a a b ab b a a b b ab

3 3 3 3

( ) ( ) 0 ( )( ) 0

⇔ − − − ≥ ⇔ − − ≥

a a b b a b a b a b

88

2

2 2 2 2

3

( ) ( ) 0 ( ) 0

2 4

 

 

⇔ − + + ≥ ⇔ − − + ≥

 

 

 

 

 

b b

a b a ab b a b a (1’)

Do bất đẳng thức (1’) đúng suy ra

4 4 3 3

2( ) ( )( )

+ ≥ + +

a b a b a b

.

b) Ta có :

(2)

4 4 4 4 3 3 3 4 3 3 3 4

3 3 3 ( )

⇔ + + − + + + + + + + +

a b c a ab ac a b b bc a c b c c

4 4 3 3 4 4 3 3 4 4 3 3

( ) ( ) ( ) 0

⇔ + − − + + − − + + − − ≥

a b a b ab b c b c bc c a a c ac

2 2 2 2 2 2

( ) ( ) ( ) ( )

a b a ab b b c b bc c

⇔ − + + + − + + +

2 2 2

( ) ( ) 0

c a c ca a

+ − + + ≥

(2’)

Do bất đẳng thức (2’) đúng suy ra

4 4 4 3 3 3

3( ) ( )( )

+ + ≥ + + + +

a b c a b c a b c

.

Bài 2. Áp dụng tính chất (a + b)

2

≤

2(a

2

+ b

2

) với mọi a, b

∈

.



Điều kiện 2014

≤

x

≤

2016, ta có :

2

( 2016 2014) 2(2016 2014)

− + − ≤ − + −x x x x

⇔

2

( 2016 2014) 2.2

− + − ≤x x = 4

⇔

2016 2014 2

− + − ≤

x x

Bài 3. Xét hiệu : (ac + bd)

2

− (a

2

+ b

2

)(c

2

+ d

2

)

= a

2

c

2

+ 2acbd + b

2

d

2

−

a

2

c

2

−

a

2

d

2

−

b

2

c

2

−

b

2

d

2

=

−

(a

2

d

2

−

2abcd + b

2

c

2

)

=

−

(ad

−

bc)

2

≤ 0 với ∀a ; b ; c ; d.

Vậy (ac + bd)

2

≤ (a

2

+ b

2

)(c

2

+ d

2

).

Bài 4. Với ∀ x ∈



, ta có :

(

)

2

3 2

+ −x

≥ 0 ⇔ x

2

+ 3

−

4

2

3

+

x

+ 4 ≥ 0

⇔ x

2

+ 7 ≥ 4

2

3

+

x

⇔

2

7

3

+

x

≥ 4

89

Bài 5. Ta có : (a

2

+ b

2

) + (c

2

+ d

2

) ≥ 2

(

)

(

)

2 2 2 2

+ +

a b c d

Nên A = ac + bd + a

2

+ b

2

+ c

2

+ d

2

= ac + bd + (a

2

+ b

2

) + (c

2

+ d

2

) ≥ ac + bd + 2

(

)

(

)

2 2 2 2

+ +

a b c d

(*)

Mà : (a

2

+ b

2

) (c

2

+ d

2

) = a

2

c

2

+ a

2

d

2

+ b

2

c

2

+ b

2

d

2

= a

2

d

2

−

2adbc + b

2

c

2

+ a

2

c

2

+ 2adbc + b

2

d

2

= (ad

−

bc)

2

+ (ac + bd)

2

= 1 + (ac + bd)

2

(do ad

−

bc = 1)

Thay vào (*) ta được : A ≥ ac + bd + 2

( )

2

1+ +

ac bd

. Đặt x = ac + bd

Suy ra : A ≥ x + 2

2

1

+

x

⇔ A

2

≥ (x + 2

2

1

+

x

)

2

= x

2

+ 4x

2

1

+

x

+ 4(x

2

+ 1) =

(

)

2 2 2

1 4 1 4 3

 

+ + + + +

 

 

x x x x

=

(

)

2

1 2

+ +

x x

+ 3 ≥ 3 ⇔ A

2

≥ 3 ⇔ A ≥

3.

Bài 6. Ta có : a

2

+ b

2

+ c

2

= 1 (giả thiết)

⇒

1 ; 1 ; 1

a b c

≤ ≤ ≤

⇒ (1 + a)(1 + b)(1 + c) ≥ 0

⇔ 1 + a + b + c + ab + bc + ca + abc ≥ 0 (1)

Mặt khác :

1

2

(a + b + c + 1)

2

=

1

2

(a

2

+ b

2

+ c

2

+ 1 + 2ab + 2ac + 2bc +

+ 2a + 2b + 2c) ≥ 0

⇔

1

2

(2 + 2ab + 2ac + 2bc + 2a + 2b + 2c) ≥ 0

⇔ 1 + ab + bc + ac + a + b + c ≥ 0 (2)

Cộng vế theo vế (1) và (2), ta suy ra :

2(1 + a + b + c + ab + bc + ca) + abc ≥ 0.

90

Bài 7. Điều kiện x

≥

0.

Ta có A =

−

2

x

+ x + 5 = (x

−

2

x

+ 1) + 4 = (

x

−

1)

2

+ 4

≥

4.

Vậy giá trị nhỏ nhất của A là 4

1 0 1 1

⇔ − = ⇔ = ⇔ =

x x x

.

Bài 8. C =

1

2 3

− −

x x

. Điều kiện : x

0

≥

.

Ta có :

(

)

2 3 2 3

− − = − − +

x x x x

=

(

)

2 1 2

 

− − + +

 

x x

=

( )

2

1 2

 

− − +

 

 

x

Do đó : C

( )

2

1

1 2

−

=

− +

x

.

Vì

(

)

2

1 2 2

− + ≥

x

với

0

∀ ≥

x

. Suy ra : C

1

2

≥ −

.

Vậy : giá trị nhỏ nhất của C là

1

1 0

2

− ⇔ − =

x

1 1

⇔ = ⇔ =

x x

thoả điều kiện.

Bài 9. a)

1 1

x y x y

+ = ⇒ = −

⇒

P =

2

1 13 13

3(1 ) 4 3 3 4 3 .

2 4 4

y y y y y

 

− − = − + − = − − − ≤ −

 

 

Vậy giá trị lớn nhất của P là

13

4

−

⇔

1

2

= =

x y

.

b)

2 2 2 2

x y x y

− = ⇒ = +

⇒

Q

2 2 2

4 8 4 2 2 2 3 6 9 2

= + + + − − + = + +

y y y y y y y

2

3 1

6( )

2 3

= + +

y y

2

3 9 11 3 11 11

6 2 6

4 16 8 4 8 8

   

= + ⋅ + − = + − ≥ −

   

   

y y y

91

Vậy giá trị nhỏ nhất của Q là

11

8

−

⇔

1

2

.

3

4

x

y



=







= −





Bài 10. Ta có : M

2

=

3 5 7 3 2 (3 5)(7 3 ) 2 2 (3 5)(7 3 ).

x x x x x x

− + − + − − = + − −

⇒

M

2

≥

⇒

M

2

≥

.

Vậy giá trị nhỏ nhất của biểu thức M là

2

⇔

5 7

.

3 3

x

≤ ≤

2. Bài tập nâng cao

Bài 1. Giả sử

, 0

a b c

≥ >

.

Khi đó ta có : (1)

2 2 2

3 ( ) ( ) ( ) 0

⇔ − + − − + − − + − ≥

abc a b c a b c a b c a b c

2 2 2

( ) ( ) ( ) 0

⇔ − − + + − − + + − − + ≥

a a ab ac bc b b bc ba ac c c ac bc ab

( )( ) ( )( ) ( )( ) 0

⇔ − − + − − + − − ≥

a a b a c b b c b a c c a c b

2 2

( )( ) ( )( ) 0

⇔ − − − + + − − ≥

a b a ac b bc c a c b c

2

( ) ( ) ( )( ) 0

⇔ − + − + − − ≥

a b a b c c a c b c

(*)

Bất đẳng thức (*) luôn đúng (Vì

, 0

a b c

≥ >

). Suy ra điều phải chứng

minh.

Bài 2. Ta có :

3 3 3 2 2 2

4( ) ( ) ( ) 4( ) ( )

a b a b a b a ab b a b

 

+ − + = + − + − +

 

2 2 2 2 2

( ) (4 4 4 ) ( 2 ) 3( )( ) 0

a b a ab b a ab b a b a b

 

= + − + − + + = + − ≥

 

Vậy

3 3 3

4( ) ( )

+ ≥ +

a b a b

với

, 0

>

a b

.

Bài 3. Ta có :

2 2 2

1 1 4 ( ) (a ) 4 2 ( )

0

( ) ( ) ( )

+ + + − − + −

+ − = = = ≥

+ + + +

b a b a b ab a ab b a b

a b a b ab a b ab a b ab a b

.

92

Suy ra

1 1 4

.

a b a b

+ ≥

+

Bài 4. Áp dụng BĐT : Nếu

0 , 0

< < >

x y m

thì

.

x x m

y y m

+

<

+

Ta có :

+

<

+ + +

a c a

a b a b c

;

+

<

+ + +

b a b

b c a b c

;

+

<

+ + +

c b c

c a a b c

2( )

2

+ +

⇒

+ + < =

+ + + + +

a b c a b c

a b b c c a a b c

(đpcm).

Bài 5. Vì hai vế của bất đẳng thức đã cho đều không âm.

( )

2

+ ≥ +

x y x y

⇔

2

2 .

+ +

x y x y

≥ (x + y)

2

⇔ x

2

+ y

2

+ 2

.

x y

≥ x

2

+ y

2

+ 2xy

⇔

.

x y

≥ xy (luôn luôn đúng).

Vậy

( )

2

.

x y x y

+ ≥ +

Đẳng thức xảy ra ⇔

xy

≥ 0 nghĩa là

x

và

y

cùng dấu.

Bài 6. A =

2

2 2 2

25 1 5 1 1

4 4 6 9 2 5 2

4 2 2 2 2

   

− + + − + = − + + = − + ≥

   

   

x x x x x x x

.

Vậy giá trị nhỏ nhất của biểu thức A =

1

2

⇔

5

2

=

x

.

Bài 7. Ta có

x

2

+ 5

y

2

+ 2

y

– 4

xy

– 3 = 0

2 2 2

( 2 ) ( 1) 4 ( 1) 4 ( 3)( 1) 0 3 1

⇔ − + + =

⇒

+ ≤

⇒

+ − ≤

⇒

− ≤ ≤

x y y y y y y

.

Vậy giá trị nhỏ nhất của y là –3

⇔

x

= – 6. Vậy cặp số (

x

;

y

) = (–6 ; –3)

là cần tìm.

Bài 8. Ta có

x

2

+ 2

xy

+ 7(

x + y

) + 2

y

2

+ 10 = 0

2 2

4 8 28 28 8 40 0

⇔ + + + + + =

x xy x y y

2 2

(2 2 7) 4 9

⇔ + + + =

x y y

93

2

(2 2 7) 9 ( 5)( 2) 0

⇔ + + ≤ ⇔ + + + + ≤

x y x y x y

5 0

2 0

+ + ≥



⇔



+ + ≤



x y

(*) (vì

2 5

+ + ≤ + +

x y x y

)

Vì S =

x + y

+ 1 nên (*)

4

⇔ − ≤

S

1

≤ −

.

Vậy giá trị nhỏ nhất của S là – 4

⇔

x

= –5,

y

= 0.

Giá trị lớn nhất của S là –1

⇔

x

= –2,

y

= 0.

Bài 9.

5 3 (4 ) 3

− > + ⇔ − >

x mx x m x

- Với

4 0 4

− ≠ ⇔ ≠

m m

*

3

4 0 4

4

− > ⇔ < ⇔ >

−

m m x

m

*

3

4 0 4

4

− < ⇔ > ⇔ <

−

m m x

m

- Với

4

=

m

bất phương trình có dạng

0. 3.

x

>

Suy ra không có giá trị nào của

x

nhân với 0 cho ta một số lớn hơn 3.

Vậy bất phương trình vô nghiệm.

Kết quả :

- Với

3

4 .

4

m x

m

<

⇒

>

−

- Với

3

4 .

4

m x

m

>

⇒

<

−

- Với

4 .

m S

=

⇒

= ∅

94

Phần hai.

HÌNH HỌC

TÍNH TOÁN CÁC ĐẠI LƯỢNG HÌNH HỌC

I. KIẾN THỨC CẦN SỬ DỤNG

1. Tam giác, tứ giác, đa giác n cạnh.

2. Đa giác đều.

3. Đường thẳng song song, cát tuyến.

4. Diện tích đa giác ; diện tích đa giác đều ; diện tích quạt tròn.

5. Hàm số lượng giác.

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

TÍNH SỐ ĐO GÓC

1. PHƯƠNG PHÁP GIẢI

− Tính chất đường phân giác của một góc, của tam giác.

− Tính chất hai đường thẳng song song, đường trung bình của tam giác, của

hình thang.

2. CÁC VÍ DỤ

Ví dụ 1. Cho nửa đường tròn (O ; R) đường kính BC. Điểm A thuộc nửa đường

tròn. Gọi D và E thứ tự là điểm chính giữa các cung nhỏ AC và AB. Gọi F là

giao điểm của BD và CE.

Ch

ChCh

Ch 

  

 

1

11

1

95

a) Tính số đo của



BFC

.

b) Tính số đo của



BFO

, biết rằng AB = 3cm ; R = 2,5cm.

Gợi ý : Sử dụng các biểu thức : tổng ba góc của tam giác, định lí Pi-ta-go,

tam giác bằng nhau, tính chất của góc nội tiếp, số đo cung, tính chất đường phân

giác.

Hướng dẫn giải

a)



BAC

là góc nội tiếp chắn nửa đường tròn (O)



0

90

⇒ =BAC



0

90 .

ABC ACB⇒ + =

Vì



=

DA DC



⇒ =

DBA DBC

nên BD là

phân giác của



ABC

.

Vì



=

EA EB



⇒ =

ECA ECB

nên CE là

phân giác của



ACB

.

Do đó



(

)

1

2

FBC FCB ABC ACB

+ = +

0 0

1

.90 45

2

= = .

T

ừ

∆

ABC

suy ra



0

135

=BFC

.

b) Tam giác ABC vuông t

ạ

i A. Áp d

ụ

ng

đị

nh lí Pi-ta-go tính

đượ

c AC = 4cm.

G

ọ

i H là giao

đ

i

ể

m c

ủ

a BD và AC. Vì BH là phân giác c

ủ

a

∆

ABC

nên

HC BC

HA BA

=

⇒

CH = 2,5cm.

D

ễ

th

ấ

y

∆ = ∆

CFH CFO

(c-g-c) (vì CH = CO = 2,5cm ; CF c

ạ

nh chung ;



=

FCH FCO

)



⇒

=

CFH CFO

, mà



0

135

=BFC

nên



0

45

=CFH

. Do

đ

ó



0

90

=BFO

.

Ví dụ 2.

Cho

đườ

ng tròn (O)

đườ

ng kính AB. G

ọ

i C là

đ

i

ể

m chính gi

ữ

a cung AB ;

D là trung

đ

i

ể

m c

ủ

a OB. Tia CD c

ắ

t

đườ

ng tròn (O)

ở

E.

a) Tính s

ố

đ

o c

ủ

a



ABE

.

b) Trên c

ạ

nh AE l

ấ

y

đ

i

ể

m F sao cho AF = BE. Tính t

ổ

ng



+

BAE BFE

.

H

F

D

E

O

B

C

A

96

Gợi ý :

Áp d

ụ

ng s

ố

đ

o cung, tính ch

ấ

t góc n

ộ

i ti

ế

p, tính ch

ấ

t

đườ

ng phân giác,

t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n (k

ế

t h

ợ

p v

ớ

i máy tính c

ầ

m tay), tam giác vuông cân,

tam giác

đồ

ng d

ạ

ng.

Hướng dẫn giải

a) Vì



=

CA CB



⇒

=

AEC BCE

⇒

EC là

phân giác c

ủ

a



AEB

Vì ED là phân giác c

ủ

a

ABE

∆

⇒ =

EA DA

EB DB

.

Mà D là trung

đ

i

ể

m OB nên DA = 3DB

⇒

EA = 3EB.

Vì AB là

đườ

ng kính c

ủ

a (O)



0

90

⇒ =AEB

.

∆

ABE

vuông t

ạ

i E

 

0

tan 3 71 34'

⇒ = = ⇒ =

EA

ABE ABE

EB

.

b) Vì AE = 3BE và AF = BE

⇒

FE = 2BE.

∆

FBE

vuông t

ạ

i E

 

0

1

tan 26 34'

2

⇒ = = ⇒ =

EB

BFE BFE

EF

Do

đ

ó



0 0 0

18 26' 26 34' 45

+ = + =BAE BFE

.

Cách khác :

D

ễ

th

ấ

y

∆

OCD



∆

EFB

(c-g-c),



=

BAE BCE

,



0

45

=OCB



0

45

⇒ + =BAE BFE

.

Ví dụ 3.

Cho

đườ

ng tròn (O)

đườ

ng kính AB.

Đ

i

ể

m C thu

ộ

c

đườ

ng tròn (O) sao

cho AC < CB. Trên dây CB l

ấ

y

đ

i

ể

m D sao cho BD = AC. G

ọ

i E là trung

đ

i

ể

m c

ủ

a CD. Tính s

ố

đ

o c

ủ

a



OEB

.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t c

ủ

a hai

đườ

ng th

ẳ

ng song song, tính ch

ấ

t tam giác

vuông cân, tính ch

ấ

t c

ủ

a góc n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn..

Hướng dẫn giải

G

ọ

i M là trung

đ

i

ể

m c

ủ

a AD.

F

E

C

D

O

A

B

97

D

ễ

th

ấ

y ME, MO th

ứ

t

ự

là

đườ

ng trung bình c

ủ

a các tam giác ACD và ABD

⇒

/ /

2

=

AC

ME ; MO/ /

2

=

BD

.

Mà BD = AC nên ME = MO (1).



ACB

là góc n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn

(O)



0

90 .

ACB⇒ =

Vì ME // AC và MO // BD nên



0

90 .

EMO =

(2)

T

ừ

(1) và (2) ta có

EMO

∆

vuông cân t

ạ

i

M



0

45

⇒ =MOE

.

Vì MO // BD



⇒ =

OEB MOE

(so le

trong)



0

45

⇒ =OEB

.

Chú ý :

Gi

ả

thi

ế

t cho bi

ế

t E là trung

đ

i

ể

m c

ủ

a CD và ta nh

ậ

n th

ấ

y O là trung

đ

i

ể

m c

ủ

a

đườ

ng kính AB. G

ợ

i ý cho ta v

ẽ

thêm

đ

i

ể

m M là trung

đ

i

ể

m c

ủ

a AD là

h

ế

t s

ứ

c quan tr

ọ

ng.

Ví dụ 4.

Cho hình vuông ABCD. G

ọ

i O là giao

đ

i

ể

m c

ủ

a hai

đườ

ng chéo. Trên

các

đ

o

ạ

n th

ẳ

ng AB và OC l

ầ

n l

ượ

t l

ấ

y các

đ

i

ể

m E và F sao cho

. 2

=AE OF

.

Tính các góc c

ủ

a tam giác DEF.

Gợi ý :

Cho thêm

đ

i

ể

m G

để

t

ạ

o ra tam giác vuông cân, hình bình hành, s

ử

d

ụ

ng ki

ế

n th

ứ

c v

ề

tam giác b

ằ

ng nhau, tính ch

ấ

t ba

đườ

ng cao, tính ch

ấ

t hình

vuông, quan h

ệ

t

ừ

vuông góc

đế

n song song

Hướng dẫn giải

Trên

đ

o

ạ

n OD l

ấ

y

đ

i

ể

m G sao cho OG = OF.

Vì ABCD là hình vuông nên

⊥

AC BD

t

ạ

i O.

Do

đ

ó tam giác OGF vuông cân t

ạ

i O. Suy ra

2

=GF OF

, mà

. 2

=AE OF

nên GF = AE.

Vì AE // = GF nên AEFG là hình bình hành

⇒

AG // = EF (1)

M

E

D

C

O

A

B

E

G

A

C

B

D

O

F

98

Vì O là giao

đ

i

ể

m hai

đườ

ng chéo AC và BD c

ủ

a hình vuông ABCD nên

AC BD

⊥

t

ạ

i O và OA = OB = OC = OD. T

ừ

đ

ó

∆ = ∆

AOG DOF

(c-g-c)

⇒

=

AG DF

(2).

T

ừ

(1), (2) suy ra EF = DF (*). D

ễ

th

ấ

y G là tr

ự

c tâm c

ủ

a

∆

ADF

(

;

⊥ ⊥

DO AF FG AD

)

⇒

⊥

AG DF

.

Mà AG // EF nên EF

⊥

DF (**). T

ừ

(*) và (**) suy ra tam giác DEF vuông

cân t

ạ

i F.

Ví dụ 5.

Cho tam giác ABC cân t

ạ

i A n

ộ

i ti

ế

p

đườ

ng tròn (O ; R). Bi

ế

t BC =

R

2

. Tính s

ố

đ

o các góc c

ủ

a tam giác ABC.

Gợi ý :

Áp d

ụ

ng

đị

nh lí Pi-ta-go

đả

o, tính ch

ấ

t góc n

ộ

i ti

ế

p, t

ổ

ng ba góc c

ủ

a

tam giác,

đị

nh ngh

ĩ

a s

ố

đ

o cung.

Hướng dẫn giải

* Tr

ườ

ng h

ợ

p 1 :

Đỉ

nh A thu

ộ

c cung l

ớ

n c

ủ

a cung BC

a) Ta có OB

2

+ OC

2

= R

2

+ R

2

= 2R

2

.

Ta l

ạ

i có BC

2

=

(

)

2

2 2

=

R R

.

∆

BOC

có BC

2

= OB

2

+ OC

2

, nên theo

đị

nh lí

Pi-ta-go

đả

o thì

∆

BOC

vuông t

ạ

i O.

Suy ra s

đ



BC

=



0

90

=BOC

⇒



1

2

=

BAC s

đ



BC

= 45

0

.

Tam giác ABC cân t

ạ

i A

⇒



(

)

0 0 0

180 45 : 2 67 30 .

ABC ACB

′

= = − =

* Tr

ườ

ng h

ợ

p 2 :

Đỉ

nh A thu

ộ

c cung nh

ỏ

c

ủ

a cung BC

S

ố

đ

o cung nh

ỏ

BC b

ằ

ng 90

0

nên s

ố

đ

o cung l

ớ

n BC b

ằ

ng 270

0

.

Khi

đ

ó



BAC

là góc n

ộ

i ti

ế

p ch

ắ

n cung l

ớ

n BC nên



0

135 .

BAC =

Tam giác ABC cân t

ạ

i A

⇒



0

22 30

ABC ACB

′

= =

.

Ví dụ 6 :

Cho t

ứ

giác ABCD n

ộ

i ti

ế

p n

ử

a

đườ

ng tròn tâm O

đườ

ng kính CD = 2R.

Bi

ế

t AC = R

3

và BD = R

2

. Tính các góc c

ủ

a t

ứ

giác ABCD.

A

H

O

B

C

99

H

B

A

O

D

C

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t góc n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn,

đị

nh lí Pi-ta-go,

t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n, tính ch

ấ

t c

ủ

a tam giác vuông cân, tính ch

ấ

t c

ủ

a t

ứ

giác n

ộ

i ti

ế

p.

Hướng dẫn giải

Góc DAC n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn tâm O

đườ

ng kính CD nên



0

90

=DAC

.

Áp d

ụ

ng

đị

nh lí Pi-ta-go tính

đượ

c : AD = R.

Tam giác DAC vuông t

ạ

i A, ta có



3 3

sin

2 2

AC R

ADC

CD R

= = =



0

60

ADC

⇒

=



0

30

⇒

=ACD

.

Góc DBC n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn

tâm O

đườ

ng kính CD nên



0

90

=DBC

.

Áp d

ụ

ng

đị

nh lí Pi-ta-go tính

đượ

c : BC = R

2

.

Do

đ

ó

DBC

∆

vuông cân t

ạ

i B



0

45

⇒

= =BDC BCD

.

T

ứ

giác ABCD n

ộ

i ti

ế

p

⇒



0 0 0 0

180 180 60 120

= − = − =ABC ADC

;



0

135

=DAB

.

Dạng 2.

TÍNH ĐỘ DÀI ĐOẠN THẲNG ; TÍNH GIÁ TRỊ CỦA BIỂU THỨC

1. PHƯƠNG PHÁP GIẢI

− Công thức tính diện tích của các hình.

− Quy về việc giải một phương trình, hoặc hệ phương trình.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác ABC có AB = 3, AC = 4, nội tiếp đường tròn (O) đường

kính BC. Gọi I là một điểm nằm trong tam giác ABC sao cho IA = IB – 1 =

IC – 2. Tính độ dài IA.

Gợi ý : Kẻ IH

⊥

AB, IK

⊥

AC. Áp dụng định lí Pi-ta-go để lập phương

trình.

100

H

K

A

O

B

C

I

K

1

H

1

H

3

K

3

H

2

K

2

C

1

B

1

C

B

G

A

1

O

Hướng dẫn giải

∆

ABC

n

ộ

i ti

ế

p

đườ

ng tròn (O)

đườ

ng kính

BC



0

90 .

BAC

⇒ =

* Kẻ IH

⊥

AB, IK

⊥

AC.

* Đặt IA =

x

, IH =

y

, IK =

z

⇒

IB = x + 1,

IC = x + 2

.

* Áp dụng định lí Pi-ta-go vào các tam giác

vuông, ta có :

x

2

= y

2

+ z

2

; y

2

+ (3 – z)

2

= (x + 1)

2

;

(4 – y)

2

+ z

2

= (x + 2)

2

.

Từ đó suy ra phương trình :

2 2

2

3 4

2 3

− −

   

= +

   

   

x x

x .

Gi

ả

i ph

ươ

ng trình trên ta tính

đượ

c OA.

Ví dụ 2.

Cho tam giác

đề

u ABC có tr

ọ

ng tâm là G. L

ấ

y

đ

i

ể

m O b

ấ

t kì trong tam

giác

đề

u khác G.

Đườ

ng th

ẳ

ng OG c

ắ

t các

đườ

ng th

ẳ

ng BC, CA, AB th

ứ

t

ự

t

ạ

i A

1

; B

1

; C

1

.

Tính t

ỉ

s

ố

1 1 1

+ +

OA OB OC

GA GB GC

.

Gợi ý :

K

ẻ

GH

1

; GH

2

; GH

3

l

ầ

n l

ượ

t vuông góc v

ớ

i BC, CA, AB. K

ẻ

OK

1

;

OK

2

; OK

3

l

ầ

n l

ượ

t vuông góc v

ớ

i BC, CA, AB. Áp d

ụ

ng

đị

nh lí Ta-lét.

Hướng dẫn giải

* K

ẻ

GH

1

; GH

2

; GH

3

l

ầ

n l

ượ

t vuông góc v

ớ

i BC, CA, AB.

* K

ẻ

OK

1

; OK

2

; OK

3

l

ầ

n l

ượ

t vuông

góc v

ớ

i BC, CA, AB.

* Áp d

ụ

ng

đị

nh lí Ta-let ta

đượ

c :

1 1

=

OA OK

GA GH

⇒

1 1 1

3

+ + =

OA OB OC

GA GB GC

101

B

A

C

D

E

D

B

A

C

Ví dụ 3.

Cho tam giác ABC có

độ

dài ba c

ạ

nh là ba s

ố

t

ự

nhiên liên ti

ế

p. Tính

độ

dài các c

ạ

nh c

ủ

a tam giác ABC, bi

ế

t r

ằ

ng



0

3. 2. 180

+ =A B

.

Gợi ý :

Áp d

ụ

ng tam giác

đồ

ng d

ạ

ng

để

l

ậ

p ph

ươ

ng trình. Chú ý xét hai

tr

ườ

ng h

ợ

p.

Hướng dẫn giải

* Ta có



0

3. 2. 180

+ =

A B

⇒



3. 2.

+ = + +

A B A B C

⇒



2

+ =

A B C

⇒



C

là góc l

ớ

n nh

ấ

t

⇒

c

ạ

nh AB là c

ạ

nh l

ớ

n nh

ấ

t.

* Trên c

ạ

nh AB l

ấ

y

đ

i

ể

m D sao cho

AD = AC.

* T

ừ

đ

ó suy ra

∆

ABC



∆

CBD

(g-g)

( )

2

.

BC AB BD AB AB AC

⇒ = = −

2

.

AB AB AC

= −

.

* Tr

ườ

ng h

ợ

p 1 :

2 ; 1 ; .

AB n BC n AC n

= + = + =

* Tr

ườ

ng h

ợ

p 2 :

2 ; ; 1.

AB n BC n AC n

= + = = +

Ví dụ 4 :

Cho tam giác ABC có



0

120

=A

; AB = a ; AC = 2a.

a) Tính

độ

dài

đườ

ng phân giác AD.

b) Hãy xét bài toán trong tr

ườ

ng h

ợ

p



0

60

=A

;



0

90

=A

;



= α

A

.

Gợi ý :

K

ẻ

DE song song v

ớ

i AB (E thu

ộ

c AC). Áp d

ụ

ng

đị

nh lí Ta-lét và tính

ch

ấ

t c

ủ

a tam giác

đề

u, tam giác cân.

Hướng dẫn giải

a) Qua D v

ẽ

đườ

ng th

ẳ

ng song

song v

ớ

i AB c

ắ

t c

ạ

nh AC t

ạ

i E. D

ễ

dàng ch

ứ

ng minh

đượ

c

∆

ADE

là tam

giác

đề

u, suy ra AD = DE = EA =

x

.

Áp d

ụ

ng

đị

nh lí Ta-lét, ta có

=

DE CE

AB AC

102

H

B

C

A

2 2

2 2 3 2

2 3

−

⇒ = ⇒ = − ⇒ = ⇒ =

x a x

ax a ax ax a x a

a a

.

b) V

ẽ

DE song song v

ớ

i AB (E

∈

AC)

⇒

DE = EA = x.

Áp d

ụ

ng

đị

nh lí Ta-lét t

ươ

ng t

ự

nh

ư

câu a), r

ồ

i v

ẽ

thêm EH

⊥

AD

để

tính

AH, t

ừ

đ

ó suy ra AD.

Ví dụ 5 :

Cho tam giác ABC có ba góc nh

ọ

n,



;

= α = β

B C , BC = a.

Tính

độ

dài

đườ

ng cao AH c

ủ

a tam giác ABC theo a,

α

,

β

.

Gợi ý :

Áp d

ụ

ng

đị

nh ngh

ĩ

a v

ề

t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n.

Hướng dẫn giải

Tam giác ABH vuông t

ạ

i H

⇒

cotB =

BH

AH

⇒

cot

α

=

.

BH

AH

(1)

Tam giác ACH vuông t

ạ

i H

⇒

cotC =

BH

AH

⇒

cot

β

=

.

CH

AH

(2)

Vì

;

α β

< 90

0

nên BH + CH = BC = a.

Do

đ

ó t

ừ

(1) và (2) suy ra

cot cot

=

α + β

a

AH

.

Ví dụ 6 :

Cho góc nh

ọ

n

α

, th

ỏ

a mãn tan

α

=

2

. Tính giá tr

ị

c

ủ

a các bi

ể

u th

ứ

c

sau :

a) sin

α

+ cos

α

; b)

sin cos

α − α

α + α

; c)

2

sin 2sin .cos

cos 3sin .cos

α − α α

α + α α

.

Gợi ý :

Áp d

ụ

ng

đị

nh ngh

ĩ

a v

ề

t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n ho

ặ

c s

ử

d

ụ

ng

các công th

ứ

c : sin

2

α

+ cos

2

α

= 1,

sin

tan

cos

α

α =

α

, …

103

B

A

C

Hướng dẫn giải

a)

* Cách 1 :

Vì tan

α

=

2

nên t

ồ

n t

ạ

i tam giác ABC vuông t

ạ

i A có



= α

B

; AB = 1 ; AC =

2

.

Tam giác ABC vuông t

ạ

i A, ta có :

tanB =

AB

AC

⇒

tan

α

=

2

1

=

.

Áp d

ụ

ng

đị

nh lí Pi-ta-go ta có

BC =

2 2

1 2 3

+ = + =AB AC

.

Do

đ

ó sin

α

=

2

3

; cos

α

=

1

3

.

V

ậ

y : sin

α

+ cos

α

=

2 1 2 1

.

3 3 3

+

+ =

* Cách 2 :

Ta có tan

α

=

2

⇒

sin

2

cos

α

=

α

⇒

sin 2.cos

α = α

.

Ta l

ạ

i có sin

2

α

+ cos

2

α

= 1 nên 2cos

2

α

+ cos

2

α

= 1

⇒

cos

α

=

1

3

> 0.

Do

đ

ó sin

α

=

2

3

, t

ừ

đ

ó tính

đượ

c : sin

α

+ cos

α

=

2 1 2 1

3 3 3

+

+ = .

b)

sin cos

α − α

α + α

=

sin

1

sin cos tan 1 2 1

cos

3 2 2

sin

sin cos tan 1

2 1

1

cos

α

−

α − α α − −

α

= = = = −

α

α + α α +

+

α

.

c)

2 2

2

sin 2sin .cos tan 2 tan 2 2 2 4 2 10

1 3tan 17

1 3 2

cos 3sin .cos

α − α α α − α − −

= = =

+ α

+

α + α α

.

Ví dụ 7 :

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (O ; R). Bi

ế

t



0

60

=A

;



0

75

=B

.

Tính

độ

dài các c

ạ

nh c

ủ

a tam giác ABC theo R.

Gợi ý :

Áp d

ụ

ng h

ệ

qu

ả

v

ề

góc n

ộ

i ti

ế

p, t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n,

đị

nh lí

Pi-ta-go.

104

I

K

H

O

B

C

A

Hướng dẫn giải



BAC

là góc n

ộ

i ti

ế

p và



BOC

là góc

ở

tâm

cùng ch

ắ

n m

ộ

t cung



 

0 0

1

2.60 120

2

⇒

=

⇒

= =BAC BOC BOC .

K

ẻ

OH

⊥

BC

2

⇒

= =

BC

HB HC (1).

∆

BOC

cân t

ạ

i O có OH là

đườ

ng cao nên

OH c

ũ

ng là phân giác c

ủ

a góc BOC



0 0

1 1

.120 60

2 2

⇒

= = =BOH BOC .

∆

BOH

vuông t

ạ

i H



0

3

.sin .sin 60

2

⇒ = = =

R

HB OB BOH R

(2)

T

ừ

(1), (2) suy ra

3

C R= .

∆

ABC

có



0

60

=A

;



0

75

=B



0

45

⇒

=C

.

T

ươ

ng t

ự



0

90

=AOB

. Áp d

ụ

ng

đị

nh lí Pi-ta-go tính

đượ

c :

2

=AB R

.

K

ẻ

BI vuông góc v

ớ

i AC. D

ễ

th

ấ

y

∆

BIC

vuông cân t

ạ

i I ;

∆

AIB

là n

ử

a tam

giác

đề

u nên

3 6

2

2 2

BC R R

IB IC= = = = ;

2

2 2

= =

AB R

IA

(

)

2 6

2

+

⇒ =

R

AC

.

Cách khác :

Sau khi tính

đượ

c BC, ta tính

đượ

c BC theo công th

ứ

c

sin sin sin

= =

BC AC AB

A B C

.

Chú ý :

T

ừ

công th

ứ

c trên ta ch

ứ

ng minh

đượ

c :

0

6 2

sin 75

4

+

=

.

105

F

E

D

B

C

A

Dạng 3.

TÍNH CHU VI ĐA GIÁC, CHU VI ĐƯỜNG TRÒN. TÍNH DIỆN TÍCH

ĐA GIÁC, TÍNH DIỆN TÍCH HÌNH TRÒN

1. PHƯƠNG PHÁP GIẢI

− Tỉ số diện tích của hai tam giác có đáy bằng nhau thì bằng tỉ số hai chiều

cao tương ứng.

− Tỉ số diện tích của hai tam giác có chiều cao bằng nhau thì bằng tỉ số hai

đáy tương ứng.

− Tỉ số chu vi của hai tam giác đồng dạng thì bằng tỉ số đồng dạng.

− Tỉ số diện tích của hai tam giác đồng dạng thì bằng bình phương tỉ số đồng

dạng.

2. CÁC VÍ DỤ

Ví dụ 1. Tính diện tích của tam giác ABC, biết rằng AB = 14cm ; AC = 35cm và

đường phân giác AD = 12cm.

Gợi ý : Kẻ DE // AB (E thuộc AC). Áp dụng tính chất định lí Ta-lét, tính chất

tam giác cân, tính chất đường phân giác của tam giác, tỉ số diện tích.

Hướng dẫn giải

Vẽ DE // AB (E

∈

AC) tính được

DE = AE = 10cm.

Vẽ EF

⊥

AD

⇒

FA = FD = 6cm

⇒

EF = 8cm.

Do đó

S

ADE

=

1 1

. .12.8 48

2 2

= =

AD EF (cm

2

)

Do AD là phân giác c

ủ

a tam giác ABC nên

DB AB

DC AC

=

14 35 7

35 5

BC AB AC

DC AC

+ +

⇒ = = =

.

Ta có

7

5

= =

ABC

ADC

S

BC

S DC

;

35 7

10 2

= = =

ADC

ADE

S

AC

S AE

106

H

B

C

A

C

2

C

1

B

2

B

1

A

2

A

1

B

C

A

O

7 7 49

.

5 2 10

⇒ = =

ABC

ADE

S

235,2

⇒

=

ABC

S (cm

2

).

Ví dụ 2.

Cho tam giác ABC vuông t

ạ

i A,

đườ

ng cao AH. Tính chu vi c

ủ

a tam giác

ABC, bi

ế

t r

ằ

ng chu vi c

ủ

a hai tam giác AHB và AHC l

ầ

n l

ượ

t b

ằ

ng 36cm và

48cm.

Gợi ý :

Áp d

ụ

ng tam giác

đồ

ng d

ạ

ng, tính ch

ấ

t t

ỉ

s

ố

chu vi b

ằ

ng t

ỉ

s

ố

đồ

ng

d

ạ

ng,

đị

nh lí Pi-ta-go.

Hướng dẫn giải

D

ễ

dàng ch

ứ

ng minh

đượ

c các tam giác

ABC ; HBA ; HAC

đồ

ng d

ạ

ng (g-g).

G

ọ

i P ; P

1

; P

2

l

ầ

n l

ượ

t là chu vi c

ủ

a các

tam giác ABC ; HBA ; HAC.

Khi

đ

ó ta có :

1

=

P

BA

P BC

và

2

.

P AC

P BC

=

Vì

∆

ABC

vuông t

ạ

i A nên

2 2 2 2 2 2 2

1 2

2 2 2 2 2 2

1

+

⇒ + = + = = =

P P BA AC BA AC BC

P P BC BC BC BC

.

Do

đ

ó

( )

2 2 2 2 2 2 2

1 2

36 48 36 48 60 cm .

P P P P= + = +

⇒

= + =

Ví dụ 3 :

Qua m

ộ

t

đ

i

ể

m O tu

ỳ

ý n

ằ

m trong tam giác ABC, v

ẽ

các

đườ

ng th

ẳ

ng

song song v

ớ

i các c

ạ

nh c

ủ

a tam giác. Các

đườ

ng th

ẳ

ng này chia tam giác

ABC thành sáu ph

ầ

n không có

đ

i

ể

m trong chung, trong

đ

ó có ba ph

ầ

n là ba

tam giác có di

ệ

n tích l

ầ

n l

ượ

t là m, n, p. Tính di

ệ

n tích c

ủ

a tam giác ABC theo

m, n, p.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t hình bình hành, t

ỉ

s

ố

di

ệ

n tích c

ủ

a hai tam giác

đồ

ng d

ạ

ng.

Hướng dẫn giải

* T

ừ

các hình bình hành AB

2

OC

1

; BC

2

OA

1

;

CA

2

OB

1

ta có C

2

O = BA

1

; OB

1

= A

2

C.

* Các tam giác OA

1

A

2

; B

2

OB

1

; C

1

C

2

O

đồ

ng

d

ạ

ng v

ớ

i

ABC

∆

.

107

H

B

C

A

* Áp d

ụ

ng “T

ỉ

s

ố

di

ệ

n tích c

ủ

a hai tam giác

đồ

ng d

ạ

ng b

ằ

ng bình ph

ươ

ng t

ỉ

s

ố

đồ

ng d

ạ

ng”.

G

ọ

i S là di

ệ

n tích c

ủ

a tam giác ABC. T

ừ

đ

ó tính

đượ

c

(

)

2

= + +

S m n p

.

Ví dụ 4.

Cho tam giác ABC có ba góc nh

ọ

n, BC = a, CA = b, AB = c.

Tính

độ

dài

đườ

ng cao AH c

ủ

a tam giác ABC theo a, b, c.

Ch

ứ

ng minh công th

ứ

c

( )( )( )

= − − −

ABC

S p p a p b p c

v

ớ

i

2

+ +

=

a b c

p

.

Gợi ý :

Áp d

ụ

ng

đị

nh lí Pi-ta-go, bi

ế

n

đổ

i

đồ

ng nh

ấ

t bi

ể

u th

ứ

c h

ữ

u t

ỉ

.

Hướng dẫn giải

a) Vì tam giác ABC có ba góc nh

ọ

n nên H n

ằ

m gi

ữ

a

B và C.

Đặ

t BH =

x

⇒

CH = a –

x

.

Áp d

ụ

ng

đị

nh lí Pi-ta-go vào các tam giác

vuông ABH, ACH ta

đượ

c :

AB

2

– BH

2

= AC

2

– CH

2

( )

2

2 2 2

⇒ − = − −

c x b a x

2 2 2 2 2

2

⇒

− = − + −

c x b a ax x

2 2 2

2

+ −

⇒ =

a c b

x

a

.

Do

đ

ó AH

2

=

2

2 2 2 2 2 2 2 2 2

2

2 2 2

    

+ − + − + −

− = − +

    

    

a c b a c b a c b

c c c

a a a

( ) ( ) ( )( )( )( )

2 2

2

.

2 2

4

− − + − + + + − + − + −

= =

b a c a c b a b c a b c b c a c a b

a a

a

Đặ

t

(

)

(

)

(

)

2

4

2

− − −

+ +

= ⇒ =

p p a p b p c

a b c

p AH

a

( )( )( )

2

.

p p a p b p c

AH

a

− − −

⇒ =

108

N

P

F

E

D

I

B

C

A

M

b) Diện tích của tam giác ABC là :

( ) ( )( )

1

.

2

= − − −

BC AH p p a p b p c

.

(Công thức tính diện tích theo độ dài ba cạnh này còn gọi là công thức

Hê-rông).

Ví dụ 5 : Cho tam giác ABC vuông tại A, AB = 15cm, AC = 20cm, ngoại tiếp

đường tròn tâm I. Giả sử đường tròn (I) tiếp xúc với cạnh BC, CA, AB thứ tự

ở D, E, F. Qua điểm M tuỳ ý trên cung nhỏ EF, vẽ tiếp tuyến của đường tròn

(I) cắt các đoạn AE, AF lần lượt ở N, P.

a) Tính chu vi của tam giác ANP.

b) Xác định vị trí của điểm M để diện tích tam giác ANP lớn nhất.

Gợi ý : Áp dụng tính chất của hai tiếp tuyến cắt nhau ; định lí Pi-ta-go ; bất

đẳng thức Cô-si.

Hướng dẫn giải

a) Theo tính chất của hai tiếp tuyến cắt nhau ta có

AE = AF, BF = BD, CD = CE,

NE = NM, PM = PF.

Do đó

AB + AC = (AF + BF) + (AE + CE)

= (AE + AE) + (BD + CD) = 2AE + BC

Tam giác ABC vuông tại A

⇒

BC = 25cm.

Từ đó suy ra AE = (AB + AC – BC) : 2 = (15 + 20 – 25) : 2 = 5 (cm).

Chu vi

∆

ANP

là :

AN + AP + NP = AN + AP + (NM + PM) = AN + AP + (NE + PF)

= (AN + NE) + (AP + DF) = AE + AF = 2AE = 10 (cm).

b) Đặt

;

= =

AN x AP y

(

0 5 ; 0 5

< < < <

x y

)

5 ; 5

⇒ = − = −

NE x PF y

.

Vì tam giác ANP vuông tại A nên ta có :

AN

2

+ AP

2

= NP

2

( )

2

2 2

10

x y x y

⇔ + = − −

50 10 10

xy x y

⇔ + = +

(1)

109

C

B

H

O'

A

O

Áp dụng bất đẳng thức Cô-si cho hai số dương

,

x y

ta đượ

c :

2+ ≥

x y xy

.

Do

đ

ó t

ừ

(1) suy ra :

(

)

2

50 20 20 100 50 10 50.

xy xy xy xy xy+ ≥ ⇔ − + ≥ ⇔ − ≥

Vì

0 5 ; 0 5

< < < <

x y

nên

10 5 2 10 5 2 150 100 2

− ≥ ⇔ ≤ − ⇔ ≤ −xy xy xy .

Đẳ

ng th

ứ

c x

ả

y ra khi và ch

ỉ

khi

10 5 2

= = −x y (tho

ả

mãn

0 5 ;

x

< <

0 5

y

< <

).

V

ậ

y maxS

ANP

=

75 50 2

−

(cm

2

),

đạ

t

đượ

c khi M là

đ

i

ể

m chính gi

ữ

a cung

nh

ỏ

EF c

ủ

a

đườ

ng tròn (I).

Ví dụ 6 :

Cho hai

đườ

ng tròn (O ; 3cm) và (O’ ; 1cm) ti

ế

p xúc ngoài v

ớ

i nhau t

ạ

i

A. V

ẽ

ti

ế

p tuy

ế

n chung ngoài BC (B

∈

(O), C

∈

(O’)).

a) Tính

độ

dài cung nh

ỏ

AB.

b) Tính di

ệ

n tích ph

ầ

n m

ặ

t ph

ẳ

ng gi

ớ

i h

ạ

n b

ở

i các cung nh

ỏ

AB, AC và

đ

o

ạ

n

th

ẳ

ng BC.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t ti

ế

p tuy

ế

n, tính ch

ấ

t hình ch

ữ

nh

ậ

t, t

ỉ

s

ố

l

ượ

ng giác

c

ủ

a góc nh

ọ

n, công th

ứ

c tính

độ

dài cung, công th

ứ

c tính di

ệ

n tích hình qu

ạ

t, tính

ch

ấ

t c

ủ

a di

ệ

n tích.

Hướng dẫn giải

a) K

ẻ

O’H

⊥

OB. Vì BC là ti

ế

p tuy

ế

n chung ngoài nên

OB

⊥

BC và O’C

⊥

BC

⇒

HBCO’ là hình ch

ữ

nh

ậ

t

⇒

HB = O’C = 1cm

⇒

OH = OB – HB = 3 – 1 = 2 (cm).

Vì (O) và (O’) ti

ế

p xúc ngoài t

ạ

i A

nên OO’ = OA + O’A

= 3 + 1 = 4 (cm).

Tam giác OHO’ vuông t

ạ

i H, ta có :

110



2 1

'

' 4 2

= = =

OH

cosHOO

OO



0

' 60

⇒

=HOO

.

Do

đ

ó



0

.3.60

180

π

= = π

AB

l

(cm).

b) Vì OB // O’C (cùng vuông góc v

ớ

i BC), mà



0

60

=AOB



0

' 120

⇒

=AO C

.

Di

ệ

n tích qu

ạ

t AOB là :

2 0

0

.3 .60 3

2

360

π π

=

(cm

2

).

Di

ệ

n tích qu

ạ

t AO’C là :

2 0

0

.1 .60

6

360

π π

=

(cm

2

).

Tam giác OHO’ vuông t

ạ

i H có



0

' 60

=HOO

, suy ra

0

' .tan 60 2 3

HO OH= = (cm)

S

OBCO’

=

(

)

3 1 2 3

4 3

2

+

=

(cm

2

).

Di

ệ

n tích c

ầ

n tìm là :

3 24 3 10

4 3

2 6 6

π π − π

 

− + =

 

 

(cm

2

).

III. BÀI TẬP VẬN DỤNG

Dạng 1. Tính số đo góc

Bài 1.

G

ọ

i I là

đ

i

ể

m n

ằ

m trong hình vuông ABCD sao cho IA : IB : IC = 1 : 2 : 3.

Tính s

ố

đ

o c

ủ

a góc AIB.

Bài 2.

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). G

ọ

i M là m

ộ

t

đ

i

ể

m trên cung

nh

ỏ

AB. K

ẻ

MD

⊥

AC ; ME

⊥

BC. G

ọ

i I và J th

ứ

t

ự

là trung

đ

i

ể

m c

ủ

a

AB và DE. Tính s

ố

đ

o c

ủ

a



MJI

.

Bài 3.

Cho tam giác ABC vuông t

ạ

i A,

đườ

ng cao AH. Bi

ế

t AB = CH. Tính s

ố

đ

o c

ủ

a các góc B và C c

ủ

a tam giác ABC (làm tròn

đế

n

độ

).

Bài 4.

Cho tam giác nh

ọ

n ABC, các

đườ

ng cao BD và CE. Tính s

ố

đ

o góc



BAC

,

bi

ế

t BC = 2DE.

Bài 5.

Tìm góc nh

ọ

n

α

, bi

ế

t r

ằ

ng :

a) sin

α

.cos

α

=

1

2

; b) sin

α

+ cos

α

=

2

.

111

c)

3

(cot

α

– 1) = 1 – tan

α

; d) 2cos

α

= 3tan

α

.

Dạng 2. Tính độ dài đoạn thẳng ; tính giá trị của biểu thức

Bài 1.

Cho tam giác

đề

u ABC n

ộ

i ti

ế

p

đườ

ng tròn (O ; R). G

ọ

i M là trung

đ

i

ể

m

c

ủ

a BC. Trên các c

ạ

nh AB và AC l

ấ

y các

đ

i

ể

m D và E sao cho



0

60

=DME

. Tính kho

ả

ng cách t

ừ

M

đế

n

đườ

ng th

ẳ

ng DE theo R.

Bài 2.

Cho tam giác

đề

u ABC n

ộ

i ti

ế

p

đườ

ng tròn (O ; R). L

ấ

y

đ

i

ể

m M tu

ỳ

ý

trong tam giác

đề

u ABC. K

ẻ

MD, ME, MF l

ầ

n l

ượ

t vuông góc v

ớ

i BC,

CA, AB. Tính t

ỉ

s

ố

+ +

MD ME MF

AF BD CE

.

Bài 3.

Cho hình vuông ABCD có c

ạ

nh b

ằ

ng 1.

Đườ

ng th

ẳ

ng qua A c

ắ

t c

ạ

nh BC t

ạ

i

E và c

ắ

t tia DC t

ạ

i F. Tính

độ

dài

đ

o

ạ

n AE, bi

ế

t EF b

ằ

ng c

ạ

nh hình vuông.

Bài 4.

Cho hai

đườ

ng tròn (O ; R) và (O’ ; r) v

ớ

i R > r, ti

ế

p xúc ngoài v

ớ

i nhau

t

ạ

i A. V

ẽ

ti

ế

p tuy

ế

n chung ngoài BC (B

∈

(O) ; C

∈

(O’)).

Tính

độ

dài BC theo R và r.

Tính kho

ả

ng cách t

ừ

A

đế

n

đườ

ng th

ẳ

ng BC theo R và r.

G

ọ

i D là giao

đ

i

ể

m c

ủ

a hai

đườ

ng th

ẳ

ng BC và OO’. Tính OD theo R và r.

Dạng 3. Tính chu vi đa giác, chu vi đường tròn.

Tính diện tích đa giác, tính diện tích hình tròn

Bài 1.

Cho t

ứ

giác ABCD n

ộ

i ti

ế

p n

ử

a

đườ

ng tròn tâm O

đườ

ng kính CD = 2R.

Bi

ế

t AC = R

3

và BD = R

2

.

a) Tính

độ

dài c

ạ

nh AB theo R.

b) Tính di

ệ

n tích t

ứ

giác ABCD theo R.

c) Tính

độ

dài cung nh

ỏ

AB theo R

.

Bài 2.

Cho tam giác ABC vuông t

ạ

i A. Các

đườ

ng trung tuy

ế

n AM và BN vuông

góc v

ớ

i nhau. Tính chu vi và di

ệ

n tích c

ủ

a tam giác ABC theo a, bi

ế

t

AC = 6a.

Bài 3.

Tính di

ệ

n tích c

ủ

a m

ộ

t t

ứ

giác, bi

ế

t

độ

dài c

ủ

a hai

đườ

ng chéo và

độ

dài

c

ủ

a

đ

o

ạ

n n

ố

i trung

đ

i

ể

m c

ủ

a hai c

ạ

nh

đố

i di

ệ

n l

ầ

n l

ượ

t là a, b, c.

112

ư

CHỨNG MINH CÁC YẾU TỐ HÌNH HỌC,

QUAN HỆ HÌNH HỌC

I. KIẾN THỨC CẦN SỬ DỤNG

1. Đường thẳng ; đoạn thẳng.

2. Quan hệ vuông góc ; quan hệ song song.

3. Tam giác ; tứ giác ; đa giác.

4. Cung tròn ; đường thẳng.

5. Vị trí tương đối giữa đường thẳng và đường tròn.

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

CHỨNG MINH HAI ĐOẠN THẲNG BẰNG NHAU, HAI GÓC

BẰNG NHAU

1. PHƯƠNG PHÁP GIẢI

− Tính chất của đường phân giác.

− Tính chất của hai đường thẳng song song.

− Các trường hợp bằng nhau của hai tam giác.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác ABC có



0

120

≠A

. Về phía ngoài tam giác ABC, vẽ các

tam giác đều ABD ; ACE và BCF . Gọi I là giao điểm của BE và CD.

a) Chứng minh rằng : BE = CD.

b) Chứng minh rằng IA là tia phân giác của góc DIE.

Gợi ý : Áp dụng tam giác bằng nhau, tính chất đường phân giác, tính chất

của góc ngoài.

Ch

ChCh

Ch 

  

 

2

22

2

113

I

D

E

B

C

A

M

N

D

E

K

I

H

B

C

A

Hướng dẫn giải

a) Vì AB = AD (

∆

ABD đều) ;

AE = AC (

∆

ACE đều) ;



0

60= = +

BAE DAC BAC

⇒

∆

ABE =

∆

ADC (c-g-c)

⇒

BE = DC.

b) Vì

∆

ABE =

∆

ADC (c-g-c)

⇒



=

ABE ADC

hay



=

ABI ADI

⇒

Tứ giác AIBD nội tiếp



⇒ =

AID ABD

, mà



0

60

=ABD

(

∆

ABD đều) nên



0

60

=AID

. Tương tự



0

60

= =BID BAD

.

Từ đó suy ra



0

60

=AIE

.

Suy ra IA là phân giác của góc DIE.

Ví dụ 2. Cho tam giác nhọn ABC, đường cao AH. Gọi D và E lần lượt là các

điểm đối xứng của H qua các cạnh AB và AC. Đường thẳng DE cắt các cạnh

AB và AC lần lượt ở M và N.

a) Chứng minh rằng





= + −

MHN B C A

.

b) Chứng minh rằng



=

ABN ACM

.

Gợi ý : Áp dụng tính chất đối xứng trục, tam giác bằng nhau, tính chất tam

giác cân, tính chất góc nội tiếp.

Hướng dẫn giải

a) Theo tính chất đối xứng trục ta có

AMH AMD

∆ = ∆

;

∆ = ∆

ANH ANE

.

⇒

AD = AH = AE

⇒

∆

ADE

cân tại A.

Từ đó suy ra





.

MHN B C A

= + −

b) Theo tính chất đối xứng trục ta có

114

ABD ABH

∆ = ∆

;

∆ = ∆

ACE ACH



;⇒ = =

ADB AHB AEC AHC

Mà



0

90

= =AHB AHC

nên



0

90

= =ADB AEC

⇒

BD // CE (cùng vuông

góc v

ớ

i DE).

T

ứ

giác AHCE có



0 0 0

90 90 180

+ = + =AHC AEC

suy ra t

ứ

giác AHCE n

ộ

i

ti

ế

p (1).

G

ọ

i I là giao

đ

i

ể

m c

ủ

a AB và HD ; K là giao

đ

i

ể

m c

ủ

a AC và HE

⇒

IH = ID ;

KH = KE.

Do

đ

ó IK là

đườ

ng trung bình c

ủ

a tam giác HDE

⇒

IK // DE



⇒ =

HKI HED

(

đồ

ng v

ị

) (2).

T

ứ

giác AKHI có



0 0 0

90 90 180

+ = + =AKH AIH

⇒

T

ứ

giác AKHI n

ộ

i ti

ế

p



⇒ =

HKI HAI

(3).

T

ừ

(2) và (3)



⇒ =

HEM HAM

⇒

T

ứ

giác AEHM n

ộ

i ti

ế

p (4).

T

ừ

(1) và (4)

⇒

5

đ

i

ể

m A, E, C, H, M cùng thu

ộ

c m

ộ

t

đườ

ng tròn



⇒ =

ACM AEM

.

T

ươ

ng t

ự

ta c

ũ

ng ch

ứ

ng minh

đượ

c :



=

ABN ADN

, mà



=

AEM ADN

nên



=

ABN ACM

.

Ví dụ 3.

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (K). K

ẻ

KM

⊥

AC ; KN

⊥

AB.

G

ọ

i G là giao

đ

i

ể

m c

ủ

a BM và CN. G

ọ

i P là m

ộ

t

đ

i

ể

m thu

ộ

c c

ạ

nh BC. V

ẽ

PE // CN (E

∈

AB) ; PF // BM (F

∈

AC). N

ố

i E v

ớ

i F c

ắ

t BM và CN l

ầ

n

l

ượ

t

ở

I và J.

Ch

ứ

ng minh r

ằ

ng IE = JF và PG

đ

i qua trung

đ

i

ể

m c

ủ

a EF.

Gợi ý :

Áp d

ụ

ng

đị

nh li Ta-lét, tính ch

ấ

t tr

ọ

ng tâm c

ủ

a tam giác,

đị

nh lí Ta-lét

đả

o, tính ch

ấ

t hình bình hành

Hướng dẫn giải

G

ọ

i R là giao

đ

i

ể

m c

ủ

a PE và BM ; S là giao

đ

i

ể

m c

ủ

a PF và CN. Vì PF // BM,

theo

đị

nh lí Ta-lét ta có

=

SF SP

GM GB

(vì cùng b

ằ

ng

CS

CG

)

1

2

⇒ = =

SF GM

SP GB

(vì G

là tr

ọ

ng tâm c

ủ

a

ABC

∆

) (1)

115

I

J

Q

O

S

R

F

E

G

N

M

K

B

C

A

P

Vì PE // CN, theo

đị

nh lí Ta-lét ta có

=

RE RP

GN GC

(vì cùng b

ằ

ng

BR

BG

)

1

2

⇒ = =

RE GN

RP GC

(vì G là tr

ọ

ng tâm

c

ủ

a

ABC

∆

) (2)

Vì RI // PF, theo Ta-lét ta có :

=

ER EI

RP IF

(3)

Vì SJ // PE, theo Ta-lét ta có :

=

FS FJ

SP JE

(4)

T

ừ

(1) ; (2) ; (3) và (4) suy ra :

= ⇒ = ⇒ = ⇒ =

+ +

EI FJ EI FJ EI FJ

EI FJ

IF JE EI IF FJ JE EF EF

(5)

T

ừ

(1) và (2) suy ra : =

SF RE

SP RP

, theo

đị

nh lí Ta-lét

đả

o suy ra RS // EF.

D

ễ

th

ấ

y t

ứ

giác PRGS là hình bình hành, do

đ

ó GP

đ

i qua trung

đ

i

ể

m O c

ủ

a

RS.

G

ọ

i Q là giao

đ

i

ể

m c

ủ

a GP và EF.

Vì IJ // RS, theo

đị

nh lí Ta-lét ta có :

=

QI QJ

OR OS

(vì cùng b

ằ

ng

GQ

GO

)

⇒

QI = QJ (6)

T

ừ

(5) và (6) suy ra GP

đ

i qua trung

đ

i

ể

m Q c

ủ

a EF.

Ví dụ 4.

Cho

đườ

ng tròn (O)

đườ

ng kính AB.

Đ

i

ể

m M n

ằ

m ngoài (O) sao cho

MA c

ắ

t (O)

ở

C. G

ọ

i N là giao

đ

i

ể

m BC và MO ; Kéo dài AN c

ắ

t MB t

ạ

i D ;

E là giao

đ

i

ể

m c

ủ

a CD và MO. Ch

ứ

ng minh r

ằ

ng EC = ED.

Gợi ý :

Áp d

ụ

ng

đị

nh lí Ta-lét, bi

ế

n

đổ

i

đồ

ng nh

ấ

t các bi

ể

u th

ứ

c h

ữ

u t

ỉ

.

116

J

I

E

D

N

C

O

A

B

M

N

M

H

F

E

D

I

B

C

A

Hướng dẫn giải

a) Qua N k

ẻ

đườ

ng th

ẳ

ng song song v

ớ

i AB c

ắ

t MA và MB th

ứ

t

ự

ở

I và J.

Áp d

ụ

ng

đị

nh lí Ta-lét ta có :

=

NI NJ

OA OB

=

MN

MO

.

Mà OA = OB nên NI = NJ. (1)

Áp d

ụ

ng

đị

nh lí Ta-lét ta có :

=

CN IN

CB AB

; =

DN NJ

DA AB

. (2)

T

ừ

(1) và (2) suy ra

CN DN

CB DA

= .

Theo

đị

nh lí Ta-lét

đả

o ta có CD // AB.

Áp d

ụ

ng

đị

nh lí Ta-lét ta có :

=

EC ED

OA OB

=

MN

MO

.

Mà OA = OB nên EC = ED.

Ví dụ 5.

Cho

đườ

ng tròn tâm I n

ộ

i ti

ế

p tam giác ABC, ti

ế

p xúc v

ớ

i các c

ạ

nh BC,

CA, AB th

ứ

t

ự

ở

D, E, F. G

ọ

i H là hình chi

ế

u c

ủ

a D lên EF. Ch

ứ

ng minh r

ằ

ng

HD là phân giác c

ủ

a tam giác BHC.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t c

ủ

a hai ti

ế

p tuy

ế

n c

ắ

t nhau, tính ch

ấ

t tam giác cân,

tam giác

đồ

ng d

ạ

ng.

Hướng dẫn giải

K

ẻ

BM và CN l

ầ

n l

ượ

t vuông

góc v

ớ

i

đườ

ng th

ẳ

ng EF.

Theo tính ch

ấ

t c

ủ

a hai ti

ế

p tuy

ế

n

c

ắ

t nhau ta có : AE = AF, BF = BD,

CD = CE.

Do

đ

ó

∆

AEF

cân t

ạ

i A



⇒ =

AEF AFE

.

Ta l

ạ

i có



=

AEF CEN

(

đố

i

đỉ

nh) ;



=

AFE BFN

(

đố

i

đỉ

nh)



=

CEN BFN

.

117

K

H

Q

N

P

M

O

B

C

A

E

T

ừ

đ

ó suy ra

∆

BFM



∆

CEN

(g-g) ⇒ = =

BM BF BD

CN CE CD

.

Vì BM // DH // CN (cùng vuông góc v

ớ

i EF), áp d

ụ

ng

đị

nh lí Ta-lét ta

đượ

c :

=

BD MH

CD NH

⇒

=

BM MH

CN NH

⇒

∆

BMH



∆

CNH

(c

-

g

-

c)



⇒

=

BHM CHN

.

Vì DH vuông góc v

ớ

i EF nên



=

BHD CHD

.

V

ậ

y HD là phân giác c

ủ

a tam giác BHC.

Ví dụ 6.

Cho tam giác nh

ọ

n ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). V

ề

phía ngoài tam giác

ABC, d

ự

ng các hình ch

ữ

nh

ậ

t ACMN và BCPQ có di

ệ

n tích b

ằ

ng nhau.

Ch

ứ

ng minh r

ằ

ng

đườ

ng th

ẳ

ng OC

đ

i qua trung

đ

i

ể

m E c

ủ

a

đ

o

ạ

n MP.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t hình ch

ữ

nh

ậ

t, tính ch

ấ

t v

ề

di

ệ

n tích, tam giác b

ằ

ng

nhau.

Hướng dẫn giải

* V

ẽ

OH

⊥

MN và OK

⊥

PQ. T

ừ

đ

ó suy

ra : HM = HN ; KP = KQ.

* D

ễ

th

ấ

y hai tam giác OCM và HCM có

di

ệ

n tích b

ằ

ng nhau (vì OH // CM).

* D

ễ

th

ấ

y hai tam giác OCP và KCP có

di

ệ

n tích b

ằ

ng nhau (vì OK // CP).

* Ta l

ạ

i có hai tam giác HCM và KCP có

di

ệ

n tích b

ằ

ng nhau (vì cùng b

ằ

ng

1

4

di

ệ

n tích

c

ủ

a các hình ch

ữ

nh

ậ

t ACMN và BCPQ).

Do

đ

ó hai tam giác OCM và OCP có di

ệ

n

tích b

ằ

ng nhau.

* T

ừ

đ

ó suy ra OC là

đườ

ng trung tuy

ế

n c

ủ

a tam giác OMP.

* Do

đ

ó

đườ

ng th

ẳ

ng OC

đ

i qua trung

đ

i

ể

m E c

ủ

a

đ

o

ạ

n MP.

118

N

M

F

E

D

B

C

A

O

Dạng 2.

CHỨNG MINH QUAN HỆ VUÔNG GÓC, QUAN HỆ SONG SONG

1. PHƯƠNG PHÁP GIẢI

− Định lí Pi-ta-go đảo, định lí Ta-lét đảo.

− Góc nội tiếp chắn nửa đường tròn.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác ABC, đường trung tuyến AD. Trên đoạn AD lấy điểm O

tuỳ ý. Tia BO cắt AC tại F. Tia CO cắt AB tại E. Chứng minh rằng EF song

song với BC.

Gợi ý : Áp dụng định lí Ta-lét đảo, biến đổi đồng nhất biểu thức hữu tỉ.

Hướng dẫn giải

* Qua O vẽ đường thẳng song song

với BC cắt các cạnh AB và AC thứ tự ở

M và N.

Áp dụng định lí Ta-lét (hoặc tam

giác đồng dạng)

*

=

OM ON

DB DC

=

AO

AD

, mà DB = DC

nên OM = ON.

*

=

MO EO

BC EC

;

=

ON FO

BC FB

⇒ =

EO FO

EC FB

.

Theo định lí Ta-let đảo ta có EF // BC.

Chú ý : Áp dụng định lí Cê-va đối với ba đường AD, BF, CE đồng quy tại O,

ta có :

. . 1

=

DB FC EA

DC FA EB

, mà DB = DC

nên . 1= ⇒ =

FC EA EA FA

FA EB EB FC

⇒

EF//BC.

119

K

I

F

E

B

C

A

O

Q

P

N

M

B

C

A

Áp dụng kết quả bài toán trên ta giải được bài toán sau :

Cho hình bình

hành ABCD. Ch

ỉ

dùng th

ướ

c th

ẳ

ng, hãy d

ự

ng m

ộ

t

đườ

ng th

ẳ

ng d

đ

i qua

đ

i

ể

m A

sao cho d // BD.

Ví dụ 2.

Cho tam giác nh

ọ

n ABC, các

đườ

ng cao BE, CF.

Đườ

ng tròn (O)

đ

i qua

hai

đ

i

ể

m B và C c

ắ

t các

đ

o

ạ

n BE và CF th

ứ

t

ự

ở

K và I. Ch

ứ

ng minh r

ằ

ng KI

song song v

ớ

i EF.

Gợi ý :

D

ấ

u hi

ệ

u nh

ậ

n bi

ế

t hai

đườ

ng th

ẳ

ng song song.

Hướng dẫn giải

Trong

đườ

ng tròn (O) ta có



CIK CBK

=

. (1)

Ta có



0

90

= =

BFC BEC

nên BFEC là t

ứ

giác n

ộ

i

ti

ế

p



.

CFE CBE

=

(2)

T

ừ

(1) và (2)



⇒ =

CIK CFE

, mà hai góc này

ở

v

ị

trí

đồ

ng v

ị

⇒

IK // EF.

Ví dụ 3.

Cho tam giác nh

ọ

n ABC. K

ẻ

BM

⊥

AC, CN

⊥

AB, MP

⊥

AB, NQ

⊥

AC

(N,P

∈

AB ; M,Q

∈

AC). Ch

ứ

ng minh r

ằ

ng PQ song song v

ớ

i BC.

Gợi ý :

Áp d

ụ

ng

đị

nh lí Ta-lét

đả

o ho

ặ

c d

ấ

u hi

ệ

u nh

ậ

n bi

ế

t hai

đườ

ng th

ẳ

ng

song song.

Hướng dẫn giải

BM // NQ (cùng vuông góc v

ớ

i AC) ;

CN // MP (cùng vuông góc v

ớ

i AB) ;

Áp d

ụ

ng

đị

nh lí Ta-lét :

=

AN AQ

AB AM

; =

AP AM

AN AC

Nhân v

ế

theo v

ế

ta

đượ

c =

AP AQ

AB AC

.

Theo

đị

nh lí Ta-lét

đả

o

⇒

PQ // BC.

120

D

I

G

M

B

C

A

Ví dụ 4.

Cho tam giác ABC có c

ạ

nh BC là trung bình c

ộ

ng c

ủ

a hai c

ạ

nh AB và

AC. G

ọ

i I là giao

đ

i

ể

m các

đườ

ng phân giác và G là tr

ọ

ng tâm c

ủ

a tam giác

ABC.

Ch

ứ

ng minh r

ằ

ng IG song song v

ớ

i BC.

Gợi ý :

Áp d

ụ

ng

đị

nh lí Ta-lét

đả

o.

Hướng dẫn giải

G

ọ

i D, M th

ứ

t

ự

là giao

đ

i

ể

m

c

ủ

a các tia AI, AG v

ớ

i c

ạ

nh BC.

Theo tính ch

ấ

t c

ủ

a

đườ

ng phân

giác trong các tam giác ABD và

ACD ta có :

ID BD CD

IA BA CA

= =

BD CD BC

BA CA BA CA

+

= =

+ +

.

Ta l

ạ

i có BC là trung bình c

ộ

ng c

ủ

a AB và AC nên

1

2

=

+

BC

BA CA

⇒

1

2

=

ID

IA

.

Vì G là tr

ọ

ng tâm c

ủ

a

∆

ABC

nên

1

2

=

GM

GA

.

Suy ra

1

2

= =

ID GM

IA GA

, theo

đị

nh lý Ta-lét

đả

o suy ra IG // BC.

Ví dụ 5.

Cho tam giác nh

ọ

n ABC,

đườ

ng trung tuy

ế

n AM. Trên n

ử

a m

ặ

t ph

ẳ

ng

b

ờ

BC có ch

ứ

a

đ

i

ể

m A, v

ẽ

các tia Bx và Cy cùng vuông góc v

ớ

i BC.

Đườ

ng

th

ẳ

ng qua M và vuông góc v

ớ

i AB c

ắ

t tia Bx t

ạ

i D.

Đườ

ng th

ẳ

ng qua M và

vuông góc v

ớ

i AC c

ắ

t tia Cy t

ạ

i E. Ch

ứ

ng minh r

ằ

ng DE vuông góc v

ớ

i AM.

Gợi ý :

Áp d

ụ

ng quan h

ệ

t

ừ

vuông góc

đế

n song song.

Hướng dẫn giải

Kéo dài EM c

ắ

t tia

đố

i c

ủ

a tia Bx t

ạ

i F.

D

ễ

th

ấ

y

∆ = ∆

BMF CME

(g-c-g)

121

y

x

N

F

E

D

M

B

C

A

E

D

C

B

A

suy ra MF = ME và



=

MFB MEC

.

Ta l

ạ

i có



=

ABM MDB

(cùng ph

ụ

v

ớ

i



ABx

) ;



=

ACM MEC

(cùng ph

ụ

v

ớ

i



ACy

).

Do

đ

ó

∆

ABC



∆

MDF

(g-g). G

ọ

i N là trung

đ

i

ể

m c

ủ

a DF

⇒

MN là

đườ

ng trung bình c

ủ

a tam

giác DEF

⇒

MN // DE (1).

Ta l

ạ

i có AM và MN th

ứ

t

ự

là các trung tuy

ế

n

t

ươ

ng

ứ

ng c

ủ

a hai tam giác

đồ

ng d

ạ

ng nói trên

nên

∆

ABM



∆

MDN

(c-g-c)



⇒

=

BAM DMN

,

mà



0

90

+ =

BAM AMD

nên



0

90

=

AMN

hay AM vuông góc v

ớ

i MN (2).

T

ừ

(1) và (2)

⇒

AM vuông góc v

ớ

i DE.

Ví dụ 6 :

Cho tam giác ABC có AD và BE là hai

đườ

ng trung tuy

ế

n. Ch

ứ

ng minh

r

ằ

ng AD và BE c

ũ

ng là các

đườ

ng cao n

ế

u



0

30

= =

DAC EBC

.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t : “M

ộ

t tam giác có m

ộ

t c

ạ

nh b

ằ

ng n

ử

a c

ạ

nh th

ứ

hai

và góc

đố

i di

ệ

n v

ớ

i c

ạ

nh

đ

ó b

ằ

ng 30

0

thì tam giác là tam giác vuông”.

Hướng dẫn giải

D

ễ

th

ấ

y

∆

ACD



∆

BCE

(g-g)

⇒

=

AC CD

BC CE

.

Mà BC = 2CD ; AC = 2CE nên AC = BC

Tam giác ACD có



0

30

=

DAC

và AC = 2CD nên tam

giác ACD là n

ử

a tam giác

đề

u



0

90

⇒

=

ADC

. T

ươ

ng t

ự



0

90

=

BEC

.

V

ậ

y AD và BE c

ũ

ng là các

đườ

ng cao c

ủ

a tam giác ABC.

122

Dạng 3.

CHỨNG MINH NHIỀU ĐIỂM CÙNG NẰM TRÊN MỘT ĐƯỜNG TRÒN

1. PHƯƠNG PHÁP GIẢI

Chứng minh nhiều điểm cùng nằm trên một đường tròn được quy về việc

chứng minh 4 điểm cùng nằm trên một đường tròn. Để chứng minh 4 điểm cùng

nằm trên một đường tròn (hay chứng minh tứ giác nội tiếp đường tròn) ta có thể

sử dụng các kiến thức sau :

- Chỉ ra một điểm cách đều tất cả các điểm đó (định nghĩa đường tròn).

- Tứ giác có tổng hai góc đối bằng 180

0

(hay một góc của tứ giác bằng góc

ngoài của góc đối diện với nó).

- Tứ giác có hai đỉnh liên tiếp cùng nhìn một cạnh dưới hai góc bằng nhau.

- Đôi khi ta cần chọn thêm điểm phụ thì việc giải bài toán sẽ thuận lợi hơn.

Chú ý :

+ Nếu hai đường chéo AC và BD của tứ giác ABCD cắt nhau tại E sao cho

EA.EC = EB.ED thì ta suy ra được

∆

AEB



∆

DEC

(c-g-c)



⇒ =

CAB CDB

⇒

tứ giác ABCD nội tiếp.

+ Nếu phần kéo dài của các cạnh AB và CD của tứ giác ABCD cắt nhau tại E

sao cho EA.EB = EC.ED thì ta suy ra được

∆

AED



∆

ECB

(c-g-c)



⇒

=

EAD ECB

⇒

tứ giác ABCD nội tiếp.

+ Hình thang cân là tứ giác nội tiếp.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác đều ABC. Trên các cạnh AB và AC lần lượt lấy các điểm

D và E sao cho AD = CE. Gọi F là giao điểm của BE và CD. Chứng minh

AEFD là tứ giác nội tiếp.

Gợi ý :

T

ứ

giác có t

ổ

ng hai góc

đố

i b

ằ

ng 180

0

(hay t

ứ

giác có m

ộ

t góc b

ằ

ng

góc ngoài t

ạ

i

đỉ

nh c

ủ

a góc

đố

i).

Hướng dẫn giải

Vì tam giác ABC đều nên AB = BC = CA ;



0

60

= = =A B C

.

123

F

E

C

B

A

D

E

D

H

B

C

A

Ta lại có AD = CE nên

ADC CEB

∆ = ∆

(c-g-c)



⇒

=

ADC CEB

⇒

AEFD là tứ giác nội tiếp.

Ví dụ 2. Cho tam giác nhọn ABC, đường cao AH. Gọi D và E thứ tự là hình chiếu

của H trên các cạnh AB và AC. Chứng minh ADHE và BDEC là các tứ giác

nội tiếp.

Gợi ý :

T

ứ

giác có t

ổ

ng hai góc

đố

i b

ằ

ng 180

0

(hay t

ứ

giác có m

ộ

t góc b

ằ

ng

góc ngoài t

ạ

i

đỉ

nh c

ủ

a góc

đố

i)

Hướng dẫn giải

Tứ giác ADHE có



0 0 0

90 90 180

+ = + =ADH AEH

⇒

ADHE là tứ giác nội tiếp.



⇒

=

ADE AHE

(hai góc nội tiếp cùng chắn



AE

)

Mà



=

AHE ACH

(cùng phụ với



EHC

)



⇒

=

ADE ACB

⇒

BDEC là tứ giác nội tiếp.

Ví dụ 3. Cho hình vuông ABCD. Trên các cạnh BC và CD lần lượt lấy các điểm

E và F sao cho



0

45

=EAF

. Đường chéo BD cắt các đoạn thẳng AE và AF thứ

tự ở M và N.

Chứng minh rằng ABEN và MEFN là các tứ giác nội tiếp.

Gợi ý :

Hai

đỉ

nh liên ti

ế

p c

ủ

a t

ứ

giác cùng nhìn m

ộ

t c

ạ

nh d

ướ

i hai góc b

ằ

ng

nhau.

Hướng dẫn giải

Vì ABCD là hình vuông, BD là đường chéo nên



0

45

DBC =

.

Do đó



0

45

= =EBN EAN

⇒

ABEN là tứ giác nội tiếp.

Mà



0

90

=ABE

nên



0

90

=ANE



0

90 .

ENF

⇒

=

(1)

124

N

M

F

A

C

B

D

E

D

H

C

B

O

A

Tương tự thì ADFM cũng là tứ giác nội tiếp.

Mà



0

90

=ADF

nên



0

90

=AMF



0

90 .

EMF

⇒

=

(2)

Từ (1) và (2)



0

90

⇒

= =ENF EMF

⇒

đpcm.

Ví dụ 4. Cho điểm A nằm ngoài đường tròn (O). Vẽ các tiếp tuyến AB, AC của

đường tròn (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Qua H

vẽ dây cung DE của đường tròn (D thuộc cung nhỏ BC). Chứng minh rằng

ADOE là tứ giác nội tiếp.

Gợi ý :

Hai

đỉ

nh liên ti

ế

p c

ủ

a t

ứ

giác cùng nhìn m

ộ

t c

ạ

nh d

ướ

i hai góc b

ằ

ng

nhau.

Hay “T

ứ

giác ABCD có hai

đườ

ng chéo AC và BD c

ắ

t nhau t

ạ

i E có EA.EC =

EB.ED”.

Hướng dẫn giải

Vì AB, AC là các tiếp tuyến (B, C là

tiếp điểm) nên AB = AC và AO là phân

giác của



BAC

⇒

AO

⊥

BC tại H và HB = HC (1).

Vì AB là tiếp tuyến (B là tiếp điểm)

nên



0

90 .

ABO =

Áp dụng hệ thức lượng trong tam giác

vuông ta có :

HB

2

= HA.HO (2)

Dễ thấy

∆

HBD



∆

HEC

(g-g)

⇒

HB.HC = HD.HE. (3)

Từ (1), (2) và (3)

⇒

HA.HO = HD.HE

⇒

ADOE là tứ giác nội tiếp.

Ví dụ 5. Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Về phía ngoài tam

giác, dựng tam giác ACD vuông cân tại A. Trên tia đối của tia EC lấy điểm F

sao cho EF = EB.

125

F

D

A

O

B

C

E

D

F

B

C

O

A

E

Chứng minh rằng BDFC là tứ giác nội tiếp.

Gợi ý :

Áp d

ụ

ng

đị

nh ngh

ĩ

a

đườ

ng tròn hay nhi

ề

u

đ

i

ể

m cách

đề

u m

ộ

t

đ

i

ể

m.

Hướng dẫn giải

Tam giác ABC cân tại A



⇒

=

ABC ACB

(1).

Ta có



=

AEC ABC

(cùng chắn



AC

).

Mà



0

180

+ =AEC AEF

(kề bù)



0

180 .

ABC AEF

⇒

+ =

(2)

Tứ giác AEBC nội tiếp (O)



0

180 .

AEB ACB

⇒

+ =

(3)

Từ (1) (2) và (3) suy ra



.

AEB AEF

=

Mà EB = EF nên

∆ = ∆

AEB AEF

(c-g-c)

⇒

AB = AF.

Dễ thấy AB = AC ; AC = AD.

Do đó AB = AC = AD = AF

⇒

đpcm.

Ví dụ 6. Cho điểm A nằm ngoài đường tròn (O). Vẽ các tiếp tuyến AB, AC của

đường tròn (B, C là các tiếp điểm). Vẽ cát tuyến ADE (D

∈

cung nhỏ BC,



<

BD DC

). Gọi F là trung điểm của DE. Chứng minh rằng 5 điểm A, B, C,

O, F cùng thuộc một đường tròn.

Gợi ý :

Các

đ

i

ể

m cùng nhìn m

ộ

t

đ

o

ạ

n d

ướ

i m

ộ

t góc vuông ho

ặ

c xét hai hay

nhi

ề

u t

ứ

giác n

ộ

i ti

ế

p.

Hướng dẫn giải

Vì AB, AC là các tiếp tuyến (B, C là các tiếp điểm) nên



0

90

ABO =

;



0

90

=ACO

.

Vì F là trung điểm của DE nên

OF DE

⊥

hay



0

90

=AFO

.

Vì



0 0 0

90 90 180

+ = + =ABO ACO

nên ABOC là tứ

giác nội tiếp. (1)

126

O

M

H

E

D

B

C

A

Vì



0 0 0

90 90 180

+ = + =AFO ACO

nên AFOC là tứ giác nội tiếp. (2)

Từ (1) và (2) suy ra 5 điểm A, B, C, O, F cùng thuộc một đường tròn.

Dạng 4.

CHỨNG MINH MỘT ĐƯỜNG THẲNG LÀ TIẾP TUYẾN

CỦA ĐƯỜNG TRÒN

1. PHƯƠNG PHÁP GIẢI

− Đường thẳng và đường tròn chỉ có một điểm chung.

− Đường thẳng vuông góc với bán kính tại một điểm trên đường tròn.

− Tia Bx nằm trên nửa mặt phẳng bờ BC không chứa điểm A sao cho



=

CBx BAC

thì tia Bx là tia tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác nhọn ABC, các đường cao BD và CE cắt nhau tại H. Gọi

M là trung điểm của BC. Chứng minh rằng MD và ME là các tiếp tuyến của

đường tròn ngoại tiếp tam giác ADE.

Gợi ý : Một đường thẳng vuông góc với bán kính tại một điểm trên đường

tròn.

Hướng dẫn giải

Tứ giác ADHE có



0 0 0

90 90 180

+ = + =ADH AEH

⇒

Tứ giác ADHE nội tiếp đường tròn tâm O đường

kính AH.

Do đó đường tròn (O) chính là đường tròn ngoại tiếp

ADE

∆

.

Tam giác AOH cân tại O (OA = OH)



.

OAD ODA

⇒

=

127

x

y

E

D

C

O

A

B

H

Tam giác BDC vuông tại D có DM là trung tuyến nên MD = MB = MC

⇒ ∆

MDC

cân tại M



.

MDC MCD

⇒ =

Vì H là trực tâm của tam giác ABC nên AH vuông góc với BC nên



0

90

OAD MCD+ =

suy ra



0

90

ODA MDC+ =



0

90

⇒ =ODM

. Vậy MD là tiếp

tuyến của đường tròn (O).

Tương tự ME là tiếp tuyến của đường tròn (O) ngoại tiếp tam giác ADE.

Ví dụ 2. Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa mặt phẳng bờ

AB chứa nửa đường tròn, vẽ các tia Ax và By cùng vuông góc với AB. Trên

các tia Ax và By lần lượt lấy các điểm C và D sao cho



0

90

=COD

. Chứng

minh rằng CD là tiếp tuyến của đường tròn (O).

Gợi ý :

K

ẻ

kho

ả

ng cách t

ừ

tâm

đế

n

đườ

ng th

ẳ

ng, r

ồ

i ch

ứ

ng minh kho

ả

ng cách

đ

ó b

ằ

ng bán kính.

Hướng dẫn giải

Kẻ OH vuông góc với CD tại H.

Gọi E là giao điểm của hai đường thẳng OC và

BD.

Dễ thấy

∆ = ∆

AOC BOE

(g-c-g)

⇒

OC = OE.

Tam giác CDE có DO vừa là đường cao, vừa là

trung tuyến nên tam giác CDE cân tại D. Suy ra DO

là phân giác của góc CDE



⇒ =

CDO EDO

⇒ ∆ = ∆

OHD OBD

(cạnh huyền-góc nhọn)

⇒

OH = OB.

Vậy CD là tiếp tuyến của đường tròn (O).

Ví dụ 3. Cho hình vuông ABCD. Trên các cạnh BC và CD lần lượt lấy các điểm

E và F sao cho



0

45

=EAF

. Chứng minh rằng đường thẳng EF là tiếp tuyến

của đường tròn tâm A bán kính AB.

Gợi ý :

K

ẻ

kho

ả

ng cách t

ừ

tâm

đế

n

đườ

ng th

ẳ

ng, r

ồ

i ch

ứ

ng minh kho

ả

ng cách

đ

ó b

ằ

ng bán kính.

128

K

F

E

A

C

B

D

H

D

O

A

B

C

Hướng dẫn giải

Kẻ AH vuông góc với EF tại H. Trên tia đối của

tia DC lấy điểm K sao cho DK = BE suy ra

ABE ADK

∆ = ∆

(c-g-c)



⇒ =

BAE DAK

và AE = AK.

Mà



0

90

+ =BAE EAD

nên



0

90

+ =EAD DAK

.

Ta có



0

45

=AEF



0

45

⇒ =KAF

⇒ ∆ = ∆

FAK FAE

(c-g-c)



⇒ =

AFK AFE

⇒ ∆ = ∆

AFD AFH

(ch-gn)

⇒

AD = AH

⇒

AH = AB.

Vậy đường thẳng EF là tiếp tuyến của đường tròn (A ; AB).

Chú ý : Trong các ví dụ 2 và 3, để chứng minh CD hay EF là tiếp tuyến ta cần

tạo ra khoảng cách từ tâm đường tròn đến CD hay EF rồi chứng minh khoảng

cách đó bằng bán kính của đường tròn.

Ví dụ 4. Cho tam giác ABC cân tại A có



0

36

=A

, đường phân giác BD. Chứng

minh BC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD.

Gợi ý :

Ch

ứ

ng minh



=

CBD BAD

.

Hướng dẫn giải

Tam giác ABC cân tại A có



0

36

=A



0 0

0

180 36

72

2

−

⇒ = = =ABC ACB .

Vì BD là phân giác của

ABC

∆



0

72

36

2 2

⇒ = = = =

ABC

ABD DBC .

Do đó



0

36

= =CBD BAD

. Tia BC nằm trên nửa mặt

phẳng bờ BD không chứa điểm A và



0

36

= =CBD BAD

nên BC là tiếp tuyến của

đường tròn tâm O ngoại tiếp tam giác ABD.

Chú ý : Đây là một dấu hiệu nhận biết tiếp tuyến cần được rèn luyện để có kĩ

năng trong việc giải bài toán chứng minh một đường thẳng là tiếp tuyến của

đường tròn.

129

B

1

C

1

I

B

C

A

1

Dạng 5.

CHỨNG MINH ĐẲNG THỨC HÌNH HỌC

1. PHƯƠNG PHÁP GIẢI

− Định lí Pi-ta-go, định lí Ta-let, tính chất đường phân giác của tam giác.

− Công thức tính diện tích của các hình.

− Vận dụng một số bất đẳng thức thường sử dụng trong phân môn đại số.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác ABC. Gọi I là giao điểm các đường phân giác trong của

tam giác ABC. Trên tia đối của tia CB lấy điểm A

1

. Đường thẳng IA

1

cắt các

cạnh AC và AB thứ tự ở B

1

; C

1

. Chứng minh hệ thức :

1 1 1

+ =

BC CA AB

IA IB IC

.

Gợi ý : Áp dụng tính chất đường phân giác của tam giác và biến đổi đồng

nhất biểu thức hữu tỉ.

Hướng dẫn giải

Vì AI là phân giác của

1 1

∆

AB C

ta có :

1 1

=

AC AB

IC IB

(1)

Vì BI là phân giác của

1 1

∆

A BC

ta có :

1 1

=

BC BA

IC IA

(2)

Vì CI là phân giác ngoài của

1 1

∆

A B C

ta có :

1 1

=

CB CA

IB IA

(3)

Lấy (2) trừ (3) vế theo vế ta được :

1 1 1 1 1 1

1 1 1 1 1 1 1

− = − ⇒ − =

BC CB BA CA BC CB

BC

IC IB IA IA IC IB IA

(4).

Cộng (1) và (4) vế theo vế ta được :

1 1 1 1

1 1 1 1 1 1 1 1

− + = + ⇒ = +

BC CB AC AB

BC AB BC CA

IC IB IC IA IB IC IA IB

130

d

B

1

C

1

D

1

A

1

A

C

B

D

O

D

E

H

B

C

A

Ví dụ 2. Cho hình vuông ABCD có cạnh bằng a. Một đường thẳng d quay quanh

tâm O của hình vuông. Chứng minh rằng tổng các bình phương của các

khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng d không đổi.

Gợi ý : Áp dụng tính chất của hình vuông, tam giác bằng nhau, định lí Pi-ta-go.

Hướng dẫn giải

Vẽ AA

1

; BB

1

; CC

1

; DD

1

lần lượt vuông góc với đường

thẳng d.

Dễ thấy

1 1

∆ = ∆

BOB OCC

(cạnh huyền-góc nhọn) nên

BB

1

= OC

1

; OB

1

= CC

1

.

Áp dụng định lí Pi-ta-go vào

tam giác vuông OBB

1

ta có

BB

1

2

+ OB

1

2

= OB

2

⇒

BB

1

2

+ CC

1

2

= OB

2

.

Tương tự AA

1

2

+ DD

1

2

= OA

2

.

Do đó : AA

1

2

+ BB

1

2

+ CC

1

2

+ DD

1

2

= 2OA

2

= AB

2

= a

2

.

Ví dụ 3. Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là

hình chiếu của H lên các cạnh AB và AC. Chứng minh rằng :

a) AD.AB = AE.AC b)

3

 

=

 

 

BD AB

CE AC

c) BD.CE.BC = AH

3

.

Gợi ý :

Áp d

ụ

ng h

ệ

th

ứ

c l

ượ

ng trong tam giác vuông, bi

ế

n

đổ

i

đồ

ng nh

ấ

t.

Hướng dẫn giải

a) Tam giác ABH vuông tại H, đường

cao HD, ta có : AH

2

= AB.AD (1)

Tam giác ACH vuông tại H, đường cao

HE, ta có : AH

2

= AC.AE (2)

Từ (1) và (2) suy ra AD.AB = AE.AC.

b) Tam giác ABC vuông tại A, đường

cao AH, ta có :

131

H

B

C

A

AB

2

= BC.BH ; AC

2

= BC.CH

⇒

2

=

BH AB

CH

AC

(*)

Tam giác ABH vuông tại H, đường cao HD, ta có : BH

2

= BD.BA. (3)

Tam giác ACH vuông tại H, đường cao HE, ta có : CH

2

= CA.CE. (4)

Từ (3) và (4) suy ra

2

=

BH AB

AC

CH

(**)

Từ (*) và (**) suy ra

3

 

=

 

 

BD AB

CE AC

.

c) Tam giác ABC vuông tại A, đường cao AH, ta có :

AH

2

= BH.CH

⇒

AH

4

= BH

2

.CH

2

= BD.BA.CA.CE = BD.CE.AB.AC (5)

Tam giác ABC vuông tại A, đường cao AH, ta có : AB.AC = BC.AH (6)

Thay (6) vào (5) ta được : AH

4

= BD.CE .BC.AH

⇒

BD.CE.BC = AH

3

.

Ví dụ 4. Cho tam giác ABC có ba góc nhọn. Chứng minh rằng :

a) S

ABC

=

1

. .sin

2

AB AC A

; b)

sin sin sin

= =

BC CA AB

A B C

;

c)

2 2 2

cotg cotg cotg cotg cotg cotg

AB BC CA

A B B C C A

= =

+ + +

;

Gợi ý : Áp dụng định nghĩa về tỉ số lượng giác của góc nhọn, công thức tính

diện tích tam giác.

Hướng dẫn giải

a) Vẽ đường cao BH của tam giác ABC

⇒

S

ABC

=

1

.

2

AC BH

(1)

Tam giác ABH vuông tại H, ta có BH = AB.sinA (2)

Thay (2) vào (1) ta được S

ABC

=

1

. .sin

2

AB AC A

.

132

b) Theo câu a) ta có :

S

ABC

=

1

. .sin

2

AB AC A

=

1

. .sin

2

BA BC B

=

1

. .sin

2

CB CA C

⇒

. .

sin sin sin 2

= = =

ABC

BC CA AB BC CA AB

A B C S

.

c)

∆

ABH

vuông tại H, ta có cotA =

AH

BH

.

∆

BCH

vuông tại H, ta có cotC =

CH

BH

. Do đó cotA + cotC =

AH

BH

+

CH

BH

=

+

=

AH CH AC

BH BH

, suy ra

cot cot

=

+

AC

BH

A C

⇒

2S

ABC

=

.

AC BH

=

2

cot cot

+

AC

A C

.

V

ậ

y :

2 2 2

2

cot cot cot cot cot cot

= = =

+ + +

ABC

AB BC CA

S

A B B C C A

.

Dạng 6.

CHỨNG MINH NHIỀU ĐIỂM THẲNG HÀNG, NHIỀU ĐƯỜNG

ĐỒNG QUY

1. PHƯƠNG PHÁP GIẢI

Chứng minh nhiều điểm thẳng hàng có thể quy về việc chứng minh ba điểm

thẳng hàng. Chứng minh nhiều đường đồng quy thực chất cũng chuyển về chứng

minh ba đường đồng quy. Bài toán chứng minh ba đường đồng quy và bài toán

chứng minh ba điểm thẳng hàng có thể biến đổi qua lại với nhau.

− Qua một điểm cho trước có duy nhất đường thẳng vuông góc với một

đường thẳng cho trước.

− Qua một điểm cho trước ở ngoài một đường thẳng cho trước có duy nhất

đường thẳng song song với đường thẳng đó.

133

M

E

D

H

N

B

C

A

− Các đường đồng quy trong tam giác.

− Tính chất đối xứng trục, đối xứng tâm.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác nhọn ABC, đường cao AH. Gọi D và E lần lượt là các

điểm đối xứng của H qua các cạnh AB và AC. Đường thẳng DE cắt các cạnh

AB và AC lần lượt ở M và N. Chứng minh rằng ba đường thẳng AH, BN, CM

đồng quy.

Gợi ý : Áp dụng tính chất đồng quy của ba đường phân giác, của ba đường

cao trong tam giác.

Hướng dẫn giải

* Theo tính chất đối xứng trục ta có

AMH AMD

∆ = ∆

;

∆ = ∆

ANH ANE

;

∆

ADE

cân tại A

⇒

HA là phân giác của



MHN

, mà HA

⊥

HC nên HC là phân giác

ngoài tại đỉnh H của

.

MHN

∆

* Dễ

th

ấ

y NC là phân giác ngoài t

ạ

i

đỉ

nh

N c

ủ

a

MHN

∆

.

* T

ừ

đ

ó suy ra MC là phân giác c

ủ

a



HMN

, mà MB là phân giác ngoài t

ạ

i

đỉ

nh M c

ủ

a tam giác MHN nên MC

⊥

MB.

T

ươ

ng t

ự

NB

⊥

NC.

* Do

đ

ó AH, BN, CM là ba

đườ

ng cao c

ủ

a tam giác ABC

⇒

đ

pcm.

Ví dụ 2.

Cho tam giác ABC có



0

120

≠A

. V

ề

phía ngoài tam giác ABC, v

ẽ

các

tam giác

đề

u ABD ; ACE và BCF . G

ọ

i I là giao

đ

i

ể

m c

ủ

a BE và CD. Ch

ứ

ng

minh r

ằ

ng IA là tia phân giác c

ủ

a góc DIE. T

ừ

đ

ó suy ra 3

đ

i

ể

m A, I, F th

ẳ

ng

hàng.

Gợi ý :

Hai tia phân giác c

ủ

a hai góc

đố

i

đỉ

nh là hai tia

đố

i nhau.

Hướng dẫn giải

D

ễ

th

ấ

y

∆

ABE =

∆

ADC (c-g-c).

134

P

Q

K

H

I

F

D

E

B

C

A

Q

P

M

H

F

D

E

B

C

A

Áp d

ụ

ng tính ch

ấ

t c

ủ

a góc ngoài tam giác tính

đượ

c



0

120

=BIC

. V

ẽ

AH

⊥

BE ; AK

⊥

CD.

Vì

∆

ABE =

∆

ADC nên AH = AK

⇒

IA là

phân giác c

ủ

a góc DIE. (1)

V

ẽ

FP

⊥

BE ; FQ

⊥

CD

⇒

∆

FPB =

∆

FQC (ch– gn)

⇒

FP = FQ

⇒

IF là phân giác c

ủ

a góc BIC. (2)

Vì



DIE

và



BIC

là hai góc

đố

i

đỉ

nh nên t

ừ

(1)

và (2) suy ra ba

đ

i

ể

m A, I, F th

ẳ

ng hàng.

Ví dụ 3.

Cho tam giác ABC vuông t

ạ

i A,

đườ

ng cao AH. V

ề

phía ngoài tam giác

v

ẽ

các tam giác vuông cân

đỉ

nh B và

đỉ

nh C là ABD và ACE.

a) Ch

ứ

ng minh r

ằ

ng ba

đ

i

ể

m D, A, E th

ẳ

ng hàng.

b) Ch

ứ

ng minh r

ằ

ng ba

đườ

ng th

ẳ

ng AH, BE, CD

đồ

ng quy.

c) G

ọ

i M là trung

đ

i

ể

m c

ủ

a DE. Ch

ứ

ng minh tam giác MBC là tam giác

vuông cân.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t c

ủ

a hai góc k

ề

bù, tính ch

ấ

t ba

đườ

ng cao c

ủ

a tam

giác thì

đồ

ng quy.

Hướng dẫn giải

a) D

ễ

th

ấ

y



+

DAB



+

BAC



0

180

=CAE

.

b) Trên tia

đố

i c

ủ

a tia AH l

ấ

y

đ

i

ể

m F sao

cho AF = BC.

C

ầ

n ch

ứ

ng minh :

∆

ABF =

∆

BDC (c-g-c) ;

∆

ACF =

∆

CEB (c-g-c), suy ra BF

⊥

CD,

CF

⊥

BE. Do

đ

ó FH, BE, CD là ba

đườ

ng

cao c

ủ

a tam giác FBC

⇒

đ

pcm.

c) V

ẽ

BP

⊥

DE ; CQ

⊥

DE

⇒

BP = PA

= PD ;

CQ = QA = QE. Do

đ

ó

∆

BPM =

∆

MQC (c-g-c)

⇒

BM = MC và



0

90

=BMC

⇒ ∆

BMC

vuông cân t

ạ

i M.

135

Q

P

M

F

N

E

D

C

A

B

Ví dụ 4.

Cho hình thang ABCD,

đ

áy l

ớ

n CD. Các

đườ

ng th

ẳ

ng k

ẻ

t

ừ

A và B l

ầ

n

l

ượ

t song song v

ớ

i CB và AD c

ắ

t các

đườ

ng chéo BD và AC t

ươ

ng

ứ

ng

ở

F

và E

đồ

ng th

ờ

i c

ắ

t

đ

áy l

ớ

n CD th

ứ

t

ự

ở

M và N. Các

đườ

ng th

ẳ

ng k

ẻ

t

ừ

M và

N l

ầ

n l

ượ

t song song v

ớ

i AC và BD c

ắ

t AD và BC th

ứ

t

ự

ở

P và Q.

a) Ch

ứ

ng minh r

ằ

ng 4

đ

i

ể

m E ; F ; P và Q th

ẳ

ng hàng.

b) Tính

độ

dài

đ

o

ạ

n th

ẳ

ng PQ, bi

ế

t r

ằ

ng AB = a ; CD = b.

Gợi ý :

Áp d

ụ

ng tiên

đề

Ơ

-clit : “Qua m

ộ

t

đ

i

ể

m

ở

ngoài m

ộ

t

đườ

ng th

ẳ

ng có

duy nh

ấ

t m

ộ

t

đườ

ng th

ẳ

ng song song v

ớ

i

đườ

ng th

ẳ

ng

đ

ó”.

Hướng dẫn giải

a) Vì AB // CD nên

=

BF AB

FN CN

. (1)

Vì AB // CD nên

=

BE AB

ED DM

. (2)

Do ABND và ABCM là các hình

bình hành nên

DN = CM = AB

⇒

DM = CN. (3)

T

ừ

(1) ; (2) và (3)

⇒

=

BE BF

ED FN

.

Theo

đị

nh lí Ta-lét

đả

o

⇒

EF song song v

ớ

i AB.

Vì MP // AC

⇒

=

AP CM

PD MD

. (4)

Vì NQ // BD

⇒

=

BQ DN

QC NC

. (5)

T

ừ

(1) ; (2) ; (3) ; (4) và (5) suy ra

= = =

AP BE BF BQ

PD ED FN QC

.

Theo

đị

nh lí Ta-lét

đả

o ta có PE // AB ; EF // AB ; FQ // CD.

Ta l

ạ

i có AB // CD nên theo tiên

đề

Ơ

-clít suy ra 4

đ

i

ể

m P ; Q ; E ; F th

ẳ

ng

hàng.

b) Vì PE // AB nên

=

PE DP

AB DA

(1). Vì PE // CD nên

=

PE AP

DM AD

(2).

136

F

E

D

O

B

C

A

M

C

ộ

ng (1) và (2) v

ế

theo v

ế

ta

đượ

c

1

+ =

PE PE

AB DM

.

Mà AB = a ; DM = DC – CM = DC – AB = b – a (vì b > a). Do

đ

ó

(

)

1

−

+ = ⇒ =

−

a b a

PE PE

PE

a b a b

. Ta l

ạ

i có ABQE là hình bình hành nên EQ =

AB = a. V

ậ

y

(

)

(

)

2

− −

= + = + =

a b a a b a

PQ PE EQ a

b b

.

Ví dụ 5.

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (O).

Đ

i

ể

m M thu

ộ

c cung nh

ỏ

BC.

G

ọ

i D, E, F l

ầ

n l

ượ

t là hình chi

ế

u vuông góc c

ủ

a M lên các

đườ

ng th

ẳ

ng BC,

CA, AB. Ch

ứ

ng minh r

ằ

ng ba

đ

i

ể

m D, E, F th

ẳ

ng hàng.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t c

ủ

a hai góc k

ề

bù,

đị

nh ngh

ĩ

a c

ủ

a hai góc

đố

i

đỉ

nh.

Hướng dẫn giải

T

ứ

giác BDMF có :



0 0 0

90 90 180

+ = + =BDM BFM

⇒

t

ứ

giác BDMF n

ộ

i ti

ế

p



⇒

=

FBM FDM

(1) (hai góc n

ộ

i ti

ế

p cùng ch

ắ

n



FM

).

T

ứ

giác MDEC có :



0

90

= =MDC MEC

.

⇒

T

ứ

giác MDEC n

ộ

i ti

ế

p

⇒



0

180

+ =MDE MEC

(2)

T

ứ

giác ABMC n

ộ

i ti

ế

p

đườ

ng tròn (O)



⇒

=

FBM ACM

(vì cùng bù v

ớ

i góc ABM) (3)

T

ừ

(1) (2) và (3) suy ra



0

180

+ =FDM MDE

.

V

ậ

y ba

đ

i

ể

m D, E, F th

ẳ

ng hàng.

Chú ý : Đườ

ng th

ẳ

ng DEF g

ọ

i là

đườ

ng th

ẳ

ng Sim-son.

Ví dụ 6.

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). G

ọ

i D, E, F th

ứ

t

ự

là

đ

i

ể

m

chính gi

ữ

a các cung nh

ỏ

BC, CA, AB. G

ọ

i I là giao

đ

i

ể

m c

ủ

a BE và CF. G

ọ

i

137

N

M

I

F

E

D

O

B

C

A

M là giao

đ

i

ể

m c

ủ

a DF và AB. G

ọ

i N là giao

đ

i

ể

m c

ủ

a DE và AC. Ch

ứ

ng

minh r

ằ

ng :

a) Ba

đ

i

ể

m A, I, D th

ẳ

ng hàng ; b) Ba

đ

i

ể

m M, I, N th

ẳ

ng hàng.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t ba

đườ

ng phân giác c

ủ

a tam giác thì

đồ

ng quy, tiên

đề

Ơ

-clít.

Hướng dẫn giải

a) Vì D, E, F th

ứ

t

ự

là

đ

i

ể

m chính gi

ữ

a

các cung nh

ỏ

BC, CA, AB nên



=

DB DC

;



=

EC EA

;



=

FA FB

.

⇒



;

DAB DAC

=



;

EBC EBA

=



FCA FCB

=

Do

đ

ó AD, BE, CF là ba

đườ

ng phân

giác c

ủ

a

ABC

∆

suy ra ba

đườ

ng th

ẳ

ng AD,

BE, CF

đồ

ng quy.

V

ậ

y ba

đ

i

ể

m A, I, D th

ẳ

ng hàng.

b) Vì



=

DB DC

;



=

FA FB

nên suy ra



=

DFB DFC

;



=

FDB FDA

⇒ ∆ = ∆

DFB DFI

(g-c-g)

⇒

DB = DI ; FB = FI.

Do

đ

ó DF là

đườ

ng trung tr

ự

c c

ủ

a

đ

o

ạ

n th

ẳ

ng BI, mà M

∈

DF nên MB = MI.

Do

đ

ó

∆

MBI

cân t

ạ

i M, suy ra



=

MBI MIB

. Ta l

ạ

i có



=

MBI IBC

(cmt) nên



=

MIB IBC

, mà hai góc này

ở

v

ị

trí so le trong nên IM // BC (1). Ch

ứ

ng minh

t

ươ

ng t

ự

ta

đượ

c IN // BC. (2)

Theo Tiên

đề

Ơ

-clit, t

ừ

(1) và (2) suy ra ba

đ

i

ể

m M, I, N th

ẳ

ng hàng.

138

G

H

F

E

A

C

B

D

Dạng 7.

CHỨNG MINH TAM GIÁC, TỨ GIÁC ĐẶC BIỆT

(Nhận dạng tam giác, tứ giác)

1. PHƯƠNG PHÁP GIẢI

Áp dụng các dấu hiệu nhận biết về các tam giác, tứ giác đặc biệt như : tam

giác vuông, tam giác cân, tam giác vuông cân, tam giác đều, hình thang cân, hình

bình hành, hình chữ nhật, hình thoi, hình vuông.

2. CÁC VÍ DỤ

Ví dụ 1. Cho hình vuông ABCD. Gọi E và F thứ tự là trung điểm của các cạnh

AB và BC. Gọi G là giao điểm của CE và DF. Chứng minh rằng tam giác

ADG là tam giác cân.

Gợi ý : Áp dụng dấu hiệu : “Tam giác có hai cạnh bằng nhau là tam giác

cân”.

Hướng dẫn giải

Dễ thấy

∆ = ∆

CBE DCF

(c-g-c)



⇒ =

BCE CDF

Mà



0

90

+ =

BCE ECD

nên



0

90

+ =

CDF ECD

.

Do đó

∆

CDG

vuông tại G



0 0

90 90

⇒ = ⇒ =

CGD DGE

.

Kéo dài CE cắt đường thẳng AD tại H.

Dễ thấy

∆ = ∆

CBE HAE

(g-c-g)

⇒

BC = AH

⇒

AH = AD.

Tam giác DGH vuông tại G có GA là đường trung tuyến

⇒

GA = AD = AH

⇒

∆

ADG

cân tại A.

Ví dụ 2. Cho tam giác ABC có AD và BE là các đường trung tuyến. Chứng minh

rằng tam giác ABC là tam giác đều nếu



0

30

= =

CAD CBE

.

139

D

E

C

B

A

D

C

B

O'

O

A

Gợi ý :

Áp d

ụ

ng d

ấ

u hi

ệ

u : “Tam giác cân có m

ộ

t góc b

ằ

ng 60

0

là tam giác

đề

u”.

Hướng dẫn giải

Dễ thấy

∆

CAD



∆

CBE

(g-g), suy ra

CA CD

CB CE

=

,

mà

;

2

CB

CD =

2

CA

CE =

nên =

CA CB

CB CA

2 2

⇒

=

⇒

=

CA CB CA CB

⇒

∆

ABC

cân t

ạ

i C.

Vì CA = CB và

2

=

CB

CD

nên

2

=

CA

CD .

Tam giác CAD có



0

30

=CAD

và

2

=

CA

CD nên

∆

CAD

là n

ử

a tam giác

đề

u



0

60

⇒

=ACD

⇒

đ

pcm.

Ví dụ 3.

Cho hai

đườ

ng tròn (O) và (O’) ti

ế

p xúc ngoài t

ạ

i A. V

ẽ

ti

ế

p tuy

ế

n chung

ngoài BC (B, C là các ti

ế

p

đ

i

ể

m, B

∈

(O), C

∈

(O’)). V

ẽ

ti

ế

p tuy

ế

n chung

trong t

ạ

i A c

ắ

t BC

ở

D. Ch

ứ

ng minh r

ằ

ng các tam giác ABC và ODO’ là các

tam giác vuông.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t hai tia phân giác c

ủ

a hai góc k

ề

bù,

đườ

ng trung

tuy

ế

n

ứ

ng v

ớ

i m

ộ

t c

ạ

nh và b

ằ

ng n

ử

a c

ạ

nh

ấ

y.

Hướng dẫn giải

Áp d

ụ

ng tính ch

ấ

t c

ủ

a hai ti

ế

p tuy

ế

n c

ắ

t nhau ta

có :

* DA = DB = DC

2

=

BC

⇒



ABC

vuông t

ạ

i A.

140

C

B

M

O

A

K

M

N

H

E

D

O

B

C

A

* DO, DO’ th

ứ

t

ự

là phân giác c

ủ

a



,

ADB ADC

.

Mà



,

ADB ADC

là hai góc k

ề

bù nên



0

' 90

=

ODO

, suy ra

'

∆

ODO

vuông t

ạ

i

D.

Ví dụ 4.

Cho

đườ

ng tròn (O ; R) bán kính A. G

ọ

i M là trung

đ

i

ể

m c

ủ

a OA. V

ẽ

dây cung BC

đ

i qua M và vuông góc v

ớ

i OA.

a) Ch

ứ

ng minh r

ằ

ng tam giác AOB là tam giác

đề

u.

b) T

ứ

giác ABOC là hình gì ? Vì sao ?

Gợi ý :

Áp d

ụ

ng d

ấ

u hi

ệ

u : “Tam giác có ba c

ạ

nh b

ằ

ng nhau là tam giác

đề

u” ; “T

ứ

giác có 4 c

ạ

nh b

ằ

ng nhau là hình thoi”.

Hướng dẫn giải

a) Tam giác AOB có BM v

ừ

a là trung tuy

ế

n, v

ừ

a là

đườ

ng cao nên tam giác AOB cân t

ạ

i B, suy ra OB = AB.

Ta l

ạ

i có OA = OB = R

nên OA = OB = AB

⇒

đ

pcm.

b) T

ươ

ng t

ự

câu a) ta suy ra OB = BA = AC = CO

⇒

ABOC là hình thoi.

Cách khác : Vì OM

⊥

BC nên MB = MC.

T

ứ

giác ABOC có MA = MO, MB = MC và OA

⊥

BC

⇒

đ

pcm.

Ví dụ 5.

Cho tam giác nh

ọ

n ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). Các

đườ

ng cao BD và

CE c

ắ

t nhau t

ạ

i H. G

ọ

i M, N th

ứ

t

ự

là trung

đ

i

ể

m c

ủ

a BC và AH. T

ứ

giác

HNOM là hình gì ? Vì sao ?

Gợi ý :

Áp d

ụ

ng d

ấ

u hi

ệ

u : “T

ứ

giác có hai c

ạ

nh

đố

i v

ừ

a song song v

ừ

a b

ằ

ng

nhau là hình bình hành”.

Hướng dẫn giải

V

ẽ

đườ

ng kính BK c

ủ

a

đườ

ng tròn (O), ta có



0

90

BAK BCK

= =

.

Theo tính ch

ấ

t ba

đườ

ng cao

⇒

AH

⊥

BC ; CH

⊥

AB.

141

y

x

H

K

E

D

O

A

B

C

Do

đ

ó AH // KC và AK // CH

⇒

AHCK là hình bình hành

⇒

AH = CK, mà NA = NH

.

2

CK

NA NH

⇒ = =

(1)

D

ễ

th

ấ

y OM là

đườ

ng trung bình c

ủ

a

∆

BCK

⇒

OM //=

.

2

CK

(2)

T

ừ

(1) và (2)

⇒

NH //= OM

⇒

AHCK là hình bình hành.

Ví dụ 6.

Cho

đ

i

ể

m C thu

ộ

c n

ử

a

đườ

ng tròn (O)

đườ

ng kính AB. Trên n

ử

a m

ặ

t

ph

ẳ

ng b

ờ

AB có ch

ứ

a

đ

i

ể

m C, v

ẽ

các tia Ax và By cùng vuông góc v

ớ

i AB.

Ti

ế

p tuy

ế

n t

ạ

i C c

ủ

a n

ử

a

đườ

ng tròn c

ắ

t các tia Ax và By th

ứ

t

ự

ở

D và E. G

ọ

i

H là giao

đ

i

ể

m c

ủ

a OD và AC ; K là giao

đ

i

ể

m c

ủ

a OE và BC.

a) T

ứ

giác OHCK là hình gì ? Vì sao ?

b)

Đ

i

ể

m C ph

ả

i th

ỏ

a mãn

đ

i

ề

u ki

ệ

n gì

để

OHCK là hình vuông ?

Gợi ý :

Áp d

ụ

ng d

ấ

u hi

ệ

u : ‘T

ứ

giác có ba góc vuông là hình ch

ữ

nh

ậ

t” ;

Hình ch

ữ

nh

ậ

t có hai c

ạ

nh k

ề

b

ằ

ng nhau ho

ặ

c có m

ộ

t

đườ

ng chéo là phân giác

c

ủ

a m

ộ

t góc ho

ặ

c có hai

đườ

ng chéo vuông góc v

ớ

i nhau là hình vuông”.

Hướng dẫn giải

a) Áp d

ụ

ng tính ch

ấ

t c

ủ

a hai ti

ế

p tuy

ế

n c

ắ

t nhau

ta có DA = DC.

Ta l

ạ

i có OA = OC = R. Do

đ

ó OD là trung tr

ự

c

ủ

a AC, suy ra OD

⊥

AC t

ạ

i H và HA = HC =

.

2

AC

T

ươ

ng t

ự

: OE

⊥

BC t

ạ

i K và KB = KC =

.

2

BC

D

ễ

th

ấ

y



0

90

=

ACB

. T

ừ

đ

ó suy ra OHCK là

hình ch

ữ

nh

ậ

t.

b) Hình ch

ữ

nh

ậ

t OHCK là hình vuông

⇔

CH = CK

⇔ = ⇔

AC BC

C là

đ

i

ể

m chính gi

ữ

a



AB

.

V

ậ

y khi C là

đ

i

ể

m chính gi

ữ

a cung AB thì OHCK là hình vuông.

142

K

H

A

B

C

D

E

Ví dụ 7.

Cho tam giác ABC vuông t

ạ

i A (AB < AC),

đườ

ng cao AH. Trên c

ạ

nh

AC l

ấ

y

đ

i

ể

m D sao cho AC = 3AD. Trên tia

đố

i c

ủ

a tia HA l

ấ

y

đ

i

ể

m E sao

cho AH = 3HE. Ch

ứ

ng minh r

ằ

ng tam giác BED là tam giác vuông.

Gợi ý :

Áp d

ụ

ng

đị

nh lí Pi-ta-go

đả

o.

Hướng dẫn giải

Qua D k

ẻ

đườ

ng th

ẳ

ng song song v

ớ

i BC

c

ắ

t AH t

ạ

i K.

Áp d

ụ

ng

đị

nh lí Talét ta có

1

3

AK AD

AH AC

= =

3

AH AK

⇒ =

(vì AC = 3AD)

Ta l

ạ

i có AH = 3HE nên AK = HE. Do

đ

ó

KE = AH.

Áp d

ụ

ng

đị

nh lí Pi-ta-go vào các tam giác vuông BHE ; DKE ; AHB ; ADK ;

ABD ta

đượ

c :

BE

2

+ FE

2

= BH

2

+ HE

2

+ KE

2

+ KD

2

= BH

2

+ AH

2

+ AK

2

+ KD

2

(vì AH = KE ; HE = AK).

= AB

2

+ AD

2

= BD

2

.

Theo

đị

nh lí Pi-ta-go

đả

o suy ra

BED

∆

vuông t

ạ

i E.

III. BÀI TẬP VẬN DỤNG

Dạng 1. Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau

Bài 1.

Cho hai

đườ

ng tròn (O) và (O’) c

ắ

t nhau t

ạ

i A và B. V

ẽ

ti

ế

p tuy

ế

n chung

ngoài CD (C

∈

(O), D

∈

(O’)). Ch

ứ

ng minh r

ằ

ng AB

đ

i qua trung

đ

i

ể

m E

c

ủ

a CD

.

Bài 2.

Cho

đ

i

ể

m A n

ằ

m ngoài

đườ

ng tròn (O). V

ẽ

hai các tuy

ế

n ABC và ADE

v

ớ

i

đườ

ng tròn (B n

ằ

m gi

ữ

a A và C ; D n

ằ

m gi

ữ

a A và E). Qua A v

ẽ

đườ

ng th

ẳ

ng d vuông góc v

ớ

i OA.

Đườ

ng th

ẳ

ng d c

ắ

t các

đườ

ng th

ẳ

ng BE

và CD th

ứ

t

ự

ở

M và N. G

ọ

i H và K l

ầ

n l

ượ

t là hình chi

ế

u c

ủ

a O lên BE

và CD. Ch

ứ

ng minh r

ằ

ng :

a)



=

AKC AHE

; b) AM = AN.

143

Bài 3.

Cho tam giác nh

ọ

n ABC.

Đườ

ng tròn

đườ

ng kính AB c

ắ

t c

ạ

nh AC

ở

H.

Đườ

ng tròn

đườ

ng kính AC c

ắ

t c

ạ

nh AB

ở

K.

Đườ

ng tròn

đườ

ng kính AB

c

ắ

t

đ

o

ạ

n CK

ở

D.

Đườ

ng tròn

đườ

ng kính AC c

ắ

t

đ

o

ạ

n BH

ở

E. Ch

ứ

ng

minh r

ằ

ng :

a) AD = AE.

b)

Đườ

ng tròn ngo

ạ

i ti

ế

p c

ủ

a hai tam giác AEB và ADC b

ằ

ng nhau.

Bài 4.

Cho hai

đườ

ng tròn (O) và (O’) ti

ế

p xúc ngoài t

ạ

i A. Dây cung BC c

ủ

a (O)

kéo dài ti

ế

p xúc v

ớ

i (O’) t

ạ

i D. Kéo dài BA c

ắ

t (O’) t

ạ

i E. Ch

ứ

ng minh

r

ằ

ng AD là phân giác c

ủ

a góc CAE.

Bài 5.

Cho

đườ

ng tròn (O)

đườ

ng kính AB, dây CD không c

ắ

t AB. Các ti

ế

p

tuy

ế

n t

ạ

i C và D c

ủ

a (O) c

ắ

t nhau

ở

E. G

ọ

i H là hình chi

ế

u c

ủ

a E trên AB.

Ch

ứ

ng minh r

ằ

ng



=

EHC EHD

.

Dạng 2. Chứng minh quan hệ vuông góc, quan hệ song song

Bài 1.

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). G

ọ

i D, E, F l

ầ

n l

ượ

t là

đ

i

ể

m

chính gi

ữ

a c

ủ

a các cung nh

ỏ

BC, CA, AB. G

ọ

i M là giao

đ

i

ể

m c

ủ

a AB và

DF ; N là giao

đ

i

ể

m c

ủ

a AD và CF.

a) Ch

ứ

ng minh r

ằ

ng AD vuông góc v

ớ

i EF.

b) Ch

ứ

ng minh r

ằ

ng MN song song v

ớ

i BC.

Bài 2.

Cho tam giác nh

ọ

n ABC n

ộ

i ti

ế

p

đườ

ng tròn (O).

Đườ

ng tròn

đườ

ng kính

BC c

ắ

t các c

ạ

nh AB, AC th

ứ

t

ự

ở

D, E. Ch

ứ

ng minh r

ằ

ng OA vuông góc

v

ớ

i DE.

Bài 3.

Cho n

ử

a

đườ

ng tròn (O)

đườ

ng kính AB. Trên n

ủ

a m

ặ

t ph

ẳ

ng b

ờ

AB ch

ứ

a

n

ử

a

đườ

ng tròn, v

ẽ

các tia A

x

và B

y

cùng vuông góc v

ớ

i AB.

Đ

i

ể

m C

thu

ộ

c n

ử

a

đườ

ng tròn. Ti

ế

p tuy

ế

n t

ạ

i C c

ắ

t A

x

và B

y

th

ứ

t

ự

ở

D và E.

a) Ch

ứ

ng minh r

ằ

ng tam giác DOE là tam giác vuông.

b) G

ọ

i F là giao

đ

i

ể

m c

ủ

a AE và BD. Ch

ứ

ng minh r

ằ

ng CF song song v

ớ

i

A

x

.

Bài 4.

Cho tam giác ABC vuông t

ạ

i A. Trên c

ạ

nh BC l

ấ

y

đ

i

ể

m D sao cho CD = AB.

G

ọ

i E là hình chi

ế

u c

ủ

a D lên AB. Tia phân giác c

ủ

a góc B c

ắ

t DE

ở

F.

Tia AF c

ắ

t BC

ở

M. G

ọ

i N là trung

đ

i

ể

m c

ủ

a AC. Ch

ứ

ng minh r

ằ

ng MN

song song v

ớ

i BF.

144

Dạng 3. Chứng minh nhiều điểm cùng nằm trên một đường tròn

Bài 1.

Cho tam giác nh

ọ

n ABC (AB < AC < BC). V

ẽ

các

đườ

ng cao AD, BE,

CF. G

ọ

i M, N, P th

ứ

t

ự

là trung

đ

i

ể

m c

ủ

a các c

ạ

nh AB, BC, CA. Ch

ứ

ng

minh r

ằ

ng 6

đ

i

ể

m D, E, F, M, N, P cùng thu

ộ

c m

ộ

t

đườ

ng tròn.

Bài 2.

Cho tam giác ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). Tia phân giác c

ủ

a góc A c

ắ

t

đườ

ng tròn t

ạ

i D. Tia phân giác c

ủ

a góc B c

ắ

t AD

ở

E. V

ẽ

tia D

x

vuông

góc v

ớ

i AD, trên tia A

x

l

ấ

y

đ

i

ể

m F sao cho DF = DC. Ch

ứ

ng minh r

ằ

ng

BECF là t

ứ

giác n

ộ

i ti

ế

p.

Bài 3.

Cho hình bình hành ABCD.

Đ

i

ể

m E n

ằ

m trong hình bình hành sao cho



=

EAD ECD

. G

ọ

i I là trung

đ

i

ể

m c

ủ

a AE. G

ọ

i F là

đ

i

ể

m

đố

i x

ứ

ng v

ớ

i D

qua I (F và D n

ằ

m khác phía

đố

i v

ớ

i AB). Ch

ứ

ng minh r

ằ

ng AFBE là t

ứ

giác n

ộ

i ti

ế

p.

Bài 4.

Cho hai

đườ

ng tròn (O) và (O’) c

ắ

t nhau t

ạ

i A và B. Trên tia

đố

i c

ủ

a tia

AB l

ấ

y

đ

i

ể

m C tu

ỳ

ý. V

ẽ

cát tuy

ế

n CDE c

ủ

a

đườ

ng tròn (O). V

ẽ

cát tuy

ế

n

CMN c

ủ

a

đườ

ng tròn (O’). Ch

ứ

ng minh r

ằ

ng 4

đ

i

ể

m D, E, M, N cùng

thu

ộ

c m

ộ

t

đườ

ng tròn.

Bài 5.

Cho

đ

i

ể

m A n

ằ

m ngoài

đườ

ng tròn (O). V

ẽ

các ti

ế

p tuy

ế

n AB, AC c

ủ

a

đườ

ng tròn (B, C là các ti

ế

p

đ

i

ể

m). V

ẽ

cát tuy

ế

n ADE (D n

ằ

m gi

ữ

a A và

E). G

ọ

i H là giao

đ

i

ể

m c

ủ

a BC và OA. Ch

ứ

ng minh r

ằ

ng DEOH là t

ứ

giác

n

ộ

i ti

ế

p.

Dạng 4. Chứng minh một đường thẳng là tiếp tuyến của đường tròn

Bài 1.

Cho tam giác ABC

đườ

ng cao AH n

ộ

i ti

ế

p

đườ

ng tròn tâm O

đườ

ng kính

BC. V

ẽ

đườ

ng tròn tâm A bán kính AH. V

ẽ

các ti

ế

p tuy

ế

n BD và CE c

ủ

a

đườ

ng tròn (A) (D, E khác

đ

i

ể

m H). Ch

ứ

ng minh r

ằ

ng DE là ti

ế

p tuy

ế

n

c

ủ

a

đườ

ng tròn (O).

Bài 2.

Cho tam giác ABC vuông t

ạ

i A (AB < AC)

đườ

ng cao AH. G

ọ

i D là

đ

i

ể

m

đố

i x

ứ

ng c

ủ

a B qua H. V

ẽ

đườ

ng tròn tâm O

đườ

ng kính CD c

ắ

t c

ạ

nh AC

t

ạ

i E. Ch

ứ

ng minh r

ằ

ng HE là ti

ế

p tuy

ế

n c

ủ

a

đườ

ng tròn (O).

Bài 3.

Cho tam giác ABC cân t

ạ

i A n

ộ

i ti

ế

p

đườ

ng tròn (O).

Đ

i

ể

m D thu

ộ

c cung

nh

ỏ

AC. Tia AD c

ắ

t

đườ

ng th

ẳ

ng BC t

ạ

i E. V

ẽ

đườ

ng tròn (O’) ngo

ạ

i ti

ế

p

tam giác BDE. Ch

ứ

ng minh r

ằ

ng AB là ti

ế

p tuy

ế

n c

ủ

a

đườ

ng tròn (O’).

145

Bài 4.

Cho hình vuông ABCD ngo

ạ

i ti

ế

p

đườ

ng tròn (O). G

ọ

i M là trung

đ

i

ể

m

c

ủ

a AB. Trên các c

ạ

nh CD và CB l

ầ

n l

ượ

t l

ấ

y các

đ

i

ể

m E và F sao cho AE

song song v

ớ

i MF. Ch

ứ

ng minh r

ằ

ng EF là ti

ế

p tuy

ế

n c

ủ

a

đườ

ng tròn (O).

Bài 5.

Cho tam giác ABC. Các tia phân giác c

ủ

a các góc B và C c

ắ

t nhau t

ạ

i I.

Đườ

ng th

ẳ

ng qua I và vuông góc v

ớ

i AI c

ắ

t các c

ạ

nh AB và AC th

ứ

t

ự

ở

D và E. Ch

ứ

ng minh r

ằ

ng DE là ti

ế

p tuy

ế

n c

ủ

a

đườ

ng tròn ngo

ạ

i ti

ế

p tam

giác BIC.

Dạng 5. Chứng minh đẳng thức hình học

Bài 1.

G

ọ

i R và r l

ầ

n l

ượ

t là bán kính

đườ

ng tròn ngo

ạ

i ti

ế

p và

đườ

ng tròn n

ộ

i

ti

ế

p c

ủ

a tam giác nh

ọ

n ABC. Ch

ứ

ng minh các

đẳ

ng th

ứ

c sau :

a)

2

sin sin sin

= = =

BC CA AB

R

A B C

; b)

. .

4

=

ABC

BC CA AB

S

R

;

c)

. .

2

=

+ +

BC CA AB

Rr

BC CA AB

.

Bài 2.

Cho tam giác ABC. G

ọ

i P là giao

đ

i

ể

m c

ủ

a ba

đườ

ng phân giác trong.

Đườ

ng th

ẳ

ng qua P và vuông góc v

ớ

i CP c

ắ

t CA và CB th

ứ

t

ự

ở

M và N.

Ch

ứ

ng minh r

ằ

ng :

a)

2

 

=

 

 

AM AP

BN BP

;

b)

2 2 2

. . . . .

+ + =

BC AP CA BP AB CP AB BC CA

.

Bài 3.

Cho tam giác nh

ọ

n ABC,

đườ

ng cao AD, tr

ự

c tâm H. Ch

ứ

ng minh r

ằ

ng :

a) tan .tan

=

AD

B C

HD

;

b)

tan tanB tanC tan .tanB.tanC

+ + =

A A

.

Dạng 6. Chứng minh nhiều điểm thẳng hàng, nhiều đường đồng quy

Bài 1.

Cho hai

đườ

ng tròn (O ; R) và (O’ ; r) v

ớ

i R > r, c

ắ

t nhau t

ạ

i A và B.

Đ

o

ạ

n n

ố

i tâm OO’ c

ắ

t các

đườ

ng tròn (O) và (O’) th

ứ

t

ự

ở

C và D. V

ẽ

các ti

ế

p tuy

ế

n chung ngoài c

ủ

a hai

đườ

ng tròn là MP và NQ (M, N

∈

(O) ;

P, Q

∈

(O’)).

146

a) Ch

ứ

ng minh ba

đườ

ng th

ẳ

ng MP, NQ và OO’

đồ

ng quy.

b) G

ọ

i E là giao

đ

i

ể

m c

ủ

a MC và PD. Ch

ứ

ng minh ba

đ

i

ể

m A, E, B th

ẳ

ng

hàng.

Bài 2.

Cho tam giác ABC vuông t

ạ

i A.

Đườ

ng tròn tâm O

đườ

ng kính AB c

ắ

t

c

ạ

nh BC t

ạ

i D. Ti

ế

p tuy

ế

n c

ủ

a

đườ

ng tròn (O) t

ạ

i D c

ắ

t c

ạ

nh AC t

ạ

i E. G

ọ

i

H là hình chi

ế

u vuông góc c

ủ

a D lên AB.

a) Ch

ứ

ng minh r

ằ

ng

đườ

ng th

ẳ

ng BE

đ

i qua trung

đ

i

ể

m K c

ủ

a DH.

b)

Đườ

ng th

ẳ

ng qua B và song song v

ớ

i AC c

ắ

t

đườ

ng th

ẳ

ng AK

ở

F.

Ch

ứ

ng minh r

ằ

ng ba

đ

i

ể

m D, E, F th

ẳ

ng hàng.

Bài 3.

V

ề

phía ngoài tam giác ABC, v

ẽ

các tam giác

đề

u ABD, BCE, CAF.

Ch

ứ

ng minh r

ằ

ng ba

đườ

ng tròn ngo

ạ

i ti

ế

p c

ủ

a các tam giác

đề

u nói trên

cùng

đ

i qua m

ộ

t

đ

i

ể

m.

Bài 4.

Cho tam giác ABC,

đườ

ng phân giác AD. Trên

đ

o

ạ

n AD l

ầ

n l

ượ

t l

ấ

y các

đ

i

ể

m E và F sao cho



=

EBA FBC

(E n

ằ

m gi

ữ

a A và F). V

ẽ

các

đườ

ng tròn

(O

1

) và (O

2

) th

ứ

t

ự

ngo

ạ

i ti

ế

p các tam giác AEB và AFC. Tia CE c

ắ

t

đườ

ng tròn (O

1

) t

ạ

i M ; Tia BF c

ắ

t

đườ

ng tròn (O

2

) t

ạ

i N. Ch

ứ

ng minh

r

ằ

ng ba

đ

i

ể

m A, M, N th

ẳ

ng hàng.

Bài 5.

Cho tam giác nh

ọ

n ABC, H là tr

ự

c tâm, O là

đ

i

ể

m cách

đề

u các

đỉ

nh c

ủ

a

tam giác. G

ọ

i M là trung

đ

i

ể

m c

ủ

a c

ạ

nh BC. G

ọ

i N là

đ

i

ể

m sao cho O là

trung

đ

i

ể

m c

ủ

a BN.

a) Ch

ứ

ng minh r

ằ

ng : CN = 2.OM và CN = AH.

b) G

ọ

i G là giao

đ

i

ể

m c

ủ

a AM và OH. Ch

ứ

ng minh r

ằ

ng G là tr

ọ

ng tâm

c

ủ

a tam giác ABC.

(

Đườ

ng th

ẳ

ng

đ

i qua 3

đ

i

ể

m O, G, H g

ọ

i là

đườ

ng th

ẳ

ng

Ơ

-le c

ủ

a tam

giác ABC).

Bài 6.

Ch

ứ

ng minh r

ằ

ng : Trong m

ộ

t t

ứ

giác,

đườ

ng th

ẳ

ng

đ

i qua trung

đ

i

ể

m c

ủ

a

hai

đườ

ng chéo và hai

đườ

ng th

ẳ

ng

đ

i qua trung

đ

i

ể

m c

ủ

a các c

ạ

nh

đố

i

di

ệ

n thì

đồ

ng quy.

Dạng 7. Chứng minh tam giác, tứ giác đặc biệt

Bài 1.

Cho tam giác nh

ọ

n ABC n

ộ

i ti

ế

p

đườ

ng tròn (O). G

ọ

i D và E th

ứ

t

ự

là

đ

i

ể

m chính gi

ữ

a các cung nh

ỏ

AB và AC. Dây DE c

ắ

t các dây AB và AC

th

ứ

t

ự

ở

M và N. G

ọ

i P là giao

đ

i

ể

m c

ủ

a BE và CD.

147

a) Ch

ứ

ng minh tam giác AMN là tam giác cân.

b) T

ứ

giác AMPN là hình gì ? Vì sao ?

Bài 2.

Cho

đườ

ng tròn (O) và hai dây AB, CD vuông góc v

ớ

i nhau. V

ẽ

đườ

ng

kính AE (E thu

ộ

c cung nh

ỏ

BD). T

ứ

giác BCDK là hình gì ? Vì sao ?

Bài 3.

Cho n

ử

a

đườ

ng tròn (O ; R) dây AB =

3

R

. Trên cung l

ớ

n AB l

ấ

y các

đ

i

ể

m C và D sao cho C thu

ộ

c cung nh

ỏ

BD. G

ọ

i M, N, P, Q th

ứ

t

ự

là trung

đ

i

ể

m c

ủ

a các dây AD, DC, CB, BA. Tính di

ệ

n tích t

ứ

giác ABCD theo R

trong tr

ườ

ng h

ợ

p MNPQ là hình vuông.

TẬP HỢP ĐIỂM

I. KIẾN THỨC CẦN SỬ DỤNG

1. Tập hợp điểm.

2. Quỹ tích cơ bản.

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

TÌM VÀ CHỨNG MINH VỀ TẬP HỢP ĐIỂM

1. PHƯƠNG PHÁP GIẢI

Cần nắm chắc các tập hợp điểm đã học sau đây :

− Tập hợp các điểm cách đều hai cạnh của một góc là tia phân giác của góc

đó.

− Tập hợp các điểm cách đều hai đầu của một đoạn thẳng là đường trung trực

của đoạn thẳng đó.

Ch

ChCh

Ch 

  

 

3

33

3

148

O

F

E

A

C

B

D

− Tập hợp các điểm cách một đường thẳng a cho trước một khoảng không đổi

h cho trước là hai đường thẳng song song với đường thẳng a và cách đường thẳng

a một khoảng bằng h.

− Tập hợp các điểm cách điểm O cố định một khoảng R > 0 không đổi là

đường tròn (O ; R).

− Tập hợp các điểm nhìn đoạn thẳng AB cố định dưới góc

α

không đổi là hai

cung tròn chứa góc

α

dựng trên đoạn AB và đối xứng với nhau qua AB.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác đều ABC. Các điểm D và E lần lượt chuyển động trên

các cạnh AB và AC sao cho AD = CE. Gọi F là giao điểm của BE và CD. Chứng

minh rằng điểm F thuộc một cung tròn cố định.

Gợi ý : Áp dụng : “Tập hợp các điểm nhìn đoạn thẳng AB cố định dưới góc

α

không đổi là hai cung tròn chứa góc

α

dựng trên đoạn AB và đối xứng với

nhau qua AB”.

Hướng dẫn giải

Tam giác ABC là tam giác đều nên AB = BC = CA và



0

60

= = =A B C

.

Xét hai tam giác ACD và CBE có :

AD = CE (gt) ; AC = CB ;



0

60

= =A C

⇒ ∆ = ∆

ACD CBE

(c-g-c)



⇒

=

ACD CBE

Mà



0

60

+ = =ACD DCB ACB

nên



0

60 .

CBE DCB+ =

Do đó trong tam giác BFC ta có



0

120

BFC =

.

Điểm F chuyển động nhìn đoạn thẳng BC cố

định dưới góc



0

120

=BFC

không đổi nên điểm F

nằm trên hai cung tròn chứa góc 120

0

dựng trên

đoạn BC cố định.

Vì D và E chuyển động trên cạnh AB và AC

nên điểm F chỉ thuộc một cung nói trên như hình

vẽ.

149

M

F

A

C

B

D

E

O'

G

M

O

A

B

C

Ví dụ 2. Cho hình vuông ABCD. Các điểm E và F lần lượt chuyển động trên các

cạnh AB và BC sao cho AE = BF. Gọi M là giao điểm của CE và DF. Chứng

tỏ rằng điểm M thuộc một cung tròn cố định.

Gợi ý :

Áp d

ụ

ng : “T

ậ

p h

ợ

p các

đ

i

ể

m nhìn

đ

o

ạ

n th

ẳ

ng AB c

ố

đị

nh d

ướ

i m

ộ

t

góc 90

0

là

đườ

ng tròn

đườ

ng kính AB”.

Hướng dẫn giải

Vì ABCD là hình vuông nên AB = BC = CD = DA, mà

AE = BF nên BE = CF.

Vì ABCD là hình vuông nên



0

90

= = = =A B C D

.

Từ đó suy ra

∆ = ∆

BCE CDF

(c-g-c), suy ra



BCE CDF

=

, mà



0

90

+ = =BCE ECD BCD

nên



0

90

+ =CDF ECD

.

Do đó

∆

CDM

vuông tại M.

Điểm M chuyển động và nhìn đoạn thẳng CD cố định dưới một góc vuông

nên điểm M thuộc đường tròn đường kính CD.

Vì các điểm E và F lần lượt chuyển động trên các cạnh AB và BC nên điểm

M chỉ thuộc cung phần tư của đường tròn nói trên như hình vẽ.

Ví dụ 3. Cho đường tròn (O ; R) và dây BC < 2R. Điểm A chuyển động trên

đường tròn (O). Chứng tỏ rằng trọng tâm G của tam giác ABC thuộc một

đường tròn cố định.

Gợi ý :

Áp d

ụ

ng

đị

nh ngh

ĩ

a

đườ

ng tròn.

Hướng dẫn giải

Vẽ trung tuyến AM của tam giác ABC, suy

ra M là trung điểm của cạnh BC cố định.

Vì G là trọng tâm của tam giác ABC nên

1

.

3

MG

MA

=

Qua G k

ẻ

đườ

ng th

ẳ

ng song song v

ớ

i AO

c

ắ

t OM

t

ạ

i O’, áp d

ụ

ng

đị

nh lí Ta-let ta có :

1

50

x

O'

E

D

O

A

B

C

' ' 1

3

O G MO MG

OA MO MA

= = =

1

' ; ' .

3 3

R

MO MO O G⇒ = =

Vì O và M c

ố

đị

nh nên O’ c

ố

đị

nh và '

3

=

R

O G .

Đ

i

ể

m G chuy

ể

n

độ

ng cách

đ

i

ể

m O’ c

ố

đị

nh m

ộ

t kho

ả

ng

3

R

không

đổ

i nên

đ

i

ể

m G thu

ộ

c

đườ

ng tròn tâm O’ bán kính

3

R

khi

đ

i

ể

m A chuy

ể

n

độ

ng trên

đườ

ng tròn (O ; R).

Ví dụ 4.

Cho

đườ

ng tròn (O ; R) và dây BC < 2R.

Đ

i

ể

m A chuy

ể

n

độ

ng trên cung

l

ớ

n BC. Trên tia BA l

ấ

y

đ

i

ể

m D sao cho BD = AC. Ch

ứ

ng t

ỏ

r

ằ

ng

đ

i

ể

m D

thu

ộ

c m

ộ

t

đườ

ng c

ố

đị

nh.

Gợi ý :

Áp d

ụ

ng : “T

ậ

p h

ợ

p các

đ

i

ể

m nhìn

đ

o

ạ

n th

ẳ

ng AB c

ố

đị

nh d

ướ

i góc

α

không

đổ

i là hai cung tròn ch

ứ

a góc

α

d

ự

ng trên

đ

o

ạ

n AB và

đố

i x

ứ

ng v

ớ

i

nhau qua AB”.

Hướng dẫn giải

Vì

đườ

ng tròn (O ; R) và dây

BC < 2R c

ố

đị

nh nên s

ố

đ

o cung nh

ỏ

BC không

đổ

i, suy ra



BAC

= α

không

đổ

i.

Trên n

ử

a m

ặ

t ph

ẳ

ng b

ờ

AB không

ch

ứ

a

đ

i

ể

m C, v

ẽ

tia Bx ti

ế

p tuy

ế

n c

ủ

a

đườ

ng tròn (O), suy ra



ABx ACB

=

(cùng b

ằ

ng n

ử

a s

ố

đ

o



AB

).

Trên tia Bx l

ấ

y

đ

i

ể

m E sao cho

BE = BC.

T

ừ

đ

ó suy ra

∆ = ∆

DEB ABC

(c-g-c)



⇒ = = α

EDB BAC

không

đổ

i.

Vì

đườ

ng tròn (O ; R) và dây BC < 2R c

ố

đị

nh nên tia Bx c

ố

đị

nh hay

đ

o

ạ

n

th

ẳ

ng BE c

ố

đị

nh.

151

G

E

C

D

F

A

B

O

Đ

i

ể

m D chuy

ể

n

độ

ng nhìn

đ

o

ạ

n BE c

ố

đị

nh d

ướ

i m

ộ

t góc b

ằ

ng

α

không

đổ

i

nên

đ

i

ể

m D thu

ộ

c hai cung tròn ch

ứ

a góc

α

d

ự

ng trên

đ

o

ạ

n BE và

đố

i x

ứ

ng qua

BE.

Tuy nhiên, vì

đ

i

ể

m A ch

ỉ

chuy

ể

n

độ

ng trên cung l

ớ

n BC nên

đ

i

ể

m D ch

ỉ

thu

ộ

c



BDE

.

Ví dụ 5.

Cho

đ

i

ể

m C thu

ộ

c

đ

o

ạ

n th

ẳ

ng AB c

ố

đị

nh sao cho AC = 3CB.

Đườ

ng

tròn (O) thay

đổ

i nh

ư

ng luôn

đ

i qua A và B. G

ọ

i D là

đ

i

ể

m chính gi

ữ

a cung

AB. Tia DC c

ắ

t

đườ

ng tròn (O) t

ạ

i E. Ch

ứ

ng minh r

ằ

ng

đ

i

ể

m E thu

ộ

c m

ộ

t

đườ

ng tròn c

ố

đị

nh.

Gợi ý :

Áp d

ụ

ng : “T

ậ

p h

ợ

p các

đ

i

ể

m nhìn

đ

o

ạ

n th

ẳ

ng AB c

ố

đị

nh d

ướ

i m

ộ

t

góc 90

0

là

đườ

ng tròn

đườ

ng kính AB”.

Hướng dẫn giải

V

ẽ

đườ

ng kính DF c

ủ

a

đườ

ng tròn (O). Tia FE

c

ắ

t

đườ

ng th

ẳ

ng AB t

ạ

i G. Vì D là

đ

i

ể

m chính

gi

ữ

a cung AB nên



DA DB

=



⇒ =

AED DEB

.

Do

đ

ó EC là phân giác c

ủ

a góc AEB. Vì



FED

ch

ắ

n n

ử

a

đườ

ng tròn (O)



0

90 .

FED⇒ =

Do

đ

ó EG là phân giác ngoài c

ủ

a tam giác

AEB, suy ra

1

3

GB CB

GA CA

= =

(vì AC = 3CB).

Mà AB c

ố

đị

nh nên G c

ố

đị

nh.

Đ

i

ể

m E chuy

ể

n

độ

ng nhìn

đ

o

ạ

n CG c

ố

đị

nh

d

ướ

i



0

90

=CEG

.

V

ậ

y

đ

i

ể

m E thu

ộ

c

đườ

ng tròn

đườ

ng kính CG c

ố

đị

nh.

Dạng 2.

CHỨNG MINH ĐƯỜNG THẲNG, ĐƯỜNG TRÒN ĐI QUA ĐIỂM

CỐ ĐỊNH

1. PHƯƠNG PHÁP GIẢI

Điểm cần tìm là giao của hai đường thẳng cố định ; của một đường thẳng và

một đường tròn cố định hoặc là giao của hai đường tròn cố định.

152

D

E

C

B

O

A

2. CÁC VÍ DỤ

Ví dụ 1. Cho điểm A nằm ngoài đường tròn (O ; R). Một cát tuyến thay đổi đi

qua A cắt đường tròn (O) tại B và C. Chứng minh rằng đường tròn ngoại tiếp tam

giác BOC luôn đi qua một điểm cố định.

Gợi ý : Dự đoán : Giao điểm E của đường tròn ngoại tiếp tam giác BOC với

đoạn OA là điểm cố định và nhận xét rằng AB.AC = AE.AO.

Hướng dẫn giải

Vẽ tiếp tuyến AD với đường tròn

(O), D là tiếp điểm, suy ra



0

90

ADO =

.

Kẻ DE

⊥

OA tại E.

Tam giác AOD vuông tại D, đường

cao DE, áp dụng hệ thức lượng trong

tam giác vuông ta có :

AE.AO = AD

2

.

AD

AE

AO

⇒ = (1)

Vì A và đường tròn (O) cố định nên

D cố định.

Do đó từ (1) suy ra điểm E cố định.

Vì AD là tiếp tuyến và ABC là cát tuyến của đường tròn (O) nên AD

2

=

AB.AC. (2)

Từ (1) và (2) suy ra AE.AO = AB.AC

⇒ =

AB AE

AO AC

⇒

∆

ABE



∆

AOC

(c-g-c)

⇒



=

AEB ACO

⇒

Tứ giác BCOE nội tiếp.

Vậy đường tròn ngoại tiếp tam giác BOC đi qua điểm E cố định.

Ví dụ 2. Cho đường tròn (O ; R) và dây BC = R

3

cố định. Điểm A chuyển động

trên cung lớn BC sao cho tam giác ABC luôn là tam giác nhọn. Gọi H là trực

tâm của tam giác ABC. Chứng minh đường thẳng đi qua A và vuông góc với

OH luôn đi qua một điểm cố định.

Gợi ý :

D

ự

đ

oán :

Đườ

ng th

ẳ

ng

đ

i qua A và vuông góc v

ớ

i OH

đ

i qua

đ

i

ể

m

chính gi

ữ

a N c

ủ

a cung nh

ỏ

BC. T

ừ

đ

ó tìm cách ch

ứ

ng minh AN là phân giác c

ủ

a

góc BAC ho

ặ

c ON

⊥

BC.

153

M

D

N

H

F

E

B

C

O

A

Hướng dẫn giải

Kẻ bán kính ON vuông góc với BC tại M suy ra

MB = MC =

3

2 2

=

BC R

.

∆

BMO

vuông tại M

⇒



3

2

sin

2

R

MB

BOM

OB R

= = =



0

60

BOM

⇒

=

.

∆

BOC

cân tại O (OB = OC = R), đường cao OM nên đồng thời cũng là phân

giác của góc BOC



0

2 120

⇒

= =BOC BOM

.

Vì



BAC

là góc nội tiếp và



BOC

là góc ở tâm cùng chắn cung nhỏ BC nên



0 0

1 1

.120 60

2 2

= = =BAC BOC

V

ẽ

các

đườ

ng cao AD, BE, CF

đồ

ng quy t

ạ

i tr

ự

c tâm H c

ủ

a tam giác ABC.

T

ứ

giác AEHF có



0 0 0

90 90 180

+ = + =AEH AFH

nên t

ứ

giác AEHF n

ộ

i ti

ế

p



0

180

⇒

+ =EAF EHF

, mà



0

60

=EAF

nên



0

120

=EHF



0

120

⇒

=BHC

(

đđ

).

Do

đ

ó



0

120

= =BHC BOC

. T

ứ

giác BHOC có hai

đỉ

nh liên ti

ế

p H và O cùng

nhìn c

ạ

nh BC d

ướ

i cùng m

ộ

t góc nên BHOC n

ộ

i ti

ế

p.

D

ễ

th

ấ

y các tam giác BON và CON là các tam giác

đề

u, suy ra

NB = NC = NO = R.

Do

đ

ó N là tâm

đườ

ng tròn ngo

ạ

i ti

ế

p t

ứ

giác BHOC

⇒

NH = R.

Vì ON và AH cùng vuông góc v

ớ

i BC nên ON // AH



⇒

=

ONA NAH

(so le

trong).

∆

AON

cân t

ạ

i O (OA = ON = R)



⇒

=

ONA OAN

⇒



=

OAN NAH

⇒

AN

là phân giác c

ủ

a



OAH

.

Ta l

ạ

i có NO = NH = R nên O và H

đố

i x

ứ

ng v

ớ

i nhau qua AN

⇒

AN

⊥

OH.

V

ậ

y

đườ

ng th

ẳ

ng qua A và vuông góc v

ớ

i OH luôn

đ

i qua

đ

i

ể

m N c

ố

đị

nh.

154

H

F

E

O

B

C

A

D

Ví dụ 3 :

Cho tam giác nh

ọ

n ABC n

ộ

i ti

ế

p

đườ

ng tròn (O).

Đ

i

ể

m D chuy

ể

n

độ

ng

trên cung nh

ỏ

BC. G

ọ

i E và F l

ầ

n l

ượ

t là chân

đườ

ng vuông góc k

ẻ

t

ừ

A

đế

n

các

đườ

ng th

ẳ

ng DB và DC. Ch

ứ

ng minh r

ằ

ng

đườ

ng th

ẳ

ng EF luôn

đ

i qua

m

ộ

t

đ

i

ể

m c

ố

đị

nh.

Gợi ý :

D

ự

đ

oán : Giao

đ

i

ể

m H c

ủ

a

đườ

ng th

ẳ

ng EF và c

ạ

nh BC là chân

đườ

ng cao k

ẻ

t

ừ

đỉ

nh A. T

ừ

đ

ó tìm cách ch

ứ

ng minh t

ứ

giác AHBE n

ộ

i ti

ế

p.

Hướng dẫn giải

G

ọ

i H là giao

đ

i

ể

m c

ủ

a hai

đườ

ng th

ẳ

ng EF và

BC.

Vì



0 0 0

90 90 180

+ = + =AEB AFB

nên t

ứ

giác

AEBF n

ộ

i ti

ế

p



⇒

=

AEF ADF

(hai góc n

ộ

i ti

ế

p

cùng ch

ắ

n



FA

). (1)

Ta có



=

ADC ABC

(góc n

ộ

i ti

ế

p cùng ch

ắ

n



AC

). (2)

T

ừ

(1) và (2) suy ra



=

AEH ABH

. T

ứ

giác AEBH có hai

đỉ

nh liên ti

ế

p E và B

cùng nhìn c

ạ

nh AH d

ướ

i hai góc b

ằ

ng nhau nên AEBH n

ộ

i ti

ế

p

G

ọ

i H là giao

đ

i

ể

m c

ủ

a hai

đườ

ng th

ẳ

ng EF và BC.

Vì



0 0 0

90 90 180

+ = + =AEB AFB

nên t

ứ

giác AEBF n

ộ

i ti

ế

p



⇒

=

AEF ADF

(hai góc n

ộ

i ti

ế

p cùng ch

ắ

n



FA

). (1)

Ta có



=

ADC ABC

(góc n

ộ

i ti

ế

p cùng ch

ắ

n



AC

). (2)

T

ừ

(1) và (2) suy ra



=

AEH ABH

. T

ứ

giác AEBH có hai

đỉ

nh liên ti

ế

p E và B

cùng nhìn c

ạ

nh AH d

ướ

i hai góc b

ằ

ng nhau nên AEBH n

ộ

i ti

ế

p. Do

đ

ó



0

180

AEB AHB+ =

, mà



0

90

=AEB

nên



0

90

=AHB

. Vì

∆

ABC

c

ố

đị

nh nên

đ

i

ể

m H c

ố

đị

nh.

V

ậ

y

đườ

ng th

ẳ

ng EF luôn

đ

i qua

đ

i

ể

m H c

ố

đị

nh.

Ví dụ 4 : Đ

i

ể

m C chuy

ể

n

độ

ng trên n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB. Trên

n

ử

a m

ặ

t ph

ẳ

ng b

ờ

BC không ch

ứ

a

đ

i

ể

m A, v

ẽ

tia Bx vuông góc v

ớ

i BC. Trên

tia Bx l

ấ

y

đ

i

ể

m D sao cho BD = 2BC. Ch

ứ

ng minh r

ằ

ng

đườ

ng th

ẳ

ng CD

luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh.

Gợi ý :

D

ự

đ

oán : Giao

đ

i

ể

m E c

ủ

a

đườ

ng th

ẳ

ng CD và n

ử

a

đườ

ng tròn (O)

là

đ

i

ể

m c

ố

đị

nh. T

ừ

đ

ó tìm cách ch

ứ

ng minh s

ố

đ

o cung AE không

đổ

i.

155

H

K

F

E

c

O

A

B

D

Hướng dẫn giải

x

E

D

O

A B

C

Tam giác BCD vuông t

ạ

i B, ta có



1

tan

2 2

= = =

⇒

= α

BC BC

D BDC

BD BC

không

đổ

i.

Kéo dài DC c

ắ

t

đườ

ng tròn t

ạ

i E. Vì



0

90

=ACB

(ch

ắ

n n

ử

a

đườ

ng tròn (O)),

suy ra



0

90

ACE BCD+ =

.

Tam giác BCD vuông t

ạ

i B nên



0

90

+ =BCD BDC

. Do

đ

ó



= α

ACE

, suy ra

s

đ



2

= α

AE

không

đổ

i, mà A và n

ử

a

đườ

ng tròn (O) c

ố

đị

nh nên

đ

i

ể

m E c

ố

đị

nh.

V

ậ

y

đườ

ng th

ẳ

ng CD luôn

đ

i qua

đ

i

ể

m E c

ố

đị

nh.

Ví dụ 5 :

G

ọ

i C là

đ

i

ể

m chính gi

ữ

a cung AB c

ủ

a n

ử

a

đườ

ng tròn tâm O

đườ

ng

kính AB.

Đ

i

ể

m D chuy

ể

n

độ

ng trên

đườ

ng kính AB. G

ọ

i E và F l

ầ

n l

ượ

t là

hình chi

ế

u vuông góc c

ủ

a D lên CA và CB. Ch

ứ

ng minh

đườ

ng th

ẳ

ng

đ

i qua

D và vuông góc v

ớ

i EF luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh.

Gợi ý :

D

ự

đ

oán : Giao

đ

i

ể

m K c

ủ

a

đườ

ng th

ẳ

ng

đ

i qua D và vuông góc v

ớ

i

EF

v

ớ

i

đườ

ng th

ẳ

ng CO là

đ

i

ể

m c

ố

đị

nh. Nh

ậ

n xét OK = OC ho

ặ

c K là

đ

i

ể

m

chính gi

ữ

a c

ủ

a n

ử

a

đườ

ng tròn (O) còn l

ạ

i.

Hướng dẫn giải

T

ứ

giác DECF có



0 0 0

90 90 180

+ = + =DEC DFC

⇒

T

ứ

giác DECF n

ộ

i ti

ế

p



.

DCF DEF

⇒

=

(1)

Gi

ả

s

ử

đườ

ng th

ẳ

ng

đ

i qua D và vuông góc

v

ớ

i EF t

ạ

i H c

ắ

t

đườ

ng th

ẳ

ng CO t

ạ

i K.

Tam giác DEH vuông t

ạ

i H



0

90 .

HED HDE

⇒

+ =

(2)

156

x

o'

E

C

o

A

B

D

Tam giác DCF vuông t

ạ

i F



0

90 .

FCD FDC

⇒

+ =

(3)

T

ừ

(1) (2) và (3)



.

HDE FDC

⇒

=

(4)

Ta có



0

90

=ACB

(góc n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn (O)).

Vì C là

đ

i

ể

m chính gi

ữ

a cung AB nên CA = CB.

Do

đ

ó tam giác ABC vuông cân t

ạ

i C, suy ra



0

45

CAB CBA= =

.

T

ừ

đ

ó suy ra



0

45 .

ADE BDF= =

(5)

T

ừ

(4) và (5) suy ra



ADH BDC

=

, mà



=

ADH BDK

(

đố

i

đỉ

nh) nên



=

BDC BDK

. (6)

Vì C là

đ

i

ể

m chính gi

ữ

a cung AB c

ủ

a n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB

nên CK

⊥

AB t

ạ

i O. (7)

T

ừ

(6) và (7) suy ra

∆

CDK

cân t

ạ

i D

⇒

DO là trung tuy

ế

n c

ủ

a

∆

CDK

⇒

OK = OC. Do

đ

ó

đ

i

ể

m K c

ố

đị

nh. V

ậ

y

đườ

ng th

ẳ

ng

đ

i qua D và vuông góc v

ớ

i

EF luôn

đ

i qua

đ

i

ể

m c

ố

đị

nh K.

Ví dụ 6 :

Cho n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB = 2R. Hai

đ

i

ể

m C và D

chuy

ể

n

độ

ng trên n

ử

a

đườ

ng tròn sao cho dây CD = R, D thu

ộ

c cung AC. G

ọ

i

E là giao

đ

i

ể

m c

ủ

a hai

đườ

ng th

ẳ

ng AD và BC. Ch

ứ

ng minh r

ằ

ng

đườ

ng

th

ẳ

ng

đ

i qua E và vuông góc v

ớ

i CD luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh.

Gợi ý :

D

ự

đ

oán :

đườ

ng th

ẳ

ng

đ

i qua E và vuông góc v

ớ

i CD

đ

i qua tâm O’

c

ủ

a

đườ

ng tròn ngo

ạ

i ti

ế

p tam giác AEB. T

ừ

đ

ó tìm cách ch

ứ

ng minh

đườ

ng tròn

(O’) c

ố

đị

nh, t

ứ

c là ch

ứ

ng minh



AEB

không

đổ

i.

Hướng dẫn giải

Tam giác COD là tam giác

đề

u (vì OC =

OD = CD = R)



0

60

⇒

=

⇒

COD

s

đ



0

60

=CD

. Góc AEB là

góc có

đỉ

nh

ở

bên ngoài

đườ

ng tròn



(

)

0 0 0

180 60 : 2 60

⇒

= − =AEB

.

D

ự

ng

đườ

ng tròn tâm O’ ngo

ạ

i ti

ế

p tam giác

157

AEB



0

' 120

⇒

=AO B

. Ta l

ạ

i có tam giác AO’B cân t

ạ

i O’ và AB c

ố

đị

nh nên O’

c

ố

đị

nh. Trên n

ử

a m

ặ

t ph

ẳ

ng b

ờ

AE không ch

ứ

a

đ

i

ể

m B, v

ẽ

tia Ex

⊥

O’E.

Ex là tia ti

ế

p tuy

ế

n t

ạ

i E c

ủ

a

đườ

ng tròn (O’)



⇒

=

ABE AEx

(cùng b

ằ

ng n

ử

a

s

đ



AE

). (1)

T

ứ

giác ABCD n

ộ

i ti

ế

p

đườ

ng tròn (O)



⇒

=

ABC EDC

(cùng bù v

ớ

i góc

ADC). (2)

T

ừ

(1) và (2)



⇒

=

AEx EDC

, mà hai góc này

ở

v

ị

trí so le trong nên E

x

// CD.

Do

đ

ó O’E

⊥

CD.

V

ậ

y

đườ

ng th

ẳ

ng

đ

i qua E và vuông góc v

ớ

i CD luôn

đ

i qua

đ

i

ể

m O’ c

ố

đị

nh.

III. BÀI TẬP VẬN DỤNG

Dạng 1. Tìm và chứng minh về tập hợp điểm

Bài 1. Cho đường tròn (O ; R) và dây BC cố định. Điểm A chuyển động trên

cung lớn BC. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng

trung điểm M của AH thuộc một đường tròn cố định.

Bài 2. Cho nửa đường tròn (O ; R) đường kính AB. Điểm C chuyển động trên

nửa đường tròn (O ; R). Về phía ngoài tam giác ABC, vẽ tam giác đều

ACE. Chứng minh rằng điểm E thuộc một đường cố định.

Bài 3. Cho điểm A nằm ngoài đường tròn (O ; R). Một đường thẳng quay quanh

điểm A cắt đường tròn (O ; R) ở B và C. Chứng minh rằng tâm đường tròn

ngoại tiếp tam giác BOC thuộc một đường cố định.

Bài 4. Cho hai đường tròn (O ; R) và (O’ ; r) với R > r tiếp xúc với nhau tại A.

Đường thẳng đi qua A cắt (O ; R) và (O’ ; r) thứ tự ở B và C. Chứng minh

rằng trung điểm M của đoạn BC thuộc một đường tròn cố định.

Dạng 2. Chứng minh đường thẳng, đường tròn đi qua điểm cố định

Bài 1. Cho đường tròn (O ; R) và dây AB. Điểm C chuyển động trên đường tròn

(O ; R). Điểm D thuộc dây BC sao cho CD = 2BD. Chứng minh rằng

đường thẳng đi qua D và vuông góc với AC luôn đi qua một điểm cố định.

158

Bài 2. Cho đoạn thẳng AB và đường thẳng d vuông với đoạn AB tại C (AC < CB).

Điểm D chuyển động trên d (D khác C). Chứng minh rằng đường tròn đi

qua trung điểm ba cạnh của tam giác ABD luôn đi qua một điểm cố định.

Bài 3. Cho tam giác ABC vuông tại A, đường cao AH (AB < AC). Điểm D

chuyển động trên đường tròn (A ; AH) sao cho D nằm ngoài đường thẳng

BC. Gọi E và F thứ tự là trung điểm của DB và DC. Chứng minh đường

tròn ngoại tiếp

∆

DEF

luôn đi qua một điểm cố định.

Bài 4. Cho tam giác nhọn ABC nội tiếp đường tròn (O) đường kính AD và ngoại

tiếp đường tròn (I). Điểm E chuyển động trên đường tròn (I). Gọi F là

điểm đối xứng với E qua I. Chứng minh đường thẳng đi qua trung điểm

của các đoạn AE và DF luôn đi qua một điểm cố định.

Bài 5. Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Một đường

thẳng quay quanh A cắt các đường tròn (O) và (O’) thứ tự ở C và D.

Chứng minh rằng đường trung trực của đoạn thẳng CD luôn đi qua một

điểm cố định.

CỰC TRỊ HÌNH HỌC

I. KIẾN THỨC CẦN SỬ DỤNG

1. Giá trị lớn nhất, nhỏ nhất của các hàm số lượng giác.

2. Bất đẳng thức cơ bản.

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1.

BẤT ĐẲNG THỨC HÌNH HỌC

1. PHƯƠNG PHÁP GIẢI

− Tính đồng biến, nghịch biến giữa góc nhọn và các tỉ số lượng giác của nó.

Ch

ChCh

Ch 

  

 

4

44

4

159

H

L

A

B

C

K

M

− Vị trí tương đối của một điểm và đường tròn, của đường thẳng và đường

tròn, của hai đường tròn.

− Liên hệ giữa đường kính và dây cung, giữa dây và khoảng cách đến tâm,

giữa dây và cung

− Vận dụng các tính chất của bất đẳng thức và một số bất đẳng thức thường

sử dụng trong phân môn đại số như : Bất đẳng thức Cô-si ; 2(x

2

+ y

2

)

≥

(x + y)

2

;

(ax + by)

2

≤

(a

2

+ b

2

)(x

2

+ y

2

) ; ...

Chú ý về điều kiện xảy ra dấu “=” của mỗi bất đẳng thức đã áp dụng.

2. CÁC VÍ DỤ

Ví dụ 1. Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, BC và CA lần

lượt lấy các điểm K, L và M sao cho tam giác KLM vuông cân tại K. Chứng

minh rằng :

1

5

≥

KLM

ABC

S

.

Gợi ý : Áp dụng bất đẳng thức : (ax + by)

2

≤

(a

2

+ b

2

)(x

2

+ y

2

), dấu “=” xảy

ra khi

=

a b

x y

.

Hướng dẫn giải

Vẽ

⊥

LH AB

. Dễ thấy

∆ = ∆

KLH MKA

(ch-gn), suy ra

HL AK x

= =

;

= =

HK AM y

.

Vì tam giác ABC vuông cân tại A nên

BHL cũng là tam giác vuông cân tại H

⇒ = =

HL HB x

.

Vì tam giác ABC vuông cân tại A nên

2

ABC

S AB

=

( )

(

)

(

)

(

)

2

2 2 2 2 2 2

2 2 1 5

x y x y x y

= + ≤ + + = +

Ví dụ 2.

Cho tam giác ABC có ba góc nh

ọ

n. Ch

ứ

ng minh r

ằ

ng :

a) S

ABC

=

1

. .sin

2

AB AC A

;

160

H

B

C

A

b)

sin sin sin

= =

BC CA AB

A B C

.

c)

2 2 2

cotg cotg cotg cotg cotg cotg

AB BC CA

A B B C C A

= =

+ + +

;

d) AB

2

+ AC

2

> BC

2

.

Gợi ý : Áp dụng định nghĩa về tỉ số lượng giác của góc nhọn, công thức tính

diện tích tam giác, tính chất của bất đẳng thức.

Hướng dẫn giải

a) Vẽ đường cao BH của tam giác ABC.

Ta có S

ABC

=

1

.

2

AC BH

(1)

Tam giác ABH vuông tại H, ta có BH = AB.sinA (2)

Thay (2) vào (1) ta được S

ABC

=

1

. .sin .

2

AB AC A

b) Theo câu a) ta có :

S

ABC

=

1

. .sin

2

AB AC A

=

1

. .sin

2

BA BC B

=

1

. .sin

2

CB CA C

⇒

. .

sin sin sin 2

= = =

ABC

BC CA AB BC CA AB

A B C S

c)

∆

ABH

vuông tại H, ta có cotgA =

AH

BH

.

∆

BCH

vuông tại H, ta có

cotgC =

CH

BH

. Do đó

cotgA + cotgC =

AH

BH

+

CH

BH

=

+

=

AH CH AC

BH BH

⇒

cotg cotg

AC

BH

A C

=

+

⇒

2S

ABC

=

.

AC BH

=

2

cotg cotg

AC

A C

+

.

161

D

A

O

M

B

C

V

ậ

y :

2 2 2

2

cotg cotg cotg cotg cotg cotg

ABC

AB BC CA

S

A B B C C A

= = =

+ + +

.

d) Ta có

2 2 2

cotg cotg cotg cotg cotg cotg

AB BC CA

A B B C C A

= =

+ + +

=

2 2

2cotg cotg cotg

AB CA

A B C

+

+ +

⇒

2 2

2

2cotg cotg cotg

1

cotg cotg

AB CA A B C

B C

BC

+ + +

= >

+

⇒

AB

2

+ AC

2

> BC

2

.

Ví dụ 3.

Cho tam giác ABC cân t

ạ

i A (



0

90

<A

), n

ộ

i ti

ế

p

đườ

ng tròn (O ; R).

Đ

i

ể

m M chuy

ể

n

độ

ng trên cung l

ớ

n BC.

Ch

ứ

ng minh r

ằ

ng MB + MC

≤

AB + AC, d

ấ

u “=” x

ả

y ra khi nào ?

Gợi ý : Tạo ra đoạn thẳng bằng tổng MB + MC hợp lí, rồi áp dụng quy tắc ba

điểm.

Hướng dẫn giải

Trên tia

đố

i c

ủ

a tia MB l

ấ

y

đ

i

ể

m D sao cho

MD = MC.

Tam giác ABC cân t

ạ

i A



.

ABC ACB

⇒ =

Ta có



=

ACB AMB

(hai góc n

ộ

i ti

ế

p cùng

ch

ắ

n



AB

).

D

ễ

th

ấ

y



0

180

+ =ABC AMC

;



0

180 .

AMB AMD+ =

T

ừ

đ

ó suy ra

AMD AMC

∆ = ∆

(c-g-c)

⇒

AD = AC.

Xét ba

đ

i

ể

m A, B, D ta có : BD

≤

AB + AD, d

ấ

u “=” x

ả

y ra khi M trùng A.

Mà BD = MB + MD = MB + MC ; AD = AC nên MB + MC

≤

AB + AC, d

ấ

u

“=” x

ả

y ra khi M

≡

A.

162

E

I

B

C

O

D

A

Ví dụ 4.

Cho

đườ

ng tròn (O ; R) và dây BC =

3

R

.

Đ

i

ể

m A chuy

ể

n

độ

ng trên

cung l

ớ

n BC. G

ọ

i (I ; r) là

đườ

ng tròn n

ộ

i ti

ế

p tam giác ABC. Ch

ứ

ng minh

IA

≤

R, d

ấ

u “=” x

ả

y ra khi nào ?

Gợi ý : Áp dụng tính chất : Trong một đường tròn thì đường kính là dây cung

lớn nhất.

Hướng dẫn giải

Tia AI c

ắ

t

đườ

ng tròn (O ; R) t

ạ

i D. V

ẽ

đườ

ng kính BE c

ủ

a (O ; R).

D

ễ

th

ấ

y

∆

BCE

vuông t

ạ

i C



0

3 3

sin 60

2 2

⇒

= = =

⇒

=

BC R

E E

BE R

.



0 0

2 2.60 120

⇒ = = =BOC BEC

⇒

s

đ



0

120

=BC

.

Vì (I ; r) là

đườ

ng tròn n

ộ

i ti

ế

p

∆

ABC

nên AI là

phân giác c

ủ

a



BAC



DAB DAC

⇒ =

⇒

s

đ



=

DB

s

đ



DC

= 60

0



0

60

⇒ =BOD

.

Tam giác BOD có OB = OD = R và



0

60

=BOD

⇒ ∆

BOD

là tam giác

đề

u

⇒

BD = R.

D

ễ

th

ấ

y



(

)

1

2

= = +

DBI DIB BAC ABC

⇒ ∆

DBI

cân t

ạ

i D

⇒

DI = DB = R.

Vì AD là dây cung c

ủ

a (O ; R) nên AD

≤

2R

⇒

AI + DI

≤

R

⇒

AI

≤

R (vì

DI = R), d

ấ

u “=” x

ả

y ra khi AD = 2R

⇔

A là

đ

i

ể

m chính gi

ữ

a cung l

ớ

n BC.

Dạng 2.

GIÁ TRỊ NHỎ NHẤT, GIÁ TRỊ LỚN NHẤT CỦA ĐẠI LƯỢNG

HÌNH HỌC

1. PHƯƠNG PHÁP GIẢI

− Áp dụng nguyên tắc về ba điểm : “Với ba điểm A, B, M ta luôn có

MA + MB

≥

AB, dấu “=” xảy ra khi và chỉ khi M nằm giữa hai điểm A và B”.

163

x

y

N

C

O

A

B

M

− Khoảng cách từ một điểm đến một đường thẳng có độ dài ngắn nhất.

2. CÁC VÍ DỤ

Ví dụ 1. Cho nửa đường tròn O đường kính AB = 2R. Gọi C là trung điểm của

OA. Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn, vẽ các tia tiếp

tuyến Ax và By. Các điểm M và N lần lượt chuyển động trên các tia Ax và By

sao cho



0

90

=MCN

. Xác định vị trí của các điểm M và N để diện tích tam

giác MCN đạt giá trị nhỏ nhất.

Gợi ý : Áp dụng điều kiện xảy ra dấu “=” trong bất đẳng thức Cô-si cho hai

số dương, khi biết tổng hoặc tích của chứng không đổi.

Hướng dẫn giải

Vì Ax và By là các tia tiếp tuyến của (O) đường kính AB nên

Ax

⊥

AB ; By

⊥

AB.

Ta có



0

90

+ =

ACM BCN

(vì



0

90

=

MCN

).

∆

ACM

vuông tại A



0

90

⇒

+ =ACM AMC

.



⇒

=

AMC BCN

⇒

∆

ACM



∆

BNC

(g-g)

⇒ =

AM BC

CM NC

(1).

∆

MCN

vuông tại C nên

1 1 1

.C .C .

2 2

.

= =

MCN

S CM N CA B

CA CB

CM CN

(*)

Ta lại có :

2 2

1

.

2

 

   

≤ +

 

   

   

 

 

CA CB CA CB

CM CN CM CN

(2)

T

ừ

(1) và (2) suy ra

2 2

1 1

.

2 2

 

   

≤ + =

 

   

   

 

 

CA CB CA AM

CM CN CM CM

(vì CA

2

+ AM

2

= CM

2

).

164

K

H

N

C

A

O

B

M

T

ừ

(*) ta có

2

3 3

.C .

2 2 4

≥ = =

MCN

R R R

S CA B

, d

ấ

u “=” x

ả

y ra khi =

CA CB

CM CN

;

= ⇔ =

AM CB

AM CA

CM CN

.

V

ậ

y

MCN

S

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t b

ằ

ng

2

3

4

R

đạ

t

đượ

c khi AM = AC =

2

R

và

BN = BC =

3

2

R

.

Ví dụ 2.

Cho

đườ

ng tròn (O ; R) và hai bán kính OA, OB vuông góc v

ớ

i nhau.

Đ

i

ể

m C là

đ

i

ể

m chính gi

ữ

a c

ủ

a cung nh

ỏ

AB.

Đườ

ng th

ẳ

ng d

đ

i qua

đ

i

ể

m C

c

ắ

t các tia OA và OB l

ầ

n l

ượ

t t

ạ

i M và N. Xác

đị

nh v

ị

trí c

ủ

a

đườ

ng th

ẳ

ng d

để

độ

dài

đ

o

ạ

n th

ẳ

ng MN ng

ắ

n nh

ấ

t.

Gợi ý :

Áp d

ụ

ng

đ

i

ề

u ki

ệ

n x

ả

y ra d

ấ

u “=” trong b

ấ

t

đẳ

ng th

ứ

c Cô-si cho hai

s

ố

d

ươ

ng, khi bi

ế

t t

ổ

ng ho

ặ

c tích c

ủ

a ch

ứ

ng không

đổ

i.

Hướng dẫn giải

V

ẽ

CH // OB (M

∈

tia OA) ;

CK // OA (K

∈

tia OB).

Vì C là

đ

i

ể

m chính gi

ữ

a c

ủ

a cung

nh

ỏ

AB nên



0

45

COA COB= =

(vì



0

90

=AOB

).

D

ễ

th

ấ

y CH = HO = OK = CK =

2

R

; MH =

x

; NK =

y

.

D

ễ

th

ấ

y

∆

MHC



∆

CKN

(g-g)

⇒

MH CH

CK NK

=

2

. .

2

R

MH NK CH CK xy

⇒

=

⇒

=

(không

đổ

i)

Tam giác OMN vuông t

ạ

i O, ta có :

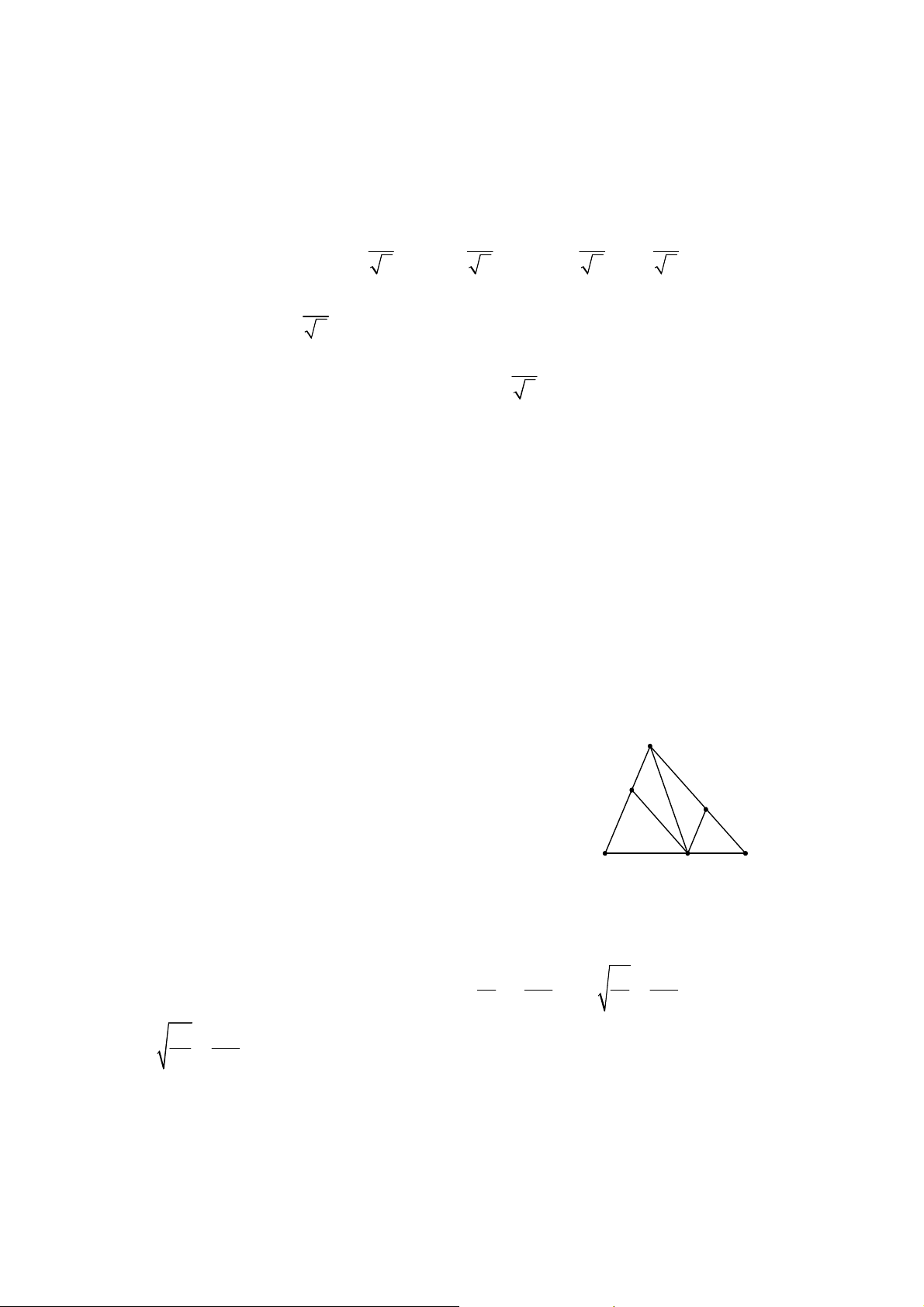
165

F

E

B

C

A

D

2 2 2

MN OM ON

= +

2 2

2

2 2 2 2

R R R R

x y x y

      

= + + + ≥ + +

      

      

( )

2 2

2 4

2

R

R x y R

 

= + + ≥

 

 

2

⇒ ≥

MN R

,

đẳ

ng th

ứ

c x

ả

y ra khi

2

= =

R

x y

⇔

d

⊥

OC t

ạ

i C.

V

ậ

y : min

2

=

MN R

khi và ch

ỉ

khi d

⊥

OC t

ạ

i C.

Ví dụ 3.

Cho tam giác ABC.

Đ

i

ể

m D chuy

ể

n

độ

ng trên c

ạ

nh BC. Trên các c

ạ

nh

AB, AC th

ứ

t

ự

l

ấ

y các

đ

i

ể

m E, F sao cho DE // AC và DF // AB. Xác

đị

nh v

ị

trí

đ

i

ể

m D

để

:

a) T

ứ

giác AEDF là hình thoi.

b) Di

ệ

n tích t

ứ

giác AEDF

đạ

t giá tr

ị

l

ớ

n nh

ấ

t.

Gợi ý :

Áp d

ụ

ng

đ

i

ề

u ki

ệ

n x

ả

y ra d

ấ

u “=” trong b

ấ

t

đẳ

ng th

ứ

c 2(x

2

+ y

2

)

≥

(x

+ y)

2

, khi bi

ế

t x + y không

đổ

i ho

ặ

c t

ổ

ng x

2

+ y

2

không

đổ

i.

Hướng dẫn giải

a) D

ễ

th

ấ

y AEDF là hình bình hành. Hình bình

hành AEDF là hình thoi

⇔

AD là phân giác c

ủ

a góc

BAC. V

ậ

y khi D là giao

đ

i

ể

m c

ủ

a tia phân giác góc

BAC và c

ạ

nh BC thì t

ứ

giác AEDF là hình thoi.

b)

Đặ

t AB = a ; AC = b ; DF = x ; DE = y.

Ta có S

AEDF

+ S

BED

+ S

CFD

= S

ABC

.

Vì S

ABC

không

đổ

i nên S

AEDF

l

ớ

n nh

ấ

t khi S

BED

+

S

CDF

nh

ỏ

nh

ấ

t.

Đặ

t S

ABC

= S ; S

BED

= S

1

; S

CDF

= S

2

.

Vì DF // AB nên

∆

BED



∆

BAC

2

1 1

 

⇒ = ⇒ =

 

 

S S

BD BD

S BC S BC

; T

ươ

ng t

ự

2

=

S

CD

S BC

.

166

y

x

d

J

I

N

B

O

M

A

Do

đ

ó

1 2

1+ = ⇒ + =

S S

S S S

S S

.

Ta l

ạ

i có

( )

(

)

2

1 2 1 2

2 + ≥ +

S S S S

nên

1 2

2

+ ≥

S

S S

, d

ấ

u “=” x

ả

y ra khi

1 2

S S

=

1 2

S S DB DC

⇔ = ⇔ = ⇔

D là trung

đ

i

ể

m c

ủ

a BC.

Nh

ư

v

ậ

y S

AEDF

l

ớ

n nh

ấ

t b

ằ

ng n

ử

a S

ABC

đạ

t

đượ

c khi D là trung

đ

i

ể

m c

ủ

a BC.

Ví dụ 4.

Cho góc nh

ọ

n xOy và

đ

i

ể

m M n

ằ

m trong góc xOy. M

ộ

t

đườ

ng th

ẳ

ng d

đ

i

qua M c

ắ

t Ox và Oy l

ầ

n l

ượ

t t

ạ

i A và B.

Xác

đị

nh v

ị

trí c

ủ

a

đườ

ng th

ẳ

ng d sao cho t

ổ

ng

1 1

+

MA MB

đạ

t giá tr

ị

l

ớ

n nh

ấ

t.

Gợi ý :

Áp d

ụ

ng tính ch

ấ

t : “Kho

ả

ng cách t

ừ

m

ộ

t

đ

i

ể

m

đế

n m

ộ

t

đườ

ng th

ẳ

ng

có

độ

dài ng

ắ

n nh

ấ

t”.

Hướng dẫn giải

D

ự

ng hình bình hành OBMN.

G

ọ

i I là giao

đ

i

ể

m c

ủ

a MN và Ox.

T

ừ

gi

ả

thi

ế

t suy ra I là

đ

i

ể

m c

ố

đị

nh.

V

ẽ

IJ // d (v

ớ

i J

∈

OM). T

ừ

hình thang OMAN, áp d

ụ

ng

đị

nh lí

Ta-lét ta

đượ

c

1 1 1

+ =

MA ON IJ

.

Vì OBMN là hình bình hành

nên ON = MB.

Do

đ

ó

1 1 1

+ =

MA MB IJ

.

T

ổ

ng

1 1

+

MA MB

đạ

t giá tr

ị

l

ớ

n nh

ấ

t

⇔

IJ

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t

⇔ ⊥ ⇔ ⊥

IJ OM d OM

.

Ví dụ 5.

Cho hình vuông ABCD có

độ

dài c

ạ

nh b

ằ

ng 2a. V

ẽ

đườ

ng tròn tâm B

bán kính b

ằ

ng a. Tìm

đ

i

ể

m E trên

đườ

ng tròn sao cho EA + 2ED

đạ

t giá tr

ị

nh

ỏ

nh

ấ

t, tính giá tr

ị

nh

ỏ

nh

ấ

t

đ

ó theo a.

167

H

E

F

A

C

B

D

E

Gợi ý :

Áp d

ụ

ng nguyên t

ắ

c v

ề

ba

đ

i

ể

m : “V

ớ

i ba

đ

i

ể

m A, B, M ta luôn có

MA + MB

≥

AB, d

ấ

u “=” x

ả

y ra khi và ch

ỉ

khi M n

ằ

m gi

ữ

a hai

đ

i

ể

m A và B”.

Hướng dẫn giải

G

ọ

i E là m

ộ

t

đ

i

ể

m thu

ộ

c

đườ

ng tròn (B ; a).

Trên c

ạ

nh AB l

ấ

y

đ

i

ể

m F sao cho BF =

2

a

.

Xét

∆

BEF

và

∆

BAE

có :



ABE

là góc

chung và

=

BF BE

BE BA

(cùng b

ằ

ng

1

2

).

Do

đ

ó

∆

BEF



∆

BAE

(c-g-c)

1

2

⇒ = ⇒ =

EF

AE EF

AE

.

Do

đ

ó EA + 2ED = 2EF + 2ED

= 2(EF + ED)

≤

DF,

đẳ

ng th

ứ

c x

ả

y ra khi E n

ằ

m gi

ữ

a D và F, suy ra E là giao

đ

i

ể

m c

ủ

a DF và

đườ

ng tròn (B ; a).

Đ

i

ề

u này luôn x

ả

y ra, vì BF =

2

a

< a ; BD = 2a

2

nên

F n

ằ

m trong còn D thì n

ằ

m ngoài

đườ

ng tròn (B ; a),

do

đ

ó DF luôn c

ắ

t

đườ

ng tròn (B ; a).

Tam giác ADF vuông t

ạ

i A nên

DF

2

=

( )

2

3 25

2

2 4

 

+ =

 

 

a a

a

5

2,5

2

⇒ = =

a

DF a

.

V

ậ

y giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a t

ổ

ng EA + 2ED

b

ằ

ng 2,5a.

Ví dụ 6.

Cho n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB = 2R. Trên cùng n

ử

a m

ặ

t

ph

ẳ

ng b

ờ

AB ch

ứ

a n

ử

a

đườ

ng tròn, v

ẽ

các tia Ax và By cùng vuông góc v

ớ

i

AB.

Đ

i

ể

m M chuy

ể

n

độ

ng trên n

ử

a

đườ

ng tròn (M khác A và B). Qua M v

ẽ

ti

ế

p tuy

ế

n v

ớ

i n

ử

a

đườ

ng tròn c

ắ

t Ax và By l

ầ

n l

ượ

t

ở

C và D.

Xác

đị

nh v

ị

trí c

ủ

a

đ

i

ể

m M trong m

ỗ

i tr

ườ

ng h

ợ

p sau :

a) Di

ệ

n tích t

ứ

giác ABDC có giá tr

ị

nh

ỏ

nh

ấ

t, tính giá tr

ị

l

ớ

n nh

ấ

t

đ

ó theo R.

b) Chu vi t

ứ

giác ABDC có giá tr

ị

nh

ỏ

nh

ấ

t, tính giá tr

ị

nh

ỏ

nh

ấ

t

đ

ó theo R.

168

x

y

D

C

O

A

B

M

c) Chu vi tam giác COD có giá tr

ị

nh

ỏ

nh

ấ

t, tính giá tr

ị

nh

ỏ

nh

ấ

t

đ

ó theo R.

Gợi ý :

Áp d

ụ

ng

đ

i

ề

u ki

ệ

n x

ả

y ra d

ấ

u “=” trong b

ấ

t

đẳ

ng th

ứ

c Cô-si cho hai

s

ố

d

ươ

ng, khi bi

ế

t tích c

ủ

a ch

ứ

ng không

đổ

i.

Hướng dẫn giải

a) Vì Ax và By cùng vuông góc v

ớ

i

đườ

ng

kính AB nên Ax và By là các tia ti

ế

p tuy

ế

n

c

ủ

a

đườ

ng tròn (O).

Theo tính ch

ấ

t c

ủ

a hai ti

ế

p tuy

ế

n c

ắ

t nhau

ta có : OC là phân giác c

ủ

a góc AOM ; OD là

phân giác c

ủ

a góc MOB.

Mà hai góc AOM và MOB k

ề

bù nên



0

90

=COD

.

Vì CD là ti

ế

p tuy

ế

n và M là ti

ế

p

đ

i

ể

m nên

OM

⊥

CD.

Tam giác COD vuông t

ạ

i O,

đườ

ng cao OM, ta có : CM.DM = OM

2

= R

2

.

Theo tính ch

ấ

t c

ủ

a hai ti

ế

p tuy

ế

n c

ắ

t nhau ta có CA = CM ; DB = DM

⇒

AC.BD = R

2

.

T

ứ

giác ABDC có



0

90

= =A B

nên ABDC là hình thang vuông. Suy ra

(

)

( )

2

+

= = +

ABDC

AC BD AB

S AC BD R

.

Áp d

ụ

ng b

ấ

t

đẳ

ng th

ứ

c Cô-si cho hai s

ố

d

ươ

ng AC và BD ta

đượ

c

2

2 . 2 2 .

AC BD AC BD R R

+ ≥ = =

Đẳ

ng th

ứ

c x

ả

y ra khi AC = BD và AC.BD = R

2

⇔

AC = BD = R

⇔

MC =

MD = R

⇔



=

MA MB

. Do

đ

ó

( )

2

= + ≥

ABDC

S AC BD R R

,

đẳ

ng th

ứ

c x

ả

y ra khi



=

MA MB

.

V

ậ

y minS

ABCD

= 2R

2

đạ

t

đượ

c khi



=

MA MB

.

b) Kí hi

ệ

u C

ABCD

là chu vi c

ủ

a t

ứ

giác ABDC ta có :

C

ABCD

= AB + BD + DC + CA = 2R + BD + (CM + DM) + CA

= 2R + 2(AC + BD).

169

Theo câu a) ta có

2

2 . 2 2

+ ≥ = =

AC BD AC BD R R

,

đẳ

ng th

ứ

c x

ả

y ra khi



=

MA MB

.

Do

đ

ó C

ABCD

≥

2R + 2.2R = 6R,

đẳ

ng th

ứ

c x

ả

y ra khi



=

MA MB

.

V

ậ

y minC

ABCD

= 6R

đạ

t

đượ

c khi



=

MA MB

.

c) Kí hi

ệ

u C

COD

là chu vi c

ủ

a tam giác COD ta có :

C

COD

= OC + OD + CD = (OC + OD) + (CM + DM)

= (OC + OD) + (AC + BD).

Áp d

ụ

ng b

ấ

t

đẳ

ng th

ứ

c Cô-si :

2 .

+ ≥

OC OD OC OD

, d

ấ

u “=” x

ả

y ra khi

OC = OD

⇔



=

MA MB

.

∆

COD

vuông t

ạ

i O,

đườ

ng cao OM, ta có :

OC.OD = OM.CD = R(CM + DM) = R(AC + BD).

Do

đ

ó C

COD

≥

( ) ( )

2 + + +

R AC BD AC BD

.

Theo câu a) ta có

2

2 . 2 2

+ ≥ = =

AC BD AC BD R R

,

đẳ

ng th

ứ

c x

ả

y ra khi



=

MA MB

.

Do

đ

ó C

COD

≥

(

)

2 .2 2 2 2 2

+ = +

R R R R

,

đẳ

ng th

ứ

c x

ả

y ra khi



=

MA MB

.

V

ậ

y minC

COD

=

(

)

2 2 2

+

R

,

đạ

t

đượ

c khi



=

MA MB

.

Ví dụ 7.

Cho

đườ

ng tròn (O ; R) dây BC =

2

R

c

ố

đị

nh.

Đ

i

ể

m A chuy

ể

n

độ

ng

trên cung l

ớ

n BC. K

ẻ

các

đườ

ng cao BD và CE c

ủ

a tam giác ABC. G

ọ

i H là

trung

đ

i

ể

m c

ủ

a

đ

o

ạ

n DE. Xác

đị

nh v

ị

trí c

ủ

a

đ

i

ể

m A

để

OH có

độ

dài ng

ắ

n

nh

ấ

t. Tính

độ

dài ng

ắ

n nh

ấ

t

đ

ó theo R.

Gợi ý :

Áp d

ụ

ng liên h

ệ

gi

ữ

a dây và kho

ả

ng cách t

ừ

dây

đế

n tâm.

Hướng dẫn giải

Áp d

ụ

ng

đị

nh lí Pi-ta-go

đả

o ta

đượ

c



BOC

vuông t

ạ

i O.

Do

đ

ó



0

45

=BAC

. T

ứ

giác BCDE n

ộ

i ti

ế

p, suy ra



ABC ADE

=

(cùng bù v

ớ

i



CDE

)

⇒ ∆

ADE



∆

ABC

(g-g)

170

H

K

D

E

B

C

O

A

0

cos 2.co 45

⇒ = = ⇒ = =

DE AD

A DE R s R

BC AB

.

K

ẻ

OK

⊥

BC

⇒

KB = KC

⇒

KH

⊥

DE

⇒

2

;

2 2

= =

R R

OK KH

.

Áp d

ụ

ng quy t

ắ

c ba

đ

i

ể

m ta có : OK

≤

OH + KH

⇔

OH

(

)

2 1

2

−

≥

R

, d

ấ

u “=” x

ả

y ra khi H

∈

OK.

V

ậ

y minOH =

(

)

2 1

2

−

R

đạ

t

đượ

c khi H

∈

OK

⇔

A là

đ

i

ể

m chính gi

ữ

a

cung l

ớ

n AB.

III. BÀI TẬP VẬN DỤNG

Dạng 1. Bất đẳng thức hình học

Bài 1. Cho tam giác ABC vuông tại A, đường cao AH = h, ngoại tiếp đường tròn

tâm I bán kính r. Chứng minh bất đẳng thức

1 2

≤ +

h

r

,

đẳ

ng th

ứ

c x

ả

y ra

khi nào ?

Bài 2.

Cho tam giác

đề

u ABC n

ộ

i ti

ế

p

đườ

ng tròn (O ; R).

Đ

i

ể

m D chuy

ể

n

độ

ng

trên

đườ

ng tròn (O ; R). Ch

ứ

ng minh b

ấ

t

đẳ

ng th

ứ

c DB + DC

≤

2R

3

,

đẳ

ng th

ứ

c x

ả

y ra khi nào ?

Bài 3.

Cho tam giác nh

ọ

n ABC,

đườ

ng cao AD, tr

ự

c tâm H. Ch

ứ

ng minh r

ằ

ng :

a) tan .tan

=

AD

B C

HD

b)

tan tanB tanC tan .tanB.tanC

+ + =

A A

.

c)

tan .tanB.tanC 3 3

≥

A

,

đẳ

ng th

ứ

c x

ả

y ra khi nào ?

Bài 4.

Cho tam giác ABC.

Đ

i

ể

m D chuy

ể

n

độ

ng trên c

ạ

nh BC. Trên các c

ạ

nh

AB, AC th

ứ

t

ự

l

ấ

y các

đ

i

ể

m E, F sao cho DE // AC và DF // AB. Xác

đị

nh

v

ị

trí

đ

i

ể

m D

để

di

ệ

n tích t

ứ

giác AEDF

đạ

t giá tr

ị

l

ớ

n nh

ấ

t.

171

Dạng 2. Giá trị nhỏ nhất, giá trị lớn nhất của đại lượng hình học

Bài 1.

Cho tam giác

đề

u ABC có

độ

dài c

ạ

nh b

ằ

ng a. G

ọ

i O là trung

đ

i

ể

m c

ủ

a

BC. Trên các c

ạ

nh AB và AC l

ấ

y các

đ

i

ể

m D và E sao cho



0

60

=

DOE

.

a) Tính kho

ả

ng cách t

ừ

O

đế

n

đườ

ng th

ẳ

ng DE theo a.

b) Xác

đị

nh v

ị

trí c

ủ

a các

đ

i

ể

m D và E

để

di

ệ

n tích tam giác DOE

đạ

t giá

tr

ị

nh

ỏ

nh

ấ

t và tính di

ệ

n tích nh

ỏ

nh

ấ

t

đ

ó theo a.

Bài 2.

Cho n

ử

a

đườ

ng tròn (O)

đườ

ng kính AB = 2R. V

ẽ

dây CD song song v

ớ

i

AB. G

ọ

i K và H th

ứ

t

ự

là hình chi

ế

u c

ủ

a C và D lên

đườ

ng kính AB. Xác

đị

nh v

ị

trí c

ủ

a dây CD

để

:

a) T

ứ

giác CDHK là hình vuông.

b) Di

ệ

n tích t

ứ

giác CDHK b

ằ

ng n

ử

a di

ệ

n tích c

ủ

a n

ử

a hình tròn (O ; R).

Bài 3.

Cho

đ

i

ể

m A n

ằ

m ngoài

đườ

ng tròn (O ; R) sao cho OA = 1,5R. V

ẽ

cát

tuy

ế

n ABC c

ủ

a

đườ

ng tròn (B n

ằ

m gi

ữ

a A và C). Xác

đị

nh v

ị

trí c

ủ

a cát

tuy

ế

n ABC

để

:

a)

Đ

i

ể

m B là trung

đ

i

ể

m c

ủ

a AC và tính

độ

dài AC theo R trong tr

ườ

ng

h

ợ

p này.

b) Di

ệ

n tích tam giác AOB g

ấ

p

đ

ôi di

ệ

n tích tam giác BOC.

Một số bài tập tổng hợp thường gặp trong các đề thi

Bài 1.

Cho

đườ

ng tròn (O ; R). Hai

đườ

ng kính AB và CD vuông góc v

ớ

i nhau.

Đ

i

ể

m E thu

ộ

c cung nh

ỏ

BC,

đ

i

ể

m F thu

ộ

c cung nh

ỏ

BD sao cho EF = R

2

.

Dây AE c

ắ

t CD và BC th

ứ

t

ự

ở

M và N ; Dây AF c

ắ

t CD và BD th

ứ

t

ự

ở

P

và Q.

a) Tính s

ố

đ

o c

ủ

a góc EAF.

b) Ch

ứ

ng minh t

ứ

giác MNQP n

ộ

i ti

ế

p

đượ

c

đườ

ng tròn.

c) Ch

ứ

ng minh r

ằ

ng NQ song song v

ớ

i EF.

d) Tính chu vi tam giác BNQ theo R.

e) Xác

đị

nh v

ị

trí c

ủ

a dây EF

để

di

ệ

n tích tam giác BNQ

đạ

t giá tr

ị

l

ớ

n

nh

ấ

t và tính giá tr

ị

l

ớ

n nh

ấ

t

đ

ó theo R.

172

Bài 2.

Cho n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB = 2R. Dây CD chuy

ể

n

độ

ng

trên n

ử

a

đườ

ng tròn sao cho CD = R

3

và D thu

ộ

c cung AC. G

ọ

i E là

giao

đ

i

ể

m c

ủ

a AD và BC.

a) Tính s

ố

đ

o c

ủ

a góc AEB.

b) G

ọ

i F là giao

đ

i

ể

m c

ủ

a AC và BD. Tính

độ

dài

đ

o

ạ

n EF theo R.

c) Xác

đị

nh v

ị

trí c

ủ

a dây CD

để

di

ệ

n tích t

ứ

giác ABCD có giá tr

ị

l

ớ

n

nh

ấ

t và tính giá tr

ị

l

ớ

n nh

ấ

t

đ

ó theo R.

d) Ch

ứ

ng minh r

ằ

ng

đ

i

ể

m F thu

ộ

c m

ộ

t cung tròn c

ố

đị

nh.

e) Ch

ứ

ng minh

đườ

ng th

ẳ

ng

đ

i qua E, vuông góc v

ớ

i CD luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh

Bài 3.

Cho

đ

i

ể

m A n

ằ

m ngoài

đườ

ng tròn (O ; R) sao cho OA = 2R. V

ẽ

các ti

ế

p

tuy

ế

n AB và AC v

ớ

i

đườ

ng tròn (B, C là các ti

ế

p

đ

i

ể

m).

Đ

i

ể

m M chuy

ể

n

độ

ng trên cung nh

ỏ

BC. Qua M v

ẽ

ti

ế

p tuy

ế

n th

ứ

ba c

ắ

t AB, AC th

ứ

t

ự

ở

D và E.

a) Tính s

ố

đ

o c

ủ

a góc DOE.

b) Tính chu vi tam giác ADE theo R.

c) Gi

ả

s

ử

BC c

ắ

t OD, OE th

ứ

t

ự

ở

P, Q. Ch

ứ

ng minh t

ứ

giác DEQP n

ộ

i

ti

ế

p.

d) Ch

ứ

ng minh r

ằ

ng DE = 2PQ và ba

đườ

ng th

ẳ

ng OM, DQ, EP

đồ

ng quy.

e) Xác

đị

nh v

ị

trí c

ủ

a

đ

i

ể

m M

để

di

ệ

n tích tam giác ADE

đạ

t giá tr

ị

l

ớ

n

nh

ấ

t và tính giá tr

ị

l

ớ

n nh

ấ

t

đ

ó theo R.

Bài 4.

Cho tam giác ABC,

đườ

ng phân giác AD. Các

đ

i

ể

m E và F chuy

ể

n

độ

ng

trên

đ

o

ạ

n AD sao cho



=

EBA FBC

(E n

ằ

m gi

ữ

a A và F). V

ẽ

các

đườ

ng

tròn (O

1

) và (O

2

) th

ứ

t

ự

ngo

ạ

i ti

ế

p các tam giác AEB và AFC. Tia CE c

ắ

t

đườ

ng tròn (O

1

) t

ạ

i M ; Tia BF c

ắ

t

đườ

ng tròn (O

2

) t

ạ

i N. Ch

ứ

ng minh

r

ằ

ng :

a) T

ứ

giác BMNC n

ộ

i ti

ế

p. T

ừ

đ

ó suy ra



.sin

2

≤

BAC

MN BC

;

b) Ba

đ

i

ể

m A, M, N th

ẳ

ng hàng ;

c)



=

ECA FCB

;

d) Tích BE.BN không

đổ

i.

173

Bài 5.

Cho tam giác nh

ọ

n ABC (AB < AC). V

ẽ

đườ

ng tròn tâm O

đ

i qua B và

ti

ế

p xúc v

ớ

i AC t

ạ

i A. V

ẽ

đườ

ng tròn tâm O’

đ

i qua C và ti

ế

p xúc v

ớ

i AB

t

ạ

i A. G

ọ

i M là giao

đ

i

ể

m th

ứ

hai c

ủ

a hai

đườ

ng tròn (O ; R) và (O’ ; R’).

a) Ch

ứ

ng minh

đẳ

ng th

ứ

c MA

2

= MB.MC.

b) G

ọ

i K là trung

đ

i

ể

m c

ủ

a OO’. G

ọ

i I là

đ

i

ể

m

đố

i x

ứ

ng c

ủ

a A qua trung

đ

i

ể

m K c

ủ

a OO’. T

ứ

giác OMIO’ là hình gì ? Vì sao ?

c) Ch

ứ

ng minh I là tâm

đườ

ng tròn ngo

ạ

i ti

ế

p tam giác ABC.

d) Ch

ứ

ng minh t

ứ

giác BMIC n

ộ

i ti

ế

p.

e) Gi

ả

s

ử



0

60

=

BAC

. Tính di

ệ

n tích t

ứ

giác OMIO’ theo a, bi

ế

t R = a và

R’ = 2a.

Bài 6.

Cho

đườ

ng tròn (O ; R) và dây BC < 2R.

Đ

i

ể

m A chuy

ể

n

độ

ng trên cung

l

ớ

n BC sao cho tam giác ABC là tam giác nh

ọ

n. Các

đườ

ng cao AD, BE,

CF c

ủ

a tam giác ABC c

ắ

t nhau t

ạ

i H.

a) Ch

ứ

ng minh r

ằ

ng các t

ứ

giác AEHF và BCEF n

ộ

i ti

ế

p.

b) Ch

ứ

ng minh r

ằ

ng bán kính

đườ

ng tròn ngo

ạ

i ti

ế

p tam giác BHC b

ằ

ng

R.

c) G

ọ

i K là giao

đ

i

ể

m c

ủ

a BE và DF. Ch

ứ

ng minh r

ằ

ng H là tâm

đườ

ng

tròn n

ộ

i ti

ế

p tam giác DEF. T

ừ

đ

ó suy ra BE.HK = BK.HE.

d)

Đườ

ng th

ẳ

ng EF c

ắ

t

đườ

ng tròn (O)

ở

M và N. Ch

ứ

ng minh r

ằ

ng tam

giác AMN là tam giác cân. T

ừ

đ

ó suy ra AM

2

= AN

2

= AH.AD.

e) Ch

ứ

ng minh r

ằ

ng

đườ

ng tròn ngo

ạ

i ti

ế

p tam giác DEF luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh.

Bài 7.

Cho

đườ

ng tròn (O ; R) và dây BC < 2R.

Đ

i

ể

m A chuy

ể

n

độ

ng trên cung

l

ớ

n BC sao cho tam giác ABC là tam giác nh

ọ

n. Các

đườ

ng trung tuy

ế

n

BD và CE c

ủ

a tam giác ABC c

ắ

t nhau t

ạ

i G. G

ọ

i H là tr

ự

c tâm c

ủ

a tam

giác ABC.

a) Ch

ứ

ng minh r

ằ

ng t

ứ

giác ADOE n

ộ

i ti

ế

p.

b) K

ẻ

đườ

ng kính AK c

ủ

a (O). Ch

ứ

ng minh HK

đ

i qua trung

đ

i

ể

m F c

ủ

a

BC.

c) Ch

ứ

ng minh r

ằ

ng

đườ

ng th

ẳ

ng GH luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh.

d) Ch

ứ

ng minh r

ằ

ng

đ

i

ể

m G thu

ộ

c m

ộ

t

đườ

ng tròn c

ố

đị

nh.

174

e) Tính giá tr

ị

c

ủ

a bi

ể

u th

ứ

c

2 2

−

AB AC

GB GC

.

Bài 8.

Cho

đ

i

ể

m A n

ằ

m ngoài

đườ

ng tròn (O ; R). V

ẽ

các ti

ế

p tuy

ế

n AB, AC c

ủ

a

đườ

ng tròn (O) (B, C là các ti

ế

p

đ

i

ể

m). M

ộ

t cát tuy

ế

n quay quanh A c

ắ

t

đườ

ng tròn (O)

ở

D và E (D n

ằ

m gi

ữ

a A, E). Các ti

ế

p tuy

ế

n t

ạ

i D và E c

ủ

a

đườ

ng tròn (O) c

ắ

t nhau

ở

F.

a) Ch

ứ

ng minh r

ằ

ng tích AD.AE không ph

ụ

thu

ộ

c vào v

ị

trí c

ủ

a cát tuy

ế

n

ADE.

b) Ch

ứ

ng minh

đẳ

ng th

ứ

c =

BD CD

BE CE

.

c) G

ọ

i H là giao

đ

i

ể

m c

ủ

a OA và BC. Ch

ứ

ng minh t

ứ

giác DHOE n

ộ

i ti

ế

p.

d) Ch

ứ

ng minh ba

đ

i

ể

m B, C, F th

ẳ

ng hàng.

e) Ch

ứ

ng minh

đẳ

ng th

ứ

c

=

BD HD

BE HE

.

Bài 9.

Cho hai

đườ

ng tròn (O ; R) và (O’ ; r) v

ớ

i R > r,

ở

ngoài nhau. V

ẽ

các ti

ế

p

tuy

ế

n chung ngoài AB và CD (A,C

∈

(O ; R) ; B,D

∈

(O’ ; r)). V

ẽ

các

ti

ế

p tuy

ế

n chung trong EF và GH (E,G

∈

(O ; R) ; F,H

∈

(O’ ; r)). Ti

ế

p

tuy

ế

n AB c

ắ

t các ti

ế

p tuy

ế

n EF và GH th

ứ

t

ự

t

ạ

i M, N. Ti

ế

p tuy

ế

n CD c

ắ

t

các ti

ế

p tuy

ế

n EF và GH th

ứ

t

ự

t

ạ

i P, Q.

a) Ch

ứ

ng minh r

ằ

ng ba

đườ

ng th

ẳ

ng EF, GH và OO’

đồ

ng quy t

ạ

i K.

b) Ch

ứ

ng minh r

ằ

ng 6

đ

i

ể

m M, N, P, Q, O, O’ cùng thu

ộ

c m

ộ

t

đườ

ng tròn.

c) Gi

ả

s

ử

OO’ = 2(R + r). Tính

độ

dài

đ

o

ạ

n th

ẳ

ng MN theo R và r.

d) G

ọ

i I là giao

đ

i

ể

m c

ủ

a BH và OO’. Ch

ứ

ng minh ba

đ

i

ể

m A, I, G th

ẳ

ng

hàng.

Bài 10.

Cho

đ

i

ể

m A n

ằ

m ngoài

đườ

ng tròn (O ; R) sao cho OA = 2R. V

ẽ

các tia

ti

ế

p tuy

ế

n AB, AC c

ủ

a

đườ

ng tròn (O) (B,C là các ti

ế

p

đ

i

ể

m).

Đ

i

ể

m D

chuy

ể

n

độ

ng trên cung nh

ỏ

BC. G

ọ

i E, F, G l

ầ

n l

ượ

t là hình chi

ế

u vuông

góc c

ủ

a

đ

i

ể

m D trên các c

ạ

nh AB, BC, CA.

a) Ch

ứ

ng minh r

ằ

ng các t

ứ

giác BEDF và CGDF n

ộ

i ti

ế

p.

b) Ch

ứ

ng minh

đẳ

ng th

ứ

c DF

2

= DE.DG.

c) Tính t

ổ

ng DE + DF + DG theo R.

175

d) G

ọ

i M là giao

đ

i

ể

m c

ủ

a BD và EF ; G

ọ

i N là giao

đ

i

ể

m c

ủ

a CD và FG.

Ch

ứ

ng minh r

ằ

ng MN song song v

ớ

i BC và MN là ti

ế

p tuy

ế

n chung c

ủ

a

hai

đườ

ng tròn ngo

ạ

i ti

ế

p c

ủ

a các tam giác DME và DNG.

e) Xác

đị

nh v

ị

trí

đ

i

ể

m D trên cung nh

ỏ

BC

để

tích BE.CG

đạ

t giá tr

ị

l

ớ

n

nh

ấ

t.

f) Ch

ứ

ng minh b

ấ

t

đẳ

ng th

ứ

c S

FEG

2

3 3.

4

≥

DF

.

Bài 11.

Cho tam giác ABC vuông t

ạ

i A,

đườ

ng cao AH. G

ọ

i (O ; r), (O

1

; r

1

), (O

2

;

r

2

) th

ứ

t

ự

là các

đườ

ng tròn n

ộ

i ti

ế

p c

ủ

a các tam giác ABC, ABH, ACH và

l

ầ

n l

ượ

t ti

ế

p xúc v

ớ

i c

ạ

nh AB

ở

D và BC

ở

E, F.

a) Ch

ứ

ng minh r

ằ

ng AH = r + r

1

+ r

2

.

b) Ch

ứ

ng minh r

ằ

ng

2 2 2

1 2

= +

r r r

.

c) Ch

ứ

ng minh r

ằ

ng O là tr

ự

c tâm c

ủ

a tam giác AO

1

O

2

.

d)

Đườ

ng th

ẳ

ng O

1

O

2

c

ắ

t các c

ạ

nh AB, AC th

ứ

t

ự

ở

M, N. Ch

ứ

ng minh

r

ằ

ng các t

ứ

giác BMO

1

H, CNO

2

H và BO

1

O

2

C n

ộ

i ti

ế

p.

e) Tính di

ệ

n tích các tam giác AMN, OO

1

O

2

, ABC, bi

ế

t

1

3 2

=r cm ;

2

4 2

=r cm.

Bài 12.

Cho tam giác ABC cân t

ạ

i A,



0

120

=A

, BC =

2 3

cm.

Đ

i

ể

m D chuy

ể

n

độ

ng trên c

ạ

nh BC. V

ẽ

đườ

ng tròn (O ; R)

đ

i qua D và ti

ế

p xúc v

ớ

i AB t

ạ

i

B. V

ẽ

đườ

ng tròn (O’ ; R’)

đ

i qua D và ti

ế

p xúc v

ớ

i AC t

ạ

i C. G

ọ

i E là

giao

đ

i

ể

m c

ủ

a hai

đườ

ng tròn (O) và (O’).

1) Ch

ứ

ng minh r

ằ

ng :

a) T

ứ

giác ABEC n

ộ

i ti

ế

p.

b)

Đườ

ng th

ẳ

ng DE luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh.

c)

3 1 1

= +

ED EB EC

.

2) Tính t

ổ

ng R + R’.

3) Xác

đị

nh v

ị

trí c

ủ

a

đ

i

ể

m D

để

DE có

độ

dài l

ớ

n nh

ấ

t. Tính

độ

dài l

ớ

n

nh

ấ

t

đ

ó.

176

Bài 13.

Cho ba

đườ

ng tròn (O

1

; 1cm), (O

2

; 2cm), (O

3

; 3cm) sao cho (O

1

; 1cm)

và (O

2

; 2cm) ti

ế

p xúc ngoài t

ạ

i A ; (O

2

; 2cm) và (O

3

; 3cm) ti

ế

p xúc

ngoài t

ạ

i B ; (O

3

; 3cm) và (O

1

; 1cm) ti

ế

p xúc ngoài t

ạ

i C.

a) Tam giác O

1

O

2

O

3

là tam giác gì ? Vì sao ?

b) Tính di

ệ

n tích c

ủ

a tam giác ABC.

c) Ch

ứ

ng minh

đườ

ng tròn ngo

ạ

i ti

ế

p

∆

ABC

là

đườ

ng tròn n

ộ

i ti

ế

p

1 2 3

∆

O O O

.

d) Ch

ứ

ng minh r

ằ

ng ba

đườ

ng th

ẳ

ng AO

3

; BO

1

; CO

2

đồ

ng quy.

Bài 14.

Cho

đườ

ng tròn (O ; R), dây BC = R

3

,

đ

i

ể

m A chuy

ể

n

độ

ng trên cung

l

ớ

n BC sao cho tam giác ABC luôn là tam giác nh

ọ

n. Các

đườ

ng cao AD,

BE, CF

đồ

ng quy t

ạ

i H. G

ọ

i I là trung

đ

i

ể

m c

ủ

a BC.

a) Ch

ứ

ng minh r

ằ

ng 4

đ

i

ể

m B, H, O, C cùng thu

ộ

c m

ộ

t

đườ

ng tròn.

b) K

ẻ

đườ

ng kính AP c

ủ

a

đườ

ng tròn (O). Ch

ứ

ng minh r

ằ

ng 3

đ

i

ể

m H, I, P

th

ẳ

ng hàng.

c) G

ọ

i K là

đ

i

ể

m chính gi

ữ

a cung nh

ỏ

BC. T

ứ

giác AOKH là hình gì ? Vì

sao ?

d)

Đườ

ng th

ẳ

ng OH c

ắ

t các c

ạ

nh AB, AC th

ứ

t

ự

ở

M, N. Tam giác AMN

là tam giác gì ?

e) Xác

đị

nh v

ị

trí

đ

i

ể

m A

để

BM + CN

đạ

t giá tr

ị

l

ớ

n nh

ấ

t. Tính giá tr

ị

l

ớ

n

nh

ấ

t

đ

ó theo R.

177

GỢI Ý - HƯỚNG DẪN GIẢI PHẦN HÌNH HỌC

Chủ đề 1. TÍNH TOÁN CÁC ĐẠI LƯỢNG HÌNH HỌC

Dạng 1. Tính số đo góc

Bài 1.

V

ề

phía ngoài hình vuông ABCD, d

ự

ng tam giác BKC b

ằ

ng tam giác

BIA. Áp d

ụ

ng

đị

nh lí Pi-ta-go

đả

o ch

ứ

ng minh tam giác IKC là tam giác

vuông.

Đ

áp s

ố

:



0

135

=AIB

.

Bài 2.

Áp d

ụ

ng tính ch

ấ

t c

ủ

a góc n

ộ

i ti

ế

p, tam giác

đồ

ng d

ạ

ng.

Đ

áp s

ố

:



0

90

=MJI

.

Bài 3.

Áp d

ụ

ng h

ệ

th

ứ

c l

ượ

ng trong tam giác vuông, t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc

nh

ọ

n, quy trình

ấ

n phím tính s

ố

đ

o góc khi bi

ế

t t

ỉ

s

ố

l

ượ

ng giác c

ủ

a nó.

Đ

áp s

ố

:



0 0

52 ; 38

≈ ≈B C .

Bài 4.

Ch

ứ

ng minh

∆

ADE



∆

ABC

, r

ồ

i áp d

ụ

ng t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n.

Đ

áp s

ố

:



0

60

=BAC

Bài 5.

Áp d

ụ

ng tính ch

ấ

t t

ỉ

s

ố

l

ượ

ng giác c

ủ

a hai góc ph

ụ

nhau, các công th

ứ

c

sin

tan

cos

α

α =

α

,

tan .cot 1

α α =

,

2 2

sin cos 1

α + α =

, t

ỉ

s

ố

l

ượ

ng giác c

ủ

a

các góc

đặ

c bi

ệ

t.

Đ

áp s

ố

: a)

0

45

α =

; b)

0

45

α =

;

c)

0

45

α =

,

0

60

α =

; d)

0

30

α =

.

Dạng 2. Tính độ dài đoạn thẳng ; tính giá trị của biểu thức

Bài 1.

Áp d

ụ

ng tính ch

ấ

t c

ủ

a tam giác

đề

u, n

ử

a tam giác

đề

u,

đị

nh lí Pi-ta-go, t

ỉ

s

ố

l

ượ

ng giác c

ủ

a góc nh

ọ

n, tam giác

đồ

ng d

ạ

ng, tam giác b

ằ

ng nhau.

Đ

áp s

ố

:

3

4

R

.

178

Bài 2.

Áp d

ụ

ng tính ch

ấ

t v

ề

di

ệ

n tích, tính ch

ấ

t tam giác

đề

u, hình thang cân ,

hình bình hành,

đị

nh lí Pi-ta-go.

Đ

áp s

ố

:

3

2

+ + =

R

MD ME MF

;

3 3

2

+ + =

R

AF BD CE

;

3

+ +

=

+ +

MD ME MF

AF BD CE

.

Bài 3.

Qua A k

ẻ

đườ

ng th

ẳ

ng vuông góc v

ớ

i AE c

ắ

t

đườ

ng th

ẳ

ng DC t

ạ

i G, áp

d

ụ

ng tính ch

ấ

t c

ủ

a hình vuông, tam giác b

ằ

ng nhau, h

ệ

th

ứ

c l

ượ

ng trong

tam giác vuông.

Đặ

t

=

AE x

thì

đượ

c ph

ươ

ng trình

( )

2 2

1 1

1

+ =

+

x

.

Đ

áp s

ố

:

5 4 2 1

2

+ −

=x .

Bài 4.

a) K

ẻ

OH vuông góc v

ớ

i OB. Áp d

ụ

ng

đị

nh lí Pi-ta-go, tính ch

ấ

t c

ủ

a hình

ch

ữ

nh

ậ

t, tính ch

ấ

t

đ

o

ạ

n n

ố

i tâm c

ủ

a hai

đườ

ng tròn ti

ế

p xúc, tính ch

ấ

t c

ủ

a

ti

ế

p tuy

ế

n.

Đ

áp s

ố

:

2=

BC Rr

.

b) K

ẻ

AK vuông góc v

ớ

i BC thì AK chính là kho

ả

ng cách t

ừ

A

đế

n BC.

G

ọ

i E là giao

đ

i

ể

m c

ủ

a AK và HO’, áp d

ụ

ng

đị

nh lí Ta-lét.

Đ

áp s

ố

:

2

=

+

Rr

AK

R r

.

c) Áp d

ụ

ng

đị

nh lí Ta-lét.

Đ

áp s

ố

:

(

)

+

=

−

R R r

DO

R r

.

Dạng 3. Tính chu vi đa giác, chu vi đường tròn.

Tính diện tích đa giác, tính diện tích hình tròn

Bài 1.

a) Áp d

ụ

ng tính ch

ấ

t góc n

ộ

i ti

ế

p ch

ắ

n n

ử

a

đườ

ng tròn, tính ch

ấ

t c

ủ

a góc

n

ộ

i ti

ế

p, tam giác vuông cân, n

ủ

a tam giác

đề

u,

đị

nh lí Pi-ta-go.

Đ

áp s

ố

:

(

)

6 2

.

2

R

AB

−

=

179

b) Áp d

ụ

ng công th

ứ

c tính di

ệ

n tích

1

. .sin

2

=

ABC

S AB AC A

.

Đ

áp s

ố

:

(

)

2

3 3

.

4

ABCD

R

S

+

=

c) Áp d

ụ

ng công th

ứ

c tính

đọ

dài cung



0

180

π

=

AB

Rn

l .

Đáp số :



0 2

0

.30

6

180

π π

= =

AB

R R

l

.

Bài 2. Áp dụng tính chất trọng tâm của tam giác, định lí Pi-ta-go, hệ thức lượng

trong tam giác vuông, công thức tính diện tích tam giác.

Đáp số :

(

)

6 3 2 3 6

= + +

ABC

C a

;

2

9 2.

=

ABC

S a

.

Bài 3. Áp dụng công thức tính diện tích tam giác

( )( )( )

,

S p p a p b p c

= − − −

trong đó a, b, c là độ dài các cạnh của tam giác,

2

+ +

=

a b c

p là nửa chu vi

của tam giác. Chú ý rằng bốn trung điểm của bốn cạnh của tứ giác tạo

thành một hình bình hành.

Chủ đề 2. Chứng minh các yếu tố hình học, quan hệ hình học

Dạng 1. Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau

Bài 1. Áp dụng tính chất góc tạo bởi tia tiếp tuyến và dây cung, tam giác đồng

dạng.

Bài 2. a) Áp dụng tính chất đường kính vuông góc với dây cung, tam giác đồng

dạng.

b) Áp dụng tính chất của tứ giác nội tiếp, tính chất, dấu hiệu nhận biết tam

giác cân.

Bài 3. a) Góc nội tiếp chắn nửa đường tròn, hệ thức lượng trong tam giác vuông,

tam giác đồng dạng.

180

b) Áp dụng công thức

2

sin sin sin

= = =

BC CA AB

R

A B C

(R là bán kính đường

tròn ngoại tiếp

ABC

∆

).

Bài 4. Qua A kẻ tiếp tuyến chung trong của (O) và (O’) cắt CD tại F. Áp dụng

tính chất của góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung.

Bài 5. Áp dụng tính chất của hai tiếp tuyến cắt nhau, tính chất của góc nội tiếp.

Dạng 2. Chứng minh quan hệ vuông góc, quan hệ song song

Bài 1. a) Gọi H là giao điểm của AD và EF. Chứng minh



0

90

=AHE

bằng cách

áp dụng tính chất góc có đỉnh ở bên trong đường tròn.

b) Áp dụng tam giác bằng nhau, dấu hiệu nhận biết hai đường thẳng song

song.

Bài 2. Áp dụng quan hệ từ vuông góc đến song song.

Bài 3. a) Áp dụng tính chất hai tia phân giác của hai góc kề bù.

b) Áp dụng định lí Ta-lét đảo.

Bài 4. Áp dụng dấu hiệu nhận biết hai đường thẳng song song.

Cần chứng minh MB = MD, sau đó gọi P là trung điểm của AD.

Dạng 3. Chứng minh nhiều điểm cùng nằm trên một đường tròn

Bài 1. Áp dụng tính chất : “Hình thang cân là tứ giác nội tiếp”.

Bài 2. Áp dụng định nghĩa đường tròn hay nhiều điểm cách đều một điểm.

Bài 3. Tứ giác có hai đỉnh liên tiếp cùng nhìn một cạnh dưới hai góc bằng nhau.

Bài 4. Hai đỉnh liên tiếp của tứ giác cùng nhìn một cạnh dưới hai góc bằng nhau.

Hay “Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại E có

EA.EC = EB.ED”.

Bài 5. Hai đỉnh liên tiếp của tứ giác cùng nhìn một cạnh dưới hai góc bằng nhau.

Hay “Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại E có

EA.EC = EB.ED”.

Dạng 4. Chứng minh một đường thẳng là tiếp tuyến của đường tròn

Bài 1. Chứng minh D, A, E thẳng hàng và OA vuông góc với DE.

181

Bài 2. Chứng minh HE

⊥

OE hay chứng minh



0

90

=HEO

.

Bài 3. Chứng minh



.

ABD AEB

=

Bài 4. Kẻ OH

⊥

EF ; OK

⊥

CD. Chứng minh OH = OK.

Bài 5. Chứng minh



=

DIB ICB

.

Dạng 5. Chứng minh đẳng thức hình học

Bài 1. a) Vẽ đường kính BD. Áp dụng góc nội tiếp chắn nửa đường tròn, tỉ số

lượng giác của góc nhọn.

b) Áp dụng công thức tính diện tích tam giác và kết quả ở câu a).

c) Áp dụng công thức tính diện tích tam giác S = pr (p là nửa chu vi và r là

bán kính đường tròn nội tiếp tam giác) và kết quả ở câu b).

Bài 2. a) Áp dụng tính chất của tam giác cân, tam giác đồng dạng.

b) Áp dụng tam giác đồng dạng, đinh lí Pi-ta-go và biến đổi các đẳng thức

một cách hợp lí.

Bài 3. a) Áp dụng tỉ số lượng giác của góc nhọn và tam giác đồng dạng.

b) Vẽ các đường cao BE, CF.

Áp dụng kết quả câu a) và đẳng thức

1

+ + =

HD HE HF

AD BE CF

.

Dạng 6. Chứng minh nhiều điểm thẳng hàng, nhiều đường đồng quy

Bài 1. a) Gọi F là giao điểm của hai đường thẳng MP và OO’. Áp dụng tính chất

của tiếp tuyến, định lí Ta-lét tính được =

−

dR

FO

R r

(trong đó d = OO’).

Gọi F’ là giao điểm của hai đường thẳng NQ và OO’, tương tự

' =

−

dR

F O

R r

⇒

đpcm.

b) Gọi I là giao điểm của hai đường thẳng AB và MP. Áp dụng tam giác

đồng dạng để chứng minh IA = IB, tính chất đường nối tâm của hai đường

tròn cắt nhau, tính chất đường trung tuyến ứng với cạnh huyền, tính chất

của tam giác cân, tính chất qua một điểm cho trước có duy nhất đường

thẳng vuông góc với một đường thẳng cho trước.

182

P

M

N

E

D

O

B

C

A

Bài 2. a) Áp dụng tính chất góc nội tiếp chắn nửa đường tròn, dấu hiệu nhận biết

tiếp tuyến, tính chất của hai tiếp tuyến cắt nhau, tính chất của tam giác

cân, tam giác vuông, định lí Ta-lét.

b) Kéo dài AD cắt đường thẳng BF tại G. Áp dụng tính chất hai góc đối

đỉnh, dấu hiệu nhận biết hai đường thẳng song song, định lí Ta-lét, tính

chất trung tuyến ứng với cạnh huyền, tính chất tam giác cân, tính chất hai

đường thẳng song song, Tiên đề Ơ-clít.

Bài 3. Gọi O

1

; O

2

; O

3

lần lượt là tâm các đường tròn ngoại tiếp các tam giác đều

ABD, BCE, CAF. Gọi M là giao điểm của hai đường tròn (O

1

) và (O

2

). Áp

dụng tính chất của tam giác đều, tính chất của tứ giác nội tiếp, dấu hiệu

nhận biết tứ giác nội tiếp.

Bài 4. Áp dụng tính chất của góc nội tiếp, tính chất tia phân giác của một góc,

tính chất của tứ giác nội tiếp, dấu hiệu nhận biết tứ giác nội tiếp để chứng

minh



=

CMN EMA

, suy ra hai tia MA và MN trùng nhau.

Bài 5. a) Áp dụng đường trung bình tam giác, tính chất hình bình bình hành.

b) Áp dụng định lí Ta-lét, tính chất trọng tâm của tam giác.

Bài 6. Vận dụng tính chất hai đường chéo của hình bình hành.

Dạng 7. Chứng minh tam giác, tứ giác đặc biệt

Bài 1. a) Ta có



;= =

DA DB EA EC



;

⇒

= =

ADE PDE AED PED

Do đó

∆ = ∆

ADE PDE

(g-c-g)

⇒

DA = DP ; EA = EP.

⇒

DE là trung trực của AP (1)

Dễ thấy BE và CD thứ tự là phân giác của các

góc



;

ABC ACB

⇒

AP là phân giác của



.

BAC

(2)

Từ (1) và (2)

⇒

tam giác AMN cân tại A.

b) Tam giác AMN cân tại A có AP là phân giác



MAN

nên AP là trung

trực của MN.

Ta lại có DE (hay MN) là trung trực của AP. Do đó tứ giác AMPN là hình

thoi.

183

Bài 2. Cần chứng minh BCDK là hình thang nội tiếp đường tròn.

Như vậy chỉ cần chứng minh BK // CD hay BK

⊥

AB.

Bài 3. Vì M, N, P, Q thứ tự là trung điểm của AD, DC, CB, BA nên dễ dàng

chứng minh được MNPQ là hình bình hành. Hình bình hành MNPQ là

hình vuông khi và chỉ khi OM = OP và



0

90

=MOP

⇔

;

= ⊥

AC BD AC BD

.

Từ đó tính được

(

)

2 6

2

+

= =

R

AC BD

⇒

(

)

2

2 3

2

+

=

ABCD

R

S

.

Chủ đề 3. Tập hợp điểm

Dạng 1. Tìm và chứng minh về tập hợp điểm

Bài 1. Gọi K là trung điểm của BC

⇒

K cố định. Cần chứng minh KM = R

⇒

đpcm.

Bài 2. Trên cùng nửa mặt phẳng bờ AB có chứa điểm C, dựng tam giác đều

ABF, suy ra F cố định. Cần chứng minh



0

90

=AEF

, từ đó suy ra đpcm.

Chú ý : Bạn đọc hãy xét bài toán trên trong các trường hợp sau : Tam giác

ACE vuông cân tại E hoặc vuông cân tại A hoặc vuông cân tại C hoặc tam

giác ACE cân tại E và có



= α

E

không đổi.

Bài 3. Dựng đường tròn (O’) ngoại tiếp tam giác BOC cắt OA tại D. Cần chứng

minh D cố định, suy ra O’ cách đều hai điểm cố định O và D

⇒

O’ thuộc

đường trung trực của OD.

Bài 4. Xét hai trường hợp : Tiếp xúc ngoài ; Tiếp xúc trong.

Gọi I là trung điểm của OO’. Hãy chứng minh điểm I cố định và IM có độ

dài không đổi.

Dạng 2. Chứng minh đường thẳng, đường tròn đi qua điểm cố định

Bài 1. Vẽ đường kính AE của đường tròn (O ; R). Gọi F là giao điểm của BF với

đường thẳng đi qua D và vuông góc với AC. Cần chứng minh điểm F cố

định.

Bài 2. Chứng minh điểm C thuộc đường tròn đi qua trung điểm ba cạnh của tam

giác ABD, tức là quy về việc chứng minh tứ giác nội tiếp.

184

Bài 3. Dự đoán đường tròn ngoại tiếp tam giác DEF đi qua điểm H. Ta cần

chứng minh tứ giác DEHF nội tiếp. Hãy dựng hình bình hành DHCG, rồi

chứng minh

∆

DHG



∆

HBD

(c-g-c).

Bài 4. Dự đoán đường thẳng đi qua trung điểm của các đoạn thẳng AE và DF đi

qua trung điểm của đoạn thẳng OI. Hãy vận dụng tính chất hai đường chéo

của hình bình hành.

Bài 5. Giả sử đường trung trực của đoạn thẳng CD đi qua điểm E. Dự đoán tứ

giác AOEO’ là hình bình hành. Từ đó dựng điểm E, rồi chứng minh tam

giác CED cân tại E, bằng cách từ O, E, O’ kẻ các đường vuông góc với

CD và vận dụng tính chất của hình bình hành, suy ra đpcm.

Chủ đề 4. Cực trị hình học

Dạng 1. Bất đẳng thức hình học

Bài 1. Kẻ ID

⊥

BC, IE

⊥

AC

⇒

ID = IE = r. Ta có AH

≤

AI + ID, dấu “=” xảy

ra khi I

∈

AH. Chú ý rằng

2

=

AI r

.

Bài 2. Xét hai trường hợp : điểm D thuộc cung lớn BC ; điểm D thuộc cung nhỏ

BC.

Áp dụng tính chất của tam giác đều, tính chất của góc góc nội tiếp, tam

giác bằng nhau, bất đẳng thức tam giác. Với chú ý rằng tam giác đều nội

tiếp đường tròn (O ; R) có cạnh bằng

3

R

.

Bài 3. a) Áp dụng tỉ số lượng giác của góc nhọn và tam giác đồng dạng.

b) Vẽ các đường cao BE, CF. Áp dụng kết quả câu a) và đẳng thức

1

+ + =

HD HE HF

AD BE CF

.

c) Áp dụng bất đẳng thức Cô-si cho 3 số dương tanA, tanB, tanC.

Bài 4. Áp dụng tính chất của diện tích đa giác, tỉ số diện tích của hai tam giác

đồng dạng, bất đẳng thức Cô-si cho 2 số dương.

Đáp số :

1

max

2

=

AEDF ABC

S S , đạt được khi D là trung điểm BC.

185

Dạng 2. Giá trị nhỏ nhất, giá trị lớn nhất

Bài 1. a) Kẻ OH

⊥

AB ; OK

⊥

DE ; OI

⊥

AC . Áp dụng tính chất của tam giác

đều, tam giác đồng dạng để chứng minh



=

BDO ODE

, từ đó tính được

2

3

4

= =

a

OK OH

.

b) Áp dụng tam giác đồng dạng, chứng minh

2

.

4

=

a

BD CE

.

Đặt DH = DK = x ; EK = EI = y.

Khi đó DE = x + y ; BD

4

= +

a

x ; CE

4

+

a

y .

Áp dụng bất đẳng thức Cô-si để tìm giá tri nhỏ nhất của

4 4

   

= + + +

   

   

a a

DE x y

.

Bài 2. a) Hình chữ nhật là hình vuông khi hình chữ nhật có hai cạnh kề bằng

nhau, áp dụng định lí Pi-ta-go để lập phương trình tính CK theo R.

Đáp số :

2

5

=

R

CK

.

b) Áp dụng công thức tính diện tích của hình chữ nhật, diện tích hình tròn,

định lí Pi-ta-go để lập hệ phương trình tính CK theo R.

Đáp số :

(

)

4 4

4

+ π ± − π

=

R

CK

.

Bài 3. a) Gọi O’ là trung điểm của OA. Áp dụng tính chất đường trung bình tam

giác để có '

2

=

R

O B , từ đó suy ra cách dựng cát tuyến ABC. Áp dụng

định lí Pi-ta-go để lập hệ phương trình, từ đó tính được

10

=AC R .

b) Ta phân tích để tìm cách xác định điểm B.

Vì diện tích tam giác AOB gấp đôi diện tích tam giác BOC nên AB =

2BC. Trên đoạn OA lấy điểm O’ sao cho O’A = 2O’O. Theo định lí Ta-lét

đảo

⇒

O’B // OC.

186

K

H

Q

P

N

M

F

D

C

O

A

B

E

Theo định lí Ta-lét tính được O’B =

2

3

R

.

Như vậy B là giao điểm của hai đường tròn (O ; R) và (O’ ;

2

3

R

).

Một số bài tập tổng hợp thường gặp trong các đề thi

Bài 1. a) Áp dụng định lí Pi-ta-go đảo để

chứng minh EOF là tam giác vuông.

b) Chứng minh



0

45

= =NAP NCP



0

90

⇒

=APN



0

90

⇒

=AMQ

⇒

tứ giác MNQP nội tiếp.

c) Chứng minh



=

AMD AFE

;



=

AMD AQN



⇒

=

AQN AFE

⇒

NQ

song song với EF.

d) Gọi H là giao điểm của MQ và NP,

kéo dài AH cắt NQ tại K. Chứng minh H là trực tâm của tam giác ANQ

⇒

∆ = ∆

AKN ACN

(ch-gn) ;

∆ = ∆

AKQ ADQ

(ch-gn)

⇒

KN = CN ; KQ

= DQ. Từ đó tính được chu vi của tam giác BNQ bằng

2 2

R

.

e) Đặt BN =

x

; BQ =

y

⇒

CN = R

2

−

x

;

DQ = R 2

−

y

và NQ = 2R 2

− −

x y

.

Áp dụng định lí Pi-ta-go lập được phương trình

( )

2

2 2 4 0

− + + =

xy x y R R

.

Áp dụng bất đẳng thức Cô-si để tìm giá trị lớn nhất của diện tích tam giác

BNQ.

Đáp số : S

BNQ

lớn nhất bằng

(

)

2

2 3 2 2

−R

đạt được khi EF // CD.

187

O'

H

F

M

E

D

C

O

A

B

Q

P

D

E

K

H

B

C

A

O

M

Bài 2. a) Vẽ đường kính CM của đường tròn (O ; R).

Áp dụng tính chất góc nội tiếp chắn nửa đường

tròn, tỉ số lượng giác của góc nhọn, tính chất

góc có đỉnh ở bên ngoài đường tròn.

Đáp số :



0

30

=AEB

b) Cần chứng minh tứ giác CEDF nội tiếp

đường tròn đường kính EF. Rồi áp dụng công

thức :

sin

=

CD

EF

E

.

c) Áp dụng tỉ số diện tích của hai tam giác

đồng dạng để chứng minh 3=

EAB ABCD

S S

⇒

S

ABCD

lớn nhất

⇔

S

EAB

lớn nhất

⇔

S

EAB

=

1

. .

2

=

AB EH R EH

lớn nhất

⇔

EH lớn nhất

⇔

H trùng O (vì E thuộc

cung chứa góc 30

0

dượng trên đoạn AB)

⇔

CD // AB.

Đáp số : S

EAB

lớn nhất bằng

(

)

2

2 3+

R

⇒

S

ABCD

lớn nhất bằng

(

)

2

2 3

3

+

R

khi CD // AB.

d) Cần chứng minh



0

150

=AFB

.

e) Gọi O’ là tâm đường tròn ngoại tiếp tam giác EAB

⇒

O’ cố định. Tìm

cách chứng minh đường thẳng đi qua E và vuông góc với CD đi qua điểm O’.

Bài 3. a) Tính chất hai tiếp tuyến cắt nhau, tỉ số

lượng giác.

Đáp số :



0

60

=DOE

.

b) Chứng minh C

ADE

= 2AB.

Đáp số : C

ADE

=

2 3

R

.

c) Cần chứng minh các tứ giác BOQD và

COPE nội tiếp



0

90

⇒

= =DPE DQE

⇒

đpcm.

188

d)

∆

OPQ



∆

OED

(g-g), tính chất ba đường cao.

e) Qua O vẽ HK // BC

2

4

.

3

⇒ =

R

HD KE

. Đặt

;

=

BD x

=

CE y

⇒ = +

DE x y

. Áp dụng bất đẳng thức Cô-si để tìm giá trị nhỏ

nhất của

= +

DE x y

.

Bài 4.

N

F

M

E

O

2

O

1

D

B

C

A

Chứng minh



=

BMC CNB

⇒

tứ giác BMNC nội tiếp. Gọi R là bán kính

đường tròn ngoại tiếp tứ giác BMNC ta có



2

sin

=

BC

R

BMC

.

Ta lại có



2

sin

2

=

BC

R

BAC

và

2

≤

MN R

⇒

đ

pcm.

b) T

ứ

giác BMNC n

ộ

i ti

ế

p



⇒ =

CBN CMN

.

Ta l

ạ

i có



;= =

CMA EBA CBF EBA



⇒ =

CMN CMA

⇒

ba

đ

i

ể

m M, A, N th

ẳ

ng hàng.

c) T

ứ

giác BMNC n

ộ

i ti

ế

p



⇒ =

BCM BNM

, mà



=

BNM FCA



⇒ =

BCM FCA



⇒ =

ECA FCB

.

d) D

ễ

th

ấ

y

∆

BEA



∆

BCN

(g-g)

⇒

=

BE BA

BC BN

⇒

BE.BN = BA.BC

không

đổ

i.

189

x

K

Q

P

N

M

H

D

F

E

O

B

C

A

Bài 5.

a) D

ễ

th

ấ

y



=

MAC MBA

;



=

MAB MCA

⇒

∆

AMB



∆

CMA

(g-g)

MA MB

MC MA

⇒

=

2

.

MA MB MC

⇒

=

b) D

ễ

th

ấ

y AOIO’ là hình

bình hành

⇒

OI = O’M.

Nh

ờ

đườ

ng trung bình c

ủ

a

tam giác

⇒

KH // MI

⇒

đ

pcm.

c) Ch

ứ

ng minh I là giao

đ

i

ể

m hai

đườ

ng trung tr

ự

c.

d) Ch

ứ

ng minh



2.=

BIC BAC

;



2.=

BMC BAC

⇒

đ

pcm.

e) OO’ =

7

a

; MI =

3 7

7

a

; MH = AH =

21

7

a

.

Bài 6.

a)



0

180

+ =AEH AFH

⇒

T

ứ

giác AEHF n

ộ

i ti

ế

p.



0

90

= =BEC BFC

⇒

T

ứ

giác BCEF n

ộ

i ti

ế

p.

b) Kéo dài AD c

ắ

t (O) t

ạ

i Q.

Ch

ứ

ng minh

∆ = ∆

BQC BHC

(g-c-g)

⇒

đ

pcm.

c) D

ễ

th

ấ

y BDHF và CDHE

đề

u là t

ứ

giác n

ộ

i ti

ế

p.

Do

đ

ó



= = =

HDF HBF HCE HCE

⇒

DH là phân giác c

ủ

a góc EDF.

T

ươ

ng t

ự

EH c

ũ

ng là phân giác c

ủ

a góc DEF.

V

ậ

y H là tâm

đườ

ng tròn n

ộ

i ti

ế

p c

ủ

a tam giác DEF.

Vì DB

⊥

DH nên DB là phân giác ngoài t

ạ

i

đỉ

nh D c

ủ

a

∆

DEF

⇒

. .

= =

⇒

=

DK HK BK

BE HK BK HE

DE HE BE

.

d) K

ẻ

ti

ế

p tuy

ế

n Ax c

ủ

a (O) r

ồ

i ch

ứ

ng minh



= =

BAx BCA AFE

⇒

EF // Ax

⇒

OA

⊥

MN

⇒

AM = AN

190

I

K

Q

P

F

H

G

E

D

O

B

C

A

⇒

Tam giác AMN cân t

ạ

i A



⇒

=

AMN ANM

,

mà



=

AMN ACN

nên



=

ACN ANE

⇒

∆

ANE



∆

ACN

(g-g)

⇒

2

.

=

⇒

=

AN AE

AN AE AC

AC AN

.

D

ễ

th

ấ

y

∆

AEH



∆

ADC

(g-g)

⇒

AE.AC = AH.AD.

Do

đ

ó AM

2

= AN

2

= AH.AD.

e) G

ọ

i P là trung

đ

i

ể

m c

ủ

a BC. Ch

ứ

ng minh



2.=

EPF EBF

;



2.=

EDF EBF

⇒

đ

pcm.

Bài 7.

a) DA = DC

⇒

OD

⊥

AC ; EA = EB

⇒

OE

⊥

AB

⇒

t

ứ

giác ADOE

n

ộ

i ti

ế

p.

b) AK là

đườ

ng kính, suy ra



0

90

= =ABK ACK

; CH

⊥

AB ;

BH

⊥

AC

⇒

BK // CH và

BH // CK

⇒

BHCK là hình bình

hành, mà FB = FC nên FH = FK.

c) D

ễ

th

ấ

y G là tr

ọ

ng tâm c

ủ

a

∆

ABC

2

3

⇒

=

GA GF

.

∆

AHK

có AF là trung tuy

ế

n và

2

3

=

GA GF

nên G là tr

ọ

ng tâm

c

ủ

a

∆

AHK

.

Vì HO là trung tuy

ế

n c

ủ

a

∆

AHK

nên 3

đ

i

ể

m H, G, O th

ẳ

ng hàng

⇒

đ

pcm.

d) K

ẻ

GI // AO

1

3

⇒

= =

FI FG

FO FA

⇒

I c

ố

đị

nh.

Ta c

ũ

ng có

1

3

= = =

FI IG FG

FO OA FA

3

⇒

=

R

IG

⇒

đ

pcm.

e) Kéo dài BD c

ắ

t (O) t

ạ

i P ; kéo dài CE c

ắ

t (O) t

ạ

i Q.

⇒

DP.DB = DA.DC =

2

4

AC

; EQ.EC = EA.EB =

2

4

AB

;

191

H

F

E

B

C

O

A

D

GB.GP = GC.GQ

⇔

2 2

3

−

=

−

AB AC

GB GC

.

Bài 8.

a) D

ễ

th

ấ

y

∆

ABD



∆

AEB

(g-g)

⇒

= =

AB AD BD

AE AB EB

(1)

2

.

⇒

=

AD AE AB

không

đổ

i

b)

∆

ACD



∆

AEC

(g-g)

⇒

= =

AC AD CD

AE AC EC

(2)

Vì AB = AC nên t

ừ

(1) và (2)

⇒

=

BD CD

BE CE

.

c) D

ễ

th

ấ

y

⊥

OA BC

t

ạ

i H và HB =

HC. C

ầ

n ch

ứ

ng minh

AH.AO = AB

2

; AH.AO = AD.AE

⇒

AD.AE =AB

2

.

T

ừ

đ

ó

⇒

∆

AHD



∆

AEO

(c-g-c)



⇒

=

AHD AEO



0

180

⇒

+ =OHD OED

⇒

đ

pcm.

d) D

ễ

th

ấ

y



0

90

= =ODF OEF

⇒

t

ứ

giác ODFE n

ộ

i ti

ế

p.

Ta l

ạ

i có t

ứ

giác DHOE n

ộ

i ti

ế

p (cmt)

⇒

5

đ

i

ể

m D, H, O, E, F cùng thu

ộ

c

đườ

ng tròn

đườ

ng kính OF



0

90

⇒

=OHF

hay

⊥

OH HF

, mà

⊥

OH BC

nên B, C, F th

ẳ

ng hàng.

e) D

ễ

th

ấ

y



=

FHD FHE

(vì FD = FE), mà

⊥

HA HF

⇒

=

AD HD

AE HE

.

Theo câu a) thì = =

AB AD BD

AE AB EB

2 2

.

   

⇒

=

⇒

=

   

   

AB AD BD AD BD

AE AB EB AE EB

.

Do

đ

ó

=

BD HD

BE HE

.

Bài 9.

a) Gi

ả

s

ử

EF c

ắ

t OO’ t

ạ

i K ; GH c

ắ

t OO’ t

ạ

i K’.

192

Vì EF là ti

ế

p tuy

ế

n chung trong nên

; ' / / O'

⊥ ⊥ ⇒

OE EF O F EF OE F

.

Áp d

ụ

ng

đị

nh lí Ta-lét ta

đượ

c

' ' '.r

'= =

⇒

=

+

KO O F r OO

KO

KO OE R R r

. T

ươ

ng

t

ự

'.r

' ' =

+

OO

K O

R r

'

⇒

≡

K K

.

V

ậ

y ba

đườ

ng th

ẳ

ng EF, GH và OO’

đồ

ng quy t

ạ

i K.

b) D

ễ

dàng ch

ứ

ng minh

đượ

c



0

' ' ' ' 90

= = = =OMO ONO OPO OQO .

V

ậ

y 6

đ

i

ể

m M, N, P, Q, O, O’ cùng thu

ộ

c

đườ

ng tròn tâm O’’

đườ

ng kính

OO’.

c) V

ẽ

O’’S vuông góc v

ớ

i MN

⇒

SM = SN.

Ta l

ạ

i có OA

⊥

AB và O’B

⊥

AB

⇒

OA // O’B // O’’S, mà

O’’O = O’’O’

⇒

SA = SB Do

đ

ó MA = NB. Vì MA = ME và MB = MF

⇒

MN = EF.

Ta có

(

)

2

'.r

' 2

+

= = =

+ +

R r r

OO

KO r

R r R r

3

⇒

=

KF r

.

T

ươ

ng t

ự

3

=KE R

(

)

3

⇒ = +EF R r

. V

ậ

y

(

)

3

= +MN R r

.

d) G

ọ

i L là giao

đ

i

ể

m c

ủ

a O’N và BH ; G

ọ

i J là giao

đ

i

ể

m c

ủ

a ON và AG.

D

ễ

th

ấ

y

∆

NOA



'

∆

O NB

(g-g) có AJ và BL là các

đườ

ng cao t

ươ

ng

ứ

ng

'

⇒

=

NJ O L

NO O N

.

Ta l

ạ

i có LI // NO (cùng vuông góc v

ớ

i O’N)

'

⇒

=

O L LI

O N NO

⇒

=

⇒

=

NJ LI

NO NO

.

Do

đ

ó JNLI là hình ch

ữ

nh

ậ

t

⇒

⊥

IJ NO

, mà

⊥

AG NO

t

ạ

i J nên A, I, G

th

ẳ

ng hàng.

Bài 10.

a)



0

90

= =BED BFD

;



0

90

= =CGD CFD

⇒

BEDF ; CGDF là các t

ứ

giác n

ộ

i ti

ế

p.

b)

∆

DEF



∆

DFG

(g-g)

2

.

⇒

=

⇒

=

DE DF

DF DE DG

DF DG

.

193

M

N

H

G

E

F

B

C

A

O

D

c) Vì AB là ti

ế

p tuy

ế

n, B là ti

ế

p

đ

i

ể

m



0

90

⇒

=ABO

.

∆

ABO

vuông t

ạ

i B

 

0

1

sin 30

2 2

⇒

= = =

⇒

=

OB R

OAB OAB

OA R

.

D

ễ

th

ấ

y

⇒

=

AB AC

và



0

30

= =OAB OAC

.

V

ậ

y tam giác ABC

đề

u có c

ạ

nh



0

.cos 2 .cos30

3

2 . 3

2

AB OA OAB R

R R

= =

.

Ta có

3

2

+ + =

⇒

+ + = =

DAB DBC DCA ABC

R

S S S S DE DF DG AH .

d) Ta có



= =

DFE DBE DCB

;



= =

DFG DCG DBC



⇒

= +

EFG DBC DCB

.

Ta l

ạ

i có



0

180

+ + =DBC DCB BDC



0

180

⇒

+ =EFG BDC

hay



0

180

+ =MFN MDN

⇒

T

ứ

giác DMFN n

ộ

i ti

ế

p



⇒

= = =

DMN DFN DCG DBC

⇒

MN // BC.

Vì



= =

DMN DBC DEF

và



= =

DNM DCB DGF

nên MN là ti

ế

p tuy

ế

n

chung c

ủ

a hai

đườ

ng tròn ngo

ạ

i ti

ế

p c

ủ

a các

∆

DME

và

∆

DNG

.

e) Tam giác ABC

đề

u



0

60

⇒

=ABC



0

120

⇒

=BDC



0

60

⇒

=MFN

⇒

∆

BEF



∆

CFG

(g-g).

BE BF

CF CG

⇒

=

2

2 2

2

3 3

. .

2 2 2 4

BF CF BC R R

BE CG BF CF

 

+

   

⇒ = ≤ = = =

 

   

 

   

 

.

Đẳng thức xảy ra khi BF = CF =

3

2 2

= ⇔

BC R

D là điểm chính giữa

cung nhỏ BC.

194

f) Ta có

S

FEG

= S

EDF

+ S

FDG

+ S

DEG

=

( )

0

1

. . . sin 60

2

+ +DE DG DE DF DF DG .

Ta lại có

. . .

DE DG DE DF DF DG

+ +

( )

2 2 2 2

2 3

DF DF DE DG DF DF DF

= + + ≥ + =

Từ đó suy ra đpcm. Dấu “=” xảy ra khi DE = DG

⇔

D là điểm chính

giữa cung nhỏ BC.

Bài 11.

K

D

N

M

E

O

1

F

O

2

O

H

B

C

A

a) Áp dụng tính chất của hai tiếp tuyến cắt nhau biến đổi được :

2AD = AB + AC – BC

Vì AO là phân giác của



BAC

⇒



0 0

1 1

.90 45

2 2

= = =DAO BAC

⇒

∆

AOD

vuông cân tại D

⇒

AD = OD = r

⇒

2r = AB + AC – BC (1)

Tương tự : 2r

1

= HB + HA – AB (2) ; 2r

2

= HA + HC – AC (3). Từ đó suy

ra AH = r + r

1

+ r

2

.

b) Ta có



=

HAB HCA

(cùng phụ với



HAC

).

Dễ thấy



0

1 2

45

= = =OAC O HA O HC

.

195

⇒

∆

AOC



1

∆

HO A



2

∆

HO C

(g-g)

⇒

1 2

= =

AC HA HC

AO HO HO

⇒

2 2 2

1 2

+

=

+

AC HA HC

AO HO HO

2 2 2

1 2

⇒ = +

r r r

.

c) Vì



=

HBA HAC

(cùng phụ với



HAB

) nên



2

ABO HAO

=



0

2

90

⇒ + =ABO BAO

2

⇒ ⊥

BO AO

hay

1 2

⊥

O O AO

(1).

Tương tự

2 1

⊥

O O AO

(2). Từ (1) và (2)

⇒

O là trực tâm của

1 2

∆

AO O

.

d) Vì O là trực tâm của

1 2

∆

AO O

nên

1 2

AO O O

⊥ hay

⊥

AO MN

⇒ ∆

AMN

vuông cân tại A



0

45

⇒ = =AMN ANM

=



0

1 2

45

= =O HB O HC

⇒

Các tứ giác BMO

1

H và CNO

2

H nội tiếp.

Dễ thấy



0

1 1 2

135

= =BMO O OO

và



1 1 2

=

MO B OO O

(đối đỉnh)



1 2 1

⇒ =

MBO OO O



1 2 1

⇒ =

O BC OO O

⇒

Tứ giác BO

1

O

2

C nội tiếp.

Cách khác : Chứng minh BO

1

O

2

C nội tiếp ta cần chứng minh

OA

2

= OO

1

.OB = OO

2

.OC.

e) Theo câu b)

(

)

(

)

2 2

2 2 2

1 2

3 2 4 2 50 5 2

= + = + = ⇒ =r r r r

⇒

AH = r + r

1

+ r

2

12 2

=

.

1 1

∆ = ∆

AO M AO H

(g-c-g)

⇒

AM = AH =

12 2

.

∆

AMN

vuông cân tại A

144

⇒ =

AMN

S (cm

2

).

Tam giác AMN vuông cân tại A có AM =

12 2

2 24

⇒ = =

MN AM

.

Giả sử AO cắt O

1

O

2

tại K.

Tam giác AMN vuông cân tại A, suy ra

1

12

2

AK MN

= =

.

Ta lại có

2 5 2. 2 10

= = =

AO r

12 10 2

⇒ = − = − =

OK AK AO

.

196

Tam giác HO

1

O

2

vuông tại H có

1 1 2 2

2 ; 2

= =HO r HO r

1 2

2 5 2. 2 10

⇒ = = =

O O r .

Do đó

1 2

10

=

OO O

S (cm

2

).

Tứ giác BMO

1

H, CNO

2

H nội tiếp



1 2 2 1

;⇒ = =

HO O HBM HO O HCN

.

Do đó

1 2

∆

HO O



∆

ABC

(g-g)

⇒

1 2 1 2

= =

HO HO O O

AB AC BC

⇒

3 4 5

= =

AB AC BC

.

Đặt AB = 3k ; AC = 4k ; BC = 5k. Từ AB.AC = BC.AH ta có k =

5 2

.

Do đó

300

=

ABC

S (cm

2

).

Bài 12.

E

O'

O

A

C

B

D

1) a) Dễ thấy



=

ABD BED

;



=

ACD CED

.

Do đó :



0

180 .

BEC BAC ABD ACD BAC+ = + + =

Suy ra tứ giác ABEC

nội tiếp.

b) Vì

∆

ABC

cân tại A



⇒ =

ABC ACB

, theo câu a) nên



BED CED

=

ta

có ED là phân giác của



BEC

(1). Tứ giác ABEC nội tiếp và AB = AC



⇒ =

BEA CEA

⇒

EA là phân giác của



BEC

(2)

197

Từ (1) và (2) suy ra DE đi qua điểm A cố định.

c) Vì

∆

ABC

cân tại A,



0

120

=A



0 0

30 30

⇒ = = ⇒ = =ABC ACB BED CED

.

Do đó

BEC BED CED

S S S= +

0 0 0

1 1 1

. .sin 60 . .sin30 . .sin 30

2 2 2

EB EC EB ED EC ED⇔ = +

1 3 1 1 1 1

. . . . . . . . .

2 2 2 2 2 2

EB EC EB ED ED EC

⇔ = +

3 1 1

. . 3 . .EB EC EB ED ED EC

ED EB EC

⇔ = + ⇔ = +

2) Vì đường tròn (O) tiếp xúc với AB tại B



0

90

=OBA

, mà



0

30

=ABC

nên



0

60

=OBD

.

Tam giác OBD cân tại O (OB = OD = R) và



0

60

=OBD

⇒ ∆

OBD

đều

⇒

R = BD (1)

Tương tự : R’ = CD (2). Từ (1) và (2)

⇒

R + R’ = BD + CD = BC =

2 3

(cm).

3) Ta có AE = AD + DE. Do đó DE lớn nhất

⇔

AE lớn nhất và AD nhỏ

nhất có thể được.

Điều này đồng thời xảy ra khi AE

⊥

BC tại D

⇒

DB = DC =

3

cm.

Dễ thấy tam giác ABD lúc này là nửa tam giác đều

⇒

AD = 1cm và

AB = 2cm.

Ta có

∆

ABE

vuông tại B, đường cao BD, suy ra

AB

2

= AD.AE

2 2

2

4

1

⇒ = = =

AB

AE

AD

(cm).

Vậy DE có độ dài lớn nhất khi D là trung điểm của BC, khi đó DE = 3cm.

198

Bài 13.

I

O

1

C

B

O

3

O

2

A

a) Áp dụng tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài

⇒

O

1

O

2

= 3cm, O

2

O

3

= 5cm, O

3

O

1

= 4cm

⇒

tam giác O

1

O

2

O

3

vuông tại

O

1

.

b) Vì tam giác O

1

O

2

O

3

vuông tại O

1

nên

1 3

2

2 3

4

sin

5

= =

O O

O

O O

;

1 2

3

2 3

3

sin

5

= =

O O

O

O O

2

2 2 2

. .sin

1,6

2

⇒ = =

ABO

O AO B O

S (cm

2

)

và

3

3 3 3

B. C.sin

2,7

2

= =

BCO

O O O

S (cm

2

)

Ta lại có

1 2 3

1 2 1 3

.

6

2

= =

O O O

O O O O

S (cm

2

) ;

1

1 1

A.

0,5

2

= =

O AC

O O C

S (cm

2

).

⇒

S

ABC

= 1,2 (cm

2

).

c) Gọi I là giao điểm các tia phân giác của các góc O

2

và O

3

⇒

O

1

I

là phân giác của góc O

1

.

Dễ thấy

2 2

∆ = ∆

O IA O IB

(c-g-c) ;

199

Q

P

N

M

H

F

E

D

B

C

I

O

K

A

3 3

∆ = ∆

O IB O IC

(c-g-c) ;

1 1

∆ = ∆

O IA O IC

(c-g-c).



1 3 1 2 1 1

; ;⇒ = = =

IAO IBO ICO IBO IAO ICO



0

2 3

90

⇒ = =IBO IBO

hay

2 3

⊥

IB O O

.

Tương tự

1 2 1 3

;⊥ ⊥

IA O O IC O O

. Ta lại có IA = IB = IC

⇒

đpcm.

d) Ta có

3

1 2

2 3 1

1 2 3

. . . . 1

2 3 1

= =

CO

AO BO

AO BO CO

.

Áp dụng định lí Cê-va đảo

⇒

đpcm.

Bài 14. a) Vì I là trung điểm của BC nên

IB = IC =

3

2 2

=

BC R

và OI

⊥

BC.

Tam giác BOI vuông tại I, ta có



3

sin

2

= =

IB

BOI

OB



0

60

⇒ =BOI

.

∆

BOC

cân tại O



0 0

2. 2.60 120

⇒ = = =BOC BOI

.



0 0

1 1

.120 60

2 2

⇒ = = =BAC BOC .

Tứ giác AEHF có :



0

90

= =AEH AFH

;



0

60

=EAF

⇒



0

120

=EHF

Ta lại có



=

BHC EHF

(đối đỉnh)



0

120

⇒ =BHC

Tứ giác BHOC có



0

120

= =BHC BOC

⇒

Tứ giác BHOC nội tiếp.

b) Dễ thấy



0

90

= =ABP ACP

⇒

CP // BH và PB // CH.

⇒

BHCP là hình bình hành, mà I là trung điểm đường chéo BC nên I

cũng là trung điểm đường chéo HP, hay 3 điểm H, I, P thẳng hàng.

c) Vì K là điểm chính giữa cung nhỏ BC

⇒

OK

⊥

BC tại I.

Tam giác BOI vuông tại I, ta có



0

.co .co 60

2

= = =

R

OI OB sBOI R s .

Dễ thấy OI là đường trung bình của tam giác AHP

⇒

AH = 2.OI = R.

200

Tứ giác AOKH có OK // AH và OK = AH = R

⇒

AOKH là hình bình

bình hành.

Hình bình hành AOKH có AH = AO = R

⇒

AOKH là hình thoi.

d) Tam giác BOC cân tại O có



0

120

=BOC



0

30

⇒ = =OBC OCB

.

Tứ giác BHOC nội tiếp



⇒ =

EHN OCB



0

30

⇒ =EHN

, mà

∆

EHN

vuông tại E



0

60

⇒ =ENH

Tam giác AMN có



0

60

= =MAN ANM

⇒

Tam giác AMN là tam giác

đều.

e) Dễ thấy



0

30

=ABE

=



0

30

=MHB

⇒ ∆

BMH

cân tại M

⇒

BM = MH (1)

Dễ thấy



0

30

=ACF

=



0

30

=NHC

⇒ ∆

CNH

cân tại N

⇒

CN = NH (2)

Cộng (1) và (2) vế theo vế ta được : BM + CN = MH + NH = MN.

Kẻ đường cao AQ của tam giác đều AMN

2

3

⇒ =

AQ

MN

⇒

BM + CN

2.

3

=

AQ

.

Mà AQ

≤

AO = R, dấu “=” xảy ra

⇔

Q

≡

H

≡

O

⇔

A là điểm chính

giữa cung BC.

Vậy : BM + CN đạt giá trị lớn nhất bằng

2

3

R

khi A là điểm chính giữa

cung lớn BC.

201

Phần ba.

SỐ HỌC

TÍNH CHIA HẾT - ĐỒNG DƯ THỨC

1. PHƯƠNG PHÁP GIẢI

− A(n)



p khi A(n) = p.A

1

(n) hoặc A(n) = pA

1

(n) +pA

2

(n) +…

− Các tính chất về phép chia hết.

− a đồng dư b theo modun m nếu a − b chia hết cho m. Kí hiệu : a

≡

b (mod m).

− Các tính chất về đồng dư thức.

2. CÁC VÍ DỤ

Ví dụ 1. Chứng minh rằng mọi số nguyên n thì :

a) n

3

– n chia hết cho 3 ;

b) n

5

– n chia hết cho 5 ;

c) n

7

– n chia hết cho 7.

Hướng dẫn giải

a) Ta có n

3

– n = (n – 1)n(n + 1) mà trong ba số nguyên liên tiếp có một số

chia hết cho 3. Vậy n

3

– n chia hết cho 3.

b) Cách 1 : Có n

5

– n = n( n

2

– 1)( n

2

+1) = n(n

2

– 1)(n

2

– 4 + 5)

= (n –2)(n – 1)n(n +1)(n + 2) + 5n(n

2

– 1)(n

2

– 4) chia hết cho 5,

vì mỗi số hạng của tổng đều chia hết cho 5.

Cách 2 : Xét số dư của n trong phép chia cho 5 (đồng dư theo mod 5).

Từ A = n

5

– n = n(n

2

– 1)(n

2

+ 1) ta có :

− Nếu n chia hết cho 5 thì A chia hết cho 5.

Ch

ChCh

Ch 

  

 

1

11

1

202

− Nếu n = 5k

±

1 (

k

∈



) thì

2 2

n 1 (25k 10k) 5

− = ±



.

−

Nếu :

n

= 5

k

±

2 (

k

∈



) thì

2 2

1 (25 20 5) 5

n k k+ = ± +



.

Trong 5 trường hợp trên, trường hợp nào cũng có một thừa số chia hết cho 5.

Vậy ta có điều phải chứng minh.

c) * Cách 1

Xét hiệu của

n

7

– n

với một số chia hết cho 7 là

(n – 3)(n – 2)(n – 1)n(n + 1)(n + 2)(n + 3).

Ta có :

n

7

– n – (n – 3)(n – 2)(n – 1)n(n + 1)(n + 2)(n + 3) = 7n(2n

4

– n

2

+ 5)



7.

* Cách 2

Ta có n

7

– n = n(n

3

+ 1)( n

3

– 1).

Xét

n 7k ; n 7k 1; n 7k 2 ; n 7k 3(k ).

= = ± = ± = ± ∈



Trong các trường hợp trên, trường hợp nào cũng có một thừa số chia hết cho 7.

Bài toán trên là các trường hợp riêng của định lí Fec-ma.

Ví dụ 2. Chứng minh rằng :

2

0

+ 2

1

+ 2

2

+ …+ 2

5n – 3

+ 2

5n – 2

+ 2

5n -1

chia hết cho 31.

Hướng dẫn giải

Tổng gồm 5n số hạng, ta nhóm thành n nhóm, mỗi nhóm 5 số hạng

2

0

+ 2

1

+ 2

2

+ …+ 2

5n – 3

+ 2

5n – 2

+ 2

5n − 1

= (2

0

+ 2

1

+…+ 2

4

) +(2

5

+ 2

6

+ …+ 2

9

) + … + (2

5n − 5

+ 2

5n − 4

+ …+ 2

5n – 1

)

= (2

0

+ 2

1

+…+ 2

4

)(1 + 2

5

+ 2

5.2

+ … +2

5( n – 1)

)

= 31(1 + 2

5

+ 2

5.2

+ … + 2

5( n – 1)

) chia hết cho 31.

Ví dụ 3. Tìm giá trị nguyên của biểu thức P =

2

1

+ +

−

x x

xy

, trong đó

x

,

y

là các số

nguyên dương.

Hướng dẫn giải

P có nghĩa khi

xy

≠

1. Xét các trường hợp sau

203

a) Với

x

= 1 và

y

≥

2 thì P =

4

1y

+

∈

−



khi y

–

1 là ước nguyên dương của 4.

Vậy P = 4 khi

x

= 1 ;

y

= 2 ;

P = 2 khi

x

= 1 ;

y

= 3 ;

P = 1 khi

x

= 1 ;

y

= 5.

b) Với y = 1 và

2

x

≥

thì P =

2

.

1 4

2

1 1

x x

x

x x

+ +

= + +

− −

Do đó P là số

nguyên khi

x

–

1 là ước nguyên dương của 4.

Vậy P = 8 khi

x

= 2 ;

y

= 1 ;

P = 7 khi

x

= 3 ;

y

= 1 ;

P = 8 khi

x

= 5 ;

y

= 1.

c) Với

2 ; 2

x y

≥ ≥

thì

y

.P =

2

2 2 1

1

1 1

x y xy y y x

x

xy xy

+ + + +

= + +

− −

Để P nguyên thì

2 1

1

y x

xy

+ +

−

= k là số nguyên dương (do

xy

–

1

≥

3).

* Nếu k = 1 thì 2y +

x

+ 1 = xy – 1

⇔

xy

–

2y – (x

−

2) = 4

⇔

(x – 2)(y

−

1) = 4

Vậy

x

= 3 ;

y

= 5 thì P = 1 ;

x

= 4 ;

y

= 3 thì P = 2 ;

x

= 6 ;

y

= 2 thì P = 4.

* Nếu k

≥

2 thì 2

y + x +

1

≥

2

xy –

2

⇔

2

xy –

2

y –

(

x –

1)

≤

4

⇔

(

x –

1)(2

y –

1)

≤

4.

Với

x

≥

2 ;

y

≥

3 thì BĐT trên không

x

ảy ra.

Với

x

= 2 ;

y

= 2 thì k không nguyên nên P không nguyên.

Vậy các giá trị nguyên của P là : 1 ; 2 ; 4 ; 7 ; 8.

Ví dụ 4. Với những giá trị nào của

a

thì các số

15

a +

và

1

15

a

−

đều là các số

nguyên ?

Hướng dẫn giải

204

Đặt

15

a +

=

x

và

1

15

a

− = y ;

,

x y Z

∈

.

Suy ra a =

15

x − và

1

15 ( 0)

y a

a

= + ≠

.

Do

đ

ó

( 15)( 15 ) 1

x y

− + =

15( ) 16

x y xy

⇔ − = −

(1)

N

ế

u

x y

≠

, ta có

16

15

xy

x y

−

=

−

vô lí vì

15

là s

ố

vô t

ỉ

và

16

xy

x y

−

là s

ố

h

ữ

u

t

ỉ

.

V

ậ

y x = y, thay vào (1) ta

đượ

c x = y = 4 ho

ặ

c x = y = –4.

V

ậ

y

{

}

4 15 ; 4 15

a ∈ − − −

.

Ví dụ 5.

Tìm hai ch

ữ

s

ố

cu

ố

i cùng c

ủ

a s

ố

A = 2

2014

.

Hướng dẫn giải

Ta tìm s

ố

d

ư

c

ủ

a A khi chia cho 100.

Ta có 100 = 4.25 và 2

10

= 1024

1( 25)

mod

≡ −

4 2010 4 10 201

2 .2 2 .(2 ) 9(mod 25)

A

⇒

= = ≡

Hi

ể

n nhiên A chia h

ế

t cho 4

16 (mod100)

A

⇒ ≡ −

.V

ậ

y hai ch

ữ

s

ố

cu

ố

i cùng

c

ủ

a A là 84.

Ví dụ 6.

Ch

ứ

ng minh r

ằ

ng n

ế

u A có ba ch

ữ

s

ố

t

ậ

n cùng là 625 thì A

n

c

ũ

ng có ba

ch

ữ

s

ố

t

ậ

n cùng là 625.

Hướng dẫn giải

T

ừ

625(mod1000)

A

≡

suy ra

625 (mod1000)

n n

A ≡ .

Ta có

1 2

625 625 625(625 1) 625.624.(625 ... 1

n n n− −

− = − = + +

)

2

390000(625 ... 1) 0(mod1000)

n−

= + + ≡ .

V

ậ

y A

n

c

ũ

ng có ba ch

ữ

s

ố

tân cùng là 625.

Ví dụ 7.

Cho A = 1

5

+ 2

5

+ 3

5

+… + 2015

5

.

Hãy tìm ch

ữ

s

ố

t

ậ

n cùng c

ủ

a A.

205

Hướng dẫn giải

Chú ý rằng :

V

ớ

i

a

∈



thì hai s

ố

a

5

và a có ch

ữ

s

ố

t

ậ

n cùng gi

ố

ng nhau.

Th

ậ

t v

ậ

y :

a

5

– a = a(a

4

– 1) = a(a

2

– 1)(a

2

+ 1) = a(a – 1)(a + 1)(a

2

– 4 + 5)

= a(a – 1)(a + 1)(a – 2)(a + 2) + 5a(a – 1 )(a + 1).

Vì tích hai s

ố

t

ự

nhiên liên ti

ế

p chia h

ế

t cho 2 và tích n

ă

m s

ố

t

ự

nhiên liên ti

ế

p

chia h

ế

t cho 5 nên a

5

– a chia h

ế

t cho 10 hay a

5

và a có ch

ữ

s

ố

t

ậ

n cùng gi

ố

ng

nhau.

Đặ

t B = 1 +2 +3 +… + 2015 thì

A = (1

5

– 1) + (2

5

– 2) + (3

5

– 3)+… + (2015

5

– 2015) + B.

Nên hai s

ố

A và B có ch

ữ

s

ố

t

ậ

n cùng gi

ố

ng nhau. Do

đ

ó ta tìm ch

ữ

s

ố

t

ậ

n

cùng c

ủ

a B.

Mà

2016

2015.

2

B = = 2.031.120 V

ậ

y ch

ữ

s

ố

cu

ố

i cùng c

ủ

a A là 0.

3. BÀI TẬP TỰ LUYỆN

Bài 1.

Ch

ứ

ng minh r

ằ

ng : n

ế

u các s

ố

nguyên a và b không chia h

ế

t cho 3 thì a

6

– b

6

chia h

ế

t cho 9.

Bài 2.

Ch

ứ

ng minh r

ằ

ng 4a

2

+ 3a + 5ch

ỉ

chia h

ế

t cho 6 n

ế

u a là m

ộ

t s

ố

nguyên

không chia h

ế

t cho 2 và c

ũ

ng không chia h

ế

t cho 3.

Bài 3.

Xét phân s

ố

2

4

5

n

A

n

+

=

+

. H

ỏ

i có bao nhiêu s

ố

t

ự

nhiên n trong kho

ả

ng t

ừ

1

đế

n 2015 sao cho phân s

ố

A ch

ư

a t

ố

i gi

ả

n.

Bài 4.

Cho a, b

∈



. Ch

ứ

ng minh :

11 2 18 5

19 19

a b a b

+ +

∈ ⇔ ∈

 

.

Bài 5.

Tìm các s

ố

t

ự

nhiên n sao cho 2

2n

+ 2

n

+ 1 chia h

ế

t cho 21.

Bài 6.

Tìm ba ch

ữ

s

ố

cu

ố

i cùng c

ủ

a A = 2

2015

.

Bài 7.

Ch

ứ

ng minh r

ằ

ng n

ế

u A có hai ch

ữ

s

ố

t

ậ

n cùng là 76 thì A

n

c

ũ

ng có hai

ch

ữ

s

ố

t

ậ

n cùng là 76.

Bài 8.

Ch

ứ

ng minh A =

2

2 5 7

n

+



1

n

∀ ≥

.

206

SỐ NGUYÊN TỐ - HỢP SỐ - SỐ CHÍNH PHƯƠNG

1. PHƯƠNG PHÁP GIẢI

−

Để

ch

ứ

ng minh A(n) là s

ố

nguyên t

ố

ta phân tích A(n) = A

1

(n).A

2

(n).

Ta có A(n) là s

ố

nguyên t

ố

khi A

1

(n) = 1 ; A

2

(n) nguyên t

ố

ho

ặ

c A

2

(n) = 1 ;

A

1

(n) là s

ố

nguyên t

ố

.

−

Để

ch

ứ

ng minh A(n) là h

ợ

p s

ố

ta c

ầ

n ch

ứ

ng minh A(n) chia h

ế

t cho m l

ớ

n

h

ơ

n 1 và A(n) l

ớ

n h

ơ

n m.

−

Để

ch

ứ

ng minh A(n) là s

ố

chính ph

ươ

ng, ta c

ầ

n ch

ứ

ng minh A(n) là bình

ph

ươ

ng c

ủ

a m

ộ

t s

ố

nguyên, ho

ặ

c c

ă

n c

ứ

vào m

ộ

t s

ố

tính ch

ấ

t v

ề

s

ố

chính ph

ươ

ng.

−

M

ộ

t s

ố

không chính ph

ươ

ng khi : ch

ữ

s

ố

t

ậ

n cùng là 2, 3, 7, 8 ; chia cho 3

d

ư

2 ; chia cho 4 d

ư

2 ho

ặ

c 3 ; n

ằ

m gi

ữ

a hai s

ố

chính ph

ươ

ng liên ti

ế

p ; ...

2. CÁC VÍ DỤ

Ví dụ 1.

Cho p là s

ố

nguyên t

ố

d

ạ

ng p = 4k + 3 (

k N

∈

). Gi

ả

s

ử

các s

ố

nguyên

x

,

y

tho

ả

mãn

x

2

+

y

2

chia h

ế

t cho p. Ch

ứ

ng minh

x

và

y

đề

u chia h

ế

t cho p.

Hướng dẫn giải

N

ế

u m

ộ

t trong hai s

ố

x

và

y

chia h

ế

t cho p, theo gi

ả

thi

ế

t

x

2

+

y

2

chia h

ế

t cho p

thì ta suy ra c

ả

hai s

ố

đề

u chia h

ế

t cho p.

Gi

ả

s

ử

c

ả

hai s

ố

đề

u không chia h

ế

t cho p. Ta có p = 4k + 3 (

k

∈



).

Theo

đị

nh lí Fer-ma thì

1 1

1(mod )

p p

x y p

− −

≡ ≡

suy ra :

4 2 4 2

2(mod )

k k

x y p

+ +

+ ≡

(1)

M

ặ

t khác :

4 2 4 2 2 2 1 2 2 1 2 2

( ) ( ) .

k k k k

x y x y x y p

+ + + +

+ = + +

 

(2)

T

ừ

(1) và (2) ta suy ra

2 2,

p p

⇒ =



vô lí vì p = 4k + 3. V

ậ

y ta có

đ

i

ề

u ch

ứ

ng

minh.

Ch

ChCh

Ch 

  

 

2

22

2

207

Ví dụ 2.

Ch

ứ

ng minh r

ằ

ng không có s

ố

chính ph

ươ

ng A nào có m

ộ

t trong hai

d

ạ

ng sau :

a) A = 4n + 2 ; b) A = 4n + 3.

Hướng dẫn giải

Xét a là s

ố

nguyên b

ấ

t kì. N

ế

u a ch

ẵ

n, a = 2n, thì a

2

= 4n

2

chia h

ế

t cho 4.

N

ế

u a l

ẻ

, a = 2n + 1, thì a

2

= 4n(n + 1) + 1

1

≡

(mod4).

Ví dụ 3.

Ch

ứ

ng minh r

ằ

ng các s

ố

có d

ạ

ng n(n + 1) và n(n + 2) không th

ể

là các s

ố

chính ph

ươ

ng v

ớ

i m

ọ

i s

ố

n nguyên d

ươ

ng.

Hướng dẫn giải

Ta bi

ế

t gi

ữ

a hai s

ố

nguyên d

ươ

ng liên ti

ế

p không còn s

ố

nguyên nào n

ữ

a,

c

ũ

ng nh

ư

gi

ữ

a hai s

ố

chính ph

ươ

ng liên ti

ế

p a

2

và (a + 1)

2

không còn s

ố

chính

ph

ươ

ng nào n

ữ

a. Mà ta có n

2

< n(n + 1) < n(n + 2) < (n + 1)

2

v

ớ

i m

ọ

i s

ố

n nguyên

d

ươ

ng nên các s

ố

n(n+ 1) và n(n + 2) không th

ể

là các s

ố

chính ph

ươ

ng v

ớ

i m

ọ

i

s

ố

n nguyên d

ươ

ng.

Ví dụ 4.

Ch

ứ

ng minh r

ằ

ng, t

ồ

n t

ạ

i vô s

ố

s

ố

nguyên d

ươ

ng a sao cho q = n

4

+ a

không là s

ố

nguyên t

ố

v

ớ

i m

ọ

i s

ố

nguyên d

ươ

ng n.

Hướng dẫn giải

Xét các s

ố

a có d

ạ

ng a = 4m

4

trong

đ

ó m là s

ố

nguyên d

ươ

ng.

Ta có q = n

4

+ a = n

4

+ 4m

4

= (n

2

+ 2m

2

)

2

– 4n

2

m

2

= (n

2

+ 2m

2

– 2nm)(n

2

+ 2m

2

+ 2nm)

V

ớ

i m > n thì n

2

+ 2m

2

– 2nm >1 và n

2

+ 2m

2

+ 2nm > 1, do

đ

ó q là h

ợ

p s

ố

.

V

ậ

y t

ồ

n t

ạ

i vô s

ố

s

ố

nguyên d

ươ

ng a = 4m

4

sao cho q không là s

ố

nguyên t

ố

v

ớ

i

m

ọ

i s

ố

nguyên d

ươ

ng n.

Ví dụ 5.

Cho p là s

ố

nguyên t

ố

l

ớ

n h

ơ

n 3 và 4p + 1 là s

ố

nguyên t

ố

.

Ch

ứ

ng minh r

ằ

ng 2p + 1 là h

ợ

p s

ố

.

Hướng dẫn giải

Vì p là s

ố

nguyên t

ố

l

ớ

n h

ơ

n 3 nên p



3. Do

đ

ó p = 3k + 1 ho

ặ

c p = 3k + 2

(k

*

∈



).

208

N

ế

u p = 3k + 2 thì 4p + 1 = 4(3k + 2) + 1 = 12k + 9



3 và l

ớ

n h

ơ

n 3 nên 4p + 1

là h

ợ

p s

ố

. Mà theo

đề

bài thì 4p + 1 là s

ố

nguyên t

ố

nên p = 3k + 1.

Khi

đ

ó 2p + 1 = 2(3k + 1) + 1 = 6k + 3



3 và l

ớ

n h

ơ

n 3. V

ậ

y 2p + 1 là h

ợ

p

s

ố

.

Ví dụ 6.

Ch

ứ

ng minh r

ằ

ng 10

6n + 4

+ 3 là h

ợ

p s

ố

v

ớ

i m

ọ

i s

ố

t

ự

nhiên n.

Hướng dẫn giải

Ta có 10

6

chia cho 7 d

ư

1 nên 10

6n

chia cho 7 c

ũ

ng d

ư

1, do

đ

ó 10

6n − 1



7.

Suy ra 10

4

(10

6n

− 1)



7

⇒

10

6n + 4

− 10

4



7

⇒

(10

6n + 4

+ 3) − (10

4

+ 3)



7.

Ta l

ạ

i có 10

4

+ 3



7 nên 10

6n + 4

+ 3



7, mà 10

6n + 4

+ 3 > 7 nên 10

6n + 4

+ 3 là

h

ợ

p s

ố

.

Ví dụ 7.

Có hay không 2009 s

ố

t

ự

nhiên liên ti

ế

p

đề

u là h

ợ

p s

ố

?

Hướng dẫn giải

Xét s

ố

t

ự

nhiên a = 1.2.3…2010 = 2010!

Xét 2009 s

ố

t

ự

nhiên liên ti

ế

p a + 2, a + 3, a + 4, …, a + 2010.

D

ễ

th

ấ

y a + k > k và a + k



k (v

ớ

i m

ọ

i k = 2, 3, 4,…, 010), suy ra a + k là h

ợ

p

s

ố

.

V

ậ

y 2009 s

ố

t

ự

nhiên liên ti

ế

p a + 2, a + 3, a + 4, …, a + 2010

đề

u là h

ợ

p s

ố

.

3. BÀI TẬP TỰ LUYỆN

Bài 1.

Tìm t

ấ

t c

ả

s

ố

t

ự

nhiên n sao cho dãy n + 1, n + 2, n + 3, …, n + 10 có

nhi

ề

u s

ố

nguyên t

ố

nh

ấ

t.

Bài 2.

Cho

; 1

n N n

∈ >

và n không chia h

ế

t cho 3.

Ch

ứ

ng minh r

ằ

ng s

ố

A = 3

2n

+ 3

n

+ 1 là h

ợ

p s

ố

.

Bài 3.

Tìm các s

ố

nguyên t

ố

p sao cho 2p + 1 b

ằ

ng l

ậ

p ph

ươ

ng c

ủ

a m

ộ

t s

ố

t

ự

nhiên.

Bài 4.

Tìm các s

ố

nguyên t

ố

p sao cho 13p + 1 b

ằ

ng l

ậ

p ph

ươ

ng c

ủ

a m

ộ

t s

ố

t

ự

nhiên.

Bài 5.

Tìm t

ấ

t c

ả

các s

ố

nguyên t

ố

p, q, r tho

ả

mãn ph

ươ

ng trình :

(p + 1)(q + 2)( r +3) =

4pqr

209

Bài 6.

Ch

ứ

ng minh r

ằ

ng v

ớ

i m

ọ

i s

ố

nguyên x, y thì

A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y

4

là s

ố

chính ph

ươ

ng.

Bài 7.

Cho S = 1.2.3 + 2.3.4 + 3.4.5 + . . . + k(k + 1)(k + 2).

Ch

ứ

ng minh r

ằ

ng 4S + 1 là s

ố

chính ph

ươ

ng.

Bài 8.

Cho a, b, c, d là các s

ố

nguyên d

ươ

ng tùy ý sao cho ac = bd.

Ch

ứ

ng minh r

ằ

ng v

ớ

i m

ọ

i s

ố

t

ự

nhiên n thì s

ố

M = a

n

+ b

n

+ c

n

+ d

n

là h

ợ

p

s

ố

.

PHƯƠNG TRÌNH NGHIỆM NGUYÊN

1. PHƯƠNG PHÁP GIẢI

Có th

ể

s

ử

d

ụ

ng m

ộ

t ho

ặ

c k

ế

t h

ợ

p các tình hu

ố

ng sau :

−

Đ

ánh giá mi

ề

n giá tr

ị

c

ủ

a bi

ế

n

x

.

−

Đư

a v

ề

ph

ươ

ng trình

ướ

c s

ố

.

− S

ử

d

ụ

ng ph

ươ

ng pháp k

ẹ

p gi

ữ

a hai s

ố

nguyên liên ti

ế

p không còn s

ố

nguyên nào n

ữ

a.

− S

ử

d

ụ

ng tính ch

ấ

t chia h

ế

t,

đồ

ng d

ư

th

ứ

c.

− Dùng ph

ươ

ng pháp c

ự

c h

ạ

n : s

ử

d

ụ

ng ph

ầ

n t

ử

l

ớ

n nh

ấ

t hay nh

ỏ

nh

ấ

t c

ủ

a

m

ộ

t t

ậ

p h

ợ

p s

ố

h

ữ

u h

ạ

n.

2. CÁC VÍ DỤ

Ví dụ 1.

Tìm nghi

ệ

m nguyên c

ủ

a ph

ươ

ng trình :

x

2

–

6

xy +

13

y

2

= 100.

G

ợi ý : Đánh giá miền giá trị của biến x.

Hướng dẫn giải

Phương trình đã cho viết được dưới dạng : (x – 3y)

2

= 4(25 – y

2

). (1)

Ch

ChCh

Ch 

  

 

3

33

3

210

Từ (1) ta suy ra :

2

25

y

≤

và

2

25

y

−

là số chính phương.

Vậy :

{

}

2

0,9,16, 25

y ∈

{

}

0, 3, 4, 5

y

⇒ ∈ ± ± ±

.

V

ậ

y ph

ươ

ng trình có 12 nghi

ệ

m :

(10 ; 0) ; (–10 ; 0) ; (17 ; 3) ; (1 ; 3) ; (–17 ; –3) ; (–1 ; –3) ; (6 ; 4) ; (18 ; 4) ;

(–18 ; –4) ; (–6, –4) ; (15 ; 5) ; (–15 ; –5).

Ví dụ 2.

Tìm nghi

ệ

m nguyên c

ủ

a ph

ươ

ng trình :

2 2 2

( 2) ( 6 8) 5 62

y x y y x y y

− + − + = − +

.

G

ợ

i ý :

Đư

a v

ề

ph

ươ

ng trình

ướ

c s

ố

.

Hướng dẫn giải

Ph

ươ

ng trình

đ

ã cho t

ươ

ng

đươ

ng v

ớ

i :

2

( 2) ( 2)( 4) ( 2)( 3) 56

y x y y x y y

− + − − = − − +

⇔

2

( 2) ( 4) ( 3) 56

y x y x y

 

− + − − − =

 

⇔

( 2)( 1)( 3) 56

y x x y

− − + − =

Nh

ậ

n th

ấ

y (y – 2) + (x – 1) = (x + y – 3), nên ta phân tích 56 thành tích ba s

ố

nguyên sao cho t

ổ

ng hai s

ố

đầ

u b

ằ

ng s

ố

còn l

ạ

i.

Nh

ư

v

ậ

y 56 = 1.7.8 = 7.1.8 = (–8).1.(–7) = 1.(–8).(–7)

= (–8).7.(–1) = 7.(–8).(–1).

T

ừ

đ

ó nghi

ệ

m c

ủ

a ph

ươ

ng trình (x ; y) là : (2 ; 9) ; (8 ; 3) ; ( –7 ; 3) ; (2 ; –6) ;

(–7 ; 9) ; (8 ; –6).

Ví dụ 3.

Tìm nghi

ệ

m nguyên c

ủ

a ph

ươ

ng trình : 1 + x + x

2

+ x

3

= y

3

.

G

ợ

i ý : S

ử

d

ụ

ng ph

ươ

ng pháp k

ẹ

p gi

ữ

a hai s

ố

nguyên liên ti

ế

p không còn s

ố

nguyên nào n

ữ

a.

Hướng dẫn giải

Vì 1 + x + x

2

> 0 v

ớ

i m

ọ

i x.

T

ừ

ph

ươ

ng trình suy ra : x

3

< y

3

< (x +2)

3

⇒

y

3

= (x + 1)

3

.

V

ậ

y ta có : 1 + x + x

2

+ x

3

= (x + 1)

3

⇔

2x

2

+ 2x = 0

⇒

x = 0 ho

ặ

c x = –1.

Ph

ươ

ng trình có nghi

ệ

m : (0 ; 1) ; (–1 ; 0).

211

Ví dụ 4.

Tìm nghi

ệ

m nguyên c

ủ

a ph

ươ

ng trình 2x

6

+ y

2

– 2x

3

y = 320.

Hướng dẫn giải

(S

ử

d

ụ

ng tính ch

ấ

t chia h

ế

t,

đồ

ng d

ư

th

ứ

c)

Vi

ế

t l

ạ

i ph

ươ

ng trình d

ướ

i d

ạ

ng : x

6

+(x

3

– y)

2

= 320.

Đặ

t u = x

3

; v = (x

3

– y) ta có u

2

+ v

2

= 320.

Do

đ

ó u, v cùng ch

ẵ

n ho

ặ

c cùng l

ẻ

.

Gi

ả

s

ử

u, v cùng l

ẻ

thì

2 2

2(mod 4)

u v+ ≡ .

Mà 320

0(mod 4)

≡

không x

ả

y ra. V

ậ

y u, v cùng ch

ẵ

n.

Đặ

t u = 2u

1

, v = 2v

1

ta

đượ

c

2 2

1 1

80

u v

+ =

.

L

ậ

p lu

ậ

n t

ươ

ng t

ự

có u

1

, v

1

cùng ch

ẵ

n

đặ

t u

1

= 2u

2

, v

1

= 2v

2

ta

đượ

c

2 2

20

u v

+ =

.

Đặ

t u

3

= 2u

2

; v

3

= 2v

2

ta có

2 2

3 3

5

u v

+ =

.

V

ậ

y các c

ặ

p (u

3

; v

3

) là (1 ; 2), (–1 ; 2), (1 ; –2) , (–1 ; –2).

Suy ra c

ặ

p nghi

ệ

m (x ; y) là : (2 ; –8) ; (–2 ; –8) ; (2 ; 24) ; (–2 ; –24).

Ví dụ 5.

Tìm nghi

ệ

m t

ự

nhiên c

ủ

a ph

ươ

ng trình x + y + z = xyz.

G

ợ

i ý : Dùng ph

ươ

ng pháp c

ự

c h

ạ

n : s

ử

d

ụ

ng ph

ầ

n t

ử

l

ớ

n nh

ấ

t hay nh

ỏ

nh

ấ

t

c

ủ

a m

ộ

t t

ậ

p h

ợ

p s

ố

.

Hướng dẫn giải

Do vai trò c

ủ

a x, y, z là nh

ư

nhau nên ta ch

ỉ

c

ầ

n tìm các nghi

ệ

m x, y, z mà

x

≥

y

≥

z, sau

đ

ó hoán v

ị

các nghi

ệ

m v

ừ

a tìm

đượ

c

để

đượ

c toàn b

ộ

nghi

ệ

m c

ủ

a

ph

ươ

ng trình.

Ta có 3x

≥

x + y + z = xyz

⇒

3

≥

yz.

+ N

ế

u z = 0 thì ta có x + y = 0

⇒

x = y = z = 0.

+ N

ế

u z > 0 thì x

≥

y

≥

z > 0.

Do yz

≤

3 nên ta có các kh

ả

n

ă

ng sau :

* y = z = 1

⇒

x + 2 = x (vô nghi

ệ

m).

* y = 2 ; z = 1

⇒

x + 3 = 2x

⇒

x = 3.

* y = 3, z = 1

⇒

x + 4 = 3x

⇒

x = 2 < y (vô nghi

ệ

m).

212

V

ậ

y ph

ươ

ng trình có 7 nghi

ệ

m là : (0, 0, 0) và (3, 2, 1) cùng v

ớ

i các hoán v

ị

c

ủ

a nó.

3. BÀI TẬP TỰ LUYỆN

Bài 1.

Tìm t

ấ

t c

ả

c

ặ

p s

ố

nguyên (x ; y) tho

ả

mãn : y(x – 1) = x

2

+ 2.

Bài 2.

Tìm t

ấ

t c

ả

c

ặ

p s

ố

nguyên d

ươ

ng (x ; y) tho

ả

mãn :

(x

2

– 9y

2

)

2

= 33y + 16.

Bài 3.

Tìm các s

ố

nguyên x, y, z tho

ả

mãn

đ

i

ề

u ki

ệ

n :

6(y

2

− 1) + 3(x

2

+ y

2

z

2

) + 2(z

2

– 9x) = 0.

Bài 4.

Tìm t

ấ

t c

ả

các c

ặ

p s

ố

nguyên (x ; y) tho

ả

mãn : x

2

(x

2

+ y

2

) = y

p+1

.

Bài 5.

Tìm các s

ố

nguyên d

ươ

ng x, y, t v

ớ

i

6

t

≤

tho

ả

mãn ph

ươ

ng trình sau :

2 2

4 2 7 2 0

x y x y t

+ − − − − =

.

TOÁN SUY LUẬN LÔ-GIC

1. PHƯƠNG PHÁP GIẢI

− Vận dụng nguyên lí Dirichlê : "Nhốt n + 1 chú thỏ vào n cái chuồng thì tồn

tại ít nhất 1 cái chuồng nhốt nhiều hơn 1 chú thỏ".

− Vận dụng nguyên lí cực hạn : "Trong một tập hợp hữu hạn các số bao giờ

cũng tồn tại số bé nhất và số lớn nhất".

− Vận dụng nguyên lí biên : "Trong mặt phẳng cho hữu hạn các điểm luôn tồn

tại một đường thẳng đi qua 2 điểm đã cho mà các điểm còn lại đều nằm về một

phía của đường thẳng đó".

− Xét các khả năng có thể xảy ra, sự sáng tạo trong việc đưa ra một mô hình

cụ thể hợp lí, sự linh hoạt trong việc vận dụng các phương pháp như : phản chứng,

nguyên lí Đirichlê, nguyên lí cực hạn, quy nạp toán học, đồ thị (đưa ra một mô

hình hợp lí), tô màu, tính chất của dãi song song, đánh giá độ lớn của một yếu tố

hình học, …

Ch

ChCh

Ch 

  

 

4

44

4

213

2. CÁC VÍ DỤ

Ví dụ 1. Cho 100 số tự nhiên tuỳ ý. Chứng minh rằng tồn tại 10 số sao cho hiệu

hai số bất kì đều chia hết cho 11.

Gợi ý : Vận dụng nguyên lí Dirichlê.

Hướng dẫn giải

Bài toán thực chất đi chứng minh có ít nhất 10 số trong 100 số đã cho có cùng

số dư khi chia cho 11.

Khi chia cho 11 ta nhận được 11 số dư : 0, 1, 2, …, 10. Ta lại có 100 = 11.9 +

1. Vậy 100 số dư xếp vào 11 cái lồng theo nguyên tắc Dirichlê thì tồn tại một lồng

chứa ít nhất 9 + 1 = 10 số dư giống nhau.

Vậy có ít nhất 10 số khi chia cho 11 có cùng số dư.

Ví dụ 2. Mỗi điểm trong mặt phẳng được tô bởi một trong hai màu xanh hoặc đỏ.

Chứng minh tồn tại hai điểm được tô cùng màu mà khoảng cách giữa chúng

bằng 1.

Gợi ý : Vận dụng nguyên lí Dirichlê.

Hướng dẫn giải

Xét tam giác đều có cạnh bằng 1. Có ba đỉnh được tô bởi hai màu nên theo

nguyên lí Dirichlê thì tồn tại hai đỉnh được tô bởi cùng một màu.

Ví dụ 3. Chứng minh rằng trong 8 số tự nhiên, mỗi số có 3 chữ số, bao giờ cũng

có thể chọn được hai số mà khi viết liền nhau ta thu được một số có 6 chữ số

chia hết cho 7.

Gợi ý : Vận dụng nguyên lí Dirichlê.

Hướng dẫn giải

Trong 8 số luôn tồn tại hai số có cùng số dư khi chia cho 7 suy ra hiệu của

chúng chia hết cho 7, gọi hai số đó là

1 2 3 1 2 3

,

a a a b b b

suy ra :

1 2 3 1 2 3

7

a a a b b b−



.

V

ậ

y :

(

)

1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

1000 1001 7

a a a b b b a a a b b b a a a a a a b b b= + = − −



(vì

1001



7).

214

C

B

A

Ví dụ 4. Có n vận động viên thi đấu bóng bàn theo thể thức vòng tròn (mỗi đấu

thủ đấu với tất cả đấu thủ còn lại). Chứng minh rằng có thể sắp xếp tất cả n vận

động viên theo hàng dọc sao cho người đứng trước thắng người đứng kề sau.

Gợi ý : Vận dụng nguyên lí cực hạn.

Hướng dẫn giải

Xét tất cả các cách xếp số vận động viên theo hàng dọc sao cho người đứng

trước thắng người đứng kề sau (các cách xếp như vậy luôn tồn tại, ví dụ xếp hai

người thì người thắng đứng trước, người thua đứng sau). Vì số cách xếp là hữu

hạn nên tồn tại một cách xếp P có nhiều vận động viên nhất. Ta chứng minh cách

xếp P có đủ n vận động viên đã thi đấu.

Giả sử trái lại, còn một vận động viên A không được xếp trong cách xếp P.

Giả sử trong cách xếp P có m người A

1

, A

2

, …., A

m

(

2 1

m n

≤ ≤ −

) sao cho A

1

th

ắ

ng A

2

, A

2

th

ắ

ng A

3

, …., A

m−1

th

ắ

ng A

m

. Vì thi

đấ

u vòng tròn nên A ph

ả

i

đấ

u

v

ớ

i A

1

. N

ế

u A th

ắ

ng A

1

thì cách x

ế

p P

1

theo thú t

ự

: A, A

1

, …, A

m

có nhi

ề

u v

ậ

n

độ

ng viên h

ơ

n cách x

ế

p P, trái v

ớ

i cách ch

ọ

n, v

ậ

y A thua A

1

.L

ậ

p lu

ậ

n t

ươ

ng t

ự

A

thua A

2

,A

3

, …A

m

. Khi

đ

ó cách x

ế

p P

2

theo th

ứ

t

ự

A

1

, A

2

,…, A

m

, A có nhi

ề

u v

ậ

n

độ

ng viên h

ơ

n cách x

ế

p P.

V

ậ

y cách x

ế

p P có

đủ

n v

ậ

n

độ

ng viên, ta có

đ

i

ề

u ph

ả

i ch

ứ

ng minh.

Ví dụ 5.

V

ề

phía trong tam giác

đề

u ABC c

ạ

nh b

ằ

ng 21cm l

ấ

y hai

đ

i

ể

m D và E

tu

ỳ

ý. Ch

ứ

ng minh r

ằ

ng t

ồ

n t

ạ

i

đ

i

ể

m M n

ằ

m trên c

ạ

nh c

ủ

a tam giác

đề

u ABC

sao cho MD và ME

đề

u có

độ

dài l

ớ

n h

ơ

n 10cm.

G

ợ

i ý :

Đồ

th

ị

(T

ạ

o ra m

ộ

t mô hình h

ợ

p lí).

Hướng dẫn giải

V

ẽ

ba

đườ

ng tròn (A), (B), (C) có bán kính

b

ằ

ng 10cm.

Vì AB = BC = CA = 21cm nên ba

đườ

ng

tròn (A), (B), (C)

đ

ôi m

ộ

t n

ằ

m ngoài nhau. Xét

hai

đ

i

ể

m D và E n

ằ

m trong tam giác

đề

u ABC thì

có các kh

ả

n

ă

ng sau : cùng n

ằ

m trong m

ộ

t hình

qu

ạ

t, cùng n

ằ

m ngoài ba hình qu

ạ

t, ch

ỉ

có m

ộ

t

đ

i

ể

m n

ằ

m trong m

ộ

t hình qu

ạ

t ho

ặ

c n

ằ

m trong

hai hình qu

ạ

t khác nhau. Trong t

ấ

t c

ả

các kh

ả

n

ă

ng có th

ể

x

ả

y ra

đ

ó thì t

ồ

n t

ạ

i

đ

i

ể

m M trùng

v

ớ

i m

ộ

t trong các

đỉ

nh A, B, C tho

ả

mãn MD > 10cm ; ME > 10cm.

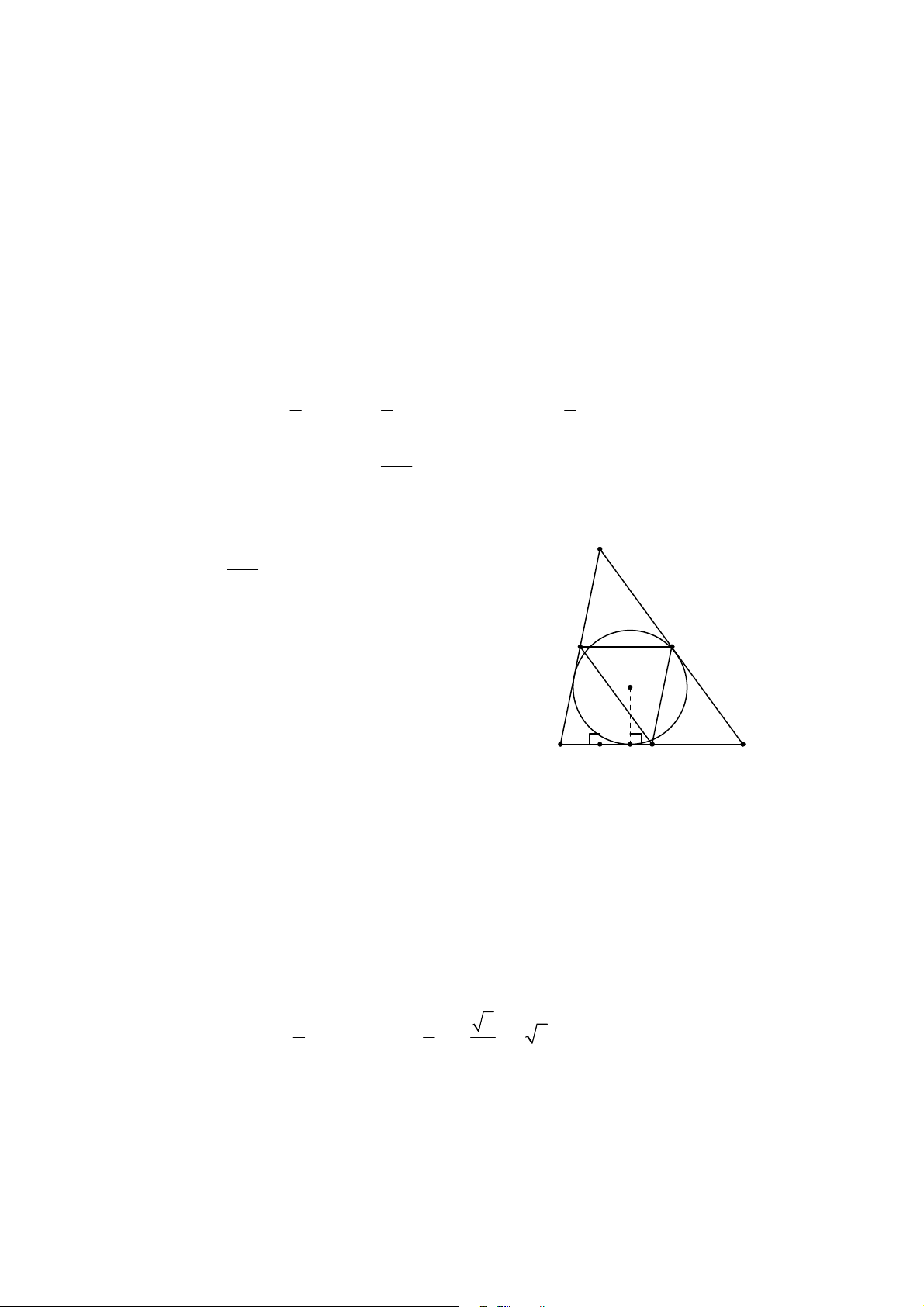
215

H

D

E

F

K

I

B

C

A

Ví dụ 6.

Ch

ứ

ng minh r

ằ

ng tâm

đườ

ng tròn n

ộ

i ti

ế

p m

ộ

t tam giác thì n

ằ

m trong

tam giác có

đỉ

nh là trung

đ

i

ể

m ba c

ạ

nh c

ủ

a tam giác

đ

ó.

G

ợ

i ý : V

ậ

n d

ụ

ng tính ch

ấ

t c

ủ

a dãi song song.

Hướng dẫn giải

G

ọ

i I là tâm

đườ

ng tròn n

ộ

i ti

ế

p c

ủ

a tam giác ABC. G

ọ

i D, E, F th

ứ

t

ự

là

trung

đ

i

ể

m các c

ạ

nh BC, CA, AB. K

ẻ

AH

⊥

BC, IK

⊥

BC.

Ta có S

ABC

=

( )

1 1 1

BC.AH BC CA AB .IK .2BC.IK

2 2 2

= + + >

.

Do

đ

ó AH > 2IK

AH

IK

2

⇒ <

.

D

ễ

th

ấ

y FE là

đườ

ng trung bình c

ủ

a tam giác

ABC nên FE // BC và kho

ả

ng cách gi

ữ

a FE và

BC b

ằ

ng

AH

2

.

⇒

I n

ằ

m trong hai

đườ

ng th

ẳ

ng song song

FE và BC (1).

T

ươ

ng t

ự

:

I n

ằ

m trong hai

đườ

ng th

ẳ

ng song song DF

và AC (2).

I n

ằ

m trong hai

đườ

ng th

ẳ

ng song song DE

và AB (3).

T

ừ

(1), (2) và (3)

⇒

I n

ằ

m trong tam giác DEF.

Ví dụ 7.

Tìm di

ệ

n tích l

ớ

n nh

ấ

t c

ủ

a m

ộ

t tam giác, bi

ế

t r

ằ

ng

độ

dài m

ỗ

i c

ạ

nh c

ủ

a

nó không v

ượ

t quá 4.

G

ợ

i ý : V

ậ

n d

ụ

ng nguyên lí c

ự

c h

ạ

n.

Hướng dẫn giải

Không m

ấ

t tính t

ổ

ng quát, gi

ả

s

ử

tam giác ABC có góc A là góc nh

ỏ

nh

ấ

t



0

A 60

⇒ ≤

.

Do

đ

ó

ABC

1 1 3

S AB.AC.sin A .4.4. 4 3

2 2 2

= ≤ =

, d

ấ

u “=” x

ả

y ra khi AB = 4,

AC = 4,



0

A 60

=

hay tam giác ABC là tam giác

đề

u c

ạ

nh b

ằ

ng 4.

216

C

B

D

A

V

ậ

y max

ABC

S 4 3

=

đạ

t

đượ

c khi tam giác ABC là tam giác

đề

u c

ạ

nh b

ằ

ng 4.

Ví dụ 8.

L

ấ

y m

ỗ

i c

ạ

nh c

ủ

a t

ứ

giác ABCD làm

đườ

ng kính, v

ẽ

n

ử

a

đườ

ng tròn

cùng phía v

ớ

i t

ứ

giác. Ch

ứ

ng minh t

ồ

n t

ạ

i ít nh

ấ

t m

ộ

t

đ

i

ể

m n

ằ

m trong ho

ặ

c

n

ằ

m trên các n

ử

a

đườ

ng tròn

đ

ó.

G

ợ

i ý :

Đ

ánh giá s

ố

đ

o m

ộ

t góc

đố

i v

ớ

i

đườ

ng tròn và ph

ươ

ng pháp ph

ả

n

ch

ứ

ng.

Hướng dẫn giải

Gi

ả

s

ử

đ

i

ể

m M n

ằ

m trong t

ứ

giác và n

ằ

m ngoài t

ấ

t c

ả

b

ố

n n

ử

a

đườ

ng tròn

đườ

ng kính AB, BC, CD,

DA thì



0

AMB 90

<

;



0

BMC 90

<

;



0

CMD 90

<

và



0

DMA 90

<



0

AMB BMC CMD DMA 360

⇒

+ + + <

, vô lí.

V

ậ

y có ít nh

ấ

t m

ộ

t

đ

i

ể

m n

ằ

m trong ho

ặ

c n

ằ

m

trên các n

ử

a

đườ

ng tròn

đườ

ng kính AB, BC, CD,

DA.

Ví dụ 9.

M

ộ

t n - giác (n > 3) có nhi

ề

u nh

ấ

t bao

nhiêu c

ạ

nh có

độ

dài b

ằ

ng

đườ

ng chéo l

ớ

n nh

ấ

t.

G

ợ

i ý : Ph

ả

n ch

ứ

ng, k

ế

t h

ợ

p v

ớ

i b

ấ

t

đẳ

ng th

ứ

c

tam giác.

Hướng dẫn giải

Xét n - giác A

1

A

2

A

3

…A

n

(n > 3) nh

ư

hình v

ẽ

sau :

Gi

ả

s

ử

đườ

ng chéo A

1

A

k

(2 < k < n) và gi

ả

s

ử

có ít nh

ấ

t 3 c

ạ

nh có

độ

dài b

ằ

ng

A

1

A

k

.

Ch

ẳ

ng h

ạ

n : A

1

A

2

, A

2

A

3

, A

3

A

4

Khi

đ

ó ta ch

ứ

ng minh

đượ

c A

1

A

3

+ A

2

A

4

> A

1

A

2

+ A

3

A

4

= 2A

1

A

k

. Nh

ư

v

ậ

y

trong hai

đườ

ng chéo A

1

A

3

và A

2

A

4

có ít nh

ấ

t m

ộ

t

đườ

ng chéo l

ớ

n h

ơ

n A

1

A

k

.

Đ

i

ề

u này vô lí, vì A

1

A

k

là

đườ

ng chéo l

ớ

n nh

ấ

t. V

ậ

y trong các n – giác (n > 3) có

nhi

ề

u nh

ấ

t có 2 c

ạ

nh có

độ

dài b

ằ

ng

đườ

ng chéo l

ớ

n nh

ấ

t.

Ch

ẳ

ng han : t

ứ

giác ABCD có

đườ

ng chéo AC l

ớ

n nh

ấ

t và có hai c

ạ

nh AB và

AD có

độ

dài b

ằ

ng AC.

Nh

ư

hình v

ẽ

sau

đ

ây :

217

A

D

B

C

A

1

A

n

A

2

A

3

A

4

A

k

A

1

A

n

A

2

A

3

A

4

A

5

A

6

A

7

Ví dụ 10. Đ

a giác có bao nhiêu c

ạ

nh thì có m

ọ

i

đườ

ng chéo

đề

u b

ằ

ng nhau.

G

ợ

i ý : Xét các tr

ườ

ng h

ợ

p

đặ

c bi

ệ

t, k

ế

t h

ợ

p v

ớ

i ph

ươ

ng pháp ph

ả

n ch

ứ

ng.

Hướng dẫn giải

V

ớ

i t

ứ

giác thì có hình ch

ữ

nh

ậ

t tho

ả

mãn

đề

bài.

V

ớ

i ng

ũ

giác thì có ng

ũ

giác

đề

u

tho

ả

mãn

đề

bài.

Ta s

ẽ

ch

ứ

ng minh v

ớ

i n – giác (n > 5)

thì không th

ể

có t

ấ

t c

ả

các

đườ

ng chéo

b

ằ

ng nhau.

Th

ậ

t v

ậ

y : Xét

đ

a giác A

1

A

2

A

3

…A

n

v

ớ

i n > 5.

Ta ch

ứ

ng minh

đượ

c A

1

A

4

+ A

2

A

6

>

A

1

A

3

+ A

4

A

6

.

Đ

i

ề

u này ch

ứ

ng t

ỏ

r

ằ

ng trong các

đườ

ng chéo A

1

A

4

; A

2

A

6

; A

1

A

3

và A

4

A

6

không th

ể

t

ấ

t c

ả

đề

u b

ằ

ng nhau.

Ví dụ 11.

Trong m

ặ

t ph

ẳ

ng cho 5

đ

i

ể

m phân bi

ệ

t. V

ẽ

t

ấ

t c

ả

các

đ

o

ạ

n th

ẳ

ng n

ố

i 2

trong 5

đ

i

ể

m

đ

ó r

ồ

i v

ẽ

các trung

đ

i

ể

m c

ủ

a chúng. Có ít nh

ấ

t bao nhiêu trung

đ

i

ể

m ?

G

ợ

i ý : V

ậ

n d

ụ

ng nguyên lí c

ự

c h

ạ

n.

Hướng dẫn giải

218

E

1

E

2

C

2

D

2

D

1

C

1

M

A

B

C

D

E

Trong 5

đ

i

ể

m phân bi

ệ

t A, B, C, D, E luôn t

ồ

n t

ạ

i 2

đ

i

ể

m có kho

ả

ng cách l

ớ

n

nh

ấ

t.

Ch

ẳ

ng h

ạ

n : A và B. G

ọ

i M là trung

đ

i

ể

m c

ủ

a AB. V

ẽ

các

đườ

ng tròn (A ;

AM) và (B ; BM). G

ọ

i C

1

; C

2

; D

1

; D

2

; E

1

; E

2

th

ứ

t

ự

là trung

đ

i

ể

m c

ủ

a CA, CB,

DA, DB, EA, EB. Vì AB l

ớ

n nh

ấ

t nên AC

1

; AD

1

; AE

1

nh

ỏ

h

ơ

n AM và BC

2

;

BD

2

; BE

2

nh

ỏ

h

ơ

n BM.

Do

đ

ó C

1

; D

1

; E

1

n

ằ

m trong

đườ

ng tròn (A ; AM) và C

2

; D

2

; E

2

n

ằ

m trong

ườ

ng tròn (B ; BM). Mà

A, B, C, D, E phân bi

ệ

t nên C

1

; D

1

;

E

1

; C

2

; D

2

; E

2

không trùng nhau.

Nh

ư

v

ậ

y s

ố

trung

đ

i

ể

m v

ẽ

đượ

c

không ít h

ơ

n 7.

B

E

2

E

C

2

D

E

1

C

A

D

1

D

2

M

C

1

Ta có th

ể

ch

ỉ

ra m

ộ

t hình v

ẽ

có

đ

úng 7 trung

đ

i

ể

m nh

ư

sau :

Các

đ

i

ể

m A, B, C, D, E th

ẳ

ng hàng và AC = CD = DE = EB khi

đ

ó ta ch

ỉ

v

ẽ

đượ

c 7 trung

đ

i

ể

m c

ủ

a các

đ

o

ạ

n th

ẳ

ng v

ẽ

đượ

c t

ừ

5

đ

i

ể

m A, B, C, D, E là M, C

1

,

C

2

, D

1

, D

2

, E

1

, E

2

.

3. BÀI TẬP TỰ LUYỆN

Bài 1.

Ch

ứ

ng minh r

ằ

ng trong 12 s

ố

nguyên t

ố

phân bi

ệ

t luôn ch

ọ

n ra

đượ

c 6 s

ố

g

ọ

i là a

1

, a

2

, … ,a

6

sao cho tích : P = (a

1

– a

2

)(a

3

– a

4

)(a

5

+ a

6

) chia h

ế

t cho

1800.

Bài 2.

Trong hình tròn tâm O bán kính b

ằ

ng 1 cho 8

đ

i

ể

m b

ấ

t kì. Ch

ứ

ng minh

r

ằ

ng trong các

đ

i

ể

m

đ

ã cho luôn t

ồ

n t

ạ

i hai

đ

i

ể

m mà kho

ả

ng cách gi

ữ

a

chúng luôn nh

ỏ

h

ơ

n 1.

Bài 3.

Cho 40 s

ố

nguyên d

ươ

ng a

1

, a

2

, … a

19

và b

1

, b

2

,…, b

21

tho

ả

mãn :

1 2 19

1 2 21

1 ... 200

a a a

b b b

≤ < < < ≤





≤ < < < ≤



Ch

ứ

ng minh r

ằ

ng t

ồ

n t

ạ

i 4 s

ố

a

i

, a

j

, b

k

, b

p

(

1 , 19,1 , 21

i j p k

≤ ≤ ≤ ≤

) sao

cho

219

i j

p k

i j p k

a a

b b

a a b b



<



<





− = −



Bài 4.

Tìm nghi

ệ

m nguyên d

ươ

ng c

ủ

a ph

ươ

ng trình :

xyz = 4(x + y + z).

Bài 5.

Bên trong

đườ

ng tròn tâm O có bán kính 1, v

ẽ

tam giác ABC có di

ệ

n tích

l

ớ

n h

ơ

n 1. Ch

ứ

ng minh r

ằ

ng tâm O n

ằ

m trong ho

ặ

c trên c

ạ

nh c

ủ

a tam giác

ABC.

Bài 6.

Cho hai

đ

i

ể

m A, B n

ằ

m trong

đườ

ng tròn (O ; R). Ch

ứ

ng minh r

ằ

ng t

ồ

n t

ạ

i

m

ộ

t

đườ

ng tròn

đ

i qua hai

đ

i

ể

m A, B và n

ằ

m trong

đườ

ng tròn (O).

Bài 7.

Trong m

ặ

t ph

ẳ

ng cho 2013

đ

i

ể

m phân bi

ệ

t sao cho b

ấ

t kì ba

đ

i

ể

m nào

c

ũ

ng t

ạ

o thành m

ộ

t tam giác có di

ệ

n tích nh

ỏ

h

ơ

n 1. Ch

ứ

ng minh r

ằ

ng có

th

ể

tìm

đượ

c m

ộ

t tam giác có di

ệ

n tích nh

ỏ

h

ơ

n 4 ch

ứ

a t

ấ

t c

ả

2013

đ

i

ể

m

đ

ã

cho.

Bài 8.

Trong tam giác

đề

u có c

ạ

nh b

ằ

ng 8,

đặ

t 193

đ

i

ể

m phân bi

ệ

t. Ch

ứ

ng minh

t

ồ

n t

ạ

i 2

đ

i

ể

m trong 193

đ

i

ể

m

đ

ã cho có kho

ả

ng cách không v

ượ

t quá

3

.

Bài 9. Đ

a giác có s

ố

đỉ

nh nhi

ề

u nh

ấ

t là bao nhiêu thì b

ấ

t kì ba

đỉ

nh nào c

ủ

a

đ

a

giác

đ

ó c

ũ

ng là ba

đỉ

nh c

ủ

a m

ộ

t tam giác giác vuông.

Bài 10.

Trong m

ặ

t ph

ẳ

ng cho 100

đ

i

ể

m phân bi

ệ

t, không có 3

đ

i

ể

m nào th

ẳ

ng

hàng và không có 4

đ

i

ể

m nào cùng thu

ộ

c m

ộ

t

đườ

ng tròn. Ch

ứ

ng minh

r

ằ

ng t

ồ

n t

ạ

i m

ộ

t

đườ

ng tròn

đ

i qua 3

đ

i

ể

m

đ

ã cho mà các

đ

i

ể

m còn l

ạ

i

đề

u

n

ằ

m ngoài

đườ

ng tròn

đ

ó.

220

GỢI Ý −

−−

− HƯỚNG DẪN GIẢI PHẦN SỐ HỌC

Chủ đề 1. TÍNH CHIA HẾT - ĐỒNG DƯ THỨC

Bài 1. Từ giả thiết ta có : a = 3m

1

±

; b = 3n

1

±

. Khi đ

ó, bi

ế

n

đổ

i bi

ể

u th

ứ

c, ta

có :

6 6

a b

− =

2

27( ) ( ) 3 9.

p q p q pq

 

− − +

 



Bài 2.

Vì a không chia h

ế

t cho 2 và 3 nên a = 6m

±

1. Xét t

ừ

ng tr

ườ

ng h

ợ

p

để

có

đ

i

ề

u ph

ả

i ch

ứ

ng minh.

Bài 3.

G

ọ

i d = (n

2

+ 4 ; n+ 5) ; d > 1. Ta có : d = 29.

Ng

ượ

c l

ạ

i n

ế

u n + 5



29 thì n + 5 = 29k (

*

k ∈



), suy ra

n

2

+ 4 = (29k – 5)

2

+ 4 = 29(29k

2

– 5k +1 )



29

⇒

A ch

ư

a t

ố

i gi

ả

n.

Nh

ư

v

ậ

y ta ch

ỉ

tìm n sao cho n + 5 = 29 k (

*

k ∈



) và tho

ả

mãn

1 2015

n

≤ ≤

1 29 5 2015 1 69

k k

≤ − ≤ ⇒ ≤ ≤

.

V

ậ

y có 69 giá tr

ị

c

ủ

a n

để

A ch

ư

a t

ố

i gi

ả

n.

Bài 4.

Ta có

11 2 18 5

5. 2

19 19

a b a b

a

+ +

− =

, suy ra

đ

i

ề

u ph

ả

i ch

ứ

ng minh.

Bài 5. Đặ

t A(n) = 2

2n

+ 2

n

+ 1. Ta tìm n sao cho A(n) chia h

ế

t cho 3 và 7.

* A(n) chia h

ế

t cho 3 khi và ch

ỉ

khi n ch

ẵ

n.

* Xét s

ố

d

ư

c

ủ

a n khi chia cho 7 ta

đượ

c :

A(n)

7 1(mod3) ; 2(mod3)

n n⇔ ≡ ≡



.

V

ậ

y n = 6k + 2, ho

ặ

c n = 6k + 4.

Bài 6.

Ta có 1000 = 8.125. Xét s

ố

d

ư

c

ủ

a A khi chia cho 125.

Bài 7.

76(mod100) 76 (mod100)

n n

A A

≡

⇒

≡ . Xét 76

n

– 76 (mod100).

Bài 8.

Có

3

2 8 1(mod 7)

= ≡ và

2

2 4 1(mod3)

n n

= ≡ .

221

V

ậ

y

2

2 3 1( )

n

k k N

= + ∈

3 1

2 5 2.8 5 2 5 0(mod 7)

k k

A

+

⇒

= + = + ≡ + ≡ .

Chủ đề 2. SỐ NGUYÊN TỐ - HỢP SỐ - SỐ CHÍNH PHƯƠNG

Bài 1.

G

ọ

i S(n) là s

ố

s

ố

nguyên t

ố

trong dãy

đ

ã cho

ứ

ng v

ớ

i n, ta có : S(0) = 4 ;

S(1) = 5 ; S(2) = 4.

Xét

3

n

≥

. Trong dãy n + 1, n +2 , …, n + 10 có 5 s

ố

ch

ẵ

n l

ớ

n h

ơ

n 3 nên

các s

ố

này không ph

ả

i là s

ố

nguyên t

ố

. Trong 5 s

ố

l

ẻ

liên ti

ế

p còn l

ạ

i có ít

nh

ấ

t m

ộ

t s

ố

chia h

ế

t cho 3, s

ố

này l

ớ

n h

ơ

n 3 nên không ph

ả

i là s

ố

nguyên

t

ố

. V

ậ

y S(n)

≤

4.

Đ

áp s

ố

: n = 1.

Bài 2.

Ch

ứ

ng minh A chia h

ế

t cho 13.

Bài 3.

Gi

ả

s

ử

2p + 1 = n

3

⇒

n l

ẻ

⇒

n = 2k + 1

⇒

p = m(4m

2

+ 6m + 3).

Do p là s

ố

nguyên t

ố

nên m = 1. V

ậ

y p = 13.

Bài 4.

p = 2 ; p = 221.

Bài 5.

Gi

ả

s

ứ

có các s

ố

nguyên t

ố

p, q, r tho

ả

mãn ph

ươ

ng trình :

(p + 1)(q + 2)( r + 3)= 4pqr.

Ta xét các giá tr

ị

c

ủ

a r (lí do c

ự

c biên) trong ba tr

ườ

ng h

ợ

p sau :

a) N

ế

u r = 2 thì ph

ươ

ng trình tr

ở

thành : 5(p + 1)(q + 2) =8pq (1).

Vì (5, 8) = 1 nên 5 ph

ả

i là

ướ

c nguyên t

ố

c

ủ

a p ho

ặ

c c

ủ

a q, do

đ

ó p = 5

ho

ặ

c q = 5.

* V

ớ

i p = 5, ph

ươ

ng trình (1) tr

ở

thành : 30(q + 2) = 40q

⇔

q = 6 (không

tho

ả

mãn).

* V

ớ

i q = 5, ph

ươ

ng trình (1) tr

ở

thành : 35(p + 1) = 40p

⇔

p = 7 (tho

ả

mãn).

b) N

ế

u r = 3, thì ph

ươ

ng trình tr

ở

thành : (p + 1)(q + 2) = 2pq,

suy ra : pq – 2p – q = 2 hay (p – 1)(q – 2) = 4 = 1.4 = 2.2.

Do p, q

đề

u là s

ố

nguyên t

ố

nên (q – 2) khác 2 và khác 4.

V

ậ

y q – 2 = 1 ta

đượ

c q = 3, p = 5.

222

c) N

ế

u r > 3 ta có 4pqr = (p + 1)(q + 2)(r + 3) < 2r(p + 1)(q + 2), suy ra :

2pq < (p + 1)(q + 2) hay (p – 1)(q – 2) < 4, suy ra p < 5 nên p = 2 ho

ặ

c p = 3.

* p = 2, ta

đượ

c 3(q + 2)(r + 3) = 8qr suy ra q là

ướ

c c

ủ

a 3 (vì r > 3) v

ậ

y

q = 3 và r = 5.

* p = 3, ta

đượ

c (q + 2)(r + 3) = 3qr suy ra 2pq – 3q – 2r = 6 hay

(q – 1)(2r – 3) = 9 = 1.9 = 3.3, mà 2r – 3 > 3 nên 2r – 3 = 9 suy ra r = 6

(không tho

ả

).

V

ậ

y ph

ươ

ng trình có nghi

ệ

m (p ; q ; r) là (7 ; 5 ; 2), (5 ; 3 ; 3), và (2 ; 3 ; 5).

Bài 6.

Vi

ế

t A v

ề

d

ạ

ng bình ph

ươ

ng

đ

úng c

ủ

a m

ộ

t s

ố

nguyên.

Bài 7.

C

ầ

n ch

ứ

ng minh r

ằ

ng S =

4

1

k(k + 1)(k + 2)(k + 3), r

ồ

i áp d

ụ

ng k

ế

t qu

ả

bài 6.

Bài 8.

G

ọ

i k =

Ư

CLN(a,d)

⇒

a = ka

1

và d = kd

1

(v

ớ

i a

1

và d

1

nguyên t

ố

cùng

nhau).

T

ừ

ac = bd ta có ka

1

c = bkd

1

⇒

a

1

c = bd

1

⇒

a

1

c



d

1

, mà a

1

và d

1

nguyên

t

ố

cùng nhau nên c



d

1

⇒

c = td

1

⇒

a

1

td

1

= bd

1

⇒

b = ta

1

.

Do

đ

ó M = a

n

+ b

n

+ c

n

+ d

n

= k

n

a

1

n

+ t

n

a

1

n

+ t

n

d

1

n

+ k

n

d

1

n

= (k

n

+ t

n

).(a

1

n

+

d

1

n

).

Vì k, t, a

1

, d

1

là các s

ố

nguyên d

ươ

ng và n

∈



nên k

n

+ t

n

> 1 và a

1

n

+ d

1

n

> 1.

V

ậ

y M = a

n

+ b

n

+ c

n

+ d

n

là h

ợ

p s

ố

.

Chủ đề 3. PHƯƠNG TRÌNH NGHIỆM NGUYÊN

Bài 1.

Ta có y = x +1 +

3

1

x

−

. V

ậ

y x – 1 là

ướ

c c

ủ

a 3.

Đ

áp s

ố

: (–2 ; –2), (0 ; –2), (4 ; 6), (2 ; 6).

Bài 2.

Do y nguyên d

ươ

ng nên v

ế

ph

ả

i d

ươ

ng.

Ph

ươ

ng trình t

ươ

ng

đươ

ng v

ớ

i :

2 2 2

(3 ) (3 ) 33 16 (3 1)

y y y y

< + + < +

2 2

(3 ) 33 16

x y y

= ± +

(*)

223

− Xét y = 1, ta có :

2

4

16

2

x

= ±



=

⇔



= ±

=



, k

ế

t h

ợ

p

đ

i

ề

u ki

ệ

n suy ra x = 4.

− Xét

2

y

≥

Rõ ràng :

2 2 2

(3 ) 33 16 (3 ) (3 ) 33 16

y y y y y

− + < < + +

.

Mà

2 2

(3 ) 33 16 (3 1) 6 1 33 16

y y y y y

− + > − ⇔ − > +

2 2

36 12 1 33 16 36 45 15 0

y y y y y

⇔ − + > + ⇔ − − >

2

36( 2) 99( 2) 39 0

y y

⇔ − + − + >

đ

úng v

ớ

i

2

y

≥

.

Và t

ươ

ng t

ự

:

2 2

(3 ) 33 16 (3 1)

y y y

+ + < +

.

Do

đ

ó

2 2 2

(3 ) (3 ) 33 16 (3 1)

y y y y

< + + < +

. S

ố

b

ị

k

ẹ

p gi

ữ

a bình ph

ươ

ng

c

ủ

a hai s

ố

t

ự

nhiên liên ti

ế

p không th

ể

là s

ố

chính ph

ươ

ng. Suy ra khi

2

y

≥

không có nghi

ệ

m x nguyên. V

ậ

y có m

ộ

t c

ặ

p s

ố

tho

ả

mãn là (4 ; 1).

Bài 3.

Ph

ươ

ng trình t

ươ

ng

đươ

ng v

ớ

i :

2 2 2 2 2

3( 3) 6 3 2 33

x y y z z

− + + + =

(1)

{ }

2 2

2

2 2

2 33 16

0 ; 9

3 3

z z

z

z z

 

≤ ≤

 

⇒ ⇒ ∈

 

 

 

 

.

N

ế

u z

2

= 0, t

ừ

(1) suy ra : (x – 3)

2

+ 2y

2

= 11.

Vì 2y

2

11

≤

{

}

2 2

5 0 ;1; 4

y y⇒ ≤ ⇒ ∈ .

* V

ớ

i y

2

= 0

⇒

(x – 3)

2

= 11 (lo

ạ

i).

* V

ớ

i y

2

= 1

⇒

(x – 3)

2

= 9

6

0.

x

=



⇒



=



* V

ớ

i y

2

= 4

⇒

(x – 3)

2

= 3 (lo

ạ

i).

N

ế

u z

2

= 9, t

ừ

(1) suy ra : (x – 3)

2

+11y

2

= 5.

Vì 11y

2

5 0

y

≤ ⇒ =

suy ra (x – 3)

2

= 5 (lo

ạ

i).

V

ậ

y có các b

ộ

s

ố

nguyên tho

ả

mãn bài toán là : (6 ; –1 ; 0) và (0 ; –1 ; 0).

Bài 4. Đặ

t x

2

= t, (

0

t

≥

).

Khi

đ

ó (*) có d

ạ

ng

2 2 1 4 1

0 4

p p

t

t y t y y y

+ +

+ − = ⇒ ∆ = + .

224

N

ế

u p = 2 thì

4 3 2

4 . ( 4)

t

y y y y y

∆ = + = +

. Do x nguyên nên t nguyên, v

ậ

y

t

∆

ph

ả

i là s

ố

chính ph

ươ

ng. Suy ra

2

( 4) ( ) ( 2 )( 2 ) 4

y y a a y a y a

+ = ∈ ⇔ + − + + =



Do (y + 2 –a) – (y + 2 + a) = –2a

2



nên y + 2 – a và y + 2 + a cùng tính

ch

ẵ

n l

ẻ

. Do

đ

ó ta có :

2 2 2 0

2 2 2 4 ; 0.

y a y a y a

+ − = + + = = =

 

⇔

 

+ − = + + = − = − =

 

* V

ớ

i y = 0, thì t = 0 suy ra x = 0.

* V

ớ

i y = –4 thì t = –8 (không tho

ả

mãn

đ

i

ề

u ki

ệ

n).

N

ế

u

3,

p

≥

đặ

t

2 1,( , 1).

p n n n

= + ∈ ≥



Khi

đ

ó

4 2 2 4 2 2

4 (1 4 )

n n

t

y y y y

+ −

∆ = + = + .

Để

t

∆

là s

ố

chính ph

ươ

ng thì

2 2

1 4

n

y

−

+ = m

2

( m

∈



)

1 1

( 2 )( 2 ) 1

n n

m y m y

− +

⇔ − + =

.

Vì m – 2y

n−1

và m + 2y

n−1

cùng tính ch

ẵ

n l

ẻ

nên :

1 1

2 2 1 0 ; 1

0 ; 1.

2 2 1

n n

m y m y y m

y m

m y m y

− −



− = + = = =



⇔



= = −

− = + = −



V

ớ

i y = 0 ta tìm

đượ

c x = 0. Vây c

ặ

p s

ố

tho

ả

mãn là (0 ; 0)

Bài 5.

Ph

ươ

ng trình (1) t

ươ

ng

đươ

ng v

ớ

i : (x – 2)

2

+ (y – 1)

2

= 7(t + 1). (2)

Nhận xét :

M

ộ

t s

ố

chính ph

ươ

ng khi chia cho 7 có s

ố

d

ư

là : 0, 1, 2 ho

ặ

c

4. Do

đ

ó t

ổ

ng hai s

ố

chính ph

ươ

ng chia h

ế

t cho 7 thì c

ả

hai s

ố

đ

ó

đề

u chia

h

ế

t cho 7.

T

ừ

(2) ta suy ra :

2 2

( 2) 7,( 1) 7 ( 2) 7,( 2) 7

x y x y− − ⇒ − −

   

Do 7 là s

ố

nguyên t

ố

nên

2 2

( 2) ( 1) 7( 1) 49

x y t− + − = +



, suy ra

( 1) 7

t +



mà

1 7

t

≤ ≤

nên t = 6.

V

ậ

y (x – 2)

2

+ (y – 1)

2

= 49 = 0

2

+ 7

2

= 7

2

+ 0

2

.

N

ế

u

2

2 2

( 2) 0

( 1) 7

x

y



− =





− =





thì

2

8

x

y

=





=



do (

*

, )

x y ∈



.

225

N

ế

u

2 2

( 2) 7

( 1) 0

x

y



− =





− =





thì

9

1

x

y

=





=



do (

*

, )

x y ∈



.

V

ậ

y có các s

ố

tho

ả

mãn

đề

bài : (2 ; 8 ; 6) và (9 ; 1 ; 6).

Chủ đề 4. TOÁN SUY LUẬN LÔ-GIC

Bài 1.

* Trong 12 s

ố

nguyên t

ố

phân bi

ệ

t luôn có ít nh

ấ

t 9 s

ố

l

ớ

n h

ơ

n 5, gi

ả

s

ử

9

s

ố

này là b

1

, b

2

, …,b

9

. M

ỗ

i s

ố

trong 9 s

ố

này khi chia cho 3 thì ch

ỉ

có s

ố

d

ư

là 1 ho

ặ

c 2. Theo nguyên t

ắ

c Dirichlê thì t

ồ

n t

ạ

i 5 s

ố

có cùng s

ố

d

ư

khi

chia cho 5, g

ọ

i các s

ố

này là b

1

, b

2

, b

3

, b

4

, b

5

.

* M

ỗ

i trong 5 s

ố

b

1

,b

2

, b

3

,b

4

, b

5

khi chia cho 5 ch

ỉ

có s

ố

d

ư

là 1, 2, 3, 4.

Theo nguyên t

ắ

c Diriclê thì t

ồ

n t

ạ

i hai s

ố

có cùng s

ố

d

ư

khia chia cho 5,

gi

ả

s

ử

hai s

ố

này là b

1

, b

2

.

Bây gi

ờ

xét các s

ố

b

3

, b

4

, b

5

, b

6

.

N

ế

u có hai s

ố

nào

đ

ó có cùng s

ố

d

ư

khi chia cho 5, ch

ẳ

ng h

ạ

n b

3

và b

4

thì

ch

ọ

n a

1

= b

1

, a

2

=b

2

, a

3

= b

3

, a

4

= b

4

, a

5

= b

5

và a

6

= b

6

.

Khi

đ

ó :

1 2 3 4

3, 3 9

a a a a P

− − ⇒

  

;

1 2 3 4

5, 5 25

a a a a P− − ⇒

  

;

1 2 3 4 5 6

2, 2, 2 8

a a a a a a P

− − + ⇒

   

.

V

ậ

y P chia h

ế

t cho 9.25.8 = 1800.

N

ế

u không có hai s

ố

nào trong 4 s

ố

b

3

, b

4

, b

5

, b

6

có cùng s

ố

d

ư

khi chia

cho 5 thì t

ồ

n t

ạ

i m

ộ

t s

ố

chia 5 d

ư

1 và m

ộ

t s

ố

chia 5 d

ư

4. G

ọ

i hai s

ố

đ

ó là

5

1(mod5)

b ≡ và

6

4(mod5)

b ≡ . Khi

đ

ó ta ch

ọ

n a

1

= b

1

, a

2

= b

2

, a

3

= b

3

,

a

4

= b

4

, a

5

= b

5

và a

6

= b

6

.

Ta có :

1 2 3 4

3, 3 9

a a a a P

− − ⇒

  

;

1 2 5 6

5, 5 25

a a a a P− + ⇒

  

;

1 2 3 4 5 6

2, 5, 2 8.

a a a a a a P

− − + ⇒

   

V

ậ

y trong tr

ườ

ng h

ợ

p này thì P c

ũ

ng chia h

ế

t cho 1800.

226

Bài 2.

N

ế

u có m

ộ

t trong 8

đ

i

ể

m

đ

ã cho trùng v

ớ

i tâm O thì rõ ràng kho

ả

ng cách

t

ừ

đ

i

ể

m

đ

ó

đế

n 7

đ

i

ể

m còn l

ạ

i

đề

u nh

ỏ

h

ơ

n 1.

Xét tr

ườ

ng h

ợ

p không có

đ

i

ể

m nào trùng v

ớ

i tâm O, ta chia hình tròn

thành 7 hình qu

ạ

t b

ằ

ng nhau có góc

ở

tâm b

ằ

ng

0

360

60

7

<

. Trong 8

đ

i

ể

m

đ

ã cho có ít nh

ấ

t hai

đ

i

ể

m ta g

ọ

i là A, B thu

ộ

c m

ộ

t trong 7 hình qu

ạ

t

đ

ã

chia. D

ễ

dàng tìm

đượ

c hình qu

ạ

t cung 60

0

ch

ử

a tr

ọ

n hình qu

ạ

t cung

0

360

7

mà có hai

đ

i

ể

m A, B. Trong hình qu

ạ

t cung 60

0

bán kính b

ằ

ng 1 rõ ràng

kho

ả

ng cách l

ớ

n nh

ấ

t gi

ữ

a hai

đ

i

ể

m b

ấ

t kì không l

ớ

n h

ơ

n 1, nên kho

ả

ng

cách AB < 1. Ta suy ra

đ

i

ề

u ph

ả

i ch

ư

ng minh.

Bài 3.

Xét các t

ổ

ng có d

ạ

ng a

i

+ b

j

. Vì có t

ấ

t c

ả

19.21 = 399 t

ổ

ng nh

ư

th

ế

. Các

t

ổ

ng này nh

ậ

n các giá tr

ị

t

ừ

2

đế

n 400.

N

ế

u các t

ổ

ng trên nh

ậ

n

đủ

399 giá tr

ị

t

ừ

2

đế

n 399 thì a

1

= b

1

= 1,

a

19

= b

21

= 200 suy ra

đ

i

ề

u ph

ả

i ch

ứ

ng minh.

N

ế

u các t

ổ

ng trên không nh

ậ

n

đủ

399 giá tr

ị

t

ừ

2

đế

n 399 thì t

ồ

n t

ạ

i hai

t

ổ

ng b

ằ

ng nhau t

ừ

đ

ó suy ra

đ

i

ề

u ph

ả

i ch

ứ

ng minh.

Bài 4.

S

ử

d

ụ

ng ph

ươ

ng pháp c

ự

c h

ạ

n, vì vai trò x, y, z nh

ư

nhau nên có th

ể

gi

ả

s

ử

x y z

≥ ≥

.

Ta có

2

4( ) 12 12 12

xyz x y z x yz z

= + + ≤ ⇒ ≤ ⇒ ≤ ⇒

{

}

1, 2,3

z ∈ .

Tr

ườ

ng h

ợ

p z = 1, ta

đượ

c xy = 4(x + y + 1)

⇔

(x – 4)(y – 4) = 20, thay

x – 4, y – 4 là các

ướ

c c

ủ

a 20 v

ớ

i

4 4 3

x y

− ≥ − ≥ −

ta

đượ

c c

ặ

p (x ; y) là

(24 ; 5), (14 ; 6), (9 ; 8).

Các tr

ườ

ng h

ợ

p còn l

ạ

i c

ũ

ng

đượ

c gi

ả

i t

ươ

ng t

ự

, ta có k

ế

t qu

ả

ph

ươ

ng

trình có nghi

ệ

m là : (24 ; 5 ; 1), (14 ; 6 ; 1), (9 ; 8 ; 1), (10 ; 3 ; 2), (6 ; 4 ; 2)

cùng v

ớ

i các hoán v

ị

c

ủ

a các b

ộ

s

ố

này.

Bài 5.

Ph

ươ

ng pháp ph

ả

n ch

ứ

ng,

đ

ánh giá di

ệ

n tích c

ủ

a m

ộ

t hình.

Gi

ả

s

ử

tâm O n

ằ

m ngoài tam giác ABC. Không m

ấ

t tính t

ổ

ng quát, gi

ả

s

ử

O và A n

ằ

m khác phía

đố

i v

ớ

i BC. V

ẽ

đườ

ng kính DE // BC. K

ẻ

AH

⊥

BC

và kéo dài c

ắ

t DE t

ạ

i K

⇒

AK

⊥

MN.

Khi

đ

ó BC < MN = 2 ; AH < AK

≤

AO = 1

1 1

. .2.1 1

2 2

ABC

S BC AH

⇒ = < =

, vô lí.

227

M

N

P

B

C

A

Q

Bài 6.

Xét các tr

ườ

ng h

ợ

p, t

ạ

o ra m

ộ

t hình h

ợ

p lí.

* Tr

ườ

ng h

ợ

p : 3

đ

i

ể

m A, O, B th

ẳ

ng hàng thì d

ễ

th

ấ

y

đườ

ng tròn

đườ

ng

kính AB tho

ả

mãn

đề

bài.

* Tr

ườ

ng h

ợ

p : 3

đ

i

ể

m A, O, B không th

ẳ

ng hàng. Không m

ấ

t tính t

ổ

ng

quát, gi

ả

s

ử

OA

≥

OB. D

ự

ng

đườ

ng trung tr

ự

c d c

ủ

a AB c

ắ

t OA

ở

C khi

đ

ó C n

ằ

m gi

ữ

a O và A. D

ễ

th

ấ

y C có th

ể

trùng v

ớ

i O nh

ư

ng không th

ể

trùng v

ớ

i A. Hãy ch

ứ

ng minh

đ

o

ạ

n n

ố

i tâm OC nh

ỏ

h

ơ

n hi

ệ

u hai bán kính.

Bài 7.

T

ạ

o ra m

ộ

t hình h

ợ

p lí. Áp d

ụ

ng nguyên lí

Đ

irichlê.

Trong các

đ

i

ể

m

đ

ã cho luôn t

ồ

n t

ạ

i tam giác có di

ệ

n tích l

ớ

n nh

ấ

t. Không

m

ấ

t tính t

ổ

ng quát, gi

ả

s

ử

đ

ó là tam giác ABC. Qua các

đỉ

nh A, B, C l

ầ

n

l

ượ

t v

ẽ

các

đườ

ng th

ẳ

ng song song v

ớ

i các c

ạ

nh BC, CA, AB chúng c

ắ

t

nhau

đ

ôi m

ộ

t

ở

M, N, P. Vì ba

đ

i

ể

m b

ấ

t kì trong 2013

đ

i

ể

m

đ

ã cho luôn

t

ạ

o thành tam giác có di

ệ

n tích

nh

ỏ

h

ơ

n 1 nên S

ABC

< 1. D

ễ

dàng suy ra S

MNP

< 4.

Ta c

ầ

n ch

ứ

ng minh t

ấ

t c

ả

2013

đ

i

ể

m

đ

ã cho không n

ằ

m ngoài

tam giác MNP. Th

ậ

t v

ậ

y :

Không m

ấ

t tính t

ổ

ng quát gi

ả

s

ử

có

đ

i

ể

m Q n

ằ

m trên n

ử

a

m

ặ

t ph

ẳ

ng b

ờ

NP không ch

ứ

a

tam giác ABC và Q

∉

đườ

ng

th

ẳ

ng NP.

Khi

đ

ó d

ễ

th

ấ

y S

QBC

> S

ABC

vô

lí, vì S

ABC

là l

ớ

n nh

ấ

t.

V

ậ

y tam giác MNP ch

ứ

a t

ấ

t c

ả

2013

đ

i

ể

m

đ

ã cho.

Bài 8.

T

ạ

o ra m

ộ

t hình h

ợ

p lí. Áp d

ụ

ng nguyên lí

Đ

irichlê.

O

M

P

N

A

B

C

228

* Chia tam giác

đề

u c

ạ

nh b

ằ

ng 8cm thành 64 tam giác

đề

u c

ạ

nh b

ằ

ng 1cm

nh

ư

hình v

ẽ

trên.

* Ta có 193 chia cho 64

đượ

c th

ươ

ng là 3 và d

ư

1. Do

đ

ó, t

ồ

n t

ạ

i ít nh

ấ

t 4

đ

i

ể

m trong các

đ

i

ể

m

đ

ã cho n

ằ

m trong tam giác

đề

u c

ạ

nh b

ằ

ng 1cm.

* Gi

ả

s

ử

đ

ó là tam giác

đề

u ABC c

ạ

nh b

ằ

ng 1. G

ọ

i O là tâm c

ủ

a tam giác

ABC, khi

đ

ó trong ba

đườ

ng tròn

đườ

ng kính OA, OB, OC ch

ư

a ít nh

ấ

t 2

trong 4

đ

i

ể

m nói trên. Do

đ

ó kho

ả

ng cách gi

ữ

a 2

đ

i

ể

m này không v

ượ

t quá

AO = BO = CO =

3

.

V

ậ

y t

ồ

n t

ạ

i 2 trong 193

đ

i

ể

m

đ

ã cho có kho

ả

ng cách không v

ượ

t quá

3

.

Bài 9.

Xét các tr

ườ

ng h

ợ

p

đặ

c bi

ệ

t,

nguyên lí c

ự

c h

ạ

n, ph

ươ

ng pháp ph

ả

n ch

ứ

ng,

nguyên lí

Đ

irichlê ?

D

ễ

th

ấ

y tam giác vuông, hình ch

ữ

nh

ậ

t là các

đ

a giác tho

ả

mãn

đề

bài.

Ta ch

ứ

ng minh m

ộ

t

đ

a giác có t

ừ

5

đỉ

nh tr

ở

lên không tho

ả

mãn

đề

bài.

Th

ậ

t v

ậ

y : Xét

đ

a giác ABCDE, không m

ấ

t tính t

ổ

ng quát gi

ả

s

ử

AB có

độ

dài l

ớ

n nh

ấ

t. V

ẽ

đườ

ng tròn

đườ

ng kính AB, suy ta các

đỉ

nh C, D, E

đề

u

thu

ộ

c

đườ

ng tròn

đườ

ng kính AB. Theo nguyên lí

Đ

irichlê thì có 2

đ

i

ể

m

cùng thu

ộ

c m

ộ

t n

ử

a

đườ

ng tròn. Ch

ẳ

ng h

ạ

n : C và D. Khi

đ

ó d

ễ

th

ấ

y

ACD

∆

ho

ặ

c

ADC

∆

là tam giác tù, vô lí.

Bài 10.

Áp d

ụ

ng tính ch

ấ

t : “Trong h

ữ

u h

ạ

n

đ

i

ể

m

đ

ã cho t

ồ

n t

ạ

i m

ộ

t

đườ

ng th

ẳ

ng

đ

i qua 2

đ

i

ể

m

đ

ã cho mà các

đ

i

ể

m còn l

ạ

i

đề

u n

ằ

m v

ề

m

ộ

t phía c

ủ

a

đườ

ng

th

ẳ

ng

đ

ó”.

Trong 100

đ

i

ể

m

đ

ã cho t

ồ

n t

ạ

i m

ộ

t

đườ

ng th

ẳ

ng

đ

i qua 2

đ

i

ể

m sao cho các

đ

i

ể

m còn l

ạ

i

đề

u n

ằ

m v

ề

m

ộ

t phía c

ủ

a

đườ

ng th

ẳ

ng

đ

ó. Ch

ẳ

ng h

ạ

n :

đ

ó là

2

đ

i

ể

m A và B. Xét t

ấ

t c

ả

các góc nhìn

đ

o

ạ

n th

ẳ

ng AB và có

đỉ

nh là m

ộ

t

trong các

đ

i

ể

m còn l

ạ

i, t

ồ

n t

ạ

i góc có s

ố

đ

o l

ớ

n nh

ấ

t. Ch

ẳ

ng h

ạ

n :

đ

ó là

đ

i

ể

m C. D

ự

ng

đườ

ng tròn tâm O ngo

ạ

i ti

ế

p tam giác ABC. Vì không có 4

đ

i

ể

m nào cùng thu

ộ

c m

ộ

t

đườ

ng tròn và t

ấ

t c

ả

các góc còn l

ạ

i

đề

u nh

ỏ

h

ơ

n

góc ACB nên t

ấ

t c

ả

các

đ

i

ể

m còn l

ạ

i

đề

u n

ằ

m ngoài

đườ

ng tròn (O). V

ậ

y

đườ

ng tròn (O) là

đườ

ng tròn tho

ả

mãn

đề

bài.

229

Phần bốn. MỘT SỐ ĐỀ THI VÀO LỚP 10 THPT

VÀ THPT CHUYÊN LÊ KHIẾT

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2009 - 2010

Môn thi : TOÁN

Thời gian làm bài : 120 phút

Bài 1. (1,5 điểm)

1) Thực hiện phép tính :

A 3 2 4 9.2.

= −

2) Cho biểu thức

a a a a

P 1 1

a 1 a 1

  

+ −

= + −

  

+ −

  

với

a 0 ; a 1.

≥ ≠

a) Chứng minh P = a

−

1.

b) Tính giá trị của P khi

a 4 2 3.

= +

Bài 2. (2,5 điểm)

1) Giải phương trình x

2

−

5x + 6 = 0.

2) Tìm m để phương trình x

2

−

5x

−

m + 7 = 0 có hai nghiệm thoả mãn hệ

thức

2 2

1 2

x x 13.

+ =

3) Cho hàm s

ố

y = x

2

có

đồ

th

ị

(P) và

đườ

ng th

ẳ

ng (d) : y =

−

x + 2.

a) V

ẽ

(P) và (d) trên cùng m

ộ

t h

ệ

tr

ụ

c to

ạ

độ

.

b) B

ằ

ng phép tính hãy tìm to

ạ

độ

giao

đ

i

ể

m c

ủ

a (P) và (d).

Bài 3.

(1,5

đ

i

ể

m)

Hai vòi n

ướ

c cùng ch

ả

y vào m

ộ

t cái b

ể

không có n

ướ

c thì trong 5 gi

ờ

s

ẽ

đầ

y b

ể

. N

ế

u vòi th

ứ

nh

ấ

t ch

ả

y trong 3 gi

ờ

và vòi th

ứ

hai ch

ả

y trong 4 gi

ờ

thì

đượ

c

2

3

b

ể

n

ướ

c.

H

ỏ

i n

ế

u m

ỗ

i vòi ch

ả

y m

ộ

t mình thì trong bao lâu m

ớ

i

đầ

y b

ể

?

230

Bài 4.

(3,5

đ

i

ể

m)

Cho

đườ

ng tròn (O ; R) và m

ộ

t

đ

i

ể

m S n

ằ

m bên ngoài

đườ

ng tròn. K

ẻ

các

ti

ế

p tuy

ế

n SA, SB v

ớ

i

đườ

ng tròn (v

ớ

i A, B là các ti

ế

p

đ

i

ể

m). M

ộ

t

đườ

ng

th

ẳ

ng

đ

i qua S (không

đ

i qua tâm O) c

ắ

t

đườ

ng trong (O : R) t

ạ

i hai

đ

i

ể

m

M và N, v

ớ

i M n

ằ

m gi

ữ

a S và N. G

ọ

i H là giao

đ

i

ể

m c

ủ

a SO và AB ; I là

trung

đ

i

ể

m c

ủ

a MN. Hai

đườ

ng th

ẳ

ng OI và AB c

ắ

t nhau t

ạ

i E.

a) Ch

ứ

ng minh IHSE là t

ứ

giác n

ộ

i ti

ế

p

đườ

ng tròn.

b) Ch

ứ

ng minh OI.OE = R

2

.

c) Cho SO = 2R và MN = R

3

. Tính di

ệ

n tích tam giác ESM theo R.

Bài 5.

(1,0

đ

i

ể

m)

Gi

ả

i ph

ươ

ng trình

2

2010 x x 2008 x 4018x 4036083.

− + − = − +

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2010 - 2011

Môn thi : TOÁN

Thời gian làm bài : 120 phút

Bài 1.

(2,0

đ

i

ể

m)

1) Th

ự

c hi

ệ

n phép tính :

.

9 + 25

2) Gi

ả

i các ph

ươ

ng trình và h

ệ

ph

ươ

ng trình sau :

a)

4 2

x 5x 4 0.

− + =

b)

2x y 88

x 2y 89.







+ =

Bài 2.

(1,5

đ

i

ể

m)

1) Cho hàm s

ố

2

1

2

=

y x

có

đồ

th

ị

là (P).

231

a) V

ẽ

(P).

b) V

ớ

i giá tr

ị

nào c

ủ

a a thì

đ

i

ể

m M(2 ; 4a) thu

ộ

c (P).

2) Cho hai

đườ

ng th

ẳ

ng (d

1

) :

2

y m x 2m 1

= + −

và (d

2

) :

y 4x m 1

= + +

.

Tìm giá tr

ị

c

ủ

a tham s

ố

m

để

hai

đườ

ng th

ẳ

ng (d

1

) và (d

2

) song song v

ớ

i

nhau.

Bài 3.

(2,0

đ

i

ể

m)

Hai xe ô tô kh

ở

i hành cùng m

ộ

t lúc v

ớ

i v

ậ

n t

ố

c không

đổ

i t

ạ

i

đị

a

đ

i

ể

m A

để

đ

i

đế

n

đị

a

đ

i

ể

m B cách nhau 300 km. Bi

ế

t r

ằ

ng m

ỗ

i gi

ờ

ô tô th

ứ

hai

đ

i

nhanh h

ơ

n ô tô th

ứ

nh

ấ

t 10 km nên ô tô th

ứ

nh

ấ

t

đế

n B ch

ậ

m h

ơ

n ô tô th

ứ

hai 1 gi

ờ

. Tính v

ậ

n t

ố

c c

ủ

a m

ỗ

i ô tô.

Bài 4.

(3,5

đ

i

ể

m)

Cho n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB. G

ọ

i C là m

ộ

t

đ

i

ể

m trên n

ử

a

đườ

ng tròn sao cho





CA < CB

. Trên n

ử

a m

ặ

t ph

ẳ

ng b

ờ

AB ch

ứ

a

đ

i

ể

m C,

k

ẻ

hai tia Ax và By cùng vuông góc v

ớ

i AB. M

ộ

t

đườ

ng tròn

đ

i qua A và C

(khác v

ớ

i

đườ

ng tròn

đườ

ng kính AB) c

ắ

t

đườ

ng kính AB t

ạ

i D và c

ắ

t tia

Ax t

ạ

i E.

Đườ

ng th

ẳ

ng EC c

ắ

t tia By t

ạ

i F.

a) Ch

ứ

ng minh BDCF là t

ứ

giác n

ộ

i ti

ế

p

đườ

ng tròn.

b) Ch

ứ

ng minh CD

2

= CE.CF

c) G

ọ

i I là giao

đ

i

ể

m c

ủ

a AC và DE ; J là giao

đ

i

ể

m c

ủ

a BC và DF. Ch

ứ

ng

minh IJ song song v

ớ

i AB.

d) Khi EF là ti

ế

p tuy

ế

n c

ủ

a n

ử

a

đườ

ng tròn

đườ

ng kính AB thì D n

ằ

m

ở

v

ị

trí nào trên AB ?

Bài 5.

(1,0

đ

i

ể

m)

G

ọ

i x

1

và x

2

là hai nghi

ệ

m c

ủ

a ph

ươ

ng trình

2

x 1005x 1 0.

+ + =

G

ọ

i y

1

và y

2

là hai nghi

ệ

m c

ủ

a ph

ươ

ng trình

2

1006y 1 0

y

+ =

+

.

Tính giá tr

ị

c

ủ

a bi

ể

u th

ứ

c :

(

)

(

)

(

)

(

)

1 1 2 1 1 2 2 2

.

M x y x y x y x y

= − − + +

232

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2011 - 2012

Môn thi : TOÁN

Thời gian làm bài : 120 phút

Bài 1.

(1,5

đ

i

ể

m)

1) Th

ự

c hi

ệ

n phép tính :

2 9 .

3 16

+

2) Gi

ả

i ph

ươ

ng trình và h

ệ

ph

ươ

ng trình sau :

a)

2

x 20x 96 0.

− + =

b)

x y 4023

x y 1.







+ =

− = −

Bài 2.

(2,5

đ

i

ể

m)

1) Cho hàm s

ố

2

y x

=

có

đồ

th

ị

là (P) và

đườ

ng th

ẳ

ng (d) :

y x 2.

= +

a) V

ẽ

(P) và (d) trên cùng m

ộ

t h

ệ

tr

ụ

c to

ạ

độ

Oxy.

b) B

ằ

ng phép tính hãy tìm to

ạ

độ

giao

đ

i

ể

m c

ủ

a (P) và (d).

2) Trong cùng m

ộ

t h

ệ

tr

ụ

c to

ạ

độ

Oxy cho 3

đ

i

ể

m : A(2 ; 4) ; B(−3 ; −1) và

C(−2 ; 1). Ch

ứ

ng minh ba

đ

i

ể

m A, B, C không th

ẳ

ng hàng.

3) Rút g

ọ

n bi

ể

u th

ứ

c M =

x 2x x

x 1 x x

−

+

− −

v

ớ

i x > 0 và x

≠

1.

Bài 3.

(1,5

đ

i

ể

m)

Hai b

ế

n sông A và B cách nhau 15 km. Th

ờ

i gian m

ộ

t ca nô xuôi dòng t

ừ

b

ế

n A

đế

n b

ế

n B, t

ạ

i b

ế

n B ca nô ngh

ỉ

20 phút r

ồ

i ng

ượ

c dòng t

ừ

b

ế

n B tr

ở

v

ề

đế

n b

ế

n A t

ổ

ng c

ộ

ng là 3 gi

ờ

.

Tính v

ậ

n t

ố

c c

ủ

a ca nô khi n

ướ

c yên l

ặ

ng, bi

ế

t v

ậ

n t

ố

c c

ủ

a dòng n

ướ

c là 3

km/h.

Bài 4.

(3,5

đ

i

ể

m)

Cho n

ử

a

đườ

ng tròn tâm O

đườ

ng kính AB. M

ộ

t

đ

i

ể

m C c

ố

đị

nh thu

ộ

c

đ

o

ạ

n th

ẳ

ng AO (C khác A và C khác O).

Đườ

ng th

ẳ

ng

đ

i qua

đ

i

ể

m C và

vuông góc v

ớ

i AO c

ắ

t n

ử

a

đườ

ng tròn

đ

ã cho t

ạ

i D. Trên cung BD l

ấ

y

đ

i

ể

m M (v

ớ

i M khác B và M khác D). Ti

ế

p tuy

ế

n c

ủ

a n

ử

a

đườ

ng tròn

đ

ã

cho t

ạ

i M c

ắ

t

đườ

ng th

ẳ

ng CD t

ạ

i E. G

ọ

i F là giao

đ

i

ể

m c

ủ

a AM và CD.

233

a) Ch

ứ

ng minh BCFM là t

ứ

giác n

ộ

i ti

ế

p

đườ

ng tròn.

b) Ch

ứ

ng minh EM = EF.

c) G

ọ

i I là tâm

đườ

ng tròn ngo

ạ

i ti

ế

p tam giác FDM. Ch

ứ

ng minh ba

đ

i

ể

m

D, I, B th

ẳ

ng hàng ; t

ừ

đ

ó suy ra góc



ABI

có s

ố

đ

o không

đổ

i khi M thay

đổ

i trên cung BD.

Bài 5.

(1,0

đ

i

ể

m)

Cho ph

ươ

ng trình (

ẩ

n x) :

( )

2

x 2m 3 x m 0

− + + =

. G

ọ

i

1

x

và

2

x

là các

nghi

ệ

m c

ủ

a ph

ươ

ng trình

đ

ã cho. Tìm giá tr

ị

c

ủ

a m

để

bi

ể

u th

ứ

c

2 2

1 2

x x

+

có giá tr

ị

nh

ỏ

nh

ấ

t.

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2012 - 2013

Môn thi : TOÁN

Thời gian làm bài : 120 phút

Bài 1.

(1,5

đ

i

ể

m)

1) Th

ự

c hi

ệ

n phép tính :

(

)

(

)

2 1 2 1 .

− +

2) Gi

ả

i h

ệ

ph

ươ

ng trình :

x y 1

.

2x 3y 7

− =





+ =



3) Gi

ả

i ph

ươ

ng trình : 9x

2

+ 8x

−

1 = 0.

Bài 2.

(2,0

đ

i

ể

m)

Cho Parabol (P) : y = x

2

và

đườ

ng th

ẳ

ng (d) : y = 2x + m

2

+ 1 (m là tham

s

ố

).

1) Xác

đị

nh t

ấ

t c

ả

các giá tr

ị

c

ủ

a m

để

(d) song song v

ớ

i

đườ

ng th

ẳ

ng (d') :

y = 2m

2

x + m

2

+ m.

234

2) Ch

ứ

ng minh r

ằ

ng v

ớ

i m

ọ

i m, (d) luôn c

ắ

t (P) t

ạ

i hai

đ

i

ể

m phân bi

ệ

t A và B.

3) Kí hi

ệ

u x

A

; x

B

là hoành

độ

c

ủ

a

đ

i

ể

m A và

đ

i

ể

m B. Tìm m sao cho

2 2

A B

x x 14.

+ =

Bài 3.

(2,0

đ

i

ể

m)

Hai xe ô tô cùng

đ

i t

ừ

c

ả

ng Dung Qu

ấ

t

đế

n khu du l

ị

ch Sa Hu

ỳ

nh, xe th

ứ

hai

đế

n s

ớ

m h

ơ

n xe th

ứ

nh

ấ

t là 1 gi

ờ

. Lúc tr

ở

v

ề

xe th

ứ

nh

ấ

t t

ă

ng v

ậ

n t

ố

c

thêm 5 km m

ỗ

i gi

ờ

, xe th

ứ

hai v

ẫ

n gi

ữ

nguyên v

ậ

n t

ố

c nh

ư

ng d

ừ

ng l

ạ

i ngh

ỉ

ở

m

ộ

t

đ

i

ể

m trên

đườ

ng h

ế

t 40 phút, sau

đ

ó v

ề

đế

n c

ả

ng Dung Qu

ấ

t cùng

lúc v

ớ

i xe th

ứ

nh

ấ

t. Tìm v

ậ

n t

ố

c ban

đầ

u c

ủ

a m

ỗ

i xe, bi

ế

t chi

ề

u dài qu

ả

ng

đườ

ng t

ừ

c

ả

ng Dung Qu

ấ

t

đế

n khu du l

ị

ch Sa Hu

ỳ

nh là 120 km và khi

đ

i

hay v

ề

hai xe

đề

u xu

ấ

t phát cùng m

ộ

t lúc.

Bài 4.

(3,5

đ

i

ể

m)

Cho

đườ

ng tròn tâm (O)

đườ

ng kính AB = 2R và C là m

ộ

t

đ

i

ể

m n

ằ

m trên

đườ

ng tròn sao cho CA > CB. G

ọ

i I là trung

đ

i

ể

m c

ủ

a OA. V

ẽ

đườ

ng th

ẳ

ng

d vuông góc v

ớ

i AB t

ạ

i I, c

ắ

t tia BC t

ạ

i M và c

ắ

t

đ

o

ạ

n th

ẳ

ng AC t

ạ

i P ; AM

c

ắ

t

đườ

ng tròn (O) t

ạ

i

đ

i

ể

m th

ứ

hai K.

1) Ch

ứ

ng minh t

ứ

giác BCPI n

ộ

i ti

ế

p

đượ

c trong m

ộ

t

đườ

ng tròn.

2) Ch

ứ

ng minh ba

đ

i

ể

m B, P, K th

ẳ

ng hàng.

3) Các ti

ế

p tuy

ế

n t

ạ

i A và C c

ủ

a

đườ

ng tròn (O) c

ắ

t nhau t

ạ

i Q. Tính di

ệ

n

tích c

ủ

a t

ứ

giác QAIM theo R khi BC = R.

Bài 5.

(1,0

đ

i

ể

m)

Cho x > 0, y > 0 tho

ả

mãn x

2

+ y

2

= 1. Tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c

2xy

A .

1 xy

−

=

+

235

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2013 - 2014

Môn thi : TOÁN

Thời gian làm bài : 120 phút

Bài 1.

(1,5

đ

i

ể

m)

1) Tính :

3 16 5 36.

+

2) Ch

ứ

ng minh r

ằ

ng v

ớ

i x > 0 và

x 1

≠

thì

x 1 x 1

.

x 1 x x x

+

− =

− −

3) Cho hàm s

ố

b

ậ

c nh

ấ

t : y = (2m + 1)x

−

6.

a) V

ớ

i giá tr

ị

nào c

ủ

a m thì hàm s

ố

đ

ã cho ngh

ị

ch bi

ế

n trên R ?

b) Tìm m

để

đồ

th

ị

c

ủ

a hàm s

ố

đ

ã cho

đ

i qua

đ

i

ể

m A(1 ; 2).

Bài 2.

(2,0

đ

i

ể

m)

1) Gi

ả

i ph

ươ

ng trình : 2x

2

+ 3x

−

5 = 0.

2) Tìm giá tr

ị

c

ủ

a tham s

ố

m

để

ph

ươ

ng trình : x

2

+ mx + m

−

2 = 0 có hai

nghi

ệ

m x

1

, x

2

tho

ả

mãn h

ệ

th

ứ

c

1 2

x x 2

− =

.

3) Gi

ả

i h

ệ

ph

ươ

ng trình :

x y xy 1

.

x 2y xy 1

+ = −





+ = +



Bài 3.

(2,0

đ

i

ể

m)

M

ộ

t t

ổ

công nhân d

ự

đị

nh làm xong 240 s

ả

n ph

ẩ

m trong m

ộ

t th

ờ

i gian nh

ấ

t

đị

nh. Nh

ư

ng khi th

ự

c hi

ệ

n, nh

ờ

c

ả

i ti

ế

n k

ỹ

thu

ậ

t nên m

ỗ

i ngày t

ổ

đ

ã làm

t

ă

ng thêm 10 s

ả

n ph

ẩ

m so v

ớ

i d

ự

đị

nh. Do

đ

ó, t

ổ

đ

ã hoàn thành công vi

ệ

c

s

ớ

m h

ơ

n d

ự

đị

nh 2 ngày. H

ỏ

i khi th

ự

c hi

ệ

n, m

ỗ

i ngày t

ổ

đ

ã làm

đượ

c bao

nhiêu s

ả

n ph

ẩ

m ?

Bài 4.

(3,5

đ

i

ể

m)

Cho

đườ

ng tròn (O) c

ố

đị

nh. T

ừ

m

ộ

t

đ

i

ể

m A c

ố

đị

nh

ở

bên ngoài

đườ

ng

tròn (O), k

ẻ

các ti

ế

p tuy

ế

n AM và AN v

ớ

i

đườ

ng tròn (v

ớ

i M ; N là các

ti

ế

p

đ

i

ể

m).

Đườ

ng th

ẳ

ng

đ

i qua A c

ắ

t

đườ

ng tròn (O) t

ạ

i hai

đ

i

ể

m B và C

(B n

ằ

m gi

ữ

a A và C). G

ọ

i I là trung

đ

i

ể

m c

ủ

a dây BC.

1) Ch

ứ

ng minh r

ằ

ng : AMON là t

ứ

giác n

ộ

i ti

ế

p.

2) G

ọ

i K là giao

đ

i

ể

m c

ủ

a MN và BC. Ch

ứ

ng minh r

ằ

ng : AK

.

AI = AB

.

AC

236

3) Khi cát tuy

ế

n ABC thay

đổ

i thì

đ

i

ể

m I chuy

ể

n

độ

ng trên cung tròn nào ?

Vì sao ?

4) Xác

đị

nh v

ị

trí c

ủ

a cát tuy

ế

n ABC

để

IM = 2IN.

Bài 5.

(1,0

đ

i

ể

m)

V

ớ

i

x 0

≠

, tìm giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c :

2

x 2x 2014

A .

x

− +

=

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2013 - 2014

Môn thi : TOÁN (Hệ Chuyên)

Thời gian làm bài : 120 phút

Bài 1.

(1,5

đ

i

ể

m)

1) Rút g

ọ

n bi

ể

u th

ứ

c

2 2

2

x x x x

A x 1

x x 1 x x 1

− +

= + + +

+ + − +

v

ớ

i

x 0.

≥

2) Ch

ứ

ng minh khi giá tr

ị

c

ủ

a m thay

đổ

i thì các

đườ

ng th

ẳ

ng (m

−

1)x +

(2m + 1)y = 4m +5 luôn

đ

i qua m

ộ

t

đ

i

ể

m c

ố

đị

nh. Tìm to

ạ

độ

c

ố

đị

nh

đ

ó.

Bài 2.

(1,5

đ

i

ể

m)

1) Tìm s

ố

chính ph

ươ

ng có 4 ch

ữ

s

ố

, bi

ế

t r

ằ

ng khi gi

ả

m m

ỗ

i ch

ữ

s

ố

m

ộ

t

đơ

n v

ị

thì s

ố

m

ớ

i

đượ

c t

ạ

o thành c

ũ

ng là m

ộ

t s

ố

chính ph

ươ

ng có 4 ch

ữ

s

ố

.

2) Tìm nghi

ệ

m nguyên c

ủ

a ph

ươ

ng trình

2 2

x xy y 3x y 1.

+ + = + −

Bài 3.

(2,5

đ

i

ể

m)

1) Tìm các giá tr

ị

c

ủ

a m

để

ph

ươ

ng trình

(

)

2

x m 2 x m 1 0

+ + − + =

có 2

nghi

ệ

m x

1

, x

2

tho

ả

mãn h

ệ

th

ứ

c

1 2

1 1 3

.

x x 10

− =

2) Gi

ả

i h

ệ

ph

ươ

ng trình

( )

x 1 x 2 y

.

y 1 y 2 x



+ =





+ =





237

3) Gi

ả

i ph

ươ

ng trình

(

)

(

)

2 3

3 x 6 8 x 1 3 .

− = − −

Bài 4.

(3,5

đ

i

ể

m)

Cho tam giác ABC có ba góc nh

ọ

n, AB < AC và

đườ

ng tròn (O ; R) ngo

ạ

i

ti

ế

p tam giác

đ

ó. Ti

ế

p tuy

ế

n t

ạ

i A c

ủ

a

đườ

ng tròn (O ; R) c

ắ

t

đườ

ng th

ẳ

ng

BC t

ạ

i

đ

i

ể

m M. K

ẻ

đườ

ng cao AH c

ủ

a tam giác ABC.

1) Ch

ứ

ng minh r

ằ

ng : BC = 2Rsin



BAC.

2)

Đ

i

ể

m N chuy

ể

n

độ

ng trên c

ạ

nh BC (N khác B và C). G

ọ

i E, F l

ầ

n l

ượ

t là

hình chi

ế

u vuông góc c

ủ

a

đ

i

ể

m N lên AB, AC. Xác

đị

nh v

ị

trí c

ủ

a

đ

i

ể

m N

để

độ

dài

đ

o

ạ

n EF ng

ắ

n nh

ấ

t.

3)

Đặ

t BC = a ; CA = b ; AB = c. Tính

độ

dài

đ

o

ạ

n th

ẳ

ng MA theo a, b, c.

4) Các ti

ế

p tuy

ế

n t

ạ

i B c

ủ

a

đườ

ng tròn (O ; R) c

ắ

t

đườ

ng th

ẳ

ng MA l

ầ

n

l

ượ

t

ở

P và Q. Ch

ứ

ng minh r

ằ

ng HA là tia phân giác c

ủ

a góc PHQ.

Bài 5.

(1,0

đ

i

ể

m)

Trong tam giác

đề

u có c

ạ

nh b

ằ

ng 8,

đặ

t 193

đ

i

ể

m phân bi

ệ

t. Ch

ứ

ng minh

t

ồ

n t

ạ

i 2

đ

i

ể

m trong 193

đ

i

ể

m

đ

ã cho có kho

ả

ng cách không v

ượ

t quá

3

.

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

TRƯỜNG THPT CHUYÊN LÊ KHIẾT

NĂM HỌC 2014 - 2015

Môn thi : TOÁN CHUYÊN

Thời gian làm bài : 150 phút

Bài 1.

(1,5

đ

i

ể

m)

a) Cho bi

ể

u th

ứ

c

– – –

3 3 +

P = + +

3 3 + +1

x x x

x x x x x

. Tìm t

ấ

t c

ả

các giá tr

ị

c

ủ

a x sao cho P > 2.

238

b) Trong m

ặ

t ph

ẳ

ng to

ạ

độ

Oxy cho parabol (P) : y = –x

2

và

đườ

ng th

ẳ

ng

(d) : y = mx –1 (m là tham s

ố

). Ch

ứ

ng minh r

ằ

ng v

ớ

i m

ọ

i giá tr

ị

c

ủ

a m,

đườ

ng th

ẳ

ng (d) luôn c

ắ

t parabol (P) t

ạ

i hai

đ

i

ể

m phân bi

ệ

t có hoành

độ

x

1

,

x

2

tho

ả

mãn

1 2

2

x x

− ≥

.

Bài 2.

(1,5

đ

i

ể

m)

a) Tìm t

ấ

t c

ả

c

ặ

p s

ố

nguyên d

ươ

ng (a ; b) sao cho

2

a 2

ab 2

−

+

là s

ố

nguyên.

b) Cho 3 s

ố

nguyên d

ươ

ng

a, b,c

tho

ả

đ

i

ề

u ki

ệ

n

a c

2 b 1

= +

và

a 1

>

. Tìm

t

ấ

t c

ả

các giá tr

ị

c

ủ

a c tho

ả

mãn

đẳ

ng th

ứ

c

đ

ã cho.

Bài 3.

(2,5

đ

i

ể

m)

a) Cho x, y là các s

ố

th

ự

c tho

ả

mãn x

2

+ 2xy + 7(x + y) + 2y

2

+ 10 = 0.

Tìm giá tr

ị

l

ớ

n nh

ấ

t và giá tr

ị

nh

ỏ

nh

ấ

t c

ủ

a bi

ể

u th

ứ

c S = x + y + 3.

b) Gi

ả

i ph

ươ

ng trình :

2 3

(x 4) 6 x 3x 13

+ − + =

.

Bài 4.

(3,5

đ

i

ể

m)

Cho hình vuông ABCD có c

ạ

nh b

ằ

ng a. Trên c

ạ

nh BC l

ấ

y

đ

i

ể

m E ;

đườ

ng

th

ẳ

ng qua B vuông góc v

ớ

i

đườ

ng th

ẳ

ng DE c

ắ

t DE t

ạ

i H và c

ắ

t DC t

ạ

i K.

G

ọ

i M là giao

đ

i

ể

m c

ủ

a DB và AH.

a) Ch

ứ

ng minh ba

đ

i

ể

m M, E, K th

ẳ

ng hàng.

b) Ch

ứ

ng minh E là tâm c

ủ

a

đườ

ng tròn n

ộ

i ti

ế

p tam giác CHM.

c) Khi E di chuy

ể

n trên c

ạ

nh BC thì

đ

i

ể

m H di chuy

ể

n trên

đườ

ng nào ?

d) Khi



0

MCH 30

=

, tính

độ

dài c

ủ

a

đ

o

ạ

n HK theo a.

Bài 5.

(1,0

đ

i

ể

m)

Cho 2014 s

ố

t

ự

nhiên b

ấ

t kì. Ch

ứ

ng minh r

ằ

ng trong s

ố

các s

ố

đ

ó có m

ộ

t

s

ố

chia h

ế

t cho 2014 ho

ặ

c có m

ộ

t s

ố

s

ố

mà t

ổ

ng c

ủ

a các s

ố

đ

ó chia h

ế

t cho

2014.

239

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

TRƯỜNG THPT CHUYÊN LÊ KHIẾT

NĂM HỌC 2014 - 2015

Môn thi : TOÁN (không chuyên)

Thời gian làm bài : 120 phút

Bài 1.

(1,5

đ

i

ể

m)

a) Th

ự

c hi

ệ

n phép tính :

2 25 3 4.

+

b) Xác

đị

nh a và b

để

đồ

th

ị

c

ủ

a hàm s

ố

y a + b

x

=

đ

i qua

đ

i

ể

m A(1 ; −2)

và

đ

i

ể

m B(3 ; 4).

c) Rút g

ọ

n bi

ể

u th

ứ

c

2 4

A :

2 2 2

x x

x x x

 

+

= +

 

+ − +

 

v

ớ

i x

≥

0 và x

≠

4.

Bài 2.

(2,0

đ

i

ể

m)

1) Gi

ả

i ph

ươ

ng trình

4 2

x 5x 36 0.

+ − =

2) Cho ph

ươ

ng trình

2 2

(1)

x (3m 1)x 2m m.1 0 − + + + =

v

ớ

i m là tham s

ố

.

a) Ch

ứ

ng minh ph

ươ

ng trình (1) luôn có hai nghi

ệ

m phân bi

ệ

t v

ớ

i m

ọ

i

giá tr

ị

c

ủ

a m.

b) G

ọ

i

1 2

x , x

là các nghi

ệ

m c

ủ

a ph

ươ

ng trình (1). Tìm m

để

bi

ể

u th

ứ

c

1 2

2 2

1 2

B x x 3x x

= + −

đạ

t giá tr

ị

l

ớ

n nh

ấ

t.

Bài 3.

(2,0

đ

i

ể

m)

Để

chu

ẩ

n b

ị

cho m

ộ

t chuy

ế

n

đ

i

đ

ánh b

ắ

t cá

ở

Hoàng Sa, hai ng

ư

dân

đả

o

Lý S

ơ

n c

ầ

n chuy

ể

n m

ộ

t s

ố

l

ươ

ng th

ự

c, th

ự

c ph

ẩ

m lên tàu. N

ế

u ng

ườ

i th

ứ

nh

ấ

t chuy

ể

n xong m

ộ

t n

ử

a s

ố

l

ươ

ng th

ự

c, th

ự

c ph

ẩ

m ; sau

đ

ó ng

ườ

i th

ứ

hai

chuy

ể

n h

ế

t s

ố

còn l

ạ

i lên tàu thì th

ờ

i gian ng

ườ

i th

ứ

hai hoàn thành lâu h

ơ

n

ng

ườ

i th

ứ

nh

ấ

t là 3 gi

ờ

. N

ế

u c

ả

hai ng

ườ

i cùng làm chung thì th

ờ

i gian

chuy

ể

n h

ế

t s

ố

l

ươ

ng th

ự

c, th

ự

c ph

ẩ

m lên tàu là

20

7

gi

ờ

. H

ỏ

i n

ế

u làm riêng

m

ộ

t mình thì m

ỗ

i ng

ườ

i chuy

ể

n h

ế

t s

ố

l

ươ

ng th

ự

c, th

ự

c ph

ẩ

m

đ

ó lên tàu

trong th

ờ

i gian bao lâu ?

240

Bài 4.

(3,5

đ

i

ể

m)

Cho n

ử

a

đườ

ng tròn tâm O,

đườ

ng kính AB = 2R. G

ọ

i M là

đ

i

ể

m chính

gi

ữ

a c

ủ

a cung AB ; P là m

ộ

t

đ

i

ể

m thu

ộ

c cung MB (P khác M và P khác B).

Đườ

ng th

ẳ

ng AP c

ắ

t

đườ

ng th

ẳ

ng OM t

ạ

i C ;

đườ

ng th

ẳ

ng OM c

ắ

t

đườ

ng

th

ẳ

ng BP t

ạ

i D. Ti

ế

p tuy

ế

n c

ủ

a n

ử

a

đườ

ng tròn

ở

P c

ắ

t CD t

ạ

i I.

a) Ch

ứ

ng minh OADP là t

ứ

giác n

ộ

i ti

ế

p

đườ

ng tròn.

b) Ch

ứ

ng minh OB.AC = OC.BD.

c) Tìm v

ị

trí c

ủ

a

đ

i

ể

m P trên cung MB

để

tam giác PIC là tam giác

đề

u.

Khi

đ

ó, hãy tính di

ệ

n tích c

ủ

a tam giác PIC theo R.

Bài 5

: (1,0

đ

i

ể

m)

Cho bi

ể

u th

ứ

c

5 4 3 2014

A (4x 4x 5x 5x 2) 2015

= + − + − + . Tính giá tr

ị

c

ủ

a

bi

ể

u th

ứ

c A khi

1 2 1

x

2

2 1

−

=

+

.

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NGÃI

KÌ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC 2014 - 2015

Môn thi : TOÁN

Thời gian làm bài : 120 phút

Bài 1.

(1,5

đ

i

ể

m)

1) Th

ự

c hi

ệ

n phép tính :

4 9 9 4.

+

2) Rút g

ọ

n bi

ể

u th

ứ

c

x x x x

P

1 x 1 x

+ −

= −

+ −

v

ớ

i

x 0 ; x 1.

≥ ≠

3) Cho

đườ

ng th

ẳ

ng (d) : y = 2014x + m. Xác

đị

nh m

để

(d)

đ

i qua

đ

i

ể

m

A(1 ;

−

1).

Bài 2.

(2,0

đ

i

ể

m)

1) Gi

ả

i ph

ươ

ng trình x

2

−

6x + 8 = 0.

241

2) Cho ph

ươ

ng trình x

2

−

2(m + 1)x + 4m

−

3 = 0 (1) (v

ớ

i m là tham s

ố

).

a) Ch

ứ

ng minh ph

ươ

ng trình (1) luôn có hai nghi

ệ

m phân bi

ệ

t v

ớ

i m

ọ

i

giá tr

ị

c

ủ

a m.

b) G

ọ

i x

1

; x

2

là nghi

ệ

m c

ủ

a ph

ươ

ng trình (1), tìm m

ộ

t h

ệ

th

ứ

c liên h

ệ

gi

ữ

a x

1

; x

2

không ph

ụ

thu

ộ

c vào m.

Bài 3.

(2,0

đ

i

ể

m)

M

ộ

t công ti d

ự

đị

nh

đ

i

ề

u

độ

ng m

ộ

t s

ố

xe chuy

ể

n 180 t

ấ

n hàng t

ừ

c

ả

ng

Dung Qu

ấ

t vào thành ph

ố

H

ồ

Chí Minh, m

ỗ

i xe ch

ở

kh

ố

i l

ượ

ng hàng nh

ư

nhau. Nh

ư

ng do nhu c

ầ

u th

ự

c t

ế

c

ầ

n chuy

ể

n thêm 28 t

ấ

n hàng nên công ti

đ

ó ph

ả

i

đ

i

ề

u

độ

ng thêm 1 xe cùng lo

ạ

i và m

ỗ

i xe bây gi

ờ

ph

ả

i ch

ở

thêm 1

t

ấ

n hàng m

ớ

i

đ

áp

ứ

ng

đượ

c nhu c

ầ

u

đặ

t ra. H

ỏ

i theo d

ự

đị

nh công ti

đ

ó c

ầ

n

đ

i

ề

u

độ

ng bao nhiêu xe ? Bi

ế

t r

ằ

ng m

ỗ

i xe không

đượ

c ch

ở

quá 15 t

ấ

n hàng.

Bài 4.

(3,5

đ

i

ể

m)

Cho n

ử

a

đườ

ng tròn (O)

đườ

ng kính AB = 2R,

đ

i

ể

m C thu

ộ

c n

ử

a

đườ

ng

tròn (CA < CB). G

ọ

i D là hình chi

ế

u c

ủ

a C trên AB.

Đ

i

ể

m E chuy

ể

n

độ

ng

trên

đ

o

ạ

n th

ẳ

ng CD (E khác C và D). Tia AE c

ắ

t

đườ

ng tròn t

ạ

i

đ

i

ể

m th

ứ

hai F.

1) Ch

ứ

ng minh r

ằ

ng :

a) T

ứ

giác BDEF n

ộ

i ti

ế

p

đượ

c

đườ

ng tròn.

b) AC

2

= AE.AF.

2) Tính AE.AF + BD.BA theo R.

3) Khi

đ

i

ể

m E chuy

ể

n

độ

ng trên

đ

o

ạ

n th

ẳ

ng CD thì tâm

đườ

ng tròn ngo

ạ

i

ti

ế

p tam giác CEF chuy

ể

n

độ

ng trên

đườ

ng nào ? Vì sao ?

Bài 5.

(1,0

đ

i

ể

m)

Cho a, b

≠

0. Tìm giá tr

ị

l

ớ

n nh

ấ

t c

ủ

a bi

ể

u th

ứ

c

( ) ( )

( )

2 2

7 a b 9 a b

M .

2 2

2014 a b

+ − −

=

+

242

MỤC LỤC

Lời nói đầu ..................................................................................................................... 3

Phần một. ĐẠI SỐ

Chủ đề 1. Biến đổi biểu thức đại số

I. Kiến thức cần sử dụng ........................................................................................... 5

II. Các dạng toán thường gặp ..................................................................................... 5

III. Bài tập vận dụng.................................................................................................. 11

Chủ đề 2. Phương trình và Hệ phương trình

I. Kiến thức cần sử dụng ......................................................................................... 14

II. Các dạng toán thường gặp ................................................................................... 15

III. Bài tập vận dụng.................................................................................................. 30

Chủ đề 3. Hàm số và đồ thị

I. Kiến thức cần sử dụng ......................................................................................... 35

II. Các dạng toán thường gặp ................................................................................... 35

III. Bài tập vận dụng.................................................................................................. 41

Chủ đề 4. Bất đẳng thức −

−−

− Bất phương trình

I. Kiến thức cần sử dụng ......................................................................................... 43

II. Các dạng toán thường gặp ................................................................................... 44

III. Bài tập vận dụng.................................................................................................. 50

Gợi ý −

−−

− Hướng dẫn giải phần Đại số .......................................................................... 52

Phần hai. HÌNH HỌC

Chủ đề 1. Tính toán các đại lượng hình học

I. Kiến thức cần sử dụng ......................................................................................... 94

II. Các dạng toán thường gặp ................................................................................... 94

III. Bài tập vận dụng................................................................................................ 110

Chủ đề 2. Chứng minh các yếu tố hình học, quan hệ hình học

I. Kiến thức cần sử dụng ....................................................................................... 112

II. Các dạng toán thường gặp ................................................................................. 112

III. Bài tập vận dụng................................................................................................ 142

243

Chủ đề 3. Tập hợp điểm

I. Kiến thức cần sử dụng ....................................................................................... 147

II. Các dạng toán thường gặp ................................................................................. 147

III. Bài tập vận dụng................................................................................................ 157

Chủ đề 4. Cực trị hình học

I. Kiến thức cần sử dụng ....................................................................................... 158

II. Các dạng toán thường gặp ................................................................................. 158

III. Bài tập vận dụng................................................................................................ 170

Gợi ý −

−−

− Hướng dẫn giải phần Hình học ................................................................... 177

Phần ba. SỐ HỌC

Chủ đề 1. Tính chia hết - Đồng dư thức

1. Phương pháp giải............................................................................................... 201

2. Các ví dụ........................................................................................................... 201

3. Bài tập tự luyện ................................................................................................. 205

Chủ đề 2. Số nguyên tố - Hợp số - Số chính phương

1. Phương pháp giải............................................................................................... 206

2. Các ví dụ........................................................................................................... 206

3. Bài tập tự luyện ................................................................................................. 208

Chủ đề 3. Phương trình nghiệm nguyên

1. Phương pháp giải............................................................................................... 209

2. Các ví dụ........................................................................................................... 209

3. Bài tập tự luyện ................................................................................................. 212

Chủ đề 4. Toán suy luận lô-gic

1. Phương pháp giải............................................................................................... 212

2. Các ví dụ........................................................................................................... 213

3. Bài tập tự luyện ................................................................................................. 218

Gợi ý −

−−

− Hướng dẫn giải phần Số học........................................................................ 220

Phần bốn. Một số đề thi vào lớp 10 THPT

và THPT Chuyên Lê Khiết....................................229

Trọng tâm kiến thức và các dạng đề ôn thi vào lớp 10 môn Toán

Tài liệu ôn thi vào 10 môn Toán 110 tài liệu

Môn Toán 1.3 K tài liệu

Bình luận

Trọng tâm kiến thức và các dạng đề ôn thi vào lớp 10 môn Toán