333 trang 7 lượt tải

Tự luận và trắc nghiệm căn thức Toán 9 Cánh Diều

14

Tài liệu gồm 333 trang, được biên soạn bởi thầy giáo Trương Ngọc Vỹ, hướng dẫn giải các dạng bài tập tự luận và trắc nghiệm chủ đề căn thức môn Toán 9 bộ sách Cánh Diều.

Chủ đề: Tài liệu chung Toán 9 129 tài liệu

Môn: Toán 9 3.4 K tài liệu

Sách: Cánh diều

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/333
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 1
CHƯƠNG 3
CĂN THỨC
BÀI 1
CĂN BẬC HAI VÀ CĂN BẬC BA CỦA SỐ THỰC
1. Căn bậc hai của số thực không âm
Định nghĩa: Căn bậc hai của số thực
a
không âm là số
x
sao cho
2
x a
.
Chú ý:
Mỗi số thực dương
0
a a
có đúng hai căn bậc hai là hai số đối nhau. Số dương kí hiệu là:
,
số âm kí hiệu là:
. Ta gọi
là căn bậc hai số học của
a
.
Số
0
có đúng 1 căn bậc hai là chính nó, ta viết
0 0
Số âm không có căn bậc hai.
Nhận xét: Với
0, 0
a b
, ta có:
Nếu
a b
thì
a b
.
Nếu
a b
thì
a b
.
2. Căn bậc ba
Căn bậc ba của số thực
a
là số thực
x
sao cho
3
x a
.
Căn bậc ba của số thực
a
được kí hiệu là:
3
.
Nhận xét:
3
3
a a
.
Nếu
a b
thì
3 3
a b
.
Nếu
3 3
a b
thì
a b
.
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 2
CHỦ ĐỀ 1
CĂN BẬC HAI CỦA SỐ THỰC
DẠNG 1
CĂN BẬC HAI CỦA SỐ THỰC
Nếu
0
a
thì các căn bậc hai của
a
là
a
.
Với số
0
a
, ta có
2 2
a a a
Bài 1. Tìm căn bậc hai của :
a)
169
b)
2,25
c)
0,64
d)
36
121
e)
7
f)
10
Bài 2. Tính:
a)
2
5
b)
2
2025
c)
2
1
2026
d)
2 2
10 8
e)
2 2
1 1
2 3
f)
2 2
2 3
3 4
Bài 3. Tính:
a)
1 5 1 5
b)
2 2
2026 2025 2026 2025
c)
1 2 1 2
2 7 2 7
d)
4 7 4 7
5 3 5 3
BÀI TẬP RÈN LUYỆN
Bài 4. Tìm căn bậc hai của :
a)
64
b)
400
c)
0,49
d)
25
169
e)
1,5
f)
17
Bài 5. Tính:
a)
2
2026
b)
2
99
c)
2
2025
2026
d)
2 2
2026 2025
e)
2 2
2 3
5 7
f)
2 2
3 4
2 5
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 3
Bài 6. Tính:
a)
3 3
17 4 17 4
b)
2025 2025
27 26 27 26
c)
2 2
3 3
11 10 11 10
24 5 24 5
d)
8 7 6 5 8 7 6 5
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
4
DẠNG 2
SO SÁNH CĂN BẬC HAI CỦA SỐ THỰC
Phương pháp
Với
0, 0
a b
, ta có:
Nếu
a b
thì
a b
.
Nếu
a b
thì
a b
.
Bài 1. So sánh các cặp số sau:
a )
24
và
5
b)
0,08
và
0,3
c)
37
và
6
Bài 2. So sánh các cặp số sau:
a)
5
và
24
5
b)
1
2
và
2
3
c)
4
5
và
5
6
Bài 3. So sánh các cặp số sau:
a)
4
và
10 1
b)
5
và
4
2
5
c)
2
và
17 2
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 5
CHỦ ĐỀ 2
CĂN BẬC BA CỦA SỐ THỰC
DẠNG 1
CĂN BẬC BA CỦA SỐ THỰC
Phương pháp
Căn bậc ba của số thực
a
là số thực
x
sao cho
3
x a
.
Căn bậc ba của số thực
a
được kí hiệu là:
3
.
3
3 3
3
a a a
.
Chú ý:
3 3 2 2 3
( ) 3 3
a b a a b ab b
,
3 3 2 2 3
( ) 3 3
a b a a b ab b
3 3 2 2
( )( )
a b a b a ab b
,
3 3 2 2
( )( )
a b a b a ab b
Bài 1. Tìm căn bậc ba của :
a)
216
b)
1
1000
c)
0,0729
d)
1
27
e)
125
64
f)
27
512
Bài 2. Tính
a)
3
0,008
b)
3
1
216
c)
3 3
2024
d)
3
3
4
5
e)
3
3
3
1
2 3 15.
125
f)
3
3 3
1 1
3 8.
3 64
Bài 3. Rút gọn các biểu thức sau
a)
3
33 3
27 4 64
A
b)
3 3
1000 1000000
B
Bài 4. Tính
a)
3 3 33 3 3
3 2 9 3. 2 4
b)
3 3 3 3 3 3
7 5 49 7. 5 25
Bài 5. Rút gọn các biểu thức sau
a)
3
2 1 3 2 2
A b)
3
4 2 3 3 1
B
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
6
BÀI TẬP RÈN LUYỆN
Bài 6. Tìm căn bậc ba của :
a)
64
b)
125
8
c)
0,512
d)
1000
216
e)
1
0,064
f)
0,027
Bài 7. Tính
a)
3
27
d)
3
729
c)
3
1
125
d)
3
3
3
1 1
216 12
e)
3 3
64 1
343 512
f)
3
3 3
1 2026
125 5
Bài 8. Rút gọn các biểu thức sau
a)
3
3 3 3
216 8 343
A b)
3 3 3
0,001 0,027 0,125
B
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
7
DẠNG 2
SO SÁNH CĂN BẬC BA CỦA SỐ THỰC
Phương pháp
Nếu
a b
thì
3 3
a b
.
Nếu
3 3
a b
thì
a b
.
Bài 1. So sánh các cặp số sau:
a)
3
2024
và
3
2025
b)
3
1
1000
và
3
1
1001
c)
8
và
3
511
Bài 2. So sánh các cặp số sau:
a)
7
và
3
342
b)
3
8
27
và
3
64
125
c)
và
3
125
216
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 1
CHƯƠNG 3
CĂN THỨC
BÀI 1
CĂN BẬC HAI VÀ CĂN BẬC BA CỦA SỐ THỰC
1. Căn bậc hai của số thực không âm
Định nghĩa: Căn bậc hai của số thực
a
không âm là số
x
sao cho
2
x a
.
Chú ý:
Mỗi số thực dương
0
a a
có đúng hai căn bậc hai là hai số đối nhau. Số dương kí hiệu là:
,
số âm kí hiệu là:
. Ta gọi
là căn bậc hai số học của
a
.
Số
0
có đúng 1 căn bậc hai là chính nó, ta viết
0 0
Số âm không có căn bậc hai.
Nhận xét: Với
0, 0
a b
, ta có:
Nếu
a b
thì
a b
.
Nếu
a b
thì
a b
.
2. Căn bậc ba
Căn bậc ba của số thực
a
là số thực
x
sao cho
3
x a
.
Căn bậc ba của số thực
a
được kí hiệu là:
3
.
Nhận xét:
3
3
a a
.
Nếu
a b
thì
3 3
a b
.
Nếu
3 3
a b
thì
a b
.
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 2
CHỦ ĐỀ 1
CĂN BẬC HAI CỦA SỐ THỰC
DẠNG 1
CĂN BẬC HAI CỦA SỐ THỰC
Nếu
0
a
thì các căn bậc hai của
a
là
a
.
Với số
0
a
, ta có
2 2
a a a
Bài 1. Tìm căn bậc hai của :
a)
169
b)
2,25
c)
0,64
d)
36
121
e)
7
f)
10
Lời giải
a)
169
Ta có
2
13 169
nên có hai căn bậc hai là
13
và
13
.
b)
2,25
Ta có
2
1,5 2,25
nên có hai căn bậc hai là
1,5
và
1,5
.
c)
0,64
Ta có
2
0,8 0,64
nên có hai căn bậc hai là
0,8
và
0,8
.
d)
36
121
Ta có
2
6 36
11 121
nên có hai căn bậc hai là
6
11
và
6
11
.
e)
7
Ta có
2
7 7
nên có hai căn bậc hai là
và
7
.
f)
10
Ta có
2
10 10
nên có hai căn bậc hai là
10
và
10
.
Bài 2. Tính:
a)
2
5
b)
2
2025
c)
2
1
2026
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 3
d)
2 2
10 8
e)
2 2
1 1
2 3
f)
2 2
2 3
3 4
Lời giải
a)
2
5 5
b)
2
2025 2025
c)
2
1 1
2026 2026
d)
2 2
10 8 10 8 2
e)
2 2
1 1 1 1 3 2 5
2 3 2 3 6 6 6
f)
2 2
2 3 2 3 8 9 1
3 4 3 4 12 12 12
Bài 3. Tính:
a)
1 5 1 5
b)
2 2
2026 2025 2026 2025
c)
1 2 1 2
2 7 2 7
d)
4 7 4 7
5 3 5 3
Lời giải
a)
2
2
1 5 1 5 1 5 1 5 4
b)
2
2 2
2026 2025 2026 2025 2026 2025 2026 2025
2
2 2
2
2026 2025 2026 2025 1
c)
2
2
1 2 1 2 1 2 1 2 7 4 3
2 7 2 7 2 7 4 7 28 28 28
d)
2 2
4 7 4 7 4 7 4 7 12 35 23
5 3 5 3 5 3 5 3 15 15 15
BÀI TẬP RÈN LUYỆN
Bài 4. Tìm căn bậc hai của :
a)
64
b)
400
c)
0,49
d)
25
169
e)
1,5
f)
17
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
4
Lời giải
a)
64
Ta có
2
8 64
nên có hai căn bậc hai là
8
và
8
.
b)
400
Ta có
2
20 400
nên có hai căn bậc hai là
20
và
20
.
c)
0,49
Ta có
2
0,7 0,49
nên có hai căn bậc hai là
0,7
và
0,7
.
d)
25
169
Ta có
2
5 25
13 169
nên có hai căn bậc hai là
5
13
và
5
13
.
e)
1,5
Ta có
2
1,5 7
nên có hai căn bậc hai là
1,5
và
1,5
.
f)
17
Ta có
2
17 17
nên có hai căn bậc hai là
17
và
17
.
Bài 5. Tính:
a)
2
2026
b)
2
99
c)
2
2025
2026
d)
2 2
2026 2025
e)
2 2
2 3
5 7
f)
2 2
3 4
2 5
Lời giải
a)
2
2026 2026
b)
2
99 99
c)
2
2025 2025
2026 2026
d)
2 2
2026 2025 2026 2025 1
e)
2 2
2 3 2 3 14 15 1
5 7 5 7 35 35 35
f)
2 2
3 4 3 4 15 8 23
2 5 2 5 10 10 10
Bài 6. Tính:
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 5
a)
3 3
17 4 17 4
b)
2025 2025
27 26 27 26
c)
2 2
3 3
11 10 11 10
24 5 24 5
d)
8 7 6 5 8 7 6 5
Lời giải
a)
3
3
3 3 2
3
2
17 4 17 4 17 4 17 4 17 4 17 16 1
b)
2025
2025
2025 2025 2 2
27 26 27 26 27 26 27 26 27 26
2025
27 26 1
c)
2
2 2
2
2 2
2
3 3 3 3 3
2
2
11 10
11 10 11 10
11 10 11 10
11 10
1
24 25
24 5 24 5
24 5 24 5
24 5
d)
2 2 2 2
8 7 6 5 8 7 6 5
8 7 8 7 6 5 6 5
8 7 6 5
1.1 1
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
6
DẠNG 2
SO SÁNH CĂN BẬC HAI CỦA SỐ THỰC
Phương pháp
Với
0, 0
a b
, ta có:
Nếu
a b
thì
a b
.
Nếu
a b
thì
a b
.
Bài 1. So sánh các cặp số sau:
a )
24
và
5
b)
0,08
và
0,3
c)
37
và
6
Lời giải
a) )
24
và
5
Ta có:
5 25
Do
24 25
nên
24 25
hay
24 5
b)
0,08
và
0,3
Ta có:
0,3 0,09
Do
0,08 0,09
nên
0,08 0,09
hay
0,08 0,3
c)
37
và
6
Ta có:
6 36
Do
37 36
nên
37 36
hay
37 6
Bài 2. So sánh các cặp số sau:
a)
5
và
24
5
b)
1
2
và
2
3
c)
4
5
và
5
6
Lời giải
a)
5
và
24
5
Ta có:
25
5
5
Do
25 24
5 5
nên
25 24
5 5
hay
24
5
5
b)
1
2
và
2
3
Ta có:
1 3
2 6
và
2 4
3 6
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
7
Do
3 4
6 6
hay
1 2
2 3
nên
1 2
2 3
c)
4
5
và
5
6
Ta có:
4 18
5 30
và
5 25
6 30
Do
18 25
30 30
hay
4 5
5 6
nên
4 5
5 6
Bài 3. So sánh các cặp số sau:
a)
4
và
10 1
b)
5
và
4
2
5
c)
2
và
17 2
Lời giải
a)
4
và
10 1
Do
9 10
nên
9 10
hay
3 10
Suy ra
4 10 1
b)
5
và
4
2
5
Do
1 4
4 5
nên
1 4
4 5
hay
1 4
2 5
Suy ra
1 4
2 2
2 5
hay
5 4
2
2 5
c)
2
và
17 2
Do
16 17
nên
16 17
hay
4 17
Suy ra
4 2 17 2
hay
2 17 2
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 8
CHỦ ĐỀ 2
CĂN BẬC BA CỦA SỐ THỰC
DẠNG 1
CĂN BẬC BA CỦA SỐ THỰC
Phương pháp
Căn bậc ba của số thực
a
là số thực
x
sao cho
3
x a
.
Căn bậc ba của số thực
a
được kí hiệu là:
3
.
3
3 3
3
a a a
.
Chú ý:
3 3 2 2 3
( ) 3 3
a b a a b ab b
,
3 3 2 2 3
( ) 3 3
a b a a b ab b
3 3 2 2
( )( )
a b a b a ab b
,
3 3 2 2
( )( )
a b a b a ab b
Bài 1. Tìm căn bậc ba của :
a)
216
b)
1
1000
c)
0,0729
d)
1
27
e)
125
64
f)
27
512
Lời giải
a) Ta có
3
6 216
nên số
6
là căn bậc ba của
216
.
b) Ta có
3
1 1
10 1000
nên số
1
10
là căn bậc ba của
1
1000
.
c) Ta có
3
0,9 0,0729
nên số
0,9
là căn bậc ba của
0,0729
.
d) Ta có
3
1 1
3 27
nên số
1
3
là căn bậc ba của
1
27
.
e) Ta có
3
5 125
4 64
nên số
5
là căn bậc ba của
125
64
.
f) Ta có
3
3 27
8 512
nên số
3
8
là căn bậc ba của
27
512
.
Bài 2. Tính
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 9
a)
3
0,008
b)
3
1
216
c)
3 3
2024
d)
3
3
4
5
e)
3
3
3
1
2 3 15.
125
f)
3
3 3
1 1
3 8.
3 64
Lời giải
a) Ta có:
3
3
3
0,008 0,8 0,8
b) Ta có:
3
33
1 1 1
216 6 6
c) Ta có:
3 3
2024 2024
d) Ta có:
3
3
4 4
5 5
e) Ta có:
3
3 3
3
3 3
33
1 1 1
2 3 15. 2 . 3 15. 8. 3 15. 21
125 5 5
f) Ta có:
3 3
3
3
33 3 3
1 1 1 1 1 1
3 8. 3 8. 27. 8. 11
3 64 3 4 3 4
Bài 3. Rút gọn các biểu thức sau
a)
3
33 3
27 4 64
A
b)
3 3
1000 1000000
B
Lời giải
a)
3
3
3 3
33 3
3
27 4 64 3 4 4 3 4 4 3
A
b)
3
3 3
3 3
3
1000 1000000 10 100 10 100 10 100 110
B
Bài 4. Tính
a)
3 3 33 3 3
3 2 9 3. 2 4
b)
3 3 3 3 3 3
7 5 49 7. 5 25
Lời giải
a)
3 3
3
3 2 2
3 3 3 3 3 33 3 3 3 3 3
3 2 9 3. 2 4 3 2 3 3. 2 2 3 2 3 2 1
b)
3 3
3 32 2
3 3 3 3 3 3 3 3 3 3 3 3
7 5 49 7. 5 25 7 5 7 7. 5 5 7 5 7 5 12
Bài 5. Rút gọn các biểu thức sau
a)
3
2 1 3 2 2
A b)
3
4 2 3 3 1
B
Lời giải
a)
2 3
3 3
3 3
2 1 3 2 2 2 1 2 2 2 1 2 1 2 1 2 1 2 1
A
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 10
b)
2 3
3 3
3 3
4 2 3 3 1 3 2 3 1 3 1 3 1 3 1 3 1 3 1
B
BÀI TẬP RÈN LUYỆN
Bài 6. Tìm căn bậc ba của :
a)
64
b)
125
8
c)
0,512
d)
1000
216
e)
1
0,064
f)
0,027
Lời giải
a) Ta có
3
4 64
nên số
4
là căn bậc ba của
64
.
b) Ta có
3
5 125
2 8
nên số
5
là căn bậc ba của
125
8
.
c) Ta có
3
0,8 0,512
nên số
0,8
là căn bậc ba của
0,512
.
d) Ta có
3
10 1000
6 216
nên số
10
6
là căn bậc ba của
1000
216
.
e) Ta có
3
1 1
0,4 0,064
nên số
1
0,4
là căn bậc ba của
1
0,064
.
f) Ta có
3
0,3 0,027
nên số
0,3
là căn bậc ba của
0,027
.
Bài 7. Tính
a)
3
27
d)
3
729
c)
3
1
125
d)
3
3
3
1 1
216 12
e)
3 3
64 1
343 512
f)
3
3 3
1 2026
125 5
Lời giải
a) Ta có:
3 3
3
27 3 3
b) Ta có:
3 3
3
729 9 9
c) Ta có:
3
33
1 1 1
125 5 5
d) Ta có:
3 3
3 3
3
1 1 1 1 1 1 2 1 3 1
216 12 6 12 6 12 12 12 12 4
e) Ta có:
3 3
3 33 3
64 1 4 1 4 1 32 7 25
343 512 7 8 7 8 56 56 56
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 11
f) Ta có:
3
3
33 3
1 2026 1 2026 1 2026 2025
405
125 5 5 5 5 5 5
Bài 8. Rút gọn các biểu thức sau
a)
3
3 3 3
216 8 343
A b)
3 3 3
0,001 0,027 0,125
B
Lời giải
a)
3
3
3 3
3 3 3
3
216 8 343 6 8 7 6 8 7 9
A
b)
3 3 3
3 3 3
3 3 3
0,001 0,027 0,125 0,1 0,3 0,5 0,1 0,3 0,5 0,1
B
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 12
DẠNG 2
SO SÁNH CĂN BẬC BA CỦA SỐ THỰC
Phương pháp
Nếu
a b
thì
3 3
a b
.
Nếu
3 3
a b
thì
a b
.
Bài 1. So sánh các cặp số sau:
a)
3
2024
và
3
2025
b)
3
1
1000
và
3
1
1001
c)
8
và
3
511
Lời giải
a) Ta có:
2024 2025
nên
3 3
2024 2025
b) Ta có:
1 1
1000 1001
nên
3 3
1 1
1000 1001
c) Ta có:
3
8 512
Do
512 511
nên
3 3
512 511
hay
3
8 511
Bài 2. So sánh các cặp số sau:
a)
7
và
3
342
b)
3
8
27
và
3
64
125
c)
và
3
125
216
Lời giải
a) Ta có:
3
7 343
Do
343 342
nên
3 3
343 342
hay
3
7 342
b)
Ta có:
3
33
8 2 2 6
27 3 3 15
và
3
33
64 4 4 12
125 5 5 15
Do
6 12
15 15
hay
2 4
3 5
nên
3 3
8 64
27 125
c) Ta có:
2 4
3 6
và
3
33
125 5 5
216 6 6
Do
4 5
6 6
hay
2 5
3 6
nên
3
2 125
3 216
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 1
BÀI 2
MỘT SỐ PHÉP TÍNH VỀ CĂN THỨC HAI CỦA SỐ THỰC
1. Căn bậc hai của một bình phương
Với mọi số
a
, ta có:
2
a a
2. Căn bậc hai của một tích
Với hai số không âm
,
a b
, ta có:
. .
a b a b
Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.
3. Căn bậc hai của một thương
Với
0, 0
a b
, ta có:
a a
b
b
4. Đưa thừa số ra ngoài dấu căn bậc hai
Cho hai số
,
a b
, với
0
b
. Khi đó:
2
a b a b
Cụ thể, ta có:
Nếu
0
a
thì
2
a b a b
Nếu
0
a
thì
2
a b a b
5. Đưa thừa số vào trong dấu căn bậc hai
Với
0
a
và
0
b
, ta có:
2
a b a b
Với
0
a
và
0
b
, ta có:
2
a b a b

Tài liệu khác của Toán 9

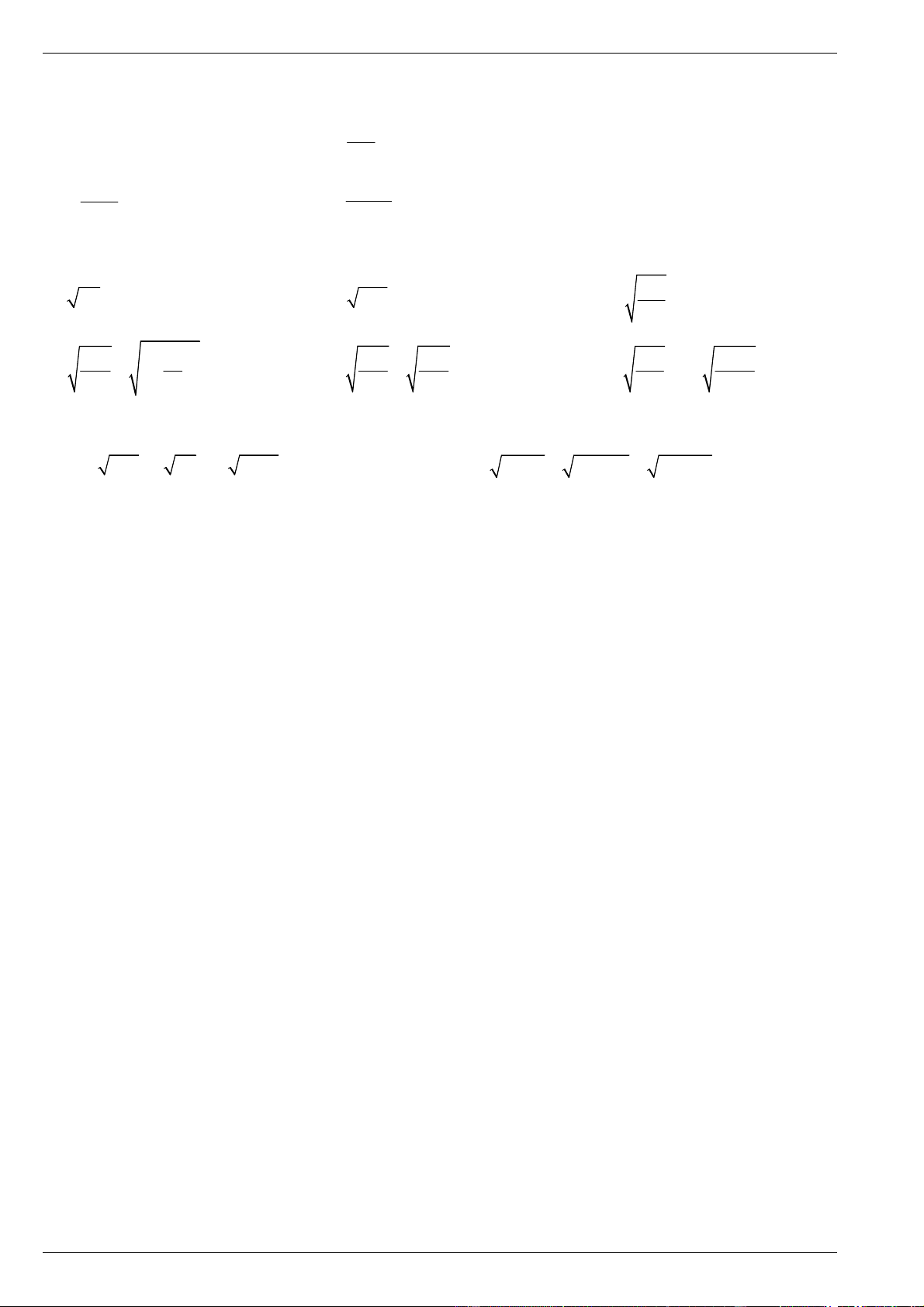
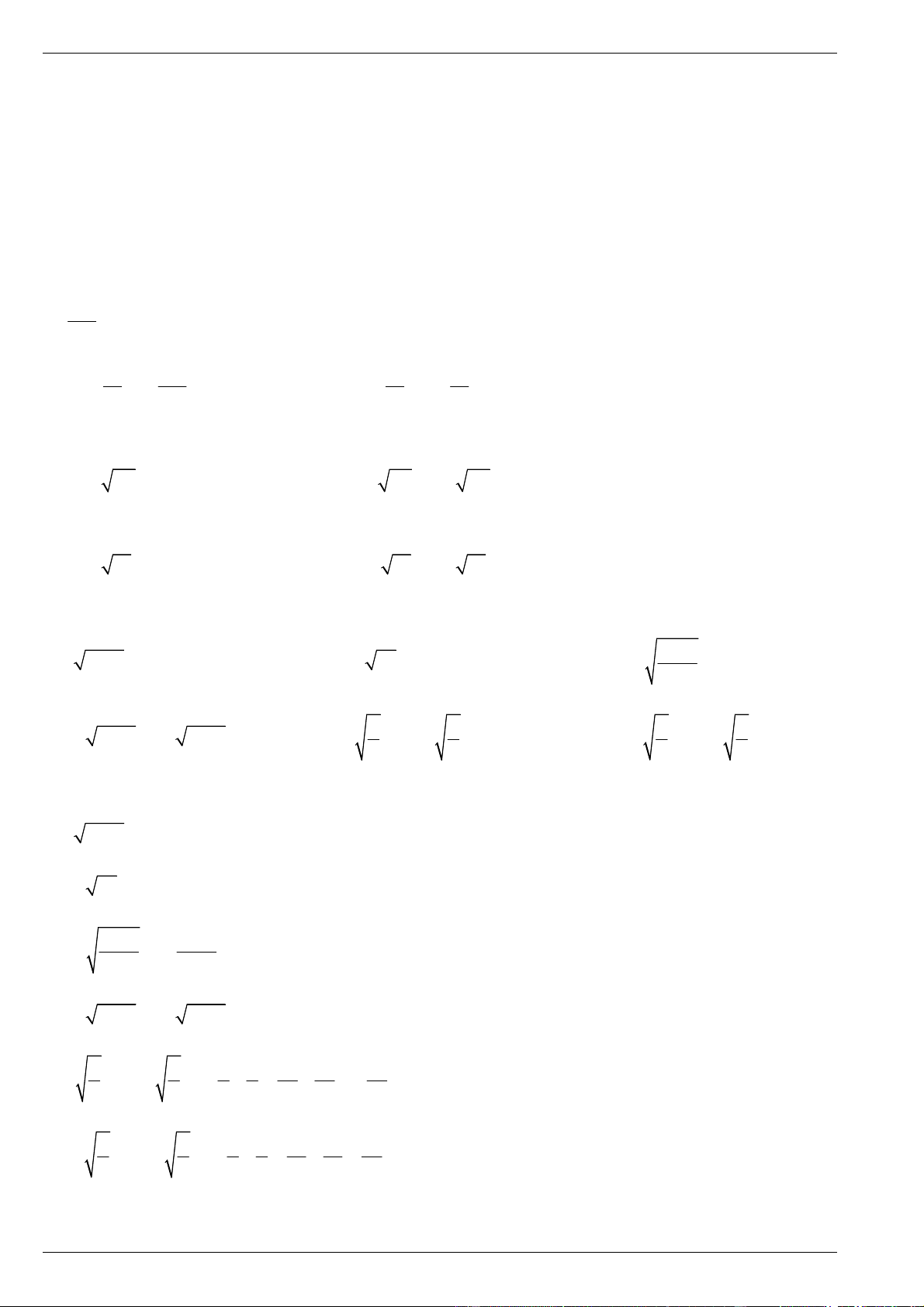
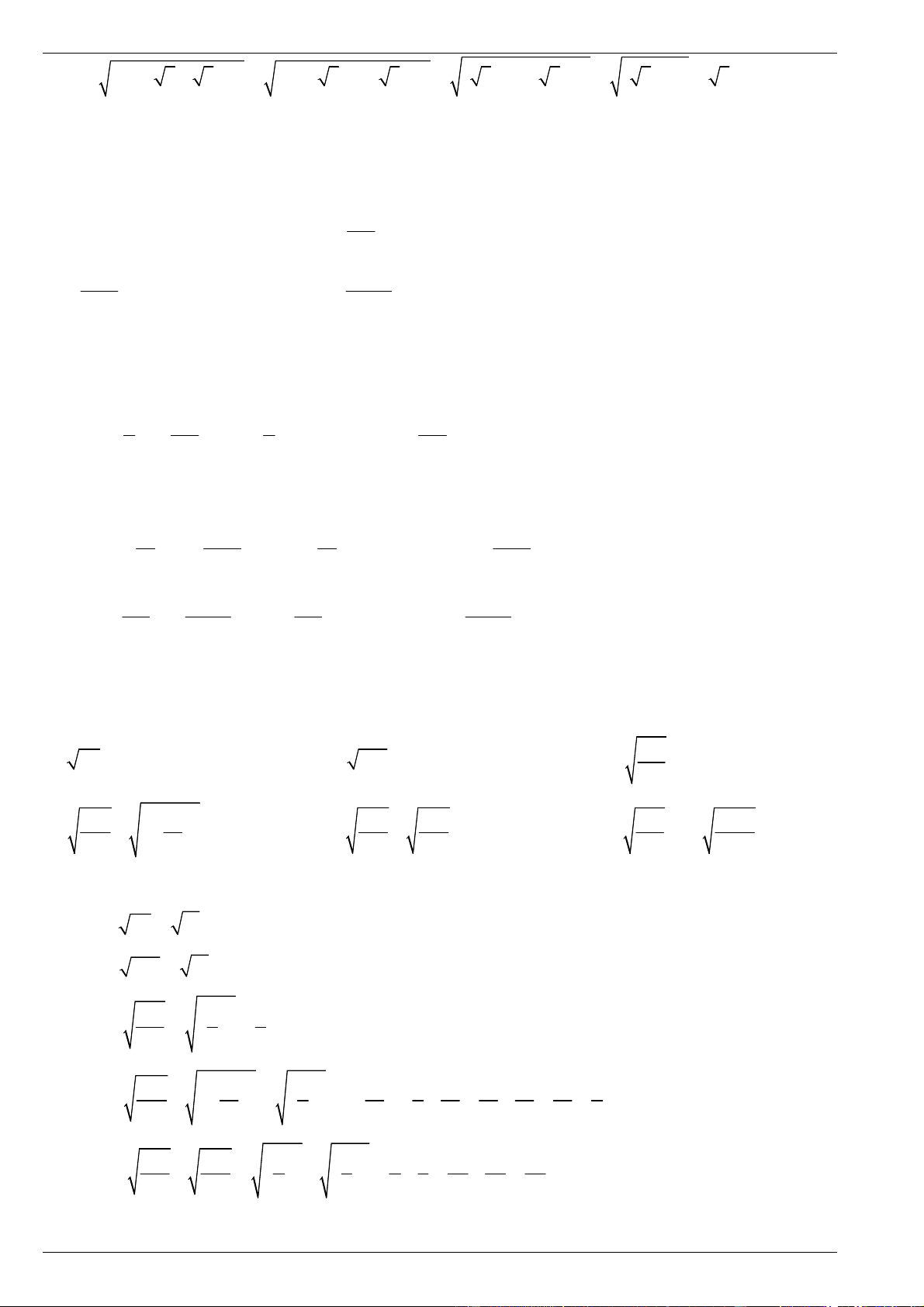
Preview text:

Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều CHƯƠNG 3 CĂN THỨC BÀI 1
CĂN BẬC HAI VÀ CĂN BẬC BA CỦA SỐ THỰC
1. Căn bậc hai của số thực không âm
Định nghĩa: Căn bậc hai của số thực a không âm là số x sao cho 2 x a . Chú ý:
 Mỗi số thực dương a a  0 có đúng hai căn bậc hai là hai số đối nhau. Số dương kí hiệu là: a ,
số âm kí hiệu là:  a . Ta gọi a là căn bậc hai số học của a .
 Số 0 có đúng 1 căn bậc hai là chính nó, ta viết 0  0
 Số âm không có căn bậc hai.
Nhận xét: Với a  0,b  0 , ta có:
 Nếu a b thì a b .
 Nếu a b thì a b . 2. Căn bậc ba
Căn bậc ba của số thực a là số thực x sao cho 3 x a .
Căn bậc ba của số thực a được kí hiệu là: 3 a . Nhận xét:   3 3 aa .
 Nếu a b thì 3 3 a b .  Nếu 3 3
a b thì a b .
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều CHỦ ĐỀ 1
CĂN BẬC HAI CỦA SỐ THỰC DẠNG 1
CĂN BẬC HAI CỦA SỐ THỰC
 Nếu a  0 thì các căn bậc hai của a là  a . 2 2
 Với số a  0 , ta có  a    a   a
Bài 1. Tìm căn bậc hai của : a) 169 b) 2, 25 c) 0, 64 36 d) e) 7 f) 10 121 Bài 2. Tính: 2  1  a)  2 5 b)  2 2025 c)     2026    2 2 2 2 2 2  1   1   2   3  d)  10    8 e)       f)         2   3          3 4     Bài 3. Tính: 2 2 a) 1 51 5
b)  2026  2025  2026  2025  1 2   1 2   4 7   4 7  c)       d)        2 7   2 7          5 3 5 3    
BÀI TẬP RÈN LUYỆN
Bài 4. Tìm căn bậc hai của : a) 64 b) 400 c) 0, 49 25 d) e) 1, 5 f) 17 169 Bài 5. Tính: 2  2025  a)  2 2026 b)  2 99 c)     2026    2 2 2 2 2 2  2   3   3   4 
d)  2026    2025 e)       f)         5   7          2 5    
https://www.facebook.com/truongngocvy8/ T r an
g 2 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều Bài 6. Tính: 3 3 2025 2025
a)  17  4  17  4 b)  27  26   27  26
 11 102  11 102 c)
d)  8  7  6  5 8  7  6  5
 24 53  24 53
https://www.facebook.com/truongngocvy8/ T r an
g 3 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều DẠNG 2
SO SÁNH CĂN BẬC HAI CỦA SỐ THỰC Phương pháp
Với a  0,b  0 , ta có:
 Nếu a b thì a b .
 Nếu a b thì a b .
Bài 1. So sánh các cặp số sau: a ) 24 và 5 b) 0, 08 và 0,3 c) 37 và 6
Bài 2. So sánh các cặp số sau: 24 1 2 4 5 a) 5 và b) và c) và 5 2 3 5 6
Bài 3. So sánh các cặp số sau: 5 4 a) 4 và 10 1 b) và  2 c) 2 và 17  2 2 5
https://www.facebook.com/truongngocvy8/ T r an
g 4 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều CHỦ ĐỀ 2
CĂN BẬC BA CỦA SỐ THỰC DẠNG 1
CĂN BẬC BA CỦA SỐ THỰC Phương pháp
Căn bậc ba của số thực a là số thực x sao cho 3 x a .
Căn bậc ba của số thực a được kí hiệu là: 3 a .  3 a 3 3 3  a a . Chú ý:  3 3 2 2 3
(a b)  a  3a b  3ab b ,  3 3 2 2 3 (a  ) b
a  3a b  3ab b  3 3 2 2
a b  (a b)(a ab b ) ,  3 3 2 2
a b  (a b)(a ab b )
Bài 1. Tìm căn bậc ba của : 1 a) 216 b)  c) 0  , 0729 1000 1 125 27 d)  e) f) 27 64 512 Bài 2. Tính 1 a) 3 0, 008 b) 3  c) 3 3  2024 216 3 3  4  1  1  1 d) 3    e) 2 33 3 3 15. f) 3 3  3    8.  5      125 3 64  
Bài 3. Rút gọn các biểu thức sau a) 3 A     3 3 3 27 4  64 b) 3 3 B  1000  1000000  Bài 4. Tính a)  3 3 3  2  3 3 3 3 9  3. 2  4  b)  3 3   3 3 3 3 7 5 49  7. 5  25 
Bài 5. Rút gọn các biểu thức sau a) 3 A   2   1 3 2 2  b) 3
B  4  2 3 3   1
https://www.facebook.com/truongngocvy8/ T r an
g 5 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều
BÀI TẬP RÈN LUYỆN
Bài 6. Tìm căn bậc ba của : 125 a) 6  4 b) c) 0,512 8 1000 1 d)  e) f) 0  , 027 216 0, 064 Bài 7. Tính 1 a) 3 27 d) 3 729 c) 3 125 3 3 1  1  64 1 1  2026  d) 3 3     e) 3 3  f) 3 3     216  12  343 512 125  5   
Bài 8. Rút gọn các biểu thức sau a) A     3 3 3 3 216 8  3  43 b) 3 3 3
B  0, 001  0, 027  0  ,125
https://www.facebook.com/truongngocvy8/ T r an
g 6 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều DẠNG 2
SO SÁNH CĂN BẬC BA CỦA SỐ THỰC Phương pháp
 Nếu a b thì 3 3 a b .  Nếu 3 3
a b thì a b .
Bài 1. So sánh các cặp số sau: 1 1 a) 3 2024 và 3 2025 b) 3 và 3 c) 8 và 3 511 1000 1001
Bài 2. So sánh các cặp số sau: 8 64 2 125 a) 7  và 3 342 b) 3 và 3 c) và 3 27 125 3 216
https://www.facebook.com/truongngocvy8/ T r an
g 7 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều CHƯƠNG 3 CĂN THỨC BÀI 1
CĂN BẬC HAI VÀ CĂN BẬC BA CỦA SỐ THỰC
1. Căn bậc hai của số thực không âm
Định nghĩa: Căn bậc hai của số thực a không âm là số x sao cho 2 x a . Chú ý:
 Mỗi số thực dương a a  0 có đúng hai căn bậc hai là hai số đối nhau. Số dương kí hiệu là: a ,
số âm kí hiệu là:  a . Ta gọi a là căn bậc hai số học của a .
 Số 0 có đúng 1 căn bậc hai là chính nó, ta viết 0  0
 Số âm không có căn bậc hai.
Nhận xét: Với a  0,b  0 , ta có:
 Nếu a b thì a b .
 Nếu a b thì a b . 2. Căn bậc ba
Căn bậc ba của số thực a là số thực x sao cho 3 x a .
Căn bậc ba của số thực a được kí hiệu là: 3 a . Nhận xét:   3 3 aa .
 Nếu a b thì 3 3 a b .  Nếu 3 3
a b thì a b .
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều CHỦ ĐỀ 1
CĂN BẬC HAI CỦA SỐ THỰC DẠNG 1
CĂN BẬC HAI CỦA SỐ THỰC
 Nếu a  0 thì các căn bậc hai của a là  a . 2 2
 Với số a  0 , ta có  a    a   a
Bài 1. Tìm căn bậc hai của : a) 169 b) 2, 25 c) 0, 64 36 d) e) 7 f) 10 121 Lời giải a) 169 Ta có 2
13  169 nên có hai căn bậc hai là 13 và 1  3 . b) 2, 25 Ta có 2
1, 5  2, 25 nên có hai căn bậc hai là 1, 5 và 1  ,5 . c) 0, 64 Ta có 2
0,8  0, 64 nên có hai căn bậc hai là 0,8 và 0  ,8 . 36 d) 121 2  6  36 6 6 Ta có   
nên có hai căn bậc hai là và  .  11  121 11 11 e) 7 Ta có  2 7
 7 nên có hai căn bậc hai là 7 và  7 . f) 10 Ta có  2 10
 10 nên có hai căn bậc hai là 10 và  10 . Bài 2. Tính: 2  1  a)  2 5 b)  2 2025 c)     2026   
https://www.facebook.com/truongngocvy8/ T r an
g 2 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều 2 2 2 2 2 2  1   1   2   3  d)  10    8 e)       f)         2   3          3 4     Lời giải a)  2 5  5 b)  2 2025  2025 2  1  1 c)      2026  2026   2 2
d)  10    8  10 8  2 2 2  1   1  1 1 3 2 5 e)             2   3  2 3 6 6 6     2 2  2   3  2 3 8 9 1 f)               3   4  3 4 12 12 12     Bài 3. Tính: 2 2 a) 1 51 5
b)  2026  2025  2026  2025  1 2   1 2   4 7   4 7  c)       d)        2 7   2 7          5 3 5 3     Lời giải a)        2 2 1 5 1 5 1 5  1 5  4  2 2 b)  2026 2025   2026 2025   2026 2025  2026 2025  2         2   2  2      2 2026 2025 2026 2025  1    2 2  1 2   1 2  1  2    1 2 7 4 3 c)                   2 7   2 7  2  7    4 7 28 28 28       2 2  4 7   4 7   4   7  4 7 12 35 23 d)                    5 3   5 3   5   3  5 3 15 15 15        
BÀI TẬP RÈN LUYỆN
Bài 4. Tìm căn bậc hai của : a) 64 b) 400 c) 0, 49 25 d) e) 1, 5 f) 17 169
https://www.facebook.com/truongngocvy8/ T r an
g 3 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều Lời giải a) 64 Ta có 2
8  64 nên có hai căn bậc hai là 8 và 8  . b) 400 Ta có 2
20  400 nên có hai căn bậc hai là 20 và 2  0 . c) 0, 49 Ta có 2
0, 7  0, 49 nên có hai căn bậc hai là 0, 7 và 0  , 7 . 25 d) 169 2  5  25 5 5 Ta có   
nên có hai căn bậc hai là và  .  13  169 13 13 e) 1, 5 Ta có  2 1, 5
 7 nên có hai căn bậc hai là 1,5 và  1, 5 . f) 17 Ta có  2 17
 17 nên có hai căn bậc hai là 17 và  17 . Bài 5. Tính: 2  2025  a)  2 2026 b)  2 99 c)     2026    2 2 2 2 2 2  2   3   3   4 
d)  2026    2025 e)       f)         5   7          2 5     Lời giải a)  2 2026  2026 b)  2 99  99 2  2025  2025 c)      2026  2026   2 2
d)  2026    2025  2026  2025  1 2 2  2   3  2 3 14 15 1 e)              5   7  5 7 35 35 35     2 2  3   4  3 4 15 8 23 f)              2   5  2 5 10 10 10     Bài 6. Tính:
https://www.facebook.com/truongngocvy8/ T r an
g 4 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều 3 3 2025 2025
a)  17  4  17  4 b)  27  26   27  26
 11 102  11 102 c)
d)  8  7  6  5 8  7  6  5
 24 53  24 53 Lời giải 3 3 3 3 2 3 a)             2 17 4 17 4 17 4 17 4 17 4            17 16  1    2025 2025 2025 2025 2 2 b)  27 26   27 26  27 26  27 26   27  26                    2025 27 26  1 2 2 2 2   
11  10 2  11  10 2     11     10 11 10 11 10        11102 c)     1   3   3      3 3 3        24 2 2 24 25 24 5 24 5 24 5 24 5   5    d)
 8  7 6  5 8  7 6  5
  8  7  8  7  6  5 6  5
 82  72  62  52             1.1  1
https://www.facebook.com/truongngocvy8/ T r an
g 5 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều DẠNG 2
SO SÁNH CĂN BẬC HAI CỦA SỐ THỰC Phương pháp
Với a  0,b  0 , ta có:
 Nếu a b thì a b .
 Nếu a b thì a b .
Bài 1. So sánh các cặp số sau: a ) 24 và 5 b) 0, 08 và 0,3 c) 37 và 6 Lời giải a) ) 24 và 5 Ta có: 5  25
Do 24  25 nên 24  25 hay 24  5 b) 0, 08 và 0,3 Ta có: 0,3  0,09
Do 0, 08  0, 09 nên 0, 08  0, 09 hay 0, 08  0, 3 c) 37 và 6 Ta có: 6  36
Do 37  36 nên 37  36 hay 37  6
Bài 2. So sánh các cặp số sau: 24 1 2 4 5 a) 5 và b) và c) và 5 2 3 5 6 Lời giải 24 a) 5 và 5 25 Ta có: 5  5 25 24 25 24 24 Do  nên  hay 5  5 5 5 5 5 1 2 b) và 2 3 1 3 2 4 Ta có:  và  2 6 3 6
https://www.facebook.com/truongngocvy8/ T r an
g 6 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều 3 4 1 2 1 2 Do  hay  nên  6 6 2 3 2 3 4 5 c) và 5 6 4 18 5 25 Ta có:  và  5 30 6 30 18 25 4 5 4 5 Do  hay  nên  30 30 5 6 5 6
Bài 3. So sánh các cặp số sau: 5 4 a) 4 và 10 1 b) và  2 c) 2 và 17  2 2 5 Lời giải a) 4 và 10 1
Do 9  10 nên 9  10 hay 3  10 Suy ra 4  10 1 5 4 b) và  2 2 5 1 4 1 4 1 4 Do  nên  hay  4 5 4 5 2 5 1 4 5 4 Suy ra  2   2 hay   2 2 5 2 5 c) 2 và 17  2
Do 16  17 nên 16  17 hay 4  17
Suy ra 4  2  17  2 hay 2  17  2
https://www.facebook.com/truongngocvy8/ T r an
g 7 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều CHỦ ĐỀ 2
CĂN BẬC BA CỦA SỐ THỰC DẠNG 1
CĂN BẬC BA CỦA SỐ THỰC Phương pháp
Căn bậc ba của số thực a là số thực x sao cho 3 x a .
Căn bậc ba của số thực a được kí hiệu là: 3 a .  3 a 3 3 3  a a . Chú ý:  3 3 2 2 3
(a b)  a  3a b  3ab b ,  3 3 2 2 3 (a  ) b
a  3a b  3ab b  3 3 2 2
a b  (a b)(a ab b ) ,  3 3 2 2
a b  (a b)(a ab b )
Bài 1. Tìm căn bậc ba của : 1 a) 216 b)  c) 0  , 0729 1000 1 125 27 d)  e) f) 27 64 512 Lời giải a) Ta có 3
6  216 nên số 6 là căn bậc ba của 216 . 3  1  1 1 1 b) Ta có      nên số  là căn bậc ba của  .  10  1000 10 1000 c) Ta có  3 0,9  0, 0729 nên số 0
 ,9 là căn bậc ba của 0  , 0729 . 3  1  1 1 1 d) Ta có     
nên số  là căn bậc ba của  .  3  27 3 27 3  5  125 5 125 e) Ta có    nên số là căn bậc ba của .  4  64 4 64 3  3  27 3 27 f) Ta có    nên số là căn bậc ba của .  8  512 8 512 Bài 2. Tính
https://www.facebook.com/truongngocvy8/ T r an
g 8 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều 1 a) 3 0, 008 b) 3  c) 3 3  2024 216 3 3  4  1  1  1 d) 3    e) 2 33 3 3 15. f) 3 3  3    8.  5      125 3 64   Lời giải
a) Ta có: 3 0, 008  0,83 3  0,8 3 1  1  1 b) Ta có: 3 3        216  6  6 c) Ta có: 3 3  2024  2  024 3  4  4 d) Ta có: 3       5  5   3 3 3 1  1  1 e) Ta có:  3 2 3  3 3 15.  2 . 3 3 3 15.  8.3 15.  21    125  5  5 3 3 3  1  1   3 1  1  1 1 f) Ta có: 3 3  3    8.   3   3 3    8.  27.   8.  11     3  64  3   4  3 4    
Bài 3. Rút gọn các biểu thức sau a) 3 A     3 3 3 27 4  64 b) 3 3 B  1000  1000000  Lời giải 3 3 a) 3 A    3   3 3 3       3 27 4 64 3
4  4  3  4  4  3 3 b) 3 3 3 3 3
B  1000  1000000  10   1  00  10   1
 00  10 100  110 Bài 4. Tính a)  3 3 3  2  3 3 3 3 9  3. 2  4  b)  3 3   3 3 3 3 7 5 49  7. 5  25  Lời giải 3 3 a)  3 3   3 3 3 3      3 3  3 2 3 3 3 2     3 3 2 9 3. 2 4 3 2 3 3. 2 2
3   3 2   3 2 1 3 3 b)  3 3   3 3 3 3      3 3  3 2 3 3 3 2     3  3 7 5 49 7. 5 25 7 5 7 7. 5 5 7 5   7  5  12
Bài 5. Rút gọn các biểu thức sau a) 3 A   2   1 3 2 2  b) 3
B  4  2 3 3   1 Lời giải 2 3 a) 3 A       3 2 1 3 2 2   2   1 2  2 2   3 1   2   1  2   3 1   2   1  2 1
https://www.facebook.com/truongngocvy8/ T r an
g 9 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều 2 3 b) 3 B       3 4 2 3 3 1  3 2 3   1  3   3 1   3   1  3   3 1   3   1  3 1
BÀI TẬP RÈN LUYỆN
Bài 6. Tìm căn bậc ba của : 125 a) 6  4 b) c) 0,512 8 1000 1 d)  e) f) 0  , 027 216 0, 064 Lời giải a) Ta có  3 4  64 nên số 4  là căn bậc ba của 6  4 . 3  5  125 5 125 b) Ta có    nên số là căn bậc ba của .  2  8 2 8 c) Ta có  3 0,8
 0,512 nên số 0,8 là căn bậc ba của 0,512 . 3  10  1000 10 1000 d) Ta có      nên số  là căn bậc ba của  .  6  216 6 216 3  1  1 1 1 e) Ta có    nên số là căn bậc ba của .  0, 4  0, 064 0, 4 0, 064 f) Ta có  3 0,3  0  , 027 nên số 0
 ,3 là căn bậc ba của 0  , 027 . Bài 7. Tính 1 a) 3 27 d) 3 729 c) 3 125 3 3 1  1  64 1 1  2026  d) 3 3     e) 3 3  f) 3 3     216  12  343 512 125  5    Lời giải a) Ta có: 3 3 3 27  3  3 b) Ta có: 3 3 3 729  9  9 3 1  1  1 c) Ta có: 3 3     125  5  5 3 3 1  1   1   1  1 1 2 1 3 1 d) Ta có: 3 3 3                  216  12   6   12  6 12 12 12 12 4 3 3 64 1  4   1  4 1 32 7 25 e) Ta có: 3 3 3 3             343 512  7   8  7 8 56 56 56
https://www.facebook.com/truongngocvy8/ T r an g
10 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều 3 3 1  2026   1  2026 1 2026 2025 f) Ta có: 3 3 3            405    125  5   5  5 5 5 5  
Bài 8. Rút gọn các biểu thức sau a) A     3 3 3 3 216 8  3  43 b) 3 3 3
B  0, 001  0, 027  0  ,125 Lời giải 3 3 a) 3 A    3   3 3 3       3 216 8 343 6
8  7  6  8  7  9  3 3 3 b) 3 3 3 3
B  0, 001  0, 027  0,125  0,  3 1   0  ,3 3   0
 , 5  0,1 0,3  0,5  0  ,1
https://www.facebook.com/truongngocvy8/ T r an g
11 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều DẠNG 2
SO SÁNH CĂN BẬC BA CỦA SỐ THỰC Phương pháp
 Nếu a b thì 3 3 a b .  Nếu 3 3
a b thì a b .
Bài 1. So sánh các cặp số sau: 1 1 a) 3 2024 và 3 2025 b) 3 và 3 c) 8 và 3 511 1000 1001 Lời giải a) Ta có: 2  024  2  025 nên 3 3 2024  2025  1 1 1 1 b) Ta có:  nên 3 3  1000 1001 1000 1001 c) Ta có: 3 8  512 Do 512  511 nên 3 3 512  511 hay 3 8  511
Bài 2. So sánh các cặp số sau: 8 64 2 125 a) 7  và 3 342 b) 3 và 3 c) và 3 27 125 3 216 Lời giải a) Ta có: 3 7   343 Do 3  43  3  42 nên 3 3 343  342  hay 3 7   342  3 3 8  2  2 6 64  4  4 12 b) Ta có: 3 3      và 3 3      27  3  3 15 125  5  5 15 6 12 2 4 8 64 Do  hay   15 15 3 5 nên 3 3 27 125 3 2 4 125  5  5 c) Ta có:  và 3 3     3 6 216  6  6 4 5 2 5 2 125 Do  hay   6 6 3 6 nên 3 3 216
https://www.facebook.com/truongngocvy8/ T r an g
12 Trương Ngọc Vỹ 0978 333 093
Đại số 9 - Chương 3: Căn thức – Tự luận phân dạng toán có lời giải Cánh Diều BÀI 2
MỘT SỐ PHÉP TÍNH VỀ CĂN THỨC HAI CỦA SỐ THỰC
1. Căn bậc hai của một bình phương
Với mọi số a , ta có: 2 a a
2. Căn bậc hai của một tích Với hai số không âm ,
a b , ta có: a.b a. b
Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.
3. Căn bậc hai của một thương a a
Với a  0,b  0 , ta có:  b b
4. Đưa thừa số ra ngoài dấu căn bậc hai Cho hai số ,
a b , với b  0 . Khi đó: 2 a b a b Cụ thể, ta có:  Nếu a  0 thì 2 a b a b  Nếu a  0 thì 2 a b  a b
5. Đưa thừa số vào trong dấu căn bậc hai
 Với a  0 và b  0 , ta có: 2 a b a b
 Với a  0 và b  0 , ta có: 2
a b   a b
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093

Tài liệu liên quan: