240 trang 5 lượt tải

Tự luận và trắc nghiệm hệ thức lượng trong tam giác vuông Toán 9 Cánh Diều

10

Tài liệu gồm 240 trang, được biên soạn bởi thầy giáo Trương Ngọc Vỹ, hướng dẫn giải các dạng bài tập tự luận và trắc nghiệm chủ đề hệ thức lượng trong tam giác vuông môn Toán 9 bộ sách Cánh Diều.

Chủ đề: Tài liệu chung Toán 9 129 tài liệu

Môn: Toán 9 3.4 K tài liệu

Sách: Cánh diều

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/240
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 1
CHƯƠNG 4
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
BÀI 1
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Tỉ số lượng giác của góc nhọn
Cho góc nhọn
0 0
0 90
. Xét
ABC
vuông tại
A
có
ABC
.
Chú ý: Với góc nhọn
, ta có:
0 sin 1; 0 cos 1
1
cot
tan
hay
tan .cot 1
2. Tỉ số lượng giác của hai góc phụ nhau
Hai góc phụ nhau là hai góc nhọn có tổng bằng
0
90
.
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Nhận xét: Với
0 0
0 90
, ta có:
0
sin(90 ) cos
0
cos(90 ) sin
0
tan(90 ) cot
0
cot(90 ) tan
Các tỉ số lượng giác của góc nhọn
Công thức
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc
, kí hiệu
sin
α
sin
AC
BC
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc
, kí hiệu
cos
cos
AB
BC
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc
, kí hiệu
tan
α
tan
AC
BC
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc
, kí hiệu
cot
α
cot
BC
AC
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 2
Bảng tỉ số lượng giác của góc đặc biệt
0 0 0
30 ,45 ,60
:
0
30
0
45
0
60
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
3
3
1
3
cot
3
1
3
3
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 3
DẠNG 1
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC
1. Với
0 0
0 90
, ta có:
0
sin(90 ) cos
0
cos(90 ) sin
0
tan(90 ) cot
0
cot(90 ) tan
0 sin 1; 0 cos 1
1
cot
tan
hay
tan .cot 1
Chú ý:
2
2
sin sin
hay tổng quát hơn:
sin sin
n
n
2. Bảng tỉ số lượng giác của một số góc đặc biệt:
0
30
0
45
0
60
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
3
3
1
3
cot
3
1
3
3
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
4
Bài 1. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau:
a)
0 0 2 0
cos45 sin 45 cot 45
A b)
2 0 0 2025 0
3
sin 60 .cos30 tan 45
8
B
c)
0 0
2 0 0
sin30 cos30
tan 45 cot30
C
d)
0 0
2026 0 0
2sin60 tan45
cot 45 tan60
D
Bài 2. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn
0
45
.
0 0 0 0
sin63 , cos72 , tan56 , cot81
Bài 3. Tính giá trị của các biểu thức sau:
a)
o o
sin23 cos67
A b)
o o
tan14 cot76
B
c)
sin15
cos75
o
o
C d)
o
o
cot72
tan18
D
e)
o o
1
tan29 .tan61
2026
E f)
o o
2025cot11 .cot79
F
Bài 4. Tính giá trị của các biểu thức sau:
a)
o o o
sin11 cos79 tan 45
A b)
o o o
1 1
tan33 cot57 sin30
2 2
B
c)
o o o
tan22 .cot60 .tan68
C d)
o
o o o
cos52
sin38 .tan 29 .tan61
D
Bài 5. Tính giá trị của các biểu thức sau:
a)
o o o o
sin35 sin67 cos23 cos55
A b)
o o o o
tan15 2025tan54 cot 75 2025cot36
B
c)
o o o o
2 o 2 o 2 o
tan 27 tan16 .tan74 cot73
sin 35 sin 45 cos 55
C
d)
2
2 o 2 o o o
o o o
tan 39 cot 51 tan39 cot51
sin39 tan 45 cos51
D
Bài 6. Tính giá trị của các biểu thức sau:
a)
o o o o o o
tan15 .tan 25 .tan35 .tan55 .tan65 .tan75
A
b)
2 o 2 o 2 2 o 2 o 2 o 2 o 2 o
cot 10 .cot 20 .cot 30.cot 40 .cot 50 .cot 60 .cot 7
0 .cot 80
B
BÀI TẬP RÈN LUYỆN
Bài 7. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau:
a)
0 0 2024 0
sin30 cos60 2tan 45
A b)
0
0 0
2025 0
sin30
cos30 .cot60
tan 45
B
c)
0
0 0
cot30
cos60 sin 45
C
d)
0 0
0 0
cos45 sin60
2sin 45 3tan30
D
e)
2 0 2 0 3 0
4 sin 45 2cos 60 3cot 45
E f)
0 0 5 0
cos30 .cot30 .tan 45
F
Bài 8. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc lớn hơn
0
45
.
0 0 0 0
sin 22 , cos13 , tan37 , cot 44
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 5
Bài 9. Tính giá trị của các biểu thức sau:
a)
2 o 2 o
sin 21 cos 69
A b)
3 o 3 o
tan 18 cot 72
B
c)
3 o 2 o 3 o
tan 13 .tan 30 .tan 77
C d)
o 2 o 2 o o
o o
sin9 .tan 29 .tan 61 .cot72
cos81 .tan8
D
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
6
DẠNG 2
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC
DÀNH CHO HỌC SINH KHÁ GIỎI
Với
0 0
0 90
, ta có:
sin
tan
cos
1
cos
cot
sin
2
2 2
sin cos 1
3
Chú ý: Công thức
1 , 2 , 3
, khi làm tự luận phải chứng minh mới được dùng.
Bài 1. Cho tam giác
ABC
vuông tại
A
, với
B
. Chứng minh:
sin
tan
cos
1
cos
cot
sin
2
2 2
sin cos 1
3
Bài 2. Tính giá trị của các biểu thức sau:
a)
2 0 2 0 2 0 2 0
sin 17 sin 25 sin 65 sin 73
A
b)
2 0 2 0 2 0 2 0
cos 24 cos 42 cos 48 cos 66
B
c)
2 0 2 0 2 0 2 0 2 0 2 0 2 0
cos 15 cos 25 cos 35 cos 45 cos 55 cos 65 cos 75
C
d)
2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
sin 10 sin 20 sin 30 sin 40 sin 50 sin 60 sin 70 sin 80
D
Bài 3. Cho
là góc nhọn tính giá trị của các biểu thức sau:
a)
4 2 2 4
sin 2sin .cos cos
A
b)
6 2 2 6
sin 3sin .cos cos
B
Bài 4. Cho
tan 2
, với
là góc nhọn. Tính giá trị của các biểu thức sau:
a)
sin cos
sin cos
A
b)
2 2
2 2
2sin 3cos
3sin 2cos
B
c)
3
3 3
cos
sin 2cos
C
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
7
DẠNG 3
TÍNH TỈ SỐ LƯỢNG GIÁC TRONG TAM GIÁC VUÔNG
1. Tỉ số lượng giác của góc nhọn
Xét
ABC
vuông tại
A
có
ABC
. Ta có tỉ số lượng giác của góc
như sau:
sin
AC
BC
cos
AB
BC
tan
AC
BC
cot
BC
AC
Chú ý:Với góc nhọn
, ta có:
0 sin 1; 0 cos 1
1
cot
tan
2. Tỉ số lượng giác của hai góc phụ nhau
Nếu
0
90
, ta có:
sin cos
cos sin
tan cot
cot tan
3. Hệ thức lượng trong tam giác vuông (kiến thức nâng cao)
C
B
H
A
Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Khi đó, ta có:
2 2 2
AB AC BC
(định lí Pythagore đã học lớp 8)
2
.
AB BH BC
1
2
.
AC CH CB
2
2
.
AH HB HC
3
. .
AH BC AB AC
4
2 2 2
1 1 1
AH AB AC
5
Công thức
1 , 2 , 3 , 4 , 5
khi dùng tự luận phải chứng minh rồi mới được dùng.
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 8
Bài 1. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
.
C
B
H
A
Chứng minh rằng:
a)
2
.
AB BH BC
b)
2
.
AC CH CB
c)
2
.
AH HB HC
d)
. .
AH BC AB AC
e)
2 2 2
1 1 1
AH AB AC
Bài 2. Cho tam giác
ABC
vuông tại
C
có
1,2 ; 0,9
BC cm AC cm
. Tính các tỉ số lượng giác của góc
B
, từ đó suy ra tỉ số lượng giác của góc
A
.
Bài 3. Cho tam giác
ABC
có
5, 3
AB a BC a
,
2
AC a
a) Chứng minh tam giác
ABC
vuông.
b) Tính các tỉ số lượng giác của góc
B
, từ đó suy ra các tỉ số lượng giác của góc
A
.
Bài 4. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
12 , 13
AC cm BC cm
.
a) Tính cạnh
AB
.
b) Tính
cos , sin
B C
.
c) Chứng minh
. .
AH BC AB AC
.
d) Tính các tỉ số lượng giác của góc
BAH
, từ đó suy ra các tỉ số lượng giác của góc
CAH
.
Bài 5. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
3 , 5
AH cm AC cm
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 9
a) Tính
tan , cot , tan , cot
C C B B
.
b) Chứng minh
2
.
AH HB HC
. Từ đó tính
HB
.
Bài 6. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
6 , 8
BH cm CH cm
.
a) Tính
AH
.
b) Tính
sin , sin
BAH CAH
.
Bài 7. Cho tam giác
ABC
vuông tại
A
có
cos 0,6
B
.
a) Chứng minh
2 2
sin cos 1
B B
.
b) Tính các tỉ số lượng giác của góc
B
còn lại.
c) Tính các tỉ số lượng giác của góc
C
.
BÀI TẬP RÈN LUYỆN
Bài 8. Cho tam giác
ABC
vuông tại
A
có
1,6 ; 1,2
AB cm AC cm
. Tính các tỉ số lượng giác của góc
B
, từ đó suy ra tỉ số lượng giác của góc
C
.
Bài 9. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
3 , 4
AB a AC a
.
a) Tính
sin
B
và
cos
C
.
b) Tính
tan , cot , tan , cot
BAH BAH CAH CAH
.
Bài 10. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
4 , 9
BH a BC a
.
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 10
a) Tính
sin
B
và
cos
C
.
b) Tính
tan
BAH
và
cot
CAH
.
Bài 11. Cho tam giác
ABC
vuông tại
A
có
1
sin
3
C
.
a) Tính các tỉ số lượng giác của góc
C
còn lại.
b) Tính các tỉ số lượng giác của góc
B
.
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 11
DẠNG 4
TÍNH CẠNH VÀ GÓC NHỌN CỦA TAM GIÁC VUÔNG
Tỉ số lượng giác của góc nhọn
Xét
ABC
vuông tại
A
có
ABC
. Ta có tỉ số lượng giác của góc
như sau:
sin
AC
BC
cos
AB
BC
tan
AC
BC
cot
BC
AC
Bài 1. Tìm
x
trong các hình sau: (kết quả làm tròn đến phần trăm của centimet)
Bài 2. Cho tam giác
ABC
vuông tại
A
có
10
BC cm
và
3
sin
2
B .
a) Tính góc
B
.
b) Tính cạnh
AC
và
AB
.
Bài 3. Cho tam giác
ABC
vuông tại
A
có
12
AC cm
và
1
cos
4
C
.
a) Tính góc
C
(kết quả làm tròn đến phần chục của độ).
b) Tính cạnh
BC
.
Bài 4. Cho tam giác
ABC
vuông tại
A
có
8
AB cm
và
4
tan
5
C
.
a) Tính góc
C
(kết quả làm tròn đến phút).
b) Tính cạnh
AC
.
Bài 5. Cho tam giác
ABC
vuông tại
A
có
6
AC cm
và
1
cot
2
B
.
a) Tính góc
B
(kết quả làm tròn đến phút).
b) Tính cạnh
AC
.
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 1
CHƯƠNG 4
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
BÀI 1
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Tỉ số lượng giác của góc nhọn
Cho góc nhọn
0 0
0 90
. Xét
ABC
vuông tại
A
có
ABC
.
Chú ý: Với góc nhọn
, ta có:
0 sin 1; 0 cos 1
1
cot
tan
hay
tan .cot 1
2. Tỉ số lượng giác của hai góc phụ nhau
Hai góc phụ nhau là hai góc nhọn có tổng bằng
0
90
.
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Nhận xét: Với
0 0
0 90
, ta có:
0
sin(90 ) cos
0
cos(90 ) sin
0
tan(90 ) cot
0
cot(90 ) tan
Các tỉ số lượng giác của góc nhọn
Công thức
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc
, kí hiệu
sin
α
sin
AC
BC
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc
, kí hiệu
cos
cos
AB
BC
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc
, kí hiệu
tan
α
tan
AC
BC
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc
, kí hiệu
cot
α
cot
BC
AC
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 2
Bảng tỉ số lượng giác của góc đặc biệt
0 0 0
30 ,45 ,60
:
0
30
0
45
0
60
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
3
3
1
3
cot
3
1
3
3
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 3
DẠNG 1
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC
1. Với
0 0
0 90
, ta có:
0
sin(90 ) cos
0
cos(90 ) sin
0
tan(90 ) cot
0
cot(90 ) tan
0 sin 1; 0 cos 1
1
cot
tan
hay
tan .cot 1
Chú ý:
2
2
sin sin
hay tổng quát hơn:
sin sin
n
n
2. Bảng tỉ số lượng giác của một số góc đặc biệt:
0
30
0
45
0
60
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
3
3
1
3
cot
3
1
3
3
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
4
Bài 1. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau:
a)
0 0 2 0
cos45 sin 45 cot 45
A b)
2 0 0 2025 0
3
sin 60 .cos30 tan 45
8
B
c)
0 0
2 0 0
sin30 cos30
tan 45 cot30
C
d)
0 0
2026 0 0
2sin60 tan45
cot 45 tan 60
D
Lời giải
a)
0 0 2 0 2
2 2
cos45 sin45 cot 45 1 1
2 2
A
b)
2
2 0 0 2025 0 2025
3 3 1 3 3 3
sin 60 .cos30 tan 45 . .1 0
8 2 2 8 8 8
B
c)
2
0 0
2 0 0
2
1 3 1 1
1 3 4 2 3
sin30 cos30 3
2 2 2 2
1
tan 45 cot30 1 3 2
1 3
1 3 1 3
C
d)
2
0 0
2026 0 0
2026
3
2. 1
1 3 1 3 4 2 3
2sin60 tan45
2
3 2
cot 45 tan 60 1 3
1 3 1 3
1 3 1 3
D
Bài 2. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn
0
45
.
0 0 0 0
sin63 , cos72 , tan56 , cot81
Lời giải
Ta có:
0 0 0 0
sin63 cos 90 63 cos27
0 0 0 0
cos72 sin 90 72 sin18
0 0 0 0
tan56 cot 90 56 cot34
0 0 0 0
cot81 tan 90 81 cos9
Bài 3. Tính giá trị của các biểu thức sau:
a)
o o
sin23 cos67
A b)
o o
tan14 cot76
B
c)
sin15
cos75
o
o
C d)
o
o
cot72
tan18
D
e)
o o
1
tan29 .tan61
2026
E f)
o o
2025cot11 .cot79
F
Lời giải
a)
o o o o o o o
sin 23 cos67 sin 90 67 cos67 cos67 cos67 0
A
b)
o o o o o o o
tan14 cot76 tan 90 76 cot76 cot76 cot76 0
B
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 5
c)
sin 90 75
sin15 cos75
1
cos75 cos75 cos75
o o
o o
o o o
C
d)
o o
o o
o o o
cot 90 18
cot72 tan18
1
tan18 tan18 tan18
D
e)
1 1 1 1
tan29 .tan61 tan 29 .tan 90 29 tan29 .cot 29
2026 2026 2026 2026
o o o o o o o
E
f)
2025cot11 .cot79 2025cot11 .cot 90 11 2025cot1
1 .tan11 2025
o o o o o o o
F
Bài 4. Tính giá trị của các biểu thức sau:
a)
o o o
sin11 cos79 tan 45
A b)
o o o
1 1
tan33 cot57 sin30
2 2
B
c)
o o o
tan22 .cot60 .tan68
C d)
o
o o o
cos52
sin38 .tan 29 .tan61
D
Lời giải
a)
o o o o o o o o
2 2 2
sin11 cos79 tan 45 sin11 sin 90 79 sin11 sin11
2 2 2
A
b)
o o o o o o o o
1 1 1 1 1 1 1 1 1
tan33 cot57 sin30 tan33 tan 90 57 tan33 tan33
2 2 2 2 2 2 2 2 2
B
c)
o o o o o o o o o
3
tan 22 .cot 60 .tan68 tan 22 .tan68 .cot60 tan22 .
cot 90 68 .
3
C
o o
3 3 3
.tan 22 .cot 22 .1
3 3 3
d)
o o
o o
o o o o o o
o o o o
sin 90 52
cos52 sin38
1
sin38 .tan29 .tan 61 sin38 .tan29 .cot 29
sin38 .tan29 .cot 90 61
D
Bài 5. Tính giá trị của các biểu thức sau:
a)
o o o o
sin35 sin67 cos23 cos55
A b)
o o o o
tan15 2025tan54 cot 75 2025cot36
B
c)
o o o o
2 o 2 o 2 o
tan 27 tan16 .tan74 cot73
sin 35 sin 45 cos 55
C
d)
2
2 o 2 o o o
o o o
tan 39 cot 51 tan39 cot51
sin39 tan 45 cos51
D
Lời giải
a)
o o o o o o o o
sin35 sin67 cos23 cos55 sin35 cos55 sin67 cos23
A
Ta có:
o o o o
cos55 cos 90 55 sin35
o o o o
cos23 sin 90 23 sin 67
Do đó:
o o o o
sin35 sin35 sin 67 sin67 0
A
b)
o o o o o o o o
tan15 2025tan54 cot75 2025cot36 tan15 cot75 20
25 tan54 cot36
B
Ta có:
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
6
o o o o
cot75 tan 90 75 tan15
o o o o
cot36 tan 90 36 tan54
Do đó:
o o o o
tan15 tan15 2025 tan54 tan54 0 2025.0 0
B
c)
o o o o o o o o
2 o 2 o 2 o 2 o 2 o 2 o
tan 27 tan16 .tan74 cot73 tan27 cot73 tan16 .tan
74
sin 35 sin 45 cos 55 sin 35 cos 55 sin 45
C
o o o o o o
o o o o
2
2 o 2 o
2 o 2 o o
tan 27 tan 90 73 tan16 .cot 90 74
tan 27 tan 27 tan16 .cot16 0 1
4
1 1
2
sin 35 sin 35 0
sin 35 sin 90 55
4 4
2
d)
2
2 o 2 o o o
o o o
tan 39 tan 51 tan39 tan51
sin39 tan45 cos51
D
2 o 2 o 2 o o o 2 o
o o o
tan 39 tan 51 tan 39 2tan39 .tan51 tan 51
sin39 cos51 tan45
o o o
o o o
o o
o o
2tan39 .cot 90 51
2
sin39 sin 90 51
2
2tan39 .cot39 2
2 2
2 2
sin39 sin39
2 2
Bài 6. Tính giá trị của các biểu thức sau:
a)
o o o o o o
tan15 .tan 25 .tan35 .tan55 .tan65 .tan75
A
b)
2 o 2 o 2 2 o 2 o 2 o 2 o 2 o
cot 10 .cot 20 .cot 30.cot 40 .cot 50 .cot 60 .cot 7
0 .cot 80
B
Lời giải
a)
o o o o o o
tan15 .tan 25 .tan35 .tan55 .tan65 .tan75
A
o o o o o o
tan15 .tan75 . tan25 tan65 . tan35 .tan55
o o o o o o o o o
tan15 .cot 90 75 . tan25 .cot 90 65 . tan35 .cot 90 6
5
o o o o o o
tan15 .cot15 . tan25 .cot 25 . tan35 .cot35 1.1.1
1
b)
2 o 2 o 2 2 o 2 o 2 o 2 o 2 o
cot 10 .cot 20 .cot 30.cot 40 .cot 50 .cot 60 .cot 7
0 .cot 80
B
2 o 2 o 2 o 2 o 2 2 o 2 o 2 o
cot 10 .cot 80 . cot 20 .cot 70 . cot 30.cot 60 . cot 4
0 .cot 50
2 2 2 2
o o o o o o o
cot10 .cot80 . cot 20 .cot70 . cot30.cot 60 . cot 4
0 .cot50
2 2 2 2
o o o o o o o
2 2 2 2
cot10 .tan10 . cot 20 .tan 20 . cot30.tan30 . cot 4
0 .tan 40
1 .1 .1 .1 1
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
7
BÀI TẬP RÈN LUYỆN
Bài 7. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau:
a)
0 0 2024 0
sin30 cos60 2tan 45
A b)
0
0 0
2025 0
sin30
cos30 .cot60
tan 45
B
c)
0
0 0
cot30
cos60 sin 45
C
d)
0 0
0 0
cos45 sin60
2sin 45 3tan30
D
e)
2 0 2 0 3 0
4 sin 45 2cos 60 3cot 45
E f)
0 0 5 0
cos30 .cot30 .tan 45
F
Lời giải
a)
0 0 2024 0 2024
1 1
sin30 cos60 2tan 45 2.1 0
2 2
A
b)
0
0 0
2025 0 2025
1
sin30 3 3 1 1
2
cos30 .cot60 . 0
tan 45 2 3 1 2 2
B
c)
0
0 0
2 3 1 2
cot30 3 3 2 3 2 6
2 3 2 6
1
cos60 sin 45 1 2
1 2
1 2 1 2
1 2
2
2 2
C
d)
2
0 0
0 0
2 3 1 1
2 3 5 2 6
cos45 sin60 5
2 2 2 2
6
2sin 45 3tan30 2 3 2
2 3
2 3 2 3
2. 3.
2 3
D
e)
2
2
2 0 2 0 3 0
2 1
4 sin 45 2cos 60 3cot 45 4 2. 3 1
2 2
E
f)
0 0 5 0 5
3 3
cos30 .cot30 .tan 45 . 3.1
2 2
F
Bài 8. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc lớn hơn
0
45
.
0 0 0 0
sin 22 , cos13 , tan37 , cot 44
Lời giải
Ta có:
0 0 0 0
sin 22 cos 90 22 cos68
0 0 0 0
cos13 sin 90 13 sin 77
0 0 0 0
tan37 cot 90 37 cot53
0 0 0 0
cot44 tan 90 44 cos46
Bài 9. Tính giá trị của các biểu thức sau:
a)
2 o 2 o
sin 21 cos 69
A b)
3 o 3 o
tan 18 cot 72
B
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 8
c)
3 o 2 o 3 o
tan 13 .tan 30 .tan 77
C d)
o 2 o 2 o o
o o
sin9 .tan 29 .tan 61 .cot72
cos81 .tan8
D
Lời giải
a)
2 o 2 o 2 o 2 o o 2 o 2 o
sin 21 cos 69 sin 21 sin 90 69 sin 21 sin 21 0
A
b)
3 o 3 o 3 o 3 o o 3 o 3 o
tan 18 cot 72 tan 18 tan 90 72 tan 18 tan 18 0
B
c)
2
3
3 o 2 o 3 o 3 o 3 o 2 o o o
3
tan 13 .tan 30 .tan 77 tan 13 .tan 77 .tan 30 tan13 .tan77 .
3
C
3
o o o o o
1 1 1
tan13 .cot 90 77 tan13 .cot13
3 3 3
d)
2
o o o o o o
o 2 o 2 o o
o o
o o o
sin9 . tan 29 .cot 90 61 .tan 90 72
sin9 .tan 29 .tan 61 .cot72
cos81 .tan8
sin 90 81 .tan8
D
2
o o o o
o o
sin9 . tan29 .cot 29 .tan8
1
sin9 .tan8
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 9
DẠNG 2
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC
DÀNH CHO HỌC SINH KHÁ GIỎI
Với
0 0
0 90
, ta có:
sin
tan
cos
1
cos
cot
sin
2
2 2
sin cos 1
3
Chú ý: Công thức
1 , 2 , 3
, khi làm tự luận phải chứng minh mới được dùng.
Bài 1. Cho tam giác
ABC
vuông tại
A
, với
B
. Chứng minh:
sin
tan
cos
1
cos
cot
sin
2
2 2
sin cos 1
3
Lời giải
Chứng minh
sin
tan
cos
1
Xét tam giác
ABC
vuông tại
A
, ta có:
sin
AC
BC
hay
.sin
AC BC
cos
AB
BC
hay
.cos
AB BC
tan
AC
AB
Suy ra:
.sin sin
tan
.cos cos
AC BC
AB BC
Vậy:
sin
tan
cos

Tài liệu khác của Toán 9

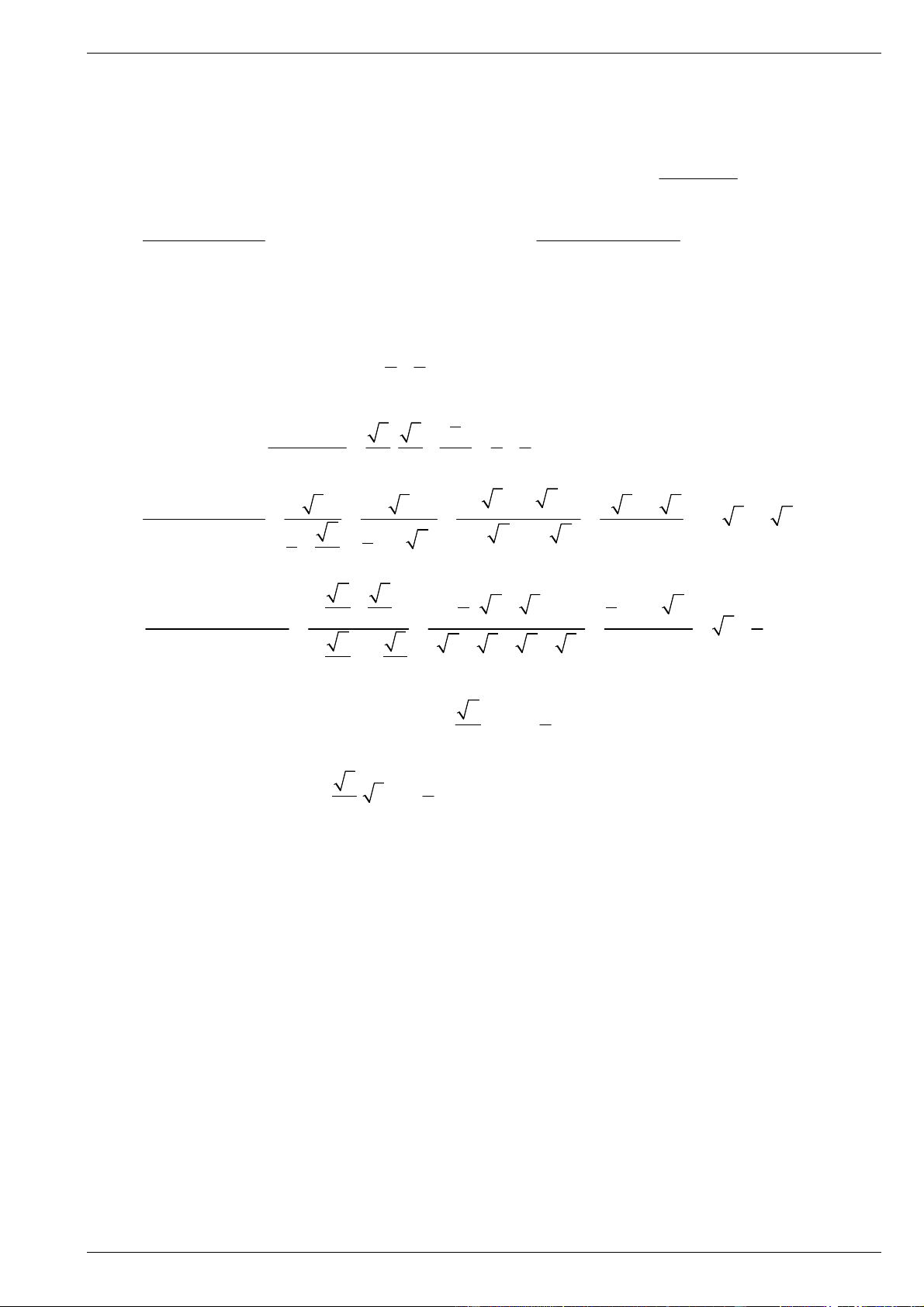
Preview text:

Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều CHƯƠNG 4
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG BÀI 1
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Tỉ số lượng giác của góc nhọn
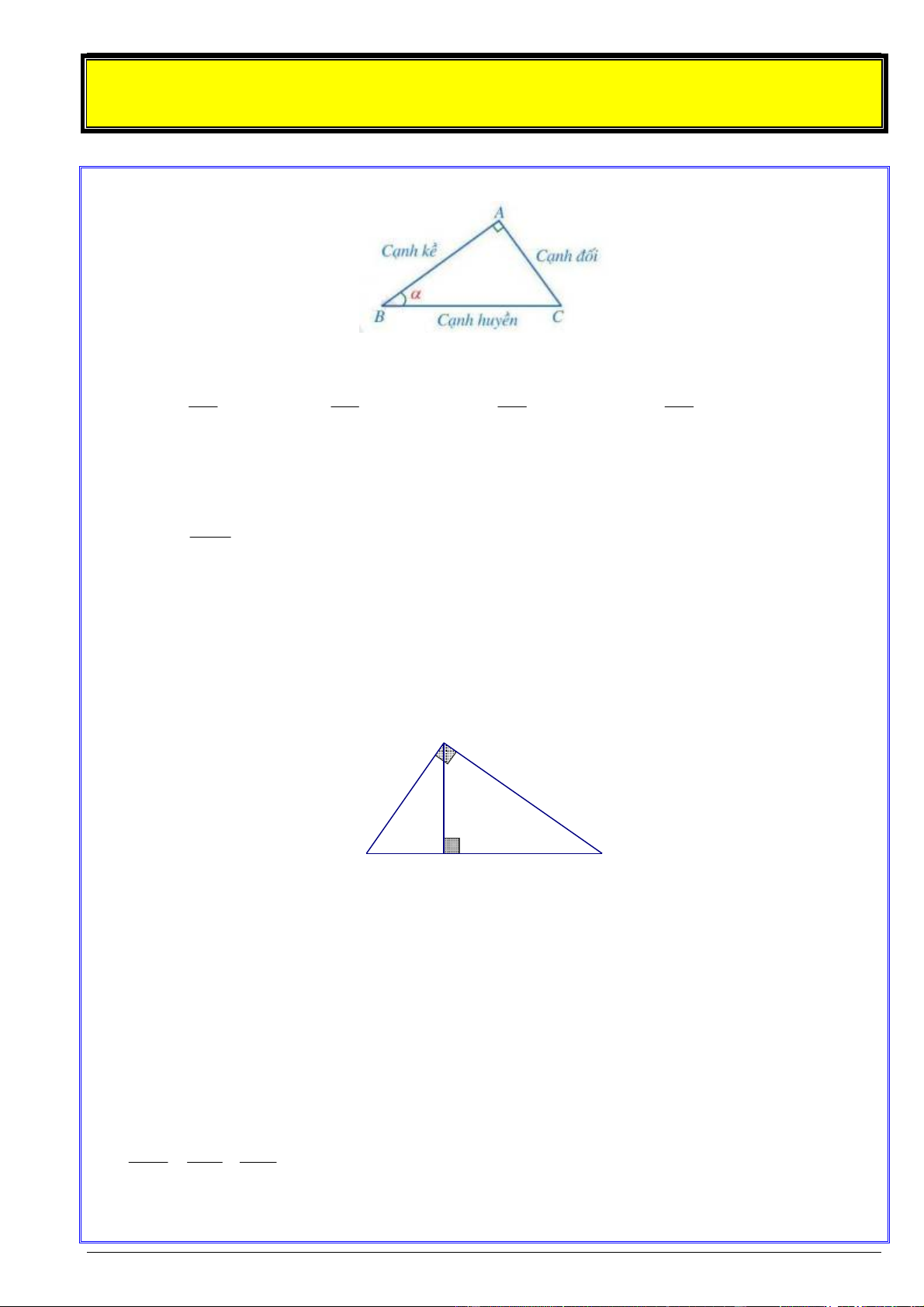
Cho góc nhọn  0 0
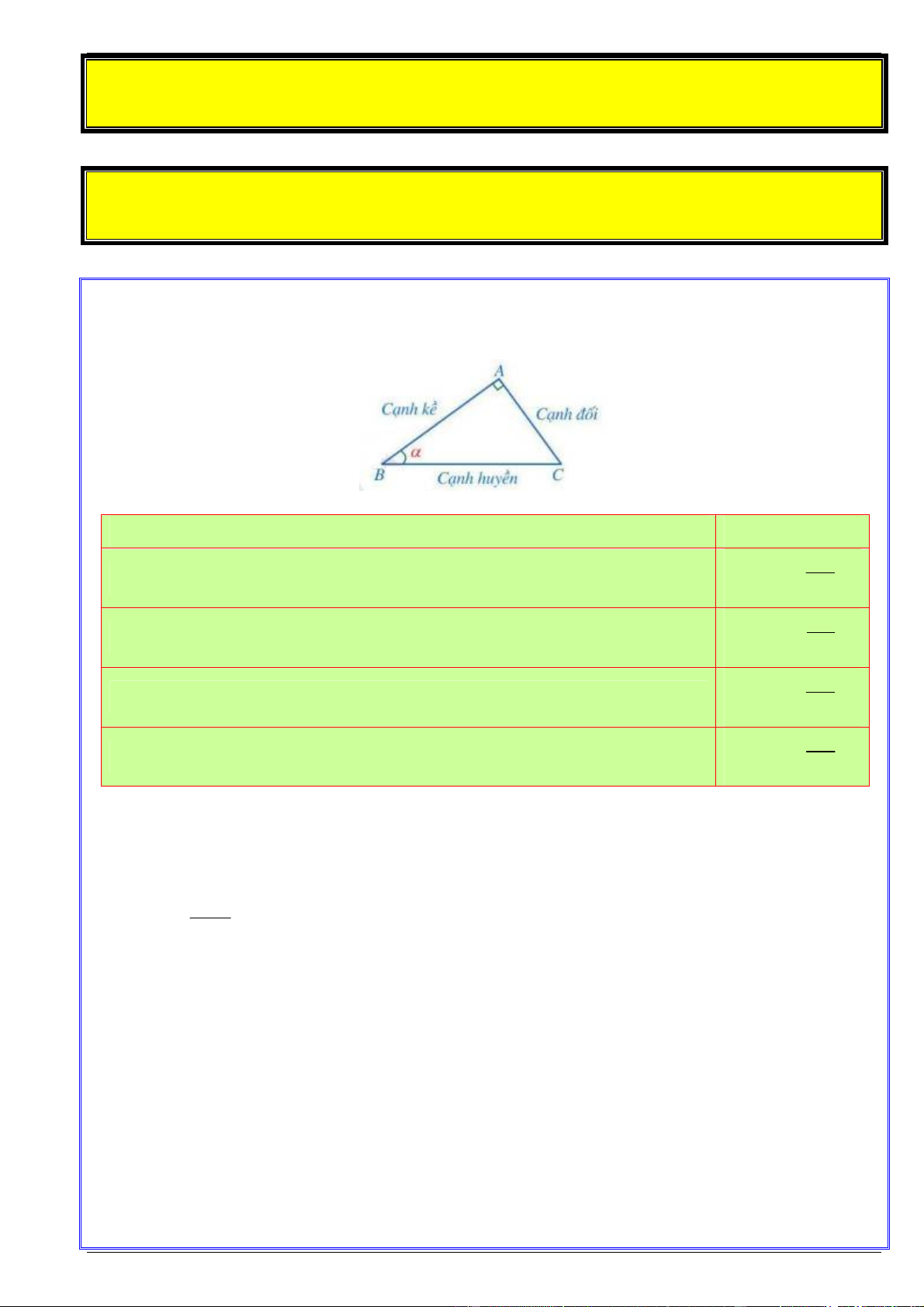
0   90  . Xét ABC vuông tại A có ABC .
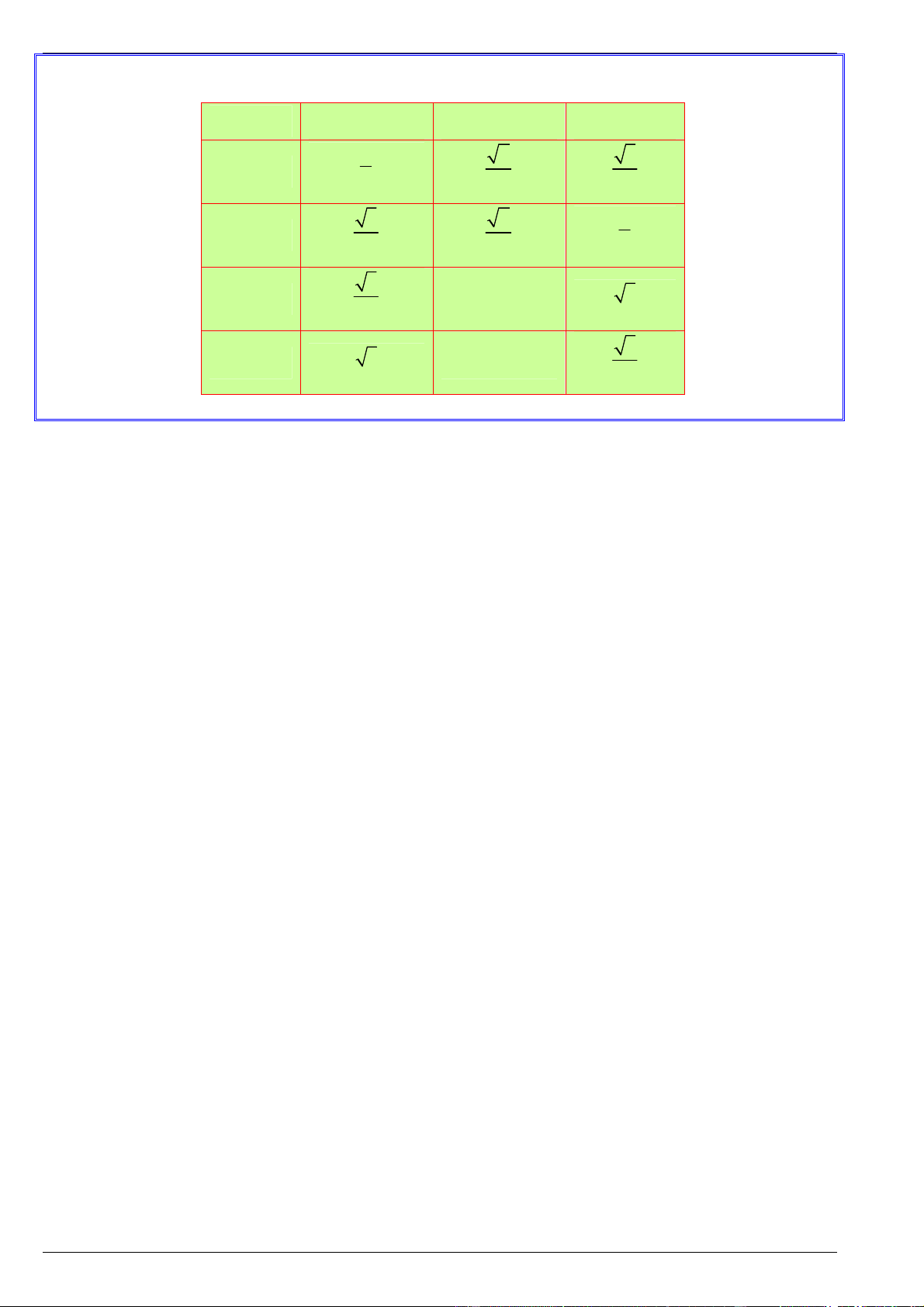
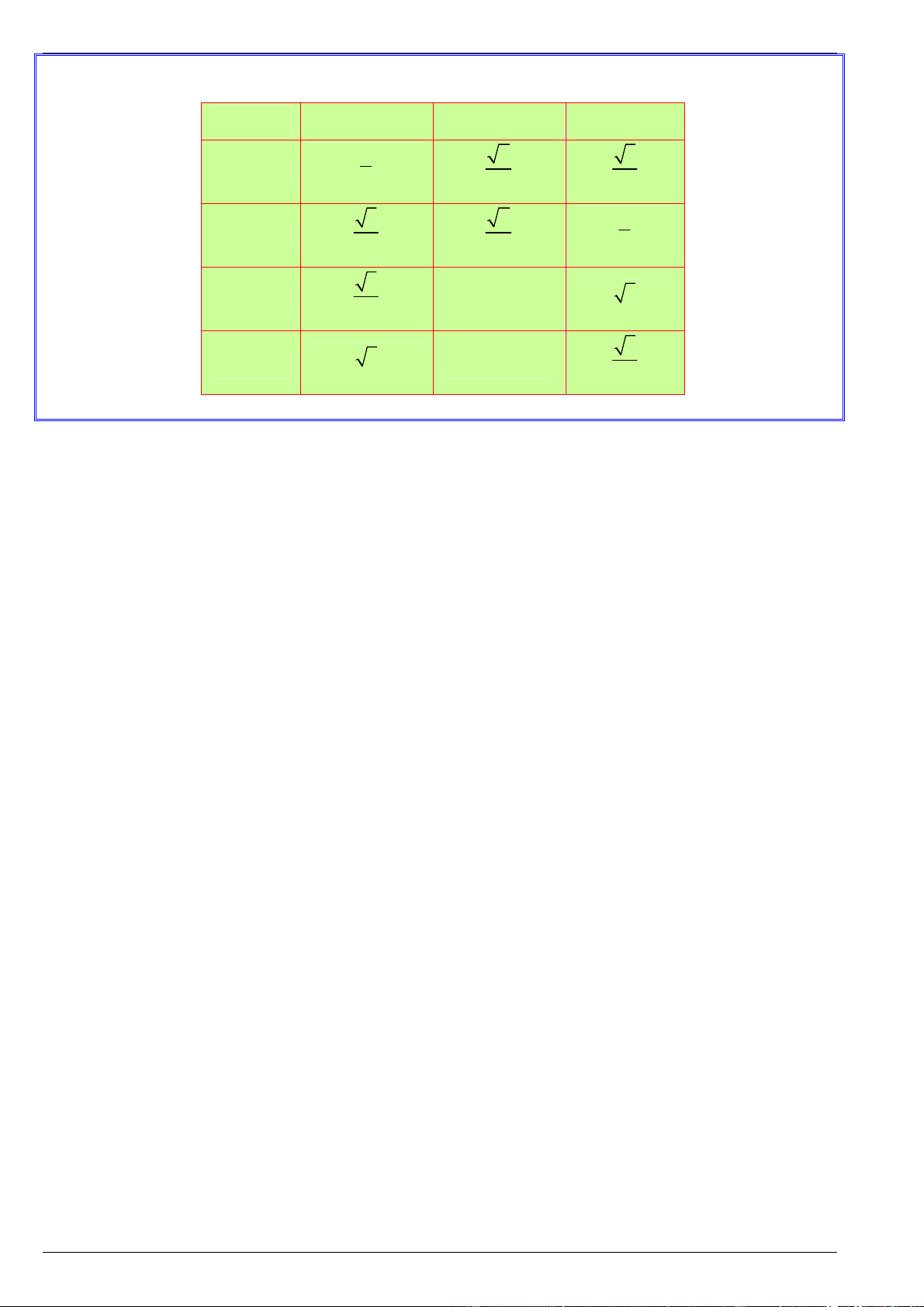
Các tỉ số lượng giác của góc nhọn Công thức AC
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc , kí hiệu sinα sinBC AB
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc , kí hiệu cos cos BC AC
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc , kí hiệu tanα tan BC BC
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc , kí hiệu cotα cot AC
Chú ý: Với góc nhọn , ta có:
 0  sin 1; 0  cos 1 1  cot
hay tan .cot 1 tan
2. Tỉ số lượng giác của hai góc phụ nhau
Hai góc phụ nhau là hai góc nhọn có tổng bằng 0 90 .
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Nhận xét: Với 0 0
0   90 , ta có:  0
sin(90  )  cos  0
cos(90  )  sin  0
tan(90  )  cot  0
cot(90  )  tan
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
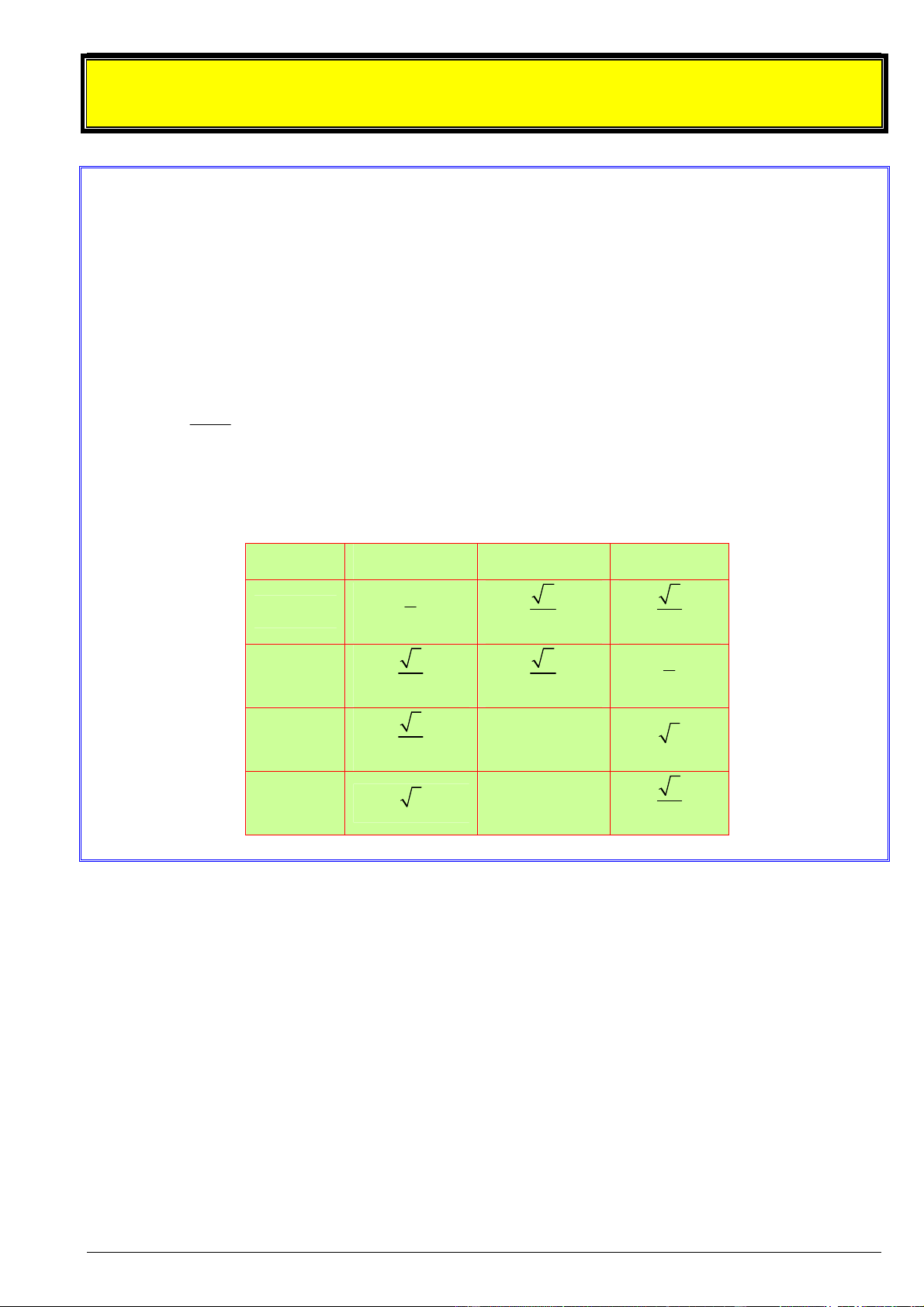
Bảng tỉ số lượng giác của góc đặc biệt 0 0 0 30 , 45 , 60 : 0 30 0 45 0 60 1 2 3 sin 2 2 2 3 2 1 cos 2 2 2 3 tan 1 3 3 3 cot 3 1 3
https://www.facebook.com/truongngocvy8/ T r an
g 2 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều DẠNG 1
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC 1. Với 0 0
0   90 , ta có:  0
sin(90  )  cos  0
cos(90  )  sin  0
tan(90  )  cot  0
cot(90  )  tan
 0  sin 1; 0  cos 1 1  cot
hay tan .cot 1 tan n Chú ý:   2 2 sin sin
hay tổng quát hơn: sinn   sin
2. Bảng tỉ số lượng giác của một số góc đặc biệt: 0 30 0 45 0 60 1 2 3 sin 2 2 2 3 2 1 cos 2 2 2 3 tan 1 3 3 3 cot 3 1 3
https://www.facebook.com/truongngocvy8/ T r an
g 3 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
Bài 1. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau: 3 a) 0 0 2 0
A  cos 45  sin 45  cot 45 b) 2 0 0 2025 0
B  sin 60 .cos 30  tan 45 8 0 0 sin 30  cos 30 0 0 2 sin 60  tan 45 c) C  d) D  2 0 0 tan 45  cot 30 2026 0 0 cot 45  tan 60
Bài 2. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 0 45 . 0 0 0 0
sin 63 , cos 72 , tan 56 , cot 81
Bài 3. Tính giá trị của các biểu thức sau: a) o o
A  sin 23  cos 67 b) o o B  tan14  cot 76 sin15o o cot 72 c) C  d) D  cos 75o o tan18 1 e) o o E  tan 29 .tan 61 f) o o
F  2025 cot11 .cot 79 2026
Bài 4. Tính giá trị của các biểu thức sau: 1 1 a) o o o
A  sin11  cos 79  tan 45 b) o o o B  tan 33  cot 57  sin 30 2 2 o cos 52 c) o o o
C  tan 22 .cot 60 .tan 68 d) D  o o o sin 38 .tan 29 .tan 61
Bài 5. Tính giá trị của các biểu thức sau: a) o o o o
A  sin 35  sin 67  cos 23  cos 55 b) o o o o
B  tan15  2025 tan 54  cot 75  2025 cot 36 o o o o
tan 27  tan16 .tan 74  cot 73
tan 39  cot 51  tan 39  cot 51 2 2 o 2 o o o c) C  d) D  2 o 2 o 2 o sin 35  sin 45  cos 55 o o o sin 39  tan 45  cos 51
Bài 6. Tính giá trị của các biểu thức sau: a) o o o o o o
A  tan15 . tan 25 . tan 35 .tan 55 .tan 65 . tan 75 b) 2 o 2 o 2 2 o 2 o 2 o 2 o 2 o
B  cot 10 .cot 20 .cot 30.cot 40 .cot 50 .cot 60 .cot 70 .cot 80
BÀI TẬP RÈN LUYỆN
Bài 7. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau: 0 sin 30 a) 0 0 2024 0
A  sin 30  cos 60  2 tan 45 b) 0 0
B  cos 30 .cot 60  2025 0 tan 45 0 cot 30 0 0 cos 45  sin 60 c) C  d) D  0 0 cos 60  sin 45 0 0 2sin 45  3 tan 30 e) 2 0 2 0 3 0
E  4  sin 45  2 cos 60  3cot 45 f) 0 0 5 0
F  cos 30 .cot 30 .tan 45
Bài 8. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc lớn hơn 0 45 . 0 0 0 0
sin 22 , cos13 , tan 37 , cot 44
https://www.facebook.com/truongngocvy8/ T r an
g 4 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
Bài 9. Tính giá trị của các biểu thức sau: a) 2 o 2 o
A  sin 21  cos 69 b) 3 o 3 o
B  tan 18  cot 72 o 2 o 2 o o sin 9 .tan 29 .tan 61 .cot 72 c) 3 o 2 o 3 o
C  tan 13 .tan 30 .tan 77 d) D  o o cos81 .tan 8
https://www.facebook.com/truongngocvy8/ T r an
g 5 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều DẠNG 2
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC
DÀNH CHO HỌC SINH KHÁ GIỎI Với 0 0
0   90 , ta có: sin  tan   1 cos cos  cot 2 sin  2 2
sin  cos  1 3
Chú ý: Công thức  
1 , 2,3 , khi làm tự luận phải chứng minh mới được dùng.
Bài 1. Cho tam giác ABC vuông tại A , với 
B . Chứng minh: sin  tan   1 cos cos  cot 2 sin  2 2
sin  cos  1 3
Bài 2. Tính giá trị của các biểu thức sau: a) 2 0 2 0 2 0 2 0
A  sin 17  sin 25  sin 65  sin 73 b) 2 0 2 0 2 0 2 0
B  cos 24  cos 42  cos 48  cos 66 c) 2 0 2 0 2 0 2 0 2 0 2 0 2 0
C  cos 15  cos 25  cos 35  cos 45  cos 55  cos 65  cos 75 d) 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
D  sin 10  sin 20  sin 30  sin 40  sin 50  sin 60  sin 70  sin 80
Bài 3. Cho là góc nhọn tính giá trị của các biểu thức sau: a) 4 2 2 4
A  sin  2 sin .cos  cos b) 6 2 2 6
B  sin  3sin .cos  cos
Bài 4. Cho tan  2 , với là góc nhọn. Tính giá trị của các biểu thức sau:
sin  cos 2 2
2 sin  3cos 3 cos a) A  b) B  c) C
sin  cos 2 2
3sin  2 cos 3 3
sin  2 cos
https://www.facebook.com/truongngocvy8/ T r an
g 6 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều DẠNG 3
TÍNH TỈ SỐ LƯỢNG GIÁC TRONG TAM GIÁC VUÔNG
1. Tỉ số lượng giác của góc nhọn
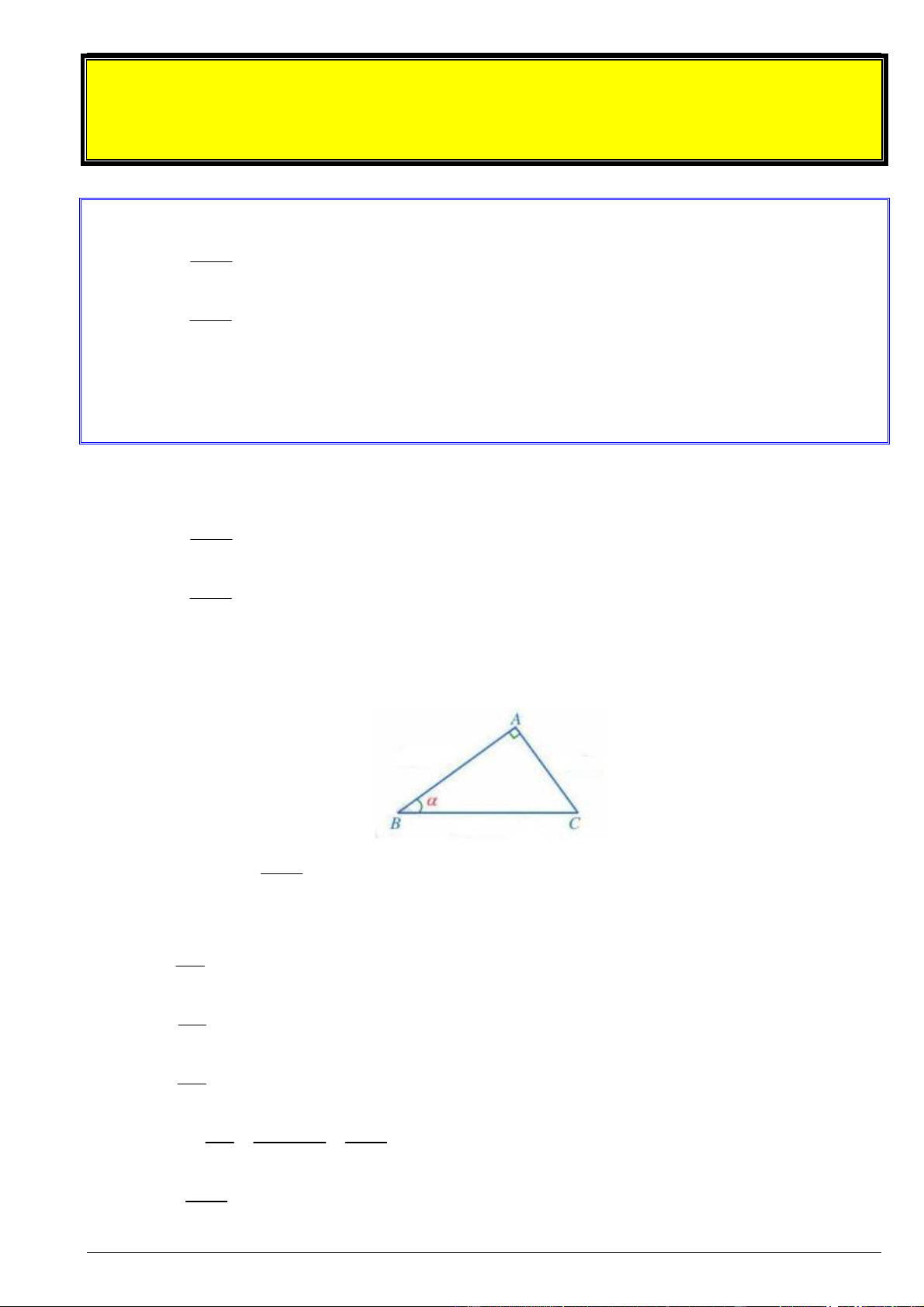
Xét ABC vuông tại A có ABC . Ta có tỉ số lượng giác của góc như sau: AC AB AC BC  sin  cos  tan   cotBC BC BC AC
Chú ý:Với góc nhọn , ta có:
 0  sin 1; 0  cos 1 1  cot tan
2. Tỉ số lượng giác của hai góc phụ nhau Nếu 0
 90 , ta có:
 sin cos  cos sin
 tan cot
 cot tan
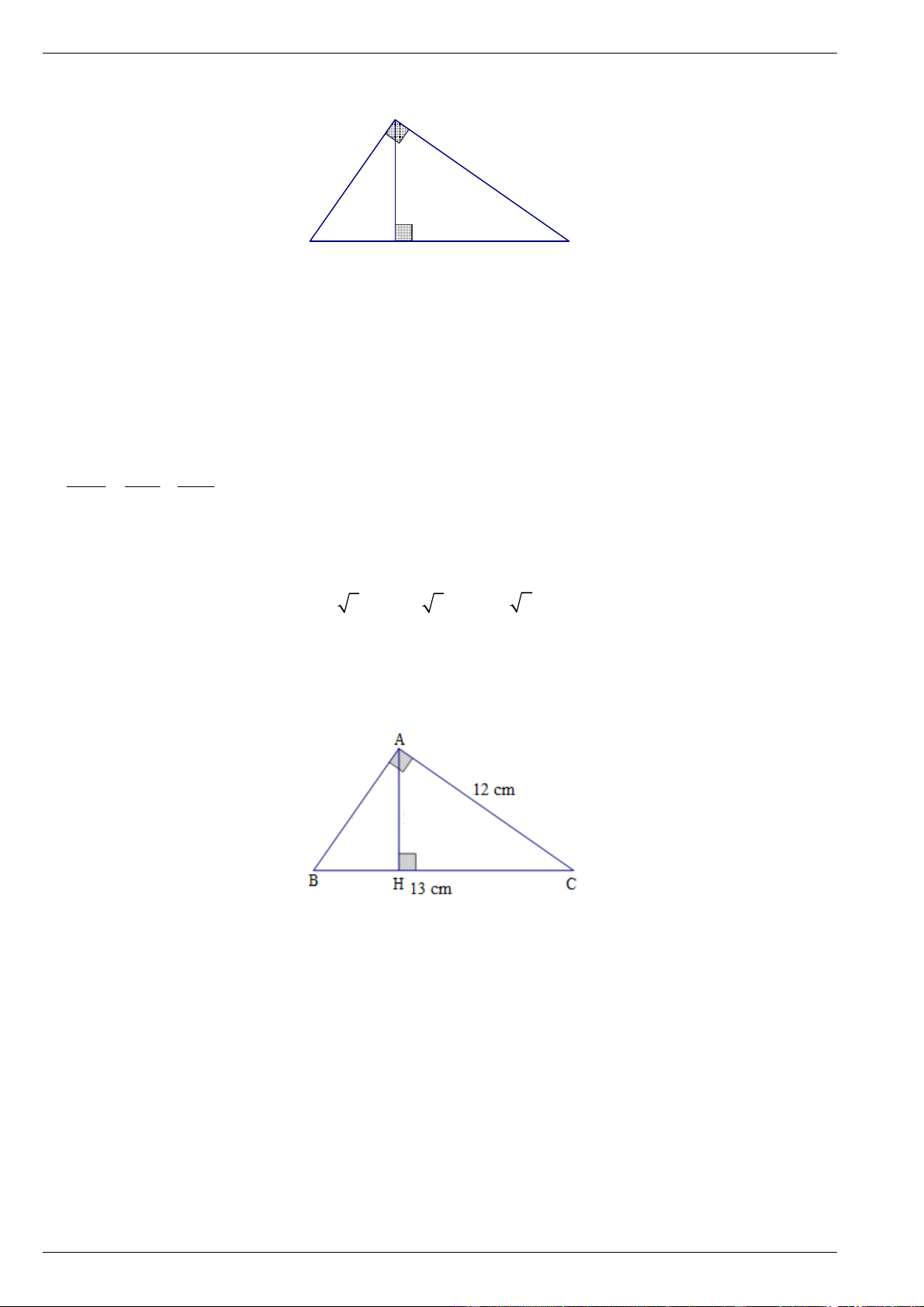
3. Hệ thức lượng trong tam giác vuông (kiến thức nâng cao) A B H C
Cho tam giác ABC vuông tại A , đường cao AH . Khi đó, ta có:  2 2 2
AB AC BC (định lí Pythagore đã học lớp 8)  2
AB BH .BC   1  2
AC CH .CB 2  2 AH H . B HC 3
AH .BC A . B AC 4 1 1 1    5 2 2 2 AH AB AC Công thức  
1 , 2,3,4 ,5 khi dùng tự luận phải chứng minh rồi mới được dùng.
https://www.facebook.com/truongngocvy8/ T r an
g 7 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
Bài 1. Cho tam giác ABC vuông tại A , đường cao AH . A B H C Chứng minh rằng: a) 2
AB BH .BC b) 2
AC CH .CB c) 2 AH H . B HC
d) AH .BC A . B AC 1 1 1 e)   2 2 2 AH AB AC
Bài 2. Cho tam giác ABC vuông tại C có BC  1, 2c ;
m AC  0, 9cm . Tính các tỉ số lượng giác của góc
B , từ đó suy ra tỉ số lượng giác của góc A .
Bài 3. Cho tam giác ABC có AB a 5, BC a 3 , AC a 2
a) Chứng minh tam giác ABC vuông.
b) Tính các tỉ số lượng giác của góc B , từ đó suy ra các tỉ số lượng giác của góc A .
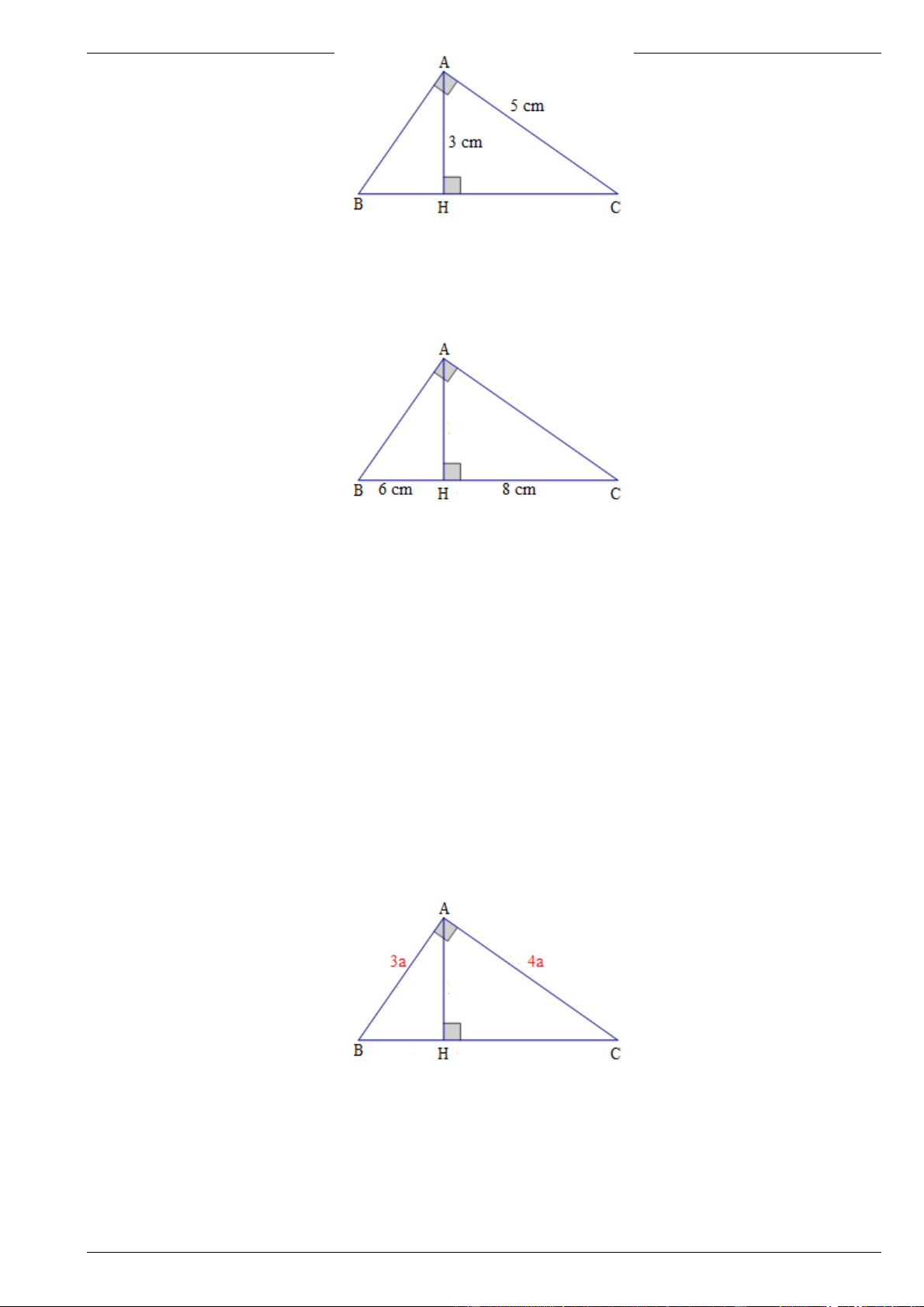
Bài 4. Cho tam giác ABC vuông tại A , đường cao AH . Biết AC  12c , m BC  13cm . a) Tính cạnh AB .
b) Tính cos B, sin C .
c) Chứng minh AH .BC A . B AC . 
d) Tính các tỉ số lượng giác của góc BAH , từ đó suy ra các tỉ số lượng giác của góc  CAH .
Bài 5. Cho tam giác ABC vuông tại A , đường cao AH . Biết AH  3c , m AC  5cm
https://www.facebook.com/truongngocvy8/ T r an
g 8 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
a) Tính tan C, cot C, tan B, cot B . b) Chứng minh 2 AH H .
B HC . Từ đó tính HB .
Bài 6. Cho tam giác ABC vuông tại A , đường cao AH . Biết BH  6c , m CH  8cm . a) Tính AH .  
b) Tính sin BAH , sin CAH .
Bài 7. Cho tam giác ABC vuông tại A có cos B  0, 6 . a) Chứng minh 2 2
sin B  cos B  1 .
b) Tính các tỉ số lượng giác của góc B còn lại.
c) Tính các tỉ số lượng giác của góc C .
BÀI TẬP RÈN LUYỆN
Bài 8. Cho tam giác ABC vuông tại A có AB  1, 6c ;
m AC  1, 2cm . Tính các tỉ số lượng giác của góc
B , từ đó suy ra tỉ số lượng giác của góc C .
Bài 9. Cho tam giác ABC vuông tại A , đường cao AH . Biết AB  3 , a AC  4a .
a) Tính sin B và cos C .    
b) Tính tan BAH , cot BAH , tan CAH , cot CAH .
Bài 10. Cho tam giác ABC vuông tại A , đường cao AH . Biết BH  4a, BC  9a .
https://www.facebook.com/truongngocvy8/ T r an
g 9 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
a) Tính sin B và cos C .  
b) Tính tan BAH và cot CAH . 1
Bài 11. Cho tam giác ABC vuông tại A có sin C  . 3
a) Tính các tỉ số lượng giác của góc C còn lại.
b) Tính các tỉ số lượng giác của góc B .
https://www.facebook.com/truongngocvy8/ T r an g
10 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều DẠNG 4
TÍNH CẠNH VÀ GÓC NHỌN CỦA TAM GIÁC VUÔNG
Tỉ số lượng giác của góc nhọn
Xét ABC vuông tại A có ABC . Ta có tỉ số lượng giác của góc như sau: AC AB AC BC  sin  cos  tan   cotBC BC BC AC
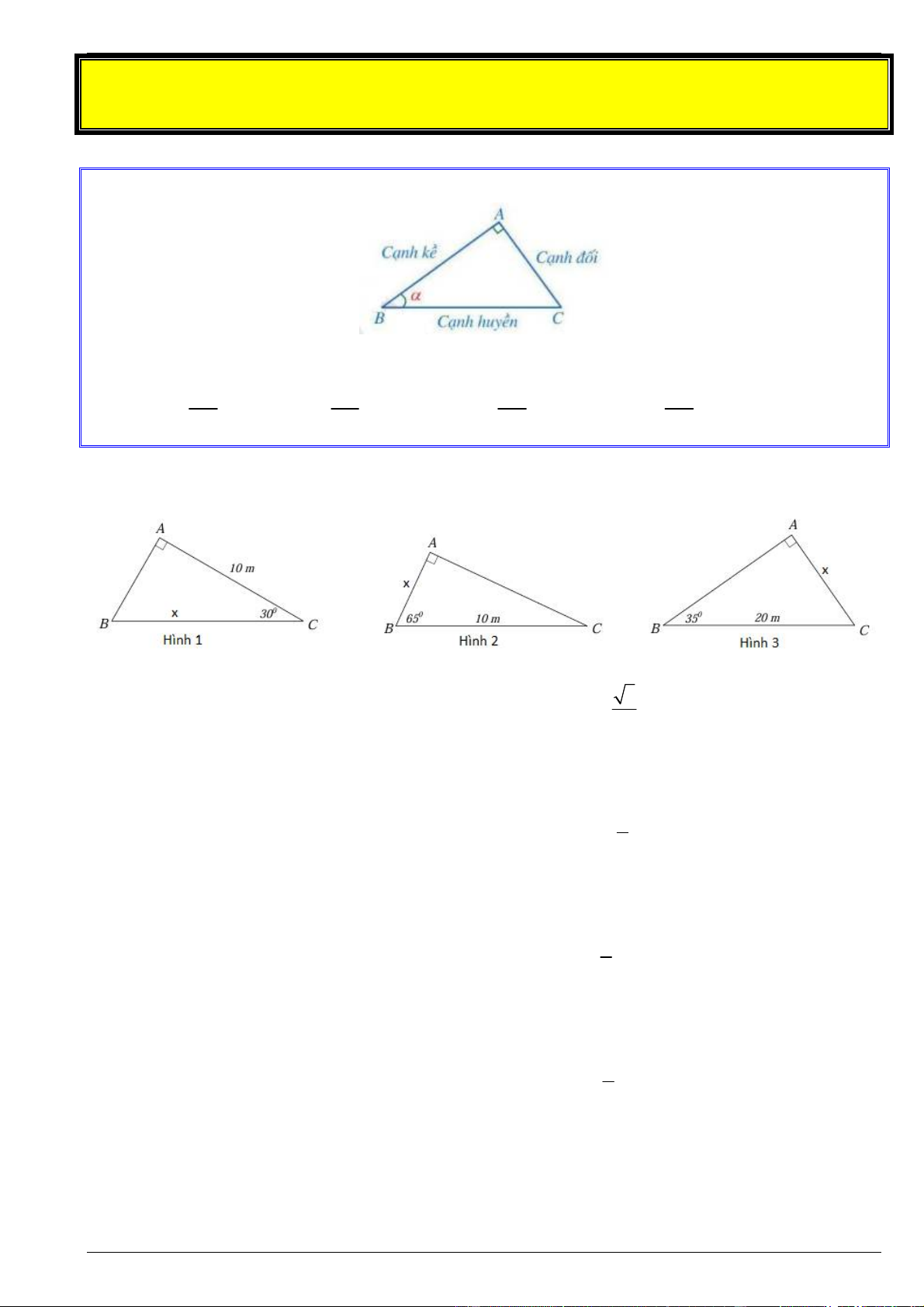
Bài 1. Tìm x trong các hình sau: (kết quả làm tròn đến phần trăm của centimet) 3
Bài 2. Cho tam giác ABC vuông tại A có BC  10cm và sin B  . 2 a) Tính góc B .
b) Tính cạnh AC và AB . 1
Bài 3. Cho tam giác ABC vuông tại A có AC  12 cm và cos C  . 4
a) Tính góc C (kết quả làm tròn đến phần chục của độ). b) Tính cạnh BC . 4
Bài 4. Cho tam giác ABC vuông tại A có AB  8cm và tan C  . 5
a) Tính góc C (kết quả làm tròn đến phút). b) Tính cạnh AC . 1
Bài 5. Cho tam giác ABC vuông tại A có AC  6 cm và cot B  . 2
a) Tính góc B (kết quả làm tròn đến phút). b) Tính cạnh AC .
https://www.facebook.com/truongngocvy8/ T r an g
11 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều CHƯƠNG 4
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG BÀI 1
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Tỉ số lượng giác của góc nhọn
Cho góc nhọn  0 0
0   90  . Xét ABC vuông tại A có ABC .
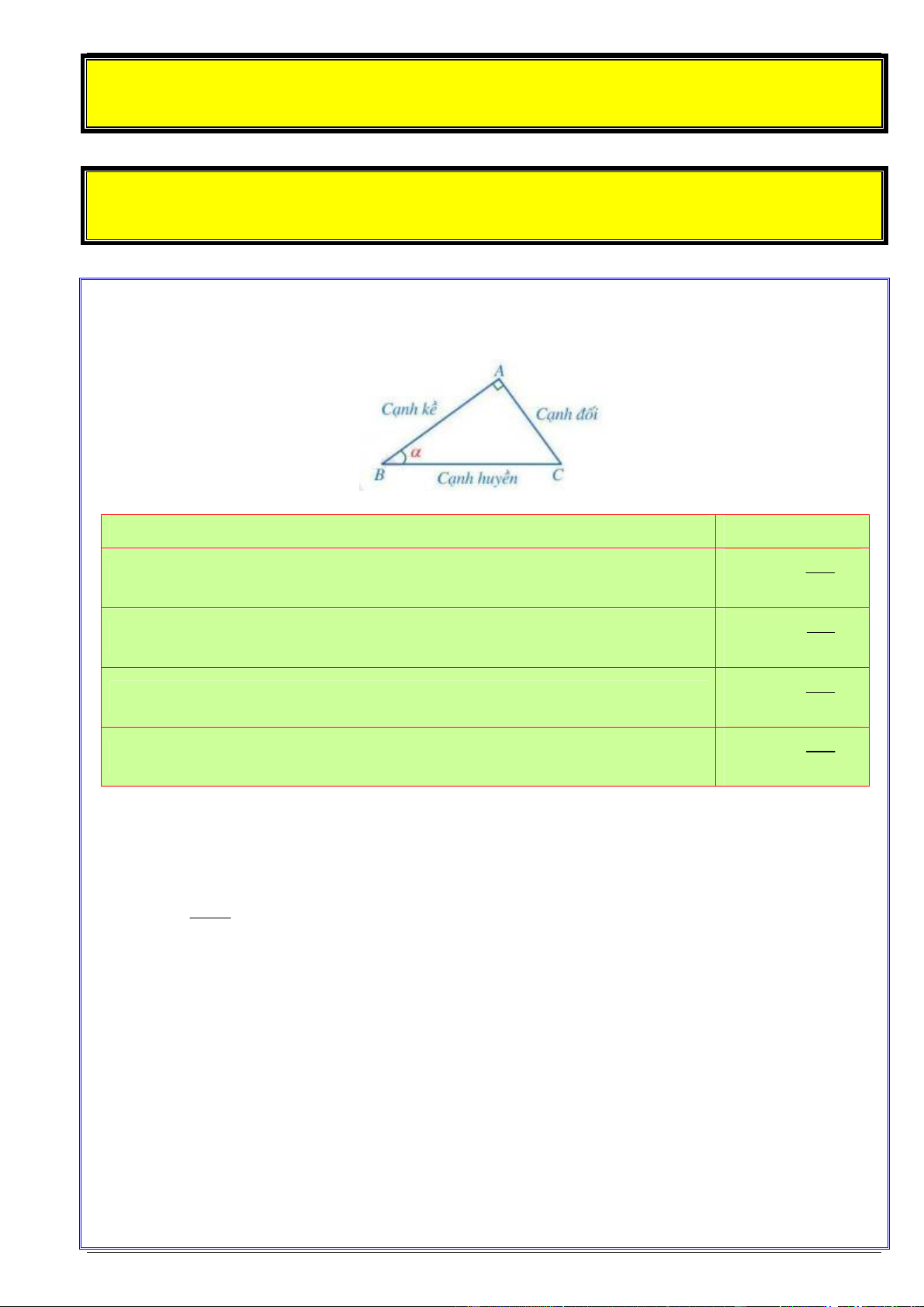
Các tỉ số lượng giác của góc nhọn Công thức AC
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc , kí hiệu sinα sinBC AB
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc , kí hiệu cos cos BC AC
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc , kí hiệu tanα tan BC BC
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc , kí hiệu cotα cot AC
Chú ý: Với góc nhọn , ta có:
 0  sin 1; 0  cos 1 1  cot
hay tan .cot 1 tan
2. Tỉ số lượng giác của hai góc phụ nhau
Hai góc phụ nhau là hai góc nhọn có tổng bằng 0 90 .
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Nhận xét: Với 0 0
0   90 , ta có:  0
sin(90  )  cos  0
cos(90  )  sin  0
tan(90  )  cot  0
cot(90  )  tan
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
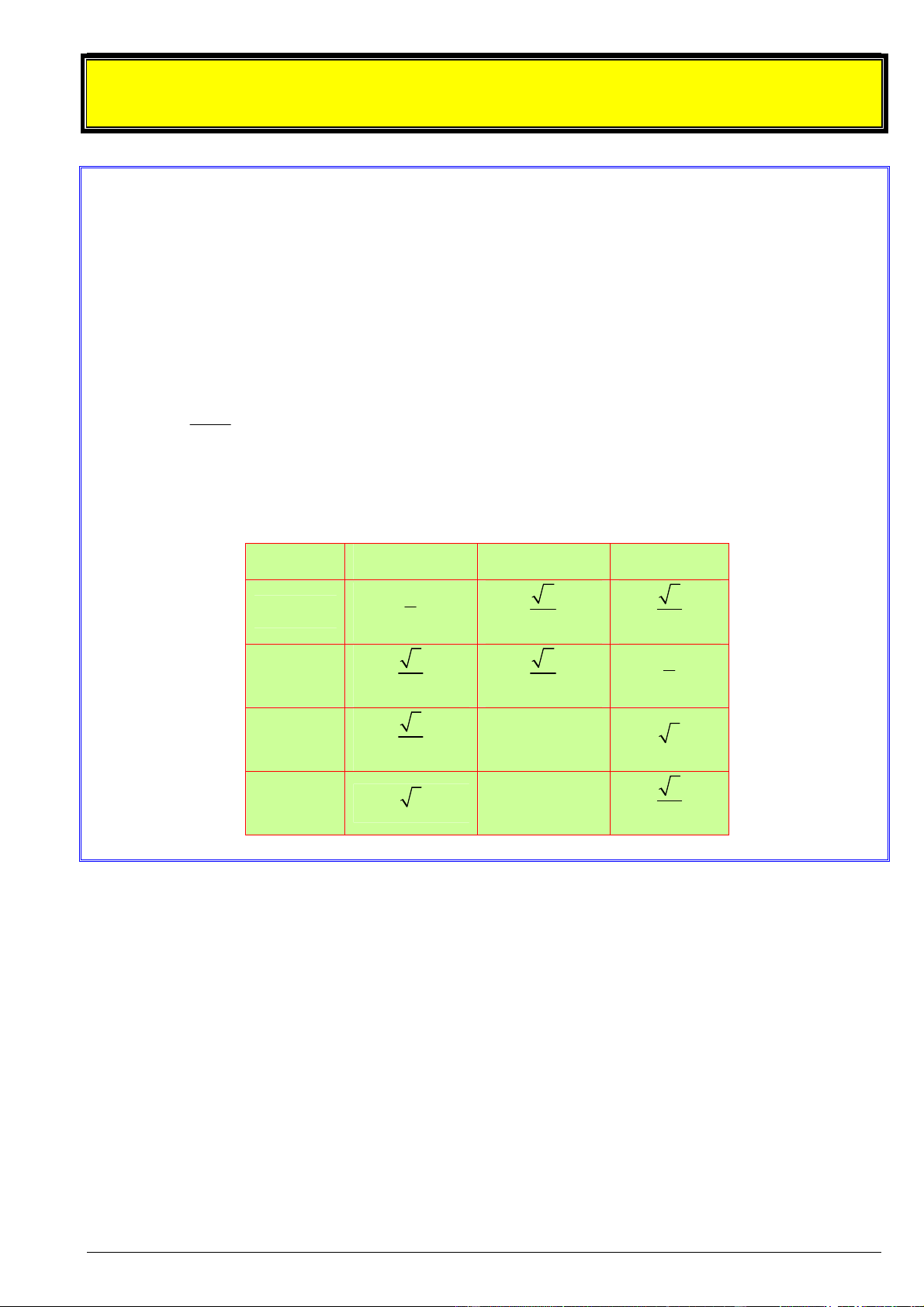
Bảng tỉ số lượng giác của góc đặc biệt 0 0 0 30 , 45 , 60 : 0 30 0 45 0 60 1 2 3 sin 2 2 2 3 2 1 cos 2 2 2 3 tan 1 3 3 3 cot 3 1 3
https://www.facebook.com/truongngocvy8/ T r an
g 2 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều DẠNG 1
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC 1. Với 0 0
0   90 , ta có:  0
sin(90  )  cos  0
cos(90  )  sin  0
tan(90  )  cot  0
cot(90  )  tan
 0  sin 1; 0  cos 1 1  cot
hay tan .cot 1 tan n Chú ý:   2 2 sin sin
hay tổng quát hơn: sinn   sin
2. Bảng tỉ số lượng giác của một số góc đặc biệt: 0 30 0 45 0 60 1 2 3 sin 2 2 2 3 2 1 cos 2 2 2 3 tan 1 3 3 3 cot 3 1 3
https://www.facebook.com/truongngocvy8/ T r an
g 3 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
Bài 1. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau: 3 a) 0 0 2 0
A  cos 45  sin 45  cot 45 b) 2 0 0 2025 0
B  sin 60 .cos 30  tan 45 8 0 0 sin 30  cos 30 0 0 2 sin 60  tan 45 c) C  d) D  2 0 0 tan 45  cot 30 2026 0 0 cot 45  tan 60 Lời giải 2 2 a) 0 0 2 0 2
A  cos 45  sin 45  cot 45    1  1 2 2 2 3  3  1 3 3 3 b) 2 0 0 2025 0 2025
B  sin 60 .cos 30  tan 45    .  .1    0 8  2  2 8 8 8   1 3 1   1 32 1 0 0 4 2 3 sin 30 cos 30  3 c) 2 2 2 2 C      1   2 0 0 2 tan 45  cot 30 1  3 1 31 3 1 3 2 3 2. 1   1 3  1 32 0 0  4  2 3 2 sin 60 tan 45  d) 2 D       3  2 2026 0 0 2026 cot 45  tan 60 1  3 1 3 1 31 3 1 3
Bài 2. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 0 45 . 0 0 0 0
sin 63 , cos 72 , tan 56 , cot 81 Lời giải Ta có: 0   0 0   0 sin 63 cos 90 63  cos 27 0   0 0   0 cos 72 sin 90 72  sin18 0   0 0   0 tan 56 cot 90 56  cot 34 0   0 0   0 cot 81 tan 90 81  cos 9
Bài 3. Tính giá trị của các biểu thức sau: a) o o
A  sin 23  cos 67 b) o o B  tan14  cot 76 sin15o o cot 72 c) C  d) D  cos 75o o tan18 1 e) o o E  tan 29 .tan 61 f) o o
F  2025 cot11 .cot 79 2026 Lời giải a) o o A     o o   o o o sin 23 cos 67 sin 90 67
 cos 67  cos 67  cos 67  0 b) o o B     o o   o o o tan14 cot 76 tan 90 76
 cot 76  cot 76  cot 76  0
https://www.facebook.com/truongngocvy8/ T r an
g 4 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều o
sin 90o  75o sin15  cos75o c) C     1 cos 75o cos 75o cos 75o cot  o o o 90 18 cot 72  o tan18 d) D     1 o o o tan18 tan18 tan18 1 o o 1 o o o 1 o o 1 e) E  tan 29 .tan 61 
tan 29 .tan 90  29   tan 29 .cot 29  2026 2026 2026 2026 f) 2025 cot11 . o cot 79o
2025 cot11o.cot 90o 11o  2025cot11 .otan11o F      2025
Bài 4. Tính giá trị của các biểu thức sau: 1 1 a) o o o
A  sin11  cos 79  tan 45 b) o o o B  tan 33  cot 57  sin 30 2 2 o cos 52 c) o o o
C  tan 22 .cot 60 .tan 68 d) D  o o o sin 38 .tan 29 .tan 61 Lời giải 2 2 2 a) o o o o
A  sin11  cos 79  tan 45  sin11  sin  o o 90  79  o o   sin11  sin11   2 2 2 1 1 1 1 1 1 1 1 1 b) o o o o B  tan 33  cot 57  sin 30  tan 33  tan  o o 90  57  o o   tan 33  tan 33   2 2 2 2 2 2 2 2 2 3 c) o o o o o o o
C  tan 22 .cot 60 .tan 68  tan 22 .tan 68 .cot 60  tan 22 .cot  o o 90  68 . 3 3 3 3 o o  .tan 22 .cot 22  .1  3 3 3 sin  o o o 90  52 cos 52  o sin 38 d) D     1 o o o o o sin 38 .tan 29 .tan 61 sin 38 . tan 29 .cot  o o 90  61  o o o sin 38 .tan 29 .cot 29
Bài 5. Tính giá trị của các biểu thức sau: a) o o o o
A  sin 35  sin 67  cos 23  cos 55 b) o o o o
B  tan15  2025 tan 54  cot 75  2025 cot 36 o o o o
tan 27  tan16 .tan 74  cot 73
tan 39  cot 51  tan 39  cot 51 2 2 o 2 o o o c) C  d) D  2 o 2 o 2 o sin 35  sin 45  cos 55 o o o sin 39  tan 45  cos 51 Lời giải a) o o o o o o o o
A  sin 35  sin 67  cos 23  cos 55  sin 35  cos 55  sin 67  cos 23 Ta có: o   o o   o cos 55 cos 90 55  sin 35 o   o o   o cos 23 sin 90 23  sin 67 Do đó: o o o o
A  sin 35  sin 35  sin 67  sin 67  0 b) o o o o o o B         o o tan15 2025 tan 54 cot 75 2025 cot 36 tan15 cot 75 2025 tan 54  cot 36  Ta có:
https://www.facebook.com/truongngocvy8/ T r an
g 5 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều o   o o   o cot 75 tan 90 75  tan15 o   o o   o cot 36 tan 90 36  tan 54 Do đó: o o B     o o tan15 tan15
2025 tan 54  tan 54   0  2025.0  0 o o o o o o o o
tan 27  tan16 .tan 74  cot 73
tan 27  cot 73  tan16 . tan 74 c) C   2 o 2 o 2 o 2 o 2 o 2 o sin 35  sin 45  cos 55 sin 35  cos 55  sin 45 o tan 27  tan  o o 90  73  o  tan16 .cot  o o 90  74  o o o o
tan 27  tan 27  tan16 .cot16 0 1     4 2 2 o 2 o 1 1   2 o 2   o o   2 sin 35  sin 35  0  sin 35 sin 90 55    4 4 2  
tan 39  tan 51  tan 39  tan 51 2 2 o 2 o o o d) D  o o o sin 39  tan 45  cos 51 2 o 2 o tan 39  tan 51   2 o o o 2 o
tan 39  2 tan 39 .tan 51  tan 51   o o o sin 39  cos 51  tan 45 o 2 tan 39 .cot  o o 90  51   2 o sin 39  sin  o o 90  51   2 o o 2 tan 39 .cot 39 2    2 2 2 2 o o sin 39  sin 39  2 2
Bài 6. Tính giá trị của các biểu thức sau: a) o o o o o o
A  tan15 . tan 25 . tan 35 .tan 55 .tan 65 . tan 75 b) 2 o 2 o 2 2 o 2 o 2 o 2 o 2 o
B  cot 10 .cot 20 .cot 30.cot 40 .cot 50 .cot 60 .cot 70 .cot 80 Lời giải a) o o o o o o
A  tan15 . tan 25 . tan 35 .tan 55 .tan 65 . tan 75   o o   o o   o o
tan15 .tan 75 . tan 25 tan 65 . tan 35 .tan 55  o    o o   o    o o   o    o o tan15 .cot 90 75 . tan 25 .cot 90 65
. tan 35 .cot 90  65          o o   o o   o o
tan15 .cot15 . tan 25 .cot 25 . tan 35 .cot 35   1.1.1 1 b) 2 o 2 o 2 2 o 2 o 2 o 2 o 2 o
B  cot 10 .cot 20 .cot 30.cot 40 .cot 50 .cot 60 .cot 70 .cot 80   2 o 2 o   2 o 2 o   2 2 o   2 o 2 o
cot 10 .cot 80 . cot 20 .cot 70 . cot 30.cot 60 . cot 40 .cot 50    2  2  2  2 o o o o o o o cot10 .cot 80 . cot 20 .cot 70 . cot 30.cot 60 . cot 40 .cot 50
 cot10 .tan10 2 .cot 20 .tan 20 2 .cot 30.tan 30 2 .cot 40 .tan 40 2 o o o o o o o 2 2 2 2  1 .1 .1 .1  1
https://www.facebook.com/truongngocvy8/ T r an
g 6 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều
BÀI TẬP RÈN LUYỆN
Bài 7. Không dùng máy tính cầm tay, chỉ dùng bảng lượng giác của các góc nhọn đặc biệt, hãy tính giá
trị của các biểu thức sau: 0 sin 30 a) 0 0 2024 0
A  sin 30  cos 60  2 tan 45 b) 0 0
B  cos 30 .cot 60  2025 0 tan 45 0 cot 30 0 0 cos 45  sin 60 c) C  d) D  0 0 cos 60  sin 45 0 0 2sin 45  3 tan 30 e) 2 0 2 0 3 0
E  4  sin 45  2 cos 60  3cot 45 f) 0 0 5 0
F  cos 30 .cot 30 .tan 45 Lời giải 1 1 a) 0 0 2024 0 2024
A  sin 30  cos 60  2 tan 45    2.1  0 2 2 1 0 sin 30 3 3 1 1 b) 0 0 2
B  cos 30 .cot 60   .     0 2025 0 2025 tan 45 2 3 1 2 2 0 2 3 1 2 cot 30 3 3  2 3  2 6 c) C       2 3  2 6 0 0 cos 60  sin 45 1 1 2     1 21 2  1 2  1 2 2 2 2 2 3 1    2  32 1 0 0 5 2 6 cos 45 sin 60  5 d) 2 2 2 2 D      6  0 0 2sin 45  3 tan 30 2 3  2  3 2  3 2  3 2 2.  3. 2 3 2 2  2   1  e) 2 0 2 0 3 0
E  4  sin 45  2 cos 60  3cot 45  4     2.  3  1    2   2    3 3 f) 0 0 5 0 5
F  cos 30 .cot 30 .tan 45  . 3.1  2 2
Bài 8. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc lớn hơn 0 45 . 0 0 0 0
sin 22 , cos13 , tan 37 , cot 44 Lời giải Ta có: 0   0 0   0 sin 22 cos 90 22  cos 68 0   0 0   0 cos13 sin 90 13  sin 77 0   0 0   0 tan 37 cot 90 37  cot 53 0   0 0   0 cot 44 tan 90 44  cos 46
Bài 9. Tính giá trị của các biểu thức sau: a) 2 o 2 o
A  sin 21  cos 69 b) 3 o 3 o
B  tan 18  cot 72
https://www.facebook.com/truongngocvy8/ T r an
g 7 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều o 2 o 2 o o sin 9 .tan 29 .tan 61 .cot 72 c) 3 o 2 o 3 o
C  tan 13 .tan 30 .tan 77 d) D  o o cos81 .tan 8 Lời giải a) 2 o 2 o 2 o 2 A      o o   2 o 2 o sin 21 cos 69 sin 21 sin 90 69  sin 21  sin 21  0 b) 3 o 3 o 3 o 3 B      o o   3 o 3 o tan 18 cot 72 tan 18 tan 90 72  tan 18  tan 18  0 2 3  3  c) 3 o 2 o 3 o 3 o 3 o 2 o
C  tan 13 .tan 30 .tan 77  tan 13 . tan 77 .tan 30   o o tan13 .tan 77  .   3    1 
tan13 .cot 90  77  3 1 1 o o o o o   tan13 .cot13  3   3 3
sin 9 . tan 29 .cot 90  61  2 o o o o  .tan  o o o 2 o 2 o o 90  72 sin 9 .tan 29 .tan 61 .cot 72    d) D   o o cos81 .tan 8 sin  o o 90  81  o .tan 8 sin 9 .tan 29 .cot 29 2 o o o o .tan 8   1 o o sin 9 .tan 8
https://www.facebook.com/truongngocvy8/ T r an
g 8 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 4: Hệ thức lượng trong tam giác vuông – Tự luận phân dạng có lời giải Cánh Diều DẠNG 2
TÍNH BIỂU THỨC CHỨA TỈ SỐ LƯỢNG GIÁC
DÀNH CHO HỌC SINH KHÁ GIỎI Với 0 0
0   90 , ta có: sin  tan   1 cos cos  cot 2 sin  2 2
sin  cos  1 3
Chú ý: Công thức  
1 , 2,3 , khi làm tự luận phải chứng minh mới được dùng.
Bài 1. Cho tam giác ABC vuông tại A , với 
B . Chứng minh: sin  tan   1 cos cos  cot 2 sin  2 2
sin  cos  1 3 Lời giải sin
 Chứng minh tan   1 cos
Xét tam giác ABC vuông tại A , ta có: AC sin
hay AC BC.sin BC AB cos
hay AB BC.cos BC AC tan AB AC BC.sin sin Suy ra: tan    AB BC.cos cos sin Vậy: tan  cos
https://www.facebook.com/truongngocvy8/ T r an
g 9 Trương Ngọc Vỹ 0978 333 093

Tài liệu liên quan: