Tuyển tập 05 đề ôn thi giữa học kỳ 1 Toán 11 KNTTvCS có đáp án và lời giải

Tài liệu gồm 64 trang, được biên soạn bởi thầy giáo Phan Nhật Linh, tuyển tập 05 đề ôn thi giữa học kỳ 1 môn Toán 11 bộ sách Kết Nối Tri Thức Với Cuộc Sống (KNTTvCS) có đáp án và lời giải chi tiết; các đề được biên soạn theo hình thức 70% trắc nghiệm kết hợp 30% tự luận

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

64 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Trong không gian, cho hai mặt phẳng phân biệt
( )
và
( )
. Có bao nhiêu vị trí tương đối giữa
( )
và
( )
?
A.
4
. B.
3
. C.
. D.
2
.
Câu 2: Tập xác định của hàm số
tanyx=
là:
A.
\,
4
kk

+


. B.
\,
2
kk

+


.
C.
\ 2 ,
2
kk

+


. D.
\,kk
.
Câu 3: Tập giá trị của hàm số
sinyx=
là
A.
1;1−
. B.
0;2
. C. . D.
2;2−
.
Câu 4: Cho dãy số
( )
n
u
với số hạng tổng quát
23
n
un=−
giá trị
2021
u
bằng
A.
6061.
B.
6065.−
C.
6061.−
D.
6065.
Câu 5: Hàm số
cosyx=
tuần hoàn với chu kỳ là
A.
3
. B.
. C.
2
. D.
2
.
Câu 6: Cho hai đường thẳng phân biệt
,ab
và mặt phẳng
( )
P
, trong đó
( )
aP⊥
. Chọn khẳng định sai
trong các khẳng định sau
A. Nếu
ab⊥
thì
( )
//bP
. B. Nếu
//ba
thì
( )
bP⊥
.
C. Nếu
( )
bP⊥
thì
//ab
. D. Nếu
( )
bP
thì
ba⊥
.
Câu 7: Hàm số nào sau đây là hàm số chẵn?
A.
tanyx=
. B.
cotyx=
. C.
sinyx=
. D.
cosyx=
.
Câu 8: Cho cấp số cộng
( )
n
u
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng:
A.
6
. B.
9
. C.
4
. D.
5
.
Câu 9: Hàm số
sinyx=
đồng biến trên khoảng nào dưới đây?
A.
( )
0;
. B.
( )
0;2
. C.
0;
2



. D.
( )
;

−
.
Câu 10: Tìm giá trị lớn nhất của hàm số
2cos 3
3
yx

= − +


?
A.
9
. B.
5
. C.
. D.
7
.
Câu 11: Phương trình nào sau đây vô nghiệm
A.
tan 3x =−
. B.
2 cos 3x−=
. C.
cos2 2x =
. D.
2sin2 1x =
.
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
01
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 12: Cho cấp số nhân
( )
n
u
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng
A.
9
. B.
5
. C.
4
. D.
6
.
Câu 13: Tìm điều kiện của
m
để phương trình sau đây vô nghiệm
cos 1mx−=
.
A.
02m
. B.
0m
hoặc
2m
. C.
20m−
. D.
2m −
hoặc
0m
Câu 14: Trên khoảng
( )
0;
, phương trình
sin 1x =
có bao nhiêu nghiệm?
A.
1
. B.
2
. C.
3
. D. Vô số.
Câu 15: Tất cả các nghiệm của phương trình
cot 0x =
là?
A.
2,
2
kk
+
. B.
2,kk

+
. C.
,
2
kk
+
. D.
2,
2
kk
− +
.
Câu 16: Cho phương trình
2
sin 3sin 4 0xx+ − =
. Ta đặt
sintx=
, phương trình thu được có dạng
A.
2
3 4 0tt− − =
. B.
2
3 4 0tt+ − =
. C.
2
3 4 0tt− + − =
. D.
2
3 4 0tt+ + =
.
Câu 17: Cho cấp số nhân
( )
n
u
với
1
2u =
và
4
16u =−
. Công bội của cấp số nhân đã cho bằng
A.
3
. B.
2
. C.
8−
. D.
2−
.
Câu 18: Số nghiệm của phương trình
22
cos sin2 1 sinx x x− = +
trên khoảng
( )
0;2
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 19: Cho cấp số nhân
( )
n
u
biết
4 10
7, 56uu==
. Tìm công bội
q
.
A.
2q =
. B.
2q =
. C.
2q =
. D.
2q =
.
Câu 20: Cho đường thẳng
a
song song mặt phẳng
( )
. Mặt phẳng
( )
chứa
a
và cắt mặt phẳng
( )
theo giao tuyến
d
. Kết luận nào sau đây đúng?
A.
a
và
d
cắt nhau. B.
a
và
d
trùng nhau.
C.
a
và
d
chéo nhau. D.
a
và
d
song song.
Câu 21: Cho dãy số
( )
n
u
với
2
1
n
u n n= + +
với
*
n
. Số
21
là số hạng thứ bao nhiêu của dãy số đã cho?
A.
5
. B.
3
. C.
6
. D.
4
.
Câu 22: Cho cấp số cộng
( )
n
u
có số hạng tổng quát là
32
n
un=−
. Tìm công sai
d
của cấp số cộng đó.
A.
3d =−
. B.
3d =
. C.
2d =
. D.
2d =−
.
Câu 23: Tổng hai nghiệm dương nhỏ nhất của phương trình
2
4cos 1x =
là
A.
. B.
7
3
. C.
6
. D.
5
3
.
Câu 24: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
5u =
, công bội
1
3
q =
. Khi đó
5
59049
là số hạng thứ mấy
của cấp số nhân?
A. 9. B. 10. C. 11. D. 12.
Câu 25: Các họ nghiệm của phương trình
sin sin 2xx=−
.
A.
2
;2
3
k
x x k

= = +
. B.
2
;
3
x k x k
= + = +
.
C.
2
2;
23
k
x k x

= + =
. D.
2
;
3
x k x k

= = +
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 26: Cho
a
và
b
lần lượt là số hạng thứ nhất và số hạng thứ năm của một cấp số cộng có công sai
0d
. Giá trị của
ba
d
−
bằng
A.
6
. B.
5
. C.
3
. D.
4
.
Câu 27: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
,
N
lần lượt là trung điểm
AD
và
BC
. Giao tuyến của hai mặt phẳng
( )
SMN
và
( )
SAC
là
A.
SG
(
G
là trung điểm
AB
). B.
SD
.
C.
SF
(
F
là trung điểm
CD
). D.
SO
(
O
là tâm hình bình hành
ABCD
).
Câu 28: Cho hai đường thẳng
a
và
b
chéo nhau. Có bao nhiêu mặt phẳng chứa
a
và song song với
b
?
A.
1
. B. Vô số. C.
2
. D.
3
Câu 29: Số điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình
( )
2 sin cos 4sin cos 2x x x x+ + =
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 30: Cho tứ diện
ABCD
. Gọi
M
là trung điểm của cạnh
AD
,
G
là trọng tâm tam giác
ABD
và
N
là điểm thuộc cạnh
BC
sao cho
2NB NC=
. Kết luận nào sau đây sai?
A.
( )
// NG BCM
. B.
( )
// NG ACD
.
C.
NG
và
AB
chéo nhau. D.
// NG CM
.
Câu 31: Cho hình hộp
. ' ' ' 'ABCD A B C D
. Khẳng định nào sau đây sai?
A.
( ) ( )
// ' ' 'ABC A D C
. B.
( ) ( )
' ' // 'AB D BCA
.
C.
( ) ( )
' ' // ' 'ADD A BCC B
. D.
( ) ( )
' ' // 'AB D BC D
.
Câu 32: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là điểm trên đoạn
AB
(
M
khác
A
và khác
B
). Qua
M
vẽ mặt phẳng
( )
song song với
( )
SBC
. Thiết diện tạo bởi mặt
phẳng
( )
và hình chóp
.S ABCD
là hình gì?
A. Hình thang. B. Hình bình hành. C. Hình tam giác. D. Ngũ giác.
Câu 33: Cho hình lăng trụ
.ABC A B C
. Gọi
I
,
J
,
K
lần lượt là trọng tâm của các tam giác
ABC
,
AA C
,
ABC
. Mặt phẳng nào sau đây song song với mặt phẳng
( )
IJK
?
A.
( )
A BC

. B.
( )
AA B
. C.
( )
BB C
. D.
( )
AA C
.
Câu 34: Cho phương trình
3sin2 cos2 1xx+=
. Phương trình trên có bao nhiêu nghiệm thuộc khoảng
3
0;
2



?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 35: Cho hình chóp
SABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
là trung điểm của cạnh
bên
SD
. Gọi
K
là giao điểm của đường thẳng
BM
với mặt phẳng
( )
SAC
. Khi đó tỷ số diện
tích
SBK
SMK
S
S
bằng
A.
4
. B.
3
. C.
. D.
2
.
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 36: (0,5 điểm) Tìm
m
để phương trình
( )( )
2sin 1 2cos2 2sin 1 2cos2x x x m x− + + = −
có đúng hai
nghiệm thuộc
0;
.
Câu 37: (1,0 điểm)
a) Biết
3
số nguyên
3
,
x
,
y
theo thứ tự đó lập thành một cấp số nhân và
3
số
x
,
y
,
9
theo
thứ tự đó lập thành một cấp số cộng. Tìm
x
và
y
?
b) Một quả bóng cao su từ độ cao
( )
15 m
so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên
một độ cao bằng hai phần năm độ cao lần rơi ngay trước đó. Biết rằng quả bóng luôn chuyển
động vuông góc với mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc
bóng không nảy nữa) bằng bao nhiêu?
Câu 38: (1,5 điểm) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi điểm
I
và
điểm
M
lần lượt là trung điểm của các đoạn thẳng
SA
và
OC
.
a) Xác định giao tuyến của hai mặt phẳng
( )
SAC
và
( )
SBD
.
b) Gọi
( )
là mặt phẳng chứa đường thẳng
IM
và song song với đường thẳng
BD
. Xác định
thiết diện của mặt phẳng
( )
với hình chóp
.S ABCD
.
c) Giả sử mặt phẳng
( )
cắt đường thẳng
SO
tại điểm
K
. Tính tỉ số
SK
KO
.
-----------------------HẾT-----------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
BẢNG ĐÁP ÁN
1.D
2.B
3.A
4.C
5.C
6.A
7.D
8.D
9.C
10.B
11.C
12.A
13.B
14.A
15.C
16.B
17.D
18.C
19.B
20.D
21.D
22.B
23.A
24.C
25.A
26.D
27.D
28.A
29.B
30.A
31.B
32.A
33.C
34.B
35.D
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Trong không gian, cho hai mặt phẳng phân biệt
( )
và
( )
. Có bao nhiêu vị trí tương đối giữa
( )
và
( )
?
A.
4
. B.
3
. C.
. D.
2
.
Lời giải
Chọn D
Các vị trí tương đối giữa 2 mặt phẳng phân biệt là: song song, cắt nhau.
Câu 2: Tập xác định của hàm số
tanyx=
là:
A.
\,
4
k k Z

+

. B.
\,
2
k k Z

+

.
C.
\ 2 ,
2
k k Z

+

. D.
\,k k Z
.
Lời giải
Chọn B
Điều kiện xác định:
cos 0
2
x x k
+
Vậy tập xác định:
\,
2
D k k Z

= +

.
Câu 3: Tập giá trị của hàm số
sinyx=
là
A.
1;1−
. B.
0;2
. C. . D.
2;2−
.
Lời giải
Chọn A
Hàm số
sinyx=
có tập giá trị là
1;1−
.
Câu 4: Cho dãy số
( )
n
u
với số hạng tổng quát
23
n
un=−
giá trị
2021
u
bằng
A.
6061.
B.
6065.−
C.
6061.−
D.
6065.
Lời giải
Chọn C
Ta có:
2021
2 3.2021 6061.u = − = −
Câu 5: Hàm số
cosyx=
tuần hoàn với chu kỳ là
A.
3
. B.
. C.
2
. D.
2
.
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Lời giải
Chọn C
Hàm số
cosyx=
tuần hoàn với chu kỳ
2
.
Câu 6: Cho hai đường thẳng phân biệt
,ab
và mặt phẳng
( )
P
, trong đó
( )
aP⊥
. Chọn khẳng định sai
trong các khẳng định sau
A. Nếu
ab⊥
thì
( )
//bP
. B. Nếu
//ba
thì
( )
bP⊥
.
C. Nếu
( )
bP⊥
thì
//ab
. D. Nếu
( )
bP
thì
ba⊥
.
Lời giải
Chọn A
Nếu
( )
( )
( )
//bP
ab
aP
bP
⊥

⊥
đáp án A sai.
Câu 7: Hàm số nào sau đây là hàm số chẵn?
A.
tanyx=
. B.
cotyx=
. C.
sinyx=
. D.
cosyx=
.
Lời giải
Chọn D
Hàm số
cosyx=
là hàm số chẵn.
Câu 8: Cho cấp số cộng
( )
n
u
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng:
A.
6
. B.
9
. C.
4
. D.
5
.
Lời giải
Chọn D
Áp dụng tính chất của cấp số cộng ta có:
1 3 2 3 2 1
2. 2. 2.3 1 5u u u u u u+ = = − = − =
.
Câu 9: Hàm số
sinyx=
đồng biến trên khoảng nào dưới đây?
A.
( )
0;
. B.
( )
0;2
. C.
0;
2



. D.
( )
;

−
.
Lời giải
Chọn C
Hàm số
sinyx=
đồng biến trên khoảng hàm số
0;
2



.
Câu 10: Tìm giá trị lớn nhất của hàm số
2cos 3
3
yx

= − +


?
A.
9
. B.
5
. C.
. D.
7
.
Lời giải
Chọn B
Ta có:
1 cos 1 2 2cos 2 1 2cos 3 5 1 5
3 3 3
x x x y
− − − − − +
Vậy
min 5 cos 1 2 ,
33
y x x k k


= − = = +


GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 11: Phương trình nào sau đây vô nghiệm
A.
tan 3x =−
. B.
2 cos 3x−=
. C.
cos2 2x =
. D.
2sin2 1x =
.
Lời giải
Chọn C
Phương trình
cos2 2x =
vô nghiệm do
21
.
Câu 12: Cho cấp số nhân
( )
n
u
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng
A.
9
. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn A
Công bội của ấp số nhân là
2
1
3
u
q
u
==
. Vậy
2
31
9u u q==
.
Câu 13: Tìm điều kiện của
m
để phương trình sau đây vô nghiệm
cos 1mx−=
.
A.
02m
. B.
0m
hoặc
2m
. C.
20m−
. D.
2m −
hoặc
0m
Lời giải
Chọn B
Ta có:
cos 1 cos 1m x x m− = = −
Phương trình vô nghiệm khi và chỉ khi
1 1 0
1 1 2
mm
mm
− −


−

.
Câu 14: Trên khoảng
( )
0;
, phương trình
sin 1x =
có bao nhiêu nghiệm?
A.
1
. B.
2
. C.
3
. D. Vô số.
Lời giải
Chọn A
sin 1 ,
2
x x k k
= = +
.
Do
( )
0;x
nên có 1 giá trị
2
x
=
thỏa mãn. Vậy phương trình có 1 nghiệm.
Câu 15: Tất cả các nghiệm của phương trình
cot 0x =
là?
A.
2,
2
kk
+
. B.
2,kk

+
. C.
,
2
kk
+
. D.
2,
2
kk
− +
.
Lời giải
Chọn C
Ta có:
cot 0 ,
2
x k k
= +
.
Câu 16: Cho phương trình
2
sin 3sin 4 0xx+ − =
. Ta đặt
sintx=
, phương trình thu được có dạng
A.
2
3 4 0tt− − =
. B.
2
3 4 0tt+ − =
. C.
2
3 4 0tt− + − =
. D.
2
3 4 0tt+ + =
.
Lời giải
Chọn B
Cho phương trình
2
sin 3sin 4 0xx+ − =
.
Đặt
sintx=
, phương trình thu được có dạng
2
3 4 0tt+ − =
.
Câu 17: Cho cấp số nhân
( )
n
u
với
1
2u =
và
4
16u =−
. Công bội của cấp số nhân đã cho bằng
A.
3
. B.
2
. C.
8−
. D.
2−
.
8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Lời giải
Chọn D
Gọi công bội của cấp số nhân đã cho là
q
.
Theo công thức số hạng tổng quát của cấp số nhân ta có
33
41
. 16 2. 2u u q q q= − = = −
.
Câu 18: Số nghiệm của phương trình
22
cos sin2 1 sinx x x− = +
trên khoảng
( )
0;2
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Ta có:
22
cos sin2 1 sinx x x− = +
22
cos sin sin2 1x x x − − =
cos2 sin2 1xx − =
2
sin 2
42
x

− =


22
44
22
44
xk
xk



− = +
− = − +
4
xk
xk
=−
= − −
.
Do
02x

02
02
4
k
k


−
− −
20
91
44
k
k
−
− −
1
2; 1
k
k
−
− −
.
Vậy phương trình có 3 nghiệm thuộc khoảng
( )
0;2
.
Câu 19: Cho cấp số nhân
( )
n
u
biết
4 10
7, 56uu==
. Tìm công bội
q
.
A.
2q =
. B.
2q =
. C.
2q =
. D.
2q =
.
Lời giải
Chọn B
Gọi
1
u
và
q
là số hạng đầu và công bội của cấp số nhân
( )
n
u
,
1
0u
,
0q
.
Ta có:
3
41
9
10 1
.7
56
u u q
u u q
==
==
4
6
10
1 7 1
56 8
u
u
q
= = =
6
82qq = =
.
Câu 20: Cho đường thẳng
a
song song mặt phẳng
( )
. Mặt phẳng
( )
chứa
a
và cắt mặt phẳng
( )
theo giao tuyến
d
. Kết luận nào sau đây đúng?
A.
a
và
d
cắt nhau. B.
a
và
d
trùng nhau.
C.
a
và
d
chéo nhau. D.
a
và
d
song song.
Lời giải
Chọn D.
Ta có
a
và
d
song song với nhau.
Câu 21: Cho dãy số
( )
n
u
với
2
1
n
u n n= + +
với
*
n
. Số
21
là số hạng thứ bao nhiêu của dãy số đã cho?
A.
5
. B.
3
. C.
6
. D.
4
.
Lời giải
Chọn D
Ta có
22
4
1 21 20 0
5
n
n n n n
n
=
+ + = + − =
=−
.
Vì
*
n
nên ta chọn
4n =
.
Vậy số
21
là số hạng thứ tư của dãy số đã cho.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 22: Cho cấp số cộng
( )
n
u
có số hạng tổng quát là
32
n
un=−
. Tìm công sai
d
của cấp số cộng đó.
A.
3d =−
. B.
3d =
. C.
2d =
. D.
2d =−
.
Lời giải
Chọn B
Ta có
( ) ( )
1
3 1 2 3 2 3 3 2 3 2 3,
nn
u u n n n n n
+
− = + − − − = + − − + =
.
Suy ra công sai của cấp số cộng đã cho là
3d =
.
Câu 23: Tổng hai nghiệm dương nhỏ nhất của phương trình
2
4cos 1x =
là
A.
. B.
7
3
. C.
6
. D.
5
3
.
Lời giải
Chọn A
Ta có
( )
2
1
4cos 1 2 1 cos2 1 cos2
23
x x x x k
= + = = − = +
.
Vậy hai nghiệm dương nhỏ nhất của phương trình là
3
và
2
3
.
Suy ra tổng hai nghiệm này là
.
Câu 24: Cho cấp số nhân
( )
n
u
có số hạng đầu
1
5u =
, công bội
1
3
q =
. Khi đó
5
59049
là số hạng thứ mấy
của cấp số nhân?
A. 9. B. 10. C. 11. D. 12.
Lời giải
Chọn C
Ta có:
1
1
1
51
. 5. 11
59049 3
n
n
n
u u q n
−
−

= = =


Vậy số
5
59049
là số hạng thứ 11 của cấp số nhân.
Câu 25: Các họ nghiệm của phương trình
sin sin2xx=−
.
A.
2
;2
3
k
x x k

= = +
. B.
2
;
3
x k x k
= + = +
.
C.
2
2;
23
k
x k x

= + =
. D.
2
;
3
x k x k

= = +
.
Lời giải
Chọn A
( )
2
22
sin sin2 sin2 sin
3
22
2
k
x x k
x
x x x x
x x k
xk


= − +
=
= − = −
= + +
=+
.
Câu 26: Cho
a
và
b
lần lượt là số hạng thứ nhất và số hạng thứ năm của một cấp số cộng có công sai
0d
. Giá trị của
ba
d
−
bằng
A.
6
. B.
5
. C.
3
. D.
4
.
Lời giải
Chọn D
10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Ta có
4b a d=+
4b a d − =
4
ba
d
−
=
.
Câu 27: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
,
N
lần lượt là trung điểm
AD
và
BC
. Giao tuyến của hai mặt phẳng
( )
SMN
và
( )
SAC
là
A.
SG
(
G
là trung điểm
AB
). B.
SD
.
C.
SF
(
F
là trung điểm
CD
). D.
SO
(
O
là tâm hình bình hành
ABCD
).
Lời giải
Chọn D
Gọi
O MN AC O=
là tâm của hình bình hành
ABCD
.
Ta có
( ) ( )
( ) ( )
( ) ( )
S SAC SMN
SO SAC SMN
O MN AC O SAC SMN

=
=
.
Câu 28: Cho hai đường thẳng
a
và
b
chéo nhau. Có bao nhiêu mặt phẳng chứa
a
và song song với
b
?
A.
1
. B. Vô số. C.
2
. D.
3
Lời giải
Chọn A
Chỉ có một mặt phẳng chứa
a
và song song với
b
.
Câu 29: Số điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình
( )
2 sin cos 4sin cos 2x x x x+ + =
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Đặt
sin cost x x=+
, khi đó:
2; 2t

−

và
2
2sin cos 1x x t=−
.
Phương trình đã cho trở thành:
( )
2
2 2 1 2tt+ − =
2
2 2 4 0tt + − =
1
2
t
t
=
=−
.
So điều kiện ta nhận
1t =
sin cos 1xx + =
2
sin
42
x

+ =


2
44
2
44
xk
xk



+ = +
+ = − +
2
2
2
xk
xk
=
=+
.
Vậy có 2 điểm biểu diễn các nghiệm của phương trình trên đường tròn lượng giác.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 30: Cho tứ diện
ABCD
. Gọi
M
là trung điểm của cạnh
AD
,
G
là trọng tâm tam giác
ABD
và
N
là điểm thuộc cạnh
BC
sao cho
2NB NC=
. Kết luận nào sau đây sai?
A.
( )
// NG BCM
. B.
( )
// NG ACD
.
C.
NG
và
AB
chéo nhau. D.
// NG CM
.
Lời giải
Chọn A
Ta có
( )
NG BCM
do
NG
không song song
( )
BCM
.
Câu 31: Cho hình hộp
. ' ' ' 'ABCD A B C D
. Khẳng định nào sau đây sai?
A.
( ) ( )
/ / ' ' 'ABC A D C
. B.
( ) ( )
' ' / / 'AB D BCA
.
C.
( ) ( )
' ' / / ' 'ADD A BCC B
. D.
( ) ( )
' ' / / 'AB D BC D
.
Lời giải
Chọn B
Vì
'AB
và
'AB
cắt nhau nên
( ) ( )
' ' / / 'AB D BCA
là một khẳng định sai.
Câu 32: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là điểm trên đoạn
AB
(
M
khác
A
và khác
B
). Qua
M
vẽ mặt phẳng
( )
song song với
( )
SBC
. Thiết diện tạo bởi mặt
phẳng
( )
và hình chóp
.S ABCD
là hình gì?
A. Hình thang. B. Hình bình hành. C. Hình tam giác. D. Ngũ giác.
Lời giải
Chọn A
Qua
M
vẽ mặt phẳng
( )
song song với
( )
SBC
:
( )
//MN BC N DC
( )
, / / ,MQ SB Q SB
( )
/ / / /QP AD BC P SD
Vậy thiết diện là hình thang.
12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 33: Cho hình lăng trụ
.ABC A B C
. Gọi
I
,
J
,
K
lần lượt là trọng tâm của các tam giác
ABC
,
AA C
,
ABC
. Mặt phẳng nào sau đây song song với mặt phẳng
( )
IJK
?
A.
( )
A BC

. B.
( )
AA B
. C.
( )
BB C
. D.
( )
AA C
.
Lời giải
Chọn C
Do
I
,
J
,
K
lần lượt là trọng tâm của các tam giác
ABC
,
AA C
,
ABC
nên:
( )
2
// //
3
AI AJ
IJ MN IJ BCC B
AM AN

= =
.
Tương tự:
( ) ( ) ( )
// //IK BCC B IJK BCC B
. Hay
( ) ( )
//IJK BB C
.
Câu 34: Cho phương trình
3sin2 cos2 1xx+=
. Phương trình trên có bao nhiêu nghiệm thuộc khoảng
3
0;
2



?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn B
Ta có:
3sin2 cos2 1xx+=
3 1 1
sin2 cos2
2 2 2
xx + =
1
sin 2
62
x

+ =


( )
22
66
5
22
66
xk
k
xk


+ = +

+ = +
( )
3
xk
k
xk
=

=+
Với
3
0;
2
x



, ta có:
3
0
2
3
0
32
k
k


+
3
0
2
17
36
k
k

−
( )
k
.
Với
xk
=
. Chọn
1k =
, suy ra
x
=
Với
3
xk
=+
. Chọn
0k =
hoặc
1k =
, suy ra
3
x
=
hoặc
4
3
x
=
Nên
4
;;
33
x




.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Phương trình có 3 nghiệm thuộc khoảng
3
0;
2



.
Câu 35: Cho hình chóp
SABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
là trung điểm của cạnh
bên
SD
. Gọi
K
là giao điểm của đường thẳng
BM
với mặt phẳng
( )
SAC
. Khi đó tỷ số diện
tích
SBK
SMK
S
S
bằng
A.
4
. B.
3
. C.
. D.
2
.
Lời giải
Chọn D
Ta có:
( ) ( )
SBD SAC SO=
.
Xét
( )
SBD
có
SO BM K=
K
là giao điểm của
BM
với
( )
SAC
.
Trong
SBD
có
,BM SO
là hai đường trung tuyến.
Mặt khác
BM SO K K =
là trọng tâm của
2SBD KM KB =
.
Ta có
sin sinSKB SKM=
.
Suy ra:
1
. .sin
2
2
1
. .sin
2
SBK
SMK
SK KB SKB
S KB
S KM
SK KM SKM
= = =
.
14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1: (0,5 điểm) Tìm
m
để phương trình
( )( )
2sin 1 2cos2 2sin 1 2cos2x x x m x− + + = −
có đúng 2
nghiệm thuộc
0;
.
Lời giải
Ta có:
( )( )
2sin 1 2cos2 2sin 1 2cos2x x x m x− + + = −
( )( )
( )
2
2sin 1 2cos2 2sin 1 2 1 2sinx x x m x − + + = − −
( )( )
2
2sin 1 2cos2 2sin 4sin 1x x x m x − + + = −
( )( ) ( )( )
2sin 1 2cos2 2sin 2sin 1 2sin 1 0x x x m x x − + + − − + =
( ) ( ) ( )
2sin 1 2cos2 2sin 2sin 1 0x x x m x − + + − + =


( )( )
2sin 1 2cos2 1 0x x m − + − =
( )
( )
1
sin 1
2sin 1 0
2
2cos2 1 0 1
cos2 2
2
x
x
x m m
x
=
−=

+ − = −
=
Phương trình
( ) ( )
0;
2
66
1
55
2
66
x
x k x
k
x k x



= + =

⎯⎯⎯→


= + =


.
Để phương trình đã cho có đúng 2 nghiệm thuộc
0;
thì phương trình
( )
2
vô nghiệm hoặc
chỉ có nghiệm
5
;
66
xx

==
.
Trường hợp 1: Phương trình
( )
2
vô nghiệm
1
1
1
2
13
1
2
m
m
mm
−
−

−
−
.
Trường hợp 2: Phương trình
( )
2
có hai nghiệm
5
;
66
xx

==
1
cos 2.
62
0
51
cos 2.
62
m
m
m
−

=


=
−

=


Vậy để phương trình
( )( )
2sin 1 2cos2 2sin 1 2cos2x x x m x− + + = −
có đúng 2 nghiệm thuộc
0;
thì
1
3
0
m
m
m
−
=
.
Câu 2: (1,0 điểm)
a) Biết
3
số nguyên
3
,
x
,
y
theo thứ tự đó lập thành một cấp số nhân và
3
số
x
,
y
,
9
theo
thứ tự đó lập thành một cấp số cộng. Tìm
x
và
y
?
Lời giải
Do
3
số nguyên
3
,
x
,
y
theo thứ tự đó lập thành một cấp số nhân nên ta có:
2
2
3
3
x
x y y= =
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Do
3
số
x
,
y
,
9
theo thứ tự đó lập thành một cấp số cộng nên ta có
( )
9
9 2 2
2
x
x y y
+
+ = =
Thay vào ta được
22
3
3 27 2 2 3 27 0
9
2
x
x x x x
x
=−
+ = − − =
=
. Do
x
là số nguyên nên
3x =−
thỏa mãn.
Vậy
9
33
2
x
xy
+
= − = =
.
b) Một quả bóng cao su từ độ cao
( )
15 m
so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên
một độ cao bằng hai phần năm độ cao lần rơi ngay trước đó. Biết rằng quả bóng luôn chuyển
động vuông góc với mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc
bóng không nảy nữa) khoảng:
Lời giải
Ta có quãng đường bóng bay bằng tổng quảng đường bóng nảy lên và quãng đường bóng rơi
xuống.
Vì mỗi lần bóng nảy lên bằng
2
5
lần nảy trước nên ta có tổng quãng đường bóng nảy lên là
23
1
2 2 2 2
15. 15. 15. 15.
5 5 5 5
n
S
= + + + + +
Đây là tổng của cấp số nhân lùi vô hạn có số hạng đầu
1
2
15. 6
5
u ==
và công bội
2
5
q =
.
Suy ra
23
1
2 2 2 2 6
15. 15. 15. 15. 10
2
5 5 5 5
1
5
n
S
= + + + + + = =
−
.
Tổng quãng đường bóng rơi xuống bằng khoảng cách độ cao ban đầu và tổng quãng đường
bóng nảy lên nên là
23
2
2 2 2 2
15 15. 15. 15. 15.
5 5 5 5
n
S
= + + + + + +
Đây là tổng của cấp số nhân lùi vô hạn có số hạng đầu
1
15u =
và công bội
2
5
q =
.
Suy ra
23
2
2 2 2 15
15 15. 15. 15. 25
2
5 5 5
1
5
n
S
= + + + + + = =
−
.
Vậy tổng quãng đường bóng bay là
( )
12
10 25 35 mSS+ = + =
.
Câu 3: (1,5 điểm) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi điểm
I
và
điểm
M
lần lượt là trung điểm của các đoạn thẳng
SA
và
OC
.
a) Xác định giao tuyến của hai mặt phẳng
( )
SAC
và
( )
SBD
.
b) Gọi
( )
là mặt phẳng chứa đường thẳng
IM
và song song với đường thẳng
BD
. Xác định
thiết diện của mặt phẳng
( )
với hình chóp
.S ABCD
.
c) Giả sử mặt phẳng
( )
cắt đường thẳng
SO
tại điểm
K
. Tính tỉ số
SK
KO
.
Lời giải
16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
a) Xác định giao tuyến của hai mặt phẳng
( )
SAC
và
( )
SBD
.
Ta có
( ) ( )
SO SAC SBD=
.
b) Gọi
( )
là mặt phẳng chứa đường thẳng
IM
và song song với đường thẳng
BD
. Xác định
thiết diện của mặt phẳng
( )
với hình chóp
.S ABCD
.
Gọi
K SO IM=
. Trong
( )
ABCD
kẻ
//Mx BD
và trong
( )
SBD
kẻ
//Ky BD
.
Gọi
, , ,E Ky SD F Ky SB P Mx BC Q Mx CD= = = =
.
Ta có thiết diện của
( )
và hình chóp là hình ngũ giác
IFPQE
.
c) Giả sử mặt phẳng
( )
cắt đường thẳng
SO
tại điểm
K
. Tính tỉ số
SK
KO
.
Ta có
K SO IM=
.
Áp dụng định lí Menelaus trong tam giác
SOA
có
. . 1
KS MO IA
KO MA IS
=
.
Mặt khác
1
3
MO
MA
=
và
1
IA
IS
=
suy ra
1
. .1 1 3
3
KS KS
KO KO
= =
.
-----------------------HẾT-----------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Trong không gian, khẳng định nào trong các khẳng định sau là đúng?
A. Luôn có một mặt phẳng đi qua bốn điểm phân biệt không thẳng hàng.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung.
C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng.
D. Không có mặt phẳng nào đi qua hai đường thẳng cắt nhau.
Câu 2: Tập giá trị của hàm số
sin 2 3yx=+
là:
A.
1;1−
. B.
2;3
. C.
3;4
. D.
2;4
.
Câu 3: Cho cấp số nhân
( )
n
u
có
1
2u =
và
2
6u =
. Giá trị của
5
u
bằng
A.
8
. B.
12
. C.
162
. D.
81
.
Câu 4: Tập xác định của hàm số
sinyx=
là
A.
D =
. B.
\,Dk

=
.
C.
\,
2
Dk


= +


. D.
\0D =
.
Câu 5: Cho khối chóp
ABCD
. Gi
G
và
E
ln lưt là trng tâm của tam giác
ABD
và
ABC
. Khẳng
định nào sau đây là khẳng định đúng?
A. Đường thẳng
GE
song song vi đường thẳng
CD
.
B. Đường thẳng
GE
cắt đường thẳng
CD
.
C. Đường thẳng
GE
và đường thẳng
AD
cắt nhau.
D. Đường thẳng
GE
và đường thẳng
CD
cho nhau.
Câu 6: Tập xác định của hàm số
cotyx=
là
A.
D =
. B.
\,Dk

=
.
C.
\,
2
Dk


= +


. D.
\0D =
.
Câu 7: Hàm số nào dưi đây có đồ thị đối xứng qua trục tung?
A.
cosyx=
. B.
cotyx=
. C.
tanyx=
. D.
sinyx=
.
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
02
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 8: Đường cong trong hình vẽ dưi đây là đồ thị của hàm số nào trong các hàm số sau?
A.
sinyx=
. B.
cosyx=
. C.
tanyx=
. D.
cotyx=
.
Câu 9: Phương trình
sin sinx
=
có nghiệm là:
A.
( )
2
,
2
xk
k
xk

=+
= − +
. B.
( )
,
xk
k
xk

=+
= − +
.
C.
( )
2
,
2
xk
k
xk

=+
= + +
. D.
( )
2
,
2
xk
k
xk

=+
= − +
.
Câu 10: Mệnh đề nào sau đây sai?
A. Qua một điểm nằm ngoài một mặt phẳng cho trưc có một và chỉ một mặt phẳng song song
vi mặt phẳng đã cho.
B. Hai mặt phẳng
( )
P
và
( )
Q
đưc gi là song song vi nhau nếu chúng không có điểm chung.
C. Nếu mặt phẳng
( )
P
chứa hai đường thẳng
,ab
và
,ab
cùng song song vi mặt phẳng
( )
Q
thì
( )
P
song song vi
( )
Q
.
D. Hai mặt phẳng phân biệt cùng song song vi mặt phẳng thứ ba thì song song vi nhau.
Câu 11: Cho cấp số cộng
( )
n
u
có số hạng đu và số hạng thứ tư ln lưt là
2;14
. Tìm công sai
d
?
A.
4d =−
. B.
3d =
. C.
3d =−
. D.
4d =
.
Câu 12: Phương trình
tan 3x =
có nghiệm là:
A.
( )
2,
3
x k k
= +
. B.
( )
2,
3
x k k
= − +
.
C.
( )
,
6
x k k
= +
. D.
( )
,
3
x k k
= +
.
Câu 13: Cho cấp số nhân
( )
n
u
vi
1
2u =
2
6u =
. Công bội của cấp số nhân này bằng
A.
3
. B.
1
3
. C.
4
. D.
12
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gi s
M
thuộc đoạn
SB
, mặt
phẳng
( )
ADM
cắt hình chóp
.S ABCD
theo thiết diện là
A. Tam giác. B. Hình thang.
C. Hình ch nhật. D. Hình bình hành.
Câu 15: Tập nghiệm của phương trình
cot 0x =
là
A.
,
2
S k k

= +

. B.
2,
2
S k k

= +

.
C.
2,S k k
=
. D.
,S k k
=
.
Câu 16: Dãy
( )
n
u
nào sau đây là dãy số gim?
A.
1
21
n
u
n
−
=
+
. B.
1
2
n
u
n
=−
. C.
2
1
n
n
u
n
−
=
. D.
sin
n
un=
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 17: Phương trình
3 tan2 3 0x −=
có nghiệm
A.
( )
32
x k k

= +
. B.
( )
62
x k k

= +
.
C.
( )
6
x k k
= +
. D.
( )
3
x k k
= +
.
Câu 18: Giá trị ln nhất của hàm số
4sin cos 1y x x=+
là
A.
4
. B.
3
. C.
1
. D.
5
.
Câu 19: Cho ba số
1x −
,
2x +
,
4x +
theo thứ tự lập thành một cấp số nhân. Giá trị của biểu thức
21Px=−
bằng
A.
8
. B.
8−
. C.
20
. D.
17−
.
Câu 20: Cho hình chóp
.S ABCD
có đáy là hình bình hành
ABCD
. Khi đó giao tuyến của hai mặt phẳng
( )
SAD
và
( )
SBC
là
A. Đường thẳng qua
S
song song vi
BC
.
B. Đường thẳng
SC
.
C. Đường thẳng qua
S
song song vi
AB
.
D. Đường thẳng
SO
, trong đó
O
là giao của
AC
và
BD
.
Câu 21: Cho phương trình
2cos 1 0x +=
. Trên đoạn
0 ; 2
phương trình đã có bao nhiêu nghiệm?
A. 0. B. 1. C. 3. D. 2.
Câu 22: Cho hai đường thẳng cho nhau
a
và
b
. Lấy
,AB
thuộc
a
và
,CD
thuộc
b
. Khẳng định nào
sau đây đúng khi nói về hai đường thẳng
AD
và
BC
?
A. Có thể song song hoặc cắt nhau. B. Song song vi nhau.
C. Chéo nhau. D. Cắt nhau.
Câu 23: Số điểm biểu diễn các nghiệm của phương trình
tan cot 2 0xx−=
trên đường tròn lưng giác là
bao nhiêu?
A. 4. B. 1. C. 3. D. 6.
Câu 24: Cho cấp số cộng
( )
n
u
có
2
4u =
và
4
2u =
. Giá trị của
6
u
bằng
A.
6
6u =
. B.
6
0u =
. C.
6
1u =−
. D.
6
1u =
.
Câu 25: Phương trình nào dưi đây không là phương trình bậc hai đối vi một hàm số lưng giác?
A.
2
sin 2 cos 1xx+=
. B.
2
tan 2tan 3 0xx+ + =
.
C.
2
sin 3sin 1 0xx− + =
. D.
2
cos 2 cos2 2 0xx− − =
.
Câu 26: Tập nghiệm của phương trình
cos2 3sin 2 0xx+ − =
là
A.
2 ; 2 ,
26
S k k k



= − + +

.
B.
5
2 ; 2 ; 2 ,
2 6 6
S k k k k

= + − + − +

.
C.
5
2 ; 2 ; 2 ,
2 6 6
S k k k k Z

= − + + +


.
D.
5
2 ; 2 ; 2 ,
2 6 6
S k k k k

= + + +

.
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 27: Gii phương trình
( )
2
tan 3 1 tan 3 0xx+ − − =
.
A.
( )
4
3
xk
k
xk
=+
= − +
. B.
( )
4
6
xk
k
xk
=+
= − +
.
C.
( )
4
6
xk
k
xk
=+
=+
. D.
( )
4
3
xk
k
xk
= − +
= − +
.
Câu 28: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gi
I
là trung điểm
SA
. Thiết diện
của hình chóp
.S ABCD
cắt bi mặt phẳng
()IBC
là
A. Tứ giác
IBCD
. B. Tam giác
IBC
.
C. Hình thang
IJCB
(
J
là trung điểm
SD
). D. Hình thang
IGBC
(
G
là trung điểm
SB
).
Câu 29: Có bao nhiêu giá trị nguyên của tham số m để phương trình
( )
1 sin 2 2cos2 2m x x m+ + =
có
nghiệm
A. 0. B.
1
. C.
2
. D. 3.
Câu 30: Cho ba số
,1 ,6x x x+−
theo thứ tự lập thành một cấp số cộng. Tìm
x
.
A.
2
. B.
4
. C.
5
. D.
3
.
Câu 31: Cho hình hộp
.ABCD A B C D
. Gi
M
là trung điểm của
AB
. Mặt phẳng
( )
MA C

cắt cạnh
BC
của hình hộp
.ABCD A B C D
tại
N
. Tính tỉ số
MN
k
AC
=

.
A.
1
2
k =
. B.
1
2
k =
. C.
1
2
k =
. D.
1
2
k =
.
Câu 32: Cho cấp số nhân
( )
n
u
biết
15
51uu+=
;
26
102uu+=
. Hỏi số hạng
12288
là số hạng thứ bao
nhiêu của cấp số nhân
( )
n
u
?
A.
12
. B.
13
. C.
11
. D.
10
.
Câu 33: Cho hình hộp
.ABCD A B C D
. Mặt phẳng
( )
AB D

song song vi mặt phẳng nào trong các mặt
phẳng sau đây?
A.
( )
BDA
. B.
( )
BC D
. C.
( )
A C C

. D.
( )
BCA
.
Câu 34: Trong đại dịch Covid-19, người ta đã thống kê hết tháng 1 năm 2020, thế gii có 2100 người t
vong, sau đó cứ tháng sau nhiều hơn tháng trưc 1000 người t vong. Đến hết tháng 12 năm
2020, tổng số người t vong trên toàn thế gii là:
A. 91200 người. B. 90000 người. C. 81200 người. D. 13100 người.
Câu 35: Cho hình hộp
.ABCD A B C D
. Một mặt phẳng
( )
cắt các cạnh bên
,AA
,BB
,CC
DD
ln
lưt tại
, , ,M N P Q
sao cho
5, 8, 7.AM BN CP= = =
Khi đó dộ dài đoạn
DQ
bằng:
A. 4. B. 6. C. 10. D. 5.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1: (0,5 điểm) Gii phương trình
2sin cos 3cos2 3x x x+=
Câu 2: (1,0 điểm)
a) Ba số
,,x y z
theo thứ tự lập thành một cấp số nhân vi công bội
q
khác
1
; đồng thời các số
, 2 , 3x y z
theo thứ tự lập thành một cấp số cộng vi công sai khác
0
. Tìm
q
?
b) Tỷ lệ tăng dân số của tỉnh
X
là
1,4%
Biết rằng dân số tỉnh
X
hiện nay là
1,8
triệu người.
Hỏi vi mức tăng như vậy thì sau
10
năm na dân số tỉnh
X
là bao nhiêu?
Câu 3: Cho hình chóp
.S ABCD
, đáy
ABCD
là hình thang
( )
// ,AD BC AD BC
. Gi
,MN
ln lươt
là các điểm thuộc các cạnh
,SB SC
sao cho
2 , 2 .SM MB SN NC==
a) Gi
.K AB CD=
Tìm thiết diện của hình chóp cắt bi mặt phẳng
( )
KMN
.
b) Cho
2.AD BC=
Tính tỉ số diện tích của tam giác
KMN
và diện tích thiết diện vừa tìm câu
trên.
-----------------------HẾT-----------------------
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
BẢNG ĐÁP ÁN
1.B
2.D
3.C
4.A
5.A
6.B
7.A
8.A
9.A
10.C
11.D
12.D
13.A
14.B
15.A
16.B
17.B
18.B
19.D
20.A
21.D
22.C
23.A
24.B
25.A
26.D
27.A
28.C
29.D
30.A
31.A
32.C
33.B
34.A
35.A
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Trong không gian, khẳng định nào trong các khẳng định sau là đúng?
A. Luôn có một mặt phẳng đi qua bốn điểm phân biệt không thẳng hàng.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung.
C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng.
D. Không có mặt phẳng nào đi qua hai đường thẳng cắt nhau.
Lời giải
Chọn B
Câu A sai vì không có mặt phẳng nào đi qua 4 đỉnh của một tứ diện.
Câu B đúng và đường thẳng đó đưc gi là giao tuyến của hai mặt phẳng.
Câu C sai vì nếu điểm đó thuộc đường thẳng thì có vô số mặt phẳng chứa đường thẳng đó.
Câu D sai vì hai đường thẳng cắt nhau xác định một mặt phẳng.
Câu 2: Tập giá trị của hàm số
sin 2 3yx=+
là:
A.
1;1−
. B.
2;3
. C.
3;4
. D.
2;4
.
Lời giải
Chọn D
Ta có
1 sin 2 1x−
2 sin 2 3 4x +
24y
.
Vậy tập giá trị của hàm số
sin 2 3yx=+
là
2;4T =
.
Câu 3: Cho cấp số nhân
( )
n
u
có
1
2u =
và
2
6u =
. Giá trị của
5
u
bằng
A.
8
. B.
12
. C.
162
. D.
81
.
Lời giải
Chọn C
Công bội:
2
1
6
3
2
u
q
u
= = =
nên
44
51
2.3 162u u q= = =
.
Câu 4: Tập xác định của hàm số
sinyx=
là
A.
D =
. B.
\,Dk

=
.
C.
\,
2
Dk


= +


. D.
\0D =
.
Lời giải
Chọn A
Tập xác định của hàm số
sinyx=
là
D =
.
Câu 5: Cho khối chóp
ABCD
. Gi
G
và
E
ln lưt là trng tâm của tam giác
ABD
và
ABC
. Khẳng
định nào sau đây là khẳng định đúng?
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
A. Đường thẳng
GE
song song vi đường thẳng
CD
.
B. Đường thẳng
GE
cắt đường thẳng
CD
.
C. Đường thẳng
GE
và đường thẳng
AD
cắt nhau.
D. Đường thẳng
GE
và đường thẳng
CD
cho nhau.
Lời giải
Chọn A
Gi
I
là trung điểm của cạnh
AB
.
Do
G
và
E
ln lưt là trng tâm của tam giác
ABD
và
ABC
nên ta có:
1
//
3
IG IE
GE CD
ID IC
= =
.
Câu 6: Tập xác định của hàm số
cotyx=
là
A.
D =
. B.
\,Dk

=
.
C.
\,
2
Dk


= +


. D.
\0D =
.
Lời giải
Chọn B
Điều kiện:
( )
sin 0x x k k
.
Câu 7: Hàm số nào dưi đây có đồ thị đối xứng qua trục tung?
A.
cosyx=
. B.
cotyx=
. C.
tanyx=
. D.
sinyx=
.
Lời giải
Chọn A
Hàm số
cosyx=
là hàm số chẵn nên có đồ thị đối xứng qua trục tung.
8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 8: Đường cong trong hình vẽ dưi đây là đồ thị của hàm số nào trong các hàm số sau?
A.
sinyx=
. B.
cosyx=
. C.
tanyx=
. D.
cotyx=
.
Lời giải
Chọn A
Dựa vào toạ độ các điểm trên đồ thị, ta xác định đưc đây là đồ thị hàm số
sinyx=
.
Câu 9: Phương trình
sin sinx
=
có nghiệm là:
A.
( )
2
,
2
xk
k
xk

=+
= − +
. B.
( )
,
xk
k
xk

=+
= − +
.
C.
( )
2
,
2
xk
k
xk

=+
= + +
. D.
( )
2
,
2
xk
k
xk

=+
= − +
.
Lời giải
Chọn A
Ta có
( )
2
sin sin ,
2
xk
xk
xk

=+
=
= − +
Câu 10: Mệnh đề nào sau đây sai?
A. Qua một điểm nằm ngoài một mặt phẳng cho trưc có một và chỉ một mặt phẳng song song
vi mặt phẳng đã cho.
B. Hai mặt phẳng
( )
P
và
( )
Q
đưc gi là song song vi nhau nếu chúng không có điểm chung.
C. Nếu mặt phẳng
( )
P
chứa hai đường thẳng
,ab
và
,ab
cùng song song vi mặt phẳng
( )
Q
thì
( )
P
song song vi
( )
Q
.
D. Hai mặt phẳng phân biệt cùng song song vi mặt phẳng thứ ba thì song song vi nhau.
Lời giải
Chọn C
Nếu
( )
,a b P
mà
,ab
cùng song song vi
( )
Q
và
a
song song
b
thì không suy ra đưc
( )
P
song song vi
( )
Q
.
Câu 11: Cho cấp số cộng
( )
n
u
có số hạng đu và số hạng thứ tư ln lưt là
2;14
. Tìm công sai
d
?
A.
4d =−
. B.
3d =
. C.
3d =−
. D.
4d =
.
Lời giải
Chọn D
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Ta có:
11
1
41
22
2
14 3 14
4
uu
u
u u d
d
==
=


= + =
=

.
Câu 12: Phương trình
tan 3x =
có nghiệm là:
A.
( )
2,
3
x k k
= +
. B.
( )
2,
3
x k k
= − +
.
C.
( )
,
6
x k k
= +
. D.
( )
,
3
x k k
= +
.
Lời giải
Chọn D
Ta có:
( )
tan 3 tan tan , .
33
x x x k k

= = = +
Câu 13: Cho cấp số nhân
( )
n
u
vi
1
2u =
2
6u =
. Công bội của cấp số nhân này bằng
A.
3
. B.
1
3
. C.
4
. D.
12
.
Lời giải
Chọn A
Công bội của cấp số nhân
2
1
6
3
2
u
q
u
= = =
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gi s
M
thuộc đoạn
SB
, mặt
phẳng
( )
ADM
cắt hình chóp
.S ABCD
theo thiết diện là
A. Tam giác. B. Hình thang.
C. Hình ch nhật. D. Hình bình hành.
Lời giải
Chọn B
Mặt phẳng
( )
ADM
cắt hình chóp
.S ABCD
theo thiết diện là hình thang
MNDA
.
Câu 15: Tập nghiệm của phương trình
cot 0x =
là
A.
,
2
S k k

= +

. B.
2,
2
S k k

= +

.
C.
2,S k k
=
. D.
,S k k
=
.
Lời giải
Chọn A
Ta có
cot 0x =
;
2
x k k
= +
.
Câu 16: Dãy
( )
n
u
nào sau đây là dãy số gim?
10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
A.
1
21
n
u
n
−
=
+
. B.
1
2
n
u
n
=−
. C.
2
1
n
n
u
n
−
=
. D.
sin
n
un=
.
Lời giải
Chọn B
Ta xt từng dãy
Xét
1
21
n
u
n
−
=
+
( )
1
11
2 1 1 2 3
n
u
nn
+
−−
==
+ + +
( )( )
( )
1
1 1 2
0 do *
2 3 2 1 2 3 2 1
nn
u u n
n n n n
+
−−
− = − =
+ + + +
dãy tăng
Xét
1
2
n
u
n
=−
1
1
2
1
n
u
n
+
=−
+
( )
( )
1
1 1 1
2 2 0 do *
11
nn
u u n
n n n n
+
−
− = − − + =
++
dãy gim chọn B
Xét
2
1
n
n
u
n
−
=
,
( )
2
1
11
1
n
n
u
n
+
+−
=
+
( ) ( )
( ) ( )
( )
22
22
1
1 1 1
11
0 do *
1 1 1
nn
n n n
n n n
u u n
n n n n n n
+
+ − + −
− + +
− = − = =
+ + +
dãy tăng
Xét
sin
n
un=
,
( ) ( ) ( )
3 4 6
u sin 3 0.14;u sin 4 0.75;u sin 6 0.27= = − = −
không gim không
tang.
Câu 17: Phương trình
3 tan2 3 0x −=
có nghiệm
A.
( )
32
x k k

= +
. B.
( )
62
x k k

= +
.
C.
( )
6
x k k
= +
. D.
( )
3
x k k
= +
.
Lời giải
Chọn B
Ta có:
3 tan2 3 0 tan2 3xx− = =
2
3
xk
= +
( )
62
x k k

= +
.
Câu 18: Giá trị ln nhất của hàm số
4sin cos 1y x x=+
là
A.
4
. B.
3
. C.
1
. D.
5
.
Lời giải
Chọn B
Ta có
2sin 2 1yx=+
.
Do
1 sin 2 1 2 2sin 2 2 1 2sin 2 1 3x x x− − − +
13y −
.
Vậy GTLN của hàm số là
3
khi
sin2 1 ,
4
x x k k
= = +
.
Câu 19: Cho ba số
1x −
,
2x +
,
4x +
theo thứ tự lập thành một cấp số nhân. Giá trị của biểu thức
21Px=−
bằng
A.
8
. B.
8−
. C.
20
. D.
17−
.
Lời giải
Chọn D
Vì ba số
1x −
,
2x +
,
4x +
theo thứ tự lập thành một cấp số nhân nên
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
( ) ( )
2
2 ( 1) 4x x x+ = − +
22
4 4 4 4 8x x x x x x + + = + − − = −
.
Suy ra
( )
2 1 2. 8 1 17Px= − = − − = −
.
Câu 20: Cho hình chóp
.S ABCD
có đáy là hình bình hành
ABCD
. Khi đó giao tuyến của hai mặt phẳng
( )
SAD
và
( )
SBC
là
A. Đường thẳng qua
S
song song vi
BC
.
B. Đường thẳng
SC
.
C. Đường thẳng qua
S
song song vi
AB
.
D. Đường thẳng
SO
, trong đó
O
là giao của
AC
và
BD
.
Lời giải
Chọn A
Ta có: Mặt phẳng
( )
SAD
và
( )
SBC
có điểm chung
S
và ln lưt chứa hai đường thẳng song
song
,AD BC
nên có giao tuyến là đường thẳng qua
S
và song song vi
,AD BC
.
Câu 21: Cho phương trình
2cos 1 0x +=
. Trên đoạn
0 ; 2
phương trình đã có bao nhiêu nghiệm?
A. 0. B. 1. C. 3. D. 2.
Lời giải
Chọn D
Ta có:
2
2
1
3
2cos 1 0 cos , .
2
2
2
3
xk
x x k
xk
=+
+ = = −
= − +
Biểu diễn các nghiệm lên đường tròn lưng giác ta đưc 2 điểm. Do vậy trên đoạn
0 ; 2
phương trình đã có 2 nghiệm.
Câu 22: Cho hai đường thẳng cho nhau
a
và
b
. Lấy
,AB
thuộc
a
và
,CD
thuộc
b
. Khẳng định nào
sau đây đúng khi nói về hai đường thẳng
AD
và
BC
?
A. Có thể song song hoặc cắt nhau. B. Song song vi nhau.
C. Chéo nhau. D. Cắt nhau.
Lời giải
Chọn C
Theo gi thuyết thì
,ab
không đồng phẳng.
Gi s
AD
và
BC
đồng phẳng.
Nếu
( ) ( )
;I AD BC I ABCD I a b=
. Mà
,ab
không đồng phẳng nên không tồn tại
điểm
I
.
Nếu
//AD BC
thì
,ab
đồng phẳng (mâu thuẫn).
Do đó
AD
và
BC
không đồng phẳng hay
AD
và
BC
chéo nhau.
Câu 23: Số điểm biểu diễn các nghiệm của phương trình
tan cot 2 0xx−=
trên đường tròn lưng giác là
bao nhiêu?
A. 4. B. 1. C. 3. D. 6.
Lời giải
Chọn A
Điều kiện
cos 0
sin2 0
sin2 0
2
x
x x k
x
.
12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
tan cot2 0 tan cot2 tan tan 2 2
2 2 6 3
x x x x x x x x k x k

− = = = − = − + = +


,
k
.
Vẽ các nghiệm lên đường tròn lưng giác và đối chiếu điều kiện ta đưc 4 điểm, tương ứng vi
các h nghiệm
6
xk
= +
.
Câu 24: Cho cấp số cộng
( )
n
u
có
2
4u =
và
4
2u =
. Giá trị của
6
u
bằng
A.
6
6u =
. B.
6
0u =
. C.
6
1u =−
. D.
6
1u =
.
Lời giải
Chọn B
Ta có:
41
1
21
2 3 2
1
5
44
u u d
d
u
u u d
= + =
=−


=
= + =

.
Từ đó:
61
50u u d= + =
.
Câu 25: Phương trình nào dưi đây không là phương trình bậc hai đối vi một hàm số lưng giác?
A.
2
sin 2 cos 1xx+=
. B.
2
tan 2tan 3 0xx+ + =
.
C.
2
sin 3sin 1 0xx− + =
. D.
2
cos 2 cos2 2 0xx− − =
.
Lời giải
Chọn A
Phương trình
2
sin 2 cos 1xx+=
không là phương trình bậc hai đối vi một hàm số lưng giác.
Phương trình
2
tan 2tan 3 0xx+ + =
là phương trình bậc hai đối vi hàm số
tanyx=
.
Phương trình
2
sin 3sin 1 0xx− + =
là phương trình bậc hai đối vi hàm số
sinyx=
.
Phương trình
2
cos 2 cos2 2 0xx− − =
là phương trình bậc hai đối vi hàm số
cos2yx=
.
Câu 26: Tập nghiệm của phương trình
cos2 3sin 2 0xx+ − =
là
A.
2 ; 2 ,
26
S k k k



= − + +

.
B.
5
2 ; 2 ; 2 ,
2 6 6
S k k k k

= + − + − +

.
C.
5
2 ; 2 ; 2 ,
2 6 6
S k k k k Z

= − + + +


.
D.
5
2 ; 2 ; 2 ,
2 6 6
S k k k k

= + + +

.
Lời giải
Chọn D
Ta có:
cos2 3sin 2 0xx+ − =
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
22
1 2sin 3sin 2 0 2sin 3sin 1 0x x x x − + − = − + − =
sin 1
1
sin
2
x
x
=
=
( )
2
2
2
6
5
2
6
xk
x k k
xk
=+
= +
=+
Câu 27: Gii phương trình
( )
2
tan 3 1 tan 3 0xx+ − − =
.
A.
( )
4
3
xk
k
xk
=+
= − +
. B.
( )
4
6
xk
k
xk
=+
= − +
.
C.
( )
4
6
xk
k
xk
=+
=+
. D.
( )
4
3
xk
k
xk
= − +
= − +
.
Lời giải
Chọn A
Ta có
( )
2
tan 3 1 tan 3 0xx+ − − =
tan 1
tan 3
x
x
=
=−
( )
4
3
xk
k
xk
=+

= − +
Câu 28: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gi
I
là trung điểm
SA
. Thiết diện
của hình chóp
.S ABCD
cắt bi mặt phẳng
()IBC
là
A. Tứ giác
IBCD
. B. Tam giác
IBC
.
C. Hình thang
IJCB
(
J
là trung điểm
SD
). D. Hình thang
IGBC
(
G
là trung điểm
SB
).
Lời giải
Chọn C
Gi
O
là giao điểm của
AC
và
BD
,
G
là giao điểm của
CI
và
SO
Khi đó
G
là trng tâm tam giác
SAC
. Suy ra
G
là trng tâm tam giác
SBD
Gi
J BG SD=
. Ta có:
( ) ( ) IJIBC SAD=
. Khi đó
J
là trung điểm
SD
.
14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
( ) ( )IBC SCD JC=
;
( ) ( )IBC ABCD BC=
;
( ) ( )IBC SAB IB=
Mặt khác:
// //IJ AD BC
Do đó thiết diện của hình chóp cắt bi
()IBC
là hình thang
IJCB
(
J
là trung điểm
SD
).
Câu 29: Có bao nhiêu giá trị nguyên của tham số m để phương trình
( )
1 sin 2 2cos2 2m x x m+ + =
có
nghiệm
A. 0. B.
1
. C.
2
. D. 3.
Lời giải
Chọn D
Phương trình
( )
1 sin 2 2cos2 2m x x m+ + =
có nghiệm khi và chỉ khi
( )
2
2
1 4 4mm+ +
22
2 1 4 4m m m + + +
2
3 2 5 0mm − −
5
1
3
m −
Mà
m
nên
1;0;1m−
.
Câu 30: Cho ba số
,1 ,6x x x+−
theo thứ tự lập thành một cấp số cộng. Tìm
x
.
A.
2
. B.
4
. C.
5
. D.
3
.
Lời giải
Chọn A
Vì
,1 ,6x x x+−
theo thứ tự lập thành một cấp số cộng nên
( )
2 1 6 2 4 2x x x x x+ = + − = =
Câu 31: Cho hình hộp
.ABCD A B C D
. Gi
M
là trung điểm của
AB
. Mặt phẳng
( )
MA C

cắt cạnh
BC
của hình hộp
.ABCD A B C D
tại
N
. Tính tỉ số
MN
k
AC
=

.
A.
1
2
k =
. B.
1
2
k =
. C.
1
2
k =
. D.
1
2
k =
.
Lời giải
Chọn A
Ta có:
//AC A C

nên
( )
//MA C AC

.
( ) ( )
MA C ABCD MN

=
do đó
// ACMN
N
là trung điểm của
BC
.
MN
là đường trung bình của
ABC
nên suy ra
1
2
MN MN
k
A C AC
= = =

.
Câu 32: Cho cấp số nhân
( )
n
u
biết
15
51uu+=
;
26
102uu+=
. Hỏi số hạng
12288
là số hạng thứ bao
nhiêu của cấp số nhân
( )
n
u
?
A.
12
. B.
13
. C.
11
. D.
10
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Lời giải
Chọn C
Gi số hạng đu của cấp số nhân là
1
u
và công bội là
q
.
Theo gi thiết, ta có
15
26
51
102
uu
uu
+=
+=
( )
( )
4
4
1
11
5
4
11
1
1 51
. 51
. . 102
. 1 102
uq
u u q
u q u q
u q q
+=
+=



+=
+=
( )
( )
4
1
4
1
1
51 1 1
102 2
1
uq
q
u q q
+
= =
+
2q=
.
Vi
2q =
, ta có
( )
4
11
1 2 51 3.uu+ = =
Gi s số
12288
là số hạng thứ
n
của cấp số nhân này.
Ta có:
1 1 1 1 12
1
. 12288 3.2 12288 2 4096 2 2 1 12 13.
n n n n
u q n n
− − − −
= = = = − = =
.
Vậy số
12288
là số hạng thứ
13
của cấp số nhân.
Câu 33: Cho hình hộp
.ABCD A B C D
. Mặt phẳng
( )
AB D

song song vi mặt phẳng nào trong các mặt
phẳng sau đây?
A.
( )
BDA
. B.
( )
BC D
. C.
( )
A C C

. D.
( )
BCA
.
Lời giải
Chọn B
Ta có:
( )
( ) ( )
//
// 1
B D BD
B D BDC
BD BDC

Ta có:
( )
( ) ( )
//
// 2
AB DC
AB BDC
DC BDC



Mà
( )
,AB B D AB D
( )
3
Từ
( ) ( )
1 , 2
và
( )
3
( ) ( )
//AB D BDC
Câu 34: Trong đại dịch Covid-19, người ta đã thống kê hết tháng 1 năm 2020, thế gii có 2100 người t
vong, sau đó cứ tháng sau nhiều hơn tháng trưc 1000 người t vong. Đến hết tháng 12 năm
2020, tổng số người t vong trên toàn thế gii là:
A. 91200 người. B. 90000 người. C. 81200 người. D. 13100 người.
Lời giải
Chọn A
Số người t vong từ tháng 1 đến tháng 12 lập thành một cấp số cộng có
1
2100u =
và công sai
1000d =
Vậy tổng số người t vong trên toàn thế gii là:
112
12
2 ( 1) 2.2100 (12 1).1000 92100
22
n
u n dS + − = + − ==
người
Câu 35: Cho hình hộp
.ABCD A B C D
. Một mặt phẳng
( )
cắt các cạnh bên
,AA
,BB
,CC
DD
ln
lưt tại
, , ,M N P Q
sao cho
5, 8, 7.AM BN CP= = =
Khi đó dộ dài đoạn
DQ
bằng
A. 4. B. 6. C. 10. D. 5.
Lời giải
Chọn A
16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Ta có:
( ) ( )
( ) ( )
( ) ( )
//
//
ABB A CDD C
ABB A MN MN PQ
CDD C PQ

=

=
Lấy
,MN

ln lưt trên
,DD CC

sao cho
5, 8.DM AM CN BN

= = = =
Khi đó:
DQ DM QM

=−
DM PN

=−
(
PQM N

là hình bình hành)
( ) ( )
5 8 7 4DM CN CP

= − − = − − =
. Vậy
4DQ =
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 4: (0,5 điểm) Gii phương trình
2sin cos 3cos2 3x x x+=
Lời giải
Ta có:
2sin cos 3cos2 3x x x+=
sin 2 3cos2 3xx + =
1 3 3
sin2 cos2
2 2 2
xx + =
3
sin 2
32
x

+ =


.
sin 2 sin
33
x


+ =


22
33
22
33
xk
xk



+ = +
+ = − +
,
6
xk
k
xk
=

=+
.
Câu 5: (1,0 điểm)
a) Ba số
,,x y z
theo thứ tự lập thành một cấp số nhân vi công bội
q
khác
1
; đồng thời các số
, 2 , 3x y z
theo thứ tự lập thành một cấp số cộng vi công sai khác
0
. Tìm
q
?
Lời giải
Ta có
,,x y z
theo thứ tự lập thành một cấp số nhân
2
y xq
z xq
=
=
Mặt khác
, 2 , 3x y z
theo thứ tự lập thành một cấp số cộng
( )
22
2
0
3
2 4 3 3 4 1 0
2
3 4 1 0
x
xz
y xq x xq x q q
qq
=
+
= = + − + =
− + =
.
Vi
0 0, 0x y z= = =
(loại do
;2 ;3x y z
theo thứ tự lập thành một cấp số cộng vi công sai
khác
0
)
Vi
2
1
3 4 1 0
1
3
q
qq
q
=
− + =
=
. Do
1q
nên
1
3
q =
.
b) Tỷ lệ tăng dân số của tỉnh
X
là
1,4%
Biết rằng dân số tỉnh
X
hiện nay là
1,8
triệu người.
Hỏi vi mức tăng như vậy thì sau
10
năm na dân số tỉnh
X
là bao nhiêu?
Lời giải
Theo gii thiết, ta thấy tỷ lệ tăng dân số hàng năm của tỉnh
X
là một cấp số nhân
( )
n
u
vi số
hạng đu
6
1
1,8.10u =
và công bội
1,4
1 1,014
100
q = + =
.
Do đó, dân số của tỉnh
X
sau
10
năm là:
( )
10
10 6
11 1
. 1,8.10 1,014u u q==
2068483
người.
Câu 6: Cho hình chóp
.S ABCD
, đáy
ABCD
là hình thang
( )
// ,AD BC AD BC
. Gi
,MN
ln lươt
là các điểm thuộc các cạnh
,SB SC
sao cho
2 , 2 .SM MB SN NC==
a) Gi
.K AB CD=
Tìm thiết diện của hình chóp cắt bi mặt phẳng
( )
KMN
.
b) Cho
2.AD BC=
Tính tỉ số diện tích của tam giác
KMN
và diện tích thiết diện vừa tìm câu
trên.
Lời giải
18
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
a) Thiết diện của hình chóp cắt bi mặt phẳng
( )
KMN
.
Trong mặt phẳng
( )
,SCD
gi
F KN SD=
thì mặt phẳng
( )
KMN
cắt hình hình chóp theo
thiết diện là tứ giác
MNFE
.
b) Tỉ số diện tích của tam giác
KMN
và diện tích thiết diện vừa tìm  câu trên.
Khi
2AD BC=
thì
BC
là đường trung bình của tam giác
KAD
.
M
là trng tâm tam giác
SAK
và
E
là trung điểm
SA
.
Tương tự
F
là trung điểm cạnh
SD
Khi đó
EF
là đường trung bình của tam giác
SAD
1
.
2
EF AD=
Mặt khác theo gi thiết, ta có
2 , 2SM MB SN NC==
21
33
MN BC AD = =
Vì
2
3
MN
EF
=
nên
2
2 4 5
;
3 9 9
KMN
KMN KEF MNFE KEF
KEF
S
S S S S
S

= = =


Vậy
4
.
5
KMN
MNFE
S
S
=
-----------------------HẾT-----------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Gi tr no sau đây mang du dương?
A.
0
cos120
B.
0
sin120
C.
0
tan120
. D.
0
cot120
.
Câu 2: Trong mặt phẳng cho ba tia
,,Ou Ov Ox
. Trong cc mnh đ sau, mnh đ no đng?
A.
( ) ( ) ( )
, , , 2 ,sd Ou Ov sd Ou Ox sd Ox Ov k k
= + +
.
B.
( ) ( ) ( )
, , , 2 ,sd Ou Ov sd Ou Ov sd Ox Ou k k
= + +
.
C.
( ) ( ) ( )
, , , 2 ,sd Ou Ov sd Ov Ox sd Ox Ou k k
= + +
.
D.
( ) ( ) ( )
, , , 2 ,sd Ou Ov sd Ov Ox sd Ou Ox k k
= + +
.
Câu 3: Trong cc khẳng đnh sau, khẳng đnh no đng?
A.
( )
cos cos cos sin sin .a b a b a b+ = −
B.
( )
cos cos cos sin sin .a b a b a b+ = +
C.
( )
cos cos sin sin cos .a b a b a b+ = +
D.
( )
cos sin cos cos sin .a b a a b b+ = +
Câu 4: Trong cc khẳng đnh sau, khẳng đnh no sai?
A.
22
sin 2 cos sina a a=−
B.
cos2 2sinaa=
C.
2
cos2 2cos 1.aa=−
D.
2
cos2 1 2sin .aa=−
Câu 5: Đồ th dưới đây l đồ th của hm số no?
A.
1 sin 2yx=+
. B.
cosyx=
. C.
sinyx=−
. D.
cosyx=−
.
Câu 6: Trong cc hm số sau, hm số no l hm số chẵn?
A.
tan .yx=
B.
cot .yx=
C.
sin .yx=
D.
cos .yx=
Câu 7: Điu kin có nghim của phương trình
sin xm=
là
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 8: Cho dãy số
( )
n
u
, biết
2
n
un=+
. Ba số hạng đầu tiên của dãy số lần lượt l
A.
3;4;5.
B.
0;1;2.
C.
2;3;4.
D.
1;2;3.
Câu 9: Trong cc dãy số sau dãy số no l dãy số hữu hạn
A.
2345
1 1 1 1 1
, , , , ....
3 3 3 3 3
B.
5,10,15,20,25....
C.
8,15,22,29,36.
D.
2,0,4,6,8,...
Câu 10: Cho cp số cộng
( )
n
u
, biết
12
2, 8uu==
. Công sai của cp số cộng l
A.
6d =
. B.
16d =
. C.
10d =
. D.
4d =
.
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
03
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 11: Cho cp số cộng
( )
n
u
, biết
1
2u =
v công sai
3d =
. Khẳng đnh no sau đây đng?
A.
2
5.u =
B.
2
2.u =
C.
2
6.u =
D.
2
3.u =
Câu 12: Cho cp số cộng
( )
n
u
. Gọi
n
S
l tổng của
n
số hạng đầu của cp số cộng. Khẳng đnh đng l
A.
( )
1
1
2
n
nn
S nu d
−
=+
. B.
( )
1
1
2
n
nu n n
Sd
+−
=
.
C.
( )
1
1
n
S nu n n d= + −
. D.
( )
1
1
2
n
n
S nu d
−
=+
.
Câu 13: Dãy số no sau đây không phải l cp số nhân?
A.
1; 3;9; 27;54−−
. B.
1;2;4;8;16
. C.
1; 1;1; 1;1−−
. D.
1; 2;4; 8;16−−
.
Câu 14: Cho cp số nhân
( )
n
u
với
1
81u =
và
4
3u =
. Tìm công bội
q
?
A.
1
3
1
3
−
. B.
1
3
−
. C.
3
. D.
3−
.
Câu 15: Cho cp số nhân
( )
n
u
với
1
2u =
v công bội
3q =
. Gi tr của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Câu 16: Trong mẫu số liu ghép nhóm, độ di mỗi nhóm
)
;ab
được tính như thế no?
A.
.ba−
B.
.
2
ab+
C.
.ab+
D.
..ab
Câu 17: Cc gi tr xut hin nhiu nht trong mẫu số liu được gọi l
A. mốt. B. số trung bình.
C. số trung v. D. tứ phân v.
Câu 18: Trong mẫu số liu ghép nhóm, gi tr đại din của nhóm
)
;ab
được tính như thế no?
A.
.
2
ab+
B.
.ba−
C.
.ab+
D.
..ab
Câu 19: Trong cc khẳng đnh sau, khẳng đnh no l đng?
A. Số trung v l
( )
( )
11
1
...
2
p
e p p p
p
n
mm
M a a a
m
+
+
− + +
= + −
.
B. Số trung v b ảnh hưởng bởi cc gi tr qu lớn hay qu bé.
C. Số trung v luôn l một số liu no đó của mẫu.
D. Số trung v chính l số trung bình.
Câu 20: Đo chiu cao (tính bằng
cm
) của
500
học sinh trong một trường THPT ta thu được kết quả như
sau:
Mẫu số liu ghép nhóm đã cho có tt cả bao nhiêu nhóm?
A.
5
. B.
6
. C.
7
. D.
12
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 21: Biết
1
sin
3
=
và
.
2


Gi tr
cos
bằng
A.
22
.
3
−
B.
23
.
3
−
C.
32
.
2
−
D.
33
.
2
−
Câu 22: Biết
1
sin
4
=
. Gi tr
cos2
bằng
A.
7
.
8
B.
8
.
7
C.
7
.
8
−
D.
8
.
7
−
Câu 23: Tập gi tr của hm số
2sinyx=
là
A.
1;1 .−
B.
0;2 .
C.
2;2 .−
D.
2;2 .−
Câu 24: Tập nghim của phương trình
cos 0x =
là
A.
2 | .
2
S k k

= +

B.
|.
2
S k k

= +

C.
2 | .S k k
=
D.
2 | .
2
S k k

= − +

Câu 25: Xét tính tăng giảm của dãy số
1 1 1 1
; ; ; .
2345
− − − −
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng không giảm D. Dãy số vừa tăng vừa giảm
Câu 26: Cho một cp số cộng có cc số hạng lần lượt l
1,6,11, .x
Khi đó gi tr của
x
là
A. 5. B. 18. C. 17. D. 16.
Câu 27: Cho cp số nhân có cc số hạng lần lượt l 1; 4; 16; 64. Gọi
n
S
l tổng của n số hạng đầu tiên
của cp số nhân đó. Mnh đ no sau đây đng?
A.
41
3
n
n
S
−
=
. B.
( )
1
14
2
n
n
n
S
−
+
=
. C.
1
4
n
n
S
−
=
. D.
( )
4 4 1
3
n
n
S
−
=
.
Câu 28: Bảng số liu ghép nhóm sau cho biết chiu cao
( )
cm
của 45 học sinh lớp
11A
.
Mẫu số liu ghép nhóm ny có số mốt l
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 29: Cơ cu dân số Vit Nam năm
2020
theo độ tuổi được cho trong bảng sau:
Chọn
85
l gi tr đại din cho nhóm trên
65
tuổi. Tính tuổi trung bình của người Vit Nam
năm
2020
.
A.
36,17
. B.
34,82
. C.
35,6
. D.
37,12
.
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 30: Khảo st chiu cao (cm) của 52 học sinh khối 11 thu được mẫu số liu ghép nhóm sau:
Nhóm chứa trung v l
A.
)
165;170
. B.
)
160;165
. C.
)
170;175
. D.
)
175;180
.
Câu 31: Tập xc đinh của hm số
sin cosy x x=+
là
A.
.
B.
\ | .kk
C.
\ | .k
D.
\ 2 | .kk
Câu 32: Phương trình
2cos 3x =−
có bao nhiêu nghim thuộc tập
;3

−
A. 4. B. 3. C. 2. D. 1.
Câu 33: Cho dãy số
( )
n
u
xc đnh bởi
2 2 2 2
1 1 1 1
...
1 2 3
n
u
n
= + + + +
. Chọn mnh đ đng?
A. Dãy số
( )
n
u
b chặn.
B. Dãy số
( )
n
u
b chặn trên, nhưng không b chặn dưới.
C. Dãy số
( )
n
u
b chặn dưới, nhưng không b chặn trên.
D. Dãy số
( )
n
u
không b chặn.
Câu 34: Gọi
1 11 111 ... 111...1S = + + + +
(
n
số
1
) thì
S
nhận gi tr no sau đây?
A.
1 10 1
10
99
n
Sn


−
=−




. B.
10 1
10
81
n
S

−
=


.
C.
10 1
10
81
n
Sn

−
=−


. D.
10 1
81
n
S
−
=
.
Câu 35: Khảo st vận tốc (dặm/h;
1
dặm
1,609km=
) của
300
xe ô tô chạy trên con đường
A
thu được
mẫu số liu ghép nhóm như sau:
Nhóm chứa tứ phân v thứ nht l
A.
)
32,5 ;37,5
. B.
)
27,5 ;32,5
. C.
)
37,5 ;42,5
. D.
)
42,5 ;47,5
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1: (1,0 điểm) Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liu trên?
Câu 2: (1,0 điểm)
a) Tìm tập xc đnh của hm số sau:
22
sin
sin cos
=
−
x
y
xx
.
b) Giải phương trình
( )
sin cos 1x
=
.
Câu 3: (1,0 điểm) Người ta trồng
2145
cây theo hình một tam gic như sau: hng thứ nht có
1
cây,
hng thứ hai có
2
cây, hng thứ ba có 3 cây,… Hỏi có tt cả bao nhiêu hng cây?
-----------------------HẾT-----------------------
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
BẢNG ĐÁP ÁN
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
A
A
B
B
D
C
A
C
A
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
A
A
A
A
A
A
A
A
A
A
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
A
A
D
B
B
D
A
A
A
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
A
A
A
A
A
C
Đáp án chi tiết
Biểu điểm
3
6
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liu trên?
Tần số lớn nht l
16
nên nhóm chứa mốt l nhóm
)
50,5;55,5
và
3j =
0,25
Ta có
3 4 4 3
50,5; 55,5 5u u h u u= = = − =
0,25
Tần số:
2 3 4
7; 16; 4n n n= = =
.
0,25
( ) ( )
( ) ( )
1
2
3
11
3
3
2 3 4
jj
oj
j j j j
n
n
M u h u h
n
n
n
n
n
n n
n
n
n
−
−+
−
−
= + = +
− + −
− + −
0
16 7
50,5 .5 52,6
(16 7) ) (16 4
M
−
= + =
−−+
0,25
3
c
7
a) Tìm tập xc đnh của hm số sau:
22
sin
sin cos
=
−
x
y
xx
.
Điu kin xc đnh của hm số l
22
sin cos 0 cos2 0 2 ;
2 4 2
k
x x x x k x k
− − + +
.
0,25
Vậy tập xc đnh của hm số l
\;
42


= +


k
Dk
0,25
b) Giải phương trnh
( )
sin cos 1x
=
.
( )
sin cos 1 cos 2 ,
2
x x k k
= = +
1
cos 2 ,
2
x k k = +
0,25
Vì
1 cos 1x−
nên
1 3 1
1 2 1
2 4 4
kk− + −
.
Do
0kk =
suy ra
1
cos 2 ,
23
x x m m
= = +
.
0,25
3
8
Người ta trồng
2145
cây theo hình một tam gic như sau: hng thứ nht có
1
cây, hng thứ hai có
2
cây, hng thứ ba có 3 cây,… Hỏi có tt cả bao nhiêu hng cây?
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Gọi số hng cây l
n
, hng thứ
n
có
n
cây.
0,25
Ta có
1 2 3 ... 2145n+ + + + =
0,25
( )
1
2145
2
nn+
=
.
0,25
65n=
0,25
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Trên đường tròn lượng giác, cho góc lượng giác có số đo
2
thì mọi góc lượng giác có cùng tia
đầu và tia cuối với góc lượng giác trên đều có số đo dạng
A.
2
. B.
( )
,
22
kk

+
. C.
( )
2,
2
kk
+
. D.
( )
,
2
kk
+
.
Câu 2: Trên đường tròn có bán kính
5r =
cm, độ dài của cung có số đo
8
là
A.
8
l
=
cm. B.
40
l
=
cm. C.
5
8
l
=
cm. D.
5.180
8
l =
cm.
Câu 3: Biểu thức
sin cos cos sinx y x y−
bằng
A.
( )
cos xy−
. B.
( )
cos xy+
. C.
( )
sin xy−
. D.
( )
sin yx−
.
Câu 4: Cho góc lượng giác
.a
Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
2
cos2 1 2sinaa=−
. B.
22
cos2 cos sina a a=−
.
C.
2
cos2 1 2cosaa=−
. D.
2
cos2 2cos 1aa=−
.
Câu 5: Tìm tập xác định của hàm số
tanyx=
.
A.
\|
2
kk

+


. B.
\|kk
.
C.
\ 2 |
2
kk

+


. D.
\ 2 |kk
.
Câu 6: Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A.
tanyx=
. B.
2
2024yx=+
. C.
sinyx=
. D.
cosyx=
.
Câu 7: Nghiệm của phương trình
sin sin
3
x
=
là
A.
( )
2
3
2
3
xk
k
xk
=+
= − +
. B.
( )
2
3
2
2
3
xk
k
xk
=+
=+
.
C.
( )
3
x k k
= +
. D.
( )
3
2
3
xk
k
xk
=+
=+
.
Câu 8: Cho các dãy số sau, dãy số nào là dãy số vô hạn?
A.
0,2,4,6,8,10.
B.
1 1 1 1
1, , , ,..., ,...
2 4 8 2
n
C.
1,4,9,16,25.
D.
1,1,1,1,1.
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
04
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 9: Cho dãy số:
5;10;15;20;25;...
Số hạng tổng quát của dãy số này là
A.
5( 1)
n
un=−
. B.
5
n
un=
. C.
5
n
un=+
. D.
51
n
un=+
.
Câu 10: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A.
1; 2; 4; 6; 8−−−−
. B.
1; 3; 6; 9; 12.− − − −
C.
1; 3; 7; 11; 15.− − − −
D.
1; 3; 5; 7; 9− − − −
.
Câu 11: Cho cấp số cộng
( )
n
u
với
52
n
un=−
. Tìm công sai của cấp số cộng.
A.
3d =
. B.
2d =−
. C.
1d =
. D.
2d =
.
Câu 12: Cho cấp số cộng
( )
n
u
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng
A.
6.
B.
9.
C.
4.
D.
5.
Câu 13: Cho các dãy số sau. Dãy số nào là dãy số giảm?
A.
1; 1; 1; 1; 1; 1.
B.
1 1 1 1
1; ; ; ; .
2 4 8 16
−−
C.
1; 3; 5; 7.
D.
11; 9; 7; 5; 3.
Câu 14: Cho dãy số
( )
n
u
có
1
n
u
n
=
. Khẳng định nào sau đây sai?
A.
1
1u =
. B. Dãy số
( )
n
u
là dãy số tăng.
C. Dãy số
( )
n
u
bị chặn trên bởi 1. D. Dãy số
( )
n
u
là dãy số giảm.
Câu 15: Cho dãy số
( )
n
u
có
21
1
n
n
u
n
−
=
+
. Khi đó,
2
u
bằng:
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 16: Đo chiều cao (tính bằng cm) của
500
học sinh trong một trường THPT ta thu được kết quả như
sau:
Các em có chiều cao 170 cm được xếp vào nhóm:
A.
)
155;160
. B.
)
160;165
. C.
)
165;170
. D.
)
170;175
.
Câu 17: Trong mẫu số liệu ghép nhóm, giá trị đại diện
i
x
của nhóm
)
1
;
ii
aa
+
được tính bằng công thức
A.
1
2
ii
i
aa
x
+
+
=
. B.
1
2
ii
i
aa
x
+
−
=
. C.
1i i i
x a a
+
=+
. D.
1i i i
x a a
+
=−
.
Câu 18: Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành hai phần, mỗi
phần chứa
50%
giá trị?
A. số trung vị. B. số trung bình. C. mốt. D. tứ phân vị.
Câu 19: Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành bốn phần, mỗi
phần chứa
25%
giá trị?
A. số trung vị. B. số trung bình. C. mốt. D. tứ phân vị.
Câu 20: Khẳng định nào sau đây sai?
A. Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc.
B. Mốt của mẫu số liệu ghép nhóm bằng mốt của mẫu số liệu gốc.
C. Mốt là một trong các số đặc trưng để đo xu thế trung tâm của mẫu số liệu.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
D. Mốt của mẫu số liệu là các giá trị xuất hiện với tần số lớn nhất.
Câu 21: Cho
1
cos
2
=
và
3
2
2


. Tính
sin
.
A.
3
2
−
. B.
3
2
. C.
2
2
. D.
2
2
−
.
Câu 22: Cho
tan 2
=
. Tính
tan
4

−


.
A.
1
3
−
. B.
1
. C.
2
3
. D.
1
3
.
Câu 23: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
4sin cos 1y x x=+
. Tính
Mm+
.
A.
2
. B.
4
. C.
3
. D.
1−
.
Câu 24: Cung lượng giác có điểm biểu diễn là
12
,MM
như hình vẽ là nghiệm của phương trình lượng
giác nào sau đây?
A.
sin 0
3
x

−=


. B.
sin 0x =
. C.
cos 0
3
x

−=


. D.
sin 0
3
x

+=


.
Câu 25: Cho dãy số
n
u
xác định bởi
1
1
2
.
1
1
3
nn
u
uu
Tìm số hạng
3
.u
A.
3
5
.
9
u
B.
3
1.u
C.
3
2
.
3
u
D.
3
14
.
27
u
Câu 26: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
0,1u =−
và công sai
0,1d =
. Số hạng thứ 7 của cấp số
cộng này là
A.
1,6
. B.
6
. C.
0,5
. D.
0,6
.
Câu 27: Cho cấp số nhân có các số hạng lần lượt là
3; ; 27; 81;...x
Tìm
x
.
A.
9−
. B. 9. C.
81−
. D.
81
.
Câu 28: Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết
quả sau:
Tính tổng số học sinh được khảo sát.
A. 40. B. 15. C. 20. D. 5.
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 29: Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết
quả sau:
Thời gian xem tivi trung bình trong tuần trước của các bạn học sinh này là
A. 9,5 giờ. B. 11,5 giờ. C. 7,5 giờ. D. 15 giờ.
Câu 30: Doanh thu bán hàng trong 30 ngày của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu
đồng):
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là
A.
)
7;9
. B.
)
5;7
. C.
)
9;11
. D.
)
9;11
.
Câu 31: Tìm tập xác định
D
của hàm số
tan 2
4
yx

=−


.
A.
3
\,
82
k
Dk


= +


. B.
3
\,
4
D k k

= +


.
C.
3
\,
42
k
Dk


= +


. D.
\,
2
D k k

= +


.
Câu 32: Phương trình
2sin 3 0x +=
có tổng nghiệm dương nhỏ nhất và nghiệm âm lớn nhất bằng
A.
4
3
. B.
2
. C.
3
. D.
.
Câu 33: Cho dãy số
( )
n
u
là cấp số cộng có
1
1; 2.ud= − =
Tìm
n
biết
483.
n
S =
A.
20=n
. B.
21=n
. C.
22=n
. D.
23=n
.
Câu 34: Cho cấp số nhân
( )
n
u
có
1
1; 2uq= = −
. Tổng của 10 số hạng đầu tiên của cấp số nhân đó bằng
A.
341−
B.
341
C.
1023
D.
1023−
Câu 35: Đo chiều cao (tính bằng cm) của
500
học sinh trong một trường THPT ta thu được kết quả như
sau:
Tính mốt của mẫu số liệu ghép nhóm trên.
A. 160. B. 164,05. C. 162,5. D. 160,94.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1: (1,0 điểm)
a) Cho
12
sin
13
=
với
2


. Tính
sin 2
.
b) Tìm tập xác định của hàm số
cos
sin 1
x
y
x
=
−
.
Câu 2: (1,0 điểm) Giải phương trình
5 4cos2 6sin .sin3x x x−=
.
Câu 3: (1,0 điểm) Ước tính dân số năm 2022 của thành phố Đà Nẵng là 579 914 người, tỷ lệ tăng dân
số 1,5% so với năm trước. Nếu lấy kết quả chính xác đến hàng nghìn thì dân số của thành phố
Đà Nẵng năm 2030 là bao nhiêu?
-----------------------HẾT-----------------------
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
BẢNG ĐÁP ÁN
1.C
2.C
3.C
4.C
5.A
6.B
7.B
8.B
9.B
10.C
11.B
12.D
13.D
14.B
15.A
16.D
17.A
18.A
19.D
20.B
21.A
22.D
23.A
24.A
25.C
26.C
27.B
28.A
29.A
30.A
31.A
32.D
33.D
34.A
35.B
PHẦN TỰ LUẬN
Câu
Ý
Đáp án
Điểm
1
(1,0 điểm)
a
2
22
12 25 5
cos 1 sin 1 cos
13 169 13

= − = − = =


Vì
2


nên
cos 0
. Suy ra
5
cos
13
=−
0,25
12 5 120
sin2 2sin .cos 2. .
13 13 169

= = − = −


0,25
b
Hàm số
os
sin 1
cx
y
x
=
−
xác định khi và chỉ khi
sin 1 2 ,
2
x x k k
+
0,25
Tập xác định của hàm số đã cho là
\ 2 ,
2
D k k

= +


0,25
2
(1,0 điểm)
Ta có:
3
3cos4x = 6sinx.sin3x
2
−
3
3cos4 3(cos2 cos4 )
2
− = −x x x
0,25
3
3cos2
2
=x
0,25
1
cos2
2
x =
0,25
x k ,k
6
= +
0,25
3
(1,0 điểm)
Đặt P
0
= 579914 và r = 1,5% = 0,015
Gọi P
n
là dân số của thành phố Đà Nẵng sau n năm nữa.
0,25
Sau 1 năm, dân số của tỉnh là:
1 0 0 0
P = P +P .r P (1+ r )=
Sau 2 năm, dân số của tỉnh là:
2
2 1 1 0
P = P + P .r P (1+r)=
…
0,25
Sau n năm, dân số của tỉnh là:
n
n n-1 n-1 0
P = P + P .r P (1+ r )=
Suy ra (P
n
) là một cấp số nhân với số hạng đầu P
0
và công bội q = 1+ r.
0,25
Do đó dân số của thành phố Đà Nẵng năm 2030 là:
88
80
P .(1 ) 579914.(1,015) 653000Pr= + =
người.
0,25
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1: Cung có số đo
250
thì có số đo theo đơn vị là radian là
A.
35
18
. B.
25
18
. C.
25
12
. D.
25
9
.
Câu 2: Cho góc
thỏa mãn
0
2

. Khẳng định nào sau đây đúng?
A.
sin 0
. B.
cot 0
. C.
sin 0
. D.
cos 0
.
Câu 3: Khẳng định nào sau đây đúng?
A.
22
sin cos 1

+=
. B.
22
sin cos 0

+=
.
C.
22
sin cos 2

+=
. D.
22
sin cos 1

+ = −
.
Câu 4:
sin 2a
bằng
A.
2sin .cosaa
. B.
sin a
. C.
cosa
. D.
cos2a
.
Câu 5: Chu kỳ tuần hoàn của hàm số
sinyx=
là
A.
2k
()k
. B.
2
. C.
. D.
2
.
Câu 6: Tập giá trị của hàm số
cos2023yx=
là
A.
1;1−
. B.
( 1;1)−
. C.
2023;2023−
. D.
11
;
22

−


.
Câu 7: Nghiệm của phương trình
tan 1x =
là
A.
,
4
x k k
= +
. B.
3
,
4
x k k
= +
.
C.
,x k k
=
. D.
,
2
x k k
= +
.
Câu 8: Cho dãy số
( )
n
u
xác định bởi
21
n
un=−
với
1n
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Câu 9: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6;4;2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Câu 10: Cho cấp số cộng
( )
n
u
với
1
3u =
và
2
5.u =
Công sai của cấp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 11: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
2
1
n
un=+
. B.
2
1
3
n
u
n
=−
. C.
sin
n
u n n=+
. D.
2
sin
n
un=
.
Câu 12: Cho
a
,
b
,
c
là ba số hạng liên tip của một cấp số cộng. Đẳng thc nào sau đây đúng?
A.
2
b ac=
. B.
2b a c=+
. C.
2a b c+=
. D.
2b c a+=
.
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
05
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 13: Dãy số nào sau đây là cấp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x
.
Câu 14: Cho cấp số cộng
( )
n
u
bit
6
48u =
và
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Câu 15: Cho cấp số nhân với và công bội . Tìm giá trị của bit số hạng tổng quát
.
A. . B. . C. . D. .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kt quả sau:
Nhóm
Chiều cao (cm)
Số học sinh
1
)
150;152
5
2
)
152;154
18
3
)
154;156
40
4
)
156;158
26
5
)
158;160
8
6
)
160;162
3
100N =
Giá trị đại diện của nhóm th tư là
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha trung vị của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
( )
n
u
1
3u =
2=−q
n
1536=−
n
u
8=n
9n =
257n =
10n =
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
T phân vị th nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8,6
.
Câu 21: Bit
4
sin
5
−
=
và
3
2


. Giá trị
cos
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
D.
9
.
5
Câu 22: Giá trị của biểu thc
sin
34
A


=+


là
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Câu 23: Hàm số nào sau đây là hàm số lẻ?
A.
2cosyx=−
. B.
2
2sin 2yx= − +
. C.
2sinyx=−
. D.
2cos 2yx= − +
.
Câu 24: Tập nghiệm của phương trình
cos 1x =−
là
A.
2 | .
2
S k k

= +

B.
2 | .
2
S k k

= − +

C.
2 | .S k k
=
D.
2 | .S k k

= +
Câu 25: Cho dãy số
1 1 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng liền trước nó). Công thc tổng
quát của dãy số đã cho là
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Câu 26: Cho cấp số cộng
( )
n
u
có
1
2; 5ud= = −
. Số hạng th
20
của cấp số cộng là
A.
93−
. B.
10
. C.
93
. D.
23
.
Câu 27: Cho cấp số nhân
( )
n
x
có
2
3x =−
và
4
27.x =−
Tính số hạng đầu
1
x
và công bội
q
của cấp số
nhân.
A.
1
1, 3xq= − = −
hoặc
1
1, 3.xq==
B.
1
1, 3xq= − =
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq= − =
D.
1
3, 1xq==
hoặc
1
3, 1.xq= − = −
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi
bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Nhóm cha trung vị là
A.
)
30;45
. B.
)
15;30
. C.
)
45;60
. D.
)
60;75
.
Câu 31: Một chic phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa
bởi hàm số
( )
5sin
5
h t t

=


, trong đó
( )
ht
là độ cao tính bằng cetimét trên mực nước biển
trung bình tại thời điểm
t
giây. Nu chic phao đang ở đỉnh của sóng thì trong bao lâu chic
phao lại ở vị trí đỉnh của cơn sóng tip theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm
số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
33
sin 3
42
x

−=


bằng
A.
.
9
B.
.
6
−
C.
.
6
D.
.
9
−
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng th nhất trồng
1
cây, hàng
th hai trồng
2
cây, hàng th ba trồng
3
cây, …, c tip tục trồng như th cho đn khi ht số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Câu 34: Một cấp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Bit
765
n
S =
. Tìm
n
.
A.
8n =
. B.
9n =
. C.
6n =
. D.
7n =
.
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đn nơi làm việc của các nhân viên một
công ty như sau:
T phân vị th nhất
1
Q
và t phân vị th ba
3
Q
của mẫu số liệu ghép nhóm này là
A.
13
1360 800
,
37 21
QQ==
. B.
13
1360 3280
,
37 83
QQ==
.
C.
13
136 3280
,
5 83
QQ==
. D.
13
136 800
,
5 21
QQ==
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1: (1,0 điểm)
a) Giải phương trình
cot 3
3
x

+=


.
b) Cho
2
sin
3
=
, tính giá trị của biểu thc
( )( )
1 3cos 1 3cosP

= − +
.
Câu 2: (1,0 điểm)
a) Giải phương trình
cos3 sin 2 0xx−=
.
b) Giải phương trình
sin cos
3
xx

=+


.
Câu 3: (1,0 điểm) Một công ty khoan ging đưa ra định mc giá như sau: Giá từ mét khoan đầu tiên là
100000
đồng và kể từ mét khoan th hai, giá mỗi mét tăng thêm
30000
đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan ging này để khoan ging sâu
20
mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan ging, gia đình đó
phải thanh toán cho cơ sở khoan ging số tiền bằng bao nhiêu?
-----------------------HẾT-----------------------
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
BẢNG ĐÁP ÁN
1.B
2.A
3.A
4.A
5.D
6.C
7.A
8.A
9.A
10.A
11.D
12.B
13.C
14.C
15.D
16.B
17.A
18.A
19.B
20.C
21.A
22.B
23.C
24.D
25.B
26.A
27.B
28.C
29.B
30.A
31.B
32.C
33.A
34.A
35.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cung có số đo
250
thì có số đo theo đơn vị là radian là
A.
35
18
. B.
25
18
. C.
25
12
. D.
25
9
.
Lời giải
Chọn B
Số đo theo đơn vị là radian là
0
0
250 . 25.
18
180

=
.
Câu 2: Cho góc
thỏa mãn
0
2

. Khẳng định nào sau đây đúng?
A.
sin 0
. B.
cot 0
. C.
sin 0
. D.
cos 0
.
Lời giải
Chọn A
Câu 3: Khẳng định nào sau đây đúng?
A.
22
sin cos 1

+=
. B.
22
sin cos 0

+=
.
C.
22
sin cos 2

+=
. D.
22
sin cos 1

+ = −
.
Lời giải
Chọn A
Câu 4:
sin 2a
bằng
A.
2sin .cosaa
. B.
sin a
. C.
cosa
. D.
cos2a
.
Lời giải
Chọn A
Câu 5: Chu kỳ tuần hoàn của hàm số
sinyx=
là
A.
2k
()k
. B.
2
. C.
. D.
2
.
Lời giải
Chọn D
Câu 6: Tập giá trị của hàm số
cos2023yx=
là
A.
1;1−
. B.
( 1;1)−
. C.
2023;2023−
. D.
11
;
22

−


.
Lời giải
Chọn C
Câu 7: Nghiệm của phương trình
tan 1x =
là
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
A.
,
4
x k k
= +
. B.
3
,
4
x k k
= +
.
C.
,x k k
=
. D.
,
2
x k k
= +
.
Lời giải
Chọn A
Ta có
tan 1 ,
4
x x k k
= = +
Câu 8: Cho dãy số
( )
n
u
xác định bởi
21
n
un=−
với
1n
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Lời giải
Chọn A
Ta có:
1
2.1 1 1u = − =
Câu 9: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6;4;2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Lời giải
Chọn A
Câu 10: Cho cấp số cộng
( )
n
u
với
1
3u =
và
2
5.u =
Công sai của cấp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Chọn A
Công sai của cấp số cộng
21
5 3 2d u u= − = − =
.
Câu 11: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
2
1
n
un=+
. B.
2
1
3
n
u
n
=−
. C.
sin
n
u n n=+
. D.
2
sin
n
un=
.
Lời giải
Chọn D
Với mọi
*
,n
ta có
2
1 sin 1 0 sin 1nn−
nên dãy số đã cho bị chặn.
Phân tch phương n nhiu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
Câu 12: Cho
a
,
b
,
c
là ba số hạng liên tip của một cấp số cộng. Đẳng thc nào sau đây đúng?
A.
2
b ac=
. B.
2b a c=+
. C.
2a b c+=
. D.
2b c a+=
.
Lời giải
Chọn B
Phân tch phương n nhiu:
8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt th tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x
.
Lời giải
Chọn C
6 3.2=
,
12 6.2=
,
24 12.2=
.
Phân tch phương n nhiu:
A. Sai do thay
21
:2uu=−
nhưng
43
:2uu=
.
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội
11q =
.
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng
( )
n
u
bit
6
48u =
và
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Lời giải
Chọn C
Ta có:
6
11
48
83
u
u
=
=
1
1
5 48
10 83
ud
ud
+=
+=
1
13
7
u
d
=
=
.
Phân tch phương n nhiu:
A. Sai vì đặt nhầm th tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm th tự
của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân với và công bội . Tìm giá trị của bit số hạng tổng quát
?
A. . B. . C. . D. .
Lời giải
Chọn D
.
.
Phân tch phương n nhiu:
A. Sai do tính .
B. Sai do nhầm công thc số hạng tổng quát .
C. Sai do tính .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kt quả sau:
( )
n
u
1
3u =
2=−q
n
1536=−
n
u
8=n
9n =
257n =
10n =
11
1
1536 . 1536 3.( 2) 1536
−−
= − = − − = −
nn
n
u u q
( )
9
1
( 2) 512 2 10
−
− = − = − =
n
n
( )
1
2 512
−
− = −
n
( )
( )
2
512 2 512:( 2) 256
2
−
= − − = − − =
−
n
n
8n=
( )
1
. 1536 2 512 9
n
n
u q n= − − = − =
( )
1
512
2 512 1 256 257
2
−
−
− = − − = = =
−
n
nn
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Nhóm
Chiều cao (cm)
Số học sinh
1
)
150;152
5
2
)
152;154
18
3
)
154;156
40
4
)
156;158
26
5
)
158;160
8
6
)
160;162
3
100N =
Giá trị đại diện của nhóm th tư là
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Lời giải
Chọn B
Giá trị đại diện của nhóm th tư là
156 158
157
2
+
=
.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Lời giải
Chọn A
Mốt
0
M
cha trong nhóm
[40;60)
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha trung vị của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Lời giải
Chọn A
Ta có:
42n =
Nên trung vị của mẫu số liệu trên là
21 22
2
2
xx
Q
+
=
Mà
)
21 22
, 40;60xx
Vậy nhóm cha trung vị của mẫu số liệu trên là
nhóm
[40;60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Lời giải
Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là
Số trung bình:
2.6 7.8 7.10 3.12 1.14
9,4
20
x
+ + + +
==
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
T phân vị th nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8,6
.
Lời giải
Chọn C
Gọi
1 2 20
, ,...,x x x
là doanh thu bán hàng trong 20 ngày xp theo th tự không giảm.
Khi đó:
)
12
, 5;7xx
,
)
39
,..., 7; 9xx
,,
)
9 16
,..., 9; 11xx
)
17 19
,..., 11; 13xx
,
)
20
13; 15x
Do đó, t phân vị th nhất
của mẫu số liệu thuộc nhóm
)
7;9
1
20, 7, 2, 7, 9
m m m
n n C u u
+
= = = = =
1
1.20
2
4
7 ( )
7
89 7 7,86Q −=+
−
Câu 21: Bit
4
sin
5
−
=
và
3
2


. Giá trị
cos
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
D.
9
.
5
Lời giải
Chọn A
Vì
3π
πα
2

nên
cosα0
. Mặt khác
22
sin α cos α 1+=
ta có
2
cosα 1 sin α= − −
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
2
1
43
55

= − − − = −


.
Câu 22: Giá trị của biểu thc
sin
34
A


=+


là
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Lời giải
Chọn B
Ta có
3 2 2 1 6 2
sin sin cos sin cos . . .
3 4 3 4 4 3 2 2 2 2 4
A
+

= + = + = + =


Câu 23: Hàm số nào sau đây là hàm số lẻ?
A.
2cosyx=−
. B.
2
2sin 2yx= − +
. C.
2sinyx=−
. D.
2cos 2yx= − +
.
Lời giải
Chọn C
Tập xác định của hàm số
( )
2siny f x x= = −
là
D =
.
Do đó, nu
x
thuộc tập xác định
D
thì
x−
cũng thuộc tập xác định
D
.
Ta có
( ) ( )
2sin( ) sinf x x x f x− = − − = = −
. Vậy
2sinyx=−
là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình
cos 1x =−
là
A.
2 | .
2
S k k

= +

B.
2 | .
2
S k k

= − +

C.
2 | .S k k
=
D.
2 | .S k k

= +
Lời giải
Chọn D
Ta có
cos 1 2 ,x x k k

= − = +
.
Câu 25: Cho dãy số
1 1 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng liền trước nó). Công thc tổng
quát của dãy số đã cho là
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Lời giải
Chọn D
Câu 26: Cho cấp số cộng
( )
n
u
có
1
2; 5ud= = −
. Số hạng th
20
của cấp số cộng là
A.
93−
. B.
10
. C.
93
. D.
23
.
Lời giải
Chọn D
20 1
19 2 19( 5) 93u u d= + = + − = −
.
12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 27: Cho cấp số nhân
( )
n
x
có
2
3x =−
và
4
27.x =−
Tính số hạng đầu
1
x
và công bội
q
của cấp số
nhân.
A.
1
1, 3xq= − = −
hoặc
1
1, 3.xq==
B.
1
1, 3xq= − =
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq= − =
D.
1
3, 1xq==
hoặc
1
3, 1.xq= − = −
Lời giải
Chọn B
2
21
3
4 1 1
1
9
3 3 3
3
27. 27. 1.
.
q
x x q q
x x q x
x
q
=
= − = − =


= − = − =
=−


Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi
bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Lời giải
Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp
)
6,5;8
nên giá trị đại diện là
6,5 8
7,25
2
+
=
.
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu
)
5;7
)
7;9
)
9;11
)
11;13
)
13;15
Số ngày
2
7
7
3
1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Lời giải
Chọn B
Số trung bình của mẫu số liệu trên là:
6.2 8.7 10.7 12.3 14.1
9,4
20
x
+ + + +
==
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Nhóm cha trung vị là
A.
)
30;45
. B.
)
15;30
. C.
)
45;60
. D.
)
60;75
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Lời giải
Chọn A
Cỡ mẫu:
9 5 15 14 7 50n = + + + + =
.
Gọi
1 50
,...,xx
là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy
này đã được sắp xp theo th tự tăng dần. Khi đó, trung vị là
25 26
2
xx+
. Do hai giá trị
25 26
,xx
thuộc nhóm
)
30;45
.
Câu 31: Một chic phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa
bởi hàm số
( )
5sin
5
h t t

=


, trong đó
( )
ht
là độ cao tính bằng cetimét trên mực nước biển
trung bình tại thời điểm
t
giây. Nu chic phao đang ở đỉnh của sóng thì trong bao lâu chic
phao lại ở vị trí đỉnh của cơn sóng tip theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm
số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Lời giải
Chọn B
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số
( )
5sin
5
h t t

=


nên để chic phao
ở vị trí đỉnh ở hai lần liên tip thì cách nhau một chu kì của sóng
( )
2
10
5
Ts
==
.
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
33
sin 3
42
x

−=


bằng:
A.
.
9
B.
.
6
−
C.
.
6
D.
.
9
−
Lời giải
Chọn C
Ta có
3
32
3 3 3
43
sin 3 sin 3 sin
3
4 2 4 3
32
43
xk
xx
xk



− = +
− = − =
− = − +
.
( )
13 2
13
32
36 3
12
.
17 17 2
32
12 36 3
xk
xk
kZ
x k x k

=+
=+
= + = +
TH1. Với
min
max
13 13
00
13 2
24 36
.
13 11
36 3
01
24 36
Cho
x k k x
xk
x k k x

− = → =
= + ⎯⎯→
− = − → = −
14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
TH2. Với
min
max
17 17
00
17 2
24 36
.
17 7
36 3
01
24 36
Cho
x k k x
xk
x k k x

− = → =
= + ⎯⎯→
− = − → = −
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là
7
36
x
=−
và nghiệm dương nhỏ nhất là
13
.
36
x
=
Khi đó tổng hai nghiệm bằng
13 7
.
36 36 6
−=
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng th nhất trồng
1
cây, hàng
th hai trồng
2
cây, hàng th ba trồng
3
cây, …, c tip tục trồng như th cho đn khi ht số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Lời giải
Chọn A
Gọi số cây ở hàng th
n
là
n
u
.
Ta có:
1
1u =
,
2
2u =
,
3
3u =
, … và
1 2 3
... 3003
n
S u u u u= + + + + =
.
Nhận xét dãy số
( )
n
u
là cấp số cộng có
1
1u =
, công sai
1d =
.
Khi đó
( )
1
21
2
n u n d
S
+−


=
3003=
( )
2.1 1 1
3003
2
nn+−


=
( )
1 6006nn + =
2
6006 0nn + − =
77
78
n
n
=
=−
77n=
(vì
n
).
Câu 34: Một cấp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Bit
765
n
S =
. Tìm
n
?
A.
8n =
. B.
9n =
. C.
6n =
. D.
7n =
.
Lời giải
Chọn A
Áp dụng công thc của cấp số nhân ta có:
( ) ( )
1
1 3. 1 2
765
1 1 2
nn
n
uq
S
q
−−
= = =
−−
8n=
.
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đn nơi làm việc của các nhân viên một
công ty như sau:
Thời gian
)
15;20
)
20;25
)
25;30
)
30;35
)
35;40
)
40;45
)
45;50
Số nhân viên
7
14
25
37
21
14
10
T phân vị th nhất
1
Q
và t phân vị th ba
3
Q
của mẫu số liệu ghép nhóm này là
A.
13
1360 800
,
37 21
QQ==
. B.
13
1360 3280
,
37 83
QQ==
.
C.
13
136 3280
,
5 83
QQ==
. D.
13
136 800
,
5 21
QQ==
.
Lời giải
Chọn D
Cỡ mẫu là
128n =
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
T phân vị th nhất
1
Q
là
32 33
2
xx+
. Do
32 33
,xx
đều thuộc nhóm
[25;30)
nên nhóm này cha
1
Q
.
Do đó,
213 3 4 3
3; 25; 25; 21, 5p a m m am a= = = = − =+
và ta có
1
21
136
4
25
8
5
5
12
25
Q
−
= + =
Với t phân vị th ba
3
Q
là
96 97
2
xx+
. Do
96 97
,xx
đều thuộc nhóm
[35;40)
nên nhóm này cha
3
Q
.
Do đó,
125 5 4 6 53
5; 35; 21; 7 14 25 37 83; 5p a m m m m m a a= = = + + + = + + + = − =
và ta có
3
3.128
83
800
4
35 5
21 21
Q
−
= + =
.
16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
PHẦN TỰ LUẬN
Câu
Đp n
Biểu điểm
1.a
Giải phương trình
cot 3
3
x

+=


.
0.5
cot 3
3 3 6
x x k

+ = + = +


0.25
6
xk
= − +
()k
.
0.25
1.b
Cho
2
sin
3
=
, tính giá trị của biểu thức
(1 3cos )(1 3cos )P

= − +
.
0.5
( )
2
2
(1 3cos )(1 3cos ) 1 3cos 1 9cosP
= − + = − = −
.
0.25
2
sin
3
=
,
2 2 2
5
sin cos 1 cos
9
+ = =
.
5
1 9. 4
9
P = − = −
.
0.25
2.a
Giải phương trình
cos3 sin 2 0xx−=
.
1.0
cos3 sin2 0 cos3 sin2 cos3 cos 2
2
x x x x x x

− = = = −


0.25
3 2 2
2
x x k

= − +


0.25
52
2
2
2
xk
xk
=+
= − +
0.25
2
10 5
()
2
2
xk
k
xk

=+

= − +
0.25
2.b
Giải phương trình
sin cos
3
xx

=+


1.0
sin cos
3
cos cos
23
xx
xx


=+


− = +
0,25
( )
2
23
2
23
x x k
k
x x k


− = + +

− = − − +
0,25
22
6
xk
− = − +
( )
k
0,25
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
12
xk
= −
( )
k
.
0,25
3
Một cơ sở khoan giếng đưa ra định mức gi như sau: Gi từ mét khoan đầu
tiên là
100000
đồng và kể từ mét khoan thứ hai, gi mỗi mét tăng thêm
30000
đồng so với gi của mét khoan ngay trước đó. Một người muốn k hợp đồng với
cơ sở khoan giếng này để khoan giếng sâu
20
mét lấy nước dùng cho sinh hoạt
gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh ton
cho cơ sở khoan giếng số tiền bằng bao nhiêu?
0.5
Giá tiền mỗi mét khoan ging lập thành một cấp số cộng với
1
100000u =
(số tiền mét khoan đầu tiên),
21
30000uu=+
(số tiền mét khoan th hai),
3 2 1
30000 2.30000u u u= + = +
(số tiền mét khoan th ba)
…
20 19 1
30000 19.30000u u u= + = +
(số tiền mét khoan th 20),
và công sai
30000d =
.
0,25
Tổng chi phí cần phải thanh toán là
20 1 2 3 20
...S u u u u= + + + +
20(2.10000 19.30000)
2
+
=
7700000=
.
0,25
| 1/64
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống ĐỀ SỐ 01
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Trong không gian, cho hai mặt phẳng phân biệt ( ) và ( ) . Có bao nhiêu vị trí tương đối giữa ( ) và ( )? A. 4 . B. 3 . C. 1. D. 2 . Câu 2:
Tập xác định của hàm số y = tan x là:     A.
\  + k ,k   . B.
\  + k ,k   .  4   2    C.
\  + k2 ,k   . D.
\k , k   .  2  Câu 3:
Tập giá trị của hàm số y = sin x là A.  1 − ;  1 . B. 0;2 . C. . D. −2;2 . Câu 4: Cho dãy số (u
với số hạng tổng quát u = 2 − 3n giá trị u bằng n ) n 2021 A. 6061. B. −6065. C. −6061. D. 6065. Câu 5:
Hàm số y = cos x tuần hoàn với chu kỳ là A. 3 . B.  . C. 2 . D. . 2 Câu 6:
Cho hai đường thẳng phân biệt a,b và mặt phẳng (P) , trong đó a ⊥ (P) . Chọn khẳng định sai
trong các khẳng định sau
A. Nếu a ⊥ b thì b / / ( P) .
B. Nếu b / /a thì b ⊥ ( P) .
C. Nếu b ⊥ ( P) thì a / /b .
D. Nếu b  ( P) thì b ⊥ a . Câu 7:
Hàm số nào sau đây là hàm số chẵn?
A. y = tan x .
B. y = cot x .
C. y = sin x .
D. y = cos x . Câu 8:
Cho cấp số cộng (u có u = 1 và u = 3. Giá trị của u bằng: n ) 1 2 3 A. 6 . B. 9 . C. 4 . D. 5 . Câu 9:
Hàm số y = sin x đồng biến trên khoảng nào dưới đây?    A. (0; ) . B. (0;2 ) . C. 0;   . D. (  − ; ).  2    
Câu 10: Tìm giá trị lớn nhất của hàm số y = 2cos x − + 3   ?  3  A. 9 . B. 5 . C. 1. D. 7 .
Câu 11: Phương trình nào sau đây vô nghiệm
A. tan x = − 3 .
B. 2 − cos x = 3 .
C. cos 2x = 2 .
D. 2sin 2x = 1 . 1 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 12: Cho cấp số nhân (u
u = 1 và u = 3 . Giá trị của u n ) có 1 2 3 bằng A. 9 . B. 5 . C. 4 . D. 6 .
Câu 13: Tìm điều kiện của m để phương trình sau đây vô nghiệm m − cos x = 1.
A. 0  m  2 .
B. m  0 hoặc m  2 . C. −2  m  0 .
D. m  −2 hoặc m  0
Câu 14: Trên khoảng (0; ) , phương trình sin x = 1 có bao nhiêu nghiệm? A. 1. B. 2 . C. 3 . D. Vô số.
Câu 15: Tất cả các nghiệm của phương trình cot x = 0 là?    A.
+ k2 ,k  .
B.  + k 2 , k  . C.
+ k ,k  . D. −
+ k2 ,k  . 2 2 2
Câu 16: Cho phương trình 2
sin x + 3sin x − 4 = 0 . Ta đặt t = sin x , phương trình thu được có dạng A. 2
t − 3t − 4 = 0 . B. 2
t + 3t − 4 = 0 . C. 2
−t + 3t − 4 = 0 . D. 2
t + 3t + 4 = 0 .
Câu 17: Cho cấp số nhân (u với u = 2 và u = −16 . Công bội của cấp số nhân đã cho bằng n ) 1 4 A. 3 . B. 2 . C. 8 − . D. −2 .
Câu 18: Số nghiệm của phương trình 2 2
cos x − sin 2x = 1 + sin x trên khoảng (0;2 ) là A. 1. B. 2 . C. 3 . D. 4 .
Câu 19: Cho cấp số nhân (u biết u = 7, u = 56 . Tìm công bội q . n ) 4 10 A. q =  2 . B. q =  2 . C. q = 2 . D. q = 2 .
Câu 20: Cho đường thẳng a song song mặt phẳng ( ) . Mặt phẳng ( ) chứa a và cắt mặt phẳng ( )
theo giao tuyến d . Kết luận nào sau đây đúng?
A. a và d cắt nhau.
B. a và d trùng nhau.
C. a và d chéo nhau.
D. a và d song song.
Câu 21: Cho dãy số (u với 2
u = n + n + 1 với * n
. Số 21 là số hạng thứ bao nhiêu của dãy số đã cho? n ) n A. 5 . B. 3 . C. 6 . D. 4 .
Câu 22: Cho cấp số cộng (u có số hạng tổng quát là u = 3n − 2 . Tìm công sai d của cấp số cộng đó. n ) n
A. d = −3.
B. d = 3 .
C. d = 2 . D. d = −2 .
Câu 23: Tổng hai nghiệm dương nhỏ nhất của phương trình 2 4cos x = 1 là 7  5 A.  . B. . C. . D. . 3 6 3
Câu 24: Cho cấp số nhân (u có số hạng đầu u = 5 , công bội 1 q = . Khi đó 5 là số hạng thứ mấy n ) 1 3 59049 của cấp số nhân? A. 9. B. 10. C. 11. D. 12.
Câu 25: Các họ nghiệm của phương trình sin x = −sin 2x . k 2 2 A. x =
; x =  + k 2 .
B. x =  + k ; x = + k . 3 3  k 2 2 C. x = + k2; x = .
D. x = k ; x = + k . 2 3 3 2 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 26: Cho a và b lần lượt là số hạng thứ nhất và số hạng thứ năm của một cấp số cộng có công sai −
d  0 . Giá trị của b a bằng d A. 6 . B. 5 . C. 3 . D. 4 .
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
AD và BC . Giao tuyến của hai mặt phẳng ( SMN ) và ( SAC ) là
A. SG ( G là trung điểm AB ). B. SD .
C. SF ( F là trung điểm CD ).
D. SO ( O là tâm hình bình hành ABCD ).
Câu 28: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 1. B. Vô số. C. 2 . D. 3
Câu 29: Số điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình
2(sin x + cos x) + 4sin x cos x = 2 là A. 1. B. 2 . C. 3 . D. 4 .
Câu 30: Cho tứ diện ABCD . Gọi M là trung điểm của cạnh AD , G là trọng tâm tam giác ABD và N
là điểm thuộc cạnh BC sao cho NB = 2NC . Kết luận nào sau đây sai?
A. NG // ( BCM ) .
B. NG // ( ACD) .
C. NG và AB chéo nhau.
D. NG // CM .
Câu 31: Cho hình hộp ABC .
D A' B 'C ' D ' . Khẳng định nào sau đây sai?
A. ( ABC ) // ( A' D 'C ') .
B. ( AB ' D ') // ( BCA') .
C. ( ADD ' A') // ( BCC ' B ') .
D. ( AB ' D ') // ( BC ' D) .
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên đoạn AB ( M
khác A và khác B ). Qua M vẽ mặt phẳng ( ) song song với ( SBC ) . Thiết diện tạo bởi mặt
phẳng ( ) và hình chóp S.ABCD là hình gì? A. Hình thang. B. Hình bình hành. C. Hình tam giác. D. Ngũ giác.
Câu 33: Cho hình lăng trụ ABC.AB C
  . Gọi I , J , K lần lượt là trọng tâm của các tam giác ABC ,
AAC , AB C
  . Mặt phẳng nào sau đây song song với mặt phẳng (IJK ) ?
A. ( ABC) .
B. ( AAB) . C. ( BB C  ).
D. ( AAC ) .
Câu 34: Cho phương trình 3 sin 2x + cos 2x = 1. Phương trình trên có bao nhiêu nghiệm thuộc khoảng  3  0;  ?  2  A. 2 . B. 3 . C. 0 . D. 1.
Câu 35: Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của cạnh
bên SD . Gọi K là giao điểm của đường thẳng BM với mặt phẳng ( SAC ) . Khi đó tỷ số diện S tích SBK bằng SSMK A. 4 . B. 3 . C. 1. D. 2 . 3 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 36: (0,5 điểm) Tìm m để phương trình (2sin x − )
1 (2 cos 2x + 2sin x + m) = 1− 2 cos 2x có đúng hai
nghiệm thuộc 0; . Câu 37: (1,0 điểm)
a) Biết 3 số nguyên 3 , x , y theo thứ tự đó lập thành một cấp số nhân và 3 số x , y , 9 theo
thứ tự đó lập thành một cấp số cộng. Tìm x và y ?
b) Một quả bóng cao su từ độ cao 15 (m) so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên
một độ cao bằng hai phần năm độ cao lần rơi ngay trước đó. Biết rằng quả bóng luôn chuyển
động vuông góc với mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc
bóng không nảy nữa) bằng bao nhiêu?
Câu 38: (1,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi điểm I và
điểm M lần lượt là trung điểm của các đoạn thẳng SA và OC .
a) Xác định giao tuyến của hai mặt phẳng ( SAC ) và ( SBD) .
b) Gọi ( ) là mặt phẳng chứa đường thẳng IM và song song với đường thẳng BD . Xác định
thiết diện của mặt phẳng ( ) với hình chóp S.ABCD .
c) Giả sử mặt phẳng ( ) cắt đường thẳng SO tại điểm K . Tính tỉ số SK . KO
-----------------------HẾT----------------------- 4 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống BẢNG ĐÁP ÁN 1.D 2.B 3.A 4.C 5.C 6.A 7.D 8.D 9.C 10.B 11.C 12.A 13.B 14.A 15.C 16.B 17.D 18.C 19.B 20.D 21.D 22.B 23.A 24.C 25.A 26.D 27.D 28.A 29.B 30.A 31.B 32.A 33.C 34.B 35.D
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Trong không gian, cho hai mặt phẳng phân biệt ( ) và ( ) . Có bao nhiêu vị trí tương đối giữa ( ) và ( )? A. 4 . B. 3 . C. 1. D. 2 .
Lời giải Chọn D
Các vị trí tương đối giữa 2 mặt phẳng phân biệt là: song song, cắt nhau. Câu 2:
Tập xác định của hàm số y = tan x là:     A.
\  + k ,k Z  . B.
\  + k ,k Z  .  4   2    C.
\  + k2 ,k Z . D.
\k , k Z .  2  Lời giải Chọn B
Điều kiện xác định: cos x  0  x  + k 2  
Vậy tập xác định: D = \  + k,k Z .  2  Câu 3:
Tập giá trị của hàm số y = sin x là A.  1 − ;  1 . B. 0;2 . C. . D. −2;2 . Lời giải Chọn A
Hàm số y = sin x có tập giá trị là  1 − ;  1 . Câu 4: Cho dãy số (u
với số hạng tổng quát u = 2 − 3n giá trị u bằng n ) n 2021 A. 6061. B. −6065. C. −6061. D. 6065.
Lời giải Chọn C Ta có: u = 2 − 3.2021 = 606 − 1. 2021 Câu 5:
Hàm số y = cos x tuần hoàn với chu kỳ là A. 3 . B.  . C. 2 . D. . 2 5 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống Lời giải Chọn C
Hàm số y = cos x tuần hoàn với chu kỳ 2 . Câu 6:
Cho hai đường thẳng phân biệt a,b và mặt phẳng (P) , trong đó a ⊥ (P) . Chọn khẳng định sai
trong các khẳng định sau
A. Nếu a ⊥ b thì b / / ( P) .
B. Nếu b / /a thì b ⊥ ( P) .
C. Nếu b ⊥ ( P) thì a / /b .
D. Nếu b  ( P) thì b ⊥ a .
Lời giải Chọn A a ⊥ bb / /  (P) Nếu     đáp án A sai. a ⊥  (P) b   (P) Câu 7:
Hàm số nào sau đây là hàm số chẵn?
A. y = tan x .
B. y = cot x .
C. y = sin x .
D. y = cos x . Lời giải Chọn D
Hàm số y = cos x là hàm số chẵn. Câu 8:
Cho cấp số cộng (u có u = 1 và u = 3. Giá trị của u bằng: n ) 1 2 3 A. 6 . B. 9 . C. 4 . D. 5 .
Lời giải Chọn D
Áp dụng tính chất của cấp số cộng ta có: u + u = 2.u u = 2.u − u = 2.3 −1 = 5. 1 3 2 3 2 1 Câu 9:
Hàm số y = sin x đồng biến trên khoảng nào dưới đây?    A. (0; ) . B. (0;2 ) . C. 0;   . D. (  − ; ).  2  Lời giải Chọn C   
Hàm số y = sin x đồng biến trên khoảng hàm số 0;   .  2    
Câu 10: Tìm giá trị lớn nhất của hàm số y = 2cos x − + 3   ?  3  A. 9 . B. 5 . C. 1. D. 7 . Lời giải Chọn B          Ta có: 1 −  cos x −  1 2 −  2cos x −
 2 1  2cos x −
+ 3  5 1  y  5        3   3   3     
Vậy min y = 5  cos x −
= 1  x = + k2,k     3  3 6 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 11: Phương trình nào sau đây vô nghiệm
A. tan x = − 3 .
B. 2 − cos x = 3 .
C. cos 2x = 2 .
D. 2sin 2x = 1 . Lời giải Chọn C
Phương trình cos 2x = 2 vô nghiệm do 2  1 .
Câu 12: Cho cấp số nhân (u
u = 1 và u = 3 . Giá trị của u n ) có 1 2 3 bằng A. 9 . B. 5 . C. 4 . D. 6 .
Lời giải Chọn A Công bội của u ấp số nhân là 2 q = = 3 . Vậy 2 u = u q = 9 . 3 1 u1
Câu 13: Tìm điều kiện của m để phương trình sau đây vô nghiệm m − cos x = 1.
A. 0  m  2 .
B. m  0 hoặc m  2 . C. −2  m  0 .
D. m  −2 hoặc m  0 Lời giải Chọn B
Ta có: m − cos x = 1  cos x = m − 1 m −1  1 − m  0
Phương trình vô nghiệm khi và chỉ khi    . m −1  1 m  2
Câu 14: Trên khoảng (0; ) , phương trình sin x = 1 có bao nhiêu nghiệm? A. 1. B. 2 . C. 3 . D. Vô số. Lời giải Chọn A
sin x = 1  x = + k ,k  . 2 
Do x  (0; ) nên có 1 giá trị x =
thỏa mãn. Vậy phương trình có 1 nghiệm. 2
Câu 15: Tất cả các nghiệm của phương trình cot x = 0 là?    A.
+ k2 ,k  .
B.  + k 2 , k  . C.
+ k ,k  . D. −
+ k2 ,k  . 2 2 2 Lời giải Chọn C  Ta có: cot x = 0  + k ,k  . 2
Câu 16: Cho phương trình 2
sin x + 3sin x − 4 = 0 . Ta đặt t = sin x , phương trình thu được có dạng A. 2
t − 3t − 4 = 0 . B. 2
t + 3t − 4 = 0 . C. 2
−t + 3t − 4 = 0 . D. 2
t + 3t + 4 = 0 . Lời giải Chọn B Cho phương trình 2
sin x + 3sin x − 4 = 0 .
Đặt t = sin x , phương trình thu được có dạng 2
t + 3t − 4 = 0 .
Câu 17: Cho cấp số nhân (u với u = 2 và u = −16 . Công bội của cấp số nhân đã cho bằng n ) 1 4 A. 3 . B. 2 . C. 8 − . D. −2 . 7 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Lời giải Chọn D
Gọi công bội của cấp số nhân đã cho là q .
Theo công thức số hạng tổng quát của cấp số nhân ta có 3 3
u = u .q  16 −
= 2.q q = −2 . 4 1
Câu 18: Số nghiệm của phương trình 2 2
cos x − sin 2x = 1 + sin x trên khoảng (0;2 ) là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C Ta có: 2 2
cos x − sin 2x = 1 + sin x 2 2
 cos x − sin x − sin 2x = 1  cos 2x − sin 2x = 1   − = +   = −     2x k 2 x k 2   4 4  sin − 2x =       .  4  2    = − −  − x k 2x =  − + k2   4 4 4
0  −k  2  2 −  k  0   k −  1 Do 0  x  2      9 1  . 0  − − k  2 −  k  − k    2 − ;−  1  4  4 4
Vậy phương trình có 3 nghiệm thuộc khoảng (0;2 ) .
Câu 19: Cho cấp số nhân (u biết u = 7, u = 56 . Tìm công bội q . n ) 4 10 A. q =  2 . B. q =  2 . C. q = 2 . D. q = 2 . Lời giải Chọn B
Gọi u và q là số hạng đầu và công bội của cấp số nhân (u , u  0 , q  0 . n ) 1 1 3
u = u .q = 7 u 1 7 1 Ta có: 4 1  4  = = = 6
q = 8  q =  2 . 9  6 u = u q = 56  u q 56 8 10 1 10
Câu 20: Cho đường thẳng a song song mặt phẳng ( ) . Mặt phẳng ( ) chứa a và cắt mặt phẳng ( )
theo giao tuyến d . Kết luận nào sau đây đúng?
A. a và d cắt nhau.
B. a và d trùng nhau.
C. a và d chéo nhau.
D. a và d song song. Lời giải Chọn D.
Ta có a và d song song với nhau.
Câu 21: Cho dãy số (u với 2
u = n + n + 1 với * n
. Số 21 là số hạng thứ bao nhiêu của dãy số đã cho? n ) n A. 5 . B. 3 . C. 6 . D. 4 .
Lời giải Chọn D n = 4 Ta có 2 2
n + n + 1 = 21  n + n − 20 = 0   . n = 5 − Vì * n
nên ta chọn n = 4 .
Vậy số 21 là số hạng thứ tư của dãy số đã cho. 8 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 22: Cho cấp số cộng (u có số hạng tổng quát là u = 3n − 2 . Tìm công sai d của cấp số cộng đó. n ) n
A. d = −3.
B. d = 3 .
C. d = 2 . D. d = −2 .
Lời giải Chọn B Ta có u u 3 n 1 2 3n 2 3n 3 2 3n 2 3, n n 1 + − = + − − − = + − − + =   . n ( ) ( )
Suy ra công sai của cấp số cộng đã cho là d = 3 .
Câu 23: Tổng hai nghiệm dương nhỏ nhất của phương trình 2 4cos x = 1 là 7  5 A.  . B. . C. . D. . 3 6 3 Lời giải Chọn A 1  Ta có 2
4cos x = 1  2(1 + cos 2x) = 1  cos 2x = −  x =  + k . 2 3  
Vậy hai nghiệm dương nhỏ nhất của phương trình là 2 và . 3 3
Suy ra tổng hai nghiệm này là .
Câu 24: Cho cấp số nhân (u có số hạng đầu u = 5 , công bội 1 q = . Khi đó 5 là số hạng thứ mấy n ) 1 3 59049 của cấp số nhân? A. 9. B. 10. C. 11. D. 12.
Lời giải Chọn C n 1 − − 5  1  Ta có: n 1 u = u .q  = 5.  n = 11 n 1   59049  3  Vậy số 5
là số hạng thứ 11 của cấp số nhân. 59049
Câu 25: Các họ nghiệm của phương trình sin x = −sin 2x . k 2 2 A. x =
; x =  + k 2 .
B. x =  + k ; x = + k . 3 3  k 2 2 C. x = + k2; x = .
D. x = k ; x = + k . 2 3 3 Lời giải Chọn A k 2  = − +  =  x = − x x = (−x) 2x x k 2 x sin sin 2 sin 2 sin    3 .
2x =  + x + k2 
x =  + k2
Câu 26: Cho a và b lần lượt là số hạng thứ nhất và số hạng thứ năm của một cấp số cộng có công sai −
d  0 . Giá trị của b a bằng d A. 6 . B. 5 . C. 3 . D. 4 .
Lời giải Chọn D 9 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống b − a
Ta có b = a + 4d b − a = 4d  = 4 . d
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
AD và BC . Giao tuyến của hai mặt phẳng ( SMN ) và ( SAC ) là
A. SG ( G là trung điểm AB ). B. SD .
C. SF ( F là trung điểm CD ).
D. SO ( O là tâm hình bình hành ABCD ).
Lời giải Chọn D
Gọi O = MN AC O là tâm của hình bình hành ABCD . S   (SAC) (SMN ) Ta có 
SO = (SAC)  (SMN ) . O
 = MN AC O   (SAC)  (SMN )
Câu 28: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 1. B. Vô số. C. 2 . D. 3 Lời giải Chọn A
Chỉ có một mặt phẳng chứa a và song song với b .
Câu 29: Số điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình
2(sin x + cos x) + 4sin x cos x = 2 là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B
Đặt t = sin x + cos x , khi đó: t  − 2; 2    và 2
2sin x cos x = t −1 . t = 1
Phương trình đã cho trở thành: t + ( 2 2 2 t − ) 1 = 2 2
 2t + 2t − 4 = 0   . t = 2 −    So điều kiện ta nhận 2
t = 1  sin x + cos x = 1  sin x + =    4  2    x + = + k2  x = k2 4 4      .    x = + k2 x + =  − + k2   2 4 4
Vậy có 2 điểm biểu diễn các nghiệm của phương trình trên đường tròn lượng giác. 10 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 30: Cho tứ diện ABCD . Gọi M là trung điểm của cạnh AD , G là trọng tâm tam giác ABD và N
là điểm thuộc cạnh BC sao cho NB = 2NC . Kết luận nào sau đây sai?
A. NG // ( BCM ) .
B. NG // ( ACD) .
C. NG và AB chéo nhau.
D. NG // CM . Lời giải Chọn A
Ta có NG  ( BCM ) do NG không song song ( BCM ) .
Câu 31: Cho hình hộp ABC .
D A' B 'C ' D ' . Khẳng định nào sau đây sai?
A. ( ABC ) / / ( A' D 'C ') .
B. ( AB ' D ') / / ( BCA') .
C. ( ADD ' A') / / ( BCC ' B ') .
D. ( AB ' D ') / / ( BC ' D) . Lời giải Chọn B
Vì AB ' và A' B cắt nhau nên ( AB ' D ') / / ( BCA') là một khẳng định sai.
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên đoạn AB ( M
khác A và khác B ). Qua M vẽ mặt phẳng ( ) song song với ( SBC ) . Thiết diện tạo bởi mặt
phẳng ( ) và hình chóp S.ABCD là hình gì? A. Hình thang. B. Hình bình hành. C. Hình tam giác. D. Ngũ giác.
Lời giải Chọn A
Qua M vẽ mặt phẳng ( ) song song với ( SBC ) : MN / /BC ( N DC ) , MQ / /SB(Q SB),
QP / / AD / / BC ( P SD)
Vậy thiết diện là hình thang. 11 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 33: Cho hình lăng trụ ABC.AB C
  . Gọi I , J , K lần lượt là trọng tâm của các tam giác ABC ,
AAC , AB C
  . Mặt phẳng nào sau đây song song với mặt phẳng (IJK ) ?
A. ( ABC) .
B. ( AAB) . C. ( BB C  ).
D. ( AAC ) . Lời giải Chọn C
Do I , J , K lần lượt là trọng tâm của các tam giác ABC , AAC , AB C   nên: AI AJ 2 =
=  IJ // MN IJ //(BCC B  ) . AM AN 3
Tương tự: IK // (BCC B
 )  (IJK )//(BCC B
 ). Hay (IJK )//(BB C  ).
Câu 34: Cho phương trình 3 sin 2x + cos 2x = 1. Phương trình trên có bao nhiêu nghiệm thuộc khoảng  3  0;  ?  2  A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn B   
Ta có: 3 sin 2x + cos 2x = 3 1 1 1  sin 2x + cos 2x = 1  sin 2x + =   2 2 2  6  2    2x + = + k2  x = k 6 6   (  k  )   (k  )   5 x = + k 2x + = + k2    3 6 6  3     3      0 k  0 k  Với 3 2 2 x  0;   , ta có:    (k  ) .  2   3  1 7  0  + k   −  k   3 2  3 6
Với x = k . Chọn k = 1, suy ra x =     Với x =
+ k . Chọn k = 0 hoặc k = 1, suy ra x = hoặc 4 x = 3 3 3  4 Nên x     ; ;  .  3 3  12 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống   
Phương trình có 3 nghiệm thuộc khoảng 3 0;  .  2 
Câu 35: Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của cạnh
bên SD . Gọi K là giao điểm của đường thẳng BM với mặt phẳng ( SAC ) . Khi đó tỷ số diện S tích SBK bằng SSMK A. 4 . B. 3 . C. 1. D. 2 . Lời giải Chọn D
Ta có: (SBD)  (SAC ) = SO .
Xét ( SBD) có SO BM = K K là giao điểm của BM với ( SAC ) .
Trong SBD có BM , SO là hai đường trung tuyến.
Mặt khác BM SO = K K là trọng tâm của SBD  2KM = KB .
Ta có sin SKB = sin SKM . 1 SK. . KB sin SKB S KB Suy ra: SBK 2 = = = 2 . S 1 KM SMK
SK.KM .sin SKM 2 13 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm) Câu 1:
(0,5 điểm) Tìm m để phương trình (2sin x − )
1 (2 cos 2x + 2sin x + m) = 1− 2 cos 2x có đúng 2
nghiệm thuộc 0; . Lời giải Ta có: (2sin x − )
1 (2 cos 2x + 2sin x + m) = 1− 2 cos 2x  ( x − )( x + x + m) = − ( 2 2sin 1 2 cos 2 2sin 1 2 1− 2sin x)  ( x − )( x + x + m) 2 2sin 1 2 cos 2 2sin = 4sin x −1  (2sin x − )
1 (2 cos 2x + 2sin x + m) − (2sin x − ) 1 (2sin x + ) 1 = 0  (2sin x − )
1 (2cos 2x + 2sin x + m) − (2sin x + ) 1  = 0   (2sin x − )
1 (2 cos 2x + m − ) 1 = 0  1 sin x = ( ) 1 2sin x −1 = 0  2    
2cos 2x + m −1 = 0 1− m cos2x = (2)  2     x = + k2 x =   6 x  6 Phương trình ( ) 1   (k  ) 0;  ⎯⎯⎯→  . 5 5   x = + k2 x =  6  6
Để phương trình đã cho có đúng 2 nghiệm thuộc 0;  thì phương trình (2) vô nghiệm hoặc   chỉ có nghiệm 5 x = ; x = . 6 6 1− m 1  m  1 2 −
Trường hợp 1: Phương trình (2) vô nghiệm     . 1− m  m  3  1 −  2     1− m cos 2. =       6  2
Trường hợp 2: Phương trình (2) có hai nghiệm 5 x = ; x =    m = 0 6 6   5  1− m cos 2. =      6  2
Vậy để phương trình (2sin x − )
1 (2 cos 2x + 2sin x + m) = 1− 2 cos 2x có đúng 2 nghiệm thuộc m  −1   0;  thì m  3  . m = 0  Câu 2: (1,0 điểm)
a) Biết 3 số nguyên 3 , x , y theo thứ tự đó lập thành một cấp số nhân và 3 số x , y , 9 theo
thứ tự đó lập thành một cấp số cộng. Tìm x và y ? Lời giải
Do 3 số nguyên 3 , x , y theo thứ tự đó lập thành một cấp số nhân nên ta có: 2 2 x x = 3y  = y . 3 14 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống x + 9
Do 3 số x , y , 9 theo thứ tự đó lập thành một cấp số cộng nên ta có x + 9 = 2 y  = y (2) 2 Thay vào ta được x = 3 − 2 2 3x 27 2x 2x 3x 27 0  + =  − − =  9 
. Do x là số nguyên nên x = −3 thỏa mãn. x =  2 + Vậy x 9 x = 3 −  y = = 3 . 2
b) Một quả bóng cao su từ độ cao 15 (m) so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên
một độ cao bằng hai phần năm độ cao lần rơi ngay trước đó. Biết rằng quả bóng luôn chuyển
động vuông góc với mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc
bóng không nảy nữa) khoảng:
Lời giải
Ta có quãng đường bóng bay bằng tổng quảng đường bóng nảy lên và quãng đường bóng rơi xuống. 2
Vì mỗi lần bóng nảy lên bằng lần nảy trước nên ta có tổng quãng đường bóng nảy lên là 5 2 3 n 2  2   2   2  S = 15. +15. +15. + +15. + 1       5  5   5   5  2 2
Đây là tổng của cấp số nhân lùi vô hạn có số hạng đầu u = 15. = 6 và công bội q = . 1 5 5 2 3 n 2  2   2   2  6 Suy ra S = 15. +15. +15. + +15. + = = 10. 1       5  5   5   5 2  1− 5
Tổng quãng đường bóng rơi xuống bằng khoảng cách độ cao ban đầu và tổng quãng đường 2 3 n  2   2   2   2 
bóng nảy lên nên là S = 15 +15. +15. +15. + +15. + 2          5   5   5   5  2
Đây là tổng của cấp số nhân lùi vô hạn có số hạng đầu u = 15 và công bội q = . 1 5 2 3 n  2   2   2  15 Suy ra S = 15 +15. +15. + +15. + = = 25 . 2        5   5   5 2  1− 5
Vậy tổng quãng đường bóng bay là S + S = 10 + 25 = 35 m . 1 2 ( ) Câu 3:
(1,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi điểm I và
điểm M lần lượt là trung điểm của các đoạn thẳng SA và OC .
a) Xác định giao tuyến của hai mặt phẳng ( SAC ) và ( SBD) .
b) Gọi ( ) là mặt phẳng chứa đường thẳng IM và song song với đường thẳng BD . Xác định
thiết diện của mặt phẳng ( ) với hình chóp S.ABCD .
c) Giả sử mặt phẳng ( ) cắt đường thẳng SO tại điểm K . Tính tỉ số SK . KO
Lời giải 15 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
a) Xác định giao tuyến của hai mặt phẳng ( SAC ) và ( SBD) .
Ta có SO = (SAC )  (SBD) .
b) Gọi ( ) là mặt phẳng chứa đường thẳng IM và song song với đường thẳng BD . Xác định
thiết diện của mặt phẳng ( ) với hình chóp S.ABCD .
Gọi K = SO IM . Trong ( ABCD) kẻ Mx / /BD và trong (SBD) kẻ Ky / /BD .
Gọi E = Ky SD, F = Ky SB, P = Mx BC, Q = Mx CD .
Ta có thiết diện của ( ) và hình chóp là hình ngũ giác IFPQE .
c) Giả sử mặt phẳng ( ) cắt đường thẳng SO tại điểm K . Tính tỉ số SK . KO
Ta có K = SO IM .
Áp dụng định lí Menelaus trong tam giác KS MO IA SOA có . . =1. KO MA IS MO 1 IA KS 1 KS Mặt khác = và = 1 suy ra . .1 = 1  = 3 . MA 3 IS KO 3 KO
-----------------------HẾT----------------------- 16 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống ĐỀ SỐ 02
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Trong không gian, khẳng định nào trong các khẳng định sau là đúng?
A. Luôn có một mặt phẳng đi qua bốn điểm phân biệt không thẳng hàng.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung.
C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng.
D. Không có mặt phẳng nào đi qua hai đường thẳng cắt nhau. Câu 2:
Tập giá trị của hàm số y = sin 2x + 3 là: A. −1;  1 . B. 2;  3 . C. 3; 4 . D. 2; 4 . Câu 3:
Cho cấp số nhân (u có u = 2 và u = 6 . Giá trị của u bằng n ) 1 2 5 A. 8 . B. 12 . C. 162 . D. 81. Câu 4:
Tập xác định của hàm số y = sin x là A. D = . B. D =
\k ,   .   C. D =
\  + k ,   . D. D = \  0 .  2  Câu 5:
Cho khối chóp ABCD . Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC . Khẳng
định nào sau đây là khẳng định đúng?
A. Đường thẳng GE song song với đường thẳng CD .
B. Đường thẳng GE cắt đường thẳng CD .
C. Đường thẳng GE và đường thẳng AD cắt nhau.
D. Đường thẳng GE và đường thẳng CD chéo nhau. Câu 6:
Tập xác định của hàm số y = cot x là A. D = . B. D =
\k ,   .   C. D =
\  + k ,   . D. D = \  0 .  2  Câu 7:
Hàm số nào dưới đây có đồ thị đối xứng qua trục tung?
A. y = cos x .
B. y = cot x .
C. y = tan x .
D. y = sin x . 1 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống Câu 8:
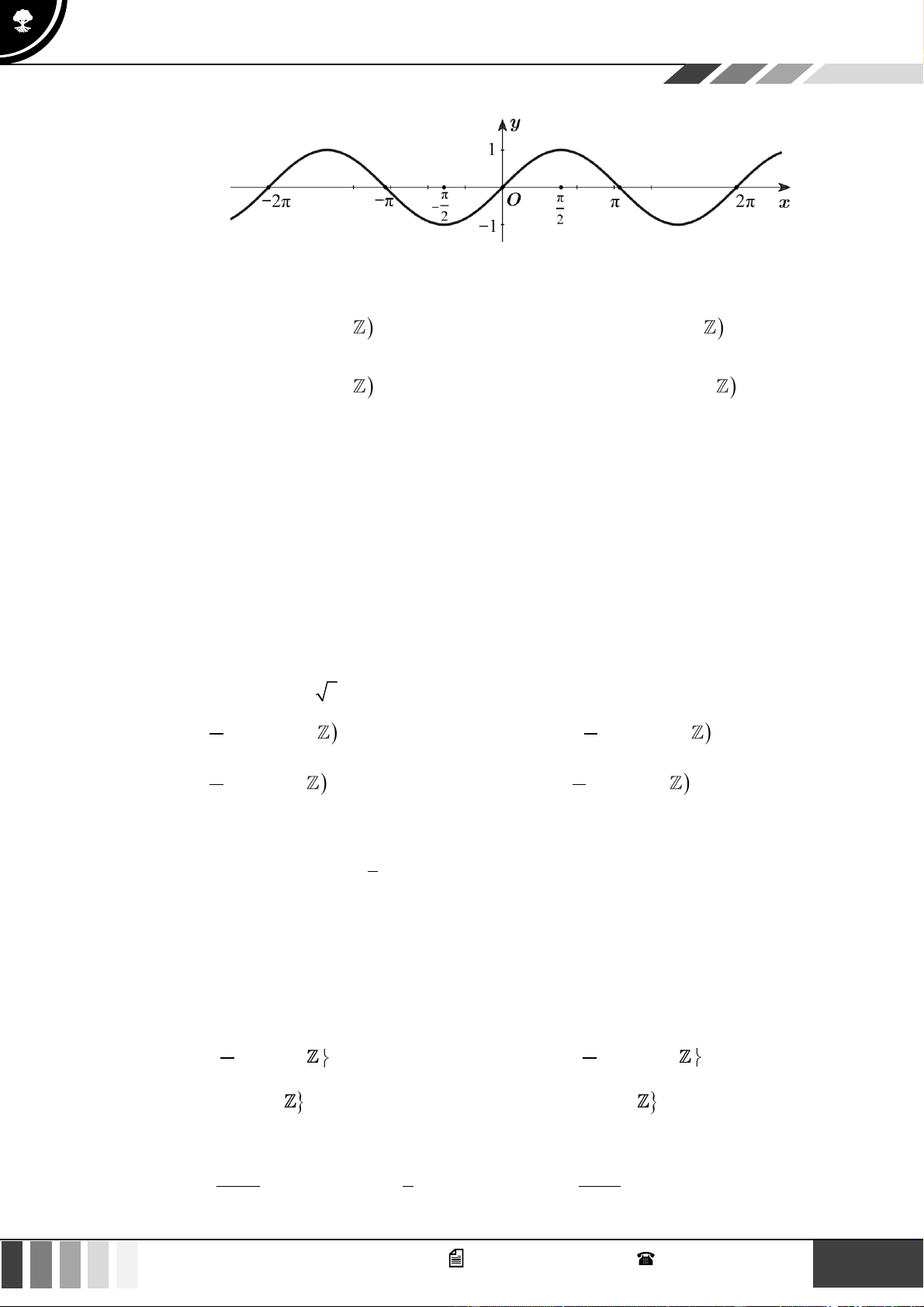
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào trong các hàm số sau?
A. y = sin x .
B. y = cos x .
C. y = tan x .
D. y = cot x . Câu 9:
Phương trình sin x = sin có nghiệm là:
x =  + k2
x =  + kA. , (k   ) . B. , (k   ) .
x =  − + k2
x =  − + k
x =  + k2
x =  + k2 C. , (k   ) . D. , (k   ) .
x =  + + k2
x =  − + k2
Câu 10: Mệnh đề nào sau đây sai?
A. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song
với mặt phẳng đã cho.
B. Hai mặt phẳng ( P) và (Q) được gọi là song song với nhau nếu chúng không có điểm chung.
C. Nếu mặt phẳng ( P) chứa hai đường thẳng a,b và a,b cùng song song với mặt phẳng (Q)
thì ( P) song song với (Q) .
D. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
Câu 11: Cho cấp số cộng (u có số hạng đầu và số hạng thứ tư lần lượt là 2;14 . Tìm công sai d ? n ) A. d = −4 . B. d = 3 . C. d = −3 . D. d = 4 .
Câu 12: Phương trình tan x = 3 có nghiệm là:   A. x =
+ k2 , (k  ). B. x = −
+ k2 , (k  ). 3 3   C. x =
+ k , (k  ) . D. x =
+ k , (k  ) . 6 3
Câu 13: Cho cấp số nhân (u với u = 2 u = 6 . Công bội của cấp số nhân này bằng n ) 1 2 1 A. 3 . B. . C. 4 . D. 12 . 3
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử M thuộc đoạn SB , mặt
phẳng ( ADM ) cắt hình chóp S.ABCD theo thiết diện là A. Tam giác. B. Hình thang.
C. Hình chữ nhật.
D. Hình bình hành.
Câu 15: Tập nghiệm của phương trình cot x = 0 là    
A. S =  + k , k   .
B. S =  + k2 , k  .  2   2 
C. S = k2 , k   .
D. S = k , k   .
Câu 16: Dãy (u nào sau đây là dãy số giảm? n ) 1 − 1 2 n −1 A. u = . B. u = − 2 . C. u = .
D. u = sin n . n 2n +1 n n n n n 2 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 17: Phương trình 3 tan 2x − 3 = 0 có nghiệm     A. x = + k (k  ). B. x = + k (k  ). 3 2 6 2   C. x =
+ k (k  ) . D. x =
+ k (k  ) . 6 3
Câu 18: Giá trị lớn nhất của hàm số y = 4 sin x cos x +1 là A. 4 . B. 3 . C. 1. D. 5 .
Câu 19: Cho ba số x −1 , x + 2 , x + 4 theo thứ tự lập thành một cấp số nhân. Giá trị của biểu thức
P = 2x −1 bằng A. 8 . B. 8 − . C. 20 . D. −17 .
Câu 20: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD . Khi đó giao tuyến của hai mặt phẳng
(SAD) và (SBC) là
A. Đường thẳng qua S song song với BC .
B. Đường thẳng SC .
C. Đường thẳng qua S song song với AB .
D. Đường thẳng SO , trong đó O là giao của AC và BD .
Câu 21: Cho phương trình 2 cos x +1 = 0 . Trên đoạn 0 ; 2  phương trình đã có bao nhiêu nghiệm? A. 0. B. 1. C. 3. D. 2.
Câu 22: Cho hai đường thẳng chéo nhau a và b . Lấy ,
A B thuộc a và C, D thuộc b . Khẳng định nào
sau đây đúng khi nói về hai đường thẳng AD và BC ?
A. Có thể song song hoặc cắt nhau.
B. Song song với nhau. C. Chéo nhau. D. Cắt nhau.
Câu 23: Số điểm biểu diễn các nghiệm của phương trình tan x − cot 2x = 0 trên đường tròn lượng giác là bao nhiêu? A. 4. B. 1. C. 3. D. 6.
Câu 24: Cho cấp số cộng (u
có u = 4 và u = 2 . Giá trị của u bằng n ) 2 4 6 A. u = 6 . B. u = 0 . C. u = −1 . D. u = 1 . 6 6 6 6
Câu 25: Phương trình nào dưới đây không là phương trình bậc hai đối với một hàm số lượng giác? A. 2
sin 2x + cos x = 1 . B. 2
tan x + 2 tan x + 3 = 0 . C. 2
sin x − 3 sin x +1 = 0 . D. 2
cos 2x − cos 2x − 2 = 0 .
Câu 26: Tập nghiệm của phương trình cos 2x + 3sin x − 2 = 0 là    
A. S = − + k2 ; + k2 , k   .  2 6    5 
B. S =  + k2 ;− + k2 ;−
+ k2 ,k   .  2 6 6     5 
C. S = − + k2 ; + k2 ;
+ k2 ,k Z .  2 6 6    5 
D. S =  + k2 ; + k2 ;
+ k2 ,k  .  2 6 6  3 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 27: Giải phương trình 2 tan x + ( 3 − ) 1 tan x − 3 = 0 .     x = + k  x = + k  4 4 A.  (k  )    . B. (k ).    x = − + k = − +   x k  3  6     x = + k  x = − + k  4 4 C.  (k  )    . D. (k ).    x = + k = − +   x k  6  3
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA . Thiết diện
của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là
A. Tứ giác IBCD .
B. Tam giác IBC .
C. Hình thang IJCB ( J là trung điểm SD ).
D. Hình thang IGBC ( G là trung điểm SB ).
Câu 29: Có bao nhiêu giá trị nguyên của tham số m để phương trình (m + )
1 sin 2x + 2 cos 2x = 2m có nghiệm A. 0. B. 1. C. 2 . D. 3.
Câu 30: Cho ba số x,1+ x, 6 − x theo thứ tự lập thành một cấp số cộng. Tìm x . A. 2 . B. 4 . C. 5 . D. 3 .
Câu 31: Cho hình hộp ABC . D AB CD
  . Gọi M là trung điểm của AB . Mặt phẳng (MA C  ) cắt cạnh
BC của hình hộp ABC . D AB CD
  tại N . Tính tỉ số MN
k = AC . 1 1 1 1 A. k = . B. k = . C. k = . D. k = . 2 2 2 2
Câu 32: Cho cấp số nhân (u biết u + u = 51 ; u + u = 102 . Hỏi số hạng 12288 là số hạng thứ bao n ) 1 5 2 6
nhiêu của cấp số nhân (u ? n ) A. 12 . B. 13 . C. 11. D. 10 .
Câu 33: Cho hình hộp ABC . D AB CD
  . Mặt phẳng ( AB D
 ) song song với mặt phẳng nào trong các mặt phẳng sau đây? A. ( BDA) . B. ( BC D  ).
C. ( AC C  ). D. ( BCA) .
Câu 34: Trong đại dịch Covid-19, người ta đã thống kê hết tháng 1 năm 2020, thế giới có 2100 người tử
vong, sau đó cứ tháng sau nhiều hơn tháng trước 1000 người tử vong. Đến hết tháng 12 năm
2020, tổng số người tử vong trên toàn thế giới là:
A. 91200 người.
B. 90000 người.
C. 81200 người.
D. 13100 người.
Câu 35: Cho hình hộp ABC . D AB CD
  . Một mặt phẳng ( ) cắt các cạnh bên AA , BB , CC , DD lần
lượt tại M , N, P,Q sao cho AM = 5, BN = 8,CP = 7. Khi đó dộ dài đoạn DQ bằng: A. 4. B. 6. C. 10. D. 5. 4 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm) Câu 1:
(0,5 điểm) Giải phương trình 2sin x cos x + 3 cos 2x = 3 Câu 2: (1,0 điểm)
a) Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1; đồng thời các số
x, 2 y, 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0 . Tìm q ?
b) Tỷ lệ tăng dân số của tỉnh X là 1,4% Biết rằng dân số tỉnh X hiện nay là 1,8 triệu người.
Hỏi với mức tăng như vậy thì sau 10 năm nữa dân số tỉnh X là bao nhiêu? Câu 3:
Cho hình chóp S.ABCD , đáy ABCD là hình thang ( AD // BC, AD BC ) . Gọi M , N lần lươt
là các điểm thuộc các cạnh SB, SC sao cho SM = 2MB, SN = 2NC.
a) Gọi K = AB C .
D Tìm thiết diện của hình chóp cắt bởi mặt phẳng ( KMN ) .
b) Cho AD = 2BC. Tính tỉ số diện tích của tam giác KMN và diện tích thiết diện vừa tìm ở câu trên.
-----------------------HẾT----------------------- 5 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống BẢNG ĐÁP ÁN 1.B 2.D 3.C 4.A 5.A 6.B 7.A 8.A 9.A 10.C 11.D 12.D 13.A 14.B 15.A 16.B 17.B 18.B 19.D 20.A 21.D 22.C 23.A 24.B 25.A 26.D 27.A 28.C 29.D 30.A 31.A 32.C 33.B 34.A 35.A
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Trong không gian, khẳng định nào trong các khẳng định sau là đúng?
A. Luôn có một mặt phẳng đi qua bốn điểm phân biệt không thẳng hàng.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung.
C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng.
D. Không có mặt phẳng nào đi qua hai đường thẳng cắt nhau. Lời giải Chọn B
Câu A sai vì không có mặt phẳng nào đi qua 4 đỉnh của một tứ diện.
Câu B đúng và đường thẳng đó được gọi là giao tuyến của hai mặt phẳng.
Câu C sai vì nếu điểm đó thuộc đường thẳng thì có vô số mặt phẳng chứa đường thẳng đó.
Câu D sai vì hai đường thẳng cắt nhau xác định một mặt phẳng. Câu 2:
Tập giá trị của hàm số y = sin 2x + 3 là: A. −1;  1 . B. 2;  3 . C. 3; 4 . D. 2; 4 . Lời giải Chọn D
Ta có −1  sin 2x  1  2  sin 2x + 3  4  2  y  4 .
Vậy tập giá trị của hàm số y = sin 2x + 3 là T = 2;4 . Câu 3:
Cho cấp số nhân (u có u = 2 và u = 6 . Giá trị của u bằng n ) 1 2 5 A. 8 . B. 12 . C. 162 . D. 81. Lời giải Chọn C Công bội: u 6 2 q = = = 3 nên 4 4
u = u q = 2.3 = 162 . u 5 1 1 2 Câu 4:
Tập xác định của hàm số y = sin x là A. D = . B. D =
\k ,   .   C. D =
\  + k ,   . D. D = \  0 .  2  Lời giải Chọn A
Tập xác định của hàm số y = sin x là D = . Câu 5:
Cho khối chóp ABCD . Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC . Khẳng
định nào sau đây là khẳng định đúng? 6 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
A. Đường thẳng GE song song với đường thẳng CD .
B. Đường thẳng GE cắt đường thẳng CD .
C. Đường thẳng GE và đường thẳng AD cắt nhau.
D. Đường thẳng GE và đường thẳng CD chéo nhau. Lời giải Chọn A
Gọi I là trung điểm của cạnh AB .
Do G và E lần lượt là trọng tâm của tam giác ABD và ABC nên ta có: IG IE 1 = =  GE//CD . ID IC 3 Câu 6:
Tập xác định của hàm số y = cot x là A. D = . B. D =
\k ,   .   C. D =
\  + k ,   . D. D = \  0 .  2  Lời giải Chọn B
Điều kiện: sin x  0  x k (k  ) . Câu 7:
Hàm số nào dưới đây có đồ thị đối xứng qua trục tung?
A. y = cos x .
B. y = cot x .
C. y = tan x .
D. y = sin x . Lời giải Chọn A
Hàm số y = cos x là hàm số chẵn nên có đồ thị đối xứng qua trục tung. 7 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống Câu 8:
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào trong các hàm số sau?
A. y = sin x .
B. y = cos x .
C. y = tan x .
D. y = cot x . Lời giải Chọn A
Dựa vào toạ độ các điểm trên đồ thị, ta xác định được đây là đồ thị hàm số y = sin x . Câu 9:
Phương trình sin x = sin có nghiệm là:
x =  + k2
x =  + kA. , (k   ) . B. , (k   ) .
x =  − + k2
x =  − + k
x =  + k2
x =  + k2 C. , (k   ) . D. , (k   ) .
x =  + + k2
x =  − + k2 Lời giải Chọn A
x =  + k2
Ta có sin x = sin  , (k   )
x =  − + k2
Câu 10: Mệnh đề nào sau đây sai?
A. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song
với mặt phẳng đã cho.
B. Hai mặt phẳng ( P) và (Q) được gọi là song song với nhau nếu chúng không có điểm chung.
C. Nếu mặt phẳng ( P) chứa hai đường thẳng a,b và a,b cùng song song với mặt phẳng (Q)
thì ( P) song song với (Q) .
D. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau. Lời giải Chọn C
Nếu a,b  (P) mà a,b cùng song song với (Q) và a song song b thì không suy ra được (P) song song với (Q) .
Câu 11: Cho cấp số cộng (u có số hạng đầu và số hạng thứ tư lần lượt là 2;14 . Tìm công sai d ? n ) A. d = −4 . B. d = 3 . C. d = −3 . D. d = 4 . Lời giải Chọn D 8 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống u  = 2 u  = 2 u  = 2 Ta có: 1 1 1      . u = 14 u + 3d = 14   d = 4 4 1
Câu 12: Phương trình tan x = 3 có nghiệm là:   A. x =
+ k2 , (k  ). B. x = −
+ k2 , (k  ). 3 3   C. x =
+ k , (k  ) . D. x =
+ k , (k  ) . 6 3 Lời giải Chọn D  
Ta có: tan x = 3  tan x = tan
x = + k ,(k  ). 3 3
Câu 13: Cho cấp số nhân (u với u = 2 u = 6 . Công bội của cấp số nhân này bằng n ) 1 2 1 A. 3 . B. . C. 4 . D. 12 . 3 Lời giải Chọn A
Công bội của cấp số nhân u 6 2 q = = = 3 . u 2 1
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử M thuộc đoạn SB , mặt
phẳng ( ADM ) cắt hình chóp S.ABCD theo thiết diện là A. Tam giác. B. Hình thang.
C. Hình chữ nhật.
D. Hình bình hành. Lời giải Chọn B
Mặt phẳng ( ADM ) cắt hình chóp S.ABCD theo thiết diện là hình thang MNDA .
Câu 15: Tập nghiệm của phương trình cot x = 0 là    
A. S =  + k , k   .
B. S =  + k2 , k  .  2   2 
C. S = k2 , k   .
D. S = k , k   . Lời giải Chọn A
Ta có cot x = 0  x = + k; k  . 2
Câu 16: Dãy (u nào sau đây là dãy số giảm? n ) 9 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống 1 − 1 2 n −1 A. u = . B. u = − 2 . C. u = .
D. u = sin n . n 2n +1 n n n n n Lời giải Chọn B Ta xét từng dãy 1 − 1 − 1 − Xét u = u = = n n 1 + 2n +1 2(n + ) 1 +1 2n + 3 1 − 1 − 2 u − u = − =
 0 do n * dãy tăng n 1 + n 2n + 3 2n +1 (2n+3)(2n+ ) ( ) 1 1 1 Xét u = − 2 u = − 2 n + n n 1 n +1 1 1 1 − u − u = − 2 − + 2 =
 0 do n * dãy giảm chọn B n 1 + n n +1 n n (n + ) ( ) 1 2 n −1 (n + )2 1 −1 Xét u = , u = n + n n 1 n +1 (n + )2 1 −1 n −1 (n+ )2 2 2 1 − n n + n +1 u − u = − = =
 0 do n * dãy tăng n 1 + n n +1 n n (n + ) 1 n (n + ) ( ) 1
Xét u = sin n , u = sin 3  0.14; u = sin 4  0 − .75;u = sin 6  0 − .27 không giảm không 3 ( ) 4 ( ) 6 ( ) n tang.
Câu 17: Phương trình 3 tan 2x − 3 = 0 có nghiệm     A. x = + k (k  ). B. x = + k (k  ). 3 2 6 2   C. x =
+ k (k  ) . D. x =
+ k (k  ) . 6 3 Lời giải Chọn B   
Ta có: 3 tan 2x − 3 = 0  tan 2x = 3  2x =
+ k  x = + k (k  ) . 3 6 2
Câu 18: Giá trị lớn nhất của hàm số y = 4 sin x cos x +1 là A. 4 . B. 3 . C. 1. D. 5 . Lời giải Chọn B
Ta có y = 2 sin 2x +1 . Do 1
−  sin 2x 1 2
−  2sin 2x  2  1
−  2sin 2x +1  3  −1  y  3. 
Vậy GTLN của hàm số là 3 khi sin 2x = 1  x = + k ,k  . 4
Câu 19: Cho ba số x −1 , x + 2 , x + 4 theo thứ tự lập thành một cấp số nhân. Giá trị của biểu thức
P = 2x −1 bằng A. 8 . B. 8 − . C. 20 . D. −17 . Lời giải Chọn D
Vì ba số x −1, x + 2 , x + 4 theo thứ tự lập thành một cấp số nhân nên 10 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống (x + )2 2
= (x −1)(x + 4) 2 2
x + 4x + 4 = x + 4x − x − 4  x = 8 − .
Suy ra P = 2x −1 = 2.( 8 − ) −1 = 17 − .
Câu 20: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD . Khi đó giao tuyến của hai mặt phẳng
(SAD) và (SBC) là
A. Đường thẳng qua S song song với BC .
B. Đường thẳng SC .
C. Đường thẳng qua S song song với AB .
D. Đường thẳng SO , trong đó O là giao của AC và BD . Lời giải Chọn A
Ta có: Mặt phẳng (SAD) và (SBC) có điểm chung S và lần lượt chứa hai đường thẳng song
song AD, BC nên có giao tuyến là đường thẳng qua S và song song với AD, BC .
Câu 21: Cho phương trình 2 cos x +1 = 0 . Trên đoạn 0 ; 2  phương trình đã có bao nhiêu nghiệm? A. 0. B. 1. C. 3. D. 2. Lời giải Chọn D  2 x = + k2 1  3
Ta có: 2 cos x +1 = 0  cos x = −   , k  . 2 2 x = − + k2  3
Biểu diễn các nghiệm lên đường tròn lượng giác ta được 2 điểm. Do vậy trên đoạn0 ; 2 
phương trình đã có 2 nghiệm.
Câu 22: Cho hai đường thẳng chéo nhau a và b . Lấy ,
A B thuộc a và C, D thuộc b . Khẳng định nào
sau đây đúng khi nói về hai đường thẳng AD và BC ?
A. Có thể song song hoặc cắt nhau.
B. Song song với nhau. C. Chéo nhau. D. Cắt nhau. Lời giải Chọn C
Theo giả thuyết thì a,b không đồng phẳng.
Giả sử AD và BC đồng phẳng.
Nếu I = AD BC I ( ABCD)  I ( ;
a b) . Mà a,b không đồng phẳng nên không tồn tại điểm I .
Nếu AD / /BC thì a,b đồng phẳng (mâu thuẫn).
Do đó AD và BC không đồng phẳng hay AD và BC chéo nhau.
Câu 23: Số điểm biểu diễn các nghiệm của phương trình tan x − cot 2x = 0 trên đường tròn lượng giác là bao nhiêu? A. 4. B. 1. C. 3. D. 6. Lời giải Chọn A cos x  0  Điều kiện 
 sin 2x  0  x k . s  in 2x  0 2 11 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống      
tan x − cot 2x = 0  tan x = cot 2x  tan x = tan
− 2x x = − 2x + k  x = + k   ,  2  2 6 3 k  .
Vẽ các nghiệm lên đường tròn lượng giác và đối chiếu điều kiện ta được 4 điểm, tương ứng với 
các họ nghiệm x =  + k . 6
Câu 24: Cho cấp số cộng (u
có u = 4 và u = 2 . Giá trị của u bằng n ) 2 4 6 A. u = 6 . B. u = 0 . C. u = −1 . D. u = 1 . 6 6 6 6 Lời giải Chọn B u  = 2 u  + 3d = 2 d = 1 − Ta có: 4 1      . u = 4 u + d = 4 u = 5    2 1 1
Từ đó: u = u + 5d = 0 . 6 1
Câu 25: Phương trình nào dưới đây không là phương trình bậc hai đối với một hàm số lượng giác? A. 2
sin 2x + cos x = 1 . B. 2
tan x + 2 tan x + 3 = 0 . C. 2
sin x − 3 sin x +1 = 0 . D. 2
cos 2x − cos 2x − 2 = 0 . Lời giải Chọn A Phương trình 2
sin 2x + cos x = 1 không là phương trình bậc hai đối với một hàm số lượng giác. Phương trình 2
tan x + 2 tan x + 3 = 0 là phương trình bậc hai đối với hàm số y = tan x . Phương trình 2
sin x − 3 sin x +1 = 0 là phương trình bậc hai đối với hàm số y = sin x . Phương trình 2
cos 2x − cos 2x − 2 = 0 là phương trình bậc hai đối với hàm số y = cos 2x .
Câu 26: Tập nghiệm của phương trình cos 2x + 3sin x − 2 = 0 là    
A. S = − + k2 ; + k2 , k   .  2 6    5 
B. S =  + k2 ;− + k2 ;−
+ k2 ,k   .  2 6 6     5 
C. S = − + k2 ; + k2 ;
+ k2 ,k Z .  2 6 6    5 
D. S =  + k2 ; + k2 ;
+ k2 ,k  .  2 6 6  Lời giải Chọn D
Ta có: cos 2x + 3sin x − 2 = 0 12 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống sin x = 1 2 2  
1− 2 sin x + 3sin x − 2 = 0  2
− sin x + 3sin x −1 = 0  1  sin x =  2   x = + k2  2     x = + k2 (k  )  6  5 x = + k2  6
Câu 27: Giải phương trình 2 tan x + ( 3 − ) 1 tan x − 3 = 0 .     x = + k  x = + k  4 4 A.  (k  )    . B. (k ).    x = − + k = − +   x k  3  6     x = + k  x = − + k  4 4 C.  (k  )    . D. (k ).    x = + k = − +   x k  6  3 Lời giải Chọn A    x = + k tan x = 1  4 Ta có 2 tan x + ( 3 − )
1 tan x − 3 = 0     (k  ) tan x = − 3 
x = − + k  3
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA . Thiết diện
của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là
A. Tứ giác IBCD .
B. Tam giác IBC .
C. Hình thang IJCB ( J là trung điểm SD ).
D. Hình thang IGBC ( G là trung điểm SB ). Lời giải Chọn C
Gọi O là giao điểm của AC và BD , G là giao điểm của CI và SO
Khi đó G là trọng tâm tam giác SAC . Suy ra G là trọng tâm tam giác SBD
Gọi J = BG SD . Ta có: (IBC)  (SAD) = IJ . Khi đó J là trung điểm SD . 13 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
(IBC)  (SCD) = JC ; (IBC)  ( ABCD) = BC ; (IBC)  (SAB) = IB
Mặt khác: IJ //AD//BC
Do đó thiết diện của hình chóp cắt bởi (IBC)
là hình thang IJCB ( J là trung điểm SD ).
Câu 29: Có bao nhiêu giá trị nguyên của tham số m để phương trình (m + )
1 sin 2x + 2 cos 2x = 2m có nghiệm A. 0. B. 1. C. 2 . D. 3. Lời giải Chọn D
Phương trình (m + )
1 sin 2x + 2 cos 2x = 2m có nghiệm khi và chỉ khi (m + )2 2 1 + 4  4m 2 2
m + 2m +1+ 4  4m 2
 3m − 2m − 5  5 0  1 −  m  3 Mà m  nên m  1 − ;0;  1 .
Câu 30: Cho ba số x,1+ x, 6 − x theo thứ tự lập thành một cấp số cộng. Tìm x . A. 2 . B. 4 . C. 5 . D. 3 . Lời giải Chọn A
Vì x,1+ x, 6 − x theo thứ tự lập thành một cấp số cộng nên
2 (1+ x) = x + 6 − x  2x = 4  x = 2
Câu 31: Cho hình hộp ABC . D AB CD
  . Gọi M là trung điểm của AB . Mặt phẳng (MA C  ) cắt cạnh
BC của hình hộp ABC . D AB CD
  tại N . Tính tỉ số MN
k = AC . 1 1 1 1 A. k = . B. k = . C. k = . D. k = . 2 2 2 2 Lời giải Chọn A
Ta có: AC // A C
  nên (MAC)// AC .
(MAC)( ABCD) = MN do đó MN // AC  N là trung điểm của BC . MN MN 1
MN là đường trung bình của ABC nên suy ra k = = = A C   . AC 2
Câu 32: Cho cấp số nhân (u biết u + u = 51 ; u + u = 102 . Hỏi số hạng 12288 là số hạng thứ bao n ) 1 5 2 6
nhiêu của cấp số nhân (u ? n ) A. 12 . B. 13 . C. 11. D. 10 . 14 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống Lời giải Chọn C
Gọi số hạng đầu của cấp số nhân là u và công bội là q . 1 Theo giả thiết, ta có  + = uu u q  ( 4 4 1+ q = 51 . 51 u ( 4 1+ q 1 ) 1 ) u  + u = 51 1 5 51 1 1  1 1      =  = u + u = 102  5 u
 .q + u .q =102  4 u  .q u q 1+ q 102 q 2 1 ( )  ( 4 1+ q = 102 1 1 1 ) 2 6  q = 2 .
Với q = 2 , ta có u ( 4 1+ 2 = 51  u = 3. 1 ) 1
Giả sử số 12288 là số hạng thứ n của cấp số nhân này. − − − − Ta có: n 1 n 1 n 1 n 1 12 u .q
=12288  3.2 =12288  2 = 4096  2 = 2  n −1 =12  n =13.. 1
Vậy số 12288 là số hạng thứ 13 của cấp số nhân.
Câu 33: Cho hình hộp ABC . D AB CD
  . Mặt phẳng ( AB D
 ) song song với mặt phẳng nào trong các mặt phẳng sau đây? A. ( BDA) . B. ( BC D  ).
C. ( AC C  ). D. ( BCA) . Lời giải Chọn B B D  //BD  Ta có:      BD  
(BDC) B D //(BDC ) ( )1 AB//DC  Ta có:     DC  
(BDC) AB //(BDC ) (2) Mà AB ,  B D    ( AB D  ) (3) Từ ( )
1 , (2) và (3)  ( AB D  ) // (BDC)
Câu 34: Trong đại dịch Covid-19, người ta đã thống kê hết tháng 1 năm 2020, thế giới có 2100 người tử
vong, sau đó cứ tháng sau nhiều hơn tháng trước 1000 người tử vong. Đến hết tháng 12 năm
2020, tổng số người tử vong trên toàn thế giới là:
A. 91200 người.
B. 90000 người.
C. 81200 người.
D. 13100 người. Lời giải Chọn A
Số người tử vong từ tháng 1 đến tháng 12 lập thành một cấp số cộng có u = 2100 và công sai 1 d = 1000
Vậy tổng số người tử vong trên toàn thế giới là: n 12 S =
2u + (n −1)d =
2.2100 + (12 −1).1000 = 92100 người 12  1    2 2
Câu 35: Cho hình hộp ABC . D AB CD
  . Một mặt phẳng ( ) cắt các cạnh bên AA , BB , CC , DD lần
lượt tại M , N, P,Q sao cho AM = 5, BN = 8,CP = 7. Khi đó dộ dài đoạn DQ bằng A. 4. B. 6. C. 10. D. 5. Lời giải Chọn A 15 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống (  ABB A  ) / /(CDD C  )  Ta có: (   )  ( ABB A
 ) = MN MN / /PQ (    )  (CDD C  ) = PQ
Lấy M , N lần lượt trên DD ,CC sao cho DM  = AM = 5,CN = BN = 8.
Khi đó: DQ = DM  − QM  = DM  − PN ( PQM N
  là hình bình hành)
= DM  − (CN − CP) = 5 − (8 − 7) = 4 . Vậy DQ = 4 . 16 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm) Câu 4:
(0,5 điểm) Giải phương trình 2sin x cos x + 3 cos 2x = 3 Lời giải
Ta có: 2 sin x cos x + 3 cos 2x = 3  sin 2x + 3 cos 2x = 3 1 3 3     sin 2x + cos 2x = 3  sin 2x + =   . 2 2 2  3  2    2x + = + k2 x = k       3 3  sin 2x + = sin       , k  .  3  3    x = + k 2x + =  − + k2   6 3 3 Câu 5: (1,0 điểm)
a) Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1; đồng thời các số
x, 2 y, 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0 . Tìm q ? Lời giải y = xq
Ta có x, y, z theo thứ tự lập thành một cấp số nhân   2 z = xq
Mặt khác x, 2 y, 3z theo thứ tự lập thành một cấp số cộng x + 3zx = 0 2  2y =
 4xq = x + 3xq x( 2 3q − 4q + ) 1 = 0   . 2 2
3q − 4q +1 = 0
Với x = 0  y = 0, z = 0 (loại do x; 2 y;3z theo thứ tự lập thành một cấp số cộng với công sai khác 0 ) q =1  1 Với 2
3q − 4q +1 = 0  1 
. Do q  1 nên q = . q =  3 3
b) Tỷ lệ tăng dân số của tỉnh X là 1,4% Biết rằng dân số tỉnh X hiện nay là 1,8 triệu người.
Hỏi với mức tăng như vậy thì sau 10 năm nữa dân số tỉnh X là bao nhiêu? Lời giải
Theo giải thiết, ta thấy tỷ lệ tăng dân số hàng năm của tỉnh X là một cấp số nhân (u với số n ) hạng đầu 6
u = 1,8.10 và công bội 1, 4 q = 1+ =1,014 . 1 100
Do đó, dân số của tỉnh X sau 10 năm là: u = u .q = 1,8.10 (1,014)10 10 6  2068483 người. 11 1 Câu 6:
Cho hình chóp S.ABCD , đáy ABCD là hình thang ( AD // BC, AD BC ) . Gọi M , N lần lươt
là các điểm thuộc các cạnh SB, SC sao cho SM = 2MB, SN = 2NC.
a) Gọi K = AB C .
D Tìm thiết diện của hình chóp cắt bởi mặt phẳng ( KMN ) .
b) Cho AD = 2BC. Tính tỉ số diện tích của tam giác KMN và diện tích thiết diện vừa tìm ở câu trên. Lời giải 17 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
a) Thiết diện của hình chóp cắt bởi mặt phẳng ( KMN ) .
Trong mặt phẳng ( SCD), gọi F = KN SD thì mặt phẳng ( KMN ) cắt hình hình chóp theo
thiết diện là tứ giác MNFE .
b) Tỉ số diện tích của tam giác KMN và diện tích thiết diện vừa tìm ở câu trên.
Khi AD = 2BC thì BC là đường trung bình của tam giác KAD .
M là trọng tâm tam giác SAK và E là trung điểm SA .
Tương tự F là trung điểm cạnh SD Khi đó 1
EF là đường trung bình của tam giác SAD EF = A . D 2
Mặt khác theo giả thiết, ta có 2 1
SM = 2MB, SN = 2NC MN = BC = AD 3 3 2 MN 2 S  2  4 5 Vì = nên KMN =  S = S ; S = S   EF 3 KMN KEF MNFE KEF S  3  9 9 KEF Vậy S 4 KMN = . S 5 MNFE
-----------------------HẾT----------------------- 18 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống ĐỀ SỐ 03
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Giá trị nào sau đây mang dấu dương? A. 0 cos120 B. 0 sin120 C. 0 tan120 . D. 0 cot120 . Câu 2:
Trong mặt phẳng cho ba tia Ou,Ov,Ox . Trong các mệnh đề sau, mệnh đề nào đúng?
A. sd (Ou,Ov) = sd (Ou,Ox) + sd (Ox,Ov) + k 2 ,k  .
B. sd (Ou,Ov) = sd (Ou,Ov) + sd (Ox,Ou ) + k 2 ,k  .
C. sd (Ou,Ov) = sd (Ov,Ox) + sd (Ox,Ou ) + k 2 ,k  .
D. sd (Ou,Ov) = sd (Ov,Ox) + sd (Ou,Ox) + k 2 ,k  . Câu 3:
Trong các khẳng định sau, khẳng định nào đúng?
A. cos (a + b) = cos a cos b − sin a sin . b
B. cos (a + b) = cos a cos b + sin a sin . b
C. cos (a + b) = cos a sin b + sin a cos . b
D. cos (a + b) = sin a cos a + cos b sin . b Câu 4:
Trong các khẳng định sau, khẳng định nào sai? A. 2 2
sin 2a = cos a − sin a
B. cos 2a = 2 sin a C. 2
cos 2a = 2 cos a −1. D. 2 cos 2a = 1− 2 sin . a Câu 5:
Đồ thị dưới đây là đồ thị của hàm số nào?
A. y = 1+ sin 2x .
B. y = cos x .
C. y = − sin x .
D. y = − cos x . Câu 6:
Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y = tan . x B. y = cot . x C. y = sin . x D. y = cos . x Câu 7:
Điều kiện có nghiệm của phương trình sin x = m là A. m  1. B. m  1. C. m  1. D. m  1. Câu 8:
Cho dãy số (u , biết u = n + 2 . Ba số hạng đầu tiên của dãy số lần lượt là n ) n A. 3; 4;5. B. 0;1; 2. C. 2;3; 4. D. 1; 2;3. Câu 9:
Trong các dãy số sau dãy số nào là dãy số hữu hạn 1 1 1 1 1 A. , , , , ....
B. 5,10,15, 20, 25.... 2 3 4 5 3 3 3 3 3
C. 8,15, 22, 29, 36.
D. 2, 0, 4, 6,8,...
Câu 10: Cho cấp số cộng (u , biết u = 2,u = 8 . Công sai của cấp số cộng là n ) 1 2 A. d = 6 . B. d = 16 . C. d = 10 . D. d = 4 . 1 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 11: Cho cấp số cộng (u , biết u = 2 và công sai d = 3 . Khẳng định nào sau đây đúng? n ) 1 A. u = 5. B. u = 2. C. u = 6. D. u = 3. 2 2 2 2
Câu 12: Cho cấp số cộng (u . Gọi S là tổng của n số hạng đầu của cấp số cộng. Khẳng định đúng là n ) n n (n − ) 1 nu + n n −1 1 ( )
A. S = nu + d . B. S = d . n 1 2 n 2 (n − ) 1
C. S = nu + n n −1 d .
D. S = nu + d . n 1 ( ) n 1 2
Câu 13: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; − 3;9; − 27;54 . B. 1; 2; 4;8;16 . C. 1; −1;1; −1;1.
D. 1; − 2; 4; − 8;16 .
Câu 14: Cho cấp số nhân (u với u = 81 và u = 3 . Tìm công bội n ) q ? 1 4 1 1 1 A. − . B. − . C. 3 . D. 3 − . 3 3 3
Câu 15: Cho cấp số nhân (u
với u = 2 và công bội q = 3 . Giá trị của u bằng n ) 1 2 2 A. 6 . B. 9 . C. 8 . D. . 3
Câu 16: Trong mẫu số liệu ghép nhóm, độ dài mỗi nhóm a;b) được tính như thế nào? a + b A. b − . a B. . C. a + . b D. . a . b 2
Câu 17: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. mốt. B. số trung bình. C. số trung vị. D. tứ phân vị.
Câu 18: Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm a;b) được tính như thế nào? a + b A. . B. b − . a C. a + . b D. . a . b 2
Câu 19: Trong các khẳng định sau, khẳng định nào là đúng?
n −(m +...+ m 1 1 + )
A. Số trung vị là 2 p M = a + a − a . e p ( p 1+ p) mp
B. Số trung vị bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.
C. Số trung vị luôn là một số liệu nào đó của mẫu.
D. Số trung vị chính là số trung bình.
Câu 20: Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau:
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5 . B. 6 . C. 7 . D. 12 . 2 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sốngCâu 21: Biết 1 sin = và
   . Giá trị cos bằng 3 2 2 2 2 3 3 2 3 3 A. − . B. − . C. − . D. − . 3 3 2 2 Câu 22: Biết 1 sin = . Giá trị cos 2 bằng 4 7 8 7 8 A. . B. . C. − . D. − . 8 7 8 7
Câu 23: Tập giá trị của hàm số y = 2 sin x là A. −1;  1 . B. 0; 2. C. −2;  2 . D. −2; 2.
Câu 24: Tập nghiệm của phương trình cos x = 0 là    
A. S =  + k2 | k  .
B. S =  + k |k  .  2   2    
C. S = k2 |k  .
D. S = − + k2 | k  .  2 
Câu 25: Xét tính tăng giảm của dãy số 1 1 1 1 − ;− ;− ;− . 2 3 4 5 A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Dãy số vừa tăng vừa giảm
Câu 26: Cho một cấp số cộng có các số hạng lần lượt là1, 6,11, .
x Khi đó giá trị của x là A. 5. B. 18. C. 17. D. 16.
Câu 27: Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64. Gọi S là tổng của n số hạng đầu tiên n
của cấp số nhân đó. Mệnh đề nào sau đây đúng? n ( n 1 1 4 − + ) 4(4n − ) 4n −1 1 A. S = . B. S = . C. 1 S 4n− = . D. S = . n 3 n 2 n n 3
Câu 28: Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 45 học sinh lớp 11A .
Mẫu số liệu ghép nhóm này có số mốt là A. 2 . B. 1. C. 0 . D. 3 .
Câu 29: Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:
Chọn 85 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020 . A. 36,17 . B. 34,82 . C. 35, 6 . D. 37,12 . 3 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 30: Khảo sát chiều cao (cm) của 52 học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 165;170) . B. 160;165) . C. 170;175) . D. 175;180) .
Câu 31: Tập xác đinh của hàm số y = sin x + cos x là A. . B.
\ k |k  . C. \  |k  . D.
\ k2 |k  .
Câu 32: Phương trình 2 cos x = − 3 có bao nhiêu nghiệm thuộc tập   − ;3  A. 4. B. 3. C. 2. D. 1. 1 1 1 1
Câu 33: Cho dãy số (u xác định bởi u = + + +...+
. Chọn mệnh đề đúng? n ) n 2 2 2 2 1 2 3 n
A. Dãy số (u bị chặn. n )
B. Dãy số (u bị chặn trên, nhưng không bị chặn dưới. n )
C. Dãy số (u bị chặn dưới, nhưng không bị chặn trên. n )
D. Dãy số (u không bị chặn. n )
Câu 34: Gọi S = 1+11+111+ ... +111...1 ( n số 1) thì S nhận giá trị nào sau đây? 1  10n −1  10n −1 A. S = 10    − n . B. S = 10  . 9   9    81  10n −1 10n −1 C. S = 10  − n . D. S = .  81  81
Câu 35: Khảo sát vận tốc (dặm/h; 1 dặm = 1, 609km ) của 300 xe ô tô chạy trên con đường A thu được
mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ nhất là A. 32,5 ;37,5) . B. 27,5 ;32,5) . C. 37,5 ; 42,5) . D. 42,5 ; 47,5) . 4 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm) Câu 1:
(1,0 điểm) Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên? Câu 2: (1,0 điểm) sin x
a) Tìm tập xác định của hàm số sau: y = . 2 2 sin x − cos x
b) Giải phương trình sin ( cos x) = 1. Câu 3:
(1,0 điểm) Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây,
hàng thứ hai có 2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
-----------------------HẾT----------------------- 5 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống BẢNG ĐÁP ÁN Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 B A A B B D C A C A Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 A A A A A A A A A A Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 A A D B B D A A A A Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 A A A A A C Đáp án chi tiết Biểu điểm 3
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau: 6
Tính mốt của mẫu số liệu trên?
Tần số lớn nhất là 16 nên nhóm chứa mốt là nhóm 50,5;55,5) và j = 3 0,25
Ta có u = 50, 5;u = 55, 5  h = u − u = 5 3 4 4 3 0,25 = = = Tần số: n 7; n 16; n 4 2 3 4 . 0,25 n − n − j j 1 − n n M = u + h = u + h o j ( 3 3 n − n + n − n n − n + n − n j j 1 − ) ( j j 1+) 2 ( 3 2) ( 3 4) 0,25 16 − 7 M = 50,5 + .5 = 52, 6 0 (16 − 7) + (16 − ) 4 3 sin x
a) Tìm tập xác định của hàm số sau: y = . c 2 2 sin x − cos x 7
Điều kiện xác định của hàm số là   k 2 2 0,25
sin x − cos x  0  − cos 2x  0  2x  + k  x  + ;k  . 2 4 2  k 
Vậy tập xác định của hàm số là D = \  + ; k    0,25 4 2 
b) Giải phương trình sin ( cos x) = 1.
sin ( cos x) = 1   cos x = + k2 , k  1
 cos x = + 2k, k 0,25 2 2 1 3 1
Vì −1  cos x  1 nên 1
−  + 2k 1  −  k  . 2 4 4 0,25 1  Do k
k = 0 suy ra cos x =  x =  + m2,m . 2 3 3
Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có 8
2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây? 6 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Gọi số hàng cây là n , hàng thứ n có n cây. 0,25
Ta có 1+ 2 + 3 + ... + n = 2145 0,25 n (n + ) 1  = 2145 . 0,25 2  n = 65 0,25 7 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống ĐỀ SỐ 04
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Trên đường tròn lượng giác, cho góc lượng giác có số đo thì mọi góc lượng giác có cùng tia 2
đầu và tia cuối với góc lượng giác trên đều có số đo dạng      A. . B.
+ k ,(k  ) . C. + k2,(k  ) . D. + k,(k  ). 2 2 2 2 2  Câu 2:
Trên đường tròn có bán kính r = 5 cm, độ dài của cung có số đo là 8  40 5 5.180 A. l = cm. B. l = cm. C. l = cm. D. l = cm. 8  8 8 Câu 3:
Biểu thức sin x cos y − cos x sin y bằng
A. cos ( x − y) .
B. cos ( x + y) .
C. sin ( x − y) .
D. sin ( y − x) . Câu 4: Cho góc lượng giác .
a Trong các khẳng định sau, khẳng định nào là khẳng định sai? A. 2
cos 2a = 1− 2sin a . B. 2 2
cos 2a = cos a − sin a . C. 2
cos 2a = 1− 2 cos a . D. 2
cos 2a = 2 cos a −1. Câu 5:
Tìm tập xác định của hàm số y = tan x .   A.
\  + k | k   . B.
\ k | k   .  2    C.
\  + k2 | k   . D.
\ k2 | k   .  2  Câu 6:
Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A. y = tan x . B. 2
y = x + 2024 .
C. y = sin x .
D. y = cos x . Câu 7:
Nghiệm của phương trình sin x = sin là 3     x = + k2  x = + k2 3  A.  (k  ) 3  . B.  (k  ) .  2 x = − + k2   = +   x k 2 3  3   = +   x k  3 C. x =
+ k (k  ) . D.  (k  ) . 3 2 x = + k  3 Câu 8:
Cho các dãy số sau, dãy số nào là dãy số vô hạn? 1 1 1 1 A. 0, 2, 4, 6,8,10. B. 1, , , ,...,
,... C. 1, 4, 9,16, 25. D. 1,1,1,1,1. 2 4 8 2n 1 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống Câu 9:
Cho dãy số: 5;10;15;20;25;... Số hạng tổng quát của dãy số này là
A. u = 5(n −1) .
B. u = 5n .
C. u = 5 + n .
D. u = 5n +1 . n n n n
Câu 10: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A. 1; −2; −4; −6; −8 . B. 1; 3 − ; 6 − ; 9 − ;−12. C. 1; 3 − ; 7 − ; 11
− ;−15. D. 1;−3;−5;−7;−9 .
Câu 11: Cho cấp số cộng (u với u = 5 − 2n . Tìm công sai của cấp số cộng. n ) n
A. d = 3 .
B. d = −2 .
C. d = 1 . D. d = 2 .
Câu 12: Cho cấp số cộng (u có u = 1 và u = 3 . Giá trị của u bằng n ) 1 2 3 A. 6. B. 9. C. 4. D. 5.
Câu 13: Cho các dãy số sau. Dãy số nào là dãy số giảm? 1 1 1 1 A. 1; 1; 1; 1; 1; 1. B. 1; − ; ; − ; . C. 1; 3; 5; 7. D. 11; 9; 7; 5; 3. 2 4 8 16 1
Câu 14: Cho dãy số (u có u =
. Khẳng định nào sau đây sai? n ) n n A. u = 1.
B. Dãy số (u là dãy số tăng. n ) 1
C. Dãy số (u bị chặn trên bởi 1.
D. Dãy số (u là dãy số giảm. n ) n ) 2n −1
Câu 15: Cho dãy số (u có u = . Khi đó, u bằng: n ) n n +1 2 A. 1 . B. 2 . C. 3 . D. 4 .
Câu 16: Đo chiều cao (tính bằng cm) của 500 học sinh trong một trường THPT ta thu được kết quả như sau:
Các em có chiều cao 170 cm được xếp vào nhóm:
A. 155;160) .
B. 160;165) .
C. 165;170) . D. 170;175) .
Câu 17: Trong mẫu số liệu ghép nhóm, giá trị đại diện x của nhóm a ; a
được tính bằng công thức i i 1 + ) i a + a a − a A. i i 1 x + = . B. i 1 i x + = .
C. x = a + a . D. x = a − a . i + + 2 i 2 i i i 1 i i 1 i
Câu 18: Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành hai phần, mỗi
phần chứa 50% giá trị?
A. số trung vị.
B. số trung bình. C. mốt. D. tứ phân vị.
Câu 19: Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành bốn phần, mỗi
phần chứa 25% giá trị?
A. số trung vị.
B. số trung bình. C. mốt. D. tứ phân vị.
Câu 20: Khẳng định nào sau đây sai?
A. Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc.
B. Mốt của mẫu số liệu ghép nhóm bằng mốt của mẫu số liệu gốc.
C. Mốt là một trong các số đặc trưng để đo xu thế trung tâm của mẫu số liệu. 2 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
D. Mốt của mẫu số liệu là các giá trị xuất hiện với tần số lớn nhất. 1 3 Câu 21: Cho cos = và
   2 . Tính sin . 2 2 3 3 2 2 A. − . B. . C. . D. − . 2 2 2 2   
Câu 22: Cho tan  = 2 . Tính tan  −  .  4  1 2 1 A. − . B. 1. C. . D. . 3 3 3
Câu 23: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số y = 4 sin x cos x +1 . Tính M + m . A. 2 . B. 4 . C. 3 . D. 1 − .
Câu 24: Cung lượng giác có điểm biểu diễn là M , M như hình vẽ là nghiệm của phương trình lượng 1 2 giác nào sau đây?          A. sin x − = 0   .
B. sin x = 0 . C. cos x − = 0   . D. sin x + = 0   .  3   3   3  u 2 1
Câu 25: Cho dãy số u u . n xác định bởi . 1 Tìm số hạng 3 u u 1 n 1 3 n 5 2 14 A. u . B. u 1. C. u . D. u . 3 9 3 3 3 3 27
Câu 26: Cho cấp số cộng (u có số hạng đầu u = −0,1và công sai d = 0,1. Số hạng thứ 7 của cấp số n ) 1 cộng này là A. 1, 6 . B. 6 . C. 0, 5 . D. 0, 6 .
Câu 27: Cho cấp số nhân có các số hạng lần lượt là 3; ;
x 27; 81;... Tìm x . A. 9 − . B. 9. C. −81. D. 81.
Câu 28: Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:
Tính tổng số học sinh được khảo sát. A. 40. B. 15. C. 20. D. 5. 3 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 29: Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:
Thời gian xem tivi trung bình trong tuần trước của các bạn học sinh này là A. 9,5 giờ. B. 11,5 giờ. C. 7,5 giờ. D. 15 giờ.
Câu 30: Doanh thu bán hàng trong 30 ngày của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là A. 7;9) . B. 5;7) . C. 9; ) 11 . D. 9; ) 11 .   
Câu 31: Tìm tập xác định D của hàm số y = tan 2x −   .  4  3 k  3  A. D = \  + , k   . B. D = \ 
+ k ,k   .  8 2   4  3 k    C. D = \  + , k   . D. D =
\  + k , k   .  4 2   2 
Câu 32: Phương trình 2 sin x + 3 = 0 có tổng nghiệm dương nhỏ nhất và nghiệm âm lớn nhất bằng 4  A. . B. 2 . C. . D.  . 3 3
Câu 33: Cho dãy số (u là cấp số cộng có u = −1; d = 2. Tìm n biết S = 483. n ) 1 n
A. n = 20 . B. n = 21. C. n = 22 . D. n = 23 .
Câu 34: Cho cấp số nhân (u có u = 1; q = −2 . Tổng của 10 số hạng đầu tiên của cấp số nhân đó bằng n ) 1 A. −341 B. 341 C. 1023 D. −1023
Câu 35: Đo chiều cao (tính bằng cm) của 500 học sinh trong một trường THPT ta thu được kết quả như sau:
Tính mốt của mẫu số liệu ghép nhóm trên. A. 160. B. 164,05. C. 162,5. D. 160,94. 4 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm) Câu 1: (1,0 điểm) 12  a) Cho sin = với
    . Tính sin 2 . 13 2
b) Tìm tập xác định của hàm số cos x y = . sin x −1 Câu 2:
(1,0 điểm) Giải phương trình 5 − 4cos 2x = 6sin .
x sin 3x . Câu 3:
(1,0 điểm) Ước tính dân số năm 2022 của thành phố Đà Nẵng là 579 914 người, tỷ lệ tăng dân
số 1,5% so với năm trước. Nếu lấy kết quả chính xác đến hàng nghìn thì dân số của thành phố
Đà Nẵng năm 2030 là bao nhiêu?
-----------------------HẾT----------------------- 5 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống BẢNG ĐÁP ÁN 1.C 2.C 3.C 4.C 5.A 6.B 7.B 8.B 9.B 10.C 11.B 12.D 13.D 14.B 15.A 16.D 17.A 18.A 19.D 20.B 21.A 22.D 23.A 24.A 25.C 26.C 27.B 28.A 29.A 30.A 31.A 32.D 33.D 34.A 35.B PHẦN TỰ LUẬN Câu Ý Đáp án Điểm 2 12  25 5 2 2 cos  = 1− sin  = 1− =  cos =    a 13  169 13 0,25  5 Vì
    nên cos  0 . Suy ra cos = − 2 13 12 5 120 sin 2 2sin.cos   = = 2. . − = −   0,25 1 13  13  169
(1,0 điểm) os c x Hàm số y =
xác định khi và chỉ khi sin x −1 0,25  b
sin x  1  x  + k2,k  2  
Tập xác định của hàm số đã cho là D = \  + k2 ,  k   2  0,25 3 Ta có: − 3cos 4 x = 6sinx.sin 3x 2 0,25  3
− 3cos 4x = 3(cos 2x − cos 4x) 2 2  3 x = 3cos 2 0,25 (1,0 điể 2 m)  1 cos 2x = 0,25 2   =  +   x k , k 0,25 6
Đặt P0 = 579914 và r = 1,5% = 0,015
Gọi Pn là dân số của thành phố Đà Nẵng sau n năm nữa. 0,25
Sau 1 năm, dân số của tỉnh là: P = P + P .r = P (1+ r ) 1 0 0 0
Sau 2 năm, dân số của tỉnh là: 2 P = P + P .r = P (1+ r ) 0,25 2 1 1 0 3 … (1,0 điể m)
Sau n năm, dân số của tỉnh là: n P = P + P .r = P (1+ r ) n n-1 n-1 0 0,25
Suy ra (Pn) là một cấp số nhân với số hạng đầu P0 và công bội q = 1+ r.
Do đó dân số của thành phố Đà Nẵng năm 2030 là: 8 8
P = P .(1+ r) = 579914.(1,015)  653000 người. 0,25 8 0 6 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống ĐỀ SỐ 05
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 KNTT
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm) Câu 1:
Cung có số đo 250 thì có số đo theo đơn vị là radian là 35 25 25 25 A. . B. . C. . D. . 18 18 12 9  Câu 2:
Cho góc  thỏa mãn 0   
. Khẳng định nào sau đây đúng? 2 A. sin   0 . B. cot   0 .
C. sin   0 .
D. cos  0 . Câu 3:
Khẳng định nào sau đây đúng? A. 2 2
sin  + cos  = 1 . B. 2 2 sin  + cos  = 0 . C. 2 2 sin  + cos  = 2 . D. 2 2 sin  + cos  = 1 − . Câu 4: sin 2a bằng A. 2 sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a . Câu 5:
Chu kỳ tuần hoàn của hàm số y = sin x là
A. k 2 (k  ) . B. . C.  . D. 2 . 2 Câu 6:
Tập giá trị của hàm số y = cos 2023x là  1 1  A. −1;  1 . B. (−1;1) . C.  2023 − ;  2023 . D. − ;   .  2 2  Câu 7:
Nghiệm của phương trình tan x = 1 là  3 A. x =
+ k , k  . B. x =
+ k , k  . 4 4 
C. x = k , k  . D. x = + k ,k  . 2 Câu 8:
Cho dãy số (u xác định bởi u = 2n −1 với n  1. Số hạng u bằng n ) n 1 A. 1. B. 2 . C. 3. D. 4 . Câu 9:
Dãy số nào sau đây là dãy tăng? A. 1;3;5; 7;9 . B. 10;8; 6; 4; 2 . C. 1;5;3; 7;9 . D. 1;1;1;1;1 .
Câu 10: Cho cấp số cộng (u
với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 .
Câu 11: Trong các dãy số (u ) sau, dãy số nào bị chặn? n 2 A. 2 u = n +1. B. u = 1− .
C. u = n + sin n . D. 2 u = sin n . n n n 3n n
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a . 1 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 13: Dãy số nào sau đây là cấp số nhân?
A. 1, −2 , 4 , 8 , −16 .
B. 2 , 22 , 222 , 22222 . C. 3 , 6 , 12 , 24 .
D. x , 2x , 3x , 4x với x  0 .
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7 − ; 1 − 3) . C. (13; 7) . D. ( 13 − ; − 7) .
Câu 15: Cho cấp số nhân (u u = 3 q = −2 n ) với và công bội
. Tìm giá trị của n biết số hạng tổng quát 1 u = 1536 − n . A. n = 8 . B. n = 9 . C. n = 257 . D. n = 10 .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 150;152) 5 2 152;154) 18 3 154;156) 40 4 156;158) 26 5 158;160) 8 6 160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156, 5 . B. 157 . C. 157, 5 . D. 158 .
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) . 2 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7, 6 . C. 8 . D. 8, 6 . 3 Câu 21: Biết 4 sin − = và     . Giá trị cos bằng 5 2 3 3 3 9 A. − . B. . C.  . D. . 5 5 5 5    
Câu 22: Giá trị của biểu thức A = sin +   là  3 4  6 − 2 6 + 2 − 6 + 2 − 6 − 2 A. . B. . C. . D. . 4 4 4 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2 . C. y = 2 − sin x . D. y = 2 − cos x + 2 .
Câu 24: Tập nghiệm của phương trình cos x = 1 − là     
A. S =  + k2 | k  . B. S = −
+ k2 |k  .  2   2 
C. S = k2 |k  .
D. S =  + k 2 | k  .
Câu 25: Cho dãy số 1 1 1 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là nn 1 − n 1   1  1 (− ) 1 A. u = . B. u = . C. u = . D. u = . n      − 3  n  3  n 3n n n 1 3
Câu 26: Cho cấp số cộng (u có u = 2; d = −5 . Số hạng thứ 20 của cấp số cộng là n ) 1 A. −93 . B. 10 . C. 93 . D. 23 .
Câu 27: Cho cấp số nhân ( x có x = −3 và x = −27. Tính số hạng đầu x và công bội q của cấp số n ) 2 4 1 nhân.
A. x = −1, q = −3 hoặc x = 1, q = 3. B. x = 1
− , q = 3 hoặc x = 1, q = −3. 1 1 1 1
C. x = 3, q = 1
− hoặc x = −3, q = 1.
D. x = 3, q = 1 hoặc x = −3, q = −1. 1 1 1 1
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6, 5 . B. 7, 5 . C. 7, 25 . D. 8 . 3 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) .
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 30;45) . B. 15;30) . C. 45;60) . D. 60;75) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa   
bởi hàm số h(t) = 5sin t
 , trong đó h(t) là độ cao tính bằng cetimét trên mực nước biển  5 
trung bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5 giây. B. 10 giây. C. 2, 5 giây. D. 20 giây.  3  3
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình sin 3x − =    4  2 bằng     A. . B. − . C. . D. − . 9 6 6 9
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 .
Câu 34: Một cấp số nhân có số hạng đầu u = 3 , công bội q = 2 . Biết S = 765 . Tìm n . 1 n A. n = 8 . B. n = 9 . C. n = 6 . D. n = 7 .
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 1360 800 1360 3280 A. Q = , Q = . B. Q = , Q = . 1 3 37 21 1 3 37 83 136 3280 136 800 C. Q = ,Q = . D. Q = , Q = . 1 3 5 83 1 3 5 21 4 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống
II. PHẦN TỰ LUẬN (3,0 điểm) Câu 1: (1,0 điểm)   
a) Giải phương trình cot x + = 3   .  3  2 b) Cho sin =
, tính giá trị của biểu thức P = (1 − 3cos )(1 + 3cos ) . 3 Câu 2: (1,0 điểm)
a) Giải phương trình cos 3x − sin 2x = 0 .   
b) Giải phương trình sin x = cos x +   .  3  Câu 3:
(1,0 điểm) Một công ty khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000 đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng sâu
20 mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó
phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
-----------------------HẾT----------------------- 5 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống BẢNG ĐÁP ÁN 1.B 2.A 3.A 4.A 5.D 6.C 7.A 8.A 9.A 10.A 11.D 12.B 13.C 14.C 15.D 16.B 17.A 18.A 19.B 20.C 21.A 22.B 23.C 24.D 25.B 26.A 27.B 28.C 29.B 30.A 31.B 32.C 33.A 34.A 35.D
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Cung có số đo 250 thì có số đo theo đơn vị là radian là 35 25 25 25 A. . B. . C. . D. . 18 18 12 9 Lời giải Chọn B 0  
Số đo theo đơn vị là radian là 250 . 25. = . 0 180 18  Câu 2:
Cho góc  thỏa mãn 0   
. Khẳng định nào sau đây đúng? 2 A. sin   0 . B. cot   0 .
C. sin   0 .
D. cos  0 . Lời giải Chọn A Câu 3:
Khẳng định nào sau đây đúng? A. 2 2
sin  + cos  = 1 . B. 2 2 sin  + cos  = 0 . C. 2 2 sin  + cos  = 2 . D. 2 2 sin  + cos  = 1 − . Lời giải Chọn A Câu 4: sin 2a bằng A. 2 sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a . Lời giải Chọn A Câu 5:
Chu kỳ tuần hoàn của hàm số y = sin x là
A. k 2 (k  ) . B. . C.  . D. 2 . 2 Lời giải Chọn D Câu 6:
Tập giá trị của hàm số y = cos 2023x là  1 1  A. −1;  1 . B. (−1;1) . C.  2023 − ;  2023 . D. − ;   .  2 2  Lời giải Chọn C Câu 7:
Nghiệm của phương trình tan x = 1 là 6 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống  3 A. x =
+ k , k  . B. x =
+ k , k  . 4 4 
C. x = k , k  . D. x = + k ,k  . 2 Lời giải Chọn A
Ta có tan x = 1  x = + k , k  4 Câu 8:
Cho dãy số (u xác định bởi u = 2n −1 với n  1. Số hạng u bằng n ) n 1 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
Ta có: u = 2.1 − 1 = 1 1 Câu 9:
Dãy số nào sau đây là dãy tăng? A. 1;3;5; 7;9 . B. 10;8; 6; 4; 2 . C. 1;5;3; 7;9 . D. 1;1;1;1;1 . Lời giải Chọn A
Câu 10: Cho cấp số cộng (u
với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 . Lời giải Chọn A
Công sai của cấp số cộng d = u − u = 5 − 3 = 2 . 2 1
Câu 11: Trong các dãy số (u ) sau, dãy số nào bị chặn? n 2 A. 2 u = n +1. B. u = 1− .
C. u = n + sin n . D. 2 u = sin n . n n n 3n n Lời giải Chọn D Với mọi * n  , ta có 2
−1  sin n  1 0  sin n  1 nên dãy số đã cho bị chặn.
Phân tích phương án nhiễu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a . Lời giải Chọn B
Phân tích phương án nhiễu: 7 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt thứ tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân?
A. 1, −2 , 4 , 8 , −16 .
B. 2 , 22 , 222 , 22222 . C. 3 , 6 , 12 , 24 .
D. x , 2x , 3x , 4x với x  0 . Lời giải Chọn C
6 = 3.2 , 12 = 6.2 , 24 = 12.2 .
Phân tích phương án nhiễu:
A. Sai do thay u : u = 2
− nhưng u : u = 2 . 2 1 4 3
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội q = 11 .
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7 − ; 1 − 3) . C. (13; 7) . D. ( 13 − ; − 7) . Lời giải Chọn C u  = 48 u  + 5d = 48 u  =13 Ta có: 6  1   1   . u = 83  u +10d = 83  d = 7 11 1
Phân tích phương án nhiễu:
A. Sai vì đặt nhầm thứ tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm thứ tự của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân (u u = 3 q = − n ) với và công bội
2 . Tìm giá trị của n biết số hạng tổng quát 1 u = 1536 − n ? A. n = 8 . B. n = 9 . C. n = 257 . D. n = 10 . Lời giải Chọn D n 1 − n 1 − u = 1 − 536  u .q = 1 − 536  3.( 2 − ) = 1 − 536 . n 1 n 1 −  ( 2 − ) = 5 − 12 = ( 2 − )9  n =10 .
Phân tích phương án nhiễu: ( n 2 − ) n− n
A. Sai do tính (− ) 1 2 = 512 −  = 5 − 12  ( 2 − ) = 5 − 12 : ( 2
− ) = 256  n = 8 . 2 − n
B. Sai do nhầm công thức số hạng tổng quát . n u q = 1 − 536  2 − = 5 − 12  n = 9 1 ( ) . n− −
C. Sai do tính (− ) 1 512 2 = 5 − 12  n −1 = = 256  n = 257 . 2 −
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: 8 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống Nhóm Chiều cao (cm) Số học sinh 1 150;152) 5 2 152;154) 18 3 154;156) 40 4 156;158) 26 5 158;160) 8 6 160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156, 5 . B. 157 . C. 157, 5 . D. 158 . Lời giải Chọn B +
Giá trị đại diện của nhóm thứ tư là 156 158 =157 . 2
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Chọn A
Mốt M chứa trong nhóm [40;60) 0
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Chọn A Ta có: n = 42 + Nên trung vị x x
của mẫu số liệu trên là 21 22 Q = 2 2
Mà x , x  40; 60 21 22  )
Vậy nhóm chứa trung vị của mẫu số liệu trên là nhóm [40;60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng): 9 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) . Lời giải Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là + + + + Số trung bình: 2.6 7.8 7.10 3.12 1.14 x = = 9,4 20
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7, 6 . C. 8 . D. 8, 6 . Lời giải Chọn C
Gọi x , x ,..., x là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm. 1 2 20
Khi đó: x , x  5;7 ,
x ,..., x  7; 9 ,,
x ,..., x  9; 11 x ,..., x  11; 13 , 17 19  ) 9 16  ) 3 9  ) 1 2  ) x  13; 15 20  )
Do đó, tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm 7;9)
n = 20, n = 7, C = 2, u = 7, u = 9 m m m 1 + 1.20 − 2 4 Q = 7 + (9 − 7)  7,86  8 1 7 4 3 Câu 21: Biết sin − = và     . Giá trị cos bằng 5 2 3 3 3 9 A. − . B. . C.  . D. . 5 5 5 5 Lời giải Chọn A 3π Vì π  α 
nên cosα  0 . Mặt khác 2 2 sin α + cos α = 1 ta có 2 cosα = − 1− sin α 2 10 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống 2  4  3 = − 1− − = −   .  5  5    
Câu 22: Giá trị của biểu thức A = sin +   là  3 4  6 − 2 6 + 2 − 6 + 2 − 6 − 2 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B         3 2 2 1 6 + 2 Ta có A = sin + = sin cos + sin cos = . + . = .    3 4  3 4 4 3 2 2 2 2 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2 . C. y = 2 − sin x . D. y = 2 − cos x + 2 . Lời giải Chọn C
Tập xác định của hàm số y = f ( x) = 2
− sin x là D = .
Do đó, nếu x thuộc tập xác định D thì −x cũng thuộc tập xác định D .
Ta có f (−x) = 2
− sin(−x) = sin x = − f (x). Vậy y = 2
− sin x là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình cos x = 1 − là     
A. S =  + k2 | k  . B. S = −
+ k2 |k  .  2   2 
C. S = k2 |k  .
D. S =  + k 2 | k  . Lời giải Chọn D Ta có cos x = 1
−  x =  + k2 ,k  .
Câu 25: Cho dãy số 1 1 1 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là nn 1 − n 1   1  1 (− ) 1 A. u = . B. u = . C. u = . D. u = . n      − 3  n  3  n 3n n n 1 3 Lời giải Chọn D
Câu 26: Cho cấp số cộng (u có u = 2; d = −5 . Số hạng thứ 20 của cấp số cộng là n ) 1 A. −93 . B. 10 . C. 93 . D. 23 . Lời giải Chọn D u
= u +19d = 2 +19( 5 − ) = −93. 20 1 11 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống
Câu 27: Cho cấp số nhân ( x có x = −3 và x = −27. Tính số hạng đầu x và công bội q của cấp số n ) 2 4 1 nhân.
A. x = −1, q = −3 hoặc x = 1, q = 3. B. x = 1
− , q = 3 hoặc x = 1, q = −3. 1 1 1 1
C. x = 3, q = 1
− hoặc x = −3, q = 1.
D. x = 3, q = 1 hoặc x = −3, q = −1. 1 1 1 1 Lời giải Chọn B 2   q = 9  x = 3 −  x q = 3 −   q = 3  2 1      3   3 x = 27 − . x q = 27 − . x = − . x = 1.  4  1   1 1   q
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6, 5 . B. 7, 5 . C. 7, 25 . D. 8 . Lời giải Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp 6,5;8) nên giá trị đại diện là 6, 5 + 8 = 7, 25. 2
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi
lại ở bảng sau (đơn vị: triệu đồng): Doanh thu 5;7) 7;9) 9; ) 11 11;13) 13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) . Lời giải Chọn B 6.2 + 8.7 +10.7 +12.3 +14.1
Số trung bình của mẫu số liệu trên là: x = = 9,4 20
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 30; 45) . B. 15;30) . C. 45; 60) . D. 60; 75) . 12 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống Lời giải Chọn A
Cỡ mẫu: n = 9 + 5 +15 +14 + 7 = 50 .
Gọi x ,..., x là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy 1 50 x + x
này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là 25
26 . Do hai giá trị x , x 2 25 26 thuộc nhóm 30; 45) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa   
bởi hàm số h(t) = 5sin t
 , trong đó h(t) là độ cao tính bằng cetimét trên mực nước biển  5 
trung bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5 giây. B. 10 giây. C. 2, 5 giây. D. 20 giây. Lời giải Chọn B   
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số h(t) = 5sin t   nên để chiếc phao  5  
ở vị trí đỉnh ở hai lần liên tiếp thì cách nhau một chu kì của sóng 2 T = =10(s)  . 5   
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3 3 sin 3x − =    4  2 bằng:     A. . B. − . C. . D. − . 9 6 6 9 Lời giải Chọn C  3  3x − = + k2 3 3 3       4 3 Ta có sin 3x − =  sin 3x − = sin       .  4  2  4  3 3    3x − =  − + k2  4 3  13  13 2 3x = + k2 x = + k   12 36 3     (k Z ). 17 17    2 3x = + k2 x = + k  12  36 3  13 13
x  0  k  −  k = 0 → x =  min 13 2 Cho 24 36 TH1. Với x = + k ⎯⎯→  . 36 3 13 11  
x  0  k  −  k = −1→ x = − max  24 36 13 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống  17 17
x  0  k  −  k = 0 → x =  min 17 2 Cho 24 36 TH2. Với x = + k ⎯⎯→  . 36 3 17 7  
x  0  k  −  k = 1 − → x = − max  24 36 
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là 7 x = −
và nghiệm dương nhỏ nhất là 36 13    x =
. Khi đó tổng hai nghiệm bằng 13 7 − = . 36 36 36 6
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 . Lời giải Chọn A
Gọi số cây ở hàng thứ n là u . n
Ta có: u = 1 , u = 2 , u = 3 , … và S = u + u + u + ... + u = 3003 . 1 2 3 1 2 3 n
Nhận xét dãy số (u là cấp số cộng có u = 1, công sai d = 1. n ) 1
n 2u + n −1 d   n 2.1+  (n − ) 1 1 1 ( ) Khi đó   S = = 3003  = 3003 2 2  =  n n (n + ) 1 = 6006 2
n + n − 6006 = 77 0  
n = 77 (vì n  ). n = 78 −
Câu 34: Một cấp số nhân có số hạng đầu u = 3 , công bội q = 2 . Biết S = 765 . Tìm n ? 1 n A. n = 8 . B. n = 9 . C. n = 6 . D. n = 7 . Lời giải Chọn A u 1 n − q 3. 1− 2n 1 ( ) ( )
Áp dụng công thức của cấp số nhân ta có: S = =
= 765  n = 8 . n 1− q 1− 2
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20) 20;25) 25;30) 30;35) 35;40) 40;45) 45;50) Số nhân viên 7 14 25 37 21 14 10
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 1360 800 1360 3280 A. Q = , Q = . B. Q = , Q = . 1 3 37 21 1 3 37 83 136 3280 136 800 C. Q = , Q = . D. Q = , Q = . 1 3 5 83 1 3 5 21 Lời giải Chọn D
Cỡ mẫu là n = 128. 14 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống +
Tứ phân vị thứ nhất x x Q là 32
33 . Do x , x đều thuộc nhóm [25;30) nên nhóm này chứa 1 32 33 2 Q . 1 128 − 21 136
Do đó, p = 3;a = 25;m = 25;m + m = 21, a − a = 5 và ta có 4 Q = 25 + 5 = 3 3 1 2 4 3 1 25 5 +
Với tứ phân vị thứ ba x x Q là 96
97 . Do x , x đều thuộc nhóm [35; 40) nên nhóm này chứa 3 96 97 2 Q . 3
Do đó, p = 5; a = 35; m = 21; m + m + m + m = 7 +14 + 25 + 37 = 83; a − a = 5 và ta có 5 5 1 2 3 4 6 5 3.128 −83 800 4 Q = 35 + 5 = . 3 21 21 15 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tuyển tập 05 đề ôn giữa học kỳ I
Kết nối trị thức với cuộc sống PHẦN TỰ LUẬN Câu Đáp án Biểu điểm    0.5
Giải phương trình cot x + = 3   .  3       0.25 1.a cot x +
= 3  x + = + k    3  3 6   0.25 x = −
+ k (k  ) . 6 2 0.5 Cho sin =
, tính giá trị của biểu thức P = (1− 3cos )(1+ 3cos ) . 3 P = −  +  = − (  )2 2 (1 3cos )(1 3cos ) 1 3cos =1− 9cos  . 0.25 1.b 2 5 0.25 sin = , 2 2 2
sin  + cos  = 1  cos  = . 3 9 5 P = 1− 9. = 4 − . 9
Giải phương trình cos 3x − sin 2x = 0 . 1.0    0.25
cos3x − sin 2x = 0  cos3x = sin 2x  cos3x = cos − 2x    2      0.25 3x =  − 2x + k2    2    0.25 5x = + k2 2.a  2   
x = − + k2  2   2 0.25 x = + k  10 5   (k  ) 
x = − + k2  2    1.0
Giải phương trình sin x = cos x +    3     sin x = cos x +    3  0,25        cos − x = cos x +      2   3  2.b  
− x = x + + k2  2 3   (k  )   0,25
 − x = −x − + k2  2 3   2
− x = − + k2 (k  ) 0,25 6 16 GV. Phan Nhật Linh - SĐT: 0817 098 716
Tu yển tập 05 đề ôn giữa học kỳ I
Kết nối tri thức với cuộc sống   x =
− k (k  ) . 0,25 12
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu
tiên là 100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000
đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng với
cơ sở khoan giếng này để khoan giếng sâu 0.5
20 mét lấy nước dùng cho sinh hoạt
gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán
cho cơ sở khoan giếng số tiền bằng bao nhiêu?
Giá tiền mỗi mét khoan giếng lập thành một cấp số cộng với
u = 100000 (số tiền mét khoan đầu tiên), 1 3
u = u + 30000 (số tiền mét khoan thứ hai), 2 1
u = u + 30000 = u + 2.30000 (số tiền mét khoan thứ ba) 0,25 3 2 1 … u
= u + 30000 = u +19.30000 (số tiền mét khoan thứ 20), 20 19 1
và công sai d = 30000 .
Tổng chi phí cần phải thanh toán là 20(2.10000 +19.30000) S
= u + u + u + ...+ u = = 7700000 . 0,25 20 1 2 3 20 2 17 GV. Phan Nhật Linh - SĐT: 0817 098 716
Document Outline

  • [Toán 11 KNTT] Đề thi giữa học kỳ I số 01_GV
  • [Toán 11 KNTT] Đề thi giữa học kỳ I số 02_GV
  • [Toán 11 KNTT] Đề thi giữa học kỳ I số 03_GV
  • [Toán 11 KNTT] Đề thi giữa học kỳ I số 04_GV
  • [Toán 11 KNTT] Đề thi giữa học kỳ I số 05_GV