Tuyển tập 181 bài tập tỷ số thể tích có đáp án và lời giải

Tài liệu gồm 134 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Word Và Biên Soạn Tài Liệu Toán, tuyển tập 181 bài tập tỷ số thể tích có đáp án và lời giải chi tiết, với đầy đủ các mức độ nhận thức: nhận biết, thông hiểu, vận dụng và vận dụng cao.

Chủ đề:

Chương 1: Khối đa diện 172 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:
134 trang 1 năm trước
Tác giả:
L
Lan Tường
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tuyển tập 181 bài tập tỷ số thể tích có đáp án và lời giải

Tài liệu gồm 134 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Word Và Biên Soạn Tài Liệu Toán, tuyển tập 181 bài tập tỷ số thể tích có đáp án và lời giải chi tiết, với đầy đủ các mức độ nhận thức: nhận biết, thông hiểu, vận dụng và vận dụng cao.

49 25 lượt tải Tải xuống

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 3.8 K tài liệu

Thông tin:

134 trang 1 năm trước

Tác giả:

Profile Lan Tường
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 1
1. KHỐI CHÓP - MỨC 1 ............................................................................................................................ 1
2. KHỐI LĂNG TRỤ - MỨC 1 .................................................................................................................. 5
3. KHỐI CHÓP - MỨC 2 ............................................................................................................................ 6
4. KHỐI LĂNG TRỤ - MỨC 2 ................................................................................................................ 24
5. KHỐI CHÓP - MỨC 3 .......................................................................................................................... 35
6. KHỐI LĂNG TRỤ - MỨC 3 ................................................................................................................ 58
7. KHỐI CHÓP - MỨC 4 .......................................................................................................................... 77
8. KHỐI LĂNG TRỤ - MỨC 4 .............................................................................................................. 122
TUYÓN TËP 1 Sè C¢U HáI LI£N QUAN
Tû Sè THÓ TÝCH
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 2 TỔNG HỢP: HOÀNG TUYÊN
1. KHỐI CHÓP - MỨC 1
Câu 1. Cho khối tứ diện
ABCD
có thể tích bằng
3
60 cm và điểm
K
trên cạnh
AB
sao cho
4 .AB KB
Tính thể tích
V
của khối tứ diện
BKCD
.
A.
3
20V cm
. B.
3
12V cm
. C.
3
30V cm
. D.
3
15V cm
.
Lời giải
Chọn D
Ta có:
3
.
. .
.
1 1 1
. . .60 15
4 4 4
B KCD
B KCD B ACD
B ACD
V
BK BC BD
V V cm
V BA BC BD
Câu 2. Cho khối chóp
.S ABCD
có đáy là hình chữ nhật và thể tích bằng 8. Thể tích của khối chóp
.S BCD
bằng:
A.
2
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn B
Ta có: Hai hình chóp
.S ABCD
và
.S BCD
có cùng chiều cao
h
là khoảng cách từ
S
đến mặt phẳng
ABCD
và
1
2
BCD ABCD
S S
1
. .
1 1
3
4.
1
2 2
. .
3
BCD
BCD
BCD ABCD
ABCD
ABCD
S h
V
V V
V
S h
Câu 3. Cho khối chóp
.S ABCD
có đáy là hình chữ nhật và thể tích bằng 8. Thể tích của khối chóp
.S BCD
bằng:
A.
2
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn B
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 3
Ta có: Hai hình chóp
.S ABCD
và
.S BCD
có cùng chiều cao
h
là khoảng cách từ
S
đến mặt phẳng
ABCD
và
1
2
BCD ABCD
S S
1
. .
1 1
3
4.
1
2 2
. .
3
BCD
BCD
BCD ABCD
ABCD
ABCD
S h
V
V V
V
S h
Câu 4. Cho khối tứ diện
ABCD
có thể tích bằng
3
60 cm
và điểm
K
trên cạnh
AB
sao cho
4 .AB KB
Tính thể tích
V
của khối tứ diện
BKCD
.
A.
3
20V cm . B.
3
12V cm . C.
3
30V cm . D.
3
15V cm .
Lời giải
Chọn D
Ta có:
3
.
. .
.
1 1 1
. . .60 15
4 4 4
B KCD
B KCD B ACD
B ACD
V
BK BC BD
V V cm
V BA BC BD
Câu 5. Cho khối chóp
.S ABC
. Gọi
A
,
B
,
C
lần lượt là trung điểm của các cạnh
SA
,
SB
,
SC
(minh
hoạ như hình vẽ). Tỉ số
.
.
S A B C
S ABC
V
V
bằng
A.
8
. B.
2
. C.
1
8
. D.
1
2
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 4 TỔNG HỢP: HOÀNG TUYÊN
Lời giải
Chọn C
Ta có:
.
.
1 1 1 1
. . . .
2 2 2 8
S A B C
S ABC
V
SA SB SC
V SA SB SC
.
Câu 6. Cho khối tứ diện
ABCD có thể tích V và điểm
E
trên cạnh
AB
sao cho 3AE EB . Tính thể tích
khối tứ diện
EBCD
theo
.V
A.
4
V
. B.
3
V
. C.
2
V
. D.
5
V
.
Lời giải
Chọn A
.
. .
.
1 1
. .
4 4
B ECD
B ECD E BCD
A BCD
V
BE AC AD
V V V
V BA AC AD
Câu 7. Cho khối chóp
.S ABC
, trên ba cạnh
SA
,
SB
,
SC
lần lượt lấy ba điểm
A
,
B
,
C
sao cho
1
2
SA SA
,
1
3
SB SB
,
1
4
SC SC
. Gọi
V
và
V
lần lượt là thể tích của các khối chóp
.S ABC
và
.S A B C
. Khi đó tỉ số
V
V
là:
A.
12
. B.
1
12
. C.
24
. D.
1
24
.
Lời giải:
Chọn D
Theo công thức tỉ số thể tích khối chóp, ta được:
1 1 1 1
. . . .
2 3 4 24
V SA SB SC
V SA SB SC
.
C'
B'
A'
A
C
B
S
B
A
D
E
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 5
2. KHỐI LĂNG TRỤ - MỨC 1
Câu 8. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
15
. Thể tích khối chóp
.A ABC
bằng
A.
5
. B.
10
. C.
3
. D.
6
.
Lời giải
Chọn A
Vì lăng trụ
.ABC A B C
và khối chóp
.A ABC
có diện tích đáy như nhau và cùng chiều cao nên
.
.
1
3
A ABC
ABC A B C
V
V
. .
1
5
3
A ABC ABC A B C
V V
.
Câu 9. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
15
. Thể tích khối chóp
.A ABC
bằng
A.
5
. B.
10
. C.
3
. D.
6
.
Lời giải
Chọn A
Vì lăng trụ
.ABC A B C
và khối chóp
.A ABC
có diện tích đáy như nhau và cùng chiều cao nên
.
.
1
3
A ABC
ABC A B C
V
V
. .
1
5
3
A ABC ABC A B C
V V
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 6 TỔNG HỢP: HOÀNG TUYÊN
3. KHỐI CHÓP - MỨC 2
Câu 10. Cho hình chóp
.S ABC
có
, 3 2, 2 3SA a SB a SC a
,
60ASB BSC CSA . Thể tích
khối chóp
.S ABC
là
A.
3
2 3a . B.
3
3
3
a
. C.
3
3a . D.
3
3 3a .
Lời giải
Chọn C
Lấy
, M SB N SC
sao cho
SA SM SN a
.
Vì
60ASB BSC CSA do đó khối chóp
SAMN
là tứ diện đều cạnh
a
nên
3
.
2
.
12
S AMN
a
V
Mặt khác
.
.
6 6
S ABC
S AMN
V
SA SB SC
V SA SM SN
3
3
. .
2
6 6 6 6 3.
12
S ABC S AMN
a
V V a
Câu 11. Cho khối chóp
.S ABC
có thể tích bằng 48. Gọi
, ,M N P
lần lượt là trung điểm của các cạnh
, ,SA SB SC
. Thể tích của khối chóp
.S MNP
bằng
A. 6. B. 8. C. 12. D. 10.
Lời giải
Chọn A
Ta có hình vẽ:
Ta có:
.
.
S ABC
S MNP
V
SA SB SC
V SM SN SP
.
Theo giả thiết ta có:
.
.
48 2 2 2
6
1 1 1
S MNP
S MNP
V
V
(đvtt).
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 7
Câu 12. Cho khối chóp
.S ABC
có thể tích bằng 48. Gọi
, ,M N P
lần lượt là trung điểm của các cạnh
, ,SA SB SC
. Thể tích của khối chóp
.S MNP
bằng
A. 6. B. 8. C. 12. D. 10.
Lời giải
Chọn A
Ta có hình vẽ:
Ta có:
.
.
S ABC
S MNP
V
SA SB SC
V SM SN SP
.
Theo giả thiết ta có:
.
.
48 2 2 2
6
1 1 1
S MNP
S MNP
V
V
(đvtt).
Câu 13. Cho hình chóp
.S ABC
có
, 3 2, 2 3SA a SB a SC a
,
60ASB BSC CSA . Thể tích
khối chóp
.S ABC
là
A.
3
2 3a . B.
3
3
3
a
. C.
3
3a . D.
3
3 3a .
Lời giải
Chọn C
Lấy
, M SB N SC
sao cho
SA SM SN a
.
Vì
60ASB BSC CSA do đó khối chóp
SAMN
là tứ diện đều cạnh
a
nên
3
.
2
.
12
S AMN
a
V
Mặt khác
.
.
6 6
S ABC
S AMN
V
SA SB SC
V SA SM SN
3
3
. .
2
6 6 6 6 3.
12
S ABC S AMN
a
V V a
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 8 TỔNG HỢP: HOÀNG TUYÊN
Câu 14. Cho khối tứ diện đều có thể tích là . Gọi , , , lần lượt là trung điểm của
, , , . Thể tích khối chóp là
A. . B. . C. . D. .
Lời giải
Chọn D
Cách 1:
Ta có: .
Mà .
Vậy .
Cách 2:
Ta có: (do là hình thoi).
Mà (do ) nên .
Vì là trung điểm của nên và .
Nên .
Suy ra .
Câu 15. Cho hình chóp
.S ABC
. Gọi
M
,
N
,
P
theo thứ tự là trung điểm của
SA
,
SB
,
SC
. Tính tỉ số
thể tích của
2
khối chóp
.S MNP
và
.S ABC
bằng
A.
1
4
. B.
1
8
. C.
1
16
. D.
1
2
.
Lời giải
Chọn B
ABCD
V
M
N
P
Q
A C
A D
BD
BC
.
AMNPQ
12
V
3
V
6
V
4
V
1
. .
4
AMNP
ACDP
V
AM AN AP
V AC AD AP
1
2
ACDP
ABCD
V
V
.
1 1 1 1
2 2. 2. . .
4 4 2 4 4
A MNPQ AMNP ACDP ABCD ABCD
V
V V V V V
.
2
A MNPQ APMQ
V V
MNPQ
APMQ BPMQ
V V
//
AB MQ
.
2
A MNPQ BPMQ
V V
P
BD
1
, ,
2
d P ABC d D ABC
1
4
BQM ABC
S S
1
, .
3
BPMQ BQM
V d P ABC S
1 1 1
. , .
3 2 4
ABC
d D ABC S
1 1
. , .
8 3
ABC
d D ABC S
8
V
4
AMNPQ
V
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 9
Ta có
.
.
1
8
S MNP
S ABC
V
SM SN SP
V SA SB SC
.
Câu 16. Cho tứ diện
ABCD
. Xét điểm
M
trên cạnh
AB
, điểm
N
trên cạnh
BC
, điểm
P
trên cạnh
CD
sao cho
3
3, 4,
2
MB NB PC
MA NC PD
. Gọi
1
V ,
2
V theo thứ tự là thể tích các khối tứ diện
MNBD
và
NPAC
. Tỉ số
1
2
V
V
bằng
A.
3
. B.
5
. C.
1
5
. D.
1
3
.
Lời giải
Chọn B
1 1 1
1
.S
3
V h
với
1 1
, ;
NBD
h d M BCD S S
.
2 2 2
1
.
3
V h S
với
2 2
, ;
CNP
h d A BCD S S
.
1 1 1
2 2 2
.
5
.
V h S
V h S
. Vì
1
2
3
4
h
h
và
1
1 2
2
4 1 3 3 20
; .
5 5 5 25 3
BCD BCD BCD
S
S S S S S
S
.
Câu 17. Cho hình chóp
.S ABC
có
, ,SA SB SC
đôi một vuông góc với nhau và
SA a
,
2SB a
và
3SC a
. Gọi
,M N
lần lượt là trung điểm của cạnh
SB
và
SC
. Tính theo
a
thể tích khối chóp
.S AMN
.
N
P
M
A
C
B
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 10 TỔNG HỢP: HOÀNG TUYÊN
A.
3
2
a
. B.
3
4
a
. C.
3
a
. D.
3
3
4
a
.
Lời giải
Chọn B
Hình vẽ
Ta có
3
.
1 1
. . .
3 6
S ABC SBC
V SA S SA SB SC a
Mặc khác
.
.
1
. .
4
S AMN
S ABC
V
SA SM SN
V SA SB SC
. Suy ra
3
. .
1
4 4
S AMN S ABC
a
V V
.
Câu 18. Cho hình chóp tam giác đều
.S ABC
. Gọi
M
,
N
lần lượt là trung điểm của
BC
,
SM
. Mặt phẳng
ABN
cắt
SC
tại
E
. Gọi
2
V là thể tích của khối chóp
.S ABE
và
1
V là thể tích khối chóp
.S ABC
. Khẳng định nào sau đây đúng?
A.
2 1
1
4
V V
. B.
2 1
1
3
V V
. C.
2 1
1
6
V V
. D.
2 1
1
8
V V
.
Lời giải
Chọn B
Gọi
I
là trung điểm của
EC
nên
IM
là đường trung bình của tam giác
BCE //MI EN
Mà
N
là trung điểm của
SM EN
là đường trung bình của tam giác
SMI
suy ra
E
là trung
điểm của
SI
.
2
2 1
1
1 1
3 3
V SE
V V
V SC
.
Câu 19. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân,
AB AC a
,
SC ABC
và
SC a
. Mặt phẳng qua
C
, vuông góc với
SB
cắt
SA
,
SB
lần lượt tại
E
và
F
. Thể tích khối
chóp
.S CEF
là
N
M
S
B
C
A
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 11
A.
3
2
12
a
. B.
3
36
a
. C.
3
2
36
a
. D.
3
18
a
.
Lời giải
Chọn B
Tam giác vuông
SCA
có
SC CA a
nên là tam giác vuông cân ở
.C
Ta có
AB AC
và
AB SC
suy ra
AB SAC
suy ra
.AB CE
1
Mặt khác theo giả thiết
SB CEF SB CE
.
2
Từ
1
và
2
suy ra
SAB CE CE SA
. Do đó
E
la trung điểm của
SA
vì tam giác
SCA
vuông cân ở
.C
Trong tam giác vuông
SCB
có
2
2
2
. .
SC SF
SC SF SB
SB SB
Từ đó ta có
2 2
.
2 2 2
.
1 1 1
. . .
2 2 2 6
S CEF
S CAB
V
SE SF SC a
V SA SB SB a a
3
. .
1 1 1 1
. . . . .
6 6 3 2 36
S CEF S CAB
a
V V a a a
Câu 20. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông. Gọi
E
,
F
lần lượt là trung điểm của
SB
,
SD
. Tỉ số
.
.
S AEF
S ABCD
V
V
bằng:
A.
1
4
. B.
3
8
. C.
1
8
. D.
1
2
.
Lời giải:
Chọn C
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 12 TỔNG HỢP: HOÀNG TUYÊN
Áp dụng công thức tỉ số thể tích hình chóp, ta có:
.
.
1
. .
4
S AEF
S ABD
V
SA SE SF
V SA SB SC
.
Suy ra
. . .
1 1 1
. .
4 4 2
S AEF S ABD S ABCD
V V V
.
Vậy
.
.
1
8
S AEF
S ABCD
V
V
.
Câu 21. Cho hình chóp tứ giác
.S ABCD
có
,M ,N ,P Q
lần lượt là trung điểm các cạnh
,SA ,SB ,SC
SD
. Biết khối chóp
.S ABCD
có thể tích là
3
16a
. Tính thể tích khối chóp
.S MNPQ
theo
a
.
A.
3
2a
. B.
3
a
. C.
3
8a
. D.
3
4a
.
Lời giải
Chọn A
Cách 1: Mặt phẳng
SAC
chia khối chóp
.S ABCD
thành hai khối chóp tam giác
.S ABC
và
.S ADC
, đồng thời cũng chia khối chóp
.S MNPQ
thành hai khối chóp
.S MNP
và
.S MQP
.
Áp dụng phương pháp tỷ số thể tích, ta có:
.
.
1
8
S MNP
S ABC
V
SM SN SP
V SA SB SC
nên
. .
1
8
S MNP S ABC
V V
; và
.
.
1
8
S MQP
S ADC
V
V
nên
. .
1
8
S MQP S ADC
V V
.
Do đó
3 3
. . . . . . .
1 1 1
.16 2
8 8 8
S MNPQ S MNP S MQP S ABC S ADC S MNPQ S ABCD
V V V V V V V a a
.
F
E
C
A
D
B
S
Q
P
N
M
A
D
B
C
S
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 13
Cách 2: Ta dễ dàng chỉ ra được tứ giác
MNPQ
đồng dạng với
ABCD
theo tỷ số
1
2
nên
2
1
.
2
MNPQ ABCD
S S
. Đồng thời
1
, ,
2
d S MNPQ d S ABCD
.
Do đó, ta có:
3 3
. .
1 1 1 1 1
. , . , .16 2
3 3 4 8 8
S MNPQ MNPQ ABCD S ABCD
V S d S MNPQ S d S ABCD V a a
.
Câu 22. Cho khối chóp
.S ABC
có các điểm
A
,
B
,
C
lần lượt thuộc các cạnh
SA
,
SB
,
SC
thoả
3SA SA
,
4SB SB
,
5 3SC SC
. Biết thể tích khối chóp
.S A B C
bằng
5
3
cm
. Tìm thể tích khối chóp
.S ABC
.
A.
120
3
cm
. B.
60
3
cm
. C.
80
3
cm
. D.
100
3
cm
.
Lời giải
Chọn D
Áp dụng tỉ lệ thể tích ta có:
.
.
. .
S A B C
S ABC
V
SA SB SC
V SA SB SC
1 1 3
. .
3 4 5
1
20
. .
20
S ABC S A B C
V V
100
3
cm
.
Câu 23. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
. Gọi
H
và
K
lần lượt là trung điểm
của
SB
,
SD
. Tỷ số thể tích
.
AOHK
S ABCD
V
V
bằng
A.
1
12
. B.
1
6
. C.
1
8
. D.
1
4
.
Lời giải
Chọn C
C'
B'
A'
S
C
B
A
O
K
H
D
A
B
C
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 14 TỔNG HỢP: HOÀNG TUYÊN
Vì
H
và
K
,
O
lần lượt là trung điểm của
SB
và
SD
,
BD
nên
1
4
OHK SBD
S S
Suy ra
. . .
.
1 1 1 1
4 4 8 8
AOHK
AOHK A SBD S ABD S ABCD
S ABCD
V
V V V V
V
.
Câu 24. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành.
M
là trung điểm
SB
và
G
là trọng tâm
của tam giác
SBC
. Gọi
V
,
V
lần lượt là thể tích của các khối chóp
.M ABC
và
.G ABD
, tính tỉ
số
V
V
.
A.
3
2
V
V
. B.
4
3
V
V
. C.
5
3
V
V
. D.
2
3
V
V
.
Lời giải
Chọn A
Cách 1:
Gọi
V
là thể tích khối chóp
.S ABCD
.
Ta có
.
.
1
2
M ABC
S ABC
V
SM
V SB
.
Mặt khác
. .
1
2
S ABC S ABCD
V V
. .
1
4
M ABC S ABCD
V V
.
Dễ thấy
1
, ,
3
d G ABCD d S ABCD
;
1
2
ABD ABCD
S S
.
Vậy
.
1
.
6
G ABD ABCD
V V
.
Suy ra,
.
.
1
3
4
1
2
6
M ABC
G ABD
V
V
.
Cách 2:
. . .
. . .
2 3
3 2
G ABD G ABC M ABC
M ABC M ABC G ABD
V V V
GC
V V MC V
Câu 25. Cho hình chóp tam giác
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA a
và
SA
vuông góc
với mặt phẳng
ABC
. Gọi
M
và
N
lần lượt là hình chiếu vuông góc của
A
trên các đường thẳng
SB
và
SC
. Thể tích
V
của khối chóp
.A BCNM
bằng
G
M
O
B
A
C
D
S
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 15
A.
3
3
.
12
a
B.
3
3
.
48
a
C.
3
3
.
24
a
D.
3
3
.
16
a
Lời giải
Chọn D
Thể tích khối chóp
.S ABC
là
2
.
1 3
.
3 4
S ABC
a
V a
3
3
12
a
.
Do
SA AB AC a
nên các tam giác
,SAC SAB
cân tại
A
.
Theo đề bài
M
,
N
là hình chiếu của
A
trên
SB
,
SC
nên
M
,
N
lần lượt là trung điểm
SB
,
SC
.
Khi đó:
3
.
. .
.
. 1 1 3
. 4 4 48
S AMN
S AMN S ABC
S ABC
V
SM SN a
V V
V SB SC
.
Vậy thể tích khối chóp
.A BCNM
là
3 3 3
. . .
3 3 3
12 48 16
A BMNC S ABC S AMN
a a a
V V V
.
Câu 26. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông góc với mặt đáy. Gọi
M
là trung điểm
BC
. Mặt phẳng
P
đi qua
A
và vuông góc với
SM
cắt
SB
,
SC
lần lượt tại
E
,
F
. Biết
. .
1
4
S AEF S ABC
V V
. Tính thể tích
V
của khối chóp
.S ABC
.
A.
3
2
a
V
. B.
3
8
a
V
. C.
3
2
5
a
V
. D.
3
12
a
V
.
Lời giải
Chọn B
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 16 TỔNG HỢP: HOÀNG TUYÊN
Ta có
BC SM
. Gọi
H
là hình chiếu vuông góc của
A
trên
SM
. Do
FE P SBC
FE SM
FE BC
và
FE
đi qua
H
.
. .
1
4
S AEF S ABC
V V
1
.
4
SE SF
SB SC
2
1
4
SH
SM
1
2
SH
SM
. Vậy
H
là trung điểm cạnh
SM
.
Suy ra
SAM
vuông cân tại
A
3
2
a
SA
.
Vậy
2
1 3 3
. .
3 2 4
SABC
a a
V
3
8
a
.
Câu 27. Cho hình chóp
.S ABCD
có đáy là hình bình hành và có thể tích bằng
1
. Trên cạnh
SC
lấy điểm
E
sao cho
2SE EC
. Tính thể tích
V
của khối tứ diện
SEBD
.
A.
2
3
V
. B.
1
6
V
. C.
1
3
V
. D.
4
3
V
.
Lời giải
Chọn C
Ta có:
2
3
SEBD
SCBD
V
SE
V SC
.
Mà:
.
1 1
2 2
SBCD S ABCD
V V
2 1 1
.
3 2 3
SEBD
V
.
Câu 28. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể
tích của khối chóp đó sẽ:
F
E
M
S
B
C
A
H
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 17
A. Không thay đổi. B. Tăng lên hai lần. C. Giảm đi ba lần. D. Giảm đi hai lần.
Lời giải
Chọn A
Nếu tăng cạnh đáy lên hai lần thì diện tích đáy tăng bốn lần. Vì giảm chiều cao đi bốn lần nên thể
tích khối chóp không thay đổi.
Câu 29. Cho tứ diện
MNPQ
. Gọi
I
;
J
;
K
lần lượt là trung điểm của các cạnh
MN
;
MP
;
MQ
. Tỉ số
thể tích
MIJK
MNPQ
V
V
bằng
A.
1
3
. B.
1
4
. C.
1
6
. D.
1
8
.
Lời giải
Chọn D
Ta có:
.
.
1 1 1 1
. . . .
2 2 2 8
M IJK
M NPQ
V
MI MJ MK
V MN MP MQ
.
Câu 30. Cho tứ diện
.ABCD
Gọi
', 'B C
lần lượt là trung điểm của
, .AB AC
Khi đó tỉ số thể tích của khối
tứ diện
' 'AB C D
và khối tứ diện
ABCD
bằng:
A.
1
8
. B.
1
2
. C.
1
4
. D.
1
6
.
Lời giải
Chọn C
K
J
I
N
Q
P
M
B'
C'
B
D
C
A
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 18 TỔNG HỢP: HOÀNG TUYÊN
Ta có
' '
' ' 1 1 1
. . .
2 2 4
AB C D
ABCD
V
AB AC
V AB AC
Câu 31. Cho tứ diện
OABC
có
,OA a 2 ,OB a
3OC a
đôi một vuông góc với nhau tại
O
. Lấy
M
là
trung điểm của cạnh
;AC
N
nằm trên cạnh
CB
sao cho
2
3
CN CB
. Tính theo
a
thể tích khối
chóp
OAMNB
.
A.
3
2a
. B.
3
1
6
a
. C.
3
2
3
a
. D.
3
1
3
a
.
Lời giải
Chọn C
Ta có:
3
1 1
; . . .
3 6
OABC OBC
V d A OBC S OAOB OC a
3
1 1 1 2 1
; . . . ; . .
3 3 2 3 3 3
MOBC OCN OBC OABC
a
V d M OBC S d M OBC S V
3 3
3
2
3 3
AOMNB OABC MOBC
a a
V V V a
.
Câu 32. Cho hình chóp
.S ABCD
. Gọi
M
,
N
,
P
,
Q
theo thứ tự là trung điểm của
SA
,
SB
,
SC
,
SD
.
Tính tỉ số thể tích của hai khối chóp
.S MNPQ
và
.S ABCD
bằng
A.
1
8
. B.
1
2
. C.
1
4
. D.
1
16
.
Lời giải
Chọn A
M
O
B
C
A
N
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 19
Ta có
. .
1
8
S MNP S ABC
V V
và
. .
1
8
S MQP S ADC
V V
. . . . . .
1 1 1
8 8 8
S MNPQ S MQP S MNP S ABC S ADC S ABCD
V V V V V V
.
.
1
8
S MNPQ
S ABCD
V
V
.
Câu 33. Cho hình chóp
.S ABC
có
SA ABC
, tam giác
ABC
đều,
AB a
, góc giữa
SB
và
ABC
bằng
60
. Gọi
M
,
N
lần lượt là trung điểm của
SA
,
SB
. Tính thể tích khối chóp
.S MNC
A.
3
8
a
. B.
3
4
a
. C.
3
3
12
a
. D.
3
16
a
.
Lời giải
Chọn D
Ta có
, , 60SB ABC SB AB SBA
.
.tan .tan 60 3SA AB SBA a a
.
2
3
.
1 1 3 1
. . . 3.
3 3 4 4
S ABC ABC
a
V SA S a a
.
Mà
.
.
1
.
4
S CMN
S CAB
V
SM SN
V SA SB
3
. .
1 1
4 16
S CMN S CAB
V V a
.
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Hai mặt bên
SAB
và
SAD
cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng
SCD
và
ABCD
bằng
45
. Gọi
Q
P
N
M
A
B
C
D
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 20 TỔNG HỢP: HOÀNG TUYÊN
1 2
;V V lần lượt là thể tích khối chóp
.S AHK
và
.S ACD
với
H
,
K
lần lượt là trung điểm của
SC
và
SD
. Tính độ dài đường cao của khối chóp
.S ABCD
và tỉ số
1
2
V
k
V
.
A.
1
;
4
h a k
. B.
1
;
6
h a k
. C.
1
2 ;
8
h a k
. D.
1
2 ;
3
h a k
.
Lời giải
Chọn A
Do
SAB
và
SAD
cùng vuông góc với mặt đáy nên
SA ABCD
.
Ta có
CD AD
CD SAD CD SD
CD SA
.
Dễ thấy góc giữa hai mặt phẳng
SCD
và
ABCD
là
45SDA .
Ta có tam giác
SAD
là tam giác vuông cân đỉnh
A
. Vậy
h SA a
.
Áp dụng công thức tỉ số thể tích có:
1
2
1
.
4
V
SH SK
V SC SD
.
Câu 35. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi và có thể tích bằng
2
. Gọi
M
,
N
lần lượt là
các điểm trên cạnh
SB
và
SD
sao cho
SM SN
k
SB SD
. Tìm giá trị của
k
để thể tích khối chóp
.S AMN
bằng
1
8
.
A.
1
8
k
. B.
2
2
k
. C.
2
4
k
. D.
1
4
k
.
Lời giải
Chọn C
S
A
B
C
D
M
N
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 21
Ta có
2
.
.
. . .
S AMN
S ABD
V
SA SM SN
k
V SA SB SD
Mà
2
. . .
1 1 1 2
, 1 .
8 2 8 4
S AMN S ABD S ABCD
V V V k k
Câu 36. Cho hình chóp
.S ABC . Gọi
M
, N lần lượt là trung điểm của SA , SB . Tính tỉ số
.
.
S ABC
S MNC
V
V
.
A.
4
. B.
1
2
C.
2
. D.
1
4
Lời giải.
Chọn A
Ta có
.
.
S ABC
S MNC
V
V
. .
4
. .
SA SB SC
SM SN SC
.
Câu 37. Cho tứ diện
ABCD
có các cạnh
AB
,
AC
,
AD
vuông góc với nhau từng đôi một và
3AB a
,
6AC a
,
4AD a
. Gọi
M
,
N
,
P
lần lượt là trung điểm các cạnh
BC
,
CD
,
BD
. Tính thể
tích khối đa diện
AMNP
.
A.
3
3a
. B.
3
12a
. C.
3
a
. D.
3
2a
.
Lời giải
Chọn A
Cách 1: Khối tứ diện
ABCD
được chia thành bốn tứ diện có thể tích bằng nhau.
Mà
3
1
. . 12
6
ABCD
V AB AC AD a
nên
3
1
3
4
AMNP ABCD
V V a
.
Cách 2: Ta có
3
1
. . 12
6
ABCD
V AB AC AD a
.
2 2
3 5BC AB AC a
;
2 2
2 13CD AC AD a
;
2 2
5BD AB AD a
.
N
C
B
A
M
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 22 TỔNG HỢP: HOÀNG TUYÊN
Diện tích tam giác
BCD
:
BCD
S p p BC p CD p BD
, với
3 5 2 13 5
2
a a a
p
2
3
12
3 29 ,
29
ABCD
BCD
BCD
V
a
S a d A BCD
S
.
Mà
M
,
N
,
P
là trung điểm các cạnh
BC
,
CD
,
BD
nên hai tam giác
BCD
và
MNP
đồng dạng
theo tỉ số
1
2
k
nên
1
4
MNP BCD
S S
Khi đó
3
1
. . , 3
3
AMNP MNP
V S d A MNP a
.
Câu 38. Cho hình chóp
.S ABC
có đáy là
ABC
vuông cân ở
,B
2,AC a
,SA ABC
.SA a
Gọi
G
là trọng tâm của
SBC
,
mp
đi qua
AG
và song song với
BC
chia khối chóp thành hai
phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
.V
A.
3
4
.
9
a
B.
3
4
.
27
a
C.
3
5
.
54
a
D.
3
2
.
9
a
Lời giải
Chọn C
Trong mặt phẳng
SBC
. Qua
G
kẻ đường thẳng song song với
BC
và lần lượt cắt
,SC SB
tại
,E F
. Khi đó ta được khối đa diện không chứa đỉnh
S
là
.ABCEF
Ta có
G
là trọng tâm của
SBC
nên
.AF
.
2 2 4
. . . .
3 3 9
S E
S ABC
V
SA SF SE
V SA SB SC
Do đó
.
.AF . . .
4 4 5
. . . .
9 9 9
S ABC
S E S ABC ABCEF S ABC S ABC
V V V V V V
Vì tam giác
ABC
vuông cân ở
,B
2AC a
nên
.AB BC a
Mặt khác
3
.
1 1
. . .
3 2 6
S ABC
a
V a a a
Suy ra
3 3
5 5
. .
9 6 54
ABCEF
a a
V
.
Câu 39. Cho hình chóp tam giác đều
.S ABC
. Gọi
M
,
N
lần lượt là trung điểm của
BC
,
SM
. Mặt phẳng
ABN
cắt
SC
tại
E
. Gọi
2
V là thể tích của khối chóp
.S ABE
và
1
V là thể tích khối chóp
.S ABC
. Khẳng định nào sau đây đúng?
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 23
A.
2 1
1
4
V V
. B.
2 1
1
3
V V
. C.
2 1
1
6
V V
. D.
2 1
1
8
V V
.
Lời giải
Chọn B
Gọi
I
là trung điểm của
EC
nên
IM
là đường trung bình của tam giác
BCE //MI EN
Mà
N
là trung điểm của
SM EN
là đường trung bình của tam giác
SMI
suy ra
E
là trung
điểm của
SI
.
2
2 1
1
1 1
3 3
V SE
V V
V SC
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 24 TỔNG HỢP: HOÀNG TUYÊN
4. KHỐI LĂNG TRỤ - MỨC 2
Câu 40. Cho lăng trụ tam giác đều . Lấy , lần lượt là tâm của hình chữ nhật và
,
là trung điểm của . Tính tỉ số thể tích của tứ diện và tứ diện .
A. . B. . C. . D. .
Lời giải
Chọn A
.
Câu 41. Cho hình hộp , gọi là giao điểm và . Thể tích khối chóp
bằng bao nhiêu lần thể tích khối hộp ?
A. . B. . C. . D. .
Lời giải
Chọn D
.
ABC A B C
H
G
B C C B
A C C A
I
C C
C H G I
CB A C
1
8
4
5
30
8
15
2
' ' '
1
. . . .
2 2 2 8
CHGI
CB A C
V
CH CG CI CH CG CI
V CB CA CC CH CG CI
G
H
B
C
A
A'
C'
B'
I
.
ABCD A B C D
O
AC
BD
.
O A B C D
.
ABCD A B C D
1
6
1
4
1
2
1
3
C
O
C'
B'
D'
D
B
A
A'
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 25
Do khối chóp và khối hộp có cùng chiều cao và diện tích đáy nên
Câu 42. Cho hình lăng trụ tam giác , biết rằng thể tích khối chóp bằng .Thể
tích khối lăng trụ bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có: Đặt
Câu 43. ( Đề Thi thử Trường Chuyên Lê Thánh Tông_Quảng Nam_2020 ) Gọi
V
là thể tích của khối
hộp
. ' ' ' 'ABCD A B C D
và
1
V là thể tích của tứ diện
'A BCD
. Hệ thức nào sau đây đúng?
A.
1
4V V . B.
1
2V V . C.
1
6V V . D.
1
3V V .
Lời giải
Chọn C
Gọi
h
là khoảng cách từ
'A
đến mp
( )ABCD
. Khi đó,
h
là chiều cao của khối hộp cũng là
chiều cao của tứ diện
'A BCD
.
Ta có:
. ' ' ' '
1 '
. 2 .
6
1 1
. .
3 3
ABCD A B C D ABCD BCD
A BCD
BCD BCD
V S h S h
V
V V
S h S h
1
6V V .
Câu 44. Cho lăng trụ tam giác có chiều cao bằng và diện tích đáy bằng . Gọi , ,
lần lượt là tâm của các mặt bên , và . Thể tích khối đa diện lồi có
các đỉnh là các điểm , , , , , bằng
A. . B. . C. . D. .
Lời giải
Chọn C
. '
. '
1
3
O A B C D
ABCD A B C D
V
V
. ' ' '
ABC A B C
. ' '
A BCC B
12
. ' ' '
ABC A B C
24
36
18
32
. ' ' '
ABC A B C
V V
' ' '
. ' ' ' ' ' '
' ' . ' ' '
. .
1 1
. .
3 3
2
12 18.
3
A B C
A A B C A B C
ABCC B A A B C
V h S
V h S V
V V V V V
.
A BC A B C
4
3
M
N
P
ABB A
B C C B
C A A C
A
B
C
M
N
P
6
9
4
9
2
3
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 26 TỔNG HỢP: HOÀNG TUYÊN
Ta có . Gọi , , lần lượt là trung điểm của , , .
.
Áp dụng bài toán tỷ số thể tích ta có:
Dễ thấy .
Vậy .
Câu 45. Nếu cạnh của một hình lập phương tăng lên 3 lần thì thể tích của hình lập phương đó tăng lên
bao nhiêu lần?
A.
27
. B.
9
. C.
6
. D.
4
.
Lời giải
Chọn A
Gọi cạnh của hình lập phương là
a
thì thể tích khối lập phương là
3
V a
.
Khi tăng cạnh lên 3 lần thì cạnh là
3a
, thể tích khối lập phương mới là
3
* 3
3 27V a a
.
Khi đó
*
27V V
.
Câu 46. Nếu cạnh của một hình lập phương tăng lên 2 lần thì thể tích của hình lập phương đó tăng lên
bao nhiêu lần?
A.
9
. B.
2
. C.
4
. D.
8
.
Lời giải
Chọn D
Gọi cạnh của hình lập phương là
a
thì thể tích khối lập phương là
3
V a
.
Khi tăng cạnh lên 2 lần thì cạnh là
2a
, thể tích khối lập phương mới là
3
* 3
2 8V a a
.
Khi đó
*
8V V
.
Câu 47. Nếu thể tích của một hình lập phương tăng lên 8 lần thì cạnh của hình lập phương đó tăng lên
bao nhiêu lần?
A.
2 2
. B.
4
. C.
2
. D.
8
.
K
J
I
P
N
M
A'
C'
B'
C
A
B
3.4 12
.
V
ABC A B C
I
J
K
AA
BB
C C
6
.
V
ABC IJK
1
.
8
.
V
AIMP
V
A A B C
. .
1 1
8 2
A IMP A A B C
V V
. . .
1
2
A IMP B MNJ C NPK
V V V
.
V
ABC M N P
3
. .
V V
ABC IJK A IM P
1 9
6 3.
2 2
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 27
Lời giải
Chọn C
Gọi cạnh của hình lập phương là
a
thì thể tích khối lập phương là
3
V a
.
Khi tăng thể tích lên 8 lần thì thể tích là
* 3
8 8V V a
.
Khi đó cạnh của hình lập phương là
2a
. Kết luận: Cạnh tăng lên 2 lần.
Câu 48. ( Đề Thi thử Trường Chuyên Lê Thánh Tông_Quảng Nam_2020 ) Gọi
V
là thể tích của khối
hộp
. ' ' ' 'ABCD A B C D
và
1
V là thể tích của tứ diện
'A BCD
. Hệ thức nào sau đây đúng?
A.
1
4V V
. B.
1
2V V
. C.
1
6V V
. D.
1
3V V
.
Lời giải
Chọn C
Gọi
h
là khoảng cách từ
'A
đến mp
( )ABCD
. Khi đó,
h
là chiều cao của khối hộp cũng là
chiều cao của tứ diện
'A BCD
.
Ta có:
. ' ' ' '
1 '
. 2 .
6
1 1
. .
3 3
ABCD A B C D ABCD BCD
A BCD
BCD BCD
V S h S h
V
V V
S h S h
1
6V V .
Câu 49. Cho hình lăng trụ tam giác
. ' ' 'ABC A B C
, biết rằng thể tích khối chóp
. ' 'A BCC B
bằng
12
.Thể
tích khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
24
. B.
36
. C.
18
. D.
32
.
Lời giải
Chọn C
Ta có: Đặt
. ' ' 'ABC A B C
V V
' ' '
. ' ' ' ' ' '
' ' . ' ' '
. .
1 1
. .
3 3
2
12 18.
3
A B C
A A B C A B C
ABCC B A A B C
V h S
V h S V
V V V V V
Câu 50. Nếu cạnh của một hình lập phương tăng lên 3 lần thì thể tích của hình lập phương đó tăng lên
bao nhiêu lần?
A.
27
. B.
9
. C.
6
. D.
4
.
Lời giải
Chọn A
Gọi cạnh của hình lập phương là
a
thì thể tích khối lập phương là
3
V a
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 28 TỔNG HỢP: HOÀNG TUYÊN
Khi tăng cạnh lên 3 lần thì cạnh là
3a
, thể tích khối lập phương mới là
3
* 3
3 27V a a
.
Khi đó
*
27V V
.
Câu 51. Nếu cạnh của một hình lập phương tăng lên 2 lần thì thể tích của hình lập phương đó tăng lên
bao nhiêu lần?
A.
9
. B.
2
. C.
4
. D.
8
.
Lời giải
Chọn D
Gọi cạnh của hình lập phương là
a
thì thể tích khối lập phương là
3
V a
.
Khi tăng cạnh lên 2 lần thì cạnh là
2a
, thể tích khối lập phương mới là
3
* 3
2 8V a a
.
Khi đó
*
8V V
.
Câu 52. Nếu thể tích của một hình lập phương tăng lên 8 lần thì cạnh của hình lập phương đó tăng lên
bao nhiêu lần?
A.
2 2
. B.
4
. C.
2
. D.
8
.
Lời giải
Chọn C
Gọi cạnh của hình lập phương là
a
thì thể tích khối lập phương là
3
V a
.
Khi tăng thể tích lên 8 lần thì thể tích là
* 3
8 8V V a
.
Khi đó cạnh của hình lập phương là
2a
. Kết luận: Cạnh tăng lên 2 lần.
Câu 53. Khối lăng trụ tam giác
.ABC A B C
có thể tích bằng
3
66 cm
. Tính thể tích khối tứ diện
.A ABC
.
A.
3
11cm
. B.
3
33cm
. C.
3
44 cm
. D.
3
22 cm
.
Lời giải
Chọn D
Ta có:
3
. .
1 1
.d , . . 22
3 3
A ABC ABC A B C ABC
V A ABC S V cm
.
Câu 54. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có thể tích bằng
V
. Các điểm
M
,
N
,
P
lần lượt thuộc
các cạnh
'AA
,
'BB
,
'CC
sao cho
1 2
,
' 2 ' ' 3
AM BN CP
AA BB CC
. Thể tích khối đa diện
.ABC MNP
bằng
A.
20
27
V
. B.
11
18
V
. C.
9
16
V
. D.
2
3
V
.
Lời giải
Chọn B
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 29
Lấy
'M
thuộc đoạn
AA '
sao cho
2
' AA'
3
AM
, khi đó ta có:
2 1 1
' ' AA ' AA' AA'
3 2 6
MM AM AM
Dễ thấy
. '
1
18
M M NP
V V
và
. '
2
3
ABC M NP
V V
Gọi thể tích khối đa diện
.ABC MNP
là
'V
Ta có
. ' . '
2 1 11
'
3 18 18
ABC M NP M M NP
V V V V V V
Câu 55. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
V
. Tính thể tích khối đa diện
ABCB C
.
A.
3
4
V
. B.
2
3
V
. C.
2
V
. D.
4
V
.
Lời giải
Chọn B
Ta có:
2
3 3 3
ABCB C B ABC C B AC
V V V
V V V
Câu 56. Cho lăng trụ tam giác
.ABC A B C
có thể tích là
V
. Tính thể tích khối chóp
.A BCC B
theo
V
.
A.
2
3
V
. B.
2
5
V
. C.
1
2
V
. D.
1
3
V
.
Lời giải
Chọn A
A
B
A
B
C
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 30 TỔNG HỢP: HOÀNG TUYÊN
Ta có
.
1 1
.
3 3
A A B C
V Sh V
Suy ra
. . .
2
3 3
A BCC B ABC A B C A A B C
V V
V V V V
.
Câu 57. Gọi
1
V là thể tích của khối lập phương
.ABCD A B C D
,
2
V là thể tích khối tứ diện
A ABD
. Hệ
thức nào sau đây là đúng?
A.
1 2
4V V . B.
1 2
6V V . C.
1 2
2V V . D.
1 2
8V V .
Lời giải
Chọn B
Cách 1: Giả sử cạnh của hình lập phương là
a
, ta có
3
1
V a
và
2
1
.
3
ABD
V AA S
3
1
6
a
suy ra
1 2
6V V .
Cách 2: Ta có
2
1
.
3
ABD
V AA S
1 1
.
3 2
ABCD
AA S
1
.
6
ABCD
AA S
1
1
6
V
1 2
6V V .
Cách 3: Ta có
. . 1 2
1 1
6 .
3 6
A ABD ABD A B D ABCD A B C D
V V V V V
Câu 58. Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông cân tại
A
,
AB AC a
,
2A A a
.
Thể tích của khối tứ diện
A BB C
là
C'
B'
A
C
B
A'
D'
D
C'
B'
A
C
B
A'
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 31
A.
3
2
3
a
. B.
3
2a
. C.
3
a
. D.
3
3
a
.
Lời giải
Chọn D
Ta có
.
1
3
A BB C ABC A B C
V V
2
1 1
2 .
3 2
a a
3
3
a
.
Câu 59. Cho hình lăng trụ
.ABC A B C
có thể tích là
V
. Gọi
M
là điểm thuộc cạnh
CC
sao cho
3CM C M
. Tính thể tích
V
của khối chóp
.M ABC
A.
4
V
. B.
3
4
V
. C.
12
V
. D.
6
V
.
Lời giải
Chọn A
Gọi
H
,
K
lần lượt là hình chiếu vuông góc của
C
và
M
lên mặt phẳng
ABC
Ta có
//C H MK
3
4
MK CM
CC CC
.
Khi đó
.
1
.
3
M ABC ABC
V MK S
.
1 3
. .
3 4 4
M ABC ABC
V
V CC S
.
Câu 60. Cho lăng trụ
.ABC A B C
có thể tích
V
. Điểm
M
là trung điểm cạnh
AA
. Tính theo
V
thể tích
khối chóp
.M BCC B
.
A.
2
3
V
. B.
3
4
V
. C.
3
V
. D.
2
V
.
B'
C'
A
C
B
A'
A
B
C
A
B
C
M
H
K
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 32 TỔNG HỢP: HOÀNG TUYÊN
Lời giải
Chọn A
Gọi:
.ABC A B C
V V
.
ABC
AA S
.
.M ABC
V
.M A B C
V
1
. .
3
ABC
MA S
1 1
. . .
3 2
ABC
AA S
1
6
V
.
Ta có:
. . .M BCC B M ABC M A B C
V V V V
1 1 2
6 6 3
V
V V V
.
Câu 61. Cho hình hộp
. ' ' ' 'ABCD A B C D
. Gọi
1 2
,V V lần lượt là thể tích khối tứ diện
ACB D
và khối hộp
.ABCD A B C D
. Tỉ số
1
2
V
V
bằng:
A.
1
.
3
B.
1
.
6
C.
1
.
2
D.
1
.
4
Lờigiải
Chọn A
Ta có
. . . . . 2
1 1
.
6 6
B ABC D ACD C B C D A A B D ABCD A B C D
V V V V V V
Suy ra
1
1 2 2 2
2
1 1 1
4. .
6 3 3
V
V V V V
V
Câu 62. Một khối lập phương có thể tích gấp
24
thể tích một khối tứ diện đều. Hỏi cạnh của hình lập
phương gấp mấy lần cạnh của hình tứ diện đều?
A.
2
. B.
2 2
. C.
2
. D.
1
.
Lời giải
Chọn A
Gọi hình lập phương có cạnh là
a
, khối tứ diện đều có cạnh là
b
.
M
B'
C'
A
B
C
A'
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 33
Khi đó, thể tích khối lập phương là:
3
1
V a
Thể tích khối tứ diện đều là:
3
2
2
12
b
V
.
Theo đề bài ta có:
1 2
24V V
3
3
2
24.
12
b
a
3 3
2 2a b 2a b
.
Câu 63. Cho khối lăng trụ
.
B C
ABC A
. Gọi
V
và
V
lần lượt là thể tích của khối lăng trụ đã cho và khối
tứ diện
ABB C
. Tỉ số
V
V
bằng
A.
1
3
. B
.
1
4
. C.
1
2
. D.
1
6
.
Lời giải
Chọn A
Ta có:
. . ' . .A BB C ABC A B C A A B C C ABC
V V V V
.
Mà
. . . '
1
.
3
A A B C C ABC ABC A B C
V V V
. Nên
. . '
1
.
3
A BB C ABC A B C
V V
.
Vậy
1
3
V
V
.
Câu 64. Cho khối hộp
.ABCD A B C D
có thể tích bằng
9
. Tính thể tích khối tứ diện
.ACB D
A.
3.
B.
9
.
2
C.
6.
D.
27
.
4
Lời giải
Chọn A.
A
B
C
D
C
D
A
B
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 34 TỔNG HỢP: HOÀNG TUYÊN
Gọi
h
và
V
lần lượt là chiều cao và thể tích khối hộp.
Ta có
.
1 1 2 1 9
4 4. . . . 3.
3 2 3 3 3
ACB D ABCD
ACB D B CD C ABCD
V S h
V V V V S h V V V
Câu 65. Cho khối lăng trụ .
ABC A B C
có thể tích bằng
V
. Tính thể tích khối đa diện
ABCB C
.
A.
3
V
. B.
2
3
V
. C.
2
V
. D.
4
V
.
Lời giải
Chọn B
Ta có:
2
3 3 3
ABCB C B ABC C B AC
V V V
V V V
A
B
A
B
C
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 35
5. KHỐI CHÓP - MỨC 3
Câu 66. Cho hình chóp có đáy là hình vuông cạnh a. Cạnh bên vuông góc với mặt đáy và
. Gọi lần lượt là hình chiếu vuông góc của trên các cạnh . Mặt phẳng
cắt cạnh tại . Tính thể tích của khối chóp
A. . B. . C. . D.
Lời giải
Chọn B
Ta có mà
vuông tại nên suy ra
Ta có và suy ra nên
Tương tự . Từ đó suy ra nên
Mà suy ra . Ta cũng có
Từ suy ra mà
Suy ra
Từ suy ra .
.
S ABCD
SA
2
SA a
;
B D
A
,
SB SD
AB D
SC
C
.
S AB C D
3
3
a
3
16
45
a
3
2
a
3
2
4
a
I
O
A
D
C
B
S
D'
B'
C'
. .
2 1
S AB C D S AB C
V V
. *
SAB C
SABC
V
SB SC
V SB SC
SAC
A
2
2
2 2 2 2
2 2 6
SC SA AC a a a
6
SC a
BC SAB BC AB
SB AB
AB SBC
AB BC
AD SC
SC AB D AB C D
SC AC
2
.
SC SC SA
2 2
2 2
4 2
6 3
SC SA a
SC SC a
2 2 2
2 2 2 2 2
4 4
4 5
SB SA SA a
SB SB SA AB a a
8
*
15
SAB C
SABC
V
V
8 8 1 8
.
15 15 2 30
SAB C SABC SABCD SABCD
V V V V
3
1 2
.
3 3
SABCD ABCD
a
V S SA
3 3
8 2 8
.
30 3 45
SAB C
a a
V
1
3
. .
16
2
45
S AB C D S AB C
a
V V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 36 TỔNG HỢP: HOÀNG TUYÊN
Câu 67. Cho khối chóp có đáy là hình bình hành . Gọi , , , lần lượt là trọng
tâm các tam giác , , , . Biết thể tích khối chóp là , khi đó thể
tích của khối chóp là:
A. . B. . C. . D. .
Hướng dẫn giải
Chọn A
Ta có .
Mặt khác gọi ta có .
Tương tự ta có .
Suy ra .
Mà .
Suy ra .
Câu 68. Cho hình chóp có đáy là hình vuông cạnh , vuông góc với đáy
, góc giữa hai mặt phẳng và bằng . Gọi , lần lượt là trung điểm của
, . Tính thể tích khối chóp .
A. . B. C. D.
Lời giải
Chọn A
.
S ABCD
ABCD
M
N
P
Q
SAB
SBC
SCD
SDA
.
S MNPQ
V
.
S ABCD
27
4
V
2
9
2
V
9
4
V
81
8
V
F
E
J
Q
P
H
N
K
M
I
O
D
S
A
B
C
,
2
3
,
d S MNPQ
SM
SI
d S ABCD
ABCD
S S
1 1 1
.
4 2 8
DEJ
BDA
S
S
1
16
DEJ
S S
1
4
JAI
DAB
S
S
1
8
JAI
S
1 1 1
1 4. 2.
16 8 2
HKIJ
S S S
2
2 4
3 9
MNPQ
HKIJ
S
S
2
9
MNPQ ABCD
S S
.
1
, .
3
S ABCD
V d S ABCD S
1 3 9 27
. , .
3 2 2 4
d S MNPQ S V
.
S ABCD
ABCD
a
SA
ABCD
SBD
ABCD
60
M
N
SB
SC
.
S ADMN
3
6
16
a
V
3
6
24
a
V
3
3 6
16
a
V
3
6
8
a
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 37
Gọi là tâm của hình vuông . Khi đó ta có là góc giữa hai mặt phẳng và
nên . Khi đó .
Ta có và .
Do đó .
Câu 69. Cho hình chóp có , là hình chữ nhật. . Góc giữa
và mặt đáy là . Gọi là trọng tâm tam giác . Tính thể tích khối chóp
là
A. . B. . C. . D. .
Lời giải
Chọn B
Vì góc giữa và mặt đáy là nên .
O
N
M
A
D
B
C
S
O
ABCD
SOA
SBD
ABCD
60
SOA
tan 60
SA
AO
2
.tan60 . 3
2
SA AO a
6
2
a
.
.
1
. .
4
S AMN
S ABC
V
SA SM SN
V SA SB SC
.
.
1
. .
2
S AND
S ACD
V
SA SN SD
V SA SC SD
. .
1 1 1
.
2 4 2
S ADMN S ABCD
V V
.
3
.
8
S ABCD
V
3
2
3 1 6 6
. . .
8 3 2 16
a a
a
.
S ABCD
SA ABCD
ABCD
2
SA AD a
SBC
ABCD
60
G
SBC
.
S AGD
3
32 3
27
a
3
8 3
27
a
3
4 3
9
a
3
16
9 3
a
G
M
D
A
B
C
S
SBC
ABCD
60
60
SBA
2
tan60
3
SA a
AB
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 38 TỔNG HỢP: HOÀNG TUYÊN
Khi đó: .
Gọi là trung điểm , khi đó: .
.
Câu 70. Cho khối tứ diện có thể tích . Gọi , , , là trọng tâm của bốn mặt của tứ diện
. Thể tích khối tứ diện là:
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi lần lượt là trung điểm của , và .
Gọi là khoảng cách từ đến , là khoảng cách từ đến .
Vì nên , .
.
Gọi , , lần lượt là diện tích các tam giác , và .
Vì lần lượt là trung điểm của , và nên:
.
Tam giác đồng dạng với tam giác với tỉ số đồng dạng là: .
(Vì tỉ số diện tích bằng bình phương tỉ số đồng dạng).
Từ và .
Thể tích khối từ diện là: .
Câu 71. Cho hình chóp , và là các điểm thuộc các cạnh và sao cho ,
, là mặt phẳng qua và song song với . Mặt phẳng chia khối chóp
2
2 4 3
. .2
3
3
ABCD
a a
S AB AD a
M
BC
2
1 2 3
2 3
ADM ABCD
a
S S
2 3
. .
2 2 1 2 3 8 3
. .2 .
3 3 3 3 27
S ADG S ADM
a a
V V a
ABCD
V
1
G
2
G
3
G
4
G
ABCD
1 2 3 4
G G G G
27
V
18
V
4
V
12
V
H
2
H
1
G
3
G
2
G
1
G
4
K
J
I
B
C
D
A
, ,
I J K
BC
BD
DC
h
A
BCD
1
h
4
G
1 2 3
G G G
1 2 3
/ /
G G G BCD
4 1 2 3 1 1 2
, ,
d G G G G d G BCD G H h
1
h AH
1 1
1
3
h KG
h KA
1
3
h
h
S
S
1
S
BCD
IJK
1 2 3
G G G
, ,
I J K
BC
BD
DC
1 1 1 1 1 1
. , . . , . . . ,
2 2 2 2 4 2 4
BC
S JK d I JK d D BC BC d D BC S
1
1 2 3
G G G
KIJ
1 2 1
2
3
G G AG
Ik Ak
2
1
2 4
3 9
S
S
1
4
9
S S
2
1
2
1
9
S
S
1 2 3 4
G G G G
1 1 1
1 1 1 1
. . . . . .
3 3 9 3 27 3 27
S h V
V S h S h
.
S ABC
M
N
SA
SB
2
MA SM
2
SN NB
MN
SC
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 39
thành hai khối đa diện và với là khối đa diện chứa điểm , là khối
đa diện chứa điểm . Gọi và lần lượt là thể tích của và . Tính tỉ số .
A. . B. . C. . D. .
Lời giải
Chọn A
Kí hiệu là thể tích khối tứ diện .
Gọi , lần lượt là giao điểm của với các đường thẳng , .
Ta có .
Khi chia khối bởi mặt phẳng , ta được hai khối chóp và .
Ta có .
; .
Do đó .
.
Do đó .
Câu 72. Cho hình chóp có đáy là hình bình hành. Gọi , lần lượt là trung điểm của
các cạnh , . Mặt phẳng chứa cắt các cạnh , lần lượt tại , . Đặt
, là thể tích của khối chóp , là thể tích của khối chóp . Tìm để
.
.
S ABC
1
H
2
H
1
H
S
2
H
A
1
V
2
V
1
H
2
H
1
2
V
V
4
5
5
4
3
4
4
3
P
N
Q
M
A
B
C
S
V
SABC
P
Q
BC
AC
// //
NP MQ SC
1
H
QNC
.
N SMQC
.
N QPC
.
.
,
,
N SMQC SMQC
B ASC SAC
d N SAC
V S
V S
d B SAC
,
2
3
,
d N SAC
NS
BS
d B SAC
2
4
.
9
AMQ
ASC
S
AM AQ AM
S AS AC AS
5
9
SMQC
ASC
S
S
.
.
2 5 10
3 9 27
N SMQC
B ASC
V
V
.
.
,
,
N QPC QPC
S ABC ABC
d N QPC
V S
V S
d S ABC
1 1 2 2
3 3 3 27
NB CQ CP
SB CA CB
. .
1
. .
N SMQC N QPC
B ASC S ABC
V V
V
V V V
10 2 4
27 27 9
1
1 2
4
9
V
V V
1 2
5 4
V V
1
2
4
5
V
V
.
S ABCD
ABCD
M
N
SA
SD
MN
SB
SC
Q
P
SQ
x
SB
1
V
.
S MNQP
V
.
S ABCD
x
1
1
2
V V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 40 TỔNG HỢP: HOÀNG TUYÊN
A. . B. . C. . D. .
Lời giải
Chọn A
Do .
(vì ).
Câu 73. Cho hình chóp tứ giác đều có đáy là hình vuông cạnh , cạnh bên tạo với đáy
một góc . Gọi là trung điểm của . Mặt phẳng đi qua và song song với cắt
tại và cắt tại . Tính thể tích khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn D
Trong mặt phẳng . Suy ra thẳng hàng.
1 33
4
x
2
x
1
2
x
1 41
4
x
N
M
O
C
A
D
B
S
P
Q
//MN BC
SBC PQ
//
PQ BC
. .
1
S MNQ S NPQ
V V
V
V V V
. .
. .
1
2 2 2
S MNQ S NPQ
S ABD S BCS
V V
V V
. . . . 1
SM SN SQ SP SN SQ
SA SD SB SC SD SB
2
1
4 2
x x
2
2 4 0
x x
1 33
4
x
0
x
.
S ABCD
ABCD
a
60
M
SC
AM
BD
SB
E
SD
F
V
.
S AEMF
3
6
36
a
V
3
6
9
a
V
3
6
6
a
V
3
6
18
a
V
F
E
I
M
O
C
A
D
B
S
:
SBD EF SO I
, ,
A M I
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 41
Trong tam giác hai trung tuyến cắt nhau tại suy ra .
Lại có .
Ta có: . .
Vậy .
Góc giữa cạnh bên và đáy của bằng góc suy ra .
Thể tích hình chóp bằng .
Vậy .
Câu 74. Cho khối chóp tứ giác có đáy là hình bình hành. Gọi là trung điểm của , mặt
phẳng chứa và song song chia khối chóp thành hai khối đa diện, đặt là thể tích
khối đa diện có chứa đỉnh và là thể tích khối đa diện có chứa đáy . Tỉ số là
A. . B. . C. . D. .
Lời giải
Chọn B
Đặt .
Gọi là giao điểm hai đường chéo và . Gọi là giao điểm của và .
Do nên cắt mặt phẳng theo giao tuyến qua và song song với ;
.
Xét tam giác có là giao điểm hai trung tuyến nên là trọng tâm.
SAC
,
AM SO
I
2
3
SI
SO
2
//
3
SE SF SI
EF BD
SB SD SO
.
1
3
S AEM
SABC
V
SE SM
V SB SC
.
1
3
S AFM
SADC
V
SF SM
V SD SC
. . .
. . .
1 1
3 3
S AEM S AFM S AEMF
S ABC S ADC S ABCD
V V V
V V V
.
S ABCD
60
SBO
6
3
2
a
SO BO
.
S ABCD
3
.
1 6
.
3 6
S ABCD ABCD
a
V SO S
3
.
6
18
S AEMF
a
V
.
S ABCD
M
SC
P
AM
BD
1
V
S
2
V
ABCD
2
1
V
V
2
1
3
V
V
2
1
2
V
V
2
1
1
V
V
2
1
3
2
V
V
.S ABCD
V V
O
AC
BD
I
SO
AM
//
P BD
P
SBD
NP
I
BD
;
N SB P SD
SAC
I
I
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 42 TỔNG HỢP: HOÀNG TUYÊN
Ta có .
Tương tự = .
Từ đó . Do đó .
Câu 75. Cho hình chóp có đáy là hình bình hành có thể tích bằng . Gọi là điểm trên
cạnh sao cho . Gọi là mặt phẳng chứa và song song với , cắt
, lần lượt tại hai điểm , . Tính theo thể tích khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi là tâm hình bình hành , , khi đó đi qua và .
Gọi là trung điểm , suy ra . Ta có .
Từ đó .
Từ đó:
.
.
Do đó
Câu 76. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm của Mặt phẳng
chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số lớn)
A. B. C. D.
Lời giải
Chọn A
.
.
.
.
S APN
S ADB
V
SP SN
V SD SB
2 2 4
.
3 3 9
. .
4
9
S APN S ADB
V V
4 1
.
9 2
V
2
9
V
.
.
. .
. .
S PMN
S DCB
V
SP SM SN
V SD SC SB
2 1 2 2
. .
3 2 3 9
. .
2
9
S PMN S DCB
V V
2 1
.
9 2
V
1
9
V
1 . .
S APN S PMN
V V V
1
3
V
2
1
2
V
V
.
S ABCD
ABCD
V
E
SC
2
EC ES
AE
BD
SB
SD
M
N
V
.
S AMEN
3
8
V
3
16
V
9
V
6
V
F
E
N
M
I
O
C
A
D
B
S
O
ABCD
I SO AE
MN
I
// D
MN B
F
EC
//
OF AE
1
2
SI SE
SO SF
1
2
SM SN SI
SB SD SO
.
.
1 1 1
. . 1. .
2 3 6
S AME
S ABC
V
SA SM SE
V SA SB SC
. .
1 1
6 12
S AME S ABC
V V V
.
.
1 1 1
. . 1. .
2 3 6
S ANE
S ADC
V
SA SN SE
V SA SD SC
. .
1 1
6 12
S ANE S ADC
V V V
. . .
1 1
12 12 6
S AMEN S AME S ANE
V
V V V V V
.
S ABCD
,
M N
, .
SA SB
( )
MNCD
3
.
5
3
.
4
1
.
3
4
.
5
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 43
Giả sử thể tích của khối chóp là
Ta có
Câu 77. Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm các
cạnh . Mặt phẳng chứa và cắt các tia lần lượt tại và . Đặt ,
là thể tích của khối chóp và là thể tích khối chóp . Tìm để .
A. . B. . C. . D. .
Lời giải
Chọn B
Ta chứng minh .
Giải sử khi đó ta có:
lần lượt là trung điểm các cạnh nên ta có
A
D
B
C
S
M
N
.
S ABCD
.
V
.
.
1
. . ;
2
S MDC
S ADC
V
SM SD SC
V SA SD SC
.
.
1
. . ;
4
S MNC
S ABC
V
SM SN SC
V SA SB SC
. . . . .
. .
1 1 3
1 1 1
2 4 4
2 2 2
S MDC S MNC S MDC S MNC S MNCD
S ADC S ABC
V V V V V
V V
V V V
.
.
3 3 5 3
.
8 8 8 5
S MNCD
S MNCD MNABCD
MNABCD
V
V V V V V V
V
.
S ABCD
ABCD
,
M N
,
SA SD
MN
,
SB SC
P
Q
SP
x
SB
1
V
.
S MNQP
V
.
S ABCD
x
1
2
V V
1
2
x
1 33
4
x
1 41
4
x
2
x
d
N
M
A
D
B
C
S
Q
P
/ /
PQ BC
SBC SAD d
// //
/ /
SBC SAD d
SBC ABCD BC
d BC, d AD.
SAD ABCD AD
BC AD
,
M N
,
SA SD
MN / / AD, MN / / d.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 44 TỔNG HỢP: HOÀNG TUYÊN
Ta lại có:
Xét tam giác có
Theo bài ra:
Mà
Cách 2
Sử dụng công thức tính nhanh tỉ lệ thể tích của khối chóp tứ giác như sau:
Cho chóp và mặt phẳng cắt các cạnh của khối chóp tại các điểm
với
Thì ta có:
Theo bài ra:
Mà
Câu 78. Cho tứ diện đều có chiều cao bằng , ở ba góc của tứ diện người ta cắt đi các tứ diện đều bằng
nhau có độ dài cạnh bằng để khối đa diện còn lại có thể tích bằng một nửa thể tích khối tứ diện
đều ban đầu. Tìm .
A. . B. . C. . D. .
Lời giải
Chọn D
/ /
SBC SAD d
SBC PQ
PQ / / MN PQ / / BC.
SAD MN
d MN
SBC
PQ / / BC,
SP
x
SB
SQ SP
= x.
SC SB
. . . .
.1
. . . .
1 . . 1 . .
2 2 2 . . 2 . .
S MNQP S MNP S NQP S NQP
S MNP
S ABCD S ABCD S ABD S DCB
V V V V
V
V
SM SN SP SN SQ SP
V V V V V SA SB SD SD SC SB
2
1 1 1 1 1 2
2 2 2 2 2 8
x x
x x x
2
2
1
1
1 33
1 2 1
4
2 2 4 0
2 8 2
1 33
4
x
V x x
V V x x
V
x
1 33
0
4
SP
x x x
SB
.
S ABCD
, , ,
SA SB SC SD
, , ,
M P Q N
SQ SP
= x,
SC SB
1
2
SM SN
SA SD
2
.
1
.
1 1
.
1 1 2
2 2
2 2
4 8
S MNPQ
S ABCD
x x
V
V
x x
V V x x
2
2
1
1
1 33
1 2 1
4
2 2 4 0 .
2 8 2
1 33
4
x
V x x
V V x x
V
x
1 33
0
4
SP
x x x
SB
h
x
x
3
6
6
h
x
3
6
2
h
x
6
6
6
h
x
6
6
2
h
x
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 45
Giả sử có tứ diện đều cạnh bằng , chiều cao .
Tam giác đều cạnh nên .
Gọi là trung điểm của thì , .
Tam giác vuông tại nên .
Thể tích tứ diện đều là: .
Gọi là thể tích của tứ diện đều cạnh , ta có .
Phần bị cắt đi có thể tích: .
Vì khối đa diện còn lại có thể tích bằng một nửa thể tích khối tứ diện đều ban đầu nên ta có:
.
Mặt khác, từ suy ra . Do đó, .
Câu 79. Cho hình chóp có đáy là hình vuông cạnh , vuông góc với đáy, .
lần lượt là hình chiếu của lên . Mặt phẳng cắt tại . Thể tích khối chóp
là
A. . B. . C. . D. .
Lời giải
ABCD
a
AO h
BCD
a
2
3
4
BCD
a
S
I
CD
3
2
a
BI
2 3
3 3
a
BO BI
ABO
O
2
2 2 2
3 6
3 3
a a
h AB BO a
ABCD
2 3
1 1 3 6 2
. . .
3 3 4 3 12
BCD
a a a
V S h
'
V
x
3
2
'
12
x
V
3
2
3 '
4
x
V
3
3 3
3
3
3
3
2
3 ' 1 3 1
4
2 2 6
2 6
12
x
V x a a
x x
V a
a
6
3
a
h
6
2
h
a
6
3 3
6 6
2
6 2 6
a h h
x
.
S ABCD
a
SA
2
SA a
', '
B D
A
,
SB SD
' '
AB D
SC
'
C
. ' ' '
S AB C D
3
2 3
3
a
V
3
2 2
3
a
V
3
2 3
9
a
V
3
2
9
a
V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 46 TỔNG HỢP: HOÀNG TUYÊN
Chọn D
Ta có .
Có
Gọi , . Khi đó .
Ta có suy ra là trọng tâm của tam giác
.
Ta có .
Ta có .
Vậy .
Câu 80. Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng . Người ta cắt khối
đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích
bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng
tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá đầu).
A. . B. . C. . D. .
Lời giải
Chọn D
3 3
. . .
1 2 2
.
3 3 6
S ABCD ABCD S ABC S ACD
a a
SA ABCD V S SA V V
2
2
3
' '
3
' '
SA a
SB SD a
SAB SAD SB SD
SB
AB AD
O AC BD
' '
H B D SO
'
C AH SC
' ' 2 2
' '
3 3
SB SD SH
B D BD
SB SD SO
H
SAC
' 1
2
SC
SC
3
. ' '
. ' ' .
.
' ' 1 1 2
.
3 3 18
S AC D
S AC D S ACD
S ACD
V
SC SD a
V V
V SC SD
3
. ' '
. ' ' .
.
' ' 1 1 2
.
3 3 18
S AB C
S AB C S ABC
S ABC
V
SC SB a
V V
V SC SB
3
. ' ' ' . ' ' . ' '
2
9
S AB C D S AB C S AC D
a
V V V
a
2
2
3
a
2
3
2
a
2
4
a
2
3
4
a
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 47
Gọi , , , lần lượt là giao điểm của mặt phẳng cắt với cạnh bên , , ,
và . Do
Đặt (Định lý Thales) và .
Ta có
Theo ycbt : .
Mặt khác
.
Câu 81. Cho khối tứ diện có thể tích bằng , thể tích của khối đa diện có đỉnh là trung điểm các
cạnh của tứ diện bằng . Tính tỉ số .
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Tương tự: , , .
M
N
P
Q
SA
SB
SC
SD
H SO MNPQ
SO ABCD
SH MNPQ
MNPQ ABCD
SH SM SN SP SQ
k
SO SA SB SC SD
0
k
.
S ABCD
V V
.
S MNPQ
V
V
.
.
. .
2 2
S MPQ
S MNP
S ABC S ACD
V
V
V V
1
. . . .
2
SM SN SP SM SP SQ
SA SB SC SA SC SD
3 3
1
2
k k
3
k
.
3
1
2
S MNPQ
V
k
V
3
1
2
k
.
1
2
S MNPQ
V
V
1
.
3
1
.
3
MNPQ
ABCD
SH S
SO S
.
MNPQ
ABCD
S
k
S
1
.
2
MNPQ ABCD
S S
k
3
2
2
.
2
a
2
3
4
a
ABCD
V
ABCD
V
V
V
1
2
V
V
1
8
V
V
1
4
V
V
3
4
V
V
1
. .
8
AEJF AEJF
ABCD
V V
AE AJ AF
V V AB AC AD
1
8
BIGE
V
V
1
8
CIHJ
V
V
1
8
DHGF
V
V
M
N
P
Q
S
A
B
C
D
H
O
A
B
D
E
F
I
H
G
J
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 48 TỔNG HỢP: HOÀNG TUYÊN
Vậy: .
Câu 82. Cho hình chóp có , . Tam giác vuông cân tại
,
. Mặt phẳng đi qua và vuông góc với , cắt , lần lượt tại , . Tính tỉ số thể
tích khối chóp và khối chóp
.
A. . B. . C. . D. .
Lời giải
Chọn B
Kẻ tại , kẻ tại .
Ta có
Ta có
Ta có
Nhận thấy qua và vuông góc với ( thỏa điều kiện bài toán)
.
Ta có: .
.
Tỉ số thể tích cần tìm là: .
1
1 4.
8
V
V
1
2
.
S ABC
SC ABC
3
SC a
A B C
B
3
AB a
C
SA
SA
SB
D
E
.
S CDE
.
S ABC
9
11
9
20
7
20
15
12
CD SA
D
CE SB
E
AB BC
AB SBC AB CE
AB SC
CE SB
CE SAB CE SA
CE AB
SA CE
SA CDE
SA CD
CDE
C
SA
CDE
2 2
3 3 6
CA a a a
2
2
2
2 2
2
3
. 3
5
6 3
a
SD SD SA SC
SA SA SA
a a
2
2
2
2 2
2
3
. 3
4
3 3
a
SE SE SB SC
SB SB SB
a a
.
.
3 3 9
. . 1. .
5 4 20
S CDE
S ABC
V
SC SD SE
V SC SA SB
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 49
Câu 83. Cho hình chóp
.S ABC
có
3
.
6
S ABC
V a
. Gọi
M
,
N
,
Q
lần lượt là các điểm trên các cạnh
SA
,
SB
,
SC
sao cho
SM MA
,
SN NB
,
2SQ QC
. Thể tích khối chóp
.S MNQ
là
A.
3
a
. B.
3
2a
. C.
3
3a
. D.
3
2
a
.
Lời giải
Chọn A
M
nằm trên các cạnh
SA
sao cho
SM MA
1
2
SM
SA
.
N
nằm trên các cạnh
SB
sao cho
SN NB
1
2
SN
SB
.
Q
nằm trên các cạnh
SC
sao cho
2SQ QC
2
3
SQ
SC
.
,.
Khi đó:
.
.
1 1 2 1
. .
2 2 3 6
S MNQ
S ABC
V
V
.
3 3
. .
1 1
.6
6 6
S MNQ S ABC
V V a a
.
Câu 84. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,M N
lần lượt là trung điểm của
các cạnh
,SA SD . Mặt phẳng
chứa
MN
cắt các cạnh ,SB SC lần lượt tại ,Q P . Đặt
SQ
x
SB
,
1
V là thể tích của khối chóp
.S MNPQ
,
V
là thể tích của khối chóp
.S ABCD
. Tìm
x
để
1
1
2
V V
.
A.
1 41
4
x
. B.
1 33
4
x
. C.
2x
. D.
1
2
x
.
Lời giải
Chọn B
M
Q
N
A
B
C
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 50 TỔNG HỢP: HOÀNG TUYÊN
Theo giả thiết ta có
MN
là đường trung bình của tam giác
SAD / / MN AD
.
ABCD
là hình bình hành nên
/ / AD BC / / MN BC
.
Có
/ /
/ /
MNPQ SBC PQ
PQ BC
MN BC
SP SQ
x
SC SB
.
Tứ giác
ABCD
là hình bình hành nên
. . .
1 1
2 2
ADC ACB ABCD S ADC S ACB S ABCD
S S S V V V
.
Ta có
.
.
. .
4
S MNP
S ADC
V
SM SN SP x
V SA SD SC
.
.
8
S MNP
S ABCD
V
x
V
và
2 2
. .
. .
. .
2 4
S MPQ S MPQ
S ACB S ABCD
V V
SM SP SQ x x
V SA SC SB V
.
Do đó
2
. .
1
8 4
S MNP S MPQ
V V
V x x
V V
.
Theo giả thiết ta có
2 2
1 1 1 33
0
4 8 2 4 8 2 4
x x x x
x
.
Vì
0x
nên
1 33
4
x
.
Câu 85. Cho khối tứ diện
ABCD
. Hai điểm
,M N
lần lượt di động trên hai đoạn thẳng
,BC BD
sao cho
2 6
BC BD
BM BN
. Gọi
1 2
,V V lần lượt là thể tích của các khối tứ diện
ABMN
và
ABCD
. Tìm giá
trị nhỏ nhất của
1
2
V
V
.
A.
5
36
.
B.
2
9
. C.
1
9
. D.
1
6
.
Lời giải
A
B
C
D
M
N
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 51
Chọn B
Đặt
; ; , 0 2 6
BC BD
x y x y x y
BM BN
9 1 2
6 2 2
2 9
xy xy
xy
1
2
1
, .
1 2
3
.
1
9
, .
3
BMN
BCD
d A BMN S
V BM BN
V BC BD xy
d A BCD S
. Vậy giá trị nhỏ nhất của
1
2
V
V
là:
2
9
Câu 86. Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2a
, mặt bên tạo với mặt đáy một góc
0
60
. Gọi
M
là trung điểm của
.SA
, thể tích của khối chóp
M.ABC
bằng
A.
3
2 3
3
a
. B.
3
4 3
3
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Lời giải
Chọn C
Gọi
O AC BD
;
H
là trung điểm
CD
Vì
.S ABCD
là hình chóp đều nên
SO ABCD
Góc giữa
SCD
và
ABCD
bằng
0
60
suy ra
60 ,SHO
SO OH.tan 3SHO a
3
2
.
1 1 1 2a 3
. . .a 3. .4
3 3 2 3
S ABC ABC
V SO S a
3
M.
M. S.
S.
1 1 a 3
.
2 2 3
ABC
ABC ABC
ABC
V
MA
V V
V SA
.
Câu 87. Cho tứ diện
.S ABC
có thể tích
V
. Gọi
, , ,H M N P
lần lượt là trung điểm của các cạnh
, , ,SA AB BC CA
. Thể tích khối chóp
.H MNP
tính theo V là
A.
1
12
V
. B.
1
16
V
. C.
1
8
V
. D.
3
8
V
.
Lời giải
Chọn C
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 52 TỔNG HỢP: HOÀNG TUYÊN
Ta có
.
. .
.
,
1 1 1
2 2 2
,
H MNP
H MNP S MNP
S MNP
d H MNP
V
V V
V
d S MNP
Ta có
.
. .
.
1 1 1
4 4 4
MNP S MNP
S MNP S ABC
ABC S ABC
S V
V V
S V
. Do đó
. .
1
8
H MNP S ABC
V V
.
Câu 88. Cho tứ diện đều
ABCD
có tất cả các cạnh bằng
a
. Gọi
G
là trọng tâm tam giác
BCD
. Gọi
S
là
điểm sao cho
AS BG
. Thể tích của khối đa diện
SABCD
là:
A.
3
2
12
a
. B.
3
2
24
a
. C.
3
5 2
36
a
. D.
3
3 2
24
a
.
Lời giải
Chọn C
Chia khối đa diện
SABCD
thành 2 khối chóp là
.A BCD
và
.S ACD
.
Ta có:
SABCD ABCD SADC
V V V
Áp dụng công thức tính nhanh khối đa diện đều:
3 3
2 2
12 12
ABCD
AB a
V
Gọi H là giao điểm giữa AM và
SB
.
1
; .
;
3
1
;
; .
3
ACD
SACD
ABCD
ACD
d S ACD S
d S ACD
V
SH
V BH
d B ACD
d B ACD S
Mặt khác theo giả thiết
/ /
AS BG
AS BG
AS BG
1 2
3 3
3
2 2
SH SA SA
BH BM
BG
3 3
3 3 3
2 2 2 2 2
.
3 3 3 12 18
2 2 5 2
12 18 36
SACD
SACD ABCD
ABCD
SABCD ABCD SACD
V
SH a a
V V
V BH
a a a
V V V
Câu 89. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
0
60BAD
và
SA
vuông góc với
mặt phẳng
ABCD
. Góc giữa 2 mặt phẳng
SBD
và
ABCD
bằng
0
45
. Gọi
M
là điểm đối
xứng của
C
qua
B
và
N
là trung điểm của
SC
. Mặt phẳng
MND
chia khối chóp
.S ABCD
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 53
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
S
có thể tích
1
V
, khối đa diện còn lại có
thể tích
2
V (tham khảo hình vẽ bên). Tính tỉ số
1
2
V
V
A.
1
2
12
7
V
V
. B.
1
2
5
3
V
V
. C.
1
2
1
5
V
V
. D.
1
2
7
5
V
V
.
Lời giải
Chọn D
Gọi
O AC BD
Khi đó góc giữa 2 mặt phẳng
SBD
và
ABCD
bằng
0
45
45
o
SOA
Ta có:
BAD
đều
3 3
2 2
a a
AO SA AO
Thể tích khối chóp
.S ABCD
bằng:
2 3
1 2 3 3
. .2 . .
3 3 2 4 4
ABD
a a a
V SA S
Ta có:
N
là trung điểm
SC
nên
;
1
2
;
d N ABCD
NC
SC
d S ABCD
Thể tích khối chóp
.N MCD
bằng thể tích khối chóp
.N ABCD
bằng:
3
1
'
2 8
a
V V
Ta có
K
là trọng tâm tam giác
SMC
;
1 1
3 3
;
d K ABCD
KB KB
SB SB
d S ABCD
Thể tích khối chóp
KMIB
bằng:
2 3
1 1 1 3 3
'' . . . .
3 3 9 2 8 48
MBI
a a a
V SA S
Khi đó:
3 3 3
2
5
' ''
8 48 48
a a a
V V V
và
3 3 3
1 2
5 7
4 48 48
a a a
V V V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 54 TỔNG HỢP: HOÀNG TUYÊN
Vậy
3
1
3
2
7
7
48
5
5
48
a
V
a
V
.
Câu 90. Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2a
, mặt bên tạo với mặt đáy một góc
0
60
. Gọi
M
là trung điểm của
.SA
, thể tích của khối chóp
M.ABC
bằng
A.
3
2 3
3
a
. B.
3
4 3
3
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Lời giải
Chọn C
Gọi
O AC BD
;
H
là trung điểm
CD
Vì
.S ABCD
là hình chóp đều nên
SO ABCD
Góc giữa
SCD
và
ABCD
bằng
0
60
suy ra
60 ,SHO
SO OH.tan 3SHO a
3
2
.
1 1 1 2a 3
. . .a 3. .4
3 3 2 3
S ABC ABC
V SO S a
3
M.
M. S.
S.
1 1 a 3
.
2 2 3
ABC
ABC ABC
ABC
V
MA
V V
V SA
.
Câu 91. Cho tứ diện
.S ABC
có thể tích
V
. Gọi
, , ,H M N P
lần lượt là trung điểm của các cạnh
, , ,SA AB BC CA
. Thể tích khối chóp
.H MNP
tính theo V là
A.
1
12
V
. B.
1
16
V
. C.
1
8
V
. D.
3
8
V
.
Lời giải
Chọn C
Ta có
.
. .
.
,
1 1 1
2 2 2
,
H MNP
H MNP S MNP
S MNP
d H MNP
V
V V
V
d S MNP
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 55
Ta có
.
. .
.
1 1 1
4 4 4
MNP S MNP
S MNP S ABC
ABC S ABC
S V
V V
S V
. Do đó
. .
1
8
H MNP S ABC
V V
.
Câu 92. Cho hình chóp
.S ABC
có
3
.
6
S ABC
V a
. Gọi
M
,
N
,
Q
lần lượt là các điểm trên các cạnh
SA
,
SB
,
SC
sao cho
SM MA
,
SN NB
,
2SQ QC
. Thể tích khối chóp
.S MNQ
là
A.
3
a
. B.
3
2a
. C.
3
3a
. D.
3
2
a
.
Lời giải
Chọn A
M
nằm trên các cạnh
SA
sao cho
SM MA
1
2
SM
SA
.
N
nằm trên các cạnh
SB
sao cho
SN NB
1
2
SN
SB
.
Q
nằm trên các cạnh
SC
sao cho
2SQ QC
2
3
SQ
SC
.
,.
Khi đó:
.
.
1 1 2 1
. .
2 2 3 6
S MNQ
S ABC
V
V
.
3 3
. .
1 1
.6
6 6
S MNQ S ABC
V V a a
.
Câu 93. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,M N
lần lượt là trung điểm của
các cạnh
,SA SD
. Mặt phẳng
chứa
MN
cắt các cạnh
,SB SC
lần lượt tại
,Q P
. Đặt
SQ
x
SB
,
1
V là thể tích của khối chóp
.S MNPQ
,
V
là thể tích của khối chóp
.S ABCD
. Tìm
x
để
1
1
2
V V
.
A.
1 41
4
x
. B.
1 33
4
x
. C.
2x
. D.
1
2
x
.
Lời giải
Chọn B
M
Q
N
A
B
C
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 56 TỔNG HỢP: HOÀNG TUYÊN
Theo giả thiết ta có
MN
là đường trung bình của tam giác
SAD / / MN AD
.
ABCD
là hình bình hành nên
/ / AD BC / / MN BC
.
Có
/ /
/ /
MNPQ SBC PQ
PQ BC
MN BC
SP SQ
x
SC SB
.
Tứ giác
ABCD
là hình bình hành nên
. . .
1 1
2 2
ADC ACB ABCD S ADC S ACB S ABCD
S S S V V V
.
Ta có
.
.
. .
4
S MNP
S ADC
V
SM SN SP x
V SA SD SC
.
.
8
S MNP
S ABCD
V
x
V
và
2 2
. .
. .
. .
2 4
S MPQ S MPQ
S ACB S ABCD
V V
SM SP SQ x x
V SA SC SB V
.
Do đó
2
. .
1
8 4
S MNP S MPQ
V V
V x x
V V
.
Theo giả thiết ta có
2 2
1 1 1 33
0
4 8 2 4 8 2 4
x x x x
x
.
Vì
0x
nên
1 33
4
x
.
Câu 94. Cho khối tứ diện
ABCD
. Hai điểm
,M N
lần lượt di động trên hai đoạn thẳng
,BC BD
sao cho
2 6
BC BD
BM BN
. Gọi
1 2
,V V lần lượt là thể tích của các khối tứ diện
ABMN
và
ABCD
. Tìm giá
trị nhỏ nhất của
1
2
V
V
.
A.
5
36
.
B.
2
9
. C.
1
9
. D.
1
6
.
Lời giải
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 57
Chọn B
Đặt
; ; , 0 2 6
BC BD
x y x y x y
BM BN
9 1 2
6 2 2
2 9
xy xy
xy
1
2
1
, .
1 2
3
.
1
9
, .
3
BMN
BCD
d A BMN S
V BM BN
V BC BD xy
d A BCD S
. Vậy giá trị nhỏ nhất của
1
2
V
V
là:
2
9
A
B
C
D
M
N
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 58 TỔNG HỢP: HOÀNG TUYÊN
6. KHỐI LĂNG TRỤ - MỨC 3
Câu 95. Cho lăng trụ có thể tích là V. Gọi M là điểm thuộc cạnh sao cho
. Thể tích của khối chóp theo V là:
A. . B. . C. . D. .
Lời giải
Chọn A
Cách 1: Thể tích của khối chóp M.ABC là:
Cách 2: Áp dụng công thức tỉ số thể tích.
.
Câu 96. Cho hình lăng trụ tam giác đều có tất cả các cạnh bằng . Gọi , lần lượt là
trung điểm của các cạnh và . Mặt phẳng cắt cạnh tại . Tính thể tích
khối đa diện .
A. B. C. D.
Lời giải
Chọn B
. ' '
ABC AB C
'
CC
3 '
CM C M
.
M ABC
4
V
3
4
V
12
V
6
V
.
. ' ' '
. . ' ' '
1
; .
3
'; .
;
1 1 1 3 1
. . . .
3 3 ' 3 4 4
';
1
.
4 4
ABC
M ABC
ABC A B C
ABC
M ABC ABC A B C
d M ABC S
V
V
d C ABC S
d M ABC
MC
C C
d C ABC
V
V V
.
.
' ' '.
1 1 3 1 1
.
3 ' 3 4 4 4
C ABM
M ABC
A B C ABC
V
CM
V V
V CC
.
ABC A B C
a
M
N
AB
B C
A MN
BC
P
V
.
MBP A B N
3
3
V .
32
a
3
7 3
.
96
a
3
7 3
.
48
a
3
7 3
.
32
a
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 59
Gọi là giao điểm của các đường ; và . Có ; ; P lần lượt là trung điểm của
các cạnh ; và .
Vì đều cạnh nên .
(1).
Vì là trung điểm của nên . Vì là trung điểm của nên
(2).
Từ (1) và (2) ta có .
Câu 97. Cho hình lăng trụ đứng có điểm và lần lượt là tâm của mặt bên và
trọng tâm của . Biết . Thể tích của khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi là trung điểm của .
Ta có:
(1)
S
A M
NP
BB
M
B
SA
SB
SN
ABC
a
2
3
4
ABC
a
S
.
. . . .
.
1 1 1 1 1 7
. . . .
2 2 2 8 8 8
S BMP
S BMP S A B N MBP A B N S A B N
S A B N
V
SB SM SP
V V V V
V SB SA SN
B
SB
. .
2.
S A B N B A B N
V V
N
B C
2 3 3
. . .
1 1 1 1 3 3 3
. . . . .
2 2 3 6 4 24 12
B A B N B A B C ABC S A B N
a a a
V V BB S a V
3 3
. .
7 7 3 7 3
.
8 8 12 96
MBP A B N S A B N
a a
V V
.
ABC A B C
O
G
' '
ABB A
ABC
3
.
270 cm
ABC A B C
V
AOGB
3
15 cm
3
30 cm
3
45 cm
3
15 cm
M
BC
'
1
.
3
AOGB
AB MB
V
AO AG
V AB AM
'
1
.
3
AOGB AB MB
V V
' '
1 1 1
. , . . , . .
2 4 4
B MB B C CB
S d B BC BM d B BC BC S
A
B
C
P
S
A
B
C
N
M
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 60 TỔNG HỢP: HOÀNG TUYÊN
(2)
(3)
Từ (1), (2) và (3), suy ra .
Vậy .
Câu 98. Cho khối lăng trụ có thể tích bằng . Gọi là tâm của hình bình hành và
là trọng tâm tam giác . Thể tích tứ diện bằng:
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi là trung điểm của .
Ta có: .
Mặt khác .
Mà .
.
Từ , , suy ra .
Câu 99. Cho hình lăng trụ . Gọi , , theo thứ tự là trung điểm các cạnh , và
, khi đó tỉ số thể tích của khối chóp với lăng trụ
là
1
. , .
1
3
1
4
. , .
3
B MB
AB MB
AB C CB
B C CB
d A B BM S
V
V
d A B C CB S
' ' '
1
.
4
AB MB AB C CB
V V
.
2
3
AB C CB ABC A B C
V V
3
. .
1 1 2 1 1
. . .270 15 cm
3 4 3 18 18
AOGB ABC A B C ABC A B C
V V V
3
15 cm
AOGB
V
.
ABC A B C
30
O
ABB A
G
A B C
COGB
7
3
15
14
5
2
10
3
I
A C
.
.
2 1 1
. . .
3 2 3
B GOC
B IAC
V
B G B O B C
V B I B A B C
. .
1
1
3
B GOC B IAC
V V
, ,
1 1 1
. .
2 2 2
IAC A AC ACC A
I AC A AC
S d AC d AC S S
.
.
1
2
B IAC IAC
B ACC A ACC A
V S
V S
. .
1
2
2
B IAC B ACC A
V V
. . . . .
1 2
.30 20 3
3 3
B ACC A ABC A B C B ABC ABC A B C ABC A B C
V V V V V
1
2
3
.
10
3
B GOC
V
.
ABC A B C
M
N
P
C C
BC
B C
.
A MN P
.
ABC A B C
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 61
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có:
+ .
+ .
(Vì: và ).
Suy ra: .
Câu 100. Cho hình hộp chữ nhật . Gọi là trung điểm của , đối xứng với qua
. Khi đó mặt phẳng chia khối hộp thành hai phần. Tính tỉ số thể tích phần lớn và phần
bé.
A. . B. . C. . D. .
Lời giải
Chọn B
1
2
1
6
1
4
1
8
.
1
. ,
3
A ABC ABC
V S d A ABC
. . .
1 2
3 3
ABC A B C A BCC B ABC A B C
V V V
.
1
. ,
3
A MNP MNP
V S d A MNP
.
1 1 1
. . ,
3 4 4
BB C C A BB C C
S d A BB C C V
1 1
2 4
MNP CC PN BB C C
S S S
, ,
d A MNP d A BB C C
. .
1
6
A MNP ABC A B C
V V
.
ABC D A B C D
N
B C
P
B
B
PAC
7
3
17
7
25
7
25
14
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 62 TỔNG HỢP: HOÀNG TUYÊN
Gọi là trung điểm của . Mặt phẳng chia khối hộp chữ nhật thành hai phần như
hình vẽ. Gọi thể tích khối hộp chữ nhật ban đầu là , phần chứa điểm có thể tích và phần
còn lại có thể tích .
Ta có .
Thể tích của khối chóp là .
Ta lại có .
Do đó .
Vậy .
Câu 101. Cho các số thực dương
x
và
y
thỏa mãn
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
. Tìm giá trị nhỏ nhất
của biểu thức
2 18x y
P
x
.
A.
9P
. B.
3 2
2
P
.
C.
1 9 2P
. D. Hàm số không có giá trị nhỏ nhất.
Lời giải
Chọn A
Từ giả thiết ta đặt
2
2t x y ,
t
.
Phương trình
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
trở thành
49 7
4 9.3 4 9 . 4 7 49 9 9. 49 0
7 3
t
t t t t
t
.
Nhận thấy
2t
là nghiệm phương trình.
Ta chứng minh
2t
là nghiệm duy nhất của phương trình.
M
A B
ACM
V
B
1
V
2
V
1
2
PB PN PM MB
PB PC PA AB
.
P ACB
.
1 1 1 1
. .2. . .
3 3 2 3
P ACB ABC
V PB S BB AB BC V
.
.
1
. .
8
P MNB
P ACB
V
PB PN PM
V PB PC PA
1 . . .
1
1 .
8
P ACB P MNB P ACB
V V V V
. .
7 7 1 7
.
8 8 3 24
P ACB ABCD A B C
V V V
1 1
2 1
7 7
7
17
24
24
V V V
V V V
V V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 63
Xét
2t
:
7 49
t
và
7
9. 49
3
t
nên vế trái phương trình luôn dương, nên phương trình vô
nghiệm.
Xét
2t
: 7 49
t
và
7
9. 49
3
t
nên vế trái phương trình luôn âm, nên phương trình vô
nghiệm.
Vậy
2
2 2t x y
2
2
2
x
y
thay vào
2
2 18 16x y x x
P
x x
. Dấu bằng đạt được khi
16
4x x
x
.
Câu 102. Cho khối lăng trụ
. ' ' 'ABC A B C
. Gọi
E
là trọng tâm tam giác
' ' 'A B C
và
F
là trung điểm
.BC
Tính tỉ số thể tích giữa khối
'.B EAF
và khối lăng trụ
. ' ' 'ABC A B C
.
A.
1
4
. B.
1
8
. C.
1
5
. D.
1
6
.
Lời giải
Chọn D
M là trung điểm của B’C’
1
2
EAF AA MF
S S
.
, ,d B AA MF d B AEF
.
. . .B AA MF ABF A B M B ABF
V V V
. . .
1 2
3 3
ABF A B M ABF A B M ABF A B M
V V V
.
Suy ra
. .
1
2
B EAF B AA MF
V V
. . .
1 2 1 1 1
. . . .
2 3 3 2 6
ABF A B M ABC A B C ABC A B C
V V V
.
Vậy
.
.
1
6
B EAF
ABC A B C
V
V
.
Câu 103. Cho lăng trụ
. ' 'ABC AB C
có thể tích là V. Gọi M là điểm thuộc cạnh
'CC
sao cho
3 'CM C M
. Thể tích của khối chóp
.M ABC
theo V là:
A.
4
V
. B.
3
4
V
. C.
12
V
. D.
6
V
.
Lời giải
Chọn A
16 16
1 2 . 1 9
x x
x x
A'
B'
C'
A
B
C
F
M
E
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 64 TỔNG HỢP: HOÀNG TUYÊN
Cách 1: Thể tích của khối chóp M.ABC là:
.
. ' ' '
. . ' ' '
1
; .
3
'; .
;
1 1 1 3 1
. . . .
3 3 ' 3 4 4';
1
.
4 4
ABC
M ABC
ABC A B C
ABC
M ABC ABC A B C
d M ABC S
V
V
d C ABC S
d M ABC
MC
C Cd C ABC
V
V V
Cách 2: Áp dụng công thức tỉ số thể tích.
.
.
' ' '.
1 1 3 1 1
.
3 ' 3 4 4 4
C ABM
M ABC
A B C ABC
V
CM
V V
V CC
.
Câu 104. Cho khối lăng trụ
. ' ' 'ABC A B C
. Gọi
E
là trọng tâm tam giác
' ' 'A B C
và
F
là trung điểm
.BC
Tính tỉ số thể tích giữa khối
'.B EAF
và khối lăng trụ
. ' ' 'ABC A B C
.
A.
1
4
. B.
1
8
. C.
1
5
. D.
1
6
.
Lời giải
Chọn D
M là trung điểm của B’C’
1
2
EAF AA MF
S S
.
, ,d B AA MF d B AEF
.
A'
B'
C'
A
B
C
F
M
E
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 65
. . .B AA MF ABF A B M B ABF
V V V
. . .
1 2
3 3
ABF A B M ABF A B M ABF A B M
V V V
.
Suy ra
. .
1
2
B EAF B AA MF
V V
. . .
1 2 1 1 1
. . . .
2 3 3 2 6
ABF A B M ABC A B C ABC A B C
V V V
.
Vậy
.
.
1
6
B EAF
ABC A B C
V
V
.
Câu 105. Cho hình hộp . Tỉ số thể tích của khối tứ diện và thể tích của khối hộp
bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Đặt
.ABCD A B C D
V V
.
Ta có
ACB D AA B D D ADC B ABC CB C D
V V V V V V
1
4.
6
V V
1
3
V
.
Vậy
1
3
ACB D
V
V
.
Câu 106. Cho khối hộp
ABCDA B C D
có thể tích V . Các điểm
, ,M N P
thỏa mãn 2AM AC
 
,
3AN AB


, 4AP AD


. Tính thể tích khối chóp
AMNP
theo
V
.
A.
6V
. B.
8V
. C.
12V
. D.
4V
.
Lời giải
Chọn B
Phân tích:
Nhận dạng bài toán: Đây là bài toán tính thể tích khối đa diện thông qua tỉ số thể tích.
Kiến thức cần nhớ: Cho khối chóp
.S ABC
. Trên các đường thẳng
, ,SA SB SC
lần lượt lấy ba
điểm
, ,A B C
khác
S
. Ta có:
.
.
. .
S A B C
S ABC
V
SA SB SC
V SA SB SC
.
.
ABCD A B C D
ACB D
.
ABCD A B C D
2
3
1
6
1
2
1
3
A'
B'
D
C
D'
C'
A
B
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 66 TỔNG HỢP: HOÀNG TUYÊN
Ta có:
.
.
. .
A MNP
A CB D
V
AM AN AP
V AC AB AD
2.3.4 24
.
.
24
A MNP
A CB D
V V
. Mặt khác:
. . . . .A CB D ABCDA B C D A A B D A B BC A D DC C C B D
V V V V V V
1
4.
6 3
V
V V
.
8
A MNP
V V
.
Câu 107. Cho khối hộp
ABCDA B C D
có thể tích
V
. Lấy điểm
M
đối xứng với
A
qua
C
, điểm
N
đối
xứng với
A
qua
B
, điểm
P
thỏa mãn
AP k AD


. Tìm
k
để thể tích khối chóp
AMNP
bằng
2
V
.
A.
3
8
k
. B.
3
8
k
. C.
1
2
k
. D.
1
2
k
.
Lời giải
Chọn B
Ta có:
.
.
. .
A MNP
A CB D
V
AM AN AP
V AC AB AD
2.2. 4k k
.
.
4
A MNP
A CB D
V k V
.
Mà:
. . . . .A CB D ABCDA B C D A A B D A B BC A D DC C C B D
V V V V V V
1
4.
6 3
V
V V
.
4
3
A MNP
V k V
.
3
2 8
A CB D
V
V k
.
Câu 108. Cho khối lăng trụ tam giác
ABCA B C
có thể tích
V
. Điểm
M
là trung điểm của
AB
. Mặt
phẳng
C B M
chia khối lăng trụ thành hai khối đa diện có thể tích là
1
V
và
2
V , biết
1
V
là khối
chứa điểm
A
. Tính
2
V theo
V
.
A.
2
7
12
V
. B.
2
5
12
V
. C.
2
5
6
V
. D.
2
17
24
V
.
Lời giải
Chọn B
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 67
Do
// (ABC)C B
nên
C B M
cắt
AC
tại điểm
N
thỏa mãn
//MN B C
N
là trung điểm
AC
.
Dễ thấy 3 đường
, ,C N B M A A
đồng quy tại
S
và
.
.
1
8
S AMN
S A B C
V V
1
.
7
8
S A B C
V V
.
Gọi
,h S
lần lượt là chiều cao và diện tích đáy của khối lăng trụ
ABCA B C
, ta có:
.
1 1 2
; . .2 .
3 3 3
S A B C
V d S A B C S h S V
, vậy
1
7
12
V V
2
5
12
V V
.
Câu 109. Cho khối lăng trụ
.ABC A B C
. Gọi
E
,
F
lần lượt là trung điểm của
AA
,
CC
. Mặt phẳng
BEF
chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó là
A.
1
3
. B.
1
. C.
1
2
. D.
2
3
.
Lời giải
Chọn C
Gọi
V
là thể tích khối lăng trụ
.ABC A B C
;
1
V là thể tích khối chóp
.B AEFC
;
2
V là thể tích khối
đa diện
BB EFC A
;
I
là trung điểm của cạnh
BB
và
h
là chiều cao của khối lăng trụ
.ABC A B C
.
Ta có:
//EIF ABC
nên
,
2
h
d B EIF
.
.
1 1 1
. . .
3 2 6 6
B IEF ABC ABC
h
V S h S V
. Do đó
1 . .
1 1 1
2 6 3
ABC EIF B EIF
V V V V V V
.
2 1
1 2
3 3
V V V V V V
. Vậy
1
2
1
2
V
V
.
Cách 2.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 68 TỔNG HỢP: HOÀNG TUYÊN
Gọi
V
là thể tích khối lăng trụ
.ABC A B C
;
1
V là thể tích khối chóp
.B AEFC
,
2
V là thể tích khối
đa diện
BB EFC A
Ta có
1 .
1 1 2 1
.
2 2 3 3
BACC A ABC A B C
V V V V
suy ra
2
2
3
V V
.
Vậy
1
2
1
2
V
V
.
Câu 110. Cho khối hộp chữ nhật
.ABCD A B C D
có thể tích là
2110
. Biết
A M MA
,
3DN ND
,
2CP C P
như hình vẽ. Mặt phẳng
MNP
chi khối hộp đã cho thành hai khối đa diện. Thể tích
khôi đa diện nhỏ hơn bằng
A.
5275
6
. B.
5275
12
. C.
7385
18
. D.
8440
9
.
Lời giải
Chọn A
Cách 1
Gọi
H
là giao điểm của mặt phẳng
MNP
với
BB
. Khi đó ta có
1 1 5
2 3 6
D N B H A M C P
DD BB AA CC
.
Khi đó ta có
.
.
1 1 5 5
.
4 2 6 12
A B C D MNPH
ABCD A B C D
V
D N B H A M C P
V DD BB AA CC
.
Vậy thể tích của khối nhỏ là
.
5 5275
.2110
12 6
A B C D MNPH
V
.
Cách 2
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 69
Gọi
H
là giao điểm của mặt phẳng
MNP
với
BB
. Khi đó ta có
1 1 5
2 3 6
D N B H A M C P
DD BB AA CC
, suy ra
7
12
B H
BB
.
Gọi
, ,E C C F A A G B B
sao cho
'D N C E A F B G
. Gọi
0
V
là thể tích
khối
A B C D ABCD
. Gọi
V
là thể tích khối
A B C D MHPN
. Gọi
1
V
là thể tích
khối
A B C D FGEN
. Gọi
2
V
là thể tích khối chóp
.N FMHG
và Gọi
3
V
là thể tích
khối chóp
.N EPHG
. Ta có
1 2 3
V V V V
.
Do
1
4
D N D D
nên suy ra
1 0
1
4
V V
.
2
1
.
3
FGHM
V S AD
mà
7
24
FGHM
ABA B
S
FM GH
S A A B B
suy ra
2 0
7
72
V V
3
1
.
3
GHPE
V S AB
mà
5
24
GHPE
BCC B
S
EP GH
S C C B B
suy ra
2 0
5
72
V V
Vậy thể tích khối cần tính là:
0
5 5275
12 6
V V
.
Câu 111. Cho khối lăng trụ tam giác
. ' ' 'ABC A B C
. Gọi
M
là trung điểm cạnh
'BB
,
N
là điểm thuộc cạnh
'AA
sao cho
' 4AA AN
. Mặt phẳng
'C MN
chia khối lăng trụ thành 2 phần, phần chứa điểm
A
có thể tích
2
V , phần còn lại có thể tích
1
V . Tỷ số
1
2
V
a
V b
với
,a b
là số tự nhiên và phân số
a
b
tối giản. Tổng
a b
bằng
A.
8
. B.
12
. C.
10
. D.
13
.
Lời giải
Chọn B
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 70 TỔNG HỢP: HOÀNG TUYÊN
Ta có:
. '
. ' ' '
1 ' 1 1 1 7
1
3 ' ' ' 3 4 2 12
ABC NMC
ABC A B C
V
AN BM CC
V AA BB CC
.
. ' . ' ' ' ' ' ' . ' ' '
7 5
12 12
ABC NMC ABC A B C NMC A B ABC A B C
V V V V
.
' ' '
1
2 . '
5
7
NMC A B
ABC NMC
V
V a
V V b
12.a b
Câu 112. Cho lăng trụ
. ' ' 'ABC A B C
có thể tích là
V
. Gọi
M
là điểm trên cạnh
'CC
sao cho
3 'CM C M
. Tính thể tích của khối chóp
.M ABC
.
A.
4
V
. B.
3
4
V
. C.
12
V
. D.
6
V
.
Lời giải
Chọn A
.
. '.
'.
3 3
' 4 4
M ABC
M ABC C ABC
C ABC
V
MC
V V
V C C
.
'.
'.
' ' '.
1 1
3 3
C ABC
C ABC
A B C ABC
V
V V
V
.
Suy ra
.
3 1
.
4 3 4
M ABC
V
V V
.
Câu 113. Cho hình lăng trụ tam giác
.ABC A B C
có thể tích là
V
và độ dài cạnh bên
6AA
đơn vị. Cho
điểm
1
A thuộc cạnh
AA
sao cho
1
2AA . Các điểm
1
B ,
1
C lần lượt thuộc cạnh
BB
,
CC
sao
cho
1 1
,BB x CC y , ở đó
,x y
là các số thực dương thỏa mãn
12.xy
Biết rằng thể tích của
khối đa diện
1 1 1
.ABC A B C bằng
1
.
2
V
Giá trị của
x y
bằng
A.
3
. B.
4
. C.
1
. D.
0
.
Lời giải
Chọn C
M
C'
B'
A
C
B
A'
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 71
Gọi
,M N
lần lượt thuộc
BB
và
CC
sao cho
2.BM CN
Khi đó ta có
1 1 1 1 1 1 1
. .ABC A B C ABC A MN A MNC B
V V V
1 4
3 12
A BCC B
x y
V V
1 4 2
.
3 12 3
x y
V V
Mặt khác theo giả thiết ta có
1 1 1
.
1
2
ABC A B C
V V
nên suy ra
1 4 2 1
3 12 3 2
x y
V V V
1 4 2 1
3 12 3 2
x y
7x y
, kết hợp với
12.xy
Ta có
3
4
x
y
hoặc
4
3
x
y
. Do đó
1.x y
Câu 114.
Cho một hình hộp chữ nhật
.
ABCD A B C D
. Trên các cạnh
AA
,
BB
,
CC
lấy lần lượt lấy ba
điểm
X
,
Y
,
Z
sao cho
2
AX A X
,
BY B Y
,
3
CZ C Z
. Mặt phẳng
XYZ
cắt cạnh
DD
ở
tại điểm
T
. Khi đó tỉ số thể tích của khối
.XYZT ABCD
và khối
.
XYZT A B C D
bằng bao nhiêu?
A.
7
24
.
B.
7
17
.
C.
17
7
.
D.
17
24
.
Lời giải
Chọn C
Xét mặt phẳng qua
H
và song song mặt phẳng
ABCD
cắt các cạnh
AA
,
BB
,
CC
,
DD
lần
lượt tại
M
,
N
,
P
,
Q
. Khi đó, hai mặt phẳng
XYZT
;
MNPQ
cùng với các mặt bên của hình
hộp chữ nhật giới hạn những khối đa diện bằng nhau và đối xứng nhau qua điểm
H
.
Khi đó,
A B C D XYZT A B C D MNPQ
V V
.
Ta có:
//MNPQ ABCD
nên
A B C D MNPQ
A B C D ABCD
V
EH
V EF
hay
XYZTABCD
A B C D XYZT
V
HF
V EH
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 72 TỔNG HỢP: HOÀNG TUYÊN
Xét hình thang
A XZC
có đường trunh bình
EH
nên
7
2 24
A X C Z
EH EF
.
Do đó
17
24
HF EF
hay
7
17
EH
HF
.
Vậy
17
7
A B C D XYZT
XYZTABCD
V
V
.
Câu 115. Cho hình lăng trụ tam giác
.
ABC A B C
. Gọi
M
,
N
lần lượt là trung điểm của
BB
,
CC
. Mặt
phẳng
A MN
chia khối lăng trụ thành hai phần, đặt
1
V là thể tích của phần đa diện chứa điểm
B
,
2
V là phần còn lại. Tính tỉ số
1
2
V
V
.
A.
1
2
7
2
V
V
. B.
1
2
2
V
V
. C.
1
2
3
V
V
. D.
1
2
5
2
V
V
.
Lời giải
Chọn B
A
B
C
A
B
C
M
N
A
B
B
C
M
N
C
A
K
Kẻ
//MK AB
suy ra
//KN AC
. Do
M
,
N
lần lượt là trung điểm của
BB
,
CC
khi đó mặt
phẳng
MKN
chia hình lăng trụ
.
ABC A B C
làm hai phần bằng nhau.
Ta có
. . . .
2
ABC A B C ABC MNK MNK A B C MNK A B C
V V V V .
Mặt khác
. . . .
MNK A B C N A B C A MNK N A B M
V V V V và
. . .
N A B C A MNK N A B M
V V V
nên
2 . . .
2
N A B C N A B M N A B C
V V V V ,
1 .
4
N A B C
V V . Vậy
1
2
2
V
V
.
Câu 116. Xét khối lăng trụ tam giác
.ABC A B C
. Mặt phẳng đi qua
C
và các trung điểm của
AA
,
BB
chia khối lăng trụ thành hai phần có tỉ số thể tích bằng
A.
2
3
. B.
1
2
. C.
1
. D.
1
3
.
Lời giải
Chọn B
F
E
B'
A'
C
A
C'
B
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 73
Gọi
E
,
F
lần lượt là các trung điểm của
AA
và
BB
khi đó ta có:
.C A B FE
V
.
1
2
C A B BA
V
.
1 2
.
2 3
ABC A B C
V
.
1
3
ABC A B C
V
.
Suy ra
.CC ABFE
V
.
2
3
ABC A B C
V
.
Vậy mặt phẳng
C EF
chia khối lăng trụ thành hai phần có tỉ số thể tích bằng
1
2
.
Câu 117. Cho khối hộp chữ nhật
.ABCD A B C D
có thể tích bằng
2110
. Biết
A M MA
,
3DN ND
,
2CP C P
như hình vẽ. Mặt phẳng
MNP
chia khối hộp đã cho thành hai khối đa diện. Thể tích
khối đa diện nhỏ hơn bằng
A.
5275
6
. B.
8440
9
. C.
7385
18
D.
5275
12
.
Lời giải
Chọn A
Gọi
Q
là giao điểm của mặt phẳng
MNP
với
BB
.
Giả sử
A M
x
AA
,
C P
y
CC
,
D N
z
DD
,
B Q
t
BB
. Khi đó
x y z t
.
.
.
3
A B D MQN
A B D ABD
V
x z t
V
.
.
6
A B D MQN
A B C D ABCD
V
x z t
V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 74 TỔNG HỢP: HOÀNG TUYÊN
.
.
3
C B D PQN
C B D CBD
V
y z t
V
.
.
6
C B D PQN
A B C D ABCD
V
y z t
V
.
.
1
2
MNPQ A D C B
ABCD A D C B
V
x y
V
.
.
1
2
MNPQ A D C B
ABCD A D C B
V
A M C P
V AA CC
1 1 1
2 2 3
5
12
. D.
5 5275
.
12 6
MNPQ A D C B ABC A D C B
V V
.
Câu 118. Cho hình hộp
.ABCD A B C D
. Tính tỉ số thể tích của khối tứ diện
A C BD
và khối hộp
.ABCD A B C D
.
A.
1
3
. B.
1
6
. C.
1
2
. D.
1
4
.
Lời giải
Chọn C
Gọi
.ABCD A B C D
V V
, ta có
' ' 'A C BD C DCB C A B B C A D D
V V V V V
1 1 1
6 6 6
V V V V
1
2
V
.
.
1
2
A C BD ABCD A B C D
V V
.
Câu 119. Cho khối lăng trụ
.ABC A B C
. Gọi
M
là trung điểm của
BB
,
N
là điểm trên cạnh
CC
sao
cho
3CN NC
. Mặt phẳng
( )AMN
chia khối lăng trụ thành hai phần có thể tích
1
V
và
2
V
như
hình vẽ. Tính tỉ số
1
2
V
V
.
A.
1
2
5
3
V
V
. B.
1
2
3
2
V
V
. C.
1
2
4
3
V
V
. D.
1
2
7
5
V
V
.
Lời giải
Chọn D
D
A
B
C
A'
D'
B'
C'
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 75
Gọi
M
là trung điểm của
CC
, ta có:
1
2
BCM M BCC B
dt dt
,
1
4
M MN BCM M
dt dt
1
8
BCC B
dt
5
8
BMNC BCC B
dt dt
2
.
A BCB C
V
V
1
, .
3
1
, .
3
BCNM
BCB C
d A BCB C dt
d A BCB C dt
5
8
.
.
.
A A B C
ABC A B C
V
V
1
; .
3
; .
A B C
A B C
d A A B C dt
d A A B C dt
1
3
.
.
2
3
A BCC B
ABC A B C
V
V
2
.
ABC A B C
V
V
5 2
.
8 3
5
12
.
Do
. 1 2ABC A B C
V V V
1
2
7
5
V
V
.
Câu 120. Cho lăng trụ
.ABC A B C
.Trên các cạnh
,AA BB
lần lượt lấy các điểm
,E F
sao cho
,AA kA E BB kB F
. Mặt phẳng
(C )EF
chia khối trụ đã cho thành hai khối đa diện bao gồm
khối chóp
( . )C A B FE
có thể tích
1
V và khối đa diện
(ABCEFC )
có thế tích
2
V . Biết rằng
1
2
2
7
V
V
, tìm k
A.
4k
. B.
3k
. C.
1k
. D.
2k
.
Lời giải
Chọn B
+) Do khối chóp
.C A B FE
và khối chóp
.C A B BA
có chung đường cao hạ từ
C
nên
.
.
2 1
2
C A B FE
A B FE A B E
C A B BA A B BA A B A
V
S S A E
V S S A A k
(1)
+) Do khối chóp
.C ABC
và khối lăng trụ
.ABC A B C
có chung đường cao hạ từ
C
và đáy là
ABC
nên
.
ABC.
1
3
C ABC
A B C
V
V
.
ABC.
2
3
C A B BA
A B C
V
V
(2)
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 76 TỔNG HỢP: HOÀNG TUYÊN
Từ (1) và (2) suy ra
.
1
1 ABC.
ABC. ABC.
2 2 2
.
3 3 3
C A B FE
A B C
A B C A B C
V
V
V V
V k V k k
+) Đặt
ABC.A B C
V V
Khi đó
1
2 1
2
.
3
2
.
3
V V
k
V V V V V
k
Mà
1
2
2
7
V
V
nên
2 2 2 2 2 2 6 2
. ( . ) (1 ) 2 6 3
3 7 3 3 7 3 7 7
V V V k k
k k k k k
Câu 121. Cho hình hộp
.ABCD A B C D
thể tích là
.V
Tính thể tích của tứ diện
ACB D
theo
.V
A.
.
6
V
B.
.
4
V
C.
.
5
V
D.
.
3
V
Lời giải
Chọn D
Ta có ngay kết quả sau
' ' '. . ' ' ' '. . ' ' '
.
ACB D B ABC C B C D D ACD A A B D
V V V V V V
Lưu ý
'. . ' ' ' '. . ' ' ' . ' ' ' ' '
1 1
. 4. .
3 3 2 6 3
B ABC C B C D D ACD A A B D ABC A B C ACB D
V V V
V V V V V V V
Câu 122. Cho khối lăng trụ đứng, mặt phẳng
P
đi qua
C
và các trung điểm của
AA
,
BB
chia khối
lăng trụ
.ABC A B C
thành hai khối đa diện có tỷ số thể tích bằng
k
với
1.k
Tìm
k
.
A.
1
.
3
B.
2
.
3
C.
1.
D.
1
.
2
Lời giải
Chọn D
Gọi
, ,D E F
lần lượt là trung điểm của
, ,AA BB CC
và
h
là độ dài chiều cao của khối lăng trụ
.ABC A B C
. Khi đó ta có
A
B
A
C
B
D
F
E
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 77
.
1 1 1
. . . . . .
3 2 6 6
C DEF DEF DEF ABC A B C
h
V S S h V
Mặt khác
.
1
. .
2
A B C DEF ABC A B C
V V
Suy ra
' . .
1 1 1
. .
2 3 2
C DEB A
C DEB A C DEF ABC A B C C DEB A ABC A B C
ABCDC E
V
V V V V V k
V
7. KHỐI CHÓP - MỨC 4
Câu 123. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm của , là
điểm trên đoạn sao cho . Mặt phẳng chứa cắt đoạn tại và cắt đoạn
tại . Tính tỉ số để thể tích khối đa diện đạt giá trị lớn nhất.
A. . B. . C. . D. .
Lời giải
Chọn D
Đặt . Ta có .
Mặt khác là hình bình hành nên có
; .
Suy ra .
Xét với ;
Bảng biến thiên:
.
S ABCD
ABCD
M
SA
N
SB
2
SN NB
R
MN
SD
Q
SC
P
SP
SC
.
.
S MNPQ
S ABCD
V
V
2
5
1
3
1
4
1
SP
x
SC
0 1
x
SM SP SN SQ
SA SC SB SD
1 2 1
2 3 6
SQ
x x
SD
1
6
x
ABCD
. . .
2 2
S ABCD S ABC S ACD
V V V
.
.
1
. .
3
S MNP
S ABC
V
SM SN SP
x
V SA SB SC
.
.
1 1
. .
2 6
S MPQ
S ACD
V
SM SP SQ
x x
V SA SC SD
. .
2
.
. . .
1 1 1 1 1
2 2 6 4 6 4 8
S MNPQ S MPQ
S MNP
S ABCD S ABC S ACD
V V
V
x x x x x
V V V
2
1 1
4 8
f x x x
1
1
6
x
1 1 1 1
0 ;1
2 8 4 6
f x x x
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 78 TỔNG HỢP: HOÀNG TUYÊN
Từ BBT ta có . Vậy đạt giá trị lớn nhất bằng khi .
Câu 124. Cho khối chóp có đáy là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn
song song với đáy và cắt các cạnh bên lần lượt tại . Gọi
lần lượt là hình chiếu vuông góc của lên mặt phẳng . Tính tỉ số để thể
tích khối đa diện đạt giá trị lớn nhất.
A. . B. . C. . D. .
Lời giải
Chọn C
Đặt với .
Xét tam giác có nên .
Xét tam giác có nên .
Kẻ đường cao của hình chóp. Xét tam giác có:
nên .
Ta có: .
Thể tích khối chóp không đổi nên đạt giá trị lớn nhất khi lớn nhất.
Ta có .
Đẳng thức xảy ra khi và chỉ khi: . Vậy .
Câu 125. Cho hình chóp có đáy là hình chữ nhật, Cạnh bên vuông góc với
đáy và Điểm là trung điểm của . Một mặt phẳng qua cắt hai cạnh và
lần lượt tại và . Tính tỉ số khi thể tích của khối chóp đạt giá trị nhỏ nhất.
1
;1
6
3
max
8
f x
.
.
S MNPQ
S ABCD
V
V
3
8
1
SP
SC
.
S ABCD
ABCD
, , ,
SA SB SC SD
, , ,
M N P Q
, , ,
M N P Q
, , ,
M N P Q
ABCD
SM
SA
.
MNPQ M N P Q
1
3
3
4
2
3
1
2
SM
k
SA
0;1
k
SAB
//
MN AB
.
MN SM
k MN k AB
AB SA
SAD
//
MQ AD
.
MQ SM
k MQ k AD
AD SA
SH
SAH
//
MM SH
1 1 1 .
MM AM SA SM SM
k MM k SH
SH SA SA SA
2
.
. . . . . . 1
MNPQ M N P Q
V MN MQ MM AB AD SH k k
.
MNPQ M N P Q
V
2
. 1
k k
3
2
2 1 . .
1 2 2 4
. 1
2 2 3 27
k k k
k k k
k k
2
2 1
3
k k k
2
3
SM
SA
.
S ABCD
, 2 .
AB a AD a
SA
3 .
SA a
P
SC
AP
SB
SD
M
N
SM
SB
.
S AMPN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 79
A. . B. . C. . D. .
Lời giải
Chọn D
Cách xác định mặt phẳng qua cắt hai cạnh , như hình vẽ. Gọi là giao điểm của hai
đường chéo hình chữ nhật và là giao điểm và .
Ta có ,
Áp dụng công thức tỉ số thể tích ta có ;
Suy ra , . Khi đó
Ta có là trọng tâm tam giác nên
Từ lần lượt kẻ các đường thẳng song song với cắt tại . Khi đó hai tam giác
(g.c.g) suy ra
Ta có ;
Từ đó suy ra suy ra . Dấu bằng xảy ra khi
.
1
1
3
4
3
2
3
AP
SB
SD
O
ABCD
I
AP
MN
3
.
1 1
. . .3 . .2 2
3 3
S ABCD
V AS AB AD a a a a
.
.
. . 1
.
. . 2
S AMP
S ABC
V
SA SM SP SM
V SA SB SC SC
.
.
. . 1
.
. . 2
S ANP
S ADC
V
SA SN SP SN
V SA SD SC SD
. .
.
4
S AMP S ABCD
SM
V V
SB
. .
.
4
S ANP S ABCD
SN
V V
SD
3
1 . .
.
2
S AMP S ANP
SM SN a
V V V
SB SD
I
SAC
2
3
SI
SO
,
B D
MN
SO
,
E F
OED OFB
OE OF
SB SF SO OF
SM SI SI
SD SE SO OE
SN SI SI
2
3
SB SD SO
SM SN SI
4 4
3
SM SN
SB SD
SB SD
SM SN
2
//
3
SM SN
MN B
B
D
SB SD
SM
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 80 TỔNG HỢP: HOÀNG TUYÊN
Vậy . Giá trị nhỏ nhất của bằng khi .
Câu 126. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm của , là
điểm trên đoạn sao cho . Mặt phẳng chứa cắt đoạn tại và cắt đoạn
tại . Tính tỉ số để thể tích khối đa diện đạt giá trị lớn nhất.
A. . B. . C. . D. .
Lời giải
Chọn D
Đặt . Ta có .
Mặt khác là hình bình hành nên có
; .
Suy ra .
Xét với ;
Bảng biến thiên:
Từ BBT ta có . Vậy đạt giá trị lớn nhất bằng khi .
Câu 127. Cho hình chóp có đáy là hình vuông cạnh cạnh bên vuông góc với đáy,
cạnh bên tạo với đáy góc . Gọi , là hình chiếu của lần lượt trên , . Mặt
phẳng cắt tại . Tính tỉ số thể tích của khối chóp và
3 3
3
1
4 2
.
2 3 2 3
SM SN a a
V a
SB SD
1
V
3
2
3
a
2
3
SM
SB
.
S ABCD
ABCD
M
SA
N
SB
2
SN NB
R
MN
SD
Q
SC
P
SP
SC
.
.
S MNPQ
S ABCD
V
V
2
5
1
3
1
4
1
SP
x
SC
0 1
x
SM SP SN SQ
SA SC SB SD
1 2 1
2 3 6
SQ
x x
SD
1
6
x
ABCD
. . .
2 2
S ABCD S ABC S ACD
V V V
.
.
1
. .
3
S MNP
S ABC
V
SM SN SP
x
V SA SB SC
.
.
1 1
. .
2 6
S MPQ
S ACD
V
SM SP SQ
x x
V SA SC SD
. .
2
.
. . .
1 1 1 1 1
2 2 6 4 6 4 8
S MNPQ S MPQ
S MNP
S ABCD S ABC S ACD
V V
V
x x x x x
V V V
2
1 1
4 8
f x x x
1
1
6
x
1 1 1 1
0 ;1
2 8 4 6
f x x x
1
;1
6
3
max
8
f x
.
.
S MNPQ
S ABCD
V
V
3
8
1
SP
SC
.
S A BC D
ABCD
,
a
SA
SB
45
B
D
A
SB
SD
AB D
SC
C
.
S ABCD
. .
S ABCD
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 81
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có:
vuông cân tại .
Mặt khác vuông cân tại có là đường cao là trung điểm .
vuông cân tại có là đường cao là trung điểm
Mà
Ta có: ; .
; .
Chứng minh tương tự ta cũng có: .
Từ và .
Xét tam giác vuông có là đường cao nên:
Đặt .
Khi đó: .
Ta có: .
.
1
8
1
12
1
6
1
3
C'
D'
O
D
A
B
C
S
B'
, 45
SB ABCD SBA
SA B
A
SA a
SA B
A
AB
B
SB
SAD
A
AD
D
.
S D
2 2 2 2
3 3 .
SC SA AC a SC a
C D AD
CD SA
( )
CD SAD CD AD
CD AD
AD SD
1
AD SCD AD SC
2
AB SC
2
SC AB C D SC AC
SAC
AC
2
2
3
.
3
SA a
SA SC SC SC
SC
.
S ABCD
V V
. . .
1 1
2 2
S ABC S ADC S ABCD
V V V V
. ' '
. ' ' .
.
3
1 1 1 1
3
. .
2 6 6 12
3
S AB C
S AB C S ABC
S ABC
a
V
SB SC
V V V
V SB SC
a
. ' '
. ' ' .
.
1 1 1
.
6 6 12
S AD C
S AD C S ADC
S ADC
V
SD SC
V V V
V SD SC
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 82 TỔNG HỢP: HOÀNG TUYÊN
Vậy .
Câu 128. Cho khối tứ diện đều Gọi , lần lượt là các điểm thỏa mãn và
Mặt phẳng chứa đường thẳng và song song với chia khối tứ diện
thành hai khối đa diện. Tính tỉ số thể tích của khối đa diện chứa đỉnh và khối đa diện
còn lại.
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi là thể tích của khối đa diện chứa đỉnh
Giả sử khối tứ diện đều có thể tích bằng .
Vì .
.
Khối đa diện chứa đỉnh được chia thành ba khối tứ diện , , do vậy
.
Xét tam giác , có .
Ta có: .
.
.
Suy ra .
Vậy .
. .
1 1
1
12 12
6
SAB C D SAB C SAC D
S ABCD S ABCD
V V
V V V
V V V
.
ABCD
M
N
0
MA MB
2 0.
NC ND
M N
A C
ABCD
A
11
18
18
11
11
A
V
.
A
ABCD
0
V
// //
AC ABC MP AC P BC
// //
AC ADC NQ AC Q AD
A
AMNQ
AMNP
ACNP
A AMNQ AMNP ACNP
V V V V
A CD
2
//
3
AQ CN
QN AC
AD CD
0 0 0
1 2 1 2 1 2 1 1
. . . . . . . . .
2 3 2 3 2 3 3 9
AMNQ ABND ABND
AM AQ DN
V V V V V V
AB AD DC
0 0 0
1 1 1 1 1
.
2 2 2 3 6
BNP
AMNP ABNP ABNP
BCD
AM S
V V V V V V
AB S
0 0 0
2 1 1
. .
3 2 3
ACNP
CN CP
V V V V
CD CB
0 0
1 1 1 11
.
9 6 3 18
A
V V V
0
0
0 0
11
11
18
11
7
18
A
A
V
V
V V
V V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 83
Câu 129. Cho khối chóp có ,
sao cho , . Mặt phẳng
đi qua hai điểm , và song song với chia khối chóp thành hai khối đa diện, có thể
tích là , với . Tỉ số là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có mặt phẳng cắt mặt phẳng theo giao tuyến ( ) và cắt mặt
phẳng
theo giao tuyến ( ). Thiết diện tạo bởi mặt phẳng với hình
chóp là hình thang .
Gọi và .
Ta có: , nên .
Suy ra: .
.
Mặt khác: , nên
.
Vậy .
Suy ra .
Câu 130. Cho hình chóp có đáy là hình bình hành có thể tích là . Gọi , , , lần
lượt là trọng tâm của các tam giác . Gọi là điểm bất kì trên mặt phẳng
đáy . Biết thể tích khối chóp bằng . Tính tỉ số .
A. . B. . C. . D. .
.
S ABC
M SA
N SB
2
MA MS
2
NS NB
M
N
SC
1
V
2
V
1 2
V V
1
2
V
V
3
5
4
9
3
4
4
5
P
Q
N
M
A
B
C
S
SAC
MQ SC
Q AC
SBC
NP SC
P B C
MNPQ
.
S ABC
V V
ABC
S S
1
3
QC
AC
2
3
PC
BC
1 2
.
3 3
PQC
S S
7
9
ABPQ PQC
S S S S
.
1
. , .
3
N ABPQ ABPQ
V d N ABC S
1 1 7 7
. , .
3 3 9 27
d S ABC S V
2
3
MA
SA
2
3
QA
CA
4
9
AMQ ASC
S S
.
1
. , .
3
N AMQ AMQ
V d N SAC S
1 2 4 8
. , .
3 3 9 27
ASC
d B SAC S V
. .
5
9
MNABPQ N ABPQ N AMQ
V V V V
4
9
SMNPQC
V V
4
5
SMNPQC
MNABPQ
V
V
.
S A BC D
V
M
N
P
Q
,
SAB
,
SBC
,
SCD
SDA
O
ABCD
.
OMNPQ
V
V
V
27
2
27
8
9
4
27
4
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 84 TỔNG HỢP: HOÀNG TUYÊN
Lời giải
Chọn A
Gọi , , , lần lượt là trung điểm của , , , .
Vì , lần lượt là trọng tâm các tam giác , nên . Suy ra
. Chứng minh tương tự ta có .
Vì lần lượt là trung điểm của nên . Chứng minh tương tự ta có
.
Từ , , , suy ra . Suy ra 4 điểm , , , đồng phẳng.
Ta có ;
.
+ .
+ .
.
.
Ta có .
Chứng minh tương tự ta có .
Khi đó .
E
F
G
K
AB
BC
CD
DA
M
N
SAB
SBC
2
3
SM SN
SE SF
MN FE
PQ KG
2
,
E F
,
AB BC
FE AC
3
KG AC
4
2
3
4
MN PQ
M
N
P
Q
//
MNPQ ABCD
2
SM
ME
, 2. ,
d S MNPQ d MNPQ ABCD
2. ,
d O MNPQ
. .
2
S MNPQ O MNPQ
V V
2
V
.
.
S MNQ
S EFK
V
SM SN SQ
V SE SF SK
2 2 2
3 3 3
8
27
. .
8
27
K
S MNQ
S EF
V V
.
.
. .
S NPQ
S FGK
V
SN SP SQ
V SF SG SK
2 2 2
. .
3 3 3
8
27
. .
8
27
S NPQ S FGK
V V
. . . .
8 8
27 27
S MNQ S NPQ S EFK S FGK
V V V V
. .
8
27
S MNPQ S EFGK
V V
. .
27 27
8 4
S EFGK S MNPQ
V V V
1
. .sin
2
1
. .sin
2
EBF
ABC
BE BF EBF
S
S
BA BC ABC
1
4
1
4
EBF ABC
S S
1
8
ABCD
S
1
8
FCG GDK KAE ABCD
S S S S
EFGK ABCD EBF FCG GDK KAE
S S S S S S
4
ABCD EBF
S S
1
2
ABCD
S
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 85
Suy ra .
Từ và suy ra hay .
CÔNG THỨC TÍNH NHANH: Cho khối chóp có đáy là hình bình hành. Mặt
phẳng cắt các cạnh , , , lần lượt tại , , , sao cho , ,
, .
Khi đó:
Áp dụng vào bài toán ta được:
Câu 131. Cho hình chóp tứ giác đều . Gọi là trung điểm của . Mặt phẳng qua
và vuông góc cắt , lần lượt tại , . Gọi , lần lượt là thể tích hai khối chóp
và . Tính tỉ số .
A. . B. . C. . D. .
Lời giải
Chọn D
.
.
1
. , .
3
1
. , .
3
EFGK
S EFGK
S ABCD
ABCD
d S EFGK S
V
V
d S ABCD S
1
2
. .
2.
S ABCD S EFGK
V V
2
2
.
27
2
S ABCD
V V
27
2
V
V
.
S A BC D
ABCD
SA
SB
SC
SD
M
N
P
Q
SA
x
SM
SB
y
SN
SC
z
SP
SD
t
SQ
.
.
4
S MNPQ
S ABCD
V
x y z t
V xyzt
.
.
8
27
S EFGK
S MNPQ
V
V
.
.
27
4
S ABCD
S MNPQ
V
V
. .
2
S MNPQ O MNPQ
V V
.
.
27
2
S ABCD
O MNPQ
V
V
27
2
V
V
.
S A BC D
C
SC
P
AC
SC
SB
SD
B
D
1
V
2
V
.
S AB C D
.
S A BC D
1
2
V
V
1
2
2
3
V
V
1
2
2
9
V
V
1
2
4
9
V
V
1
2
1
3
V
V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 86 TỔNG HỢP: HOÀNG TUYÊN
Do là hình chóp tứ giác đều nên hình chiếu của lên mặt phẳng trùng với
tâm của hình vuông .
Vì là trung điểm của và là trung điểm nên là trọng tâm
.
Ta có:
, mà ; .
Vì
;
và suy ra .
Mặt khác:
, , .
Do đó:
.
Ta có:
.
Vậy .
CÔNG THỨC TÍNH NHANH: Cho khối chóp có đáy là hình bình hành. Mặt
phẳng cắt các cạnh , , , lần lượt tại , , , sao cho , ,
, .
.
S A BC D
S
ABCD
H
ABCD
C
SC
H
A C
I AC SH
SA C
2
3
SI SH
B D AC
B D S H
BD SAC
B D SC
BD P
P SC
//
BD P
BD SBD
SBD P B D
//
BD P
//
BD B D
P SBD BD
I AC P
I SH SBD
I B D
SB
SB
SD
SD
SI
SH
2
3
.1
2 .
S AB C D
S ABCD
V
V
V V
. .
.
S AB C S AC D
S ABCD
V V
V
. .
. .
2 2
S AB C S AC D
S ABC S ACD
V V
V V
1 1
2 2
SA SB SC SA SC SD
SA SB SC SA SC SD
1 2 1 1 1 2
1 1
2 3 2 2 2 3
1
3
1
2
1
3
V
V
.
S A BC D
ABCD
SA
SB
SC
SD
M
N
P
Q
SA
x
SM
SB
y
SN
SC
z
SP
SD
t
SQ
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 87
Ta có:
Áp dụng vào bài toán ta có
Câu 132. Cho tứ diện có là trọng tâm tứ diện, mặt phẳng quay quanh cắt các cạnh ,
lần lượt tại , . Giá trị nhỏ nhất của tỉ số là
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi , lần lượt là trung điểm , khi đó trung điểm của là trọng tâm của tứ diện
. Điểm là giao điểm của và . Qua dựng đường thẳng cắt các cạnh ,
lần lượt tại , . Suy ra là mặt phẳng quay quanh thỏa mãn yêu cầu bài toán.
.
.
4
S MNPQ
S ABCD
V
x y z t
V xyzt
.1
2 .
S AB C D
S ABCD
V
V
V V
3 3
1 2
1
2 2
3 3
3
4 4 1 2
2 2
SA SD SC SB
SA SD SC SB
SA SD SC SB
SA SD SC SB
SA B C
G
A G
SB
SC
M
N
.
.
S AMN
S ABC
V
V
4
9
3
8
1
3
1
2
E
F
BC
SA
G
EF
SA B C
I
A G
SE
I
SB
SC
M
N
AMN
A G
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 88 TỔNG HỢP: HOÀNG TUYÊN
Dựng , suy ra là trung điểm .
. Mà .
Cách 1:
Dựng , , .
Ta có: ; .
Ta có: , và là trung điểm của
(đúng cả trong trường hợp ).
Ta có: .
Dấu xảy ra khi và chỉ khi . Hay .
Vậy tỉ số nhỏ nhất là .
Cách 2:
Đặt ; , với , .
Ta có: .
Do , , thẳng hàng nên .
Ta có: .
Dấu xảy ra khi và chỉ khi .
Vậy tỉ số nhỏ nhất là .
Câu 133. Cho tứ diện , trên các cạnh , , lần lượt lấy các điểm , , sao cho
, , . Mặt phẳng chia khối tứ diện thành hai
phần có thể tích là , với . Tính tỉ số .
A. . B. . C. . D. .
Lời giải
Chọn B
//
GK SE
K SA
K
FS
KG
SI
AK
AS
3
4
1
2
KG
SE
2
3
SI
SE
//
B P M N
//
CQ MN
,
P Q SE
SM SI
SB SP
SN SI
SC SQ
//
BP QC
E PQ BC
EB EC
BEP CEQ
E
PQ
2
SP SQ SE
P Q E
.
.
S AMN
S ABC
V
V
. .
SA SM SN
SA SB SC
1. .
SI SI
SP SQ
AM GM
2
2
4
SI
SP SQ
2
2
SI
SE
2
SI
SE
4
9
" "
SP
SQ
SE
P
Q
E
//
MN BC
4
9
SB
SM
x
SC
SN
y
0
x
0
y

SI
2
3

SE
1
3
SB SC
1
. .
3

x SM y SN
. .
3 3
 
x y
SM SN
I
M
N
3 3
x y
1
x y
3
.
.ABC
S AMN
S
V
V
. .
SA SM SN
SA SB SC
1
xy
AM GM
2
1
4
x y
4
9
" "
x
y
3
2
//
MN BC
4
9
ABCD
B C
B D
A C
M
N
P
3
B C B M
3
2
BD BN
2
AC AP
MNP
ABCD
1
V
2
V
1 2
V V
2
1
V
T
V
26
13
T
26
19
T
26
21
T
26
15
T
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 89
Gọi , , suy ra .
Thiết diện của tứ diện được cắt bởi mặt phẳng là tứ giác .
Có ; và ; .
Áp dụng định lí Menelaus trong các tam giác và ta có:
.
Và .
Áp dụng bài toán tỉ số thể tích của hai khối chóp tam giác ta có:
và
. Suy ra
.
.
Suy ra thể tích phần thứ nhất là: .
Do đó thể tích phần còn lại là: .
Vậy .
Câu 134. Cho hình chóp tứ giác đều có tất cả các cạnh bằng , tâm của đáy là . Gọi ,
tương ứng là trung điểm các cạnh , . Gọi là giao điểm của và mặt phẳng .
Tính thể tích của khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn D
Q
I
N
M
P
A
B
C
D
ABCD
V V
I M N C D
Q IP AD
Q AD MNP
ABCD
MNP
MNQP
3
2
BD BN
2
NB
ND
3
B C B M
2
MC
MB
2
AC AP
1
PC
PA
1
2
AP
AC
B C D
A CD
. . 1
NB ID MC
ND IC MB
2. .2 1
ID
IC
1
4
ID
IC
. . 1
ID PC QA
IC PA QD
1
.1. 1
4
QA
QD
4
QA
QD
4
5
AQ
AD
ANCD
ABCD
V
ND
V BD
1
3
1
3
ANCD
V V
2
3
CBNA
V V
ANPQ
ANCD
V
V
. .
AN AP AQ
AN AC AD
1 4
1. .
2 5
2
5
2
5
ANPQ ANCD
V V
2
15
V
.
1 2
3 15
N PQDC
V V V
1
5
V
CMNP
CBNA
V
V
. .
CM CN CP
CB CN CA
2 1
.1.
3 2
1
3
1
3
CMNP CBNA
V V
2
9
V
1 .
N PQDC CMNP
V V V
1 2
5 9
V V
19
45
V
2 1
V V V
26
45
V
T
2
1
26
19
V
V
.
S ABCD
a
O
M
N
SA
SC
E
SD
BMN
V
.
O BMEN
3
2
18
a
V
3
2
24
a
V
3
2
12
a
V
3
2
36
a
V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 90 TỔNG HỢP: HOÀNG TUYÊN
Cách 1:
Trong mặt phẳng gọi . Trong mặt phẳng gọi .
Khi đó .
Vì , lần lượt là trung điểm của , nên là đường trung bình tam giác .
Suy ra là trung điểm .
Áp dụng định lý Menelaus tam giác với ba điểm thẳng hàng , , , ta có:
.
Ta có , suy ra .
Vì hình chóp là hình chóp đều nên .
Ta có .
Thể tích khối là (vì là trung điểm ).
.
.
.
Vậy .
Cách 2: Làm trắc nghiệm.
SAC
I MN SO
SBD
E BI SD
E SD BMN
M
N
SA
SC
MN
SAC
I
SO
SOD
B
I
E
. . 1
ES BD IO
ED BO IS
.2.1 1
ES
ED
1
2
ES
ED
2 2
2
AC AB BC a
2
2
a
AO
.
S ABCD
SO ABCD
2
2 2 2
2 2
2 2
a a
SO SA AO a
OBMEN
0 . . .
BMEN S BMEN S BMN S EMN
V V V V
I
SO
.
.
1
. .
4
S BMN
S BAC
V
SB SM SN
V SB SA SC
3
. .
1 1 1 1 2
. . . . .
4 4 3 2 48
S BMN S BAC
a
V V SO AB BC
.
.
1
. .
12
S EMN
S DAC
V
SE SM SN
V SD SA SC
3
. .
1 1 1 1 2
. . . . .
12 12 3 2 144
S EMN S DAC
a
V V SO AD DC
3 3 3
. .
2 2 2
48 144 36
SBMEN S BMN S EMN
a a a
V V V
3
0
2
36
BMEN
a
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 91
Đặt ; ; ; .
Điều kiện để bốn điểm , , , đồng phẳng là:
.
Ta có
.
Suy ra .
Mà .
Vậy .
Cách 3:
.
Lại có .
; ; . Suy ra tam giác vuông tại .
.
Kẻ . Suy ra
Do đó .
.
Vậy .
Câu 135. Cho hình chóp có đáy là hình bình hành. Gọi , lần lượt là trung điểm của
các cạnh , . Điểm thuộc đoạn . Biết mặt phẳng chia khối chóp
thành hai phần, phần chứa đỉnh có thể tích bằng lần phần còn lại. Tính tỉ số .
A. . B. . C. . D. .
Lời giải
Chọn D
1
2
SM
x
SA
1
SB
y
SB
1
2
SN
z
SC
SE
t
SD
B
M
E
N
1 1 1 1
x z y t
1 1
2 2 1
3
t
t
.
.
1 1 1 1 1
4
S BMEN
S BADC
V
xyzt
V x y z t
1 1 1 1 1
. .1. . . 2 1 2 3
4 2 2 3 6
3
. .
1 1 1 1 1 2 2
. . . . . . . .
6 6 3 6 3 2 36
S BMEN S BADC
a a
V V SO AB BC a a
3
0 .
2
36
BMEN S BMEN
a
V V
3
0
2
36
BMEN
a
V
0
BMEN BOMN OMNE
V V V
OMNE SMNE
V V
2
a
OM ON
2
2
a
MN
2
2
a
BO
OMN
O
3
1 1 2 1 2
. . . .
3 3 2 2 2 2 48
BOMN OMN
a a a a
V BO S
// BE
OF
1
;
SI SE
SO SF
1
.
2
DF DO
DE DB
1
3
SE SD
2 3
1 1 1 1 1 1 1 2 2
. . . . .
3 2 2 12 12 12 3 2 2 144
SMNE
SMNE SACD
SACD
V
a a a
V V
V
3 3 3
0
2 2 2
48 144 36
BMEN BOMN OMNE
a a a
V V V
.
S ABCD
ABCD
M
N
AB
BC
K
SA
MNK
.
S ABCD
S
7
13
KA
t
KS
1
2
t
3
4
t
1
3
t
2
3
t
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 92 TỔNG HỢP: HOÀNG TUYÊN
Trong mặt phẳng , kéo dài cắt , lần lượt tại , .
Trong mặt phẳng , gọi . Trong mặt phẳng , gọi .
Suy ra thiết diện là ngũ giác và .
Đặt
Ta có: .
Áp dụng định lý Menelaus cho tam giác , suy ra
Mặt khác:
Suy ra thể tích của khối đa diện không chứa đỉnh S là
Phần thể tích của khối đa diện không chứa đỉnh bằng phần còn lại suy ra thể tích của khối
đa diện không chứa đỉnh S bằng thể tích khối chóp
.
Câu 136. Cho tứ diện có trọng tâm là . Một mặt phẳng qua cắt các tia và theo thứ
tự tại . Đặt . Đẳng thức nào sau đây đúng
A. . B. .
ABCD
MN
DA
DC
F
E
( )
SAD
FK SD Q
SCD
QE SC P
MNPQK
// //
MN AC PK
,
h d S ABCD
, , .
1 1
KA KA t t
t d K ABCD d P ABCD h
KS SA t t
1
3
2
FD
FA BN AD
FA
SAD
1 3 3
. . 1 .3. 1 ,
3 3 1 3 1
QS FD KA QS QS QD t t
t d Q ABCD h
QD FA KS QD QD t SD t t
1 1 9
4 8 8
FAM NCE BMN ABC ABCD DEF ABCD
S S S S S S S
1 3 9 1 1
. . .
3 3 1 8 1 8 1 8
QDEF KAMF PECN
t t t
V V V V h S S S
t t t
1 27 2
. . .
3 8 3 1 8 1
ABCD
t t
h S
t t
27 2
8 3 1 8 1
ABCD
t t
V V
t t
S
7
13
13
20
.
S ABCD
27 2 13 2
8 3 1 8 1 20 3
t t
t
t t
SABC
G
G
,
SA SB
SC
, ,
A B C
, ,
SA SB SC
m n p
SA SB SC
2 2 2
1 1 1
1
m n p
1 1 1
4
mn np pm
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 93
C. . D. .
Lời giải
Chọn C
Gọi lần lượt là trung điểm các cạnh , là trọng tâm tam giác . Khi đó, ta có:
.
Xét tam giác có:
và .
Ta có: (1)
(2)
(3)
Cộng (1),(2),(3) vế theo vế ta được:
.
Bình luận: Nếu làm trắc nghiệm, ta chọn mp qua và cắt là mp ,ta có ngay
đáp án:
1 1 1
4
m n p
4
m n p
G
A
C
B
S
N
M
O
A'
B'
C'
,
M N
,
BC SA
O
ABC
G SO MN
SAM
1 1 1 1
2
2 2 2 4
SG SN SM SA SM SA SM

1 2 1 4 3
2
3 3 3 3 4
SG
SO SA SM SA SM SG
SO
  
3 3
. . . . .
4 4
SA GC SAOC
SA GC
SAOC
V V
SA SG SC
m p V mnp
V SA SO SC n
3 3
. . . . .
4 4
SA GB SAOB
SA GB
SAOB
V V
SA SG SB
m n V mnp
V SA SO SB p
3 3
. . . . .
4 4
SB GC SBOC
SB GC
SBOC
V V
SB SG SC
n p V mnp
V SB SO SC m
3 1 1 1
. . .
4
SA B C SAOC SAOB SBOC
V mnp V V V
n p m
3 1 1 1
. . .
4
SA B C SAOC SAOB SBOC
SABC SABC SABC SABC
V V V V
mnp
V n V p V m V
3 1 1 1
. . .
4
AOC AOB BOC
ABC ABC ABC
S S S
mnp mnp
n S p S m S
; ; ;
4 1 1 1 4 1 1 1 1 1 1
. . . . . .
3 ; ; ; 3 3 3 3
d O AC d O AB d O BC
n d B AC p d C AB m d A BC n p m
1 1 1
4
m n p
G
, ,
SA SB SC
NBC
1 1 1
4.
m n p
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 94 TỔNG HỢP: HOÀNG TUYÊN
Câu 137. Cho khối chóp có đáy là tứ giác lồi, tam giác đều cạnh , tam giác
cân tại và , và . Mặt phẳng đi qua và vuông góc với
cắt lần lượt tại . Tính thể tích khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn A
Giả thiết: cân tại và
.
vuông tại có .
Giả thiết: cân và đều.
Tứ giác có và
.
.
.
Giả thiết: vuông góc với cắt lần lượt tại .
Ta có: .
Mặt khác vuông cân tại là trung điểm .
tương tự .
.
.
S ABCD
ABCD
ABD
a
BCD
C
0
120
BCD
SA ABCD
SA a
P
A
SC
, ,
SB SC SD
, ,
M N P
.
S AMNP
3
3
42
a
3
2 3
21
a
3
3
14
a
3
3
12
a
BCD
C
0
; 120
BD a BCD
2 2 2
2 . .cos
BD BC CD BC CD BCD
2 2
3
3
3
a
a BC BC
ABC
B
3
,
3
a
AB a BC
2
2 2 2
2 3
3 3
a a
AC AB BC a
BCD
ABD
ABCD
AC BD
ABC ADC
2
1 1 2 3 3
. . .
2 2 3 3
ABCD
a a
S AC BD a
2 3
.
1 1 3 3
. . .
3 3 3 9
S ABCD ABCD
a a
V SA S a
3
. ..
1 3
2 18
S ACS D SAB CDC AB
a
VV V
P
SC
, ,
SB SC SD
, ,
M N P
1
AM SB
BC SA
BC AM
BC AB
AM SC
SAB
S
M
1
2
SM
SB
SB
2
1
2
SP
SD
3
SC AN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 95
Mặt khác vuông tại có .
.
Ta có: .
.
.
Câu 138. Cho tứ diện đều có cạnh bằng . Gọi là hai điểm thay đổi lần lượt thuộc cạnh
sao cho mặt phẳng luôn vuông góc với mặt phẳng . Gọi lần lượt
là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện . Tính .
A. . B. . C. . D. .
Lời giải
Chọn A
Cách 1:
Gọi lần lượt là trung điểm của các đoạn thẳng . là trọng tâm .
Tứ diện đều, G là tâm tam giác đề .
Ta có .
Đặt .
Ta có .
.
SAC
A
2 3
,
3
a
SA a AC
2 2
2 2 2
2
7 3
3 7
a SN SA
SC SA AC
SC SC
.
.
1 3 3
. .
2 7 14
S AMN
S ABC
V
SM SN
V SB SC
3 3
. .
3 3 3 3
. .
14 14 18 84
S AMN S ABC
a a
V V
3 3
.
. .
.
3 3 3 3 3
. .
14 14 14 18 84
S APN
S APN S ADC
S ADC
V
SP SN a a
V V
V SD SC
3 3
. . .
3 3
2.
84 42
S AMNP S APN S AMN
a a
V V V
ABCD
1
,
M N
,
BC BD
AMN
( )
BCD
1 2
;
V V
ABMN
1 2
V V
17 2
216
17 2
72
17 2
144
2
12
, ,
I J K
, ,
BC BD CD
G
ABC
ABCD
BCD AG BCD
AMN BCD AMN AG G MN
1
, , 1
2
BM x BN y x y
2
2 2 2
3 6
1
3 3
AG AB BG
BMN BGM BGN
S S S
1 1 1
. .sin . .
2 2 2
BM BN B BM GI BN GJ
0
1 1 3 1 3
. . sin 60 . .
2 2 6 2 6
x y x y
3 1
x
y
x
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 96 TỔNG HỢP: HOÀNG TUYÊN
Thể tích tứ diện là: .
Xét hàm số .
Vậy .
Cách 2:
Gọi lần lượt là trung điểm của các đoạn thẳng . là trọng tâm .
Tứ diện đều, G là tâm tam giác đề .
Ta có .
.
.
Dễ thấy diện tích Tam giác nhỏ nhất khi và chỉ khi tam giác đều, khi đó
.
.
Diện tích tam giác lớn nhất khi và chỉ khi hoặc
.
Khi đó: .
.
Vậy .
Câu 139. Cho tứ diện đều có cạnh bằng . Gọi , lần lượt là trọng tâm của các tam giác
, và là điểm đối xứng với qua điểm . Mặt phẳng chia khối tứ diện
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh có thể tích . Tính .
ABMN
2 2
1 1 3 6 2
. . . .
3 3 4 3 1 3 12 3 1
ABMN BMN
x x
V S AG
x x
2
2 1
. , ;1
12 3 1 2
x
f x x
x
2
'
2
0
3 2
0
2
3 1
3
x L
x x
f x
x N
x
1
1
;1
2
2
max 1
24
x
V f x f
2
1
;1
2
2 2
min
3 27
x
V f x f
1 2
17 2
216
V V
, ,
I J K
, ,
BC BD CD
G
ABC
ABCD
BCD AG BCD
AMN BCD AMN AG G MN
2
2 2 2
3 6
1
3 3
AG AB BG
1
.
3
ABMN BMN
V S AG
BMN
BMN
/ /
MN CD
2 2 2
3 3 3
BM BG
BM BC
BC BK
min
2
2 3 3
.
3 4 9
BMN
S
BMN
M C
N D
max
1 3
2 8
ABC
BMN
S S
max
1
1 1 6 3 2
. . .
3 3 3 8 24
BMN
V AG S
min
2
1 1 6 3 2
. . .
3 3 3 9 27
BMN
V AG S
1 2
17 2
216
V V
ABCD
a
M
N
ABD
ABC
E
B
D
MNE
ABCD
A
V
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 97
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích khối tứ diện đều cạnh là .
Gọi ; . Trong mặt phẳng đường thẳng cắt ,
lần lượt tại , . Khi đó mặt phẳng chia khối tứ diện đã cho phần chứa đỉnh là tứ
diện .
Gọi là trung điểm . Xét ta có: (định lý Menelaus) .
Tương tự ta có:
Xét ta có: .
Mặt khác ta có: .
Câu 140. Cho hình chóp tứ giác đáy là hình bình hành có thể tích bằng . Lấy điểm , lần
lượt là trung điểm của cạnh và . Mặt phẳng qua cắt cạnh tại . Khi đó thể
tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn D
3
2
96
a
3
3 2
80
a
3
3 2
320
a
3
9 2
320
a
a
3
2
12
a
P ME AD
T ME AB
ABC
TN
AC
BC
Q
F
MNE
A
ATPQ
I
BD
AID
. . 1
ED MI PA
EI MA PD
3
PA
PD
3
QA
QC
AIB
. . 1
EI TB MA
EB TA MI
2
3
TB
TA
3 3 3 27
. . . .
5 4 4 80
ATPQ
ABCD
V
AT AP AQ
V AB AD AC
3 3
27 2 9 2
.
80 12 320
ATPQ
a a
V
.
S ABCD
V
B
D
SB
SD
AB D
SC
C
.
S AB C D
3
V
2
3
V
3
3
V
6
V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 98 TỔNG HỢP: HOÀNG TUYÊN
Gọi là giao điểm của hai đường chéo và thì . Khi đó là trung điểm
của và .
Trong mặt phẳng : Ta kẻ và cắt tại . Khi đó áp dụng tính đồng dạng
của các tam giác ta có: ; .
Vì nên ta có và
.
Suy ra .
Lưu ý :Có thể sử dụng nhanh công thức
Câu 141. Cho hình chóp có đáy là hình bình hành, là trung điểm của . Gọi là
giao của với mặt phẳng chứa và song song với . Tính tỉ số thể tích của hai khối chóp
và .
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi .
.
S
A
B
C
D
B
D
C
O
H
A
C
O
H
S
C
K
d
O
AC
BD
SO B D H
H
SO
C AH SO
SAC
//
d AC
AC
d
K
1
OH OA
SK OA
SH SK
1
2
SK
AC
1
2
SK SC
AC CC
1
3
SC
SC
. . .
1
.
2 2
S ABD S BCD S ABCD
V
V V V
.
.
1
4
S AB D
S ABD
V
SA SB SD
V SA SB SD
.
1
8
S AB D
V V
.
.
1
4
S B C D
S BCD
V
SB SC SD SC
V SB SC SD SC
.
8
S B C D
SC V
V
SC
. . .
1
1
8 8 8 6
S AB C D S AB D S B C D
SC V V SC V
V V V V
SC SC
SA SC SB SD
SA SC SB SD
.
S ABCD
ABCD
M
AD
S
SC
BM
SA
.
S BCDM
.
S ABCD
2
3
1
2
1
4
3
4
S'
G
M
C
A
B
D
S
G BM AC
1
//
2
AG AM
AM BC AGM CGB
GC BC
( ) ( )
//
( ) , //( )
SAC S BM S G
S G SA
SAC SA SA S BM
CS GC
SC AC
2
3
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 99
Do đó: .
Ta có
.
Do vậy:
.
Câu 142. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm của . Mặt phẳng qua
cắt các cạnh , lần lượt tại và . Gọi , theo thứ tự là thể tích khối chóp
và khối chóp . Giá trị nhỏ nhất của tỉ số bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Đặt , , , , có .
Áp dụng công thức tính nhanh tỉ lệ thể tích: , với .
Suy ra: . Khi đó , dấu bằng xảy ra khi .
Vậy giá trị nhỏ nhất của tỉ số bằng khi .
Chứng minh bài toán:
Cho hình chóp có đáy là hình bình hành. Các điểm , , , lần lượt nằm trên
các cạnh , , , . Đặt , , , .
Chứng minh rằng:: và .
Lời giải
( ,( )
( ,( ))
d S ABCD S C
d S ABCD SC
2
3
( , ). . ( , ).
ABM ABCD
S d M AB AB d D AB AB S
1 1 1 1
2 2 2 4
BCDM ABCD ABCD ABCD
S S S S
1 3
4 4
.
( ',( ). . ( ,( )).
BCDM ABCD
S BCDM
V d S ABCD S d S ABCD S
1 1 2 3
3 3 3 4
.
. ( ,( )).
ABCD S ABCD
d S ABCD S V
1 1 1
2 3 2
'S BCDM
SABCD
V
V
1
2
.
S ABCD
K
SC
AK
SB
SD
M
N
1
V
V
.
S AMKN
.
S ABCD
1
V
V
1
2
2
3
1
3
3
8
K
N
M
D
C
B
A
S
1
SA
a
SA
SB
b
SM
2
SC
c
SK
SD
d
SN
3
a c
.1
.
4
S AMKN
S ABCD
V
V
a b c d
V V abcd
a c b d
3
b d
1
2
6 3 3 1
8 4 3
4
2
V
V bd bd
b d
3
2
b d
1
V
V
1
3
3
2
SB SD
SM SN
.
S ABCD
A
B
C
D
SA
SB
SC
SD
SA
a
SA
SB
b
SB
SC
c
SC
SD
d
SD
.
.
4
S A B C D
S ABCD
V
a b c d
V abcd
a c b d
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 100 TỔNG HỢP: HOÀNG TUYÊN
Ta có: là hình bình hành nên: .
Khi đó: .
.
Suy ra: .
Chứng minh tương tự như trên ta cũng có: .
Từ và suy ra: .
.
Vậy: .
Câu 143. Cho hình chóp tam giác đều . Gọi là trọng tâm tam giác , biết góc tạo bởi và
bằng . Mặt phẳng chứa và vuông góc với chia khối chóp đã cho thành hai
phần có thể tích , trong đó là phần thể tích chứa điểm . Tỉ số bằng
A. . B. . C. . D. .
Lời giải
Chọn B
D
B
C
A
S
B'
D'
A'
C'
ABCD
. .
2 2
ABCD ABD S ABCD S ABD
S S V V
.
. . .
.
1 1 1
. . . .
2
S A B D
S A B D S ABD S ABCD
S ABD
V
SA SB SD
V V V
V SA SB SD abd abd abd
.
. . .
.
1 1 1
. . . .
2
S B C D
S B C D S BCD S ABCD
S BCD
V
SB SC SD
V V V
V SB SC SD bcd bcd bcd
.
. . . . .
1 1
. .
2 2 2
S ABCD
S A B C D S A B D S B C D S ABCD S ABCD
a c V
V V V V V
abd bcd abcd
1
.
.
2
S ABCD
S A B C D
b d V
V
abcd
2
1
2
a c b d
. . .
.
2
2 4 4
S ABCD S ABCD S ABCD
S A B C D
b d V b d V a b c d V
V
abcd abcd abcd
.
.
4
S A B C D
S ABCD
V
a b c d
V abcd
.
S ABC
G
ABC
SG
SBC
30
BC
SA
1
V
2
V
1
V
S
1
2
V
V
6
1
6
6
7
7
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 101
Gọi là trung điểm , , trong đó là mặt phẳng chứa và vuông góc
, là hình chiếu của lên . Ta có: , nên .
Vì là hình chóp tam giác đều nên là đường cao hình chóp ứng với đáy và
là tam giác đều.
Ta có:
vừa là đường trung tuyến, vừa là đường cao trong tam giác đều nên .
, nên .
và .
Suy ra (vì ).
Do đó: .
Ta lại có: là hình chiếu vuông góc của lên .
.
Giả sử cạnh của tam giác đều là .
Xét tam giác vuông tại , ta có: .
Xét tam giác vuông tại , ta có: .
Trong tam giác , ta có: .
Xét tam giác vuông tại , ta có: .
M
BC
F SA
BC
SA
H
G
SM
SA
FM
SA FM
.
S ABC
SG
ABC
ABC
AM
AM BC
SG ABC
BC ABC
SG BC
AM SG G
,
AM SG SAM
BC SAM
BC GH
GH SAM
,
GH SM
GH BC
GH SBC
SM BC M
SM BC SBC
SG SBC S
SH
SH SBC
SG
SBC
, , 30
SG SBC SG SH GSH
ABC
a
SGM
G
3
cot30 . 3
6 2
a a
SG GM
SAG
G
2 2
2 2
21
3 4 6
a a a
SA AG SG
SAM
3
.
. 3 7
2 2
14
21
6
a a
SG AM a
MF
SA
a
AFM
F
2 2
2 2
3 3 7 21
2 14 7
a a a
FA AM FM
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 102 TỔNG HỢP: HOÀNG TUYÊN
Suy ra .
Mà
(vì ).
Do đó .
Câu 144. Cho hình chóp tam giác
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
2SA a
,
SA
vuông góc
với mặt phẳng
ABC
. Gọi
M
và
N
lần lượt là hình chiếu vuông góc của
A
lên các đường thẳng
,SB SC
. Tính
3
50 3V
a
, với
V
là thể tích khối chóp
.A BCNM
.
A.
12
. B.
10
. C.
11
. D.
9
.
Lời giải
Chọn D
Thể tích khối chóp
.S ABC
là
3
.
1 1 1 3 3
. .2 . . . .
3 3 2 2 6
S ABC ABC
a
V SA S a a a
.
Tam giác
SAB
vuông tại
A
và có
AM
là đường cao nên
2
. SM SB SA
2 2 2
2 2 2 2 2
4 4
4 5
SM SA SA a
SB SB SA AB a a
.
Tam giác
SAC
vuông tại
A
và có
AN
là đường cao nên
2 2 2
2 2 2 2 2
4 4
4 5
SN SA SA a
SC SC SA AC a a
.
Ta có
.
.
4 4 16
. .
5 5 25
S AMN
S ABC
V
SM SN
V SB SC
. .
16
25
S AMN S ABC
V V
21
6 1
7
1 1 1
7 7
21
6
a
SF FA
SA SA
a
.
1 . .
.
1 1
7 7
S FBC
S FBC S ABC
S ABC
V
SF
V V V
V SA
2 .
6
7
S ABC
V V
. . 1 2
S ABC S FBC FABC
V V V V V
1
2
1
6
V
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 103
Suy ra
3 3
. . . . .
16 9 9 3 3 3
.
25 25 25 6 50
ABCNM S ABC S AMN S ABC S ABC S ABC
a a
V V V V V V V
.
Vậy
3
50 3
9
V
a
.
Câu 145. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
,
N
,
K
lần lượt là trung điểm
của các cạnh
AB
,
BC
,
SA
. Biết mặt phẳng
MNK
chia khối chóp
.S ABCD
thành hai phần có
thể tích là
1 2
,V V
1 2
V V
. Tính tỉ số
1
2
V
V
.
A.
49
71
. B.
17
67
. C.
7
13
. D.
9
23
.
Lời giải
Chọn D
Trong mặt phẳng
ABCD
, kéo dài
MN
cắt
DA
,
DC
lần lượt tại
F
,
E
.
Trong mặt phẳng
( )SAD
, gọi
FK SD Q
. Trong mặt phẳng
SCD
, gọi
QE SC P
.
Suy ra thiết diện là ngũ giác
MNPQK
và
// // MN AC PK
.
Đặt
,h d S ABCD
1
, ,
2
d K ABCD d P ABCD h
Ta có:
1
3
2
FD
FA BN AD
FA
.
Áp dụng định lý Menelaus cho tam giác
SAD
, suy ra
1 3 3
. . 1 ,
3 4 4
QS FD KA QS QD
d Q ABCD h
QD FA KS QD SD
Mặt khác:
1 1 9
4 8 8
FAM NCE BMN ABC ABCD DEF ABCD
S S S S S S S
Suy ra thể tích của khối đa diện không chứa đỉnh S là
1 3 9 1 1 1 1
. . .
3 4 8 2 8 2 8
QDEF KAMF PECN
V V V V h S h S h S
2
1 23 23
. . .
3 32 32
ABCD ABCD
h S V V
1
1
2
9 9
32 23
V
V
V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 104 TỔNG HỢP: HOÀNG TUYÊN
Câu 146. Cho hình chóp tứ giác đều
.S ABCD
, đáy
ABCD
là hình vuông cạnh
,a
cạnh bên tạo với đáy góc
60
. Gọi
M
là trung điểm
SC
. Mặt phẳng đi qua
AM
và song song với
BD
, cắt
SB
tại
E
và
cắt
SD
tại
F
. Tính thể tích khối chóp
. .S AEMF
A.
3
6
12
a
. B.
3
6
27
a
. C.
3
6
36
a
. D.
3
6
18
a
.
Lời giải
Chọn D
, , 60 .SC ABCD SC OC SCO
Gọi
I SO AM I
là trọng tâm của tam giác
SAC
.
Ta có
.
. .
.
1 2 2 2 2
. . . . .
2 3 3 9 9
S AEM
S AEM S ABC
S ABC
V
SM SE SI
V V
V SC SB SO
Mà:
. .
2
S AEMF S AEM
V V
và
. .
2
S ABCD S ABC
V V
nên
. .
2
. 1
9
S AEMF S ABCD
V V
Trong
:SOC
6
tan60 .tan60 .
2
SO a
SO OC
OC
Khi đó
3
2
.
1 1 6 6
. . . . .
3 3 2 6
S ABCD ABCD
a a
V S SO a
Thay vào
3
.
6
1 : .
18
S AEMF
a
V
Câu 147. Cho tứ diện
ABCD
có thể tích
V
với
,M N
lần lượt là trung điểm
,AB CD
. Gọi
1 2
,V V lần lượt là
thể tích của
MNBC
và
MNDA
. Tính tỉ lệ
1 2
V V
V
.
A.
1
. B.
1
2
. C.
1
3
. D.
2
3
.
Lời giải
Chọn B
60
0
I
O
S
F
E
M
D
C
B
A
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 105
Vì
,M N
lần lượt là trung điểm
,AB CD
nên ta có:
, , ; , ,d A MCD d B MCD d C NAB d D NAB
, do đó:
.
. . 1 . .
; ;
2 2 4
B MCD
A MCD B MCD MNBC C MNB D MNB
V
V V
V V V V V V
.
2 . .
2 4
A MCD
MNAD D MNA C MNA
V
V
V V V V
.
1 2
1
4 4
2
V V
V V
V V
.
Câu 148. Cho khối chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích
12V
. Gọi
,M N
lần lượt
trung điểm
, ;SA SB P
là điểm thuộc cạnh
SC
sao cho
2PS PC
. Mặt phẳng
MNP
cắt cạnh
SD
tại
Q
. Tính thể tích khối chóp
.S MNPQ
bằng
A.
5
18
. B.
7
3
. C.
4
3
. D.
12
25
.
Lời giải
Chọn B
Ta có
2
PQ/ / .
3
SQ SP
CD
SD SC
Khi đó ta có:
1 1 2 1 1
. . . V.
2 2 3 6 12
SMNP
SMNP
SABC
V
SM SN SP
V
V SA SB SC
1 2 2 2 1
. . .
2 3 3 9 9
SMPQ
SMPQ
SACD
V
V V
V
Vậy
.
7 7
.
36 3
S MNPQ
V V
N
D
C
B
M
A
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 106 TỔNG HỢP: HOÀNG TUYÊN
Câu 149. Cho tứ diện
ABCD
có
3, 4, 6AB AC AD
,
o
60 ,BAC
o
90 ,CAD
o
120BAD . Thể tích
của khối tứ diện
ABCD
bằng
A.
27 2
8
. B.
9 2
4
. C.
6 2
. D. 6 6 .
Lời giải
Chọn C
Lấy các điểm
,C
D
lần lượt trên cạnh và
,AC
AD
sao cho
3AB AC AD
.
Áp dụng định lí Côsin ta có:
2 2 2
1
' 2 . 'cos 9 9 2.9. 9.3 27 3 3
2
BD AB AD AB AD BAD BD
.
Tam giác
BAC
là tam giác đều nên
3BC
, tam giác
D AC
vuông tại
A
nên
3 2C D
.
Xét tam giác
BD C
có
2 2 2
BD BC C D
, nên tam giác vuông tại
C
.
Gọi
H
là hình chiếu vuông góc của
A
trên
BD C
, vì
AB AC AD
nên
HB HC HD
.
Mặt khác, tam giác
BD C
vuông tại
C
nên
H
là trung điểm của
BD
.
Ta có,
2
2
27 3
9
4 4 2
BD
AH AB
.
Thể tích khối tứ diện
ABC D
bằng
1 1 3 1 9 2
. . . .3.3 2
3 3 2 2 4
ABC D BC D
V AH S
Áp dụng công thức tỉ số thể tích ta có
. 3 3 9 24
. 6 2
. 4 6 24 9
ABC D
ABCD ABC D
ABCD
V
AC AD
V V
V AC AD
.
Câu 150. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M, N
lần lượt là trung điểm của
,SA SD
. Mặt phẳng
chứa
MN
và cắt các cạnh
,SB SC
lần lượt tại
,Q P
. Đặt
SQ
x
SB
,
1
V là
thể tích khối chóp
.S MNPQ
,
V
là thể tích khối chóp
.S ABCD
. Tìm
x
để
1
1
2
V V
.
A.
1 41
4
x
. B.
1 33
4
x
. C.
2x
. D.
1
2
x
.
Lời giải
Chọn B
H
C'
D'
A
B
C
D
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 107
Vì
/ /
MN
MN SBC
SBC PQ
nên
/ / PQMN
, do đó
SP SQ
x
SC SB
.
Ta có:
.
. .
.
1 1 1
. . . . . . .
2 2 4 4 4 2 8
S MNP
S MNP S ACD
S ACD
V SM SN SP x x x xV
x V V V
V SA SD SC
.
2 2 2 2
.
. .
.
1 1
. . . . . .
2 2 2 2 2 4
S MQP
S MQP S ABC
S ABC
V
SM SQ SP x x x x V
x x V V V
V SA SB SC
.
2
2
. 1 . .
2
8 4 8
S MNPQ S MNP S MPQ
x x V
xV x V
V V V V
.
Do đó:
2
2
1
1 33
2
1 1
4
2 4 0
2 8 2
1 33
4
x
x x V
V V V x x
x
Rõ ràng
0x
nên
1 33
4
x
.
Câu 151. Cho hình chóp
. .S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
.a
Cạnh bên
SA a
và vuông
góc với mặt phẳng đáy. Gọi
, , ,M N P Q
lần lượt là trung điểm các cạnh
, , , .SA SB SC SD
Thể tích
của khối chóp cụt
.MNPQ ABCD
bằng
A.
3
6
a
. B.
3
7
24
a
. C.
3
3
a
. D.
3
4
a
.
Lời giải
Chọn B
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 108 TỔNG HỢP: HOÀNG TUYÊN
Ta có
2
3
.
1
. .
3 3
S ABCD
a
V a a
Theo định lý tỷ số thể tích ta có :
3 3
.
. . .
.
1 1 1 1 1 1 1 1
. . . . . . .
2 2 2 8 8 8 2 16 3 48
S MNQ
S MNQ S ABD S ABCD
S ABD
V
SM SN SQ a a
V V V
V SA SB SD
Tương tự ta có
3 3
. . .
1 1 1 1
. . .
8 8 2 16 3 48
S NPQ S BCD S ABCD
a a
V V V
Ta có
3 3 3
. . .
.
48 48 24
S MNPQ S MNQ S NPQ
a a a
V V V
3 3 3
. . .
7
.
3 24 24
MNPQ ABCD S ABCD S MNPQ
a a a
V V V
Câu 152. Cho khối chóp .
S ABC
. Gọi
M
là điểm trên cạnh
SB
, mặt phẳng
P
đi qua
,
A M
và song song
với
BC
chia khối chóp thành hai phần có cùng thể tích. Tìm tỷ số
SM
MB
.
A.
2 1
. B.
1
. C.
1
2
. D.
1 2
.
Lời giải
Chọn D
Do mặt phẳng
P
song song với
BC
nên mặt phẳng
P
cắt cạnh
SC
tại
N
và
//
MN BC
.
Đặt
0
SM SN
x x x
SB SC
.
Ta có
2
.
.
.
S AMN
S ABC
V
SM SN
x
V SB SC
.
Nên
2
.
.
1 1 1
2 2
2
S AMN
S ABC
V
ycbt x x
V
.
Do đó
1 2 1
2 2
SM SB MB SB SM SB
.
Vậy
1
2 1
2 1
SM
MB
.
Câu 153. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,
M N
lần lượt là trung điểm của
các cạnh
,
SA SD
. Mặt phẳng
chứa
MN
cắt các cạnh
,
SB SC
lần lượt tại
,
Q P
. Đặt
1
,
SQ
x V
SB
là thể tích khối chóp
. ,
S MNQP V
là thể tích khối chóp
.
S ABCD
. Tìm
x
để
1
1
2
V V
.
A.
1 41
.
4
x
B.
1 33
.
4
x
C.
2.
x D.
1
.
2
x
Lời giải
Chọn B
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 109
Ta có
MN AD BC
SBC PQ MN
MN
SP SQ
x
SC SB
Khi đó
. . .
1
. .
S MNQP S MNQ S NQP
S ABCD S ABCD
V V V
V
V V V
. .
. .
1
2 2 2
S MNQ S NQP
S ABD S ABC
V V
V V
. .
. .
1
S MNQ S NQP
S ABD S ABC
V V
V V
2
1 1 1 1 33
. . . . 1 2 4 0
2 2 2 4
x x x x x x
(vì
0x
)
Câu 154. Cho hình chóp đều
.S ABCD
có độ dài cạnh đáy bằng
a
. Gọi
G
là trọng tâm tam giác
SAC
. Mặt
phẳng chứa
AB
và đi qua
G
cắt các cạnh
SC
,
SD
lần lượt tại
M
và
N
. Biết mặt bên của hình
chóp tạo với đáy một góc bằng
60
. Thể tích khối chóp
.S ABMN
bằng
A.
3
3
4
a
. B.
3
3
8
a
. C.
3
3
16
a
. D.
3
3
3
16
a
.
Lời giải
Chọn B
Vì
G
là trọng tâm tam giác
SAC
nên
AG
cắt
SC
tại trung điểm
M
của
SC
, tương tự
BG
cắt
SD
tại trung điểm
N
của
SD
.
Gọi
O
là tâm của hình vuông
ABCD
và
I
là trung điểm của
AB
. Suy ra góc giữa mặt bên
SAB
và mặt đáy
ABCD
là
60SIO . Do đó
3
.tan 60
2
a
SO OI
.
Suy ra
3
2
.
1 1 3 3
.
3 3 2 6
S ABCD ABCD
a a
V S SO a
.
a
I
N
G
M
O
C
A
B
D
S
A
B
C
D
M
Q
P
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 110 TỔNG HỢP: HOÀNG TUYÊN
Mặt khác
. .
2
S ABCD S ABC
V V , ta lại có
.
.
1
2
S ABM
S ABC
V
SA SB SM
V SA SB SC
. .
1
.
2
S ABM S ABC
V V
.
.
.
1 1 1
2 2 4
S AMN
S ACD
V
SA SN SM
V SA SD SC
. .
1
.
4
S AMN S ACD
V V
.
Vậy
3 3
. .
3 3 3 3
4 4 6 8
S ABMN S ABCD
a a
V V
.
Câu 155. Cho khối chóp
.S ABC
có
SA SB SC a
và
30 ASB BSC CSA Mặt phẳng
qua
A
và cắt hai cạnh
SB
,
SC
tại
B
,
C
sao cho chu vi tam giác
AB C
nhỏ nhất. Tính
.
.
S AB C
S ABC
V
k
V
.
A.
2 2 k
. B. 4 2 3 k . C.
1
4
k
. D.
2 2 2 k .
Lời giải
Chọn B
Cắt hình chóp theo cạnh
SA
rồi trải các mặt bên ra ta được hình như hình vẽ (
A
là điểm sao cho
khi gấp lại thành hình chóp thì trùng với
A
).
Khi đó chu vi tam giác
AB C
bằng
AB B C C A
nhỏ nhất khi
A
,
B
,
C
,
A
thẳng hàng hay
AB B C C A AA
.
Khi đó tam giác
SAA
có
90
SAA ASB B SC C SA nên vuông cân tại
S
và có
SA a
,
SB SC
,
45
SAB .
Ta có
sin 45
3 1
sin105 sin 45 sin105
SA SB SB
SA
.
Do đó
.
.
. 3 1 3 1 4 2 3
S AB C
S ABC
V
SB SC
k
V SB SC
.
Câu 156. Cho tứ diện
DABC
. Gọi
'B
và
'C
lần lượt là trung điểm của
AB
và
AC
. Khi đó tỉ số thể tích
của khối tứ diện AB’C’D và khối tứ diện ABCD bằng:
A.
1
8
B.
1
6
C.
1
4
D.
1
2
Lời giải
Chọn C
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 111
Ta có:
' '
'. '. 1 1 1
.
. . 2 2 4
AB C D
ABCD
V
AB AC AD
V AB AC AD
Câu 157. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
. Mặt bên của hình chóp tạo với mặt
đáy một góc
60
. Mặt phẳng
P
chứa
AB
và đi qua trọng tâm
G
của tam giác
SAC
cắt
SC
,
SD
lần lượt tại
M
và
N
. Thể tích khối chóp
.S ABMN
là
A.
3
3
2
a
.
B.
3
3
4
a
.
C.
3
3
3
a
.
D.
3
3a .
Lời giải
Chọn A
Gọi
H
là trung điểm cạnh
CD
và
O
là tâm hình vuông
ABCD
.
Ta có
.S ABCD
là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử
, 60SCD ABCD SHO
Tam giác
SHO
vuông tại
O
có
.tan 60 3SO OH a
.
3
.
1 4 3
. .
3 3
S ABCD ABCD
a
V S SO
.
Mặt khác:
, // //
//
P SCD MN
AB P MN SCD MN CD AB
AB CD
Mà
G
là trọng tâm tam giác
SAC
nên
G
cũng là trọng tâm tam giác
SBD
1
2
SM SN
SC SD
.
Ta lại có
1 1
2 4
SABM
SABM SABC SABCD
SABC
V
SM
V V V
V SC
S
A
B
C
D
O
N
M
P
60
G
H
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 112 TỔNG HỢP: HOÀNG TUYÊN
1 1
.
4 8
SAMN
SAMN SACD SABCD
SACD
V
SM SN
V V V
V SC SD
Khi đó
3
1 1 3 3
4 8 8 2
SABMN SABCD SABCD
a
V V V
.
Câu 158. Cho khối tứ diện có thể tích
V
. Gọi
V
là thể tích khối đa diện có các đỉnh là trung điểm các cạnh
của khối tứ diện đã cho. Tính tỉ số
V
V
.
A.
2
3
V
V
. B.
1
4
V
V
. C.
5
8
V
V
. D.
1
2
V
V
.
Lời giải
Chọn D
Gọi khối tứ diện đã cho là
ABCD
.
Gọi
E
,
F
,
G
,
H
,
I
,
J
lần lượt là trung điểm của
AD
,
AB
,
AC
,
BC
,
CD
,
BD
.
Khi đó ta có:
.
4.
A FEG
V V V
.
Mặt khác
.
1
8
A FEG
V V
.
Suy ra
1 1
2 2
V
V V V
V
.
Câu 159. Cho hình chóp
.S ABCD
có đáy là hình bình hành và có thể tích là
V
. Điểm
P
là trung điểm của
SC
, một mặt phẳng qua
AP
cắt các cạnh
SD
và
SB
lần lượt tại
M
và
N
. Gọi
1
V là thể tích khối
chóp
.S AMPN
. Tìm giá trị nhỏ nhất của
1
V
V
?
A.
1
8
. B.
2
3
. C.
3
8
. D.
1
3
.
Lời giải
Chọn D
H
G
E
F
J
B
D
C
A
I
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 113
Đặt
SM
x
SB
,
SN
y
SD
,
0 x
,
1y
.
Vì
SA SC SB SD
SA SP SM SN
nên
1 1
1 2
3 1
x
y
x y x
Khi đó
. .1
. .
1 1 1 1 1 1
. . . . . . . . . .
2 2 2 2 2 2 2 2
S ANP S AMP
S ADC S ABC
V V
V SA SN SP SA SM SP
y x
V V V SA SD SC SA SB SC
1 1
4 4 3 1
x
x y x
x
Vì
0x
,
0y
nên
1
1
3
x
Xét hàm số
1
4 3 1
x
f x x
x
trên
1
;1
3
Ta có
2
1 1
1
4
3 1
f x
x
;
2
0
3
f x x
.
Bảng biến thiên
Vậy giá trị nhỏ nhất của
1
V
V
bằng
1
3
.
Câu 160. Cho tứ diện
ABCD
có thể tích
V
, gọi
M
,
N
,
P
,
Q
lần lượt là trọng tâm tam giác
ABC
,
ACD
,
ABD
và
BCD
. Thể tích khối tứ diện
MNPQ
bằng
A.
4
9
V
. B.
27
V
. C.
9
V
. D.
4
27
V
.
Lời giải
Chọn C
Gọi
E
,
F
,
I
lần lượt là trung điểm các đoạn thẳng
BC
,
CD
,
BD
.
Ta có
8 8 2
9 9 9
AMNP
AMNP AEFI
AEFI
V
V V V
V
.
I
O
N
M
P
D
C
B
A
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 114 TỔNG HỢP: HOÀNG TUYÊN
1 1 1 1 1
, . , . , .
3 3 2 6 2 9
MNPQ MNP MNP MNP AMNP
V
V d Q MNP S d A MNP S d Q MNP S V
.
Câu 161. Cho hình chóp
.S ABCD
có đáy là hình vuông, cạnh bên
SA
vuông góc với đáy. Gọi
M
,
N
là
trung điểm của
SA
,
SB
. Mặt phẳng
MNCD
chia hình chóp đã cho thành hai phần. tỉ số thể tích
hai phần
.S MNCD và MNABCD là
A.
3
4
. B.
3
5
. C.
4
5
. D.
1
.
Lời giải
Chọn B
Ta có
. . .
1
2
S ABC S ACD S ABCD
V V V
;
và
. . .
1
4
S MNC S ABC S ABC
SM SN SC
V V V
SA SB SC
;
. . .
1
2
S MCD S ACD S ACD
SM SD SC
V V V
SA SD SC
.
Suy ra
. . . . .
3 3
4 8
S MNCD S MNC S MCD S ABC S ABCD
V V V V V
.
Đồng thời
. . .
5
8
MNABCD S ABCD S MNCD S ABCD
V V V V
.
Vậy tỉ số thể tích hai phần
.S MNCD
và
MNABCD
là
3
5
.
Câu 162. Cho khối chóp
.S ABC
có
M SA
,
N SB
sao cho
2MA MS
,
2NS NB
. Mặt phẳng
qua hai điểm
M
, N và song song với SC chia khối chóp thành hai khối đa diện. Tính tỉ số thể
tích của hai khối đa diện đó ( số bé chia số lớn ).
A.
3
5
. B.
4
9
. C.
3
4
. D.
4
5
.
Lời giải
Chọn D
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 115
Cách 1: Ta có mặt phẳng
cắt các mặt
SAC
theo giao tuyến
MQ SC
và cắt mặt
SBC
theo giao tuyến
NP SC
. Thiết diện tạo bởi mặt phẳng
với hình chóp là hình thang
MNPQ
.
Do
. .MNABPQ N ABPQ N AMQ
V V V
, gọi
.S ABC
V V và
ABC
S S
ta có:
.
1
. , .
3
N ABPQ ABPQ
V d N ABC S
1 1 1 2 7
. , .
3 3 3 3 27
d S ABC S S V
.
.
1
. , .
3
N AMQ AMQ
V d N SAC S
1 2 4 8
. , .
3 3 9 27
ASC
d B SAC S V
.
Vậy
. .
5
9
MNABPQ N ABPQ N AMQ
V V V V
4
9
SMNPQC
V V
.
Suy ra
4
5
SMNPQC
MNABPQ
V
V
.
Cách 2:
Gọi
I MN AB
,Áp dụng định lý Me-ne-la-us cho tam giác
SAB
, ta có
1
1
4
MS IA NB IB
MA IB NS IA
.
Áp dụng định lý Me-ne-la-us cho tam giác
AMI
, ta có:
1
BI SA NM
BA SM NI
1
NM
NI
.
Tương tự ta có:
1
PI
PQ
. Vì
2
//
3
AM AQ
MQ SC
AS AC
.
P
Q
N
M
A
B
C
S
I
P
Q
N
M
A
B
C
S
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 116 TỔNG HỢP: HOÀNG TUYÊN
Khi đó:
.
.
1 1 1 1
4 2 2 16
I BNP
I AMQ
V
IB IN IP
V IA IM IQ
. .
15
.
16
AMQ NBP I AMQ
V V
.
Mà
.
.
;
;
M AIQ AIQ
S ABC ABC
d M ABC
V S
V S
d S ABC
với
;
2
3
;
d M ABC
MA
SA
d S ABC
và
4 2 8
3 3 9
AIQ
ABC
S
AI AQ
S AB AC
.
Suy ra
. . .
15 2 8 5
16 3 9 9
AMQ NBP S ABC S ABC
V V V
.
Vậy tỉ số thể tích cần tìm là:
5
1
4
9
5
5
9
.
Câu 163. Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn
song song với đáy và cắt các cạnh bên
, , ,SA SB SC SD
lần lượt tại
, , ,M N P Q
. Gọi
, , ,M N P Q
lần lượt là hình chiếu vuông góc của
, , ,M N P Q
lên mặt phẳng
ABCD
. Tính tỉ số
SM
SA
để thể
tích khối đa diện
.MNPQ M N P Q
đạt giá trị lớn nhất.
A.
1
3
. B.
3
4
. C.
2
3
. D.
1
2
.
Lời giải
Chọn C
Đặt
SM
k
SA
với
0;1k
.
Xét tam giác
SAB
có
//MN AB
nên
.
MN SM
k MN k AB
AB SA
.
Xét tam giác
SAD
có
//MQ AD
nên
.
MQ SM
k MQ k AD
AD SA
.
Kẻ đường cao
SH
của hình chóp. Xét tam giác
SAH
có:
//MM SH
nên
1 1 1 .
MM AM SA SM SM
k MM k SH
SH SA SA SA
.
Ta có:
2
.
. . . . . . 1
MNPQ M N P Q
V MN MQ MM AB AD SH k k
.
Thể tích khối chóp không đổi nên
.MNPQ M N P Q
V
đạt giá trị lớn nhất khi
2
. 1k k
lớn nhất.
Ta có
3
2
2 1 . .
1 2 2 4
. 1
2 2 3 27
k k k
k k k
k k
.
Đẳng thức xảy ra khi và chỉ khi:
2
2 1
3
k k k
. Vậy
2
3
SM
SA
.
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 117
Câu 164. Cho hình chóp đáy là hình vuông cạnh , có và vuông góc với mặt đáy. Gọi
, lần lượt là trọng tâm của tam giác , . Tính thể tích khối tứ diện .
A. . B. . C. . D. .
Lời giải
Chọn B
+Gọi , lần lượt là trung điểm của cạnh , .
+Ta có .
+Vì , lần lượt là trong tâm tam giác , .
+Ta xét: .
+Ta xét: .
+Từ , .
Câu 165. Cho khối chóp tứ giác đều . Gọi là điểm đối xứng của qua , là trung điểm
cạnh . Mặt phẳng chia khối chóp thành hai khối đa diện. Tỉ số thể tích của
khối đa diện chứa đỉnh và khối chóp bằng:
A. . B. . C. . D. .
Lời giải
Chọn C
.
S AB C D
a
2
SA a
M
N
SAB
S C D
.
S M N C
3
1
27
a
3
2
27
a
3
1
13
a
3
2
13
a
P
Q
AB
CD
.S ABCD
V
1
. .
3
ABCD
SA S
3
2
3
a
M
N
SAB
S C D
2
3
SM SN
SP SQ
.
.
4
. .
9
S MNC
S PQC
V
SM SN SC
V SP SQ SC
. .
4
9
S MNC S PQC
V V
1
.
.
S PQC
S ABCD
V
V
1
. .
3
1
. .
3
PQC
ABCD
SA S
SA S
1
4
PQC
ABCD
S
S
. .
1
4
S PQC S ABCD
V V
2
2
.S MNC
V
.
1
9
S ABCD
V
3
2
27
.
S A BC D
M
C
B
N
SC
MDN
.
S A BC D
S
.
S A BC D
5
7
5
12
7
12
6
7
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 118 TỔNG HỢP: HOÀNG TUYÊN
Gọi . Tam giác có và là các đường trung tuyến nên là trọng tâm
của tam giác .
Gọi , do , nên tứ giác là hình bình hành suy ra
là trung điểm của .
Ta có:
.
Mà: .
Do đó: .
.
Vậy tỉ số thể tích cần tính: .
Câu 166. Cho hình chóp có , là trung điểm của , . Mặt phẳng chia hình
chóp đã cho thành hai phần. Tỉ số thể tích khối chóp và khối đa diện là:
A. . B. . C. . D. .
Lời giải
Chọn C
P M N SB
SM C
M N
SB
P
SM C
Q MD AB
//
AD BM
AD BM
ADBM
Q
MD
. . . . . .
1 1 2 5
. 1 . .
2 2 3 6
BCDQPN M CDN M BQP M CDN M CDN M CDN M CDN
MB MQ MP
V V V V V V V
MC MD MN
. . . . .
2
1
.
,
1 1
2
. . .
2 2
,
MCD
M CDN N MCD S ABCD S ABCD S ABCD
ABCD
CD CM
d N ABCD
S
V V V V V
S CD
d S ABCD
.
5
12
BCDQPN S ABCD
V V
. .
7
12
SANPQD S ABCD BCDQNP S ABCD
V V V V
.
7
12
SANPQD
S ABCD
V
V
.
S A BC D
M
N
SA
SB
MNCD
.
S MNCD
MNABCD
5
8
3
8
3
5
5
3
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 119
Ta có:
.
Khi đó: .
.
Vậy .
Câu 167. Cho hình chóp tứ giác có đáy là hình bình hành. Gọi là trung điểm cạnh các
điểm lần lượt là điểm đối xứng của qua và Mặt phẳng cắt các cạnh
lần lượt tại các điểm Tính tỉ số thể tích của khối đa diện và .
A. . B. . C. . D. .
Lời giải
Chọn C
.
. . .
.
1 1 1 1 1
. . . .1
2 2 4 4 8
S MNC
S MNC S ABC S ABCD
S ABC
V
SM SN SC
V V V
V SA SB SC
.
. . .
.
1 1 1 1
. . .1.1
2 2 2 4
S MCD
S MCD S ACD S ABCD
S ACD
V
SM SC SD
V V V
V SA SC SD
. . . .
3
8
S MNCD S MNC S MCD S ABCD
V V V V
. . .
5
8
MNABCD S ABCD S MNCD S ABCD
V V V V
.
3
5
S MNCD
MNABCD
V
V
.
S A BC D
M
,
SA
,
E F
A
B
.
D
MEF
,
SB SD
, .
N P
ABCDMNP
.
S AEF
1
2
2
3
1
3
3
4
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 120 TỔNG HỢP: HOÀNG TUYÊN
Ta có ; có , lần lượt là trọng tâm vì nó giao điểm của hai đường trung tuyến.
Vì vậy và có .
Ta có .
Tương tự ta có .
Do đó .
Mặt khác nên (1).
Ta lại có , lần lượt là trung điểm của , nên và .
Suy ra .
Mà nên (2).
Từ (1) và (2) suy ra .
Câu 168. ( Quốc Học Huế_Lần 1_2020 ) Cho khối chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
1
.
Gọi
,M N
lần lượt thuộc các cạnh
,BC CD
sao cho
MN
luôn bằng
1
. Tìm giá trị nhỏ nhất của
thể tích khối tứ diện
SAMN
.
A.
2
12
. B.
3
12
. C.
1 2
12
. D.
4 2
24
.
Lời giải
Chọn D
SAE
SA F
N
P
2
3
SN SP
SB SD
C E F
.
.
.
S MNC
S ABC
V
SM SN
V SA SB
1 2 1
.
2 3 3
. .
1
3
S MNC S ABC
V V
.
1 1
.
3 2
S ABCD
V
.
1
6
S ABCD
V
.
.
.
S MPC
S ADC
V
SM SP
V SA SD
1 2 1
.
2 3 3
. .
1
3
S MPC S ADC
V V
.
1 1
.
3 2
S ABCD
V
.
1
6
S ABCD
V
. . .
1 1
6 6
S MNCP S ABCD S ABCD
V V V
.
1
3
S ABCD
V
. .
ABCDMNP S ABCD S MNCP
V V V
.
2
3
ABCDMNP S ABCD
V V
B
D
AE
A F
ABC EBC
S S
ADC FCD
S S
2
AEF ABCD
S S
.
1
, .
3
S AEF AEF
V d S ABCD S
.
1
, .2
3
S AEF ABCD
V d S ABCD S
.
2
S ABCD
V
.
1
3
ABCDMNP
S AEF
V
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 121
Gọi
O AC BD
. Vì
.S ABCD
là hình chóp đều nên
SO ABCD
và
2 2
2
.
2
SO SA AO
Ta có:
1
. . .
3
SAMN AMN
V SO S
Đặt
, 0 1 .CM x x
Ta có:
2 2 2 2
1 ; 1 ; 1 1BM x CN MN CM x DN x
2 2
1 1 1
1 .1. 1 .1. 1 1 . . 1
2 2 2
AMN ABCD ABM ADN CMN
S S S S S x x x x
2 2
1
1 1
2
x x x x
.
Xét hàm số
2 2
1
1 1 , 0 1
2
f x x x x x x
.
Có:
2 2 2
2
2 2 2
1 1 2 1
1 1
2
1 1 2 1
x x x x x
f x x
x x x
2 2 2 2
0 1 2 1 0 1 2 1f x x x x x x x
2
2
2 2
0 1
0 1
2
2 2 1 1 0
2
1 2 1
x
x
x
x x x
x x x
.
Bảng biến thiên:
Do đó,
min
2 2 1
4
AMN
S
đạt được khi
2
2
x
.
Ta có:
min min
1 1 2 2 2 1 4 2
. . .
3 3 2 4 24
SAMN AMN
V SO S
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 122 TỔNG HỢP: HOÀNG TUYÊN
8. KHỐI LĂNG TRỤ - MỨC 4
Câu 169. ( Đề Thi Thử Trường Chuyên KHTN_HN_2020 ) Cho khối lập phương
D. ' ' ' 'ABC A B C D
cạnh
1
. Gọi
, , ,LM N P
lần lượt là tâm các hình vuông
' '; ' ' ' '; DD' 'ABB A A B C D A A
và
DD' 'C C
. Gọi
Q
là trung điểm của
BL
. Tính thể tích khối tứ diện
MNPQ
(tham khảo hình vẽ).
A.
1
24
. B.
1
16
. C.
2
27
. D.
3
27
.
Lời giải
Chọn A
Do
D. ' ' ' 'ABC A B C D
là hình lập phương cạnh 1 ' 3A C .
/ / M D ' ' ' / / ' ' , , ' ' A, ' '
1 3
' .
3 3
BL AB D BL AB D d Q MNP d B AB D d AB D
A C
Ta có:
' 'AB D
đều
2
' ' ' '
3 3 1 1 3 3
2 . .
4 2 4 4 2 8
AB D MNP AB D
S S S
.
.
1 1 3 3 1
. , . .
3 3 8 3 24
Q MNP MNP
V S d Q MNP
Chọn A.
Câu 170. ( Quốc Học Huế_Lần 1_2020 ) Cho khối chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
1
.
Gọi
,M N
lần lượt thuộc các cạnh
,BC CD
sao cho
MN
luôn bằng
1
. Tìm giá trị nhỏ nhất của
thể tích khối tứ diện
SAMN
.
A.
2
12
. B.
3
12
. C.
1 2
12
. D.
4 2
24
.
Lời giải
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 123
Chọn D
Gọi
O AC BD
. Vì
.S ABCD
là hình chóp đều nên
SO ABCD
và
2 2
2
.
2
SO SA AO
Ta có:
1
. . .
3
SAMN AMN
V SO S
Đặt
, 0 1 .CM x x
Ta có:
2 2 2 2
1 ; 1 ; 1 1BM x CN MN CM x DN x
2 2
1 1 1
1 .1. 1 .1. 1 1 . . 1
2 2 2
AMN ABCD ABM ADN CMN
S S S S S x x x x
2 2
1
1 1
2
x x x x
.
Xét hàm số
2 2
1
1 1 , 0 1
2
f x x x x x x
.
Có:
2 2 2
2
2 2 2
1 1 2 1
1 1
2
1 1 2 1
x x x x x
f x x
x x x
2 2 2 2
0 1 2 1 0 1 2 1f x x x x x x x
2
2
2 2
0 1
0 1
2
2 2 1 1 0
2
1 2 1
x
x
x
x x x
x x x
.
Bảng biến thiên:
Do đó,
min
2 2 1
4
AMN
S
đạt được khi
2
2
x
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 124 TỔNG HỢP: HOÀNG TUYÊN
Ta có:
min min
1 1 2 2 2 1 4 2
. . .
3 3 2 4 24
SAMN AMN
V SO S
.
Câu 171. ( Đề Thi Thử Trường Chuyên KHTN_HN_2020 ) Cho khối lập phương
D. ' ' ' 'ABC A B C D
cạnh
1
. Gọi
, , ,LM N P
lần lượt là tâm các hình vuông
' '; ' ' ' '; DD' 'ABB A A B C D A A
và
DD' 'C C
. Gọi
Q
là trung điểm của
BL
. Tính thể tích khối tứ diện
MNPQ
(tham khảo hình vẽ).
A.
1
24
. B.
1
16
. C.
2
27
. D.
3
27
.
Lời giải
Chọn A
Do
D. ' ' ' 'ABC A B C D
là hình lập phương cạnh 1 ' 3A C .
/ / M D ' ' ' / / ' ' , , ' ' A, ' '
1 3
' .
3 3
BL AB D BL AB D d Q MNP d B AB D d AB D
A C
Ta có:
' 'AB D
đều
2
' ' ' '
3 3 1 1 3 3
2 . .
4 2 4 4 2 8
AB D MNP AB D
S S S
.
.
1 1 3 3 1
. , . .
3 3 8 3 24
Q MNP MNP
V S d Q MNP
Chọn A.
Câu 172. Cho hình lăng trụ có chiều cao bằng 6 và diện tích đáy bằng 8. Gọi , lần lượt
là trung điểm của các cạnh , và , lần lượt thuộc các cạnh , sao cho
. Thể tích của khối đa diện lồi có các đỉnh là các điểm , , , , và
bằng
A. . B. . C. . D. .
.
ABC A B C
M
N
AB
AC
P
Q
A C
A B
3
4
A P A Q
A C A B
A
A
M
N
P
Q
18
19
27
36
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 125
Lời giải
Chọn B
+) Vì , lần lượt là trung điểm của cạnh , .
+) , lần lượt thuộc các cạnh , sao cho .
+) Vì là hình lăng trụ nên .
Do đó 4 điểm , , , đồng phẳng.
Ta có , ,
3 đường thẳng , , đồng quy hoặc đôi một song song.
Hơn nữa, vì và nên cắt . Do đó ,
, đồng quy tại .
Ta có .
Mà , nên .
Suy ra, .
Gọi là thể tích của khối đa diện lồi có các đỉnh là các điểm , , , , , . Khi đó:
.
Gọi , lần lượt là hình chiếu vuông góc của lên các mặt phẳng , .
Do nên , , thẳng hàng. Suy ra là chiều cao của lăng trụ
. Hơn nữa, .
Theo đầu bài nên .
M
N
AB
AC
//
MN BC
P
Q
A C
A B
3
4
A P A Q
A C A B
//
QP B C
.
ABC A B C
//
BC B C
//
MN QP
M
N
P
Q
ABB A ACC A AA
ABB A MNPQ MQ
ACC A MNPQ NP
AA
MQ
NP
//
AM A Q
1 3 3
2 4 4
AM AB AB A B A Q
AA
MQ
AA
MQ
NP
S
.
.
. .
S AMN
S A QP
V
SA SM SN
V SA SQ SP
//
AM A Q
//
AN A P
1
2
2
3
3
4
AB
SA SM SN AM
SA SQ SP A Q
A B
3
.
.
2 8
. .
3 27
S AMN
S A QP
V
SA SM SN
V SA SQ SP
. .
8
27
S AMN S A QP
V V
V
A
A
M
N
P
Q
. . . . .
8 19
27 27
S A QP S AMN S A QP S A QP S A QP
V V V V V V
H
K
S
AMN
A QP
//
AMN A QP
S
H
K
HK
.
ABC A B C
2
3
SH SA
SK SA
2
3
SH SK
2 1
3 3
HK SK SH SK SK SK
3
SK HK
6
HK
3 18
SK HK
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 126 TỔNG HỢP: HOÀNG TUYÊN
Lại có, .
Theo đầu bài nên . Do đó .
Vậy .
Bài toán trên có thể tổng quát hơn như sau: Cho hình lăng trụ có thể tích bằng
. Gọi , lần lượt là trung điểm của các cạnh , và , lần lượt thuộc các cạnh
, sao cho . Tính thể tích của khối đa diện lồi có các đỉnh là các
điểm , , , , , theo .
Lời giải:
Gọi là thể tích của khối đa diện lồi có các đỉnh là các điểm , , , , , .
Ta xét các trường hợp:
+) Với , giải tương tự như trên ta được công thức .
+) Với , giải tương tự như trên ta được công thức .
+) Với , dễ thấy công thức đúng.
Vậy: .
Cách khác:
+ Ta có hình vẽ:
2
1
. .sin
3 9
2
.
1
4 16
. .sin
2
A QP
A B C
A Q A P A
S
A Q A P
S A B A C
A B A C A
9
16
A QP A B C
S S
8
A B C
S
9 9
16 2
A QP A B C
S S
.
1 1 9
. . .18 27
3 3 2
S A QP A QP
V S SK
.
19 19
.27 19
27 27
S A QP
V V
.
ABC A B C
V
M
N
AB
AC
P
Q
A C
A B
A P A Q
k
A C A B
0 1
k
A
A
M
N
P
Q
V
V
A
A
M
N
P
Q
1
2
k
2
4 2 1
.
12
k k
V V
1
2
k
2
4 2 1
.
12
k k
V V
1
2
k
4
V
V
2
4 2 1
.
12
k k
V V
2
4 2 1
.
12
k k
V V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 127
+ Theo đề ta có: .
+ Do .
+ Do .
+ Hình chóp cụt có chiều cao và hai đáy là , nên thể tích được tính bởi công
thức
.
Câu 173. Cho hình hộp chữ nhật . Trên các cạnh , , lần lượt lấy các điểm
, , sao cho , , . Mặt phẳng cắt cạnh tại . Gọi
, lần lượt là thể tích của các khối đa diện và . Khi đó
bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Lấy , lần lượt là tâm của và .
Gọi . Vậy .
Đặt ; ; và .
Ta có: nên .
Mặt khác ta có
.
Suy ra
0
8
ABC A B C
S S S
1
2
AM AN
AB AC
2
1
1
. 2
2
AMN ABC
S S S
3
4
A Q A P
A B A C
2
2
3 9
.
4 2
A PQ A B C
S S S
AMNA QP
h
1
S
2
S
V
1 2 1 2
6 9 9
. 2 2.
3 3 2 2
h
V S S S S
19
.
ABCD A B C D
AA
BB
CC
M
N
P
4
5
AM
AA
1
2
BN
BB
3
4
CP
CC
MNP
DD
Q
1
V
2
V
MNPQABCD
MNPQA B C D
1
2
V
V
31
9
9
31
40
9
40
31
O
O
ABCD
A B C D
I OO MP
NI DD Q
DD MNP Q
AM
x
AA
BN
y
BB
CP
z
CC
DQ
w
DD
2
MA PC NB QD OI
x z y w
. . .
. .
2
MNPQ ABCD ABC MNP ACD MPQ
ABCD A B C D ABC A B C
V V V
V V
.
.
. .
1
2
ACD MPQ
ABC MNP
ABC A B C ACD A C D
V
V
V V
1
2 3 3
x y z x z w
1
2 2
6
x y z w
2
x z
4 3
5 4
2
31
40
. .
31
40
MNPQ ABCD ABCD A B C D
V V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 128 TỔNG HỢP: HOÀNG TUYÊN
Lại có .
Vậy khi đó , , suy ra
Câu 174. Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua
'B
và vuông góc với
'A C
chia lăng trụ thành hai khối. Biết thể tích của hai khối là V
1
và V
2
với
1 2
V V . Tỉ số
1
2
V
V
bằng:
A.
1
47
. B.
1
23
. C.
1
11
. D.
1
7
.
Lời giải
Chọn A
Gọi H là trung điểm của
' 'A C
.
Ta có:
'
' ' ' ' '
' '
B H AC
B H ACC A B H A C
B H AA
.
Trong
mp ACC A
, kẻ
' , 'HE A C HE AA I
.
Vậy mặt phẳng (P) cắt lăng trụ là mặt phẳng
'B HI
.
'A EH
đồng dạng
' 'A C C
.
.
' ' ' ' . ' ' 5
2
'
' ' ' 10
5
a
a
A E A C A H A C a
A E
A H A C A C
a
.
'A IH
đồng dạng
' 'C A C
.
. 5
' ' . ' 5
2
' ' ' 2 4
a
a
IH A H A H A C a
IH
A C C C C C a
.
2
'
1 1 5 5
' . .
2 2 10 4 16
A IH
a a a
S A E IH
.
Thể tích khối chóp
2 3
1 '. ' '
1 1 3 3
. ' . . .
3 3 2 16 96
B A HI A HI
a a a
V V B H S
.
Thể tích khối lăng trụ là:
2 3
. ' ' '
3 3
'. 2 .
4 2
ABC A B C ABC
a a
V AA S a
.
Thể tích phần còn lại
2 . ' ' ' 1ABC A B C
V V V
. . .
MNPQ A B C D ABCD A B C D MNPQ ABCD
V V V
. . .
31 9
40 40
ABCD A B C D ABCD A B C D ABCD A B C D
V V V
1 .
31
40
ABCD A B C D
V V
2 .
9
40
ABCD A B C D
V V
1
2
31
.
9
V
V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 129
3 3 3
1
2
3 3 47 3 1
2 96 96 47
Va a a
V
.
Câu 175. Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua
'B
và vuông góc với
'A C
chia lăng trụ thành hai khối. Biết thể tích của hai khối là V
1
và V
2
với
1 2
V V . Tỉ số
1
2
V
V
bằng:
A.
1
47
. B.
1
23
. C.
1
11
. D.
1
7
.
Lời giải
Chọn A
Gọi H là trung điểm của
' 'A C
.
Ta có:
'
' ' ' ' '
' '
B H AC
B H ACC A B H A C
B H AA
.
Trong
mp ACC A
, kẻ
' , 'HE A C HE AA I
.
Vậy mặt phẳng (P) cắt lăng trụ là mặt phẳng
'B HI
.
'A EH
đồng dạng
' 'A C C
.
.
' ' ' ' . ' ' 5
2
'
' ' ' 10
5
a
a
A E A C A H A C a
A E
A H A C A C
a
.
'A IH
đồng dạng
' 'C A C
.
. 5
' ' . ' 5
2
' ' ' 2 4
a
a
IH A H A H A C a
IH
A C C C C C a
.
2
'
1 1 5 5
' . .
2 2 10 4 16
A IH
a a a
S A E IH
.
Thể tích khối chóp
2 3
1 '. ' '
1 1 3 3
. ' . . .
3 3 2 16 96
B A HI A HI
a a a
V V B H S
.
Thể tích khối lăng trụ là:
2 3
. ' ' '
3 3
'. 2 .
4 2
ABC A B C ABC
a a
V AA S a
.
Thể tích phần còn lại
2 . ' ' ' 1ABC A B C
V V V
3 3 3
1
2
3 3 47 3 1
2 96 96 47
V
a a a
V
.
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 130 TỔNG HỢP: HOÀNG TUYÊN
Câu 176. [TT-SGD-HA-TINH-19-20] Cho hình lập phương ABCD.A’B’C’D’ có thể tích V. Gọi M là điểm
thuộc cạnh BB’ sao cho MB=2MB’. Mặt phẳng
đi qua M và vuông góc với AC’ cắt các cạnh
DD’, DC, BC lần lượt tại N, P, Q. Gọi
1
V
là thể tích của khối đa diện CPQMNC’. Tính tỉ số
1
V
V
A.
35
162
B.
11
162
C.
33
162
D.
13
162
Câu 177. [TT-SGD-HA-TINH-19-20] Cho hình lập phương ABCD.A’B’C’D’ có thể tích V. Gọi M là điểm
thuộc cạnh BB’ sao cho MB=2MB’. Mặt phẳng
đi qua M và vuông góc với AC’ cắt các cạnh
, ,DD DC BC
lần lượt tại
, ,N P Q
. Gọi
1
V
là thể tích của khối đa diện
CPQMNC
. Tính tỉ số
1
V
V
A.
35
162
B.
11
162
C.
33
162
D.
13
162
Lời giải
Gọi a là cạnh của hình lập phương, ta có
3
V a
.
Vì
' 'BDA AC
nên
/ /( ')BDA
, do đó ta có
/ / ' ; / / 'MQ B C NP CD
.
Gọi I là giao điểm CC’, MQ, NP (3 đường thẳng này đồng quy). Ta có
1 . ' .I MNC L CPQ
V V V
.
Mặt khác
3
. ' . ' '
1 1 1 4 2
( ;( )). . . .
3 3 2 3 9
' '
I MNC M IC N IC N
CV V d M CDD S a a a a
3
.
1 1
. . . .
3 2 3 3 3 162
I CPQ
a a a a
V
Vậy
3
3 3
1
1 . ' .
2 35 35
9 162 162 162
I MNC L CPQ
Va
V V V a a
V
Câu 178. Cho khối lăng trụ có thể tích bằng 2020. Gọi , lần lượt là trung điểm của
; và điểm nằm trên cạnh sao cho . Thể tích của khối đa diện lồi có các
đỉnh là các điểm , , , , , bằng:
A. . B. . C. . D. .
Lời giải
Chọn D
Giả sử .
I
Q
P
N
M
D'
C'
B'
A'
D
B
C
A
.
ABC A B C
M
N
AA
BB
P
CC
3
PC PC
A
B
C
M
N
P
2020
3
5353
3
2525
3
3535
3
.
2020
ABC A B C
V V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 131
Ta có .
Lại có .
Ta có .
Mà và .
Suy ra .
Vậy .
Cách 2: Dùng công thức giải nhanh
Ta có: .
Câu 179. Cho lăng trụ có đáy là tam giác đều cạnh , góc giữa cạnh bên với mặt phẳng
đáy bằng và cách đều 3 điểm , , . Gọi là trung điểm của ; thỏa
mãn và sao cho . Thể tích của khối đa diện lồi có các đỉnh là các
điểm , , , , , bằng:
A. . B. . C. . D. .
Lời giải
Chọn B
. .
1 2
; .
3 3 3
C ABC ABC C ABB A
V
V d C ABC S V V
.
.
.
1
. ; .
;
3 1
3
1
4 4
;
. ; .
3
ABC
P ABC
P ABC
C ABC
ABC
d P ABC S
d P ABC
V
PC
V V
V CC
d C ABC
d C ABC S
.
.
1
. ; .
3
1
. ; .
3
ABNM
P ABNM
C ABB A
ABB A
d P ABB A S
V
V
d C ABB A S
; ;
d P ABB A d C ABB A
1
2
ABNM ABB A
S S
.
.
.
1 1
2 3
P ABNM
P ABNM
C ABB A
V
V V
V
. . .
7 3535
12 3
ABC MNP P ABNM P ABC
V V V V
.
.
1
3
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC
.
2020 1 1 3 3535
3 2 2 4 3
ABC MNP
V
.
ABC A B C
ABC
a
60
A
A
B
C
M
AA
N BB
4
NB NB
P CC
3
PC PC
A
B
C
M
N
P
3
3
4
a
3
41 3
240
a
3
23 3
144
a
3
19 3
240
a
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 132 TỔNG HỢP: HOÀNG TUYÊN
Gọi là thể tích của khối đa diện có các đỉnh là các điểm , , , , , .
là thể tích của khối lăng trụ . Gọi là trọng tâm của tam giác . Vì điểm
cách đều các điểm , , nên .
Hơn nữa nên .
Suy ra
Do đó (đvtt)
Mà .
Từ
Suy ra
.
.
Và (vì là trung điểm của ).
Vậy thể tích cần tìm là (đvtt).
Cách 2: Dùng công thức giải nhanh
V
A
B
C
M
N
P
1
V
.
ABC A B C
H
ABC
A
A
B
C
A H ABC
AA ABC A
, 60
AA ABC A AH
.tan 60 tan 60
3
a
A H AH a
2 3
1
3 3
. .
4 4
ABC
a a
V S A H a
1 1
. .
2
1
.
3 3 3
A ABC ABC A BCC B
V V
V S A H V
4
4
5
3
3 3
4 4
NB BB
NB NB
PC PC
PC CC BB
1
,
2
BCPN
S NB PC d BB CC
1 4 3
,
2 5 4
BB BB d BB CC
31
. ,
40
BB d BB CC
31
.
40
BCC B
S
. . . 1
31 31 31
40 40 60
M BCPN M BCC B A BCC B
V V V V
. . 1
1 1 1 1
.
3 2 2 6
M ABC ABC A ABC
V S A H V V
M
AA
3
. . 1
41 41 3
60 240
M ABC M BCPN
a
V V V V
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 133
Ta có: .
Câu 180. Cho khối lăng trụ có thể tích . Gọi là trung điểm của ; thuộc cạnh
sao cho và thuộc cạnh sao cho . Thể tích của khối đa diện lồi có
các đỉnh là các điểm , , , , , theo bằng:
A. . B. . C. . D. .
Lời giải
Chọn C
Cách 1. Tự luận
Gọi , lần lượt là trung điểm của , .
Ta có .
.
.
1
3
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC
3 3
.
3 1 4 3 41 3
12 2 5 4 240
ABC MNP
a a
V
.
ABC A B C
V
M
AA
N
BB
4
NB NB
P
CC
3
PC PC
A
B
C
M
N
P
V
101
180
V
5
8
V
41
60
V
5
7
V
E
D
P
N
M
C'
B'
A
B
C
A'
D
E
BB
CC
. . .
1
2
ABCMNP ABCMDE M DEPN M DEP M PDN
V V V V V V
1 1 3 3
2 5 10 20
PDN BCC B
DN DB NB BB BB S S
. .
1 1 3 3 3 2 1
, . , . .
3 3 20 20 20 3 10
M DPN PDN BCC B A BCC B
V d M BCC B S d A BCC B S V V V
1 1 1 1
2 4 4 8
DEP BCC B
EP EC PC CC CC S S
. .
1 1 1 1 1 2 1
, . , . .
3 3 8 8 8 3 12
M DEP DEP BCC B A BCC B
V d M BCC B S d A BCC B S V V V
HÌNH KHÔNG GIAN:K12 NHÓM WORD BIÊN SOẠN TOÁN THPT
Trang 134 TỔNG HỢP: HOÀNG TUYÊN
Vậy .
Cách 2: Dùng công thức giải nhanh
Ta có: .
Câu 181.
Cho hình lăng trụ
.ABC A B C
và
,M N
là hai điểm lần lượt trên cạnh
,CA CB
sao cho
MN
song
song với
AB
và
CM
k
CA
. Mặt phẳng
( )MNB A
chia khối lăng trụ
.ABC A B C
thành hai phần
có thể tích
1
V (phần chứa điểm
C
) và
2
V sao cho
1
2
2
V
V
. Khi đó giá trị của
k
là
A.
1 5
2
k
. B.
1
2
k
. C.
1 5
2
k
. D.
3
3
k
.
Lời giải
Chọn A
+ Vì ba mặt phẳng
( ),( ),( )MNB A ACC A BCC B
đôi một cắt nhau theo ba giao tuyến phân biệt
, ,A M B N CC
và
,A M CC
không song song nên
, ,A M B N CC
đồng qui tại
S
.
Ta có
CM MN MN SM SN SC
k
CA AB A B SA SB SC
+ Từ đó
3 3
. . 1 . .
1
S MNC S A B C MNC A B C S A B C
V k V V V k V
.
+ Mặt khác
.
. ' ' '
3
3
3 1
ABC A B C
S A B C
SC SC
V
CC
k
V SC SC
.
.
3 1
ABC A B C
S A B C
V
V
k
Suy ra
2
.
3
.
1
1 .
1
3 1 3
ABC A B C
ABC A B C
k k V
V
V k
k
.
+ Vì
1
2
2
V
V
nên
2
2
1 .
2 1 2 1 5
1 0 ( 0)
3 3 3 2
ABC A B C
k k
V V k k k k
.
Vậy
1 5
2
k
.
1 1 1 41
2 10 12 60
ABCMNP
V V V
.
.
1
3
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC
.
1 4 3 41
3 2 5 4 60
ABC MNP
V
V V
| 1/134

Tài liệu khác của Toán 12

Preview text:

NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
TUYÓN TËP 1 Sè C¢U HáI LI£N QUAN Tû Sè THÓ TÝCH
1. KHỐI CHÓP - MỨC 1 ............................................................................................................................ 1
2. KHỐI LĂNG TRỤ - MỨC 1 .................................................................................................................. 5
3. KHỐI CHÓP - MỨC 2 ............................................................................................................................ 6
4. KHỐI LĂNG TRỤ - MỨC 2 ................................................................................................................ 24
5. KHỐI CHÓP - MỨC 3 .......................................................................................................................... 35
6. KHỐI LĂNG TRỤ - MỨC 3 ................................................................................................................ 58
7. KHỐI CHÓP - MỨC 4 .......................................................................................................................... 77
8. KHỐI LĂNG TRỤ - MỨC 4 .............................................................................................................. 122
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 1 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1. KHỐI CHÓP - MỨC 1
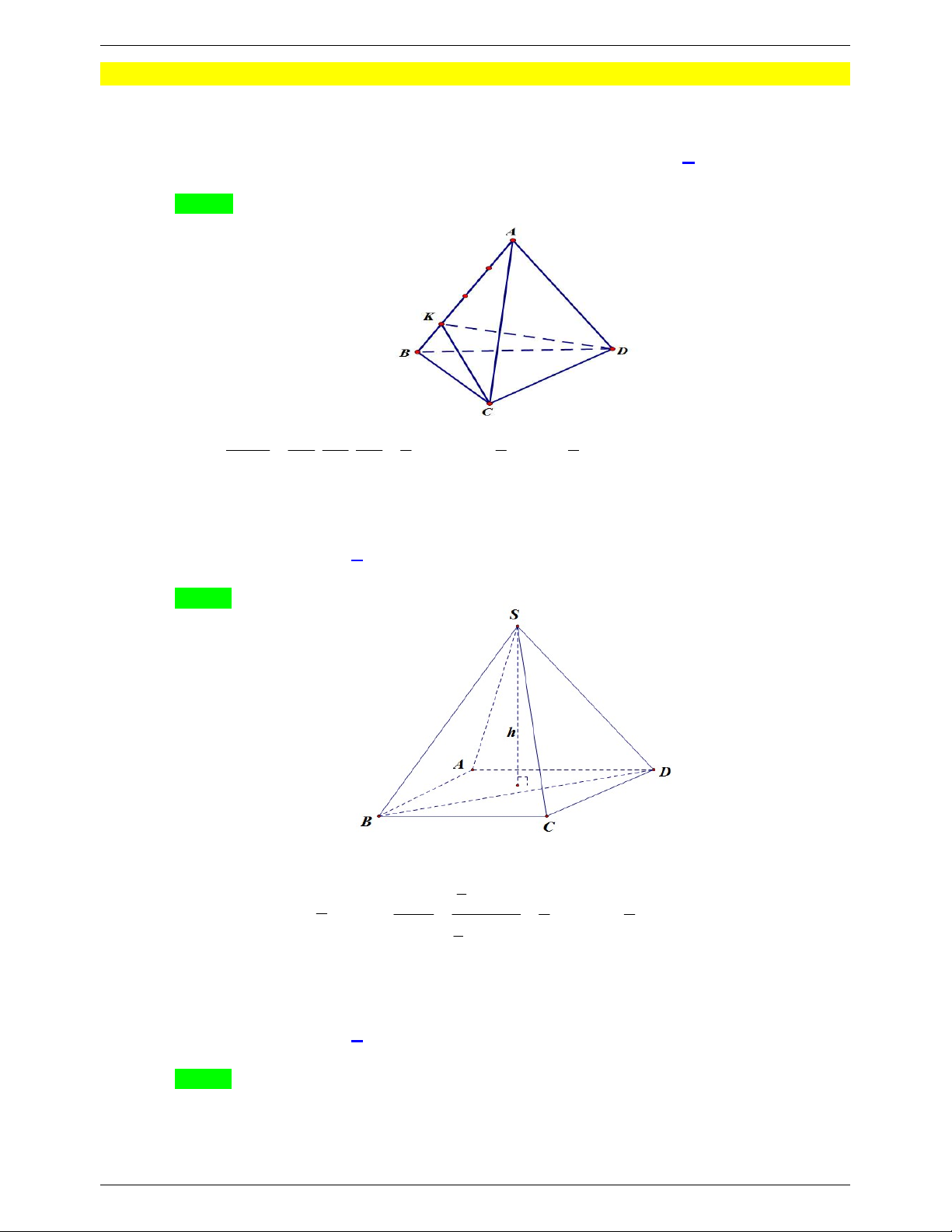
Câu 1. Cho khối tứ diện ABCD có thể tích bằng 3
60 cm và điểm K trên cạnh AB sao cho AB  4KB.
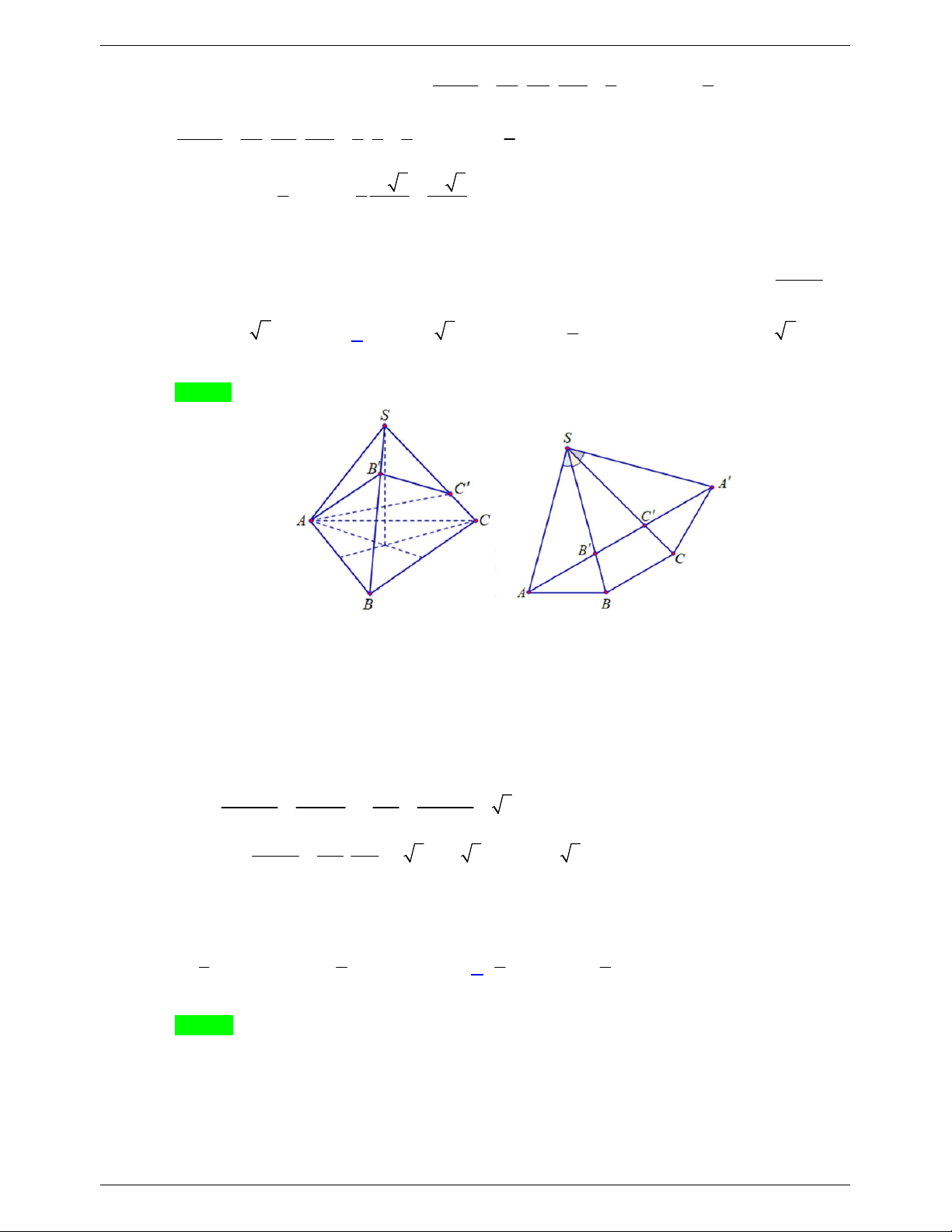
Tính thể tích V của khối tứ diện BKCD . A. 3 V  20cm . B. 3 V  12cm . C. 3 V  30 cm . D. 3 V  15cm . Lời giải Chọn D V BK BC BD 1 1 1 Ta có: B.KCD  . .  V  V  .60  15 cm B.KCD B.ACD  3 V BA BC BD 4 4 4 B.ACD
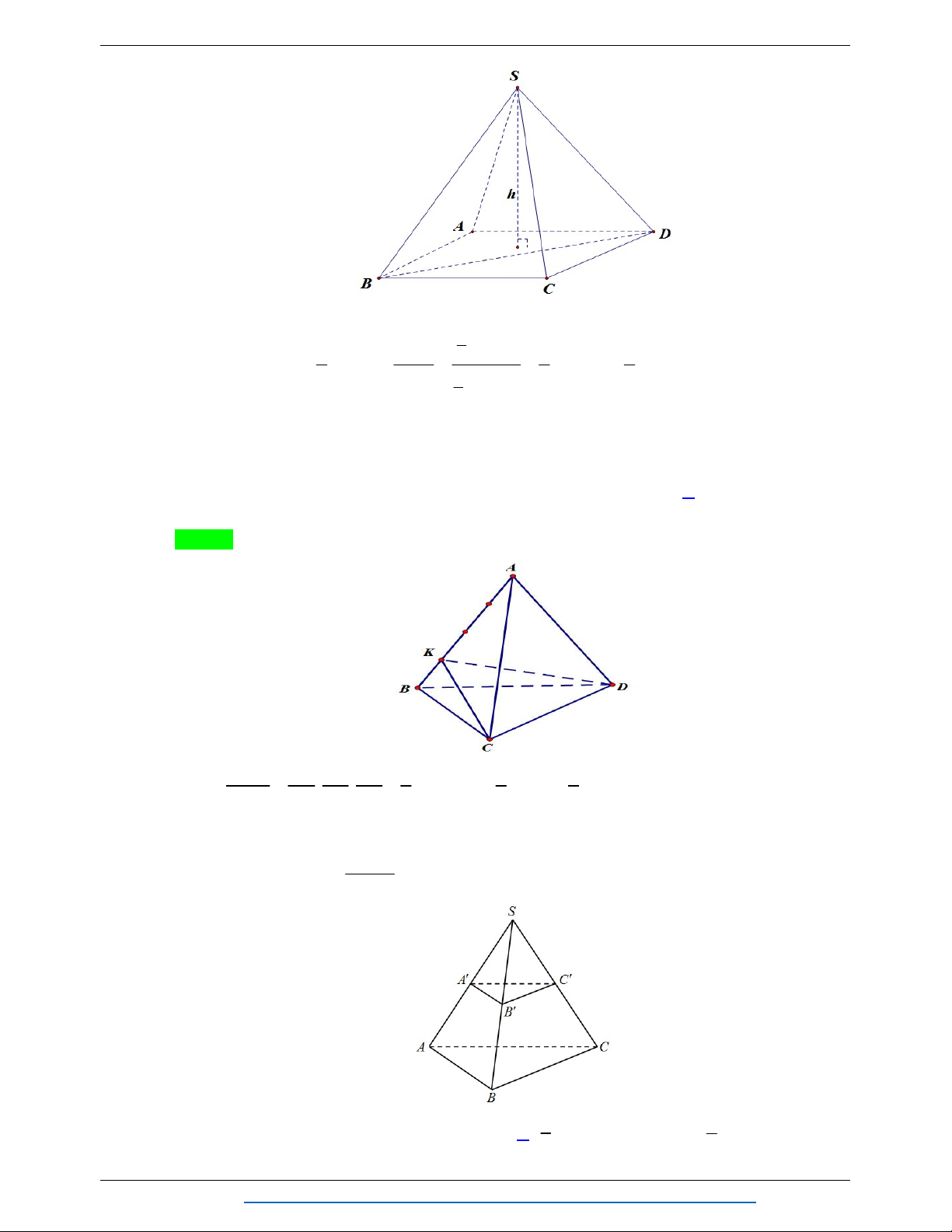
Câu 2. Cho khối chóp S.ABCD có đáy là hình chữ nhật và thể tích bằng 8. Thể tích của khối chóp S.BCD bằng: A. 2 . B. 4 . C. 6 . D. 3 . Lời giải Chọn B
Ta có: Hai hình chóp S.ABCD và S.BCD có cùng chiều cao h là khoảng cách từ S đến mặt phẳng 1 .S .h  1 BCD V 1 1 ABCD và S  S BCD 3     V  V  4. BCD 2 ABCD V 1 2 BCD 2 ABCD ABCD .S .h 3 ABCD
Câu 3. Cho khối chóp S.ABCD có đáy là hình chữ nhật và thể tích bằng 8. Thể tích của khối chóp S.BCD bằng: A. 2 . B. 4 . C. 6 . D. 3 . Lời giải Chọn B Trang 2 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Ta có: Hai hình chóp S.ABCD và S.BCD có cùng chiều cao h là khoảng cách từ S đến mặt phẳng 1 .S .h  1 BCD V 1 1 ABCD và S  S BCD 3     V  V  4. BCD 2 ABCD V 1 2 BCD 2 ABCD ABCD .S .h 3 ABCD
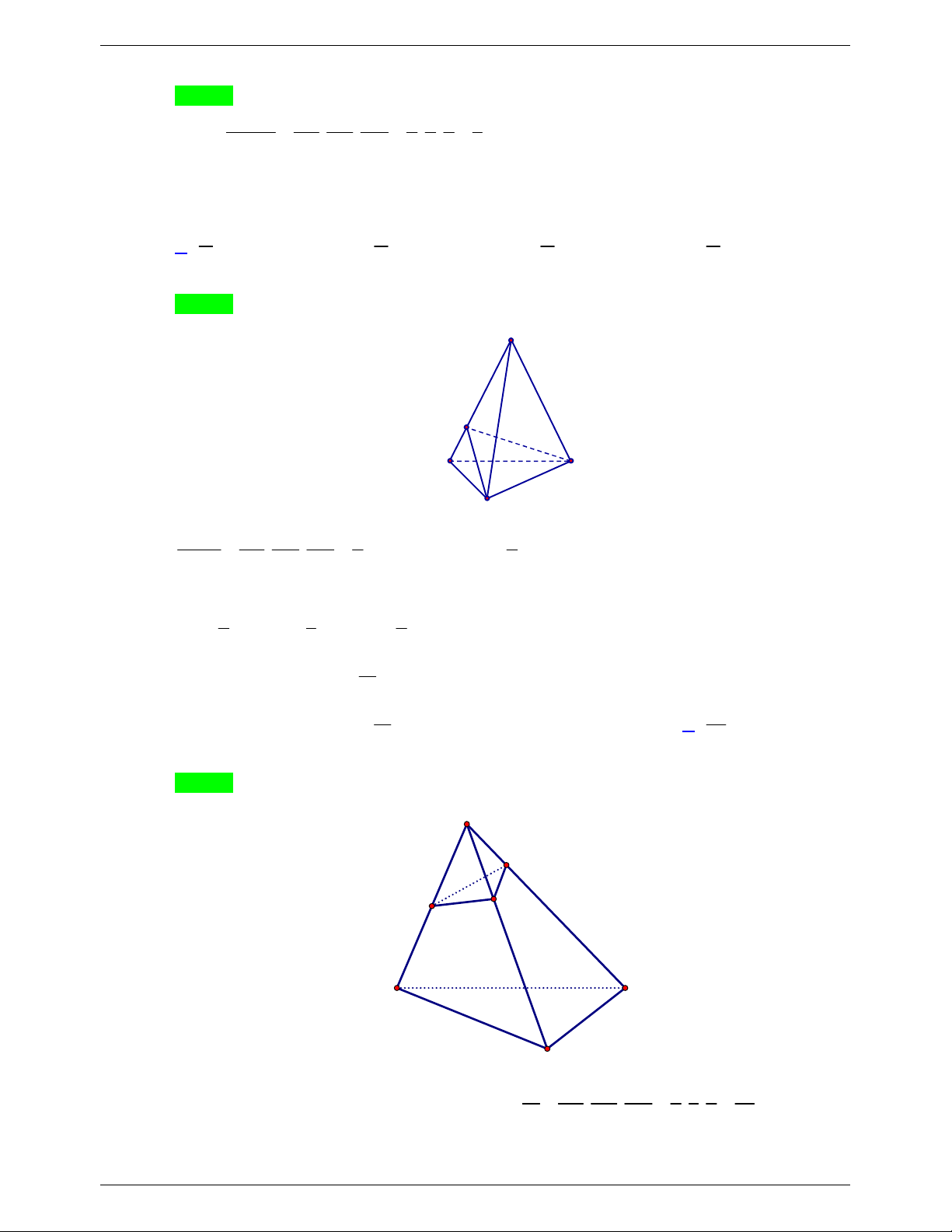
Câu 4. Cho khối tứ diện ABCD có thể tích bằng 3
60 cm và điểm K trên cạnh AB sao cho AB  4KB.
Tính thể tích V của khối tứ diện BKCD . A. 3 V  20cm . B. 3 V  12cm . C. 3 V  30 cm . D. 3 V  15cm . Lời giải Chọn D V BK BC BD 1 1 1 Ta có: B.KCD  . .  V  V  .60  15 cm B.KCD B.ACD  3 V BA BC BD 4 4 4 B.ACD
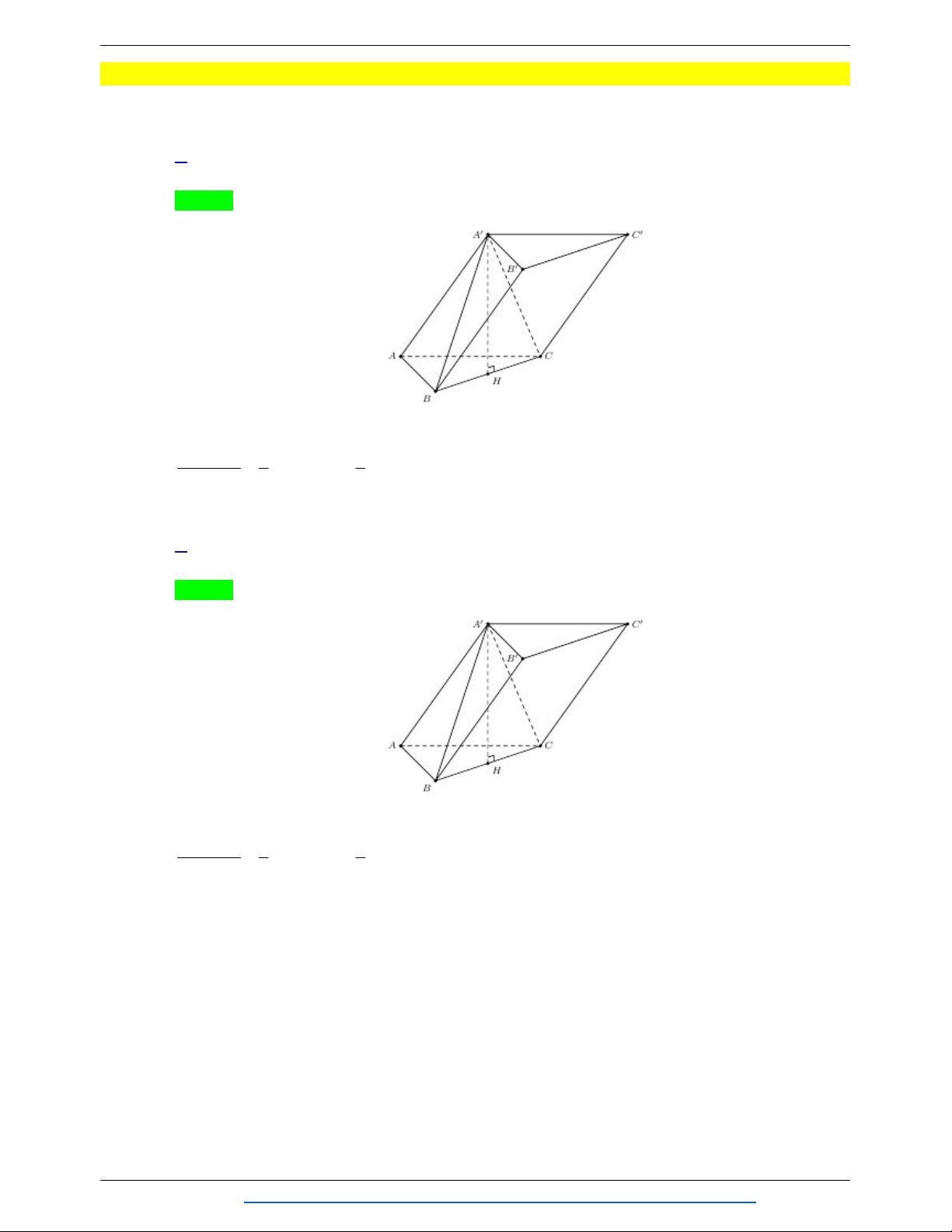
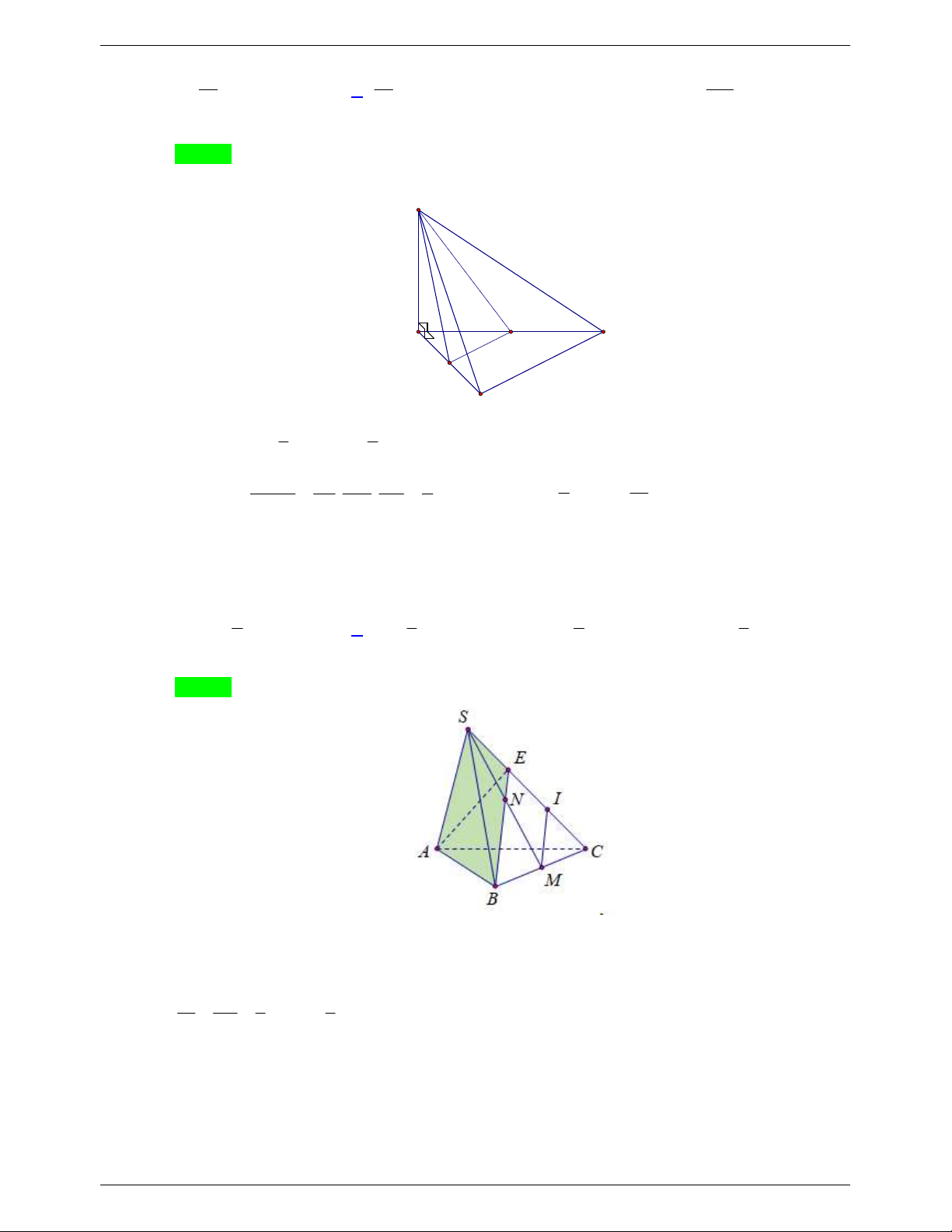
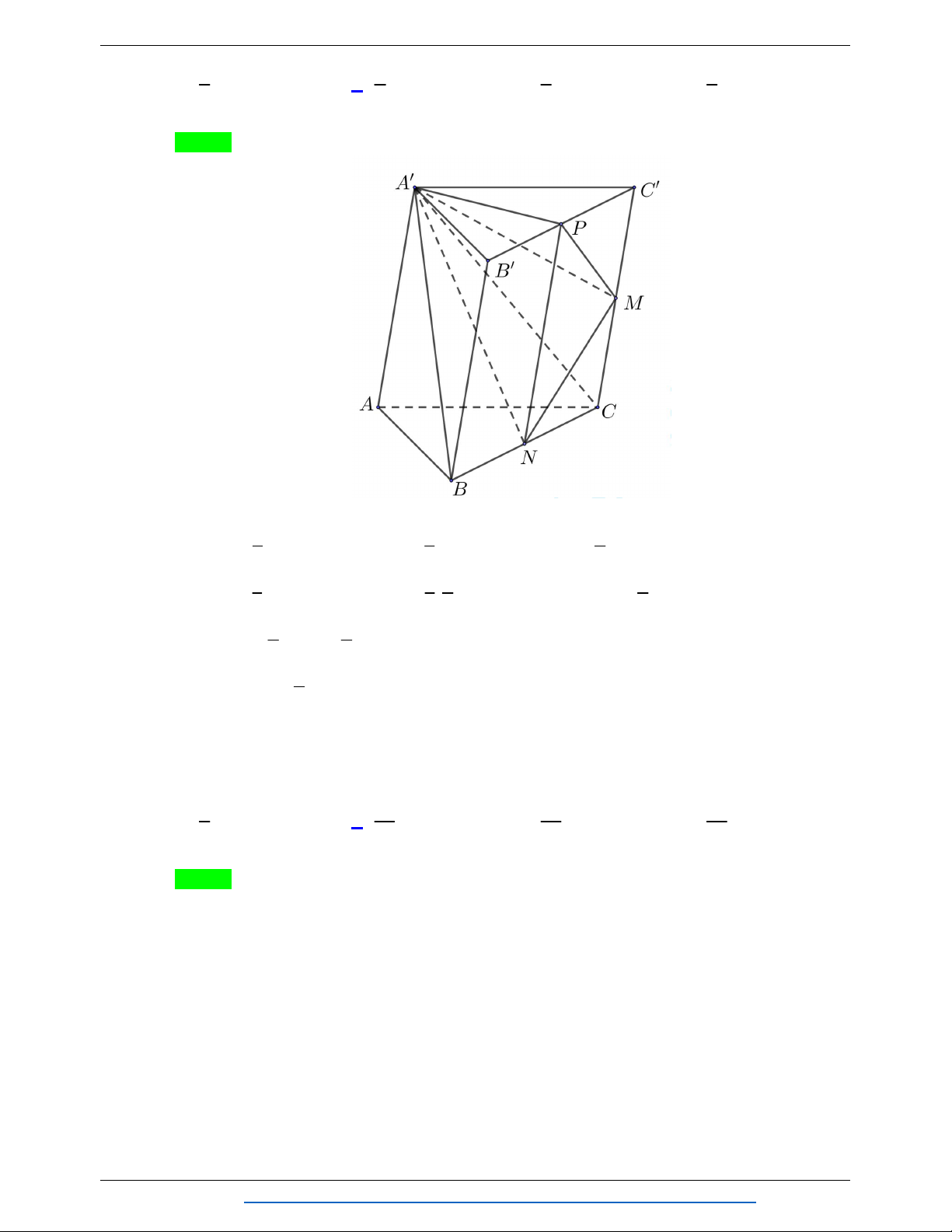
Câu 5. Cho khối chóp S.ABC . Gọi A , B , C lần lượt là trung điểm của các cạnh SA , SB , SC (minh V
hoạ như hình vẽ). Tỉ số S.A B C bằng VS.ABC 1 1 A. 8 . B. 2 . C. . D. . 8 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 3 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT Lời giải Chọn C V       SA SB SC 1 1 1 1 Ta có: S.A B C  . .  . .  . V SA SB SC 2 2 2 8 S.ABC
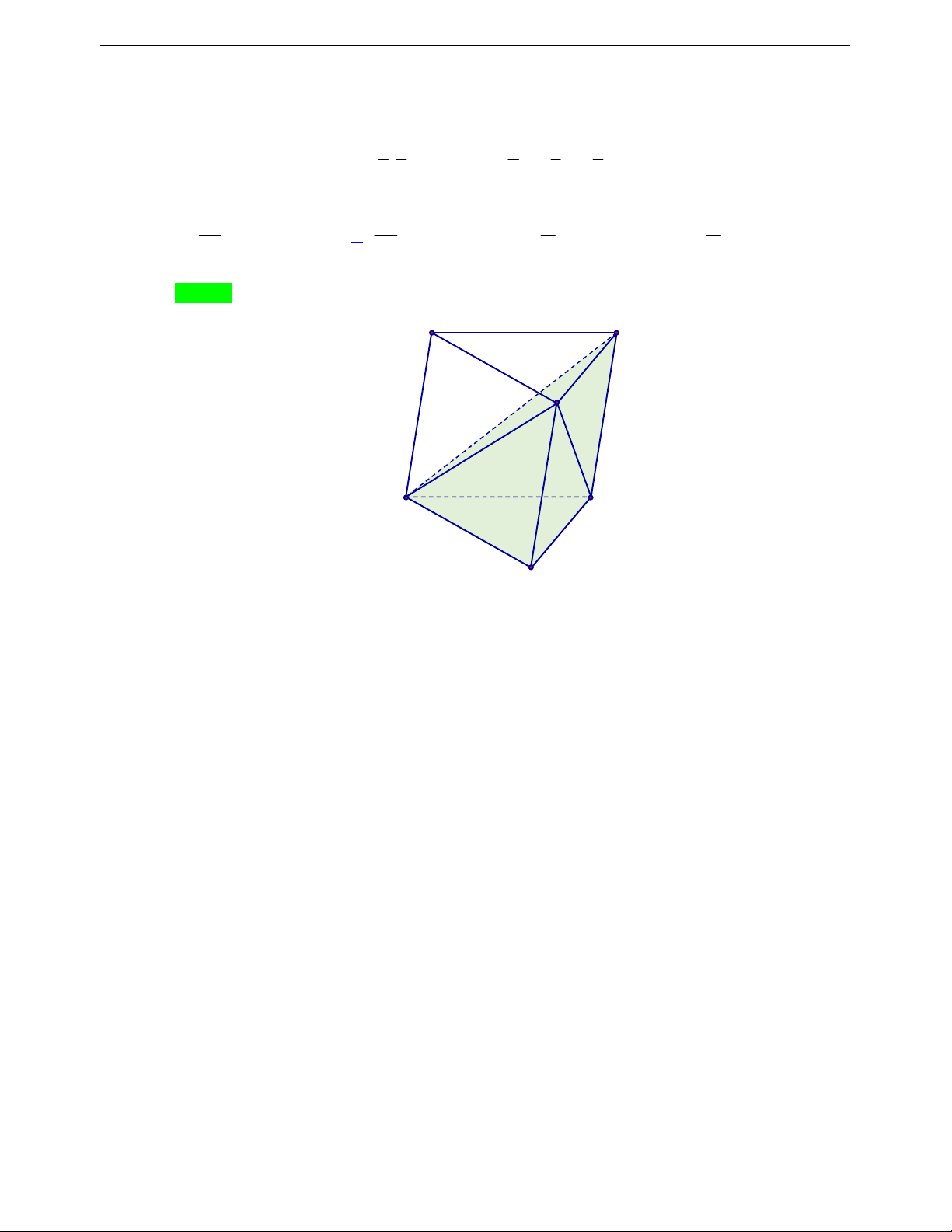
Câu 6. Cho khối tứ diện ABCD có thể tích V và điểm E trên cạnh AB sao cho AE  3EB . Tính thể tích
khối tứ diện EBCD theo V . V V V V A. . B. . C. . D. . 4 3 2 5 Lời giải Chọn A A E B D C V BE AC AD 1 1 B.ECD  . .   V  V  V B.ECD E. V BA AC AD 4 BCD 4 . A BCD
Câu 7. Cho khối chóp S.ABC , trên ba cạnh SA , SB , SC lần lượt lấy ba điểm A , B , C sao cho 1 1 1
SA  SA , SB  SB , SC  SC . Gọi V và V  lần lượt là thể tích của các khối chóp S.ABC 2 3 4 V  và S.A B  C
 . Khi đó tỉ số là: V 1 1 A. 12 . B. . C. 24 . D. . 12 24 Lời giải: Chọn D S C' B' A' A C B V  SA SB SC 1 1 1 1
Theo công thức tỉ số thể tích khối chóp, ta được:  . .  . .  . V SA SB SC 2 3 4 24 Trang 4 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
2. KHỐI LĂNG TRỤ - MỨC 1
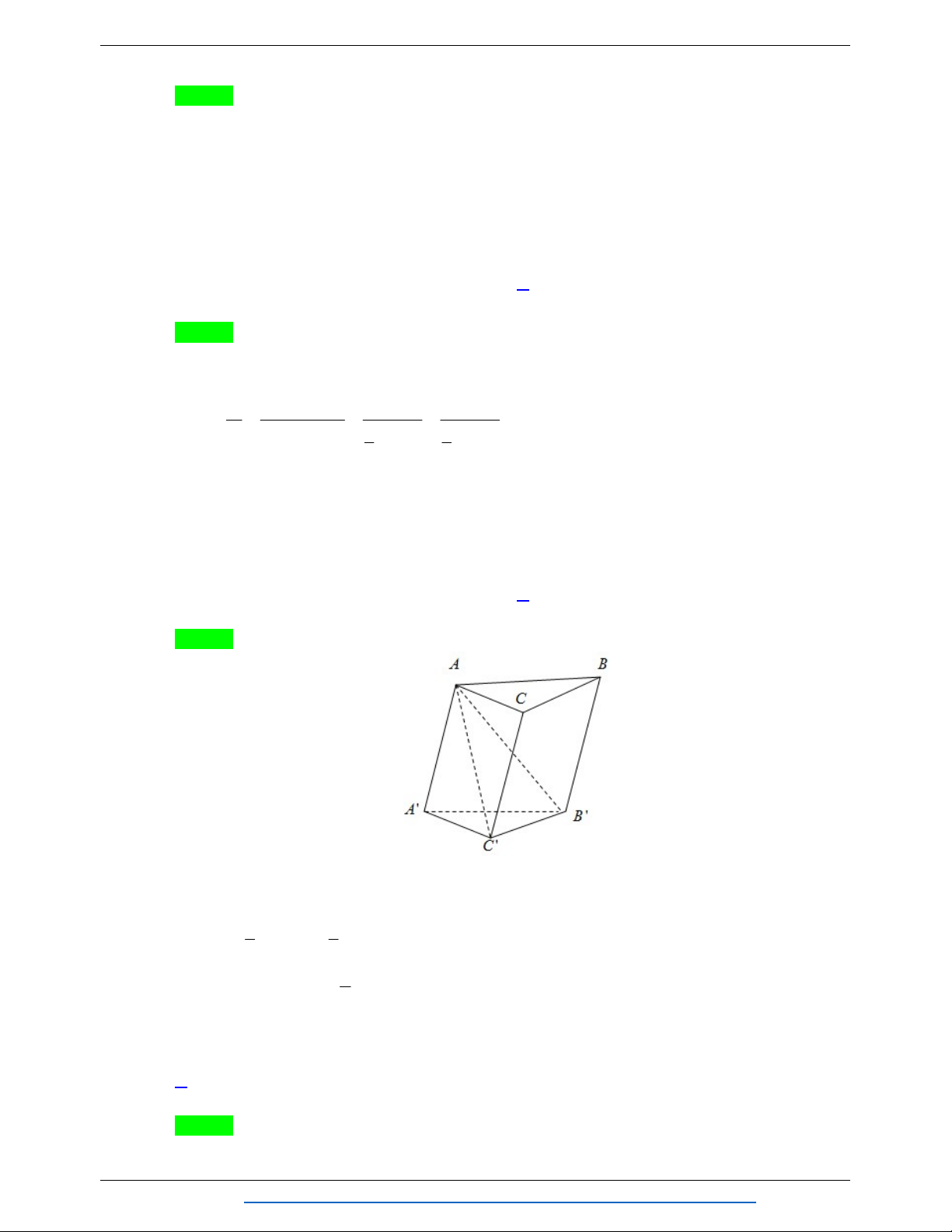
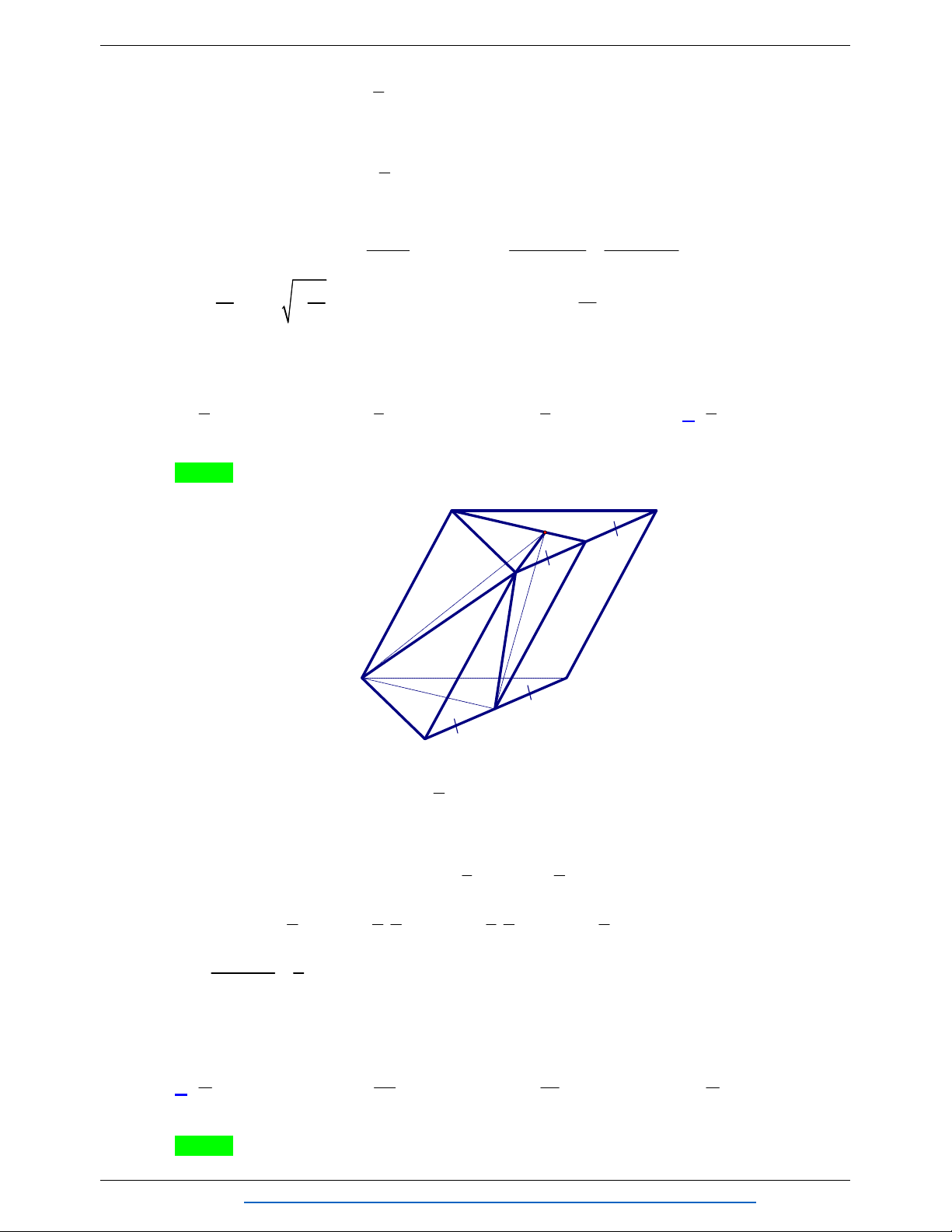
Câu 8. Cho khối lăng trụ ABC.A B  C
 có thể tích bằng 15. Thể tích khối chóp A .ABC bằng A. 5 . B. 10 . C. 3 . D. 6 . Lời giải Chọn A Vì lăng trụ ABC.AB C
 và khối chóp A .ABC có diện tích đáy như nhau và cùng chiều cao nên V  1 1 A .ABC  V    V    5 . V A .ABC ABC.A B C    3 3 ABC.A B C
Câu 9. Cho khối lăng trụ ABC.A B  C
 có thể tích bằng 15. Thể tích khối chóp A .ABC bằng A. 5 . B. 10 . C. 3 . D. 6 . Lời giải Chọn A Vì lăng trụ ABC.AB C
 và khối chóp A .ABC có diện tích đáy như nhau và cùng chiều cao nên V  1 1 A .ABC  V    V    5 . V A .ABC ABC.A B C    3 3 ABC.A B C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 5 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3. KHỐI CHÓP - MỨC 2
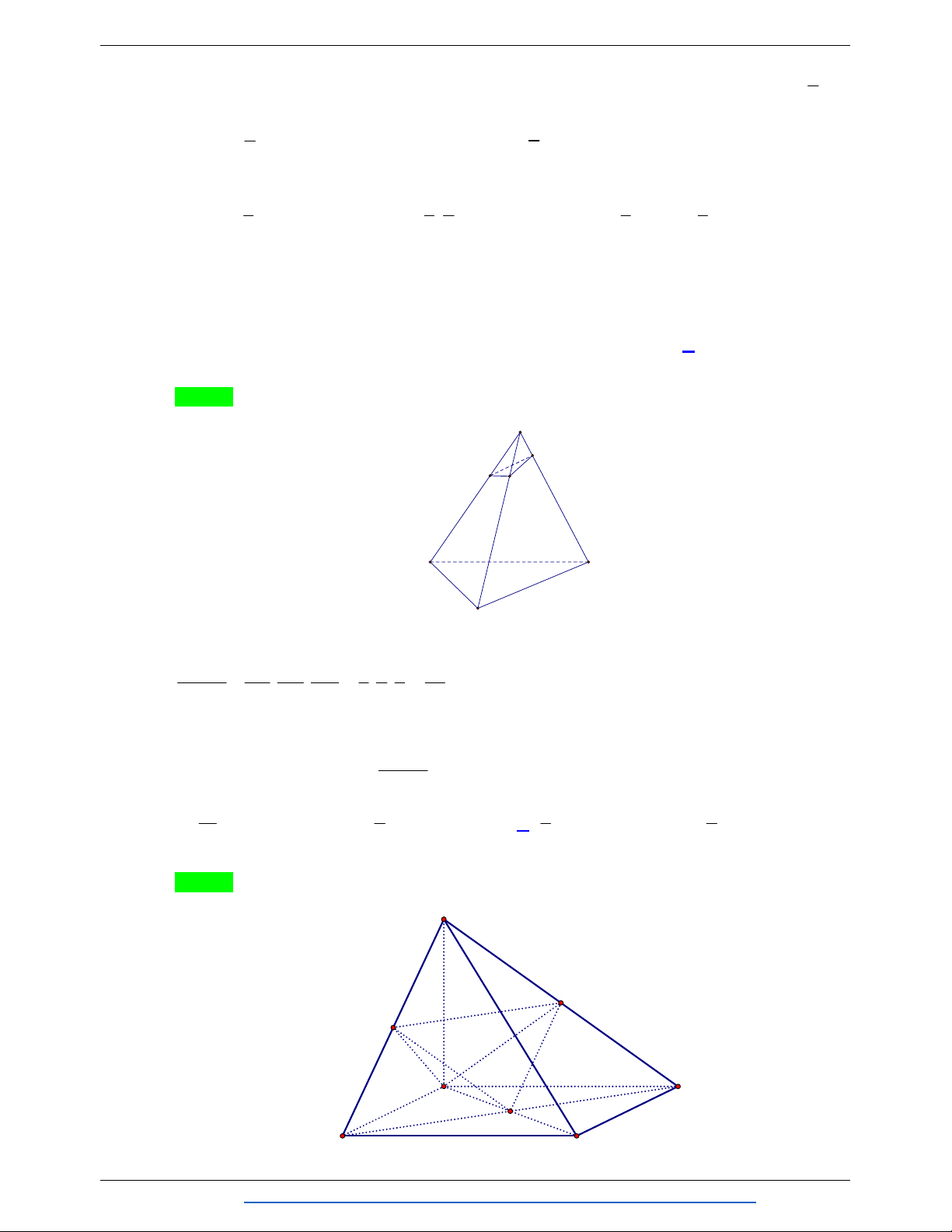
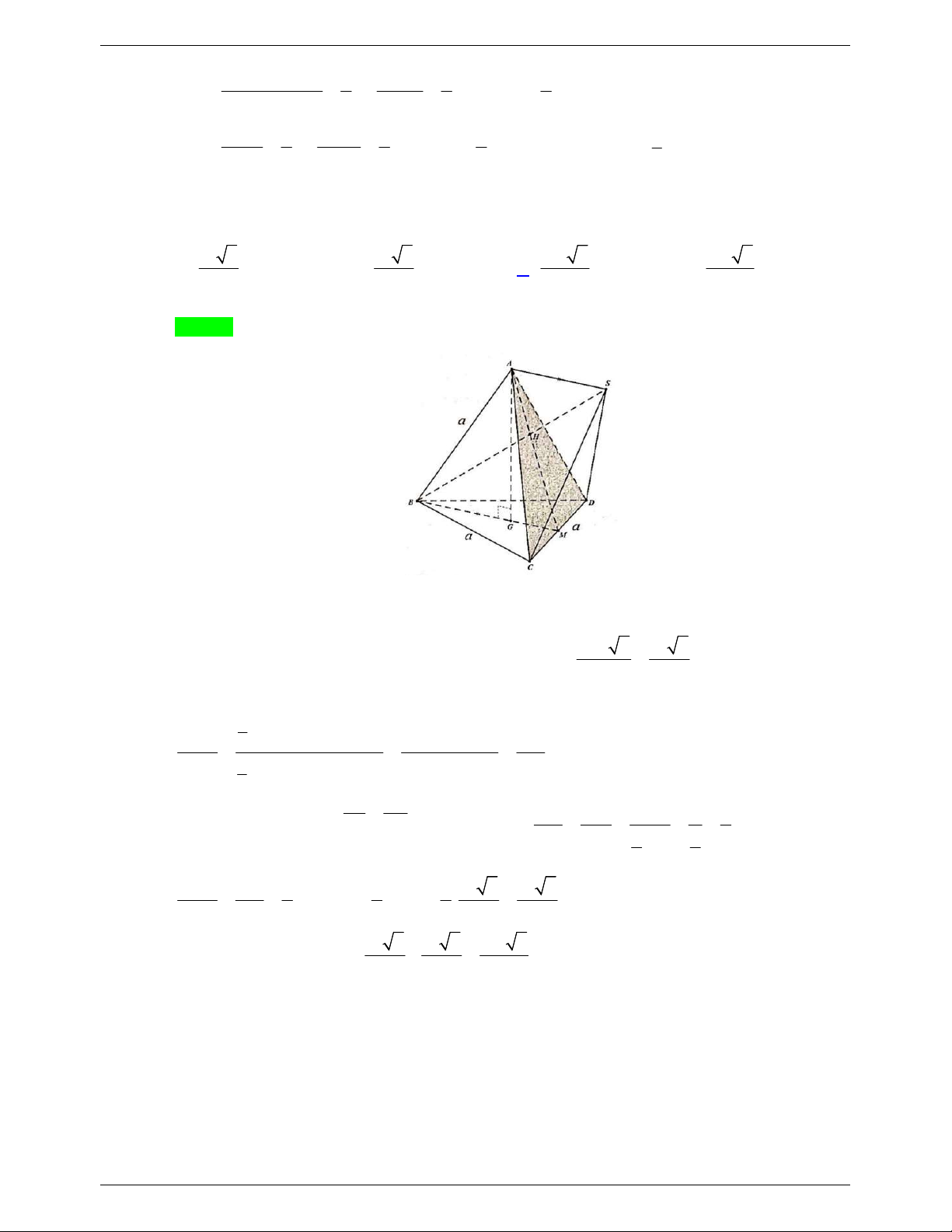
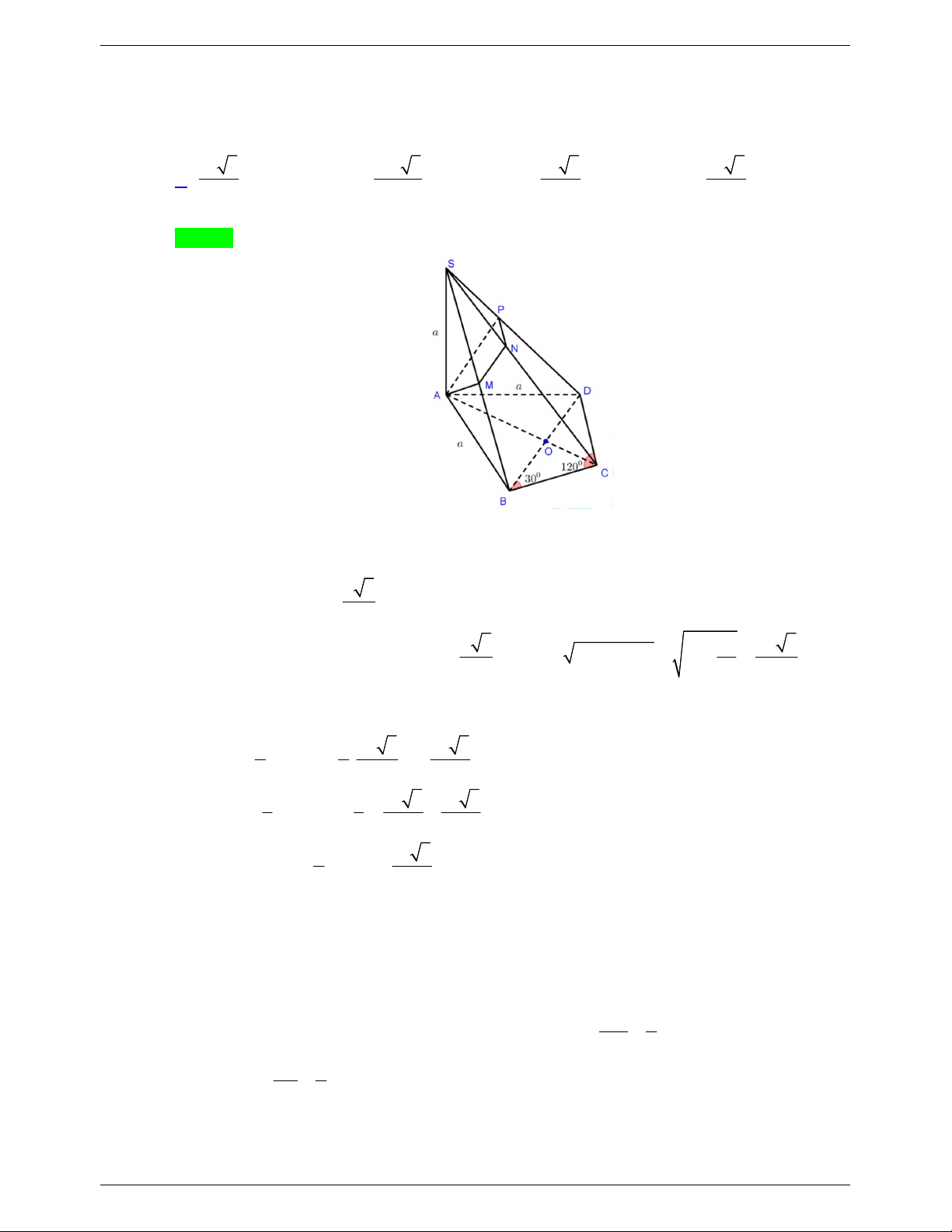
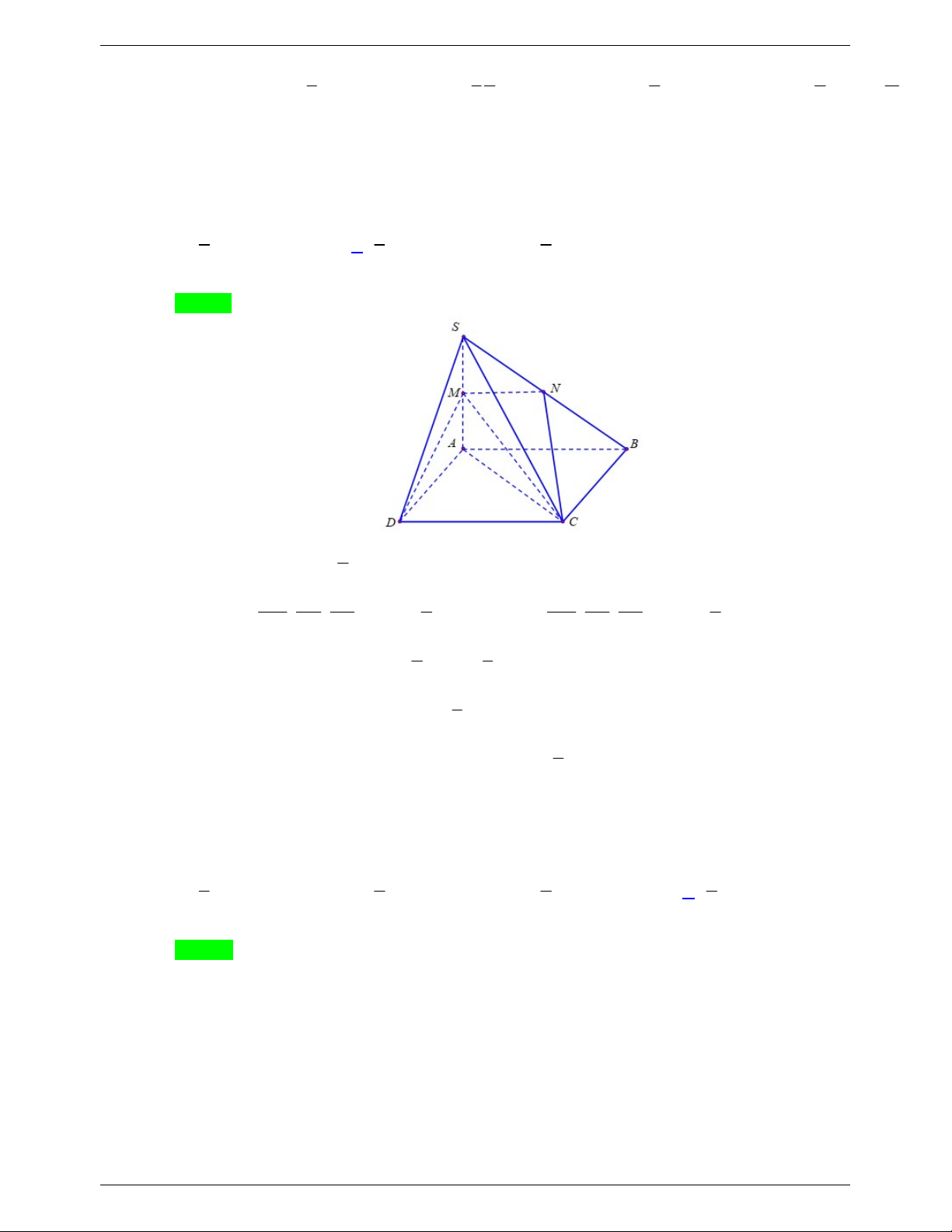
Câu 10. Cho hình chóp S.ABC có SA  a, SB  3a 2, SC  2a 3 ,  ASB   BSC   CSA  60. Thể tích khối chóp S.ABC là 3 a 3 A. 3 2a 3 . B. . C. 3 a 3 . D. 3 3a 3 . 3 Lời giải Chọn C Lấy M  S ,
B N  SC sao cho SA  SM  SN  a . 3 a 2 Vì  ASB   BSC  
CSA  60do đó khối chóp SAMN là tứ diện đều cạnh a nên V  . S.AMN 12 V SA SB SC 3 a 2 Mặt khác S.ABC     6 6 3 V  6 6V  6 6  a 3. S.ABC S.AMN V SA SM SN 12 S.AMN
Câu 11. Cho khối chóp S.ABC có thể tích bằng 48. Gọi M , N , P lần lượt là trung điểm của các cạnh S ,
A SB, SC . Thể tích của khối chóp S.MNP bằng A. 6. B. 8. C. 12. D. 10. Lời giải Chọn A Ta có hình vẽ: V SA SB SC Ta có: S.ABC    . V SM SN SP S.MNP 48 2 2 2 Theo giả thiết ta có:     V  6 (đvtt). . V 1 1 1 S MNP S.MNP Trang 6 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Câu 12. Cho khối chóp S.ABC có thể tích bằng 48. Gọi M , N , P lần lượt là trung điểm của các cạnh S ,
A SB, SC . Thể tích của khối chóp S.MNP bằng A. 6. B. 8. C. 12. D. 10. Lời giải Chọn A Ta có hình vẽ: V SA SB SC Ta có: S.ABC    . V SM SN SP S.MNP 48 2 2 2 Theo giả thiết ta có:     V  6 (đvtt). . V 1 1 1 S MNP S.MNP
Câu 13. Cho hình chóp S.ABC có SA  a, SB  3a 2, SC  2a 3 ,  ASB   BSC   CSA  60. Thể tích khối chóp S.ABC là 3 a 3 A. 3 2a 3 . B. . C. 3 a 3 . D. 3 3a 3 . 3 Lời giải Chọn C Lấy M  S ,
B N  SC sao cho SA  SM  SN  a . 3 a 2 Vì  ASB   BSC  
CSA  60do đó khối chóp SAMN là tứ diện đều cạnh a nên V  . S.AMN 12 V SA SB SC 3 a 2 Mặt khác S.ABC     6 6 3 V  6 6V  6 6  a 3. S.ABC S.AMN V SA SM SN 12 S.AMN
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 7 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
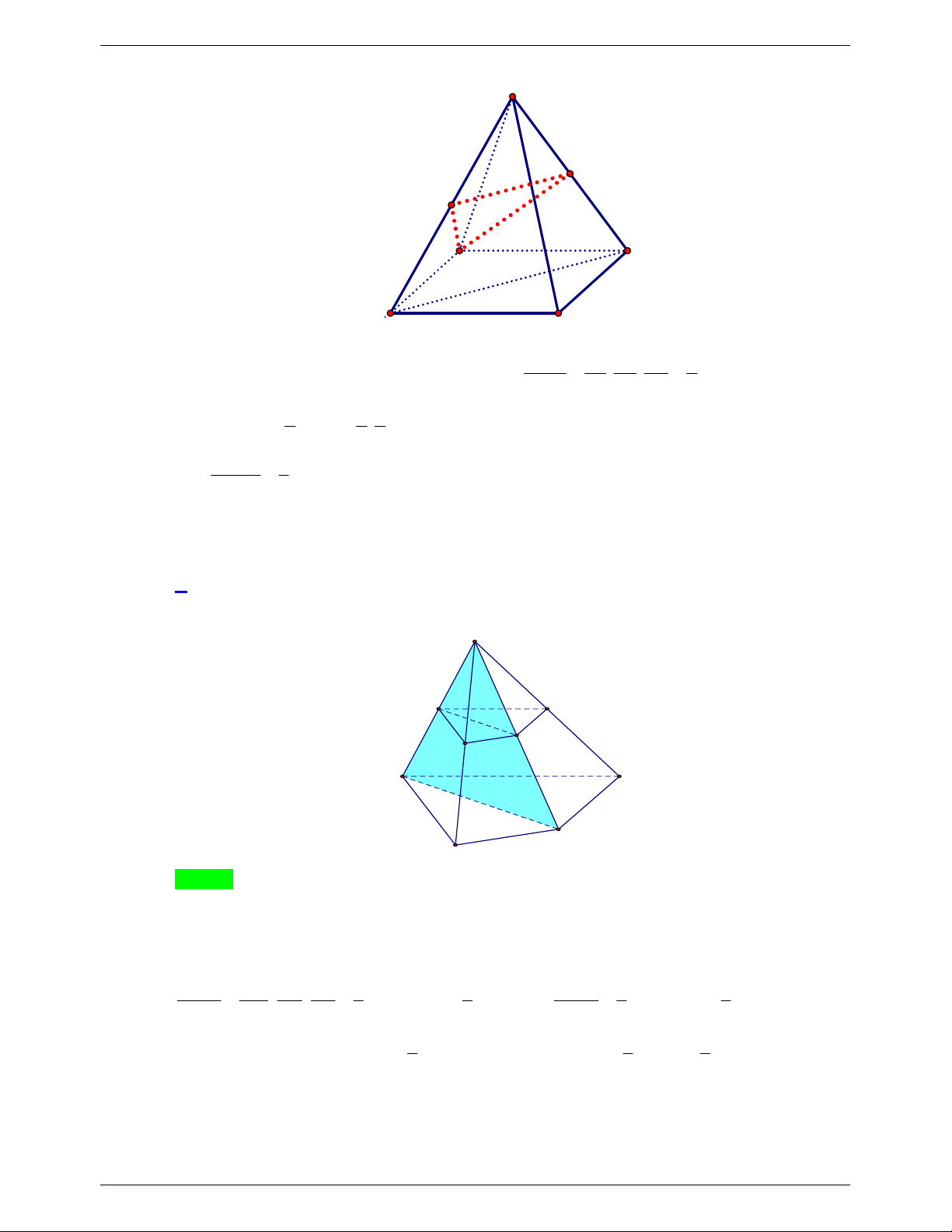
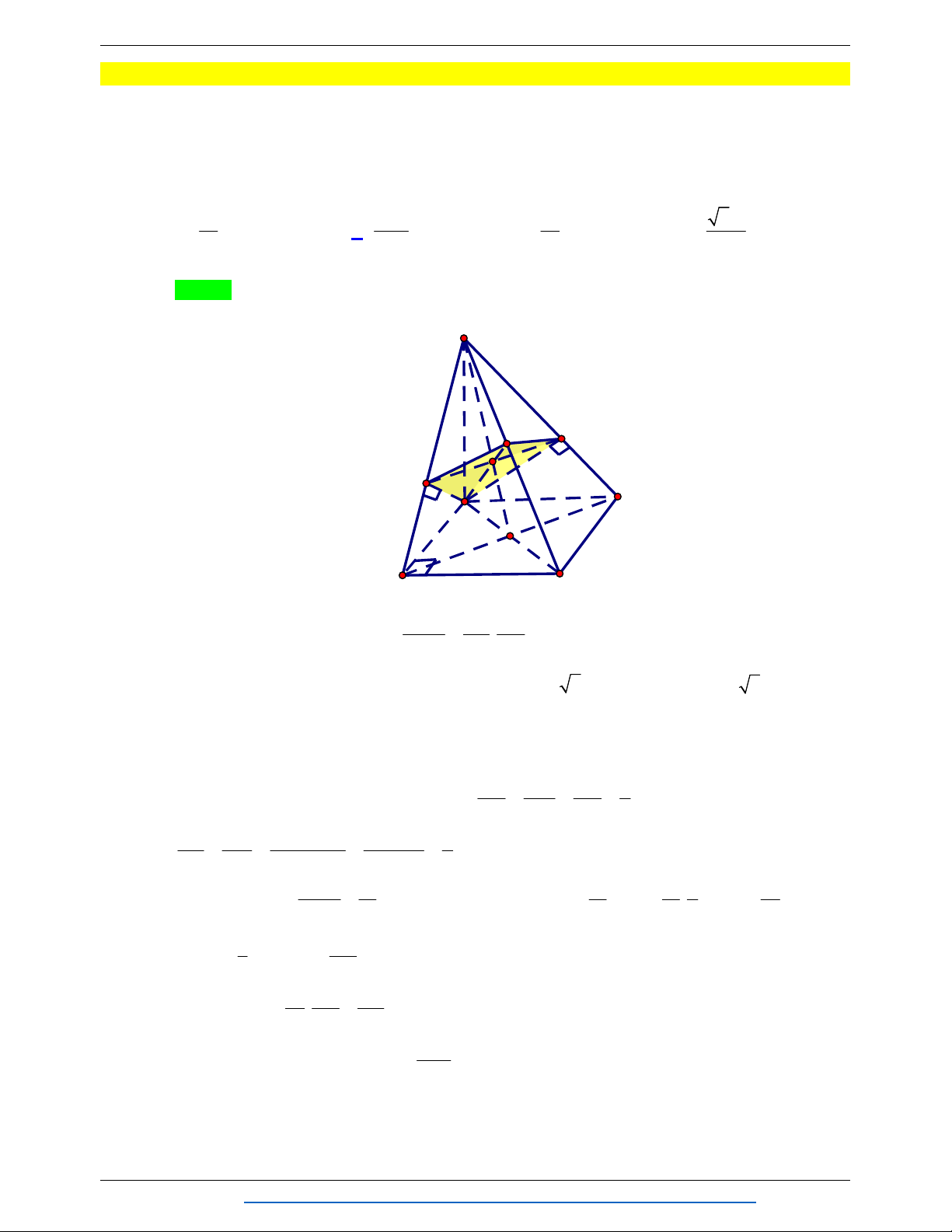
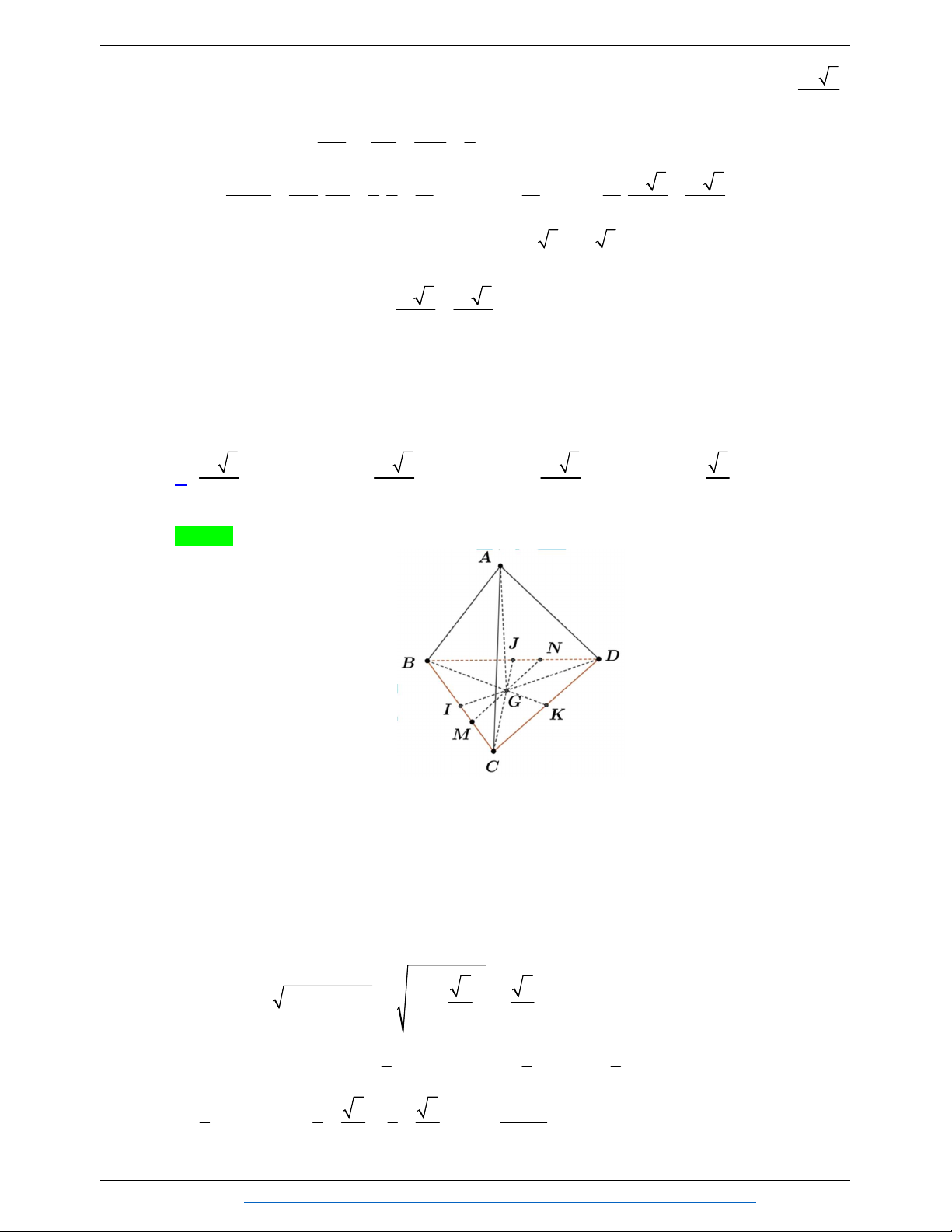
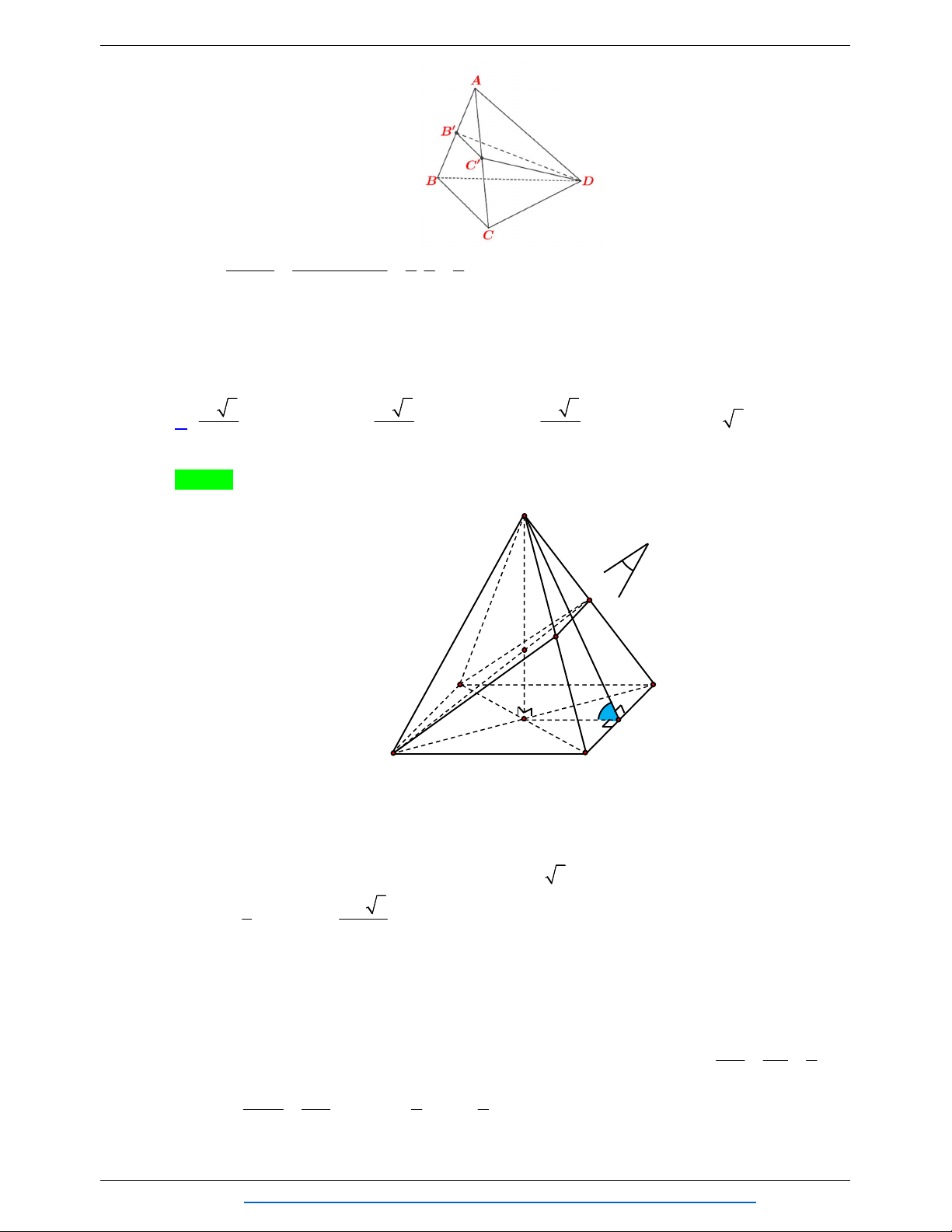
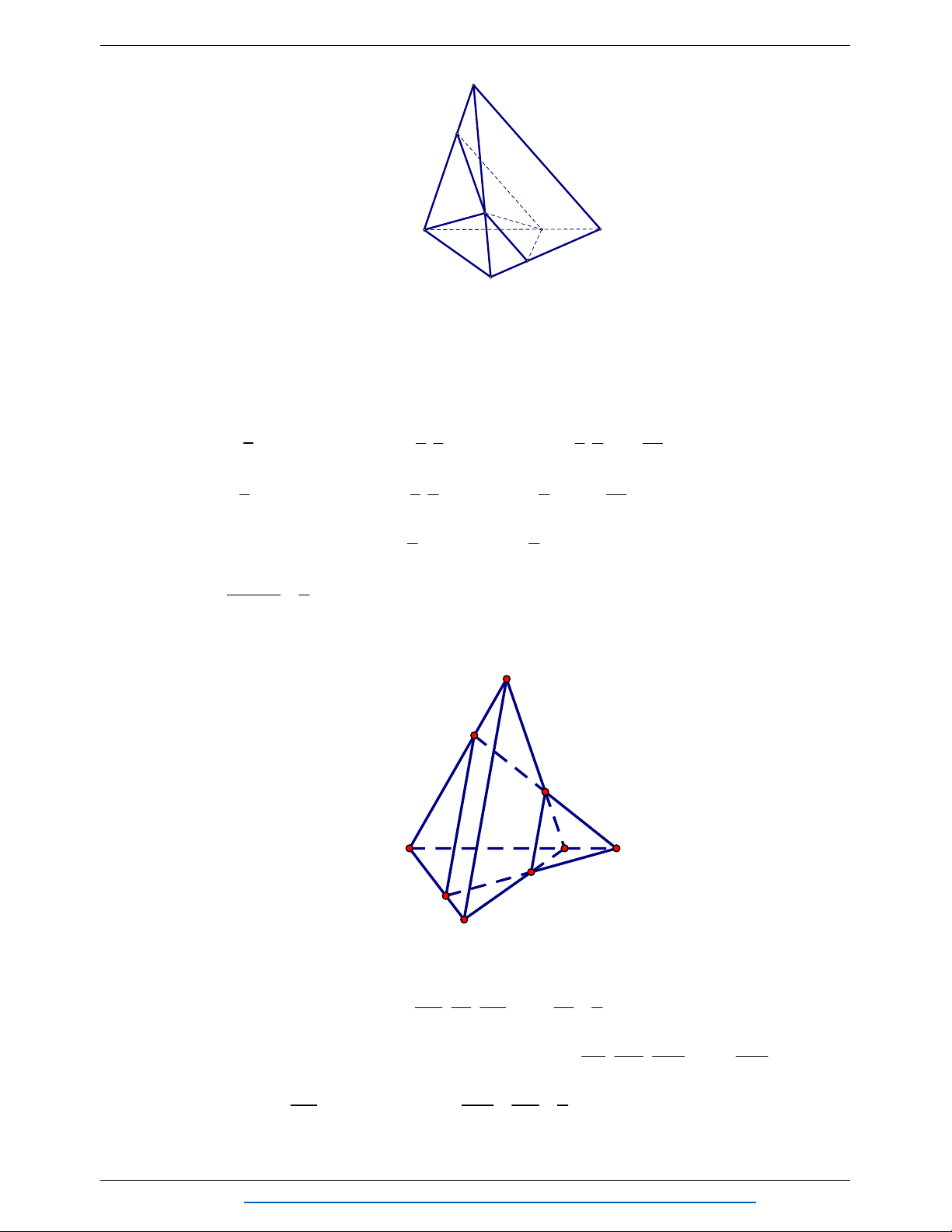
Câu 14. Cho khối tứ diện đều ABCD có thể tích là V . Gọi M , N , P , Qlần lượt là trung điểm của A C , A D , BD , BC . AMNPQ . Thể tích khối chóp là V V V V A. . B. . C. . D. . 12 3 6 4 Lời giải Chọn D Cách 1: V AM AN AP 1 Ta có: AMNP  . .  . V AC AD AP 4 ACDP V 1 Mà ACDP  . V 2 ABCD Vậy 1 1 1 1 V V  2V  2. V  2. . .V  V  . A.MNPQ AMNP 4 ACDP 4 2 ABCD 4 ABCD 4 Cách 2: Ta có: V  2V (do MNPQlà hình thoi). A.MNPQ APMQ Mà V  V (do AB// MQ) nên V  2V . APMQ BPMQ A.MNPQ BPMQ Vì 1
P là trung điểm của BD nên d P, ABC   1 d D, ABC  và S  S . 2 BQM 4 ABC Nên 1 1 1 1 1 1 V V  d P ABC S  . d D, ABC. S  . d D, ABC .S  BPMQ  , . . 3 BQM 3 2 4 ABC 8 3 ABC 8 Suy ra V V  . AMNPQ 4
Câu 15. Cho hình chóp S.ABC . Gọi M , N , P theo thứ tự là trung điểm của SA , SB , SC . Tính tỉ số
thể tích của 2 khối chóp S.MNP và S.ABC bằng 1 1 1 1 A. . B. . C. . D. . 4 8 16 2 Lời giải Chọn B Trang 8 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S P M N A C B V SM SN SP 1 Ta có S.MNP     . V SA SB SC 8 S.ABC
Câu 16. Cho tứ diện ABCD . Xét điểm M trên cạnh AB , điểm N trên cạnh BC , điểm P trên cạnh CD MB NB PC 3 sao cho  3,  4,
 . Gọi V , V theo thứ tự là thể tích các khối tứ diện MNBD và MA NC PD 2 1 2 V NPAC . Tỉ số 1 bằng V2 1 1 A. 3 . B. 5 . C. . D. . 5 3 Lời giải Chọn B 1
V  h .S với h  d M , BCD ; S  S . 1    1 1 1 3 1 N  BD 1 V  h .S với h  d , A BCD ; S  S . 2    2 2 2 3 2 C  NP V h .S h 3 4 1 3 3 S 20 1 1 1   5 . Vì 1  và 1 S  S ; S  . S  S   . V h .S h 4 1 B  CD 2 5 5 5 B  CD 25 B  CD S 3 2 2 2 2 2
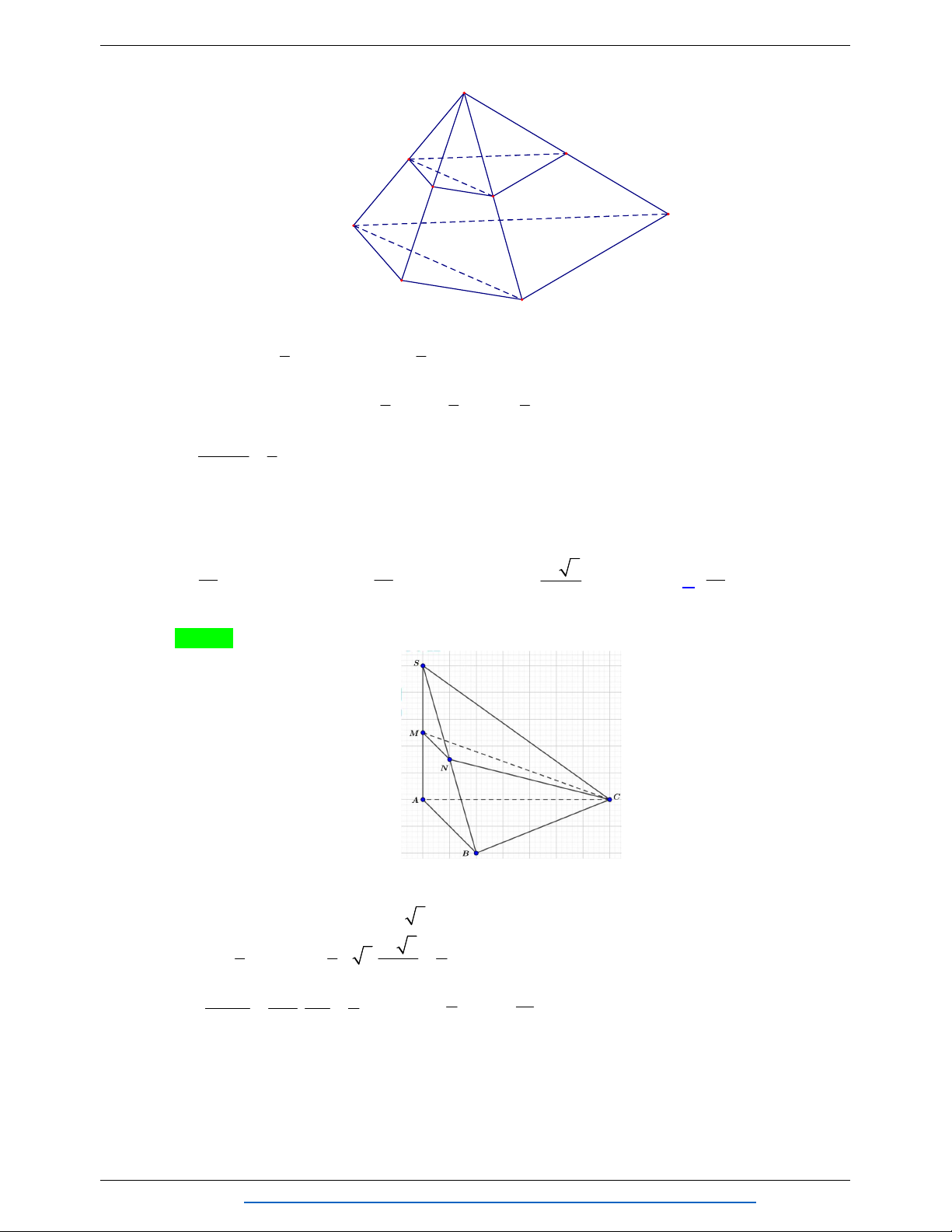
Câu 17. Cho hình chóp S.ABC có S ,
A SB, SC đôi một vuông góc với nhau và SA  a , SB  2a và
SC  3a . Gọi M , N lần lượt là trung điểm của cạnh SB và SC . Tính theo a thể tích khối chóp S.AMN .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 9 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3 a 3 a 3 3a A. . B. . C. 3 a . D. . 2 4 4 Lời giải Chọn B Hình vẽ A N S C M B 1 1 Ta có 3 V  . SA S  S . A S . B SC  a S.ABC 3 SB  C 6 V SA SM SN 1 3 1 a Mặc khác S.AMN  . .  . Suy ra V  V  . V SA SB SC 4 S.AMN S. 4 ABC 4 S.ABC
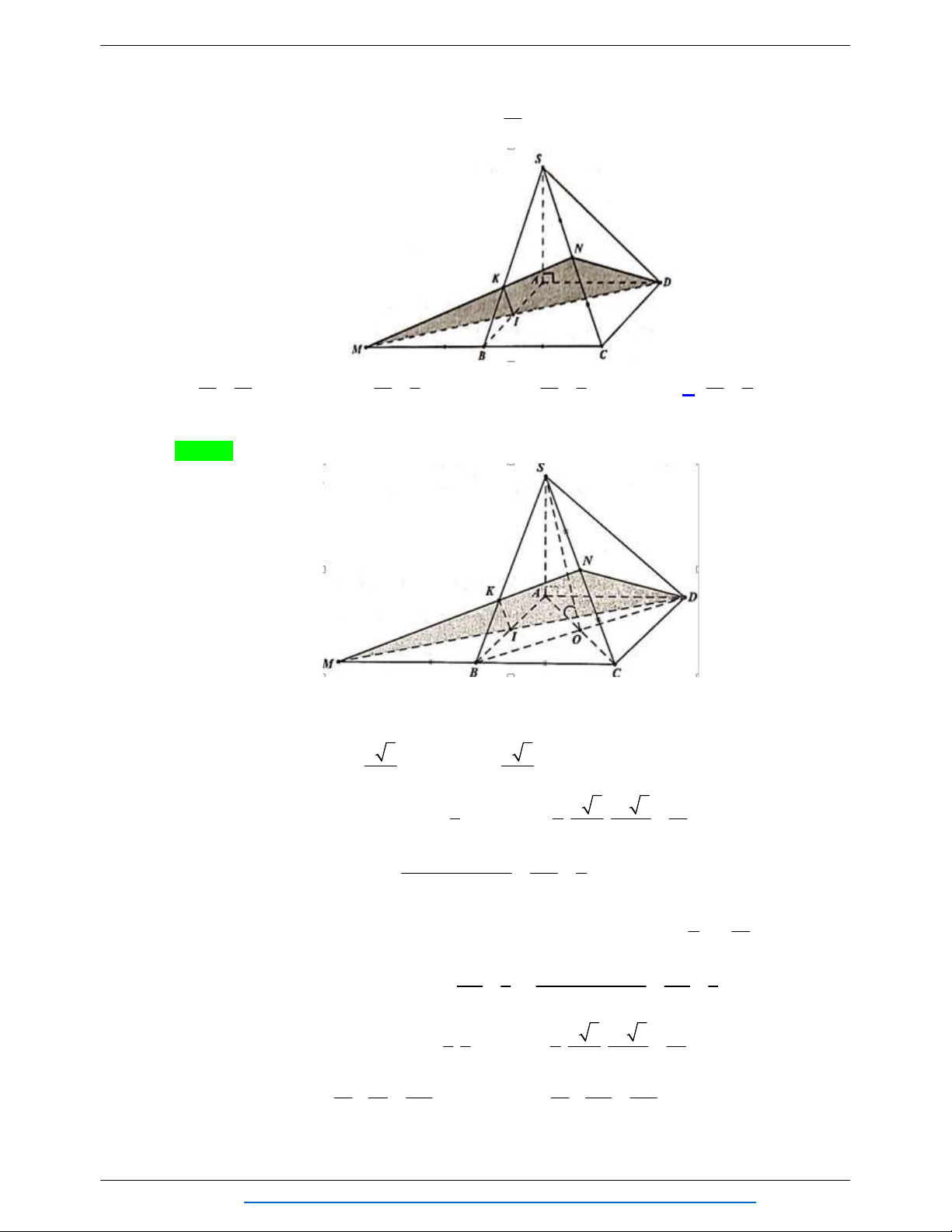
Câu 18. Cho hình chóp tam giác đều S.ABC . Gọi M , N lần lượt là trung điểm của BC , SM . Mặt phẳng
 ABN  cắt SC tại E . Gọi V là thể tích của khối chóp S.ABE và V là thể tích khối chóp S.ABC 2 1
. Khẳng định nào sau đây đúng? 1 1 1 1 A. V  V . B. V  V . C. V  V . D. V  V . 2 1 4 2 1 3 2 1 6 2 1 8 Lời giải Chọn B
Gọi I là trung điểm của EC nên IM là đường trung bình của tam giác BCE  MI //EN
Mà N là trung điểm của SM  EN là đường trung bình của tam giác SMI suy ra E là trung điểm của SI . V SE 1 1 2    V  V . 2 1 V SC 3 3 1
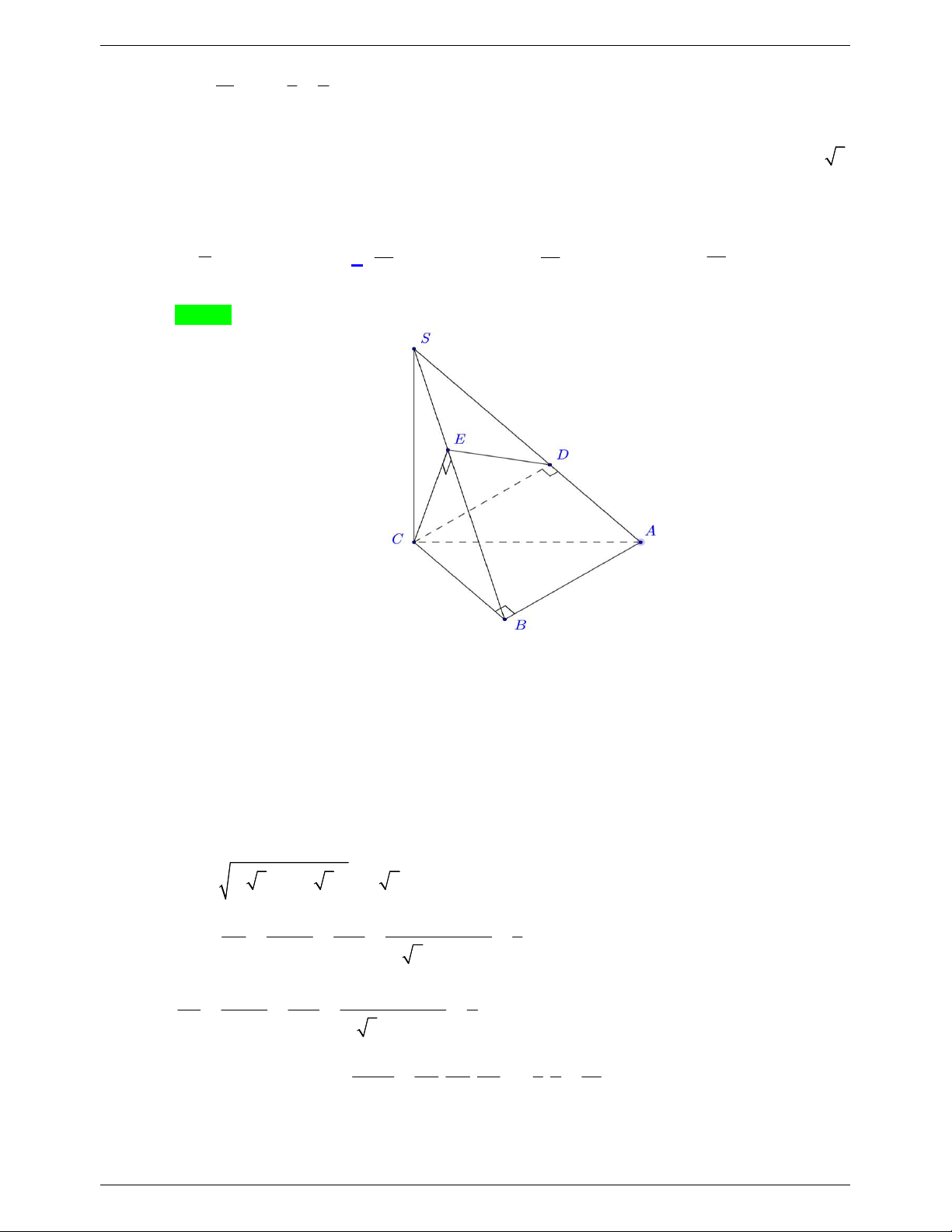
Câu 19. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB  AC  a , SC   ABC  và
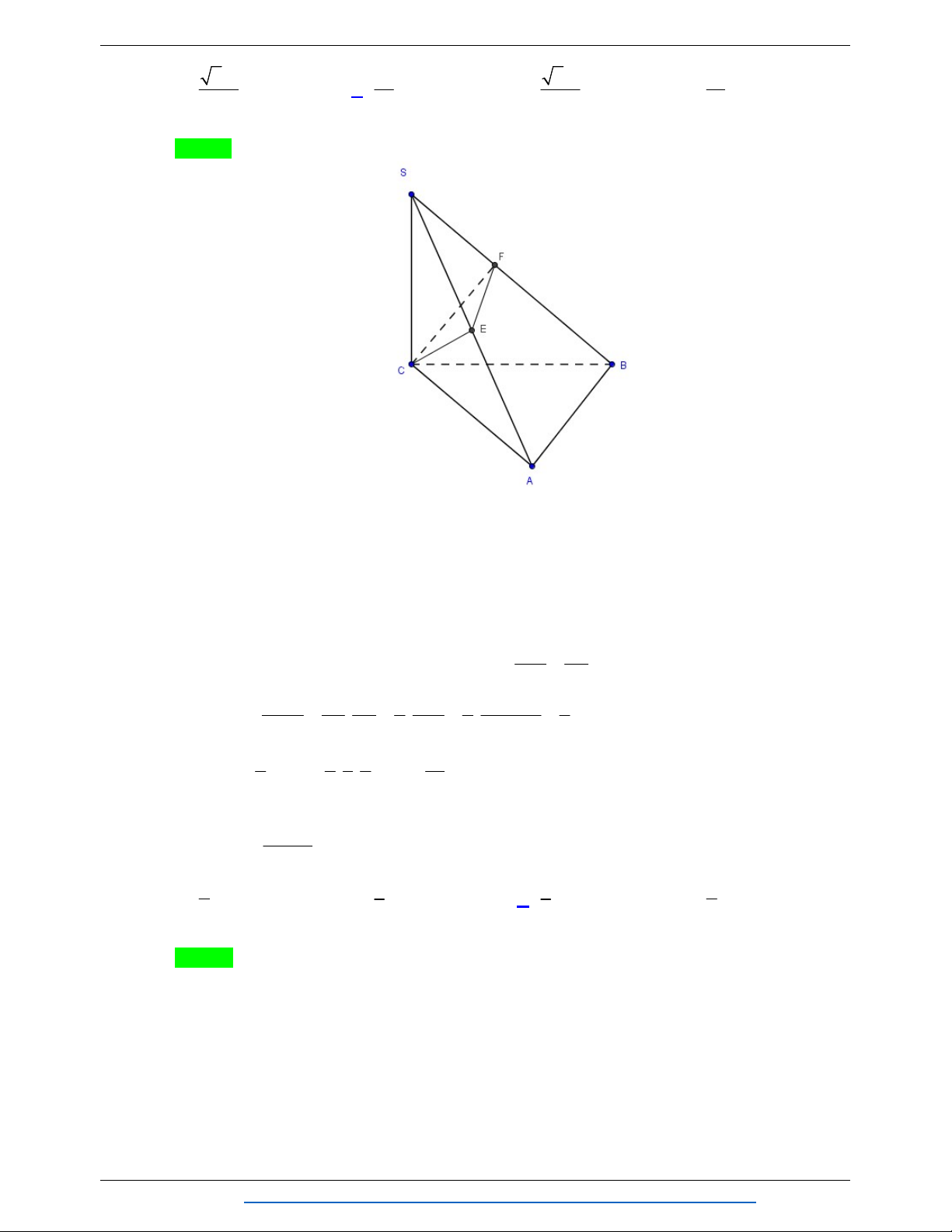
SC  a . Mặt phẳng qua C , vuông góc với SB cắt SA , SB lần lượt tại E và F . Thể tích khối chóp S.CEF là Trang 10 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 3 2a 3 a 3 2a 3 a A. . B. . C. . D. . 12 36 36 18 Lời giải Chọn B
Tam giác vuông SCA có SC  CA  a nên là tam giác vuông cân ở C.
Ta có AB  AC và AB  SC suy ra AB  SAC suy ra AB  CE.   1
Mặt khác theo giả thiết SB  CEF   SB  CE . 2 Từ  
1 và 2 suy ra SAB  CE  CE  SA. Do đó E la trung điểm của SA vì tam giác SCA vuông cân ở C. 2 SC SF
Trong tam giác vuông SCB có 2 SC  SF.SB   . 2 SB SB 2 2 V SE SF 1 SC 1 a 1 Từ đó ta có S.CEF  .  .  .  2 2 2 V SA SB 2 SB 2 a  2a 6 S.CAB 3 1 1 1 1 a  V  V  . . . a . a a  . S.CEF S. 6 CAB 6 3 2 36
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi E , F lần lượt là trung điểm của SB V
, SD . Tỉ số S.AEF bằng: VS.ABCD 1 3 1 1 A. . B. . C. . D. . 4 8 8 2 Lời giải: Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 11 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT S F E A D B C V SA SE SF 1
Áp dụng công thức tỉ số thể tích hình chóp, ta có: S.AEF  . .  . V SA SB SC 4 S.ABD 1 1 1 Suy ra V  V  . .V . S.AEF S.ABD S. 4 4 2 ABCD V 1 Vậy S.AEF  . V 8 S.ABCD
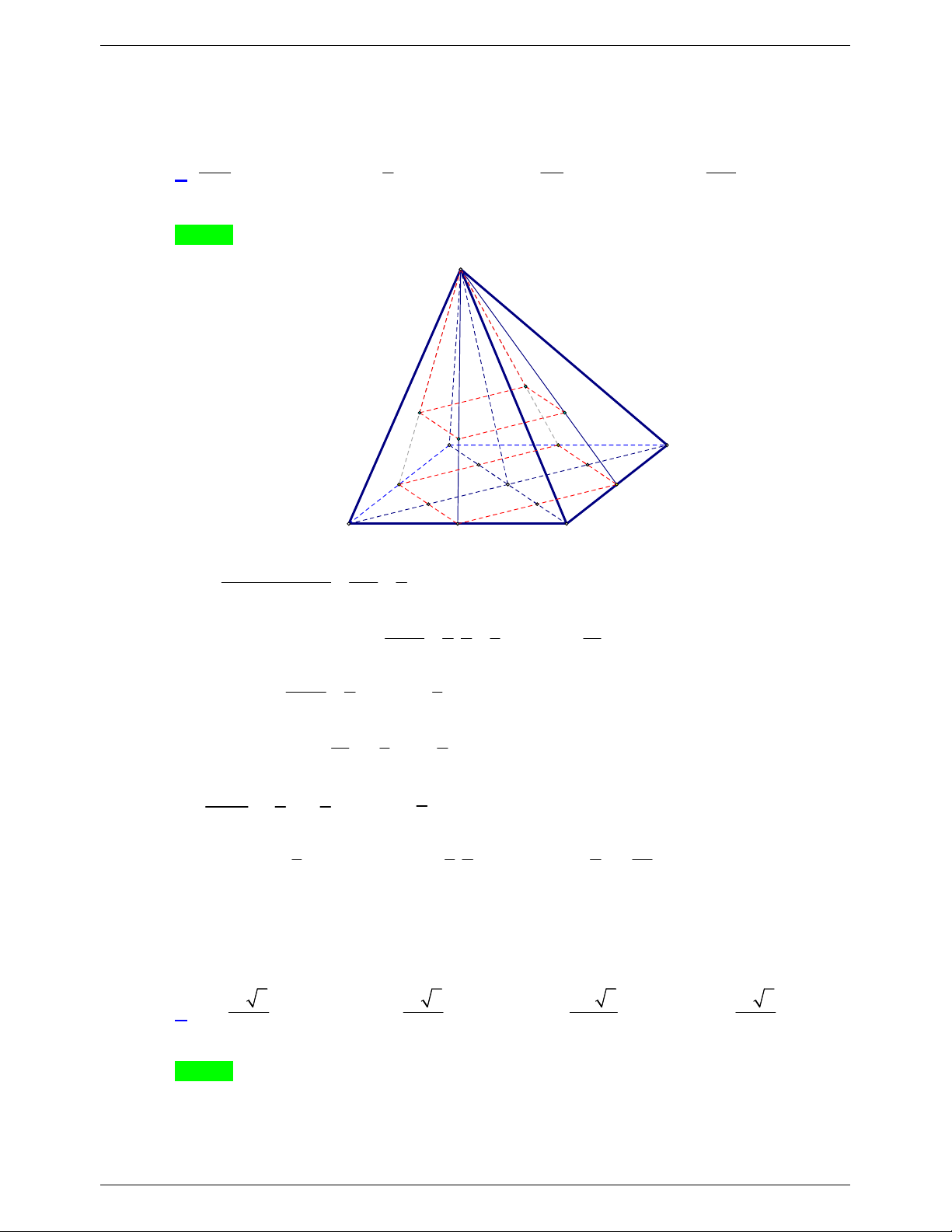
Câu 21. Cho hình chóp tứ giác S.ABCD có M , N, P, Q lần lượt là trung điểm các cạnh , SA SB, SC, SD
. Biết khối chóp S.ABCD có thể tích là 3
16a . Tính thể tích khối chóp S.MNPQ theo a . A. 3 2a . B. 3 a . C. 3 8a . D. 3 4a . Lời giải S M Q P N A D C B Chọn A
Cách 1: Mặt phẳng SAC  chia khối chóp S.ABCD thành hai khối chóp tam giác S.ABC và
S.ADC , đồng thời cũng chia khối chóp S.MNPQ thành hai khối chóp S.MNP và S.MQP .
Áp dụng phương pháp tỷ số thể tích, ta có: V SM SN SP 1 1 VS MQP 1 1 S.MNP     nên V  V ; và .  nên V  V . V SA SB SC 8 S.MNP S . 8 ABC V 8 S.MQP S. 8 ADC S.ABC S.ADC 1 1 1 Do đó V  V V  V V  V  V  a  a . S MNPQ S MNP S MQP  S ABC S ADC  3 3 .16 2 . . . . . S.MNPQ S. 8 8 ABCD 8 Trang 12 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1
Cách 2: Ta dễ dàng chỉ ra được tứ giác MNPQ đồng dạng với ABCD theo tỷ số nên 2 2  1  1 S  .S
. Đồng thời d S,MNPQ  d S, ABCD . MNPQ    2 ABCD  2 Do đó, ta có: 1 V  S .d S MNPQ   S d S ABCD  V  a  a . S MNPQ MNPQ  ,  1 1 . ABCD  ,  1 1 3 3 .16 2 . S. 3 3 4 8 ABCD 8
Câu 22. Cho khối chóp S.ABC có các điểm A, B, C lần lượt thuộc các cạnh SA , SB , SC thoả 3SA  SA
, 4SB  SB , 5SC  3SC . Biết thể tích khối chóp S.AB C  bằng 5  3
cm  . Tìm thể tích khối chóp S.ABC . A. 120  3 cm  . B. 60  3 cm  . C. 80  3 cm  . D. 100  3 cm  . Lời giải Chọn D S C' A' B' A C B
Áp dụng tỉ lệ thể tích ta có: V       SA SB SC S.A B C  1 1 3 . .  1 . .   V  20V 100  3 cm  . V SA SB SC 3 4 5 20 S.ABC S .AB C   S.ABC
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O . Gọi H và K lần lượt là trung điểm V
của SB , SD . Tỷ số thể tích AOHK bằng VS.ABCD 1 1 1 1 A. . B. . C. . D. . 12 6 8 4 Lời giải Chọn C S K H D A O B C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 13 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1
Vì H và K , O lần lượt là trung điểm của SB và SD , BD nên S  S OHK 4 SBD 1 1 1 V 1 Suy ra AOHK V  V  V  V   . AOHK . A SBD S.ABD S. 4 4 8 ABCD V 8 S.ABCD
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm SB và G là trọng tâm
của tam giác SBC . Gọi V ,V  lần lượt là thể tích của các khối chóp M .ABC và G.ABD , tính tỉ V số . V  V 3 V 4 V 5 V 2 A.  . B.  . C.  . D.  . V  2 V  3 V  3 V  3 Lời giải S M G D C O B A Chọn A Cách 1:
Gọi V là thể tích khối chóp S.ABCD . V SM 1 Ta có M.ABC   . V SB 2 S.ABC 1 1 Mặt khác V  V  V  V . S.ABC S. 2 ABCD M .ABC S. 4 ABCD 1 1
Dễ thấy d G, ABCD  d S, ABCD ; S  S . 3 ABD 2 ABCD 1 Vậy V  .V . G.ABD 6 ABCD 1 V 3 Suy ra, M.ABC 4   . V 1 2 G.ABD 6 Cách 2: V V GC 2 V 3 G.ABD G.ABC M .ABC      V V MC 3 V 2 M .ABC M .ABC G.ABD
Câu 25. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , SA  a và SA vuông góc
với mặt phẳng  ABC  . Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng
SB và SC . Thể tích V của khối chóp . A BCNM bằng Trang 14 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 48 24 16 Lời giải Chọn D 2 1 a 3 3 a 3
Thể tích khối chóp S.ABC là V  . a  . S.ABC 3 4 12
Do SA  AB  AC  a nên các tam giác SAC, SAB cân tại A .
Theo đề bài M , N là hình chiếu của A trên SB , SC nên M , N lần lượt là trung điểm SB , SC . 3 V SM.SN 1 1 a 3 Khi đó: S.AMN    V  V  . S.AMN S. V . SB SC 4 4 ABC 48 S.ABC 3 3 3 a 3 a 3 a 3
Vậy thể tích khối chóp . A BCNM là V  V V    . . A BMNC S.ABC S .AMN 12 48 16
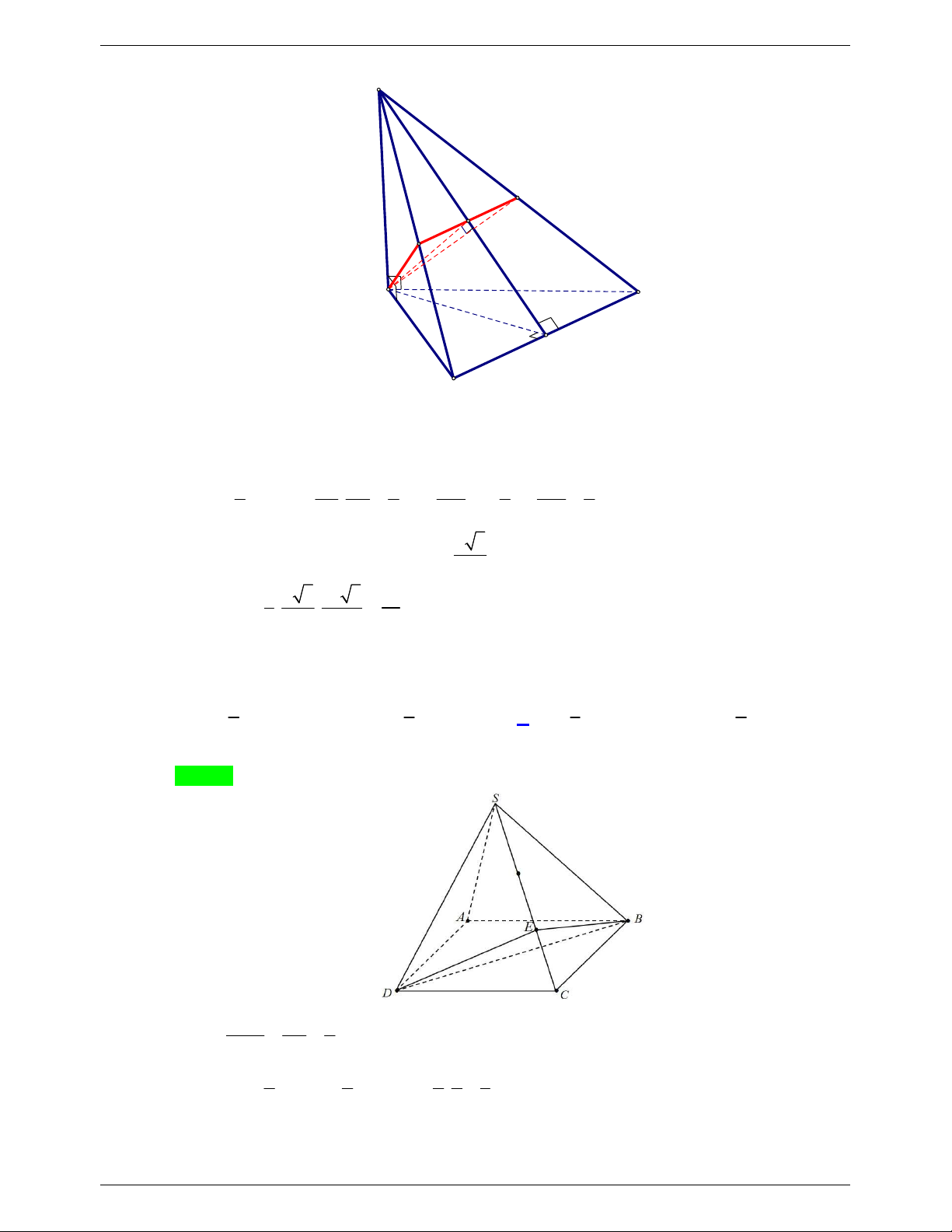
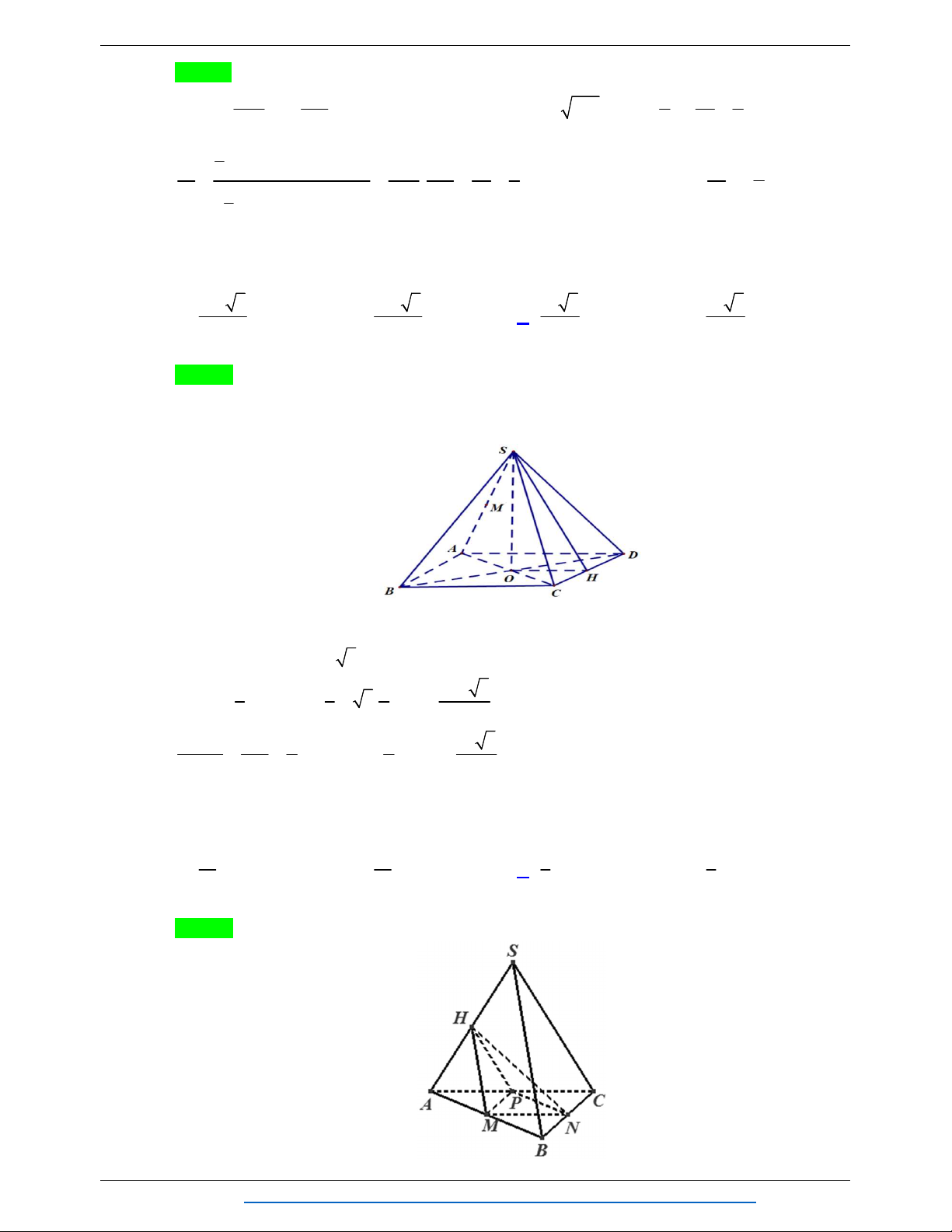
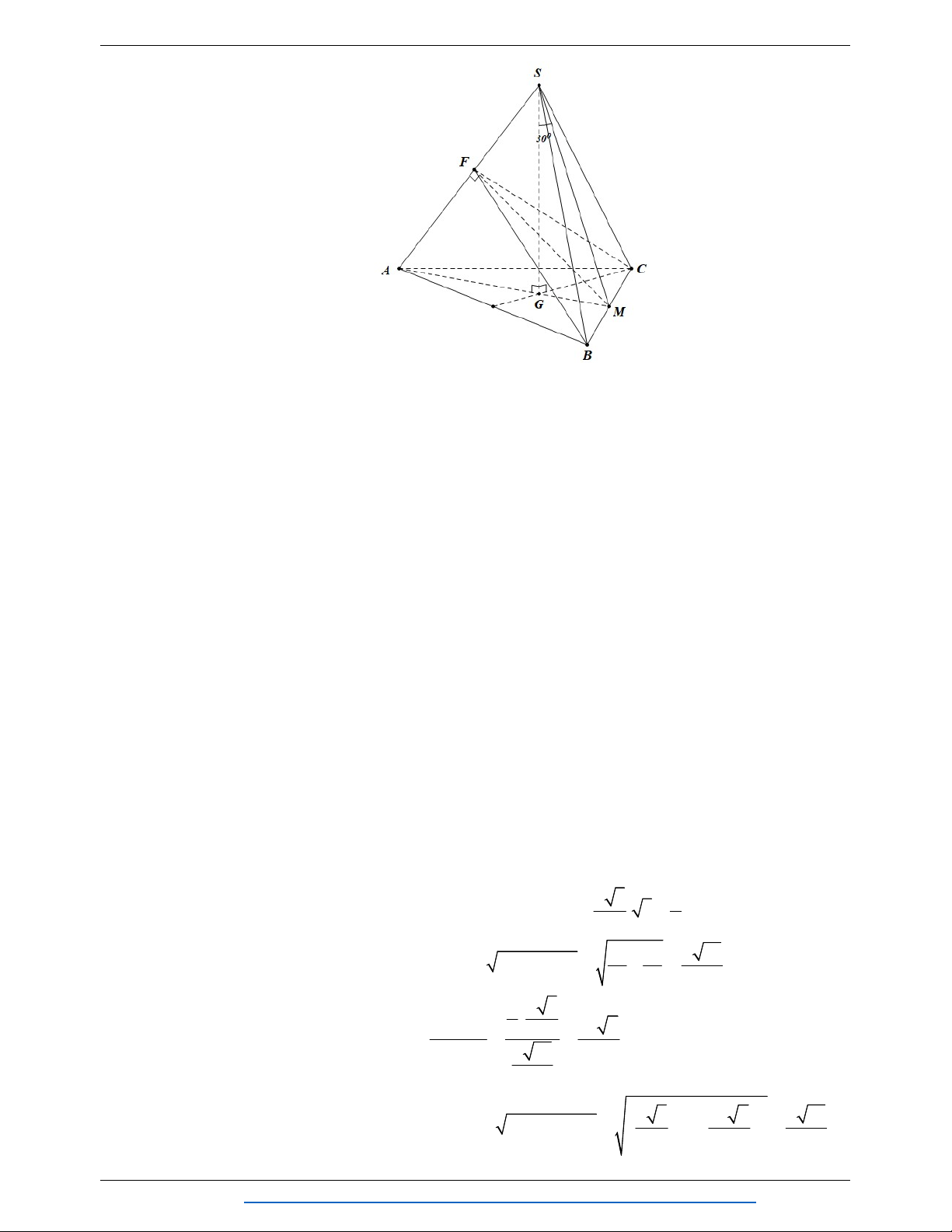
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt đáy. Gọi M
là trung điểm BC . Mặt phẳng P đi qua A và vuông góc với SM cắt SB , SC lần lượt tại E , 1 F . Biết V  V
. Tính thể tích V của khối chóp S.ABC . S.AEF S . 4 ABC 3 a 3 a 3 2a 3 a A. V  . B. V  . C. V  . D. V  . 2 8 5 12 Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 15 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT S F H E A C M B
Ta có BC  SM . Gọi H là hình chiếu vuông góc của A trên SM . Do FE  P  SBC
 FE  SM  FE  BC và FE đi qua H . 1 SE SF 2  SH  1 SH 1 V  1 V  .    
 . Vậy H là trung điểm cạnh SM . S.AEF S.   4 ABC SB SC 4  SM  4 SM 2 a 3
Suy ra SAM vuông cân tại A  SA  . 2 2 1 a 3 a 3 3 a Vậy V  . .  . SABC 3 2 4 8
Câu 27. Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm
E sao cho SE  2EC . Tính thể tích V của khối tứ diện SEBD . 2 1 1 4 A. V  . B. V  . C. V  . D. V  . 3 6 3 3 Lời giải Chọn C V SE 2 Ta có: SEBD   . V SC 3 SCBD 1 1 Mà: V  V  2 1 1  V  .  . SBCD S. 2 ABCD 2 SEBD 3 2 3
Câu 28. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể
tích của khối chóp đó sẽ: Trang 16 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 A. Không thay đổi. B. Tăng lên hai lần. C. Giảm đi ba lần. D. Giảm đi hai lần. Lời giải Chọn A
Nếu tăng cạnh đáy lên hai lần thì diện tích đáy tăng bốn lần. Vì giảm chiều cao đi bốn lần nên thể
tích khối chóp không thay đổi.
Câu 29. Cho tứ diện MNPQ . Gọi I ; J ; K lần lượt là trung điểm của các cạnh MN ; MP ; MQ . Tỉ số V thể tích MIJK bằng VMNPQ 1 1 1 1 A. . B. . C. . D. . 3 4 6 8 Lời giải Chọn D M I K J N Q P VM IJK MI MJ MK 1 1 1 1 Ta có: .  . .  . .  . V MN MP MQ 2 2 2 8 M .NPQ Câu 30. Cho tứ diện ABC .
D Gọi B ',C ' lần lượt là trung điểm của AB, AC. Khi đó tỉ số thể tích của khối
tứ diện AB 'C ' D và khối tứ diện ABCD bằng: 1 1 1 1 A. . B. . C. . D. . 8 2 4 6 Lời giải Chọn C A B' C' B D C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 17 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V AB ' AC ' 1 1 1 Ta có AB'C'D  .  .  . V AB AC 2 2 4 ABCD
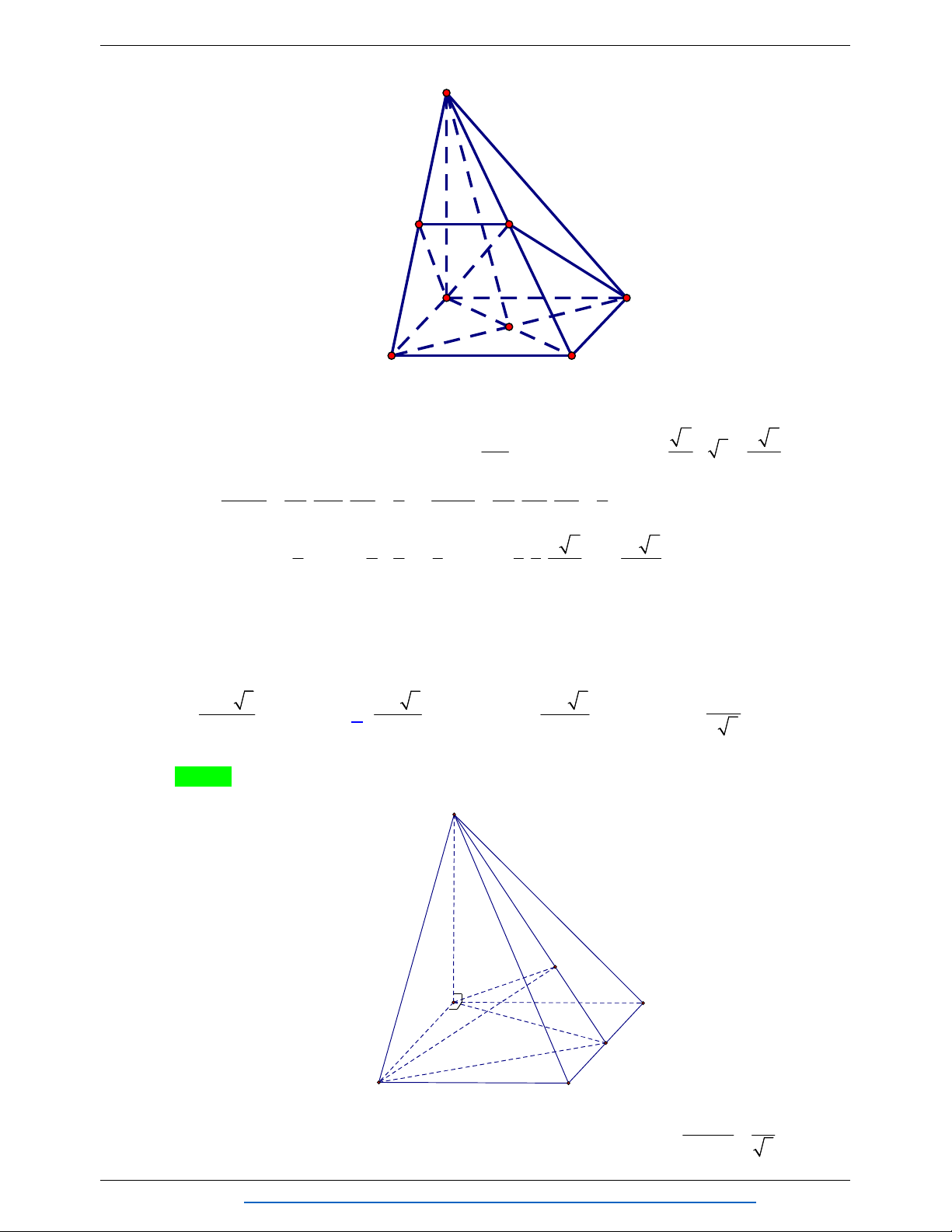
Câu 31. Cho tứ diện OABC có OA  a, OB  2a, OC  3a đôi một vuông góc với nhau tại O . Lấy M là 2
trung điểm của cạnh AC; N nằm trên cạnh CB sao cho CN  CB . Tính theo a thể tích khối 3 chóp OAMNB . 1 2 1 A. 3 2a . B. 3 a . C. 3 a . D. 3 a . 6 3 3 Lời giải Chọn C Ta có: A M O C N B 1 V  d A OBC S  OAOB OC  a OABC  ;  1 3 . . . 3 O  BC 6 a V  d M OBC S  d M OBC S  V  MOBC    OCN    3 1 1 1 2 1 ; . . . ; . . 3 3 2 3 O  BC 3 OABC 3 3 3 a 2a 3 V  V V  a   . AOMNB OABC MOBC 3 3
Câu 32. Cho hình chóp S.ABCD . Gọi M , N , P , Q theo thứ tự là trung điểm của SA , SB , SC , SD .
Tính tỉ số thể tích của hai khối chóp S.MNPQ và S.ABCD bằng 1 1 1 1 A. . B. . C. . D. . 8 2 4 16 Lời giải Chọn A Trang 18 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S Q M N P D A B C 1 1 Ta có V  V và V  V S.MNP S. 8 ABC S.MQP S. 8 ADC 1 1 1  V  V V  V  V  V S.MNPQ S.MQP S.MNP S.ABC S.ADC S. 8 8 8 ABCD VS.MNPQ 1   . V 8 S.ABCD
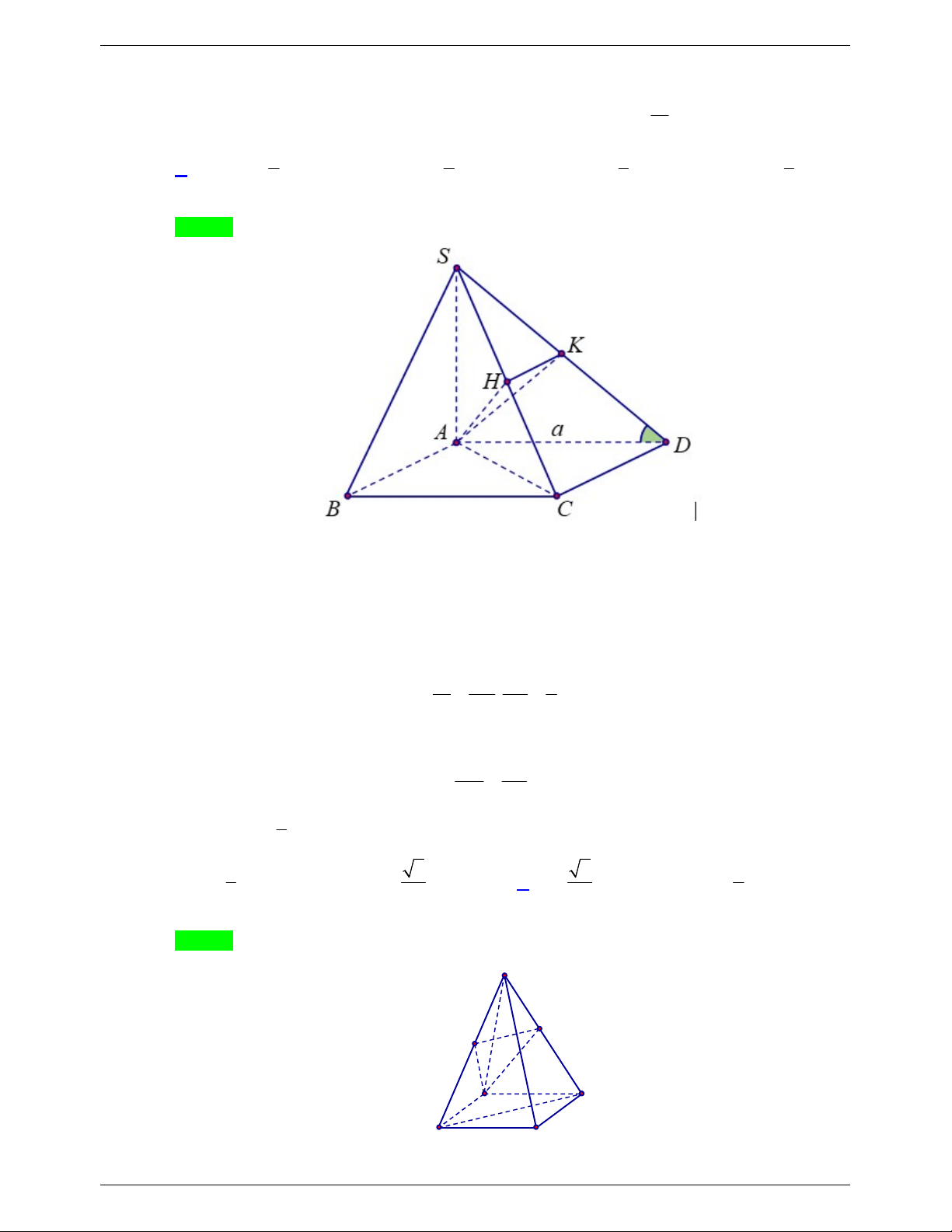
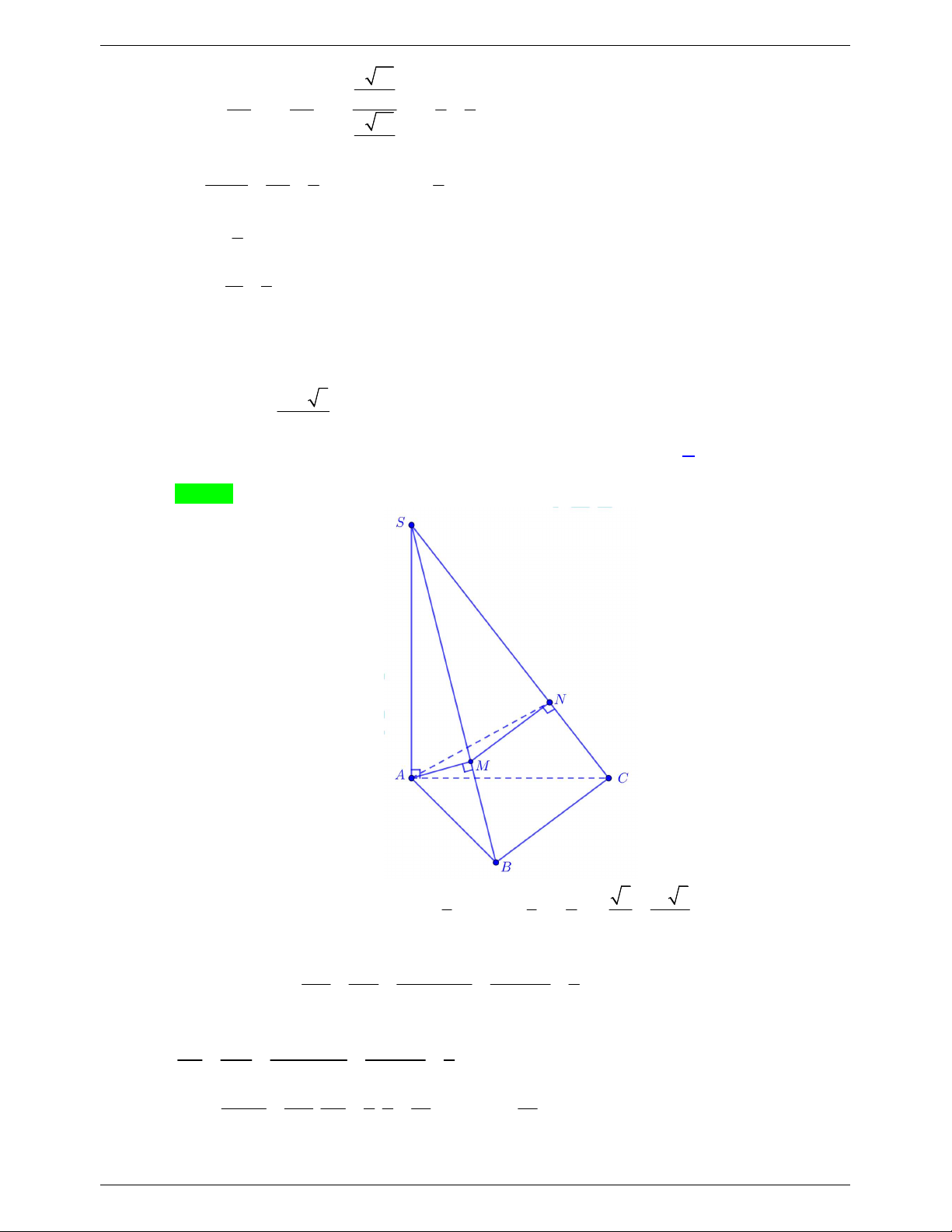
Câu 33. Cho hình chóp S.ABC có SA   ABC , tam giác ABC đều, AB  a , góc giữa SB và  ABC
bằng 60 . Gọi M , N lần lượt là trung điểm của SA , SB . Tính thể tích khối chóp S.MNC 3 a 3 a 3 3 a A. . B. . C. a 3 . D. . 8 4 12 16 Lời giải Chọn D Ta có S , B  ABC  S ,BAB   SBA  60 . SA  AB.tan  SBA  . a tan 60  a 3 . 2 1 1 a 3 1 3 V  .S . A S  .a 3.  a . S . ABC 3 ABC 3 4 4 1 1 Mà V SM SN 1 S .CMN  .  3 V  V  a . V SA SB 4 S.CMN S. 4 CAB 16 S .CAB
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hai mặt bên SAB và SAD
cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng SCD và  ABCD bằng 45. Gọi
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 19 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
V ;V lần lượt là thể tích khối chóp S.AHK và S.ACD với H , K lần lượt là trung điểm của SC 1 2 V
và SD . Tính độ dài đường cao của khối chóp S.ABCD và tỉ số 1 k  . V2 1 1 1 1 A. h  ; a k  . B. h  ; a k  . C. h  2 ; a k  . D. h  2 ; a k  . 4 6 8 3 Lời giải Chọn A
Do SAB và SAD cùng vuông góc với mặt đáy nên SA   ABCD . C  D  AD Ta có 
 CD  SAD  CD  SD . C  D  SA
Dễ thấy góc giữa hai mặt phẳng SCD và  ABCD là  SDA  45 .
Ta có tam giác SAD là tam giác vuông cân đỉnh A . Vậy h  SA  a . V SH SK 1
Áp dụng công thức tỉ số thể tích có: 1  .  . V SC SD 4 2
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có thể tích bằng 2 . Gọi M , N lần lượt là SM SN
các điểm trên cạnh SB và SD sao cho 
 k . Tìm giá trị của k để thể tích khối chóp SB SD 1 S.AMN bằng . 8 1 2 2 1 A. k  . B. k  . C. k  . D. k  . 8 2 4 4 Lời giải Chọn C S N M A D B C Trang 20 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 V SA SM SN Ta có S.AMN 2  . .  k . V SA SB SD S.ABD 1 1 1 2 Mà 2 V  , V  V  1  k  k  . S. AMN S.ABD S. 8 2 ABCD 8 4 V
Câu 36. Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của SA , SB . Tính tỉ số S.ABC . VS.MNC 1 1 A. 4 . B.  C. 2 . D.  2 4 Lời giải. Chọn A S M N C A B V SA SB SC Ta có S.ABC  . .  4 . V SM .SN.SC S.MNC
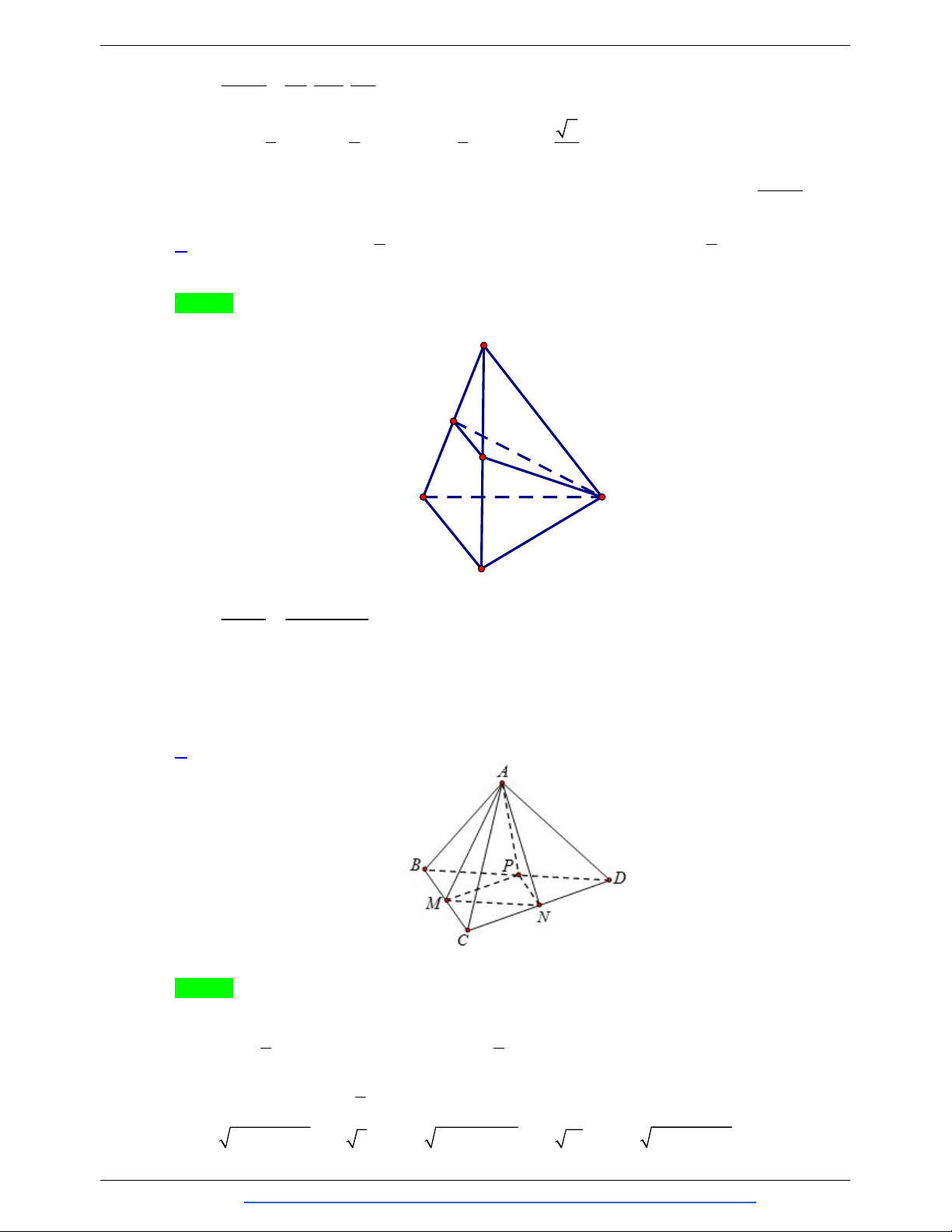
Câu 37. Cho tứ diện ABCD có các cạnh AB , AC , AD vuông góc với nhau từng đôi một và AB  3a ,
AC  6a , AD  4a . Gọi M , N , P lần lượt là trung điểm các cạnh BC , CD , BD . Tính thể
tích khối đa diện AMNP . A. 3 3a . B. 3 12a . C. 3 a . D. 3 2a . Lời giải Chọn A
 Cách 1: Khối tứ diện ABCD được chia thành bốn tứ diện có thể tích bằng nhau. 1 1 Mà 3 V  A . B AC.AD 12a nên 3 V  V  3a . ABCD 6 AMNP 4 ABCD 1  Cách 2: Ta có 3 V  . AB AC.AD  12a . ABCD 6 2 2 BC  AB  AC  3a 5 ; 2 2 CD  AC  AD  2a 13 ; 2 2 BD  AB  AD  5a .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 21 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3a 5  2a 13  5a Diện tích tam giác BCD : S
 p p  BC p  CD p  BD , với p  BCD     2 3V 12a 2  S  3a 29  d  , A BCD ABCD   . BCD SBCD 29
Mà M , N , P là trung điểm các cạnh BC , CD , BD nên hai tam giác BCD và MNP đồng dạng 1 1 theo tỉ số k  nên S  S 2 MNP 4 BCD 1 Khi đó V  .S .d A MNP  a . AMNP MNP  ,  3 3 3
Câu 38. Cho hình chóp S.ABC có đáy là A
 BC vuông cân ở B, AC  a 2, SA   ABC, SA  . a Gọi G là trọng tâm của S
 BC , mp đi qua AGvà song song với BC chia khối chóp thành hai
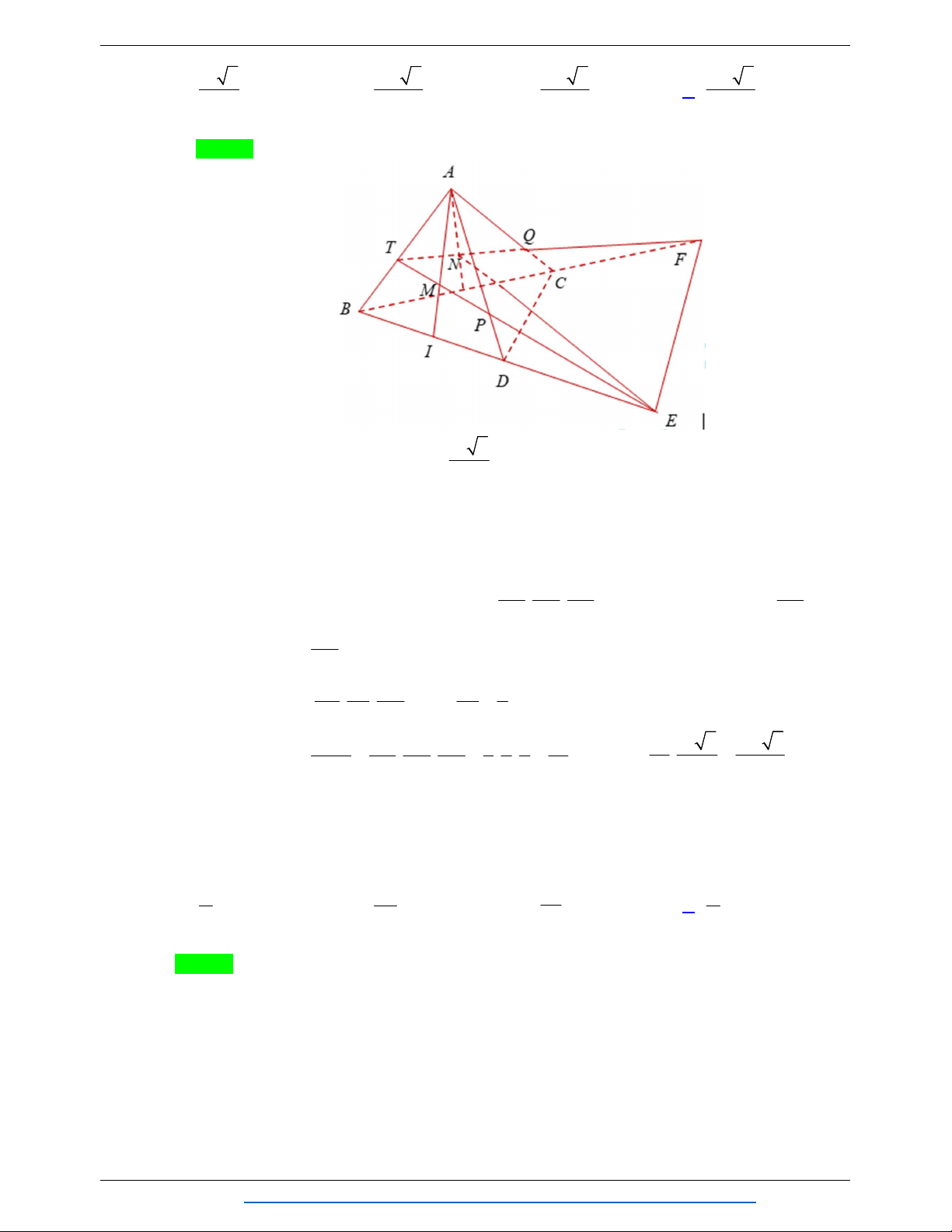
phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S . Tính V. 3 4a 3 4a 3 5a 3 2a A. . B. . C. . D. . 9 27 54 9 Lời giải Chọn C
Trong mặt phẳng SBC  . Qua G kẻ đường thẳng song song với BC và lần lượt cắt SC, SB tại
E, F . Khi đó ta được khối đa diện không chứa đỉnh S là ABCEF. V SA SF SE 2 2 4
Ta có G là trọng tâm của S  BC nên S.AFE  . .  .  . V SA SB SC 3 3 9 S.ABC 4 4 5 Do đó V  .V  V  V  .V  .V . S .AFE S .ABC ABCEF S . S .ABC S . 9 ABC 9 9 ABC Vì tam giác A
 BC vuông cân ở B, AC  a 2 nên AB  BC  . a 3 1 1 a 3 3 5 a 5a Mặt khác V  . a . a a  .Suy ra V  .  . . S.ABC 3 2 6 ABCEF 9 6 54
Câu 39. Cho hình chóp tam giác đều S.ABC . Gọi M , N lần lượt là trung điểm của BC , SM . Mặt phẳng
 ABN  cắt SC tại E . Gọi V là thể tích của khối chóp S.ABE và V là thể tích khối chóp S.ABC 2 1
. Khẳng định nào sau đây đúng? Trang 22 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 1 1 1 A. V  V . B. V  V . C. V  V . D. V  V . 2 1 4 2 1 3 2 1 6 2 1 8 Lời giải Chọn B
Gọi I là trung điểm của EC nên IM là đường trung bình của tam giác BCE  MI //EN
Mà N là trung điểm của SM  EN là đường trung bình của tam giác SMI suy ra E là trung điểm của SI . V SE 1 1 2    V  V . 2 1 V SC 3 3 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 23 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
4. KHỐI LĂNG TRỤ - MỨC 2
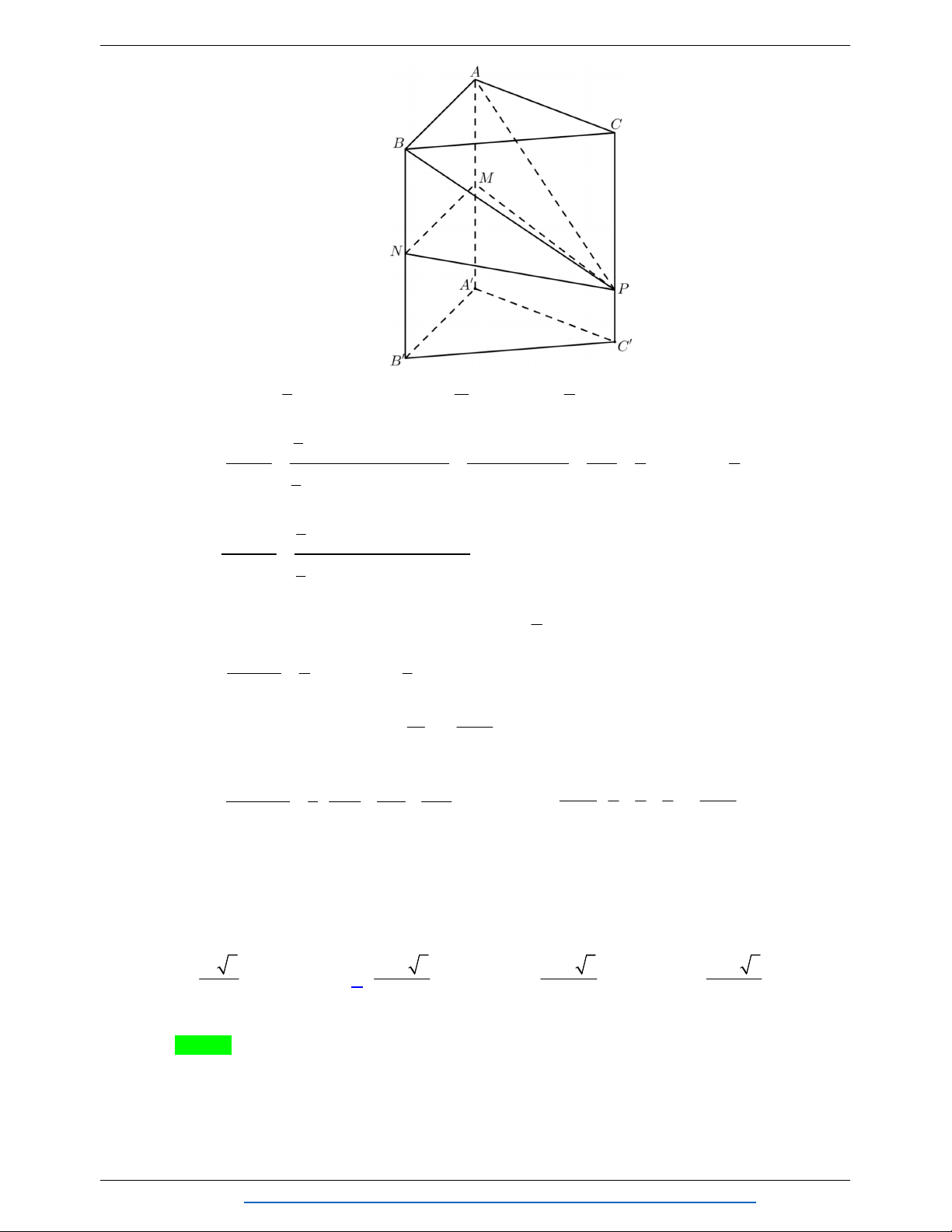
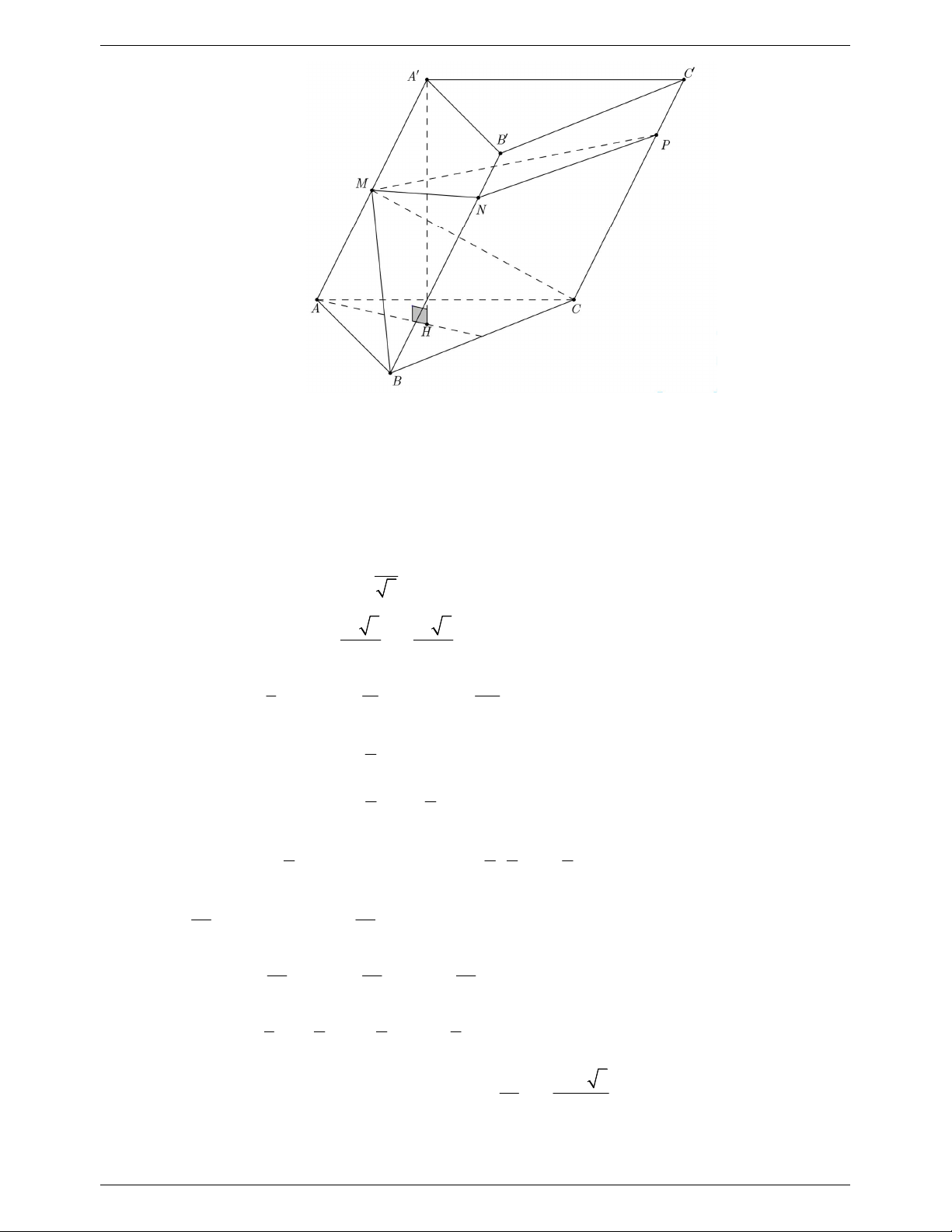
Câu 40. Cho lăng trụ tam giác đều ABC.AB C
  . Lấy H , G lần lượt là tâm của hình chữ nhật B C C B   và A C C A
  , I là trung điểm của CC  . Tính tỉ số thể tích của tứ diện CHGI và tứ diện CB AC . 1 4 30 15 A. . B. . C. . D. . 8 5 8 2 Lời giải Chọn A V CH CG CI CH CG CI 1 CHGI  . .  . .  . V CB CA CC 2CH 2CG 2CI 8 CB' A'C ' B C H A I G B' C' A'
Câu 41. Cho hình hộp ABCD.AB C  D
  , gọi O là giao điểm AC và BD . Thể tích khối chóp O.AB C  D
  bằng bao nhiêu lần thể tích khối hộp ABCD.AB C  D   ? 1 1 1 1 A. . B. . C. . D. . 6 4 2 3 Lời giải Chọn D C B O D A C' B' A' D' Trang 24 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 V    1
Do khối chóp và khối hộp có cùng chiều cao và diện tích đáy nên O.A B C D '  VABCD.AB C D  ' 3
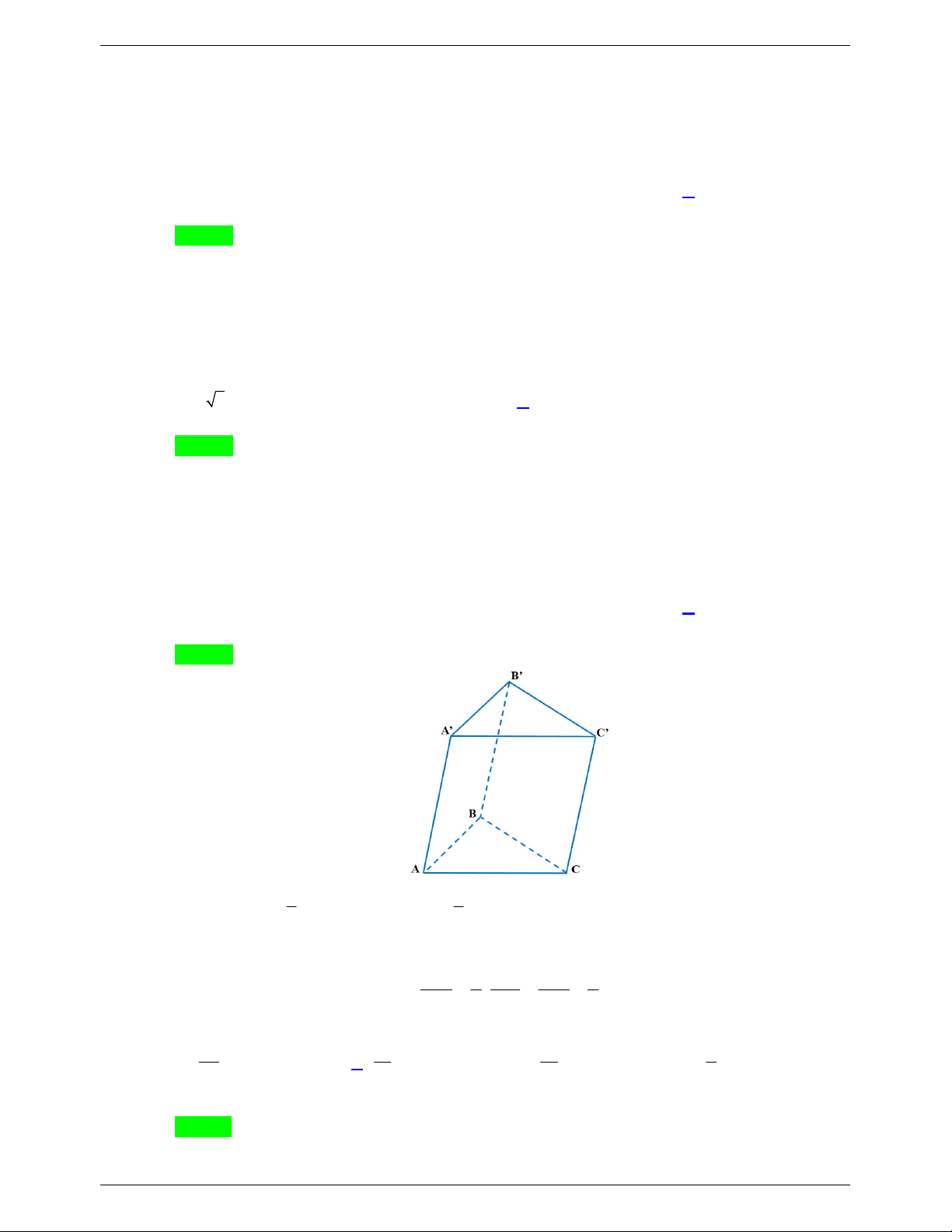
Câu 42. Cho hình lăng trụ tam giác AB .
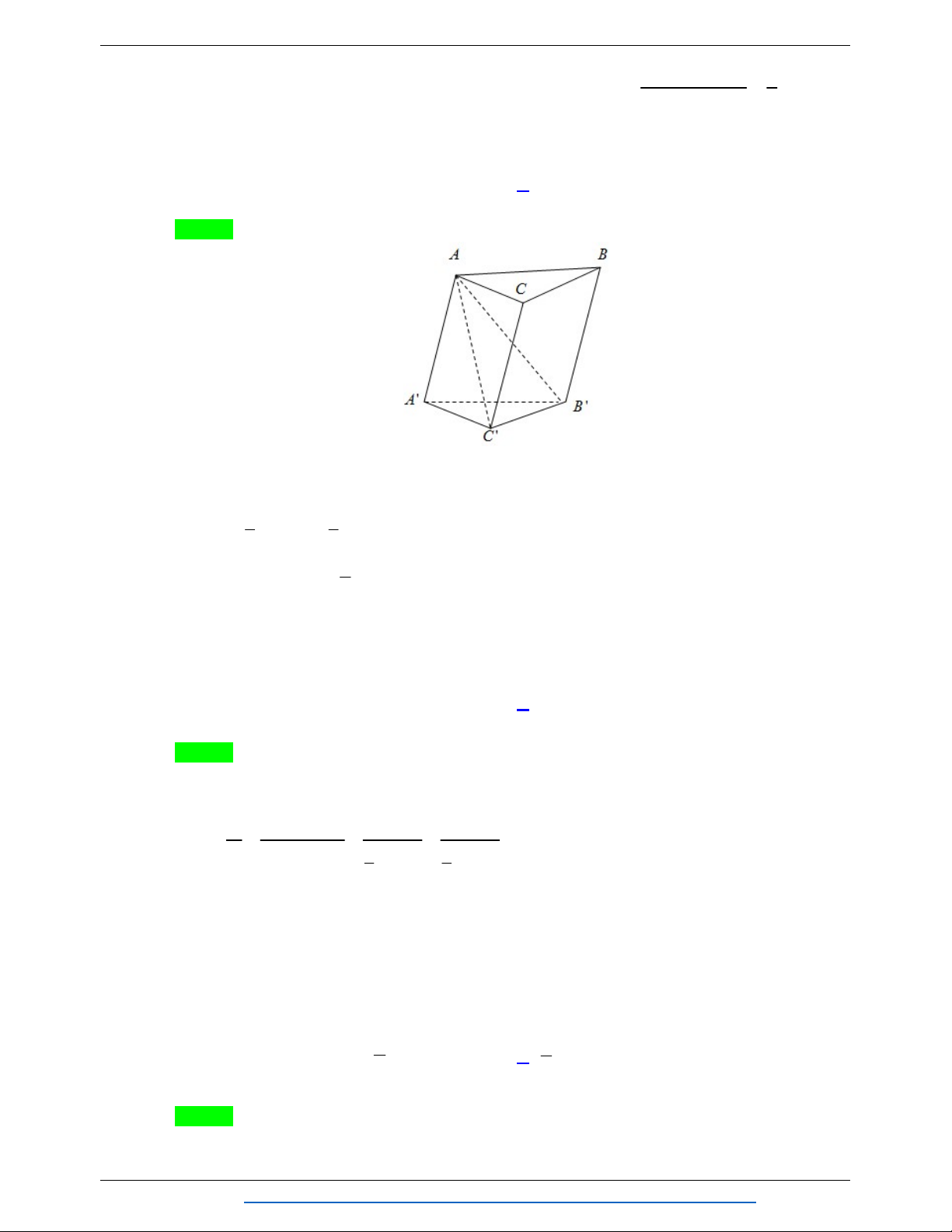
C A' B 'C ' , biết rằng thể tích khối chóp . A BCC ' B ' bằng 12 .Thể
tích khối lăng trụ ABC.A' B 'C 'bằng A. 24 . B. 36 . C. 18 . D. 32 . Lời giải Chọn C
Ta có: Đặt V  VABC.A'B'C' V  . h S . A'B'C ' 1 1 V  . h S  V. . A A'B 'C ' A'B 'C ' 3 3 2 V  V V  V  12  V 18. ABCC ' B' . A A' B 'C ' 3
Câu 43. ( Đề Thi thử Trường Chuyên Lê Thánh Tông_Quảng Nam_2020 ) Gọi V là thể tích của khối hộp ABC .
D A' B 'C ' D ' và V là thể tích của tứ diện A' BCD . Hệ thức nào sau đây đúng? 1 A. V  4V . B. V  2V . C. V  6V . D. V  3V . 1 1 1 1 Lời giải Chọn C
Gọi h là khoảng cách từ A ' đến mp (ABCD) . Khi đó, h là chiều cao của khối hộp cũng là
chiều cao của tứ diện A' BCD . V V S .h 2S .h Ta có: ABCD.A'B 'C 'D ' ABCD BCD     6 V V 1 1 1 A'BCD S .h S .h 3 BCD 3 BCD  V  6V . 1
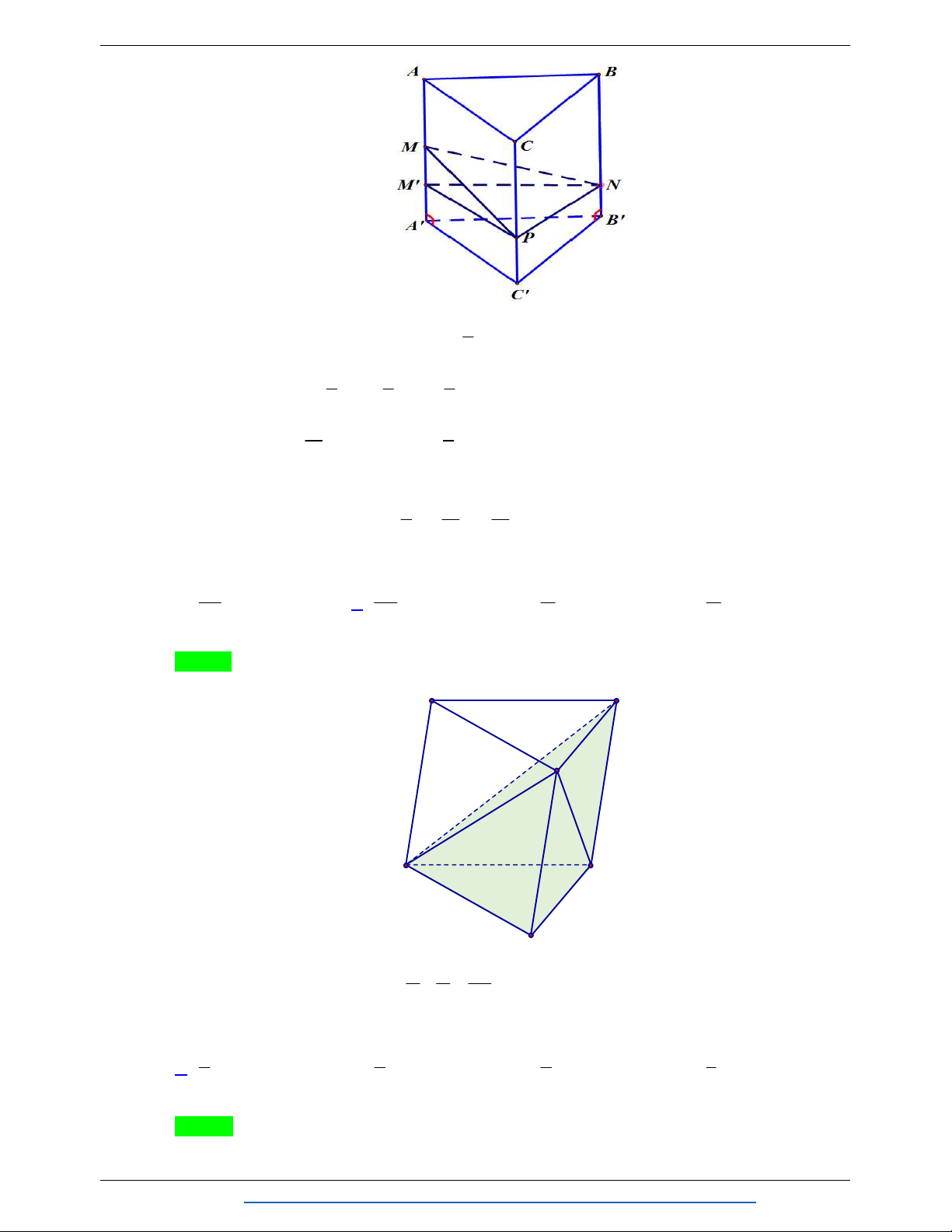
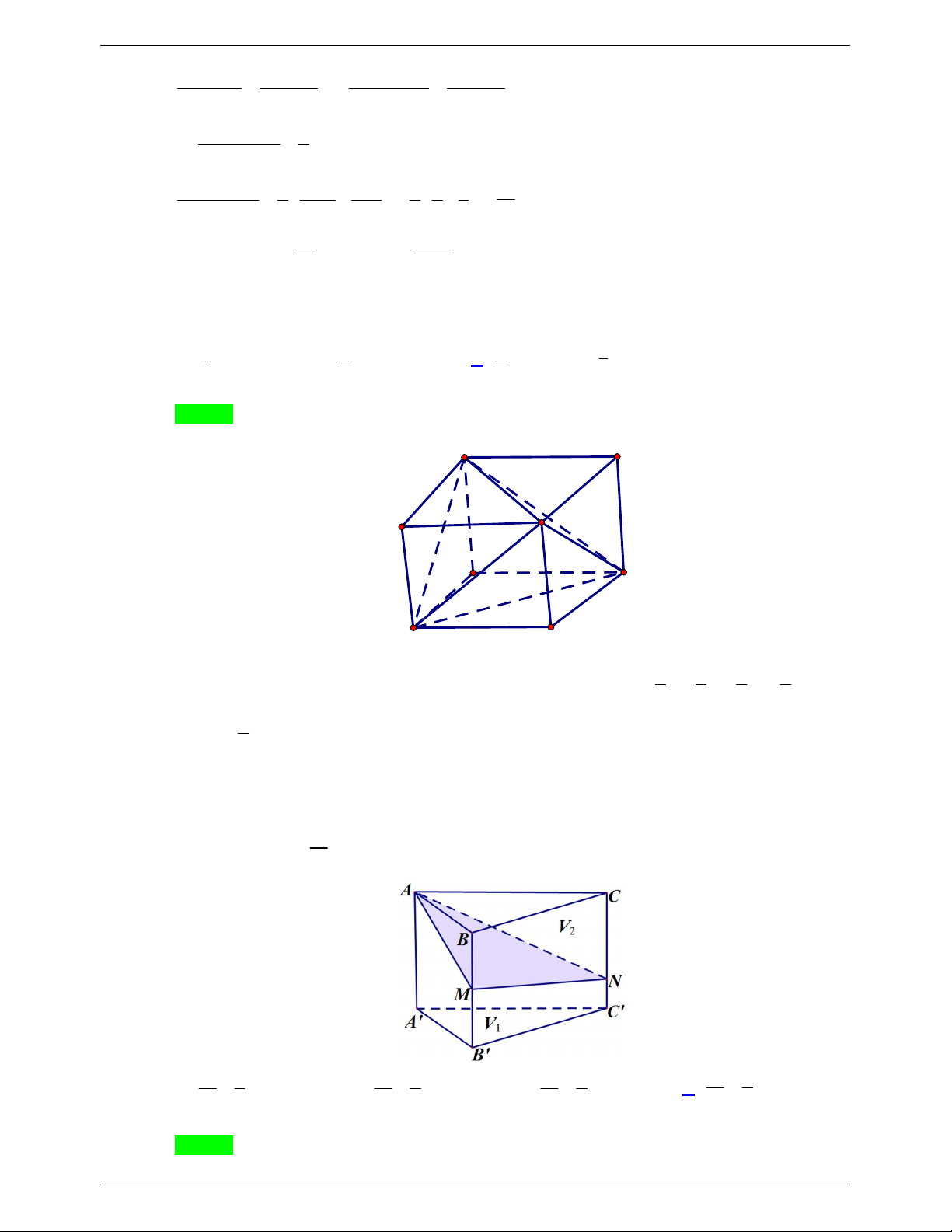
Câu 44. Cho lăng trụ tam giác A B C .AB C  có chiều cao bằng 4 và diện tích đáy bằng 3 . Gọi M , N ,
P lần lượt là tâm của các mặt bên ABB A   , B C C B
  và C A AC  . Thể tích khối đa diện lồi có
các đỉnh là các điểm A , B , C , M , N , P bằng 9 9 A. 6 . B. . C. . D. 3 . 4 2 Lời giải Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 25 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT C A B P K I N M J C' A' B' Ta có V  3.4  12 . Gọi , ,
lần lượt là trung điểm của , , . ABC .AB C  I J K AA BB  C C   V  6 . A BC .IJK V 1 1 1
Áp dụng bài toán tỷ số thể tích ta có: . AIMP   V  V  V 8 A.IMP A.AB C   . A A B  C   8 2 1 Dễ thấy V  V  V  . A.IMP B.MNJ C.NPK 2 1 9 Vậy V  V  3V  6  3.  . ABC .M N P ABC .IJK A.IM P 2 2
Câu 45. Nếu cạnh của một hình lập phương tăng lên 3 lần thì thể tích của hình lập phương đó tăng lên bao nhiêu lần? A. 27. B. 9. C. 6. D. 4. Lời giải Chọn A
Gọi cạnh của hình lập phương là athì thể tích khối lập phương là 3 V  a .
Khi tăng cạnh lên 3 lần thì cạnh là 3a , thể tích khối lập phương mới là V   a3 * 3 3  27a . Khi đó * V  27V .
Câu 46. Nếu cạnh của một hình lập phương tăng lên 2 lần thì thể tích của hình lập phương đó tăng lên bao nhiêu lần? A. 9. B. 2. C. 4. D. 8. Lời giải Chọn D
Gọi cạnh của hình lập phương là athì thể tích khối lập phương là 3 V  a .
Khi tăng cạnh lên 2 lần thì cạnh là 2a, thể tích khối lập phương mới là V   a3 * 3 2  8a . Khi đó * V  8V .
Câu 47. Nếu thể tích của một hình lập phương tăng lên 8 lần thì cạnh của hình lập phương đó tăng lên bao nhiêu lần? A. 2 2 . B. 4. C. 2. D. 8. Trang 26 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 Lời giải Chọn C
Gọi cạnh của hình lập phương là athì thể tích khối lập phương là 3 V  a .
Khi tăng thể tích lên 8 lần thì thể tích là * 3 V  8V  8a .
Khi đó cạnh của hình lập phương là 2a. Kết luận: Cạnh tăng lên 2 lần.
Câu 48. ( Đề Thi thử Trường Chuyên Lê Thánh Tông_Quảng Nam_2020 ) Gọi V là thể tích của khối hộp ABC .
D A' B 'C ' D ' và V là thể tích của tứ diện A' BCD . Hệ thức nào sau đây đúng? 1 A. V  4V . B. V  2V . C. V  6V . D. V  3V . 1 1 1 1 Lời giải Chọn C
Gọi h là khoảng cách từ A ' đến mp (ABCD) . Khi đó, h là chiều cao của khối hộp cũng là
chiều cao của tứ diện A' BCD . V V S .h 2S .h Ta có: ABCD.A'B 'C 'D ' ABCD BCD     6 V V 1 1 1 A'BCD S .h S .h 3 BCD 3 BCD  V  6V . 1
Câu 49. Cho hình lăng trụ tam giác AB .
C A' B'C ', biết rằng thể tích khối chóp . A BCC ' B'bằng 12 .Thể tích khối lăng trụ AB . C A' B'C 'bằng A. 24 . B. 36 . C. 18 . D. 32 . Lời giải Chọn C
Ta có: Đặt V  VABC.A'B'C' V  . h S . A'B 'C ' 1 1 V  . h S  V. . A A' B'C ' A'B'C ' 3 3 2 V  V V  V  12  V  18. ABCC 'B ' . A A'B 'C ' 3
Câu 50. Nếu cạnh của một hình lập phương tăng lên 3 lần thì thể tích của hình lập phương đó tăng lên bao nhiêu lần? A. 27. B. 9. C. 6. D. 4. Lời giải Chọn A
Gọi cạnh của hình lập phương là athì thể tích khối lập phương là 3 V  a .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 27 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Khi tăng cạnh lên 3 lần thì cạnh là 3a , thể tích khối lập phương mới là V   a3 * 3 3  27a . Khi đó * V  27V .
Câu 51. Nếu cạnh của một hình lập phương tăng lên 2 lần thì thể tích của hình lập phương đó tăng lên bao nhiêu lần? A. 9. B. 2. C. 4. D. 8. Lời giải Chọn D
Gọi cạnh của hình lập phương là athì thể tích khối lập phương là 3 V  a .
Khi tăng cạnh lên 2 lần thì cạnh là 2a, thể tích khối lập phương mới là V   a3 * 3 2  8a . Khi đó * V  8V .
Câu 52. Nếu thể tích của một hình lập phương tăng lên 8 lần thì cạnh của hình lập phương đó tăng lên bao nhiêu lần? A. 2 2 . B. 4. C. 2. D. 8. Lời giải Chọn C
Gọi cạnh của hình lập phương là athì thể tích khối lập phương là 3 V  a .
Khi tăng thể tích lên 8 lần thì thể tích là * 3 V  8V  8a .
Khi đó cạnh của hình lập phương là 2a. Kết luận: Cạnh tăng lên 2 lần.
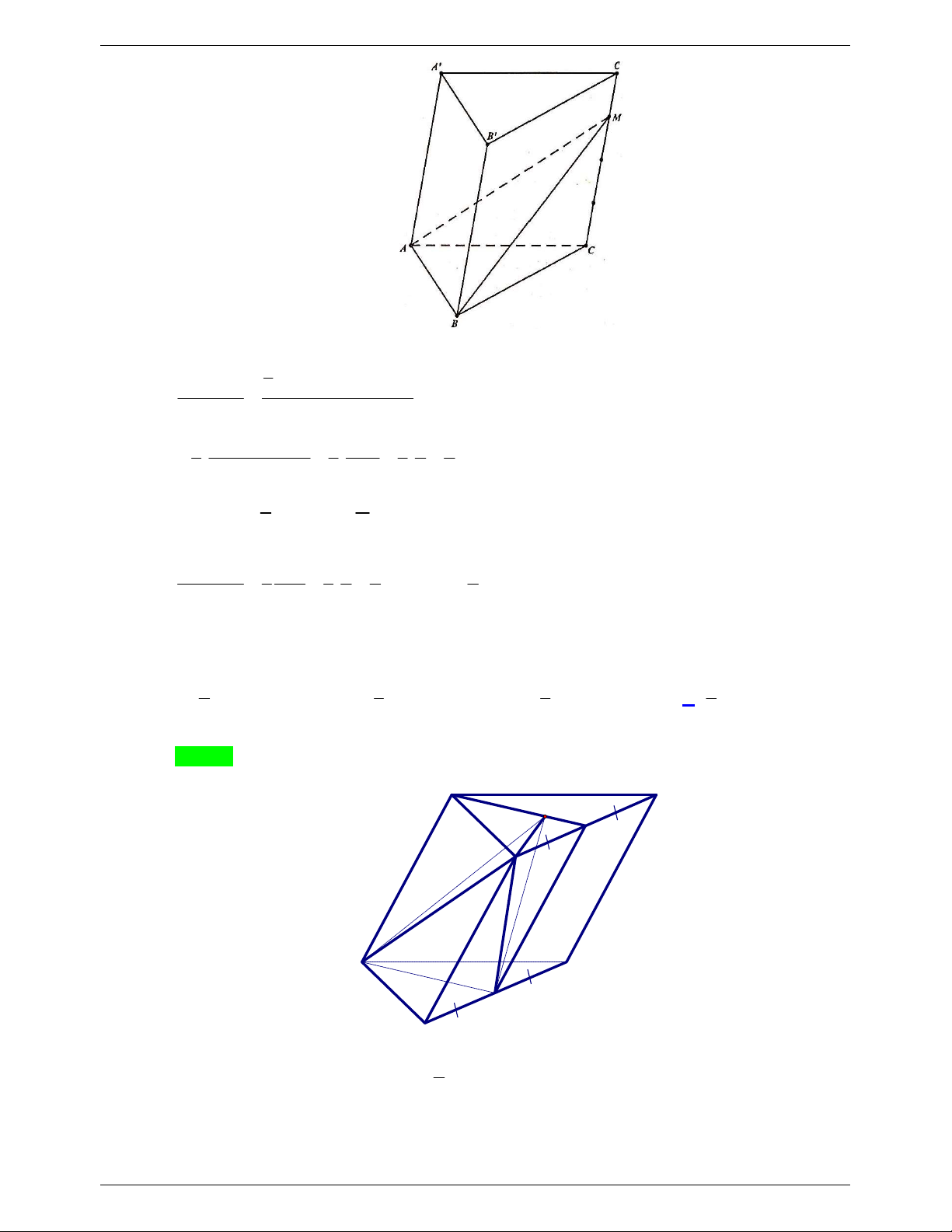
Câu 53. Khối lăng trụ tam giác AB . C AB C  có thể tích bằng 3
66 cm . Tính thể tích khối tứ diện A .ABC . A. 3 11cm . B. 3 33cm . C. 3 44 cm . D. 3 22 cm . Lời giải Chọn D 1 1 Ta có: V   A ABC S  V   .d cm . A ABC  ,  3 . . ABC  A BC 22 . . 3 3 ABC
Câu 54. Cho hình lăng trụ đứng ABC.A ' B 'C ' có thể tích bằng V . Các điểm M , N , P lần lượt thuộc AM 1 BN CP 2
các cạnh AA' , BB ' , CC 'sao cho  , 
 . Thể tích khối đa diện ABC.MNP AA' 2 BB ' CC ' 3 bằng 20 11 9 2 A. V . B. V . C. V . D. V . 27 18 16 3 Lời giải Chọn B Trang 28 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 2
Lấy M ' thuộc đoạn AA ' sao cho AM '  AA' , khi đó ta có: 3 2 1 1
MM '  AM ' AM  AA ' AA '  AA ' 3 2 6 1 2 Dễ thấy V  V và V  V M .M ' NP 18 ABC.M ' NP 3
Gọi thể tích khối đa diện ABC.MNP là V ' 2 1 11 Ta có V '  V V  V  V  V ABC.M 'NP M .M ' NP 3 18 18
Câu 55. Cho khối lăng trụ AB . C A B  C
 có thể tích bằng V . Tính thể tích khối đa diện ABCB C   . 3V 2V V V A. . B. . C. . D. . 4 3 2 4 Lời giải Chọn B A C  B A C B V V 2V Ta có: V        V  V ABCB C B ABC C B  A  C 3 3 3
Câu 56. Cho lăng trụ tam giác ABC.A B  C
 có thể tích là V . Tính thể tích khối chóp . A BCC B   theo V . 2 2 1 1 A. V . B. V . C. V . D. V . 3 5 2 3 Lời giải Chọn A
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 29 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT A' C' B' A C B 1 1 Ta có V  Sh  V    . . A A B C 3 3 V 2V Suy ra V        V    V    V . . A BCC B ABC.A B C . A A B C 3 3
Câu 57. Gọi V là thể tích của khối lập phương ABC . D A B  C  D
  , V là thể tích khối tứ diện A A  BD . Hệ 1 2
thức nào sau đây là đúng? A. V  4V . B. V  6V . C. V  2V . D. V  8V . 1 2 1 2 1 2 1 2 Lời giải Chọn B A' C' D' B' A C D B 1 1
Cách 1: Giả sử cạnh của hình lập phương là a , ta có 3 V  a và V  AA .S 3  a suy ra 1 2 3 ABD 6 V  6V . 1 2 1 1 Cách 2: Ta có V  1 1 AA .S  1 AA . S  AA .S  V  V  6V . 2 3 ABD 3 2 ABCD 6 ABCD 1 6 1 2 1 1 Cách 3: Ta có V      V    V     V 6V . A ABD ABD.A B D ABCD.A B C D 1 2 3 6
Câu 58. Cho lăng trụ đứng ABC.A B  C
 có đáy là tam giác vuông cân tại A , AB  AC  a , A A   2a .
Thể tích của khối tứ diện ABB C  là Trang 30 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 3 2a 3 a A. . B. 3 2a . C. 3 a . D. . 3 3 Lời giải Chọn D A' C' B' A C B 1 1 1 3 a Ta có V  2     V 2 . a a . A BB C ABC. 3 AB C   3 2 3
Câu 59. Cho hình lăng trụ ABC.A B  C
 có thể tích là V . Gọi M là điểm thuộc cạnh CC sao cho CM  3C M
 . Tính thể tích V của khối chóp M.ABC V 3V V V A. . B. . C. . D. . 4 4 12 6 Lời giải Chọn A A C M B A C H K B
Gọi H , K lần lượt là hình chiếu vuông góc của C và M lên mặt phẳng  ABC  MK CM Ta có C H  3 // MK    . CC CC 4 1 1 3 V Khi đó V  MK.S  V  . CC .S  . M .ABC 3 ABC M .ABC 3 4 ABC 4
Câu 60. Cho lăng trụ ABC.A B  C
 có thể tích V . Điểm M là trung điểm cạnh AA . Tính theo V thể tích khối chóp M .BCC B   . 2V 3V V V A. . B. . C. . D. . 3 4 3 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 31 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT Lời giải Chọn A A' C' B' M A C B Gọi: V  V  AA .S . ABC.A B  C   A  BC V V 1  1 1 .M . A S  1 . .AA .S  V . M .ABC M .AB C   3 ABC 3 2 ABC 6 V Ta có: V    1 1 2   V V V  V  V  V  . M .BCC B M .ABC M .A B  C   6 6 3 Câu 61. Cho hình hộp ABC .
D A' B 'C ' D ' . Gọi V , V lần lượt là thể tích khối tứ diện ACB D   và khối hộp 1 2 V ABC . D A B  C  D   . Tỉ số 1 bằng: V2 1 1 1 1 A. . B. . C. . D. . 3 6 2 4 Lờigiải Chọn A 1 1 Ta có V       V  V    V    V     V . B .ABC D .ACD C.B C D . A A B D ABCD.A B C D 2 6 6 1 1 V 1 Suy ra 1 V  V  4. V  V   . 1 2 2 2 6 3 V 3 2
Câu 62. Một khối lập phương có thể tích gấp 24 thể tích một khối tứ diện đều. Hỏi cạnh của hình lập
phương gấp mấy lần cạnh của hình tứ diện đều? A. 2 . B. 2 2 . C. 2 . D. 1. Lời giải Chọn A
Gọi hình lập phương có cạnh là a , khối tứ diện đều có cạnh là b . Trang 32 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Khi đó, thể tích khối lập phương là: 3 V  a 1 3 b 2
Thể tích khối tứ diện đều là: V  . 2 12 3 b
Theo đề bài ta có: V  24V 3 2  a  24. 3 3  a  2 2b  a  2b . 1 2 12
Câu 63. Cho khối lăng trụ ABC.A B  C
  . Gọi V và V lần lượt là thể tích của khối lăng trụ đã cho và khối V  tứ diện ABB C   . Tỉ số bằng V 1 1 1 1 A. . B. . C. . D. . 3 4 2 6 Lời giải Chọn A Ta có: V      V   V    V . . A BB C ABC.A'B C . A A B C C .ABC 1 1 Mà V       V  .V . Nên V   .V . . A A B C C .ABC ABC.A' 3 B C   . A BB C ABC.A' 3 B C   V  1 Vậy  . V 3
Câu 64. Cho khối hộp ABC . D AB C  D
  có thể tích bằng 9 . Tính thể tích khối tứ diện ACB D  . 9 27 A. 3. B. . C. 6. D. . 2 4 Lời giải Chọn A. A D B C D A B C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 33 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Gọi h và V lần lượt là chiều cao và thể tích khối hộp. Ta có V    S .h ACB D ABCD 1 1 2 1 9 V            V 4V    V 4. . .S .h V V V 3. ACB D B CD C 3 2 ABCD 3 3 3
Câu 65. Cho khối lăng trụ AB . C A B  C
 có thể tích bằng V . Tính thể tích khối đa diện ABCB C   . 3V 2V V V A. . B. . C. . D. . 4 3 2 4 Lời giải Chọn B A C  B A C B V V 2V Ta có: V        V  V ABCB C B ABC C B  A  C 3 3 3 Trang 34 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 5. KHỐI CHÓP - MỨC 3
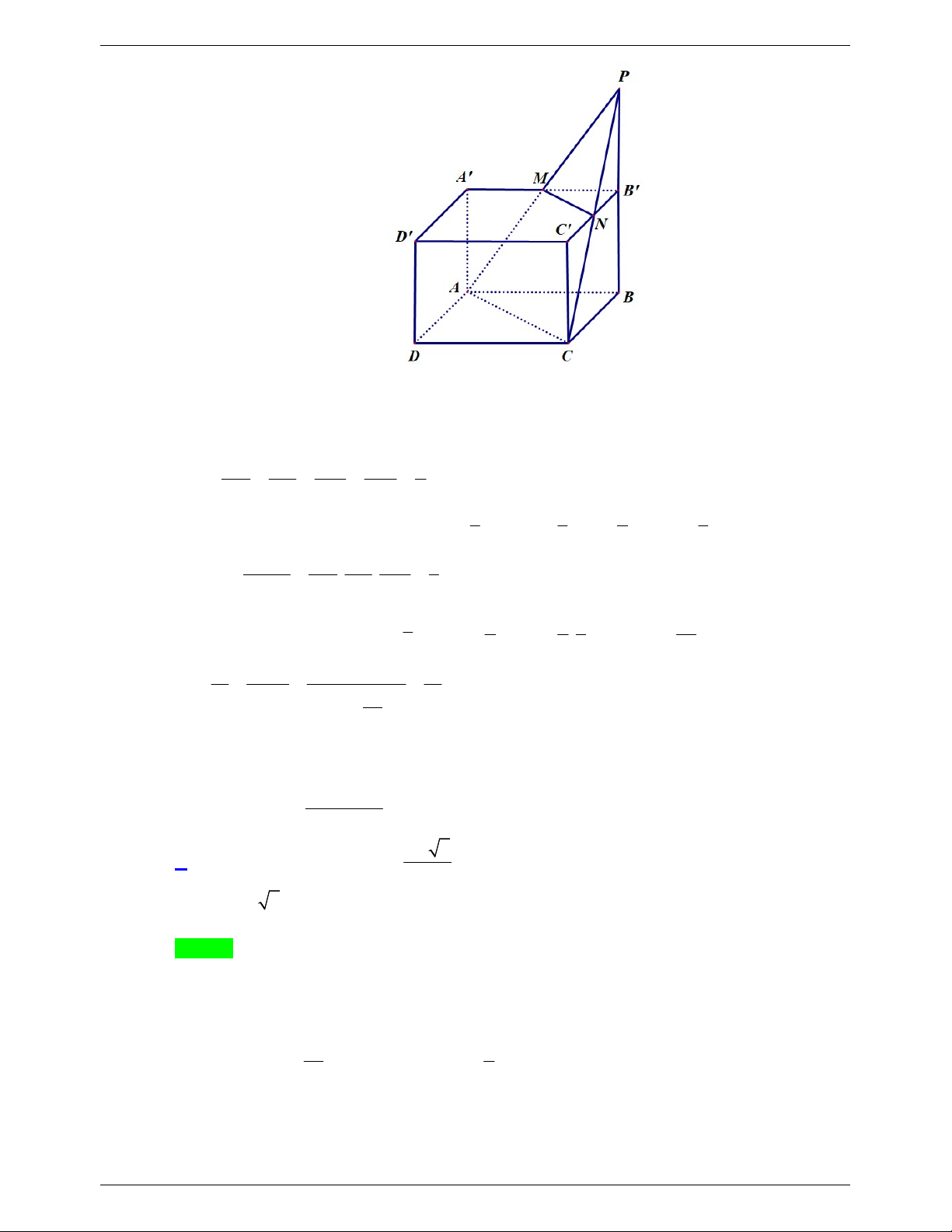
Câu 66. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và
SA  2a . Gọi B ; D lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SD . Mặt phẳng
 ABD cắt cạnh SC tại C . Tính thể tích của khối chóp S.ABCD 3 a 3 16a 3 a 3 2a A. . B. . C. . D. 3 45 2 4 Lời giải Chọn B S C' B' I D' B A O D C V SB SC Ta có V  V SABC  .   * S ABCD 2 S ABC 1 . .   mà V SB SC SABC
SAC vuông tại A nên SC  SA  AC   a  a 2 2 2 2 2 2 2 2  6a suy ra SC  a 6
Ta có BC  SAB  BC  AB và SB  AB suy ra AB  SBC  nên AB  BC
Tương tự AD  SC . Từ đó suy ra SC   ABD   ABCD nên SC  AC 2 2 SC SA 4a 2 Mà 2 SC .SC  SA suy ra    . Ta cũng có 2 2 SC SC 6a 3 2 2 2 SB SA SA 4a 4     2 2 2 2 2 SB SB SA  AB 4a  a 5 V 8 8 1 8 Từ   SABC 8 *   suy ra V  V  V  V SABC . mà V 15 15 SABC 15 2 SABCD 30 SABCD SABC 3 1 2  a V S .SA  SABCD 3 ABCD 3 3 3 8 2a 8a Suy ra V   SABC . 30 3 45 3 16a Từ   1 suy ra V  V  S ABCD 2 . . S.ABC 45
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 35 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
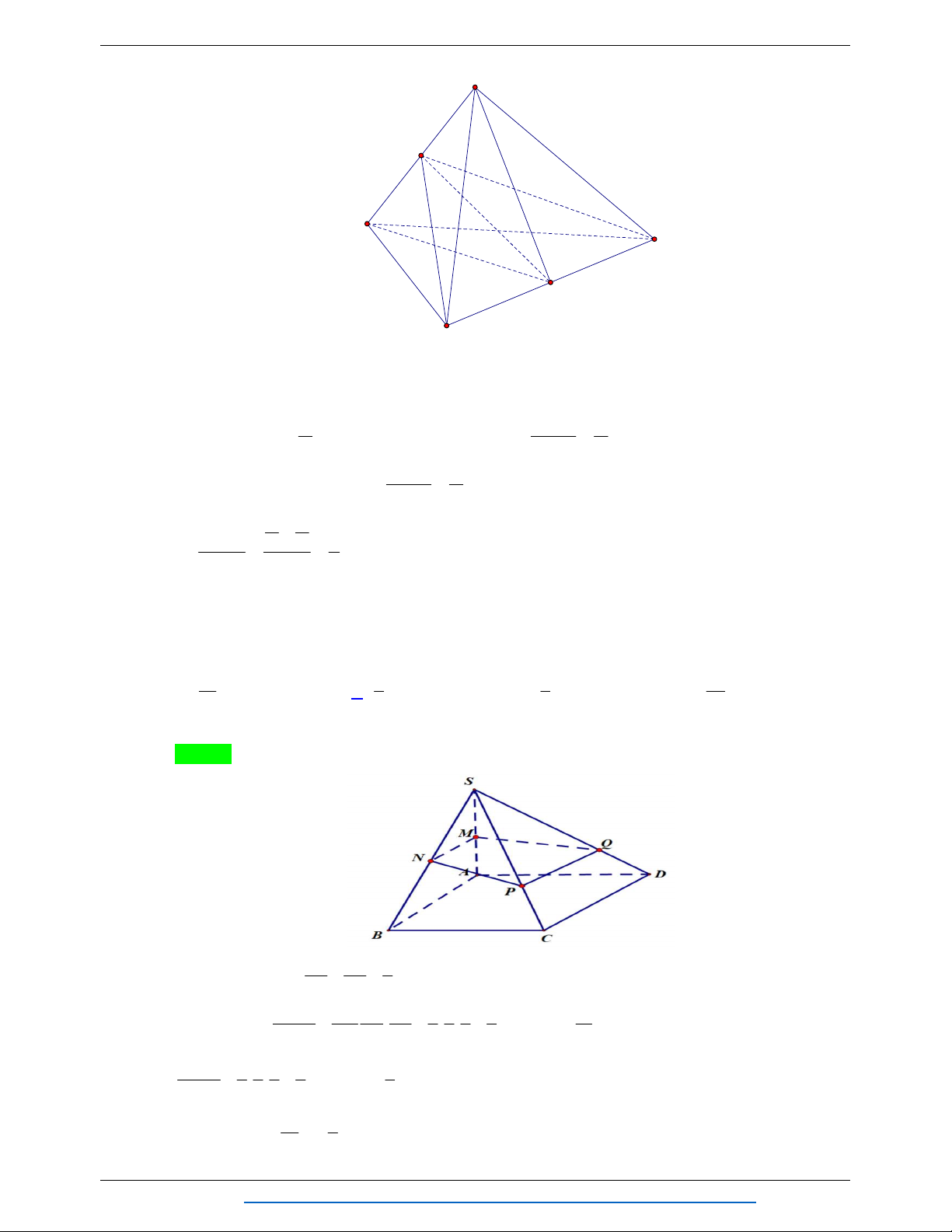
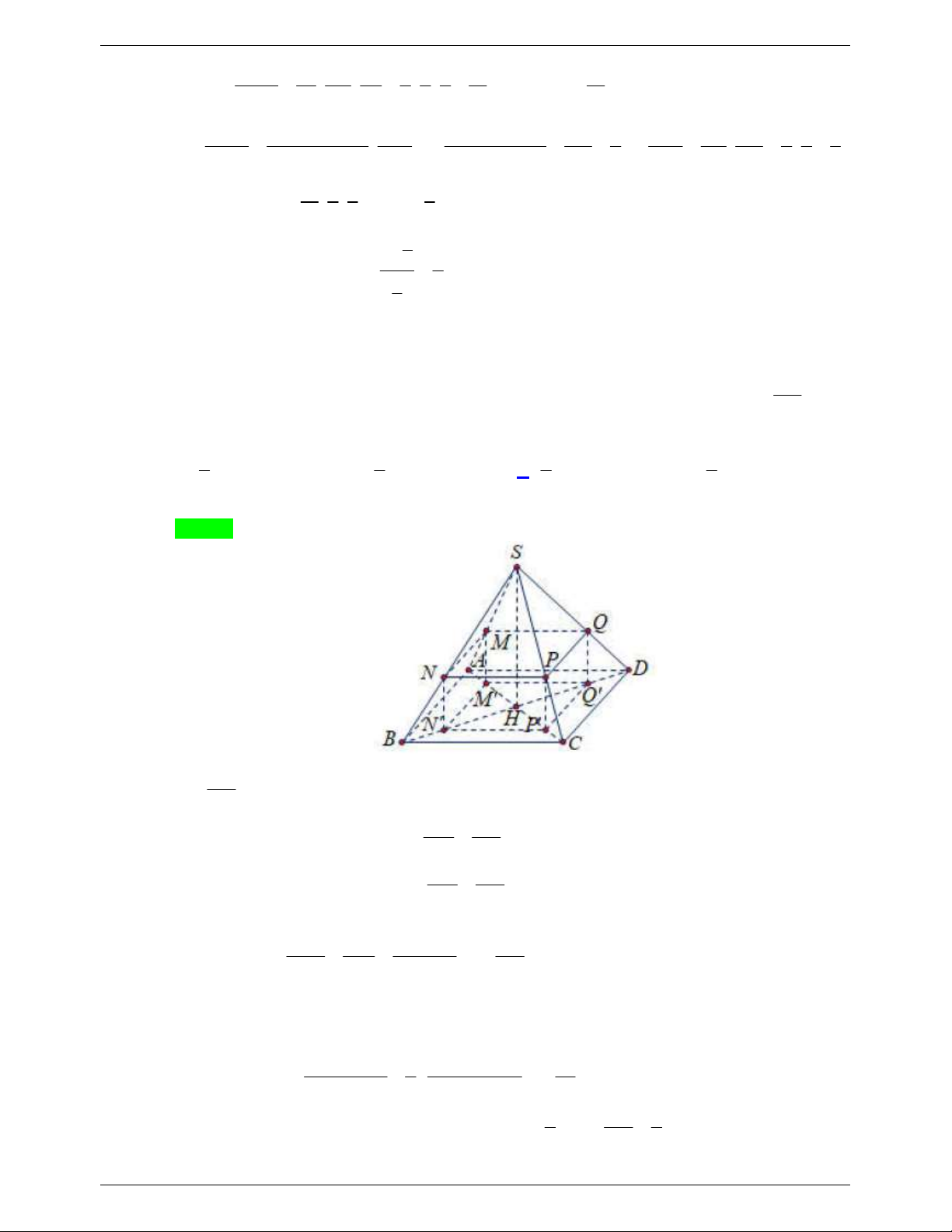
Câu 67. Cho khối chóp S.ABCD có đáy là hình bình hành ABCD . Gọi M , N , P , Q lần lượt là trọng
tâm các tam giác SAB , SBC , SCD , SDA . Biết thể tích khối chóp S.MNPQ là V , khi đó thể
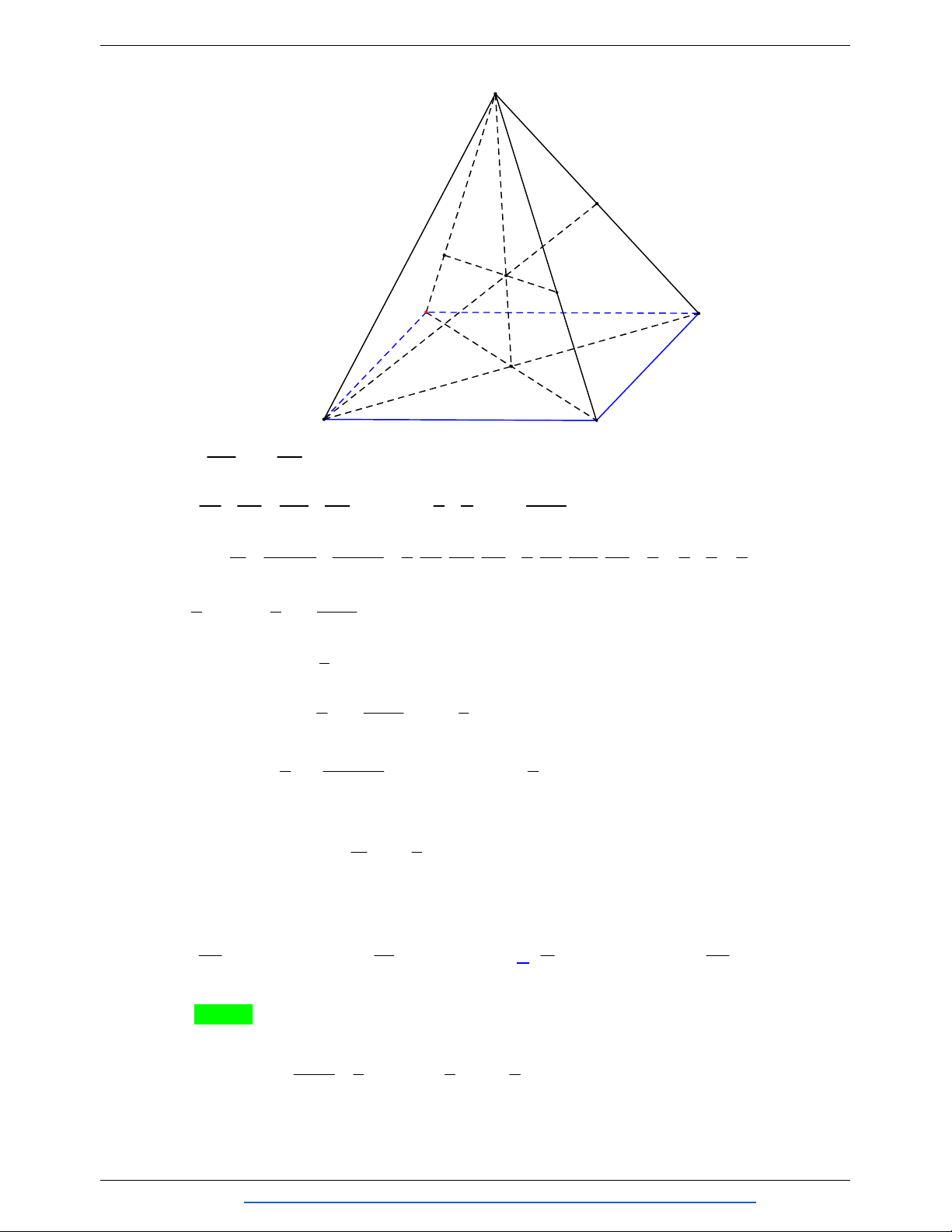
tích của khối chóp S.ABCD là: 27V 2  9  9V 81V A. . B. V   . C. . D. . 4  2  4 8 Hướng dẫn giải Chọn A S N M P Q C K B H F O I E D J A d S,MNPQ SM 2 Ta có   . d S, ABCD SI 3 S Mặt khác gọi S  1 1 1 S ta có D  EJ  .  1  S  S . ABCD S 4 2 8 DE  J 16 B  DA S 1 Tương tự ta có J  AI  1  S   . S 4 JAI 8 D  AB   1 1  1 Suy ra S  1 4.  2. S  S . HKIJ     16 8    2 2 SMNPQ  2  4 2 Mà    S  S .   S  3  9 MNPQ 9 ABCD HKIJ 1 1 3 9 27 Suy ra V
 d S, ABCD .S  . d S,MNPQ. S  V S.ABCD    . 3 3 2 2 4
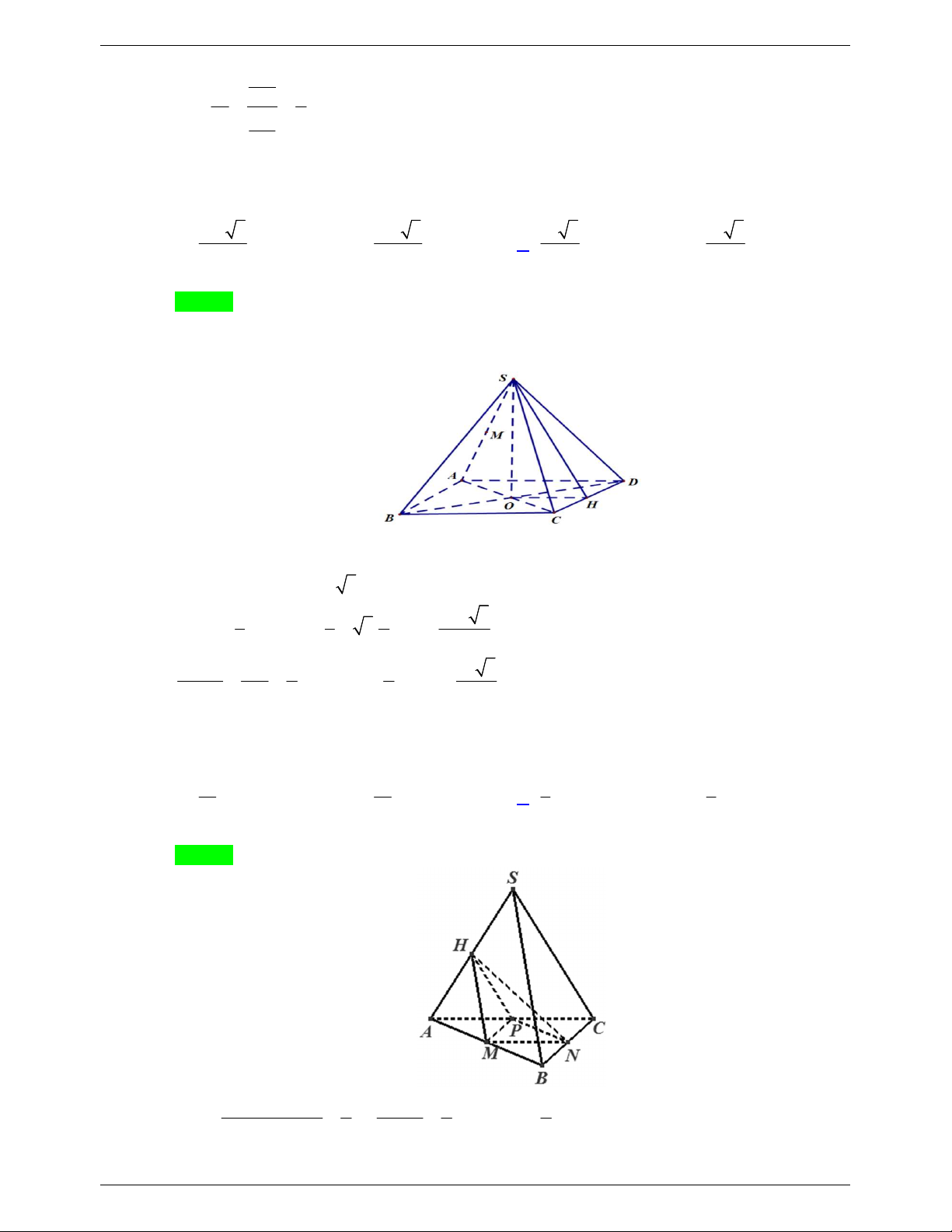
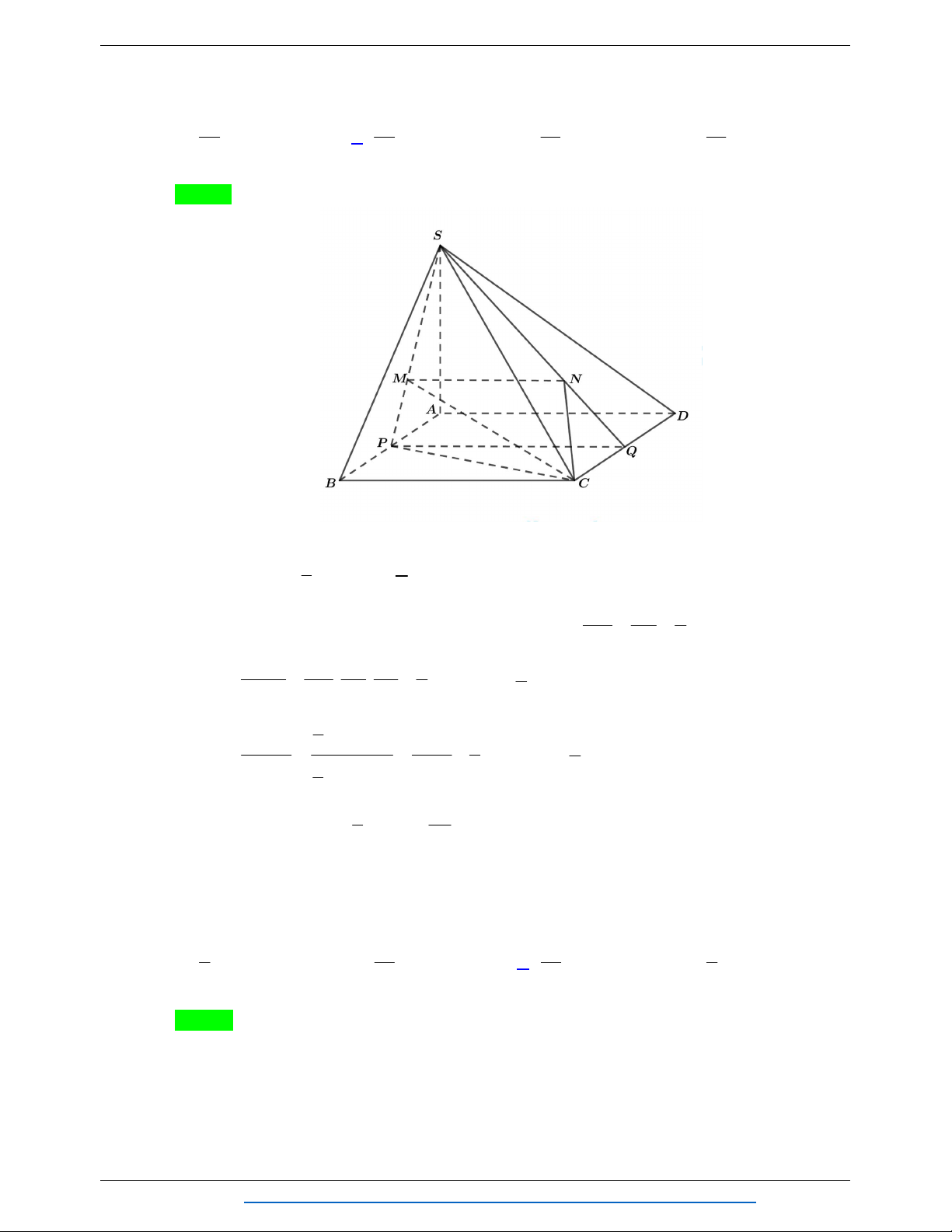
Câu 68. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy  ABCD
, góc giữa hai mặt phẳng SBD và  ABCD bằng 60 . Gọi M , N lần lượt là trung điểm của
SB , SC . Tính thể tích khối chóp S.ADMN . 3 a 6 3 a 6 3 3a 6 3 a 6 A. V  . B. V   C. V   D. V   16 24 16 8 Lời giải Chọn A Trang 36 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S N M A D O B C
Gọi O là tâm của hình vuông ABCD . Khi đó ta có 
SOA là góc giữa hai mặt phẳng SBD và  SA a ABCD nên 
SOA  60 . Khi đó tan 60  2  SA  A . O tan 60  6 . a 3  . AO 2 2 V SA SM SN 1 V SA SN SD 1 Ta có S.AMN  . .  và S.AND  . .  . V SA SB SC 4 V SA SC SD 2 S.ABC S.ACD 1  1 1  3 3 3 1 a 6 a 6 Do đó V  V .     .V 2  . . .a  . S.ADMN S. 2 ABCD  4 2  . 8 S ABCD 8 3 2 16
Câu 69. Cho hình chóp S.ABCD có SA   ABCD , ABCD là hình chữ nhật. SA  AD  2a . Góc giữa
SBC và mặt đáy  ABCD là 60. Gọi G là trọng tâm tam giác SBC . Tính thể tích khối chóp S.AGD là 3 32a 3 3 8a 3 3 4a 3 3 16a A. . B. . C. . D. . 27 27 9 9 3 Lời giải Chọn B S G B A M D C SA 2a
Vì góc giữa SBC  và mặt đáy  ABCD là 60 nên  SBA  60  AB   . tan 60 3
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 37 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 2 2a 4a 3 Khi đó: S  A . B AD  .2a  . ABCD 3 3 2 1 2a 3
Gọi M là trung điểm BC , khi đó: S  S  . ADM 2 ABCD 3 2 3 2 2 1 2a 3 8a 3  V  V  . .2 . a  . S.ADG S. 3 ADM 3 3 3 27
Câu 70. Cho khối tứ diện ABCD có thể tích V . Gọi G , G , G , G là trọng tâm của bốn mặt của tứ diện 1 2 3 4
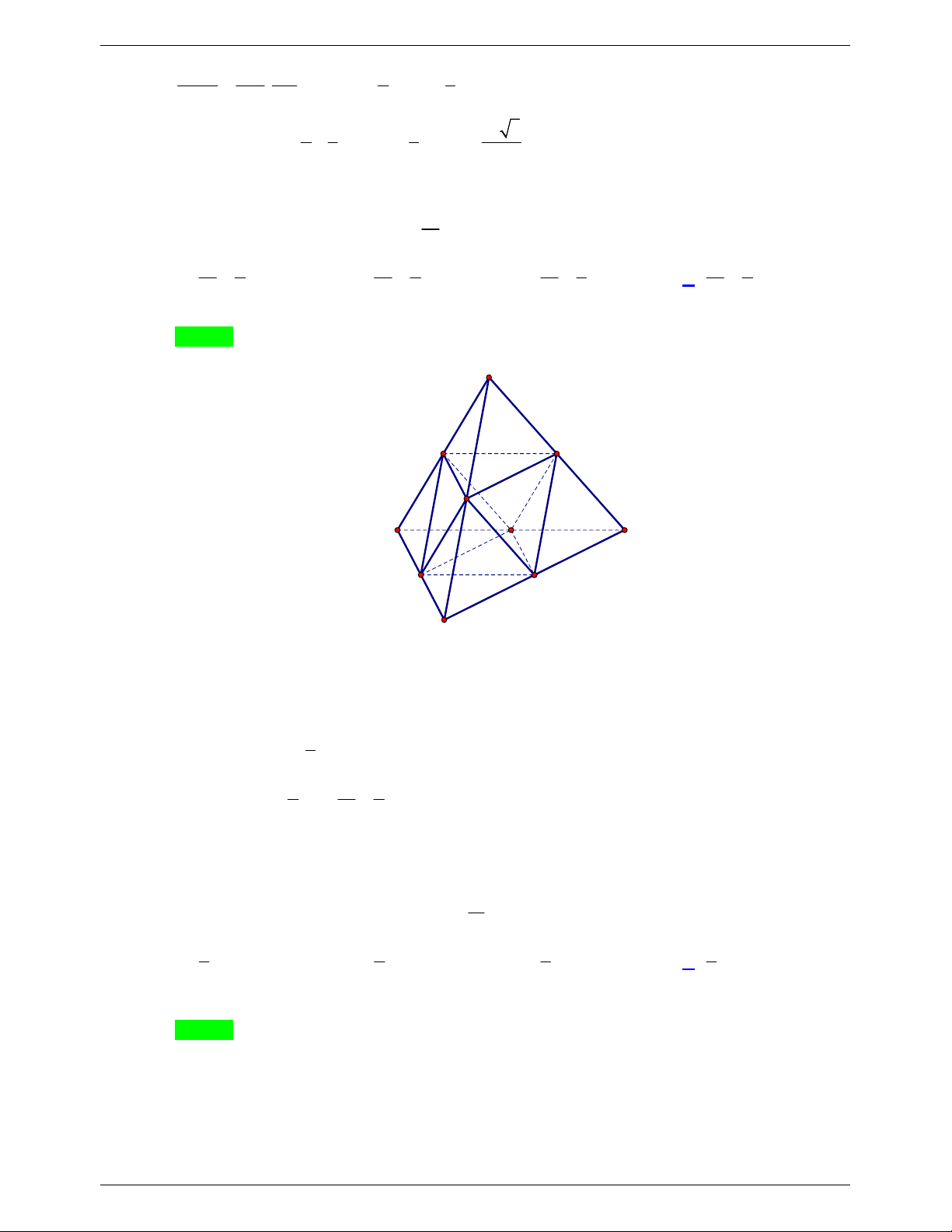
ABCD . Thể tích khối tứ diện G G G G là: 1 2 3 4 V V V V A. . B. . C. . D. . 27 18 4 12 Lời giải Chọn A A G2 G3 G1 I C B G4 H1 H2 K J D
Gọi I, J , K lần lượt là trung điểm của BC , BD và DC .
Gọi h là khoảng cách từ A đến BCD , h là khoảng cách từ G đến G G G 1 2 3  . 1 4 Vì G G G / / BCD
d G , G G G  d G , BCD  G H  h h  AH 4  1 2 3   1   1 2 3    nên , . 1 2 1 h KG 1 h 1 1     h  . h KA 3 1 3
Gọi S , S , S lần lượt là diện tích các tam giác BCD , IJK và G G G . 1 1 2 3
Vì I, J , K lần lượt là trung điểm của BC , BD và DC nên: 1
S  JK d I JK  1 BC 1  d D BC 1 1  BC d D BC 1 . , . . , . . . ,  S   1 . 2 2 2 2 4 2 4 G G AG 2
Tam giác G G G đồng dạng với tam giác KIJ với tỉ số đồng dạng là: 1 2 1   . 1 2 3 Ik Ak 3 2 S  2  4 4 1  
  S  S 2 (Vì tỉ số diện tích bằng bình phương tỉ số đồng dạng).   S  3  9 1 9 S Từ   1 và 2  S  . 1 9 1 1 S h 1  1  V
Thể tích khối từ diện G G G G là: V  S .h  . .  . .S.h  . 1 2 3 4 1 1 1   3 3 9 3 27  3  27
Câu 71. Cho hình chóp S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  2SM ,
SN  2NB ,   là mặt phẳng qua MN và song song với SC . Mặt phẳng   chia khối chóp Trang 38 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
S.ABC thành hai khối đa diện H H H S  H2  1  2  1  và với
là khối đa diện chứa điểm , là khối V
đa diện chứa điểm A . Gọi V và V lần lượt là thể tích của H H 1 2  1  và . Tính tỉ số . 1 2 V2 4 5 3 4 A. . B. . C. . D. . 5 4 4 3 Lời giải Chọn A S M N C A Q P B
Kí hiệu V là thể tích khối tứ diện SABC .
Gọi P , Q lần lượt là giao điểm của   với các đường thẳng BC , AC . Ta có NP // MQ // SC . Khi chia khối H QNC N.SMQC N.QPC 1  bởi mặt phẳng
, ta được hai khối chóp và . V d N, SAC S N .SMQC    Ta có SMQC   . V d B, SAC S B.ASC    SAC d  N,SAC NS 2 2 S S   AMQ AM AQ  AM  4 SMQC 5 ;  .     . d B,SAC BS 3   S AS AC  AS  9 S 9 ASC ASC VN SMQC 2 5 10 Do đó .    . V 3 9 27 B.ASC V d N, QPC S N .QPC    QPC   NB  CQ CP  1  1 2  2        .     V d S, ABC S
SB  CA CB  3  3 3  27 S.ABC    ABC V V V 10 2 4 V 4 V 4 Do đó 1 N .SMQC N .QPC      1    5V  4V 1   . V V V 27 27 9 V V 9 1 2 V 5 B.ASC S.ABC 1 2 2
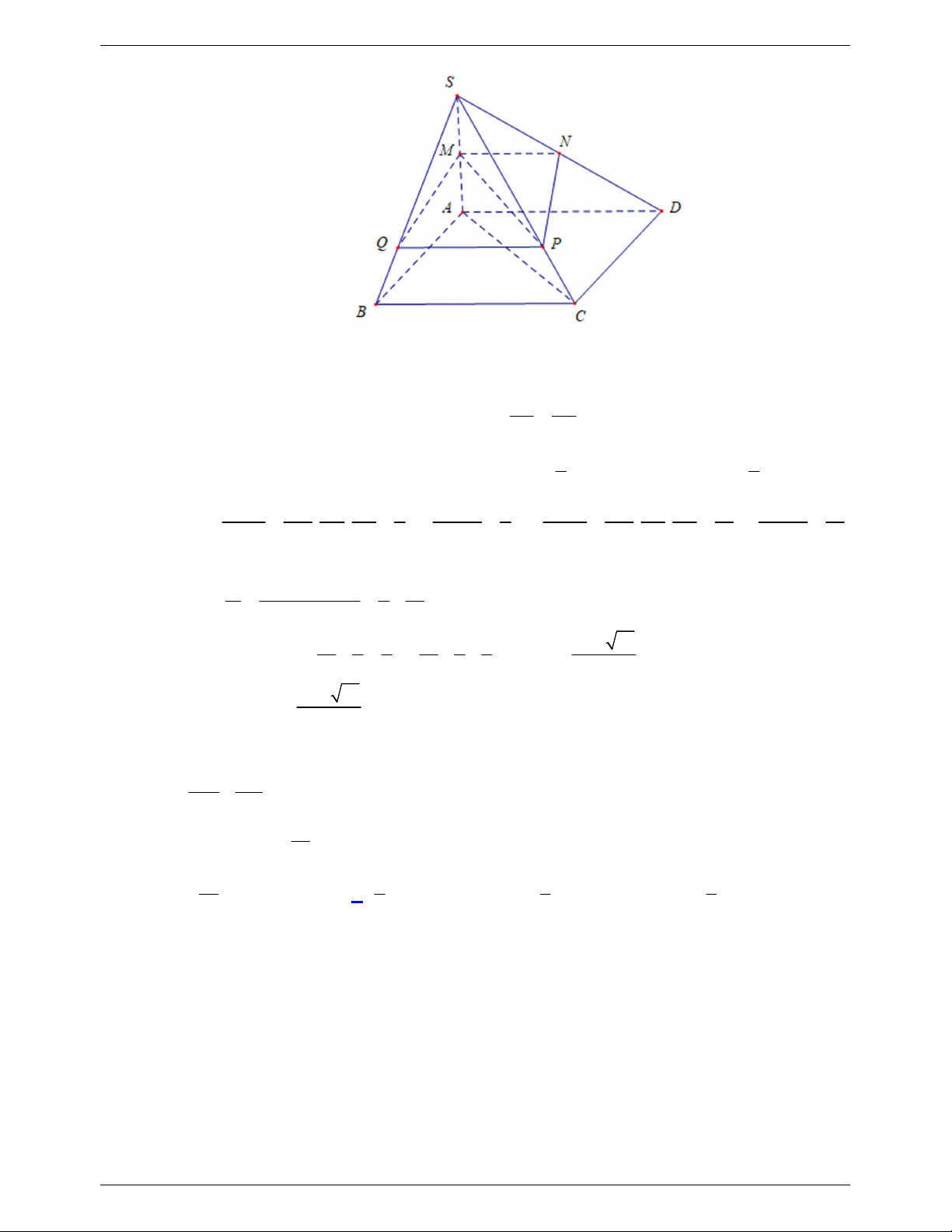
Câu 72. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của
các cạnh SA , SD . Mặt phẳng   chứa MN cắt các cạnh SB , SC lần lượt tại Q , P . Đặt
SQ  x , V là thể tích của khối chóp S.MNQP , V là thể tích của khối chóp S.ABCD . Tìm x để SB 1 1 V  V . 1 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 39 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1   33   A. x  . B. x  1 2 . C. x  1 41 . D. x  . 4 2 4 Lời giải Chọn A S P Q M N B C O A D MN // BC  Do   PQ // BC .      SBC  PQ V V V V 2 S.MNQ S.NPQ V S MNQ S NPQ 1 SM SN SQ SP SN SQ x x 1    . .    . .  . .  1   1 V V V 2V 2V 2 SA SD SB SC SD SB 4 2 S.ABD S.BCS   2  2x  x  4  1 33 0  x  (vì x  0 ). 4
Câu 73. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên tạo với đáy
một góc 60 . Gọi M là trung điểm của SC . Mặt phẳng đi qua AM và song song với BD cắt
SB tại E và cắt SD tại F . Tính thể tích V khối chóp S.AEMF . 3 a 6 3 a 6 3 a 6 3 a 6 A. V  . B. V  . C. V  . D. V  . 36 9 6 18 Lời giải Chọn D S M F E I D A O B C
Trong mặt phẳng SBD : EF  SO  I . Suy ra , A M , I thẳng hàng. Trang 40 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 SI 2
Trong tam giác SAC hai trung tuyến AM , SO cắt nhau tại I suy ra  . SO 3 SE SF SI 2 Lại có EF // BD     . SB SD SO 3 V SE SM 1 V SF SM 1 Ta có: S.AEM    . S.AFM    . V SB SC 3 V SD SC 3 SABC SADC V V 1 V 1 Vậy S.AEM S.AFM S .AEMF    . V V 3 V 3 S.ABC S.ADC S.ABCD a 6
Góc giữa cạnh bên và đáy của S.ABCD bằng góc 
SBO  60 suy ra SO  BO 3  . 2 3 1 a 6
Thể tích hình chóp S.ABCD bằng V  . SO S  . S.ABCD 3 ABCD 6 3 a 6 Vậy V  . S.AEMF 18
Câu 74. Cho khối chóp tứ giác S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC , mặt
phẳng P chứa AM và song song BD chia khối chóp thành hai khối đa diện, đặt V là thể tích 1 V
khối đa diện có chứa đỉnh S và V là thể tích khối đa diện có chứa đáy ABCD . Tỉ số 2 là 2 V1 V V V V 3 A. 2  3 . B. 2  2 . C. 2  1. D. 2  . V V V V 2 1 1 1 1 Lời giải Chọn B Đặt V  V . S.ABCD
Gọi O là giao điểm hai đường chéo AC và BD . Gọi I là giao điểm của SO và AM .
Do P //BD nên P cắt mặt phẳng SBD theo giao tuyến NP qua I và song song với BD ; N SB;P SD .
Xét tam giác SAC có I là giao điểm hai trung tuyến nên I là trọng tâm.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 41 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V S . P SN 4 Ta có S.APN  2 2 4  .   V  4 1 V  2 . V  V . V . SD SB 3 3 9 S.APN S. 9 ADB 9 2 9 S.ADB V . SP SM .SN 2 Tương tự S.PMN  2 1 2 2 = . .   V  2 1 V  1 . V  V . V . SD SC.SB 3 2 3 9 S.PMN S . 9 DCB 9 2 9 S.DCB 1 V Từ đó V  V V  V . Do đó 2  2 . 1 S .APN S.PMN 3 V1
Câu 75. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có thể tích bằng V . Gọi E là điểm trên
cạnh SC sao cho EC  2ES . Gọi   là mặt phẳng chứa AE và song song với BD ,   cắt SB
, SD lần lượt tại hai điểm M , N . Tính theo V thể tích khối chóp S.AMEN . 3V 3V V V A. . B. . C. . D. . 8 16 9 6 Lời giải Chọn D S E N I M A F D O B C
Gọi O là tâm hình bình hành ABCD , I  SO  AE , khi đó MN đi qua I và MN //BD . SI SE 1
Gọi F là trung điểm EC , suy ra OF //AE . Ta có   . SO SF 2 SM SN SI 1 Từ đó    . SB SD SO 2 Từ đó: V SA SM SE 1 1 1 1 1 S.AME  . . 1. .   V  V  V . V SA SB SC 2 3 6 S.AME S . 6 ABC 12 S.ABC V SA SN SE 1 1 1 1 1 S.ANE  . . 1. .   V  V  V . V SA SD SC 2 3 6 S.ANE S. 6 ADC 12 S.ADC 1 1 V Do đó V  V V  V  V  S.AMEN S.AME S .ANE 12 12 6
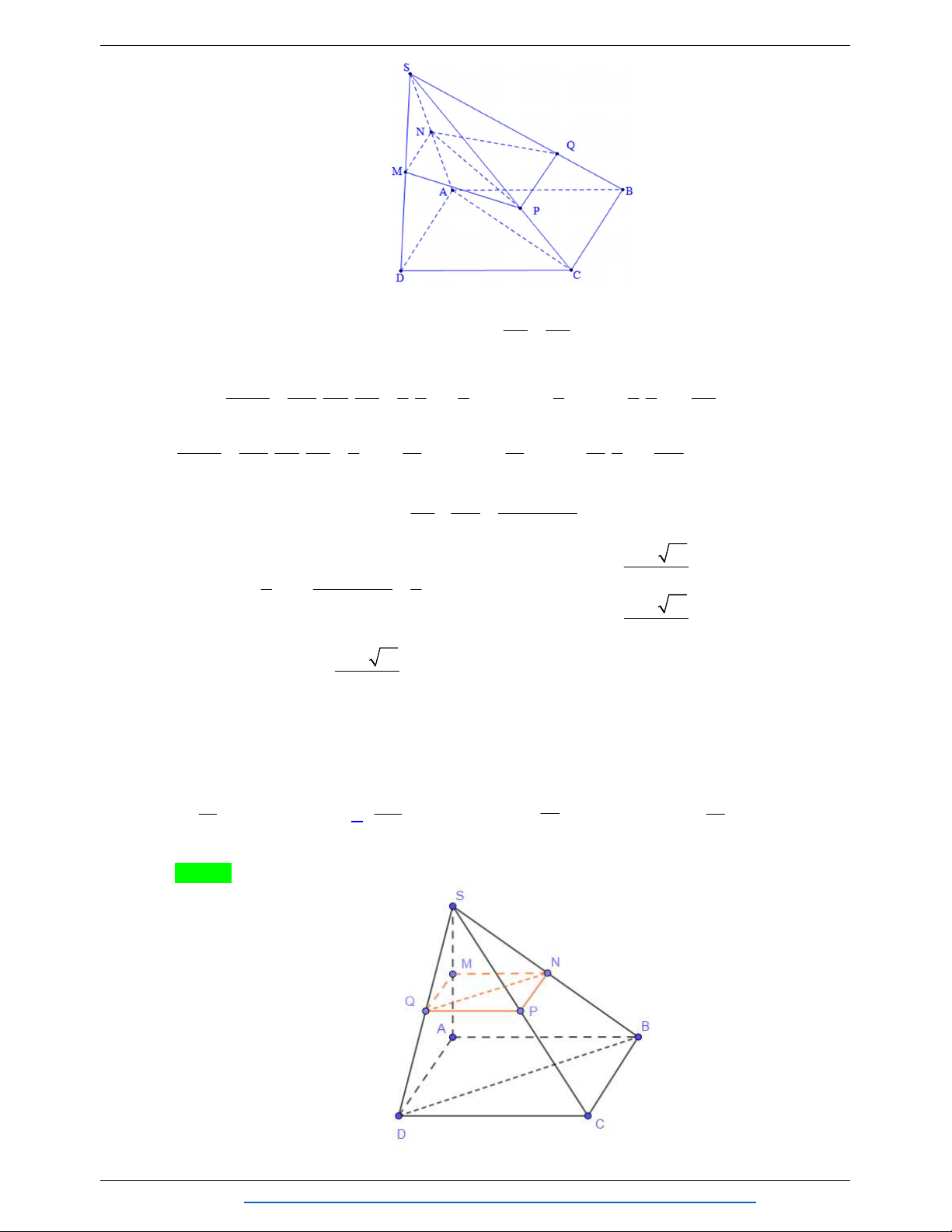
Câu 76. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N là trung điểm của S , A S . B Mặt phẳng
(MNCD) chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số lớn) 3 3 1 4 A. . B. . C. . D. . 5 4 3 5 Lời giải Chọn A Trang 42 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S M N A B D C
Giả sử thể tích của khối chóp S.ABCD là V . V SM SD SC 1 V SM SN SC 1 Ta có S.MDC  . .  ; S.MNC  . .  ; S V . SA SD SC 2 ADC S V . SA SB SC 4 ABC S V .MDC S V .MNC S V .MDC S V .MNC S V . 1 1 3 MNCD        V V 1 1 1 S.ADC S. 2 4 4 ABC V V V 2 2 2 3 3 5 S V . 3 MNCD  V  V  V  V  V  V   . S.MNCD 8 MNABCD 8 8 V 5 MNABCD
Câu 77. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm các SP cạnh S ,
A SD . Mặt phẳng   chứa MN và cắt các tia SB,SC lần lượt tại P và Q . Đặt  x , SB
V là thể tích của khối chóp S.MNQP và V là thể tích khối chóp S.ABCD . Tìm x để V  2V . 1 1 1 1   33   A. x  . B. x  1 41 . C. x  . D. x  2 . 2 4 4 Lời giải Chọn B d S M N A D P Q B C Ta chứng minh PQ / /BC .   SBC SAD  d  
 SBC  ABCD  BC
Giải sử SBC  SAD  d khi đó ta có:   d //BC, d //AD. 
 SAD   ABCD  AD  BC / / AD
M , N lần lượt là trung điểm các cạnh S ,
A SD nên ta có MN / / AD, MN / / d.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 43 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT   SBC  SAD  d  
 SBC     PQ Ta lại có:   PQ / / MN  PQ / / BC. 
 SAD     MN  d / /MN SP
Xét tam giác SBC có PQ / / BC,  SQ SP x   = x. SB SC SB V V V V V V S MNQP S MNP S NQP SM SN SP SN SQ SP S MNP S NQP 1 . . 1 . . 1 . . . . .         V V V 2V 2V 2 . SA . SB SD 2 . SD SC.SB S.ABCD S.ABCD S .ABD S.DCB 2 1 1 1 1 1 x  2x
    x    x  x   2 2 2 2 2 8  1 33 x  2 V 1 x  2x 1 Theo bài ra: 1 2 4 V  2V   
  2x  x  4  0   1 V 2 8 2  1 33 x   4 SP 1 33 Mà  x  x  0  x   SB 4 Cách 2
Sử dụng công thức tính nhanh tỉ lệ thể tích của khối chóp tứ giác như sau:
Cho chóp S.ABCD và mặt phẳng   cắt các cạnh S ,
A SB, SC, SD của khối chóp tại các điểm SQ SP SM SN M , P,Q, N với  1 = x,    SC SB SA SD 2 1 1 . x x   2 V V    S MNPQ 1 1 x 2x Thì ta có: 1 . 2 2     2  2     V V 4  x x  8 S.ABCD  1   33 x  2 V 1 x  2x 1 Theo bài ra: 1 2 4 V  2V   
  2x  x  4  0   . 1 V 2 8 2  1   33 x   4 SP 1   33 Mà  x  x  0  x  SB 4
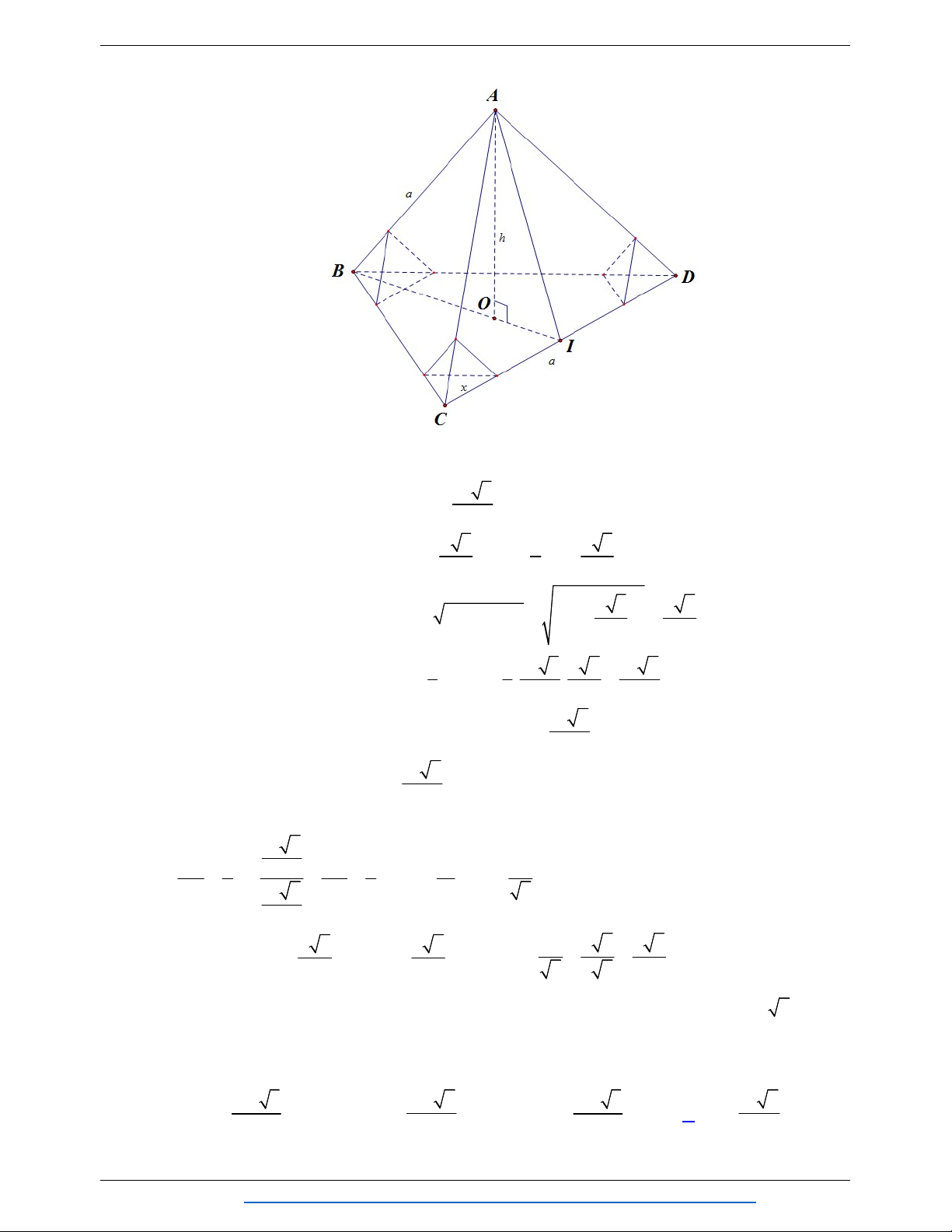
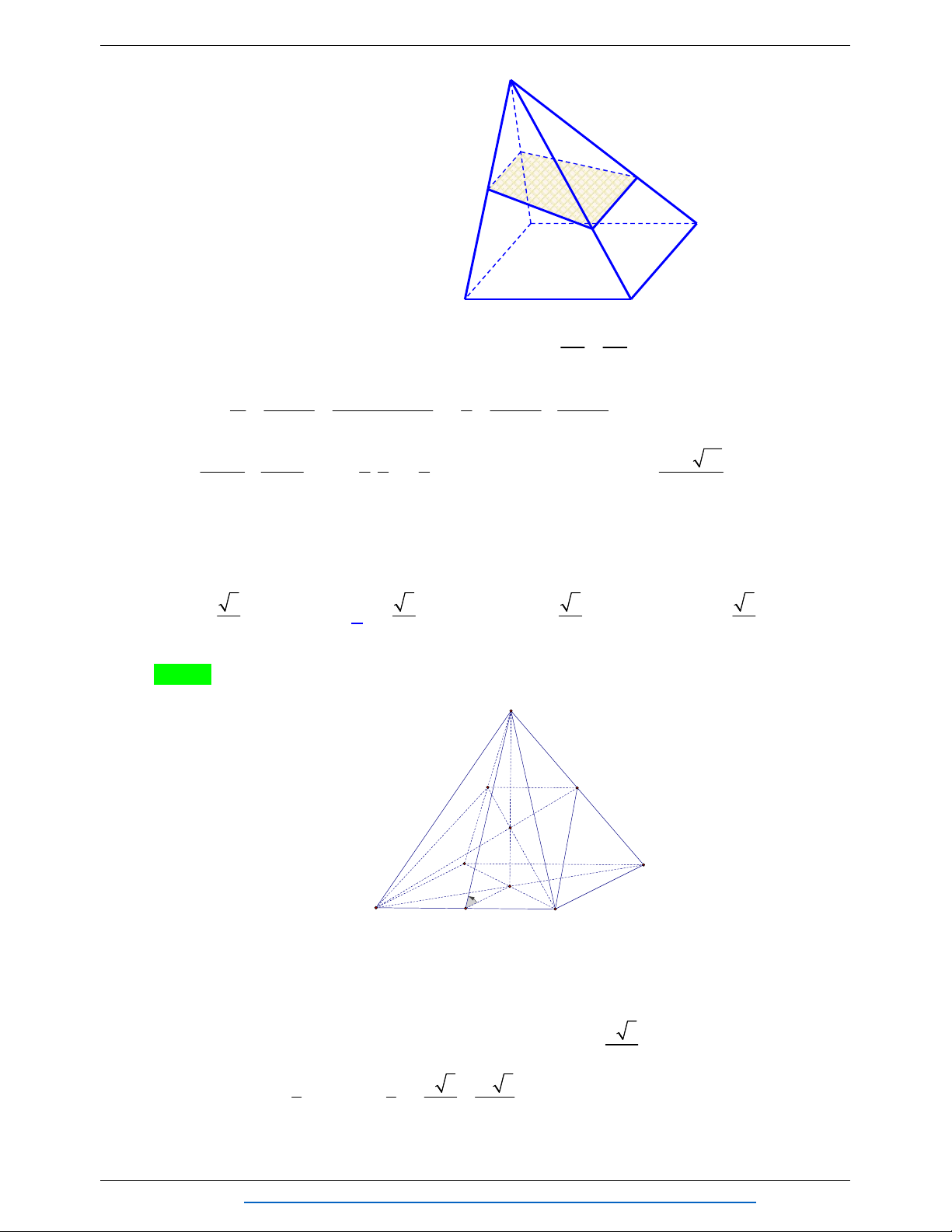
Câu 78. Cho tứ diện đều có chiều cao bằng h , ở ba góc của tứ diện người ta cắt đi các tứ diện đều bằng
nhau có độ dài cạnh bằng x để khối đa diện còn lại có thể tích bằng một nửa thể tích khối tứ diện đều ban đầu. Tìm x . 3 h 6 3 h 6 6 h 6 6 h 6 A. x  . B. x  . C. x  . D. x  . 6 2 6 2 Lời giải Chọn D Trang 44 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Giả sử có tứ diện đều ABCD cạnh bằng a , chiều cao AO  h . 2 a 3
Tam giác BCD đều cạnh a nên S  . BCD 4 a a
Gọi I là trung điểm của CD 3 thì BI  2 3 , BO  BI  . 2 3 3 2  a 3  a 6
Tam giác ABO vuông tại O nên 2 2 2 h  AB  BO  a     .  3  3   2 3 1 1 a 3 a 6 a 2
Thể tích tứ diện đều ABCD là: V  S .h  . .  . 3 BCD 3 4 3 12 3 x 2
Gọi V ' là thể tích của tứ diện đều cạnh x , ta có V '  . 12 3 x 2
Phần bị cắt đi có thể tích: 3V '  . 4
Vì khối đa diện còn lại có thể tích bằng một nửa thể tích khối tứ diện đều ban đầu nên ta có: 3 x 2 3 3 3V ' 1 3x 1 4 a a 3      x   x  . 3 3 3 V 2 a 2 a 2 6 6 12 a 6 h 6 a h 6 h 6 Mặt khác, từ h  6 suy ra a  . Do đó, x    . 3 2 3 3 6 2 6 2
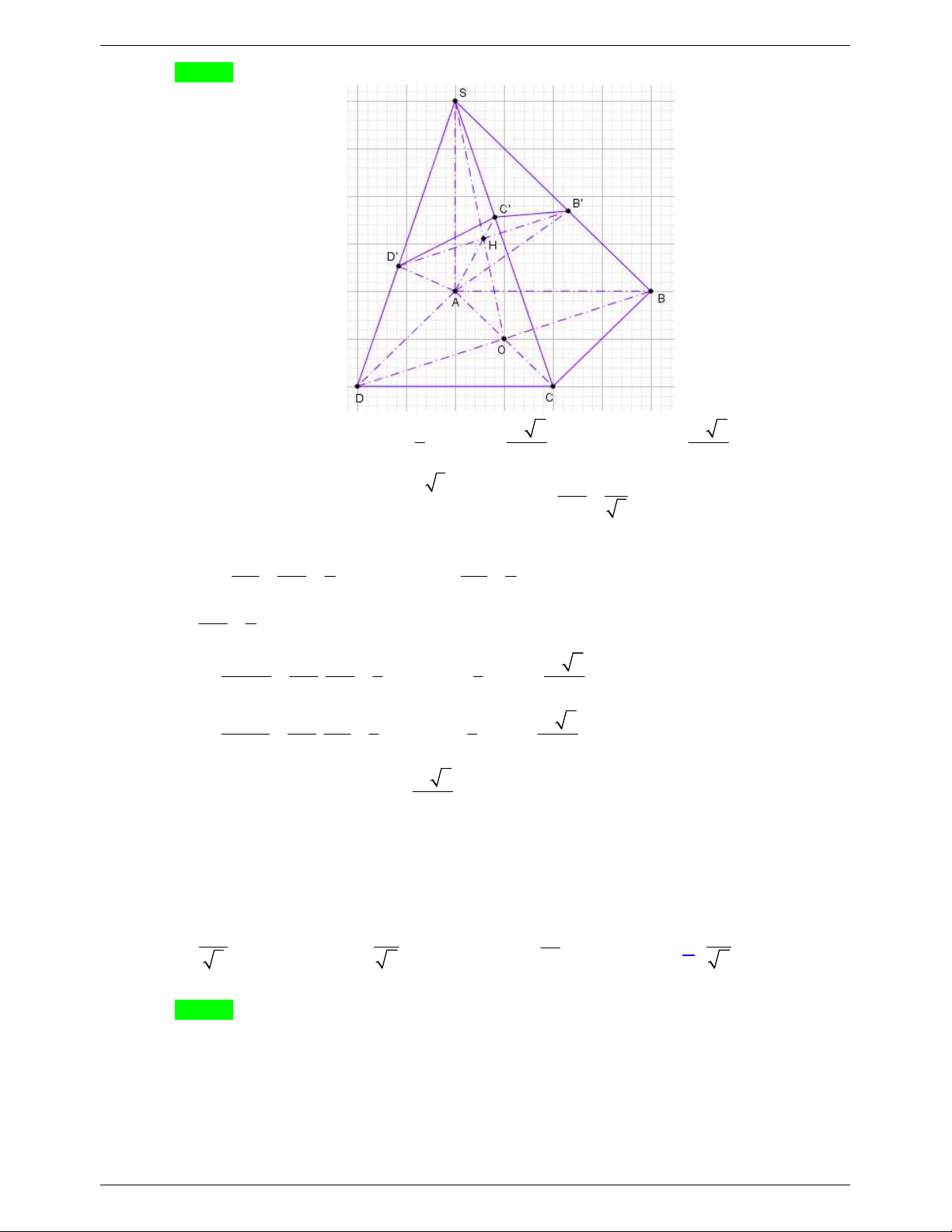
Câu 79. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, SA  a 2 . B ', D '
lần lượt là hình chiếu của A lên SB, SD . Mặt phẳng  AB ' D ' cắt SC tại C ' . Thể tích khối chóp S.AB 'C ' D ' là 3 2a 3 3 2a 2 3 2a 3 3 a 2 A. V  . B. V  . C. V  . D. V  . 3 3 9 9 Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 45 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT Chọn D 3 3 1 a 2 a 2
Ta có SA   ABCD  V  S .SA   V  V  . S .ABCD ABCD S .ABC S . 3 3 ACD 6 2 SB  SD  a 3 SA 2a Có SA  B  SA  D    SB '  SD '   AB '  AD' SB 3
Gọi O  AC  BD , H  B ' D ' SO . Khi đó C '  AH  SC . SB ' SD ' 2 SH 2 Ta có    B ' D '  BD 
 suy ra H là trọng tâm của tam giác SAC SB SD 3 SO 3 SC ' 1   . SC 2 3 V SC ' SD ' 1 1 a 2 Ta có S.AC'D'  .   V  V  . S.AC ' D' S. V SC SD 3 3 ACD 18 S.ACD 3 V SC ' SB ' 1 1 a 2 Ta có S.AB'C'  .   V  V  . S.AB 'C ' S. V SC SB 3 3 ABC 18 S.ABC 3 a 2 Vậy V  V V  . S .AB 'C 'D ' S .AB 'C ' S.AC 'D ' 9
Câu 80. Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a . Người ta cắt khối
đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích
bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng
tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá đầu). 2 2a 2 a 2 a 2 a A. . B. . C. . D. . 3 3 2 4 3 4 Lời giải Chọn D Trang 46 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S M Q N H P A D O B C
Gọi M , N , P , Q lần lượt là giao điểm của mặt phẳng cắt với cạnh bên SA , SB , SC , SD SO    ABCD
và H  SO  MNPQ . Do   SH  MNPQ   MNPQ     ABCD SH SM SN SP SQ Đặt    
 k k  0 (Định lý Thales) và V  V . SO SA SB SC SD S.ABCD V V V 1  SM SN SP SM SP SQ  1 Ta có S.MNPQ S.MNP S.MPQ    . .  . .     3 3 k  k  3  k V 2V 2V 2  SA SB SC SA SC SD  2 S.ABC S.ACD VS MNPQ 1 1 Theo ycbt : . 3  k   k  . V 2 3 2 1 1 V SH.SMNPQ S Mặt khác S.MNPQ  3   k. MNPQ 2 V 1 . SO S SABCD 3 ABCD 1 3 2 2 a  S  .S 2  .a  . MNPQ 2 ABCD k 2 3 4
Câu 81. Cho khối tứ diện ABCD có thể tích bằng V , thể tích của khối đa diện có đỉnh là trung điểm các 
cạnh của tứ diện ABCD bằng V  V . Tính tỉ số . V V  1 V  V  V  A.  1 . B.  1 . C.  3 . D.  . V 2 V 8 V 4 V 4 Lời giải Chọn A A E F J G B D I H C V V AE AJ AF 1 Ta có AEJF AEJF   . .  . V V AB AC AD 8 ABCD V 1 V V Tương tự: BIGE  1 , CIHJ  1 , DHGF  . V 8 V 8 V 8
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 47 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V  1 Vậy: 1 1 4.  . V 8 2
Câu 82. Cho hình chóp S.ABC có SC  ABC , SC  3a . Tam giác AB C vuông cân tại   B , AB  a 3
. Mặt phẳng  đi qua C và vuông góc với SA , cắt SA , SB lần lượt tại D , E . Tính tỉ số thể  
tích khối chóp S.CDE và khối chóp S.ABC . 9 9 7 15 A. . B. . C. . D. . 11 20 20 12 Lời giải Chọn B
Kẻ CD  SA tại D , kẻ CE  SB tại E . AB  BC Ta có 
 AB  SBC AB  CE AB   SC  C  E  SB Ta có 
 CE SAB CE  SA C  E   AB  SA  CE Ta có   SA  CDE SA   CD 
Nhận thấy CDE qua C và vuông góc với SA ( thỏa điều kiện bài toán)    CDE  2 2 CA  a 3  a 3  a 6 .     SD S . D SA SC 3a2 2 3 Ta có:     . 2 2 SA SA SA a 2 a2 5 6 3 SE S . E SB SC 3a2 2 3     . 2 2 SB SB SB a 2 a2 4 3 3 V SC SD SE 3 3 9
Tỉ số thể tích cần tìm là: S.CDE  . . 1. .  . V SC SA SB 5 4 20 S.ABC Trang 48 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Câu 83. Cho hình chóp S.ABC có 3 V
 6a . Gọi M , N , Q lần lượt là các điểm trên các cạnh SA , S .ABC
SB , SC sao cho SM  MA , SN  NB , SQ  2QC . Thể tích khối chóp S.MNQ là 3 a A. 3 a . B. 3 2a . C. 3 3a . D. . 2 Lời giải Chọn A S M Q N A C B SM
M nằm trên các cạnh SA sao cho SM  1 MA   . SA 2 SN
N nằm trên các cạnh SB sao cho SN  1 NB   . SB 2 SQ
Q nằm trên các cạnh SC sao cho SQ  2 2QC   . SC 3 ,. VS MNQ 1 1 2 1 Khi đó: .  . .  . V 2 2 3 6 S.ABC 1 1 3 3  V  V  .6a  a . S .MNQ S . 6 ABC 6
Câu 84. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SQ các cạnh ,
SA SD . Mặt phẳng   chứa MN cắt các cạnh SB, SC lần lượt tại , Q P . Đặt  x , SB 1
V là thể tích của khối chóp S.MNPQ , V là thể tích của khối chóp S.ABCD . Tìm x để V  V 1 1 2 . 1   41 1   33 1 A. x  . B. x  . C. x  2 . D. x  . 4 4 2 Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 49 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Theo giả thiết ta có MN là đường trung bình của tam giác SAD  MN / / AD .
ABCD là hình bình hành nên AD / / BC  MN / / BC . 
 MNPQ SBC  PQ SP SQ Có   PQ / / BC    x . MN / / BC SC SB 1 1
Tứ giác ABCD là hình bình hành nên S  S  S  V  V  V . ADC ACB ABCD S .ADC S .ACB S. 2 2 ABCD V SM SN SP x V x 2 2 V SM SP SQ x V x Ta có S.MNP  . .  S.MNP   và S.MPQ S.  . . MPQ    V SA SD SC 4 V 8 V SA SC SB 2 V 4 S.ADC S.ABCD S.ACB S.ABCD . 2 V V V x x Do đó 1 S.MNP S.MPQ    . V V 8 4 2 2 x x 1 x x 1 1   33 Theo giả thiết ta có       0  x  . 4 8 2 4 8 2 4 1 33 Vì x  0 nên x  . 4
Câu 85. Cho khối tứ diện ABCD . Hai điểm M , N lần lượt di động trên hai đoạn thẳng BC, BD sao cho BC BD 2 
 6 . Gọi V ,V lần lượt là thể tích của các khối tứ diện ABMN và ABCD . Tìm giá BM BN 1 2 V trị nhỏ nhất của 1 . V2 5 2 1 1 A. . B. . C. . D. . 36 9 9 6 Lời giải A B D N M C Trang 50 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 Chọn B BC BD Đặt x  ; y 
; x, y  0  2x  y  9 1 2
6  6  2 2xy  xy    BM BN 2 xy 9
1 d  ,ABMN.S BMN V BM BN 1 2 V 2 1 3   . 
 . Vậy giá trị nhỏ nhất của 1 là: V 1 BC BD xy 9 V 9 2 d  , A BCD.S 2 3 B  CD
Câu 86. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a , mặt bên tạo với mặt đáy một góc 0 60 . Gọi M là trung điểm của S .
A , thể tích của khối chóp M.ABC bằng 3 2a 3 3 4a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 3 3 6 Lời giải Chọn C
Gọi O  AC  BD ; H là trung điểm CD
Vì S.ABCD là hình chóp đều nên SO   ABCD
Góc giữa SCD và  ABCD bằng 0 60 suy ra  SHO  60 ,  SO  OH.tan  SHO  a 3 3 1 1 1 2a 3 2 V  . . SO S  .a 3. .4a  S.ABC 3 ABC 3 2 3 3 V MA 1 1 a 3 M.ABC    V  .V  . M.ABC S. V SA 2 2 ABC 3 S.ABC
Câu 87. Cho tứ diện S.ABC có thể tích V . Gọi H , M , N, P lần lượt là trung điểm của các cạnh ,
SA AB, BC,CA . Thể tích khối chóp H.MNP tính theo V là 1 1 1 3 A. V . B. V . C. V . D. V . 12 16 8 8 Lời giải Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 51 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT d H,MNP 1 V 1 1 Ta có      d  H MNP V V S,MNP . H .MNP S . 2 V 2 2 MNP S.MNP S 1 V 1 1 1 Ta có M  NP S.MNP     V  V . Do đó V  V . S.MNP S. S 4 V 4 4 ABC H .MNP S. 8 ABC A  BC S.ABC
Câu 88. Cho tứ diện đều ABCD có tất cả các cạnh bằng a . Gọi G là trọng tâm tam giác BCD. Gọi S là  
điểm sao cho AS  BG . Thể tích của khối đa diện SABCD là: 3 a 2 3 a 2 3 5a 2 3 3a 2 A. . B. . C. . D. . 12 24 36 24 Lời giải Chọn C
Chia khối đa diện SABCD thành 2 khối chóp là . A BCD và S.ACD . Ta có: V  V V SABCD ABCD SADC 3 3 AB 2 a 2
Áp dụng công thức tính nhanh khối đa diện đều: V   ABCD 12 12
Gọi H là giao điểm giữa AM và SB . 1 d S;ACD.S V 3 ACD d S ACD SH SACD  ;     V 1 d B ACD BH ABCD d  ; B  ACD  ;  .S 3 ACD AS  BG SH SA SA 1 2
Mặt khác theo giả thiết AS  BG        AS / /BG BH BM 3 3 3 BG 2 2 3 3 V SH 2 2 2 a 2 a 2 SACD    V  V  .  V BH 3 SACD 3 ABCD 3 12 18 ABCD 3 3 3 a 2 a 2 5a 2  V  V V    SABCD ABCD SACD 12 18 36  0
Câu 89. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , BAD  60 và SA vuông góc với
mặt phẳng  ABCD . Góc giữa 2 mặt phẳng SBD và  ABCD bằng 0
45 . Gọi M là điểm đối
xứng của C qua B và N là trung điểm của SC . Mặt phẳng MND chia khối chóp S.ABCD Trang 52 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V , khối đa diện còn lại có 1 V
thể tích V (tham khảo hình vẽ bên). Tính tỉ số 1 2 V2 V 12 V 5 V 1 V 7 A. 1  . B. 1  . C. 1  . D. 1  . V 7 V 3 V 5 V 5 2 2 2 2 Lời giải Chọn D Gọi O  AC  BD
Khi đó góc giữa 2 mặt phẳng SBD và  ABCD bằng 0 45    45o SOA a 3 a 3
Ta có: BAD đều AO   SA  AO  2 2 2 3 1 2 a 3 a 3 a
Thể tích khối chóp S.ABCD bằng:V  . .2 SA S  . .  3 A  BD 3 2 4 4 d  N; ABCD NC 1
Ta có: N là trung điểm SC nên   d S; ABCD SC 2 3 1 a
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng:V '  V  2 8 KB 1 d K; ABCD KB 1
Ta có K là trọng tâm tam giác SMC      SB 3 d S; ABCD SB 3 2 3 1 1 1 a 3 a 3 a
Thể tích khối chóp KMIB bằng: V '  . . SA S  . .  3 3 MB  I 9 2 8 48 3 3 3 a a 5a 3 3 3 a 5a 7a Khi đó: V  V 'V '    và V  V V    2 8 48 48 1 2 4 48 48
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 53 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3 7a V 7 Vậy 1 48   . 3 V 5a 5 2 48
Câu 90. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a , mặt bên tạo với mặt đáy một góc 0 60 . Gọi M là trung điểm của S .
A , thể tích của khối chóp M.ABC bằng 3 2a 3 3 4a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 3 3 6 Lời giải Chọn C
Gọi O  AC  BD ; H là trung điểm CD
Vì S.ABCD là hình chóp đều nên SO   ABCD
Góc giữa SCD và  ABCD bằng 0 60 suy ra  SHO  60 ,  SO  OH.tan  SHO  a 3 3 1 1 1 2a 3 2 V  . . SO S  .a 3. .4a  S.ABC 3 ABC 3 2 3 3 V MA 1 1 a 3 M.ABC    V  .V  . M.ABC S. V SA 2 2 ABC 3 S.ABC
Câu 91. Cho tứ diện S.ABC có thể tích V . Gọi H , M , N, P lần lượt là trung điểm của các cạnh ,
SA AB, BC,CA . Thể tích khối chóp H.MNP tính theo V là 1 1 1 3 A. V . B. V . C. V . D. V . 12 16 8 8 Lời giải Chọn C d H,MNP 1 V 1 1 Ta có      d  H MNP V V S,MNP . H .MNP S . 2 V 2 2 MNP S.MNP Trang 54 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S 1 V 1 1 1 Ta có M  NP S.MNP     V  V . Do đó V  V . S.MNP S. S 4 V 4 4 ABC H .MNP S. 8 ABC A  BC S.ABC
Câu 92. Cho hình chóp S.ABC có 3 V
 6a . Gọi M , N , Q lần lượt là các điểm trên các cạnh SA , S .ABC
SB , SC sao cho SM  MA , SN  NB , SQ  2QC . Thể tích khối chóp S.MNQ là 3 a A. 3 a . B. 3 2a . C. 3 3a . D. . 2 Lời giải Chọn A S M Q N A C B SM
M nằm trên các cạnh SA sao cho SM  1 MA   . SA 2 SN
N nằm trên các cạnh SB sao cho SN  1 NB   . SB 2 SQ
Q nằm trên các cạnh SC sao cho SQ  2 2QC   . SC 3 ,. VS MNQ 1 1 2 1 Khi đó: .  . .  . V 2 2 3 6 S.ABC 1 1 3 3  V  V  .6a  a . S .MNQ S . 6 ABC 6
Câu 93. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SQ các cạnh ,
SA SD . Mặt phẳng   chứa MN cắt các cạnh SB, SC lần lượt tại , Q P . Đặt  x , SB 1
V là thể tích của khối chóp S.MNPQ , V là thể tích của khối chóp S.ABCD . Tìm x để V  V 1 1 2 . 1   41 1   33 1 A. x  . B. x  . C. x  2 . D. x  . 4 4 2 Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 55 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Theo giả thiết ta có MN là đường trung bình của tam giác SAD  MN / / AD .
ABCD là hình bình hành nên AD / / BC  MN / / BC . 
 MNPQ SBC  PQ SP SQ Có   PQ / / BC    x . MN / / BC SC SB 1 1
Tứ giác ABCD là hình bình hành nên S  S  S  V  V  V . ADC ACB ABCD S .ADC S .ACB S. 2 2 ABCD V SM SN SP x V x 2 2 V SM SP SQ x V x Ta có S.MNP  . .  S.MNP   và S.MPQ S.  . . MPQ    V SA SD SC 4 V 8 V SA SC SB 2 V 4 S.ADC S.ABCD S.ACB S.ABCD . 2 V V V x x Do đó 1 S.MNP S.MPQ    . V V 8 4 2 2 x x 1 x x 1 1   33 Theo giả thiết ta có       0  x  . 4 8 2 4 8 2 4 1 33 Vì x  0 nên x  . 4
Câu 94. Cho khối tứ diện ABCD . Hai điểm M , N lần lượt di động trên hai đoạn thẳng BC, BD sao cho BC BD 2 
 6 . Gọi V ,V lần lượt là thể tích của các khối tứ diện ABMN và ABCD . Tìm giá BM BN 1 2 V trị nhỏ nhất của 1 . V2 5 2 1 1 A. . B. . C. . D. . 36 9 9 6 Lời giải Trang 56 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 A B D N M C Chọn B BC BD Đặt x  ; y 
; x, y  0  2x  y  9 1 2
6  6  2 2xy  xy    BM BN 2 xy 9
1 d  ,ABMN.S BMN V BM BN 1 2 V 2 1 3   . 
 . Vậy giá trị nhỏ nhất của 1 là: V 1 BC BD xy 9 V 9 2 d  , A BCD.S 2 3 B  CD
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 57 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
6. KHỐI LĂNG TRỤ - MỨC 3
Câu 95. Cho lăng trụ ABC.AB 'C ' có thể tích là V. Gọi M là điểm thuộc cạnh CC ' sao cho CM  3C ' M
. Thể tích của khối chóp M .ABC theo V là: V 3V V V A. . B. . C. . D. . 4 4 12 6 Lời giải Chọn A
Cách 1: Thể tích của khối chóp M.ABC là: 1 d M;ABC.SABC VM.ABC 3  V d C '; ABC .S ABC.A'B 'C '    ABC 1 d M ; ABC  1 MC 1 3 1  .    d C '; ABC . . . 3 3 C 'C 3 4 4 1 V  V  V  . M .ABC ABC.A'B 'C ' 4 4
Cách 2: Áp dụng công thức tỉ số thể tích. V 1 CM 1 3 1 1 C.ABM   .   V  V . M . V 3 CC ' 3 4 4 ABC 4 A' B'C '.ABC
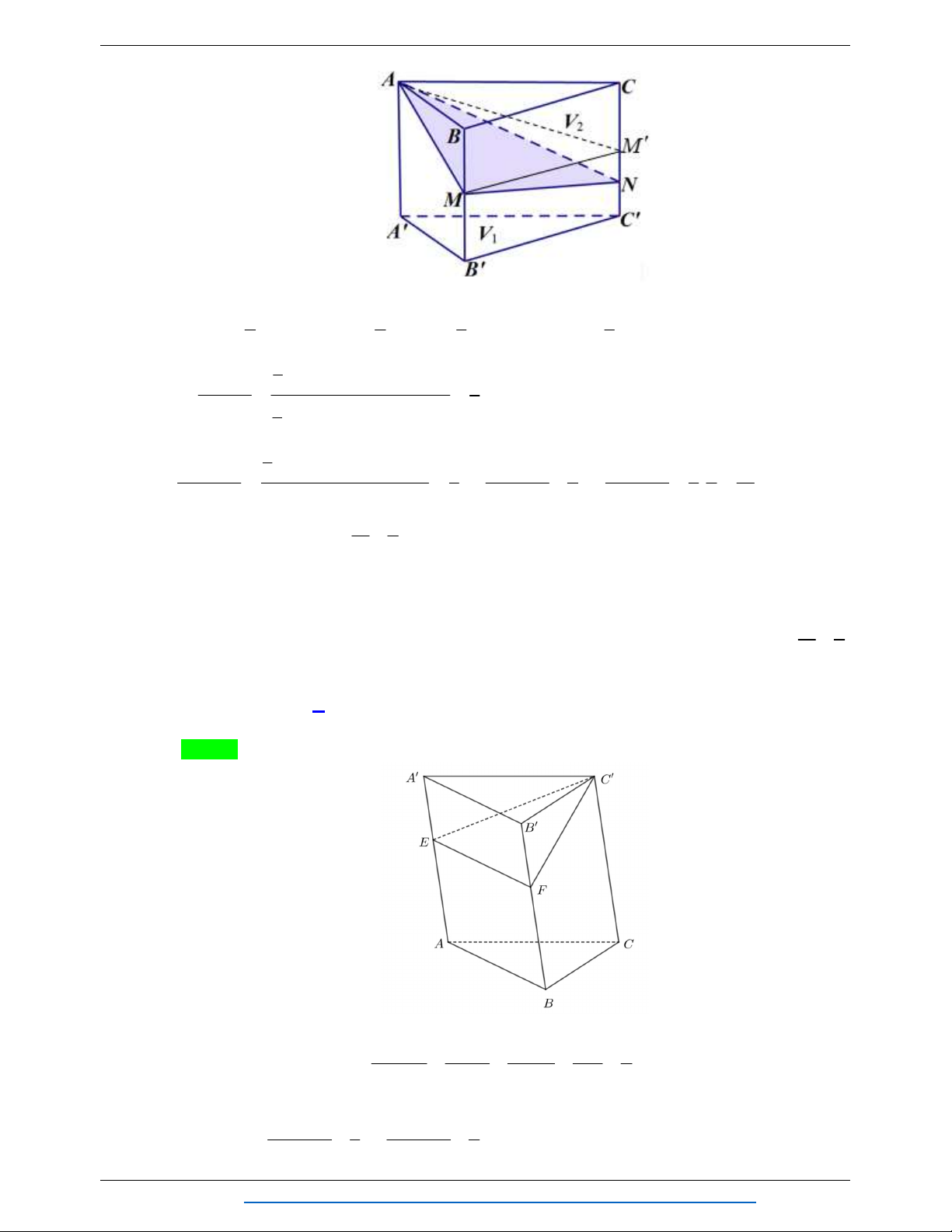
Câu 96. Cho hình lăng trụ tam giác đều ABC.A B  C
  có tất cả các cạnh bằng a . Gọi M , N lần lượt là
trung điểm của các cạnh AB và B C
  . Mặt phẳng  AMN  cắt cạnh BC tại P . Tính thể tích V khối đa diện MB . P AB N  . 3 3a 3 7 3a 3 7 3a 3 7 3a A. V  . B. . C. . D. . 32 96 48 32 Lời giải Chọn B Trang 58 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 A C  B  N A C M B P S
Gọi S là giao điểm của các đường AM ; NP và BB . Có M ; B ; P lần lượt là trung điểm của
các cạnh SA ; SB và SN . 2 a 3
Vì ABC đều cạnh a nên S  . ABC 4 V SB SM SP 1 1 1 1 1 7 S.BMP  . .  . .   V  V     V   V S.BMP S.A B N MBP.A B N S.A B  N  (1). V     SB SA SN 2 2 2 8 8 8 S.A B N
Vì B là trung điểm của SB nên V   
2.V   . Vì N là trung điểm của B C   nên S.A B N B.A B N 2 3 3 1 1 1 1 a 3 a 3 a 3 V  V  . .BB .S  . . a   V         (2). B.A B N B.A B C ABC S. 2 2 3 6 4 24 A B N 12 3 3 7 7 a 3 7 3a Từ (1) và (2) ta có V  V  .      . MBP.A B N S. 8 A B N 8 12 96
Câu 97. Cho hình lăng trụ đứng AB . C A B  C
  có điểm O và G lần lượt là tâm của mặt bên ABB' A' và trọng tâm của A  BC . Biết 3 V  AOGB   
270 cm . Thể tích của khối chóp bằng ABC.A B C A. 3 15 cm . B. 3 30 cm . C. 3 45 cm . D. 3 15 cm . Lời giải Chọn A
Gọi M là trung điểm của BC . Ta có: V AO AG 1  1 AOGB  .  V  .V (1) V AB AM 3 AOGB AB' 3 MB AB'MB 1  S        d B BC BM d B BC BC S B MB   1   1 . , . . , . . B'C' 2 4 4 CB
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 59 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
1 .d A,B BM .SBMB V  1 1 AB MB 3     V  .V (2) V 1 AB 'MB AB 'C ' 4 CB AB C  C  B d  A B C  C  B 4 . , .S 3 B C  C  B 2  V    V (3) AB C CB ABC. 3 AB C   1 1 2 1 1 Từ (1), (2) và (3), suy ra 3 V  . . V       V    .270 15 cm . AOGB ABC.A B C ABC. 3 4 3 18 A B C 18 Vậy 3 V 15 cm . AOGB
Câu 98. Cho khối lăng trụ ABC.A B  C
  có thể tích bằng 30. Gọi O là tâm của hình bình hành ABB A   và
G là trọng tâm tam giác A B  C
 . Thể tích tứ diện COGB bằng: 7 15 5 10 A. . B. . C. . D. . 3 14 2 3 Lời giải Chọn D
Gọi I là trung điểm của AC . V     B G B O B C 2 1 1 1 Ta có: B .GOC  . .  .   V   V  1 B .GOC B .IAC   . V     B I B A B C 3 2 3 3 B .IAC 1 1 1 Mặt khác S  d .AC  d .AC  S      S   . IAC I , AC A , AC 2 2 A AC 2 ACC A V  S 1 1 Mà B .IAC I  AC    V   V    2 B .IAC B .ACC A   . V    S   2 2 B .ACC A ACC A 1 2 V          V    V  V    V    .30 20 3 B .ACC A ABC.A B C B .ABC ABC.A B C ABC.A B C   . 3 3 10 Từ  
1 , 2 , 3 suy ra  V   . B .GOC 3
Câu 99. Cho hình lăng trụ ABC.AB C
  . Gọi M , N , P theo thứ tự là trung điểm các cạnh C C  , BC và B C
  , khi đó tỉ số thể tích của khối chóp A .MN P với lăng trụ ABC.AB C   là Trang 60 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 1 1 1 A. . B. . C. . D. . 2 6 4 8 Lời giải Chọn B Ta có: + 1 1 2 V       S .d A , ABC V    V    V A . ABC ABC    . 3 ABC. A B C A .BCC B ABC. 3 3 AB C   + 1 1 1 1 V    . S       .d A BB C C V BB C C  ,   S .d A , MNP A .MNP MNP    . 3 A. 3 4 4 BB C  C  1 1 (Vì: S  S 
d  A, MNP   d  A, BB C  C     S và ). MNP 2 CC PN 4 BB C C Suy ra: 1 V   V . A .MNP ABC. 6 AB C  
Câu 100. Cho hình hộp chữ nhật ABC D.AB C D
  . Gọi N là trung điểm của B C
  , P đối xứng với B qua
B. Khi đó mặt phẳng PAC  chia khối hộp thành hai phần. Tính tỉ số thể tích phần lớn và phần bé. A. 7 . B. 17 . C. 25 . D. 25 . 3 7 7 14 Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 61 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Gọi M là trung điểm của AB . Mặt phẳng  ACM  chia khối hộp chữ nhật thành hai phần như
hình vẽ. Gọi thể tích khối hộp chữ nhật ban đầu là V , phần chứa điểm Bcó thể tích V và phần 1
còn lại có thể tích V . 2 PB PN PM MB 1 Ta có     . PB PC PA AB 2 1 1 1 1
Thể tích của khối chóp P.ACB là V  P . B S  .2.BB . A . B BC  V . P.ACB 3 ABC 3 2 3 V   PB PN PM 1 Ta lại có P.MNB  . .  . V PB PC PA 8 P.ACB  1 7 7 1 7 Do đó V  V V    1 .V    V  . V     V . 1 P.ACB P.MNB .  8 P ACB  P.ACB ABCD. 8 8 3 A B C 24 Vậy V V 7V 7 1 1    . V V V  7  17 2 1 24 V  V    24 
Câu 101. Cho các số thực dương x và y thỏa mãn 2 x  y    2 x  y   2 2 2 2 yx 2 4 9.3 4 9 .7 . Tìm giá trị nhỏ nhất x  2y 18 của biểu thức P  . x 3  2 A. P  9 . B. P  . 2 C. P  1 9 2 .
D. Hàm số không có giá trị nhỏ nhất. Lời giải Chọn A Từ giả thiết ta đặt 2 t  x  2y , t   . Phương trình 2 x  y    2 x  y   2 2 2 2 yx 2 4 9.3 4 9 .7 trở thành   t  t  49               . t  t  t 7 t 4 9.3 4 9 . 4 7 49 9 9. 49 0 7   3   
Nhận thấy t  2 là nghiệm phương trình.
Ta chứng minh t  2 là nghiệm duy nhất của phương trình. Trang 62 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 7 t  
 Xét t  2 : 7t  49 và 9.  49  
nên vế trái phương trình luôn dương, nên phương trình vô  3  nghiệm. 7 t  
 Xét t  2 : 7t  49 và 9.  49  
nên vế trái phương trình luôn âm, nên phương trình vô  3  nghiệm. 2 x  2 2 x  2y 18 x  x 16 Vậy 2 t  x  2y  2  y  thay vào P   2 x x 16 16 16  x  1  2 . x
1  9 . Dấu bằng đạt được khi x   x  4 . x x x
Câu 102. Cho khối lăng trụ AB .
C A' B 'C '. Gọi E là trọng tâm tam giác A' B'C ' và F là trung điểm B . C
Tính tỉ số thể tích giữa khối B '.EAF và khối lăng trụ AB . C A' B 'C '. 1 1 1 1 A. . B. . C. . D. . 4 8 5 6 Lời giải Chọn D A' C' E M B' C A F B 1
M là trung điểm của B’C’  S  S . EAF 2 AA MF  d B , AA M
 F   d B , AEF . 1 2 V        V   V V V V . B .AA MF ABF .A B M B .ABF ABF .AB M  ABF .A B  M  ABF . 3 3 A B  M  1 1 2 1 1 1 Suy ra V      V . .V   . .V    V . B .EAF B . 2  AAMF ABF .A B M ABC.A B C ABC. 2 3 3 2 6 AB C   V  1 Vậy B .EAF  . V    6 ABC.A B C
Câu 103. Cho lăng trụ ABC.AB 'C ' có thể tích là V. Gọi M là điểm thuộc cạnh CC ' sao cho CM  3C ' M
. Thể tích của khối chóp M .ABC theo V là: V 3V V V A. . B. . C. . D. . 4 4 12 6 Lời giải Chọn A
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 63 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Cách 1: Thể tích của khối chóp M.ABC là: 1 d M;ABC.SABC VM.ABC 3  V d C '; ABC .S ABC.A'B 'C '    ABC 1 d M ; ABC 1 MC 1 3 1  .    d C '; ABC . . . 3 3 C 'C 3 4 4 1 V  V  V  . M .ABC ABC.A'B'C ' 4 4
Cách 2: Áp dụng công thức tỉ số thể tích. V 1 CM 1 3 1 1 C.ABM   .   V  V . M . V 3 CC ' 3 4 4 ABC 4 A' B 'C '.ABC
Câu 104. Cho khối lăng trụ AB .
C A' B 'C '. Gọi E là trọng tâm tam giác A' B'C ' và F là trung điểm B . C
Tính tỉ số thể tích giữa khối B '.EAF và khối lăng trụ AB . C A' B 'C '. 1 1 1 1 A. . B. . C. . D. . 4 8 5 6 Lời giải Chọn D A' C' E M B' C A F B 1
M là trung điểm của B’C’  S  S . EAF 2 AA MF  d B , AA M
 F   d B , AEF . Trang 64 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 2 V        V   V V   V   V . B .AA MF ABF .A B M B .ABF ABF .A B M ABF .A B M ABF . 3 3 A B  M  1 1 2 1 1 1 Suy ra V      V . .V   . .V    V . B .EAF B . 2  AAMF ABF .A B M ABC.A B C ABC. 2 3 3 2 6 AB C   V  1 Vậy B .EAF  . V    6 ABC.A B C
Câu 105. Cho hình hộp ABC . D A B  C  D
  . Tỉ số thể tích của khối tứ diện ACB D
  và thể tích của khối hộp ABC . D A B  C  D   bằng 2 1 1 1 A. . B. . C. . D. . 3 6 2 3 Lời giải Chọn D A' D' B' C' A D B C Đặt V  V . ABCD.AB C  D   Ta có V      1   1  .   V V    V  V  V V 4. V V ACB D AA B D D ADC B ABC CB C  D   6 3 V   1 Vậy ACB D  . V 3  
Câu 106. Cho khối hộp ABCDAB C  D
  có thể tích V . Các điểm M , N , P thỏa mãn AM  2AC ,    
AN  3AB , AP  4AD . Tính thể tích khối chóp AMNP theo V . A. 6V . B. 8V . C. 12V . D. 4V . Lời giải Chọn B Phân tích:
 Nhận dạng bài toán: Đây là bài toán tính thể tích khối đa diện thông qua tỉ số thể tích.
 Kiến thức cần nhớ: Cho khối chóp S.ABC . Trên các đường thẳng SA, SB , SC lần lượt lấy ba V SA SB SC
điểm A, B,C khác S . Ta có: S.AB C  . . . V SA SB SC S.ABC
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 65 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V AM AN AP Ta có: . A MNP  . .   V  24V . Mặt khác: V AC AB AD 2.3.4 24 . A MNP . A CB D   . A CB D   V V V V V V  1 V V 4. V  V  8V . . A CB D   ABCDAB C  D   A.AB D   . A B B  C . A D DC  C.C B  D   6 3 . A MNP
Câu 107. Cho khối hộp ABCDAB C  D
  có thể tích V . Lấy điểm M đối xứng với A qua C , điểm N đối  
xứng với A qua B , điểm P thỏa mãn AP  k AD . Tìm k để thể tích khối chóp AMNP bằng V . 2 3 3 1 1 A. k  . B. k   . C. k  . D. k   . 8 8 2 2 Lời giải Chọn B V AM AN AP Ta có: . A MNP  . .  k  k V  4 k V . V AC AB AD 2.2. 4 . A MNP . A CB D   . A CB D   V Mà: V V V V V  1 V V 4. V  . A CB D   ABCDAB C  D   A.AB D   . A B B  C A.D DC  C.C B  D   6 3 4  V 3 V  k V V   k  . A.MNP 3 A.CBD 2 8
Câu 108. Cho khối lăng trụ tam giác ABCAB C
  có thể tích V . Điểm M là trung điểm của AB . Mặt phẳng C B  M
 chia khối lăng trụ thành hai khối đa diện có thể tích là V và V , biết V là khối 1 2 1
chứa điểm A . Tính V theo V . 2 7 5 5 17 A. V  . B. V  . C. V  . D. V  . 2 12 2 12 2 6 2 24 Lời giải Chọn B Trang 66 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 Do C B
  // (ABC) nên C B M
 cắt AC tại điểm N thỏa mãn MN // B C
   N là trung điểm AC . 1 7 Dễ thấy 3 đường C N  ,B M
 , AA đồng quy tại S và V  V V  V . S .AMN S. 8 AB C   1 . 8 S AB C
Gọi h, S lần lượt là chiều cao và diện tích đáy của khối lăng trụ ABCAB C   , ta có: 1 1 2 7 5 V  d S ; AB C
  .S  .2 .hS  V , vậy V  V V  V . S .AB C      3 3 3 1 12 2 12
Câu 109. Cho khối lăng trụ ABC.AB C
 . Gọi E , F lần lượt là trung điểm của AA , CC . Mặt phẳng
BEF chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó là 1 1 2 A. . B. 1. C. . D. . 3 2 3 Lời giải Chọn C
Gọi V là thể tích khối lăng trụ ABC.AB C
 ; V là thể tích khối chóp .
B AEFC ; V là thể tích khối 1 2 đa diện BB E  FC A
 ; I là trung điểm của cạnh BB và h là chiều cao của khối lăng trụ ABC.AB C  . h
Ta có: EIF  //  ABC nên d B,EIF   . 2 1 h 1 1 1 1 1 V  . .S  . h S  V . Do đó V  V V  V  V  V . B.IEF 3 2 ABC 6 ABC 6 1 ABC.EIF B.EIF 2 6 3 1 2 V 1
V  V V  V  V  V . Vậy 1  . 2 1 3 3 V 2 2 Cách 2.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 67 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Gọi V là thể tích khối lăng trụ ABC.AB C
 ; V là thể tích khối chóp .
B AEFC , V là thể tích khối 1 2 đa diện BB EFC  A   1 1 2 1 2 Ta có V  V      . V    V suy ra V V . 1 BACC A ABC. 2 2 3 A B C 3 2 3 V 1 Vậy 1  . V 2 2
Câu 110. Cho khối hộp chữ nhật ABC . D AB C  D
  có thể tích là 2110 . Biết AM  MA , DN  3ND , CP  2C P
 như hình vẽ. Mặt phẳng MNP chi khối hộp đã cho thành hai khối đa diện. Thể tích
khôi đa diện nhỏ hơn bằng 5275 5275 7385 8440 A. . B. . C. . D. . 6 12 18 9 Lời giải Chọn A Cách 1
Gọi H là giao điểm của mặt phẳng MNP với BB . Khi đó ta có D N  B H  A M  C P  1 1 5       . DD BB AA CC 2 3 6 V          1 D N B H A M C P  1 5 5
Khi đó ta có A B C D .MNPH      .    . V          4 DD BB AA CC  2 6 12 ABCD.A B C D 5 5275
Vậy thể tích của khối nhỏ là V       .2110 . A B C D .MNPH 12 6 Cách 2 Trang 68 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Gọi H là giao điểm của mặt phẳng MNP với BB . Khi đó ta có D N  B H  A M  C P  1 1 5        B H 7 , suy ra  . DD BB AA CC 2 3 6 BB 12
    Gọi E C C  , F  A , A G  B B  sao cho D N   C E   A' F  B G  . Gọi V là thể tích 0 khối A B  C  D  A
 BCD . Gọi V là thể tích khối A B  C  D  M
 HPN . Gọi V là thể tích 1 khối A B  C  D  F
 GEN . Gọi V là thể tích khối chóp N.FMHG và Gọi V là thể tích 2 3
khối chóp N.EPHG . Ta có V  V  V  V . 1 2 3 1 1 Do D N   D D  nên suy ra V  V . 4 1 0 4 1 S FM  GH 7 7 V  S .AD mà FGHM   suy ra V  V 2 3 FGHM S    2 0   A A B B 24 72 ABA B 1 S EP  GH 5 5 V  S .AB mà GHPE   suy ra V  V 3 3 GHPE S    2 0   C C B B 24 72 BCC B 5 5275
Vậy thể tích khối cần tính là: V  V  . 0 12 6
Câu 111. Cho khối lăng trụ tam giác ABC.A ' B 'C '. Gọi M là trung điểm cạnh BB ' , N là điểm thuộc cạnh
AA ' sao cho AA '  4 AN . Mặt phẳng C 'MN  chia khối lăng trụ thành 2 phần, phần chứa điểm V a a
A có thể tích V , phần còn lại có thể tích V . Tỷ số 1  với a,b là số tự nhiên và phân số 2 1 V b b 2
tối giản. Tổng a  b bằng A. 8 . B. 12 . C. 10 . D. 13 . Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 69 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V 1  AN BM CC '  1  1 1  7 Ta có: ABC.NMC'      1      . V
3  AA' BB ' CC '  3  4 2  12 ABC.A'B 'C ' 7 5  V  V  V  V . ABC.NMC ' ABC.A'B 'C ' NMC ' A'B' ABC.A'B 'C ' 12 12 V V 5 a 1 NMC ' A'B '      a  b  12. V V 7 b 2 ABC.NMC '
Câu 112. Cho lăng trụ ABC.A' B 'C 'có thể tích là V . Gọi M là điểm trên cạnh CC 'sao cho CM  3C ' M
. Tính thể tích của khối chóp M .ABC . V 3V V V A. . B. . C. . D. . 4 4 12 6 Lời giải Chọn A A' C' M B' A C B V MC 3 3 M .ABC    V  V . M .ABC C '. V C 'C 4 4 ABC C '.ABC V 1 1 C '.ABC   V  V . C '. V 3 ABC 3 A' B 'C '.ABC 3 1 V Suy ra V  . V  . M .ABC 4 3 4
Câu 113. Cho hình lăng trụ tam giác ABC.AB C
 có thể tích là V và độ dài cạnh bên AA  6 đơn vị. Cho
điểm A thuộc cạnh AA sao cho AA  2 . Các điểm B , C lần lượt thuộc cạnh BB , CC sao 1 1 1 1
cho BB  x, CC  y , ở đó x, y là các số thực dương thỏa mãn xy  12.Biết rằng thể tích của 1 1 1
khối đa diện ABC.A B C bằng V .Giá trị của x  y bằng 1 1 1 2 A. 3 . B. 4 . C. 1. D. 0 . Lời giải Chọn C Trang 70 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Gọi M , N lần lượt thuộc BB và CC sao cho BM  CN  2. Khi đó ta có x  y  x  y  V  V  1 4 V  V  1 4 2 V  V   V. ABC.    1 A 1 B 1 C ABC. 1 A MN 1 A MN 1 C 1 B 3 12 A BCC B 3 12 3 1
Mặt khác theo giả thiết ta có V  V nên suy ra ABC. 1 A 1 B 1 C 2 1 x  y  4 2 1 x  y  V   V  1 4 2 1 V  
   x  y  7 , kết hợp với xy  12.Ta có 3 12 3 2 3 12 3 2 x  3 x  4  hoặc  . Do đó x  y  1.  y  4  y  3
Câu 114. Cho một hình hộp chữ nhật ABC . D 
A BCD . Trên các cạnh A 
A , BB , CC lấy lần lượt lấy ba
điểm X , Y , Z sao cho AX  2 
A X , BY  BY , CZ  3CZ . Mặt phẳng  XYZ  cắt cạnh DDở
tại điểm T . Khi đó tỉ số thể tích của khối XYZT.ABCD và khối XYZT.  A BC  D bằng bao nhiêu? A. 7 . B. 7 . C. 17 . D. 17 . 24 17 7 24 Lời giải Chọn C
Xét mặt phẳng qua H và song song mặt phẳng  ABCD cắt các cạnh A  A , BB , CC , D  D lần
lượt tại M , N , P , Q . Khi đó, hai mặt phẳng  XYZT  ; MNPQ cùng với các mặt bên của hình
hộp chữ nhật giới hạn những khối đa diện bằng nhau và đối xứng nhau qua điểm H . Khi đó, V   V . A BCDXYZT  A BCDMNPQ V V HF Ta có:  EH MNPQ //  ABCD nên  A BCDMNPQ  hay XYZTABCD  . V V EH  EF A BCDABCD  A BCDXYZT
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 71 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT  A X  C Xét hình thang  Z
A XZC có đường trunh bình EH nên 7 EH   EF . 2 24 Do đó 17 EH HF  EF hay 7  . 24 HF 17 V ABCD 17 Vậy XYZT  . V 7 XYZTABCD
Câu 115. Cho hình lăng trụ tam giác ABC. 
A BC. Gọi M , N lần lượt là trung điểm của BB , CC . Mặt phẳng  
A MN  chia khối lăng trụ thành hai phần, đặt V là thể tích của phần đa diện chứa điểm 1 V
B , V là phần còn lại. Tính tỉ số 1 . 2 V2 V 7 V V V 5 A. 1  . B. 1  2 . C. 1  3. D. 1  . V 2 V V V 2 2 2 2 2 Lời giải Chọn B B C B C A A M N M N B C B K C A A
Kẻ MK // AB suy ra KN // AC . Do M , N lần lượt là trung điểm của B  B , CC khi đó mặt
phẳng MKN chia hình lăng trụ ABC. 
A BClàm hai phần bằng nhau. Ta có V  V V  V . ABC  A BC ABC MNK MNK  A BC 2 . . . MNK .  A BC Mặt khác V  V V V và V  V  V MNK .ABC N .ABC  A .MNK N .  A BM N .  A BC A .MNK N .  A BM V nên V  V V  V , V  4V . Vậy 1  2 . N  A BC N  A B 2 2 . . M N .  A BC 1 N .ABC V2
Câu 116. Xét khối lăng trụ tam giác ABC.AB C
 . Mặt phẳng đi qua C và các trung điểm của AA , BB
chia khối lăng trụ thành hai phần có tỉ số thể tích bằng 2 1 1 A. . B. . C. 1. D. . 3 2 3 Lời giải Chọn B C' B' A' F E C B A Trang 72 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Gọi E , F lần lượt là các trung điểm của AA và BB khi đó ta có: 1 1 2 1 V  V  . V  V . C .AB F  E . 2 C AB BA . 2 3 ABC A B C . 3 ABC A B C 2 Suy ra V  V . CC .ABFE . 3 ABC A B C 1 Vậy mặt phẳng C E
 F  chia khối lăng trụ thành hai phần có tỉ số thể tích bằng . 2
Câu 117. Cho khối hộp chữ nhật ABC . D AB C  D
  có thể tích bằng 2110 . Biết AM  MA , DN  3ND , CP  2C P
 như hình vẽ. Mặt phẳng MNP chia khối hộp đã cho thành hai khối đa diện. Thể tích
khối đa diện nhỏ hơn bằng 5275 8440 7385 5275 A. . B. . C. D. . 6 9 18 12 Lời giải Chọn A
Gọi Q là giao điểm của mặt phẳng MNP với BB . A M  C P  D N  B Q  Giả sử  x ,  y ,  z ,
 t . Khi đó x  y  z  t . AA CC DD BB V   V   A B  D  .MQN x z t     x z t A B D .MQN   V    3 V     6 A B D .ABD A B C D .ABCD
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 73 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V   V   C B  D  .PQN y z t     y z t C B D .PQN   V 3 V 6 C B  D  .CBD AB C  D  .ABCD VMNPQ.A D C B 1    x  y V 2 ABCD.AD C  B   V    MNPQ.A D  C  B   1 A M C P    1  1 1  5        V        2 AA CC  2  2 3  12 ABCD.A D C B 5 5275  V       .V . MNPQ.A D C B AB D C . 12 A D  C  B   6
Câu 118. Cho hình hộp ABC . D A B  C  D
  . Tính tỉ số thể tích của khối tứ diện AC BD  và khối hộp ABC . D A B  C  D   . 1 A. 1 . B. 1 . C. 1 . D. . 3 6 2 4 Lời giải Chọn C A' B' C' D' A B D C Gọi V  V , ta có V     1 1 1     1    V V V   V V V V V V . ABCD.AB C  D   A C BD C'DCB C'A B B C'A D  D  6 6 6 2 1 V    V . A C BD ABCD. 2 A B  C  D  
Câu 119. Cho khối lăng trụ ABC.AB C
 . Gọi M là trung điểm của BB , N là điểm trên cạnh CC sao
cho CN  3NC . Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích V và V như 1 2 V
hình vẽ. Tính tỉ số 1 . V2 V 5 V 3 V 4 V 7 A. 1  . B. 1  . C. 1  . D. 1  . V 3 V 2 V 3 V 5 2 2 2 2 Lời giải Chọn D Trang 74 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Gọi M  là trung điểm của CC , ta có: 1 1 dt   1  5    dt , dt  dt dt dt dt BCM M 2 BCC B M MN 4 BCM M 8 BCC B BMNC 8 BCC B 1 d  ,ABCBC V .dtBCNM 5 2  3   . V 1 8 . A BCBC d  , A BCBC.dt 3 BCBC
1 d  ;A ABC V .dt ABC 1 V   2 V 5 2 . A  A BC 3   . A BCC B   2   5 .  . V d  ; A   A BC.dt 3 V    3 V 8 3 12 ABC.ABC  A BC ABC.A B C ABC.  A BC V 7 Do V   1      V V . ABC.A B C 1 2 V 5 2
Câu 120. Cho lăng trụ ABC.AB C
  .Trên các cạnh AA , BB lần lượt lấy các điểm E, F sao cho
AA  kAE, BB  kB F
 . Mặt phẳng (C EF ) chia khối trụ đã cho thành hai khối đa diện bao gồm V 2 khối chóp (C .AB F
 E) có thể tích V và khối đa diện (ABCEFC ) có thế tích V . Biết rằng 1  1 2 V 7 2 , tìm k A. k  4 . B. k  3 . C. k  1 . D. k  2 . Lời giải Chọn B
+) Do khối chóp C .AB F
 E và khối chóp C .AB B
 A có chung đường cao hạ từ C nên V     S   2S   A E 1 C .A B FE A B FE A B E     (1) V     S   2S   A A k C .A B BA A B BA A B A
+) Do khối chóp C .ABC và khối lăng trụ ABC.AB C
  có chung đường cao hạ từ C và đáy là V  1 V    2 ABC nên C .ABC  C .A B BA   (2) V    3 V    3 ABC.A B C ABC.A B C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 75 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V    2 V 2 2
Từ (1) và (2) suy ra C .A B FE 1     V  .V 1 ABC. V    3k V    3k 3 A B  C k   ABC.A B C ABC.A B C  2 V  .V  1  +) Đặt V  V Khi đó 3k ABC.AB C    2 V  V V V  .V 2 1  3k V 2 2 2 2 2 2 2 6 2 Mà 1  nên .V  (V  .V )   (1 )    2k  6  k  3 V 7 3k 7 3k 3k 7 3k 7k 7 2 Câu 121. Cho hình hộp ABC . D AB C  D
  thể tích là V. Tính thể tích của tứ diện ACB D   theo V. V V V V A. . B. . C. . D. . 6 4 5 3 Lời giải Chọn D Ta có ngay kết quả sau V  V  V V V V . ACB'D '  B'.ABC C.B'C'D' D'.ACD . A A'B 'D '  1 1 V V V Lưu ý V  V  V  V  V  . V V  4.  . B '.ABC C.B 'C 'D' D '.ACD . A A' B'D ' ABC.A'B'C ' ACB'D ' 3 3 2 6 3 Câu 122.
Cho khối lăng trụ đứng, mặt phẳng P đi qua C và các trung điểm của AA , BB chia khối lăng trụ ABC.AB C
 thành hai khối đa diện có tỷ số thể tích bằng k với k  1.Tìm k . 1 2 1 A. . B. . C. 1. D. . 3 3 2 Lời giải Chọn D A B C D E F A B C
Gọi D, E, F lần lượt là trung điểm của AA , BB , CC và h là độ dài chiều cao của khối lăng trụ ABC.AB C  . Khi đó ta có Trang 76 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 h 1 1 V     .S . .S .h .V     . C DEF DEF DEF ABC. 3 2 6 6 A B C 1 Mặt khác V     .V   . A B C DEF ABC. 2 A B C 1 1 V    1 Suy ra V           V . C DEB A V    V    V    k . C DEB A C 'DEF ABC.A B C C DEB A ABC. 2 3 A B C V  2 ABCDC E 7. KHỐI CHÓP - MỨC 4
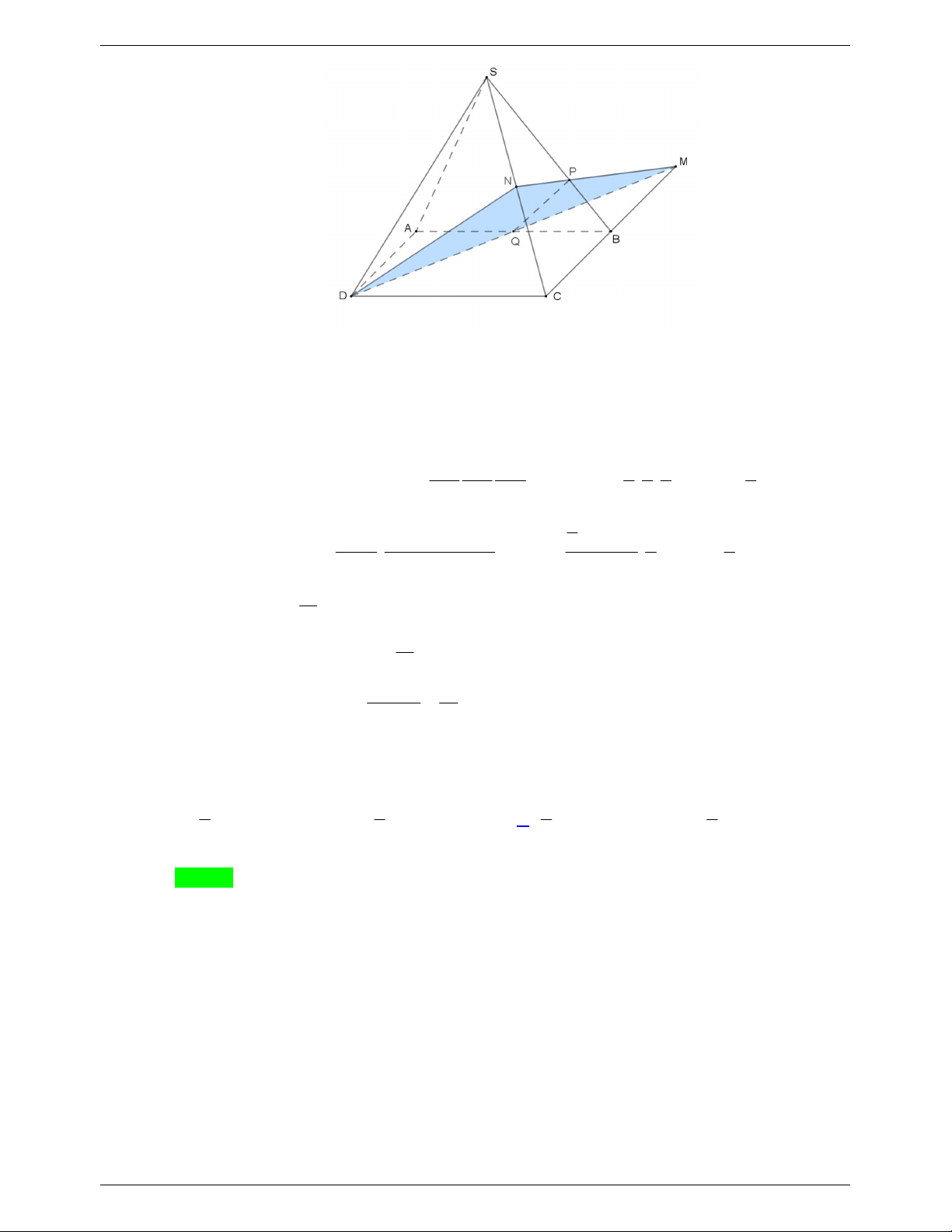
Câu 123. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA , N là
điểm trên đoạn SB sao cho SN  2NB . Mặt phẳng  R chứa MN cắt đoạn SD tại Q và cắt đoạn SC V tại P SP . Tính tỉ số
để thể tích khối đa diện S.MNPQ đạt giá trị lớn nhất. SC VS.ABCD 2 1 1 A. . B. . C. . D. . 1 5 3 4 Lời giải Chọn D SP SQ   Đặt  x 0  x  SM SP SN SQ 1. Ta có    1 2 1    x   x  1 x  .   SC SA SC SB SD SD 2 3 6  6 
Mặt khác ABCD là hình bình hành nên có V  2V  2V S.ABCD S.ABC S.ACD V SM SN SP 1 VS MPQ SM SP SQ 1  1  S.MNP  . .  x ; .  . .  x x  .   V SA SB SC 3 V SA SC SD 2  6  S .ABC S.ACD V V V S MNPQ   S MNP S MPQ 1 1 1 1 1 Suy ra . . . 2    x  x x   x  x .   V 2V 2V 6 4  6  4 8 S.ABCD S.ABC S .ACD 1 1   Xét f x 2  x  1
x với  x  1 ; f  x 1 1 1 1
 x   0  x    ;1  4 8 6 2 8 4 6    Bảng biến thiên:
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 77 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3 V 3 SP
Từ BBT ta có max f  x  . Vậy S.MNPQ đạt giá trị lớn nhất bằng khi  1.  1  ;1 8 V 8 SC  S .ABCD 6   
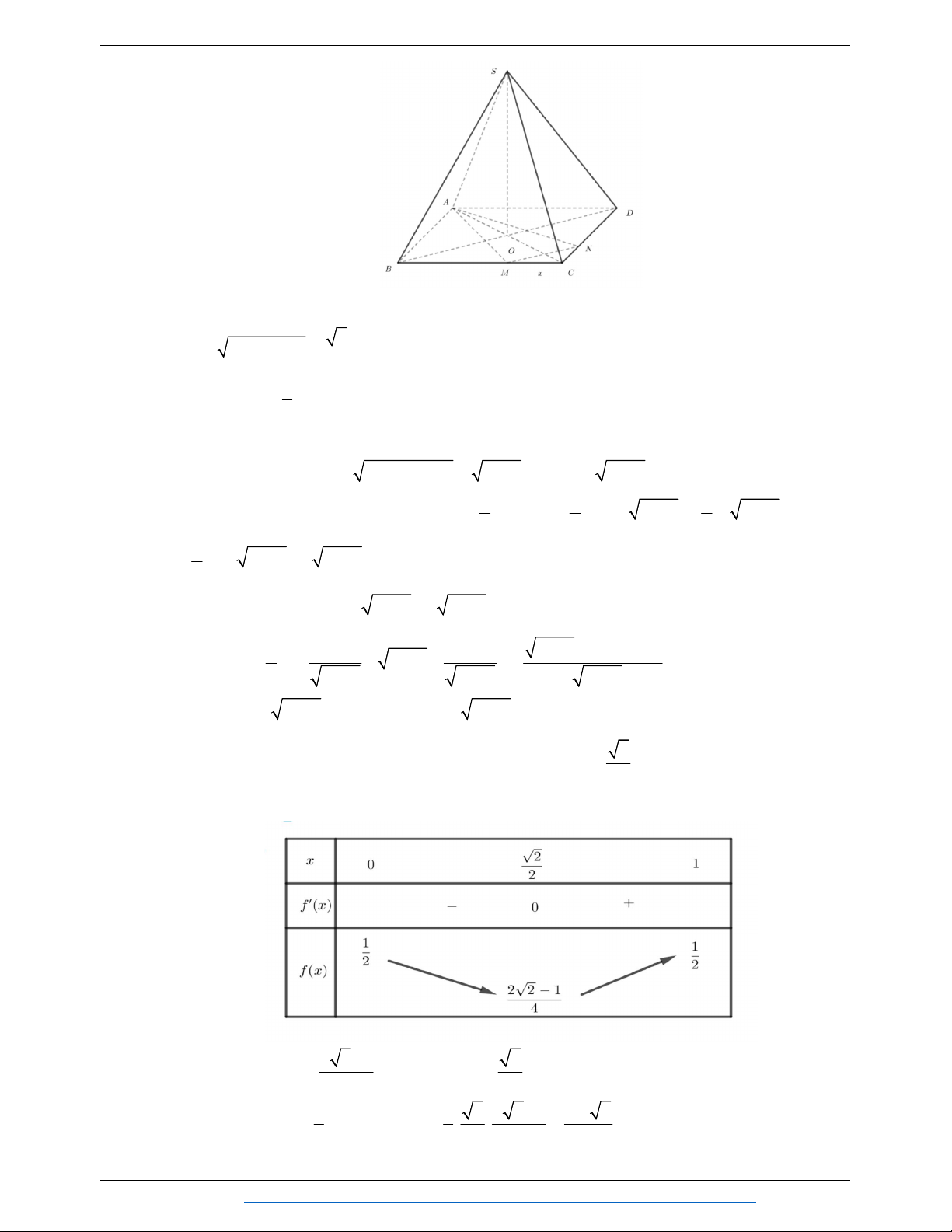
Câu 124. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn
song song với đáy và cắt các cạnh bên S , A S ,
B SC,SD lần lượt tại M, N, ,
P Q . Gọi M , N , P ,Q SM
lần lượt là hình chiếu vuông góc của M, N, ,
P Q lên mặt phẳng  ABCD . Tính tỉ số để thể SA tích khối đa diện MNP . Q M N  P  Q
 đạt giá trị lớn nhất. 1 3 2 1 A. . B. . C. . D. . 3 4 3 2 Lời giải Chọn C SM Đặt  k với k 0;  1 . SA MN SM
Xét tam giác SAB có MN //AB nên   k  MN  k.AB . AB SA MQ SM
Xét tam giác SAD có MQ//AD nên   k  MQ  k.AD . AD SA
Kẻ đường cao SH của hình chóp. Xét tam giác SAH có:   MM //SH MM AM SA SM SM nên    1
 1 k  MM   1 k .SH . SH SA SA SA Ta có: 2 V         MN.M . Q MM A . B A . D SH.k . 1 k MNPQ.M N P Q   .
Thể tích khối chóp không đổi nên V
đạt giá trị lớn nhất khi 2
k .1 k  lớn nhất. MNPQ.M N  P  Q   2 1 k .k.k 1  2  2k  k  k  4 Ta có k .1 k    3 2    .   2 2  3  27 SM
Đẳng thức xảy ra khi và chỉ khi:   k  2 2 1  k  k  2 . Vậy  . 3 SA 3
Câu 125. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  a, AD  2 .
a Cạnh bên SA vuông góc với đáy và SA  3 .
a Điểm P là trung điểm của SC . Một mặt phẳng qua AP cắt hai cạnh SB và SD lần lượt tại M và N SM . Tính tỉ số
khi thể tích của khối chóp S.AMPN đạt giá trị nhỏ nhất. SB Trang 78 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 4 2 A. . 1 1 B. . C. . D. . 3 3 3 Lời giải Chọn D
Cách xác định mặt phẳng qua AP cắt hai cạnh SB , SD như hình vẽ. Gọi O là giao điểm của hai
đường chéo hình chữ nhật ABCD và I là giao điểm AP và MN . 1 1 Ta có 3 V  AS.A . B AD  .3 . a .2 a a  2a , S.ABCD 3 3 V S . A SM .SP 1 SM
Áp dụng công thức tỉ số thể tích ta có S .AMP   . ; V S . A SB.SC 2 SC S .ABC V S . A SN.SP 1 SN S .ANP   . V S . A . SD SC 2 SD S .ADC SM SN Suy ra V  .V , V  .V . Khi đó S.AMP S. 4 ABCD SB S.ANP S. 4 ABCD SD 3  SM SN  a V  V V   . 1 S.AMP S.ANP    SB SD  2 SI 2
Ta có I là trọng tâm tam giác SAC nên  SO 3 Từ ,
B Dlần lượt kẻ các đường thẳng song song với MN cắt SO tại , E F . Khi đó hai tam giác
OED  OFB (g.c.g) suy ra OE  OF SB SF SO  OF  Ta có   SD SE SO OE ;   SM SI SI SN SI SI SB SD 2SO SM SN Từ đó suy ra    4 4 3suy ra  
 . Dấu bằng xảy ra khi SM SN SI SB SD SB SD 3  SM SN SM SN SM 2   MN //BD   . SB SD SB 3
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 79 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3 3  SM SN  a 4 a 2 2 SM 2 Vậy 3 V   .   a  
. Giá trị nhỏ nhất của V bằng 3 a khi  . 1  SB SD  2 3 2 3 1 3 SB 3
Câu 126. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA , N là
điểm trên đoạn SB sao cho SN  2NB . Mặt phẳng  R chứa MN cắt đoạn SD tại Q và cắt đoạn SC V tại P SP . Tính tỉ số
để thể tích khối đa diện S.MNPQ đạt giá trị lớn nhất. SC VS.ABCD 2 1 1 A. . B. . C. . D. 1. 5 3 4 Lời giải Chọn D SP SQ   Đặt  x 0  x  SM SP SN SQ 1. Ta có    1 2 1    x   x  1 x  .   SC SA SC SB SD SD 2 3 6  6 
Mặt khác ABCD là hình bình hành nên có V  2V  2V S.ABCD S.ABC S.ACD V SM SN SP 1 VS MPQ SM SP SQ 1  1  S.MNP  . .  x ; .  . .  x x  .   V SA SB SC 3 V SA SC SD 2  6  S .ABC S.ACD V V V S MNPQ   S MNP S MPQ 1 1 1 1 1 Suy ra . . . 2    x  x x   x  x .   V 2V 2V 6 4  6  4 8 S.ABCD S.ABC S .ACD 1 1   Xét f  x 2  x  1
x với  x  1 ; f  x 1 1 1 1
 x   0  x    ;1  4 8 6 2 8 4 6    Bảng biến thiên: 3 V 3 SP
Từ BBT ta có max f  x  . Vậy S.MNPQ đạt giá trị lớn nhất bằng khi  1.  1  ;1 8 V 8 SC  S .ABCD 6   
Câu 127. Cho hình chóp S .A BC D có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy,
cạnh bên SB tạo với đáy góc 45 . Gọi B  , D  là hình chiếu của A lần lượt trên SB , SD . Mặt phẳng AB D
  cắt SC tại C . Tính tỉ số thể tích của khối chóp . S ABC  D  và   S .ABC D. Trang 80 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 1 1 1 A. . B. . C. . D. . 8 12 6 3 Lời giải Chọn C S C' D' B' D A O B C Ta có: S , B  ABCD   
SBA  45   SAB vuông cân tại A  SA  a .
Mặt khác  SA B vuông cân tại A có AB  là đường cao  B  là trung điểm SB .
SAD vuông cân tại A có AD  là đường cao  D  là trung điểm S D . Mà 2 2 2 2
SC  SA  AC  3a  SC  3a.
Ta có: C D  AD ; CD  SA  CD  (SA ) D CD  AD .
CDAD; ADSD  AD  SCD  AD  SC .     1
Chứng minh tương tự ta cũng có: AB   SC 2 .  
Từ 1 và 2  SC  ABC D    SC  AC  .   SA a Xét tam giác vuông 2 3 SAC có AC 2
là đường cao nên: SA  S . C SC  SC   SC 3 Đặt V  V . S . ABCD Khi đó: 1 1 V  V  V  V . S . ABC S . ADC S . 2 ABCD 2 a 3 V SB SC 1 1 1 1 Ta có: S.AB'C' 3  .  .  V  V  V . S.AB'C ' S. V SB SC 2 S ABC a 3 6 6 ABC 12 . V SD SC 1 1 1 S.AD'C '  .  V  V  V . S.AD'C ' S. V SD SC 6 6 ADC 12 S.ADC
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 81 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1 1 V  V V     V   V S AB C D SAB C SAC D   1 Vậy 12 12    . V V V 6 S.ABCD S.ABCD   
Câu 128. Cho khối tứ diện đều ABCD. Gọi M , N lần lượt là các điểm thỏa mãn MA MB  0 và   
NC  2ND  0.Mặt phẳng   chứa đường thẳng M N và song song với A C chia khối tứ diện
ABC D thành hai khối đa diện. Tính tỉ số thể tích của khối đa diện chứa đỉnh A và khối đa diện còn lại. 11 7 7 1 1 A. . B. . C. . D. . 18 18 1 1 7 Lời giải Chọn D
Gọi V là thể tích của khối đa diện chứa đỉnh . A A
Giả sử khối tứ diện đều ABCD có thể tích bằng V . 0
Vì   // AC      ABC   MP // AC P  BC  .
 // AC     ADC   NQ // AC Q  AD .
Khối đa diện chứa đỉnh A được chia thành ba khối tứ diện AMNQ , AMNP , ACNP do vậy V  V V V . A AMNQ AMNP ACNP Xét tam giác AQ CN 2 A C D , có QN // AC    . AD CD 3 Ta có: AM AQ 1 2 1 2 DN 1 2 1 1 V  . .V  . .V  . . V  . . .V  V . AMNQ ABND ABND 0 0 0 AB AD 2 3 2 3 DC 2 3 3 9 AM 1 1 S 1 1 1 BNP V  V  V  V  . V  V AMNP ABNP ABNP 0 0 0 . AB 2 2 S 2 3 6 BCD CN CP 2 1 1 V  . V  . V  V . ACNP 0 0 0 CD CB 3 2 3  1 1 1  11 Suy ra V    V  .V . A   0 0  9 6 3 18 11V0 V 11 Vậy A 18   . V V 11 7 0 A V  V 0 0 18 Trang 82 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12    
Câu 129. Cho khối chóp S.ABC có M  SA , N  SB sao cho MA  2  MS , NS  2  NB . Mặt phẳng
  đi qua hai điểm M , N và song song với SC chia khối chóp thành hai khối đa diện, có thể V  1 tích là V V V V 1 , 2 với 1 2 . Tỉ số là V2 3 4 3 4 A. . B. . C. . D. . 5 9 4 5 Lời giải Chọn D S M N Q C A P B
Ta có mặt phẳng   cắt mặt phẳng SAC  theo giao tuyến MQ SC (Q  AC ) và cắt mặt
phẳng SBC  theo giao tuyến NP  SC (P  BC ). Thiết diện tạo bởi mặt phẳng   với hình chóp là hình thang MNPQ. Gọi V  V và S  S . S.ABC A  BC QC 1 PC Ta có:  2 ,  1 2 nên S   . S . AC 3 BC 3 PQC 3 3 Suy ra: S  S S  7 S . ABPQ PQC 9 1 1 1 7 7 V  .d N , ABC .S
 . d S, ABC . S  V N . ABPQ    . 3 ABPQ 3 3 9 27 MA 2 QA Mặt khác:  2 ,  nên 4 SA 3 CA 3 S  S AMQ 9 ASC 1 1 2 4 8 V  .d N , SAC .S  . d B,SAC . S  V N . AMQ    . 3 AMQ 3 3 9 ASC 27 Vậy 5 V  V  V  4 V  V  V . MNABPQ N .ABPQ N . AMQ 9 SMNPQC 9 VSMNPQC 4 Suy ra  . V 5 MNABPQ
Câu 130. Cho hình chóp S .A BC D có đáy là hình bình hành có thể tích là V  . Gọi M , N , P , Qlần
lượt là trọng tâm của các tam giác SA , B SBC, SC ,
D SDA . Gọi O là điểm bất kì trên mặt phẳng  đáy  V
ABCD  . Biết thể tích khối chóp .
OMNPQ bằng V . Tính tỉ số . V A. 27 . B. 27 . C. 9 . D. 27 . 2 8 4 4
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 83 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT Lời giải Chọn A
Gọi E , F , G , K lần lượt là trung điểm của AB , BC , CD , DA . SM SN 2
Vì M , N lần lượt là trọng tâm các tam giác SAB , SBC nên   . Suy ra MN  FE SE SF 3
1 . Chứng minh tương tự ta có PQ  KG 2 . Vì ,
E F lần lượt là trung điểm của A ,
B BC nên FE  AC 3 . Chứng minh tương tự ta có KG  AC 4 .
Từ 1 , 2 , 3 , 4 suy ra MN  PQ . Suy ra 4 điểm M , N , P , Qđồng phẳng. SM Ta
có MNPQ  //  ABCD  ;
 2  d S,MNPQ  2.d  MNPQ, ABCD ME  2.d  , O MNPQ  V  2V  2V . S .MNPQ O.MNPQ V SM SN SQ + S.MNQ    2 2 2    8  8  V  V . V SE SF SK 3 3 3 27 S .MNQ S . 27 EFK S.EFK V SN SP SQ + S.NPQ  2 2 2 8 . .  8 . .   V  V . V SF SG SK 3 3 3 27 S .NPQ S . 27 FGK S .FGK 8 8  8 V V  V  V  V  V . S .MNQ S .NPQ S.EFK S . 27 27 FGK S .MNPQ S . 27 EFGK 27 27  V  V  V 1 . S .EFGK S . 8 MNPQ 4 1 BE.BF.sin  EBF S Ta có E  BF 2  1  1  S  1 S  S . S 1 EBF ABC  4 4 8 ABCD ABC B . A BC.sin  ABC 2
Chứng minh tương tự ta có 1 S  S  S  S . FCG GDK KAE 8 ABCD Khi đó S  S  S  S  S  S  S  1 4S  S EFGK ABCD  EBF FCG GDK KAE  . ABCD EBF 2 ABCD Trang 84 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 .d S ,EFGK.SEFGK V Suy ra S.EFGK 3  1   V  2.V 2 . V 1 2 S.ABCD S.EFGK S.ABCD .d S , ABCD.S 3 ABCD  Từ  27 V 27 1 và 2 suy ra V  V hay  . S . ABCD 2 V 2
CÔNG THỨC TÍNH NHANH: Cho khối chóp S .A B C D có đáy ABCD là hình bình hành. Mặt
phẳng cắt các cạnh SA , SB , SC , SD lần lượt tại M , N , P , Q SA sao cho  SB x ,  y , SM SN SC SD  z , t . SP SQ V x  y  z  t Khi đó: S.MNPQ  V 4xyzt S.ABCD
Áp dụng vào bài toán ta được: V V S.MNPQ 8   S.MNPQ 4   V 27 V 27 S.EFGK S. ABCD VO MNPQ 2 V  V  2V .   27   S. MNPQ O. MNPQ V 27 V 2 S.ABCD
Câu 131. Cho hình chóp tứ giác đều S .A BC D . Gọi C  là trung điểm của SC . Mặt phẳng  P qua AC 
và vuông góc SC cắt SB , SD lần lượt tại B, D  . Gọi V , V lần lượt là thể tích hai khối chóp 1 2 V S .AB C  D
  và S .A B C D . Tính tỉ số 1 . V2 V 2 V 2 V 4 V 1 A. 1  . B. 1  . C. 1  . D. 1  . V 3 V 9 V 9 V 3 2 2 2 2 Lời giải Chọn D
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 85 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Do S .A B C D là hình chóp tứ giác đều nên hình chiếu của S lên mặt phẳng  ABC  D trùng với
tâm H của hình vuông ABCD .
Vì C  là trung điểm của SC và H là trung điểm A C nên I  AC   SH là trọng tâm  S A C 2  SI  SH . 3 Ta có:
B D  A C , B D  S H BDSA 
C  BD  SC mà BD  P ;   P SC B / D /  P . Vì BD  SBD  BD// 
; SBD    P   B D   và P suy ra BD// B D   . Mặt khác:   P SB  D  BD  , I AC  P , I SH SB  D  I  BD . Do đó: SB SD   SI  2  . SB SD SH 3 Ta có: V V V 
1 SA SB SC 1 SA SC SD   V V   V 1 S.AB C  D    S.AB C S.AC D    S.AB C S.AC D             V V V 2V 2V 2 SA SB SC 2 SA SC SD 2 S.ABCD S.ABCD S.ABC S.ACD 1 2 1 1 1 2  1     1    1  . 2 3 2 2 2 3 3 V 1 Vậy 1  . V 3 2
CÔNG THỨC TÍNH NHANH: Cho khối chóp S .A BC D có đáy ABCD là hình bình hành. Mặt phẳng cắt các cạnh SA
SA , SB , SC , SD lần lượt tại M , N , P , Q sao cho  SB x ,  y , SM SN SC SD  z , t . SP SQ Trang 86 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 V x  y  z  t Ta có: S.MNPQ  V 4xyzt S.ABCD SA SD SC SB 3 3 V V    1  2     1
Áp dụng vào bài toán ta có 1 S.AB C  D    SA SD SC SB 2 2    V V SA SD SC SB 3 3 3 2 S.ABCD 4    41  2  SA SD SC SB 2 2
Câu 132. Cho tứ diện S A B C có G là trọng tâm tứ diện, mặt phẳng quay quanh A G cắt các cạnh SB , SC V
lần lượt tại M , N . Giá trị nhỏ nhất của tỉ số S.AMN là VS.ABC 4 3 1 1 A. . B. . C. . D. . 9 8 3 2 Lời giải Chọn A
Gọi E , F lần lượt là trung điểm BC , SA khi đó trung điểm G của EF là trọng tâm của tứ diện
S A B C . Điểm I là giao điểm của A G và SE . Qua I dựng đường thẳng cắt các cạnh SB , SC
lần lượt tại M , N . Suy ra  AMN  là mặt phẳng quay quanh A G thỏa mãn yêu cầu bài toán.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 87 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Dựng GK // SE , K  SA suy ra K là trung điểm FS .  KG  AK  3 KG 1 SI . Mà   2  . SI AS 4 SE 2 SE 3 Cách 1: Dựng B P //M N , C / Q /MN , P , Q  SE  . SN SI Ta có: SM  SI ;  . SB SP SC SQ Ta có: B /
P /QC , E  PQ BC và EB  EC BEP  CEQ  E là trung điểm của PQ
SP SQ  2SE (đúng cả trong trường hợp P  Q  E ). V 2 SA SM SN SI SI 2 AM GM SI SI SI Ta có: S.AMN  . . 1. .   2    4 .  V   SA SB SC SP SQ SPSQ2 2 SE SE 9 S.ABC   4
Dấu "  " xảy ra khi và chỉ khi SP  SQ  SE . Hay P  Q  E  MN // BC . 4
Vậy tỉ số nhỏ nhất là . 9 Cách 2: SB Đặt  x SC ;
 y , với x  0 , y  0. SM SN   1   1   x  y 
Ta có: SI  2 SE  SB  SC  x.SM  y.SN   .SM  .SN . 3 3 3 3 3 x y
Do I , M , N thẳng hàng nên  1  x  y  3 . 3 3 V AM GM Ta có: S.AMN  SA SM SN . .  1 1  4 .  V SA SB SC xy 9 S.ABC x  y2 4
Dấu "  " xảy ra khi và chỉ khi x  y  3  MN // BC . 2
Vậy tỉ số nhỏ nhất là 4 . 9
Câu 133. Cho tứ diện ABCD , trên các cạnh B C , B D , A C lần lượt lấy các điểm M , N , P sao cho 3 B C  3 B M , BD 
BN , AC  2 AP . Mặt phẳng  MNP chia khối tứ diện ABCD thành hai 2 V
phần có thể tích là V , V với V  V . Tính tỉ số 2 T  . 1 2 1 2 V1 A. 26 26 26 26 T  . B. T  . C. T  . D. T  . 13 19 21 15 Lời giải Chọn B Trang 88 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 A Q I P D N B M C Gọi V
V , I  M N  CD , Q  IP ADsuy ra Q  AD   MN  P . ABCD
Thiết diện của tứ diện ABCD được cắt bởi mặt phẳng MNP là tứ giác MNQP . 3 NB MC PC AP Có BD  BN   2 ; B C  3B M   2 và AC  2 AP   1 1 ;  . 2 ND MB PA AC 2
Áp dụng định lí Menelaus trong các tam giác B C D và A C D ta có: NB ID MC ID ID . .  1  2. .2  1 1   . ND IC MB IC IC 4 AQ 4 Và ID PC QA QA QA . .  1 1  .1.  1   4   . IC PA QD 4 Q D QD AD 5
Áp dụng bài toán tỉ số thể tích của hai khối chóp tam giác ta có: V ND ANCD  1  1  V  2 V và V  V V BD 3 ANCD 3 CBNA 3 ABCD VANPQ AN AP AQ  1 4 1 2 . .  2 1. .  2  V  2 V  V . Suy ra V  V  V V AN AC AD 2 5 5 ANPQ 5 ANCD 15 N .PQDC 3 15 ANCD 1  V . 5 VCMNP CM CN CP  2 1 1 . .  1 .1.   V  2 V  V . V CB CN CA 3 2 3 CMNP 3 CBNA 9 CBNA
Suy ra thể tích phần thứ nhất là: V  V  1 2 V  V  19 V  V . 1 N .PQDC CMNP 5 9 45
Do đó thể tích phần còn lại là: V  V  26 V  V . 2 1 45 V 26 Vậy T  2  . V 19 1
Câu 134. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a , tâm của đáy là O . Gọi M , N
tương ứng là trung điểm các cạnh SA , SC . Gọi E là giao điểm của SD và mặt phẳng  BMN  .
Tính thể tích V của khối chóp . O BMEN . 3 a 2 3 a 2 3 a 2 3 a 2 A. V  . B. V  . C. V  . D. V  . 18 24 12 36 Lời giải Chọn D
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 89 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT Cách 1:
Trong mặt phẳng SAC gọi I  MN  SO . Trong mặt phẳng SBD gọi E  BI  SD .
Khi đó E  SD  BMN  .
Vì M , N lần lượt là trung điểm của SA , SC nên MN là đường trung bình tam giác SAC .
Suy ra I là trung điểm SO .
Áp dụng định lý Menelaus tam giác SOD với ba điểm thẳng hàng B , I , E , ta có: ES BD IO ES ES . .  1  .2.1  1 1   . ED BO IS ED ED 2 a 2 Ta có 2 2
AC  AB  BC  a 2 , suy ra AO  . 2
Vì hình chóp S.ABCD là hình chóp đều nên SO   ABCD . 2  a 2  a 2 Ta có 2 2 2 SO  SA  AO  a     .  2  2   Thể tích khối OBMEN là V  V  V V
(vì I là trung điểm SO ). 0BMEN S .BMEN S.BMN S .EMN V SB SM SN 1 3 1 1 1 1 a 2 S .BMN  . .   V  V  . .S . O .A . B BC  . V SB SA SC 4 S .BMN S . 4 BAC 4 3 2 48 S .BAC V SE SM SN 1 3 1 1 1 1 a 2 S .EMN  . .   V  V  . .S . O .A . D DC  . V SD SA SC 12 S .EMN S . 12 DAC 12 3 2 144 S .DAC 3 3 3 a 2 a 2 a 2 V  V V    . SBMEN S .BMN S .EMN 48 144 36 3 a 2 Vậy V  . 0 BMEN 36
Cách 2: Làm trắc nghiệm. Trang 90 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 SM 1 SB SN Đặt  x  ;  y  1 1;  z  SE ;  t . SA 2 SB SC 2 SD
Điều kiện để bốn điểm B , M , E , N đồng phẳng là: 1 1 1 1    1 1
 2  2  1  t  . x z y t t 3 V 1  1 1 1 1 Ta có S.BMEN  xyzt      V 4  x y z t S.BADC  1 1 1 1       1 . .1. . . 2 1 2 3  . 4 2 2 3 6 3 1 1 1 1 1 a 2 a 2 Suy ra V  V  . .S . O A . B BC  . . . . a a  . S .BMEN S . 6 BADC 6 3 6 3 2 36 3 a 2 Mà V  V  . 0 BMEN S .BMEN 36 3 a 2 Vậy V  . 0 BMEN 36 Cách 3: V  V V 0BMEN BOMN OMNE . Lại có V  V . OMNE SMNE a a a OM  ON  2 ; MN  2 ; BO 
. Suy ra tam giác OMN vuông tại O . 2 2 2 3 1 1 a 2 1 a a a 2 V  B . O S  . . .  . BOMN OMN 3 3 2 2 2 2 48 SI SE 1 DF DO Kẻ OF // BE . Suy ra   1 ;   1 . Do đó SE  SD . SO SF 2 DE DB 2 3 2 3 V 1 1 1 1 1 1 1 a 2 a a 2 SMNE  . .   V  V  . . .  SMNE SACD . V 3 2 2 12 12 12 3 2 2 144 SACD 3 3 3 a 2 a 2 a 2 Vậy V  V V    . 0 BMEN BOMN OMNE 48 144 36
Câu 135. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của
các cạnh AB , BC . Điểm K thuộc đoạn SA . Biết mặt phẳng MNK  chia khối chóp S.ABCD 7 KA
thành hai phần, phần chứa đỉnh S có thể tích bằng
lần phần còn lại. Tính tỉ số t  . 13 KS 1 A. t  3 . B. t  1 . C. t  2 . D. t  . 2 4 3 3 Lời giải Chọn D
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 91 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Trong mặt phẳng  ABCD , kéo dài MN cắt DA , DC lần lượt tại F , E .
Trong mặt phẳng (SAD) , gọi FK  SD  Q . Trong mặt phẳng SCD , gọi QE  SC  P .
Suy ra thiết diện là ngũ giác MNPQK và MN // AC // PK .
Đặt h  d S, ABCD KA KA t      t t
d K, ABCD  d P, ABCD  .h KS SA t 1 t 1 1 FD Ta có: FA  BN  AD   3 . 2 FA
Áp dụng định lý Menelaus cho tam giác SAD , suy ra QS FD KA QS QS 1 QD 3t   t       d Q  ABCD 3t . . 1 .3. 1 ,  h QD FA KS QD QD 3t SD 3t 1 3t 1 1 1 9 Mặt khác: S  S  S  S  S  S  S FAM NCE BMN 4 ABC 8 ABCD DEF 8 ABCD
Suy ra thể tích của khối đa diện không chứa đỉnh S là 1  3t 9 t 1 t 1  V  V V V  . h S  . S  . S QDEF KAMF PECN   3  3t 1 8 t 1 8 t 1 8  1  27t 2t   .     t  t  . .hS 3 8 3 1 8 1 ABCD       27t 2t   V    V
 83t 1 8t 1 ABCD      7
Phần thể tích của khối đa diện không chứa đỉnh S bằng
phần còn lại suy ra thể tích của khối 13 13
đa diện không chứa đỉnh S bằng
thể tích khối chóp S.ABCD 20 27t 2t 13 2     t  . 83t   1 8t   1 20 3
Câu 136. Cho tứ diện SABC có trọng tâm là G . Một mặt phẳng qua G cắt các tia S , A SB và SC theo thứ SA SB SC
tự tại A, B,C . Đặt  m,  n,
 p . Đẳng thức nào sau đây đúng SA SB SC 1 1 1 A.    1 1 1 1. B.    4 . 2 2 2 m n p mn np pm Trang 92 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 1 1 C.    4 . D. mn p  4 . m n p Lời giải Chọn C S N C' A' G A C O B' M B
Gọi M , N lần lượt là trung điểm các cạnh BC , SA , O là trọng tâm tam giác ABC . Khi đó, ta có:   G  SO  MN .
 1   1  1   1  
Xét tam giác SAM có: SG  SN  SM   SA  SM    SA2SM  2 2  2  4
 1  2  1   4  SG 3
và SO  SA  SM  SA  2SM   SG   . 3 3 3 3 SO 4 V     SA SG SC 3 3 V Ta có: SA GC  . .  . m .p  V    . SAOC mnp (1) V SA SO SC 4 SA GC 4 n SAOC V     SA SG SB 3 3 V SA GB  . .  . m .n  V    m . SAOB np (2) V SA SO SB 4 SA GB 4 p SAOB V     SB SG SC 3 3 V SB GC  . .  . n .p  V    . SBOC mnp (3) V SB SO SC 4 SB GC 4 m SBOC
Cộng (1),(2),(3) vế theo vế ta được: 3  1 1 1  V       mnp .V .V .V SA B C   4 SAOC SAOB SBOC  n p m  V      3 1 V 1 V 1 V SA B C 
 mnp . SAOC  . SAOB  . SBOC  V 4 n V p V m V SABC  SABC SABC SABC  3  1 S 1 S 1 S 
 mnp  mnp  . AOC  . AOB  . BOC  4 n S p S m S  ABC ABC ABC 
4  1 d O; AC  1 d  ; O AB 1 d O; BC 4 1 1 1 1 1 1    .        n d  B AC . p d C AB . m d  A BC . . . 3 ; ; ; 3 n 3 p 3 m 3  1 1 1     4 . m n p
Bình luận: Nếu làm trắc nghiệm, ta chọn mp qua G và cắt ,
SA SB, SC là mp  NBC ,ta có ngay 1 1 1 đáp án:    4. m n p
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 93 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Câu 137. Cho khối chóp S.ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a , tam giác BCD SA   ABCD  P cân tại C  0 và BCD  120 , và SA a . Mặt phẳng
đi qua A và vuông góc với
SC cắt SB,SC,SDlần lượt tại M, N,P . Tính thể tích khối chóp S.AMNP . 3 a 3 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. . 42 21 14 12 Lời giải Chọn A
Giả thiết: BCD cân tại C và BD  a  0 ; BCD  120 2 2 2
 BD  BC  CD  2BC.C . D cos  BCD a 3 2 2  a  3BC  BC  . 3 a 3 2 a 2a 3
 ABC vuông tại B có AB  a, BC  2 2 2  AC  AB  BC  a   . 3 3 3
Giả thiết: BCD cân và ABD đều.
 Tứ giác ABCD có AC  BD và ABC  ADC 2 1 1 2a 3 a 3  S  AC.BD  . .a  . ABCD 2 2 3 3 2 3 1 1 a 3 a 3  V  S . A S  . . a  . S.ABCD 3 ABCD 3 3 9 3 1 a 3  V  V  V  . S.ABC S .ACD S. 2 A C B D 18
Giả thiết: P  vuông góc với SC cắt SB, SC,SD lần lượt tại M, N, P .  BC  SA      BC  AM  Ta có:   1 AM  SB BC  AB .      AM SC    SM 1 Mặt khác S
 AB vuông cân tại S  M là trung điểm SB   . SB 2  SP 1 2 tương tự  . SD 2 3 SC  AN . Trang 94 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 2a 3 Mặt khác SAC vuông tại A có SA  a, AC  . 3 2 2 7a SN SA 3 2 2 2 SC  SA  AC     . 2 3 SC SC 7 V SM SN 1 3 3 3 3 3 3 a 3 a 3 Ta có: S.AMN  .  .   V  .V  .  . V SB SC 2 7 14 S.AMN S. 14 ABC 14 18 84 S.ABC 3 3 V SP SN 3 3 3 a 3 a 3 S .APN  .   V  V  .  . S .APN S . V SD SC 14 14 ADC 14 18 84 S .ADC 3 3 a 3 a 3  V  V V  2.  . S.AMNP S.APN S .AMN 84 42
Câu 138. Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M,N là hai điểm thay đổi lần lượt thuộc cạnh
BC, BD sao cho mặt phẳng AMN luôn vuông góc với mặt phẳng (BCD) . Gọi V ;V lần lượt   1 2
là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN . Tính V V . 1 2 17 2 17 2 17 2 2 A. . B. . C. . D. . 216 72 144 12 Lời giải Chọn A Cách 1:
Gọi I,J,K lần lượt là trung điểm của các đoạn thẳng BC, , BD CD . G là trọng tâm A  BC .
Tứ diện ABCD đều, G là tâm tam giác đề BCD  AG  BCD .  
Ta có AMN  BCD  AMN  AG  G  MN .       1 
Đặt BM  x ,BN  y   x,y  1 . 2  2     Ta có 2 2 2 3 6
AG  AB BG  1      .  3    3  1 1 1 S  S  S
 BM.BN.sinB  BM.GI  BN.GJ BMN BGM BGN 2 2 2 1 0 1 3 1 3  x.y.sin 60  x.  y. x  y  . 2 2 6 2 6 3x 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 95 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 2 2 1 1 3 x 6 2 x
Thể tích tứ diện ABMN là: V  S .AG  . .  . . ABMN 3 B  MN 3 4 3x 1 3 12 3x 1 x   Xét hàm số f x  x   .   2 2 1 . , ;1 12 3x 1 2     2 x  0 3  2  L x x  ' f x   0    x  2 2 3 1 x   N  3 2   V  max f x  f 1  2   2
V  min f x  f    2    1    1 1        x ;1 24 x  3 27  ;1 2    2    17 2 Vậy V V  . 1 2 216 Cách 2:
Gọi I,J,K lần lượt là trung điểm của các đoạn thẳng BC, , BD CD . G là trọng tâm A  BC .
Tứ diện ABCD đều, G là tâm tam giác đề BCD  AG  BCD .  
Ta có AMN  BCD  AMN  AG  G  MN .       2   2 2 2  3 6
AG  AB BG  1      .  3    3  1 V  S .AG . ABMN 3 B  MN
Dễ thấy diện tích Tam giác BMN nhỏ nhất khi và chỉ khi tam giácBMN đều, khi đó MN / /CD BM BG 2 2 2    BM  BC  . BC BK 3 3 3 2 2   3 3  S    .  . B  MN   min 3 4 9
Diện tích tam giác BMN lớn nhất khi và chỉ khi M  C hoặc N  D 1 3  S  S  . B  MN AB  C max 2 8 1 1 6 3 2 Khi đó: V  AG.S  . .  . 1 B  MNmax 3 3 3 8 24 1 1 6 3 2 V  AG.S  . .  . 2 B  MNmin 3 3 3 9 27 17 2 Vậy V V  . 1 2 216
Câu 139. Cho tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trọng tâm của các tam giác ABD
, ABC và E là điểm đối xứng với B qua điểm D . Mặt phẳng MNE  chia khối tứ diện ABCD
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V . Trang 96 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 3 a 2 3 3a 2 3 3a 2 3 9a 2 A. . B. . C. . D. . 96 80 320 320 Lời giải Chọn D 3 a 2
Thể tích khối tứ diện đều cạnh a là . 12
Gọi P  ME  AD ; T  ME  AB . Trong mặt phẳng  ABC  đường thẳng TN cắt AC , BC
lần lượt tại Q , F . Khi đó mặt phẳng MNE  chia khối tứ diện đã cho phần chứa đỉnh A là tứ diện ATPQ . ED MI PA PA
Gọi I là trung điểm BD . Xét AID ta có: . . 1(định lý Menelaus)  3 . EI MA PD PD QA Tương tự ta có:  3 QC EI TB MA TB 2 Xét AIB ta có: . . 1   . EB TA MI TA 3 V 3 3 ATPQ AT AP AQ 3 3 3 27 27 a 2 9a 2 Mặt khác ta có:  . .  . .   V  .  . V AB AD AC 5 4 4 80 ATPQ 80 12 320 ABCD
Câu 140. Cho hình chóp tứ giác S.ABCD đáy là hình bình hành có thể tích bằng V . Lấy điểm B , D lần
lượt là trung điểm của cạnh SB và SD . Mặt phẳng qua  AB D
  cắt cạnh SC tại C . Khi đó thể tích khối chóp S.AB C  D   bằng V 2V 3 V V A. . B. . C. . D. . 3 3 3 6 Lời giải Chọn D
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 97 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT S S K C D C d B H H A D A B O O C C
Gọi O là giao điểm của hai đường chéo AC và BD thì SO  B D
   H . Khi đó H là trung điểm
của SO và C  AH  SO .
Trong mặt phẳng SAC  : Ta kẻ d  //AC và AC cắt d  tại K . Khi đó áp dụng tính đồng dạng OH OA SK SK SC SC 1 của các tam giác ta có:   1 SK  OA  1  1 ;     . SH SK AC 2 AC CC 2 SC 3 1 V V     SA SB SD 1 1 Vì V  V  .V  nên ta có S.AB D      V    V và S.ABD S .BCD S. 2 ABCD 2 V SA SB SD 4 S .AB D 8 S.ABD V         SB SC SD 1 SC SC V S.B C D       V      . V SB SC SD 4 SC S .B C D SC 8 S.BCD 1 SC V V  SC  V Suy ra V            V   V    V 1   . S.AB C D S.AB D S.B C D 8 SC 8 8  SC  6 SA SC SB SD
Lưu ý :Có thể sử dụng nhanh công thức    SA SC SB SD
Câu 141. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của AD . Gọi S là
giao của SC với mặt phẳng chứa BM và song song với SA . Tính tỉ số thể tích của hai khối chóp S .BCDM và S.ABCD . 2 1 1 3 A. . B. . C. . D. . 3 2 4 4 Lời giải Chọn B S S' D A M G B C AG AM 1
Gọi G  BM  AC . AM //BC  A  GM  C  GB    GC BC 2 (
 SAC)(S BM )  S G      S G  //SA S C GC    2 . (  SAC)   , SA SA//(S B  M )  SC AC 3 Trang 98 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 d (S,(ABCD) S C  Do đó:   2 . d (S,( ABCD)) SC 3 1 1 1 1 Ta có S
 d(M, AB).AB  . d(D, AB).AB  S ABM ABCD 2 2 2 4  1 3 S  S  S  S BCDM ABCD ABCD ABCD . 4 4 1 1 2 3 Do vậy: V d(S ',(ABCD).S . d (S,(ABCD)). S S    .BCDM BCDM ABCD 3 3 3 4  1 1 1 V . d(S,(ABCD)).S  V S ' BCDM   1 . ABCD S.ABCD 2 3 2 V 2 SABCD
Câu 142. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm của SC . Mặt phẳng qua
AK cắt các cạnh SB , SD lần lượt tại M và N . Gọi V , V theo thứ tự là thể tích khối chóp 1 V
S.AMKN và khối chóp S.ABCD . Giá trị nhỏ nhất của tỉ số 1 bằng V 1 2 1 3 A. . B. . C. . D. . 2 3 3 8 Lời giải Chọn C S N K A D M C B SA SC Đặt a   SB 1, b  , c   SD 2 , d  , có a  c  3 . SA SM SK SN V V a  b  c  d
Áp dụng công thức tính nhanh tỉ lệ thể tích: 1 S.AMKN   , với a  c  b  d . V V 4abcd S.ABCD V 6 3 3 1 3
Suy ra: b  d  3 . Khi đó 1   
 , dấu bằng xảy ra khi b  d  . 2 V 8bd 4bd  b  d  3 2 4   2  V 1 SB SD 3
Vậy giá trị nhỏ nhất của tỉ số 1 bằng khi   . V 3 SM SN 2 Chứng minh bài toán:
Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm A , B , C , D lần lượt nằm trên SA SB SC SD
các cạnh SA , SB , SC , SD . Đặt a  , b  , c  , d  . SA SB SC SD V        a b c d
Chứng minh rằng:: S.A B C D  và a  c  b  d . V 4abcd S.ABCD Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 99 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT S A' B' D' C' A D B C
Ta có: ABCD là hình bình hành nên: S  2S V  2V . ABCD A  BD S.ABCD S.ABD V       SA SB SD 1 1 1 Khi đó: S.A B D  . .   V      .V .V S.A B D S.ABD S.ABCD . V SA SB SD abd abd 2abd S.ABD V       SB SC SD 1 1 1 S.B C D  . .   V      .V .V S.B C D S.BCD S.ABCD . V SB SC SD bcd bcd 2bcd S.BCD 1 1 a  cV Suy ra: S . V            V    V    .V . ABCD V 1 . S.A B C D S .A B D S .B C D S .ABCD S . 2abd 2 ABCD bcd 2abcd b  d V
Chứng minh tương tự như trên ta cũng có: S . ABCD V  2     . S . A B C D 2abcd Từ  
1 và 2 suy ra: a  c  b  d . b  d V 2 b  d V a  b  c  d V S .ABCD   S.ABCD   S.ABCD V        . S . A B C D 2abcd 4abcd 4abcd V        a b c d Vậy: S.A B C D  . V 4abcd S.ABCD
Câu 143. Cho hình chóp tam giác đều S.ABC . Gọi G là trọng tâm tam giác ABC , biết góc tạo bởi SG và
SBC bằng 30. Mặt phẳng chứa BC và vuông góc với SA chia khối chóp đã cho thành hai V
phần có thể tích V , V trong đó V là phần thể tích chứa điểm S . Tỉ số 1 bằng 1 2 1 V2 1 6 A. 6 . B. . C. . D. 7 . 6 7 Lời giải Chọn B Trang 100 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Gọi M là trung điểm BC , F  SA    , trong đó   là mặt phẳng chứa BC và vuông góc SA
, H là hình chiếu của G lên SM . Ta có: SA    , FM    nên SA  FM .
Vì S.ABC là hình chóp tam giác đều nên SG là đường cao hình chóp ứng với đáy  ABC và ABC là tam giác đều. Ta có:
 AM vừa là đường trung tuyến, vừa là đường cao trong tam giác đều nên AM  BC .
 SG   ABC  BC   ABC , nên SG  BC .
 AM  SG  G và AM , SG  SAM  .
Suy ra BC  SAM   BC  GH (vì GH  SAM  ). G  H  SM G  H  BC  Do đó:   GH  SBC . SM  BC  M  SM , BC   SBC SG   SBC  S Ta lại có: 
 SH là hình chiếu vuông góc của SG lên SBC . SH   SBC  SG,SBC     SG,SH  GSH  30 .
Giả sử cạnh của tam giác đều ABC là a . a 3 a
Xét tam giác SGM vuông tại G , ta có: SG  GM cot 30  . 3  . 6 2 2 2 a a a 21
Xét tam giác SAG vuông tại G , ta có: 2 2 SA  AG  SG    . 3 4 6 a a 3 . . SG AM 3a 7 Trong tam giác SAM , ta có: 2 2 MF    . SA a 21 14 6 2 2  a 3   3a 7  a 21
Xét tam giác AFM vuông tại F , ta có: 2 2 FA  AM  FM        .  2   14  7    
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 101 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT a 21 SF FA 6 1 Suy ra 7  1  1  1  . SA SA a 21 7 7 6 V SF 1 1 Mà S.FBC    V  V  V 1 S .FBC S . V SA 7 7 ABC S.ABC 6  V  V (vì V  V V  V V ). 2 . 7 S ABC S.ABC S .FBC FABC 1 2 V 1 Do đó 1  . V 6 2
Câu 144. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , SA  2a , SA vuông góc
với mặt phẳng  ABC . Gọi M và N lần lượt là hình chiếu vuông góc của A lên các đường thẳng 50V 3 SB, SC . Tính
, với V là thể tích khối chóp . A BCNM . 3 a A. 12 . B. 10 . C. 11. D. 9 . Lời giải Chọn D 3 1 1 1 3 a 3
Thể tích khối chóp S.ABC là V  . SA S  .2 . a . . a . a  . S.ABC 3 ABC 3 2 2 6
Tam giác SAB vuông tại A và có AM là đường cao nên 2 2 2 SM SA SA 4a 4 2 SM .SB  SA      . 2 2 2 2 2 SB SB SA  AB 4a  a 5
Tam giác SAC vuông tại A và có AN là đường cao nên 2 2 2 SN SA SA 4a 4     . 2 2 2 2 2 SC SC SA  AC 4a  a 5 V SM SN 4 4 16 16 Ta có S.AMN  .  .   V  V V SB SC 5 5 25 S .AMN S . 25 ABC S.ABC Trang 102 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 3 3 16 9 9 a 3 3a 3 Suy ra V  V  V V  V  V  V  .  . ABCNM S.ABC S.AMN S .ABC S.ABC S. 25 25 ABC 25 6 50 50V 3 Vậy  9 . 3 a
Câu 145. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N , K lần lượt là trung điểm
của các cạnh AB , BC , SA . Biết mặt phẳng MNK  chia khối chóp S.ABCD thành hai phần có V
thể tích là V ,V V V . Tính tỉ số 1 . 1 2  1 2 V2 49 17 7 9 A. . B. . C. . D. . 71 67 13 23 Lời giải Chọn D
Trong mặt phẳng  ABCD , kéo dài MN cắt DA , DC lần lượt tại F , E .
Trong mặt phẳng (SAD) , gọi FK  SD  Q . Trong mặt phẳng SCD , gọi QE  SC  P .
Suy ra thiết diện là ngũ giác MNPQK và MN // AC // PK .
Đặt h  d S, ABCD  d K  ABCD  d P  ABCD 1 , ,  h 2 1 FD Ta có: FA  BN  AD   3 . 2 FA
Áp dụng định lý Menelaus cho tam giác SAD , suy ra QS FD KA QS 1 QD 3    
  d Q  ABCD 3 . . 1 ,  h QD FA KS QD 3 SD 4 4 1 1 9 Mặt khác: S  S  S  S  S  S  S FAM NCE BMN 4 ABC 8 ABCD DEF 8 ABCD
Suy ra thể tích của khối đa diện không chứa đỉnh S là 1  3 9 1 1 1 1  V  V V V  . h S  . h S  . h S QDEF KAMF PECN   3  4 8 2 8 2 8  1 23 23  . . . h S  V  V ABCD ABCD 2 3 32 32 9 V 9 1  V    1 32 V 23 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 103 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Câu 146. Cho hình chóp tứ giác đều S.ABCD , đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy góc
60 . Gọi M là trung điểm SC . Mặt phẳng đi qua AM và song song với BD , cắt SB tại E và
cắt SD tại F . Tính thể tích khối chóp S.AEMF. 3 a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 12 27 36 18 Lời giải Chọn D S M F I E D 600 C O A B
SC,ABCD SC,OC   SCO  60.
Gọi I  SO  AM  I là trọng tâm của tam giác SAC . V SM SE SI 1 2 2 2 2 Ta có S.AEM  . .  . .  V  V . S.AEM S. V SC SB SO 2 3 3 9 9 ABC S.ABC 2 Mà: V  2V và V  2V nên V  .V 1 S.AEMF S.ABCD   S.AEMF S.AEM S. ABCD S .ABC 9 SO a 6 Trong SOC : tan 60   SO  OC.tan60  . OC 2 3 1 1 a 6 a 6 3 a 6 Khi đó 2 V  .S .SO  .a .  .Thay vào   1 :V  . S.ABCD 3 ABCD 3 2 6 S.AEMF 18
Câu 147. Cho tứ diện ABCD có thể tích V với M, N lần lượt là trung điểm A ,
B CD . Gọi V , V lần lượt là 1 2 V V
thể tích của MNBC và MNDA . Tính tỉ lệ 1 2 . V 1 1 2 A. 1. B. . C. . D. . 2 3 3 Lời giải Chọn B Trang 104 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 A M B D N C Vì M, N lần lượt là trung điểm A , B CD nên ta có: d  , A MCD  d  ,
B MCD; d C, NAB  d  , D  NAB , do đó: V V V B. V  V  ; MCD V  V  V  V   ; . A MCD B.MCD 1 MNBC C.MNB D. 2 MNB 2 4 V V A.MCD V  V  V  V   . 2 MNAD D.MNA C.MNA 2 4 V V  V V 1 1 2 4 4    . V V 2
Câu 148. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V 12 . Gọi M , N lần lượt trung điểm S , A S ;
B P là điểm thuộc cạnh SC sao cho PS  2PC . Mặt phẳng MNP cắt cạnh SD
tại Q . Tính thể tích khối chóp S.MNPQ bằng 5 7 4 12 A. . B. . C. . D. . 18 3 3 25 Lời giải Chọn B SQ SP 2 Ta có PQ / / CD    . SD SC 3 Khi đó ta có: V SM SN SP 1 1 2 1 1 SMNP  .  . .   V  V. V SA SB SC 2 2 3 6 SMNP 12 SABC S V MPQ 1 2 2 2 1  . .  V  V. V 2 3 3 9 SMPQ 9 SACD 7 7 Vậy   S V . V . MNPQ 36 3
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 105 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Câu 149. Cho tứ diện ABCD có AB  3, AC  4, AD  6 ,  o BAC  60 ,  o CAD  90 ,  o BAD  120 . Thể tích
của khối tứ diện ABCD bằng 27 2 9 2 A. . B. . C. 6 2 . D. 6 6 . 8 4 Lời giải Chọn C A D' C' H B C D
Lấy các điểm C , D lần lượt trên cạnh và AC, AD sao cho AB  AC AD  3.
Áp dụng định lí Côsin ta có:  1 2 2 2 
BD '  AB  AD  2 A . B AD 'cos  BAD  9  9  2.9. 
 9.3  27  BD  3 3   .  2 
Tam giác BAC là tam giác đều nên BC  3 , tam giác D A
 C vuông tại A nên C D    3 2 . Xét tam giác BD C   có 2 2 2 BD  BC  C D
  , nên tam giác vuông tại C .
Gọi H là hình chiếu vuông góc của A trên BD C
  , vì AB  AC  ADnên HB  HC  HD. Mặt khác, tam giác BD C
  vuông tại C nên H là trung điểm của BD . 2 BD 27 3 Ta có, 2 AH  AB   9   . 4 4 2
Thể tích khối tứ diện ABC D   bằng 1 1 3 1 9 2 V      AH.S   . . .3.3 2 ABC D 3 BC D 3 2 2 4
Áp dụng công thức tỉ số thể tích ta có V     AC .AD 3 3 9 24 ABC D   .   V  V    6 2 . V AC.AD 4 6 24 ABCD 9 ABC D ABCD
Câu 150. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SQ
SA, SD . Mặt phẳng   chứa MN và cắt các cạnh SB , SC lần lượt tại Q, P . Đặt  x , V là SB 1 1
thể tích khối chóp S.MNPQ , V là thể tích khối chóp S.ABCD . Tìm x để V  V . 1 2 1 41 1 33 1 A. x    . B. x    . C. x  2 . D. x  . 4 4 2 Lời giải Chọn B Trang 106 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12     MN  SP SQ
Vì  MN / / SBC  nên MN / / PQ , do đó   x .    SC SB    SBC  PQ V SM SN SP 1 1 x x x 1 xV Ta có: S.MNP  . .  . .x   V  .V  . .V  . S .MNP S . V SA SD SC 2 2 4 4 ACD 4 2 8 S.ACD 2 2 2 2 VS.MQP SM SQ SP 1 x x x 1 x V  . .  . . x x   V  .V  . V  . S.MQP S. V SA SB SC 2 2 2 ABC 2 2 4 S.ABC xV x V  2 2 x  2x V  V  V  V V    . S.MNPQ 1 S .MNP S.MPQ 8 4 8    x  1  1 33 2 x  2x V 1 Do đó: 2 4 V  V 
 V  2x  x  4  0   1 2 8 2  1 33 x   4 1 33 Rõ ràng x  0 nên x  . 4
Câu 151. Cho hình chóp S.ABC .
D có đáy ABCD là hình vuông cạnh bằng .
a Cạnh bên SA  a và vuông
góc với mặt phẳng đáy. Gọi M , N, P,Q lần lượt là trung điểm các cạnh , SA SB, SC, . SD Thể tích của khối chóp cụt MNP . Q ABCD bằng 3 a 3 7a 3 a 3 a A. . B. . C. . D. . 6 24 3 4 Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 107 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 3 1 a Ta có 2 V  . . a a  S.ABCD 3 3 Theo định lý tỷ số thể tích ta có : 3 3 VS.MNQ SM SN SQ 1 1 1 1 1 1 1 1 a a  . .  . .   V  V  . V  .  . S.MNQ S.ABD S . V SA SB SD 2 2 2 8 8 8 2 ABCD 16 3 48 S.ABD 3 3 1 1 1 1 a a Tương tự ta có V  V  . V  .  . S.NPQ S.BCD S. 8 8 2 ABCD 16 3 48 3 3 3 a a a Ta có V  V  V    . S.MNPQ S.MNQ S.NPQ 48 48 24 3 3 3 a a 7a  V  V V    . MNPQ.ABCD S.ABCD S.MNPQ 3 24 24
Câu 152. Cho khối chóp S.ABC . Gọi M là điểm trên cạnh SB , mặt phẳng P đi qua , A M và song song SM
với BC chia khối chóp thành hai phần có cùng thể tích. Tìm tỷ số . MB 1 A. 2 1. B. 1. C. . D. 1 2 . 2 Lời giải Chọn D
Do mặt phẳng P song song với BC nên mặt phẳng P cắt cạnh SC tại N và MN //BC . SM SN Đặt  x   x x  0 . SB SC V SM SN Ta có S.AMN 2  .  x . S V .ABC SB SC V 1 1 1 Nên S.AMN 2 ycbt    x   x  . S V . 2 2 ABC 2 1 2 1 Do đó SM  SB  MB  SB  SM  SB . 2 2 SM 1 Vậy   2 1. MB 2 1
Câu 153. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SQ các cạnh ,
SA SD . Mặt phẳng   chứa MN cắt các cạnh SB, SC lần lượt tại Q, P . Đặt  x,V1 SB 1
là thể tích khối chóp S.MNQP,V là thể tích khối chóp S.ABCD . Tìm x để V  V . 1 2 1   41 1   33 1 A. x  . B. x  . C. x  2. D. x  . 4 4 2 Lời giải Chọn B Trang 108 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S M Q N A B P D C MN  AD  BC  Ta có   SP SQ    x            SBC PQ MN MN SC SB V V V V 1 V V Khi đó 1 S.MNQP S.MNQ S.NQP   S.MNQ S.NQP    V V V 2 2V 2V S.ABCD S.ABCD S.ABD S .ABC V V   S.MNQ S.NQP    1 1 1 1 33 1 2  . .x  . .
x x  1  2x  x  4  0  x  (vì x  0 ) V V 2 2 2 4 S.ABD S .ABC
Câu 154. Cho hình chóp đều S.ABCD có độ dài cạnh đáy bằng a . Gọi G là trọng tâm tam giác SAC . Mặt
phẳng chứa AB và đi qua G cắt các cạnh SC , SD lần lượt tại M và N . Biết mặt bên của hình
chóp tạo với đáy một góc bằng 60 . Thể tích khối chóp S.ABMN bằng 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 4 8 16 16 Lời giải Chọn B S N M G C D a O A I B
Vì G là trọng tâm tam giác SAC nên AG cắt SC tại trung điểm M của SC , tương tự BG cắt
SD tại trung điểm N của SD .
Gọi O là tâm của hình vuông ABCD và I là trung điểm của AB . Suy ra góc giữa mặt bên SAB a 3
và mặt đáy  ABCD là 
SIO  60 . Do đó SO  OI.tan 60  . 2 3 1 1 a 3 a 3 Suy ra 2 V  S .SO  a   . S.ABCD 3 ABCD 3 2 6
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 109 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V SA SB SM 1 1 Mặt khác V  2V , ta lại có S.ABM      V  .V . S.ABCD S.ABC V SA SB SC 2 S.ABM S. 2 ABC S.ABC V SA SN SM 1 1 1 1 S.AMN        V  .V . V SA SD SC 2 2 4 S.AMN S. 4 ACD S.ACD 3 3 3 3 a 3 a 3 Vậy V  V   . S.ABMN S. 4 ABCD 4 6 8
Câu 155. Cho khối chóp S.ABC có SA  SB  SC  a và  ASB   BSC  
CSA  30 Mặt phẳng   qua A V
và cắt hai cạnh SB , SC tại B, C sao cho chu vi tam giác ABCnhỏ nhất. Tính .   k  S AB C . VS.ABC 1 A. k  2  2 . B. k  4  2 3 . C. k  . D. k  22  2. 4 Lời giải Chọn B
Cắt hình chóp theo cạnh SA rồi trải các mặt bên ra ta được hình như hình vẽ (  A là điểm sao cho
khi gấp lại thành hình chóp thì trùng với A ).
Khi đó chu vi tam giác ABC bằng AB  BC  CA nhỏ nhất khi A , B, C ,  A thẳng hàng hay
AB  BC  CA  A  A . Khi đó tam giác SA  A có  SAA   ASB   BSC   C 
SA  90 nên vuông cân tại S và có SA  a , SB  SC ,  SAB  45 . SA SB SB sin 45 Ta có     3 1. sin105 sin 45 SA sin105 V SB SC Do đó S.ABC k   .   3   1  3   1  4  2 3 . V SB SC S.ABC
Câu 156. Cho tứ diện ABCD . Gọi B ' và C ' lần lượt là trung điểm của AB và AC . Khi đó tỉ số thể tích
của khối tứ diện AB’C’D và khối tứ diện ABCD bằng: 1 1 1 1 A. B. C. D. 8 6 4 2 Lời giải Chọn C Trang 110 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 V AB '.AC '.AD 1 1 1 Ta có: AB'C'D   .  V . AB AC.AD 2 2 4 ABCD
Câu 157. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a . Mặt bên của hình chóp tạo với mặt
đáy một góc 60 . Mặt phẳng P chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC ,
SD lần lượt tại M và N . Thể tích khối chóp S.ABMN là 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 2 4 3 Lời giải Chọn A S P M G N B C 60 O H A D
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD .
Ta có S.ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử SCD, ABCD     SHO  60
Tam giác SHO vuông tại O có SO  OH.tan 60  a 3 . 3 1 4a 3 V  .S .SO  . S.ABCD 3 ABCD 3   P SCD  MN 
Mặt khác: AB  P, MN  SCD  MN // CD // AB AB //CD  SM SN 1
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD    . SC SD 2 V SM 1 1 Ta lại có SABM   V  V  V SABM V SC 2 SABC 4 SABCD SABC
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 111 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V SM SN 1 1 SAMN  .  V  V  V SAMN V SC SD 4 SACD 8 SABCD SACD 3  1 1  3 a 3 Khi đó V   V  V  . SABMN    4 8 SABCD  8 SABCD 2
Câu 158. Cho khối tứ diện có thể tích V . Gọi V  là thể tích khối đa diện có các đỉnh là trung điểm các cạnh V 
của khối tứ diện đã cho. Tính tỉ số . V V  2 V  1 V  5 V  1 A.  . B.  . C.  . D.  . V 3 V 4 V 8 V 2 Lời giải Chọn D A F E G J B D H I C
Gọi khối tứ diện đã cho là ABCD .
Gọi E , F , G , H , I , J lần lượt là trung điểm của AD , AB , AC , BC , CD , BD .
Khi đó ta có: V  V   4.V . . A FEG 1 Mặt khác V  V . . A FEG 8 1 V  1 Suy ra V  V   V   . 2 V 2
Câu 159. Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V . Điểm P là trung điểm của
SC , một mặt phẳng qua AP cắt các cạnh SD và SB lần lượt tại M và N . Gọi V là thể tích khối 1 V
chóp S.AMPN . Tìm giá trị nhỏ nhất của 1 ? V 1 2 3 1 A. . B. . C. . D. . 8 3 8 3 Lời giải Chọn D Trang 112 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S P N I M D C O A B SM SN Đặt  x ,  y , 0  x , y  1. SB SD SA SC SB SD 1 1 x Vì    nên 1 2    y  SA SP SM SN x y 3x 1 V V V 1 SA SN SP 1 SA SM SP 1 1 1 1 Khi đó 1 S.ANP S .   AMP  . . .  . . .  . . y  . . x V 2V 2V 2 SA SD SC 2 SA SB SC 2 2 2 2 S.ADC S.ABC 1 x y 1 x     x    4 4  3x 1 1
Vì x  0 , y  0 nên  x  1 3  x   1  Xét hàm số f  x 1  x    trên ;1  4  3x 1 3    1  1 
Ta có f  x  1  ; f x 2  0  x  . 4  3x 2 1     3 Bảng biến thiên V 1
Vậy giá trị nhỏ nhất của 1 bằng . V 3
Câu 160. Cho tứ diện ABCD có thể tích V , gọi M , N , P , Q lần lượt là trọng tâm tam giác ABC , ACD
, ABD và BCD . Thể tích khối tứ diện MNPQ bằng 4V V V 4V A. . B. . C. . D. . 9 27 9 27 Lời giải Chọn C
Gọi E , F , I lần lượt là trung điểm các đoạn thẳng BC , CD , BD . V 8 8 2 Ta có AMNP   V  V  V . V 9 AMNP 9 AEFI 9 AEFI
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 113 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1 V V  d Q MNP S  d A MNP S  d Q MNP S  V  MNPQ    1 1 MNP    1 MNP    1 , . , . , . 3 3 2 6 MNP 2 AMNP 9 .
Câu 161. Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy. Gọi M , N là
trung điểm của SA , SB . Mặt phẳng MNCD chia hình chóp đã cho thành hai phần. tỉ số thể tích
hai phần S.MNCD và MNABCD là 3 3 4 A. . B. . C. . D. 1. 4 5 5 Lời giải Chọn B 1 Ta có V  V  V ; S.ABC S.ACD S. 2 ABCD SM SN SC 1 SM SD SC 1 và V    V  V ; V    V  V . S.MNC S.ABC S. SA SB SC 4 ABC S.MCD S.ACD S. SA SD SC 2 ACD 3 3 Suy ra V  V V  V  V . S.MNCD S.MNC S.MCD S.ABC S. 4 8 ABCD 5 Đồng thời V  V V  V . MNABCD S.ABCD S.MNCD S. 8 ABCD 3
Vậy tỉ số thể tích hai phần S.MNCD và MNABCD là . 5    
Câu 162. Cho khối chóp S.ABC có M  SA , N  SB sao cho MA  2  MS , NS  2
 NB . Mặt phẳng  
qua hai điểm M , N và song song với SC chia khối chóp thành hai khối đa diện. Tính tỉ số thể
tích của hai khối đa diện đó ( số bé chia số lớn ). 3 4 3 4 A. . B. . C. . D. . 5 9 4 5 Lời giải Chọn D Trang 114 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 S M N Q C A P B
Cách 1: Ta có mặt phẳng   cắt các mặt SAC  theo giao tuyến MQ  SC và cắt mặt SBC 
theo giao tuyến NP  SC . Thiết diện tạo bởi mặt phẳng   với hình chóp là hình thang MNPQ . Do V  V V , gọi V  V và S  S ta có: MNABPQ N .ABPQ N .AMQ S.ABC A  BC 1 1 1  1 2  7 V  .d N, ABC .S
 . d S, ABC S  . S  V . N .ABPQ      3 ABPQ 3 3  3 3  27 1 1 2 4 8 V  .d N, SAC .S  . d B,SAC. S  V . N .AMQ    3 A  MQ 3 3 9 A  SC 27 5 Vậy V  V V  4 V  V  V . MNABPQ N .ABPQ N .AMQ 9 SMNPQC 9 VSMNPQC 4 Suy ra  . V 5 MNABPQ Cách 2: S M N B A I P Q C
Gọi I  MN  AB ,Áp dụng định lý Me-ne-la-us cho tam giác SAB , ta có MS IA NB IB 1   1  . MA IB NS IA 4 BI SA NM NM
Áp dụng định lý Me-ne-la-us cho tam giác A  MI , ta có:   1   1. BA SM NI NI PI AM AQ 2 Tương tự ta có: 1. Vì MQ//SC    . PQ AS AC 3
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 115 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT V IB IN IP 1 1 1 1 15 Khi đó: I.BNP         V  .V . V IA IM IQ 4 2 2 16 AMQ.NBP I . 16 AMQ I .AMQ V d M ; ABC S d M ; ABC  S M .AIQ    MA 2 AIQ AI AQ 4 2 8 Mà AIQ   với   và      . V d S; ABC S d S; ABC SA 3 S AB AC 3 3 9 S.ABC    ABC ABC 15 2 8 5 Suy ra V    V  V . AMQ.NBP S.ABC S. 16 3 9 9 ABC 5 1 4
Vậy tỉ số thể tích cần tìm là: 9  . 5 5 9
Câu 163. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn
song song với đáy và cắt các cạnh bên S , A S ,
B SC, SD lần lượt tại M, N, ,
P Q . Gọi M , N , P ,Q SM
lần lượt là hình chiếu vuông góc của M, N, ,
P Q lên mặt phẳng  ABCD . Tính tỉ số để thể SA tích khối đa diện MNP . Q M N  P  Q
 đạt giá trị lớn nhất. 1 3 2 1 A. . B. . C. . D. . 3 4 3 2 Lời giải Chọn C SM Đặt  k với k 0;  1 . SA MN SM
Xét tam giác SAB có MN //AB nên   k  MN  k.AB . AB SA MQ SM
Xét tam giác SAD có MQ//AD nên   k  MQ  k.AD . AD SA
Kẻ đường cao SH của hình chóp. Xét tam giác SAH có:   MM//SH MM AM SA SM SM nên    1
 1 k  MM   1 k .SH . SH SA SA SA Ta có: 2 V         MN.M . Q MM A . B A . D SH.k . 1 k . MNPQ.M N P Q  
Thể tích khối chóp không đổi nên V 2 k . 1 k lớn nhất. MNPQ.M N  P  Q
  đạt giá trị lớn nhất khi   2 1 k .k.k 1  2  2k  k  k  4 Ta có k .1 k    3 2      . 2 2  3  27 SM 2
Đẳng thức xảy ra khi và chỉ khi:   k  2 2 1  k  k  . Vậy  . 3 SA 3 Trang 116 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12
Câu 164. Cho hình chóp S .AB C D đáy là hình vuông cạnh a , có SA  2a và vuông góc với mặt đáy. Gọi
M , N lần lượt là trọng tâm của tam giác SAB , SC D . Tính thể tích khối tứ diện S .M NC . 1 2 1 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 27 27 13 13 Lời giải Chọn B
+Gọi P , Qlần lượt là trung điểm của cạnh AB , CD . +Ta có 2 V  1 . . SA S 3  a . S .ABCD 3 ABCD 3 SM SN 2
+Vì M , N lần lượt là trong tâm tam giác SAB , S C D    . SP SQ 3 V SM SN SC 4 4 +Ta xét: S.MNC  . .   V  V . 1 V SP SQ SC 9 S .MNC S . 9 PQC S .PQC 1 V .S . A SPQC S P  QC 1 1 +Ta xét: S .PQC  3    V  V . 2 V 1 S 4 S .PQC S . 4 ABCD S .ABCD .S . A S ABCD 3 ABCD +Từ  1 2 1 , 2 V  V 3  a . S .MNC . 9 S ABCD 27
Câu 165. Cho khối chóp tứ giác đều S .A BC D . Gọi M là điểm đối xứng của C qua B , N là trung điểm
cạnh SC . Mặt phẳng M DN chia khối chóp S .A BC D thành hai khối đa diện. Tỉ số thể tích của  
khối đa diện chứa đỉnh S và khối chóp S .A BC D bằng: A. 5 . B. 5 . C. 7 . D. 6 . 7 12 12 7 Lời giải Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 117 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Gọi P  M N  SB . Tam giác SM C có M N và SB là các đường trung tuyến nên P là trọng tâm của tam giác SM C .
Gọi Q  MD AB, do AD // BM , AD  BM nên tứ giác ADBM là hình bình hành suy ra Q là trung điểm của MD . Ta có: MB MQ MP  1 1 2  5 V V V V  .V  1 . . V  V BCDQPN M .CDN M .BQP M .CDN M .CDN   M.CDN M .CDN . MC MD MN  2 2 3  6 CD CM S d N ABCD MCD  1   . , Mà: 1 1 2 V  V  . .V  . V  V . M .CDN N .MCD S d S, ABCD S.ABCD 2 S . ABCD S . CD 2 2 ABCD ABCD 5 Do đó: V  V . BCDQPN S . 12 ABCD 7  V  V V  V . SANPQD S. ABCD BCDQNP S . 12 ABCD VSANPQD 7
Vậy tỉ số thể tích cần tính:  . V 12 S .ABCD
Câu 166. Cho hình chóp S .A BC D có M , N là trung điểm của SA , SB . Mặt phẳng MNCD chia hình  
chóp đã cho thành hai phần. Tỉ số thể tích khối chóp S .M NCD và khối đa diện M NABCD là: 5 3 3 5 A. . B. . C. . D. . 8 8 5 3 Lời giải Chọn C Trang 118 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 V SM SN SC 1 1 1 1 1 Ta có: S.MNC  . .  . .1 V  V  V S.MNC S.ABC S. V SA SB SC 2 2 4 4 8 ABCD S.ABC V SM SC SD 1 1 1 1 S.MCD  . .  .1.1 V  V  V S.MCD S.ACD S.ABCD . V SA SC SD 2 2 2 4 S.ACD 3 Khi đó: V  V V  V . S .MNCD S .MNC S .MCD S . 8 ABCD 5  V  V V  V . MNABCD S . ABCD S .MNCD S . 8 ABCD V 3 Vậy S.MNCD  . V 5 MNABCD
Câu 167. Cho hình chóp tứ giác S .A BC D có đáy là hình bình hành. Gọi M là trung điểm cạnh S , A các điểm ,
E Flần lượt là điểm đối xứng của A qua B và D . Mặt phẳng MEF cắt các cạnh   S , B SD
lần lượt tại các điểm N, .
P Tính tỉ số thể tích của khối đa diện ABCDMNP và S.AEF . 1 2 1 3 A. . B. . C. . D. . 2 3 3 4 Lời giải Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 119 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Ta có SAE ;  S A F có N , P lần lượt là trọng tâm vì nó giao điểm của hai đường trung tuyến. SN SP 2 Vì vậy   và có C  E F . SB SD 3 V SM SN 1 2 1 1 1 1 1 Ta có S.MNC  .  .   V  V  . V  V . V SA SB 2 3 3 S.MNC S. 3 ABC . 3 2 S ABCD . 6 S ABCD S.ABC V SM SP 1 2 1 1 1 1 1 Tương tự ta có S.MPC  .  .   V  V  . V  V . V SA SD 2 3 3 S.MPC S. 3 ADC . 3 2 S ABCD . 6 S ABCD S.ADC 1 1 1 Do đó V  V  V  V . S.MNCP S .ABCD S . 6 6 ABCD . 3 S ABCD 2 Mặt khác V  V V nên V  V (1). ABCDMNP S.ABCD S.MNCP ABCDMNP S . 3 ABCD
Ta lại có B , D lần lượt là trung điểm của AE , A F nên S  S và S  S . A  BC E  BC A  DC F  CD Suy ra S  2S . A  EF ABCD Mà 1 1 V  d S , ABCD .S V  d S , ABCD .2S  2V S.AEF    S.AEF    nên (2). 3 AEF 3 ABCD S.ABCD V 1
Từ (1) và (2) suy ra ABCDMNP  . V 3 S.AEF
Câu 168. ( Quốc Học Huế_Lần 1_2020 ) Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 1.
Gọi M , N lần lượt thuộc các cạnh BC, CD sao cho MN luôn bằng 1. Tìm giá trị nhỏ nhất của
thể tích khối tứ diện SAMN . 2 3 1 2 4  2 A. . B. . C. . D. . 12 12 12 24 Lời giải Chọn D Trang 120 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 Gọi O  AC  BD . Vì S.ABCD là hình chóp đều nên SO   ABCD và 2 2 2 SO  SA  AO  . 2 1 Ta có: V  .SO.S . SAMN 3 AMN
Đặt CM  x, 0  x   1 . Ta có: 2 2 2 2 BM  1 ;
x CN  MN  CM  1 x ; DN  1 1 x 1 S  S  S  S  S  1 .1.  x    x  x  x AMN ABCD ABM ADN CMN 1  1 .1. 1 2 1 1  2 . . 1 2 2 2 1   2 2
x  1 x  x 1 x  . 2 1
Xét hàm số f  x   2 2
x  1 x  x 1 x , 0  x   1 . 2 2 2 2 1  x x  1 x  2x  x 1 Có: f  x 2  1  1 x    2 2 2 2  1 x 1 x  2 1 x f  x 2 2 2 2
 0  1 x  2x  x 1  0  1 x  2  x  x 1 0  x  1 0  x  1   2      x  . 2 1 x    2 2  x  x  2 1 2x   2 2x   1  x   1  0 2 Bảng biến thiên: 2 2 1 2 Do đó, S  đạt được khi x  . A  MN min 4 2 1 1 2 2 2 1 4  2 Ta có: V  SO S   . SAMN  . A  MN  . . min min 3 3 2 4 24
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 121 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
8. KHỐI LĂNG TRỤ - MỨC 4
Câu 169. ( Đề Thi Thử Trường Chuyên KHTN_HN_2020 ) Cho khối lập phương ABCD.A' B 'C ' D '
cạnh 1. Gọi M , N, P, L lần lượt là tâm các hình vuông ABB ' A'; A' B 'C ' D '; D A D ' A' và CDD 'C '
. Gọi Q là trung điểm của BL . Tính thể tích khối tứ diện MNPQ (tham khảo hình vẽ). 1 1 2 3 A. . B. . C. . D. . 24 16 27 27 Lời giải Chọn A
Do ABCD.A' B 'C ' D 'là hình lập phương cạnh 1 A'C  3 .
BL / / M D '   AB ' D '  BL / /  AB ' D '  d Q,MNP  d B, AB ' D '  d A, AB 'D ' 1 3  A'C  . 3 3 3 3 1 1 3 3
Ta có: AB ' D ' đều  S    S  S   . AB D  22. . ' ' M  NP A  B'D ' 4 2 4 4 2 8 1 1 3 3 1 V  S .d Q, MNP  . .   Chọn A. Q.MNP MN  P    3 3 8 3 24
Câu 170. ( Quốc Học Huế_Lần 1_2020 ) Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 1.
Gọi M , N lần lượt thuộc các cạnh BC, CD sao cho MN luôn bằng 1. Tìm giá trị nhỏ nhất của
thể tích khối tứ diện SAMN . 2 3 1 2 4  2 A. . B. . C. . D. . 12 12 12 24 Lời giải Trang 122 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 Chọn D Gọi O  AC  BD . Vì S.ABCD là hình chóp đều nên SO   ABCD và 2 2 2 SO  SA  AO  . 2 1 Ta có: V  .SO.S . SAMN 3 AMN
Đặt CM  x, 0  x   1 . Ta có: 2 2 2 2 BM  1 ;
x CN  MN  CM  1 x ; DN  1 1 x 1 S  S  S  S  S  1 .1.  x    x  x  x AMN ABCD ABM ADN CMN 1  1 .1. 1 2 1 1  2 . . 1 2 2 2 1   2 2
x  1 x  x 1 x  . 2 1
Xét hàm số f  x   2 2
x  1 x  x 1 x , 0  x   1 . 2 2 2 2 1  x x  1 x  2x  x 1 Có: f  x 2  1  1 x    2 2 2 2  1 x 1 x  2 1 x f  x 2 2 2 2
 0  1 x  2x  x 1  0  1 x  2  x  x 1 0  x  1 0  x  1   2      x  . 2 1 x    2 2  x  x  2 1 2x   2 2x   1  x   1  0 2 Bảng biến thiên: 2 2 1 2 Do đó, S  đạt được khi x  . A  MN min 4 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 123 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1 1 2 2 2 1 4  2 Ta có: V  SO S   . SAMN  . A  MN  . . min min 3 3 2 4 24
Câu 171. ( Đề Thi Thử Trường Chuyên KHTN_HN_2020 ) Cho khối lập phương ABCD.A' B 'C ' D '
cạnh 1. Gọi M , N, P, L lần lượt là tâm các hình vuông ABB ' A'; A' B 'C ' D '; D A D ' A' và CDD 'C '
. Gọi Q là trung điểm của BL . Tính thể tích khối tứ diện MNPQ (tham khảo hình vẽ). 1 1 2 3 A. . B. . C. . D. . 24 16 27 27 Lời giải Chọn A
Do ABCD.A' B 'C ' D 'là hình lập phương cạnh 1 A'C  3 .
BL / / M D '   AB ' D '  BL / /  AB ' D '  d Q,MNP  d B, AB ' D '  d A, AB 'D ' 1 3  A'C  . 3 3 3 3 1 1 3 3
Ta có: AB ' D ' đều  S    S  S   . AB D  22. . ' ' M  NP A  B'D ' 4 2 4 4 2 8 1 1 3 3 1 V  S .d Q, MNP  . .   Chọn A. Q.MNP MN  P    3 3 8 3 24
Câu 172. Cho hình lăng trụ ABC.A B  C
 có chiều cao bằng 6 và diện tích đáy bằng 8. Gọi M , N lần lượt
là trung điểm của các cạnh AB , AC và P , Q lần lượt thuộc các cạnh AC , A B   sao cho AP AQ 3 
 . Thể tích của khối đa diện lồi có các đỉnh là các điểm A , A , M , N , P và Q AC AB 4 bằng A. 18. B. 19. C. 27 . D. 36 . Trang 124 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 Lời giải Chọn B
+) Vì M , N lần lượt là trung điểm của cạnh AB , AC  MN // BC . AP A Q 
+) P , Q lần lượt thuộc các cạnh AC , A B   3 sao cho    QP // B C   . A C   A B   4 +) Vì AB . C A B  C
 là hình lăng trụ nên BC // B C   .
Do đó MN // QP  4 điểm M , N , P , Q đồng phẳng. Ta có  ABB A   ACC A
   AA ,  ABB A
 MNPQ  MQ ,  ACC A  MNPQ  NP
 3 đường thẳng AA , MQ , NP đồng quy hoặc đôi một song song. Hơn nữa, vì AM // A 1 3 3 Q và AM  AB  AB  AB  A Q
 nên AA cắt MQ . Do đó AA , 2 4 4 MQ , NP đồng quy tại S . V SA SM SN Ta có S.AMN  . . . V   SA SQ SP S .A QP 1 AB SA SM SN AM 2 Mà AM // AQ , AN // A P  nên 2      . SA SQ SP AQ 3 3 AB 4 3 V SA SM SN  2  8 8 Suy ra, S.AMN  . .    V  V  .   V  S.AMN S. 27 A QP  SA SQ SP  3  27 S.A QP
Gọi V là thể tích của khối đa diện lồi có các đỉnh là các điểm A , A , M , N , P , Q . Khi đó: 8 19 V  V      V V  V  V  . S.A QP S.AMN S.A QP S.A QP S . 27 27 A QP
Gọi H , K lần lượt là hình chiếu vuông góc của S lên các mặt phẳng  AMN  ,  AQP . Do  AMN  //  A Q
 P nên S , H , K thẳng hàng. Suy ra HK là chiều cao của lăng trụ AB . C A B  C   SH SA 2 2 . Hơn nữa,    SH  2 1
SK  HK  SK  SH  SK  SK  SK  SK  3HK . SK SA 3 3 3 3
Theo đầu bài HK  6 nên SK  3HK 18 .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 125 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 1 A . Q A . P sin A 2 S   A  QP A Q A P  3  9 9 Lại có, 2   .    S    S    .   S 1     A QP 16 A B C     A B A C  4  16 A B C A B  .AC .sin A 2 1 1 9 Theo đầu bài S  9 9 S   V     S  .SK . .18 27   S     8 nên     . Do đó . A B C A QP 16 A B C 2 S.A QP 3 A QP 3 2 19 19 Vậy V  V    .27 19 . S. 27 A QP 27
Bài toán trên có thể tổng quát hơn như sau: Cho hình lăng trụ AB . C A B  C
  có thể tích bằng V
. Gọi M , N lần lượt là trung điểm của các cạnh AB , AC và P , Q lần lượt thuộc các cạnh AC   , A B   A P A Q sao cho   k 0  k  
1 . Tính thể tích của khối đa diện lồi có các đỉnh là các AC AB
điểm A , A, M , N , P , Q theo V . Lời giải:
Gọi V  là thể tích của khối đa diện lồi có các đỉnh là các điểm A , A , M , N , P , Q . Ta xét các trường hợp: 1 2  4k  2k 1
+) Với k  , giải tương tự như trên ta được công thức V   .V   . 2 12   1 2  4k  2k 1
+) Với k  , giải tương tự như trên ta được công thức V    .V . 2 12   1 V 2  4k  2k 1
+) Với k  , dễ thấy V    công thức V   .V   đúng. 2 4 12   2  4k  2k 1 Vậy: V   .V   . 12   Cách khác: + Ta có hình vẽ: Trang 126 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 + Theo đề ta có: S  S  S       8 . 0 ABC A B C AM AN 1 2  1  + Do    S  S  .S  2     . AB AC 2 1 AMN  2 ABC  AQ AP 3 2  3  9 + Do    S  S     .S       . AB A C   4 2 A PQ  4 A B C  2
+ Hình chóp cụt AMNAQP có chiều cao h và hai đáy là S , S nên thể tích V được tính bởi công 1 2 thức h   V   6 9 9
S  S  S .S   2   2.  19 1 2 1 2   . 3 3  2 2   
Câu 173. Cho hình hộp chữ nhật ABC . D A B  C  D
  . Trên các cạnh AA , BB , CC lần lượt lấy các điểm AM 4 BN 1 CP 3 M , N , P sao cho  ,  ,
 . Mặt phẳng MNP cắt cạnh DD tại Q . Gọi AA 5 BB 2 CC 4 V
V , V lần lượt là thể tích của các khối đa diện MNPQABCD và MNPQA B  C  D   . Khi đó 1 1 2 V2 bằng 31 9 40 40 A. . B. . C. . D. . 9 31 9 31 Lời giải Chọn A
Lấy O , O lần lượt là tâm của ABCD và A B  C  D   .
Gọi I  OO  MP  NI  DD  Q . Vậy DD MNP  Q . AM BN CP DQ Đặt  x ;  y ;  z và  w . AA BB CC DD
Ta có: MA  PC  NB  QD  2OI nên x  z  y  w . V V V 1  V V  Mặt khác ta có MNPQ.ABCD ABC.MNP ACD.MPQ  ABC.MNP ACD.MPQ     V     2V 2 V     V ABCD.A B C D ABC.A B  C   ABC.A B C ACD.A C  D    4 3 
1  x  y  z x  z  w     1   x z 2x  y  2z  w  5 4  31  .   2  3 3  6 2 2 40 31 Suy ra V  V MNPQ.ABCD ABCD. 40 AB C  D  
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 127 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT 31 9 Lại có V    V       V     V     V     V     . MNPQ.A B C D ABCD.A B C D MNPQ.ABCD ABCD.A B C D ABCD.A B C D ABCD. 40 40 A B C D 31 9 V 31 Vậy khi đó V  V  1      , V V     , suy ra . 1 . 40 ABCD A B C D 2 . 40 ABCD A B C D V 9 2
Câu 174. Cho lăng trụ tam giác đều ABC.A ' B 'C ' cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua
B ' và vuông góc với A'C chia lăng trụ thành hai khối. Biết thể tích của hai khối là V1 và V2 với V V  V . Tỉ số 1 bằng: 1 2 V2 1 1 1 1 A. . B. . C. . D. . 47 23 11 7 Lời giải Chọn A
Gọi H là trung điểm của A 'C ' . B ' H  AC  Ta có:
  B ' H   ACC ' A'  B ' H  A'C . B ' H  AA' Trong mp  ACC A
  , kẻ HE  A'C, HE  AA'  I .
Vậy mặt phẳng (P) cắt lăng trụ là mặt phẳng  B ' HI  . A
 ' EH đồng dạng A'C 'C . a . ' ' ' ' . ' ' a A E A C A H A C a 5 2    A' E    . A' H A'C A'C a 5 10 A
 ' IH đồng dạng C ' A'C . a .a 5 IH A' H A' H.A'C a 5 2    IH    . A'C C 'C C 'C 2a 4 2 1 1  a 5   a 5  a  S  A' . E IH   .   . A'IH 2 2  10   4  16     2 3 1 1 a 3 a a 3
Thể tích khối chóp V  V  .B ' H.S  . .  . 1 B '.A'HI A' 3 HI 3 2 16 96 2 3 a 3 a 3
Thể tích khối lăng trụ là: V  AA'.S  2 . a  . ABC.A' B 'C ' ABC 4 2
Thể tích phần còn lại V  V V 2 ABC.A'B 'C ' 1 Trang 128 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 3 3 3 a 3 a 3 47a 3 V 1 1      . 2 96 96 V 47 2
Câu 175. Cho lăng trụ tam giác đều ABC.A ' B 'C ' cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua
B ' và vuông góc với A'C chia lăng trụ thành hai khối. Biết thể tích của hai khối là V1 và V2 với V V  V . Tỉ số 1 bằng: 1 2 V2 1 1 1 1 A. . B. . C. . D. . 47 23 11 7 Lời giải Chọn A
Gọi H là trung điểm của A 'C ' . B ' H  AC  Ta có:
  B ' H   ACC ' A'  B ' H  A'C . B ' H  AA' Trong mp  ACC A
  , kẻ HE  A'C, HE  AA'  I .
Vậy mặt phẳng (P) cắt lăng trụ là mặt phẳng  B ' HI  . A
 ' EH đồng dạng A'C 'C . a . ' ' ' ' . ' ' a A E A C A H A C a 5 2    A' E    . A' H A'C A'C a 5 10 A
 ' IH đồng dạng C ' A'C . a .a 5 IH A' H A' H.A'C a 5 2    IH    . A'C C 'C C 'C 2a 4 2 1 1  a 5   a 5  a  S  A' . E IH   .   . A'IH 2 2  10   4  16     2 3 1 1 a 3 a a 3
Thể tích khối chóp V  V  .B ' H.S  . .  . 1 B '.A'HI A' 3 HI 3 2 16 96 2 3 a 3 a 3
Thể tích khối lăng trụ là: V  AA'.S  2 . a  . ABC.A' B 'C ' ABC 4 2
Thể tích phần còn lại V  V V 2 ABC.A'B 'C ' 1 3 3 3 a 3 a 3 47a 3 V 1 1      . 2 96 96 V 47 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 129 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Câu 176. [TT-SGD-HA-TINH-19-20] Cho hình lập phương ABCD.A’B’C’D’ có thể tích V. Gọi M là điểm
thuộc cạnh BB’ sao cho MB=2MB’. Mặt phẳng  đi qua M và vuông góc với AC’ cắt các cạnh V
DD’, DC, BC lần lượt tại N, P, Q. Gọi V là thể tích của khối đa diện CPQMNC’. Tính tỉ số 1 1 V 35 11 33 13 A. B. C. D. 162 162 162 162
Câu 177. [TT-SGD-HA-TINH-19-20] Cho hình lập phương ABCD.A’B’C’D’ có thể tích V. Gọi M là điểm
thuộc cạnh BB’ sao cho MB=2MB’. Mặt phẳng  đi qua M và vuông góc với AC’ cắt các cạnh V
DD , DC, BC lần lượt tại N, P,Q . Gọi V là thể tích của khối đa diện CPQMNC . Tính tỉ số 1 1 V 35 11 33 13 A. B. C. D. 162 162 162 162 Lời giải I B Q C P A D M B' C' N A' D'
Gọi a là cạnh của hình lập phương, ta có 3 V  a .
Vì BDA'  AC 'nên  / /(BDA') , do đó ta có MQ / /B 'C; NP / /CD '.
Gọi I là giao điểm CC’, MQ, NP (3 đường thẳng này đồng quy). Ta có V  V V . 1 I .MNC ' L.CPQ 1 1 1 4 2 Mặt khác 3 V  V  d(M ;(CDD 'C )').S  . a . . a a  a I .MNC ' M .IC ' N IC ' 3 N 3 2 3 9 3 1 1 a a a a V  . . . .  I .CPQ 3 2 3 3 3 162 3 2 a 35 V 35 Vậy 3 3 1 V  V V  a   a   1 I .MNC ' L.CPQ 9 162 162 V 162
Câu 178. Cho khối lăng trụ AB . C A B  C
 có thể tích bằng 2020. Gọi M , N lần lượt là trung điểm của AA
; BB và điểm P nằm trên cạnh CC sao cho PC  3PC . Thể tích của khối đa diện lồi có các
đỉnh là các điểm A , B , C , M , N , P bằng: 2020 5353 2525 3535 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D Giả sử V  V     2020 . ABC.A B C Trang 130 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 1 V 2 Ta có V       d C ; ABC .S V     V C .ABC    . ABC C . 3 3 ABB A 3
1 .d P;ABC.S ABC V d P; ABC PC 3 1 P.ABC 3    Lại có      V  V . V 1 P ABC    d C ABC CC C ABC .d C; ABC  ;  . 4 4 . .S 3 A  BC
1 .d P;ABB A.SABNM V Ta có P.ABNM 3  . V 1 C.ABB A   .d C ; ABB A  .S 3 ABB A   Mà d P; ABB A    1 d C ; ABB A  và S  S   . ABNM 2 ABB A V 1 1 Suy ra P.ABNM   V  V . P. V    2 ABNM 3 C .ABB A 7 3535 Vậy V  V V  V  . ABC.MNP P.ABNM P.ABC 12 3
Cách 2: Dùng công thức giải nhanh V 1 AM BN CP 2020  1 1 3  3535 ABC MNP   Ta có: .     V     ABC MNP   .   V AA BB CC . 3  2 2 4  3 ABC A B C        3  . Câu 179. Cho lăng trụ AB . C A B  C
 có đáy ABC là tam giác đều cạnh a , góc giữa cạnh bên với mặt phẳng
đáy bằng 60 và A cách đều 3 điểm A , B , C . Gọi M là trung điểm của AA ; N  BB thỏa
mãn NB  4NB và P CCsao cho PC  3PC . Thể tích của khối đa diện lồi có các đỉnh là các
điểm A , B , C , M , N , P bằng: 3 a 3 3 41a 3 3 23a 3 3 19a 3 A. . B. . C. . D. . 4 240 144 240 Lời giải Chọn B
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 131 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT
Gọi V là thể tích của khối đa diện có các đỉnh là các điểm A , B , C , M , N , P .
V là thể tích của khối lăng trụ AB . C A B  C
 . Gọi H là trọng tâm của tam giác ABC . Vì điểm 1
A cách đều các điểm A , B , C nên AH   ABC .
Hơn nữa AA   ABC   A nên  AA, ABC   AAH  60 . a
Suy ra AH  AH.tan 60  tan 60  a 3 2 3 a 3 a 3 Do đó V  S .A H   .a  (đvtt) 1 ABC 4 4 1 V 2V Mà 1 1 V       S .A H V    . A .ABC ABC A . 3 3 BCC B 3  4 NB  BB NB  4NB  Từ 5    PC  3PC  3 3 PC  CC  BB  4 4 1 1  4 3  Suy ra S  NB  PC d BB CC  BB  BB d   BB,CC BCPN    ,  2 2  5 4  31  31 BB .d BB,CC  .S   . 40 40 BCC B 31 31 31  V  V     V    V . M .BCPN M .BCC B A .BCC B 1 40 40 60 1 1 1 1 Và V  S . AH  V  
V (vì M là trung điểm của AA ). M .ABC ABC A . ABC 1 3 2 2 6 3 41 41a 3
Vậy thể tích cần tìm là V  V V  V  (đvtt). M .ABC M .BCPN 1 60 240
Cách 2: Dùng công thức giải nhanh Trang 132 TỔNG HỢP: HOÀNG TUYÊN
NHÓM WORD BIÊN SOẠN TOÁN HÌNH KHÔNG GIAN:K12 V 1 AM BN CP 3 3 a 3  1 4 3  41a 3 ABC MNP   Ta có: .     V     ABC MNP   .   V AA BB CC . 12  2 5 4  240 ABC A B C        3  .
Câu 180. Cho khối lăng trụ AB . C A B  C
 có thể tích V . Gọi M là trung điểm của AA ; N thuộc cạnh BB
sao cho NB  4NB và P thuộc cạnh CC sao cho PC  3PC . Thể tích của khối đa diện lồi có
các đỉnh là các điểm A , B , C , M , N , P theo V bằng: 101 5 41 5 A. V . B. V . C. V . D. V . 180 8 60 7 Lời giải Chọn C A C B M E P D A' C' N B' Cách 1. Tự luận
Gọi D , E lần lượt là trung điểm của BB , CC . 1 Ta có V V V  V V V . ABCMNP ABCMDE M .DEPN M .DEP M . 2 PDN  1 1  3 3 DN  DB  NB   BB  BB  S  S    2 5  10 PDN 20 BCC B 1 1 3 3 3 2 1  V  d M , BCC B   .S  d A, BCC B   . S      V   . V V M .DPN    PDN    BCC B A. 3 3 20 20 BCC B 20 3 10  1 1  1 1 EP  EC  PC   CC  CC  S  S      2 4  4 DEP 8 BCC B 1 1 1 1 1 2 1  V  d M , BCC B   .S  d A, BCC B   . S      V   . V V M .DEP    DEP    BCCB A. 3 3 8 8 BCC B 8 3 12
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 133 HÌNH KHÔNG GIAN:K12
NHÓM WORD BIÊN SOẠN TOÁN THPT  1 1 1  41 Vậy V    V  V   . ABCMNP  2 10 12  60
Cách 2: Dùng công thức giải nhanh V 1 AM BN CP V  1 4 3  41 ABC MNP   Ta có: .     V     V ABC MNP   .   V AA BB CC . 3  2 5 4  60 ABC A B C        3  .
Câu 181. Cho hình lăng trụ ABC.A B  C
 và M , N là hai điểm lần lượt trên cạnh C , A CB sao cho MN song CM song với AB và  k . Mặt phẳng (MNB A
 ) chia khối lăng trụ ABC.A B  C  thành hai phần CA V
có thể tích V (phần chứa điểm C ) và V sao cho 1  2 . Khi đó giá trị của k là 1 2 V 2 1   5 1 1 5 3 A. k  . B. k  . C. k  . D. k  . 2 2 2 3 Lời giải Chọn A + Vì ba mặt phẳng (MNB A  ),(ACC A  ),(BCC B
 )đôi một cắt nhau theo ba giao tuyến phân biệt AM , B N  ,CC và A M
 ,CC không song song nên AM , B N
 ,CC đồng qui tại S . CM MN MN SM SN SC Ta có k       CA AB A B   SA SB SC + Từ đó 3 V  k V        V V    k V . MNC S A B C MNC A B C  3 1 S. . 1 .  S.ABC V    V    3CC 3 SC SC ABC.A B C   + Mặt khác    31 k ABC.A B  C  V    V SC SC S.AB C   31 k  S.A'B 'C ' V  2k k  1.V Suy ra V  1 k  ABC. 3 . A B  C ABC A B C       . 1 31 k  3 V 2 2 k  k 1 2 1   5 + Vì 1  2 nên 2 V  V             k k 1 0 k (k 0) . V 1 ABC. 3 A B C 3 3 2 2 1   5 Vậy k  . 2 Trang 134 TỔNG HỢP: HOÀNG TUYÊN