Ứng dụng hình học của tích phân xác định | Giải tích 1 | Đại học Bách Khoa Hà Nội

Ứng dụng hình học của tích phân xác định | Giải tích 1 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 1

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

7 trang 6 tháng trước

Tác giả:

Profile Thùy Dương
1
Ứ ỌNG DỤNG HÌNH H C CỦA TPXĐ
I. Các ng d ng hình h ứ ụ ọc của tpxđ:
1. Diệ ề ẳn tích mi n ph ng
( ), 0
:
,
( )
b
a
y f x y
D
x a x b
S f x dx
( ), ( )
:
,
( ) g(x)
b
a
y f x y g x
D
x a x b
S f x dx
2. Thể ậ tích v t thể tròn xoay:
2
0
0
( ), 0
:
( )
2 ( )
b
x
a
b
y
a
y f x y
D
a x b
V f x dx
V xf x dx
2 2
0
0
( ), ( )
:
( ) ( )
2 ( ) ( )
b
x
a
b
y
a
y f x y g x
D
a x b
V f x g x dx
V x f x g x dx
Chú ý:
+ Khi quay quanh Ox thì mi n D ph m v 1 phía so v i Ox và khi quay ề ải nằ ề ớ
quanh Oy thì mi n D ph i n m về ả ằ ề 1 phía so v i Oy. ớ
+ Tính đối x i xứng: Miền D đố ứng qua Ox, D là ph n phía trên Ox c a D
1
ầ ủ
a
b
y=f(x)
y=f(x)
y=g(x)
a
b
y=f(x)
a
b
y=g(x)
y=f(x)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2
3. Độ dài cung:
Đường cong C :
2
2
: ( ), 1 '( )
: (y), 1 g'(y)
b
a
d
c
C y f x a x b L f x dx
C x g c y d L dy
4. Diệ ặn tích m t tròn xoay:
- Khi C quay quanh Ox t o thành di n tích :ạ ệ
2
2 ( ) 1 '( )
b
x
a
S f x f x dx
- Khi C quay quanh Oy t o thành di n tích: ạ ệ
2
2 g(y) 1 g'(y)
d
y
c
S dy
II. SỬ D NG QU TÍNH GIÁ TR X P X C Ụ I TẮC ĐỂ Ị Ấ Ỉ ỦA TPXĐ:
- Không ph i t t c u có thả ấ ả các TP đề ể được tính toán, điển hình là TPXĐ
2
2
0
x
I e dx
nên ta s ẽ dùng phương pháp để ước tính giá trị của TPXD.
1
1
2
x x
y y
V D V D
V D V D
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3
- c tính Ta có 3 phương pháp khác nhau để ướ
( ) dx
b
a
f x
, b ng cách xem tích phân ằ
như là diệ ạng đã biết để ện tích dưới đườn tích và sử dụng hình d ước tính di ng cong.
Ba phương pháp đó là
Qui t m ắc trung điể
Qui t c hình thang ắ
Qui t c Simpson ắ
1. Qui tắc trung điểm:
Qui t c quen thu c nên ta s chia các kho ng [a,b] thành n các kho ng nh có chiắ ộ ẽ ả ả ỏ ều
rộng bằng nhau:
b a
x
n
, ta có các phân đoạn như sau:
0 1 1 2 2 3 1
, , , , , ,..., , ,
n n
x x x x x x x x
với
0
,
n
x a x b
.
Khi đó,
* * *
1 2
* * *
1 2
( )dx ...
...
b
n
a
n
f x xf x xf x xf x
x f x f x f x
- Xét t ng Riemann: ổ
1
( ).
n
n i
i
R f x x
1
( ) lim lim ( ).
b
n
n i
n n
i
a
f x dx R f x x
 
2. Qui t c hình thang: ắ
CuuDuongThanCong.com https://fb.com/tailieudientucntt
4
- Qui t chia kho ng [a,b] ắc này cũng giống như qui tắc trung điểm, ta cũng sẽ ả
thành n kho ng nh có chi u rả ỏ ề ộng b ng nhau ằ
b a
x
n
,
-
- Ta tính di n tích th c t x p x c a m ng cong. Và di n tích ệ ự ế ấ ỉ ủ ỗi hình thang dưới đườ ệ
hình thang trong khoảng
1
,
i i
x x
i công th c sau: được đưa ra bở ứ
1
2
i i i
x
A f x f x
Vì v y, ch ng ta s d ng n kho ng thì tích phân x p x ậ ứ ử ụ ả ấ ỉ là :
0 1 1 2 1
( ) ( ) ( ) ( ) ( ) ... ( ) ( )
2 2 2
b
n n
a
x x x
f x dx f x f x f x f x f x f x
3. Qui t c Simpson: ắ
- ch [a,b] thành n n con b ng nhau v i n Phương pháp này ta cũng phân hoạ đoạ ằ ớ
chẵn. Độ r ng m i kho ng là ộ ỗ ả
b a
x
n
với
0
,
n
x a x b
- X p x n tích trên khoấ ỉ diệ ảng kép
1
,
i i
x x
và
1
,
i i
x x
là
1 1
4
3
i i i i
x
A f x f x f x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
5
- V y, thì tích phân x p x : ới 2n đoạn con như vậ ấ ỉ
0 1 2 2 3 4 2 1
( ) 4 4 ... 4
3 3 3
b
n n n
a
x x x
f x dx f x f x f x f x f x f x f x f x f x
Ví d : Tính ụ
2
2
0
x
I e dx
với n = 4 theo 3 phương pháp lấy xấp xỉ
Giá tr cị ủa
2
2
0
16.45262776
x
e dx
Với :
2 0 1
4 2
x
và nh ng kho ng chia là : [0; 0,5], [0,5; 1], [1; 1,5], [1,5 ; 2]ữ ả
Qui t m ắc trung điể
Sai s 1.96701523 ố:
Qui t c hình thang: ắ
Sai s : 4.19193129 ố
Qui t c Simpson: ắ
Sai số: 0.90099869
CuuDuongThanCong.com https://fb.com/tailieudientucntt
6
III. BÀI TẬP:
1. Cho mi n ph ng ề ẳ
2 2
: 0, 3, 4D y y x x y
. Tính th tích v t th c t o ra ể ậ ể đượ ạ
khi D quay quanh Ox.
2. Tính th tích v t thể ậ ể được t o ra khi mi n D gi i h n bạ ề ớ ạ ởi
2 , x y, y 0y x
quay quanh Oy.
3. Tính th tích v t th t o ra khi mi n ph ng gi i h n bể ậ ể ạ ề ẳ ớ ạ ởi các đường
2
2
6, , 0, 0
2
x
y x y x y
quay quanh Oy.
4. Tính di n tích mi n phệ ề ẳng Oxy được giới hạn bởi:
2
1 , 1, 0
2
x
y x y y
5. Cho đường cong (C):
2
4x y
. Vi p tuy n (d) c ng cong ết phương trình tiế ế ủa đườ
này t i (0;2). G i D là mi n ph ng gi i h n b ng cong (C), ti p tuy n d và ạ ọ ề ẳ ớ ạ ởi đườ ế ế
trục Ox. Tính th tích v o ra khi quay quanh Ox. ể ật thể được tạ
6. Cho mi n ph ng D gi i h n b i: ề ẳ ớ ạ ở
2 2
2 3, 2 1, 1y x x y x x y
. Tính diện
tích mi n D. ề
7. Cho mi n D gi i h n bề ớ ạ ởi
2 2 2 2
0, 2, 2y x y x y y
. Tính th tích v t th t o ra ể ậ ể ạ
khi quay mi n D quanh tr c Oy ề ụ
8. Cho mi n ph ng D gi i h n bề ẳ ớ ạ ởi
2
2 , 2 , 0 1y x x y x x
. Tính di n tích b ệ ề
mặt của vật thể tạo ra khi miền D quay quanh tr c Ox (k c ụ ể ả đáy)
9. Cho mi n ph ng D: ề ẳ
2
0 , 2y x x y
. Tính th tích v t th t o ra khi quay D ể ậ ể ạ
quanh tr c Ox và quanh tr c Oy. ụ ụ
CuuDuongThanCong.com https://fb.com/tailieudientucntt
7
10. Tính di n tích ph n m t ph ng Oxy gi i h n bệ ầ ặ ẳ ớ ạ ởi
2 2 2 2
2, 4 4, 4y x y y x y
CuuDuongThanCong.com https://fb.com/tailieudientucntt
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ỨNG DỤNG HÌNH HỌC CỦA TPXĐ
I. Các ứng dụng hình học của tpxđ:
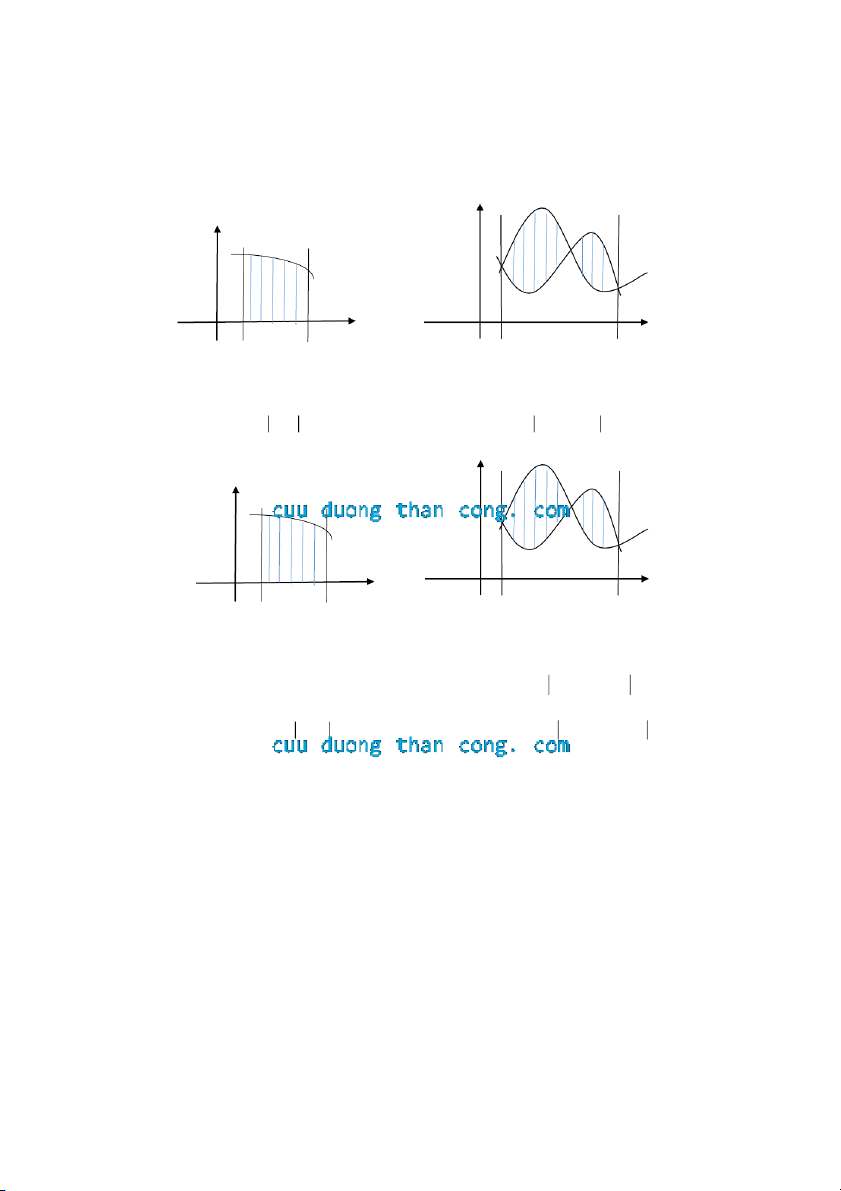
1. Diện tích miền phẳng y=f(x) y=f(x) y=g(x) a b a b y f ( ) x , y  0 y f ( )
x , y g( x) D :  D :  x  , a x   b x  , a x   b b bS f ( ) x dx   S f ( ) x g(x) dxa a
2. Thể tích vật thể tròn xoay: y=f(x) y=f(x) y=g(x) a a b b y f ( ) x , y  0
y f (x), y g (x) D :  D : 
a x b
a x bb b 2
V  f (x)dx  2 2
V  f (x)  g (x) dx  0x 0x a a b b V  2 xf ( ) x dxV  2 x f ( )
x g(x) dx  0 y   0 y a a Chú ý:
+ Khi quay quanh Ox thì miền D phải nằm về 1 phía so với Ox và khi quay
quanh Oy thì miền D phải nằm về 1 phía so với Oy.
+ Tính đối xứng: Miền D đối xứng qua Ox, D ầ ủ
1 là ph n phía trên Ox c a D 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt VD V Dx   x  1  V D V D  y   2 y  1
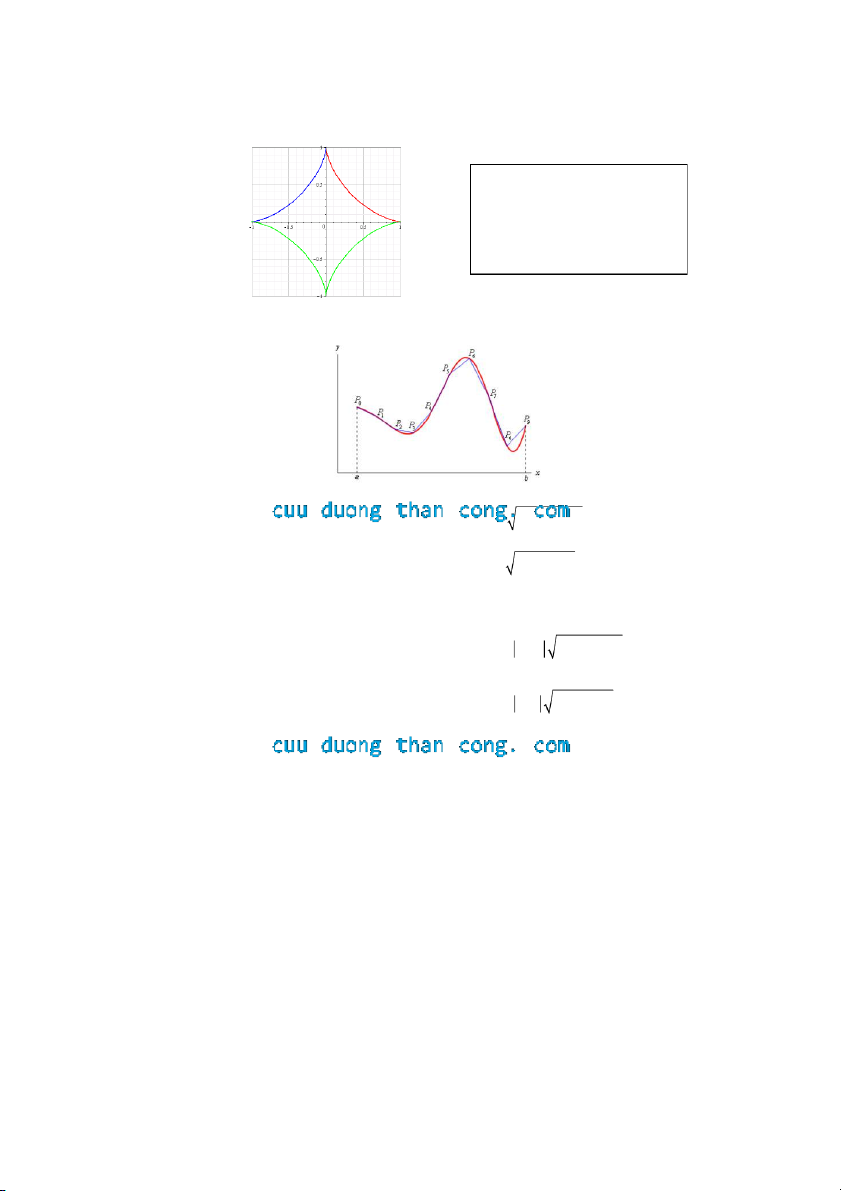
3. Độ dài cung: b
C : y f (x), a x bL  1 
f '(x)2dx Đường cong C : a d
C : x g (y), c y dL  1   g'(y)2dy c
4. Diện tích mặt tròn xoay: b
- Khi C quay quanh Ox tạo thành diện tích : S   f xf x dx x  2 2 ( ) 1 '( )  a d
- Khi C quay quanh Oy tạo thành diện tích: S    dy y  2 2 g(y) 1 g'(y) c
II. SỬ DỤNG QUI TẮC ĐỂ TÍNH GIÁ TRỊ XẤP XỈ CỦA TPXĐ: 2
- Không phải tất cả các TP đều có thể được tính toán, điển hình là TPXĐ 2 x I e dx  0
nên ta sẽ dùng phương pháp để ước tính giá trị của TPXD. 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt b
- Ta có 3 phương pháp khác nhau để ước tính f (x) dx 
, bằng cách xem tích phân a
như là diện tích và sử dụng hình dạng đã biết để ước tính diện tích dưới đường cong. Ba phương pháp đó là  Qui tắc trung điểm  Qui tắc hình thang  Qui tắc Simpson
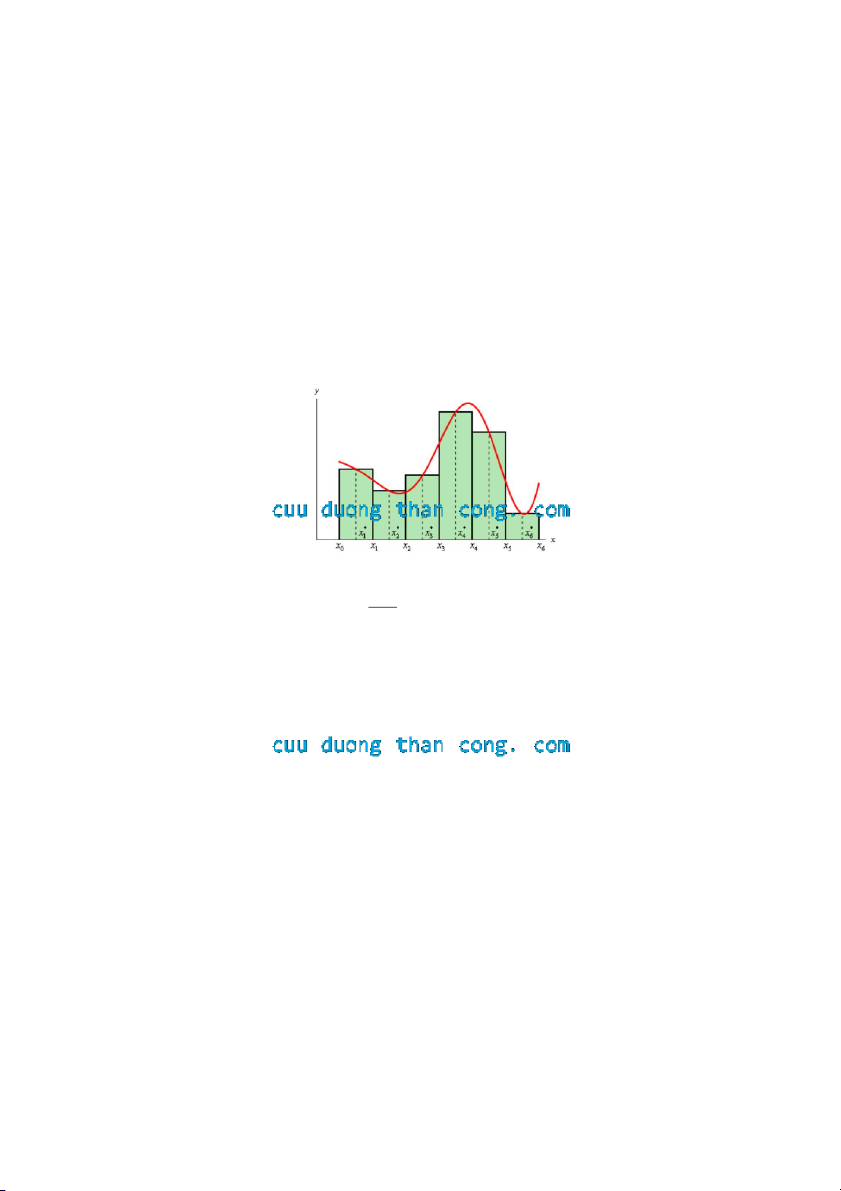
1. Qui tắc trung điểm:
Qui tắc quen thuộc nên ta sẽ chia các khoảng [a,b] thành n các khoảng nhỏ có chiều b a rộng bằng nhau: x  
, ta có các phân đoạn như sau: n
x , x , x , x , x , x ,..., x , x , x  , a x b . 0 1   1 2   2 3   n 1 với n  0 n b
f (x) dx  xf
 *x xf  *x  ...xf  *x 1 2 n Khi đó, ax   f   *
x   f  *
x  ...  f  * x  1 2 n  n
- Xét tổng Riemann: R
f ( x ).xn i i 1  b n
f (x)dx  lim R  lim f   (x ).x n i n  n  i 1 a
2. Qui tắc hình thang: 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
- Qui tắc này cũng giống như qui tắc trung điểm, ta cũng sẽ chia khoảng [a,b] 
thành n khoảng nhỏ có chiều rộng bằ b a ng nhau x   , n -
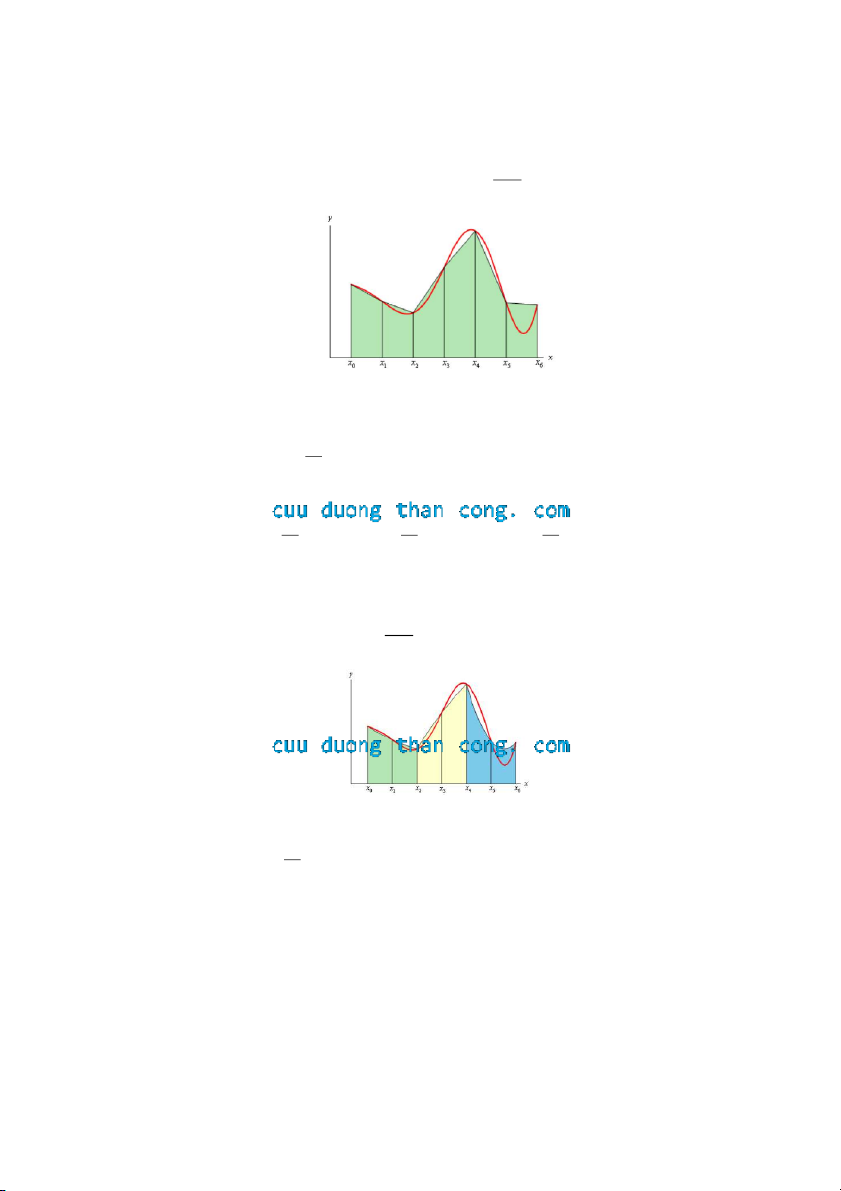
- Ta tính diện tích thực tế xấp xỉ của mỗi hình thang dưới đường cong. Và diện tích
hình thang trong khoảng  x được đưa ra bở ứ  , x i công th c sau: i 1 i xA f xf x i   i1  i  2
Vì vậy, chứng ta sử dụng n khoảng thì tích phân xấp xỉ là : b xxx
f (x)dx
f (x )  f (x ) 
f ( x )  f (x )  ... f (x )  f ( x )  0 1   1 2   n 1  n  2 2 2 a
3. Qui tắc Simpson:
- Phương pháp này ta cũng phân hoạch [a,b] thành n đoạn con bằng nhau với n 
chẵn. Độ rộng mỗi khoả b a ng là x  với x  , a x b n 0 n
- Xấp xỉ diện tích trên khoảng kép  x , x x , x l à i và  i i 1  1 i xA f xf x f x i    4 i 1   i   i1 3 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
- Với 2n đoạn con như vậy, thì tích phân xấp xỉ : b xxx
f (x)dx  
f x  4 f x f x f x
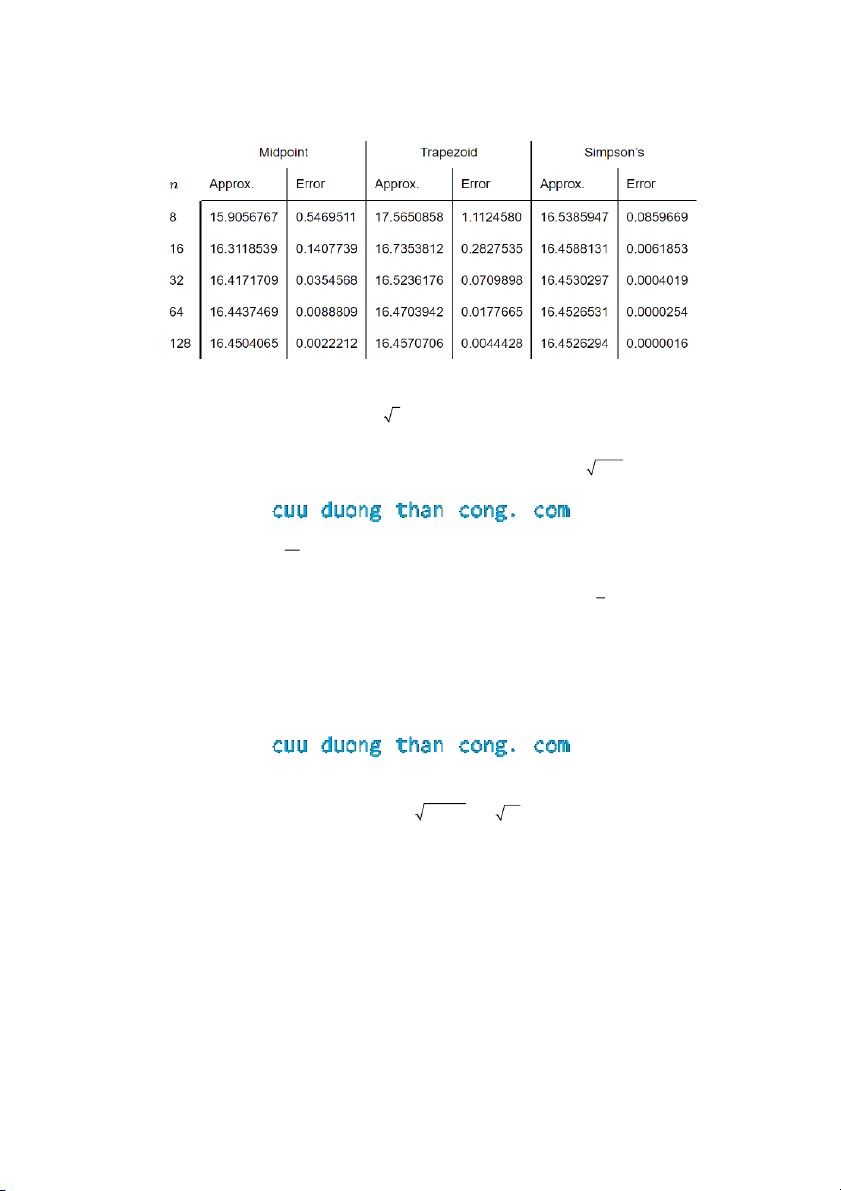
 4 f x f x  ... f x    4 f x f x 0   1  2   2   3   4    n 2  n 1  n  3 3 3 a 2 Ví dụ 2 : Tính x I e dx
với n = 4 theo 3 phương pháp lấy xấp xỉ 0 2 2 Giá trị của x e dx 16.45262776  0 2  0 1
Với :x
 và những khoảng chia là : [0; 0,5], [0,5; 1], [1; 1,5], [1,5 ; 2] 4 2
Qui tắc trung điểm Sai số: 1 .96701523
Qui tắc hình thang: Sai số: 4.19193129
Qui tắc Simpson: Sai số: 0.90099869 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
III. BÀI TẬP: 1. Cho miền phẳng 2 2
D : y  0, y x 3, x y  4 . Tính thể tích vật thể được tạo ra khi D quay quanh Ox.
2. Tính thể tích vật thể được tạo ra khi miền D giới hạn bởi y  2  x, x  y, y  0 quay quanh Oy.
3. Tính thể tích vật thể tạo ra khi miền phẳng giới hạn bởi các đường 2 x 2
y  x  6, y
, x  0, y  0 quay quanh Oy. 2 x
4. Tính diện tích miền phẳng Oxy được giới hạn bởi: y  x  2 1 , y   1, y  0 2 5. Cho đường cong (C): 2
x y  4 . Viết phương trình tiếp tuyến (d) của đường cong
này tại (0;2). Gọi D là miền phẳng giới hạn bởi đường cong (C), tiếp tuyến d và
trục Ox. Tính thể tích vật thể được tạo ra khi quay quanh Ox.
6. Cho miền phẳng D giới hạn bởi: 2 2
y  x  2x  3, y x  2x 1, y  1 . Tính diện tích miền D.
7. Cho miền D giới hạn bởi 2 2 2 2
y  0, x y  2, x y  2 y . Tính thể tích vật thể tạo ra
khi quay miền D quanh trục Oy
8. Cho miền phẳng D giới hạn bởi 2 y
2x x , y  2x, 0  x 1 . Tính diện tích bề
mặt của vật thể tạo ra khi miền D quay quanh trục Ox (kể cả đáy) 9. Cho miền phẳng D: 2 0  y  ,
x x  2  y . Tính thể tích vật thể tạo ra khi quay D
quanh trục Ox và quanh trục Oy. 6 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
10. Tính diện tích phần mặt phẳng Oxy giới hạn bởi 2 2 2 2
y  2, x y  4y  4, x y  4 7 CuuDuongThanCong.com
https://fb.com/tailieudientucntt