Viết phương trình mặt cầu Toán 12

Viết phương trình mặt cầu Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 355

 Phương trình mặt cầu (S) dạng 1:

Để viết phương trình mặt cầu ( ),S ta cần tìm tâm ( ; ; )I a b c và bán kính

Khi đó:

2 2 2 2

Tâm: ( ; ; )

( ) : ( ) : ( ) ( ) ( ) .

Bán kí

n : h

I a b c

S S x a y b z c R





      









 Phương trình mặt cầu (S) dạng 2:

2 2 2

( ) : 2 2 2 0 .S x y z ax by cz d      

Với

2 2 2

0a b c d    là phương trình mặt cầu dạng 2

Tâm ( ; ; ),I a b c bán kính:

2 2 2

0.R a b c d    

BÀI TẬP MẪU

Trong không gian Oxyz , cho mặt cầu

 

S có tâm là điểm

 

0;0; 3I  và đi qua điểm

 

4;0;0M . Phương

trình của

 

S là

 

2 2

3 25x y z    . B.

 

2 2

3 5x y z    .

 

2 2

3 25x y z   

. D.

 

2 2

3 5x y z   

Phân tích hướng dẫn giải

1. DẠNG TOÁN: Đây là dạng toán viết phương trình của mặt cầu.

2. HƯỚNG GIẢI:

B1:

2 2 2 2

Tâm: ( ; ; )

( ) : ( ) : ( ) ( ) ( ) .

Bán kí

n : h

I a b c

S S x a y b z c R





      









B2:

     

2 2 2

4 0 0 0 0 3 5R IM       

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn A

Theo bài ta có bán kính của mặt cầu

 

là

     

2 2 2

4 0 0 0 0 3 5R IM        .

Từ đó ta có phương trình mặt cầu

   

2 2

: 3 25S x y z    .

VIẾT PHƯƠNG TRÌNH MẶT CẦU

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 356

Bài tập tương tự và phát triển:

Câu 33.1: Viết phương trình mặt cầu có tâm





1;2;3

và đi qua giao điểm của đường thẳng

: 2

x t

d y t

z t

 





 





 



với mặt phẳng





Oxy

2 2 2

( 1) ( 2) ( 3) 27

     

x y z B.

2 2 2

( 1) ( 2) ( 3) 27

     

x y z

2 2 2

( 1) ( 2) ( 3) 3 3

     x y z

2 2 2

( 1) ( 2) ( 3) 3 3

     x y z

Lời giải

Chọn B

Mặt phẳng

Oxyz

là :



Gọi

( ) 3 ( 2;5; 0)

A d Oxyz t A

      

Vì điểm

nằm trên mặt cầu nên bán kính của mặt cầu là

2 2 2

( 3) 3 ( 3) 3 3

      R IA

Phương trình mặt cầu





tâm





1;2;3

I và bán kính

3 3

R

là

 

2 2

( 1) ( 2) 3 27

     

x y z .

Câu 33.2: Trong không gian

Oxyz

, cho mặt cầu





có tâm là điểm





1;2; 3

 

và tiếp xúc với trục

. Phương trình của





là:













2 2 2

1 2 3 13

x y z     













2 2 2

1 2 3 13

x y z     













2 2 2

1 2 3 13

x y z      D.













2 2 2

1 2 3 13

x y z     

Lời giải

Chọn C

Gọi

là hình chiếu của

lên trục

Ox A(-1;0;0)



Vì điểm

nằm trên mặt cầu nên bán kính của mặt cầu là

2 2 2

0 ( 2) ( 3) 13

      R IA .

Phương trình mặt cầu





tâm





1;2; 3

 

và bán kính

R là

 

2 2

( 1) ( 2) 3 13

     

x y z

Câu 33.3: Mặt cầu





tâm





1; 2; 3

 

I và tiếp xúc với mặt phẳng





: 2 2 1 0

   

P x y z có phương

trình:

     

2 2 2

1 2 3 .

     

x y z

     

2 2 2

1 2 3 .

     

x y z

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 357

     

2 2 2

1 2 3 .

     

x y z

     

2 2 2

1 2 3 .

     

x y z

Lời giải

Chọn B

 Bán kính mặt cầu là :

 

2 2 2

1 2.2 2.( 3) 1

1 2 2

    

  

 

R d I P .

 Phương trình mặt cầu là:

2 2 2

( 1) ( 2) ( 3)

     

x y z

Câu 33.4: Mặt cầu





tâm





2;1;5

I và tiếp xúc với mặt cầu





2 2 2

: ( 1) 3

   

S x y z có phương trình:

2 2 2

( 2) ( 1) ( 5) 12

( 2) ( 1) ( 5) 48



     



     



x y z

2 2 2

( 2) ( 1) ( 5) 2 3

( 2) ( 1) ( 5) 4 3



     



     





x y z

2 2 2

( 2) ( 1) ( 5) 12

( 2) ( 1) ( 5) 48



     



     



x y z

2 2 2

( 2) ( 1) ( 5) 2 3

( 2) ( 1) ( 5) 4 3



     



     





x y z

Lời giải

Chọn A

Từ





2 2 2

: ( 1) 3

    

S x y z

Tâm

(1; 0;0)

và bán kính

r 

1 1

27 3

II r

  

vậy điểm

(2;1;5)

I nằm ngoài mặt cầu





2 2 2

: ( 1) 3

   

S x y z

Ta có pt đường thẳng

là

x t

y t

z t

 





 





 



Gọi

1 1

( ) (1 ; ; 5 )

A II S A t t t

     

. Do

( )

A S



nên

2 2 2 2

2 1 5

; ; 4 3

3 3 3

1 1

25 3

9 3

4 1 5

; ; 2 3

3 3 3

A AI

t t t t t

A AI



 

   

 



 



        



 

 



 

 



 Bán kính mặt cầu là :

2 3

R .

 Phương trình mặt cầu là:

2 2 2

( 2) ( 1) ( 5) 12

     

x y z

 Bán kính mặt cầu là :

4 3

R

 Phương trình mặt cầu là:

2 2 2

( 2) ( 1) ( 5) 48

     

x y z .

Câu 33.5: Mặt cầu





tâm





1; 2; 4

I và tiếp xúc với mặt phẳng





2 2 2

: ( 1) ( 2) 27

S x y z

    

có

phương trình:













2 2 2

1 2 4 3.

     

x y z













2 2 2

1 2 4 3.

     x y z













2 2 2

1 2 4 3.

     

x y z D.













2 2 2

1 2 4 3.

     x y z

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 358

Lời giải

Chọn C

Từ





2 2 2

: ( 1) ( 2) 27

S x y z

    

Tâm

( 1;0; 2)

I và bán kính

3 3

R 

1 1

2 3 3 3

II R

  

vậy điểm





1; 2; 4

nằm trong mặt cầu









và





tiếp xúc

1 1

5 3

3 3 2 3

R R II R





      









 Bán kính mặt cầu là :

R .

 Phương trình mặt cầu là:

2 2 2

( 1) ( 2) ( 4) 3

x y z

     

Câu 33.6: Mặt cầu





tâm





1; 2;3

I 

và tiếp xúc với mặt phẳng tọa độ (Oyz) có phương trình:

     

2 2 2

1 2 3 1

x y z

     

     

2 2 2

1 2 3 14

     

x y z

     

2 2 2

1 2 3 1

x y z

     

     

2 2 2

1 2 3 14

     

x y z

Lời giải

ChọnC

 PT mp

( ): 0

Oyz x



Bán kính mặt cầu là :

 

2 2 2

, 1

( 1) 0 0

R d I Oyz



  

  

 Phương trình mặt cầu là:

2 2 2

( 1) ( 2) ( 3) 1

     

x y z

Câu 33.7: Trong không gian

Oxyz

, cho hai điểm









1;3; 2 , 3;5;0

A B

. Phương trình mặt cầu đường

kính AB là:

2 2 2

( 2) ( 4) ( 1) 3.

     

x y z B.

2 2 2

( 2) ( 4) ( 1) 12.

     

x y z

2 2 2

( 2) ( 4) ( 1) 12.

     x y z D.

2 2 2

( 2) ( 4) ( 1) 3.

     

x y z

Lời giải

Chọn A

 Trung điểm của đoạn thẳng

là





2;4;1

2 2 2

2 2 ( 2) 2 3

AB     

 Mặt cầu đường kính

có tâm





2;4;1

, bán kính

 

 Vậy phương trình của mặt cầu là:

2 2 2

( 2) ( 4) ( 1) 3.

     

x y z

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 359

Câu 33.8: Trong không gian

Oxyz

, Viết phương trình mặt cầu (S) biết (S) có bán kính R=3 và tiếp xúc với

mặt phẳng (Oxy) tại điểm M(1;2;0)

2 2 2

4 2 6 5 0

      

x y z x y z

2 2 2

4 2 6 5 0

      

x y z x y z

2 2 2

4 2 6 11 0

      

x y z x y z

2 2 2

4 2 6 11 0

      

x y z x y z

Lời giải

Chọn A

 Giả sử mặt cầu (S) có tâm





; ;

I a b c

Do mặt cầu (S) tiếp xúc với mặt phẳng (Oxy) tại điểm M(1;2;0) nên M là hình chiếu của





; ;

I a b c

lên mp (Oxy) suy ra





2;1;

I c

Ta có mp(Oxy) có pt là



Ta có

( ,(Ox )) 3

d I y c

   

 Với



Mặt cầu





2;1;3

, bán kính



có phương trình là:

2 2 2 2 2 2

( 2) ( 1) ( 3) 9 4 2 6 5 0

             

x y z x y z x y z .

 Với

 

Mặt cầu





2;1; 3



, bán kính



có phương trình là:

2 2 2 2 2 2

( 2) ( 1) ( 3) 9 4 2 6 5 0

x y z x y z x y z

             

Câu 33.9: Phương trình mặt cầu

( )

đi qua

(1; 2;3), (4; 6; 2)

A B



và có tâm

thuộc trục

là

2 2 2

( ) : ( 7) 6.

S x y z

   

2 2 2

( ) : ( 7) 36.

S x y z   

2 2 2

( ) : ( 7) 6.

S x y z

   

2 2 2

( ) : ( 7) 49.

S x y z   

Lời giải

Chọn D

Vì

I Ox



nên gọi

( ;0;0).

I x

( )

đi qua

;

A B

nên

IA IB



2 2

(1 ) 4 9 (4 ) 36 4 7.

x x x

         

Suy ra

(7;0;0) 7.

I R IA

  

Do đó

2 2 2

( ) : ( 7) 49.

S x y z   

Câu 33.10: Phương trình mặt cầu

( )

đi qua

(2;0; 2), ( 1;1; 2)

A B

 

và có tâm

thuộc trục

là

2 2 2

( ) : 2 8 0.

S x y z y

    

2 2 2

( ) : 2 8 0.

S x y z y

    

2 2 2

( ) : 2 8 0.

S x y z y

    

2 2 2

( ) : 2 8 0.

S x y z y

    

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 360

Lời giải

Chọn A

Vì

I Oy



nên gọi

(0; ; 0).

I y

( )

đi qua

;

A B

nên

IA IB



2 2

4 ( ) 4 1 (1 ) 4 1.

y y y

          

Suy ra

(0; 1; 0) 3.

I R IA

   

Do đó

 

2 2 2 2 2

( ) : 1 9 2 8 0.

S x y z x y z y

         

Câu 33.11: Phương trình mặt cầu

( )

đi qua

(1;2; 4), (1; 3;1), (2;2;3)

A B C

 

và tâm

( )

I Oxy



là.

2 2 2

( 2) ( 1) 26.

x y z

    

2 2 2

( 2) ( 1) 9.

x y z

    

2 2 2

( 2) ( 1) 26.

x y z

    

2 2 2

( 2) ( 1) 9.

x y z

    

Lời giải

Chọn A

Vì

( )

I Oxy



nên gọi

( ; ;0).

I x y

Ta có:

IA IB

IA IC



















2 2 2 2 2 2

( 1) ( 2) 4 ( 1) ( 3) 1

( 1) ( 2) 4 ( 2) ( 2) 3

x y x y





        









        





10 10 2

( 2;1;0) 26.

2 4 1

y x

I R IA

x y

 

 

  

 

      

 

 

  

 

 

2 2 2

( 2) ( 1) 26.

x y z

     

Câu 33.12: Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm M(2;1;1)



     



     





2 2 2

( 1) ( 1) ( 1) 1

( 3) ( 3) ( 3) 9

x y z

. B.



     



     





2 2 2

( 1) ( 1) ( 1) 1

( 3) ( 3) ( 3) 9

x y z

2 2 2

( 1) ( 1) ( 1) 3

( 3) ( 3) ( 3) 1

x y z



     



     





. D.

2 2 2

( 1) ( 1) ( 1) 3

( 3) ( 3) ( 3) 1

x y z



     



     





Lời giải

Chọn B

Gỉa sử





; ;

I a b c

là tâm mặt cầu

( )

tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm

(2;1;1).

Vì mặt cầu

( )

tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm

(2;1;1)

M có các thành phần

tọa độ đều dương nên

a b c r

  

Phương trình mặt cầu

( )

là

2 2 2 2

( ) ( ) ( )

x a y a z a a

     

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 361

Vì mặt cầu

( )

đi qua điểm M(2;1;1) nên

2 2 2 2 2

(2 ) (1 ) (1 ) 2 8 6 0

a a a a a a

         



       





       





2 2 2

1 ( ): ( 1) ( 1) ( 1) 1

3 ( ):( 3) ( 3) ( 3) 9

a S x y z

Câu 33.13: Cho mặt cầu





có tâm





1; 2; 4



và thể tích bằng

36 .



Phương trình của





là

     

2 2 2

1 2 4 9.

x y z

     

     

2 2 2

1 2 4 9.

x y z

     

     

2 2 2

1 2 4 9.

x y z

     

     

2 2 2

1 2 4 3.

x y z

     

Lời giải

Chọn A

Ta có:

3 3

4 4

36 3

3 3

V R R R

  

    

Khi đó

 

Tâm: (1; 2; 4)

Bán kính :













       

2 2 2

: 1 2 4 9.

S x y z

      

Câu 33.14: Cho mặt cầu





có tâm





1; 2;3

và diện tích bằng

32 .



Phương trình của





là

     

2 2 2

1 2 3 16.

x y z     

     

2 2 2

1 2 3 16.

x y z     

     

2 2 2

1 2 3 8.

x y z

     

     

2 2 2

1 2 3 8.

x y z

     

Lời giải

Chọn C

Ta có:

2 2

4 4 32 8

S R R R

  

    

Khi đó

 





Tâm: 1; 2;3

Bán kính:















       

2 2 2

: 1 2 3 8.

S x y z

      

Câu 33.15: Cho mặt cầu





có tâm

(1;2;0).

I Một mặt phẳng

( )

cắt





theo giao tuyến là một đường

tròn





Biết diện tích lớn nhất của





bằng

3 .



Phương trình của





là

 

2 2

2 3.

x y z

   

   

2 2

1 2 3.

x y z

    

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 362

     

2 2 2

1 2 1 9.x y z     

   

2 2

1 2 9.x y z    

Lời giải

Chọn B

Nhận xét : Mặt phẳng

( )P

cắt

 

S theo giao tuyến là một đường tròn

 

C và diện tích của

 

C lớn nhất khi ( )P qua tâm I của ( ).S

Ta có:

3 3S R R

 

   

Khi đó

 

Tâm: 1;2; 0

(

) :

Bán kí : 3















     

2 2

: 1 2 3.S x y z     

Câu 33.16: Cho mặt cầu

 

S có tâm

 

1;1;1I . Một mặt phẳng ( )P cắt

 

S theo giao tuyến là một đường

tròn

 

C . Biết chu vi lớn nhất của

 

C bằng 2 2.



Phương trình của

 

S là

     

2 2 2

1 1 1 4.x y z     

     

2 2 2

1 1 1 2.x y z     

     

2 2 2

1 1 1 4.x y z     

     

2 2 2

1 1 1 2.x y z     

Lời giải

Chọn D

Đường tròn

 

C đạt chu vi lớn nhất khi

 

C đi qua tâm

của mặt cầu

 

S .

Ta có: 2 2 2 2C R R

 

    .

Khi đó

 

Tâm: 1;1;1

(

) :

Bán kí : 2















       

2 2 2

: 1 1 1 2.S x y z      

Câu 33.17: Cho

 

1; 2;3I  . Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai điểm A và B sao cho

2 3AB  .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 363

2 2 2

( 1) ( 2) ( 3) 16

x y z

     

. B.

)3(

)2(

)1(  zyx

)3(

)2(

)1(  zyx

)3(

)2(

)1(  zyx

Lời giải

Chọn A

Gọi M là hình chiếu vuông góc của I (1; -2;3) trên trục Ox



M (1;0;0) và

là trung điểm của AB

Ta có:

     

2 2 2

1 1 0 2 0 3 13, 3

IM AM        

IMA



vuông tại

2 2

13 3 4 4

M IA IM AM R

       

Phương trình mặt cầu cần tìm là:

     

2 2 2

1 2 3 16

x y z

     

Câu 33.18: Trong không gian với hệ toạ độ

Oxyz

, Viết phương trình mặt cầu đi qua













2 ;3 ; 3 , 2; 2 ; 2 , 3 ;3 ;4

A B C 

và có tâm nằm trên mặt phẳng





Oxy

2 2 2

( 6) ( 1) 29

x y z

    

. B.

2 2 2

( 6) ( 1) 29

x y z

    

2 2 2

( 6) ( 1) 29

x y z

    

. D.

2 2 2

( 6) ( 1) 29

x y z

    

Lời giải

Chọn A

Giả sử





; ;0 ( )



I a b Oxy

và

là tâm và bán kính của mặt cầu

( )

và đi qua













2 ;3 ; 3 , 2; 2 ; 2 , 3 ;3 ;4

A B C 

Phương trình mặt cầu

( )

là

2 2 2 2

( ) ( )

x a y b z r

    

Vì mặt cầu ñi qua













2 ;3 ; 3 , 2; 2 ; 2 , 3 ;3 ;4

A B C 

nên

2 2 2 2

2 2 2 2 2 2 2 2 2

(2 ) (3 ) ( 3)

10 10 0 1

(2 ) ( 2 ) 2 2 12 0 6

(3 ) (3 ) 4 (3 ) (3 ) 4 29

a b r

b b

a b r a a

a b r a b r r



     

    



 

          

  

  

          

 



Vậy phương trình mặt cầu

( )

là

2 2 2

( 6) ( 1) 29

x y z

    

Câu 33.19: Trong không gian O xyz cho 4 điểm

















1; 2; 4 , 1; 3;1 , 2; 2;3 , 1; 0;4

 A B C D

. Viết

phương trình mặt cầu ngoại tiếp tứ diện ABCD

   

2 2

2 1 26

x y z

    

. B.

   

2 2

2 1 26

    

x y z

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 364

   

2 2

2 1 26

    x y z . D.

   

2 2

2 1 26

    x y z .

Lời giải

Chọn A

Giả sử









2 2 2 2 2 2

: 2 2 2 0 0

S x y z ax by cz d a b c d

          

là phương trình mặt cầu

ngoại tiếp tứ diện

ABCD

. Thay lần lượt tọa độ của

, , ,

A B C D

vào phương trình ta được

2 2 2

1 2 4 2 4 8 0

1 3 1 2 6 2 0 1

2 2 3 4 4 6 0

1 0 4 2 0 8 0

a b c d

a b c d b

a b c d

a c d



      

 





       

 



 



      

 

 

      



Do đó:





2;1; 0

I  và bán kính

2 2 2

R a b c d     .

Vậy (S) :

   

2 2

2 1 26

x y z

    

Câu 33.20: Viết phương trình mặt cầu





có tâm





I 1; 0;3

và cắt

1 1 1

2 1 2

  

 

x y z

tại hai

điểm A, B sao cho tam giác

IAB

vuông tại

   

2 2

1 3

    x y z

. B.

   

2 2

1 3

    x y z

   

2 2

2 10

1 3

    x y z . D.

   

2 2

2 10

1 3

    x y z .

Lời giải

Chọn A

Đường thẳng

có một vectơ chỉ phương





2;1; 2





u và





1; 1;1

 

P d

Ta có:





0; 1; 2

  



 

, 0; 4;2

u IP

 

  

 





. Suy ra:

 

d ;

 

 

 





u IP

I d



IAB

vuông tại I

IAB

 

vuông cân tại I

 

2d , .

IA I d 

Vậy (S) :

   

2 2

1 3

    x y z .

Bấm Tải xuống để xem toàn bộ.

| 1/10

| | Tải xuống

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
VIẾT PHƯƠNG TRÌNH MẶT CẦU
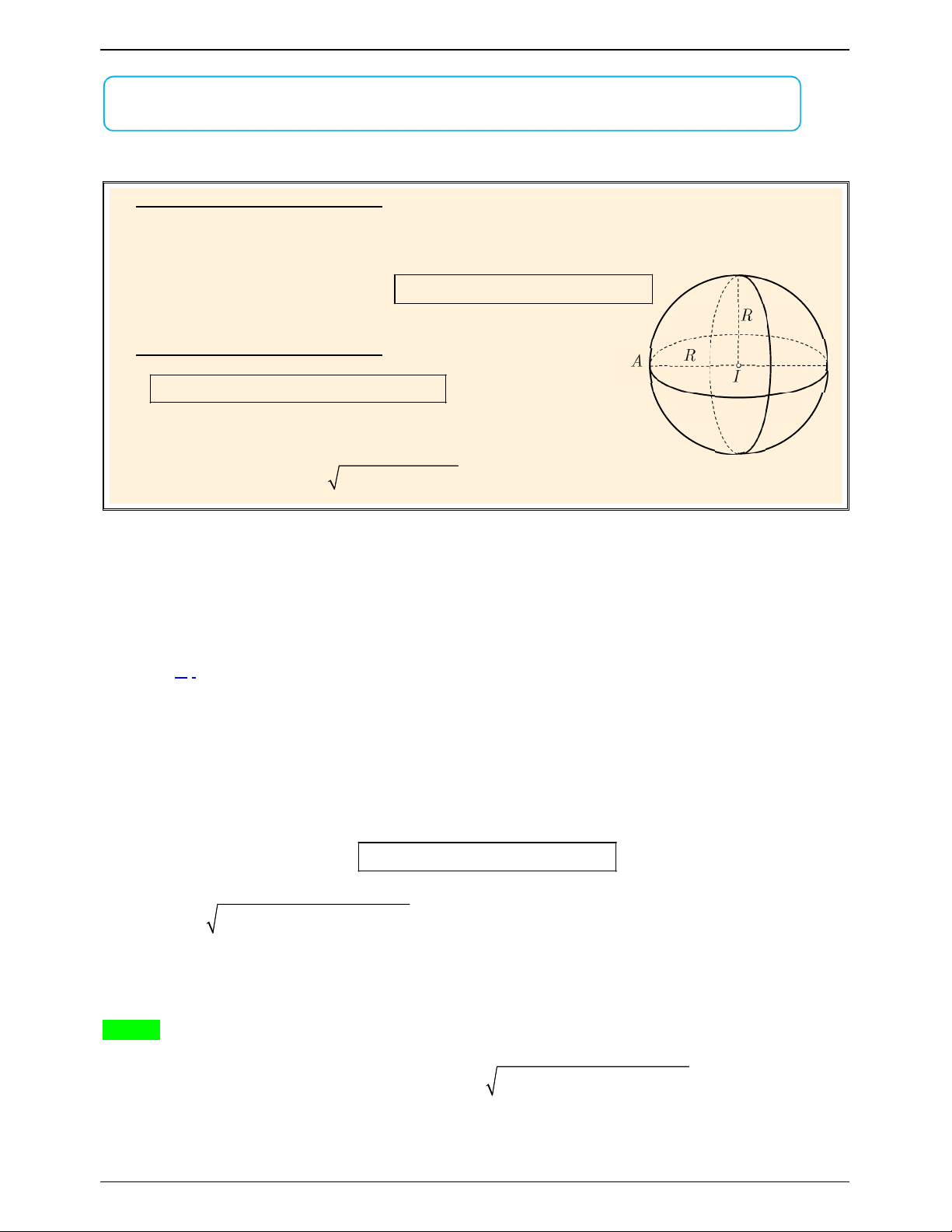
 Phương trình mặt cầu (S) dạng 1:
Để viết phương trình mặt cầu (S ), ta cần tìm tâm I (a;b;c) và bán kính . R
 Tâm: I(a; ; b c)  Khi đó: 2 2 2 2 (S) : 
 (S) : (x a)  (y b)  (z c)  R .   Bán kính: R 
 Phương trình mặt cầu (S) dạng 2: 2 2 2
(S) : x  y  z  2ax  2by  2cz  d  0 . 2 2 2
Với a  b  c d  0 là phương trình mặt cầu dạng 2 Tâm I (a; ; b c), bán kính: 2 2 2
R  a  b  c d  0. BÀI TẬP MẪU
Trong không gian Oxyz , cho mặt cầu S  có tâm là điểm I 0;0; 3 và đi qua điểm M 4; 0;0 . Phương
trình của S  là
A. x  y   z  2 2 2 3  25 .
B. x  y   z  2 2 2 3  5 .
C. x  y   z  2 2 2 3  25 .
D. x  y   z  2 2 2 3  5 .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán viết phương trình của mặt cầu. 2. HƯỚNG GIẢI:  T âm: I(a; ; b c)  B1: 2 2 2 2 (S) : 
 (S) : (x  a)  (y b)  (z c)  R .   B án kính: R  2 2 2
B2: R  IM  4  0  0  0  0  3  5
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn A 2 2 2
Theo bài ta có bán kính của mặt cầu  S  là R  IM  4  0  0  0  0  3  5 .
Từ đó ta có phương trình mặt cầu S  x  y   z  2 2 2 : 3  25 . Trang 355
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Bài tập tương tự và phát triển: Câu 33.1:
Viết phương trình mặt cầu có tâm I 1; 2;3 và đi qua giao điểm của đường thẳng x  1 t 
d :  y  2  t với mặt phẳng Oxy . z  3 t  A. 2 2 2
(x 1)  ( y  2)  (z  3)  27 B. 2 2 2
(x 1)  ( y  2)  (z  3)  27 C. 2 2 2
(x 1)  ( y  2)  (z  3)  3 3 D. 2 2 2
( x  1)  ( y  2)  ( z  3)  3 3 Lời giải Chọn B
Mặt phẳng Oxyz là : z  0
Gọi A  d  (Oxyz)  t  3  ( A 2;5; 0)
Vì điểm A nằm trên mặt cầu nên bán kính của mặt cầu là 2 2 2 R  IA  ( 3  )  3  ( 3  )  3 3 .
Phương trình mặt cầu  S  tâm I 1; 2;3 và bán kính R  3 3 là x   y    z  2 2 2 ( 1) ( 2) 3  27 . Câu 33.2:
Trong không gian Oxyz , cho mặt cầu S  có tâm là điểm I 1;2;3 và tiếp xúc với trục
Ox . Phương trình của S  là: 2 2 2 2 2 2 A. x   1  y  
2  z  3  13 B. x  
1  y  2  z  3  13 2 2 2 2 2 2 C. x   1  y  
2  z  3  13 D. x  
1  y  2  z  3  13 Lời giải Chọn C
Gọi A là hình chiếu của I lên trục Ox  A(-1;0;0) .
Vì điểm A nằm trên mặt cầu nên bán kính của mặt cầu là 2 2 2
R  IA  0  ( 2  )  ( 3  )  13 .
Phương trình mặt cầu  S  tâm I 1;2;3 và bán kính R  13 là x   y    z  2 2 2 ( 1) ( 2) 3  13 .
Câu 33.3: Mặt cầu S  tâm I 1; 2; 3 và tiếp xúc với mặt phẳng P : x  2 y  2z 1  0 có phương trình: 2 2 2 4 2 2 2 4 A.  x  
1   y  2   z  3  . B.  x  
1   y  2   z  3  . 9 9 Trang 356
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 2 2 2 2 2 2 C.  x  
1   y  2   z  3  . D.  x  
1   y  2   z  3  . 3 3 Lời giải Chọn B 1   2.2  2.(3) 1 2
 Bán kính mặt cầu là : R  d I,P   . 2 2 2 3 1  2  2 4
 Phương trình mặt cầu là: 2 2 2
( x 1)  ( y  2)  (z  3)  . 9
Câu 33.4: Mặt cầu S  tâm I 2;1;5 và tiếp xúc với mặt cầu S  2 2 2
: (x 1)  y  z  3 có phương trình: 1 2 2 2
(x  2)  ( y 1)  (z  5)  12 2 2 2
(x  2)  ( y 1)  (z  5)  2 3 A.  B.  2 2 2
(x  2)  ( y 1)  (z  5)  48  2 2 2
(x  2)  ( y 1)  (z  5)  4 3  2 2 2
(x  2)  ( y 1)  (z  5)  12 2 2 2
(x  2)  ( y 1)  (z  5)  2 3 C.  D.  2 2 2
(x  2)  ( y 1)  (z  5)  48 2 2 2 
(x  2)  ( y 1)  (z  5)  4 3  Lời giải Chọn A Từ S  2 2 2
: (x 1)  y  z  3  Tâm I (1; 0; 0) và bán kính r  3 1 1 1 Do II 
27  3  r vậy điểm I (2;1;5) nằm ngoài mặt cầu S : (x 1)  y  z  3 1  2 2 2 1 1 x  1 t 
Ta có pt đường thẳng II là  y  t 1 z  5t 
Gọi A  II  (S )  (
A 1 t; t
 ; 5t) . Do A  (S ) nên 1 1 1   2 1 5  A ;  ;   AI  4 3    1 1  3 3 3 2 2 2 2  t t 25t 3 t t           9 3   4 1 5  A ; ;  AI  2 3      3 3 3 
 Bán kính mặt cầu là : R  2 3 .
 Phương trình mặt cầu là: 2 2 2
(x  2)  ( y 1)  (z  5) 12.
 Bán kính mặt cầu là : R  4 3 .
 Phương trình mặt cầu là: 2 2 2
(x  2)  ( y 1)  (z  5)  48 .
Câu 33.5: Mặt cầu S  tâm I 1; 2; 4 và tiếp xúc với mặt phẳng S  2 2 2
: (x  1)  y  (z  2)  27 có 1 phương trình: 2 2 2 2 2 2 A.  x  
1   y  2   z  4  3. B.  x  
1   y  2   z  4  3. 2 2 2 2 2 2 C.  x  
1   y  2   z  4  3. D.  x  
1   y  2   z  4  3. Trang 357
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn C Từ S  2 2 2
: (x  1)  y  (z  2)  27 Tâm I (1;0; 2) và bán kính R  3 3 . 1 1 1
Do II  2 3  3 3  R vậy điểm I 1; 2; 4 nằm trong mặt cầu S . 1  1 1 R  5 3
S  và S tiếp xúc  R  R  II  R  3 3  2 3   1  1 1 R  3 
 Bán kính mặt cầu là : R  3 .
 Phương trình mặt cầu là: 2 2 2
(x 1)  ( y  2)  (z  4)  3 . Câu 33.6:
Mặt cầu S  tâm I  1
 ; 2;3 và tiếp xúc với mặt phẳng tọa độ (Oyz) có phương trình: 2 2 2 2 2 2 A.  x   1
  y  2   z  3  1 B.  x   1
  y  2   z  3  14 2 2 2 2 2 2 C.  x   1
  y  2   z  3  1 D.  x   1
  y  2   z  3  14 Lời giải ChọnC
 PT mp (Oyz) : x  0 1
Bán kính mặt cầu là : R  d I,Oyz   1 . 2 2 2 (1)  0  0
 Phương trình mặt cầu là: 2 2 2
(x 1)  ( y  2)  (z  3)  1. Câu 33.7:
Trong không gian Oxyz , cho hai điểm A1;3; 2, B 3;5;0 . Phương trình mặt cầu đường kính AB là: A. 2 2 2
(x  2)  ( y  4)  (z 1)  3. B. 2 2 2
(x  2)  ( y  4)  (z 1)  12. C. 2 2 2
(x  2)  ( y  4)  (z 1)  12. D. 2 2 2
(x  2)  ( y  4)  (z 1)  3. Lời giải Chọn A
 Trung điểm của đoạn thẳng AB là I 2;4  ;1 , 2 2 2 AB  2  2  ( 2  )  2 3 AB
 Mặt cầu đường kính AB có tâm I 2;4  ;1 , bán kính R   3 2
 Vậy phương trình của mặt cầu là: 2 2 2
(x  2)  ( y  4)  (z 1)  3. Trang 358
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Câu 33.8: Trong không gian Oxyz , Viết phương trình mặt cầu (S) biết (S) có bán kính R=3 và tiếp xúc với
mặt phẳng (Oxy) tại điểm M(1;2;0) A. 2 2 2
x  y  z  4x  2 y  6z  5  0 B. 2 2 2
x  y  z  4x  2 y  6z  5  0 C. 2 2 2
x  y  z  4x  2 y  6z  11  0 D. 2 2 2
x  y  z  4x  2 y  6z 11  0 Lời giải Chọn A
 Giả sử mặt cầu (S) có tâm I a;b;c ,
Do mặt cầu (S) tiếp xúc với mặt phẳng (Oxy) tại điểm M(1;2;0) nên M là hình chiếu của I a; ; b c 
lên mp (Oxy) suy ra I 2;1;c
Ta có mp(Oxy) có pt là z  0 c
Ta có d (I , (Oxy))   c  3  . 1  Với c  3
Mặt cầu I 2;1;3 , bán kính R  3 có phương trình là: 2 2 2 2 2 2
(x  2)  ( y 1)  (z  3)  9  x  y  z  4x  2y  6z  5  0 .  Với c  3
Mặt cầu I 2;1; 3 , bán kính R  3 có phương trình là: 2 2 2 2 2 2
(x  2)  ( y 1)  (z  3)  9  x  y  z  4x  2 y  6z  5  0 .
Câu 33.9: Phương trình mặt cầu (S) đi qua (
A 1; 2;3), B(4; 6; 2) và có tâm I thuộc trục Ox là A. 2 2 2
(S ) : (x  7)  y  z  6. B. 2 2 2
(S ) : (x  7)  y  z  36. C. 2 2 2
(S ) : (x  7)  y  z  6. D. 2 2 2
(S ) : (x  7)  y  z  49. Lời giải Chọn D
Vì I  Ox nên gọi I ( ; x 0; 0).
Do (S) đi qua A; B nên IA  IB 2 2
 (1 x)  4  9  (4  x)  36  4  x  7.
Suy ra I (7;0; 0)  R  IA  7. Do đó 2 2 2
(S ) : (x  7)  y  z  49.
Câu 33.10: Phương trình mặt cầu (S) đi qua (
A 2;0; 2), B(1;1; 2) và có tâm I thuộc trục Oy là A. 2 2 2
(S) : x  y  z  2y 8  0. B. 2 2 2
(S) : x  y  z  2y 8  0. C. 2 2 2
(S) : x  y  z  2 y  8  0. D. 2 2 2
(S) : x  y  z  2 y  8  0. Trang 359
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn A
Vì I Oy nên gọi I (0; y; 0).
Do (S) đi qua A; B nên IA  IB 2 2
 4  ( y)  4  1 (1 y)  4  y  1. 
Suy ra I (0; 1; 0)  R  IA  3. Do đó S
x   y  2 2 2 2 2 2 ( ) :
1  z  9  x  y  z  2 y  8  0.
Câu 33.11: Phương trình mặt cầu (S ) đi qua (
A 1; 2; 4), B(1; 3
 ;1), C(2; 2;3) và tâm I  (Oxy) là. A. 2 2 2
(x  2)  (y  1)  z  26. B. 2 2 2
(x  2)  (y  1)  z  9. C. 2 2 2
(x  2)  (y  1)  z  26. D. 2 2 2
(x  2)  (y  1)  z  9. Lời giải Chọn A I  A  IB 
Vì I  (Oxy) nên gọi I (x;y; 0). Ta có: I  A  IC   2 2 2 2 2 2
 (x  1)  (y  2)  4  (x  1)  (y  3)  1    2 2 2 2 2 2
 (x  1)  (y  2)  4  (x  2)  (y  2)  3  1  0y  10 x   2      
 I(2;1;0)  R  IA  26. 2  x  4 y   1   2 2 2
 (x  2)  (y  1)  z  26.
Câu 33.12: Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm M(2;1;1) (x  2 1)  (y  2 1)  (z  2 1)  1 (x  2 1)  (y  2 1)  (z  2 1)  1 A.  . B.  . (x  2 3)  (y  2 3)  (z  2 3)  2 2 2  9
(x  3)  (y  3)  (z  3)   9 2 2 2
(x 1)  (y 1)  (z 1)  3 2 2 2 (
 x 1)  (y 1)  (z 1)  3 C.  . D.  . 2 2 2
(x  3)  (y  3)  (z  3)  1 2 2 2  (
 x  3)  (y  3)  (z  3)  1  Lời giải Chọn B Gỉa sử I  ;
a b;c  là tâm mặt cầu (S) tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm M (2;1;1).
Vì mặt cầu (S) tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm M (2;1;1) có các thành phần
tọa độ đều dương nên a  b  c  r . 2 2 2 2
Phương trình mặt cầu (S) là (x a)  (y a)  (z a)  a Trang 360
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Vì mặt cầu (S) đi qua điểm M(2;1;1) nên 2 2 2 2 2
(2 a)  (1a)  (1a)  a  2a  8a  6  0
a  1  (S) : (x  2 1)  (y  2 1)  (z  2 1)  1
 a  3 (S):(x  2 3)  (y  2 3)  (z  2 3)   9
Câu 33.13: Cho mặt cầu S  có tâm I 1; 2; 4 và thể tích bằng 36 . Phương trình của S  là 2 2 2 2 2 2 A.  x  
1   y  2   z  4  9. B.  x  
1   y  2   z  4  9. 2 2 2 2 2 2 C.  x  
1   y  2   z  4  9. D.  x  
1   y  2   z  4  3. Lời giải Chọn A 4 4 Ta có: 3 3 V   R 
 R  36  R  3 . 3 3  T âm: I (1; 2; 4  )
Khi đó S  :  B án kính: R  3 
  S  x  2   y  2   z  2 : 1 2 4  9.
Câu 33.14: Cho mặt cầu S  có tâm I 1; 2;3 và diện tích bằng 32 . Phương trình của S  là 2 2 2 2 2 2 A.  x  
1   y  2   z 3 16. B.  x  
1   y  2   z  3 16. 2 2 2 2 2 2 C.  x  
1   y  2  z   3  8. D.  x  
1   y  2   z   3  8. Lời giải Chọn C Ta có: 2 2
S  4 R  4 R  32  R  8 .  Tâm: I  1; 2;3
Khi đó S  :  Bán kính: R  8 
  S  x  2   y  2   z  2 : 1 2 3  8.
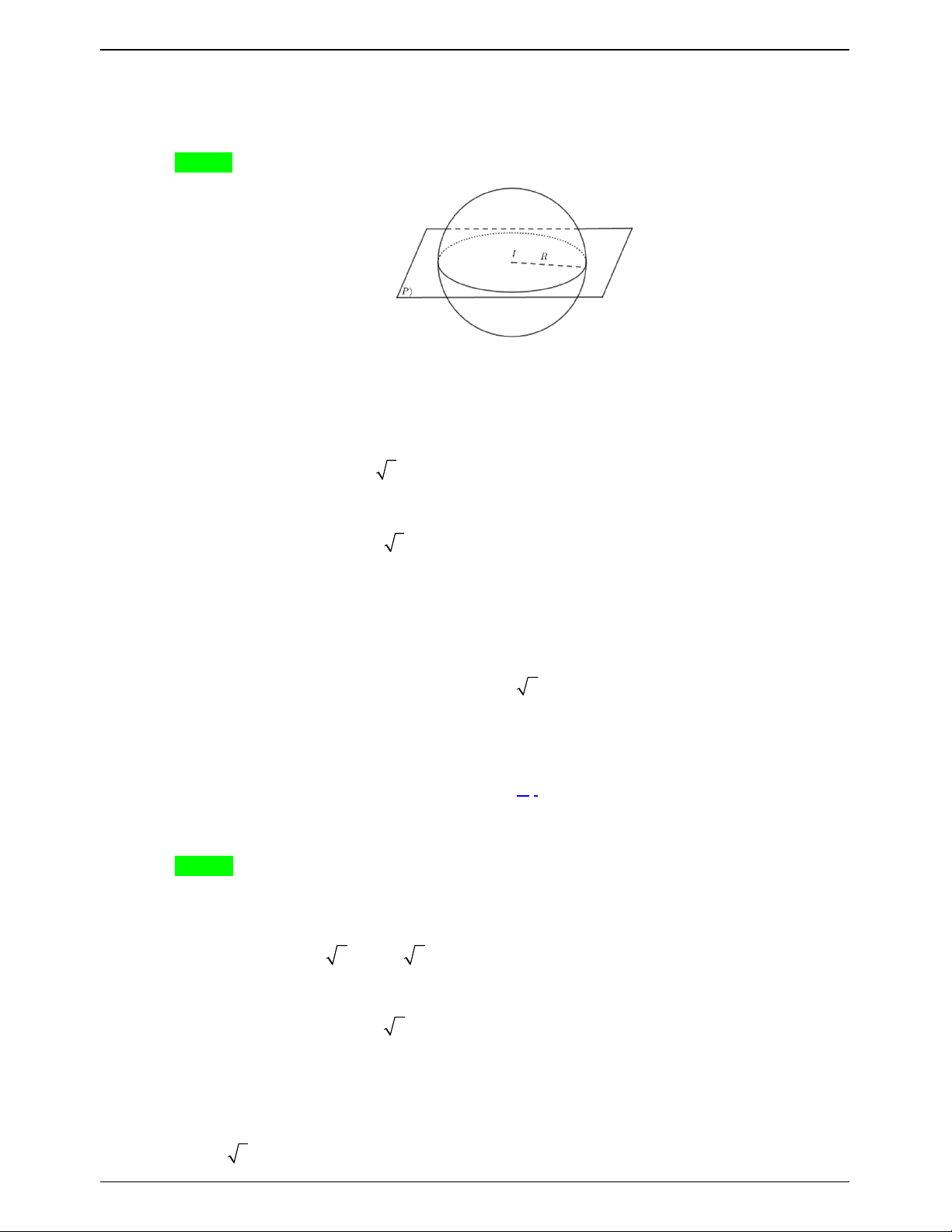
Câu 33.15: Cho mặt cầu S  có tâm I (1; 2;0). Một mặt phẳng (P) cắt S  theo giao tuyến là một đường
tròn C  Biết diện tích lớn nhất của C  bằng 3 . Phương trình của S  là 2 2
A. x   y  2 2 2 2  z  3.
B.  x     y   2 1 2  z  3. Trang 361
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 2 2 2 C.  x  
1   y  2   z   1  9.
D.  x     y   2 1 2  z  9. Lời giải Chọn B
Nhận xét : Mặt phẳng (P) cắt S  theo giao tuyến là một đường tròn C  và diện tích của
C  lớn nhất khi (P) qua tâm I của (S). Ta có: 2
S   R  3  R  3 .  T âm: I  1;2;0 
Khi đó (S ) :  Bán kín : h R  3 
 S   x  2   y  2 2 : 1 2  z  3.
Câu 33.16: Cho mặt cầu S  có tâm I 1;1 
;1 . Một mặt phẳng (P) cắt S  theo giao tuyến là một đường
tròn C  . Biết chu vi lớn nhất của C  bằng 2 2. Phương trình của S  là 2 2 2 2 2 2 A.  x   1   y   1   z   1  4. B.  x   1   y   1   z   1  2. 2 2 2 2 2 2 C.  x   1   y   1   z   1  4. D.  x   1   y   1   z   1  2. Lời giải Chọn D
Đường tròn C  đạt chu vi lớn nhất khi C  đi qua tâm I của mặt cầu S  .
Ta có: C  2 R  2 2  R  2 .  Tâm: I  1;1;  1
Khi đó (S ) :  Bán kín : h R  2 
 S   x  2   y  2   z  2 : 1 1 1  2.
Câu 33.17: Cho I 1; 2
 ;3 . Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai điểm A và B sao cho AB  2 3 . Trang 362
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 2 2 2 2
A. (x 1)  ( y  2)  (z  3)  16 . B. (x  ) 1  (y  ) 2  (z  ) 3  20 . 2 2 2 2 2 2 C. (x  ) 1  (y  ) 2  (z  ) 3  25. D. (x  ) 1  (y  ) 2  (z  ) 3  9 . Lời giải Chọn A
Gọi M là hình chiếu vuông góc của I (1; -2;3) trên trục Ox
 M (1;0;0) và M là trung điểm của AB 2 2 2 AB
Ta có: IM  1  1
 0  2  0  3  13, AM   3 . 2 IMA vuông tại 2 2 M  IA 
IM  AM  13  3  4  R  4 . 2 2 2
Phương trình mặt cầu cần tìm là:  x  
1   y  2   z  3  16 .
Câu 33.18: Trong không gian với hệ toạ độ Oxyz , Viết phương trình mặt cầu đi qua
A2 ;3 ; 3, B 2; 2 ; 2, C 3 ;3 ; 4 và có tâm nằm trên mặt phẳng Oxy . 2 2 2 2 2 2
A. (x  6)  (y 1)  z  29 .
B. (x  6)  (y  1)  z  29 . 2 2 2 2 2 2
C. (x  6)  (y 1)  z  29 .
D. (x  6)  (y  1)  z  29 . Lời giải Chọn A Giả sử I  ;
a b ;0 (Oxy) và r là tâm và bán kính của mặt cầu (S) và đi qua
A2 ;3 ; 3, B 2; 2 ; 2, C 3 ;3 ; 4 2 2 2 2
Phương trình mặt cầu (S) là (x a)  (y b)  z  r
Vì mặt cầu ñi qua A2 ;3 ; 3, B 2; 2 ; 2, C 3 ;3 ; 4 nên 2 2 2 2
(2  a)  (3  b)  ( 3  )  r 10b 10  0 b   1  2 2 2 2   (2  a)  ( 2
  b)  2  r  2a 12  0  a  6  2 2 2 2  2 2 2 2  2
(3  a)  (3  b)  4  r
(3  a)  (3  b)  4  r r  29    2 2 2
Vậy phương trình mặt cầu (S) là (x  6)  (y 1)  z  29 .
Câu 33.19: Trong không gian O xyz cho 4 điểm A1; 2; 4, B 1; 3 
;1 , C 2; 2;3, D 1; 0; 4 . Viết
phương trình mặt cầu ngoại tiếp tứ diện ABCD 2 2 2 2
A.  x     y   2 2 1  z  26 .
B.  x     y   2 2 1  z  26 . Trang 363
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 2 2
C.  x     y   2 2 1  z  26 .
D.  x     y   2 2 1  z  26 . Lời giải Chọn A Giả sử S  2 2 2
x  y  z  ax  by  cz  d   2 2 2 : 2 2 2
0 a  b  c  d  0 là phương trình mặt cầu
ngoại tiếp tứ diện ABCD . Thay lần lượt tọa độ của ,
A B, C, D vào phương trình ta được 2 2 2 1 
 2  4  2a  4b  8c  d  0 a  2  2 2 2  1 
 3 1  2a  6b  2c  d  0 b   1    2 2 2
2  2  3  4a  4b  6c  d  0 c  0    2 2 2 d  2  1
1  0  4  2a  0  8c  d  0  
Do đó: I 2;1; 0 và bán kính 2 2 2 R 
a  b  c  d  26 . 2 2
Vậy (S) :  x     y   2 2 1  z  26 . x 1 y 1 z 1
Câu 33.20: Viết phương trình mặt cầu   S có tâm I1; 0;  3 và cắt d :   tại hai 2 1 2
điểm A, B sao cho tam giác IAB vuông tại I 2 2 40 2 2 40 A.  x   2
1  y   z  3  . B.  x   2
1  y   z  3  . 9 9 2 2 2 10 2 2 2 10 C.  x   2
1  y   z  3  . D.  x   2
1  y   z  3  . 3 3 Lời giải Chọn A 
Đường thẳng d có một vectơ chỉ phương u  2;1; 2 và P 1; 1   ;1  d .      u, IP   20 Ta có: IP  0; 1  ; 2    u  , IP  0; 4  ; 2 . Suy ra: .  
d I; d     u 3 40
IAB vuông tại I  IAB vuông cân tại I IA  2d  I , d   . 3 2 2 40
Vậy (S) :  x   2
1  y   z  3  . 9 Trang 364

Viết phương trình mặt cầu Toán 12

Thông tin :

Tài liệu liên quan:

Bài giảng vectơ và hệ trục tọa độ trong không gian Toán 12 KNTTVCS

Toán ứng dụng thực tế vectơ và hệ trục toạ độ trong không gian

Chuyên đề hình học giải tích không gian – Lưu Huy Thưởng Toán 12

Chuyên đề HH giải tích không gian – Trung tâm LTĐH Vĩnh Viễn Toán 12

Bài tập tọa độ không gian phân theo dạng có lời giải chi tiết – Trần Sĩ Tùng Toán 12