
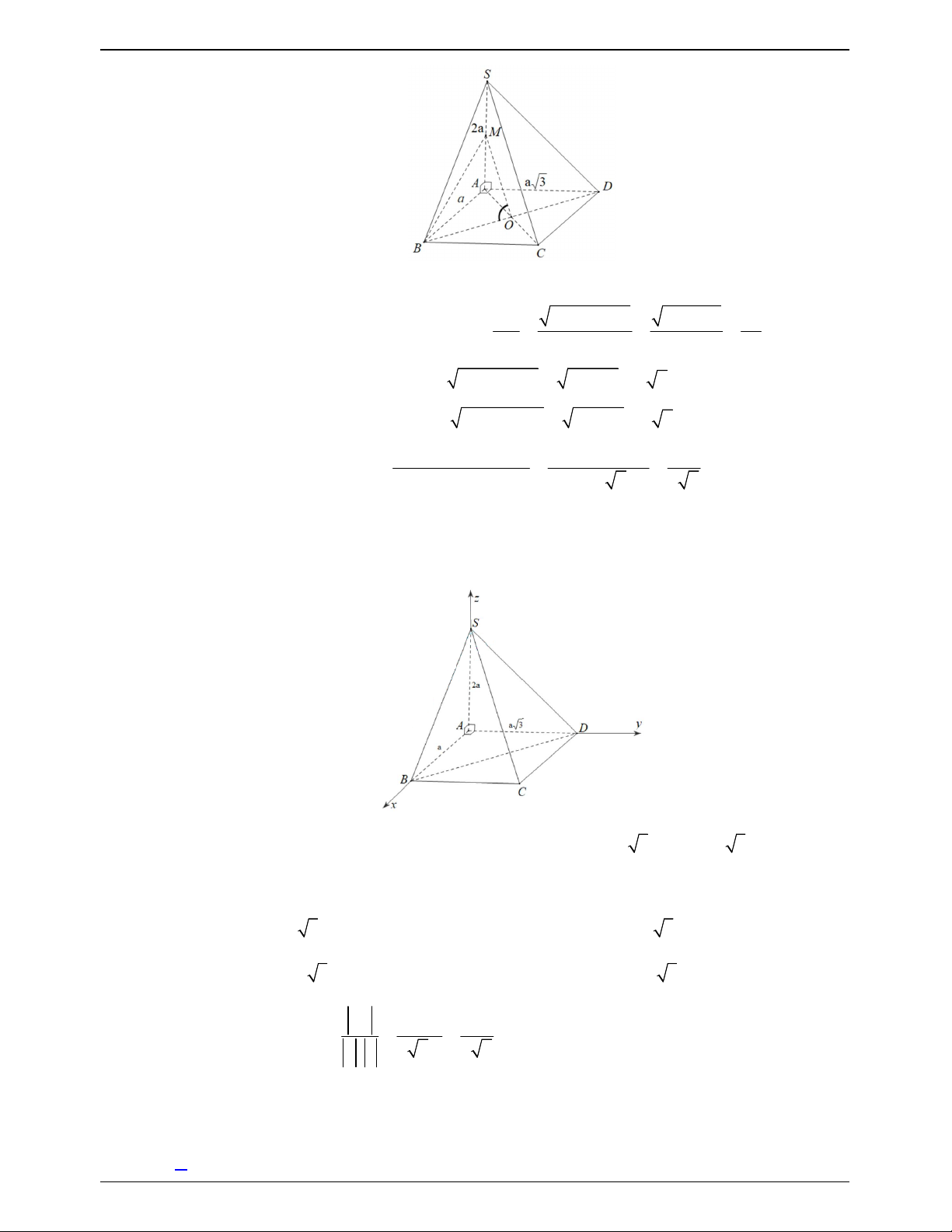

Preview text:
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 XÁC ĐỊNH GÓC
GIỮA HAI ĐƯỜNG THẲNG - ĐƯỜNG THẲNG VÀ MẶT PHẲNG - HAI MẶT PHẲNG
KIẾN THỨC CẦN NHỚ:
1) Góc giữa hai đường thẳng
Phương pháp 1: Sử dụng định lý hàm số cosin hoặc tỉ số lượng giác.
Phương pháp 2: Sử dụng tích vô hướng: nếu u và v lần lượt là hai vectơ chỉ phương của hai
đường thẳng a và b thì góc của hai đường thẳng này được xác định bởi công thức . u v
cos cos u,v . u . v
2) Góc giữa đường thẳng và mặt phẳng: a a' P
Muốn xác định góc của đường thẳng a và P ta tìm hình chiếu vuông góc a của a trên P .
Khi đó, a P a a , , '
3) Góc giữa hai mặt phẳng:
Phương pháp 1: Dựng hai đường thẳng a , b lần lượt vuông góc với hai mặt phẳng và .
Khi đó, góc giữa và là ,
a,b . Tính góc a,b.
Phương pháp 2: β b φ c a α
Xác định giao tuyến c của hai mặt phẳng và .
Dựng hai đường thẳng a , b lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao
tuyến c tại một điểm trên c . Khi đó: , a,b . Trang 162
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Cách khác: Ta xác định mặt phẳng phụ vuông góc với giao tuyến c mà a ,
b . Suy ra , a,b .
4) Sử dụng phương pháp tọa độ trong không gian:
Chọn hệ trục thích hợp và cụ thể hóa tọa độ các điểm.
a) Giả sử đường thẳng a và b lần lượt có vectơ chỉ phương là a,b . . a b Khi đó: co s a, b
a,b a . b
b) Giả sử đường thẳng a có vectơ chỉ phương là a và P có vectơ pháp tuyến là n . . a n
Khi đó: sina, P
a,P a . n
c) Giả sử mặt phẳng và lần lượt có vectơ pháp tuyến là a,b . . a b Khi đó: co
s ,
, a . b BÀI TẬP MẪU
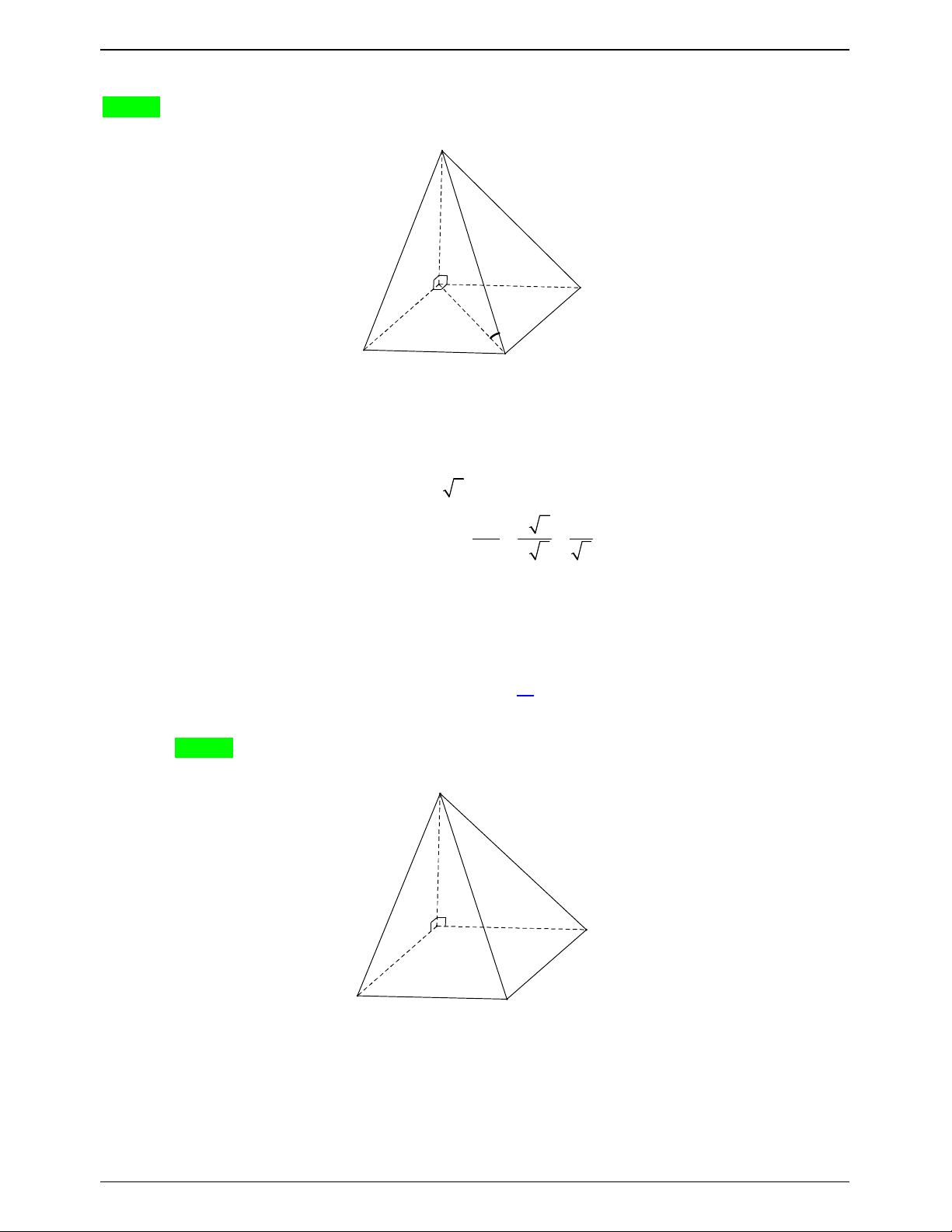
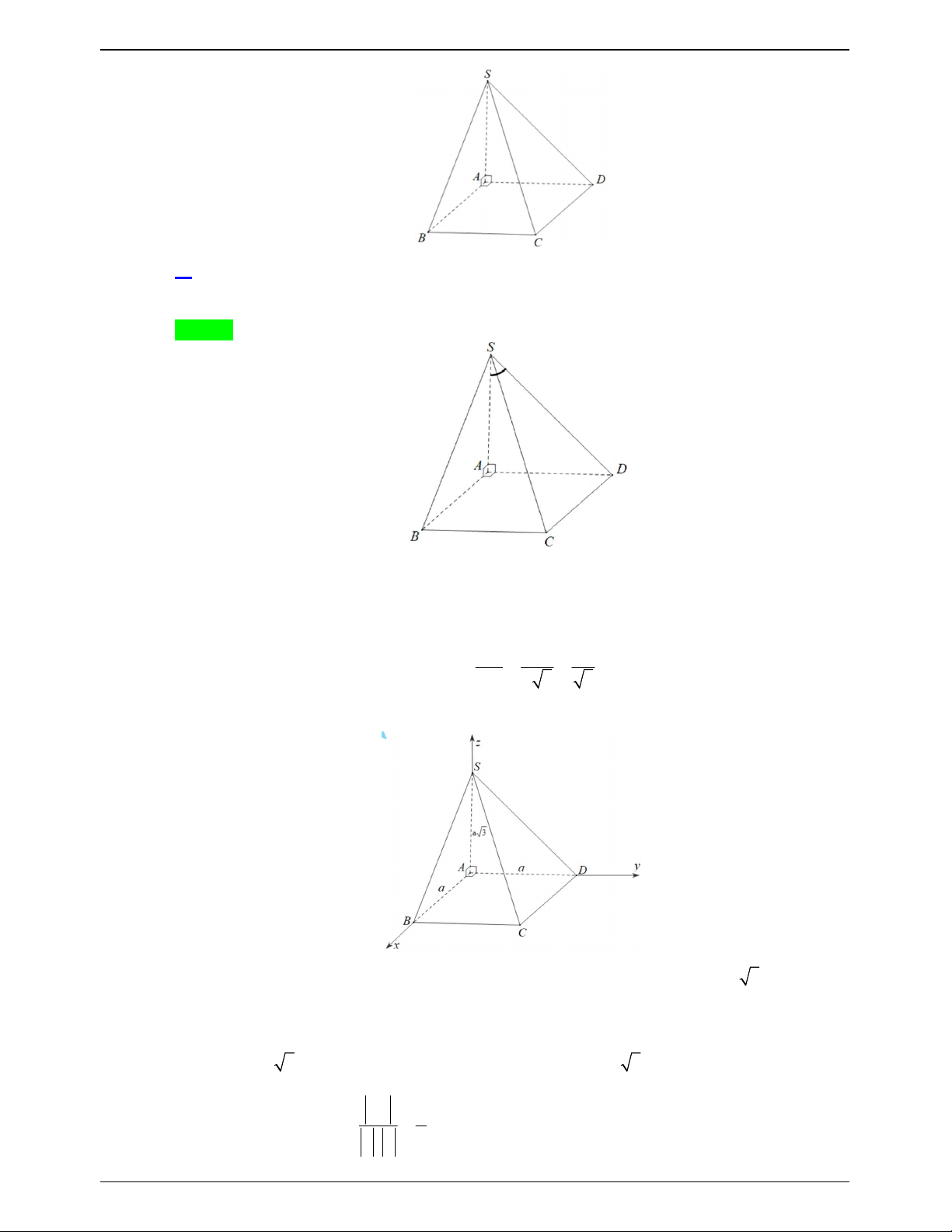
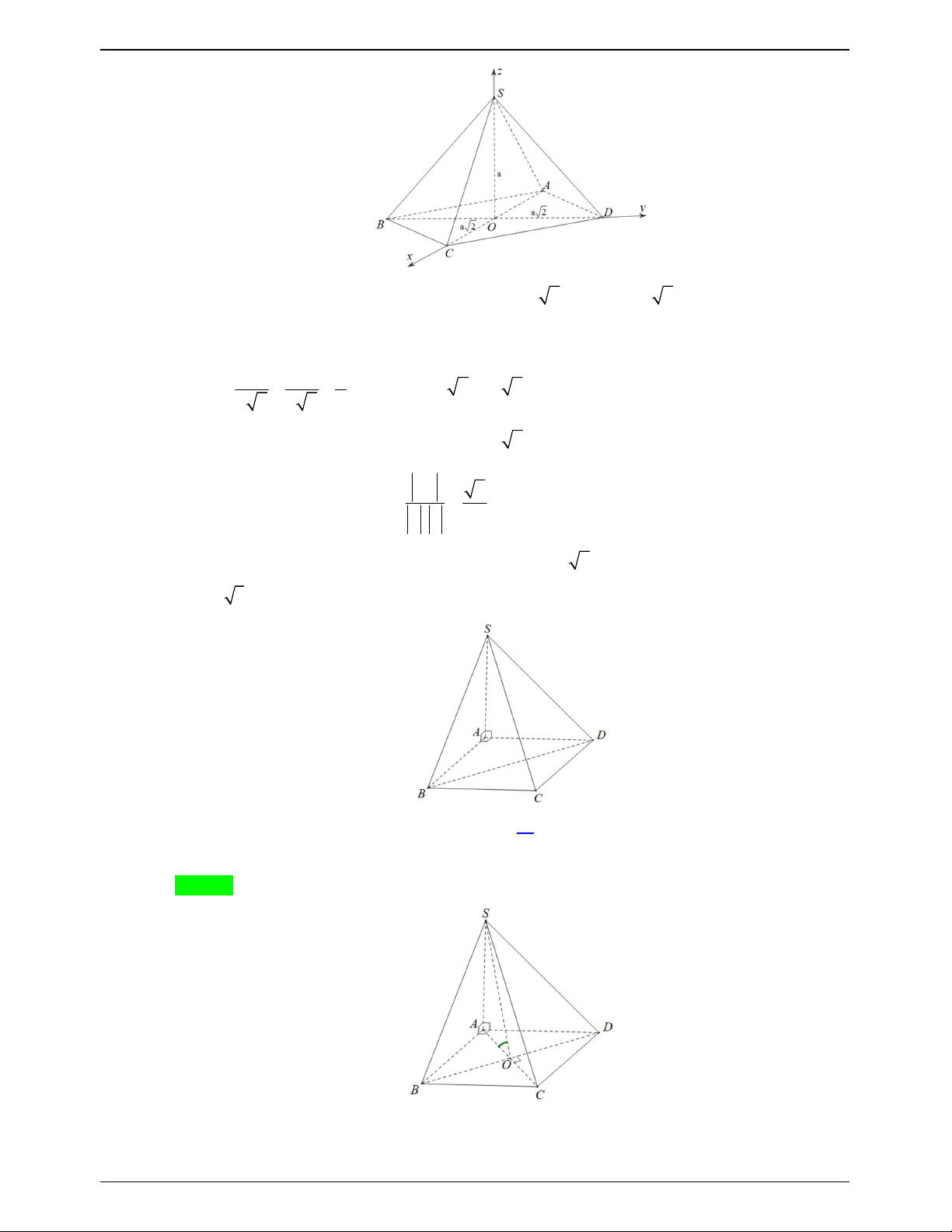
(ĐỀ MINH HỌA BDG 2019-2020) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3 , SA vuông
góc với mặt phẳng đáy, SA a 2 (minh họa như hình vẽ). Góc giữa đường thẳng SC và mặt phẳng ABCD bằng: A. 30 . B. 45 . C. 60 . D. 90 .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tính góc giữa đường thẳng và mặt phẳng. 2. HƯỚNG GIẢI:
B1: Xác định hình chiếu của SC trên mặt phẳng ABCD
B2: Tính góc giữa SC và hình chiếu của nó.
Từ đó, ta có thể giải bài toán cụ thể như sau: Trang 163
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn A S A D B C
Ta có: SA ABCD nên AC là hình chiếu của SC trên mặt phẳng ABC .
Do đó: SC ABCD SC AC , , SC . A
Xét hình vuông ABCD ta có: AC a 6. SA a 2 1
Xét SAC vuông tại A , ta có: o tan SCA SCA 30 . AC a 6 3
Bài tập tương tự và phát triển:
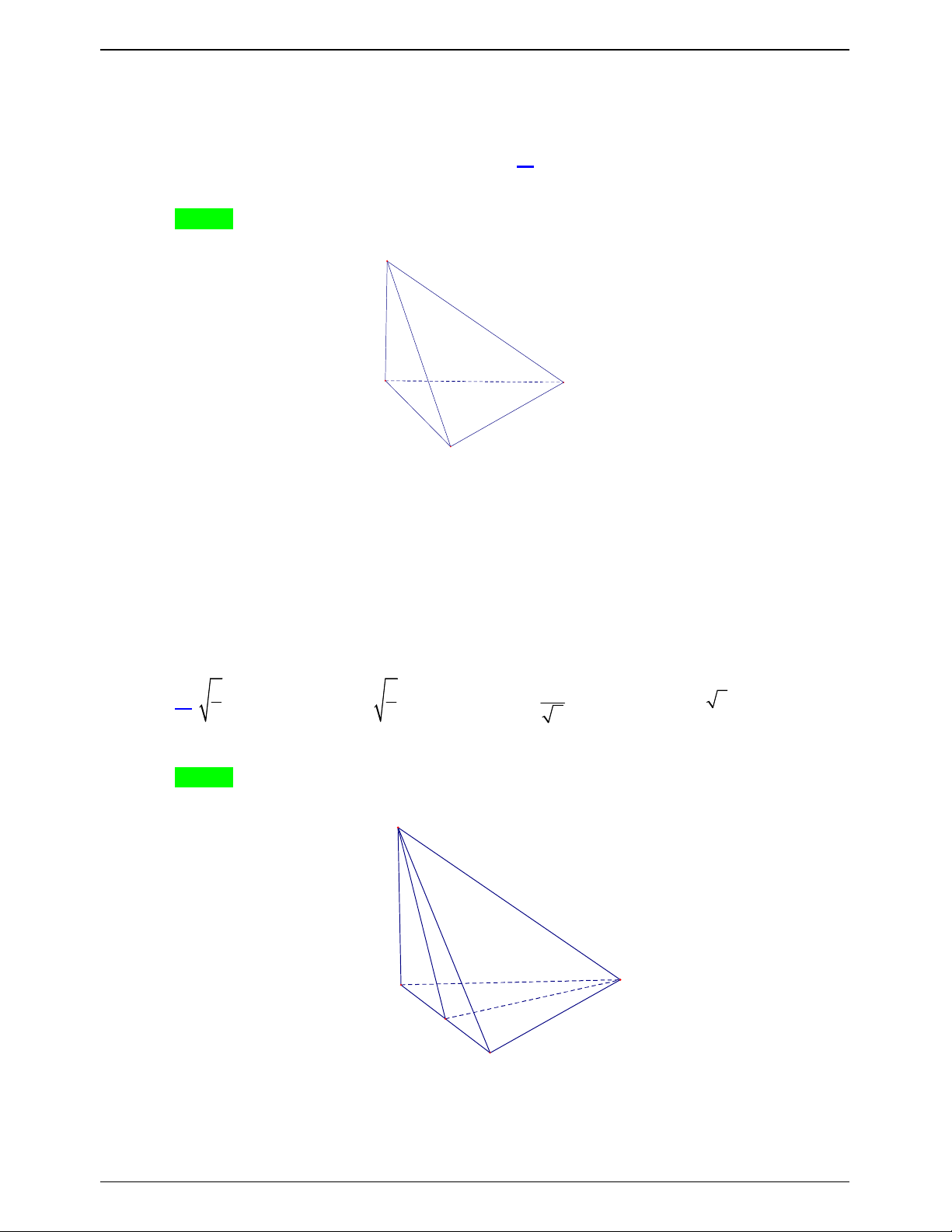
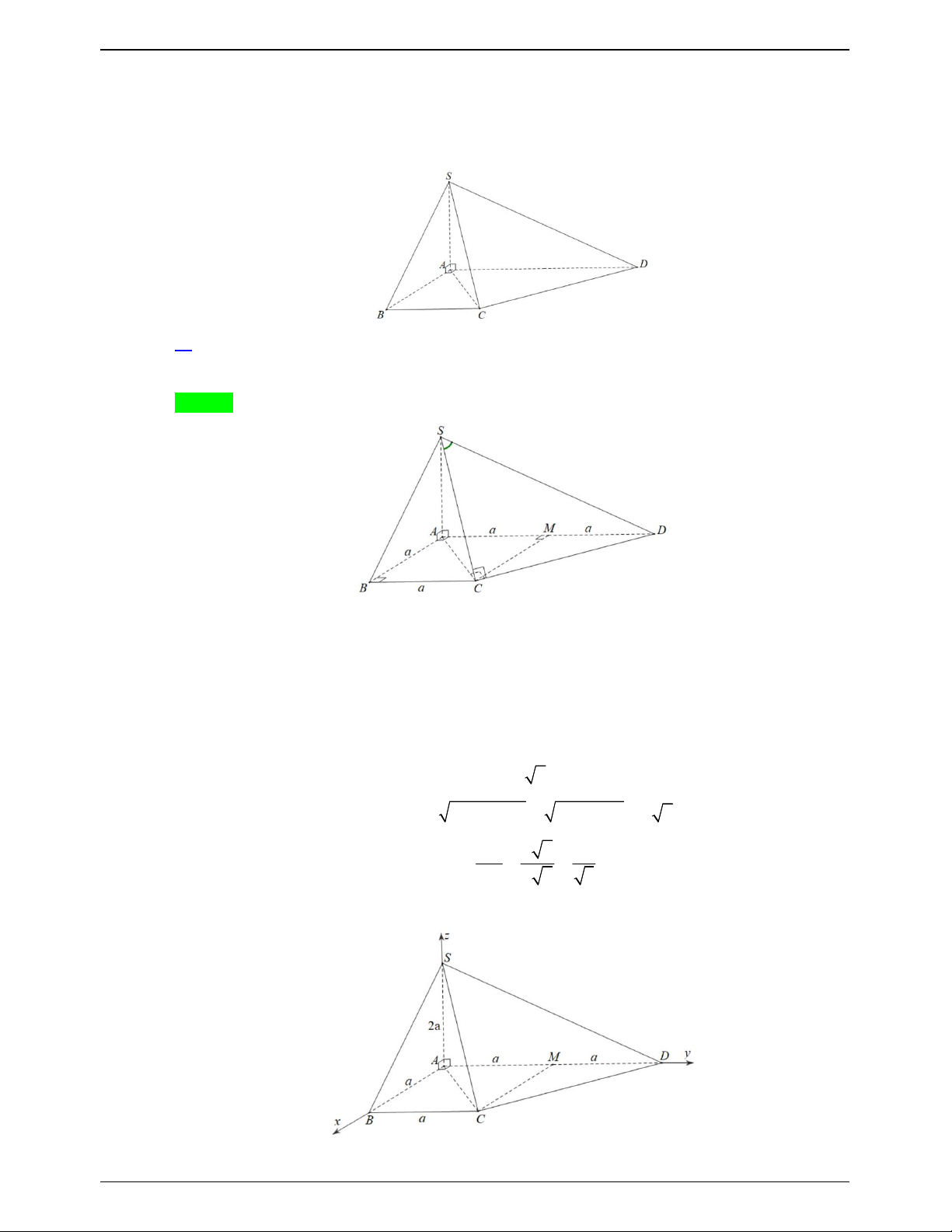
Câu 17.1: Cho một hình thoi ABCD cạnh a và một điểm S nằm ngoài mặt phẳng chứa hình thoi sao cho
SA a và vuông góc với ABC . Tính góc giữa SD và BC A. 60 . B. 90 . C. 45 . D. 30 . Lời giải Chọn C S A D B C Ta có: AD
BC SD BC SD AD 0 / / , , ADS 45 .
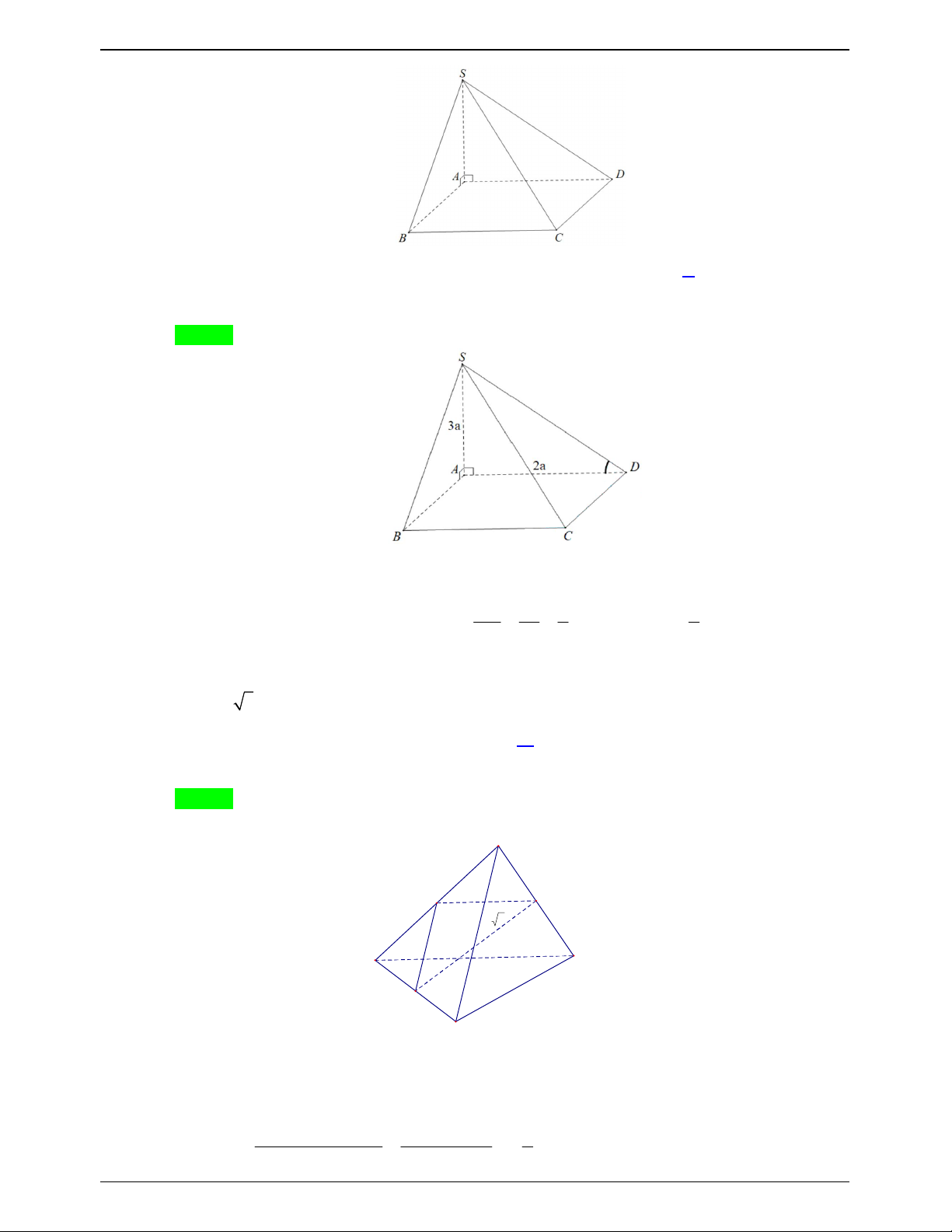
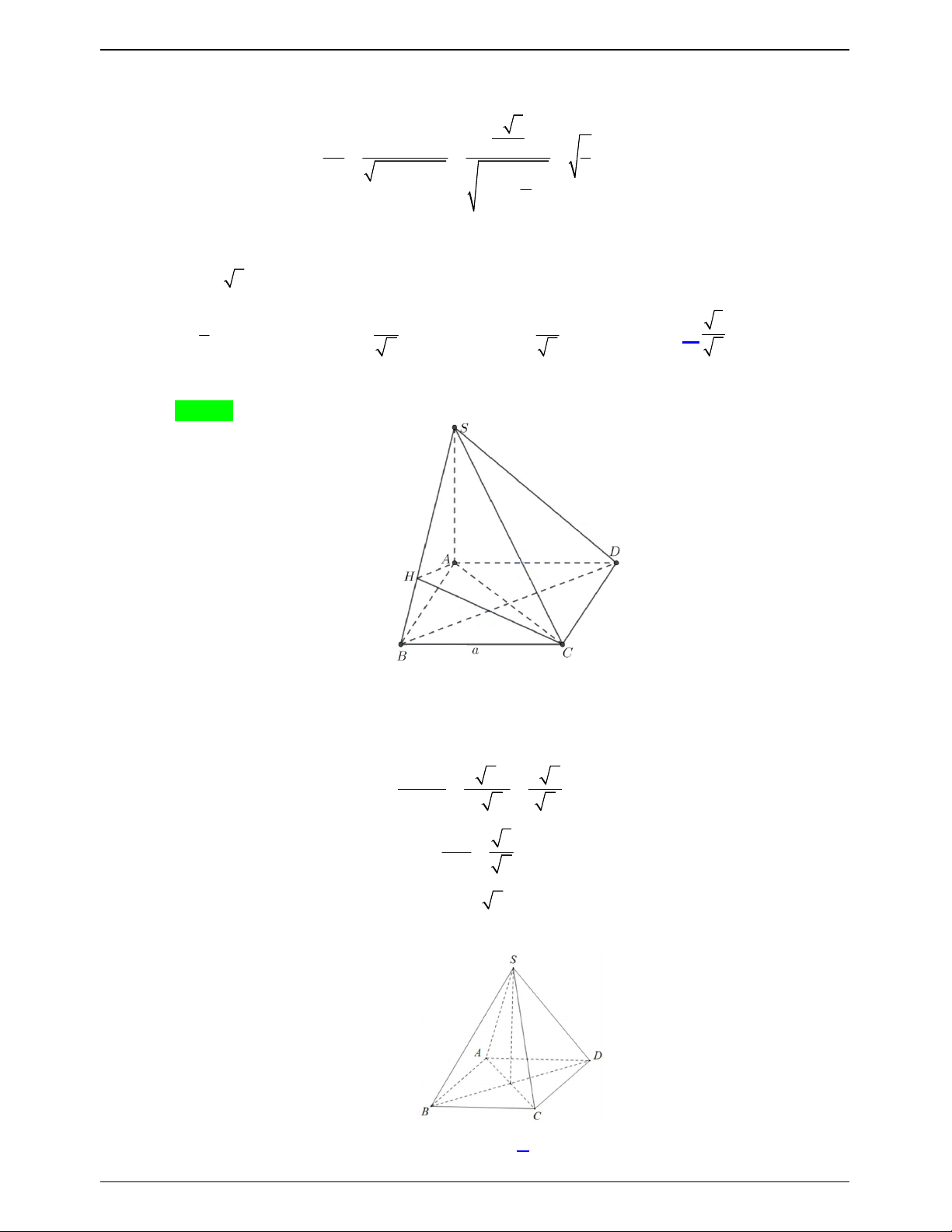
Câu 17.2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với BC 2a, SA vuông góc với mặt
phẳng đáy, SA 3a (minh họa như hình vẽ). Góc giữa hai đường thẳng SD và BC nằm trong khoảng nào? Trang 164
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 20 ; 30 . B. 30 ; 40 . C. 40 ; 50 . D. 50 ; 60 . Lời giải Chọn D Ta có: BC
AD SD BC SD AD / / , ,
SDA ( Do SAD vuông tại A nên 90o SDA ) SA 3a 3 3
Xét SAD vuông tại A , ta có: tan SDA SDA arctan 56 . o AD 2a 2 2
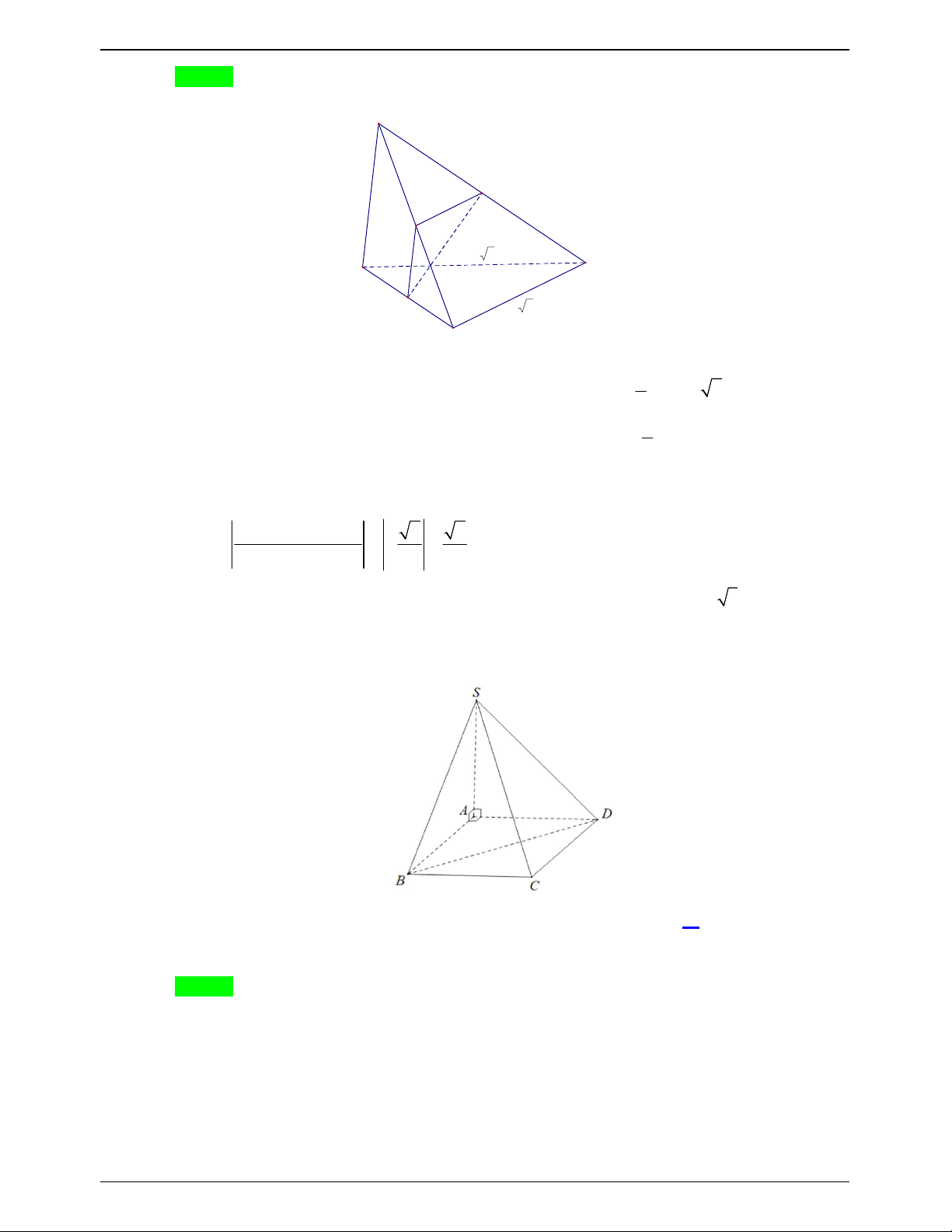
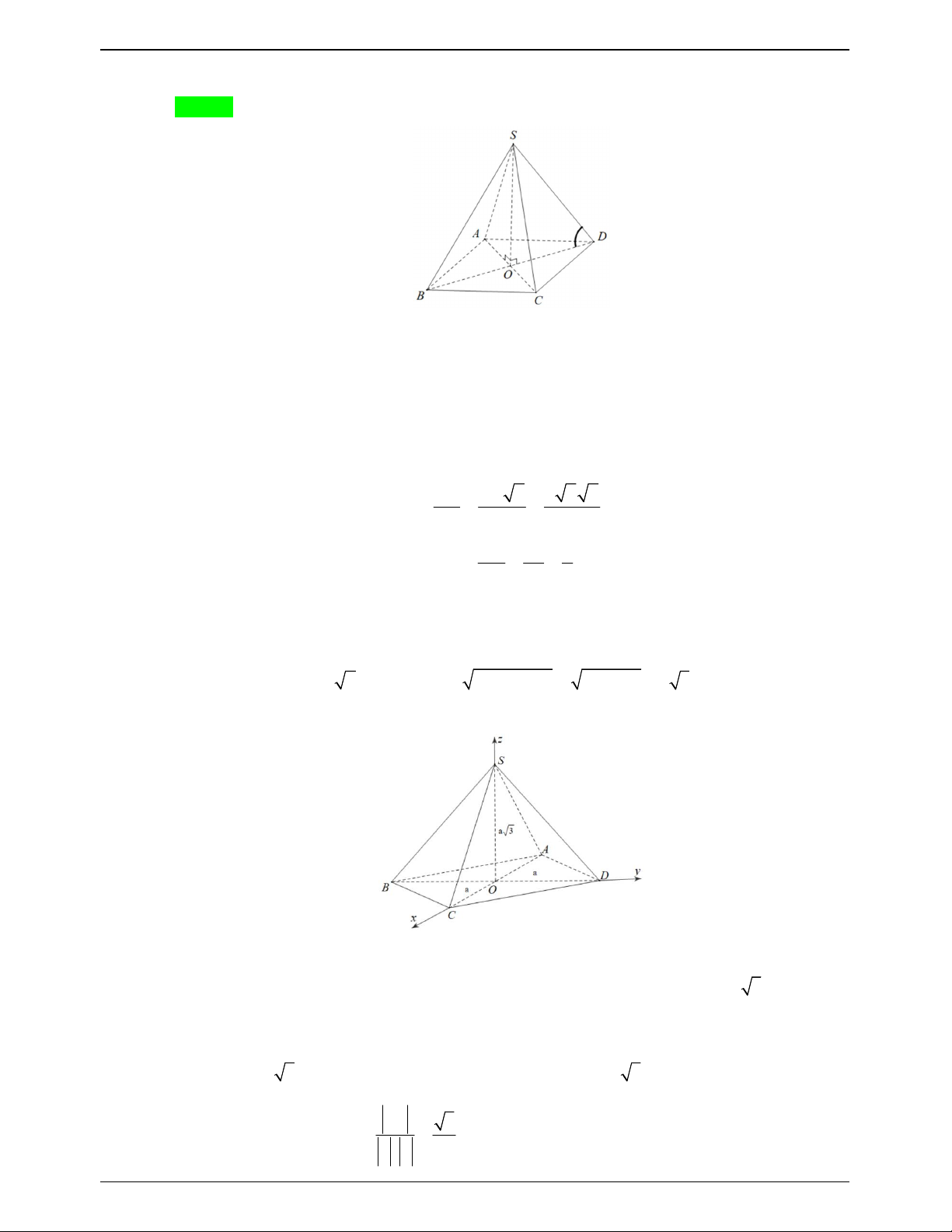
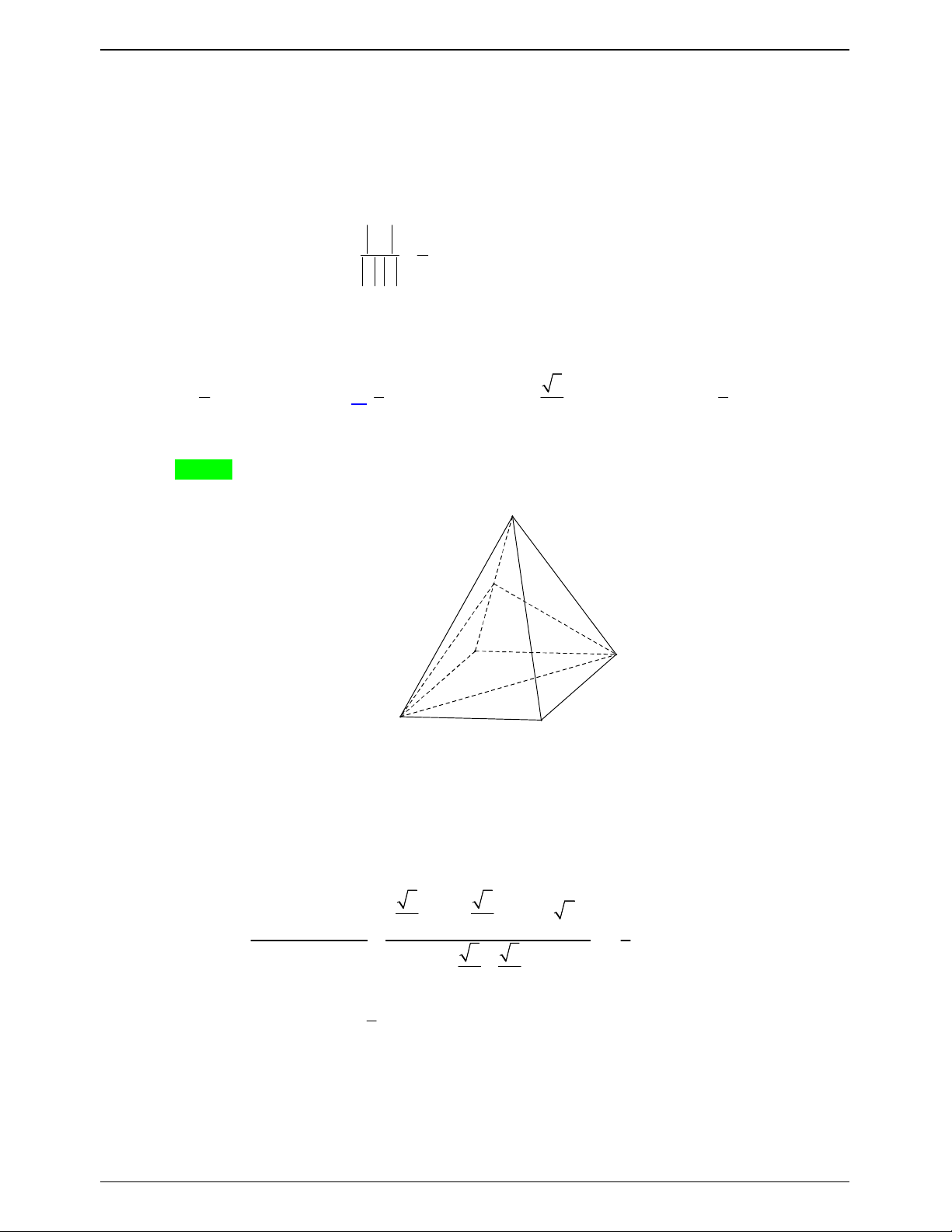
Câu 17.3: Cho tứ diện ABCD có AC BD 2 .
a Gọi M , N lần lượt là trung điểm BC, AD . Biết rằng
MN a 3. Tính góc của AC và BD . A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 . Lời giải Chọn C A I a N a 3 a 2a B D 2a M C
Gọi I là trung điểm của AB . Ta có IM IN a .
Áp dụng định lý cosin cho I MN ta có: 2 2 2 2 2 2
IM IN MN
a a 3a 1 0 cos MIN MIN 120 . 2.IM .IN 2. . a a 2 Trang 165
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Vì IM AC IN
BD AC BD IM IN 0 0 0 / / , / / , , 180 120 60 .
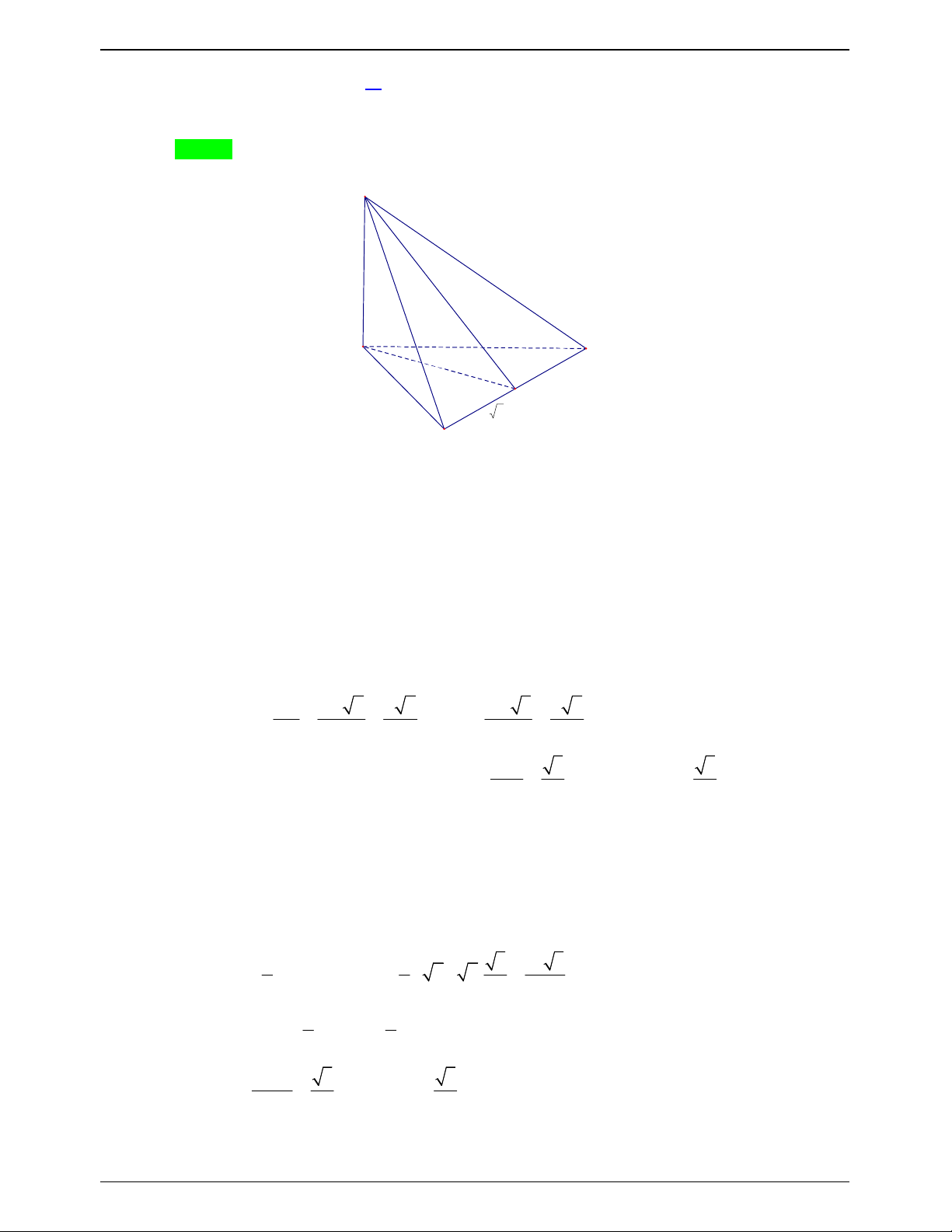
Câu 17.4: Cho tứ diện đều ABCD cạnh a . Gọi O là tâm đường tròn ngoại tiếp BCD . Gọi M là trung
điểm CD . Tính cosin góc của AC và BM . 3 3 3 2 A. . B. . C. . D. . 4 6 2 2 Lời giải Chọn B
AC.BM
AC.CM CB
cos AC, BM
cosAC,BM AC . BM a 3 . a 2 2 2 2
a a a 0 0 . a cos120 . a . a cos120 a
AC.CM AC.CB 2 4 2 3 4 . 2 2 2 2 a 3 a 3 a 3 a 3 6 2 2 2 2
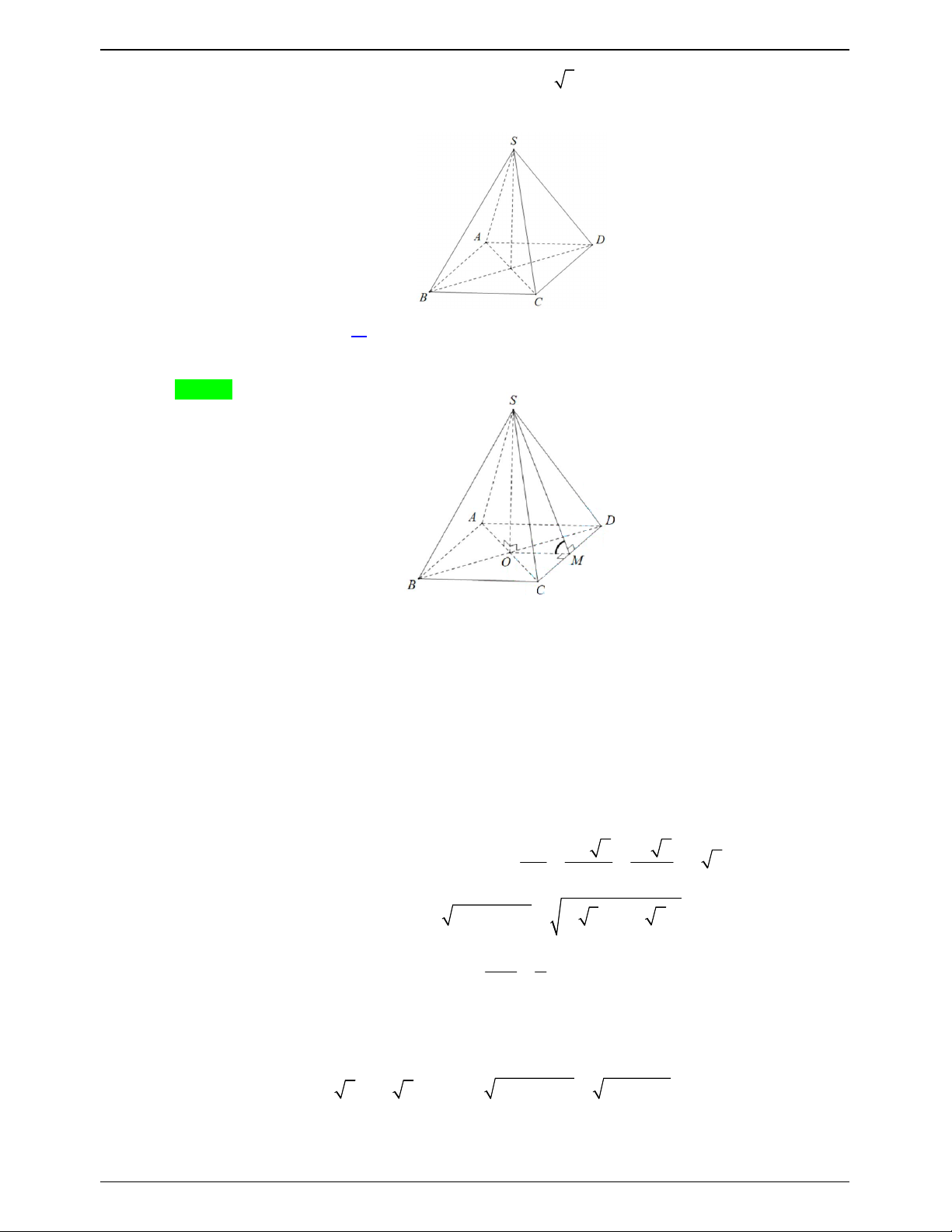
Câu 17.5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 2a , BC a . Các cạnh bên
của hình chóp cùng bằng a 2 . Khi đó, góc giữa hai đường thẳng AB và SC bằng: A. 45 . B. 30 . C. 60 . D. 90 . Lời giải Chọn A S A D M B C
Ta có: AB//CD nên AB SC CD SC , , SCD .
Gọi M là trung điểm của CD . Tam giác SCM vuông tại M và có SC a 2 , CM a nên
là tam giác vuông cân tại M nên
SCD 45 . Vậy
AB,SC 45 .
Câu 17.6: Cho tứ diện ABCD . Gọi M , N , I lần lượt là trung điểm của BC , AD và AC . Cho AB 2a,
CD 2a 2 và MN a 5 . Tính góc
AB,CD A. 135 . B. 60 . C. 90 . D. 45 . Lời giải Trang 166
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn D A N 2a I a a 5 B D 2a 2 M C 1 IN / /C ; D IN CD a 2 2
Theo tính chất đường trung bình trong tam giác: 1
IM / / AB; IM AB a 2
AB CD IM IN , ,
. Áp dụng định lý cosin ta có: 2 2 2
IM IN MN 2 2 0 cos 45 . 2.IM .IN 2 2
Câu 17.7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD a 3, SA vuông góc
với mặt phẳng đáy, SA 2a (minh họa như hình vẽ). Góc giữa hai đường thẳng SC và BD nằm trong khoảng nào? A. 30 ; 40 . B. 40 ; 50 . C. 50 ; 60 . D. 60 ; 70 . Lời giải Chọn D Trang 167
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Gọi O AC BD và M là trung điểm SA . 2 2 2 2 BD AB AD a 3a 2a
Xét hình chữ nhật ABCD , ta có: OB OA . a 2 2 2 2
Xét MAB vuông tại A , ta có: 2 2 2 2 MB
AB MA a a a 2.
Xét MAO vuông tại A , ta có: 2 2 2 2 MO AO MA
a a a 2. 2 2 2 2 2 2
OB OM BM
a 2a 2a 1
Xét MBO , ta có: cosMOB
MOB 69o. 2.O . B OM 2. . a a 2 2 2 Ta có: / / , , 69o SC MO SC BD MO BD MOB ( Do 90o MOB ).
Cách khác: Sử dụng phương pháp tọa độ
Chọn hệ trục Axyz như hình vẽ với A0; 0;0, B a; 0;0,C ;
a a 3;0, D 0; a 3;0 và
S 0;0; 2a .
Ta có: SC a;a 3;2a SC có một vectơ chỉ phương là u 1; 3;2. BD ;
a a 3; 0 BD có một vectơ chỉ phương là v 1; 3;0. . u v 2 1
Suy ra: cos SC, BD SC, BD 69 .o u . v 2 2.2 2 2
Câu 17.8: Cho hình chóp S.ABC có các A
BC và SBC là các tam giác đều và nằm trong hai mặt phẳng
vuông góc với nhau. Góc giữa đường thẳng SA và ABC bằng A. 45 . B. 75 . C. 60 . D. 30 . Trang 168
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn A S A C H B
Theo giả thiết ta có ABC SBC .
Trong mặt phẳng SBC kẻ SH BC SH ABC nên AH là hình chiếu của SA trên
ABC . Do đó, SA ABC SA AH , , SAH . Giả sử AB . a a 3
Ta có: SBC và ABC là tam giác đều nên H là trung điểm của BC và AH SH . 2 SH
Xét tam giác vuông SHA ta có tan SAH 1 SAH 45 . AH
Vậy SA ABC , 45 .
Câu 17.9: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy,
SA a 2 (minh họa như hình vẽ). Góc giữa đường thẳng SC và mặt phẳng SAB bằng: A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn A Trang 169
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 BC SA Ta có:
BC SAB nên SB là hình chiếu của SC trên mặt phẳng SAB . BC AB
Do đó: SC SAB SC SB , , BSC.
Xét SAB vuông tại A , ta có: SB SA AB a 2 2 2 2 2 a a 3. BC a 1
Xét SBC vuông tại B , ta có: tan BSC BSC 30o. SB a 3 3
Cách khác: Sử dụng phương pháp tọa độ
Chọn hệ trục Axyz như hình vẽ với A0; 0;0, B a;0; 0,C a; a;0 và S 0;0;a 2 .
Ta có: SAB : y 0 vectơ pháp tuyến của SAB là j 0;1;0. SC ;
a a; a 2 SC có một vectơ chỉ phương là u 1;1; 2 . j.u 1
Suy ra: sin SC, SAB
SC,SAB 30 .o j . u 2
Câu 17.10:Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy,
SA a 3 (minh họa như hình vẽ). Góc giữa đường thẳng SD và mặt phẳng SAB bằng: Trang 170
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn A
Ta có: AD SAB nên SA là hình chiếu của SD trên mặt phẳng SAB .
Do đó: SD SAB SD SA , , AS . D AD a 1
Xét SAD vuông tại A , ta có: tan ASD ASD 30o. SA a 3 3
Cách khác: Sử dụng phương pháp tọa độ
Chọn hệ trục Axyz như hình vẽ với A0; 0;0, B a;0; 0, D 0; ;
a 0 và S 0;0;a 3 .
Ta có: SAB : y 0 vectơ pháp tuyến của SAB là j 0;1;0.
SD 0;a;a 3 SD có một vectơ chỉ phương là u 0;1; 3. j.u 1
Suy ra: sin SD, SAB
SD,SAB 30 .o j . u 2 Trang 171
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Câu 17.11:Cho hình chóp S.ABC có SA ABC , SA a , A
BC đều cạnh a . Tính góc giữa SB và ABC A. o 30 . B. 60 . C. 45 . D. 90 . Lời giải Chọn C S A C B
Ta có SA ABC AB là hình chiếu của SB trên mặt phẳng ABC
ASB SD AD 0 , 45 .
Câu 17.12:Cho hình chóp S.ABC có SA ABC , SA a , A
BC đều cạnh a . Gọi là góc giữa SC
và mặt phẳng SAB . Khi đó, tan bằng 3 5 1 A. . B. . C. . D. 2 . 5 3 2 Lời giải Chọn A S a a A C a I B C I AB
Gọi I là trung điểm của AB . Ta có:
CI SAB CI SA Trang 172
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
SI là hình chiếu của SC trên mặt phẳng SAB SC SAB SC SI , , CSI a 3 CI CI 3 2
tan tan CSI . 2 2 2 SI 5 SA AI a 2 a 2
Câu 17.13:Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với ABCD cà
SA a 6 . Tính sin của góc tạo bởi AC và mặt phẳng SBC . 1 1 1 3 A. . B. . C. . D. . 3 6 7 7 Lời giải Chọn D
Kẻ AH SB BC AH AH SBC
AH là hình chiếu của AC lên mặt phẳng SBC AC SBC AC HC , , ACH . S . A AB a 6.a a 6
Tam giác SAB vuông AH SB a 7 7 AH 3 Vì A
HC vuông tại H sin ACH . AC 7
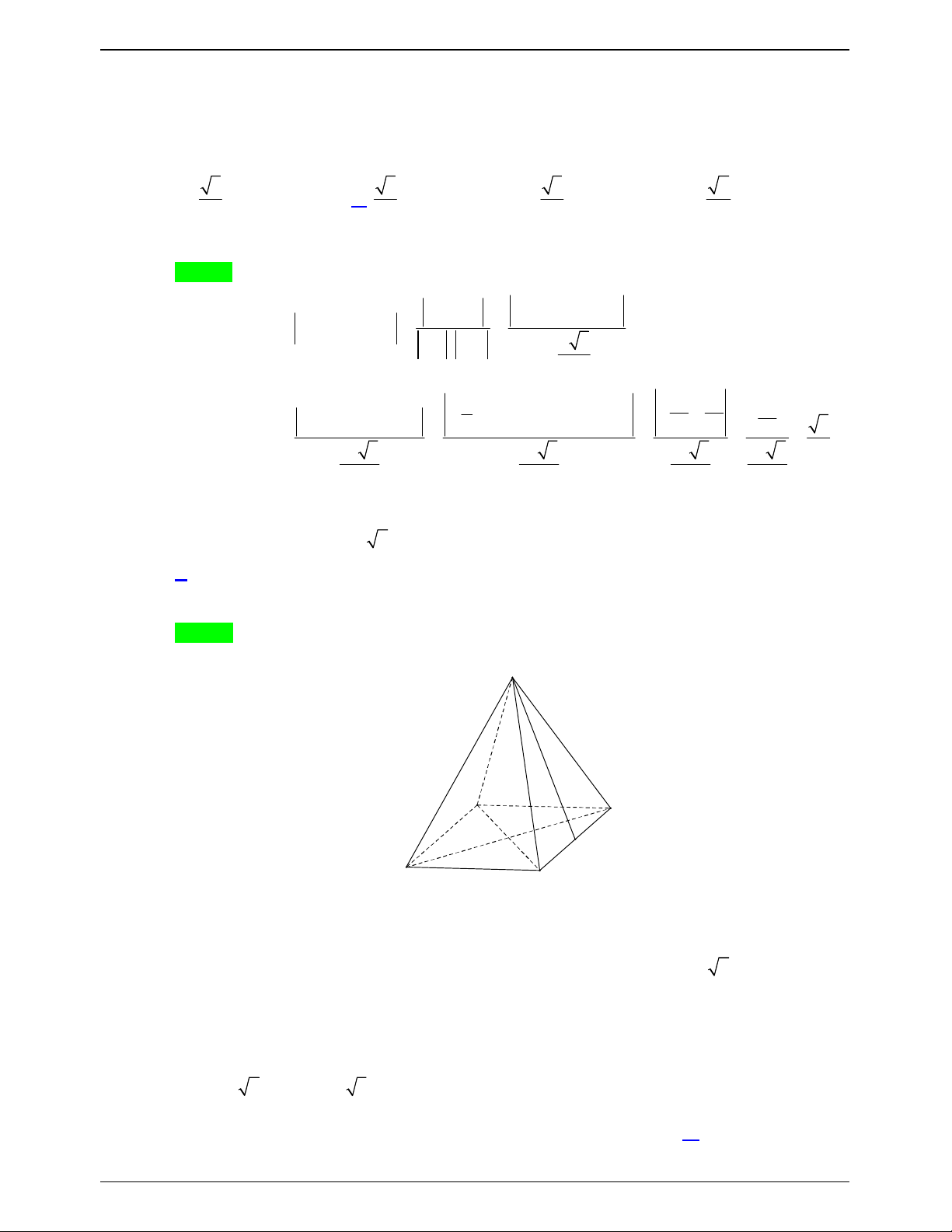
Câu 17.14:Cho hình chóp đều S.ABCD có cạnh đá a 2 , cạnh bên 2a (minh họa như hình vẽ). Góc giữa
cạnh bên và mặt đáy bằng: A. 30 . B. 45 . C. 60 . D. 90 . Trang 173
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn C
Ta có: góc giữa cạnh bên và mặt đáy là góc giữa SD và ABCD.
Gọi O AC B .
D Vì S.ABCD là hình chóp đều nên SO ABCD.
OD là hình chiếu của SD trên ABCD.
Do đó: SD ABCD SD OD , , SD . O BD AB 2 a 2 2
Xét hình vuông ABCD ta có: OD . a 2 2 2 OD a 1
Xét SOD vuông tại O , ta có: cosSDO SDO 60 . o SD 2a 2
Cách khác: Sử dụng phương pháp tọa độ
Gọi O AC B .
D Vì S.ABCD là hình chóp đều nên SO ABCD.
Ta có: AC BD AB 2 2a và 2 2 2 2 SO
SD OD 4a a a 3.
Chọn hệ trục Oxyz như hình vẽ với O 0; 0; 0,C a;0; 0, D 0; ;
a 0 và S 0;0;a 3 .
Ta có: ABCD : z 0 ABCD có một vectơ pháp tuyến là k 0;0; 1 .
SD 0;a;a 3 SD có một vectơ chỉ phương là u 0;1; 3. k.u 3
Suy ra: sin SD, ABCD
SD, ABCD 60o. k . u 2 Trang 174
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
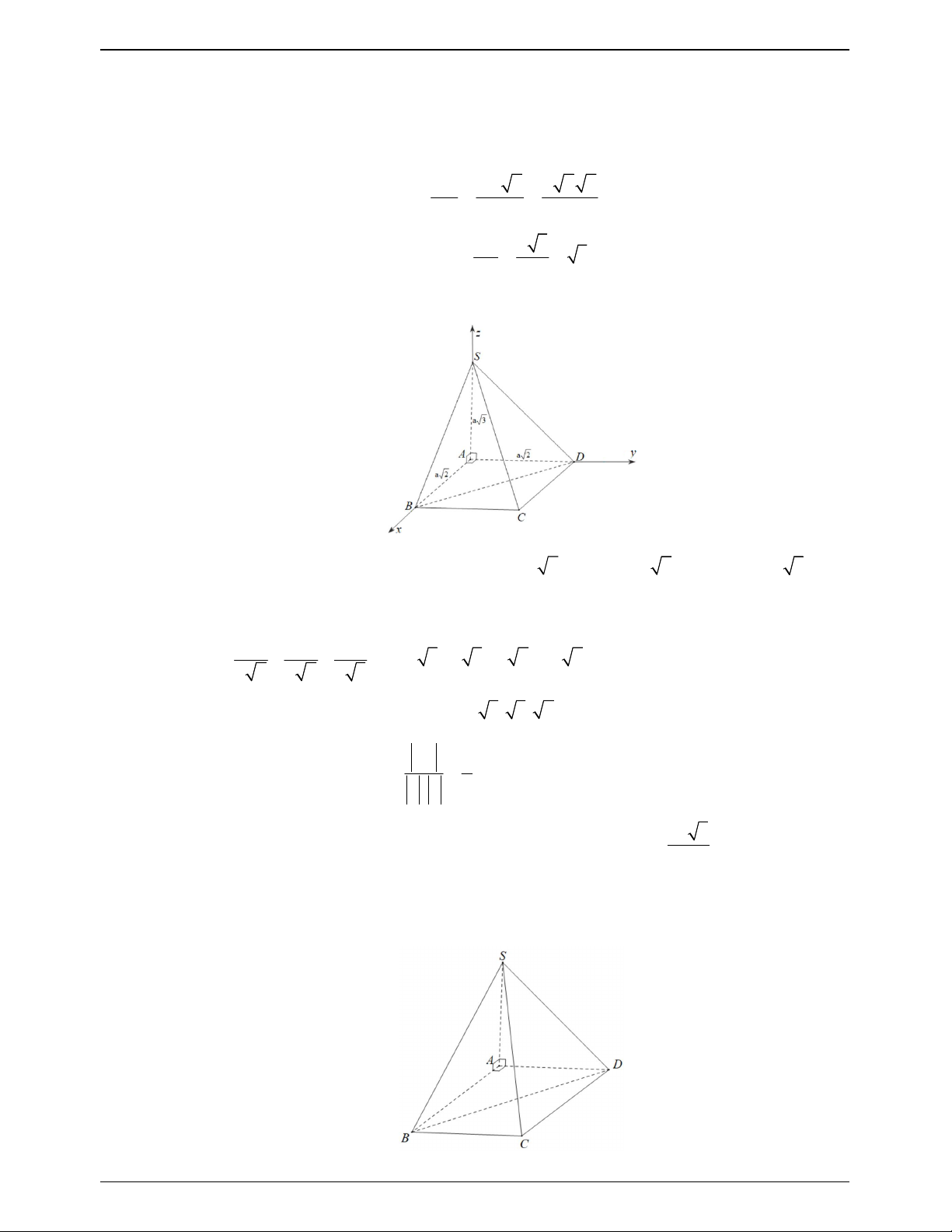
Câu 17.15:Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với
AD 2 AB 2BC 2 ;
a SA vuông góc với mặt phẳng đáy, SA 2a (minh họa như hình vẽ).
Góc giữa đường thẳng SD và mặt phẳng SAC bằng: A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn A
Gọi M là trung điểm AD. Ta có: ACM và DCM vuông cân tại M .
45o 45o 90o ACD ACM DCM
CD AC mà CD SA nên CD SAC .
SC là hình chiếu của SD trên mặt phẳng SAC .
Do đó: SD SAC SD SC , , CS . D
Xét ACD vuông cân tại C , ta có: AC CD a 2.
Xét SAC vuông tại A , ta có: 2 2 2 2 SC SA AC
4a 2a a 6. CD a 2 1
Xét SCD vuông tại C , ta có: tan CSD CSD 30o SC a 6 3
Cách khác: Sử dụng phương pháp tọa độ
Chọn hệ trục Axyz như hình vẽ với A0; 0;0, B a;0;0,C ;
a a; 0, D 0; 2 ;
a 0 và S 0; 0; 2a . Trang 175
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Ta có: SD 0;2a;2a SD có một vectơ chỉ phương là u 0;1; 1 .
AS 0;0; 2a
AS, AC 2 2 2
a ; 2a ; 0 AC ; a ; a 0
SAC có một vectơ pháp tuyến là n 1;1;0. u.n 1
Suy ra: sin SD,SAC
SD,SAC 30o. u . n 2
Câu 17.16:Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng a và SA SB SC SD a . Khi đó, cosin
góc giữa hai mặt phẳng SAB và SAD bằng 1 1 3 1 A. . B. . C. . D. . 4 3 2 3 Lời giải Chọn B S I A D B C
Gọi I là trung điểm SA . BI SA
Do tam giác SAD và SAB đều nên
SAB, SAD
BI, DI . DI SA
Áp dụng định lý cosin cho tam giác BID ta có: 2 2 3 3 a a a 2 2 2 2 2
IB ID BD 2 2 1 cos BID . 2I . B ID 3 3 3 2. . a a 2 2 Vậy
SAB SAD 1 cos , . 3
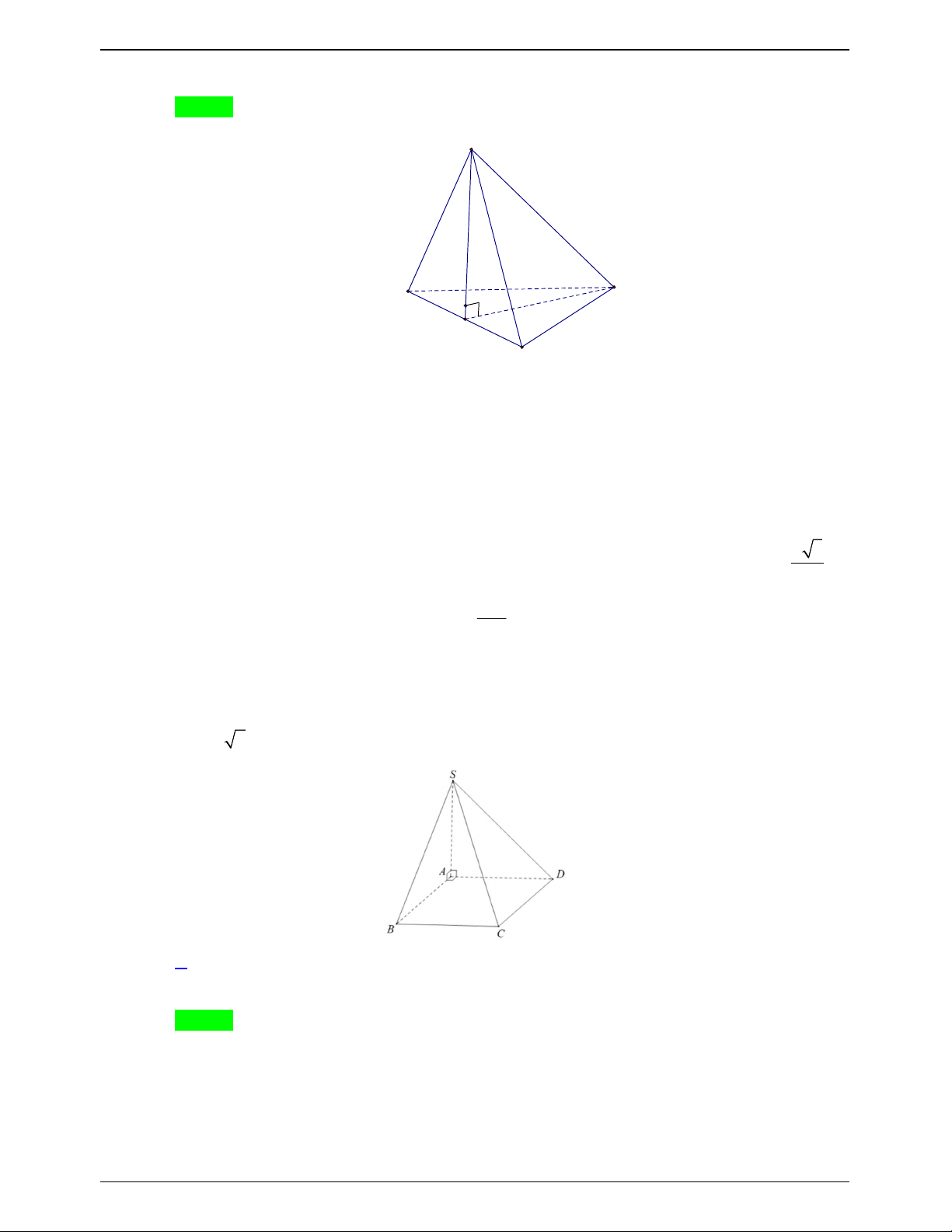
Câu 17.17:Cho tam giác ABC vuông cân tại A có AB a , trên đường thẳng d vuông góc với ABC
tại điểm A ta lấy một điểm D sao cho DBC đều. Khi đó, góc giữa hai mặt phẳng ABC và
DBC nằm trong khoảng nào? Trang 176
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. o o 40 ;50 . B. o o 50 ; 60 . C. o o 60 ;70 . D. o o 70 ;80 . Lời giải Chọn B D a A C a M a 2 B
Gọi M là trung điểm BC. BC DM Ta có:
BC DMA BC DA
ABD DBC BC DMA BC Mặt khác:
ABC DBC AM DM , , DMA DMA
ABC AM
DMA DBC DM BC AB 2 a 2 BC 3 a 6 Ta có: AM , DM 2 2 2 2 2 AM 3 3
Xét ADM vuông tại A , ta có: cos AMD AMD arccos 54o. DM 3 3 Cách khác:
Gọi là góc giữa hai mặt phẳng ABC và DBC .
Theo công thức diện tích hình chiếu của đa giác. Ta có: S S .cos ABC D BC 2 1 1 3 a 3 Mà: 0 S D . B DC.sin 60 a 2.a 2. DBC 2 2 2 2 1 1 Mặt khác: 2 S A . B AC a A BC 2 2 S 3 3 A BC o cos arccos 54 . S 3 3 DBC Trang 177
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
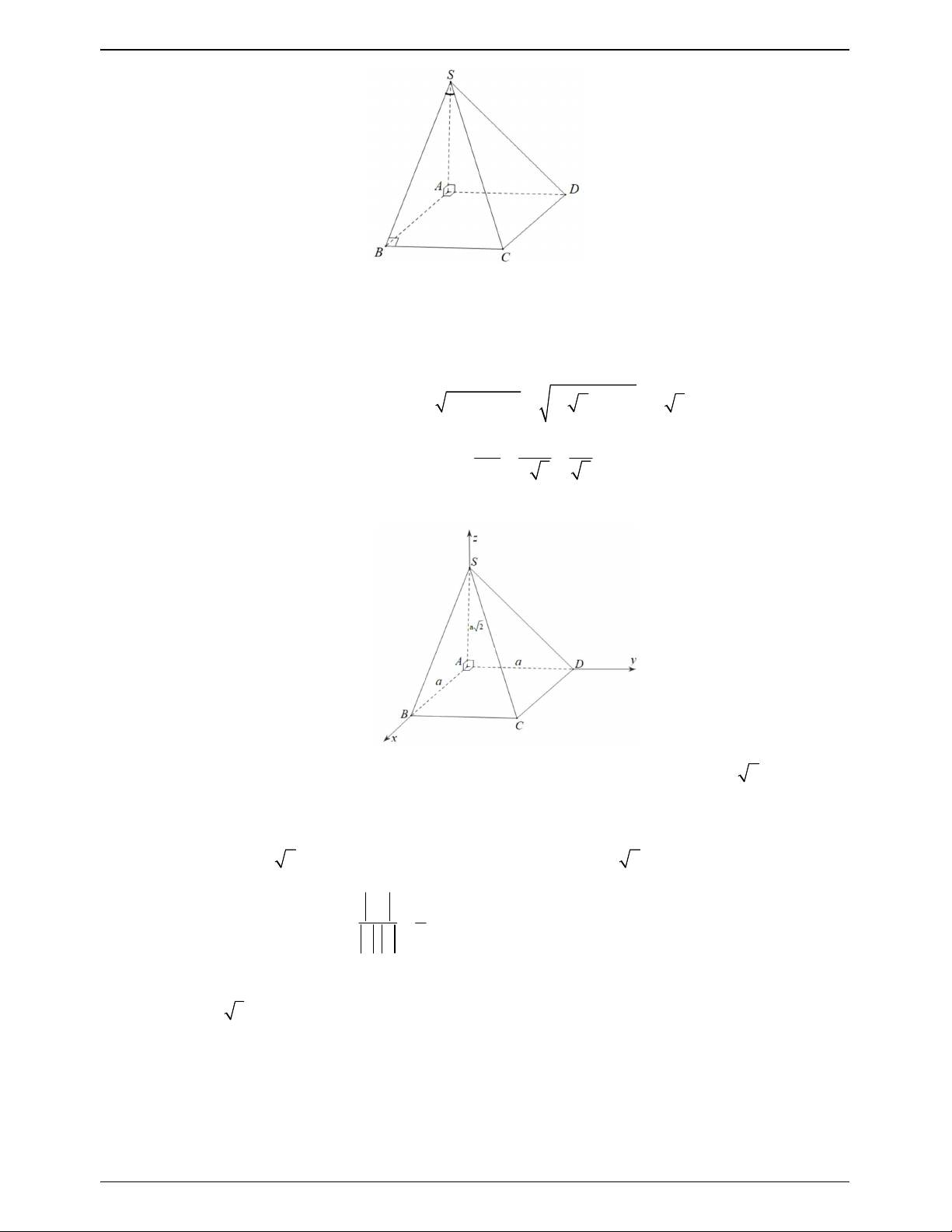
Câu 17.18:Cho hình chóp đều S.ABCD có cạnh 2a , cạnh bên a 3 (minh họa như hình vẽ). Góc giữa mặt bên và mặt đáy bằng: A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn B
Ta có: góc giữa mặt bên và mặt đáy là góc giữa SCD và ABCD.
Gọi O AC B .
D Vì S.ABCD là hình chóp đều nên SO ABCD. CD SM
Gọi M là trung điểm C . D Ta có:
CD SOM . CD OM C
D SOM
SCD ABCD CD Do đó: SCD ABCD
SM OM SMO
SOM SCD , , . SM SOM
ABCD OM BD AB 2 2a 2
Xét hình vuông ABCD ta có: OM a và OD a 2. 2 2 2 2 2
Xét SOD vuông tại O , ta có: 2 2 SO
SD OD a 3 a 2 . a SO a
Xét SOM vuông tại O , ta có: tan SMO
1 SMO 45o. OM a
Cách khác: Sử dụng phương pháp tọa độ
Gọi O AC B .
D Vì S.ABCD là hình chóp đều nên SO ABCD.
Ta có: AC BD AB 2 2a 2 và 2 2 2 2 SO
SD OD 3a 2a . a Trang 178
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Chọn hệ trục Oxyz như hình vẽ với O 0;0;0,C a 2;0;0, D0;a 2;0 và S 0;0;a .
Ta có: ABCD : z 0 ABCD có một vectơ pháp tuyến là k 0;0; 1 . x y z SCD :
1 x y 2z a 2 0 a 2 a 2 a
SCD có một vectơ pháp tuyến là n 1;1; 2. k.n 2
Suy ra: cos SCD, ABCD
SCD, ABCD 45o. k . n 2
Câu 17.19:Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 , SA vuông góc với mặt phẳng đáy,
SA a 3 (minh họa như hình vẽ). Góc giữa hai mặt phẳng SBD và ABCD bằng: A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn C BD SA
Gọi O AC B . D Ta có:
BD SAC . BD AC Trang 179
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
BD SAC
SBD ABCD BD Do đó:
SBD ABCD SO AC , , SO . A SAC SBD SO SAC
ABCD AC AC AB 2 a 2 2
Xét hình vuông ABCD ta có: OA . a 2 2 2 SA a 3
Xét SAO vuông tại A , ta có: tan SOA
3 SOA 60o. OA a
Cách khác: Sử dụng phương pháp tọa độ
Chọn hệ trục Axyz như hình vẽ với A0;0;0, B a 2;0;0, D 0;a 2;0 và S 0;0;a 3 .
Ta có: ABCD : z 0 ABCD có một vectơ pháp tuyến là k 0;0; 1 . x y z SBD : 1
3x 3y 2z a 6 0 a 2 a 2 a 3
SBD có một vectơ pháp tuyến là n 3; 3; 2. k.n 1
Suy ra: cos SBD, ABCD
SBD,ABCD 60 .o k . n 2 2a 3
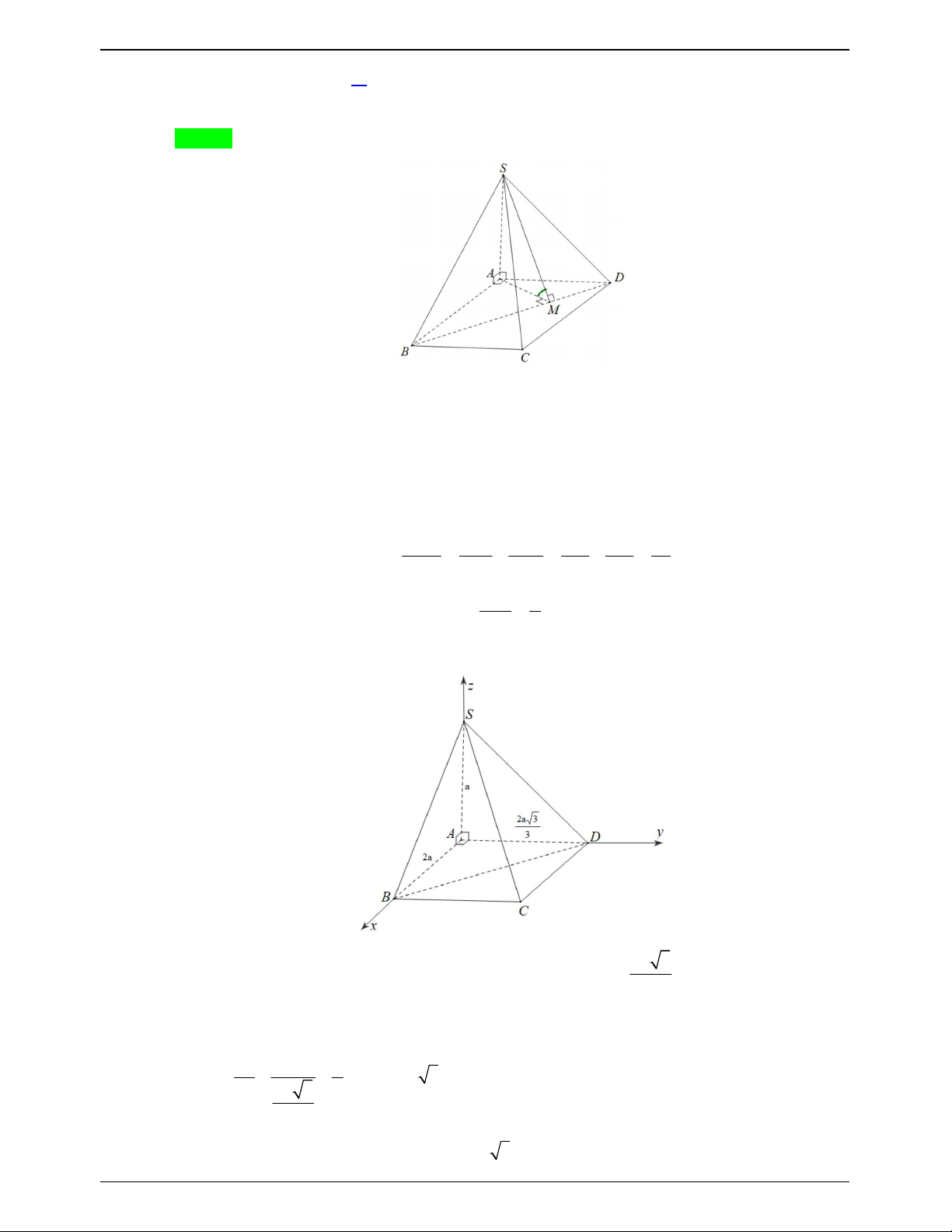
Câu 17.20:Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB 2a, AD
, SA vuông góc với 3
mặt phẳng đáy, SA a (minh họa như hình vẽ). Góc giữa hai mặt phẳng SBD và ABCD bằng: Trang 180
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn B BD SA
Vẽ AM BD tại M . Ta có:
BD SAM . BD AM
BD SAM
SBD ABCD BD Do đó: SBD ABCD
SM AM SMA
SAM SBD , , . SM SAM
ABCD AM 1 1 1 1 3 1
Xét ABD vuông tại A , ta có: AM . a 2 2 2 2 2 2 AM AB AD 4a 4a a SA a
Xét SAM vuông tại A , ta có: tan SMA 1 SMA 45 . o AM a
Cách khác: Sử dụng phương pháp tọa độ 2a 3
Chọn hệ trục Axyz như hình vẽ với A0; 0;0, B 2 ;
a 0; 0, D 0;
; 0 và S 0;0; a . 3
Ta có: ABCD : z 0 ABCD có một vectơ pháp tuyến là k 0;0; 1 . x y z SBD :
1 x 3 y 2z 2a 0 2a 2a 3 a 3
SBD có một vectơ pháp tuyến là n 1; 3;2. Trang 181
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 k.n 1
Suy ra: cos SBD, ABCD
SBD, ABCD 45o. k . n 2 Trang 182




