Xác định hệ số của hàm số khi biết bảng biến thiên hoặc đồ thị Toán 12

Xác định hệ số của hàm số khi biết bảng biến thiên hoặc đồ thị Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

56 28 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

31 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
VÍ DỤ MINH HỌA VÀ PHƯƠNG PHÁP GIẢI TOÁN
ĐỀ MINH HỌA TỐT NGHIỆP THPT 2020:
Cho hàm số
( )
1ax
fx
bx c
+
=
+
( )
,,abc
có bảng biến thiên
như sau:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A.
2
. B. 3. C. 1. D. 0.
PHÂN TÍCH VÀ HƯỚNG DẪN GIẢI
1. DẠNG TOÁN: Đây là bài toán ở dạng vận dụng: Từ bảng biến thiên xác định dấu các hệ số a, b và c
của hàm số
( )
1ax
fx
bx c
+
=
+
.
2. KIẾN THỨC CẦN NHỚ:
Cho hàm số
( )
ax b
fx
cx d
+
=
+
Đồ thị hàm số
( )
ax b
fx
cx d
+
=
+
có tiệm cận đứng là đường thẳng
d
x
c
=−
.
Đồ thị hàm số
( )
ax b
fx
cx d
+
=
+
có tiệm cận ngang là đường thẳng
a
y
c
=
.
Đạo hàm của hàm số
( )
ax b
fx
cx d
+
=
+
là
( )
( )
2
'
ad bc
fx
cx d
−
=
+
.
3. HƯỚNG GIẢI:
B1: Từ công thức của hàm số
( )
1ax
fx
bx c
+
=
+
chỉ ra phương trình đường thẳng của tiệm cận đứng, tiệm
cận ngang và công thức tính đạo hàm của nó.
B2: Từ bảng biến thiên chỉ ra tiệm cận đứng, tiệm cận ngang của đồ thị hàm số và chiều biến thiên của
hàm số đó.
B3: Thay các dữ kiện ở bước 1 vào bước 2 ta sẽ xác định được dấu của các hệ số a, b và c.
Từ đó, ta có thể giải bài toán cụ thể như sau:
LỜI GIẢI CHI TIẾT
XÁC ĐỊNH HỆ SỐ CỦA HÀM SỐ KHI BIẾT BẢNG BIẾN THIÊN HOẶC ĐỒ THỊ
Chọn C
Đồ thị hàm số
( )
1ax
fx
bx c
+
=
+
có đường tiệm cận đứng là đường thẳng
và đường tiệm cận ngang
là đường thẳng
a
y
b
=
.
Từ bảng biến thiên ta có:
2
2
1
c
c
b
ab
a
b
−=
= = −
=
(1)
Mặt khác:
( )
( )
2
'
ac b
fx
bx c
−
=
+
.
Vì hàm số đã cho đồng biến trên các khoảng
( )
;2−
và
( )
2;+
nên
( )
( )
2
' 0 0
ac b
f x ac b
bx c
−
= −
+
(2)
Thay (1) vào (2), ta được:
2
2
0 0 0 1
22
cc
c c c− + − +
.
Suy ra c là số dương và a, b là số âm.
BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN - PHẦN 1
Câu 1: Cho hàm số
( )
2
4ax m
fx
bx c
++
=
+
( )
, , ,a b c m
có bảng biến thiên như sau:
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn C
Tiệm cận đứng:
30x =
0
c
b
−
0bc
.
Tiệm cận ngang:
10y =
0
a
b

0ab
.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
30x 
2
4
0
m
a
+
−
0a
0b
0c
.
Câu 2: Cho hàm số
( )
9ax
fx
bx c
+
=
+
( )
,,abc
có bảng biến thiên như sau:
x
−
3
+
( )
fx
+
+
( )
fx
1
+
−
1
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn B
Tiệm cận đứng:
20x = −
0
c
b
−
0bc
.
Tiệm cận ngang:
30y =
0
a
b

0ab
.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
20x −
9
0
a
−
0a
0b
0c
.
Câu 3: Cho hàm số
( )
ax b
fx
cx d
+
=
+
( )
, , , , 0a b c d a
có bảng biến thiên như sau:
Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A.
0b
,
0c
,
0d
. B.
0b
,
0c
,
0d
.
C.
0b
,
0c
,
0d
. D.
0b
,
0c
,
0d
.
Lời giải
Chọn A
Tiệm cận ngang:
20y =
0
a
c

, mà
0a
0c
.
Tiệm cận đứng:
10x = −
0
d
c
−
0
d
c

, mà
0c
0d
.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
10x −
0
b
a
−
0
b
a

0b
.
Câu 4: Cho hàm số
( )
ax b
fx
cx d
+
=
+
( )
, , , , 0a b c d a
có bảng biến thiên như sau:
x
−
1
+
( )
fx
+
+
( )
fx
2
+
−
2
x
−
1−
+
( )
fx
–
–
( )
fx
2
−
+
2
x
−
2−
+
( )
fx
–
–
( )
fx
3
−
+
3
Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A.
0b
,
0c
,
0d
. B.
0b
,
0c
,
0d
.
C.
0b
,
0c
,
0d
. D.
0b
,
0c
,
0d
.
Lời giải
Chọn D
Tiệm cận ngang:
20y =
0
a
c

, mà
0a
0c
.
Tiệm cận đứng:
10x =
0
d
c
−
0
d
c

, mà
0c
0d
.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
10x 
0
b
a
−
0
b
a

0b
.
Câu 5: Cho hàm số
( )
2ax
fx
bx c
−
=
+
( )
, , ,a b c m
có bảng biến thiên như sau:
Trong các số
a
,
b
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn A
Tiệm cận đứng:
10x =
0
c
b
−
0bc
.
Tiệm cận ngang:
10y =
0
a
b

0ab
.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
10x 
2
0
a

0a
0b
0c
.
Câu 6: Cho hàm số
( ) ( )
2020
,,
ax
f x a b c
bx c
+
=
+
có bảng biến thiên như sau:
Kết quả nào sau đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.a b c
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
Lời giải
Chọn B
+ Tiệm cận đứng:
4 0 0 0
c
x bc
b
= −
x
−
4
+
y
+
+
y
1
3
−
+
−
1
3
−
x
−
1
+
( )
fx
+
+
( )
fx
1
+
−
1
+ Tiệm cận ngang:
1
0 0 0
3
a
y ab
b
= −
+ Đồ thị hàm số cắt trục hoành tại điểm
2020
4 0 0 0 0 0x x a b c
a
−
.
Câu 7: Cho hàm số
42
0y ax bx c a
có bảng biến thiên dưới đây:
Tính
2 3 .P a b c
A.
3.P
B.
6P
. C.
2P
. D.
2P
.
Lời giải
Chọn C
Ta có
32
4 2 2 (2 )y ax bx x ax b
= + = +
,
0y
=
2
0
2
x
b
x
a
=
=−
.
Căn cứ vào bảng biến thiên ta thấy
0a
;
0b
, hàm đạt cực đại tại
1x =
và
( )
12y =
, hàm
đạt cực tiểu tại
0x =
và
( )
01y =
. Suy ra,
1
2
2
1
b
a
abc
c
−=
+ + =
=
1
2
1
a
b
c
=−
=
=
.
Do đó:
2 3 2P a b c= − + = −
.
Câu 8: Cho đồ thị hàm số
( )
42
f x ax bx c= + +
như hình vẽ.
Mệnh đề nào sau đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0abc
.
C.
0, 0, 0a b c
. D.
0, 0, 0abc
.
Lời giải
Chọn A
Ta có:
lim
x
y
→+
= +
nên
0a
.
Đồ thị hàm số cắt
Oy
tại điểm
( )
0;3
do đó
30c =
.
Đồ thị hàm số có 3 điểm cực trị nên:
00ab b
.
Câu 9: Cho hàm số
( ) ( )
32
, , , , 0, 0f x ax bx cx d a b c d a d= + + +
có bảng biến thiên như sau:
x
−
1−
0
1
+
y
−
0
+
0
−
0
+
y
+
0
3
0
+
Trong các số
,ab
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn A
Từ dạng đồ thị suy ra
0a
.
Ta có
2
32y ax bx c
Vì hàm số có 2 cực trị nên
0y
có 2 nghiệm phân biệt
12
,xx
.
Nên theo công thức Vi-ét ta có:
12
12
2
3
.
3
b
xx
a
c
xx
a
.
Dựa vào hoành độ 2 điểm cực trị ta có:
2
0
0
3
0
0
3
b
b
a
cc
a
.
Câu 10: Cho hàm số
( ) ( )
32
, , , , 0f x ax bx cx d a b c d a= + + +
có bảng biến thiên như sau:
Trong các số
,ab
và
c
có bao nhiêu số âm?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn A
Từ dạng đồ thị suy ra
0a
.
0 1 0x y d d= = = −
.
Ta có
2
32y ax bx c
Vì hàm số có 2 cực trị nên
0y
có 2 nghiệm phân biệt
12
,xx
.
Nên theo công thức Vi-ét ta có:
12
12
2
3
.
3
b
xx
a
c
xx
a
.
Dựa vào hoành độ 2 điểm cực trị ta có:
2
0
0
3
0
0
3
b
b
a
cc
a
.
Câu 11: Cho hàm số
( ) ( )
32
, , , , 0f x ax bx cx d a b c d a= + + +
có bảng biến thiên như sau:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn A
Từ dạng đồ thị suy ra
0a
.
00x y d= =
.
Ta có
2
32y ax bx c
Vì hàm số có 2 cực trị nên
0y
có 2 nghiệm phân biệt
12
,xx
.
Nên theo công thức Vi-ét ta có:
12
12
2
3
.
3
b
xx
a
c
xx
a
.
Dựa vào hoành độ 2 điểm cực trị ta có:
2
0
0
3
0
0
3
b
b
a
cc
a
.
Câu 12: Cho hàm số
ax b
y
xc
+
=
−
có đồ thị như hình vẽ bên.
Tìm khẳng định đúng trong các khẳng định sau
A.
0, 0,c 0ab
. B.
0, 0,c 0ab
. C.
0, 0,c 0ab
. D.
0, 0,c 0ab
.
Lời giải
Chọn D
❖ Từ hàm số
ax b
y
xc
+
=
−
suy ra:
+ Tiệm cận đứng của đồ thị là đường thẳng có phương trình
xc=
.
O
x
y
+ Tiệm cận ngang của đồ thị là đường thẳng có phương trình
ya=
.
+ Giao điểm với trục hoành là
;0
b
A
a

−


,
0a
.
+ Giao điểm với trục tung là
0;
b
B
c

−


,
0c
.
❖ Từ đồ thị hàm số ta có:
+ Đường tiệm cận đứng nằm bên trái
Oy
nên
0c
.
+ Đường tiệm cận ngang nằm trên
Ox
nên
0a
.
+ Giao điểm với trục
Ox
có hoành độ dương nên
. Vì
0a
nên
0b
.
Câu 13: Cho hàm số
( )
1
, , 1 0
ax
y a d ad
xd
−
= +
+
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0
0
a
d
B.
0
0
a
d
C.
0
0
a
d
D.
0
0
a
d
Lời giải
Chọn A
+ Phương trình tiệm cận đứng:
xd=−
. Dựa vào đồ thị ta có
00dd−
+ Phương trình tiệm cận ngang:
ya=
. Dựa vào đồ thị ta có
0a
Câu 14: Cho hàm số
( )
32
y f x ax bx cx d= = + + +
có đồ thị như hình vẽ ở bên. Mệnh đề nào
sau đây đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
Chọn C
Ta có
2
32y ax bx c
= + +
Dựa vào đồ thị ta thấy nhánh cuối cùng bên phải hướng lên trên suy ra
0a
.
Đồ thị cắt trục tung tại điểm
1x =
10d =
.
Hàm số có 2 điểm cực trị
1
10x =
,
2
30x =
12
0xx +
2
0
3
b
a
−
0b
.
12
0xx
0
3
c
a

0c
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 15: Đồ thị hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ sau. Mệnh đề nào sau đây đúng.
A.
0; 0; 0; 0a b c d
. B.
0; 0; 0; 0a b c d
.
C.
0; 0; 0; 0a b c d
. D.
0; 0; 0; 0a b c d
.
Lời giải
Chọn A
Có
0a
do điểm cuối đồ thị có hướng đi xuống.
0d
do giao điểm của đồ thị với
Oy
nằm phía trên
Ox
.
Đồ thị có 2 cực trị trái dấu nên
3 . 0ac
0c
.
Hoành độ điểm uốn dương nên
00
3
b
b
a
−
.
Câu 16: Cho hàm số
( )
42
,,y ax bx c a b c= + +
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0; 0; 0.abc
B.
0; 0; 0.a b c
C.
0; 0; 0.abc
D.
0; 0; 0.a b c
Lời giải
Chọn D
+ Dựa vào dạng đồ thị ta thấy:
0a
.
+ Dựa vào đồ thị ta thấy đồ thị hàm số có 3 điểm cực trị nên:
00ab b
.
+ Với
0x =
ta có:
( )
00yc=
.
Câu 17: Cho hàm số
( )
42
,,y ax bx c a b c= + +
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0; 0; 0.abc
B.
0; 0; 0.a b c
C.
0; 0; 0.a b c
D.
0; 0; 0.a b c
Lời giải
Chọn B
+ Dựa vào dạng đồ thị ta thấy:
0a
.
+ Dựa vào đồ thị ta thấy đồ thị hàm số có 3 điểm cực trị nên:
00ab b
.
+ Với
0x =
ta có:
( )
00yc=
.
Câu 18: Cho hàm số
( )
42
f x ax bx c= + +
với
0a
có đồ thị như hình vẽ:
Tìm mệnh đề đúng trong các mệnh đề sau?
A.
0a
;
0b
;
0c
. B.
0a
;
0b
;
0c
.
C.
0a
;
0b
;
0c
. D.
0a
;
0b
;
0c
.
Lời giải
Chọn A
Ta có nhánh bên phải đồ thị đi xuống, suy ra
0a
.
Mặt khác do đồ thị có ba cực trị suy ra
0ab
mà
00ab
.
Mà giao điểm của đồ thị với trục
Oy
tại điểm có tung độ
0yc=
.
Vậy chọn đáp án A.
Câu 19: 2 Cho hàm số
32
y ax bx cx d= + + +
có đồ thị là đường cong như hình vẽ bên. Mệnh đề nào
dưới đây đúng?
A.
0, 0, 0, 0a b c d =
. B.
0, 0, 0, 0a b c d =
.
C.
0, 0, 0, 0a b c d =
. D.
0, 0, 0, 0a b c d =
.
Lời giải
Chọn A
Do nhánh cuối của đồ thị đi lên nên ta có
0a
.
Ta có
2
32y ax bx c
= + +
. Do cực tiểu của hàm số thuộc trục tung và có giá trị âm nên
0d
và
0x =
là nghiệm của phương trình
00yc
= =
.
Lại có
2
0
2
3 2 0 0 0, 0
2
3
3
x
b
ax bx a b
b
a
x
a
=
+ = −
=−
.
Câu 20: Cho hàm số bậc ba
( )
32
= + + +f x x bx cx d
. Biết đồ thị của hàm số
( )
=y f x
như hình vẽ.
Giá trị của
c
b
là:
A.
1
3
−
. B.
3
4
. C.
1
3
. D.
3
4
−
.
Lời giải
Chọn D
Tập xác định
=D
.
Đạo hàm cấp 1
( )
2
32
= + +f x ax bx c
Dựa vào đồ thị của hàm số
( )
=y f x
ta có bảng thiên của hàm số
( )
fx
x
y
3
2
1
2
O
1
Ta có
13
24

= + +


a
f b c
và
3 27
3
24

= + +


a
f b c
.
Dựa vào bảng biến thiên ta có
3 4 4 0 27 36 36 0
27 12 4 0 27 12 4 0
+ + = + + =


+ + = + + =

a b c a b c
a b c a b c
.
3
24 32 0
4
+ = = −
c
bc
b
.
Vậy
3
4
=−
c
b
.
BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN - PHẦN 2
Mức độ 3
Câu 43.1. Cho hàm số
()y f x=
có đạo hàm
()fx
, biết rằng đồ thị của hàm số
()fx
như hình vẽ.
Biết
( ) 0fa
, hỏi đồ thị hàm số
()y f x=
cắt trục hoành tại nhiều nhất bao nhiêu
điểm?
A. 4. B. 2. C. 3. D. 1
Lời giải
Chọn B
Dựa vào đồ thị của hàm số
()fx
, ta có bảng biến thiên của hàm số
()y f x=
như sau:
Vì
( ) 0fa
nên ta xét các trường hợp sau:
・ Nếu
( )
0fc
thì toàn bộ đồ thị hàm số nằm ở phía trên trục hoành, do đó đồ thị hàm số
không cắt trục hoành.
・ Nếu
( ) 0fc=
thì đồ thị hàm số và trục hoành có một điểm chung duy nhất
・ Nếu
( ) 0fc
thì đồ thị hàm số và trục hoành có hai điểm chung
Vây đồ thị hàm số
()y f x=
cắt trục hoành nhiều nhất tại hai điểm.
Câu 43.2. Cho hàm số
()y f x=
ax b
cx d
+
=
+
có đồ thị hàm số
( )
fx
như trong hình vẽ dưới đây:
Biết rằng đồ thị hàm số
()fx
đi qua điểm
( )
0;4A
. Khẳng định nào dưới đây là đúng?
A.
( )
12f =
. B.
( )
11
2
2
f =
. C.
( )
7
1
2
f =
. D.
( )
26f =
.
Lời giải
Chọn D
Đồ thị hàm số
()fx
đi qua
( )
0;4A
nên
4bd=
( )
1
.
Ta có:
( )
( )
2
ad bc
fx
cx d
−
=
+
.
Căn cứ theo đồ thị hàm số
( )
fx
ta có
1
d
c
− = −
cd=
( )
2
.
Đồ thị hàm số
( )
fx
đi qua
(0;3)
nên
2
3
ad bc
d
−
=
2
3ad bc d − =
( )
3
.
Thay
( )
1
,
( )
2
vào
( )
3
ta được
22
43ad d d−=
7ad=
( )
0d
vì nếu
0d =
thì
ab=
c=
d=
0=
(vô lí ).
Do đó
( )
74dx d
fx
dx d
+
=
+
74
1
x
x
+
=
+
.
Vậy
( )
26f =
.
Câu 43.3. Cho hàm số
( )
+
==
+
ax b
y f x
cx d
, (
a
,
b
,
c
,
d
,
0c
,
0d
) có đồ thị
( )
C
. Đồ thị của
hàm số
( )
=y f x
như hình vẽ dưới đây. Biết
( )
C
cắt trục tung tại điểm có tung độ bằng
2
.
Tiếp tuyến của
( )
C
tại giao điểm của
( )
C
với trục hoành có phương trình là
A.
3 2 0+ + =xy
. B.
3 2 0+ − =xy
. C.
3 2 0− − =xy
. D.
3 2 0− + =xy
.
Lời giải
Chọn B
-1
y
-2
-3
O
1
Xét hàm số
( )
+
==
+
ax b
y f x
cx d
có
( )
( )
( )
2
2
−
=
+
ad bc
fx
cx d
.
Ta có đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
2
nên
( )
02=f
2=
b
d
2=bd
. Từ đồ thị
( )
=y f x
nhận đường thẳng
1=−x
làm tiệm cận đứng nên
1− = − =
d
dc
c
( )
( )
( )
2
22
22
1
−−
= =
++
ad d a d
fx
dx d d x
.
Mặt khác ta lại có đồ thị
( )
=y f x
đi qua điểm
( )
2; 3−−
nên
( )
23
=f
2
3
−
= −
ad
d
= −ad
.
Vậy
( )
22
1
− + − +
==
++
dx d x
fx
dx d x
.
Đồ thị
( )
C
cắt trục
Ox
tại điểm
( )
2;0
và
( )
1
2
3
=−f
.
Vậy phương trình tiếp tuyến của
( )
C
tại giao điểm của
( )
C
và trục
Ox
là
( )
1
2
3
= − −yx
3 2 0 + − =xy
.
Câu 43.4. Xác định
a
,
b
,
c
để hàm số
1ax
y
bx c
−
=
+
có đồ thị như hình vẽ bên. Chọn đáp án đúng?
A.
2, 1, 1.a b c= = = −
B.
2, 1, 1.a b c= = =
C.
2, 2, 1.a b c= = = −
D.
2, 1, 1.a b c= = − =
Lời giải
Chọn A
Nhận xét: đồ thị hàm số có đường tiệm cận đứng
b
x
c
−
=
và tiệm cận ngang
a
y
b
=
.
Dựa vào đồ thị ta có
( ) ( )
1
2
1
0;1 :
b
c
a
b
ax
M C y
bx c
−
=
=
−
=
+
0
2
1
1
bc
ab
c
+=
=
−
=
0
2
1
bc
ab
c
+=
=
=−
22
1
1
ab
bc
c
==
= − =
=−
.
Câu 43.5. Đường cong ở hình bên là đồ thị hàm số
2ax
y
cx b
+
=
+
với
a
,
b
,
c
là các số thực.
Mệnh đề nào sau đây đúng?
A.
1a =
;
2b =−
;
1c =
. B.
1a =
;
2b =
;
1c =
. C.
1a =
;
1b =
;
1c =−
. D.
2a =
;
2b =
;
1c =−
.
Lời giải:
Chọn A
Đồ thị hàm số đã cho cắt trục hoành tại điểm có tọa độ
( )
2;0−
nên ta có:
22
01
2
a
a
cb
−+
= =
−+
. Vậy loại D
Đồ thị hàm số đã cho có tiệm cận ngang là đường thẳng
1 1 1
a
y c a
c
= = = =
. Vậy loại C
Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng
2 2 2 2
b
x b c
c
= − = = − = −
.
Câu 43.6. Cho hàm số
32
y ax bx cx d= + + +
có đồ thị là đường cong trong hình dưới đây. Mệnh đề
nào sau đây đúng?
A.
0a
,
0c
,
0d
. B.
0a
,
0c
,
0d
.
C.
0a
,
0c
,
0d
. D.
0a
,
0c
,
0d
.
Lời giải:
Chọn B
Dựa vào hình dạng đồ thị: đồ thị hàm bậc ba có hệ số
0a
, đồ thị cắt trục tung tại điểm có
tung độ dương nên
0d
.
Ta có:
2
32y ax bx c
= + +
. Đồ thị có hai điểm cực trị cùng nằm bên phải trục tung nên
0y
=
có 2 nghiệm dương phân biệt.
x
y
O
Suy ra
2
2
2
0
0
0
0
30
3
0
0
3
3
0
a
a
b
b
a
b ac
ac
c
a
b
c


−


−
−
.
Câu 43.7. Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị là đường cong như hình vẽ.
Tính tổng
S a b c d= + + +
.
A.
4S =−
. B.
2S =
. C.
0S =
. D.
6S =
.
Lời giải:
Chọn C
Ta có
( )
2
32f x ax bx c
= + +
. Hàm số
( )
32
f x ax bx cx d= + + +
liên tục trên ; đồ thị hàm
số có hai điểm cực trị là
( )
2; 2−
và
( )
0;2
( )
( )
( )
( )
22
20
02
00
f
f
f
f
=−
=
=
=
8 4 2 2
12 4 0
2
0
a b c d
a b c
d
c
+ + + = −
+ + =
=
=
1
3
0
2
a
b
c
d
=
=−
=
=
0S=
.
Câu 43.8. Cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải:
Chọn A
3 2 2
32y ax bx cx d y ax bx c
= + + + = + +
.
Từ đồ thị ta có: hàm số có hai điểm cực trị
12
12
0xx
xx

, đồ thị cắt trục tung tại điểm có tung độ
âm và
lim
x
y
→+
= −
.
Suy ra
12
12
0
0
0
0
2
0
0
3
0
.0
3
a
a
d
d
b
xx
b
a
cc
xx
a


+ = −


=
.
Câu 43.9. Cho hàm số
42
y ax bx c= + +
( 0)a
và có bảng biến thiên như hình sau:
.
Khẳng định nào sau đây là khẳng định đúng?
A.
0a
và
0b
. B.
0a
và
0b
. C.
0a
và
0b
. D.
0a
và
0b
.
Lời giải:
Chọn C
.
Dựa vào bảng biến thiên
0a
.
Hàm số có một cực trị
. 0 0ab b
. Vậy KĐ “
0a
và
0b
” là đúng.
Câu 43.10. Cho hàm số
42
y ax bx c= − +
có đồ thị như hình vẽ sau.
Khẳng định nào sau đây đúng?
A.
0, 0, 0abc
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Lời giải:
Chọn A
Ta có
3
4 2 0y ax bx
= − =
.
Dựa vào đồ thị ta thấy
0a
và
0y
=
có 3 nghiệm phân biệt nên.
( )
2
0
0 2 2 0
2
2
x
b
y x ax b x
a
b
x
a
=
= − = =
=−
với
0, 0ab
loại B và C.
Thay
00x y c= =
loại D.
Câu 43.11. Cho hàm số
( )
32
y f x ax bx cx d= = + + +
có đạo hàm là hàm số
( )
y f x
=
với đồ thị
như hình vẽ bên. Biết rằng đồ thị hàm số
( )
y f x=
tiếp xúc với trục hoành tại điểm có hoành
độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?
A. 4. B. 1. C.
4−
. D. 2.
Lời giải
Chọn C
Nhìn đồ thị ta thấy
0
0
2
x
y
x
=
=
=−
. Do đó, hàm số
( )
y f x=
đạt cực trị tại
0x =
và
2x =−
.
Đồ thị hàm số
( )
y f x=
tiếp xúc với trục hoành tại điểm có hoành độ âm nên suy ra hàm số
( )
y f x=
đạt cực trị bằng 0 tại điểm có hoành độ âm
( )
20f − =
. (1)
Mặt khác
( )
2
32f x ax bx c
= + +
.
Đồ thị hàm số
( )
y f x
=
đi qua các điểm có tọa độ
( )
0;0
,
( )
2;0−
,
( )
1; 3−−
. (2)
Từ (1), (2) lập được hệ phương trình
01
12 4 0 3
3 2 3 0
8 4 2 0 4
ca
a b c b
a b c c
a b c d d
==


− + = =


− + = − =


− + − + = = −

( )
32
34f x x x = + −
.
Đồ thị hàm số
( )
y f x=
cắt trục tung tại điểm có tung độ
( )
0yf=
= -
4
.
Câu 43.12. Cho hàm số
1−
=
+
ax
y
cx d
có tiệm cận đứng
1=x
, tiệm cận ngang
2=y
và đi qua điểm
( )
2; 3−A
. Lúc đó hàm số
1+
=
+
ax
y
cx d
là hàm số nào trong bốn hàm số sau:
A.
3 2 1
..
51
−+
=
−
x
y
x
B.
21
1
−
=
−
x
y
x
. C.
21
.
1
−−
=
−+
x
y
x
D.
21
.
1
−
=
−
x
y
x
Lời giải:
Chọn B
Đồ thị hàm số
1−
=
+
ax
y
c x d
có tiệm cận đứng
=−
d
x
c
, tiệm cận ngang
=
a
y
c
Theo đề bài ta có
2
2 2 0 2
2 2 2 0 1
2 1 6 3 2 6 3 1 1
.2 1
3
.2
=
= − = =
− = − = + = = −
− = − − + + = =
−
=−
+
a
c
a c a c a
d
d c c d c
c
a c d a c d d
a
cd
Câu 43.13. Cho hàm số
1+
=
+
mx
y
xm
. Các đồ thị nào dưới đây có thể là đồ thị biểu diễn hàm số đã cho?
Hãy chọn đáp án sai?
A. Hình (I) và (III). B. Hình (III). C. Hình (I). D. Hình (II).
Lời giải
Chọn D
Hàm số
1+
=
+
mx
y
xm
có tập xác định
\=−
Dm
.
Ta có
( )
2
2
1
'
−
=
+
m
y
xm
,
2
' 0 1 0 1 1 − − y m m
;
2
1
' 0 1 0
1
−
−
m
ym
m
. Hình
(I) có
( )
1
1;1
2
= − −m
nên
'0y
suy ra hàm số nghịch biến, do đó Hình (I) đúng. Hình (II) có
3
1
2
= − −m
nên
'0y
suy ra hàm số đồng biến, do đó Hình (II) sai. Hình (III) có
21= − −m
nên
'0y
suy ra hàm số đồng biến, do đó Hình (III) đúng.
Câu 43.14. Hàm số có đồ thị như hình vẽ bên. Mệnh đề nào sau đây
là đúng?
bx c
y
xa
−
=
−
(
0;a
)
, , a b c
A. B.
C. D.
Lời giải
Chọn A
Đồ thị hàm số có tiệm cận đứng ; tiệm cận ngang
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác
định của nó nên
Vậy .
Câu 43.15. Cho hàm số
( ) ( )
32
0y f x ax bx cx d a= = + + +
có đồ thị như hình vẽ.
Phương trình
( )
( )
0f f x =
có bao nhiêu nghiệm thực?
A. 3. B. 7. C. 5. D. 9.
Lời giải
Chọn D
Từ đồ thị hàm số đã cho trong hình vẽ ta có phương trình
( )
0fx=
có ba nghiệm phân biệt
1
x
,
2
x
và
3
x
thuộc khoảng
( )
2;2−
hay
( )
1
2
3
0
xx
f x x x
xx
=
= =
=
với
1
x
,
2
x
và
3
x
thuộc khoảng
( )
2;2−
.
Đặt
( )
t f x=
ta có
( )
1
2
3
0
tt
f t t t
tt
=
= =
=
hay
( )
( )
( )
1
2
3
f x t
f x t
f x t
=
=
=
với
1
t
,
2
t
và
3
t
thuộc khoảng
( )
2;2−
Dựa vào đồ thị ta thấy ba đường thẳng phân biệt
1
yt=
,
2
yt=
và
3
yt=
mỗi đường thẳng luôn
cắt đồ thị hàm số tại ba điểm.
Vậy phương trình
( )
( )
0f f x =
có
9
nghiệm.
x
y
y
O
0, 0, 0.a b c ab −
0, 0, 0.a b c ab −
0, 0, 0.a b c ab − =
0, 0, 0.a b c ab −
0xa
0.yb
2
0, 0.
c ab
y x a c ab
xa
0, 0, 0.a b c ab
Câu 43.16. Cho hàm số
4 3 2
y f x mx nx px qx r
, trong đó
, , , ,m n p q r
. Biết hàm
số
y f x
có đồ thị như hình bên dưới. Số nghiệm của phương trình
16 8 4 2f x m n p q r
là
A. 4. B. 5. C. 2. D. 3.
Lời giải
Chọn A
* Dựa vào đồ thị ta có
0m
và
32
4 (x 1)(x 1)(x 4) 4 16 4 16 .f x m mx mx mx m
* Mà
32
4 3 2f x mx nx px q
. Suy ra
16
3
2
16
nm
pm
qm
.
* Phương trình
16 8 4 2f x m n p q r
.
4 3 2
16 128
2 16 16 8 32
33
mx mx mx mx r m m m m r
4 3 2
16 8
2 16 0
33
m x x x x
32
2
10 26 4
0
3 3 3
x
x x x
.
Phương trình
32
10 26 4
0
3 3 3
x x x
có 3 nghiệm phân biệt khác
2
.
Vậy phương trình
16 8 4 2f x m n p q r
có 4 nghiệm.
Câu 43.17. Cho các hàm số
( )
4 3 2
f x mx nx px qx r= + + + +
và
( )
32
g x ax bx cx d= + + +
( )
, , , , , , , ,m n p q r a b c d
thỏa mãn
( ) ( )
00fg=
. Các hàm số
( )
y f x
=
và
( )
gx
có đồ thị
như hình vẽ bên.
Tập nghiệm của phương trình
( ) ( )
f x g x=
có số phần tử là
A. 4. B. 2. C. 1. D. 3.
Lời giải:
Chọn B
+ Từ đồ thị hàm số
( )
y f x
=
0m
.
+
( ) ( )
00f g r d= =
.
+ Ta có
( ) ( ) ( ) ( )
32
4 3 2f x g x mx n a x p b x q c

− = + − + − + −
( )
1
.
Mặt khác từ đồ thị hai hàm số
( )
y f x
=
và
( )
gx
ta có
( ) ( ) ( )( )( )
4 1 1 2f x g x m x x x

− = + − −
hay
( ) ( )
32
4 8 4 8f x g x mx mx mx m

− = − − +
( )
2
.
Từ
( )
1
và
( )
2
ta suy ra
( )
( )
38
24
8
n a m
p b m
q c m
− = −
− = −
−=
.
+ Phương trình
( ) ( )
4 3 2 3 2
f x g x mx nx px qx r ax bx cx d= + + + + = + + +
4 3 2 3 2
mx nx px qx ax bx cx + + + = + +
( ) ( )
32
0x mx n a x p b x q c

+ − + − + − =

32
8
2 8 0
3
m
x mx x mx m

− − + =


32
32
0
8
2 8 0
8
3
2 8 0
3
x
mx x x x
x x x
=

− − + =

− − + =

.
Phương trình
32
8
2 8 0
3
x x x− − + =
có đúng một nghiệm thực khác 0.
Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 43.18. Cho hàm số
4 3 2
()f x ax bx cx dx e= + + + +
có đồ thị của hàm số
()y f x
=
như hình vẽ
bên. Phương trình
1
()
2
f x f

=


có bao nhiêu nghiệm thực phân biệt?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải:
Chọn A
Ta có
32
( ) 4 3 2f x ax bx cx d
= + + +
là một đa thức bậc ba có đồ thị cắt trục hoành tại ba điểm
có hoành độ lần lượt -1;1;2. Vì vậy
32
( ) 4 3 2 4 ( 1)( 1)( 2).f x ax bx cx d a x x x
= + + + = + − −
Mặt khác
1
(0) 2 4 (0 1)(0 1)(0 2) 2
4
f a a
= + − − = =
.
Vậy ta có
32
( ) 4 3 2 ( 1)( 1)( 2),f x ax bx cx d x x x x
= + + + = + − −
3 2 3 2
4 3 2 2 2,ax bx cx d x x x x + + + = − − +
432
4 1
32
1 2 1 1 2 1
( ; ; ; ) ; ; ;2 ( ) 2
21
4 3 2 4 3 2
2
a
b
a b c d f x x x x x e
c
d
=
=−

= − − = − − + +

=−

=
Khi đó
432
1 1 2 1 155
( ) 2 0
2 4 3 2 192
f x f x x x x

= − − + − =


4 nghiệm. Chọn đáp án A.
Câu 43.19. Hỏi có bao nhiêu cặp số nguyên dương
( )
;ab
để hàm số
2
4
xa
y
xb
−
=
−
có đồ thị trên
( )
1; +
như hình vẽ dưới đây?
A.
3
. B.
4
. C.
2
. D.
1
.
Hướng dẫn giải
Chọn D
Hàm số không xác định tại điểm
4
b
x =
. Theo đồ thị ta có tiệm cận đứng nhỏ hơn
1
14
4
b
b
. Do
b
nguyên dương nên
1,2,3b
.
Ta có
( )
2
42
4
ab
y
xb
−
=
−
. Hàm số nghịch biến nên
4 2 0ab−
2ba
. Do
a
là số nguyên
dương và
1,2,3b
nên ta có một cặp
( )
,ab
thỏa mãn là
( )
1,3
Câu 43.20. Cho hàm số
( )
32
( ) , , , , 0y f x ax bx cx d a b c d a= = + + +
có đồ thị là
( )
C
. Biết rằng đồ
thị
( )
C
đi qua gốc tọa độ và đồ thị hàm số
'( )y f x=
cho bởi hình vẽ bên. Tính giá trị
(4) (2)H f f=−
?
A.
64H =
. B.
51H =
. C.
58H =
. D.
45H =
.
Hướng dẫn giải
Chọn C
Theo bài ra
( )
32
( ) , , , , 0y f x ax bx cx d a b c d a= = + + +
do đó
( )
y f x
=
là hàm bậc hai
có dạng
( )
2
y f x a x b x c
= = + +
.
Dựa vào đồ thị ta có:
1
4
4
c
a b c
abc
=
− + =
+ + =
3
0
1
a
b
c
=
=
=
( )
2
31y f x x
= = +
.
Gọi
S
là diện tích phần hình phẳng giới hạn bởi các đường
( )
y f x
=
, trục
Ox
,
4,x =
2x =
.
Ta có
( )
4
2
2
3 1 dx 58Sx= + =
.
Lại có:
( ) ( ) ( ) ( )
4
4
2
2
dx 4 2S f x f x f f
= = = −
.
Do đó:
( ) ( )
4 2 58H f f=−=
.
Câu 43. 21. Cho hàm số
1
ax b
y
x
−
=
−
có đồ thị như hình dưới.
Khẳng định nào dưới đây là đúng?
O
x
y
1−
1
2−
2
A.
0ba
. B.
0 ba
. C.
0ba
. D.
0 ab
.
Lời giải
Chọn C
Nhìn vào đồ thị ta thấy : Đồ thị hàm số có tiệm cận ngang
ya=
và tiệm cận đứng
1x =
.Đồ thị
cắt trục hoành tại điểm có hoành độ
1
b
x
a
=
. Ta có :
1
1
10
1
a
ba
b
a
=
−
= −
.
Câu 43.22. Giả sử hàm số
42
y ax bx c= + +
có đồ thị là hình bên dưới.
Khẳng định nào sau đây là khẳng định đúng?
A.
0, 0, 1a b c =
. B.
0, 0, 1abc =
.
C.
0, 0, 1a b c =
. D.
0, 0, 0abc
.
Lời giải
Chọn A
Dựa vào đồ thị ta có:
+ Đồ thị hướng lên nên
0a
, loại đáp án C.
+Với
0x =
1yc = =
nên loại đáp án D.
+Có 3 cực trị nên
0ab
suy ra
0b
.
Câu 43.23. Cho hàm số
32
y ax bx cx d= + + +
. Hỏi hàm số luôn đồng biến trên khi nào?
A.
2
0, 0
0; 3 0
a b c
a b ac
= =
−
. B.
2
0
0; 3 0
abc
a b ac
= = =
−
.
C.
2
0, 0
0; 3 0
a b c
a b ac
= =
−
. D.
2
0, 0
0; 3 0
a b c
a b ac
= =
−
.
Lời giải
Chọn C
Hàm số luôn đồng biến trên khi
2
' 3 2 0,y ax bx c x= + +
Trường hợp 1:
0, 0a b c= =
Trường hợp 1:
0a
, giải
2
3b ac
= −
O
x
y
1−
1
1
Hàm số luôn đồng biến trên
' 0,yx
0
0
a

2
0
30
a
b ac
−
Câu 43. 24. Cho hàm số
1
ax b
y
x
+
=
+
có đồ thị như hình vẽ bên.
Tìm khẳng định đúng trong các khẳng định sau
A.
0ba
. B.
0 ab
. C.
0ab
. D.
0 ba
.
Lời giải
Chọn B
( )
2
1
ab
y
x
−
=
+
. Dựa vào đồ thị hàm số ta thấy hàm số nghịch biến trên từng khoảng xác định và
có đường tiệm cận ngang
1y =
.
Suy ra:
0
lim 1
xy
y
→
=
0
1
ab
a
−
=
1
1
a
b
=
. Vậy
0 ab
.
Câu 43.25. cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
x
y
1
1
O
1−
x
y
1
O
A.
0, 0, 0, 0.a b c d =
B.
0, 0, 0, 0.a b c d =
C.
0, 0, 0, 0.a b c d
. D.
0, 0, 0, 0.a b c d
.
Lời giải
Chọn A
32
y ax bx cx d= + + +
( )
2
' 3 2f x ax bx c= + +
.
Cho
0x =
, ta có
( )
0 0.fd=
Từ hình dáng đồ thị ta thấy
0a
Đồ thị hàm số có điểm cực đại và cực tiểu, suy ra
( )
'0fx=
có hai nghiệm phân biệt, từ đồ thị
có hoành độ hai điểm cực trị không âm do đó
12
12
0
0
2
00
3
0
0
3
a
a
b
x x b
a
c
c
xx
a

+ = −


=
==
Câu 43.26. Hàm số
42
y ax bx c= + +
có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
A.
0a
;
0b
;
0c
. B.
0a
;
0b
;
0c
. C.
0a
;
0b
;
0c
. D.
0a
;
0b
;
0c
.
Lời giải:
Chọn A
Đồ thị hàm số có dạng đồ thị của hàm số bậc bốn hệ số
a
âm, giao điểm của đồ thị với trục
tung nằm trên điểm
O
nên hệ số
c
dương. Đồ thị hàm số có ba cực trị nên hệ số
b
trái dấu với
hệ số
a
, hay hệ số
b
dương.
O
x
y
Câu 43.27. Đồ thị hàm số
1ax
y
cx d
−
=
+
(
a
,
c
,
d
: hằng số thực ) như hình vẽ.
Khẳng định nào đúng
A.
0, 0, 0d a c
. B.
0, 0, 0d a c
. C.
0, 0, 0d a c
. D.
0, 0, 0d a c
.
Lời giải
Chọn C
Ta có
1
0 0 0x y d
d
= = −
.
1
0 0 0y x a
a
= =
.
Hàm số
1ax
y
cx d
−
=
+
có tiệm cận ngang
00
a
yc
c
=
.
Vậy
0, 0, 0d a c
.
Câu 43.28. Đồ thị hàm số
32
y ax bx cx d= + + +
(
a
,
b
,
c
,
d
là các hằng số thực và
0a
) như hình vẽ.
Khẳng định nào đúng
A.
0, 0bc
. B.
0, 0bc
. C.
0, 0bc
. D.
0, 0bc
.
Lời giải
Chọn C
Từ đồ thị hàm số ta thấy
lim
x
y
→−
= +
nên
0a
.
O
x
y
O
x
y
Nhận thấy
2
0 3 2 0y ax bx c
= + + =
có hai nghiệm dương phân biệt nên
0
0
3
20
0
3
c
P
c
a
bb
S
a
=

= −
.
Câu 43.29. Giả sử tồn tại hàm số
( )
y f x=
xác định trên
\ 1;2−
, liên tục trên mỗi khoảng xác định
và có bảng biến thiên như sau:
Câu 43.30. Cho hàm số bậc ba
( )
32
, , , , 0y ax bx cx d a b c d a= + + +
có đồ thị như hình vẽ. Mệnh
đề nào dưới đây đúng?
A.
2
0; 0; 0; 0; 3 .a b c d b ac
B.
2
0; 0; 0; 0; 3 .a b c d b ac
C.
2
0; 0; 0; 0; 3 .a b c d b ac
D.
2
0; 0; 0; 0; 3 .a b c d b ac
Lời giải
Chọn C
2
32y ax bx c
= + +
.
2
3b ac
= −
.
12
b
S x x
a
= + = −
.
Ta có
lim ( )
x
fx
→−
= −
nên
0a
.
( )
1
Nhìn vào ĐTHS khi
0x =
thì
0yd=
.
( )
4
Phương trình có hai cực trị dương nghiệm nên
0
0
0
S
P

( )
( )
( )
2
3 0 5
0 0 2
0 0 3
b ac
b
b
a
c
c
a
−
−
.
Câu 43.31. Cho hàm số
1
−
=
+
ax b
y
bx
có đồ thị
( )
C
. Nếu
( )
C
có tiệm cận ngang là đường thẳng
2=y
và
tiệm cận đứng là đường thẳng
1
3
=x
thì các giá trị của a và b lần lượt là
A.
1
2
−
và
1
6
−
. B.
3−
và
6−
. C.
1
6
−
và
1
2
−
. D.
6−
và
3−
.
y
O
x
x
−
2−
1−
1
2
3
+
y
−
0
+
+
0
−
−
0
+
y
1
3−
+
−
2
−
+
1
3
Lời giải
Chọn D
Điều kiện
1
0
−
x
b
b
.
Ta có tiệm cận đứng của đồ thị hàm số có phương trình
1
=−x
b
, tiệm cận ngang của đồ thị hàm
số có phương trình
=
a
y
b
.
Yêu cầu bài toán thỏa mãn khi
11
3
3
2
6
1
.0
−=
=−
=

=−

− +


b
b
a
a
b
ab
b
.
Câu 43.32. Cho hàm số
1
ax b
y
x
+
=
−
có đồ thị cắt trục tung tại điểm
( )
0;1A
, tiếp tuyến tại
A
có hệ số góc
3−
. Khi đó giá trị
a
,
b
thỏa mãn điều kiện sau:
A.
0ab+=
. B.
1ab+=
. C.
2ab+=
. D.
3ab+=
.
Lời giải
Chọn D
Ta có
( )
2
1
ab
y
x
−−
=
−
.
Đồ thị hàm số
1
ax b
y
x
+
=
−
cắt trục tung tại điểm
( )
0;1A
nên:
11
1
b
b= = −
−
.
Vì tiếp tuyến tại
A
có hệ số góc bằng
3−
nên:
( )
( )
2
0 3 3 4
1
ab
ya
−−
= − = − =
−
.
Vậy
3ab+=
.
-------------------- HẾT --------------------
https://toanmath.com/
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

XÁC ĐỊNH HỆ SỐ CỦA HÀM SỐ KHI BIẾT BẢNG BIẾN THIÊN HOẶC ĐỒ THỊ
VÍ DỤ MINH HỌA VÀ PHƯƠNG PHÁP GIẢI TOÁN +
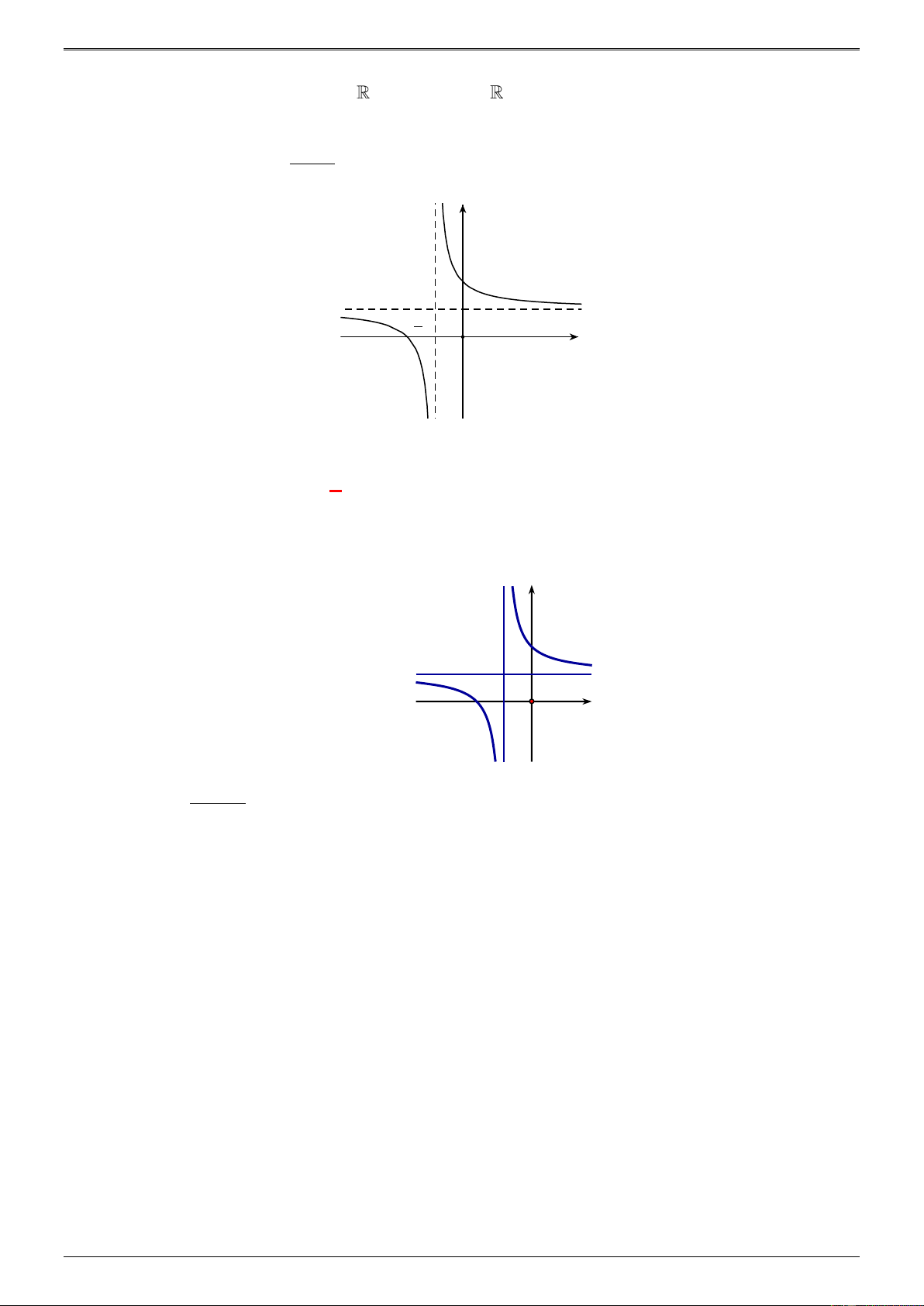
ĐỀ MINH HỌA TỐT NGHIỆP THPT 2020: Cho hàm số f (x) ax 1 =
(a, ,bc ) có bảng biến thiên bx + c như sau:
Trong các số a, b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0.
PHÂN TÍCH VÀ HƯỚNG DẪN GIẢI
1. DẠNG TOÁN: Đây là bài toán ở dạng vận dụng: Từ bảng biến thiên xác định dấu các hệ số a, b và c +
của hàm số f ( x) ax 1 = bx+ . c
2. KIẾN THỨC CẦN NHỚ: + Cho hàm số ( ) ax b
f x = cx + d +
Đồ thị hàm số ( ) ax b d f x = x = − . cx +
có tiệm cận đứng là đường thẳng d c +
Đồ thị hàm số ( ) ax b a f x = y = . cx +
có tiệm cận ngang là đường thẳng d c + −
Đạo hàm của hàm số ( ) ax b ad bc f x = f ' x = . cx + là ( ) d (cx + d)2 3. HƯỚNG GIẢI: ax +
B1: Từ công thức của hàm số f ( x) 1
= bx+ chỉ ra phương trình đường thẳng của tiệm cận đứng, tiệm c
cận ngang và công thức tính đạo hàm của nó.
B2: Từ bảng biến thiên chỉ ra tiệm cận đứng, tiệm cận ngang của đồ thị hàm số và chiều biến thiên của hàm số đó.
B3: Thay các dữ kiện ở bước 1 vào bước 2 ta sẽ xác định được dấu của các hệ số a, b và c.
Từ đó, ta có thể giải bài toán cụ thể như sau: LỜI GIẢI CHI TIẾT Chọn C + Đồ ax c
thị hàm số f ( x) 1 = x = −
và đường tiệm cận ngang
bx + có đường tiệm cận đứng là đường thẳng c b là đườ a ng thẳng y = . bc − = 2  b c
Từ bảng biến thiên ta có: 
a = b = − (1) a 2  =1 b ac − b
Mặt khác: f '( x) = ( . bx + c)2
Vì hàm số đã cho đồng biến trên các khoảng ( ; − 2) và (2;+) nên ac − b f '( x) =   −  ( (2) bx + c) 0 ac b 0 2 2 Thay (1) vào (2), ta đượ c c c: 2 −
+  0  −c + c  0  0  c 1. 2 2
Suy ra c là số dương và a, b là số âm.
BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN - PHẦN 1 ax + m + Câu 1:
Cho hàm số f ( x) 2 4 =
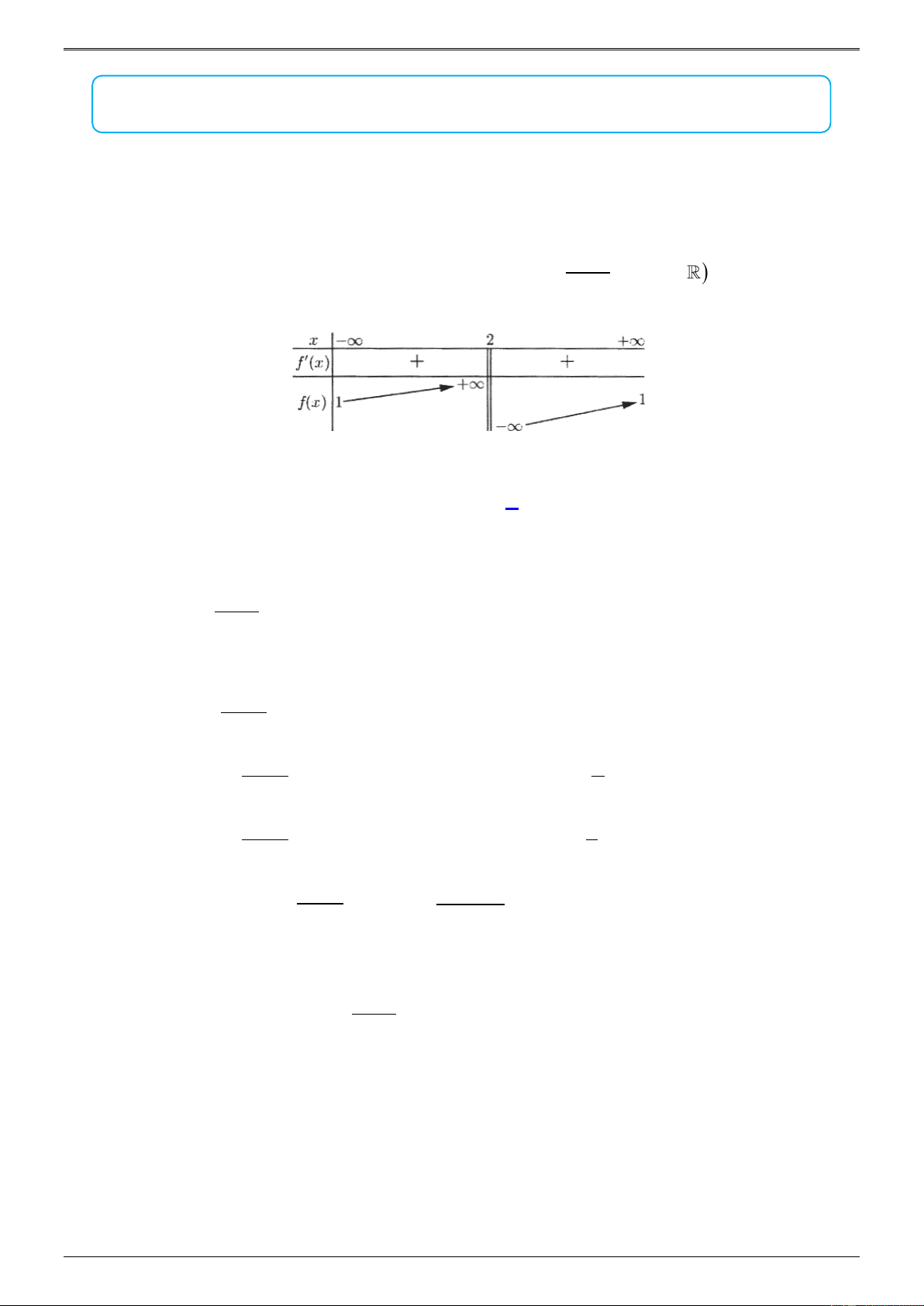
(a, ,b ,cm ) có bảng biến thiên như sau: bx + c x − 3 + f ( x) + + + 1 f ( x) 1 −
Trong các số a , b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn C c
Tiệm cận đứng: x = 3  0  −  0  bc  0 . b a
Tiệm cận ngang: y = 1  0   0  ab  0 . b 2 + Đồ m 4
thị hàm số cắt trục hoành tại điểm có hoành độ x  3  0  −
 0  a  0 b  0 ac  0. ax + Câu 2:
Cho hàm số f ( x) 9 =
(a, ,b c ) có bảng biến thiên như sau: bx + c x − 2 − + f ( x) – – 3 + f ( x) − 3
Trong các số a , b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn B c
Tiệm cận đứng: x = 2
−  0  −  0  bc  0. b a
Tiệm cận ngang: y = 3  0   0  ab  0 . b Đồ 9
thị hàm số cắt trục hoành tại điểm có hoành độ x  2
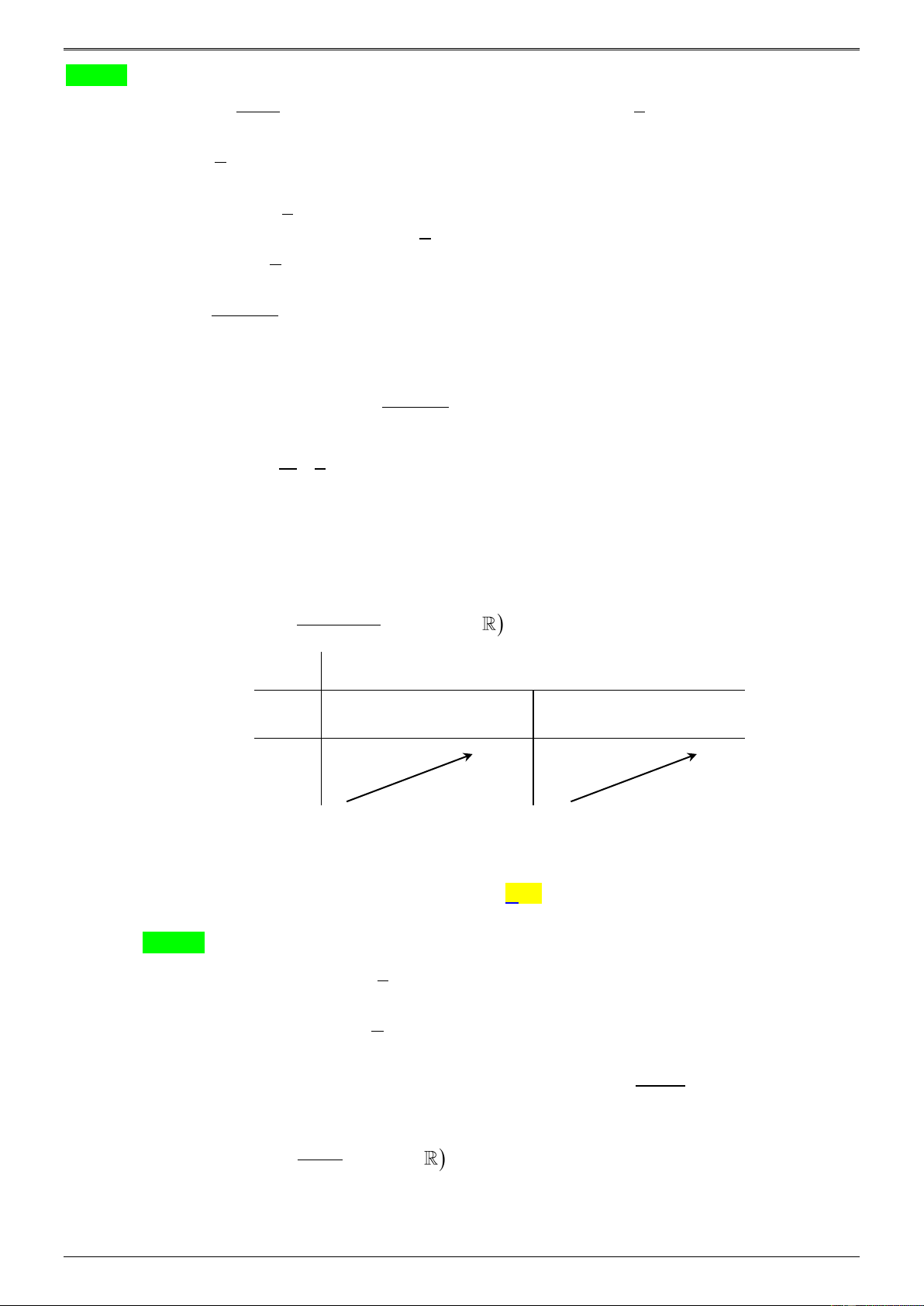
−  0  −  0  a  0  b  0 ac  0. + Câu 3: Cho hàm số ( ) ax b f x =
( ,a ,b ,cd  ,a  0) có bảng biến thiên như sau: cx + d x − −1 + f ( x) – – 2 + f ( x) − 2
Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. b  0, c  0 , d  0 .
B. b  0 , c  0 , d  0 .
C. b  0 , c  0 , d  0 .
D. b  0 , c  0 , d  0 . Lời giải Chọn A a
Tiệm cận ngang: y = 2  0 
 0 , mà a  0  c  0. c d d
Tiệm cận đứng: x = 1
−  0  −  0   0 , mà c  0  d  0. c c Đồ b b
thị hàm số cắt trục hoành tại điểm có hoành độ x  1
−  0  −  0   0  b  0 . a a + Câu 4: Cho hàm số ( ) ax b f x =
( ,a ,b ,cd  ,a  0) có bảng biến thiên như sau: cx + d x − 1 + f ( x) + + + 2 f ( x) 2 −
Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. b  0, c  0 , d  0 .
B. b  0 , c  0 , d  0 .
C. b  0 , c  0 , d  0 .
D. b  0 , c  0 , d  0 . Lời giải Chọn D a
Tiệm cận ngang: y = 2  0 
 0 , mà a  0  c  0 . c d d
Tiệm cận đứng: x =1  0  −  0 
 0 , mà c  0  d  0. c c Đồ b b
thị hàm số cắt trục hoành tại điểm có hoành độ x 1  0  −
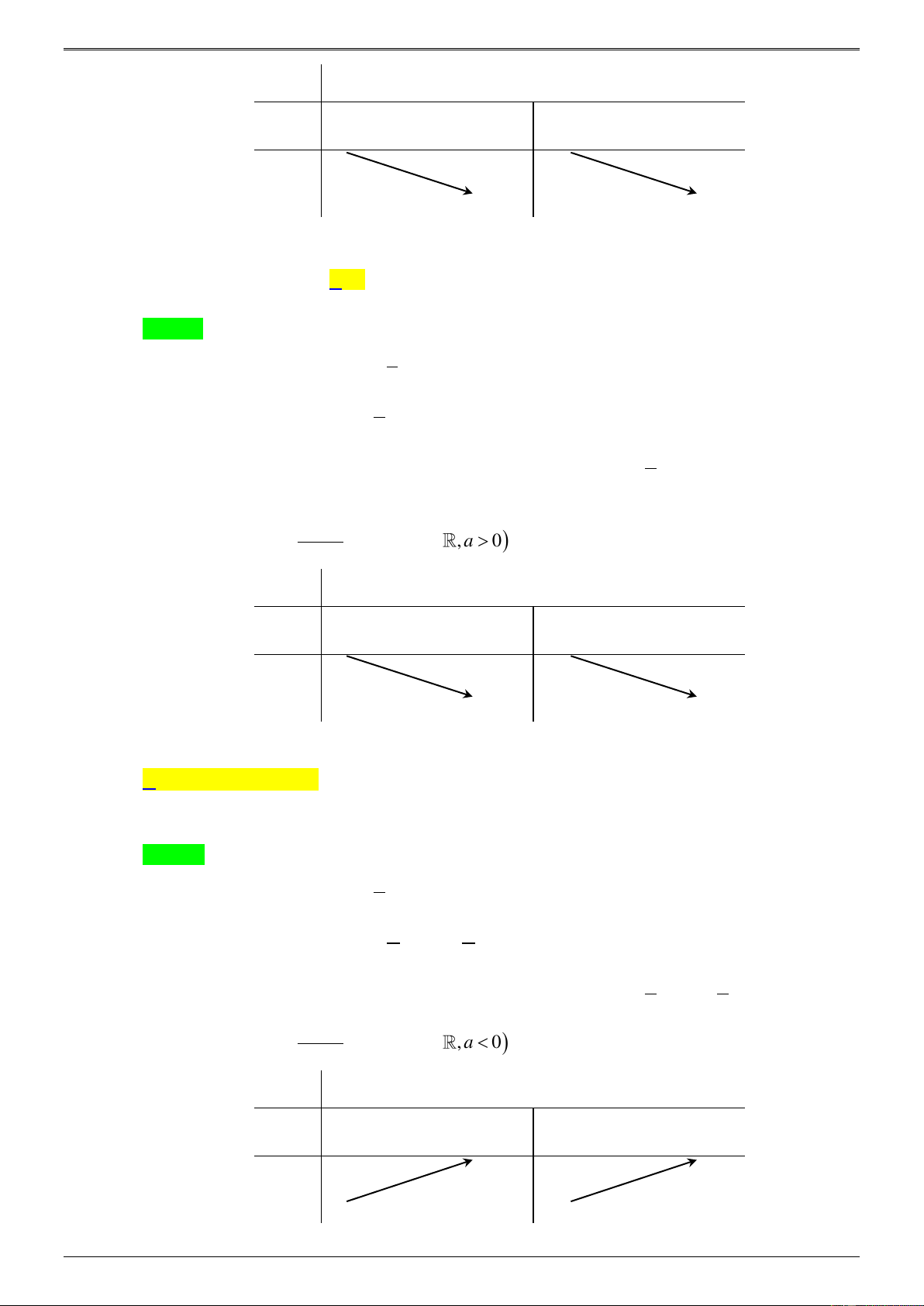
 0   0  b  0 . a a ax − Câu 5:
Cho hàm số f ( x) 2 =
(a, ,b ,cm ) có bảng biến thiên như sau: bx + c x − 1 + f ( x) + + + 1 f ( x) 1 −
Trong các số a , b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn A c
Tiệm cận đứng: x =1  0  −  0  bc  0 . b a
Tiệm cận ngang: y = 1  0   0  ab  0 . b Đồ 2
thị hàm số cắt trục hoành tại điểm có hoành độ x 1  0 
 0  a  0  b  0 ac  0 . ax + 2020 Câu 6:
Cho hàm số f ( x) = (a, ,bc ) bx +
có bảng biến thiên như sau: c x − 4 + y + + + 1 y 1 − − 3 − 3
Kết quả nào sau đây đúng?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0.
D. a  0, b  0, c  0. Lời giải Chọn B c
+ Tiệm cận đứng: x = 4  0  −  0  bc  0 b 1 a
+ Tiệm cận ngang: y = −
 0   0  ab  0 3 b + Đồ 2020
thị hàm số cắt trục hoành tại điểm x  4  x  0  −
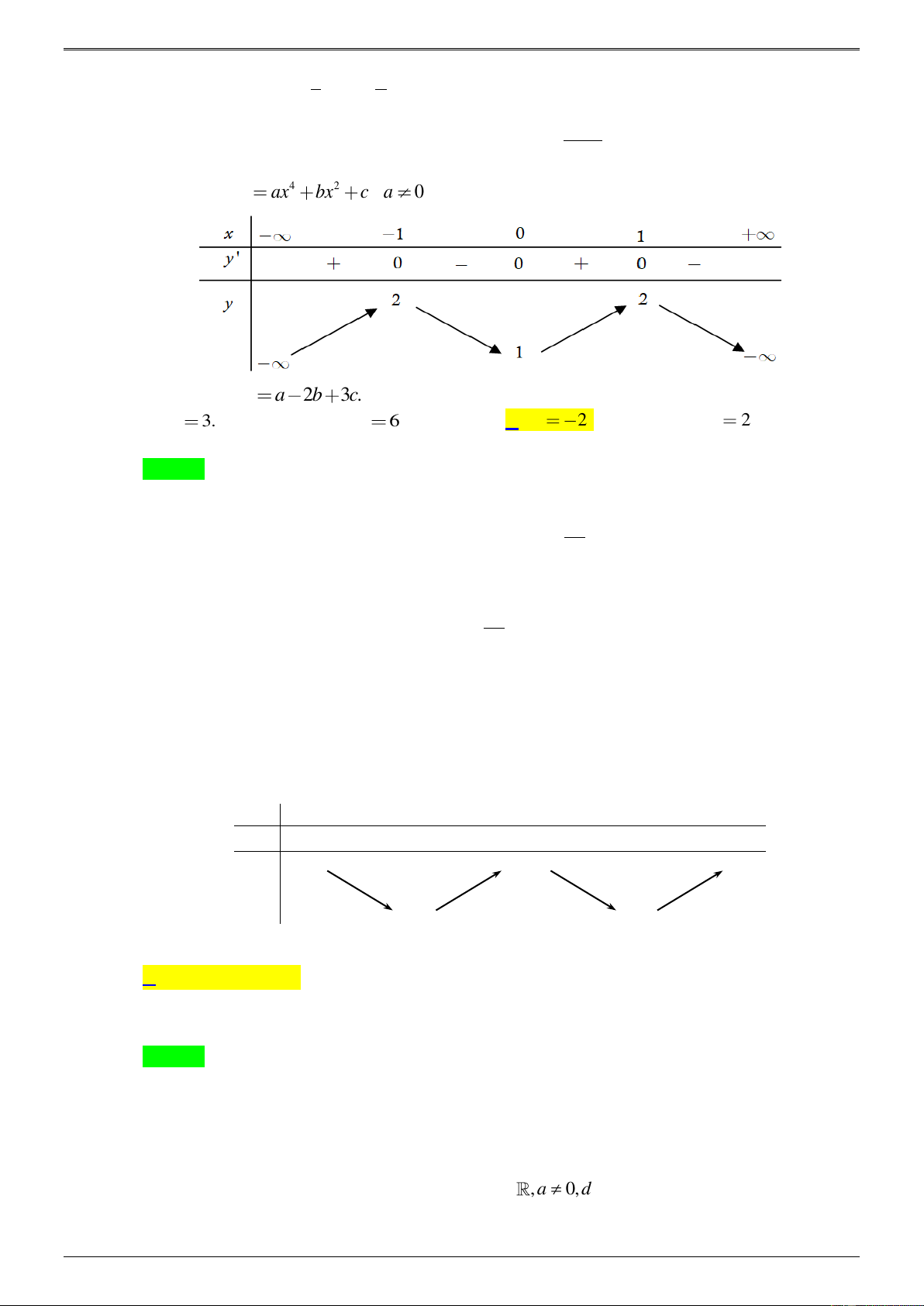
 0  a  0  b  0  c  0 . a Câu 7: Cho hàm số 4 2 y ax bx c a
0 có bảng biến thiên dưới đây: Tính P a 2b 3 . c A. P 3. B. P 6 . C. P 2 . D. P 2 . Lời giải Chọn C x = 0 Ta có 3 2
y = 4ax + 2bx = 2x(2ax + b) , y = 0   b . 2 x = −  2a
Căn cứ vào bảng biến thiên ta thấy a  0 ; b  0, hàm đạt cực đại tại x = 1  và y ( ) 1 = 2 , hàm  b − = 1   = − 2a a 1  
đạt cực tiểu tại x = 0 và y (0) =1. Suy ra, a + b + c = 2  b  = 2 .   c = 1  c = 1  
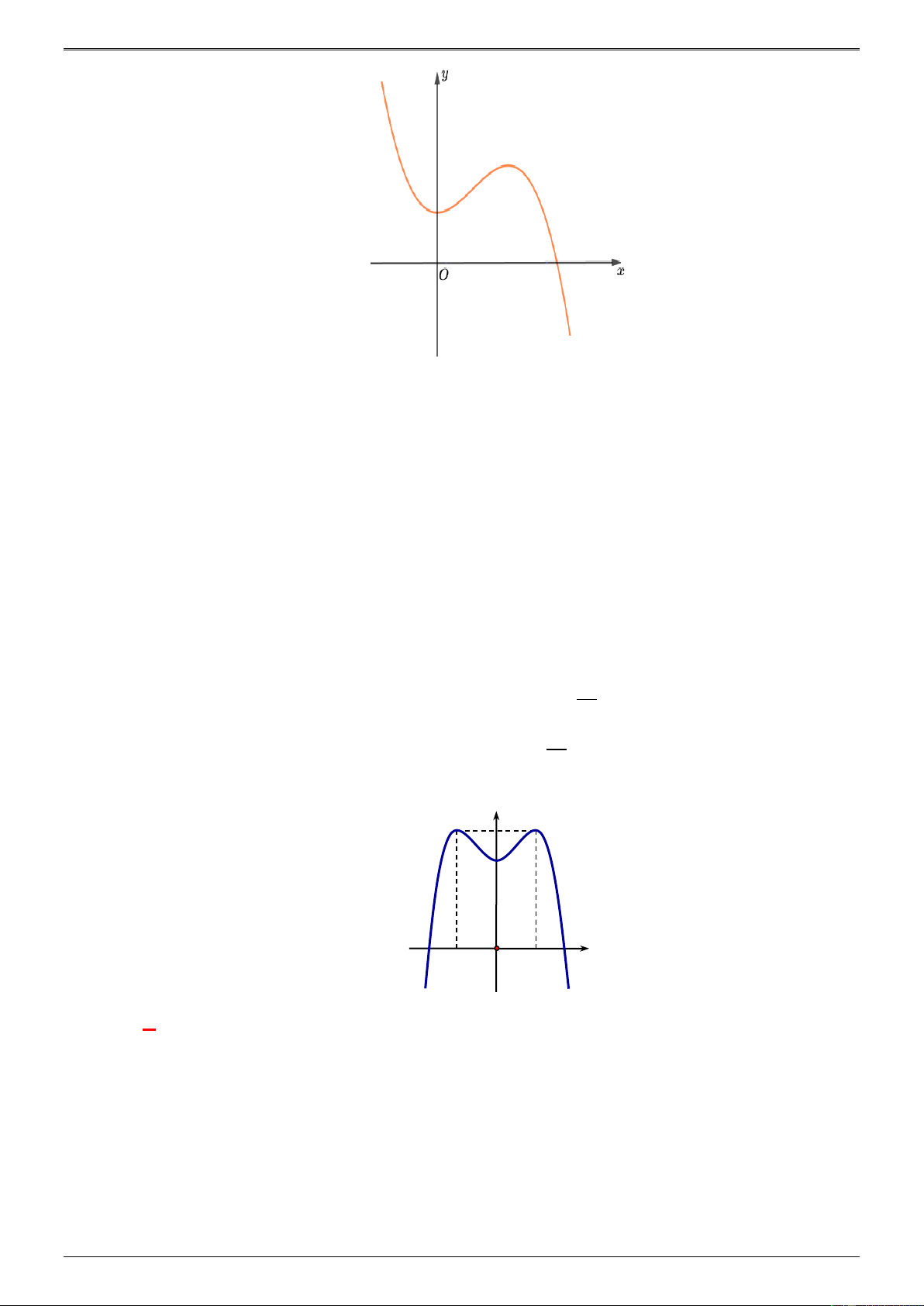
Do đó: P = a − 2b +3c = 2 − . Câu 8: Cho đồ thị hàm số ( ) 4 2
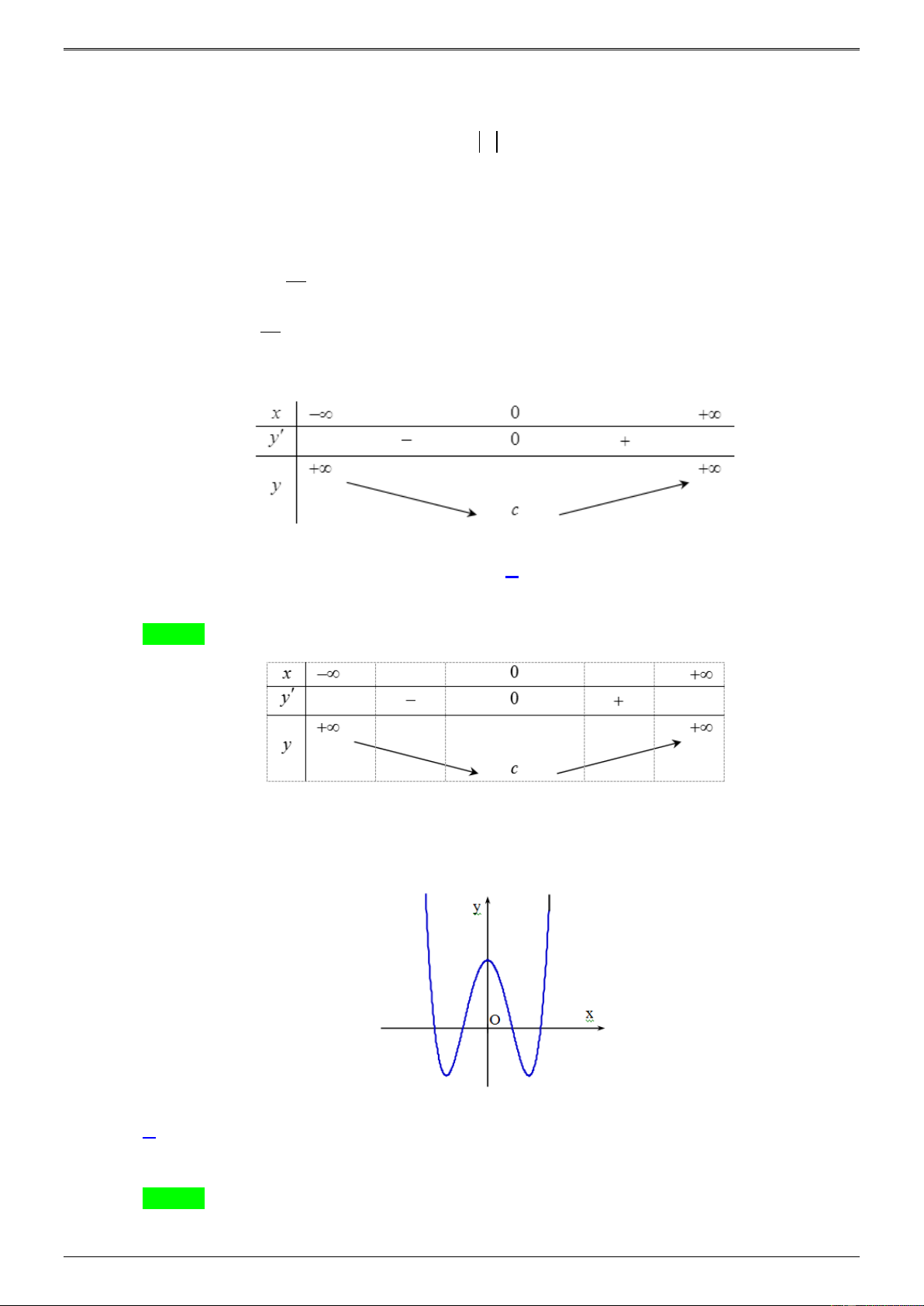
f x = ax + bx + c như hình vẽ. x − −1 0 1 + y − 0 + 0 − 0 + + 3 + y 0 0
Mệnh đề nào sau đây đúng?
A. a  0, b  0, c  0 .
B. a  0, b  0, c  0 .
C. a  0, b  0, c  0 .
D. a  0, b  0, c  0 . Lời giải Chọn A
Ta có: lim y = + nên a  0 . x→+
Đồ thị hàm số cắt Oy tại điểm (0;3) do đó c = 3  0.
Đồ thị hàm số có 3 điểm cực trị nên: ab  0  b  0 . Câu 9:
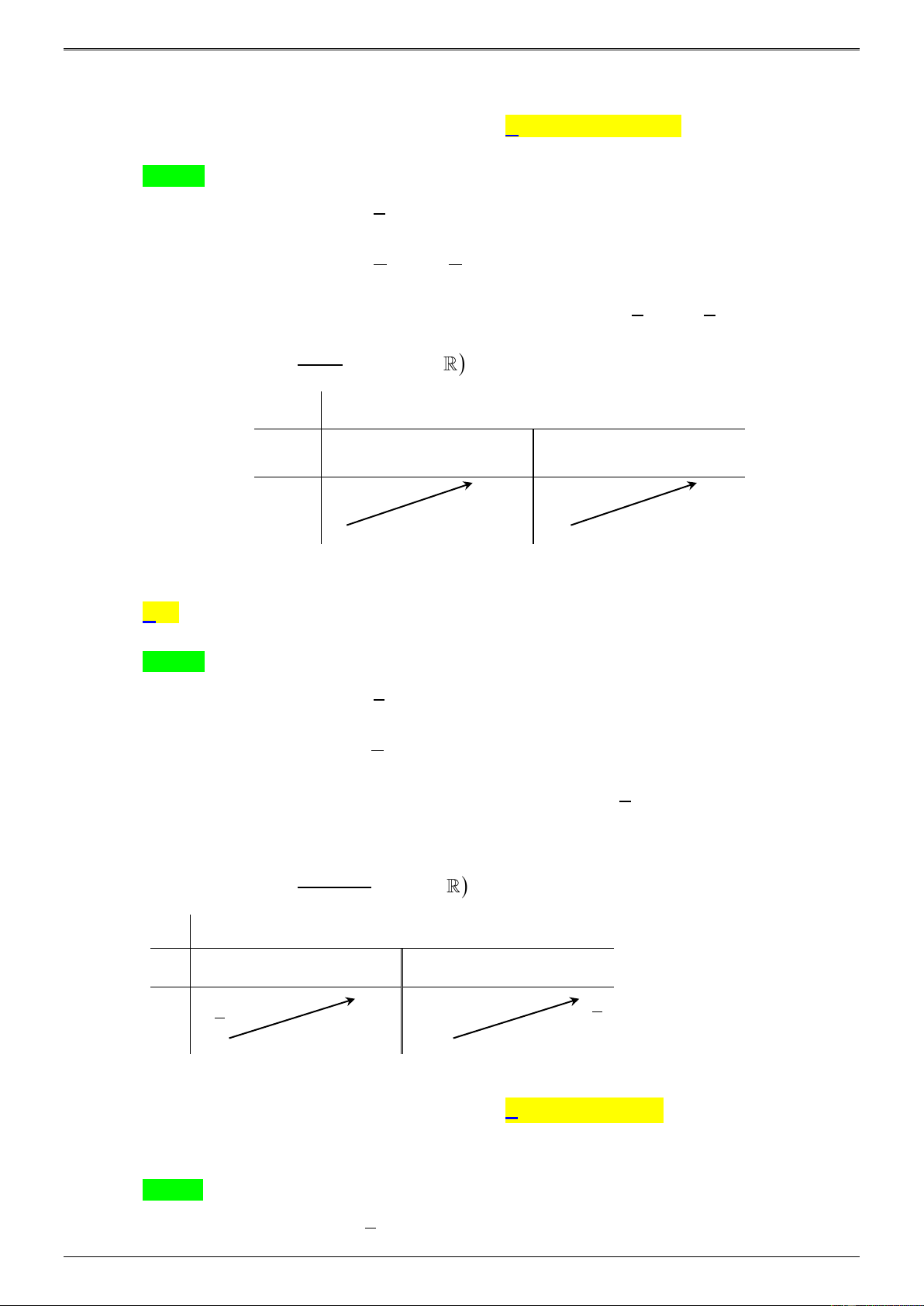
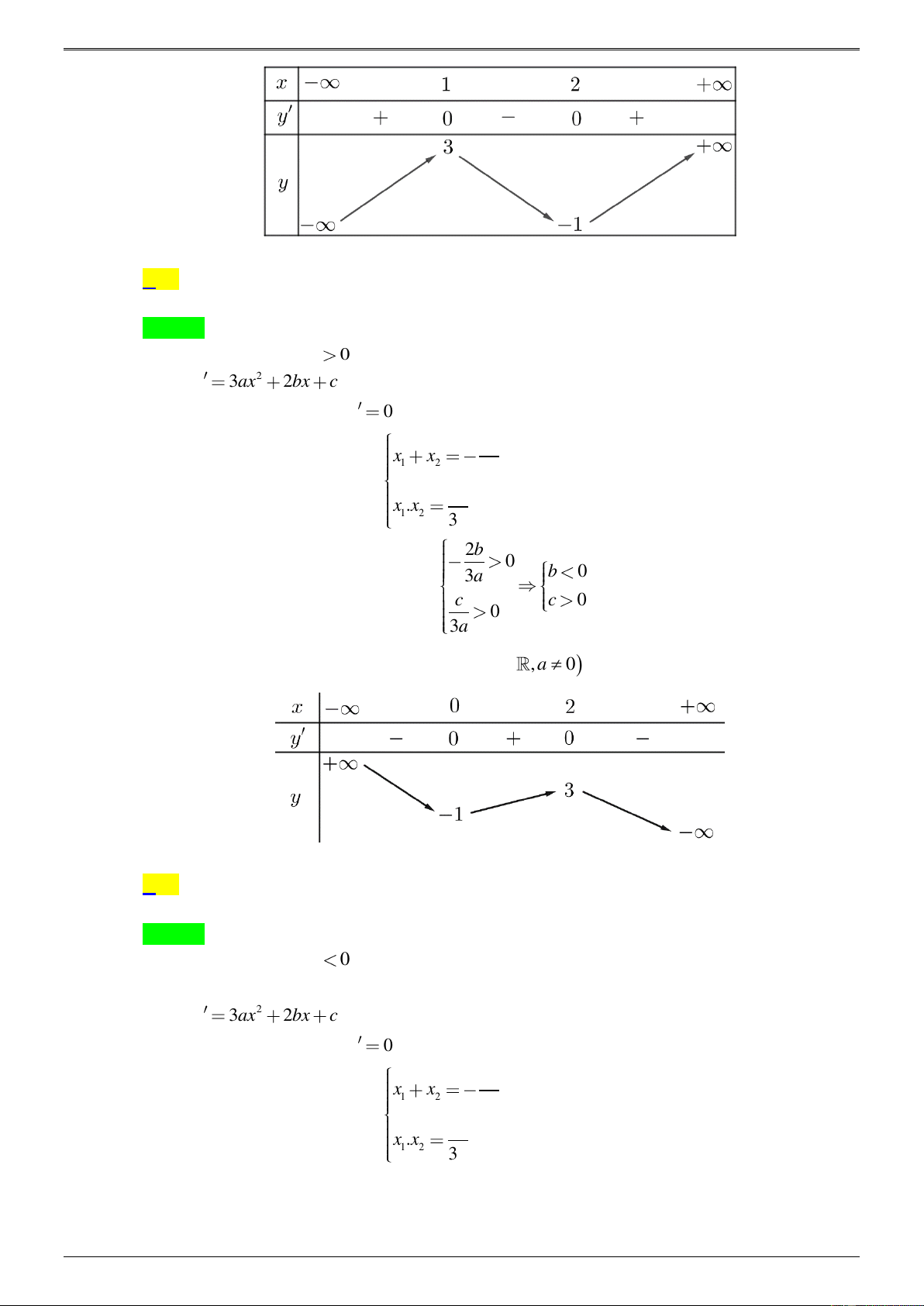
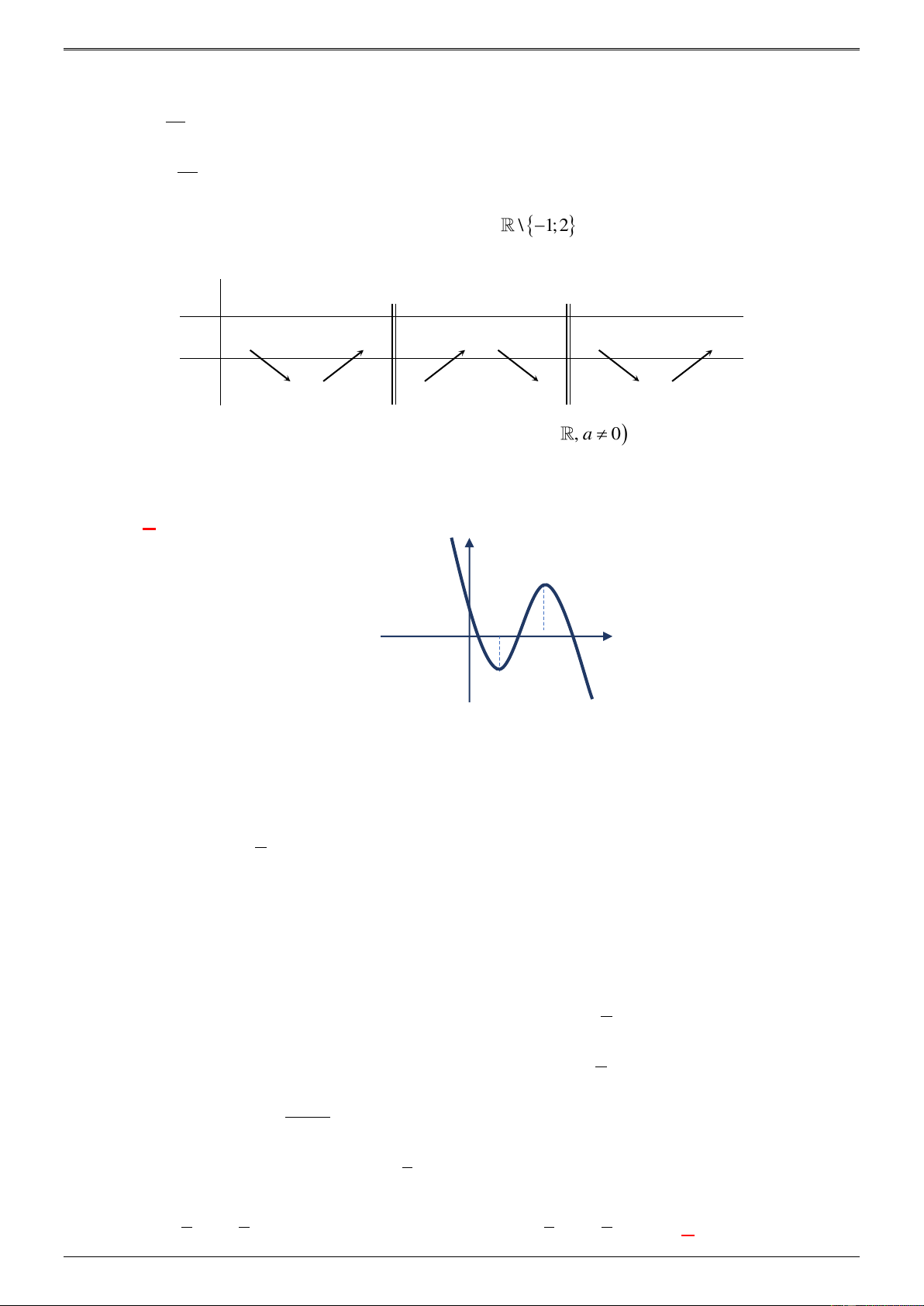
Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a, ,
b c, d  , a  0, d  0) có bảng biến thiên như sau:
Trong các số a, b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn A
Từ dạng đồ thị suy ra a 0 . Ta có 2 y 3ax 2bx c
Vì hàm số có 2 cực trị nên y
0 có 2 nghiệm phân biệt x , x . 1 2 2b x x 1 2 3a
Nên theo công thức Vi-ét ta có: . c x .x 1 2 3a 2b 0 b 0 3a
Dựa vào hoành độ 2 điểm cực trị ta có: . c c 0 0 3a
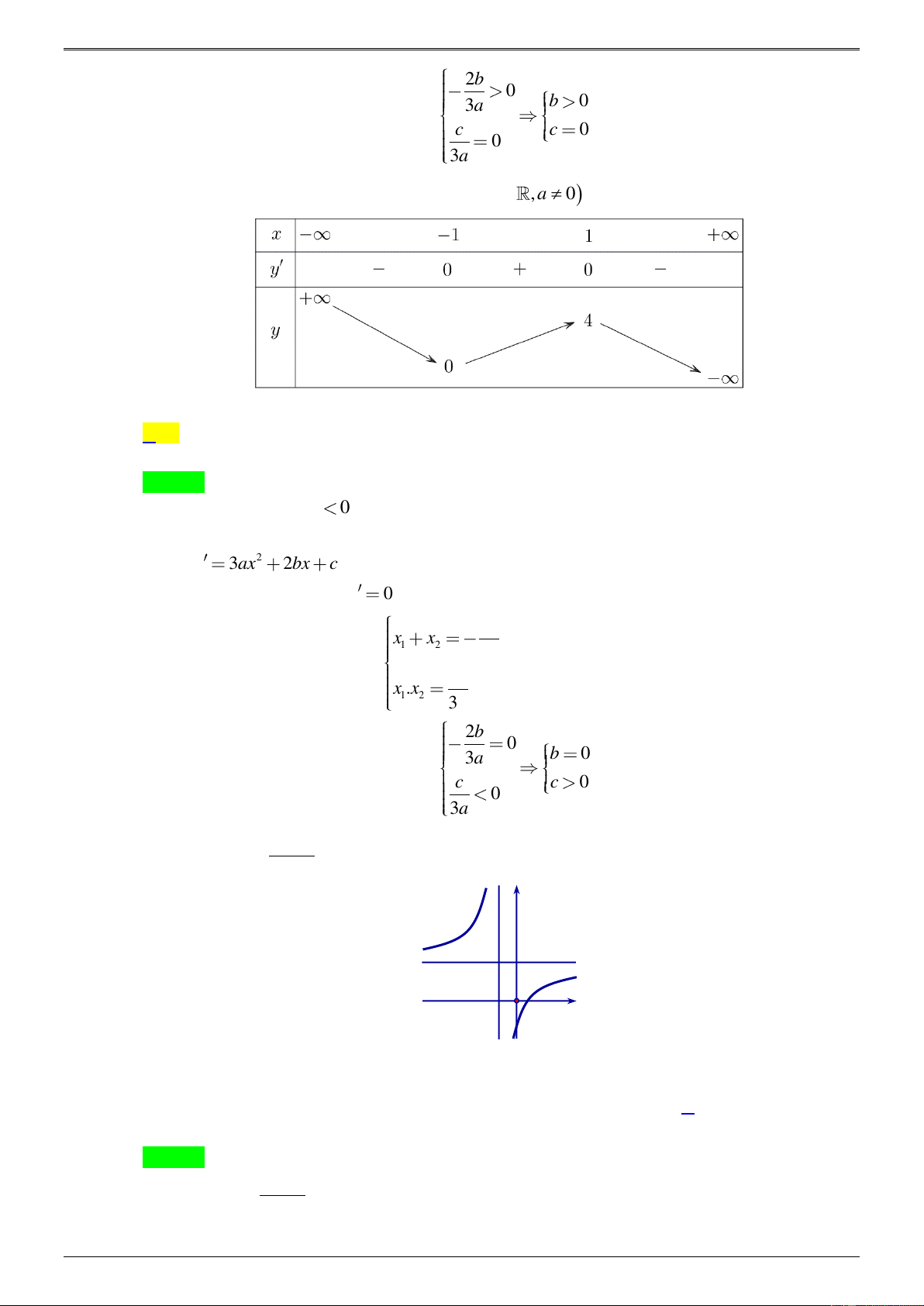
Câu 10: Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a, , b ,
c d  , a  0) có bảng biến thiên như sau:
Trong các số a, b và c có bao nhiêu số âm? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn A
Từ dạng đồ thị suy ra a 0 .
x = 0  y = d = 1 −  d  0 . Ta có 2 y 3ax 2bx c
Vì hàm số có 2 cực trị nên y
0 có 2 nghiệm phân biệt x , x . 1 2 2b x x 1 2 3a
Nên theo công thức Vi-ét ta có: . c x .x 1 2 3a 2b 0 b 0 3a
Dựa vào hoành độ 2 điểm cực trị ta có: . c c 0 0 3a
Câu 11: Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a, , b ,
c d  , a  0) có bảng biến thiên như sau:
Trong các số a, b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn A
Từ dạng đồ thị suy ra a 0 .
x = 0  y = d  0 . Ta có 2 y 3ax 2bx c
Vì hàm số có 2 cực trị nên y
0 có 2 nghiệm phân biệt x , x . 1 2 2b x x 1 2 3a
Nên theo công thức Vi-ét ta có: . c x .x 1 2 3a 2b 0 b 0 3a
Dựa vào hoành độ 2 điểm cực trị ta có: . c c 0 0 3a ax + b
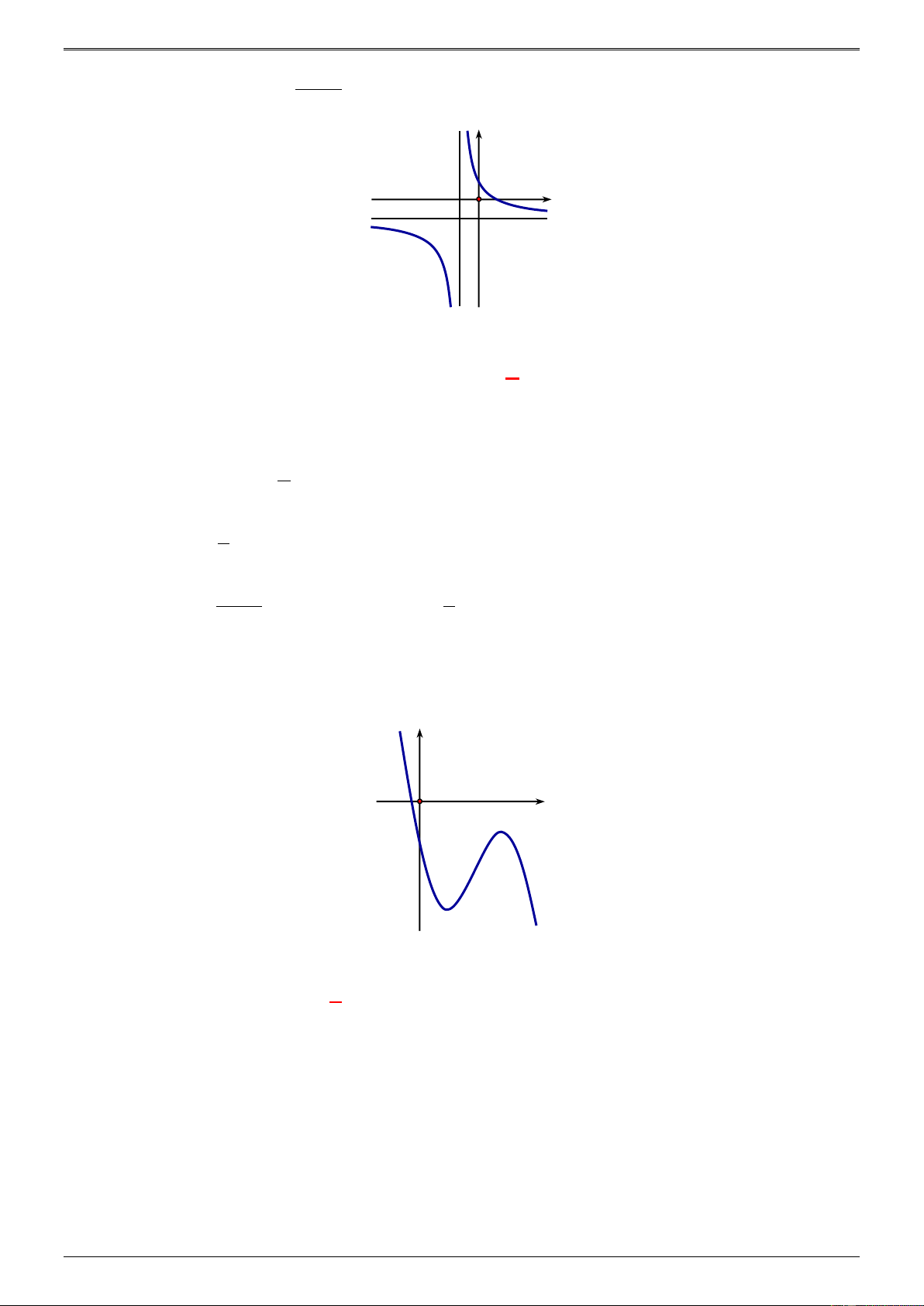
Câu 12: Cho hàm số y =
có đồ thị như hình vẽ bên. x − c y O x
Tìm khẳng định đúng trong các khẳng định sau
A. a  0, b  0, c  0 .
B. a  0, b  0, c  0 . C. a  0, b  0, c  0 . D. a  0, b  0, c  0 . Lời giải Chọn D + ❖ Từ hàm số ax b y = suy ra: x − c
+ Tiệm cận đứng của đồ thị là đường thẳng có phương trình x = c .
+ Tiệm cận ngang của đồ thị là đường thẳng có phương trình y = a .   + Giao điể b
m với trục hoành là A − ;0   , a  0 .  a    + Giao điể b
m với trục tung là B 0; −   , c  0.  c
❖ Từ đồ thị hàm số ta có:
+ Đường tiệm cận đứng nằm bên trái Oy nên c  0 .
+ Đường tiệm cận ngang nằm trên Ox nên a  0 . + Giao điể b
m với trục Ox có hoành độ dương nên −
 0 . Vì a  0 nên b  0. a ax −1
Câu 13: Cho hàm số y =
(a,d  ,ad +1 0) x +
có đồ thị như hình bên. d
Mệnh đề nào dưới đây đúng? a  0 a  0 A. B.  d  0 d  0 a  0 a  0 C. D.  d  0 d  0 Lời giải Chọn A
+ Phương trình tiệm cận đứng: x = d
− . Dựa vào đồ thị ta có d −  0  d  0
+ Phương trình tiệm cận ngang: y = a . Dựa vào đồ thị ta có a  0 Câu 14: Cho hàm số = ( ) 3 2 y
f x = ax + bx + cx + d có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây đúng?
A. a  0 , b  0, c  0 , d  0 .
B. a  0 , b  0 , c  0 , d  0 .
C. a  0 , b  0 , c  0 , d  0 .
D. a  0 , b  0 , c  0 , d  0 . Lời giải Chọn C Ta có 2
y = 3ax + 2bx + c
Dựa vào đồ thị ta thấy nhánh cuối cùng bên phải hướng lên trên suy ra a  0 .
Đồ thị cắt trục tung tại điểm x =1  d =1 0 . b
Hàm số có 2 điểm cực trị x = 1  0 , x = 3  0  x + x  2 0  −
 0 b  0. 1 2 1 2 3a c x x  0 
 0  c  0. 1 2 3a
Vậy a  0 , b  0 , c  0 , d  0 .
Câu 15: Đồ thị hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ sau. Mệnh đề nào sau đây đúng.
A. a  0;b  0; c  0; d  0 .
B. a  0;b  0; c  0; d  0 .
C. a  0;b  0; c  0; d  0 .
D. a  0;b  0; c  0; d  0 . Lời giải Chọn A
Có a  0 do điểm cuối đồ thị có hướng đi xuống.
d  0 do giao điểm của đồ thị với Oy nằm phía trên Ox .
Đồ thị có 2 cực trị trái dấu nên 3 .
a c  0  c  0 . b
Hoành độ điểm uốn dương nên −  0  b  0 . 3a Câu 16: Cho hàm số 4 2
y = ax + bx + c (a, ,
b c  ) có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A. a  0;b  0; c  0.
B. a  0;b  0; c  0.
C. a  0;b  0; c  0.
D. a  0;b  0; c  0. Lời giải Chọn D
+ Dựa vào dạng đồ thị ta thấy: a  0 .
+ Dựa vào đồ thị ta thấy đồ thị hàm số có 3 điểm cực trị nên: ab  0  b  0 .
+ Với x = 0 ta có: y (0) = c  0. Câu 17: Cho hàm số 4 2
y = ax + bx + c (a, ,
b c  ) có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A. a  0;b  0; c  0.
B. a  0;b  0; c  0.
C. a  0;b  0; c  0.
D. a  0;b  0; c  0. Lời giải Chọn B
+ Dựa vào dạng đồ thị ta thấy: a  0 .
+ Dựa vào đồ thị ta thấy đồ thị hàm số có 3 điểm cực trị nên: ab  0  b  0 .
+ Với x = 0 ta có: y (0) = c  0 . Câu 18: Cho hàm số ( ) 4 2
f x = ax + bx + c với a  0 có đồ thị như hình vẽ:
Tìm mệnh đề đúng trong các mệnh đề sau?
A. a  0 ; b  0 ; c  0 .
B. a  0 ; b  0 ; c  0 .
C. a  0 ; b  0 ; c  0 .
D. a  0 ; b  0 ; c  0 . Lời giải Chọn A
Ta có nhánh bên phải đồ thị đi xuống, suy ra a  0 .
Mặt khác do đồ thị có ba cực trị suy ra ab  0 mà a  0  b  0 .
Mà giao điểm của đồ thị với trục Oy tại điểm có tung độ y = c  0 .
Vậy chọn đáp án A.
Câu 19: 2 Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị là đường cong như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c = 0, d  0 .
B. a  0, b = 0, c  0, d  0 .
C. a  0, b = 0, c  0, d  0 .
D. a  0, b = 0, c  0, d  0 . Lời giải Chọn A
Do nhánh cuối của đồ thị đi lên nên ta có a  0 . Ta có 2
y = 3ax + 2bx + c . Do cực tiểu của hàm số thuộc trục tung và có giá trị âm nên d  0
và x = 0 là nghiệm của phương trình y = 0  c = 0 . x = 0 2b Lại có 2  3ax + 2bx = 0 2b  −
 0  a  0,b  0  . x = − 3a  3a
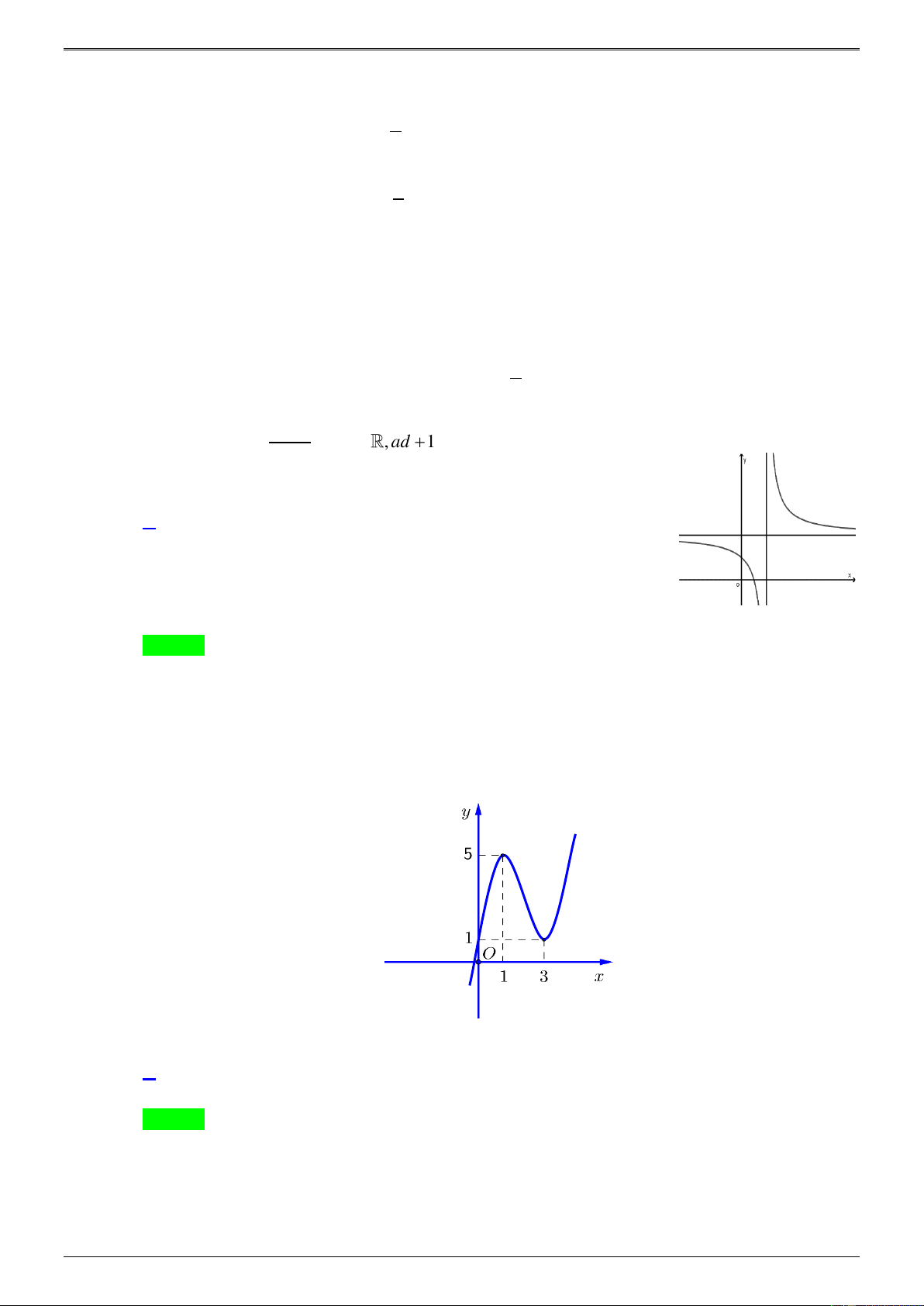
Câu 20: Cho hàm số bậc ba f ( x) 3 2
= x + bx + cx + d . Biết đồ thị của hàm số y = f (x) như hình vẽ. c Giá trị của là: b y x O 1 1 3 2 2 1 3 1 3 A. − . B. . C. . D. − . 3 4 3 4 Lời giải Chọn D
Tập xác định D = .
Đạo hàm cấp 1 f (x) 2
= 3ax + 2bx + c
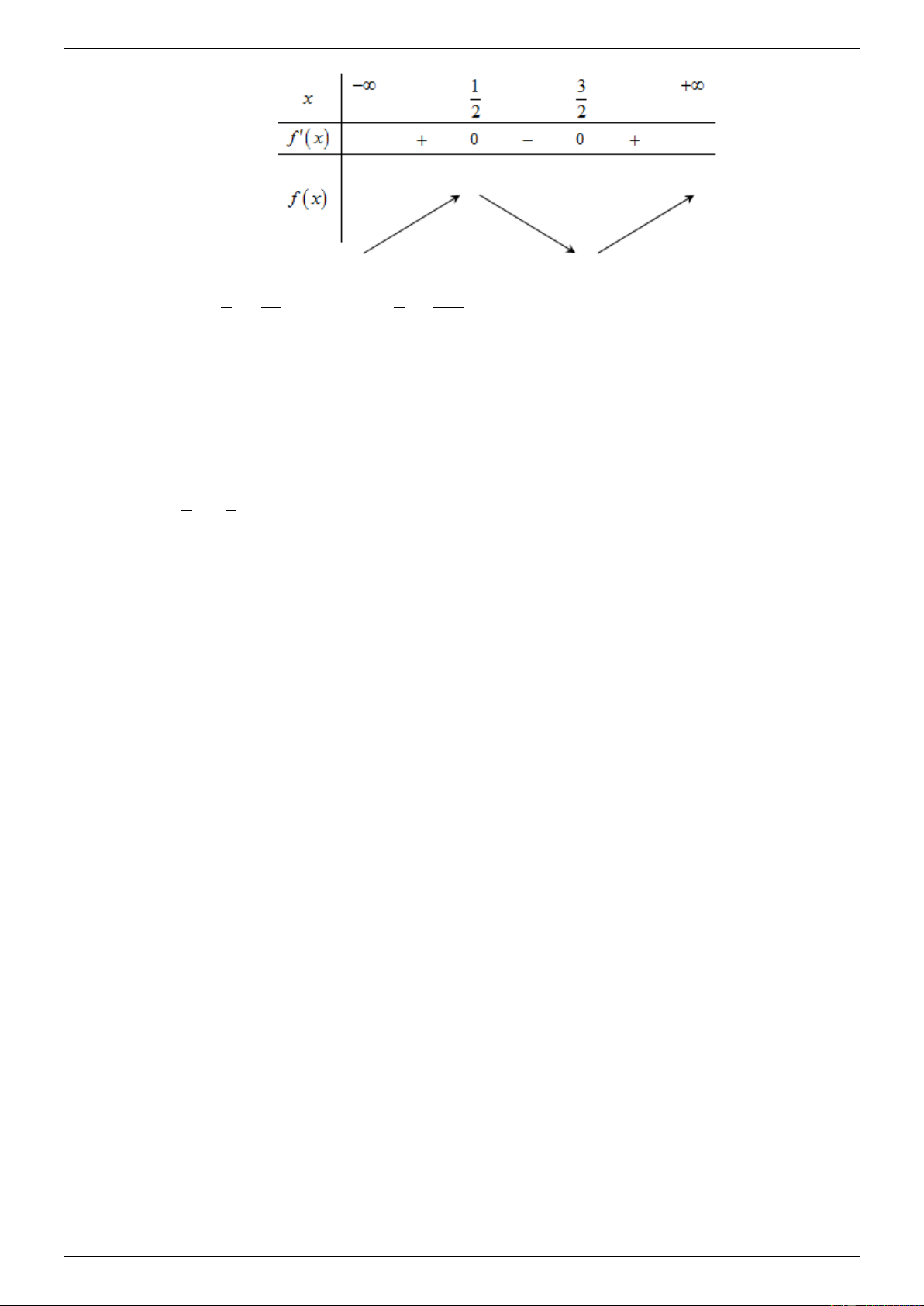
Dựa vào đồ thị của hàm số y = f ( x) ta có bảng thiên của hàm số f ( x)  1  3a  3  27a Ta có f  = + b +   c và f  = + 3b +   c .  2  4  2  4 3
a + 4b + 4c = 0
27a + 36b + 36c = 0
Dựa vào bảng biến thiên ta có    .
27a +12b + 4c = 0
27a +12b + 4c = 0 c 3
 24b + 32c = 0  = − . b 4 c 3 Vậy = − . b 4
BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN - PHẦN 2Mức độ 3  
Câu 43.1.
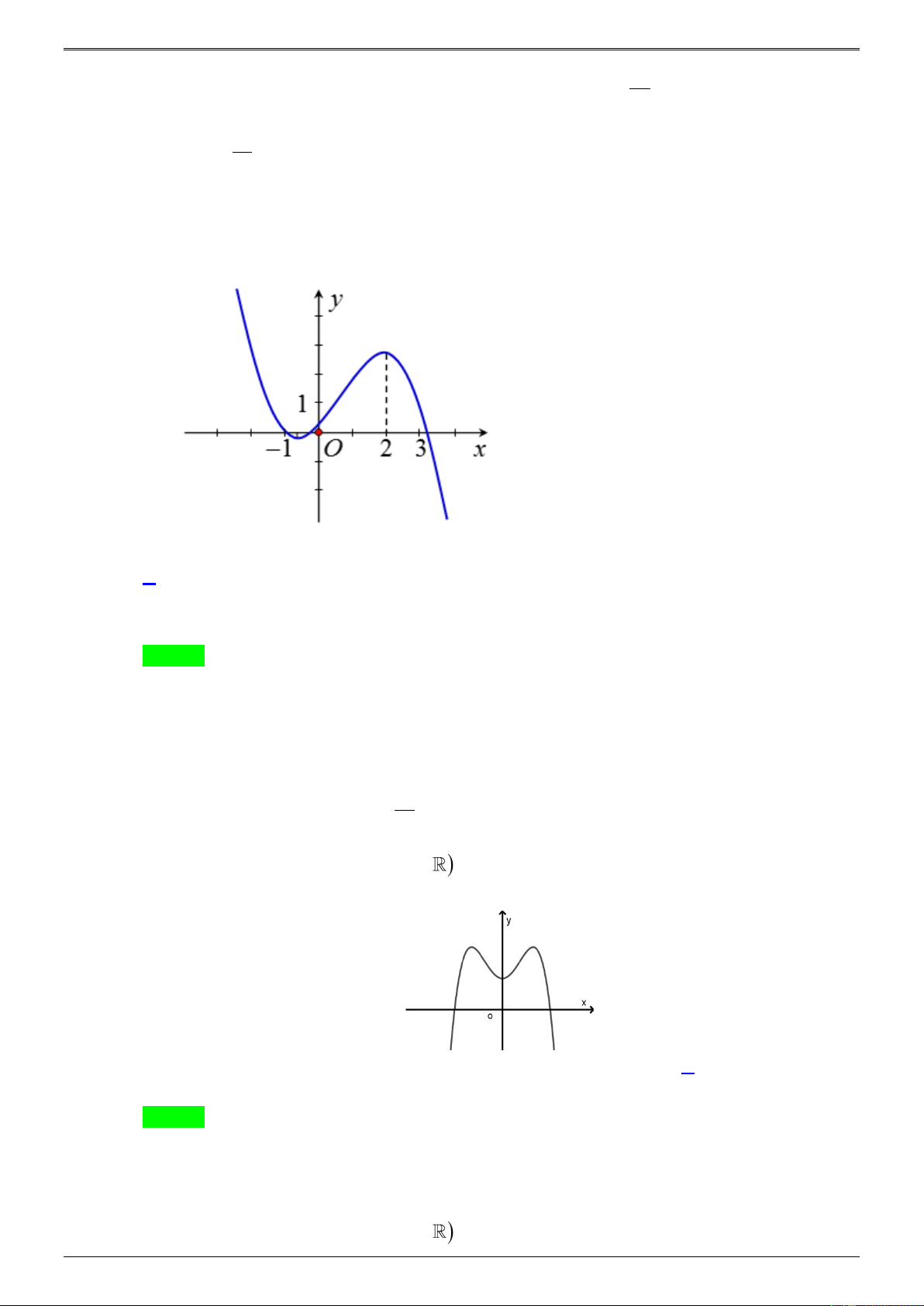
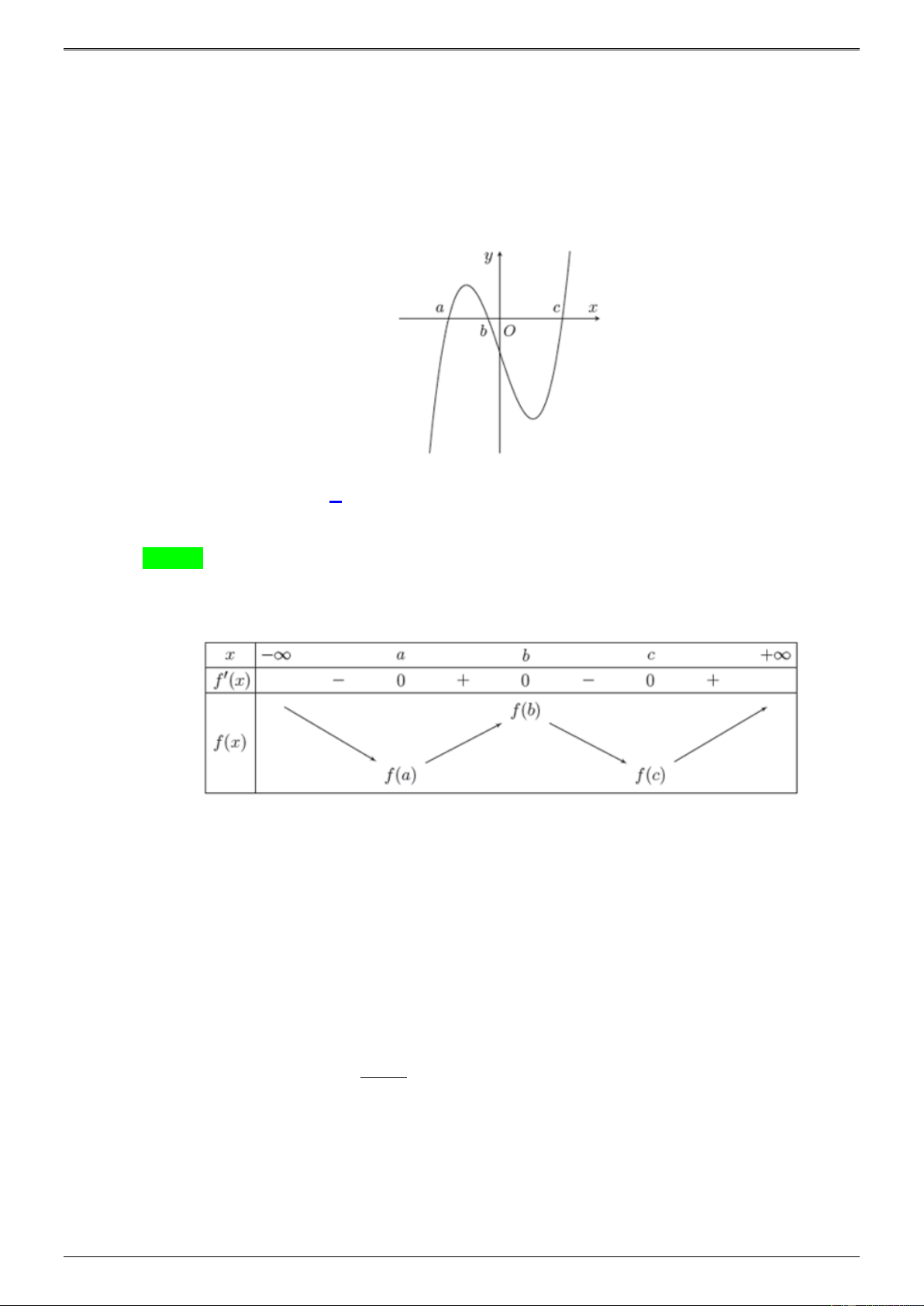
Cho hàm số y = f (x) có đạo hàm f (x) , biết rằng đồ thị của hàm số f (x) như hình vẽ. Biết
f (a)  0 , hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm? A. 4. B. 2. C. 3. D. 1 Lời giải Chọn B
Dựa vào đồ thị của hàm số f (x) , ta có bảng biến thiên của hàm số y = f (x) như sau:
Vì f (a)  0 nên ta xét các trường hợp sau:
・ Nếu f (c)0 thì toàn bộ đồ thị hàm số nằm ở phía trên trục hoành, do đó đồ thị hàm số không cắt trục hoành.
・ Nếu f (c) = 0 thì đồ thị hàm số và trục hoành có một điểm chung duy nhất
・ Nếu f (c)  0 thì đồ thị hàm số và trục hoành có hai điểm chung
Vây đồ thị hàm số y = f (x) cắt trục hoành nhiều nhất tại hai điểm. +
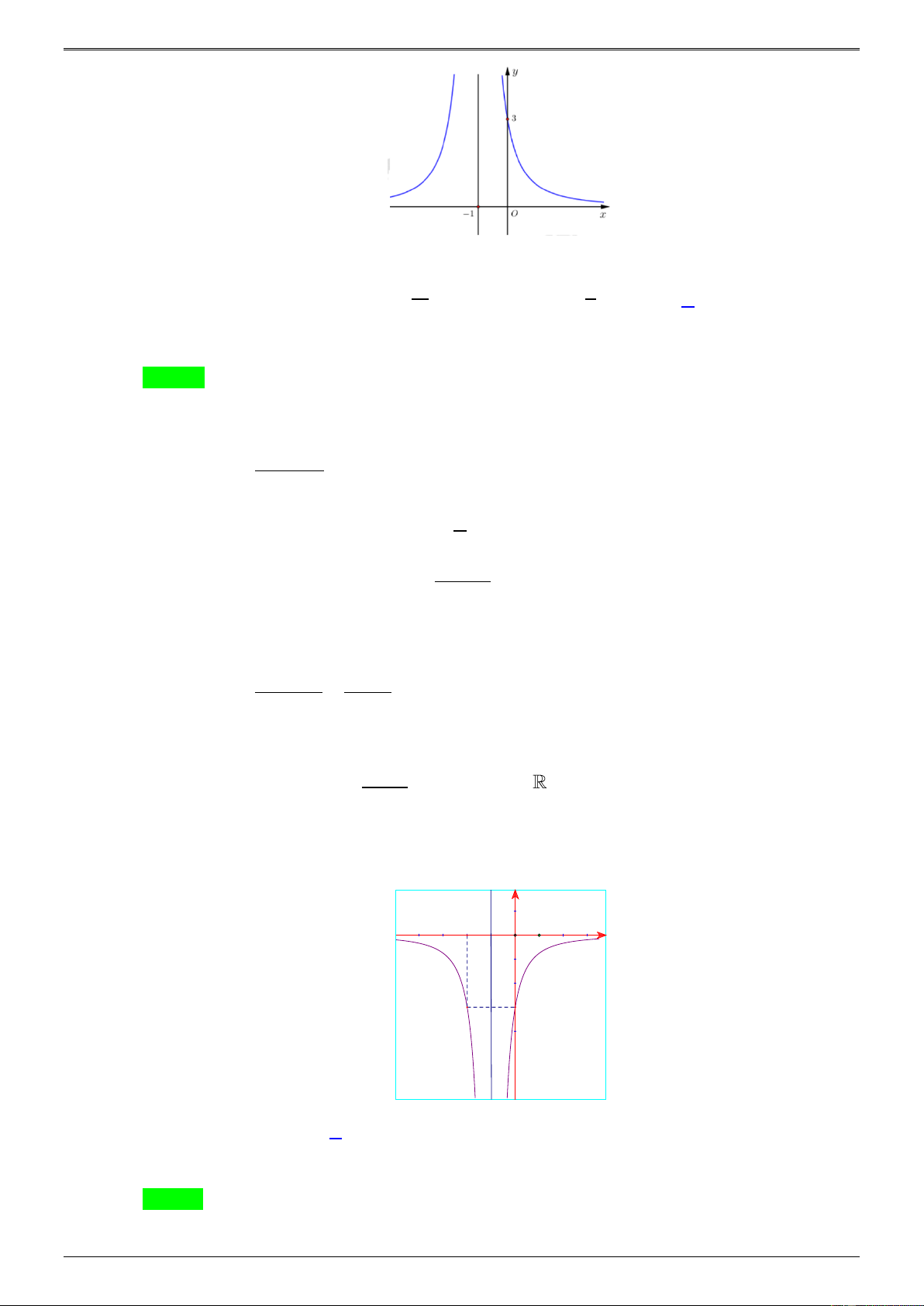
Câu 43.2. Cho hàm số y = ax b f (x) =
có đồ thị hàm số f ( x) như trong hình vẽ dưới đây: cx + d
Biết rằng đồ thị hàm số f (x) đi qua điểm A(0;4) . Khẳng định nào dưới đây là đúng? A. f ( ) 1 = 2 . B. f ( ) 11 2 = . C. f ( ) 7 1 = . D. f (2) = 6 . 2 2 Lời giải Chọn D
Đồ thị hàm số f (x) đi qua A(0;4) nên b = 4d ( ) 1 . ad − bc
Ta có: f ( x) = ( . cx + d )2 Căn cứ d
theo đồ thị hàm số f ( x) ta có −
= −1  c = d (2) . c − Đồ ad bc
thị hàm số f ( x) đi qua (0;3) nên = 3 2
ad − bc = 3d (3) . 2 d Thay ( ) 1 , (2) vào (3) ta được 2 2
ad − 4d = 3d a = 7d (d  0) vì nếu d = 0 thì a = b = c = d = 0 (vô lí ). + +
Do đó ( ) 7dx 4d 7 x 4 f x = = . dx + d x + 1 Vậy f (2) = 6 . ax b
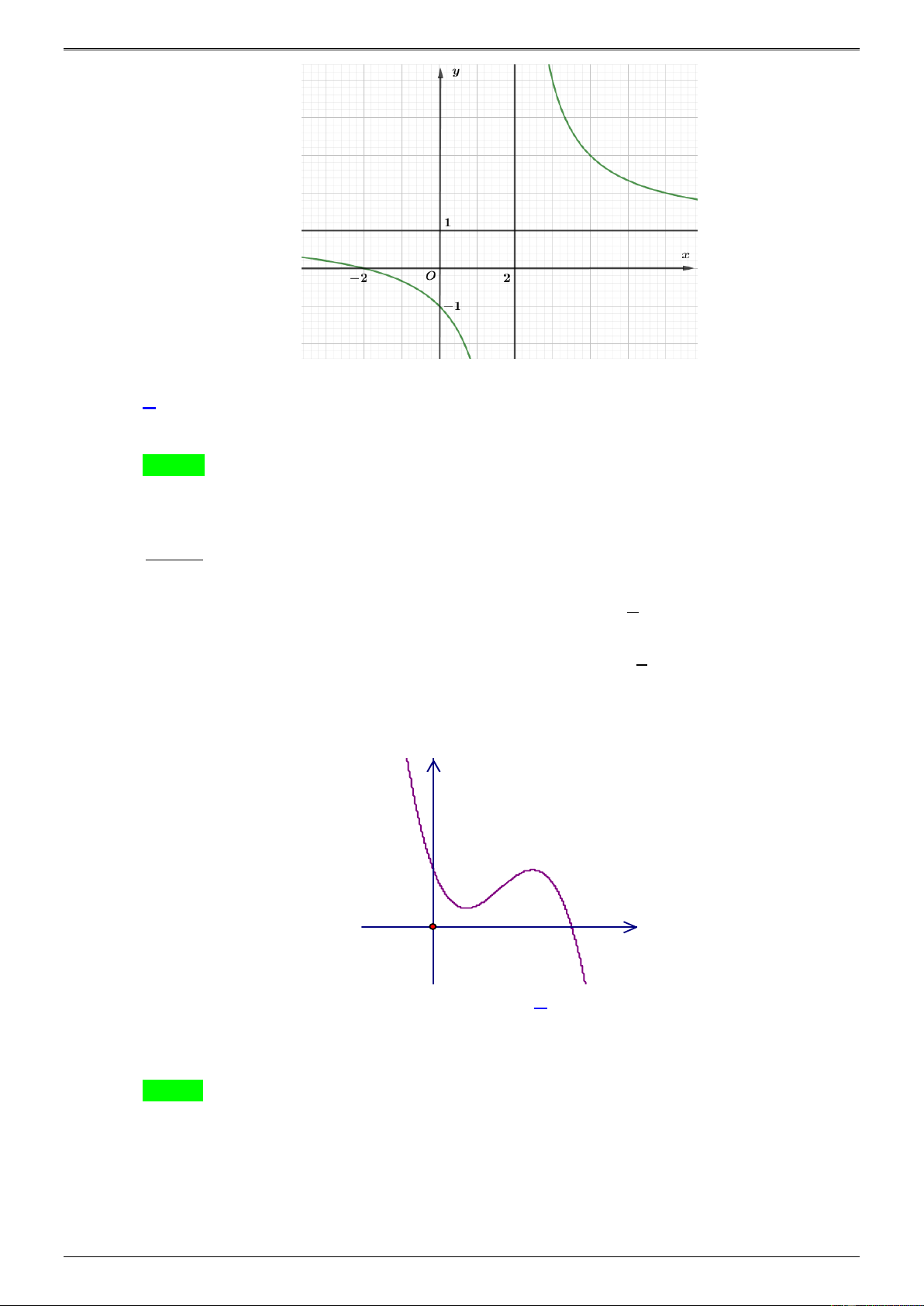
Câu 43.3. Cho hàm số y f ( x) + = =
, ( a , b , c , d
, c  0 , d  0 ) có đồ thị (C) . Đồ thị của cx + d
hàm số y = f ( x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2 .
Tiếp tuyến của (C) tại giao điểm của (C) với trục hoành có phương trình là y -1 -2 1 O -3
A. x + 3y + 2 = 0 .
B. x + 3y − 2 = 0 .
C. x − 3y − 2 = 0 .
D. x − 3y + 2 = 0 . Lời giải Chọn B 2 ax b ad − bc Xét hàm số y f ( x) + = = có f ( x) ( ) = . cx + d (cx + d)2 Ta có đồ b
thị hàm số cắt trục tung tại điểm có tung độ bằng 2 nên f (0) = 2  = 2  b = 2d d d
. Từ đồ thị y = f ( x) nhận đường thẳng x = 1
− làm tiệm cận đứng nên − = −1  d = c c  ( ) 2 ad − 2d a − 2 = = d f x ( . dx + d )2 d ( x + )2 1 a − 2d
Mặt khác ta lại có đồ thị y = f ( x) đi qua điểm ( 2 − ; 3
− ) nên f (2) = 3  = −3 da = −d . −dx + d −x + Vậy f ( x) 2 2 = = . dx + d x +1
Đồ thị (C) cắt trục Ox tại điểm (2;0) và f ( ) 1 2 = − . 3 1
Vậy phương trình tiếp tuyến của (C) tại giao điểm của (C) và trục Ox là y = − ( x − 2) 3
x + 3y − 2 = 0 . ax −
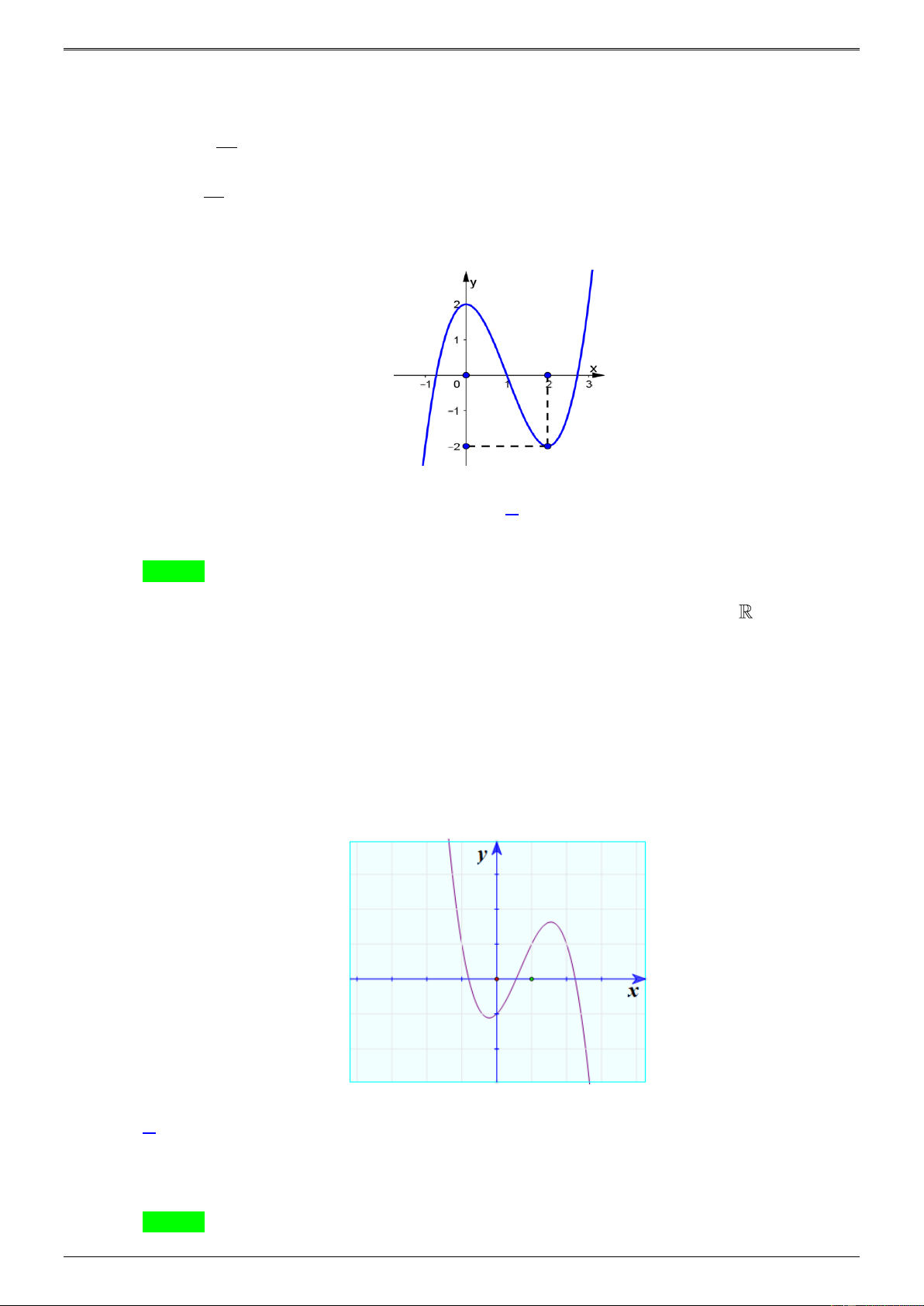
Câu 43.4.
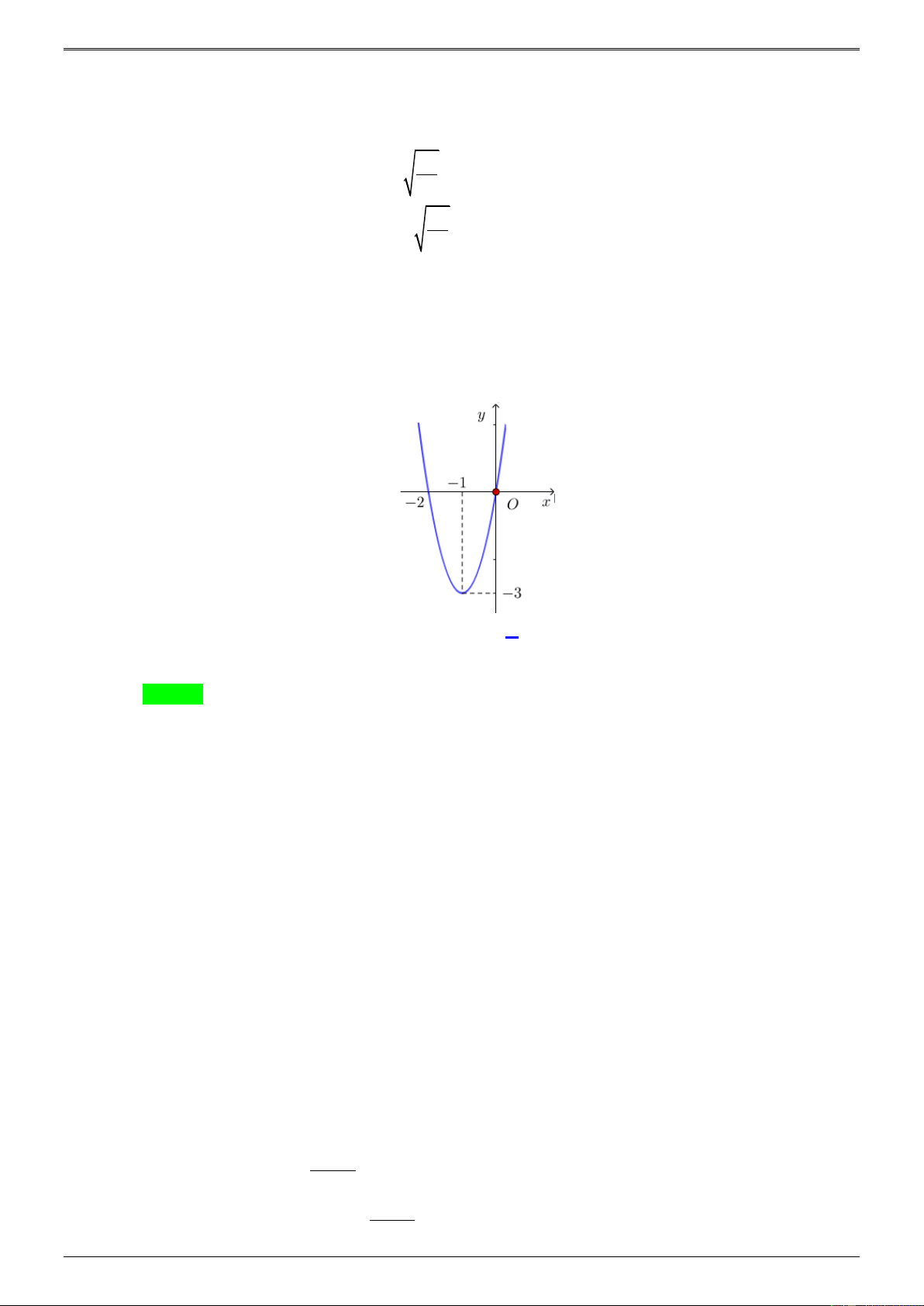
Xác định a , b , c để hàm số 1 y =
có đồ thị như hình vẽ bên. Chọn đáp án đúng? bx + c
A. a = 2, b = 1, c = 1. −
B. a = 2, b = 1, c = 1.
C. a = 2, b = 2, c = 1. −
D. a = 2, b = 1 − ,c = 1. Lời giải Chọn A −
Nhận xét: đồ thị hàm số có đường tiệm cận đứng b x = và tiệm cận ngang a y = . c bb − =1   cb  + c = 0 b  + c = 0 a = 2b = 2    
Dựa vào đồ thị ta có a  = 2
 a = 2b  a = 2b b  = −c =1 . b   −    − 1 c = 1 −  c = 1 −  1  = M ( )(C) ax 1 0;1 : y =    c bx + c ax + 2
Câu 43.5.
Đường cong ở hình bên là đồ thị hàm số y = cx+ với a , b , c là các số thực. b
Mệnh đề nào sau đây đúng?
A. a =1; b = 2
− ; c =1. B. a =1; b = 2 ; c =1. C. a =1; b =1; c = 1
− . D. a = 2 ;b = 2 ; c = 1 − . Lời giải: Chọn A
Đồ thị hàm số đã cho cắt trục hoành tại điểm có tọa độ ( 2 − ;0) nên ta có:
−2a + 2 = 0  a =1. Vậy loại D 2 − c + b a
Đồ thị hàm số đã cho có tiệm cận ngang là đường thẳng y = 1
= 1 c = a = 1. Vậy loại C c b
Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng x = 2  − = 2  b = −2c = −2 . c
Câu 43.6. Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị là đường cong trong hình dưới đây. Mệnh đề nào sau đây đúng? y O x
A. a  0 , c  0 , d  0 .
B. a  0 , c  0 , d  0 .
C. a  0 , c  0 , d  0 .
D. a  0 , c  0 , d  0 . Lời giải: Chọn B
Dựa vào hình dạng đồ thị: đồ thị hàm bậc ba có hệ số a  0 , đồ thị cắt trục tung tại điểm có
tung độ dương nên d  0 . Ta có: 2
y = 3ax + 2bx + c . Đồ thị có hai điểm cực trị cùng nằm bên phải trục tung nên
y = 0 có 2 nghiệm dương phân biệt. a  0  2 −  a  0 b 3ac 0   2  b  − 3ac  0 Suy ra 2b −  0   . b  0  3a   c c  0   0 3a
Câu 43.7. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d có đồ thị là đường cong như hình vẽ.
Tính tổng S = a +b + c + d . A. S = 4 − . B. S = 2 . C. S = 0 . D. S = 6 . Lời giải: Chọn C Ta có f ( x) 2
= 3ax + 2bx + c . Hàm số ( ) 3 2
f x = ax + bx + cx + d liên tục trên ; đồ thị hàm
số có hai điểm cực trị là (2; 2 − ) và (0;2)  f (2) = 2 −  + + + = −  =  8a 4b 2c d 2 a 1    f (2) = 0  + + =  = −  12a 4b c 0 b 3       S = 0 . f  (0) = 2 d = 2  c = 0     f   (0) = 0 c = 0 d = 2
Câu 43.8. Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . Lời giải: Chọn A 3 2 2
y = ax + bx + cx + d y = 3ax + 2bx + c . x  0  x
Từ đồ thị ta có: hàm số có hai điểm cực trị 1 2 
, đồ thị cắt trục tung tại điểm có tung độ  x x  1 2
âm và lim y = − . x→+ a  0   a  0 d 0    d  0 Suy ra 2bx + x = −  0   . 1 2 b  0  3a   c c  0 x .x =  0 1 2  3a
Câu 43.9. Cho hàm số 4 2
y = ax + bx + c (a  0) và có bảng biến thiên như hình sau: .
Khẳng định nào sau đây là khẳng định đúng?
A. a  0 và b  0 .
B. a  0 và b  0 .
C. a  0 và b  0 .
D. a  0 và b  0 . Lời giải: Chọn C .
Dựa vào bảng biến thiên  a  0.
Hàm số có một cực trị  .
a b  0  b  0 . Vậy KĐ “ a  0 và b  0 ” là đúng.
Câu 43.10. Cho hàm số 4 2
y = ax − bx + c có đồ thị như hình vẽ sau.
Khẳng định nào sau đây đúng?
A. a  0, b  0, c  0 .
B. a  0, b  0, c  0 . C. a  0, b  0, c  0 . D. a  0, b  0, c  0 . Lời giải: Chọn A Ta có 3
y = 4ax − 2bx = 0 .
Dựa vào đồ thị ta thấy a  0 và y = 0 có 3 nghiệm phân biệt nên.  x = 0   b
y = 0  2x ( 2
2ax − b) = 0  x = 
với a  0, b  0 loại B và C. 2a   bx = −  2a
Thay x = 0  y = c  0 loại D.
Câu 43.11. Cho hàm số = ( ) 3 2 y
f x = ax + bx + cx + d có đạo hàm là hàm số y = f ( x) với đồ thị
như hình vẽ bên. Biết rằng đồ thị hàm số y = f ( x) tiếp xúc với trục hoành tại điểm có hoành
độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu? A. 4. B. 1. C. 4 − . D. 2. Lời giải Chọn C x = 0
Nhìn đồ thị ta thấy y = 0  
. Do đó, hàm số y = f ( x) đạt cực trị tại x = 0 và x = 2 − x = 2 − .
Đồ thị hàm số y = f ( x) tiếp xúc với trục hoành tại điểm có hoành độ âm nên suy ra hàm số
y = f ( x) đạt cực trị bằng 0 tại điểm có hoành độ âm  f ( 2 − ) = 0 . (1)
Mặt khác f ( x) 2
= 3ax + 2bx + c .
Đồ thị hàm số y = f (x) đi qua các điểm có tọa độ (0;0) , ( 2 − ;0) , ( 1 − ;− ) 3 . (2) c = 0 a = 1   1
 2a − 4b + c = 0 b = 3
Từ (1), (2) lập được hệ phương trình     f (x) 3 2
= x + 3x − 4 .
3a − 2b + c = −3 c = 0    8
− a + 4b − 2c + d = 0 d = −4
Đồ thị hàm số y = f ( x) cắt trục tung tại điểm có tung độ y = f (0) = - 4 . ax −
Câu 43.12. Cho hàm số 1 y =
có tiệm cận đứng x =1, tiệm cận ngang y = 2 và đi qua điểm cx + d ax + A(2; 3 − ) . Lúc đó hàm số 1 y =
là hàm số nào trong bốn hàm số sau: cx + d −3 2x +1 2x −1 2 − x −1 2x −1 A. y = . . B. y = . C. y = . D. y = . 5 x −1 1− x −x +1 x −1 Lời giải: Chọn B a x −1
Đồ thị hàm số y =
có tiệm cận đứng = − d x
, tiệm cận ngang = a y c x + d c ca = 2  ca = 2ca − 2c = 0 a = 2  d   
Theo đề bài ta có − = 2  −d = 2c
 2c + d = 0  c = 1 −  c    2a −1 = 6 − c − 3d
2a + 6c + 3d = 1 d = 1     . a 2 −1 = 3 −  .2 c + d mx +
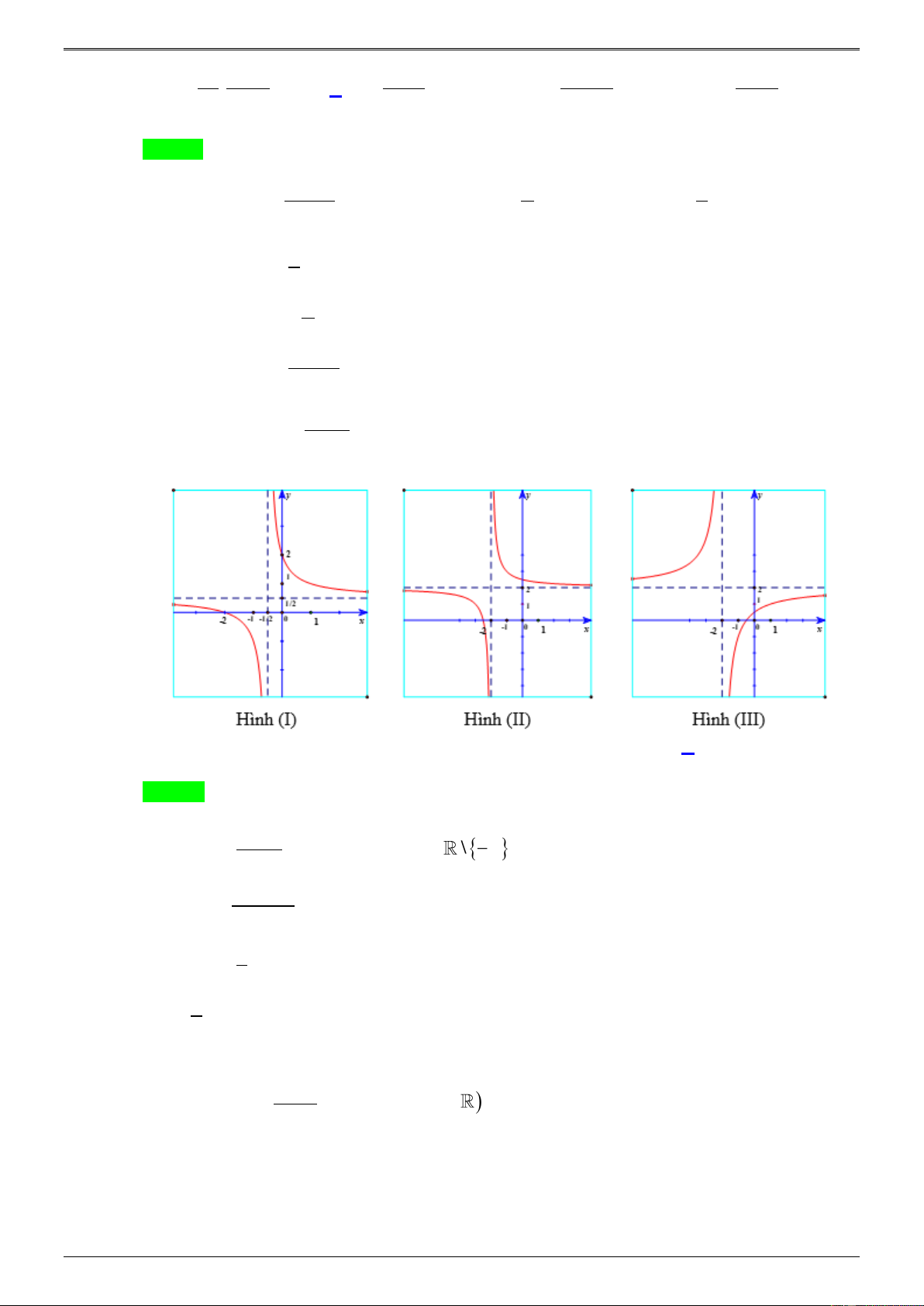
Câu 43.13. Cho hàm số 1 y =
. Các đồ thị nào dưới đây có thể là đồ thị biểu diễn hàm số đã cho? x + m
Hãy chọn đáp án sai? A. Hình (I) và (III). B. Hình (III). C. Hình (I). D. Hình (II). Lời giải Chọn D mx + Hàm số 1 y =
có tập xác định D = \ −  m . x + m 2 m −1 m 1 Ta có y ' =
y   m −   −  m
y   m −   ( , 2 ' 0 1 0 1 1; 2 ' 0 1 0  . Hình x + m)2 m  1 − 1
(I) có m = −  (−1 )
;1 nên y '  0 suy ra hàm số nghịch biến, do đó Hình (I) đúng. Hình (II) có 2 3 m = −
 −1 nên y '  0 suy ra hàm số đồng biến, do đó Hình (II) sai. Hình (III) có 2 m = 2 −  1
− nên y '  0 suy ra hàm số đồng biến, do đó Hình (III) đúng. bx − c
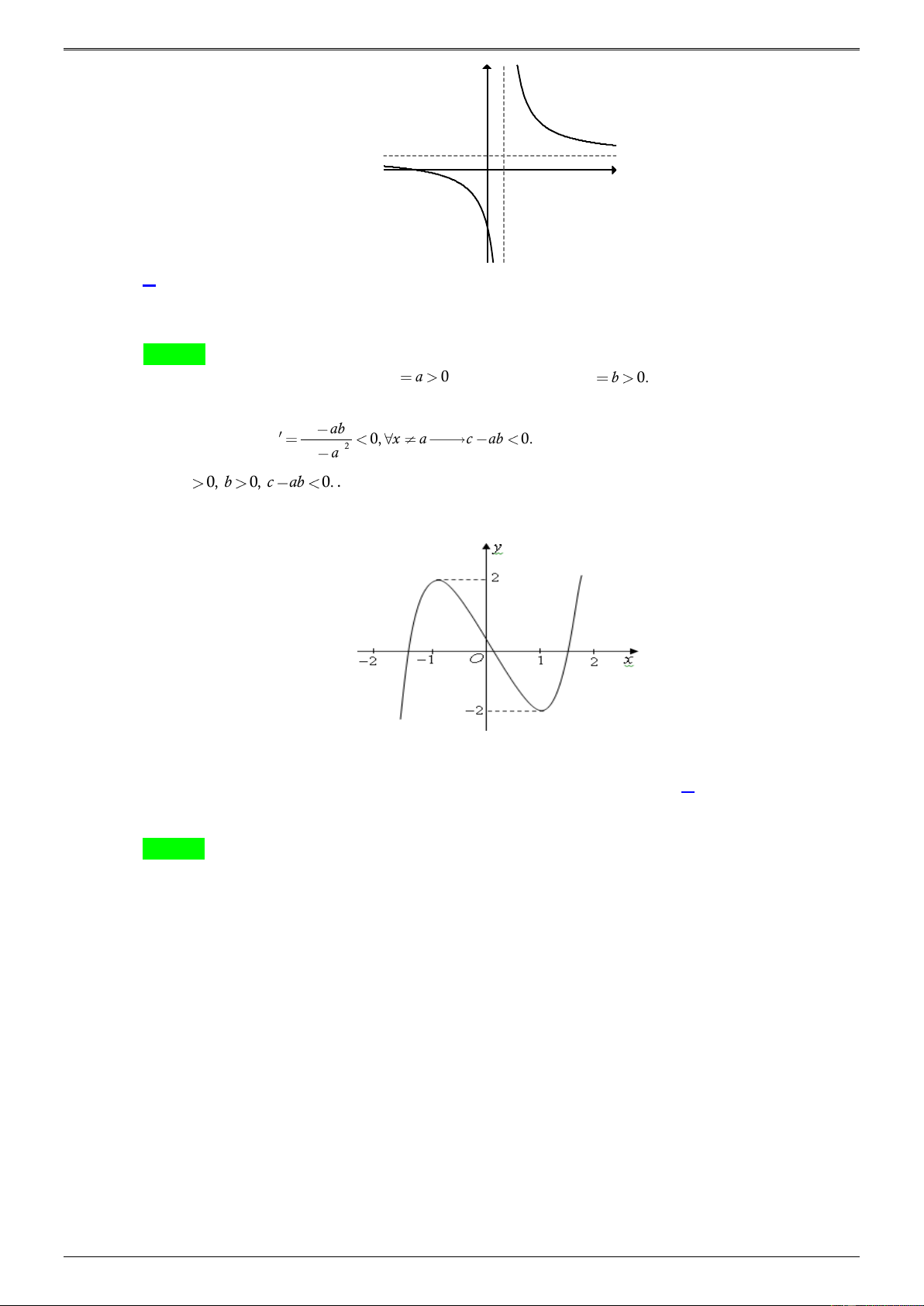
Câu 43.14. Hàm số y =
(a  0; a, ,b c ) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây x − a là đúng? y y O x
A. a  0, b  0, c − ab  0.
B. a  0, b  0, c − ab  0.
C. a  0, b  0, c − ab = 0.
D. a  0, b  0, c − ab  0. Lời giải Chọn A
Đồ thị hàm số có tiệm cận đứng x a 0 ; tiệm cận ngang y b 0.
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên c ab y 0, x a c ab 0. 2 x a
Vậy a 0, b 0, c ab 0. .
Câu 43.15.
Cho hàm số y = f ( x) 3 2
= ax + bx + cx + d (a  0) có đồ thị như hình vẽ.
Phương trình f ( f (x)) = 0 có bao nhiêu nghiệm thực? A. 3. B. 7. C. 5. D. 9. Lời giải Chọn D
Từ đồ thị hàm số đã cho trong hình vẽ ta có phương trình f ( x) = 0 có ba nghiệm phân biệt x , 1 x = x1 
x và x thuộc khoảng ( 2
− ;2) hay f (x) = 0  x = x với x , x và x thuộc khoảng 2 3 2  1 2 3 x = x  3 ( 2 − ;2) . t = t
f (x) = t 1  1 
Đặt t = f (x) ta có f (t) = 0  t = t hay  f ( x) = t với t , t và t thuộc khoảng ( 2 − ;2) 2  2 1 2 3   t = tf  ( x) = 3 t3
Dựa vào đồ thị ta thấy ba đường thẳng phân biệt y = t , y = t và y = t mỗi đường thẳng luôn 1 2 3
cắt đồ thị hàm số tại ba điểm.
Vậy phương trình f ( f ( x)) = 0 có 9 nghiệm.
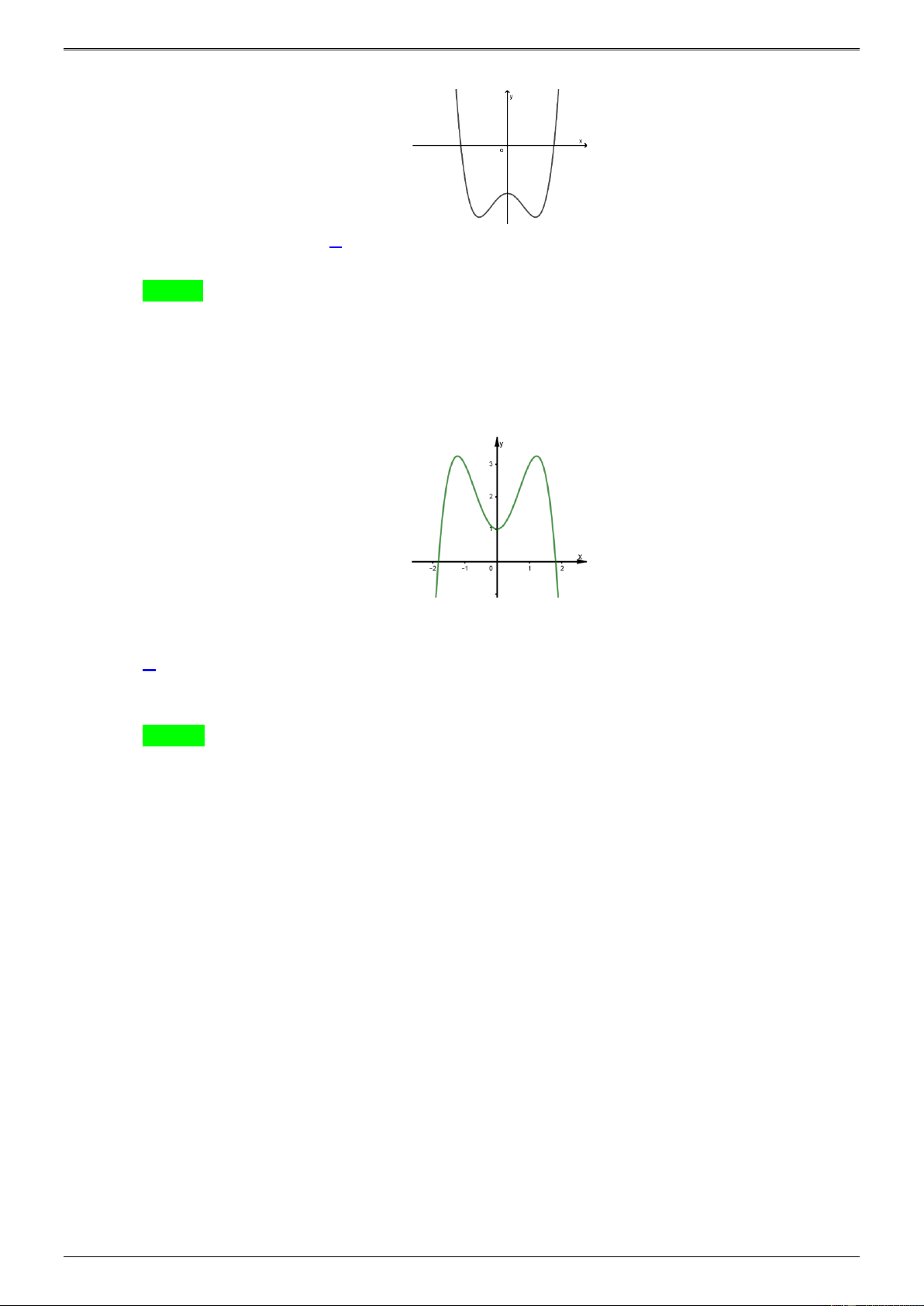
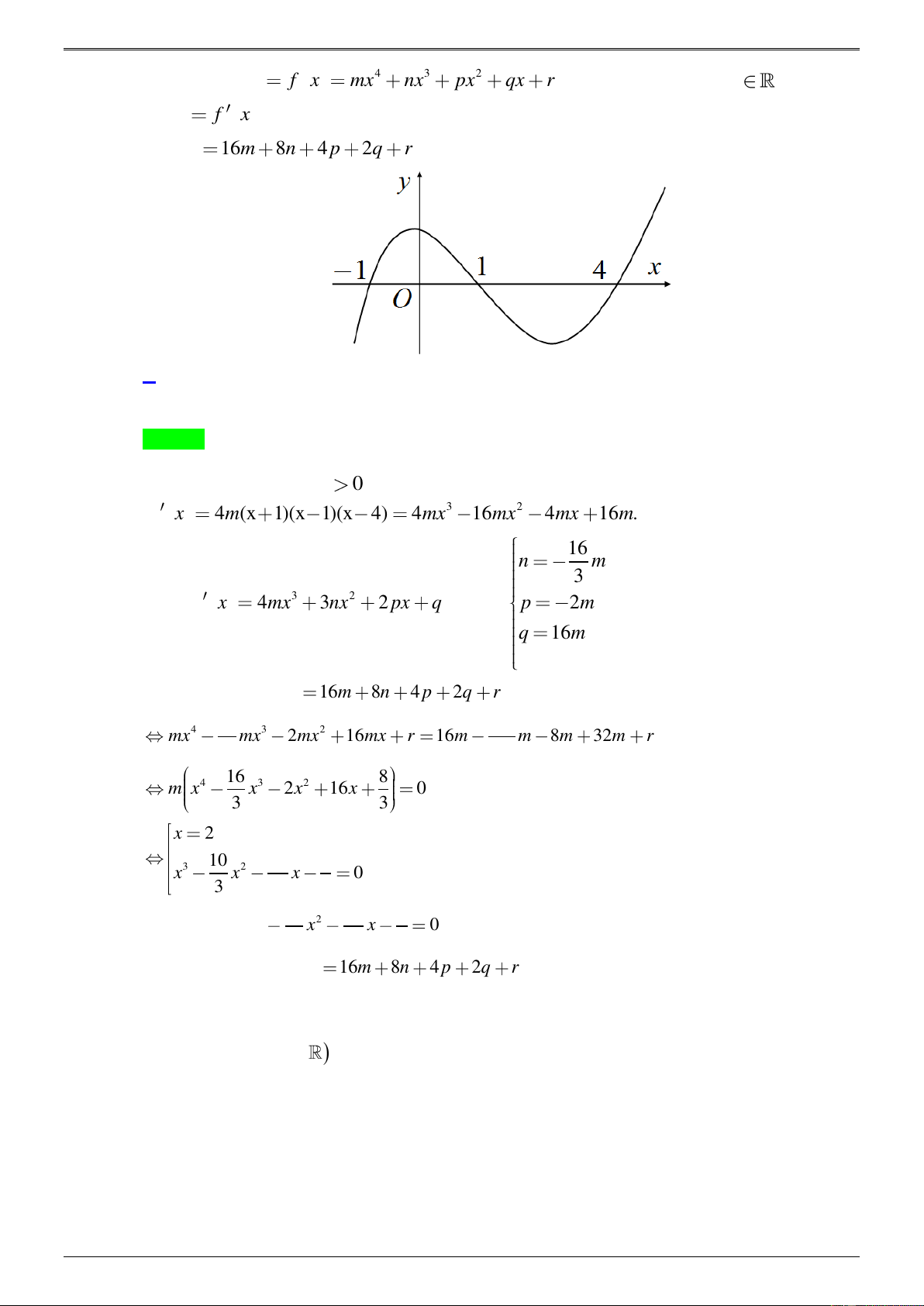
Câu 43.16. Cho hàm số 4 3 2 y f x mx nx px qx r , trong đó , m , n , p , q r . Biết hàm số y f x
có đồ thị như hình bên dưới. Số nghiệm của phương trình f x 16m 8n 4 p 2q r là A. 4. B. 5. C. 2. D. 3. Lời giải Chọn A
* Dựa vào đồ thị ta có m 0 và 3 2 f x 4m(x 1)(x 1)(x 4) 4mx 16mx 4mx 16 . m 16 n m 3 * Mà 3 2 f x 4mx 3nx 2 px q . Suy ra p 2m . q 16m * Phương trình f x 16m 8n 4 p 2q r . 16 128 4 3 2 mx mx 2mx 16mx r 16m m 8m 32m r 3 3 16 8 4 3 2 m x x 2x 16x 0 3 3 x 2 10 26 4 . 3 2 x x x 0 3 3 3 Phương trình 10 26 4 3 2 x x x
0 có 3 nghiệm phân biệt khác 2 . 3 3 3
Vậy phương trình f x 16m 8n 4 p 2q r có 4 nghiệm.
Câu 43.17. Cho các hàm số ( ) 4 3 2
f x = mx + nx + px + qx + r và ( ) 3 2
g x = ax + bx + cx + d ( , m ,
n p, q, r, a, , b ,
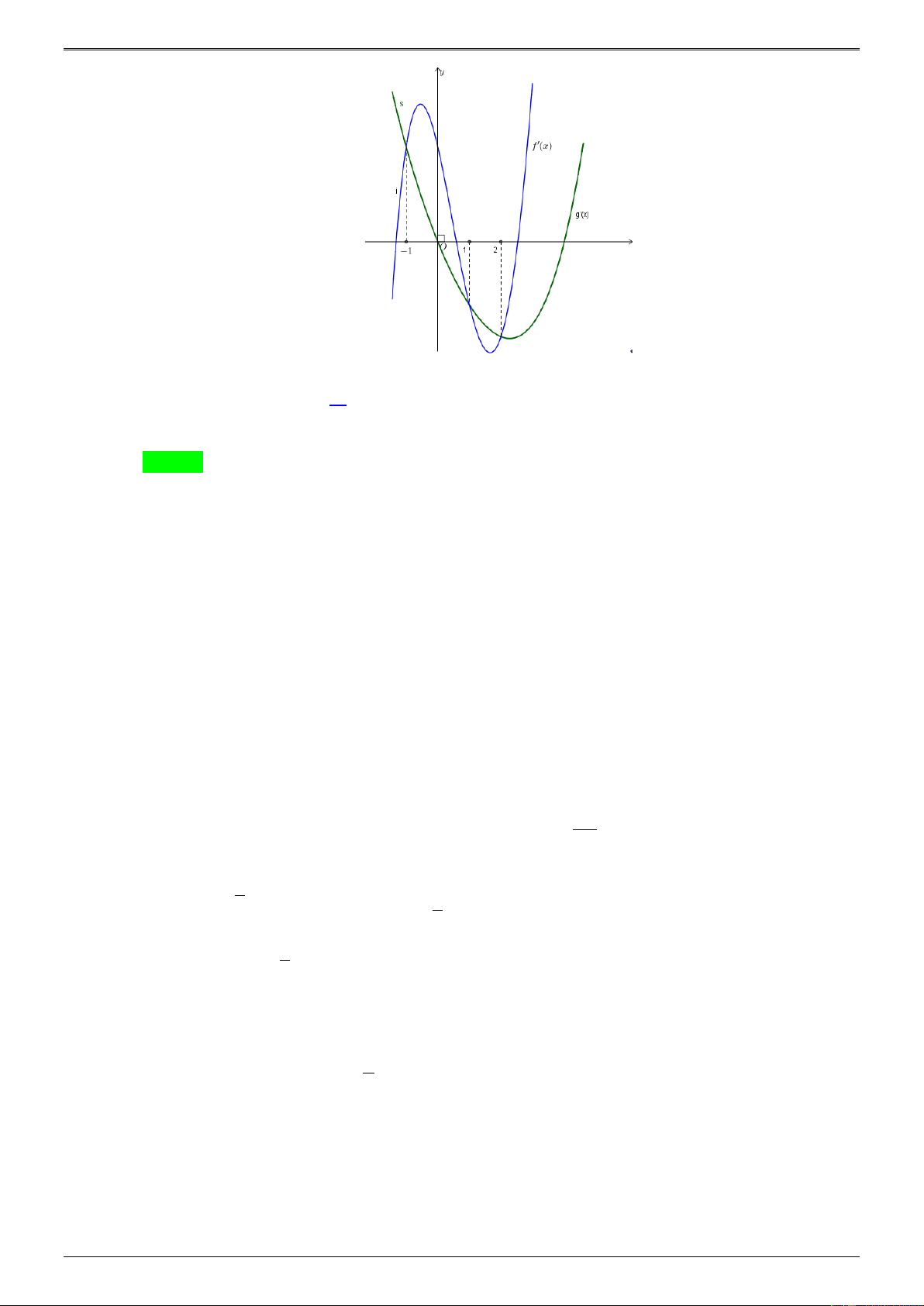
c d  ) thỏa mãn f (0) = g (0) . Các hàm số y = f ( x) và g( x) có đồ thị như hình vẽ bên.
Tập nghiệm của phương trình f ( x) = g ( x) có số phần tử là A. 4. B. 2. C. 1. D. 3. Lời giải: Chọn B
+ Từ đồ thị hàm số y = f ( x)  m  0 .
+ f (0) = g (0)  r = d .
+ Ta có f ( x) − g( x) 3
= mx + (n − a) 2 4 3
x + 2( p − b) x + q − c ( ) 1 .
Mặt khác từ đồ thị hai hàm số y = f ( x) và g( x) ta có f ( x) − g( x) = 4m( x + ) 1 ( x − ) 1 ( x − 2)
hay f ( x) − g( x) 3 2
= 4mx −8mx − 4mx +8m (2) . 3
 (n − a) = −8m  Từ ( )
1 và (2) ta suy ra 2( p − b) = −4m .
q −c = 8m  + Phương trình ( ) = ( ) 4 3 2 3 2 f x
g x mx + nx + px + qx + r = ax + bx + cx + d 4 3 2 3 2
mx + nx + px + qx = ax + bx + cx  8m  3
x mx + (n − a) 2
x + ( p − b) x + q − c = 0   3 2  x mx −
x − 2mx + 8m = 0    3  x = 0  8  3 2 
mx x − x − 2x + 8 = 0    8 . 3 2  3 
x − x − 2x +8 = 0  3 8 Phương trình 3 2 x −
x − 2x + 8 = 0 có đúng một nghiệm thực khác 0. 3
Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 43.18. Cho hàm số 4 3 2
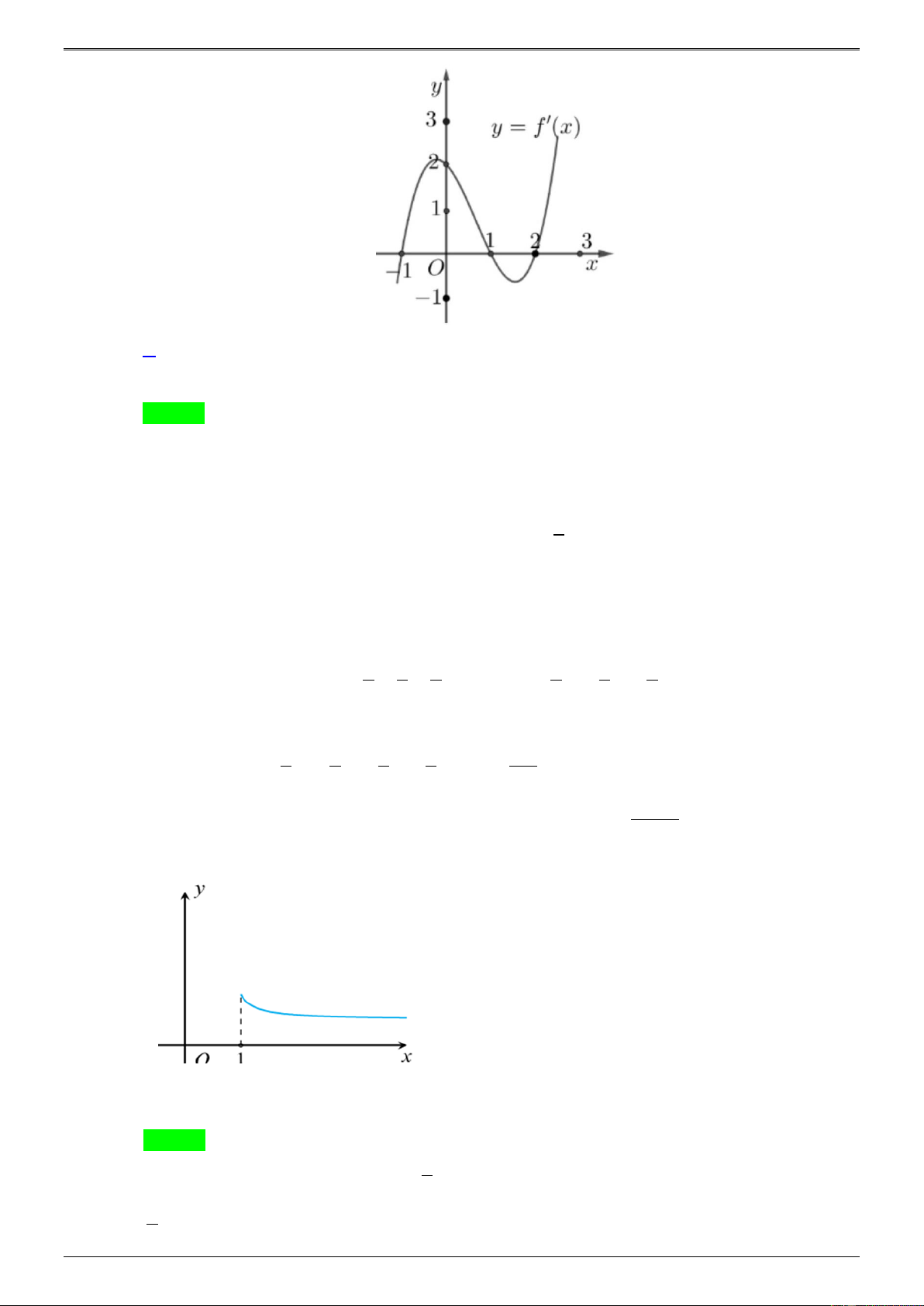
f (x) = ax + bx + cx + dx + e có đồ thị của hàm số y = f (  x) như hình vẽ   bên. Phương trình 1
f (x) = f   có bao nhiêu nghiệm thực phân biệt?  2  A. 4 . B. 1. C. 3 . D. 2 . Lời giải: Chọn A Ta có 3 2 f (
x) = 4ax + 3bx + 2cx + d là một đa thức bậc ba có đồ thị cắt trục hoành tại ba điểm
có hoành độ lần lượt -1;1;2. Vì vậy 3 2 f (
x) = 4ax + 3bx + 2cx + d = 4a(x +1)(x −1)(x − 2). 1 Mặt khác f (
 0) = 2  4a(0 +1)(0 −1)(0 − 2) = 2  a = . 4 Vậy ta có 3 2 f (
x) = 4ax + 3bx + 2cx + d = (x +1)(x −1)(x − 2), x  3 2 3 2
 4ax + 3bx + 2cx + d = x − 2x − x + 2, x  4a =1 3  b = 2 −  1 2 1  1 2 1 4 3 2    ( ; a ; b ; c d ) =
; − ; − ; 2  f (x) = x − x −
x + 2x + e   2c = 1 −   4 3 2  4 3 2 d = 2   Khi đó 1 1 2 1 155 4 3 2 f (x) = f
x − x − x + 2x − = 0    4 nghiệm. Chọn đáp án A.  2  4 3 2 192 2x − a
Câu 43.19. Hỏi có bao nhiêu cặp số nguyên dương (a;b) để hàm số y =
có đồ thị trên (1;+ ) 4x − b
như hình vẽ dưới đây? A. 3 . B. 4 . C. 2 . D. 1. Hướng dẫn giải Chọn D b
Hàm số không xác định tại điểm x =
. Theo đồ thị ta có tiệm cận đứng nhỏ hơn 1  4
b 1 b  4. Do b nguyên dương nên b1,2,  3 . 4 4a − 2b Ta có y =
. Hàm số nghịch biến nên −    ( 4a 2b 0 b
2a . Do a là số nguyên 4x − b)2
dương và b 1,2, 
3 nên ta có một cặp (a,b) thỏa mãn là (1,3)
Câu 43.20. Cho hàm số 3 2
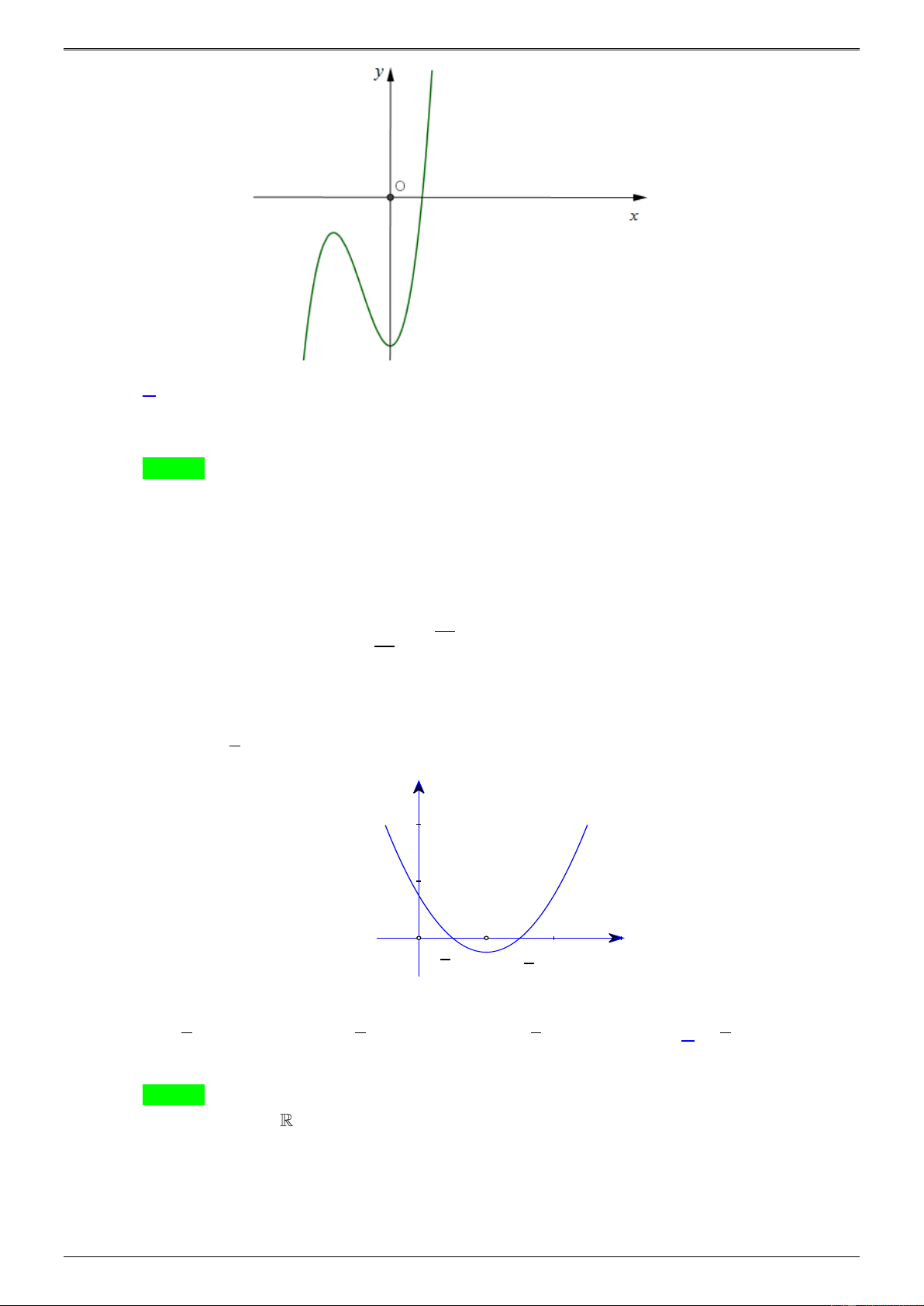
y = f (x) = ax + bx + cx + d (a, ,
b c, d  , a  0) có đồ thị là (C ) . Biết rằng đồ
thị (C ) đi qua gốc tọa độ và đồ thị hàm số y = f '(x) cho bởi hình vẽ bên. Tính giá trị H = f (4) − f (2) ?
A. H = 64 .
B. H = 51.
C. H = 58 .
D. H = 45 . Hướng dẫn giải Chọn C Theo bài ra 3 2
y = f (x) = ax + bx + cx + d (a, ,
b c, d  , a  0) do đó y = f ( x) là hàm bậc hai có dạng = ( ) 2 y f x = a x  + b x  + c. c =1 a = 3  
Dựa vào đồ thị ta có: a − b + c = 4  b
  = 0  y = f (x) 2 = 3x +1.  
a + b + c = 4  c = 1 
Gọi S là diện tích phần hình phẳng giới hạn bởi các đường y = f (x) , trục Ox , x = 4, x = 2 . 4 Ta có S = ( 2 3x + ) 1 dx = 58 . 2 4 4
Lại có: S = f
 (x)dx = f (x) = f (4)− f (2). 2 2
Do đó: H = f (4) − f (2) = 58 . ax − b
Câu 43. 21. Cho hàm số y = x − có đồ thị như hình dưới. 1 y 1 2 x O −1 2 −
Khẳng định nào dưới đây là đúng?
A. b  0  a .
B. 0  b a .
C. b a  0 .
D. 0  a b . Lời giải Chọn C
Nhìn vào đồ thị ta thấy : Đồ thị hàm số có tiệm cận ngang y = a và tiệm cận đứng x =1.Đồ thị  a =1 b  1 −
cắt trục hoành tại điểm có hoành độ x = 1. Ta có :   b a = 1 −  0 . a b  1 a
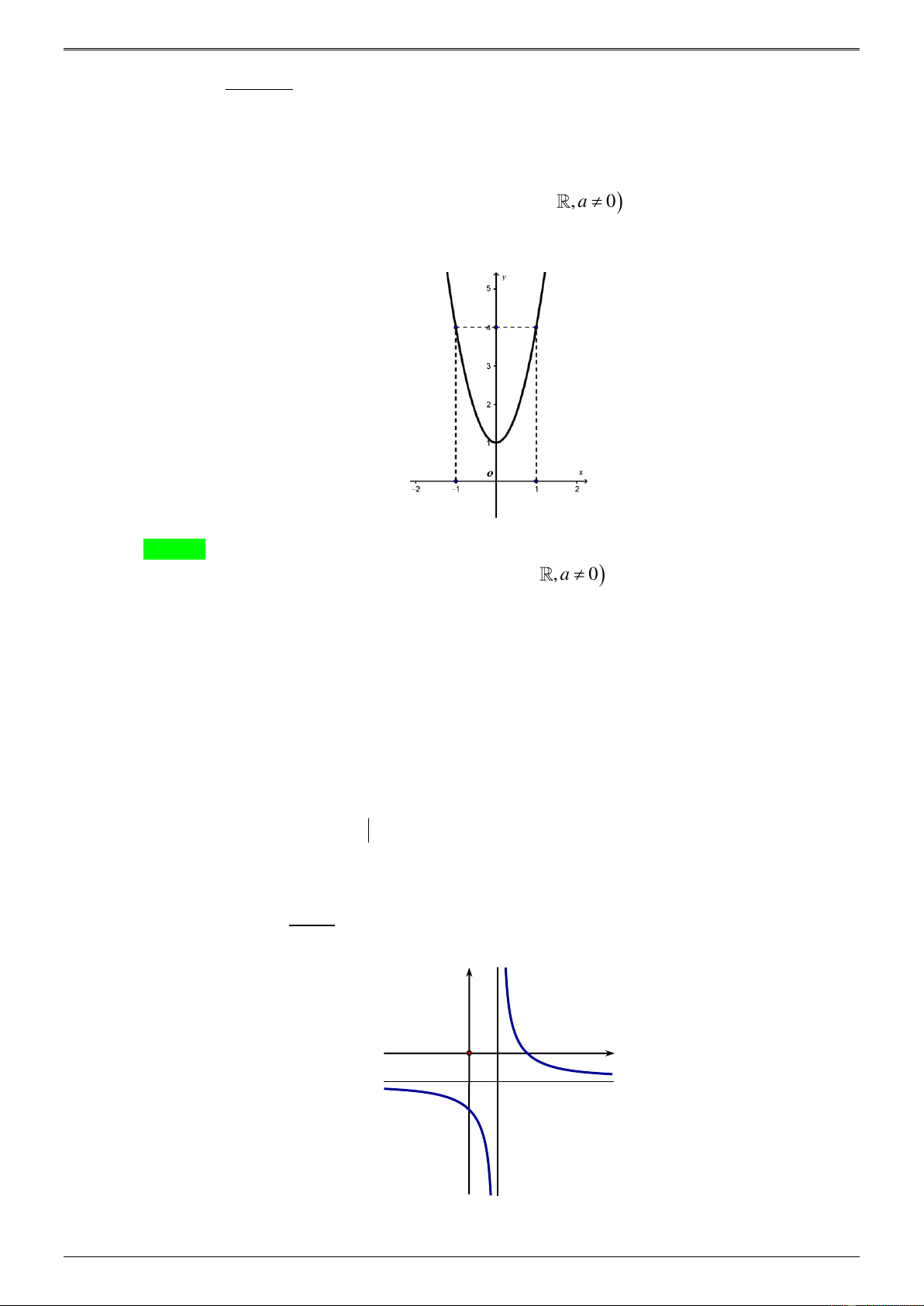
Câu 43.22. Giả sử hàm số 4 2
y = ax + bx + c có đồ thị là hình bên dưới. y 1 −1O x 1
Khẳng định nào sau đây là khẳng định đúng?
A. a  0, b  0, c = 1 .
B. a  0, b  0, c = 1 .
C. a  0, b  0, c = 1.
D. a  0, b  0, c  0 . Lời giải Chọn A
Dựa vào đồ thị ta có:
+ Đồ thị hướng lên nên a  0 , loại đáp án C.
+Với x = 0  y = c = 1nên loại đáp án D.
+Có 3 cực trị nên ab  0 suy ra b  0 .
Câu 43.23. Cho hàm số 3 2
y = ax + bx + cx + d . Hỏi hàm số luôn đồng biến trên khi nào?
a = b = 0,c  0
a = b = c = 0 A.  . B.  . 2
a  0;b − 3ac  0 2
a  0; b − 3ac  0
a = b = 0,c  0
a = b = 0,c  0 C.  . D.  . 2
a  0;b − 3ac  0 2
a  0;b − 3ac  0 Lời giải Chọn C
Hàm số luôn đồng biến trên khi 2
y ' = 3ax + 2bx + c  0, x  
Trường hợp 1: a = b = 0,c  0
Trường hợp 1: a  0 , giải 2
 = b − 3aca  a  0
Hàm số luôn đồng biến trên  y '  0, x   0        0 2 b  − 3ac  0 ax + b
Câu 43. 24. Cho hàm số y = x + có đồ thị như hình vẽ bên. 1 y 1 1 O x
Tìm khẳng định đúng trong các khẳng định sau
A. b  0  a .
B. 0  a b .
C. a b  0 .
D. 0  b a . Lời giải Chọn B y 1 −1 x O a − b y = (
. Dựa vào đồ thị hàm số ta thấy hàm số nghịch biến trên từng khoảng xác định và x + )2 1
có đường tiệm cận ngang y = 1. y  0  a −b  0 a =1 Suy ra:     
. Vậy 0  a b . lim = 1  a =1 b  1 x→ y
Câu 43.25. cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c = 0, d  0.
B. a  0, b  0, c = 0, d  0.
C. a  0, b  0, c  0, d  0. .
D. a  0, b  0, c  0, d  0. . Lời giải Chọn A 3 2
y = ax + bx + cx + d f ( x) 2 '
= 3ax + 2bx + c .
Cho x = 0 , ta có f (0) = d  0. Từ hình dáng đồ thị ta thấy a  0
Đồ thị hàm số có điểm cực đại và cực tiểu, suy ra f '( x) = 0 có hai nghiệm phân biệt, từ đồ thị  a  0  a  0   có hoành độ 2b
hai điểm cực trị không âm do đó x + x = −  0  b   0 1 2 3a  c = 0   c x x = = 0  1 2  3a
Câu 43.26. Hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng? y O x
A. a  0 ; b  0 ; c  0 . B. a  0 ; b  0 ; c  0 . C. a  0 ; b  0 ; c  0 . D. a  0 ; b  0 ; c  0 . Lời giải: Chọn A
Đồ thị hàm số có dạng đồ thị của hàm số bậc bốn hệ số a âm, giao điểm của đồ thị với trục
tung nằm trên điểm O nên hệ số c dương. Đồ thị hàm số có ba cực trị nên hệ số b trái dấu với
hệ số a , hay hệ số b dương. ax −1
Câu 43.27. Đồ thị hàm số y = cx + (a , c , d : hằng số thực ) như hình vẽ. d y x O Khẳng định nào đúng
A. d  0, a  0, c  0 .
B. d  0, a  0, c  0 . C. d  0, a  0, c  0 . D. d  0, a  0, c  0 . Lời giải Chọn C 1
Ta có x = 0  y = −  0  d  0 . d 1 y = 0  x =  0  a  0 . a ax −1 a Hàm số y = y =   c  . cx + có tiệm cận ngang 0 0 d c
Vậy d  0, a  0, c  0 .
Câu 43.28. Đồ thị hàm số 3 2
y = ax + bx + cx + d ( a , b , c , d là các hằng số thực và a  0 ) như hình vẽ. y O x Khẳng định nào đúng
A. b  0, c  0 .
B. b  0, c  0 .
C. b  0, c  0 .
D. b  0, c  0 . Lời giải
Chọn C
Từ đồ thị hàm số ta thấy lim y = + nên a  0 . x→− Nhận thấy 2
y = 0  3ax + 2bx + c = 0 có hai nghiệm dương phân biệt nên  c P =  0  c  0 3a    . 2b b    0 S = −  0  3a
Câu 43.29. Giả sử tồn tại hàm số y = f ( x) xác định trên \  1 − ; 
2 , liên tục trên mỗi khoảng xác định
và có bảng biến thiên như sau: x − 2 − −1 1 2 3 + y − 0 + + 0 − − 0 + 1 + 2 + 3 y 3 − − − 1
Câu 43.30. Cho hàm số bậc ba 3 2
y = ax + bx + cx + d (a, ,
b c, d  , a  0) có đồ thị như hình vẽ. Mệnh
đề nào dưới đây đúng? A. 2
a  0;b  0; c  0; d  0;b  3a . c B. 2
a  0;b  0; c  0; d  0;b  3a . c C. 2
a  0;b  0; c  0; d  0;b  3a . c D. 2
a  0;b  0; c  0; d  0;b  3a . c y O x Lời giải Chọn C 2
y = 3ax + 2bx + c . 2
 = b − 3ac . b
S = x + x = − . 1 2 a
Ta có lim f (x) = − nên a  0 . ( ) 1 x→−
Nhìn vào ĐTHS khi x = 0 thì y = d  0 . (4)  2
b − 3ac  0(5)   0    Phương trình có hai cự b
c trị dương nghiệm nên  S  0  −  0  b  0(2) .  aP  0 
c  0  c  0  (3)  a ax − b
Câu 43.31. Cho hàm số y =
có đồ thị (C) . Nếu (C) có tiệm cận ngang là đường thẳng y = 2 và bx +1 1
tiệm cận đứng là đường thẳng x =
thì các giá trị của a và b lần lượt là 3 1 1 1 1 A. − và − . B. 3 − và 6 − . C. − và − . D. 6 − và 3 − . 2 6 6 2 Lời giải Chọn D  1 x  − Điều kiện  b . b  0 1
Ta có tiệm cận đứng của đồ thị hàm số có phương trình x = −
, tiệm cận ngang của đồ thị hàm b số có phương trình = a y . b  1 1 − =  b 3  ab = 3 −
Yêu cầu bài toán thỏa mãn khi  = 2   . ba = 6 −   1  . a − + b  0      b ax + b
Câu 43.32. Cho hàm số y =
có đồ thị cắt trục tung tại điểm A(0; )
1 , tiếp tuyến tại A có hệ số góc x −1 3
− . Khi đó giá trị a , b thỏa mãn điều kiện sau:
A. a + b = 0.
B. a + b =1.
C. a + b = 2 .
D. a + b = 3 . Lời giải Chọn D −a − b Ta có y = ( . x − )2 1 ax + b b
Đồ thị hàm số y = A 0;1 nên: 1 =  b = −1 x −
cắt trục tung tại điểm ( ) 1 − . 1 −a − b
Vì tiếp tuyến tại A có hệ số góc bằng 3 − nên: y(0) = 3 −  = −  = ( . − ) 3 a 4 2 1
Vậy a + b = 3.
-------------------- HẾT -------------------- https://toanmath.com/