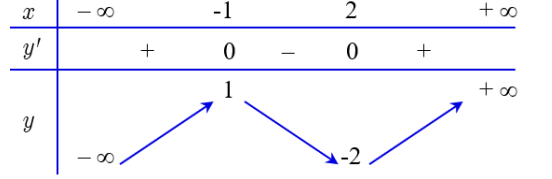
Câu hỏi:
12/04/2025 132Cho hàm số có đồ thị (C) và hai điểm A(4;-1), B(10;5). Gọi M() là điểm thuộc đồ thị (C) sao cho diện tích tam giác MAB nhỏ nhất. Tính diện tích S của hình phẳng được giới hạn bởi đồ thị hàm số (C), trục Ox và các đường thẳng x = 0, x = x0.
A
B
Đáp án chính xác
C
D
Trả lời:
 Trả lời bởi Docx
Trả lời bởi Docx
là điểm thuộc đồ thị (C) nên .
Phương trình đường thẳng AB : x-y-5=0
Từ đó ta có
Vậy diện tích hình phẳng cần tính là
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu hỏi 1 / 15
Xem đáp án »
12/04/2025
473
Câu hỏi 3 / 15
Xem đáp án »
09/04/2025
246
Câu hỏi 5 / 15
Xem đáp án »
09/04/2025
224
Câu hỏi 8 / 15
Xem đáp án »
12/04/2025
208
Câu hỏi 9 / 15
Xem đáp án »
10/04/2025
208
Câu hỏi 10 / 15
Xem đáp án »
12/04/2025
194
Câu hỏi 14 / 15
Xem đáp án »
09/04/2025
174