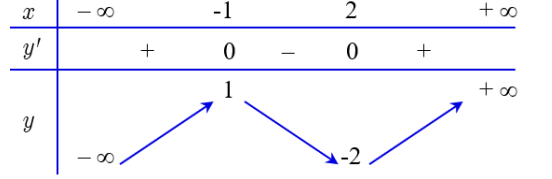
Trả lời:
 Trả lời bởi Docx
Trả lời bởi Docx
Xét . Đặt .
Đổi cận:
Vì
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu hỏi 1 / 15
Xem đáp án »
12/04/2025
473
Câu hỏi 3 / 15
Xem đáp án »
09/04/2025
246
Câu hỏi 5 / 15
Xem đáp án »
09/04/2025
224
Câu hỏi 8 / 15
Xem đáp án »
12/04/2025
208
Câu hỏi 9 / 15
Xem đáp án »
10/04/2025
208
Câu hỏi 10 / 15
Xem đáp án »
12/04/2025
194
Câu hỏi 14 / 15
Xem đáp án »
09/04/2025
174