









Preview text:
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
BÀI TOÁN KH O SÁT S BI N THIÊN L uy VÀ V TH HÀM S en th TRONG THI BGD i tra c 2016 - 2021 n gh iem
Câu 1: (Câu 26 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị hàm số 3 2 y = 2 − x + 3x − 5 .vn
cắt trục tung tại điểm có tung độ bằng Ⓐ. −5 . Ⓑ. 0 . Ⓒ. −1. Ⓓ. 2 . Lời giải Chọn A
Đồ thị hàm số cắt trục tung tại điểm có tung độ 3 2 y = 2 − .0 + 3.0 − 5 = 5 − .
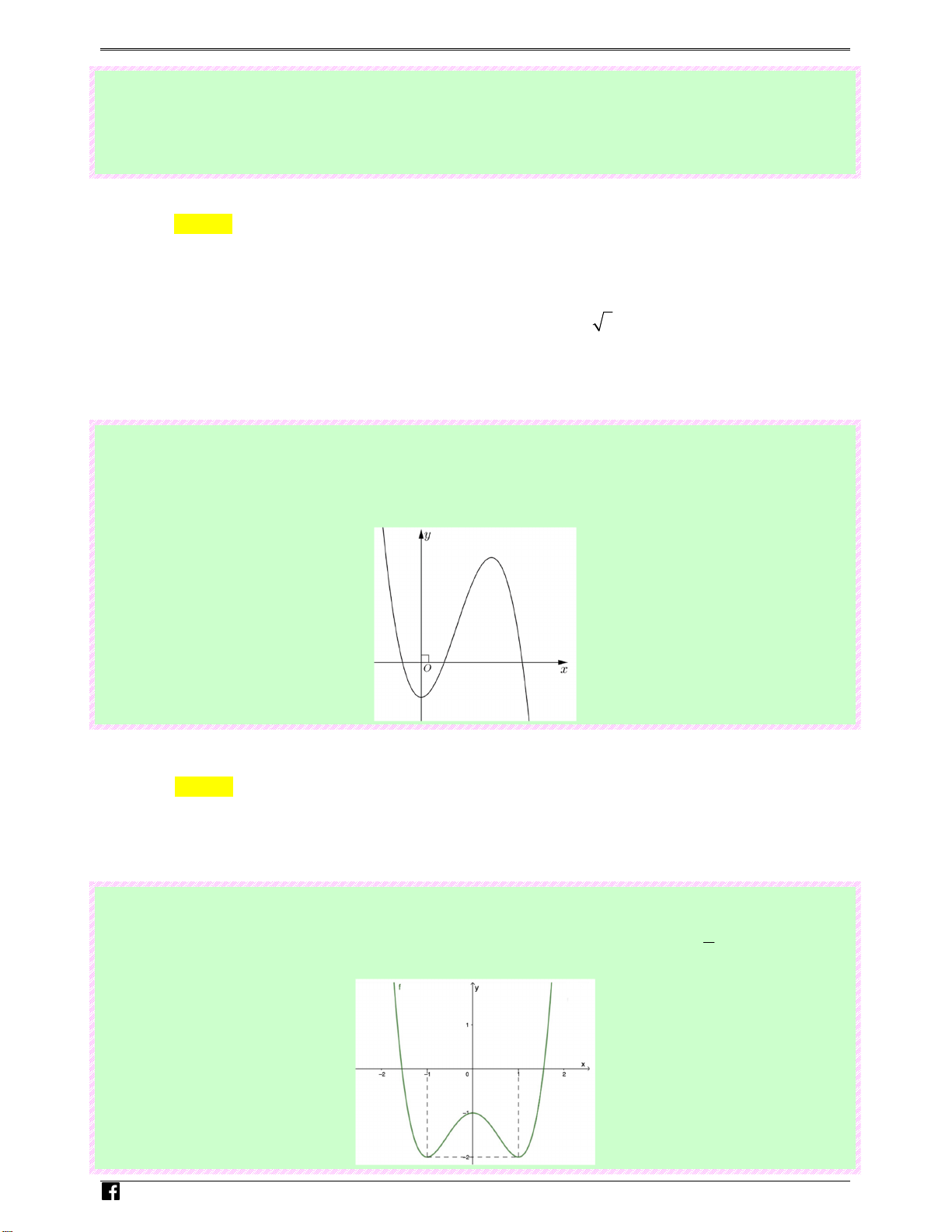
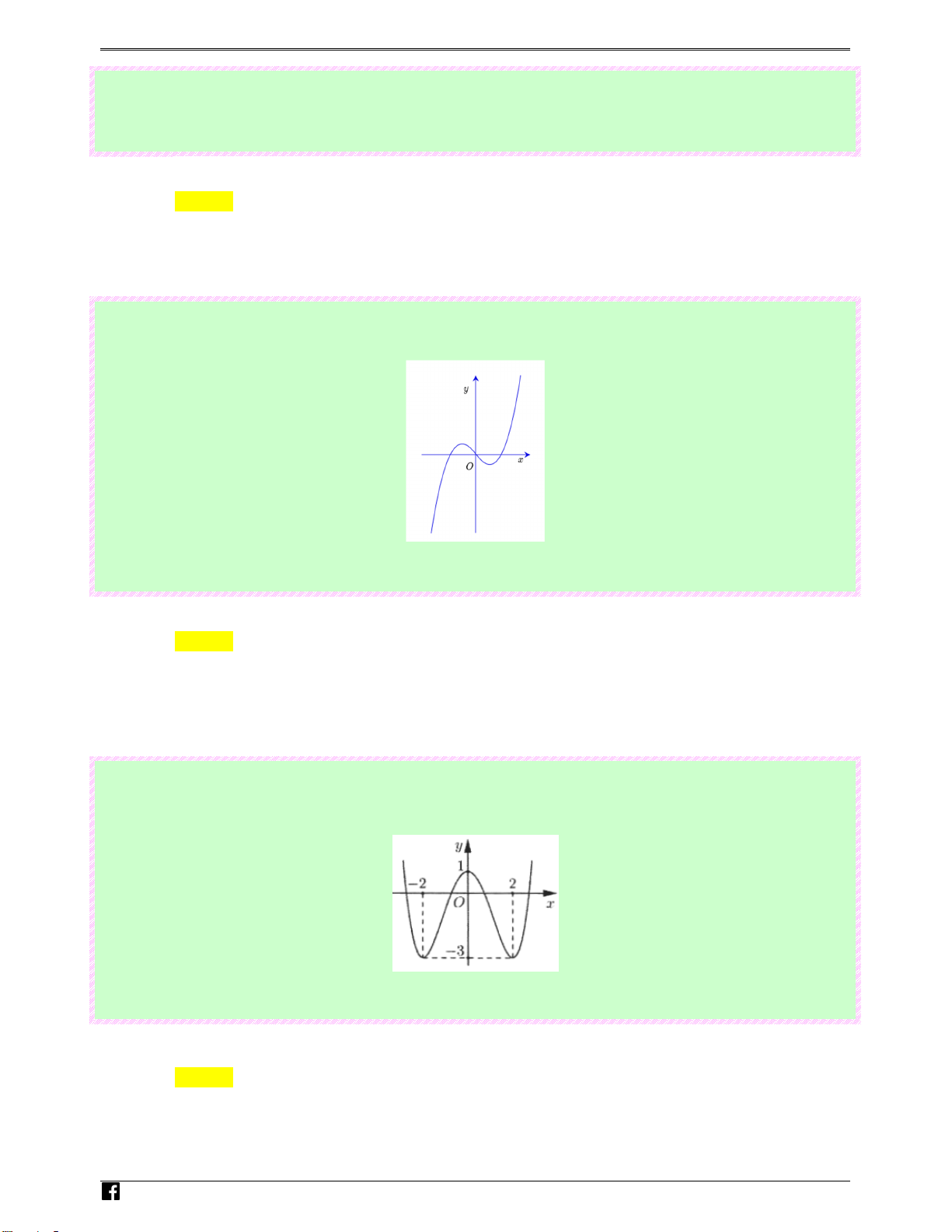
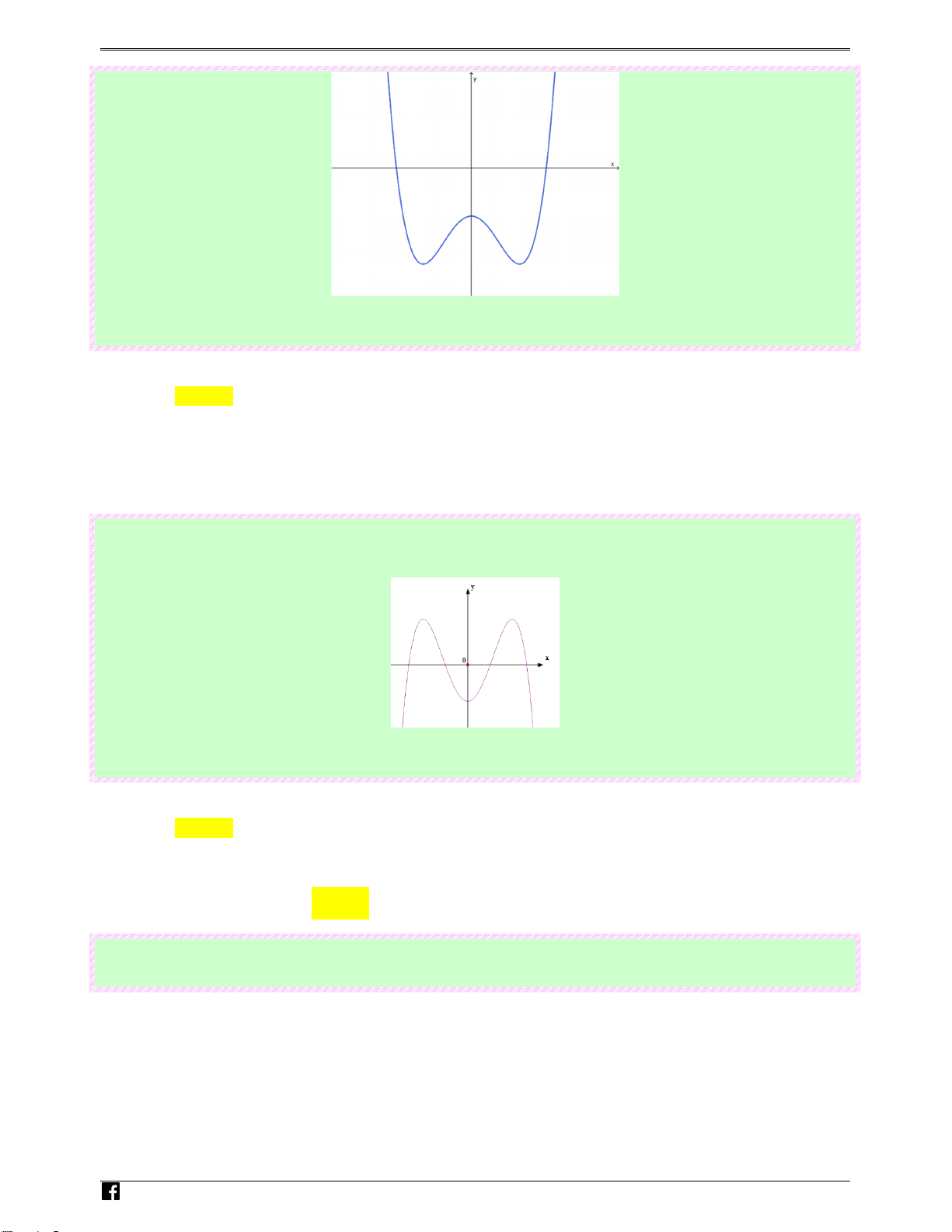
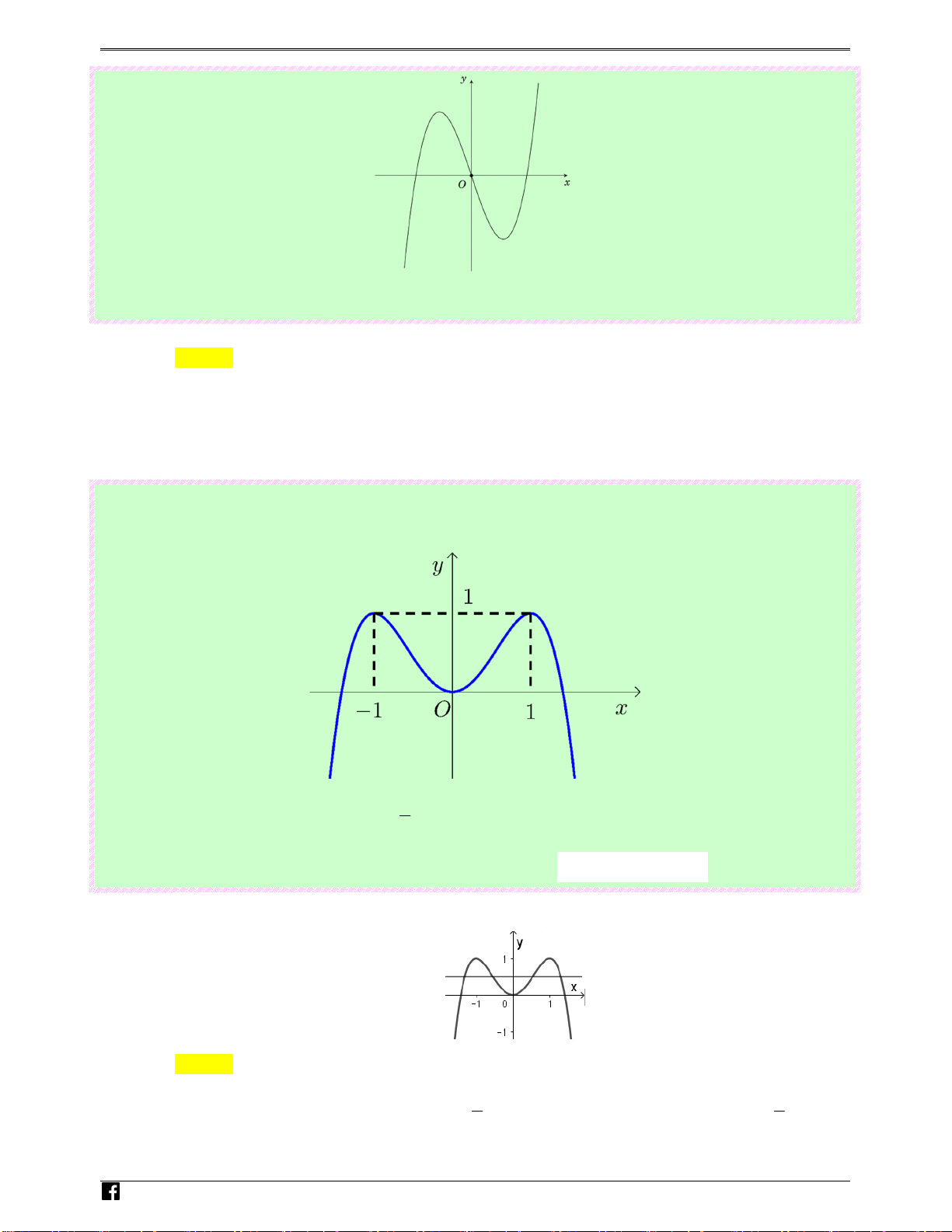
Câu 2: (Câu 1 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong hình bên? N guy-n Ho àng Ⓐ. 3 1
y = −x − 2x + . Ⓑ. 3 1
y = x − 2x + . Ⓒ. 4 2 1
y = −x + 2x + . Ⓓ. 4 2 1
y = x + 2x + . V 2 2 2 2 i0t Lời giải Chọn B
Dễ thấy đường cong có dạng đồ thị của hàm số bậc ba với hệ số a dương.
Câu 3: (Câu 16 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị hàm số 3 2
y = −x + 2x −1cắt
trục tung tại điểm có tung độ bằng Ⓐ. 3. Ⓑ. 1. Ⓒ. −1. Ⓓ. 0 . Lời giải Chọn C
Ta có x = 0 ⇒ y = 1 − Vậy đồ thị hàm số 3 2
y = −x + 2x −1cắt trục tung tại điểm có tung độ bằng −1 .
https://www.facebook.com/vietgold Trang 1
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
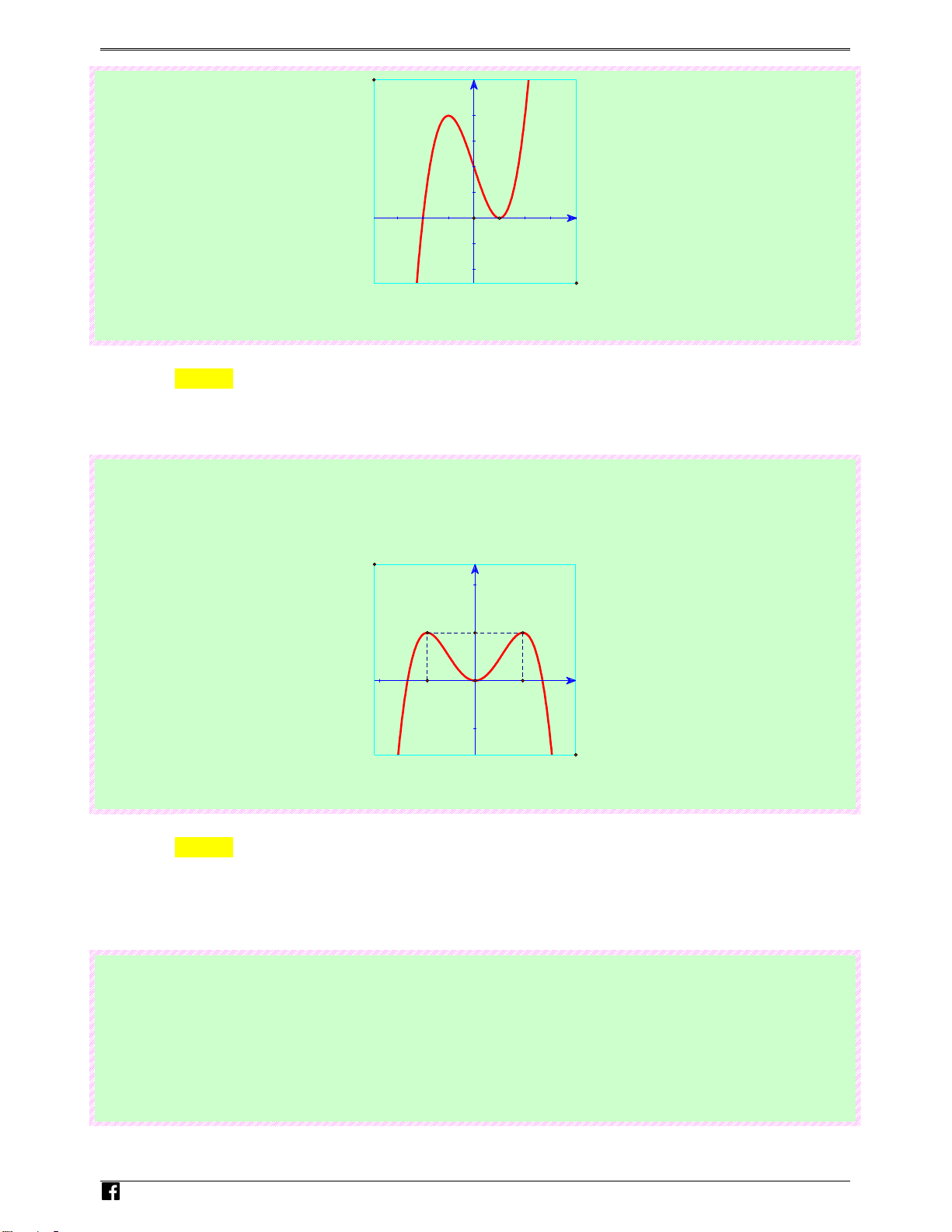
Câu 4: (Câu 15 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong hình bên? Luyenthi trac Ⓐ. 3
y = x − 3x + 1 . Ⓑ. 4 2
y = −2 x + 4 x + 1 . nghi Ⓒ. 3
y = − x + 3x + 1 . Ⓓ. 4 2
y = 2 x − 4 x + 1. em . Lời giải vn Chọn D
Dựa vào đồ thị ta thấy đây là đồ thị hàm trùng phương và có hệ số a > 0 .
Câu 5: (Câu 18 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị của hàm số 4 2
y = −x − 2x + 3
cắt trục tung tại điểm có tung độ bằng Ⓐ. 1. Ⓑ. 0 . Ⓒ. 2 . Ⓓ. 3. Lời giải Chọn D
Ta có x = 0 ⇒ y = 3
Vậy đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3.
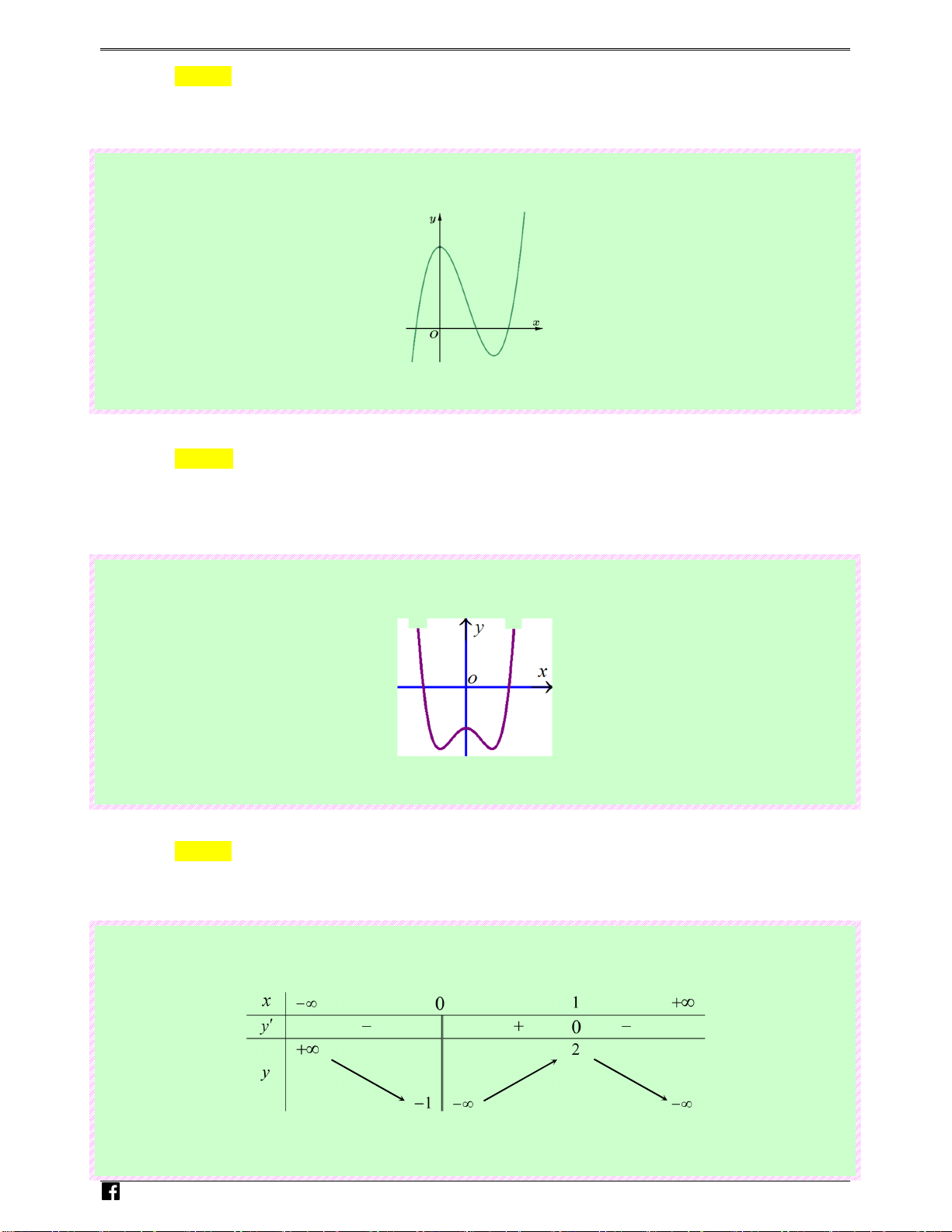
Câu 6: (Câu 6 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị hàm số nào dưới đây có dạn g N
như đường cong trong hình bên? guy-n Hoàng Vi0t Ⓐ. 4 2 y = 2
− x + 4x −1. Ⓑ. 3
y = −x + 3x −1 . Ⓒ. 4 2
y = 2x − 4x −1. Ⓓ. 3
y = x − 3x −1. Lời giải Chọn A
Đồ thị hàm số nhận Oy làm trục đối xứng nên loại đáp án B và Ⓓ.
Từ đồ thị hàm số ta thấy lim y = −∞ nên loại đáp án Ⓒ. x→+∞
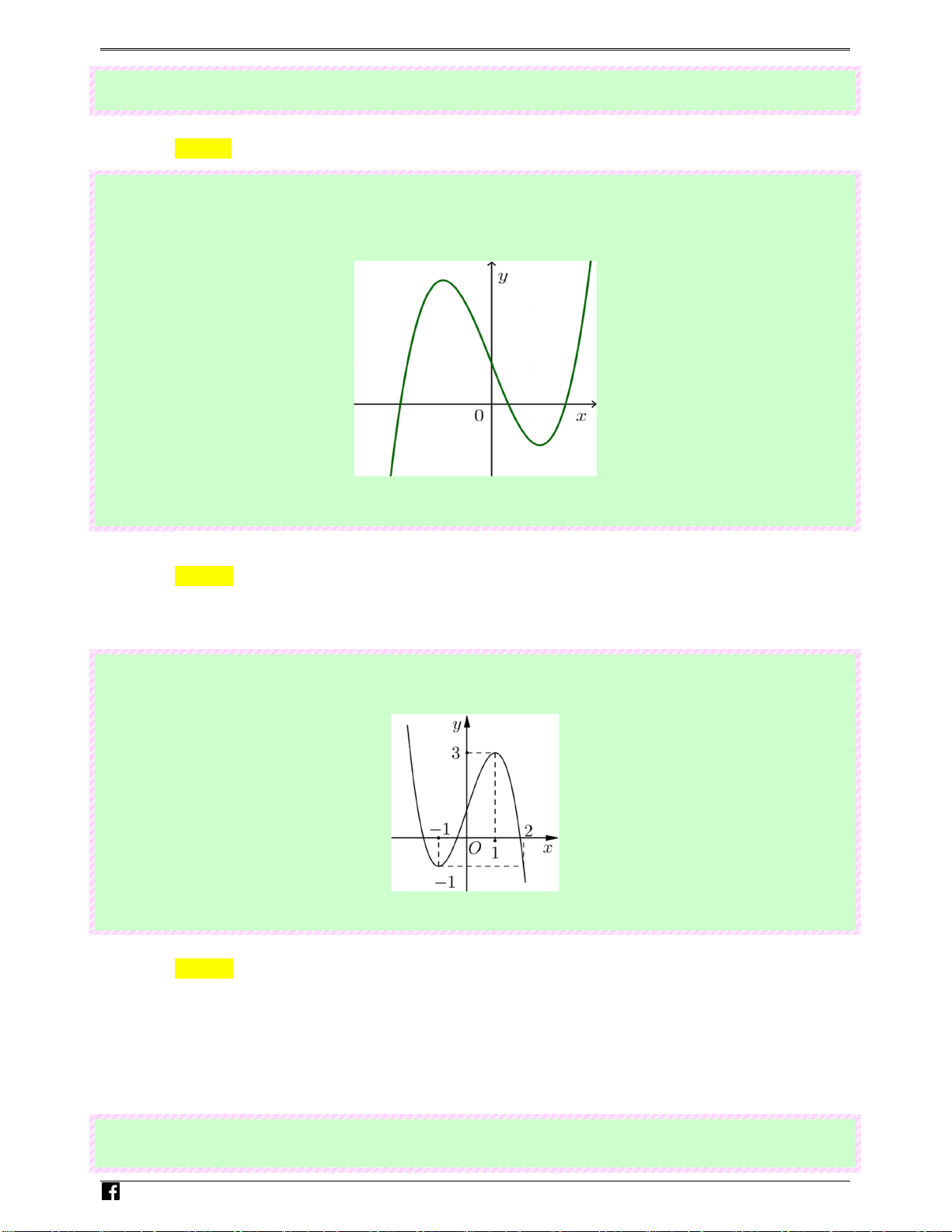
Câu 7: (Câu 7 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị của hàm số 4 2
y = −x + 4x − 3
cắt trục tung tại điểm có tung độ bằng Ⓐ. 0 . Ⓑ. 3. Ⓒ. 1. Ⓓ. 3 − .
https://www.facebook.com/vietgold Trang 2
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Lời giải Chọn D
Gọi M ( x ; y là giao điểm của đồ thị hàm số 4 2
y = −x + 4x − 3 và trục Oy M M ) Luy
Ta có x = 0 ⇒ y = 3 − . M M enth Câu 8:
(Câu 7 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Đồ thị của hàm số nào dưới đây có dạng itr
như đường cong trong hình sau acnghiem.vn Ⓐ. 4 2
y = −x + 2x −1. Ⓑ. 4 2
y = x − 2x −1. Ⓒ. 3 2
y = x − 3x −1. Ⓓ. 3 2
y = −x + 3x −1. Lời giải Chọn B
Dựa vào đồ thị hàm số ta thấy đây là đồ thị của hàm số bậc 4 trùng phương với hệ số a > 0 . Do đó nhận đáp án 4 2
y = x − 2x −1. Câu 9:
(Câu 8 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Đồ thị của hàm số 3
y = x − 3x + 2 c ắt N g
trục tung tại điểm có tung độ bằng uy-n Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 2 − . Ho Lời giải àng Chọn C Vi0t Gọi M ( x ;
x = 0 ⇒ y = 2 . 0 y
là giao điểm của đồ thị hàm số với trục tung. Ta có 0 ) 0 0
Câu 10: (Câu 20 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong vẽ bên Ⓐ. 3
y = x − 3x +1 . Ⓑ. 4 2
y = x − 2x +1. Ⓒ. 4 2
y = −x + 2x +1. Ⓓ. 3
y = −x + 3x +1.
https://www.facebook.com/vietgold Trang 3
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Lời giải Chọn A
Đường cong đã cho là đồ thị của hàm số bậc 3 có dạng 3 2
y = ax + bx + cx + d (a ≠ 0). Suy ra Lu
chọn đáp án A hoặc D yent
y = +∞ ⇒ a > ⇒ h Từ đồ thị ta có lim 0 Chọn đáp án A i x→+∞ tracn
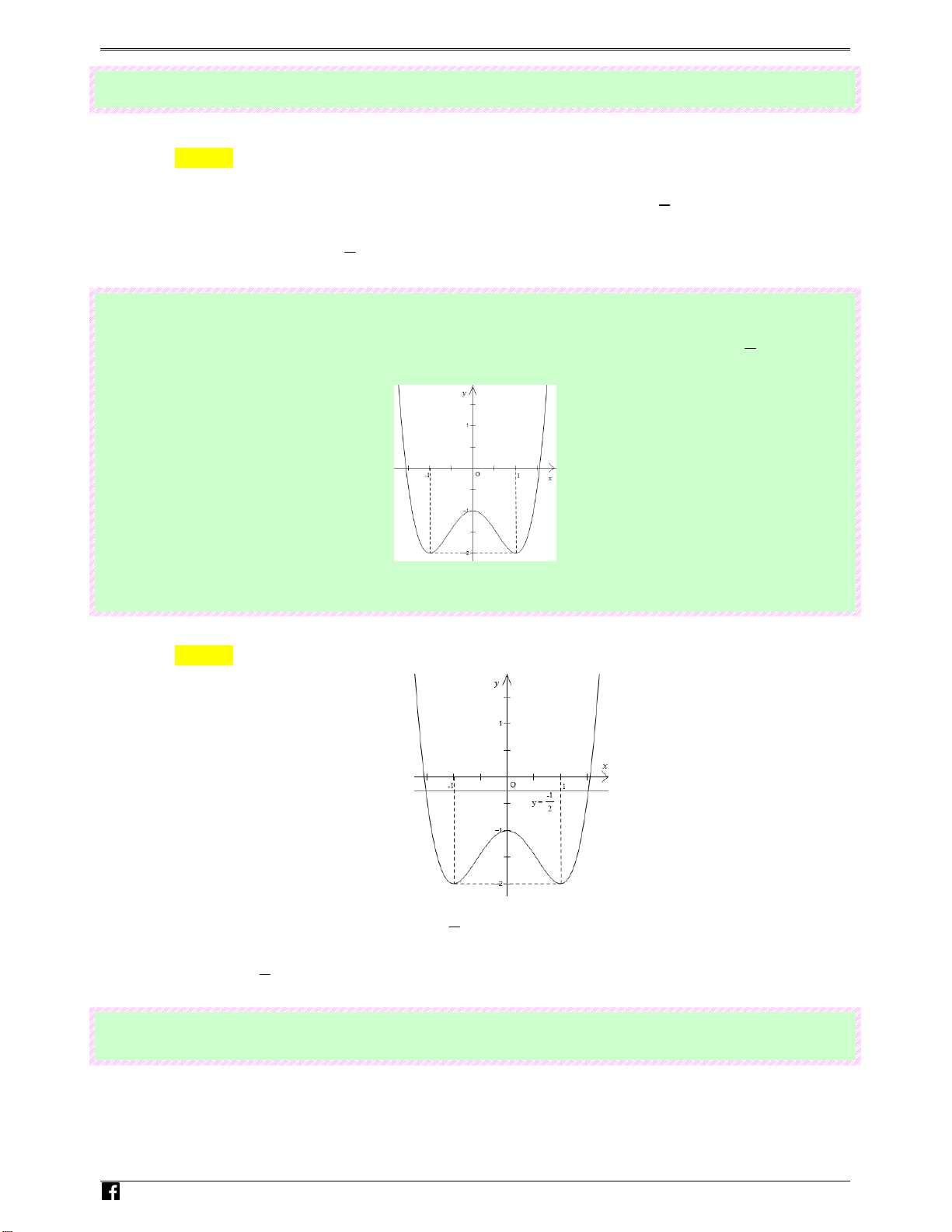
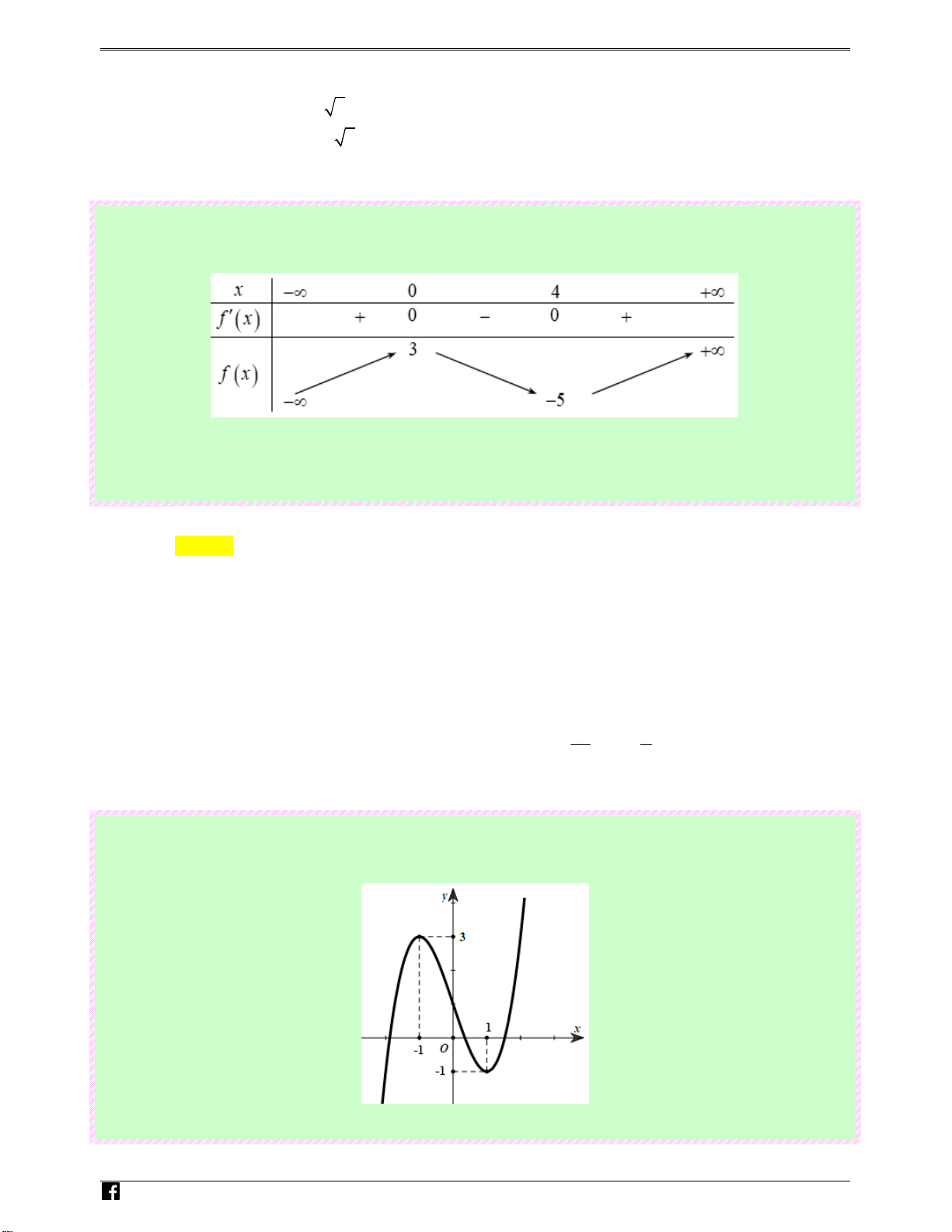
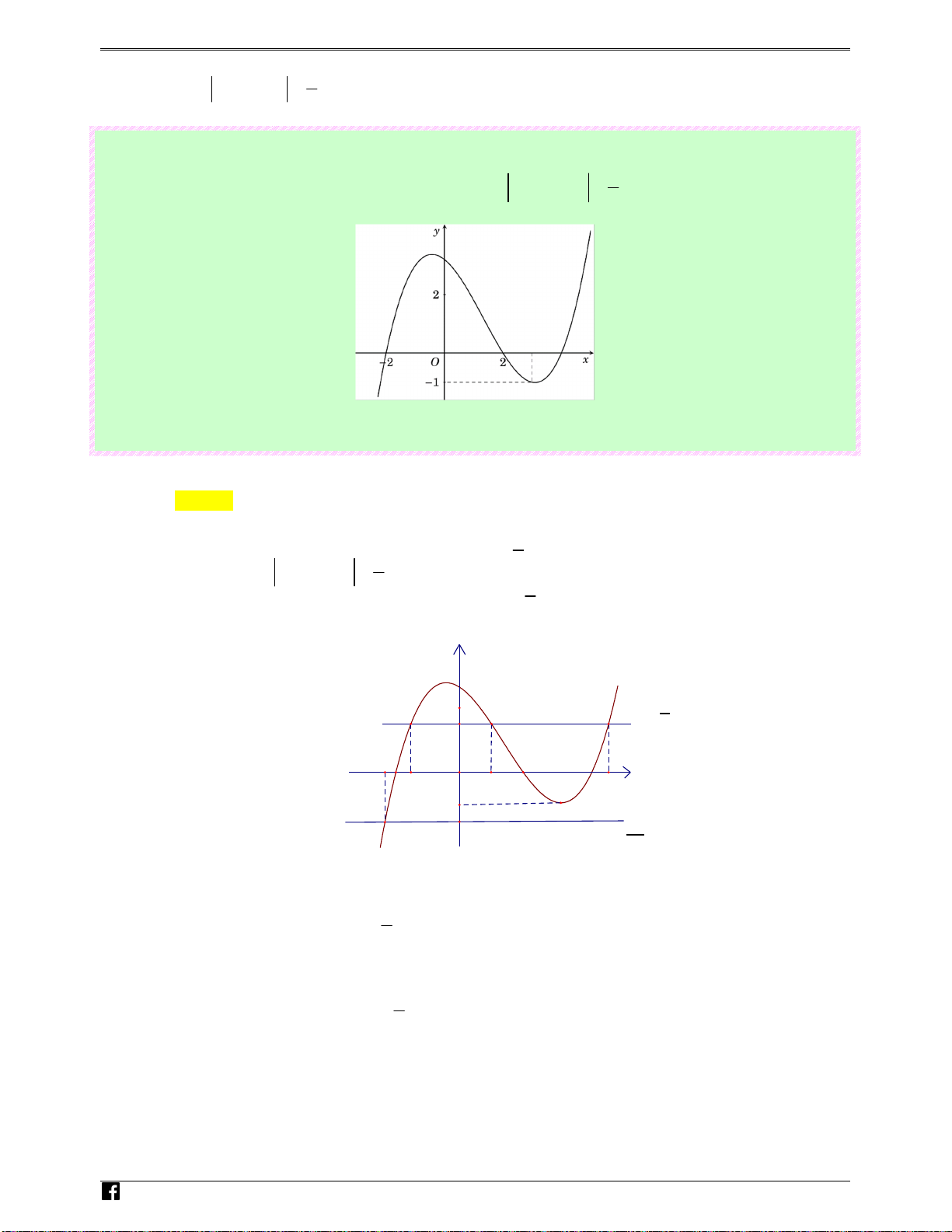
Câu 11: (Câu 25 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số bậc bốn y = f ( x) có gh
đồ thị là đường cong trong hình bên. iem.vn
Số nghiệm của phương trình f ( x) 1 = là 2 Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 1. Ⓓ. 3. N g Lời giải uy- Chọn A n Hoàng Vi0t
Số nghiệm của phương trình f ( x) 1
= bằng số giao điểm của đồ thị hàm số đã cho với đường 2 1 1
thẳng y = . Căn cứ vào đồ thị ta thấy đường thẳng y = cắt đồ thi hàm số đã cho tại 2 điểm 2 2
phân biệt nên phương trình f ( x) 1
= có 2 nghiệm phân biệt. 2
https://www.facebook.com/vietgold Trang 4
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 12: (Câu 27 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3
y = −x + 3x với trục hoành là L Ⓐ. 2 . Ⓑ. 0 . Ⓒ. 3. Ⓓ. 1. uye Lời giải nth Chọn C itra
Ta có hoành độ giao điểm của đồ thị hàm số 3
với trục hoành là nghiệm của c
y = −x + 3x ng x = 0 h 2
⇔ −x x − 3 = 0 ⇔ i phương trình: 3
−x + 3x = 0 (1) ( ) . e x = ± 3 m .vn
Phương trình (1) có ba nghiệm phân biệt, do đó đồ thị hàm số 3
y = −x + 3x cắt trục hoành tại ba điểm phân biệt.
Câu 13: (Câu 4 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong hình bên? Ⓐ. 4 2
y = − x + 2x −1. Ⓑ. 4 2
y = x − 2x −1. Ⓒ. 3 2
y = x − 3x −1 . Ⓓ. 3 2
y = −x + 3x −1. N guy- n H Lời giải oàn Chọn D g Vi0
Quan sát đồ thị hàm số ta có đây là đồ thị của hàm số bậc ba có hệ số a < 0 nên chọn đáp án t Ⓓ.
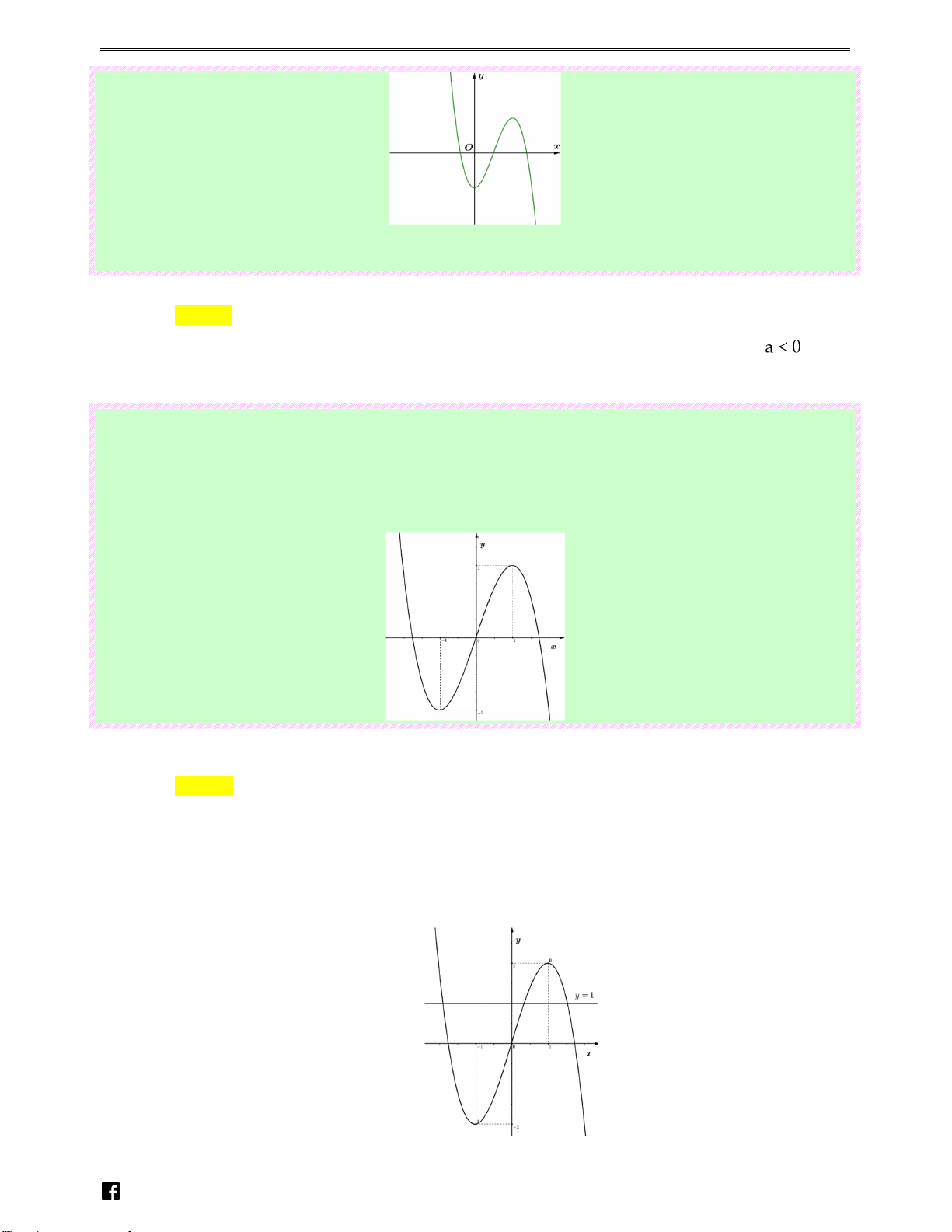
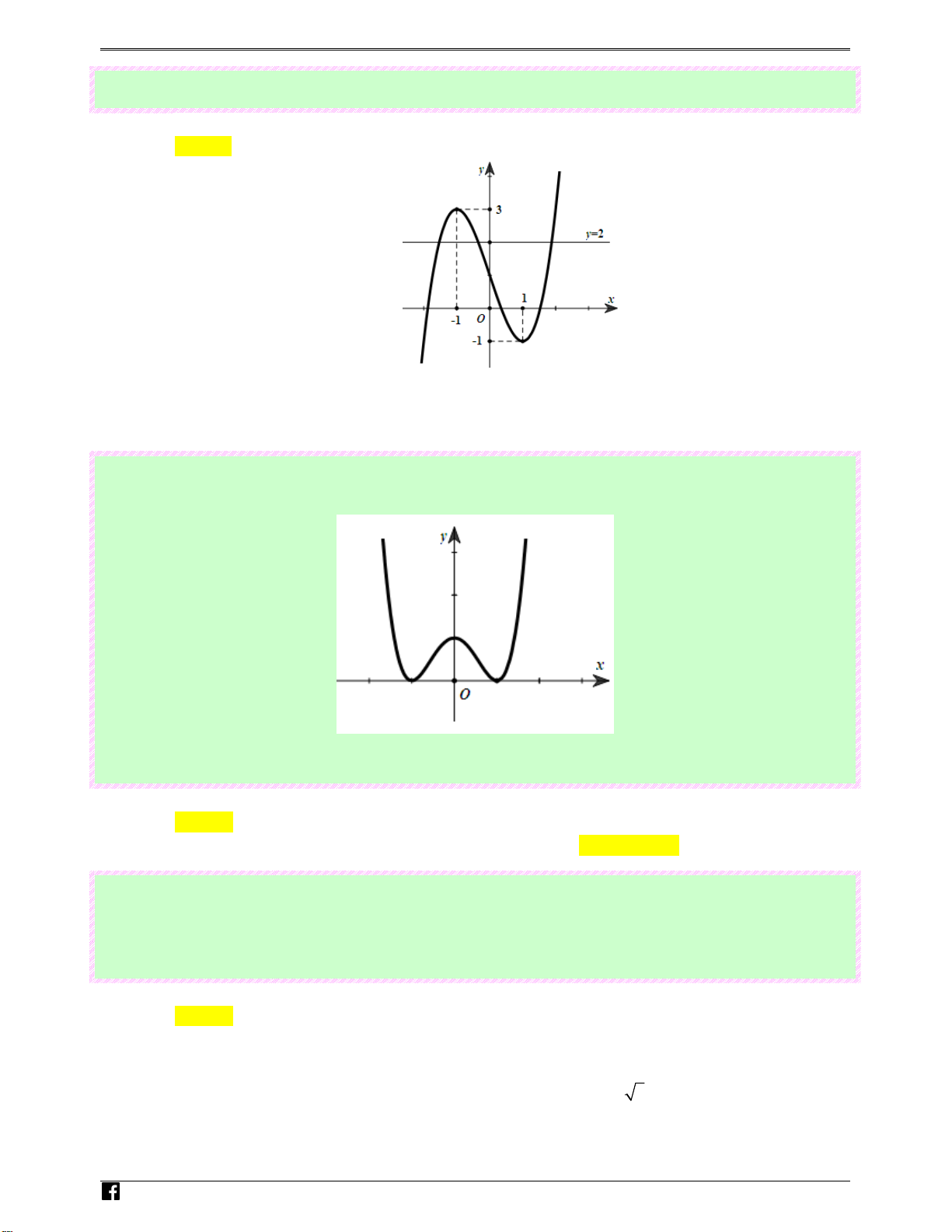
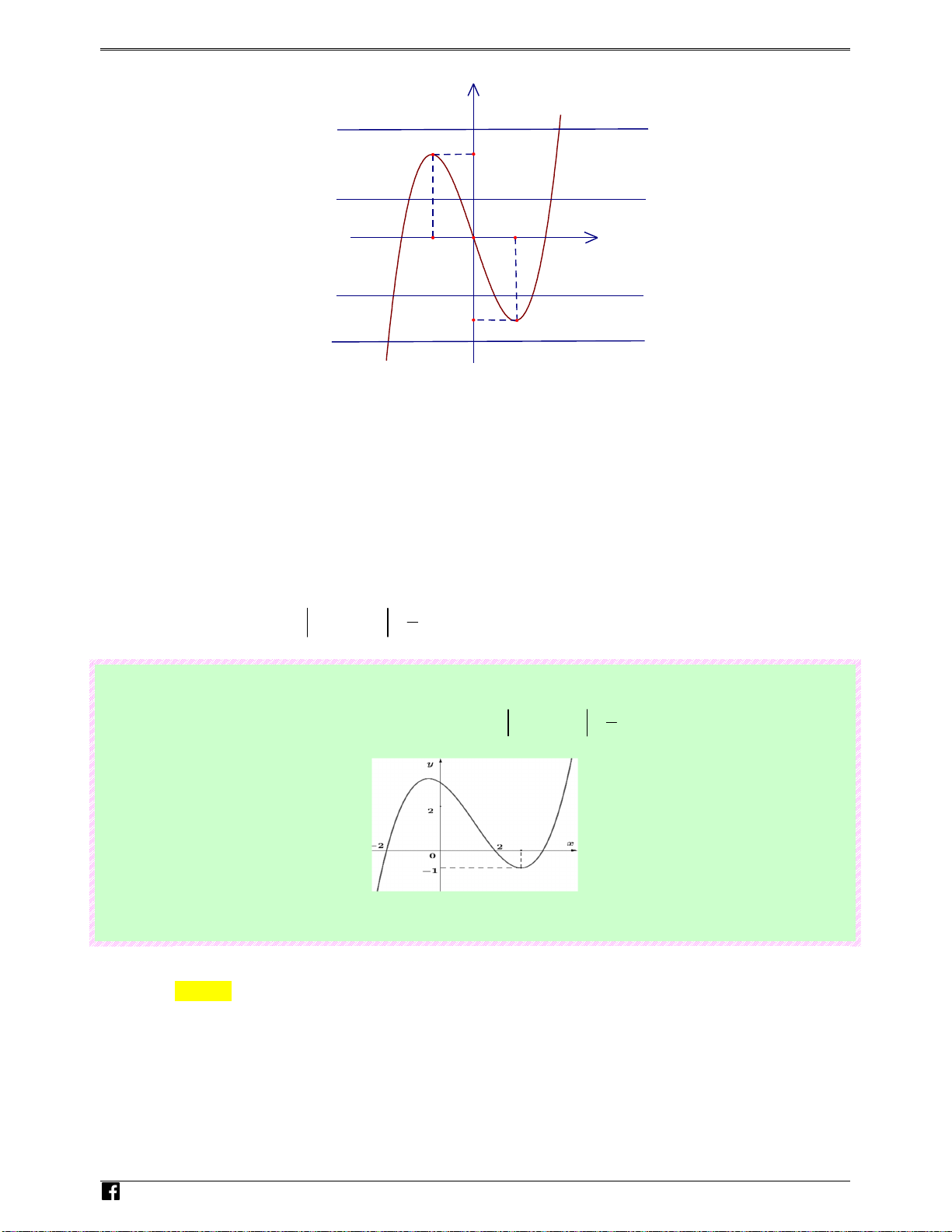
Câu 14: (Câu 17 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số bậc bốn y = f ( x) có
đồ thị là đường cong hình bên. Số nghiệm thực của phương trình f ( x) 3 = − là? 2
https://www.facebook.com/vietgold Trang 5
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Ⓐ. 4 Ⓑ. 1 Ⓒ. 2 Ⓓ. 3 Lời giải L Chọn A uye 3 n
Số giao điểm của đồ thị hàm số y = f ( x) và đồ thị hàm số y = − chính là số nghiệm của t 2 hitr
phương trình. f ( x) 3 = − ac 2 ngh
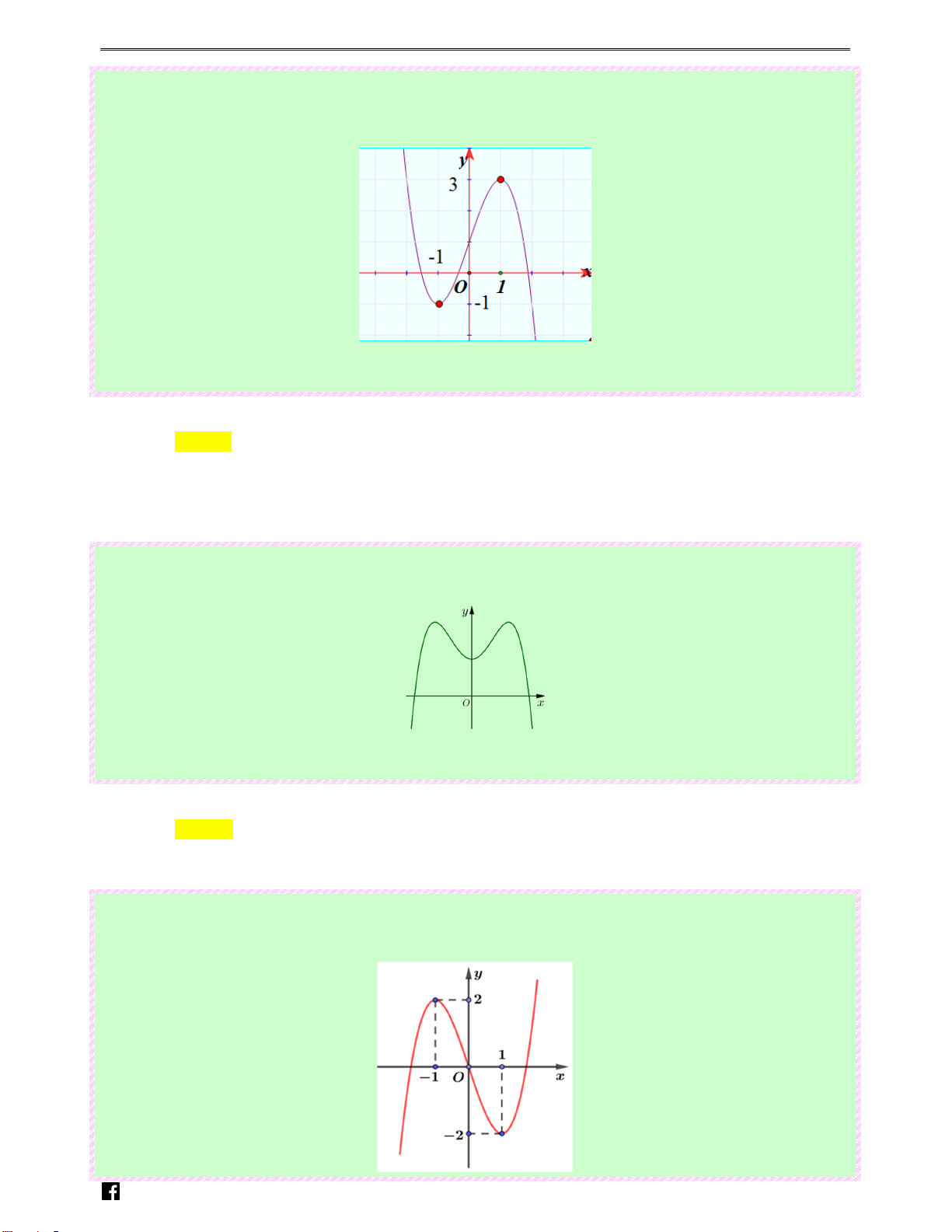
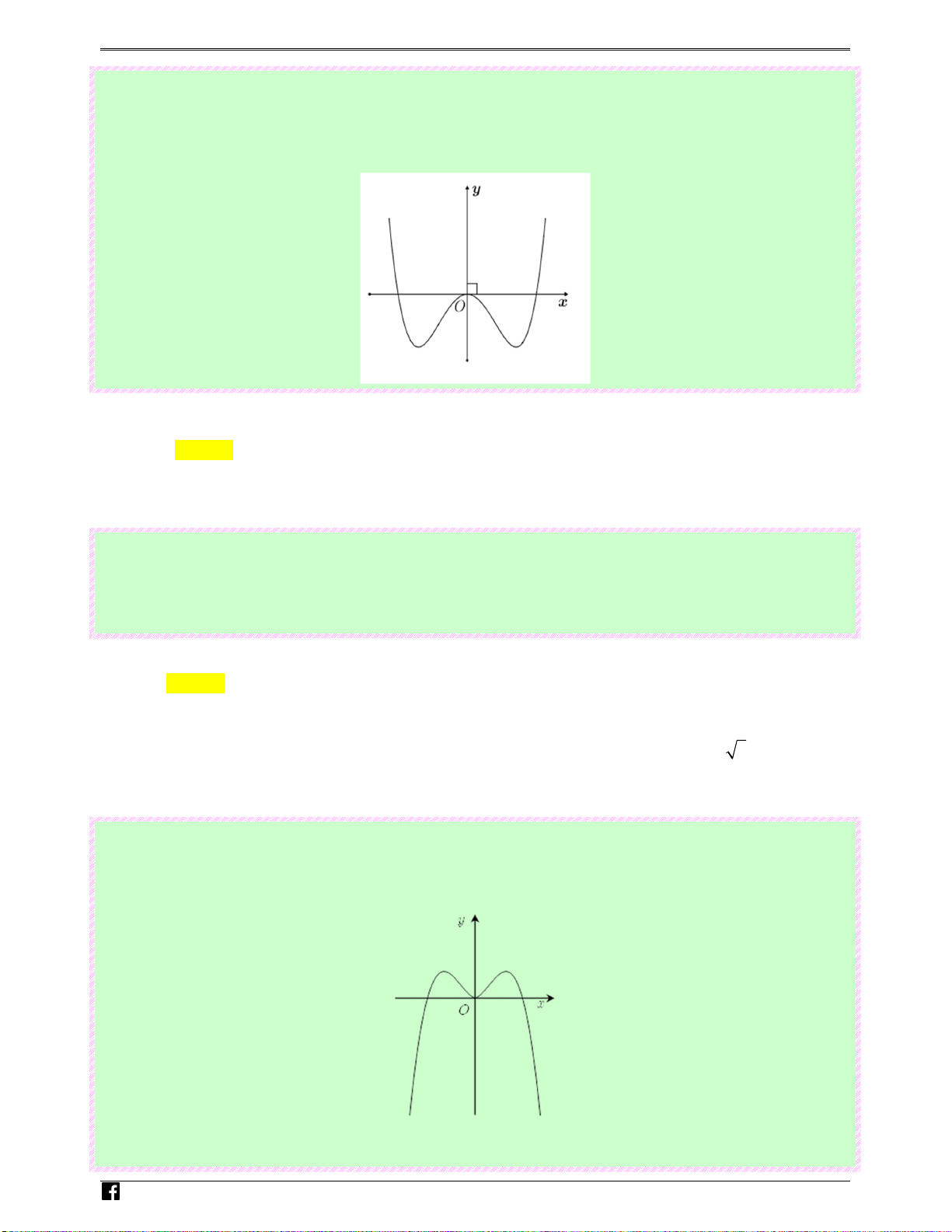
Câu 15: (Câu 1 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số bậc bốn y = f x có i ( ) em .
đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình f ( x) 1 = − là vn 2 Ⓐ. 3. Ⓑ. 4 . Ⓒ. 2 . Ⓓ. 1. Lời giải Chọn C N guy-n Hoàng Vi0t
Số nghiệm của phương trình f ( x) 1
= − là số giao điểm của đồ thị hàm số y = f ( x) và đường 2 1
thẳng y = − . Vậy phương trình đã cho có 2 nghiệm thực phân biệt. 2
Câu 16: (Câu 21 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
đường cong như trong hình vẽ
https://www.facebook.com/vietgold Trang 6
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenth itr
y = x − x − .
y = −x + x − .
y = x − x − .
y = −x + x − . a Ⓐ. 4 2 2 2 Ⓑ. 3 2 3 2 Ⓒ. 3 2 3 2 Ⓓ. 4 2 2 2 cng Lời giải hie Chọn B m .
Dựa vào hình dáng đồ thị hàm số ta nhận thấy đó là đồ thị hàm số bậc 3 và có hệ số nên vn
chọn đáp án Ⓑ.
Câu 17: (Câu 15 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc ba y = f ( x) có
đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình f ( x) =1 là Ⓐ. 1. Ⓑ. 0. Ⓒ. 2. Ⓓ. 3. N guy- n H Lời giải oàn Chọn D g Vi0
Số nghiệm thực của phương trình f ( x) =1 là số giao điểm của đường thẳng y = 1 và đồ thị t
hàm số y = f ( x) . Nhìn vào hình vẽ ta thấy đường thẳng y = 1 cắt đồ thị tại 3 điểm phân biệt.
Vậy phương trình f ( x) =1 có 3 nghiệm thự Ⓒ.
https://www.facebook.com/vietgold Trang 7
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 18: (Câu 11 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc ba y = f ( x) có
đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình f ( x) = 1 là. Luyenthitracnghiem .vn Ⓐ. 0 Ⓑ. 3 Ⓒ. 1 Ⓓ. 2 Lời giải Chọn B
Ta thấy đường thẳng y = 1 cắt đồ thị hàm số y = f ( x) tại 3 điểm phân biệt. Nên phương trình
f ( x) = 1 có 3 nghiệm thực phân biệt.
Câu 19: (Câu 1 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong hình bên? N guy-n Ho Ⓐ. 3 2
y = x − 3x +1. Ⓑ. 3 2
y = −x + 3x +1 . Ⓒ. 4 2
y = −x + 2x +1. Ⓓ. 4 2
y = x − 2x +1. àng Lời giải Vi0 Chọn C t
Ta có: Dựa vào đồ thị của hàm số ta thấy đây là hàm trùng phương và có hệ số a âm.
Câu 20: (Câu 16 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc ba y = f ( x) có
đồ thị là đường cong trong hình bên.
https://www.facebook.com/vietgold Trang 8
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Số nghiệm thực của phương trình f ( x) = −1 là Ⓐ. 3. Ⓑ. 1. Ⓒ. 0 . Ⓓ. 2 . Lu Lời giải yen Chọn A thit
Số nghiệm của phương trình f ( x) = 1
− bằng số giao điểm của đường cong y = f ( x) với đường rac thẳng y = 1
− . Nhìn hình vẽ ta thấy có 3 giao điểm nên phương trình đã cho có 3 nghiệm. nghi
Câu 21: (Câu 14 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có em
dạng như đường cong trong hình dưới? .vn Ⓐ. 3
y = x − 3x . Ⓑ. 3
y = −x + 3x . Ⓒ. 4 2
y = x − 2x . Ⓓ. 4
y = −x + 2x . Lời giải Chọn A N 3 2 g
Ta thấy đây là đồ thị của hàm số y = ax + bx + cx + d (a ≠ 0) và a > 0. uy-n
Nên chọn. Ⓐ. Hoàn
Câu 22: (Câu 17 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Cho hàm số y = f ( x) có đồ thị trong g V
hình vẽ bên. Số nghiệm của phương trình f (x) = 1 − là i0t Ⓐ. 3. Ⓑ. 2. Ⓒ. 1. Ⓓ. 4. Lời giải Chọn D
Số nghiệm của phương trình f (x) = 1
− bằng số giao điểm của đồ thị hàm số y = f ( x) với đường
thẳng y = −1 . Dựa vào đồ thị hàm số y = f ( x) suy ra số nghiệm của phương trình bằng 4.
https://www.facebook.com/vietgold Trang 9
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 23: (Câu 30 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3
y = x − 3x +1 và trục hoành là Ⓐ. 3. Ⓑ. 0. Ⓒ. 2. Ⓓ. 1. Luy Lời giải enth Chọn A itr 3 2 a
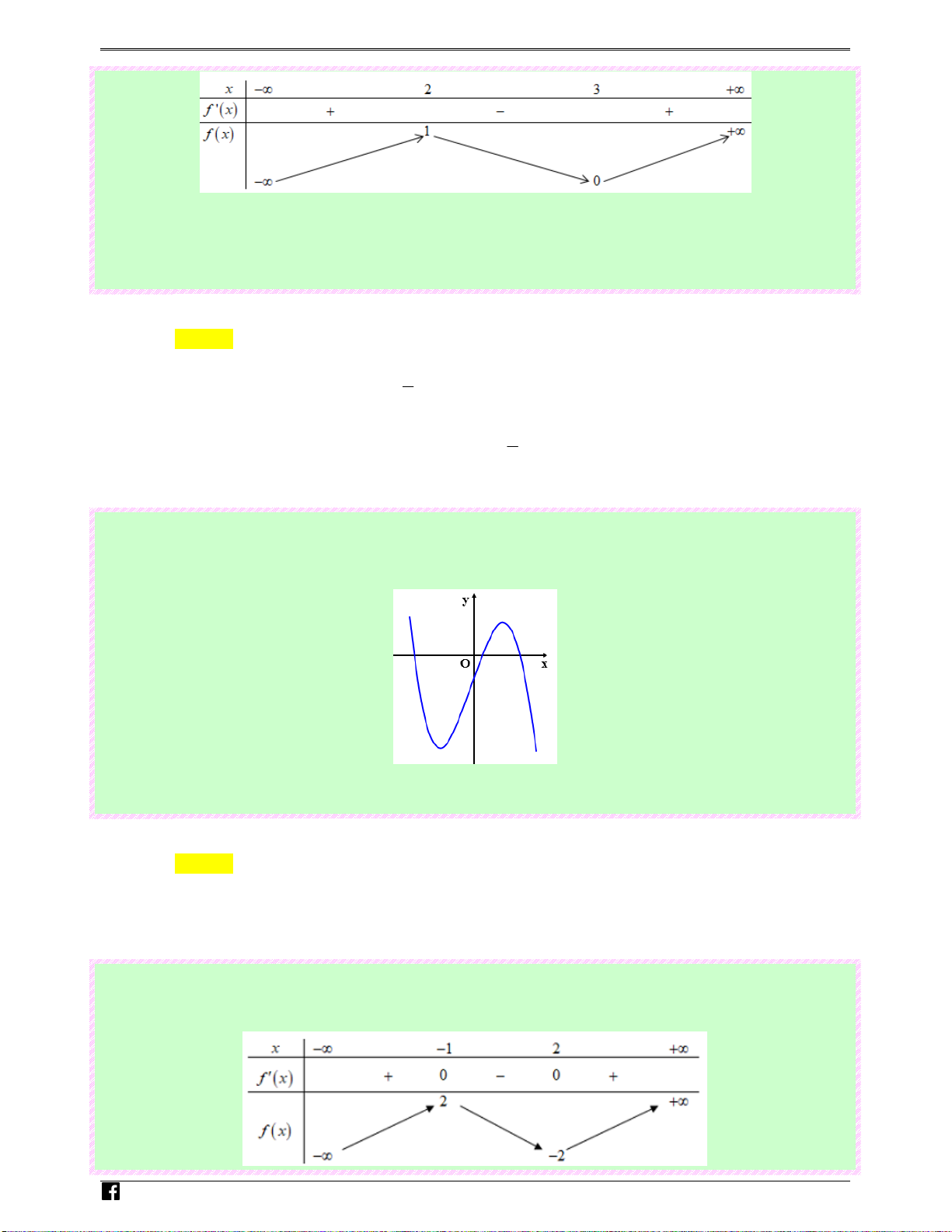
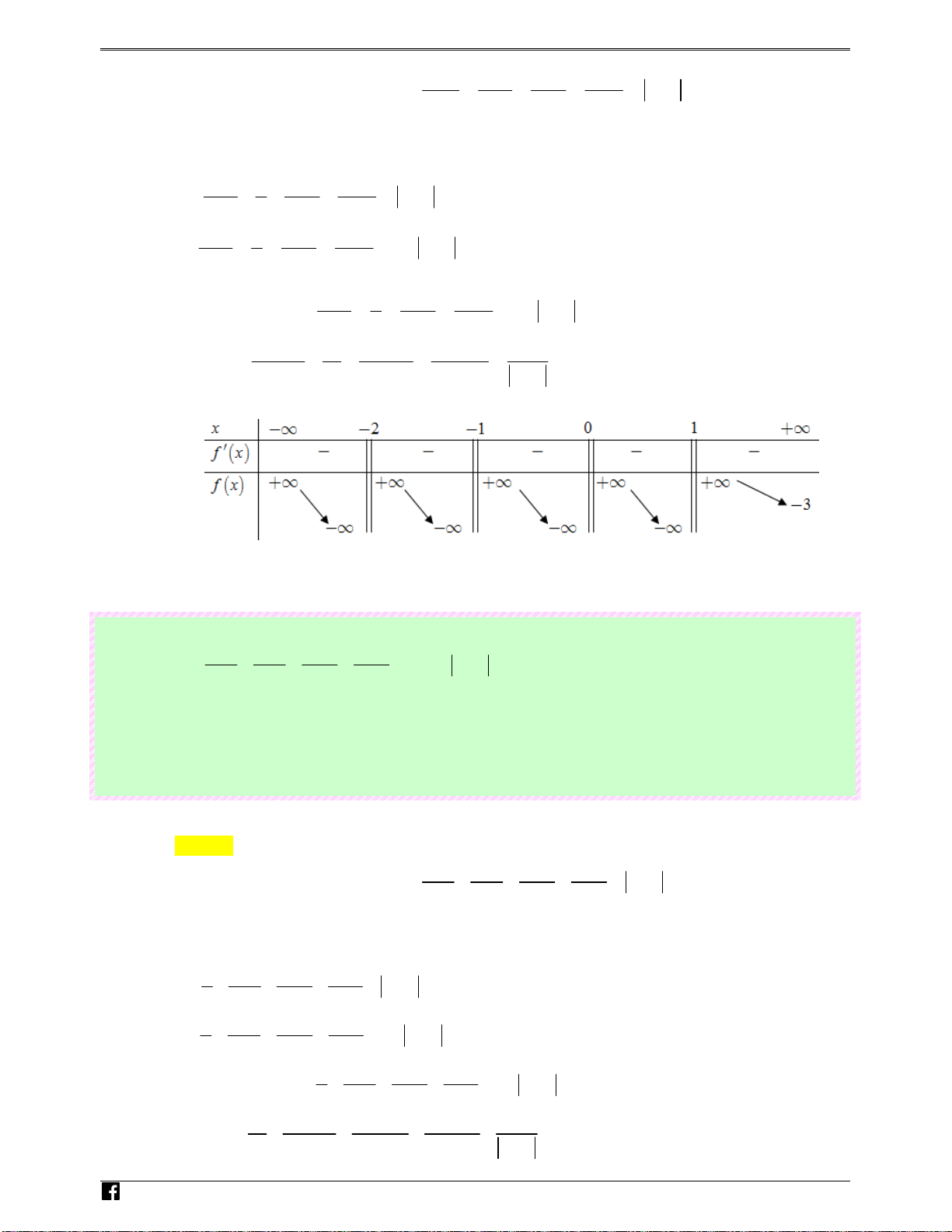
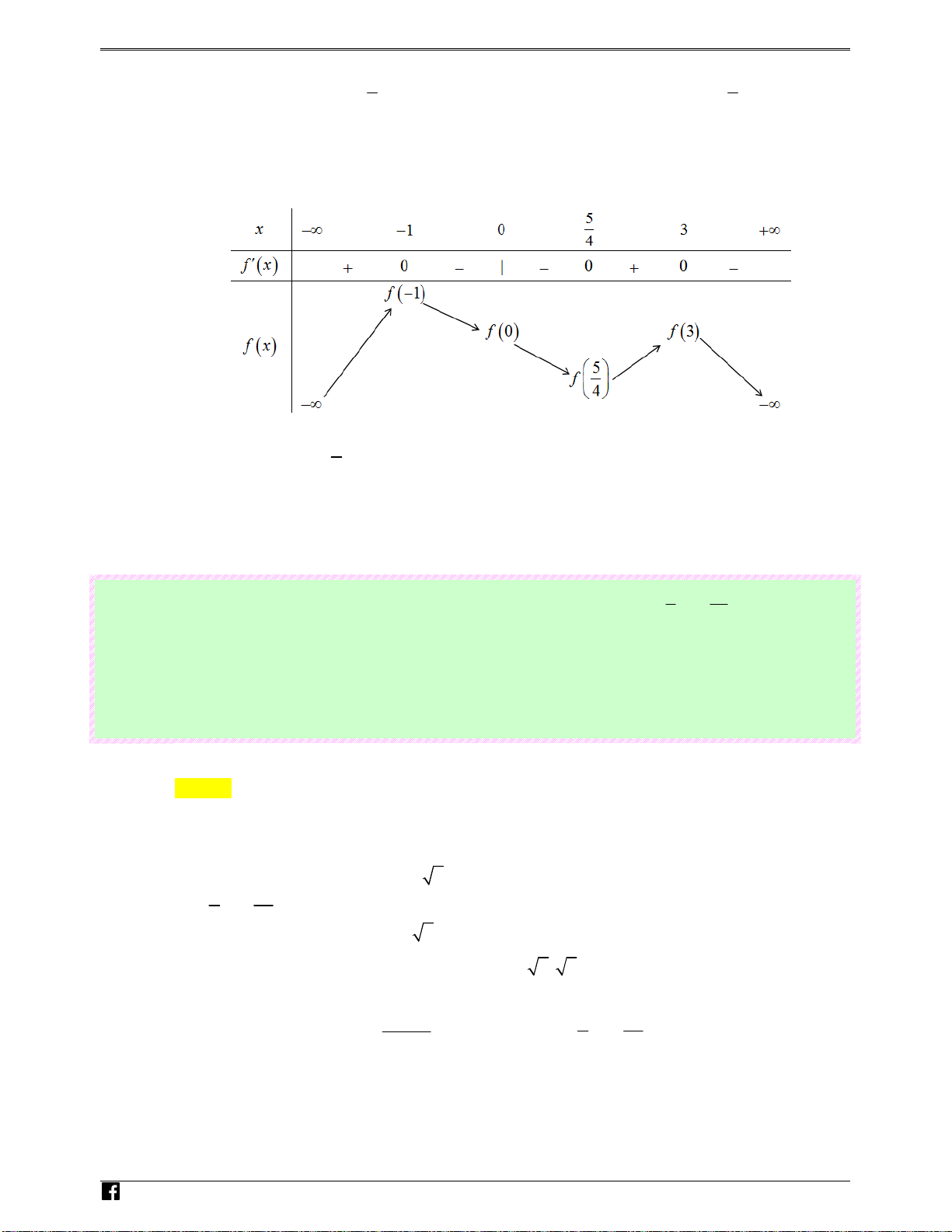
y = x −3x +1⇒ y′ = 3x − 3 = 3( x − ) 1 (x + ) 1 . cngh x = 1 − i y′ = 0 ⇔ e m x = 1 .v Ta có bảng biến sau: n
Nhìn vào bảng biến thiên ta thấy đồ thị hàm số f (x) cắt trục hoành
tại ba điểm phân biệt.
Câu 24: (Câu 9 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có dạng
như đường cong trong hình bên? N guy-n Hoàng Vi0t Ⓐ. 4 2
y = −x + 2x . Ⓑ. 4 2
y = x − 2x . Ⓒ. 3 2
y = x − 3x . Ⓓ. 3 2
y = −x + 3x . Lời giải Chọn A
Đồ thị trên là đồ thị của hàm số dạng 4 2
y = ax + bx + c với a < 0 .
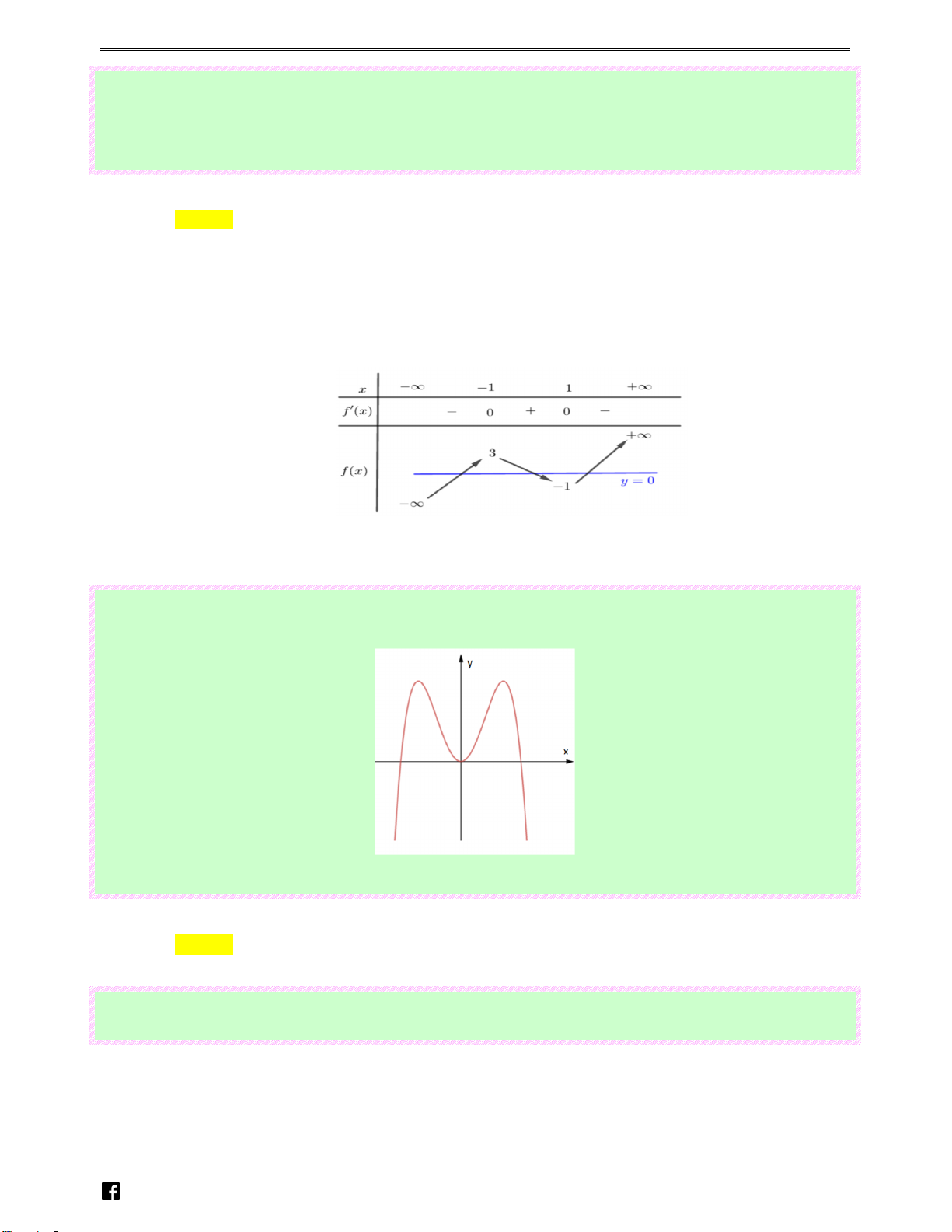
Câu 25: (Câu 9 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Đồ thị của hàm số nào dưới đây có dạng như
đường cong trong hình vẽ bên?
https://www.facebook.com/vietgold Trang 10
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenth itrac Ⓐ. 3
y = 2x − 3x +1. Ⓑ. 4 2 y = 2
− x + 4x +1. Ⓒ. 4 2
y = 2x − 4x +1 . Ⓓ. 3 y = 2 − x + 3x +1. ngh Lời giải ie Chọn B m .
Do nhánh cuối đi xuống nên hệ số a < 0 , loại , A C . vn
Đồ thị có ba cực trị, loại D .
Câu 26: (Câu 2 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Đồ thị của hàm số nào dưới đây có dạng như
đường cong trong hình vẽ bên? Ⓐ. 3 2
y = x − 3x − 2 . Ⓑ. 4 2
y = x − 2x − 2 . Ⓒ. 3 2
y = −x + 3x − 2 . Ⓓ. 4 2
y = −x + 2x − 2 . N Lời giải gu Chọn B y-
Ta dựa vào đồ thị chọn a > 0 . n H
Đồ thị cắt trục tung tại điểm có tung độ âm nên c < 0 . oà
Do đồ thị hàm số có 3cực trị nên b < 0 . ng Vi
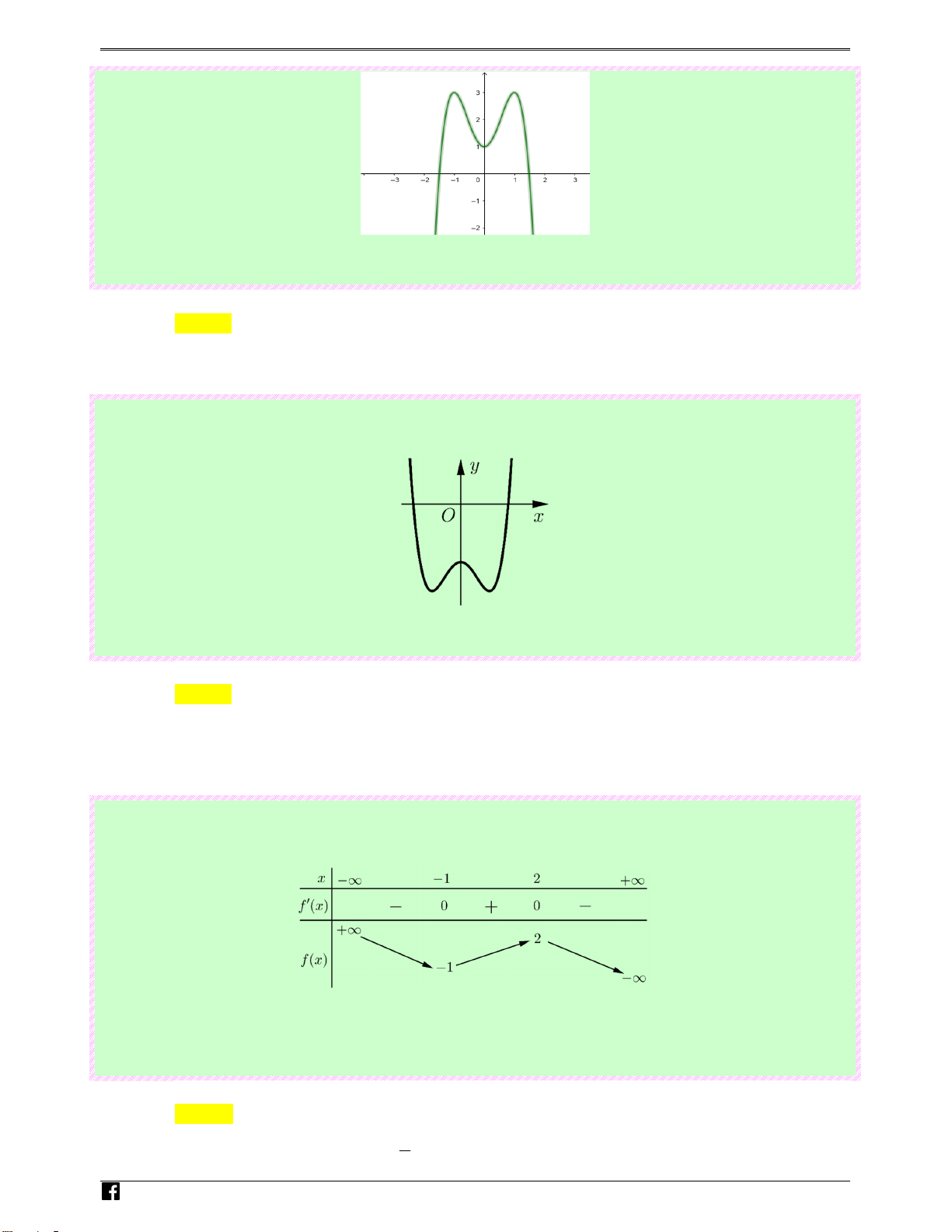
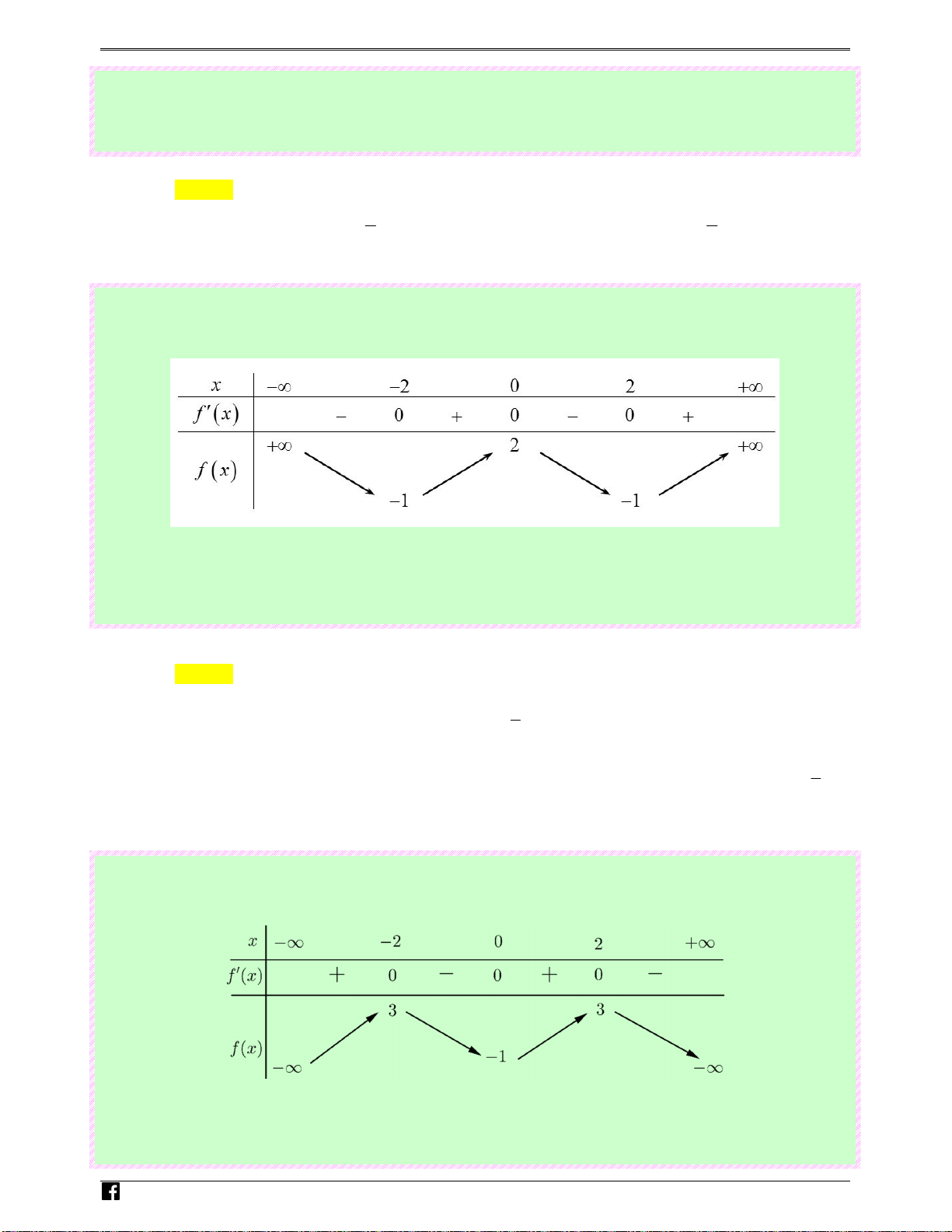
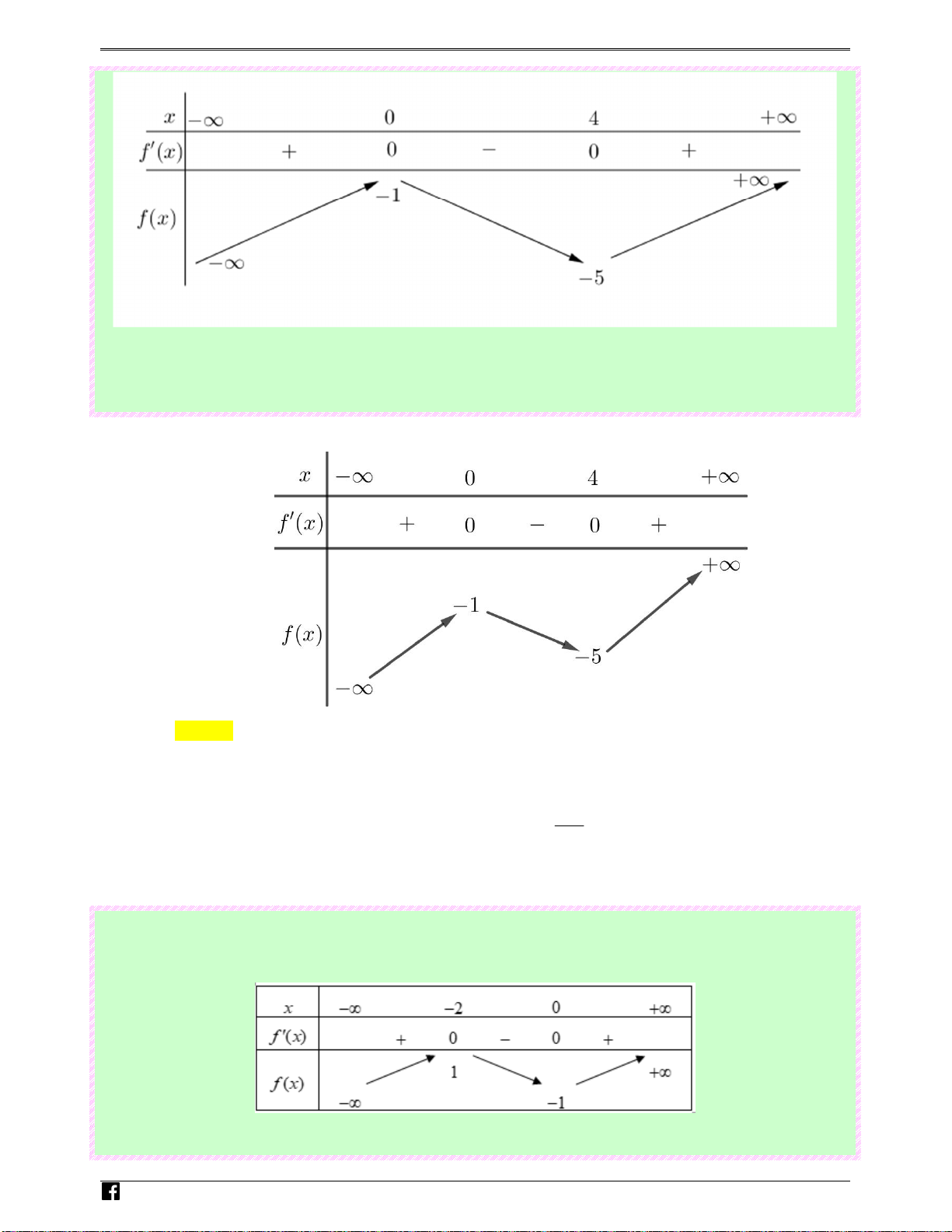
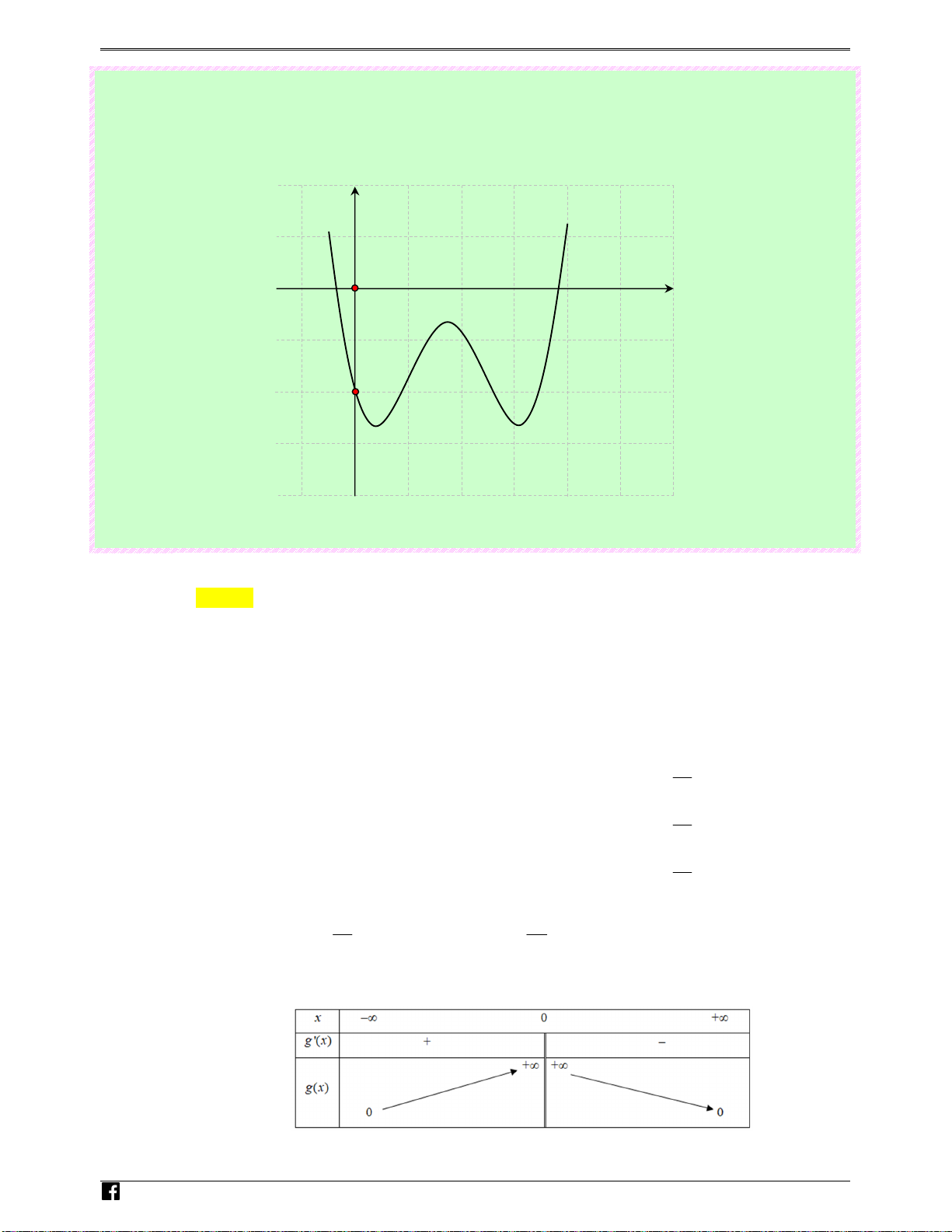
Câu 27: (Câu 16 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên như 0t sau:
Số nghiệm thực của phương trình 2 f ( x) − 3 = 0 là Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3. Ⓓ. 0. Lời giải Chọn C
Ta có f ( x) − = ⇔ f ( x) 3 2 3 0 = . 2
https://www.facebook.com/vietgold Trang 11
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Dựa vào bảng biến thiên: Suy ra phương trình f (x) 3
= có ba nghiệm thực phân biệt 2
Câu 28: (Câu 10 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Đồ thị của hàm số nào dưới đây có dạng L
như đường cong trong hình vẽ bên? uyenthitracnghiem.vn Ⓐ. 4 2 y = x − +2x 1 + . Ⓑ. 3 y = x − +3x 1 + . Ⓒ. 3
y = x −3x 1 + . Ⓓ. 4 2
y = x −2x 1 + . Lời giải Chọn B
Căn cứ vào đồ thị hàm số và các phương án ta loại các phương án hàm số bậc bốn trùng phương là ,
A D . Còn lại các phương án hàm số bậc b Ⓐ.
Từ đồ thị ta có: lim y = +∞, lim y = −∞ nên hàm số 3 y = x − +3x 1 + có đường cong như x→−∞ x→+∞ trong hình vẽ. N gu
Câu 29: (Câu 6 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Đồ thị của hàm số nào dưới đây có dạng như y-
đường cong hình vẽ bên n Hoàng Vi0t Ⓐ. 3 2
y = x −3x +3. Ⓑ. 3 2 y = x
− +3x +3. Ⓒ. 4 2
y = x −2x +3. Ⓓ. 4 2 y = x − +2x +3. Lời giải Chọn A
Đồ thị hàm số có hai điểm cực trị nên loại C và Ⓓ.
Câu 30: (Câu 15 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
https://www.facebook.com/vietgold Trang 12
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthi trac 2x −1 x +1 n Ⓐ. y = . Ⓑ. y = . Ⓒ. 4 2
y = x +x +1. Ⓓ. 3
y = x − 3x −1 . g x −1 x −1 hie Lời giải m .v Chọn B n
Dựa vào đồ thị thấy hàm số đã cho không xác định tại x =1 nên loại đáp án C, Ⓓ. x +1
Mặt khác lim y = 1 nên đường cong trong hình bên là đồ thị của hàm số y = . x→+∞ x −1
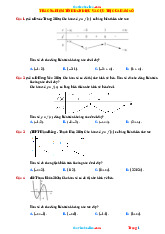
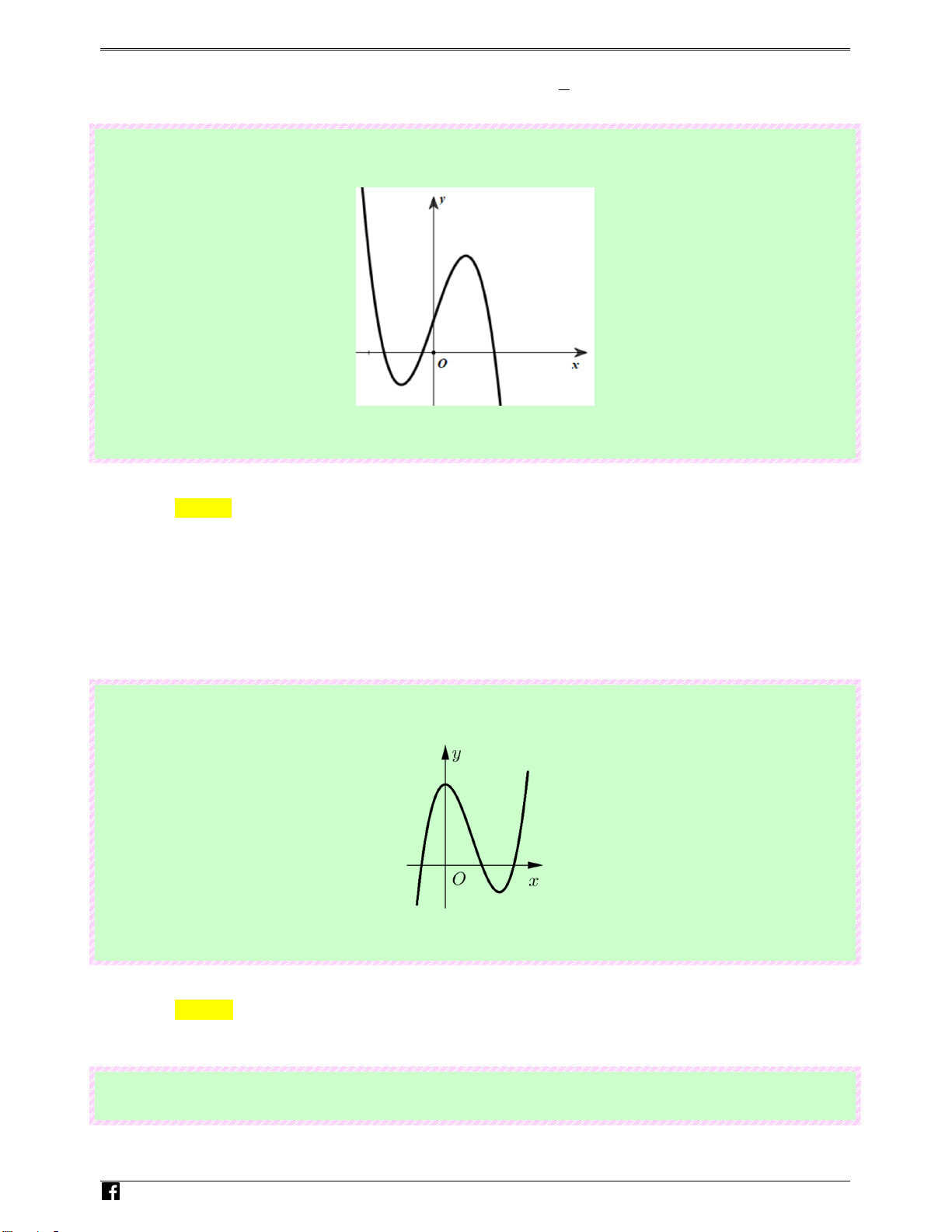
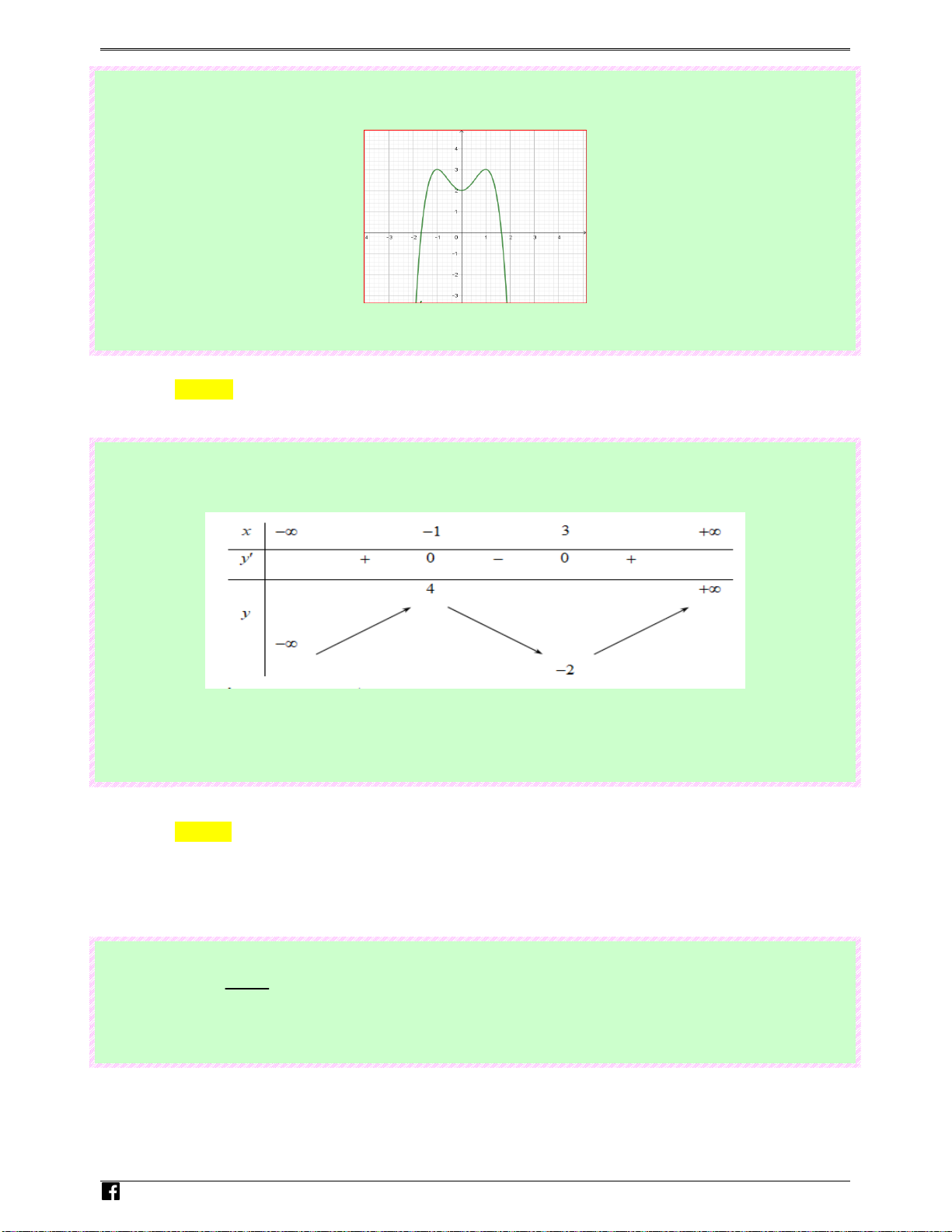
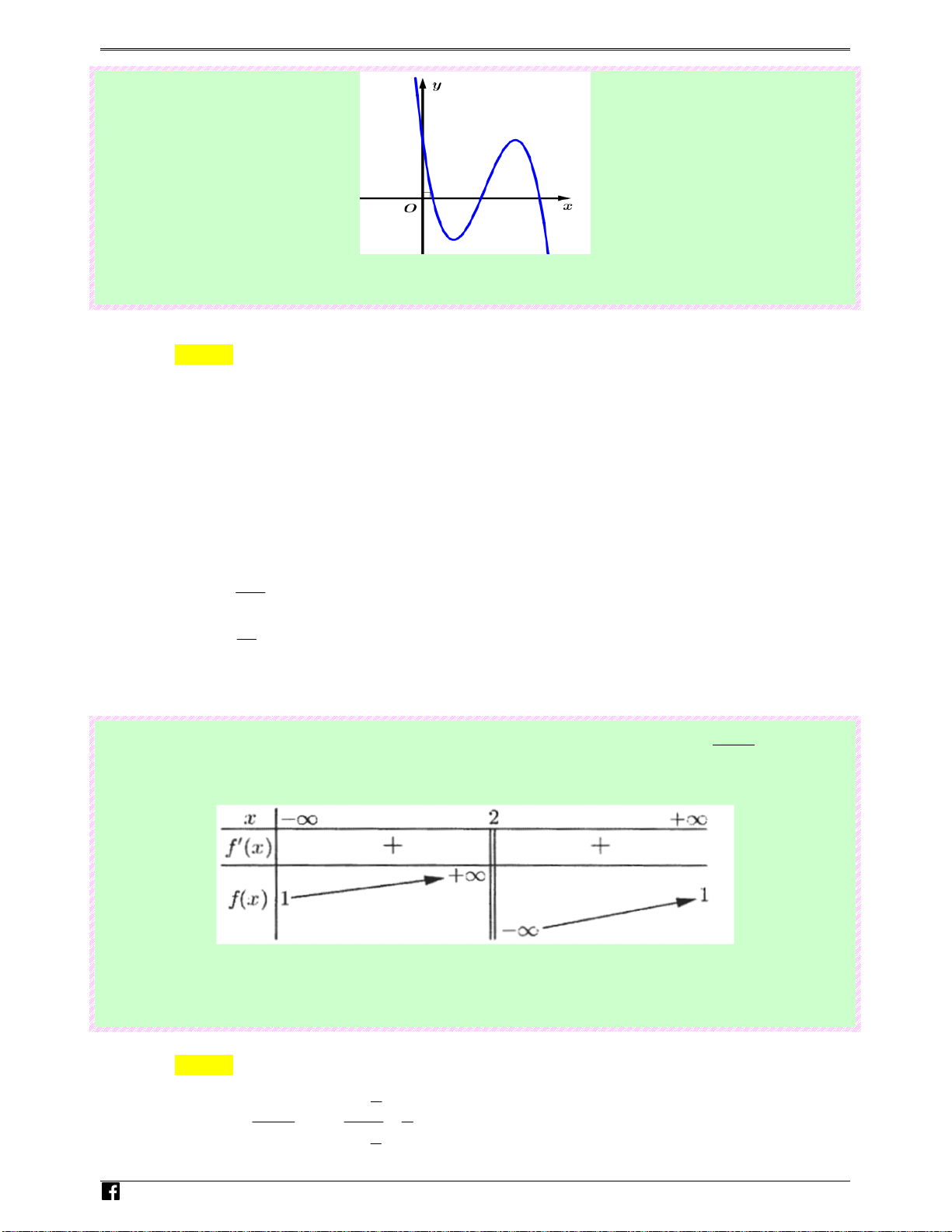
Câu 31: (Câu 6 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y x N O guy-n Ho àng Ⓐ. 4 2
y = −x + x −1. Ⓑ. 4 2
y = x − 3x −1. Ⓒ. 3
y = −x − 3x −1. Ⓓ. 3
y = x − 3x −1 Vi0 Lời giải t Chọn D
Đồ thị hàm số là đồ thị của hàm số bậc ba nên loại A và. Ⓑ.
Đồ thi hàm số bậc ba có hệ số a > 0 nên D đúng.
Câu 32: (Câu 8 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
https://www.facebook.com/vietgold Trang 13
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracng hiem Ⓐ. 4 2
y = x − 2x −1. Ⓑ. 4 2
y = −x + 2x −1. Ⓒ. 3 2
y = x − x −1 . Ⓓ. 3 2
y = −x + x −1 .vn Lời giải Chọn A
Dựa vào hình vẽ suy ra hàm số đã cho có 3 cực trị → loại C,. Ⓓ.
Mặt khác nhánh bên tay phải của đồ thị hàm số đi lên suy ra hệ số a > 0 → Chọn. Ⓐ.
Câu 33: (Câu 11 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? N guy-n Ho Ⓐ. 4 2
y = x − 3x −1 Ⓑ. 3 2
y = x − 3x −1 Ⓒ. 3 2
y = −x + 3x −1 Ⓓ. 4 2
y = −x + 3x −1 àng Lời giải Vi0 Chọn D t
+ Nhìn đồ thị khẳng định đồ thị hàm trùng phương loại B, C
+ lim y = −∞ nên Chọn D x→±∞
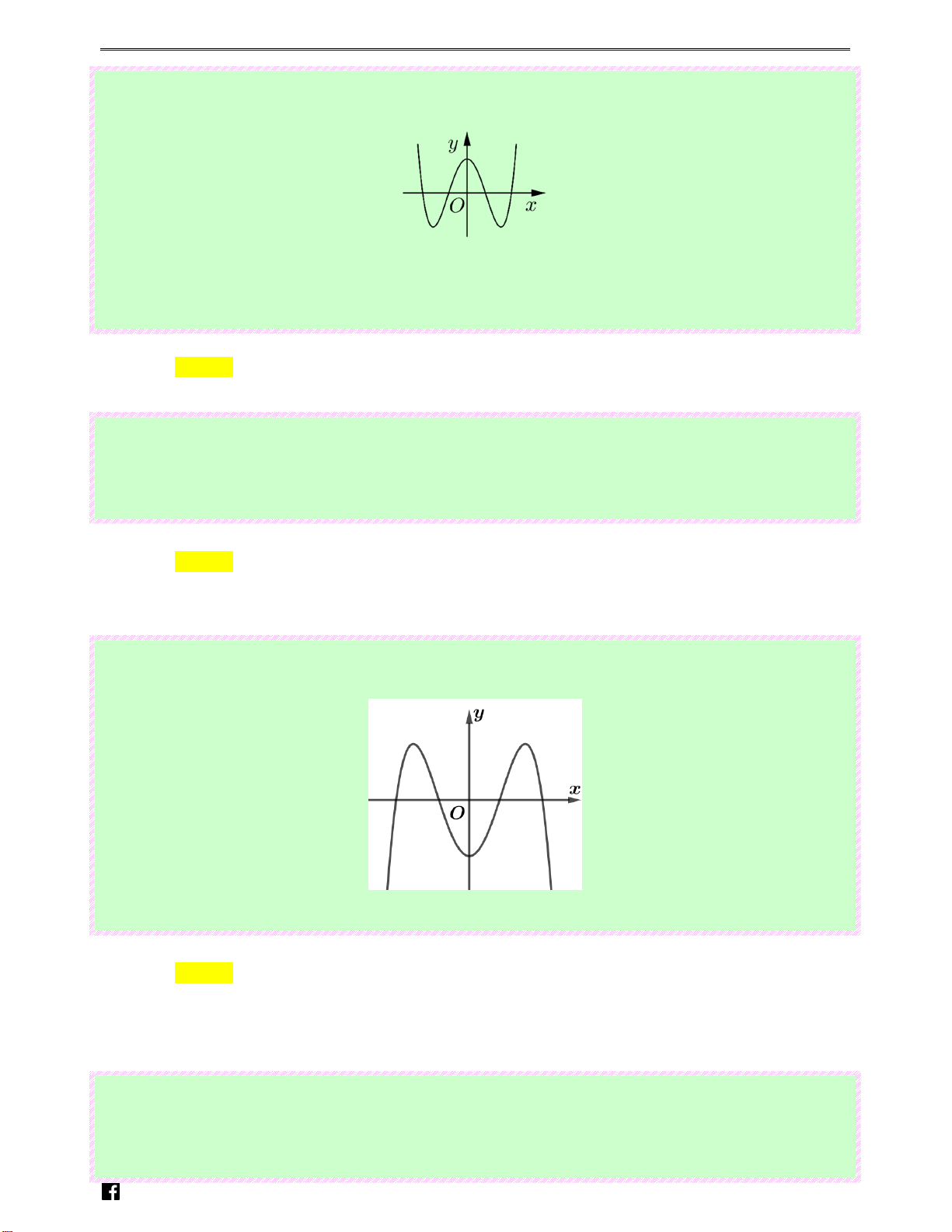
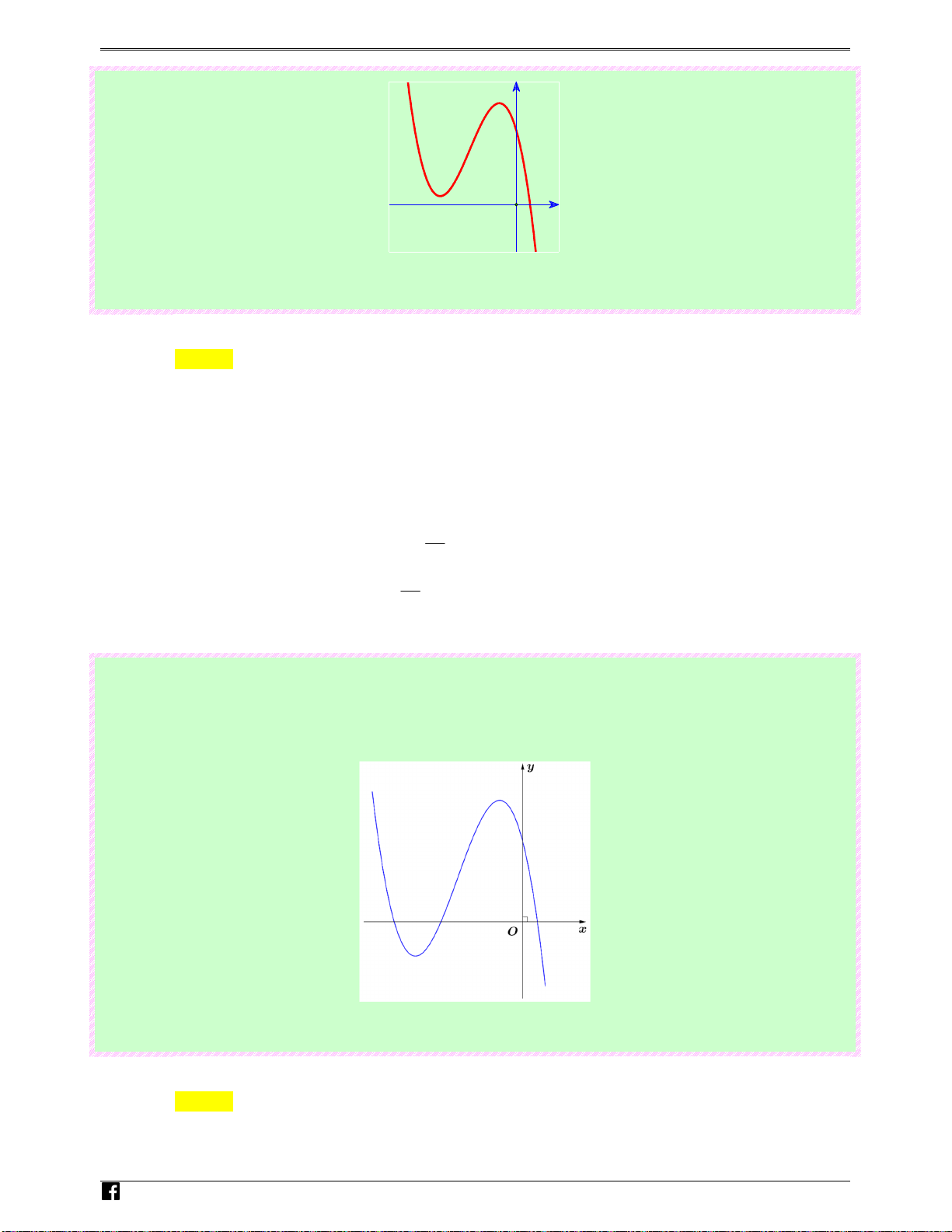
Câu 34: (Câu 6 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Đường cong hình bên là đồ thị của một
trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
https://www.facebook.com/vietgold Trang 14
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 y Luyenth O x itracn ghie Ⓐ. 3
y = x − 3x + 2 . Ⓑ. 4 2
y = x − x +1. Ⓒ. 4 2
y = x + x +1. Ⓓ. 3
y = −x + 3x + 2 . m .v Lời giải n Chọn A
Đồ thị hình bên là đồ thị hàm số bậc ba đi qua điểm A(0;2) có hệ số a > 0 nên chỉ có đáp án
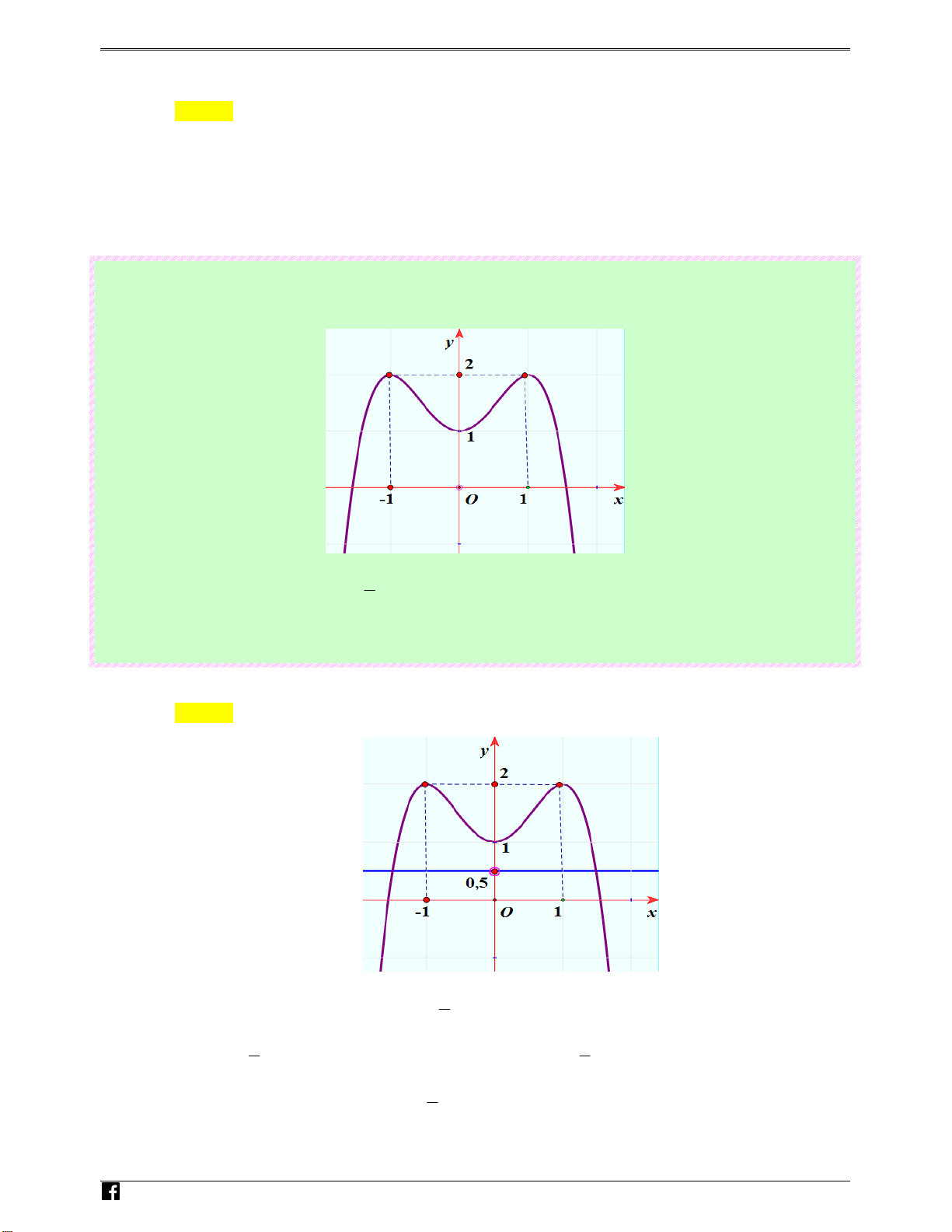
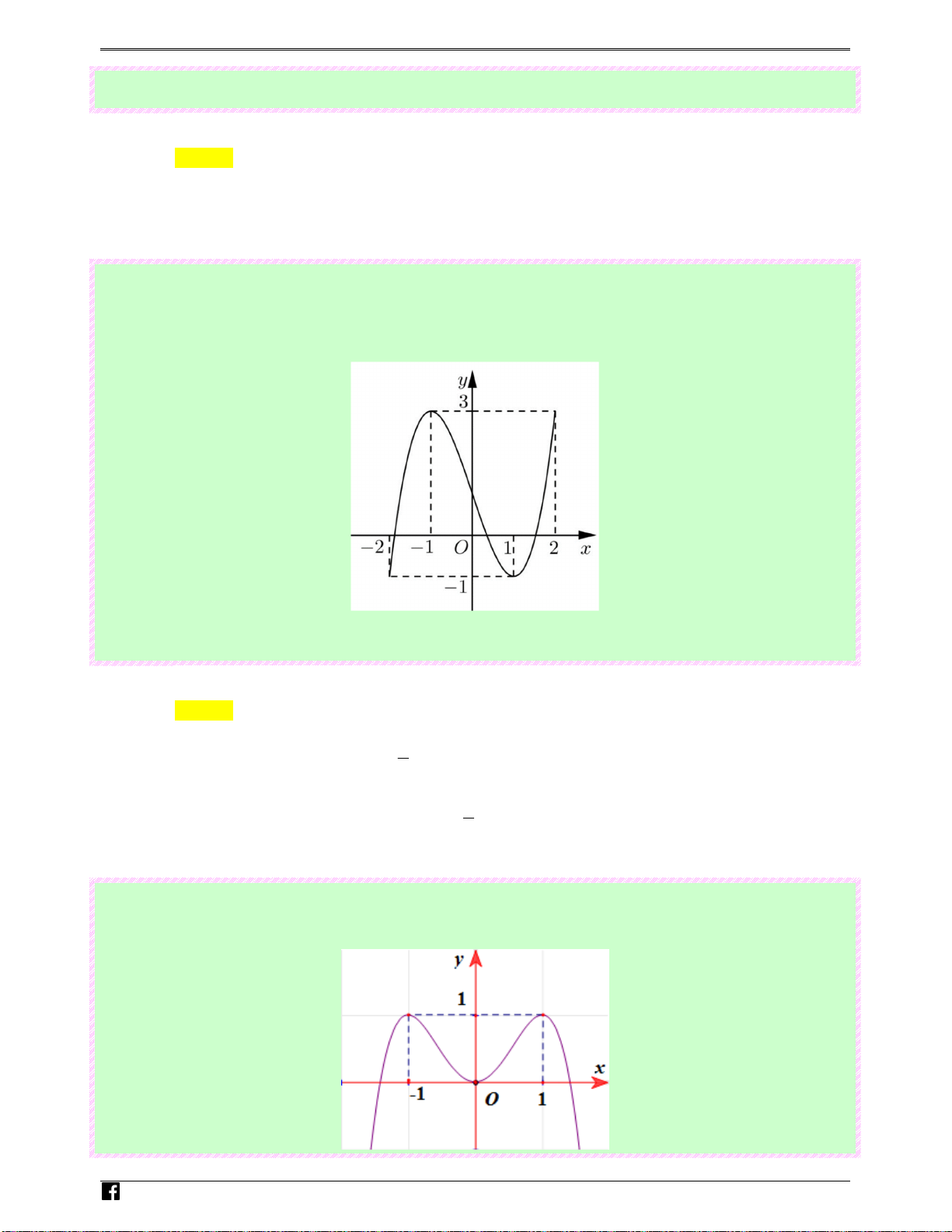
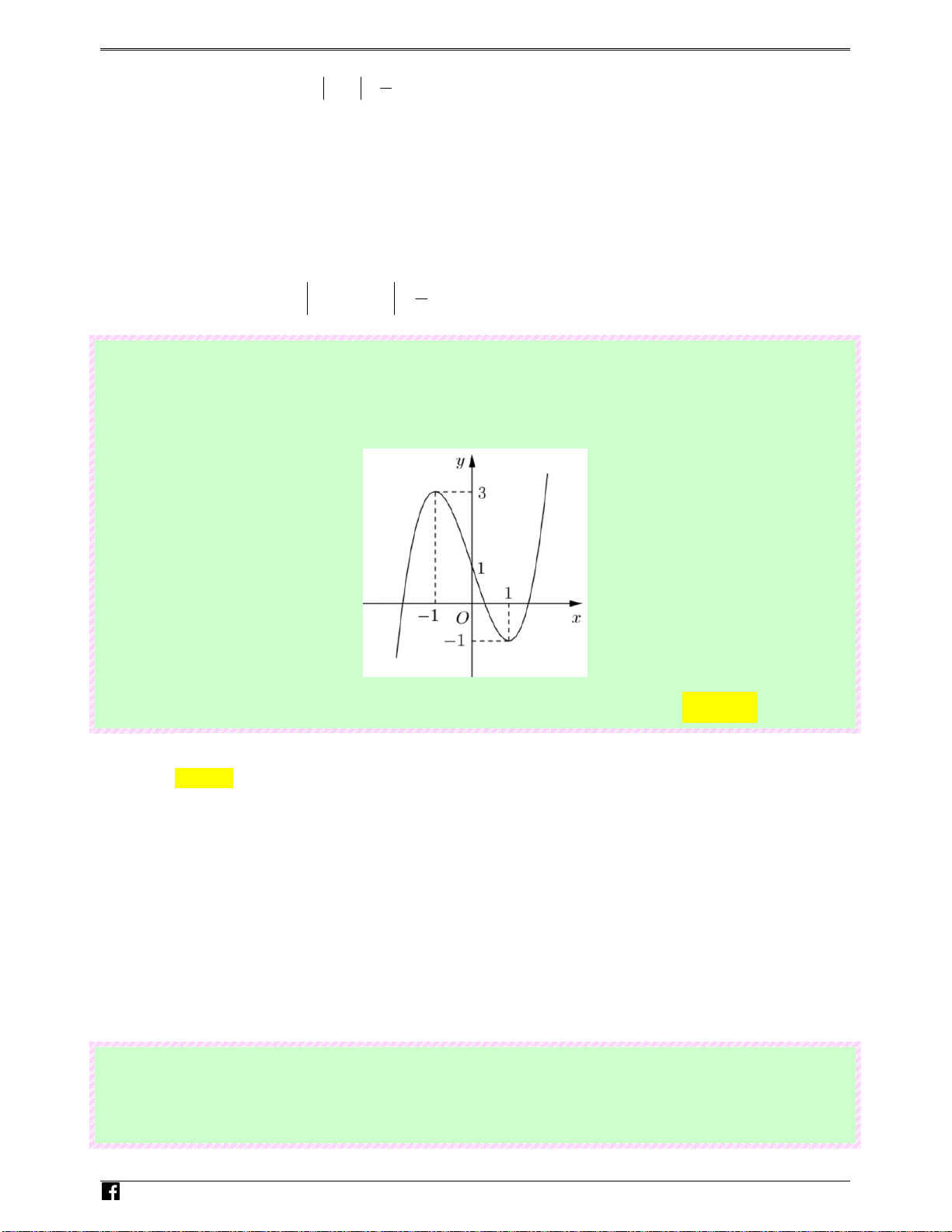
A thỏa mãn điều kiện trên. Câu 35: (Câu 24 - Cho hàm số 4 2
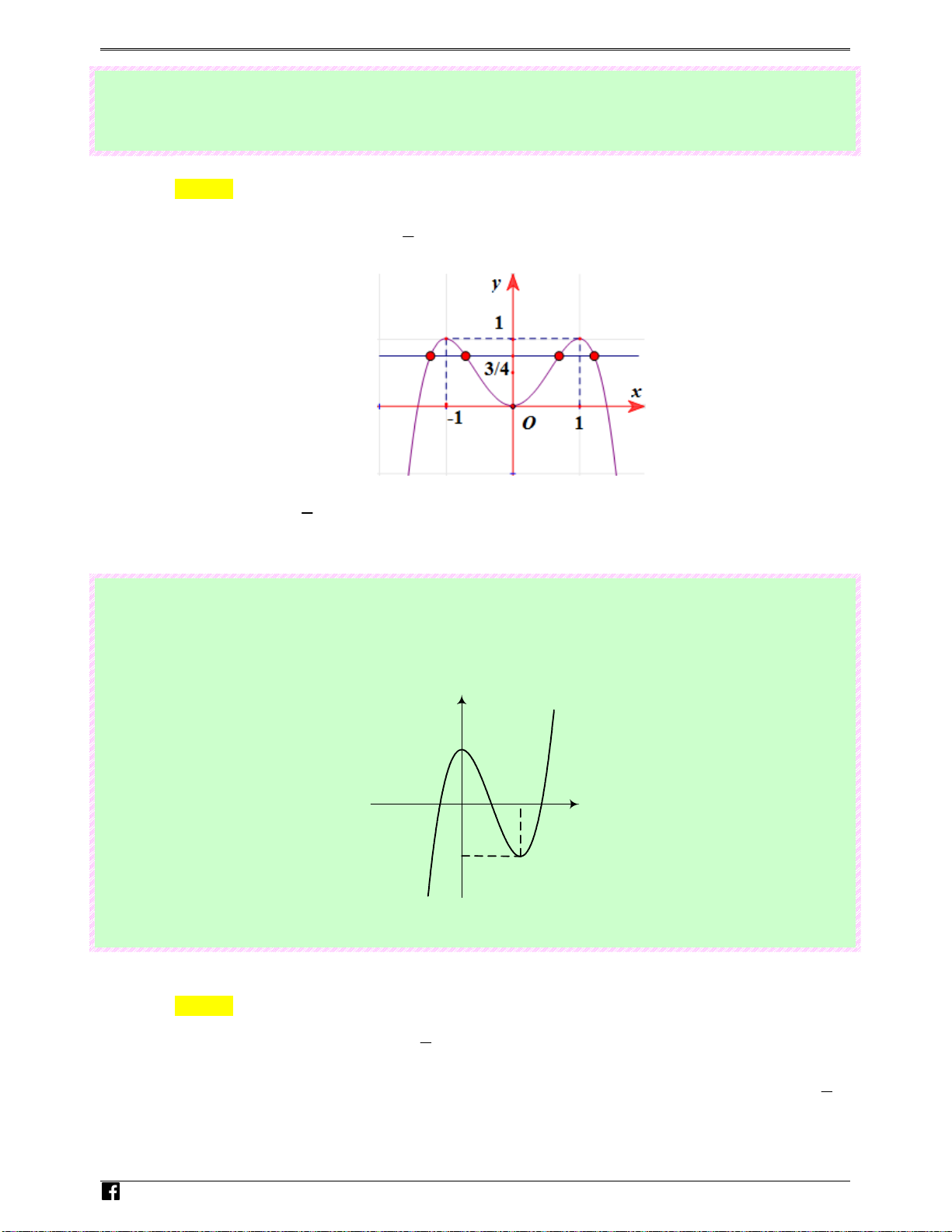
y = −x + 2x có đồ thị như
MĐ 104 - BGD&ĐT - NĂM 2016 - 2017)
hình bên.Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
−x + 2x = m có bốn nghiệm thực phân biệt. y 1 N -1 1 g 0 u x y-n Ho àng
Ⓐ. m > 0.
Ⓑ. 0 ≤ m ≤1.
Ⓒ. 0 < m <1 Ⓓ. m <1. Vi0 Lời giải t Chọn C
Số nghiệm thực của phương trình 4 2
−x + 2x = m chính là
số giao điểm của đồ thị hàm số 4 2
y = −x + 2x và đường thẳng y = m . Dựa vào đồ thị suy ra 4 2
−x + 2x = m có bốn nghiệm thực phân biệt khi 0 < m < 1 .
Câu 36: (Câu 1 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số y = ( x − )( 2 2 x + ) 1 có đồ thị
(C). Mệnh đề nào dưới đây đúng?
Ⓐ. (C) cắt trục hoành tại hai điểm.
Ⓑ. (C) cắt trục hoành tại một điểm.
Ⓒ. (C) không cắt trục hoành.
Ⓓ. (C) cắt trục hoành tại ba điểm. Lời giải
https://www.facebook.com/vietgold Trang 15
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Chọn B
Dễ thấy phương trình ( x − )( 2 2 x + )
1 = 0 có 1 nghiệm x = 2 ⇒ (C) cắt trục hoành tại một điểm. L
Câu 37: (Câu 5 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Đường cong ở hình bên dưới là đồ thị của uy
một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? enthitracnghiem.v n Ⓐ. 4 2
y = x − 2x +1 Ⓑ. 4 2
y = −x + 2x +1 Ⓒ. 3 2
y = −x + 3x +1 Ⓓ. 3 2
y = x − 3x + 3 Lời giải Chọn D
Dựa vào đồ thị ta thấy đây là hình ảnh đồ thị của hàm số bậc ba nên loại đáp án A và B; Mặt khác
dựa vào đồ thị ta có lim y = +∞ nên hệ số của 3
x dương nên ta chọn đáp án 3 2
y = x − 3x + 3 x→+∞
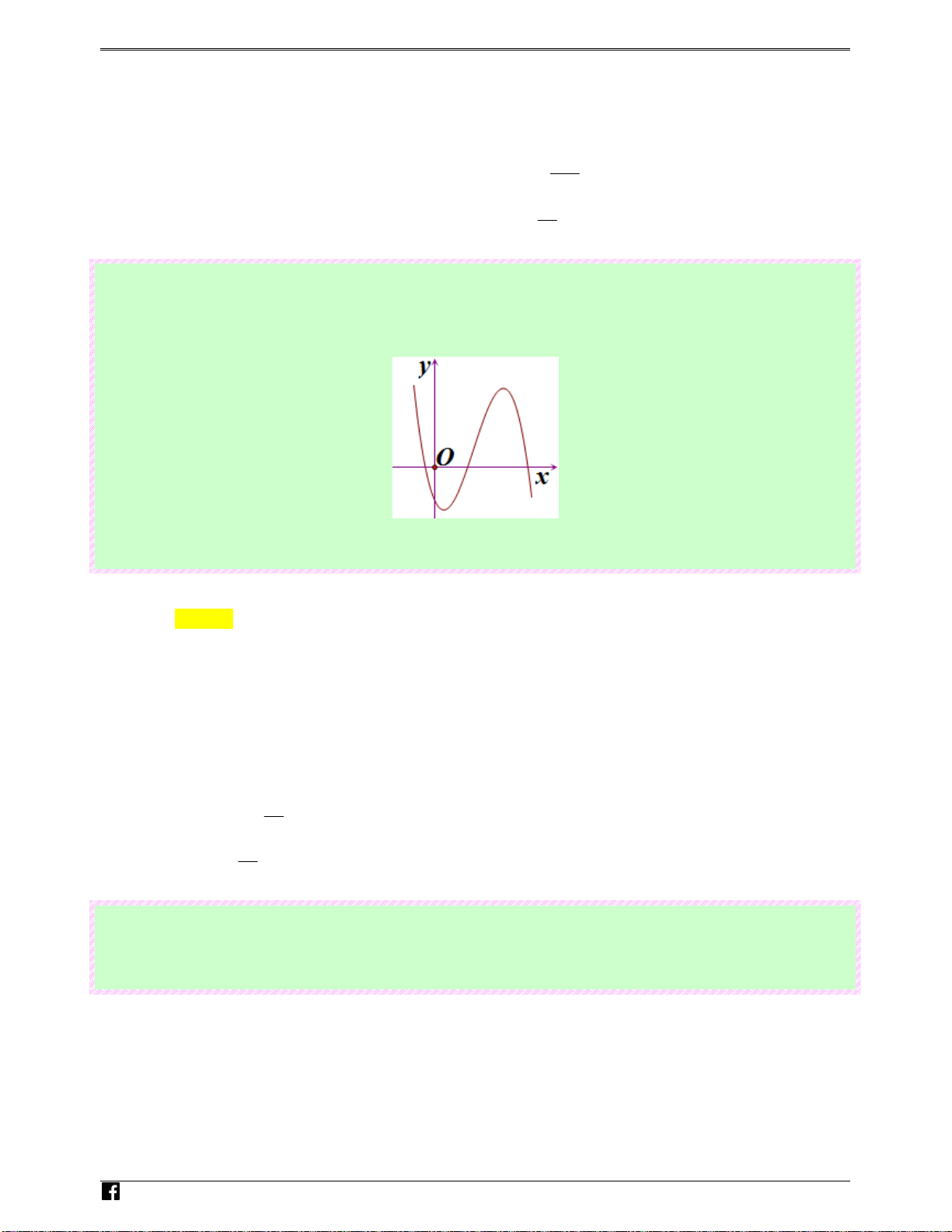
Câu 38: (Câu 5 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Đường cong ở hình bên là đồ thị của một
trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? N guy-n H oàn Ⓐ. 3 2
y = −x + x − 1 . Ⓑ. 4 2
y = x − x − 1 . Ⓒ. 3 2
y = x − x − 1 . Ⓓ. 4 2
y = − x + x − 1. g Vi0 Lời giải t Chọn B
Đặc trưng của đồ thị là hàm bậc 4 ⇒ Loại đáp án A, C
Dáng điệu của đồ thị ⇒ Loại đáp án D
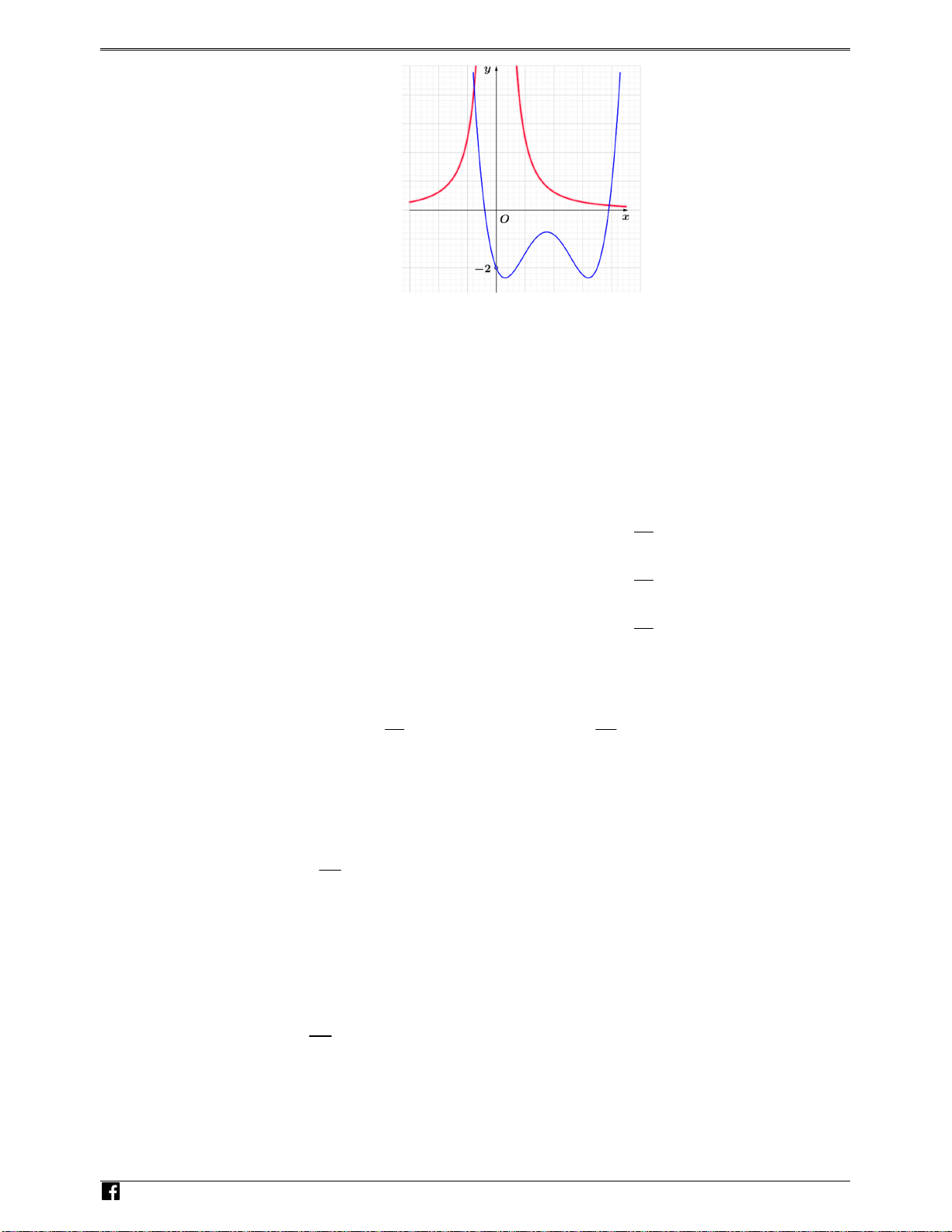
Câu 39: (Câu 5 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Cho hàm số y = f (x) xác định trên ℝ \ { } 0 ,
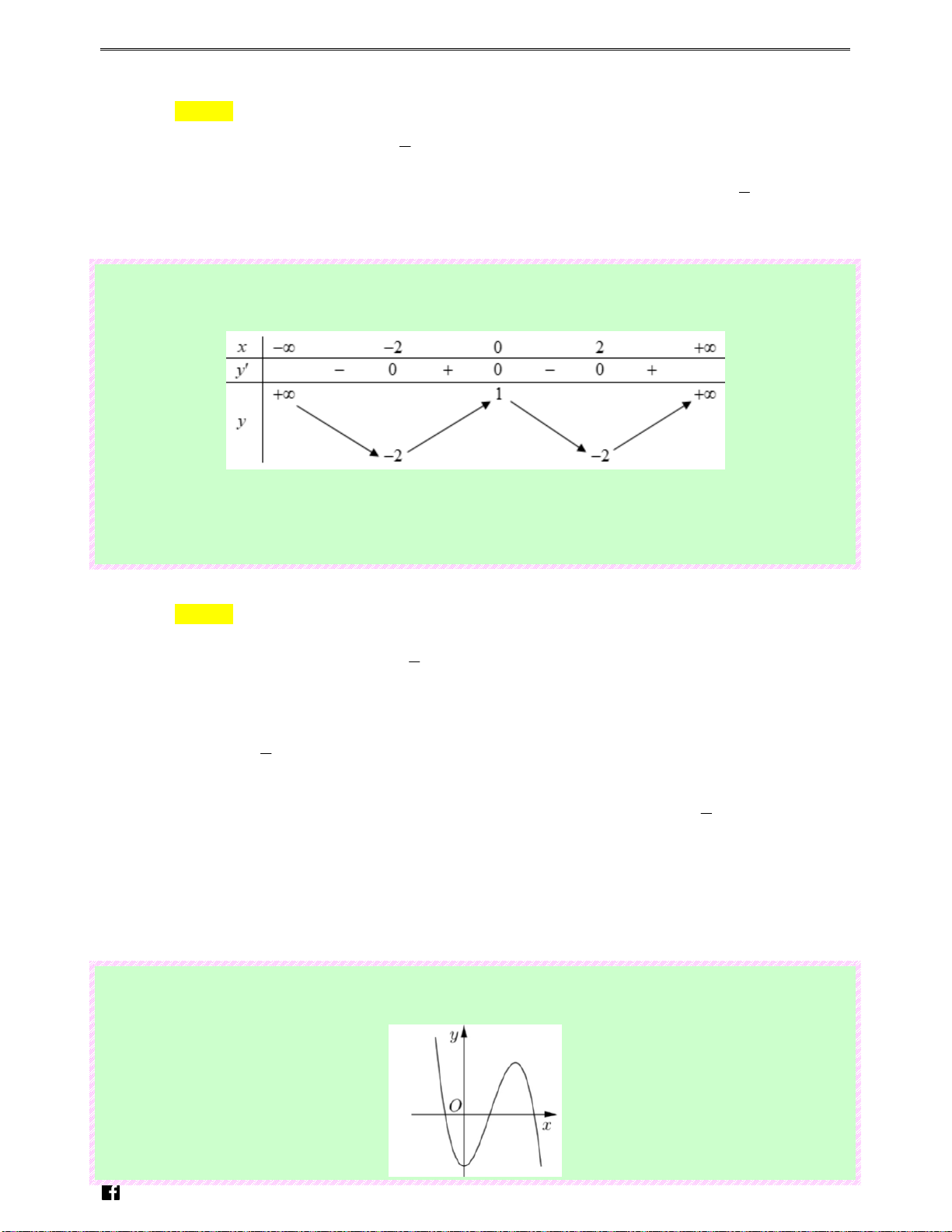
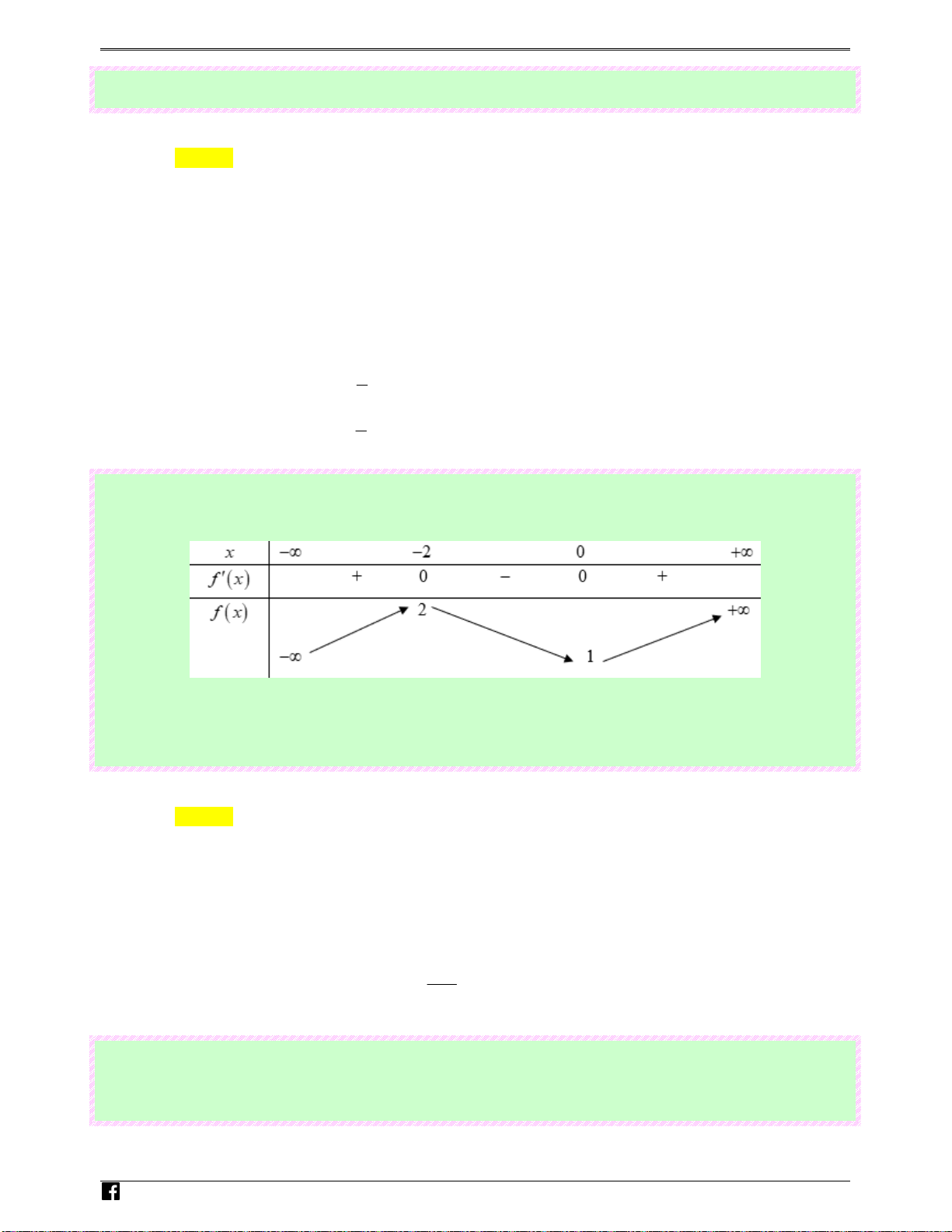
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
Tìm tập hợp tất cả các giá trị của tham số thực
m sao cho phương trình f ( x) = m có ba nghiệm thực phân biệt.
https://www.facebook.com/vietgold Trang 16
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Ⓐ. [ 1 − ;2].
Ⓑ. (−1; 2) . Ⓒ. (−1;2].
Ⓓ. (−∞;2] . Lời giải Chọn B Luy
Câu 40: (Câu 1 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Đường cong trong hình bên là đồ thị của một en
hàm số trong bốn hàm số được liệt kê ở bốn phương án ,
A B,C, D dưới đây. Hỏi hàm số đó là thi hàm số nào? tracnghiem.vn Ⓐ. 2
y = −x + x −1 Ⓑ. 3
y = −x + 3x +1 Ⓒ. 4 2
y = x − x +1 Ⓓ. 3
y = x − 3x +1 Lời giải Chọn D
Từ đồ thị : lim y = +∞ và đây là đồ thị hàm bậc ba nên ta chọn phương án 3
y = x − 3x +1. x→+∞ N
Câu 41: (Câu 2 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Đồ thị của hàm số nào dưới đây có gu
dạng như đường cong trong hình bên? y-n Hoàng Vi0t Ⓐ. 3
y = x − 3x +1. Ⓑ. 4 2
y = x + 4x +1 . Ⓒ. 3
y = −x + 3x +1. Ⓓ. 4 2
y = −x + 2x +1. Lời giải Chọn C
Nhận dạng đồ thị: Đồ thị hàm số bậc 3 với:
- Nhánh phải đồ thị đi xuống nên nhận xét hệ số a < 0
- Hai điểm cực trị trái dấu nên: .
a c < 0 mà a < 0 nên c > 0
- Đồ thị hàm số cắt trục tung Oy tại điểm có tung độ dương nên d > 0
Chỉ có đáp án C thỏa mãn.
Câu 42: (Câu 18 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong hình bên?
https://www.facebook.com/vietgold Trang 17
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitrac ngh Ⓐ. 4 2
y = x + 2x . Ⓑ. 3
y = −x − 3x . Ⓒ. 3
y = x − 3x . Ⓓ. 4 2
y = −x + 2x . iem Lời giải .v Chọn C n
+) Đồ thị trên là đồ thị hàm số bậc 3 nên loại đáp án A, Ⓓ.
+) Đồ thị hàm số có 2 điểm cực trị nên loại đáp án B vì hàm số 3
y = −x − 3x không có điểm cực trị.
Câu 43: (Câu 25 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số bậc bốn y = f ( x) có
đồ thị là đường cong trong hình vẽ bên. N guy-n Hoà ng V
Số nghiệm thực của phương trình i f ( x) 1 = là 0 2 t Ⓐ. 4. Ⓑ. 2. Ⓒ. 1. Ⓓ. 3. Lời giải Chọn A 1
Số nghiệm thực của phương trình f ( x) 1
= bằng số giao điểm của đường thẳng y = và có 2 2
đồ thị hàm số y = f ( x) .
https://www.facebook.com/vietgold Trang 18
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 1
Ta thấy đường thẳng y = cắt đồ thị hàm số tại 4 điểm nên phương trình f ( x) 1 = có 4 2 2 nghiệm. L
Câu 44: (Câu 28 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số uy 3 e
y = −x + 5x với trục hoành là nthi t Ⓐ. 3. Ⓑ. 2. Ⓒ. 0. Ⓓ. 1. rac Lời giải ngh Chọn A iem
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là .vn x = 0 3
−x + 5x = 0 ⇔ x ( 2
−x + 5) = 0 ⇔ x = 5 . x = − 5
Vậy số giao điểm của đồ thị hàm số 3
y = −x + 5x với trục hoành là 3.
Câu 45: (Câu 35 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3
y = −x + 7 x với trục hoành là Ⓐ. 0. Ⓑ. 3. Ⓒ. 2 . Ⓓ. 1. Lời giải N Chọn B guy
Hoành độ giao điểm của đồ thị hàm số 3
y = −x + 7 x với trục hoành là nghiệm phương trình: -n x = 0 H 3 o x 7x 0 − + = ⇔ x = − 7 . à n g x = 7 Vi0t
Khi đó giao điểm của đồ thị hàm số 3
y = −x + 7 x với trục hoành tại 3 điểm
A(0;0), B(− 7;0),C ( 7;0) . Vậy nên có 3 giao điểm của đồ thị với trục hoành.
Câu 46: (Câu 26 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3
y = − x + 6x với trục hoành là: Ⓐ. 2 . Ⓑ. 3. Ⓒ. 1. Ⓓ. 0 . Lời giải Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số 3
y = − x + 6x với trục hoành là:
https://www.facebook.com/vietgold Trang 19
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 x = 0 3
−x + 6x = 0 ⇔ x = 6 . x = − 6 Lu Vậy đồ thị hàm số 3
y = − x + 6x cắt trục hoành tại 3 điểm phân biệt. yent
Câu 47: (Câu 45 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số hi 3 2 t
f x = ax + bx + cx + d a; ; b c; Î
có bảng biến thiên như sau: r ( ) ( d ℝ) acnghiem.vn
Có bao nhiêu số dương trong các số ; a ; b ; c d ? Ⓐ. 2 . Ⓑ. 3. Ⓒ. 1. Ⓓ. 4 . Lời giải Chọn A f (x) 3 2
= ax + bx + cx + d (a; ;
b c; d Î ℝ) . Ta có: f ¢(x) 2
= 3ax + 2bx + c . +) lim f ( )
x = +¥ Þ a > 0 . x®+¥ +) f ( )
0 = 3 Þ d = 3 > 0 . N gu +) f ¢( )
x = 0 có nghiệm x = 0 Þ c = 0 . y-n 2 ¢ b b do a> H
+) Tổng 2 nghiệm của phương trình f ( ) x = 0 là 0 4 Þ - > 0 Þ
< 0 ¾¾¾¾¾¾¾¾® b < 0 . o 3a a àn Vậy trong các số ; a ; b ;
c d có 2 số dương. g Vi0
Câu 48: (Câu 4) (MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho đồ thị hàm số bậc ba y = f x t ( )
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f ( x) = 2 là
https://www.facebook.com/vietgold Trang 20
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Ⓐ. 0 . Ⓑ. 3. Ⓒ. 1. Ⓓ. 2 . Lời giải Chọn B Luyenthitracnghiem.vn
Đường thẳng y = 2 cắt đồ thị hàm số y = f ( x) tại 3 điểm phân biệt nên phương trình
f ( x) = 2 có 3 nghiệm thự Ⓒ.
Câu 49: (Câu 10 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
dạng như đường cong trong hình bên? N guy-n Hoà Ⓐ. 4 2
y = x − 2x +1. Ⓑ. 3 2
y = −x + 3x +1. Ⓒ. 3 2
y = x −3x +1. Ⓓ. 4 2
y = −x + 2x +1. ng Lời giải Vi0 Chọn A t
Hình vẽ bên là đồ thị của hàm số bậc 4 có hệ số a > 0 ⇒ chọn A đúng.
Câu 50: (Câu 37 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3 2
y = x − x và đồ thị hàm số 2
y = −x + 3x là Ⓐ. 1. Ⓑ. 0. Ⓒ. 2. Ⓓ. 3. Lời giải Chọn D
Số giao điểm của hai đồ thị là số nghiệm thực phân biệt của phương trình hoành độ giao điểm x = 0 sau: 3 2 2 3
x − x = − x + 3x ⇔ x − 3x = 0 ⇔ x ( 2 x − 3) = 0 ⇔ . x = ± 3
Vậy số giao điểm của hai đồ thị hàm số đã cho là 3 .
https://www.facebook.com/vietgold Trang 21
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 51: (Câu 19 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Đồ thị của hàm số nào dưới đây có
dạng đường cong như hình bên Ⓐ. 4 2
y = −x + 2x . Ⓑ. 3 2
y = x − 3x . Ⓒ. 4 2
y = x − 2x . Ⓓ. 3 2
y = −x + 3x . Luyenthitracnghiem.vn Lời giải Chọn C
Vì đồ thị hàm số có 3 cực trị nên ta loại đáp án B và D . Ta lại thấy khi x → +∞ thì y → +∞ . Nên hệ số trước 4 x phải dương.
Câu 52: (Câu 38 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3 2
y = x + x và đồ thị hàm số 2
y = x + 5x Ⓐ. 3. Ⓑ. 0 . Ⓒ. 1. Ⓓ. 2 . Lời giải N g Chọn A uy-n x = 0
Xét phương trình hoành độ giao điểm: 3 2 2 3
x + x = x + 5x ⇔ x − 5x = 0 ⇔ H x = ± 5 o àng
Vậy có 3giao điểm. Vi0t
Câu 53: (Câu 20 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Đồ thị hàm số nào dưới đây có dạng
như đường cong trong hình bên? Ⓐ. 4 2
y = − x + 2 x . Ⓑ. 3
y = − x + 3x . Ⓒ. 4 2
y = x − 2x . Ⓓ. 3
y = x − 3x .
https://www.facebook.com/vietgold Trang 22
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Lời giải Chọn A
Từ hình dáng đồ thị ta thấy đó là đồ thị hàm số bậc bốn trùng phương. Suy ra loại đáp án B, Lu Ⓓ. yenth
Hàm số có hệ số a < 0 . Suy ra loại đáp án Ⓒ. itrac
Câu 54: (Câu 33 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số ng 3 2 = − = − + h y x
x và đồ thị hàm số 2 y x 5x là: iem Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0. .vn Lời giải Chọn B
Xét phương trình hoành độ giao điểm
x = 0 ⇒ y = 0 3 2 2 3
x − x = −x + 5x ⇔ x − 5x = 0 ⇔ x = 5 ⇒ y = 5 − + 5
x = − 5 ⇒ y = −5− 5
Vậy số giao điểm của đồ thị hàm số 3 2
y = x − x và đồ thị hàm số 2
y = −x + 5x là 3.
Câu 55: (Câu 26 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Số giao điểm của đồ thị hàm số 3 2
y = x + 3x và đồ thị hàm số 2
y = 3x + 3x là N guy Ⓐ. 3. Ⓑ. 1. Ⓒ. 2 . Ⓓ. 0 . -n Lời giải H oà Chọn A ng 3 2 2 V
Số giao điểm của đồ thị hàm số y = x + 3x và đồ thị hàm số y = 3x + 3x là số nghiệm phân i0t 3 2 2
biệt của phương trình x + 3x = 3x + 3x ( ) 1 . x = 0 ( ) 3
1 ⇔ x − 3x = 0 ⇔ x = 3 . x = − 3
Phương trình (1) có 3 nghiệm phân biệt.
Vậy số giao điểm của đồ thị hàm số y = 3 x + 2
3x và đồ thị hàm số y = 2 3x + 3x là 3.
Câu 56: (Câu 23 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến thiên như sau:
https://www.facebook.com/vietgold Trang 23
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luy enth
Số nghiệm của phương trình 3 f ( x) − 2 = 0 là itrac Ⓐ. 2. Ⓑ. 0. Ⓒ. 3. Ⓓ. 1. ngh Lời giải iem Chọn C .vn
Ta có: f ( x) − = ⇔ f ( x) 2 3 2 0 = . 3 2
Từ bảng biến thiên ta thấy đường thẳng d : y = cắt đồ thị hàm số y = f ( x) tại 3điểm phân 3
biệt nên phương trình đã cho có 3 nghiệm phân biệt.
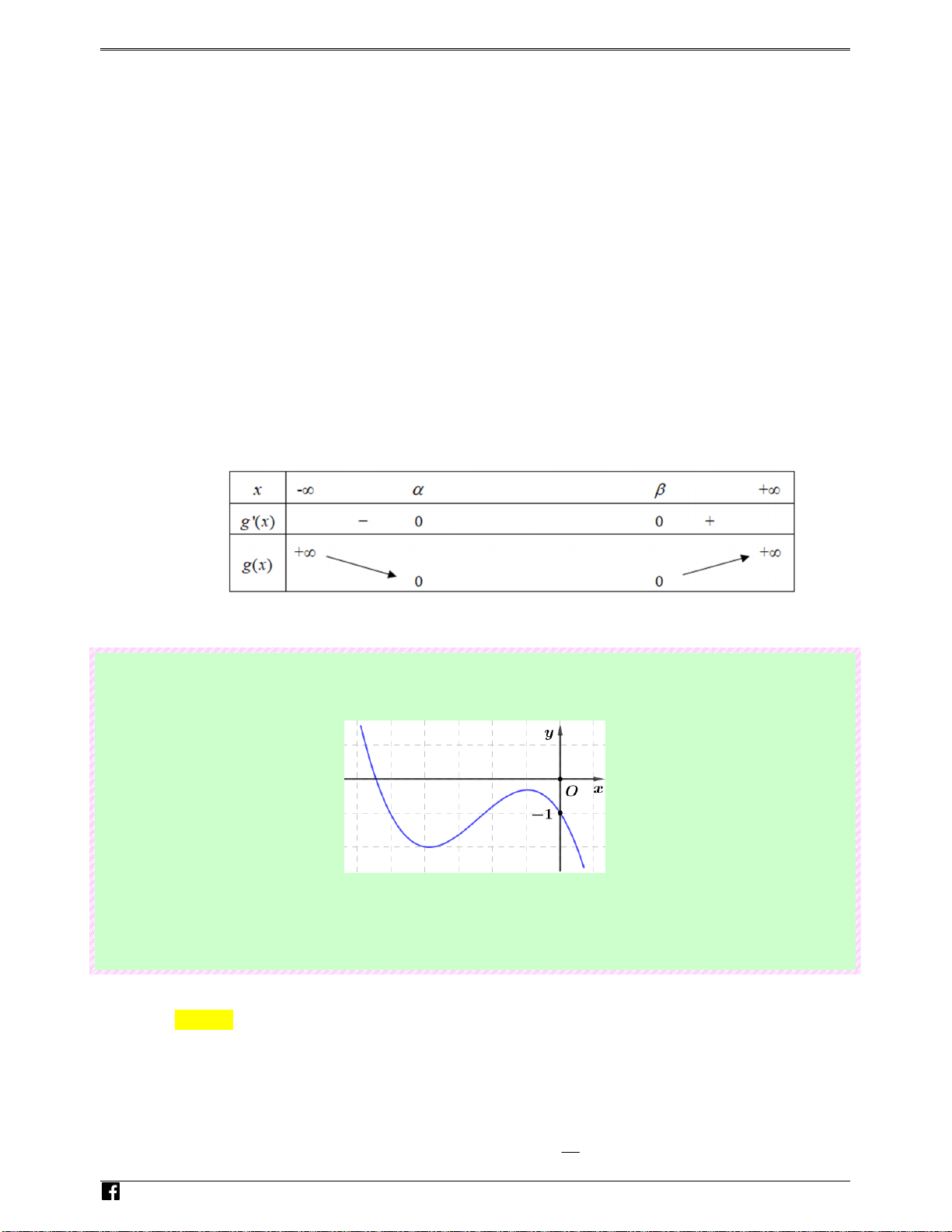
Câu 57: (Câu 28 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Cho hàm số 3
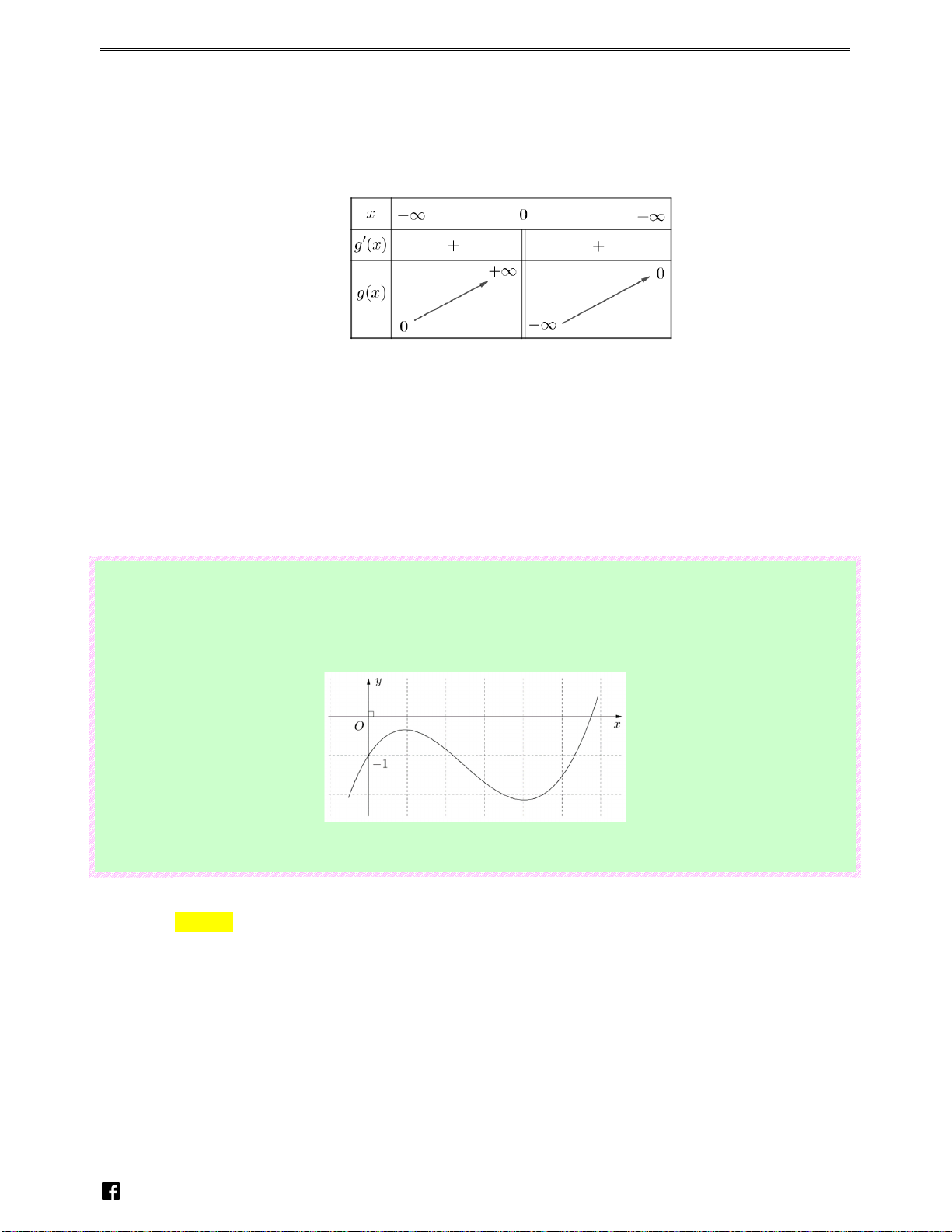
y = ax + 3x + d
( ,ad ∈ℝ) có đồ thị như hình bên.Mệnh đề nào dưới đây đúng? N guy-n Ho àng
Ⓐ. a > 0,d > 0 .
Ⓑ. a < 0,d > 0 .
Ⓒ. a > 0;d < 0 .
Ⓓ. a < 0;d < 0 . Vi0 Lời giải t Chọn D
Do nhánh tiến đến +∞ của đồ thị hàm số đi xuống ⇒ a < 0 .
Do đồ thị cắt trục tung tại điểm có tung độ nhỏ hơn 0 ⇒ d < 0 .
Câu 58: (Câu 29 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên như sau:
https://www.facebook.com/vietgold Trang 24
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Số nghiệm của phương trình 2 f ( x) + 3 = 0 là Ⓐ. 3. Ⓑ. 1. Ⓒ. 2 . Ⓓ. 0 . Lu Lời giải ye Chọn A nt 3 h
f ( x) + = ⇔ f ( x) 3 2 3 0
= − . Từ bảng biến thiên ta thấy f ( x) đạt giá trị − tại ba giá trị x it 2 2 ra
khác nhau. Suy ra phương trình có 3 nghiệm. cngh
Câu 59: (Câu 23 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên như iem sau: .vn
Số nghiệm thực của phương trình 3 f ( x) − 5 = 0 là Ⓐ. 2. Ⓑ. 3. Ⓒ. 4. Ⓓ. 0. Lời giải N Chọn C guy-
Ta có 3 f ( x) − 5 = 0 ⇔ 3 f ( x) = 5 ⇔ = . n f ( x ) 5 3 Hoàn
Số nghiệm của phương trình là số giao điểm của hai đồ thị y = f ( x) và đường thẳng 5 y = . g 3 Vi0
Vậy phương trình có 4 nghiệm thực phân biệt. t
Câu 60: (Câu 16 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f ( x) − 3 = 0 là Ⓐ. 2. Ⓑ. 1. Ⓒ. 4. Ⓓ. 3.
https://www.facebook.com/vietgold Trang 25
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Lời giải Chọn C
Ta có f (x) − = ⇔ f ( x) 3 2 3 0 = . L 2 uye
Dựa vào bảng biến thiên ta thấy đồ thị hàm số y = f ( x) cắt đường thẳng 3 y = tại bốn điểm n 2 thi
phân biệt. Do đó phương trình 2 f ( x) − 3 = 0 có 4 nghiệm phân biệt. tracn
Câu 61: (Câu 29 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có bảng biến thiên như gh sau: iem.vn
Số nghiệm thực của phương trình 2 f ( x) + 3 = 0 là Ⓐ. 4. Ⓑ. 3. Ⓒ. 2. Ⓓ. 1. Lời giải Chọn A
Ta có f ( x) + = ⇔ f ( x) 3 2 3 0 = − (*) . N 2 guy-
Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số y = f ( x) và đường n H 3 thẳng o y = − . à 2 ng 3 V
Dựa vào bảng biến thiên của hàm số y = f ( x) , ta thấy đường thẳng y = − cắt đồ thị hàm số i0 2 t
y = f ( x) tại 4 điểm phân biệt.
Do đó phương trình (*) có 4 nghiệm phân biệt. Vậy phương trình đã cho có 4 nghiệm thự Ⓒ.
Câu 62: (Câu 4 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
https://www.facebook.com/vietgold Trang 26
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Ⓐ. 3 2
y = x − 3x − 2 Ⓑ. 4 2
y = x − x − 2 Ⓒ. 4 2
y = − x + x − 2 Ⓓ. 3 2
y = − x + 3x − 2 Lời giải L Chọn D uye
Dựa trên hình dáng đồ thị, ta loại 3 2
y = x − 3x − 2 và 4 2
y = x − x − 2 Mặt khác từ đồ thị, ta thấy nth
lim y = −∞ nên loại 4 2
y = − x + x − 2 i x→+∞ tracn
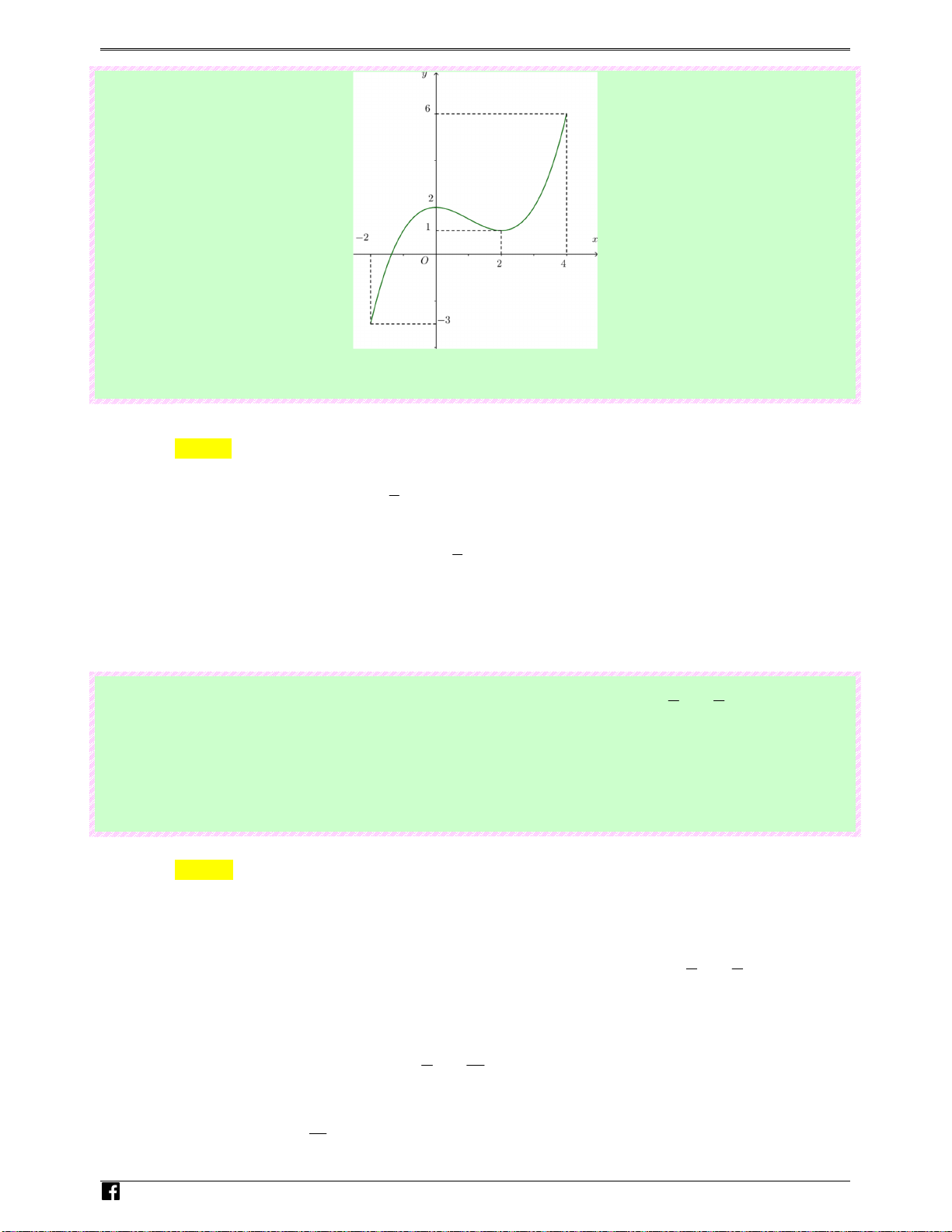
Câu 63: (Câu 22 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) liên tục trên [−2;2] gh
và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình trên đoạn i
3 f ( x) − 4 = 0 [−2;2] em là .vn Ⓐ. 3. Ⓑ. 1. Ⓒ. 2 . Ⓓ. 4 . N Lời giải guy- Chọn A n Ho
Ta có f ( x) − = ⇔ f ( x) 4 3 4 0 = . à 3 ng V 4 i
Dựa vào đồ thị, ta thấy đường thẳng y = cắt y = f ( x) tại 3 điểm phân biệt nên phương trình 0t 3
đã cho có 3 nghiệm phân biệt.
Câu 64: (Câu 16 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số f ( x ) 4 2
= ax + bx + c (a,b, c ∈ ℝ) . Đồ thị của hàm số y = f ( x) như hình vẽ bên.
https://www.facebook.com/vietgold Trang 27
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Số nghiệm của phương trình 4 f ( x) − 3 = 0 là Ⓐ. 4 . Ⓑ. 3. Ⓒ. 2 . Ⓓ. 0 L Lời giải u ye Chọn A nthi
Ta có 4 f x − 3 = 0 ⇔ f ( x) 3 = t ( ) r 4 acnghiem.vn 3
Đường thẳng y = cắt đồ thị hàm số y = f ( x) tại 4 điểm phân biệt nên phương trình đã cho 4 có 4 nghiệm phân biệt.
Câu 65: (Câu 17 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số f ( x) 3 2
= ax +bx + cx + d (a,b,c,d ∈ℝ) . Đồ thị của hàm số y = f (x) như hình vẽ bên. Số
nghiệm thực của phương trình 3 f ( x) + 4 = 0 là N guy y -n H 2 oàng O 2 Vi x 0t −2 Ⓐ. 3 Ⓑ. 0 Ⓒ. 1 Ⓓ. 2 Lời giải Chọn A
Ta có: 3 f ( x) + 4 = 0 ⇔ f ( x) 4 = − ( ) * 3 ( ) 4
* là phương trình hoành độ giao điểm của đồ thị hàm số y = f ( x) và đường thẳng y = − . 3
Dựa vào đồ thị hàm số, ta thấy ( ) * có 3 nghiệm.
https://www.facebook.com/vietgold Trang 28
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 66: (Câu 11 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây? Luyenthitracngh iem Ⓐ. 4 2
y = −x + 2x + 2 Ⓑ. 4 2
y = x − 2x + 2 Ⓒ. 3 2
y = x − 3x + 2 Ⓓ. 3 2
y = −x + 3x + 2 .vn Lời giải Chọn A
Đồ thị hàm số trên là đồ thị hàm trùng phương có 3 cực trị và có a < 0
Câu 67: (Câu 17 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) có bảng biến thiên như sau: N g uy-
Số nghiệm của phương trình f ( x) − 2 = 0 là: n Ho Ⓐ. 0 Ⓑ. 3 Ⓒ. 1 Ⓒ. 2 àng Lời giải Vi0t Chọn B
Dựa vào bảng biến thiên ta thấy f ( x) − 2 = 0 ⇔ f ( x) = 2∈( 2 − ,4) nên phương trình
f ( x) − 2 = 0 có ba nghiệm phân biệt.
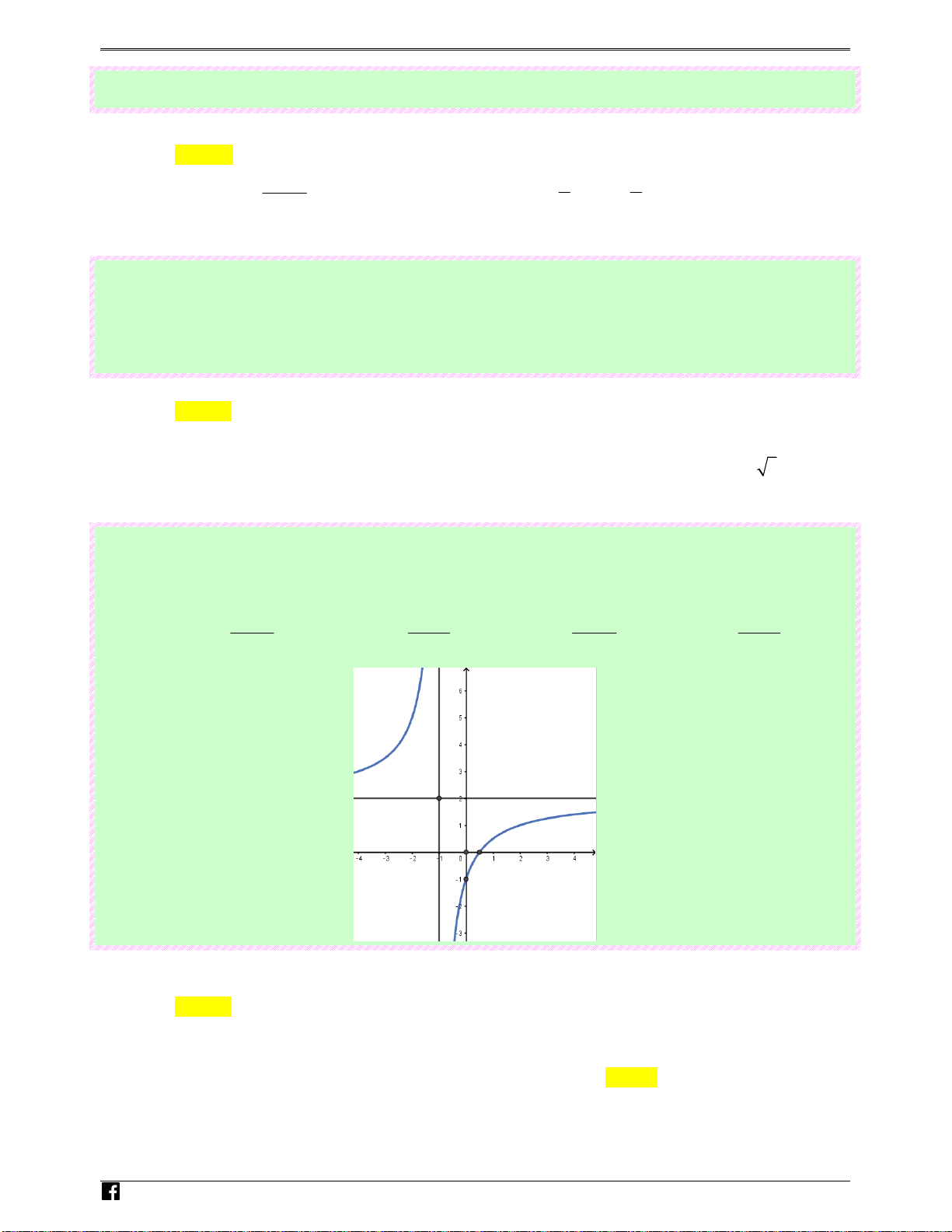
Câu 68: (Câu 24 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Đường cong ở hình bên là đồ thị của hàm + số ax b y =
với a , b , c , d là các số thự Ⓒ. Mệnh đề nào dưới đây đúng? cx + d
Ⓐ. y′ < 0, x ∀ ≠ 2.
Ⓑ. y′ < 0, x ∀ ≠1.
Ⓒ. y′ > 0, x ∀ ≠ 2.
Ⓓ. y′ > 0, x ∀ ≠1.
https://www.facebook.com/vietgold Trang 29
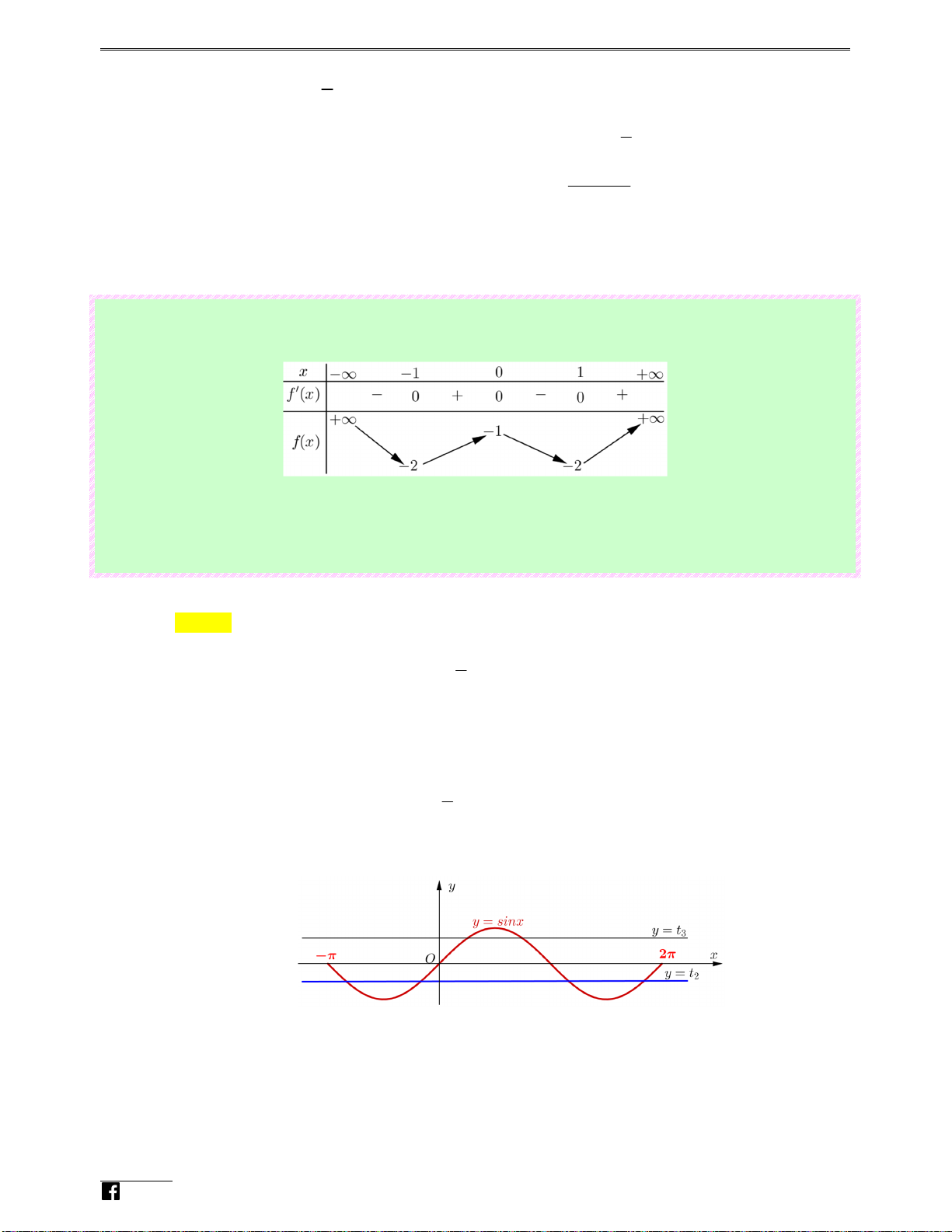
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracng hiem Lời giải .v Chọn A n Hàm số giảm trên (− ;
∞ 2) và (2;+∞) nên y′ < 0, x ∀ ≠ 2.
Câu 69: (Câu 14 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Đường cong ở hình bên là đồ thị của hàm số 4 2
y = ax + bx + c , với a, b, c là các số thự
Ⓒ. Mệnh đề nào dưới đây đúng?
Ⓐ. Phương trình y′ = 0 có đúng ba nghiệm thực phân biệt N gu
Ⓑ. Phương trình y′ = 0 có đúng hai nghiệm thực phân biệt y-n H
Ⓒ. Phương trình y′ = 0 có đúng một nghiệm thực oàn
Ⓓ. Phương trình y′ = 0 vô nghiệm trên tập số thực g Vi Lời giải 0t Chọn A
Dựa vào hình dáng của đồ thị hàm số 4 2
y = ax + bx + c ta thấy đây là đồ thị của hàm số bậc bốn
trùng phương có 3 điểm cực trị nên phương trình y′ = 0 có ba nghiệm thực phân biệt.
Câu 70: (Câu 28 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Đường cong ở hình bên là đồ thị của hàm + số ax b y =
với a, b, c, d là các số thự Ⓒ. Mệnh đề nào dưới đây đúng? cx + d
https://www.facebook.com/vietgold Trang 30
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Ⓐ. y′ > 0,∀x ∈ ℝ
Ⓑ. y′ < 0,∀x ∈ ℝ
Ⓒ. y′ > 0,∀x ≠ 1
Ⓓ. y′ < 0,∀x ≠ 1 Lời giải L Chọn D uy + d d e Hàm số ax b y =
đồng biến/nghịch biến trên − ; ∞ − và − ;+ ∞
⇒ Loại đáp án A, B n cx + d c c thi
Đồ thị nằm ở góc phần tư thứ nhất ⇒ y′ < 0. Loại đáp án C tracn
Câu 71: (Câu 1 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Cho hàm số 3
y = x − 3x có đồ thị (C ) . Tìm số gh
giao điểm của (C ) và trục hoành. iem.v Ⓐ. 2 Ⓑ. 3 Ⓒ. 1 Ⓓ. 0 n Lời giải Chọn B x = 0
Xét phương trình hoành độ giao điểm của (C ) và trục hoành: 3
x − 3x = 0 ⇔ x = ± 3
Vậy số giao điểm của (C) và trục hoành là 3.
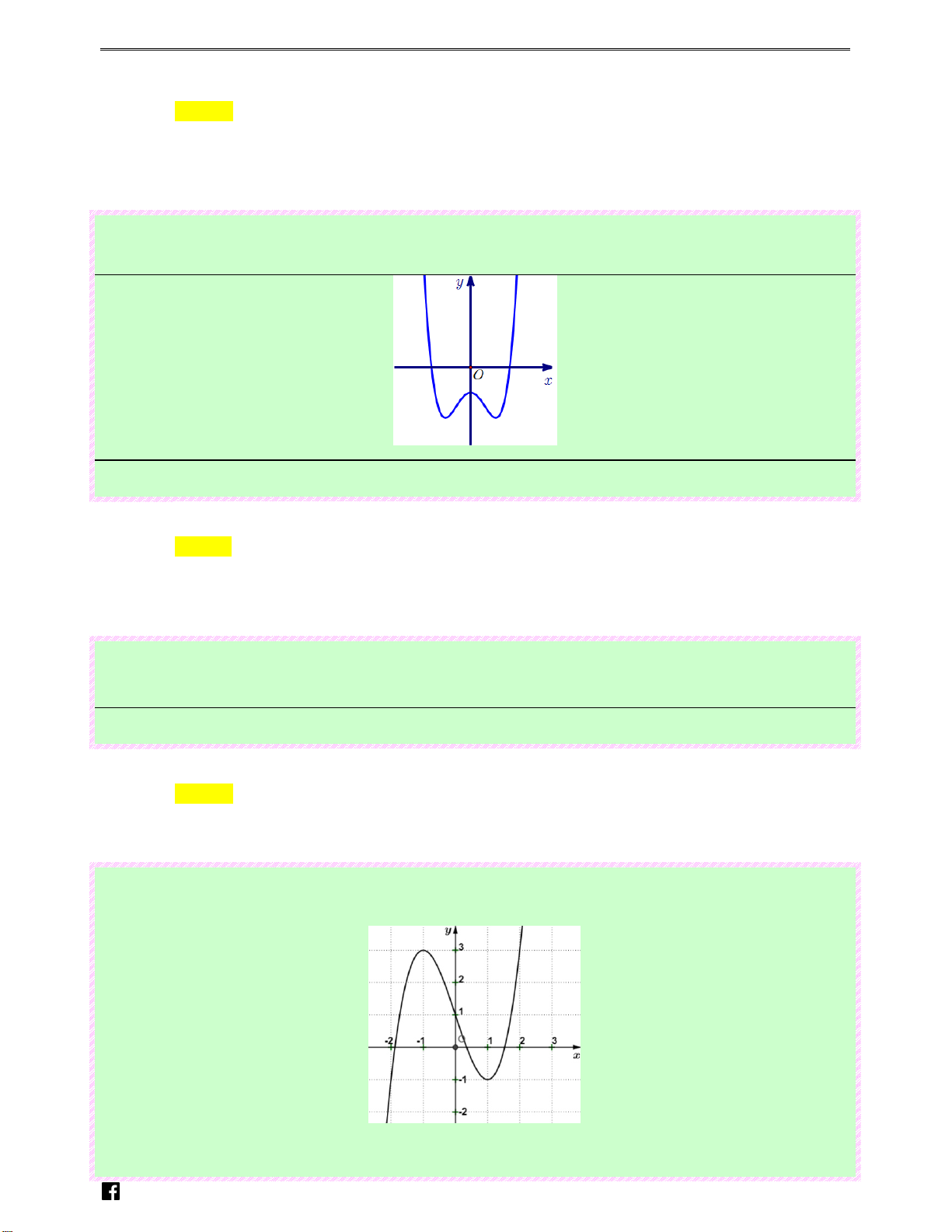
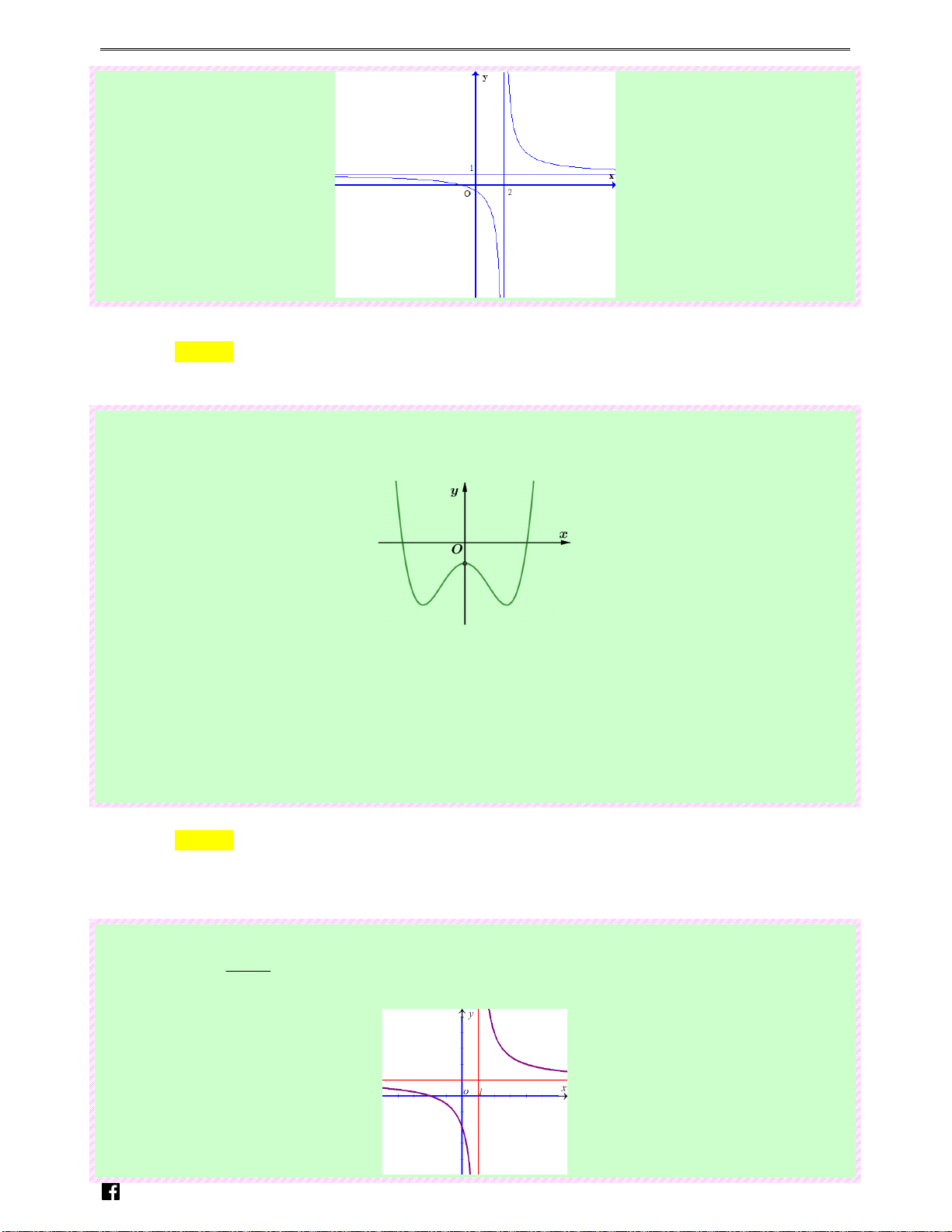
Câu 72: (Câu 23 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Cho đường cong hình vẽ bên là đồ thị của một
hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x + 3 2x −1 2x − 2 2x +1 Ⓐ. y = Ⓑ. y = Ⓒ. y = Ⓓ. y = x +1 x + 1 x −1 x −1 N guy-n Hoàng Vi0t Lời giải Chọn B
Dựa vào đồ thị suy ra tiệm cận đứng x = 1 − loại C, D
Đồ thị hàm số giao với trục hoành có hoành độ dương suy ra chọn B
https://www.facebook.com/vietgold Trang 31
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitrac ngh
Câu 73: (Câu 2 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Đồ thị của hàm số 4 2
y = x − 2x + 2 và đồ thị iem của hàm số 2
y = −x + 4 có tất cả bao nhiêu điểm chung? .vn Ⓐ. 0 Ⓑ. 4 Ⓒ. 1 Ⓓ. 2 Lời giải Chọn D x = 2
Phương trình hoành độ giao điểm: 4 2 2 4 2
x − 2x + 2 = −x + 4 ⇔ x − x − 2 = 0 ⇔ . x = − 2
Vậy hai đồ thị có tất cả 2 điểm chung.
Câu 74: (Câu 7 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Biết rằng đường thẳng y = 2
− x + 2 cắt đồ thị hàm số 3
y = x + x + 2 tại điểm duy nhất; kí hiệu ( x ; 0 y
là tọa độ của điểm đó. Tìm 0 ) 0 y . N
Ⓐ. y = 4
Ⓑ. y = 0
Ⓒ. y = 2 Ⓓ. y = 1 − 0 0 0 0 guy Lời giải -n H Chọn C oàn
Xét phương trình hoành độ giao điểm: 3 3 2
− x + 2 = x + x + 2 ⇔ x + 3x = 0 ⇔ x = 0 g V
Với x = 0 ⇒ y = 2 . i 0 0 0t
Câu 75: (Câu 39 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số bậc bốn y = f ( x) có
đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f ( f ( x)) = 0 là: Ⓐ. 12. Ⓑ. 10. Ⓒ. 8. Ⓓ. 4 .
https://www.facebook.com/vietgold Trang 32
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Lời giải Chọn B
f ( x) = a(a < − ) 1 ( ) 1 L f
( x) = b (−1 < b < 0) (2) u
Ta có: f ( f ( x)) = 0 ⇔ . y
f ( x) = c (0 < c < ) 1 (3) e nt
f (x) = d (d > ) 1 (4) hitracnghiem.vn
Từ đồ thị hàm số ta thấy:
Phương trình (1) có: 2 nghiệm
Phương trình (2) có: 4 nghiệm
Phương trình (3) có: 4 nghiệm
Phương trình (4) vô nghiệm
Vậy phương trình f ( f (x)) = 0 có tất cả 10 nghiệm thực phân biệt.
Câu 76: (Câu 41 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số bậc bốn y = f ( x) có
đồ thị là đường cong trong hình bên dưới. N guy-n Hoàng Vi0
Số nghiệm thực phân biệt của phương trình f ( f (x)) = 0 là t Ⓐ. 4 . Ⓑ. 10. Ⓒ. 12 . Ⓓ. 8. Lời giải Chọn B
https://www.facebook.com/vietgold Trang 33
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
f (x) = a (a < − ) 1
f ( x) = b ( 1 − < b < 0)
Ta có: f ( f (x)) = 0 ⇔ .
f ( x) = c (0 < c < ) 1 L u
f ( x) = d (d > ) 1 yen
Phương trình f ( x) = a với a < 1 − vô nghiệm. thi
Phương trình f ( x) = b với 1
− < b < 0 có 4 nghiệm phân biệt. trac
Phương trình f ( x) = c với 0 < c <1 có 4 nghiệm phân biệt. ngh
Phương trình f ( x) = d với d >1 có 2 nghiệm phân biệt. iem
Vậy phương trình f ( f (x)) = 0 có 10 nghiệm. .vn
Câu 77: (Câu 41 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số bậc ba y = f ( x) có
đồ thị là đường cong trong hình trên. Số nghiệm thực phân biệt của phương trình f ( f (x)) =1 là N g Ⓐ. 9. Ⓑ. 7 . Ⓒ. 3. Ⓓ. 6 . uy- Lời giải n Chọn B H oàng Vi0t
f ( x) = a, (a < − ) 1
Từ f ( f ( x)) =1 ⇔ f ( x) = 0 f ( x) = ,
b (1 < b < 2)
i f ( x) = a với a < −1 phương trình có một nghiệm
i f ( x) = 0 phương trình có ba nghiệm phân biệt
i f ( x) = b với 1< b < 2 phương trình có 3 nghiệm phân biệt.
Vậy số nghiệm thực phân biệt của phương trình f ( f (x)) =1 là 7 .
https://www.facebook.com/vietgold Trang 34
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 78: (Câu 41 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số bậc ba y = f (x) có đồ
thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f ( f (x)) =1 là Luyenthitracnghiem.vn Ⓐ. 9. Ⓑ. 3. Ⓒ. 6 . Ⓓ. 7 . Lời giải Chọn D
Từ đồ thị hàm số ta có N guy-n Hoàn g V
f (x) = x và x < 1 − (1) 1 1 i0
f (x) = 0 (2) t
f ( f ( x)) = 1 ⇔
f (x) = x và 1< x < 2 (3) 2 2
Dựa vào đồ thị, (1) có đúng 1 nghiệm, (2) và (3) mỗi phương trình có 3 nghiệm phân biệt và
7 nghiệm trên phân biệt nhau.
Câu 79: (Câu 48 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a,b,c,d ∈ ℝ) có bảng biến thiên như sau:
https://www.facebook.com/vietgold Trang 35
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracnghie m.v
Có bao nhiêu số dương trong các số a,b,c,d? n Ⓐ. 4. Ⓑ. 2. Ⓒ. 3. Ⓓ. 1. Lời giải N gu y-n Chọn D Hoà
Từ bảng biến thiên ta thấy: lim f ( x) = −∞ nên a > 0 . n x→−∞ g Vi − b 0 f ′( x) 2
= 3ax + 2bx + c ; f ′( )= ⇒ c = f ′ ( ) 2 0 0 0; 4 = 0 ⇒
= 4⇒ ab < 0 ⇒ b > 0 t 3a
Lại có f (0) = −1⇒ d < 0 . Vậy trong các số a,b,c,d có đúng 1 số dương.
Câu 80: (Câu 43 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số 3 2
f (x) = ax + bx + cx + d ( a, b, c ∈ R ) có bảng biến thiên như sau
Có bao nhiêu số dương trong các số a, b, c, d ?
https://www.facebook.com/vietgold Trang 36
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Ⓐ. 3. Ⓑ. 4 . Ⓒ. 2 . Ⓓ. 1. Lời giải L Chọn C uy 2 e f (
′ x) = 3ax + 2bx + c nthi 1
2a − 4b + c = 0 tr
Đồ thị hàm số có điểm cực đại là (−2; ) 1 suy ra a − + − + = c
8a 4b 2c d 1 ngh 3 . a 0 + 2 . b 0 + c = 0 c = 0 ie
Đồ thị hàm số có điểm cực tiểu là (0; −1) suy ra ⇒ m . a 0 + . b 0 + . c 0 + d = 1 − d = 1 − .vn 1 1 = 2 a a − 4b = 0 ⇒ 2 ⇒ . 8 − a + 4b = 2 3 b = 2
Câu 81: (Câu 47 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a,b,c, d ∈ ℝ) có bảng biến thiên như sau: N guy
Có bao nhiêu số dương trong các số a, b, c, d ? -n H Ⓐ. 2. Ⓑ. 4. Ⓒ. 1. Ⓓ. 3. oàn Lời giải g Vi Chọn D 0t
Từ bảng biến thiên hàm số, ta có lim f ( x) = +∞ ⇒ a > 0 . x→+∞
Khi x = 0 thì y = d = 1 > 0 . x = −
Mặt khác f ′( x) 2
= 3ax + 2bx + c . Từ bảng biến thiên ta có f ′( x) 2 = 0 ⇔ . x = 0 −2 Từ đó suy ra b
f ′(0) = 0 ⇒ c = 0 và
= −2 ⇒ b = 3a > 0 . 3a
Vậy có 3 số dương là a, b, d .
Câu 82: (Câu 48 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số 3 2
y = ax + bx + cx + d
( a, b , c , d ∈ ℝ ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a
, b , c , d ?
https://www.facebook.com/vietgold Trang 37
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 y Luyent O x hitra cng Ⓐ. 4 . Ⓑ. 2 . Ⓒ. 1. Ⓓ. 3. hiem Lời giải .vn Chọn C
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương ⇒ d > 0 .
lim y < 0 ⇒ a < 0 . x→ +∞ Ta có: 2
y′ = 3ax + 2bx + c .
Đồ thị hàm số có 2 điểm cực trị nằm về bên trái trục tung nên phương trình y′ = 0 có 2 nghiệm
phân biệt x < x < 0 . 1 2 2b x + x = − < 0 1 2 Khi đó theo Viet ta có: 3a
. Từ đó suy ra b < 0 và c < 0 . . c x x = > 0 1 2 3a
Vậy trong các số a, b , c , d có 1 số dương. N
Câu 83: (Câu 46 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số gu 3 2 y
y = ax + bx + cx + d ( , a , b ,
c d ∈ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số -n
dương trong các số a, , b , c d ? H oàng Vi0t Ⓐ. 4. Ⓑ. 2. Ⓒ. 1. Ⓓ. 3. Lời giải Chọn C 2
y′ = 3ax + 2bx + c .
https://www.facebook.com/vietgold Trang 38
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Do lim y = −∞ nên a < 0 . x→+∞
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d > 0 . L 2 − b u x + x = < 0 1 2 y 3 b < 0 a e
Hàm số có điểm cực trị x < x < 0 , suy ra ⇒ . n 1 2 c c < 0 t h x .x = > 0 1 2 i 3a tracn
Câu 84: (Câu 46 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số g 3 2 h
f ( x) = ax + bx + cx + d (a, b, c, d ∈ ℝ ) có đồ thị là đường cong như hình vẽ bên. Có bao nhiêu iem
số dương trong các số a,b, c, d ? .vn Ⓐ. 4. Ⓑ. 3. Ⓒ. 1. Ⓓ. 2. Lời giải Chọn C
Quan sát hình dáng đồ thị ta thấy a < 0 . N gu
Đồ thị cắt trục Oy tại điểm A(0; d ) nằm bên dưới trục Ox nên d < 0 . y-n
Lại thấy hàm số đạt cực trị tại hai điểm x , = (
1 x là hai số dương nên phương trình y ' 0 2 H o 2 y ' = 3ax + 2
+ ) có hai nghiệm x , x là hai số dương, do đó theo Vi – et ta có à bx c 1 2 ng V 2b i x + x = − > 0 1 2 0 3 b > 0 a t ⇔
. Vậy có một số dương là Ⓑ. c c < 0 x .x = > 0 1 2 3a
Câu 85: (Câu 45 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số
dương trong các số a, , b c, d ?
https://www.facebook.com/vietgold Trang 39
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitr acng Ⓐ. 4 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 3 . hie Lời giải m .v Chọn C n Ta có 2
y ' = 3ax + 2bx + c . Từ đồ thị hàm số đề cho, suy ra: + a < 0 .
+ Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d > 0 .
+ Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ dương
⇒ Phương trình y ' = 0 có 2 nghiệm phân biệt dương −2b S = > 0 3 b > 0 a ⇒ ⇒ (Vì a < 0 ). c c < 0 P = > 0 3a N gu
Vậy có 2 số dương trong các số a, , b c, d . y-n ax + H
Câu 86: (Câu 43 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Cho hàm số f ( x) 1 =
(a,b,c ∈ ℝ) o bx + c àn
có bảng biến thiên như sau g Vi0t
Trong các số a,b và c có bao nhiêu số dương? Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0. Lời giải Chọn C 1 + ax +1 a Ta có lim = lim a x = . x→+∞ x bx + c →+∞ c b b + x
https://www.facebook.com/vietgold Trang 40
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Theo gỉa thiết, ta có a = 1 ⇒ a = b ( ) 1 . b
Hàm số không xác định tại c
x = 2 nên suy ra 2b + c = 0 ⇒ b = − (2) . 2 Lu ac − b y
Hàm số đồng biến trên các khoảng xác định ⇒ f ′( x) = > 0 3 với mọi 2 ( ) x khác 2 . en (bx + c) thi
Nếu a = b > 0 thì từ (2) suy ra c < 0 . Thay vào (3) , ta thấy vô lý nên trường hợp này không trac xảy r
Ⓐ. Suy ra, chỉ có thể xảy ra khả năng a = b < 0 và c > 0 . nghi
Câu 87: (Câu 45 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Cho hàm số f (x) có bảng biến thiên em như sau: .vn
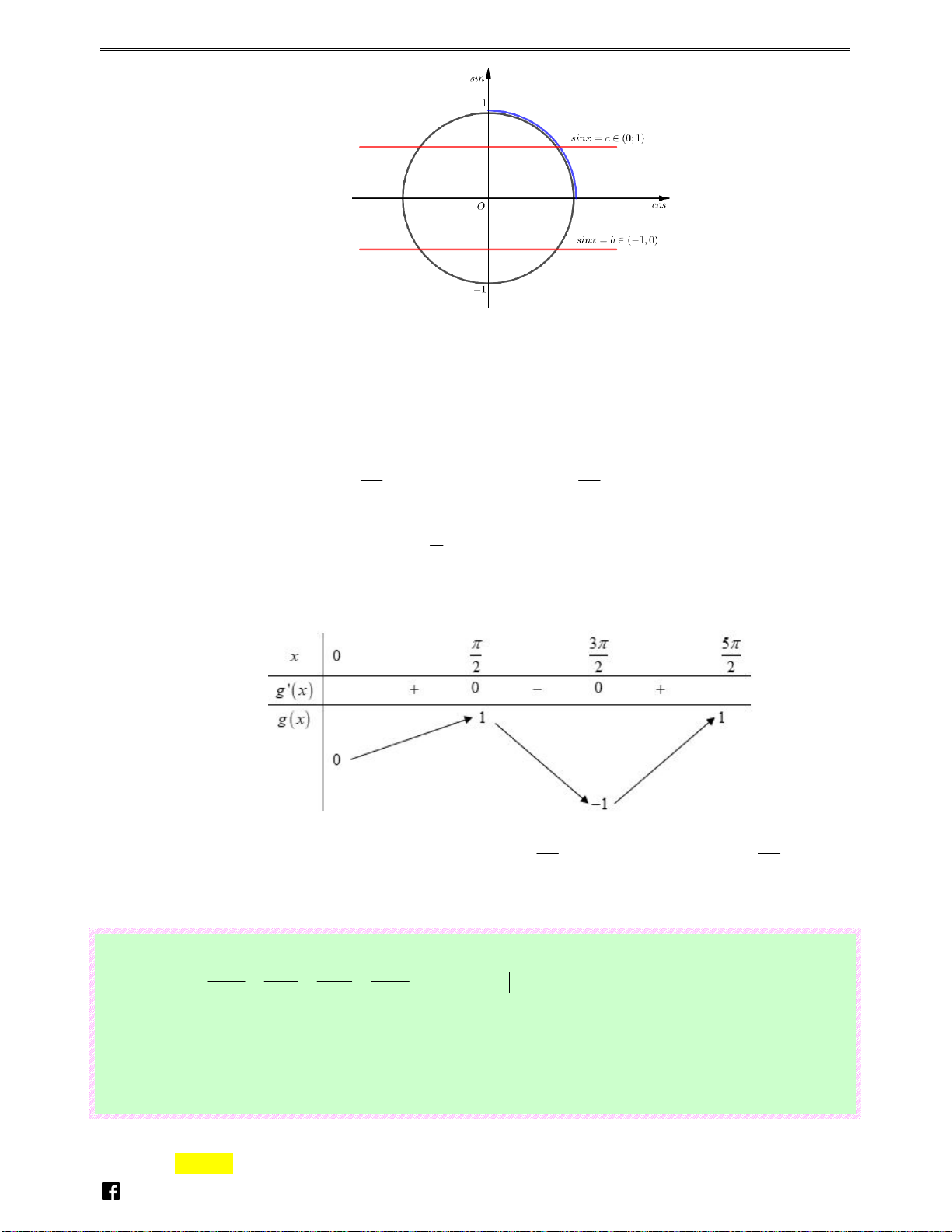
Số nghiệm thuộc đoạn [ π
− ;2π ] của phương trình 2 f (sin x) +3 = 0 là Ⓐ. 4. Ⓑ. 6. Ⓒ. 3. Ⓓ. 8. Lời giải Chọn B N Ta có f ( x) + = ⇔ f ( x) 3 2 sin 3 0 sin = − . g 2 uy-
Dựa vào bảng biến thiên ta có: n Ho
sin x = t ∈ − ; ∞ −1 1 1 ( ) ( ) à n 3 sin x = t ∈ 1 − ;0 2 2 ( ) ( ) g
f (sin x) = − ⇔ V i 2
sin x = t ∈ 0;1 3 3 ( ) ( ) 0 t
sin x = t ∈ 1;+∞ 4 4 ( ) ( ) Phương trình ( ) 1 và (4) vô nghiệm.
Phương trình (2) có 4 nghiệm phân biệt
Phương trình (3) có hai nghiệm phân biệt khác các nghiệm của (2).
Do đó tổng số nghiệm của phương trình đã cho là 6.
https://www.facebook.com/vietgold Trang 41
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
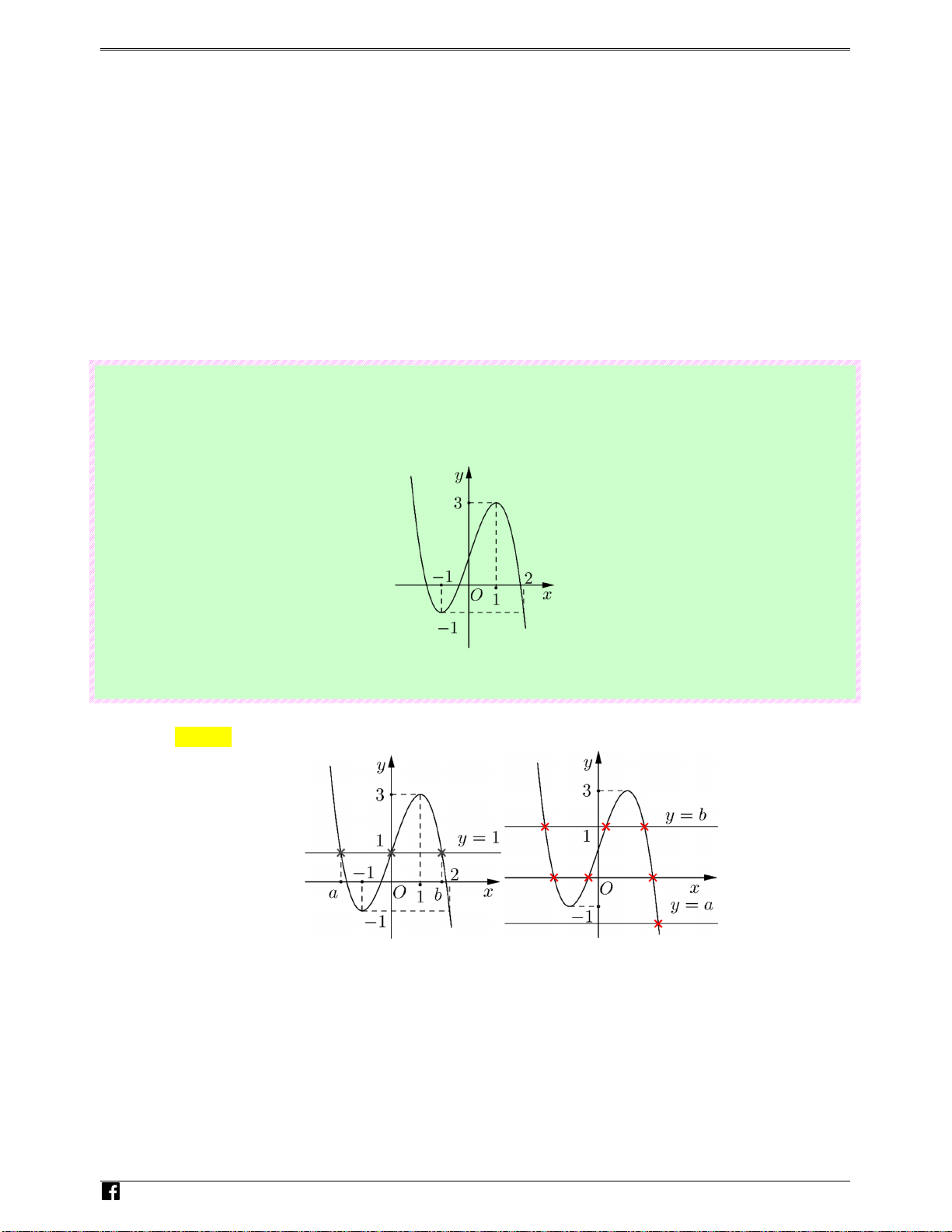
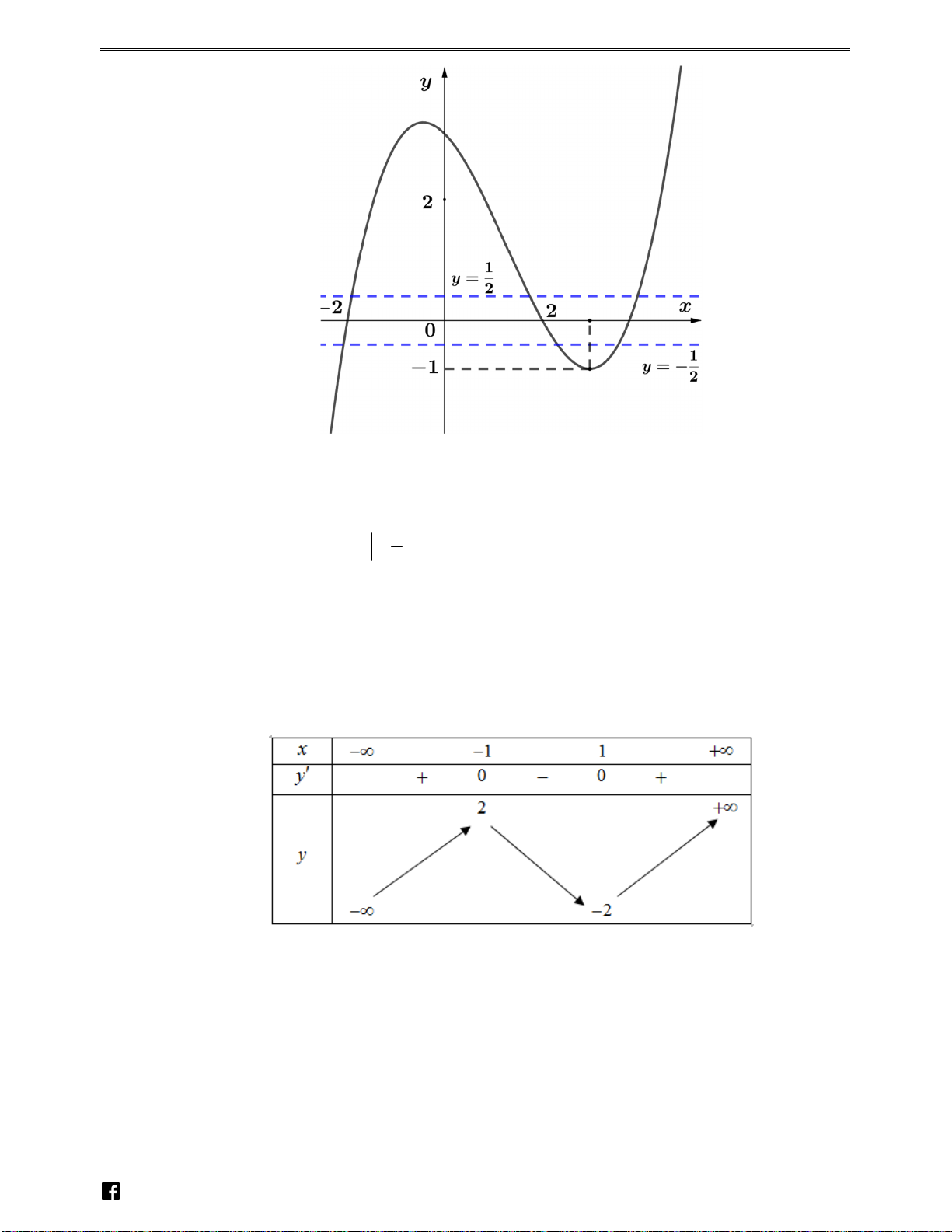
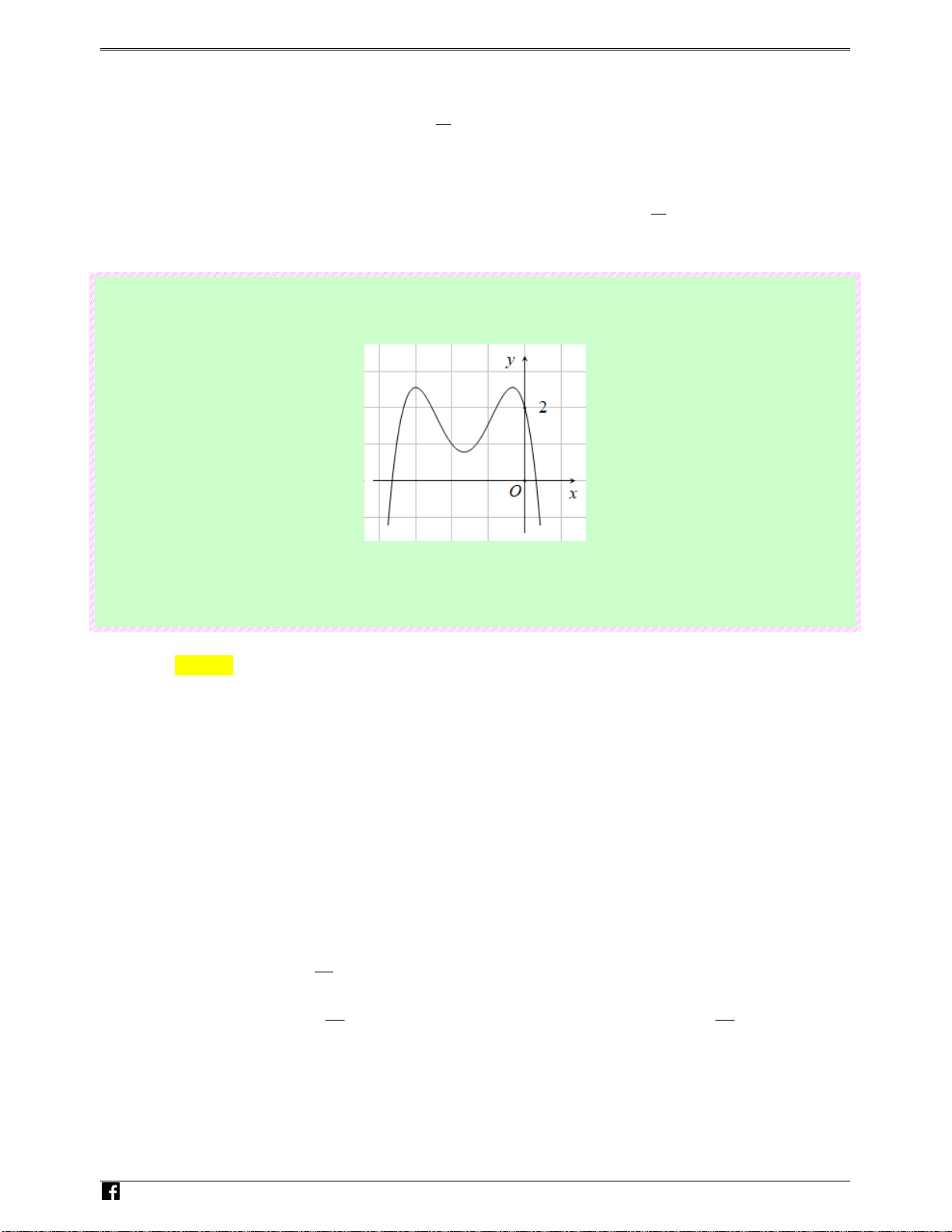
Câu 88: (Câu 42 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số bậc ba y = f ( x) có đồ thị như 2
hình vẽ bên. Số nghiệm thực của phương trình f ( 3 x − 3x) = là 3 Luyenthitracnghiem.v n Ⓐ. 6 . Ⓑ. 10. Ⓒ. 3. Ⓓ. 9. Lời giải Chọn B Cách 1
Đặt t = g ( x) 3 = x − 3x (1) Ta có g ( x) 2 '
= 3x − 3 = 0 ⇔ x ±1 Bảng biến thiên N guy-n Hoàn g V
Dựa vào bảng biến thiên ta có i0t
Với t ∈ (−2;2) phương trình 3
t = x − 3x có 3 nghiệm phân biệt. Với t ∈{−2; } 2 phương trình 3
t = x − 3x có 2 nghiệm phân biệt Với t ∈ (− ;
∞ −2) ∪ (2;+∞) phương trình 3
t = x − 3x có 1 nghiệm. f (t) 2 = 2 2 3 Phương trình f ( 3
x − 3x) = (2) trở thành f (t) = ⇔ 3 3 f (t) 2 = − 3
Dựa vào đồ thị ta có:
+ Phương trình f (t) 2 = có 3 nghiệm thỏa mãn 2
− < t < t < 2 < t ⇒ phương trình (2) có 7 3 1 2 3 nghiệm phân biệt.
https://www.facebook.com/vietgold Trang 42
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
+ Phương trình f (t) 2
= − có 3 nghiệm thỏa mãn t < 2
− < 2 < t < t ⇒ phương trình (2) có 3 3 4 5 6 nghiệm phân biệt. L
Vậy phương trình đã cho có 10 nghiệm phân biệt. uye Cách 2. nth 2 i 3 t
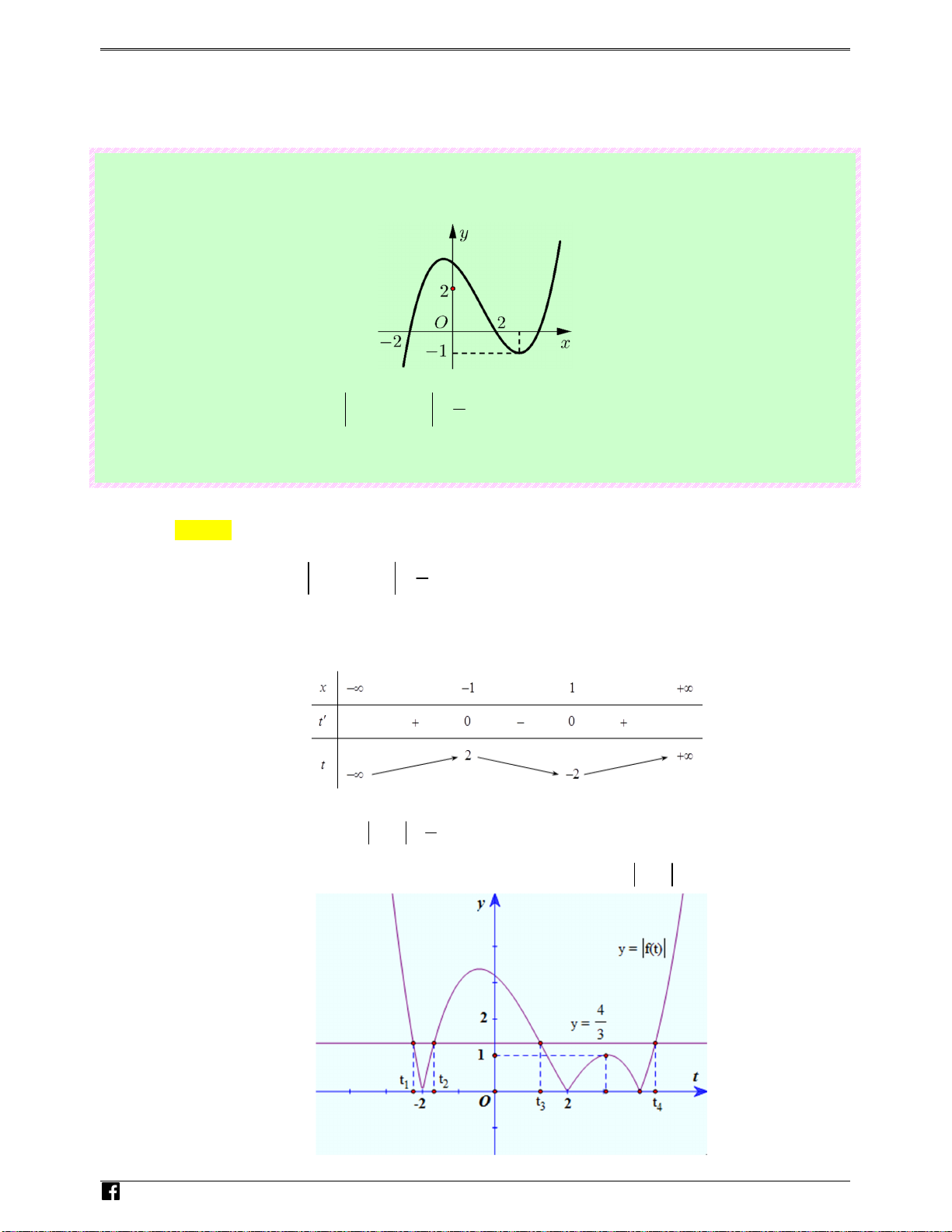
Xét phương trình f (x − 3x) = ra 3 cng Đặt 3 2 t = x − 3 ,
x t ' = 3x − 3,t ' = 0 ⇔ x = 1 ± hiem Bảng biến thiên: .vn 2
Phương trình trở thành: f (t) = ,t ∈ ℝ 3 Từ đồ thị f ( )
x ban đầu, ta suy ra đồ thị hàm số y = f (t) như sau: N guy-n Hoàng Vi0t 2
Suy ra: phương trình f (t) = có các nghiệm t < 2
− < t < t < 2 < t < t < t . 3 1 2 3 4 5 6 3
x − 3x = t co 1 nghiem x 1 1 3
x − 3x = t co 1 nghiem x 4 2 3
x − 3x = t co 3 nghiem x , x , x
Từ bảng biến thiên ban đầu, ta có: 2 3 4 5
đều là các nghiệm phân 3
x −3x = t co 3 nghiem x , x , 3 6 7 8 x 3
x − 3x = t co 1 nghiem x 5 9 3
x − 3x = t co 1 nghiem x 6 10 biệt.
https://www.facebook.com/vietgold Trang 43
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 2 Vậy 3
f (x − 3x) =
có 10 nghiệm phân biệt. 3
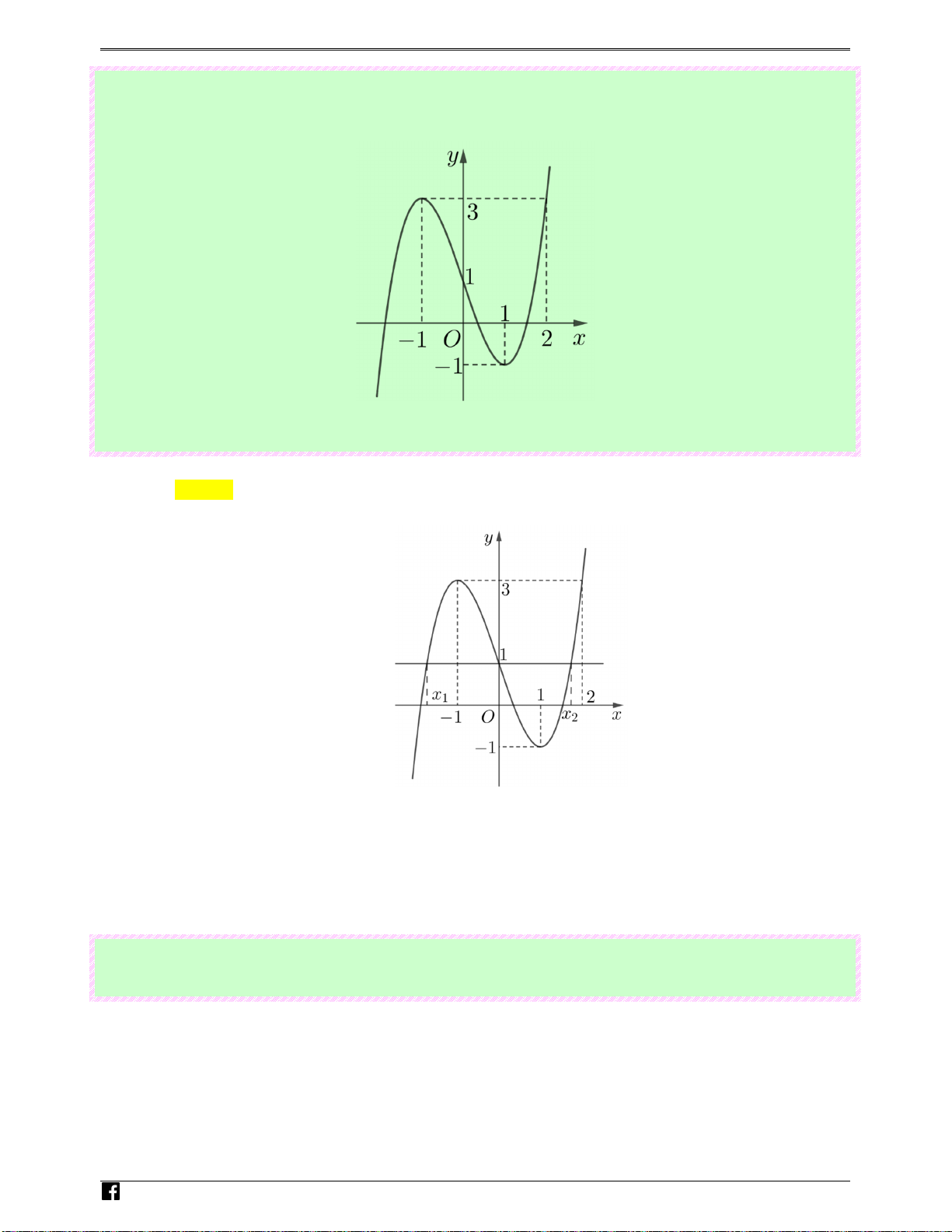
Câu 89: (Câu 45 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số bậc ba y = f ( x) có đồ thị như Lu 3 3 y
hình vẽ bên. Số nghiệm thực của phương trình f x − 3x = là e ( ) n 2 thitracnghiem.vn Ⓐ. 8. Ⓑ. 4. Ⓒ. 7. Ⓓ. 3. Lời giải Chọn A f ( 3 3 x − 3x) = 3 Phương trình f ( 3 x − x) 2 3 = ⇔ . 2 f ( 3 3 x − 3x) = − 2 y N guy 3 2 - y = n 2 Ho a4 àn a -2 1 O a 2 a x 2 3 g V -1 i0 - 3 t y = 2 3
x − 3x = a , −2 < a < 0 1 ( 1 ) 3 * Phương trình f ( 3 x − 3x) 3
= ⇔ x − 3x = a , 0 < a < 2 . 2 ( 2 ) 2 3
x − 3x = a , a > 2 3 ( 3 ) 3 * Phương trình f ( 3 x − 3x) 3
= − ⇔ x − 3x = a , a < 2 − . 4 ( 4 ) 2 Đồ thị hàm số 3
y = x − 3x có dạng như hình vẽ sau:
https://www.facebook.com/vietgold Trang 44
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 y y = a 2 3 Luyen y = a t 2 hitr O -1 1 a x cngh y = a i 1 e -2 m .v y = a n 4
Dựa vào đồ thị trên ta có: - Phương trình 3 x − 3x = có 3 nghiệm phân biệt. 1 a - Phương trình 3
x − 3x = a có 3 nghiệm phân biệt. 2 - Phương trình 3
x − 3x = a có 1 nghiệm. 3 - Phương trình 3
x − 3x = a có 1 nghiệm. 4 3
Vậy phương trình f ( 3
x − 3x) = có 8 nghiệm phân biệt. 2 N g
Câu 90: (Câu 41 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số bậc ba y = f ( x) có đồ thị như uy- 1 3 n
hình vẽ bên. Số nghiệm thực của phương trình f (x − 3x) = là 2 H oàng Vi0t Ⓐ. 6. Ⓑ. 10. Ⓒ. 12. Ⓓ. 3. Lời giải Chọn B
https://www.facebook.com/vietgold Trang 45
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracnghiem.vn 3 x −3x = , a ( 2 − < a < − ) 1 3 x − 3x = ,
b (1 < b < 2) f ( 1 3 x − 3x ) = 3 1 x − 3x = , c (c > 2) Ta có f ( 3 x − x ) 2 3 = ⇔ ⇔ . 2 3
x − 3x = d, (d < 2 − ) f ( 3 x − 3x ) 1 = − 2 3
x −3x = ,e (2 < e < 3) 3
x −3x = f , ( f > 3) N Xét hàm số 3
y = x −3x ; có 2 y' =3x −3 guy- Bảng biến thiên n Hoàng Vi0t
Dựa vào bảng biến thiên ta có Phương trình: 3
x − 3 x = a có 3 nghiệm. Phương trình: 3
x − 3 x = b có 3 nghiệm. Phương trình: 3
x − 3 x = c có 1 nghiệm. Phương trình: 3
x − 3 x = d có 1 nghiệm. Phương trình: 3
x − 3 x = e có 1 nghiệm.
https://www.facebook.com/vietgold Trang 46
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Phương trình: 3
x −3x = f có 1 nghiệm.
Vậy tổng có 10 nghiệm. Lu
Câu 91: (Câu 43 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số bậc ba y = f ( x) có đồ thị như ye hình vẽ bên. nthitracnghiem.vn 4
Số nghiệm thực của phương trình f ( 3 x − 3x) = là 3 Ⓐ. 3. Ⓑ. 8. Ⓒ. 7. Ⓓ. 4. Lời giải Chọn B 4
Xét phương trình: f ( 3 x − 3x) = ( )1 . 3 Đặt 3
t = x − 3x , ta có: 2
t ′ = 3 x − 3 ; t′ = 0 ⇔ x = 1 ± . Bảng biến thiên: N guy-n Hoàng Vi0t Phương trình ( )
1 trở thành f (t) 4 = với t ∈ ℝ . 3
Từ đồ thị hàm số y = f ( x) ban đầu, ta suy ra đồ thị hàm số y = f (t ) như sau:
https://www.facebook.com/vietgold Trang 47
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Suy ra phương trình f (t ) 4
= có các nghiệm t < 2
− <t <t <2<t . 3 1 2 3 4
Từ bảng biến thiên ban đầu ta có: +) 3
x −3x =t có 1 nghiệm L 1 1 x . uy +) 3
x −3x = t có 1 nghiệm e 4 2 x . nth +) 3 x −3x = x , x , x 2
t có 3 nghiệm 3 3 5 . itra +) 3 x − 3x = x , x , x 3 t có 3 nghiệm 6 7 8 . cng 4 3 h
Vậy phương trình f ( x − 3x) = có 8 nghiệm. i 3 em .v
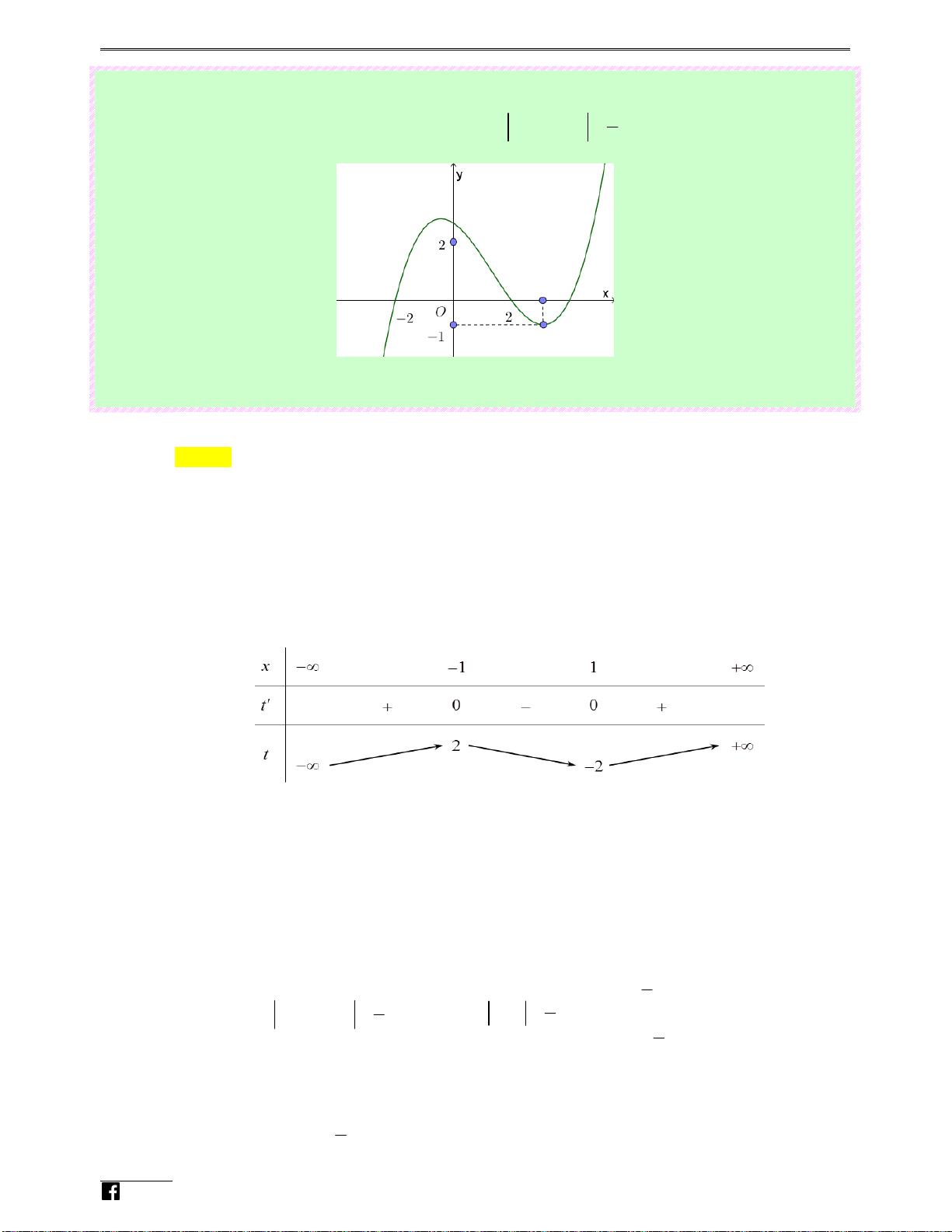
Câu 92: (Câu 43 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) liên tục trên R và có n
đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sin x) = m
có nghiệm thuộc khoảng (0;π ) là N guy Ⓐ. 1 − ;3 . Ⓑ. ( 1 − ; ) 1 . Ⓒ. ( 1 − ; ) 3 . Ⓓ. 1 − ;1 . - [ ) [ ) n H Lời giải oàn Chọn D g Vi
Đặt t = sin x , với x ∈(0;π ) ⇒ t ∈(0; ] 1 . 0t
Khi đó phương trình f (sin x) = m trở thành f (t) = m .
Phương trình f (sin x) = m có nghiệm x ∈(0;π ) khi và chỉ khi phương trình f (t) = m có nghiệm t ∈(0; ]
1 . Điều này xảy ra khi và chỉ khi đường thẳng y = m có điểm chung với đồ thị
hàm số y = f (t) trên nửa khoảng (0; ] 1 .
Dựa vào đồ thị đã cho ta có tập hợp tất cả các giá trị thực của tham số m là nửa khoảng [−1; ) 1 .
Câu 93: (Câu 24 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f (x) liên tục trên đoạn [ 2 − ; ]
4 và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình 3 f (x) − 5 = 0 trên đoạn [ 2 − ; ] 4 là
https://www.facebook.com/vietgold Trang 48
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracnghiem .vn Ⓐ. 0 Ⓑ. 3 Ⓒ. 2 Ⓓ. 1 Lời giải Chọn B 5
Ta có 3 f (x) − 5 = 0 ⇔ f (x) = . 3 5
Dựa vào đồ thị ta thấy đường thẳng y = cắt đồ thị hàm số y = f (x) tại ba điểm phân biệt thuộc 3 đoạn [ 2 − ; ] 4 .
Do đó phương trình 3 f (x) − 5 = 0 có ba nghiệm thự Ⓒ. N gu 1 7
Câu 94: (Câu 45 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số 4 2 y = x −
x có đồ thị (C) . y- 6 3 n
Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt H oà
M ( x ; y , N x ; y − y = 4 − 1 1 ) ( 2 y ( M , 2 )
N khác A ) thỏa mãn 1 2 ( 1x 2x ) ng V Ⓐ. 3 Ⓑ. 0 Ⓒ. 1 Ⓓ. 2 i0t Lời giải Chọn D
Đường thẳng MN có VTCP là NM = (x − x ; y − y ) = (x − x ; 4(x − x )) . 1 2 1 2 1 2 1 2
Chọn VTCP là u = (1; 4) ⇒ VTPT n = (4; −1) . 1 7
Phương trình đường thẳng 2 4
MN : 4(x − x ) − ( y − y ) = 0 ⇔ y = 4x − 4 + − . 1 1 1 x 1 x 1 x 6 3
Đường thẳng MN còn tiếp xúc với đồ thị (C) tại điểm A . Như vậy, nếu A có hoành độ là 0 x x = −1 2 14 thì x −
x = 4 ⇔ x − 7x − 6 = 0 ⇔ x = −2 0
x là nghiệm của phương trình 3 3 3 3 x = 3 13 + x = 1 − : A −1; − 6
https://www.facebook.com/vietgold Trang 49
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Vì đường thẳng MN tiếp xúc với đồ thị (C) tại A nên ta có: 13 1 7 −
= −4 + x − x − 4x ⇔ ( x + )2 4 2 1 ( 2
x − 2x −11 = 0 (1) 1 1 1 1 1 1 ) 6 6 3
có 1 nghiệm kép và 2 nghiệm đơn phân biệt nên đường thẳng MN tiếp xúc với đồ thị (C) tại A Lu
và cắt đồ thị tại 2 điểm phân biệt M , y N khác A . en 20 t + − − h x = −2 : A 2; i 3 tra
Vì đường thẳng MN tiếp xúc với đồ thị (C) tại A nên ta có: cn 20 1 7 2 g 4 2 2 −
= −8 + x − x − 4x ⇔ x + 2
x − 4x − 4 = 0 (2) h 1 1 1 ( 1 ) ( 1 1 ) i 3 6 3 em
có 1 nghiệm kép và 2 nghiệm đơn phân biệt nên đường thẳng MN tiếp xúc với đồ thị (C) tại A .vn
và cắt đồ thị tại 2 điểm phân biệt M , N khác A . 15 + x = 3: A 3;− 2
Vì đường thẳng MN tiếp xúc với đồ thị (C) tại A nên ta có: 15 1 7 −
= 12 + x − x − 4x ⇔ ( x − 3)2 4 2 ( 2
x + 6x +13 = 0 (3) 1 1 1 1 1 1 ) 2 6 3
chỉ có 1 nghiệm kép nên đường thẳng MN chỉ tiếp xúc với đồ thị (C) tại A nên loại.
Vậy có 2 điểm A thỏa mãn yêu cầu đề bài. 1 7
Câu 95: (Câu 40 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số 4 2 y = x −
x có đồ thị (C ) . 4 2
Có bao nhiêu điểm A thuộc (C ) sao cho tiếp tuyến của (C ) tại A cắt (C ) tại hai điểm phân
biệt M x ; y ; N x ;
y − y = 6(x − x ) N ( 1 1 ) ( 2 y khác 2 ) A thỏa mãn 1 2 1 2 guy- Ⓐ. 1 Ⓑ. 2 Ⓒ. 0 Ⓓ. 3 n Ho Lời giải àng Chọn B V 1 7 i 0 Ta có A ∈ (C) 4 2
⇒ A t; t − t t 4 2 3
y′ = x − 7x ⇒ y′(t ) 3 = t − 7t
Phương trình tiếp tuyến của (C ) tại A là 3 7 y = ( 1 7 3
t − 7t )( x − t ) 4 2
+ t − t ⇔ y = ( 3t − 7t) 4 2 x − t + t 4 2 4 2
Phương trình hoành độ giao điểm: 1 7 3 7 4 2 x − x = ( 3 t − 7t ) 4 2 x − t + t 4 2 4 2 4 2
⇔ x − x − ( 3t − t) 4 2 14 4
7 x + 3t −14t = 0
⇔ ( x − t )2 ( 2 2
x + 2tx + 3t − 14) = 0 x = t ⇔ 2 2
x + 2tx + 3t −14 = 0 ( ) 1
https://www.facebook.com/vietgold Trang 50
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Tiếp tuyến cắt đồ thị (C ) tại hai điểm phân biệt M ( x ; y ; N x ; 1 1 ) ( 2 y khác 2 ) A khi phương trình ( )
1 có hai nghiệm phân biệt khác t 2 2 − 7 < t < 7 L t − (3t −14) > 0 u ⇔ ⇔ 21 (2) y 2 2 2 e t
+ 2t + 3t −14 ≠ 0 t ≠ ± n 3 th Khi dó itra 3 7 3 4 2 c y = t − 7 − + 1 ( t ) x + x = 2 − t 1 x t t n 1 2 4 2 3 ⇒ − = − − g và y y t 7 1 2 ( t )( 1 x 2 x ) 2 h x x = 3t −14 3 7 1 2 3 4 2 i y = t − 7 − + 2 ( t ) 2 x t t e 4 2 m . 3 v
Ta có y − y = 6(x − x ) ⇔ (t − 7t)(x − x = 6 − 1 2 ) ( 1x 2x ) 1 2 1 2 n t = 1 − (n) t +1 = 0 3
⇔ t − 7t − 6 = 0 ⇔ (t + )( 2
1 t − t − 6) = 0 ⇔ ⇔ t = 2 − (n) 2
t − t − 6 = 0 t = 3 (l) 13
Với t = −1 ta có A 1 − ;− 4
Với t = −2 ta có A( 2 − ; 1 − 0)
⇒ có hai điểm thỏa yêu cầu bài toán.
Câu 96: (Câu 35 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
m + 3 m + 3 sin x = sin x có nghiệm thực N guy Ⓐ. 5 Ⓑ. 2 Ⓒ. 4 Ⓒ. 3 -n H Lời giải o Chọn A àng 3 3 3 V Ta có: 3
m + 3 m + 3sin x = sin x ⇔ m + 3 m + 3sin x = sin x . i0t Đặt 3 3
m + 3sin x = u ⇒ m + 3sin x = u thì phương trình trên trở thành 3
m + 3u = sin x
Đặt sin x = v thì ta được 3
m + 3v = u
⇒ 3(v − u) + (v −u)( 2 2
v + uv + u ) = 0 ⇔ (v − u)( 2 2
3 + v + uv + u = 0 Do 3 )
m + 3u = v 2 2
3+ v + uv + u > 0, u
∀ ,v nên phương trình trên tương đương u = v . Suy ra 3 3
m + 3sin x = sin x ⇔ m = sin x − 3sin x .
Đặt sin x = t ( 1 − ≤ t ≤ )
1 và xét hàm f (t) 3
= t −3t trên [ 1 − ; ] 1 có f ′(t) 2
= 3t −3 ≤ 0, t ∀ ∈[ 1 − ; ] 1
Nên hàm số nghịch biến trên [ 1 − ; ] 1 ⇒ 1 − = f ( )
1 ≤ f (t) ≤ f (− ) 1 = 2 ⇒ 2 − ≤ m ≤ 2. Vậy m∈{ 2 − ; 1 − ;0;1; } 2 .
https://www.facebook.com/vietgold Trang 51
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 −x + 2
Câu 97: (Câu 40 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y =
có đồ thị (C) và điểm x − 1 ( A ;
a 1) . Gọi S là tập hợp tất cả các giá trị thực của tham số a để có đúng một tiếp tuyến của L
(C) đi qua A . Tổng tất cả các giá trị các phần tử của S là uyent Ⓐ. 1 Ⓑ. 3 Ⓒ. 5 Ⓓ. 1 h 2 2 2 itra Lời giải cn Chọn C ghie −1 m
ĐK: x ≠ 1 ; y' = . (x − 2 1) vn
Đường thẳng d qua A có hệ số góc k là y = ( k x − ) a + 1 −x +
k(x − a) + 1 = 2 (1) x − 1
d tiếp xúc với (C ) ⇔ có nghiệm. − k = 1 (2) (x − 2 1) −1 −x + 2 Thế (2) vào ( ) 1 ta có: (x − ) a + 1 = ⇔ −x + a + 2
x − 2x + 1 = − 2
x + 3x − 2, x ≠ 1 (x − 2 1) x −1 ⇔ 2
2x − 6x + a + 3 = 0 (3)
Để đồ thị hàm số có một tiếp tuyến qua A thì hệ là số nghiệm của hệ phương trình trên c ó N g
nghiệm duy nhất ⇔ phương trình ( )
3 có nghiệm duy nhất khác 1 uy-n
∆' = 9 − 2a − 6 = 0 H 3 o 1 − 6 + a + 3 ≠ 0 a 2 = à
⇔ 2x − 6x + a + 3 = 0 (3) ⇔ ⇒ n 2
∆' = 9 − 2a − 6 > g 0 a = 1 Vi 2 − 6 + a + 3 = 0 0t −1
Cách 2: TXĐ : D = R \{ } 1 ; y′ = (x − )2 1
Giả sử tiếp tuyến đi qua A( ; a )
1 là tiếp tuyến tại điểm có hoành độ x = , khi đó phương trình 0 x 1 − −x + 2
tiếp tuyến có dạng : y = x − x + d 2 ( ) 0 0 ( ) (x − ) 1 x −1 0 0
Vì A ∈ d nên thay tọa độ điểm A vào phương trình đường thẳng d ta có : 2 1 − −x + 2
2x − 6x + 3+ a = 0 1 1 = a − x + ⇔ 2 ( 0 ) 0 0 0 ( ) ( x −1 x −1 x ≠ 1 0 ) 0 0
Để chỉ có một tiếp tuyến duy nhất đi qua A thì phương trình ( )
1 có nghiệm duy nhất khác 1
https://www.facebook.com/vietgold Trang 52
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
∆′ = 9 − 2a − 6 = 0 3 1− 6 + a + 3 ≠ 0 a = ⇔ ⇒ 2
∆′ = 9 − 2a − 6 > 0 a = 1 L 2 − 6 + a + 3 = 0 uyen
Câu 98: (Câu 45 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Tìm tất cả các giá trị thực của tham số m thi để đường thẳng = −
cắt đồ thị của hàm số 3 2
y = x − 3x − m + 2 tại ba điểm phân biệt , A , t y mx B C rac
sao cho AB = BC . ngh Ⓐ. m∈(− ; ∞ ) 3 Ⓑ. m∈(− ; ∞ − ) 1
Ⓒ. m∈(−∞: +∞)
Ⓓ. m∈(1: +∞) iem Lời giải . vn Chọn A
Hoành độ giao điểm là nghiệm của phương trình x = 1 3 2
x − x − m + = −mx ⇔ ( x − )( 2 3 2
1 x − 2x + m − 2) = 0 ⇔ 2
x − 2x + m − 2 = 0
Đặt nghiệm x = 1. Từ giải thiết bài toán trở thành tìm 2
m để phương trình có 3 nghiệm lập thành cấp số cộng. Khi đó phương trình 2
x − 2x + m − 2 = 0 phải có 2 nghiệm phân biệt Vậy ta chỉ cần ′
∆ =1−(m−2) > 0 ⇔ m < 3
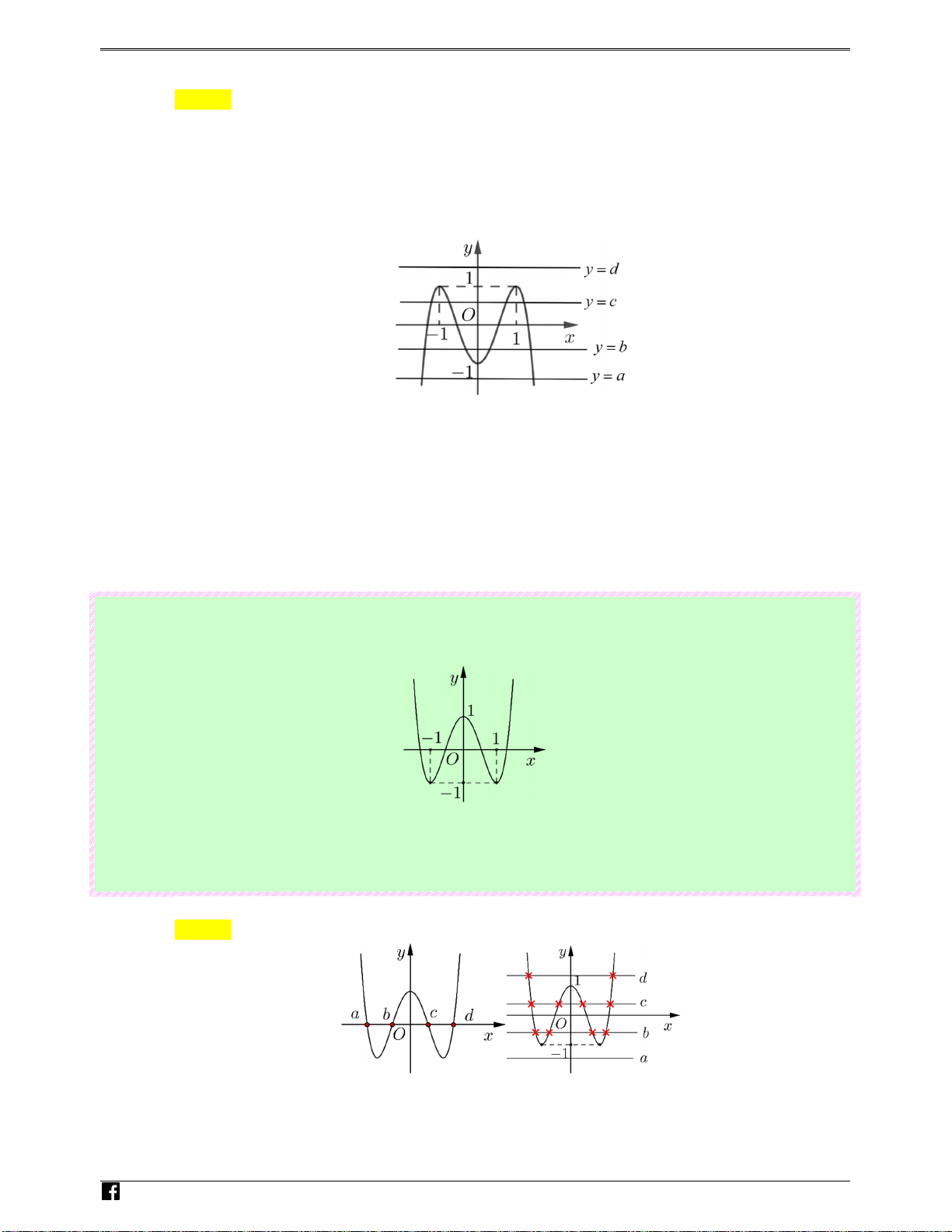
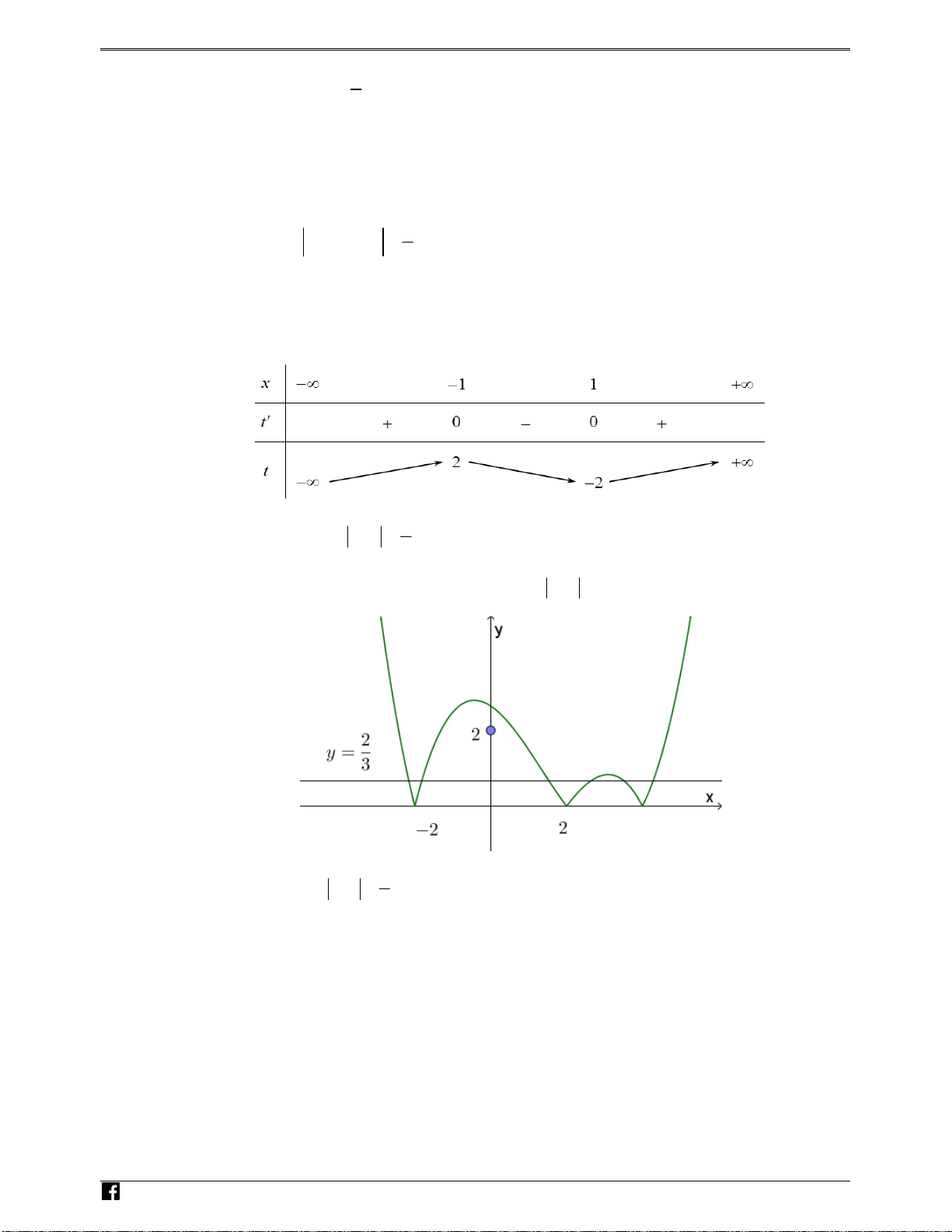
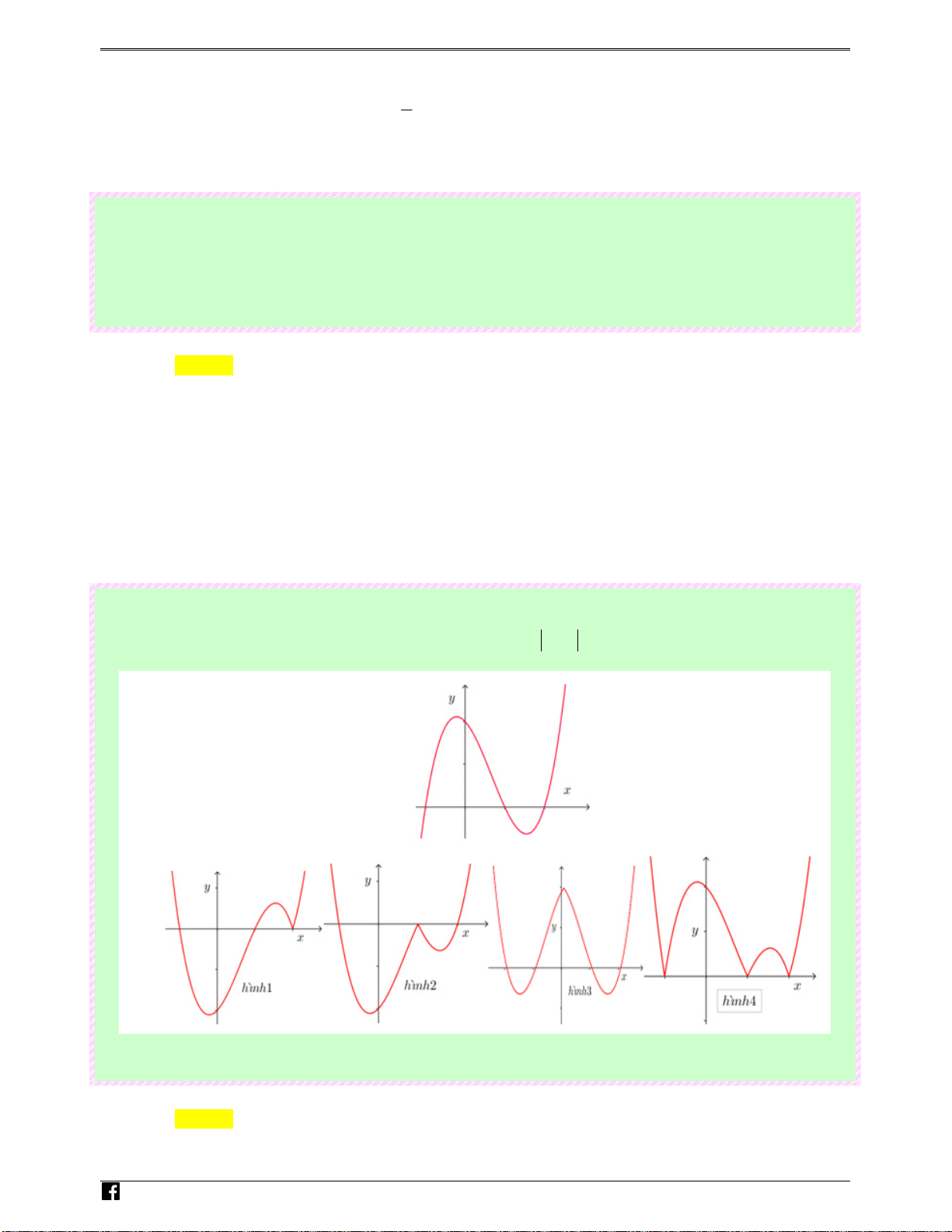
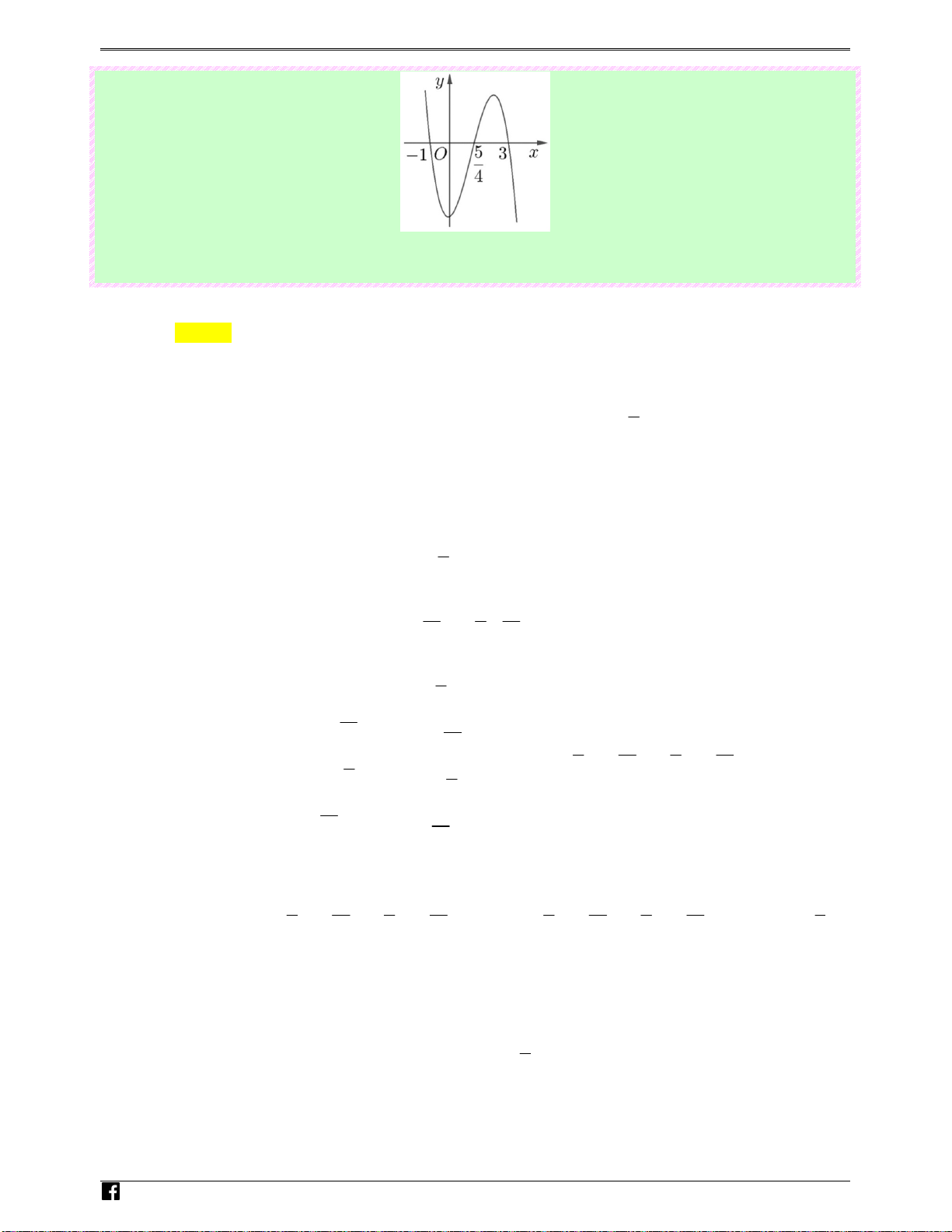
Câu 99: (Câu 32 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Hàm số y = ( x − )( 2 2 x − ) 1 có đồ thị như hình
vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x − ( 2 2 x − ) 1 ? N guy-n Hoàng Vi0t Ⓐ. Hình 1 Ⓑ. Hình 2 Ⓒ. Hình 3 Ⓓ. Hình 4 Lời giải Chọn A
https://www.facebook.com/vietgold Trang 53
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 (
x − 2)( 2x − ) x ≥ y = x − 2 ( 1 , 2 2 x − ) 1 =
Đồ thị gồm 2 phần: −( x − 2)
( 2x − )1,x < 2
+) Giữ nguyên phần đồ thị đã cho ứng với x ≥ 2 . Lu
+) Lấy đối xứng phần đồ thị đã cho ứng với x < 2 qua trục Ox ye 2 n
Hình 1 nhận vì đồ thị là hàm y = x − 2 (x − ) 1 thitr
Hình 2 loại vì đồ thị là hàm y = ( x − 2) x −1 ( x +1) acng
Hình 3 loại vì đồ thị hàm số 2 y = x − 2 x −1 h ( )( ) iem
Hình 4 loại vì đồ thị hàm y = ( x − ) 2 2 x −1 . ( ) vn
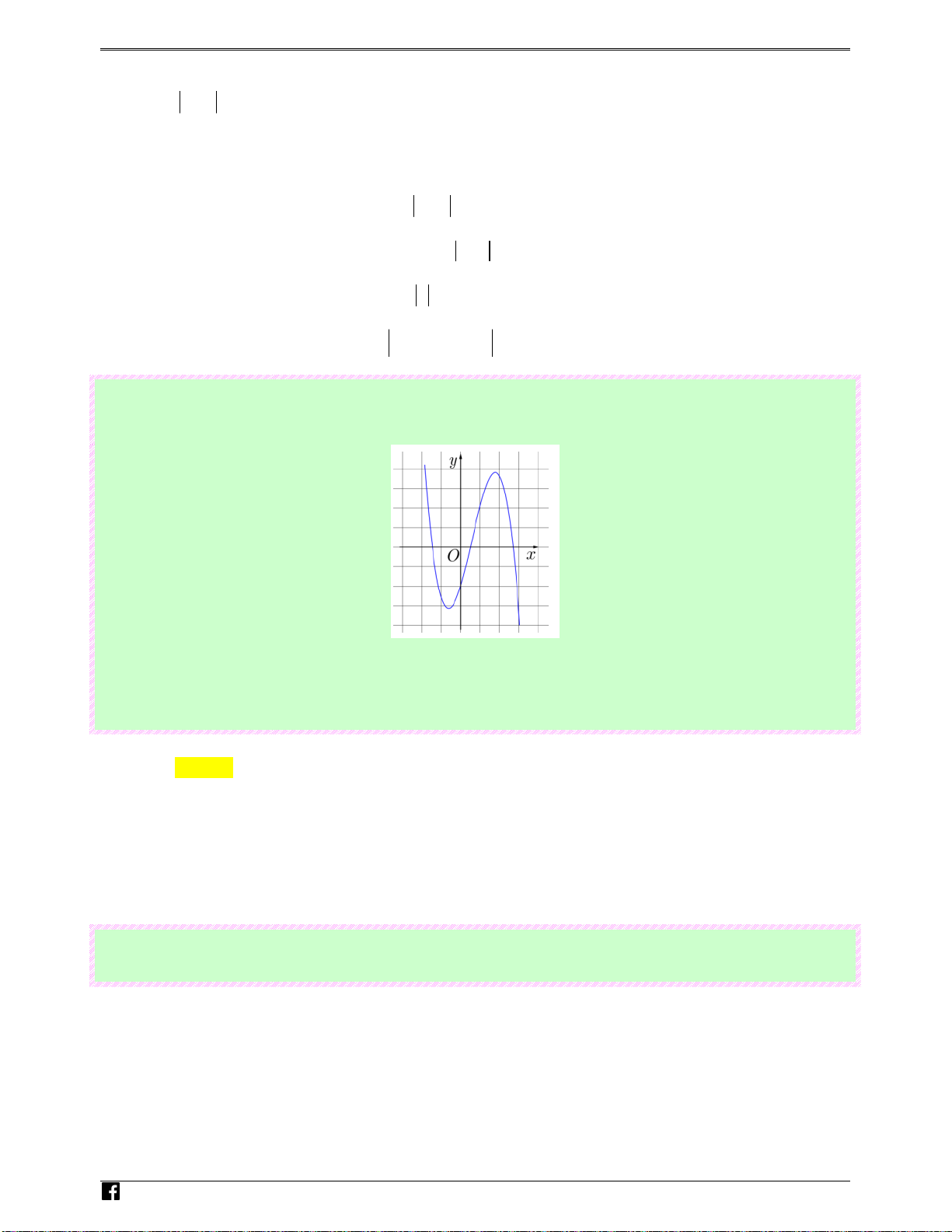
Câu 100: (Câu 11 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị
như hình vẽ bên. Mệnh đề nào dưới đây đúng? N
Ⓐ. a < 0, b > 0, c > 0, d < 0
Ⓑ. a < 0, b < 0, c > 0, d < 0 . guy-
Ⓒ. a > 0, b < 0, c < 0, d > 0
Ⓓ. a < 0, b > 0, c < 0, d < 0 . n H Lời giải oà Chọn A ng
Dựa vào đồ thị suy ra hệ số a < 0 ⇒ loại phương án C Vi0 2 t
y′ = 3ax + 2bx + c = 0 có 2 nghiệm x , x trái dấu (do hai điểm cực trị của đồ thị hàm số nằm 1 2
hai phía với Oy ) ⇒ 3 .
a c < 0 ⇒ c > 0 ⇒ loại phương án Ⓓ. Do
(C )∩ Oy = D (0;d ) ⇒ d < 0.
Câu 101: (Câu 50 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số f (x) có bảng biến thiên như sau:
https://www.facebook.com/vietgold Trang 54
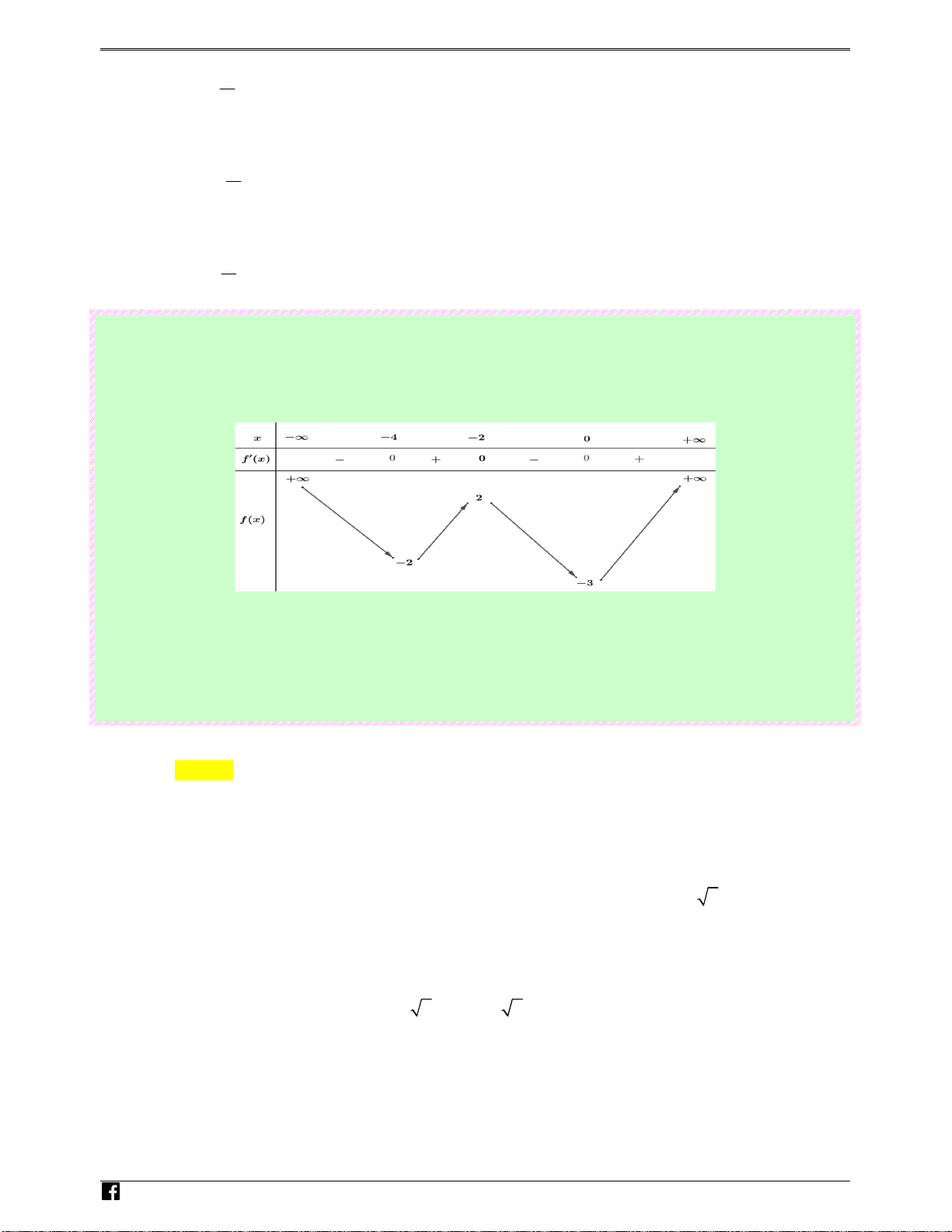
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 x - ∞ - 4 - 2 0 + ∞ L f '(x) 0 + + 0 0 uyen + ∞ + ∞ t 2 hi f(x) tracn - 2 gh - 3 ie m .v − = n
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 4 f (x 4 ) x
m có ít nhất 3 nghiệm thực phân
biệt thuộc khoảng (0;+∞)? Ⓐ. 16. Ⓑ. 19. Ⓒ. 20. Ⓓ. 17 . Lời giải Chọn C + Đặt 2
t = x − 4x . Ta có bảng biến thiên sau: N guy-n H oàn Khi t ∈( 4
− ;0) có 2 giá trị x ∈(0;+∞) thỏa mãn 2 t = x − 4x . g Vi0
Khi t ∈[0;+∞) ∪{− }
4 có 1 giá trị x ∈ (0;+∞) thỏa mãn 2 t = x − 4x . t + Xét phương trình 4 (t) = ⇔ (t) m f m f = , (*) 4 x - ∞ - 4 - 2 0 + ∞ f '(x) 0 + + 0 0 + ∞ + ∞ 2 f(x) - 2 - 3
https://www.facebook.com/vietgold Trang 55
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
* Khi m ∈ (−3;2] ⇔ m ∈(−12;8] , (*) có ít nhất 1 nghiệm t ∈( 4
− ;0) và một nghiệm t ∈(0;+∞) 4 . Suy ra 2 4 f (x − 4 )
x = m có ít nhất 3 nghiệm thực phân biệt thuộc khoảng (0;+∞) . Lu m y * Khi ∈ (2;+∞) ∪{− }
3 ⇔ m ∈ (8; +∞) ∪{−1 }
2 , (*) có đúng 1 nghiệm t ∈[0;+∞) . Suy ra e 4 nt 2 h 4 f (x − 4 )
x = m có đúng 1 nghiệm thực thuộc khoảng (0; +∞) . itrac
* Khi m ∈ −∞; −3 ⇔ m ∈ −∞; −12 , có (*) vô nghiệm. Suy ra 2 4 f (x − 4 )
x = m vô nghiệm. n ( ) ( ) g 4 hiem
Câu 102: Vậy có 20 giá trị nguyên của tham số m để phương trình 2 4 f (x − 4 )
x = m có ít nhất 3 nghiệm .vn
thực phân biệt thuộc khoảng (0;+∞).(Câu 49 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 -
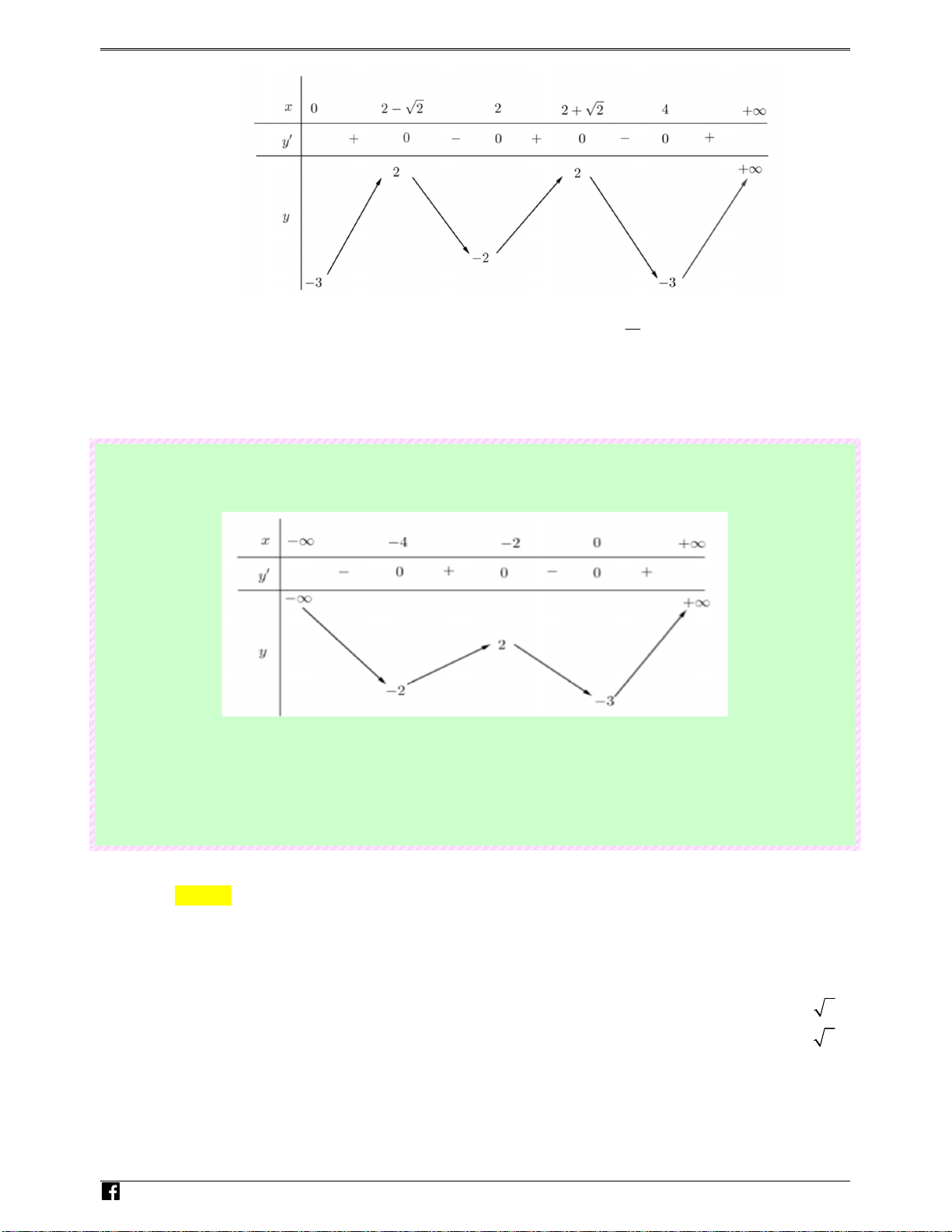
2020) Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 2 3
x − 4x) = m có ít nhất ba nghiệm thực
phân biệt thuộc khoảng (0;+ ∞) ? N guy Ⓐ. 15. Ⓑ. 12. Ⓒ. 14. Ⓓ. 13. -n Lời giải H oà Chọn A ng 2 2 V
Đặt: y = g ( x) = f ( x − 4x) ⇒ g '( x) = (2x − 4) f '( x − 4x) . i0t x = 2 2 2x − 4 = 0 − = − g′( x) x 4x 4 = 0 ⇔ ⇔ ⇔ x ∈ ± f ' ( 2; 2 2;0;4 . 2 x − 4x) 2 { } = 0 x − 4x = 2 − 2 x − 4x = 0
Ta có: g (0) = f (0) = 3
− ; g (2 − 2 ) = g (2 + 2 ) = f (−2) = 2 ; g (2) = f ( 4 − ) = 2
− ; g (4) = f (0) = −3 .
Nhận thấy g '(5) = 6 f '(5) > 0 và tất cả các nghiệm của phương trình g '( x) = 0 đều là nghiệm
bội lẻ, từ đó ta có bảng biến thiên của hàm số y = g ( x) như sau:
https://www.facebook.com/vietgold Trang 56
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Lu yenthitracnghie m m
Từ bảng biến thiên ta được: yêu cầu bài toán tương đương −3 < ≤ 2 3 .vn ⇔ 9 − < m ≤ 6 .
Vậy có tất cả 15 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Câu 103: (Câu 50 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số y = f ( x) có bảng biến thiên như sau N guy- n 2 H
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 f (x − 4x) = m có ít nhất 3 nghiệm thực oàn
phân biệt thuộc khoảng (0;+∞) ? g Vi0 Ⓐ. 25 . Ⓑ. 30 . Ⓒ. 29 . Ⓓ. 24 . t Lời giải Chọn B
Đặt g ( x) = f ( 2
x − x) ⇒ g′( x) = ( x − ) f ′( 2 4 2 4 . x − 4x) . x = 2 2x − 4 = 0 x = 2+ 2 2 2x − 4 = 0 ⇒ ′( ) x − x = −
g x = 0 ⇔ (2x − 4). f ′( 4 4 2 x − 4x) = 0 ⇔ ⇔ ⇔ = − . f ′ ( 2 x − x) 2 x 2 2 4 = 0 x − 4x = 2 − 2 x = 0 x − 4x = 0 x = 4 Ta có bảng biến thiên:
https://www.facebook.com/vietgold Trang 57
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitra cn m g
Yêu cầu của bài toán ⇔ =
có ít nhất 3 nghiệm thực phân biệt thuộc khoảng 0; +∞ h g ( x) ( ) i 6 em ⇔ −3 m <
≤ 2 ⇔ −18 < m ≤ 12 mà m ∈
m ∈ −17; −16; ...;11;12 . . ℤ nên { } v 6 n
Câu 104: Vậy có 30 giá trị nguyên của m thỏa mãn yêu cầu bài toán.(Câu 49 - MĐ 101 - BGD&ĐT -
Đợt 2 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến thiên như sau: N
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 2 5
x − 4x) = m có ít nhất 3 nghiệm thực guy
phân biệt thuộc khoảng (0;+∞) ? -n H Ⓐ. 24. Ⓑ. 21. Ⓒ. 25. Ⓓ. 20. oàn Lời giải g Vi Chọn C 0t
Từ bảng biến thiên của hàm số y = f ( x) và sự biến thên của của hàm số 2
y = x − 4x trên khoảng
(0;+∞) ta có bảng biến thiên của hàm số y = f ( 2x − 4x) trên khoảng (0;+∞) như sau
https://www.facebook.com/vietgold Trang 58
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Số nghiệm của phương trình f ( 2 5
x − 4x) = m bằng số giao điểm của đồ thị hàm số m y = f ( 2
x − 4x) và đường thẳng y = . 5 L 2 2 u
Từ bảng biến thiên của hàm số y = f ( x − 4x) ta có phương trình 5 f (x − 4x) = m có ít nhất 3 yen m t
nghiệm thực phân biệt thuộc khoảng (0;+∞) khi và chỉ khi 3 − < ≤ 2 ⇔ 1
− 5 < m ≤ 10 , mặt h 5 itr
khác m∈ℤ nên có 25 giá trị của tham số m thỏa mãn bài toán. acng
Câu 105: (Câu 50 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc bốn y = f ( x) có hie
đồ thị là đường cong trong hình bên. m .vn
Số nghiệm thực của phương trình f ( 2
x f ( x)) − 2 = 0 là Ⓐ. 6 . Ⓑ. 12. Ⓒ. 8. Ⓓ. 9. Lời giải N Chọn D g 2 2 u
Ta có f (x f (x)) −2 = 0 ⇔ f (x f (x)) = 2. y-n
Dựa vào đồ thị ta thấy: H 2 x f x = 0 1 o ( ) ( ) à n 2
x f ( x) = a ( 1 − < a < 0)(2) g . V 2
x f x = b −3 < b < −2 3 i ( ) ( )( ) 0t 2 x f
(x) = c(−4 < c < −3)(4) x = 0 x = 0 Giải ( ) 1
⇔ ( ) ⇔ x = (có 3 nghiệm phân biệt). 1 x f x 0 = x = 2 x Giải (2) ⇔ ( ) a f x = . 2 x Vẽ đồ thị hàm số a a y =
lên cùng hệ tọa độ Oxy . Ta thấy đồ thị hàm số y = cắt đồ thị hàm 2 x 2 x
số y = f ( x) tại 2 nghiệm phân biệt.
Tương tự với (3) và (4) đều có 2 nghiệm phân biệt.
https://www.facebook.com/vietgold Trang 59
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Câu 106: Vậy có phương trình f ( 2
x f ( x)) = 2 có 9 nghiệm phân biệt.(Câu 50) (MĐ 103 - BGD&ĐT -
Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f ( 2
x f (x)) + 2 = 0 là Luye y nthitracngh O x iem.vn −2 Ⓐ. 8. Ⓑ. 12. Ⓒ. 6. Ⓓ. 9. Lời giải Chọn D Cách 1: N gu y - x = 0 n 2 x f (x) = 0 H f (x) = 0 (1) o 2
x f (x) = a ∈ (0;1) à 2 a n
Ta có f (x f (x)) + 2 = 0 ⇔ ⇔ f (x) = , a ∈(0;1) (2) 2 2 g
x f (x) = b ∈ (2;3) x V b i 2 0
x f (x) = c ∈ (3; 4) f (x) = , b ∈(2;3) (3) 2 t x ( ) c f x = , c ∈ (3;4) (4) 2 x 2 Xét hàm số ( ) k g x =
(k > 0) , Ta có '( ) k g x = − . 2 x 3 x Bảng biến thiên
Đồ thị của f (x) và g (x) được mô tả như sau:
https://www.facebook.com/vietgold Trang 60
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracng hie
Do đó ta có: (1), (2), (3) và (4) mỗi phương trình có 2 nghiệm phân biệt. m .v
Suy ra phương trình đã cho có 9 nghiệm. n Cách 2: x = 0 2 x f (x) = 0 f (x) = 0 (1) 2
x f (x) = a ∈ (0;1) a Ta có f ( 2
x f ( x)) + 2 = 0 ⇔ ⇔ f (x) − = 0, a ∈(0;1) (2) 2 2
x f (x) = b ∈ (2;3) x 2 b
x f (x) = c ∈ (3;4) f (x) − = 0, b∈(2;3) (3) 2 x ( ) c f x − = 0, c ∈(3;4) (4) 2 x N g
(1) có 2 nghiệm phân biệt là x = α < 0, x = β > 3 . uy- k 2 n
Xét hàm số g(x) = f (x) −
(k > 0) có '( ) = '( ) k g x f x + . Ta có: 2 3 H x x oàn
* x∈[α;β] thì g(x) < 0 nên các phương trình (2), (3) và (4) không có nghiệm x∈[α;β] . g Vi0 lim g(x) = +∞ t x→−∞ * lim ( ) k g x = −
< 0 ⇒ Mỗi phương trình (2), (3) và (4) chỉ có đúng một nghiệm − 2 x α → α
g '(x) < 0, x ∀ ∈ (− ; ∞ α) x ∈(− ; ∞ α ) lim g(x) = +∞ x→+∞ * lim ( ) k g x = − < 0
⇒ Mỗi phương trình (2), (3) và (4) đều chỉ có đúng một + 2 x→β β
g '(x) > 0, x
∀ ∈ (β;+∞), β >3 nghiệm x∈(β;+∞)
Suy ra mỗi phương trình (1), (2), (3) và (4) có 2 nghiệm phân biệt.
https://www.facebook.com/vietgold Trang 61
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021
Vậy phương trình đã cho có 9 nghiệm. Cách 3: 2 x f (x) = 0 (1) L u 2 y
x f (x) = a ∈ (0;1) (2) 2 e
Ta có f (x f (x)) + 2 = 0 ⇔ n 2
x f (x) = b ∈ (2;3) (3) t hi 2 t
x f (x) = c ∈ (3; 4) (4) r acn
Ta có (1) có ba nghiệm phận biệt là x = 0, x = α < 0, x = β > 3 . ghie Xét 2
g(x) = x f (x) có 2
g '(x) = 2xf (x) + x f '(x) m .vn
Với x ∈[α;β ] thì 2
g(x) = x f (x) ≤ 0 nên (2), (3), (4) không có nghiệm x ∈[α; β ] . Với x ∈(− ;
∞ α ) ta có: g '(x) < 0. Và với x∈(β;+∞) , β >3, thì g '(x) > 0 nên ta có bảng
biến thiên của g(x) Câu 1.
Do đó các phương trình (2), (3), (4) đều có 2 nghiệm phân biệt. N
Câu 107: Vậy phương trình đã cho có 9 nghiệm phân biệt.(Câu 50 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm gu
2019 - 2020) Cho hàm số bậc ba y = f ( x) có đồ thị là đường cong trong hình bên. y-n Hoàng Vi0t
Số nghiệm thực phân biệt của phương trình f ( 3
x f ( x)) +1 = 0 là Ⓐ. 6 . Ⓑ. 4 . Ⓒ. 5. Ⓓ. 8. Lời giải Chọn A 3
x f (x) = a ( 3 − < a < − ) 1 ( ) 1 Ta có f ( 3
x f ( x)) +1 = 0 ⇔ f ( 3 x f ( x)) 3 = 1
− ⇔ x f (x) = b ( 6 − < b < 3 − )(2) . 3 x f ( x) = 0 (3) + Với m
m < 0 , xét phương trình 3
x f ( x ) = m ⇔ f ( x ) = . 3 x
https://www.facebook.com/vietgold Trang 62
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 −3 Đặt ( ) m m g x = , g′( x) = > 0,∀x ≠ 0 . 3 x 4 x
lim g ( x) = 0 , lim g ( x) = +∞ , lim g ( x) = −∞ . x→±∞ − + x→0 x→0 Lu Ta có bảng biến thiên yenthitracnghiem .vn
Dựa vào bảng biến thiên và đề bài, suy ra trong mỗi khoảng (−∞;0) và (0; +∞ ) phương trình
f ( x ) = g ( x ) có đúng một nghiệm.
Suy ra mỗi phương trình (1) và (2) có 2 nghiệm và các nghiệm đều khác nhau. x = 0 x = 0 + Xét phương trình ( ) 3
3 : x f ( x) = 0 ⇔ ⇔
, với c khác các nghiệm của f ( x) = 0 x = c < 0 (1) và (2) .
Câu 108: Vậy phương trình f ( 3
x f ( x)) +1 = 0 có đúng 6 nghiệm.(Câu 50 - MĐ 101 - BGD&ĐT - Đợt
1 - Năm 2019 - 2020) Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. Số
nghiệm thực phân biệt của phương trình f ( 3
x f (x)) +1 = 0 là N guy-n Hoàng Vi 0t Ⓐ. 8. Ⓑ. 5. Ⓒ. 6 . Ⓓ. 4 . Lời giải Chọn C Cách 1: 3 x f (x) = 0 ( ) 1 Ta có f ( 3
x f (x)) +1= 0 ⇔ f ( 3 x f (x)) 3 = 1
− ⇔ x f (x) = a∈(2;3) (2) 3
x f (x) = b∈(5;6) (3)
https://www.facebook.com/vietgold Trang 63
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitrac ngh x = 0 x = 0 ie Ta có ( ) 1 ⇔ ⇔ . m f ( x) = 0 x = c .vn 3 Xét ( ) k k g x =
, với k > 0 . Ta có g '( x) = − < 0, x ∀ ≠ 0 . 3 x 4 x Bảng biến thiên
Với k = a , dựa vào đồ thị suy ra phương trình (2) có hai nghiệm phân biệt khác 0 và c. N
Với k = b , dựa vào đồ thị suy ra phương trình (3) có hai nghiệm phân biệt khác 0 , c và khác guy
hai nghiệm của phương trình (2) . -n Hoàng Vi0t
Vậy phương trình f ( 3
x f (x)) +1 = 0 có 6 nghiệm phân biệt. Cách 2: Ta có:
https://www.facebook.com/vietgold Trang 64
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 x = 0 3 f (x) = 0 x f (x) = 0 ( 3 ( )) 1 0 ( 3 ( )) 3 1 ( ) 0 + = ⇔ = − ⇔ = > ⇔ ( ) a f x f x f x f x x f x a f x = (do x ≠ 0) 3 L 3 x = > u x f (x) b 0 y b e f (x) = (do x ≠ 0) 3 n x thitracnghiem.vn
* f (x) = 0 có một nghiệm dương x = c . * Xét phương trình ( ) k f x =
với x ≠ 0, k > 0 . 3 x 3 Đặt ( ) = ( ) k g x f x − ; ( ′ ) = '( ) k g x f x + . 3 x 4 x
TH 1: Với x > c , đồ thị hàm f (x) đồng biến trên ( ; c +∞) nên f (
′ x) > 0, x ∈( ; c + ∞) 3 ⇒ (′ ) = ( ′ ) k g x f x + > 0, x ∈ ; c + ∞ 4 ( ) N x guy g(c) < 0 - n Mà
và g(x) liên tục trên (c;+ ∞) lim g(x) = +∞ H x→+∞ oà
⇒ g(x) = 0 có duy nhất nghiệm trên (c;+∞) . ng Vi0
TH 2: Với 0 < x < c thì ( ) < 0 k f x <
⇒ g(x) = 0 vô nghiệm trên (0;c). 3 t x
TH 3: Với x < 0 , đồ thị hàm f (x) đồng biến trên (−∞;0) nên f (′x) > 0, x ∈(− ; ∞ 0) 3 ⇒ (′ ) = ( ′ ) k g x f x + > 0, x ∈ − ; ∞ 0 4 ( ) x
lim g(x) > 0 Mà − x→0
và g(x) liên tục trên (−∞;0) .
lim g(x) = −∞ x→−∞
⇒ g(x) = 0 có duy nhất nghiệm trên (−∞;0).
Do đó: g(x) = 0 có đúng hai nghiệm trên ℝ \ { } 0 . * Phương trình ( ) a f x =
k = a có 2 nghiệm phân biệt khác 0 và khác c. 3 ( ) x
https://www.facebook.com/vietgold Trang 65
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 * Phương trình ( ) b f x =
k = b có 2 nghiệm phân biệt khác 0 và khác c. 3 ( ) x
Câu 109: Kết luận: Phương trình f ( 3
x f (x)) +1= 0 có đúng 6 nghiệm.(Câu 46 - ĐTK - BGD&ĐT - Lần Luy
2 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến thiên như sau: enthitracnghiem .vn 5π
Số nghiệm thuộc đoạn 0;
của phương trình f (sin x) =1 là 2 Ⓐ. 7. Ⓑ. 4. Ⓒ. 5. Ⓓ. 6. Lời giải Chọn C
x = a ∈ (− ; ∞ − ) 1 x = b∈ (−1;0)
Dựa vào bảng biến thiên, ta có f ( x) = 1 ⇔ . x = c ∈ (0; ) 1
x = d ∈(1;+∞ )
sin x = a ∈ (− ; ∞ − ) 1 ( ) 1 N gu sin x = b ∈ (−1;0) (2) y
Như vậy f (sin x) = 1 ⇔ . -
sin x = c ∈ (0; ) 1 (3) n H
sin x = d ∈(1;+∞ ) (4) oàng π Vì x ∈ [ ] 5 sin 0;1 , x ∀ ∈ 0; nên ( ) 1 và (4) vô nghiệm. V i 2 0t 5π
Cần tìm số nghiệm của (2) và ( ) 3 trên 0; . 2 Cách 1.
https://www.facebook.com/vietgold Trang 66
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthitracngh iem 5π 5π .
Dựa vào đường tròn lượng giác: (2) có 2 nghiệm trên 0; , ( ) 3 có 3 nghiệm trên 0; . v n 2 2
Vậy phương trình đã cho có tất cả 5 nghiệm. Cách 2. 5π 5π
Xét g ( x) = sin x,∀x ∈ 0;
⇒ g '( x) = cos x, x ∀ ∈ 0; . 2 2 π x = Cho g ( x) 2 '
= 0 ⇔ cos x = 0 ⇔ . Bảng biến thiên: 3π x = 2 N guy-n Hoàng V i0t 5π 5π
Dựa vào bảng biến thiên: (2) có 2 nghiệm trên 0; , ( ) 3 có 3 nghiệm trên 0; . 2 2
Vậy phương trình đã cho có tất cả 5 nghiệm.
Câu 110: (Câu 47 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hai hàm số x −2 x 1 − x x +1 y = + + +
và y = x +1 − x − m ( m là tham số thực) có đồ thị lần lượt x 1 − x x +1 x + 2 là ( và
. Tập hợp tất các các giải trịcủa và
cắt nhau tại đúng 4 điểm 1 C ) ( 2 C ) m để ( 1 C ) ( 2 C ) phân biệt là Ⓐ. ( 3 − ;+∞) . Ⓑ. (− ; ∞ 3 − ) . Ⓒ. [ 3 − ; +∞) . Ⓓ. (−∞;− ] 3 . Lời giải Chọn D
https://www.facebook.com/vietgold Trang 67
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 x −2 x 1 − x x +1
Phương trình hoành độ giao điểm: + + +
= x +1 − x −m . x 1 − x x +1 x + 2
Tập xác định: D = ℝ \ {1;0;−1;− } 2 . L
Với điều kiện trên, phương trình trở thành: uy 1 1 1 1 e 4− − − −
= x +1 − x −m( ) * n x 1 − x x +1 x + 2 thi 1 1 1 1 tr ⇔ + + +
−4 + x +1 − x = m a x 1 − x x +1 x + 2 cngh 1 1 1 1 i
Xét hàm số f (x)= + + +
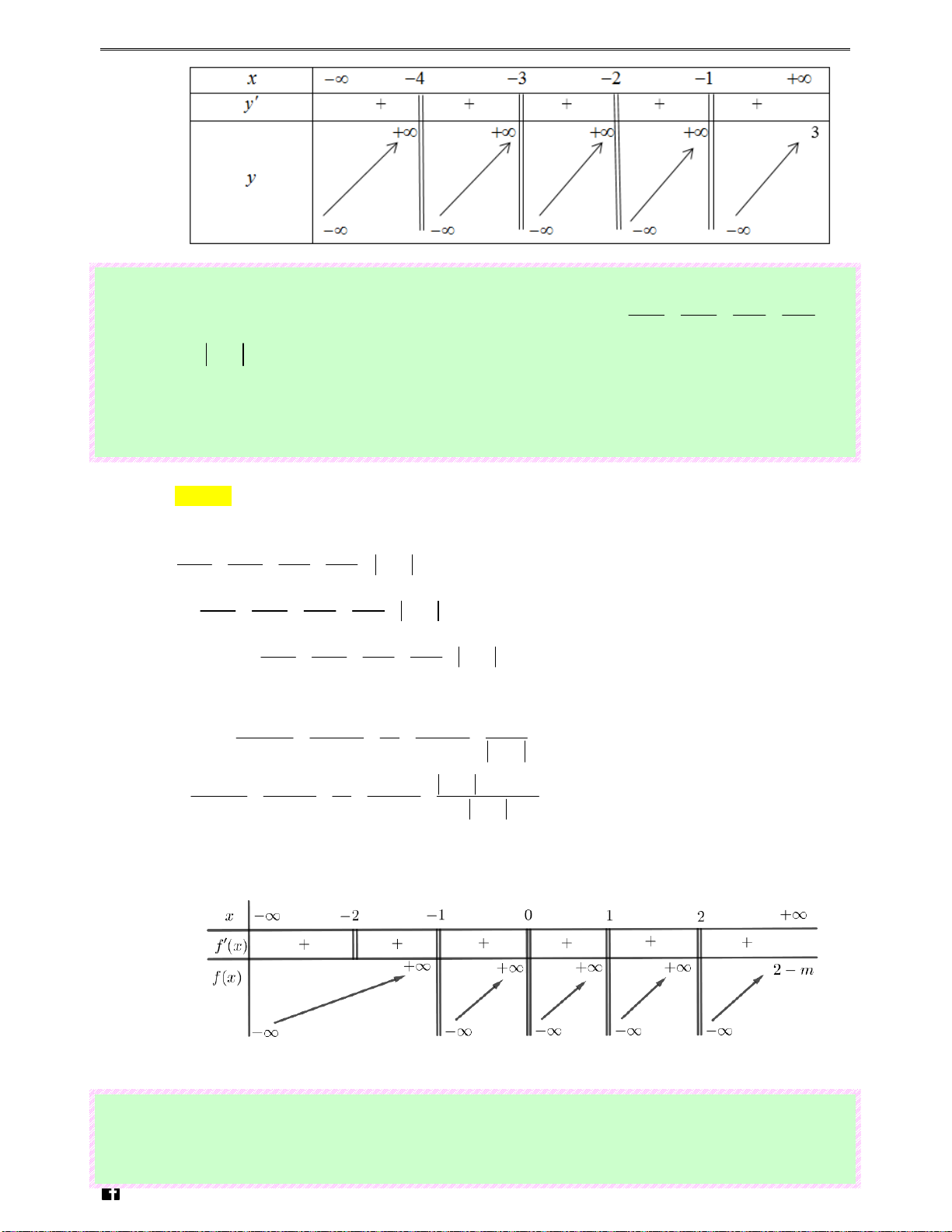
−4 + x +1 − x với tập xác định D , ta có: e x 1 − x x +1 x + 2 m .v 1 1 1 1 x +1 n f ′(x) = − − − − + 1 − < 0, ∀x ∈ . D 2 2 2 2 (x− ) 1 x (x + ) 1 (x + ) 2 x +1 Bảng biến thiên: Để ( và (
cắt nhau tại đúng 4 điểm phân biệt thì phương trình ( )
* có 4 nghiệm phân biệt. 2 C ) 1 C )
Từ bảng biến thiên suy ra tất cả các giá trị m cần tìm là m ≤ 3 − .
Câu 111: (Câu 50 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hai hàm số x −1 x x +1 x + 2 N y = + + +
và y = x + 2 − x − m ( m là tham số thực) có đồ thị lần lượt là g x x +1 x + 2 x + 3 uy ( và (
. Tập hợp tất cả các giá trị của và (
cắt nhau tại đúng 4 điểm phân 2 C ) 2 C ) 1 C ) m để ( 1 C ) -n biệt là H oà −2; +∞ . . . −∞;−2 . n Ⓐ. [ ) Ⓑ. (−∞ : −2) Ⓒ. (−2 : +∞) Ⓓ. ( ] g V Lời giải i0t Chọn D x −1 x x +1 x + 2
Phương trình hoành độ giao điểm: + + +
= x + 2 − x − m . x x +1 x + 2 x + 3
Tập xác định: D = ℝ \{ 3 − ; 2 − ; 1 − ; } 0
Với điều kiện trên, phương trình trở thành 1 1 1 1 4 − − − −
= x + 2 − x − m ( ) * x x +1 x + 2 x + 3 1 1 1 1 ⇔ + + +
− 4 + x + 2 − x = m . x x +1 x + 2 x + 3
Xét hàm số f ( x) 1 1 1 1 = + + +
− 4 + x + 2 − x với tập xác định D . Ta có x x +1 x + 2 x + 3 + f ′( x) 1 1 1 1 x 2 = − − − − + −1 < 0, x ∀ ∈ D . 2 x (x + )2 1
(x + 2)2 (x +3)2 x + 2
https://www.facebook.com/vietgold Trang 68
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Bảng biến thiên Luyent hit Câu 112: Để ( và (
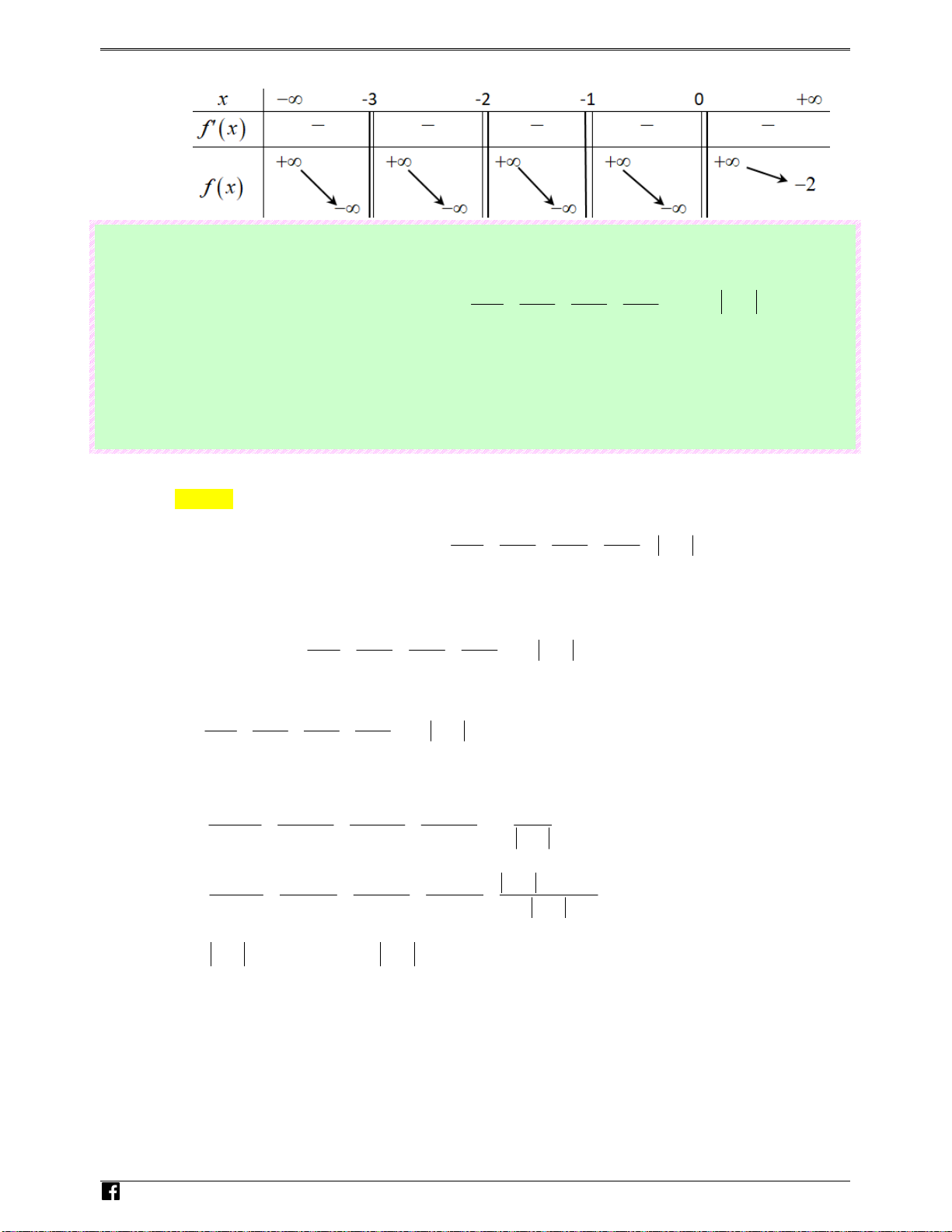
cắt nhau tại đúng 4 điểm phân biệt thì phương trình (*) có 4 nghiệm phân biệt. 2 C ) 1 C ) rac
Từ bảng biến thiên suy ra tất cả các giá trị m cần tìm là m ≤ 2
− .(Câu 50 - MĐ 102 - BGD&ĐT ng x x + x + x + h
- Năm 2018 - 2019) Cho hai hàm số 1 2 3 y = + + +
và y = x +1 − x + m ( m ie x + 1 x + 2 x + 3 x + 4 m .
là tham số thực) có đồ thị lần lượt là ( 1 C ) và ( 2
C ). Tập hợp tất cả các giá trị của m để ( 1 C ) và vn ( 2
C ) cắt nhau tại đúng bốn điểm phân biệt là
Ⓐ. (3;+ ∞) . Ⓑ. (−∞; ] 3 . Ⓒ. (− ; ∞ ) 3 . Ⓓ. [3;+ ∞). Lời giải Chọn D
Xét phương trình hoành độ giao điểm: x x + 1 x + 2 x + 3 + + +
= x +1 − x + m (*) x + 1 x + 2 x + 3 x + 4
Điều kiện: x∈ℝ \{ 1 − ; 2 − ; 3 − ;− } 4 . Ta có (*) x x + 1 x + 2 x + 3 ⇔ m = + + + + x − x + 1 . x + 1 x + 2 x + 3 x + 4 N gu
Số nghiệm của phương trình (*) bằng số giao điểm của hai đồ thị y- x x + 1 x + 2 x + 3 n y = + + +
+ x − x +1 và y = m. H x + 1 x + 2 x + 3 x + 4 oàn Ta có: g V 1 1 1 1 x +1 i0 y′ = + + + +1− 2 2 2 2 t (x + ) 1
(x + 2) (x + 3) (x + 4) x +1 1 1 1 1
x + 1 − ( x + 1) y′ = + + + + > 0 x ∀ ∈ℝ\{ 1 − ; 2 − ; 3 − ;− } 4 .
(x +1)2 (x + 2)2 (x + 3)2 (x + 4)2 x + 1
, (vì x +1 > x +1 x ∀ ≠ 1
− ⇒ x +1 −( x+ ) 1 > 0 x ∀ ≠ 1 − ). BBT
https://www.facebook.com/vietgold Trang 69
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenthit racn
Câu 113: Từ bảng biến thiên, để phương trình có 4 nghiệm phân biệt thì m ≥ 3 .(Câu 49 - MĐ 101 - gh x − x − x − x i
BGD&ĐT - Năm 2018 - 2019) Cho hai hàm số 3 2 1 = + + + và e y m x − 2 x − 1 x x + 1 .v
y = x + 2 − x + m ( m là tham số thực) có đồ thị lần lượt là ( 1
C ) và (C2 ) . Tập hợp tất cả các n
giá trị của m để ( 1
C ) và (C2 ) cắt nhau tại 4 điểm phân biệt là Ⓐ. (− ; ∞ ] 2 . Ⓑ. [2;+ ) ∞ . Ⓒ. (− ; ∞ ) 2 . Ⓓ. (2;+ ) ∞ . Lời giải Chọn B
Phương trình hoành độ giao điểm của ( 1 C ) và (C2 ) : x − 3 x − 2 x −1 x + + +
= x + 2 − x + m x − 2 x − 1 x x + 1 x − 3 x − 2 x − 1 x ⇔ + + +
− x + 2 + x − m = 0 . x − 2 x − 1 x x + 1 − − −
Đặt ( ) x 3 x 2 x 1 x f x = + + +
− x + 2 + x − m . N x − 2 x −1 x x + 1 gu
Tập xác định D = ℝ \{ 1 − ;0;1; } 2 . y-n 1 1 1 1 x + 2 f ′( x) = + + + − +1 H 2 2 2 2 x − 2 x −1 x x +1 x + 2 o ( ) ( ) ( ) àn 1 1 1 1
x + 2 − ( x + 2) g = + + + + 2 2 2 2 V (x − 2) (x − ) 1 x (x + ) 1 x + 2 i0t
⇒ f ′(x) > 0, x ∀ ∈ , D x ≠ 2 − . Bảng biến thiên
Yêu cầu bài toán ⇔ có 4 nghiệm phân biệt ⇔ 2 − m ≤ 0 ⇔ m ≥ 2 .
Câu 114: (Câu 50 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) 4 3 2
= mx + nx + px + qx + r ( ,
m n, p, q, r ∈ ℝ ) . Hàm số y = f ′( x) có đồ thị như hình vẽ
bên. Tập nghiệm của phương trình f ( x) = r có số phần tử là
https://www.facebook.com/vietgold Trang 70
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 Luyenth itrac Ⓐ. 4 . Ⓑ. 3. Ⓒ. 1. Ⓓ. 2 . ngh Lời giải iem Chọn B .vn Cách 1: 5
Dựa trên đồ thị hàm số y = f ′( x) ta có f ′( x) = k ( x + ) 1 x −
( x − 3), k < 0. 4 Mặt khác 3 2 f (
′ x) = 4mx + 3nx + 2 px + . q Đồng nhất ta có 5 3 2
4mx + 3nx + 2 px + q = k ( x + )
1 x − (x −3), x ∀ 4 13 x 15 3 2 3 2
⇔ 4mx + 3nx + 2 px + q = k x − x − + , x ∀ 4 2 4 N 1 g 4m = k m = k u 4 y - 13 n 3n = − k 13 n = − k 4 H 12 1 13 1 15 o ⇔ 1 ⇔ ⇒ f ( x) 4 3 2 = k x − x − x + x + r. à 2 p = − k 1 4 12 4 4 n 2 p = − k g 4 V 15 i q = k 15 0 4 q = k t 4 x = 0 f ( x) 1 13 1 15 1 13 1 15 5 4 3 2 4 3 2 = r ⇔ k x − x − x +
x + r = r ⇔ x − x − x +
x = 0 ⇔ x = − . 4 12 4 4 4 12 4 4 3 x = 3 Chọn đáp án B x = −1 5
Cách 2: Xét hàm số f ( x) có f ′( x) = 0 ⇔ x = 4 x = 3
Ta đi so sánh f (0) với f (3) .
https://www.facebook.com/vietgold Trang 71
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 3 3 5 5
Ta có: f ′( x) = k ( x + ) 1 x − ( x − ) 3 ⇒ f ( )
3 − f (0) = f (′ ) x dx = k ∫ ∫ (x+ )1 x− ( x − ) 3 dx = 0 4 4 0 0
⇒ f (0) = f (3). Lu Bảng biến thiên: yenthitracnghiem.vn 5
Ta có r = f (0)∈ f ; f (− ) 1 . 4
Đường thẳng y = f (0) cắt đồ thị hàm số f ( x) tại 3 điểm phân biệt. Do đó phương trình
f ( x) = r = f (0) có 3 nghiệm phân biệt. Chọn đáp án B 1 14
Câu 115: (Câu 50 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số 4 2 y = x −
x có đồ thị (C ) 3 3
. Có bao nhiêu điểm A thuộc (C ) sao cho tiếp tuyến của (C ) tại A cắt (C ) tại hai điểm phân N biệt M ( x ; , N ( x ; y − y = 8 − ? 2 y
( M , N khác A ) thỏa mãn 1 2 ( 1x x2 ) 2 ) 1 1 y ) guy- n Ⓐ. 1. Ⓑ. 2 . Ⓒ. 0 . Ⓓ. 3 Ho Lời giải àng Chọn B Vi Cách 1: 0t
Gọi d là tiếp tuyến của (C ) tại A . x = − 7 4 28 3 y′ = x −
x ⇒ y′ = 0 ⇔ x = 0 . 3 3 x = 7
Do tiếp tuyến tại A cắt (C ) tại M , N ⇒ x ∈(− 7; 7 . A ) x = 3 − 4 28 A Ta có:
y − y = 8( x − x ) 1 y y2 ⇒ = 8 ⇒ k = 8. Suy ra 3 x − x = 8 ⇔ x = 1 − . 1 2 1 2 d − 3 A 3 A A 1 x 2 x x = 2 − A x = 1 −
Đối chiếu điều kiện: A
. Vậy có 2 điểm A thỏa ycbt. x = 2 − A Cách 2:
https://www.facebook.com/vietgold Trang 72
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 1 14 Gọi 4 2 A a; a − a
là tọa độ tiếp điểm 3 3 4 28 1 14
Phương trình tiếp tuyến tại A là 3 d : y = a − a ( x − a) 4 2 + a − a L 3 3 3 3 uy
Phương trình hoành độ giao điểm của (C ) và d là: ent 1 28 4 28 1 14 4 2 3 4 2 h x − x = a − a
( x − a) + a − a it 3 3 3 3 3 3 rac = 2 x a n ⇔ (x − a) 2 2
x + 2ax + 3a −14 = 0 ⇔ g ( ) 2 2 h
x + 2ax + 3a −14 = 0 ( ) 1 iem
Để (C ) cắt d tại 3 điểm phân biệt ⇔ Phương trình (1) có hai nghiệm phân biệt khác a .vn ∆ > 0 7 ⇔
⇔ a ∈ − 7; 7 \ ± . 2 ( ) 6a −14 ≠ 0 3 4 28
Theo đề bài: y − y = 8( x − x ) 3 ⇔ a − a x − x = 8 − 1 2 1 2 ( 1 2 ) ( 1x 2x ) 3 3 a = 3 4 28 3 ⇔ a − a = 8 ⇔ a = 1 − . 3 3 a = 2 − a = 1 −
Đối chiếu điều kiện:
. Vậy có 2 điểm A thỏa đề bài. a = 2 − 1 7
Câu 116: (Câu 50 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số 4 2 y = x −
x có đồ thị (C ) N 8 4 gu
. Có bao nhiêu điểm A thuộc đồ thị (C ) sao cho tiếp tuyến của (C ) tại A cắt (C ) tại hai điểm y-n
phân biệt M ( x ; ; N ( x ; y − y = 3 − . 2 y
( M , N khác A ) thỏa mãn 1 2 ( 1x x2 ) 2 ) 1 1 y ) Hoàn Ⓐ. 0 . Ⓑ. 2 . Ⓒ. 3. Ⓓ. 1 g V Lời giải i0t Chọn B − −
Phương trình đường thẳng x x y y MN có dạng 2 2 =
⇒ hệ số góc của đường thẳng MN − − 1 x 2 x 1 y y2 − là 1 y y2 k = = 3 . − 1 x 2 x 1 7 1 7 Vậy tiếp tuyến tại 4 2 A x ; −
có hệ số góc k = 3 ⇔ 3 f ′ ( x = 3 ⇔ x − x = 3 0 ) 0 0 x 0 x 8 4 0 0 2 2 x = 1 − 1 7 0 3 ⇔ x −
x − 3 = 0 ⇔ x = 3 . 0 0 2 2 0 x = 2 − 0 13 11 +) Với x = 1 − ⇒ A 1 − ;−
⇒ Phương trình tiếp tuyến y = 3 + . 0 x 8 8
https://www.facebook.com/vietgold Trang 73
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 1 7 11 1 7 11
Xét phương trình hoành độ giao điểm 4 2 x − x = 3x + 4 2
⇔ x − x − 3x − = 0 8 4 8 8 4 8 x = 1 − 13 L ⇔ x = 1+ 3 ⇒ A 1 − ; − thỏa mãn đề bài. u 8 y x = 1− 3 e nth 171 195
+) Với x = 3 ⇒ A 3; −
⇒ Phương trình tiếp tuyến y = 3x − . i 0 t 8 8 r ac 1 7 195 1 7 195 n
Xét phương trình hoành độ giao điểm 4 2 x − x = 3x − 4 2
⇔ x − x − 3x + = 0 g 8 4 8 8 4 8 hie 2 171 2 m
⇔ ( x − 3) (x + 6x +13) = 0 ⇔ x = 3 ⇒ Tiếp tuyến cắt đồ thị tại một điểm ⇒ A 3;− 8 . vn Không thỏa mãn. +) Với x = 2
− ⇒ A(−2;−5) ⇒ Phương trình tiếp tuyến: y = 3x +1. 0 1 7 1 7
Xét phương trình hoành độ giao điểm 4 2 x − x = 3x +1 4 2
⇔ x − x − 3x −1 = 0 8 4 8 4 x = 2 − ⇔ ( x + )2 ( 2 2
x − 4x − 2) = 0 ⇔ x = 2 + 6
⇒ A (−2; −5) Thỏa mãn đề bài. x = 2 − 6
Vậy có hai điểm thỏa mãn yêu cầu bài toán.
Câu 117: (Câu 48 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Tìm tất cả các giá trị thực của tham số m
để đường thẳng y = mx − m + 1 cắt đồ thị của hàm số 3 2
y = x − 3x + x + 2 tại ba điểm A, B, C N
phân biệt sao cho AB = BC guy
Ⓐ. m ∈ (−∞;0]∪[4;+∞) Ⓑ. m∈ℝ -n H 5 o
Ⓒ. m∈ − ;+∞
Ⓓ. m ∈ (−2;+∞) à 4 ng V Lời giải i 0t Chọn D
Phương trình hoành độ giao điểm: 3 2
x − 3x + x + 2 = mx − m +1 3 2
⇔ x − 3x + x +1− ( x − )
1 m = 0 ⇔ ( x − ) 1 ( 2 x − 2x − ) 1 − ( x − ) 1 m = 0 ⇔ ( − ) x = x 1 ( 1 2
x − 2x −1 − m) = 0 ⇔ 2
x − 2x −1 − m = 0 (2)
Đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt ⇔ PT có 3 nghiệm phân biệt.
⇔ PT có 2 nghiệm phân biệt khác 1.
1− 2 −1− m ≠ 0 m ≠ 2 − ⇔ ⇔ ⇔ m > − ∆ ' = (− ) 2 2 1 +1+ m > 0 m > −2
Mà x = 1 cũng là hoành độ điểm uốn của đồ thị hàm số và AB = BC nên B (1; 1 ) là trung điểm
của AC, A( x ;mx − m +1 ,C x ;mx − m +1 với x , x là hai nghiệm của PT. 1 1 ) ( 2 2 ) 1 2
Theo Viet, ta có: x + x = 2 1 2
https://www.facebook.com/vietgold Trang 74
Luyenthitracnghiem.vn 117 BTOÁN KS VÀ V Đ TH HÀM S" TRONG Đ% THI BGD T( 2016 - 2021 x + x x + x 1 2 A C x = 1 = B Suy ra 2 2 ⇔
(lu«nlu«ndóng m ∀ ) y + y m x + x − m + A C ( 2 2 1 2 ) y = 1 = B 2 L 2 uy
Kết hợp với điều kiện m > −2 , ta được m > −2 . en thi tracnghiem.vn N guy-n Hoàng Vi0t
https://www.facebook.com/vietgold Trang 75