138 bài toán chọn lọc tính đơn điệu của hàm hợp – Nguyễn Hoàng Việt Toán 12

138 bài toán chọn lọc tính đơn điệu của hàm hợp – Nguyễn Hoàng Việt Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 1/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Câu 1: Cho hàm số

 

y f x

. Đồ thị hàm số

 

y f x





như hình vẽ bên. Hàm số

     

21g x f x x  

đồng biến trên khoảng nào?

 

3;1

. B.

 

1;3

. C.

 

;3

. D.

 

3; 

Lời gii

Chọn B

Ta có

   

2 2 2 0 1y f x x f x x

  

       

Kẻ đường thẳng

1yx  

qua các điểm

     

3;2 , 2;1 ; 3; 4  

Ta có

 

1f x x



  













138

BÀI TOÁN CHỌN LỌC

TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 2/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Xét khoảng mà đồ thị hàm số

 

y f x





nằm bên trên đường thẳng

1yx  

suy ra

hàm số

 

y g x

đồng biến trên khoảng

 

1;3

Câu 2: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ bên. Hàm số

 

2y f x

đồng biến trên khoảng

 

1;3

. B.

 

2;

. C.

 

2;1

. D.

 

;2 

Lời gii

Chọn C

Ta có

   

2 0 2 0

1 2 4

y f x f x

  



  

       















  



Do đó, hàm số

 

2y f x

đồng biến trên khoảng

 

2;1

Câu 3: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ bên. Hàm số

 

2y f x

đồng biến trên khoảng

 

0; 6

. B.

 

0;1

. C.

 

3;0

. D.

 

1; 3

Lời gii

Chọn D

Ta có

 

2 . 2 0y x f x



  

* Nếu

0x 

thì

 

20fx





1 2 1 1 3 1 3

2 4 6

x x x





       

  





  









* Nếu

0x 

thì

 

20fx





1 2 4 3 6

2 1 1

  





    

  





   

   





Chuyên đề: Tính đơn điệu của hàm hợp

Trang 3/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Do đó, trong các đáp án đã cho thì hàm số

 

2y f x

đồng biến trên khoảng

 

1; 3

Câu 4: Cho hàm số

 

y f x

có đạo hàm

 

14y x x x  

. Hàm số

 

2y f x

đồng biến

trên khoảng

 

;0

. B.

 

0;1

. C.

 

2;

. D.

 

1;4

Lời gii

Chọn B

Ta có

         

 

2 2 . 2 2 . 2 2 1 2 4y f x x f x x x x x

  

         

Do đó

   

 

2 1 4y x x x x



    

Suy ra

  

 

0 1 2 4 0

y x x x x







      







Vậy, từ các đáp án đã cho ta có hàm số đồng biến trên khoảng

 

0;1

Câu 5: Cho hàm số

 

y f x

có bảng biến thiên như sau

Hàm số

 

2y f x

nghịch biến trên khoảng nào dưới đây

 

2;0

. B.

 

2;

. C.

 

0;2

. D.

 

;0

Lời gii

Chọn B

Ta có

 

   

2 2 . 2 2 . 2 0y f x x f x x f x

   

      

* Nếu

0x 

thì





 

20fx



  

2 2 0





   











* Nếu

0x 

thì





 

20fx



  

0 2 2



  

     



  



Do đó, đáp án đúng trong các đáp án đã cho hàm khoảng

 

2;

Câu 6: Cho hàm số

 

y f x

có đạo hàm

     

12f x x x x



  

. Hỏi hàm số











đồng biến trên khoảng nào dưới đây?

 

;2 

. B.

 

0;2

. C.

 

2;4

. D.

 

2;1

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 4/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Lời gii

Chọn C

Ta có:

 

2 22

5x 5

5 5 5

4 4 4

x x x



   

  

   

  

   





   





   



   

Do đó:

    

2 2 2

4 5 4 5 2 8 0 2 4

x x x x x xy







        



  







Đối chiếu các phương án ta chọn

Câu 7: Cho hàm số

 

y f x

có đạo hàm trên và có đồ thị hàm số

 

y f x





như hình vẽ.

Đặt

 

2g x f x

. Mệnh đề nào dưới đây sai?

A. Hàm số

 

đồng biến trên khoảng

 

2;

B. Hàm số

 

nghịch biến trên khoảng

 

0;2

C. Hàm số

 

nghịch biến trên khoảng

 

1;0

D. Hàm số

 

nghịch biến trên khoảng

 

;2 

Lời gii

Chọn C

Ta có:

 

( ) 2 2 0

g x xf x









































     



  



































Đối chiếu các phương án ta chọn

Câu 8: Cho hàm số

 

y f x

có bảng biến thiên như hình vẽ dưới đây

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 5/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

3y f x

đồng biến trên khoảng nào dưới đây?

 

;0

. B.

 

4;6

. C.

 

1;5

. D.

 

0;4

Lời gii

Chọn D

Ta có

   

3 0 3 0 1 3 3 0 4y f x f x x x

  

              

Vậy hàm số

 

3y f x

đồng biến trên khoảng

 

0;4

Câu 9: Cho hàm số

 

y f x

có đạo hàm

      

14f x x x x g x



  

, trong đó

 

0,g x x

Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

 

;2 

. B.

 

1;1

. C.

 

2; 1

. D.

 

1;2

Lời gii

Chọn C

Ta có

        

2 2 2 2 2

2 2 1 4y xf x x x x x g x



   

    

 

2 1 2 1 2x x x x x g x    

Ta có

' 0 2 1







     







Vậy hàm số

 

y f x

đồng biến trên mỗi khoảng

     

2; 1 , 0;1 , 2;  

Câu 10: Cho hàm số

 

y f x

có đồ thị

 



như hình vẽ bên

Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

 

;1 

. B.

 

1;

. C.

 

1;1

. D.

 

0;1

Lời gii



1













2



Chuyên đề: Tính đơn điệu của hàm hợp

Trang 6/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Chọn B

Ta có

 

3y x f x





3 0,xx  

nên





 









  



  



Suy ra hàm số

 

y f x

đồng biến trên khoảng

 

1;

Câu 11: Cho hàm số

 

y f x

có đạo hàm

 

14f x x x x



  

. Hàm số

 

3y f x

đồng

biến trên khoảng nào dưới đây?

 

2;3

. B.

 

1;3

. C.

 

4;

. D.

 

3;4

Lời gii

Chọn D

Ta có

       

3 3 3 1 3 4 0

y f x x x x

  







           









Câu 12: Cho hàm số

 

y f x

có đạo hàm

   

 

15f x xx x x mx



   

. Có bao nhiêu số

nguyên âm

để hàm số

 

y f x

đồng biến trên khoảng

 

1; 

. B.

. C.

. D.

Lời gii

Chọn A

Ta có

         

2 2 2 4 2 5 2 4 2

2 2 1 5 2 1 5y xf x x x x x mx x x x mx



        

Yêu cầu bài toán





1x

  

5 2 4 2

2 1 5x x x mx   

1x

x 5 0, 1 , 1

x m x m x



          

. Đặt

 

55x

g x x





    





Ta có

25x



 

25gx  

1x

 

Max 2 5gx



  

khi

5x 

 

m g x



  

1x

 

Max 2 5 4,4m g x



    

Vậy có

giá trị nguyên âm thỏa mãn bài toán.

Câu 13: Cho hàm số

 

y f x

có đạo hàm

   

 

1 3 1f x x x x mx



   

. Có bao nhiêu giá trị

nguyên âm

để hàm số

 

y f x

đồng biến trên khoảng

 

0;

. B.

. C.

. D.

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 7/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Lời gii

Chọn D

Ta có

      

2 2 2 8 6

2 2 1 3 1y xf x x x x x mx



    

Yêu cầu bài toán





0x

3 1 0x mx   

0x

 

31x

m g x



   

Ta có

2 2 2 2

34x x x x

     

 

4gx  

0x

 

Max 4gx



  

khi

1x 

 

31x

m g x



  

0x

 

Max 4m g x



   

Vậy có

giá trị nguyên âm thỏa mãn bài toán.

Câu 14: Cho hàm số

 

y f x

có đạo hàm

   

 

19f x x x x mx



   

. Có bao nhiêu số

nguyên dương

để hàm số

 

3y f x

đồng biến trên khoảng

 

3; 

. B.

. C.

. D.

Lời gii

Chọn A

Đặt

   

3g x f x

Ta có

   

3g x f x



  

      

3 3 1 3 3 9 0x x x m x



         



Yêu cầu bài toán tương đương

 

0gx





3x

   

3 3 9 0x m x     

3x

 

m h x



  



3x

 

h x x



    





 

Min 6hx





khi

6x 

 

m h x



  



3x

 

Min 6m h x



  

Vậy có

giá trị nguyên dương

thỏa mãn.

Câu 15: Cho hàm số

 

y f x

có đồ thị

 



như hình vẽ

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 8/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

đồng biến khoảng nào dưới đây?

 

;1 

. B.

 

1;0

. C.

 

0;1

. D.

 

1; 

Lời gii

Chọn B

Đặt

 

g x f x

 

2g x xf x





 

g x x

















    















Bảng biến thiên của

 

Dựa vào bảng biến thiên hàm số đồng biến trong khoảng

 

1;0

Câu 16: Cho hàm số

 

y f x

có đồ thị của hàm số

 

y f x





như hình vẽ bên. Hàm số

 

3y f x

đồng biến trên khoảng

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 9/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

2;3

. B.

 

2; 1

. C.

 

0;1

. D.

 

1;0

Lời gii

Chọn D

Ta có

   

2 3 0 3 0y xf x xf x

  

      

Với

 

0 3 0

1 3 2

x f x



  



    



   















Với

 

6 3 1

0 3 0

x f x



    



    









  







   



Đối chiếu Chọn D

Câu 17: Cho hàm số

 

y f x

. Đồ thị của hàm số

 

y f x





như hình vẽ bên. Đặt

 

( ) 2h x f x x

. Hàm số

 

y h x

đồng biến trên khoảng nào dưới đây?

 

;2 

. B.

 

2;4

. C.

 

2;2

. D.

 

2;

Lời gii

Chọn C

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 10/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

( ) 2 ( ) 2 0 ( )h x f x x f x x

  

    

Kẻ đường thẳng

yx

đi qua các điểm

( 2 ; 2) ;(2 ; 2) ;(4 ; 4)

ta thấy đường

thẳng này cắt đồ thị hàm số

()y f x





tại ba điểm có hoành độ

2; 2, 4x x x   

Nhìn đồ thị ta có

()

f x x

  













Đối chiếu đáp án Chọn C

Câu 18: Cho hàm số

 

y f x

. Đồ thị của hàm số

 

y f x





như hình vẽ bên. Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

 

1;0

. B.

 

1;2

. C.

 

;2 

. D.

 

2; 1

Lời gii

Chọn D

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 11/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta đi giải bất phương trình

 

20y xf x





Với

 

x f x



  



























Với

 

1 4

x f x









   









   

Đối chiếu với Chọn D

Câu 19: Cho hàm số

 

có đạo hàm cấp

xác định và liên tục trên thỏa mãn

( ) ( ) ( 1)( 2),f x f x x x x x



    

. Hàm số

 

( ) ( ) 2 ( ) ( )g x f x f x f x

 



đồng

biến trên khoảng nào?

 

0;1

. B.

 

1;0

. C.

 

4;

. D.

 

;1 

Lời gii

Chọn B

Ta có

 

( ) 2 ( ) ( ) 2 ( ) ( ) ( ) ( )g x f x f x f x f x f x f x

     

  

 

2 ( ) ( ) 2 1 ( 4)f x f x x x x



     

Vậy

 

( ) 0 2 1 ( 4) 0

g x x x x

  





      







Đối chiếu Chọn B

Câu 20: Cho hàm số

 

có đạo hàm cấp

xác định và liên tục trên thỏa mãn

 

( ) ( ) ( ) ( 1)( 2),f x f x f x x x x x

 

     

. Hàm số

( ) ( ) ( )g x f x f x





đồng

biến trên khoảng nào?

 

0;2

. B.

 

;0

. C.

 

2;

. D.

 

1;2

Lời gii

Chọn C

Ta có

 

( ) ( ) ( ) ( ) ( 1)( 2) 0

g x f x f x f x x x x





  

      







Chuyên đề: Tính đơn điệu của hàm hợp

Trang 12/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Đối chiếu đáp án Chọn C

Câu 21: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

 

;2 

. B.

 

2;0

. C.

 

1; 

. D.

 

2; 2

Lời gii

Chọn B

Ta có

 

20y xf x





 

2 2 2 0x x x



    



 

20xx  









  





Đối chiếu các đáp án. Chọn B

Câu 22: Cho hàm số

   

61f x x mx m x    

. Có bao nhiêu số nguyên dương

để hàm

số





1y f x x  

đồng biến trên khoảng

 

; 

. B.

. C.

. D.

Lời gii

Chọn B

Ta có yêu cầu bài toán









 

1 1 0, 1 0, 1

y f x x x f x x x



  

           







Đặt

 

1 0; ,t x x x     

và

 

3 2 6f x x mx m



   

Do vậy:

       

1 0, 0; 3 2 6 0, 0;f t t t mt m t



            

 

, 0;



    







   

min 1 3 1,2,3

m y y m







     







Chọn B

Câu 23: Cho ham số

   

61f x x mx m x    

. Có bao nhiêu số nguyên không âm

để

hàm số





1y f x x  

nghịch biến trên khoảng

 

; 

. B.

. C.

. D.

-2

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 13/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Lời gii

Chọn D

Ta có, yêu cầu bài toán





1 . 1 0,

y f x x x





      











 

1 1 0, 1f x x



    

Đặt

 

1 ; 0; ,t x x t x      

và

 

3 2 6f x x mx m



   

Do vậy

       

 









   

1 ' 0, 0; 3 2 6 0, 0;

3 6 3 6

, 0; , 0;

2 1 2 1

min 1 3 0,1,2,3

f t t t mt m t

m t m t

m y y m



            



         







     







Câu 24: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình bên. Hàm số

 

y f e

đồng biến trên khoảng

 

,ab

. Giá trị lớn nhất của

ba

bằng

. B.

. C.

. D.

Lời gii

Chọn B

Ta có:

   

3 7 3 7

' 2 ' 5 2 0 ' 5 2 0 2 5 2 2 ln ln

2 2 2 2

x x x x x

y e f e f e e e x                 

Vậy

 

max

7 3 7

ln ln ln

2 2 3

ba   

Câu 25: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình vẽ. Hàm số

 

3y f x

đồng biến trên khoảng nào dưới đây?

-2

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 14/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

2;3

. B.

 

0;1

. C.

 

2; 1

. D.

 

1;0

Lời gii

Chọn D

   

' 2 ' 3 0 ' 3 0y xf x xf x      

 

  

2 2 2

3 6 3 1 3 2 0x x x x         







   







  







Câu 26: Cho hàm số

 

y f x

có đồ thị của hàm số

 



y f x

như hình vẽ bên. Hàm số

1 2tan











đồng biến trên khoảng nào dưới đây?

; arctan











. B.

;arctan 2











. C.

arctan ;











. D.

;arctan











Lời gii

Chọn C

Ta có hàm số

1 2tan











tuần hoàn với chu kỳ



T

nên ta chỉ cần xét trên

khoảng

;











có

-6

-1

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 15/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

2 1 1 2tan 1 2tan

. 0 0

3 cos 2 3



   

  

    

   

   

y f f

1 2tan























tan 2

tan 1











   



arctan 2

arctan













   





Câu 27: Cho hàm số

 

4 3 2

    f x ax bx cx dx e

với

, , , ,a b c d e

là các số nguyên không âm

nhỏ hơn

và

 

6 2019f

. Hàm số

 

   

y f x x

đồng biến trên khoảng nào

dưới đây?

;







. B.







. C.

;









. D.

;







Lời gii

Chọn A

Ta có

 

4 3 2

6 2019 .6 .6 .6 .6 2019      f a b c d e

4 3 2 4 3 2 1 0

.6 .6 .6 .6 6 3.6 2.6 0.6 3.6        a b c d e

   

13203 1, 3, 2, 0, 3       abcde a b c d e

Suy ra

 

4 3 2

3 2 3   f x x x x

Khi đó

       

 

1 1 4 1 9 1 4 1 1



             y f x x x x x x

   

1 2 4 9 0



       y x x x x

hoặc

12x

Câu 28: Cho hàm số

 

   f x ax bx cx d

với

, , ,a b c d

là các số nguyên không âm nhỏ hơn

và

 

9 2019f

. Hàm số

 

  y f x x x

nghịch biến trên khoảng nào dưới đây?

;



 





. B.

;



 





. C.









. D.









Lời gii

Chọn C

Ta có

 

3 2 1

9 2019 .9 .9 .9 2019     f a b c d

3 2 1 3 2 1

.9 .9 .9 2.9 6.9 8.9 1      a b c d

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 16/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

   

2681 2, 6, 8, 1      abcd a b c d

Suy ra

 

2 6 8 1   f x x x x

Khi đó

     

2 2 11

1 2 6 12 8 1 2 0 1

3 3 9



             y f x x x x x x

Câu 29: Cho hàm số

 

y f x

có bảng biến tiên như hình vẽ bên dưới đây. Hàm số

   

6





y f x f x

nghịch biến trên khoảng nào dưới đây?

 

1;1

. B.

 

6;

. C.

 

1;6

. D.

 

;2 

Lời gii

Chọn D

Ta có

           

2 6 2 3 . 0 0





    

       











y f x f x f x f x f x f x

Vì dựa vào bảng biến thiên ta có

   

3, 3 0,       f x x f x x

Câu 30: Cho hàm số

 

y f x

. Hàm số











y f x

có đồ thị như hình bên. Hàm số

 

21y f x

nghịch biến trên khoảng

5 11

;







. B.







. C.

;







. D.

9 15

;







Lời gii

Chọn D

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 17/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

   

2 2 1 0 *



  y f x

Đặt

1 2 1

2 1 3

2 3 3

     x t t x

Khi đó

 

trỏ thành









  















  













  







Câu 31: Cho hàm số

( ) 3 1f x x x

. Có bao nhiêu số nguyên không âm

để hàm số

y = f(m - x)+(m - 1)x

đồng biến trên khoảng có độ dài không vượt quá

. B.

. C.

. D.

Lời gii

Chọn A

Ta có

2 2 2

( ) 1 3( ) 3 1 3 6 3 2y f m x m m x m x mx m m

Ta có

luôn có hai nghiệm phân biệt vì

9 3 3 2 3( 2) 0, 0m m m m m

Do đó hàm đồng biến trên khoảng

;xx

theo yêu cầu bài toán ta có

2 1 2 1 1 2 1 2

4 16 4 16 0x x x x x x x x

4 4 16 0 10

Vậy

0;2;....;10m

. Có

số nguyên không âm

thỏa mãn.

Câu 32: Cho hàm số

( ) 3 1f x x x

. Có bao nhiêu số nguyên

để hàm số

y = f(m - x)+(m - 1)x

đồng biến trên khoảng

8;9

. B.

. C.

. D.

Lời gii

Chọn D

Ta có

2 2 2

( ) 1 3( ) 3 1 ( ) 3 6 3 2y f m x m m x m g x x mx m m

Với

9 3 3 2 3( 2)m m m m

TH1:

0 2 0,m y x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 18/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

TH2:

02m

Khi đó phương trình có hai nghiệm phân biệt

và hàm số đồng bến trên

;xx

Theo yêu cầu bài toán ta có:

1 2 1 2

3 (8) 0 3 49 190 0

(8;9) ; 8 9

3 (9) 0

3 55 241 0

55 133

g m m

x x x x

Vậy

{8,9,10}m

.Có

số nguyên

thỏa mãn.

Câu 33: Cho hàm số

( ) 3 1f x x x

. Số thực

nhỏ nhất để hàm số

y = f(m - x)+(m - 1)x

đồng biến trên khoảng

8;9

là

, với

,,a b c

là các số

nguyên dương và

tối giản. Giá trị của biểu thức

a b c

bằng:

194

. B.

. C.

193

. D.

Lời gii

Chọn A

Ta có

2 2 2

( ) 1 3( ) 3 1 ( ) 3 6 3 2y f m x m m x m g x x mx m m

Với

9 3 3 2 3( 2)m m m m

TH1:

0 2 0,m y x

TH2:

02m

Khi đó phương trình có hai nghiệm phân biệt

và hàm số đồng bến trên

;xx

Theo yêu cầu bài toán ta có:

1 2 1 2

3 (8) 0 3 49 190 0

(8;9) ; 8 9

3 (9) 0

3 55 241 0

55 133

g m m

x x x x

a=55, b=133, c=6

và

a+b+c=194

Câu 34: Cho hàm số

()y f x

có bảng biến thiên như sau:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 19/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Có bao nhiêu số nguyên

40;40m

để hàm số

y = f(x )

đồng biến trên khoảng

. B.

. C.

. D.

Lời gii

Chọn A

2 0, 2 , 2

6, 2 4 6 2

ycbt y xf x x x

x m x m m

Vì số nguyên

40;40m

nên

{ 39, 38,..., 2}m

.Có

số nguyên

thỏa mãn.

Câu 35: Cho hàm số

( ), ( )y f x y g x

có đồ thị

'( ), '( )y f x y g x

như hình vẽ dưới.

4m 

6m 

1

















Chuyên đề: Tính đơn điệu của hàm hợp

Trang 20/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

( ) ( )y f x g x

đồng biến trên khoảng nào dưới đây

;









. B.







. C.







. D.

;









Lời gii

Chọn C

Ta có

( ) ( ) 0 ( ) ( ) 6

0,25

y f x g x f x g x x

. Đối chiếu Chọn C

Câu 36: Cho hàm số

y f x

có đạo hàm

1 4 ,fx xxx

. Hàm số

cosy xf

đồng biến trên khoảng nào dưới đây?

;

. B.

;

. C.

. D.

;

Lời gii

Chọn B

Hàm số

cosy xf

tuàn hoàn chu kỳ

. Do vậy ta chỉ xét trên đoạn

;

sin . cos sin co c 04ss1 ox f x x x xy

0 sin

sin 1 sin 4sin 3 0

1 sin

x x x x

Chú ý: Chúng ta có thể tính đạo hàm tại một điểm trong khoảng trong các đáp án để

chọn được đáp án đúng.

Câu 37: Cho hàm số

,y f x y g x

có đồ thị của hàm số

,y f x y g x

như hình vẽ

bên. Hàm số

2 3 6 18

y f x g x x

nghịch biến trên khoảng nào dưới đây?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 21/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

;

. B.

;

. C.

. D.

1 11

;

Lời gii

Chọn D

Có

0 2 2 3 3 6 18 0 2 2 3 3 6 18

f x g f x gy xx

Quan sát đồ thị đã cho có

0;6

max 6fx

và

min 2gx

Do vậy ta chỉ cần chọn

0 2 6

1 11

x x

thì

2 2 3 6 11

3 82f x xg

Vậy hàm số

2 3 6 18

y f x g x x

nghịch biến trên khoảng

1 11

;

Câu 38: Cho hàm số

y f x

có đồ thị của hàm số

y f x

như hình vẽ bên. Hàm số

2 3 2 2y f x xxx

đồng biến trên khoảng nào dưới dây?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 22/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

. B.

;

. C.

;

. D.

Lời gii

Chọn A

Ta cần giải

2 3 20 20

2 3 2 2

f x x x x

2 2 2 2

1 2 2 2 3 2 3 2 2 0x x x x x f x x x x

1 2 3 2 2 0x f x x x x

2 2 2 2

1 2 3 2 2 1 2 3 2 2 2 0 1x x x x x x x x x x

Câu 39: Cho hàm số

4 4 2

axfx bx cx dx

thỏa mãn

1 100, 2 200, 3 300f f f

Hàm số

100

f x x

nghịch biến trên một khoảng có đồ dài lớn nhất bằng?

. B.

. C.

. D.

Lời gii

Chọn B

Có

4 3 2

100 100axg x f x x x cbx xd

và theo giả thiết ta có:

1 2 3 0g g g

do đó

1 2 3 1001 2 3g x x m x x x f x x m x x x x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 23/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Đồng nhất hệ số tự do của

ta có

1 2 3 00

6 1

m f x x x x xd xm

Vậy

100

1 2 3

3 12 11 0

f x x

y x x x x

Câu 40: Cho hàm số

y f x

có đồ thị hàm số

y f x

như hình vẽ bên. Hàm số

3 2 1y f x x

đồng biến trên khoảng nào dưới đây?

. B.

. C.

;

. D.

Lời gii

Chọn D

Có

3 3 2 2 1

y f x x

Đặt

32x

t x

, bất phương trình trở thành

f t t

Kẻ trên đồ thị đường thẳng

qua hai điểm

và

5;0

Suy ra

1 1 1

5 3 2 5 1

9 2

t x xf t t

Câu 41: Cho hàm số

()y f x

có đồ thị của hàm số

'(x)yf

như hình vẽ bên

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 24/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

39 ( ) 8 45 276 1y f x x x x    

đồng biến trên khoảng nào dưới đây?

1; .











 





;









;









Lời gii

Chọn A

Ta có:

' 39 '( ) 24 90 276y f x x x   

Hàm số đã cho đồng biến

24 90 276

' 0 '( )

y f x



   

Gọi

 

là đồ thị hàm số

24 90 276





. Ta có đồ thị hàm số

'( )fx

và

 

được

thể hiện trong hình sau:

Từ đồ thị trên ta thấy đồ thị hàm số

'( )fx

nằm phía trên parabol

 

trên khoảng









Vậy

24 90 276 11

'( ) 1;

39 2

f x x





   





Chuyên đề: Tính đơn điệu của hàm hợp

Trang 25/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Vậy Chọn A

Câu 42: Cho hàm số

()fx

có bảng xét dấu của đạo hàm như sau:

Hàm số

3 ( 2) 3y f x x x   

đồng biến trên khoảng nào dưới đây?

 

1; .

 

; 1 . 

 

1;0 .

 

0;2 .

Lời gii

Chọn C

Ta có:

' 3 '( 2) 3 3y f x x   

Đặt

22t x x t    

khi đó ta có:

 

' 3 '(t) 3 2 3 3 '( ) ( 4 3)y f t f t t t



       



Ta có bảng xét dấu như sau:

Vậy ta thấy

   

' 0 1;3 1;1y t x     

nên hàm số đã cho đồng biến trên

 

1;0

Câu 43: Cho hàm số

()fx

. Hàm số

()y f x





có bảng xét dấu:

Hàm số

( 2 )y f x x

nghịch biến trên khoảng nào dưới đây?

 

4; 3

. B.

 

0;1

. C.

 

2; 1

. D.

 

2;1

Lời gii

Chọn C

Ta có

 

( 2 ) 2 2 2y f x x x f x x





    

Xét bất phương trình

 

0 2 2 2 0y x f x x



    

TH1:

 

2 2 3

f x x











      

  





  

   







Chuyên đề: Tính đơn điệu của hàm hợp

Trang 26/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

TH2:

2 2 (vn)

( 2 ) 0

f x x















   

  

  

   

















Vậy hàm số nghịch biến trên mỗi khoảng

 

3; 1

và

 

1; 



Hàm số nghịch biến trên

 

2; 1

Câu 44: Cho hàm số

()fx

có bảng xét dấu đạo hàm

()fx



như sau:

Hàm số

3 9 1

3 ( 2) e

x x x

y f x

  

   

nghịch biến trên khoảng nào dưới đây?

 

2;1

. B.

 

2;

. C.

 

0;2

. D.

 

;2 

Lời gii

Chọn A

Ta có:

 

3 2 3 2

3 9 1 2 3 9 1

3 ( 2) e 3 2 3 6 9

x x x x x x

y f x f x x x e

     





          

Đặt

2tx  

2xt  

Khi đó

2 9 15 3

3 ( ) 3( 6 5).

t t t

y f t t t e

   



    

Ta có bảng xét dấu:

Từ đó suy ra, với

 

1;5t 

thì





Từ

 

1;5t 

1 2 5 3 1xx        



Trên

 

3;1

, hàm số

3 9 1

3 ( 2) e

x x x

y f x

  

   

nghịch biến.



Hàm số nghịch biến trên

 

2;1

Câu 45: Cho hàm số

 

có bảng biến thiên như sau

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 27/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

3y f x f x

nghịch biến trên khoảng nào dưới đây?

 

2;3

. B.

 

1;2

. C.

 

3;4

. D.

 

;1 

Lời gii

Chọn A

Ta có

   

 

3 2 .y f x f x f x





Dựa vào bảng biến thiên ta có trên

 

2;3

thì

     

0, 2 0, 0f x f x f x



   

Do đó





hay hàm số nghịch biến trên

 

2;3

Câu 46: Cho hàm số

 

có bảng xét dấu đạo hàm như sau

Xét hàm số

   

x x x

g x f x



  

. Khẳng định nào sau đây đúng?

A. Hàm số

 

đồng biến trên khoảng

;







B. Hàm số

 

đồng biến trên khoảng

 

0;2

C. Hàm số

 

đồng biến trên khoảng

 

3; 

D. Hàm số

 

nghịch biến trên khoảng

 

0;1

Lời gii

Chọn C

Ta có

   

 

1 3 3 2 ln3

x x x

g x f x x x





     

Hàm số

 

đồng biến khi

   

 

0 1 3 3 2 ln3 0

x x x

g x f x x x





       

Ta có

   

0 1 1 0 1

1 0 1 0

1 2 3

f x f x

    





       



   



Và

 

3 3 2 ln3 0

x x x







   







Suy ra trên

 

3; 

thì

 

0gx





Chuyên đề: Tính đơn điệu của hàm hợp

Trang 28/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Do đó hàm số

 

đồng biến trên khoảng

 

3; 

Câu 47: Cho hàm số

 

có đạo hàm liên tục trên và có đồ thị như hình vẽ bên dưới.

Có bao nhiêu số nguyên

 

10;10m

để hàm số

 

3 1 3y f x x mx   

đồng biến trên

khoảng

 

2;1

. B.

. C.

. D.

Lời gii

Chọn B

Ta có

 

' 3 ' 3 1 3 3y f x x m   

Để hàm số đồng biến trên khoảng

 

2;1

thì

   

' 3 ' 3 1 3 3 0 2;1y f x x m x       

           

' 3 1 0 2;1 ' 3 1 , 2;1 *f x x m x m g x f x x x               

Ta có:

     

' 3 1 ' 1 4, 0 ' 3 1 4f x f x f x x          

Suy ra điều kiện (*) tương đương:

 

   

2;1

4 9; 8; 7; 6; 5; 4m Min g x m



          

Vậy có 6 giá trị nguyên thỏa mãn điều kiện đề bài.

Câu 48: Cho hàm số

 

có bảng xét dấu đạo hàm như sau:

hàm số

 

2 2 2

y f x e  

nghịch biến trên khoảng nào dưới đây?

 

;1 

. B.

 

2;0

. C.

 

0;1

. D.

 

1; 

Lời gii

Chọn C

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 29/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

 

' 2 ' 2 2 2

y f x e  

Để hàm số nghịch biến thì điều kiện cần là:

 

' 2 2 0

2 2 6 2

' 2 2 0

4 2 2 0 1 1

2 0 ( )

e L D

  

    





    





      









Suy ra Chọn C

Câu 49: Cho hàm số

 

có bảng xét dấu đạo hàm như sau

Hàm số

 

6 1 2 3y f x x x   

đồng biến trên khoảng nào dưới đây?

 

2;

. B.

 

1;0

. C.

 

;1 

. D.

 

0;1

Lời gii

Chọn D

Ta có:

 

6. 1 6 6y f x x x



   

 

01y f x x x



    

Đặt

11t x x t    

Khi đó ta có phương trình:

         

1 1 *f t t t f t t t



      

Nhận thấy phương trình

 

có nghiệm

0; 1tt  

Trên khoảng

 

1;0

thì

 

0ft





và

0tt

nên

 

0f t t t



  

Nên hàm số

 

đồng biến trên khoảng

 

1;0

Suy ra hàm số

 

đồng biến trên khoảng

 

0;1

Câu 50: Cho hai hàm số

   

,y f x y g x

có đạo hàm trên và có đồ thị như hình vẽ bên,

trong đó đường cong đậm hơn là đồ thị của hàm số

 

y f x

. Biết rằng hai hàm số

 

21y f x  

và

   

,,y g ax b a b  

có cùng khoảng đồng biến. Giá trị của

2ab

bằng:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 30/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

. B.

. C.

. D.

Lời gii

Chọn C

+) Xét hàm số:

 

21y f x  

có:

 

2. 2 1y f x



   

Hàm số đồng biến

   

0 2. 2 1 0 2 1 0y f x f x

  

          

0 2 1 2

xx        

+) Xét hàm số:

   

,,y g ax b a b  

có

 

.y a g ax b





TH1: Nếu

0a 

Hàm số

   

,,y g ax b a b  

đồng biến





   

. 0 0a g ax b g ax b



     

ax b

ax b b









  







  











Không thỏa mãn giả thiết hàm số

 

21y f x  

và

   

,,y g ax b a b  

có cùng

khoảng đồng biến.

TH2: Nếu

0a 

thì

 

y g b

là hàm hằng.

Không thỏa mãn giả thiết hàm số

 

21y f x  

và

   

,,y g ax b a b  

có cùng

khoảng đồng biến.

TH3: Nếu

0a 

: Hàm số

   

,,y g ax b a b  

đồng biến





   

. 0 0a g ax b g ax b



     

ax b x

  

       

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 31/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

21y f x  

và

   

,,y g ax b a b  

có cùng khoảng đồng biến

1 1 0































Vậy

22ab

Câu 51: Cho hàm số

 

có đồ thị

 

'y f x

như hình vẽ bên. Hàm số

 

cosy f x x x  

đồng biến trên khoảng:

 

1;2

. B.

 

1;0

. C.

 

0;1

. D.

 

2; 1

Lời gii

Chọn A

Ta có:

+ Vì mà

+ Suy ra hay hàm số tăng trên

Câu 52: Cho hàm số

 

y f x

có bảng xét dấu đạo hàm như hình vẽ

Hàm số

 

2 1 1y f x x x    

nghịch biến trên khoảng nào:

 

;1

. B.

 

;2 

. C.

 

3; 2

. D.

 

2;0

Lời gii

Chọn D

 

' 2 ' 1 1 0

y f x

     



 

' sin . ' cos 2 1y x f x x   

 

 

 

cos 1;1 sin . ' cos 1;1x x f x     

2 1 1 1xx   

 

' sin . ' cos 2 1 0, 1y x f x x x      

[1; )

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 32/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có:

1 0,

   



Khi:

1 1 3 2 0xx      

thì

   

' 1 0 2 ' 1 0f x f x     

Vậy

   

2 ' 1 1 0, 2;0

f x x

       



. Hàm số nghịch biến trên

 

2;0

Câu 53: [2D1-1.4-3] Cho hàm số

()y f x

có đạo hàm liên tục trên . Đồ thị hàm số

()y f x





như hình vẽ

Hàm số

( ) ( 2 1) ( 1)( 2 4)g x f x x x      

đồng biến trên khoảng nào dưới đây









. B.

( ;2)

. C.

;



  





. D.









Lời gii

Chọn A

Xét hàm số

( ) ( 2 1) ( 1)( 2 4)g x f x x x      

Tập xác định: .

( ) 2 ( 2 1) 4 2g x f x x



     

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 33/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

( ) 0gx







2 ( 2 1) 4 2 0f x x



     



( 2 1) 2 1f x x



    

(hay

()f t t





, với

21tx  

)

Từ đồ thị ta thấy

( 2 1) 2 1f x x



    



2 1 3

2 2 1 5

   





   











   



Hay

( ) 0gx













   



Như vậy trên mỗi khoảng









 

2;

hàm số

()y g x

đồng biến.

Soi các phương án ta thấy phương án A thỏa yêu cầu đề bài.

Câu 54: [2D2-4.3-3] Cho hàm số

()y f x

có đạo hàm trên . Đồ thị hàm số

()y f x





như

hình vẽ bên dưới.

Hàm số

(1 2 )

()











nghịch biến trên khoảng nào dưới đây

 

0;1

. B.

( ;0)

. C.

 

1;0

. D.

 

1; 

Lời gii

Chọn D

Xét hàm số

(1 2 )

()











Tập xác định: .

   

(1 2 )

( ) 1 2 . 1 2 . .ln

g x x f x



   





  

   

   

 

(1 2 )

( ) 2ln 2. 1 2 .

g x f x













( ) 0gx







(1 2 ) 0fx





Từ đồ thị của hàm số

()y f x





ta thấy

(1 2 ) 0fx







1 2 1

1 1 2 2

  





  











  



Chuyên đề: Tính đơn điệu của hàm hợp

Trang 34/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hay

( ) 0gx













  



Như vậy trên mỗi khoảng









 

1;

hàm số

()y g x

nghịch biến.

Soi các phương án ta thấy phương án D thỏa yêu cầu đề bài.

Câu 55: Cho hàm số

()fx

có đồ thị của

'( )fx

như hình vẽ bên. Có bao nhiêu số nguyên

[ 5;5]m

để hàm số

()f x m

nghịch biến trên khoảng

(1;2)?

Lời gii

Chọn D

Đặt

( ) ( ).g x f x m

Ta có

'( ) '( ).g x f x m

YCBT

'( ) 0, (1;2)f x m x

'( ) 0, (1 ;2 )f t t m m

với

t x m

2 1 3

1 1 2 3 0 1

m m m

Vì

[ 5;5]m

nên

{ 5; 4; 3;0;1}.m

Câu 56: Cho hàm đa thức bậc ba

()y f x

có đồ thị hàm số

'( )y f x

như hình vẽ. Hàm số

( ) ( )g x f x x

nghịch biến trên khoảng nào dưới đây?

;0 .

( 1;0).

( 2; 1).

(1;2).

Lời gii

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 35/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Chọn D

'( ) ( 1 2 ) '( )g x x f x x

'( ) 0 0 0

g x x x x

Bảng biến thiên

Vậy Chọn D

Câu 57: Cho hàm số

 

y f x

có bảng xét dấu của đạo hàm như sau

Đặt

 

1 1 3

2 3 2

g x f x x x





    





. Mệnh đề nào dưới đây sai?

A. Hàm số

 

nghịch biến trên khoảng

 

1;0

B. Hàm số

 

đồng biến trên khoảng

 

0;2

C. Hàm số

 

nghịch biến trên khoảng

 

4; 1

D. Hàm số

 

nghịch biến trên khoảng

 

7;

Lời gii

Chọn B

Ta có

 

1 1 1 1

3 2 2 6 4

2 2 2 2

g x f x x f x x

   

   

  

       

   



   



Chuyên đề: Tính đơn điệu của hàm hợp

Trang 36/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số nghịch biến

khi

 

0 2 6 4 0

g x f x x







     





2 6 4 0



   























5 1 1

222























  

































  













  

















Từ đó suy ra B sai.

Câu 58: Cho hàm số

 

y f x

liên tục, nhận giá trị dương trên và có bảng xét dấu đạo hàm

như hình bên. Hàm số

   

 

log 2g x f x

đồng biến trên khoảng

 

1;2

. B.

 

;1 

. C.

 

1;0

. D.

 

1;1

Lời gii

Chọn A

Ta có

 

2 ln2





Hàm số đồng biến khi

 

1 2 1

0 2 0

2 ln2

g x f x





  







     











Câu 59: Cho hàm số

 

y f x

liên tục trên có

 

00f 

và đồ thị hàm số

 

y f x





như hình

vẽ dưới đây.

Hàm số

 

3y f x x

đồng biến trên khoảng

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 37/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

2;

. B.

 

;2

. C.

 

0;2

. D.

 

1;3

Lời gii

Chọn C

Xét hàm số

   

3g x f x x

có

     

3 3 0g x f x x f x x

  

    

Vẽ đồ thị hàm số

yx

cắt đồ thị

 

y f x





tại 3 điểm

0, 1, 2x x x  

(như hình vẽ).

Từ đây ta có bảng biến thiên của hàm số

 

y g x

(như hình trên).

Dùng phép đối xứng đồ thị, ta thu được hàm số

 

y g x

đồng biến trên khoảng

 

0;2

và

 

;a 

với

2a 

Câu 60: Cho hàm số

 

y f x

có bảng xét dấu đạo hàm như hình vẽ.

Biết rằng

 

13fx

x

. Hàm số

 

61y f f x x x   





nghịch biến trên

khoảng

 

3;4

. B.

 

3; 2

. C.

 

1;3

. D.

 

2;1

Lời gii

Chọn A

Ta có

   

0 . 3 12 0y f x f f x x x

  

    





(*)

Theo đề bài

 

13fx

x

nên

 

0f f x









x

Vậy ta chỉ cần các điều kiện sau để thỏa (*) là

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 38/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

   

 

   

;1 3;4

0;1 3;4

0;4

3 12 0



  







   











Câu 61: Cho đồ thị hàm số

 

2y f x

như hình vẽ

Hàm số

 

3y f x

nghịch biến trên khoảng nào dưới đây?

 

0;1

. B.

 

1;3

. C.

 

;1 

. D.

 

1;0

Lời gii

Chọn A

Gọi

 

là đồ thị hàm số

   

2  y g x f x

Tịnh tiến

 

sang trái 2 đơn vị ta được đồ thị hàm số

   

2   y g x f x

Lấy đối xứng đồ thị hàm số

 

y f x

qua Oy ta được đồ thị hàm số

 

y f x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 39/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

   

3 2 . 3



    y f x y x f x

 

0 3 0 3

















       



















y x x

Bảng xét dấu



Vậy hàm số

 

3y f x

nghịch biến trên khoảng

 

0;1

Câu 62: Cho hàm số

 

có bảng xét dấu đạo hàm

 



như sau:

Hàm số

 

2y f x x

nghịch biến trên khoảng nào dưới đây?

 

2;1

. B.

 

4; 3

. C.

 

0;1

. D.

 

2; 1

Lời gii

Chọn D

Đặt:

 

2y g x f x x  

;

 

2g x f x x





 

2 2 . 2x f x x



  

 

0gx





 

2 2 . 2 0x f x x



   

 

2 2 0

f x x

















 







  















vo ânghieäm

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 40/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688







  



   













. (

12x   

là các nghiệm bội chẵn của phương trình:

21xx

Ta có bảng biến thiên:

Dựa vào bảng biến thiên, suy ra hàm số

 

2y f x x

nghịch biến trên khoảng

 

2; 1

Chú ý: Cách xét dấu

 



Chọn giá trị

 

0 1; 1 2x     

20xx  

   

0 0 0gf



  

(dựa theo bảng xét

dấu của hàm

 



). Suy ra

 

0gx





 

1; 1 2x    

. Sử dụng quy tắc xét dấu đa

thức “lẻ đổi, chẵn không” suy ra dấu của

 



trên các khoảng còn lại.

Câu 63: Cho hàm số

 

y f x

liên tục trên và hàm số

 

y f x





có đồ thị như hình vẽ.

Hàm số

 

1 2 2020y g x f x x    

đồng biến trên khoảng nào dưới đây?

 

1;0

. B.

 

0;1

. C.

 

2;3

. D.

 

3;5

Lời gii

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 41/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Chọn B

Ta có

   

 

2 2 . 1 2g x x f x x



   

 

2 2 0

1 2 0

f x x













  





1 2 2

1 2 1







    



   

























Bảng biến thiên:

Dựa vào bảng biến thiên hàm số

 

đồng biến trên khoảng

 

;1 

và

 

1 3;1

và

 

1 3;3

Mà

(0;1) (1 3;1)

nên hàm số

 

1 2 2020y g x f x x    

đồng biến trên

(0;1)

Câu 64: Cho hàm số

 

y f x

có đạo hàm

     

. 2 5f x x x x



  

. Hàm số

   

10 5g x f x

đồng biến trên khoảng nào dưới đây?

 

;1

. B.

 

1;2

. C.

 

2;

. D.

 

1;3

Lời gii

Chọn B

Ta có

       



  

     g x x f x f x10 5 . 10 5 5. 10 5

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 42/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

   

10 5 0

0 10 5 0 10 5 2

10 5 5

g x f x x x













         













Bảng xét dấu

()gx



Vậy hàm số

 

đồng biến trên khoảng

 

1;2

Câu 65: Cho hàm số

()y f x

có đạo hàm

( ) ( 1) ( 2)



  f x x x x

với mọi giá trị thực của

. Xét

hàm số

()











g x f

. Trong các khẳng định sau khẳng định nào đúng?

A. Hàm số đồng biến trên khoảng

(0;1)

. B. Hàm số nghịch biến trên khoảng

(0;4)

C. Hàm số đạt cực đại tại

0x

. D. Hàm số đạt giá trị nhỏ nhất tại

1x

Lời gii

Sưu tầm:Phạm Hải Dương; Fb: Duongpham

Chọn C

Ta có:

 

g x f



   





   



   

 

2 2 2

20 5 5 5 5

1 2 ,

4 4 4

x x x x

x x x



    

    

    

  

    



 

20 5

( ) 0



















































Bảng biến thiên của hàm số

()y g x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 43/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Vậy hàm số

()y g x

đạt cực đại tại

0x

Câu 66: Cho hàm số

 

. Hàm số

 

y f x





có đồ thị như hình bên.

Hỏi hàm số

 

2 6 3g x f x x x x   

đồng biến trên khoảng nào dưới đây?









. B.







. C.

 

0;1

. D.

 

;0

Lời gii

Chọn A

Ta có:

 

2 6 3g x f x x x x   

   

 

4 1 2 12 3g x x f x x x



     

 

4 1 2 3x f x x





   



Chuyên đề: Tính đơn điệu của hàm hợp

Trang 44/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

4 1 0

f x x













  





 







  

















2 1 voânghieäm

2 2 nghieäm keùp

 











































1 17

nghieäm keùp

1 17

nghieäm keùp

Ta có :

   

   ' 2 9 '(10) 3gf

dựa vào đồ thì

 

'fx

ta thấy

   

    ' 10 3 ' 10 3 0ff

 

  ' 2 0g

Ta có bảng xét dấu như sau:

Xét dấu

 



ta được

 

1 1 1 1 17 1 17

0, ;0 ; 1; ;

2 4 2 4 4

g x x

   



   



       

   

   

Suy ra

 

đồng biến trên các khoảng









và

;







và

1 17









và

1 17

;











Chuyên đề: Tính đơn điệu của hàm hợp

Trang 45/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Mà

;0 ;0

   

  

   

   

nên hàm số

 

2 6 3g x f x x x x   

đồng biến trên khoảng









Câu 67: Cho hàm số

 

y f x

có đạo hàm

     

' (3 ) 10 3 2f x x x x   

với mọi

.x

Hàm

số

   

3 ( 1)

g x f x x   

đồng biến trên khoảng nào trong các khoảng sau?

 

;0 .

 

0;1 .

 

1; .



 





Lời gii

Chọn D

Ta có

   

' ' 3 ( 1)g x f x x x    

Theo giả thiết

     

' (3 ) 10 3 2f x x x x   

nên

     

' 3 3 1 1f x x x x   

Từ đó suy ra

     

' 3 1 1 ( 1)g x x x x x x     

2 2 2 2 2

( 1) (3 1) ( 1) ( 1) ( 8 4 )



         



x x x x x x x x

( 1) ( 8 4)   x x x

Khi đó

 









  









0( )

' 0 1( )

x nghiÖm kÐp

g x x nghiÖm kÐp

Bảng biến thiên

Khi đó hàm số đồng biến trên



 





Câu 68: Cho hàm số

 

có bảng biến thiên như sau

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 46/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

3y f x f x

nghịch biến trên khoảng nào dưới đây?

 

2;3

. B.

 

1;2

. C.

 

3;4

. D.

 

;1 

Lời gii

Chọn A

Ta có

 

     

3 . 6 .y f x f x f x f x

  



     

3 . 2y f x f x f x









 

y f x











  







 

























;

 













;

 

1;2

x x x

  



















+ Bảng xét dấu của



Từ bảng xét dấu suy ra hàm số

 

3y f x f x

nghịch biến trên khoảng

 

2;3

Câu 69: Cho hàm số

 

y f x

, hàm số

   

,,f x x ax bx c a b c



    

có đồ thị như hình vẽ

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 47/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

   

 

g x f f x





nghịch biến trên khoảng nào dưới đây?

 

1; 

. B.

 

;2 

. C.

 

1;0

. D.

;









Lời gii

Chọn B

Vì các điểm

     

1;0 , 0;0 , 1;0

thuộc đồ thị hàm số

 

y f x





nên ta có hệ:

   

1 0 0

0 1 '' 3 1

1 0 0

a b c a

c b f x x x f x x

a b c c

     







         





    



Ta có:

   

 

   

 

. ''g x f f x g x f f x f x

   

  

Xét

     

 

  

0 ' . 0 3 1 0

3 1 0

g x g x f f x f x f x x x











    

        



  







( 1,325 )

( 1,325)

x x x













  



  









Bảng biến thiên

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 48/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Dựa vào bảng biến thiên ta có

 

nghịch biến trên

 

;2 

Câu 70: Cho hàm số

 

y f x

liên tục có đạo hàm trên . Biết hàm số

 

'fx

có đồ thị cho như

hình vẽ. Có bao nhiêu giá trị nguyên của

thuộc

 

2019;2019

để hàm só

 

2019 2

g x f mx  

đồng biến trên

 

0;1

2028

. B.

2019

. C.

2011

. D.

2020

Lời gii

Chọn D

Ta có

 

' 2019 ln2019. ' 2019

g x f m

Ta lại có hàm số

2019

y 

đồng biến trên

 

0;1

Với

 

0;1x

thì

 

2019 1;2019



mà hàm

 

'y f x

đồng biến trên

 

1; 

nên hàm

 

' 2019

yf

đồng biến trên

 

0;1

Mà

 

 

2019 1; ' 2019 0 0;1

fx   

nên hàm

 

2019 ln2019. ' 2019

h x f

đồng

biến trên

 

0;1

Hay

   

 

0 0, 0;1h x h x   

Do vậy hàm số

 

đồng biến trên đoạn

 

0;1

 

 

' 0, 0;1g x x   

 

 

2019 ln2019. ' 2019 , 0;1

m f x   

 

   

0;1

min 0 0

m h x h



   

Vì

nguyên và

 

2019;2019m  

có

2020

giá trị

thỏa mãn yêu cầu bài toán.

Câu 71: Cho hàm số

 

y f x

có đạo hàm trên và có đồ thị hàm

 



như hình vẽ dưới

đây. Hàm số

 

g x f x x

đồng biến trên khoảng nào?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 49/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688







. B.

 

1;2

. C.









. D.

 

;1 

Lời gii

Sưu tầm: Nguyễn Thị Thu; Fb:Nguyễn Thu

Chọn C

 

g x f x x

   

 

21g x x f x x



   

 

2 1 0

0 0 1

g x x x x

f x x



























      

























Từ đồ thị

 



ta có

 

f x x x x







     







Xét dấu

 



Từ bảng xét dấu ta có hàm số

 

đồng biến trên khoảng









Chuyên đề: Tính đơn điệu của hàm hợp

Trang 50/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Câu 72: Cho hàm số

 

y f x

có đạo hàm trên . Biết hàm số

 

y f x





liên tục trên và có

đồ thị như hình vẽ. Hàm số





1y f x

đồng biến trong khoảng nào dưới đây?

   

; 3 , 0; 3 

. B.

   

; 3 , 3;  

   

3;0 , 3; 

. D.

 

; 3 , 0;  

Lời gii

Sưu tầm: Nguyễn Thị Thu; Fb:Nguyễn Thu

Chọn C

Xét hàm số





1y f x





y f x



  































  



  

















  















  













  







Bảng biến thiên

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 51/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Vậy hàm số





1y f x

đồng biến trên các khoảng

   

3;0 , 3; 

Câu 73: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

y f x x

nghịch biến trên khoảng nào dưới đây.

;



 





. B.

;



 





. C.

;









. D.

;









Lời gii

Sưu tầm:Chu Minh; Fb:Minhchu

Chọn D

Đặt

 

y g x f x x  

 

   

 

2 2 2

. 1 2g x f x x x x x f x x



  

      

Cho

 

0gx





 

1 2 0

f x x

















 

1 2 0

1 ptvn

2 ptvn







  







x

Ta có

 

' 0 0

x x x

f x f x x



  



     









( Luôn đúng với mọi

x

)

Vậy

 

' 0 1 2 0

g x x x     

Hay hàm số

 

g x f x x

nghịch biến trên khoảng

;









Câu 74: Cho ham số

 

y f x

có đạo hàm trên . Đường cong trong hình vẽ bên là đồ thị của

hàm số

 

y f x





(

 

y f x





liên tục trên ). Xét hàm số

 

3g x f x

. Mệnh đề

nào dưới đây sai?

2

1

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 52/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

A. Hàm số

 

đồng biến trên

 

1;0

. B. Hàm số

 

nghịch biến trên

 

;1 

C. Hàm số

 

nghịch biến trên

 

1;2

. D. Hàm số

 

đồng biến trên

 

2;

Lời gii

Sưu tầm:Chu Minh; Fb:Minhchu

Chọn C

 

3g x f x





   

33x f x



  

 

23xf x





Ta có

 

0fx





2x  

nên

f '(x

-3) < 0

32x   

1x

11x   

Ta có bảng xét dấu:



2

1



f '(x

-3)

g '(x)

Từ bảng xét dấu ta thấy Chọn C đúng

Câu 75: Cho hàm số

 

y f x

có đồ thị nằm trên trục hoành và có đạo hàm trên , bảng xét

dấu của biểu thức

 



như bảng dưới đây.

Hàm số

 

f x x

y g x

f x x







nghịch biến trên khoảng nào dưới đây?

 

;1

. B.









. C.

 

1;3

. D.

 

2;

Lời gii

Chọn C

 

   

 

2 2 2

2 . 2 2 2 . 2

2 1 2 1

x x f x x x f x x

f x x f x x





   





   

 

2 2 0

g x x

f x x















  



     







  















Chuyên đề: Tính đơn điệu của hàm hợp

Trang 53/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có bảng xét dấu của

 



Dựa vào bảng xét dấu ta có hàm số

 

y g x

nghịch biến trên các khoảng

 

;1 

và

 

1;3

Câu 76: Cho hàm số

 

có bảng biến thiên như sau:

Hàm số

 

3.y f x f x

nghịch biến trên khoảng nào dưới đây?

 

1; 2

. B.

 

3; 4

. C.

 

; 1

. D.

 

2; 3

Lời gii

Sưu tầm: Lê Liên;Fb: Lien Le

Chọn D

Ta có

 

     

3. . 6. .y f x f x f x f x

  



     

= 3 . . 2f x f x f x









   

2 3 4 1 2 3 4

0 ,4| 1

0 2 , ,3, | 1 2;4

' 0 1,2,3,4

f x x x x

y f x x x x x x x x x

f x x

   







         



  



Lập bảng xét dấu ta có

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 54/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Do đó ta có hàm số nghịch biến trên khoảng

 

2; 3

Câu 77: Cho hàm số

 

y f x

đạo hàm liên tục trên có đồ thị hàm số

 



như hình vẽ

Hỏi hàm số

 

2y f x x

đồng biến trên khoảng nào sau đây?

 

1;0

. B.

 

0;1

. C.

 

1;3

. D.

 

2;

Lời gii

Chọn A

Có

 

2 2 2y x f x x



  

Do đó





 

f x x























  











  

























Ta có bảng xét dấu đạo hàm như sau

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 55/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Dựa vào bảng xét dấu đạo hàm, hàm số

 

2y f x x

đồng biến trên các khoảng

     

1;0 , 1;2 , 3; 

Câu 78: Cho hàm số

 

có đạo hàm, liên tục trên , có đồ thị như hình vẽ

Hỏi hàm số

 

y f x





nghịch biến trên khoảng nào sau đây?

 

1;1

. B.







. C.







. D.

 

2; 1

Lời gii

Chọn C

Có

   

2y f x f x





. Do đó





 







































Ta có bảng xét dấu đạo hàm như sau

Dựa vào bảng xét dấu đạo hàm, hàm số

 

y f x





nghịch biến trên các khoảng

   

; 2 , 1;0 , ;4



  





Câu 79: Cho hàm số

y f x

có bảng biến thiên như sau

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 56/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Có bao nhiêu số nguyên

2019m

để hàm số

2g x f x x m

đồng biến trên

khoảng

A. 2016. B. 2015. C. 2017. D. 2018.

Lời gii

Chọn A

Ta có

2 2 2

2 2 2 1 2g x x x m f x x m x f x x m

Hàm số

y g x

đồng biến trên khoảng

khi và chỉ khi

0, 1;g x x

và

0gx

tại hữu hạn điểm

2 1 2 0, 1;x f x x m x

2 0, 1;f x x m x

2 2, 1;

2 0, 1;

x x m x

Xét hàm số

2y x x m

, ta có bảng biến thiên

Dựa vào bảng biến thiên ta có

TH1:

2 2, 1; 1 2 3x x m x m m

TH2:

2 0, 1;x x m x

: Không có giá trị

thỏa mãn.

Vậy có 2016 số nguyên

2019m

thỏa mãn yêu cầu bài toán.

Câu 80: Cho hàm số

()y f x

có bảng biến thiên như sau:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 57/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

( ) (3 )g x f x

nghịch biến trên khoảng nào trong các khoảng sau?

( 2;5)

. B.

(1;2)

. C.

(2;5)

. D.

(5; )

Lời gii

Chọn C

Từ bảng biến thiên suy ra

( ) 0, (3 ) 0,f x x f x x       

Ta có

'( ) 2 '(3 ). (3 )g x f x f x   

Xét

2 3 1 2 5

0 2 3 . 3 0 3 0

3 2 1

g x f x f x f x

Suy ra hàm số

nghịch biến trên các khoảng

( ;1)

và

(2;5)

Câu 81: Cho hàm số

 

y f x

có đồ thị như hình vẽ. Hàm số đồng biến trong

khoảng nào dưới đây?

 

0;1

. B.

 

1;1

. C.

 

0;2

. D.

 

1;2

Lời gii

Chọn D

Thực hiện liên hoàn biến đổi đồ thị

 

y f x

thành đồ thị

 

y f x

, sau đó biến đổi

đồ thị

 

y f x

thành đồ thị

 

y f x

 

y f x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 58/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Dựa vào đồ thị hàm số

 

y f x

ta suy ra hàm số đồng biến trên khoảng

 

1;2

Câu 82: Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên dưới

Hàm số

 

3g x f x

đồng biến trên khoảng nào trong các khoảng sau?

 

; 1 . 

 

1;2 .

 

2;3 .

 

4;7 .

Lời gii

Chọn B

Dựa vào đồ thị, suy ra

 

  













và

 















 Với

3x 

khi đó

   

3g x f x  

   

30g x f x



  

1 3 1

   























. Do đó hàm số

 

đồng biến trên các khoảng

 

3;4 ,

 

7; .

 Với

3x 

khi đó

         

3 3 0 3 0g x f x g x f x f x

  

         

 

1 3 4

x loai





  







  

  



. Do đó hàm số

 

đồng biến trên khoảng

 

1;2 .

Câu 83: Cho hàm số bậc ba

 

y f x

, hàm số

 

y f x





có đồ thị như hình vẽ. Hỏi hàm số

 

1g x f x

nghịch biến trên khoảng nào dưới đây?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 59/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

1, 

. B.

 

1,0

. C.

 

1,2

. D.

 

,1

Lời gii

Chọn B

Ta có:

 

g x f x





Xét

 

1 ( )

0 1 0

g x f x













  



      































Ta có bảng biến thiên:

Từ bảng biến thiên thì ta có

 

1g x f x

nghịch biến trên khoảng

 

1,1

và đồng

biến trên khoảng

   

, 1 1,   

Câu 84: Có bao nhiêu giá trị nguyên của tham số

nhỏ hơn 10 để hàm số

4 3 2

3 4 12y x x x m

nghịch biến trến khoảng

. B.

. C.

. D.

Lời gii

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 60/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Chọn D

Xét hàm số

4 3 2 3 2

3 4 12 12 12 24f x x x x m f x x x x

f x x

BBT:

Để hàm số

y f x

nghịch biến trên

; 1 5 0 5mm

Do yêu cầu

là số nguyên nhỏ hơn

nên ta có

5;6;7;8;9m

Vậy có 5 giá trị m thỏa yêu cầu.

Câu 85: Cho hàm số

 

y f x

. Đồ thị hàm số

 

y f x





như hình vẽ sau:

Hàm số

 

42g x f x

nghịch biến trên khoảng nào sau đây?

;







. B.

 

;2

. C.







. D.

;







Lời gii

Chọn A

Trường hợp 1:

2x 

. Khi đó

   

42g x f x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 61/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

   

2 4 2g x f x



  

   

4 2 2

4 2 0

1 4 2 3

fgx x





  







    





  







So điều kiện

2x 

ta được

 

nghịch biến trên

;







Trường hợp 2:

2.x 

Khi đó

   

24g x f x

Ta có

   

2 2 4g x f x





   

2 2 4 1

2 4 00

2 4 3 7







   





    



















So điều kiện

2x 

ta được

 

nghịch biến trên

;;

;







  



  

   

Câu 86: Cho hàm số

 

y f x

có đạo hàm

   

 

12f x x x x



  

, với

x

. Số giá trị

nguyên của tham số

để hàm số

 

3g x f x x m  

có

điểm cực trị là

. B.

. C.

. D.

Lời gii

Chọn C

Ta có

 

   

2 3 2

3 6 . 3g x x x f x x m



   

 

3 6 0

0 3 1

x x m

g x x x m

x x m















  





     



  



  



  





  



Vì khi đi qua các nghiệm của phương trình

31x x m  

(nếu có) dấu của

 

3f x x m





không đổi nên dấu của

 



chỉ phụ thuộc các nghiệm của hai

phương trình còn lại.

Vậy hàm số

 

y g x

có 8 điểm cực trị khi và chỉ khi mỗi phương trình

30x x m  

và

32x x m  

phải có ba nghiệm phân biệt (khác

và khác

Xét hàm số

 

3h x x x  

, ta có

 

36h x x x



  

;

 















Bảng biến thiên của hàm số

 

y h x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 62/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Dựa vào bảng biến thiên, ta thấy điều kiện để mỗi phương trình

3x x m  

và

32x x m   

phải có ba nghiệm phân biệt (khác

và khác

) là

0 2 4 2 4m m m      

Vậy chỉ có một giá trị nguyên của

thỏa mãn là

3m 

Câu 87: Cho hàm số xác định trên R và hàm số có đồ thị như hình bên

dưới và với mọi . Đặt . Có bao

nhiêu giá trị dương của tham số để hàm số có đúng hai điểm cực trị?

A. 4. B. 7. C. 8. D. 9.

Lời gii

Chọn C

Ta có ; . Để hàm số có

đúng hai điểm cực trị khi và chỉ khi phương trình có hai nghiệm bội lẻ phân

biệt . Khi đó

 

1,2,3,4,5,10,11,12m

. Vậy có

giá trị của thỏa mãn yêu

cầu đề bài.

Câu 88: Cho hàm số đa thức bậc bốn

 

y f x

, biết hàm số có ba điểm cực trị

3, 3, 5   x x x

. Có tất cả bao nhiêu giá trị nguyên của tham số

sao cho hàm số

 

3



g x f e m

có đúng

điểm cực trị

Lời gii

 

y f x

 

'y f x

 

'0fx

   

; 3,4 9;x    

   

5g x f x mx  

 

   

g x f x m





   

00g x f x m



   

 

f x m





 

y g x

 

0gx





10 13





























Chuyên đề: Tính đơn điệu của hàm hợp

Trang 63/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Chọn D

Ta có:

 

3 2 3 2

2 3 3

3 6 .











x x x x

g x x x e f e m

 

3 2 3 2

2 3 3

0 3 6 . 0





    

x x x x

g x x x e f e m











   









 

3 1

5 3













  













Hàm số

 

có

điểm cực trị khi và chỉ khi tổng số nghiệm đơn và bội lẻ, khác

và

2

của các phương trình

     

1 , 2 , 3

là

Xét hàm số

 

3



h x e

có

 







h x x x e

Ta có

 















Bảng biến thiên:

Khi đó có

trường hợp sau:

Trường hợp 1:

Khi đó:

3 3 51,6

1 3 4 3 57,6



    





      



m e m e

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 64/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

nguyên nên

 

52;53;54;55;56;57m

Trường hợp 2:

Khi đó:

5 5 49,6

1 3 2 3

0 3 1 3 4



    



         





    



m e m e

m e m e m

Trường hợp 3:

Khi đó:

3 1

3 0



  













4 5 49,6



    



    









Vậy có

giá trị nguyên của tham số

thỏa yêu cầu bài toán.

Câu 89: Cho hàm số

)(xfy 

có đạo hàm

 

  





xxxxxf

x

. Tính tổng tất cả các

giá trị nguyên của tham số m để hàm số

 

mxfxg 

có 3 cực trị.

A. 0. B. 6. C. 3. D. 2.

Lời gii

Chọn C

Ta có

     













031

xxxxf

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 65/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Lại có

 













































3 3

2 1

0.2

mxf

mxfxxg

 

có nghiệm luôn là nghiệm bội chẵn; các phương trình

 

có nghiệm không

chung nhau và

mm  3

nên:

Hàm số

 

có 3 cực trị

 

0



 xg

có 3 nghiệm bội lẻ













 m

Vì

m

 

2;1;0 m

. Vậy tổng các giá trị nguyên bằng 3.

Câu 90: Cho hàm số

 

y f x

liên tục trên và có đồ thị như hình vẽ.

Xét hàm số

 

2 1 .g x f x x m   

Tìm

để

 

 

0;1

max 10.gx

3m 

. B.

12m 

. C.

13m 

. D.

6m 

Lời gii

Chọn C

Đặt

 

21t x x x  

với

 

0;1 .x

Ta có

 

 

6 1 0, 0;1 .t x x x



    

Suy ra hàm số

 

đồng biến nên

   

0;1 1;2 .xt   

Từ đồ thị hàm số ta có

 

 

 

 

1;2 1;2

max 3 max 3 .f t f t m m



    





Theo yêu cầu bài toán ta cần có:

3 10 13.mm     

Câu 91: Cho hàm số

 

có đạo hàm trên là

    

13f x x x



  

. Có bao nhiêu giá trị

nguyên của tham số

thuộc đoạn

 

10;20

để hàm số

 

3y f x x m  

đồng biến

trên khoảng

 

0;2

. B.

. C.

. D.

Lời gii

Chọn A

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 66/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

 

3 2 3 3y f x x m x f x x m

  

      

Theo đề bài ta có:

    

13f x x x



  

suy ra

 















và

 

0 3 1f x x



    

Hàm số đồng biến trên khoảng

 

0;2

khi

 

0, 0;2yx



  

 

2 3 3 0, 0;2x f x x m x



      

 

0;2x

nên

 

2 3 0, 0;2xx   

. Do đó, ta có:

 

3 3 3 3

0, 0;2 3 0

3 1 3 1

x x m m x x

y x f x x m

x x m m x x



      



        



     



 

 

 

 

0;2

max 3 3

min 3 1

m x x



  













  







 

10;20m

m

nên có

giá trị nguyên của

thỏa yêu cầu đề bài.

Câu 92: Cho các hàm số

 

4f x x x m  

và

 

    

2 2 2

2018 2019 2020g x x x x   

. Có bao

nhiêu giá trị nguyên của tham số

 

2020;2020m

để hàm số

 

g f x

đồng biến trên

 

2;

2005

. B.

2037

. C.

4016

. D.

4041

Lời gii

Chọn B

Ta có

 

4f x x x m  

 

    

2 2 2 12 10 2

12 10 2 0

2018 2019 2020 ...g x x x x a x a x a x a        

Suy ra

 

34f x x





 

11 9

12 10 2

12 10 ... 2g x a x a x a x



   

Và

 

   

 

11 9

12 10 2

12 10 ... 2g f x f x a f x a f x a f x







   



     

 





10 8

12 10 2

12 10 ... 2f x f x a f x a f x a



   

Dễ thấy

12 10 2 0

; ;...; ; 0a a a a 

và

 

3 4 0f x x



  

2x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 67/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Do đó

   

 





10 8

12 10 2

12 10 ... 2 0f x a f x a f x a



   

2x

Hàm số

 

g f x

đồng biến trên

 

2;

khi

 

0g f x









2x



 

0fx

2x



40x x m  

3x



4m x x  

2x







 

max 4 16m x x



    

Vì

 

2020;2020m

và

m

nên có 2037 giá trị thỏa mãn

Câu 93: Cho hàm số có đạo hàm

1 2 1f x x x x mx

với mọi Có bao

nhiêu số nguyên âm

để hàm số

21g x f x

đồng biến trên khoảng

3;5

Lời gii

Chọn A

Ta có:

 

2 '(2 1) 2(2 1)(2 2) [(2 1) 2 (2 1) 1]g x f x x x x m x



        

Đặt

21tx

Để hàm số đồng biến trên khoảng

3;5

khi và chỉ khi

0, 3;5g x x

( 2 1) 0, 7;11 2 1 0, 7;11 2 , 7;11

t t mt t t mt t m t

Xét hàm số

()





trên

 

7;11

, có

'( )





BBT:

Dựa vào BBT ta có

7;11

1 50

2 , 7;11 2 max

m t m h t m

Vì

{ 3; 2; 1}mm



     

Câu 94: Cho hàm số

 

xác định và liên tục trên

. Hàm số

 

y f x





liên tục trên và có

đồ thị như hình vẽ.

y f x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 68/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Xét hàm số

     

2 2 2020

g x f x m m x    

, với

là tham số thực. Gọi

là tập

hợp các giá trị nguyên dương của

để hàm số

 

y g x

nghịch biến trên khoảng

 

3;4

. Hỏi số phần tử của

bằng bao nhiêu?

. B.

. C.

. D. Vô số.

Lời gii

Chọn B

Ta có

     

' ' 2 2g x f x m m x   

Đặt

     

'h x f x x  

. Từ đồ thị hàm số

 

'y f x

và đồ thị hàm số

yx

trên hình

vẽ suy ra:

   

h x f x x

  



    







Chuyên đề: Tính đơn điệu của hàm hợp

Trang 69/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

   

3 2 1 2 3 2 1

' 2 0

2 3 2 3

x m m x m

g x h x m

x m x m

       



    



   



Suy ra hàm số

 

y g x

nghịch biến trên các khoảng

 

2 3;2 1mm

và

 

2 3;m 

Do đó hàm số

 

y g x

nghịch biến trên khoảng

 

3;4

2 3 3

2 1 4

2 3 3

  





























Mặt khác, do

nguyên dương nên

   

2;3 2;3mS  

. Vậy số phần tử của

bằng

Từ đó Chọn B

Câu 95: Cho hàm số

 

liên tục trên và có đạo hàm

   

 

26f x x x x x m



   

với mọi

. Có bao nhiêu số nguyên

thuộc đoạn

 

2020;2020

để hàm số

1g x f x

nghịch biến trên khoảng

 

;1 

2016

. B.

2014

. C.

2012

. D.

2010

Lời gii

Chọn C

Ta có:

           

1 1 1 1 6 1g x f x x x x x m





          



1 1 4 5x x x x m

Hàm số

 

nghịch biến trên khoảng

 

;1 

 

0, 1g x x



    

, (dấu

xảy ra tại hữu hạn điểm).

Với

1x 

thì

 

10x 

và

10x

nên

4 5 0, 1x x m x

4 5, 1m x x x

Xét hàm số

45y x x

trên khoảng

 

;1 

, ta có bảng biến thiên:

Từ bảng biến thiên suy ra

9m 

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 70/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Kết hợp với

thuộc đoạn

 

2020;2020

và

nguyên nên

 

9;10;11;...;2020m

Vậy có

2012

số nguyên

thỏa mãn đề bài.

Câu 96: Cho hàm số

()y f x

có đồ thị

()fx



như hình vẽ. Có bao nhiêu giá trị nguyên

 

2020;2020m

để hàm số

   

 

2 3 ln 1 2g x f x x mx    

đồng biến trên







2020

. B.

2019

. C.

2021

. D.

2018

Lời gii

Chọn B

+ Ta có

   

2 2 3 2

g x f x m



   



Hàm số

 

đồng biến trên







khi và chỉ khi

     

0, 1;2 2 3 , ;2

g x x m f x x





         







 

min 2 3

m f x













   







 

+ Đặt

23tx

, khi đó

 

;2 2;1



   





Từ đồ thị hàm

 



suy ra

   

0, 2;1f t t



   

và

 

0ft





khi

1t 

Tức là

 

2 3 0, ;2

f x x





   





 

min 2 3 0











  

khi

1x 

 

+ Xét hàm số

 





trên khoảng







. Ta có

 









và

 

0 1 0 1h x x x



      

-2

-1

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 71/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Bảng biến thiên của hàm số

 

trên







như sau:

Từ bảng biến thiên suy ra

 

hx

 

min









  

khi

1x 

 

Từ

 

và

 

suy ra

m 

Kết hợp với

m

 

2020;2020m

thì

 

2019; 2018;....; 2; 1m    

Vậy có tất cả

2019

giá trị

cần tìm.

Câu 97: Cho hàm số

 

y f x

liên tục trên và có đồ thị như hình vẽ.

Hàm số

 

2 3 2

4 3 6 2020g x f x x x x x     

đồng biến trên khoảng nào sau đây?









. B.

 

2;0

. C.

 

1; 

. D.

 

0;1

Lời gii

Chọn D

Ta có

   

 

2 1 12 6 6g x x f x x x x



     

Từ đồ thị hàm số

 

y f x

suy ra

 

0 1 2f x x



    

. Do đó

 

1 1 0;

0 2 1

2 2 0

x x x x x

f x x x

x x x x



       





       



    





Chuyên đề: Tính đơn điệu của hàm hợp

Trang 72/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có bảng xét dấu

 



Vậy hàm số

 

đồng biến trên khoảng









Câu 98: Cho hàm số

 

y f x

xác định trên và có bảng xét dấu đạo hàm như sau:

Biết

 

2,f x x  

. Xét hàm số

   

 

3 2 3 2020g x f f x x x    

. Khẳng định nào

sau đây đúng?

A. Hàm số

 

đồng biến trên khoảng

 

2; 1

B. Hàm số

 

nghịch biến trên khoảng

 

0;1

C. Hàm số

 

đồng biến trên khoảng

 

3;4

D. Hàm số

 

nghịch biến trên khoảng

 

2;3

Lời gii

Chọn D

Ta có:

     

 

' 2 ' ' 3 2 3 6g x f x f f x x x    

Vì

 

2,f x x  

nên

 

3 2 1fx  

x

Từ bảng xét dấu

 

'fx

suy ra

 

' 3 2 0,f f x x   

Từ đó ta có bảng xét dấu sau:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 73/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Từ bảng xét dấu trên, loại trừ đáp án suy ra hàm số

 

nghịch biến trên khoảng

 

2;3

Câu 99: Cho hàm số

()y f x

xác định trên . Hàm số

 

( ) ' 2 3 2y g x f x   

có đồ thị là một

parabol với tọa độ đỉnh

 

2; 1I 

và đi qua điểm

 

1;2A

. Hỏi hàm số

()y f x

nghịch

biến trên khoảng nào dưới đây?

 

5;9

. B.

 

1;2

. C.

 

;9

. D.

 

1;3

Lời gii

Chọn A

Xét hàm số

 

( ) ' 2 3 2g x f x  

có đồ thị là một Parabol nên có phương trình dạng:

 

()y g x ax bx c P   

Vì

 

có đỉnh

 

2; 1I 

nên

 

4 4 0

4 2 1 4 2 1

b a a b

a b c a b c







   







  

       









 

đi qua điểm

 

1;2A

nên

 

1 2 2g a b c    

Ta có hệ phương trình

4 0 3

4 2 1 12

2 11

a b a

a b c b

a b c c

  





      





   



nên

 

3 12 11g x x x  

Đồ thị của hàm

()y g x

là

Theo đồ thị ta thấy

'(2 3) 0 '(2 3) 2 2 1 3f x f x x        

Đặt

t x x



   

khi đó

'( ) 0 1 3 5 9

f t t



      

Vậy

()y f x

nghịch biến trên khoảng

 

5;9

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 74/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Câu 100: Cho hàm số

 

y f x

có đạo hàm cấp

liên tục trên và thỏa mãn

       

. 1 4f x f x x x x



  

với mọi

x

và

       

2.g x f x f x f x

 







. Hàm số

 

2h x g x x

đồng biến trên khoảng nào dưới đây?

 

;1

. B.

 

2;

. C.

 

0;1

. D.

 

1;2

Lời gii

Chọn D

Ta có

                 

2 2 . 2 . 2 . ;g x f x f x f x f x f x f x f x f x

      

    

Khi đó

 

    

2 2 2 2

2 2 2 2 2 2 2 2 1 2 4h x x g x x x x x x x x x



          

 



























Ta có bảng xét dấu của

 



Suy ra hàm số

 

2h x g x x

đồng biến trên khoảng

 

1;2

Câu 101: Cho hàm số

()y f x

liên tục trên . Biết rằng hàm số

'( )y f x

có đồ thị như hình vẽ.

Hàm số

( 5)y f x

nghịch biến trên khoảng nào sau đây?

( 1;0)

. B.

(1;2)

. C.

( 1;1)

. D.

(0;1)

Lời gii

Chọn D

+ Đặt

( ) ( 5) ( ), 5g x f x f u u x    

'( ) ( 5)' '( ) 2 '( 5)g x x f u xf x   

+ Hàm số

()y g x

nghịch biến khi

'( ) 0gx

và dấu bằng xảy ra tại hữu hạn điểm

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 75/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

()

'( 5) 0

2 '( 5) 0

()

'( 5) 0

xf x

















   



















Giải (I): Từ đồ thị hàm số

'( )y f x

ta có

()

4 5 1

1 2 1







  



























  











   











     

     



















Xét (II): Từ đồ thị

'( )y f x

ta có

5 4 1 1 1

()

4 2 2

1 5 2 7 2 2 7

7 7 7

7 2 2 7

x x x









        











     





            







    













  





  

















  





      







Vậy hàm số đồng biến trên mỗi khoảng:

 

   

 

; 7 ; 2; 1 ; 0;1 ; 2; 7   

. Chọn D

Câu 102: Cho hàm số

()y f x

. Hàm số

'( )y f x

có đồ thị như hình vẽ bên.

Hàm số

()y f x

đồng biến trên khoảng

;

0;2

2; 1

Lời gii

Chọn C

'( )y f x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 76/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Xét hàm

'( ) ( 1)( 1)( 4)f x x x x

. Đặt

()g x f x

Có

2 2 2 2

'( ) 2 '( ) 2 ( 1)( 1)( 4)g x xf x x x x x

. Suy ra

'( ) 0 1

g x x

Xét dấu

'( )gx

Câu 103: Cho hàm số

 

.y f x

Hàm số

 

y f x





có đồ thị như hình bên.

Hàm số

 

32y f x

nghịch biến trên khoảng

 

1; 

 

0;2

 

;1 

 

1;3

Lời gii

Chọn C

Ta có

   

2 3 2 2

2. 3 2 ; 0 3 2 0

3 2 5

y f x y f x



   







   

        











Vậy hàm số

 

32y f x

nghịch biến trên các khoảng

 

;1 

và







Câu 104: Cho hàmsố

()y f x

có đạo hàm trên . Đường cong trong hình vẽ dưới là đồ thị của

hàm số

'( )y f x

. Xét hàm số

( ) (3 )g x f x

-4 -3 -2 -1 1 2 3 4 5 6 7

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 77/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Mệnh đề nào dưới đây là đúng?

A. Hàm số

()gx

đồng biến trên

( ;1)

B. Hàm số

()gx

đồng biến trên

(0;3)

C. Hàm số

()gx

nghịch biến trên

( 1; ) 

D. Hàm số

()gx

nghịch biến trên

( ; 2) 

và

(0;2)

Lời gii

Chọn D

Ta có

 

' 2 ' 3g x xf x  

 

3 1 2

' 3 0



    



   









Ta có bảng xét dấu:

Hàm số

()gx

nghịch biến trên

( ; 2) 

và

(0;2)

Câu 105: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ. Hàm số

 

y f e

nghịch biến trên khoảng nào sau đây?

f(x)=x^3-3x^2

f(x)=-4

x(t)=2 , y(t)=t

T?p h?p 1

-







 

0;

. B.

 

;0

. C.

 

1;3

. D.

 

2;1

-1

(

)

∞

(3-

)

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 78/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Lời gii

Phân tích

Dựa vào đồ thị hàm

 

y f x





, suy ra nghiệm

 

0fx





và dấu của

 



Dùng tính chất hàm hợp xét dấu

 





, suy ra dấu của

 

e f e





. Từ đó chọn

đáp án.

Chọn B

Ta có

 















Xét

 

y f e

, có

 

y e f e





;

 

0 . 2 0

y e f e



   





  







Mặt khác,

 

0 . 2 0

y e f e



   

2 3 0

ex    

Do đó hàm số

 

y f e

nghịch biến trên

 

;0

Câu 106: Cho hàm số

 

có đạo hàm liên tục trên và có đồ thị của hàm

 



y f x

như

hình vẽ. Xét hàm số

 

( ) 2g x f x

. Mệnh đề nào dưới đây sai?

A. Hàm số

()gx

đồng biến trên

 

2; .

B. Hàm số

()gx

nghịch biến trên

 

0;2 .

C. Hàm số

()gx

nghịch biến trên

 

1;0 .

D. Hàm số

()gx

nghịch biến trên

 

; 2 . 

Lời gii

Chọn C

Dựa vào đồ thị hàm số

 















và

 



  f x x

Xét

 

2g x f x

có tập xác định

   

' 2 .



g x x f t

với

2tx

1

4

2

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 79/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

' 0 2 1 1











        





  



g x t x x

Lại có

 

0 2 2







     







f t t x

Do đó, ta có bảng xét dấu

 

'gx



2

1



 











Từ bảng xét dấu ta chọn phát biểu sai là C

Câu 107: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

2y f x

đồng biến trên khoảng:

 

1;3

. B.

 

2;

. C.

 

2;1

. D.

 

;2

Lời gii

Chọn C

Ta có:

 

     

2 2 . 2 2f x x f x f x





      

Hàm số đồng biến khi

 

2 1 3

2 0 2 0

1 2 4 2 1

f x f x

   





      



     



Câu 108: Cho hàm số

 

y f x

có đạo hàm là hàm số

 



trên . Biết rằng hàm số

 

22y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

nghịch biến trên

khoảng nào?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 80/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

;2

. B.

 

1;1

. C.

;







. D.

 

2;

Lời gii

Chọn B

Hàm số

 

22y f x



  

có đồ thị

 

như sau:

Dựa vào đồ thị

 

ta có:

       

2 2 2, 1;3 2 0, 1;3f x x f x x



         

Đặt

*2xx

thì

   

* 0, * 1;1



   f x x

Vậy: Hàm số

 

nghịch biến trên khoảng

 

1;1

Cách khác:

Tịnh tiến sang trái hai đơn vị và xuống dưới 2 đơn vị thì từ đồ thị

 

sẽ thành đồ thị

của hàm

 



y f x

. Khi đó:

   

0, 1;1f x x



   

Vậy: Hàm số

 

nghịch biến trên khoảng

 

1;1

Phân tích: Cho biết đồ thị của hàm số

 



sau khi đã tịnh tiến và dựa vào đó để xét

sự đồng biến của hàm số

 

Câu 109: Cho hàm số

 

y f x

có đạo hàm là hàm số

 



trên . Biết rằng hàm số

 

22y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

đồng biến trên khoảng

nào?

   

;3 , 5; 

. B.

   

; 1 , 1;  

. C.

 

1;1

. D.

 

3;5

Lời gii

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 81/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Chọn B

Hàm số

 

22y f x



  

có đồ thị

 

như sau:

Dựa vào đồ thị

 

ta có:

           

2 2 2, ;1 3; 2 0, ;1 3;f x x f x x



             

Đặt

*2xx

suy ra:

     

* 0, * ; 1 1;f x x



     

Vậy: Hàm số

 

đồng biến trên khoảng

   

; 1 , 1;  

Câu 110: Cho hàm số

 

y f x

có đạo hàm là hàm số

 



trên . Biết rằng hàm số

 

22y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

nghịch biến trên

khoảng nào?

   

3; 1 , 1;3

. B.

   

1;1 , 3;5

. C.

   

; 2 , 0;2 

. D.

   

5; 3 , 1;1  

Lời gii

Chọn B

Hàm số

 

22y f x



  

có đồ thị

 

như sau:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 82/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Dựa vào đồ thị

 

ta có:

           

2 2 2, 3; 1 1;3 2 0, 3; 1 1;3f x x f x x



              

Đặt

*2xx

suy ra:

     

* 0, * 1;1 3;5f x x



   

Vậy: Hàm số

 

đồng biến trên khoảng

   

1;1 , 3;5

Câu 111: Cho hàm số

 

có đạo hàm cấp một là

    

12f x x x x



  

. Khi đó hàm số

 

21fx

không đồng biến trên khoảng nào dưới đây?

 

0;1

. B.









. C.

 

1;3

. D.

 

2;

Lời gii

Chọn A

Xét hàm số

 

21y f x

ta có

     

2 2 1 2 2 1 .2 . 2 1y f x x x x



    

  

4 2 1 2 1x x x  

Hàm số

 

21fx

đồng biến





;0 ;

   

    

   

   

Do đó trên các khoảng









 

1;3

 

2;

hàm số đồng biến. Trên khoảng

 

0;1

hàm số vừa đồng biến vừa nghịch biến.

Câu 112: Cho hàm số

 

có đạo hàm xác định trên . Biết rằng hàm số

 

và các hàm số

 

f ax b

 

2f x bx a

đều đồng biến trên , với

là tham số thực khác

và

là

tham số thực. Kết luận đúng và đủ nhất về các tham số thực

,ab

là:

0; 0ab

. B.

0; 0ab

. C.

0; 0ab

. D.

0; 0ab

Lời gii

Chọn A

Có

 

0,f x x



  

   

. 0,f ax b a f ax b x



     





     

3 2 3

2 3 2 0,f x bx a x b f x bx a x







        



Suy ra

3 0,

x b x











   



Câu 113: [2D1-4] Cho hàm số

 

y f x

có đồ thị hàm số

 



y f x

như hình vẽ. Hàm số

 

2  g x f x x

đồng biến trên khoảng nào?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 83/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

1;2

. B.

 

3; 

. C.







. D.

 

1; 

Lời gii

Chọn A

Dựa vào đồ thị hàm số

 



y f x

, ta có bảng biến thiên sau





 









 





Ta có

 

2  g x f x x



   

 

2 2 2



    g x x f x x

ycbt



 

0gx







 

2 2 0

f x x

   











  









  













  











2 2 0

   



























  







  









  







 

2 2 0

x x luôn đúng















































   





























































Nhận xét: Chọn A thỏa mãn yêu cầu bài toán.

Câu 114: [2D1-4] Cho hàm số

 

y f x

có đạo hàm

    



  f x x x x

x

. Với tham số

thực

thuộc khoảng nào sau đây thì hàm số

 

g x f x m

đồng biến trên

 

1; 







. B.

 

1;4

. C.







. D.

 

0;1

Lời gii

Chọn B

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 84/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

 

     

2 3 2 3 3 3

3 . 3 . 1 2



       g x x f x m x x m x m x m

Hàm số

 

đồng biến khi

 



gx

   

2 3 3 3

3 1 2 0      x x m x m x m



3 3 3

1 ; 2 ;x m m m

  

       

  

Hàm số đồng biến trên

 

1; 

khi

2 1 1mm   

hay





1;m 

Nhận xét:

 

1;4

thỏa mãn yêu cầu bài toán.

Câu 115: Cho hàm số

 

y f x

có đạo hàm liên tục trên . Đồ thị hàm số

 

y f x





như hình

vẽ. Hàm số

   

21g x f x

đồng biến trên khoảng nào?

 

2;3

. B.

 

1; 

. C.

 

0;1

. D.

 

3; 

Lời gii

Chọn B

   

2 2 1g x f x





   

0 2 2 1 0 2 1 1 1g x f x x x



        

Hàm số

   

21g x f x

đồng biến trên khoảng

 

1; 

Câu 116: Cho hàm số

 

y f x

có đạo hàm

    

13f x x x m x



   

. Có bao nhiêu số nguyên

âm

để hàm số

 

y f x

đồng biến trên khoảng

 

1; 

. B.

. C.

. D.

Lời gii

Chọn.

    

2 4 2 2

2 2 . . 1 3y xf x x x x m x



    

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 85/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688









   







Hàm số

 

y f x

đồng biến trên khoảng

 

1; 

 

0, 1;yx



    

  

   

5 2 2 2

2 . 1 3 0, 1; 3 0, 1;x x m x x m x x              

 

3 max

 

   

không có giá trị

thỏa mãn

Câu này bị sai ko có đáp án mong th cô xem xét cẩn thận giúp

Câu này thầy giải chính xác rồi. Không có đáp án đúng.

Câu 117: Cho hàm số

 

y f x

có đạo hàm liên tục trên . Đồ thị hàm số

 

y f x





có đồ thị

như hình vẽ. Hỏi hàm số

   

g x f x x   

nghịch biến trên khoảng nào sau đây?

 

3;1

. B.

 

2;0

. C.









. D.

 

1;3

Lời gii

Chọn B

Ta có

   

11g x f x x



    

Vậy

 

0gx





 

11f x x



   

Ta có đồ thị

 

1y f x





màu xanh là ảnh của đồ thị

   

:C y f x





qua phép lấy đối

xứng qua

và tịnh tiến qua phải 1 đơn vị.

1

3

1

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 86/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Đồ thị

1yx

là đường thẳng màu đỏ đi qua hai điểm

 

4;3

;

 

2; 3

và

 

0; 1

Hàm số

 

nghịch biến hay

 

0gx





Căn cứ vào đồ thị ta được đáp án là B.

Câu 118: Cho hai hàm số

 

và

 

có đồ thị các đạo hàm cho như hình vẽ với

 



(màu

hồng) và

 



(màu xanh) có đồ thị như hình vẽ. Hỏi hàm số

     

12h x f x g x  

đồng biến trên khoảng nào sau đây?

 

1;0

. B.







. C.









. D.







Lời gii

Chọn B



1

2

3

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 87/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

     

1 2 2h x f x g x

  

  

Đồ thị hàm

 

1y f x





là sự tịnh tiến sang phải 1 đơn vị của đồ thị hàm

 

y f x





Đồ thị hàm

 

2y g x





sự co lại 2 đơn vị theo trục

của đồ thị hàm

 

y g x





Đồ thị hàm

 

22y g x





sự lớn lên 2 đơn vị theo trục

của đồ thị hàm

 

2y g x





Ta có

 

2 1 3 4 1 0

h f g



   

  

       

   

   

loại A.

Loại ngay C, D vì hình vẽ.

Ta Chọn B

Câu 119: Cho hàm số

 

có đồ thị như hình vẽ. Hàm số

 

32fx

nghịch biến trên khoảng

 

;



. Khi đó giá trị lớn nhất của





là:

. B.

. C.

. D.

Lời gii

Chọn D

Ta có:

   

3 2 3. 3 2y f x y f x



    

 

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 88/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số

 

32y f x

nghịch biến

   

0 3. 3 2 0 3 2 0y f x f x

  

       

1 3 2 4 1 2xx      

Vậy khoảng

 

;



lớn nhất là

 

1;2

Câu 120: Cho hai hàm số

 

và

 

có đồ thị như hình vẽ. Biết rằng hai hàm số

 

21fx

và

 

g ax b

có cùng khoảng nghịch biến. Khi đó giá trị của biểu thức

 

4ab

bằng:

. B.

2

. C.

4

. D.

Lời gii

Chọn C

+) Hàm số

 

y f x

nghịch biến trên khoảng

 

1;3

Hàm số

 

21y f x

có

 

2 2 1y f x





Với

   

0 2. 2 1 0 2 1 0 1 2 1 3 1 2y f x f x x x

  

             

Vậy hàm số

 

21y f x

nghịch biến trên khoảng

 

1;2

+) Hàm số

 

y g ax b

có đạo hàm

 

.y a g ax b





 

ax b

y a g ax b

ax b b













    



  











+ Nếu



   

Hàm số nghịch biến trên các khoảng

; ; ;



   

  

   

   

(không thỏa mãn).

+ Nếu



   

 

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 89/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Hàm số nghịch biến trên khoảng

;











Do hàm số có cùng khoảng nghịch biến là

 

1;2

nên

b b b





  











  







   





Vậy

44ab  

Câu 121: Cho hai hàm số

 

và

 

có đồ thị biễu diễn đạo hàm

 



và

 



như hình

vẽ.

Biết rằng hàm số

   

2y f x g x  

đồng biến trong khoảng

 

;



thỏa giá trị lớn

nhất của





; phương trình tiếp tuyến với đồ thị hàm số

 

y g x

tại điểm có

hoành độ

11x 

là

32yx

và phương trình tiếp tuyến với đồ thị hàm số

 

y f x

tại điểm có hoành độ

9x 

là

1y ax

. Giá trị của

 

bằng

. C.

26

. D.

Lời gii

Chọn B

Đặt

     

2h x f x g x  

Ta có

     

2h x f x g x

  

  

Cách 1

Theo hình vẽ ta có

   

13fg





nên

     

1 1 3 0h f g

  

  

Do hàm số

 

đồng biến trong khoảng

 

;



và giá trị lớn nhất của biểu thức





bằng

nên

 

90h





   

9 11 0fg



  

30a  

3a

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 90/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Mặt khác điểm

 

9;9 1Ma

là tiếp điểm giữa tiếp tuyến

1y ax

với đồ thị của hàm

 

nên

 

9 9 1 27 1 28fa    

Cách 2

 

0hx





   

2f x g x



  

 

Để hàm số

 

tồn tại khoảng đồng biến

 

;



thì phương trình

 

có hai nghiệm

phân biệt





và





Lại có đồ thị hàm số

 

2gx





có được bằng cách tịnh tiến đồ thị hàm số

 



qua trái

đơn vị. Từ hình vẽ, ta suy ra phương trình

 

có hai nghiệm phân biệt là

1x 

và















Theo đề bài









, hay

   

9 9 2fg





3a

Từ đó tiếp tuyến của đồ thị hàm số

 

y f x

tại điểm có hoành độ

9x 

là

31yx

nên

 

9 1 9 28fa  

Câu 122: Cho hàm số

 

y f x

có đạo hàm

 



xác định trên và có bảng biến thiên như

hình vẽ. Khi đó hàm số

 

2f x x

nghịch biến trên khoảng nào dưới đây?







. B.

 

1;2

. C.

 

1;1 3

. D.

 

2;2

Lời gii

Chọn C

Ta có:

 

2 0 2 2 2 0f x x x f x x







     



 

2 2 0

f x x

  















































Chuyên đề: Tính đơn điệu của hàm hợp

Trang 91/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

1 2 2

x x Vn











  































   





1 3 1 3













































   







1 1 3









  





Do đó: hàm số

 

2f x x

nghịch biến trên các khoảng

 

;1 3 

và

 

1;1 3

Câu 123: (4) Cho hai hàm số

 

và

 

có một phần đồ thị biểu diễn đạo hàm

 



và

 



như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số

để hàm số

   

2019y f x g x a x   

tồn tại một khoảng đồng biến

 

;



. B.

. C.

. D.

Lời gii

Chọn C

Đặt

     

2019h x f x g x a x   

     

h x f x g x a

  

   

Xét

 

0hx





   

f x g x a



  

 

Trong đó đồ thị

 

g x a





có được bằng cách tịnh tiến đồ thị

 



lên trên

đơn vị.

Từ đồ thị, để tồn tại một khoảng đồng biến

 

;



thì phương trình

 

cần có hai

nghiệm phân biệt









Do đó

0 11a

0 11a  

(do

0a 

)

Vì

nguyên dương nên

 

1;2;3a

Câu 124: (4) Cho hàm số

 

y f x

có đồ thị đạo hàm

 



được cho như hình vẽ bên dưới.

Hàm số

 

3 2 2 2019y f x x x    

đồng biến trên khoảng nào dưới đây?

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 92/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688









. B.

 

0;1

. C.

 

1;0

. D.

;









Lời gii

Chọn B

Đặt

   

3 2 2 2019g x f x x x    

   

3 3 2 2 2g x f x x



    

   

2 10

3 3 2 3 2

f x x



    

 

0gx





   

2 10

3 2 3 2

f x x



    

 

Xét đường thẳng

2 10

yx  

, dễ thấy



đi qua các điểm có tọa độ









và

 

5;0

hay phương trình

 

2 10

f x x





có hai nghiệm phân biệt là

x 

và

5x 

Từ đó phương trình

 

3 2 5





























Chuyên đề: Tính đơn điệu của hàm hợp

Trang 93/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Bảng biến thiên:

Vậy hàm số

 

đồng biến trên khoảng









nên Chọn B

Câu 125: Cho hàm số

 

y f x

có đồ thị đạo hàm

 



được cho như hình vẽ bên dưới. Hàm

số

 

3 1 3 2020y f x x x    

đồng biến trên khoảng

 

;ab

. Giá trị lớn nhất của

ba

bằng

. B.

. C.

. D.

Lời gii

Chọn C

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 94/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có

 

3 3 1 3 3y f x x



   

 

3 3 1 1 1f x x





   



Đặt

31tx





 



   

 

y f t







   





Vẽ đồ thị hàm số

 





trên cùng hệ trục tọa độ với đồ thị của hàm số

 



Dựa vào đồ thị ta có:

 

4;5t

thì đồ thị hàm số

 



nằm trên đồ thị hàm số

 





nên





hay

 

y f t







  





đồng biến trên khoảng

 

4;5

tức là hàm số

 

3 1 3 2020y f x x x    

đồng biến trên khoảng

 

1;2

do đó

1; 2 3a b b a     

Câu 126: Cho hàm số

 

y f x

có biểu thức đạo hàm là

    

12f x x x x



  

, với

x

. Hỏi

hàm số

 

1 2 2018y f x x   

đồng biến trên khoảng nào sau đây?

 

2;

. B.

 

1;2

. C.

 

1; 

. D.

 

;1 

Lời gii

Chọn A

Ta có

 

2 1 2y xf x



  

   

2 2 2

2 . 1 . . 1 2x x x x   

Đặt

 

   

2 2 2

2 . 1 . . 1 2h x x x x x   

2 2 2xx  

 

14 6h x x x





 

0hx



















Bảng biến thiên

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 95/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Vì

















nên loại các Chọn B, C, D.

Mặt khác

 

20h 

và

 

0 2h x x  

do đó

0 2yx



  

, Chọn A thỏa mãn.

Câu 127: Cho hàm số

y f x

có đạo hàm

2 1 2018f x x x x g x

và

0gx

với

. Hỏi hàm số

1 2018h x f x x

đồng biến trên khoảng nào

sau đây?

 

1;2

. B.

 

1;2

. C.

 

2;

. D.

 

1; 

Lời gii

Chọn B

Ta có:

1 2018h x f x x

1 2018h x f x

1 1 2 1x x x g x

0gx

với

nên

10gx

với

0hx

nên ta có bảng biến thiên của hàm số

như sau:

Vậy hàm số

đồng biến trên khoảng

1;2

. Chọn B

Câu 128: Cho hàm số

 

y f x

có đạo hàm

   

 

19f x x x x mx



   

x

. Có bao nhiêu

số nguyên dương

để hàm số

   

3g x f x

đồng biến trên khoảng

 

3; 

. B.

. C.

. D.

Lời gii

Chọn B

Ta có

   

3g x f x



  

Đặt

3tx

, ta thấy

3x 

khi và chỉ khi

0t 

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 96/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Suy ra hàm số

   

3g x f x

đồng biến trên khoảng

 

3; 



hàm số

 

y f x

nghịch biến trên khoảng

 

;0

Vì

   

 

19f x x x x mx



   

, mà

 

1 0,xx   

nên

   

0, ;0f x x



    

9 0,x mx x   

hoặc

90x mx  

có hai nghiệm dương phân biệt.

TH1:

9 0,x mx x   

36 0m    

 

6;6m  

, mà

nguyên dương nên

 

1;2;3;4;5;6m

TH2:

90x mx  

có hai nghiệm dương phân biệt

36 0







  









6m  

, mà

nguyên dương nên

m

Câu 129: Cho hàm số

 

y f x

có đồ thị như hình vẽ bên. Hỏi hàm số

 

1g x f x

đồng

biến trên khoảng nào sau đây?

 

;1 

. B.

 

2; 1

. C.

 

1;0

. D.

 

0;2

Lời gii

Chọn C

Từ đồ thị của hàm số

 

y f x

ta suy ra đồ thị của hàm số

 

1g x f x

có hình

dạng như sau:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 97/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Dựa vào đồ thị ta Chọn C

Câu 130: Cho hàm số

 

y f x

có đạo hàm

   

 

1 3 1f x x x x mx



   

x

. Có bao nhiêu

giá trị nguyên âm của tham số

để hàm số

 

g x f x

đồng biến trên khoảng

 

0;

. B.

. C.

. D.

Lời gii

Chọn B

Ta có

 

     

2 3 2 8 6

2 . 2 1 3 1g x x f x x x x mx



    

Hàm số

 

đồng biến trên khoảng

 

0;

khi

   

0, 0;g x x



   

Hay

 

3 1 0, 0;x mx x     

 

3 , 0;m x x

      

Xét hàm số

   

3 , 0;h x x x

    

ta có:

 

6 , 0;

h x x x





     

 

01h x x



  

Dựa vào bảng biến thiên ta được:

 

3 , 0; 4m x x m

        

Vì





nên

 

4; 3; 2; 1m    

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 98/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Câu 131: Cho hàm số

 

y f x

có đồ thị hàm số

 

y f x





như hình vẽ bên. Hỏi hàm số

 





đồng biến trên khoảng nào sau đây?

 

;2

. B.

 

1;3

. C.

 

1;4

. D.

 

2; 1

Lời gii

Chọn C

Ta có

 













 

2 2 2 .2 .ln2







. Hàm số

 

đồng biến khi

 

0gx





 

2 2 0fx



  

2 2 4

0 2 2 2









  











  



Câu 132: Cho hàm số

 

có biểu thức đạo hàm là

    

11f x x x x



  

. Khi đó hàm số

 

sinfx

đồng biến trên khoảng nào dưới đây?







. B.

 

; 10 

. C.

 

2;4

. D.







Lời gii

Chọn D

Xét hàm số

 

siny f x

Ta có:

     

sin sin . siny f x x f x











  

cos .sin . sin 1 sin 1x x x x  

 

sin2 . 1 sin

xx  

sin2 .cos

xx

Cho

0 sin2 .cos 0y x x



   

sin2 0

cos 0





























 

k 





 

k 

Ta thấy:

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 99/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688



;3 ;



   

  

   

   

sin2 0x



hàm số

 

siny f x

đồng biến trên







Câu 133: Cho hàm số

 

có biểu thức đạo hàm là

 

'2f x x ax  

. Biết rằng hàm số

 

sinfx

nghịch biến trên khoảng

;









. Hỏi có bao nhiêu giá trị nguyên của

 

2019;2019a

thỏa mãn bài toán?

2022

. B. 2023. C. 2021. D. 2020.

Lời gii

Chọn B

Đặt

sinux

;

 

; 0;1





  





Ta có

' 2sin .cos 0, ;

u x x x





   





và

 

   

' sin ' ' . '

x x u

f x f u u f u

Để hàm số

 

' siny f x

nghịch biến trên khoảng

;









thì

 

' sin 0, ;

f x x





  





 

' . ' 0, ;

u f u x





   





   

' 0, 0;1

f u u   

 

2 0, 0;1u au u     

 

, 0;1a u u

     

 

 

0;1

max 3a g u a    

Kết hợp

 

2019;2019a

suy ra

3 2019a  

. Vậy có 2023 số nguyên thỏa mãn ycbt.

Câu 134: Cho hàm số

 

có biểu thức đạo hàm là

 

200

f x x x



  

. Biết rằng hàm số

 

cosfx

đồng biến trên khoảng

;









. Hòi có bao nhiêu giá trị nguyên

 

2019;2019b

thỏa mãn bài toán?

1969

. B.

1968

. C.

1970

. D.

1971

Lời gii

Chọn C

Xét

 

cosy f x

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 100/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Ta có:

 

2sin .cos . cos 0, ;

y x x f x x







    





với

; cos 0, sin 0

x x x







   





Suy ra

 

2 4 2

cos 0 cos cos 0 ;

200 2 6

f x x x x







      





, đặt

cos 0

t x t   

Suy ra

, 0;

200 4

t t t



   





 

max

200

tt  

200 4

b   

Nên

 

50,51,...,2019b

có 1970 số nguyên.

Câu 135: Cho hàm số

 

đồng biến trên . Khi đó hàm số

   

y f x f x  

đồng biến trên

khoảng nào dưới đây?

 

;0

. B.

 

1;1

. C.

 

0;

. D. .

Lời gii

Chọn D

Ta có: hàm số

 

đồng biến trên

 

' 0,f x x   

 

' 0,f x x    

   

 

   

' ' ' ' 0,y f x f x f x f x x         

Vậy hàm số đồng biến trên .

Câu 136: Cho hàm số

 

có đạo hàm xác định trên ? Biết rằng hàm số

   

y f x f x  

đồng biến trên khoảng

 

2;5

. Hỏi hàm số

   

y f x f x  

luôn đồng biến trên

khoảng nào dưới đây?

 

1;4

. B.

 

;5 

. C. . D.

 

4; 3

Lời gii

Chọn D

Ta có: hàm số

   

y f x f x  

đồng biến trên khoảng

 

2;5

     

' ' ' 0, 2;5y f x f x x      

Đặt

   

( ) ' 'g x f x f x  

Ta thấy

()gx

là hàm số chẵn trên

nên

     

( ) ' ' 0, 5; 2g x f x f x x       

 

' 0, 5; 2yx     

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 101/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

 

' 0, 4; 3yx     



Hàm số luôn đồng biến trên

 

4; 3

. Chọn D

Câu 137: Cho hàm số

()fx

liên tục và xác định trên

có đồ thị biểu diễn đạo hàm

'( )fx

như

hình vẽ. Khi đó hàm số

( ) ( )y f x f x  

đồng biến trên khoảng nào dưới đây?

 

0;

. B.

 

3;0

. C.

 

1;4

 

5; 2

Lời gii

Chọn B

Ta có:

' '( ) '( )y f x f x  

' 0 4







  







Hàm số đồng biến trên

 

4;0

. Chọn B

Chuyên đề: Tính đơn điệu của hàm hợp

Trang 102/102

Giáo viên: Nguyễn Hoàng Việt

Website: http://luyenthitracnghiem.vn

 0905193688

Câu 138: Cho hàm số

()fx

liên tục và xác định trên

, có biểu thức đạo hàm

'( )

fx



. Biết

rằng hàm số

1 2 3 2018

...

2019 2019 2019 2019 2019

x x x x a x

y f f f f

   

       

     

       

       

luôn đồng

biến trên

và

là tham số nguyên. Hỏi có tất cả bao nhiêu số chính phương

thỏa

yêu cầu bài toán?

. B.

. C.

. D.

Lời gii

Chọn B

1 1 2 3 2018

' ' ' ' ... ' 0,

2019 2019 2019 2019 2019

x x x x

y f f f f a x R

     

       

       

       



       



9 9 3

'(1 )

9 3 9 3.9 3 9

a a a



   

  

'(1 ) ( ) 1f a f a  

Do đó:

(*) 1009 0 1009 1009 31,765a a a       

là số chính phương nên

 

1;4;9;16;25a

. Chọn B

Bấm Tải xuống để xem toàn bộ.

| 1/102

| | Tải xuống

Preview text:

Chuyên đề: Tính đơn điệu của hàm hợp Trang 1/102 138
BÀI TOÁN CHỌN LỌC
TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP Câu 1:
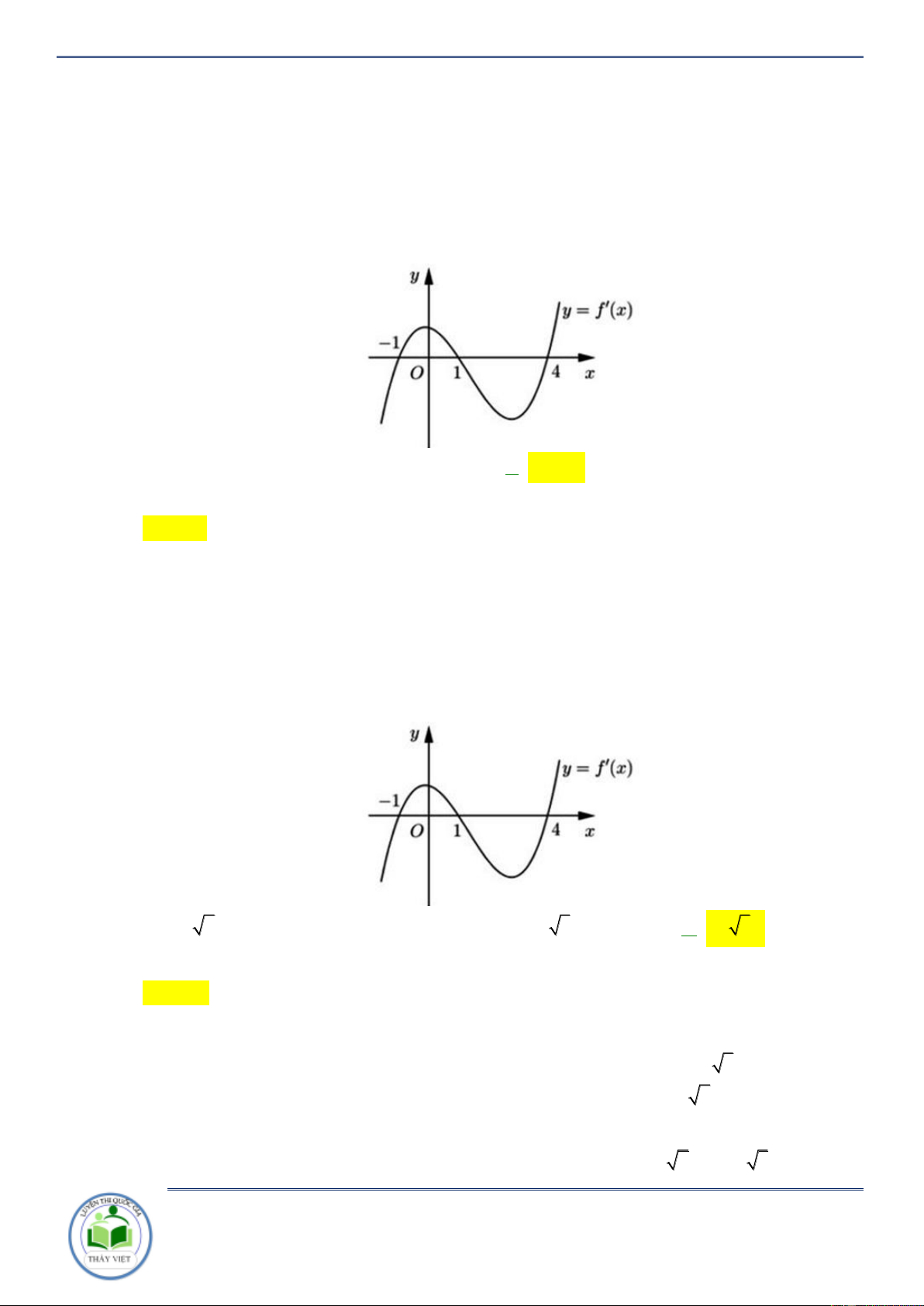
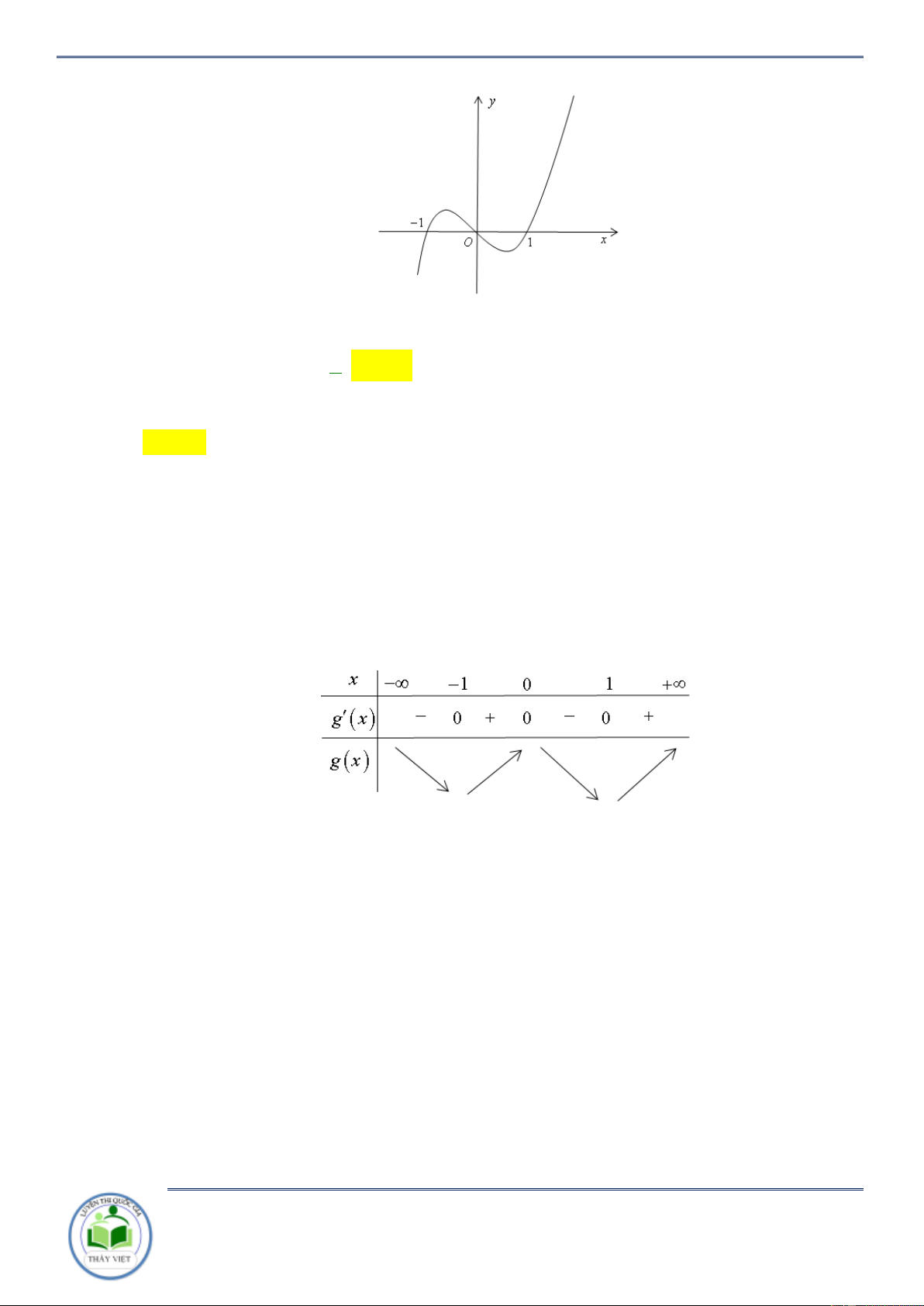
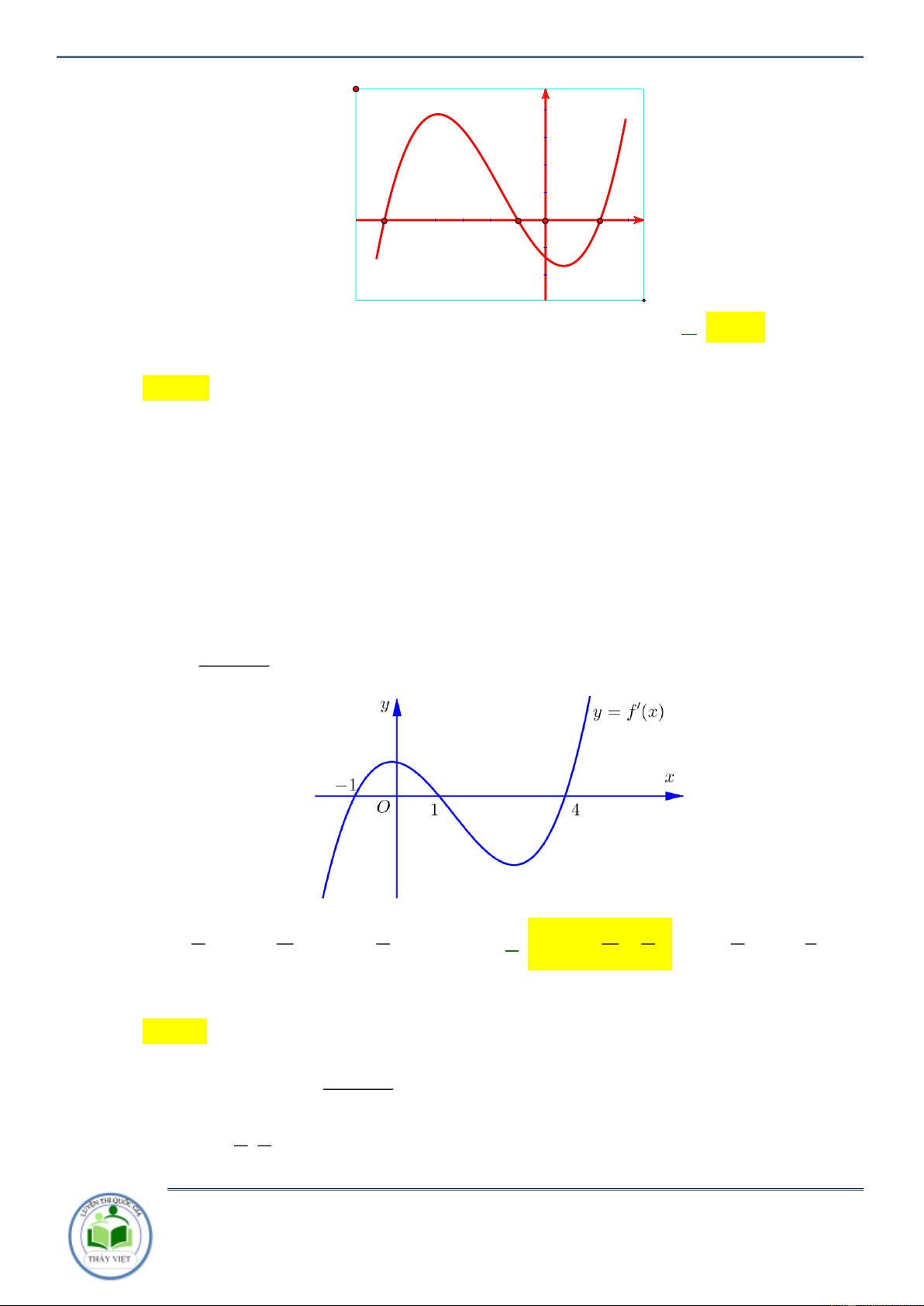
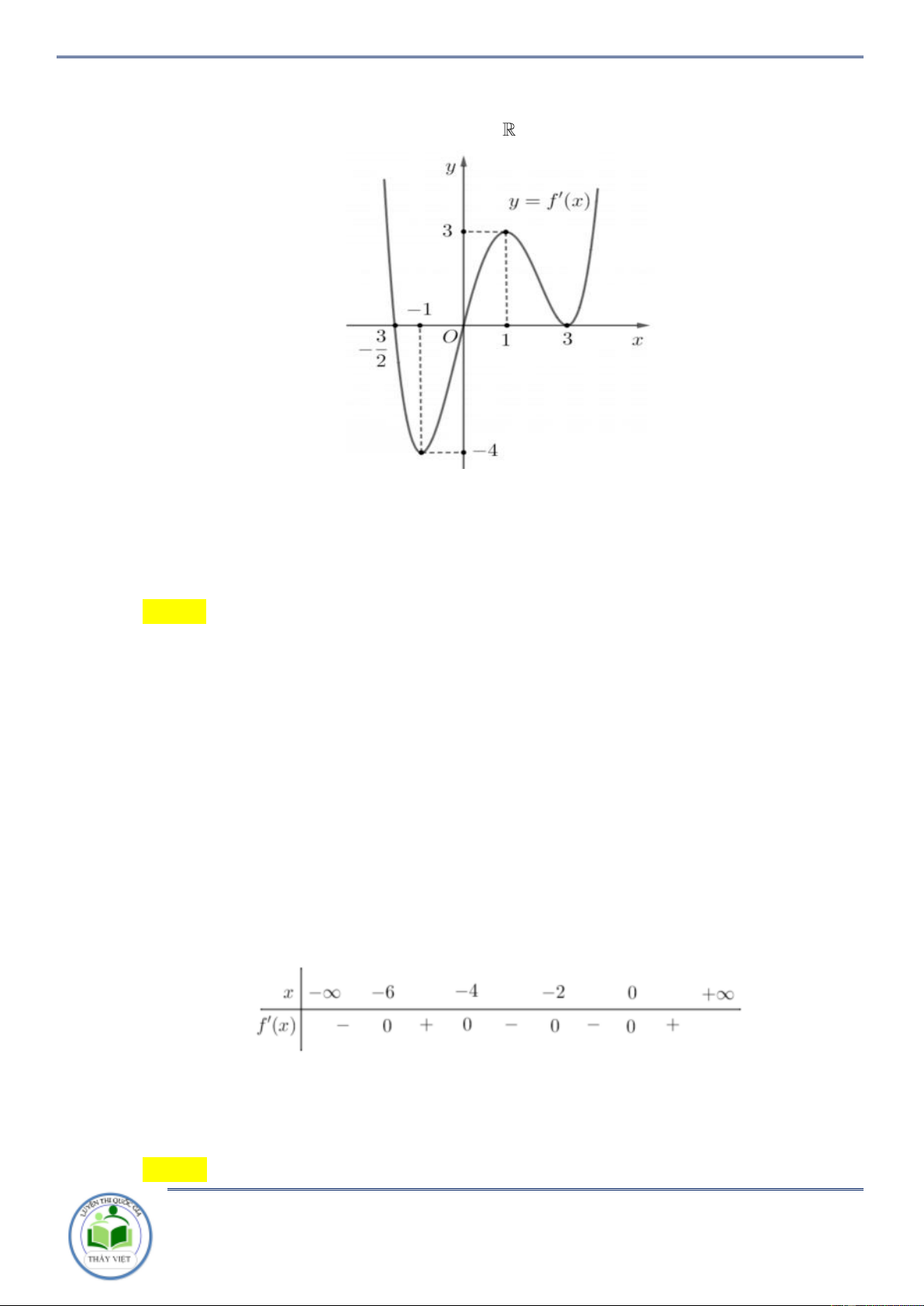
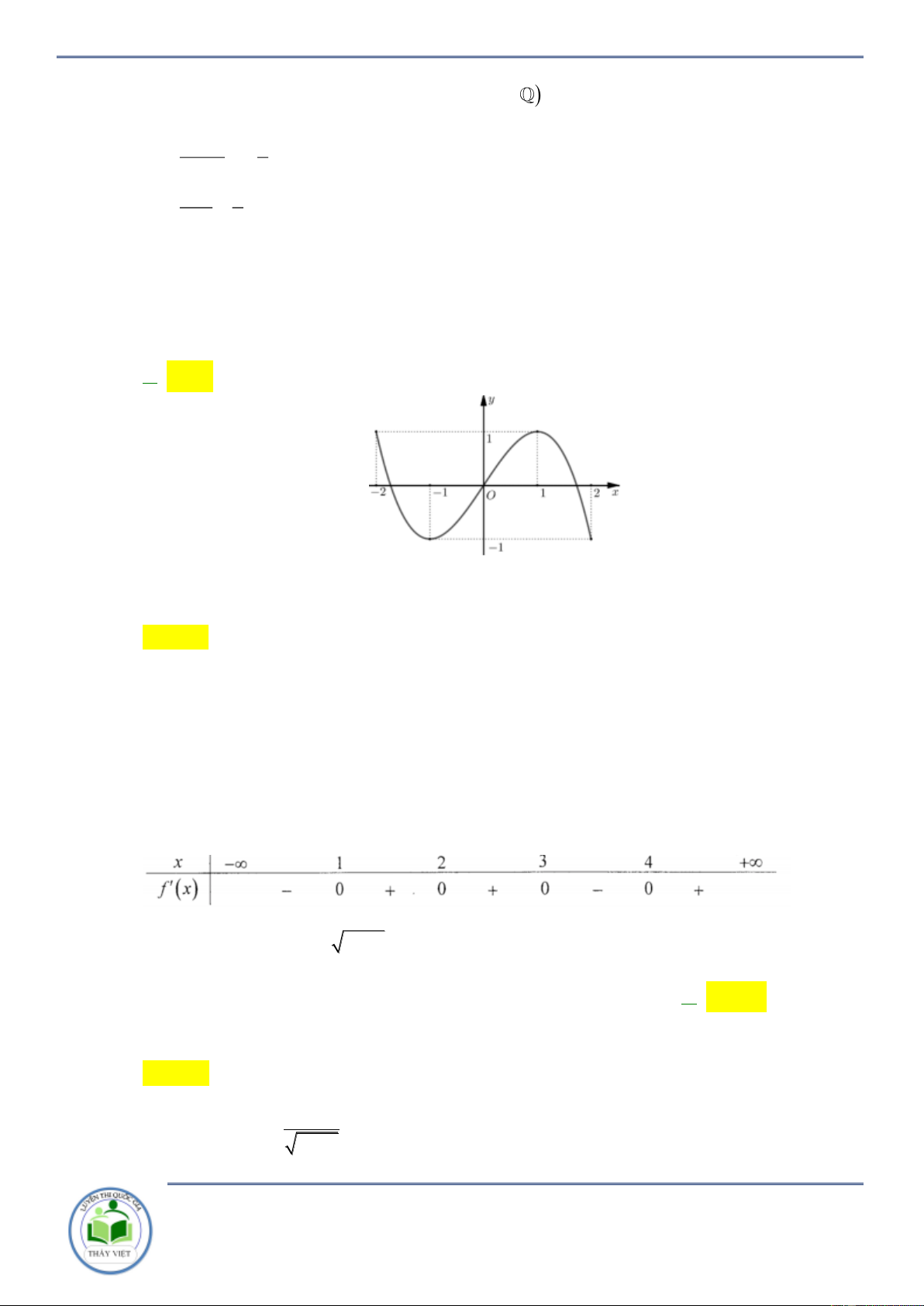
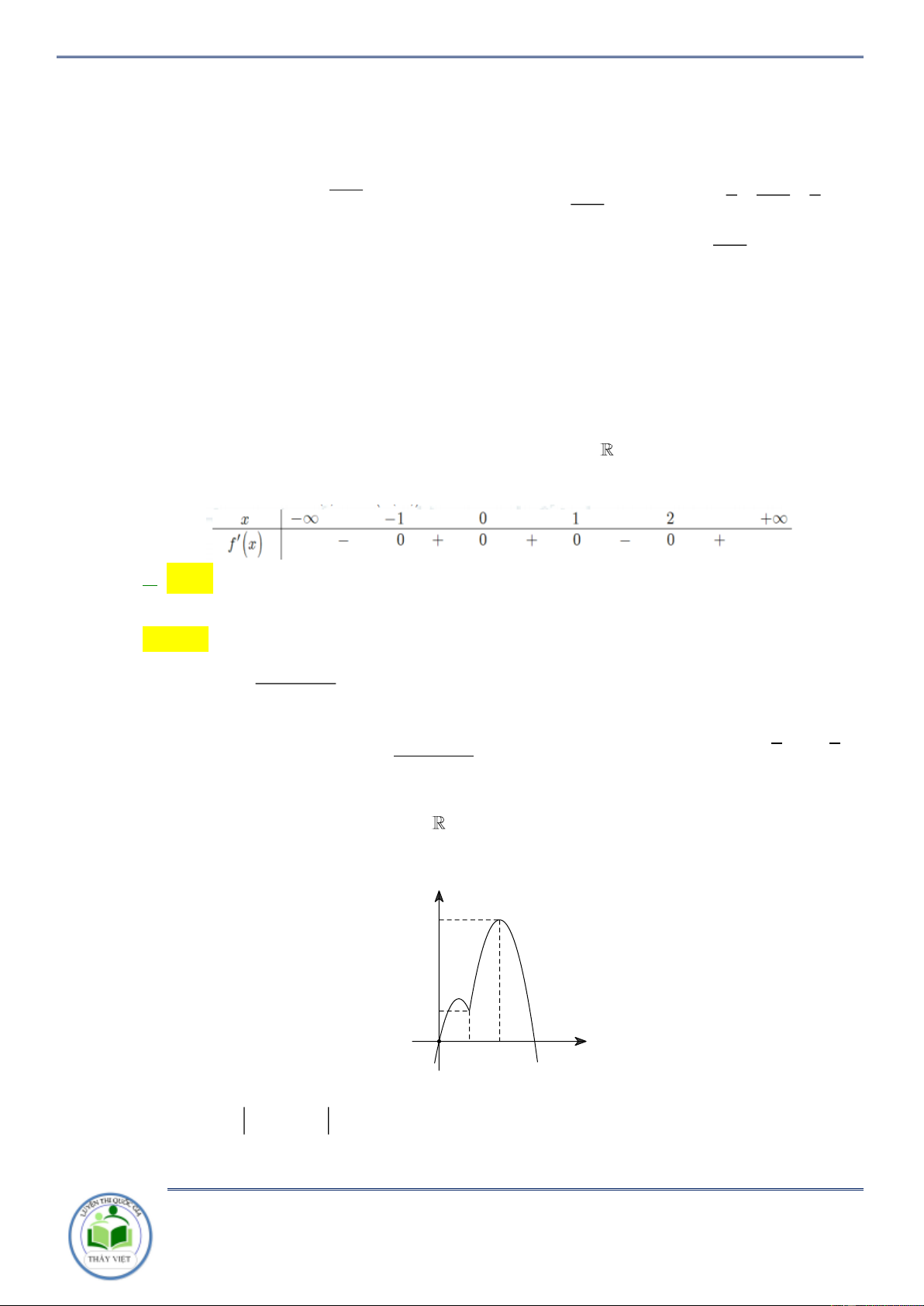
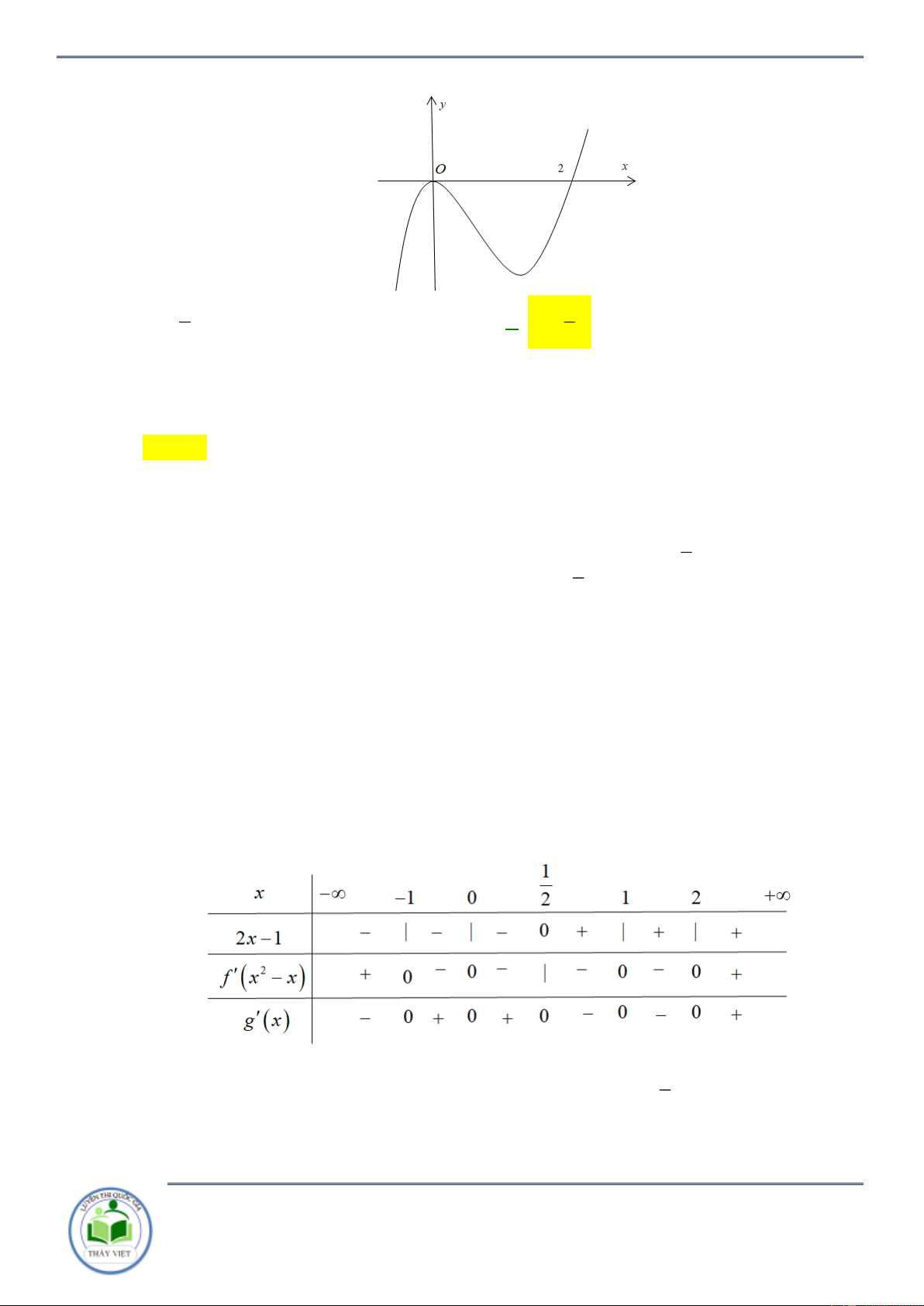
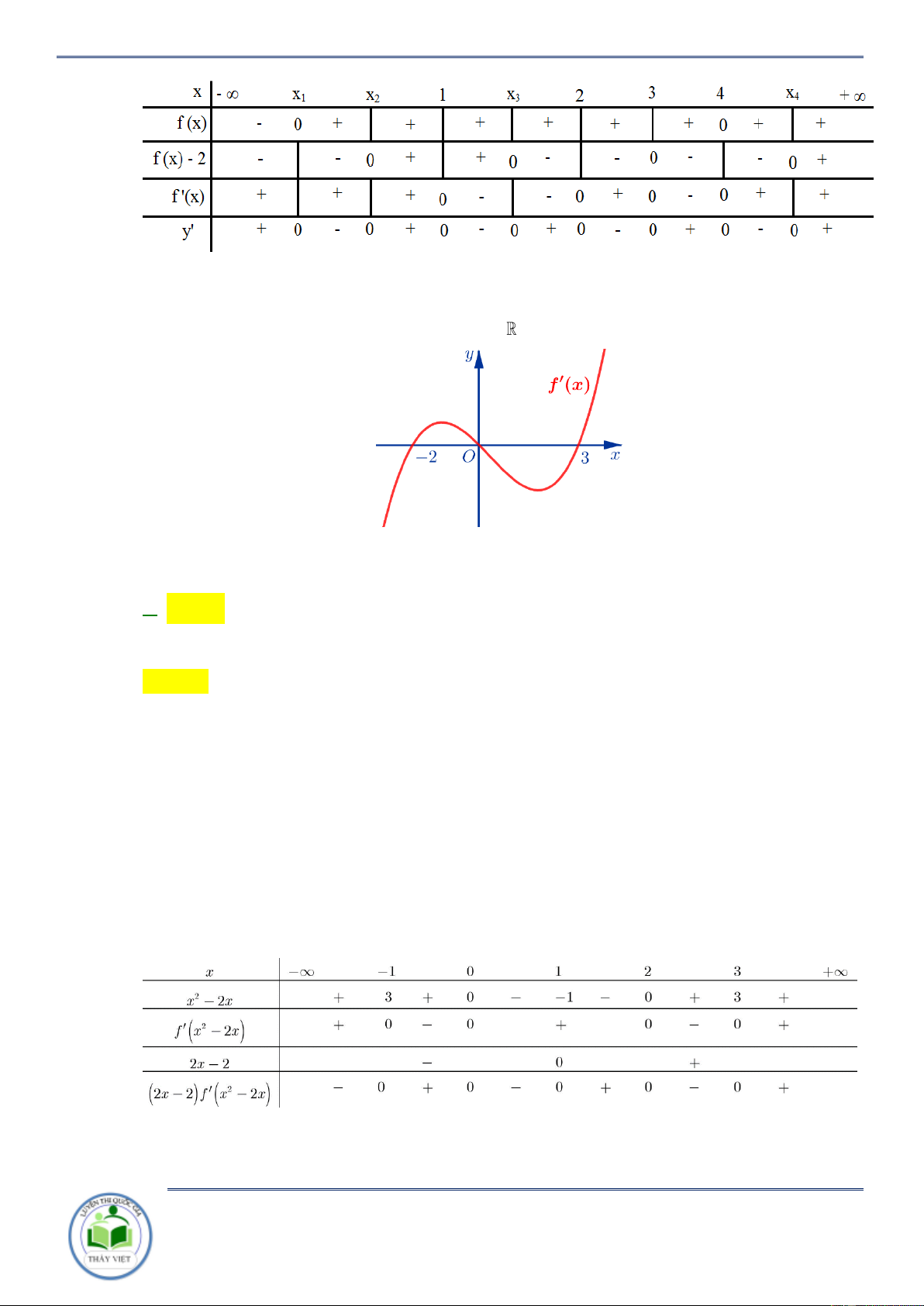
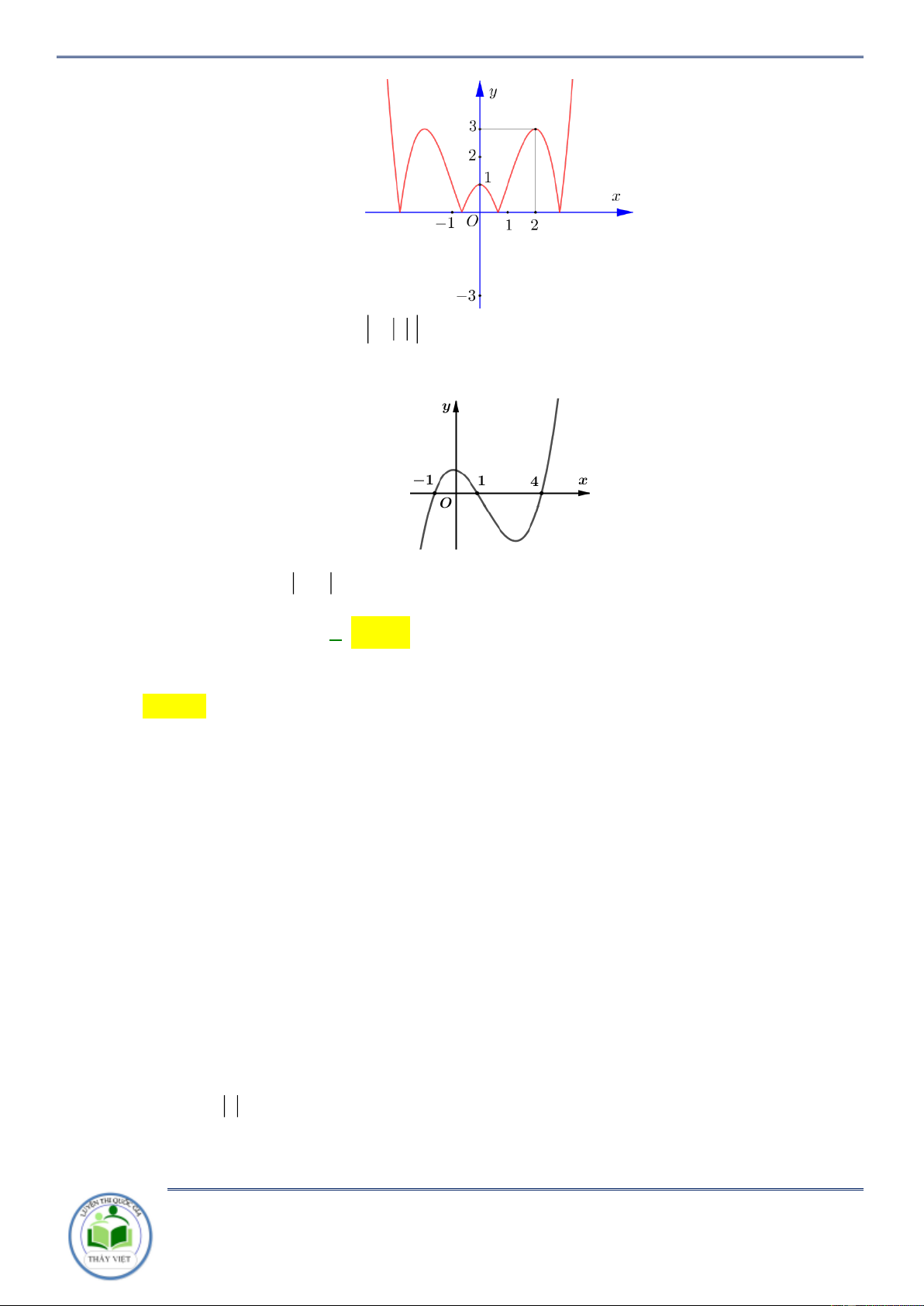
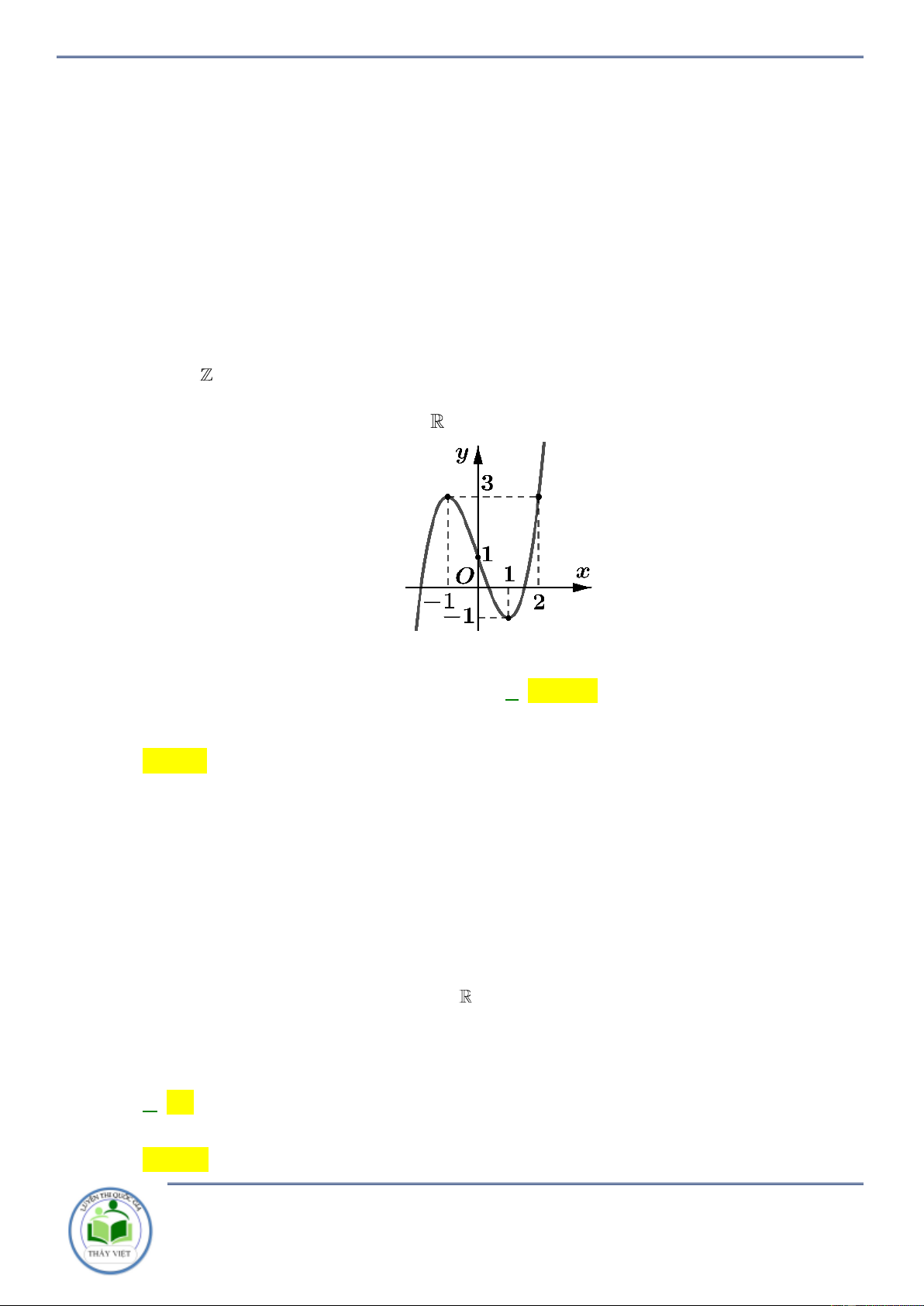
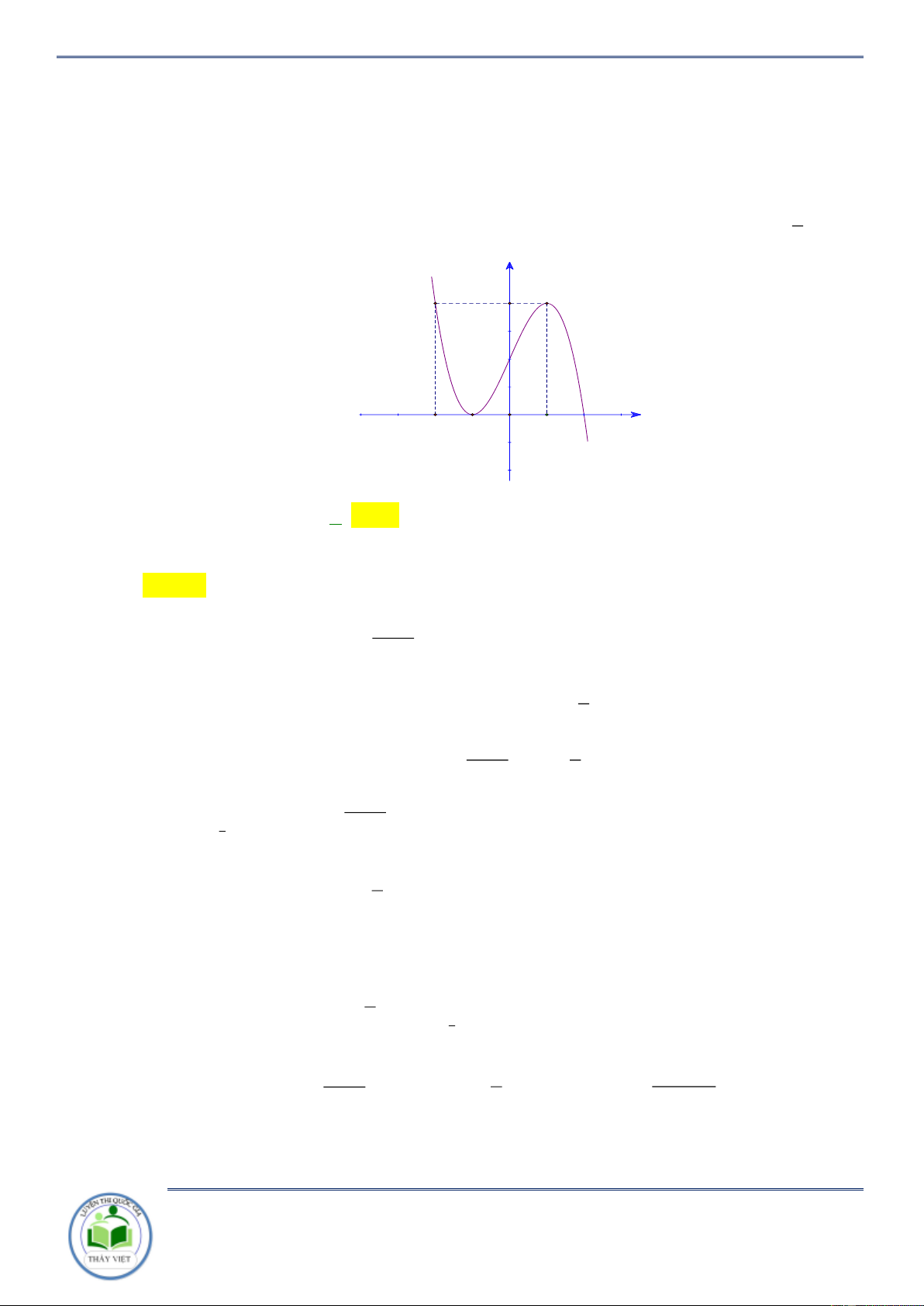
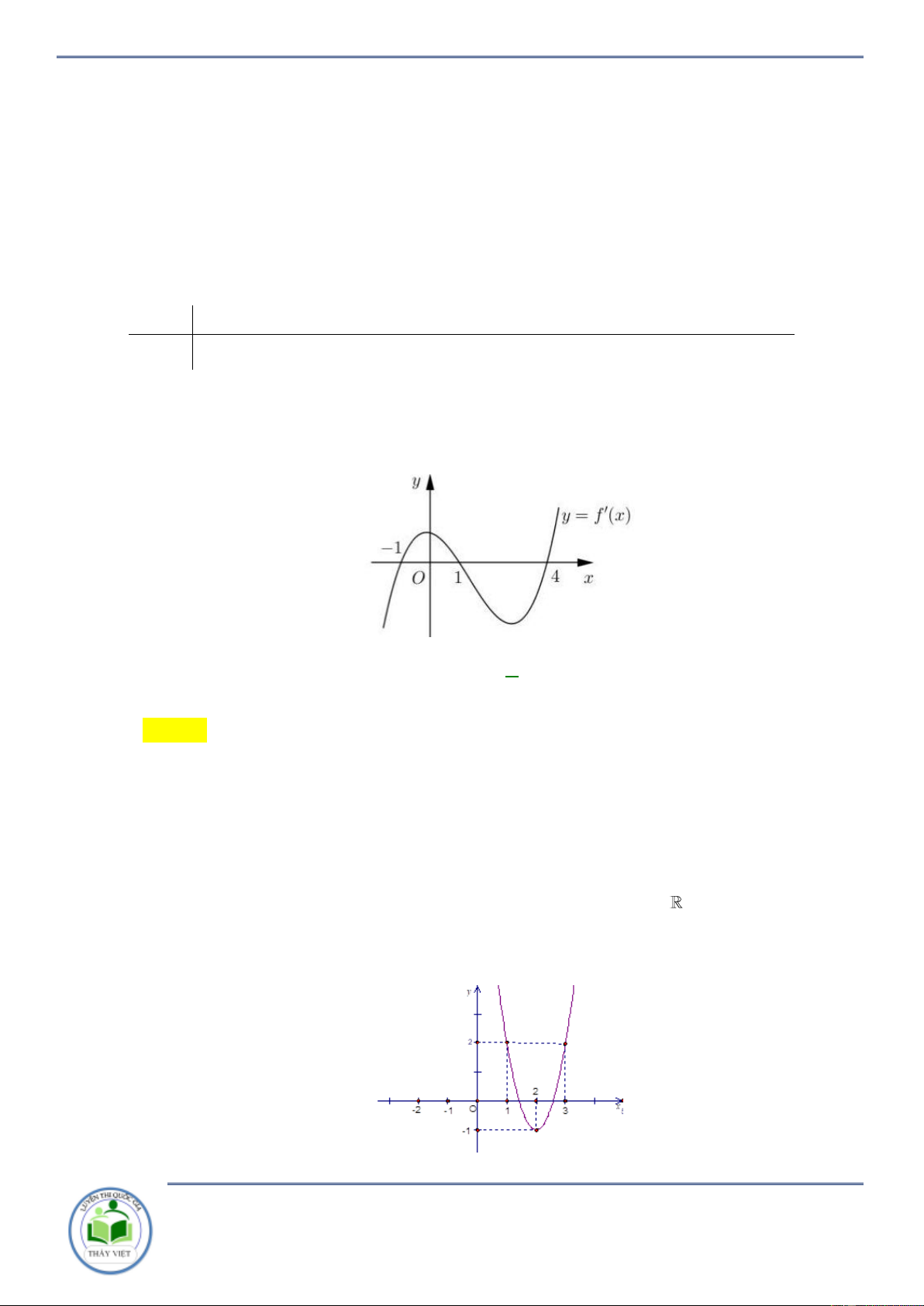
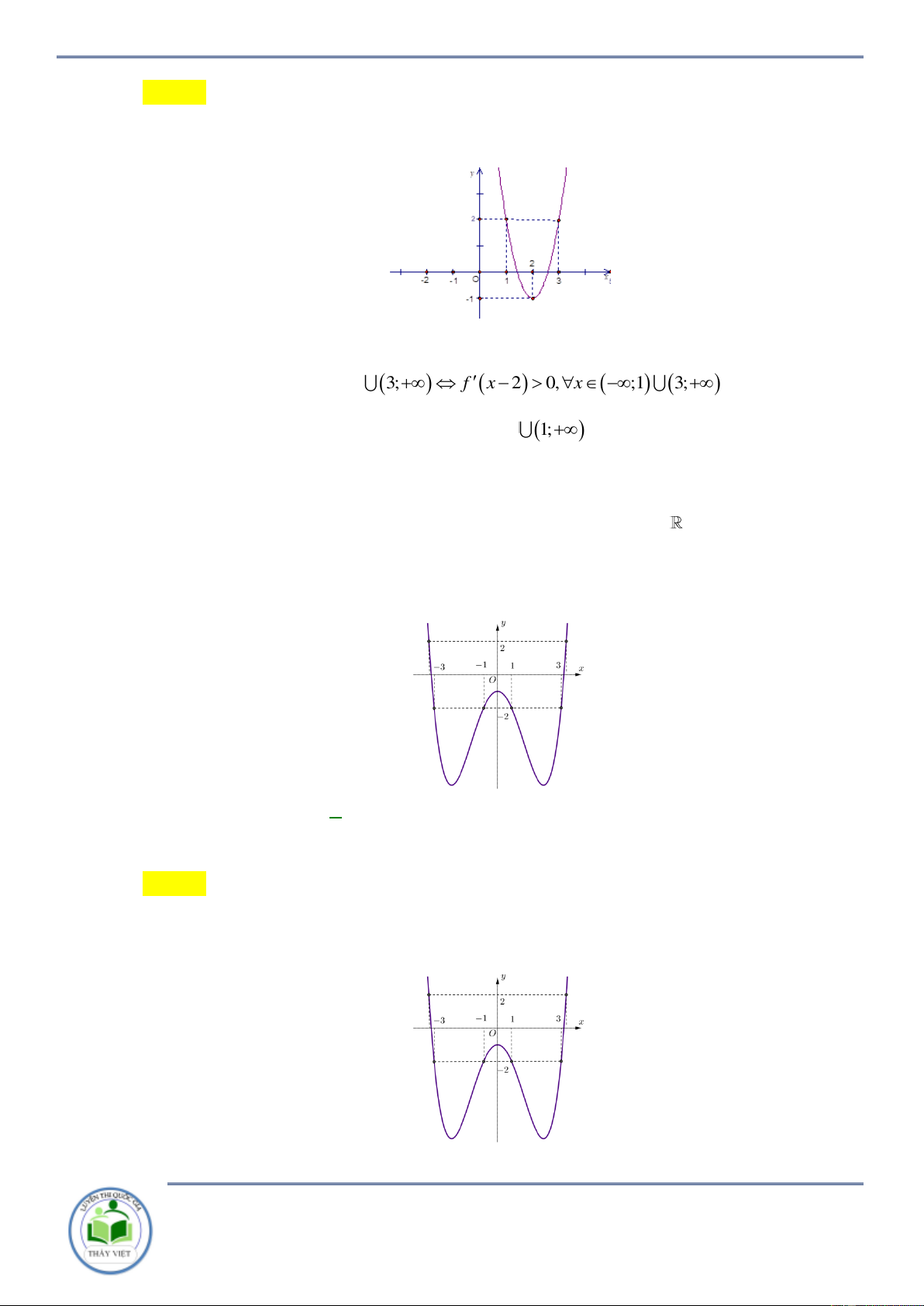
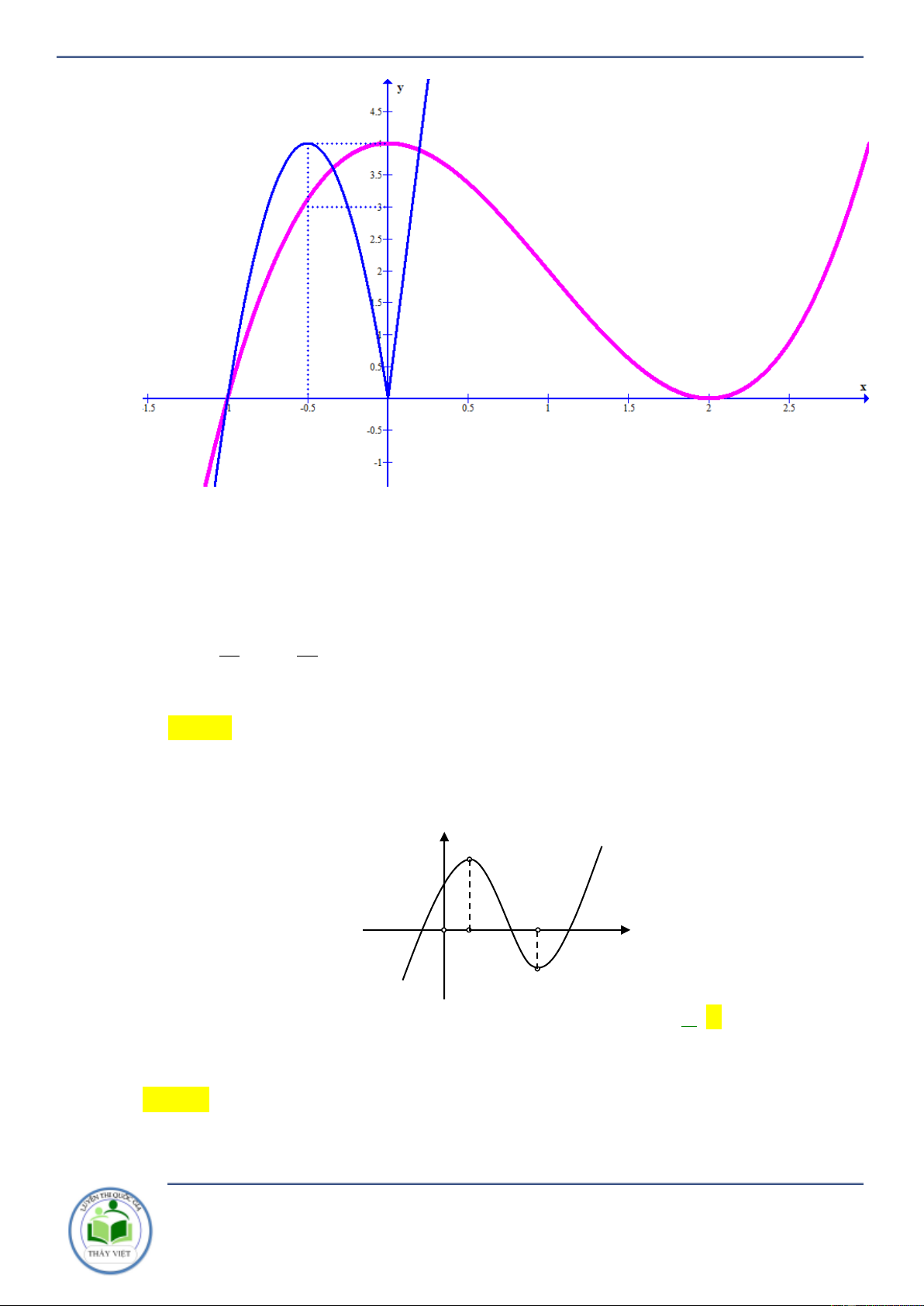
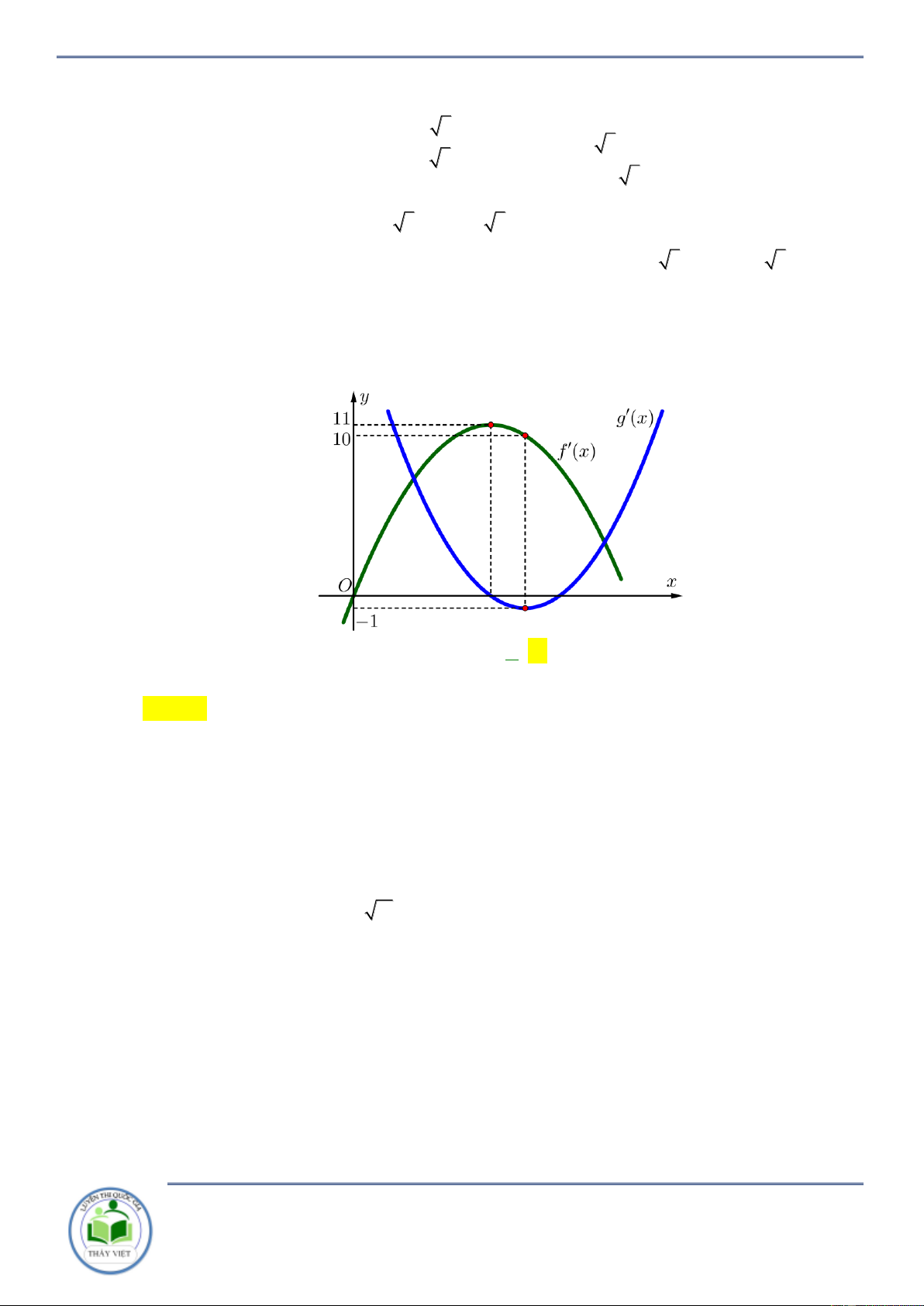
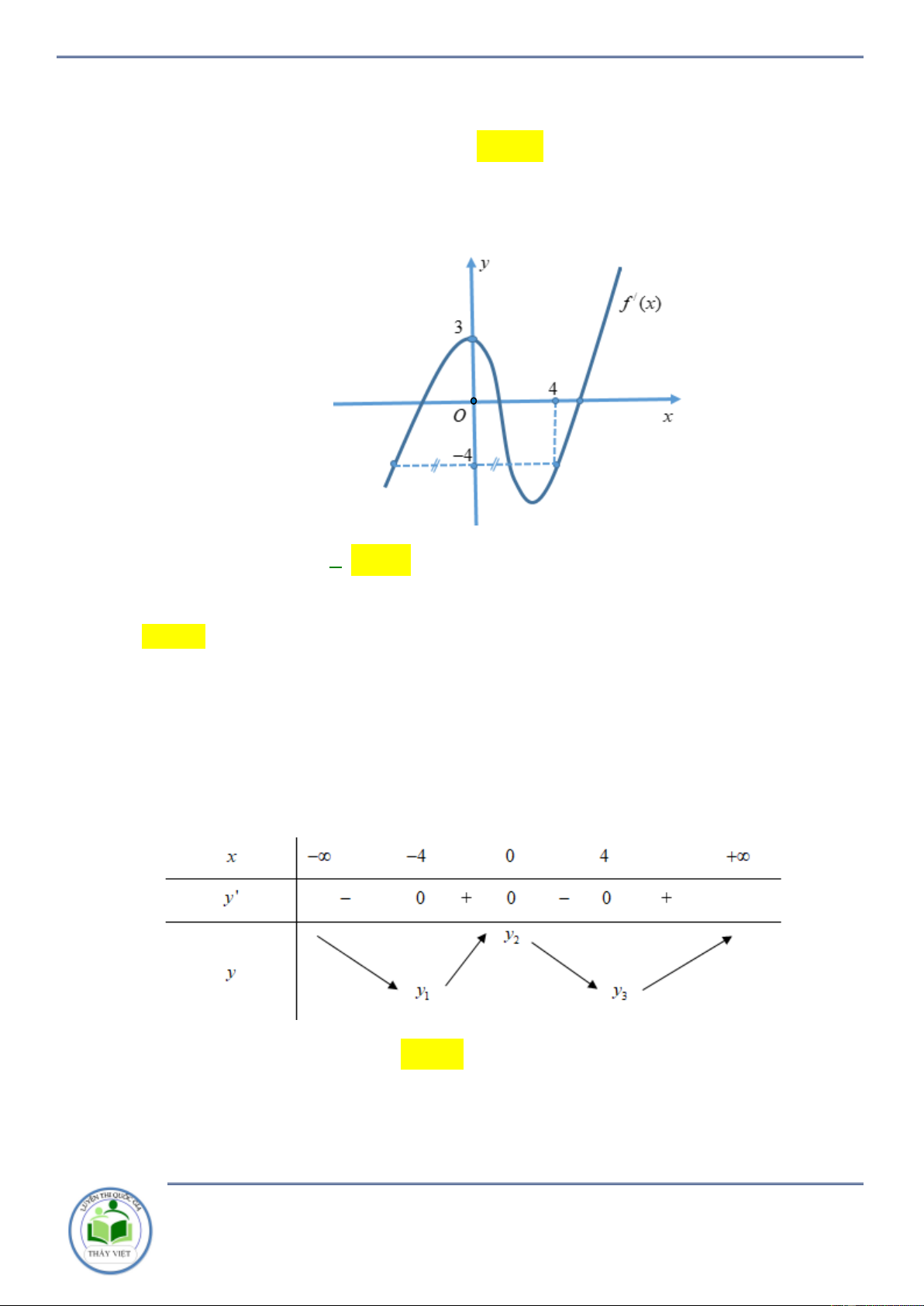
Cho hàm số y  f  x . Đồ thị hàm số y  f  x như hình vẽ bên. Hàm số
g  x  f  x   x  2 2
1 đồng biến trên khoảng nào? A.  3   ;1 . B. 1;3 . C.  ;3   . D. 3; . Lời giải Chọn B
Ta có y  2 f  x  2x  2  0  f  x  x 1.
Kẻ đường thẳng y  x 1 qua các điểm  3  ;2, 2  ;  1 ;3; 4   x  3 
Ta có f  x  x 1   . 1   x  3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 2/102
Xét khoảng mà đồ thị hàm số y  f  x nằm bên trên đường thẳng y  x 1 suy ra
hàm số y  g  x đồng biến trên khoảng 1;3 . Câu 2:
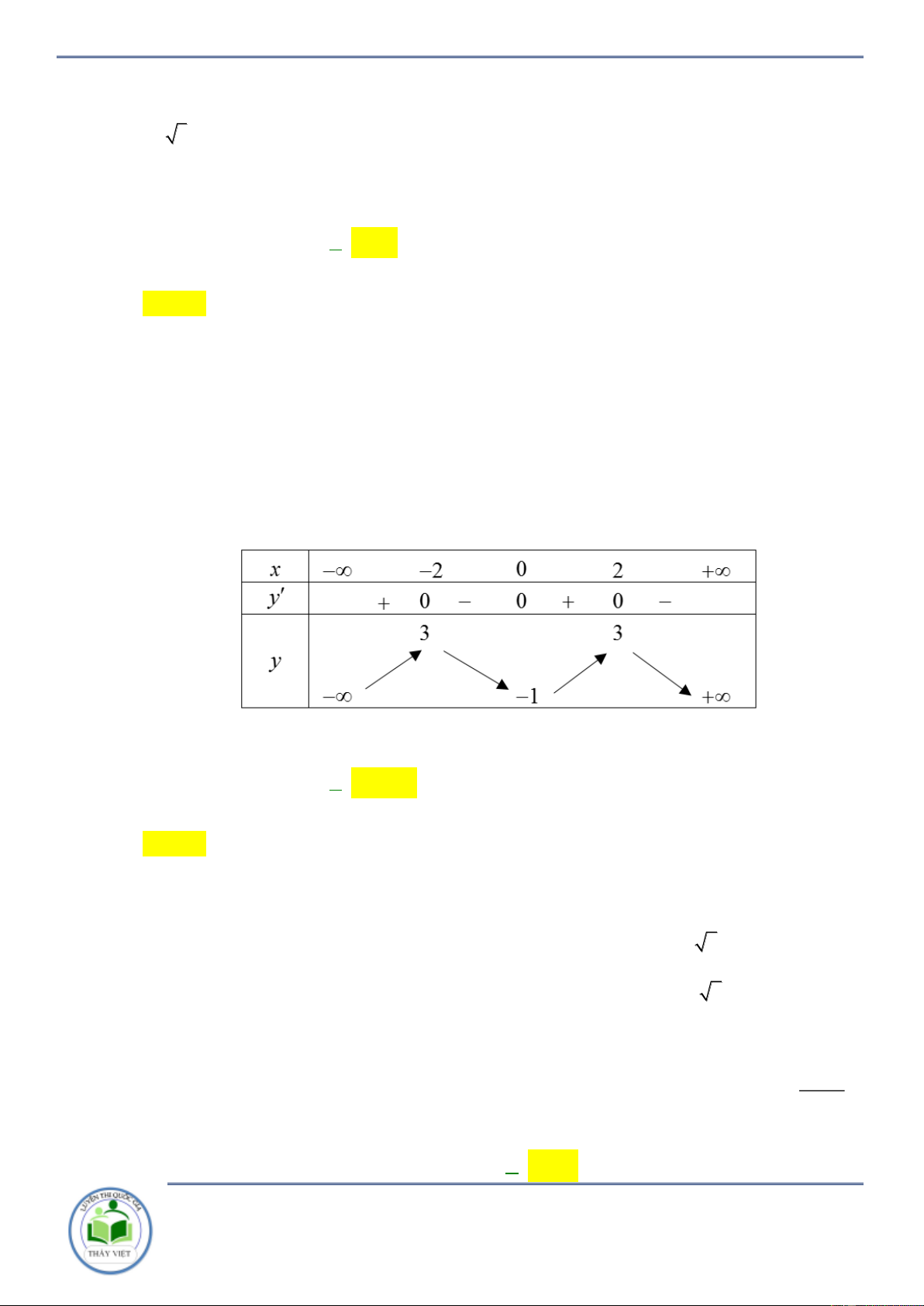
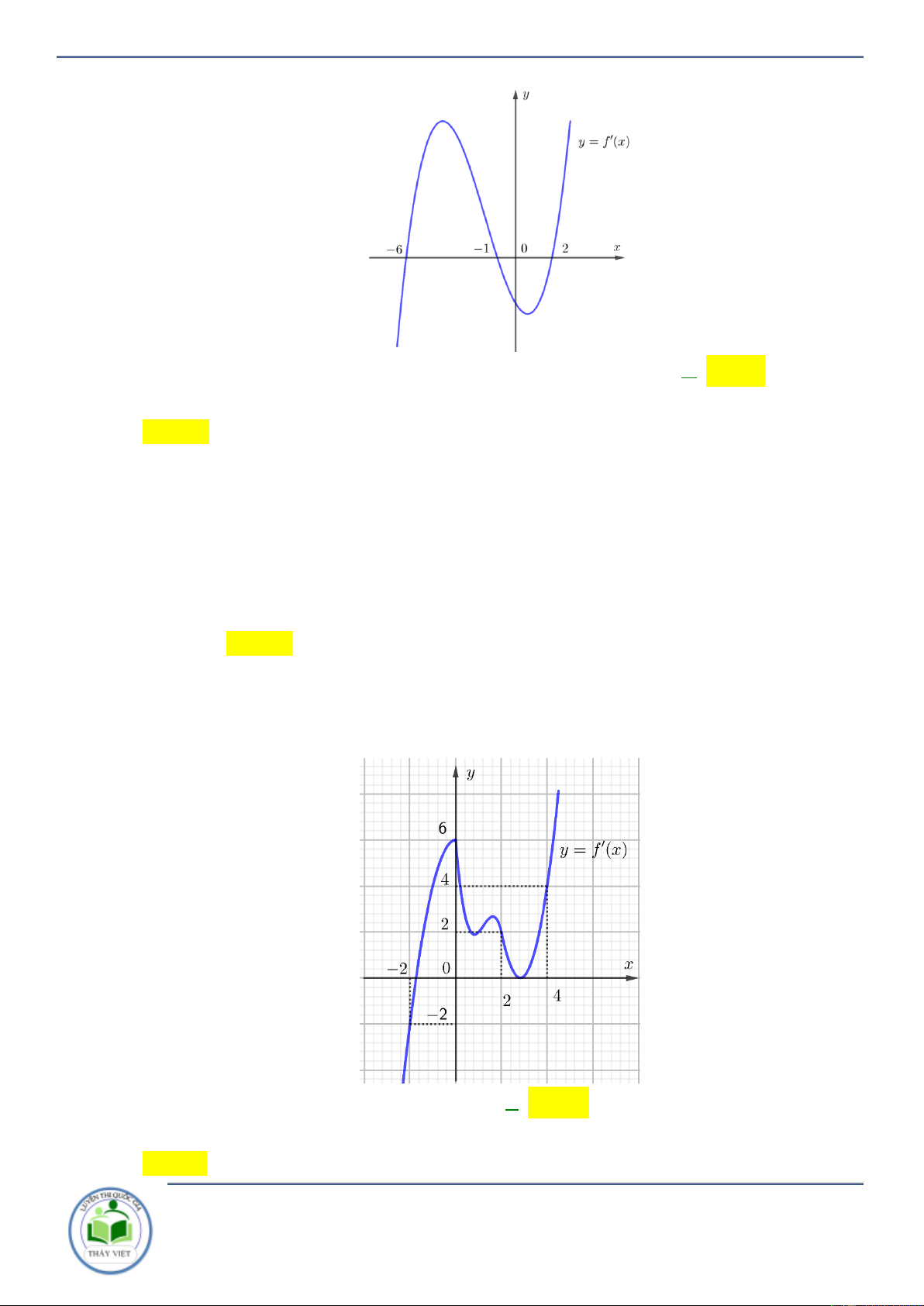
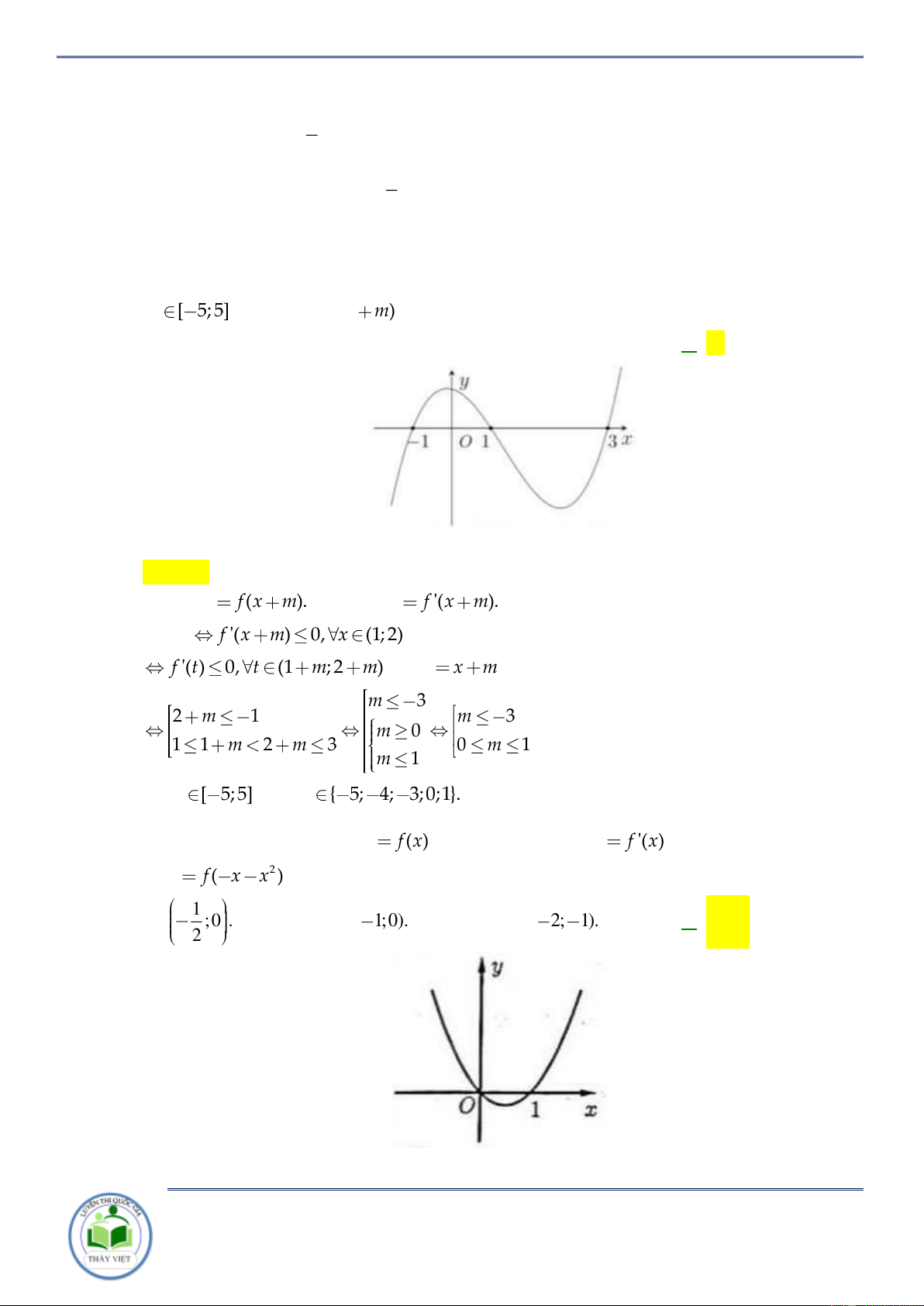
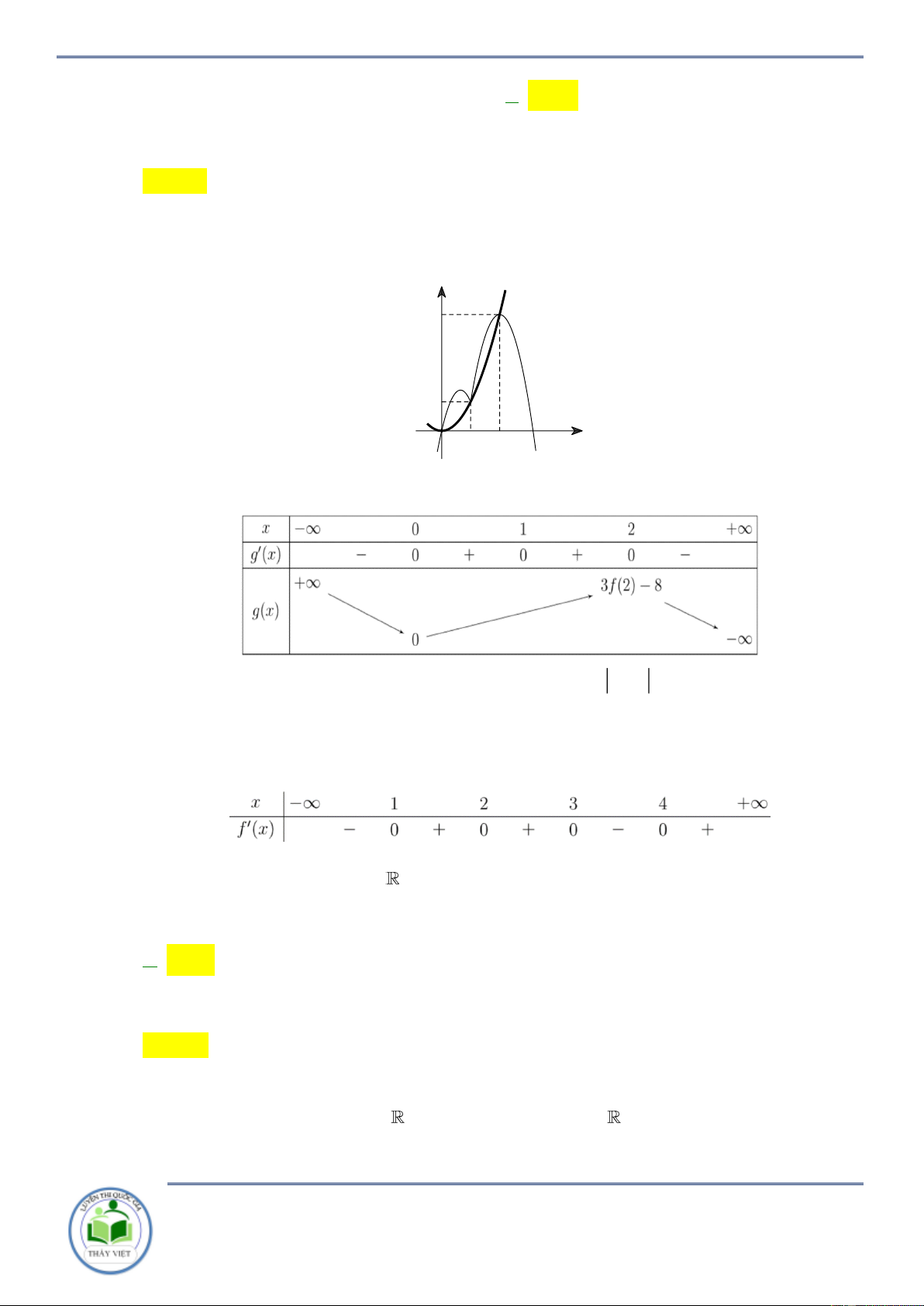
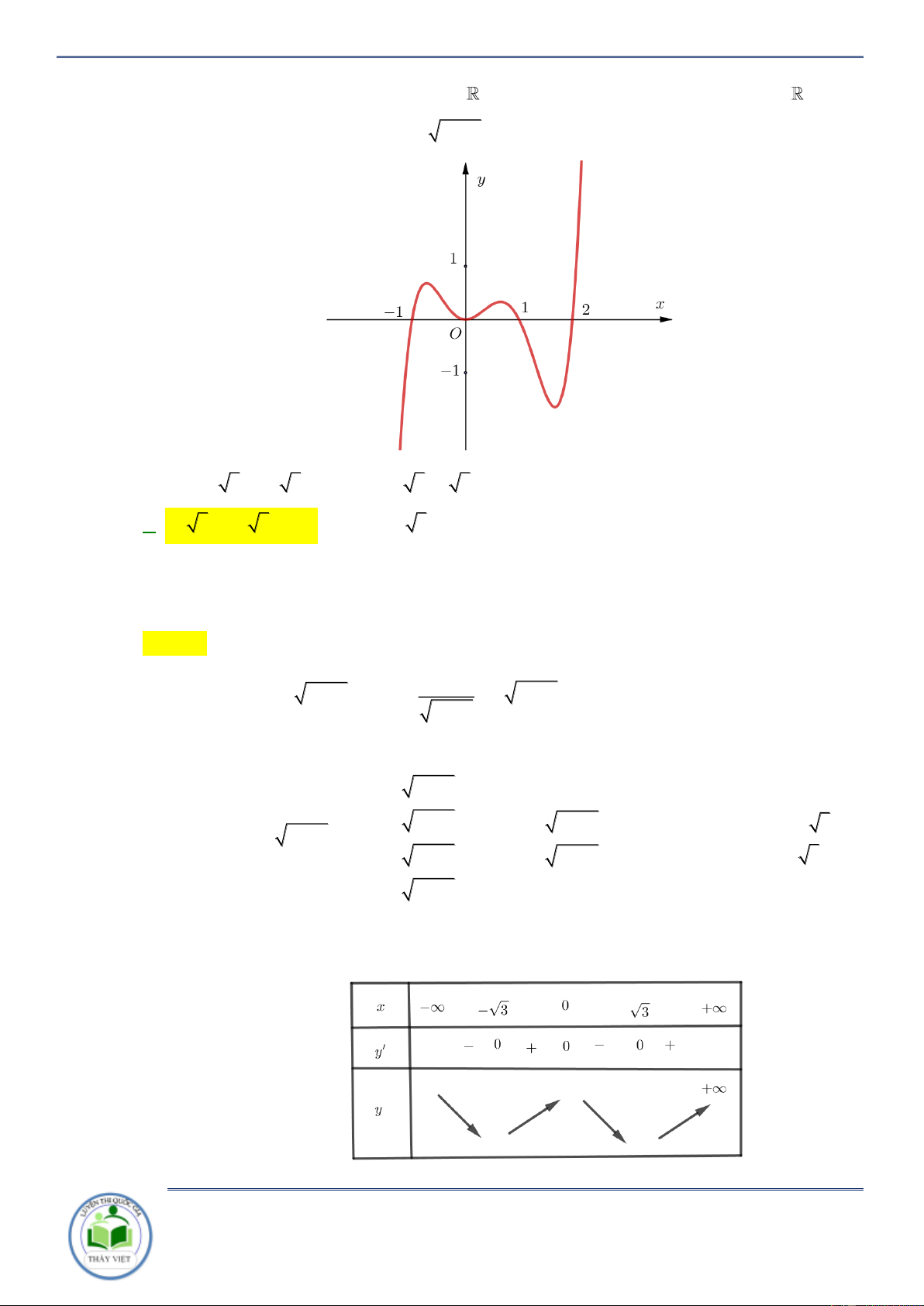
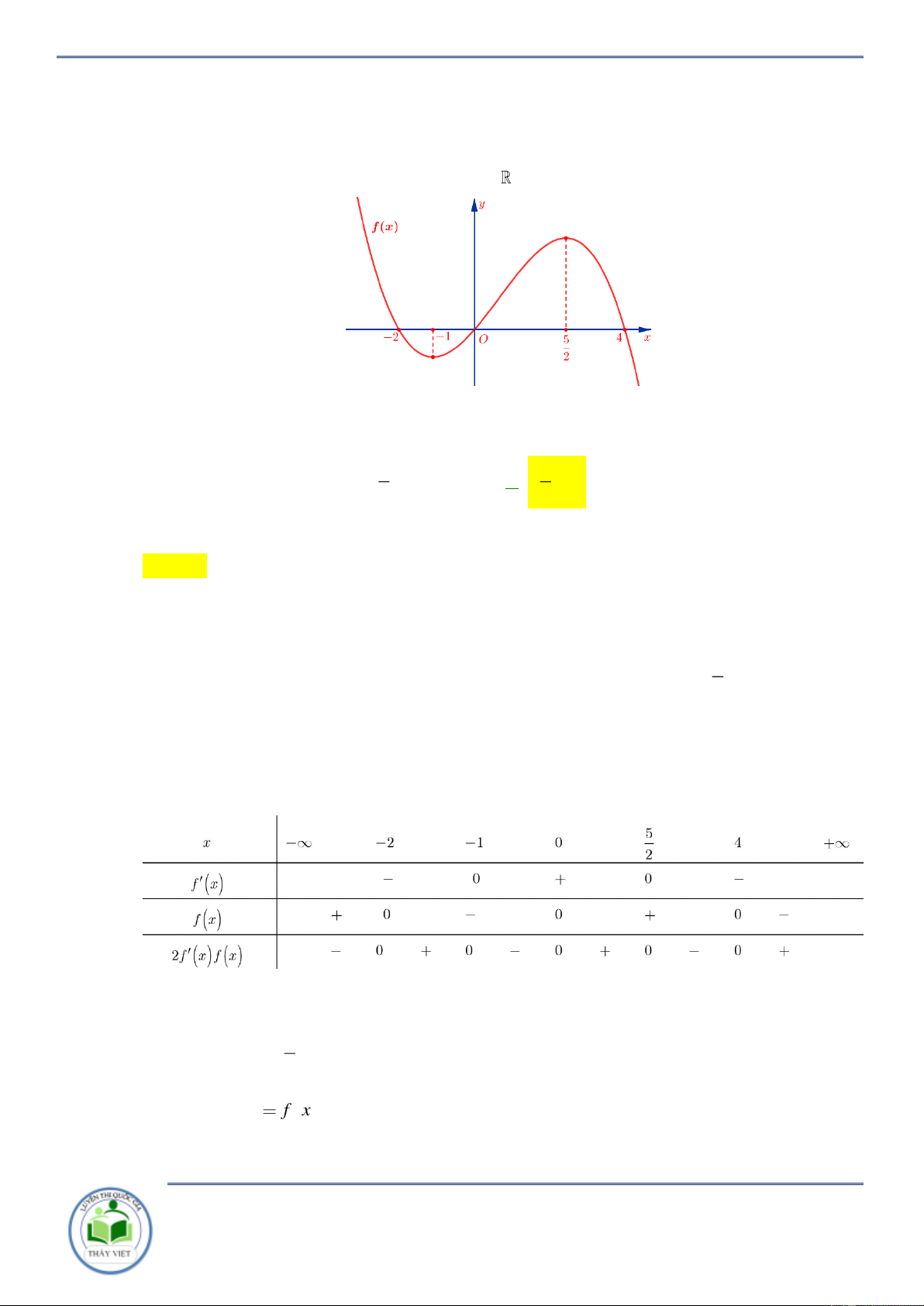
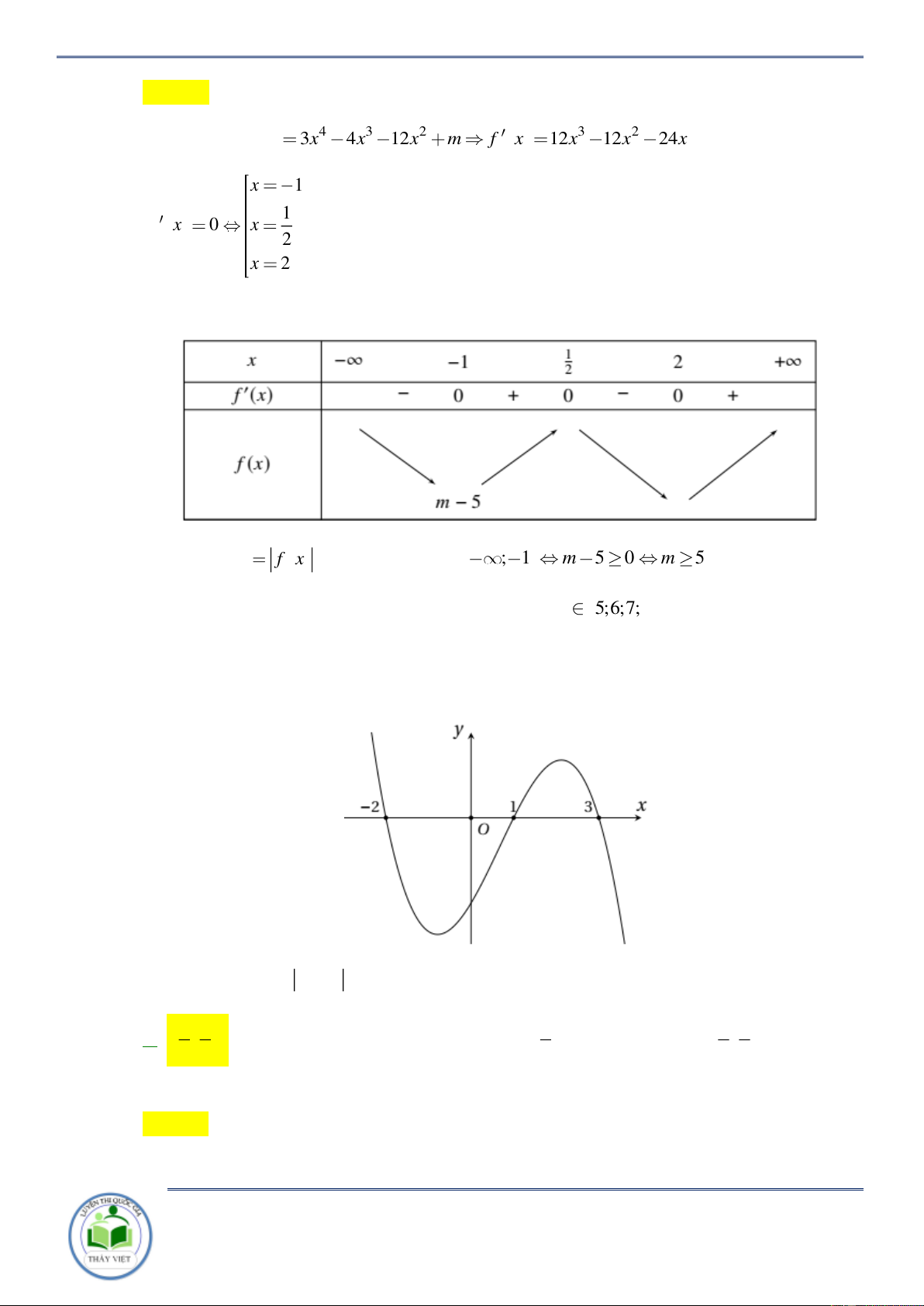
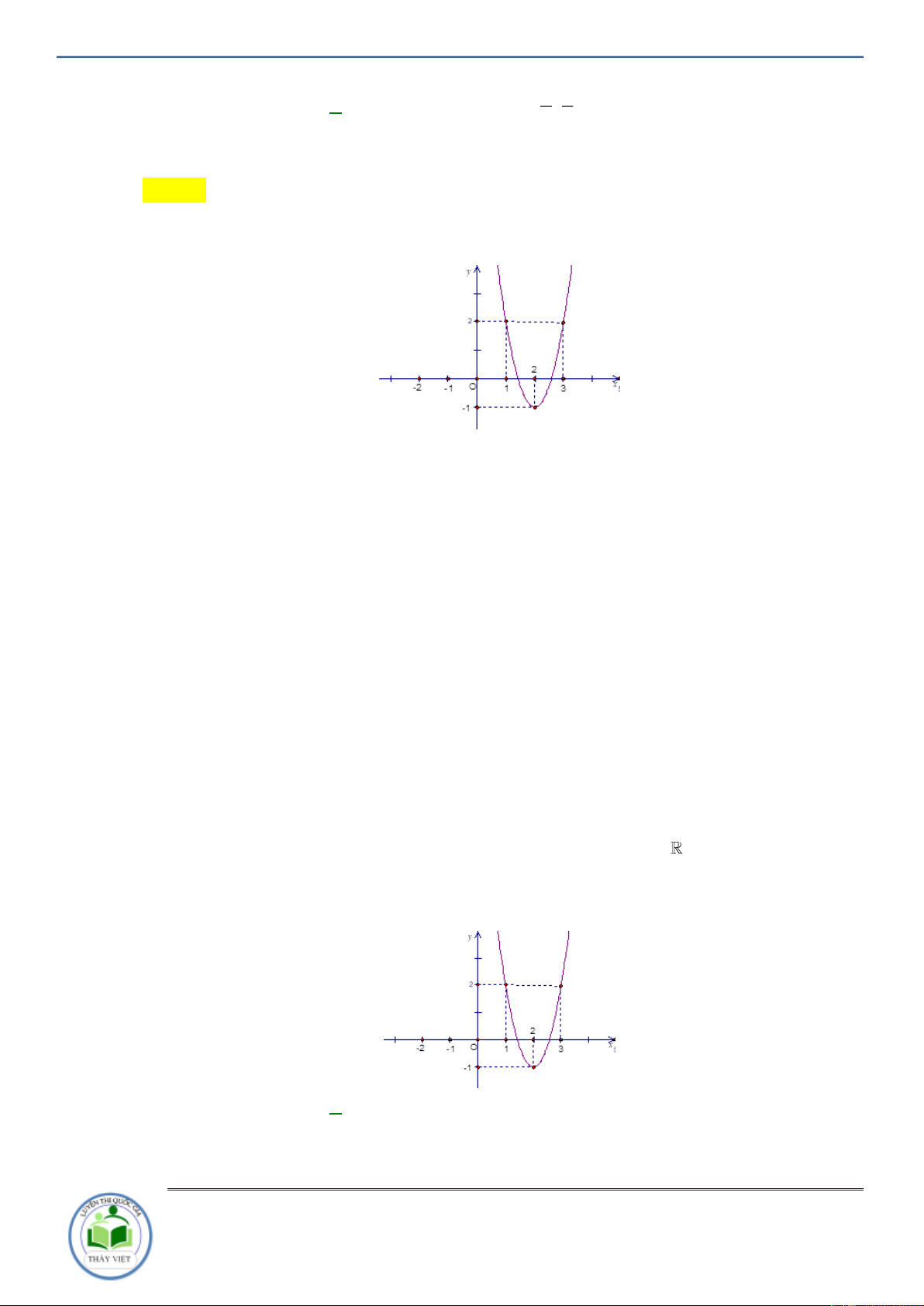
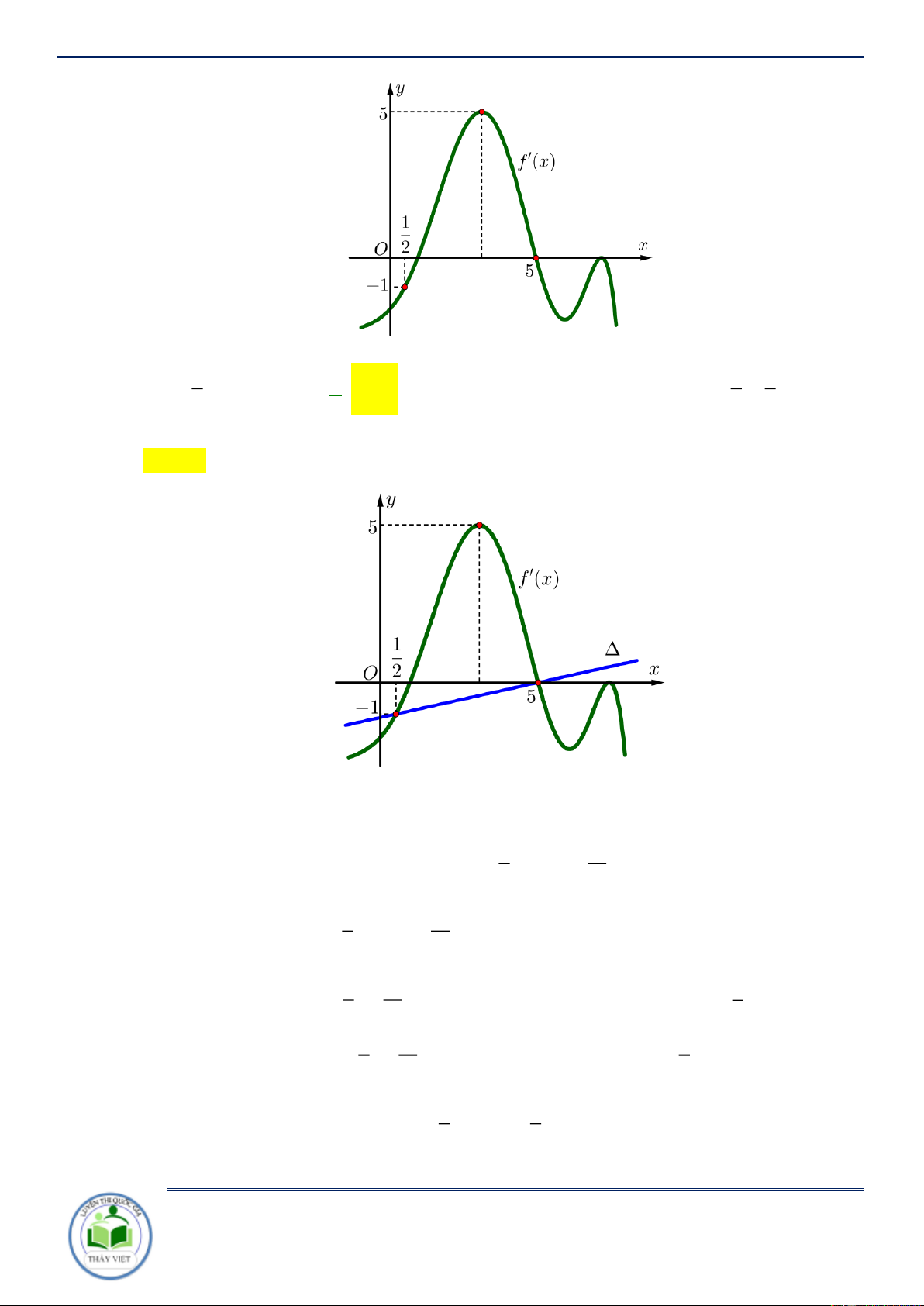
Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số
y  f 2  x đồng biến trên khoảng A. 1;3 . B. 2; . C.  2   ;1 . D.  ;  2   . Lời giải Chọn C   x   x  3
Ta có y   f   x   f   x 2 1 2 0 2  0     . 1   2  x  4  2   x 1
Do đó, hàm số y  f 2  x đồng biến trên khoảng  2   ;1 . Câu 3:
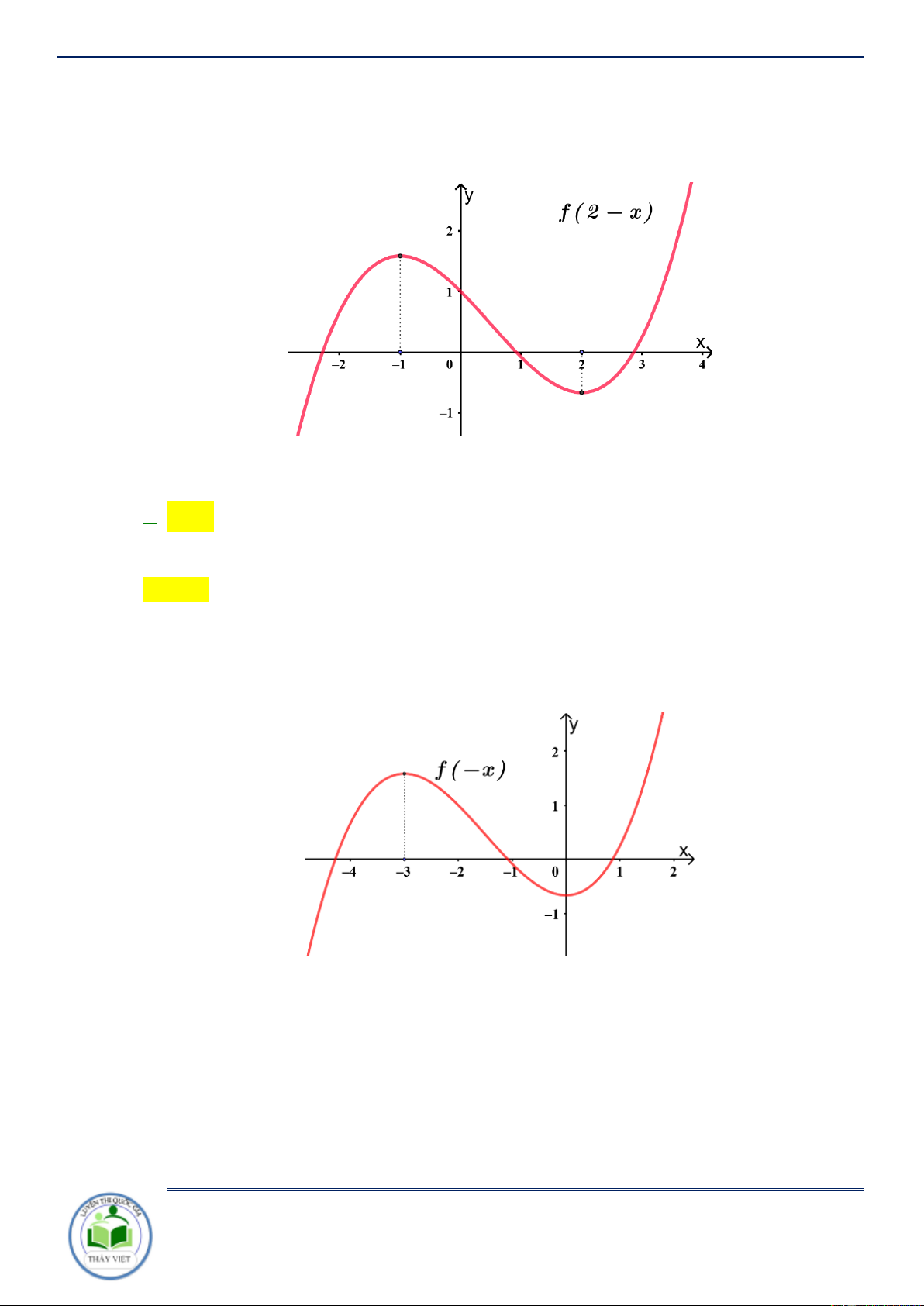
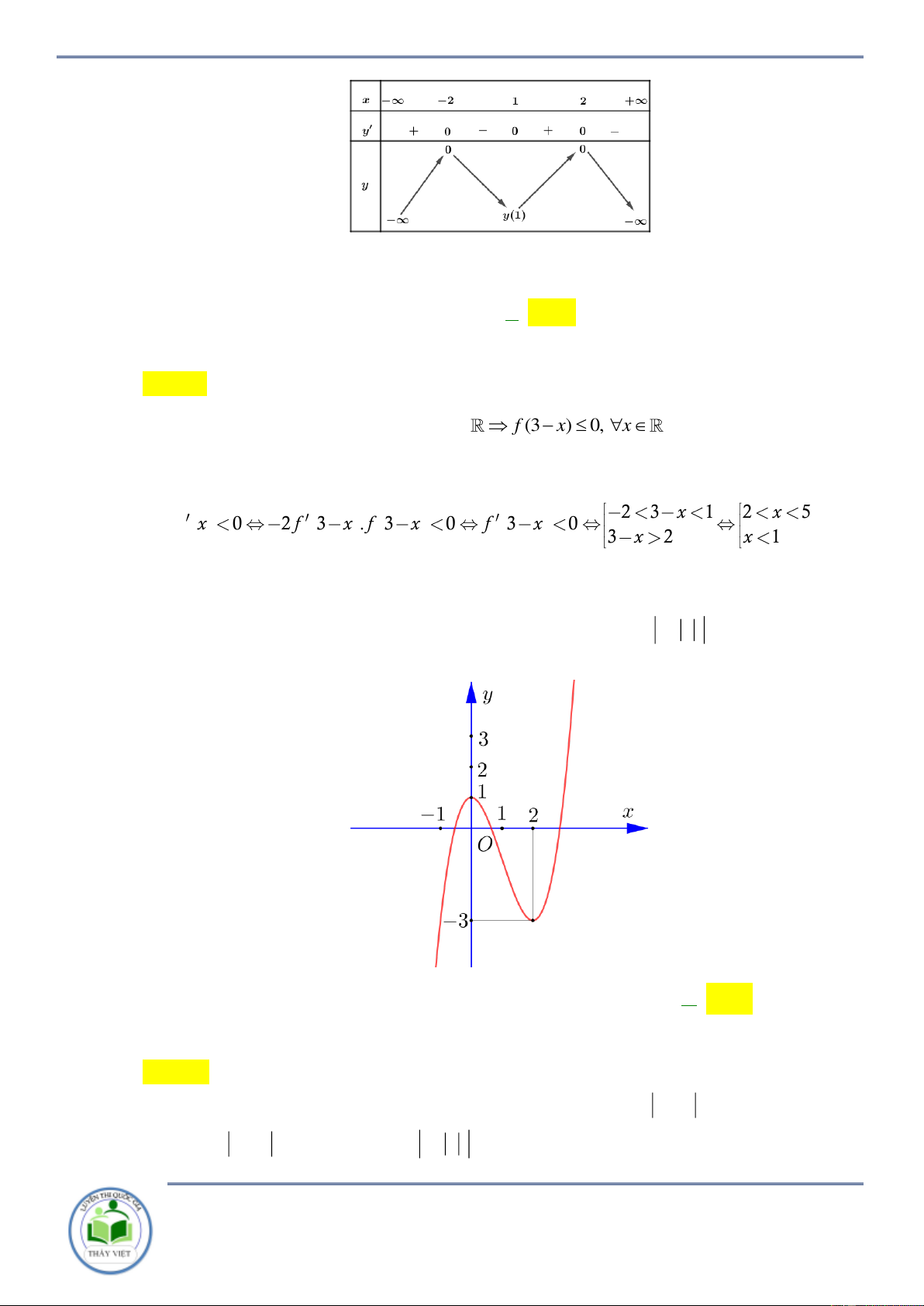
Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số y  f  2
x  2 đồng biến trên khoảng A. 0; 6 . B. 0  ;1 . C.  3;0 . D. 1; 3 . Lời giải Chọn D
Ta có y  x f  2 2 . x  2  0 2 2  1   x  2 1 1   x  3 1   x  3
* Nếu x  0 thì f  2
x  2  0       . 2 2 x  2  4 x  6 x  6 2 2 1   x  2  4 3  x  6  1   x  0
* Nếu x  0 thì f  2
x  2  0       . 2 2 x  2  1  x 1
 6  x   3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 3/102
Do đó, trong các đáp án đã cho thì hàm số y  f  2
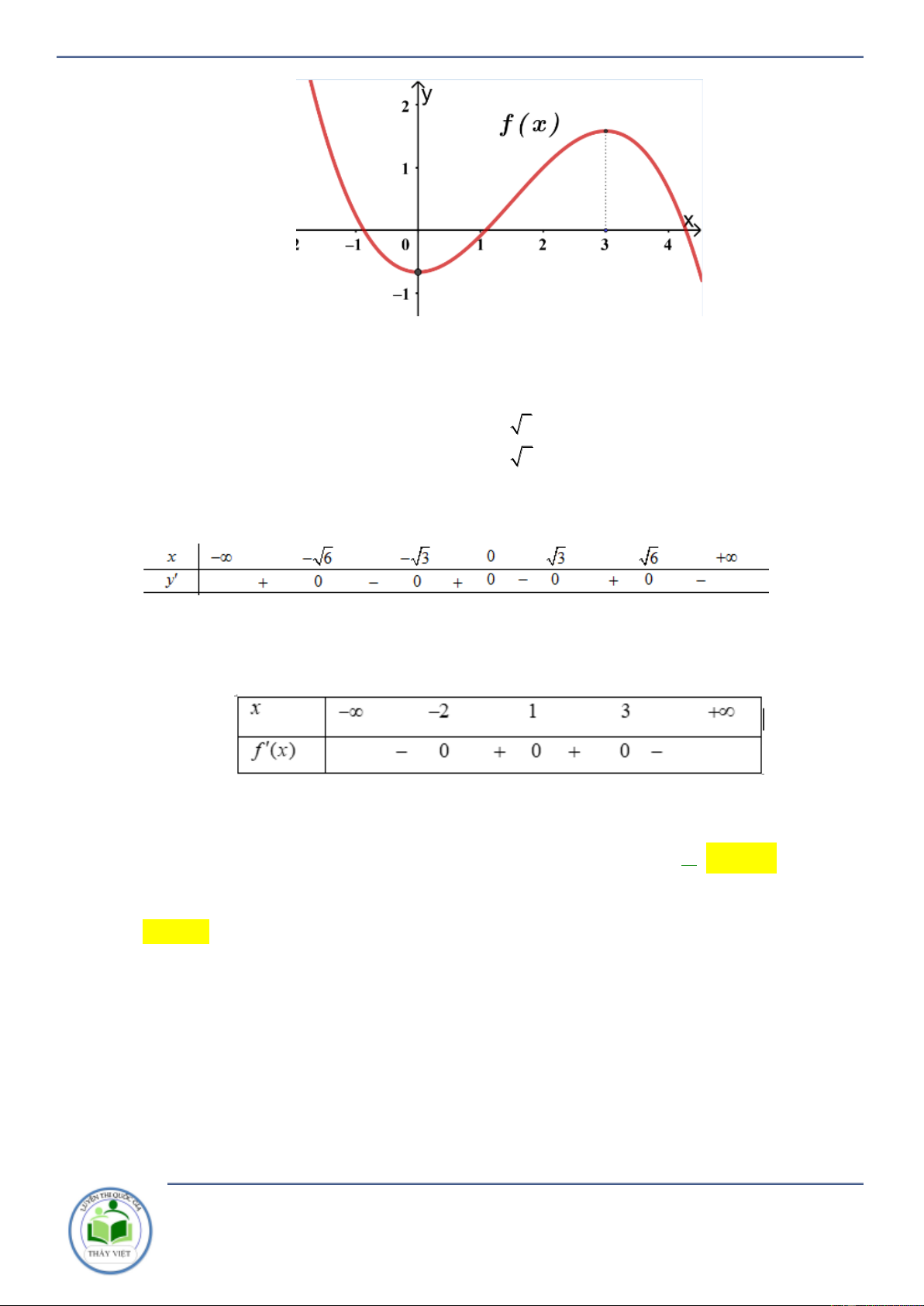
x  2 đồng biến trên khoảng 1; 3. Câu 4:
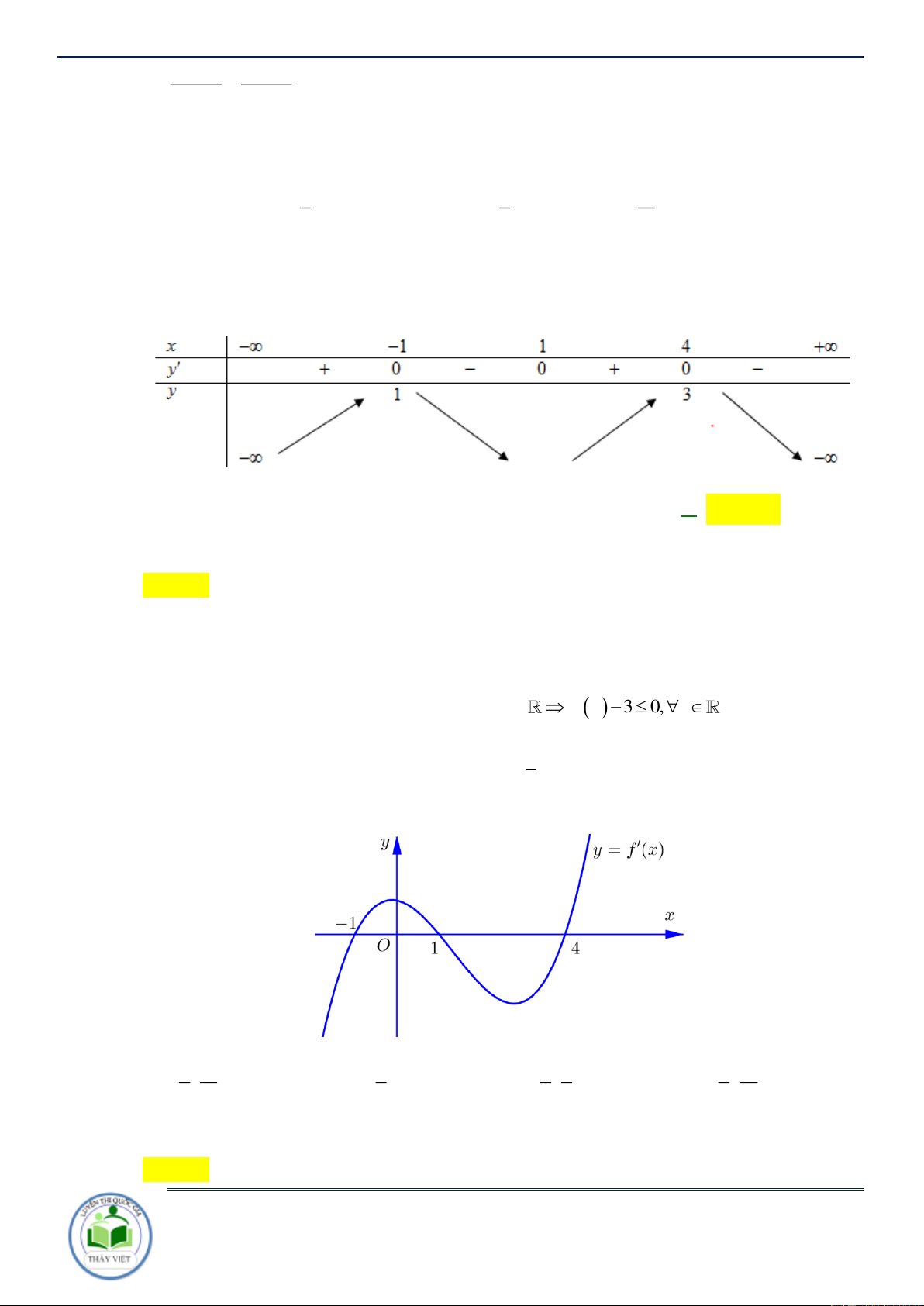
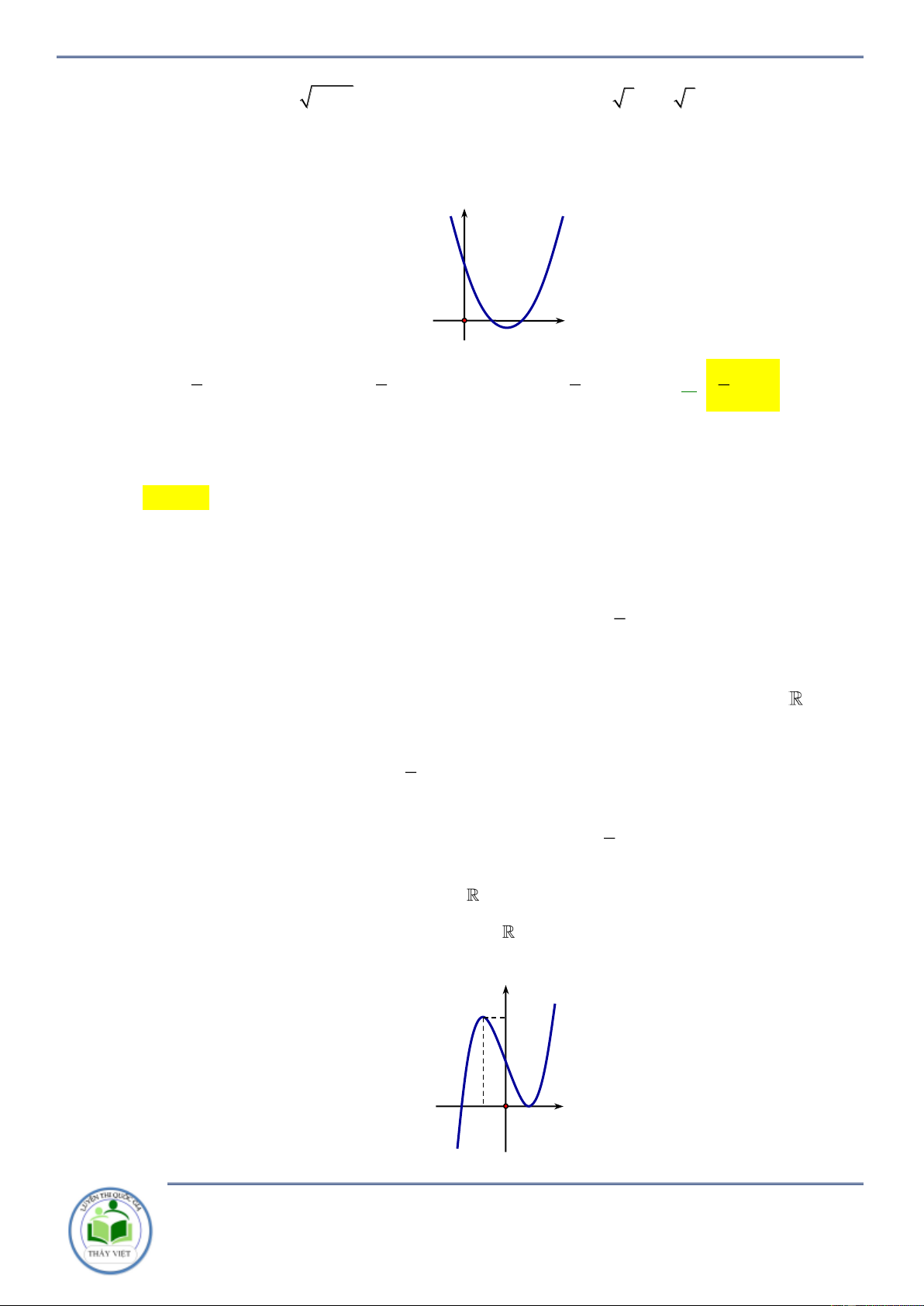
Cho hàm số y  f  x có đạo hàm 2
y  x  x   2
1 x  4. Hàm số y  f 2  x đồng biến trên khoảng A.  ;  0. B. 0  ;1 . C. 2; . D. 1;4 . Lời giải Chọn B 2 2
Ta có y  f 2  x  2 .
x f 2  x  2 .
x 2  x 2  x  
1  2  x  4
Do đó y    x2   x 2 2 1 x  4x.    2 0 x 1
Suy ra y  0   x   1  x  2  2
x  4x  0   x  4
Vậy, từ các đáp án đã cho ta có hàm số đồng biến trên khoảng 0  ;1 . Câu 5:
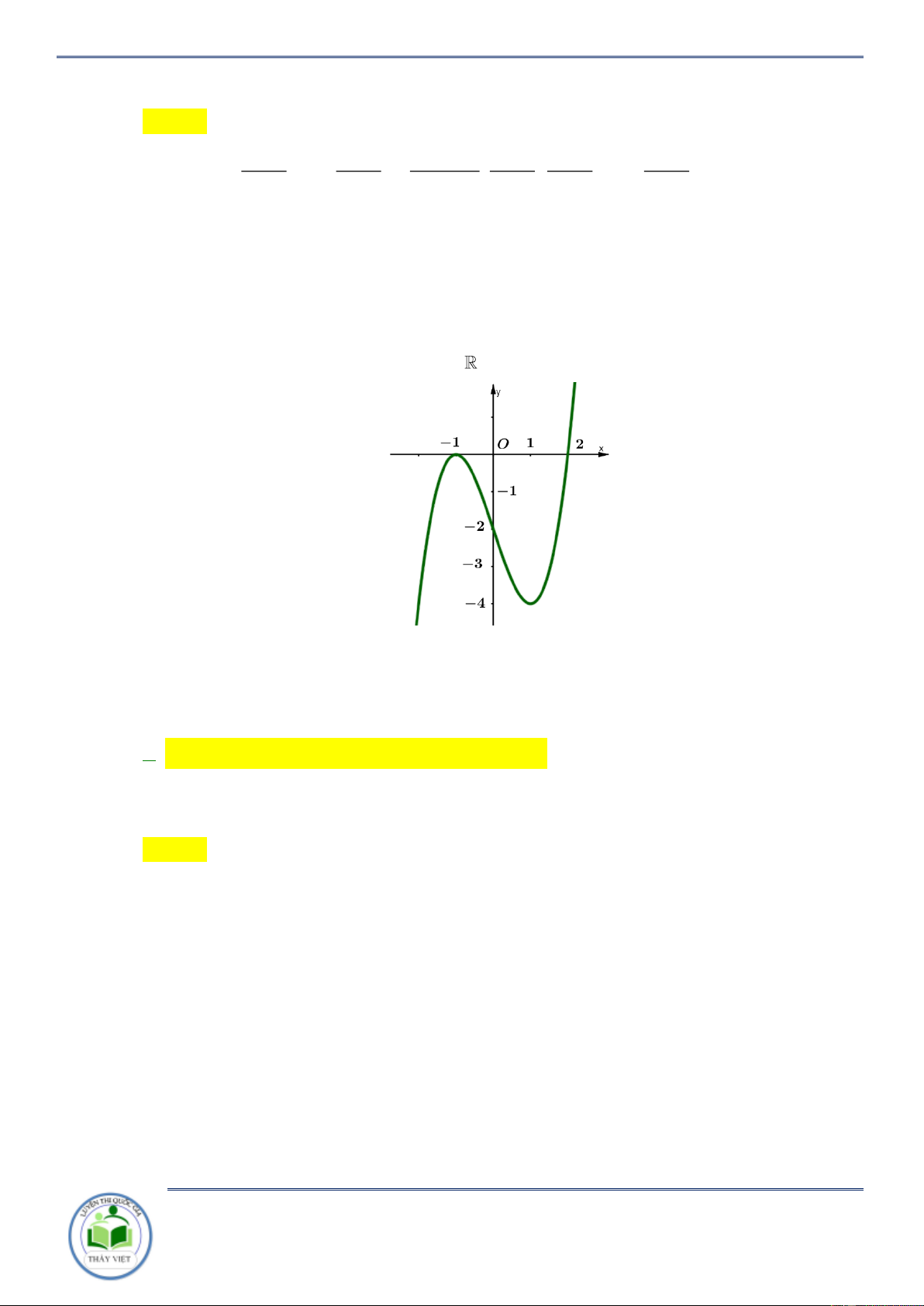
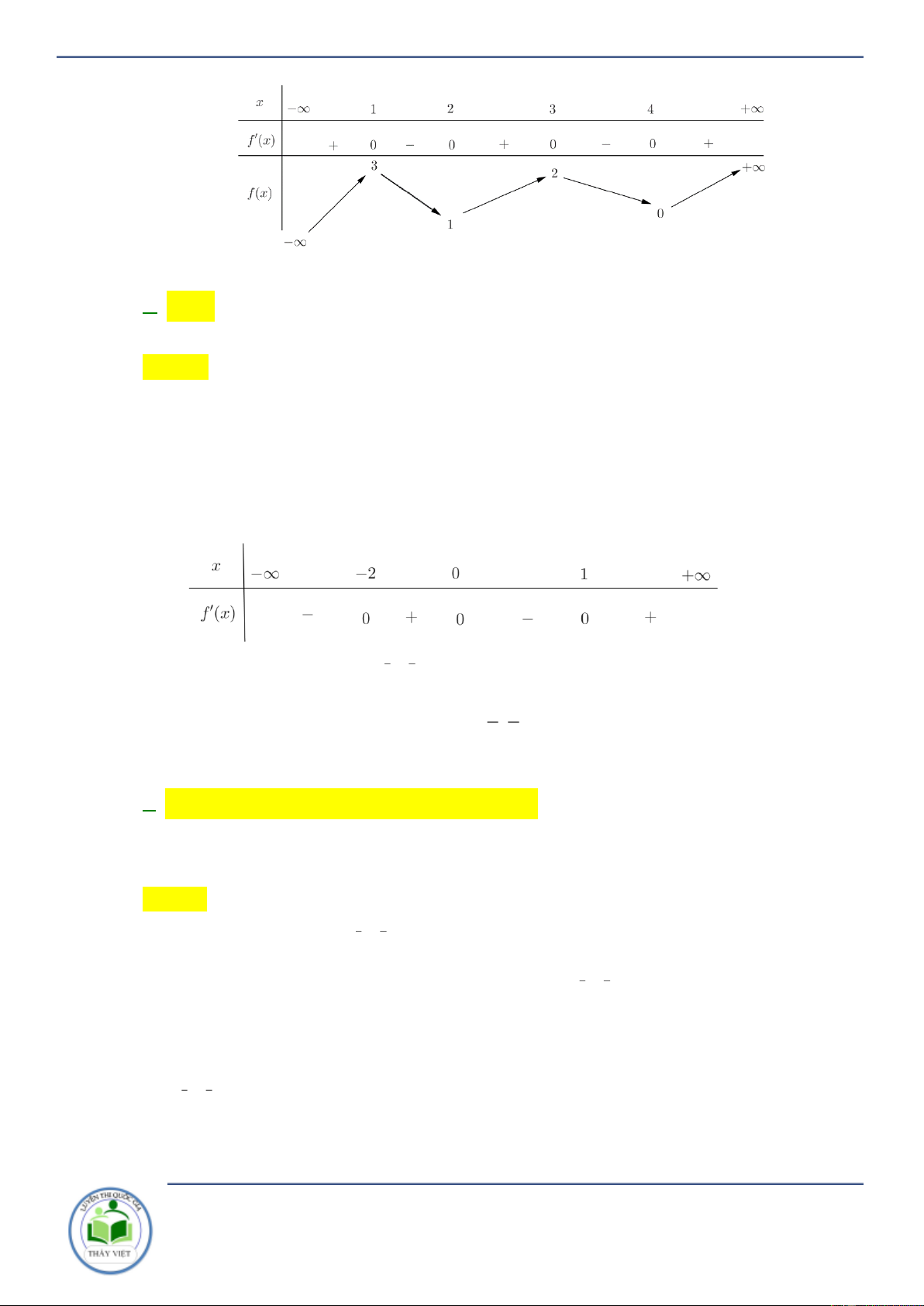
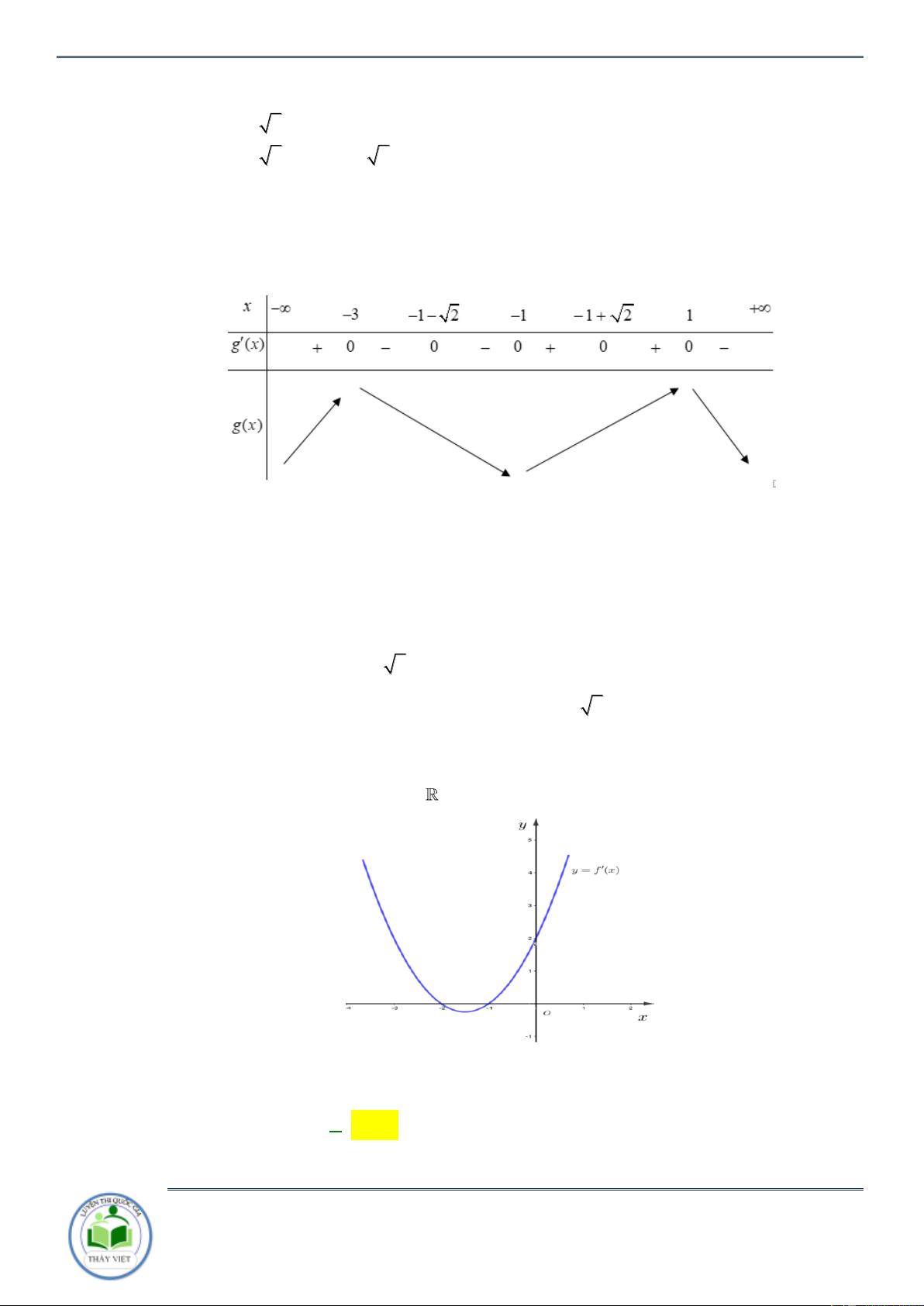
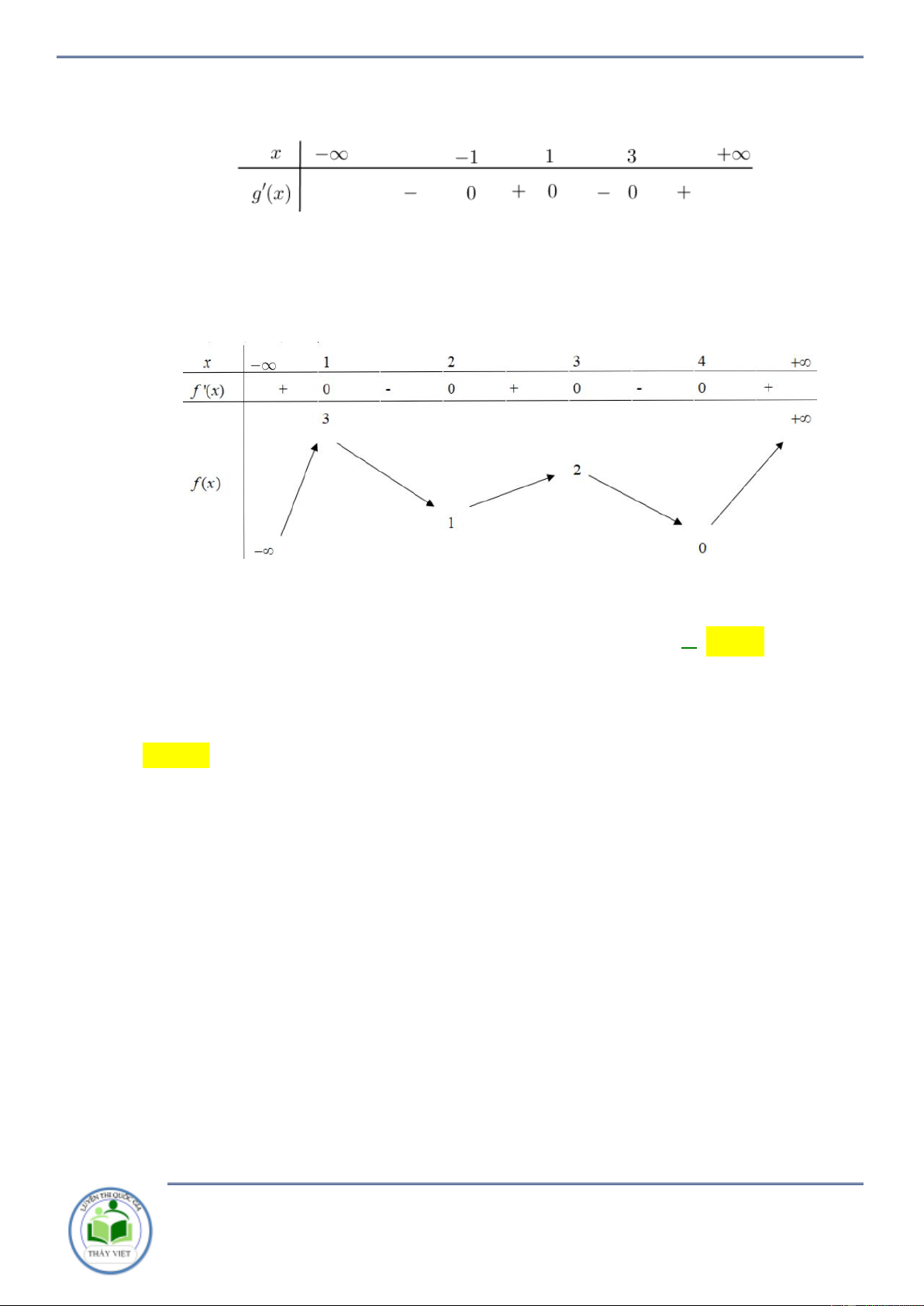
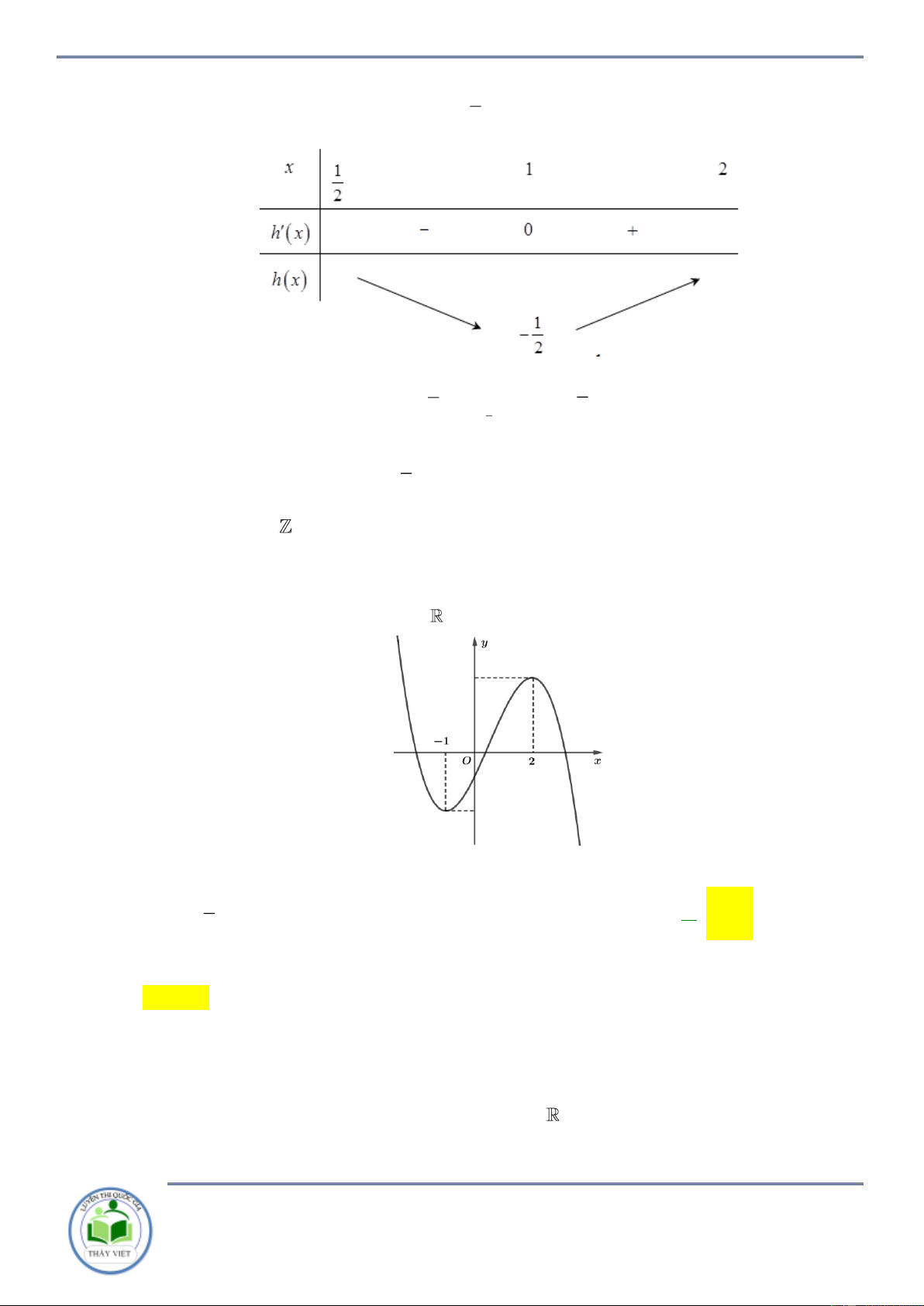
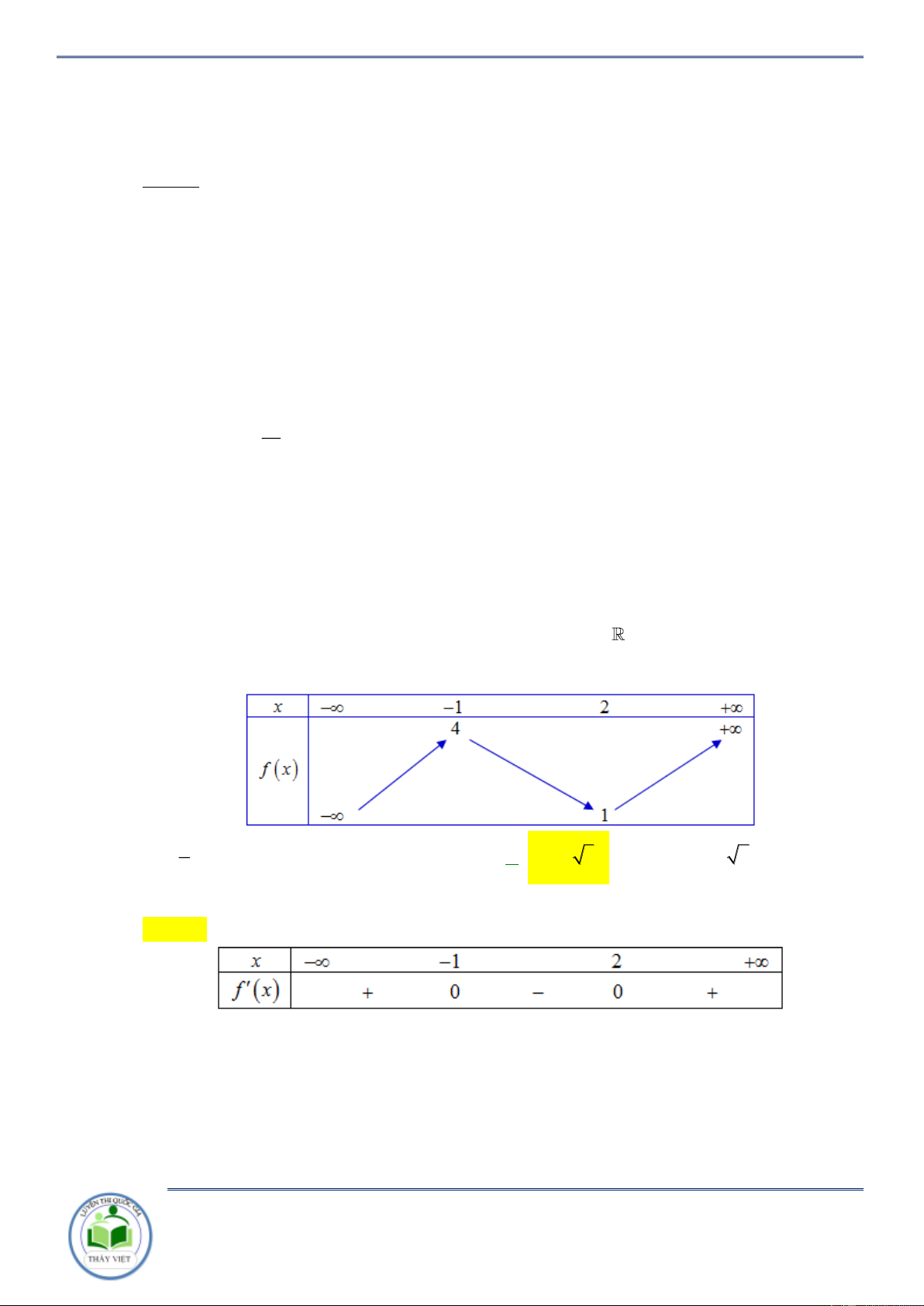
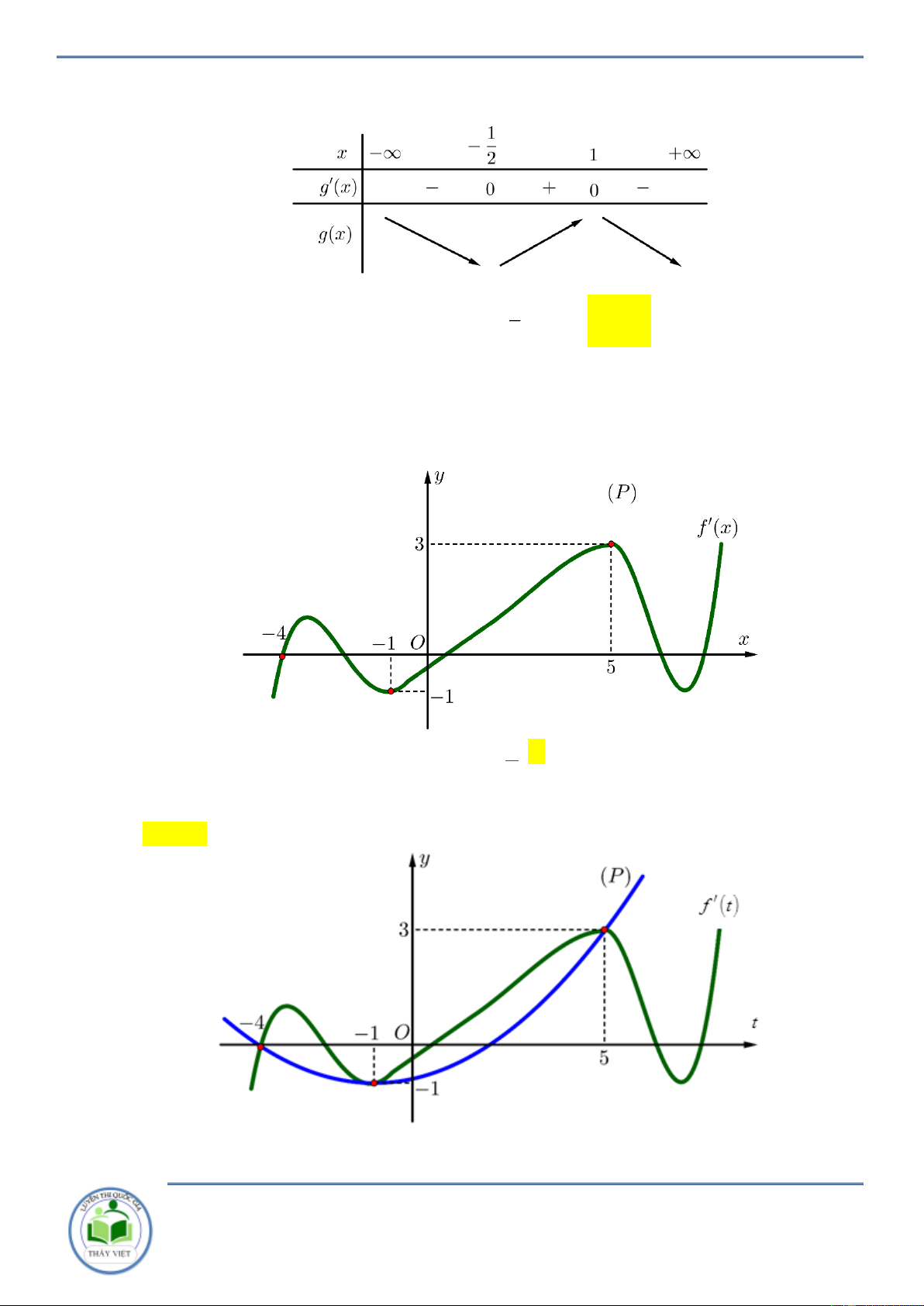
Cho hàm số y  f  x có bảng biến thiên như sau
Hàm số y  f  2
x  2 nghịch biến trên khoảng nào dưới đây A.  2  ;0 . B. 2; . C. 0; 2 . D.  ;  0. Lời giải Chọn B
Ta có y  f   x  x f  2
x    x f  2 2 2 . 2 2 . x  2  0 2  2   x  2  0 x  2
* Nếu x  0 thì y  0  f  2
x  2  0     . 2 x  2  2 0  x  2 2 x  2  2 
* Nếu x  0 thì y  0  f  2
x  2  0    2   x   2 . 2 0  x  2  2
Do đó, đáp án đúng trong các đáp án đã cho hàm khoảng 2; . 2  5x  Câu 6:
Cho hàm số y  f  x có đạo hàm f  x  x x  
1  x  2 . Hỏi hàm số y  f   2  x  4 
đồng biến trên khoảng nào dưới đây? A.  ;  2  . B. 0; 2 . C. 2; 4 . D.  2   ;1 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 4/102 Lời giải Chọn C   5x   5 5 x   2 4  x  2 5x  5x   5x  Ta có: y  . f    1  2         . 2 2  x  4 
 x  4  x  2 2 2 2 2
x  4  x  4   x  4 4  x  4 2 
Do đó: y  0   2 4  x  2
5x  x  4  2
5x  2x  8  0  2  x  4  .  2   x  0 
Đối chiếu các phương án ta chọn C . Câu 7:
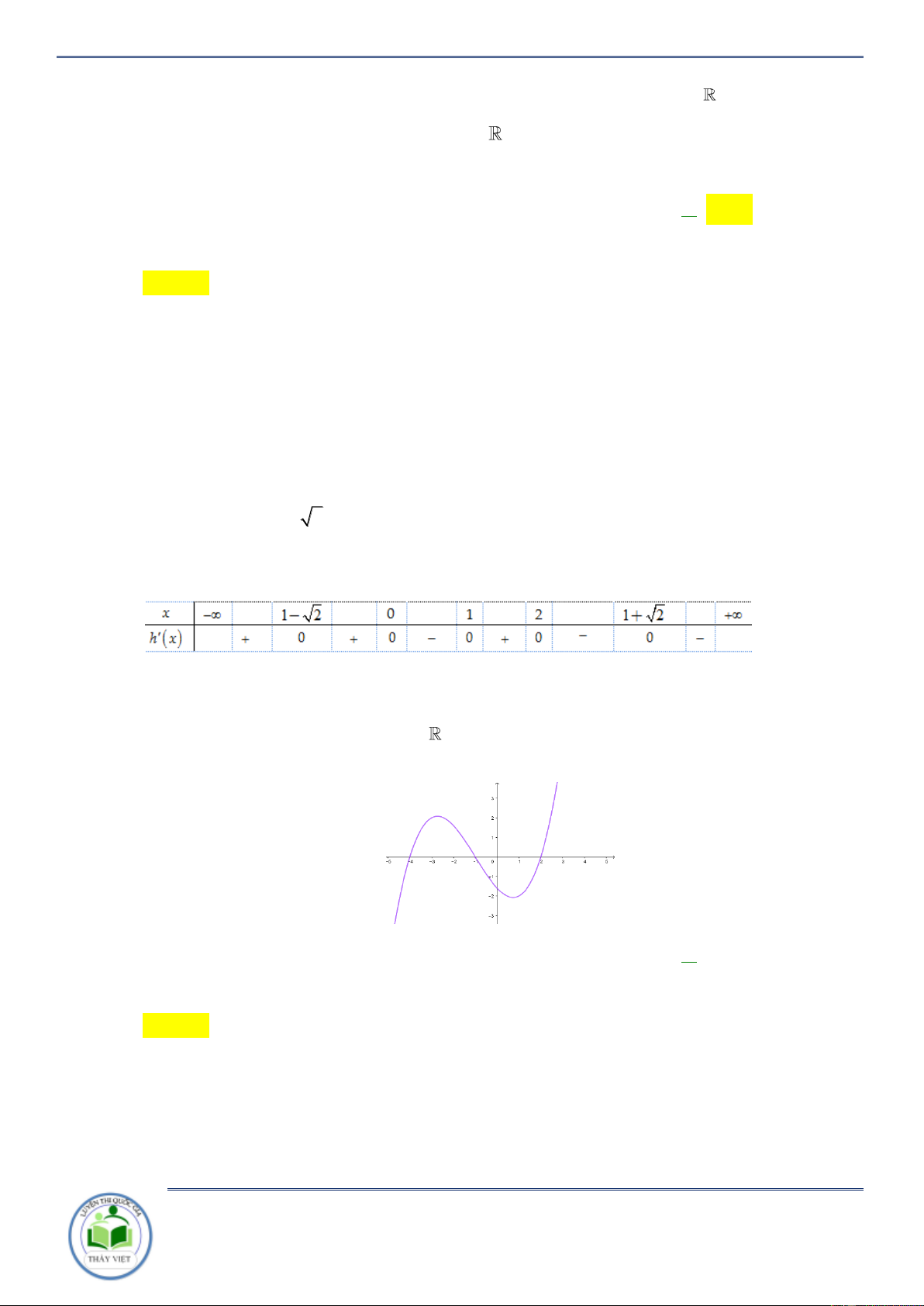
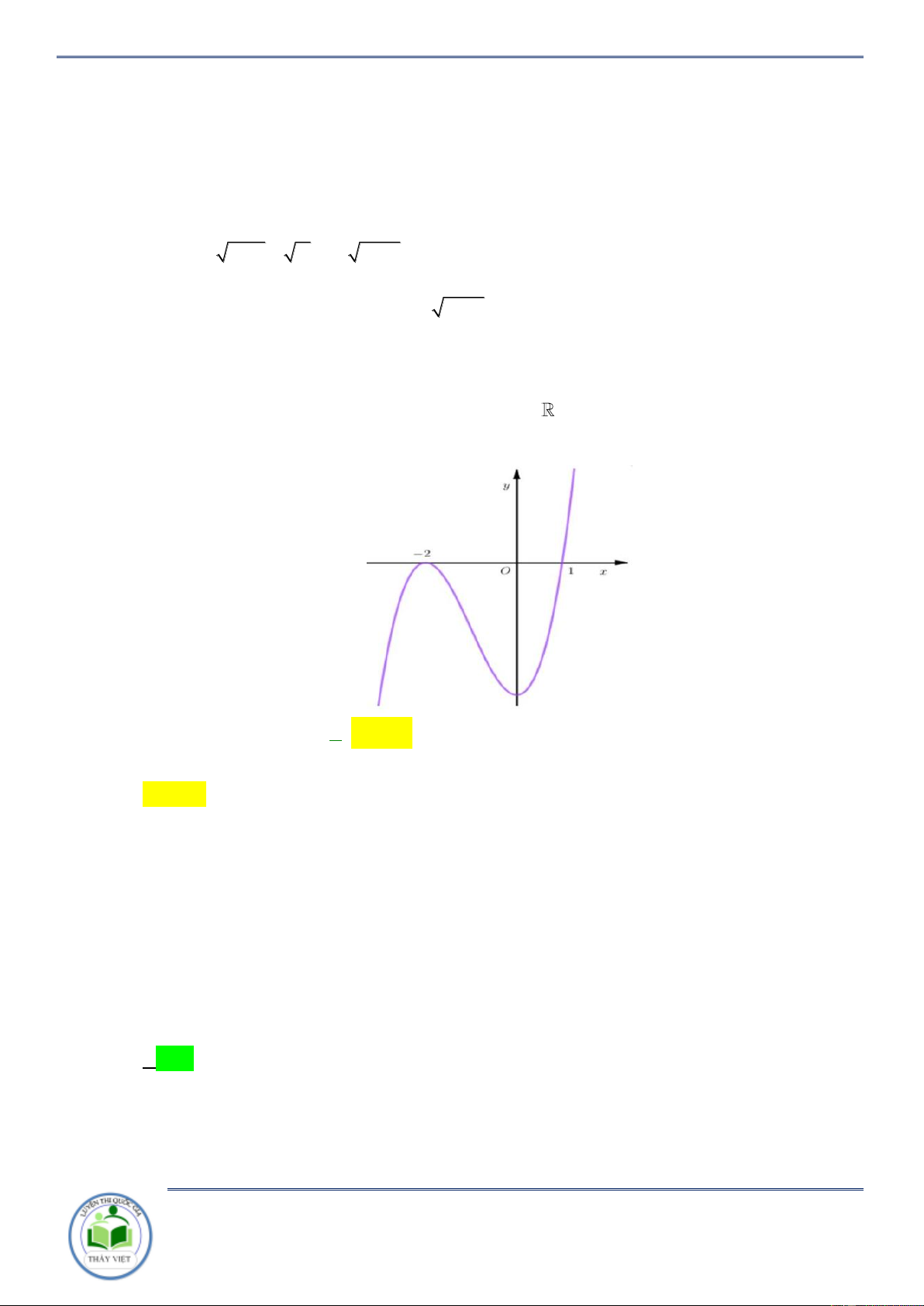
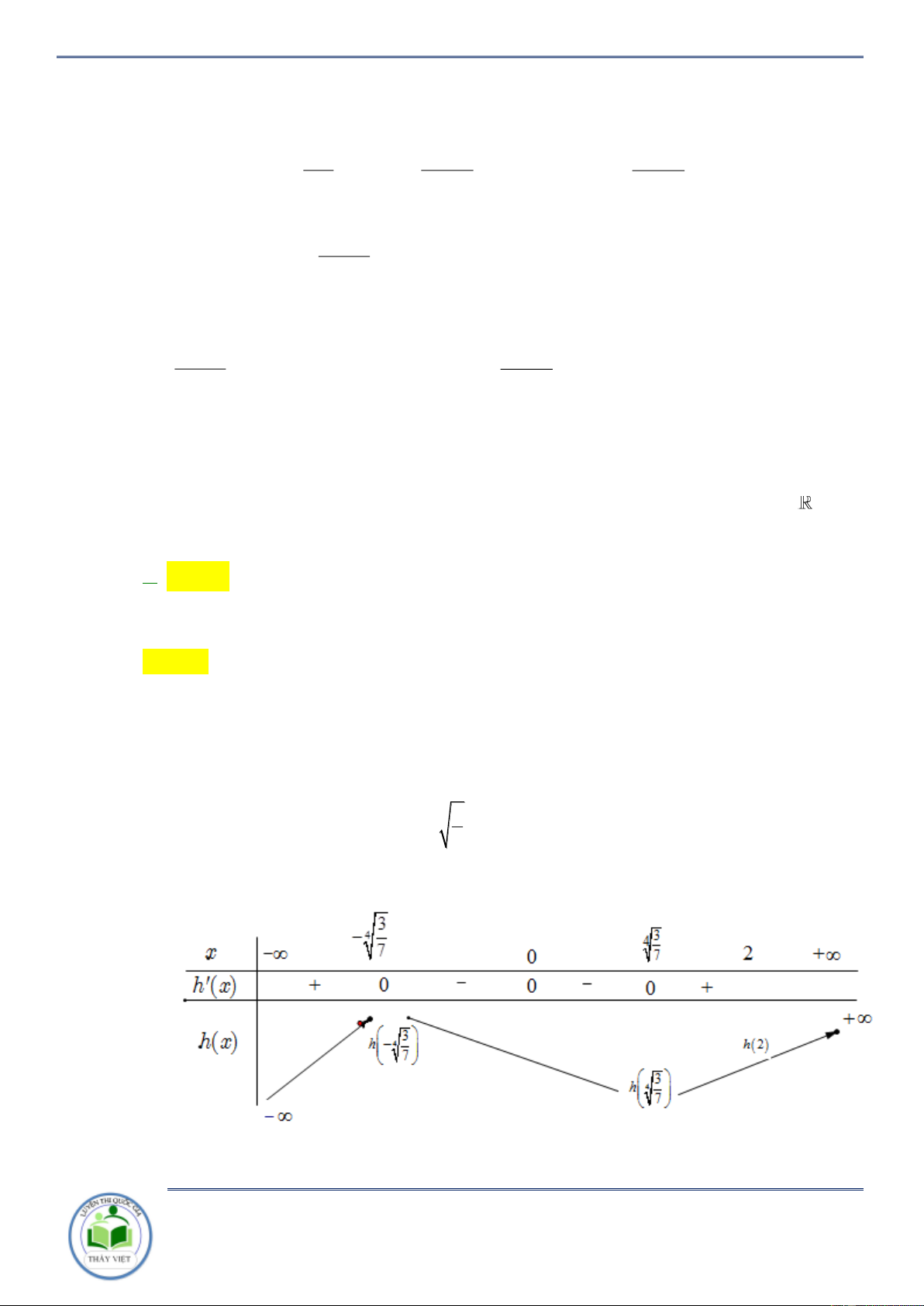
Cho hàm số y  f  x có đạo hàm trên và có đồ thị hàm số y  f  x như hình vẽ.
Đặt g  x  f  2
x  2 . Mệnh đề nào dưới đây sai?
A. Hàm số g  x đồng biến trên khoảng 2; .
B. Hàm số g  x nghịch biến trên khoảng 0; 2 .
C. Hàm số g  x nghịch biến trên khoảng  1  ;0 .
D. Hàm số g  x nghịch biến trên khoảng  ;  2  . Lời giải Chọn C x  0  x  0    f    2 x  2 2  0 x  2  2 x  2 Ta có: g (
 x)  2xf  2
x  2  0       . x  0 x  0   2   x  0    f    2 x  2 2  0 x 2  2
Đối chiếu các phương án ta chọn C . Câu 8:
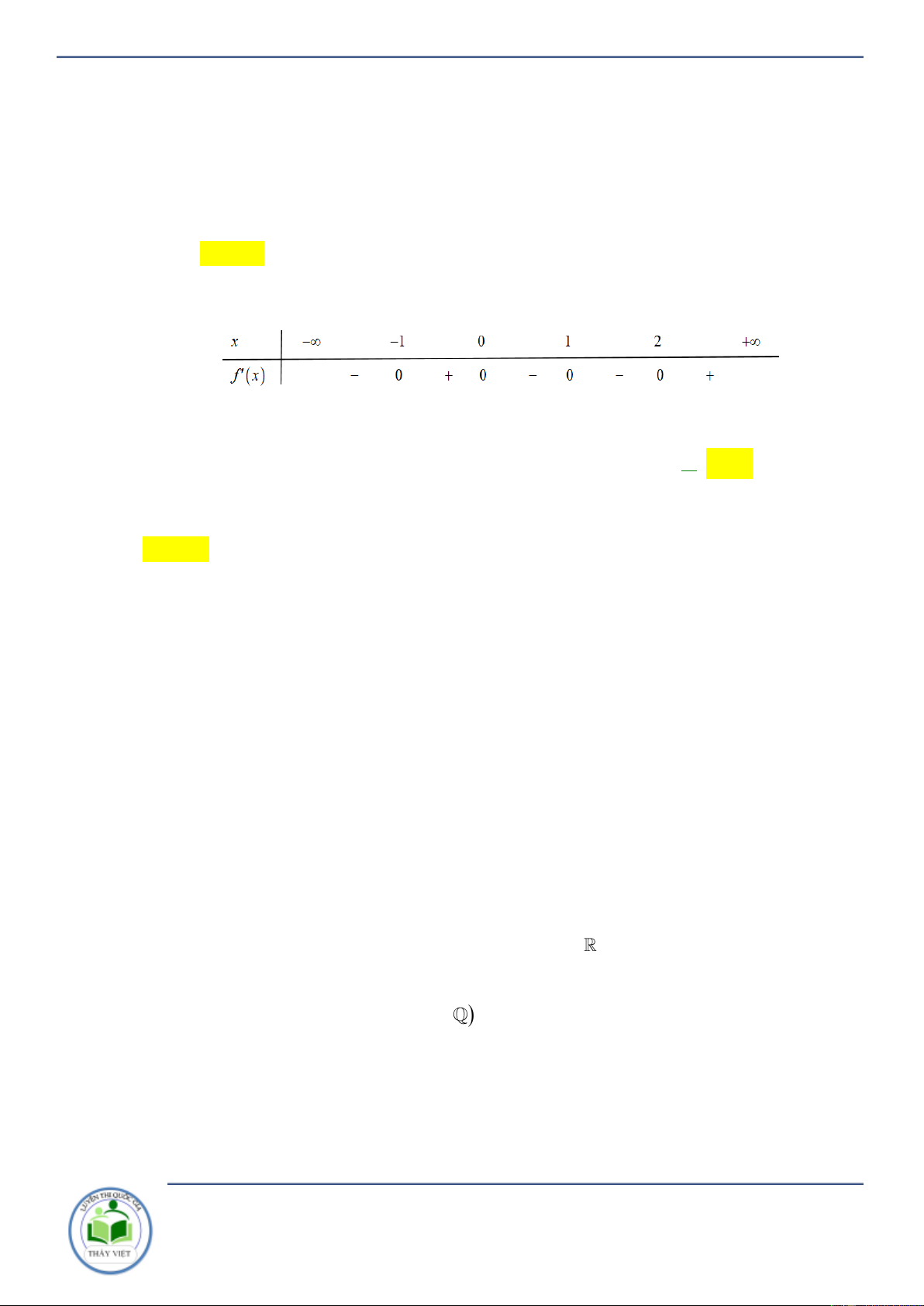
Cho hàm số y  f  x có bảng biến thiên như hình vẽ dưới đây
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
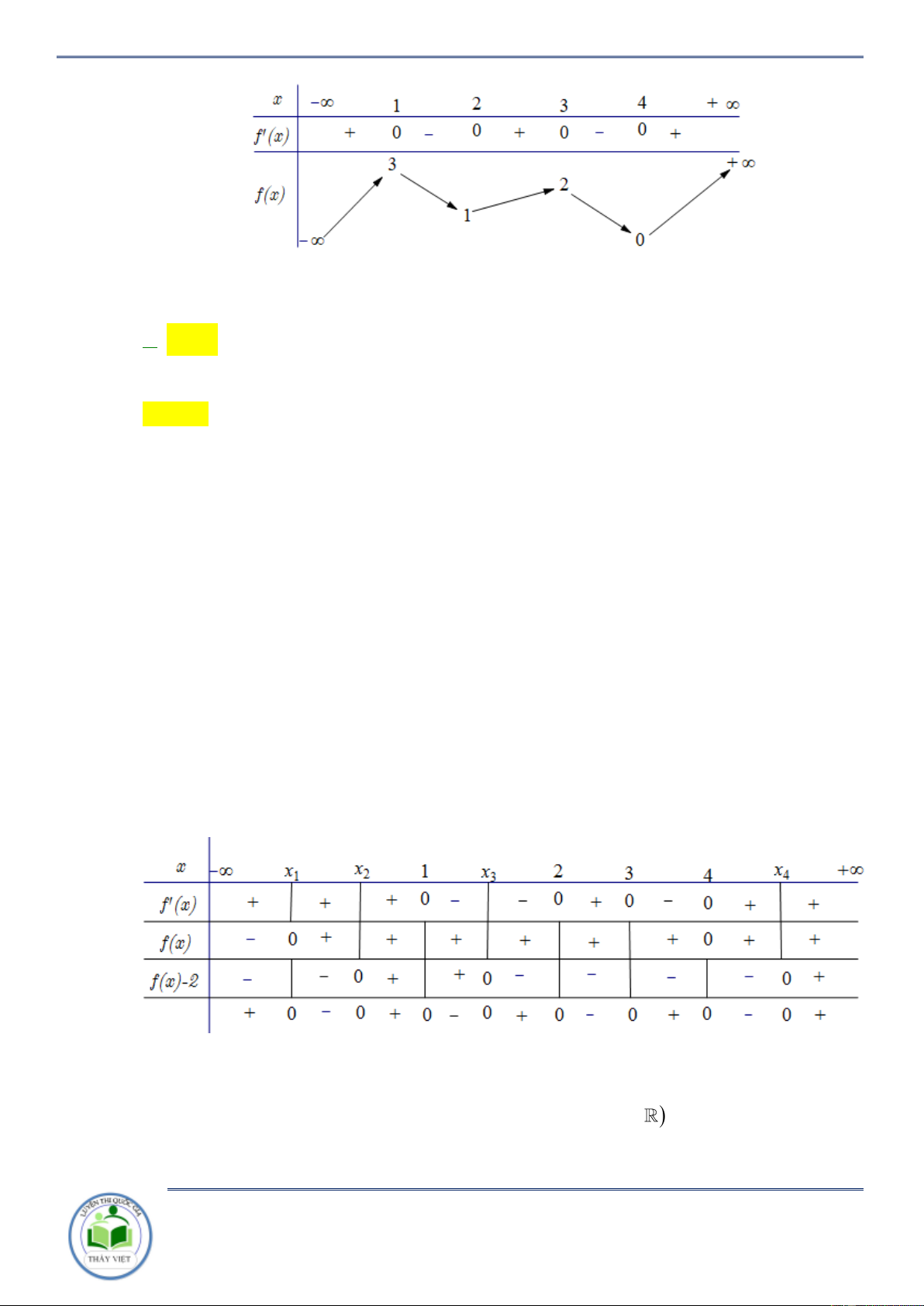
Chuyên đề: Tính đơn điệu của hàm hợp Trang 5/102 x  1  3  y  0  0   y 4
Hàm số y  f 3 x  đồ
ng biến trên khoảng nào dưới đây 2  ? A. ;0 . B. 4;6 . C.  1  ;5 . D. 0;4 . Lời giải Chọn D
Ta có y   f 3 x  0  f 3 x  0  1
  3 x  3  0  x  4 .
Vậy hàm số y  f 3 x đồng biến trên khoảng 0;4 . Câu 9:
Cho hàm số y  f  x có đạo hàm f  x 2
 x x  
1  x  4 g  x , trong đó g  x  0, x  . Hàm số   2 y
f x  đồng biến trên khoảng nào dưới đây?
A. ; 2 . B.  1   ;1 . C.  2  ;  1 . D. 1;2 . Lời giải Chọn C 2
Ta có y  xf  2 x   x 2 x   2 x   2
x   g  2 2 2 1 4 x  5
 x x  x  x  x   g  2 2 1 2 1 2 x  x  2  Ta có y '  0  2   x  1   . 0  x 1  Vậy hàm số   2 y
f x  đồng biến trên mỗi khoảng  2  ;  1 ,0;  1 ,2;   .
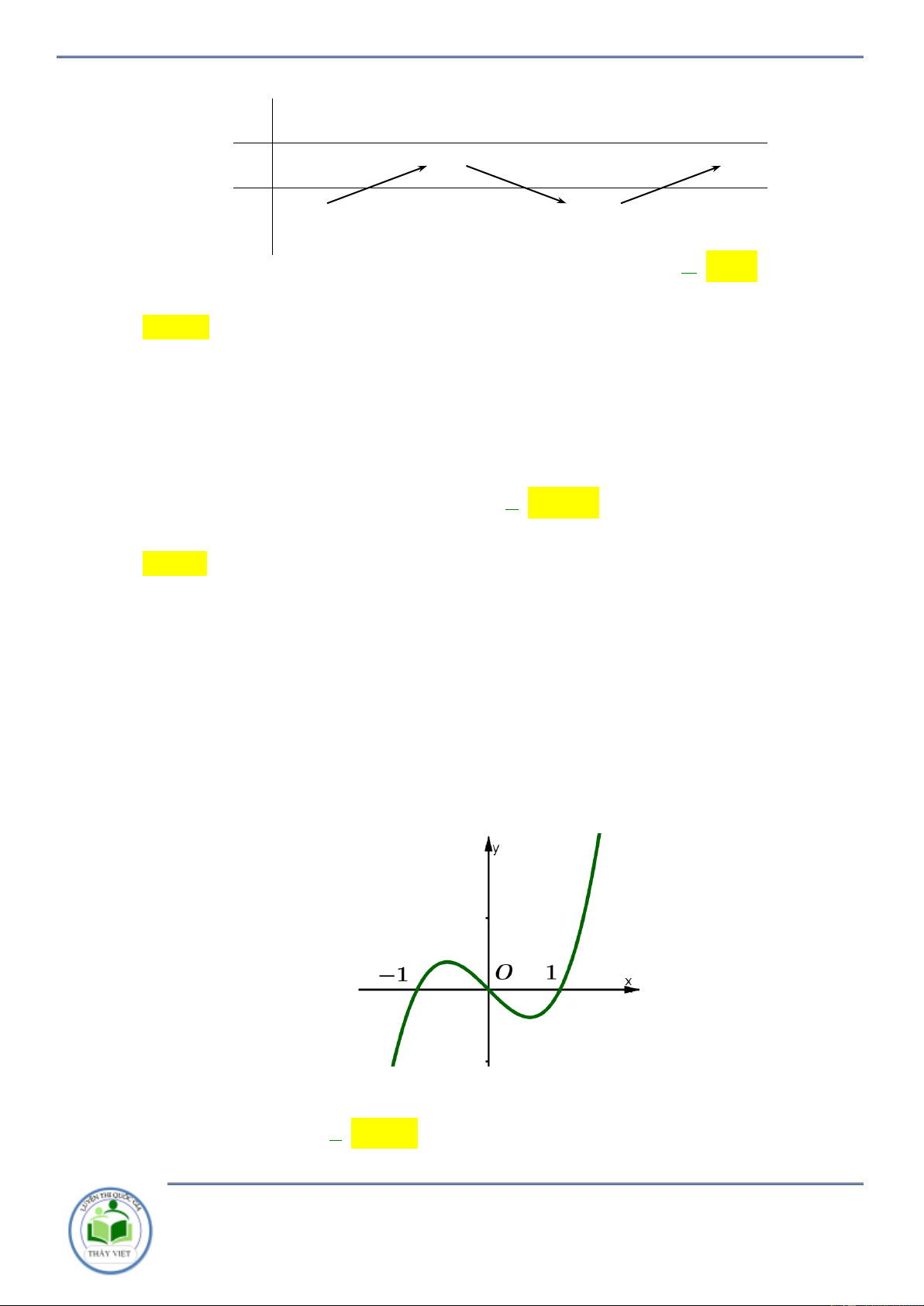
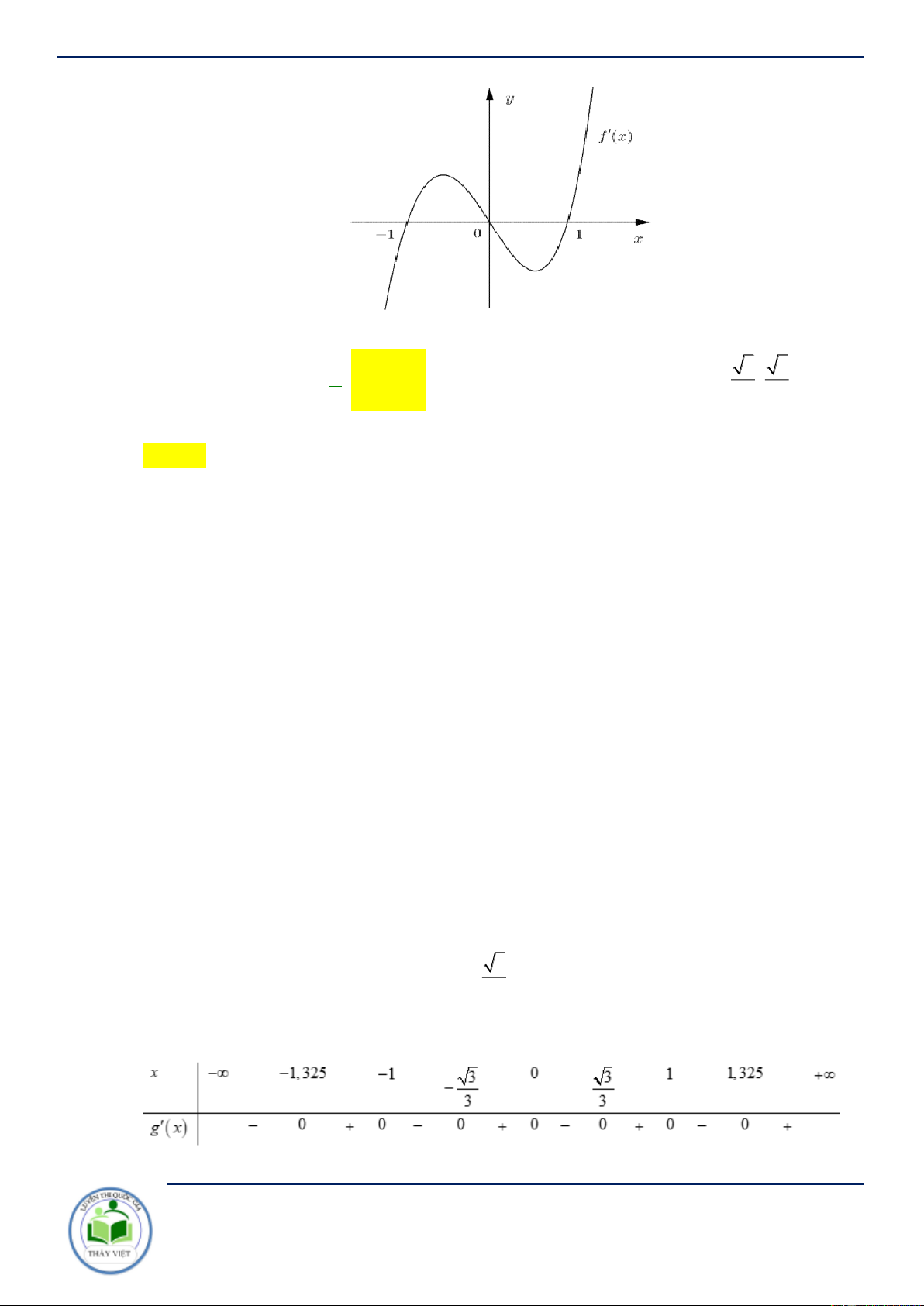
Câu 10: Cho hàm số y  f  x có đồ thị f  x như hình vẽ bên Hàm số   3 y
f x  đồng biến trên khoảng nào dưới đây? A. ;  1 . B. 1;  . C.  1   ;1 . D. 0  ;1 . Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 6/102 Chọn B Ta có 2
y  x f  3 3 x  . x 1 x 1 Do 2 3x  0, x
  nên y  0  f x  3 3  0     . 3  1   x  0  1   x  0 Suy ra hàm số   3 y
f x  đồng biến trên khoảng 1;  .
Câu 11: Cho hàm số y  f  x có đạo hàm f  x  x 2 x  
1  x  4 . Hàm số y  f 3  x đồng
biến trên khoảng nào dưới đây? A. 2;3 . B.  1  ;3. C. 4; . D. 3;4 . Lời giải Chọn D    2 1 x 2
Ta có y   f 3  x  3 x 3 x 13 x  4  0     . 3  x  4
Câu 12: Cho hàm số y  f  x có đạo hàm f  x 2
 xx x   2
1 x  mx  5 . Có bao nhiêu số
nguyên âm m để hàm số   2 y
f x  đồng biến trên khoảng 1; . A. 4 . B. 5 . C. 7 . D. 3 . Lời giải Chọn A 2
Ta có y  xf  2 x   x 2 x   2 x   4 2 x  mx   5  x  2 x   4 2 2 2 1 5 2
1 x  mx  5 . Yêu cầu bài toán  y  0, x  1 5  x  2 x   4 2 2
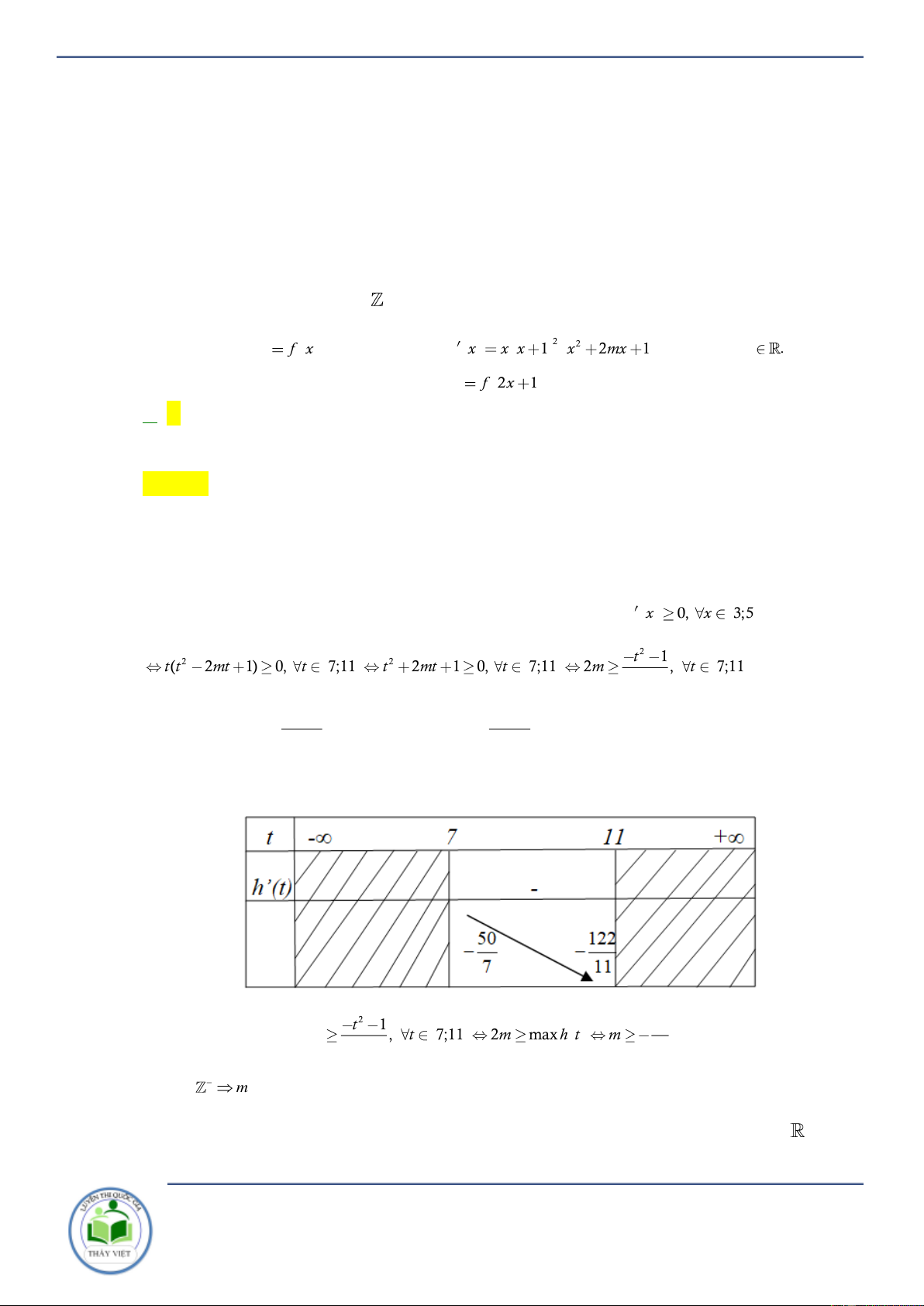
1 x  mx  5 , 4 x  5 x  5  5  x  1 4 2  x  x m  5  0, x  1  m   , x
  1. Đặt g x 4 2     x    2 x 2 2 x  x  5 Ta có 2 x 
 2 5  g x  2  5 , x
 1  Max g x  2  5 khi 4 x  5 . 2 x 1; 4 x  5 m  
 g x , x
 1  m  Max g x  2  5 4  ,4 . 2 x 1;
Vậy có 4 giá trị nguyên âm thỏa mãn bài toán. 2
Câu 13: Cho hàm số y  f  x có đạo hàm f  x  x x    4 3 1
3x  mx   1 . Có bao nhiêu giá trị
nguyên âm m để hàm số   2 y
f x  đồng biến trên khoảng 0; . A. 3 . B. 5 . C. 6 . D. 4 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 7/102 Lời giải Chọn D 2
Ta có y  xf  2 x   x 2 x  2 x    8 6 2 2 1
3x  mx   1 . 8 3x 1
Yêu cầu bài toán  y  0, x   0 8 6
 3x  mx 1 0 , x   0  m    g x . 6 x 1 1 Ta có 2 2 2 2 3x 
 x  x  x 
 4  g x  4  , x
  0  Max g x  4  khi x 1. 6 6 x x 0; 8 3x 1 m  
 g x , x
  0  m  Max g x  4  . 6 x 0;
Vậy có 4 giá trị nguyên âm thỏa mãn bài toán. Câu 14: 2
Cho hàm số y  f  x có đạo hàm f  x  x x    2 1
x  mx  9 . Có bao nhiêu số
nguyên dương m để hàm số y  f 3 x đồng biến trên khoảng 3; ? A. 6 . B. 8 . C. 5 . D. 7 . Lời giải Chọn A
Đặt g  x  f 3 x . 2 2
Ta có g x   f 3 x  3 x3 x   1
3 x  m3 x9  0  
Yêu cầu bài toán tương đương 2
g x  0 , x
  3  x 3  mx 3 9  0, x  2 3  9 x   3  m   hx x   x  , 3 3  
h  x  x 2 3 9 9   x  3
 6  Min hx  6 khi x  6 . x  3 x  3 3; x  2 3  9  m   hx x
   m  Min hx  6 . x  , 3 3 3;
Vậy có 6 giá trị nguyên dương m thỏa mãn.
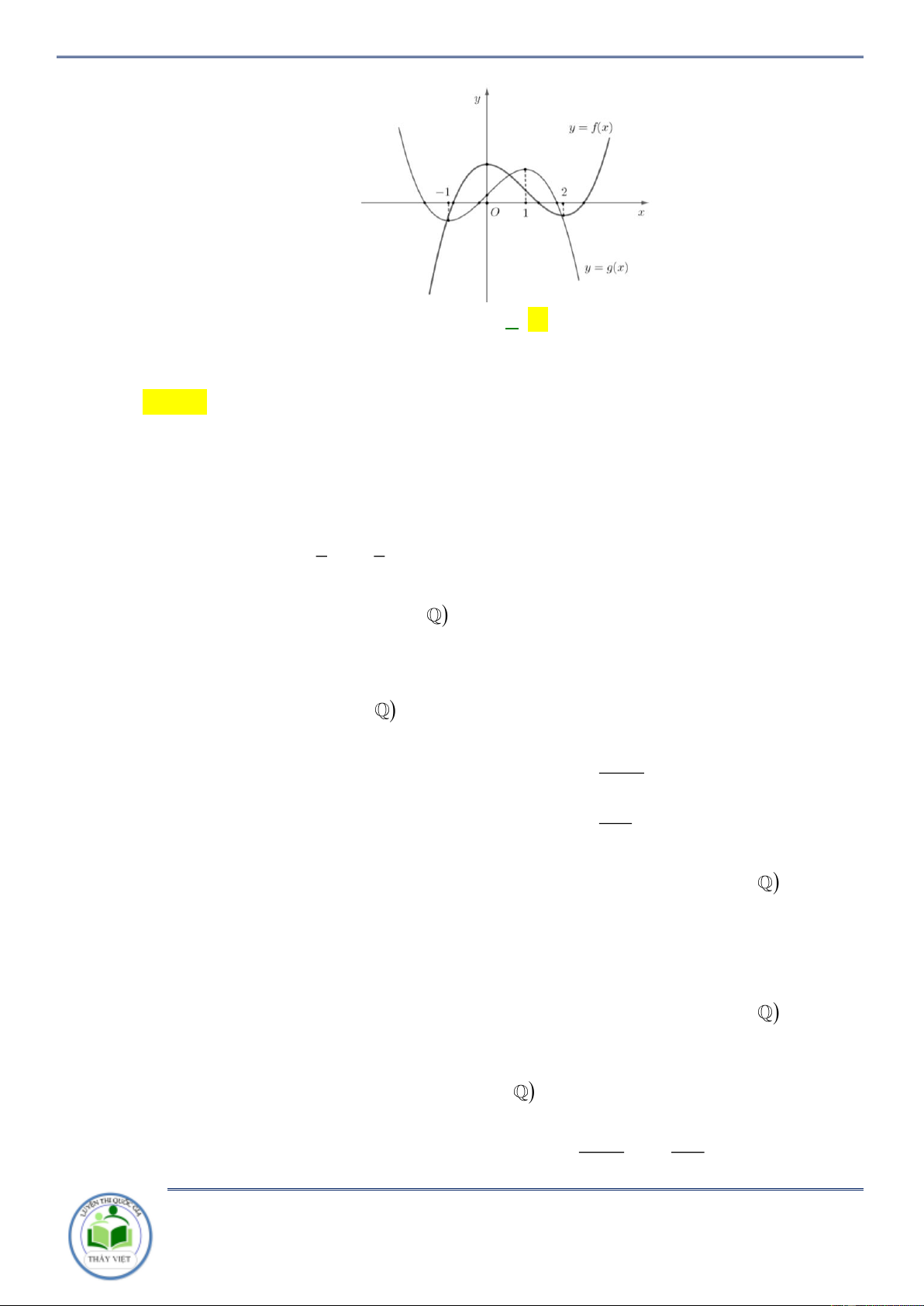
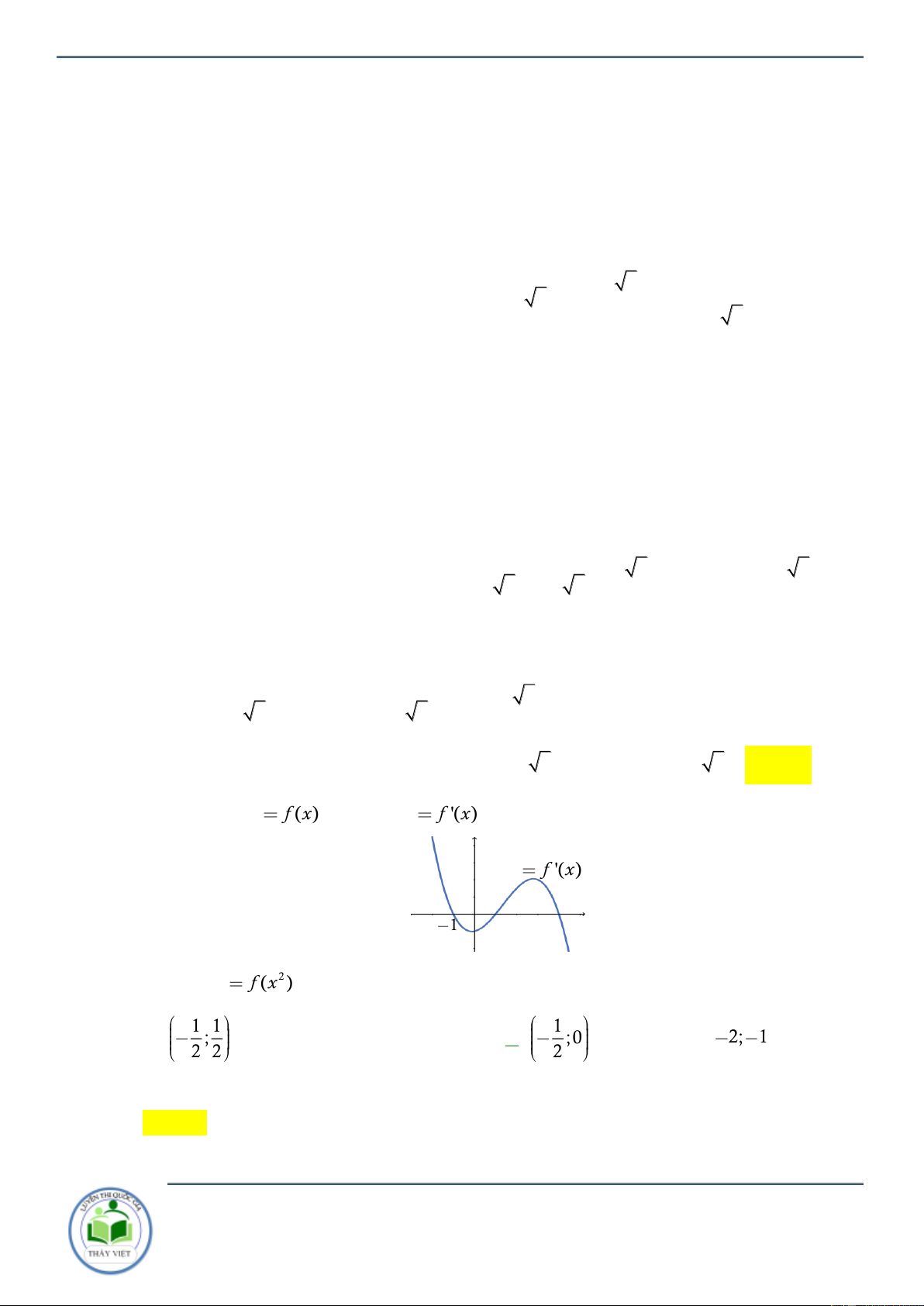
y  f  x f  x Câu 15: Cho hàm số có đồ thị như hình vẽ
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
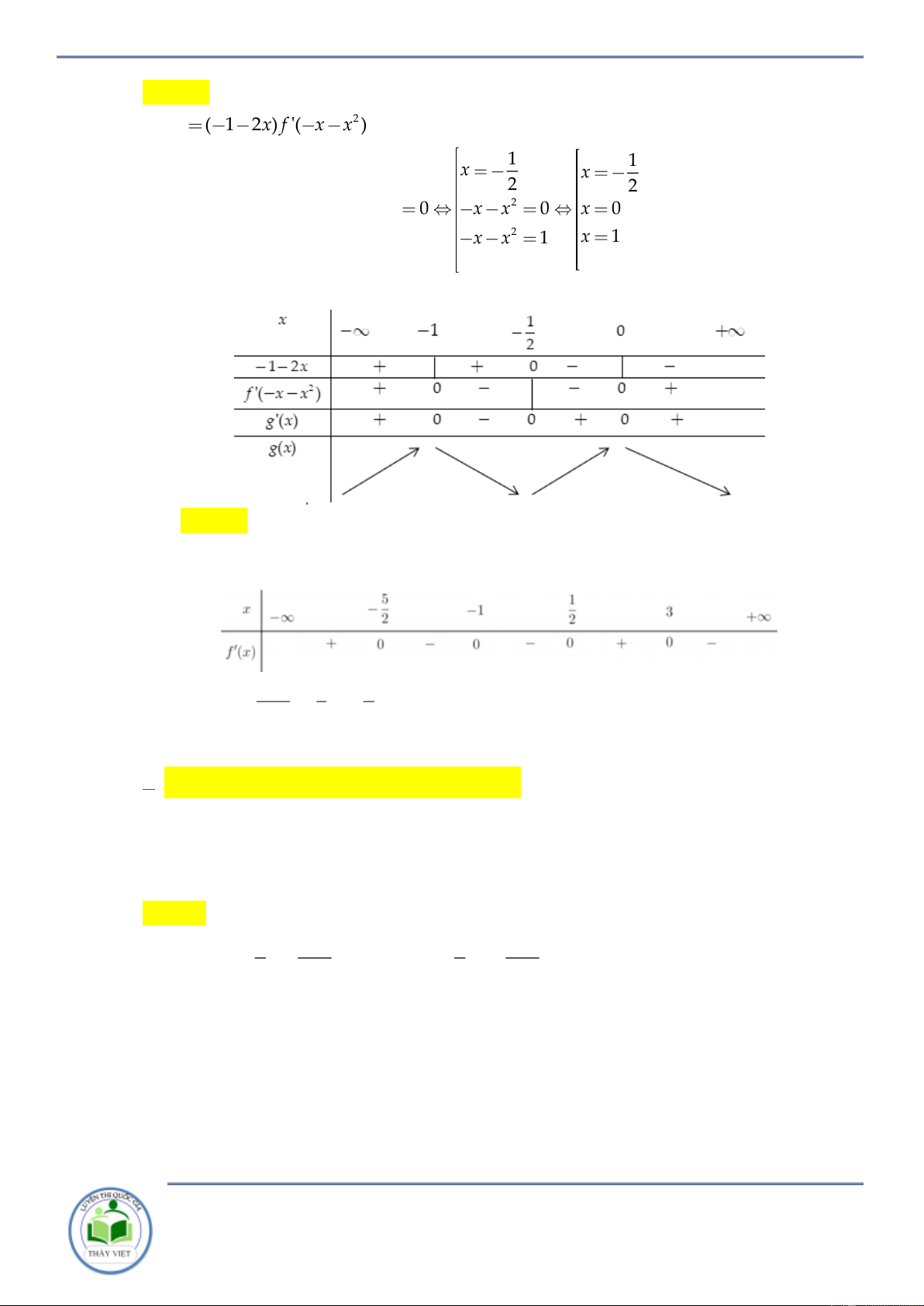
Chuyên đề: Tính đơn điệu của hàm hợp Trang 8/102 Hàm số  2
f x  đồng biến khoảng nào dưới đây? A.  ;    1 . B.  1  ;0 . C. 0  ;1 . D.  1  ; . Lời giải Chọn B Đặt     2 g x f x . x  0  x  0 2 x  1   
g x  xf  2 2
x   g x  0   x 1  . 2  x  0  x  1   2 x 1
Bảng biến thiên của g  x . 0
Dựa vào bảng biến thiên hàm số đồng biến trong khoảng  1  ;0 .
Câu 16: Cho hàm số y  f  x có đồ thị của hàm số y  f  x như hình vẽ bên. Hàm số y  f  2
3  x  đồng biến trên khoảng
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 9/102 A. 2;3 . B.  2  ;  1 . C. 0  ;1 . D.  1  ;0 . Lời giải Chọn D
Ta có y   xf  2
 x    xf  2 2 3 0 3  x   0. 3  x  6  x  3 
Với x  0  f 3  x  2 2  0   x 0   . 2  1   3  x  2 1   x  2  6   3  x  1   1   x  0 
Với x  0  f 3  x  2 2  0   x 0   . 2 3  x  2  3   x  2 
Đối chiếu Chọn D
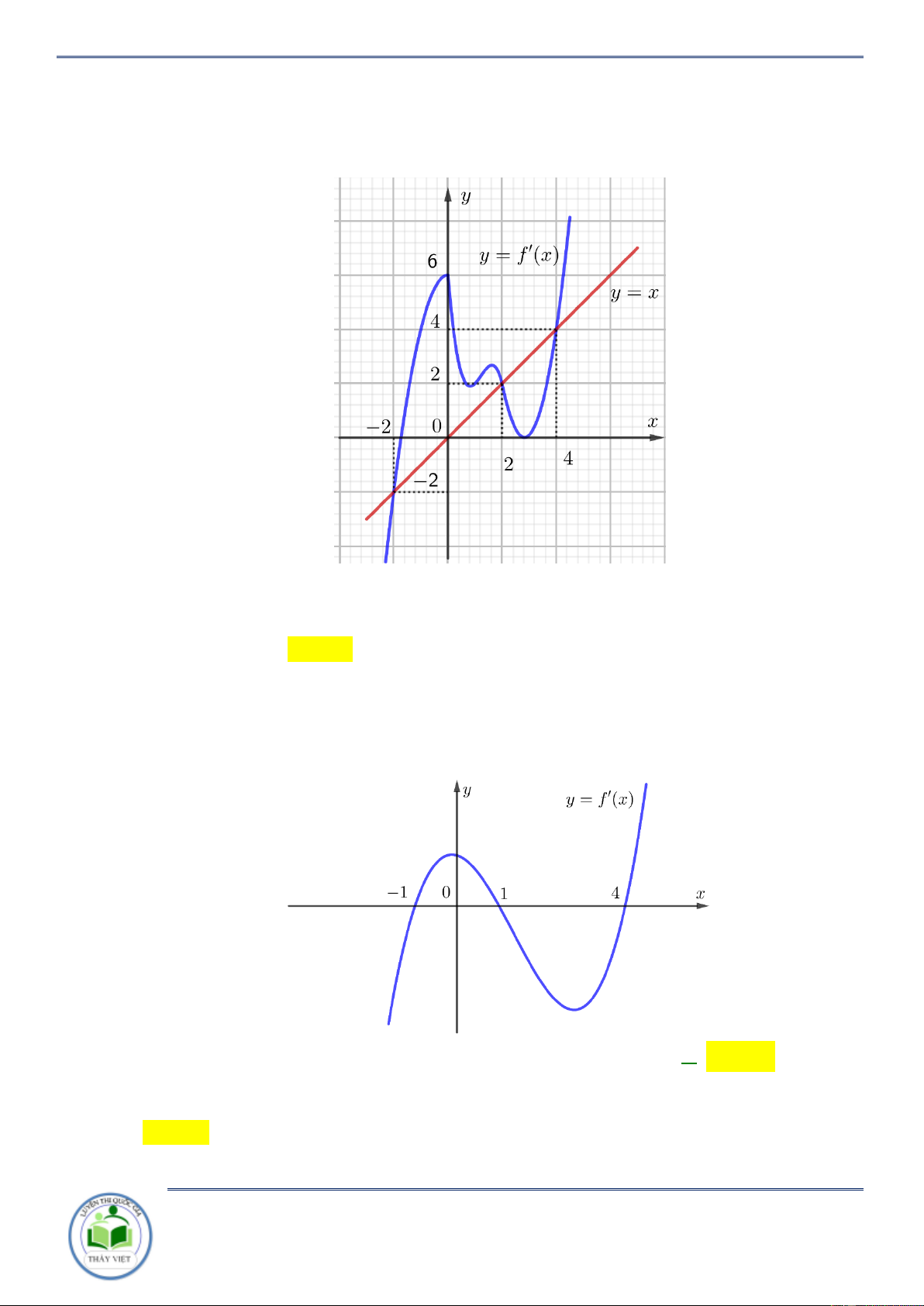
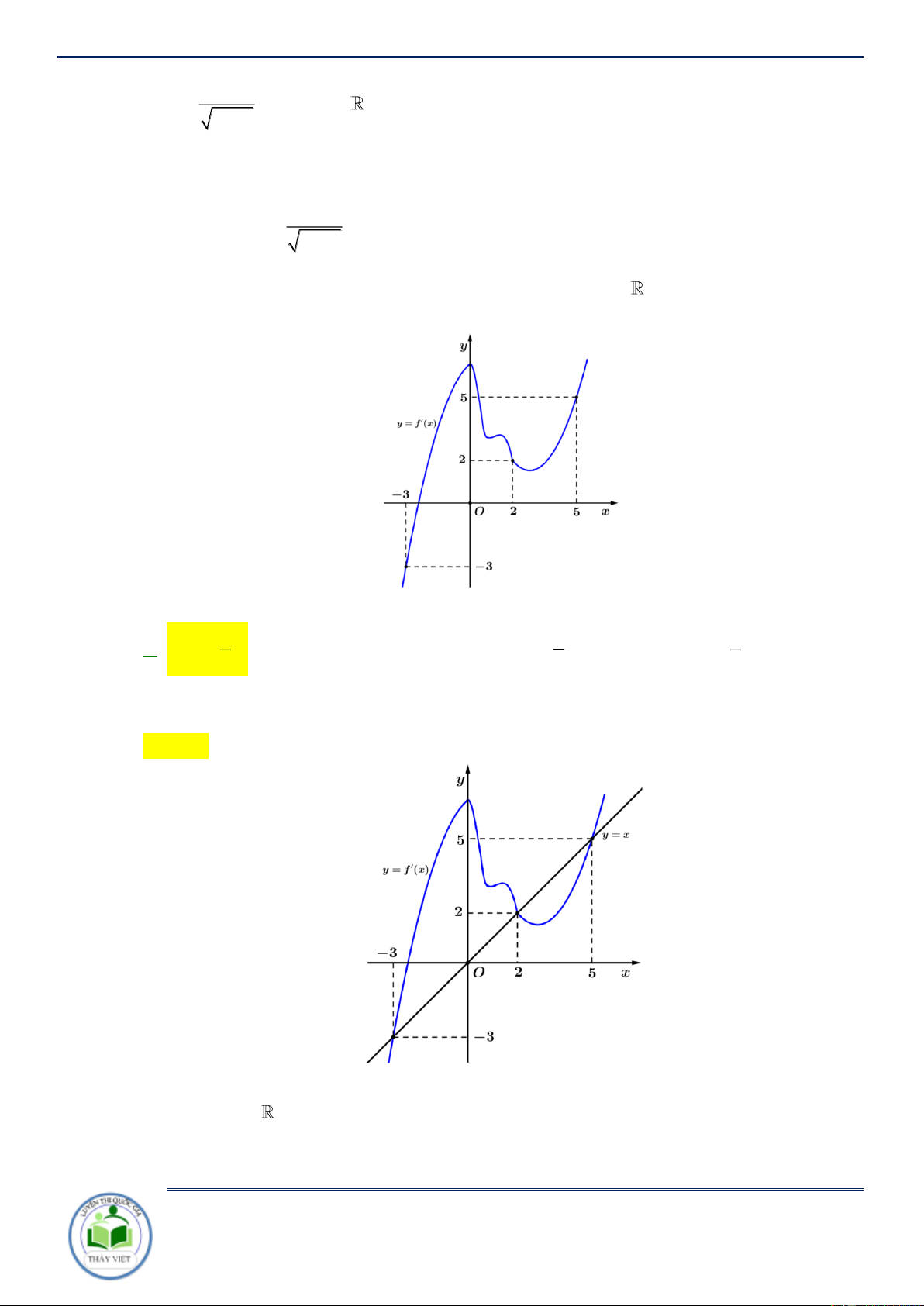
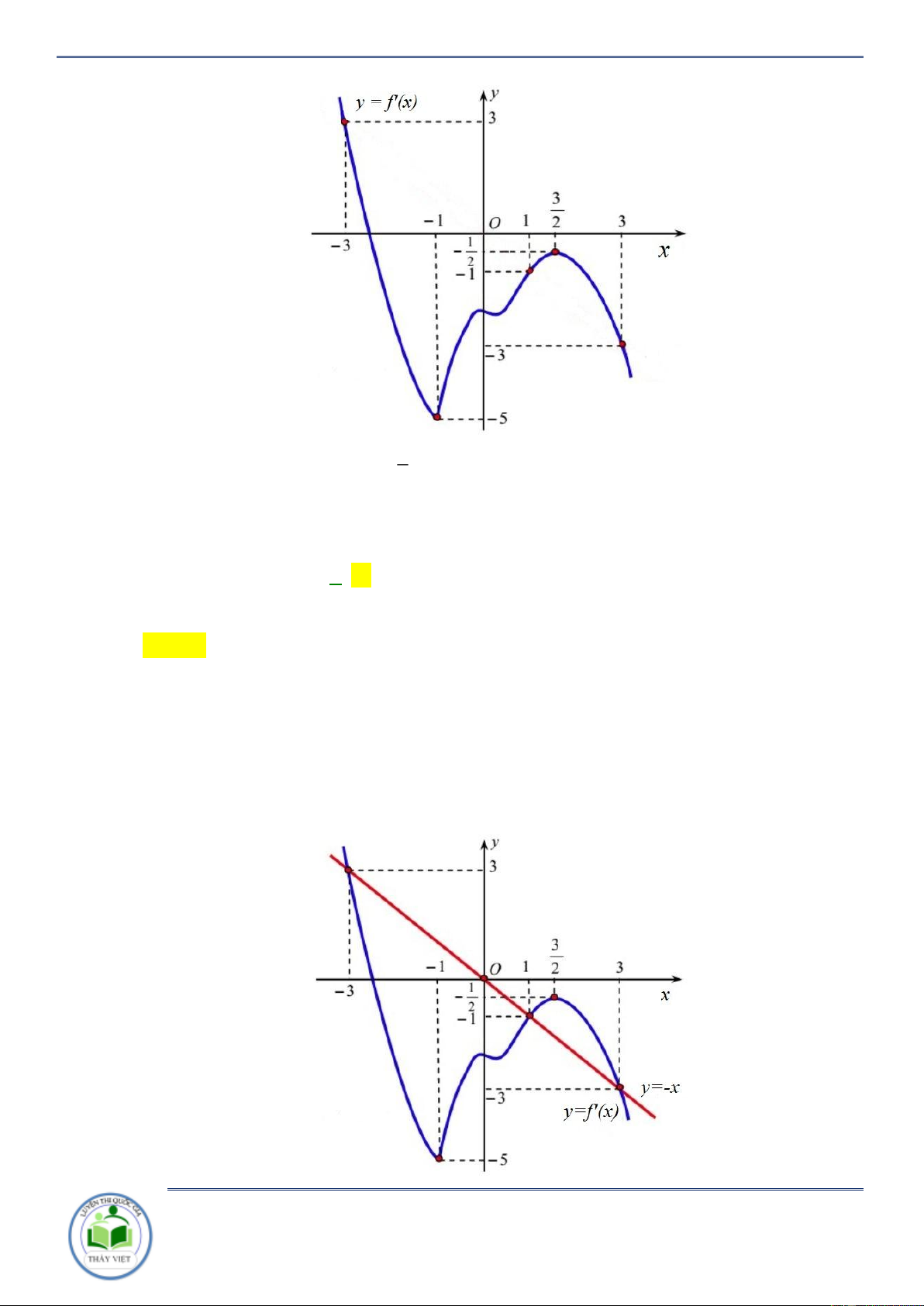
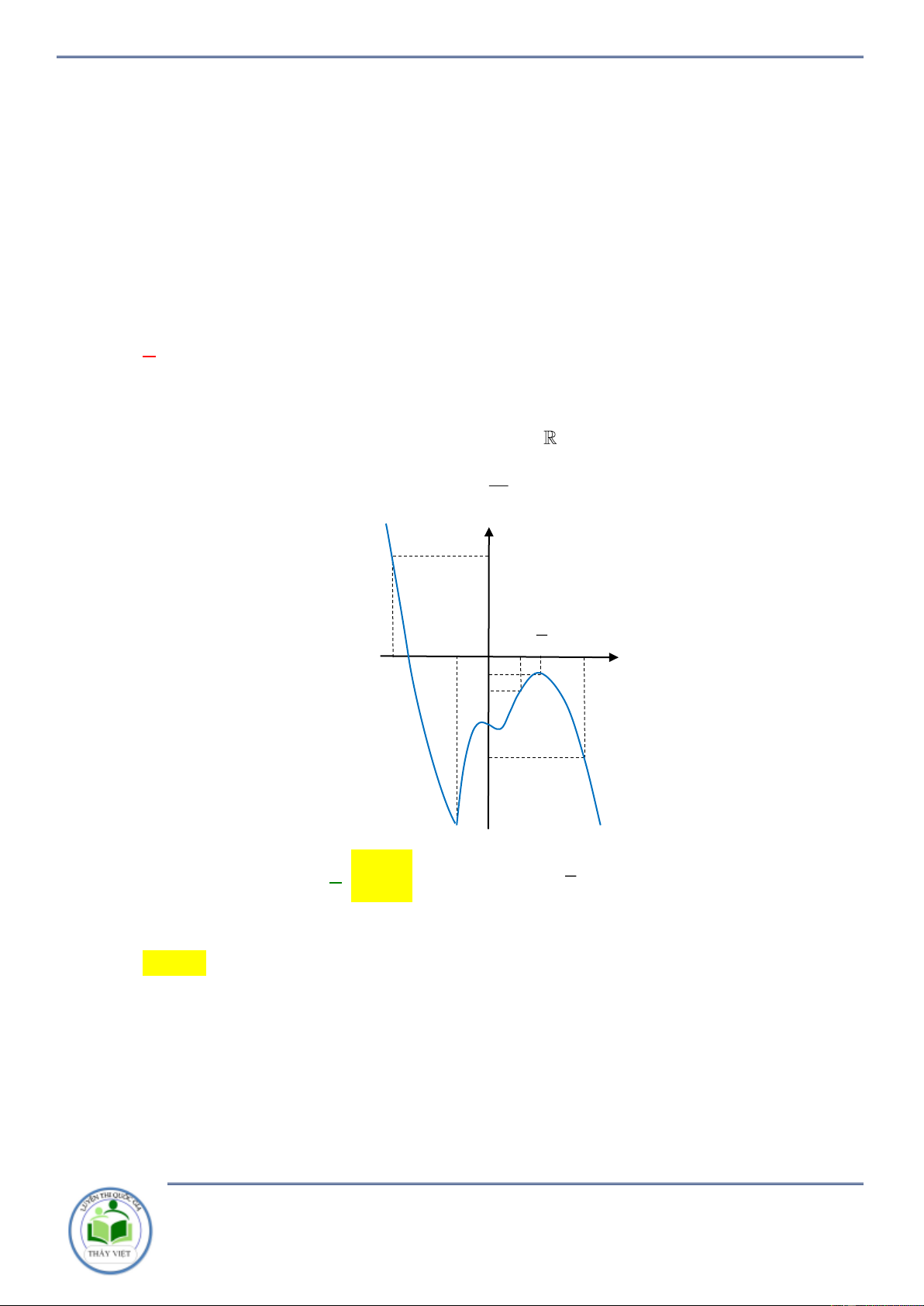
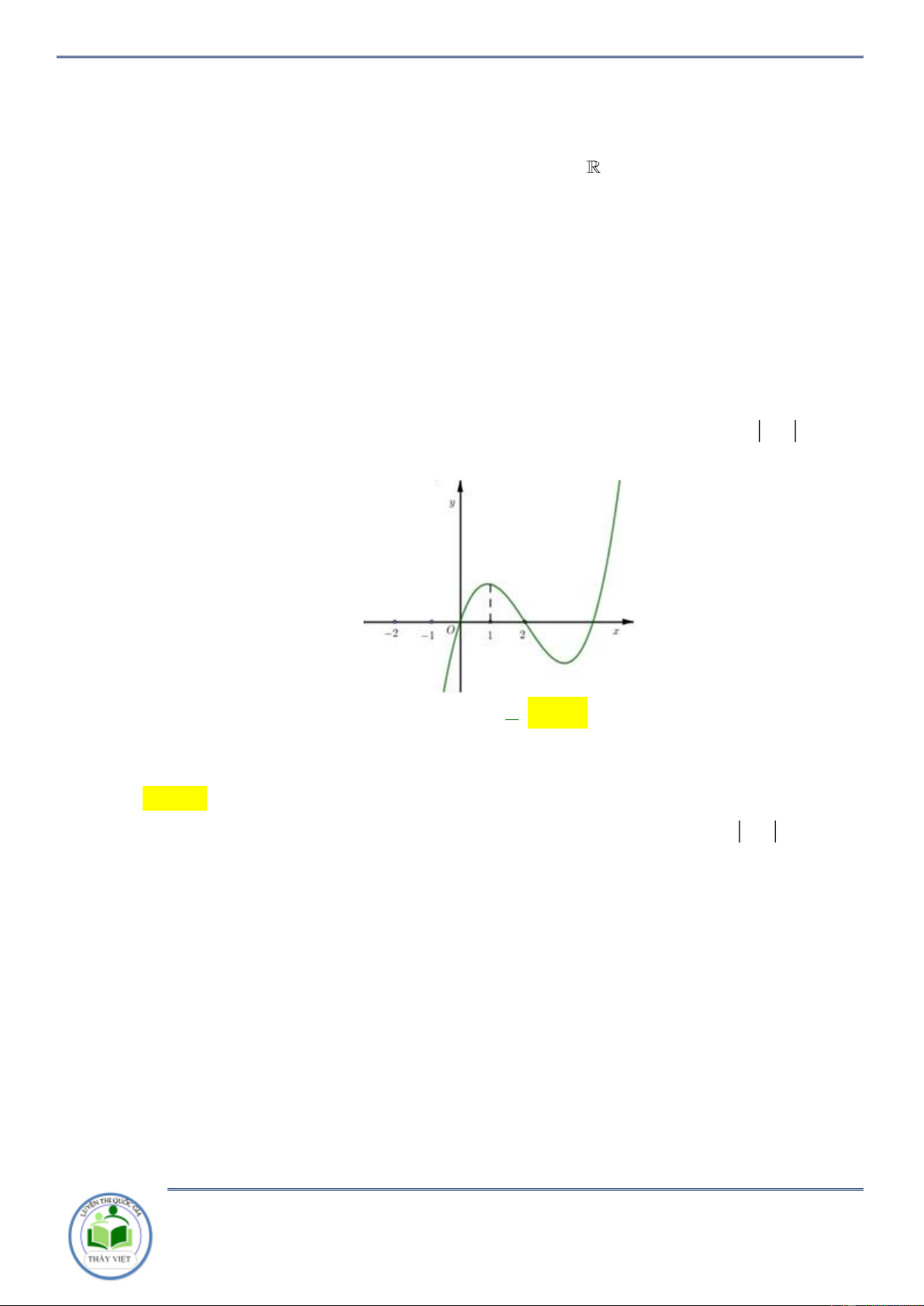
Câu 17: Cho hàm số y  f  x . Đồ thị của hàm số y  f  x như hình vẽ bên. Đặt
h x  f  x 2 ( ) 2
 x . Hàm số y  hx đồng biến trên khoảng nào dưới đây? A.  ;  2  . B. 2; 4 . C.  2  ;2 . D. 2; . Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 10/102 Ta có h (  ) x  2 f (  )
x  2x  0  f (  ) x  x .
Kẻ đường thẳng y  x đi qua các điểm ( 2  ; 2
 ) ;(2 ; 2) ;(4 ; 4) ta thấy đường
thẳng này cắt đồ thị hàm số y  f (
 x) tại ba điểm có hoành độ x  2
 ;x  2, x  4.  2   x  2
Nhìn đồ thị ta có f (
 x)  x   . x  4
Đối chiếu đáp án Chọn C
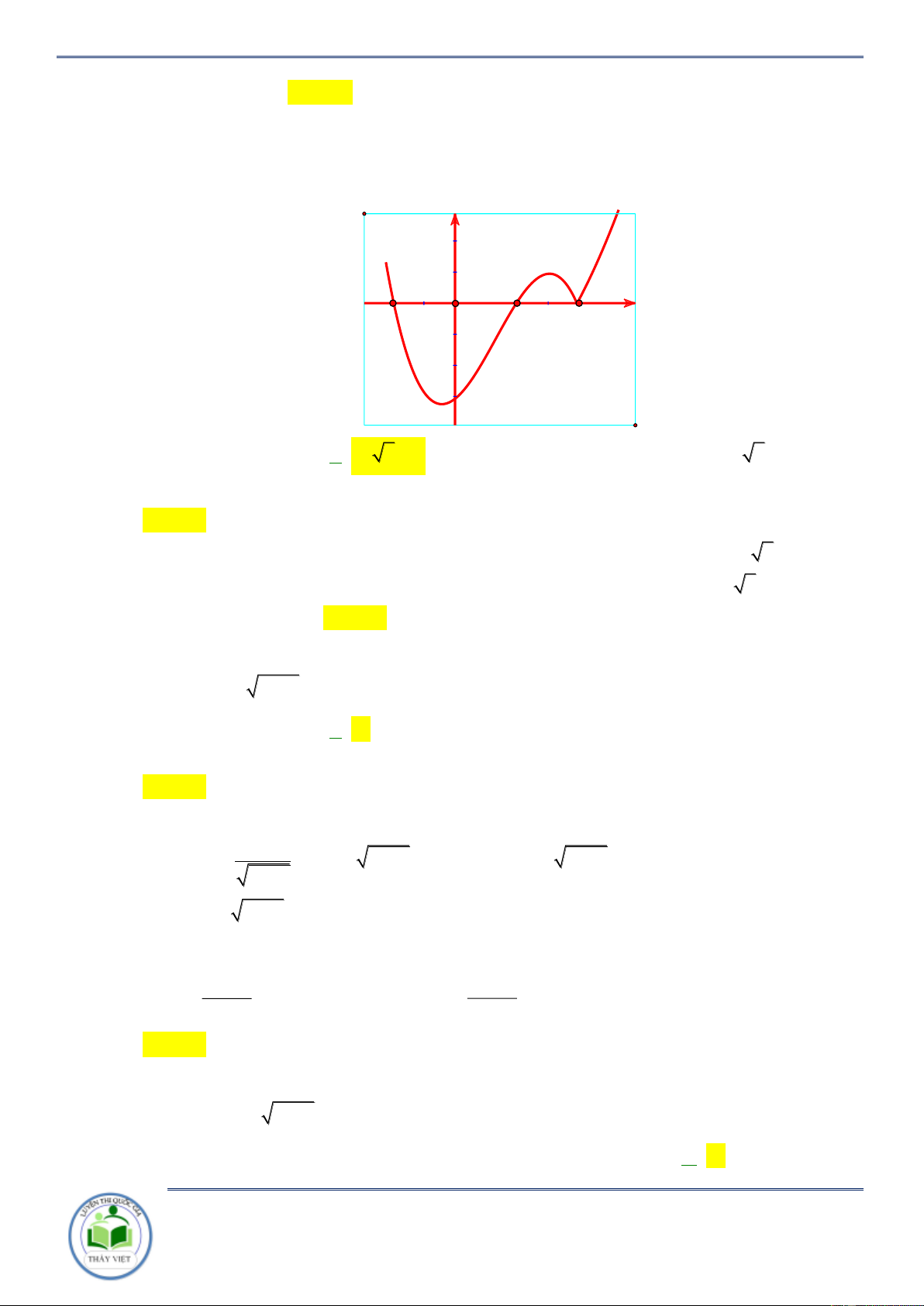
Câu 18: Cho hàm số y  f  x . Đồ thị của hàm số y  f  x như hình vẽ bên. Hàm số   2 y
f x  đồng biến trên khoảng nào dưới đây? A.  1  ;0 . B. 1;2 . C.  ;  2   . D.  2  ;  1 . Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 11/102
Ta đi giải bất phương trình
y  xf  2 2 x   0  1   x 1 0  x 1 
Với x  0  f  x  2 2  0   x 0   . 2 x  4 x  2 x  1  
Với x  0  f  x  2 2  0   x 0   2   x  1  . 2 1   x  4
Đối chiếu với Chọn D
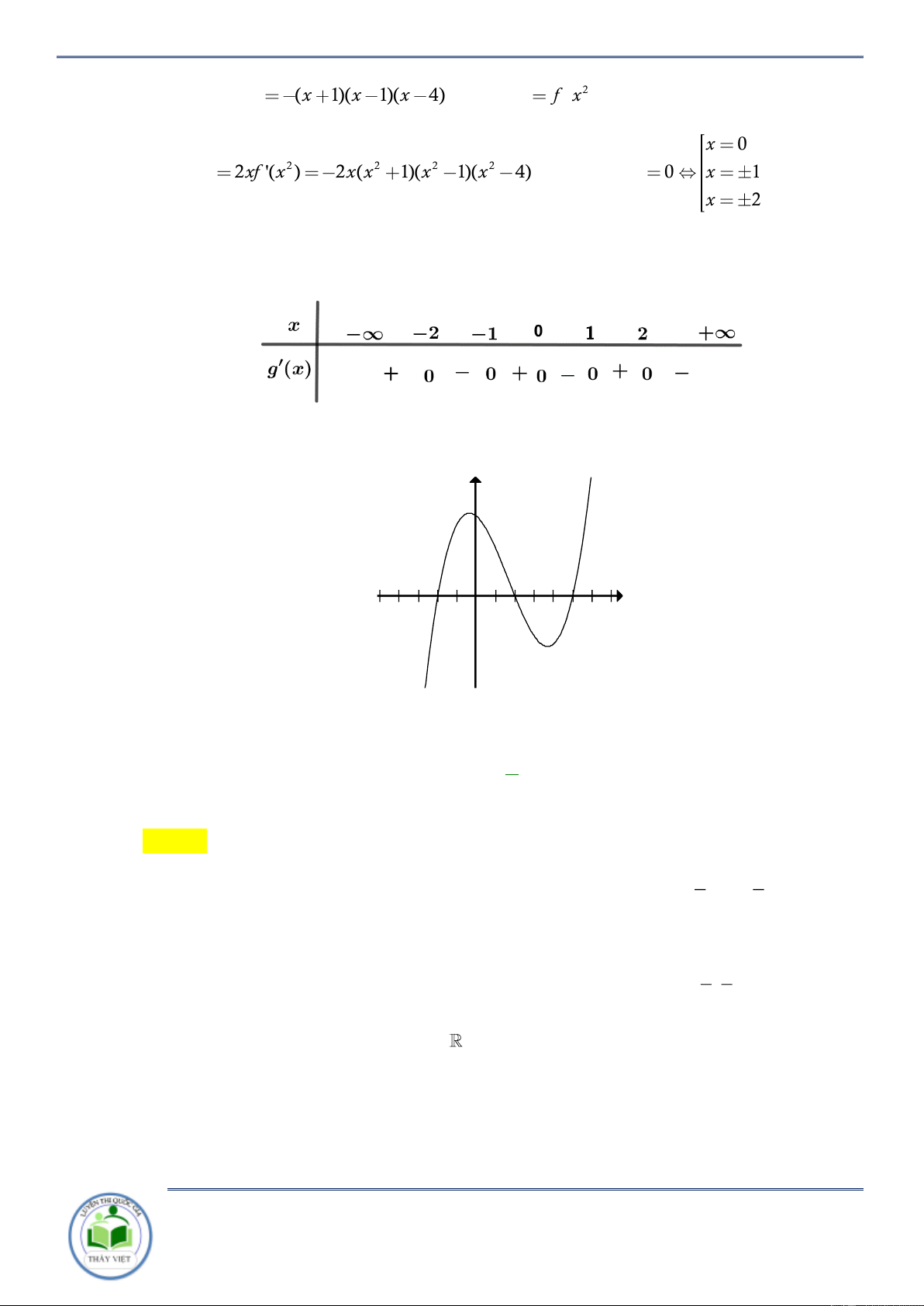
Câu 19: Cho hàm số f  x có đạo hàm cấp 3 xác định và liên tục trên thỏa mãn f (x) f (
 x)  x(x 1)(x  2), x
  . Hàm số g x   f  x 2 ( ) ( )
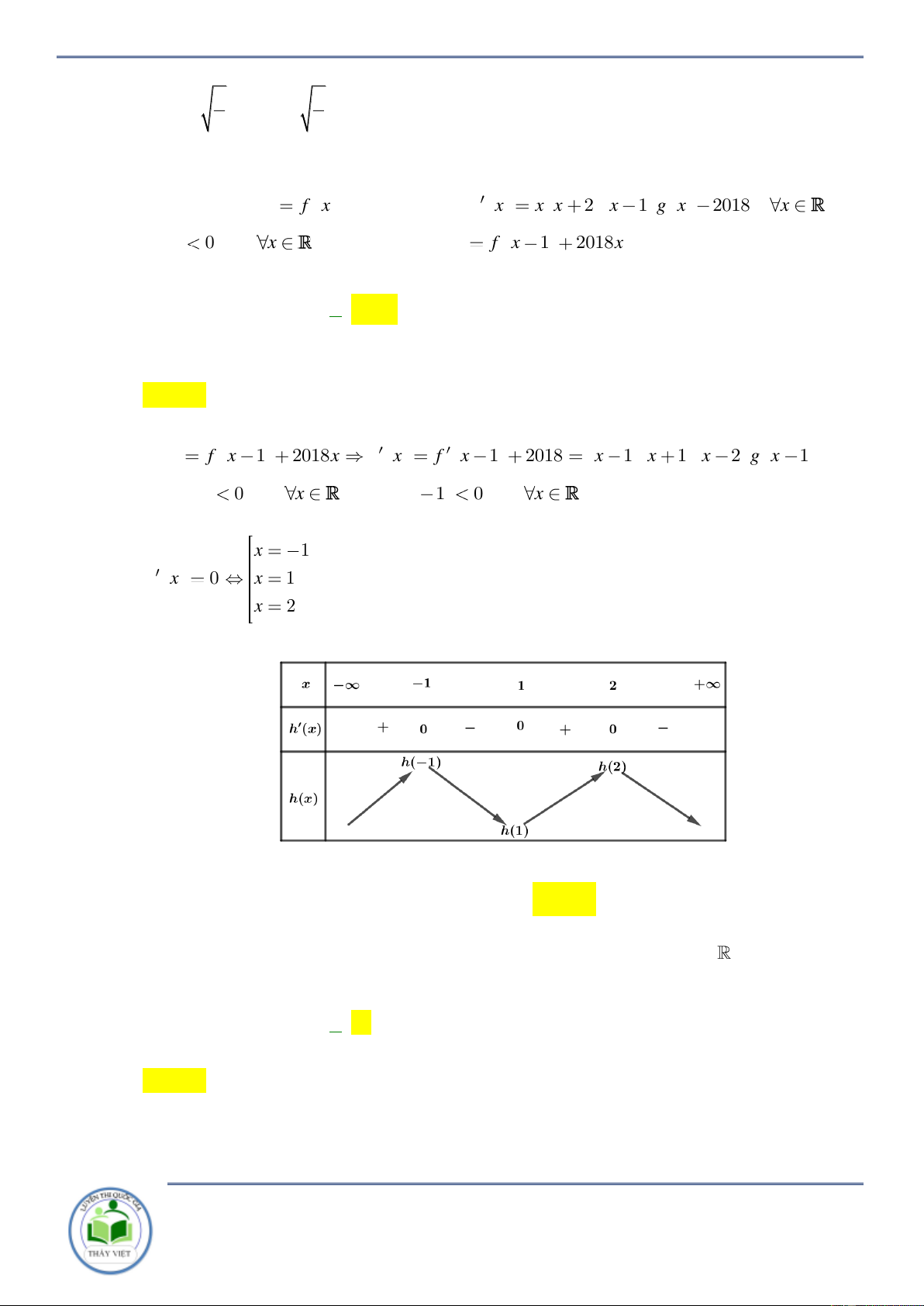
 2 f (x) f  (x) đồng biến trên khoảng nào? A. 0  ;1 . B.  1  ;0 . C. 4; . D.  ;    1 . Lời giải Chọn B Ta có g (
 x)  2 f (x) f  (x)  2 f ( ) x f  (  ) x  f ( ) x f  (  ) x 
  f x f  x   x 2 2 ( ) ( ) 2 x   1 (x  4) .  1   x  0 Vậy g (  x)  0  2  x 2 x  
1 (x  4)  0   .  1 x  4
Đối chiếu Chọn B
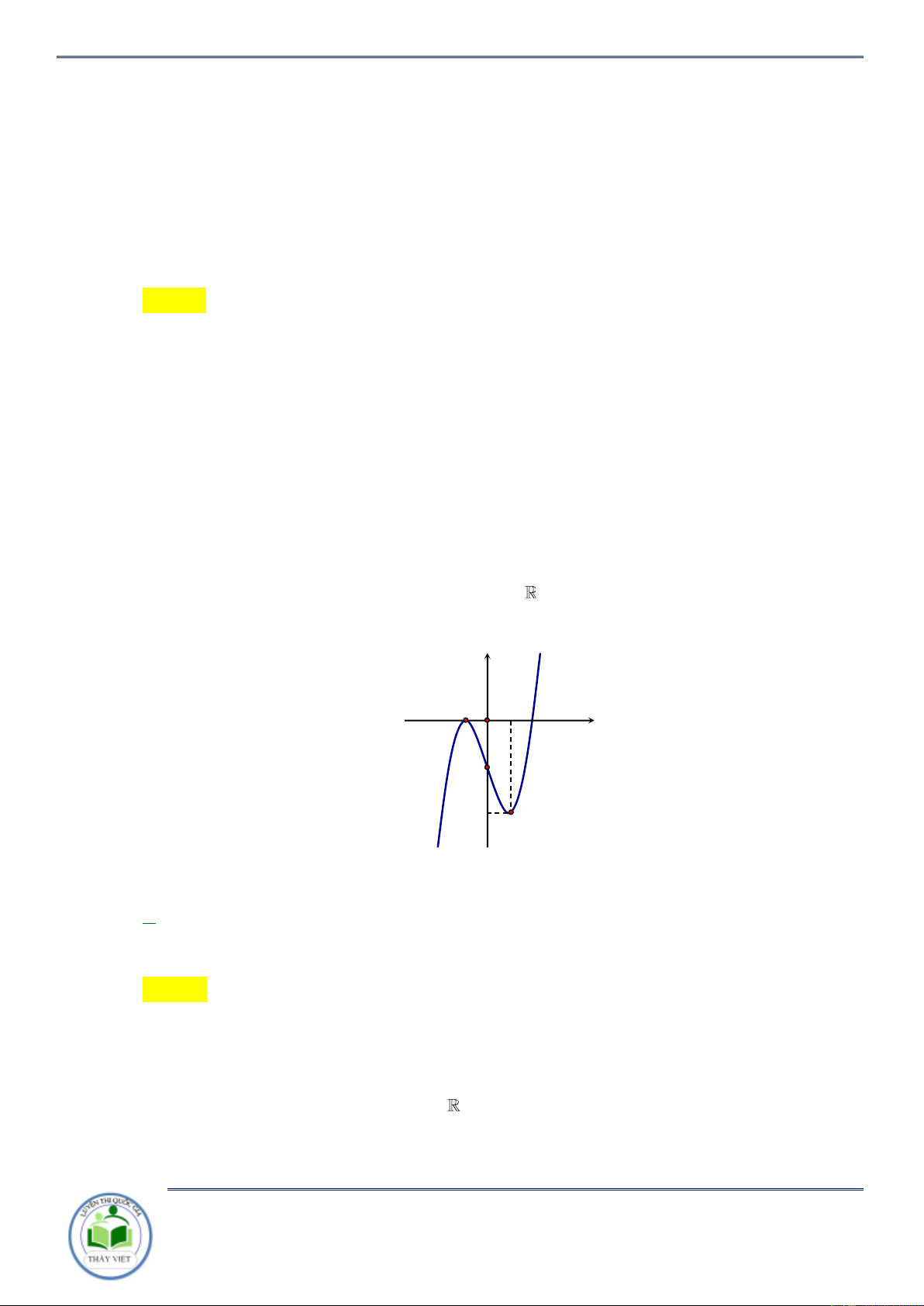
Câu 20: Cho hàm số f  x có đạo hàm cấp 2 xác định và liên tục trên thỏa mãn  f  x 2 ( )
 f (x) f  (x)  x(x 1)(x  2), x
  . Hàm số g(x)  f (x) f (x) đồng biến trên khoảng nào? A. 0; 2 . B.  ;  0. C. 2; . D. 1;2 . Lời giải Chọn C Ta có  
g x   f  x 2 x 2 ( ) ( )
 f (x) f  (x)  x(x 1)(x  2)  0   . 0  x 1
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 12/102
Đối chiếu đáp án Chọn C
Câu 21: Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình bên. Hàm số   2 y f x 
đồng biến trên khoảng nào dưới đây? y -2 O 2 4 x A.  ;  2  . B.  2;0 . C. 1; . D.  2  ; 2 . Lời giải Chọn B x  2
Ta có y  xf  2 2 x   0 2
 x x     2 2 2
x  2  0  x 2
x  2  0   .  2  x  0
Đối chiếu các đáp án. Chọn B
Câu 22: Cho hàm số f  x 3 2
 x  mx m6 x 1. Có bao nhiêu số nguyên dương m để hàm số y  f  2
x  x 1 đồng biến trên khoảng  ;   . A. 2 . B. 3 . C. 5 . D. 4 . Lời giải Chọn B Ta có yêu cầu bài toán  x   y  1  f  2
x  x 1  0, x   f  2
x  x 1  0, x  1 . 2     x 1  Đặt 2
t  x  x 10;, x
 và f x 2
 3x  2mx  6  m .
Do vậy:    f t  t    2 1 0, 0;
 3t  2mt  6  m  0, t  0; 2 3t  6 2     3t 6 m  , t
 0; m  min y    y  
1  3  m 1, 2,  3 . 2t 1 0;  2t 1  Chọn B
Câu 23: Cho hàm số f  x 3 2
 x  mx m6 x 1. Có bao nhiêu số nguyên không âm m để
hàm số y  f  2
x 1  x nghịch biến trên khoảng  ;   A. 6 . B. 3 . C. 5 . D. 4 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 13/102 Lời giải Chọn D Ta có, yêu cầu bài toán  x   y  
1. f  2x 1 x  0, x
  f  2x 1 1  0, x    1 . 2   x 1  Đặt 2 t  x 1  ;
x t 0; , x
 và f x 2
 3x  2mx  6  m . Do vậy
 1  f 't  0, t  0; 2
 3t  2mt  6  m  0, t  0; 2 3t  6   m  t    2 3t 6 , 0;  m  , t  0; 2t 1 2t 1 2  3t  6 
 m  min y    y  
1  3  m0,1, 2,  3 0;  2t 1 
Câu 24: Cho hàm số y  f  x . Hàm số y  f ' x có đồ thị như hình bên. Hàm số  5  2 x y f e 
đồng biến trên khoảng a,b . Giá trị lớn nhất của b  a bằng y -2 O 2 4 x 10 7 5 7 A. ln . B. ln . C. ln . D. ln . 3 3 2 2 Lời giải Chọn B Ta có: x
y   e f  x
 e    f  x  e  x 3 x 7 3 7 ' 2 ' 5 2 0 ' 5 2  0  2
  5  2e  2   e   ln  x  ln 2 2 2 2 7 3 7
Vậy b  a  ln  ln  ln max 2 2 3
Câu 25: Cho hàm số y  f  x . Hàm số y  f ' x có đồ thị như hình vẽ. Hàm số y  f  2 3  x 
đồng biến trên khoảng nào dưới đây?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 14/102 y -6 O -1 2 x A. 2;3 . B. 0  ;1 . C.  2  ;  1 . D.  1  ;0 . Lời giải Chọn D y   xf  2
 x    xf  2 ' 2 ' 3 0
' 3  x   0 x  3       3 x 2 x  2
 x   2
 x   2 3 6 3 1
3  x  2  0   1   x  0  1   x  2
Câu 26: Cho hàm số y  f  x có đồ thị của hàm số y  f  x như hình vẽ bên. Hàm số 1 2 tan x  y  f 
 đồng biến trên khoảng nào dưới đây?  3    11     11     1  A.  ; arc tan   . B.  ;arc tan 2   . C. arc tan ;    . D.  ;arc tan   .  2 2   4   2 4   4 2  Lời giải Chọn C 1 2 tan x 
Ta có hàm số y  f 
 tuần hoàn với chu kỳ T   nên ta chỉ cần xét trên  3      khoảng  ;   có  2 2 
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 15/102 2 1 1 2 tan x  1 2 tan x  y   . f   0  f   0     2 3 cos x  2   3  1 2 tan x    1   tan x  2 arc tan 2  x   3     2 11   . 1 2 tan  x   tan x  1  11   1   4  arc tan  x     2 3  2 4
Câu 27: Cho hàm số f  x 4 3 2
 ax  bx  cx  dx  e với , a , b ,
c d, e là các số nguyên không âm x
nhỏ hơn 6 và f 6  2019 . Hàm số y  f   x 2 1 
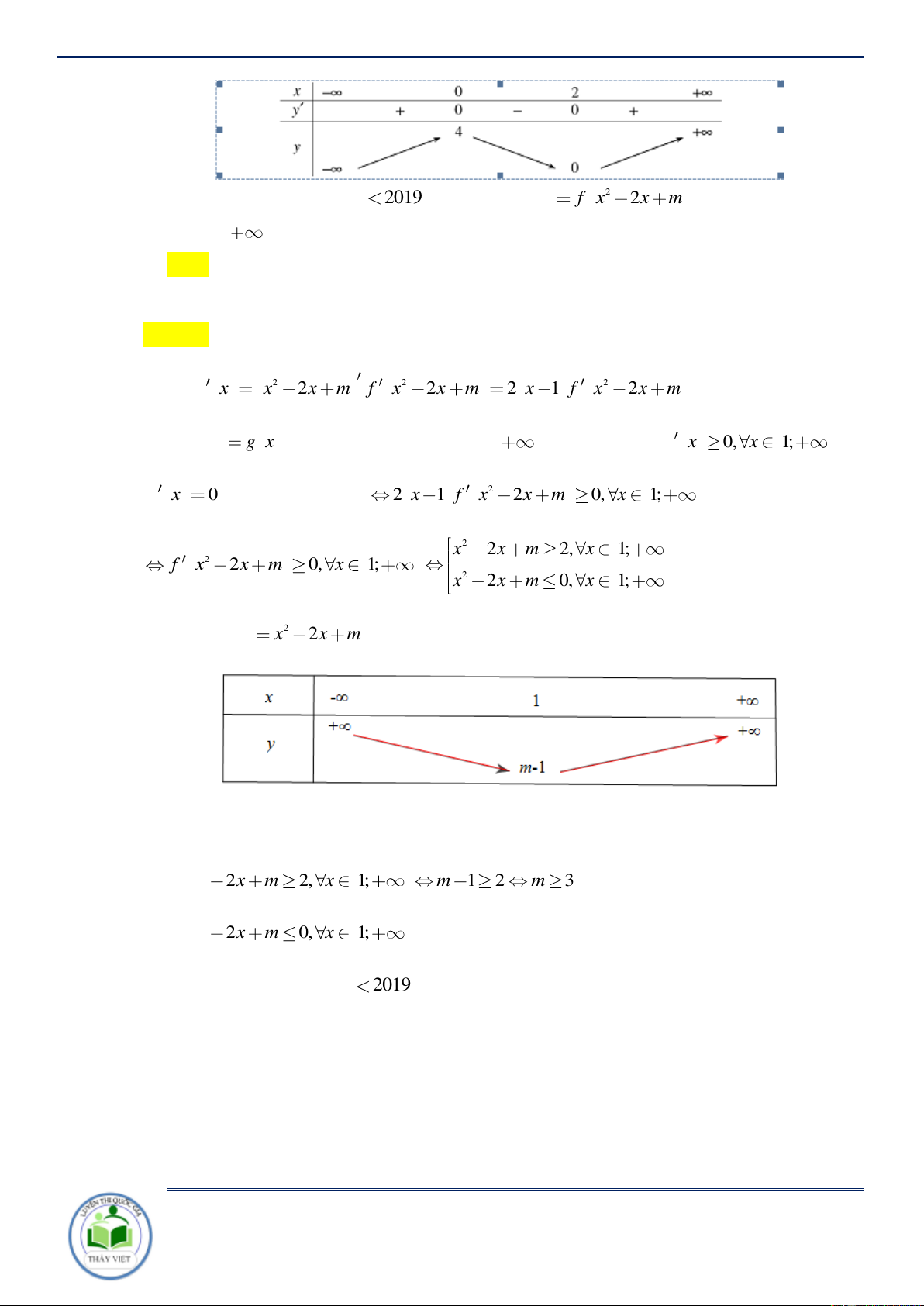
 x đồng biến trên khoảng nào 2 dưới đây?  5 7   9   9   3 5  A. ;   . B. 2;   . C. ;    . D. ;   .  4 4   4   4   4 4  Lời giải Chọn A Ta có f   4 3 2 6  2019  . a 6  . b 6  .
c 6  d.6  e  2019 4 3 2 4 3 2 1 0 . a 6  . b 6  .
c 6  d.6  e  6  3.6  2.6  0.6  3.6
 abcd e 13203  a 1, b  3, c  2, d  0, e  3 6 6
Suy ra f  x 4 3 2
 x  3x  2x  3. Khi đó
y   f   x  x      x3    x2 1 1 4 1 9 1
 41 x x1
 y  x  x   x   9 1 2 4 9  0  x  hoặc 1 x  2 . 4
Câu 28: Cho hàm số f  x 3 2
 ax  bx  cx  d với , a , b ,
c d là các số nguyên không âm nhỏ hơn 2
9 và f 9  2019. Hàm số y  f  x   2
x  x  nghịch biến trên khoảng nào dưới đây? 3  6   1   11   5  A.  ;     . B.  ;    . C.  ; 1    . D.  ;0   .  5   2   9   6  Lời giải Chọn C Ta có f   3 2 1 9  2019  . a 9  . b 9  .
c 9  d  2019 3 2 1 3 2 1 . a 9  . b 9  .
c 9  d  2.9  6.9  8.9 1
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 16/102
 abcd  2681  a  2, b  6, c  8, d 1 9 9
Suy ra f  x 3 2
 2x  6x 8x 1. 2 2 11
Khi đó y  f  x  1 2x 2
 6x 12x  8  1 2x  0    x  1  . 3 3 9
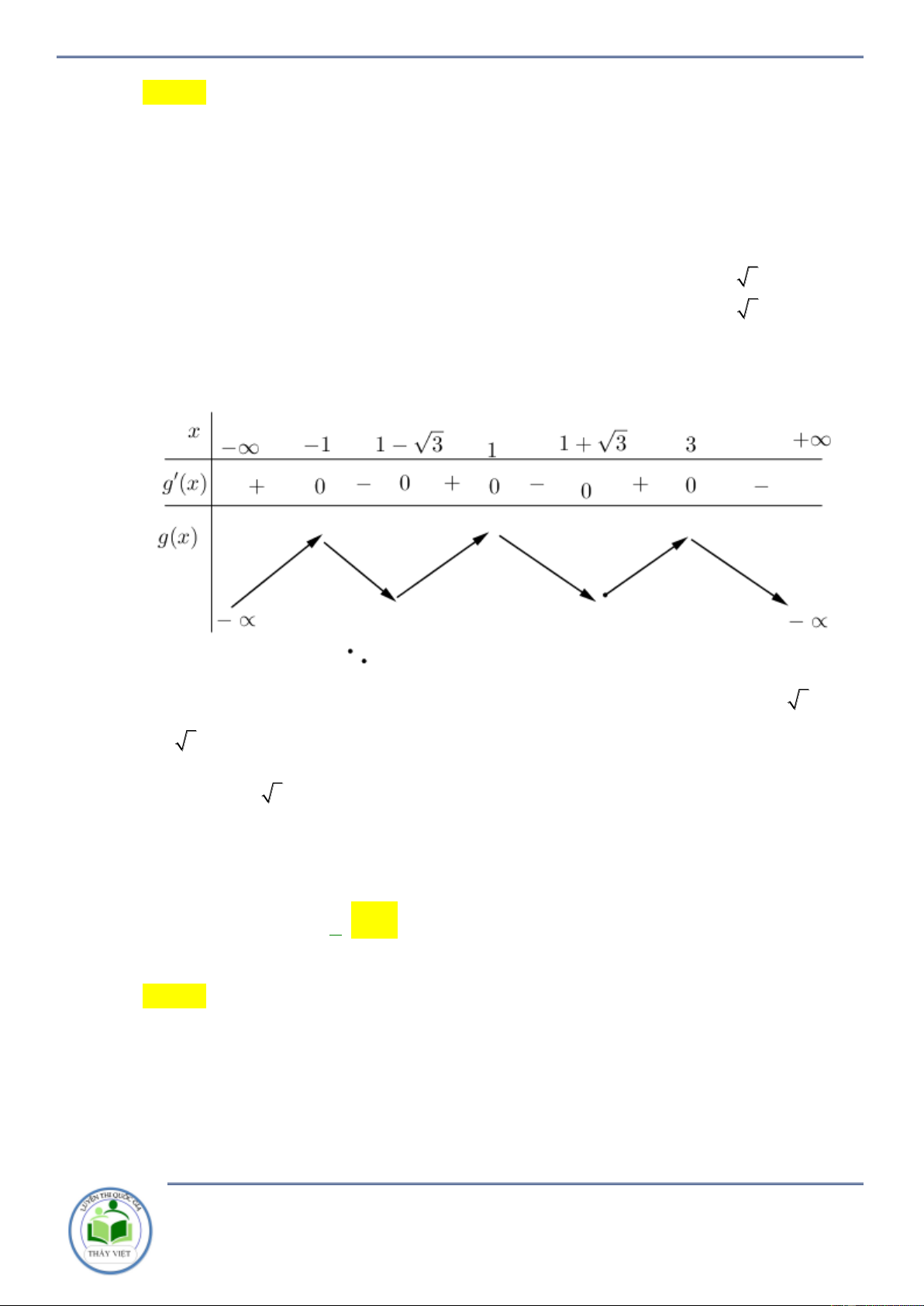
Câu 29: Cho hàm số y  f  x có bảng biến tiên như hình vẽ bên dưới đây. Hàm số
y   f x 2   6 
f  x nghịch biến trên khoảng nào dưới đây? A.  1   ;1 . B. 6; . C. 1;6 . D.  ;  2   . Lời giải Chọn D x  
Ta có y  f  x f  x  f  x   f x   f  
x   f x 1 2 6 2 3 . 0  0   1   x  4
Vì dựa vào bảng biến thiên ta có f  x  3,x   f  x  3  0,x  .  1 
Câu 30: Cho hàm số y  f  x . Hàm số y  f  3x  
 có đồ thị như hình bên. Hàm số  2 
y  f 2x  
1 nghịch biến trên khoảng  5 11  5   1 3   9 15  A. ;   . B. 1;   . C. ;   . D. ;   .  4 4   2   2 2   4 4  Lời giải Chọn D
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 17/102
Ta có y  2 f 2x   1  0  * . 1 2 1
Đặt 2x 1  3t   t  x  2 3 3 2 1 x    x    1 1 1  t  1  3 3
Khi đó * trỏ thành f  3t   0         .  13 2  1   t  4 2 1   2  x  1  x   4  2  3 3 Câu 31: Cho hàm số 3 f (x) x 3x
1. Có bao nhiêu số nguyên không âm m để hàm số
y = f(m - x)+(m - 1)x đồng biến trên khoảng có độ dài không vượt quá 4 . A. 11. B. 2 . C. 10 . D. 3 . Lời giải Chọn A Ta có 2 2 2 y f (m x) m 1 3(m x) 3 m 1 3x 6mx 3m m 2
Ta có y ' luôn có hai nghiệm phân biệt vì x x 2 2 9m 3 3m m 2 3(m 2) 0, m 0 1 2
Do đó hàm đồng biến trên khoảng x ;x theo yêu cầu bài toán ta có 1 2 2 2 x x 4 x x 16 x x 4x x 16 0 2 1 2 1 1 2 1 2 2 3m m 2 2 4m 4 16 0 m 10 . 3 Vậy m
0;2;....;10 . Có 11 số nguyên không âm m thỏa mãn. Câu 32: Cho hàm số 3 f (x) x 3x
1. Có bao nhiêu số nguyên m để hàm số
y = f(m - x)+(m - 1)x đồng biến trên khoảng 8;9 . A. 4 . B. 2 . C. 1. D. 3 . Lời giải Chọn D Ta có 2 2 2 y f (m x) m 1 3(m x) 3 m 1 g(x) 3x 6mx 3m m 2 Với 2 2 9m 3 3m m 2 3(m 2) TH1: 0 m 2 y 0, x .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 18/102 TH2: 0 m 2 .
Khi đó phương trình có hai nghiệm phân biệt x
x và hàm số đồng bến trên x ;x . 1 2 1 2
Theo yêu cầu bài toán ta có: 2 3g(8) 0 3m 49m 190 0 (8;9) x ;x x 8 9 x 1 2 1 2 2 3g(9) 0 3m 55m 241 0 55 133 m 10 6 Vậym
{8,9,10} .Có 3 số nguyên m thỏa mãn. Câu 33: Cho hàm số 3 f (x) x 3x
1. Số thực m nhỏ nhất để hàm số a b
y = f(m - x)+(m - 1)x đồng biến trên khoảng 8;9 là , với , a , b c là các số c a
nguyên dương và tối giản. Giá trị của biểu thức a b c bằng: c A. 194 . B. 72 . C. 193 . D. 75 . Lời giải Chọn A Ta có 2 2 2 y f (m x) m 1 3(m x) 3 m 1 g(x) 3x 6mx 3m m 2 Với 2 2 9m 3 3m m 2 3(m 2) TH1: 0 m 2 y 0, x . TH2: 0 m 2 .
Khi đó phương trình có hai nghiệm phân biệt x
x và hàm số đồng bến trên x ;x . 1 2 1 2
Theo yêu cầu bài toán ta có: 2 3g(8) 0 3m 49m 190 0 (8;9) x ;x x 8 9 x 1 2 1 2 2 3g(9) 0 3m 55m 241 0 55 133 m 10 6
a=55, b=133, c=6 và a+b+c=194 .
Câu 34: Cho hàm số y
f (x)có bảng biến thiên như sau:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 19/102 x  m  4 m  6  y  0  0   0 y 1  
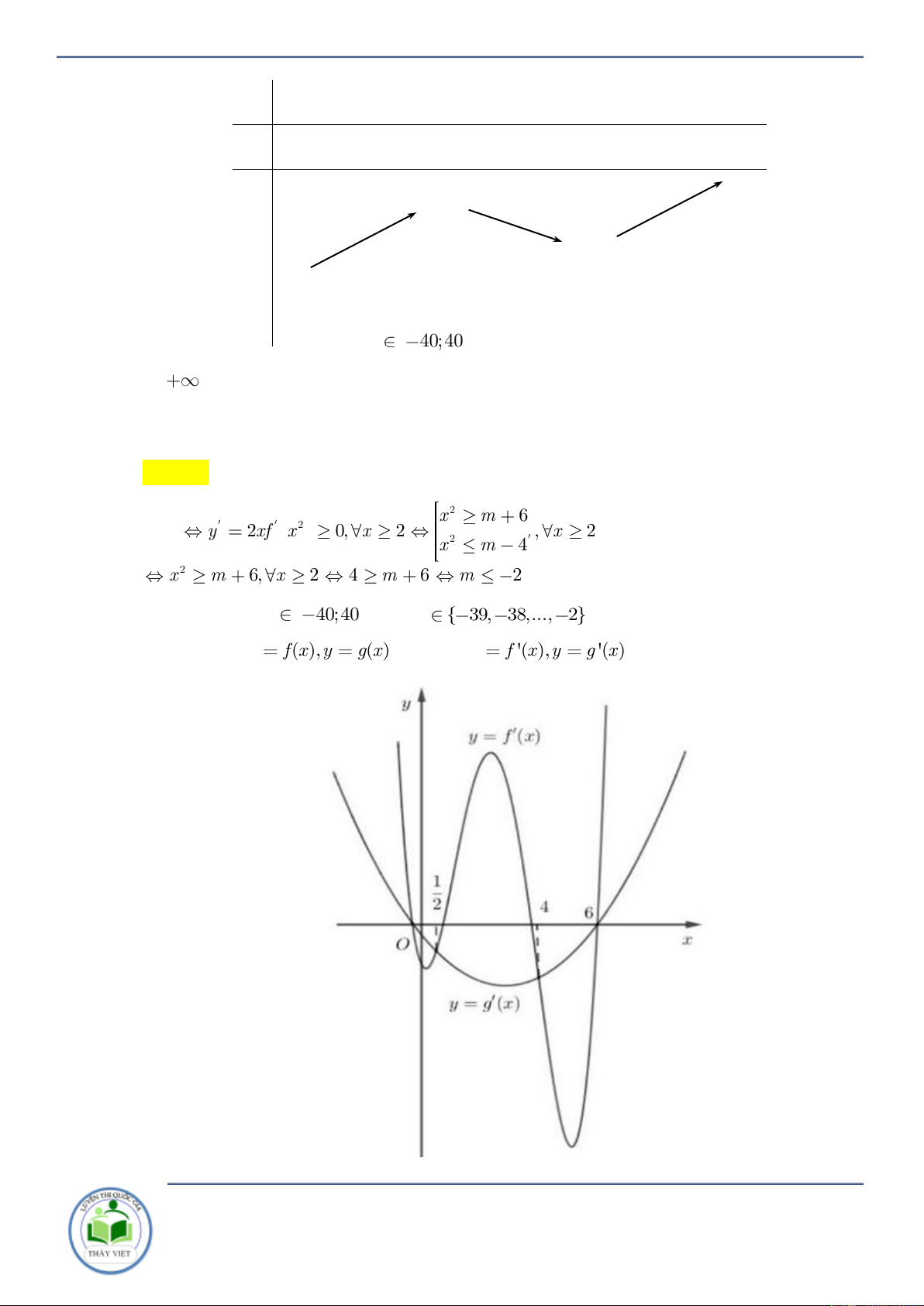
Có bao nhiêu số nguyên m 40;40 để hàm số 2
y = f(x ) đồng biến trên khoảng 2; . A. 37 . B. 39 . C. 36 . D. 76 . Lời giải Chọn A 2 x m 6 2 ycbt y 2xf x 0, x 2 , x 2 2 x m 4 2 x m 6, x 2 4 m 6 m 2 Vì số nguyên m
40;40 nên m { 39, 38,..., 2} .Có 38 số nguyên m thỏa mãn.
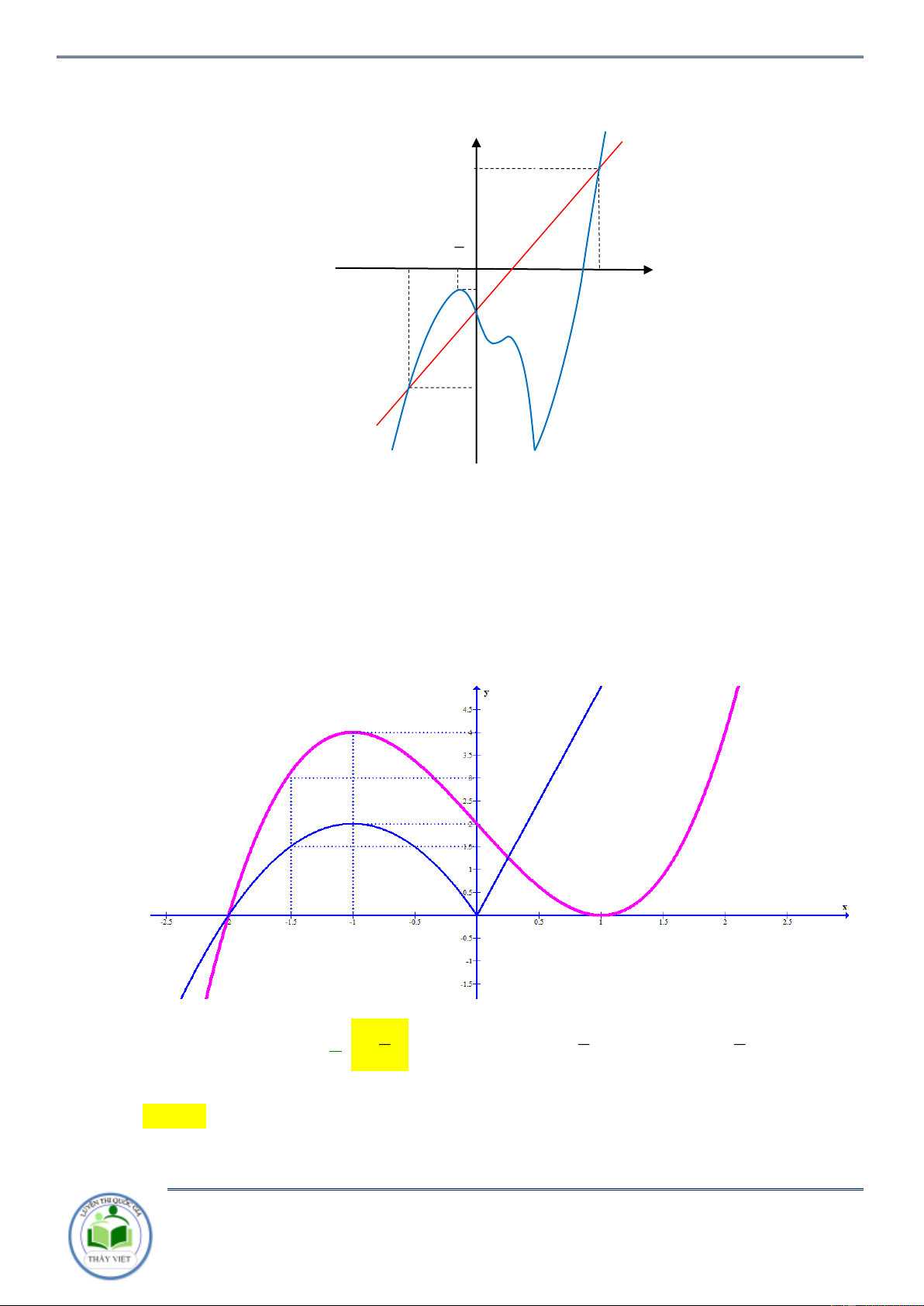
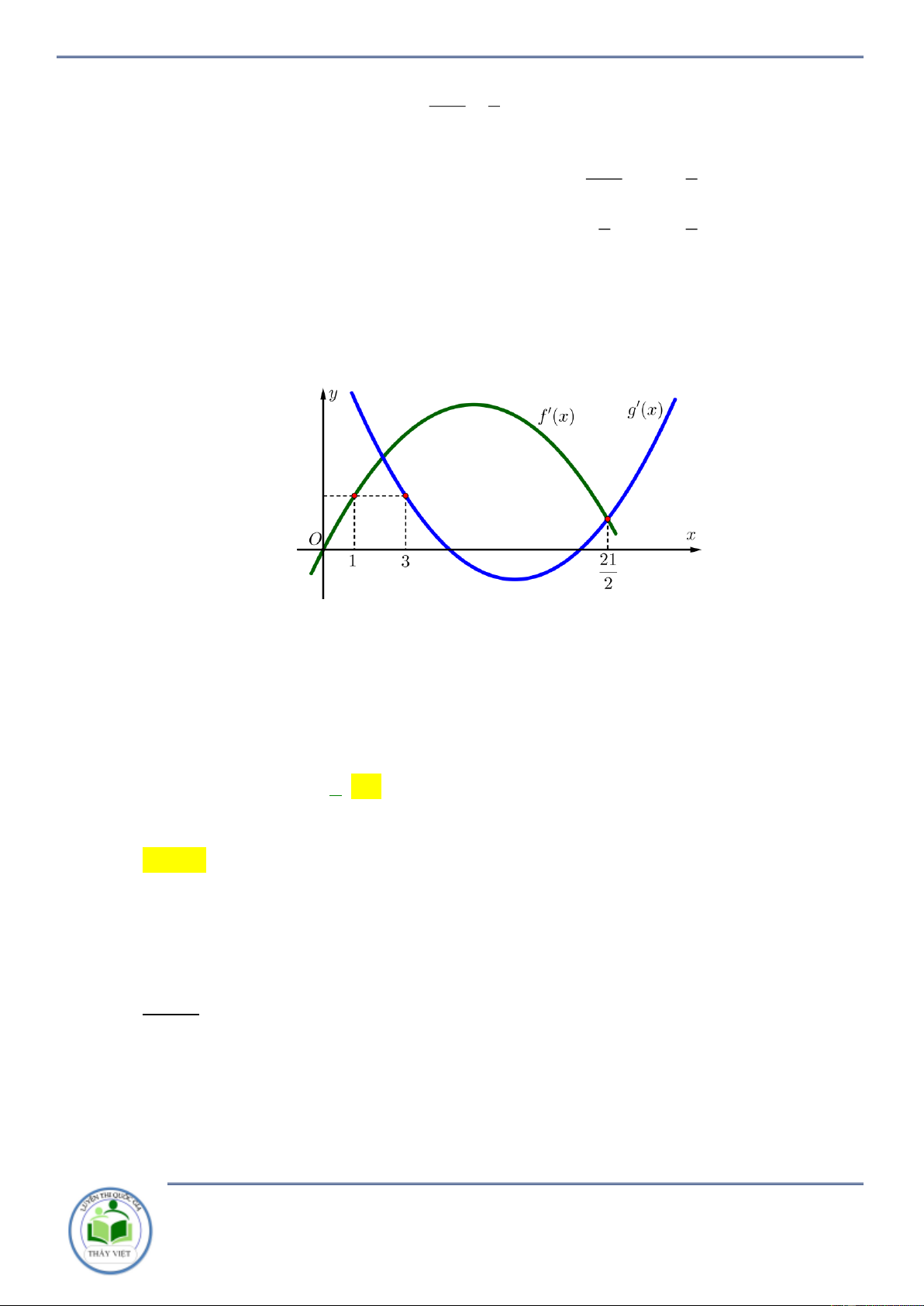
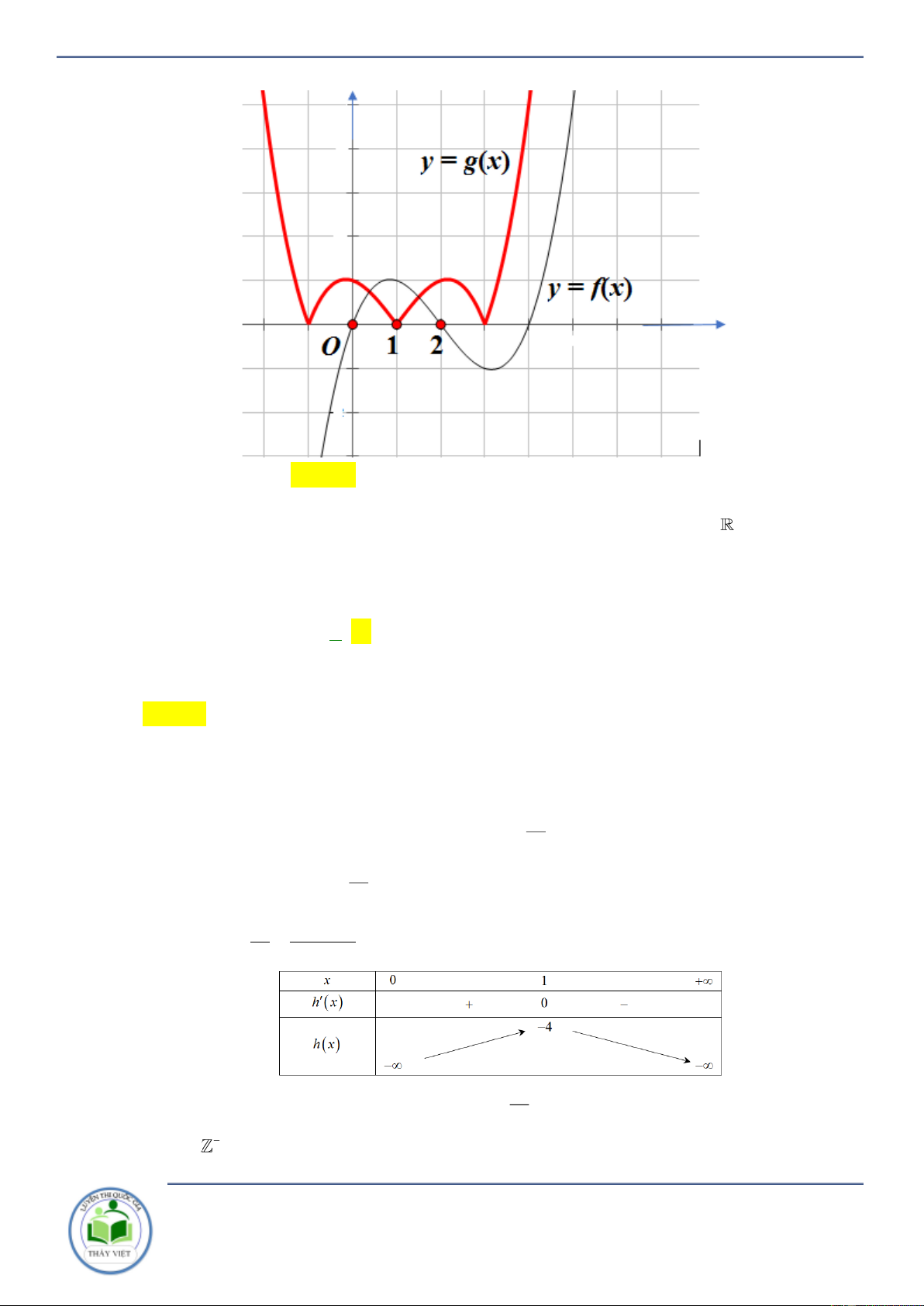
Câu 35: Cho hàm số y f (x),y (
g x)có đồ thị y f '(x),y
g '(x)như hình vẽ dưới.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
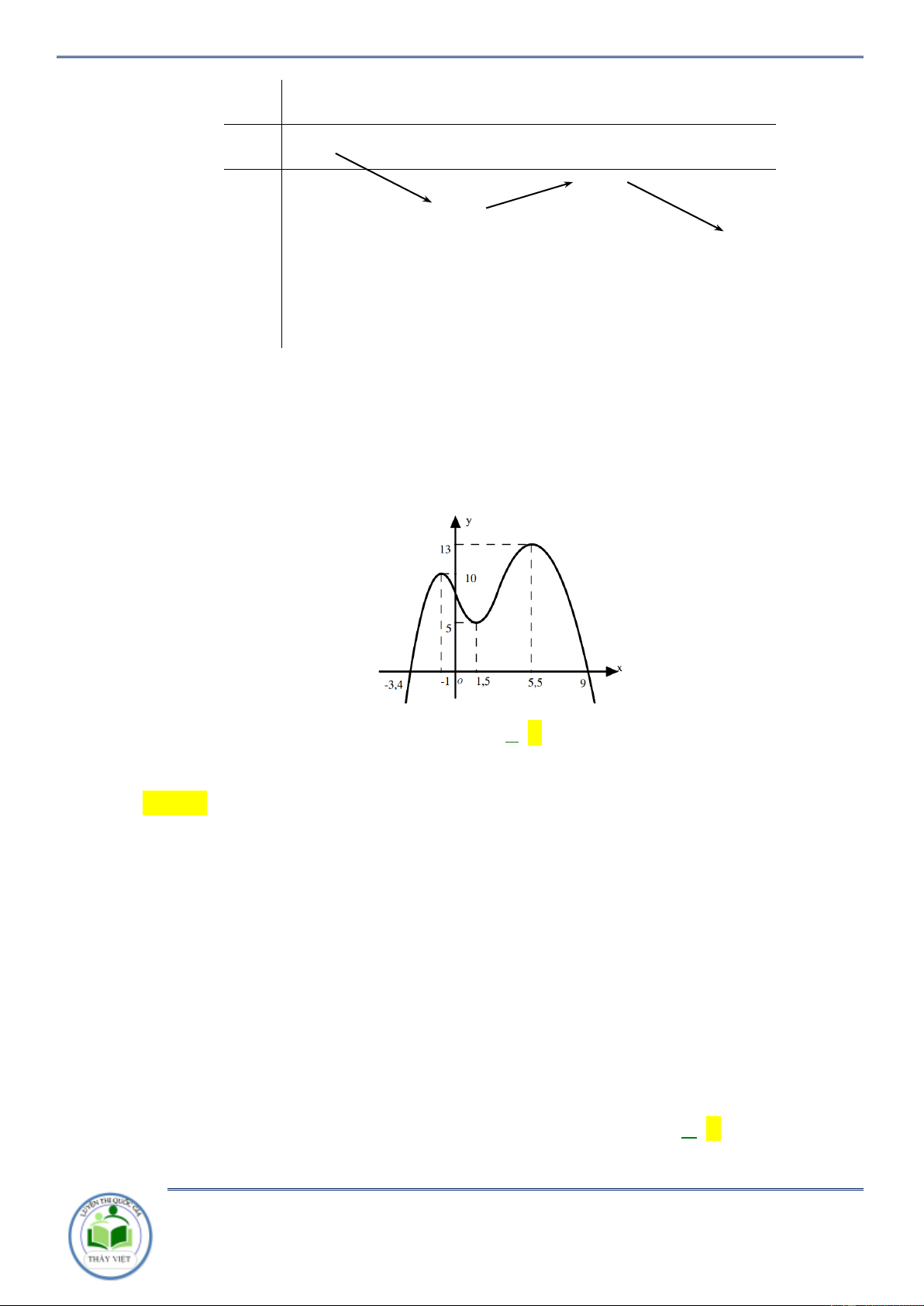
Chuyên đề: Tính đơn điệu của hàm hợp Trang 20/102 Hàm số y
f (x) g(x)đồng biến trên khoảng nào dưới đây  1 1   9   3  11  A.  ;   . B. ; 6   . C. ; 4   . D. ;    .  2 2   2   2   2  Lời giải Chọn C 1 x 4 2 Ta có y
f (x) g (x) 0 f (x) g (x) x 6
. Đối chiếu Chọn C x a 0,25
Câu 36: Cho hàm số y f x có đạo hàm 2 2 f x x 1 4x , x . Hàm số y f cos x
đồng biến trên khoảng nào dưới đây? 2 2 A. ; . B. ; . C. ; 0 . D. ; . 3 3 3 3 6 6 Lời giải Chọn B Hàm số y
f cos x tuàn hoàn chu kỳ T
2 . Do vậy ta chỉ xét trên đoạn ; . 2 2 y sin . x f cos x
sin x cos x 1 4c s o x 0 0 x 3 3 0 sin x 2 2 2 2
sin x 1 sin x 4sin x 3 0 x . 3 3 1 sin x 2 2 x 3
Chú ý: Chúng ta có thể tính đạo hàm tại một điểm trong khoảng trong các đáp án để
chọn được đáp án đúng.
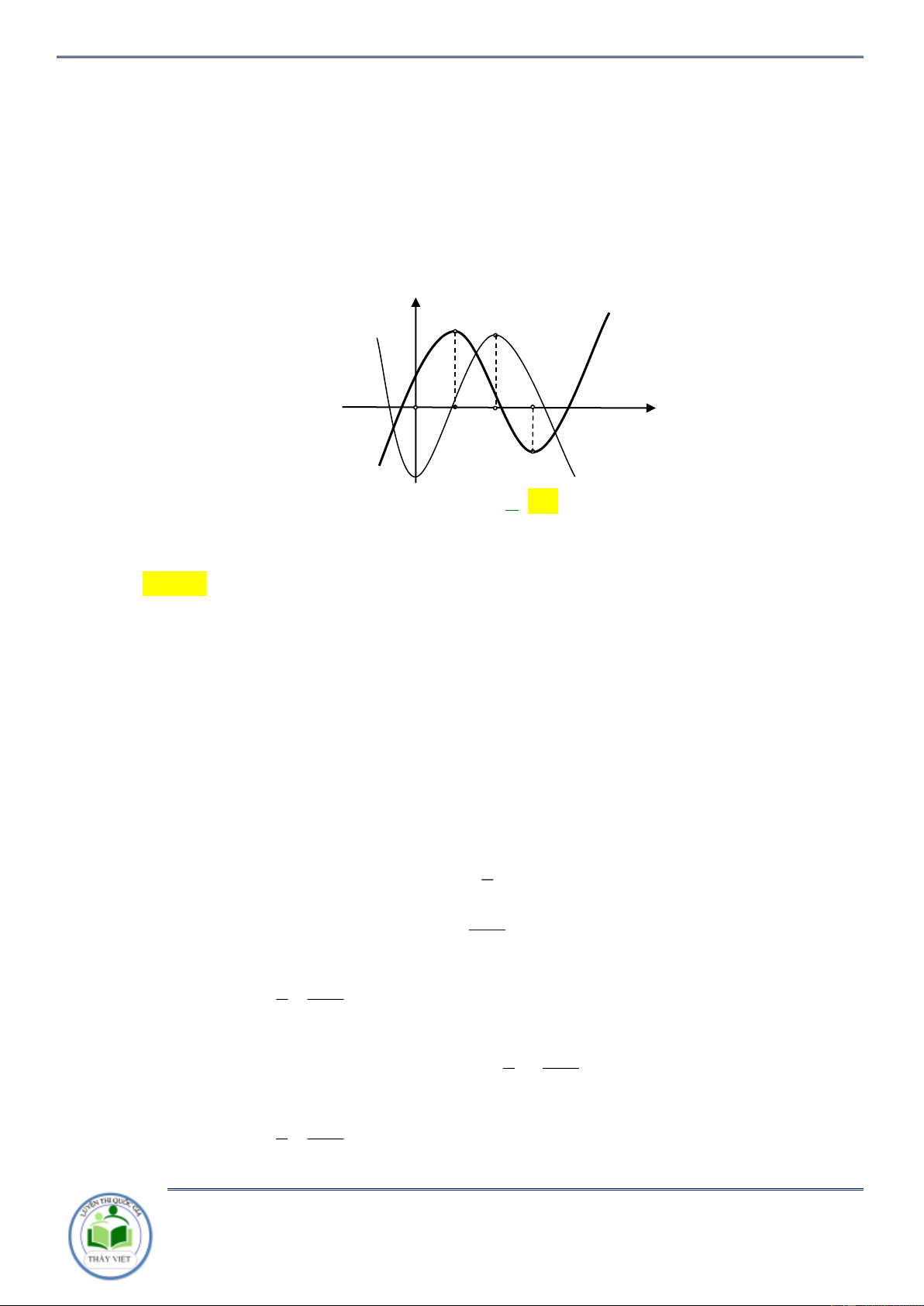
Câu 37: Cho hàm số y f x , y
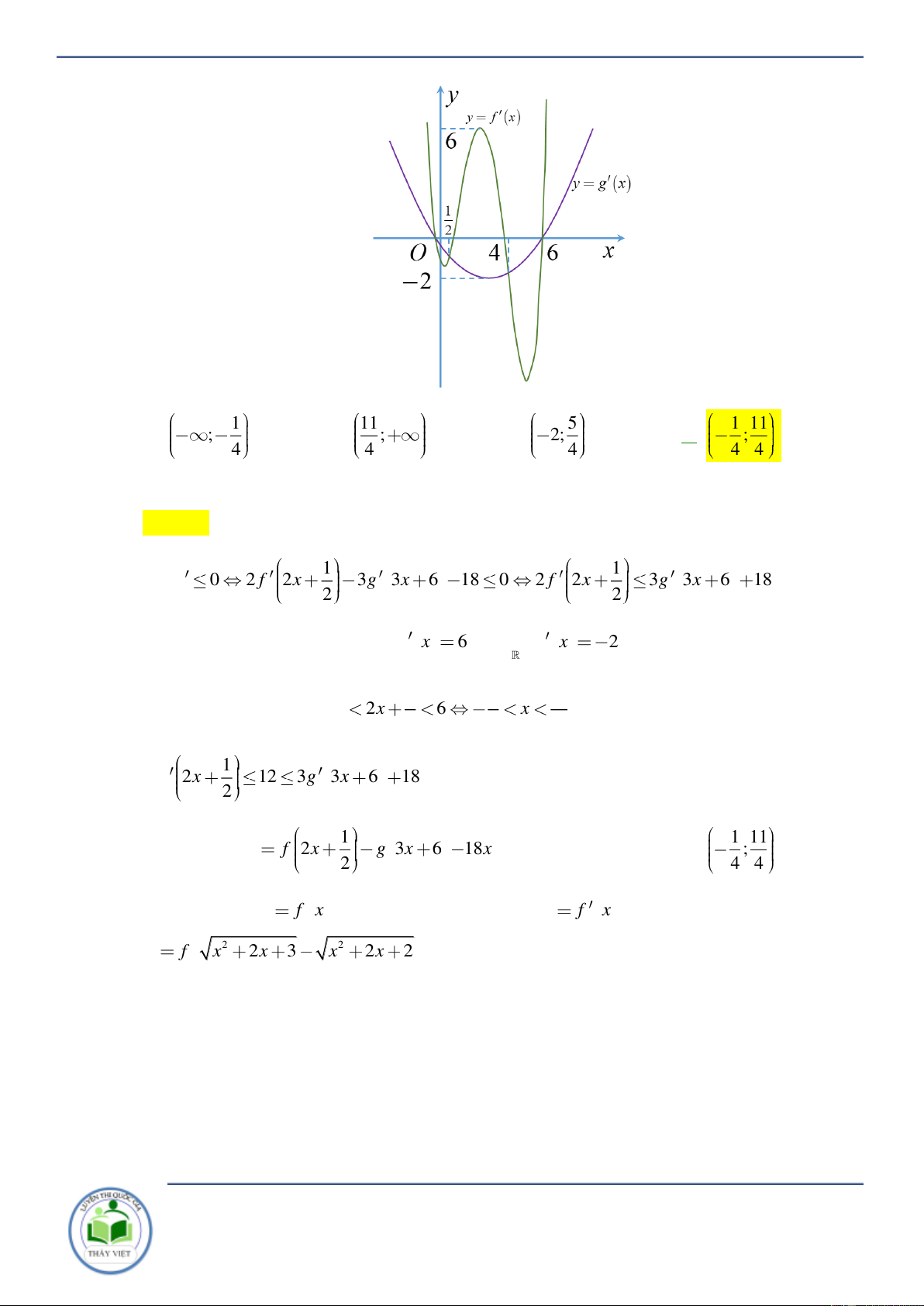
g x có đồ thị của hàm số y f x , y g x như hình vẽ 1 bên. Hàm số y f 2x g 3x 6
18x nghịch biến trên khoảng nào dưới đây? 2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 21/102 1 11 5 1 11 A. ; . B. ; . C. 2; . D. ; . 4 4 4 4 4 Lời giải Chọn D 1 1 Có y 0 2 f 2x 3g 3x 6 18 0 2 f 2x 3g 3x 6 18 2 2
Quan sát đồ thị đã cho có max f x 6 và min g x 2 0;6 1 1 11
Do vậy ta chỉ cần chọn 0 2x 6 x thì 2 4 4 1 2 f 2x 12 3g 3x 6 18 2 1 1 11 Vậy hàm số y f 2x g 3x 6
18x nghịch biến trên khoảng ; . 2 4 4
Câu 38: Cho hàm số y
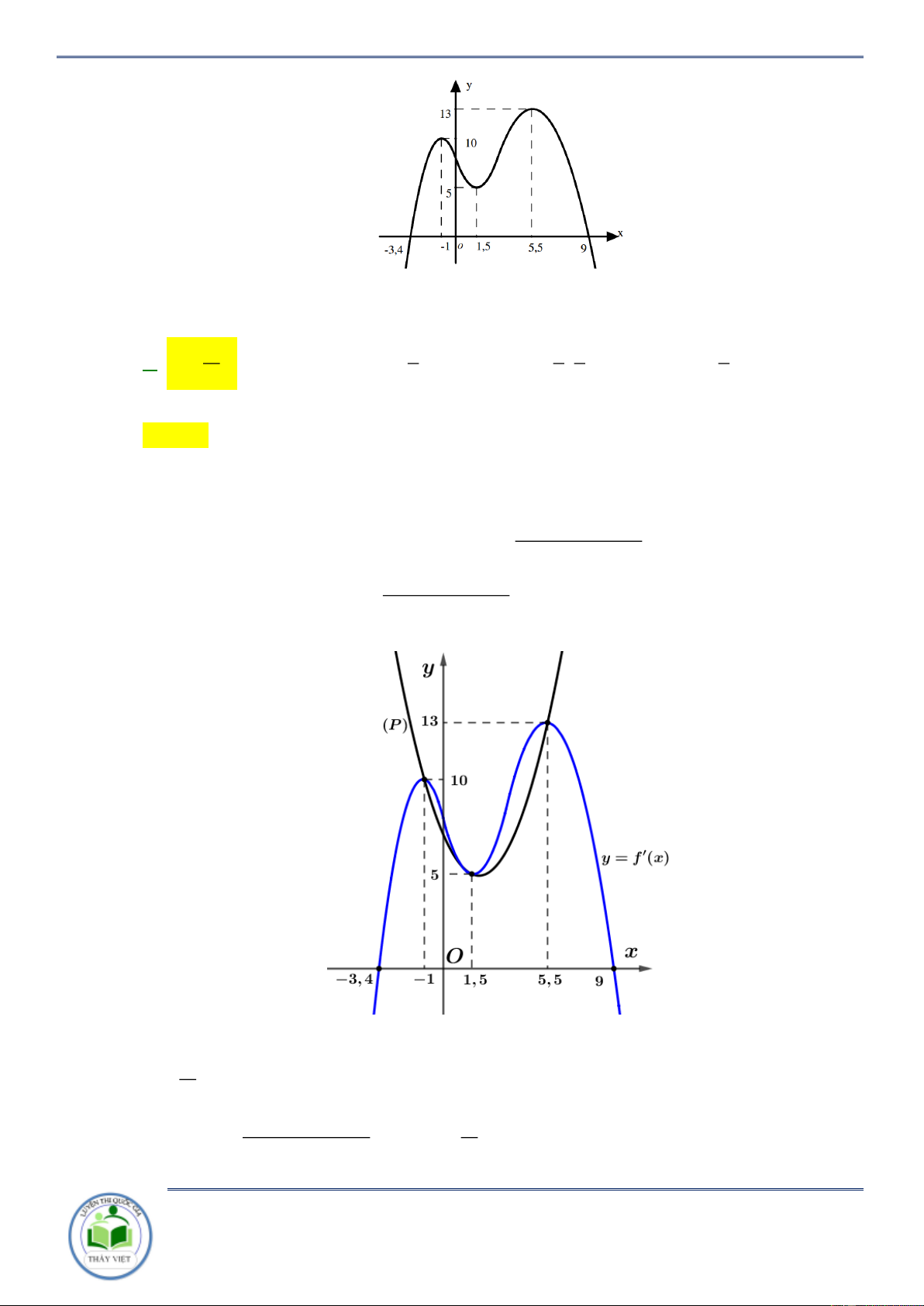
f x có đồ thị của hàm số y f
x như hình vẽ bên. Hàm số 2 2 y f x 2x 3 x 2x
2 đồng biến trên khoảng nào dưới dây?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 22/102 1 1 A. ; 1 . B. ; . C. ; . D. 1; . 2 2 Lời giải Chọn A Ta cần giải x 1 x 1 2 2 y 0 f x 2x 3 x 2x 2 0 2 2 x 2x 3 x 2x 2 2 2 2 2 x 1 x 2x 2 x 2x 3 f x 2x 3 x 2x 2 0 2 2 x 1 f x 2x 3 x 2x 2 0 2 2 2 2 x 1 x 2x 3 x 2x 2 1 x 2x 3 x 2x 2 2 0 x 1. Câu 39: Cho hàm số 4 4 2 f x x ax bx cx
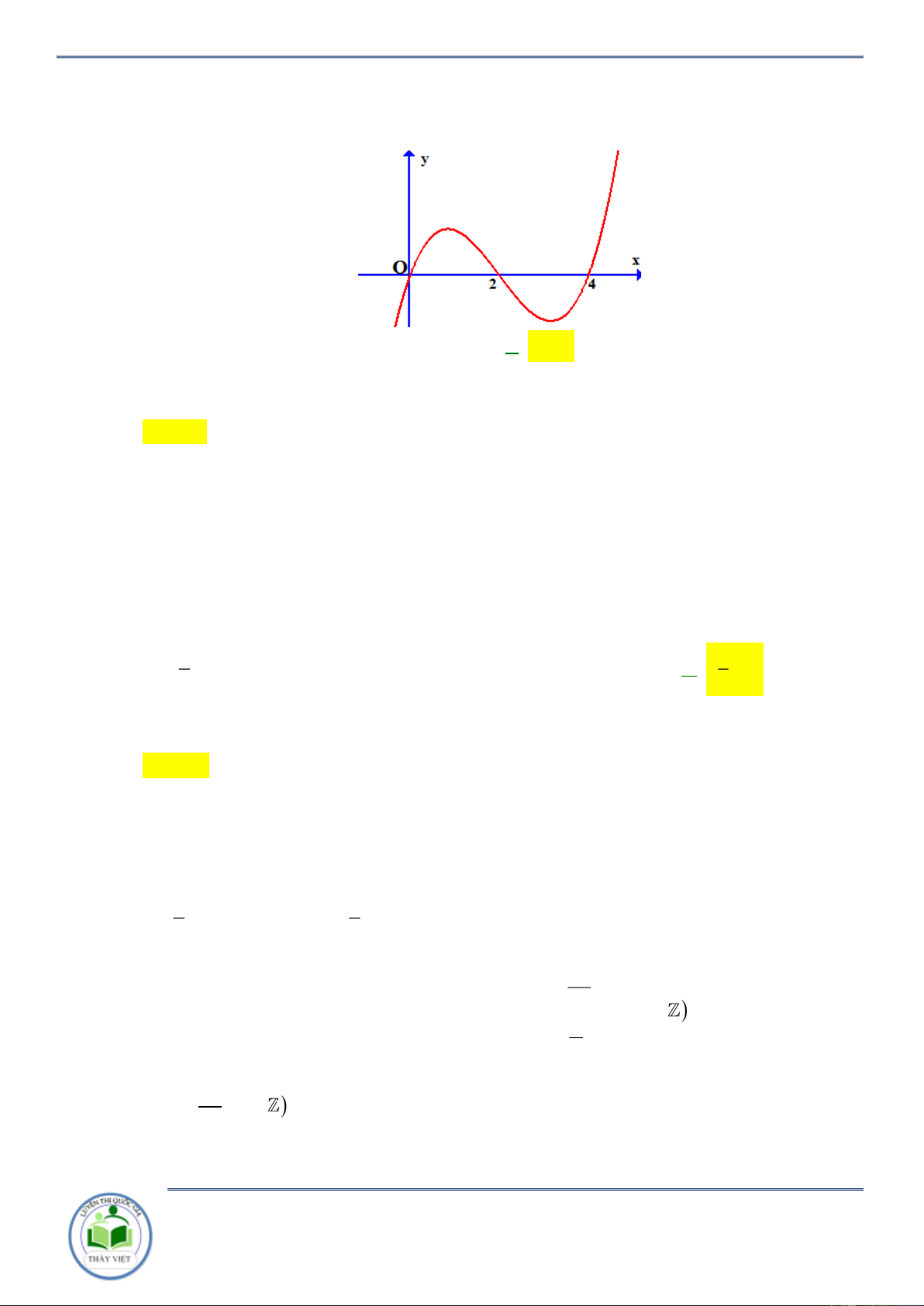
d thỏa mãn f 1 100, f 2 200, f 3 300 . f x 100x Hàm số f
nghịch biến trên một khoảng có đồ dài lớn nhất bằng? 6x d 2 3 3 A. 4 . B. . C. 2 . D. . 3 3 Lời giải Chọn B Có 4 3 2 g x f x 100x x ax bx c 100 x
d và theo giả thiết ta có: g 1 g 2 g 3 0 do đó g x x m x 1 x 2 x 3 f x x m x 1 x 2 x 3 100x
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 23/102
Đồng nhất hệ số tự do của f x ta có d d 6m d m f x x x 1 x 2 x 3 0 1 0x 6 6 f x 100x 1 1 Vậy 2 y x 1 x 2 x 3 y 3x 12x 11 0 6x d 6 6 1 1 2 x 2 . 3 3
Câu 40: Cho hàm số y
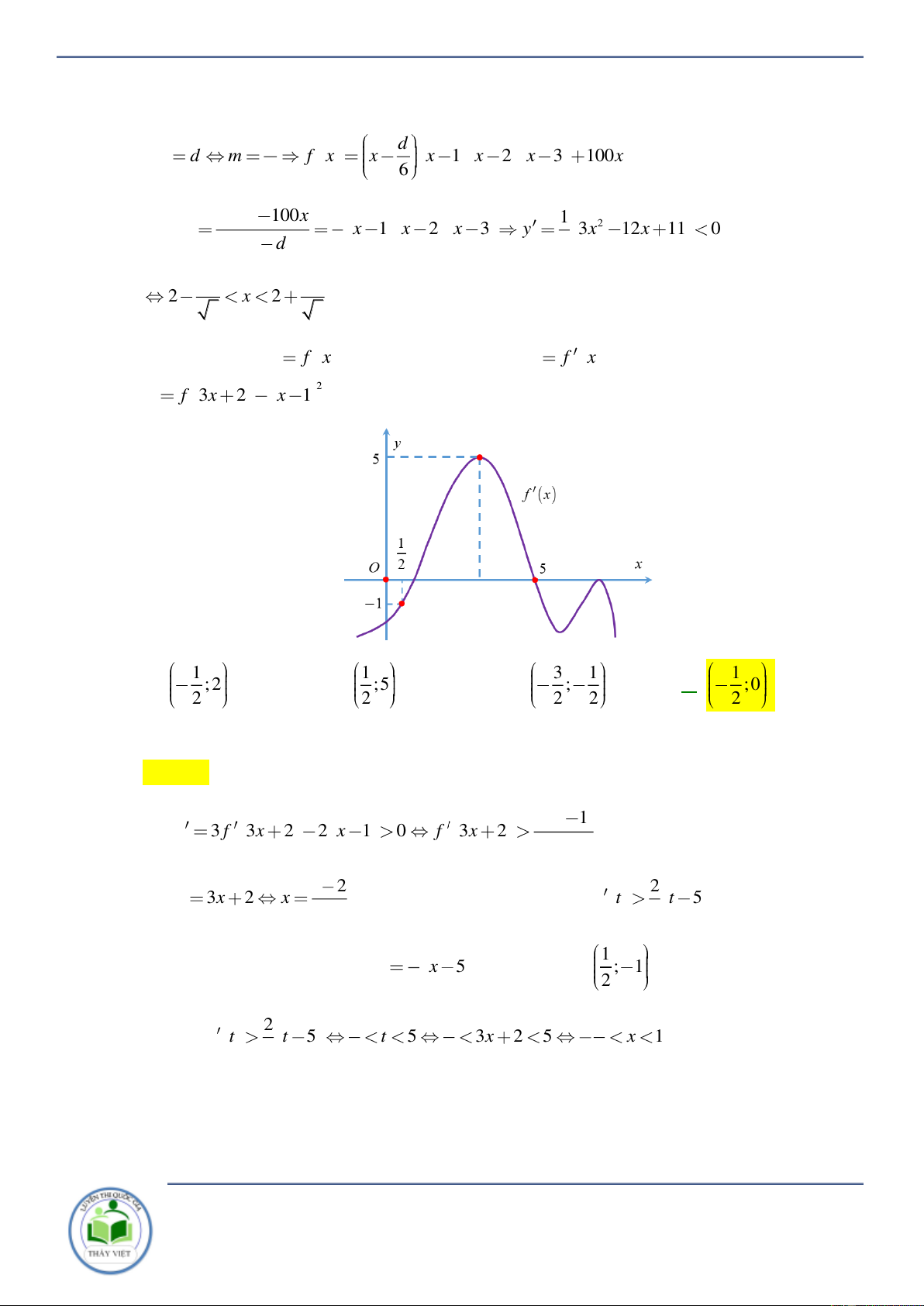
f x có đồ thị hàm số y f
x như hình vẽ bên. Hàm số 2 y f 3x 2
x 1 đồng biến trên khoảng nào dưới đây? 1 1 3 1 1 A. ; 2 . B. ;5 . C. ; . D. ; 0 . 2 2 2 2 2 Lời giải Chọn D 2 x 1 Có y 3 f 3x 2 2 x 1 0 f 3x 2 3 t 2 2 Đặt t 3x 2 x
, bất phương trình trở thành f t t 5 3 9 2 1
Kẻ trên đồ thị đường thẳng y x 5 qua hai điểm ; 1 và 5;0 . 9 2 2 1 1 1 Suy ra f t t 5 t 5 3x 2 5 x 1. 9 2 2 2
Câu 41: Cho hàm số y  f (x) có đồ thị của hàm số y  f '(x) như hình vẽ bên
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 24/102 Hàm số 3 2
y  39 f (x)  8x  45x  276x 1 đồng biến trên khoảng nào dưới đây?  11   3   3 9   9  A. 1  ; .   B.  ;   .   C.  ;   D. ;     2   2   2 2   2  Lời giải Chọn A Ta có: 2
y '  39 f '(x)  24x  90x  276 2
24x  90x  276
Hàm số đã cho đồng biến  y '  0  f '(x)  39 2
24x  90x  276
Gọi  P là đồ thị hàm số y 
. Ta có đồ thị hàm số f '(x) và  P được 39 thể hiện trong hình sau:
Từ đồ thị trên ta thấy đồ thị hàm số f '(x) nằm phía trên parabol  P trên khoảng  11  1  ;   .  2  2
24x  90x  276  11  Vậy f '(x)   x  1  ;   39  2 
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 25/102 Vậy Chọn A
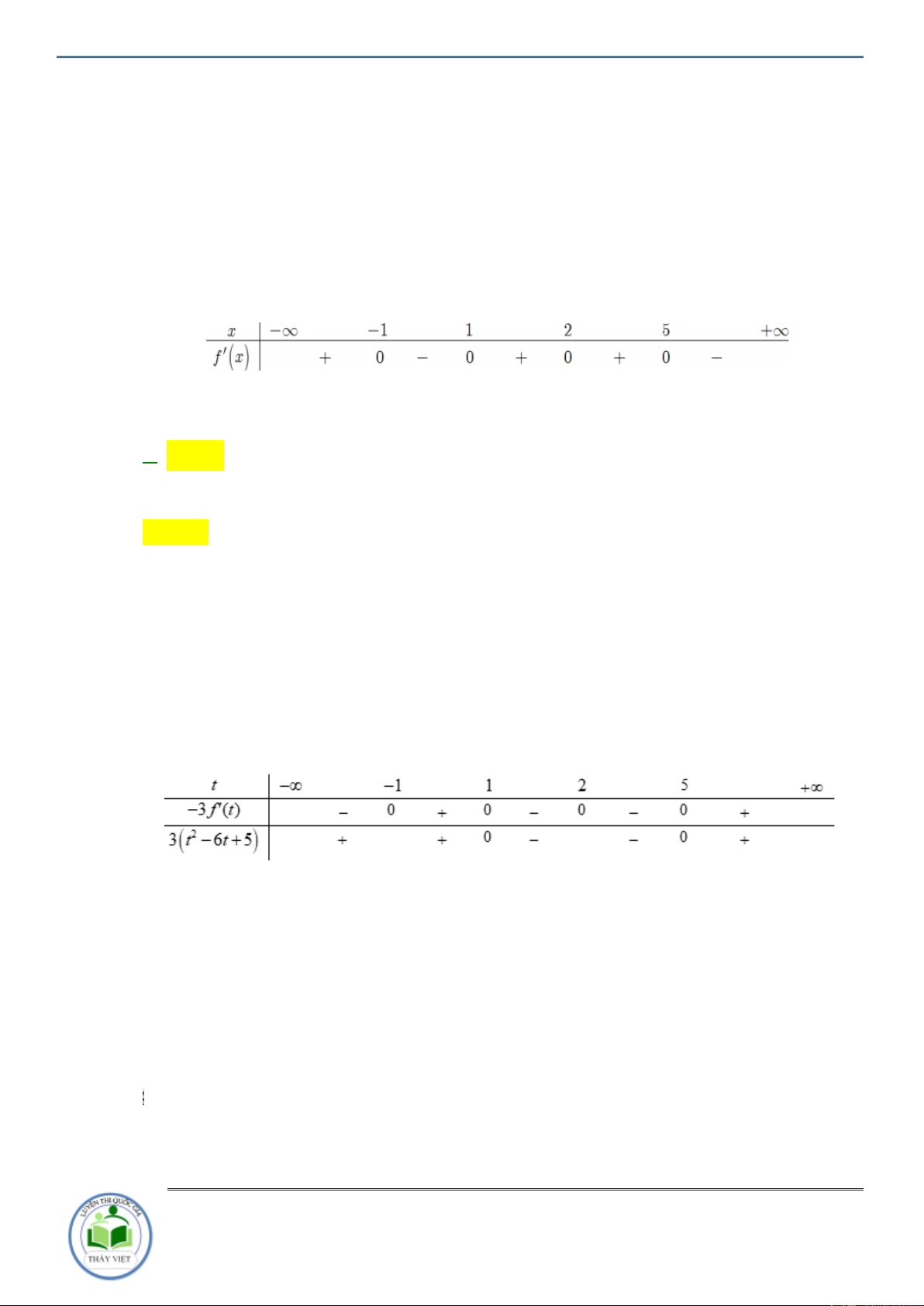
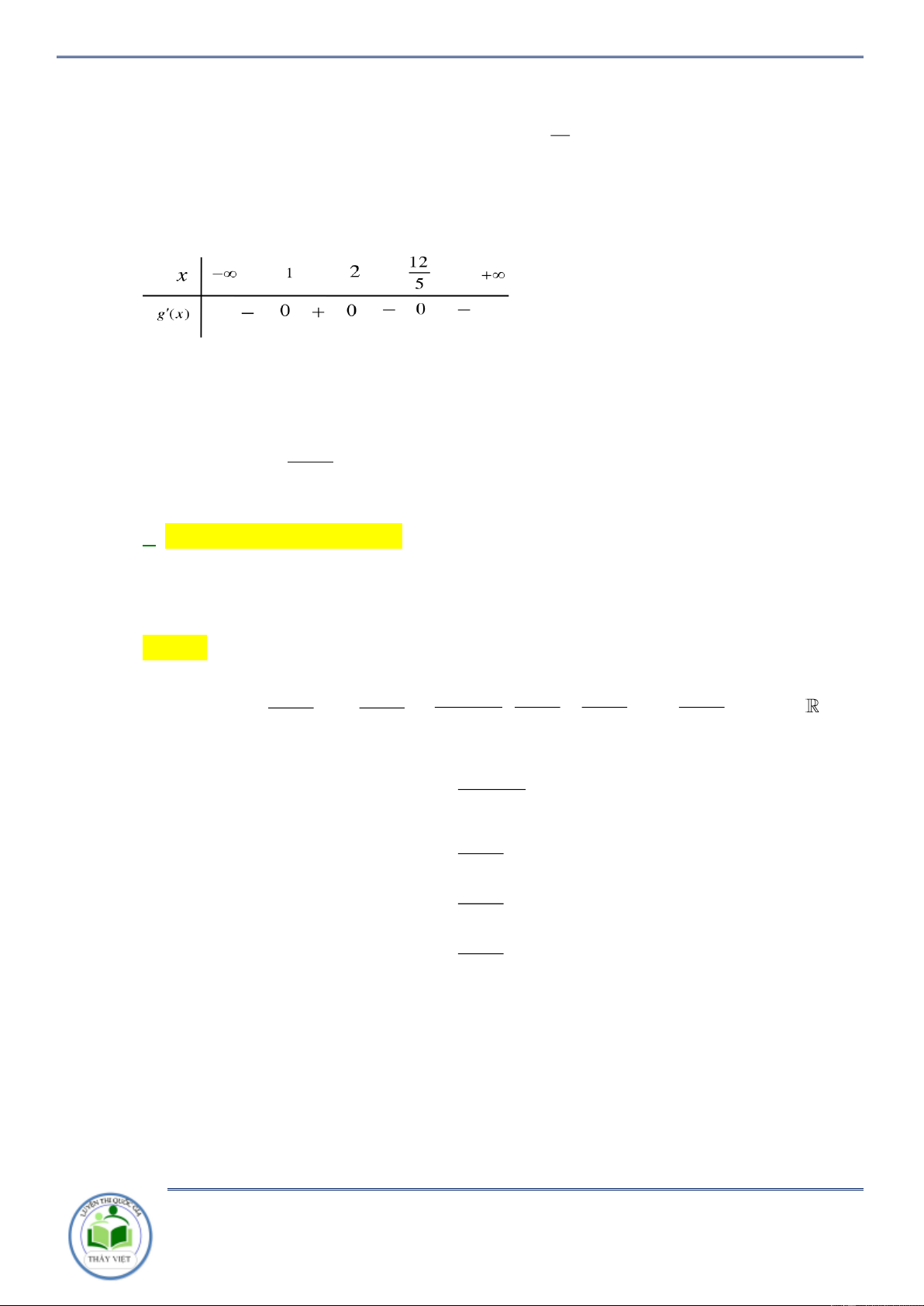
Câu 42: Cho hàm số f (x) có bảng xét dấu của đạo hàm như sau: Hàm số 3
y  3 f (x  2)  x  3x đồng biến trên khoảng nào dưới đây?
A. 1;. B.  ;    1 . C.  1  ;0. D. 0;2. Lời giải Chọn C Ta có: 2
y '  3 f '(x  2)  3x  3
Đặt t  x  2  x  t  2 khi đó ta có: y  f  t  2 2 ' 3 '(t) 3 2
 3  3 f '(t)  (t  4t  3)  
Ta có bảng xét dấu như sau:
Vậy ta thấy y '  0  t 1;  3  x  1  ; 
1 nên hàm số đã cho đồng biến trên  1  ;0 .
Câu 43: Cho hàm số f (x) . Hàm số y  f (
 x) có bảng xét dấu: Hàm số 2
y  f (x  2x) nghịch biến trên khoảng nào dưới đây? A.  4  ; 3   . B. 0  ;1 . C.  2  ;  1 . D.  2   ;1 . Lời giải Chọn C  Ta có y   2
f x  x    x   f  2 ( 2 ) 2 2 x  2x .
Xét bất phương trình y    x   f  2 0 2 2
x  2x  0 x 1 0  x  1  x  1  TH1:           f    3 x 1 2 x  2x 2  0  2
  x  2x  3  3   x 1
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 26/102 x  1  x 1 0  x  1  TH2: 2 
 x  2x  2  (vn)    x 1 2
 f (x  2x)  0  x  3   x 1 2
x  2x  3
Vậy hàm số nghịch biến trên mỗi khoảng  3  ;  1 và 1; 
Hàm số nghịch biến trên  2  ;  1 .
Câu 44: Cho hàm số f (x) có bảng xét dấu đạo hàm f (  x) như sau: 3 2 Hàm số 3 9 1 3 ( 2) ex x x y f x       
nghịch biến trên khoảng nào dưới đây? A.  2   ;1 . B. 2; . C. 0; 2 . D.  ;  2   . Lời giải Chọn A  3 2 3 2 Ta có: y  
x 3x 9 x 1 f x   
  fx  2x  x  x 3x 9x 1 3 ( 2) e 3 2 3 6 9 e 
Đặt t  x  2  x  2  t 3 2 Khi đó 2 9 15 3  3 
( )  3(  6  5). t t t y f t t t e      Ta có bảng xét dấu:
Từ đó suy ra, với t 1;  5 thì y  0 . Từ t 1; 
5 1 x  2  5  3   x 1  3 2 Trên  3   ;1 , hàm số 3 9 1 3 ( 2) ex x x y f x        nghịch biến.
 Hàm số nghịch biến trên  2   ;1 .
Câu 45: Cho hàm số f  x có bảng biến thiên như sau
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 27/102 3 2
Hàm số y   f  x  3 f  x nghịch biến trên khoảng nào dưới đây? A. 2;3 . B. 1;2 . C. 3;4 . D.  ;    1 . Lời giải Chọn A
Ta có y  3 f  x f x  2. f x .
Dựa vào bảng biến thiên ta có trên 2;3 thì f  x  0, f  x  2  0, f  x  0 .
Do đó y  0 hay hàm số nghịch biến trên 2;3 .  
Câu 46: Cho hàm số f  x có bảng xét dấu đạo hàm như sau 1 3
x  x 2 x
Xét hàm số g  x  f   x 3 2 3 2 1  3
. Khẳng định nào sau đây đúng?  1 3 
A. Hàm số g  x đồng biến trên khoảng ;   .  2 2 
B. Hàm số g  x đồng biến trên khoảng 0; 2 .
C. Hàm số g  x đồng biến trên khoảng 3; .
D. Hàm số g  x nghịch biến trên khoảng 0  ;1 . Lời giải Chọn C 1 3 3 2
x  x 2 x
Ta có g x   f   x   2 3 2 1 3
x  3x  2ln 3 . 1 3 3 2
x  x 2 x
Hàm số g  x đồng biến khi g x    f   x   2 3 2 0 1 3
x  3x  2ln 3  0 .    x    x 
Ta có  f   x   f   x 0 1 1 0 1 1 0 1  0     1   x  2  x  3 1 3 3 2
x  x 2 x x 1 Và 3  2 3 2
x  3x  2ln 3  0   . x  2
Suy ra trên 3; thì g x  0 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 28/102
Do đó hàm số g  x đồng biến trên khoảng 3; .
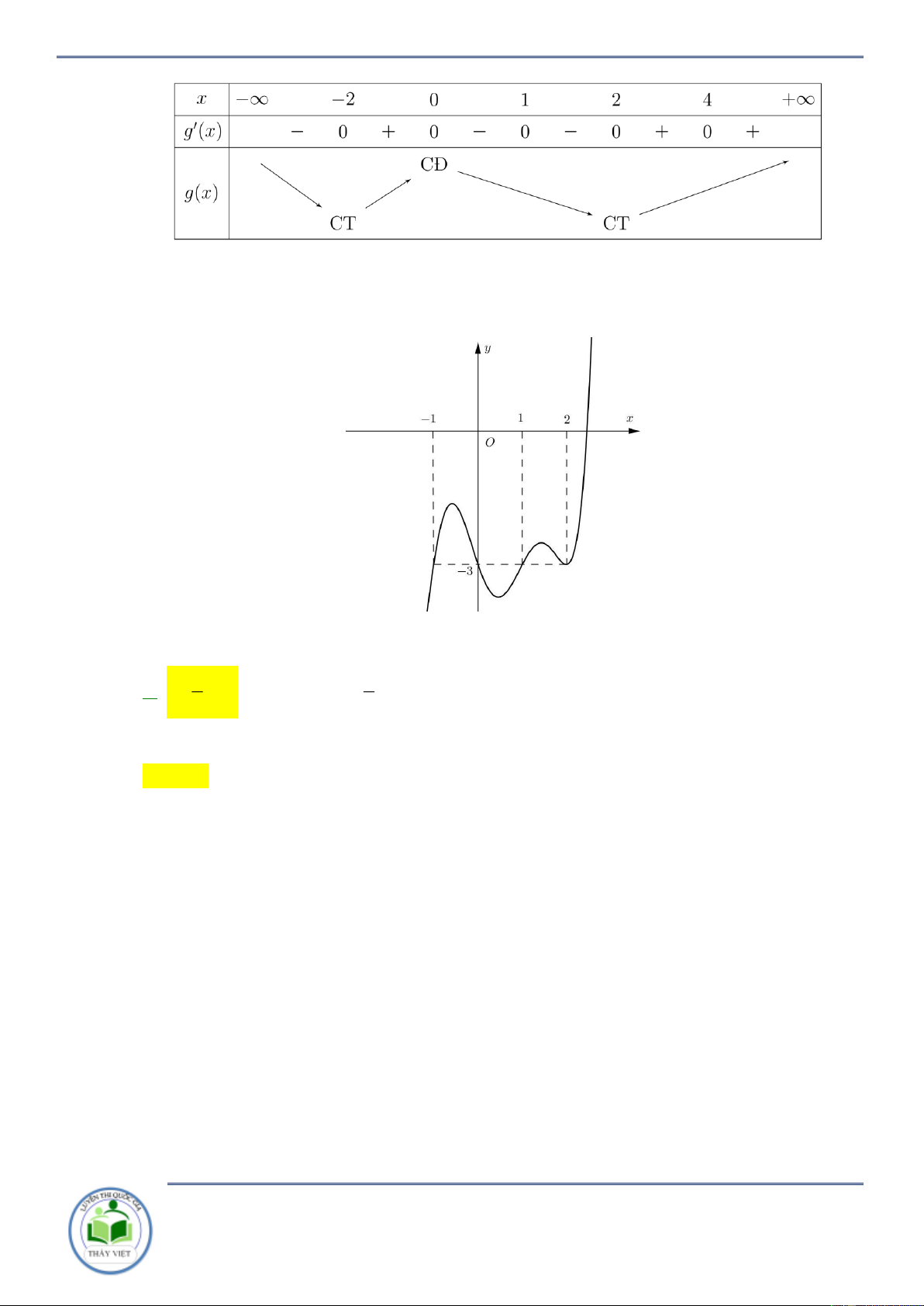
Câu 47: Cho hàm số f  x có đạo hàm liên tục trên và có đồ thị như hình vẽ bên dưới.
Có bao nhiêu số nguyên m 1
 0;10 để hàm số y  f  x   3 3
1  x  3mx đồng biến trên khoảng  2   ;1 . A. 8 . B. 6 . C. 10 . D. 13 . Lời giải Chọn B
Ta có y  f  x   2 ' 3 ' 3
1  3x  3m .
Để hàm số đồng biến trên khoảng  2  
;1 thì y  f  x   2 ' 3 ' 3
1  3x  3m  0 x   2  ;  1
 f  x   2  x  m  x
    m  g x  f  x   2 ' 3 1 0 2;1 ' 3 1  x , x   2  ;  1   *
Ta có: f  x    f   2
  x   f  x   2 ' 3 1 ' 1 4, 0 ' 3 1  x  4  .
Suy ra điều kiện (*) tương đương: m  Min g x  4   m  9  ; 8  ; 7  ; 6  ; 5  ; 4  2  ;1      
Vậy có 6 giá trị nguyên thỏa mãn điều kiện đề bài.
Câu 48: Cho hàm số f  x có bảng xét dấu đạo hàm như sau: hàm số  2 22 x y f x
e nghịch biến trên khoảng nào dưới đây? A.  ;    1 . B.  2  ;0 . C. 0  ;1 . D. 1; . Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 29/102
Ta có '  2 '2  2  2 x y f x e Để hàm số nghịch biến thì điều kiện cần là:
 f '2x  2  0        
 f  x   2x 2 6 x 2 ' 2 2  0      2 x
 e  0 (L D)  4   2x  2  0  1   x 1 Suy ra Chọn C
Câu 49: Cho hàm số f  x có bảng xét dấu đạo hàm như sau
Hàm số y  f  x   3 2 6
1  2x  3x đồng biến trên khoảng nào dưới đây? A. 2; . B.  1  ;0 . C.  ;    1 . D. 0  ;1 . Lời giải Chọn D
Ta có: y  6. f  x   2          1 6x 6x . y f  x  2 0 1 x x
Đặt t  x 1 x  t 1. 2
Khi đó ta có phương trình: f t   t    t    f t  2 1 1
 t  t   * .
Nhận thấy phương trình * có nghiệm t  0;t  1  . Trên khoảng  1
 ;0 thì f t  0 và 2t t  0 nên f t  2t t  0 .
Nên hàm số y t  đồng biến trên khoảng  1  ;0 .
Suy ra hàm số y  x đồng biến trên khoảng 0  ;1
Câu 50: Cho hai hàm số y  f  x, y  g  x có đạo hàm trên
và có đồ thị như hình vẽ bên,
trong đó đường cong đậm hơn là đồ thị của hàm số y  f  x . Biết rằng hai hàm số y  f  2  x  
1 và y  g ax  b, , a b 
 có cùng khoảng đồng biến. Giá trị của a 2b bằng:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 30/102 A. 3 . B. 4 . C. 2 . D. 6 . Lời giải Chọn C
+) Xét hàm số: y  f  2  x   1 có: y  2  . f  2  x   1 .
Hàm số đồng biến  y  0  2  . f  2  x   1  0  f  2  x   1  0 . 1 1  0  2
 x 1 2    x  . 2 2
+) Xét hàm số: y  g ax  b, , a b 
 có y  .agax b . TH1: Nếu a  0 :
Hàm số y  g ax  b, , a b 
 đồng biến  y  0  1   b x        ax b 1 a .
a gax  b  0  gax  b  0     . ax  b 1 1 b x   a
Không thỏa mãn giả thiết hàm số y  f  2  x  
1 và y  g ax  b, , a b   có cùng khoảng đồng biến.
TH2: Nếu a  0 thì y  g b là hàm hằng.
Không thỏa mãn giả thiết hàm số y  f  2  x  
1 và y  g ax  b, , a b   có cùng khoảng đồng biến.
TH3: Nếu a  0 : Hàm số y  g ax  b, , a b 
 đồng biến  y  0    b  b .
a gax  b  0  gax  b  1 1 0  1
  ax  b 1   x  . a a
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 31/102
Hàm số y  f  2  x  
1 và y  g ax  b, , a b 
 có cùng khoảng đồng biến  1   b 1    a  2 a 2     . 1 b 1 b    0   a 2
Vậy a  2b  2 .
Câu 51: Cho hàm số f  x có đồ thị y  f ' x như hình vẽ bên. Hàm số y  f  x 2 cos  x  x
đồng biến trên khoảng: A. 1;2 . B.  1  ;0 . C. 0  ;1 . D.  2  ;  1 . Lời giải Chọn A
Ta có: y '  sin .
x f 'cos x  2x 1 + Vì cos x  1  ;  1  sin .
x f 'cos x 1  ; 
1 mà 2x 11  x 1
+ Suy ra y '  sin .
x f 'cos x  2x 1 0, x
 1 hay hàm số tăng trên [1;)
Câu 52: Cho hàm số y  f  x có bảng xét dấu đạo hàm như hình vẽ
Hàm số y  f   x 2 2 1
 x 1  x nghịch biến trên khoảng nào: A.   ;1  . B.  ;   2. C.  3  ; 2   . D.  2  ;0 . Lời giải Chọn D x y '  2
 f '1 x  1 0 . 2 x 1
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 32/102 x Ta có: 1 0, x   . 2 x 1
Khi: 11 x  3  2
  x  0 thì f '1 x  0  2
 f '1 x  0. x Vậy 2
 f '1 x  1 0, x   2
 ;0 . Hàm số nghịch biến trên  2  ;0 . 2 x 1
Câu 53: [2D1-1.4-3] Cho hàm số y  f (x) có đạo hàm liên tục trên
. Đồ thị hàm số y  f (  x) như hình vẽ Hàm số g( ) x  f ( 2
 x 1)  (x 1)( 2
 x  4) đồng biến trên khoảng nào dưới đây  1   1   1  A. 2;     . B. (;2) . C.  ;     . D.  ; 2   .  2   2   2  Lời giải Chọn A Xét hàm số g( ) x  f ( 2
 x 1)  (x 1)( 2  x  4) Tập xác định: . g (  x)  2  f (  2
 x 1)  4x  2 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 33/102 g (  x)  0  2  f (  2
 x 1)  4x  2  0  f (  2  x 1)  2  x 1(hay f (  t)  t , với t  2  x 1)  x  2 x    Từ đồ thị ta thấy  f (  2  x 1)  2  x 1  2 1 3   1 . 2  2  x 1 5  2   x    2 x  2 Hay  g (  x)  0  1  2   x    2  1 
Như vậy trên mỗi khoảng 2;   
 , 2;  hàm số y  g(x) đồng biến.  2 
Soi các phương án ta thấy phương án A thỏa yêu cầu đề bài.
Câu 54: [2D2-4.3-3] Cho hàm số y  f (x) có đạo hàm trên
. Đồ thị hàm số y  f (  x) như hình vẽ bên dưới. f (12 x)  1 
Hàm số g(x)   
nghịch biến trên khoảng nào dưới đây  2  A. 0  ;1 . B. (;0) . C.  1  ;0 . D. 1; . Lời giải Chọn D f (12 x)  1 
Xét hàm số g(x)     2  Tập xác định: . f (12 x) f (12 x)       1 
g x    x f   x 1 1 ( ) 1 2 . 1 2 . .ln  
  = g (x)  2ln 2. f 1 2x.   2   2   2  g (
 x)  0  f (1 2x)  0.
Từ đồ thị của hàm số y  f (  x) ta thấy   x  1 x    f (
 1 2x)  0  1 2 1   1 . 1  1 2x  2   x  0  2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 34/102 x  1 Hay  g (  x)  0  1  .   x  0  2  1 
Như vậy trên mỗi khoảng  ;0 
 , 1;  hàm số y  g(x) nghịch biến.  2 
Soi các phương án ta thấy phương án D thỏa yêu cầu đề bài.
Câu 55: Cho hàm số f (x) có đồ thị của f '(x) như hình vẽ bên. Có bao nhiêu số nguyên
m [ 5; 5] để hàm số f (x )
m nghịch biến trên khoảng (1; 2)? A. 4. B. 3. C. 6. D. 5. Lời giải Chọn D Đặt ( g ) x f (x ) m . Ta có g'( ) x f '(x ) m . YCBT f '(x ) m 0, x (1; 2) f '(t) 0, t (1 ; m 2 ) m với t x m m 3 2 m 1 m 3 m 0 1 1 m 2 m 3 0 m 1 m 1
Vì m [ 5; 5] nên m { 5; 4; 3; 0;1}.
Câu 56: Cho hàm đa thức bậc ba y f ( )
x có đồ thị hàm số y f '( )
x như hình vẽ. Hàm số 2 ( g ) x
f ( x x ) nghịch biến trên khoảng nào dưới đây? 1 A. ; 0 . B. ( 1;0). C. ( 2; 1). D. (1; 2). 2 Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 35/102 Chọn D 2 g'( ) x ( 1 2 ) x f '( x x ) 1 1 x x 2 2 2 g '(x) 0 x x 0 x 0 2 x x 1 x 1 Bảng biến thiên Vậy Chọn D
Câu 57: Cho hàm số y  f  x có bảng xét dấu của đạo hàm như sau  x 1 1 3
Đặt g  x 3 2  f
 x  x  2x  3  
. Mệnh đề nào dưới đây sai?  2  3 2
A. Hàm số g  x nghịch biến trên khoảng  1  ;0 .
B. Hàm số g  x đồng biến trên khoảng 0;2 .
C. Hàm số g  x nghịch biến trên khoảng  4  ;  1 .
D. Hàm số g  x nghịch biến trên khoảng 7; . Lời giải Chọn B 1  x 1 1   x 1 
Ta có g x 2 2  f 
 x  3x  2  f 
 2x  6x  4       . 2  2  2   2  
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 36/102 Hàm số nghịch biến x 1    2  x 2 2
 x  6x  4  0  x 1    khi g x 2  0  f 
 2x  6x  4  0        5 x 1 1       x 1 2  f   0        2 2 2 2    x 1    3   2 x 1  x  2  4   x  1     .  4   x  2 x  7  x  7 Từ đó suy ra B sai.
Câu 58: Cho hàm số y  f  x liên tục, nhận giá trị dương trên
và có bảng xét dấu đạo hàm
như hình bên. Hàm số g  x  log f 2x
đồng biến trên khoảng 2    A. 1;2 . B.  ;    1 . C.  1  ;0 . D.  1   ;1 . Lời giải Chọn A 2 f  2x
Ta có g x    . f 2x ln 2  1 1 2 f  2x  1   2x 1   x 
Hàm số đồng biến khi g x            . f  f x 2x 0 2  0 2 2 ln 2 2x  2  x 1
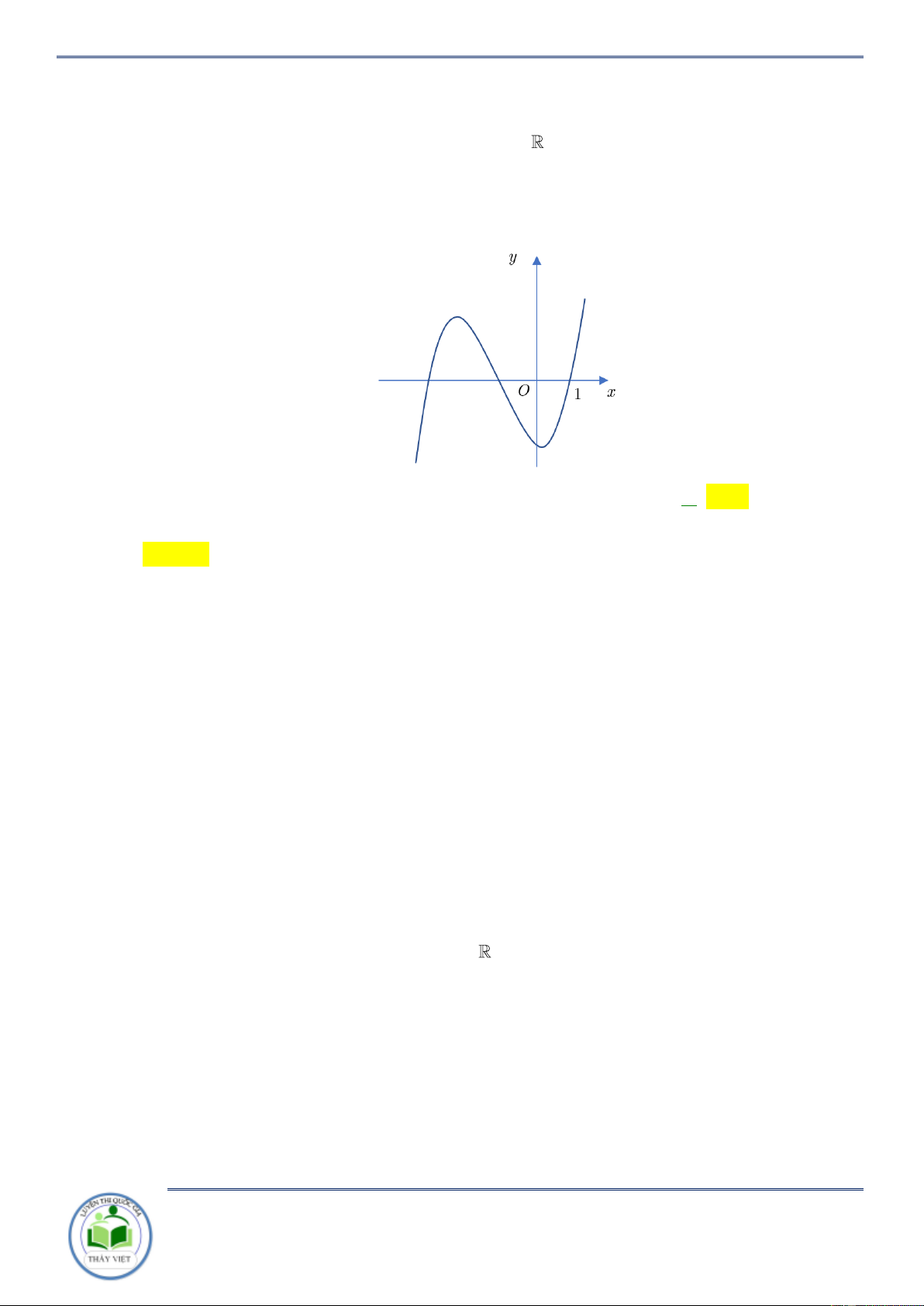
Câu 59: Cho hàm số y  f  x liên tục trên có f 0  0 và đồ thị hàm số y  f  x như hình vẽ dưới đây. y 4 1 x O 1 2
Hàm số y  f  x 3 3
 x đồng biến trên khoảng
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 37/102 A. 2; . B.  ;  2 . C. 0; 2 . D. 1;3 . Lời giải Chọn C
Xét hàm số g  x  f  x 3 3
 x có gx  f x 2
 x   f x 2 3 3 0  x . Vẽ đồ thị hàm số 2
y  x cắt đồ thị y  f  x tại 3 điểm x  0, x 1, x  2 (như hình vẽ). y 4 1 x O 1 2
Từ đây ta có bảng biến thiên của hàm số y  g  x (như hình trên).
Dùng phép đối xứng đồ thị, ta thu được hàm số y  g  x đồng biến trên khoảng
0;2 và  ;a với a  2.
Câu 60: Cho hàm số y  f  x có bảng xét dấu đạo hàm như hình vẽ.
Biết rằng 1  f  x  3 , x
  . Hàm số y  f  f  x 3 2
  x  6x 1  nghịch biến trên khoảng A. 3;4 . B.  3  ; 2   . C. 1;3 . D.  2   ;1 . Lời giải Chọn A
Ta có y   f  x f   f  x 2 0 .
  3x 12x  0  (*)
Theo đề bài 1  f  x  3 , x
  nên f  f  x  0  , x   .
Vậy ta chỉ cần các điều kiện sau để thỏa (*) là
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 38/102
 f x  0 x     ;1  3; 4     x 0  ;1  3; 4 . 2 3
 x 12x  0 x   0;4
Câu 61: Cho đồ thị hàm số y  f 2  x như hình vẽ
Hàm số y  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. 0  ;1 . B. 1;3 . C.  ;    1 . D.  1  ;0 . Lời giải Chọn A
Gọi C là đồ thị hàm số y  g  x  f 2  x .
Tịnh tiến C sang trái 2 đơn vị ta được đồ thị hàm số y  g  x  2  f x .
Lấy đối xứng đồ thị hàm số y  f x qua Oy ta được đồ thị hàm số y  f  x .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 39/102
Ta có y  f  2
x    y  x f  2 3 2 . x  3 . x  0 x  0 x  0   y  0   . f  x x           x  3 2 3 0 3 2  0 2   x  3  3  x   6  Bảng xét dấu y
Vậy hàm số y  f  2
x  3 nghịch biến trên khoảng 0  ;1 .
Câu 62: Cho hàm số f  x có bảng xét dấu đạo hàm f  x như sau:
Hàm số y  f  2
x  2x nghịch biến trên khoảng nào dưới đây? A.  2   ;1 . B.  4  ;3 . C. 0  ;1 . D.  2  ;  1 . Lời giải Chọn D
Đặt: y  g  x  f  2
x  2x; g x   f  2
x  2x    x   f  2 2 2 . x  2x . x  1    2x  2  0 2 x  2x  2   vo ânghieäm
g x  0   x   f  2 2 2 .
x  2x  0    f      2
x  2x  0 2 x  2x  1  2
x  2x  3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 40/102 x  1 x  1 2    x  1 2  . ( x  1
  2 là các nghiệm bội chẵn của phương trình: 2
x  2x  1). x 1 x  3  Ta có bảng biến thiên:
Dựa vào bảng biến thiên, suy ra hàm số y  f  2
x  2x nghịch biến trên khoảng  2  ;  1 .
Chú ý: Cách xét dấu g x :
Chọn giá trị x  0 1  ;1 2 2
 x  2x  0  g0  f 0  0 (dựa theo bảng xét
dấu của hàm f  x ). Suy ra g x  0 , x   1
 ;1 2. Sử dụng quy tắc xét dấu đa
thức “lẻ đổi, chẵn không” suy ra dấu của g x trên các khoảng còn lại.
Câu 63: Cho hàm số y  f  x liên tục trên và hàm số y  f  x có đồ thị như hình vẽ.
Hàm số y  g  x  f  2
1 2x  x   2020 đồng biến trên khoảng nào dưới đây? A.  1  ;0 . B. 0  ;1 . C. 2;3 . D. 3;5 . Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 41/102 Chọn B
Ta có g x    x f  2 2 2 .
1 2x  x  . x   1      x 1 x  1   g x 2 2x 0  0   2
 1 2x  x  2    x  3 . f      2
1 2x  x   0 2
1 2x  x  1   x 1  3 x 1 3 Bảng biến thiên:
Dựa vào bảng biến thiên hàm số g  x đồng biến trên khoảng ;  1 và 1 3;  1 và 1 3;3.
Mà (0;1)  (1 3;1) nên hàm số y  g  x  f  2
1 2x  x   2020 đồng biến trên (0;1) . 2 3
Câu 64: Cho hàm số y  f x có đạo hàm f x  x.x  2 x  
5 . Hàm số gx  f 10  5x
đồng biến trên khoảng nào dưới đây?   ;1 1;2 2; 1;3 A. . B. . C. . D. . Lời giải Chọn B 
Ta có gx  10  5x . f 10  5x  5. f 10  5x .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 42/102 x  2 10   5x  0 
gx   f   x  12 0
10 5  0  10  5x  2   x   .  5 10   5x  5  x 1  Bảng xét dấu g (  x)
Vậy hàm số g x đồng biến trên khoảng 1;2 .
Câu 65: Cho hàm số y  f (x) có đạo hàm 2 f (
 x)  x(x 1) (x  2) với mọi giá trị thực của x . Xét  5x 
hàm số g(x)  f 
 . Trong các khẳng định sau khẳng định nào đúng? 2  x  4 
A. Hàm số đồng biến trên khoảng (0;1) .
B. Hàm số nghịch biến trên khoảng (0; 4) .
C. Hàm số đạt cực đại tại x  0 .
D. Hàm số đạt giá trị nhỏ nhất tại x  1. Lời giải
Sưu tầm:Phạm Hải Dương; Fb: Duongpham Chọn C   2 5x   5x  2
20  5x  5x  5x   5x 
Ta có: g x  f       1  2 , x        . 2 2  x  4 
 x  4  x  2 2 2 2 2
 x  4  x  4   x  4 4  2  20  5x    x  4 0 2 2  x  2 5x    0 x  0 2 g (
 x)  0   x  4      . 5x x 1   1  2    x  4 x 4  5x   2 2  x  4
Bảng biến thiên của hàm số y  g(x) :
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 43/102
Vậy hàm số y  g(x) đạt cực đại tại x  0 .
Câu 66: Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình bên.
Hỏi hàm số g  x  f  2 x  x 2 2
 6x 3x đồng biến trên khoảng nào dưới đây?  1   1  A.  ;0   . B. ;1   . C. 0  ;1 . D.  ;  0.  4   4  Lời giải Chọn A
Ta có: g  x  f  2 x  x 2 2  6x 3x
 gx   x   f  2 4 1
2x  x 12x  3   x    f    2 4 1
2x  x  3 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 44/102  1 x    4     2
2x  x  1voânghieäm g x 4x 1 0  0     2 f  2
2x  x  3  
2x  x  1  2 2x  x   0  2 2x  x   2nghieäm keùp  1 x    4 x  1   1 x    2 x  0   .  1 x   2   1 17 x  nghieäm keùp  4   1 17 x  nghieäm keùp  4
Ta có : g'2  9 f '(10)  3 dựa vào đồ thì f ' x ta thấy f '10  3  f '10  3  0
 g'2  0 .
Ta có bảng xét dấu như sau:          
Xét dấu g x ta được g x 1 1 1 1 17 1 17  0, x    ;0  ;      1;   ;       .  2   4 2  4 4      1   1 1   1 17 
Suy ra g  x đồng biến trên các khoảng  ;0   và ;   và 1;  và    2   4 2  4   1 17   ;     . 4  
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 45/102  1   1  Mà  ;0   ;0   
 nên hàm số g x  f  2 x  x 2 2
 6x 3x đồng biến trên khoảng  4   2   1   ;0   .  4  Câu 67: 2 2
Cho hàm số y  f  x có đạo hàm f ' x  (3 x)10  3x  x  2 với mọi x  . Hàm 1
số g  x  f 3  x 2 3
 (x 1) đồng biến trên khoảng nào trong các khoảng sau? 6  1  A.  ;  0. B. 0;  1 . C. 1;. D.  ;   .    2  Lời giải Chọn D
Ta có g  x   f   x 2 2 ' ' 3  x(x 1) . Theo giả thiết 2 2 f  x 
 x   x2 x  2 ' (3 ) 10 3
2 nên f '3  x  x3x   1 1 x Từ đó suy ra
g  x  x x  2   x2 2 2 ' 3 1 1  x(x 1) 2 2 2 2 2
 x(x 1)  (
 3x 1)  (x 1)   x(x 1) ( 8  x  4x)   2 2
 x (x 1) ( 8  x  4) 
x  0(nghiÖmkÐp) 
Khi đó g ' x  0  x   1(nghiÖm kÐp)  x   1  2 Bảng biến thiên  1 
Khi đó hàm số đồng biến trên  ;   .    2 
Câu 68: Cho hàm số f  x có bảng biến thiên như sau
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 46/102 3 2
Hàm số y   f  x  3 f  x nghịch biến trên khoảng nào dưới đây? A. 2;3 . B. 1;2 . C. 3; 4 . D. ;  1 . Lời giải Chọn A 2
Ta có y  3 f  x . f  x  6 f x. f x .
y  3 f  x. f  x  f  x  2   .
 f x  0 
y  0   f  x  0 .  f   x  2 x 1
x  x  x ;1 2  1    x  2 x  x 1
x  x  1;2 3  
+ f  x  0        ; f  x 1 0  ; f  x 2 . x  3 x  4     x x 4 4  x  4 x  3
+ Bảng xét dấu của y 3 2
Từ bảng xét dấu suy ra hàm số y   f  x  3 f  x nghịch biến trên khoảng 2;3 .
Câu 69: Cho hàm số y  f  x , hàm số f  x 3 2
 x  ax  bx  ca, , b c 
 có đồ thị như hình vẽ
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 47/102
Hàm số g  x  f  f  x nghịch biến trên khoảng nào dưới đây?  3 3  A. 1; . B.  ;  2   . C.  1  ;0 . D.   ;    . 3 3   Lời giải Chọn B Vì các điểm  1
 ;0,0;0,1;0 thuộc đồ thị hàm số y  f x nên ta có hệ:  1
  a  b  c  0 a  0   c  0  b   1
  f x 3
 x  x  f ' x 2  3x 1  
1 a  b  c  0 c  0  
Ta có: g  x  f  f x  gx  f  f x. f ' x 3 x  x  0  3 x  x  1 
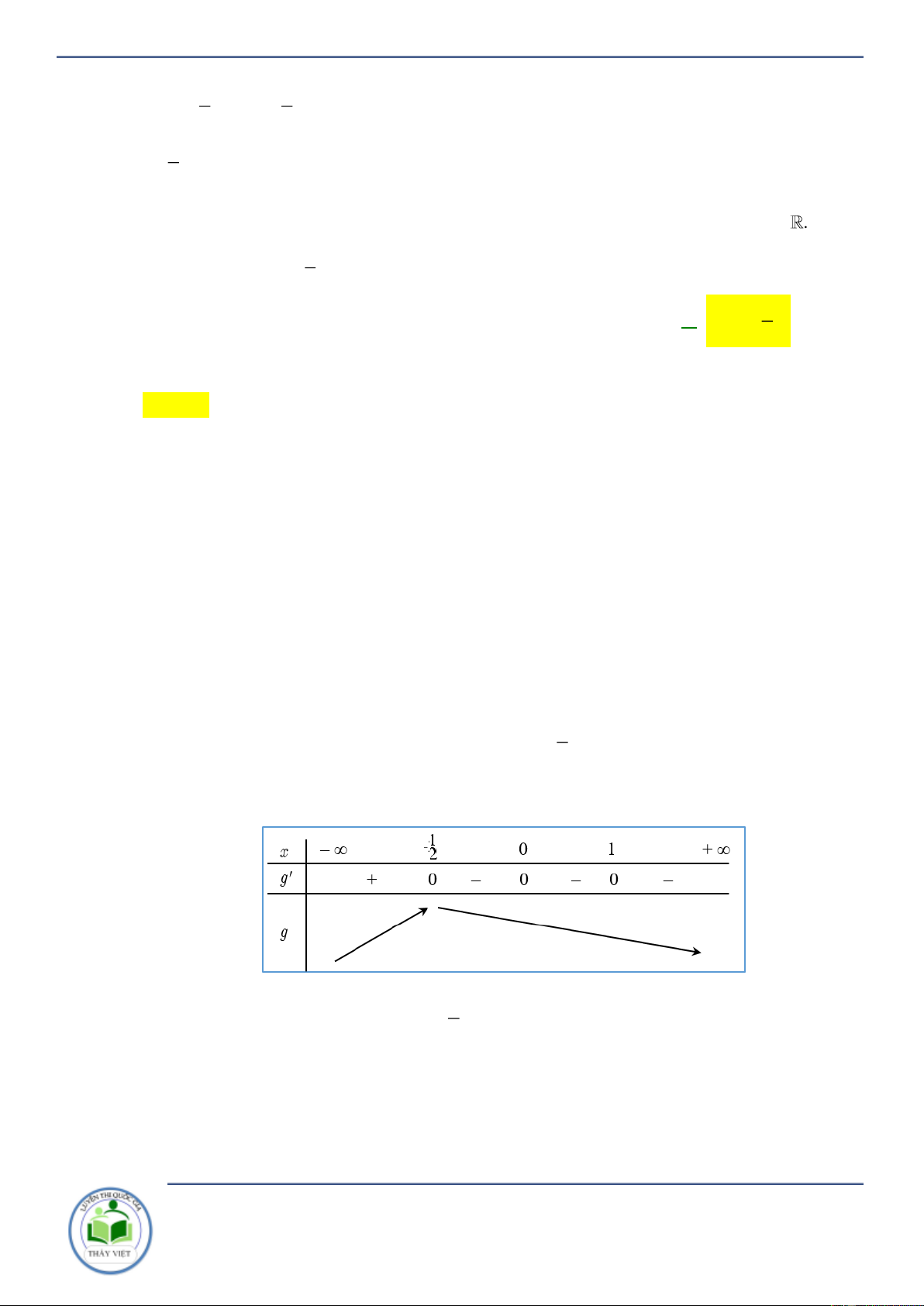
Xét g x  0  g x  f  f ' x. f   x  0  f  3 x  x 2 3x   1  0   3 x  x  1   2 3x 1 0  x  1   x  0 
 x  x (x 1,325 ) 1 1 
x  x (x  1  ,325) 2 2   3 x    3 Bảng biến thiên
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 48/102
Dựa vào bảng biến thiên ta có g  x nghịch biến trên  ;  2  
Câu 70: Cho hàm số y  f  x liên tục có đạo hàm trên . Biết hàm số f ' x có đồ thị cho như
hình vẽ. Có bao nhiêu giá trị nguyên của m thuộc  2  019;201  9 để hàm só    2019x g x f
mx2 đồng biến trên 0  ;1 A. 2028 . B. 2019 . C. 2011. D. 2020 Lời giải Chọn D
Ta có '   2019x ln 2019. '2019x g x f m. Ta lại có hàm số 2019x y  đồng biến trên 0  ;1 . Với x 0; 
1 thì 2019x 1;2019 mà hàm y  f ' x đồng biến trên 1; nên hàm  '2019x y f
 đồng biến trên 0  ;1
Mà 2019x  1; '2019x f
  0x0; 1 nên hàm    2019x ln2019. '2019x h x f  đồng biến trên 0  ;1
Hay h x  h0  0, x 0;  1
Do vậy hàm số g  x đồng biến trên đoạn0 
;1  g ' x  0, x 0;  1
  2019x ln 2019. '2019x m f
,x0; 1  m min hx  h0  0 x   0;  1
Vì m nguyên và m 2
 019;2019  có 2020 giá trị m thỏa mãn yêu cầu bài toán.
Câu 71: Cho hàm số y  f  x có đạo hàm trên
và có đồ thị hàm f  x như hình vẽ dưới
đây. Hàm số     2 g x
f x  x đồng biến trên khoảng nào?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 49/102  1   1  A. ;1   . B. 1;2 . C. 1  ;   . D.  ;    1 .  2   2  Lời giải
Sưu tầm: Nguyễn Thị Thu; Fb:Nguyễn Thu Chọn C     2 g x
f x  x  g x   x   f  2 2 1 x  x .  1 x    1 2 x    2 x  0      g x 2x 1 0  0          . f 
 x  x 2 x x 0 x 1 2  0   2 x  x  2 x  1     x  2   x  2
Từ đồ thị f  x ta có f  2 x  x 2
 0  x  x  2   , x  1 
Xét dấu g x :  1 
Từ bảng xét dấu ta có hàm số g  x đồng biến trên khoảng 1  ;   .  2 
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 50/102
Câu 72: Cho hàm số y  f  x có đạo hàm trên . Biết hàm số y  f  x liên tục trên và có
đồ thị như hình vẽ. Hàm số y  f  2
x 1 đồng biến trong khoảng nào dưới đây? A.  ;
  3,0; 3 . B.  ;
  3, 3; .
C.  3;0, 3; . D.  ;   3,0; . Lời giải
Sưu tầm: Nguyễn Thị Thu; Fb:Nguyễn Thu Chọn C x
Xét hàm số y  f  2
x 1  y  f  2 x 1 . 2  x 1 x  0  2        x 1 1 x 0   x  0 x  0 x 0     y  0   2   x 1  0 2   x 1 1 2
 x 1  1  x   3    f    2 x 1  0     2 2 x 1  1  2  x 1  2  x 1  4  x  3   2 x 1  2  Bảng biến thiên
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 51/102
Vậy hàm số y  f  2
x 1 đồng biến trên các khoảng  3;0, 3; .
Câu 73: Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình bên. Hàm số   2 y f x  x 
nghịch biến trên khoảng nào dưới đây. y 2 O 1 2 x  1   3   3   1  A.  ;    . B.  ;    . C. ;    . D. ;    .  2   2   2   2  Lời giải
Sưu tầm:Chu Minh; Fb:Minhchu Chọn D  Đặt      2 y g x
f x  x   g x  f  2 x  x   2
x  x     x f  2 . 1 2 x  x  1   2x  0 1   2x  0  1
Cho g x  0   2
 x  x 1ptvn  x  . f    2
x  x   0  2 2 x  x  2  ptvn x 1 x  x 1
Ta có f ' x  0   f  x x  2 2  0  
( Luôn đúng với mọi x  ) 2 x  2 x  x  2 Vậy g  x 1 '
 0 1 2x  0  x  . 2  1  Hay hàm số     2 g x
f x  x  nghịch biến trên khoảng ;    .  2 
Câu 74: Cho hàm số y  f  x có đạo hàm trên . Đường cong trong hình vẽ bên là đồ thị của
hàm số y  f  x ( y  f  x liên tục trên
). Xét hàm số g  x  f  2
x  3 . Mệnh đề
nào dưới đây sai? y 4 2 2  1  O 1 x
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 52/102
A. Hàm số g  x đồng biến trên  1  ;0 .
B. Hàm số g  x nghịch biến trên  ;    1 .
C. Hàm số g  x nghịch biến trên 1; 2 .
D. Hàm số g  x đồng biến trên 2;  . Lời giải
Sưu tầm:Chu Minh; Fb:Minhchu Chọn C  
g x   f  2 x  3   2
x   f  2 3
x  3  xf  2 2 x  3
Ta có f  x  0  x  2
 nên f '(x2 - 3) < 0 2  x  3  2  2  x 1  1   x 1. Ta có bảng xét dấu: x  2  1  0 1 2  2x - | - | - 0 + | + | + f '(x2 - 3) + 0 + 0 - | - 0 + 0 + g '(x) - 0 - 0 + 0 - 0 + 0 +
Từ bảng xét dấu ta thấy Chọn C đúng
Câu 75: Cho hàm số y  f  x có đồ thị nằm trên trục hoành và có đạo hàm trên , bảng xét
dấu của biểu thức f  x như bảng dưới đây. f  2 x  2x
Hàm số y  g  x 
nghịch biến trên khoảng nào dưới đây? f  2 x  2x 1  5  A.   ;1  . B. 2;    . C. 1;3 . D. 2; .  2  Lời giải Chọn C   2
x  2x . f  2 x  2x
2x  2.f  2x  2x g x    .
f  x  2x  2 1
 f x 2x 2 2 2 1 x  1          g x 2 x 1 2x         f  2 0 x 2x 2 0 2 x  x 2 x 1 2  0
x  2x  1   x  3  2 
x  2x  3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 53/102
Ta có bảng xét dấu của g x :
Dựa vào bảng xét dấu ta có hàm số y  g  x nghịch biến trên các khoảng ;  1 và 1;3 .
Câu 76: Cho hàm số f  x có bảng biến thiên như sau: 3 2
Hàm số y   f  x  3. f  x nghịch biến trên khoảng nào dưới đây? A. 1; 2 .
B. 3 ; 4 . C.  ;  1 . D. 2 ; 3 . Lời giải
Sưu tầm: Lê Liên;Fb: Lien Le Chọn D 2
Ta có y  3. f  x . f  x  6. f x. f x
= 3f  x. f  x. f  x  2  
 f x  0  xx ,4 | x 1 1 1  
y  0   f  x  2  x x , x ,3, x | x  x  1  x  2;4  x 2 3 4 1 2 3 4 
 f 'x  0  x  1,2,3,  4
Lập bảng xét dấu ta có
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 54/102
Do đó ta có hàm số nghịch biến trên khoảng 2 ; 3 .
Câu 77: Cho hàm số y  f  x đạo hàm liên tục trên có đồ thị hàm số f  x như hình vẽ
Hỏi hàm số y  f  2
x  2x đồng biến trên khoảng nào sau đây? A.  1  ;0 . B. 0  ;1 . C. 1;3 . D. 2; . Lời giải Chọn A
Có y   x   f  2 2 2 x  2x .  x  1 x  1    x  0 x  1 2 x  2x  2   
Do đó y  0     x  2 . f      2
x  2x  0 2 x  2x  0  x  1   2
x  2x  3 x  3 
Ta có bảng xét dấu đạo hàm như sau
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 55/102
Dựa vào bảng xét dấu đạo hàm, hàm số y  f  2
x  2x đồng biến trên các khoảng  1
 ;0,1;2,3;.
Câu 78: Cho hàm số f  x có đạo hàm, liên tục trên , có đồ thị như hình vẽ
Hỏi hàm số     2 y f x  
 nghịch biến trên khoảng nào sau đây?  5   5  A.  1   ;1 . B. 0;  . C. ; 4   . D.  2  ;  1 .  2   2  Lời giải Chọn C x  2 x  0 
 f x  0  5
Có y  2 f  x f  x . Do đó y  0    x   .  f   x  0 2  x  4 x  1 
Ta có bảng xét dấu đạo hàm như sau
Dựa vào bảng xét dấu đạo hàm, hàm số     2 y f x  
 nghịch biến trên các khoảng
       5   ; 2 , 1;0 , ; 4   .  2 
Câu 79: Cho hàm số y
f x có bảng biến thiên như sau
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 56/102
Có bao nhiêu số nguyên m 2019 để hàm số 2 g x f x 2x
m đồng biến trên khoảng 1; ? A. 2016. B. 2015. C. 2017. D. 2018. Lời giải Chọn A Ta có 2 2 2 g x x 2x m f x 2x m 2 x 1 f x 2x m . Hàm số y
g x đồng biến trên khoảng 1; khi và chỉ khi g x 0, x 1; và g x 0 tại hữu hạn điểm 2 2 x 1 f x 2x m 0, x 1; 2 x 2x m 2, x 1; 2 f x 2x m 0, x 1; 2 x 2x m 0, x 1; Xét hàm số 2 y x 2x
m , ta có bảng biến thiên
Dựa vào bảng biến thiên ta có TH1: 2 x 2x m 2, x 1; m 1 2 m 3. TH2: 2 x 2x m 0, x 1;
: Không có giá trị m thỏa mãn.
Vậy có 2016 số nguyên m
2019 thỏa mãn yêu cầu bài toán.
Câu 80: Cho hàm số y  f (x) có bảng biến thiên như sau:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 57/102
Hàm số g x   f  x 2 ( ) (3
) nghịch biến trên khoảng nào trong các khoảng sau? A. ( 2  ;5) . B. (1; 2) . C. (2;5) . D. (5; )  . Lời giải Chọn C
Từ bảng biến thiên suy ra f (x)  0, x
   f (3 x)  0, x   .
Ta có g '(x)  2
 f '(3 x). f (3 x) . 2 3 x 1 2 x 5 Xét g x 0
2 f 3 x . f 3 x 0 f 3 x 0 3 x 2 x 1 .
Suy ra hàm số g x nghịch biến trên các khoảng ( ;  1) và (2;5)
Câu 81: Cho hàm số y  f  x có đồ thị như hình vẽ. Hàm số y  f  x  đồng biến trong khoảng nào dưới đây? A. 0  ;1 . B.  1   ;1 . C. 0; 2 . D. 1;2 . Lời giải Chọn D
Thực hiện liên hoàn biến đổi đồ thị y  f  x thành đồ thị y  f  x , sau đó biến đổi
đồ thị y  f  x thành đồ thị y  f  x  .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 58/102
Dựa vào đồ thị hàm số y  f  x  ta suy ra hàm số đồng biến trên khoảng 1;2 .
Câu 82: Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới
Hàm số g  x  f  3 x  đồng biến trên khoảng nào trong các khoảng sau? A.  ;    1 . B.  1  ;2. C. 2;3. D. 4;7. Lời giải Chọn B   x  x  
Dựa vào đồ thị, suy ra f  x 1 1  0  
và f  x 1  0  .  x  4 1   x  4  1   x  3 1
 Với x  3 khi đó g  x  f  x   3 
 gx  f x 3  0   x  3  4 2  x  4  
. Do đó hàm số g  x đồng biến trên các khoảng 3;4, 7;. x  7
 Với x  3 khi đó g  x  f 3 x 
gx   f 3 x  0  f 3 x  0 3 x  1 
x  4 loai    
. Do đó hàm số g  x đồng biến trên khoảng  1  ;2. 1   3 x  4  1   x  2
Câu 83: Cho hàm số bậc ba y  f  x , hàm số y  f  x có đồ thị như hình vẽ. Hỏi hàm số
g  x  f  x  
1 nghịch biến trên khoảng nào dưới đây?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 59/102 A. 1,  . B.  1  ,0 . C.  1  ,2 . D.   ,1  . Lời giải Chọn B x
Ta có: g x 
f  x   1 . x  x x  0 x  0  0 x   
Xét g x  0 
f  x   1  0 x    x 1  0     x  1  (L)  . x      f    x   1  0  x 1  2   x 1  x  0   x  1   .  x 1 Ta có bảng biến thiên:
Từ bảng biến thiên thì ta có g  x  f  x  
1 nghịch biến trên khoảng  1  ,  1 và đồng biến trên khoảng  ,    1  1,  .
Câu 84: Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số 4 3 2 y 3x 4x 12x
m nghịch biến trến khoảng ; 1 ? A. 4 . B. 6 . C. 3 . D. 5 . Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 60/102 Chọn D Xét hàm số 4 3 2 3 2 f x 3x 4x 12x m f x 12x 12x 24x x 1 1 f x 0 x 2 x 2 BBT: Để hàm số y
f x nghịch biến trên ; 1 m 5 0 m 5
Do yêu cầu m là số nguyên nhỏ hơn 10 nên ta có m 5;6;7;8;9
Vậy có 5 giá trị m thỏa yêu cầu.
Câu 85: Cho hàm số y  f  x . Đồ thị hàm số y  f  x như hình vẽ sau:
Hàm số g  x  f  4  2x  nghịch biến trên khoảng nào sau đây?  1 3   5   3 5  A. ;   . B.  ;  2  . C. ; 7   . D. ;   .  2 2   2   2 2  Lời giải Chọn A
Trường hợp 1: x  2 . Khi đó g  x  f 4  2x .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 61/102 x  3 4  2x  2 
Ta có g x  2
 f 4 2x, gx  0  f 4  2x  0     1 3 1   4  2x  3   x  2 2  1 3 
So điều kiện x  2 ta được g  x nghịch biến trên ;   .  2 2 
Trường hợp 2: x  2. Khi đó g  x  f 2x  4 .  5 1  x   2   2x  4 1  2
Ta có g x  2 f 2x  4 , g x  0  f 2x  4  0     2x  4  3 7 x   2  5   7 
So điều kiện x  2 ta được g  x nghịch biến trên 2; ; ;       .  2   2 
Câu 86: Cho hàm số y  f  x có đạo hàm f  x   x  2  2 1
x  2x , với x   . Số giá trị
nguyên của tham số m để hàm số g  x  f  3 2
x  3x  m có 8 điểm cực trị là A. 2 . B. 3 . C. 1. D. 4 . Lời giải Chọn C
Ta có g x   2
x  x f  3 2 3 6 .
x  3x  m . x  0 2
3x  6x  0   x  2  3 2     g x x 3x m 1 3 2  0  
 x  3x  m 1  . 3 2
x  3x  m  0  3 2 
x  3x  m  0 3 2
x 3x  m  2  3 2
x  3x  m  2
Vì khi đi qua các nghiệm của phương trình 3 2
x  3x  m  1 (nếu có) dấu của f  3 2
x  3x  m không đổi nên dấu của g x chỉ phụ thuộc các nghiệm của hai phương trình còn lại.
Vậy hàm số y  g  x có 8 điểm cực trị khi và chỉ khi mỗi phương trình 3 2
x  3x  m  0 và 3 2
x  3x  m  2 phải có ba nghiệm phân biệt (khác 0 và khác 2 ). x 
Xét hàm số h x 3 2
 x  3x , ta có hx 2  3
 x  6x ; hx 0  0   . x  2
Bảng biến thiên của hàm số y  h x
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 62/102 x  0 2  y  0  0   y 4
Dựa vào bảng biế n thiên, ta thấy điề 0 u kiện đ ể mỗi ph ương t rình 3 2  x  3 x  m và 3 2
x  3x  m  2 phải có ba nghiệm phân biệt (khác 0 và khác 2 ) là 
0  m  2  m  4  2  m  4 .
Vậy chỉ có một giá trị nguyên của m thỏa mãn là m  3 .
Câu 87: Cho hàm số y  f  x xác định trên R và hàm số y  f ' x có đồ thị như hình bên
dưới và f ' x  0 với mọi x  ;  3
 ,49; . Đặt g x  f x  mx 5. Có bao
nhiêu giá trị dương của tham số m để hàm số g  x có đúng hai điểm cực trị? A. 4. B. 7. C. 8. D. 9. Lời giải Chọn C
Ta có g x  f  x  m ; g x  0  f  x  m  0  f  x  m . Để hàm số y  g  x có
đúng hai điểm cực trị khi và chỉ khi phương trình g x  0 có hai nghiệm bội lẻ phân m  5 biệt  
. Khi đó m1, 2,3, 4,5,10,11,1 
2 . Vậy có 8 giá trị của m thỏa mãn yêu 1  0  m 13 cầu đề bài.
Câu 88: Cho hàm số đa thức bậc bốn y  f  x , biết hàm số có ba điểm cực trị x  3
 , x  3, x  5 . Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số     3 2 x 3x g x f e
 m có đúng 7 điểm cực trị A. 3 B. 4 C. 5 D. 6 Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 63/102 Chọn D 3 2 3 2
Ta có:     2 
 x 3x  x 3 3 6 . x g x x x e f e  m   x  0 x  0   x  2   x  2          3 2  x  x  3 2 2 3 x 3 3 2 3 2 0 3 6 . x g x x x e f e  m  0 x 3  x  e  m  3 x 3x    e  m  3   1  3 2  x 3x 3 2 e  m  3 x 3x  e  m  3 2 3 2  x 3  x e  m  5 3 2 x 3x e  m  5   3
Hàm số g  x có 7 điểm cực trị khi và chỉ khi tổng số nghiệm đơn và bội lẻ, khác 0 và 2
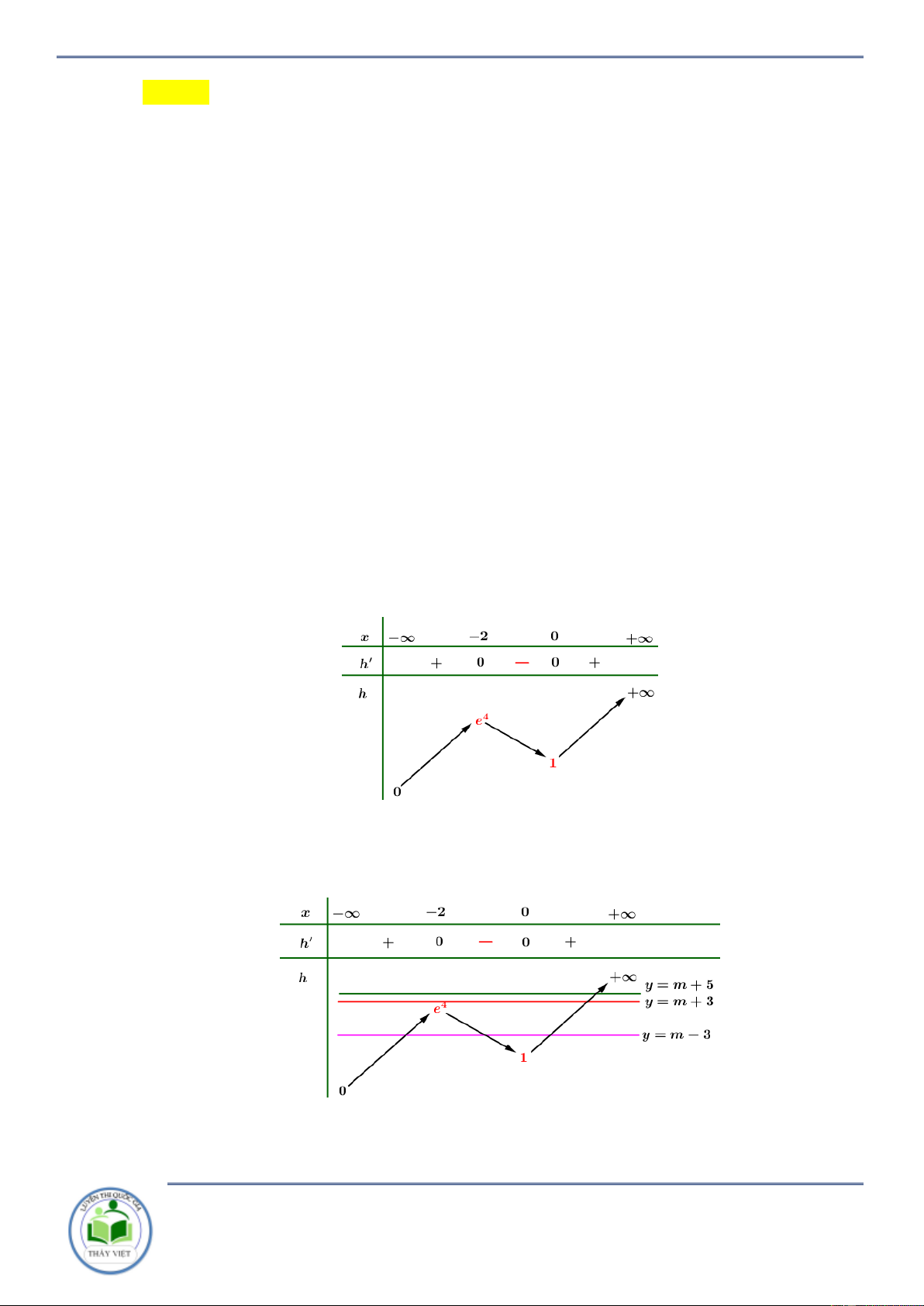
 của các phương trình   1 ,2,3 là 5 . Xét hàm số   3 2 3  x x h x e có     3 2 2 3 3 6     x x h x x x e .  x  Ta có  h  x 0  0   . x  2  Bảng biến thiên:
Khi đó có 3 trường hợp sau: Trường hợp 1: 4 4
m  3  e
m  e  3  51,6 Khi đó:    4 4
 1 m  3  e
 4  m  e  3  57,6
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 64/102
Do m nguyên nên m52;53;54;55;56;5  7 . Trường hợp 2: 4 4 m  5  e
m  e  5  49,6   Khi đó: 4 4 1
  m  3  e   2
  m  e  3  m .   0  m  3  1 3  m  4   Trường hợp 3: 4
 1 m  5  e 4  4
  m  e  5  49,6  
Khi đó: m  3  1  m  2   m .   m  3  0  m  3 
Vậy có 6 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 89: Cho hàm số y  f (x) có đạo hàm f   x   2 x  x 2 x  4x   3 , x
  . Tính tổng tất cả các
giá trị nguyên của tham số m để hàm số gx  f x2  m có 3 cực trị. A. 0. B. 6. C. 3. D. 2. Lời giải Chọn C x  0  Ta có f 
 x  xx   1 2 x   3  0  x 1 x  3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 65/102 x  0 x  0  2  x  0 x  m  0 2 x  m   2   1 Lại có g   x  2 . x f 
 x  m 0    f  2 x  m    2   0 x  m  1 2 x  1 m  2    2 x  m  3    2
x  3  m   3
Do 2 có nghiệm luôn là nghiệm bội chẵn; các phương trình  
1 , 3 có nghiệm không
chung nhau và  m  3 m nên: 3   m  0
Hàm số gx có 3 cực trị  g 
 x  0 có 3 nghiệm bội lẻ    0  m  3  m  0 Vì m  m  2 ; 1 ; 0
. Vậy tổng các giá trị nguyên bằng 3.
Câu 90: Cho hàm số y  f  x liên tục trên
và có đồ thị như hình vẽ.
Xét hàm số g  x  f  3 2x  x   1  .
m Tìm m để max g  x  1  0. 0; 1
A. m  3 . B. m  12  . C. m  13  . D. m  6 . Lời giải Chọn C
Đặt t  x 3
 2x  x 1 với x0; 
1 . Ta có t x 2
 6x 1 0, x  0;  1 .
Suy ra hàm số t  x đồng biến nên x 0;  1  t  1  ;2.
Từ đồ thị hàm số ta có max f t  3  max  f
 t  m  3 . m   1  ;2  1  ;2
Theo yêu cầu bài toán ta cần có: 3 m  1  0  m  1  3.
Câu 91: Cho hàm số f  x có đạo hàm trên
là f  x   x   1  x   3 . Có bao nhiêu giá trị
nguyên của tham số m thuộc đoạn  1
 0;20 để hàm số y  f  2
x  3x  m đồng biến trên khoảng 0; 2 ? A. 18 . B. 17 . C. 16 . D. 20 . Lời giải Chọn A
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 66/102
Ta có y  f  2
x  x  m   x   f  2 3 2 3
x  3x  m.
Theo đề bài ta có: f  x   x   1  x   3 x  
suy ra f  x 3  0  
và f  x  0  3   x 1. x 1
Hàm số đồng biến trên khoảng 0; 2 khi y  0, x  0;2
  x   f  2 2 3
x  3x  m  0, x  0;2.
Do x 0;2 nên 2x  3  0, x
 0;2 . Do đó, ta có:
x  x  m  
m  x  x  y  0, x
 0;2  f x 3x  m 2 2 3 3 3 3 2  0     2 2
x  3x  m 1
m  x  3x 1
m  max  2x 3x 3     0;2 m 13     . m  
 2x  x  m  1 min 3 1   0;2 Do m 1
 0;20 , m nên có 18 giá trị nguyên của m thỏa yêu cầu đề bài. 2 3
Câu 92: Cho các hàm số f  x 3
 x  4x  m và g x   2 x   2x    2 2018 2019
x  2020 . Có bao
nhiêu giá trị nguyên của tham số m 2  020;202 
0 để hàm số g  f  x đồng biến trên 2; ? A. 2005 . B. 2037 . C. 4016 . D. 4041. Lời giải Chọn B
Ta có f  x 3
 x  4x  m,
g  x  x  2018x  20192 x  20203 2 2 2 12 10 2
 a x  a x ... a x  a . 12 10 2 0
Suy ra f  x 2
 3x  4 , gx 11 9
12a x 10a x ... 2a x . 12 10 2 11 9  Và g
  f x  f x 1  2a f x 10a f x ... 2a f x  12     10    2    
 f x f x12a  f x10 10a  f x8 ...2a . 12 10 2 
Dễ thấy a ;a ;...; a ; a  0 và f  x 2
 3x  4  0 , x   2. 12 10 2 0
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 67/102 10 8
Do đó f  x12a f x 10a f x
... 2a  0 , x   2. 12    10    2  
Hàm số g  f  x đồng biến trên 2; khi g
  f x  0  , x
  2  f x  0 , x   2.  3
x  4x  m  0 , x   3  3
m  x  4x , x
  2  m  max 3
x  4x  1  6 . 2; Vì m 2  020;202 
0 và m nên có 2037 giá trị thỏa mãn m .
Câu 93: Cho hàm số y f x có đạo hàm 2 2 f x x x 1 x
2mx 1 với mọi x . Có bao
nhiêu số nguyên âm m để hàm số g x
f 2x 1 đồng biến trên khoảng 3;5 ? A. 3 B. 2 C. 4 D. 6 Lời giải Chọn A
Ta có: gx 2 2
 2 f '(2x 1)  2(2x 1)(2x  2) [(2x 1)  2 (
m 2x 1) 1]
Đặt t  2x 1
Để hàm số g x đồng biến trên khoảng 3;5 khi và chỉ khi g x 0, x 3;5 2 t 1 2 2 t(t 2mt 1) 0, t 7;11 t 2mt 1 0, t 7;11 2m , t 7;11 t 2 t  1 2 t  1
Xét hàm số h(t)  trên 7;1 
1 , có h '(t)  t 2 t BBT: 2 t 1 50
Dựa vào BBT ta có 2m , t 7;11 2m max h t m 7;11 t 14 Vì m    m{3; 2  ; 1  }.
Câu 94: Cho hàm số f  x xác định và liên tục trên R . Hàm số y  f  x liên tục trên và có đồ thị như hình vẽ.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 68/102 1
Xét hàm số g  x  f  x  2m  2m  x2  2020 , với m là tham số thực. Gọi S là tập 2
hợp các giá trị nguyên dương của m để hàm số y  g  x nghịch biến trên khoảng
3;4. Hỏi số phần tử của S bằng bao nhiêu? A. 4 . B. 2 . C. 3 . D. Vô số. Lời giải Chọn B
Ta có g ' x  f ' x  2m  2m  x .
Đặt h x  f ' x  x . Từ đồ thị hàm số y  f ' x và đồ thị hàm số y  x trên hình   x 
vẽ suy ra: h x   f  x 3 1 0 '  x   . x  3
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 69/102
  x  m 
 m   x  m 
Ta có g  x  h x  m 3 2 1 2 3 2 1 ' 2  0     .
x  2m  3
x  2m  3
Suy ra hàm số y  g  x nghịch biến trên các khoảng 2m  3;2m  
1 và 2m  3; . 2m  3  3 3   m  3 Do đó hàm số 
y  g  x nghịch biến trên khoảng 3; 4  2m 1 4  2  .    m  0 2m 3 3
Mặt khác, do m nguyên dương nên m2;  3  S  2; 
3 . Vậy số phần tử của S bằng 2. Từ đó Chọn B
Câu 95: Cho hàm số f  x liên tục trên và có đạo hàm f  x 2
 x x   2 2
x  6x  m với mọi x
. Có bao nhiêu số nguyên m thuộc đoạn  2  020;202  0 để hàm số g x f 1 x
nghịch biến trên khoảng  ;    1 ? A. 2016 . B. 2014 . C. 2012 . D. 2010 . Lời giải Chọn C 2 2
Ta có: g x  f 1 x  1 x x  
1 1 x  61 x  m   2 2 x 1 x 1 x 4x m 5
Hàm số g  x nghịch biến trên khoảng  ;    1
 gx  0, x   1
 * , (dấu " "xảy ra tại hữu hạn điểm). Với x  1  thì x  2 1
 0 và x 1 0 nên * 2 x 4x m 5 0, x 1 2 m x 4x 5, x 1. Xét hàm số 2 y x 4x 5 trên khoảng  ;   
1 , ta có bảng biến thiên:
Từ bảng biến thiên suy ra m  9 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 70/102
Kết hợp với m thuộc đoạn  2  020;202 
0 và m nguyên nên m9;10;11;...;202  0 .
Vậy có 2012 số nguyên m thỏa mãn đề bài.
Câu 96: Cho hàm số y  f (x) có đồ thị f (
 x) như hình vẽ. Có bao nhiêu giá trị nguyên  1  m  2  020;2020 2     
để hàm số g  x f 2x  3
ln 1 x  2mx đồng biến trên ; 2   ?  2  y 4 -2 -1 0 1 x A. 2020 . B. 2019 . C. 2021. D. 2018 . Lời giải Chọn B 2x
+ Ta có g x  2 f 2x  3   2m . 2 1 x  1  Hàm số g  x đồng biến trên ; 2   khi và chỉ khi  2    g x  x
    m  f  x   x 1 0, 1; 2 2 3  , x   ; 2   2 1 x  2   x 
 m  min f 2x 3     1 2   1     x ;2 1 x    2   1 
+ Đặt t  2x  3 , khi đó x  ; 2  t  2     ;1 .  2 
Từ đồ thị hàm f  x suy ra f t   0, t   2  ; 
1 và f t   0 khi t  1  .  
Tức là f  x   1 2 3  0, x   ; 2 
  min f 2x  3  0 khi x 1. 2  2   1  x ;2    2  x  1  2 x 1
+ Xét hàm số h x   trên khoảng ; 2 
 . Ta có h x  và 2 1 x  2  1 x 2 2 h x 2
 0  x 1 0  x  1  .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 71/102  1 
Bảng biến thiên của hàm số h  x trên ; 2   như sau:  2  1
Từ bảng biến thiên suy ra h x 1
   min hx   khi x 1. 3 2  1  x ;2 2    2  1 Từ  
1 , 2 và 3 suy ra m   . 2
Kết hợp với m , m 2
 020;2020 thì m 2  019; 2018;....; 2  ;  1 .
Vậy có tất cả 2019 giá trị m cần tìm.
Câu 97: Cho hàm số y  f  x liên tục trên và có đồ thị như hình vẽ.
Hàm số g  x  f  2 x  x 3 2
 4x  3x  6x  2020 đồng biến trên khoảng nào sau đây?  1  A. 1  ;   . B.  2  ;0 . C. 1; . D. 0  ;1 .  2  Lời giải Chọn D
Ta có g x   x   f  2 x  x 2 2 1
12x  6x  6 .
Từ đồ thị hàm số y  f  x suy ra f  x  0  1
  x  2 . Do đó          
f  x  x 2 2 x x 1 x x 1 0; x 2  0      2   x 1. 2 2
x  x  2
x  x  2  0
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 72/102
Ta có bảng xét dấu g x :  1 
Vậy hàm số g  x đồng biến trên khoảng  ;1   .  2 
Câu 98: Cho hàm số y  f  x xác định trên và có bảng xét dấu đạo hàm như sau:
Biết f  x  2, x
  . Xét hàm số g x  f   f x 3 2 3 2
 x  3x  2020 . Khẳng định nào sau đây đúng?
A. Hàm số g  x đồng biến trên khoảng  2  ;  1 .
B. Hàm số g  x nghịch biến trên khoảng 0  ;1 .
C. Hàm số g  x đồng biến trên khoảng 3;4 .
D. Hàm số g  x nghịch biến trên khoảng 2;3 . Lời giải Chọn D
Ta có: g  x   f  x f   f x 2 ' 2 ' ' 3 2 3x  6x .
Vì f  x  2, x
  nên 3 2 f x  1  x  
Từ bảng xét dấu f ' x suy ra f '3 2 f  x  0, x  
Từ đó ta có bảng xét dấu sau:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 73/102
Từ bảng xét dấu trên, loại trừ đáp án suy ra hàm số g  x nghịch biến trên khoảng 2;3.
Câu 99: Cho hàm số y  f (x) xác định trên
. Hàm số y  g(x)  f '2x  3  2 có đồ thị là một
parabol với tọa độ đỉnh I 2; 
1 và đi qua điểm A1; 2 . Hỏi hàm số y  f (x) nghịch
biến trên khoảng nào dưới đây? A. 5;9 . B. 1;2 . C.  ;9  . D. 1;3 . Lời giải Chọn A
Xét hàm số g(x)  f '2x  3  2 có đồ thị là một Parabol nên có phương trình dạng: 2
y  g(x)  ax  bx  c P  b    2  b   4a
4a  b  0
Vì  P có đỉnh I 2;  1 nên 2a     .            g   4a 2b c 1 4a 2b c 1 2  1  
P đi qua điểm A1;2 nên g 
1  2  a  b  c  2
4a  b  0 a  3  
Ta có hệ phương trình 4a  2b  c  1   b   1
 2 nên g x 2
 3x 12x 11.  
a  b  c  2 c  11  
Đồ thị của hàm y  g(x) là 8 6 4 2 15 10 5 5 10 15 2 4
Theo đồ thị ta thấy f '(2x  3)  0  f '(2x6  3)  2  2 1 x  3. t  3 t  3
Đặt t  2x  3  x 
khi đó f '(t)  0  8 1 
 3  5  t  9 . 2 2
Vậy y  f (x) nghịch biến trên khoảng 5;9 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 74/102
Câu 100: Cho hàm số y  f  x có đạo hàm cấp 3 liên tục trên và thỏa mãn 2
f  x f  x  x  x  2  x  3 . 1 4 với mọi x 
và g  x   f 
 x  2 f 
x.f  x . Hàm số
h  x  g  2
x  2x đồng biến trên khoảng nào dưới đây? A.   ;1  .
B. 2; . C. 0  ;1 . D. 1;2 . Lời giải Chọn D
Ta có g x  2 f   x f  x  2 f  x. f   x  2 f x. f x  2
 f x.f x; 2 3 
Khi đó h x   x   g 2
x  x    x   2 x  x 2
x  x    2 2 2 2 2 2 2 2 2 1
x  2x  4  x  0    h x x 1  0   x  2  x 1 2
Ta có bảng xét dấu của h x
Suy ra hàm số h x  g  2
x  2x đồng biến trên khoảng 1;2 .
Câu 101: Cho hàm số y  f (x) liên tục trên
. Biết rằng hàm số y  f '(x) có đồ thị như hình vẽ. Hàm số 2
y  f (x 5
 ) nghịch biến trên khoảng nào sau đây? A. ( 1  ;0) . B. (1; 2) . C. ( 1  ;1) . D. (0;1) Lời giải Chọn D + Đặt 2 2
g(x)  f (x  5)  f (u),u  x  5 + 2 2
g '(x)  (x  5) ' f '(u)  2xf '(x  5)
+ Hàm số y  g(x) nghịch biến khi g '(x)  0 và dấu bằng xảy ra tại hữu hạn điểm
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 75/102 x  0  (I ) 2
 f '(x  5)  0 2
 2xf '(x  5)  0   x  0  (II ) 2
 f '(x 5)  0
Giải (I): Từ đồ thị hàm số y  f '(x) ta có x  0    x   7 2 x  0 x  7    x   7 2
(I )  x  5  2  x  0       2   x  1  2 2  4   x  5  1  x 1  2   x  1  2  x  4 
Xét (II): Từ đồ thị y  f '(x) ta có x  0  2 2 x  5  4   x  1  1   x  1  (II )   2 
x  4  x  2 x  2 2 1
  x  5  2   
  7  x  2  2  x  7 2 
x  7   7  x  7 x  0   0  x  1  1   x  1  x  0    2  x  7
 7  x  2   2  x  7
Vậy hàm số đồng biến trên mỗi khoảng:  ;   7 ; 2  ;  1 ;0; 
1 ;2; 7  . Chọn D
Câu 102: Cho hàm số y
f (x) . Hàm số y
f '(x) có đồ thị như hình vẽ bên. y y f '(x) O 1 1 4 x Hàm số 2 y
f (x ) đồng biến trên khoảng 1 1 1 A. ; B. 0;2 C. ;0 D. 2; 1 2 2 2 Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 76/102 Xét hàm f '(x)
(x 1)(x 1)(x 4) . Đặt 2 g(x) f x x 0 Có 2 2 2 2 g '(x) 2xf '(x ) 2x(x 1)(x 1)(x
4) . Suy ra g '(x) 0 x 1 x 2
Xét dấu g '(x)
Câu 103: Cho hàm số y  f  x. Hàm số y  f  x có đồ thị như hình bên. y x -4 -3 -2 -1 1 2 3 4 5 6 7
Hàm số y  f 3 2x nghịch biến trên khoảng A.  1  ; B. 0; 2 C.  ;    1 D. 1;3 Lời giải Chọn C 1 5  2   3 2x  2  x  Ta có y  2
 . f 3 2x; y  0  f 3 2x  0     2 2 3 2x  5  x  1   1 5 
Vậy hàm số y  f 3 2x nghịch biến trên các khoảng  ;    1 và ; .    2 2 
Câu 104: Cho hàmsố y  f (x) có đạo hàm trên
. Đường cong trong hình vẽ dưới là đồ thị của
hàm số y  f '(x) . Xét hàm số 2
g(x)  f (3  x ) .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 77/102 y -1 O 3 x
Mệnh đề nào dưới đây là đúng?
A. Hàm số g(x) đồng biến trên ( ;  1) .
B. Hàm số g(x) đồng biến trên (0;3) .
C. Hàm số g(x) nghịch biến trên ( 1  ; )  .
D. Hàm số g(x) nghịch biến trên ( ;  2  ) và (0;2) . Lời giải Chọn D
Ta có g  x   xf  2 ' 2 ' 3  x    x   x  
f '3  x  2 3 1 2 2  0     2 3 x  3 x  0 Ta có bảng xét dấu: x ∞ 2 0 2 + ∞ x + + 0 f(3-x2) 0 + + 0 g'(x) + 0 0 0 +
Hàm số g(x) nghịch biến trên ( ;  2  ) và (0;2) .
Câu 105: Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ. Hàm số  2 x y f  e 
nghịch biến trên khoảng nào sau đây? f(x)=x^3-3x^2 f(x)=-4 x(t)=2 , y(t)=t y T ?p h?p 1 x - A. 0; . B.  ;  0. C.  1  ;3 . D.  2   ;1 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 78/102 Lời giải Phân tích
Dựa vào đồ thị hàm y  f  x , suy ra nghiệm f  x  0 và dấu của f  x .
Dùng tính chất hàm hợp xét dấu 2 x f
 e  , suy ra dấu của x. 2 x e f
 e  . Từ đó chọn đáp án. Chọn B x 
Ta có f  x 0  0   . x  3 2 x  e  0 Xét  2 x y f  e  , có x   . 2 x y e f
 e  ;   0 x  . 2 x y e f  e   0    x  0 . 2 x  e  3 Mặt khác,   0 x  . 2 x y e f
 e   0  2 x
 e  3  x  0 . Do đó hàm số  2 x y f
 e  nghịch biến trên  ;  0.
Câu 106: Cho hàm số f  x có đạo hàm liên tục trên
và có đồ thị của hàm y  f  x như
hình vẽ. Xét hàm số g x  f  2 ( )
x  2 . Mệnh đề nào dưới đây sai? y O 1 x 1  2 2  4 
A. Hàm số g(x) đồng biến trên 2;.
B. Hàm số g(x) nghịch biến trên 0;2.
C. Hàm số g(x) nghịch biến trên  1  ;0.
D. Hàm số g(x) nghịch biến trên  ;  2  . Lời giải Chọn C x  
Dựa vào đồ thị hàm số f  x 1  0  
và f  x  0  x  2 x  2
Xét g  x  f  2
x  2 có tập xác định
g ' x  2 .
x f t  với 2 t  x  2
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 79/102 x  0 x  0   g ' x 2
 0  t  x  2  1   x  1    2
t  x  2  2 x  2    x  2
Lại có f t  2
 0  t  x  2  2   x  2 
Do đó, ta có bảng xét dấu g ' x x  2  1  0 1 2  g x  0  0  0  0  0 
Từ bảng xét dấu ta chọn phát biểu sai là C
Câu 107: Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình bên. Hàm số y  f 2  x
đồng biến trên khoảng: A. 1;3 . B. 2; . C.  2   ;1 . D.  ;  2 . Lời giải Chọn C  Ta có:  
f 2  x  2  x . f 2  x   f 2  x    x   x 
Hàm số đồng biến khi  f   x   f   x 2 1 3 2 0 2  0     . 1   2  x  4  2   x 1
Câu 108: Cho hàm số y  f  x có đạo hàm là hàm số f  x trên . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x nghịch biến trên khoảng nào?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 80/102  3 5  A.  ;  2 . B.  1   ;1 . C. ;   . D. 2; .  2 2  Lời giải Chọn B
Hàm số y  f  x  2  2 có đồ thị C  như sau:
Dựa vào đồ thị C  ta có: f  x  2  2  2, x
 1;3  f x  2  0, x  1;3 . Đặt *
x  x  2 thì f x  *  0, * x  1  ;  1 .
Vậy: Hàm số f  x nghịch biến trên khoảng  1   ;1 . Cách khác:
Tịnh tiến sang trái hai đơn vị và xuống dưới 2 đơn vị thì từ đồ thị C  sẽ thành đồ thị
của hàm y  f  x . Khi đó: f  x  0, x   1  ;  1 .
Vậy: Hàm số f  x nghịch biến trên khoảng  1   ;1 .
Phân tích: Cho biết đồ thị của hàm số f  x sau khi đã tịnh tiến và dựa vào đó để xét
sự đồng biến của hàm số f  x .
Câu 109: Cho hàm số y  f  x có đạo hàm là hàm số f  x trên . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x đồng biến trên khoảng nào? A.  ;  3, 5; . B.  ;   
1 , 1;  . C.  1   ;1 . D. 3;5 . Lời giải
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 81/102 Chọn B
Hàm số y  f  x  2  2 có đồ thị C  như sau:
Dựa vào đồ thị C  ta có:
f  x  2  2  2, x   ;   1
3;  f x2  0, x   ;   1 3; . Đặt *
x  x  2 suy ra: f  x  *  0, * x  ;    1 1;.
Vậy: Hàm số f  x đồng biến trên khoảng  ;    1 , 1;  .
Câu 110: Cho hàm số y  f  x có đạo hàm là hàm số f  x trên . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x nghịch biến trên khoảng nào? A.  3  ;  1 , 1;3 . B.  1  ;  1 , 3;5 . C.  ;  2
 , 0;2. D.  5  ; 3  ,  1  ;  1 . Lời giải Chọn B
Hàm số y  f  x  2  2 có đồ thị C  như sau:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 82/102
Dựa vào đồ thị C  ta có:
f  x  2  2  2  , x   3  ;  1
1;3  f x  2  0, x   3  ;  1 1;3. Đặt *
x  x  2 suy ra: f  x  *  0, * x  1  ;  1 3;5 .
Vậy: Hàm số f  x đồng biến trên khoảng  1  ;  1 , 3;5 .
Câu 111: Cho hàm số f  x có đạo hàm cấp một là f  x  x x  
1  x  2 . Khi đó hàm số f 2x  
1 không đồng biến trên khoảng nào dưới đây?  1  A. 0  ;1 . B.  ;0   . C. 1;3 . D. 2; .  3  Lời giải Chọn A
Xét hàm số y  f 2x  
1 ta có y  2 f 2x   1  22x   1 .2 . x 2x  
1  4x 2x   1 2x   1 .  1   1 
Hàm số f 2x  
1 đồng biến  y  0  x   ;0  ;      .  2   2   1 
Do đó trên các khoảng  ;0 
 , 1;3 , 2; hàm số đồng biến. Trên khoảng 0  ;1  3 
hàm số vừa đồng biến vừa nghịch biến.
Câu 112: Cho hàm số f  x có đạo hàm xác định trên
. Biết rằng hàm số f  x và các hàm số
f ax  b , f  3
x  bx  2a đều đồng biến trên , với a là tham số thực khác 0 và b là
tham số thực. Kết luận đúng và đủ nhất về các tham số thực a,b là:
A. a  0; b  0 .
B. a  0; b  0 .
C. a  0; b  0 .
D. a  0; b  0 . Lời giải Chọn A
Có f  x  0, x   .   f
 ax  b  . a f  
ax b  0, x   
 f  3x bx  a   2
x  b f  3 2 3
x  bx  2a  0, x     a  0 a  0 Suy ra    . 2 3
 x  b  0, x   b   0
Câu 113: [2D1-4] Cho hàm số y  f  x có đồ thị hàm số y  f  x như hình vẽ. Hàm số
g  x  f  2
x  2x đồng biến trên khoảng nào?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 83/102  9  A. 1;2 . B. 3; . C. 3;   . D. 1; .  2  Lời giải Chọn A
Dựa vào đồ thị hàm số y  f  x , ta có bảng biến thiên sau x  0 2 
f  x  0  0  
f  x 
Ta có g  x  f  2
x  2x  gx   x   f  2 2 2 x  2x 2x  2  0   2  x  2  0   x   0    f    2
x  2x  0 x  2
ycbt  gx   0     2  x  2  0  2x  2  0   2 f  
x  x    2
x  2x  0 2 0  2
x  2x  2  x  1  x  1 x  0   x  0 x  2  x  0        x 2 .   x  1  1   x  2  x  1 0  x  2   0  x  2 2
x  2x  2  0 
luôn đúng 
Nhận xét: Chọn A thỏa mãn yêu cầu bài toán.
Câu 114: [2D1-4] Cho hàm số y  f  x có đạo hàm f  x  x x  2 x   1 , x  . Với tham số
thực m thuộc khoảng nào sau đây thì hàm số g  x f  3 
x  m đồng biến trên 1; .  1   1  A. 0;  . B. 1;4 . C. ;1   . D. 0  ;1 .  2   2  Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 84/102
Ta có g x 2  x f  3 x  m 2  x  3
x   m 3 x  m 3 3 . 3 . 1
x  m  2 .
Hàm số g  x đồng biến khi g x  0 2  x  3
x   m 3 x  m 3 3 1
x  m  2  0. 3 3 3
 x 1 m; m   2  m;    .
Hàm số đồng biến trên 1; khi 3 2  m 1  m 1 hay m1; .
Nhận xét: 1;4 thỏa mãn yêu cầu bài toán.
Câu 115: Cho hàm số y  f  x có đạo hàm liên tục trên
. Đồ thị hàm số y  f  x như hình
vẽ. Hàm số g  x  f 2x  
1 đồng biến trên khoảng nào? A.  2  ;3 . B. 1; . C. 0  ;1 . D.  3;   . Lời giải Chọn B
g x  2 f 2x   1 .
g x  0  2 f 2x  
1  0  2x 1  1  x  1.
Hàm số g  x  f 2x  
1 đồng biến trên khoảng 1;  .
Câu 116: Cho hàm số y  f  x có đạo hàm f  x 2
 x x  
1 m  x  
3 . Có bao nhiêu số nguyên
âm m để hàm số   2 y
f x  đồng biến trên khoảng 1; ? A. 4 . B. 5 . C. 2 . D. 3 . Lời giải Chọn.
y  xf  2 x  4  x x  2 x   2 2 2 . .
1 m  x  3 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 85/102 x  0
y  0  x  1  . 2
x  3m Hàm số   2 y
f x  đồng biến trên khoảng 1;  y  0, x  1; 5  x  2 x   2
m  x    x    2 2 . 1 3 0, 1;
 m  x 3  0, x  1; 2
 m  3  max x  không có giá trị m thỏa mãn x   1:
Câu này bị sai ko có đáp án mong th cô xem xét cẩn thận giúp
Câu này thầy giải chính xác rồi. Không có đáp án đúng.
Câu 117: Cho hàm số y  f  x có đạo hàm liên tục trên
. Đồ thị hàm số y  f  x có đồ thị x
như hình vẽ. Hỏi hàm số g  x  f   x 2 1 
 x nghịch biến trên khoảng nào sau đây? 2 y 3 3 1  1 2 3 3  O x 1  3   3  A.  3   ;1 . B.  2  ;0 . C. 1  ;   . D. 1;3 .  2  Lời giải Chọn B
Ta có g x   f 1 x  x 1.
Vậy g x  0  f 1 x  x 1.
Ta có đồ thị y  f 1 x màu xanh là ảnh của đồ thị C : y  f  x qua phép lấy đối
xứng qua Oy và tịnh tiến qua phải 1 đơn vị.
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 86/102
Đồ thị y  x 1 là đường thẳng màu đỏ đi qua hai điểm 4;3 ;  2  ; 3   và 0;  1  . y 3 1  2  2 O 2 4 x 1  3 
Hàm số g  x nghịch biến hay g x  0 .
Căn cứ vào đồ thị ta được đáp án là B.
Câu 118: Cho hai hàm số f  x và g  x có đồ thị các đạo hàm cho như hình vẽ với f  x (màu
hồng) và g x (màu xanh) có đồ thị như hình vẽ. Hỏi hàm số h x  f  x  
1  g 2x
đồng biến trên khoảng nào sau đây?  1   1   5  A.  1  ;0 . B. 0;   . C. 1  ;   . D. 2;   .  2   2   2  Lời giải Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 87/102
h x  f  x  
1  2g2x
Đồ thị hàm y  f  x  
1 là sự tịnh tiến sang phải 1 đơn vị của đồ thị hàm y  f  x .
Đồ thị hàm y  g2x sự co lại 2 đơn vị theo trục Ox của đồ thị hàm y  g x .
Đồ thị hàm y  2g2x sự lớn lên 2 đơn vị theo trục Oy của đồ thị hàm y  g2x .  1    3   Ta có h  f   2g       1  3  4  1   0 loại A.  2   2 
Loại ngay C, D vì hình vẽ. Ta Chọn B
Câu 119: Cho hàm số f  x có đồ thị như hình vẽ. Hàm số f 3x  2 nghịch biến trên khoảng
;  . Khi đó giá trị lớn nhất của   là: y f  x 4 O 1 x A. 9 . B. 3 . C. 6 . D. 1. Lời giải Chọn D
Ta có: y  f 3x  2  y  3. f 3x  2 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 88/102
Hàm số y  f 3x  2 nghịch biến  y  0  3. f 3x  2  0  f 3x  2  0 .
1 3x  2  4 1 x  2 .
Vậy khoảng ;   lớn nhất là 1;2 .
Câu 120: Cho hai hàm số f  x và g  x có đồ thị như hình vẽ. Biết rằng hai hàm số f 2x   1 và
g ax  b có cùng khoảng nghịch biến. Khi đó giá trị của biểu thức 4a  b bằng: y f  x O 1 2 3 x g  x A. 0 . B. 2  . C. 4  . D. 3 . Lời giải Chọn C
+) Hàm số y  f  x nghịch biến trên khoảng 1;3 .
Hàm số y  f 2x  
1 có y  2 f 2x   1
Với y  0  2. f 2x  
1  0  f 2x  
1  0 1  2x 1  3 1  x  2 .
Vậy hàm số y  f 2x  
1 nghịch biến trên khoảng 1; 2 .
+) Hàm số y  g ax  b có đạo hàm y  .
a gax  b .  b x      
  a gax  b ax b 0 a y .  0    
ax  b  2 2  b x   a b 2  b
+ Nếu a  0    . a a 
b   2  b 
Hàm số nghịch biến trên các khoảng  ;   ; ;      (không thỏa mãn).  a   a  b 2  b + Nếu a  0    . a a
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 89/102  2  b b 
Hàm số nghịch biến trên khoảng ;    .  a a  2  b 2 1  1      a  2 a a 
Do hàm số có cùng khoảng nghịch biến là 1;2 nên      . b b b     4   2  2   a a
Vậy 4a  b  4  .
Câu 121: Cho hai hàm số f  x và g  x có đồ thị biễu diễn đạo hàm f  x và g x như hình vẽ.
Biết rằng hàm số y  f  x  g  x  2 đồng biến trong khoảng ;   thỏa giá trị lớn
nhất của    8 ; phương trình tiếp tuyến với đồ thị hàm số y  g  x tại điểm có
hoành độ x  11 là y  3x  2 và phương trình tiếp tuyến với đồ thị hàm số y  f  x 1
tại điểm có hoành độ x  9 là y  ax 1. Giá trị của f 9 bằng 2 A. 13 B. 28 . C. 26  . D. 22 . Lời giải Chọn B
Đặt h x  f  x  g x  2.
Ta có h x  f  x  g x  2 . Cách 1
Theo hình vẽ ta có f  
1  g3 nên h  1  f  
1  g3  0 .
Do hàm số h  x đồng biến trong khoảng ;   và giá trị lớn nhất của biểu thức
  bằng 8 nên h9  0  f 9 g1 
1  0  a  3  0  a  3 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 90/102
Mặt khác điểm M 9;9a  
1 là tiếp điểm giữa tiếp tuyến y  ax 1 với đồ thị của hàm
f  x nên f 9  9a 1  27 1  28. Cách 2
h x  0  f  x  g x  2 *
Để hàm số h  x tồn tại khoảng đồng biến ;   thì phương trình * có hai nghiệm
phân biệt x   và x   .
Lại có đồ thị hàm số g x  2 có được bằng cách tịnh tiến đồ thị hàm số g x qua trái
2 đơn vị. Từ hình vẽ, ta suy ra phương trình * có hai nghiệm phân biệt là x  1 và  21  x   1      .  2 
Theo đề bài  1  8    9 , hay f 9  g9  2  a  3 .
Từ đó tiếp tuyến của đồ thị hàm số y  f  x tại điểm có hoành độ x  9 là y  3x 1
nên f 9 1 9a  28 .
Câu 122: Cho hàm số y  f  x có đạo hàm f  x xác định trên
và có bảng biến thiên như
hình vẽ. Khi đó hàm số f  2
x  2x nghịch biến trên khoảng nào dưới đây?  5  A. ;3   . B.  1  ;2 . C. 1;1 3 . D.  2;2 .  2  Lời giải Chọn C 2x  2  0   2   f 
 x  2x  0 Ta có:  f   2
x  x    x   f    2 2 0 2 2
x  2x  0   2x  2  0   f    2
x  2x  0
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 91/102 x 1 x 1   2 
 x  2x  1  Vn   x 1 3     x 1 3 2  
x  2x  2   x 1 3   .  1   x 1 3   x  1  x 1    2  1
  x  2x  2  1
  3  x 1 3
Do đó: hàm số f  2
x  2x nghịch biến trên các khoảng  ;
 1 3 và 1;1 3 .
Câu 123: (4) Cho hai hàm số f  x và g  x có một phần đồ thị biểu diễn đạo hàm f  x và
g x như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số a để hàm số
y  f  x  g  x 2
 a x  2019 tồn tại một khoảng đồng biến ;  ? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Đặt h x  f  x  g  x 2
 a x  2019          2 h x f x g x  a .
Xét h x  0       2 f x
g x  a * .
Trong đó đồ thị   2
g x  a có được bằng cách tịnh tiến đồ thị g x lên trên 2 a đơn vị.
Từ đồ thị, để tồn tại một khoảng đồng biến ;   thì phương trình * cần có hai
nghiệm phân biệt x   , x   . Do đó 2
0  a  11  0  a  11 (do a  0 )
Vì a nguyên dương nên a 1;2;  3 .
Câu 124: (4) Cho hàm số y  f  x có đồ thị đạo hàm f  x được cho như hình vẽ bên dưới.
Hàm số y  f  x   2 3
2  x  2x  2019 đồng biến trên khoảng nào dưới đây?
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 92/102  1   3 1  A.  ; 2   . B. 0  ;1 . C.  1  ;0 . D.  ;    .  2   2 2  Lời giải Chọn B
Đặt g  x  f  x   2 3
2  x  2x  2019  2 10
g x  3 f 3x  2  2x  2  3 f 3x  2  3x  2  . 3 3 2 10
g x  0  f 3x  2  3x  2  * . 9 9 2 10  1 
Xét đường thẳng  : y  x 
, dễ thấy  đi qua các điểm có tọa độ ; 1   và 5;0 9 9  2  1
hay phương trình f  x 2 10  x 
có hai nghiệm phân biệt là x  và x  5. 9 9 2  1  1 3x  2  x  
Từ đó phương trình *    2   2  . 3x  2  5 x 1
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 93/102 Bảng biến thiên:  1 
Vậy hàm số g  x đồng biến trên khoảng  ;1   nên Chọn B  2 
Câu 125: Cho hàm số y  f  x có đồ thị đạo hàm f  x được cho như hình vẽ bên dưới. Hàm
số y  f  x   3 3
1  x  3x  2020 đồng biến trên khoảng  ;
a b . Giá trị lớn nhất của b  a bằng A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 94/102
Ta có y  f  x     2 3 3 1
3x  3   f  x     2 3 3 1 x   1 1  .    t  t 1 t 2  2
Đặt t  3x  1 1  x   x 1 
1  y   f t  2 1 3  1 3 9  9    t  2 1
Vẽ đồ thị hàm số y 
1 trên cùng hệ trục tọa độ với đồ thị của hàm số f t . 9
Dựa vào đồ thị ta có: t  4  ; 
5 thì đồ thị hàm số f t  nằm trên đồ thị hàm số t  2 1  t   y 
1 nên y  0 hay y   f t  2 1 3 
1 đồng biến trên khoảng  4  ;5 , 9  9   
tức là hàm số y  f  x   3 3
1  x  3x  2020 đồng biến trên khoảng  1  ;2 do đó a  1
 ;b  2  b  a  3 .
Câu 126: Cho hàm số y  f  x có biểu thức đạo hàm là f  x  x x  
1  x  2 , với x   . Hỏi
hàm số y  f  2 x  
1  2x  2018 đồng biến trên khoảng nào sau đây? A. 2; . B.  1  ;2 . C.  1  ; . D.  ;    1 . Lời giải Chọn A
Ta có y  xf  2 2 x   1  2  x  2 x   2 x  2 2 . 1 . . x   1  2 .
Đặt h x  x  2 x   2 x  2 2 . 1 . . x   1  2 7 3
 2x  2x  2 x  0  h x 6 2
14x  6x , hx  0  3  . 4 x    7 Bảng biến thiên
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 95/102  3   3  Vì 4 h     0   , 4 h    0  
nên loại các Chọn B, C, D. 7   7  
Mặt khác h2  0 và h x  0 x
  2 do đó y  0 x
  2 , Chọn A thỏa mãn.
Câu 127: Cho hàm số y
f x có đạo hàm f x x x 2 x 1 g x 2018 , x và g x 0 với x . Hỏi hàm số h x f x 1
2018x đồng biến trên khoảng nào sau đây? A.  1  ;2 . B. 1;2 . C. 2; . D.  1  ; . Lời giải Chọn B Ta có: h x f x 1 2018x h x f x 1 2018 x 1 x
1 x 2 g x 1 Do g x 0 với x nên g x 1 0 với x . x 1 h x 0 x
1 nên ta có bảng biến thiên của hàm số h x như sau: x 2
Vậy hàm số h x đồng biến trên khoảng 1;2 . Chọn B 2
Câu 128: Cho hàm số y  f  x có đạo hàm f  x  x x    2 1
x  mx  9 , x   . Có bao nhiêu
số nguyên dương m để hàm số g  x  f 3 x đồng biến trên khoảng 3; . A. 5 . B. 6 . C. 7 . D. 8 . Lời giải Chọn B
Ta có g x   f 3 x .
Đặt t  3 x , ta thấy x  3 khi và chỉ khi t  0 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 96/102
Suy ra hàm số g  x  f 3 x đồng biến trên khoảng 3;  hàm số y  f  x
nghịch biến trên khoảng  ;  0.
Vì f  x  x x  2  2 1
x  mx  9 , mà  x  2 1  0, x
  nên f x  0, x   ;  0  2
x  mx  9  0, x  hoặc 2
x  mx  9  0 có hai nghiệm dương phân biệt. TH1: 2
x  mx  9  0, x  2
   m 36  0  m 6
 ;6, mà m nguyên dương nên m 1;2;3;4;5;  6 . 2 m  36  0  TH2: 2
x  mx  9  0 có hai nghiệm dương phân biệt  m  0  m  6  , mà m 9  0 
nguyên dương nên m .
Câu 129: Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hỏi hàm số g  x  f  x 1  đồng
biến trên khoảng nào sau đây? A.  ;    1 . B.  2  ;  1 . C.  1  ;0 . D. 0; 2 . Lời giải Chọn C
Từ đồ thị của hàm số y  f  x ta suy ra đồ thị của hàm số g  x  f  x 1  có hình dạng như sau:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 97/102
Dựa vào đồ thị ta Chọn C 2
Câu 130: Cho hàm số y  f  x có đạo hàm f  x  x x    4 3 1
3x  mx   1 , x   . Có bao nhiêu
giá trị nguyên âm của tham số m để hàm số     2 g x
f x  đồng biến trên khoảng 0;? A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B 2
Ta có g x  x f  2 x  3  x  2 x    8 6 2 . 2 1
3x  mx   1 .
Hàm số g  x đồng biến trên khoảng 0; khi g x  0, x  0;. 1 Hay 8 6
3x  mx 1  0, x  0; 2  m  3  x  , x   0; . 6   x 1
Xét hàm số h x 2  3  x 
, x  0;  ta có: 6   x 6 8 1 6  x 
h x  6  x  
, x  0;  , h x  0  x 1. 7 7   x x 1
Dựa vào bảng biến thiên ta được: 2 m  3  x  , x
  0;  m  4  . 6   x Vì m   nên m 4  ; 3  ; 2  ;  1 .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 98/102
Câu 131: Cho hàm số y  f  x có đồ thị hàm số y  f  x như hình vẽ bên. Hỏi hàm số   2 2  2f x g x
đồng biến trên khoảng nào sau đây? A.  ;  2 . B.  1  ;3 . C. 1;4 . D.  2  ;  1 . Lời giải Chọn C   Ta có   2 2    2 f x g x  f 2 x 2 
  2 f 2x  2   .2
.ln 2 . Hàm số g  x đồng biến khi  x   x 1
g x  0  f 2x  2  2 2 4 0     . 0  2x  2  2  1   x  0
Câu 132: Cho hàm số f  x có biểu thức đạo hàm là f  x  x x   1  x   1 . Khi đó hàm số
f sin x đồng biến trên khoảng nào dưới đây?  3   8  A. ; 2   . B.  ;  1  0. C. 2; 4 . D. ;3   .  2   5  Lời giải Chọn D
Xét hàm số y  f sin x  
Ta có: y   f  sin x  
sin x .f sin x  cos .xsin .xsin x   1 sin x   1 1   1 sin 2 . x  2 1 sin x 2   sin 2 . x cos x . 2 2  k x  sin 2x  0  2 Cho 2
y  0  sin 2 .
x cos x  0     k    cos x  0 
 x   k  2 k  x  k   . 2 Ta thấy:
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 99/102         8 8 x   ;3  ;   
  sin 2x  0  hàm số y  f sin x đồng biến trên ;3   .  5   2   5 
Câu 133: Cho hàm số f  x có biểu thức đạo hàm là f  x 2 '
 x  ax  2. Biết rằng hàm số    f  2
sin x nghịch biến trên khoảng ; 
. Hỏi có bao nhiêu giá trị nguyên của  2  a  2  019;201 
9 thỏa mãn bài toán? A. 2022 . B. 2023. C. 2021. D. 2020. Lời giải Chọn B    Đặt 2
u  sin x ; x  ;  u    0  ;1 .  2     Ta có u '  2sin .
x cos x  0, x   ; và f  2
' sin x  f ' u  u ' . f ' u . x x u   x    2       
Để hàm số y  f  2
' sin x nghịch biến trên khoảng ;   thì f  2
' sin x  0, x   ;   .  2   2    
 u ' . f ' u  x  
  f ' u  u   . u   0, 0;  1 x u   0, ;    2  2 2
 u  au  2  0, u  0;  1  a  u   , u  0 
;1  a  max g u  a  3  . u 0; 1 Kết hợp a  2  019;201  9 suy ra 3
  a  2019 . Vậy có 2023 số nguyên thỏa mãn ycbt. b
Câu 134: Cho hàm số f  x có biểu thức đạo hàm là f  x 2  x  x  . Biết rằng hàm số 200   5  f  2
cos x đồng biến trên khoảng ; 
 . Hòi có bao nhiêu giá trị nguyên  2 6  b  2  019;201  9 thỏa mãn bài toán? A. 1969. B. 1968. C. 1970 . D. 1971. Lời giải Chọn C Xét y  f  2 cos x .
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 100/102   5  Ta có: y  2  sin . x cos . x f  2
cos x  0, x   ;   với  2 6       x  ;
 cos x  0, sin x  0   .  2 6  b   5  3 Suy ra f  2 cos x 4 2
 0  cos x  cos x   0 x   ;   , đặt 2
t  cos x  0  t  . 200  2 6  4 b  3  b b 1 Suy ra 2
 t  t , t   0;      2
max t  t     b  50 . 200  4  200 200 4
Nên b 50,51,..., 201  9 có 1970 số nguyên.
Câu 135: Cho hàm số f  x đồng biến trên
. Khi đó hàm số y  f  x  f x đồng biến trên khoảng nào dưới đây? A.  ;  0. B.  1   ;1 . C. 0; . D. . Lời giải Chọn D
Ta có: hàm số f  x đồng biến trên
 f 'x  0, x  
 f 'x  0, x   .
 y '   f x f x'  f 'x f 'x  0, x   .
Vậy hàm số đồng biến trên .
Câu 136: Cho hàm số f  x có đạo hàm xác định trên
? Biết rằng hàm số y  f  x  f x
đồng biến trên khoảng 2;5 . Hỏi hàm số y  f  x  f x luôn đồng biến trên khoảng nào dưới đây? A. 1;4 . B.  ;  5   . C. . D.  4  ; 3   . Lời giải Chọn D
Ta có: hàm số y  f  x  f x đồng biến trên khoảng 2;5
 y '  f 'x  f 'x  0, x  2;5 .
Đặt g(x)  f 'x  f ' x
Ta thấy g(x) là hàm số chẵn trên R nên g(x)  f 'x  f ' x  0, x   5  ; 2   .  y'  0, x   5  ; 2  
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 101/102  y'  0, x   4  ; 3  
Hàm số luôn đồng biến trên  4  ; 3   . Chọn D
Câu 137: Cho hàm số f (x) liên tục và xác định trên R có đồ thị biểu diễn đạo hàm f '(x) như
hình vẽ. Khi đó hàm số y  f (x)  f (x) đồng biến trên khoảng nào dưới đây? A. 0; . B.  3  ;0 . C. 1;4 D.  5  ; 2   . Lời giải Chọn B
Ta có: y '  f '(x)  f '( ) x x  0 
y '  0  x  4  x  4  
Hàm số đồng biến trên  4  ;0. Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn
Chuyên đề: Tính đơn điệu của hàm hợp Trang 102/102 9x
Câu 138: Cho hàm số f (x) liên tục và xác định trên R , có biểu thức đạo hàm f '(x)  . Biết 9x  3 2  1 x   2  x   3 x   2018  x  a x
rằng hàm số y   f  f  f ...  f          luôn đồng  2019   2019   2019   2019  2019
biến trên R và a là tham số nguyên. Hỏi có tất cả bao nhiêu số chính phương a thỏa yêu cầu bài toán? A. 6 . B. 5 . C. 11. D. 63 . Lời giải Chọn B 1   1 x   2  x   3 x   2018  x   2 y '  f '  f '  f ' ...  f '  a  0, x   R           2019   2019   2019   2019   2019   1 9 a 9 3 f '(1 a)    1 9 a  3 9  3.9a 3  9a
f '(1 a)  f (a)  1 Do đó: 2 2
(*)  1009  a  0  a  1009  a  1009  31,765
Do a là số chính phương nên a 1;4;9;16;2  5 . Chọn B
Giáo viên: Nguyễn Hoàng Việt  0905193688
Website: http://luyenthitracnghiem.vn

138 bài toán chọn lọc tính đơn điệu của hàm hợp – Nguyễn Hoàng Việt Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số