150 Trắc nghiệm Nguyên Hàm Tích Phân Ứng Dụng Mức Thông Hiểu

150 trắc nghiệm nguyên hàm tích phân ứng dụng mức thông hiểu được biên soạn dưới dạng file PDF gồm 30 trang. Tài liệu gồm 3 dạng khác nhau: Nguyên hàm, Tích phân, Ứng dụng của tích phân. Mỗi dạng gồm 2 phần lý thuyết và trắc nghiệm từ cơ bản đến nâng cao khác nhau. Mời các em tham khảo thêm nhé!

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

30 trang 6 tháng trước

Tác giả:

Profile ha phan
Trang1
BÀI TẬP TRẮC NGHIỆM NGUYÊN HÀM TÍCH PHÂN MỨC NHẬN BIẾT THÔNG HIỂU
Định nghĩa:
f x dx F x C
'F x f x
Tính chất của nguyên hàm
Tính chất 1:
f x dx f x
và
'f x dx f x C
Tính chất 2:
kf x dx k f x dx

với
k
là hằng số khác
0
.
Tính chất 3:
Bảng nguyên hàm của một số hàm số sơ cấp
Nguyên hàm của hàm số sơ cấp
Nguyên hàm của hàm số hợp
u u x
dx x C
du u C
1
1
1
1
x dx x C

1
1
1
1
u du u C

1
lndx x C
x

1
lndu u C
u

xx
e dx e C
uu
e du e C
0, 1
ln
x
x
a
a dx C a a
a
0, 1
ln
u
u
a
a du C a a
a
sin cosxdx x C
sin cosudu u C
cos sinxdx x C
cos sinudu u C
2
1
tan
cos
dx x C
x

2
1
tan
cos
du u C
u

2
1
cot
sin
dx x C
x
2
1
cot
sin
du u C
u
Phương pháp đổi biến số:
'f u x u x dx F u x C
Hệ quả: Nếu
0u ax b a
thì ta có
1
f ax b dx F ax b C
a
Phương pháp nguyên hàm từng phần:
udv uv vdu

Một số cách đặt thường gặp:
Dạng
sin
cos . d
e,
xx
x
I x P x x
a





. Đặt
u P x
,
sin
d cos d
e,
xx
x
v x x
a





, với
Px
là đa thức.
Dạng
ln
.d
log
a
x
I P x x
x



. Đặt
ln
d
log
a
x
ux
x



;
ddv P x x
, với
Px
là đa thức.
DẠNG 1: NGUYÊN HÀM
Trang2
Câu 1. Nguyên hàm của hàm số
3
32f x x x
là hàm số nào trong
các hàm số sau?
A.
42
2
42
xx
F x x C
. B.
4
2
32
3
x
F x x x C
.
C..
42
3
2
42
xx
F x x C
D.
2
33F x x x C
.
Câu 2. Hàm số
32
5 4 7 120F x x x x C
là họ nguyên hàm của
hàm số nào sau đây?
A.
2
5 4 7f x x x
. B.
2
5 4 7f x x x
.
C.
2 3 2
5 4 7
4 3 2
x x x
fx
. D.
2
15 8 7f x x x
.
Câu 3. Họ nguyên hàm của hàm số:
2
1
3y x x
x
là
A.
3
2
3
ln
32
x
F x x x C
. B.
3
2
3
ln
32
x
F x x x C
.
C.
3
2
3
ln
32
x
F x x x C
.D.
2
1
23 F x x C
x
.
Câu 4. Tìm nguyên hàm của hàm số
12f x x x
A.
3
2
3
2
32
x
F x x x C
. B.
3
2
2
2
33
x
F x x x C
.
C.
23 F x x C
. D.
3
2
2
2
33
x
F x x x C
.
Câu 5. Nguyên hàm
Fx
của hàm số
2
2 2 3
52
fx
xxx
là hàm số
nào?
A.
3
ln 5 2 2lnF x x x C
x
.
B.
3
ln 5 2 2lnF x x x C
x
.
C.
3
ln 5 2 2lnF x x x C
x
.
D.
3
ln 5 2 2lnF x x x C
x
.
Câu 6. Tìm nguyên hàm của hàm số
( ) sin2f x x
A.
sin2 cos2xdx x C
. B.
1
sin 2 cos2
2
xdx x C
.
C.
1
sin 2 cos2
2
xdx x C
. D.
sin2 cos2xdx x C
.
Câu 7. Tìm nguyên hàm của hàm số
( ) cos 3
6
f x x




.
A.
1
( ) sin 3
36
f x dx x C



. B.
( ). sin 3
6
f x dx x C



.
CÂU HỎI TRẮC NGHIỆM
Trang3
C.
1
( ) sin 3
36
f x dx x C



. D.
1
( ) sin 3
66
f x dx x C



.
Câu 8. Tìm nguyên hàm của hàm số
2
( ) 2 .3
xx
fx
.
A.
21
.
9 ln2 ln9
x
f x dx C




.B.
91
.
2 ln2 ln9
x
f x dx C




.
C.
21
.
3 ln2 ln9
x
f x dx C




. D.
21
.
9 ln2 ln9
x
f x dx C




.
Câu 9. Tìm nguyên hàm của hàm số
()
xx
f x e e

.
A.
xx
f x dx e e C
.B.
xx
f x dx e e C
.
C.
xx
f x dx e e C
.D.
xx
f x dx e e C
.
Câu 10. Họ nguyên hàm của hàm số
( ) (3 )
xx
f x e e

là
A.
1
( ) 3
x
x
F x e C
e
. B.
( ) 3 ln
x x x
F x e e e C
.
C.
( ) 3
x
F x e x C
. D.
( ) 3
x
F x e x C
.
Câu 11. Nguyên hàm của hàm số
1
()
21
fx
x
là
A.
2 2 1f x dx x C
. B.
2 2 1f x dx x C
.
C.
21
2
x
f x dx C

. D.
21f x dx x C
.
Câu 12. Tìm nguyên hàm của hàm số
1
()
3
fx
x
.
A.
33f x dx x C
. B.
3f x dx x C
.
C.
23f x dx x C
. D.
23f x dx x C
.
Câu 13. Tìm nguyên hàm của hàm số
3
( ) 2f x x
.
A.
3
3
22
4
f x dx x x C
.B.
3
3
22
4
f x dx x x C
.
C.
2
22
3
f x dx x x
. D.
2
3
1
2
3
f x dx x C
.
Câu 14. Biết một nguyên hàm của hàm số
1
1
13
fx
x

là hàm số
Fx
thỏa mãn
2
1
3
F 
. Khi đó
Fx
là hàm số nào sau đây?
A.
2
1 3 3
3
F x x x
B.
2
1 3 3
3
F x x x
C.
2
1 3 1
3
F x x x
D.
2
4 1 3
3
F x x
Trang4
Câu 15. Nếu
Fx
là một nguyên hàm của hàm số
1
()
1
fx
x
và
21F
thì
3F
bằng
A.
ln2 1
. B.
3
ln
2
. C.
ln2
. D.
1
2
.
Câu 16. Nguyên hàm
Fx
của hàm số
2
1
2
sin
f x x
x

thỏa mãn
1
4
F




là
A.
2
2
cot
16
xx
. B.
2
2
cot
16
xx
.
C.
2
cot xx
. D.
2
2
cot
16
xx
.
Câu 17. Một nguyên hàm
()Fx
của hàm số
2
( ) ( )
xx
f x e e

thỏa mãn
điều kiện
(0) 1F
là
A.
22
11
( ) 2 1
22
xx
F x e e x
. B.
22
( ) 2 2 2 1
xx
F x e e x
.
C.
22
11
( ) 2
22
xx
F x e e x
. D.
22
11
( ) 2 1
22
xx
F x e e x
.
Câu 18. Một nguyên hàm
()Fx
của hàm số
( ) cos2f x a b x
thỏa mãn
(0)
2
F
,
26
F




,
12 3
F




là
A.
27
( ) sin 2
3 9 2
F x x x

. B.
27
( ) sin 2
39
F x x x
.
C.
27
( ) sin 2
3 9 2
F x x x

. D.
27
( ) sin 2
3 9 2
F x x x

.
Câu 19. Cho hàm số
32
( ) 1F x ax bx cx
là một nguyên hàm của hàm
số
()fx
thỏa mãn
(1) 2,f
(2) 3, (3) 4ff
. Hàm số
()Fx
là
A.
2
1
( ) 1
2
F x x x
. B.
2
1
( ) 1
2
F x x x
.
C.
2
1
( ) 1
2
F x x x
. D.
2
1
( ) 1
2
F x x x
.
Câu 20. Một nguyên hàm
()Fx
của hàm số
3
( ) 2sin5
5
f x x x
thỏa
mãn đồ thị của hai hàm số
()Fx
và
()fx
cắt nhau tại một điểm
nằm trên trục tung là
A.
2 2 3
( ) cos5 1
5 3 5
F x x x x x
.
B.
2 2 3
( ) cos5 1
5 3 5
F x x x x x
.
C.
13
( ) 10cos5 1
5
2
F x x x
x
.
D.
2 2 3
( ) cos5
5 3 5
F x x x x x
.
Câu 21. Hàm số
2
( ) ( )
x
F x ax bx c e
là một nguyên hàm của hàm số
Trang5
2
()
x
f x x e
thì
abc
bằng:
A.
1
. B.
2
. C.
3
. D.
2
.
Câu 22. Cho
fx
,
gx
là các hàm số xác định và liên tục trên
. Trong
các mệnh đề sau, mệnh đề nào sai?
A.
d d . df x g x x f x x g x x
.
B.
2 d 2 df x x f x x

.
C.
d d df x g x x f x x g x x


.
D.
dddf x g x x f x x g x x


.
Câu 23. Nếu
1
ld n xC
x
f x x
thì
fx
là
A.
lnf xCx x
. B.
1
lnx x C
x
fx
.
C.
2
1
lnf C
x
x x
. D.
2
1
fx
x
x
.
Câu 24. Tìm họ nguyên hàm của hàm số
2
1
1

xx
fx
x
.
A.
1
1

xC
x
. B.
2
1
1
1

C
x
.
C.
2
ln 1
2
x
xC
. D.
2
ln 1 x x C
.
Câu 25. Biết
Fx
là một nguyên hàm của hàm số
1
1
fx
x
và
21F
. Tính
3F
.
A.
3 ln2 1F 
. B.
3 ln2 1F 
.
C.
1
3
2
F
. D.
7
3
4
F
.
Câu 26. Cho hàm số
fx
thỏa mãn đồng thời các điều kiện
sinf x x x

và
01f
. Tìm
fx
.
A.
2
cos 2
2
x
f x x
. B.
2
cos 2
2
x
f x x
.
C.
2
cos
2
x
f x x
. D.
2
1
cos
22
x
f x x
.
Câu 27. Họ nguyên hàm của hàm số
3
1f x x
là
A.
4
1
1
4
xC
. B.
3
1
1
4
xC
.
C.
31xC
. D.
4
41xC
.
Câu 28. Tính
( ) sinF x x xdx
bằng
A.
( ) sin cosF x x x x C
. B.
( ) sin cosF x x x x C
.
Trang6
C.
( ) sin cosF x x x x C
. D.
( ) sin cosF x x x x C
.
Câu 29. Tính
( ) sin cosF x x x xdx
. Chọn kết quả đúng:
A.
1
( ) sin 2 cos2
84
x
F x x x C
. B.
1
( ) cos2 sin 2
42
x
F x x x C
.
C.
1
( ) sin 2 cos2
48
x
F x x x C
. D.
1
( ) sin 2 cos2
48
x
F x x x C
.
Câu 30. Tìm nguyên hàm của hàm số
2
( ) cos .sinf x x x
.
A.
2
sin
()
2
x
f x dx C
. B.
3
cos
()
3
x
f x dx C
.
C.
2
sin
()
2
x
f x dx C
. D.
3
cos
()
3
x
f x dx C
.
Câu 31. Tìm nguyên hàm của hàm số
sin 2
()
cos2 1
x
fx
x
.
A.
( ) ln sinf x dx x C
. B.
( ) ln cos2 1f x dx x C
.
C.
( ) ln sin2f x dx x C
. D.
( ) ln sinf x dx x C
.
Câu 32. Tính
.2
x
x dx
bằng:
A.
2
.2 2
ln2 ln 2
xx
x
C
. B.
21
ln2
x
x
C
.
C.
2 ( 1)
x
xC
. D.
2 ( 1)
x
xC
.
Câu 33. Tính
2 ln( 1)x x dx
bằng:
A.
2
2
( 1)ln( 1)
2
x
x x x C
. B.
2
2
ln( 1)
2
x
x x x C
.
C.
2
2
( 1)ln( 1)
2
x
x x x C
. D.
2
2
( 1)ln( 1)
2
x
x x x C
.
Câu 34. Họ nguyên hàm của
5
23
1f x x x
là
A.
6
3
1
1
18
F x x C
. B.
6
3
18 1F x x C
.
C.
6
3
1F x x C
. D.
6
3
1
1
9
F x x C
.
Câu 35. Họ nguyên hàm của hàm số
23
3
1x x x
fx
x
là hàm số nào?
A.
2
11
ln
2
F x x x C
xx
.
B.
2
11
ln
2
F x x x C
xx
.
C.
32
3
ln
32
xx
F x x C
.
D.
32
3
ln
32
xx
F x x C
.
Câu 36. Xét tích phân
2dI x x x
. Nếu đặt
2tx
thì ta được
Trang7
A.
42
2dI t t t
. B.
42
2 4 dI t t t
.
C.
42
2dI t t t
. D.
42
4 2 dI t t t
.
Câu 37. Cho
1
x
x
e
I dx
e
, khi đặt
1
x
te
ta có:
A.
2
2I t dt
. B.
2I dt
. C.
2
dt
I
. D.
2
I t dt
.
Câu 38. Tìm họ nguyên hàm của hàm số
1
()
( 1)
fx
xx
A.
( ) ln ( 1)f x dx x x C
. B.
( ) ln
1
x
f x dx C
x

.
C.
1
( ) ln
x
f x dx C
x

.D.
( ) ln
1
x
f x dx C
x

Câu 39. Cho hàm số
sin2f x x x
. Trong các khẳng định sau, khẳng
định nào đúng?
A.
1
d 2 cos2 sin 2
4
f x x x x x C
.
B.
1
d 2 cos2 sin 2
4
f x x x x x C
.
C.
1
d 2 cos2 sin 2
4
f x x x x x C
.
D.
1
d 2 cos2 sin 2
4
f x x x x x C
.
Câu 40. Trong các khẳng định sau, khẳng định nào sai?
A.
x
2e d 2 e
x
xC
. B.
1
d lnx x C
x

.
C.
4
3
d
4
xC
xx
. D. .
Câu 41. Biết
Fx
là nguyên hàm của
1
1
fx
x
và
21F
. Tính
3F
.
A.
ln2 1
. B.
ln2
. C.
3
ln
2
. D.
1
2
.
Câu 42.
()Fx
là một nguyên hàm của hàm số
e2
x
f x x
thỏa
mãn
02F
. Tìm
()Fx
.
A.
2
e3
x
F x x
. B.
2
2e 1
x
F x x
.
C.
2
e2
x
F x x
. D.
2
e1
x
F x x
Câu 43. Cho biết
Fx
là một nguyên hàm của hàm số
fx
. Tìm
2 1 dI f x x


.
sin d cosx x C x
Trang8
A.
21I F x C
. B.
21I xF x C
.
C.
2I xF x x C
. D.
2I F x x C
.
Câu 44. Tính
1
d
ln
Ix
xx
bằng cách đặt
lntx
. Mệnh đề nào dưới
đây đúng?
A.
dIt
. B.
2
1
dIt
t
.
C.
dI t t
. D.
1
dIt
t
.
Câu 45. Tìm nguyên hàm của hàm số
.e
x
yx
.
A.
e d .e
xx
x x x C
. B.
e d .e e
x x x
x x x C
.
C.
e d e
xx
x x C
. D.
e d .e e
x x x
x x x C
.
Câu 46. Tính nguyên hàm của hàm số
5
2018e
e 2017
x
x
fx
x




.
A.
4
2018
d 2017e
x
f x x C
x
.
B.
4
504,5
d 2017e
x
f x x C
x
.
C.
4
504,5
d 2017e
x
f x x C
x
.
D.
4
2018
d 2017e
x
f x x C
x
.
Câu 47. Nguyên hàm
Fx
của
x
f x xe
thỏa mãn
01F
là:
A.
11
x
F x x e
. B.
12
x
F x x e
.
C.
11
x
F x x e
. D.
1
x
F x x e

.
Câu 48. Tính
( ) sin2F x x xdx
. Chọn kết quả đúng?
A.
1
( ) (2 cos2 sin 2 )
4
F x x x x C
.
B.
1
( ) (2 cos2 sin 2 )
4
F x x x x C
.
C.
1
( ) (2 cos2 sin 2 )
4
F x x x x C
.
D.
1
( ) (2 cos2 sin 2 )
4
F x x x x C
.
Câu 49. Họ nguyên hàm của hàm số
2018
3f x x x
là
A.
2019
673
x
xC
B.
2019
3
2
2019
x
xC
Trang9
C.
2019
1
673
x
C
x

D.
2017
1
6054
2
xC
x

Câu 50. Cho hai hàm số
fx
,
gx
là hàm số liên tục, có
Fx
,
Gx
lần lượt là nguyên hàm của
fx
,
gx
. Xét các
mệnh đề sau:
I
.
F x G x
là một nguyên hàm của
f x g x
.
II
.
.k F x
là một nguyên hàm của
.k f x
với
k
.
III
.
.F x G x
là một nguyên hàm của
.f x g x
.
Các mệnh đề đúng là
A.
II
và
III
. B. Cả
3
mệnh đề.
C.
I
và
III
. D.
I
và
II
.
DẠNG 2: TÍCH PHÂN
Trang10
Định nghĩa:
d
b
b
a
a
f x x F x F b F a
Tên gọi:
d
b
a
f x x
đọc là: “Tích phân từ
a
đến
b
của
df x x
”
a
và
b
gọi là hai cận tích phân, trong đó
a
là cận dưới,
b
là cận trên.
Tính chất:
(1)
0
a
a
fx
(2)
dd
ab
ba
f x x f x x

(3)
dd
bb
aa
kf x x k f x x k

(4)
d d d
c b c
a a b
f x x f x x f x x
(5)
d d d
b b b
a a a
f x g x x f x x g x x


(6)
0fx
trên
d; 0
b
a
a f x xb 
(7)
f x g x
trên
d; d
bb
aa
fxa x x g xb 

(8)
m f x M
trên
; – d
a
b
fxa b m b a x M b a
(9)
t
biến thiên trên
d;
t
a
a b G t f x x
là một nguyên hàm của
ft
và
0Ga
.
Phương pháp đổi biến số:
Phương pháp đổi biến dạng 1: Tính
d
b
a
I g x x
Bước 1: Phân tích
d . d dg x x f u x u x x f u x u x

Đặt
t u x
Bước 2: Đổi cận Với
xa
thì
t u a
Với
xb
thì
t u b
Bước 3: Khi đó
dd
ub
b
ub
ua
a u a
I g x x f t t F t F u b F u a

.
Phương pháp đổi biến dạng 2:
d
b
a
I f x x
(với
fx
liên tục trên
;ab
)
Bước 1: Chọn
xt
, trong đó
t
là hàm số được lựa chọn một cách thích hợp.
Bước 2: Lấy vi phân
ddx t t
, giả sử
t
liên tục.
Bước 3: Ta chọn một trong hai hướng:
Hướng 1: Nếu tínhđược các cận
và
tương ứng theo
a
và
b
(
a

và
b

) thì ta được
.dI f t t t



Phương pháp nguyên hàm từng phần:
bb
b
a
aa
udv uv vdu

Trang11
Câu 1. Cho
2
0
d3I f x x
. Khi đó
2
0
4 3 dJ f x x


bằng:
A.
2
. B.
6
. C.
8
. D.
4
.
Câu 2. Biết
2 1 d 1
b
a
xx
. Khẳng định nào sau đây là đúng?
A.
1ba
. B.
22
1a b a b
.
C.
22
1b a b a
. D.
1ab
.
Câu 3. Cho hàm số
fx
liên tục trên đoạn
0;10
và
10
0
d7f x x
và
6
2
d3f x x
. Tính
2 10
06
ddP f x x f x x

.
A.
7P
. B.
4P 
. C.
4P
. D.
10P
.
Câu 4. Nếu
2
1
d3f x x
,
5
2
d1f x x 
thì
5
1
df x x
bằng
A.
2
. B.
2
. C.
3
. D.
4
.
Câu 5. Cho hàm số
fx
liên tục trên
và
Fx
là nguyên hàm
của
fx
, biết
9
0
d9f x x
và
03F
. Tính
9F
.
A.
96F 
. B.
96F
.
C.
9 12F
. D.
9 12F 
.
Câu 6. Cho hàm số
fx
có
fx
liên tục trên đoạn
1;3
,
13f 
và
3
1
( )d 10f x x
giá trị của
3f
bằng
A.
13
. B.
7
. C.
13
. D.
7
.
Câu 7. Cho
1
0
d2f x x
,
2
1
d4f x x
, khi đó
2
0
df x x
?
A.
6
. B.
2
. C.
1
. D.
3
.
Câu 8. Cho
2
1
d2f x x
và
2
1
d1g x x

. Tính
2
1
2 3 dI x f x g x x


bằng
A.
11
2
I
. B.
7
2
I
. C.
17
2
I
. D.
5
2
I
.
Câu 9. Biết
8
1
d2f x x 
;
4
1
d3f x x
;
4
1
d7g x x
. Mệnh đề
nào sau đây sai?
CÂU HỎI TRẮC NGHIỆM
Trang12
A.
8
4
d1f x x
. B.
4
1
d 10f x g x x


.
C.
8
4
d5f x x 
. D.
4
1
4 2 d 2f x g x x


.
Câu 10. Biết
8
1
d2f x x 
;
4
1
d3f x x
;
4
1
d7g x x
. Mệnh đề
nào sau đây sai?
A.
8
4
d1f x x
. B.
4
1
d 10f x g x x


.
C.
8
4
d5f x x 
. D.
4
1
4 2 d 2f x g x x


.
Câu 11. Cho hàm số
fx
liên tục trên
và có
1
0
d2f x x
;
3
1
d6f x x
. Tính
3
0
dI f x x
.
A.
8I
. B.
12I
. C.
36I
. D.
4I
.
Câu 12. Cho hàm số
fx
liên tục trên
và có
1
0
d2f x x
;
3
1
d6f x x
. Tính
3
0
dI f x x
.
A.
8I
. B.
12I
. C.
36I
. D.
4I
.
Câu 13. Cho hàm số
fx
liên tục trên
0;1
và
1 0 2ff
.
Tính tích phân
1
0
df x x
.
A.
1I 
. B.
1I
. C.
2I
. D.
0I
.
Câu 14. Giá trị nào của
b
để
1
2 6 d 0
b
xx
?
A.
0b
hoặc
3b
. B.
0b
hoặc
1b
C.
5b
hoặc
0b
. D.
1b
hoặc
5b
.
Câu 15. Cho
2
0
d3f x x
. Tính
2
0
1df x x
?
A.
4
. B.
5
. C.
7
. D.
1
.
Câu 16. Kết quả của tích phân
2
0
2 1 sin dx x x

được viết ở dạng
1
1
ab




a
,
b
. Khẳng định nào sau đây là sai?
A.
28ab
.B.
5ab
. C.
2 3 2ab
. D.
2ab
.
Trang13
Câu 17. Cho
x
26
0
f x d k
. Tính

x
3
23
1
2 . 1I x f x d
theo
k
?
A.
3
k
I
. B.
2Ik
.C.
6Ik
. D.
2
3
k
I
.
Câu 18. Cho
0
3
m
x
K dx
. Định
m
để
10
ln 3
K
?
A.
3
log 10m
.B.
2m
.C.
11m
. D.
3
log 11m
.
Câu 19. Cho

2
1
(3 2)M f x dx
. Đặt
32tx
ta có:
A.
7
1
1
()
3
M f t dt
. B.
3
1
3 ( )M f t dt
.
C.
7
1
3 ( )M f t dt
. D.
3
1
1
()
3
M f t dt
.
Câu 20. Cho


5 12
22
( ) 7; 3 ( ) 57f x dx f x dx
. Tính
12
5
()K f x dx
.
A.
50
B.
50
3
. C.
12
. D.
64
3
.
Câu 21. Biết
2
2
2
1
d ln5
9
xa
x
b
x

với
,ab
và
a
b
là phân số tối giản.
Khi đó
ab
?
A.
4
. B.
8
. C.
10
. D.
7
.
Câu 22. Cho
1
2
5f x dx
,
1
2
4g x dx

.
Thì
1
2
32I f x g x dx


A.
23
. B.
2
. C.
7
. D.
13
.
Câu 23. Tính
3
2
23
4
x
I dx
x
ta được
ln6I a b
với
,ab
.
Lúc đó
ab
A.
15
. B.
10
. C.
7
. D.
17
.
Câu 24. Cho hàm số
2 2 khi 1
ln
khi 1
xx
fx
x
x
x

. Biết tích phân
2
2
0
1
d ln 2f x x a
b

trong đó
,ab
. Tính giá trị
S a b
.
A.
3S
. B.
5S
. C.
3S 
. D.
1S
.
Câu 25. Biết
22
00
d 6, 3 d 10f x x x f x g x x

.
Trang14
Tính
2
0
2 3 d .I f x g x x
A.
12I
. B.
16I
. C.
10I
. D.
14.I
Câu 26. Cho hàm số
fx
có đạo hàm liên tục trên
và thỏa mãn
2 16f
,
1
0
2 d 6f x x
.Tính
2
0
.dI x f x x
ta được kết quả
A.
14.I
. B.
20.I
C.
10.I
D.
4.I
Câu 27. Tính tích phân
2
2
1
21I x x dx
, băng ca
ch đă
t
2
1tx
.
Mê
nh đê na
o dươ
i đây đu
ng?
A.
2
1
I t dt
. B.
2
1
1
2
I t dt
.
C.
3
0
2I t dt
. D.
3
0
I t dt
.
Câu 28. Cho
7
1
d5f x x
. Tính
2
0
3 1 dI f x x
.
A.
1
2
I
. B.
2I
. C.
7
3
I
. D.
5
3
I
.
Câu 29. Cho tích phân
1
0
2 3 d
x
I x e x ae b
, với
,ab
. Mệnh đề
nào dưới đây là đúng.
A.
3ab
. B.
2ab
. C.
21ab
. D.
33
28ab
.
Câu 30. Cho
5
2
d 10f x x
. Kết quả
2
5
2 4 df x x


bằng:
A.
32
. B.
34
. C.
36
. D.
40
.
Câu 31. Biết
11
1
d 18.f x x
Tính
2
2
0
2 3 1 d .I x f x x


A.
10.I
B.
5.I
C.
7.I
D.
8.I
Câu 32. Cho hàm số
()fx
có đạo hàm trên đoạn
3;1
,
( 3) 17f
và
(1) 1f 
. Tính
1
3
3 ' 2f x dx
.
A.
58
. B.
44
. C.
48
. D.
56
.
Câu 33. Cho hàm số
y f x
có đạo hàm
'fx
liên tục trên
1;4
,
1 12f
và
4
1
' 17f x dx
. Giá trị của
f 4
bằng
A.
19
. B.
9
. C.
29
. D.
5
.
Câu 34. Kết quả của tích phân
1
0
23
x
I x e dx
được viết dưới dạng
I ae b
, với
,ab
là các số hữu tỉ. Tìm khẳng định đúng trong
Trang15
các khẳng định sau.
A.
2ab
B.
33
28ab
C.
3ab
D.
21ab
Câu 35. Cho
, 5, 2
bb
ac
a b c f x dx f x dx

. Tính
c
a
f x dx
.
A.
3
c
a
f x dx
. B.
2
c
a
f x dx 
.
C.
1
c
a
f x dx
. D.
7
c
a
f x dx
.
Câu 36. Biết
11
1
d 18f x x
. Tính
2
2
0
2 3 1 dI x f x x


.
A.
5I
. B.
8I
. C.
7I
. D.
10I
.
Câu 37. Cho hàm số
fx
có đạo hàm
fx
liên tục trên
1;3 , 1 3f
và
3
1
10f x dx
. Giá trị của
3f
bằng
A. -13. B. 13. C. 7. D. -7.
Câu 38. Cho
,abZ
thỏa mãn
5
2
1
3
ln5 ln 2.
3
dx a b
xx

Mệnh đề
nào sau đây đúng?
A.
20ab
. B.
0ab
.
C.
0ab
. D.
20ab
.
Câu 39. Cho hàm số
Fx
là một nguyên hàm của hàm số
fx
trên
đoạn
1;2
. Biết
2
1
d1f x x
và
11F
. Tính
2F
.
A.
20F
. B.
23F
.
C.
21F
. D.
22F
.
Câu 40. Biết
4
1
1
d
2
f x x
và
0
1
1
d
2
f x x

. Tính tích phân
4
2
0
4e 2 d
x
f x x


.
A.
8
4.e
. B.
8
2.e
. C.
8
2. 4e
. D.
8
4. 2e
.
Câu 41. Biết
a
là số thực dương thỏa mãn
22
0
22
ln3
12
a
x x a
dx a
x

. Giá trị của
a
là?
A.
3
. B.
5
. C.
2
. D.
4
.
Câu 42. Cho hàm số
fx
liên tục trên
và
Trang16
1
0
0 2018, 1f f x dx
. Tính
1
0
1 . 'I x f x dx
.
A.
2018I 
. B.
2018I
.
C.
2017I
. D.
2019I
.
Câu 43. Biết
2
0
d6f x x x


và
2
0
3 d 10f x g x x


. Tính
2
0
2 +3 dI f x g x x


.
A.
12I
. B.
16I
. C.
10I
. D.
14I
.
Câu 44. Cho
3
0
( )df x x a
,
3
2
( )df x x b
. Khi đó
2
0
( )df x x
bằng:
A.
ab
. B.
ba
.
C.
ab
. D.
ab
.
Câu 45. Biết
3
2
1f x dx
và
3
2
3g x dx
. Khi đó
3
2
f x g x dx


bằng
A.
4
. B.
2
. C.
2
. D.
3
.
Câu 46. Cho
2
0
3 2 1 d 6
m
x x x
. Giá trị của tham số m thuộc
khoảng nào sau đây?
A.
1;2
. B.
;0
. C.
0;4
. D.
3;1
.
Câu 47. Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;5
và
5 10f
,
5
0
d 30xf x x
. Tính
5
0
df x x
.
A.
20
. B.
30
. C.
20
. D.
70
.
Câu 48. Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;2
và
0 2 2022.ff
Tính
2
0
f x dx
.
A.
2022
.B.
2022
.C.
1011
. D.
4044
.
Câu 49. Cho hàm số
2
01
.
1
2 1 1 3
khi x
y f x
x
x khi x


Tính tích phân
3
0
d.f x x
A.
6 ln2
. B.
4 ln 4
.
C.
6 ln4
. D.
2 2ln2
.
Câu 50. Biết
6
0
2 sin3 d
a
x x x
b

. Biết
,a
b
nguyên tố cùng nhau khi
Trang17
đó giá trị
a
bằng
A.
3
. B.
4
. C.
5
. D.
6
.
DIỆN TÍCH HÌNH PHẲNG
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
liên tục trên đoạn
;ab
, trục hoành và hai đường thẳng
xa
,
xb
:
DẠNG 3:ỨNG DỤNG CỦA TÍCH PHÂN
Trang18
Chú ý:
Nếu trên đoạn
;ab
, hàm số
fx
không đổi dấu thì:
dd
bb
aa
f x x f x x

.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
11
:C y f x
,
22
:C y f x
liên tục trên đoạn
;ab
và hai đường thẳng
xa
,
xb
:
Chú ý:
Nếu phương trình
f x g x
vô nghiệm trên
;ab
thì
dd
bb
aa
S f x g x x f x g x x



Nếu phương trình
f x g x
có nghiệm
xc
trên
;ab
thì
d d d
b c b
a a c
S f x g x x f x g x x f x g x x
THỂ TÍCH
Bài toán 1: Gọi
B
là phần vật thể giới hạn bởi hai mặt phẳng
P
và
Q
cùng vuông góc
với trục
Ox
tại các điểm
a
và
b
;
Sx
là diện tích thiết diện của vật thể bị cắt bởi mặt
phẳng vuông góc với trục
Ox
tại điểm
x
,
a x b
. Giả sử
Sx
là hàm số liên tục trên
đoạn
;ab
.
12
d
b
a
S f x f x x
O
x
y
a
1
c
2
c
b
1
C
2
C
11
22
:
:
:
C y f x
C y f x
H
xa
xb
d
b
a
S f x x
0
:
y f x
y
H
xa
xb
()y f x
O
x
y
a
1
c
2
c
b
3
c
Trang19
Bài toán 2: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
y f x
,
0y
xa
,
xb
(
ab
) quanh trục
Ox
:
Bài toán 3: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
1
y f x
,
2
y g x
,
xa
,
xb
(với
ab
và
21
0 yy
,
;x a b
) quanh trục
Ox
:
BÀI TOÁN CHUYỂN ĐỘNG
Mối liên hệ giữa quãng đường, vận tốc và gia tốc:
Cho một chất điểm chuyển động với quãng đường là một hàm số theo biến số thời gian
t
là
st
. Khi đó:
Vận tốc của chất điểm là
dv t s t s t v t t
.
Gia tốc của chất điểm là
da t v t v t a t t
.
Câu 1. Cho hai hàm số
y f x
,
y g x
liên tục trên
;ab
và có đồ thị
1
C
và
2
C
tương ứng thì công thức tính diện tích hình phẳng giới hạn bởi
1
C
,
2
C
và hai đường thẳng
,x a x b
là
A.
d
b
a
S g x f x x


. B.
d
b
a
S f x g x x
.
1
2
y f x
y g x
xa
xb
22
d
b
a
V f x g x x

O
x
y
1
y f x
a
b
2
y g x
O
x
y
y f x
xa
xb
0
y f x
y
xa
xb
2
d
b
a
V f x x


d
b
B
a
S x xV
P
Q
x
Sx
a
b
O
x
CÂU HỎI TRẮC NGHIỆM
Trang20
C.
d
b
a
S g x f x x


. D.
dd
bb
aa
S f x x g x x

.
Câu 2. Cho hàm số
y f x
liên tục trên
;ab
. Diện tích hình phẳng giới
hạn bởi đồ thị hàm số, đường thẳng
xa
, đường thẳng
x b b a
và trục
hoành là
A.
d
b
a
S f x x
. B.
d
b
a
S f x x
.
C.
2
d
b
a
S f x x
. D.
d
b
a
S f x x
.
Câu 3. Cho hàm số
y f x
liên tục trên đoạn
;.ab
Gọi
D
là hình phẳng
giới hạn bởi đồ thị
:,C y f x
trục hoành, hai đường thẳng
,xa
xb
(như hình vẽ bên dưới). Giả sử
D
S
là diện tích của hình phẳng
.D
Chọn công
thức đúng trong các phương án A, B, C, D dưới đây?
A.
0
0
dd
b
D
a
S f x x f x x

.
B.
0
0
dd
b
D
a
S f x x f x x

.
C.
0
0
dd
b
D
a
S f x x f x x

.
D.
0
0
dd
b
D
a
S f x x f x x

.
Câu 4. Hình phẳng giới hạn bởi các đường
1x 
,
2x
,
0y
,
2
2y x x
có diện tích được tính theo công thức:
A.
2
2
1
2dS x x x

. B.
02
22
10
2 d 2 dS x x x x x x

.
C.
02
22
10
2 d 2 dS x x x x x x

. D.
2
2
0
2dS x x x
.
Câu 5. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số trên
đoạn và trục hoành.
A. . B. . C. . D. .
Câu 6. Tính diện tích
S
của miền hình phẳng giới hạn bởi đồ thị của hàm số
32
3y x x
và trục hoành.
A.
13
2
S
. B.
29
4
S
. C.
27
4
S 
. D.
27
4
S
.
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
2y x x
và các
đường thẳng
0y
,
1x 
,
1x
là
32
2y x x x
1; 2
37
12
28
3
8
3
9
4
O
x
b
a
y
y f x
Trang21
A.
2
3
. B.
2
. C.
4
3
. D.
8
3
.
Câu 8. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
3
;2y x x y x
và các đường
1; 1xx
được xác định bởi công thức.
A.
1
3
1
3 d .S x x x

B.
1
3
1
3 d .S x x x

C.
01
33
10
3 d 3 d .S x x x x x x

D.
01
33
10
3 d 3 d .S x x x x x x

Câu 9. Tính diện tích của hình phẳng
H
giới hạn bởi các đường
yx
,
6yx
và trục hoành.
A.
20
3
. B.
25
3
. C.
16
3
. D.
22
3
.
Câu 10. Diện tích hình phẳng giới hạn bởi các đường
2yx
,
4yx
và trục
Ox
được tính bởi công thức:
A.
44
00
2 d 4 dx x x x

. B.
24
02
2 d 4 dx x x x

.
C.
4
0
2 4 dx x x
. D.
2
0
4 2 dx x x
.
Câu 11. Diện tích hình phẳng giới hạn bởi các đường
2
yx
và
2
2–yx
là:
A.
1
2
1
1dxx
. B.
1
2
0
1dxx
. C.
1
2
1
1dxx
. D.
1
2
0
1dxx
.
Câu 12. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
2
:2P y x
và đường thẳng
:d y x
quay xung quanh trục
Ox
được tính bởi
công thức nào dưới đây?
A.
11
22
24
00
d 4 dV x x x x



. B.
1
2
2
0
2dV x x x

.
C.
1
2
2
2
0
2dV x x x

. D.
11
22
24
00
ddV x x x x


.
Câu 13. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
2
:P y x
và đường thẳng
:d y x
quay xung quanh trục
Ox
bằng:
A.
11
24
00
ddx x x x


. B.
11
24
00
ddx x x x


.
C.
1
2
2
0
dx x x
. D.
1
2
0
dx x x
.
Câu 14. Thể tích
V
của khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi đồ thị hàm số
2
yx
và các đường thẳng
0y
,
1x
,
2x
xung
Trang22
quanh trục hoành là
A.
7
3
V
. B.
31
5
V
. C.
7
3
V
. D.
31
5
V
.
Câu 15. Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị
các hàm số
2
2y x x
và
2
yx
quay quanh trục
Ox
.
A.
4
3
. B.
4
3
. C.
3
. D.
1
3
.
Câu 16. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
2
:P y x
và đường thẳng
:2d y x
quay xung quanh trục
Ox
bằng
A.
2
2
2
0
2dx x x
. B.
2
2
0
2dx x x
.
C.
22
24
00
4 d dx x x x


. D.
22
24
00
4 d dx x x x


.
Câu 17. Cho đồ thị hàm số
y f x
. Diện tích hình phẳng (phần tô đậm
trong hình dưới) là
-8 -6 -4 -2 2 4 6 8
-8
-6
-4
-2
2
4
6
8
x
y
A.
2
2
df x x
. B.
02
20
ddf x x f x x

.
C.
02
20
ddf x x f x x

. D.
02
20
ddf x x f x x

.
Câu 18. Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục hoành, đường thẳng
xa
,
xb
(như hình bên dưới). Hỏi cách tính
S
nào dưới đây đúng?
A.
d d .
cb
ac
S f x x f x x

B.
d d .
cb
ac
S f x x f x x

C.
dd
cb
ac
S f x x f x x

.
D.
d.
b
a
S f x x
Câu 19. Tính diện tích
S
của phần hình phẳng gạch sọc (bên dưới) giới hạn
O
a
c
b
x
y
y f x
Trang23
bởi đồ thị hàm số bậc ba
32
y ax bx cx d
và trục hoành
A.
31
5
S
.
B.
27
4
S
.
C.
19
3
.
D.
31
5
.
Câu 20. Diện tích hình phẳng (phần gạch sọc) trong hình sau bằng
A.
3
2
1
2 3 dS x x x
.B.
3
2
1
2 3 dS x x x
.
C.
3
2
1
2 3 dS x x x
.D.
3
2
1
4 3 dS x x x
.
Câu 21. Phần hình phẳng
H
được gạch chéo trong hình vẽ dưới đây được
giới hạn bởi đồ thị hàm số
y f x
,
2
4y x x
và hai đường thẳng
2x 
,
0x
.
Biết
0
2
4
d
3
f x x
, diện tích hình phẳng
H
là
A.
7
3
. B.
16
3
. C.
4
3
. D.
20
3
.
Trang24
Câu 22. Cho hàm số
y f x
có đồ thị như hình vẽ. Diện tích phần tô đậm
bằng
A.
1
2
df x x
. B.
1
0
df x x
. C.
2
0
df x x
. D.
0
1
df x x
.
Câu 23. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số
2
yx
,
yx
và các đường thẳng
0x
,
1x
bằng
A.
0
2
1
d
x x x
. B.
1
2
0
d
x x x
. C.
0
2
1
d
x x x
. D.
1
2
0
d
x x x
.
Câu 24.Diện tích S của hình phẳng giới hạn bởi các đường
2
5y x x
,
2
y x x
,
1x
và
2x
bằng
A.
13
3
S
. B.
9S
. C.
7
3
S
. D.
14
3
S
.
Câu 25.Cho hình phẳng giới hạn các đường
5 , 0, 2
x
y y x
và
2x
.
Thể tích khối tròn xoay tạo thành do hình phẳng
D
quay quanh trục hoành
được tính theo công thức nào dưới đây?
A.
2
2
2
5d
x
Vx
. B.
2
2
25 d
x
Vx
. C.
2
2
5d
x
Vx
. D.
2
2
5d
x
Vx
.
Câu 26.Hình phẳng giới hạn bởi đường cong
2
1yx
và
Ox
khi quay quanh
Oy
tạo thành vật thể có thể tích là
A.
2
V
. B.
16
15
V
. C.
16
15
V
. D.
1
2
V
.
Câu 27.Thể tích của khối tròn xoay do đồ thị giới hạn bởi đồ thị của hàm số
()y f x
liên tục và không âm trên đoạn
1;3
, trục
Ox
và hai đường thẳng
1, 3xx
quay quanh trục
Ox
được tính theo công thức:
A.
3
1
( ) .V f x dx
B.
3
2
1
( ) .V f x dx
C.
3
1
( ) .V f x dx
D.
3
2
1
( ) .V f x dx
Câu 28.Cho hàm số
y f x
liên tục trên
. Gọi
S
là diện tích hình phẳng
Trang25
giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường thẳng
1,x 
4x
(như hình vẽ bên dưới). Mệnh đề nào dưới đây đúng.
A.
14
11
d d .S f x x f x x


B.
14
11
d d .S f x x f x x

C.
14
11
d d .S f x x f x x

D.
14
11
d d .S f x x f x x


Câu 29.Cho hình phẳng
H
giới hạn bởi các đường
y f x x
,
2y g x x
và trục hoành (như hình vẽ bên dưới). Tính thể tích
V
của
khối tròn xoay tạo thành khi quay hình
H
quanh trục hoành.
A.
8
3
V
. B.
6
3
1
V
. C.
8V
. D.
10V
.
Câu 30.Trong không gian
Oxyz
, cho vật thể nằm giữa hai mặt phẳng
0x
và
3x
. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
0 3x
là một hình vuông cạnh là
2
9 x
.
Tính thể tích
V
của vật thể.
A.
18V
. B.
171V
. C.
171V
. D.
18V
.
Câu 31. Diện tích
S
của hình phẳng giới hạn bởi các đường
, 0, 2y f x y x
và
1x
(phần tô đậm trong hình bên) được tính bởi
công thức nào dưới đây?
Trang26
A.
11
21
ddSxxfxx f


. B.
11
21
ddSxxfxx f



.
C.
11
21
ddxS f x f x x



. D.
11
21
ddxS f x f x x


.
Câu 32. Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số
2
3 6 ,y x x
trục hoành và hai đường thẳng
2; 0xx
bằng
A.
4
. B.
20
. C.
20
. D.
4
.
Câu 33.Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số
2
,y x y x
và các đường thẳng
0, 1xx
bằng
A.
1
2
0
x x dx
. B.
0
2
1
x x dx
. C.
1
2
0
x x dx
. D.
0
2
1
x x dx
.
Câu 34.Cho hình phẳng D giới hạn bởi đồ thị hàm số
6yx
và các đường
thẳng
0, 1, 2 y x x
. Thể tích khối tròn xoay tạo thành khi quay D quanh
trục hoành bằng
A.
2
1
6dxx
. B.
2
2
1
6dxx
. C.
2
2
0
6dxx
. D.
1
2
0
6dxx
.
Câu 35.Cho hàm số
y f x
có đồ thị như hình vẽ. Diện tích phần tô đậm
bằng
x
y
-2
2
1
O
Trang27
A.
1
2
f x dx
. B.
1
0
f x dx
. C.
2
0
f x dx
. D.
0
2
f x dx
.
Câu 36.Thể tích của khối tròn xoay khi quay hình phẳng được giới hạn bởi đồ
thị hàm số
2 1, 0, 0, 3y x y x x
quanh trục hoành bằng
A.
21.
B.
6.
C.
6.
D.
21 .
Câu 37. Diện tích
S
của hình phẳng được tô đậm trong hình bên dưới bằng
A.
14
11
.S f x dx f x dx

B.
14
11
.S f x dx f x dx


C.
14
11
.S f x dx f x dx


D.
14
11
.S f x dx f x dx

Câu 38.Cho hàm số
fx
liên tục trên
. Gọi
S
là diện tích hình phẳng giới
hạn bởi các đường
, 0, 1, 2y f x y x x
(như hình vẽ). Mệnh đề nào
dưới đây đúng?
A.
12
11
ddS f x x f x x


. B.
12
11
ddf x x f x x

.
C.
2
1
df x x
. D.
2
1
df x x
.
Câu 39. Cho đồ thị hàm số
y f x
như hình vẽ.
Diện tích
S
của hình phẳng được giới hạn bởi đồ thị hàm số
y f x
và trục
Trang28
Ox
( phần in đậm) được tính bởi công thức
A.
13
31
d dS f x x f x x


. B.
13
31
d dS f x x f x x


.
C.
3
3
dS f x x
. D.
3
3
dS f x x
.
Câu 40. Cho hàm số
y f x
liên tục trên đoạn
3;3
. Hình phẳng
H
giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường thẳng
3, 3xx
được cho như hình vẽ dưới. Biết
0
3
df x x a
,
3
0
df x x b
.
Diện tích của hình phẳng
H
bằng
A.
ab
. B.
ba
. C.
ab
. D.
ab
.
Câu41.Cho hình phẳng giới hạn bởi các đường
2
2yx
,
2
4yx
quay xung
quanh trục
Ox
. Thể tích của khối tròn xoay tạo thành bằng
A.
6
5
V
.B.
9
70
V
.C.
4
3
V
. D.
88
5
V
.
Câu42. Diện tích phần gạch chéo trong hình bên dưới được tính theo công
thức
Trang29
A.
0
0
dd

b
a
f x x f x x
. B.
0
0
dd

b
a
f x x f x x
.
C.
0
0
dd

b
a
f x x f x x
. D.
0
0
dd

b
a
f x x f x x
.
Câu43. Một chất điểm chuyển động trên trục
Ox
với vận tốc thay đổi theo
thời gian
2
36v t t t
(m/s). Tính quãng đường chất điểm đó đi được từ thời
điểm
1
0 t
(s),
2
4t
(s).
A.
16.
B.
24.
C.
8.
D.
12.
Câu44.Bạn An ngồi trên máy bay đi du lịch thế giới vận tốc chuyển động của
máy bay là
2
3 5 m/sv t t
. Quãng đường máy bay đi được từ giây thứ
4
đến giây thứ
10
là
A.
996 m
. B.
876 m
. C.
966 m
. D.
1086 m
.
Câu45.Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi
công thức
51v t t
, thời gian tính theo đơn vị giây, quãng đường vật đi
được tính theo đơn vị mét. Quãng đường vật đó đi được trong 10 giây đầu tiên
là:
A.
15 m
. B.
620 m
. C.
51m
. D.
260 m
.
Câu46.Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc
1
7 m/s .v t t
Đi được
5s
, người lái xe phát hiện chướng ngại vật và
phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc
2
70 m/s .a 
Tính quãng đường
S
m
đi được của ô tô từ lúc bắt đầu
chuyển bánh cho đến khi dừng hẳn.
A.
95,70 mS
. B.
96,25 mS
.
C.
87,50 mS
. D.
94,00 mS
.
Câu47.Một ô tô đang chạy với vận tốc
10m/s
thì người lái đạp phanh. Từ thời
điểm đó ô tô chuyển động chậm dần đều với vận tốc
10 5v t t
m/s
với
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng
đường đi được của ô tô từ lúc đạp phanh đến khi dừng hẳn.
Trang30
A.
10 m
. B.
20 m
.
C.
2m
. D.
0,2 m
.
Câu48.Giả sử một vật từ trạng thái nghỉ khi
0 st
chuyển động thẳng với
vận tốc
5 m/sv t t t
. Tìm quảng đường vật đi được cho tới khi nó
dừng lại.
A.
20,8 m
. B.
20,83 m
.
C.
125
m
6
. D.
20,83333 m
.
Câu49.Một vật chuyển động theo quy luật
32
6s t t
, với
t
(giây) là khoảng
thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi
được trong thời gian đó. Kể từ lúc bắt đầu chuyển động đến lúc vận tốc đạt giá
trị lớn nhất thì quãng đường vật đi được là bao nhiêu?
A.
12 m
. B.
16 m
.
C.
20 m
. D.
24 m
.
Câu50.Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi
công thức
32v t t
, thời gian tính theo đơn vị giây, quãng đường vật đi
được tính theo đơn vị mét. Biết tại thời điểm
2st
thì vật đi được quãng
đường là
10m.
Hỏi tại thời điểm
30st
thì vật đi được quãng đường là bao
nhiêu?
A.
240m.
B.
1140m.
C.
300m.
D.
1410m.
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP TRẮC NGHIỆM NGUYÊN HÀM TÍCH PHÂN MỨC NHẬN BIẾT THÔNG HIỂU DẠNG 1: NGUYÊN HÀM
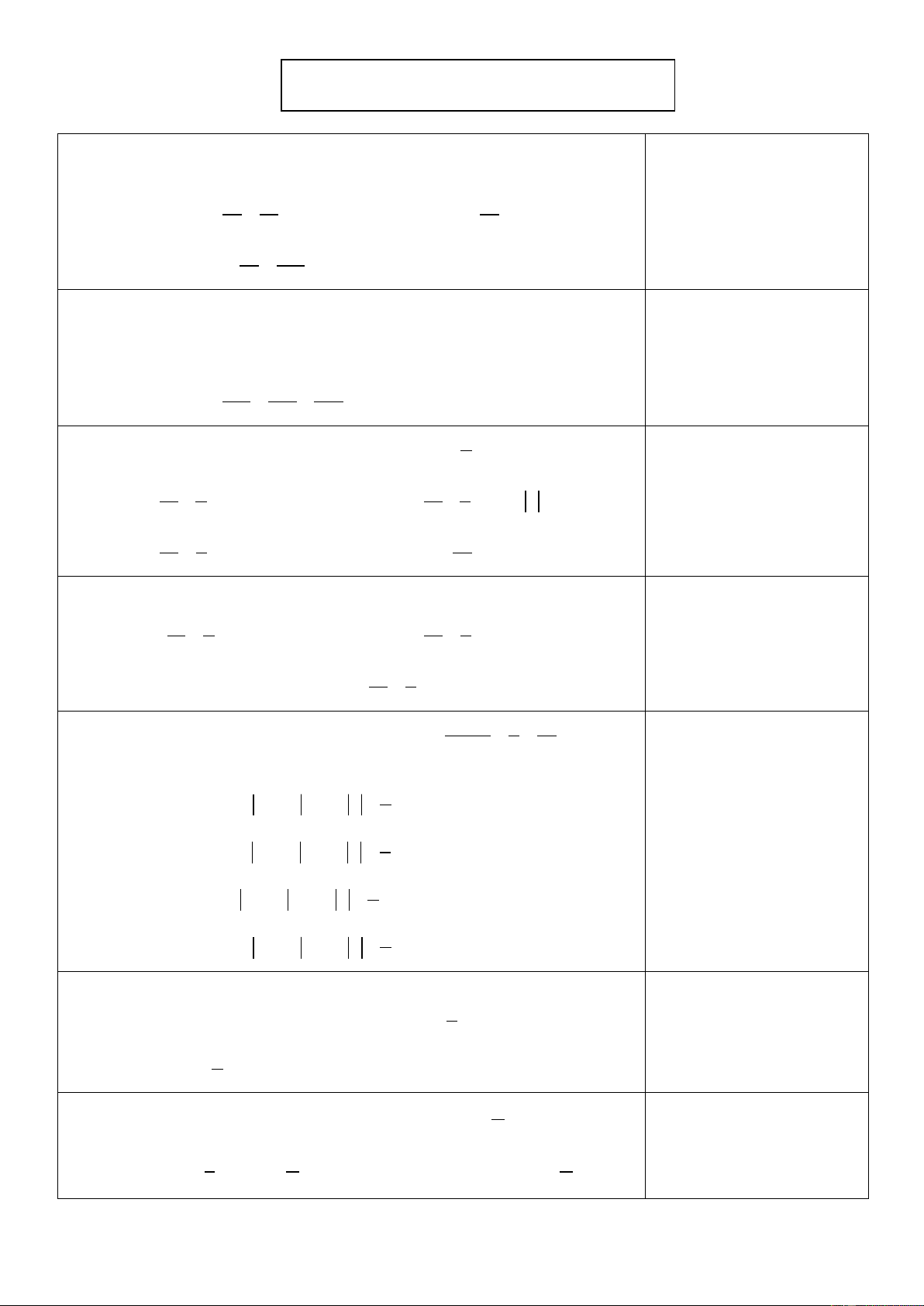
Định nghĩa: f
 xdx FxC F 'x  f x
Tính chất của nguyên hàm
Tính chất 1: f
 xdx  f x và f '
 xdx f xC
Tính chất 2: kf
 xdx k f
 xdx với k là hằng số khác 0 .
Tính chất 3: f
 x gxdx f
 xdxg  xdx
Bảng nguyên hàm của một số hàm số sơ cấp
Nguyên hàm của hàm số sơ cấp
Nguyên hàm của hàm số hợp u u x
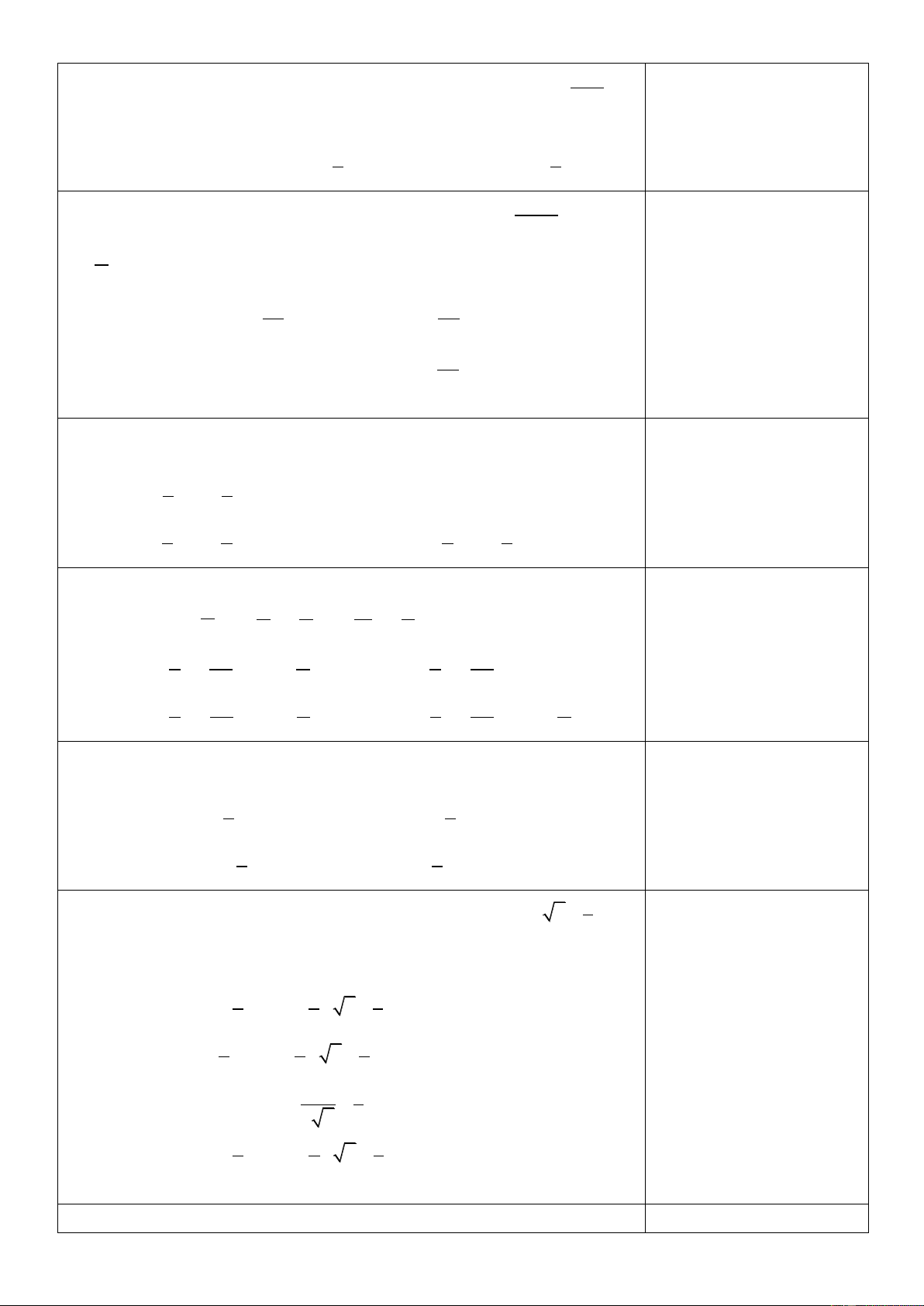
dx x C
du u C   1   1 1 x dx x    C      1  1 u du u    C      1  1  1 1 1
dx  ln x C
du  ln u Cx u x x
e dx e Cu u
e du e Cx a u a x a dx
C a  0,a    1 u a du
C a  0,a    1 ln a ln a
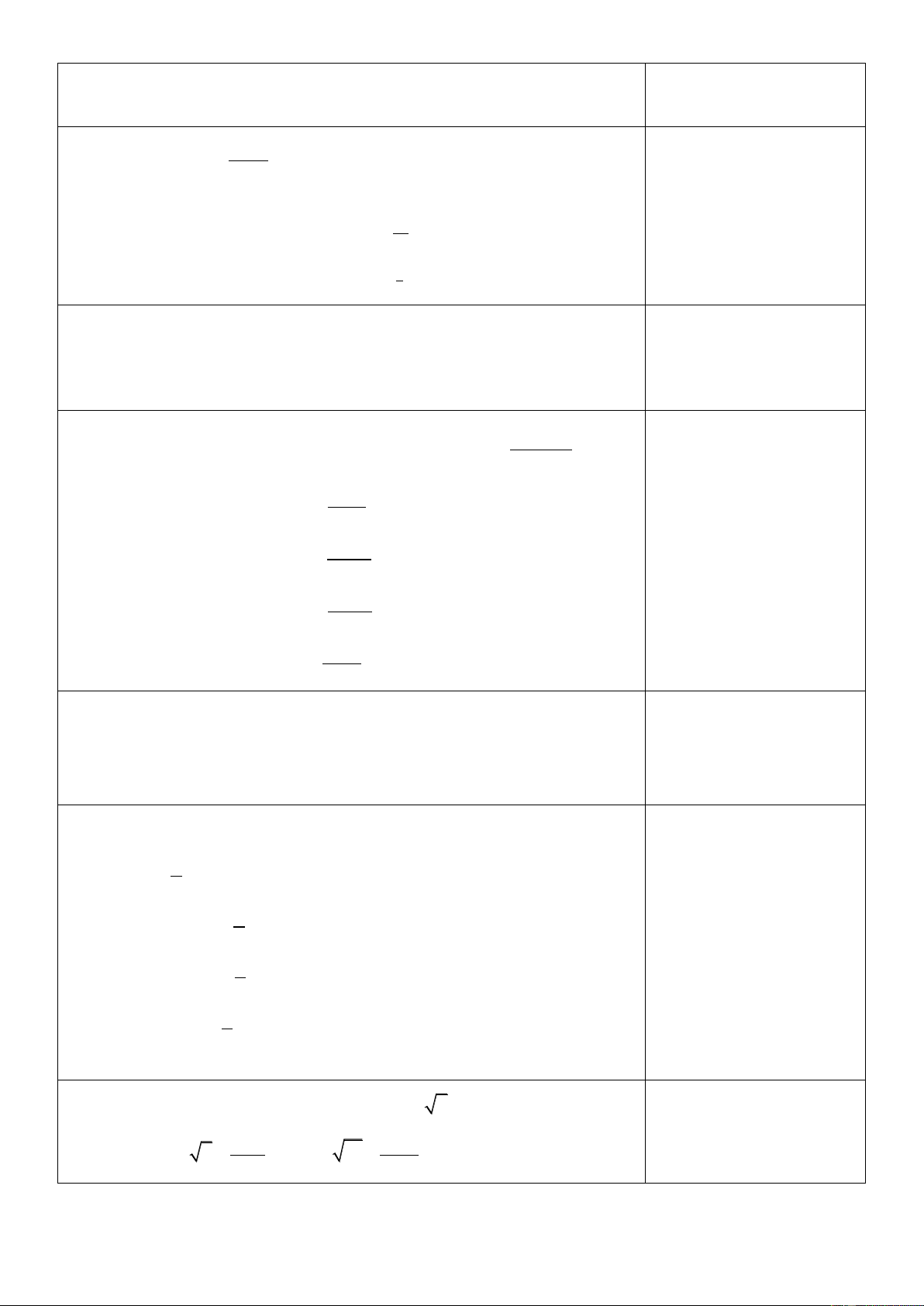
sin xdx   cos x C
sin udu   cos u C
cos xdx  sin x C
cos udu  sin u C  1 1
dx  tan x C
du  tan u C  2 cos x 2 cos u 1 1
dx   cot x C
du   cot u C  2 sin x 2 sin u
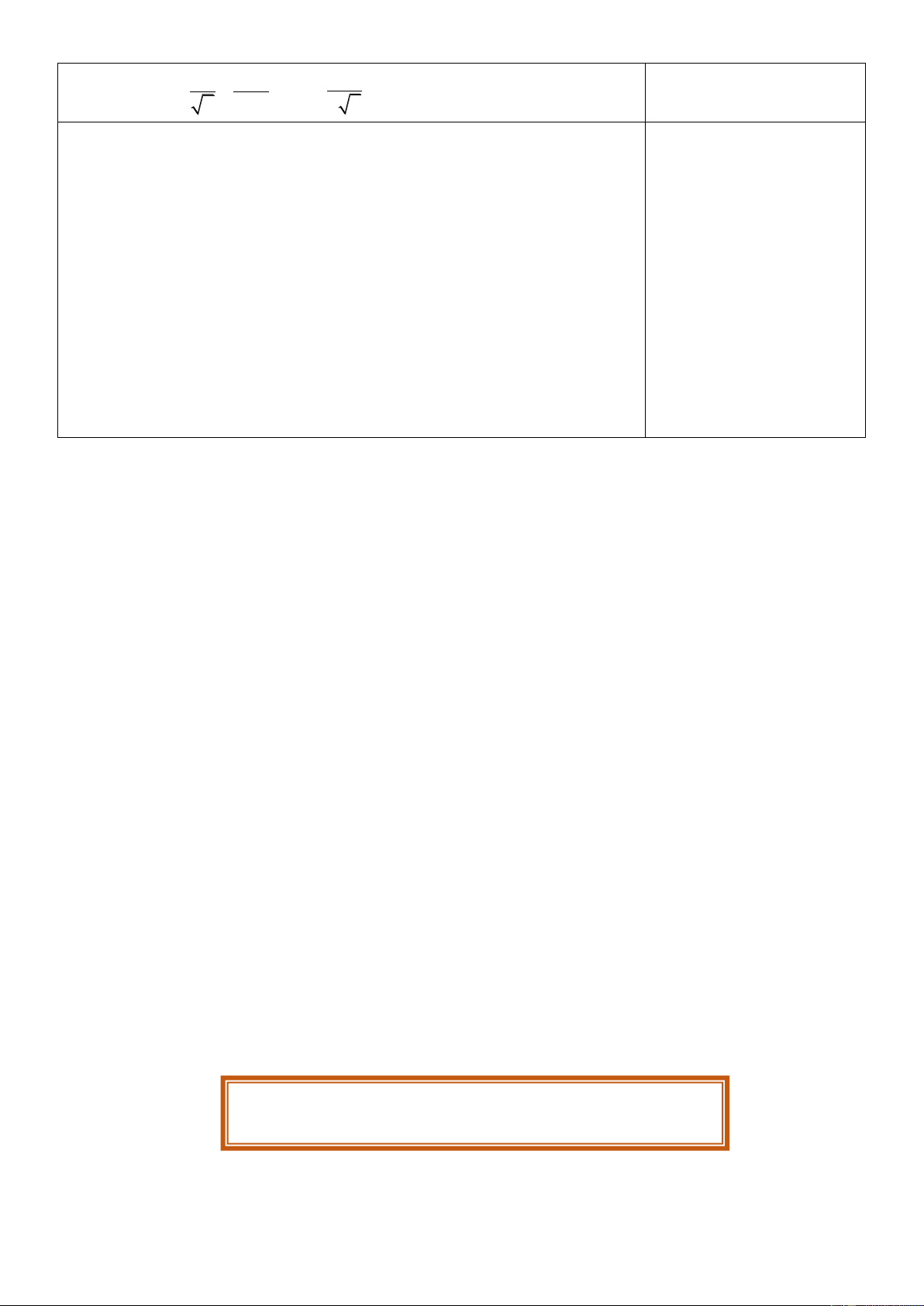
Phương pháp đổi biến số: f
 uxu'xdx F uxC Hệ quả: 1
Nếu u ax b a  0 thì ta có f
 ax bdx F ax bC a
Phương pháp nguyên hàm từng phần: udv uv vdu  
 Một số cách đặt thường gặp: sin x  sin x       Dạng I  cos x .P  xdx  
. Đặt u P x , dv  cos x dx  
, với P x là đa thức. ex, x a    ex, x a    ln x  ln x   Dạng I  .P 
  xdx . Đặt u  dx  
; dv P x dx , với P x là đa thức. log x  log x a   aTrang1 CÂU HỎI TRẮC NGHIỆM Câu 1.
Nguyên hàm của hàm số f x 3
x  3x  2 là hàm số nào trong các hàm số sau? x x x
A. F x 4 2    2x C .
B. F x 4 2 
 3x  2x C . 4 2 3 x x
C.. F x 4 2 3  
 2x C D. F x 2
 3x  3x C . 4 2 Câu 2.
Hàm số F x 3 2
 5x  4x  7x 120  C là họ nguyên hàm của hàm số nào sau đây?
A. f x 2
 5x  4x  7 .
B. f x 2
 5x  4x  7 . x x x
C. f x 2 3 2 5 4 7    .
D. f x 2
15x  8x  7 . 4 3 2 1 Câu 3.
Họ nguyên hàm của hàm số: 2
y x  3x  là x x 3 x 3
A. F x 3 2 
x  ln x C .
B. F x 3 2 
x  ln x C . 3 2 3 2 x 3 1
C. F x 3 2 
x  ln x C .D. F x  2x  3  C . 3 2 2 x Câu 4.
Tìm nguyên hàm của hàm số f x   x   1  x  2 x 3 x 2
A. F x 3 2 
x  2x C .
B. F x 3 2 
x  2x C . 3 2 3 3 x 2
C. F x  2x  3  C .
D. F x 3 2 
x  2x C . 3 3 2 2 3 Câu 5.
Nguyên hàm F x của hàm số f x    là hàm số 2 5  2x x x nào?
A. F x 3
  ln 5  2x  2ln x   C . x
B. F x 3
  ln 5  2x  2ln x   C . x
C. F x 3
 ln 5  2x  2ln x   C . x
D. F x 3
  ln 5  2x  2ln x   C . x Câu 6.
Tìm nguyên hàm của hàm số f (x)  sin 2x 1
A. sin 2xdx  cos 2x C
. B. sin 2xdx  cos 2x C. 2 1
C. sin 2xdx   cos 2x C
. D. sin 2xdx   cos 2x C. 2    Câu 7.
Tìm nguyên hàm của hàm số f (x)  cos 3x    .  6  1     A.
f (x)dx   sin 3x   C     . B.
f (x).dx  sin 3x   C     . 3  6   6  Trang2 1   1   C.
f (x)dx  sin 3x   C     . D.
f (x)dx  sin 3x   C     . 3  6  6  6  Câu 8.
Tìm nguyên hàm của hàm số 2 ( ) 2 .3 x x f x   . x   x   A. f  x 2 1 dx  .  C   .B. f  x 9 1 dx  .  C   .  9  ln 2  ln 9  2  ln 2  ln 9 x   x   C. f  x 2 1 dx  .  C   . D. f  x 2 1 dx  .  C   .  3  ln 2  ln 9  9  ln 2  ln 9 Câu 9.
Tìm nguyên hàm của hàm số ( ) x x f x e e   . A.    xx f x dx e
  e C .B.    xx
f x dx e eC . C.    xx
f x dx e e
C .D.    xx f x dx e
  e C .
Câu 10. Họ nguyên hàm của hàm số ( ) x (3 x f x e e   ) là 1
A. F (x)  3 x e
C . B. ( )  3 x x  ln x F x e e e C . x e C. ( )  3 x F x
e x C . D. ( )  3 x F x
e x C .
Câu 11. Nguyên hàm của hàm số 1 f (x)  là 2x 1 A. f
 xdx  2
 2x 1  C . B. f
 xdx  2 2x1C . x C. f  x 2 1 dx   C . D. f
 xdx  2x1C . 2
Câu 12. Tìm nguyên hàm của hàm số 1 f (x)  . 3  x A. f
 xdx  3
 3 x C . B. f
 xdx   3 x C . C. f
 xdx  2 3 x C . D. f
 xdx  2
 3 x C .
Câu 13. Tìm nguyên hàm của hàm số 3 f ( ) x x  2 . 3 3 A. f
 xdx   x 2 3 x 2 C .B. f
 xdx  x 2 3 x 2 C . 4 4 2 1  C. f
 xdx  x 2 x 2 . D. f
 xdx  x2 23 C . 3 3
Câu 14. Biết một nguyên hàm của hàm số f x 1  1 là hàm số 1 3x
F x thỏa mãn F   2 1 
. Khi đó F x là hàm số nào sau đây? 3
A. F x 2  x
1 3x  3 B. F x 2  x  1 3x  3 3 3
C. F x 2  x
1 3x 1D. F x 2  4  1 3x 3 3 Trang3
Câu 15. Nếu F x là một nguyên hàm của hàm số 1 f (x)  và x 1
F 2  1 thì F 3 bằng 3 1
A. ln 2 1. B. ln . C. ln 2 . D. . 2 2 1
Câu 16. Nguyên hàm F x của hàm số f x  2x  thỏa mãn 2 sin x    F  1    là  4  2  2  A. 2
 cot x x  . B. 2 cot x x  . 16 16 2  C. 2
 cot x x . D. 2 cot x x  . 16
Câu 17. Một nguyên hàm 
F (x) của hàm số x x 2
f (x)  (ee ) thỏa mãn
điều kiện F(0)  1 là 1  x 1 A. 2 2 ( ) x F x   e
e  2x 1. B. 2  x 2 ( )  2   2 x F x e e  2x 1. 2 2 1  1  x 1 x 1 C. 2 2 ( ) x F x   e
e  2x . D. 2 2 ( ) x F x   e
e  2x 1. 2 2 2 2
Câu 18. Một nguyên hàm F (x) của hàm số f (x)  a b cos 2x thỏa mãn          F (0)  , F    , F    là 2  2  6 12  3 2 7  2 7
A. F (x)   x  sin 2x
. B. F (x)   x  sin 2x . 3 9 2 3 9 2 7  2 7 
C. F (x)   x  sin 2x
. D. F (x)   x  sin 2x  . 3 9 2 3 9 2 Câu 19. Cho hàm số 3 2
F (x)  ax bx cx 1là một nguyên hàm của hàm
số f (x) thỏa mãn f (1)  2, f (2)  3, f (3)  4 . Hàm số F (x) là 1 1 A. 2 F (x) 
x x 1. B. 2 F (x)   x x 1 . 2 2 1 1 C. 2 F (x)  
x x 1. D. 2 F (x)  x x 1 . 2 2
Câu 20. Một nguyên hàm F (x) của hàm số 3
f (x)  2 sin 5x x  thỏa 5
mãn đồ thị của hai hàm số F (x) và f (x) cắt nhau tại một điểm nằm trên trục tung là 2 2 3
A. F (x)   cos 5x x x x 1 . 5 3 5 2 2 3
B. F (x)  cos 5x x x x 1 . 5 3 5 1 3
C. F (x)  10 cos 5x   x 1. 2 x 5 2 2 3
D. F (x)   cos 5x x x x . 5 3 5 Câu 21. Hàm số 2 ( )  (   ) x F x ax bx
c e là một nguyên hàm của hàm số Trang4 2 ( ) x
f x x e thì a b c bằng:
A.1. B. 2 . C. 3 . D. 2  .
Câu 22. Cho f x , g x là các hàm số xác định và liên tục trên  . Trong
các mệnh đề sau, mệnh đề nào sai? A. f
 xgxdx f
 xd .x g  xdx. B. 2 f
 xdx  2 f  xdx . C. f
 x gxdx f
 xdxg  xdx . D. f
 x gxdx f
 xdxg  xdx. Câu 23. Nếu f  x 1 dx
 ln x C thì f x là x
A. f x  x  ln x C .
B. f x 1
  x   ln x C . x 1 x 1
C. f x  
 ln x C .
D. f x  . 2 x 2 x x x
Câu 24. Tìm họ nguyên hàm của hàm số f x 2 1  . x 1 1 1 A. x  C . B.1  C . x 1 x  2 1 2 x C.
 ln x 1  C . D. 2
x  ln x 1  C . 2
Câu 25. Biết F x là một nguyên hàm của hàm số f x 1  và x 1
F 2  1. Tính F 3 .
A. F 3  ln 2 1.
B. F 3  ln 2 1. C. F   1 3  . D. F   7 3  . 2 4
Câu 26. Cho hàm số f x thỏa mãn đồng thời các điều kiện
f  x  x  sin x và f 0  1. Tìm f x . x x
A. f x 2 
 cos x  2 . B. f x 2   cos x  2 . 2 2 x x
C. f x 2 
 cos x . D. f x 2 1   cos x  . 2 2 2
Câu 27. Họ nguyên hàm của hàm số f x   x  3 1 là 1 1
A. x  4 1  C .
B. x  3 1  C . 4 4
C. 3 x   1  C .
D. x  4 4 1  C .
Câu 28. Tính F(x)  x sin xdx  bằng
A. F (x)  x sin x  cos x C . B. F (x)  sin x x cos x C . Trang5
C. F (x)  sin x x cos x C . D. F (x)  x sin x  cos x C .
Câu 29. Tính F(x)  x sin x cos xdx  . Chọn kết quả đúng: 1 x 1 x
A. F (x)  sin 2x
cos 2x C . B. F (x)  cos 2x  sin 2x C . 8 4 4 2 1 x 1 x
C. F (x)  sin 2x
cos 2x C . D. F (x)  sin 2x  cos 2x C . 4 8 4 8
Câu 30. Tìm nguyên hàm của hàm số 2 f (x)  cos . x sin x . 2 sin x 3 cos x A.
f (x)dx   C  . B.
f (x)dx   C  . 2 3 2 sin x 3 cos x C.
f (x)dx    C  . D.
f (x)dx    C  . 2 3 x
Câu 31. Tìm nguyên hàm của hàm số sin 2 f (x)  . cos 2x 1 A.
f (x)dx   ln sin x C  . B.
f (x)dx  ln cos 2x 1  C  . C.
f (x)dx  ln sin 2x C  . D.
f (x)dx  ln sin x C  . Câu 32. Tính .2x x dx  bằng: .2x 2x x 2x x   1 A.   C . B.C . 2 ln 2 ln 2 ln 2 C.
2x (x 1)  C . D. 2x (x 1)  C .
Câu 33. Tính 2x ln(x 1)dx  bằng: 2 x 2 x A. 2
(x 1) ln(x 1) 
x C . B. 2 x ln(x 1)   x C . 2 2 2 x 2 x C. 2
(x 1) ln(x 1) 
x C . D. 2
(x 1) ln(x 1)   x C . 2 2
Câu 34. Họ nguyên hàm của f x  x x  5 2 3 1 là 1
A. F x  x  6 3 1  C .
B. F x  x  6 3 18 1  C . 18 1
C. F x  x  6 3 1  C .
D. F x   x  6 3 1  C . 9
x x x 1
Câu 35. Họ nguyên hàm của hàm số f x 2 3  là hàm số nào? 3 x 1 1
A. F x  ln x   x   C . 2 x 2x 1 1
B. F x  ln x   x   C . 2 x 2x x x
C. F x 3 2 3  
 ln x C . 3 2 x x
D. F x 3 2 3  
 ln x C . 3 2
Câu 36. Xét tích phân I x x  2dx  . Nếu đặt t
x  2 thì ta được Trang6
A. I   4 2
t  2t dt .
B. I   4 2
2t  4t dt .
C. I   4 2
2t t dt .
D. I   4 2
4t  2t dt . x e
Câu 37. Cho I dx  , khi đặt x
t e 1 ta có: x e 1 dt A. 2 I  2t dt
. B. I  2dt
 . C. I   . D. 2 I t dt  . 2 1
Câu 38. Tìm họ nguyên hàm của hàm số f (x)  x(x 1) x A.
f (x)dx  ln x(x 1)  C  . B.
f (x)dx  ln  C  . x 1 x 1 x C.
f (x)dx  ln  C  .D.
f (x)dx  ln  Cx x 1
Câu 39. Cho hàm số f x  x sin 2x . Trong các khẳng định sau, khẳng định nào đúng? 1 A. f
 xdx   2xcos2x sin2xC . 4 1 B. f
 xdx  2xcos2x sin2xC . 4 1 C. f
 xdx  2xcos2x sin2xC . 4 1 D. f
 xdx   2xcos2x sin2xC . 4
Câu 40. Trong các khẳng định sau, khẳng định nào sai? 1 A. x 2e d  2  ex xC . B.
dx  ln x C  . x 4 x C C. 3 x dx   . D. sin d
x x C  cos x .  4
Câu 41. Biết F x là nguyên hàm của f x 1 
và F 2  1. Tính x 1 F 3 . 3 1
A. ln 2 1. B. ln 2 . C. ln . D. . 2 2
Câu 42. F (x) là một nguyên hàm của hàm số    ex f x  2x thỏa
mãn F 0  2 . Tìm F (x) .
A. F xx 2
 e  x  3 . B. F xx 2
 2e  x 1.
C. F xx 2
 e  x  2 . D. F xx 2  e  x 1
Câu 43. Cho biết F x là một nguyên hàm của hàm số f x . Tìm I  2 f
 x1dx  . Trang7
A. I  2F x 1 C . B. I  2xF x 1 C .
C. I  2xF x  x C . D. I  2F x  x C . 1
Câu 44. Tính I  dx
bằng cách đặt t  ln x . Mệnh đề nào dưới x ln x đây đúng? 1
A. I  dt  . B. I  dt  . 2 t 1 C. I  d t t  . D. I  dt  . t
Câu 45. Tìm nguyên hàm của hàm số  .ex y x . A. exd  .ex x x xC. B.
exd  .ex  ex x x xC. C. exd  ex x xC. D.
exd  .ex  ex x x xC  .    x 2018e x
Câu 46. Tính nguyên hàm của hàm số f x  e  2017   . 5  x  2018
A.   d  2017ex f x x   C . 4 x 504, 5
B.   d  2017ex f x x   C . 4 x 504, 5
C.   d  2017ex f x x   C . 4 x 2018
D.   d  2017ex f x x   C . 4 x
Câu 47. Nguyên hàm F x của   x f x xe 
thỏa mãn F 0  1 là: A.     1 x F x x e    1. B.    1 x F x x e     2 . C.    1 x F x x e   1. D.    1 x F x x e   .
Câu 48. Tính F(x)  x sin 2xdx
. Chọn kết quả đúng? 1
A. F (x) 
(2x cos 2x  sin 2x)  C . 4 1
B. F (x)  
(2x cos 2x  sin 2x)  C . 4 1
C. F (x)  
(2x cos 2x  sin 2x)  C . 4 1
D. F (x) 
(2x cos 2x  sin 2x)  C . 4
Câu 49. Họ nguyên hàm của hàm số f x 2018  3 x x là 2019 x 2019 x A. x   C B. 3 2 x   C 673 2019 Trang8 2019 1 x 1 C.   C D. 2017  6054xC x 673 2 x
Câu 50. Cho hai hàm số f x , g x là hàm số liên tục, có F x ,
G x lần lượt là nguyên hàm của f x , g x . Xét các mệnh đề sau:
I . F xGx là một nguyên hàm của f x g x.
II  . k.F x là một nguyên hàm của k.f x với k .
III  . F x.Gx là một nguyên hàm của f x.g x . Các mệnh đề đúng là
A. II  và  III  .
B. Cả 3 mệnh đề.
C. I  và  III  .
D. I  và  II  . DẠNG 2: TÍCH PHÂN Trang9Định nghĩa: b f
 xdx F xb F b F a a     a b Tên gọi: 
f x dx
đọc là: “Tích phân từ a đến b của f x dx ” a
a và b gọi là hai cận tích phân, trong đó a là cận dưới, b là cận trên.  Tính chất: a a b (1) f  x  0 (2) f
 xdx   f  xdx a b a b b c b c (3)
kf x dx k f x dx k      (4) f
 xdx f
 xdxf  xdx a a a a b b b b b (5)  f
 x gxdx f
 xdxg
 xdx(6)
f x  0 trên  ;
a b  f
 xdx  0 a a a a b b (7)
f x  g x trên  ;
a b  f
 xdx g  xdx a a a
(8) m f x  M trên  ;
a b  mb – a  f
 xdx M bab t (9)
t biến thiên trên  ;
a b  G t   f
 xdx là một nguyên hàm của f t và Ga  0. a
Phương pháp đổi biến số: b
Phương pháp đổi biến dạng 1: Tính I g
 xdx a
Bước 1:  Phân tích g xdx f u
 x.uxdx f u
 xd u  x      
 Đặt t u x
Bước 2: Đổi cận
 Với x a thì t u a
 Với x b thì t u bub bub
Bước 3: Khi đó I g
 xdx f
 tdt F t  F ubF ua     . uaa uab
Phương pháp đổi biến dạng 2: I f
 xdx (với f x liên tục trên  ;ab) a
Bước 1: Chọn x   t , trong đó  t là hàm số được lựa chọn một cách thích hợp.
Bước 2: Lấy vi phân dx  tdt , giả sử t liên tục.
Bước 3: Ta chọn một trong hai hướng:
Hướng 1: Nếu tínhđược các cận  và  tương ứng theo a và b ( a     và 
b     ) thì ta được I f  
  t.  tdt b bb
Phương pháp nguyên hàm từng phần: udv uv vdu   a a a Trang10 CÂU HỎI TRẮC NGHIỆM 2 2 Câu 1. Cho I f
 xdx  3. Khi đó J  4 f
 x3dx  bằng: 0 0 A. 2 . B. 6 . C. 8 . D. 4 . b Câu 2. Biết 2x  
1 dx  1. Khẳng định nào sau đây là đúng? a
A. b a 1. B. 2 2
a b a b 1 . C. 2 2
b a b a 1 .
D. a b 1. Câu 3.
Cho hàm số f x liên tục trên đoạn 0;10 và 10 6 2 10 f
 xdx  7 và f
 xdx 3. Tính P f
 xdxf  xdx. 0 2 0 6
A. P  7 . B. P  4
 . C. P  4 .
D. P  10. 2 5 5 Câu 4. Nếu f
 xdx 3, f xdx  1   thì
f xdx  bằng 1 2 1 A. 2  . B. 2 . C. 3 . D. 4 . Câu 5.
Cho hàm số f x liên tục trên  và F x là nguyên hàm 9
của f x , biết f
 xdx  9 và F0 3. Tính F 9. 0
A. F 9  6
 . B. F 9  6 .
C. F 9  12 .
D. F 9  1  2 . Câu 6.
Cho hàm số f x có f  x liên tục trên đoạn  1  ;  3 , 3 f   1  3 và f (  x)dx 10 
giá trị của f 3 bằng 1  A. 13  . B. 7  . C.13 . D. 7 . 1 2 2 Câu 7. Cho f
 xdx  2, f
 xdx  4, khi đó f xdx   ? 0 1 0 A. 6 . B. 2 . C.1. D. 3 . 2 2 Câu 8. Cho f
 xdx  2 và
g xdx  1   . Tính 1  1  2 I  x  2 f  
x3gxdx  bằng 1  11 7 17 5 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 8 4 4 Câu 9.
Biết f xdx  2   ; f
 xdx 3; g
 xdx  7. Mệnh đề 1 1 1
nào sau đây sai? Trang11 8 4 A. f
 xdx 1. B. f
 x gxdx 10  . 4 1 8 4 C.
f xdx  5   . D. 4 f
 x2gxdx  2   . 4 1 8 4 4 Câu 10.
Biết f xdx  2   ; f
 xdx 3; g
 xdx  7. Mệnh đề 1 1 1
nào sau đây sai? 8 4 A. f
 xdx 1. B. f
 x gxdx 10  . 4 1 8 4 C.
f xdx  5   . D. 4 f
 x2gxdx  2   . 4 1 1 Câu 11.
Cho hàm số f x liên tục trên  và có f
 xdx  2; 0 3 3 f
 xdx  6. Tính I f  xdx . 1 0
A. I  8 . B. I  12 . C. I  36 .
D. I  4 . 1 Câu 12.
Cho hàm số f x liên tục trên  và có f
 xdx  2; 0 3 3 f
 xdx  6. Tính I f  xdx . 1 0
A. I  8 . B. I  12 . C. I  36 .
D. I  4 . Câu 13.
Cho hàm số f x liên tục trên 0;  1 và f  
1  f 0  2 . 1 Tính tích phân f
 xdx. 0 A. I  1
 . B. I 1 . C. I  2 .
D. I  0 . b Câu 14.
Giá trị nào của b để 2x 6dx  0? 1
A. b  0 hoặc b  3 .
B. b  0 hoặc b 1
C. b  5 hoặc b  0 .
D. b 1 hoặc b  5 . 2 2 Câu 15. Cho f
 xdx 3. Tính  f x  1dx ? 0 0 A. 4 . B. 5 . C. 7 . D.1. 2 Câu 16.
Kết quả của tích phân 2x 1sin xdx được viết ở dạng 0  1     1  
a , b  . Khẳng định nào sau đây là sai?  a b
A. a  2b  8 .B. a b  5.
C. 2a 3b  2 .
D. a b  2. Trang12 26 3 Câu 17. Cho
f xd   x k . Tính I  2 2 x . f  3 x  
1 xd theo k ? 0 1 k k A. I
. B. I  2k .C. I  6k .
D. I  2 . 3 3 m Câu 18. Cho  3x K
dx . Định m để K  10 ? ln 3 0
A. m  log 10 .B. m  2 .C. m  11.
D. m  log 11 . 3 3 2
Câu 19. Cho M f (3x  
2)dx . Đặt t  3x  2 ta có: 1 7 1 3
A. M   f(t)dt . B. M  3 f(t)dt . 3 1 1 7 3 1
C. M  3 f(t)dt .
D. M   f(t)dt . 3 1 1 5 12 12
Câu 20. Cho f (x)dx  7; 3 f (x)dx   
57 . Tính K   f (x)dx . 2 2 5 50 64 A. 50 B. . C. 12 . D. . 3 3 2 x 1 a a Câu 21. Biết dx   ln 5 
với a, b   và là phân số tối giản. 2 x  9 b b 2 
Khi đó a b  ? A. 4 . B. 8 . C. 10 . D. 7 . 1 1 Câu 22. Cho f
 xdx  5, gxdx  4   . 2  2  1 Thì I  3 f
  x2gxdx   2  A. 23. B. 2  . C. 7 . D. 13 . 3 2x  3
Câu 23. Tính I dx
ta được I a bln 6 với a , b   . x  4 2 
Lúc đó a b A. 15 . B. 10 . C. 7 . D. 17 .
2x  2 khi x 1 Câu 24. Cho hàm số
f x  ln x . Biết tích phân khi x  1  x 2 f  x 1 2 dx a
ln 2 trong đó a, b   . Tính giá trị S a b . b 0
A. S  3. B. S  5. C. S  3  .
D. S  1. 2 2
Câu 25. Biết  f
 x xdx  6, 3f
 x gxdx 10  . 0 0 Trang13 2
Tính I   2 f x  3g xd . x 0
A. I  12 . B. I 16 . C. I 10 .
D. I 14.
Câu 26. Cho hàm số f x có đạo hàm liên tục trên  và thỏa mãn 1 2
f 2  16 , f
 2xdx  6.Tính I  .xf  
xdx ta được kết quả 0 0
A. I 14. . B. I  20. C. I 10.
D. I  4. 2
Câu 27. Tính tích phân 2
I  2x x 1 dx  , bằng cách đă ̣t 2 t x 1. 1
Mê ̣nh đề nào dưới đây đúng? 2 2 1 A. I t dt  . B. I t dt  . 2 1 1 3 3 C. I  2 t dt  . D. I t dt  . 0 0 7 2 Câu 28. Cho f
 xdx 5. Tính I f 3x   1 dx . 1 0 1 7 5 A. I
. B. I  2 . C. I  . D. I  . 2 3 3 1
Câu 29. Cho tích phân  2 3 x I x
e dx ae b , với a, b   . Mệnh đề 0
nào dưới đây là đúng.
A. ab  3. B. a b  2. C. a  2b 1. D. 3 3
a b  28 . 5 2 Câu 30. Cho f
 xdx 10. Kết quả 24 f  x d  x  bằng: 2 5 A. 32 . B. 34 . C. 36 . D. 40 . 11 2 Câu 31. Biết f
 xdx 18. Tính I x2 f   2 3x   1 d .x  1  0
A. I 10. B. I  5. C. I  7.
D. I  8.
Câu 32. Cho hàm số f (x) có đạo hàm trên đoạn  3  
;1 , f (3)  17 và 1 f (1)  1
 . Tính  3f 'x 2dx. 3 
A. 58 . B. 44 . C. 48. D. 56 .
Câu 33. Cho hàm số y f x có đạo hàm f ' x liên tục trên1;4, 4 f   1  12 và f '
 xdx 17 . Giá trị của f   4 bằng 1
A. 19 . B. 9 . C. 29 . D. 5. 1
Câu 34. Kết quả của tích phân  2 3 x I x
e dx được viết dưới dạng 0
I ae b, với a, b là các số hữu tỉ. Tìm khẳng định đúng trong Trang14 các khẳng định sau.
A. a b  2B. 3 3
a b  28 C. ab  3
D. a  2b 1 b b c
Câu 35. Cho a b c, f
 xdx  5, f
 xdx  2. Tính f xdx  . a c a c c A. f
 xdx  3. B.
f xdx  2   . a a c c C. f
 xdx 1. D. f
 xdx  7. a a 11 2 Câu 36. Biết f
 xdx 18. Tính I x2 f   2 3x   1dx  . 1  0
A. I  5 . B. I  8 . C. I  7 .
D. I 10 . Câu 37. Cho hàm số
f x có đạo hàm f  x liên tục trên  3 1  ;  3 , f   1  3 và f
 xdx 10. Giá trị của f 3 bằng 1  A. -13. B. 13. C. 7. D. -7. 5 3
Câu 38. Cho a, b Z thỏa mãn
dx a ln 5  b ln 2.  Mệnh đề 2 1 x  3x nào sau đây đúng?
A. 2a b  0.
B. a b  0.
C. a b  0.
D. a  2b  0 .
Câu 39. Cho hàm số F x là một nguyên hàm của hàm số f x trên 2 đoạn  1  ;2 . Biết f
 xdx 1 và F  1  1  . Tính F 2. 1 
A. F 2  0 .
B. F 2  3 .
C. F 2  1.
D. F 2  2 . 4 1 0 1 Câu 40. Biết
f xdx   và
f xdx    . Tính tích phân 2 2 1  1  4 2 4e x  2 f  x d  x   . 0 A. 8 4.e . B. 8 2.e . C. 8 2.e  4 . D. 8 4.e  2 . a 2 2 x  2x  2 a
Câu 41. Biết a là số thực dương thỏa mãn dx   a  ln 3  x1 2 0
. Giá trị của a là? A. 3 . B. 5 . C. 2 . D. 4 . Câu 42. Cho hàm số f x liên tục trên  và Trang15 1 1
f 0  2018, f xdx  1  
. Tính I   x  
1.f 'xdx . 0 0 A. I  2018  . B. I  2018. C. I  2017 .
D. I  2019 . 2 2 Câu 43. Biết  f
 x xdx 6  và 3 f
 x gxdx 10  . Tính 0 0 2 I  2 f
 x+3gxdx  . 0
A. I  12 . B. I  16 . C. I 10 .
D. I  14 . 3 3 2
Câu 44. Cho f (x)dx a
, f (x)dx b
. Khi đó f (x)dx  bằng: 0 2 0 A. a  b.
B. b a .
C. a b .
D. a b . 3 3 3
Câu 45. Biết f
 xdx 1 và g
 xdx 3. Khi đó  f
 x gxdx  2 2 2 bằng
A. 4 . B. 2 . C. 2  . D. 3 . m Câu 46. Cho  2
3x  2x  
1 dx  6 . Giá trị của tham số m thuộc 0 khoảng nào sau đây? A.  1  ;2 . B.  ;0
 . C. 0;4 . D.  3   ;1 .
Câu 47. Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;5 5 5
và f 5 10 , xf
 xdx  30. Tính f xdx  . 0 0 A. 20 . B. 30  . C. 20  . D. 70 .
Câu 48. Cho hàm số y f x có đạo hàm liên tục trên đoạn 0; 2 và 2
f 0  f 2  2022. Tính f   xdx . 0 A. 2022 .B. 2022  .C. 1011. D. 4044 . 2 
khi 0  x  1
Câu 49. Cho hàm số y f x   x 1 .
2x 1 khi1 x  3 3 Tính tích phân f x d . x 0 A. 6  ln 2. B. 4  ln 4 . C. 6  ln 4.
D. 2  2 ln 2 . 6 a
Câu 50. Biết 2  xsin 3 d x x  
. Biết a, b nguyên tố cùng nhau khi b 0 Trang16
đó giá trị a bằng A. 3 . B. 4 . C. 5 . D. 6 .
DẠNG 3:ỨNG DỤNG CỦA TÍCH PHÂN
DIỆN TÍCH HÌNH PHẲNG
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x liên tục trên đoạn
a;b, trục hoành và hai đường thẳng x a , x b : Trang17 y
y f (x)
y f x  b    H y 0 :  S f
 xdx x aa b x b O a c c c x 1 2 3  Chú ý: b b Nếu trên đoạn  ;
a b , hàm số f x không đổi dấu thì: f
 x dx f  xdx . a a
Diện tích hình phẳng giới hạn bởi đồ thị hàm số C : y f x , C : y f x 2 2   1 1  
liên tục trên đoạn a;b và hai đường thẳng x a , x b : yC1 
C : y f x 1  1    bC
C : y f x 2  2   2  H : S f
x f
x dx  
1  2   x a a x b O a c c x 1 2 bChú ý:
 Nếu phương trình f x  g x vô nghiệm trên  ; a b thì b b S f
 x gx dx   f
 x gxdxa a
 Nếu phương trình f x  g x có nghiệm x c trên  ; a b thì b c b S f
 x gx dx   f
 x gxdx   f
 x g xdxa a c THỂ TÍCH
Bài toán 1: Gọi B là phần vật thể giới hạn bởi hai mặt phẳng  P và Q cùng vuông góc
với trục Ox tại các điểm a và b ; S x là diện tích thiết diện của vật thể bị cắt bởi mặt
phẳng vuông góc với trục Ox tại điểm x , a x b . Giả sử S x là hàm số liên tục trên đoạn  ; a b . Trang18 P Q S xb
V S x xB  d a a x O b x
Bài toán 2: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y f x ,
y  0 x a , x b ( a b ) quanh trục Ox : y
y f x
y f x   b y  0 
V    f
  x2dxO x x aa x b x a x b
Bài toán 3: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y f x 1  
, y g x , x a , x b (với a b và 0  y y , x   ;
a b ) quanh trục Ox : 2   2 1 y y f x 1    y f x 1     y g x b 2 2 2   y g x 2    V    f
  x  g
  x dx  x a aa bx b O x
BÀI TOÁN CHUYỂN ĐỘNG
Mối liên hệ giữa quãng đường, vận tốc và gia tốc:
Cho một chất điểm chuyển động với quãng đường là một hàm số theo biến số thời gian
t là s t  . Khi đó:
 Vận tốc của chất điểm là vt  st  st  v  tdt .
 Gia tốc của chất điểm là at  vt  vt  a  tdt .
CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hai hàm số y f x , y g x liên tục trên  ;
a b và có đồ thị
C và C tương ứng thì công thức tính diện tích hình phẳng giới hạn bởi 2  1 
C , C và hai đường thẳng x a, x b là 2  1  b b
A. S  g
 x f xdx  . B. S f
 x gx dx. a a Trang19 b b b C. S  g
 x f xdx  . D. S f
 xdxg
 xdx . a a a
Câu 2. Cho hàm số y f x liên tục trên ;
a b . Diện tích hình phẳng giới
hạn bởi đồ thị hàm số, đường thẳng x a , đường thẳng x bb a và trục hoành là b b
A. S   f  xdx . B. S f  xdx. a a b b C. 2 S   f  xdx. D. S f
 x dx. a a
Câu 3. Cho hàm số y f x liên tục trên đoạn  ;
a b. Gọi D là hình phẳng
giới hạn bởi đồ thị C  : y f x, trục hoành, hai đường thẳng x a, x b
(như hình vẽ bên dưới). Giả sử S là diện tích của hình phẳng . D Chọn công D
thức đúng trong các phương án A, B, C, D dưới đây? 0 b A. S f x x f x x   . D  d  d y
y f xa 0 0 b
B. S   f x x f x x   . D  d  d a 0 a O x 0 b C. S f x x f x x   . b D  d  d a 0 0 b
D. S   f x x f x x   . D  d  d a 0
Câu 4. Hình phẳng giới hạn bởi các đường x  1
 , x  2 , y  0 , 2
y x  2x
có diện tích được tính theo công thức: 2 0 2
A. S    2
x  2xdx .
B. S    2
x  2xdx   2
x  2xdx . 1  1  0 0 2 2
C. S    2
x  2xdx   2
x  2xdx . D. 2 S
x  2x dx  . 1  0 0
Câu 5. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x x  2x trên đoạn  1  ; 2 và trục hoành. 37 28 8 9 A. . B. . C. . D. . 12 3 3 4 Câu 6.
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số 3 2
y x  3x và trục hoành. 13 29 27 27 A. S  . B. S  . C. S   . D. S  . 2 4 4 4
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x và các
đường thẳng y  0 , x  1  , x 1 là Trang20 2 4 8 A. . B. 2 . C. . D. . 3 3 3
Câu 8. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 3 y x  ; x y  2x
và các đường x  1; x  1 được xác định bởi công thức. 1 1
A. S    3
3x x dx . B. S    3 3x x d . x 1 1  0 1 0 1
C. S    3
x  3xdx   3 3x x d .
x D. S    3
3x x dx   3 x  3xd . x 1  0 1  0
Câu 9. Tính diện tích của hình phẳng  H  giới hạn bởi các đường y x ,
y  6  x và trục hoành. 20 25 16 22 A. . B. . C. . D. . 3 3 3 3
Câu 10. Diện tích hình phẳng giới hạn bởi các đường y  2x , y  4  x và trục
Ox được tính bởi công thức: 4 4 2 4 A. 2xdx  
4 xdx. B. 2xdx  
4 xdx. 0 0 0 2 4 2
C.  2x  4  xdx . D. 4  x  2x dx. 0 0
Câu 11. Diện tích hình phẳng giới hạn bởi các đường 2 y x và 2
y  2 – x là: 1 1 1 1 A.   2
1 x dx . B.  2
1 x dx . C.  2 x  
1dx. D.  2x   1dx. 1  0 1  0
Câu 12. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol P 2
: y  2x và đường thẳng d : y x quay xung quanh trục Ox được tính bởi
công thức nào dưới đây? 1 1 1 2 2 2 A. 2 4
V   x dx  4 x dx  
. B. V    2
x  2x dx . 0 0 0 1 1 1 2 2 2 2
C. V    2
2x x dx . D. 2 4
V   x dx    x dx   . 0 0 0 Câu 13.
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol P 2
: y x và đường thẳng d  : y x quay xung quanh trục Ox bằng: 1 1 1 1 A. 2 4
x dx  x dx   . B. 2 4
x dx  x dx   . 0 0 0 0 1 1 2 C.   2
x x dx . D.   2
x x dx . 0 0 Câu 14.
Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi đồ thị hàm số 2
y x và các đường thẳng y  0 , x 1, x  2 xung Trang21 quanh trục hoành là 7 31 7 31 A. V  . B. V  . C. V  . D. V  . 3 5 3 5 Câu 15.
Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị các hàm số 2
y x  2x và 2
y  x quay quanh trục Ox . 4 4  1 A. . B. . C. . D. . 3 3 3 3 Câu 16.
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol P 2
: y x và đường thẳng d : y  2x quay xung quanh trục Ox bằng 2 2 2 A.   2
x  2x dx . B.   2
2x x dx . 0 0 2 2 2 2 C. 2 4
 4x dx  x dx   . D. 2 4
 4x dx  x dx   . 0 0 0 0
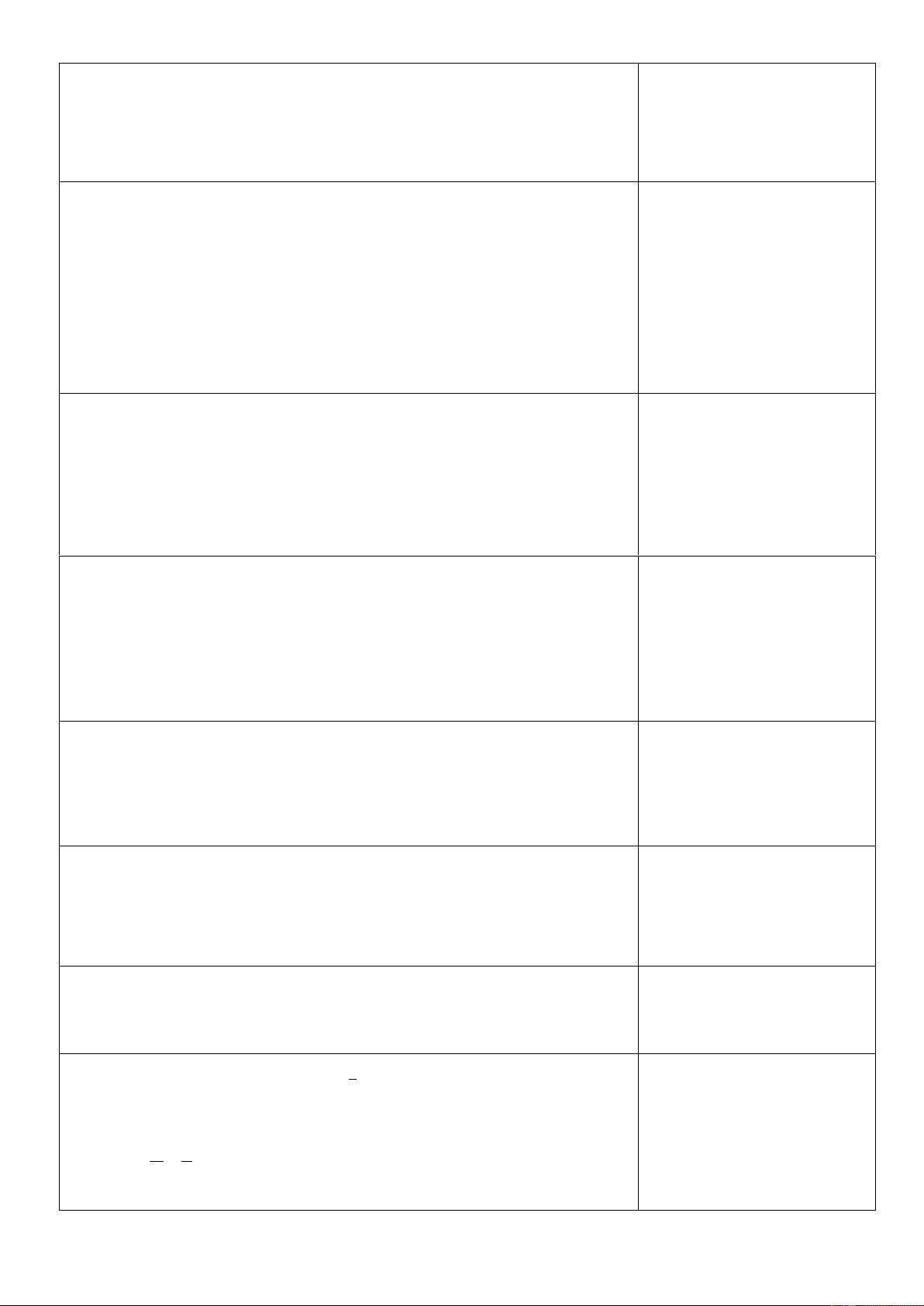
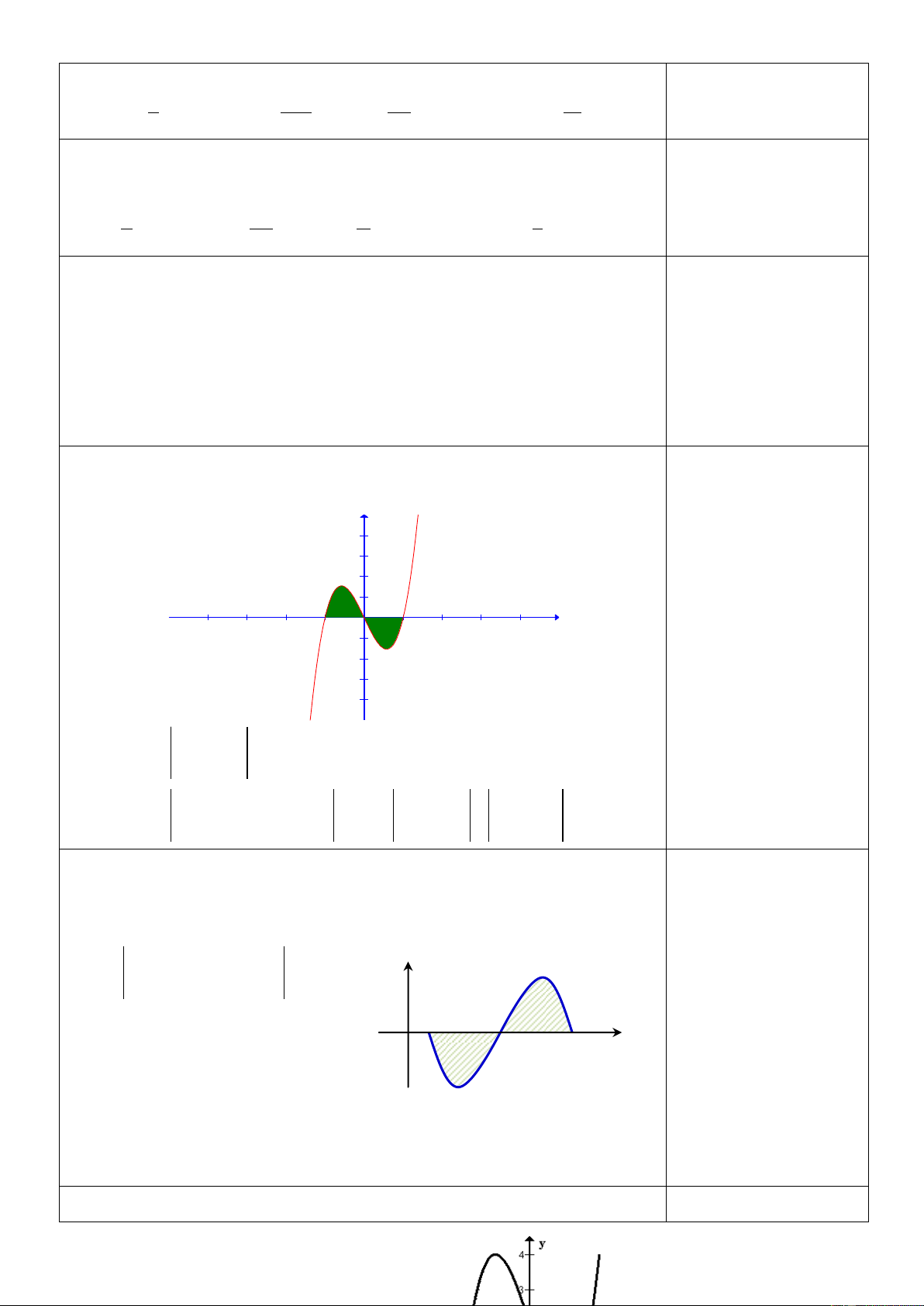
Câu 17. Cho đồ thị hàm số y f x . Diện tích hình phẳng (phần tô đậm trong hình dưới) là y 8 6 4 2 x -8 -6 -4 -2 2 4 6 8 -2 -4 -6 -8 2 0 2 A. f
 xdx . B. f
 xdxf  xdx. 2 2  0 0 2 0 2 C. f
 xdxf
 xdx . D. f
 xdx f
 xdx . 2  0 2  0
Câu 18. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x
, trục hoành, đường thẳng x a , x b (như hình bên dưới). Hỏi cách tính S nào dưới đây đúng? c b A. S f
 xdxf  xdx . y a c c b B. S f
 xdxf  xd .x O a c b x a c c b
y f x
C. S   f
 xdxf  xdx . a c b D. S f
 xd .x a
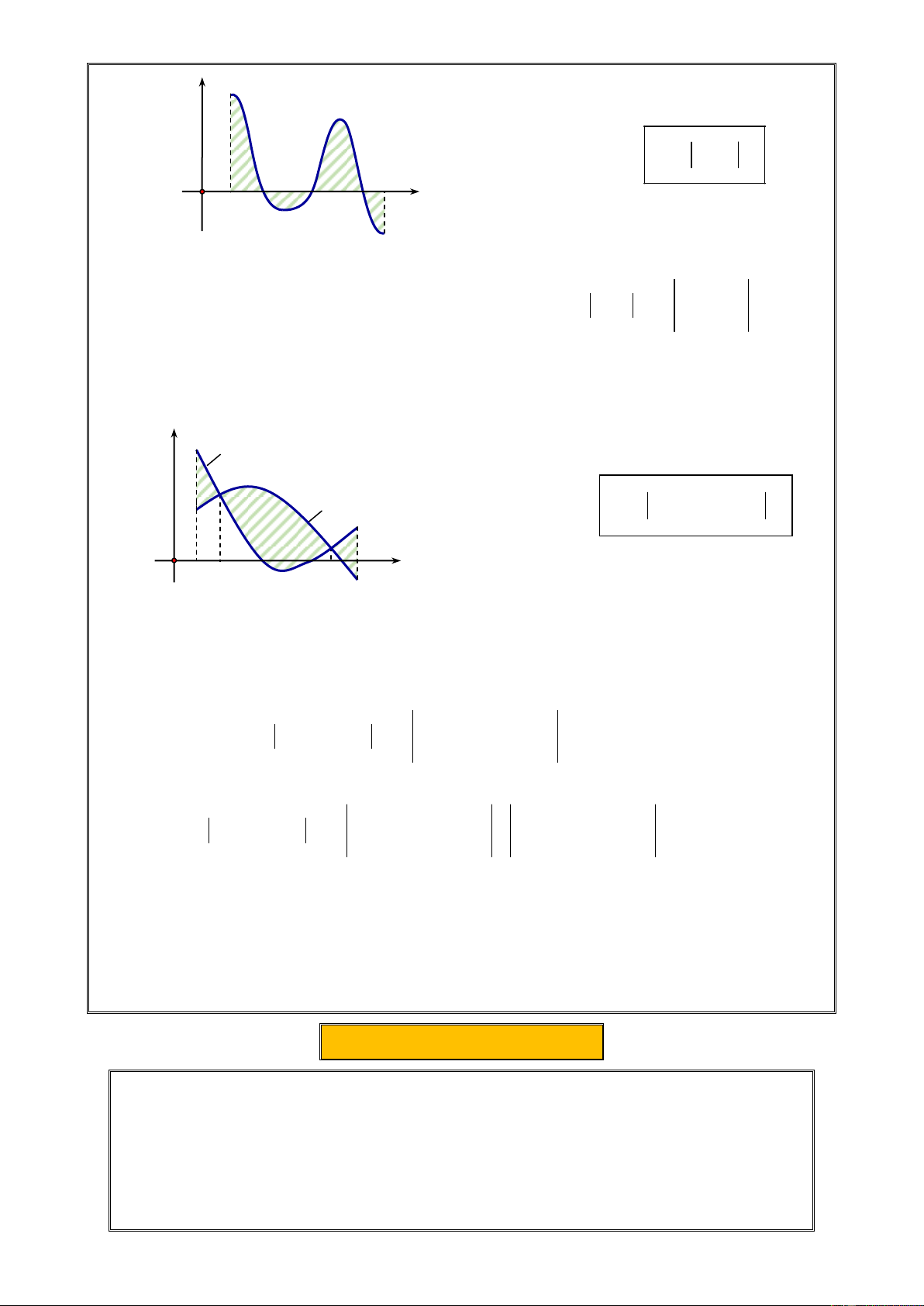
Câu 19. Tính diện tích S của phần hình phẳng gạch sọc (bên dưới) giới hạn Trang22
bởi đồ thị hàm số bậc ba 3 2
y ax bx cx d và trục hoành 31 A. S   . 5 27 B. S  . 4 19 C. . 3 31 D. . 5
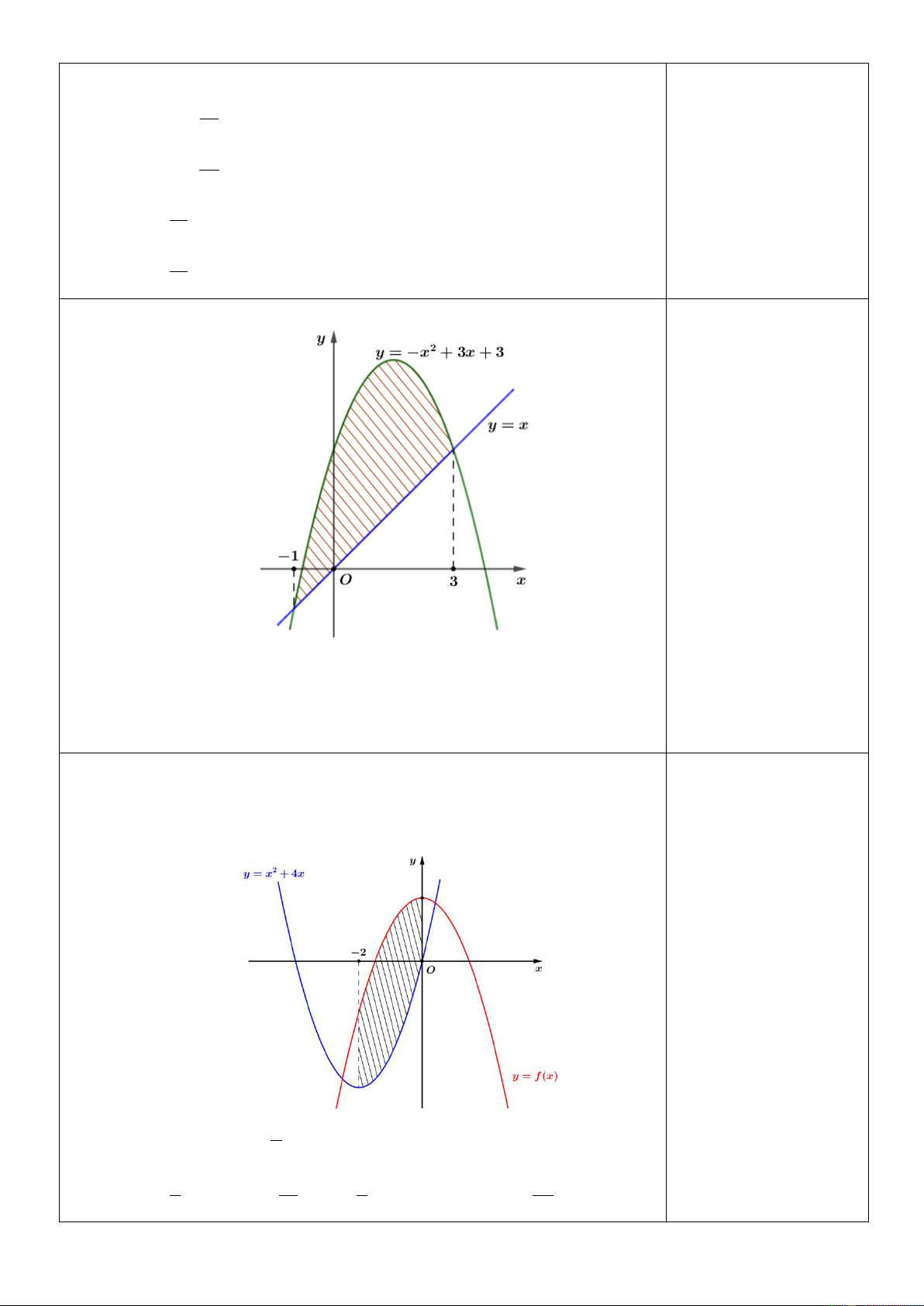
Câu 20. Diện tích hình phẳng (phần gạch sọc) trong hình sau bằng 3 3
A. S    2
x  2x  3dx .B. S    2x 2x 3dx . 1  1  3 3
C. S    2
x  2x 3dx .D. S    2
x  4x  3dx . 1  1 
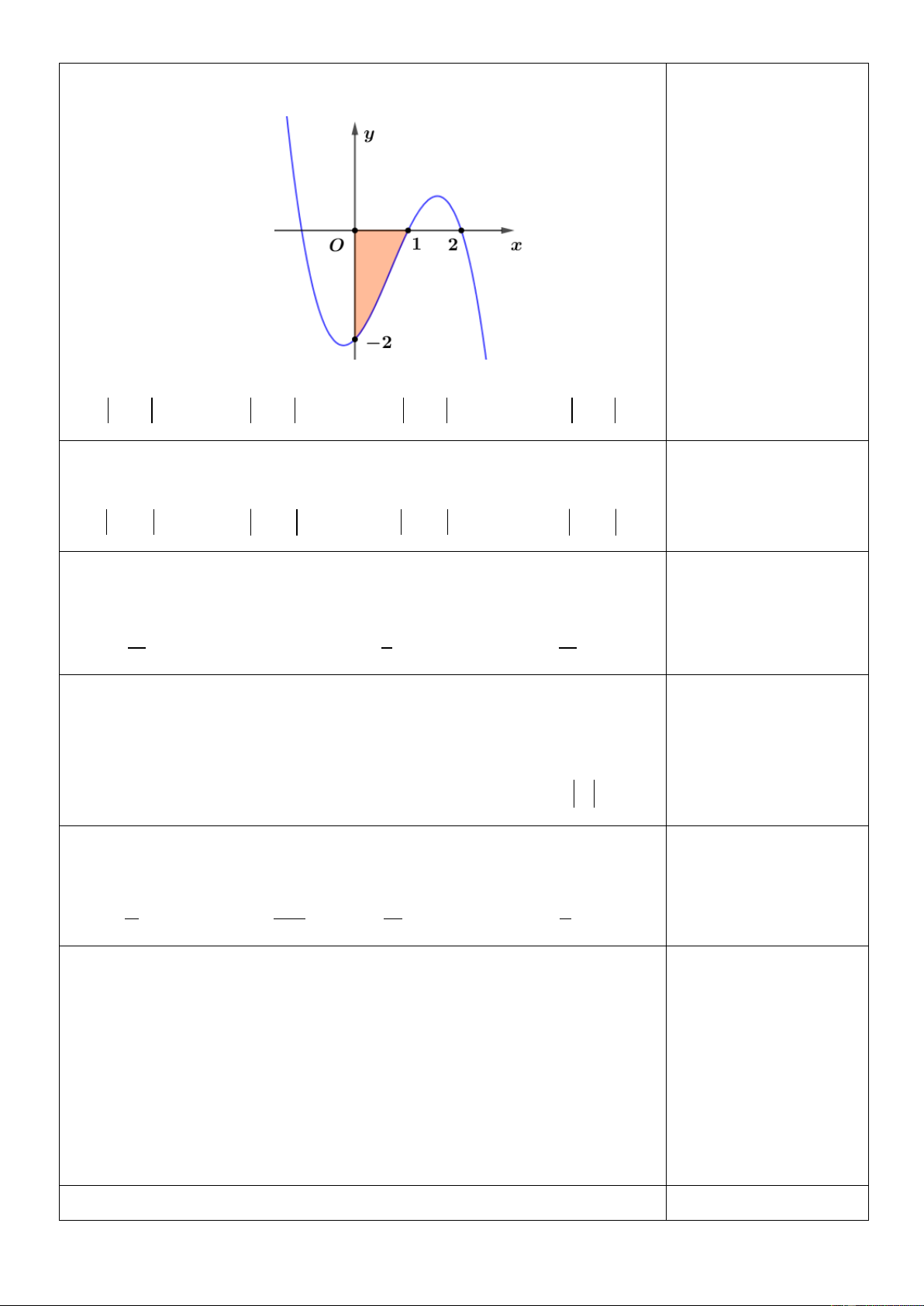
Câu 21. Phần hình phẳng  H  được gạch chéo trong hình vẽ dưới đây được
giới hạn bởi đồ thị hàm số y f x , 2
y x  4x và hai đường thẳng x  2  , x  0 . 0 Biết f x 4 dx  
, diện tích hình phẳng H  là 3 2  7 16 4 20 A. . B. . C. . D. . 3 3 3 3 Trang23
Câu 22. Cho hàm số y f x có đồ thị như hình vẽ. Diện tích phần tô đậm bằng 1 1 2 0 A. f
 x dx. B. f x dx  . C.
f x dx  . D. f
 x dx. 2  0 0 1 
Câu 23. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số 2
y x ,
y x và các đường thẳng x  0 , x 1 bằng 0 1 0 1 A. 2  d
x x x. B. 2  d
x x x . C. 2  d  x x x . D. 2  d  x x x . 1 0 1 0
Câu 24.Diện tích S của hình phẳng giới hạn bởi các đường 2
y x  5x , 2
y x x , x 1 và x  2 bằng 13 7 14 A. S  . B. S  9 . C. S  . D. S  . 3 3 3
Câu 25.Cho hình phẳng giới hạn các đường  5x y
, y  0, x  2  và x  2 .
Thể tích khối tròn xoay tạo thành do hình phẳng D quay quanh trục hoành
được tính theo công thức nào dưới đây? 2 2 2 2 A. 2  5 x V dx  . B.   25x V dx  . C.   5x V dx  . D.  5x V dx  . 2  2  2  2 
Câu 26.Hình phẳng giới hạn bởi đường cong 2
y  1 x và Ox khi quay quanh
Oy tạo thành vật thể có thể tích là  16 16 1 A. V  . B. V  . C.V  . D.V  . 2 15 15 2
Câu 27.Thể tích của khối tròn xoay do đồ thị giới hạn bởi đồ thị của hàm số
y f (x) liên tục và không âm trên đoạn 1; 
3 , trục Ox và hai đường thẳng
x  1, x  3 quay quanh trục Ox được tính theo công thức: 3 3 2 A. V   f (x)d . x
B. V   f (x) d .x 1 1 3 3 2 C. V f (x)d . x
D. V    f (x) d .x 1 1
Câu 28.Cho hàm số y f x liên tục trên  . Gọi S là diện tích hình phẳng Trang24
giới hạn bởi đồ thị hàm số
y f x , trục hoành và hai đường thẳng x  1
 , x  4 (như hình vẽ bên dưới). Mệnh đề nào dưới đây đúng. 1 4 1 4 A. S f
 xdxf
 xd .xB. S   f
 xdxf  xd .x 1  1 1  1 1 4 1 4
C. S   f
 xdxf
 xd .xD. S f
 xdxf  xd .x 1  1 1  1
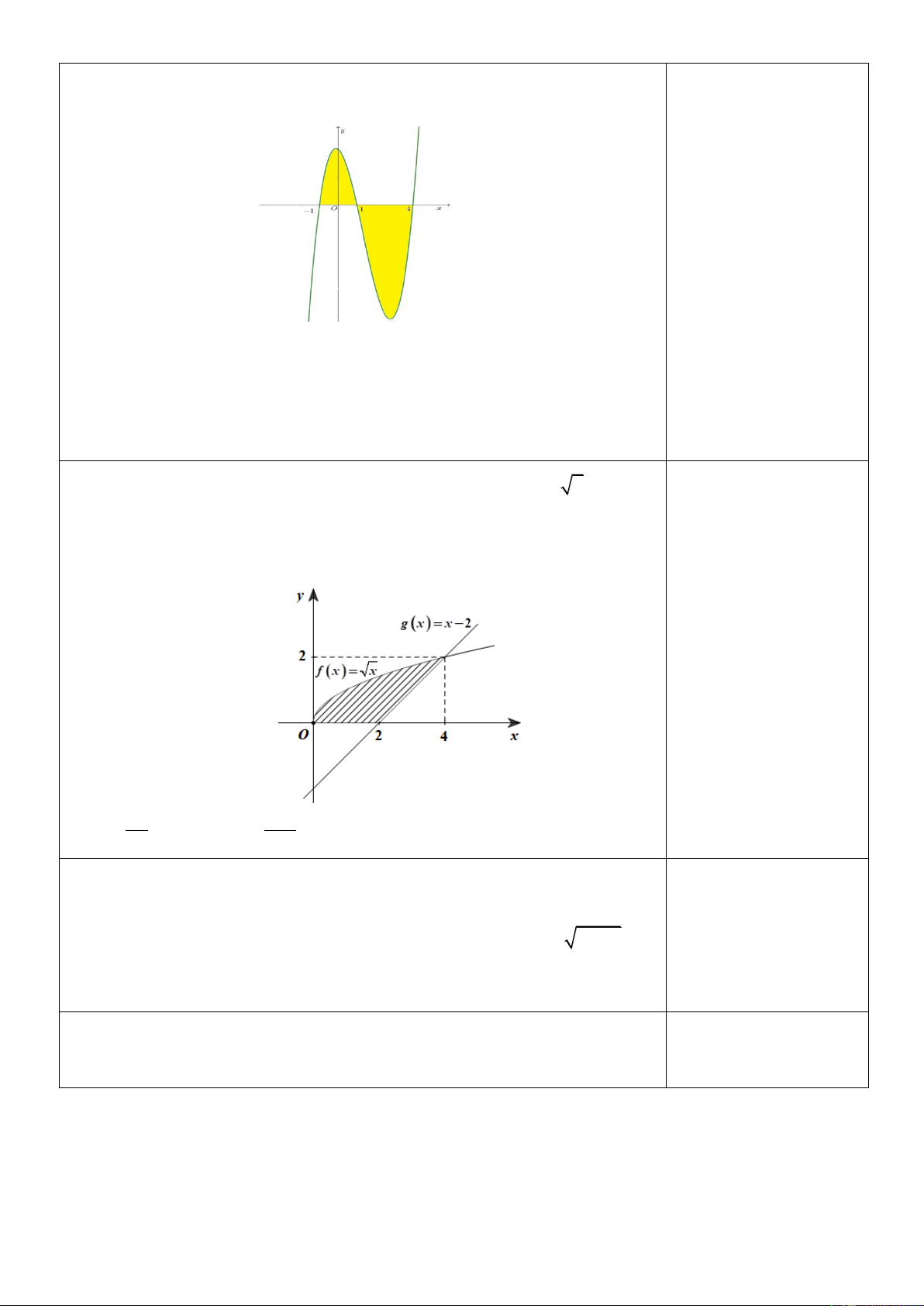
Câu 29.Cho hình phẳng  H  giới hạn bởi các đường y f x  x ,
y g x  x  2 và trục hoành (như hình vẽ bên dưới). Tính thể tích V của
khối tròn xoay tạo thành khi quay hình  H  quanh trục hoành. 8 16 A. V  . B. V  . C.V  8 .
D.V 10 . 3 3
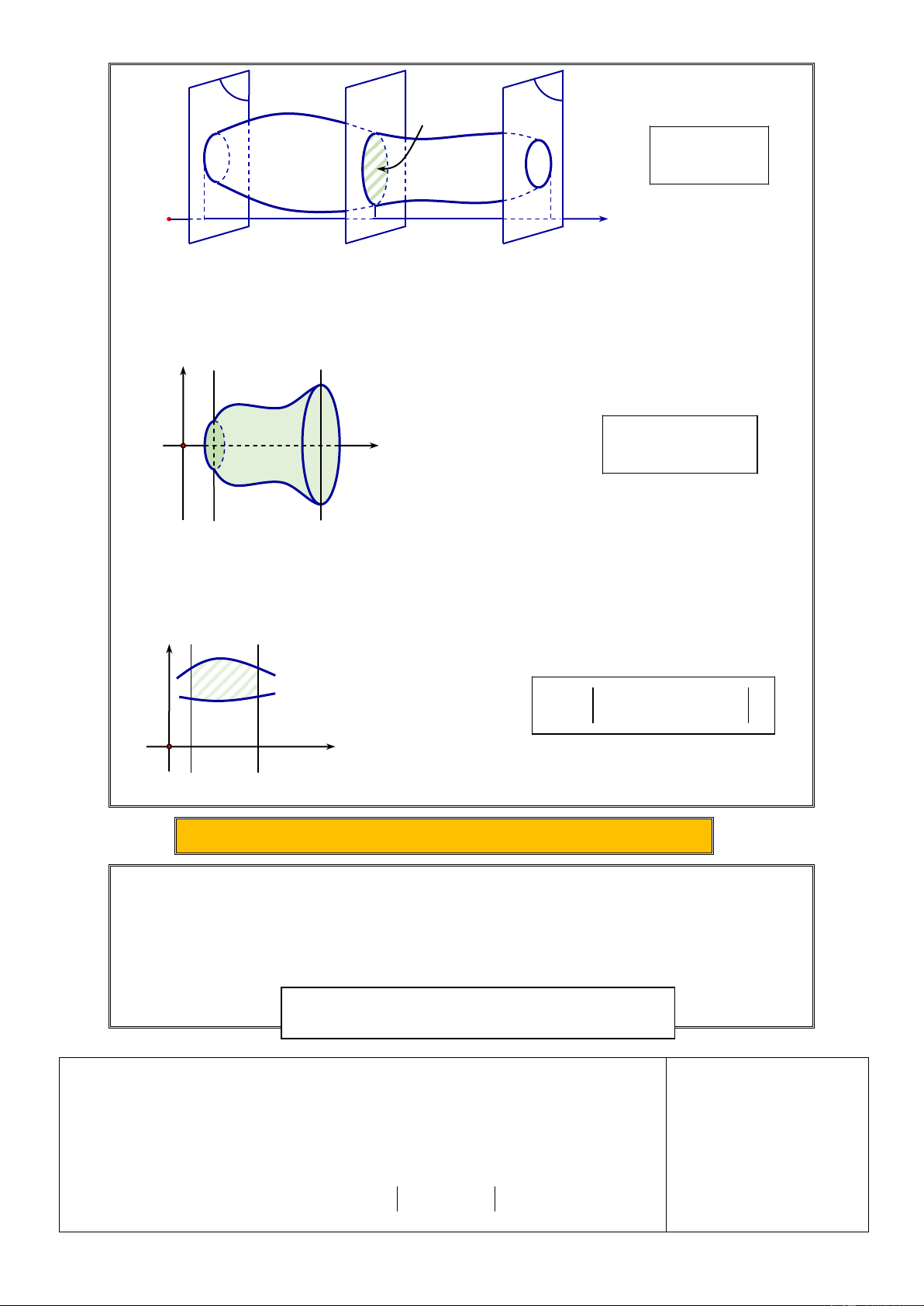
Câu 30.Trong không gian Oxyz , cho vật thể nằm giữa hai mặt phẳng x  0 và
x  3. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục
Ox tại điểm có hoành độ x 0  x  3 là một hình vuông cạnh là 2 9  x .
Tính thể tích V của vật thể.
A. V 18 . B. V 171. C.V 171 .
D.V  18.
Câu 31. Diện tích S của hình phẳng giới hạn bởi các đường
y f x, y  0, x  2
 và x 1 (phần tô đậm trong hình bên) được tính bởi
công thức nào dưới đây? Trang25 1  1 1  1 A. S   f
 xdxf
 xdx . B. S   f
 xdxf  xdx. 2  1  2  1  1  1 1  1 C. S f
 xdxf
 xdx. D.S f
 xdxf  xdx. 2  1  2  1 
Câu 32. Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số 2
y  3x  6x,
trục hoành và hai đường thẳng x  2; x  0 bằng
A. 4 . B. 20 . C. 20 . D. 4 .
Câu 33.Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số 2
y x , y x
và các đường thẳng x  0, x  1 bằng 1 0 1 0 A. 2 x x dx  . B. 2 x x dx  . C. 2 x x dx  . D. 2 x x dx  . 0 1  0 1 
Câu 34.Cho hình phẳng D giới hạn bởi đồ thị hàm số y  6x và các đường
thẳng y  0, x  1, x  2 . Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành bằng 2 2 2 1 A.  6 d x x  . B. 2  6x dx  . C. 2  6x dx  . D. 2  6x dx  . 1 1 0 0
Câu 35.Cho hàm số y f x có đồ thị như hình vẽ. Diện tích phần tô đậm bằng y O 1 2 x -2 Trang26 1 1 2 0 A. f
 xdx . B. f xdx  . C.
f xdx  . D. f
 xdx . 2  0 0 2 
Câu 36.Thể tích của khối tròn xoay khi quay hình phẳng được giới hạn bởi đồ
thị hàm số y  2x 1, y  0, x  0, x  3 quanh trục hoành bằng
A. 21.B. 6 . C. 6. D. 21.
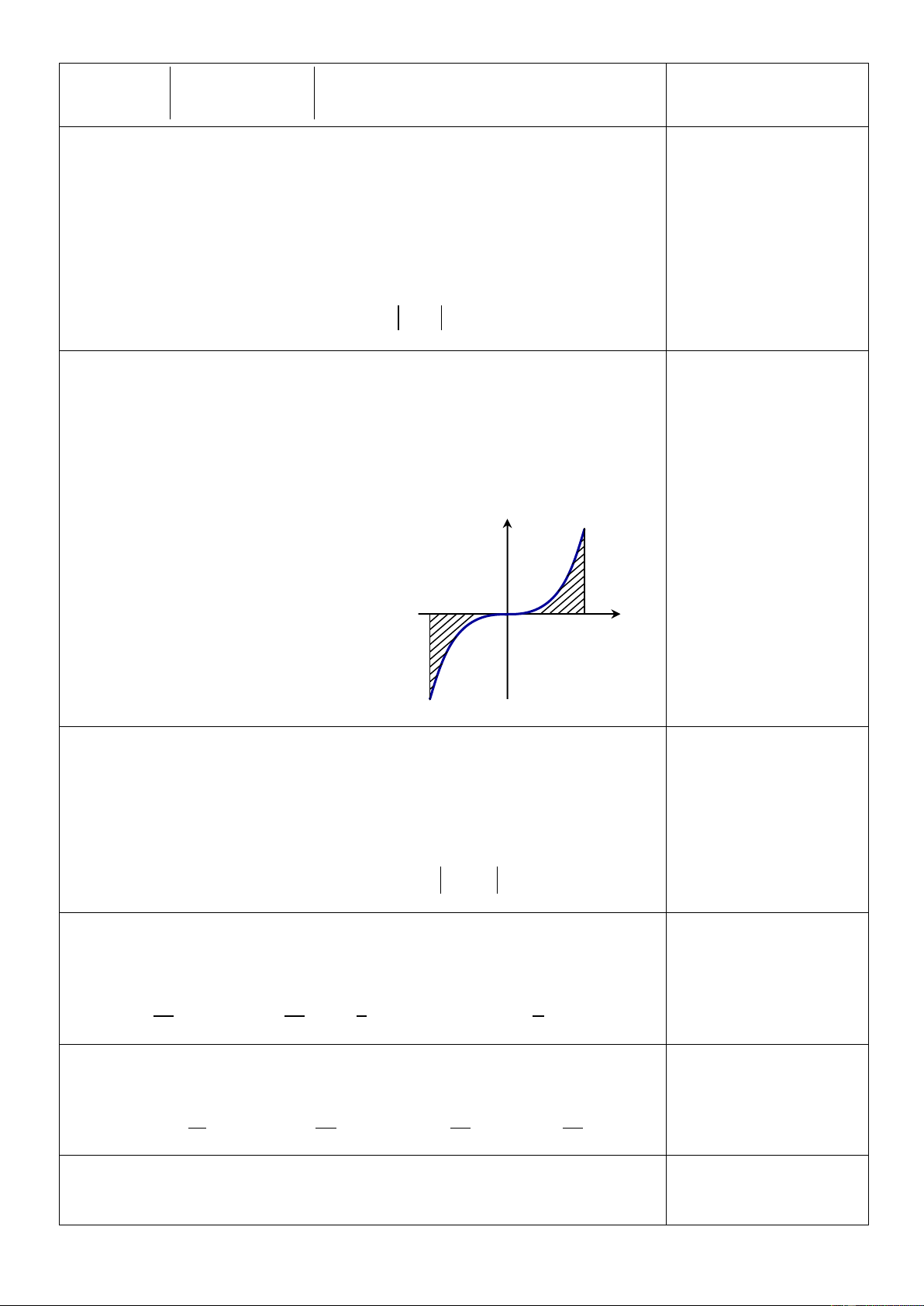
Câu 37. Diện tích S của hình phẳng được tô đậm trong hình bên dưới bằng 1 4 1 4
A. S   f
 xdxf
 xd .x B. S f
 xdxf
 xd .x 1  1 1  1 1 4 1 4 C. S f
 xdxf
 xd .x
D. S   f
 xdxf
 xd .x 1  1 1  1
Câu 38.Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới
hạn bởi các đường y f x, y  0, x 1, x  2 (như hình vẽ). Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S f
 xdxf
 xdx . B. f
 xdxf  xdx. 1  1 1  1 2 2 C. f  xdx. D. f
 xdx. 1  1 
Câu 39. Cho đồ thị hàm số y f x như hình vẽ.
Diện tích S của hình phẳng được giới hạn bởi đồ thị hàm số y f x và trục Trang27
Ox ( phần in đậm) được tính bởi công thức 1 3 1 3 A. S f
 x dxf
 x dx. B. S f
 x dxf
 x dx . 3  1 3  1 3 3 C. S f  x dx. D. S f
 x dx . 3  3 
Câu 40. Cho hàm số y f x liên tục trên đoạn  3  ; 
3 . Hình phẳng  H
giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng 0 3
x  3, x  3 được cho như hình vẽ dưới. Biết f
 xdx a, f
 xdx b. 3  0
Diện tích của hình phẳng  H  bằng
A. a b . B. b a . C. a  b.
D. a b .
Câu41.Cho hình phẳng giới hạn bởi các đường 2 y  2x , 2
y  4x quay xung
quanh trục Ox . Thể tích của khối tròn xoay tạo thành bằng 6 9 4 88 A. V  .B. V  .C. V  . D. V  . 5 70 3 5
Câu42. Diện tích phần gạch chéo trong hình bên dưới được tính theo công thức Trang28 0 b 0 b A.
f x dx  
f xdx . B. f xdx 
f xdx . a 0 a 0 0 b 0 b C.
f x dx  
f xdx . D. f xdx 
f xdx . a 0 a 0
Câu43. Một chất điểm chuyển động trên trục Ox với vận tốc thay đổi theo
thời gian v t  2
 3t  6t (m/s). Tính quãng đường chất điểm đó đi được từ thời
điểm t  0 (s), t  4 (s). 1 2 A. 16. B. 24. C. 8. D. 12.
Câu44.Bạn An ngồi trên máy bay đi du lịch thế giới vận tốc chuyển động của
máy bay là v t  2
 3t  5m/s. Quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 là
A. 996 m . B. 876 m . C. 966 m . D. 1086 m .
Câu45.Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi
công thức v t  5t 1, thời gian tính theo đơn vị giây, quãng đường vật đi
được tính theo đơn vị mét. Quãng đường vật đó đi được trong 10 giây đầu tiên là:
A. 15 m . B. 620 m . C. 51 m . D. 260 m .
Câu46.Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc
v t  7t m/s . Đi được 5s , người lái xe phát hiện chướng ngại vật và 1    
phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a    2
70 m/s . Tính quãng đường S m đi được của ô tô từ lúc bắt đầu
chuyển bánh cho đến khi dừng hẳn.
A. S  95, 70m .
B. S  96, 25m .
C. S  87,50m .
D. S  94, 00m .
Câu47.Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh. Từ thời
điểm đó ô tô chuyển động chậm dần đều với vận tốc vt 10 5t m/s với t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng
đường đi được của ô tô từ lúc đạp phanh đến khi dừng hẳn. Trang29 A. 10 m . B. 20 m . C. 2 m . D. 0, 2 m .
Câu48.Giả sử một vật từ trạng thái nghỉ khi t  0 s chuyển động thẳng với
vận tốc vt  t 5 t m/s . Tìm quảng đường vật đi được cho tới khi nó dừng lại. A. 20,8 m . B. 20,83 m . 125 C. m . D. 20,83333 m . 6
Câu49.Một vật chuyển động theo quy luật 3 2 s t
  6t , với t (giây) là khoảng
thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi
được trong thời gian đó. Kể từ lúc bắt đầu chuyển động đến lúc vận tốc đạt giá
trị lớn nhất thì quãng đường vật đi được là bao nhiêu? A. 12 m . B. 16 m . C. 20 m . D. 24 m .
Câu50.Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi
công thức vt  3t  2 , thời gian tính theo đơn vị giây, quãng đường vật đi
được tính theo đơn vị mét. Biết tại thời điểm t  2s thì vật đi được quãng
đường là10 m.Hỏi tại thời điểm t  30s thì vật đi được quãng đường là bao nhiêu? A . 240 m. B. 1140 m. C . 300 m. D . 1410 m. Trang30