166 bài toán cực trị hàm số bậc ba trong các đề thi thử THPT môn Toán

166 bài toán cực trị hàm số bậc ba trong các đề thi thử THPT môn Toán được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

“Nơi nào có ý chí, nơi đó có con đường.”

Ngày đã rạng, bình minh đang tỉnh giấc!

“Khi nào em cảm thấy muốn phê phán và chê bai một ai đó,

hãy nhớ rằng không phải ai trên thế giới này cũng có những

thuận lợi trong cuộc sống mà em có được."

166

BÀI TOÁN CỰC TRỊ

HÀM SỐ BẬC BA

TRONG CÁC ĐỀ THI THỬ 17-21

Họ và Tên học sinh: ………………………………..................

Trường:…………………………………………. Lớp: ……….

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 1: (Câu 25 - Chuyên Hạ Long - Quảng Ninh - Lần 1 - Năm 2020 - 2021) Tìm tất cả các giá trị

của tham số

để hàm số

32y x x mx    

có cực đại và cực tiểu?

Ⓐ.

3m 

. Ⓑ.

3m 

. Ⓒ.

3m 

. Ⓓ.

3m 

Lời giải

Chọn B



 

' 3 6 1y x x m   

Để hàm số có cực đại, cực tiểu thì phương trình

 

có

nghiệm phân biệt

0 9 3 0 3mm



        

Câu 2: (Câu 37 - Chuyên Thoại Ngọc Hầu - An Giang - Đề A - Năm 2020 - 2021) Tìm tất cả các giá

trị thực của tham số

để hàm số

 

3 2 2

1 4 3 1

y x m x m m x      

có hai điểm cực trị.

Ⓐ.

51m   

. Ⓑ.

15m

. Ⓒ.

51m  

. Ⓓ.

15m  

Lời giải

Chọn B

 

2 2 1 4 3y x m x m m



     

Hàm số có hai điểm cực trị



phương trình





có hai nghiệm phân biệt

 

2 2 1 4 3 0x m x m m      

có hai nghiệm phân biệt

 

0 1 2 4 3 0 6 5 0 1 5m m m m m m



               

Vậy

15m

thỏa yêu cầu bài toán.

Câu 3: (Câu 32 - THPT Lương Thế Vinh - Hà Nội - Lần 01 - Năm 2020 - 2021) Tất cả các giá trị của

tham số

để hàm số

y mx mx    

có hai điểm cực trị là

Ⓐ.











. Ⓑ.

02m

. Ⓒ.

2m 

. Ⓓ.

0m 

Lời giải

Chọn A

Ta có

22y x mx m



   

Hàm số đã cho có hai điểm cực trị khi và chỉ khi phương trình





có 2 nghiệm phân biệt



Phương trình

2 2 0x mx m   

có 2 nghiệm phân biệt









    







Câu 4: (Câu 6 - THPT Yên Phong 1 - Bắc Ninh - Lần 1 - Năm 2020 - 2021) Tất cả các giá trị của

tham số

để hàm số

   

3 1 3 3 7 1y x m x m x     

có cực trị là

Ⓐ.











. Ⓑ.











. Ⓒ.











. Ⓓ.

23m  

Lời giải

Chọn A

Ta có

       

3 2 2

3 1 3 3 7 1 ' 3 6 1 3 3 7y x m x m x y x m x m           

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Để hàm số

   

3 1 3 3 7 1y x m x m x     

có cực trị thì

'0y 

có 2 nghiệm phân biệt

' 0 9 9 54 0





       







Câu 5: (Câu 45 - Chuyên Lê Qúy Đôn - Bà Rịa Vũng Tàu - Lần 1 - Năm 2020 - 2021) Tìm số giá trị

nguyên của tham số

để hàm số

 

2 3 2

1 3 1

y m x mx x    

có cực đại

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

 

1 2 3y m x mx



   

Trường hợp 1.

1m 

ta có

23yx





Xét dấu



1m

loại

Trường hợp 2.

1m 

ta có

23yx



  



  

1m  

thỏa mãn

1m 

Hàm số có cực đại



phương trình





có hai nghiệm phân biệt



  

 

3 1 0mm   

3 2 0

mm      

Vì

m

nên

 

1;0;1m

kết hợp với điều kiện ta được

0m 

Vậy có 2 giá trị nguyên của

thỏa mãn bài toán.

Câu 6: (Câu 10 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Biết

 

0;2M

 

2; 2N 

là các điểm cực trị

của đồ thị hàm số

y ax bx cx d   

. Tính giá trị của hàm số tại

2x 

Ⓐ.

 

22y 

. Ⓑ.

 

2 22y 

. Ⓒ.

 

26y 

. Ⓓ.

 

2 18y   

Lời giải

Chọn D

Ta có:

32y ax bx c



  

Vì

 

0;2M

 

2; 2N 

là các điểm cực trị của đồ thị hàm số nên:

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

 

12 4 0

a b c

















  











 

8 4 2 2

a b c d















    









Từ

 

và

 

suy ra:

 

3 2 2 18

y x x y











       











Câu 7: (Câu 2 - THPT Lý Thái Tổ - Bắc Ninh - Lần 2 - Năm 2020 - 2021) Tìm tất cả các giá trị của

tham số

để hàm số

y x mx x   

đạt cực trị tại

,xx

thỏa mãn

1 2 1 2

3x x x x  

Ⓐ.

4m

. Ⓑ.

2m

Ⓒ.

3m 

. Ⓓ. Không có giá trị

Lời giải

Chọn D

Ta có:

1y x mx



  

Để hàm số đạt cực trị tại

,xx

thì phương trình





có hai nghiệm phân biệt

   

0 4 0 ; 2 2;mm           

 

Khi đó, phương trình

 

có hai nghiệm

,xx

theo hệ thức viet

x x m











Theo bài ra ta có:

 

1 2 1 2

3 1 3 2 2x x x x m m       

Từ

 

và

 

suy ra không có giá trị

nào thỏa mãn yêu cầu bài toán

Câu 8: (Câu 40 - THPT Ngô Gia Tự - Vĩnh Phúc - Năm 2020 - 2021) Biết

là giá trị tham số

để hàm số

31y x x mx   

có hai điểm cực trị

,xx

sao cho

1 2 1 2

13x x x x  

. Mệnh đề

nào sau đây đúng?

Ⓐ.

 

7; 1m   

. Ⓑ.

 

7;10m 

. Ⓒ.

 

1;7m 

. Ⓓ.

 

15; 7m   

Lời giải

Chọn D

Để hàm số có 2 điểm cực trị thì





có 2 nghiệm phân biệt.

3 6 0x x m   

có 2 nghiệm phân biệt

36 12 0 3mm      

Theo bài ra:

1 2 1 2

13x x x x  

 

1 2 1 2

3 13 *x x x x   

Mà theo định lý Viét ta có















thay vào

ta được:

4 3. 13 9

m    

(

/tm

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 9: (Câu 41 - THPT Kim Liên - Hà Nội - Lần 1 - Năm 2020 - 2021) Biết

là giá trị của tham số

để hàm số

31y x x mx   

có hai điểm cực trị

,xx

sao cho

1 2 1 2

10x x x x  

. Mệnh

đề nào dưới đây là đúng?

Ⓐ.

( 15; 7)m   

. Ⓑ.

( 1;7)m 

. Ⓒ.

( 7; 1)m   

. Ⓓ.

(7;10)m 

Lời giải

Chọn C

Ta có:

3 6 0 3 6 0y x x m y x x m



        

(1)

Để hàm số có hai điểm cực trị thì phương trình

(1)

có hai nghiệm phân biệt

,xx

Điều kiện

0 9 3 0 3mm



      

Theo Viet















(*)

Theo bài ra

2 2 2

1 2 1 2 1 2 1 2

10 ( ) 3 10x x x x x x x x      

(**)

Từ

(*)

và

(**)

ta được

4 10 6mm    

thoả mãn điều kiện.

Vậy

6 ( 7; 1)m     

Câu 10: (Câu 36 - SGD Phú Thọ - Lần 1 - Năm 2020 - 2021) Biết hàm số

2 3 2

1 3 5 1y m x m x x

có hai điểm cực trị

,xx

thỏa mãn

. Khẳng

định nào sau đây là đúng?

Ⓐ.

5; 2m

. Ⓑ.

4;5m

. Ⓒ.

1;1m

. Ⓓ.

3;7m

Lời giải

Chọn C

Ta có :

3 1 6 5 1y m x m

Có ac<0 nên hàm số đã cho luôn có 2 điểm cực trị

8xx

1 1 2 2

2 . 64x x x x

1 2 1 2 1 2

2 2 64x x x x x x

64xx

4 1 0

4 9 0

1 17

Câu 11: (Câu 44 - SGD Thái Nguyên - Lần 1 - Năm 2020 - 2021) Có bao nhiêu giá trị thực của tham

số

để hàm số

 

3 2 2

3 2 2 3 1 2

y x m x m m x      

có điểm cực đại

CĐ

và điểm cực

tiểu

thoả mãn

CCĐ T

xx

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ⓐ. 2. Ⓑ. 1. Ⓒ. 3. Ⓓ. 4.

Lời giải

Chọn A

 Tập xác định:

D 

Ta có:

 

3 2 2 3 1y x m x m m



     

. Cho















Hàm số đã cho có điểm cực đại và điểm cực tiểu

1 2 1 0m m m     

 Trường hợp 1:

1 2 1 0m m m    

Khi đó:

CĐ

xm

CCĐ T

xx

   

3 1 4 2 1mm   

3 2 1 0mm   

 















 Trường hợp 2:

2 1 1 0m m m    

Khi đó

CĐ

xm

CCĐ T

xx

   

3 2 1 4 1mm   

12 8 1 0mm   

 





















Vậy có 2 giá trị của

thoả yêu cầu bài toán.

Câu 12: (Câu 33 - Chuyên Ngữ - Hà Nội - lần 1 - Năm 2020 - 2021) Hàm số

31y x x mx   

có

hai điểm cực trị

,xx

thỏa

3xx

khi

Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

2m 

. Ⓓ.

1m 

Lời giải

Chọn B

Hàm số

31y x x mx   

Tập xác định

D 

 

3 6 , 3, 6, , 36 12y x x m a b c m m



         

Để hàm số có hai điểm cực trị

,xx

thì

03m   

Theo đề bài

 

1 2 1 2 1 2

3 2 3 4 3

x x x x x x m m          

. (nhận)

Câu 13: (Câu 17 - Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - Lần 1 - Năm 2020 - 2021) Cho hàm

số

 

3 2 2

2 4 3 6 9

y x m x m m x m       

. Tìm giá trị của tham số

để đồ thị hàm số

 

có cực đại tại

, đạt cực tiểu tại

sao cho

2xx

Ⓐ.

4m 

. Ⓑ.

2m 

. Ⓒ.











. Ⓓ.

5m 

Lời giải

Chọn D

Tập xác định

D 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 

2 2 4 3y x m x m m



     

Hàm số đạt cực đại tại

, đạt cực tiểu tại

khi và chỉ khi

 

0 2 4 3 0 1 0m m m



         

, m















Theo đề bài ta có:

   

2 1 2 3 5 0

x x m m m





        









Câu 14: (Câu 5 - Chuyên Khoa Học Tự Nhiên - Lần 1 - Năm 2020 - 2021) Cho hàm số

3 2 2

8y x mx m x   

. Có bao nhiêu giá trị m nguyên để hàm số có điểm cực tiểu nằm hoàn toàn

phía trên trục hoành?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

32y x mx m



  

2 2 2

34m m m



   

Do đó phương trình





có hai nghiệm là





m m m



  

Để hàm số có cực trị thì

0m 

Trường hợp 1:

0m 

, khi đó

xx

, hàm số đạt cực tiểu tại

xm

Để hàm số có điểm cực tiểu nằm hoàn toàn phía trên trục hoành

 

0fx

Hay

3 3 3 3

8 0 8 0 2m m m m m        

Kết hợp điều kiện ta được

02m

. Do m nguyên nên

1.m

Trường hợp 2:

0m 

, khi đó

xx

, hàm số đạt cực tiểu tại

x 

Để hàm số có điểm cực tiểu nằm hoàn toàn phía trên trục hoành

 

0fx 

Hay

3 3 3

5 216

8 0 8 0

27 9 3 27 5

m m m

mm          

Kết hợp điều kiện ta được

216

m  

. Do m nguyên nên

 

3; 2; 1 .m   

Vậy có 4 giá trị nguyên của m thỏa mãn đề bài.

Câu 15: (Câu 50 - Chuyên PTNK - HCM - Lần 1 - Năm 2020 - 2021) Cho

 

|0 20A n n   

và

là tập hợp các hàm số

3 2 2 2

( ) (2 5) 6 8f x x m x x m    

có

mA

. Chọn ngẫu nhiên một hàm

số

()fx

thuộc

. Tính xác suất để đồ thị hàm số

()y f x

có hai điểm cực trị nằm khác phía

đối với trục

.Ox

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

+ Không gian mẫu

21

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

+ Ta có:

2 2 2

( ) 0

(2 3) 4 0(*)

x m x m









   



+ Đồ thị hàm số

()y f x

có hai điểm cực trị nằm khác phía đối với trục



(*) có hai nghiệm phân biệt khác 2

 

2 2 2

7 2 10

2,58

(2 3) 16 0 0;3;4;...;20

7 2 10

2 (2 3).2 4 0

0 0,58

m m m

























      











   

  















Vậy xác suất là:

P 

Câu 16: (Câu 40 - THPT Ngô Quyền - Ba Vì - Hà Nội - Lần 2 - Năm 2020 - 2021) Cho hàm số

 

3 2 2

3 2 1 4 1y m x m m x m x       

. Gọi

là tập hợp tất cả các giá trị nguyên của

để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục

. Tổng các phần tử của

là

Ⓐ.

3

. Ⓑ.

4

. Ⓒ.

. Ⓓ.

2

Lời giải

Chọn A

Ta có

 

3 3 4 1 4 0y m x m m x m



       

Đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục



Phương trình





có hai nghiệm phân biệt

thỏa mãn

0xx

  

3 3 4 0 4 3m m m       

Kết hợp điều kiện

m

ta được

 

3; 2; 1;0;1;2m   

 

3; 2; 1;0;1;2S    

Vậy tổng các phần tử của

là

3

Câu 17: (Câu 46 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Gọi

là tập hợp tất cả các giá trị thực của

tham số

để đồ thị của hàm số

 

3 2 2

y x mx m x   

có hai điểm cực trị

và

sao cho

,AB

nằm khác phía và cách đều đường thẳng

: 5 9d y x

. Tính tổng tất cả các phần tử của

Ⓐ.

Ⓑ.

Ⓒ.

6

Ⓓ.

Lời giải

Chọn A

Cách 1: Ta có

 

' 2 1y x mx m   

' 0 1;

y A m









    











và











Dễ thấy phương trình đường thẳng

 

AB y x



  

nên

không thể song song hoặc

trùng với

,AB

cách đều đường thẳng

: 5 9d y x

nếu trung điểm

của

nằm trên

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

; 5 9 18 27 0

m m m m

I m d m m m





       





3 3 5



















Với

3,m A B

thỏa điều kiện nằm khác phía so với

Với

3 3 5

m A B





thỏa điều kiện nằm khác phía so với

Tổng các phần tử của

bằng 0.

Câu 18: (Câu 35 - SGD Hà Nội- Lần 1 - Năm 2020 - 2021) Gọi

là tập hợp các giá trị thực của tham

số

để đồ thị của hàm số

 

3 2 2

y x mx m x   

có hai điểm cực trị

và

sao cho

,AB

nằm khác phía và cách đều đường thẳng

: 5 9d y x

. Tổng các phần tử của

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

6

Lời giải

Chọn A

Ta có:

 

21y x mx m



   

0 1;

y A m











    











và











Dễ thấy phương trình đường thẳng

2 ( 1)

AB y x



 

nên

không thể song song hoặc

trùng với

: 5 9d y x

nếu trung điểm

của

nằm trên

; 5 9 19 27 0

3 3 5

m m m m

I m d m m m











        















Với

3,m A B

thỏa mãn điều kiện nằm khác phía so với

Với

3 3 5

m A B





thỏa mãn điều kiện nằm khác phía so với

Vậy Tổng các phần tử của

bằng

Câu 19: (Câu 36 - THPT Ba Đình - Thanh Hóa - Lần 2 - Năm 2020 - 2021) Gọi

là các giá trị

của tham số

để đồ thị hàm số

2 3 1y x x m   

có hai điểm cực trị là

sao cho tam

giác

OBC

có diện tích bằng

,với

là gốc tọa độ. Tính

.mm

Ⓐ.

. Ⓑ.

15

. Ⓒ.

. Ⓓ.

20

Lời giải

Chọn B

Hàm số xác định với mọi

x

66y x x





0; 1

1; 2

x y m

  









  



Bảng biến thiên:

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Vậy

 

0; 1Bm

 

1; 2Cm

 

1; 1 2BC BC   

 

đi qua

 

0; 1Bm

và nhận

 

1;1n 

làm một vectơ pháp tuyến nên có phương trình

   

1 0 1 1 0 1 0x y m x y m         

 

;

d O BC





 

1 4 3

; . . . 2 2 1 4

1 4 5

OBC

S d O BC BC m

   





       



   



Vậy

. 15mm

Câu 20: (Câu 35 - THPT Hoàn Kiếm và Hai Bà Trưng - Hà Nội - Năm 2020 - 2021) Cho hàm số

31y x mx  

(1) và điểm

 

2;3A

. Biết

là một giá trị để đồ thị hàm số (1) có hai điểm cưc

trị

và

sao cho tam giác

ABC

cân tại

. Diện tích tam giác

ABC

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

Ta có

3 3 .y x m





Đồ thị hàm số (1) có hai điểm cưc trị

và

khi và chỉ khi phương trình





có hai nghiệm

phân biệt, suy ra

0m 

Khi đó, không giảm tổng quát suy ra

 

( ;1 2 );C ;2 1 ; 2;3B m m m m m m A  

Tam giác

ABC

cân tại

suy ra

AB AC

       

        

2 2 2 2

2 2 2 2 2 2AB AC m m m m m m

 







   









0 lo¹i v× 0

8 16 0

tháa m·n

m m m

Với

m 

thì

2 2 3

(2 ) (4 ) 4 16 4. 16. 2

BC m m m m m      

Thử lại thấy ba điểm

,,A B C

không thẳng hàng.

Gọi

là trung điểm của

, suy ra

 

0;1I

và

2 (3 1) 2 2IA    

Vậy diện tích tam giác

ABC

bằng

. . .2 2.2 2 2

IABC 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 21: (Câu 44 - THPT Hoàn Kiếm và Hai Bà Trưng - Hà Nội - Năm 2020 - 2021) Có bao nhiêu giá

trị nguyên của tham số

để đồ thị hàm số

 

3 2 2 3

3 3 1y x mx m x m m     

có hai điểm cực

trị

, AB

và

OA OB

đạt giá trị nhỏ nhất?

Ⓐ. Vô số. Ⓑ. 2. Ⓒ. 3. Ⓓ. 1.

Lời giải

Chọn C

Ta có

   

3 3 3y x m x m y x m



       

 

y x m







    







Đồ thị hàm số đã cho có hai điểm cực trị





có hai nghiệm phân biệt

11m m m     

Với

   

1 1 3 1 2 2 1; 2 2 .x m y m m m A m m             

Với

   

1 1 3 1 2 2 1; 2 2 .x m y m m m B m m              

Ta có

       

2 2 2 2

1 2 2 1 2 2OA OB m m m m          

5 10 5 5 10 5m m m m     

     

min

5 1 5 1 5. 1 1 2 5 2 5.m m m m OA OB             

Dấu

""

xảy ra

    

1 1 0 1 1 0; 1 .m m m m           

Câu 22: (Câu 45 - THPT Hồng Lĩnh - Hà Tĩnh - Lần 1 - Năm 2020 - 2021) Cho hàm số

 

3 2 2

y x mx m m x     

. Có bao nhiêu giá trị nguyên của tham số thực

để hàm số

đạt cực trị tại

, xx

thỏa mãn

2 3 5 0x mx m m    

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

Ta có:

' 2 1y x mx m m    

Hàm số đạt cực trị tại

, xx

khi và chỉ khi phương trình

'0y 

có

nghiệm phân biệt



' 1 0m   

1m  

 

Khi đó

x x m

x x m m







  



Theo đề bài:

2 3 5 0x mx m m    

 

1 1 2 2

3 5 0x x x x m m      

2 2 2

1 1 2 2

3 5 0x x x x m m      

 

1 2 1 2

3 5 0x x x x m m      

2 2 2

4 1 3 5 0m m m m m       

2 4 0m  

2m

Kết hợp với

 

ta được

12m  

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

nguyên nên

 

0,1,2m

Vậy có

giá trị

thỏa mãn yêu cầu bài toán.

Câu 23: (Câu 38 - THPT Lương Tài - Bắc Ninh - Lần 1 - Năm 2020 - 2021) Biết rằng đồ thị hàm số

y x mx x   

có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh của

tam giác vuông có cạnh huyền

. Hỏi có mấy giá trị của

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

 Ta có:

'1y x mx  

' 0 1 0y x mx    

 Đồ thị hàm số có hai điểm cực trị



phương trình có hai nghiệm phân biệt

' 4 0m    

Khi đó, gọi các nghiệm của là

,xx

thì

,xx

chính là hoành độ hai điểm cực trị. Theo Viet ta

có

1 2 1 2

; . 1x x m x x  

Theo bài ra ta có:

 

2 2 2 2

1 2 1 2 1 2

7 2 7 2 7 9 3x x x x x x m m m             

Vậy có 2 giá trị của

thỏa mãn yêu cầu.

Câu 24: (Câu 38 - SGD Thái Nguyên - Lần 1 - Năm 2020 - 2021) Cho hàm số

 

3 2 2 3

3 3 1y x mx m x m    

, với

là tham số. Gọi

 

là đồ thị của hàm số đã cho. Biết

rằng khi

thay đổi, điểm cực tiểu của đồ thị

 

luôn nằm trên đường thẳng cố định. Hệ số

góc của đường thẳng

bằng

Ⓐ.



. Ⓑ.

. Ⓒ.

3

. Ⓓ.

Lời giải

Chọn C

Tập xác định

D 

Ta có:

 

3 6 3 1y x mx m



   

0 2 1 0

y x mx m







      







Vì hàm số có hệ số bậc ba dương nên hàm số có điểm cực tiểu

xm

Mặt khác ta lại có:

     

3 3 3y x m x m mx mx x m x



      



Suy ra:

     

3 3 3

CT CT CT CT CT CT CT

y x m x m mx mx x m x



      



 

1 3 3 3

CT CT CT CT

y mx mx x   

x

Vậy tọa độ điểm cực tiểu thỏa mãn phương trình đường thẳng

31yx  

hay đường thẳng

có hệ số góc bằng

3

Câu 25: (SGD Hưng Yên-Năm 2019-2020) Tất cả các giá trị thực của tham số

để hàm số

2 3 2 5y x mx mx   

không có cực trị là

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ⓐ.

m

. Ⓑ.

m

. Ⓒ.

m  

. Ⓓ.

m  

Lời giải

Chọn A

Tập xác định

D 

. Ta có

6 6 2y x mx m



  

Để hàm số đã cho không có cực trị thì phương trình

6 6 2 0x mx m  

vô nghiệm hoặc có

nghiệm kép

9 12 0 0

m m m



       

Câu 26: (SGD Vĩnh Phúc-2019-2020) Cho hàm số

 

22y x m x   

(với

là tham số). Hàm số

đã cho có cực tiểu khi và chỉ khi

Ⓐ.

1m 

. Ⓑ.

2m 

. Ⓒ.

0m 

. Ⓓ.

3m 

Lời giải

Chọn B

Ta thấy

   

3 2 2 3 2 2y x m x x x m



     





 

0 3 2 2 0

y x m x









     











Vì hàm số đã cho là hàm bậc 3 nên hàm số có cực tiểu khi và chỉ khi hàm số có 2 điểm cực trị



phương trình





có hai nghiệm phân biệt



 



   

Câu 27: (THPT Nguyễn Tất Thành - Hà Nội - Năm 2019-2020) Tìm tất cả các giá trị thực của tham số

để hàm số

 

3 3 6y x mx m x    

có cực trị.

Ⓐ.

32m  

. Ⓑ.

3m 

hoặc

2m 

. Ⓒ.

3m 

hoặc

2m 

. Ⓓ.

32m  

Lời giải

Chọn B

Ta có:

 

3 6 3 6y x mx m



    

Hàm số có cực trị

 

0 9 3.3 6 0 6 0

m m m m









           







Câu 28: (TN12-THPT Nguyễn Tất Thành 2019-2020) Tìm tất cả các giá trị thực của tham số

để

hàm số

 

3 3 6y x mx m x    

có cực trị.

Ⓐ.

32m  

. Ⓑ.

3m 

hoặc

2m 

. Ⓒ.

3m 

hoặc

2m 

. Ⓓ.

32m  

Lời giải

Chọn B

Ta có:

 

3 6 3 6y x mx m



    

Hàm số có cực trị

 

0 9 3.3 6 0 6 0

m m m m









           







 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 29: (THPT Võ Thị Sáu- TPHCM- năm 2019-2020) Tập hợp các số thực

để hàm số

 

6 9 1

y mx m    

có cực trị là

Ⓐ.

 

. Ⓑ. . Ⓒ.

 

\ 3;3

. Ⓓ.

 

\3

Lời giải

Chọn D

Để hàm số

y ax bx cx d   

có cực trị thì

30b ac

   

 

3. 6 9 0

6 9 0



     



   

  

  

  

Câu 30: (THPT Nguyễn Gia Thiều- Năm 2019 -2020) Cho hàm số

     

2 2 1 1y f x x a x a x      

. Tìm mệnh đề nào sai.

Ⓐ. Hàm số luôn có cực đại, cực tiểu

a

. Ⓑ. Hàm số luôn có cực đại, cực tiểu

1a  

Ⓒ. Hàm số đồng biến khi

1a 

. Ⓓ. Hàm số luôn có cực đại, cực tiểu

1a  

Lời giải

Chọn B

   

3 2 2 2 1 .y x a x a



    

     

' 2 3 2 1 2 1 1 .a a a a a         





có 2 nghiệm phân biệt khi

1.a 

Vậy hàm số luôn có cực đại, cực tiểu

1a  

Câu 31: (THPT Nguyễn Khuyến - TP HCM - Lần 02 - Năm 2019 - 2020) Tìm tất cả các giá trị của

tham số thực

để hàm số

21y mx x m   

có điểm cực tiểu.

Ⓐ.

0m 

. Ⓑ.

0m 

. Ⓒ.

0m 

. Ⓓ.

0m 

Lời giải

Chọn A

Tập xác định:

.D 

Ta có:

3 2.y mx





Để hàm số đã cho có điểm cực tiểu thì phương trình

'0y 

phải có hai nghiệm phân biệt

3 .2 0 0.mm   

Câu 32: (Chuyên Hùng Vương - Phú Thọ - Năm 2019 - 2020) Cho hàm số

2)56()1(

223

 xmmxmxy

. Gọi

);( baS 

là tập hợp các giá trị của tham số m để

hàm số có cực trị, giá trị của

ba

bằng :

Ⓐ. 7 Ⓑ. 6 Ⓒ. 8 Ⓓ. 9

Lời giải

Chọn C

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

56)1(23'

 mmxmxy

Để hàm số có cực trị

0' y

có 2 nghiệm phân biệt

0)56(3)1('

 mmm

014162

 mm

71  m

)7;1( S

. Vậy,

8 ba

Câu 33: Với giá trị thực nào của tham số

thì hàm số

 

3 2 3 5y m x x mx    

có hai điểm cực

trị?

Ⓐ.

 

1;4m

. Ⓑ.

   

; 1 4;m    

Ⓒ.

   

1;4 \ 3m

. Ⓓ.

     

; 1 4; 3m     

Lời giải

Chọn C

Ta có

 

3 3 4 3y m x x m



   

Hàm số có hai cực trị khi và chỉ khi





có hai nghiệm phân biệt

 

   

1;4 \ 3

3 9 12 0

2 3 3 3 0











     

  

  

   

  







Vậy

   

1;4 \ 3m

thỏa mãn yêu cầu bài toán.

Câu 34: (Vted - Đề số 21 - Năm 2019 - 2020) Hàm số

 

31f x x x  

có hai điểm cực trị

,xx

. Giá

trị của

xx

bằng

Ⓐ.

6

. Ⓑ.

2

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Có

 

3 6 0 0 2 2

f x x x x x







        







Câu 35: (THPT Nguyễn Khuyến - TP HCM - Lần 02 - Năm 2019 - 2020) Tìm tất cả các giá trị thực

của tham số

để đồ thị hàm số

 

y x m x x m     

không có điểm cực trị.

Ⓐ.

31m  

. Ⓑ.

11m  

. Ⓒ.

1m 

. Ⓓ.

31m  

Lời giải

Chọn D

Ta có

 

3 2 1

y x m x



   

Hàm số không có cực trị khi và chỉ khi



không đổi dấu

 

0 1 4 0 2 3 0 3 1m m m m



              

Câu 36: (THPT Triệu Sơn 4 - Thanh Hóa - Lần 3 - Năm - 2019 2020) Có bao nhiêu giá trị nguyên của

để hàm số

 

2 6 1f x x x m   

có các giá trị cực trị trái dấu?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Tập xác định

D 

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có

6 12 0

y x x y







    







;

   

0 1 , 2 7f m f m    

Hàm số

 

2 6 1f x x x m   

có các giá trị cực trị trái dấu

       

0 . 2 0 1 . 7 0 7 1f f m m m          

Mà

 

6; 5; 4; 3; 2; 1;0mm        

. Có 7 giá trị thỏa mãn.

Câu 37: (THPT Tam Dương - Vĩnh Phúc - Năm học 2019 - 2020) Có bao nhiêu giá trị thực của tham

số

để đồ thị hàm số

 

5 3 1 2 1 1

y m m x m x      

có hai điểm cực trị

,AB

sao

cho

,AB

cách đều đường thẳng

: 1 0x  

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

Tập xác định:

D 

Đạo hàm:

 

' 2 5 3 1 2 1y x m m x m     

'0y 

 

2 5 3 1 2 1 0 1x m m x m      

Đồ thị hàm số có hai điểm cực trị

,AB

khi và chỉ khi

 

có hai nghiệm phân biệt.

Khi đó:

 

   

' 0 5 3 1 2 1 0 *m m m       

Với điều kiện

 

, phương trình

 

có hai nghiệm phân biệt

,xx

thỏa mãn:

 

2 5 3 1

. 2 1

x x m m

x x m



   











(theo định lý Vi-ét).

Giả sử tọa độ hai điểm cực trị

 

1 1 1

; 5 3 1 2 1 1

A x m m x m x



     





 

2 2 2

; 5 3 1 2 1 1

B x m m x m x



     





Theo giả thiết, hai điểm cực trị cách đều đường thẳng

: 1 0x  

nên ta có:

   

,,d A d B  

11xx   

2xx  

(do

xx

Kết hợp với hệ

 

suy ra:

 

2 5 3 1 2mm  

5 3 2 0mm   















Kiểm tra với điều kiện

 

thấy

m 

thỏa mãn.

Vậy có

giá trị thực của tham số

thỏa mãn yêu cầu bài toán.

Câu 38: (THPT Liên Trường - Nghệ An - Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham số

để hàm số

y x mx mx    

có hai điểm cực trị

,xx

nằm về hai phía trục

.Oy

Ⓐ.

0m

. Ⓑ.

0m

. Ⓒ.

  m

. Ⓓ.











 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Lời giải

Chọn B

Tập xác định:

.D

Ta có

4y x mx m



   

Để hàm số có hai điểm cực trị

,xx

nằm về hai phía trục

thì phương trình

40   x mx m

có hai nghiệm phân biệt

,xx

trái dấu

0 0.    mm

Câu 39: (THPT chuyên Biên Hòa - Hà Nam - 2020) Có tất cả bao nhiêu giá trị thực của tham số

để

đồ thị hàm số

 

3 2 2

2 3 1

y x mx m x    

có hai điểm cực trị có hoành độ

,xx

sao cho

 

1 2 1 2

21x x x x  

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

TXĐ:

D 

 

2 2 2 3 1y x mx m



   

 

0 3 1 0 1y x mx m



     

Đồ thị hàm số đã cho có hai điểm cực tri khi và chỉ khi phương trình

 

có hai nghiệm phân biệt

 

2 2 2

0 4 3 1 0 13 4 0

m m m







           











Theo định lý Vi-et:

1 2 1 2

3 1;x x m x x m    

Theo đề bài, ta có:

 

1 2 1 2

nhaän

2 1 3 1 2 1

0 loaïi

x x x x m m







        









Vậy có

giá trị thực của

thoả yêu cầu bài toán.

Câu 40: (THPT Thái Phục- Thái Bình- Lần 3- 2020) Cho hàm số

   

3 2 2

2,f x x ax a x b a b    

có

điểm cực trị

và

. Biết tam giác

OAB

vuông cân tại

(

là gốc tọa độ ), giá trị của

biểu thức

P a b

bằng

Ⓐ.

25.

Ⓑ.

Ⓒ.

40.

Ⓓ.

10.

Lời giải

Chọn D

Ta có

34y x ax a



  

 









  







 

,A a b

và

;

3 27









 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có

3 27

9 27

OAOB

OA OB

a b b





  



















  

  



   

  













   













10P a b   

Câu 41: (THPT-Quốc Học Huế- Lần 1- 2020) Tìm các giá trị nguyên của tham số

thuộc khoảng

 

2019;2020

để điểm cực tiểu của đồ thị hàm số

1y x x mx   

nằm bên phải trục tung.

Ⓐ.

2020

. Ⓑ.

2019

. Ⓒ. 2017. Ⓓ.

2018

Lời giải

Chọn D

Ta có:

' 3 2y x x m  

Hàm số có cực trị thì

' 0 1 3 0

mm      

Điểm cực tiểu của đồ thị hàm số

1y x x mx   

nằm bên phải trục tung

'0y

có ít nhất

một nghiệm dương.

Mà

3 2 0x x m  

có 2 nghiệm

;xx

thỏa mãn:





  













0m

Vậy có 2018 giá trị nguyên

thỏa mãn.

Câu 42: (Chuyên KHTN - Hà Nội - Lần 3 - Năm 2019-2020) Có bao nhiêu giá trị nguyên của tham số

để đồ thị hàm số

(2 1) 2 1y mx m x mx m     

có hai điểm cực trị nằm về hai phía của trục hoành.

Ⓐ. 4. Ⓑ. 2. Ⓒ. 1. Ⓓ. 3.

Lời giải

Chọn C

Để đồ thị hàm số

(2 1) 2 1y mx m x mx m     

có hai điểm cực trị nằm về hai phía của trục

hoành thì phương trình

(2 1) 2 1 0 (1)mx m x mx m     

có ba nghiệm phân biệt.

Ta có:

(2 1) 2 1 0mx m x mx m     

 

( 1) (1 ) 1 0

( ) (1 ) 1 0 2

x mx m x m

f x mx m x m



      











     





Để phương trình

(1)

có ba nghiệm phân biệt thì

(2)

có hai nghiệm phân biệt khác

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 

   

0 1 4 1 0

1 1 0

3 2 3 3 2 3

3 6 1 0

m m m









       







    













   



       















Mặt khác ta có

1mm   

Câu 43: (SGD Hưng Yên - Năm 2019-2020) Cho hàm số

   

2 3 1 6 2 1y x m x m x     

với

là tham số thựⒸ. Tìm tất cả các giá trị của tham số

để hàm số có các điểm cực đại và cực tiểu

của hàm số nằm trong khoảng

 

2;3

Ⓐ.

 

1;3m

. Ⓑ.

   

1;3 3;4m  

Ⓒ.

 

1;4m

. Ⓓ.

 

3;4m

Lời giải

Chọn B

Ta có

   

6 6 1 6 2y x m x m



    















Để hàm số có các điểm cực đại đều thuộc khoảng

 

2;3

thì

2 1 3

2 2 3 1 4

   







      



Vậy

   

1;3 3;4m  

Câu 44: (THPT Nam Đàn 2 - Lần 1 - Năm 2019-2020) Cho hàm số

32y x x mx m    

có đồ thị

 

. Giá trị của tham số thực

để

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành

là

Ⓐ.

3m 

. Ⓑ.

15m

. Ⓒ.

23m

. Ⓓ.

3m 

Lời giải

Chọn A

Cách 1:

Ta có:

32y x x mx m    

 

1 2 2x x x m    

 

0 1 2 2 0y x x x m      

 

2 2 0 1

x x m



   









Để đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành

0y

có ba nghiệm phân biệt



phương trình

 

có hai nghiệm phân biệt khác

1

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

1 2 2 0









   





   



Vậy

3m 

thì đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành.

Cách 2:

Ta có:

36y x x m  

;

0y 

3 6 0x x m   

 



Hàm số có cực đại, cực tiểu



phương trình

 



có hai nghiệm phân biệt

0  

9 3 0 3mm    

 

Gọi

,xx

là nghiệm của phương trình

 



. Theo định lý viet ta có

  













Gọi

,yy

là giá trị cực trị tương ứng của hàm số.

Vì

 

1 1 2

. 2 1

3 3 3

y y x m x

   

    

   

   

nên

 

y m x



  





;

 

y m x



  





Để đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành

.0yy

   

2 1 . 2 1 0

m x m x

   

     

   

   

 

1 2 1 2

2 . 1 0

m x x x x



     





2 1 0

   

   

   

   





  







 

Từ

 

và

 

suy ra

3m 

thì đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành.

Câu 45: (THPT Tam Dương - Vĩnh Phúc - Năm 2019-2020) Có bao nhiêu giá trị thực của tham số

để đồ thị hàm số

 

5 3 1 2 1 1

y m m x m x      

có hai điểm cực trị

,AB

sao cho

,AB

cách đều đường thẳng

: 1 0x  

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

Tập xác định:

D 

Đạo hàm:

 

' 2 5 3 1 2 1y x m m x m     

'0y 

 

2 5 3 1 2 1 0 1x m m x m      

Đồ thị hàm số có hai điểm cực trị

,AB

khi và chỉ khi

 

có hai nghiệm phân biệt.

Khi đó:

 

   

' 0 5 3 1 2 1 0 *m m m       

Với điều kiện

 

, phương trình

 

có hai nghiệm phân biệt

,xx

thỏa mãn:

 

2 5 3 1

. 2 1

x x m m

x x m



   











(theo định lý Vi-ét).

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Giả sử tọa độ hai điểm cực trị

 

1 1 1

; 5 3 1 2 1 1

A x m m x m x



     





 

2 2 2

; 5 3 1 2 1 1

B x m m x m x



     





Theo giả thiết, hai điểm cực trị cách đều đường thẳng

: 1 0x  

nên ta có:

   

,,d A d B  

11xx   

2xx  

(do

xx

Kết hợp với hệ

 

suy ra:

 

2 5 3 1 2mm  

5 3 2 0mm   















Kiểm tra với điều kiện

 

thấy

m 

thỏa mãn.

Vậy có

giá trị thực của tham số

thỏa mãn yêu cầu bài toán.

Câu 46: (THPT Nghi Sơn - Thanh Hóa - Lần 01 - Năm 2019-2020) Tìm tổng tất cả các giá trị thực của

tham số

sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

   

2 3 1 6 1 2y x m x m m x    

song song đường thẳng

4yx

Ⓐ.



. Ⓑ.



. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

TXĐ:

D 

Gọi

     

: 2 3 1 6 1 2C y x m x m m x    

Có:

   

' 6 6 1 6 1 2y x m x m m    

Có:

   

 

36 1 4 1 2 36 9 6 1 36 3 1

m m m m m m



         



Để hàm số có hai cực trị thì:

 

0 3 1 0

mm      

Có:

 

  

'. 1 9 6 1 1 2 1

y y x m m m x m m m



         





Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị

 

là:

 

   

9 6 1 1 2 1y m m x m m m d      

Để đường thẳng

 

song song với đường thẳng

4yx

thì:

  

9 6 1 4

1 2 1 0

0; 1;

m m m











    









   





  







  



Vậy

m 

là giá trị cần tìm.

Câu 47: (THPT Việt Nam Ba Lan - Hà Nội - Năm 2019-2020) Số các giá trị nguyên của tham số

sao cho hàm số

   

2 3 1 6 2 2019y x m x m x     

có hai điểm cực trị nằm trong khoảng

 

5;5

bằng

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

Ta có:

   

6 6 1 6 2y x m x m



    















Để hàm số

   

2 3 1 6 2 2019y x m x m x     

có hai điểm cực trị nằm trong khoảng

 

5;5

thì

2 1 3

5 2 5 3 7

   







      



Mà

 

2; 1;0;1;2;4;5;6mm    

Câu 48: (THPT Việt Nam Ba Lan - Hà Nội - Năm 2019-2020) Tìm tất cả các giá trị thực của tham số

để hàm số

   

 

3 2 2

2 1 8 2f x x m x m x      

đạt cực tiểu tại

1x 

Ⓐ.

3m 

. Ⓑ. Không tìm được

Ⓒ.

9m 

. Ⓓ.

2m 

Lời giải

Chọn B

Ta có

   

 

3 2 2 1 8f x x m x m



     

và

   

6 2 2 1f x x m



   

Hàm số đạt cực tiểu tại

1x 

 





















4 9 0

4 4 0



   









 

2 5 0



   













(vô

nghiệm).

Vậy không tìm được

Câu 49: (THPT Lý Tự Trọng - TPHCM - Năm 2019 - 2020) Cho hàm số

32y x mx m   

có đồ

thị

 

và đường thẳng

yx

. Tập hợp các giá trị thực của tham số

để

 

có

điểm cực trị đối xứng với nhau qua đường thẳng

là:

Ⓐ.

 

. Ⓑ.

 

1

. Ⓒ.

 

1;1

. Ⓓ.



Lời giải

Chọn D

TXĐ :

D 

36y x mx





 

32x x m

Để đồ thị hàm số có

điểm cực trị thì





có hai nghiệm phân biệt

20m

0m

Khi đó:















, đồ thị hàm số có hai điểm cực trị là

 

0; 2Am

 

2 ; 4 2B m m m  

Gọi

 

; 2 2I m m m  

là trung điểm của

Ta có:

 

2;1

u 

;

 

2 ; 4AB m m

và

đối xứng nhau qua đường thẳng

khi và chỉ khi:

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

d AB











u AB

















2 2 3

4 4 0

m m m



    











4 2 0

4 4 0



   













Hệ phương trình vô nghiệm nên không có giá trị

thoả yêu cầu bài toán.

Câu 50: (Chuyên Nguyễn Trãi - Hải Dương- Lần 04 - Năm 2019 - 2020) Cho hàm số

 

3y x m x m   

( với

là tham số ).

là điểm cực đại của đồ thị hàm số ứng với giá

trị m thích hợp đồng thời là điểm cực tiểu của đồ thị hàm số ứng với một giá trị khác của

. Hỏi

số điểm

có tính chất như vậy là bao nhiêu?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Hàm số

 

3y x m x m   

TXĐ:

D 

 

33y x m



  

 

6y x m





 

0 3 3 0

y x m







     







Ta có:

 

6 1 6 0

y m m





    

;

 

6 1 6 0

y m m





     

   

1 ; 1 3 1 3 2

C CD

CT CT

x m y m m m m m m



          







          





Gọi

là 1 điểm cực đại ứng với giá trị

và là điểm cực tiểu ứng với giá trị

Yêu cầu bài toán

   

1 1 2 2

2 2 2 2

3 2 3 2

2 3 2 2 3 2

m m m m





  









    

      





;









  

















Câu 51: (Chuyên Lương Văn Chánh - Lần 02 - Năm 2019 - 2020) Biết hàm số

 

f x x ax bx c   

đạt cực đại tại điểm

 

3, 3 28xf   

và đồ thị của hàm số cắt trục tung tại điểm có tung độ

bằng

. Tính

2 2 2

S a b c  

Ⓐ.

89S 

. Ⓑ.

225

S 

. Ⓒ.

619

S 

. Ⓓ.

91S 

Lời giải

Ta có

   

3 2 ; 6 2f x x ax b f x x a

 

    

Hàm số

 

đạt cực đại tại điểm

3x 

khi và chỉ khi

 

6 27







   





















Mà

   

3 28 9 3 55 2f a b c     

Ngoài ra, đồ thị của hàm số

 

cắt trục tung tại điểm có tung độ bằng

nên

 

13c 

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Từ

     

1 , 2 , 3

suy ra

6 27 3

9 3 55 9

a b a

a b c b

    





    















Do đó

 

3 9 1 89S     

Câu 52: (THPT Phó Cơ Điều - An Giang - Năm 2019 - 2020) Cho hàm số

 

3 2 2

2 1 2 1

y x mx m x m     

(

là tham số ). Xác định khoảng cách lớn nhất từ gốc tọa

độ

0;0O

đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số trên.

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Đặt

   

3 2 2

2 1 2 1

y f x x mx m x m      

   

41f x x mx m



    

Hàm số có hai cực trị



Phương trình

 

0fx





có hai nghiệm phân biệt

   

1 15

4 1 0 2 0,

4 16

2 1 1 0

m m m m













           









  









Tìm được phương trình đường thẳng qua 2 điểm cực trị:

 

8 2 2 8 2

3 3 3 3 3

y m m x m m





      





Cách 1: Theo đề bài ta có:

 

8 2 8 2 2 1

3 3 3 3 3 3

8 2 2 8 2 2

3 3 3 3 3 3

m m m m

    

  



   

     

   

   

Ta có:

 

8 2 2 2 2 1 5

4 1 2 0,

3 3 3 3 3 4 8

m m m m m m



          





Áp dụng bất đẳng thức Ⓑ. Ⓒ. S cho 2 số dương:

2 2 2

8 2 2 1 1 8 2 2

1. .1 1 1

3 3 3 3 3 3 3 3

m m m m

   

     

       

   

     

     

   

   

8 2 2 1

1. .1

3 3 3 3

1 10

8 2 2

3 3 3



  









   















  











 

dO  

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Vậy giá trị lớn nhất của

 

dO

8 2 2 8 2 7

3 3 3 3 3 3

m m m m



       





1 57





















Cách 2:

Tìm được điểm cố định mà



luôn đi qua với mọi

là









có vec tơ chỉ phương là



8 2 2

3 3 3



  





Ta có

 

,d O OA

Dấu “=” xảy ra

1 8 2 2

. 0 1 0

3 3 3 3

OA OAu m m





          





1 57





















Vậy giá trị lớn nhất của

 

dO

1 57





















Câu 53: (THPT Minh Khai – Hà Nội - Lần 01 - Năm 2019 - 2020) Hàm số

 

1 5 4

y x m x m    

có điểm cực tiểu lớn hơn

khi

Ⓐ.

2m 

. Ⓑ.

 

1;3m

. Ⓒ.

3m 

. Ⓓ.

1m 

Lời giải

Chọn A

Ta có

   

2 1 ; 0 2 1 0

y x m x y x m x







        







Nếu

2 2 0 1mm   

thì hàm số đạt cực tiểu tại

02x 

. Không thỏa mãn.

Để hàm có điểm cực tiểu lớn hơn

thì ta phải có

2 2 2 2x m m    

Vậy

2m 

thì hàm số có điểm cực tiểu lớn hơn

Câu 54: (THPT Nghi Xuân - Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham số

sao cho đường

thẳng đi qua hai điểm cực trị của đồ thị hàm số

   

2 3 1 6 1 2y x m x m m x    

song song

đường thẳng

4yx

Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

1m 

. Ⓓ.

m 

Lời giải

Chọn A

Ta có

   

6 6 1 6 1 2y x m x m m



    

Điều kiện để hàm số có hai điểm cực trị là:

 

0 9 9 6 1 0

m m m



       

(*).

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Chia

cho



ta được phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là

 

  

9 6 1 1 1 2y m m x m m m      

Để đường thẳng đi qua hai điểm cực trị song song với đường thẳng

4yx

ta phải có

  

9 6 1 4

1 1 2 0

0; 1;

m m m











    









   





  







  



Kiểm tra điều kiện (*) ta được

m 

Câu 55: (THPT NGHI XUÂN - NĂM 2019-2020) Tìm tất cả các giá trị thực của tham số

sao cho

đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

   

2 3 1 6 1 2y x m x m m x    

song

song đường thẳng

4yx

Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

1m 

. Ⓓ.

m 

Lời giải

Chọn A

Ta có

   

6 6 1 6 1 2y x m x m m



    

Điều kiện để hàm số có hai điểm cực trị là:

 

0 9 9 6 1 0

m m m



       

(*).

Chia

cho



ta được phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là

 

  

9 6 1 1 1 2y m m x m m m      

Để đường thẳng đi qua hai điểm cực trị song song với đường thẳng

4yx

ta phải có

  

9 6 1 4

1 1 2 0

0; 1;

m m m











    









   





  







  



Kiểm tra điều kiện (*) ta được

m 

Câu 56: (THPT Hàm Rồng - Năm 2019 - 2020) Có bao nhiêu giá trị nguyên của tham số

để hàm số

 

3 2 2 2

23y x m x m m x m      

 

có hai giá trị cực trị trái dấu.

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

Ta có

 

3 2 2 2

2 3 0 2x m x m m x m      

   

1 3 0x x m x m



     



     

3 0 3

f x x m x m









    



 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Hàm số

 

có hai giá trị cực trị trái dấu



Đồ thị hàm số

 

cắt trục hoành tại ba điểm phân biệt.



Phương trình

 

có ba nghiệm phân biệt.



Phương trình (3) có hai nghiệm phân biệt khác

 

3 6 9 0





   



     





  





Mà

m

nên

 

0;1;2m

Vậy có ba số nguyên

thoả mãn yêu cầu bài toán.

Câu 57: (THPT Thạch Thành 2 - Thanh Hóa - Năm 2019 - 2020) Gọi

là tập hợp tất cả các giá trị

thực của tham số

để đồ thị hàm số

 

3 2 2

y x mx m x   

có hai điểm cực trị

,AB

sao

cho

,AB

nằm khác phía và cách đều đường thẳng

59yx

. Tính tổng tất cả các phần tử của

Ⓐ.

. Ⓑ.

. Ⓒ.

6

. Ⓓ.

Lời giải

Chọn A

Ta có:

21y x mx m



   

1 1 0mm



     

nên

phương trình





 

1 1 1

y m m m m







      























      



Vậy

3 2 3 2 4

1; ; 1; 2;

3 3 3

m m m m

A m B m AB

   

   



    

   





   

nên đường thẳng

không

song song hoặc trùng với đường thẳng

 

: 5 9d y x

,AB

cách đều đường thẳng

 

nếu trung điểm

của

nằm trên đường thẳng

 

; 5 9 18 27 0

3 3 5

m m m m

I m d m m m











        















Cả ba giá trị của

đều thỏa mãn

,AB

nằm khác phía so với

 

. Vậy tổng tất cả các phần tử

của

là 0.

Câu 58: (THPT Lê Lợi - Thanh Hóa - Năm 2019 - 2020) Biết rằng đồ thị hàm số

 

f x x mx x   

có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh

của tam giác vuông có cạnh huyền là

. Hỏi có mấy giá trị của

Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. Không có

Lời giải

Chọn A

1y x mx



  

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Để hàm số có hai cực trị thì





có 2 nghiệm phân biệt

  

  

  









Giả sử hai điểm cực trị có hoành độ

,xx

Theo đề ra, ta có

 

1 2 1 2 1 2

7 2 7 2 7 3x x x x x x m m           

So với điều kiện, ta có 2 giá trị của

là

3m 

và

3m 

Câu 59: (THPT Lê Lợi - Thanh Hóa - Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham số

để

đồ thị hàm số

32y x mx  

có 2 điểm cực trị

và

sao cho các điểm

,AB

và

 

1; 2



thẳng hàng.

Ⓐ.

2.m 

Ⓑ.

2; 2.mm  

Ⓒ.

2.m 

Ⓓ.

2.m 

Lời giải

Chọn B

 

3 6 .

0 3 6 0 1

y x mx











    







Đồ thị hàm số có 2 điểm cực trị



phương trình

 

có hai nghiệm phân biệt

0m

Khi đó, giả sử

 

0;2

2 ;2 4

mm

Cách 1:

Phương trình đường thẳng

:4 2 0.AM x y  

Ba điểm

,,A B M

thẳng hàng

B AM

0 (l)

8 4 0







   









Cách 2: Ta có

 

1; 4 ; 2 ; 4AM AB m m   

Ba điểm

,,A B M

thẳng hàng

2 0 2

m m m m



        



So với điều kiện

0m 

ta được

2m 

Vậy

2.m













Câu 60: (THPT Lê Xoay - Vĩnh Phúc - Lần 1 – Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham

số m để hàm số

y x x mx   

có 2 điểm cực trị thoả mãn

CD CT

xx

Ⓐ.

2m 

. Ⓑ.

02m

. Ⓒ.

20m  

. Ⓓ.

22m  

Lời giải

Chọn B

Ta có

4y mx x m  



Để hàm sỗ đã cho có 2 điểm cực trị thỏa mãn

CD CT

xx

thì

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Δ0

4 0 2 2













    

  



    







Câu 61: (THTP Nam Đàn 2 - Nghệ An - năm 2019 - 2020) Cho hàm số

32y x x mx m    

có đồ

thị

 

. Giá trị của tham số thực

để

 

có điểm cực đại, cực tiểu nằm về hai phía trục

hoành là

Ⓐ.

3m 

. Ⓑ.

15m

. Ⓒ.

23m

. Ⓓ.

3m 

Lời giải

Chọn A

Cách 1:

Ta có:

32y x x mx m    

 

1 2 2x x x m    

 

0 1 2 2 0y x x x m      

 

2 2 0 1

x x m



   









Để đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành

0y

có ba nghiệm phân biệt



phương trình

 

có hai nghiệm phân biệt khác

1

1 2 2 0









   





   



Vậy

3m 

thì đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành.

Cách 2:

Ta có:

36y x x m  

;

0y 

3 6 0x x m   

 



Hàm số có cực đại, cực tiểu



phương trình

 



có hai nghiệm phân biệt

0  

9 3 0 3mm    

 

Gọi

,xx

là nghiệm của phương trình

 



. Theo định lý viet ta có

  













Gọi

,yy

là giá trị cực trị tương ứng của hàm số.

Vì

 

1 1 2

. 2 1

3 3 3

y y x m x

   

    

   

   

nên

 

y m x



  





;

 

y m x



  





Để đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành

.0yy

   

2 1 . 2 1 0

m x m x

   

     

   

   

 

1 2 1 2

2 . 1 0

m x x x x



     





2 1 0

   

   

   

   





  







 

Từ

 

và

 

suy ra

3m 

thì đồ thị

 

có điểm cực đại, cực tiểu nằm về hai phía trục hoành.

Câu 62: (THPT Triệu Sơn 4 - Thanh Hóa - Lần 3 - Năm - 2019 2020) Cho hàm số

3 2 2 3

3 3( 1)     y x mx m x m m

có đồ thị (C) và điểm

 

1;1I

. Biết rằng có hai giá trị của

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

tham số m ( kí hiệu

,mm

với

mm

) sao cho hai điểm cực trị của (C) cùng với I tạo ra một

tam giác có bán kính đường tròn ngoại tiếp bằng

. Tính

5.P m m

Ⓐ.

2P

. Ⓑ.

P

. Ⓒ.

P

. Ⓓ.

2P

Lời giải

Chọn A

*TXĐ:

.D

* Ta có

' 3 6 3( 1);

' 0 .

   













y x mx m

Giả sử hai điểm cực trị của (C) là A và B, khi đó:

   

1; 2 2 ; 1; 2 2 2 5 2        A m m B m m AB R

( Với R là bán kính đường tròn ngoại

tiếp tam giác ABI). Vậy tam giác ABI vuông tại I.

Ta có

   

1; 2 2 ; 1; 2 2 2 5 2 ,

; 2 3 , 2; 2 1 ;

. 0 5 2 3 0 .

        

      







     







A m m B m m AB R

IA m m IB m m

IA IB m m

Theo giả thiết ta có

1, 2.

    m m P

Câu 63: (THPT Hoàng Văn Thụ - Nam Định - Lần 2 - Năm 2019 - 2020) Cho hàm số

, ( là tham số). Gọi

là hai điểm cực trị của đồ thị hàm

số và . Tổng tất cả các số để ba điểm tạo thành tam giác nội tiếp đường tròn

có bán kính bằng là

Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .

Lời giải

Chọn C

Tập xác định: .

Ta có ;

Đồ thị hàm số đã cho có hai điểm cực trị là và

+) là ba đỉnh của một tam giác .

+) Nhận thấy là tam giác vuông tại

Phương trình luôn có 2 nghiệm phân biệt, khác 1.

 

3 2 2 3

3 3 1y x mx m x m m     

,AB

 

2; 2I 

,,I A B



D 

 

3 6 3 1y x mx m



   

0 2 1 0

y x mx m







      









 

1; 4 2A m m  

 

1; 4 2B m m  

     

2; 4 , 3; 4 4 , 1; 4AB IA m m IB m m         

,,I A B



   



2 5 2AB R IAB  

.0IAIB

    

3 1 4 4 4 0m m m m      

17 20 3 0mm   

 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Theo Vi – et, ta có tổng hai nghiệm bằng .

Câu 64: (THPT Quảng Xương 1 - Thanh Hoá - Năm học 2019 - 2020) Cho hàm số

   

2 1 3f x x m x mx m    

có đồ thị

 

. Có bao nhiêu giá trị nguyên của tham số

thuộc





2020;2020

để đồ thị

 

có hai điểm cực trị nằm khác phía so với trục hoành.

Ⓐ.

4037

. Ⓑ.

4038

. Ⓒ.

4039

. Ⓓ.

4040

Lời giải

Chọn B

 Đồ thị

 

có hai điểm cực trị nằm khác phía so với trục hoành khi

 

cắt trục hoành tại

ba điểm phân biệt, điều này xảy ra khi phương trình hoành độ giao điểm của

 

và trục hoành

có ba nghiệm phân biệt.

 Xét phương trình hoành độ giao điểm của

 

và trục hoành:

 

2 1 3 0x m x mx m    

 

3 2 2

2 3 1 0x x m x x     

 

1 2 0x x mx m    

 

2 0 *

x mx m









  



 Để yêu cầu bài toán xảy ra thì phương trình (*) phải có hai nghiệm phân biệt khác

1 2 .1 0



   







  





   

;0 1;

   















   

;0 1;m    

 Do





 

2019; 2018; ; 1;2;3; ;2020

2020;2020







    









 Ta đếm được

4038

giá trị

thỏa mãn.

Câu 65: (HSG - Thái Bình - Năm 2019 - 2020) Tìm tất cả các giá trị của tham số

để đồ thị của hàm

số

3 2 2

33y x mx m

có hai điểm cực trị cùng với gốc tọa độ tạo thành một tam giác có diện

tích bằng

192

(đvdt).

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

Hàm số

3 2 2

33y x mx m

có

ĐTX : D

. Ta có

36y x mx

;

Để đồ thị hàm số có hai điểm cực trị thì

. Khi đó hai điểm cực trị của đồ thị hàm số là

0;3Am

2 ; 4 3B m m m

Tam giác

OAB

có

0Ay

nên

. ; . 2 . 3

OAB

S d B Oy OA m m

Theo yêu cầu bài toán, ta có:

2 . 3 192

OAB

S m m

64 4mm

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 66: (Chuyên Bắc Giang - Lần 01 - Năm 2018-2019) Tập hợp các giá trị của

để hàm số

 

y x mx m x    

có hai cực trị là:

Ⓐ.



 



; 1 2;   

Ⓑ.

   

; 1 2;   

Ⓒ.

 

1;2

Ⓓ.

 

1;2

Lời giải

Chọn B

Ta có

22y x mx m



   

. Để hàm số có hai cực trị thì





có hai nghiệm phân biệt nên

0 0 2 0

y m m







        







Câu 67: (GK1 - K12 - THPT Nghĩa Hưng - Nam Định - Năm 2018 -2019) Giá trị của tham số

để

hàm số

31y x x mx   

có hai cực trị

,xx

thỏa mãn

6xx

là

Ⓐ.

. Ⓑ.

1

. Ⓒ.

. Ⓓ.

3

Lời giải

Chọn D

Ta có:

' 3 6 0y x x m   

 

Để hàm số có hai cực trị

,xx

thì phương trình

 

có hai nghiệm phân biệt,

Khi đó:

' 9 3 0 3mm     

 

Mà theo yêu cầu bài toán

,xx

thỏa mãn:

 

1 2 1 2 1 2

6 2 6x x x x x x     

 

Mặt khác theo Viet ta có:















, thay vào

 

ta được:

4 2. 6 3

m    

, thỏa mãn

điều kiện

 

Vậy

3m 

Câu 68: (THPT Ba Đình - Hà Nội - Lần 2 - Năm 2018-2019) Tìm tất cả các giá trị của tham số

để

hàm số

32y x x mx m   

có cực đại và cực tiểu?

Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

m 

. Ⓓ.

m 

Lời giải

Chọn A

+ TXĐ:

D 

3 6 2y x x m



  

+ Hàm số có cực đại và cực tiểu





có 2 nghiệm phân biệt.

36 24 0

mm      

Câu 69: (THPT Hùng Vương-Bình Phước-Lần 01-Năm 2018-2019) Tìm tất cả các giá trị của tham số

để hàm số

y mx mx    

có hai điểm cực trị.

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ⓐ.

02m

. Ⓑ.

2m 

. Ⓒ.

0m 

. Ⓓ.











Lời giải

Chọn D

Ta có:

22y x mx m



   

Hàm số

y mx mx    

có hai điểm cực trị





có hai nghiệm phân biệt







     







Câu 70: (THPT Yên Khánh - Ninh Bình - Năm 2018-2019) Cho hàm số

   

3 1 3 7 3y x m x m x    

. Gọi

là tập các giá trị nguyên của tham số m để hàm số

không có cực trị. Số phần tử của

là

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ. Vô số.

Lời giải

Chọn B

Ta có:

   

3 6 1 3 7 3y x m x m



    

 

0 2 1 7 3 0y x m x m



      

Để hàm số không có cực trị thì

   

0 1 7 3 0mm



      

5 4 0mm   

14m  

 

1;2;3;4mS  

. Vậy

có 4 phần tử.

Câu 71: (SGD Bà Rịa Vũng Tàu - Năm 2018-2019) Cho hàm số

 

4 4 1

y x mx m x     

. Mệnh

đề nào sau đây sai?

Ⓐ.

2m

thì hàm số có hai điểm cực trị. Ⓑ.

m

thì hàm số có cực đại và cực tiểu.

Ⓒ.

2m

thì hàm số có cực trị. Ⓓ.

2m

thì hàm số có cực đại và cực tiểu.

Lời giải

Chọn B

Ta có

 

2 4 4y x mx m



    

 

4 4 2 0m m m



      

+) Với

2m

thì





nên hàm số đã cho sẽ có 2 cực trị (trong đó có 1 cực đại và một cực

tiểu).

+) Với

2m 

thì





do đó





với

x

nên hàm số đã cho không có cực trị.

Vậy B là phương án sai.

Câu 72: (THPT Lê Quý Đôn – Điệ n Biên - Lầ n 01- Nă m 2018-2019 ) Cho hàm số

   

1 3 2 2018

     y mx m x m x

vớ i

là tham số . Tổ ng bình phương tấ t cả

các giá trị củ a

để hàm số có hai điể m cự c trị

;xx

thỏ a mãn

21xx

bằ ng

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn A

Ta có

   

' x 2 1 3 2    y m m x m

Để hàm số có hai điểm cực trị thì phương trình

   

x 2 1 3 2 0    m m x m

phải có hai

nghiệm phân biệt.

   

2 4 1 0

1 3 2 0

















   

     





m m m

Theo định lý Vi-ét ta có

 





















Theo bài ta có hệ phương trình

 



































 

    

 

3 4 2

. 3 2 3 4 2 0











        









m t m

m m m m

m m m

m t m

Vậy

mm

Câu 73: (THPT Lê Quý Đôn – Điện Biên - Lần 01- Năm 2018-2019 ) Cho hàm số

2 3 1 6 2 1y x m x m x

với

là tham số thựⒸ. Tìm tất cả các giá trị của

để

hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng

2; 3

Ⓐ.

1; 3 3;4m

. Ⓑ.

1;3m

. Ⓒ.

3;4m

. Ⓓ.

1;4m

Lời giải

Chọn A

Ta có:

' 6 6 1 6 2y x m x m

Để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng

2; 3

'0y

có 2 nghiệm

thuộc khoảng

2; 3

1 2 0x m x m

có 2 nghiệm thuộc khoảng

2; 3

1 2 0x x m

1 2; 3

2 1 3

2 2 3 1 4

YCBT

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 74: (ĐTD - Đề số 8 - Năm 2018 - 2019) Tìm các giá trị của sao cho đồ thị hàm số

có các điểm cực đại và cực tiểu nằm cùng một phía đối với trục

tung.

Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .

Lời giải

Chọn C

Tập xác định: .

Đạo hàm: .

Đồ thị hàm số có các điểm cực đại và cực tiểu nằm cùng một phía đối với trục tung khi phương

trình có 2 nghiệm phân biệt cùng dấu.

ĐK: .

Câu 75: (GK1-K12-THPT Lương Thế Vinh-Hà Nội-2018-2019) Tìm tất cả cả các giá trị của tham số

m để

y x 3x mx 1   

đạt cực trị tại

,xx

thỏa mãn

6xx

Ⓐ.

3m

Ⓑ.

3m

Ⓒ.

1m

Ⓓ.

1m

Lời giải

Chọn A

y' 3x 6x m  

. Hàm số đạt cực trị tại

,xx

.Vậy

,xx

là nghiệm của phương trình

y' 0

Theo viet ta có















2 2 2

1 2 1 2 1 2

( ) 2   x x x x x x



  

3  m

Câu 76: (GK1 - K12 - Lương Thế Vinh - Hà Nội - Năm 2018 - 2019) Tìm tất cả giá trị của tham số m

để hàm số

31y x x mx   

đạt cực trị tai

,xx

thỏa mãn

6.xx

Ⓐ.

3m 

. Ⓑ.

3m 

. Ⓒ.

1m 

. Ⓓ.

1m 

Hướng dẫn giải

Chọn A

31y x x mx   

TXĐ:

' 3 6 .y x x m  

Hàm số đạt cực trị tại

,xx

phương trình y’=0 có hai nghiệm phân biệt

,xx

' 9 3 0

    



 

6 9 12

    y x mx m x

2m

   m















m

D

2 6 9



   y x mx m



y

6 9 0









    











   







 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Khi đó có:

 

1 2 1 2 1 2

2 4 2

x x x x x x     

vì















Theo đề bài có:

4 2 6 3

m    

Câu 77: (GK1 - K12 - Lương Thế Vinh - Hà Nội - Năm 2018 - 2019) Tìm tất cả giá trị của tham số m

để hàm số

31y x x mx   

đạt cực trị tai

,xx

thỏa mãn

6.xx

Ⓐ.

3m 

. Ⓑ.

3m 

. Ⓒ.

1m 

. Ⓓ.

1m 

Hướng dẫn giải

Chọn A

31y x x mx   

TXĐ:

' 3 6 .y x x m  

Hàm số đạt cực trị tại

,xx

phương trình y’=0 có hai nghiệm phân biệt

,xx

' 9 3 0

    



Khi đó có:

 

1 2 1 2 1 2

2 4 2

x x x x x x     

vì















Theo đề bài có:

4 2 6 3

m    

Câu 78: (THCS -THPT Nguyễn Khuyến - Lần 1 - Năm 2018-2019) Giá trị lớn nhất của

để hàm số

 

3 1 1    y mx mx m x

không đạt cực trị là

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

TXĐ:

DR

Ta có:

 

3 6 1y mx mx m



   

Với

0m

thì

' 1 0y   

hàm số

 

3 1 1    y mx mx m x

đồng biến trên



0m

thì

hàm số đã cho không đạt cực trị.

Với

0m

, hàm số

 

3 1 1    y mx mx m x

không đạt cực trị







vô nghiệm hoặc

có nghiệm kép

 

' 9 3 1 0

12 3 0











     

  

    













m m m



Hàm số

 

3 1 1    y mx mx m x

không đạt cực trị khi

m

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Vậy giá trị lớn nhất của

thỏa mãn yêu cầu bài toán là

m

Câu 79: (THPT YÊN LẠC NĂM 2018-2019) Cho hàm số

31y x x mx   

với

là tham số thự

Ⓒ. Tìm tất cả các giá trị của tham số

để hàm số đạt cực trị tại hai điểm

thỏa

6xx

Ⓐ.

. Ⓑ.

1

. Ⓒ.

. Ⓓ.

3

Lời giải

Chọn D

Ta có:

36y x x m



  

có

93m



  

Để hàm số đạt cực trị tại hai điểm

thì phương trình





có 2 nghiệm phân biệt, nghĩa

là:

9 3 0 3





    









. Khi đó theo định lý Vi-et ta có:

S x x

P x x

  













Ta có:

2 2 2

6 2 6 4 2. 6 0 3

x x S P m           

(nhận).

Câu 80: (THPT Đoàn Thượng - Hải Dương - Năm 2018 - 2019) Tìm tất cả các giá trị của m để hàm số

( 2)

y x mx m x   

có cực trị và các điểm cực đại, điểm cực tiểu nhận giá trị dương.

Ⓐ.

2m 

. Ⓑ.

2m 

. Ⓒ.

02m

. Ⓓ.

2m 

Lời giải

Chọn B

Ta có

2 ( 2)y x mx m



   

Hàm số đã cho có các điểm cực đại và cực tiểu dương khi và chỉ khi phương trình





có hai nghiệm phân biệt dương

0 2 0 2

x x m m







  



      











Câu 81: (THPT chuyên Bắc Ninh - L01 - 2018-2019) Gọi S là tập các giá trị dương của tham số

sao

cho hàm số

3 27 3 2y x mx x m    

đạt cực trị tại

,xx

thỏa mãn

5xx

. Biết





;S a b

. Tính

2T b a

Ⓐ.

51 6T 

Ⓑ.

61 3T 

Ⓒ.

61 3T 

Ⓓ.

51 6T 

Lời giải

Chọn C

+) Ta có

3 6 27y x mx



  

0 2 9 0y x mx



    

(1)

+) Theo giả thiết hàm số đạt cực trị tại

,xx



phương trình

(1)

có

nghiệm phân biệt



  





   







(*)

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

+) Với điều kiện (*) thì phương trình

(1)

có

nghiệm

,xx

, theo Vi-ét ta có:

x x m











+) Ta lại có

5xx

   

1 2 1 2 1 2

25 4 25 0x x x x x x       

61 61

4 61 0

mm      

(**)

+) Kết hợp (*), (**) và điều kiện

dương ta được:

m

2 61 3

T b a







     









Câu 82: (THPT chuyên Lam Sơn - Thanh Hóa - L01 - 2018-2019) Có tất cả bao nhiêu giá trị nguyên

của

, 2019mm

để phương trình

3 2 3

3 4 1 0x mx m   

có ba nghiệm phân biệt?

Ⓐ.

2020

Ⓑ.

2021

Ⓒ.

2030

Ⓓ.

2019

Lời giải

Chọn D

Để phương trình

3 2 3

3 4 1 0x mx m   

có ba nghiệm phân biệt khi và chỉ khi hàm số

3 2 3

3 x 4 1y x m m   

cắt

tại ba điểm phân biệt

CD CT

yy

' 3x 6 x ' 0

y m y





    







   

0 4 1; 2 1 . 0 4 1 0

CD CT

y m y m y y m m          

Vậy có:

 

1 2019 1 2019    

giá trị nguyên của

thỏa mãn điều kiện đề bài

Câu 83: (THPT chuyên Lam Sơn - Thanh Hóa - L01 - 2018-2019) Tổng tất cả các giá trị thực của tham

số m để hàm số:

 

3 2 1 3 5y x m x mx m     

có hai điểm cực trị

;xx

đồng thời

   

.0y x y x 

là:

Ⓐ.

21

Ⓑ.

39

Ⓒ.

8

Ⓓ.

3 11 13

Lời giải

Chọn A

+) Để hàm số có hai cực trị thì phương trình





phải có hai nghiệm phân biệt:

 

9 4 1 3y x m x m



   

có hai nghiệm phân biệt

 

4 1 27 0mm



     

+) Xét

   

.0y x y x 

nên ta có

 

3 2 1 3 5y x m x mx m     

phải tiếp xúc với trục hoành

 

3 2 1 3 5 0x m x mx m      

phải có nghiệm kép

     

1 3 2 5 5 0 1x x m x m



      



phải có nghiệm kép

+) TH1: Phương trình

 

3 2 5 5 0x m x m    

có một nghiệm

1 13xm   

+) TH2: Phương trình

 

3 2 5 5 0x m x m    

có nghiệm kép khác

   

2 5 12 5 0 4 32 35 0 8m m m m m m              

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

1 2 3

21m m m    

Câu 84: (Chuyên Thái Bình - Lần 01 - Năm 2018 - 2019) Có bao nhiêu giá trị nguyên của tham số

để đồ thị hàm số

 

3 2 2 2

8 11 2 2y x x m x m     

có hai điểm cực trị nằm về hai phía của trục

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn D

Yêu cầu bài toán



đồ thị hàm số cắt trục hoành tại ba điểm phân biệt

 

3 2 2 2

8 11 2 2 0x x m x m      

có ba nghiệm phân biệt

 

3 2 2 2

8 11 2 2 0x x m x m     

 

2 6 1 0x x x m     

6 1 0(*)

x x m









   



Suy ra phương trình (*) có hai nghiệm phân biệt khác

' 10 0



   













10 10











  





Vậy có

giá trị nguyên của tham số thỏa mãn đề bài.

Câu 85: (Vted-Đề số 1-Năm học 2018-2019) Có bao nhiêu giá trị nguyên của tham số

để đồ thị hàm

số

 

3 2 2 2

1 2 3y x m x m x m      

có hai điểm cực trị và hai điểm cực trị đó nằm về

cùng một phía đối với trục hoành?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Ta có

 

' 3 2 1 2y x m x m    

Điều kiện để hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành là

 

   

2 2 7 0

1 3 2 0

; 2 2;

3 2 0

   



    



  



  



    









   

1 15 1 15

;

1 15 1 15

; 2 ; 2

; 2 2;



  





   





    





   

   



    



Vì

nguyên nê chỉ có giá trị

2m 

là thỏa mãn yêu cầu.

Câu 86: (ĐỀ 02 VTED NĂM HỌC 2018 - 2019) Có bao nhiêu giá trị nguyên của tham số

để đồ thị

hàm số

 

3 2 2 2

1 2 3      y x m x m x m

có hai điểm cực trị và hai điểm cực trị đó nằm về

cùng một phía đối với trục hoành.

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Ta có

 

' 3 2 1 2    y x m x m

Hàm số có hai cực trị khi và chỉ khi phương trình

'0y

có hai nghiệm phân biệt

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

 

1 3 2 0 2 2 7 0

1 15 1 15

         



  

m m m m

 

1;0;1;2   mm

Phương trình đường thẳng qua hai điểm cực trị là

   

2 3 2

' 4 4 14 8 2 25

      y m m x m m m

Hai điểm cực trị nằm về cùng phía đối với trục hoành khi và chỉ khi

.0

CD CT

Bằng cách thử đáp án ta nhận ba giá trị của

Câu 87: (Vted - Đề số 04 - Năm 2018 - 2019) Biết đồ thị hàm số

y x ax bx c   

có hai điểm cưc

trị

   

1 1 2 2

; , ;M x y N x y

thỏa mãn

   

1 1 2 1 1 2

x y y y x x  

. Giá trị nhỏ nhất của biểu thức

23P abc ab c  

bằng

Ⓐ.



Ⓑ.



Ⓒ.

841



Ⓓ.



Lời giải

Chọn A

Ta có

32y x ax b



  

Chia

cho



ta được

1 1 2

3 9 9 3 9

a b ab

y y x a x c





      





   

1 1 2 2

; , ;M x y N x y

là hai điểm cực trị nên

   

0, 0y x y x





Do đó

1 1 2 2

;

9 3 9 9 3 9

a b ab a b ab

y x c y x c

   

         

   

   

Theo giả thiết

   

1 1 2 1 1 2 1 2 2 1

x y y y x x x y x y    

1 2 2 1

9 3 9 9 3 9

a b ab a b ab

x x c x x c

   

   

         

   

   

   

   

1 2 1 2

0( ) 9

9 9 9

ab ab ab

x c x c c x x ab c

   

         

   

   

Ta có:

7 49 49

2 3 9 21 3

2 4 4

P abc ab c c c c



         





Vậy giá trị nhỏ nhất của biểu thức

23P abc ab c  

bằng



Câu 88: (ĐTD - Đề Số 20 - Năm 2018 - 2019) Cho hàm số

   

y x m x m C   

. Biết rằng điểm

 

;M a b

là điểm cực đại của

 

ứng với một giá trị

thích hợp đồng thời là điểm cực tiểu

của

 

ứng với một giá trị khác của

. Tính tổng

2018 2020S a b

Ⓐ.

5004

. Ⓑ.

504

. Ⓒ.

504

. Ⓓ.

12504

Lời giải

Chọn C

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có:

 

' 3 3 0

y x m





    







1 1 1

1; 3 2a m b m m     

Gọi

là giá trị đó mà

 

;M a b

đạt cực tiểu nên ta có

2 2 2

1; 3 2a m b m m    

Nên ta có hệ

1 2 1 2

3 3 4 0

m m m m







  









  

  

    











Vậy

;

ab   

1009 505 504S   

Câu 89:

(ĐTD - Đề số 8 - Năm 2018 - 2019) Tìm tất cả các giá trị thực của tham số sao cho hàm số

đạt cực trị tại , thỏa mãn: .

Ⓐ. Ⓑ. Ⓒ. Ⓓ.

Lời giải

Chọn B

Ta có .

Để thỏa yêu cầu bài toán ta phải có

Câu 90: (VDC - Đề Số 12 - Năm 2018 - 2019) Tìm các giá trị của tham số

để đồ thị hàm số

2 3(2 1) 6 ( 1) 1y x m x m m x     

có hai điểm cực trị cách đều trục tung.

Ⓐ. Không tồn tại giá trị nào. Ⓑ.

m 

Ⓒ.

2.m 

Ⓓ.

2; .

mm  

Lời giải

Chọn B

Kí hiệu

   

1 1 1 2 2 2

; , ;A x y A x y

là hai điểm cực trị của đồ thị hàm số. Để

,AA

cách đều trục tung

điêu cận cần và đủ là

0xx

. Cần tìm

để



có hai nghiệm phân biệt có tổng bằng

Câu 91: (Đề VDC -Đề số 16 - Năm 2018 - 2019)

Tìm tất cả

sao cho điểm cực tiểu của đồ thị hàm số

1y x x mx   

nằm bên phải trục tung.

Ⓐ. Không tồn tại

. Ⓑ.

m

. Ⓒ.

m 

. Ⓓ.

0m 

Lời giải

Chọn D

y x x ax   

1 2 2 1

( 2 )( 2 ) 9x x a x x a    

2.a 

4.a 

3.a 

1.a 

2 2 2 3 3

1 2 1 2

0 1 1 2 ; 1 3

y x x a S x x a x x a

  







            









 

2 2 2 2 2 3 3

1 2 1 2 1 2 1 2 1 2

4 2 2 2 2 9

0a x x x x a x x x x x x         













 

2 2

1 4 0

2 4 2 14 9 03

a a a aa

a       











    











   



 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Để hàm số có cực tiểu, tức hàm số có hai cực trị thì phương trình





có hai nghiệm phân biệt

3 2 0 (1)x x m  

có hai nghiệm phân biệt

1 3 0



     

Khi đó

(1)

có hai nghiệm phân biệt

CĐ

là hoành độ hai điểm cực trị. Theo định lí Viet ta

có

0 (2)

. (3)

CĐ



   













, trong đó

CĐ CT

xx

vì hệ số của

lớn hơn 0.

Để cực tiểu của đồ thị hàm số nằm bên phải trục tung thì phải có:

x 

, kết hợp

(2)

và

(3)

suy ra

(1)

có hai nghiệm trái dấu

. 0 0

CCĐ T

x x m    

Câu 92: (ĐTD - Đề 24 - Năm 2018 - 2019) Cho hàm số . Tập hợp tất cả

các giá trị của tham số sao cho đồ thị của hàm số đã cho có 2 điểm cực trị, đồng thời hoành

độ điểm cực đại không nhỏ hơn là

Ⓐ. . Ⓑ. .

Ⓒ. . Ⓓ. .

Lời giải

Chọn C

Tập xác định . Ta có . Vậy

(*)

Đồ thị của hàm số đã cho có 2 điểm cực trị (*) có 2 nghiệm phân biệt

(1)

Gọi , là 2 nghiệm của (*), sao cho . Ta có bảng biến thiên

Vậy là điểm cực đại của hàm số đã cho.

Đặt . Yêu cầu bài toán tương đương hai nghiệm phân biệt , của phương trình

phải thỏa , nghĩa là

(2)

Từ (1) và (2) suy ra .

   

2 1 1y x m x m x    

1

 





 







 

; 2;





  





;











 





 





D 

 

3 2 2 1 1y x m x m



    

 

0 3 2 2 1 1 0y x m x m



      





  

4 7 2 0mm   

















xx

   

*VT f x

 

1 xx  

 











   









  











 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 93: (ĐTD - ĐỀ 02 - NĂM 2018-2019) Biết rằng đồ thị hàm số

   

2 3 3 2 2

3 1 1 3 4y a x b x c x d     

có hai điểm cực trị là

 

1; 7

 

2; 8

. Hãy xác định tổng

2 2 2 2

M a b c d   

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

18

Lời giải

Chọn A

Đao hàm:

   

2 2 3 2

3 3 1 2 1 3y a x b x c



    

Theo giả thiết ta có hệ:

 

   

 

   

 

   

 

   

2 3 2

1 3 3 1 2 1 3 0

2 12 3 1 4 1 3 0

1 3 1 1 3 4 7

2 8 3 1 4 1 6 4 8

y a b c

y a b c d





     





     





       



       





Xét hệ phương trình

3 2 0

12 4 0

8 4 2 8

x y z

x y z t

  





  





    



    



với





















Giải hệ phương trình trên ta tìm được

2 2 2 2

a b c d













     















Câu 94: (ĐTD - ĐỀ 02 - NĂM 2018-2019) Cho hàm số

31y x mx  

(1). Cho

 

2; 3A

, tìm

để

đồ thị hàm số (1) có hai điểm cực trị

và

sao cho tam giác

ABC

cân tại

Ⓐ.





. Ⓑ.





. Ⓒ.

m 

. Ⓓ.

m 

Lời giải

Chọn C

Ta có

33y x m





. Hàm số có hai điểm cực trị khi và chỉ khi

0m 

















Đồ thị hàm số có hai điểm cực trị

 

; 2 1B m m m

 

;2 1C m m m

. Suy ra

 

2 ;4BC m m m

Gọi

là trung điểm của

thì

(0;1)M

, nên

( 2; 2)AM   

Vậy tam giác

ABC

là tam giác cân khi và chỉ khi.

Câu 95:

   

. 0 ( 2). 2 ( 2). 4 0

AM BC AM BC m m m m          

.(ĐTD - ĐỀ TUẦN 1

- NĂM 2018-2019) Với giá trị thực dương của tham số m để đồ thị hàm số

3 3 1y x mx x   

có các điểm cực trị A và B sao cho tam giác

OAB

có diện tích bằng

thì mệnh đề nào sau

đây là đúng?

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ⓐ.

12m

Ⓑ.

m

Ⓒ.

34m

Ⓓ.

1m 

Lời giải

Chọn B

Đường thẳng qua hai điểm cực trị

 

2 2 1y m x m px q     

Điều kiện có hai điểm cực trị là

1m 

. Gọi hai điểm cực trị của đồ thị hàm số là

 

;A x px q

và

 

;B x px q

   

1 2 2 1

OAB

S x px q x px q



    

OAB

S q x x



  

 

1 2 1 2

. 1. 4

OAB

S m x x x x



    

. 1. 4 4

OAB

S m m



   

1. 1 8 2

OAB

S m m



    

  

2 1 1 128m m m    

 

3 5 15 43 0m m m m     

3m

. Chọn B

Câu 96: (TT học mãi - Thầy Lê Anh Tuấn - Năm 2018 - 2019) Có bao nhiêu giá trị nguyên của tham

số

để điểm

(2 ; )M m m

tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số

2 3(2 1) 6 ( 1) 1 ( )y x m x m m x C     

một tam giác có diện tích nhỏ nhất?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ. không tồn tại

Lời giải

Chọn B

Ta có

' 6 6(2 1) 6 ( 1)y x m x m m    

y m R





    







, hàm số luôn có CĐ, CT

Tọa độ các điểm CĐ, CT của đồ thị là

3 2 3 2

( ;2 3 1), ( 1;2 3 )A m m m B m m m   

Suy ra

2AB 

và phương trình đường thẳng

: 2 3 1 0AB x y m m m     

Do đó, tam giác

MAB

có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ

tới

nhỏ nhất

Ta có

3 1 1

( , )

d M AB





, dấu "=" khi

0m 

Câu 97: (Chuyên Thái Bình- Lần 03- Năm 2018- 2019) Gọi

,xx

là hai điểm cực trị của hàm số

4 10

y x mx x   

. Tìm giá trị lớn nhất của biểu thức

  

11S x x  

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

Ta có:

3 2 2

4 10 ' 4

y x mx x y x mx       

' 0 4 0y x mx    

16 0,mm    

nên phương trình

'0y 

luôn có hai nghiệm phân biệt

,xx

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Áp dụng định lí viet:

x x m





  







  





2 2 2 2

1 2 1 2 1 2 1 2

( 1)( 1) ( ) [( ) 2 . ] 1S x x x x x x x x       

16 ( 8) 1 9 9mm      

Câu 98: (THPT Sơn Tây - Hà Nội - Lần 01- Năm 2018-2019 ) Ta xác định được các số

,,abc

để đồ thị

hàm số

y x ax bx c   

đi qua điểm

 

0;1

và có điểm cực trị

 

2;0

. Tính giá trị của biểu

thức

4T a b c  

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

TXĐ:

y x ax bx c   

;

32y x ax b



  

Đồ thị hàm số qua điểm

 

0;1

nên

1c 

Đồ thị hàm số có điểm cực trị

 

2;0

 







  











8 4 2 0

12 4 0

a b c







     





  



















Do đó:

4 4. 5 1 23

T a b c      

Câu 99: (THPT KIM LIÊN - HÀ NỘI - Lần 03 - Năm 2018-2019) Cho hàm số

64y x mx  

có đồ

thị

 

. Gọi

là giá trị của

để đường thẳng đi qua điểm cực đại, điểm cực tiểu của

 

cắt đường tròn tâm

 

1;0I

, bán kính

tại hai điểm phân biệt

,AB

sao cho tam giác

IAB

có

diện tích lớn nhất. Chọn khẳng định đúng

Ⓐ.

 

3;4m 

. Ⓑ.

 

1;2m 

. Ⓒ.

 

0;1m 

. Ⓓ.

 

2;3m 

Lời giải

Chọn C

Xét hàm số

64y x mx  

có tập xác định .

3 6 ; ' 0 2y x m y x m



    

Đồ thị hàm số có 2 điểm cực trị





đổi dấu

lần





có hai nghiệm phân biệt

0m

Ta có

'. 4 4

y y x mx  

Gọi

   

1 1 2 2

; , ;M x y N x y

là hai điểm cực trị của đồ thị hàm số.

Ta có

   

1 1 1 1 1

2 2 2 2 2

. 4 4

y x y x

y mx

y y x y x x mx

y mx

y y x y x x mx









  







    



  







   





 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Suy ra

,MN

thuộc đường thẳng

có phương trình

44y mx  

Vậy phương trình đường thẳng qua hai điểm cực trị của

 

là:

44y mx  

Gọi

 

là đường tròn có tâm

 

1;0I

và bán kính

2R 

Đường thẳng

cắt đường tròn tại hai điểm phân biệt

,AB

và tạo thành tam giác

IAB

   

0 , 0 , 2d I d R d I d     

16 1





















(*).

Cách 1: (Nguyễn Công Định)

Do đường thẳng

luôn đi qua điểm

 

0;4K

17IK R

K

nằm ngoài đường tròn nên

tồn tại hai điểm

,AB

là giao điểm của

với đường tròn để tam giác

IAB

vuông tại

Do đó:

. .sin .

IAB

S IA IB AIB IA IB

Dấu bằng xảy ra

IA IB

 

d I d  

(thỏa mãn (*)).

16 1



   



Bình luận: Nếu đường thẳng

luôn đi qua điểm

cố định mà

IK 

thì sẽ không có vị trí

của đường thẳng

để tam giác

IAB

vuông tại

. Khi đó, nếu làm như trên sẽ bị sai. Trong

trường hợp đó thì ta phải đặt

   

,0d I d t t l  

, với

là độ dài đoạn thẳng

, rồi tính

 

IAB

S f t





và tìm giá trị lớn nhất của

 

trên nửa khoảng





0;l

Cách 2: Phương trình đường tròn là:

 

12xy  

 

Xét hệ

 

   

16 1 2 16 1 15 0 1

m x m x

y mx



  



     



  





cắt

 

tại hai điểm phân biệt

,AB

 

1

có 2 nghiệm phân biệt

,ab

   

16 1 15 16 1 0mm    

Khi đó

   

 

1; 4 4

; 4 4 , ; 4 4

1; 4 4

IA a ma

A a ma B b mb

IB b mb



   



    



   



   

. 16 1 1 0IAIB ab a b m ab m a b



         



   

16 16 17 0ab a b m ab m a b       

 

  

16 1 16 1 17 0m ab m a b      

   

2 16 1 16 1

15 17 0 16

16 1 16 1 32



       



Câu 100: (THPT KIM LIÊN - HÀ NỘI - Lần 03 - Năm 2018-2019) Tìm tất cả các giá trị thực của tham

số

để hàm số

 

3 2 2

2 1 7 5

y x m x m m x m       

có hai điểm cực trị là độ dài hai

cạnh góc vuông của một tam giác vuông có cạnh huyền bằng

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ⓐ.

3m 

. Ⓑ.











. Ⓒ.

2m 

. Ⓓ.











Lời giải

Chọn A

2(2 1) 7y x m x m m



     

Xét phương trình





2(2 1) 7 0x m x m m      

(*).

Yêu cầu bài toán



pt (*) có hai nghiệm phân biệt

;xx

sao cho











































 

3 3 6 0

4 2 0

4 2 2 7 74

m m m



  









  



    



3 3 6 0

4 2 0



  











  



  



3 3 6 0

4 2 0



  







  

  





















Câu 101: (THPT Nguyễn Khuyến - Thành Phố Hồ Chí Minh - Năm 2018-2019) Tìm số thực

để đồ

thị hàm số

2  y x kx k

có ba điểm cực trị tạo thành một tam giác nhận điểm







làm

trọng tâm.

Ⓐ.

  kk

. Ⓑ.

kk

Ⓒ.

kk

. Ⓓ.

;

kk

Lời giải

Chọn C

Ta có:

 

4 4 4



   y x kx x x k

 













Đồ thị hàm số có ba điểm cực trị



y

có ba nghiệm phân biệt và



đổi dấu khi

đi qua

3 nghiệm đó

 

1 PT

có hai nghiệm phân biệt khác không

0k

. Khi đó ba điểm cực trị

của đồ thị hàm số là

 

0;Ak

 

;B k k k

 

; C k k k

Từ yêu cầu bài toán ta có:

   

3 3 3

   



  

A B C

k k k k k

yyy

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

2 3 1 0







     







Câu 102: (Chuyên KHTN - Năm 2018 - 2019 - Lần 01) Có bao nhiêu giá trị nguyên của tham số

để

đồ thị của hàm số

 

3 2 2 2

1 2 3y x m x m x m      

có hai điểm cực trị và hai điểm cực trị

đó nằm về hai phía khác nhau đối với trục hoành?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải

Chọn B

Ta có

 

0 3 2 1 2 0y x m x m



      

Để hàm số có hai điểm cực trị

 

1 15 1 15

0 2 2 7 0 *

m m m





          

Ta lần lượt thử bốn giá trị nguyên của

thỏa mãn

 

là

1;0;1;2

Ta được bốn hàm số

3 3 2 3 2 3 2

2; 2 3; 2 2; 3 1y x x y x x x y x x x y x x x              

Khi đó ta nhận thấy chỉ có

1m 

thỏa mãn yêu cầu bài toán.

Câu 103: (THPT LÝ THÁI TỔ - BẮC NINH -LẦN 1- NĂM 2018 - 2019) Cho hàm số

2 3 1 2 1

y x m m x m

. Gọi

là tập hợp tất cả các giá trị của

tham số

sao cho ham số

 

đạt cực đại, cực tiểu tại

C§

sao cho



C§

. Khi đó,

tổng các phần tử của tập

bằng?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

TXĐ:

D 

Ta có

 

' 3 2 2 3 1y x m x m m     

Hàm số đạt cực đại, cực tiểu khi

'0y 

có hai nghiệm phân biệt

,xx

 

3 2 4 2 3 1 0, 0m m m m m          



  



  

 Trường hợp

0m 

   

C§ CT

1, 2 1x m x m

   







         









C§

3 4 3 1 4 2 1 3 2 1 0

x x m m m m

Vì

0m 

nên

1m 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 Trường hợp

0m 

   

C§ CT

2 1, 1x m x m

   









         











C§

3 4 3 2 1 4 1 12 8 1 0

x x m m m m

Vì

0m 

nên





Vậy

2 7 4 7

  

  

Câu 104: (THPT Ischool Nha Trang – Khánh Hoà - Lần 01 - Năm 2018 - 2019) Tìm các giá trị thực

của tham số

để đồ thị hàm số

   

1 3 1 2y x m x     

có hai điểm cực trị cách đều

gốc tọa độ.

Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

5m 

. Ⓓ.

5m 

Lời giải

Chọn B

Ta có

 

' 3 1 3y x m   

   

0 3 1 3 0 1

x m x m

y x m x m

x m x m

   





          



    



Để hàm số có 2 cực trị thì

0m 

Gọi

,AB

là hai điểm cực trị của đồ thị hàm số có hoành độ lần lượt là

1 ; 1

x m x m   

Khi đó

   

1 ;2 2 ; 1 ; 2 2A m m B m m    

Hai điểm cực trị cách đều gốc tọa độ nên

OA OB OA OB  

 

1 2 2 1 2 2m m m m        

 

m ktm

m tm







   









Vậy

m 

Câu 105: (Chuyên Thái Bình - Lần 04 - Năm 2018 - 2019) Cho hàm số

3 2 3

33  y x mx m

. Biết rằng

có hai giá trị của tham số

để đồ thị hàm số có hai điểm cực trị

,AB

và tam giác

OAB

có diện

tích bằng 48. Khi đó tổng hai giá trị của

là

Ⓐ.

. Ⓑ.

2

. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

Tập xác định của hàm số là

.D

Ta có

3 6 , 0







   







y x mx y

Hàm số đã cho có hai điểm cực trị



y

có hai nghiệm phân biệt

0.m

Khi đó tọa độ hai điểm cực trị của đồ thị hàm số là

   

0 ; 3 ; 2 ; .A m B m m

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Phương trình đường thẳng

là

2 3 0.  m x y m

 

48 . ; 48 4 16 96



     



OAB

AB d O AB m m

36 96





  







( Thỏa mãn điều kiện

0m

)

Vậy tổng hai giá trị của

là

Câu 106: (Chuyên Lam Sơn - Lần 2 - Năm 2018 - 2019) Cho hàm số

 

3 2 2 3

3 3 1y x mx m x m m     

(

là tham số). Gọi

là hai điểm cực trị của đồ thị

hàm số và

 

2; 2I 

. Tổng tất cả các giá trị của

để ba điểm

tạo thành tam giác nội

tiếp đường tròn có bán kính bằng

là

Ⓐ.

. Ⓑ.



. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

+) Xét hàm số

 

3 2 2 3

3 3 1y f x x mx m x m m      

. TXĐ:

D 

 

3 6 3 1 3 1y x mx m x m





      



x m x m

   





  



    



+) Suy ra

m

, đồ thị hàm số

 

y f x

luôn có 2 điểm cực trị là:

 

1; 4 2A m m  

 

1; 4 2B m m  

+) Ta có

 

2 4 2 5AB    

; Bán kính đường tròn ngoại tiếp

IAB

là

5R 

+)Theo định lý sin trong

IAB

ta có:

2 sin 1 90

sin

R AIB AIB

AIB

     

     

. 0 1 3 4 4 4 0 17 20 3 0

IA IB m m m m m m







              







Vậy tổng các giá trị của

là:

3 20

17 17



Câu 107: (THPT Nình Bình - Bạc Liêu - Lần 04 - Năm 2018 - 2019) Có bao nhiêu số nguyên

để hàm

số

34y x x mx   

có hai điểm cực trị thuộc khoảng

 

3;3

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

Ta có:

' 3 6y x x m  

Để hàm số

34y x x mx   

có hai điểm cực trị thuộc khoảng

 

3;3

thì phương trình

'0y 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

hay

3 6 0x x m  

có hai nghiệm phân biệt thuộc khoảng

 

3;3

Cách 1:

Khi đó, đặt

 

36f x x x m  

thì

 

9 3 0

. 3 0

45 0

. 3 0

3 1 3



















    







  







Do đó có 11 giá trị nguyên của

thỏa mãn yêu cầu bài toán.

Cách 2:

Khi đó, đặt

 

36f x x x m  

thì

9 3 0

3 9 3 3 9 3











    



   

   







Do đó có 11 giá trị nguyên của

thỏa mãn yêu cầu bài toán.

Cách 3: Admin Nguyễn Văn Thịnh

Ta có:

36y x x m



  

Hàm số

34y x x mx   

có hai điểm cực trị thuộc khoảng

 

3;3



Phương trình





hay

36x x m

có hai nghiệm phân biệt thuộc khoảng

 

3;3

Đặt

   

3 6 , 3;3f x x x x   

. Ta có:

 

66f x x





;

 

01f x x



  

Bảng biến thiên:

Yêu cầu bài toán

39m   

Vậy có 11 giá trị nguyên của

thỏa mãn yêu cầu bài toán.

Câu 108: (THPT Nguyễn Huệ - Huế - Lần 02 - Năm 2018 - 2019) Cho hàm số

   

1 3 2 2019

y mx m x m x     

với

là tham số. Tổng bình phương tất cả các giá trị

của

để hàm số có hai điểm cực trị

,xx

thỏa mãn

21xx

bằng

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn C

Ta có:

   

' 2 1 3 2y mx m x m    

Để hàm số có hai điểm cực trị

' 2 4 1 0









     



 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có:

 

1 2 2

2 1 1

x x x

















     



























 

2 2 2

3 1 3 1

m m m







    

      



    

    









Vậy

mm

Câu 109: (SGD Bắc Giang - Lần 01 - Năm 2018 - 2019) Gọi

là tập hợp các giá trị nguyên của tham

số

để hàm số

y x mx   

có hai điểm cực trị

,4xx

. Số phần tử của

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Hàm số có hai điểm cực trị

,xx

thì phương trình

'0y 

có hai nghiệm phân biệt

' 0 4 0 4mm       

Khi đó giả sử

xx



  





  





Yêu cầu bài toán trở thành

4 2 4 4 0 4x m m       

Kết hợp với

4m 

ta được

04m

. Do

nguyên nên

 

0;1;2;3m

. Vậy có 4 giá trị của

thỏa mãn yêu cầu bài toán.

Câu 110: (SGD Hưng Yên - Năm 2018 - 2019) Cho hàm số

   

2 3 1 6 2 1y x m x m x     

với

là tham số thựⒸ. Tìm tất cả các giá trị của

để hàm số có điểm cực đại và điểm cực tiểu nằm

trong khoảng

 

2;3

Ⓐ.

   

1;4 \ 3m

. Ⓑ.

 

3;4m

. Ⓒ.

 

1;3m

. Ⓓ.

 

1;4m

Lời giải

Chọn A

Ta có

   

6 6 1 6 2y x m x m



    

   

0 1 2 0

y x m x m







       



  



Để hàm số có điểm cực đại cực tiểu nằm trong khoảng

 

2;3

thì





có hai nghiệm phân biệt

nằm trong khoảng

 

2;3

2 1 3

2 2 3 1 4

    







       



 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 111: (SGD Kiên Giang - Năm 2018 - 2019) Gọi

là số thực âm để đồ thị hàm số

3 2 3

6 32y x mx m  

có hai điểm cực trị đối xứng với nhau qua đường phân giác của góc phần

tư thứ nhất của hệ trục tọa độ

Oxy

. Chọn khẳng định đúng trong các khẳng định sau.

Ⓐ.



  





. Ⓑ.



  





. Ⓒ.



  





. Ⓓ.









Lời giải

Chọn D

Ta có

3 12y x mx

















Hàm số có hai cực trị khi

0m 

. Khi đó, gọi

 

0;32 ; 4 ;0A m B m

là tọa độ 2 điểm cực trị của

đồ thị hàm số. Hai điểm này đối xứng với nhau qua đường thẳng

: yx

khi và chỉ khi:

   

32 4

;;

4 32 0

d A d B





  





   















(vì

0m 

Vì

0m 

nên ta chọn





Cách 2:

Chú ý: Hai điểm

   

; , '; 'A x y B x y

đối xứng nhau qua đường phân giác góc phần tư thứ nhất

khi và chỉ khi











Câu 112:

 

0;32 ; 4 ;0A m B m

đối xứng nhau qua đường phân giác góc phần tư thứ nhất khi và chỉ khi

32 4mm

(với

0m 

)

m  

. Đối chiếu các phương án, ta chọn phương án D

(SGD Phú Thọ - Lần 02 - Năm 2018 - 2019) Tập hợp tất cả các giá trị tham số thực

để đồ

thị hàm số

 

3 2 2 3

3 3 1y x mx m x m    

có hai điểm cực trị nằm về hai phía trục hoành là

 

;ab

. Khi đó giá trị

2ab

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Ta có

' 3 6 3( 1)y x mx m   

Xét

3 6 3( 1) 0

x mx m

  



    



  



Hai nghiệm trên phân biệt với mọi

Đường thẳng qua 2 điểm cực trị của đồ thị là

2y x m  

Vậy nên các giá trị cực trị

( 1) 3 2y m m   

( 1) 3 2y m m   

Theo yêu cầu bài toán ta phải có

  

3 2 3 2 0

m m m      

Vậy

ab

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 113: (SGD Quảng Nam - Năm 2018 - 2019) Có bao nhiêu giá trị thực của tham số

để đồ thị hàm

số

3 2 3

y x mx m  

có hai điểm cực trị đối xứng nhau qua đường thẳng

yx

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn C

Ta có

' 3 3y x mx

;













Hàm số có hai điểm cực trị khi và chỉ khi

'0y 

có hai nghiệm phân biệt

0m

Với điều kiện

0m 

, giả sử hai điểm cực trị của đồ thị hàm số là







 

;0Bm

;

AB m m









và

;







là trung điểm của đoạn thẳng

Yêu cầu bài toán

AB u













  

  

  

















Đối chiếu điều kiện ta được

2m 

Câu 114: (SGD Vĩnh Phúc - Lần 2 - Năm 2018 - 2019) Tìm tất cả các giá trị của tham số

để hàm số

   

3 2 3

3 4 3

y x m x m x m m      

đạt cực trị tại

x ,x

thỏa mãn

1 xx  

Ⓐ.

31m  

. Ⓑ.

m   

. Ⓒ.











. Ⓓ.

m   

Lời giải

Chọn B

Ta có

   

2 3 4 3y x m x m



    

Đặt

11t x x t    

. Khi đó

 

2 2 2 7y t m t m



    

Hàm số đạt cực trị tại

x ,x

thỏa mãn

1 xx  

   

2 3 4 3 0x m x m     

có hai

nghiệm phân biệt

x ,x

thỏa mãn

1 xx  

 

2 2 2 7 0t m t m     

có hai nghiệm phân

biệt dương. Điều này tương đương với

 

2 3 0

2 2 0 2 3

2 7 0

S m m m

  













    





           





  











Cách 2:

Ta có

   

2 3 4 3y f (x) x m x m



     

Hàm số đạt cực trị tại

x ,x

thỏa mãn

1 xx  

   

2 3 4 3 0x m x m     

có hai

nghiệm phân biệt

x ,x

thỏa mãn

1 xx  

. Điều này tương đương với

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

. ( 1) 0





















2 3 0

1 2( 3) 4( 3) 0

2( 3)





  



     













  













  













  

. Chọn B

Câu 115: (ĐTD-Đề 5- Năm 2018-2019) Xác định các giá trị của tham số thực

để đồ thị hàm số

y x x mx m   

có các điểm cực đại và cực tiểu

và

sao cho tam giác

ABC

vuông

tại

trong đó tọa độ điểm







Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

m 

. Ⓓ.

m 

Lời giải

Chọn B

Ta có tam giác ABC vuông tại C nên gọi M là điểm uốn của đồ thị hám số đồng thời là trung

điểm của AB, Khi đó tam giác vuông có đường trung tuyến bằng nửa cạnh huyền do vậy ta có

phương trình sau:

 

2 1 1 2

MC AB p x x x x    

(*). Thay số:

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hệ số góc đường thẳng qua hai cực trị:

 

pm

Ta có:

y x x m

x x m





   







Tọa độ điểm uốn









(Chú ý điểm uốn



Vậy ta có: (*)

 

5 1 4 1

1 1 4 4

3 2 9 2

m m m      

Câu 116: (ĐTD- Đề VDC 9 - 10- Tuần 15 - Năm 2018-2019) Có bao nhiêu giá trị nguyên của tham số

để đồ thị hàm số

 

3 2 2 2

8 11 2 2y x x m x m     

có hai điểm cực trị nằm về hai phía của trục

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

Đồ thị hàm số

 

3 2 2 2

: 8 11 2 2C y x x m x m     

có hai điểm cực trị nằm về hai phía

của trục



phương trình

 

3 2 2 2

8 11 2 2 0, 1x x m x m     

có 3 nghiệm phân biệt.

Ta có

   

 

   

1 2 6 1 0

6 1 0, 2

x x x m

f x x x m





      



    



Suy ra phương trình

 

phải có

nghiệm phân biệt khác

 

9 1 0

10 10

2 4 12 1 0





    



  











    







. Do

 

2; 1;0mm    

Câu 117: (Chuyên Hùng Vương - Gia Lai - Lần 01 - Năm 2018 - 2019) Cho hàm số

 

3 2 2 3

3 3 1y x mx m x m m     

, với

là tham số. Gọi

là hai điểm cực trị của đồ thị

hàm số và

 

2; 2I 

. Giá trị thực

1m 

để ba điểm

tạo thành tam giác nội tiếp đường

tròn có bán kính bằng

là

Ⓐ.

m 

. Ⓑ.

m 

. Ⓒ.

m 

Ⓓ.

m 

Lời giải

Chọn B

   

3 2 2 3 2 2

3 3 1 3 6 3 1y x mx m x m m y x mx m



          

 

1 4 2

0 3 6 3 1 0

1 4 2

x m y m

y x mx m

x m y m

    





       



    



Khi đó đồ thị hàm số có 2 điểm cực trị

   

1; 4 2 , 1; 4 2A m m B m m     

   

1; 4 4 , 3; 4IA m m IB m m     

Ta có:

 

2;4AB 

25AB

do đó

là đường kính của đường tròn ngoại tiếp tam giác

IAB

nên

90AIB





hay

AI BI

.0IAIB

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

     

1 3 4 4 4 0 17 20 3 0

m m m m m m







            







1m 

nên chọn

m 

Câu 118: (Chuyên Lê Hồng Phong - Nam Định - Lần 2 - Năm 2018) Tìm tham số

để hàm số

 

2 2018

y x mx m x    

không có cực trị.

Ⓐ.

1m 

hoặc

2m 

Ⓑ.

1m 

Ⓒ.

2m 

Ⓓ.

12m  

Lời giải

Chọn D

Ta có:

22y x mx m



   

Để hàm số đã cho không có cực trị khi phương trình





vô nghiệm hoặc có nghiệm kép hay





 

20mm   

12m   

Câu 119: (THPT LƯƠNG NGỌC QUYẾN - THÁI NGUYÊN - LẦN 02 - NĂM 2017-2018) Cho hàm

số

   

2 3 1 6 2 1y x m x m x     

. Với điều kiện nào của tham số

thì hàm số trên có

cực trị?

Ⓐ.

3m 

. Ⓑ. Với mọi

. Ⓓ.

3m 

Lời giải

Chọn D

   

6 6 1 6 2y x m x m



    

Hàm số có cực trị





có 2 nghiệm phân biệt

   

1 4 2 0mm    

6 9 0 3m m m     

Câu 120: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Biết rằng đồ thị hàm số

 

y f x ax bx c   

có hai điểm cực trị là

 

0;3A

và

 

2; 13B 

. Giá trị của

 

là

Ⓐ.

 

14f 

Ⓑ.

 

18f 

Ⓒ.

 

12f 

Ⓓ.

 

16f 

Lời giải

Chọn A

Ta có

 

42f x ax bx





   

0 3 2 15; , ;AB

là hai điểm cực trị nên ta có:

 

3 8 0 1

2 0 32 4 0 4 4 8

16 4 13 3 3

2 15

c a b a

f a b a b b

a b c c c





  

   



   



          

   

   

     



  





 

83f x x x   

 

1 1 8 3 4f     

Chú ý:

 Như bình thường với một điểm

 

;M x y

là điểm cực trị của đồ thị hàm số

 

y f x

ta sẽ

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

khai thác được phương trình

 

0fx

f x y

















. Nhưng hàm trùng phương,với điểm cực trị thuộc trục

tung

thì dữ kiện

 

0fx





luôn đúng (ở đây

0x 

và

 

0 0 0 0f



  

). Do đó ta chỉ có

được

phương trình (ở bài toán trên ta có được 1 phương trình là

 

03fy

 Ở bài toán này đề bài cho biết tọa độ 2 điểm cực trị (trong khi thực tế hàm số có tới 3 cực trị)

nên việc tìm điểm cực trị thứ ba (nếu cần) là không khó khi ta biết

 

03;A Oy

thì suy ra điểm

cực trị thứ ba sẽ đối xứng với

 

2 15;B 

qua trục

, hay điểm cực trị thứ ba có tọa độ

 

2 15;C 

. Nhưng với bài toán này, dữ kiện điểm cực trị thứ ba không cần thiết nên ta không

khai thá

Ⓒ.

Câu 121: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Biết đồ thị

 

của hàm số

y ax bx c  

có

 

14;A

và

 

03;B

là các điểm cực trị. Hỏi trong các điểm sau đây, đâu là

điểm thuộc đồ thị

 

Ⓐ.

 

25;M 

Ⓑ.

 

14;N 

Ⓒ.

 

3 15;P 

Ⓓ.

 

25;Q 

Lời giải

Chọn D

Ta có

 

42f x ax bx





. Do

 

14;A

và

 

03;B

là hai điểm cực trị nên ta có:

 

4 2 0 2 0 1

1 4 4 1 2

3 3 3

a b a b a

f a b c a b b

c c c







  

     



   

         

   

   

  



  





 

23f x x x    

Chỉ có điểm

 

25;Q 

thỏa mãn

   

25f Q T   

Câu 122: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tìm tất cả các giá trị của

sao cho hàm

số

3 3 1y x mx m   

có hai điểm cực trị

Ⓐ.

0m 

Ⓑ.

0m 

Ⓒ.

0m 

Ⓓ.

0m 

Lời giải

Chọn D

Cách 1: Ta có

3 6 ;y x mx



















Để hàm số có hai điểm cực trị thì phương trình trên có hai nghiệm phân biệt

2 0 0mm  

Cách 2: Do hàm số dạng bậc ba nên điều kiện để hàm số có hai điểm cực trị là

30b ac

90m

0m

Câu 123: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Cho hàm số

 

3 2 2

2 2 1 1 2y x m x m x      

. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số

để

hàm số đã cho có hai điểm cực trị

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn B

Do hàm số bậc ba nên điều kiện hàm số có hai điểm cực trị là

 

2 2 2

3 0 2 1 6 1 0 2 4 7 0b ac m m m m          

2 3 2 2 3 2

   

  

. Do

m

nên

 

3; 2; 1;0;1m   

Vậy có

giá trị nguyên của

thỏa mãn.

Câu 124: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tìm tất cả các giá trị của tham số

để

hàm số

 

1 3 3 1y m x x x    

có cực trị.

Ⓐ.

1m 

Ⓑ.

1m 

Ⓒ.

01m

Ⓓ.

0m 

Lời giải

Chọn D

+) Với

1m 

hàm số có dạng

3 3 1y x x   

là hàm số bậc 2 nên có một cực trị (thỏa mãn).

+) Với

1m 

, hàm số có cực trị

3 0 9 0 0b ac m m      

Vậy

0m 

Ch : Hàm số bc ba số cực trị có thể là

hoc

. Do đó câu hi tìm

để hàm bc ba có

cực trị hay có hai cực trị là như nhau. Song nếu hàm số có hệ số

chứa tham số thì ta phi xt

thêm

0a 

(Hàm số không có dng bc 3), khi đó có thể hàm số có 1 cực trị v như câu trên.

Câu 125: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Cho hàm số

 

2 1 1

y x mx m x    

. Trong các mệnh đề sau, đâu là mệnh đề sai?

Ⓐ. Với

1m

thì hàm số có hai điểm cực trị.

Ⓑ. Hàm số luôn có cực đại và cực tiểu.

Ⓒ.

Với

1m

thì hàm số có cực đại và cực tiểu.

Ⓓ. Với

1m

thì hàm số có cực trị.

Lời giải

Chọn B

Vì hàm số có dạng bậc ba nên ta xét

   

3 2 1 1b ac m m m     

Hàm số có hai cực trị khi và chỉ khi

 

3 0 1 0 1b ac m m      

nên đáp án B sai.

Ch : Ở bài toán này mệnh đề A, D đúng vì

1m

thì hàm số có cực đi và cực tiểu (Có hai

cực trị hay có cực trị) nên cng tha mn với

1m

hoc

1m

Câu 126: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tất cả các giá trị của

để hàm số

 

2 4 2

1 1 3y m x m x    

có đúng một cực trị là

Ⓐ.

1m 

Ⓑ.

1m 

Ⓒ.

1m 

và

1m 

Ⓓ.

1m 

và

1m 

Lời giải

Chọn D

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hàm số có một cực trị khi và chỉ khi











 

1 1 0



  







   





 

   

1 1 0

1 1 1 0



  









   































Chú ý: Trong bài toán này, có thể rất nhiều bạn sẽ mắc phải lỗi không cho điều kiện

0ab

dẫn đến kết quả không đúng. Vì với

00a b a b y c      

sẽ không có cực trị.

Vì vậy các bạn cần nhớ: Hàm số

y ax bx c  

với

chứa tham số

 không có cực trị

0ab  

 có một cực đại và không có cực tiểu













hoặc











(hay viết gọn thành

















 có một cực tiểu và không có cực đại













hoặc











(hay viết gọn thành

















 có một cực đại

















hoặc











 có một cực tiểu

















hoặc











 có một cực trị













 có hai cực đại và một cực tiểu













 có hai cực tiểu và một cực đại













 có ba cực trị

0ab

Câu 127: (NXBGD - Phạm Đức Tài- Đề số 2 - Năm 2017-2018) Tìm tất cả các giá trị thực của tham số



để hàm số

   

2 1 sin 1 cos2

y x x x



    

có cực trị.

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ⓐ.







. Ⓑ.





. Ⓒ.







. Ⓓ.





Lời giải

Chọn A

   

' 4 4 1 sin 1 cos2y x x



    

có hai nghiệm phân biệt

  

  

1 sin 3 sin 0



   

sin 1 2 ,



  

     

Câu 128: (Chuyên Hùng Vương - Phú Thọ - Lần 1 - Năm 2018) Biết

là giá trị của tham số

để

hàm số

31y x x mx   

có hai điểm cực trị

,xx

sao cho

1 2 1 2

13x x x x  

. Mệnh đề nào

dưới đây đúng?

Ⓐ.

 

1;7m 

. Ⓑ.

 

7;10m 

. Ⓒ.

 

15; 7m   

. Ⓓ.

 

7; 1m   

Lời giải

Chọn C

TXĐ:

D 

36y x x m



  

Xét

0 3 6 0y x x m



    

;

93m



  

Hàm số có hai điểm cực trị

03m



    

Hai điểm cực trị

;xx

là nghiệm của





nên:

1 2 1 2

2; .

x x x x  

Để

 

1 2 1 2 1 2 1 1

13 3 . 13x x x x x x x x      

4 13 9mm     

. Vậy

 

9 15; 7m     

Câu 129: (THPT Lương Thế Vinh - Hà Nội - Lần 03 - Năm 2018) Cho hàm số

f x x x ax b

có đồ thị là

. Biết

có điểm cực tiểu là

1;2A

. Giá trị

2ab

bằng

Ⓐ.

1

Ⓑ.

Ⓒ.

5

Ⓓ.

Lời giải

Chọn C

Ta có

f x x x ax b

32f x x x a

Đồ thị hàm số có điểm cực tiểu là

1;2A

Ta được

Vậy

2 2 3 5ab     

Câu 130: (THPT Nguyễn Khuyến - TP HCM - Năm 2018) Tìm tất cả các giá trị của tham số thực

để

đồ thị hàm số

 

21y x x m x m    

có hai điểm cực trị nằm về hai phía đối với trục hoành.

Ⓐ.

m  

Ⓑ.

0m 

Ⓒ.

m  

Ⓓ.

m 

Lời giải

Chọn A

TXĐ:

D 

, có

 

3 4 1y x x m



   

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hai điểm cực trị nằm về hai phía đối với trục hoành thì

0y 

có ba nghiệm phân biệt.

Suy ra

   

 

3 2 2

2 1 0 1 0x x m x m x x x m         

có ba nghiệm phân biệt.

Nên

1 4 0

1 1 0





   



  



Câu 131: (THPT Nguyễ n Khuyế n - TP HCM - Năm 2018) Biết hàm số

   

1 2 1

y m x m x     

đạt cực trị tại

1x 

(

là tham số thực). Khi đó điểm cực trị

của hàm số khác

là

Ⓐ.

1

Ⓑ.

2

Ⓒ.

Ⓓ. Đáp số khác

Lời giải

Chọn C

Ta có:

 

2 1 2y x m x m



    

Hàm số đạt cực trị tại

1x 

 

10y





10m   

1m

Với

1m 

ta có:

2 3 1

y x x   

và

4 3 0y x x



   













Suy ra điểm cực trị còn lại là

3x 

Câu 132: (THPT Kinh Môn 2 - Hải Dương - Năm 2018) Cho

 

3 2 2

3 2 1 4 1y m x m m x m x       

. Gọi

là tập tất cả các giá trị nguyên của

để

đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục

có bao nhiêu phần tử?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn C

Ta có

 

3 3 4 1 4y m x m m x m



      





 

3 3 4 1 4 0m x m m x m       

Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục

thì phương trình





có hai nghiệm phân biệt trái dấu.

Suy ra

 

   

3 3 0

3 3 . 4 0









  





43m   

Mà

m

nên

 

3; 2; 1;0;1;2m    

. Vậy

có

phần tử.

Câu 133: (Chuyên Hạ Long - Quảng Ninh - Lần 01 - Năm 2018) Tìm tất cả các giá trị thực của tham số

để hàm số

 

3 1 2y x x m x    

có hai điểm cực trị.

Ⓐ.

2m 

. Ⓑ.

2m 

. Ⓒ.

2m 

. Ⓓ.

4m 

Lời giải

Chọn B

Ta có

3 6 1y x x m



   

. Hàm số có hai điểm cực trị khi





có hai nghiệm phân biệt.





 

9 3 1 0m   

2m

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 134: (THPT THỰC HÀNH TÂY NGUYÊN - LẦN 02 - 2018) Tìm các giá trị thực của tham số

để hàm số

3 2 1

y x mx x m    

đạt cực tiểu tại

1x 

Ⓐ.

2m 

. Ⓑ. Không tồn tại

. Ⓒ.

1m 

. Ⓓ.

3m 

Lời giải

Chọn B

23y x mx



  

22y x m





Xét

 





















4 2 0

2 2 0























Vậy không tồn tại

thỏa mãn bài toán.

Câu 135: (Pen M - Nguyễn Thanh Tùng) Tìm tất cả các giá trị thực của tham số

để đồ thị hàm số

 

3 2 2

4 1 1y x x m x    

có hai điểm cực trị nằm về hai phía khác nhau đối với trục tung.

Ⓐ.

m  

. Ⓑ.











. Ⓒ.

11m  

. Ⓓ.

11m  

Lời giải

Chọn B

 

3 8 1y x x m



   

Yêu cầu bài toán







có hai nghiệm trái dấu



 

3 1 0m













Câu 136: (Chuyên Nam Sơn - Thanh Hóa - Lần 03 - Năm 2018 - 2019) Gọi

là tập các giá trị dương

của tham số

sao cho hàm số

3 . 9y x m x x m   

đạt cực trị tại

thỏa mãn

2xx

. Biết





;S a b

. Tính

T b a

Ⓐ.

23T 

Ⓑ.

13T 

Ⓒ.

23T 

Ⓓ.

33T 

Lời giải

Chọn C

Ta có

3 6 . 9y x m x



  

Hàm số có hai cực trị khi và chỉ khi





9 27 0m  















Ta có:

2xx

 

4xx  

 

1 2 1 2

44x x x x   

4 12 4m  

16m

22m   

Từ, mà

0m 

theo giả thiết ta được



3;2S







Vậy

T b a

2 3.

Câu 137: (NXBGD - Đề số 3 - PHẠM ĐỨC TÀI - Năm 2017 - 2018) Tìm tất cả các giá trị thực của tham

số

để hàm số

   

1 2 1 1

y x m x m x m      

có cực trị.

Ⓐ.

0m 

. Ⓑ.

m

. Ⓒ.

0m 

. Ⓓ. không có

Lời giải

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Chọn C

Tập xác định

D 

Để hàm số có cực trị thì phương trình





có hai nghiệm phân biệt

 

2 1 2 1y x m x m



    

Ta có

 

1 2 1 0m m m



      

0m

Câu 138: (NXBGD - ĐOÀN QUỲNH - Đề số 05 - Năm 2021) Tìm các giá trị của tham số

để đồ thị

hàm số

3y x x m  

có hai điểm cực trị

,AB

sao cho gốc tọa độ

cùng với

và

là ba

đỉnh của tam giác vuông tại

Ⓐ. Không có giá trị nào của

. Ⓑ.

4m 

Ⓒ.

0, 4mm  

. Ⓓ.

1, 4mm

Lời giải

Chọn C

Tập xác định

3 6 ; 0

y x x y







   







Hàm số luôn có hai điểm cực trị với

m

Hai điểm cực trị của đồ thị hàm số

   

0; , 2; 4A m B m

   

0;, , 2; 4OA m OB m   

OAB

vuông tại

 

.. 0 4 0

OA OB m m





     







Câu 139: (THPT Triệu Sơn - Thanh Hóa - Năm 2018) Cho hàm số

 

3y x m x m   

có đồ thị là

 

với

 

;M a b

là điểm cực đại của

 

ứng với một giá trị

thích hợp, đồng thời là điểm cực tiểu của

 

ứng với một giá trị khác của

. Tổng

2018 2020S a b

bằng

Ⓐ.

504

. Ⓑ.

504

. Ⓒ.

12504

. Ⓓ.

5004

Lời giải

Chọn A

Vì điểm

 

;M a b

thuộc đồ thị

 

nên ta có:

 

3,a m a m b m     

 

Xét

 

33y x m



  

;

















Bảng biến thiên

Dựa vào bảng biến thiên, ta có: Nếu

là giá trị của tham số

để đồ thị hàm số nhận điểm

 

;M a b

là điểm cực đại thì

1am

. Nếu

là giá trị của tham số

để đồ thị hàm số nhận

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

điểm

 

;M a b

là điểm cực tiểu thì

1am

Mà

phải thỏa mãn

 

nên ta có:

 

1 3 1

a a b



    





   























Vậy

2018 2020 504S a b  

Câu 140: (Chuyên ĐHSP Hà Nội - Lần 01 - Năm 2017 - 2018) Tìm tất cả các giá trị của tham số

để

hàm số

3 2 2

2 9 12 1y x ax a x   

có cực đại, cực tiểu và hoành độ điểm cực tiểu của đồ thị hàm

số bằng

Ⓐ.

a 

. Ⓑ.

1a 

. Ⓒ.

a 

. Ⓓ.

1a 

Lời giải

Chọn A

TXĐ:

D 

6 18 12y x ax a



  

 

Để hàm số có cực đại, cực tiểu thì





2 2 2

81 72 9 0a a a   

luôn đúng

a

Do đó

là nghiệm của phương trình

 

. Từ giả thiết

x 

thay vào phương trình

 

có:

12 18 6 0aa  















+ Với

1a 

2 9 12 1y x x x   

6 18 12y x x



  















Bảng biến thiên

Dựa vào BBT ta thấy hàm số không đạt cực tiểu tại

1x 

. Do đó

1a 

không thỏa mãn.

+ Với

a 

2 3 1

y x x x   

6 9 3y x x



  

















Bảng biến thiên

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Dựa vào BBT ta thấy hàm số đạt cực tiểu tại

1x 

. Do đó

a 

thỏa mãn.

Câu 141: (Chuyên Hạ Long - Quảng Ninh - Lần 01 - Năm 2018) Tìm tất cả giá trị thực của tham số

để đồ thị hàm số

32y x mx  

có hai điểm cực trị

và

sao cho các điểm

và

 

1; 2M 

thẳng hàng.

Ⓐ.

2m 

. Ⓑ.

2m 

. Ⓒ.

2m 

. Ⓓ.

2m 

;

2m 

Lời giải

Chọn D

Ta có:

36y x mx





;







3 6 0x mx



0x 

2xm

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình





có hai nghiệm phân biệt



20m 



0m 

Khi đó hai điểm cực trị là

 

0;2A

 

2 ;2 4B m m

Ta có

 

1;4MA 

 

2 1;4 4MB m m  

Ba điểm

và

 

1; 2M 

thẳng hàng



cùng phương



2 1 4 4

mm







2 1 1

mm







2 1 1mm  



2mm



2m 



2m 

Câu 142: (THPT SỐ 02 AN NHƠN - BÌNH ĐỊNH - LẦN 2 - 2018) Cho hàm số

   

1 3 2 2018

y mx m x m x     

với

là tham số. Tổng bình phương tất cả các giá trị

của

để hàm số có hai điểm cực trị

thỏa mãn

22xx

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

Ta có:

   

2 1 3 2y mx m x m



    

Hàm số có hai điểm cực trị





có hai nghiệm phân biệt

a 













2 4 1 0









   



 

Theo định lý Viet:

 

21m

S x x



  

 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 

P x x





 

Theo giả thiết:

22xx

 

Từ

 

và

 



và

24m





Từ

 

2 2 4

m m m





3 10 8 0mm   















So điều kiện

 

, ta nhận

2m 

;

m 

Câu 143: (Chuyên Vĩnh Phúc - Lần 3 - MĐ234 - Năm 2018) Với giá trị nào của tham số

thì đồ thị

hàm số

   

2 3 1 6 2 1y x m x m x     

có cực đại, cực tiểu thỏa mãn

CTĐ C

xx

Ⓐ.

1m 

Ⓑ.

2m 

Ⓒ.

1m 

Ⓓ.

2m 

Lời giải

Chọn C

Ta có

   

6 6 1 6 2y x m x m



    

Giải phương trình





   

6 6 1 6 2 0x m x m     













Để đồ thị hàm số có cực đại cực tiểu thì

21m  

3m

Theo giả thiết ta có

CTĐ C

xx

12m  









  



 

m t m

m loai















Vậy

1m 

Câu 144: (Chuyên Hoàng Văn Thụ - Hòa Bình - Năm 2018) Tìm tất cả các giá trị thực của tham số

để hàm số

 

3 1 12 3 4y x m x mx m     

có hai điểm cực trị

thỏa mãn

3xx

Ⓐ.

1m 

Ⓑ.

1m 

Ⓒ.

m 

Ⓓ.

m 

Lời giải

Chọn D

Ta có

 

3 6 1 12y x m x m



   

   

0 3 6 1 12 0 2 1 4 0

y x m x m x m x m







           







Bởi vậy, hàm số đã cho có hai điểm cực trị

thỏa mãn

3xx

khi và chỉ khi

232

mm   

Câu 145: (THPT QUẢNG XƯƠNG - THANH HÓA - LẦN 04 - NĂM HỌC 2017-2018) Cho hàm số

   

2 1 3f x x m x mx m    

có đồ thị

 

. Có bao nhiêu giá trị nguyên của tham số

thuộc





2018;2018

để đồ thị

 

có hai điểm cực trị nằm khác phía so với trục hoành.

Ⓐ.

4033

. Ⓑ.

4034

. Ⓒ.

4035

. Ⓓ.

4036

Lời giải

Chọn B

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

- Xét phương trình

 

0fx

 

2 1 3 0x m x mx m    

 

1 2 0x x mx m    

x mx m









  



Suy ra đồ thị

 

có hai điểm cực trị nằm khác phía so với trục hoành khi và chỉ khi phương

trình

20x mx m  

có hai nghiệm phân biệt khác





   





















hay

   

;0 1;m   

Lại do:





2018;2018















nên

 

2017; 2016;...; 1;2;3;...;2018m   

Vậy có tất cả 4034 giá trị của

thỏa mãn yêu cầu bài toán.

Câu 146: (THPT THÁI PHIÊN - HẢI PHÒNG - LẦN 04 - NĂM 2017-2018) Cho hàm số

   

1 3 2 2018

y mx m x m x     

với

là tham số. Tổng bình phương tất cả các giá trị

của

để hàm số có hai điểm cực trị thỏa mãn

22xx

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

   

2 1 3 2y mx m x m



    

Hàm số có hai cực trị

   

1 3 2 0

m m m













     





2 4 1 0









   



2 6 2 6

;



























Theo Vi-et, ta có:

 





;

 





Từ giả thiết

22xx  

. Thay vào

 

, ta được:







24m





Thay vào

 

, ta được:

2 2 4 3 6

m m m





4 8 3 6m m m   

3 10 8 0mm   















Vậy tổng bình phương tất cả các giá trị của

là:

4 52









--- HẾT ---

Câu 147: (Chuyên Hà Tĩnh - Lần 01 - Năm 2018 - 2019) Tổng tất cả các giá trị của tham số thực

sao

cho đồ thị hàm số

3 2 3

34y x mx m  

có điểm cực đại và cực tiểu đối xứng với nhau qua đường

phân giác của góc phần tư thứ nhất là

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn C

Ta có:

36y x mx



















Để hàm số có cực đại cực tiểu thì

0m 

Khi đó các điểm cực trị của đồ thị hàm số là

 

0;4Am

 

2 ;0Bm

Ta có

 

;2I m m

là trung điểm của đoạn thẳng

Đường phân giác của góc phần tư thứ nhất là

:0d x y

Do đó để điểm cực đại và cực tiểu đối xứng với nhau qua

thì:

2 4 0

1 2 0







     









Vậy tổng tất cả các giá trị của tham số thực

là

Câu 148: (Chuyên Trần Phú - Hải Phòng - Lần 02 - Năm 2017 - 2018) Gọi

là các giá trị của

tham số

để đồ thị hàm số

2 3 1y x x m   

có hai điểm cực trị là

sao cho tam giác

OBC

có diện tích bằng

, với

là gốc tọa độ. Tính

Ⓐ.

15

Ⓑ.

Ⓒ.

Ⓓ.

20

Lời giải

Chọn A

Ta có

' 6 6 0y x x  

 

0 1 0; 1

1 2 1; 2

x y m B m

x y m C m

     







     





 

0; 1

1; 2

OB m

OC m

















OBC

S

   

0. 2 1 .1

mm   

m

Bài ra

OBC

S 

m  













15mm  

Câu 149: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tìm tất cả các giá trị của tham số

để

hàm số

31y x x mx   

có điểm cực trị

,xx

thỏa mãn

3xx

Ⓐ.

3

Ⓑ.

Ⓒ.



Ⓓ.

Lời giải

Chọn D

Ta có

3 6 ; 0 3 6 0y x x m y x x m



       

Để hàm số có hai điểm cực trị thì

9 3 0 3mm



     

(1)

Theo viet ta có:















Khi đó

 

2 2 2

1 2 1 2 1 2

2 3 2 2. 3

x x x x x x m         

thỏa mãn điều kiện.

Ch : Với những bài thuộc dng này ta có thể tìm điều kiện (1) sau. V như bài toán này khi ra

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

kết qu

m 

thì ta cng chc chn rng kết qu đó đúng (Vì các phương án của bài toán cho

một kết qu

) mà không cần th li điều kiện. Do đó trong một số bài toán ta không cần kiểm

tra điều kiên (1).

Câu 150: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) (Chuyên Thái Bình – lần 3) Tìm tất cả

các giá trị thực của tham số a sao cho hàm số

   y x x ax

đạt cực trị tại

,xx

thỏa

mãn

1 2 2 1

( 2 )( 2 ) 9    x x a x x a

Ⓐ.

2a

Ⓑ.

4a

Ⓒ.

3a

Ⓓ.

1a

Lời giải

Chọn B

Ta có:

; 0 0



       y x x a y x x a

(*)

Cách 1: ( Giải xuôi)

Để hàm số có hai điểm cực trị thì

1 4 0

aa     

(2*)

Với

,xx

là nghiệm của (*) nên ta có

1









x x a

(3*)

Biến đổi

2 2 2 3 3 2 2 2

1 2 2 1 1 2 1 2 1 2 1 2 1 2

( 2 )( 2 ) ( ) ( ) 2 ( ) 4            x x a x x a x x x x a x x x x x x a

2 3 2 2

1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2

( ) ( ) 3 ( ) 2 ( ) 2 4



           



x x x x x x x x a x x x x x x x x a

(2*)

2 2 2 2

1 3 2 (1 2 1) 4 2 1 ( 1) .            a a a a a a a a a

Khi đố điều kiện của bài toán tương đương:

(2*)

( 1) 9 4





      







Chọn B

Cách 2: ( Giải ngược)

+) Thử

2a

(*)

có dạng

20  xx

(vô nghiệm), vậy

2a

không thỏa mãn.

+) Thử

4a

(*)

có dạng

1 17









   











Lúc này sử dụng casio, gán

1 17



xA

và

1 17



xB

Sau đó nhập biểu thức

( 8)( 8)   A B B A

vào máy:

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta được kết quả là

(thỏa mãn)



Chọn B

Chú ý:Nếu bài toán này câu hi là “Tìm giá trị gần

nhất “ thì ta không gii được theo chiều

ngượ

Ⓒ.

Câu 151: (Chuyên Hùng Vương - Gia Lai - Lần 2 - 2018) Gọi

là hai điểm cực trị của đồ thị hàm

số

 

3f x x x m  

với

là tham số thực khác

. Tìm tất cả các giá trị thực của tham số

để trọng tâm tam giác

OAB

thuộc đường thẳng

3 3 8 0xy  

Ⓐ.

5m 

. Ⓑ.

2m 

. Ⓒ.

6m 

. Ⓓ.

4m 

Lời giải

Chọn A

TXĐ:

D 

 

36f x x x





 

0fx















Tọa độ 2 điểm cực trị là

 

0;Am

;

 

2; 4Bm

Tọa độ trọng tâm

của tam giác

OAB

là

2 2 4

;









Điểm

thuộc đường thẳng:

3 3 8 0xy  

nên:

2 2 4 8 0m   

5m

Câu 152: (Chuyên Hạ Long - Lần 03 - Năm 2017 - 2018) Gọi

là tập hợp tất cả các giá trị thực của

tham số

để đồ thị của hàm số

 

3 2 2

y x mx m x   

có hai điểm cực trị là

và

sao

cho

nằm khác phía và cách đều đường thẳng

59yx

. Tính tích các phần tử của

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

27

Lời giải

Chọn D

Ta có:

21y x mx m



   

  

11x m x m    

;

















Vì

11mm  

với mọi giá trị

nên đồ thị hàm số luôn có hai điểm cực trị là

A m m



  





và

B m m



  





nằm khác phía và cách đều đường thẳng

59yx



: 5 9A d y x  

và trung điểm

;

I m m









của

thuộc

5 5 9



    









  





18 27 0mm   

4,9

1,9







  







 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Vậy tích các phần tử của

bằng

27

Câu 153: (Chuyên Quốc Học Huế - Lần 03 - Năm 2017 - 2018) Cho hàm số

( ) 1 3

f x x m x mx

với

của

thuộc khoảng

20;18

sao cho đồ thị của hàm số đã cho có hai điểm cực trị nằm cùng

một phía đối với trục hoành?

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Ta có

 

( ) 3 3 1 3f x x m x m



   

 















Hàm số có cực trị thì

1m 

Đồ thị của hàm số đã cho có hai điểm cực trị nằm cùng một phía đối với trục hoành

   

 

1 . 0 3 3 0 0

y y m m m m m         

Suy ra

0m 

và

1m 

Vậy trong khoảng

20;18

có

giá trị nguyên của

thỏa mãn bài toán.

Câu 154: (Chuyên Lê Hồng Phong - HCM - Năm 2017 - 2018) Tìm tổng tất cả các giá trị thực của

sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

   

2 3 1 6 1 2y x m x m m x    

song song với đường thẳng

4yx

Ⓐ.

1m 

. Ⓑ.

m 

. Ⓒ.

m 

. Ⓓ.

m 

Lời giải

Chọn B

   

2 3 1 6 1 2y x m x m m x    

   

' 6 6 1 6 1 2y x m x m m    

     

' 9 1 36 1 2 81 54 9 9 3m m m m m m         

Hàm số có hai điểm cực trị

m

Ta có phương trình đường thẳng qua hai điểm cực trị có dạng:

3 3 9

b bc

y c x d



   





 

2 3 2

9 6 1 2 3y m m x m m m       

Để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

   

2 3 1 6 1 2y x m x m m x    

song song với đường thẳng

4yx

thì:

3 2 3 2

9 6 1 4 9 6 3 0

2 3 0 2 3 0

2 3 0

m m m m

m m m m m m

m m m













        

  





   

  



     







  



 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Tìm tổng tất cả các giá trị thực của

là



Câu 155: (NXBGD - Đề số 4 - ĐOÀN QUỲNH - Năm 2017 - 2018) Tìm các giá trị của tham số

để đồ

thị hàm số

   

2 3 2 1 6 1 1y x m x m m x     

có hai điểm cực trị cách đều trục tung.

Ⓐ. Không tồn tại giá trị nào. Ⓑ.

m 

Ⓒ.

2m 

. Ⓓ.

mm  

Lời giải

Chọn B

Tập xác định

D 

   

6 6 2 1 6 1y x m x m m    

Để hàm số có hai điểm cực trị cách đều trục tung





có hai nghiệm phân biệt

;xx

thỏa

mãn

0xx

32 32 1 0

2 1 0







   



    







Câu 1. Câu 156: (NXBGD - ĐOÀN QUỲNH - Đề số 05 - Năm 2021) Tìm các giá trị của tham

số

sao cho đồ thị hàm số

3 2 3

34y x mx m  

có hai điểm cực trị đối xứng nhau qua đường thẳng

yx

Câu 2. Ⓐ.

0m 

. Ⓑ.

m 

. Ⓒ.

m 

. Ⓓ.

1m 

Lời giải

Chọn C

Ta có

 

' 3 6 3 2 ; ' 0

y x mx x x m y





     







Để đồ thị hàm số có hai điểm cực trị

'0y

có hai nghiệm phân biệt

0m

Gọi

,AB

là hai điểm cực trị của đồ thị hàm số và giả sử

 

0;4 , 2 ;0A m B m

Theo giả thiết

,AB

đối xứng với nhau qua đường thẳng

yx

nên ta có

m m m m     

Câu 157: (NXBGD - Đoàn Quỳnh - Đề số 07 - Năm 2018) Tìm các giá trị của tham số

sao cho đồ thị

hàm số

2 12 13mxy xx

có các điểm cực đại, cực tiểu và các điểm đó có khoảng cách

bằng nhau đến trục tung.

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn A

126 2yxmx

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Phương trình

có

nên luôn có hai nghiệm phân biệt

;x x

Do đó hàm số luôn có hai cực trị

Các điểm cực đại và cực tiểu có khoảng cách đến trục tung bằng nhau nên

x x

Hay

0x x

Câu 158: (NXBGD - Đề số 14 - Năm 2018) Cho đồ thị

 

của hàm số

 

3 2 2 2

3 3 1 1y x mx m x m     

và điểm

 

2;2 .M 

Biết đồ thị

 

có hai điểm cực trị

,AB

và tam giác

ABM

vuông tại

Hỏi giá trị nào của

cho cưới đây thoả mãn bài toán đã

cho?

Ⓐ.

1.m 

Ⓑ.

1.m 

Ⓒ. Không có

1.m 

Ⓓ. Có vô số giá trị của

Lời giải

Chọn A

 

3 6 3 1y x mx m



   

   

 

1; 3 3 , 1; 3 1

1; 3 1

3; 3 3

. 0 10 10 0 .

y x m

A m m B m m

MA m m

MB m m

MA MB m m

  



   

     

   

   





    







Câu 159: (NXBGD - Phạm Đức Tài - Đề 20 - Năm 2017-2018) Tìm tất cả các giá trị thực của tham số

để đồ thị

 

của hàm số

3 2 3

32y x mx m   

có hai điểm cực trị

,MN

sao cho dường

thẳng

vuông góc với đường thẳng

:2d y x

Ⓐ.

;









. Ⓑ.

;









. Ⓒ.

;









. Ⓓ.

;









Lời giải

Chọn A

Phương trình đường thẳng

22y m x m

2 .( 2) 1

MN d m m m         

Câu 160: (Vted - Đề số 16 - Năm 2017 - 2018) Khi đồ thị hàm số có hai điểm cực trị A,

B và đường tròn cắt đường thẳng AB tại hai điểm phân biệt M,N sao

cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN.

Ⓐ. Ⓑ. Ⓒ. Ⓓ.

Lời giải

Chọn D

32y x mx  

( ) :( 1) ( 1) 3C x y   

3.MN 

1.MN 

2.MN 

2 3.MN 

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có điều kiện để hàm số có hai điểm cực trị là và

Đường tròn (C) có tâm Ta có

Dấu bằng đạt tại

Câu 161: (Đề 20- Vted- Năm 2017-2018) Có bao nhiêu số thực

để đồ thị hàm số

22y x mx  

có

ba điểm cực trị

, , A B C

sao cho tứ giác

ABCD

nội tiếp với

;







Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn B

44y x mx





;

 

0 4 0y x x m



   

Suy ra đồ thị hàm số có ba điểm cực trị

0m

. Khi đó ba điểm cực trị của đồ thị hàm số là

 

0;2A

 

;2B m m

 

;2C m m

Gọi

 

0;Ih

là tâm đường tròn ngoại tiếp tứ giác

ABCD

Ta có:

 

2 2 2

22IA IB h m h m      





Lại có:

 

25 5

IA ID h h h



       





Vậy suy ra

4 1 2 0m m m   

2 1 0





    



  



. Phương trình này có ba

nghiệm trong đó có hai nghiệm dương. Vậy Chọn B

Nhận xét: Bài toán trên là bài toán liên quan đến cực trị của hàm bậc 4 trùng phương và một

rồi dựa vào đặc điểm của chúng để thiết lập các mối quan hệ (phương trình) thỏa yêu cầu bài

toán.

Các bài tương tự: Tìm điều kiện để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều;

tam giác cân có góc ở đỉnh bằng

120

,…; tam giác có bán kính đường tròn ngoại tiếp bằng 2;

….

Câu 162: (ĐTD - Đề thi thử đại học - Năm 2017 - 2018) Tìm tất cả các giá trị thực của tham số

để

 

2;M m m

cùng với hai điểm cực trị của đồ thị hàm số

   

2 3 2 1 6 1 1y x m x m m x   

tạo thành một tam giác có diện tích nhỏ nhất.

Ⓐ.

2m 

. Ⓑ.

0m 

. Ⓒ.

1m 

. Ⓓ.

1m 

Lời giải

Chọn B

   

6 6 2 1 6 1y x m x m m



    

   

0 6 6 2 1 6 1 0y x m x m m



      

   

2 1 1 0x m x m m     

0m 

: 2 2.AB y mx  

(1;1), 3.IR

2 1 4 2 1

2 ( , ) 2 3 2 2 2 3.

m m m

MN R d I AB



   

     







m 

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có

10m    

nên đồ thị luôn có 2 cực trị.

Phương trình đường thẳng đi qua hai điểm cực trị

2 3 1y x m m m     

Hai điểm cực trị có tọa độ là

 

1;2 3A m m m

 

;2 3 1B m m m

 

1 1 1

, 3 1

2 2 2

ABC

S MA MB m



    



min

ABC

S 

0m

Câu 163: (WORD VD - VDC - Đề 05- NĂM 2018) Tìm tất cả các giá trị thực của tham số

để điểm

 

2 ; 1M m m

cùng với hai điểm cực trị của đồ thị hàm số

   

2 3 2 1 6 1    y x m x m m x

tạo thành một tam giác có diện tích nhỏ nhất.

Ⓐ.

1m

Ⓑ.

2m

Ⓒ.

0m

Ⓓ.

1m

Lời giải

Chọn C

Ta có

   

' 6 6 2 1 6 1    y x m x m m

và













Lại có :

  

1 2 1

. ' 1 2 1





     





y x y x m m m

suy ra phương trình đường thẳng đi qua 2

cực trị là :

  

1 2 1    y x m m m

Suy ra CT

  

 

; 1 2 1  A m m m m m

;

CĐ :

  

 

1; 1 2 1 1    B m m m m m

2AB

Có

 

;







M AB

Mà

 

;

1 3 1 1

2 2 2 2



   

MAB

M AB

S AB d

Dấu ‘=’xảy ra khi

0.m

Câu 164: (NXBGD - PHẠM ĐỨC TÀI - ĐỀ 12 - NĂM 2018 ) Tìm tất cả các giá trị thực của tham số

để đồ thị hàm số

3 2 3

34y x mx m  

có hai điểm cực trị

,AB

sao cho

20AB 

Ⓐ.

 

1;2m

. Ⓑ.

 

1;1m

. Ⓒ.





. Ⓓ.

 

2;1m

Lời giải

Chọn B

Ta có

 

' 3 6 3 2 ; ' 0

y x mx x x m y





     







Để đồ thị hàm số có hai điểm cực trị

0m

Giả sử

 

0;4 , 2 ;0A m B m

Theo giả thiết

2 2 6

20 20 4 16 20AB AB m m     

   

2 2 2

4 5 0 1 1m m m m        

(thỏa mãn).

 Quảng Thuận – Ba Đồn – Quảng Bình Cực trị hàm số bậc ba trong các đề thi 2017 - 2021

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 165: (THPT An Lão - Hải Phòng - Năm 2018) Cho hàm số

   

1 3 2 2018

y mx m x m x     

với

là tham số. Tổng bình phương tất cả các giá trị

của

để hàm số có hai điểm cực trị

thỏa mãn

21xx

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Chọn D

Ta có

   

2 1 3 2 0y mx m x m



     

 

Hàm số có hai điểm cực trị

thỏa mãn

21xx

khi và chỉ khi

 

2 1 2



















Ta có

   

2 6 2 6

1 2 4 1 0 *

m m m



       

Mặt khác ta có

 

21m





 

Từ

 

và

 

ta có

2 m





mà

là nghiệm của

 

nên

Vì

 

2 1 . 3 6 0 3 8 4 0

m m m m m





        



















thỏa mãn

 

Vậy tổng bình phương các giá trị của

là:

2 40









Câu 166: (Vted - Đề số 09 - Năm 2017 - 2018) Biết hàm số

()f x x x mx  

có một cực trị bằng 1.

Cực trị còn lại của hàm số đã cho bằng

Ⓐ.



Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn A

Theo giả thiết

 

0f x





có hai nghiệm phân biệt

,xx

và

 

1,f x 

ta cần tìm

 

Ta có

( ) 0 3 2 0f x x x m



    

phương trình này có hai nghiệm phân biệt khi và chỉ khi

1 3 0 .



     

Khi đó theo vi-ét ta có







  







và

1 1 1 1

( ) 1 1,f x x x mx    

Khi đó rút

1 2 1 1 1 1

3 3 2 3

m x x x x x x



      





và thay vào đẳng thức cuối có

3 2 2 3 2

1 1 1 1 1 1 1 1

( 2 3 ) 1 2 1 0 1 1x x x x x x x x m              

(thoả mãn điều kiện).

 Quảng Thuận – Ba Đồn – Quảng Bình “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

THAM GIA LỚP LUYỆN THI

CHẤT LƯỢNG CAO

MR.VIỆT MATH CLASS

LIÊN

HỆ

82 Võ Thị Sáu - TDP Bến Chợ – Phường Q.Thuận - T.xã Ba

Đồn –Tỉnh Quảng Bình

http://luyenthitracnghiem.vn

0905 193 688 (Điện thoại hoặc nhắn tin)

Facebook: https:// www.facebook.com/vietgold

Vậy

1 2 2

2 1 1 1 1 5

( ) , 1, 1 ( ) .

3 3 3 3 3 27

f x x x x x x f x

     

              

     

     

Bấm Tải xuống để xem toàn bộ.

| 1/78

| | Tải xuống

Preview text:

 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
“Nơi nào có ý chí, nơi đó có con đường.” BÀI TOÁN CỰC TRỊ h ttp 166 HÀM SỐ BẬC BA s://
TRONG CÁC ĐỀ THI THỬ 17-21 lu ye n th it racngh
Ngày đã rạng, bình minh đang tỉnh giấc! ie m.vn
“Khi nào em cảm thấy muốn phê phán và chê bai một ai đó,
hãy nhớ rằng không phải ai trên thế giới này cũng có những
thuận lợi trong cuộc sống mà em có được."
Họ và Tên học sinh: …
…………………………….................. http s://www
Trường:……………………
……………………. Lớp: ………. .fa ceboo k.com /vietgold 0
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” Câu 1:
(Câu 25 - Chuyên Hạ Long - Quảng Ninh - Lần 1 - Năm 2020 - 2021) Tìm tất cả các giá trị
của tham số m để hàm số 3 2
y  x  3x  mx  2 có cực đại và cực tiểu?
Ⓐ. m  3 .
Ⓑ. m  3.
Ⓒ. m  3 .
Ⓓ. m  3 . Lời giải Chọn B  2 y '  3
 x  6x  m   1 . m.vn
Để hàm số có cực đại, cực tiểu thì phương trình   ie 1 có 2 nghiệm phân biệt gh  
  0  93m  0  m  3  . racn Câu 2:
(Câu 37 - Chuyên Thoại Ngọc Hầu - An Giang - Đề A - Năm 2020 - 2021) Tìm tất cả các giá it 2 th
trị thực của tham số m để hàm số 3 y 
x  m   2 1 x   2
m  4m  3 x 1 có hai điểm cực trị. n 3 ye lu Ⓐ. 5   m  1  .
Ⓑ. 1  m  5. Ⓒ. 5   m 1. Ⓓ. 1   m  5. s:// Lời giải ttp Chọn B h 2
y  x  m   2 2 2
1 x  m  4m  3
Hàm số có hai điểm cực trị  phương trình y  0 có hai nghiệm phân biệt 2
 x  m   2 2 2
1 x  m  4m  3  0 có hai nghiệm phân biệt 
   m 2   2 m  m   2 0 1 2 4
3  0  m  6m  5  0  1  m  5 .
Vậy 1 m  5 thỏa yêu cầu bài toán.
Câu 3: (Câu 32 - THPT Lương Thế Vinh - Hà Nội - Lần 01 - Năm 2020 - 2021) Tất cả các giá trị của 3 x
tham số m để hàm số 2 y  
 mx  2mx 1 có hai điểm cực trị là /vietgold 3 m  2 k.com Ⓐ.  .
Ⓑ. 0  m  2. Ⓒ. m  2 . Ⓓ. m  0. m  0 ceboo Lời giải .fa Chọn A Ta có 2
y  x  2mx  2m .
Hàm số đã cho có hai điểm cực trị khi và chỉ khi phương trình y  0 có 2 nghiệm phân biệt  Phương trình 2
x  2mx  2m  0 có 2 nghiệm phân biệt https://www    m 2 2
  m  2m  0   . m  0 Câu 4:
(Câu 6 - THPT Yên Phong 1 - Bắc Ninh - Lần 1 - Năm 2020 - 2021) Tất cả các giá trị của
tham số m để hàm số 3
y  x  m   2 3
1 x  33m  7 x 1có cực trị là          Ⓐ. m 2 m m  . Ⓑ. 3  . Ⓒ. 2  . Ⓓ. 2   m  3. m  3 m  2 m  3 Lời giải Chọn A Ta có 3
y  x  m   2
x   m   2 3 1 3 3
7 x 1 y '  3x  6m  
1 x  33m  7 . 1
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Để hàm số 3
y  x  m   2 3
1 x  33m  7 x 1có cực trị thì y '  0 có 2 nghiệm phân biệt m  2  2
  '  0  9m  9m  54  0   . m  3 Câu 5:
(Câu 45 - Chuyên Lê Qúy Đôn - Bà Rịa Vũng Tàu - Lần 1 - Năm 2020 - 2021) Tìm số giá trị 1
nguyên của tham số m để hàm số y   2 m   3 2
1 x  mx  3x 1 có cực đại 3 h Ⓐ. 2 . Ⓑ. 0 . Ⓒ. 1. Ⓓ. 3 . ttp Lời giải s:// Chọn A lu 2 2 ye
y  m  
1 x  2mx  3 n  th
Trường hợp 1. m 1 ta có y  2x  3 it Xét dấu y racngh ie m.vn  m 1 loại
Trường hợp 2. m  1 ta có y  2  x  3 3
y  0  x  2  m  1  thỏa mãn http ? m  1  s://www
Hàm số có cực đại  phương trình y  0 có hai nghiệm phân biệt    0 2 2 .fa
 m  3m   1  0 ceboo 6 6 2
 3  2m  0    m  k.com 2 2 Vì m  nên m 1  ;0; 
1 kết hợp với điều kiện ta được m  0 /viet
Vậy có 2 giá trị nguyên của m thỏa mãn bài toán. gold Câu 6:
(Câu 10 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Biết M 0;2 , N 2; 2
  là các điểm cực trị của đồ thị hàm số 3 2
y  ax  bx  cx  d . Tính giá trị của hàm số tại x  2. Ⓐ. y 2    2 . Ⓑ. y 2    22. Ⓒ. y 2    6 . Ⓓ. y 2    1  8 . Lời giải Chọn D Ta có: 2
y  3ax  2bx  c .
Vì M 0;2 , N 2; 2
  là các điểm cực trị của đồ thị hàm số nên: 2
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” y  0  0 c  0      y  2 1  0 1
 2a  4b  c  0 y  0  2 d  2    2 y  2  2  8
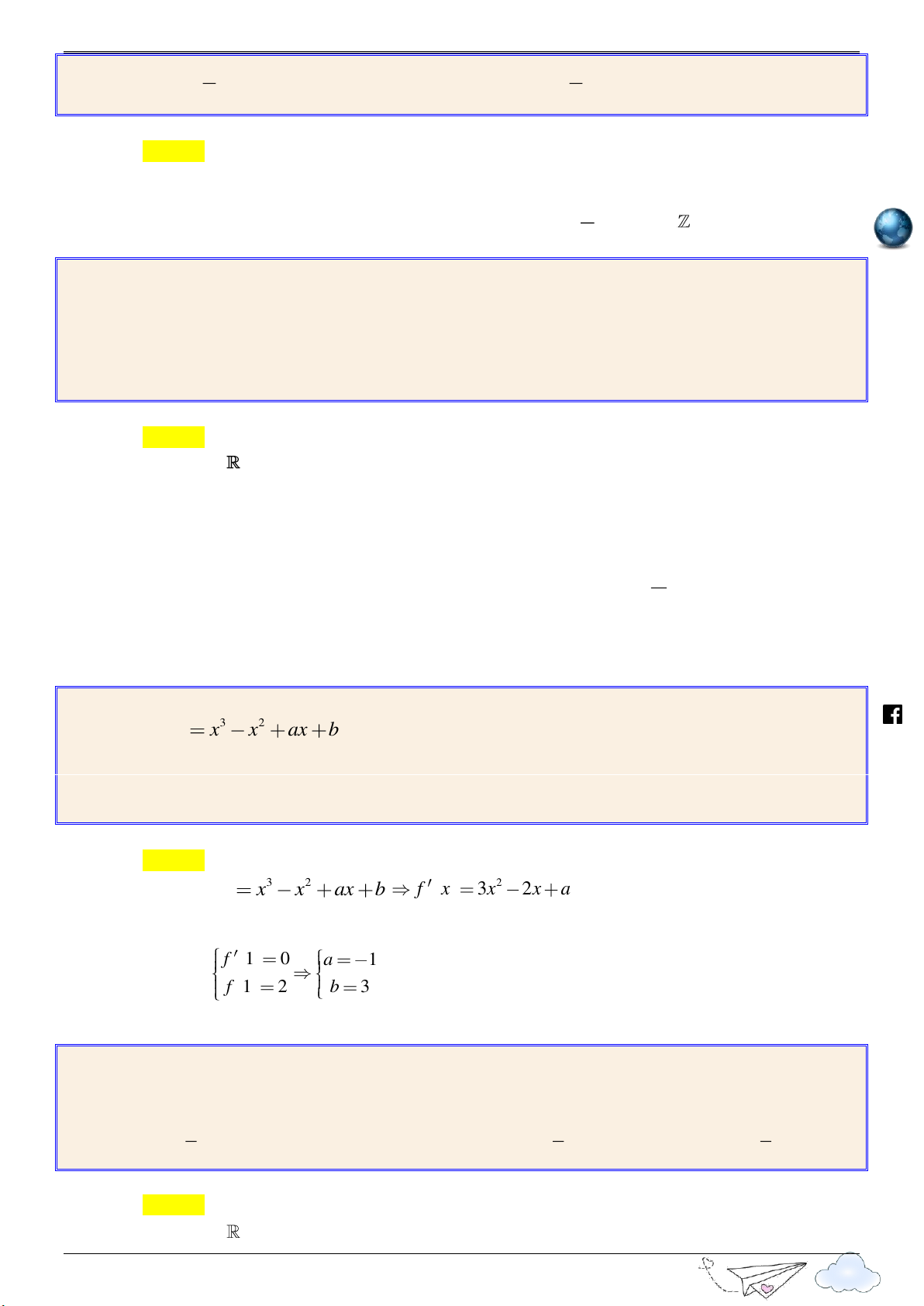
 a  4b  2c  d  2  a 1 b   3  Từ   3 2          m.vn 1 và 2 suy ra: y x 3x 2 y  2 18 . c  0 ie    gh d 2 racn Câu 7:
(Câu 2 - THPT Lý Thái Tổ - Bắc Ninh - Lần 2 - Năm 2020 - 2021) Tìm tất cả các giá trị của it 1 1        th
tham số m để hàm số 3 2 y x mx x
2 đạt cực trị tại x , x thỏa mãn x x x x 3 1 2 1 2 1 2 n 3 2 ye Ⓐ. m  4  .
Ⓑ. m  2 . lu s://
Ⓒ. m  3 .
Ⓓ. Không có giá trị m . ttp h Lời giải Chọn D Ta có: 2
y  x  mx 1
Để hàm số đạt cực trị tại x , x thì phương trình y  0 có hai nghiệm phân biệt 1 2 2
   0  m  4  0  m ;  2
 2;   1
Khi đó, phương trình  
1 có hai nghiệm x , x . 1 2
x  x  m theo hệ thức viet 1 2  . x .x  1  1 2 /vietgold
Theo bài ra ta có: x  x  x x  3  m 1  3  m  2 2 . 1 2 1 2   k.com Từ  
1 và 2 suy ra không có giá trị m nào thỏa mãn yêu cầu bài toán Câu 8:
(Câu 40 - THPT Ngô Gia Tự - Vĩnh Phúc - Năm 2020 - 2021) Biết m là giá trị tham số m ceboo o .fa để hàm số 3 2
y  x  3x  mx 1 có hai điểm cực trị x , x sao cho 2 2
x  x  x x  13 . Mệnh đề 1 2 1 2 1 2 nào sau đây đúng? Ⓐ. m  7  ; 1  .
Ⓑ. m  7;10 . Ⓒ. m  1  ;7 . Ⓓ. m  1  5; 7  . 0   0   0   0   https://www Lời giải Chọn D
Để hàm số có 2 điểm cực trị thì y  0 có 2 nghiệm phân biệt. 2
 3x  6x  m  0 có 2 nghiệm phân biệt    3612m  0  m  3 Theo bài ra: 2 2
x  x  x x  13   x  x  3x x 13 * . 1 2 2 1 2 1 2 1 2 x  x  2 1 2 
Mà theo định lý Viét ta có 
m thay vào * ta được: x .x   1 2  3 m 4  3. 13  m  9  (t / m ). 3 3
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Câu 9:
(Câu 41 - THPT Kim Liên - Hà Nội - Lần 1 - Năm 2020 - 2021) Biết m0 là giá trị của tham số m 3 2 2 2
để hàm số y  x  3x  mx 1 có hai điểm cực trị x , x
x  x  x x 10 1 2 sao cho . Mệnh 1 2 1 2
đề nào dưới đây là đúng? Ⓐ. m ( 1  5; 7  ) m ( 1  ;7) m ( 7  ; 1  ) m (7;10) 0 . Ⓑ. 0 . Ⓒ. 0 . Ⓓ. 0 . Lời giải Chọn C h 2 2 ttp
Ta có: y  3x  6x  m  y  0  3x  6x  m  0 (1) . s://
Để hàm số có hai điểm cực trị thì phương trình (1) có hai nghiệm phân biệt x , x 1 2 . lu Điều kiện 
  0  93m  0  m  3. ye n x  x  2 1 2 th  Theo Viet  m (*) . it x x   1 2 r  3 acn 2 2 2
Theo bài ra x  x  x x  10  (x  x )  3x x  10 (**) . gh 1 2 1 2 1 2 1 2 ie
Từ (*) và (**) ta được 4  m 10  m  6
 thoả mãn điều kiện. m.vn Vậy m  6  ( 7  ; 1  ) 0 .
Câu 10: (Câu 36 - SGD Phú Thọ - Lần 1 - Năm 2020 - 2021) Biết hàm số 1 1 2 3 2 y m 1 x 3 m 5 x x
1 có hai điểm cực trị x , x thỏa mãn 8 . Khẳng 1 2 x x 1 2
định nào sau đây là đúng? Ⓐ. m 5; 2 . Ⓑ. m 4;5 . Ⓒ. m 1;1 . Ⓓ. m 3;7 . Lời giải http Chọn C s://www Ta có : 2 2 y 3 m 1 x 6 m 5 1
Có ac<0 nên hàm số đã cho luôn có 2 điểm cực trị .fa ceboo m 5 x x 2 1 2 2 m 1 k.com x .x 1 1 2 1 1 x x 2 1 2 2 /v 8 8 x x 8 x 2 x .x x 64 2 1 1 1 2 2 iet x x x .x 1 2 1 2 gold x x 8 2 4m m 1 0 2 2 1 2 x x 2x x 2 x x 64 x x 64 1 2 1 2 1 2 1 2 x x 8 2 1 2 4m m 9 0 1 17 m . 8
Câu 11: (Câu 44 - SGD Thái Nguyên - Lần 1 - Năm 2020 - 2021) Có bao nhiêu giá trị thực của tham 1 1
số m để hàm số 3 y  x 
3m 2 2x  2
2m  3m  
1 x  2 có điểm cực đại x và điểm cực CĐ 3 2 tiểu x thoả mãn 2 3x  4x ? CT CĐ CT 4
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” Ⓐ. 2. Ⓑ. 1. Ⓒ. 3. Ⓓ. 4. Lời giải Chọn A
 Tập xác định: D  .  x  m 1 Ta có: 2
y  x   m   x   2 3 2
2m  3m  
1 . Cho y  0   . x  2m 1
Hàm số đã cho có điểm cực đại và điểm cực tiểu  m 1 2m 1 m  0 . m.vn ie
 Trường hợp 1: m 1 2m 1 m  0 . gh Khi đó: x
 m 1, x  2m 1. CĐ CT
 m 1 N  racn  it 2 2 3x
 4x  3m   1  42m   1 2
 3m  2m1 0  CĐ CT 1
m   L th  n  3 ye
 Trường hợp 2: 2m 1 m 1 m  0 . lu Khi đó x
 2m 1, x  m 1. CĐ CT s://  2   7 ttp m  L h 2 2 6 3x
 4x  32m   1  4m   1 2
12m 8m 1 0   CĐ CT  2   7 m  N   6
Vậy có 2 giá trị của m thoả yêu cầu bài toán.
Câu 12: (Câu 33 - Chuyên Ngữ - Hà Nội - lần 1 - Năm 2020 - 2021) Hàm số 3 2
y  x  3x  mx 1 có 2 2 hai điể x , x x  x  3 m cực trị 1 2 thỏa 1 2 khi 1 3 Ⓐ. m  . Ⓑ. m  .
Ⓒ. m  2. Ⓓ. m 1. 2 2 /vietgold Lời giải Chọn B k.com Hàm số 3 2
y  x  3x  mx 1 ceboo
Tập xác định D  . .fa 2
y  3x  6x  ,
m a  3,b  6  ,c  ,
m   36 12m .
Để hàm số có hai điểm cực trị x , x thì   0  m  3. 1 2 2 3
Theo đề bài x  x  3   x  x 2 2 2
 2x x  3  4  m  3  m  . (nhận) 1 2 1 2 1 2 3 2
https://www Câu 13: (Câu 17 - Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - Lần 1 - Năm 2020 - 2021) Cho hàm 1 số 3 y 
x  m  2 2 x   2
m  4m  3 x  6m  9 . Tìm giá trị của tham số m để đồ thị hàm số 3
C có cực đại tại x , đạt cực tiểu tại x sao cho 2 x  2x . 1 2 1 2 m  4 Ⓐ. m  4 . Ⓑ. m  2  . Ⓒ.  .
Ⓓ. m   5 . m  2  Lời giải Chọn D
Tập xác định D  . 5
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 2
y  x  m   2 2
2 x  m  4m  3.
Hàm số đạt cực đại tại x , đạt cực tiểu tại x khi và chỉ khi 1 2 
   m 2  2 0 2 m  4m   3  0  1  0 , m   . x  m  3 y  0   . x  m 1 m   5
Theo đề bài ta có: x  2x  m  2 2 1  2m  3 2
 m  5  0   . 1 2 h m  5 ttp s://
Câu 14: (Câu 5 - Chuyên Khoa Học Tự Nhiên - Lần 1 - Năm 2020 - 2021) Cho hàm số lu 3 2 2
y  x  mx  m x  8 . Có bao nhiêu giá trị m nguyên để hàm số có điểm cực tiểu nằm hoàn toàn ye phía trên trục hoành? n th it Ⓐ. 3. Ⓑ. 5. Ⓒ. 4 . Ⓓ. 6 . rac Lời giải n gh Chọn C ie 2 2
y  3x  2mx  m m.vn 2 2 2 
  m  3m  4m .   m 2m m 2m m
Do đó phương trình y  0 có hai nghiệm là x   m x    1 , . 3 2 3 3
Để hàm số có cực trị thì m  0
Trường hợp 1: m  0 , khi đó x  x , hàm số đạt cực tiểu tại x  m . 1 2 1
Để hàm số có điểm cực tiểu nằm hoàn toàn phía trên trục hoành f x  0 . 1  Hay 3 3 3 3
m  m  m  8  0  8  m  0  m  2 .
Kết hợp điều kiện ta được 0  m  2 . Do m nguyên nên m 1. http m s://www
Trường hợp 2: m  0 , khi đó x  x , hàm số đạt cực tiểu tại x   . 1 2 2 3
Để hàm số có điểm cực tiểu nằm hoàn toàn phía trên trục hoành f  x  0 . 2  .fa 3 3 3 m m m 5 216 3 3 ceboo Hay     8  0 
m  8  0  m   . 27 9 3 27 5 k.com
Kết hợp điều kiện ta được 216 3 
 m  0 . Do m nguyên nên m 3  ; 2  ;  1 . 5 /v
Vậy có 4 giá trị nguyên của m thỏa mãn đề bài. ietgold
Câu 15: (Câu 50 - Chuyên PTNK - HCM - Lần 1 - Năm 2020 - 2021) Cho A  n  | 0  n  2  0 và
F là tập hợp các hàm số 3 2 2 2
f (x)  x  (2m  5)x  6x  8m có m  A . Chọn ngẫu nhiên một hàm
số f (x) thuộc F . Tính xác suất để đồ thị hàm số y  f (x) có hai điểm cực trị nằm khác phía đối với trục . Ox 18 19 9 19 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 21 20 10 21 Lời giải Chọn D
+ Không gian mẫu   21 6
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” x  2
+ Ta có: f (x)  0   2 2 2
x  (2m  3)x  4m  0(*)
+ Đồ thị hàm số y  f (x) có hai điểm cực trị nằm khác phía đối với trục Ox  (*) có hai nghiệm phân biệt khác 2 m A   7  2 10 m A m   2,58  m.vn   2 2 2  2
 (2m 3) 16m  0  
 m0;3;4;...;  20 ie    2 2 2 7  2 10      gh 2 (2m 3).2 4m 0  0  m   0,58  2  racn  m   it th Vậy xác suất là: 19 n P  . 21 ye lu
Câu 16: (Câu 40 - THPT Ngô Quyền - Ba Vì - Hà Nội - Lần 2 - Năm 2020 - 2021) Cho hàm số s://
y  m   3 x   2
m  m   2 3 2
1 x  m  4 x 1 . Gọi S là tập hợp tất cả các giá trị nguyên của m ttp để h
đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục Oy . Tổng các phần tử của S là Ⓐ. 3  . Ⓑ. 4  . Ⓒ. 0 . Ⓓ. 2  . Lời giải Chọn A
Ta có y  m   2 x   2 3 3
4 m  m  
1 x  m  4  0 .
Đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục Oy  Phương trình y  0
có hai nghiệm phân biệt x , x thỏa mãn x  0  x  3m 3m  4  0  4   m  3 . 1 2 1 2 /vietgold
Kết hợp điều kiện m ta được m 3  ; 2;1;0;1;  2  S   3  ; 2;1;0;1;  2 . k.com
Vậy tổng các phần tử của S là 3  .
Câu 17: (Câu 46 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Gọi S là tập hợp tất cả các giá trị thực của ceboo .fa 1
tham số m để đồ thị của hàm số 3 2 y 
x  mx   2 m  
1 x có hai điểm cực trị A và B sao cho 3 ,
A B nằm khác phía và cách đều đường thẳng d : y  5x  9 . Tính tổng tất cả các phần tử của S . https://www Ⓐ. 0 Ⓑ. 6 Ⓒ. 6  Ⓓ. 3 Lời giải Chọn A Cách 1: Ta có 2
y  x  mx   2 ' 2 m   1 3 x  m 1 
m  3m  2  3      m 3m 2 y '  0   A   m 1;
 và B m 1;  x  m 1  3   3  m 2 m   1 2
Dễ thấy phương trình đường thẳng AB : y   x 
nên AB không thể song song hoặc 3 3 trùng với d  ,
A B cách đều đường thẳng d : y  5x  9 nếu trung điểm I của AB nằm trên d 7
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 m  3 3 3  m  3m  m  3m 3  I  ; m d 
 5m  9  m 18m  27  0     3  3 3 3 5 m   2 Với m  3 ,
A B thỏa điều kiện nằm khác phía so với d .   Với 3 3 5 m   ,
A B thỏa điều kiện nằm khác phía so với d . 2
Tổng các phần tử của S bằng 0. h ttp
Câu 18: (Câu 35 - SGD Hà Nội- Lần 1 - Năm 2020 - 2021) Gọi S là tập hợp các giá trị thực của tham s:// 1
số m để đồ thị của hàm số 3 2 y 
x  mx   2 m  
1 x có hai điểm cực trị A và B sao cho , A B lu 3 ye
nằm khác phía và cách đều đường thẳng d : y 5x 9 . Tổng các phần tử của S bằng n th Ⓐ. 0 . Ⓑ. 6 . Ⓒ. 2 . Ⓓ. 6  . it ra Lời giải cn Chọn A gh Ta có: 2
y  x  mx   2 2 m   1 . ie m.vn 3 x  m 1 
m  3m  2  3      m 3m 2 y  0   A   m 1;
 và B m 1;  x  m 1  3   3  2 
Dễ thấy phương trình đường thẳng 2 m(m 1) AB : y   x 
nên AB không thể song song hoặc 3 3
trùng với d : y 5x 9 nếu trung điểm I của AB nằm trên d m 3 3 3  m  3m  m  3m 3  I  ; m d 
5m  9 m 19m  27 0 3  3 5  3  3 m  2 ht Với m3 ,
A B thỏa mãn điều kiện nằm khác phía so với d . tps://www 3  3 5 Với m   ,
A B thỏa mãn điều kiện nằm khác phía so với d . 2
Vậy Tổng các phần tử của S bằng 0 . .fa ceboo
Câu 19: (Câu 36 - THPT Ba Đình - Thanh Hóa - Lần 2 - Năm 2020 - 2021) Gọi m , m là các giá trị 1 2
của tham số m để đồ thị hàm số 3 2
y  2x  3x  m 1 có hai điểm cực trị là B , C sao cho tam k.com
giác OBC có diện tích bằng 2 ,với O là gốc tọa độ. Tính m .m . 1 2 /viet Ⓐ. 6 . Ⓑ. 15  . Ⓒ. 12 . Ⓓ. 20  . gold Lời giải Chọn B
Hàm số xác định với mọi x  . 2
y  6x  6x .
x  0; y  m 1 y  0   .
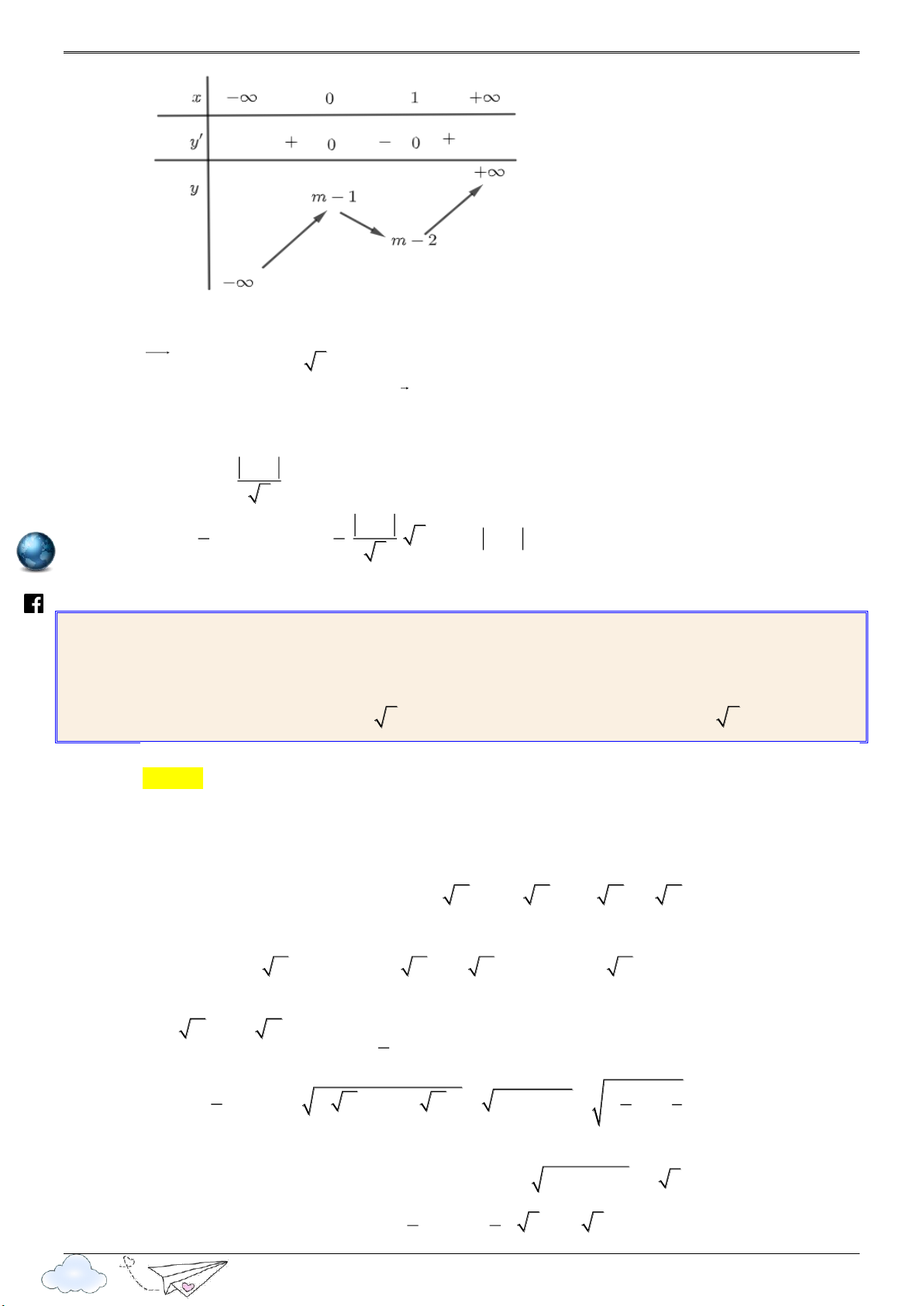
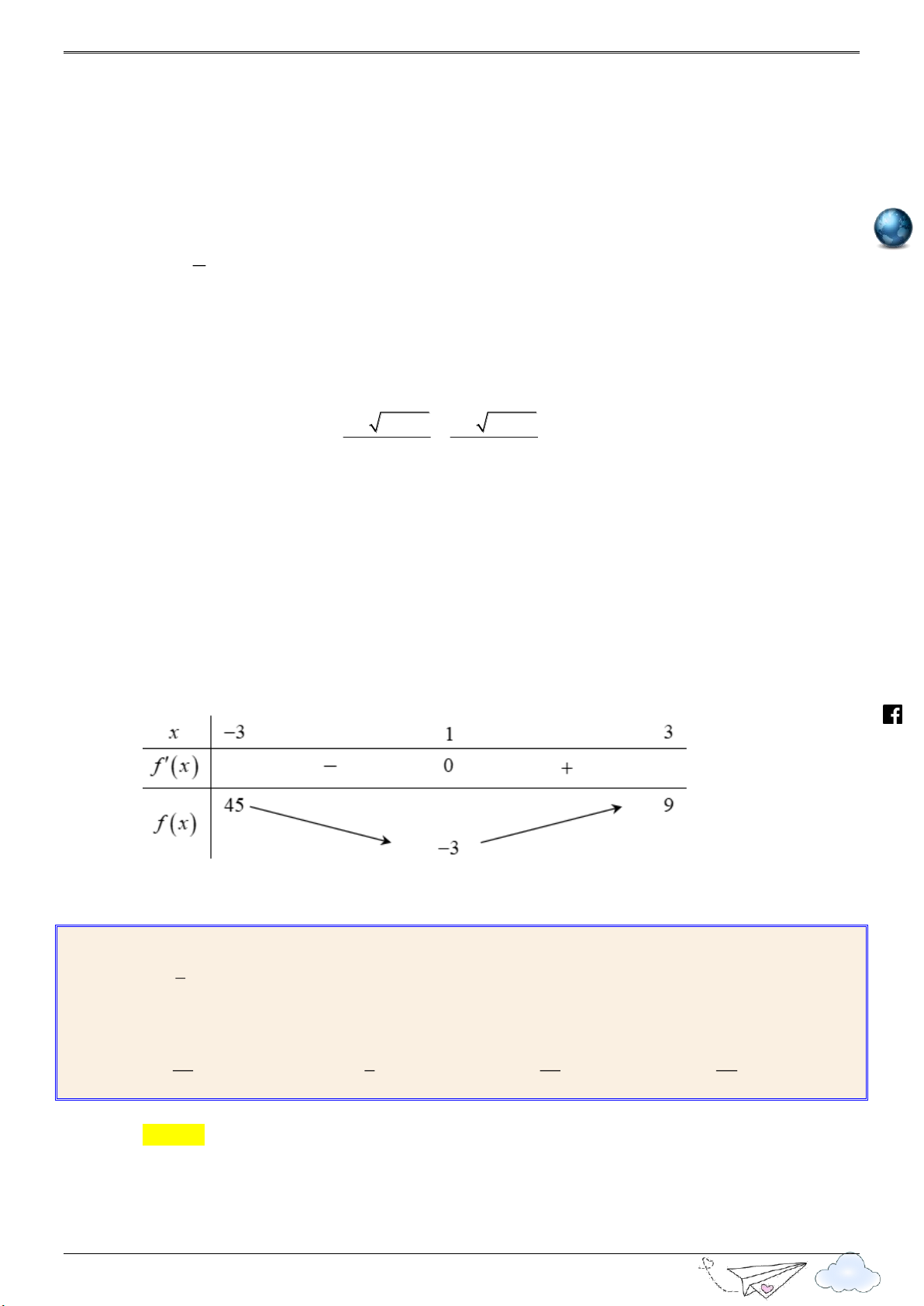
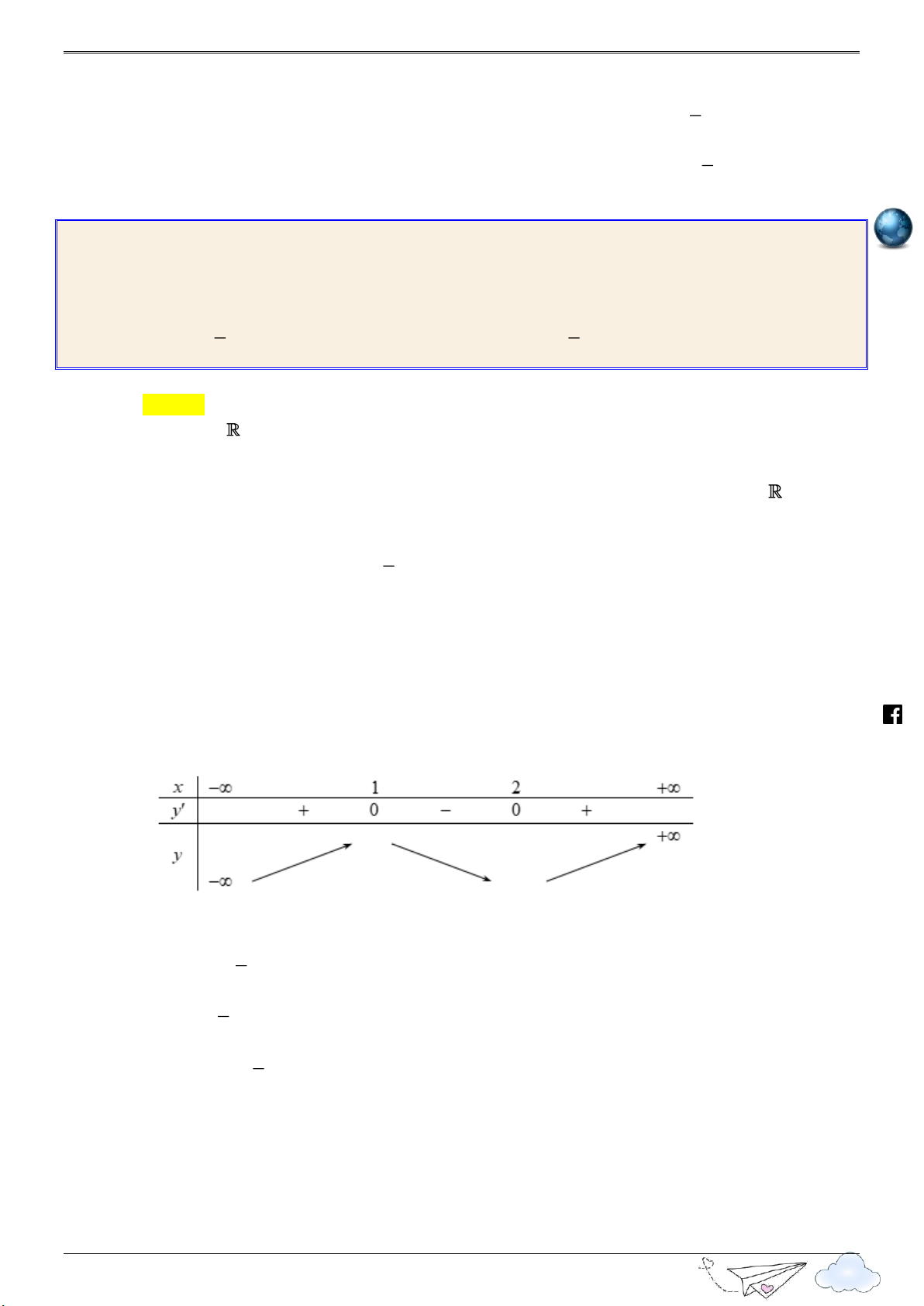
x 1; y  m  2 Bảng biến thiên: 8
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” m.vn ie gh
Vậy B0;m  
1 , C 1;m  2 . racn BC  1;  it 1  BC  2 . th n
BC đi qua B0;m 1 và nhận n  1; 1 làm một vectơ pháp tuyến nên có phương trình ye  1 x  0  
1 y  m  
1  0  x  y  m 1  0 . lu  s:// O BC 1 m d ;  . ttp 2 h 1  m   m  m   S  d O BC BC     m    . OBC  ;  1 1 1 4 3 . . . 2 2 1 4   2 2 2 1   m  4  m  5 Vậy m .m  1  5. 1 2
Câu 20: (Câu 35 - THPT Hoàn Kiếm và Hai Bà Trưng - Hà Nội - Năm 2020 - 2021) Cho hàm số 3
y  x  3mx 1 (1) và điểm A2; 
3 . Biết m là một giá trị để đồ thị hàm số (1) có hai điểm cưc
trị B và C sao cho tam giác ABC cân tại A . Diện tích tam giác ABC bằng Ⓐ. 6 . Ⓑ. 2 2 . Ⓒ. 3. Ⓓ. 2 . /vietgold Lời giải Chọn B k.com Ta có 2
y  3x  3 . m
Đồ thị hàm số (1) có hai điểm cưc trị B và C khi và chỉ khi phương trình y  0 có hai nghiệm ceboo .fa
phân biệt, suy ra m  0 .
Khi đó, không giảm tổng quát suy ra B( m;1 2m m);C m;2m m   1 ; A2;3 .
Tam giác ABC cân tại A suy ra AB  AC .
AB  AC   m  2    m m 2   m  2    m m 2 2 2 2 2 2 2 2 2 https://www
m  0 lo¹i v× m  0  
 8 m 16m m  0   m  1 tháa m·n  2 1 Với 1 1 m  thì 2 2 3
BC  (2 m)  (4m m)  4m 16m  4. 16.  2 . 2 2 8
Thử lại thấy ba điểm , A ,
B C không thẳng hàng.
Gọi I là trung điểm của BC , suy ra I 0  ;1 và 2 2
IA  2  (3 1)  2 2 . 1 1
Vậy diện tích tam giác ABC bằng .I . A BC  .2 2.2  2 2 . 2 2 9
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
Câu 21: (Câu 44 - THPT Hoàn Kiếm và Hai Bà Trưng - Hà Nội - Năm 2020 - 2021) Có bao nhiêu giá
trị nguyên của tham số m để đồ thị hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m  m có hai điểm cực trị ,
A B và OA  OB đạt giá trị nhỏ nhất? Ⓐ. Vô số. Ⓑ. 2. Ⓒ. 3. Ⓓ. 1. Lời giải Chọn C 3 2 h
Ta có y   x  m  3x  m  y  3 x  m  3. ttp    s:// y 
 x  m2 x m 1 0 1     lu x m 1 ye
Đồ thị hàm số đã cho có hai điểm cực trị  y  0 có hai nghiệm phân biệt n th
 m 1 m 1 m . it
Với x  m 1 y 1 3m   1  m  2
 m  2  Am1; 2  m  2. racn
Với x  m 1 y  1  3m  1  m  2
 m  2  Bm1; 2  m  2. gh 2 2 2 2 ie
Ta có OA  OB  m   1   2
 m  2  m  1   2  m  2 m.vn 2 2
 5m 10m  5  5m 10m  5
 5 m 1  5 m 1  5. m   1  m  
1  2 5  OA  OB  2 5. min
Dấu "  " xảy ra  m   1 m   1  0  1
  m 1 m0;  1 .
Câu 22: (Câu 45 - THPT Hồng Lĩnh - Hà Tĩnh - Lần 1 - Năm 2020 - 2021) Cho hàm số 1 3 2 y 
x  mx   2 m  m  
1 x 1. Có bao nhiêu giá trị nguyên của tham số thực m để hàm số 3
đạt cực trị tại x , x thỏa mãn 2 2
x  2mx 3m  m  5  0? 1 2 1 2 https://www Ⓐ. 9 . Ⓑ. 3 . Ⓒ. 7 . Ⓓ. 4 . Lời giải Chọn B .fa Ta có: 2 2
y '  x  2mx  m  m 1. ceboo
Hàm số đạt cực trị tại x , x khi và chỉ khi phương trình y '  0 có 2 nghiệm phân biệt 1 2 k.com
 '  m1 0  m  1  . * /v
x  x  2m iet Khi đó 1 2  2
x .x  m  m 1 gold  1 2 Theo đề bài: 2 2
x  2mx 3m  m  5  0 1 2 2
 x x  x  2
x  3m  m  5  0 1 1 2 2 2 2 2
 x  x x  x 3m  m5  0 1 1 2 2
 x  x 2 2
 x x 3m  m5  0 1 2 1 2 2 2 2
 4m m  m13m  m5  0
 2m4  0  m  2.
Kết hợp với * ta được 1   m  2 . 10
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Do m nguyên nên m 0,1,  2 .
Vậy có 3 giá trị m thỏa mãn yêu cầu bài toán.
Câu 23: (Câu 38 - THPT Lương Tài - Bắc Ninh - Lần 1 - Năm 2020 - 2021) Biết rằng đồ thị hàm số 1 1 3 2 y  x 
mx  x  2 có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh của 3 2
tam giác vuông có cạnh huyền 7 . Hỏi có mấy giá trị của m ? m.vn Ⓐ. 0 . Ⓑ. ie 2 . Ⓒ. 3. Ⓓ. 1. gh Lời giải Chọn B racn it  Ta có: 2
y '  x  mx 1. th 2      n y ' 0 x mx 1 0 . ye
 Đồ thị hàm số có hai điểm cực trị  phương trình có hai nghiệm phân biệt 2
 '  m  4  0 lu . s://
Khi đó, gọi các nghiệm của là x , x thì x , x chính là hoành độ hai điểm cực trị. Theo Viet ta 1 2 1 2 ttp h có x  x  ; m x .x  1. 1 2 1 2
Theo bài ra ta có: x  x
 7  x  x 2 2 2 2 2
 2x x  7  m  2  7  m  9  m  3  ). 1 2 1 2 1 2
Vậy có 2 giá trị của m thỏa mãn yêu cầu.
Câu 24: (Câu 38 - SGD Thái Nguyên - Lần 1 - Năm 2020 - 2021) Cho hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m , với m là tham số. Gọi C  là đồ thị của hàm số đã cho. Biết
rằng khi m thay đổi, điểm cực tiểu của đồ thị C  luôn nằm trên đường thẳng cố định. Hệ số
góc của đường thẳng d bằng /vietgold 1 1 Ⓐ.  . Ⓑ. 3 . Ⓒ. 3  . Ⓓ. . 3 3 k.com Lời giải Chọn C ceboo
Tập xác định D  . .fa Ta có: 2
y  x  mx   2 3 6 3 m   1 . x  m 1 2 2
y  0  x  2mx  m 1  0   . x  m 1 https://www
Vì hàm số có hệ số bậc ba dương nên hàm số có điểm cực tiểu x  m 1. CT
Mặt khác ta lại có: y  x  m 
 x  m2 3mx 3mxx m3x   2 Suy ra: y
 x  m 
 x  m 3mx  3mx x m3x CT CT CT CT CT CT CT   y
 13mx 3mx 3x 13x 13x CT CT CT CT CT CT
Vậy tọa độ điểm cực tiểu thỏa mãn phương trình đường thẳng y  3
 x 1 hay đường thẳng d có hệ số góc bằng 3  .
Câu 25: (SGD Hưng Yên-Năm 2019-2020) Tất cả các giá trị thực của tham số m để hàm số 3 2
y  2x  3mx  2mx  5 không có cực trị là 11
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 4 4 4 4
Ⓐ. 0  m  .
Ⓑ. 0  m  .
Ⓒ.   m  0 .
Ⓓ.   m  0 . 3 3 3 3 Lời giải Chọn A
Tập xác định D  . Ta có 2
y  6x  6mx  2m .
Để hàm số đã cho không có cực trị thì phương trình 2
6x  6mx  2m  0 vô nghiệm hoặc có 4 nghiệm kép 2  
  9m 12m  0  0  m  . h 3 ttp
Câu 26: (SGD Vĩnh Phúc-2019-2020) Cho hàm số 3
y  x  m   2
2 x  2 (với m là tham số). Hàm số s://
đã cho có cực tiểu khi và chỉ khi lu ye Ⓐ. m 1. Ⓑ. m  2  . Ⓒ. m  0 . Ⓓ. m  3  . n th Lời giải it r Chọn B ac 2 n
Ta thấy y  3x  2m  2 x  x 3
 x  2m  2   . gh ie  x  0 m.vn 2 
y  0  3x  2 m  2 x  0  2m  2  . x   3
Vì hàm số đã cho là hàm bậc 3 nên hàm số có cực tiểu khi và chỉ khi hàm số có 2 điểm cực trị 2m  2
 phương trình y  0 có hai nghiệm phân biệt   0  m  2  . 3
Câu 27: (THPT Nguyễn Tất Thành - Hà Nội - Năm 2019-2020) Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  x  3mx  3m  6 x có cực trị.     
Ⓐ. 3 m 2 .
Ⓑ. m  3 hoặc m  2.
Ⓒ. m  3 hoặc m  2 http . Ⓓ. 3   m  2 . s://www Lời giải Chọn B .fa Ta có: 2 y  3
 x  6mx  3m  6 . ceboo m  3  Hàm số có cực trị 2              0 9m 3.3 m m m . y  6 2 0 6 0    k.com m 2
Câu 28: (TN12-THPT Nguyễn Tất Thành 2019-2020) Tìm tất cả các giá trị thực của tham số m để /v hàm số 3 2
y  x  3mx  3m  6 x có cực trị. ietgold Ⓐ. 3
  m  2 . Ⓑ. m  3  hoặc m  2 . Ⓒ. m  3  hoặc m  2 . Ⓓ. 3   m  2 . Lời giải Chọn B Ta có: 2 y  3
 x  6mx  3m  6 . m  3  Hàm số có cực trị 2              0 9m 3.3 m m m . y  6 2 0 6 0  m  2 12
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Câu 29: (THPT Võ Thị Sáu- TPHCM- năm 2019-2020) Tập hợp các số thực m để hàm số 3 x 2 y 
 mx  6m  9 1 có cực trị là 3 Ⓐ. \  3 . Ⓑ. . Ⓒ. \ 3  ;  3 . Ⓓ. \  3  . Lời giải Chọn D m.vn Để hàm số 3 2
y  ax  bx  cx  d có cực trị thì 2 b  3ac  0 ie 2 1 gh
 m  3. 
 6m  9  0  3 racn 2
 m  6m  9  0 it 2 th  m  3  0 n  m  3  0 ye lu  m  3.  s://
Câu 30: (THPT Nguyễn Gia Thiều- Năm 2019 -2020) Cho hàm số ttp
y  f  x 3
 x a   2
2 x  2a   h
1 x 1. Tìm mệnh đề nào sai.
Ⓐ. Hàm số luôn có cực đại, cực tiểu a  .
Ⓑ. Hàm số luôn có cực đại, cực tiểu a   1  .
Ⓒ. Hàm số đồng biến khi a  1  .
Ⓓ. Hàm số luôn có cực đại, cực tiểu a   1  . Lời giải Chọn B 2
y  3x  2a  2 x  2a   1 .
  a  2   a    a  a   a  2 2 ' 2 3 2 1 2 1 1 . /vietgold
 y  0 có 2 nghiệm phân biệt khi a  1.
 Vậy hàm số luôn có cực đại, cực tiểu a   1  .
Câu 31: (THPT Nguyễn Khuyến - TP HCM - Lần 02 - Năm 2019 - 2020) Tìm tất cả các giá trị của k.com
tham số thực m để hàm số 3 2
y  mx  2x  m 1 có điểm cực tiểu. ceboo .fa Ⓐ. m  0. Ⓑ. m  0. Ⓒ. m  0 . Ⓓ. m  0 . Lời giải Chọn A
Tập xác định: D  . Ta có: 2
y  3mx  2. https://www
Để hàm số đã cho có điểm cực tiểu thì phương trình y '  0 phải có hai nghiệm phân biệt  3 .
m 2  0  m  0.
Câu 32: (Chuyên Hùng Vương - Phú Thọ - Năm 2019 - 2020) Cho hàm số 3
y  x  (m  ) 1 2 x  ( 2 m  6m  )
5 x  2 . Gọi S  (a ; )
b là tập hợp các giá trị của tham số m để
hàm số có cực trị, giá trị của a  b bằng : Ⓐ. 7 Ⓑ. 6 Ⓒ. 8 Ⓓ. 9 Lời giải Chọn C 13
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 y'  3 2 x  ( 2 m  ) 1 2
x  m  6m  5
Để hàm số có cực trị  y' 0 có 2 nghiệm phân biệt  '   (m  ) 1 2  3( 2 m  6m  ) 5  0  2 2
 m 16m 14  0 1 m  7  S  ) 7 ; 1 (
. Vậy, a  b  8
Câu 33: Với giá trị thực nào của tham số m thì hàm số y  m   3 2
3 x  2 3x  mx  5 có hai điểm cực trị? Ⓐ. m 1  ;4 .
Ⓑ. m ;    1 4; . h ttp Ⓒ. m 1  ;4 \  3 .
Ⓓ. m ;    1 4;   3 . s:// Lời giải lu ye Chọn C n
Ta có y  m   2 3
3 x  4 3x  m . th it
Hàm số có hai cực trị khi và chỉ khi y  0 có hai nghiệm phân biệt rac m  3  0  m  3 m  3 n          gh  m . 2 3  2  1;4 \   3m 3 3 2 m  0  3
 m  9m 12  0  1   m  4 ie m.vn Vậy m  1  ;4 \ 
3 thỏa mãn yêu cầu bài toán.
Câu 34: (Vted - Đề số 21 - Năm 2019 - 2020) Hàm số f  x 3 2
 x 3x 1 có hai điểm cực trị x , x . Giá 1 2
trị của x  x bằng 1 2 Ⓐ. 6  . Ⓑ. 2  . Ⓒ. 3 . Ⓓ. 2 . Lời giải Chọn D x  0           Có f  x 2 3x 6x 0 x x 0 2 2  . 1 2 ht x  2 tps://www
Câu 35: (THPT Nguyễn Khuyến - TP HCM - Lần 02 - Năm 2019 - 2020) Tìm tất cả các giá trị thực 4
của tham số m để đồ thị hàm số 3
y  x  m   2 1 x 
x  2  m không có điểm cực trị. 3 .fa ceboo Ⓐ. 3   m 1. Ⓑ. 1   m 1. Ⓒ. m 1. Ⓓ. 3   m 1. k.com Lời giải Chọn D /v 4 Ta có 2
y  3x  2m   1 x  . iet 3 gold
Hàm số không có cực trị khi và chỉ khi y không đổi dấu  
   m 2 2 0
1  4  0  m  2m  3  0  3   m 1.
Câu 36: (THPT Triệu Sơn 4 - Thanh Hóa - Lần 3 - Năm - 2019 2020) Có bao nhiêu giá trị nguyên của
m để hàm số f  x 3 2
 2x  6x  m 1 có các giá trị cực trị trái dấu? Ⓐ. 2 . Ⓑ. 9 . Ⓒ. 3 . Ⓓ. 7 . Lời giải Chọn D
Tập xác định D  . 14
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” x  0 Ta có 2
y  6x 12x  y  0  
; f 0 1 m, f 2  7   m . x  2 Hàm số f  x 3 2
 2x  6x  m 1 có các giá trị cực trị trái dấu
 f 0. f 2  0  1 m. 7
  m  0  7   m 1. Mà m  m 6
 ;5; 4;3; 2;1; 
0 . Có 7 giá trị thỏa mãn.
Câu 37: (THPT Tam Dương - Vĩnh Phúc - Năm học 2019 - 2020) Có bao nhiêu giá trị thực của tham m.vn 3 x ie 2 2
số m để đồ thị hàm số y 
5m 3m 
1 x  2m  
1 x 1 có hai điểm cực trị , A B sao gh 3 cho ,
A B cách đều đường thẳng  : x 1  0 ? racn it Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0 . th n Lời giải ye Chọn C lu
Tập xác định: D  . s:// Đạo hàm: 2 y  x   2 '
2 5m  3m   1 x  2m 1 ttp h y '  0 2  x   2
2 5m  3m  
1 x  2m 1  0   1
Đồ thị hàm số có hai điểm cực trị ,
A B khi và chỉ khi  
1 có hai nghiệm phân biệt.
Khi đó:     m  m 2 2 ' 0 5 3 1  2m   1  0   *
Với điều kiện * , phương trình  
1 có hai nghiệm phân biệt x , x 1 2 thỏa mãn:
x  x  2 2 5m  3m 1 1 2     ** (theo định lý Vi-ét).
 x .x  2m 1  1 2 3  x  /vietgold
Giả sử tọa độ hai điểm cực trị 1 A x ;
 5m  3m 1 x  2m 1 x 1 1  2  21   1  3  k.com 3  x  2 B  x ;
 5m  3m 1 x  2m 1 x 1. 2  2  22   2  3  ceboo
Theo giả thiết, hai điểm cực trị cách đều đường thẳng  : x 1  0 nên ta có: .fa d  ,
A   d  ,
B   x 1  x 1  x  x  2 (do x  x ). 1 2 1 2 1 2 m  1 Kết hợp với hệ   ** suy ra:  2 
2 5m  3m   1  2 2
 5m  3m  2  0  2  . m    https://www 5 2
Kiểm tra với điều kiện * thấy m   thỏa mãn. 5
Vậy có 1 giá trị thực của tham số m thỏa mãn yêu cầu bài toán.
Câu 38: (THPT Liên Trường - Nghệ An - Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham số m để 1 hàm số 3 2
y   x  2mx  mx 1 có hai điểm cực trị x , x nằm về hai phía trục . Oy 3 1 2  1 1 m   
Ⓐ. m  0. Ⓑ. m  0.
Ⓒ.   m  0 . Ⓓ. 4 . 4  m  0 15
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Lời giải Chọn B
Tập xác định: D  . Ta có 2
y  x  4mx  m .
Để hàm số có hai điểm cực trị x , x nằm về hai phía trục Oy thì phương trình 1 2 2
x  4mx  m  0 có hai nghiệm phân biệt x , x trái dấu  m  0  m  0. 1 2
Câu 39: (THPT chuyên Biên Hòa - Hà Nam - 2020) Có tất cả bao nhiêu giá trị thực của tham số m để h 2 2 3 2 2 ttp
đồ thị hàm số y  x  mx  23m   1 x 
có hai điểm cực trị có hoành độ x , x sao cho 3 3 1 2 s://
x x  2 x  x 1? 1 2  1 2 lu ye Ⓐ. n 1. Ⓑ. 0 . Ⓒ. 3 . Ⓓ. 2 . th it Lời giải ra Chọn A cn TXĐ: D  . gh 2
y  x  mx   2 2 2 2 3m   1 . ie m.vn 2 2
y  0  x  mx  3m 1  0  1 .
Đồ thị hàm số đã cho có hai điểm cực tri khi và chỉ khi phương trình  
1 có hai nghiệm phân biệt  2 m   2
    m   2  m   2 13 0 4 3
1  0  13m  4  0   .  2  m   13 Theo định lý Vi-et: 2 x x  3
 m 1; x  x  m . 1 2 1 2 Theo đề bài, ta có: http  2 s://www m  nhaän x x 2 x x 1 3m 1 2m 1           3 1 2  1 2 2    . m  0  loaïi .fa
Vậy có 1 giá trị thực của m thoả yêu cầu bài toán. ceboo
Câu 40: (THPT Thái Phục- Thái Bình- Lần 3- 2020) Cho hàm số f  x 3 2 2
 x  2ax  a x  ba,b  k.com
có 2 điểm cực trị A và B . Biết tam giác OAB vuông cân tại O ( O là gốc tọa độ ), giá trị của biểu thức 2 2
P  a  b bằng /viet 10 Ⓐ. 25. Ⓑ. . Ⓒ. 40. Ⓓ. 10. gold 3 Lời giải Chọn D Ta có 2 2
y  3x  4ax  a x  a   y  0  a a  0  . x   3 3  a 4a 
Aa,b và B  ;  b  3 27  16
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” 2 3 a  4a  2 2   b  b  0 a  9b 2  3     27 O . A OB 0   a  9 Ta có 2 3          2 a 4a 2 2 3 O  A  OB     b    b  0 a 4a b  1 2 2 a  b      b 3    27  9   27  2 2
 P  a  b 10 .
Câu 41: (THPT-Quốc Học Huế- Lần 1- 2020) Tìm các giá trị nguyên của tham số m thuộc khoảng m.vn  2
 019;2020 để điểm cực tiểu của đồ thị hàm số 3 2
y  x  x  mx 1 nằm bên phải trục tung. ie gh Ⓐ. 2020 . Ⓑ. 2019 . Ⓒ. 2017. Ⓓ. 2018 . racn Lời giải it Chọn D th n Ta có: 2
y '  3x  2x  m . ye 1 lu
Hàm số có cực trị thì  '  0  1 3m  0  m  3 s://
Điểm cực tiểu của đồ thị hàm số 3 2
y  x  x  mx 1 nằm bên phải trục tung  y '  0 có ít nhất ttp h một nghiệm dương.  2  x  x   0  1 2  3 Mà 2
3x  2x  m  0 có 2 nghiệm x ; x thỏa mãn:   m  0 1 2 m x .x  1 2  3
Vậy có 2018 giá trị nguyên m thỏa mãn.
Câu 42: (Chuyên KHTN - Hà Nội - Lần 3 - Năm 2019-2020) Có bao nhiêu giá trị nguyên của tham số
m để đồ thị hàm số 3 2
y  mx  (2m 1)x  2mx  m 1 có hai điểm cực trị nằm về hai phía của trục hoành. /vietgold Ⓐ. 4. Ⓑ. 2. Ⓒ. 1. Ⓓ. 3. k.com Lời giải ceboo Chọn C .fa
Để đồ thị hàm số 3 2
y  mx  (2m 1)x  2mx  m 1 có hai điểm cực trị nằm về hai phía của trục hoành thì phương trình 3 2
mx  (2m 1)x  2mx  m 1  0 (1) có ba nghiệm phân biệt. Ta có: 3 2
mx  (2m 1)x  2mx  m 1  0 2 2
 (x 1) mx  (1 m)x  m 1  0   https://www x 1   2 2
 f (x)  mx  (1 m)x  m 1  0  2
Để phương trình (1) có ba nghiệm phân biệt thì (2) có hai nghiệm phân biệt khác 1 17
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021   m  0 m 0      0  
 1 m2  4mm   1  0   f    1  0
m 1 m  m 1  0  m  0 m  0       2 3 2 3 3 2 3   3
 m  6m 1  0    m  3 3   m  2   m  2   h ttp Mặt khác ta có m  m  1  . s://
Câu 43: (SGD Hưng Yên - Năm 2019-2020) Cho hàm số 3
y  x  m   2 2 3
1 x  6m  2 x 1 với m lu ye
là tham số thựⒸ. Tìm tất cả các giá trị của tham số m để hàm số có các điểm cực đại và cực tiểu n th
của hàm số nằm trong khoảng  2  ;3 it ra   c
Ⓐ. m1;3.
Ⓑ. m 1;3 3;4 . n gh  ie
Ⓒ. m 1;4 .
Ⓓ. m3;4 . m.vn Lời giải Chọn B Ta có 2
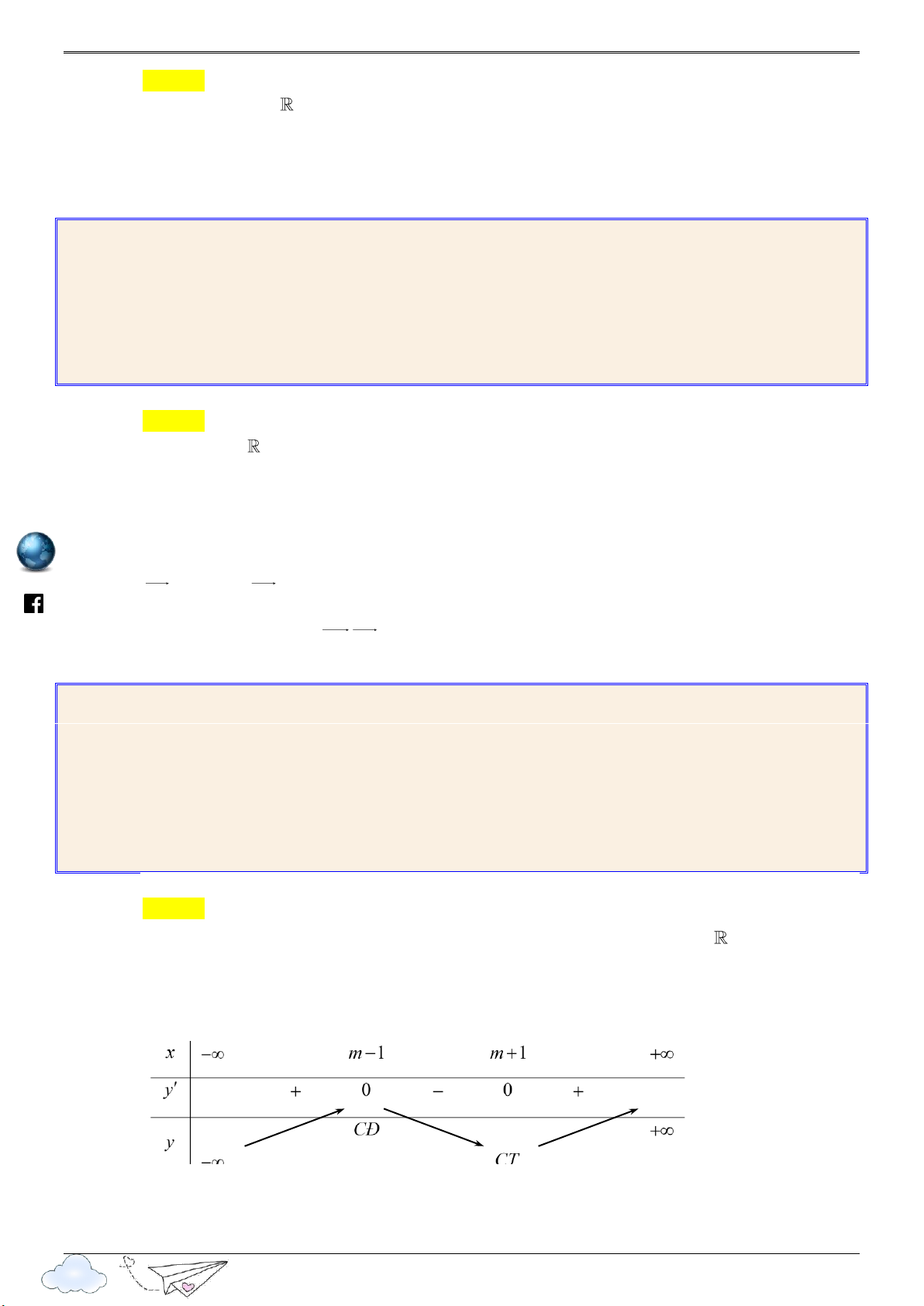
y  6x  6m  
1 x  6m  2 x  1  y  0   x  2  m
Để hàm số có các điểm cực đại đều thuộc khoảng  2  ;3 thì 2  m  1  m  3    .  2   2  m  3  1   m  4 http   s://www Vậy m  1;3 3;4
Câu 44: (THPT Nam Đàn 2 - Lần 1 - Năm 2019-2020) Cho hàm số 3 2
y  x  3x  mx  m  2 có đồ thị
C . Giá trị của tham số thực m để C có điểm cực đại, cực tiểu nằm về hai phía trục hoành m  m  .fa ceboo là k.com
Ⓐ. m  3 .
Ⓑ. 1 m  5.
Ⓒ. 2  m  3. Ⓓ. m  3. Lời giải /v Chọn A ietgold Cách 1: Ta có: 3 2
y  x  3x  mx  m  2   x   2
1 x  2x  m  2 2
x  2x  m  2  0   1 y   x   2 0
1 x  2x  m  2  0   x  1 
Để đồ thị C có điểm cực đại, cực tiểu nằm về hai phía trục hoành m 
 y  0 có ba nghiệm phân biệt  phương trình  
1 có hai nghiệm phân biệt khác 1  18
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” '   0 m  3      m  3 1
  2  m  2  0 m  3
Vậy m  3 thì đồ thị C
có điểm cực đại, cực tiểu nằm về hai phía trục hoành. m  Cách 2: 2      Ta có: ' 2
y  3x  6x  m ; ' y  0 3x 6x m 0  
Hàm số có cực đại, cực tiểu  phương trình  có hai nghiệm phân biệt m.vn '
   0  93m  0  m  3   1 ie gh x  x  2  1 2 
Gọi x , x là nghiệm của phương trình  . Theo định lý viet ta có  1 2 m racn x .x   1 2 it  3 th
Gọi y , y là giá trị cực trị tương ứng của hàm số. n 1 2 ye  1 1   2   2   2  Vì ' y  y . x  
m  2  x     
1 nên y  m2 x 1 ; y  m2 x 1 . 2   2  1   1  lu  3 3   3   3   3  s://
Để đồ thị C có điểm cực đại, cực tiểu nằm về hai phía trục hoành  y . y  0 m  1 2 ttp h  2     m    2 2 x 1 . m  2 x 1  0 1    2   3   3  2  2   m  2 
  x  x  x .x 1  0 1 2 1 2   3  2  2   m  m  3  m  2 1  0        m  3 2  3   3  m  3 Từ  
1 và 2 suy ra m  3 thì đồ thị C
có điểm cực đại, cực tiểu nằm về hai phía trục hoành. m 
Câu 45: (THPT Tam Dương - Vĩnh Phúc - Năm 2019-2020) Có bao nhiêu giá trị thực của tham số m /vietgold 3 x để 2 2
đồ thị hàm số y 
5m 3m 
1 x  2m  
1 x 1 có hai điểm cực trị , A B sao cho , A B 3 k.com
cách đều đường thẳng  : x 1  0 ? ceboo Ⓐ. 2 . Ⓑ. 3 . Ⓒ. 1. Ⓓ. 0 . .fa Lời giải Chọn C
Tập xác định: D  . Đạ 2 2
o hàm: y '  x  25m  3m   1 x  2m 1 https://www y '  0 2  x   2
2 5m  3m  
1 x  2m 1  0  1
Đồ thị hàm số có hai điểm cực trị ,
A B khi và chỉ khi  
1 có hai nghiệm phân biệt.
Khi đó:     m  m 2 2 ' 0 5 3 1  2m   1  0   *
Với điều kiện * , phương trình  
1 có hai nghiệm phân biệt x , x thỏa mãn: 1 2
x  x  2 2 5m  3m 1 1 2     ** (theo định lý Vi-ét).
 x .x  2m 1  1 2 19
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 3  x 
Giả sử tọa độ hai điểm cực trị 1 A x ;
 5m  3m 1 x  2m 1 x 1 1  2  21   1  3  3  x  2 B  x ;
 5m  3m 1 x  2m 1 x 1. 2  2  22   2  3 
Theo giả thiết, hai điểm cực trị cách đều đường thẳng  : x 1  0 nên ta có: d  ,
A   d  ,
B   x 1  x 1  x  x  2 (do x  x ). 1 2 1 2 1 2 m 1 h 2    2   ttp Kết hợp với hệ   ** suy ra: 25m 3m
1 2 5m 3m20 2  . m   s://  5 lu 2
Kiểm tra với điều kiện * thấy m   thỏa mãn. ye 5 n
Vậy có 1 giá trị thực của tham số m thỏa mãn yêu cầu bài toán. th it
Câu 46: (THPT Nghi Sơn - Thanh Hóa - Lần 01 - Năm 2019-2020) Tìm tổng tất cả các giá trị thực của ra
tham số m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số cn 3 2        gh y 2x 3m  1 x
6m1 2m x song song đường thẳng y 4x . ie 1 2 2 m.vn Ⓐ.  . Ⓑ.  . Ⓒ. 1. Ⓓ. . 3 3 3 Lời giải Chọn A TXĐ: D  . Gọi C 3
y  x  m   2 : 2 3
1 x  6m1 2m x . Có: 2
y '  6x  6m  
1 x  6m1 2m . 2 2 Có:   36   m 
1  4m1 2m  36 2
9m  6m 1  36 3m 1 y '      . ht 1 tp
Để hàm số có hai cực trị thì:   0  m    m  . y 3 2 1 0 ' s://www 3  1 1  Có: y  y '. x  m  1   2 9
 m  6m  
1 x  m m   1 2m     1 .  3 6  .fa
Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị C là: ceboo y   2 9
 m  6m  
1 x  mm   1 2m   1 d  . k.com Để đường thẳng
d  song song với đường thẳng y  4  x thì: /v m 1 iet  2 1 gold  9
 m  6m 1  4  m   1  .        m   
m m 1 2m   3 1  0 3  1
m  0;m 1;m   2 1
Vậy m   là giá trị cần tìm. 3
Câu 47: (THPT Việt Nam Ba Lan - Hà Nội - Năm 2019-2020) Số các giá trị nguyên của tham số m sao cho hàm số 3
y  x  m   2 2 3
1 x  6m  2 x  2019 có hai điểm cực trị nằm trong khoảng  5  ;5 bằng 20
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” Ⓐ. 7 . Ⓑ. 8 . Ⓒ. 6 . Ⓓ. 5 . Lời giải Chọn B Ta có: 2
y  6x  6m  
1 x  6m  2 . x  1  y  0   . x  2  m m.vn Để hàm số 3
y  x  m   2 2 3
1 x  6m  2 x  2019 có hai điểm cực trị nằm trong khoảng ie       gh  2 m 1 m 3 5  ;5 thì    .  5   2  m  5  3   m  7 racn it Mà m  m 2  ; 1  ;0;1;2;4;5;  6 . th n
Câu 48: (THPT Việt Nam Ba Lan - Hà Nội - Năm 2019-2020) Tìm tất cả các giá trị thực của tham số ye
m để hàm số f  x 3
 x   m   2 x   2 2 1
m  8 x  2 đạt cực tiểu tại x  1  . lu s:// Ⓐ. m  3.
Ⓑ. Không tìm được m . ttp h Ⓒ. m  9  . Ⓓ. m  2  . Lời giải Chọn B
Ta có f  x 2
  x   m   x  2 3 2 2 1
m  8 và f  x  6
 x  22m  1 .  f     1  0 2
m  4m  9  0 m  2 2  5  0
Hàm số đạt cực tiểu tại x  1        (vô  f  
 1  0 4m 4  0 m  1  nghiệm).
Vậy không tìm được m .
/vietgold Câu 49: (THPT Lý Tự Trọng - TPHCM - Năm 2019 - 2020) Cho hàm số 3 2
y  x  3mx  m  2 có đồ 1 k.com
thị C  và đường thẳng d : y 
x  3 . Tập hợp các giá trị thực của tham số m để C  có 2 2
điểm cực trị đối xứng với nhau qua đường thẳng d là: ceboo .fa Ⓐ.   1 . Ⓑ.   1  . Ⓒ.  1   ;1 . Ⓓ.  . Lời giải Chọn D TXĐ : D  . https://www 2
y  3x  6mx  3x  x  2m .
Để đồ thị hàm số có 2 điểm cực trị thì y  0 có hai nghiệm phân biệt  2m  0  m  0 . x  Khi đó: y  0 0  
, đồ thị hàm số có hai điểm cực trị là A0;m  2 , x  2m B  3 2 ;
m  4m  m  2. Gọi I  3 ;
m  2m  m  2 là trung điểm của AB . Ta có: u  2;  1 ; AB   3 2 ; m  4m  . d
A và B đối xứng nhau qua đường thẳng d khi và chỉ khi: 21
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021   1 I  d I  d  3  2
 m  m  2  m  3 3  4
 m  m  2  0     2   d  AB u  .AB  0  3
4m  4m  0 d 3
4m  4m  0
Hệ phương trình vô nghiệm nên không có giá trị m thoả yêu cầu bài toán.
Câu 50: (Chuyên Nguyễn Trãi - Hải Dương- Lần 04 - Năm 2019 - 2020) Cho hàm số
y   x  m3 2
3x  m ( với m là tham số ). M là điểm cực đại của đồ thị hàm số ứng với giá
trị m thích hợp đồng thời là điểm cực tiểu của đồ thị hàm số ứng với một giá trị khác của m . Hỏi h
số điểm M có tính chất như vậy là bao nhiêu? ttp s:// Ⓐ. 0 . Ⓑ. 2 . Ⓒ. 1. Ⓓ. 3 . lu Lời giải ye n
Hàm số y   x  m3 2 3x  m th TXĐ: it D  ra
y   x  m2 3 3 cngh
y  6 x  m ie    m.vn x m
y  0  3 x  m2 1 1  3  0   x  m 1  2 Ta có: y
 6 m 1 m  6  0; y  6 m 1 m  6   0 m 1    m 1       
x  m 1 ; y  m   m  m   m  m  m   C CD  1 3 3  2 2 1 3 2 D  
x  m 1 ; y  m   m  m   m  m  m   CT CT  1 3 3  2 2 1 3 2
Gọi M là 1 điểm cực đại ứng với giá trị m và là điểm cực tiểu ứng với giá trị m . 1 2
m 1  m 1 m  m  2  1 2 1 2 Yêu cầu bài toán     2 ht 2 2
m  3m  2  m  3m  2    m  2   3m  2 2
 2  m  3m  2 1 1 2 2 2 2 2 2 tps://www  3 m   1  2  1 1     M ;    . 1    2 4  .fa m  2  2 ceboo
Câu 51: (Chuyên Lương Văn Chánh - Lần 02 - Năm 2019 - 2020) Biết hàm số   3 2
f x  x  ax  bx  c k.com
đạt cực đại tại điểm x  3  , f  3
   28 và đồ thị của hàm số cắt trục tung tại điểm có tung độ /v bằng 1. Tính 2 2 2
S  a  b  c . ietgold 225 619 Ⓐ. S  89. Ⓑ. S  . Ⓒ. S  . Ⓓ. S  91. 4 8 Lời giải
Ta có f  x 2
 3x  2ax  ;
b f   x  6x  2a .  f    3    0  6
 a  b  2  7
Hàm số f  x đạt cực đại tại điểm x  3  khi và chỉ khi      .  f    3   1  0 a  9 Mà f  3
   28  9a 3b  c  55 2 .
Ngoài ra, đồ thị của hàm số f  x cắt trục tung tại điểm có tung độ bằng 1 nên c 1 3 . 22
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”  6
 a  b  2  7 a  3   9
 a  3b  c  55 b   9  Từ  
1 , 2, 3 suy ra    . c  1 c  1   a  9 a  9 Do đó S    2 2 2 3 9 1  89 .
Câu 52: (THPT Phó Cơ Điều - An Giang - Năm 2019 - 2020) Cho hàm số m.vn 1 3 2 y 
x  2mx  m   2
1 x  2m 1 ( m là tham số ). Xác định khoảng cách lớn nhất từ gốc tọa ie 3 gh
độ O 0;0 đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số trên. racn it 2 10 Ⓐ. 3 . Ⓑ. . Ⓒ. 2 3 . Ⓓ. . th 9 3 n ye Lời giải lu Chọn D s:// Đặ 1
t y  f  x 3 2
 x  2mx  m   2
1 x  2m 1 ttp 3 h  f x 2
 x  4mx  m   1
Hàm số có hai cực trị  Phương trình f  x  0 có hai nghiệm phân biệt 2   1   0 a 0   1  15 2    
 m  m    m    m      .   0 2m   4 1 0 2 0, 2 1m   1  0  4  16
Tìm được phương trình đường thẳng qua 2 điểm cực trị:   8  2 2  8 2 2 2 : y  m  m  x  m  m 1    3 3 3  3 3
Cách 1: Theo đề bài ta có: /vietgold 8 2 8 2 2 1 2 2 m  m 1 m  m   k.com d O  3 3 3 3 3 3 ,   2 2  8  2 2   8 2 2  2 2 ceboo m  m  1 m  m  1      3 3 3   3 3 3  .fa 8 2 2 2 2  1  5 Ta có: m  m 
 4m  m   2 2 2 1  2m    0, m     . 3 3 3 3 3  4  8
Áp dụng bất đẳng thức Ⓑ.
Ⓒ. S cho 2 số dương: https://www 2 2 8 2 2 1  1   8 2 2        2 2 2 1. m  m   .1  1  
      m  m  1     3 3 3  3   3       3 3 3     8 2 2  1 2 1. m  m   .1   2  3 3 3  3  1    10 2   1       2     3      3 8 2 2  2  m  m  1     3 3 3   
 d O  10 ,  . 3 23
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021  8 2 2  8 2 7
Vậy giá trị lớn nhất của d O  10 ,  2 2  m  m 
 3  m  m   0   3  3 3 3  3 3 3  1 57 m  8   .  1 57 m   8 Cách 2: h  1  ttp
Tìm được điểm cố định mà  luôn đi qua với mọi m là A 1;   .  3  s://  8 2 2  2 lu
 có vec tơ chỉ phương là u     1; m m   . ye  3 3 3  n Ta có d  ,
O   OA . th it  1 57 ra m  c 1  8 2 2  8 n Dấu “=” xảy ra 2
 OA    O . A u  0  1   m  m   0      . gh 3  3 3 3   1 57 m  ie  8 m.vn  1 57 m  8
Vậy giá trị lớn nhất của d O  10 ,    . 3  1 57 m   8
Câu 53: (THPT Minh Khai – Hà Nội - Lần 01 - Năm 2019 - 2020) Hàm số 1 3 y 
x  m   2
1 x  5m  4 có điểm cực tiểu lớn hơn 2 khi 3
Ⓐ. m  2 .
Ⓑ. m1;3 .
Ⓒ. m  3. Ⓓ. m 1. http Lời giải s://www Chọn A x  0 Ta có 2
y  x  2m   2 1 ;
x y  0  x  2m   1 x  0   . .fa
x  2m  2 ceboo
Nếu 2m  2  0  m 1 thì hàm số đạt cực tiểu tại x  0  2 . Không thỏa mãn.
Để hàm có điểm cực tiểu lớn hơn 2 thì ta phải có x  2m  2  2  m  2. k.com
Vậy m  2 thì hàm số có điểm cực tiểu lớn hơn 2 .
Câu 54: (THPT Nghi Xuân - Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham số m sao cho đường /viet
thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y  x  m   2 2 3
1 x  6m1 2m x song song gold
đường thẳng y  4  x . 1 2 2
Ⓐ. m   .
Ⓑ. m   . Ⓒ. m 1. Ⓓ. m  . 3 3 3 Lời giải Chọn A Ta có 2
y  6x  6m  
1 x  6m1 2m . Điề 1
u kiện để hàm số có hai điểm cực trị là:    0  9 2
9m  6m   1  0  m  (*). 3 24
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Chia y cho y ta được phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là y   2 9
 m  6m  
1 x  mm   1 1 2m .
Để đường thẳng đi qua hai điểm cực trị song song với đường thẳng y  4  x ta phải có m 1  2 1  9
 m  6m 1  4  m   1  .        m   
m m 1 1 2m 3  0 3  1 m.vn
m  0;m 1;m  ie  2 gh 1
Kiểm tra điều kiện (*) ta được m   . 3 racn it
Câu 55: (THPT NGHI XUÂN - NĂM 2019-2020) Tìm tất cả các giá trị thực của tham số m sao cho th 3 2 n
đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  2x  3m  
1 x  6m1 2m x song ye
song đường thẳng y  4  x . lu s:// 1 2 2
Ⓐ. m   .
Ⓑ. m   . Ⓒ. m 1. Ⓓ. m  . ttp 3 3 3 h Lời giải Chọn A Ta có 2
y  6x  6m  
1 x  6m1 2m . Điề 1
u kiện để hàm số có hai điểm cực trị là:    0  9 2
9m  6m   1  0  m  (*). 3
Chia y cho y ta được phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là y   2 9
 m  6m  
1 x  mm   1 1 2m .
Để đường thẳng đi qua hai điểm cực trị song song với đường thẳng y  4  x ta phải có /vietgold m 1  2 1  k.com  9
 m  6m 1  4  m   1  .        m   
m m 1 1 2m 3  0 3  ceboo 1
m  0;m 1;m  .fa  2 1
Kiểm tra điều kiện (*) ta được m   . 3
Câu 56: (THPT Hàm Rồng - Năm 2019 - 2020) Có bao nhiêu giá trị nguyên của tham số m để hàm số https://www 3
y  x  m   2 x   2 m  m   2 2
3 x  m  
1 có hai giá trị cực trị trái dấu. Ⓐ. 1. Ⓑ. 4 . Ⓒ. 3 . Ⓓ. 2 . Lời giải Chọn C Ta có 3
x  m   2 x   2 m  m   2 2
3 x  m  0 2  x   2
x  m  2 1
3 x  m   0   x 1   f   x 2
 x  m  3 2
x  m  0 3 25
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Hàm số  
1 có hai giá trị cực trị trái dấu
 Đồ thị hàm số  
1 cắt trục hoành tại ba điểm phân biệt.
 Phương trình 2 có ba nghiệm phân biệt.
 Phương trình (3) có hai nghiệm phân biệt khác 1. 2   0   3
 m  6m  9  0         .  f    1 m 3 2 1  0
m  m  4  0 h Mà m  nên m 0;1;  2 . ttp
Vậy có ba số nguyên m thoả mãn yêu cầu bài toán. s://
Câu 57: (THPT Thạch Thành 2 - Thanh Hóa - Năm 2019 - 2020) Gọi S là tập hợp tất cả các giá trị lu ye 1
thực của tham số m để đồ thị hàm số 3 2 y 
x  mx   2 m  
1 x có hai điểm cực trị , A B sao n 3 th cho ,
A B nằm khác phía và cách đều đường thẳng y  5x  9 . Tính tổng tất cả các phần tử của it ra S . cngh Ⓐ. 0 . Ⓑ. 6 . Ⓒ. 6  . Ⓓ. 3 . ie m.vn Lời giải Chọn A Ta có: 2 2
y  x  2mx  m 1, 2 2 
  m  m 11 0 nên  m  3 1       m  m  y
m m 1  m   1 m   3 2 3 2 2 1  x  m 1 phương trình  3 3 y  0    x  m 1  m  3 1      m  m   y
m m 1  m   1 m   3 2 3 2 2 1   3 3 3 3 
m  3m  2  
m  3m  2   4 
Vậy A m 1;
; B m 1;   AB  2  ; 
 nên đường thẳng AB không ht  3   3   3  tps://www
song song hoặc trùng với đường thẳng d  : y  5x  9 . ,
A B cách đều đường thẳng d  nếu trung điểm I của AB nằm trên đường thẳng d  . m  3 .fa 3 3  m  3m  m  3m 3  ceboo I  ; m d  
 5m  9  m 18m  27  0  3   3 5 .  3  3 m   2 k.com
Cả ba giá trị của m đều thỏa mãn ,
A B nằm khác phía so với d  . Vậy tổng tất cả các phần tử /v của S là 0. iet
Câu 58: (THPT Lê Lợi - Thanh Hóa - Năm 2019 - 2020) Biết rằng đồ thị hàm số gold f  x 1 1 3 2
 x  mx  x  2 có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh 3 2
của tam giác vuông có cạnh huyền là 7 . Hỏi có mấy giá trị của m ? Ⓐ. 2. Ⓑ. 3. Ⓒ. 1.
Ⓓ. Không có m . Lời giải Chọn A 2
y  x  mx 1 26
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Để hàm số có hai cực trị thì y  0 có 2 nghiệm phân biệt    0 2  m  4  0  m  2   m  2
Giả sử hai điểm cực trị có hoành độ x , x 1 2 Theo đề ra, ta có 2 2 x
 x  7  x  x
 2x x  7  m  2  7  m  3  . 1 2  1 22 2 m.vn 1 2 ie
So với điều kiện, ta có 2 giá trị của m là m  3  và m  3 . gh
Câu 59: (THPT Lê Lợi - Thanh Hóa - Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham số m để racn đồ thị hàm số 3 2
y  x  3mx  2 có 2 điể 
m cực trị A và B sao cho các điểm ,
A B và M 1; 2 it thẳng hàng. th n ye Ⓐ. m  2.
Ⓑ. m   2; m  2. Ⓒ. m  2.
Ⓓ. m   2. lu Lời giải s:// Chọn B ttp 2    h y 3x 6m . x x  0 2
y  0  3x  6mx  0  
1  x  2m
Đồ thị hàm số có 2 điểm cực trị  phương trình  
1 có hai nghiệm phân biệt  m  0 .
Khi đó, giả sử A0;2 B 3 , 2 ;
m 2  4m  . Cách 1:
Phương trình đường thẳng AM : 4x  y  2  0. m  0 (l)  Ba điểm , A ,
B M thẳng hàng  B  AM 3
 8m  4m  0  m  2 . /vietgold   m   2. k.com
Cách 2: Ta có AM     AB   3 1; 4 ; 2 ; m  4m  . ceboo 3  Ba điể 2m 4m m , A , B M thẳng hàng 3  
 m  2m  m  0  m   2 . .fa 1 4 
So với điều kiện m  0 ta được m   2 . m  2 Vậy  m   2.
https://www Câu 60: (THPT Lê Xoay - Vĩnh Phúc - Lần 1 – Năm 2019 - 2020) Tìm tất cả các giá trị thực của tham m số m để hàm số 3 2 y 
x  2x  mx 1 có 2 điểm cực trị thoả mãn x  x ? 3 CD CT Ⓐ. m  2.
Ⓑ. 0  m  2 . Ⓒ. 2   m  0 . Ⓓ. 2   m  2 . Lời giải Chọn B Ta có 2
y  mx  4x  m
Để hàm sỗ đã cho có 2 điểm cực trị thỏa mãn x  x thì CD CT 27
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 m  0 m  0 m  0     
 0  m  2 2 Δ  0 4  m  0    2   m  2 ,
Câu 61: (THTP Nam Đàn 2 - Nghệ An - năm 2019 - 2020) Cho hàm số 3 2
y  x  3x  mx  m  2 có đồ thị C
. Giá trị của tham số thực m để C
có điểm cực đại, cực tiểu nằm về hai phía trục m  m  hoành là Ⓐ. m  3 .
Ⓑ. 1 m  5.
Ⓒ. 2  m  3. Ⓓ. m  3 . h ttp Lời giải s:// Chọn A Cách 1: lu 2 ye Ta có: 3 2
y  x  3x  mx  m  2   x  
1  x  2x  m  2 n th 2
x  2x  m  2  0   1 2 it
y  0   x  
1  x  2x  m  2  0   r x  1  acn
Để đồ thị C có điểm cực đại, cực tiểu nằm về hai phía trục hoành m  gh ie
 y  0 có ba nghiệm phân biệt m.vn  phương trình  
1 có hai nghiệm phân biệt khác 1  '   0 m  3      m  3 1
  2  m  2  0 m  3
Vậy m  3 thì đồ thị C
có điểm cực đại, cực tiểu nằm về hai phía trục hoành. m  Cách 2: Ta có: ' 2
y  3x  6x  m ; ' y  0 2
 3x  6x  m  0 
Hàm số có cực đại, cực tiểu  phương trình  có hai nghiệm phân biệt ht '
   0  9 3m  0  m  3   1 tps://www x  x  2  1 2 
Gọi x , x là nghiệm của phương trình  . Theo định lý viet ta có  1 2 m x .x   1 2  3 .fa
Gọi y , y là giá trị cực trị tương ứng của hàm số. ceboo 1 2  1 1   2   2   2  Vì ' y  y . x  
m  2  x     
1 nên y  m2 x 1 ; y  m2 x 1 . 2   2  1   1  k.com  3 3   3   3   3 
Để đồ thị C có điểm cực đại, cực tiểu nằm về hai phía trục hoành  y . y  0 m  /v 1 2 iet  2   2  gold  m  2   x 1 . m  2 x 1  0 1    2   3   3  2  2   m  2 
  x  x  x .x 1  0 1 2 1 2   3  2  2   m  m  3  m  2 1  0        m  3 2  3   3  m  3 Từ  
1 và 2 suy ra m  3 thì đồ thị C
có điểm cực đại, cực tiểu nằm về hai phía trục hoành. m 
Câu 62: (THPT Triệu Sơn 4 - Thanh Hóa - Lần 3 - Năm - 2019 2020) Cho hàm số 3 2 2 3
y  x  3mx  3(m 1)x  m  m có đồ thị (C) và điểm I 1 
;1 . Biết rằng có hai giá trị của 28
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
tham số m ( kí hiệu m , m với m  m ) sao cho hai điểm cực trị của (C) cùng với I tạo ra một 1 2 1 2
tam giác có bán kính đường tròn ngoại tiếp bằng 5 . Tính P  m  5m . 1 2 5 5
Ⓐ. P  2 .
Ⓑ. P  .
Ⓒ. P   . Ⓓ. P  2  . 3 3 Lời giải Chọn A *TXĐ: D  . m.vn ie 2 2
y '  3x  6mx  3(m 1); gh * Ta có x  m 1 y '  0  .  x  m 1 racn it Giả sử hai điểm cực trị của (C) là A và B, khi đó: th
Am 1; 2m  2; B m 1; 2m  2 n
 AB  2 5  2R ( Với R là bán kính đường tròn ngoại ye
tiếp tam giác ABI). Vậy tam giác ABI vuông tại I. lu
Am 1;  2m  2; B m 1;  2m  2  AB  2 5  2R, s:// Ta có IA   ; m 2
 m  3, IB  m  2; 2  m   1 ; ttp h m  1  2  I .
A IB  0  5m  2m  3  0  3 . m   5 3
Theo giả thiết ta có m  1,
 m   P  2. 1 2 5
Câu 63: (THPT Hoàng Văn Thụ - Nam Định - Lần 2 - Năm 2019 - 2020) Cho hàm số 3 2 2 3
y  x  3mx  3m  
1 x  m  m , ( m là tham số). Gọi , A B là hai điể
m cực trị của đồ thị hàm số và I 2; 2
  . Tổng tất cả các số m để ba điểm I, ,
A B tạo thành tam giác nội tiếp đường tròn /vietgold có bán kính bằng 5 là 4 2 14 k.com Ⓐ. . Ⓑ.  20 . Ⓒ. . Ⓓ. . 17 17 17 17 ceboo Lời giải .fa Chọn C
Tập xác định: D  . x  m 1 Ta có 2
y  x  mx   2 3 6 3 m   1 ; 2 2
y  0  x  2mx  m 1  0   x  m 1 https://www
 Đồ thị hàm số đã cho có hai điểm cực trị là Am 1; 4m  2 và Bm 1; 4m  2
 AB  2; 4, IA  m 3;4m  4, IB  m 1;4m m 1 4  m +) I , ,
A B là ba đỉnh của một tam giác    m  1 . 2 4 
+) Nhận thấy AB  2 5  2R  IAB là tam giác vuông tại I  I . A IB  0  m   3 m   1  4m 4  m  4  0 2
17m  20m 3  0 *
Phương trình * luôn có 2 nghiệm phân biệt, khác 1. 29
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 20
Theo Vi – et, ta có tổng hai nghiệm bằng . 17
Câu 64: (THPT Quảng Xương 1 - Thanh Hoá - Năm học 2019 - 2020) Cho hàm số f  x 3
 x  m   2 2
1 x  3mx  m có đồ thị C
. Có bao nhiêu giá trị nguyên của tham số m m  thuộc  2
 020;2020 để đồ thị C có hai điểm cực trị nằm khác phía so với trục hoành. m  Ⓐ. 4037 . Ⓑ. 4038 . Ⓒ. 4039 . Ⓓ. 4040 . h Lời giải ttp Chọn B s://
 Đồ thị C có hai điểm cực trị nằm khác phía so với trục hoành khi C cắt trục hoành tại m  m  lu ye
ba điểm phân biệt, điều này xảy ra khi phương trình hoành độ giao điểm của C và trục hoành m  n th có ba nghiệm phân biệt. it
 Xét phương trình hoành độ giao điểm của C và trục hoành: m  rac 3
x   m   2 2
1 x  3mx  m  0 n gh 3 2
 x  x  m 2
2x  3x   1  0 ie m.vn  x   2
1 x  2mx  m  0 x 1   2
x  2mx  m  0    *
 Để yêu cầu bài toán xảy ra thì phương trình (*) phải có hai nghiệm phân biệt khác 1 2
'  m  m  0 m ;  01;     2 1   2 . m 1 m  0 m 1  m ;  01; . ht m  tp  Do   m 2  019; 2  018; ; 1  ;2;3; ;2020 . s://www m   2  020;2020  
 Ta đếm được 4038 giá trị m thỏa mãn.
Câu 65: (HSG - Thái Bình - Năm 2019 - 2020) Tìm tất cả các giá trị của tham số m để đồ thị của hàm .fa 3 2 2 ceboo số y x 3mx
3m có hai điểm cực trị cùng với gốc tọa độ tạo thành một tam giác có diện
tích bằng 192 (đvdt). k.com Ⓐ. m 4 . Ⓑ. m 3 . Ⓒ. m 1. Ⓓ. m 2 . /v Lời giải ietgold Chọn A x 0 3 2 2 2 Hàm số y x 3mx 3m có T Đ X : D . Ta có y 3x 6mx ; y 0 . x 2m
Để đồ thị hàm số có hai điểm cực trị thì m
0 . Khi đó hai điểm cực trị của đồ thị hàm số là 2 A 0;3m , 3 2 B 2 ; m 4m 3m . 1 1
Tam giác OAB có A 0y nên 2 S
.d B;Oy .OA 2m . 3m OAB 2 2 1
Theo yêu cầu bài toán, ta có: 2 S 2m . 3m 192 3 m 64 m 4 m 4 OAB . 2 30
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Câu 66: (Chuyên Bắc Giang - Lần 01 - Năm 2018-2019) Tập hợp các giá trị của m để hàm số 1 3 2 y 
x  mx  m  2 x 1 có hai cực trị là: 3 Ⓐ.  ;   
1 2; Ⓑ.  ;   
1  2; Ⓒ.  1  ;2 Ⓓ.  1  ;2 Lời giải Chọn B m.vn Ta có 2
y  x  2mx  m  2 . Để hàm số có hai cực trị thì y  0 có hai nghiệm phân biệt nên ie m  1  gh 2
y  0    0  m  m  2  0   m  2 racn it
Câu 67: (GK1 - K12 - THPT Nghĩa Hưng - Nam Định - Năm 2018 -2019) Giá trị của tham số m để th n hàm số 3 2
y  x  3x  mx 1 có hai cực trị x , x thỏa mãn 2 2
x  x  6 là 1 2 1 2 ye lu Ⓐ. 1. Ⓑ. 1  . Ⓒ. 3 . Ⓓ. 3  . s:// Lời giải ttp Chọn D h Ta có: 2
y '  3x  6x  m  0   1 .
Để hàm số có hai cực trị x , x thì phương trình  
1 có hai nghiệm phân biệt, 1 2
Khi đó: '  9 3m  0  m  3 * .
Mà theo yêu cầu bài toán x , x thỏa mãn: x  x  6  x  x
 2x x  6 2 . 1 2  1 22 2 2 1 2 1 2 x  x  2 1 2  m
Mặt khác theo Viet ta có: 
m , thay vào 2 ta được: 4  2.  6  m  3  , thỏa mãn x x   3 1 2  3 /vietgold điều kiện * . Vậy m  3  .
k.com Câu 68: (THPT Ba Đình - Hà Nội - Lần 2 - Năm 2018-2019) Tìm tất cả các giá trị của tham số mđể ceboo hàm số 3 2
y  x  3x  2mx  m có cực đại và cực tiểu? .fa 3 3 3 3
Ⓐ. m  .
Ⓑ. m   .
Ⓒ. m   . Ⓓ. m  . 2 2 2 2 Lời giải Chọn A https://www + TXĐ: D  + 2
y  3x  6x  2m
+ Hàm số có cực đại và cực tiểu  y  0 có 2 nghiệm phân biệt. 3
   36  24m  0  m  . 2
Câu 69: (THPT Hùng Vương-Bình Phước-Lần 01-Năm 2018-2019) Tìm tất cả các giá trị của tham số 3 x m để hàm số 2 y  
 mx  2mx 1 có hai điểm cực trị. 3 31
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 m  2
Ⓐ. 0  m  2. Ⓑ. m  2. Ⓒ. m  0 . Ⓓ.  . m  0 Lời giải Chọn D Ta có: 2
y  x  2mx  2m 3 x Hàm số 2 y  
 mx  2mx 1 có hai điểm cực trị  y  0 có hai nghiệm phân biệt 3 h m  2 ttp 2
   m  2m  0   . m  0 s:// lu Câu 70: (THPT Yên Khánh - Ninh Bình -
Năm 2018-2019) Cho hàm số ye 3
y  x  m   2 3
1 x  37m  3 x . Gọi S là tập các giá trị nguyên của tham số m để hàm số n th
không có cực trị. Số phần tử của S là it rac Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 0 . Ⓓ. Vô số. n gh Lời giải ie Chọn B m.vn Ta có: 2
y  3x  6m  
1 x  37m  3 . 2
y  0  x  2m  
1 x  7m  3  0 .
Để hàm số không có cực trị thì 
   m 2 0
1  7m  3  0 2
 m 5m  4  0 1 m  4. Do m   S  1;2;3; 
4 . Vậy S có 4 phần tử. http 1 3 2 s://www
Câu 71: (SGD Bà Rịa Vũng Tàu - Năm 2018-2019) Cho hàm số y  
x  mx  4 4m x 1 3 . Mệnh
đề nào sau đây sai? .fa Ⓐ. m
  2 thì hàm số có hai điểm cực trị. Ⓑ. m
  thì hàm số có cực đại và cực tiểu. ceboo Ⓒ. m
  2 thì hàm số có cực trị. Ⓓ. m
  2 thì hàm số có cực đại và cực tiểu. k.com Lời giải /v Chọn B iet Ta có 2
y  x  2mx  4 4m . 
  m  m   m  2 2 4 4 2  0 . gold +) Với m   2 thì 
  0 nên hàm số đã cho sẽ có 2 cực trị (trong đó có 1 cực đại và một cực tiểu).
+) Với m  2 thì 
  0 do đó y  0 với x
  nên hàm số đã cho không có cực trị.
Vậy B là phương án sai.
Câu 72: (THPT Lê Quý Đôn – Điệ n Biên - Lầ n 01- Nă m 2018-2019 ) Cho hàm số 1 3 y 
mx  m   2
1 x  3m  2 x  2018 vớ i m là tham số . Tổ ng bình phư ơ ng tấ t cả 3
các giá trị củ a m để hàm số có hai điể m cự c trị x ; x thỏ a mãn x  2x  1 bằ ng 1 2 1 2 32
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” Ⓐ. 40 Ⓑ. 22 Ⓒ. 25 Ⓓ. 8 9 9 4 3 Lời giải Chọn A Ta có 2 y '  x m  2m  
1 x  3m  2
Để hàm số có hai điểm cực trị thì phương trình 2 x m  2m  
1 x  3m  2  0 phải có hai nghiệm phân biệt. m.vn ie m  0  m  0     gh    m  2 1
 3mm  2 2  0  2
 m  4m 1  0 racn  2 m   1 it x .  x  1 2  th  m n
Theo định lý Vi-ét ta có 3  m  2 ye x .x  1 2  m lu  3m  4 s://  2m   1 x   1 x .  x   m ttp 1 2  m   h
Theo bài ta có hệ phương trình 2m   1 2 x     m 2x  1  x  1   1 2 2  m m m  t m 3m  4 2  m 3m  2 2 /    . 
 32  mm  3m  42  m  0  2  m m m m  t / m  3 40 Vậy 2 2 m  m  . 1 2 9
Câu 73: (THPT Lê Quý Đôn – Điện Biên - Lần 01- Năm 2018-2019 ) Cho hàm số /vietgold 3 2 y 2x 3 m 1 x
6 m 2 x 1 với m là tham số thựⒸ. Tìm tất cả các giá trị của m để
hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng 2; 3 . k.com ceboo Ⓐ. m 1; 3 3; 4 . Ⓑ. m 1; 3 . Ⓒ. m 3;4 . Ⓓ. m 1; 4 . .fa Lời giải Chọn A Ta có: 2 y' 6x 6 m 1 x 6 m 2
Để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng 2; 3 pt y' 0 có 2 nghiệm https://www thuộc khoảng 2; 3 2 x m 1 x m 2
0 có 2 nghiệm thuộc khoảng 2; 3 x 1 x m 2 0 x 1 2; 3 x 2 m 2 m 1 m 3 YCBT 2 2 m 3 1 m 4 33
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
Câu 74: (ĐTD - Đề số 8 - Năm 2018 - 2019) Tìm các giá trị của m sao cho đồ thị hàm số 1 3 2 y 
x  mx  6m  9 x 12 có các điểm cực đại và cực tiểu nằm cùng một phía đối với trục 3 tung.  3 3 m   3 Ⓐ. m  2  . Ⓑ. 3   m   . Ⓒ.  2 .
Ⓓ. m   . 2  2 m  3 h Lời giải ttp Chọn C s://
Tập xác định: D  . lu Đạo hàm: 2 
y  x  2mx  6m  9 . ye n
Đồ thị hàm số có các điểm cực đại và cực tiểu nằm cùng một phía đối với trục tung khi phương th trình 
y  0 có 2 nghiệm phân biệt cùng dấu. it r m  3  a 2  
  m  m   c 6 9 0  n ĐK:    3  . gh P  6  m  9  0 m   2 ie m.vn
Câu 75: (GK1-K12-THPT Lương Thế Vinh-Hà Nội-2018-2019) Tìm tất cả cả các giá trị của tham số m để 3 2
y  x  3x  mx 1 đạt cực trị tại x , x thỏa mãn 2 2
x  x  6 1 2 1 2 Ⓐ. m  3  Ⓑ. m  3 Ⓒ. m  1  Ⓓ. m 1 Lời giải Chọn A 2
y '  3x  6x  m . Hàm số đạt cực trị tại x , x .Vậy x , x là nghiệm của phương trình y '  0 1 2 1 2 x  x  2 1 2 ht  tp Theo viet ta có  m s://www x .x   1 2  3 2 2 2
x  x  (x  x )  2x x 1 2 1 2 1 2 .fa 2  m 4  m 2  4   6  m  3  ceboo 3 3 k.com
Câu 76: (GK1 - K12 - Lương Thế Vinh - Hà Nội - Năm 2018 - 2019) Tìm tất cả giá trị của tham số m để hàm số 3 2
y  x  3x  mx 1đạt cực trị tai x , x thỏa mãn 2 2 x  x  6. 1 2 1 2 /viet Ⓐ. m  3  . Ⓑ. m  3 .
Ⓒ. m 1. Ⓓ. m  1  . gold Hướng dẫn giải Chọn A 3 2
y  x  3x  mx 1 TXĐ: 2
y '  3x  6x  . m
Hàm số đạt cực trị tại x , x  phương trình y’=0 có hai nghiệm phân biệt x , x 1 2 1 2
  '  9  3m  0  m  3 34
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” x  x  2 1 2 
Khi đó có: x  x   x  x 2 m 2 2
 2x x  4  2 vì  1 2 1 2 1 2 m 3 x .x   1 2  3 Theo đề m bài có: 4  2  6  m  3  3
Câu 77: (GK1 - K12 - Lương Thế Vinh - Hà Nội - Năm 2018 - 2019) Tìm tất cả giá trị của tham số m m.vn để hàm số 3 2
y  x  3x  mx 1đạt cực trị tai x , x thỏa mãn 2 2 x  x  6. 1 2 1 2 ie gh Ⓐ. m  3  . Ⓑ. m  3 .
Ⓒ. m 1. Ⓓ. m  1  . racn Hướng dẫn giải it th Chọn A n ye 3 2
y  x  3x  mx 1 TXĐ: lu 2
y '  3x  6x  . m s:// ttp
Hàm số đạt cực trị tại x , x  phương trình y’=0 có hai nghiệm phân biệt x , x h 1 2 1 2
  '  9  3m  0  m  3 x  x  2 1 2 
Khi đó có: x  x   x  x 2 m 2 2
 2x x  4  2 vì  1 2 1 2 1 2 m 3 x .x   1 2  3 Theo đề m bài có: 4  2  6  m  3  3
/vietgold Câu 78: (THCS -THPT Nguyễn Khuyến - Lần 1 - Năm 2018-2019) Giá trị lớn nhất của m để hàm số 3 2
y  mx  3mx  m  
1 x 1 không đạt cực trị là k.com 1 1 ceboo Ⓐ. . Ⓑ. 0 . Ⓒ. . Ⓓ. 1. 4 2 .fa Lời giải Chọn A
TXĐ: D  R Ta có: 2
y  3mx  6mx  m   1 . https://www Với 3 2
m  0 thì y '  1  0  hàm số y  mx  3mx  m  
1 x 1 đồng biến trên R  m  0 thì
hàm số đã cho không đạt cực trị. Với 3 2
m  0 , hàm số y  mx  3mx  m  
1 x 1 không đạt cực trị  y  0 vô nghiệm hoặc m  0 m  0  m  0  1 có nghiệm kép       1  0  m  . 2  '  9m  3  m m   2 1  0 1
 2m  3m  0 0  m  4  4  1 Hàm số 3 2
y  mx  3mx  m  
1 x 1 không đạt cực trị khi 0  m  . 4 35
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 1
Vậy giá trị lớn nhất của m thỏa mãn yêu cầu bài toán là m  . 4
Câu 79: (THPT YÊN LẠC NĂM 2018-2019) Cho hàm số 3 2
y  x  3x  mx 1 với m là tham số thự
Ⓒ. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x , x thỏa 1 2 2 2 x  x  6 . 1 2 Ⓐ. 3 . Ⓑ. 1  . Ⓒ. 1. Ⓓ. 3  . h ttp Lời giải s:// Chọn D lu Ta có: 2
y  3x  6x  m có    9 3m. ye Để x x n
hàm số đạt cực trị tại hai điểm ,
thì phương trình y  0 có 2 nghiệm phân biệt, nghĩa 1 2 th
S  x  x  2 it 3   0 1 2  r       a là: 9 3m 0 m
3 . Khi đó theo định lý Vi-et ta có:  m . c    0 P  x x  n  1 2  3 gh m ie Ta có: 2 2 2
x  x  6  S  2P  6  4  2.  6  0  m  3  (nhận). 1 2 m.vn 3
Câu 80: (THPT Đoàn Thượng - Hải Dương - Năm 2018 - 2019) Tìm tất cả các giá trị của m để hàm số 1 3 2 y 
x  mx  (m  2)x có cực trị và các điểm cực đại, điểm cực tiểu nhận giá trị dương. 3
Ⓐ. m  2. Ⓑ. m  2 .
Ⓒ. 0  m  2 . Ⓓ. m  2 . Lời giải Chọn B  Ta có 2
y  x  2mx  (m  2) . http
Hàm số đã cho có các điểm cực đại và cực tiểu dương khi và chỉ khi phương trình y  0 s://www
có hai nghiệm phân biệt dương 2   0
m  m  2  0   .fa
 x  x  0  2m  0  m  2 . 1 2 ceboo   x .x  0 m  2  0   1 2 k.com
Câu 81: (THPT chuyên Bắc Ninh - L01 - 2018-2019) Gọi S là tập các giá trị dương của tham số m sao cho hàm số 3 2
y  x  3mx  27x  3m  2 đạt cực trị tại x , x thỏa mãn x  x  5 . Biết 1 2 1 2 /viet S   ;
a b . Tính T  2b  a . gold
Ⓐ. T  51  6
Ⓑ. T  61  3
Ⓒ. T  61 3
Ⓓ. T  51  6 Lời giải Chọn C +) Ta có  2
y  3x  6mx  27 ,  2
y  0  x  2mx  9  0 (1)
+) Theo giả thiết hàm số đạt cực trị tại x , x  phương trình (1) có 2 nghiệm phân biệt 1 2       m 3 0 2
 m  9  0   (*) m  3  36
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
x  x  2m
+) Với điều kiện (*) thì phương trình (1) có 2 nghiệm x , x , theo Vi-ét ta có: 1 2  1 2 x x  9  1 2 2 2
+) Ta lại có x  x  5   x  x
 25  x  x  4x x  25  0 1 2   1 2 1 2 1 2 61 61 2
 4m  61 0    m  (**) 2 2 61 +) Kết hợp (*), (**) và điều kiện m dương ta được: 3  m  m.vn 2 ie a  3 gh   
 T  2b  a  61  3 61 . b   racn  2 it th
Câu 82: (THPT chuyên Lam Sơn - Thanh Hóa - L01 - 2018-2019) Có tất cả bao nhiêu giá trị nguyên n ye của , m m  2
 019 để phương trình 3 2 3
x  3mx  4m 1  0 có ba nghiệm phân biệt? lu s:// Ⓐ. 2020 Ⓑ. 2021 Ⓒ. 2030 Ⓓ. 2019 ttp Lời giải h Chọn D Để phương trình 3 2 3
x  3mx  4m 1  0 có ba nghiệm phân biệt khi và chỉ khi hàm số 3 2 3 y  x  3 x m
 4m 1 cắt Ox tại ba điểm phân biệt  y .y  0 CD CT x  0 2 y '  3x  6 x
m  y '  0   x  2m 1 y 0 3
 4m 1; y 2m 3
1 y .y  0  4m 1 0  m   CD CT 3 4 Vậy có: 1   2
 019 1 2019 giá trị nguyên của m thỏa mãn điều kiện đề bài
/vietgold Câu 83: (THPT chuyên Lam Sơn - Thanh Hóa - L01 - 2018-2019) Tổng tất cả các giá trị thực của tham k.com số m để hàm số: 3
y  x  m   2 3 2
1 x  3mx  m  5 có hai điểm cực trị x ; x đồng thời 1 2
y  x .y x  0 là: 1   2 ceboo .fa Ⓐ. 21  Ⓑ. 39  Ⓒ. 8  Ⓓ. 3 11 13 Lời giải Chọn A
+) Để hàm số có hai cực trị thì phương trình y  0 phải có hai nghiệm phân biệt: https://www 2
y  9x  4m  
1 x  3m có hai nghiệm phân biệt     m  2 4 1  27m  0
+) Xét y  x .y x  0 nên ta có 3
y  x  m   2 3 2
1 x  3mx  m  5 phải tiếp xúc với trục hoành 1   2 3
 x  m  2 3 2
1 x  3mx  m  5  0 phải có nghiệm kép  x   2 1 3
 x  2m5 x  m5  0  1   phải có nghiệm kép +) TH1: Phương trình 2
3x  2m  5 x  m  5  0 có một nghiệm x 1 m  1  3 1 +) TH2: Phương trình 2
3x  2m  5 x  m  5  0 có nghiệm kép khác 1
   2m 52 125 m 2
 0  4m  32m 35  0  m  m  8  2 3 37
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
 m  m  m  21  1 2 3
Câu 84: (Chuyên Thái Bình - Lần 01 - Năm 2018 - 2019) Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2
y  x  x   2 m   2 8
11 x  2m  2 có hai điểm cực trị nằm về hai phía của trục Ox . Ⓐ. 4. Ⓑ. 5. Ⓒ. 6. Ⓓ. 7. Lời giải h ttp Chọn D
Yêu cầu bài toán  đồ thị hàm số cắt trục hoành tại ba điểm phân biệt s:// 3 2 2 2 lu
 x 8x  m 1 
1 x  2m  2  0 có ba nghiệm phân biệt ye 3 2
x  x   2 m   2 8
11 x  2m  2  0   x   2 2 2
x  6x  m   1  0 n th x  2 it  r  2 2 a
x  6x  m 1  0(*) cngh
Suy ra phương trình (*) có hai nghiệm phân biệt khác 2 ie 2
' 10  m  0 m  2  2 m.vn     2 m 8  0
 10  m  10
Vậy có 7 giá trị nguyên của tham số thỏa mãn đề bài.
Câu 85: (Vted-Đề số 1-Năm học 2018-2019) Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3
y  x   m   2 x   2 m   2 1
2 x  m  3 có hai điểm cực trị và hai điểm cực trị đó nằm về
cùng một phía đối với trục hoành? Ⓐ. 4 . Ⓑ. 1. Ⓒ. 3 . Ⓓ. 2 . Lời giải http Chọn D s://www Ta có 2
y  x   m   2 ' 3 2 1 x  m  2
Điều kiện để hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành là 2 2 2            .fa ' 0
 m 1 3 m 2 0 2m 2m 7 0       ceboo  P  0 3   2 m  2   0 m    ;
  2    2;    1  15 1  15  k.com m  ;     1  15   1  15   2 2     m  ; 2  ; 2     2 2      /v m    ;   2    2;   ietgold
Vì m nguyên nê chỉ có giá trị m  2 là thỏa mãn yêu cầu.
Câu 86: (ĐỀ 02 VTED NĂM HỌC 2018 - 2019) Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3
y  x  m   2 x   2 m   2 1
2 x  m  3 có hai điểm cực trị và hai điểm cực trị đó nằm về
cùng một phía đối với trục hoành. Ⓐ. 4 . Ⓑ. 1. Ⓒ. 3 . Ⓓ. 2 Lời giải Ta có 2
y  x  m   2 ' 3 2 1 x  m  2
Hàm số có hai cực trị khi và chỉ khi phương trình y '  0 có hai nghiệm phân biệt 38
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
 m  2   2 m   2 1 3 2  0  2
 m  2m  7  0 1 15 1 15   m  2 2 Do m   m   1  ;0;1;  2 Phương trình đường thẳng qua hai điểm cực trị là 1 y '   1 2
4m  4m 14 x   3 2
m  8m  2m  25 9 9 m.vn ie
Hai điểm cực trị nằm về cùng phía đối với trục hoành khi và chỉ khi y .y  0 CD CT gh
Bằng cách thử đáp án ta nhận ba giá trị của m . racn
Câu 87: (Vted - Đề số 04 - Năm 2018 - 2019) Biết đồ thị hàm số 3 2
y  x  ax  bx  c có hai điểm cưc it th
trị M  x ; y , N x ; y thỏa mãn x y  y  y x  x . Giá trị nhỏ nhất của biểu thức 1  1 2  1  1 2  1 1   2 2 n    ye P
abc 2ab 3c bằng lu 49 25 841 7 Ⓐ.  Ⓑ.  Ⓒ.  Ⓓ.  s:// 4 4 36 6 ttp h Lời giải Chọn A Ta có 2
y  3x  2ax  b 2  1 1   a 2b  ab
Chia y cho y ta được y  y x  a        x  c  .  3 9  9 3 9  
Do M  x ; y , N x ; y là hai điểm cực trị nên y x  0, y x  0 1   2 1 1   2 2 2 2     Do đó a 2b ab a 2b ab y      x  c  ; y      x  c  1 1 2 2 9 3 9 9 3 9     /vietgold
Theo giả thiết x y  y
 y x  x  x y  x y 1  1 2  1  1 2  1 2 2 1 2 2  a 2b  ab   a 2b  ab  k.com
 x    x  c    x    x  c   1 2 2 1 9 3 9 9 3 9       ceboo  ab   ab  ab           .fa x c x c c 0(x x ) ab 9c 1   2   1 2  9   9  9 2  7  49 49 Ta có: 2
P  abc  2ab  3c  9c  21c  3c        2  4 4    49  https://www
Vậy giá trị nhỏ nhất của biểu thức P
abc 2ab 3c bằng 4 3
Câu 88: (ĐTD - Đề Số 20 - Năm 2018 - 2019) Cho hàm số y   x  m 2
3x  m C . Biết rằng điểm m  M  ;
a b là điểm cực đại của C
ứng với một giá trị m thích hợp đồng thời là điểm cực tiểu m  của C
ứng với một giá trị khác của m . Tính tổng S  2018a  2020b m  Ⓐ. 5004. Ⓑ. 504  . Ⓒ. 504. Ⓓ. 12504. Lời giải Chọn C 39
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 x  m 
Ta có: y   x  m2 1 ' 3  3  0   2
 a  m 1;b  m 3m  2 x  m 1 1 1 1
Gọi m là giá trị đó mà M  ;
a b đạt cực tiểu nên ta có 2
a  m 1;b  m  3m  2 2 2 2 2  1 m           1 m m 2 m m 1  1 2 2 Nên ta có hệ 1 2      2 2
m  m  3m  3m  4  0 m  m  2  3   1 2 1 2 1 2 m  2  2 h 1 1 ttp
Vậy a   ;b  
 S 1009505  504 . 2 4 s:// a lu
Câu 89: (ĐTD - Đề số 8 - Năm 2018 - 2019) Tìm tất cả các giá trị thực của tham số sao cho hàm số ye 1 1 3 2 y  x 
x  ax 1 đạt cực trị tại x , x thỏa mãn: 2 2
(x  x  2a)(x  x  2a)  9 . 1 2 1 2 2 1 n 3 2 th it    r Ⓐ. a  2. Ⓑ. a  4. Ⓒ. a  3. Ⓓ. a  1. acn Lời giải gh Chọn B ie m.vn  1 4a  Ta có 2 2 2 3 3
y  x  x  a  0  S  1
 x  x 1 2 ;
a x  x  1 3a . 1 2 1 2 P  a  Để thỏa yêu cầu bài toán ta phải có   0   2 4a    2 2
2x  2x  2x  2x  2 2 3 3
a  x x  x  x  x x  9  0 1 2 1 2 1 2 1 2 1 2  1 1   4a  0  a      4  a  4.  2 2          4a  
2 4a 2a a 1 3a a 9 0  ht
a  2  a  4  tps://www
Câu 90: (VDC - Đề Số 12 - Năm 2018 - 2019) Tìm các giá trị của tham số m để đồ thị hàm số 3 2
y  2x  3(2m 1)x  6 (
m m 1)x 1 có hai điểm cực trị cách đều trục tung. 1 .fa
Ⓐ. Không tồn tại giá trị nào.
Ⓑ. m   . ceboo 2 1 Ⓒ. m  2.
Ⓓ. m  2;m   . k.com 2 Lời giải /v Chọn B ietgold
Kí hiệu A x ; y , A x ; y
là hai điểm cực trị của đồ thị hàm số. Để A , A cách đều trục tung 1  1 1  2  2 2  1 2
điêu cận cần và đủ là x  x  0 . Cần tìm m để y có hai nghiệm phân biệt có tổng bằng 0 . 1 2
Câu 91: (Đề VDC -Đề số 16 - Năm 2018 - 2019) Tìm tất cả m sao cho điểm cực tiểu của đồ thị hàm số 3 2
y  x  x  mx 1nằm bên phải trục tung. 1 1
Ⓐ. Không tồn tại m .
Ⓑ. 0  m  .
Ⓒ. m  . Ⓓ. m  0 . 3 3 Lời giải Chọn D 40
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Để hàm số có cực tiểu, tức hàm số có hai cực trị thì phương trình y  0 có hai nghiệm phân biệt 1 2
3x  2x  m  0 (1) có hai nghiệm phân biệt 
 1 3m  0  m  . 3
Khi đó (1) có hai nghiệm phân biệt x , x là hoành độ hai điểm cực trị. Theo định lí Viet ta CĐ CT  2 x  x    0 (2)  CĐ CT  3 có 
, trong đó x  x vì hệ số của 3 x lớn hơn 0. m CĐ CT x .x  (3) m.vn CĐ CT  3 ie
Để cực tiểu của đồ thị hàm số nằm bên phải trục tung thì phải có: x  0 , kết hợp (2) và (3) gh CT m
suy ra (1) có hai nghiệm trái dấu  x .x   0  m  0. racn CĐ CT 3 it th
Câu 92: (ĐTD - Đề 24 - Năm 2018 - 2019) Cho hàm số 3
y  x   m   2 2
1 x  1 m x . Tập hợp tất cả n ye
các giá trị của tham số m sao cho đồ thị của hàm số đã cho có 2 điểm cực trị, đồng thời hoành lu
độ điểm cực đại không nhỏ hơn 1  là s://  1    1   Ⓐ.  ;      2 . Ⓑ.  ;  2;   .  ttp  4   4  h  1    1   Ⓒ. ;  . Ⓓ.  ;       2 .    4   4  Lời giải Chọn C
Tập xác định D  . Ta có 2
y  3x  22m  
1 x 1 m . Vậy 2
y  0  3x  22m      1 x 1 m 0 (*)
Đồ thị của hàm số đã cho có 2 điểm cực trị  (*) có 2 nghiệm phân biệt  1   /vietgold     m 0 2  
4m  7m  2  0  4 (1)  m  2 k.com
Gọi x , x là 2 nghiệm của (*), sao cho x  x . Ta có bảng biến thiên 1 2 1 2 ceboo .fa https://www
Vậy x là điểm cực đại của hàm số đã cho. 1 Đặt VT  
*  f  x . Yêu cầu bài toán tương đương hai nghiệm phân biệt x , x của phương trình 1 2 * phải thỏa 1
  x  x , nghĩa là 1 2  f   1  0  m  2     m  2 (2) b 2  m 1  1     m  2  2a 3 1 
Từ (1) và (2) suy ra m  . 4 41
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Câu 93: (ĐTD - ĐỀ 02 - NĂM 2018-2019) Biết rằng đồ thị hàm số y   2 a   3 x   3 b   2 2 3 1
1 x  3c x  4d có hai điểm cực trị là 1; 7   , 2; 8
  . Hãy xác định tổng 2 2 2 2
M  a  b  c  d Ⓐ. 18. Ⓑ. 8 . Ⓒ. 15. Ⓓ. 18  . Lời giải Chọn A 2 2 3 2 h
Đao hàm: y  33a  
1 x  2b   1 x  3c . ttp 2 3 2  s:// y  1  33a   1  2 b   1  3c  0  lu y2 12   2 3a   1  4  3 b   2 1  3c  0 ye
Theo giả thiết ta có hệ:  . 2 3 2 n y   1  3a   1  b  
1  3c  4d  7  th  2 3 2 it y 2  8 
3a  14b  16c 4d  8  rac 2 n 3
 x  2y  z  0 x  3a 1 gh   1
 2x  4y  z  0 3  y  b 1 ie Xét hệ phương trình  với  . 2 m.vn
x  y  z  t  7   z  3c 8
 x  4y  2z t  8  t  4d 2 x  2 a 1   2 y  9 b   4
Giải hệ phương trình trên ta tìm được 2 2 2 2   
 a  b  c  d  18 . 2 z  12  c  4     2 t 12 d  9
Câu 94: (ĐTD - ĐỀ 02 - NĂM 2018-2019) Cho hàm số 3
y  x  3mx 1 (1). Cho A2; 3 , tìm m để ht
đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A tps://www 1  3  1 3 Ⓐ. m  . Ⓑ. m  . Ⓒ. m  . Ⓓ. m  . 2 2 2 2 Lời giải .fa Chọn C ceboo Ta có 2
y  3x  3m . Hàm số có hai điểm cực trị khi và chỉ khi m  0 . k.com x  m y  0   .
x   m /viet
Đồ thị hàm số có hai điểm cực trị B m; 2  m m  
1 , C  m;2m m   1 . Suy ra gold   BC
 2 m;4m m.
Gọi M là trung điểm của BC thì M (0;1) , nên AM  ( 2  ; 2  ) .
Vậy tam giác ABC là tam giác cân khi và chỉ khi.
Câu 95: AM  BC  AM BC 
   m   m m 1 . 0 ( 2). 2 ( 2). 4
 0  m  .(ĐTD - ĐỀ TUẦN 1 2
- NĂM 2018-2019) Với giá trị thực dương của tham số m để đồ thị hàm số 3 2
y  x  3mx  3x 1
có các điểm cực trị A và B sao cho tam giác O
 AB có diện tích bằng 8 2 thì mệnh đề nào sau đây là đúng? 42
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” 7
Ⓐ. 1 m  2
Ⓑ. 2  m 
Ⓒ. 3  m  4 Ⓓ. m 1 2 Lời giải Chọn B
Đường thẳng qua hai điểm cực trị y   2
2  2m  x  m 1  px  q
Điều kiện có hai điểm cực trị là 2
m  1. Gọi hai điểm cực trị của đồ thị hàm số là A x ; px  q 1 1  1 1 m.vn
và B  x ; px  q  S
 . x px  q  x px  q  S
 . q . x  x O  AB 1  2  2  1  2 2  O  AB 1 2 ie 2 2 gh 1  1 S
 . m 1 . x  x  x x 2  S
 . m 1 . 4m  4 O  AB  2 4 1 2 1 2  2 OAB 2 racn it 2  S
 m 1 . m 1  8 2   2
m  m   2 2 1 m   1  128 O  AB th n  m   3 2
3 m  5m 15m  43  0  m  3. Chọn B ye lu
Câu 96: (TT học mãi - Thầy Lê Anh Tuấn - Năm 2018 - 2019) Có bao nhiêu giá trị nguyên của tham s:// số m để điểm 3 M (2m ; )
m tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số ttp 3 2       h y 2x 3(2m 1)x 6 (
m m 1)x 1 (C) một tam giác có diện tích nhỏ nhất? Ⓐ. 0 Ⓑ. 1 Ⓒ. 2
Ⓓ. không tồn tại Lời giải Chọn B Ta có 2
y '  6x  6(2m 1)x  6 ( m m 1) x  m y '  0   m   R  , hàm số luôn có CĐ, CT x  m 1
Tọa độ các điểm CĐ, CT của đồ thị là 3 2 3 2 ( A ;
m 2m  3m 1), (
B m 1;2m  3m ) /vietgold
Suy ra AB  2 và phương trình đường thẳng 3 2
AB : x  y  2m  3m  m 1  0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất k.com 2 3m 1 1
Ta có d (M , AB)  
, dấu "=" khi m  0 ceboo 2 2
.fa Câu 97: (Chuyên Thái Bình- Lần 03- Năm 2018- 2019) Gọi x ,x là hai điểm cực trị của hàm số 1 2 1 1 3 2 y  x 
mx  4x 10 . Tìm giá trị lớn nhất của biểu thức S   2 x   1  2 x 1 . 1 2  3 2 https://www Ⓐ. 9 . Ⓑ. 4 . Ⓒ. 0 . Ⓓ. 8 . Lời giải Chọn A 1 1 Ta có: 3 2 2 y  x 
mx  4x 10  y '  x  mx  4 . 3 2 2
y '  0  x  mx  4  0 . 2
  m 16  0, m
 nên phương trình y '  0 luôn có hai nghiệm phân biệt x , x . 1 2 43
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021  b x  x   m 1 2  a
Áp dụng định lí viet:  . c
 x .x   4  1 2  a 2 2 2 2
S  (x 1)(x 1)  (x x )  [(x  x )  2x .x ] 1 2 2
 16  (m  8) 1  9  m  9 . 1 2 1 2 1 2 1 2
Câu 98: (THPT Sơn Tây - Hà Nội - Lần 01- Năm 2018-2019 ) Ta xác định được các số a, , b c để đồ thị hàm số 3 2
y  x  ax  bx  c đi qua điểm 0 
;1 và có điểm cực trị  2
 ;0 . Tính giá trị của biểu http
thức T  4a  b  c . s:// Ⓐ. 20 . Ⓑ. 23. Ⓒ. 24 . Ⓓ. 22 . lu ye Lời giải n Chọn B th it TXĐ: r 3 2 a
y  x  ax  bx  c ; 2
y  3x  2ax  b . cngh
Đồ thị hàm số qua điểm 0  ;1 nên c  1 ie 2
a  3b  0 2    m.vn a 3b 0    17 a 
Đồ thị hàm số có điểm cực trị  2  ;0  y 2    0   8
  4a  2b  c  0   4 .      y   2    0
12  4a  b  0  b 5 Do đó: 17
T  4a  b  c  4.  51 23. 4
Câu 99: (THPT KIM LIÊN - HÀ NỘI - Lần 03 - Năm 2018-2019) Cho hàm số 3
y  x  6mx  4 có đồ thị C
. Gọi m là giá trị của m để đường thẳng đi qua điểm cực đại, điểm cực tiểu của C m  m  0
cắt đường tròn tâm I 1;0 , bán kính 2 tại hai điểm phân biệt ,
A B sao cho tam giác IAB có http
diện tích lớn nhất. Chọn khẳng định đúng s://www
Ⓐ. m  3;4 .
Ⓑ. m  1;2 .
Ⓒ. m  0;1 .
Ⓓ. m  2;3 . 0   0   0   0   .fa Lời giải ceboo Chọn C Xét hàm số 3
y  x  6mx  4 có tập xác định . k.com 2 2
y  3x  6m; y '  0  x  2m . /v
Đồ thị hàm số có 2 điểm cực trị  y đổi dấu 2 lần iet
 y  0 có hai nghiệm phân biệt  m  0 . gold 1 Ta có y 
y '.x  4mx  4 . 3
Gọi M  x ; y , N x ; y là hai điểm cực trị của đồ thị hàm số. 1 1   2 2 
yx  y x  0 1   2   1 y  4  mx  4
Ta có  y  y  x   y x  1 1
.x  4mx  4   . 1 1 1 1 1 3 y  4  mx  4   2 2  1 y  y x
 y x .x  4mx  4  2  2  2 2 2  3 44
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Suy ra M , N thuộc đường thẳng d có phương trình y  4  mx  4.
Vậy phương trình đường thẳng qua hai điểm cực trị của C là: y  4  mx  4. m 
Gọi T  là đường tròn có tâm I 1;0 và bán kính R  2 .
Đường thẳng d cắt đường tròn tại hai điểm phân biệt ,
A B và tạo thành tam giác IAB m  1  
0  d I, d   R  0  d I, d   2   4  m  4  (*). 2  m.vn 2  16m 1 ie
Cách 1: (Nguyễn Công Định) gh
Do đường thẳng d luôn đi qua điểm K 0;4 , IK  17  R  K nằm ngoài đường tròn nên racn it tồn tại hai điểm ,
A B là giao điểm của d với đường tròn để tam giác IAB vuông tại I . th n Do đó: 1 1 S  I . A I . B sin AIB  I . A IB . IAB 2 2 ye lu R
Dấu bằng xảy ra  IA  IB  d  I, d   1 (thỏa mãn (*)). s:// 2 ttp 4  m  4 15 h  1  m  . 2  32 16m 1 R
Bình luận: Nếu đường thẳng d luôn đi qua điểm K cố định mà IK 
thì sẽ không có vị trí 2
của đường thẳng d để tam giác IAB vuông tại I . Khi đó, nếu làm như trên sẽ bị sai. Trong
trường hợp đó thì ta phải đặt d I,d   t 0  t  l , với l là độ dài đoạn thẳng IK , rồi tính S
 f t và tìm giá trị lớn nhất của f t trên nửa khoảng 0;l. IAB   
Cách 2: Phương trình đường tròn là:  x  2 2
1  y  2 C  2 2  /vietgold   x   1  y  2 Xét hệ    2 16m   2
1 x  216m   1 x 15  0   1 . y  4  mx  4 k.com
d cắt C  tại hai điểm phân biệt , A B   
1 có 2 nghiệm phân biệt a,b ceboo   m 2 16 1 1516m   1  0 . .fa
IA  a 1; 4  ma  4 Khi đó A ; a 4
 ma  4, B ; b 4  mb  4   IB   b 1; 4  mb  4
 IA IB  ab a b 2 .
16m ab  ma b 1 1 0   https://www
 ab a b 2
16m ab 16ma b 17  0   2 16m  
1 ab  16m  
1 a  b 17  0 216m  2 1 16m 2 1 15 15  17  0  16  m  2 2 16m 1 16m  . 1 32
Câu 100: (THPT KIM LIÊN - HÀ NỘI - Lần 03 - Năm 2018-2019) Tìm tất cả các giá trị thực của tham 1 số 3 2 2
m để hàm số y 
x  2m  
1 x  m  m  7 x  m  5 có hai điểm cực trị là độ dài hai 3
cạnh góc vuông của một tam giác vuông có cạnh huyền bằng 74 . 45
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 m  3  m  3 Ⓐ. m  3. Ⓑ.  . Ⓒ. m  2 . Ⓓ.  . m  2 m  2  Lời giải Chọn A 2 2
y  x  2(2m 1)x  m  m  7 .
Xét phương trình y  0 2 2
 x  2(2m 1)x  m  m  7  0 (*). x  0 h 1  ttp
Yêu cầu bài toán  pt (*) có hai nghiệm phân biệt x ; x sao cho x  0 1 2 2 s://  2 2 x  x  74  1 2 lu 2 3
 m  3m  6  0 2 ye   0 3
 m  3m  6  0    n x  x  0  4m  2  0  4m  2  0 th  1 2     2     2 it x .x  0 m m 7 0    1 2   m m 7 0  r 2 a 2 2
x  x  74  2       2     c  4m 2 2  m m 7 74 1 2 m m 6 0 n gh 2 3
 m  3m  6  0 ie  m.vn 4m  2  0   2
 m  m  7  0  m  3. m  3  m  2 
Câu 101: (THPT Nguyễn Khuyến - Thành Phố Hồ Chí Minh - Năm 2018-2019) Tìm số thực k để đồ  1  thị hàm số 4 2
y  x  2kx  k có ba điểm cực trị tạo thành một tam giác nhận điểm G 0;   làm  3  trọng tâm. http 1 1 Ⓐ. k  1  ;k  .
Ⓑ. k 1;k  . s://www 2 3 1 1 1
Ⓒ. k 1;k  .
Ⓓ. k  ;k  . .fa 2 3 2 ceboo Lời giải Chọn C k.com Ta có: 3
y  x  kx  x  2 4 4 4 x  k  . /v x  0 iet y '  0   . 2 x   k   1 gold
Đồ thị hàm số có ba điểm cực trị  y  0 có ba nghiệm phân biệt và y đổi dấu khi x đi qua
3 nghiệm đó  PT  
1 có hai nghiệm phân biệt khác không  k  0 . Khi đó ba điểm cực trị
của đồ thị hàm số là
A0; k  , B  2
 k ;k  k  , C 2
k ; k  k  .   k   2
k  k    2 1 k  k y y y 
Từ yêu cầu bài toán ta có: y  A B C   G 3 3 3 46
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” k 1 2 2k 3k 1 0        1  . k   2
Câu 102: (Chuyên KHTN - Năm 2018 - 2019 - Lần 01) Có bao nhiêu giá trị nguyên của tham số m để đồ 3 2 2 2       
thị của hàm số y x m  1 x
m 2x m 3 có hai điểm cực trị và hai điểm cực trị
đó nằm về hai phía khác nhau đối với trục hoành? m.vn Ⓐ. 2 . Ⓑ. 1. ie gh Ⓒ. 3 . Ⓓ. 4 . racn Lời giải it th Chọn B n Ta có 2
y   x  m   2 0 3 2
1 x  m  2  0 . ye lu   Để 1 15 1 15
hàm số có hai điểm cực trị 2     0  2
 m  2m  7  0   m    * . s:// 2 2 ttp
Ta lần lượt thử bốn giá trị nguyên của m thỏa mãn * là 1  ;0;1;2 . h Ta được bốn hàm số 3 3 2 3 2 3 2
y  x  x  2; y  x  x  2x  3; y  x  2x  x  2; y  x  3x  x 1 .
Khi đó ta nhận thấy chỉ có m 1 thỏa mãn yêu cầu bài toán.
Câu 103: (THPT LÝ THÁI TỔ - BẮC NINH -LẦN 1- NĂM 2018 - 2019) Cho hàm số 2 1 3m 2 x 3 2 y x 2m 3m 1 x m
2 1 . Gọi S là tập hợp tất cả các giá trị của 3 2
tham số m sao cho ham số  
1 đạt cực đại, cực tiểu tại x , x sao cho 2 3x  4x . Khi đó, C§ CT C§ CT
tổng các phần tử của tập S bằng? /vietgold 4 7 4 7 4 7 4 7 S S S S k.com Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 6 6 6 6 ceboo Lời giải .fa Chọn D TXĐ: D  . Ta có 2
y  x   m   x   2 ' 3 2
2m  3m   1 .
Hàm số đạt cực đại, cực tiểu khi y '  0 có hai nghiệm phân biệt x , x 1 2 https://www 2 2
    m     m  m  2 3 2 4 2 3 1  m  0, m   0 . 3m  2  m x   2m 1 1 2 3m  2  m x   m 1 2 2
 Trường hợp m  0: x  m 1, x  2m 1. C§ CT m  1 3x 4x 3 m 1 4 2m 1 3m 2m 1 0 C§ CT  2 2   2             m  1  3
Vì m  0 nên m  1. 47
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
 Trường hợp m  0: x  2m 1,x  m 1. C§ CT  2  7 m  x  x  6 3 4 3 2m 1 4 m 1 12m 8m 1 0 C§ CT   2 2      2      2 m  7  6 2   7
Vì m  0 nên m  . 6 h 2   7 4  7 ttp Vậy S  1  . 6 6 s://
Câu 104: (THPT Ischool Nha Trang – Khánh Hoà - Lần 01 - Năm 2018 - 2019) Tìm các giá trị thực lu 3 2 ye
của tham số m để đồ thị hàm số y   x  
1  3m  x  
1  2 có hai điểm cực trị cách đều n th gốc tọa độ. it 1 1 r Ⓐ. m   . Ⓒ. m  5  . Ⓓ. m  5. a m   . Ⓑ. c 3 2 n gh Lời giải ie Chọn B m.vn Ta có
y    x  2 2 ' 3 1  3m . x   m x   m y  0  3  x  2
1  3m  0   x  2 1 1 2 2 1  m     .
x 1  m x 1 m
Để hàm số có 2 cực trị thì m  0 .
Gọi A, B là hai điểm cực trị của đồ thị hàm số có hoành độ lần lượt là x  1 m; x  1 m . A B Khi đó A 3
 m m   B 3 1 ;2 2 ;
1 m;  2m  2 .
Hai điểm cực trị cách đều gốc tọa độ nên 2 2
OA  OB  OA  OB http
m  0ktm s://www    
m   m  2    m   m  2 2 2 3 3 1 2 2 1 2 2 3
 4m  m  0  1  .
m   tm  2 .fa 1 Vậy m   . ceboo 2 k.com
Câu 105: (Chuyên Thái Bình - Lần 04 - Năm 2018 - 2019) Cho hàm số 3 2 3
y  x  3mx  3m . Biết rằng
có hai giá trị của tham số m để đồ thị hàm số có hai điểm cực trị ,
A B và tam giác OAB có diện /v iet
tích bằng 48. Khi đó tổng hai giá trị của m là gold Ⓐ. 2 . Ⓑ. 2  . Ⓒ. 0 . Ⓓ. 2 . Lời giải Chọn C
Tập xác định của hàm số là D  . x  0 Ta có 2
y  3x  6mx, y  0  x  2m
Hàm số đã cho có hai điểm cực trị  y  0 có hai nghiệm phân biệt  m  0.
Khi đó tọa độ hai điểm cực trị của đồ thị hàm số là A 3 m  B 3 0 ; 3 ; 2m ;  m . 48
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Phương trình đường thẳng AB là 2 3
2m x  y  3m  0. 3  m  48  A .
B d O ; AB 3 1 2 6
 48  4m 16m  96 S OAB 4 2 4m  1 m  2 8 2  36m  96  
( Thỏa mãn điều kiện  m  0 ) m  2  m.vn
Vậy tổng hai giá trị của m là 0. . ie Câu 106: (Chuyên
Lam Sơn - Lần 2 - Năm 2018 - 2019) Cho hàm số gh 3 2
y  x  mx   2 m   3 3 3
1 x  m  m ( m là tham số). Gọi A , B là hai điểm cực trị của đồ thị racn it
hàm số và I 2; 2 . Tổng tất cả các giá trị của m để ba điểm I , A , B tạo thành tam giác nội th n
tiếp đường tròn có bán kính bằng 5 là ye lu 20 2 4 14 Ⓐ. . Ⓑ.  . Ⓒ. . Ⓓ. . s:// 17 17 17 17 ttp Lời giải h Chọn C
+) Xét hàm số y  f  x 3 2
 x  mx   2 m   3 3 3
1 x  m  m . TXĐ: D  . +) 2
y  x  mx   2 3 6 3 m   1  3 
 x  m2 1   . x  m 1 x  m 1 +) y  0     . x  m  1  x  m 1 +) Suy ra m
  , đồ thị hàm số y  f x luôn có 2 điểm cực trị là:
Am 1; 4m  2 , Bm 1; 4m  2 . /vietgold
+) Ta có AB   2 2 2
 4  2 5 ; Bán kính đường tròn ngoại tiếp I
 AB là R  5 . k.com AB 2 5
+)Theo định lý sin trong I  AB ta có:
 2R  sin AIB  1  AIB  90 ceboo sin AIB 2 5 .fa m 1   I .
A IB  0  m  
1 m  3   4  m 4  m  4 2
 0  17m  20m  3  0  3  . m   17 3 20
Vậy tổng các giá trị của m là: 1   . https://www 17 17
Câu 107: (THPT Nình Bình - Bạc Liêu - Lần 04 - Năm 2018 - 2019) Có bao nhiêu số nguyên m để hàm số 3 2
y  x  3x  mx  4 có hai điểm cực trị thuộc khoảng  3  ;3 ? Ⓐ. 12. Ⓑ. 11. Ⓒ. 13 . Ⓓ. 10 . Lời giải Chọn B Ta có: 2
y '  3x  6x  m Để hàm số 3 2
y  x  3x  mx  4 có hai điểm cực trị thuộc khoảng  3
 ;3 thì phương trình y'  0 49
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 hay 2
3x  6x  m  0 có hai nghiệm phân biệt thuộc khoảng  3  ;3 . Cách 1:
Khi đó, đặt f x 2
 3x  6x  m thì  '  0     a f   9 3m 0 . 3  0       a f   45 m 0     3   m  9 . 3 0 9  m  0    S  h     3  1 3 3 3 ttp  2 s://
Do đó có 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán. lu Cách 2: ye
Khi đó, đặt f x 2
 3x  6x  m thì n th 9   3m  0 it  '  0  r     3   m  9 3  9  3m 3  9  3m a 3
  x  x  3   3     3 c 1 2 n  3 3 gh
Do đó có 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán. ie
Cách 3: Admin Nguyễn Văn Thịnh m.vn Ta có: 2
y  3x  6x  m Hàm số 3 2
y  x  3x  mx  4 có hai điểm cực trị thuộc khoảng  3
 ;3  Phương trình y  0 hay 2
3x  6x  m có hai nghiệm phân biệt thuộc khoảng  3  ;3 . Đặt f x 2  3x  6 , x x  3  ;3 . Ta có:
f  x  6x  6 ; f  x  0  x 1. Bảng biến thiên: https://www .fa ceboo Yêu cầu bài toán  3   m  9 .
Vậy có 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán. k.com
Câu 108: (THPT Nguyễn Huệ - Huế - Lần 02 - Năm 2018 - 2019) Cho hàm số /v 1 3 2 iet y 
mx  m  
1 x  3m  2 x  2019 với m là tham số. Tổng bình phương tất cả các giá trị gold 3
của m để hàm số có hai điểm cực trị x , x thỏa mãn x  2x  1 bằng 1 2 1 2 22 8 40 25 Ⓐ. Ⓑ. Ⓒ. Ⓓ. 9 3 9 4 Lời giải Chọn C Ta có: 2
y '  mx  2m  
1 x  3m  2 . m  0
Để hàm số có hai điểm cực trị   2  '  2
 m  4m 1  0 50
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”    m   2 2 1 x  3   1 x  x  1 2 m m    2
Ta có: x  2x  1  x  1   1 2 2 m   3m  2 x x    2  1 2  x x  3 1     m 1 2   m   1 m  m.vn 2 2 2       2  3 1    3 1        N  ie  m  m   m  2   gh m  3 racn 40   it Vậy 2 2 m m . 1 2 9 th n
Câu 109: (SGD Bắc Giang - Lần 01 - Năm 2018 - 2019) Gọi S là tập hợp các giá trị nguyên của tham ye 3 lu x
số m để hàm số 2 y 
 2x  mx  3 có hai điểm cực trị x , x  4 . Số phần tử của S bằng 1 2 s:// 3 ttp h Ⓐ. 5 . Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 4 . Lời giải Chọn D
Hàm số có hai điểm cực trị x , x thì phương trình y '  0 có hai nghiệm phân biệt 1 2
 '  0  4  m  0  m  4 .
 x  2  4  m
Khi đó giả sử x  x , 1 y '  0   1 2
x  2  4  m  2
Yêu cầu bài toán trở thành x  4  2  4  m  4  0  m  4 . 2 /vietgold
Kết hợp với m  4 ta được 0  m  4 . Do m nguyên nên m 0;1;2; 
3 . Vậy có 4 giá trị của m
thỏa mãn yêu cầu bài toán.
k.com Câu 110: (SGD Hưng Yên - Năm 2018 - 2019) Cho hàm số 3
y  x  m   2 2 3
1 x  6m  2 x 1 với m ceboo .fa
là tham số thựⒸ. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng  2  ;3 . Ⓐ. m 1  ;4 \  3 .
Ⓑ. m3;4 .
Ⓒ. m1;3. Ⓓ. m 1  ;4 . https://www Lời giải Chọn A Ta có 2
y  6x  6m  
1 x  6m  2 . x  1  2
y  0  x  m  
1 x  m  2  0   .
x  m  2
Để hàm số có điểm cực đại cực tiểu nằm trong khoảng  2
 ;3 thì y  0 có hai nghiệm phân biệt m  2  1  m  3 nằm trong khoảng  2  ;3     .  2
  m  2  3  1   m  4 51
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
Câu 111: (SGD Kiên Giang - Năm 2018 - 2019) Gọi m là số thực âm để đồ thị hàm số 3 2 3
y  x  6mx  32m có hai điểm cực trị đối xứng với nhau qua đường phân giác của góc phần
tư thứ nhất của hệ trục tọa độ Oxy . Chọn khẳng định đúng trong các khẳng định sau.  3   1   3   1 
Ⓐ. m  ;1   . Ⓑ. m 1;     . Ⓒ. m 2;     . Ⓓ. m  ;0   .  2   2   2   2  Lời giải Chọn D h ttp Ta có 2
y  3x 12mx s:// x  0 y '  0  . lu  x  4m ye 3 n
Hàm số có hai cực trị khi m  0 . Khi đó, gọi A0;32m ; B4m;0 là tọa độ 2 điểm cực trị của th it
đồ thị hàm số. Hai điểm này đối xứng với nhau qua đường thẳng  : y  x khi và chỉ khi: ra      c
d  A;  d  B;  3  32m  4m 1 n     m   (vì m  0 ). gh 3 AB      2 2 4m 32m 0 ie m.vn 1 
Vì m  0 nên ta chọn m  . 2 2 Cách 2:
Chú ý: Hai điểm A ;
x y, B  x '; y ' đối xứng nhau qua đường phân giác góc phần tư thứ nhất x '  y khi và chỉ khi  .  y '  x Câu 112: A 3
0;32m ; B4m;0 đối xứng nhau qua đường phân giác góc phần tư thứ nhất khi và chỉ khi 3 1 ht
32m  4m (với m  0 )  m  
. Đối chiếu các phương án, ta chọn phương án D tp 2 2 s://www
(SGD Phú Thọ - Lần 02 - Năm 2018 - 2019) Tập hợp tất cả các giá trị tham số thực m để đồ thị hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m có hai điểm cực trị nằm về hai phía trục hoành là .fa
a;b . Khi đó giá trị a 2b bằng ceboo 3 4 2 Ⓐ. . Ⓑ. . Ⓒ. 1. Ⓓ. . k.com 2 3 3 Lời giải /v Chọn D ietgold Ta có 2 2
y '  3x  6mx  3(m 1) .
x  m 1 Xét 2 2
3x  6mx  3(m 1)  0   .
x  m 1
Hai nghiệm trên phân biệt với mọi m .
Đường thẳng qua 2 điểm cực trị của đồ thị là y  2  x  m .
Vậy nên các giá trị cực trị y(m 1)  3m  2 , y(m 1)  3m  2 .
Theo yêu cầu bài toán ta phải có  m   m   2 2 3 2 3 2  0    m  . 3 3 2
Vậy a  2b  . 3 52
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Câu 113: (SGD Quảng Nam - Năm 2018 - 2019) Có bao nhiêu giá trị thực của tham số m để đồ thị hàm 3 1 số 3 2 3 y  x  mx 
m có hai điểm cực trị đối xứng nhau qua đường thẳng y  x ? 2 2 Ⓐ. 1 Ⓑ. 3 Ⓒ. 2 Ⓓ. 0 Lời giải Chọn C m.vn x  0   y '  0  ie Ta có 2 y ' 3x 3mx ;  x  m gh
Hàm số có hai điểm cực trị khi và chỉ khi y '  0 có hai nghiệm phân biệt  m  0 . racn  1  it
Với điều kiện m  0 , giả sử hai điểm cực trị của đồ thị hàm số là 3 A 0; m   , B ;0 m  .  2  th n  1  3  m m  ye 3  AB ; m  m   và I  ;
 là trung điểm của đoạn thẳng AB . lu  2   2 4  s://  1 3 m  m  0       ttp A . B u 0 m   d 2 2      h Yêu cầu bài toán  3 I d m m  m  0   2 4
Đối chiếu điều kiện ta được m   2 .
Câu 114: (SGD Vĩnh Phúc - Lần 2 - Năm 2018 - 2019) Tìm tất cả các giá trị của tham số m để hàm số 1 3 y 
x  m  3 2
x  4m  3 3
x  m  m đạt cực trị tại x ,x thỏa mãn 1
  x  x . 3 1 2 1 2 7 m  3  7 Ⓐ. 3   m 1.
Ⓑ.   m  3  . Ⓒ.  .
Ⓓ.   m  2  . 2 m 1 2 /vietgold Lời giải Chọn B k.com Ta có 2
y  x  2m  
3 x  4m  3 ceboo
Đặt t  x 1 x  t 1. Khi đó 2
y  t  2m  2t  2m  7 .fa
Hàm số đạt cực trị tại x ,x thỏa mãn 1   x  x 2
 x  2m  
3 x  4m  3  0 có hai 1 2 1 2
nghiệm phân biệt x ,x thỏa mãn 1   x  x 2
 t  2m  2t  2m  7  0 có hai nghiệm phân 1 2 1 2
biệt dương. Điều này tương đương với https://www m  3   2
  m  2m  3  0 m 1  
S   m   7 2 2  0
 m  2    m  3 . 2  
P  2m  7  0 7  m    2  Cách 2: Ta có 2
y  f (x)  x  2m  
3 x  4m  3
Hàm số đạt cực trị tại x ,x thỏa mãn 1   x  x 2
 x  2m  
3 x  4m  3  0 có hai 1 2 1 2
nghiệm phân biệt x ,x thỏa mãn 1
  x  x . Điều này tương đương với 1 2 1 2 53
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 m  3         m 1 0 2
m  2m  3  0    7 7   . a f ( 1  )  0  1
  2(m  3)  4(m  3)  0  m   
 m  3 . Chọn B   2  2 S     2(m 3) 1    1  m  3  2  2  
Câu 115: (ĐTD-Đề 5- Năm 2018-2019) Xác định các giá trị của tham số thực m để đồ thị hàm số h 1 ttp 3 2 y 
x  x  mx  m có các điểm cực đại và cực tiểu A và B sao cho tam giác ABC vuông 3 s://  2  lu
tại C trong đó tọa độ điểm C ; 0   ? ye  3  n th it racngh ie m.vn 1 1 1 1
Ⓐ. m  .
Ⓑ. m  .
Ⓒ. m  .
Ⓓ. m  . 3 2 6 4 Lời giải http Chọn B s://www .fa ceboo k.com /vietgold
Ta có tam giác ABC vuông tại C nên gọi M là điểm uốn của đồ thị hám số đồng thời là trung
điểm của AB, Khi đó tam giác vuông có đường trung tuyến bằng nửa cạnh huyền do vậy ta có phương trình sau: 1 1 MC  AB  1 p x  x 2 2
 4x x (*). Thay số: 2 1 1 2 2 2 54
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” 2
Hệ số góc đường thẳng qua hai cực trị: p  m  1 . 3 x  x  2 Ta có: 2 2 1
y '  x  2x  m   . x x  m  1 2  2  b
Tọa độ điểm uốn M 1,  
 (Chú ý điểm uốn x   ).  3  3a 5 1 4 1 m.vn Vậy ta có: (*)   1 m 2 1
4  4m  m  . ie 3 2 9 2 gh
Câu 116: (ĐTD- Đề VDC 9 - 10- Tuần 15 - Năm 2018-2019) Có bao nhiêu giá trị nguyên của tham số m 3 2 2 2 racn
để đồ thị hàm số y  x 8x  m 1 
1 x  2m  2 có hai điểm cực trị nằm về hai phía của trục it th Ox . n ye Ⓐ. 4 . Ⓑ. 5 . Ⓒ. 6 . Ⓓ. 7 . lu Lời giải s:// Chọn B ttp
Đồ thị hàm số C 3 2
y  x  x   2 m   2 : 8
11 x  2m  2 có hai điểm cực trị nằm về hai phía h
của trục Ox  phương trình 3 2
x  x   2 m   2 8
11 x  2m  2  0,  
1 có 3 nghiệm phân biệt. x  2 Ta có  
1   x  2 2 2
x  6x  m   1  0   . f   x 2 2
 x  6x  m 1  0,2
Suy ra phương trình 2 phải có 2 nghiệm phân biệt khác 2 .   9    2 m   1  0   10  m  10     . Do m   m 2  ; 1  ;  0 .  f  2 2
 4 12  m 1  0 m  3 
/vietgold Câu 117: (Chuyên Hùng Vương - Gia Lai - Lần 01 - Năm 2018 - 2019) Cho hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m  m , với m là tham số. Gọi A , B là hai điểm cực trị của đồ thị k.com hàm số và I 2; 2
  . Giá trị thực m 1 để ba điểm I , A , B tạo thành tam giác nội tiếp đường ceboo
tròn có bán kính bằng 5 là .fa 2 3 4 5 Ⓐ. m  . Ⓑ. m  . Ⓒ. m  . Ⓓ. m  . 17 17 17 17 Lời giải Chọn B https://www 3 2
y  x  mx   2 m   3 2
x  m  m  y  x  mx   2 3 3 1 3 6 3 m   1 x  m 1 y  4  m  2 2
y  0  3x  6mx  3 2 m   1  0     . x  m 1 y  4  m  2
Khi đó đồ thị hàm số có 2 điểm cực trị Am 1; 4
 m  2, Bm1; 4  m  2
 IAm 1; 4
 m  4, IBm 3; 4  m Ta có: AB  2
 ;4  AB  2 5 do đó AB là đường kính của đường tròn ngoại tiếp tam giác  I
 AB nên AIB  90 hay AI  BI  I . A IB  0 55
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 m 1    m  
1 m  3   4  m 4  m  4 2
 0  17m  20m  3  0  3  . m   17 3
Do m  1 nên chọn m  . 17
Câu 118: (Chuyên Lê Hồng Phong - Nam Định - Lần 2 - Năm 2018) Tìm tham số m để hàm số 1 3 2 y 
x  mx  m  2 x  2018 không có cực trị. h 3 ttp s:// Ⓐ. m  1
 hoặc m  2 Ⓑ. m  1  Ⓒ. m  2 Ⓓ. 1   m  2 lu Lời giải ye Chọn D n th Ta có: 2
y  x  2mx  m  2 it r
Để hàm số đã cho không có cực trị khi phương trình y  0 vô nghiệm hoặc có nghiệm kép hay ac 2 n 
  0  m m 2  0  1   m  2. gh ie
Câu 119: (THPT LƯƠNG NGỌC QUYẾN - THÁI NGUYÊN - LẦN 02 - NĂM 2017-2018) Cho hàm m.vn số 3
y  x  m   2 2 3
1 x  6m  2 x 1 . Với điều kiện nào của tham số m thì hàm số trên có cực trị? Ⓐ. m  3.
Ⓑ. Với mọi m .
Ⓒ. Không tồn tại m . Ⓓ. m  3. Lời giải Chọn D 2
y  6x  6m  
1 x  6m  2 .
Hàm số có cực trị  y  0 có 2 nghiệm phân biệt 2 2 ht  m  
1  4m  2  0  m  6m  9  0  m  3 . tps://www
Câu 120: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Biết rằng đồ thị hàm số    4 2 y
f x  ax  bx  c A0;3 B 2; 1  3 f   1
có hai điểm cực trị là và . Giá trị của là .fa ceboo Ⓐ. f   1  4 Ⓑ. f   1  8  Ⓒ. f   1  2 Ⓓ. f   1  6  Lời giải k.com Chọn A    /v
Ta có f  x 3 4ax 2bx . ietgold
Do A0;3,B2; 1
 5 là hai điểm cực trị nên ta có:  f 0  3 c  3 8
 a  b  0 a  1    
 f 2  0  3
 2a  4b  0
 4a  b  4   b   8            f    16a 4b c 13 c 3 c 3 2  1  5     f x 4 2
 x  8x  3  f   1  1 8  3  4  . Chú ý:
 Như bình thường với một điểm M x ; y là điểm cực trị của đồ thị hàm số y  f x ta sẽ 0 0  56
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”  f    x  0
khai thác được phương trình 
. Nhưng hàm trùng phương,với điểm cực trị thuộc trục  f   x  y 0  0
tung Oy thì dữ kiện f  x  0 luôn đúng (ở đây x  0 và f 0  0  0  0 ). Do đó ta chỉ có 0  0
được 1 phương trình (ở bài toán trên ta có được 1 phương trình là f 0  y  3). 0
 Ở bài toán này đề bài cho biết tọa độ 2 điểm cực trị (trong khi thực tế hàm số có tới 3 cực trị)
nên việc tìm điểm cực trị thứ ba (nếu cần) là không khó khi ta biết A0;3Oy thì suy ra điểm m.vn ie
cực trị thứ ba sẽ đối xứng với B2; 1
 5 qua trục Oy , hay điểm cực trị thứ ba có tọa độ gh C  2  ; 1
 5. Nhưng với bài toán này, dữ kiện điểm cực trị thứ ba không cần thiết nên ta không racn it khai tháⒸ. th n ye
Câu 121: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Biết đồ thị T  của hàm số lu 4 2
y  ax  bx  c có A1;4 và B0;3 là các điểm cực trị. Hỏi trong các điểm sau đây, đâu là s:// điể ttp
m thuộc đồ thị T  ? h Ⓐ. M  2  ;5 Ⓑ. N  1  ; 4   Ⓒ. P3; 1  5 Ⓓ. Q2; 5   Lời giải Chọn D
Ta có f  x 3
 4ax  2bx . Do A1;4 và B0;3 là hai điểm cực trị nên ta có:  f   1  0          4a 2b 0 2a b 0 a 1      f  
1  4  a  b  c  4  a  b  1  b   2        f    c 3 c 3 c 3 0  3    /vietgold  f x 4 2
 x  2x  3 . k.com
Chỉ có điểm Q2; 5
  thỏa mãn f 2  5
  QT .
ceboo Câu 122: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tìm tất cả các giá trị của m sao cho hàm .fa số 3 2
y  x  3mx  3m 1có hai điểm cực trị Ⓐ. m  0 Ⓑ. m  0 Ⓒ. m  0 Ⓓ. m  0 Lời giải https://www Chọn D x  0 Cách 1: Ta có 2
y  3x  6m ;
x y  0   x  2m
Để hàm số có hai điểm cực trị thì phương trình trên có hai nghiệm phân biệt 2m  0  m  0 .
Cách 2: Do hàm số dạng bậc ba nên điều kiện để hàm số có hai điểm cực trị là 2 b  3ac  0 2
 9m  0  m  0 Câu 123: (Pen M - Nguyễn Thanh Tùng -
Năm 2017 - 2018) Cho hàm số 3
y   x   m   2 x   2 2 2 1 m  
1 x  2 . Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để
hàm số đã cho có hai điểm cực trị 57
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Ⓐ. 4 Ⓑ. 5 Ⓒ. 3 Ⓓ. 6 Lời giải Chọn B
Do hàm số bậc ba nên điều kiện hàm số có hai điểm cực trị là b  ac    m  2 2   2 m   2 3 0 2 1 6
1  0  2m  4m  7  0 2   3 2 2   3 2   m  . Do m  nên m  3  ; 2  ; 1  ;0;  1 . 2 2 h ttp
Vậy có 5 giá trị nguyên của m thỏa mãn. s://
Câu 124: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tìm tất cả các giá trị của tham số m để lu
hàm số y    m 3 2 1
x  3x  3x 1 có cực trị. ye n th Ⓐ. m 1 Ⓑ. m  1 
Ⓒ. 0  m 1 Ⓓ. m  0 it ra Lời giải cn Chọn D gh
+) Với m  1 hàm số có dạng 2 y  3
 x  3x 1 là hàm số bậc 2 nên có một cực trị (thỏa mãn). ie m.vn
+) Với m  1, hàm số có cực trị 2
 b 3ac  0  9m  0  m  0 . Vậy m  0 .
Chú ý: Hàm số bậc ba số cực trị có thể là 2 hoặc 0 . Do đó câu hỏi tìm m để hàm bậc ba có
cực trị hay có hai cực trị là như nhau. Song nếu hàm số có hệ số a chứa tham số thì ta phải xét
thêm a  0 (Hàm số không có dạng bậc 3), khi đó có thể hàm số có 1 cực trị ví như câu trên. 1
Câu 125: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Cho hàm số 3 2 y 
x  mx  2m   1 x 1 3
. Trong các mệnh đề sau, đâu là mệnh đề sai? ht Ⓐ. Với m
 1 thì hàm số có hai điểm cực trị. tps://www
Ⓑ. Hàm số luôn có cực đại và cực tiểu. Ⓒ. Với m
 1 thì hàm số có cực đại và cực tiểu. .fa ceboo Ⓓ. Với m
 1 thì hàm số có cực trị. k.com Lời giải Chọn B /v
Vì hàm số có dạng bậc ba nên ta xét b  ac  m   m    m  2 2 2 3 2 1 1 ietgold
Hàm số có hai cực trị khi và chỉ khi b  ac   m 2 2 3 0 1
 0  m 1 nên đáp án B sai.
Chú ý: Ở bài toán này mệnh đề A, D đúng vì m
 1 thì hàm số có cực đại và cực tiểu (Có hai
cực trị hay có cực trị) nên cũng thỏa mãn với m  1 hoặc m  1
Câu 126: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tất cả các giá trị của m để hàm số y   2 m   4
x  m   2 1
1 x  3 có đúng một cực trị là Ⓐ. m  1  Ⓑ. m  1 
Ⓒ. m 1 và m  1  Ⓓ. m  1  và m  1 Lời giải Chọn D 58
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”   2  m    ab  0 1 m   1  0
Hàm số có một cực trị khi và chỉ khi    2 2 a  b  0 m   2 1  m  2 2 1  0  2  m   1 m   1  0         m 1 0 m 1        m  2 1 m  2 1 1  0 m  1 m  1    a  b  m.vn
Chú ý: Trong bài toán này, có thể rất nhiều bạn sẽ mắc phải lỗi không cho điều kiện 2 2 0 ie
dẫn đến kết quả không đúng. Vì với 2 2
a  b  0  a  b  0  y  c sẽ không có cực trị. gh
Vì vậy các bạn cần nhớ: Hàm số 4 2
y  ax  bx  c với a chứa tham số racn
 không có cực trị  a  b  0 . it a  0 a  0 th   n
có một cực đại và không có cực tiểu  hoặc  (hay viết gọn thành b   0 b   0 ye lu a  0  s:// b   0 ). ttp  2 2 h a  b  0 a  0 a  0
 có một cực tiểu và không có cực đại   hoặc  (hay viết gọn thành b   0 b   0 a  0 b   0 ).  2 2    a b 0 a  0  a  0
 có một cực đại  b   0 hoặc  . /vietgold  b   0 2 2 a  b  0 k.com a  0  a  0 ceboo
 có một cực tiểu  b   0 hoặc  . b   0 .fa  2 2 a  b  0 ab  0
 có một cực trị   . 2 2 a  b  0 https://www a  0
 có hai cực đại và một cực tiểu   . b   0 a  0
 có hai cực tiểu và một cực đại   . b   0
 có ba cực trị  ab  0.
Câu 127: (NXBGD - Phạm Đức Tài- Đề số 2 - Năm 2017-2018) Tìm tất cả các giá trị thực của tham số  để 4 hàm số 3 y 
x  21 sin  2
x  1 cos 2  x có cực trị. 3 59
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021  
Ⓐ.    k2 .
Ⓑ.   k .
Ⓒ.    k2 .
Ⓓ.   k . 2 2 Lời giải Chọn A 2
y '  4x  41 sin  x  1 cos 2  có hai nghiệm phân biệt 
   0  1sin 3sin   0  sin 1    k2,k  . y ' 2 h ttp
Câu 128: (Chuyên Hùng Vương - Phú Thọ - Lần 1 - Năm 2018) Biết m là giá trị của tham số m để 0 s:// hàm số 3 2
y  x  3x  mx 1 có hai điểm cực trị x , x sao cho 2 2
x  x  x x  13 . Mệnh đề nào 1 2 1 2 1 2 lu dưới đây đúng? ye n Ⓐ. m  1  ;7 .
Ⓑ. m  7;10 . Ⓒ. m  1  5; 7
 . Ⓓ. m  7  ; 1  . 0   0   0   0   th it Lời giải rac Chọn C n gh TXĐ: D  2 ie
y  3x  6x  m . m.vn Xét 2
y  0  3x  6x  m  0 ;    9 3m.
Hàm số có hai điểm cực trị     0  m  3. Hai điể m
m cực trị x ; x là nghiệm của y  0 nên: x  x  2; x .x  . 1 2 1 2 1 2 3
Để x  x  x x 13  x  x 2 2 2  3x .x 13 1 2 1 2 1 2 1 1
 4 m 13  m  9  . Vậy m  9   1  5; 7  . 0  
Câu 129: (THPT Lương Thế Vinh - Hà Nội - Lần 03 - Năm 2018) Cho hàm số 3 2 f x x x ax
b có đồ thị là C . Biết C có điểm cực tiểu là A 1; 2 . Giá trị 2a  b http bằng s://www Ⓐ. 1  Ⓑ. 1 Ⓒ. 5  Ⓓ. 5 Lời giải .fa ceboo Chọn C Ta có 3 2 f x x x ax b 2 f x 3x 2x a k.com
Đồ thị hàm số có điểm cực tiểu là A 1;2 /v f 1 0 a 1 iet Ta được f 1 2 b 3 gold
Vậy 2a  b  2  3  5  .
Câu 130: (THPT Nguyễn Khuyến - TP HCM - Năm 2018) Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số 3 2
y  x  2x  1 m x  m có hai điểm cực trị nằm về hai phía đối với trục hoành. 1 1 1
Ⓐ.   m  0
Ⓑ. m  0
Ⓒ.   m  0 Ⓓ. m   4 4 4 Lời giải Chọn A TXĐ: D  , có 2
y  3x  4x  1 m . 60
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Hai điểm cực trị nằm về hai phía đối với trục hoành thì y  0 có ba nghiệm phân biệt. Suy ra 3 2
x  x    m x  m    x   2 2 1 0
1 x  x  m  0 có ba nghiệm phân biệt. 1   4m  0 1 Nên     m  0 . 1  1 m  0 4
Câu 131: (THPT Nguyễ n Khuyế n - TP HCM - Năm 2018) Biết hàm số 3 x y   m   2
1 x  m  2 x 1 đạt cực trị tại x  1 ( m là tham số thực). Khi đó điểm cực trị m.vn 3 ie của hàm số khác 1 là gh Ⓐ. 1  Ⓑ. 2  Ⓒ. 3 Ⓓ. Đáp số khác racn it Lời giải th n Chọn C 2 ye
Ta có: y  x  2m  
1 x  m  2 . lu
Hàm số đạt cực trị tại x  1  y  1  0  m
 1 0  m 1. s:// 3 x x 1 ttp Với m  1 ta có: 2 y 
 2x  3x 1 và 2
y  x  4x  3  0   . h 3 x  3
Suy ra điểm cực trị còn lại là x  3. Câu 132: (THPT Kinh Môn 2 - Hải Dương - Năm 2018) Cho
y  m   3 x   2
m  m   2 3 2
1 x  m  4 x 1 . Gọi S là tập tất cả các giá trị nguyên của m để
đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục Oy . S có bao nhiêu phần tử? Ⓐ. 4 . Ⓑ. 5 . Ⓒ. 6 . Ⓓ. 7 . Lời giải /vietgold Chọn C
Ta có y  m   2 x   2 3 3
4 m  m   1 x  m  4 k.com
y  0  m   2 x   2 3 3
4 m  m  
1 x  m  4  0 . ceboo
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục Oy thì phương trình y  0 .fa
có hai nghiệm phân biệt trái dấu. 3
 m 3  0 Suy ra   4   m  3 . 3
 m 3.m  4  0 Mà m  nên m   3  ; 2  ; 1  ;0;1; 
2 . Vậy S có 6 phần tử.
https://www Câu 133: (Chuyên Hạ Long - Quảng Ninh - Lần 01 - Năm 2018) Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  x  3x  m  
1 x  2 có hai điểm cực trị. Ⓐ. m  2. Ⓑ. m  2. Ⓒ. m  2 . Ⓓ. m  4  . Lời giải Chọn B Ta có 2
y  3x  6x  m 1 . Hàm số có hai điểm cực trị khi y  0 có hai nghiệm phân biệt. 
  0  9 3m  1  0  m  2 . 61
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
Câu 134: (THPT THỰC HÀNH TÂY NGUYÊN - LẦN 02 - 2018) Tìm các giá trị thực của tham số m để 1 hàm số 3 2 y 
x  mx  3x  2m 1 đạt cực tiểu tại x  1 . 3 Ⓐ. m  2 .
Ⓑ. Không tồn tại m . Ⓒ. m 1. Ⓓ. m  3 . Lời giải Chọn B 2
y  x  2mx  3, y  2x  2m . h ttp y    1  0   m  m  Xét   4 2 0   2  . s:// y    1  0 2  2m  0 m 1 lu
Vậy không tồn tại m thỏa mãn bài toán. ye n
Câu 135: (Pen M - Nguyễn Thanh Tùng) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số th 3 2 2 it
y  x  4x  1 m  x 1 có hai điểm cực trị nằm về hai phía khác nhau đối với trục tung. racn 1 1 m  1 gh
Ⓐ.   m  . Ⓑ.  . Ⓒ. 1   m 1. Ⓓ. 1   m 1. 3 3 m  1  ie m.vn Lời giải Chọn B 2
y  x  x   2 3 8 1 m  m 1
Yêu cầu bài toán  y  0 có hai nghiệm trái dấu   2
3 1 m   0   . m  1 
Câu 136: (Chuyên Nam Sơn - Thanh Hóa - Lần 03 - Năm 2018 - 2019) Gọi S là tập các giá trị dương
của tham số m sao cho hàm số 3 2 y  x  3 .
m x  9x  m đạt cực trị tại x , x thỏa mãn 1 2
x  x  2 . Biết S   ;
a b . Tính T  b  a . ht 1 2 tps://www
Ⓐ. T  2  3
Ⓑ. T 1 3
Ⓒ. T  2  3
Ⓓ. T  3 3 Lời giải Chọn C .fa  ceboo Ta có 2 y  3x  6 . m x  9 m  2 k.com
Hàm số có hai cực trị khi và chỉ khi 
  0  9m  27  3 0   m   3 /v
Ta có: x  x  2   x  x
 4  x  x  4x x  4 2  4m 12  4 1 2 2 1 2 2 1 2 1 2 iet gold 2  m 16  2   m  2
Từ, mà m  0 theo giả thiết ta được S   3;2 .
Vậy T  b  a  2  3.
Câu 137: (NXBGD - Đề số 3 - PHẠM ĐỨC TÀI - Năm 2017 - 2018) Tìm tất cả các giá trị thực của tham 1
số m để hàm số 3 y 
x  m   2
1 x  2m  
1 x  m 1 có cực trị. 3 Ⓐ. m  0. Ⓑ. m   . Ⓒ. m  0 .
Ⓓ. không có m . Lời giải 62
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” Chọn C
Tập xác định D  .
Để hàm số có cực trị thì phương trình y  0 có hai nghiệm phân biệt 2
y  x  2m  
1 x  2m 1. Ta có    m  2 2
1  2m 1  m  0  m  0 .
Câu 138: (NXBGD - ĐOÀN QUỲNH - Đề số 05 - Năm 2021) Tìm các giá trị của tham số m để đồ thị    m.vn hàm số 3 3 y x 3x
m có hai điểm cực trị ,
A B sao cho gốc tọa độ O cùng với A và B là ba ie
đỉnh của tam giác vuông tại O . gh
Ⓐ. Không có giá trị nào của m . Ⓑ. m  4  . racn it
Ⓒ. m  0,m  4  .
Ⓓ. m  1,m  4 . th n Lời giải ye Chọn C lu Tập xác định s:// x  0 2 2
y  3x  6x ; y  0   ttp x  2  h
Hàm số luôn có hai điểm cực trị với m 
Hai điểm cực trị của đồ thị hàm số A0;m, B 2  ;m  4.
OA  0;, m, OB   2  ;m  4 m  O
 AB vuông tại O  OA OB   mm   0 . 0 4  0   . m  4 
Câu 139: (THPT Triệu Sơn - Thanh Hóa - Năm 2018) Cho hàm số y xm3 2
3x  m có đồ thị là
C với m là tham số thựⒸ. Biết điểm M  ;a b là điểm cực đại của C ứng với một giá trị m  m  /vietgold
m thích hợp, đồng thời là điểm cực tiểu của C
ứng với một giá trị khác của m . Tổng m  k.com
S  2018a  2020b bằng ceboo Ⓐ. 504. Ⓑ. 504  . Ⓒ. 12504. Ⓓ. 5004. .fa Lời giải Chọn A Vì điểm M  ;
a b thuộc đồ thị C
nên ta có: a  m3 2
3a  m  , b m   .   1 m  x  m 1 https://www
Xét y   x  m2 3
3 ; y  0   . x  m 1 Bảng biến thiên
Dựa vào bảng biến thiên, ta có: Nếu m là giá trị của tham số m để đồ thị hàm số nhận điểm 1 M  ;
a b là điểm cực đại thì a  m 1. Nếu m là giá trị của tham số m để đồ thị hàm số nhận 1 2 63
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 điểm M  ;
a b là điểm cực tiểu thì a  m 1. 2  1  a  1   3a   a  2 1  b  2
Mà m , m phải thỏa mãn   1 nên ta có:    . 1 2 1   3a   a  2 1  b 1 b     4
Vậy S  2018a  2020b  504 .
Câu 140: (Chuyên ĐHSP Hà Nội - Lần 01 - Năm 2017 - 2018) Tìm tất cả các giá trị của tham số a để h hàm số 3 2 2
y  2x  9ax 12a x 1 có cực đại, cực tiểu và hoành độ điểm cực tiểu của đồ thị hàm ttp số bằng 1. s:// 1 1 lu
Ⓐ. a   . Ⓑ. a 1. Ⓒ. a  . Ⓓ. a  1  . ye 2 2 n Lời giải th it Chọn A ra TXĐ: D  cn + 2 2
y  6x 18ax 12a   1 gh 2 2 2 ie
Để hàm số có cực đại, cực tiểu thì 
  0  81a  72a  9a  0 luôn đúng a   . m.vn
Do đó x là nghiệm của phương trình  
1 . Từ giả thiết x
1 thay vào phương trình   1 ta CT CT  1 a    có: 2
12a 18a  6  0  2  a  1  + Với a  1  3 2
y  2x  9x 12x 1, 2
y  6x 18x 12 x 1 y  0   x  2 ht Bảng biến thiên tps://www .fa ceboo k.com
Dựa vào BBT ta thấy hàm số không đạt cực tiểu tại x  1 . Do đó a  1 không thỏa mãn. /v 1 + Với a   iet 2 gold 9 3 2 y  2x  x  3x 1 , 2
y  6x  9x  3 2  1 x  y  0   2  x 1 Bảng biến thiên 64
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” m.vn
Dựa vào BBT ta thấy hàm số đạt cực tiểu tại x  1 . Do đó 1 a   thỏa mãn. ie 2 gh
Câu 141: (Chuyên Hạ Long - Quảng Ninh - Lần 01 - Năm 2018) Tìm tất cả giá trị thực của tham số m racn để đồ thị hàm số 3 2
y  x  3mx  2 có hai điểm cực trị A và B sao cho các điểm A , B và it th
M 1; 2 thẳng hàng. n ye Ⓐ. m  2 .
Ⓑ. m   2 . Ⓒ. m  2 .
Ⓓ. m   2 ; m  2 lu s:// . ttp Lời giải h Chọn D Ta có: 2
y  3x  6mx ; y  0  2
3x  6mx  0  x  0 , x  2m .
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình y  0 có hai nghiệm phân biệt 
2m  0  m  0 .
Khi đó hai điểm cực trị là A0;2 , B 3 2 ;
m 2  4m  . Ta có MA   1  ;4 , MB   3
2m 1; 4  4m  .
Ba điểm A , B và M 1; 2 thẳng hàng  MA , MB cùng phương 3   3    2m 1 4 4m 2m 1 1 m     3
2m 1  m 1  3 m  2m /vietgold 1  4 1  1  2
m  2  m   2 .
k.com Câu 142: (THPT SỐ 02 AN NHƠN - BÌNH ĐỊNH - LẦN 2 - 2018) Cho hàm số ceboo 1 3 y 
mx  m   2
1 x  3m  2  .fa x
2018 với m là tham số. Tổng bình phương tất cả các giá trị 3
của m để hàm số có hai điểm cực trị x ; x thỏa mãn 2x  x  2 bằng 1 2 1 2 52 10 73 34 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 9 9 16 9 https://www Lời giải Chọn A Ta có: 2
y  mx  2m  
1 x  3m  2
Hàm số có hai điểm cực trị  y  0 có hai nghiệm phân biệt x ; x . 1 2 a  0    m 0    *    0 2  2
 m  4m 1  0 2m   1
Theo định lý Viet: S  x  x   1 1 2 m 65
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 3m  2
P  x .x  2 1 2 m
Theo giả thiết: 2x  x  2 3 1 2 2 2m  4 Từ   1 và 3  x  và x  1 m 2 m  m  2 2 2m  4 3m  2 Từ 2  .  2  
3m 10m  8  0  4 m m m m  h  3 ttp 4 s://
So điều kiện * , ta nhận m  2 ; m  . 3 lu
Câu 143: (Chuyên Vĩnh Phúc - Lần 3 - MĐ234 - Năm 2018) Với giá trị nào của tham số m thì đồ thị ye 3 2 n
hàm số y  2x  3m  
1 x  6m  2 x 1 có cực đại, cực tiểu thỏa mãn x  x  2 CĐ T C th it r Ⓐ. m 1 Ⓑ. m  2 Ⓒ. m  1  Ⓓ. m  2  acn Lời giải gh Chọn C ie Ta có 2
y  6x  6m  
1 x  6m  2 m.vn x  
Giải phương trình y  0 2
 6x  6m 
1 x  6m  2  1 0   x  2  m
Để đồ thị hàm số có cực đại cực tiểu thì 2  m  1   m  3   m  m  1  t / m
Theo giả thiết ta có x
 x  2  1 m  1 2 2    CĐ T C 1m  2  m  3  loai Vậy m  1 
Câu 144: (Chuyên Hoàng Văn Thụ - Hòa Bình - Năm 2018) Tìm tất cả các giá trị thực của tham số m ht để hàm số 3
y  x  m   2 3
1 x 12mx  3m  4 có hai điểm cực trị x , x thỏa mãn x  3  x . 1 2 1 2 tps://www 3 3 Ⓐ. m 1 Ⓑ. m 1 Ⓒ. m  Ⓓ. m  2 2 .fa Lời giải ceboo Chọn D Ta có 2
y  3x  6m   1 x 12m . k.com x  2 2
y  0  3x  6m   2
1 x 12m  0  x  2m  
1 x  4m  0   . /v x  2m iet
Bởi vậy, hàm số đã cho có hai điểm cực trị x , x thỏa mãn x  3  x khi và chỉ khi gold 1 2 1 2 3
2  3  2m  m  . 2
Câu 145: (THPT QUẢNG XƯƠNG - THANH HÓA - LẦN 04 - NĂM HỌC 2017-2018) Cho hàm số f  x 3
 x  m   2 2
1 x  3mx  m có đồ thị C
. Có bao nhiêu giá trị nguyên của tham số m m  thuộc  2  018;201 
8 để đồ thị C
có hai điểm cực trị nằm khác phía so với trục hoành. m  Ⓐ. 4033. Ⓑ. 4034 . Ⓒ. 4035 . Ⓓ. 4036 . Lời giải Chọn B 66
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
- Xét phương trình f  x  0  3
x   m   2 2
1 x  3mx  m  0   x   2
1 x  2mx  m  0 x 1   . 2
x  2mx  m  0
Suy ra đồ thị C có hai điểm cực trị nằm khác phía so với trục hoành khi và chỉ khi phương m  trình 2
x  2mx  m  0 có hai nghiệm phân biệt khác 1 2
  m  m  0    m 0     m.vn   hay m  ;0 1; . 1   m  0 m 1 ie gh m  Lại do:  nên m 2  017; 2  016;...; 1  ;2;3;...;201  8 . m   2  018;2018 racn it
Vậy có tất cả 4034 giá trị của m thỏa mãn yêu cầu bài toán. th n
Câu 146: (THPT THÁI PHIÊN - HẢI PHÒNG - LẦN 04 - NĂM 2017-2018) Cho hàm số ye 1 3 y 
mx  m   2
1 x  3m  2 x  2018 với m là tham số. Tổng bình phương tất cả các giá trị lu 3 s://
của m để hàm số có hai điểm cực trị thỏa mãn 2x  x  2 . 1 2 ttp h 52 34 10 73 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 9 9 9 16 Lời giải Chọn A 2
y  mx  2m  
1 x  3m  2 . m  0  m  0
Hàm số có hai cực trị        m 2
1  3m m  2  0 2  2
 m  4m 1  0 m  0  /vietgold    2  6 2  6  . m    ;    2 2    k.com 2m   1 3m  2
Theo Vi-et, ta có: x  x  1 ; x x  2 . 1 2   1 2   ceboo m m .fa 2m  2 2 2m  4
Từ giả thiết  x  2  2x . Thay vào  
1 , ta được: 2  x   x   x  2 1 1 m 1 m 2 m 2 2m  4 3m  6
Thay vào 2 , ta được: .  m m m https://www m  2 2  
4m  8  3m  6m 2
 3m 10m 8  0  4  . m   3 2  4  52
Vậy tổng bình phương tất cả các giá trị của m là: 2 2     .  3  9 --- HẾT ---
Câu 147: (Chuyên Hà Tĩnh - Lần 01 - Năm 2018 - 2019) Tổng tất cả các giá trị của tham số thực m sao cho đồ thị hàm số 3 2 3
y  x  3mx  4m có điểm cực đại và cực tiểu đối xứng với nhau qua đường
phân giác của góc phần tư thứ nhất là 67
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 2 1 1 Ⓐ. Ⓑ. Ⓒ. 0 Ⓓ. 2 2 4 Lời giải Chọn C x  0 Ta có: 2
y  3x  6mx , y  0   . x  2m
Để hàm số có cực đại cực tiểu thì m  0 . 3 h
Khi đó các điểm cực trị của đồ thị hàm số là A0;4m  , B2m;0 . ttp 3 s://
Ta có I m;2m  là trung điểm của đoạn thẳng AB . lu
Đường phân giác của góc phần tư thứ nhất là d : x  y  0. ye
Do đó để điểm cực đại và cực tiểu đối xứng với nhau qua d thì: n 3 th
2m  4m  0 2 2 
 1 2m  0  m   . it 3
m  2m  0 2 rac
Vậy tổng tất cả các giá trị của tham số thực m là 0 . n gh
Câu 148: (Chuyên Trần Phú - Hải Phòng - Lần 02 - Năm 2017 - 2018) Gọi m , m là các giá trị của ie 1 2 m.vn
tham số m để đồ thị hàm số 3 2
y  2x  3x  m 1 có hai điểm cực trị là B , C sao cho tam giác
OBC có diện tích bằng 2 , với O là gốc tọa độ. Tính m m . 1 2 Ⓐ. 15  Ⓑ. 12 Ⓒ. 6 Ⓓ. 20  Lời giải Chọn A
x  0  y  m 1 B0;m   1 O
 B  0;m    1 Ta có 2
y '  6x  6x  0    
x 1 y  m  2  C  1;m2 O  C   1;m 2 ht 1 1 tp  S
 0.m  2 m   1 .1  m 1 . OBC s://www 2 2 m  Bài ra S  1 2  m 1  5 2   m m  15  . OBC  2 m  3  1 2 .fa
Câu 149: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) Tìm tất cả các giá trị của tham số m để ceboo hàm số 3 2
y  x  3x  mx 1 có điểm cực trị x , x thỏa mãn 2 2 x  x  3 . 1 2 1 2 k.com 3 3 Ⓐ. 3  Ⓑ. 3 Ⓒ.  Ⓓ. /v 2 2 iet Lời giải gold Chọn D Ta có 2 2
y  3x  6x  ;
m y  0  3x  6x  m  0
Để hàm số có hai điểm cực trị thì 
  93m  0  m  3 (1) x  x  2 1 2  Theo viet ta có:  m x x   1 2  3 Khi đó m 3 x  x
 x  x 2 2 2 2
 2x x  3  2  2.  3  m  thỏa mãn điều kiện. 1 2 1 2 1 2 3 2
Chú ý: Với những bài thuộc dạng này ta có thể tìm điều kiện (1) sau. Ví như bài toán này khi ra 68
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” 3 kết quả m 
thì ta cũng chắc chắn rằng kết quả đó đúng (Vì các phương án của bài toán cho 2
một kết quả m ) mà không cần thử lại điều kiện. Do đó trong một số bài toán ta không cần kiểm tra điều kiên (1).
Câu 150: (Pen M - Nguyễn Thanh Tùng - Năm 2017 - 2018) (Chuyên Thái Bình – lần 3) Tìm tất cả 1 1
các giá trị thực của tham số a sao cho hàm số 3 2 y  x 
x  ax 1 đạt cực trị tại x , x thỏa 3 2 1 2 m.vn mãn 2 2
(x  x  2a)(x  x  2a)  9 ie 1 2 2 1 gh Ⓐ. a  2 Ⓑ. a  4  Ⓒ. a  3  Ⓓ. a  1  racn Lời giải it Chọn B th n Ta có: 2 2
y  x  x  ;
a y  0  x  x  a  0 (*) ye
Cách 1: ( Giải xuôi) lu 1 s://
Để hàm số có hai điểm cực trị thì  1 4a  0  a  (2*) 4 ttp h x  x 1
Với x , x là nghiệm của (*) nên ta có 1 2  (3*) 1 2 x x   a 1 2 Biến đổi 2 2 2 3 3 2 2 2
(x  x  2a)(x  x  2a)  (x x )  (x  x )  2a(x  x  x  x )  x x  4a $$ 1 2 2 1 1 2 1 2 1 2 1 2 1 2 2 3 2 2
 (x x )  (x  x ) 3x x (x  x )  2a (x  x )  2x x  x  x   x x  4a 1 2 1 2 1 2 1 2  1 2 1 2 1 2  1 2 (2*) 2 2 2 2
 a 13a  2a(1 2a 1)  a  4a  a  2a 1 (a 1) . (2*) a  2
Khi đố điều kiện của bài toán tương đương: 2 (a 1)  9  a  4    Chọn B a  4  Cách 2: ( Giải ngược) /vietgold
+) Thử a  2 , (*) có dạng 2
x  x  2  0 (vô nghiệm), vậy a  2 không thỏa mãn. k.com  1 17 x  1 2 2 x  x     ceboo 4 0 +) Thử a  4  , (*) có dạng   .fa 1 17 x  2  2 1 17 1 17
Lúc này sử dụng casio, gán x   A và x   B 1 2 2 2 https://www Sau đó nhập biểu thức 2 2
(A  B  8)(B  A  8) vào máy: 69
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
Ta được kết quả là 9 (thỏa mãn)  Chọn B
Chú ý:Nếu bài toán này câu hỏi là “Tìm giá trị gần a nhất “ thì ta không giải được theo chiều h ttp ngượⒸ. s://
Câu 151: (Chuyên Hùng Vương - Gia Lai - Lần 2 - 2018) Gọi A , B là hai điểm cực trị của đồ thị hàm lu ye số f  x 3 2
 x 3x  m với m là tham số thực khác 0 . Tìm tất cả các giá trị thực của tham số nth
m để trọng tâm tam giác OAB thuộc đường thẳng 3x  3y 8  0 . it ra
Ⓐ. m  5.
Ⓑ. m  2 .
Ⓒ. m  6. Ⓓ. m  4 . cngh Lời giải ie Chọn A m.vn x 
TXĐ: D  , f x 2
 3x  6x , f x  0 0   . x  2
Tọa độ 2 điểm cực trị là A0; m ; B2; m  4 .  2 2m  4 
Tọa độ trọng tâm G của tam giác OAB là G ;   .  3 3 
Điểm G thuộc đường thẳng: 3x  3y 8  0 nên: 2  2m  4 8  0  m  5 .
Câu 152: (Chuyên Hạ Long - Lần 03 - Năm 2017 - 2018) Gọi S là tập hợp tất cả các giá trị thực của 1 3 2 2
tham số m để đồ thị của hàm số y 
x  mx  m  
1 x có hai điểm cực trị là A và B sao ht 3 tps://www
cho A , B nằm khác phía và cách đều đường thẳng y  5x  9 . Tính tích các phần tử của S . Ⓐ. 3 Ⓑ. 0 Ⓒ. 18 Ⓓ. 27  .fa Lời giải ceboo Chọn D x  m  k.com Ta có: 2 2
y  x  2mx  m 1   x  m  
1  x  m   1 ; y  1 0   . x  m 1 /v
Vì m 1  m 1 với mọi giá trị m nên đồ thị hàm số luôn có hai điểm cực trị là iet 3  m 2  3  m 2  gold A m 1;
 m   và Bm 1;  m   .  3 3   3 3 
A , B nằm khác phía và cách đều đường thẳng y  5x  9 . 3    m
A d : y  5x  9 và trung điểm I  ; m
 m của AB thuộc d .  3  3 m 2
 m   5m  5  9  m  3  3 3    3
 m 18m  27  0  m  4  ,9 3 
m  m  5m 9   m  1, 9   3 70
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Vậy tích các phần tử của S bằng 27  .
Câu 153: (Chuyên Quốc Học Huế - Lần 03 - Năm 2017 - 2018) Cho hàm số 3 3m 3 2 f (x) x m 1 x 3mx
với m là tham số thựⒸ. Có tất cả bao nhiêu giá trị nguyên 2 2
của m thuộc khoảng
20;18 sao cho đồ thị của hàm số đã cho có hai điểm cực trị nằm cùng
một phía đối với trục hoành? m.vn Ⓐ. 1. Ⓑ. 19. Ⓒ. 20 . Ⓓ. 18. ie Lời giải gh Chọn D    racn x 2         it Ta có f (x) 3x 3m 
1 x 3m , f  x 1 0  . x  m th n
Hàm số có cực trị thì m  1  . ye
Đồ thị của hàm số đã cho có hai điểm cực trị nằm cùng một phía đối với trục hoành lu
 y   ym 1 1 .  0   m 2
m  3m  3    s:// 0 m 0 . 4 ttp
Suy ra m  0 và m  1  . h Vậy trong khoảng
20;18 có 18 giá trị nguyên của m thỏa mãn bài toán.
Câu 154: (Chuyên Lê Hồng Phong - HCM - Năm 2017 - 2018) Tìm tổng tất cả các giá trị thực của m
sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y  x  m   2 2 3
1 x  6m1 2m x song song với đường thẳng y  4  x . 1 2 2 Ⓐ. m 1.
Ⓑ. m   . Ⓒ. m  .
Ⓓ. m   . 3 3 3 Lời giải /vietgold Chọn B 3
y  x  m   2 2 3
1 x  6m1 2m x . k.com 2
y '  6x  6m  
1 x  6m1 2m . ceboo
  m  2  m  m  m  m    m  2 2 ' 9 1 36 1 2 81 54 9 9 3 . .fa 1
Hàm số có hai điểm cực trị  m  . 3
Ta có phương trình đường thẳng qua hai điểm cực trị có dạng: 2 2  b  bc https://www y  c   x  d  3  3a  9a  y   2
 m  m   3 2 9 6
1 x  2m  3m  m
Để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y  x  m   2 2 3
1 x  6m1 2m x
song song với đường thẳng y  4  x thì: m 1  2 2   9
 m  6m 1  4   9
 m  6m  3  0  1 1      m    m   3 2 3 2
2m 3m  m  0
2m 3m  m  0  3 3  3 2
2m 3m  m  0 71
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 1
Tìm tổng tất cả các giá trị thực của m là . 3
Câu 155: (NXBGD - Đề số 4 - ĐOÀN QUỲNH - Năm 2017 - 2018) Tìm các giá trị của tham số m để đồ thị hàm số 3
y  x   m   2 2 3 2
1 x  6mm  
1 x 1 có hai điểm cực trị cách đều trục tung. 1
Ⓐ. Không tồn tại giá trị nào.
Ⓑ. m   . 2 h 1 ttp Ⓒ. m  2 .
Ⓓ. m  2,m   . 2 s:// Lời giải lu Chọn B ye
Tập xác định D  n th 2
y  6x  62m  
1 x  6mm   1 it ra
Để hàm số có hai điểm cực trị cách đều trục tung  y  0 có hai nghiệm phân biệt x ; x thỏa 1 2 cn   gh mãn x x 0 1 2 ie 2   0  3
 2m  32m 1  0 1 m.vn      m   . x  x  0  2m 1  0 2 1 2 Câu 1. Câu 156:
(NXBGD - ĐOÀN QUỲNH - Đề số 05 - Năm 2021) Tìm các giá trị của tham
số m sao cho đồ thị hàm số 3 2 3
y  x  3mx  4m có hai điểm cực trị đối xứng nhau qua đường thẳng y  x . 2 Câu 2. Ⓐ. m  0. Ⓑ. m  . Ⓒ. 2 2 m   . Ⓓ. m 1. ht 2 tps://www Lời giải Chọn C x  0 .fa Ta có 2
y '  3x  6mx  3x  x  2m; y '  0   . ceboo x  2m
Để đồ thị hàm số có hai điểm cực trị  y '  0 có hai nghiệm phân biệt  m  0 . k.com Gọi ,
A B là hai điểm cực trị của đồ thị hàm số và giả sử A 3
0; 4m , B2 ; m 0 . /v Theo giả thiết ,
A B đối xứng với nhau qua đường thẳng
y  x nên ta có ietgold 1 2 3 2
4m  2m  m   m   . 2 2
Câu 157: (NXBGD - Đoàn Quỳnh - Đề số 07 - Năm 2018) Tìm các giá trị của tham số m sao cho đồ thị hàm số 3 2 y 2x mx
12x 13 có các điểm cực đại, cực tiểu và các điểm đó có khoảng cách
bằng nhau đến trục tung.
Ⓐ. m 0.
Ⓑ. m 1.
Ⓒ. m 2 . Ⓓ. m 3 . Lời giải Chọn A 2 y 6x 2mx 12 72
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” Phương trình y 0 có P
0 nên luôn có hai nghiệm phân biệt x ;x 1 2
Do đó hàm số luôn có hai cực trị
Các điểm cực đại và cực tiểu có khoảng cách đến trục tung bằng nhau nên x x 1 2 2m Hay x x 0 0 m 0 1 2 . 6
Câu 158: (NXBGD - Đề số 14 - Năm 2018) Cho đồ thị C của hàm số m  3 2 2 2 m.vn
y  x  3mx  3m  
1 x  m 1 và điểm M  2
 ;2. Biết đồ thị C có hai điểm cực trị m  ie ,
A B và tam giác ABM vuông tại M . Hỏi giá trị nào của m cho cưới đây thoả mãn bài toán đã gh cho? racn it Ⓐ. m  1.  Ⓑ. m 1. th n
Ⓒ. Không có m 1.
Ⓓ. Có vô số giá trị của . m ye lu Lời giải s:// Chọn A ttp 2
y  x  mx   2 3 6 3 m   1 h   0 x 
y  0  x  m 1 Am 1; 3
 m  3, Bm 1; 3  m   1
MA  m 1; 3  m   1
MB  m  3; 3  m  3 m  0 2 M .
A MB  0  10m 10m  0  .  m  1 
/vietgold Câu 159: (NXBGD - Phạm Đức Tài - Đề 20 - Năm 2017-2018) Tìm tất cả các giá trị thực của tham số
m để đồ thị C của hàm số 3 2 3
y  x  3mx  2m có hai điểm cực trị M , N sao cho dường m  k.com
thẳng MN vuông góc với đường thẳng d : y  2  x . ceboo  1 1  1 1  1 1  1 1 .fa
Ⓐ. m ; .
Ⓑ. m ; .
Ⓒ. m ; .
Ⓓ. m ; .  2 2  4 2  2 4  4 4 Lời giải Chọn A
Phương trình đường thẳng MN : 2 3
y  2m x  2m . https://www 1 1 2 2
MN  d  2m .( 2  )  1
  m   m   . 4 2
Câu 160: (Vted - Đề số 16 - Năm 2017 - 2018) Khi đồ thị hàm số 3
y  x  3mx  2 có hai điểm cực trị A, B và đường tròn 2 2
(C) : (x 1)  ( y 1)  3 cắt đường thẳng AB tại hai điểm phân biệt M,N sao
cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN.
Ⓐ. MN  3.
Ⓑ. MN  1.
Ⓒ. MN  2.
Ⓓ. MN  2 3. Lời giải Chọn D 73
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021
Ta có điều kiện để hàm số có hai điểm cực trị là m  0 và AB : y  2  mx  2.
Đường tròn (C) có tâm I(1;1), R  3. Ta có 2 2  2  m 1 
 4m  2m 1 2 2
MN  2 R  d (I , AB)  2 3     2 2   2 3. 2 2     4m  1 4m 1  1
Dấu bằng đạt tại m  . 2    h
Câu 161: (Đề 20- Vted- Năm 2017-2018) Có bao nhiêu số thực m để đồ thị hàm số 4 2 y x 2mx 2 có ttp  3 9  s:// ba điểm cực trị , A ,
B C sao cho tứ giác ABCD nội tiếp với D ;   .  5 5  lu ye Ⓐ. 4 . Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 1. n th Lời giải it Chọn B ra 3 2 c
y  4x  4mx ; y  0  4x  x  m  0 . n gh
Suy ra đồ thị hàm số có ba điểm cực trị  m  0 . Khi đó ba điểm cực trị của đồ thị hàm số là ie 2 2 m.vn
A0;2 , B m;2  m  , C  m;2  m .
Gọi I 0; h là tâm đường tròn ngoại tiếp tứ giác ABCD . 3 4m  m 1
Ta có: IA  IB    h  m    h  m 2 2 2 2 2 2 2  h  . 2m 2 2 9  9  Lại có: 2 2
IA  ID  2  h    h  h 1   . 25  5  m 1 Vậy suy ra 3
4m  m 1 2m  0 3
 2m  m 1  0   . Phương trình này có ba 2
m  m 1  0 http
nghiệm trong đó có hai nghiệm dương. Vậy Chọn B s://www
Nhận xét: Bài toán trên là bài toán liên quan đến cực trị của hàm bậc 4 trùng phương và một
điều kiện hình họⒸ. Phương pháp giải là ta xác định tọa độ các điểm cực trị của đồ thị hàm số
rồi dựa vào đặc điểm của chúng để thiết lập các mối quan hệ (phương trình) thỏa yêu cầu bài .fa toán. ceboo
Các bài tương tự: Tìm điều kiện để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều;
tam giác cân có góc ở đỉnh bằng 120 ,…; tam giác có bán kính đường tròn ngoại tiếp bằng 2; k.com …. /v
Câu 162: (ĐTD - Đề thi thử đại học - Năm 2017 - 2018) Tìm tất cả các giá trị thực của tham số m để iet 3 3 2 gold
M 2m ;m cùng với hai điểm cực trị của đồ thị hàm số y  2x 32m  
1 x  6mm   1 x 1
tạo thành một tam giác có diện tích nhỏ nhất. Ⓐ. m  2 . Ⓑ. m  0. Ⓒ. m 1. Ⓓ. m  1  . Lời giải Chọn B 2
y  6x  62m  
1 x  6mm   1 2
y  0  6x  62m  
1 x  6mm   1  0 2
 x 2m  
1 x  mm   1  0 74
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng”
Ta có   1  0 m
  nên đồ thị luôn có 2 cực trị.
Phương trình đường thẳng đi qua hai điểm cực trị 3 2
y  x  2m  3m  m 1
Hai điểm cực trị có tọa độ là A 3 2
m 1; 2m  3m  , B 3 2 ;
m 2m  3m   1 1 1  S  M , A MB  m   ABC    1 2 3 1 2 2 2 1 min S   m  0 . ABC 2 m.vn ie
Câu 163: (WORD VD - VDC - Đề 05- NĂM 2018) Tìm tất cả các giá trị thực của tham số m để điểm gh M  3 2m ; m  
1 cùng với hai điểm cực trị của đồ thị hàm số 3
y  x   m   2 2 3 2
1 x  6mm   1 x racn
tạo thành một tam giác có diện tích nhỏ nhất. it th Ⓐ. m 1 Ⓑ. m  2 Ⓒ. m  0 Ⓓ. m  1  n ye Lời giải lu Chọn C s:// x  m Ta có 2
y '  6x  62m  
1 x  6mm   1 và y '  0   . ttp x  m 1 h  1 2m 1 Lại có : y  x 
.y ' x  m m   1 2m    
1 suy ra phương trình đường thẳng đi qua 2  3 6 
cực trị là : y  x  mm   1 2m   1 . Suy ra CT A ; m mm   1 2m   1  m ;
CĐ : Bm 1; mm   1 2m   1  m   1  AB  2 . 2 2 3
 m 1 3m 1 Có d   . M ; AB /vietgold 2 2 2 1 3m 1 1 S  AB d    k.com Mà .  MAB  . M ; AB 2 2 2 2
Dấu ‘=’xảy ra khi  m  0. ceboo
.fa Câu 164: (NXBGD - PHẠM ĐỨC TÀI - ĐỀ 12 - NĂM 2018 ) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 3 2 3
y  x  3mx  4m có hai điểm cực trị ,
A B sao cho AB  20 . Ⓐ. m 1  ;  2 . Ⓑ. m 1  ;  1 . Ⓒ. m . Ⓓ. m 2  ;  1 . Lời giải https://www Chọn B x  0 Ta có 2
y '  3x  6mx  3x  x  2m; y '  0   . x  2m
Để đồ thị hàm số có hai điểm cực trị  m  0 . Giả sử A 3
0; 4m , B2 ; m 0 . Theo giả thiết 2 2 6
AB  20  AB  20  4m 16m  20  m 3 2   2 m  2 4
5  0  m 1 m  1  (thỏa mãn). 75
 Quảng Thuận – Ba Đồn – Quảng Bình
Cực trị hàm số bậc ba trong các đề thi 2017 - 2021 Câu 165: (THPT An Lão - Hải Phòng - Năm 2018) Cho hàm số 1 3 y 
mx  m   2
1 x  3m  2 x  2018 với m là tham số. Tổng bình phương tất cả các giá trị 3
của m để hàm số có hai điểm cực trị x , x thỏa mãn x  2x  1 bằng 1 2 1 2 25 22 8 40 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 4 9 3 9 Lời giải h Chọn D ttp Ta có 2        * s:// y mx 2m  1 x 3m 2 0 lu m  0 ye 
Hàm số có hai điểm cực trị x , x thỏa mãn x  2x  1 khi và chỉ khi   0   1 . 1 2 1 2 n th x  2x 1 2  1 2   it ra 2  6 2  6 2 c Ta có   1  2
 m  4m 1  0   m    * . n 2 2 gh 2m   1 ie
Mặt khác ta có x  x  3 1 2 m.vn m 2  m
Từ 2 và 3 ta có x  mà * nên 2 2
x là nghiệm của   m   2  m 2 2  m  2  m Vì m  2   m  2 1 .
 3m  6  0  3m 8m  4  0   thỏa mãn * .  2 m  m m   3 2  2  40
Vậy tổng bình phương các giá trị của m là: 2 2     .  3  9 ht
Câu 166: (Vted - Đề số 09 - Năm 2017 - 2018) Biết hàm số 3 2
f (x)  x  x  mx có một cực trị bằng 1. tps://www
Cực trị còn lại của hàm số đã cho bằng 5 13 11 5 Ⓐ.  . Ⓑ. . Ⓒ. . Ⓓ. . 27 27 27 27 .fa Lời giải ceboo Chọn A k.com
Theo giả thiết f  x  0 có hai nghiệm phân biệt x , x và f  x  1, ta cần tìm f  x 2  1  1 2 Ta có 2 f (
 x)  0  3x  2x  m  0 phương trình này có hai nghiệm phân biệt khi và chỉ khi /viet 1 
 1 3m  0  m  . gold 3  2 x  x    1 2  Khi đó theo vi 3 -ét ta có  và 3 2
f (x )  1  x  x  mx  1, m  1 1 1 1 x x  1 2  3   Khi đó rút 2 2
m  3x x  3x   x  2
 x  3x và thay vào đẳng thức cuối có 1 2 1  1  1 1  3  3 2 2 3 2
x  x  x ( 2
 x 3x ) 1 2x  x 1 0  x  1   m  1
 (thoả mãn điều kiện). 1 1 1 1 1 1 1 1 76
 Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không với lười biếng” 3 2 2 1  1   1   1  5 Vậy 3 2
f (x)  x  x  x, x  1
 , x   1   f (x )      . 1 2 2       3 3  3   3   3  27 m.vn ie
THAM GIA LỚP LUYỆN THI gh CHẤT LƯỢNG CAO racn it MR.VIỆT MATH CLASS th n ye lu
82 Võ Thị Sáu - TDP Bến Chợ – Phường Q.Thuận - T.xã Ba
Đồn –Tỉnh Quảng Bình s:// ttp h LIÊN
http://luyenthitracnghiem.vn HỆ
0905 193 688 (Điện thoại hoặc nhắn tin)
Facebook: https://www.facebook.com/vietgold /vietgold k.com ceboo .fa https://www 77

166 bài toán cực trị hàm số bậc ba trong các đề thi thử THPT môn Toán

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số