



























































































Preview text:
GV. LƯƠNG ANH NHẬT CHUYÊN ĐỀ
NGUYÊN HÀM – TÍCH PHÂN – ỨN 3 G DỤNG
TỪ ĐỀ CÁC TRƯỜNG CHUYÊN 2020 - 2021 GV. LƯƠNG ANH NHẬT
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 NGUYÊN HÀM
ĐỊNH NGHĨA – TÍNH CHẤT – NGUYÊN HÀM CƠ BẢN Câu 1:
(CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Mệnh đề nào sau đây sai? Ⓐ 1
dx = ln x + C . Ⓑ x x
e dx = e + C . x 2 + Ⓒ x 1 xdx = + C . Ⓓ
sin xdx = cos x + C . 2 Câu 2:
(CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Hàm số f ( x) 4 2 = x −3x có họ nguyên hàm là Ⓐ F ( x) 3
= x − 6x + C. Ⓑ F (x) 5 3
= x + x + C. x x Ⓒ F ( x) 5 3 = + x + C. Ⓓ F ( x) 5 3 = − x + C. 5 5 Câu 3:
(CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Họ nguyên hàm của hàm số ( ) 2 x
f x = e là Ⓐ ( ) 2x F x = e + C. Ⓑ ( ) 3x
F x = e + C. Ⓒ ( ) 1 2 = 2 x F x e + C. Ⓓ ( ) 2 x F x = e + C. 2 Câu 4:
(CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Họ nguyên hàm của hàm số
y = 5 − 3x là: Ⓐ 2 ( 2 2 1 5 − 3x)3 + C. Ⓑ − 5 − 3x + C. Ⓒ −
(5−3x)3 +C. Ⓓ 5 − 3x + C. 9 3 9 2 Câu 5: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) 3 2
= 4x − 3x + 2x −1. Trong các khẳng định sau, khẳng định nào đúng? Ⓐ f (x) 4 3 2
dx = 4x − x + x − x +C . Ⓑ f (x) 4 3 2
dx = x − x + x − x +C . Ⓒ f (x) 1 4 3 2
dx = x − x + x − x + C . Ⓓ f (x) 4 3 2
dx =12x −6x + x − x +C . 4 Câu 6:
(CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) = sin 3x . Trong
các khẳng định sau, khẳng định nào đúng? Ⓐ f (x)dx = 3 − cos3x +C . Ⓑ f
(x)dx =3cos3x+C. Ⓒ f (x) 1
dx = − cos3x + C . Ⓓ f (x) 1
dx = cos3x + C . 3 3 Câu 7:
(CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho F ( x) là
một nguyên hàm của hàm số f ( x) = sin 2x và F =1 . Tính F . 4 6 1 5 3 Ⓐ F = . Ⓑ F = . Ⓒ F = . Ⓓ F = 0 . 6 2 6 4 6 4 6
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 1 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Câu 8:
(CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Họ tất cả các 2
nguyên hàm của hàm số f (x) = sin x + . x Ⓐ 2 cos x − + C .
Ⓑ − cos x + 2ln x + C . 2 x
Ⓒ − cos x − 2ln x + C .
Ⓓ cos x + 2ln x + C . Câu 9:
(CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho C là
một hằng số. Trong các mệnh đề sau, mệnh đề nào sai ? Ⓐ 2
2x dx = x + C . Ⓑ
sinx dx = cos x + C . 1 Ⓒ
dx = ln | x | +C . Ⓓ ex d = ex x −C . x
Câu 10: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho hàm số
f ( x) = sin 3x . Trong các khẳng định sau, khẳng định nào đúng? Ⓐ f
(x)dx =3cosx+C . Ⓑ f (x) 1 dx = cos x + C . 3 Ⓒ f
(x)dx =3cos3x+C. Ⓓ f (x) 1
dx = − cos 3x + C . 3
Câu 11: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Họ nguyên hàm của hàm số ( ) = ex f x + x là: 2 2 2 Ⓐ 1 x x x 1 + 1 x ex + + C .
Ⓑ ex +1+ C . Ⓒ e +
+ C . Ⓓ ex + + C . 2 x +1 2 2 2
Câu 12: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tìm họ nguyên hàm 1 x + dx x −1 2 Ⓐ 2 1 x 1
x + ln x −1 + C . Ⓑ x + + C . Ⓒ
+ ln x −1 + C . Ⓓ 1− + C . x −1 2 (x − )2 1
Câu 13: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số F ( x) , f ( x) liên
tục trên khoảng K , khi đó F ( x) là một nguyên hàm của hàm f ( x) trên khoảng K
nếu với mọi x K ta có
Ⓐ F ( x) = f ( x).
Ⓑ F (x) = f (x) .
Ⓒ F( x) = f ( x).
Ⓓ F (x) = f (x) .
Câu 14: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số
f ( x) = cos 2x . Trong các khẳng định sau, khẳng định nào đúng? x x Ⓐ f (x) sin 2 dx = − + C . Ⓑ f (x) sin 2 dx = + C . 2 2 Ⓒ f (x)dx = 2
− sin 2x + C . Ⓓ f
(x)dx = 2sin2x+C .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 2 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 15: Tìm họ nguyên hàm của hàm số f ( x) 2 = 3x . Ⓐ f
(x)dx = 6x+C. Ⓑ f
(x)dx = x+C. 1 Ⓒ f (x) 3
dx = x + C . Ⓓ f (x) 3 dx = x + C . 3
Câu 16: Tìm họ nguyên hàm của hàm số f (x) = 2x + cos 2 . x 1 Ⓐ 2
x − sin 2x + C . Ⓑ 2 x + sin 2x + C . 2 1 Ⓒ 2
x + sin 2x + C . Ⓓ 2 x − sin 2x + C . 2
Câu 17: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) tan d x x bằng 1 1 Ⓐ − + C .
Ⓑ ln cos x + C . Ⓒ + C .
Ⓓ −ln cos x + C . 2 sin x 2 cos x
Câu 18: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Một nguyên 1
hàm của hàm số f (x) = là F(x) bằng 2x − 3 Ⓐ 2 1 1 − ( . Ⓑ . Ⓒ 2ln 2x − 3 . Ⓓ ln 2x − 3 . 2x − 3)2 2 (2x − 3)2 2
Câu 19: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Họ nguyên hàm của hàm số ( ) 2 x f x = e là Ⓐ 1 1 x e + C . Ⓑ 2 x e + C . Ⓒ 2 2 x e + C . Ⓓ 2 x e + C . 2 2
Câu 20: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Họ các
nguyên hàm của hàm số ( ) = 5x f x − x là x 2 5 x 2 x 5x Ⓐ − + C . Ⓑ 2
5x − x + C . Ⓒ 5x ln 2 − + C . Ⓓ −1+ C . ln 5 2 2 ln 5
Câu 21: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Họ
nguyên hàm của hàm số f ( x) = sin x + 4x là Ⓐ 2
−cos x + 4x +C . Ⓑ 2
cos x + 4x + C . Ⓒ 2
−cos x + 2x +C . Ⓓ 2
cos x + 2x + C .
Câu 22: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Tìm
nguyên hàm của hàm số f ( x) 1 = 3x− . 2 Ⓐ dx dx 1
= ln 3x − 2 + C . Ⓑ
= − ln 3x − 2 + C . 3x − 2 3x − 2 2 Ⓒ dx 1 dx 1 = ln 3x + 2 + C . Ⓓ
= ln 2 − 3x + C . 3x − 2 3 3x − 2 3
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 3 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 23: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Nguyên hàm
của hàm số f ( x) 3 = 2x −9 là. 1 Ⓐ 1 4
x − 9x + C . Ⓑ 3
4x − 9x + C . Ⓒ 4
4x − 9x + C . Ⓓ 4 x + C . 2 4
Câu 24: Tìm mệnh đề sai trong các mệnh đề sau 4 x + C Ⓐ 3 x dx = . Ⓑ 2exd = 2 (ex x + C). 4 1 Ⓒ sin d
x x = C − cos x . Ⓓ
dx = ln x + C . x
Câu 25: Họ nguyên hàm của hàm số f ( x) = 2x + sin 2x là Ⓐ 2 1 x −
cos 2x + C . Ⓑ 2
x + 2 cos 2x + C . 2 Ⓒ 2 1 x +
cos 2x + C . Ⓓ 2
x − 2 cos 2x + C . 2
Câu 26: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Họ tất cả các nguyên hàm
của hàm số f (x) = 2x + 3 là
Ⓐ 2x2 + 3x + C . Ⓑ x2 2 + C . Ⓒ x2 + C .
Ⓓ x2 + 3x + C .
Câu 27: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho hàm số f ( x) 1
= 2x + +1. F (x) là một nguyên hàm của f ( x) thỏa mãn F ( ) 1 = 0 . Trong các x
khẳng định sau khẳng định nào đúng? Ⓐ F (x) 2
= x + x + ln x − 2 . Ⓑ F (x) 2
= x + x + ln x + 2 . Ⓒ F (x) 2
= x + x − ln x − 2 . Ⓓ F (x) 2
= x − x + ln x + 2 .
Câu 28: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Một nguyên hàm của hàm số 2
f (x) = 3x +1 là: Ⓐ 6x . Ⓑ 3 x +1. Ⓒ 3 x + x . Ⓓ 3 3x + x .
Câu 29: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Cho hàm số f ( x) 3
= 4x + 3. Mệnh đề nào sau đây đúng ? Ⓐ 1 f (x) 4
dx = x + 3x + . C Ⓑ f (x) 4 dx =
x + 3x + C. 4 Ⓒ f (x) 4
dx = 4x + 3x + . C Ⓓ f (x) 3
dx = 12x + 3x + . C
Câu 30: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Họ tất cả các x − 2
nguyên hàm của hàm số f (x) = trên khoảng (0; ) + là x 2 2 Ⓐ x + + C .
Ⓑ x − 2ln x + C .
Ⓒ x + 2ln x + C . Ⓓ x − + C . 2 x 2 x
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 4 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 31: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Họ nguyên hàm của hàm số 2
f (x) = 3x − sin x là
Ⓐ 6x − cos x + C . Ⓑ 3
x − cos x + C . Ⓒ 3
x + cos x + C . Ⓓ 3
x − sin x + C
Câu 32: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Tìm họ nguyên hàm của hàm số f ( x) 2
= 3x + sin x (C là hằng số) Ⓐ 3 x − cos x + . C
Ⓑ 6x + cos x + C. Ⓒ 3 x + cos x + . C
Ⓓ 6x − cos x + C.
Câu 33: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Tìm họ nguyên hàm của hàm số ( ) 3x
f x = e ( C là hằng số) 3x e Ⓐ ( ) 3 d = 3 x f x x e + C . Ⓑ f (x) x d = + C . 3 3x 1 + e Ⓒ ( ) 3x f x x d = e + C . Ⓓ f (x) x d = + C . 3x + 1 Câu 34:
(CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Một nguyên hàm của hàm số f ( x) 2 = 3x +1 là Ⓐ 6x . Ⓑ 3 x +1. Ⓒ 3 x + x . Ⓓ 3 3x + x .
Câu 35: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Tìm mệnh đề sai trong các mệnh đề sau 4 x + C Ⓐ 3 x dx = . Ⓑ 2 x = 2( x e dx e + C) . 4 Ⓒ 1
sin xdx = C − cos x . Ⓓ
dx = ln x + C . x
Câu 36: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Họ nguyên hàm của hàm số
f ( x) = 2x + sin 2x là: 1 1 Ⓐ 2
x − cos 2x + C . Ⓑ 2
x + 2cos 2x + C . Ⓒ 2 x +
cos 2x + C . Ⓓ 2
x − 2cos 2x + C 2 2
Câu 37: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Họ tất cả nguyên
hàm của hàm số f ( x) = cos 2x 1 1
Ⓐ 2sin 2x + C .
Ⓑ − sin 2x + C . Ⓒ
sin 2x + C . Ⓓ 2
− sin 2x + C . 2 2
Câu 38: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Cho f (x) 2
dx = 3x + 2x − 3 + C . Hỏi
f ( x) là hàm số nào?
Ⓐ f ( x) = 6x + 2 . Ⓑ f ( x) 3 2
= x + x −3x + C .
Ⓒ f ( x) = 6x + 2 + C . Ⓓ f ( x) 3 2
= x + x − 3x .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 5 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 39: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Họ tất cả các nguyên hàm của hàm
số f ( x) =1+ sin x là
Ⓐ 1+ cos x + C .
Ⓑ 1− cos x + C .
Ⓒ x + cos x + C .
Ⓓ x − cos x + C .
Câu 40: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Họ tất cả các nguyên hàm của hàm số ( ) 2x f x = e là 2 x x Ⓐ x e e e + C . Ⓑ 2x e + C . Ⓒ + C . Ⓓ + C . 2 2
Câu 41: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Họ các nguyên hàm của hàm
số f (x) = sin3x là 1 1
Ⓐ − cos3x + C .
Ⓑ −cos3x + C .
Ⓒ cos3x + C .
Ⓓ cos3x + C . 3 3
Câu 42: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số + f ( x) 2x 1 =
, x 1. Trong các khẳng định sau, khẳng định nào đúng? x −1 Ⓐ f
(x)dx =3ln x−1 +C, x 1. Ⓑ f
(x)dx =3ln(x− )1+C, x 1. Ⓒ f
(x)dx = 2x+3ln x−1 +C, x 1. Ⓓ f
(x)dx =3ln(x− )1+C, x 1. ( ) 2
f x dx = x + C f (2x)dx Câu 43: Biết . Tính 1 1 Ⓐ f (2x) 2 dx = x + C . Ⓑ f (2x) 2 dx = x + C . 2 4 Ⓒ f ( x) 2 2
dx = 2x + C . Ⓓ f ( x) 2 2
dx = 4x + C .
Câu 44: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Tìm nguyên hàm ( 3 4x + 2x + )1dx. 4 Ⓐ x 4 2
4x + 2x + x + C . Ⓑ 4 2
x + 2x + x + C . Ⓒ 4 2
x + x + x + C . Ⓓ 2
+ x + x + C . 4
Câu 45: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Biết rằng F ( x) là
một nguyên hàm của f ( x) = cos 2x trên
và F (0) = 0. Tính giá trị của biểu thức T = F + 2F . 2 4 Ⓐ 1 T = 2. Ⓑ T = 3. Ⓒ T = . Ⓓ T = 1. 2
Câu 46: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tính nguyên hàm 2 tan 2 d x x . 1 1
Ⓐ tan 2x − x + C . Ⓑ
tan 2x − x + C . Ⓒ
tan 2x + x + C . Ⓓ tan 2x + x + C . 2 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 6 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 47: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Cho 1
hàm số f ( x) xác định trên
\ thỏa mãn f ( x) 3 ' = ,
f (0) =1. Giá trị của 3 3x −1 f (− ) 1 bằng: Ⓐ 3ln 2 + 3. Ⓑ 2ln 2 +1. Ⓒ 3ln 2 + 4 . Ⓓ 12ln 2 + 3 .
Câu 48: (THPT CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021 LẦN 01) Với mọi hàm số f ( x)
; g ( x) liên tục trên
, cho các khẳng định sau: (I ) . f
(x)−g(x)dx = f
(x)dx− g (x)dx . (II ) . f
(x).g(x)dx =
( f (x)dx).( g(x)dx). (III ) . Nếu f
(x)dx = F(x)+C thì f
(u)du = F(u)+C . (IV ). kf
(x)dx = k f
(x)dx với mọi hằng số k .
Có bao nhiêu khẳng định sai? Ⓐ 4 . Ⓑ 1. Ⓒ 2 . Ⓓ 3 .
Câu 49: (THPT CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021 LẦN 01) Biết rằng ( a a 3 3 cos . x sin 3x + sin .
x cos 3x)dx = cos 4x + C với , a b , là phân số tối giản b b
(a 0,b 0), tính 2a +b . Ⓐ −13 . Ⓑ 13 . Ⓒ −10 . Ⓓ 10 .
Câu 50: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Cho F ( x) là một nguyên hàm của hàm số ( ) x
f x = e + 2x thỏa mãn F ( ) 3 0 = . Tìm F ( x) . 2 x 1 x 5 Ⓐ F ( x) 2 = e + x + . Ⓑ F ( x) 2 = 2e + x − . 2 2 x 1 x 3 Ⓒ F ( x) 2 = e + x + . Ⓓ F ( x) 2 = e + x + . 2 2
Câu 51: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho hàm số f ( x) 2
=1− 2cos x . Tìm nguyên hàm của f ( x) ? Ⓐ sin 2x sin 2x − + C . Ⓑ + C .
Ⓒ sin 2x + C .
Ⓓ −sin 2x + C . 2 2
Câu 52: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho F ( x) là một
nguyên hàm của hàm số f ( x) 1 =
F 0 = 1 . Giá trị F ( 2 − ) bằng 2x − , biết ( ) 1 1 1 1 Ⓐ 1+ ln 5 . Ⓑ (1+ ln5). Ⓒ 1+ ln 3 . Ⓓ 1+ ln 5 . 2 2 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 7 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 53: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Họ tất cả các
nguyên hàm của hàm số f ( x) 2 = 1; + là 4x − trên khoảng ( ) 3 1 1 Ⓐ 2ln (4x −3) + . C Ⓑ
ln (4x − 3) + C. Ⓒ
ln (4x − 3) + C.
Ⓓ 4ln (4x −3) + . C 2 4
Câu 54: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Họ các nguyên hàm của hàm số ( ) 2 1 3 x f x − = là x x x x Ⓐ 9 9 9 9 + C . Ⓑ + C . Ⓒ + C . Ⓓ + C . 3 3ln 3 6ln 3 6 1
Câu 55: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho F ( x) = là một 2 2x f ( x) nguyên hàm của hàm số
. Họ nguyên hàm của hàm số f ( x)ln x là x ln x 1 Ⓐ f (x) ln x 1 ln d x x = + + C . Ⓑ f (x)ln d x x = − + + C . 2 2 x x 2 2 x x ln x 1 Ⓒ ln x 1 f (x)ln d x x = − + + C . Ⓓ f (x)ln d x x = + + C . 2 2 x 2x 2 2 x 2x
Câu 56: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f ( x) thỏa mãn
( f (x))2 + f (x) f (x) 4 2 .
=15x +12x +1, x và
f (0) = 0. Tính giá trị của 2
A = 3 f (3) − 678 . Ⓐ 2018 . Ⓑ 2021. Ⓒ 2022 . Ⓓ 2019 .
Câu 57: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Cho hàm số
f ( x) xác định trên
, thỏa mãn f '( x) = 2x −1 và f (3) = 5 . Giả sử phương trình
f ( x) = 999 có hai nghiệm x và x . Tính tổng S = log x + log x . 1 2 1 2 Ⓐ 5 . Ⓑ 999 . Ⓒ 3 . Ⓓ 1001.
Câu 58: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Cho hàm số f x
có đạo hàm liên tục trên
và thoả mãn f x sin x 1
f x cos x với mọi số thực x . Tính f . 6 3 1 Ⓐ 1. Ⓑ 1. Ⓒ . Ⓓ . 2 2
Câu 59: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f ( x) thỏa mãn 1 1
(x+ )1 f (x)dx =10 và 2 f ( )1− f (0) = 2. Tính I = f (x)dx . 0 0 Ⓐ I =1. Ⓑ I = 8 . Ⓒ I = 8 − . Ⓓ I = 12 − .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 8 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 60: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tính nguyên hàm 2 3 2
x (2x −1) dx ( x − )3 3 2 1 ( x − )3 3 2 1 ( x − )3 3 2 1 ( x − )3 3 2 1 Ⓐ + C. Ⓑ + C. Ⓒ + C. Ⓓ + C. 18 3 6 9
Câu 61: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Khi tính x − 3 nguyên hàm dx
, bằng cách đặt u = x +1 ta được nguyên hàm nào? x +1 Ⓐ 2
2u(u − 4)du . Ⓑ 2 2(u −1)du . Ⓒ 2 2(u − 4)du . Ⓓ 2 (u − 4)du . dx
Câu 62: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Tính nguyên hàm x x+4
bằng cách đặt t = x + 4 ta thu được nguyên hàm nào? 2tdt 2d Ⓐ 2dt dt . Ⓑ . Ⓒ t . Ⓓ . 2 t − 4 ( 2t −4) ( 2t −4)t 2 t − 4
Câu 63: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Cho F(x) là một nguyên hàm của hàm f (x) trên . Hỏi 2
F (x ) là nguyên hàm của hàm số nào dưới đây: Ⓐ 2 . x f ( ) x . Ⓑ 2 .
x f (x ) . Ⓒ 2 f (x ) . Ⓓ 2 2 . x f (x ) .
Câu 64: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Cho F ( x) là một nguyên
hàm của hàm số f ( x) trên . Hỏi ( 2
F x ) là một nguyên hàm của hàm số nào dưới đây? Ⓐ 2 . x f ( x). Ⓑ ( 2 . x f x ). Ⓒ ( 2 f x ) . Ⓓ ( 2 2 . x f x ) .
Câu 65: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Cho hàm số
y = f (x) có đạo hàm và liên tục trên 1;2 , thỏa mãn 2
f (x) = xf (
x) − x . Biết
f (1) = 3. Tính f (2) . Ⓐ 16 . Ⓑ 2 . Ⓒ 8 . Ⓓ 4 .
Câu 66: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Cho f ( x) 2x 2 4
dx = e − x + . C Khi đó f
(−x)dx bằng 2 x x x 2 − x − x Ⓐ e 1 1 2 + 4x + C . Ⓑ 2 2 4e − x + C . Ⓒ 2 2 4
− e + x + C . Ⓓ 2 −e + + C 4 4 4 4 Câu 67: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Biết ( + ) 1 ln ln 2 ( ) = ln + + mx x n px dx x C với , m , n ,
p C là các số thựⒸ Khi đó, m + n + p 2 x x bằng Ⓐ e +1. Ⓑ e + 2 . Ⓒ 2e −1. Ⓓ 2e − 2 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 9 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 68: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho F(x) là một nguyên hàm của (x+ x +1)2021 2
hàm số f (x) =
và F (0) =1.Giá trị của F ( ) 1 bằng 2 x +1 ( + )2020 1 2 − 2021 ( + )2021 1 2 + 2020 Ⓐ . Ⓑ . 2020 2021 ( + )2020 1 2 + 2021 ( + )2021 1 2 − 2020 Ⓒ . Ⓓ . 2020 2021
Câu 69: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Cho hàm số f (x) liên tục và có đạo hàm trên (− 2; 2) \
0 , thỏa mãn f (1) = 0 và x 1
f '(x) + x ( f (x) e + 2) +
= 0 . Giá trị của f bằng f ( x) e 2 Ⓐ ln 3 . Ⓑ ln 6 . Ⓒ ln 7 . Ⓓ ln 5 .
Câu 70: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hai hàm số
u ( x),v( x) có đạo hàm lien tục trên . Chọn mệnh đề đúng? Ⓐ u
(x).v'(x)dx =u(x).v(x)+ u'
(x).v'(x)dx . Ⓑ u
(x).v'(x)dx =u(x).v(x)− u'
(x).v'(x)dx . Ⓒ u
(x).v'(x)dx =u(x).v(x)+ u'
(x).v(x)dx . Ⓓ u
(x).v'(x)dx =u(x).v(x)− u'
(x).v(x)dx .
Câu 71: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tính nguyên hàm 1 A
dx bằng cách đặt t
ln x . Mệnh đề nào dưới đây đúng? x ln x Ⓐ 1 1 A dt . Ⓑ A dt . Ⓒ A dt . Ⓓ A tdt . 2 t t
Câu 72: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Một nguyên
hàm của ln x bằng 1
Ⓐ x − x ln x . Ⓑ .
Ⓒ x + x ln x .
Ⓓ 1− x + x ln x . x
Câu 73: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tìm nguyên hàm (2x − )1ln d x x x x Ⓐ (x − x) 2 2 ln x − − x + C . Ⓑ (x − x ) 2 2 ln x + − x + C . 2 2 x x Ⓒ (x − x) 2 2 ln x + + x + C . Ⓓ (x − x) 2 2 ln x − + x + C . 2 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 10 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 74: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Cho ( ) = ( 2 + − ) 2ex F x ax bx c
là một nguyên hàm của hàm số ( ) = ( 2 + − ) 2 2020 2022 1 e x f x x x
trên khoảng (−;+ ) . Tính T = a − 2b + 4c . Ⓐ T = 1012 . Ⓑ T = 2012 − . Ⓒ T = 1004 . Ⓓ T = 1018 .
Câu 75: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Cho ( ) 2 F x = x là
một nguyên hàm của hàm số ( ) 2x
f x e . Họ tất cả các nguyên hàm của hàm số ( ) 2x f x e là Ⓐ 2
−x + 2x +C . Ⓑ 2
−x + x +C . Ⓒ 2 2
− x + 2x + C . Ⓓ 2
2x − 2x + C .
Câu 76: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Giả sử hàm số f ( x) có đạo
hàm liên tục trên. Biết rằng ( ) 3
G x = x là một nguyên hàm của ( ) 2 − x g x = e f ( x) trên
. Họ tất cả các nguyên hàm của 2 − x e f ( x) là Ⓐ 3 2 2
− x +3x +C . Ⓑ 3 2
2x + 3x + C . Ⓒ 3 2
x + 3x + C . Ⓓ 3 2
−x +3x +C .
Câu 77: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Cho hai hàm số f ( x), g ( x) có đạo hàm trên
và thỏa mãn f ( x) + g ( x) = , x
g( x) + f ( x) = −x x
. Biết f (0) = g (0) =1, tính f ( ) 1 . 2 2 − 2 + Ⓐ 1 e 2 e 2 − 2 . Ⓑ e + − 2 . Ⓒ . Ⓓ . e e 2e 2e
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 11 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 TÍCH PHÂN
ĐỊNH NGHĨA – TÍNH CHẤT – TÍCH PHÂN CƠ BẢN 1
Câu 78: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Cho f (x)dx = 2, 0 2 2 f
(x)dx =1. Tích phân f (x)dx bằng 0 1 Ⓐ 1. Ⓑ 2 . Ⓒ 1 − . Ⓓ 3 . Câu 79: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Cho 1 1 1 f
(x)−2g(x) dx =12 và g
(x)dx = 5. Khi đó f (x)dx bằng 0 0 0 Ⓐ 2 − . Ⓑ 12 . Ⓒ 22 . Ⓓ 2 . 2
Câu 80: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Giá trị của sin d x x 0 bằng Ⓐ 0 . Ⓑ 1. Ⓒ 1 − . Ⓓ . 2 1
Câu 81: (CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Tích phân 2020 x dx bằng 1 − 1 2 Ⓐ 2 . Ⓑ . Ⓒ . Ⓓ 0 . 2021 2021 2020 1 3 Câu 82:
(CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Nếu f
(x)dx = 3 và f (x)dx = 7 0 0 3
thì f ( x) dx bằng 1 Ⓐ 10 . Ⓑ 4 . Ⓒ 4 − . Ⓓ 21.
Câu 83: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho hàm số 2
y = f (x) có đạo hàm trên đoạn [0; 2], f (0) =1 và f '(x)dx = 3 − . Tính f (2) 0 Ⓐ f (2) = 4 − . Ⓑ f (2) = 3 − . Ⓒ f (2) = 2 − . Ⓓ f (2) = 4 .
Câu 84: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho 1
f ( x), g ( x) là các hàm số liên tục trên R thoả mãn f (x)dx = 3; 0 2 2 2 f
(x)−3g(x)dx = 4 và 2 f
(x)+ g(x)dx =8
. Tính f ( x)dx . 0 0 1 Ⓐ I = 0 . Ⓑ I = 2 . Ⓒ I =1. Ⓓ I = 3 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 12 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2
Câu 85: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Nếu f (x)dx = 5 1 2 2 và g
(x)dx = 9 thì 2 f
(x)+ g(x)dx bằng 1 1 Ⓐ 19 . Ⓑ 28 . Ⓒ 14 . Ⓓ 4 .
Câu 86: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Nếu 3 3 f
(x)−2xdx =5 thì f ( x)dx bằng 1 1 Ⓐ 9 . Ⓑ 13 . Ⓒ 10 . Ⓓ 12.
Câu 87: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Tích phân π 2 cos d x x bằng 0 Ⓐ 1. Ⓑ 0 . Ⓒ 2 . Ⓓ 2 . 1
Câu 88: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tích phân 2 x e dx bằng 0 2 e −1 Ⓐ e −1 2 e −1. Ⓑ . Ⓒ ( 2 2 e − ) 1 . Ⓓ . 2 2 Câu 89:
(CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f ( x) liên tục trên
;ab và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai. b a Ⓐ f
(x)dx = F(b)−F(a) . Ⓑ f (x)dx = 0. a a b Ⓒ b f (x) a dx = − f (x)dx. Ⓓ f
(x)dx = F(a)−F(b) . a b a 2
Câu 90: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Nếu f (x)dx = 3 1 2 2
và g ( x) dx = 1 − thì 2 f
(x)+3g(x)dx bằng 1 1 Ⓐ 2 . Ⓑ 9 . Ⓒ 3 . Ⓓ 0 .
Câu 91: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Tích phân 2 sin xdx bằng 0 Ⓐ − . Ⓑ 1. Ⓒ 1 − . Ⓓ . 2 2
Câu 92: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Cho hàm số 1 1 1
f ( x), g ( x) liên tục trên 0
;1 và f (x)dx = 1
− , g (x)dx = 2 . Tính 2
f (x)+3g(x)d x 0 0 0 Ⓐ 4 . Ⓑ 1. Ⓒ 2 − . Ⓓ 5 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 13 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 93: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Cho hàm số 6 4
f (x) liên tục trên đoạn 0;6 thoả mãn f (x)dx = 10
và f (x)dx = 6. Tính giá trị 0 2 2 6 của biểu thức P = f (x)dx + f (x)d . x 0 4 Ⓐ 4. Ⓑ 8. Ⓒ 16. Ⓓ 10. 1 Câu 94: Tính 3 = e x I dx . 0 3 e −1 1 Ⓐ 3 I = e −1. Ⓑ I = e −1. Ⓒ I = . Ⓓ 3 I = e + . 3 2 2 5 5 Câu 95: Nếu f
(x)dx = 3 và f (x)dx = 1 −
thì f ( x) dx bằng 1 2 1 Ⓐ 2 − . Ⓑ 4 . Ⓒ 2 . Ⓓ 3 . 2 2
Câu 96: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Tích phân dx 2 sin x 4 bằng Ⓐ 2 . Ⓑ 3 . Ⓒ 1. Ⓓ . 4 5
Câu 97: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Nếu f (x)dx = 10 và 2 9 9
f (x)dx = 7
thì f (x)dx bằng 2 5 Ⓐ −3 . Ⓑ 3 . Ⓒ 17 . Ⓓ −17 . 4
Câu 98: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Tính tích phân I = xdx . 1 Ⓐ 14 13 11 . Ⓑ . Ⓒ 4 . Ⓓ . 3 3 3
Câu 99: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Tích phân 2
( 2x + x)dx bằng 0 14 14 Ⓐ − . Ⓑ −5 . Ⓒ 5 . Ⓓ . 3 3 0
Câu 100: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Tích phân ( 5 6x + )1dx 2 − bằng Ⓐ 62. − Ⓑ 64. Ⓒ 68. Ⓓ 68. −
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 14 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2
Câu 101: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Giá trị của sin xdx bằng bao 0 nhiêu? Ⓐ 1. Ⓑ 1 − . Ⓒ . Ⓓ 0 . 2
Câu 102: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Cho hàm số f ( x) liên tục trên 6 10 10
thỏa mãn f ( x)dx = 7,
f ( x)dx = 1 − . Tính I = f (x)dx . 0 6 0 Ⓐ I = 5 . Ⓑ I = 8 . Ⓒ I = 7 . Ⓓ I = 6 . 4
Câu 103: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Tính tích phân I = xdx . 1 14 13 11 Ⓐ . Ⓑ . Ⓒ 4 . Ⓓ . 3 3 3
Câu 104: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Trong không gian Oxyz , cho điểm A(2; 2 − ; ) 1 , B (1; 1
− ;3) .Tọa độ của vectơ AB là Ⓐ (3; 3 − ;4) . Ⓑ ( 1 − ;1;2) . Ⓒ ( 3 − ;3; 4 − ) . Ⓓ (1; 1 − ; 2 − ). 1
Câu 105: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Tính 3x I = e dx 0 3 − 1 Ⓐ e 1 3
I = e −1. Ⓑ I = e −1. Ⓒ I = . Ⓓ 3 I = e + . 3 2 2 5
Câu 106: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Nếu f x dx 3 ; f x dx 1 thì 1 2 5 f x dx bằng 1 Ⓐ 2 − . Ⓑ 4 . Ⓒ 2 . Ⓓ 3 .
Câu 107: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Cho hàm số f ( x) 3
có f (2) = 2, f (3) = 5 ; hàm số f ( x) liên tục trên đoạn 2; 3 . Khi đó f
(x)dx bằng 2 Ⓐ 3 . Ⓑ 10 . Ⓒ −3 . Ⓓ 7 . 3 3
Câu 108: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Biết f
(x)dx =5 và g(x)dx = 7 − . 1 1 3 Giá trị của 3 f
(x)−2g(x)dx bằng 1 Ⓐ −29 . Ⓑ 1. Ⓒ 29 . Ⓓ 31 − .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 15 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 109: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hàm số f (x) liên tục trên đoạn 1 2 2 0;2 thỏa mãn f
(x) dx = 3 và f
(x) dx = 2. Khi đó f (x)dx bằng 0 1 0 Ⓐ 6 . Ⓑ 1. Ⓒ 1 − . Ⓓ 5 . 1 1
Câu 110: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Biết
f ( x)dx = và 3 0 1 1 g ( x) 4 dx =
. Khi đó (g (x) − f (x))dx bằng 3 0 0 5 5 Ⓐ − . Ⓑ . Ⓒ 1 − . Ⓓ 1. 3 3 Câu 111: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Nếu 4 4 5 f
(x)−3dx =5 thì f x dx bằng 1 − 1 14 Ⓐ 4 . `Ⓑ 3 . Ⓒ 2 . Ⓓ . 5 2021 2021
Câu 112: (CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Nếu f
(x)dx =12 và f (x)dx = 2 2 2020 2020 thì f ( x)dx bằng 2 Ⓐ −10 . Ⓑ 10 . Ⓒ 14 . Ⓓ 24. 1
Câu 113: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho 5 f (x) 2021 + x + x x d = 20 . 1 − 1 Tính f (x) x d . 1 − Ⓐ 5 . Ⓑ 4 . Ⓒ 1. Ⓓ 0 .
Câu 114: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tìm giá trị của a để 4 1 dx = ln a . x −1 x − 2 3 ( )( ) Ⓐ 3 1 4 . Ⓑ . Ⓒ 12 . Ⓓ . 4 3 3 Câu 115: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Biết rằng 2 3
x −1 dx = a +bln3+cln 2 với , a ,
b c là các số hữu tỉ. Tính 2a + 3b − 4c . 2 x + x 1 Ⓐ −19 . Ⓑ 19 . Ⓒ 5 . Ⓓ −5 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 16 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Câu 116: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Biết 8 f (x) 4 dx = 2 − ; f (x) 4 dx = 3; g
(x)dx = 7. Mệnh đề nào sau đây là sai? 1 1 1 8 4 4 Ⓐ f
(x)dx+ g (x)dx =8. Ⓑ f
(x)+ g(x)dx =10 . 4 1 1 8 4 Ⓒ
f ( x) dx = 5 − . Ⓓ 4 f
(x)−2g(x)dx = 2 − . 4 1 2 2
Câu 117: Nếu (2x −3 f (x))dx = 3 thì f (x)dx bằng 0 0 1 5 5 1 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 3 2 2 3 4
Câu 118: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho f (x)dx =10. 1 −
Biết F ( x) là một nguyên hàm của f ( x) và F (− ) 1 = 4
− . Tính F (4). Ⓐ F (4) = 6 . Ⓑ F (4) =14 . Ⓒ F (4) = 1 − 4 . Ⓓ F (4) = 6 − .
Câu 119: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Nếu 1 1 3 f
(x)+ x x d = 2 f (x) x d = 2 0 thì 0 bằng Ⓐ 1 1 2 − . Ⓑ . Ⓒ 2 . Ⓓ . 2 2 3 1
Câu 120: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Nếu f (x) x d = 2 1 − 2 2 và f (x) x
d = 8 thì f ( x) x d bằng 1 − 1 Ⓐ 4 . Ⓑ 10 . Ⓒ 6 . Ⓓ 16 . 2
Câu 121: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho 2 và g(x) = 1 − . 1 − 2
Tính I = [x + 2 f (x) + 3g(x)] bằng? 1 − 11 7 17 5 Ⓐ I = .
Ⓑ I = . Ⓒ I = . Ⓓ I = . 2 2 2 2 3
Câu 122: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Nếu
f (x)dx = 3 và 1 3 2
f (x)dx = 4
thì f (x)dx bằng: 2 1 Ⓐ −7 . Ⓑ 7 Ⓒ 1 − . Ⓓ 1.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 17 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 2
Câu 123: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Nếu (2x −3 f (x))dx = 3 thì f (x)dx 0 0 bằng Ⓐ 1 5 5 1 − . Ⓑ − . Ⓒ . Ⓓ 3 2 2 3
Câu 124: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Biết F ( x) = cos x là một nguyên
hàm của hàm số f ( x) trên . Giá trị của 3 f
(x)+ 2dx bằng 0 Ⓐ 2 − 6 . Ⓑ 4 − . Ⓒ 2 . Ⓓ 2 .
Câu 125: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hàm số f ( x) có đạo hàm liên 3 tục trên đoạn 1; 3 , và f '
(x)dx = 6. Tính f ( )1 1 Ⓐ 10 . Ⓑ 11. Ⓒ 1. Ⓓ 1 − .
Câu 126: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hai hàm số f ( x), g ( x) liên tục 2 2
trên đoạn 1;2 và thỏa mãn 3 f
(x)+2g(x)dx =1 , 2 f
(x)− g(x)dx = 3 − . Khi đó, 1 1 2 f ( x) dx bằng 1 6 16 11 5 Ⓐ . Ⓑ . Ⓒ . Ⓓ − . 7 7 7 7
Câu 127: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Cho hàm số 2021 f ( ) x = x
+ sinx + 2021. Biết rằng có duy nhất giá trị của a m m = − để ' ( .
x f (m− x) − f (x))dx = 1
. Tìm a + b . b 0
Ⓐ a + b = 2021.
Ⓑ a + b = 2023.
Ⓒ a + b = 2020 .
Ⓓ a + b = 2022 .
PHƯƠNG PHÁP ĐỔI BIẾN SỐ
Câu 128: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f x liên tục trên 6 3 và f x dx 10 , thì
f 2x dx bằng 0 0 Ⓐ 30 . Ⓑ 20 . Ⓒ 10 . Ⓓ 5 . 2 e ln x
Câu 129: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Tích phân dx x e bằng Ⓐ 3 3. Ⓑ . Ⓒ 1. Ⓓ 2. 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 18 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 dx
Câu 130: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Tính tích phân I = bằng cách đặt 1 x + e 0 x
t = e , ta được: e 1 e 1 Ⓐ dt dt dt tdt I = . Ⓑ I = . Ⓒ I = . Ⓓ I = . 1+ t 1+ t t 1+ t 1+ t 1 ( ) 1 0 0 1 dx
Câu 131: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Tính tích phân I = 1 x + e 0 bằng cách đặt x
t = e , ta được e 1 e 1 Ⓐ dt dt dt tdt I = . Ⓑ I = . Ⓒ I = . Ⓓ I = . 1+ t 1+ t t t +1 1+ t 1 ( ) 1 0 0
Câu 132: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Cho hàm số 4 2 −
x + 2x −1 khi x 2 e 1 x f (x) = . Giá trị của I = . f ln ( 2
x +1 dx thuộc khoảng 2 )
x + 5 khi x 2 x +1 0 nào dưới đây ? Ⓐ ( 2 − ;3) . Ⓑ (5;7) . Ⓒ (10;1 ) 1 . Ⓓ (8;9) . Câu 133: (CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Cho hàm số + 1 f ( x) 2x 1 khi x 3 =
( a là tham số thực). Nếu f ( xe + ) x 2
1 e dx = e thì a bằng
ax − 3a + 7 khi x 3 0 2 + − Ⓐ 3e 4e 6 . Ⓑ 6e − 6 Ⓒ 6e + 6 Ⓓ 6 − e + 6 e −1
Câu 134: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho hàm số 2 f ( x) 2
= x −1 . Tích phân f (3cos x − )1.sin xdx bằng 0 8 7 Ⓐ 10 . Ⓑ . Ⓒ . Ⓓ 11 . 9 9 9 9
Câu 135: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Có bao nhiêu giá trị ln a 1 3
thực dương của tham số a để dx = ln ?. x e + 2 x e− − 3 2 ln 3 Ⓐ 3 . Ⓑ 2 . Ⓒ 4 . Ⓓ 1.
Câu 136: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho hàm số − − ln 4 f ( x) 2 x 8x 5 khi x 8 =
. Tích phân (2 x + 3) x f e e dx bằng −x + 3 khi x 8 0 123 123 Ⓐ 39 39 . Ⓑ . Ⓒ − . Ⓓ − . 2 4 2 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 19 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 137: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Cho hàm số y = f ( x) có 4
f (0) = 0 và f ( x) 4 2
= tan x + tan x , x 0;
. Tính I = f (x)dx. 2 0 1 1 1− ln 2 1− ln 2 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 12 6 6 3
Câu 138: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Biết rằng ln 4 dx
= a + bln 2 + c ln 3 với , a ,
b c . Tính a + b + c . + 0 1 x e Ⓐ –2. Ⓑ 3. Ⓒ 2. Ⓓ –1.
PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN
Câu 139: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho 2 x + ln x a 1 a I = = − ( với , a ,
b c là các số nguyên dương và là phân số tối x + ) dx ln 2 2 1 b c b 1 a + b
giản.Tính giá trị S = c 2 1 1 5 Ⓐ S = . Ⓑ S = . Ⓒ S = . Ⓓ S = . 3 2 3 6 e
Câu 140: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tính tích phân I = x ln d x x , 1 2 e + a
ta được kết quả I =
, với a , b là các số nguyên. Tính 3 3 a + b . b Ⓐ 35 . Ⓑ 65 . Ⓒ 28 . Ⓓ 9 .
Câu 141: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Cho hàm số 1
f ( x) có đạo hàm f '( x) và thỏa (2x + )
1 f '( x)dx = 10, 3 f ( )
1 − f (0) = 12 . Tính 0 1 I = f (x)dx 0 Ⓐ I = 1 − . Ⓑ I =1. Ⓒ I = 2 . Ⓓ I = 2 − .
Câu 142: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Cho hàm số f (x) có đạo 1
hàm liên tục trên thỏa mãn f (3) = 3 21,
f (x)dx = 9 . Tính tích phân I = x f ( 3x)dx 0 0 Ⓐ I = 15 . Ⓑ I = 6 . Ⓒ I = 12. Ⓓ I = 9 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 20 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 143: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Cho hàm số f (x) có đạo
hàm cấp 2 liên tục trên đoạn 0; 1 thỏa mãn f (1) = 0; f ( 1) =1và 1 2
10 f (x) − 5xf (
x) + x f (x) = 0với mọi x0
;1 . Khi đó tích phân f (x)dx bằng 0 − − − − Ⓐ 1 2 1 1 . Ⓑ . Ⓒ . Ⓓ . 15 3 10 17
Câu 144: Cho hàm số f ( x) có đạo hàm f ( x) trên đoạn 0; 1 thỏa mãn f ( ) 1 = 4 và 1 1 f
(x)dx = 3. Tích phân 3x f ( 2x) x d bằng 0 0 1 1 Ⓐ − . Ⓑ 1. Ⓒ . Ⓓ 1 − . 2 2
Câu 145: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Cho hàm số f ( x) có đạo hàm liên tục trên
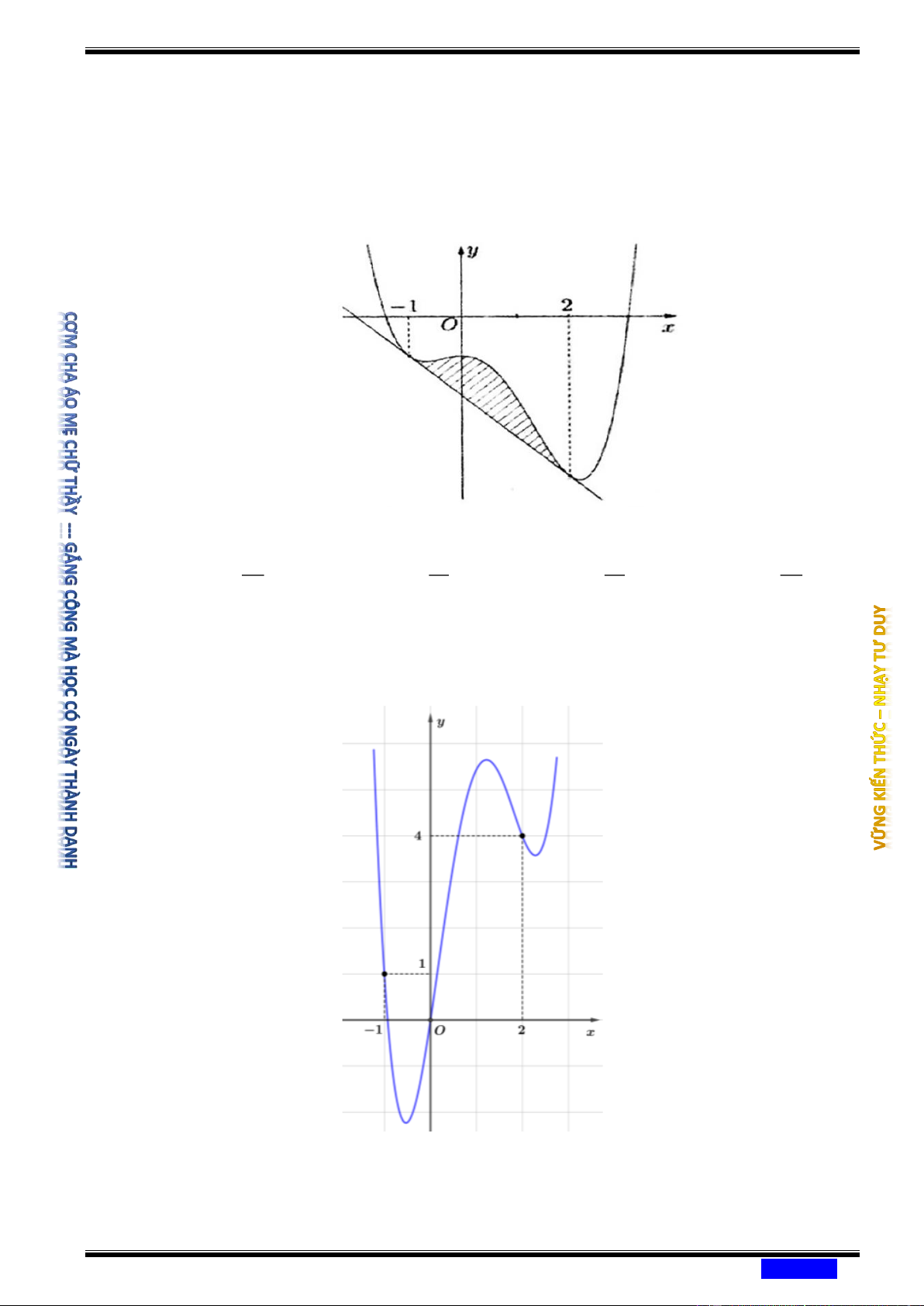
và có đồ thị như hình bên. 1 Đặt K = xf
(x)f '(x)dx, khi đó K thuộc khoảng nào sau đây? 0 Ⓐ ( 3 2 3 2 3 − ;− 2) . Ⓑ −2; − . Ⓒ − ;0 . Ⓓ − ;− . 2 3 2 3
Câu 146: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Cho hàm số f ( x) có đạo hàm f ( x) 1 1 trên đoạn 0; 1 thỏa mãn f ( )
1 = 4 và f (x)dx = 3. Tích phân 3
x f ( 2x)dx bằng 0 0 Ⓐ 1 1 − . Ⓑ 1. Ⓒ . Ⓓ −1. 2 2
Câu 147: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Giả sử f ( x) là hàm có đạo
hàm liên tục trên khoảng (0; ) và f '( x)sin x = x + f ( x)cos x, x (0; ). Biết 1 f =1, f =
(a+bln2+c 3), với ,a ,b c là các số nguyên. Giá trị a+b+c 2 6 12 bằng Ⓐ 1 − . Ⓑ 1. Ⓒ 11. Ⓓ 11 − .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 21 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
TÍCH PHÂN HÀM ẨN – TÍCH PHÂN ĐẶC BIỆT
Câu 148: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Cho f ( x) là hàm số 1 1 liên tục trên
và f (x)dx = 6. Tính tích phân I =
f (2x− )1+2xd x . 1 − 0 Ⓐ I = 4 . Ⓑ I = 13 . Ⓒ I = 7 . Ⓓ I = 5 .
Câu 149: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Cho hàm số y = f ( x) có đạo hàm trên (0;+) . Biết 2
x là một nguyên hàm của 2
x f '( x) trên (0; +) và f ( ) 1 = 1. Tính f (e) . Ⓐ 2 . Ⓑ 3 . Ⓒ 2e +1 . Ⓓ e .
Câu 150: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) có đạo hàm liên tục trên
và thỏa mãn các điều kiện sau: f (0) = 2 − và ( 2 x + )
1 f ( x) + xf ( x) = −x , 3 x
. Tính tích phân I = xf
(x)dx . 0 Ⓐ 5 3 3 5 I = .
Ⓑ I = − .
Ⓒ I = .
Ⓓ I = − . 2 2 2 2
Câu 151: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho hàm số
y = f ( x) liên tục và có đạo hàm trên thỏa mãn 1 a
f ( x) − f ( − x) = ( 2 5 7 1
3 x − 2x), x
. Biết rằng tích phân I = .
x f '( x) dx = − . Tính b 0 T =3a − . b Ⓐ T =0. Ⓑ T =− 48. Ⓒ T 16. = Ⓓ T =1.
Câu 152: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số f (x)
có đạo hàm liên tục trên R và thỏa mãn 3
f (x + 3x +1) = 3x + 2, x
R . Tích phân 5 xf ( x)dx bằng 1 −31 33 17 49 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 4 4 4 4
Câu 153: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Cho hàm số f ( x) liên tục trên ( 0; +) và thỏa mãn ( ) 1 2 f x + xf = x với mọi x 0 . x 2
Tính f ( x) dx . 1 2 7 7 9 3 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 12 4 4 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 22 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 154: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Cho hàm số f ( x) liên tục trên và thoả mãn ( ) ( ) 1 ( ) x xf x x f x e− + + =
với mọi x . Tính f (0) . 1 Ⓐ 1. Ⓑ 1 − . Ⓒ e . Ⓓ . e
Câu 155: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Biết 8 4 3
f (x)dx = 10; f (x)dx = 4 − . Tính f
( 3x−1)dx. 0 0 1 − Ⓐ 2 . Ⓑ 1. Ⓒ 0 . Ⓓ 4 .
Câu 156: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Cho hàm số f (x) có f (0) = 0 và 4 f ( x) 4 2
= tan x + tan x , x 0;
. Tính I = f (x)dx . 2 0 − − Ⓐ 1 1 1 ln 2 1 ln 2 . Ⓑ . Ⓒ . Ⓓ . 12 6 6 3
Câu 157: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Cho hai hàm số f ( x), g ( x) có đạo hàm
trên R và thỏa mãn f ( x) + g ( x) = x , g( x) + f ( x) = − , x x
. Biết f (0) = g (0) =1. Tính f ( ) 1 . 2 e − 2 2 e + 2 Ⓐ 2 1 − 2 .
Ⓑ e + − 2 . Ⓒ . Ⓓ . e e 2e 2e
Câu 158: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Cho hàm số y = f ( x) có đạo hàm
liên tục trên 1;4 , đồng biến trên 1;4 và thỏa mãn đẳng thức 4
x + xf ( x) = f ( x) 2 / 2 , x
1;4 . Biết rằng f ( ) 3 1 = . Tính I = f (x)dx . 2 1 1222 1201 1174 1186 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 45 45 45 45
Câu 159: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Cho hàm số f ( x) 1 2 liên tục trên
và có một nguyên hàm là hàm số g ( x) 2
= x − x +1. Khi đó f ( 2 x ) dx 2 1 bằng 2 4 4 2 Ⓐ . Ⓑ − . Ⓒ . Ⓓ − . 3 3 3 3
Câu 160: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Cho hàm số y = f ( x) có đạo hàm trên thỏa mãn f ( )
1 = 1và f ( x) − xf ( 2 x ) 3 2
= 5x − 2x −1với mọi x Tính tích phân 2 I = xf '
(x)d .x 1 Ⓐ I = 3. Ⓑ I = 1. − Ⓒ I = 2. Ⓓ I = 5.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 23 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 161: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) liên tục trên và thỏa mãn ( ) = ( )− ( ) 2 0 1; = . x f f x xf x x e , x . Tích phân 1 xf
( x+1)dx bằng 0 Ⓐ 2 e − e .
Ⓑ 4 e − 2e . Ⓒ 1. Ⓓ e .
Câu 162: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Cho hàm số f ( x) 1 4
có đạo hàm liên tục trên . Biết f ( 2
x ) = f ( x) 4 2
+ x − 4x, x
và f (x)dx = , khi 3 0 1 đó 2 x f (x)dx bằng 0 7 8 7 2 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 6 15 10 3
Câu 163: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Cho hàm số f (x)
có đạo hàm liên tục trên
và thỏa mãn f (0) = 3 và 2
f (x) + f (2 − x) = x − 2x + 2 , 2 x . Tích phân .
x f '(x)dx bằng 0 − 5 − −11 7 − Ⓐ 10 . Ⓑ . Ⓒ . Ⓓ . 3 3 3 3
Câu 164: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hàm số y = f ( x) có đạo hàm .
x f (t ) − t. f ( x)
liên tục trên khoảng (0;+) và thỏa mãn lim
=1 với mọi t 0 . Biết 2 2 x→t x − t rằng f ( )
1 = 1, tính f (e) . 3e +1 Ⓐ . Ⓑ 3e . Ⓒ 2e . Ⓓ −e . 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 24 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
ỨNG DỤNG TÍCH PHÂN
DIỆN TÍCH HÌNH PHẲNG GIỚI HẠN BỞI CÁC ĐỒ THỊ
Câu 165: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Diện tích hình phẳng giới hạn
bởi hai đường thẳng x = 0, x = , đồ thị hàm số y = cos x và trục Ox là
Ⓐ S = cos x d . x Ⓑ S = cos d x . x Ⓒ 2 S = cos d x . x
Ⓓ S = cos x d . x 0 0 0 0
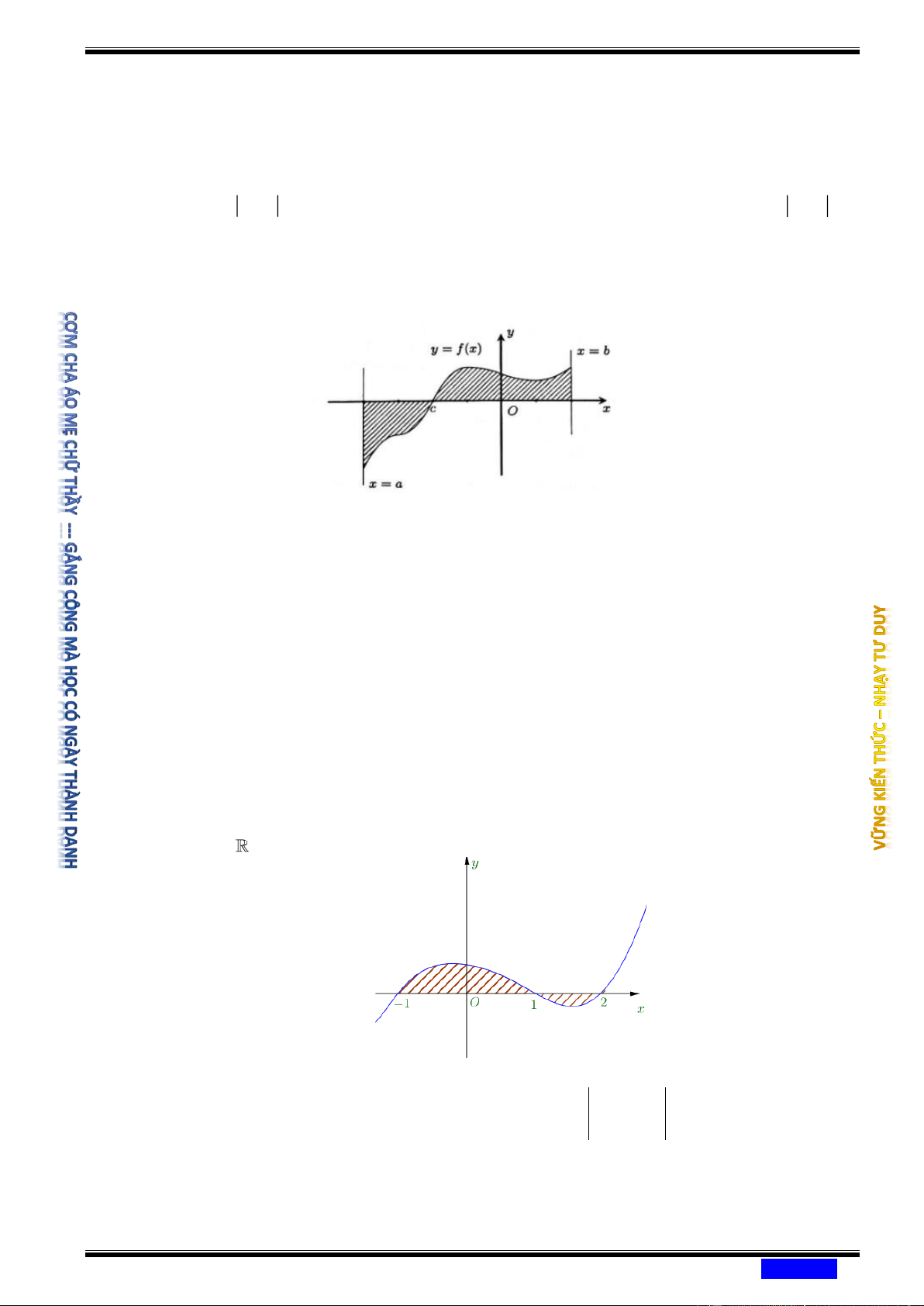
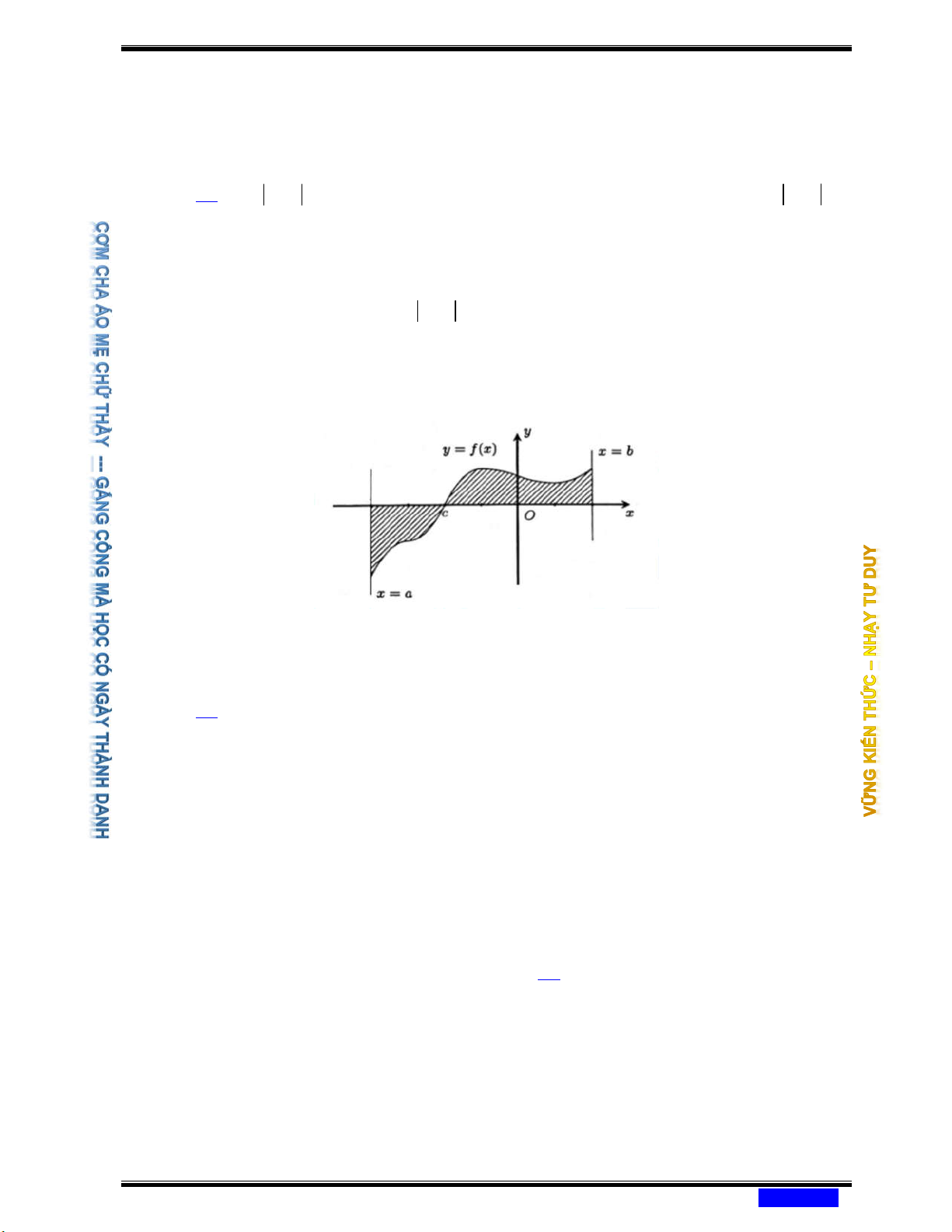
Câu 166: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Hình phẳng giới hạn bởi
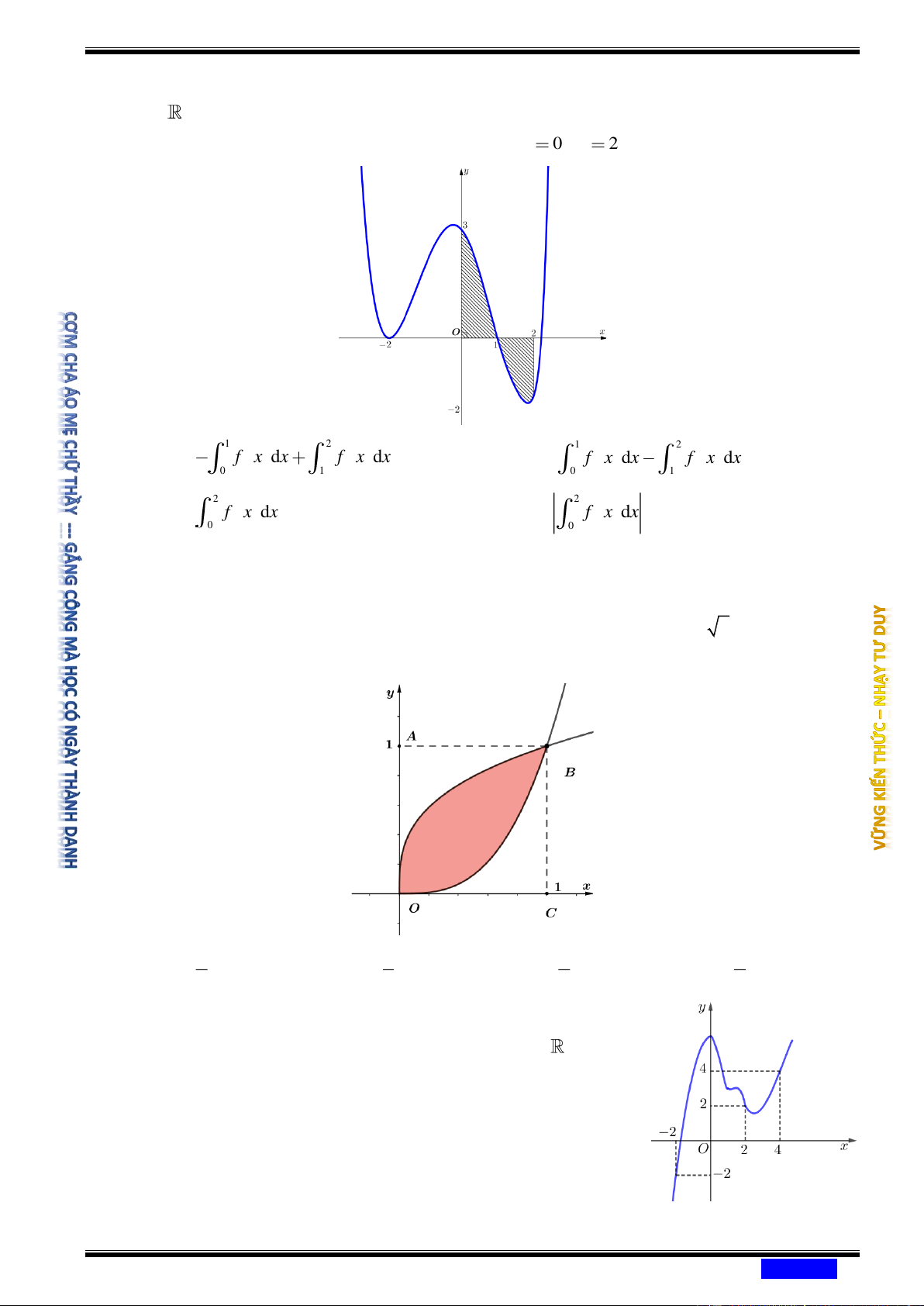
đồ thị hàm số y = f ( x) , trục hoành và hai đường thẳng x = ,
a x = b trong hình dưới
đây (phần gạch sọc có diện tích S bằng c b c b Ⓐ f
(x)dx + f (x)dx . Ⓑ f
(x)dx − f (x)dx. a c a c c b c b Ⓒ − f
(x)dx + f (x)dx . Ⓓ − f
(x)dx − f (x)dx. a c a c
Câu 167: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Tìm công thức tính diện
tích hình phẳng giới hạn bởi các đường 4 y = x , 2 y = x . 1 1 1 1 Ⓐ ( 4 2
x − x )dx . Ⓑ ( 2 4
x − x )dx . Ⓒ ( 2 4
x − x )dx . Ⓓ ( 4 2
x − x )dx . 0 0 1 − 1 −
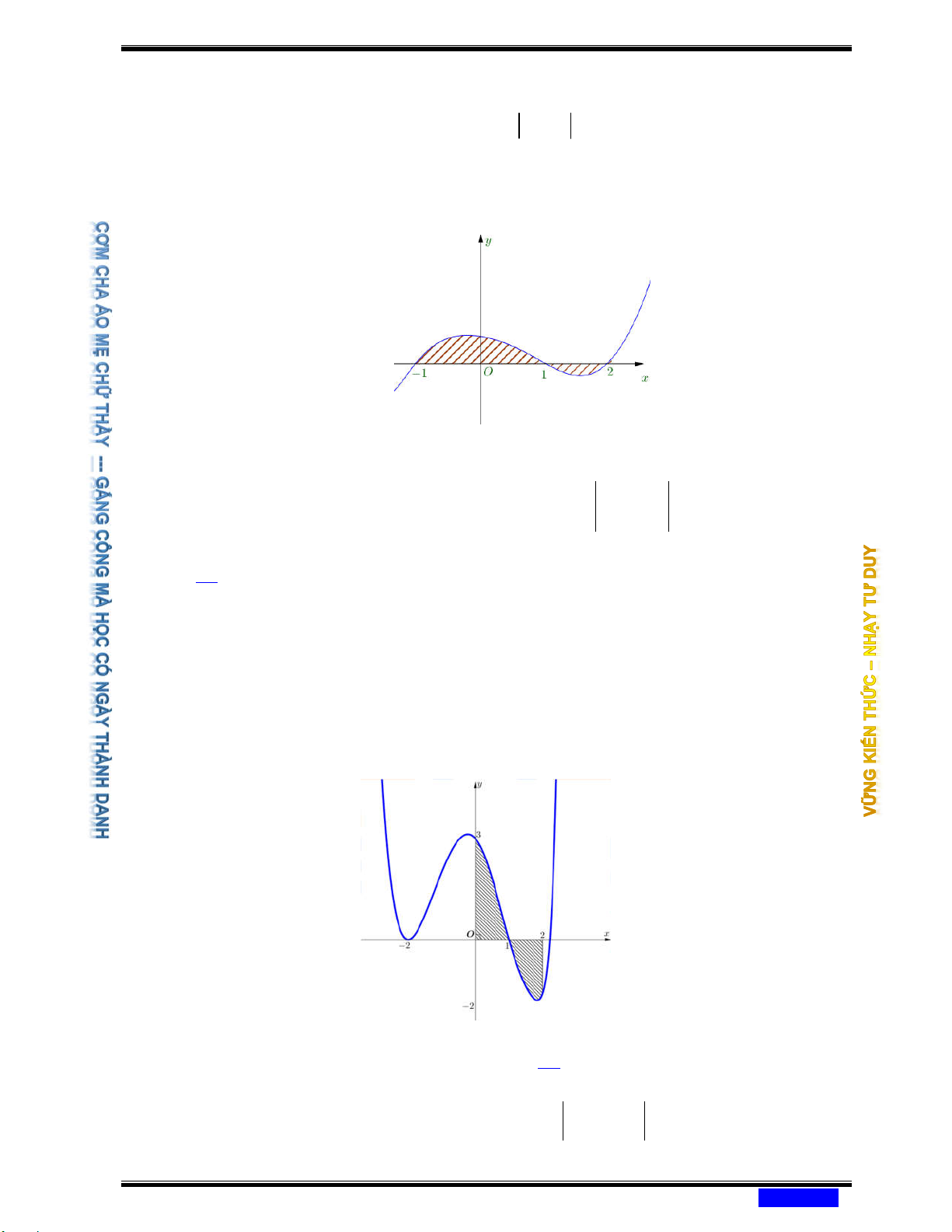
Câu 168: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Gọi S là diện tích
miền hình phẳng được gạch chéo trong hình vẽ dưới đây, với y = f ( x) là hàm số liên tục trên
Công thức tính S là 2 2 Ⓐ S = − f
(x)dx . Ⓑ S = f
(x)dx . 1 − 1 − 1 2 2 Ⓒ S = f
(x)dx− f
(x)dx. Ⓓ f (x)dx . 1 − 1 1 −
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 25 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
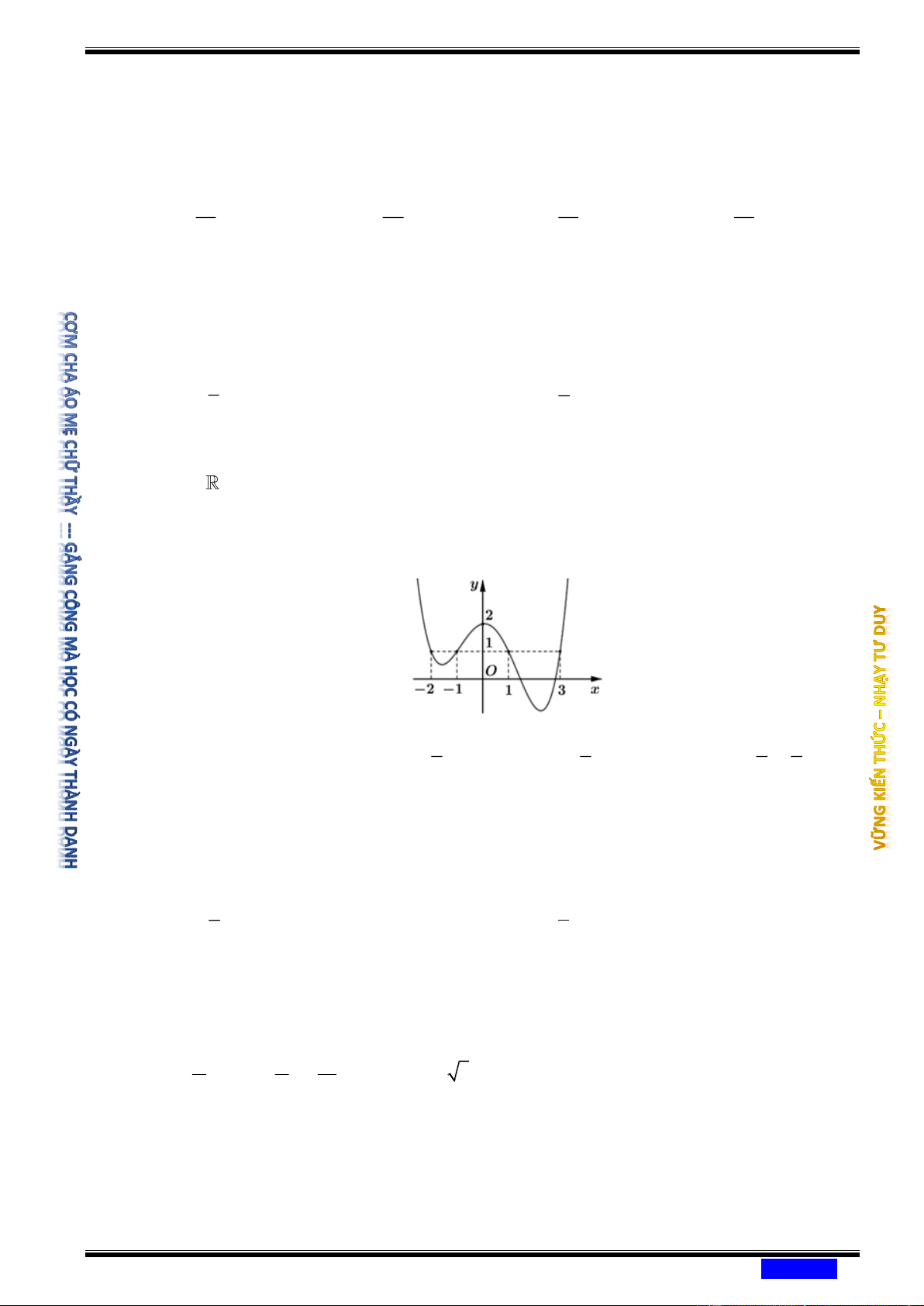
Câu 169: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f x liên tục trên
và có đồ thị C là đường cong như hình bên, Diện tích hình phẳng giới hạn bởi
đồ thị C , trục hoành và hai đường thẳng x 0 , x 2 là 1 2 1 2 Ⓐ f x dx f x dx . Ⓑ f x dx f x dx . 0 1 0 1 2 2 Ⓒ f x dx . Ⓓ f x dx . 0 0
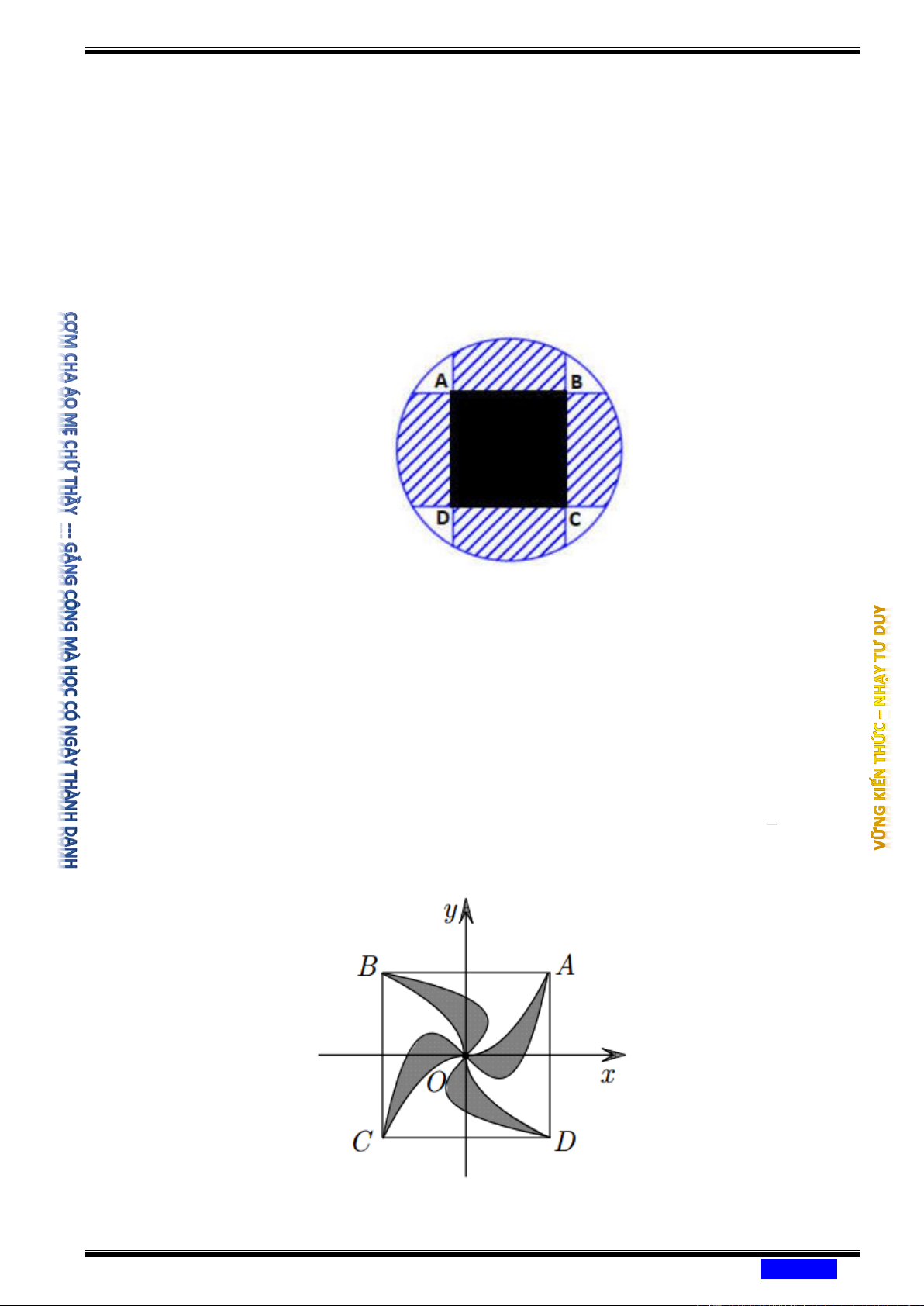
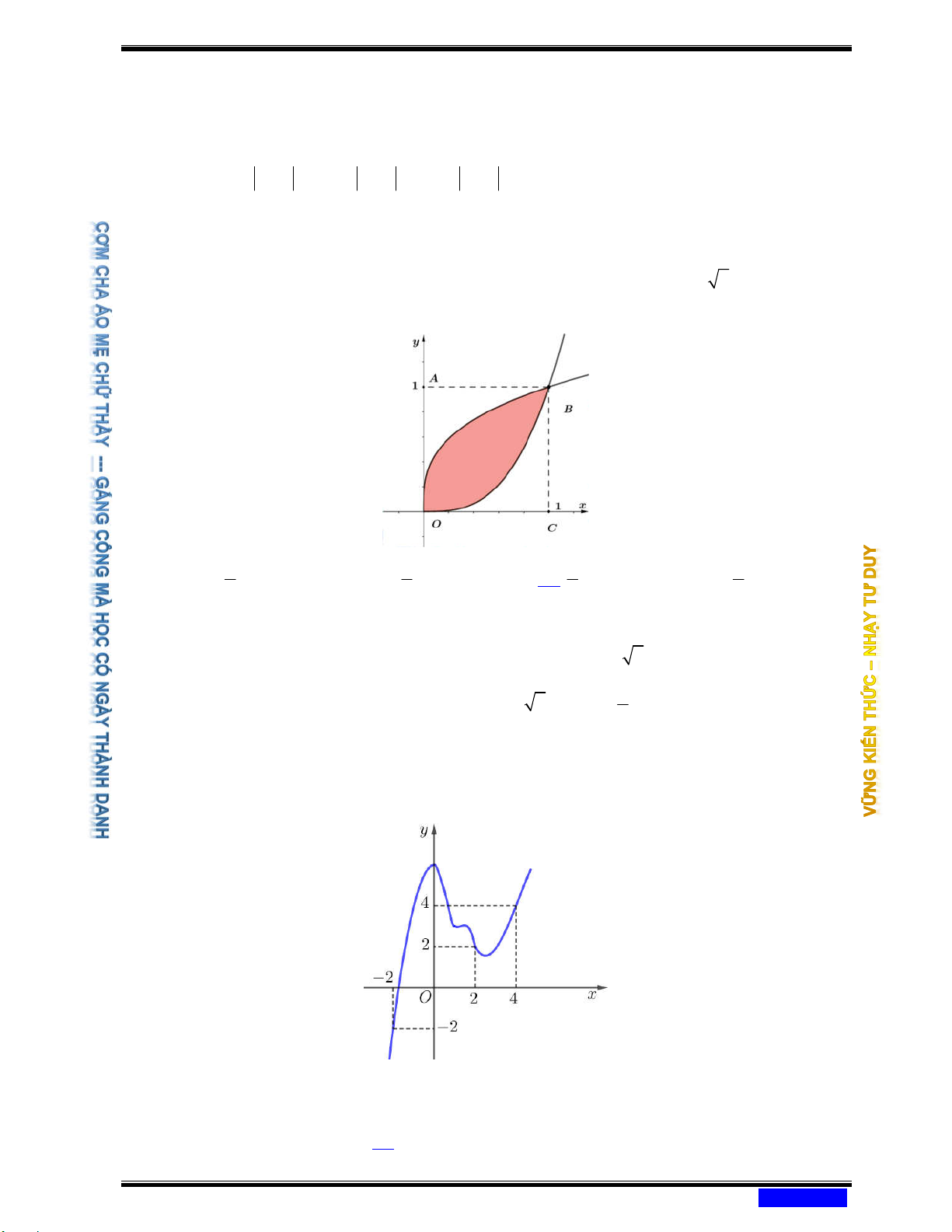
Câu 170: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho một viên gạch men có
dạng hình vuông OABC như hình vẽ. Sau khi tọa độ hóa, ta có O (0;0) , A(0 ) ;1 , B (1; ) 1
, C (1;0) và hai đường cong lần lượt là đồ thị hàm số 3 y = x và 3
y = x . Tính diện tích
phần tô đậm trên viên gạch men. Ⓐ 5 1 1 4 . Ⓑ . Ⓒ . Ⓓ . 4 3 2 5
Câu 171: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021)
Cho hàm số y = f ( x) có đạo hàm liên tục trên và có đồ thị như hình vẽ bên. 2 4 Giá trị của f
(x+2)dx+ f
(x−2)dx bằng 0 0 Ⓐ 4 . Ⓑ 6 . Ⓒ 4 − . Ⓓ 2 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 26 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 172: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Diện tích hình phẳng giới hạn
bởi đường thẳng y = x + 3 và parabol 2
y = 2x − x −1 bằng: 13 9 13 Ⓐ . Ⓑ . Ⓒ 9 . Ⓓ . 6 2 3
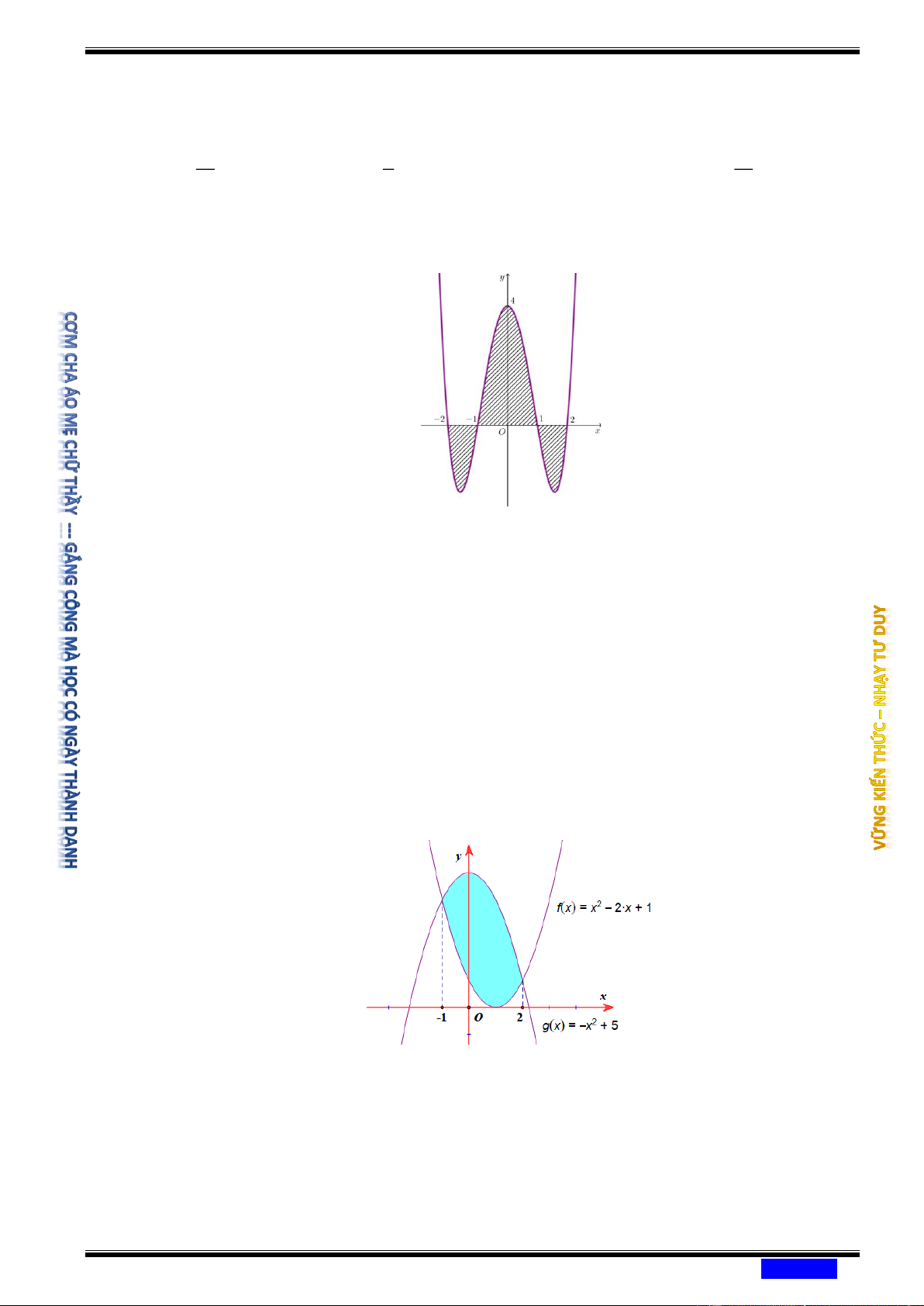
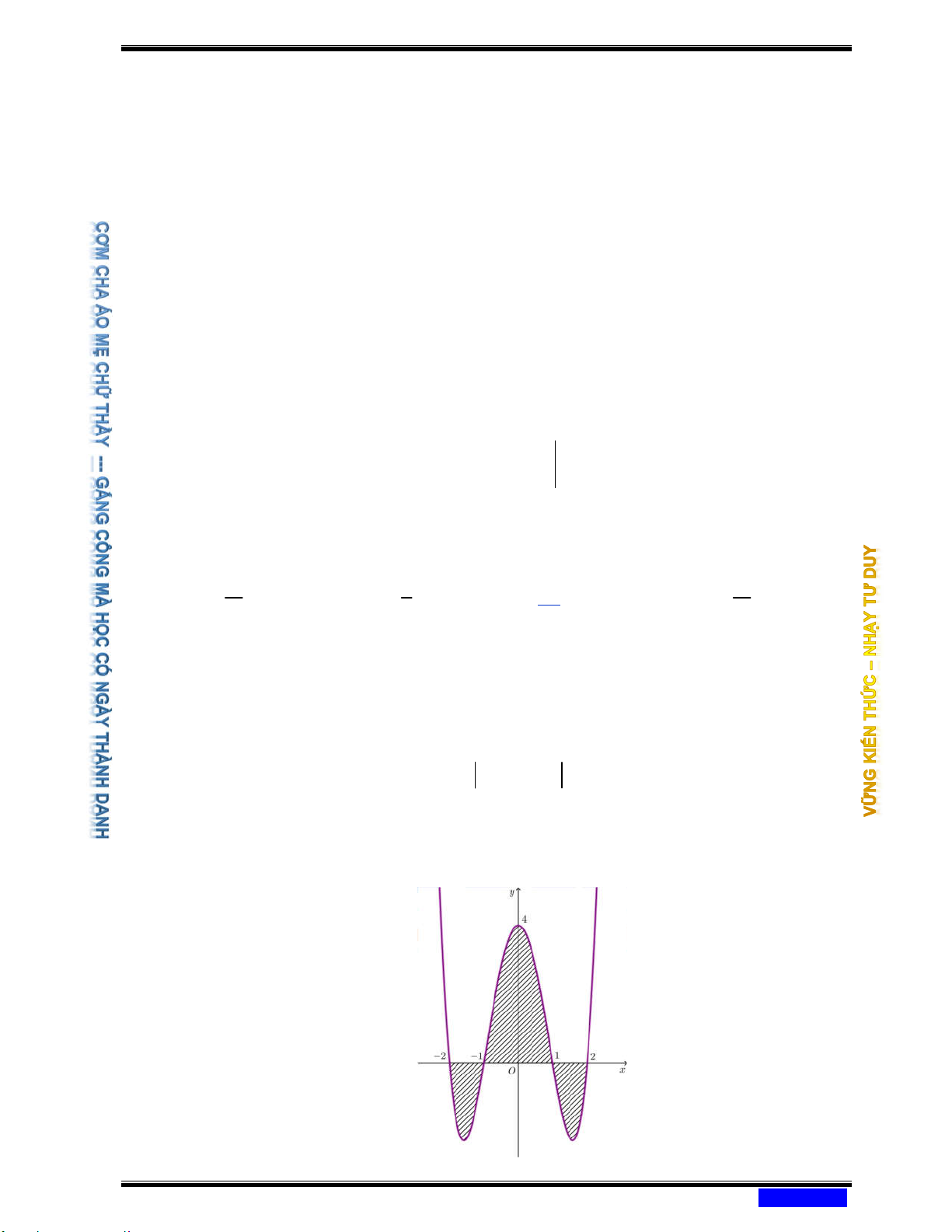
Câu 173: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho hàm số = ( ) 4 2 y
f x = ax + bx + c có đồ thị như hình vẽ.
Diện tích S của miền được tô xiên như hình được tính theo công thức nào? 1 − 1 2 1 − 1 2 Ⓐ S = − f
(x)dx+ f
(x)dx− f
(x)dx . Ⓑ S = f
(x)dx+ f
(x)dx+ f
(x)dx . 2 − 1 − 1 2 − 1 − 1 1 − 1 2 1 − 1 2
Ⓒ S = − f
(x)dx+ f
(x)dx+ f
(x)dx . Ⓓ S = f
(x)dx− f
(x)dx+ f (x)dx . 2 − 1 − 1 2 − 1 − 1
Câu 174: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Tìm công thức tính diện tích hình phẳng
giới hạn bởi các đường 4 2
y = x , y = x 1 1 1 1 Ⓐ ( 4 2
x − x )dx . Ⓑ ( 2 4
x − x )dx . Ⓒ ( 2 4
x − x )dx . Ⓓ ( 4 2
x − x )dx . 0 0 1 − 1 −
Câu 175: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Diện tích hình
phẳng được tô đậm trong hình bên bằng 2 2 Ⓐ ( 2 2
− x + 2x − 4) x d . Ⓑ ( 2
2x − 2x − 4) x d . 1 − 1 − 2 2 Ⓒ ( 2 2
− x − 2x + 4) x d . Ⓓ ( 2 2
− x + 2x + 4) x d . 1 − 1 −
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 27 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 176: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Diện tích hình phẳng giới hạn bởi
hai đường y = ( x − )( 2
1 x − 5x + 6) và hai trục tọa độ bằng Ⓐ 11 11 1 . Ⓑ . Ⓒ . Ⓓ . 2 4 4 2
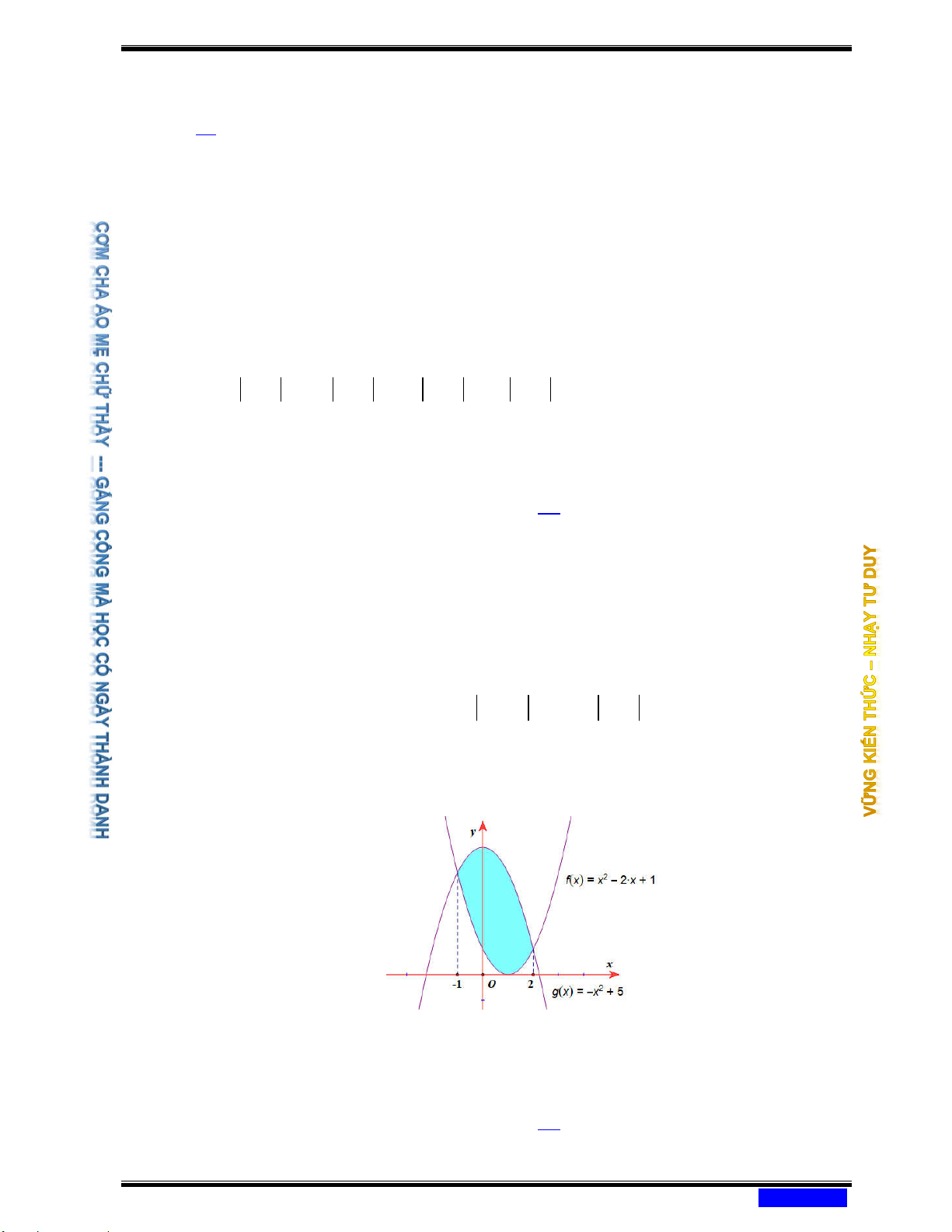
Câu 177: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hai hàm số f ( x) 3 2
= ax + bx + cx − 2, g (x) 2
= dx + ex + 2 , (a, , b , c d, e
) . Biết đồ thị hàm số
y = f ( x) và y = g ( x) cắt nhau tại ba điểm phân biệt có hoành độ lần lượt là 2 − ; 1 − ;1
. Tính diện tích hình phẳng giới hạn bởi hai đồ thị. Ⓐ 37 13 9 37 . Ⓑ . Ⓒ . Ⓓ . 6 2 2 12
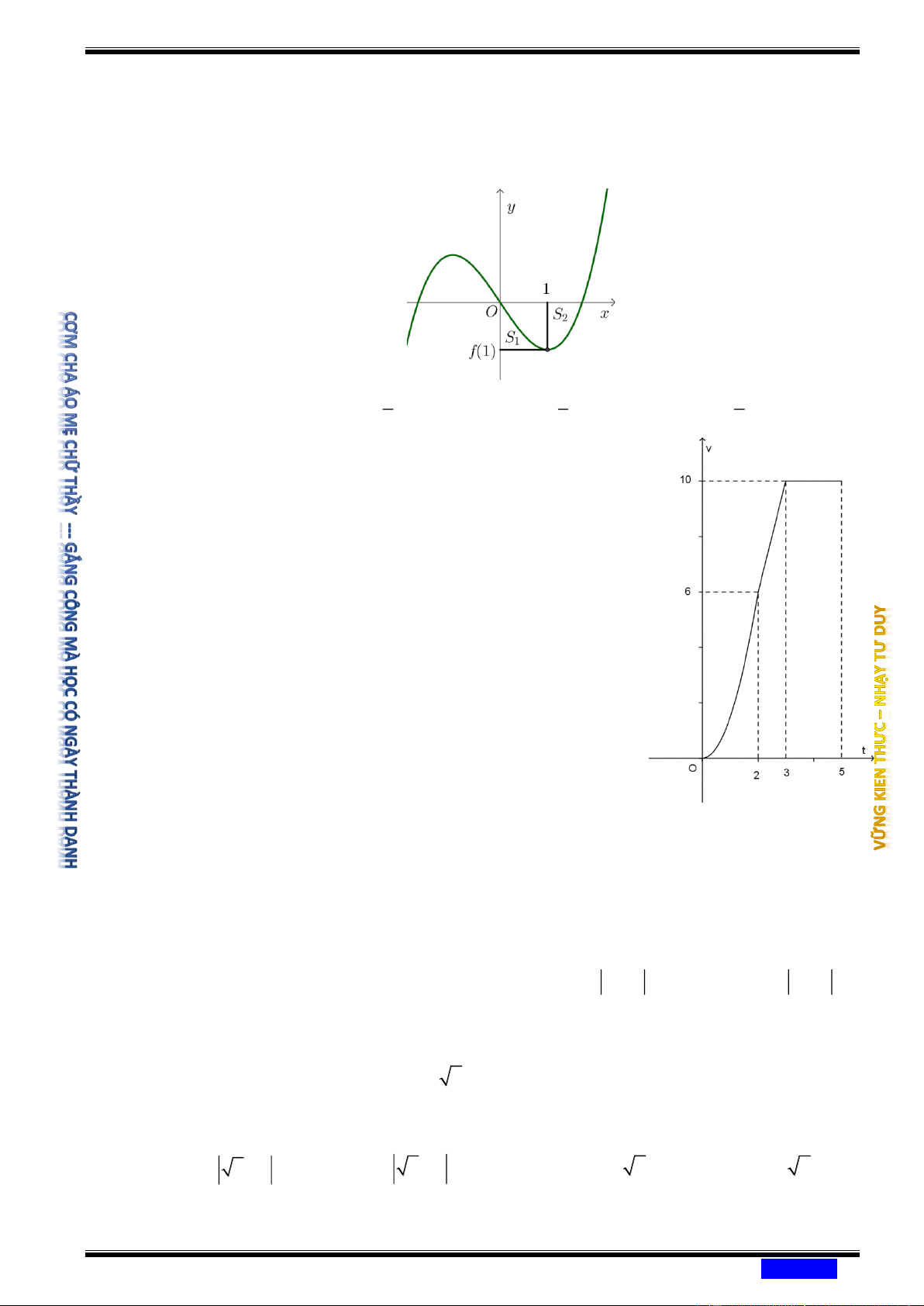
Câu 178: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho hàm số
y = f ( x) 1 3
= x + ax có đồ thị như hình bên. Gọi S , S lần lượt là diện tích của hai 3 1 2
hình phẳng được gạch chéo trong hình vẽ bên. S 7 Khi 1 =
thì a thuộc khoảng nào dưới đây? S 40 2 Ⓐ 3 5 1 1 1 1 3 ; . Ⓑ ; . Ⓒ 0; . Ⓓ ; . 4 4 3 2 3 2 4
Câu 179: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho parabol ( P) có phương trình 2
y = x và đường thẳng d đi qua điểm A(1;3) . Giả sử khi đường thẳng d có hệ
số góc k thì diện tích hình phẳng giới hạn bởi parabol ( P) và đường thẳng d nhỏ
nhất. Giá trị thực của k thuộc khoảng nào sau đây? Ⓐ (0 ) ;1 . Ⓑ ( ;3 − ) . Ⓒ ( 3 − ;0) . Ⓓ (3;+) .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 28 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
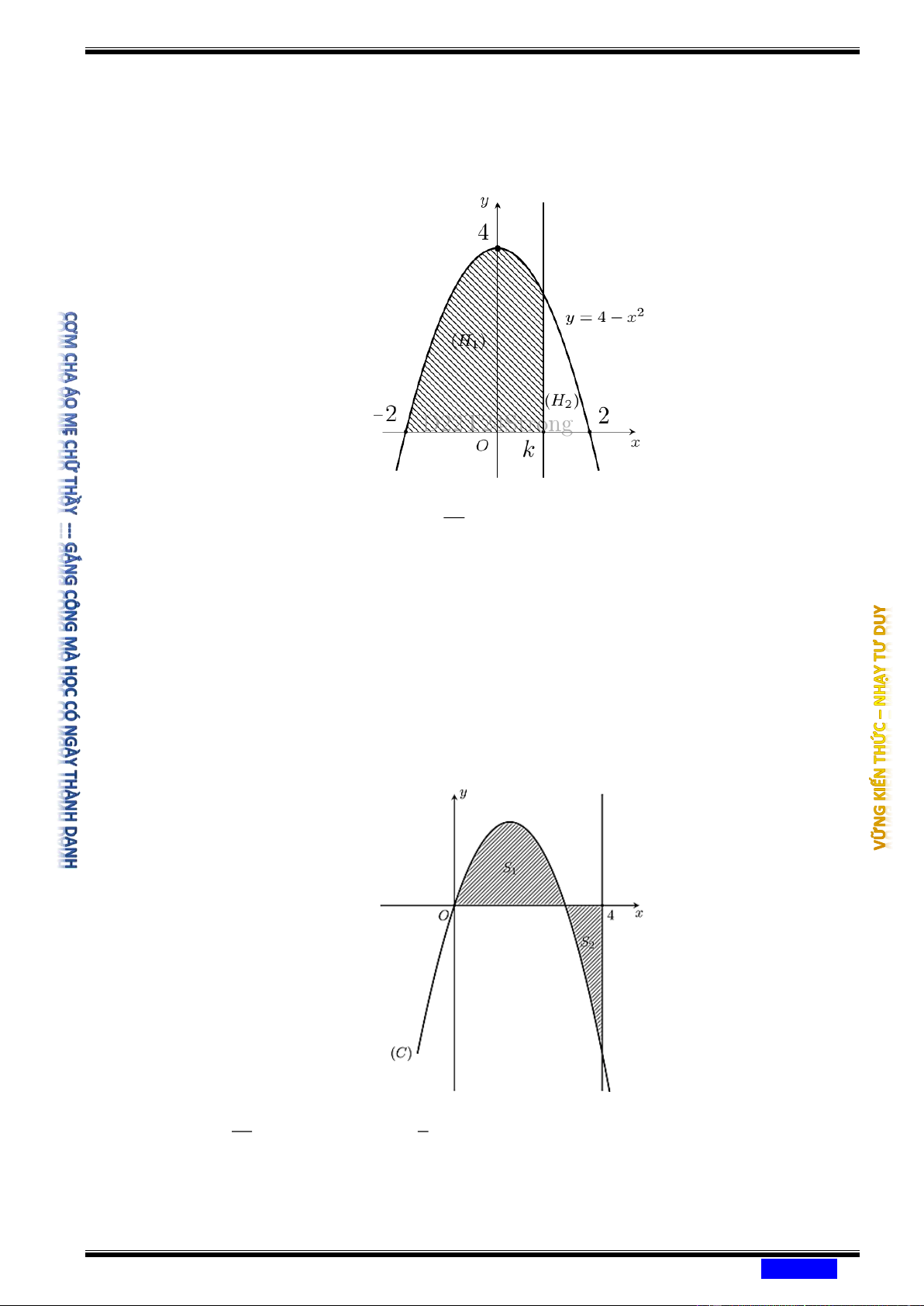
Câu 180: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Trong mặt phẳng
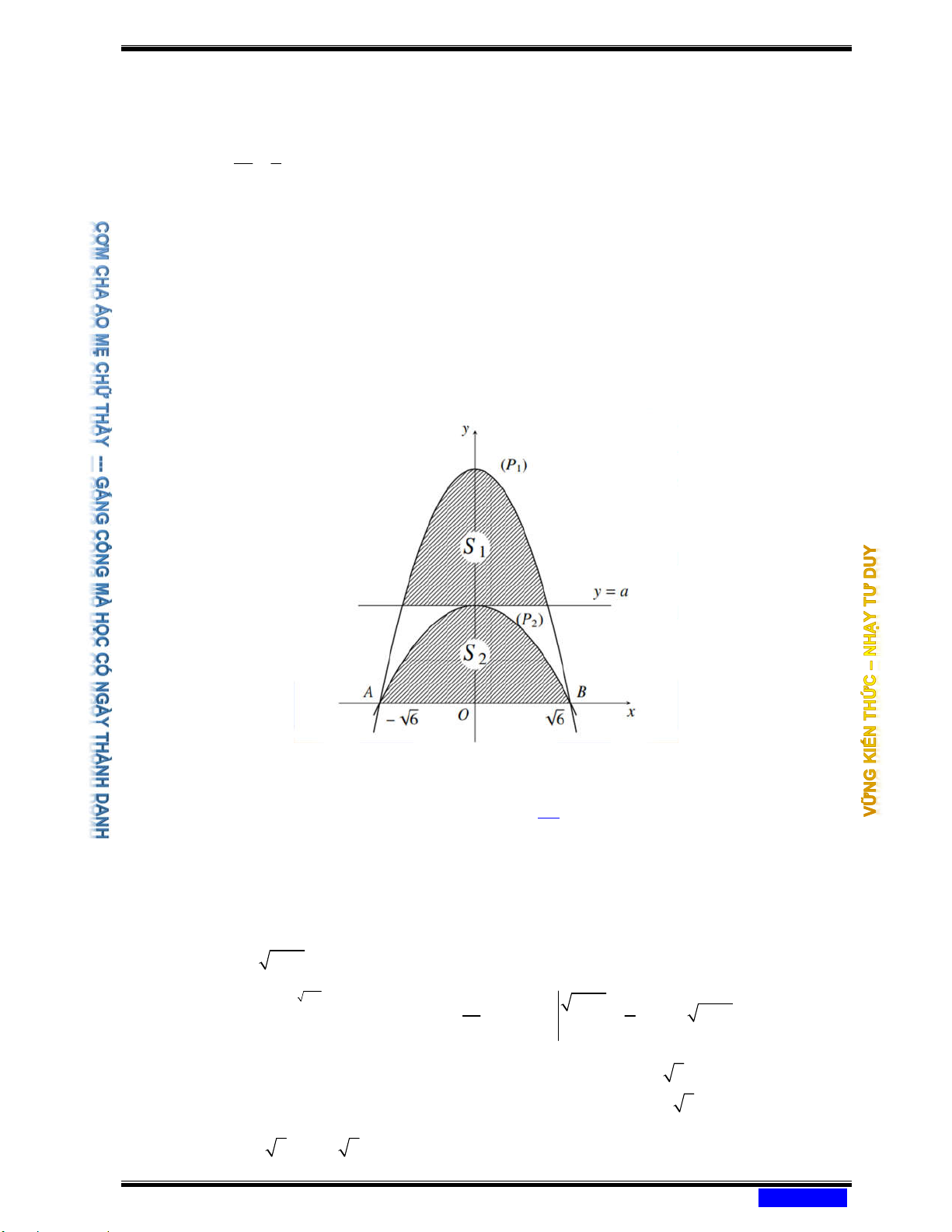
Oxy cho (H ) là hình phẳng giới hạn bởi parabol 2
y = 4 − x và trục hoành. Đường
thẳng x = k ( 2
− k 2) chia (H) thành hai phần (H ) , (H ) như hình vẽ 1 2 20
Biết rằng diện tích hình (H ) gấp
lần diện tích của hình (H ) , hỏi giá trị k thuộc 1 7 2 khoảng nào sau đây? Ⓐ ( 2 − ; 1 − ). Ⓑ (0;1) . Ⓒ ( 1 − ;0) . Ⓓ (1;2) .
Câu 181: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Cho hàm số 2
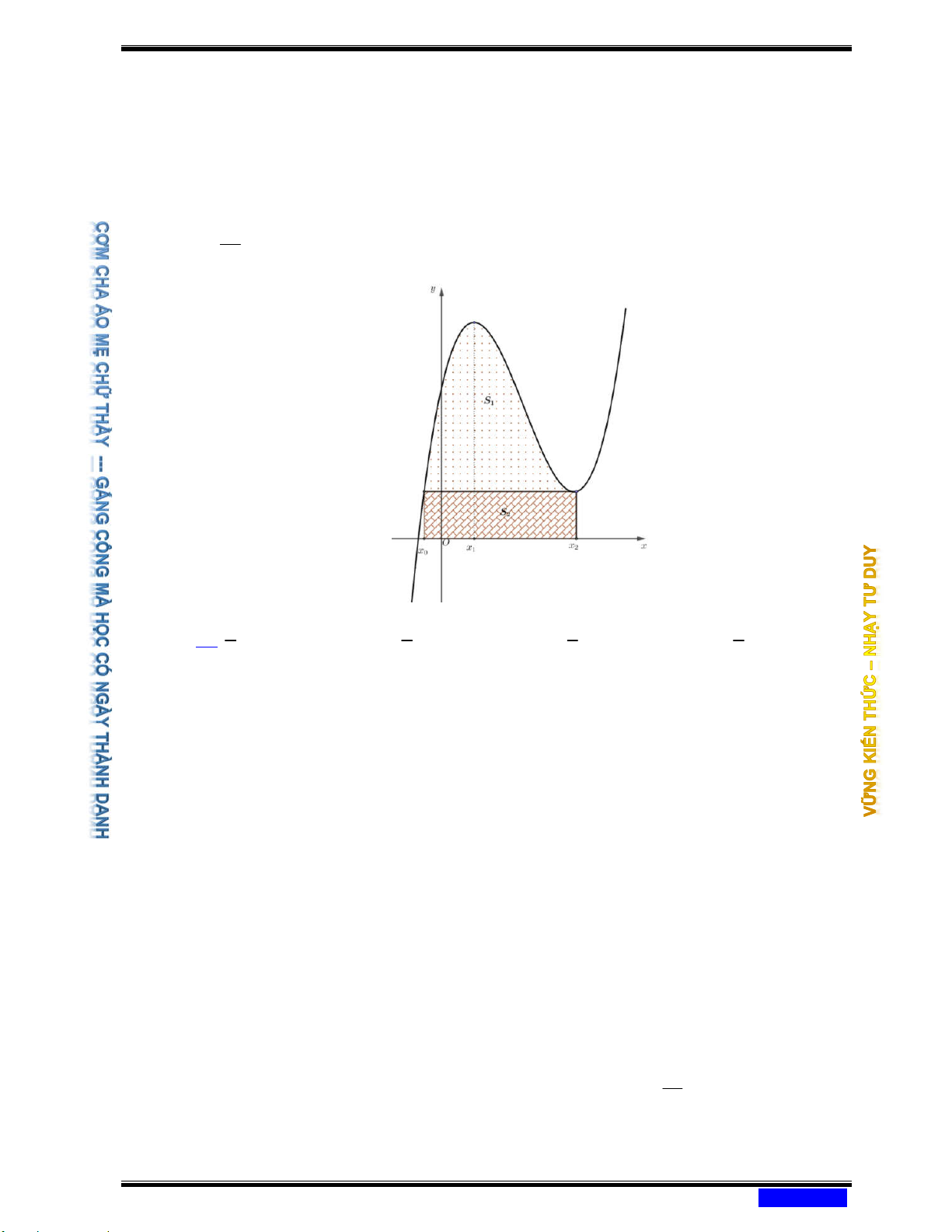
y = mx − x
(0 m 4) có đồ thị (C) . Gọi S + S là diện tích của hình phẳng giới 1 2
hạn bởi (C ) , trục hoành, trục tung và đường thẳng x = 4 . Giá trị m để S = S là 1 2 10 8 Ⓐ m = .
Ⓑ m = . Ⓒ m = 3. Ⓓ m = 2. 3 3
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 29 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 182: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Cho hai hàm số f ( x) 4 3 2
= ax + bx + cx + dx −1 và g (x) = ex − 2 ( , a , b ,
c d, e là các số thực cho trước).
Biết rằng đồ thị của hai hàm số y = f ( x) và y = g ( x) tiếp xúc nhau tại hai điểm có
hoành độ lần lượt là 1 − ;2 .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 81 81 81 81 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 20 4 10 40
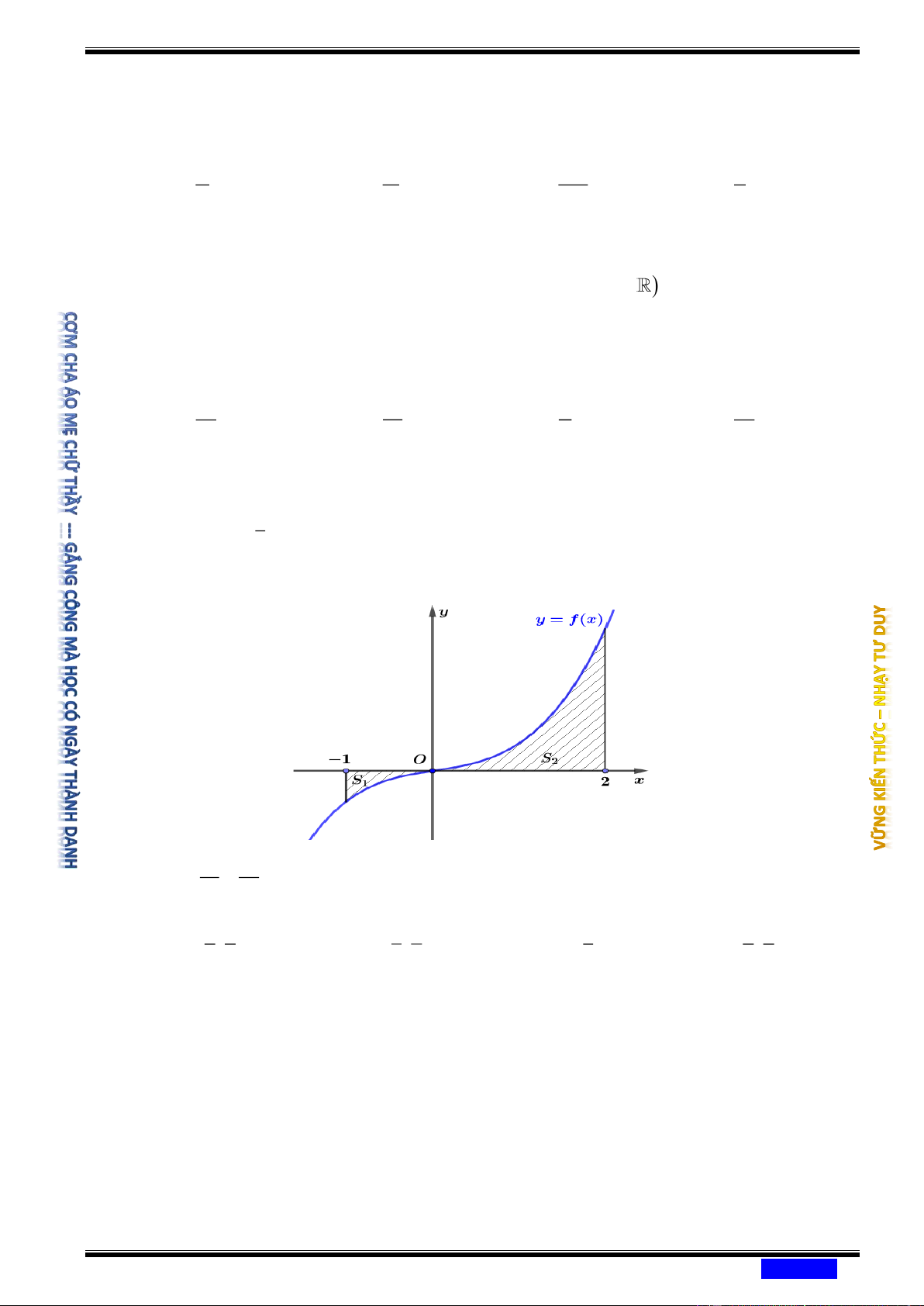
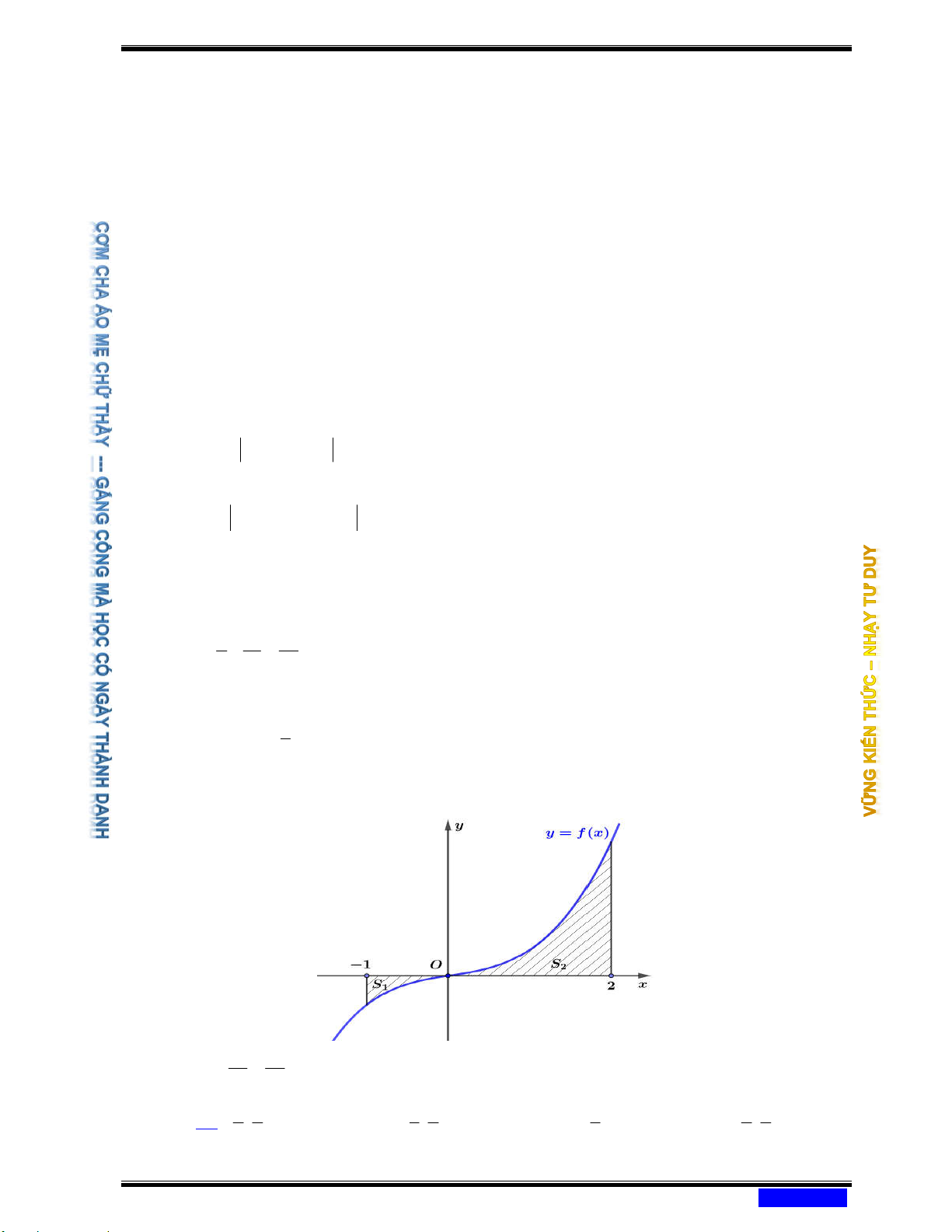
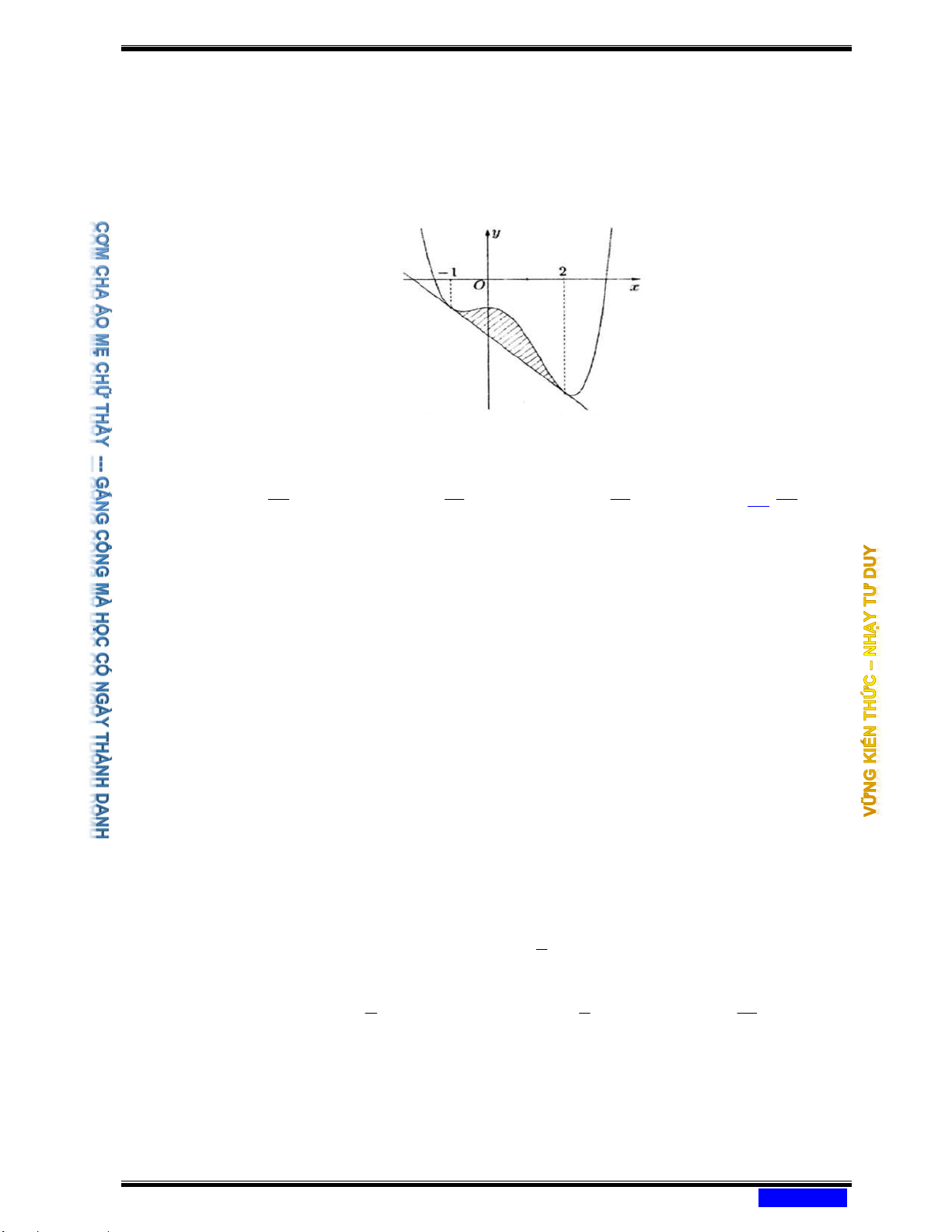
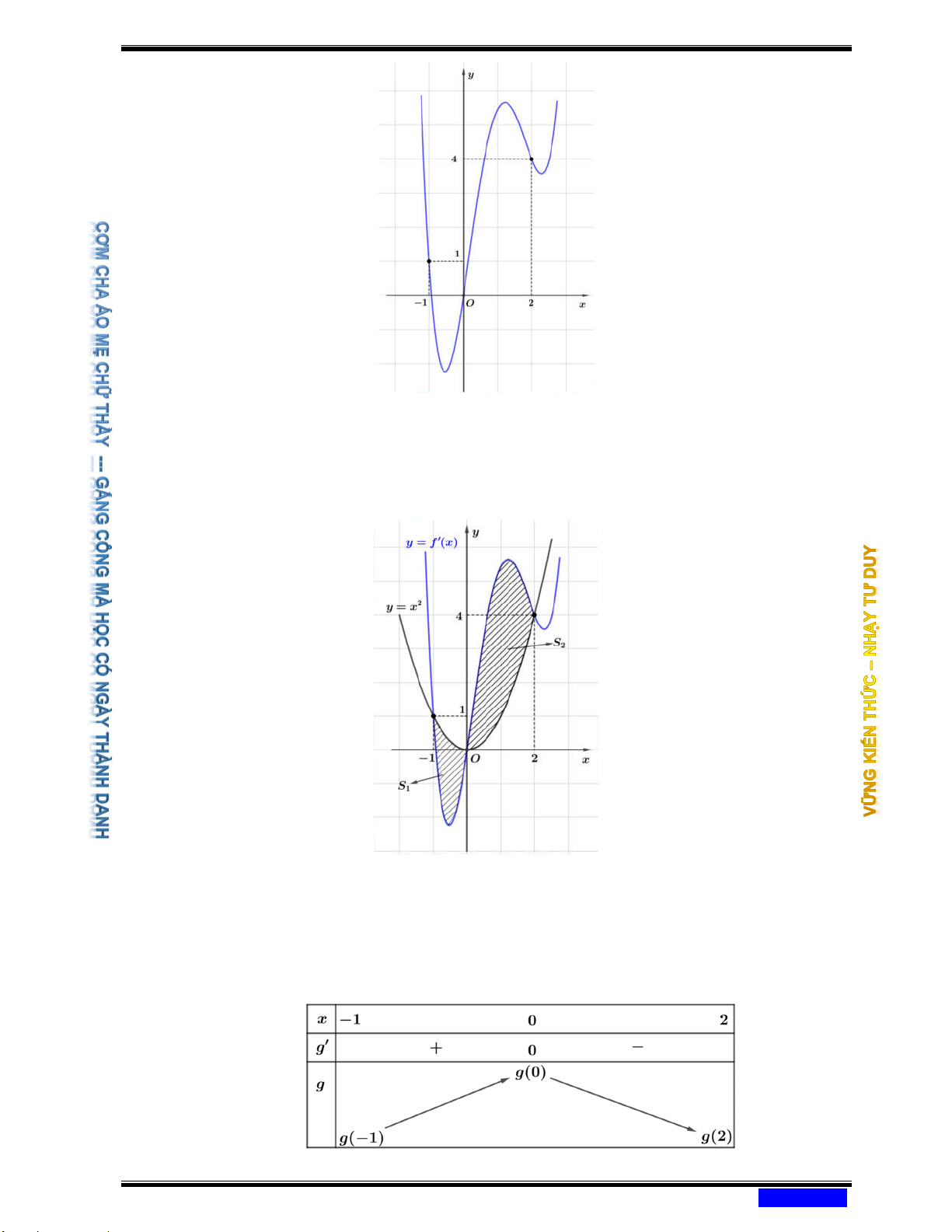
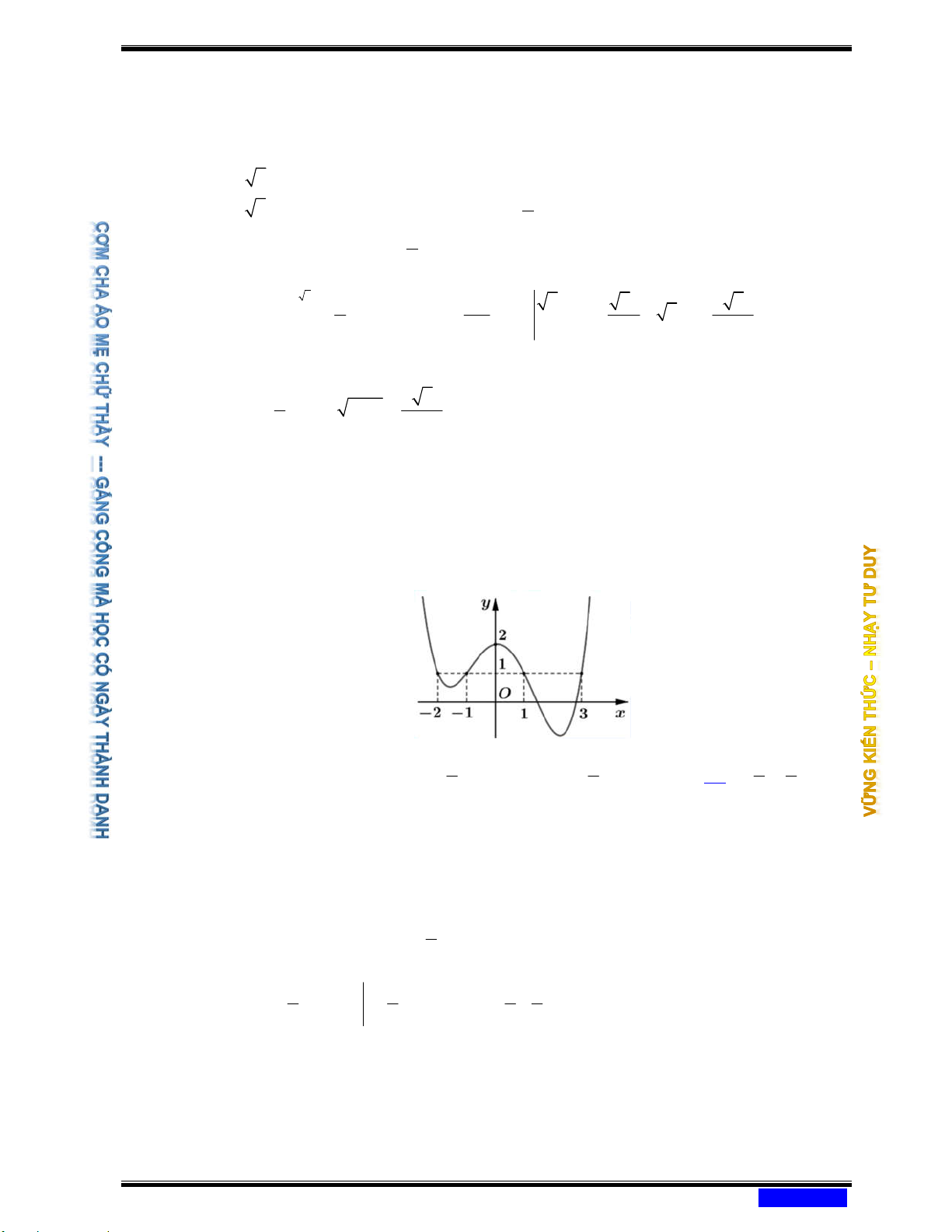
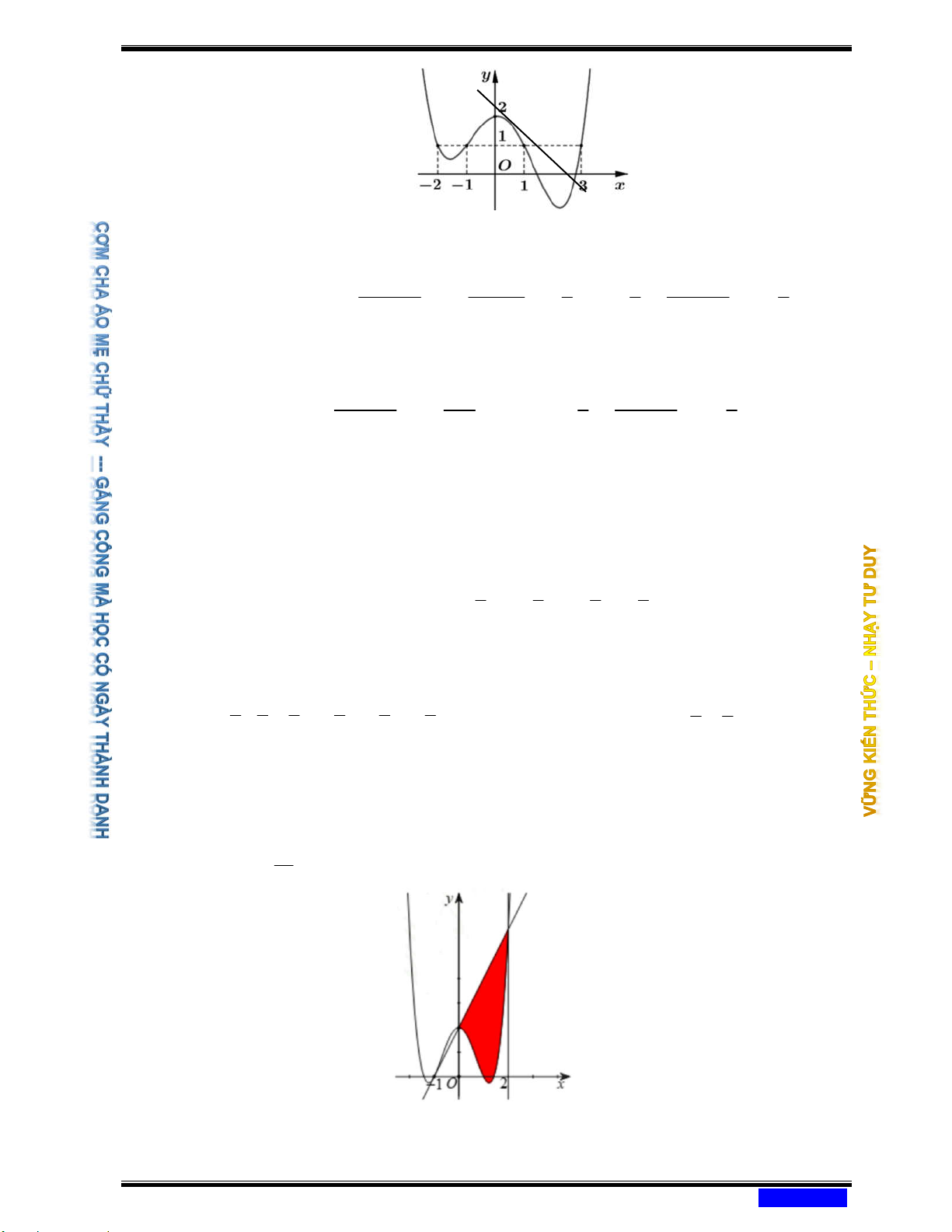
Câu 183: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Cho hàm số y = f ( ) x . Đồ thị hàm số y = f ( )
x như hình bên. Đặt 3
g(x) = x − 3 f (x). Mệnh đề nào dưới đây đúng?
Ⓐ g(2) g( 1 − ) g(0).
Ⓑ g(0) g( 1 − ) g(2). Ⓒ g( 1
− ) g(0) g(2).
Ⓓ g(2) g(0) g( 1 − ) .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 30 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
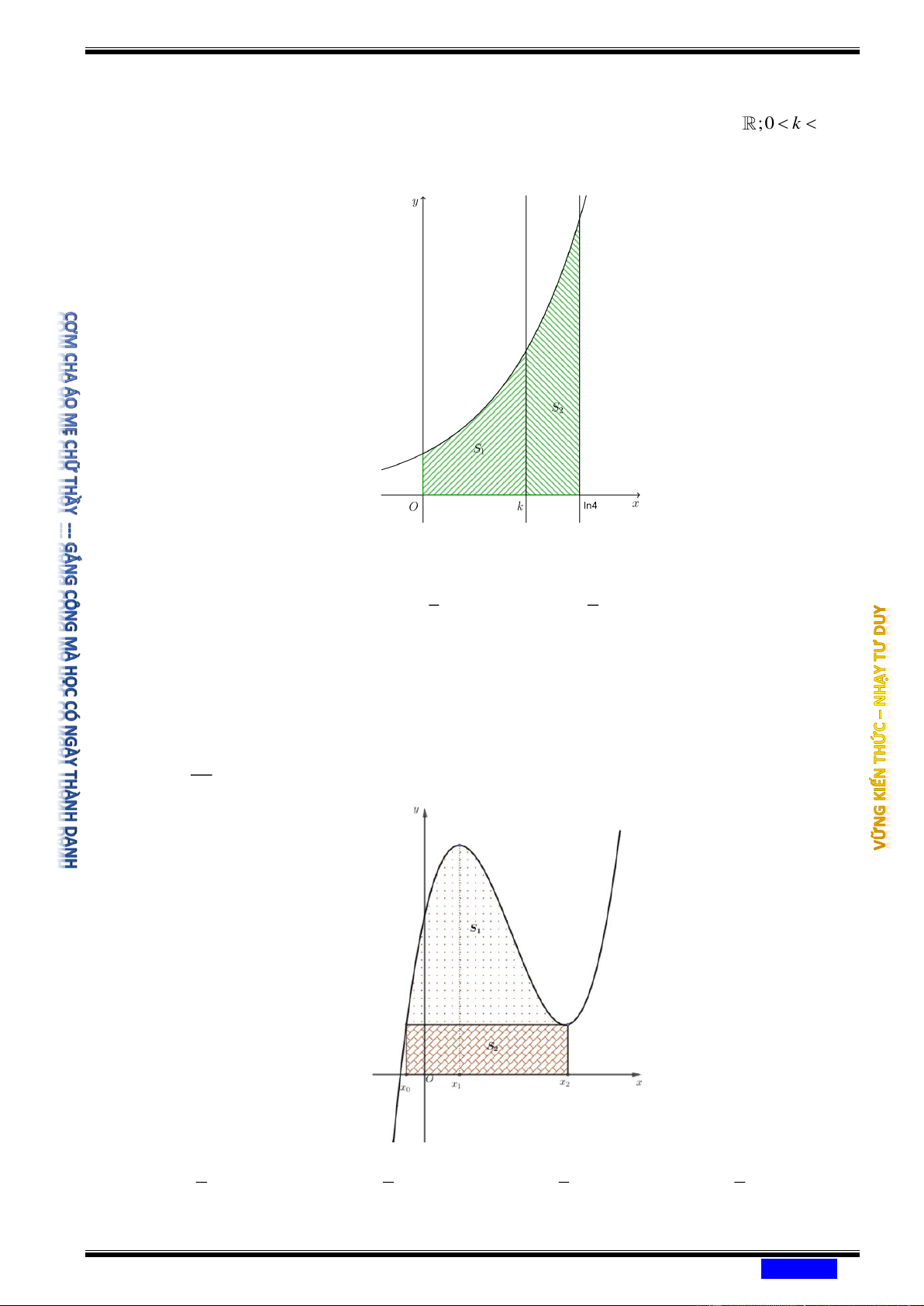
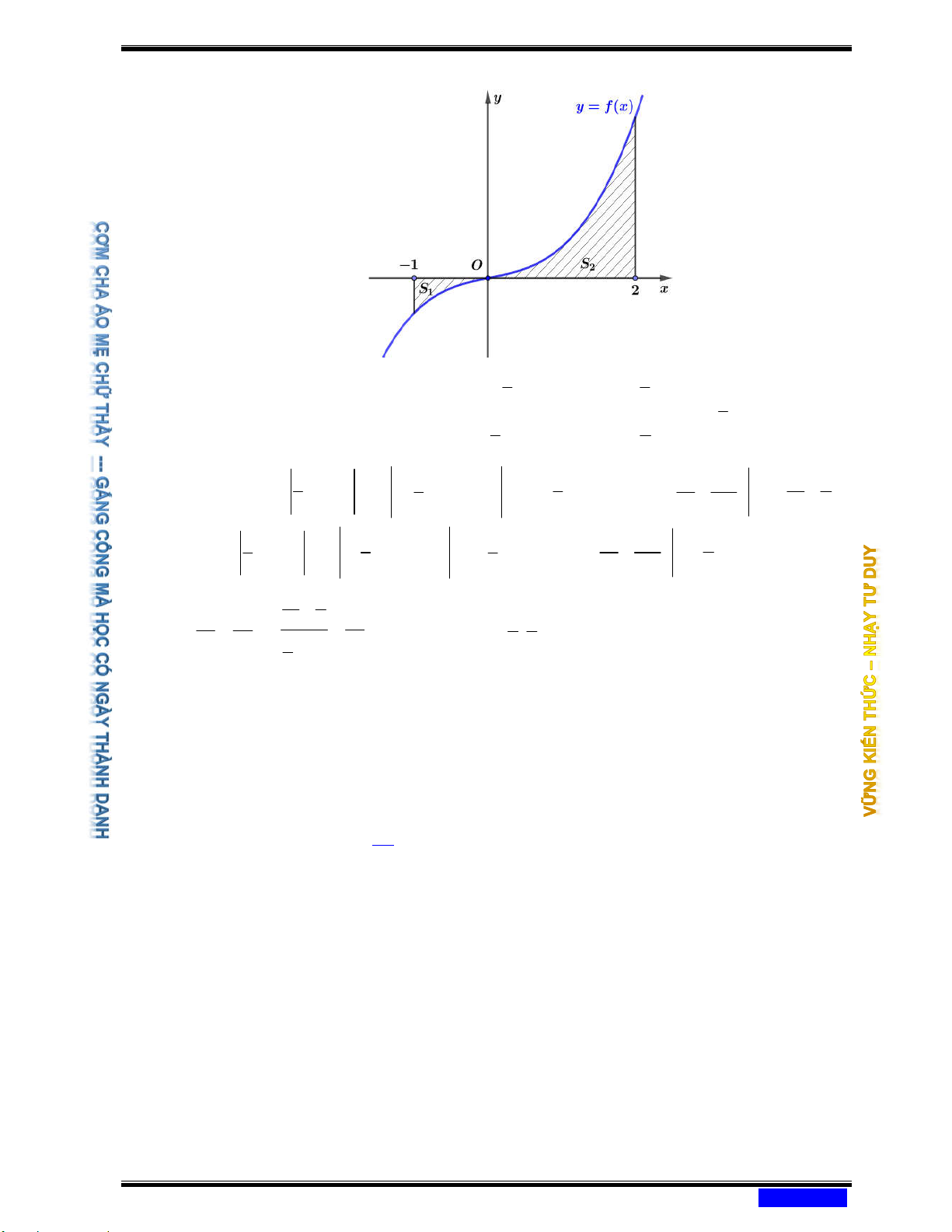
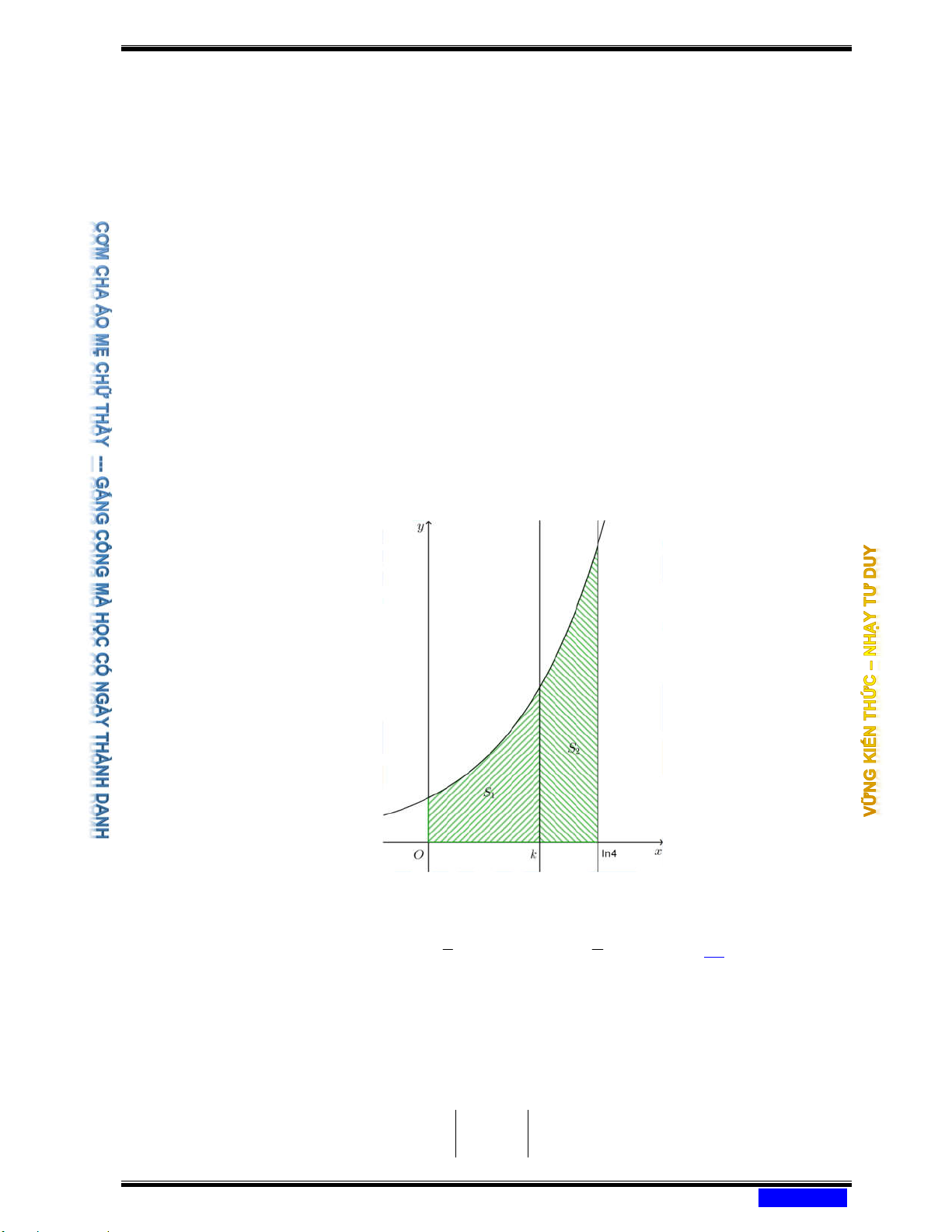
Câu 184: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hình phẳng ( H ) được giới hạn bởi các đường ex y =
; y = 0 ; x = 0 và x = ln 4 . Đường thẳng x = k (k ;0 k ln 4)
chia hình phẳng ( H ) thành hai phần có diện tích là S ; S (xem hình vẽ). 1 2
Tìm k để S = 2S . 2 1 8 2 Ⓐ k = ln 3. Ⓑ k = ln . Ⓒ k = ln 4 . Ⓓ k = ln 2 . 3 3
Câu 185: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Cho hàm số bậc ba
y = f ( x) có đồ thị là đường cong bên dưới. Gọi x ; x lần lượt là hai điểm cực trị thỏa 1 2
mãn x = x + 2 và f ( x − 3 f x = 0 . Đường thẳng song song với trục Ox và đi qua 1 ) ( 2 ) 2 1
điểm cực tiểu cắt đồ thị hàm số tại điểm thứ hai có hoành độ x và x = x +1. Tính tỉ 0 1 0 S
số 1 ( S và S lần lượt là diện tích hai hình phẳng được gạch ở hình bên dưới). S 1 2 2 Ⓐ 9 5 3 3 . Ⓑ . Ⓒ . Ⓓ . 8 8 8 5
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 31 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
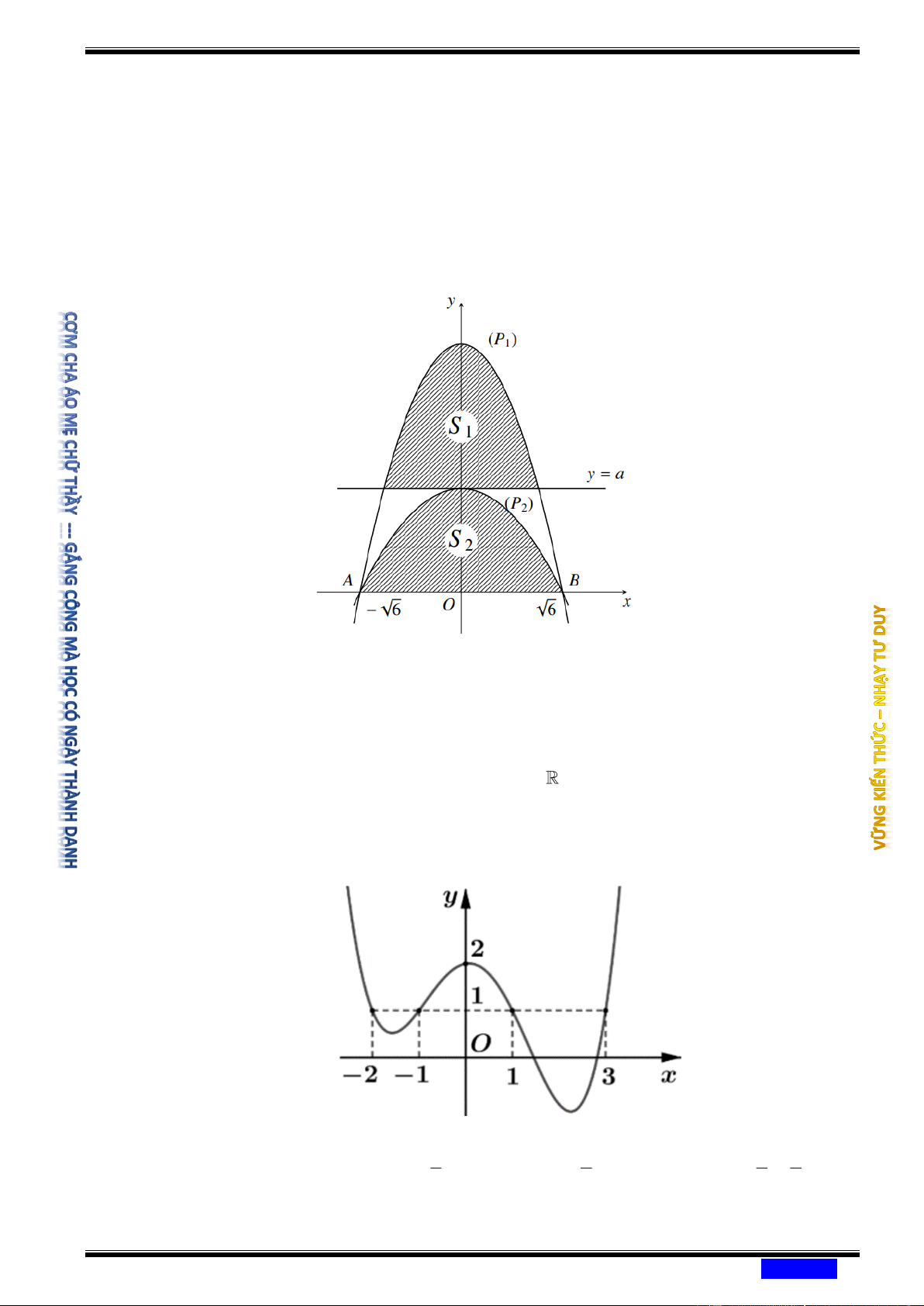
Câu 186: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho parabol (P ) 2
: y = −x + 6 cắt trục hoành tại hai điểm phân biệt ,
A B và đường thẳng d : y = a 1
(0 a 6) . Xét parabol (P đi qua ,
A B và có đỉnh thuộc đường thẳng y = a . Gọi S 2 ) 1
là diện tích hình phẳng giới hạn bởi ( P và d ; S là diện tích hình phẳng giới hạn 1 ) 2
bởi ( P và trục hoành (tham khảo hình vẽ). 2 )
Biết S = S , tính 3 2
T = a −12a +108a . 1 2 Ⓐ T = 218 . Ⓑ T = 219 . Ⓒ T = 216 . Ⓓ T = 217 .
Câu 187: Cho hàm số y = f ( x) có đạo hàm liên tục trên và có đồ thị như hình bên. Biết rằng 1 tích phân K = . x f
(x).f (x)dx có giá trị thuộc khoảng nào sau đây? 0 Ⓐ ( 3 2 3 2 3 − ; 2 − ) . Ⓑ 2; − − . Ⓒ − ;0 . Ⓓ − ; − . 2 3 2 3
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 32 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
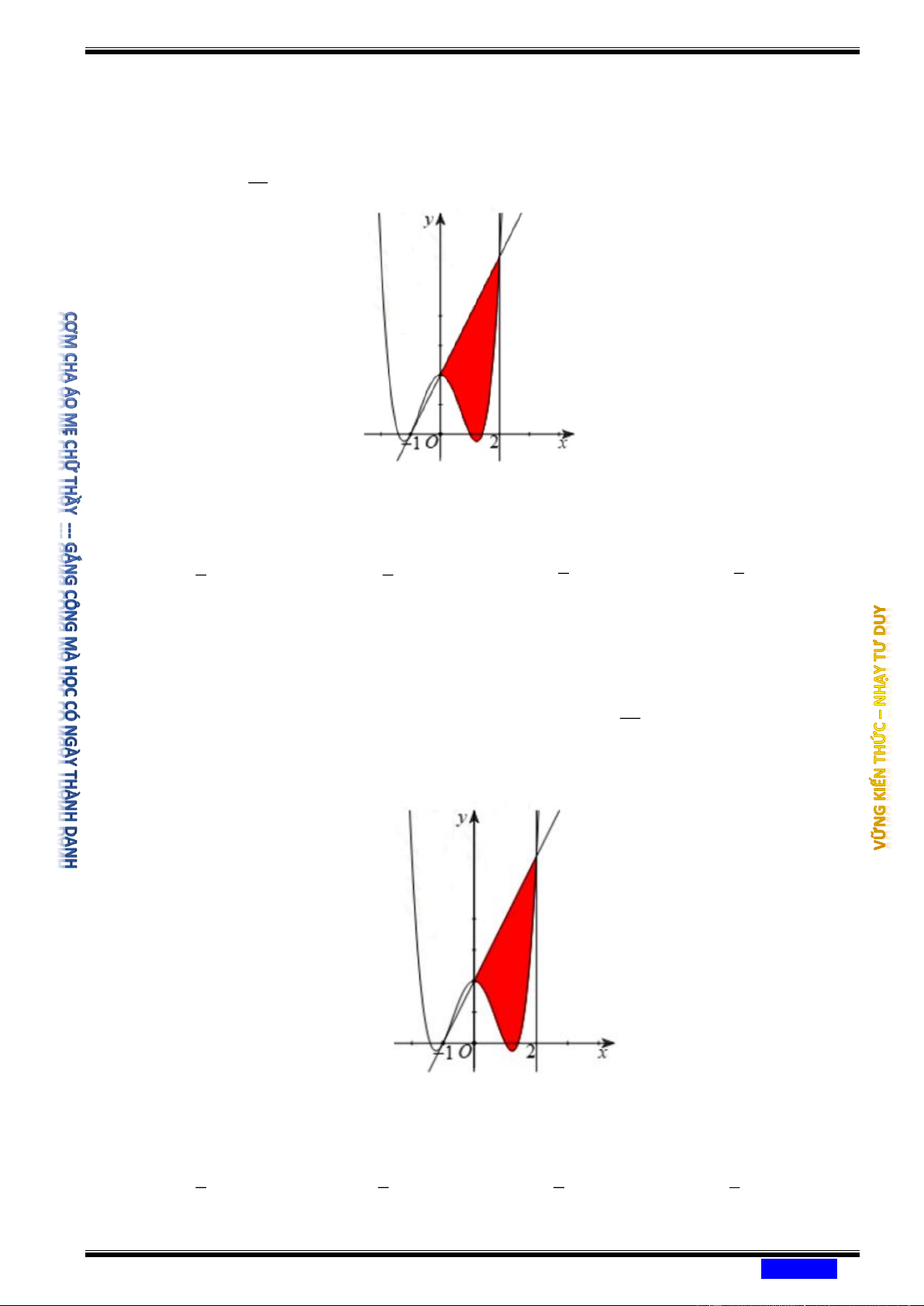
Câu 188: Cho hàm số 4 2
y = ax + bx + c có đồ thị (C) , biết rằng (C) đi qua điểm A( 1 − ;0) , tiếp
tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2 và diện
tích hình phẳng giới hạn bởi d , đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện 28 tích bằng
(phần tô màu trong hình vẽ). 5
Diện tích hình phẳng giới hạn bởi (C) và hai đường thẳng x = 1
− ; x = 0 có diện tích bằng 2 6 Ⓐ 2 1 . Ⓑ . Ⓒ . Ⓓ . 5 4 9 5
Câu 189: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Cho hàm số 4 2
y = ax + bx + c có đồ thị
(C), biết rằng (C) đi qua điểm A( 1
− ;0) , tiếp tuyến d tại A của (C) cắt (C) tại hai
điểm có hoành độ lần lượt là 0 và 2 và diện tích hình phẳng giới hạn bởi d , đồ thị ( 28
C ) và hai đường thẳng x = 0; x = 2 có diện tích bằng (phần tô màu trong hình 5 vẽ).
Diện tích hình phẳng giới hạn bởi (C) , d và hai đường thẳng x = 1 − ; x = 0 có diện tích bằng Ⓐ 2 1 2 1 . Ⓑ . Ⓒ . Ⓓ . 5 4 9 5
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 33 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 190: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Bồn hoa của một trường X có dạng
hình tròn bán kính bằng 8m . Người ta chia bồn hoa thành các phần như hình vẽ dưới
đây và có ý định trồng hoa như sau: Phần diện tích bên trong hình vuông ABCD để
trồng hoⒶ Phần diện tích kéo dài từ 4 cạnh của hình vuông đến đường tròn dùng
để trồng cỏ. Ở bốn góc còn lại, mỗi góc trồng một cây cọ. Biết AB = 4m , giá trồng hoa
là 200.000 đ/m2, giá trồng cỏ là 100.000 đ/m2, mỗi cây cọ giá 150.000 đ. Hỏi số tiền để
thực hiện việc trang trí bồn hoa như miêu tả ở trên gần bằng giá trị nào nhất?
Ⓐ 14.465.000 đồng. Ⓑ 14.865.000 đồng. Ⓒ 13.265.000 đồng. Ⓓ 12.218.000 đồng.
Câu 191: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Mặt sàn của một thang máy
có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một
hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ tọa độ Oxy với O là tâm hình vuông sao cho A(1; )
1 như hình vẽ bên thì các đường cong OA có phương trình 2 y = x 1 và 3
y = ax + bx . Tính giá trị ab biết rằng diện tích trang trí màu sẫm chiếm diện tích 3 mặt sàn. Ⓐ 2 − . Ⓑ −3 . Ⓒ 2 . Ⓓ 3 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 34 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 192: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho hàm số bậc ba có
đồ thị như hình vẽ, biết f ( x) đạt cực tiểu tại điểm x = 1 và thỏa mãn f ( x) +1 và
f (x) −1
lần lượt chia hết cho (x − )2 1 và (x + )2
1 . Gọi S , S lần lượt là diện tích hình 1 2
phẳng như hình bên dưới. Tính 2S − S 1 2 3 1 1 Ⓐ 4 . Ⓑ . Ⓒ . Ⓓ . 4 2 4
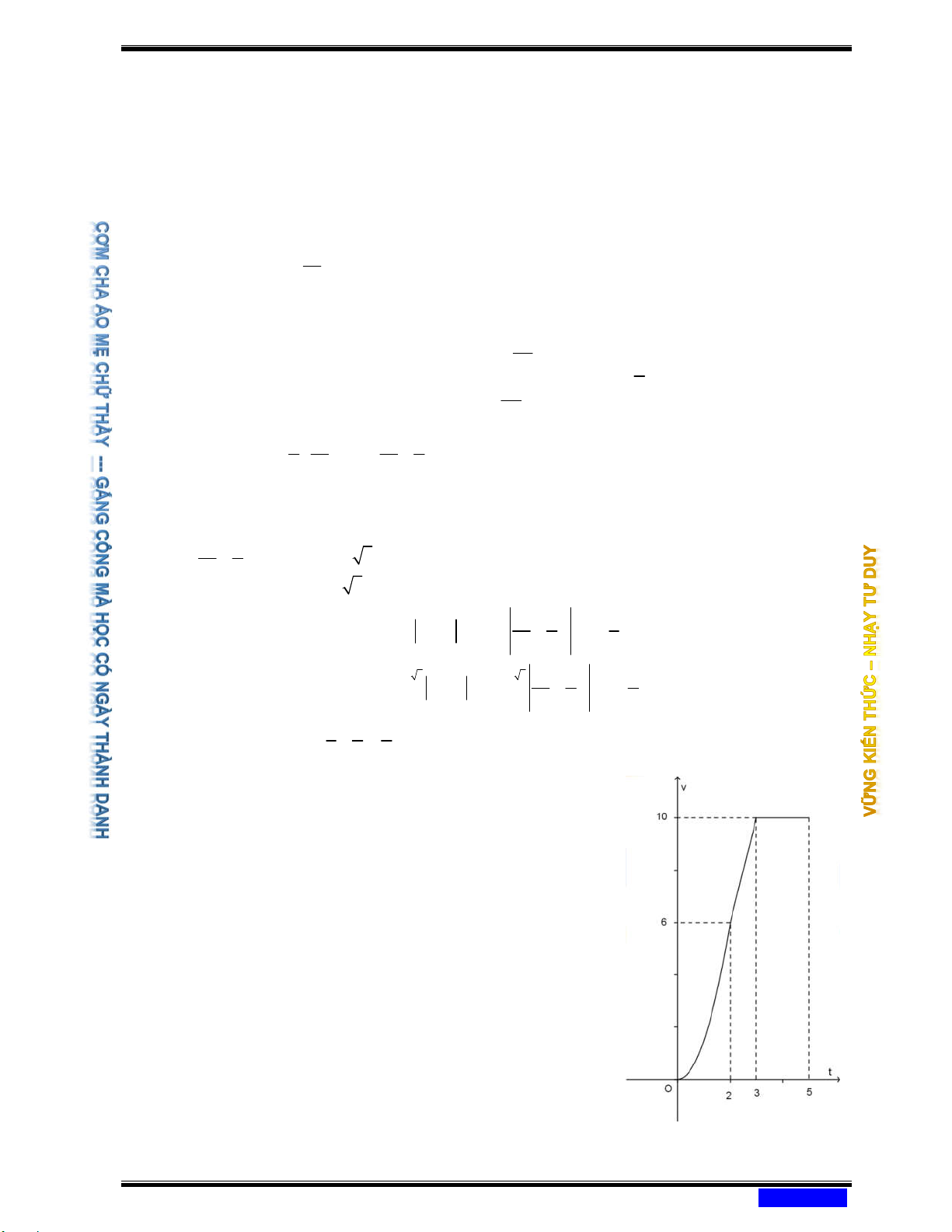
Câu 193: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021
LẦN 01) Một chiếc xe đua F đạt tới vận tốc lớn 1
nhất là 360km / h . Đồ thị bên biểu thị vận tốc v
của xe trong 5 giây đầu tiên kể từ lúc xuất phát.
Đồ thị trong 2 giây đầu tiên là một phần của
parabol đỉnh tại gốc tọa độ O , giây tiếp theo là
đoạn thẳng và sau đúng 3 giây thì xe đạt vận
tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành
biểu thị 1 giây, mỗi đơn vị trục tung biểu thị
10m / s và trong 5 giây đầu xe chuyển động
theo đường thẳng. Hỏi trong 5 giây đó xe đã đi
được quãng đường là bao nhiêu? Ⓐ 340 (mét). Ⓑ 420 (mét). Ⓒ 400 (mét). Ⓓ 320 (mét).
Câu 194: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Thể tích vật thể tròn xoay do
hình phẳng giới hạn bởi đồ thị y = f ( x) , trục Ox và các đường thẳng x = a , x = b ,
(a b) quay quanh trục Ox được tính theo công thức b b b b Ⓐ 2 V = f (x)dx. Ⓑ 2 V = f
(x)dx. Ⓒ V = f
(x) dx . Ⓓ V = f (x) dx a a a a
Câu 195: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Gọi (H ) là hình
phẳng giới hạn bởi các đồ thị y = x − ,
x y = 0 trong mặt phẳng Oxy . Quay hình (H )
quanh trục hoành ta được một khối tròn xoay có thể tích bằng 1 1 1 1 2 2 Ⓐ
x − x dx . Ⓑ
x − x dx . Ⓒ x
(1− x) dx . Ⓓ x
(1− x) dx . 0 0 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 35 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 196: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Gọi ( D) là hình phẳng giới
hạn bởi các đường y = 1 và 2
y = 2 − x . Thể tích khối tròn xoay giới hạn được tạo thành
khi quay ( D) xung quanh trục Ox được tính theo công thức 2 1 2 Ⓐ 2 V = ( 2 2 − x ) dx . Ⓑ V = ( 2 2 − x ) dx . − 2 1 − 1 2 2 Ⓒ 2 V = ( 2
2 − x ) dx − 2 .
Ⓓ V = ( 2
2 − x ) dx − 4 . 1 − − 2
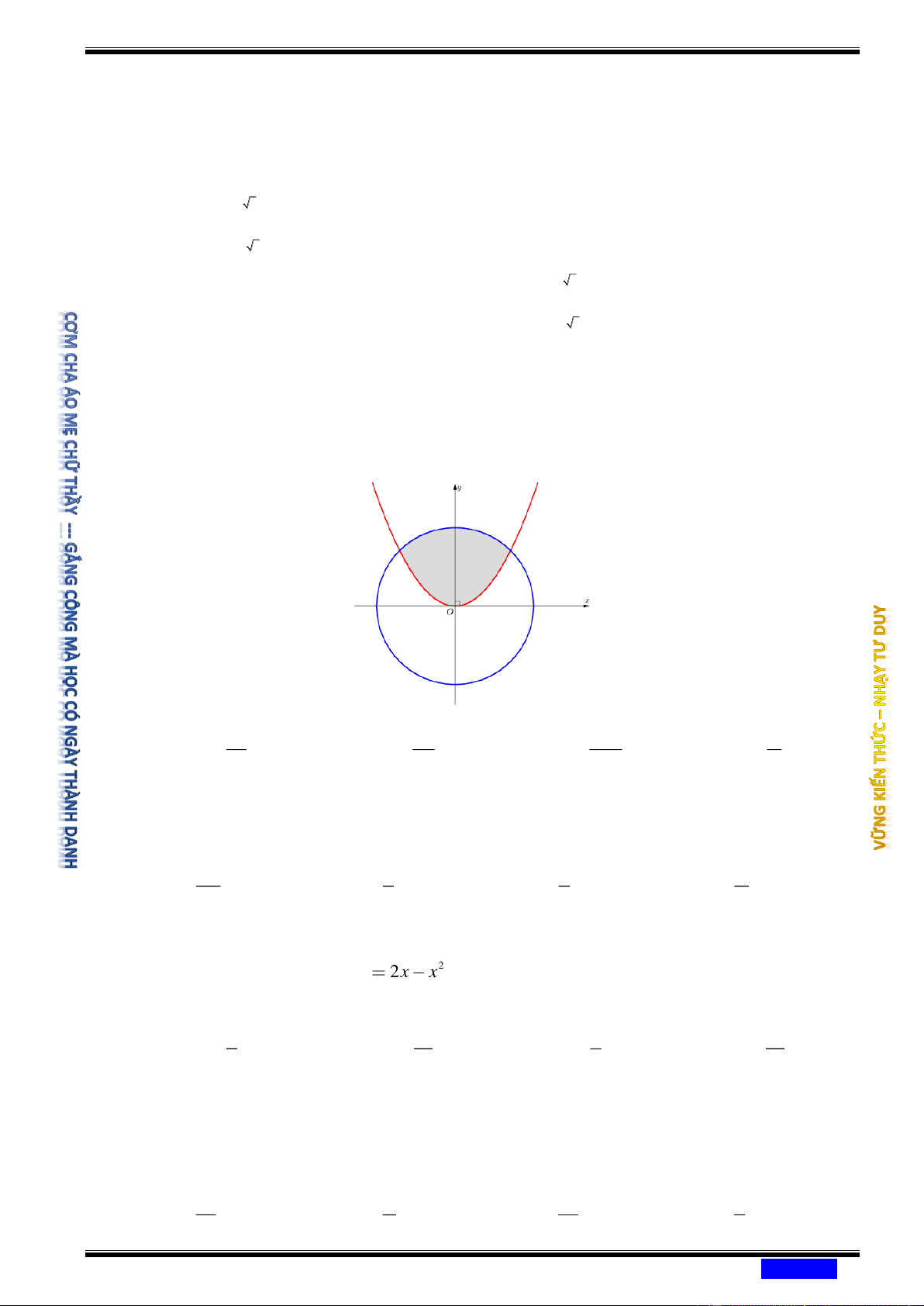
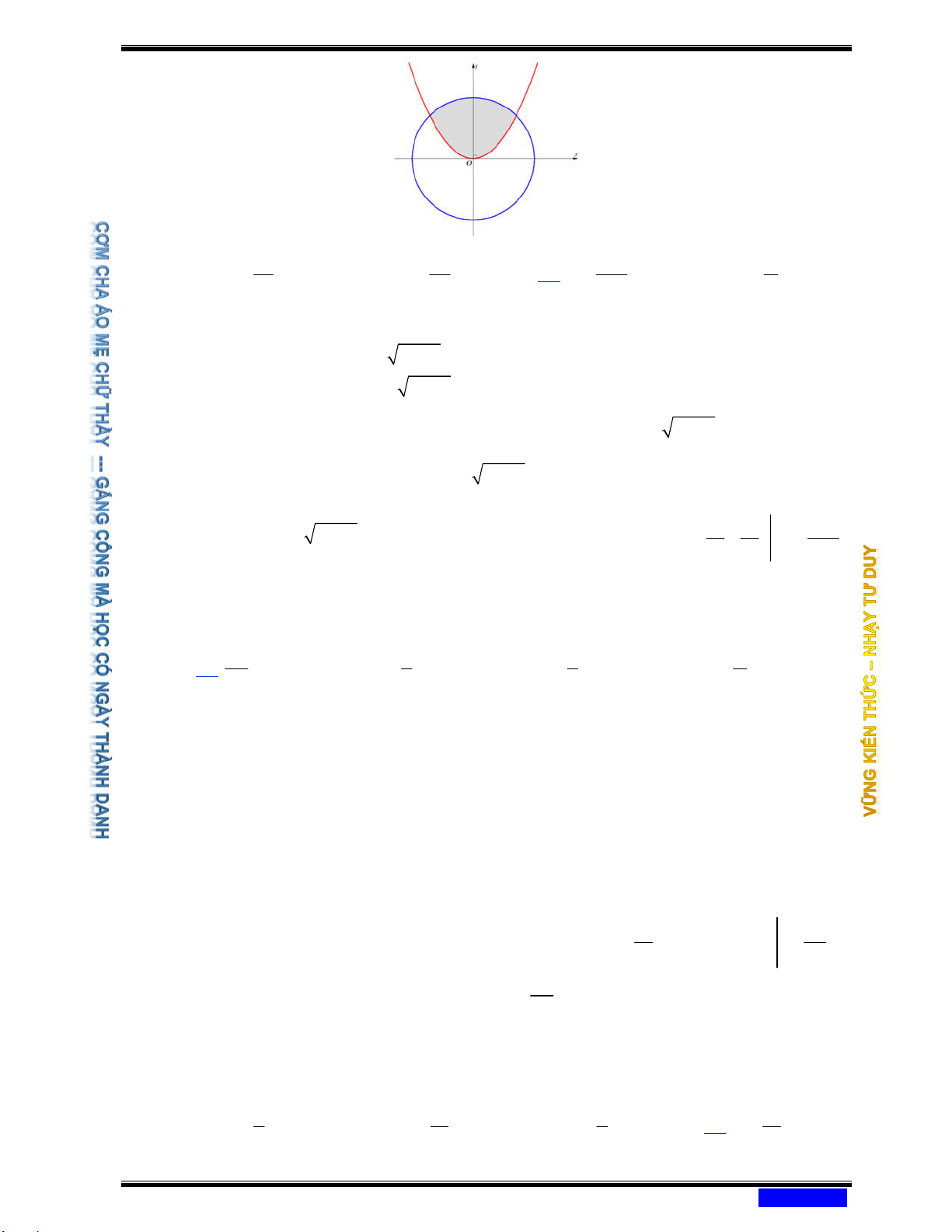
Câu 197: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho (H ) là hình phẳng giới hạn bởi parabol 2
y = x và đường tròn 2 2
x + y = 2 . Thể tích V của vật thể tròn xoay
tạo thành khi quay (H ) quanh trục hoành là Ⓐ 44 5 44 V = . Ⓑ V = . Ⓒ V = . Ⓓ V = . 15 3 15 5
Câu 198: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tính thể tích của khối tròn xoay
khi cho hình phẳng giới hạn bởi đường thẳng y = 3x − 2 và đồ thị hàm số 2 y = x quay quanh trục Ox . 4 1 4 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 5 6 5 6
Câu 199: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Cho hình phẳng H giới
hạn bởi đồ thị hàm số 2 y 2x
x và trục hoành. Tính thể tích V vật thể tròn xoay
sinh ra khi cho H quanh quay trục Ox . Ⓐ 4 16 4 16 V = . Ⓑ V = . Ⓒ V = . Ⓓ V = . 3 15 3 15
Câu 200: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Gọi ( H ) là hình phẳng giới hạn bởi 2
y = −x + x và trục hoành. Thể tích của khối tròn xoay tạo thành
khi quay hình ( H ) quanh trục hoành bằng Ⓐ 1 1 . Ⓑ . Ⓒ . Ⓓ . 30 6 30 6
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 36 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 201: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Thể tích của khối
tròn xoay do hình phẳng giới hạn bởi y = ln x , trục Ox và đường thẳng x = 2 quay xung quanh trục Ox là Ⓐ 2ln 2 −1. Ⓑ 2 ln 2 + . Ⓒ 2 ln 2 − . Ⓓ 2ln 2 −1.
Câu 202: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Một vật chuyển động có
phương trình vận tốc: v(t ) 3
= t −3t +1 . Quãng đường vật đi được từ thời điểm t = 0 đến khi t = 3 là Ⓐ 39 15 m . Ⓑ 19m . Ⓒ 20m . Ⓓ . 4 4
Câu 203: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Một chiếc máy bay
vào vị trí cất cánh chuyển động trên đường băng với vận tốc v (t ) 2
= t + 2t (m/s) với t
là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết
máy bay đạt vận tốc 120(m/s) thì nó rời đường băng. Quãng đường máy bay đã di
chuyển trên đường băng gần nhất với giá trị nào dưới đây? Ⓐ 1200(m). Ⓑ 1100(m). Ⓒ 430(m). Ⓓ 330(m).
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 37 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
HƯỚNG DẪN GIẢI NGUYÊN HÀM – TÍCH PHÂN TRONG ĐỀ CHUYÊN 2020-2021 NGUYÊN HÀM
ĐỊNH NGHĨA – TÍNH CHẤT – NGUYÊN HÀM CƠ BẢN Câu 1:
(CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Mệnh đề nào sau đây sai? Ⓐ 1
dx = ln x + C . Ⓑ x x
e dx = e + C . x 2 + Ⓒ x 1 xdx = + C . Ⓓ
sin xdx = cos x + C . 2 Lời giải
Ta có: sin xdx = −cos x + C . Suy ra đáp án D sai. Câu 2:
(CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Hàm số f ( x) 4 2 = x −3x có họ nguyên hàm là Ⓐ F ( x) 3
= x − 6x + C. Ⓑ F (x) 5 3
= x + x + C. x x Ⓒ F ( x) 5 3 = + x + C. Ⓓ F ( x) 5 3 = − x + C. 5 5 Lời giải x
Áp dụng bảng nguyên hàm, ta có: (x − x ) 5 4 2 3 3 dx = − x + C. 5 Câu 3:
(CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Họ nguyên hàm của hàm số ( ) 2 x f x = e là Ⓐ ( ) 2x F x = e + C. Ⓑ ( ) 3x
F x = e + C. Ⓒ ( ) 1 2 = 2 x F x e + C. Ⓓ ( ) 2 x F x = e + C. 2 Lời giải x 1
Áp dụng bảng nguyên hàm, ta có: ( ) 2 2 x
F x = e dx = e + C. 2 Câu 4:
(CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Họ nguyên hàm của hàm số y = 5 − 3x là: Ⓐ 2 ( 2 2 1 5 − 3x)3 + C. Ⓑ − 5 − 3x + C. Ⓒ −
(5−3x)3 +C. Ⓓ 5 − 3x + C. 9 3 9 2 Lời giải 1 d 5 − 3x Ta có: 5 − 3xdx = (5−3x) ( ) 2 3 − 1 1 ( − x)3 = − ( 2 5 3 2
5 − 3x)12 d (5 − 3x) = − . + C = − (5−3x)3 + C. 3 3 3 9 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 38 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Câu 5: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) 3 2
= 4x − 3x + 2x −1. Trong các khẳng định sau, khẳng định nào đúng? Ⓐ f (x) 4 3 2
dx = 4x − x + x − x +C . Ⓑ f (x) 4 3 2
dx = x − x + x − x +C . Ⓒ f (x) 1 4 3 2
dx = x − x + x − x + C . Ⓓ f (x) 4 3 2
dx =12x −6x + x − x +C . 4 Lời giải Ta có f
(x)dx = ( 3 2
x − x + x − ) 4 3 2 4 3 2
1 dx = x − x + x − x + C . Câu 6:
(CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) = sin 3x . Trong
các khẳng định sau, khẳng định nào đúng? Ⓐ f (x)dx = 3 − cos3x +C . Ⓑ f
(x)dx =3cos3x+C. Ⓒ f (x) 1
dx = − cos3x + C . Ⓓ f (x) 1
dx = cos3x + C . 3 3 Lời giải 1
Ta có sin 3x dx = − cos 3x + C . 3 Câu 7:
(CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho F ( x) là
một nguyên hàm của hàm số f ( x) = sin 2x và F =1 . Tính F . 4 6 1 5 3 Ⓐ F = . Ⓑ F = . Ⓒ F = . Ⓓ F = 0 . 6 2 6 4 6 4 6 Lời giải
Ta có: F ( x) = sin 2 d x x 1
= − cos 2x + C . 2 1 Vì F =1 − cos 2
+ C = 1 C =1 F (x) 1 = − cos 2x +1. 4 2 4 2 1 3 Vậy F = − cos 2 +1 = . 6 2 6 4 Câu 8:
(CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Họ tất cả các 2
nguyên hàm của hàm số f (x) = sin x + . x Ⓐ 2 cos x − + C .
Ⓑ − cos x + 2ln x + C . 2 x
Ⓒ − cos x − 2ln x + C .
Ⓓ cos x + 2ln x + C .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 39 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Ta có: f ( )
x dx = − cos x + 2ln x + C . Câu 9:
(CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho C là
một hằng số. Trong các mệnh đề sau, mệnh đề nào sai ? Ⓐ 2
2x dx = x + C .
Ⓑ sinx dx = cos x + C . 1 Ⓒ
dx = ln | x | +C . Ⓓ ex d = ex x −C . x Lời giải
Ta có sinxdx = −cos x + C
Câu 10: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho hàm số
f ( x) = sin 3x . Trong các khẳng định sau, khẳng định nào đúng? Ⓐ f
(x)dx =3cosx+C . Ⓑ f (x) 1 dx = cos x + C . 3 Ⓒ f
(x)dx =3cos3x+C. Ⓓ f (x) 1
dx = − cos 3x + C . 3 Lời giải Ta có f (x) 1 dx = sin 3 d
x x = − cos 3x + C . 3
Câu 11: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Họ nguyên hàm của hàm số ( ) = ex f x + x là: 2 2 1 x 2 Ⓐ x x 1 + 1 x ex + + C .
Ⓑ ex +1+ C . Ⓒ e +
+ C . Ⓓ ex + + C . 2 x +1 2 2 2 Lời giải x Ta có ( + x) 2 e dx = e + + x x C . 2
Câu 12: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tìm họ nguyên hàm 1 x + dx x −1 2 Ⓐ 2 1 x 1
x + ln x −1 + C . Ⓑ x + + C
+ ln x −1 + C . Ⓓ 1− + C . x − . Ⓒ 1 2 (x − )2 1 Lời giải 1 x Ta có x + dx 2 =
+ ln x −1 + C . x −1 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 40 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 13: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số F ( x) , f ( x) liên
tục trên khoảng K , khi đó F ( x) là một nguyên hàm của hàm f ( x) trên khoảng K
nếu với mọi x K ta có
Ⓐ F ( x) = f ( x).
Ⓑ F (x) = f (x) .
Ⓒ F( x) = f ( x).
Ⓓ F (x) = f (x) . Lời giải
Hàm số F ( x) là một nguyên hàm của hàm f ( x) trên khoảng K nếu với mọi x K
ta có F( x) = f ( x).
Câu 14: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số
f ( x) = cos 2x . Trong các khẳng định sau, khẳng định nào đúng? x x Ⓐ f (x) sin 2 dx = − + C . Ⓑ f (x) sin 2 dx = + C . 2 2 Ⓒ f (x)dx = 2
− sin 2x + C . Ⓓ f
(x)dx = 2sin2x+C . Lời giải
Ta có nếu F(x) là một nguyên hàm của hàm số f (x) thì 1
f (ax + b)dx = F (ax +b)+C a sin 2x Vậy cos 2 d x x = + C . 2
Câu 15: Tìm họ nguyên hàm của hàm số f ( x) 2 = 3x . Ⓐ f
(x)dx = 6x+C. Ⓑ f
(x)dx = x+C. 1 Ⓒ f (x) 3
dx = x + C . Ⓓ f (x) 3 dx = x + C . 3 Lời giải Chọn C 1 Ta có f (x) 2 3 3
dx = 3x dx = 3. x + C = x + C . 3
Câu 16: Tìm họ nguyên hàm của hàm số f (x) = 2x + cos 2 . x 1 Ⓐ 2
x − sin 2x + C . Ⓑ 2 x +
sin 2x + C . Ⓒ 2
x + sin 2x + C . Ⓓ 2 1 2 x − sin 2x + C . 2 Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 41 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Chọn B 1
Ta có: (2x + cos2x) 2
dx = 2xdx + cos 2xdx = x + sin 2x + C . 2
Câu 17: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) tan d x x bằng 1 1 Ⓐ − + C .
Ⓑ ln cos x + C . Ⓒ + C .
Ⓓ −ln cos x + C . 2 sin x 2 cos x Lời giải Chọn D sin x d (cos x) Ta có: tan d x x = dx = −
= −ln cos x + C . cos x cos x
Câu 18: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Một nguyên 1
hàm của hàm số f (x) = là F(x) bằng 2x − 3 Ⓐ 2 1 1 − ( . Ⓑ . Ⓒ 2ln 2x − 3 . Ⓓ ln 2x − 3 . 2x − 3)2 2 (2x − 3)2 2 Lời giải Chọn D 1 1 I = f (x)dx = dx
. Đặt: u = 2x − 3 du = 2dx dx = du . 2x − 3 2 1 du 1 Khi đó, I = = ln u + C . 2 u 2 1
Thay u = 2x − 3 ta được I = ln 2x − 3 + C . 2
Câu 19: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Họ nguyên hàm của hàm số ( ) 2 x f x = e là Ⓐ 1 1 x e + C . Ⓑ 2 x e + C . Ⓒ 2 2 x e + C . Ⓓ 2 x e + C . 2 2 Lời giải x 1 kx 1 Ta có d kx e x = e + C . Vậy 2 2 d x e x = e + C . k 2
Câu 20: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Họ các
nguyên hàm của hàm số ( ) = 5x f x − x là
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 42 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 x 2 5 x 2 x 5x Ⓐ − + C . Ⓑ 2
5x − x + C . Ⓒ 5x ln 2 − + C . Ⓓ −1+ C . ln 5 2 2 ln 5 Lời giải Chọn A x x
Ta có (5x − x) 2 5 dx = − + C . ln 5 2 Câu 21:
(THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Họ
nguyên hàm của hàm số f ( x) = sin x + 4x là Ⓐ 2
−cos x + 4x +C . Ⓑ 2
cos x + 4x + C . Ⓒ 2
−cos x + 2x +C . Ⓓ 2
cos x + 2x + C . Lời giải Chọn C Ta có ( + x) 2
sinx 4 dx = −cos x + 2x + C .
Câu 22: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Tìm
nguyên hàm của hàm số f ( x) 1 = 3x− . 2 Ⓐ dx dx 1
= ln 3x − 2 + C . Ⓑ
= − ln 3x − 2 + C . 3x − 2 3x − 2 2 Ⓒ dx 1 dx 1 = ln 3x + 2 + C . Ⓓ
= ln 2 − 3x + C . 3x − 2 3 3x − 2 3 Lời giải Chọn D dx 1 d (3x − 2) 1 Ta có =
= ln 3x − 2 + C 1
= ln 2 − 3x + C . 3x − 2 3 3x − 2 3 3
Câu 23: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Nguyên hàm
của hàm số f ( x) 3 = 2x −9 là. 1 Ⓐ 1 4
x − 9x + C . Ⓑ 3
4x − 9x + C . Ⓒ 4
4x − 9x + C . Ⓓ 4 x + C . 2 4 Lời giải 2 1 Ta có ( 3 2x − 9) 4 4 dx =
x − 9x + C =
x − 9x + C . 4 2
Câu 24: Tìm mệnh đề sai trong các mệnh đề sau 4 x + C Ⓐ 3 x dx = . Ⓑ 2exd = 2 (ex x + C). 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 43 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 Ⓒ sin d
x x = C − cos x . Ⓓ
dx = ln x + C x . Lời giải Chọn D 1 1
Ta có công thức đúng là
dx = ln x + C , còn
dx = ln x + C
chỉ đúng khi x 0 . x x
Câu 25: Họ nguyên hàm của hàm số f ( x) = 2x + sin 2x là Ⓐ 2 1 x −
cos 2x + C . Ⓑ 2
x + 2 cos 2x + C . Ⓒ 2 1 x +
cos 2x + C . Ⓓ 2 2 2
x − 2 cos 2x + C . Lời giải Chọn A f (x) 2 1 x
d = 2x + sin 2x x d = x − cos 2x + C 2
Câu 26: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Họ tất cả các nguyên hàm
của hàm số f (x) = 2x + 3 là
Ⓐ 2x2 + 3x + C . Ⓑ x2 2 + C . Ⓒ x2 + C .
Ⓓ x2 + 3x + C . Lời giải
Họ nguyên hàm của f (x) = 2x + 3 là (2x + ) 3 dx = 2xdx + dx 3
= x2 + 3x + C .
Câu 27: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho hàm số f ( x) 1
= 2x + +1. F (x) là một nguyên hàm của f ( x) thỏa mãn F ( ) 1 = 0 . Trong các x
khẳng định sau khẳng định nào đúng? Ⓐ F (x) 2
= x + x + ln x − 2 . Ⓑ F (x) 2
= x + x + ln x + 2 . Ⓒ F (x) 2
= x + x − ln x − 2 . Ⓓ F (x) 2
= x − x + ln x + 2 . . Lời giải Chọn A 1 Ta có: f (x) 2 dx = 2x +
+1 dx = x + ln x + x + C . x Do F ( ) 1 = 0 , nên C = 2
− . Vậy F (x) 2
= x + ln x + x − 2 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 44 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 28: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Một nguyên hàm của hàm số 2
f (x) = 3x +1 là: Ⓐ 6x . Ⓑ 3 x +1. Ⓒ 3 x + x . Ⓓ 3 3x + x . Lời giải Chọn C F x = f x dx = ( 2x + ) 3 ( ) ( ) 3
1 dx = x + x + C Chọn C = 0 thì 3
F (x) = x + x .
Câu 29: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Cho hàm số f ( x) 3
= 4x + 3. Mệnh đề nào sau đây đúng ? Ⓐ 1 f (x) 4
dx = x + 3x + . C Ⓑ f (x) 4 dx =
x + 3x + C. 4 Ⓒ f (x) 4
dx = 4x + 3x + . C Ⓓ f (x) 3
dx = 12x + 3x + . C Lời giải Chọn A Vì ( 4
x + x + C ) 3 3 = 4x + 3.
Câu 30: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Họ tất cả các nguyên x − 2
hàm của hàm số f (x) = trên khoảng (0; ) + là x 2 2 Ⓐ x + + C .
Ⓑ x − 2ln x + C .
Ⓒ x + 2ln x + C . Ⓓ x − + C . 2 x 2 x Lời giải x − 2 2 Trên khoảng (0; ) + = − = − + ta có dx 1 dx x 2 ln x C . x x
Câu 31: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Họ nguyên hàm của hàm số 2
f (x) = 3x − sin x là
Ⓐ 6x − cos x + C . Ⓑ 3
x − cos x + C . Ⓒ 3
x + cos x + C . Ⓓ 3
x − sin x + C Lời giải Chọn C Ta có ( 2 x − x) 3 3 sin
dx = x + cos x + C
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 45 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 32: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Tìm họ nguyên hàm của hàm số f ( x) 2
= 3x + sin x (C là hằng số) Ⓐ 3 x − cos x + . C
Ⓑ 6x + cos x + C. Ⓒ 3 x + cos x + . C
Ⓓ 6x − cos x + C. Lời giải Chọn A ( 2x + x) 3 3 sin
dx = x − cos x + . C
Câu 33: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Tìm họ nguyên hàm của hàm số ( ) 3x
f x = e ( C là hằng số) 3x e Ⓐ ( ) 3 d = 3 x f x x e + C . Ⓑ f (x) x d = + C . 3 3x 1 + e Ⓒ ( ) 3x f x x d = e + C . Ⓓ f (x) x d = + C . 3x + 1 Lời giải Chọn B 3x ( ) e f x x d = + C . 3
Câu 34: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Một nguyên hàm của hàm số f ( x) 2 = 3x +1 là Ⓐ 6x . Ⓑ 3 x +1. Ⓒ 3 x + x . Ⓓ 3 3x + x . Lời giải Ta có f
(x) x = ( 2x + ) 3 d 3
1 dx = x + x + C .
Cho C = 0 ta được một nguyên hàm của hàm số f ( x) là 3
x + x . Chọn đáp án Ⓒ
Câu 35: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Tìm mệnh đề sai trong các mệnh đề sau 4 x + C Ⓐ 3 x dx = . Ⓑ 2 x = 2( x e dx e + C)
. Ⓒ sin xdx = C − cos x . Ⓓ 4
1dx = ln x +C . x Lời giải Chọn D Áp dụng công thức dx = x + 1 ln C x .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 46 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 36: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Họ nguyên hàm của hàm số
f ( x) = 2x + sin 2x là: 1 1 Ⓐ 2
x − cos 2x + C . Ⓑ 2
x + 2cos 2x + C . Ⓒ 2 x +
cos 2x + C . Ⓓ 2
x − 2cos 2x + C 2 2 . Lời giải Chọn A 1
Ta có (2x + sin 2x) 2 dx = x − cos 2x + C ; 2
Câu 37: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Họ tất cả nguyên
hàm của hàm số f ( x) = cos 2x 1 1
Ⓐ 2sin 2x + C .
Ⓑ − sin 2x + C . Ⓒ
sin 2x + C . Ⓓ 2
− sin 2x + C . 2 2 Lời giải Chọn C 1 Ta có cos 2 d x x = sin 2x + C . 2
Câu 38: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Cho f (x) 2
dx = 3x + 2x − 3 + C . Hỏi
f ( x) là hàm số nào?
Ⓐ f ( x) = 6x + 2 . Ⓑ f ( x) 3 2
= x + x −3x + C .
Ⓒ f ( x) = 6x + 2 + C . Ⓓ f ( x) 3 2
= x + x − 3x . Lời giải Chọn A
Ta có f ( x) = ( 2
3x + 2x − 3 + C ) = 6x + 2 .
Câu 39: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Họ tất cả các nguyên hàm của hàm
số f ( x) =1+ sin x là
Ⓐ 1+ cos x + C .
Ⓑ 1− cos x + C .
Ⓒ x + cos x + C .
Ⓓ x − cos x + C . Lời giải Chọn D
F ( x) = f
(x)dx = x−cosx+ . C
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 47 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 40: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Họ tất cả các nguyên hàm của hàm số ( ) 2x f x = e là 2 x x Ⓐ e e x e + C . Ⓑ 2x e + C . Ⓒ + C . Ⓓ + C . 2 2 Lời giải Chọn C
Áp dụng công thức nguyên hàm ta chọn C
Câu 41: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Họ các nguyên hàm của hàm
số f (x) = sin3x là 1 1
Ⓐ − cos3x + C .
Ⓑ −cos3x + C .
Ⓒ cos3x + C .
Ⓓ cos3x + C . 3 3 Lời giải Chọn A cos 3x 1
Ta có f (x)dx = sin 3xdx = −
+ C = − cos3x + C. 3 3
Câu 42: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số + f ( x) 2x 1 =
, x 1. Trong các khẳng định sau, khẳng định nào đúng? x −1 Ⓐ f
(x)dx =3ln x−1 +C, x 1. Ⓑ f
(x)dx =3ln(x− )1+C, x 1. Ⓒ f
(x)dx = 2x+3ln x−1 +C, x 1. Ⓓ f
(x)dx =3ln(x− )1+C, x 1. Lời giải x + Ta có f (x) 2 1 3 dx = dx = 2 +
dx = 2x + 3ln x −1 + C, x 1 . x −1 x −1 Câu 43: Biết ( ) 2
f x dx = x + C . Tính f (2x)dx 1 1 Ⓐ f (2x) 2 dx = x + C . Ⓑ f (2x) 2 dx = x + C . 2 4 Ⓒ f ( x) 2 2
dx = 2x + C . Ⓓ f ( x) 2 2
dx = 4x + C . Lời giải Chọn C Ta có: f (x) 2
dx = x + C f (x) = 2x . Suy ra: f ( x) 2 2
dx = 2.2xdx = 2x + C .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 48 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 44: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Tìm nguyên hàm ( 3 4x + 2x + )1dx. 4 Ⓐ x 4 2
4x + 2x + x + C . Ⓑ 4 2
x + 2x + x + C . Ⓒ 4 2
x + x + x + C . Ⓓ 2
+ x + x + C . 4 Lời giải Ta có: ( 3x + x+ ) 3 4 2 4 2
1 dx = 4x dx + 2 d
x x + 1dx = x + x + x + C .
Câu 45: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Biết rằng F ( x) là
một nguyên hàm của f ( x) = cos 2x trên
và F (0) = 0. Tính giá trị của biểu thức T = F + 2F . 2 4 Ⓐ 1 T = 2. Ⓑ T = 3. Ⓒ T = . Ⓓ T = 1. 2 Lời giải Ta có F ( x) 1 = cos 2 d x x = sin 2x + C. 2
Mà F (0) = 0 nên C = 0. Suy ra F ( x) 1 = sin 2 . x 2 1 1 1 Do đó F = sin = 0 và F = sin = . 2 2 4 2 2 2 1 Vậy T = F + 2F = 0 + 2. = 1. 2 4 2
Câu 46: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tính nguyên hàm 2 tan 2 d x x . 1 1
Ⓐ tan 2x − x + C . Ⓑ
tan 2x − x + C . Ⓒ
tan 2x + x + C . Ⓓ tan 2x + x + C . 2 2 Lời giải Chọn B 1 1 1 Ta có: 2 tan 2 d x x = −1 dx = dx − dx =
tan 2x − x + C. 2 2 cos 2x cos 2x 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 49 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 47: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Cho 1
hàm số f ( x) xác định trên
\ thỏa mãn f ( x) 3 ' = ,
f (0) =1. Giá trị của 3 3x −1 f (− ) 1 bằng: Ⓐ 3ln 2 + 3. Ⓑ 2ln 2 +1. Ⓒ 3ln 2 + 4 . Ⓓ 12ln 2 + 3 . Lời giải Chọn B
Ta có: f ( x) = f (x) 3 ' dx =
dx = ln 3x −1 + C 3x−1
Vì : f (0) =1 C =1 f ( x) = ln 3x −1 +1 Vậy: f (− ) 1 = ln 4 +1 = 2 ln 2 +1
Câu 48: (THPT CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021 LẦN 01) Với mọi hàm số f ( x)
; g ( x) liên tục trên
, cho các khẳng định sau: (I ) . f
(x)−g(x)dx = f
(x)dx− g (x)dx . (II ) . f
(x).g(x)dx =
( f (x)dx).( g(x)dx). (III ) . Nếu f
(x)dx = F(x)+C thì f
(u)du = F(u)+C . (IV ). kf
(x)dx = k f
(x)dx với mọi hằng số k .
Có bao nhiêu khẳng định sai? Ⓐ 4 . Ⓑ 1. Ⓒ 2 . Ⓓ 3 . Lời giải Chọn C
Các khẳng định sai là ( II ) ; ( IV ) .
Câu 49: (THPT CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021 LẦN 01) Biết rằng ( a a 3 3 cos . x sin 3x + sin .
x cos 3x)dx = cos 4x + C với , a b , là phân số tối giản b b
(a 0,b 0), tính 2a +b . Ⓐ −13 . Ⓑ 13 . Ⓒ −10 . Ⓓ 10 . Lời giải Chọn D Ta có:
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 50 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 3 3 3 x x + x x = x ( 3 x − x) 3 + x ( 3 cos .sin 3 sin .cos3 cos . 3sin 4sin sin
. 4cos x − 3cos x) 3 3 3 3 3 3 = 3cos . x sin x − 4sin . x cos x + 4sin . x cos x + 3sin . x cos x 3 3 = 3cos . x sin x + 3sin . x cos x = x x ( 2 2
3sin .cos . cos x − sin x) 3 = sin 2 . x ( 2 2 cos x − sin x) 2 3 3 = sin 2 . x cos 2x = sin 4x 2 4 ( 3 3 a 3 3 cos . x sin 3x + sin .
x cos 3x)dx = sin 4 d x x = − cos 4x + C = cos 4x + C . 4 16 b a 0 a = 3 − Vì: b 0
2a + b =10 . b =16 a,b
Câu 50: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Cho F ( x) là một nguyên hàm của hàm số ( ) x
f x = e + 2x thỏa mãn F ( ) 3 0 = . Tìm F ( x) . 2 x 1 x 5 Ⓐ F ( x) 2 = e + x + . Ⓑ F ( x) 2 = 2e + x − . 2 2 x 1 x 3 Ⓒ F ( x) 2 = e + x + . Ⓓ F ( x) 2 = e + x + . 2 2 Lời giải
Ta có F ( x) = f
(x) x = ( xe + x) x 2 d
2 dx = e + x + C . Mà F ( ) 3 1 0 = C = . 2 2 x 1 Vậy F ( x) 2 = e + x + . 2
Câu 51: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho hàm số f ( x) 2
=1− 2cos x . Tìm nguyên hàm của f ( x) ? sin 2x sin 2x Ⓐ − + C . Ⓑ + C .
Ⓒ sin 2x + C .
Ⓓ − sin 2x + C . 2 2 Lời giải Chọn A
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 51 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 Ta có: f (x)dx = ( 2
1− 2 cos x) dx = − cos 2xdx = − sin 2x + C . 2
Câu 52: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho F ( x) là một
nguyên hàm của hàm số f ( x) 1 =
F 0 = 1 . Giá trị F ( 2 − ) bằng 2x − , biết ( ) 1 1 1 1 Ⓐ 1+ ln 5 . Ⓑ (1+ ln5). Ⓒ 1+ ln 3 . Ⓓ 1+ ln 5 . 2 2 2 Lời giải Chọn A Ta có F ( x) 1 1 = dx = ln 2x −1 + C . 2x −1 2 1 1
Với F (0) = C = 1 F ( x) = ln 2x −1 +1 F ( 2 − ) = ln5+1. 2 2
Câu 53: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Họ tất cả các nguyên
hàm của hàm số f ( x) 2 = 1; + là 4x − trên khoảng ( ) 3 1 1 Ⓐ 2ln (4x −3) + . C Ⓑ
ln (4x − 3) + C. Ⓒ
ln (4x − 3) + C.
Ⓓ 4ln (4x −3) + . C 2 4 Lời giải Chọn B 1
Đặt t = 4x − 3 dt = 4dx dx = dt . Vì x (1;+) nên t 0. 4 2 1 1 dt 1 1 1
Ta có: f (x)dx = . dt =
= ln t + C = ln t + c = ln (4x −3)+C. t 4 2 t 2 2 2
Câu 54: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Họ các nguyên hàm của hàm số ( ) 2 1 3 x f x − = là x x x x Ⓐ 9 9 9 9 + C . Ⓑ + C . Ⓒ + C . Ⓓ + C . 3 3ln 3 6ln 3 6 Lời giải Chọn C 2 x 1 − x− 3 9x Ta có: 2 1 3 dx = + C = + C . 2.ln 3 6ln 3
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 52 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1
Câu 55: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho F ( x) = là một 2 2x f ( x) nguyên hàm của hàm số
. Họ nguyên hàm của hàm số f ( x)ln x là x ln x 1 Ⓐ f (x) ln x 1 ln d x x = + + C . Ⓑ f (x)ln d x x = − + + C . 2 2 x x 2 2 x x ln x 1 Ⓒ ln x 1 f (x)ln d x x = − + + C . Ⓓ f (x)ln d x x = + + C . 2 2 x 2x 2 2 x 2x Lời giải 1 f ( x) Do F ( x) =
là một nguyên hàm của hàm số nên ta có: 2 2x x f (x) = F(x) f ( x) 1 = − f ( x) 1 = − 3 2 x x x x . f (x) f x 1 f (x) dx = F (x) ( ) 1 + C dx = + C dx = + C 2 2 x x 2x x 2x Suy ra : f
(x) x x = x
( f (x)) = f (x) f ( x) ln x 1 ln x 1 ln d ln d ln x − dx = − − + C = − + + C 2 2 2 2 x x 2x x 2x
Câu 56: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f ( x) thỏa mãn
( f (x))2 + f (x) f (x) 4 2 .
=15x +12x +1, x và f (0) = 0. Tính giá trị của 2
A = 3 f (3) − 678 . Ⓐ 2018 . Ⓑ 2021. Ⓒ 2022 . Ⓓ 2019 . Lời giải 2
Ta có ( f ( x)) + f ( x) f ( x) 4 2 . =15x +12x +1 f
( x) f ( x) 4 2 . =15x +12x +1
f (x). f (x) 5 3
= 3x + 4x + x + C1
f (0). f (0) = C C = 0, . 1 1
Do đó ta có : f ( x) f ( x) 5 3 .
= 3x + 4x + x f
(x) f (x) x = ( 5 3 . d
3x + 4x + x)dx 1 1 1 2 f (x) 6 4 2
= x + x + x + C2 2 2 2 1 2
f (0) = C C = 0, . 2 2 2 Do đó ta có 2 f ( x) 6 4 2
= x + 2x + x . Vậy 2
A = 3 f (3) − 678 = 2022 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 53 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 57: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Cho hàm số
f ( x) xác định trên
, thỏa mãn f '( x) = 2x −1 và f (3) = 5 . Giả sử phương trình
f ( x) = 999 có hai nghiệm x và x . Tính tổng S = log x + log x . 1 2 1 2 Ⓐ 5 . Ⓑ 999 . Ⓒ 3 . Ⓓ 1001. Lời giải Chọn C
Ta có: f ( x) = x − f ( x) 2 ' 2 1
= x − x + C . Do f (3) = 5 nên 2
3 − 3+ C = 5 C = 1 − Vậy: f ( x) 2 2
= 999 x − x −1= 999 x − x −1000 = 0 ( ) *
Nhận thấy phương trình ( )
* có hai nghiệm x , x mà x x = −1000 . 1 2 1 2
Khi đó: S = log x + log x = log x .x = log1000 = 3. 1 2 1 2
Câu 58: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Cho hàm số f x
có đạo hàm liên tục trên
và thoả mãn f x sin x 1
f x cos x với mọi số thực x . Tính f . 6 3 1 Ⓐ 1. Ⓑ 1. Ⓒ . Ⓓ . 2 2 Lời giải
Ta có: f x sin x 1 f x cos x f x sin x f x cos x cos x f x sin x cos x
Suy ra: f x sin x sin x C Chọn x 0 C 0 f x .sin x sin x f .sin sin f 1 . 6 6 6 6
PHƯƠNG PHÁP ĐỔI BIẾN SỐ
Câu 59: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f ( x) thỏa mãn 1 1
(x+ )1 f (x)dx =10 và 2 f ( )1− f (0) = 2. Tính I = f (x)dx . 0 0 Ⓐ I =1. Ⓑ I = 8 . Ⓒ I = 8 − . Ⓓ I = 12 − . Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 54 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 Ta có (x + )
1 f ( x)dx = 10 . 0
Đặt u = x +1 du = dx .
dv = f ( x)dx , ta chọn v = f ( x). 1 1 1 Khi đó (x + )
1 f ( x)dx = ( x + )
1 f ( x) − f (x)d .x 0 0 0 1 1 1
Suy ra f ( x)dx =
(x + )1 f (x) − (x + )1 f (x)dx = = 2 f ( )
1 − f (0) −10 2 −10 = 8 − . 0 0 0 1
Vậy I = f ( x)dx = 8 − . 0
Câu 60: HẾT (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tính nguyên hàm 2 3 2
x (2x −1) dx . ( x − )3 3 2 1 ( x − )3 3 2 1 ( x − )3 3 2 1 ( x − )3 3 2 1 Ⓐ + C. Ⓑ + C. Ⓒ + C. Ⓓ + C. 18 3 6 9 Lời giải Chọn A 2x −1 1 2 3 2 3 2 3 ( )3 3
Vì x (2x −1) dx =
(2x −1) d(2x −1) = + C. 6 18
Câu 61: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Khi tính x − 3 nguyên hàm dx
, bằng cách đặt u = x +1 ta được nguyên hàm nào? x +1 Ⓐ 2
2u(u − 4)du . Ⓑ 2 2(u −1)du . Ⓒ 2 2(u − 4)du . Ⓓ 2 (u − 4)du . Lời giải x − 3 Ta có: I = dx . Đặt 2 2 u =
x +1 u = x +1 x = u −1 2 . u du = dx . x +1 2 u −1− 3 Khi đó I = 2 . u du = 2
( 2u −4).du . u dx
Câu 62: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Tính nguyên hàm x x+4
bằng cách đặt t = x + 4 ta thu được nguyên hàm nào? 2tdt 2d Ⓐ 2dt dt . Ⓑ . Ⓒ t . Ⓓ . 2 t − 4 ( 2t −4) ( 2t −4)t 2 t − 4 Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 55 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Đặt 2 t =
x + 4 t = x + 4 2tdt = dx và 2
x = t − 4 . Ta có: dx 2 d t t 2 = = dt . x x + 4 ( 2t −4) 2 t t − 4
Câu 63: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Cho F(x) là một nguyên hàm của hàm f (x) trên . Hỏi 2
F (x ) là nguyên hàm của hàm số nào dưới đây: Ⓐ 2 . x f ( ) x . Ⓑ 2 .
x f (x ) . Ⓒ 2 f (x ) . Ⓓ 2 2 . x f (x ) . Lời giải Chọn D F( ) x = f ( ) x dx 2 2
t = x dt = 2xdx = d (x ) 2 2 2
F(x ) = F(t) = f (t)dt =
f (x ).2xdx = 2 .
x f (x )dx . Câu 64:
(CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Cho F ( x) là một nguyên
hàm của hàm số f ( x) trên . Hỏi ( 2
F x ) là một nguyên hàm của hàm số nào dưới đây? Ⓐ 2 . x f ( x). Ⓑ ( 2 . x f x ). Ⓒ ( 2 f x ) . Ⓓ ( 2 2 . x f x ) . Lời giải
F ( x) là một nguyên hàm của hàm số f ( x) trên
F(x) = f (x), x . Ta có F ( 2 x ) = ( 2 x ) F( 2 x ) = x f ( 2 . 2 . x ), x . Vậy ( 2
F x ) là một nguyên hàm của hàm số ( 2 2 . x f x ) .
Câu 65: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Cho hàm số
y = f (x) có đạo hàm và liên tục trên 1;2 , thỏa mãn 2
f (x) = xf (
x) − x . Biết
f (1) = 3. Tính f (2) . Ⓐ 16 . Ⓑ 2 . Ⓒ 8 . Ⓓ 4 . Lời giải Chọn C xf (
x) − f (x) Theo bài 2 2
f (x) = xf (
x) − x xf (x) − f (x) = x =1 2 x ' f (x) f (x) 2 =1
= 1.dx = x + C f (x) = x + Cx . x x
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 56 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Mà 2 f (1) = 3 1 + .
C 1 = 3 C = 2 . Vậy 2
f (x) = x + 2x . Suy ra 2 f (2) = 2 + 2.2 = 8 .
Câu 66: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Cho f ( x) 2x 2 4
dx = e − x + . C Khi đó f
(−x)dx bằng 2 x x x 2 x − − x Ⓐ e 1 1 2 + 4x + C . Ⓑ 2 2 4e − x + C . Ⓒ 2 2 4
− e + x + C . Ⓓ 2 −e + + C 4 4 4 4 Lời giải Chọn C Ta có ( ) 2 x 2 = − + ( ) = ( 2x 2 − + ) 2 4 d 4 = 2 x f x x e x C f x e x C e − 2 . x 1 1 − t 1
Đặt x = − t suy ra f (4x) = f ( t − ) 2 = 2e + t. 4 2 1 − x 1
Khi đó f (−x) 2 = 2e + . x 2 1 − 1 x x − 1 Ta có f (−x) 2 2 2 dx = 2e + x dx = 4
− e + x + C. 2 4 Câu 67: (THPT CHUYÊN PHÚ THỌ NĂM 2020-2021 LẦN 02) Biết ( + ) 1 ln ln 2 ( ) = ln + + mx x n px dx x C với , m , n ,
p C là các số thựⒸ Khi đó, m + n + p 2 x x bằng Ⓐ e +1. Ⓑ e + 2 . Ⓒ 2e −1. Ⓓ 2e − 2 . Lời giải (mx + ) 1 ln x ln x ln = + x dx m dx dx = I + I . 2 2 1 2 x x x ln * Tính = x I m dx 1 x 1
Đặt t = ln x dt = dx x 2 2 mt m ln x I = m tdt = + C = + C 1 1 1 2 2 ln *Tính = x I dx 2 2 x
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 57 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1
u = ln x du = dx x 1 1 −
dv = dx v = 2 x x 1 1 1 1 −ln (ex) I = − ln x + dx = − ln x − + C = + C 2 2 2 2 x x x x x ( + ) 1 ln m −ln 2 ( ) Suy ra dx = ln x + + mx x ex C 2 x 2 x m = 2,n = 1
− , p = e m+ n + p =1+ e .
Câu 68: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho F(x) là một nguyên hàm của (x+ x +1)2021 2
hàm số f (x) =
và F (0) =1.Giá trị của F ( ) 1 bằng 2 x +1 ( + )2020 1 2 − 2021 ( + )2021 1 2 + 2020 Ⓐ . Ⓑ . 2020 2021 ( + )2020 1 2 + 2021 ( + )2021 1 2 − 2020 Ⓒ . Ⓓ . 2020 2021 Lời giải Chọn B 2 x + x +1 Đặt 2
t = x + x +1 dt = d . x 2 x +1 (x+ x +1)2021 + + t (x x 1)2021 2 2 2021 2020 F(x) = dx = t dt = + C = + C. 2 2021 2021 x +1 (x+ x + )2021 2 1 2020
Lại có F (0) = 1 F (x) = + . 2021 2021 ( + )2021 1 2 + 2020 F(1) = . 2021 Câu 69:
(CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Cho hàm số f (x) liên tục và có đạo hàm trên (− 2; 2) \
0 , thỏa mãn f (1) = 0 và x 1
f '(x) + x ( f (x) e + 2) +
= 0 . Giá trị của f bằng f ( x) e 2 Ⓐ ln 3 . Ⓑ ln 6 . Ⓒ ln 7 . Ⓓ ln 5 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 58 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn C
Ta có phương trình trên tương đương với: x
f '(x) + x ( f (x) e + 2) f ( x) f ( x) + = 0 + e
f '(x) + xe e + + x = f x ( f(x) 2 0 ( ) ) e f x e
f '(x) + x ( f x e + 2 f x e + ) 1 = 0 f x e
f '(x) + x ( f x e + )2 ( ) 2 ( ) ( ) ( ) ( ) 1 = 0 f ( x) −e f '(x) ( = x f x e + )2 ( ) 1
Đến đây ta nguyên hàm hai vế, ta được như sau: f ( x) 2 2 −e f '(x) 1 x 1 x = ( + ) dx xdx d = + C = + C 2 f x f x f x + 1 ( ( ) e )1 2 ( ( ) ( ) e e + ) 1 2 2 1 x 2
Mà f (1) = 0 nên ta suy ra C = 0 ( = f (x) = ln −1 f ( x) e + ) 2 1 2 x 1 Từ đó suy ra f = ln 7 2
PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
Câu 70: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hai hàm số
u ( x),v( x) có đạo hàm lien tục trên . Chọn mệnh đề đúng? Ⓐ u
(x).v'(x)dx =u(x).v(x)+ u'
(x).v'(x)dx . Ⓑ u
(x).v'(x)dx =u(x).v(x)− u'
(x).v'(x)dx . Ⓒ u
(x).v'(x)dx =u(x).v(x)+ u'
(x).v(x)dx . Ⓓ u
(x).v'(x)dx =u(x).v(x)− u'
(x).v(x)dx . Lời giải
Ta có theo công thức tính nguyên hàm của hàm hợp ta có u
(x).v'(x)dx =u(x).v(x)− u'
(x).v(x)dx
Câu 71: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tính nguyên hàm 1 A
dx bằng cách đặt t
ln x . Mệnh đề nào dưới đây đúng? x ln x Ⓐ 1 1 A dt . Ⓑ A dt . Ⓒ A dt . Ⓓ A tdt . 2 t t Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 59 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 Xét A dx . x ln x 1 Đặt t ln x dt dx . x 1 1 1 1 Suy ra A dx . dx dt . x ln x ln x x t
Câu 72: (THPT CHUYÊN NAM SƠN THANH HÓA NĂM 2020-2021 LẦN 01) Một nguyên
hàm của ln x bằng 1
Ⓐ x − x ln x . Ⓑ .
Ⓒ x + x ln x .
Ⓓ 1− x + x ln x . x Lời giải Chọn D 1 u = ln x du = dx Đặt x dv = dx v = x
Ta có: ln xdx = x ln x − dx = x ln x − x + C
Vậy một nguyên hàm của ln x bằng 1− x + x ln x .
Câu 73: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tìm nguyên hàm (2x − )1ln d x x x x Ⓐ (x − x) 2 2 ln x − − x + C . Ⓑ (x − x ) 2 2 ln x + − x + C . 2 2 x x Ⓒ (x − x) 2 2 ln x + + x + C . Ⓓ (x − x) 2 2 ln x − + x + C . 2 2 Lời giải Chọn D 1 u = ln x du = dx Đặt . = ( x dv 2x − ) 1 dx 2 v = x − x 1 Ta có (2x − ) 1 ln d x x = ( 2
x − x)ln x − ( 2
x − x) dx x x
= (x − x) x − (x − ) x =(x − x) 2 2 2 ln 1 d ln x − + x + C . 2
Câu 74: (THPT CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021 LẦN 01) Cho ( ) = ( 2 + − ) 2ex F x ax bx c
là một nguyên hàm của hàm số ( ) = ( 2 + − ) 2 2020 2022 1 e x f x x x
trên khoảng (−;+ ) . Tính T = a − 2b + 4c . Ⓐ T = 1012 . Ⓑ T = 2012 − . Ⓒ T = 1004 . Ⓓ T = 1018 . Lời giải Chọn A
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 60 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Xét ( ) = ( 2 + − ) 2 2020 2022 1 e x F x x x dx . = + 2 du (4040x 2022)dx u
= 2020x + 2022x −1 Đặt . x 1 2 2 dv = e dx v = e x 2 1 x 1 Do đó ( ) = ( 2 2020 + 2022 − ) 2 1 e
− (4040 + 2022) 2ex F x x x x dx + C . 2 2 Đặt = ( + ) 2 4040 2022 e x I x dx . d u = 4040dx 1 u = 4040x + 2022 Đặt 1 . x 1 2 2 dv = e dx v = e x 1 1 2 Do đó 1 = ( 1 4040 + 2022) 2x 2 e − 2020 e x I x dx = (4040 + 2022) 2x 2 e −1010e x x = ( + ) 2 2020 1 e x x . 2 2 ( ) 1 = ( x 1 2 2020 + 2022 − ) 2 1 e − (2020 + ) 2 1 e x F x x x x + C 2 2 x x 1 x x 1 2 2 2 2 2 2
=1010 e +1011 e − e −1010 e − e x x x x + C 2 2 2 2x 2x 2 =1010 e + e − e x x x + C = ( 2 + − ) 2 1010 1 e x x x + C .
Theo đề bài, ta có a = 1010 , b = 1, c = 1, C = 0 . Vậy T = 1010 − 2 + 4 = 1012 .
Câu 75: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Cho ( ) 2 F x = x là
một nguyên hàm của hàm số ( ) 2x
f x e . Họ tất cả các nguyên hàm của hàm số ( ) 2x f x e là Ⓐ 2
−x + 2x +C . Ⓑ 2
−x + x +C . Ⓒ 2 2
− x + 2x + C . Ⓓ 2
2x − 2x + C . Lời giải Chọn C 2 x 2 = = 2 x u e du e dx Đặt dv = f (x)dx v = f (x) ( ) 2x 2x = ( )− ( ) 2x 2x f x e x e f x f x e
x = e f ( x) 2 d 2 d
− 2x +C = I Ta lại có ( ) 2
F x = x là một nguyên hàm của hàm số ( ) 2x f x e ( ) 2x f x e = ( 2 x ) = 2x 2
I = 2x − 2x +C Câu 76:
(CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Giả sử hàm số f ( x) có đạo
hàm liên tục trên. Biết rằng ( ) 3
G x = x là một nguyên hàm của ( ) 2 − x g x = e f ( x) trên
. Họ tất cả các nguyên hàm của 2 − x e f ( x) là Ⓐ 3 2 2
− x +3x +C . Ⓑ 3 2
2x + 3x + C . Ⓒ 3 2
x + 3x + C . Ⓓ 3 2
−x +3x +C .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 61 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12 NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn B
Dùng công thức nguyên hàm từng phần ta có: 2 − x ( ) 2 − x = ( ) 2 d + 2 − x e f x x e f x e f (x)dx 2 − x = e f (x) 3
+ x + C = G(x) 3 2 3 2
+ 2x + C = 3x + 2x + C
Câu 77: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Cho hai hàm số f ( x), g ( x) có đạo hàm trên
và thỏa mãn f ( x) + g ( x) = , x
g( x) + f ( x) = −x x
. Biết f (0) = g (0) =1, tính f ( ) 1 . 2 2 − 2 + Ⓐ 1 e 2 e 2 − 2 . Ⓑ e + − 2 . Ⓒ . Ⓓ . e e 2e 2e Lời giải
Đặt h( x) = f ( x) + g ( x) .
Từ giả thiết ta có h( x) + h( x) = 0 x
( ). x + ( ). x h x e h x e = 0 x ( ( ). x h x e ) = 0 x . Suy ra ( ). x
h x e = C . Do f (0) = g (0) h(0) = 0 C = 0. 2 2 2
Do đó f ( x) + g ( x) = g x =
− f x g x = − − f x . x ( ) x ( ) ( ) x ( ) e e e 2 2
Kết hợp với giả thiết ta có: −
− f x + f x = −x f x − f x = x − x ( ) ( ) ( ) ( ) x e e −x −x −x 2 − x − x 2
f ( x).e − f ( x).e = . x e −
( f (x).e ) = .xe − . 2 x e 2 x e − x − x 2 − x 2 − x 1
Suy ra f ( x).e = . x e − dx= . x e dx − dx= − . x d e + 2 x 2 x ( ) 2x e e e − x − x 1 − x − x 1 = − ( . x e − e .dx
)+ = −xe −e + +C . 2 x 2 x 1 e e
Do f (0) =1 nên ta có C = 1 . Do đó f ( x) 1 = −x −1 x + + e . 1 x e Vậy f ( ) 1 1 = 2 − + + e . e
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 62 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 TÍCH PHÂN
ĐỊNH NGHĨA – TÍNH CHẤT – TÍCH PHÂN CƠ BẢN 1
Câu 78: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Cho f (x)dx = 2, 0 2 2 f
(x)dx =1. Tích phân f (x)dx bằng 0 1 Ⓐ 1. Ⓑ 2 . Ⓒ 1 − . Ⓓ 3 . Lời giải 2 2 1 Ta có f
(x)dx = f
(x)dx − f
(x)dx =1−2 = 1 − . 1 0 0 Câu 79: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Cho 1 1 1 f
(x)−2g(x) dx =12 và g
(x)dx = 5. Khi đó f (x)dx bằng 0 0 0 Ⓐ 2 − . Ⓑ 12 . Ⓒ 22 . Ⓓ 2 . Lời giải 1 1 1 f
(x)−2g(x) dx =12 f
(x)dx −2 g (x)dx =12 0 0 0 1 1 f
(x)dx =12+2 g
(x)dx =12+2.5 = 22 . 0 0 2
Câu 80: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Giá trị của sin d x x 0 bằng Ⓐ 0 . Ⓑ 1. Ⓒ 1 − . Ⓓ . 2 Lời giải 2 = − 2 sin d x x cos x =1 . 0 0 1
Câu 81: (CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Tích phân 2020 x dx bằng 1 − 1 2 Ⓐ . Ⓑ . Ⓒ 2 . Ⓓ 0 . 2021 2021 2020 Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 63 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 1 2021 x 1 1 − 2 2020 x dx = = − = . 2021 2021 2021 2021 1 − 1 − 1 3
Câu 82: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Nếu f
(x)dx = 3 và f (x)dx = 7 0 0 3
thì f ( x) dx bằng 1 Ⓐ 10 . Ⓑ 4 . Ⓒ 4 − . Ⓓ 21. Lời giải 3 1 3 3 3 1 Ta có: f
(x)dx = f
(x)dx + f
(x)dx f
(x)dx = f
(x)dx − f
(x)dx = 7−3= 4. 0 0 1 1 0 0
Câu 83: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho hàm số 2
y = f (x) có đạo hàm trên đoạn [0; 2], f (0) = 1 và
f '(x)dx = 3 − . Tính f (2) 0 Ⓐ f (2) = 4 − . Ⓑ f (2) = 3 − . Ⓒ f (2) = 2 − . Ⓓ f (2) = 4 . Lời giải 2 Ta có 2
f '(x)dx = f (x) = f (2) − f (0) = 3 − f (2) = 3 − + f (0) = 2 − 0 0
Câu 84: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho 1
f ( x), g ( x) là các hàm số liên tục trên R thoả mãn f (x)dx = 3; 0 2 2 2 f
(x)−3g(x)dx = 4 và 2 f
(x)+ g(x)dx = 8
. Tính f ( x)dx . 0 0 1 Ⓐ I = 0 . Ⓑ I = 2 . Ⓒ I =1. Ⓓ I = 3 . Lời giải 2 2 f
(x)dx−3 g (x)dx = 4 2 2 0 0 Do f
(x)−3g(x)dx = 4 và 2 f
(x)+ g(x)dx = 8 nên 2 2 0 0 2 f
(x)dx+ g (x)dx =8 0 0 2 Vì vậy f (x)dx = 4 . 0 2 2 1 Ta có f
(x)dx = f
(x)dx − f (x)dx =1. 1 0 0
Câu 85: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Nếu 2 2 2 f
(x)dx = 5 và g
(x)dx = 9 thì 2 f
(x)+ g(x)dx bằng 1 1 1
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 64 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ 19 . Ⓑ 28 . Ⓒ 14 . Ⓓ 4 . Lời giải 2 2 2 Ta có 2 f
(x)+ g(x)dx = 2 f
(x)dx+ g
(x)dx = 2.5+9 =19. 1 1 1
Câu 86: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Nếu 3 3 f
(x)−2xdx =5 thì f ( x)dx bằng 1 1 Ⓐ 9 . Ⓑ 13 . Ⓒ 10 . Ⓓ 12 . Lời giải 3 3 3 3 3 Ta có: f
(x)−2xdx = f (x)dx− 2 d x x = 5 f (x) 2 dx = 5 + x = 5 + 8 =13. 1 1 1 1 1
Câu 87: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Tích phân π 2 cos d x x bằng 0 Ⓐ 1. Ⓑ 0 . Ⓒ 2 . Ⓓ 2 . Lời giải π 2 π π Ta có 2 cos d x x sin x sin sin 0 1 . 0 2 0 1
Câu 88: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tích phân 2 x e dx bằng 0 2 e −1 Ⓐ e − 2 e −1. Ⓑ 1 . Ⓒ ( 2 2 e − ) 1 . Ⓓ . 2 2 Lời giải 1 2 e − x 1 1 x 1 Ta có 2 2 e dx = e = . 2 0 2 0
Câu 89: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f ( x) liên tục trên
;ab và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai. b a Ⓐ f
(x)dx = F(b)−F(a) . Ⓑ f (x)dx = 0. a a b Ⓒ b = − f (x) a dx = − f (x)dx. Ⓓ f
(x)dx F(a) F(b) . a b a Lời giải b
Theo định nghĩa tích phân, ta có f
(x)dx = F(b)−F(a) . a
Vậy D là khẳng định sai.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 65 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2
Câu 90: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Nếu f (x)dx = 3 1 2 2
và g ( x) dx = 1 − thì 2 f
(x) +3g(x)dx bằng 1 1 Ⓐ 2 . Ⓑ 9 . Ⓒ 3 . Ⓓ 0 . Lời giải 2 2 2 2 f
(x)+3g(x)dx = 2 f (x)dx 3 + g
(x)dx = 2.3+3(− )1 = 3. 1 1 1 Câu 91:
(CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Tích phân 2 sin xdx bằng 0 Ⓐ − . Ⓑ 1. Ⓒ 1 − . Ⓓ . 2 2 Lời giải 2 = − 2 sin xdx cos x = −cos + cos0 = 1 . 0 2 0
Câu 92: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Cho hàm số 1 1
f ( x), g ( x) liên tục trên 0 ;1 và
f (x)dx = 1
− , g (x)dx = 2 . Tính 0 0 1 2
f (x)+3g(x)d x 0 Ⓐ 4 . Ⓑ 1. Ⓒ 2 − . Ⓓ 5 . Lời giải 1 1 1 Ta có : 2
f (x)+3g(x)d
x = 2 f (x)dx + 3 g (x)dx = 2(− ) 1 + 3.2 = 4 . 0 0 0 Câu 93:
(CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Cho hàm số 6 4
f ( x) liên tục trên đoạn 0;6 thoả mãn
f (x)dx = 10 và
f (x)dx = 6. Tính giá trị 0 2 2 6 của biểu thức P =
f (x)dx + f (x)d . x 0 4 Ⓐ 4. Ⓑ 8. Ⓒ 16. Ⓓ 10. Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 66 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 6 2 4 6
Ta có f (x)dx = f (x)dx + f (x)dx + f (x)dx = 10 0 0 2 4 2 6 4 Suy ra P =
f (x)dx + f (x)dx = 10 − f (x)dx = 10 − 6 = 4 . 0 4 2 1 Câu 94: Tính 3 = e x I dx . 0 3 e −1 Ⓐ 1 3 I = e −1. Ⓑ I = e −1. Ⓒ I = . Ⓓ 3 I = e + . 3 2 Lời giải Chọn C 1 1 x 1 x 1 Ta có 3 e dx = ( 3e ) = ( 3e − )1. 0 3 3 0 2 5 5 Câu 95: Nếu f
(x)dx = 3 và f (x)dx = 1 −
thì f ( x) dx bằng 1 2 1 Ⓐ 2 − . Ⓑ 4 . Ⓒ 2 . Ⓓ 3 . Lời giải Chọn C 5 2 5 f
(x)dx = f
(x)dx+ f
(x)dx = 3+(− )1 = 2. 1 1 2 2 2
Câu 96: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Tích phân dx 2 sin x 4 bằng Ⓐ 2 . Ⓑ 3 . Ⓒ 1. Ⓓ . 4 Lời giải Chọn A 2 2 Tích phân 2 dx = 2 − cot x = 2 − cot − cot = 2 . 2 sin x 2 4 4 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 67 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 5
Câu 97: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Nếu f (x)dx = 10 và 2 9 9
f (x)dx = 7
thì f (x)dx bằng 2 5 Ⓐ −3 . Ⓑ 3 . Ⓒ 17 . Ⓓ −17 . Lời giải Chọn A 9 9 5
Ta có: f (x)dx = f (x)dx − f (x)dx = 7 −10 = 3 − . 5 2 2 4
Câu 98: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Tính tích phân I = xdx . 1 Ⓐ 14 . Ⓑ 13 . Ⓒ 4 . Ⓓ 11 . 3 3 3 Lời giải Chọn A 4 14 Ta có I = xdx = . 3 1
Câu 99: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Tích phân 2
( 2x + x)dx bằng 0 Ⓐ 14 − . Ⓑ −5 . Ⓒ 5 . Ⓓ 14 . 3 3 Lời giải Chọn D 2 2 3 2 3 2 x x 2 2 8 14 Ta có ( 2
x + x)dx = + = + = + 2 = . 3 2 3 2 3 3 0 0 0
Câu 100: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Tích phân ( 5 6x + )1dx 2 − bằng Ⓐ 62. − Ⓑ 64. Ⓒ 68. Ⓓ 68. − Lời giải Chọn A
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 68 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 0 0 Ta có (6x + )
1 dx = ( x + x) = − ( 2 − )6 5 6 − 2 = 6 − 2. 2 − 2 − 2
Câu 101: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Giá trị của sin
xdx bằng bao nhiêu? 0 Ⓐ 1. Ⓑ 1 − . Ⓒ . Ⓓ 0 . 2 Lời giải Chọn A 2 Ta có: 2 sin = −cos = − cos − cos0 = 1 xdx x . 0 2 0
Câu 102: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Cho hàm số f ( x) liên tục trên 6 10 10
thỏa mãn f ( x)dx = 7,
f ( x) dx = 1 − . Tính I = f (x)dx . 0 6 0 Ⓐ I = 5 . Ⓑ I = 8 . Ⓒ I = 7 . Ⓓ I = 6 . Lời giải Chọn Ⓓ 10 6 10 Ta có I = f
(x)dx = f
(x)dx + f
(x)dx = 7 −1= 6 . 0 0 6 4
Câu 103: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Tính tích phân I = xdx 1 . Ⓐ 14 . Ⓑ 13 . Ⓒ 4 . Ⓓ 11 . 3 3 3 Lời giải 4 4 4 1 3 4 2 2 14 Ta có 2 2 I =
xdx = x dx = x = x x = . 3 3 3 1 1 1 1
Câu 104: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Trong không gian Oxyz , cho điểm A(2; 2 − ; ) 1 , B (1; 1
− ;3) .Tọa độ của vectơ AB là Ⓐ (3; 3 − ;4) . Ⓑ ( 1 − ;1;2) . Ⓒ ( 3 − ;3; 4 − ) . Ⓓ (1; 1 − ; 2 − ). Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 69 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Chọn B
Tọa độ của vectơ AB là ( 1 − ;1;2) . 1
Câu 105: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Tính 3x I = e dx 0 3 e −1 Ⓐ 3 1
I = e −1. Ⓑ I = e −1. Ⓒ I = . Ⓓ 3 I = e + . 3 2 Lời giải Chọn C 1 3 1 e − x 1 x 1 Ta có: 3 3 I = e dx = e = 0 3 3 0 2 5
Câu 106: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Nếu f x dx 3 ; f x dx 1 thì 1 2 5 f x dx bằng 1 Ⓐ 2 − . Ⓑ 4 . Ⓒ 2 . Ⓓ 3 . Lời giải Chọn C 5 2 5 Ta có f x dx f x dx f x dx 3 1 2 . 1 1 2
Câu 107: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Cho hàm số f ( x) 3
có f (2) = 2, f (3) = 5 ; hàm số f ( x) liên tục trên đoạn 2; 3 . Khi đó f
(x)dx bằng 2 Ⓐ 3 . Ⓑ 10 . Ⓒ −3 . Ⓓ 7 . Lời giải Chọn A 3 3 Ta có f
(x)dx = f (x) = f (3)− f (2) = 5−2 = 3. 2 2 3 3
Câu 108: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Biết f
(x)dx =5 và g(x)dx = 7 − . 1 1 3 Giá trị của 3 f
(x)−2g(x)dx bằng 1 Ⓐ −29 . Ⓑ 1. Ⓒ 29 . Ⓓ 31 − .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 70 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn C 3 3 3 3 3 3 f
(x)−2g(x)dx = 3f
(x)dx − 2g
(x)dx =3 f
(x)dx −2 g
(x)dx =3.5−2.( 7 − ) = 29 1 1 1 1 1 .
Câu 109: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hàm số f (x) liên tục trên đoạn 1 2 2 0; 2 thỏa mãn f
(x) dx = 3 và f
(x) dx = 2. Khi đó f (x)dx bằng 0 1 0 Ⓐ 6 . Ⓑ 1. Ⓒ 1 − . Ⓓ 5 . Lời giải Chọn D 2 1 2 f
(x)dx = f
(x)dx + f
(x)dx = 3+2 = 5 . 0 0 1 1 1
Câu 110: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Biết
f ( x)dx = và 3 0 1 1 g ( x) 4 dx =
. Khi đó (g (x) − f (x))dx bằng 3 0 0 Ⓐ 5 − . Ⓑ 5 . Ⓒ 1 − . Ⓓ 1. 3 3 Lời giải Chọn D 1 ( 1 1
g ( x) − f ( x))dx = g
(x)dx− f (x) 4 1 dx = − = 1, 3 3 0 0 0 Câu 111: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Nếu 4 4 5 f
(x)−3dx = 5 thì f x dx bằng 1 − 1 14 Ⓐ 4 . `Ⓑ 3 . Ⓒ 2 . Ⓓ . 5 Lời giải 4 4 4 4 Ta có 5 f
(x)−3dx = 5 5 f
(x)dx−3 dx= 5 f (x)dx = 4. 1 − 1 − 1 − 1 −
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 71 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2021 2021
Câu 112: (CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Nếu f
(x)dx =12 và f (x)dx = 2 2 2020 2020 thì f ( x)dx bằng 2 Ⓐ −10 . Ⓑ 10 . Ⓒ 14 . Ⓓ 24. Lời giải 2021 2020 Ta có
f ( x)dx = 2
f ( x)dx = 2 − 2020 2021 2020 2021 2020 2020 f
(x)dx = f
(x)dx + f
(x)dx =12−2 =10. Vậy f (x)dx =10. 2 2 2021 2 1
Câu 113: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho 5 f (x) 2021 + x + x x d = 20 . 1 − 1 Tính f (x) x d . 1 − Ⓐ 5 . Ⓑ 4. Ⓒ 1. Ⓓ 0 . Lời giải 1 1 1 1 1 2022 2 Ta có 5 f (x) 2021 + x
+ x dx = 5 f (x) 2021 dx + x + x dx = 5 ( )d x x f x x + + 2022 2 1 − 1 − 1 − 1 − 1 − 1 = 5 f (x)dx . 1 − 1 1 Do đó 5 f
(x)dx = 20 f (x)dx = 4. 1 − 1 −
Câu 114: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tìm giá trị của a để 4 1 dx = ln a . x −1 x − 2 3 ( )( ) Ⓐ 3 . Ⓑ 1 . Ⓒ 12 . Ⓓ 4 . 4 3 3 Lời giải 4 4 1 1 1 4 − Ta có 4 x 2 4 dx = − dx
= (ln(x − 2) − ln(x − ) 1 ) = ln = ln . x −1 x − 2
x − 2 x −1 3 x −1 3 3 ( )( ) 3 3 Do đó 4 4 ln a = ln a = . 3 3 Câu 115: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Biết rằng 2 3
x −1 dx = a +bln3+cln 2 với , a ,
b c là các số hữu tỉ. Tính 2a + 3b − 4c . 2 x + x 1
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 72 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ −19 . Ⓑ 19 . Ⓒ 5 . Ⓓ −5 . Lời giải Chọn B Ta có: 2 3 2 x −1 x −1 dx = x −1+ dx 2 2 x + x x + x 1 1 2 1 1 = 2 x −1+ − dx 1 1 1 = x −1+ − − dx x +1 x x +1 x +1 x x +1 1 ( ) 1 2 2 2 1 1 2 = x −1+ − dx =
x − x + 2 ln x +1 − ln x x +1 x 2 1 1 1
= 2 − 2 + 2ln 3 − ln 2 − +1− 1 2 ln 2 = + 2ln 3 − 3ln 2 2 2 1
a = ;b = 2;c = 3 − 2
2a + 3b − 4c =1+ 6 +12 =19 Câu 116: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Biết 8 f (x) 4 dx = 2 − ; f (x) 4 dx = 3; g
(x)dx = 7. Mệnh đề nào sau đây là sai? 1 1 1 8 4 4 Ⓐ f
(x)dx+ g (x)dx =8. Ⓑ f
(x)+ g(x)dx =10 . 4 1 1 8 4 Ⓒ
f ( x) dx = 5 − . Ⓓ 4 f
(x)−2g(x)dx = 2 − . 4 1 Lời giải 8 4 8
Từ f ( x) dx = 2
− ; f (x)dx = 3 f (x)dx = 5 − . 1 1 4 8 4 Do đó f
(x)dx+ g (x)dx = 5 − + 7 = 2 4 1 2 2
(2x−3f (x))dx = 3 f ( x) dx Câu 117: Nếu 0 thì 0 bằng Ⓐ 1 . Ⓑ 5 . Ⓒ 5 . Ⓓ 1 . 3 2 2 3 Lời giải Chọn D 2 2 2
Ta có (2x −3 f (x))dx = 3 2 d x x − 3 f (x)dx = 3 0 0 0 2 2 2 x − 3 f (x)dx = 3 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 73 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 4 − 3 f (x)dx = 3 0 2 f (x) 1 dx = 3 0 4
Câu 118: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho f (x)dx =10. 1 −
Biết F ( x) là một nguyên hàm của f ( x) và F (− ) 1 = 4
− . Tính F (4). Ⓐ F (4) = 6 . Ⓑ F (4) =14. Ⓒ F (4) = 1 − 4 . Ⓓ F (4) = 6 − . Lời giải Chọn A 4 Ta có f
(x)dx =10 F(4)−F(− )1 =10 F(4) =10+ F(− )1 =10−4 = 6. 1 −
Câu 119: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Nếu 1 1 3 f
(x)+ x x d = 2 f (x) x d = 2 0 thì 0 bằng Ⓐ 1 − . Ⓑ 1 . Ⓒ 2 . Ⓓ 2 . 2 2 3 Lời giải Chọn B 1 1 1 1 1 2 x Ta có 3 f
(x)+ x x d = 2 3 f (x) x d + x x d = 2 3 f (x) x d + = 2 2 0 0 0 0 0 1 1 1 f ( x) 1 x d = − f ( x) 3 x d = f (x) 1 3 2 3 x d = . 2 2 2 0 0 0 1 f (x) x d = 2
Câu 120: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Nếu 1 − 2 2 f (x) x d = 8 f ( x) x d và 1 − thì 1 bằng Ⓐ 4 . Ⓑ 10 . Ⓒ 6 . Ⓓ 16 . Lời giải Chọn C
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 74 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 1 2 2 1 Ta có f (x) x d = 8 f (x) x d + f (x) x d = 8 f (x) x d = 8 − f (x) x d = 8 − 2 = 6 . 1 − 1 − 1 1 1 − 2
Câu 121: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho 2 và g(x) = 1 − . 1 − 2
Tính I = [x + 2 f (x) + 3g(x)] bằng? 1 − Ⓐ 11 I = . Ⓑ 7 I = . Ⓒ 17 I = . Ⓓ 5 I = . 2 2 2 2 Lời giải Chọn D 2 2 2 2 3 5
Vì I = [x + 2 f (x) + 3g(x)]dx = xdx + 2 f (x)dx + 3 g(x)dx = + 2.2 + 3.( 1 − ) = . 2 2 1 − 1 − 1 − 1 − 3
Câu 122: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Nếu
f (x)dx = 3 và 1 3 2
f (x)dx = 4
thì f (x)dx bằng: 2 1 Ⓐ −7 . Ⓑ 7 Ⓒ 1 − . Ⓓ 1. Lời giải Chọn C 2 3 3
Ta có f (x)dx = f (x)dx − f (x)dx = 3 − 4 = 1 − . 1 1 2 2 2
Câu 123: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Nếu (2x −3 f (x))dx = 3 thì f (x)dx 0 0 bằng Ⓐ 1 − . Ⓑ 5 − . Ⓒ 5 . Ⓓ 1 3 2 2 3 Lời giải Chọn D 2 ( 2 2 2 2
x − f ( x)) x = x x −
f ( x) x = −
f ( x) x = f ( x) 1 2 3 d 3 2 d 3 d 3 4 3 d 3 dx = . 3 0 0 0 0 0
Câu 124: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Biết F ( x) = cos x là một nguyên
hàm của hàm số f ( x) trên
. Giá trị của 3 f
(x)+ 2dx bằng 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 75 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ 2 − 6 . Ⓑ 4 − . Ⓒ 2 . Ⓓ 2 . Lời giải Chọn A Ta có: 3 f
(x)+ 2dx = 3 f
(x)dx + 2 dx
= 3F (x) + 2x =3cosx +2x = 2 −6. 0 0 0 0 0 0 0
Câu 125: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hàm số f ( x) có đạo hàm liên 3 tục trên đoạn 1; 3 , và f '
(x)dx = 6. Tính f ( )1 1 Ⓐ 10 . Ⓑ 11. Ⓒ 1. Ⓓ 1 − . Lời giải Chọn D 3 Ta có : f '
(x)dx = f (3)− f ( )1 = 6 f ( )1 = f (3)−6 =5−6 = 1 − 1
Câu 126: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hai hàm số f ( x), g ( x) liên tục 2 2
trên đoạn 1; 2 và thỏa mãn 3 f
(x)+2g(x)dx =1 , 2 f
(x)− g(x)dx = 3 − . Khi đó, 1 1 2 f ( x) dx bằng 1 Ⓐ 6 . Ⓑ 16 . Ⓒ 11 . Ⓓ 5 − . 7 7 7 7 Lời giải Chọn D 2 2 2 2
f (x) g(x) x
f (x) x g (x) + = + x = f (x) 5 3 2 d 1 3 d 2 d 1 dx = − 7 1 1 1 1 Theo đề: . 2 2 2 2
f (x) g(x) x
f (x) x g(x) − = − − x = − g(x) 11 2 d 3 2 d d 3 dx = 7 1 1 1 1
Câu 127: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Cho hàm số 2021 f ( ) x = x
+sinx + 2021. Biết rằng có duy nhất giá trị của a m m = − để ' ( .
x f (m− x) − f (x))dx = 1
. Tìm a + b . b 0
Ⓐ a + b = 2021.
Ⓑ a + b = 2023.
Ⓒ a + b = 2020 .
Ⓓ a + b = 2022 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 76 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải m m m Ta có ' ( .
x f (m− x) − f (x))dx = 1 ' .
x f (m− x)dx −
f (x)dx = 1 0 0 0 m m m − . x f
(m − x) + f
(m− x)dx − f (x)dx =1 o 0 0 0 m
−mf (0) − f (t)dt − f (x)dx = 1 m 0 m m 2
− 021m + f (t)dt − f (x)dx =1 o 0 1 m = −
. Vậy a =1;b = 2021 a + b = 2022 . 2021
PHƯƠNG PHÁP ĐỔI BIẾN SỐ
Câu 128: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f x liên tục trên 6 3 và f x dx 10 , thì
f 2x dx bằng 0 0 Ⓐ 30 . Ⓑ 20 . Ⓒ 10 . Ⓓ 5 . Lời giải 3 Xét I
f 2x dx . 0 Đặt t 2x dt 2dx . Đổi cận: x 0 t 0 . x 3 t 6 . 6 6 6 Lúc đó: 1 1 1 1 I f t . dt f t dt . f x dx .10 5 . 0 0 0 2 2 2 2 2 e Câu 129: ln x
(CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Tích phân dx x e bằng Ⓐ 3. Ⓑ 3 . Ⓒ 1. Ⓓ 2. 2 Lời giải 2 2 2 e e e Ta có ln x x = x ( x) 1 = ( x)2 3 d ln d ln ln = . x 2 2 e e e 1 dx
Câu 130: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Tính tích phân I = bằng cách đặt 1 x + e 0 x
t = e , ta được:
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 77 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 e 1 e 1 Ⓐ dt dt dt tdt I = . Ⓑ I = . Ⓒ I = . Ⓓ I = . 1+ t 1+ t t 1+ t 1+ t 1 ( ) 1 0 0 Lời giải Chọn C Đặt x = d x t e
t = e dx .
x = 0 t =1
Đổi cận x =1t = e 1 e dx dt Ta có: I = = . 1 x + e t(1+ t) 0 1 1 dx
Câu 131: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Tính tích phân I = 1 x + e 0 bằng cách đặt x
t = e , ta được e 1 e 1 Ⓐ dt dt dt tdt I = . Ⓑ I = . Ⓒ I = . Ⓓ I = . 1+ t 1+ t t t +1 1+ t 1 ( ) 1 0 0 Lời giải Đặt x t = e d x
t = e dx .
Đổi cận: x = 0 t = 1.
x = 1 t = e . 1 1 x e dt Khi đó: dx e .dx I = = = . 1 x x + e e 1 x + e t 1+ t 1 ( ) 0 0 ( )
Câu 132: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Cho hàm số 4 e 1 − 2
x + 2x −1 khi x 2 x 2 = + f (x) = . Giá trị của I . f ln x 1 dx thuộc khoảng 2 ( )
x + 5 khi x 2 x +1 0 nào dưới đây ? Ⓐ ( 2 − ;3) . Ⓑ (5;7) . Ⓒ (10;1 ) 1 . Ⓓ (8;9) . Lời giải Đặt = ( 2x + ) 2x u ln 1 du = dx . 2 x +1
Đổi cận: x = 0 u = 0 ; 4
x = e −1 u = 4 . 4 e 1 − x I = . f ln (x + ) 4 2 4 1 1 1 2 1 dx =
f (u) du =
f (u) du + f (u) du 2 x +1 2 2 2 0 0 0 2 2 1 = (u +2u − ) 4 1 31 2 1 du + (u +5)du = . 2 2 3 0 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 78 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Suy ra: I (10;1 ) 1 . Câu 133: (CHUYÊN ĐHSP HÀ NỘI NĂM 2020-2021) Cho hàm số + 1 f ( x) 2x 1 khi x 3 =
( a là tham số thực). Nếu f ( xe + ) x 2
1 e dx = e thì a bằng
ax − 3a + 7 khi x 3 0 2 3e + 4e − 6 Ⓐ e − Ⓒ 6e + 6 Ⓓ 6 − e + 6 e − . Ⓑ 6 6 1 Lời giải Đặt x = +1 x t e
dt = e dx . Nếu x = 0 t = 2, Nếu x =1 t = e +1 Suy ra: 1 + + + f ( xe + ) e 1 3 e 1 3 e 1 1 x e dx = f
(t)dt = f
(t)dt + f
(t)dt = (at −3a +7)dt + (2t + )1dt 0 2 2 3 2 3 3 2 e at + =
− 3at + 7t + (t + t) 1 2 = 2 2 2 2 2 .3 a .2 a = − 3 .3 a + 7.3 − − 3 .2
a + 7.2 + ( e + )2 1 + e + ) 1 − ( 2 3 + 3) 2 2 −a 2 = + e + 3e − 3 2 1 Theo giả thiết: f ( xe + ) x 2
1 e dx = e nên ta có phương trình: 0 −a a 2 2
+ e + 3e − 3 = e
= 3e − 3 a = 6e − 6 2 2
Câu 134: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho hàm số 2 f ( x) 2
= x −1 . Tích phân f (3cos x − )1.sin xdx bằng 0 Ⓐ 8 . Ⓑ 10 . Ⓒ 7 . Ⓓ 11 . 9 9 9 9 Lời giải 2 x −1 , x (− ; − ) 1 ( 1 − ;+ ) Ta có f ( x) 2 = x −1 = . 2 −x +1 , x 1 − ; 1
Đặt 3cos x −1 = t 3
− sin xdx = dt .
Khi x = 0 thì t = 2 ; Khi x = thì t = 1 − . 2 Vậy
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 79 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 1 − 2 f ( x − ) 1 xdx = − f (t) 1 3cos 1 .sin dt = f (t)dt 3 3 0 2 1 − 1 2 1 2 1 = f
(t)dt + f (t) 1 dt = ( 8 2 t
− +1 )dt + ( 2t − )1dt = 3 3 9 1 − 1 1− 1
Câu 135: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Có bao nhiêu giá trị ln a 1 3
thực dương của tham số a để dx = ln ?. x e + 2 x e− − 3 2 ln 3 Ⓐ 3 . Ⓑ 2 . Ⓒ 4 . Ⓓ 1. Lời giải ln a dx Xét I = x e + 2 x e− − 3 ln 3 Đặt x x
t = e dt = e dx Đổi cận x ln 3 ln a t 3 a ln a a a a dx dt dt t − 2 a − 2 1 I = = = = ln = ln − ln x −x 2 e + 2e − 3 t − 3t + 2
(t −1)(t − 2) t −1 a −1 2 ln 3 3 3 3 3 a − 2 1 3 a − 2 3 I = ln ln − ln = ln ln = ln 2 a −1 2 2 a −1 4 − Ta có a 2 3 = a = 5 a − 2 3 −
4a − 8 = 3a − 3 a 1 4 = 11 a −1 4 a − 2 3 − 4a −8 = 3 − a + 3 a = = 7 a −1 4 1 11 Khi 11 a =
thì hàm số f (t) = ;3 nên 7 (t − )1(t −
không liên tục trên khoảng 2) 7 không thỏa mãn.
Vậy có 1 giá trị của a thỏa mãn yêu cầu bài toán.
Câu 136: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho hàm số − − ln 4 f ( x) 2 x 8x 5 khi x 8 =
. Tích phân (2 x + 3) x f e e dx bằng −x +3 khi x 8 0 Ⓐ 39 . Ⓑ 39 . Ⓒ 123 − . Ⓓ 123 − . 2 4 2 4 Lời giải Chọn B
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 80 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 ln 4
Ta có: = (2 x + 3) x I f e e dx . 0 Đặt = 2 x + 3 = 2 x u e du e dx . Đổi cận:
x = 0 u = 5; x = ln 4 u = 11 11 11 11 8 11 I = f (u) du 1 = f (u) 1 du = f (x) 1 dx = f (x) 1 . dx + f (x)dx 2 2 2 2 2 5 5 5 5 8 8 11 8 11 1 = ( x x −x + 3) 1 dx + (x −8x−5) 2 3 1 2 2 dx =
− +3x + − 4x −5x . 2 2 2 2 3 5 8 5 8 1 5 286 376 39 = 8 − − − + = . 2 2 3 3 4
x − x + khi x
Đổi đề do hàm số f ( x) 2 1 8 =
không liên tục tại x = 8 . −x +3 khi x 8
Câu 137: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Cho hàm số y = f ( x) có 4
f (0) = 0 và f ( x) 4 2
= tan x + tan x , x 0;
. Tính I = f (x) . dx 2 0 − − Ⓐ 1 . Ⓑ 1 . Ⓒ 1 ln 2 . Ⓓ 1 ln 2 . 12 6 6 3 Lời giải Ta có: f (x)dx = ( 1 4 2 tan x + tan x) 2 dx = tan x ( 2 tan x + ) 2 1 dx = tan . x dx 2 cos x x = tan d x (tan x) 3 tan 2 = + C . 3 x x Suy ra f ( x) 3 tan =
+ C ; f (0) = 0 C = 0. Do đó f (x) 3 tan = . 3 3 4 4 4 4 4 1 1 1 1 sin x Ta có I = f (x) 3 dx = tan d x x = tan x −1 dx = tan d x tan x − dx 2 ( ) 3 3 cos x 3 cos x 0 0 0 0 0 2 1 tan x 1 1 1 1− ln 2 = + ln cos x 4 = − ln 2 = . 3 2 3 2 2 6 0 4 1− ln 2
Vậy I = f ( x)dx = . 6 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 81 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 138: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Biết rằng ln 4 dx
= a + bln 2 + c ln 3 với , a , b c
. Tính a + b + c . + 0 1 x e Ⓐ –2. Ⓑ 3. Ⓒ 2. Ⓓ –1. Lời giải ln 4 dx ln 4 x e ◦ Ta có: I = = dx . + x x + 0 e (1 e ) 0 1 x e ◦ Đặt = 1 x t + e x
e = (t − )2 1 . ◦ Suy ra: x
e dx = 2(t − ) 1 dt .
◦ Đổi cận: x = 0 t = 2 và x = ln 4 t = 3 . 3 3 2(t − ) 3 1 dt − ◦ Khi đó: 1 t 1 2 1 I = = = = − ( 2 ln 2 ln 2 ln t − ) 2 dt 2 1 t t −1 t t 3 2 2 2 ( ) 2
= 2ln 2 − 2ln 3+ 2ln 2 = 4ln 2 − 2ln 3.
◦ Vậy: a = 0,b = 4,c = 2
− → a + b + c = 2.
PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN
Câu 139: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho 2 x + ln x a 1 I = = − với là phân số tối ( , a ,
b c là các số nguyên dương và a x + ) dx ln 2 2 1 b c b 1 + giản.Tính giá trị a b S = c Ⓐ 2 S = . Ⓑ 1 S = . Ⓒ 1 S = . Ⓓ 5 S = . 3 2 3 6 Lời giải x +1 u = x + ln x du = dx Đặt x 1 dv = ( x + ) dx 2 1 1 v = − x +1 2 2 2 1 1 1 1 2 1 Ta được I = −
(x +ln x) + dx = −
(2+ln2)+ +ln x = ln2− . x +1 1 x 3 2 1 3 6 1
Suy ra: a = 2,b = 3,c = 6 . Vậy 5 S = . 6
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 82 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 e
Câu 140: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Tính tích phân I = x ln d x x , 1 2 e + a
ta được kết quả I =
, với a , b là các số nguyên. Tính 3 3 a + b . b Ⓐ 35 . Ⓑ 65 . Ⓒ 28 . Ⓓ 9 . Lời giải e I = x ln d x x 1 1 du = dx u = ln x Đặt , ta có x . d v = d x x 2 x v = 2 e e 2 e 2 2 2 2 2 x ln x x e x e e 1 e +1 Ta có I = − dx = − = − − = . 2 2 2 4 2 4 4 4 1 1 1
Suy ra a = 1, b = 4 . Vậy 3 3 3 3
a + b = 1 + 4 = 65 .
Câu 141: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Cho hàm số 1
f ( x) có đạo hàm f '( x) và thỏa (2x + )
1 f '( x)dx = 10, 3 f ( )
1 − f (0) = 12. Tính 0 1 I = f (x)dx 0 Ⓐ I = 1 − . Ⓑ I =1. Ⓒ I = 2 . Ⓓ I = 2 − . Lời giải 1
Từ giả thiết: (2x + )
1 f '( x) dx = 10 . 0 u = 2x +1 du = 2dx Đặt . dv = f ' (x)dx v = f (x) 1 1 1
Khi đó ta có: (2x + )
1 f '( x) dx = 10 (2x + )
1 f ( x) − 2 f (x)dx =10 . 0 0 0 1 −
f (x) − f ( ) − f (x) 12 10 3 0 2 dx = 10 I = = 1. 2 0
Câu 142: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Cho hàm số f (x) có đạo 3 1 hàm liên tục trên thỏa mãn = f (3) = 21,
f (x)dx = 9 . Tính tích phân I
x f (3x)dx 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 83 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ I = 15. Ⓑ I = 6 . Ⓒ I =12. Ⓓ I = 9 . Lời giải 1 1 3 Xét có: 1 I = x f x x = x f x ( x) 1 (3 )d 3 (3 )d 3 = t f ( t)dt 0 0 0 9 9 u = t du = dt Đặt dv = f
(t)dt v = f (t) 3 3 3
Do đó 9I = t. f (t ) − f
(t)dt = 3f (3)− f
(x)dx = 3.21−9 = 54 I = 6. 0 0 0
Câu 143: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Cho hàm số f (x) có đạo
hàm cấp 2 liên tục trên đoạn
0; 1 thỏa mãn f (1) = 0; f (1) =1và 1 2
10 f (x) − 5xf (
x) + x f (x) = 0với mọi x0
;1 . Khi đó tích phân f (x)dx bằng 0 − − − − Ⓐ 1 . Ⓑ 2 . Ⓒ 1 . Ⓓ 1 . 15 3 10 17 Lời giải 1 1 1 Ta đặt 2 I = f (x)d ; x J = xf ( x)d ; x K = x f ( x)dx . 0 0 0
Theo đề ta có 10I = 5J − K . Hơn nữa, dùng phương pháp tích phân từng phần ta được : 1 1 2 K = x f (
x) − 2 xf (x)dx =1− 2J 0 0 1 1
J = x f (x) −
f (x)dx = 0 − I = −I 0 0 − Suy ra 10I = 5
− I − (1+ 2I) = 7 − I −1. Do đó 1 I = . 17
Câu 144: Cho hàm số f ( x) có đạo hàm f ( x) trên đoạn 0; 1 thỏa mãn f ( ) 1 = 4 và 1 1 f
(x)dx = 3. Tích phân 3x f ( 2x) xd bằng 0 0 Ⓐ 1 − . Ⓑ 1. Ⓒ 1 . Ⓓ 1 − . 2 2 Lời giải Chọn C Đặt 2
t = x dt = 2 d x x .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 84 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 1 1 Khi đó 3 x f ( 2x) x d = t. f (t) td . 2 0 0 u = t u d = t d Đặt v d = f
(t) td v = f (t) 1 1 1 1 Suy ra t. f
(t) td = t.f (t) − f
(t) td = f ( )1− f (x) x d = 4 − 3 =1. 0 0 0 0 1 1 Vậy 3 x f ( 2 x ) x = d 2 0
Câu 145: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Cho hàm số f ( x) có đạo hàm liên tục trên
và có đồ thị như hình bên. 1 Đặt K = xf
(x)f '(x)dx, khi đó K thuộc khoảng nào sau đây? 0 3 2 3 2 Ⓐ ( 3 − ;− 2) . Ⓑ −2; − . Ⓒ − ;0 . Ⓓ − ; − . 2 3 2 3 Lời giải Chọn D du = dx u = x Đặt = ( ) f x dv f x f '( x) 2 ( ) dx v = 2 1 1 2 1 1 xf x 1 1 1 Khi đó K = xf
(x)f '(x) ( ) 2 dx = − f (x) 2 dx = − f (x)dx. 2 2 2 2 0 0 0 0 Từ đồ thị ta thấy: · 2 1 2 1 1 2 −
f ( x) − x x f ( x) (2 x) 7 1 f ( x) 2 2 , 0;1 dx dx = K = − dx − . 2 2 6 2 2 3 0 0 0 1 2 1 1 2 f x 1 f x 3 ·
f ( x) 2, x 0 ( ) ( ) ;1
dx 2dx = 2 K = − dx − . 2 2 2 2 0 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 85 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Vậy 3 2 − K − . 2 3
Câu 146: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Cho hàm số f ( x) có đạo hàm f ( x) 1 1 trên đoạn 0; 1 thỏa mãn f ( )
1 = 4 và f (x)dx = 3. Tích phân 3
x f ( 2x)dx bằng 0 0 Ⓐ 1 − . Ⓑ 1. Ⓒ 1 . Ⓓ −1. 2 2 Lời giải Chọn C Đặt 2
t = x dt = 2 d x x
Đổi cận: x = 0 t = 0, x =1 t =1. Do đó 1 x . f (x ) 1 1 1 1 3 2 dx = t. f (t)dt = . x f (x)dx 2 2 0 0 0 u = x du = d x Đặt dv = f
(x)dx v = f ( x) Khi đó 1 x . f (x ) 1 1 1 1 1 1 1 3 2 dx = . x f
(x)dx = .x f (x) 1 − f (x)dx = ( f ( )1−3) = (4−3) = . 2 2 0 2 2 2 0 0 0
Câu 147: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 01) Giả sử f ( x) là hàm có đạo
hàm liên tục trên khoảng (0; ) và f '( x)sin x = x + f ( x)cos x, x (0; ). Biết 1 f =1, f =
(a+bln2+c 3), với + + , a ,
b c là các số nguyên. Giá trị a b c 2 6 12 bằng Ⓐ 1 − . Ⓑ 1. Ⓒ 11. Ⓓ 11 − . Lời giải Chọn A x
(0; ) , ta có: f '(x)sin x = x + f (x)cos x, x (0; ).
f '( x)sin x − f ( x)cos x x = 2 2 sin x sin x
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 86 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 f (x) ' x = 2 sin x sin x f ( x) x = dx = − .
x cot x + ln sin x + C 2 sin x sin x
f (x) = − .xcos x +sin .xln sin x +C.sin x Ta lại có: f =1 C =1 2 3 1 1 1 1 f = − . + .ln + = (6−6ln2− 3) 6 2 6 2 2 2 12 a = 6, b = 6 − , c = 1 − .
Vậy a + b + c = 1 − .
TÍCH PHÂN HÀM ẨN – TÍCH PHÂN ĐẶC BIỆT
Câu 148: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Cho f ( x) là hàm số 1 1 liên tục trên
và f (x)dx = 6. Tính tích phân I =
f (2x − )1+ 2xd x . 1 − 0 Ⓐ I = 4 . Ⓑ I = 13 . Ⓒ I = 7 .
Ⓓ I = 5 . Lời giải Ta có : 1 1 1 I =
f (2x − )1+ 2xdx =
f (2x − )1dx + 2xd x . 0 0 0 1 Xét I = f 2x −1 d x đặt 1
u = 2x −1 du = 2dx dx = du . 1 ( ) 2 0 Đổi cận: 1 1 1 1 I = f u du = f x dx = 3. Vậy I = 3 +1 = 4 . 1 ( ) ( ) 2 2 1 − 1 −
Câu 149: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Cho hàm số y = f ( x) có đạo hàm trên (0;+) . Biết 2 2
x là một nguyên hàm của x f '( x) trên (0; +) và f ( ) 1 = 1. Tính f (e) .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 87 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ 2 . Ⓑ 3 . Ⓒ 2e +1. Ⓓ e . Lời giải Vì 2 2
x là một nguyên hàm của x f '( x) trên (0; +) nên ta có 2 x f ( x) = ( 2 '
x )' = 2x f ( x) 2 ' = . x e e 2 e Ta có f '
(x)dx = dx = 2ln x = 2lne−2ln1= 2 = f (e)− f ( ) 1 . x 1 1 1
2 = f (e)−1 f (e) = 2+1= 3.
Câu 150: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) có đạo hàm liên tục trên
và thỏa mãn các điều kiện sau: f (0) = 2
− và ( 2x + )1 f (x)+ xf (x) = −x , 3 x
. Tính tích phân I = xf
(x)dx . 0 Ⓐ 5 I = . Ⓑ 3 I = − . Ⓒ 3 I = . Ⓓ 5 I = − . 2 2 2 2 Lời giải • ( 2 x + )
1 f ( x) + xf ( x) = −x x x 2
x +1. f (x) + . f ( x) = − 2 2 x +1 x +1 2 x f ( x) + = ( 2 1. − x +1) 2
x + f (x) 2 1.
= − x +1 + C . • f (0) = 2
− 1. f (0) = − 1 + C C = 1 − . • 1 2
x +1. f ( x) 2
= − x +1 −1 f (x) = −1− . 2 x +1 Khi đó: 3 3 3 I = xf (x) x 1 3 5 2 2
dx = −x−
dx = − x − x +1 = − − 3+1 − (−0 − ) 1 = − . 2 + 2 2 2 0 0 x 1 0
Câu 151: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho hàm số
y = f ( x) liên tục và có đạo hàm trên thỏa mãn
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 88 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 a
f ( x) − f ( − x) = ( 2 5 7 1
3 x − 2x), x
. Biết rằng tích phân I = .
x f '( x) dx = − . Tính b 0 T = 3a − . b Ⓐ T =0. Ⓑ T =− 48. Ⓒ T 16. = Ⓓ T =1. Lời giải 1 1 1 1 Ta có: I = . x f '
(x)dx = .xd f
(x) = I = .x f (x)1 − f
(x)dx = f ( )1− f (x)d .x 0 0 0 0 0
Theo giả thiết: f ( x) − f ( − x) = ( 2 5 7 1 3 x − 2x) 1 1 5 f
(x)−7 f (1− x)dx =3
( 2x −2x)dx 0 0 1 1 1 1 1 5 f
(x)dx −7 f
(1− x)dx =3( 2x −2x)dx 5 f
(x)dx −7 f
(1− x)dx =−2. 0 0 0 0 0 1 0 1 1
Bằng cách đổi biến t =1 x − , ta có f
(1− x)dx =− f
(t)dt = f
(t)dt = f (x)dx . 0 1 0 0 1 1 1 Thay vào , ta có 5 f
(x)dx −7 f
(x)dx =− 2 f (x)dx =1. 0 0 0
Mặt khác do f ( x) − f ( − x) = ( 2 5 7 1
3 x − 2x) nên lần lượt chọn x =0, x =1 ta có 5 f (0) −7 f ( ) 1 = 0 f ( ) 5 1 = . 5 f ( ) 1 − 7 f (0) = 3 − 8 1 1 5 3 Thay f ( ) 5 1 = và f
(x)dx =1 vào ta có I = f ( )1− f
(x)dx = −1=− . 8 8 8 0 0
Vậy a = 3; b =8 T =3a −b =9 −8 1 = .
Câu 152: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số f (x) 3
có đạo hàm liên tục trên R + + = +
và thỏa mãn f (x
3x 1) 3x 2, x R . Tích phân 5 xf ( x)dx bằng 1 − Ⓐ 31 . Ⓑ 33 . Ⓒ 17 . Ⓓ 49 . 4 4 4 4 Lời giải 3 2 3 2
Ta có f (x + 3x +1) = 3x + 2 (3x + 3) f (x + 3x +1) = (3x + 3)(3x + 2) .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 89 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 1 59 2 3 2
(3x + 3) f (x + 3x +1)dx = (3x + 3)(3x + 2)dx = . 4 0 0 1 5 5 59 59 3 3
f (x + 3x +1)d(x + 3x +1) =
hay f (t)dt = f (x)dx = . 4 4 0 1 1 5 5 5 59 59 33 Do đó xf (
x)dx = xf (x) − f (x)dx = 5 f (5) − f (1) − = 5.5 − 2 − = . 1 4 4 4 1 1
Câu 153: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Cho hàm số f ( x) liên tục trên ( 0;+) và thỏa mãn ( ) 1 2 f x + xf = x với mọi x 0 . x 2
Tính f ( x) dx . 1 2 Ⓐ 7 . Ⓑ 7 . Ⓒ 9 . Ⓓ 3 . 12 4 4 4 Lời giải Chọn D 1 1
Xét 2 f ( x) + xf = x 4 f (x)+ 2xf = 2x ( )1 x x 1 1 1 1 1 1 1 1
Đặt x = 2 f + f (t) = 2 f + f (x) = 2xf + f (x) =1 (2) t t t t x x x x − Từ ( )
1 và (2) f ( x) 2x 1 = 3 2 2 2 2 2x −1 x − x 2 1 3 Khi đó: f (x)dx = dx = = + = . 3 3 1 3 12 4 1 1 2 2 2
Câu 154: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Cho hàm số f ( x) liên tục trên và thoả mãn ( ) ( )1 ( ) x xf x x f x e− + + =
với mọi x . Tính f (0) . Ⓐ 1. Ⓑ 1 − . Ⓒ e . Ⓓ 1 . e Lời giải Chọn B − Ta có: ( )+( + ) 1 ( ) x xf x x f x = e ( )1 x ( )1 x ( ) x e xf
x + e ( x + ) 1 f ( x) =1 x ( )+( x x e xf x
e x + e ) f (x) =1
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 90 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 x ( ) + ( x e xf x
e x) f ( x) =1 ( x e . x f ( x)) =1. Suy ra: ( x e .
x f ( x)) dx = dx x e .
x f ( x) = x + C (2) . Do đẳng thức ( )
1 đúng với mọi x nên ( )
1 cũng đúng với x = 0 . Thay x = 0 vào ( )
1 ta được f (0) =1.
Thay x = 0 vào ( 2) 0 = 0 + C C = 0 x
e xf (x) = x f (x) 1 = với x 0 . x e − Mà: f ( ) 1 0 = ( ) x f x = e x . 0 e Suy ra: ( ) x f x e− = − f (0) = 1 − .
Câu 155: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Biết 8 4 3
f (x)dx = 10; f (x)dx = 4 − . Tính f
( 3x−1)dx. 0 0 1 − Ⓐ 2 . Ⓑ 1. Ⓒ 0 . Ⓓ 4 . Lời giải Chọn A 1 3 3 3 Ta có I = f
( 3x−1)dx = f
(3x− )1dx+ f (1−3x)dx 1 − 1 1 − 3 1 3 1 I = f
( x− ) ( x− ) 3 1 3 1 d 3 1 − f
(1−3x)d(1−3x) 3 3 1 1 − 3 . 8 0 8 4 1 − I = f (u) 1 u − f (t) 1 t = f (u) 1 u + f (t) 10 4 d d d dt = = 2 3 3 3 3 3 0 4 0 0
Câu 156: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Cho hàm số f (x) có f (0) = 0 và 4 f ( x) 4 2
= tan x + tan x , x 0; . Tính = I f (x)dx . 2 0 − − Ⓐ 1 . Ⓑ 1 . Ⓒ 1 ln 2 . Ⓓ 1 ln 2 . 12 6 6 3 Lời giải Chọn C
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 91 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 ' 4 2
Ta có f (x) = tan x + tan x
Nguyên hàm hai vế, ta được 4 2 2 2 f ( ) x = (tan x + tan ) x dx = tan .
x (tan x +1)dx Đặt t = tan x 1 2 dt =
dx = (1+ tan x)dx 2 cos x 3 t 1 Khi đó: 2 3
f (x) = t dt =
+ C = tan x + C , mà 1
f (0) = 0 nên C = 0 . Vậy 3 f (x) = tan x 3 3 3 4 4 1 Tính 3 I = f (x)dx = tan xdx 3 0 0 Đặt t = tan x 1 2 dt =
dx = (1+ tan x)dx 2 cos x Đổi cận: 1 1 1 dt 1 t 3 I = t . = t − dt 2 2 3 1+ t 3 t +1 0 0 1 1 1 1 1 1 t 1 1 1 I = tdt − dt = tdt − d ( 2 1+ t 2 2 ) 3 3 1+ t 3 6 1+ t 0 0 0 0 2 1 t 1 1 1 − 2 I = . − ln t + 1 ln 2 1 = . 3 2 0 6 0 6
Câu 157: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Cho hai hàm số f ( x), g ( x) có đạo hàm
trên R và thỏa mãn f ( x) + g ( x) = x , g( x) + f ( x) = − , x x
. Biết f (0) = g (0) =1. Tính f ( ) 1 . 2 e − 2 2 e + 2 Ⓐ 2 − 2 . Ⓑ 1 e + − 2 . Ⓒ . Ⓓ . e e 2e 2e Lời giải Chọn B
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 92 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 f
(x) + g (x) = x f
(x) + g (x) + g(x) + f (x) = 0 g
(x) + f (x) = −x f
(x) + g (x) − g(x) − f (x) = 2x x e f (x) x
+ e g (x) x
+ e g(x) x + e f (x) = 0 −x e f (x) −x
+ e g (x) −x
− e g(x) −x
−e f (x) = 2 −x xe x e f
( x) + g ( x) + ( x e ) f
( x) + g ( x) = 0 − x e f
( x) − g ( x) + ( −x e ) f
( x) − g ( x) = 2 −x xe 1 + e
( f (x) + g (x)) x x e =
( f ( x) g (x)) dx=0 0 0 − x − e
( f (x) g(x)) 1 = 2 −x −x xe e ( 1
f ( x) − g ( x)) dx= 2 −x xe dx 0 0 e f ( ) 1 + g ( ) 1 − f
(0) + g (0) = 0 2 f ( ) 1 + g ( ) 1 = e − 4 − 1 e f ( ) 1 − g ( ) 1 − f
(0) − g (0) = + 2 f ( ) 1 − g ( ) 1 = 4 − + 2e e f ( ) 1 1 = e + − 2. e
Câu 158: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Cho hàm số y = f ( x) có đạo hàm
liên tục trên 1; 4 , đồng biến trên 1; 4 và thỏa mãn đẳng thức 4
x + xf ( x) = f ( x) 2 / 2 , x
1;4 . Biết rằng f ( ) 3 1 = . Tính I = f (x)dx . 2 1 Ⓐ 1222 . Ⓑ 1201 . Ⓒ 1174 . Ⓓ 1186 . 45 45 45 45 Lời giải Chọn D
Vì hàm số y = f ( x) có đạo hàm liên tục trên 1; 4 , đồng biến trên 1; 4 ; f ( ) 3 1 = . 2
Nên từ đẳng thức x + xf ( x) = f ( x) 2 / 2 , x 1;4 / / f x f x /
f (x) = x(1+ 2 f (x)) ( ) ( ) = x dx = xdx 1+ 2 f ( x) 1+ 2 f ( x) + f ( x) 2 1 2
= x x + C , mà f ( ) 3 1 = nên 4 C = 3 2 3 2 2 4 1 2 4
Vậy 1+ 2 f ( x) = x x +
f (x) = x x + −1 3 3 2 3 3
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 93 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 4 1186 Vậy I = f (x)dx = . 45 1
Câu 159: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Cho hàm số f ( x) liên tục trên
và có một nguyên hàm là hàm số g ( x) 1 2
= x − x +1. Khi đó 2 2 f ( 2 x ) dx bằng 1 Ⓐ 2 . Ⓑ 4 − . Ⓒ 4 . Ⓓ 2 − . 3 3 3 3 Lời giải Chọn C
Ta có f ( x) = g
(x) = x − f ( 2x) 2 1 = x −1. 2 2 2 3 x 4 Khi đó f
( 2x)dx = ( 2x − )1dx = − x = . 3 3 1 1 1
Câu 160: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Cho hàm số y = f ( x) có đạo hàm trên thỏa mãn f ( )
1 = 1và f ( x) − xf ( 2 x ) 3 2
= 5x − 2x −1với mọi x Tính tích 2 phân I = xf '
(x)d .x 1 Ⓐ I = 3. Ⓑ I = 1. − Ⓒ I = 2. Ⓓ I = 5. Lờigiải 2 2 2 2 Ta có: I = xf '
(x)dx = xd
( f (x)) = xf (x) − f (x)d .x 1 1 1 1 Từ giả thiết 1 1 1
f (2x) − xf ( 2 x ) 3
= 5x − 2x −1 f
(2x)dx − xf
( 2x)dx = ( 3 5x − 2x − ) 1 dx = 1. 0 0 0 1 2 2 1 1 Đặt K = f
(2x)d .xĐổi biến t = 2x dt = 2dx K = f (t)dt = f (x)d .x 2 2 0 0 0 1 1 1 1 1 Đặt L = xf
( 2x)d .xĐổi biến 2
t = x dt = 2xdx L = f (t)dt = f (x)d .x 2 2 0 0 0 2 1 2 1 2 1 1 1 Khi đó f
(x)dx− f
(x)dx =1 f
(x)dx− f
(x)dx =1 f (x)dx = 2. 2 2 2 0 0 0 0 1
Từ giả thiết f ( x) − xf ( 2 x ) 3 2
= 5x − 2x −1 ta suy ra f (2) = 3.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 94 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 2 2
Như vậy: I = xf ( x) − f
(x)dx = 2.f (2)−1.f ( )1− f
(x)dx = 2.3−1.1−2 =3. 1 1 1
Câu 161: (CHUYÊN HÙNG VƯƠNG PHÚ THỌ NĂM 2020-2021 LẦN 04) Cho hàm số f ( x) liên tục trên và thỏa mãn ( ) = ( )− ( ) 2 0 1; = . x f f x xf x x e , x . Tích phân 1 xf
( x +1)dx bằng 0 Ⓐ 2 e − e .
Ⓑ 4 e − 2e . Ⓒ 1. Ⓓ e . Lời giải 2 2 2 2 2 x x x x x − − −
Ta có f ( x) − xf ( x) 2 x 2 = x e e f ( x) 2 − xe f ( x) 2 2 = x e e f ( x) 2 . . = . x e 2 2 2 2 2 2 x x x x x x − − − e
f ( x) = x e x e f (x) 2 x 2 2 2 2 2 = e e f ( x) 2 . d d = e + C. 2
Theo bài ra f (0) =1 C = 0 . Từ đó suy ra ( ) 2 x f x = e . 1 1 1 1 1 1 Do đó xf ( x+1) x 1 dx = . x e + dx = d x ( x 1 e + ) x 1 + x 1 + 2 x 1 + 2 2 = . x e
− e dx = e −e
= e − e + e = e 0 0 0 0 0 0 .
Câu 162: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Cho hàm số f ( x) 1 4
có đạo hàm liên tục trên . Biết f ( 2
x ) = f ( x) 4 2
+ x − 4x, x
và f ( x) dx = , khi 3 0 1 2 đó x f (x)dx bằng 0 Ⓐ 7 . Ⓑ 8 . Ⓒ 7 . Ⓓ 2 . 6 15 10 3 Lời giải Chọn A Ta có: f ( 2
x ) = f ( x) 4
+ x − x xf ( 2
x ) = xf ( x) 5 2 2 4 2 4 + 2x − 8x . 1 2xf (x ) 1 1 2 dx = 4 xf
(x)dx+( 5 2
2x − 8x )dx . 0 0 0 1 1 1 2 2 4
Đặt: x = t 2xdx = dt 2xf ( x )dx = f (t)dt = f ( x)dx = . 3 0 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 95 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 1 2 d x x = dv x = v 1 1 1 1 2 1 2 Đặt . Nên xf
(x)dx = x f (x) − x f (x)dx. f ( x) 2 = u 2 2 f
( x)dx = du 0 0 0 1 1 4 = 2x f (x)1 2 2 − 2 x f (x)dx+ ( 5 2
2x − 8x )dx 0 3 0 0 1 4 = f ( ) 2 − x f (x) 7 2 1 2 dx − 3 3 0 1 2 x f (x) 11 2 dx = − + 2 f ( ) 1 3 0 Với f ( ) 1 = 2 f ( ) 1 +1− 4 f ( ) 1 = 3 . 1 2 7
Vậy x f ( x) dx = . 6 0
Câu 163: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Cho hàm số f (x) 2
có đạo hàm liên tục trên và thỏa mãn + − = − +
f (0) = 3 và f (x) f (2 x) x 2x 2 , 2 x . Tích phân .
x f '(x)dx bằng 0 − − − − Ⓐ 10 . Ⓑ 5 . Ⓒ 11 . Ⓓ 7 . 3 3 3 3 Lời giải Chọn A u = x d u = dx 2 2 2 2 Đặt I = .
x f '(x)dx = xf
(x) − f (x)dx = 2 f (2) − f (x)dx . d
v = f '(x)dx v = f (x) 0 0 0 0 2
Ta có f (x) + f (2 − x) = x − 2x + 2 thế x = 0 vào ta được f (0) + f (2) = 2 f (2) = 1 − (1) 2 2 2 2 3 x 8
Ta lại có f (x)dx + f (2 − x)dx = ( 2x −2x+2) 2 dx =
− x + 2x = . 3 3 0 0 0 0 2 0 2 2
Mặt khác đặt t = 2 − x ta có f (x)dx = − f (2 − t)dt = f (2 − t)dt = f (2 − x)dx 0 2 0 0 2 2 2 2 8 4
Nên suy ra f (x)dx + f (2 − x)dx = 2 f (x)dx = f (x)dx = (2) 3 3 0 0 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 96 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 2 4 10
Từ (1) và (2) suy ra I = .
x f '(x)dx = 2 f (2) −
f (x)dx = 2 − − = − . 3 3 0 0
Câu 164: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hàm số y = f ( x) có đạo hàm .
x f (t ) − t. f ( x)
liên tục trên khoảng (0;+) và thỏa mãn lim =1 t . Biết 2 2 x→t x − với mọi 0 t rằng f ( )
1 = 1, tính f (e) . Ⓐ 3e +1 . Ⓑ 3e . Ⓒ 2e . Ⓓ −e . 2 Lời giải Chọn D Ta có: .
x f (t ) − t. f ( x) .
x f (t ) − t. f (t ) + t. f (t ) − t. f ( x)
f (t) t( f (t) − f (x)) lim = lim = lim + 2 2 x→t x t x − t →
(x −t)(x +t) x t → x + t
(x −t)(x +t) f (t ) f (t ) = − . 2t 2 .
x f (t) − t. f ( x) f (t ) f (t ) Theo đề lim =1 −
=1 f t −t. f t = 2t, t 0. 2 2 ( ) ( ) x t → x − t 2t 2 Như vậy ta có f ( x) − .
x f ( x) = 2x, x 0 1 1 2 1 2 − f x + f x = − f x = − . 2 ( ) ( ) ( ) x x x x x Suy ra 1 f ( x) 2 = − dx = 2 − ln x + C . x x Theo đề f ( )
1 = 1 nên C =1. Suy ra f ( x) = x( 2 − ln x + ) 1 .
Vậy f (e) = − . e
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 97 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
ỨNG DỤNG TÍCH PHÂN
DIỆN TÍCH HÌNH PHẲNG GIỚI HẠN BỞI CÁC ĐỒ THỊ
Câu 165: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Diện tích hình phẳng giới hạn
bởi hai đường thẳng x 0, x , đồ thị hàm số y cos x và trục Ox là
Ⓐ S cos x d . x Ⓑ S cos d x . x Ⓒ 2 S cos d x . x
Ⓓ S cos x d . x 0 0 0 0 Lời giải
Diện tích hình phẳng giới hạn bởi hai đường thẳng x 0, x , đồ thị hàm số
y cos x và trục Ox là S cos x d . x 0
Câu 166: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Hình phẳng giới hạn bởi
đồ thị hàm số y f x , trục hoành và hai đường thẳng x a, x b trong hình dưới
đây (phần gạch sọc có diện tích S bằng c b c b Ⓐ
f x dx f x dx . Ⓑ
f x dx f x dx . a c a c c b c b
Ⓒ f xdx f xdx .
Ⓓ f xdx f xdx . a c a c Lời giải Từ hình ta thấy : c b c b
S f x dx f x dx f x dx f x dx . a c a c
Câu 167: (CHUYÊN LÊ QUÝ ĐÔN VŨNG TÀU NĂM 2020-2021) Tìm công thức tính diện
tích hình phẳng giới hạn bởi các đường 4 y x , 2 y x . 1 1 1 1 Ⓐ 4 2
x x dx . Ⓑ 2 4
x x dx . Ⓒ 2 4
x x dx . Ⓓ 4 2
x x dx . 0 0 1 1 Lời giải
Hoành độ giao điểm của hai đồ thị hàm số 4 y x , 2
y x là nghiệm của phương x 1 trình: 4 2 4 2 2
x x x x 0 x . 2 x 1 0 x 0 . x 1
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 98 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ta có 4 2 2
x x x 2
. x 1 0 , x 1 ;1 . 1 1
Suy ra diện tích hình phẳng cần tính là: 4 2 x x dx 2 4
x x dx . 1 1
Câu 168: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 02) Gọi S là diện tích
miền hình phẳng được gạch chéo trong hình vẽ dưới đây, với y f x là hàm số liên tục trên
Công thức tính S là 2 2
Ⓐ S f x dx . Ⓑ S
f x dx . 1 1 1 2 2
Ⓒ S f x dx f x dx . Ⓓ
f x dx . 1 1 1 Lời giải Chọn C
Câu 169: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số f x liên tục trên
và có đồ thị C là đường cong như hình bên, Diện tích hình phẳng giới hạn bởi
đồ thị C, trục hoành và hai đường thẳng x 0 , x 2 là 1 2 1 2 Ⓐ
f xdx
f xdx . Ⓑ
f xdx
f xdx . 0 1 0 1 2 2 Ⓒ
f xdx . Ⓓ
f xdx . 0 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 99 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải
Diện tích hình phẳng giới hạn bởi đồ thị C, trục hoành và hai đường thẳng x 0 , x 2 là 2 S f x 1 dx f x 2 dx f x 1 dx f x 2 dx
f xdx . 0 0 1 0 1
Câu 170: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho một viên gạch men có
dạng hình vuông OABC như hình vẽ. Sau khi tọa độ hóa, ta có O 0;0 , A0 ;1 , B 1 ;1
, C 1;0 và hai đường cong lần lượt là đồ thị hàm số 3 y x và 3
y x . Tính diện tích
phần tô đậm trên viên gạch men. Ⓐ 5 . Ⓑ 1 . Ⓒ 1 . Ⓓ 4 . 4 3 2 5 Lời giải
Phần tô đậm là hình phẳng giới hạn bời các đường 3 y x , 3
y x , x 0 , x 1 . 1 1
Suy ra diện tích phần hình phẳng là S 3 3
x x dx . 2 0
Câu 171: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho hàm số y f x có đạo
hàm liên tục trên và có đồ thị như hình vẽ bên. 2 4
Giá trị của f x 2dx f x 2 dx bằng 0 0 Ⓐ 4 . Ⓑ 6 . Ⓒ 4 . Ⓓ 2 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 100 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải 2
+) Xét I f x 2 dx
. Đặt t x 2 dt dx . 0
Đổi cận: x 0 t 2 và x 2 t 4 . 4 4 I f ( t)dt f ( x)dx . 2 2 4
+) Xét J f x 2 dx
. Đặt t x 2 dt dx . 0
Đổi cận: x 0 t 2
và x 4 t 2 . 2 2 J f ( t)dt f ( x)dx . 2 2 Suy ra: 4 2 4 4 I J
f x dx f x dx
f x dx f x
f 4 f 2 4 2 6 . 2 2 2 2
Câu 172: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Diện tích hình phẳng giới hạn
bởi đường thẳng y x 3 và parabol 2
y 2x x 1 bằng: 13 9 13 Ⓐ . Ⓑ . Ⓒ 9 . Ⓓ . 6 2 3 Lời giải Chọn C x 1 Xét phương trình: 2 2
x 3 2x x 1 2x 2x 4 0 . x 1 2 2
Diện tích hình phẳng cần tìm: 2 S
2x 2x 4 dx 2 2
x 2x 4 dx 9 . 1 1
Câu 173: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Cho hàm số 4 2 y
f x ax bx c có đồ thị như hình vẽ.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 101 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Diện tích S của miền được tô xiên như hình được tính theo công thức nào? 1 1 2 1 1 2
Ⓐ S f x dx f xdx f x dx . Ⓑ S
f x dx
f x dx f x dx . 2 1 1 2 1 1 1 1 2 1 1 2
Ⓒ S f x dx f xdx f xdx . Ⓓ S
f x dx
f x dx f x dx . 2 1 1 2 1 1 Lời giải Chọn A
Diện tích S của miền được tô xiên như hình là: 2 1 1 2 1 1 2 S
f x dx
f x dx
f x dx
f x dx f x dx
f x dx f xdx . 2 2 1 1 2 1 1
Câu 174: (SGD&ĐT LAI CHÂU NĂM 2020-2021) Tìm công thức tính diện tích hình phẳng
giới hạn bởi các đường 4 2
y x , y x 1 1 1 1 Ⓐ 4 2
x x dx . Ⓑ 2 4
x x dx . Ⓒ 2 4
x x dx . Ⓓ 4 2
x x dx . 0 0 1 1 Lời giải Chọn C x 0
Xét phương trình hoành độ giao điểm 4 2
x x x 1 1 1 1
Do đó diện tích hình phẳng là 4 2 2 2 S
x x dx x x 1 dx 2 4
x x dx . 1 1 1
Câu 175: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Diện tích hình
phẳng được tô đậm trong hình bên bằng 2 2 Ⓐ 2
2 x 2 x 4 dx . Ⓑ 2
2 x 2 x 4 dx . 1 1 2 2 Ⓒ 2
2 x 2 x 4 dx . Ⓓ 2
2 x 2 x 4 dx . 1 1
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 102 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn D
Trên 1; 2 ta có g x f x nên diện tích hình phẳng là: 2 2 g
x f x dx 2
2 x 2 x 4 dx . 1 1
Câu 176: (CHUYÊN HẠ LONG NĂM 2020-2021 LẦN 02) Diện tích hình phẳng giới hạn bởi
hai đường y x 2
1 x 5x 6 và hai trục tọa độ bằng Ⓐ . Ⓑ 11 . Ⓒ 11 . Ⓓ 1 . 2 4 4 2 Lời giải Chọn B
y x 2
1 x 5x 6
Ta có diện tích hình phẳng giới hạn bởi y 0 x 0 x 1
Xét phương trình hoành độ giao điểm: 2
(x 1)(x 5x 6) 0 x 2 x 3
Diện tích hình phẳng là: 3 S x 1 2
x 5x 6dx 0 1 2 3 x 1 2
x 5x 6dx x 1 2
x 5x 6dx x 1 2
x 5x 6dx 0 1 2 1 2 3 x 1 2
x 5x 6dx x 1 2
x 5x 6dx x 1 2
x 5x 6dx 0 1 2 9 1 1 11 4 4 4 4
Câu 177: (CHUYÊN THÁI BÌNH NĂM 2020-2021 LẦN 04) Cho hai hàm số f x 3 2
ax bx cx 2 , g x 2
dx ex 2 , a,b, c, d, e . Biết đồ thị hàm số
y f x và y g x cắt nhau tại ba điểm phân biệt có hoành độ lần lượt là 2 ; 1 ;1
. Tính diện tích hình phẳng giới hạn bởi hai đồ thị. Ⓐ 37 . Ⓑ 13 . Ⓒ 9 . Ⓓ 37 . 6 2 2 12
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 103 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải
Phương trình hoành độ giao điểm của đồ thị hàm số y f x và y g x là:
f x g x f x g x 0 3
ax b d 2
x c e x 4 0 * Ta có 2 ; 1
;1 là ba nghiệm của phương trình * nên ta có hệ phương trình: 8
a 4b d 2c e 4 a 2
a b d c e 4 b d 4
a b d c e 4 c e 2
Do đó f x g x 3 2
2x 4x 2x 4 0
Vậy diện tích hình phẳng giới hạn bởi hai đồ thị trên là: 1 S
f x g x dx 2 1 3 2
2x 4x 2x 4 dx 2 1 1 3 2
2x 4x 2x 4dx 3 2
2x 4x 2x 4dx 2 1 5 16 37 . 6 3 6
Câu 178: (CHUYÊN NGUYỄN BÌNH KHIÊM QUẢNG NAM NĂM 2020-2021) Cho hàm số 1
y f x 3
x ax có đồ thị như hình bên. Gọi S , S 3 1
2 lần lượt là diện tích của hai
hình phẳng được gạch chéo trong hình vẽ bên. S 7 Khi 1
thì a thuộc khoảng nào dưới đây? S 40 2 Ⓐ 3 5 ; . Ⓑ 1 1 ; . Ⓒ 1 0; . Ⓓ 1 3 ; . 4 4 3 2 3 2 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 104 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải 1 1 a 0 a f 1 0 3 3 1
Dựa vào đồ thị suy ra: a . f 2 0 8 4 3 2a 0 a 3 3 0 1 0 0 1 1 4 2 x ax 0 1 a Ta có: 3 S
x axdx 3
x ax dx 3
x ax dx . 1 3 3 3 12 2 1 12 2 1 1 1 2 1 2 1 2 1 4 2 x ax 2 4 3 S
x axdx 3
x ax dx 3
x ax dx 2a . 2 3 3 3 12 2 0 3 0 0 0 1 a S 7 7 1 3 5 12 2
a 1. Vậy a ; . S 40 4 40 4 4 2 2a 3
Câu 179: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho parabol P có phương trình 2
y x và đường thẳng d đi qua điểm A1;3 . Giả sử khi đường thẳng d có hệ
số góc k thì diện tích hình phẳng giới hạn bởi parabol P và đường thẳng d nhỏ
nhất. Giá trị thực của k thuộc khoảng nào sau đây? Ⓐ 0 ;1 . Ⓑ ; 3 . Ⓒ 3 ;0 . Ⓓ 3; . Lời giải
Đường thẳng d đi qua điểm A1;3 , có hệ số góc k có phương trình dạng
y kx k 3 .
Phương trình hoành độ giao điểm của d và P : 2
x kx k 3 2
x kx k 3 0 * . Do 2
k 4k 12 0, k nên d luôn cắt parabol P tại hai điểm phân biệt.
Gọi x , x là hai nghiệm phân biệt của phương trình * , x x . 1 2 1 2
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 105 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
x x k 1 2
Ta có: x x k 3 . 1 2 2 x x k 4k 12 2 1
Gọi S diện tích hình phẳng giới hạn bởi parabol P và đường thẳng d . Parabol P quay bề lõm lên trên suy ra x x 2 2 2 S
x kx k dx kx k 2 3 3 x dx 1 x 1 x 2 x 1 1 1 1 1 S x
kx 3 k x
x x x x 2 3 2 x x k x x 3 k 2 1 1 2 1 2 1 2 3 2 3 3 2 1 x 1 1 1 2 2
k 4k 12. k k 3 2 k 3 k 3 3 2 3 1 k k 3 3 1 1 8 2 . 4 12 . k 22 2 8 . 8 , k 6 6 6 3 8 2 Do đó min S
, đạt được khi k 2 . 3
Câu 180: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Trong mặt phẳng
Oxy cho (H ) là hình phẳng giới hạn bởi parabol 2
y 4 x và trục hoành. Đường
thẳng x k ( 2
k 2 ) chia (H ) thành hai phần (H ) , (H ) như hình vẽ 1 2 20
Biết rằng diện tích hình (H ) gấp
lần diện tích của hình (H ) , hỏi giá trị k thuộc 1 7 2 khoảng nào sau đây? Ⓐ ( 2 ; 1 ) . Ⓑ (0;1) . Ⓒ ( 1 ;0) . Ⓓ (1;2) . Lời giải
Gọi S , S lần lượt là diện tích hình (H ) , (H ) . 1 2 1 2 Khi đó
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 106 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 k 3 k 16 2 3 k 16 2 S
(4 x )dx 4k 2
S (4 x )dx 4k 1 và . 3 3 2 3 3 2 k Theo giả thiết, có 3 3 20 k 16 20 k 16 3 S S 4k 4k
27k 324k 208 0 . 1 2 7 3 3 7 3 3 2 1 105
Giải phương trình trên, ta có k ; k . 3 3 2
Đối chiếu với điều kiện, suy ra k . 3
Câu 181: (CHUYÊN NGUYỄN QUANG DIỆU ĐỒNG THÁP NĂM 2020-2021) Cho hàm số 2
y mx x 0 m 4 có đồ thị C . Gọi S S là diện tích của hình phẳng giới 1 2
hạn bởi C , trục hoành, trục tung và đường thẳng x 4 . Giá trị m để S S là 1 2 10 8 Ⓐ m . Ⓑ m . Ⓒ m 3 . Ⓓ m 2 . 3 3 Lời giải Phương trình hoành độ giao điểm của
C và trục Ox là: x 0 2
mx x 0 x m 0 m 4 m m m 2 3 3 mx x m Ta có: 2 S
mx x dx 2
mx x dx . 1 2 3 6 0 0 0 4 4 4 3 2 3 x mx m 64 Lại có: 2 S
mx x dx 2
x mx dx 8m . 2 3 2 6 3 m m m 3 3 m m 64 8
Theo giả thiết ta có: S S 8m m . 1 2 6 6 3 3
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 107 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 182: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Cho hai hàm số f x 4 3 2
ax bx cx dx 1 và g x ex 2 ( a,b, c, d , e là các số thực cho trước).
Biết rằng đồ thị của hai hàm số y f x và y g x tiếp xúc nhau tại hai điểm có
hoành độ lần lượt là 1; 2 .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 81 81 81 81 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 20 4 10 40 Lời giải
y f x, y g x
Hình phẳng H : . x 1 , x 2 2
Dựa vào hình vẽ trên diện tích hình phẳng H là: S f x g xdx . 1
Ta có: f x g x 4 3 2
ax bx cx d e x 1
Do đồ thị của hai hàm số y f x và y g x tiếp xúc nhau tại hai điểm có hoành
độ lần lượt là 1; 2 nên x 1, x 2 là hai nghiệm bội chẵn của phương trình
f x g x 0. 2 2
Suy ra f x g x 4 3 2
ax bx cx d e x 1 a x 1 x 2 . 1
Đồng nhất hệ số tự do ta được: 1 4a a . 4 1 2 2 2 1 2 2 81
Do đó f x g x x
1 x 2 hay S x
1 x 2 dx . 4 4 40 1
Câu 183: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Cho hàm số y f (x). Đồ thị hàm
số y f (x) như hình bên. Đặt 3
g(x) x 3 f (x). Mệnh đề nào dưới đây đúng?
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 108 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Ⓐ g(2) g( 1 ) g(0).
Ⓑ g(0) g( 1 ) g(2). Ⓒ g( 1
) g(0) g(2).
Ⓓ g(2) g(0) g( 1 ) . Lời giải x 1 Ta có: 2
g x x f x 2 ( ) 3 3 ( ) 3 x f ( x) . Suy ra: 2 g (
x) 0 x f (
x) x 0 x 2 BBT:
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 109 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Từ BBT suy ra max g(x) g(0). 1;2 Theo hình vẽ thì 0 2 0 2
S S 2 x f (
x)dx 2 x f (
x)dx 3 2 x f (
x)dx 3 2 x f ( x) dx 1 2 1 0 1 0 0 2 g (
x)dx g ( x)dx 1 0
g(0) g (1) g (2) g(0)
g(1) g (2).
Tóm lại: g(0) g(1) g(2). Ta chọn đáp án Ⓐ
Câu 184: (CHUYÊN QUỐC HỌC HUẾ NĂM 2020-2021) Cho hình phẳng H được giới hạn bởi các đường ex y
; y 0 ; x 0 và x ln 4 . Đường thẳng x k k ; 0 k ln 4
chia hình phẳng H thành hai phần có diện tích là S ; S (xem hình vẽ). 1 2
Tìm k để S 2S . 2 1 8 2 Ⓐ k ln 3. Ⓑ k ln . Ⓒ k ln 4 . Ⓓ k ln 2 . 3 3 Lời giải Chọn D Ta có ln 4 k ln 4 k S 2S
exdx 2 exdx ex 2ex 4 ek 2ek
2 ek 2 k ln 2 . 2 1 k 0 k 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 110 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 185: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2020-2021) Cho hàm số bậc ba
y f x có đồ thị là đường cong bên dưới. Gọi x ; x lần lượt là hai điểm cực trị thỏa 1 2
mãn x x 2 và f x 3 f x 0 . Đường thẳng song song với trục O x và đi qua 1 2 2 1
điểm cực tiểu cắt đồ thị hàm số tại điểm thứ hai có hoành độ x và x x 1. Tính tỉ 0 1 0 S
số 1 ( S và S lần lượt là diện tích hai hình phẳng được gạch ở hình bên dưới). S 1 2 2 Ⓐ 9 . Ⓑ 5 . Ⓒ 3 . Ⓓ 3 . 8 8 8 5 Lời giải
Do f x là hàm số bậc ba nên f x 3 2
ax bx cx d a f x 2 , 0
3ax 2bx c
Mặt khác do hàm số y f x có hai điểm cực trị x ; x thỏa mãn x x 2 nên 1 2 2 1
f x 3a x x x x 3a x x x x 2 3a x x 2 6a x x . 1 2 1 1 1 1 3 2
Mặt khác f x f xdx
f x a x x 3a x x C , khi đó và 1 1
f x C 1
f x f x 2 a x 2 x 3 3a x 2 x 2 C 4 a C . 2 1 1 1 1 1
Mà f x 3 f x 0 C 3 4a C 0 C 6a f x 2a . 1 2 2 f x
a x x 3 3 x x 2 6 . 1 1 2 x 1 x 2 3 2 27 Do S f x f x d x a x x 3 x x 4 d x a 1 2 1 1 . 4 x x 1 0 1
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 111 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 x 1 x 2 S f x dx 2 d a x 6a 2 2 . x x 1 0 1 S 9 Vậy 1 . S 8 2
Câu 186: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021 LẦN 02) Cho parabol P 2
: y x 6 cắt trục hoành tại hai điểm phân biệt ,
A B và đường thẳng d : y a 1
0 a 6 . Xét parabol P đi qua ,
A B và có đỉnh thuộc đường thẳng y a . Gọi S 2 1
là diện tích hình phẳng giới hạn bởi P và d ; S là diện tích hình phẳng giới hạn 1 2
bởi P và trục hoành (tham khảo hình vẽ). 2
Biết S S , tính 3 2
T a 12a 108a . 1 2 Ⓐ T 218 . Ⓑ T 219 . Ⓒ T 216 . Ⓓ T 217 . Lời giải
Xét phương trình hoành độ giao điểm: 2 x 6 a 2
x 6 a
x 6 a . 6a 3 x 6 a 4
Khi đó S 2 2
x 6 a 2 6x ax 6 a 6 a . 1 3 0 3 0 2
y x 6
x 6 y 0 Tọa độ giao điểm ,
A B là nghiệm của hệ . y 0
x 6 y 0
Vậy A 6;0, B 6;0 .
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 112 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Gọi P 2
: y mx nx p . 2
Vì parabol P đi qua ,
A B và có đỉnh thuộc đường thẳng y a nên 2
6m 6n p 0 n 0 a
6m 6n p 0 p a P 2 : y x a . 2 6 p a a m 6 6 3 a ax 6 6a 4 6a Do đó 2 S 2
x a dx 2 ax 2 6a . 2 6 18 0 3 3 0 Theo đề bài 4 4 6a S S
6 a 6 a 6 a3 2 2 3 2
6a 216 108a 18a a 6a 1 2 3 3 3 2
a 12a 108a 216 .
Câu 187: Cho hàm số y f x có đạo hàm liên tục trên và có đồ thị như hình bên. Biết 1
rằng tích phân K .
x f x. f x dx
có giá trị thuộc khoảng nào sau đây? 0 Ⓐ 3; 2 . Ⓑ 3 2 ; . Ⓒ 2 ; 0 . Ⓓ 3 2 ; . 2 3 2 3 Lời giải Chọn D u
x du dx Đặt 1 .
dv f x. f x dx v f x 2 2 1 1 1 x 2 1 2 1 1 2 Khi đó K
f x
f x dx
f x dx . 2 2 2 2 0 0 0
Cách 1. Từ đồ thị ta thấy
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 113 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Đồ thị y f x nằm trên đường thẳng y 2 x trên 0; 1 . f x 2 2 2 x2 1 1 1 7 1
f x 2
Nên f x 2 x dx dx K dx . 2 2 6 2 2 3 0 0 0
Đồ thị y f x nằm dưới đường thẳng y 2 trên 0; 1 . f x 2 2 22 1 1 1 1
f x 3
Nên f x 2 dx dx 2 K dx . 2 2 2 2 2 0 0 0
Cách 2. [Khi có rất nhiều điểm thuộc đồ thị trên hình] Chọn 4 3 2
f x ax bx cx dx e . Dựa vào độ thị ta có hệ phương trình f 2 1 f 1 1 1 1 7 1
f 0 2 a
, b , c , d , e 2 . 6 6 6 6 f 1 1 f 3 1 1 2 1 1 1 1 7 1 4 3 2 3 2 K x x x
x 2 dx 0, 968
. Suy ra K ; . 2 2 6 4 6 6 2 3 0
Câu 188: Cho hàm số 4 2
y ax bx c có đồ thị C , biết rằng C đi qua điểm A1; 0 , tiếp
tuyến d tại A của C cắt C tại hai điểm có hoành độ lần lượt là 0 và 2 và diện
tích hình phẳng giới hạn bởi d , đồ thị C và hai đường thẳng x 0; x 2 có diện 28 tích bằng
(phần tô màu trong hình vẽ). 5
Diện tích hình phẳng giới hạn bởi C và hai đường thẳng x 1
; x 0 có diện tích bằng
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 114 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 2 6 Ⓐ 2 . Ⓑ 1 . Ⓒ . Ⓓ . 5 4 9 5 Lời giải Chọn D
Từ đồ thị ta có phương trình hoành độ giao điểm là:
a x 2 x 4 2 1
2 x 0 ax 3ax 2ax 0 , a 0
Diện tích hình phẳng giới hạn bởi d , đồ thị C và hai đường thẳng x 0; x 2 bằng 28 2 5 28 ax 2 28 nên: 4 2 3 2
ax 3ax 2ax dx ax ax a 1 8 5 5 0 5 0
Suy ra phương trình hoành độ giao điểm là: 4 2
x 3x 2x 0
Từ đồ thị ta thấy d đi qua điểm A1;0 và B 0; k nên phương trình đường thẳng d là:
y kx k . Suy ra hàm số C có dạng: 4 2
y x 3x 2 k x k 0 . Mà đồ thị hàm số
C là hàm trùng phương 4 2
y ax bx c nên 2 k 0 k 2 0 6
Vậy diện tích cần tìm là: 4 2
x 3x 2dx . 5 1
Câu 189: (THPT CHUYÊN BẾN TRE NĂM 2020-2021) Cho hàm số 4 2
y ax bx c có đồ thị
C , biết rằng C đi qua điểm A1;0 , tiếp tuyến d tại A của C cắt C tại hai
điểm có hoành độ lần lượt là 0 và 2 và diện tích hình phẳng giới hạn bởi d , đồ thị 28
C và hai đường thẳng x 0; x 2 có diện tích bằng (phần tô màu trong hình 5 vẽ).
Diện tích hình phẳng giới hạn bởi C , d và hai đường thẳng x 1; x 0 có diện tích bằng Ⓐ 2 . Ⓑ 1 . Ⓒ 2 . Ⓓ 1 . 5 4 9 5 Lời giải
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 115 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Gọi phương trình đường thẳng d có dạng y mx n .
Diện tích hình phẳng giới hạn bởi C, d và hai đường thẳng x 0, x 2 là 2 2 28 28 4 2
| a x bx c mx n | dx 4 2
a x bx c mx ndx * 5 5 0 0
Vì C và d tiếp xúc tại điểm x 1
và giao nhau tại các điểm có hoành độ 2
x 0; x 2 nên ta có 4 2
ax bx c mx n a x x x a 4 2 2 1
x 3x 2x . Khi đó: 2 5 28 x 2 28 28 28
* a 4 2
x 3x 2x 3 2 dx . a x x a a 1. 5 5 0 5 5 5 0
Vậy diện tích hình phẳng giới hạn bởi C, d và hai đường thẳng x 1, x 0 là 0 1 4 2
S | x 3x 2x | dx . 5 1
Lưu ý: Đề bài trên đã bổ sung thêm yếu tố giới hạn bởi đồ thị C với đường thẳng d vào
câu hỏi so với đề bài gốc vì nếu đề bài gốc là tính diện tích hình phẳng giới hạn bởi C và hai
đường thẳng x 1; x 0 là không hợp lí vì hình phẳng hở nên không tính được diện tích, 6
nếu chọn bổ sung giới hạn với trục Ox thì đáp án là không có trong 4 đáp án. 5
BÀI TOÁN THỰC TẾ SỬ DỤNG DIỆN TÍCH HÌNH PHẲNG
Câu 190: (CHUYÊN LONG AN NĂM 2020-2021 LẦN 03) Bồn hoa của một trường X có dạng
hình tròn bán kính bằng 8m . Người ta chia bồn hoa thành các phần như hình vẽ dưới
đây và có ý định trồng hoa như sau: Phần diện tích bên trong hình vuông ABCD để
trồng hoⒶ Phần diện tích kéo dài từ 4 cạnh của hình vuông đến đường tròn dùng
để trồng cỏ. Ở bốn góc còn lại, mỗi góc trồng một cây cọ. Biết AB 4m , giá trồng hoa
là 200.000 đ/m2, giá trồng cỏ là 100.000 đ/m2, mỗi cây cọ giá 150.000 đ. Hỏi số tiền để
thực hiện việc trang trí bồn hoa như miêu tả ở trên gần bằng giá trị nào nhất?
Ⓐ 14.465.000 đồng. Ⓑ 14.865.000 đồng. Ⓒ 13.265.000 đồng. Ⓓ 12.218.000 đồng.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 116 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn C
Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với tâm hình tròn, suy ra phương trình đường tròn là: 2 2
x y 64 .
Diện tích hình vuông ABCD là: S 2 4 4 16 m . ABCD
Số tiền để trồng hoa là: T 16 200.000 3.200.000 . 1 2
Diện tích trồng cỏ là: S 4 2
64 x 2dx 94,654 2 m . 2
Số tiền trồng cỏ là: T 94, 654100.000 9.465.000 . 2
Số tiền trồng 4 cây cọ là: T 150.000 4 600.000 . 3
Vậy tổng số tiền để thực hiện việc trang trí bồn hoa là:
T T T T 13.265.000 . 1 2 3
Câu 191: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Mặt sàn của một thang máy
có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một
hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ tọa độ Oxy với O là tâm hình
vuông sao cho A1
;1 như hình vẽ bên thì các đường cong OA có phương trình 2 y x 1 và 3
y ax bx . Tính giá trị ab biết rằng diện tích trang trí màu sẫm chiếm diện tích 3 mặt sàn.
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 117 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ 2 . Ⓑ 3 . Ⓒ 2 . Ⓓ 3 . Lời giải
Vì đường cong OA có phương trình 3
y ax bx đi qua điểm A1 ;1 nên
a b 1 b 1 a 3
y ax 1 a x
Diện tích mặt sàn hình vuông là: 2 S 2 2 4 m ABCD
Diện tích hình một cánh màu sẫm là: 1 1 2 3 S
x ax 1 a x dx 2 3
x ax ax x dx 0 0 1 3 4 2 2 x ax ax x 1 a a 1 a 1 3 4 2 2 3 4 2 2 4 6 0 1 a 1
Theo đề bài, ta có: 4S S 12S S 12 4 a 2 b 1 3 ABCD ABCD 4 6 Do đó: ab 2 .
Câu 192: (CHUYÊN LÊ QUÝ ĐÔN QUẢNG NINH NĂM 2020-2021) Cho hàm số bậc ba có
đồ thị như hình vẽ, biết f x đạt cực tiểu tại điểm x 1 và thỏa mãn f x 1 và
f x 1
lần lượt chia hết cho x 2 1 và x 2
1 . Gọi S , S lần lượt là diện tích hình 1 2
phẳng như hình bên dưới. Tính 2S S 1 2 3 1 1 Ⓐ 4 . Ⓑ . Ⓒ . Ⓓ . 4 2 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 118 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn B
f x 1 x 2 1
f x 1 x 1 f
x x 1 Theo giả thiết, ta có:
2
f x x f x x f x x 1 1 1 1 1
f x có dạng: f x a x x a 2 1 1 x 1 a 0 3 x
Và f x a x C 3
Theo hình vẽ, f 0 0 C 0 2a f x x 2 f 1 0 1 1 1 1 0 3 3 a
1 2 1 f f x x 1 1 0 2a 2 1 0 3 3 3 3 x x 3
Vậy f x x x 2 3 2 2
* Phương trình giao điểm của của C : y f x với trục hoành: x 0 3 x 3
x 0 x 3 2 2 x 3 3 1 1 x 3 5
Diện tích hình phẳng S f x dx x dx 1 0 0 2 2 8 3 3 3 x 3 1
Diện tích hình phẳng S f x dx x dx 2 1 1 2 2 2 5 1 3
Vậy: 2S S 2. 1 2 8 2 4
Câu 193: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021
LẦN 01) Một chiếc xe đua F đạt tới vận tốc lớn 1
nhất là 360 km / h . Đồ thị bên biểu thị vận tốc v
của xe trong 5 giây đầu tiên kể từ lúc xuất phát.
Đồ thị trong 2 giây đầu tiên là một phần của
parabol đỉnh tại gốc tọa độ O , giây tiếp theo là
đoạn thẳng và sau đúng 3 giây thì xe đạt vận
tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành
biểu thị 1 giây, mỗi đơn vị trục tung biểu thị
10 m / s và trong 5 giây đầu xe chuyển động
theo đường thẳng. Hỏi trong 5 giây đó xe đã đi
được quãng đường là bao nhiêu? Ⓐ 340 (mét). Ⓑ 420 (mét). Ⓒ 400 (mét). Ⓓ 320 (mét).
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 119 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải Chọn D
Giả sử A2;6 ; B3;10 3
Theo gt thì phương trình của parabol là 2 y
x ; phương trình đường thẳng AB là 2 y 4x 2
Vậy trong 5 giây đó xe đã đi được quãng đường là: 2 3 3 2 S 10
x dx 4x 2dx 2.10 320 (mét). 2 0 2
THỂ TÍCH GIỚI HẠN BỞI CÁC ĐỒ THỊ (TRÒN XOAY)
Câu 194: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Thể tích vật thể tròn xoay do
hình phẳng giới hạn bởi đồ thị y f x , trục Ox và các đường thẳng x a , x b ,
a b quay quanh trục Ox được tính theo công thức b b b b Ⓐ 2 V
f x dx . Ⓑ 2
V f x dx . Ⓒ V
f x dx .
Ⓓ V f x dx a a a a . Lời giải
Thể tích vật thể tròn xoay do hình phẳng giới hạn bởi đồ thị y f x , trục Ox và
các đường thẳng x a , x b , a b quay quanh trục Ox được tính theo công b thức 2
V f x dx . a
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 120 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021
Câu 195: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2020-2021) Gọi (H ) là hình
phẳng giới hạn bởi các đồ thị y x x, y 0 trong mặt phẳng Oxy . Quay hình (H )
quanh trục hoành ta được một khối tròn xoay có thể tích bằng 1 1 1 1 2 2 Ⓐ
x x dx . Ⓑ
x x dx . Ⓒ x
1 x dx . Ⓓ x
1 x dx . 0 0 0 0 Lời giải x 0 x 0
Xét phương trình x x 0 x x . 2 x x x 1 Ta có thể tích khối tròn xoay là 1 1 1 V
x x2 dx x 1 x 2 dx x
1 x 2 dx . 0 0 0
Câu 196: (CHUYÊN ĐẠI HỌC VINH NĂM 2020-2021 LẦN 02) Gọi D là hình phẳng giới
hạn bởi các đường y 1 và 2
y 2 x . Thể tích khối tròn xoay giới hạn được tạo thành
khi quay D xung quanh trục Ox được tính theo công thức 2 1 2 Ⓐ 2 V 2
2 x dx . Ⓑ V 2
2 x dx . 2 1 1 2 2 2 Ⓒ V 2
2 x dx 2 . Ⓓ V 2
2 x dx 4 . 1 2 Lời giải
Ta có phương trình hoành độ giao điểm 2
1 2 x x 1 .
Thể tích khối tròn xoay giới hạn được tạo thành khi quay D xung quanh trục Ox
được tính theo công thức 1 1 2 2 V 2 2 x 2 1 dx 2 2 x 1dx 1 1 1 1 1 1 2 1 2
2 x 2 2 dx dx 2
2 x dx x 2
2 x dx 2 . 1 1 1 1 1
Câu 197: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Cho H là hình phẳng giới hạn bởi parabol 2
y x và đường tròn 2 2
x y 2 . Thể tích V của vật thể tròn xoay
tạo thành khi quay H quanh trục hoành là
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 121 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Ⓐ 44 5 44 V . Ⓑ V . Ⓒ V . Ⓓ V . 15 3 15 5 Lời giải 2
y 2 x Ta có: 2 2
x y 2 . 2
y 2 x
Hình H là hình phẳng giới hạn bởi đồ thị của hàm số 2 y 2 x và 2 y x . x 1
Phương trình hoành độ giao điểm: 2 2 4 2
2 x x x x 2 0 . x 1 1 1 1 3 5 2 2 x x 1 44
Ta có V 2
2 x dx 2
x dx 2 4
2 x x dx 2x . 3 5 1 15 1 1 1
Câu 198: (THPT CHUYÊN KHTN NĂM 2020-2021 LẦN 01) Tính thể tích của khối tròn xoay
khi cho hình phẳng giới hạn bởi đường thẳng y 3x 2 và đồ thị hàm số 2 y x quay quanh trục Ox . 4 1 4 Ⓐ . Ⓑ . Ⓒ . Ⓓ . 5 6 5 6 Lời giải Chọn A
Hoành độ giao điểm là nghiệm của phương trình: x 1 2 x 3x 2 2
x 3x 2 0 x 2 Mà 2
x 3x 2 với x
1; 2 Thể tích của khối tròn xoay khi cho hình phẳng giới
hạn bởi đường thẳng y 3x 2 và đồ thị hàm số 2
y x quay quanh trục Ox là: 2 2 2 5 x 4 V 3x 22 4 x dx 4 2
x 9x 12x 4 3 2 dx
3x 6x 4x 5 5 1 1 1 4
Vậy thể tích của khối tròn xoay cần tính là . 5
Câu 199: (CHUYÊN LÊ HỒNG PHONG TPHCM NĂM 2020-2021) Cho hình phẳng H giới
hạn bởi đồ thị hàm số 2
y 2x x và trục hoành. Tính thể tích V vật thể tròn xoay
sinh ra khi cho H quanh quay trục Ox . Ⓐ 4 16 4 16 V . Ⓑ V . Ⓒ V . Ⓓ V . 3 15 3 15
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 122 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải
Hoành độ giao điểm của đồ thị hàm số 2
y 2x x và trục hoành là nghiệm của phương trình: x 0 2
2x x 0 . x 2 2 V .
2x x 2 16 2 dx . 15 0
Câu 200: (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2020-2021) Gọi H là hình phẳng giới hạn bởi 2
y x x và trục hoành. Thể tích của khối tròn xoay tạo thành
khi quay hình H quanh trục hoành bằng Ⓐ 1 1 . Ⓑ . Ⓒ . Ⓓ . 30 6 30 6 Lời giải Chọn A
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y x x và trục hoành là x 0 2
x x 0 . x 1 1 2
Thể tích của khối tròn xoay cần tìm là V 2
x x dx . 30 0
Câu 201: (CHUYÊN LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2020-2021 LẦN 02) Thể tích của khối
tròn xoay do hình phẳng giới hạn bởi y ln x , trục Ox và đường thẳng x 2 quay
xung quanh trục Ox là Ⓐ 2ln 2 1. Ⓑ 2 ln2 . Ⓒ 2 ln2 . Ⓓ 2ln 2 1. Lời giải
Ta có: ln x 0 x 1 Thể tích mặt tròn xoay: 2 2 2
V ln x 2 2
dx ln x dx .
x ln x dx 2 2 .
x ln x x 2 ln 2 . 1 1 1 1 1 1
ỨNG DỤNG TÍCH PHÂN VÀO CÁC BÀI TOÁN CHUYỂN ĐỘNG
Câu 202: (CHUYÊN NGUYỄN DU ĐĂKLẮC NĂM 2020-2021) Một vật chuyển động có
phương trình vận tốc: v t 3
t 3t 1 . Quãng đường vật đi được từ thời điểm t 0 đến khi t 3 là Ⓐ 39 m . Ⓑ 19m . Ⓒ 20m . Ⓓ 15 . 4 4
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 123 | HNT.E
TÀI LIỆU LUYỆN THI LỚP 12
NGUYÊN HÀM TÍCH PHÂN TRONG ĐỀ THI CHUYÊN 2020-2021 Lời giải
Quãng đường vật đi được từ thời điểm t 0 đến khi t 3 là: 3 4 2 t t 3 39 S 3 t 3t 1 dt 3 t m . 4 2 0 4 0
Câu 203: (CHUYÊN LAM SƠN THANH HÓA NĂM 2020-2021 LẦN 03) Một chiếc máy bay
vào vị trí cất cánh chuyển động trên đường băng với vận tốc v t 2
t 2t m/s với t
là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết
máy bay đạt vận tốc 120m/s thì nó rời đường băng. Quãng đường máy bay đã di
chuyển trên đường băng gần nhất với giá trị nào dưới đây? Ⓐ 1200m. Ⓑ 1100m. Ⓒ 430m. Ⓓ 330m. Lời giải Chọn C
Máy bay đạt vận tốc 120m/s tại thời điểm thỏa mãn pt: 2
t 2t 120 0 t 10. 10 1300
Khi đó quãng đường máy bay di chuyển là s 2t 2tdt m 430m. 3 0
LƯƠNG ANH NHẬT – 0968373054 – CHĂM CHỈ THÀNH TÀI MIỆT MÀI TẤT GIỎI 124 | HNT.E
GV. LƯƠNG ANH NHẬT HNT EDUCATION
VỮNG KIẾN THỨC – NHẠY TƯ DUY
Nguyên hàm – Tích phân – Ứng dụng
Giảng dạy Toán lớp 6 – 12 + Luyện thi đại học LƯU HÀNH NỘI BỘ
Điện thoại: 0968 373 054 HNT.E - 20082021




