321 bài toán trắc nghiệm nguyên hàm, tích phân – Nguyễn Tiến Chinh Toán 12

321 bài toán trắc nghiệm nguyên hàm, tích phân – Nguyễn Tiến Chinh Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

36 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
1
Chuyên đề 5 – Nguyên Hàm – Tích phân
Câu 1: Biết F(x) là một nguyên hàm của hàm số:
f(x) sin x x .
2 3
2
Giá trị của
//
F
2
là?
A.
2
3
1
4
B.
2
3
1
4
C.
2
3
4
D.
2
3
4
Câu 2: Nguyên hàm của hàm số:
f(x) x x
2
1 là?
A.
F(x) x C
3
2
1
1
3
B.
F(x) x C
3
2
1
1
3
C.
F(x) x C
2
1
D.
F(x) x C
3
2
1
1
2
Câu 3: Nguyên hàm của hàm số:
x
f(x) xe
2
là?
A.
x
F(x) ( x )e C
2
2 1
B.
x
F(x) ( x )e C
2
1
2 1
4
C.
x
F(x) (x )e C
2
1
D.
x
F(x) (x )e C
2
1
Câu 4: Giá trị của
x x
dx
x
2
2
1
3
là?
A.
3
2
B.
3
2
C. 3 D. –2
Câu 5: Diện tích hình phẳng giới hạn bởi (C): y = x
3
–3x
2
+1 và (D): y = 1 là?
A. 3 B.
13
2
C. 9 D.
27
4
Câu 6: Thể tích của khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi hai đường: y = x
2
–x, y = 0
quanh trục Ox là?
A.
1
6
B.
1
6
C.
1
30
D.
30
Câu 7: Một chiếc xe ô tô sẽ chạy trên đường với vận tốc tăng dần đều với vận tốc v = 10t (m/s) t là khoảng
thời gian tính bằng giây, kể từ lúc bắt đầu chạy. Hỏi quảng đường xe phải đi là bao nhiêu từ lúc xe bắt
đầu chạy đến khi đạt vận tốc 20 (m/s)?
A. 10m B. 20m C. 30m D. 40m
Câu 8.
Giá trị của tích phân
x dx
I
x
7
3
3
2
0 1
được viết dưới dạng
a
b
. Khi đó giá trị của a-7b bằng
A.
2
B.
0
C.
1
D.
-1
Câu 9
.
Cho hình phẳng giới hạn bởi các đường
y x,y x
. Quay xung quanh trục ox. Thể tích khối
tròn xoay tạo thành bằng
A.
6
B.
3
C.
D.
4
Câu 10.
Công thức nào sau đây đúng với k là hằng số
A.
b a
a b
k.f (x)dx f(x) kdx
B.
b b
a a
k.f(x)dx k f(x)dx
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
2
C.
b a
a b
k.f(x)dx k f (x)dx
D.
b b
a a
k.f(x)dx k f (x)dx
Câu 11.
Diện tích hình phẳng giới hạn bởi các đường cong y=x+sinx và y=x
x
0 2
A.
5
B.
3
C.
4
D.
4
Câu 12.
Cho
M x . x dx
2 3
4
chọn câu đúng
A.
M x C
3
3
2
4
9
B.
M x C
3
3
2 4
C.
M x C
3
2 4
D.
M x C
3
3
1
4
9
Câu 13.
Cho
dx
A
x(x )
1
1
2
1
. Kết quả nào sau đây đúng
A.
0<A<1
B.
1<A<2
C.
A<0
D.
2<A<3
Câu 14.
Biết
lnm
x
x
e dx
ln
e
0
2
2
Khi đó giá trị m là
A.
1
B.
2
C.
3
D.
4
Câu 15.
Gọi F(x) là nguyên hàm của hàm số
x
f(x)
x
2
8
thỏa mãn F(2)=0. Khi đó phương trình F(x)=x
có nghiệm là
A.
1 3
B.
1
C.
-1
D.
0
Câu 16: Tìm nguyên hàm của hàm số f(x) =
x
x
4
2
2 3
A.
x x
dx C
x
x
4 3
2
2 3 2 3
3
B.
x x
dx C
x
x
4 3
2
2 3 2 3
3
C.
x x
dx C
x x
4
2 3
2 3 2 3
3
D.
x x
dx C
x x
4
2 3
2 3 2 3
3
Câu 17
: Tính tích phân
e
lnx
I dx
x(lnx )
2
1
2
A.
I ln
1 3
3 2
B.
I ln
1 3
3 2
C.
I ln
1 3
3 2
D.
I ln
1 3
3 2
Câu 18: Tính tích phân
sinx
I (e cosx)cosxdx.
2
0
A.I e
1
4
B. I e
1
4
C.I e
1
4
D.I e
1
4
Câu 19:Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f(x)
liên tục trên đoạn
a;b
,trục hoành, hai
đường thẳng
x a,x b
có công thức là:
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
3
A.
b
a
S f(x) dx
B.
b
a
S f(x)dx
C.
b
a
S [ f(x)] dx
2
D.
a
b
S f(x) dx
Câu 20: Diện tích hình phẳng giới hạn bởi đồ hai thị hàm số y x x ,y x
2
2 2
và hai đường thẳng
x ,x
1 3
.
A.
20
3
B.
34
3
C.
20
3
D.
34
3
Câu 21: Cho hình (H) giới hạn bởi : y sinxcosx,y ,x ,x
0 0
2
. Thể tích khối tròn xoay khi cho hình
(H) quay quanh trục Ox .
A.
2
8
B.
2
2
C.
2
16
D.
2
4
Câu 22: Một vật chuyển động với gia tốc đầu bằng 0, vận tốc biến đổi theo quy luật
a , (m/ s )
2
0 3 .Xác
định quãng đường vật đó đi được trong 40 phút đầu tiên.
A. 1200m B. 240m C. 3600m D.3200m
Câu 23: Tích phân
sin x cos x
I dx
sinx cosx
2
0
1 2 2
bằng:
A.
I
2
B. I
1
C. I
2
D. I
1
Câu 24: Tích phân
I x.sinxdx.
2
0
bằng:
A. I
3
B. I
2
C.
I
1
D. I
1
Câu 25: Họ nguyên hàm của hàm số:
x
y xe dx
là:
A.
x
xe C
B.
x x
xe e C
C.
x x
xe e C
D.
x
xe C
Câu 26: Họ nguyên hàm của hàm số: y = cos
2
x.sinx là:
A.
cos x C
3
1
3
B.
cos x C
3
C.
sin x C
3
1
3
D.
cos x C
3
1
3
Câu 27: Họ nguyên hàm của hàm số:
y lnxdx
là:
A.
xlnx x C
B.
x lnx C
C.
xlnx x C
D.
lnx x C
Câu 28: Diện tích hình phẳng được giới hạn bởi hai đường y x
2
2
và
y x
là:
A. S =
9
3
B. S=
9
4
C. S=
2
9
D. S =
9
3
Câu 29: Thể tích khối tròn xoay được tạo bởi phép quay quanh trục 0x hình phẳng giới hạn bởi hai đường
y x
2
và
y x
2
là:
A. V
3
10
B. V
5
C. V
10
D. V
7
10
Câu 30: Biết
dx
I
x
2 1 4
=
a. x b.ln x C
2 1 2 1 4
. Tính a + b
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
4
A. -2 B. -3 C. 1 D. 2
Câu 31: Biết
x
L e cosxdx
0
= a.e
+ b. Tính a + b
A. 0 B. 1 C. -2 D. 3
Câu 32: Biết
L x x dx a. b
1
2
0
1 2
. Tính a - b
A. 1 B. 1/3 C. 2 D. 3
Câu 33: Diện tích hình phẳng giới hạn bởi các đường y = x
2
và y = x + 2 là
A. 3/2 ; B. 9/2 ; C. 15/2 ; D. 21/2
Câu 34: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 2 – x
2
,
y
1
quanh trục
Ox là:
A. 56/15 ; B. 86/15 ; C. 16/15 ; D. 16/7
Câu 35: Diện tích hình phẳng giới hạn bởi các đường y = x – 1 +
x
1
lnx, y = x – 1, x = e là :
A.
1
2
; B.
1
3
; C.
1
8
; D.
2
3
Câu 36: Giá trị của
dx
I
x x
1
2
0
5 6
là:
A. I = 1 B.
I ln
3
4
C. I = ln2 D. I = ln(4/3)
Câu 37
: Cho hai hàm số
y f(x), y g(x)
liên tục trên đoạn
a;b
. Diện tích hình phẳng giới hạn bởi đồ
thị hai hàm số đó và các đường thẳng
x a, x b
được tính theo công thức:
A.
b
a
S g(x) f(x) dx
B.
b
a
S f(x) g(x) dx
C.
b
a
S f(x) g(x) dx
D.
b
a
S f(x) g(x)dx
Câu 38: Cho hàm số
f(x)
x
1
2 1
. Khi đó
F(x) f(x)dx
là
A. F(x) x
1
2 1
2
B.
F(x) x C
2 1
C.
F(x) x C
1
2 1
2
D. F(x) x
2 1
Câu 39: Một hòn đá rơi tự do từ đỉnh của một vách núi thẳng đứng và chạm vào mặt đất với vận tốc 98
m/s. Hỏi đỉnh núi cao bao nhiêu mét so với mặt đất? (lấy gia tốc rơi tự do bằng 9,8 m/s
2
)
A. 490 m B. 430 m C. 400 m D. 460 m
Câu 40: Giá trị tích phân
I (x )sinxdx
2
0
1
là
A.
I
2
B.
I
3
C.
I
1
D.
I
2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
5
Câu 41: Giá trị tích phân
e
I x lnxdx
2
1
là
A.
e
I
3
1 2
9
B.
e
I
3
2 1
9
C.
e
I
3
2 1
9
D.
e
I
3
2 1
9
Câu 42: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y x x
2
6
và đồ thị hàm số
y x
2
6
là
A. 10 B. 8 C. 7 D. 9
Câu 43: Kí hiệu (H) là hình phẳng giới hạn bởi hai đồ thị hàm số
y x
2
2 1 và
y ( x)
2 1
. Thể tích V
của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là
A.
V
3
B. V
5
3
C. V
4
3
D. V
2
3
Câu 44
: Tính tích phân
dx
I
x x
0
2
1
3 2
A.
ln
5
6
B.
ln
3
4
C.
ln
3
2
D.
ln
2
3
Câu 45: Tính tích phân
x
I dx
( x)
1
3
0
1 2
A
1
18
B.
1
15
C.
1
11
D.
1
8
Câu 46: Tính tích phân
x dx
I
x
1
3
2
8
0
4
A.
ln
1 3
2 2
B.
ln
1 3
6 12
C.
ln
1 3
9 28
D.
ln
1 3
96 128
Câu 47: Tính tích phân
I x dx
2
2
2
1
2
1
A.
3 1
12 4
B.
3 1
12 4
C.
2 3
24 8
D.
2 3
24 8
Câu 48: Tính tích phân
I x dx
2
2
1
4
A.
1 3
2
B.
16 3 3
12
C.
3 3 1
6
D.
6 2 2
9
Câu 49: Tính tích phân
e
I cos(lnx)dx
1
A.
e
1
1
4
B.
e
1
1
2
C.
e
1
1
2
D.
e
1
1
2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
6
Câu 50: Tính diện tích hình phẳng giới hạn bởi các đường thẳng
x ,x ,y
0 1 0
và đồ thị hàm số
x x
y
x
2
3 1
1
A.
ln
1
2
2
B.
ln
1
3
2
C.
ln
3
2
2
D.
ln
3
3
2
Câu 51: Tính diện tích hình phẳng giới hạn bởi các đồ thị
y x x,y x
2
2 3
A.
125
2
B.
125
3
C.
125
6
D.
125
8
Câu 52: Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số
y sin x,y cos x
3 3
và trục Oy với
x
0
4
A.
2 1
B.
2 2 1
C.
4 2 5
D.
5 2 4
Câu 53: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi:
y xlnx,y ,x ,x e
0 1
A.
e
3
1
3
B.
e
3
1
2
C.
e
3
3
27
D.
e
3
5 3
27
Câu 54: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi: y ,y cos x sin x ,x ,x
6 6
0 0
2
A.
2
3
B.
2
2
C.
2
5
6
D.
2
5
16
Câu 55: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi:
y x ,y x
2
A.
10
B.
3
C.
3
D.
2
3
Câu 56: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi: y x x ,y x x
2 2
4 6 2 6
A.
B.
2
C.
3
D.
8
Câu 57: Công thức nào sau đây sai?
A. 1. 0
dx C
B.
dx x C
C.
ln
x
x
a
a dx C
a
D. cos sinx
xdx C
Câu 58: Hàm số
2
1
sin
y
x
có nguyên hàm là:
A.
cot
x C
B.
cot
x C
C.
tan
x C
D.
tan
x C
Câu 59: Nguyên hàm của hàm số
2
( )
x x
f x
x
là:
A.
3
2
4
( ) .
3
f x dx x x C
B.
3
2
3
( ) .
4
f x dx x x C
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
7
C.
3
2
( )
f x dx x x C
D.
3
2
4
( ) .
3
f x dx x C
Câu 60: Nuyên hàm của hàm số
2 3
( )
1
x
f x
x
là:
A. ( ) 2 5ln 1
f x dx x x C
B. ( ) 2 5ln 1
f x dx x x C
C. ( ) 5ln 1
f x dx x x C
D. ( ) 2 3 5ln 1
f x dx x x C
Câu 61: Nguyên hàm của hàm số
( ) sin(3 5 )
f x x
là:
A.
1
( ) os(3 5 )
5
f x dx c x C
B.
1
( ) os(3 5 )
5
f x dx c x C
C. ( ) 5 os(3 5 )
f x dx c x C
C. ( ) 5 os(3 5 )
f x dx c x C
Câu 62: Nguyên hàm
3 2
4
x dx
x
là:
A.
3 5
3
4ln
5
x x C
B.
3 5
5
4ln
3
x x C
C.
3 5
4ln
x x C
D.
3 5
4ln
x x C
Câu 63: Nguyên hàm
2
3
2
x x dx
x
là:
A.
3
3
4
3ln
3 3
x
x x C
B.
3
4
2 3ln
3
x x x C
C.
3
3
4
3ln
3 3
x
x x C
D.
3
3
3
3ln
3 4
x
x x C
Câu 64: Nguyên hàm
1
( 3)
dx
x x
là:
A
.
1
ln
3 3
x
C
x
B.
1
ln
3 3
x
C
x
C.
1 3
ln
3
x
C
x
D.
1 3
ln
3
x
C
x
Câu 65: Nguyên hàm
2
(1 sin )
x dx
là:
A.
3 1
2cos sin 2
2 4
x x x C
B.
3 1
2cos sin 2
2 4
x x x C
C.
3 1
2cos sin
2 4
x x x C
C.
3 1
2cos sin
2 4
x x x C
Câu 66: Nguyên hàm ln
xdx
là:
A.
ln
x x x C
B.
ln
x x x C
C.
ln
x x x C
D.
ln
x x x C
Câu 67: Theo định nghĩa tích phân thì:
A.
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
B.
( ) ( ) (a) (b)
b
b
a
a
f x dx F x F F
C.
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
C.
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x f b f a
Câu 68: Tính chất nào sau đây sai?
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
8
A.
( ) ( ) ( ) , ( )
b c b
a a c
f x dx f x dx f x dx a c b
B.
( ) ( ) ( ) , ( )
b c b
a a c
f x dx f x dx f x dx a c b
C.
. ( ) ( ) ,
b b
a a
k f x dx k f x dx
k là hằng số D.
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx
Câu 69: Nếu
( )
u u x
và
( )
v v x
là hai hàm số có đạo hàm liên tục trên đoạn
[ ; ]
a b
thì:
A.
u( )v'( ) (u( ) v( )) u'( )v( )
b b
b
a
a a
x x dx x x x x dx
B.
u( )v'( ) (u'( ) v'( )) u'( ) v( )
b b
b
a
a a
x x dx x x x x dx
C.
u( )v'( ) (u( ) v'( )) u'( ) v( )
b b
b
a
a a
x x dx x x x x dx
D.
u( )v'( ) (u( ) v( )) u'( ) v( )
b b
b
a
a a
x x dx x x x x dx
Câu 70:
Giá trị của tích phân
1
3 1
0
x
I e dx
là:
A
.
4
1
( )
3
I e e
B.
4
1
( )
3
I e e
C.
4
3( )
I e e
D.
4
3( )
I e e
Câu 71: Cho
3
2
1
2 3 1
2
x x
I dx
x
. Kết quả nào sau đây sai?
A.
3
6 3ln
5
I B.
5
6 3ln
3
I
C.
6 3ln5 3ln3
I
D.
(9 3 3ln5) (1 1 3ln3)
I
Câu 72: Giá trị của tích phân
2
2
sin3 cos5
I x xdx
là:
A
.
0
I
B.
1
I
C.
2
I
D.
3
I
Câu 73: Giá trị của tích phân
1
3
0
1
I x xdx
là:
A
.
9
28
I B.
28
9
I C.
0
I
D.
1
I
Câu 74: Giá trị của tích phân
2
5
0
sin
I xdx
là:
A.
8
15
I
B.
2
9
I
C.
1
I
D.
1
I
Câu 75: Giá trị của tích phân
2
0
(2 1) os
I x c xdx
là:
A.
1
I
B.
1I
C.
I
D.
2
I
Câu 76: Giá trị của tích phân
2
2
1
ln
I x xdx
là:
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
9
A.
1
(24ln2 7)
9
B.
1
(24ln 2 7)
9
C.
8 8 1
ln2
3 9 9
D.
8 8 1
ln2
3 9 9
Câu 77: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
( )
f x
liên tục, trục hoành và hai đường
thẳng ,
x a x b
được tính theo công thức:
A
.
( )
b
a
S f x dx
B.
( )
b
a
S f x dx
C.
2
( )
b
a
S f x dx
D.
(a) (b)
b
a
S f f dx
Câu 78: Cho hàm số
y f x
liên tục trên đoạn
[ ; ]
a b
. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường thẳng x = a, x = b. Khi D quay xung quanh Ox ta được một khối tròn
xoay có thể tích là:
A.
2
( )d
b
a
V f x x
B.
( )d
b
a
V f x x
C.
2
( )d
b
a
V f x x
D.
( )d
b
a
V f x x
Câu 79: Diện tích hình phẳng giới hạn bởi các đường sau
sinx
y
, trục hoành, trục tung và đường
thẳng
x
là:
A.
2
S
B.
2
S
C.
2
S
D.
2
S
Câu 80: Diện tích hình phẳng giới hạn bởi các đường sau
3
3 ,
y x x y x
là:
A.
8
S
B.
8
S
C.
4
S
D.
4
S
Câu 81: Diện tích hình phẳng giới hạn bởi các đường sau
3 2
3 , 2
y x x y x
, được tính bằng tích
phân sau
A.
2
3 2
0
3 2
S x x xdx
B.
2
3 2
1
3 2
S x x xdx
C.
2
3 2
0
( 3 2 )
S x x xdx
D.
2
3 2
1
( 3 2 )
S x x xdx
Câu 82: Diện tích hình phẳng giới hạn bởi các đường sau cos , 0, 0,
4
y x y x x
, được tính bằng
tích phân sau
A.
4
0
cos
S xdx
B.
4
0
cos
S xdx
C.
2
0
cos
2
x
S dx
D.
4
2
0
cos
S xdx
Câu 83: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau: Trục Ox,
sinx, (0 )
y x
, quay xung quanh trục Ox là:
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
10
A.
2
2
V
B.
2
4
V
C.
2
2
V
D.
2
4
V
Câu 84: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau:
2
2 , 0
y x x y
,
quay xung quanh trục Ox là:
A.
16
15
V
B.
15
16
V
C.
2
16
15
V
D.
2
15
16
V
Câu 85: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau:
2
1, 0
y x y
, quay
xung quanh trục Ox được tính bởi:
A.
1
2 2
1
( 1)
V x dx
B.
1
2 2 2
1
( 1)
V x dx
C.
1
2 2
1
( 1)
V x dx
D.
1
2
1
( 1)
V x dx
Câu 86: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau:
sinx, 0, 0,
4
y y x x
, quay xung quanh trục Ox được tính bởi:
A.
4
2
0
sin
V xdx
B.
4
2 2
0
sin
V xdx
C.
4
0
sin
V xdx
D.
4
2
0
sin
V xdx
Câu 88
. Họ nguyên hàm của hàm số
2
1 1
( )f x
x x
là:
A.
2
ln ln
x x C
B. lnx –
1
x
+ C C. ln|x| +
1
x
+ C D. lnx +
1
x
+ C
Câu 89. Họ nguyên hàm của hàm số
f x 1 cos3
x
là:
A.
1
sin3
3
x x C
B.
1
sin3
3
x x C
C. sin3
x x C
D. sin3
x x C
Câu 90. Họ nguyên hàm của hàm số: y =
2
x
x
e
e
là:
A. 2ln( 2)
x
e C
B.
ln( 2)
x
e
+ C C.
e ln( 2)
x x
e
+ C D.
2
x
e
+ C.
Câu 91. Kết quả của
2
3 2
dx
x x
là:
A.
1
ln
2
x
C
x
B.
1
ln
2
x
C
x
C.
2
ln
1
x
C
x
D.
ln 1 2
x x C
Câu 92. Họ nguyên hàm của hàm số:
sin .cos
y x x
là:
A.
1
cos2
2
x
+C B. cos2
x C
C.
1
sin 2
4
x C
D.
1
cos2
4
x C
Câu 93. Kết quả của
1
1 2
dx
x
là:
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
11
A.
1
ln 1 2
2
x C
B.
ln 1 2
x C
C.
1
ln 1 2
2
x C
D.
1
ln 1 2
2
x C
Câu 94. Họ nguyên hàm của hàm số
2
(tanx cot )
y x
là:
A.
3
1
(tanx cot )
3
x C
B. tan cot
x x C
C.tanx cot 2
x x C
D.tan cot 2
x x x C
Câu 95. Tích phân I =
2
1
1
0
.
x
x e dx
có giá trị là:
A.
2
2
e e
B.
2
3
e e
C.
2
2
e e
D.
2
3
e e
Câu 96. Biến đổi
3
0
1 1
x
dx
x
=
2
1
f t dt
, với 1
t x
. Khi đó f(t) là hàm nào trong các hàm số sau:
A.
2
2 2
f t t t
B.
2
f t t t
C.
2
f t t t
D.
2
2 2
f t t t
Câu 97 .Diện tích hình phẳng được giới hạn bởi các đường
2
2
y x x
và đường thẳng
2
x y
là:
A.
1
6
dvdt
B.
5
2
dvdt
C.
6
5
dvdt
D.
1
2
dvdt
Câu 98. Diện tích hình phẳng giới hạn bởi
3
, 0, 1, 2
y x y x x
có kết quả là:
A.
17
4
B.
4
C.
15
4
D.
14
4
Câu 99. Cho hình (H) giới hạn bởi các đường
y x
;
4
x
; trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
15
B.
14
3
C.
8
D.
16
3
Câu 100. Tìm nguyên hàm của hàm số f(x) =
x
xe
2
2
.
A.
x
f(x)dx x e C
2
2
. B.
x
f(x)dx e C
2
.
C.
x
f(x)dx x e C
2
2
. D.
x
f(x)dx e C
2
2
.
Câu 101. Cho hàm số f(x) = 2x + sinx + 2cosx. Một nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 là:
A. F(x) = x
2
+ cosx – 2sinx. B. F(x) = x
2
– cosx + 2sinx – 2.
C. F(x) = x
2
+ cosx – 2sinx + 2. D. F(x) = x
2
– cosx + 2sinx + 2.
Câu 102. Tính tích phân I =
x
x
e
dx
e
1
0
1
.
A. I = 1. B. I =
ln( e)
1
1
2
. C. I =
e
ln
1
2
. D. I = ln
e
2
1
.
Câu 103
. Tính tích phân I =
sinx
e cosx cosxdx
2
0
.
A. I =
4
+ e – 1. B. I =
4
+ 1. C. I = e – 1. D. I =
4
– 1.
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
12
Câu 104. Tính tích phân I =
x
dx
sin x
2
2
4
.
A. I =
4
+ ln2. B. I =
ln
1
2
4 2
. C. I =
4
– 2ln2. D. I =
4
+ 2ln2.
Câu 105. Đặt In =
n
tan xdx
4
0
. Mệnh đề nào sau đây là đúng:
A. In + In + 1 =
n
1
. B. In – In + 1 =
n
1
1
. C. In – In + 2 =
n
1
. D. In + In + 2 =
n
1
1
.
Câu 106. Diện tích hình phẳng giới hạn bởi hai đường y = x
3
và y = x được tính bởi công thức nào sau
đây:
A.
x x dx
1
3
1
. B. 2
x x dx
1
3
0
. C.
x x dx
1
3
1
. D.
x x dx
1
3
1
.
Câu 107. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x x
3 2
2 1
3 3
và trục Ox là:
A.
9
32
. B.
32
9
. C.
9
13
. D.
12
11
.
Câu 108. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị các hàm số y =
x
xe
, y = 0,
x = 0 và x = 1 quanh trục Ox là:
A.
e
2
1
. B.
e
2
4 1
. C.
e
2
1
4
. D.
e
2
4
.
Câu 109 .Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị các hàm số y = 1 – x
2
, y = 0
quanh trục Ox có kết quả dạng
a
b
. Khi đó a + b bằng:
A. 17. B. 11. C. 25. D. 31.
Câu 110: Hàm số F(X) ln x x
2
1 2016
là một nguyên hàm của hàm số
A. f(x)
x
2
1
1
B.
x
f(x)
x
2
1
C. f(x) x
2
1
D. f(x) x
2
1 2016
Câu 111: Hàm số
sin x
F(X) e
2
là một nguyên hàm của hàm số
A.
sin x
sin x.e
2
2
B.
sin x
sin x.e
2
2 1
C.
sin x
cos x.e
2
2
D.
sin x
e
2
Câu 112: Hàm số
F(X) ln lnx C
1
là họ nguyên hàm của hàm số
A.
x( lnx)
1
1
B.
xlnx
1
C.
xln( x)
1
1
D.
lnx
1
1
Câu 113: Tích phân
cosx
e sinxdx
2
0
bằng
A.
e
1
B.
e
1
C.
e
1
2
D.
e
2
1
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
13
Câu 114: Tích phân
e
e
dx
x(lnx)
2
2
bằng
A.
e
e
lnx
2
1
B.
e
e
x
2
1
C.
e
e
x
2
3
3
D.
e
e
lnx
2
1
Câu 115: Cho
I ( x x )dx
3
3
1
1
thì I bằng
A.
x x x
3
4
3
3
2
1
3 2
4 3
B.
x x
3
4
3
3
2
1
3 2
1
4 3
C.
x x x
3
4
3
3
2
1
D.
x x x
3
4
3
3
2
1
3 2
4 3
Câu 116: Tích phân
e
xlnxdx
1
bằng:
A.
e
xlnx x
1
B.
e
x x
lnx
2
1
2 2
C.
e
x x
lnx
2
1
2 2
D.
e
(lnx)
2
1
2
Câu 117: Tích phân
x dx
1
2
0
2 1
bằng
A.
( )
2
8 1
3
B.
( )
3
1
4 1
3
C.
( )
1
8 1
2
D.
( )
1
8 1
3
Câu 118: Diện tích hình phẳng giới hạn bởi các đường
y x x
2
2
,
x y
0
là
A.
9
2
B.
5
2
C.
7
2
D.
11
2
Câu 119: Diện tích hình phẳng giới hạn bởi các đường
x
y
2
,
y
2
,
x
0
được tính bởi công thức
A.
x
dx
1
0
2 2
B.
x
dx
1
0
2 2
C.
x
dx
2
0
2 2
D.
x
dx
2
0
2 2
Câu 120: Diện tích hình phẳng (H) giới hạn bởi các đường
y lnx
,
y
1
,
x e
2
được tính bởi công thức
A.
e
e
lnx dx
2
1
B.
e
lnx dx
2
1
1
C.
e
e
lnx dx
2
1
D.
e
lnx dx
2
0
1
Câu 121
: Tìm nguyên hàm của hàm
số
x x dx
x
2
3
2
A.
x
ln x x C
3
3
4
3
3 3
B.
x
lnx x
3
3
4
3
3 3
C.
x
ln x x C
3
3
4
3
3 3
D.
x
ln x x C
3
3
4
3
3 3
Câu 122: Giá trị
m
để hàm số F(x) mx ( m )x x
3 2
3 2 4 3
là một nguyên hàm của hàm số
f(x) x x
2
3 10 4
là:
A.
m
3
B.
m
0
C.
m
1
D.
m
2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
14
Câu 123: Tính tích
phân
sin x
dx
sin x
3
4
2
6
1
A.
3 2
2
B.
3 2 2
2
C.
3 2
2
D.
3 2 2 2
2
Câu 124: Tính tích
phân
e
x.lnxdx
1
A.
e
2
1
1
4
B.
e
2
1
4
C. e
2
1
1
4
D.
e
1
1
4
Câu 125: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm
số
y x
2
2
và
y x
A. 5 B. 7 C.
9
2
D.
11
2
Câu 126: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm
số
y x x
2
2
và
y
0
. Tính thể tích vật thể
tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục
Ox
A.
16
15
B.
17
15
C.
18
15
D.
19
15
Câu 127 : Tìm họ nguyên hàm của hàm số
f(x) x( x)
20
1
A.
(x ) (x )
f(x)dx C
22 21
1 1
22 21
B.
(x ) (x )
f(x)dx C
22 21
1 1
23 22
C.
(x )
f(x)dx C
21
1
22
D.
(x )
f(x)dx C
22
1
23
Câu 128: Tính tích phân
x lnx
I dx
x
2
2
1
2
.
A.
I ln
2
2
B.
I ln
3
2
2
C.
I ln
2
3
2
2
D.
I ln
2
Câu 129 : Gọi (D) là miền giới hạn bởi
y x x
2
2
và trục hoành. Tính thể tích của vật thể tròn xoay
sinh ra bởi hình (D) khi nó quay xung quanh trục
Ox
.
A.
V
16
B. V
16
25
C. V
1
25
D. V
16
5
Câu 130 : Tìm họ nguyên hàm của hàm số
(lnx)
f(x)
x
4
A.
f(x)dx (lnx) C
5
1
5
B.
f(x)dx (lnx) C
4
1
4
C.
f(x)dx (lnx) C
5
1
4
D.
f(x)dx (lnx) C
4
1
5
Câu 131 : Tính diện tích hình phẳng giới hạn bởi trục hoành,
y x x
2
2
và đường thẳng
x ,x
1 2
A. 16 B. 0 C. 8 D.
8
3
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
15
Câu 132 : Cho hình phẳng (D) giới hạn bởi các đường
y (x )
2
2
và
y
4
. Tính thể tích của vật thể
tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục
Ox
.
A.
V
16
25
B. V
26
25
C. V
256
5
D. V
16
25
Câu 133 : Gọi (D) là miền giới hạn bởi
y xsinx cos x
2
, trục hoành và đường thẳng x ,x
0
2
.
Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục
Ox
.
A.
V ( )
2
4
4
B.
V ( )
4
4
C.
V ( )
2
4
4
D.
V ( )
4
4
Câu 134 : Tính tích phân
x x
I dx
x x
2
2
2
1
3 1
.
A.
I ln
3 1
B.
I ln
3
C.
I ln
1 3
D.
I ln
1 3
Câu 135 : Tính tích phân
I x x dx
1
2
0
2
.
A. I
1 2 2
3
B. I
2 2 1
3
C. I
2 2 1
3
D.
I
2 2
Câu 136 : Tính tích phân
e
dx
I
x lnx
1
1
.
A.
I
1
B.
I ln
1 3
C.
I
2 2 2
D.
I ln
2
Câu 137: Tính thể tích V khối tròn xoay tạo thành khi quay hình phẳng được giới hạn bởi các đường
y , y , x
x
1
0 0
1 4 3
và
x
1
xung quanh trục hoành.
A. V ln
3
6 1
9 2
B. V ln
3
6 1
9 2
C. V ln
1 3
6 1
9 2
D. V ln
1 3
6 1
9 2
Câu 138 : Tính tích phân
x
I dx
x
2
1
2
0
1
1
.
A.
I ln
2 1
B.
I ln
1 2
C.
I ln
2
D.
I ln
1 2
Câu 139 : Tính tích phân
ln
x x
I e e dx
2
2
0
1
.
A. I e
2
1
3
B. I e
2
1
3
C. I
1
3
D.
I e
Câu 140 : Tính tích phân
I x sin xdx
4
0
1 2
.
A.
I
3
4
B.
I
C.
I
2
D. I
3
2
Câu 141 :
Tính tích phân
I cos xsin xdx
2
2
0
2
.
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
16
A.
I
2
B. I
1
2
C.
I
0
D. I
2
2
Câu 142 : Tính diện tích hình phẳng giới hạn bởi hai đường cong
y x
3
và
y x
2
A. 12 B. 1 C. 0 D.
1
12
Câu 143 : Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x x
2
3
và đồ thị hàm số
y x
2 1
.
A. I
1
36
B.
I
6
C.
I
36
D. I
1
6
Câu 144 : Tính tích phân
I x sin x dx
4
0
1 2
.
A. I
2
1
32 4
B. I
2
32
C. I
32
D. I
1
32 4
Câu 145 : Tìm họ nguyên hàm của hàm số
x x x
f(x)
x x
4 2
2
2 2
1
A.
x x
f(x)dx x C
3 2
3 2
B.
x x
f(x)dx x C
3 2
2
3 2
C.
x
f(x)dx x x C
3
2
2
3
D.
x
f(x)dx x x C
2
3
2
2
Câu 146 : Tính tích phân
x x
I ( e e )xdx
2
1
0
2
. .
A.
I e
3
B. I = e C.
I e
1
D.
I e
2
Câu 147 : Hàm số
F x ln sinx cosx
là một nguyên hàm của hàm số:
A.
sinx cosx
sinx cosx
B.
sinx-cosx
sinx+cosx
C.
sinx+cosx
1
D.
sinx cosx
1
Câu 148 : Nguyên hàm của
f x
x x
2
1
3 2
là:
A.
ln (x )(x ) C
1 2
B.
x
ln C
x
2
1
C.
x
ln C
x
1
2
D.
x
ln C
x x
2
2 3
3 2
Câu 149: Thể tích của vật thể được tạo ra khi quay hình phẳng giới hạn bởi hai đường y x
2
1
và y = 0
quanh trục
Ox
là :
A.
15
6
B.
15
6
C.
8
15
D.
8
15
Câu 150: Diện tích hình phẳng giới hạn bởi hai đường
y x
2
và
y x
2
2
là:
A.
8
15
B.
8
3
C.
4
3
D. 2
Câu 151: Thể tích của vật thể được tạo ra khi quay hình phẳng giới hạn bởi hai đường
y x x
2
và y =
0 quanh trục
Ox
là :
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
17
A.
4
B.
5
C.
6
D.
3
C©u 152 :
Cho ha hàm số
y f x
1
và
y f x
2
liên tục trên đoạn
a;b
. Gọi D là hình phẳng giới hạn bởi
đồ thị hai hàm số đó và các đường thẳng x=a, x=b. Giả sử
f x f x , x a;b
1 2
. Khi đó diện tích
của hình D là :
A.
b
a
f x .f x dx
1 2
B.
b
a
f x f x dx
1 2
C.
b
a
f x f x dx
1 2
D.
b
a
f x f x dx
1 2
Câu 153: Cho tam giác vuông OPM có cạnh OP nằm trên
Trục Ox (Hình bên). Đặt
POM ,OM R , R .
0 0
3
Tính thể tích của V theo
và R.
A.
R
V (cos cos )
3
3
3
. B.
V R (cos cos )
3 3
.
C.
R
V (cos cos )
3
2
3
. D.
V R (cos cos )
3 2
.
Câu 154. Tìm nguyên hàm của hàm số
f(x) x dx
9
4 2
.
A.
x
f(x) x dx C
10
9
4 2
4 2
4
. B.
x
f(x) x dx C
10
9
4 2
4 2
8
.
C.
x
f(x) x dx C
9
9
4 2
4 2
4
. D.
x
f(x) x dx C
9
9
4 2
4 2
8
.
Câu 155. Tính tích phân
I sin xcosxdx
2
0
.
A. I
1
2
. B. I
3
1
4
. C.
I
0
. D. I
2
3
.
Câu 156
. Tính tích phân
x
I x e dx
1
0
1
.
A.
I e
2
. B.
I e
. C.
I e
2
. D.
I e
2 1
.
Câu 157. Tính tích phân
sinx
I e cosx cosxdx
2
0
.
A.
I e
1
2
. B.
e
I
1
. C. I e
4
. D. I e
1
4
.
Câu 158
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x x
3 2
5 1
và đồ thị hàm số
y x
8 3
.
A.
95
12
. B.
28
3
. C.
17
12
. D.
1
12
.
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
18
Câu 159. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
1
2
, trục tung. Tính thể tích V của
khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A.
V ln
4 3 4
. B.
V (ln )
4 3 1
. C.
V ln
4 3 4
. D.
V (ln )
4 3 1
.
Câu 160: Tính nguyên hàm
x
x
e
dx
e
3
1
1
A.
x x
e e x C
2
1
2
B.
x C
C.
x x
e e x C
2
1
2
D.
x
e x C
2
1
2
Câu 161: Tính tích phân
ln
x
xe dx
2
0
A.
ln
2 2 1
B.
ln
2 1
C.
ln
2 2 1
D.
ln
1 2 2
Câu 162: Tính diện tích hình phẳng giới hạn bởi đồ thị (C)
x
y
x
3
1
, trục tung, trục hoành.
A.
ln
4 4 3
B.
ln
4 4 4
C.
ln
3 4 4
D.
ln
4 4 3
.
Câu 163
: Xét hình phẳng giới hạn bởi
y x , y ( x)
2
2 1 2 1
. Tính diện tích hình phẳng.
A.
2
B.
1
C.
1
2
D.
1
2
Câu 164: Cho hình phẳng giới hạn bởi đường cong y = sinx, trục Ox, x = 0, x = .
Tính thể tích khối tròn xoay thu được khi quay hình này xung quanh trục Ox.
A.
1
2
B.
3
2
C.
2
D.
2
2
Câu 165: Tính tích phân
x
I dx.
x
2
2
0
1
A. I ln
2
4
2
B. I ln
2
1 4
2 4
C. I ln
2
1 4
2 2
D. I ln
2
4
4
Câu 166: Xét hình phẳng giới hạn bởi
y x , y ( x)
2
2 1 2 1
. Tính thể tích khối tròn xoay tạo thành khi
quay hình phẳng quanh trục Ox.
A.
1
2
B.
4
3
C.
1
D.
2
Câu 167: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
y x .e
1 1
2 2
,x=1, x=2, y=0
quanh trục Ox là:
A.
(e e)
2
B.
(e e)
2
C.
e
2
D.
e
3
2
Câu 168: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y
x
4
, y=0, x=1, x=4
quanh trục Ox là:
A.
6
B.
4
C.
12
D.
8
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
19
Câu 169: Giá trị của
( tanx) . dx
cos x
4
4
2
0
1
1
bằng :
A.
1
5
B.
1
3
C.
1
2
D.
1
4
Câu 170: Kết quả của
x
dx
x
2
1
là:
A.
x C
2
1
B.
C
x
2
1
1
C.
C
x
2
1
1
D. -
x C
2
1
Câu 171: diện tích hình phẳng giới hạn bởi đồ thị hàm số
y x
2
và đường thẳng y=2x là:
A.
4
3
B.
3
2
C.
5
3
D.
23
15
Câu 172. Tìm nguyên hàm của hàm số
10
( ) 3 1
f x x dx
.
A.
11
10
3 1
( ) 3 1
3
x
f x x dx C
B.
10
10
3 1
( ) 3 1
33
x
f x x dx C
C.
11
10
3 1
( ) 3 1
11
x
f x x dx C
D.
11
10
3 1
( ) 3 1
33
x
f x x dx C
Câu 173. Tính tích phân
2
2
0
sin cos
I x xdx
.
A.
3
1
12
I
B. I
3
1
4
C.
1
3
I
D. I
2
3
Câu 174. Tính tích phân
1
0
x
I xe dx
.
A.
2 1
I e
B.
1
I
C.
1
I
D.
I e
2 1
Câu 175. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
5
y x
và đồ thị hàm số
3
y x
.
A.
10
3
B.
9
2
C.
27
2
D.
7
3
Câu 176. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
3
8
y x
, trục tung và truch hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A.
12
V
B.
12
V
C.
20
V
D.
4
V
Câu 177: Một nguyên hàm của hàm
x
f x e
là:
A.
x
x.e
B.
x
x .e
2 1
C.
x
e
D.
x
e
1
Câu 178: Một nguyên hàm của hàm
f x
sinx
1
là:
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
20
A.
x
ln tan
2
B.
sinx
1
C.
x
ln sin
2
D.
ln tanx
Câu 179: Tính tích phân:
x
I dx
x x
1
2
0
4 11
5 6
A.
ln
9
2
B.
ln
9
C.
ln
6
D.
ln
11
2
Câu 180: Tính tích phân:
I x dx
4
2
1
1
A.
9
2
B.
7
6
C.
ln
7
6
D.
11
2
Câu 181: Tính diện tích hình phẳng giới hạn bởi
y x x
2
2
và
y x x
2
4
A. 3 B. 6 C. 9 D. 12
Câu 182 : Tìm họ nguyên hàm F(x) =
dx
x
8 1
A. F(x) = ln|1-8x| +C B. F(x) =
ln| x|
1
1 8
8
C. F(x) =- ln|1-8x| + C D.F(x) =
ln| x| C
1
1 8
8
Câu 183 :Gọi F(x) =
( x ) dx
11
2 1
. F(x) bằng biểu thức nào sau đây
A.
( x ) C
12
1
2 1
24
B.
( x ) C
12
1
2 1
22
C.
( x ) C
12
1
2 1
12
D.
ln( x ) C
12
1
2 1
12
Câu 184: Tính tích phân I=
x
x.e dx
1
2
0
A.
(e )
2
1
1
4
B.
(e )
2
1
1
4
C.
(e )
2
1
1
2
D.
(e )
2
1
1
2
Câu 185: Tính tích phân I =
x dx
1
2
2
2
1
A.
1
8 4
B.
3
2 4
C.
1
8 4
D.
3
2 4
Câu 186: Tính tích phân I =
( sinx)
cosx.e dx
2
1
0
A. 2e-1 B.e
2
– 1 C. e
2
–e D.
e
1
2
Câu 187: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=
x
x
3 5
2 2
, trục hoành và các đường thẳng
x = 0 ; x= 2
A. S = ln3 + 3 B. S = ln3 C.S= ln2+ 3 D. S = ln3-2
Câu 188: Tính diện tích hình phẳng giới hạn bởi các đường y +x
2
-5 = 0; x + y – 3 = 0
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
21
A. S = 9 B. S=
9
2
C. S =
11
2
D.
7
2
Câu189 : Tính thể tích vật thể giới hạn bởi các đường y = -x
2
+ 5 và y = 3 – x khi quay quanh trục Ox
A. 2
B.
53
15
C.
153
5
D.
31
13
Câu 190: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi
y=
x
1
3
2 1
,x = 0 , y = 3, quay quanh trục oy
A. V =
480
7
B.V =
460
5
C.
450
3
D. V =
490
9
Câu 191: Viết công thức thể tích khối tròn xoay tạo thành khi quay hình thang cong , giới hạn bởi đồ thị
hàm số x = g(y) , trục oy và 2 đường thẳng y = a; y = b (a < b) , xung quanh trục Oy.
A.
b
a
V g (y)dy
2
B.
b
a
V g (y)dy
2
C.
b
a
V g (y)dy
D.
b
a
V |g(y)|dy
Câu 192. Hàm số
x
f(x)
2
có nguyên hàm là :
A.
x
.ln C
2 2
B.
x
C
ln
2
2
C.
x
.lnx C
2
D.
x
C
lnx
2
Câu 193. Hàm số
f(x) ( x)
5
1 có nguyên hàm là:
A.
( x)
6
1
1
6
B.
( x)
6
1
1
6
C.
( x)
6
1 D.
( x)
6
1
Câu 194
. Tích phân
x x
(x e )e dx
1
0
bằng :
A.0 B.1 C.
e
2
1
D.
(e )
2
1
1
2
Câu 195. Tích phân
x dx
2
2
0
4
bằng :
A.
B.
2
C.
2
D.
3
2
Câu 196. Tích phân
sin x
dx
cos x
2
2
0
2
4
bằng :
A .2ln2 + ln3 B.ln3 – 2ln2 C. 2ln2-ln3 D.ln2 – ln3
Câu 197. Diện tích giới hạn bởi
y x
2
,
y x
2 3
và hai đường thẳng x =0, x=2.
A.1 B. 2 C. 3 D. 4
Câu 198. Tính thể tích vật thể tròn xoay sinh ra khi quay hình (D) quanh trục Ox biết (D) giới hạn bởi
y x
2
1
và y = 0
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
22
A. V
2
B. V
3
2
C. V
16
15
D. V
15
16
Câu 199: Nguyên hàm của hàm số
x x
f(x) e ( e )
2
1 3
bằng:
A.
x x
F(x) e e C
3
B.
x x
F(x) e e C
3
C.
x x
F(x) e e C
2
3
D.
x x
F(x) e e C
3
3
Câu 200: Cho
M x x dx
2 3
4
. Chọn câu đúng trong các câu sau:
A.
M x C
3
2
4
9
B.
M ( x ) C
3 2
2 4
C.
M ( x ) C
3 3
2
4
9
D.
M ( x ) C
3 2
1
4
9
Câu 201: Gọi
F(x)
là nguyên hàm của hàm số
x
f(x)
x
2
8
thỏa mãn
F( )
2 0
.Khi đó phương trình
F(x) x
có nghiệm là:
A.
x
0
B.
x
1
C.
x
1
D.x
1 3
Câu 202: Cho
dx
M .
x(x )
4
1
1
Bất đẳng thức nào sau đây là đúng?
A.
M
0 1
B.
M
1 2
C.
M
0
D.
M
2 3
Câu 203: Cho
x dx
P .
x
2
2
1
1
Giá trị của P là:
A.
ln
1
2
2
B. ln
1
2
2
C.
2
D.
ln
1
2
2
Câu 204
: Với
t ( ; )
1 1
ta có
t
dx
ln .
x
2
0
1
3
2
1
Khi đó giá trị của t là:
A.
1
3
B.
1
2
C.
0
D.
1
3
Câu 205: Các đường cong
y sinx,
y cosx
với x
0
2
và trục Ox tạo thành một hình phẳng. Diện
tích của hình phẳng này là:
A.
2 2
B.
2 2
C.
2
D. Đáp số khác
.
Câu 206: Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số
y lnx
và các đường thẳng
y ,
0
x ,
1
x e
2
là:
A.
e
2
3 1
B.
e
2
2 1
C.
e
2
2 1
D.
e
2
1
Câu 207: Cho đồ thị hàm số
y x x x.
3 2
3 9
Diện tích của hình phẳng giới hạn bởi đồ thị, tiếp tuyến của
nó tại điểm
( ; )
2 2
và trục tung là:
A.
30
B.
24
C.
28
D.
20
Câu 208: Diện tích của hình phẳng giới hạn bởi
y x
2
4
và
y x
3
là:
A.
5
2
B.
13
3
C.
17
6
D.
3
2
Câu 209. Tìm nguyên hàm của hàm số
f(x) cos( x )
4 1
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
23
A.
cos( x )dx sin( x ) C
1
4 1 4 1
4
B.
cos( x )dx sin( x ) C
1
4 1 4 1
4
C.
cos( x )dx cos( x ) C
1
4 1 4 1
2
D.
cos( x )dx sin( x ) C
1
4 1 4 1
2
Câu 210. Tính
I x ( x ) dx
3 4 3
5
:
A.
I ( x ) C
4 4
1
5
16
B.
I ( x ) C
4 4
1
5
16
C.
I ( x ) C
4 4
1
5
4
D.
I ( x ) C
4 4
1
5
4
Câu 211. Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường
y
0
và
y x x
2
2
khi
nó quay quanh trục
Ox
bằng bao nhiêu?
A.
V
3
8
B. V
8
3
C. V
15
16
D. V
16
15
Câu 212. Tính
x
I dx
x
1
0
1
1
A.
I ln
4
B.
I ln
1 4
C.
I ln
4 1
D.
I ln
1 4
Câu 213. Tính
x
I xe dx
1
2
0
A.
e
I
2
1
4
B.
I e
2
1
C.
e
I
2
1
4
D.
I e
2
1
Câu 215. Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số
y lnx
, trục hoành và các đường
thẳng x
e
1
,
x e
là:
A.0 B. -2e C.
e
2
-2e D.
e
2
Câu 216: Nguyên hàm của y
x(x )
1
3
là
A.
x
ln C
x
2
3 3
B.
x
ln C
x
1
3 3
C.
x
ln C
x
1 3
3
D.
x
ln C
x
1
3 3
Câu 217: Nguyên hàm của hàm số
x
y e x
x
2
1
3
là.
A.
x
e x lnx c
3
B.
x
e x lnx c
3
C.
x
e x lnx c
3
D.
x
e x lnx c
3
Câu 218: Cho hàm
y f(x)
và
y g(x)
liên tục trên
a : b
khi đó diện tích hình phẳng giới hạn bởi hàm
số
y f(x)
và
y g(x)
và 2 đường thẳng
x a,x b,(a b)
là.
A.
b
a
S f (x) g(x).dx
B.
b
a
S f (x) g(x).dx
C.
b
a
S f (x).dx
D.
b
a
S g(x) .dx
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
24
Câu 219: Tính tích phân
I ( cos x)sin xdx
6
0
1 3 3
A. I
1
3
B. I
1
6
C. I
1
3
D.I
1
6
Câu 220: Tính tích phân
I ( x )cosxdx
2
0
2 1
A.
I
3
B.
I
3
C.
I
D.
I
3
Câu 221: Tính tích phân
x
I dx
x x
1
2
0
4 2
1
A.
I ln
2
B.
I ln
2 3
C.
I ln
3 2
D.
I ln
2 2
Câu 222: Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đường
y x x
2
2
và
y
0
khi
quay xung quanh trục
ox
bằng.
A.
16
15
( đvdt) B.
15
16
( đvdt) C.
5
6
( đvdt) D.
6
5
( đvdt)
Câu 223. Diện tích hình phẳng giới hạn bởi các đường cong
y f(x),y g(x)
và các đường thẳng
x a,x b
là:
A.
b
a
S f(x) g(x)dx
B.
b
a
S f(x) g(x) dx
C.
b
a
S f(x) g(x) dx
D.
b
a
S f(x) g(x) dx
Câu 224. Trong các công thức sau đây, công thức nào sai:
A.
b b b
a a a
f(x).g(x) dx f(x)dx. g(x)dx
B.
b b b
a a a
f(x) g(x) dx f(x)dx g(x)dx
C.
b b b
a a a
f(x) g(x) dx f (x)dx g(x)dx
D.
b c b
a a c
f(x)dx f(x)dx f(x)dx (a c b)
Câu 225. Nguyên hàm của hàm
f(x) x
2
2 1
là:
A.
f(x)dx c
( x )
1
2 2 1
B.
f(x)dx c
( x )
1
2 2 1
C.
f(x)dx c
( x )
2
2 1
D.
f(x)dx c
( x )
2
2 1
Câu 226. Nguyên hàm của hàm
f(x) x
1
1 2
là:
A.
f(x)dx ln x c
1
1 2
2
B.
f(x)dx ln( x) c
1
1 2
2
C.
f(x)dx ln( x) c
1
1 2
2
D.
f(x)dx c
( x )
2
1
2 2 1
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
25
Câu 227. Tính tích phân
I sin x( cos x)dx
2
2
0
2 2 1
A. 1 B. -1 C. 2 D
. -2
Câu 228
. Tính tích phân
I x( sinx)dx
0
2 1
A.
2
2
B.
2
2
C.
2
2
D.
2
2
Câu 229. Tính tích phân
I sin x( sin x)dx
2
2
0
2 2 1
A. 1 B. -1 C. 2 D. -2
Câu 230. Tính tích phân
e
I x( lnx)dx
1
2 1
A.
e
2
3 1
2 2
B.
e
2
5 3
2 2
C.
e
2
3 1
2 2
D.
e
2
5 3
2 2
Câu 231. Tìm a>0, biết:
a
a
x x
I dx ln
x
3
2 2 3 1
3 2
3
A. 1 B. 2 C. e D. 2e
Câu 232. Tìm a>0, biết:
a
a
I dx ln
x(x )
4
1 8
1 5
A. 4 B. 3 C. 3e D. 4e
Câu 233. Hình phẳng giới hạn bởi các đường cong:
f(x) x x
2
2
và
g(x) x
2
có diện tích là:
A.
9
2
B.
19
2
C.
7
2
D.
17
2
Câu 234. Hình phẳng giới hạn bởi các đường cong: f(x) x x
2
2 1
,
g(x) x
1
và các đường thẳng:
x , x
1 1
có diện tích là:
A. 3 B.
2
3
C.
3
2
D.
1
3
Câu 235. Khối tròn xoay sinh ra khi xoay quanh trục hoành phần hình phẳng giới hạn bởi các đường :
y cosx,y ,x ,x
0 0
có thể tích là:
A.
2
2
B.
2
4
C.
2
3
2
D.
2
3
4
Câu 236. Khối tròn xoay sinh ra khi xoay quanh trục hoành phần hình phẳng giới hạn bởi các đường :
y x ,y x
2
1 1
có thể tích là:
A.
7
15
B.
28
15
C.
2
7
15
D.
2
28
15
Một vật chuyển động với biểu thức vận tốc
v x
trong thời gian từ
t
Quang.duong.di.duoc
t
t t S v x dx

2
1
1 2
Câu 237
. Một ô tô đang chuyển động với vận tốc
m / s
12
thì người lái xe bất ngờ tăng tốc cho xe chạy
nhanh dần đều , sau
s
15
thì xe đạt vận tốc
m / s
15
.Tính quãng đường xe đi được sau
s
30
kể từ khi tăng
tốc
A. 270m B. 450m C. 360m D. 540m
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
26
Câu 238. Một lực có độ lớn 40 N (newton) cần thiết để kéo căng một chiếc lò xo có độ dài tự nhiên 10 cm
lên 15 cm. Biết rằng theo định luật
Hooke
trong Vật lý, khi một chiếc lò xo bị kéo căng thêm
x
(đơn vị độ
dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho bởi công thức
f x kx N
, trong đó
k
là hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo lò xo
có độ dài từ 15 cm đến 18 cm ? (kí hiệu
J Jun
là đơn vị của công)
A.
, J
1 56
. B.
J
0,94
. C.
J
1,78
. D.
J
2,03
.
Câu 239
. Một vật chuyển động chậm dần với vận tốc
160 10 m/s
v t t
. Hỏi rằng trong
3s
trước khi dừng hẳn
vật di chuyển được bao nhiêu mét ?
A. 16 m. B. 130 m. C. 435 m. D. 170 m.
Câu 240: Bạn Nhớ đang chở hai người bạn gái của mình là Ty và Sương trên chiếc xe thể thao hiệu
Lamborghini Aventador chạy trên một đường đua thẳng có độ dài 4km. Xe tăng tốc từ 0km/h đến
100km/h trong 3 giây đầu tiên đi hết 260m và sau đó xe chuyển động nhanh dần đều với gia tốc
20 /
m s
.
Tính thời gian để xe hoàn thành đường đua biết vận tốc của chuyển động nhanh dần đều có công thức
o
v at v
với
,
o
a v
là gia tốc và vận tốc đầu.
A. 21s B. 11s C. 14s D. 18s
Câu 241. Một vật đang chuyển động thẳng nhanh dần đều có vận tốc là
18 /
km h
. Trong giây thứ 5 mật
đi được quãng đường là
5,9
m
> tính quãng đường vật đi được sau
10
s
kể từ lúc bắt đầu chuyển động
A.
132
5
m
B.
103,6
m
C.
60
m
D. đáp án khác
Câu 242. Bạn Phương vừa nhai quần đùi vừa thả một hòn bi chuyển động trên một rãnh nằm ngang để
tạo một dao động điều hòa với phương trình chuyển động là
x cos t cm
4 4
3
, cùng lúc đó ở máng
bên cạnh bạn Hợp cũng đang điều khiển chiếc xe hơi đồ chơi mới mượn được của bạn Nhớ và cũng
đang dao động điều hòa với phương trình dao động là
x cos t cm
2 2
2
.Nếu gọi
S
1
là quãng
đường hòn bi của Phương đi được trong khoảng thời gian là
, s
0 25
kể từ lúc xuất phát và
S
2
là quãng
đường chiếc siêu xe của bạn hợp chạy được trong khoảng thời gian
, s
2 875
kể từ lúc xuất phát. Khi đó
i.
S S
1 2
ii.
S S
1 2
iii.
S S
1 2
4i.S S
2 1
12
Có bao nhiêu khẳng định đúng
A. 1 B. 2 C. 3 D. 0
Câu 243. Cho
b
a
f x g x
2 19
và
b
a
f x g x dx
5 3 30
khi đó
b b
a a
f x dx A; g x dx B
thì
A và B có giá trị là bao nhiêu
Câu 244. Cho
b
a
f x g x
2 1
và
b
a
f x g x dx
3 30
khi đó
b
a
f x g x dx ?
11 12
Câu 245. Cho
b
a
f x g x
10
và
b
a
f x g x dx
3 15
khi đó
b b
a a
f x dx g x dx
2016 2017
Câu 246. Cho
f x dx
3
0
15
. Hãy tính
x x f x dx
3
2
0
5
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
27
Câu 247. Cho
f x dx
4
0
4
, Hãy tính
sin x f x dx
4
0
2 3
Câu 248: Cho
x ;khi:x 0
f x
5x+1;khi:x<0
2
1
Hãy tính tích
f x dx
5
3
Câu 249. Cho
x ;Khi:x<-1
f x
x x ;Khi : x
2
6
5 1
Hãy tính tích
f x dx
2
3
Câu 250. Cho Cho
x ;khi : x
f x
x ;khi : x
2
2 1 0
1 0
, Hãy tính tích
f x dx
1
1
Câu 251.Cho
x
I dx a lnc b ln c ;a;b;c Q
x x
2
2
2 2
2
1
1 1
7 12
, Khi đó , hãy tính kết quả của
P a b c
A.
P
43
B.
P
11
C.
P
3
D.
P
3
Câu 252.Cho
dx a a b a
I lnb ln a b ,a;b Q
b b b
x x
2
5 3
1
4
hãy chọn phát biểu sai
A.
a b
B.
a b
1
C.
a b
2 2
5
D.
a b
2 10
Câu 253. Cho
x
I dx
x x x
5
2
3 2
4
3 1
2 5 6
, Chọn phát biểu đúng ?
A.
I ln ln ln
2 4 13 7 14
2
3 3 15 6 5
B.
I ln ln ln C
2 4 13 7 14
2
3 3 15 6 5
C.
I ln ln ln
2 4 13 7 14
2
3 3 15 6 5
D.
I ln ln ln
2 4 13 7 14
2
3 3 15 6 5
Câu 254
. Tính
xdx
I
(x )
1
0
3
1
, Chọn phát biểu đúng ?
A.
1
B.
1
3
C.
1
8
D.
2
3
Câu 255. Cho
(x )
I dx
( x )
2
4
1
2 1
, Phát biểu nào sau đây là sai
A.
x
I C
x
3
1 1
9 2 1
B.
x x
I d
x x
2
1 1 1
3 2 1 2 1
C.
'
(x ) x
I . dx
x
( x )
2
2
1 1 1
3 2 1
2 1
D.
'
x x
I . dx
x x
2
1 1
2 1 2 1
Câu 256
. Tính
x
I dx
x
99
1
101
0
7 1
2 1
, chọn kết quả đúng
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
28
A.
I
100
1
2 1
900
B.
I
100
1
2 1
700
C.
I
100
1
2 1
100
D. kết quả khác
Câu 257. Tính
x
I dx
(x )
1
2 2
0
5
4
, chọn phát biểu sai
A. I
1
8
B.
Đặt
t x
2
4
,
t ;
1 5
C.
Đặt
dt
t x I
t
1
2
0
2
5
4
2
D. .
Đặt
dt
t x I
t
5
2
1
2
5
4
2
Câu 258. Cho
x
I dx
( x )
1
7
2 5
0
1
, Bạn Phương đã giải bài toán như sau
Bước 1.
t x dt xdx
2
1 2
Bước 2.
(t )
I dx
t
2
3
5
1
1 1
2
Bước 3.
I .
5
1 1
4
2
Hãy cho biết lời giải trên đúng hay sai , nếu sai thì sai ở bước nào?
A. Bước 1 B. Bước 2 C. Bước 3 D. Không sai
Câu 259. Cho
I x ( x ) dx ;a,b,c Q
abc
1
5 3 6
0
1
1
.Hãy tính
P a b c
2 3
A.
35
B.
36
C.
37
D.
38
Câu 260. Cho
b
I dx ln ,a;b;c Q
a c
x(x )
4
3
4
1
1 1
1
, Chọn phát biểu sai?
A.
b b c
2
2 5
B.
a b c
C.
a b c
2 2 2
1
D.
a b c
Câu 261. Tính
x
I dx
x( x )
2
7
7
1
1
1
( x ).x
I dx
x .( x )
2
7 6
7 7
1
1
1
. Đặt
t x
7
t
I dt
t( t)
128
1
1 1
7 1
Câu 262. Khi tính
I x dx
1
2
0
1 một học sinh đã thực hiện các bước như sau:
Bước I.
I x dx x x
1 1
2
2
0 0
1 2 1
Bước II.
x
I x x
1
3
2
0
3
Bước III.
I
3
2
1
7
1 1 0
3 3
Lời giải trên đã đúng chưa ? Nếu sai thì sai từ bước nào ?
A. Sai từ bước I. B. Sai từ bước II. C. Sai từ bước III. D. Lời giải đúng
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
29
Câu 263. Tính thể tích khối cầu bán kính R là khối tròn xoay thu đc khi quay nửa hình tròn giới hạn bởi
đường
2 2
y R x R x R
và đường thẳng
0
y
xung quanh trục Ox
A.
3
3
4
R
. B.
3
3
4
R
. C.
3
4
3
R
. D.
3
4
3
R
.
Câu 264. Tích phân
x
I dx a bln , a;b
cos x
3
2
0
2
3
. Khi đó tổng
a b
gần với gía trị nào nhất sau
đây ?
A.
3
. B.
3
. C.
1
. D.
1
.
Câu 265
. Cho
f x
là hàm số liên tục và lẻ trên
, biết rằng
f x dx
16
0
3
. Khi đó tích phân
f x dx
0
16
bằng
A. -3. B. 2016. C. 3. D. -2016.
Câu 267. Vòm cửa lớn của trường Đại Học Bôn Ba có dạng hình Parabol. Người ta dự định lắp cửa kính
cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp biết rằng vòm cửa cao 8 m và rộng 8 m ?
A.
m
2
128
3
. B.
m
2
64
3
. C.
m
2
32
3
. D.
m
2
16
3
.
Câu 268. Tính diện tích hình phẳng giới hạn bởi đường cong
2
2
y x x
, trục Oy và đường thẳng
3
x
.
A.
15
2
S B.
59
6
S C.
15
2
S
B.
Câu 269. Kí hiệu (H) là hình phẳng giới hạn bởi hai đường cong
x
y e
trục Oy và đường thẳng
ln4
x
.
Tính thể tích khối tròn xoay thu được khi cho (H) xoay quanh trục Oy.
A.
V e
B.
3
2
V
C.
2
V
D.
4
V
Câu 270.
x dx a
I
b
x x
1
2
0
(3 1) 5
3ln
6
6 9
vậy phát biểu nào sau là đúng
1.
a b
7
2.
a b
7
3.
a b
4.
a b
A. chỉ 1 và 3 đúng B. chỉ
2
và 3 đúng
C. Chỉ 1 và 4 đúng D. không đáp án nào đúng
Câu 271. Chọn đáp án đúng khi tính tích phân
3
4 2
2
2
3 2
1
x x
I dx
x
A. I
3
23 ln
2
B. I
3
23 ln
2
C.
I
3
ln
2
D.
I
23
Câu 272. Cho
I xdx
2
5
0
cos
, Đâu là kết quả của tích phân trên trong các số dưới đây
A.
8
15
B.
8
15
C.
8
15 4
D.
8
15 2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
30
Câu 273. Thể tích vật thể khối tròn xoay giới hạn bởi các đường
2
ln
y x x
, trục hoành,
x e
khi xoay
quanh trục hoành được tính bới công thức nào dưới đây?
A.
x
V x lnx e dx
1
2
0
0
B.
e
Vox x lnxdx
2
1
C.
e
Vox x lnx dx
2
2
1
D.
e
Vox x lnxdx
2
1
A.
36
B.
36
C.
9
D.
9
Câu 276. Cho hình phẳng giới hạn bởi đường cong
y sinx
, trục hoành và hai đường thẳng
x ,x
0
.
Thể tích của khối tròn xoay thu được khi quay hình này quanh trục Ox:
A.
V sin xdx
3
0
. B.
V sin xdx
2
0
.
C.
V sin xdx
2
0
. D.
V sin xdx
2
0
.
Câu 277. Cho hình phẳng (H) giới hạn bởi trục hoành và Parabol
C : y ax x a
2
0
. Thể tích tính theo
a
sinh ra khi quay hình phẳng (H) quanh trục
Ox
là:
A.
a
3
30
(đvtt). B.
a
5
20
(đvtt). C.
a
5
15
(đvtt). D.
a
5
30
(đvtt).
Câu 278. Biết rằng tích phân
x
dx a bln cln , a;b;c
x x
5
1
2 1 3
2
5
2 3 2 1 1
. Khi đó giá trị
A a b c
2
là
A.
8
B.
0
C.
4
D.
7
Câu 279. Trong hệ tọa độ
Oxy,
cho Parabol
C
và
d
là tiếp tuyến
của
C
tại điểm
A ;
1 1
như hình vẽ. Diện tích của phần tô vàng
như hình vẽ là:
A.
1
3
. B.
2
3
.
C.
4
3
. D.
1
.
Câu 274. Diện tích hình phẳng giới hạn bởi các đường y x
2
2x và y x
2
4x có kết quả nào dưới
đây
A.
81
B.
9
C.
9
D.
81
Câu 275. Cho hình phẳng
H
được giới hạn bởi các đường y x
2
4x6;y 0;x 2;x 4 .Diện tích
hình phẳng
H
có giá trị là
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
31
Câu 280. Tính diện tích hình phẳng giới hạn bởi hai đường thẳng
0,
x
x
và đồ thị hai hàm số
sin , cos .
y x y x
A. 2. B.
2 2
. C.
2 3
. D. 1.
Câu 281. Tính diện tích hình phẳng giới hạn bởi đường cong có phương trình
2
1
y x
, tiếp tuyến với
đường này tại điểm
2;5
M và trục tung.
A. 3. B.
5
3
. C.
8
3
. D. 6.
Câu 282. Tính thể tích vật thể nằm giữa hai mặt phẳng có phương trình
0
x
và
2
x
, biết rằng thiết
diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
0;2
x
là một phần tư
đường tròn bán kính
2
2
x
, ta được kết quả nào sau đây?
A.
32 .
V
B.
64 .
V
C.
16
.
5
V
D.
8 .
V
Câu 283 . Tính tích phân
1
2
0
2
d
1
x
I x
x
.
A.
1
2
I . B.
ln2
I
. C.
1
I
. D.
ln2
2
I .
Câu 284. Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
2
4
y x , trục hoành và hai đường thẳng
1, 1
x x .
A.
406
15
S . B.
22
3
S . C.
22
3
S . D.
11
3
S .
Câu 285. Cho hình
được giới hạn bởi đồ thị
: 2 1 .ln
C y x x
, trục hoành và đường thẳng
2
x
. Tính
thể tích khối tròn xoay được tạo thành khi quay
quanh trục hoành.
A.
5
2
V . B.
5
ln64
2
V . C.
ln64 4
V . D.
143
9
V .
Câu 286. Tìm nguyên hàm của hàm số
2
sin
y x
.
A.
2
cos
F x x C
. B.
2 sin2
4
x x
F x C
.
C.
cos2
F x x x C
. D.
2
1
cot
F x C
x
.
Câu 287
F x
là một nguyên hàm của hàm số
ln
x
y
x
. Nếu
2
4
F e
thì
ln
d
x
x
x
bằng:
A.
2
ln
2
x
F x C
. B.
2
ln
2
2
x
F x
.
C.
2
ln
2
2
x
F x
. D.
2
ln
2
x
F x x C
.
Câu 288. Trong giải tích, với hàm số
y f x
liên tục trên miền
,
D a b
có đồ thị là một đường cong
C
, người ta
có thể tính độ dài của
C
bằng công thức
2
1 ' d
b
a
L f x x
. Với thông tin đó, hãy tính độ dài của đường cong
C
cho bởi hàm số
2
ln
8
x
y x
trên
1;2
.
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
32
A.
3 8ln2
8
. B.
31
ln4
24
. C.
3 8ln2
8
. D.
31
ln4
24
.
Câu 289 . Giá trị của
d 12
b
a
f x x
và
d 8
b
c
f x x
. Khi đó
d
c
a
I f x x
có giá trị bằng :
A.
20
I
. B.
20
I
. C.
4
I
. D.
4
I
.
Câu 290
. Cho
ln
0
ln2
2
m
x
x
e dx
I
e
. Khi đó, giá trị của số thực
m
bằng :
A.
0
4
m
m
. B.
2
m
. C.
4
m
. D.
m e
.
Câu 291. Cho
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
3 2
6 9
y x x x
và trục
Ox
. Tìm số nguyên
lớn nhất không vượt quá giá trị của
S
.
A.
10
. B.
6
. C.
7
. D.
27
.
Câu 292 Sơ đồ ở bên phải phác thảo của một khung cửa sổ.
Diện tích của cửa sổ được tính bằng công thức nào sau đây?
A.
1
2
2
1
2
5
4 d
2
S x x
. B.
1
2
2
1
2
5
2 d
2
S x x
.
C.
1
2
2
1
2
2 d
S x x
. D.
1
2
2
1
2
1 4 d
S x x
.
x
y
1
2
1
2
O
2
5
2
y x
2
2
y x
Câu 293. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol
2
4
y x
và
2
2
y x
quay
quanh trục
Ox
là kết quả nào sau đây?
A.
10 .
V
B.
12 .
V
C.
14 .
V
D.
16 .
V
Câu 294. Tính tích phân
1
2
0
1
x
I x e dx
A.
2
3
1
4
I e
B.
2
3 1
4
e
I
C.
2
3 1
4
e
I
D.
2
1
1
4
I e
Câu 295: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3 2
2
y x x
và đồ thị hàm
số
2
3
y x x
.
A.
27
4
B.
21
4
C. 0 D.
9
2
Câu 296: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
3 2 ln
y x x
và trục
hoành. Tính thể tích khối tròn xoay thu được khi cho hình (H) xoay quanh trục Ox.
A.
8ln2 16
V
B.
24ln2 16
V
C.
24ln2 16
V
D.
8ln2 16
V
Câu 297. Giá trị của :
x x dx
2
2
1
3 2 3
bằng :
A.6. B. 7. C. 8 . D. 9.
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
33
Câu 298. Diện tích hình phẳng giới hạn bởi các đường
y x
2
, trục
Ox
và đường thẳng
x
2
là
A.
8
. B.
8
3
C.
16
. D.
16
3
.
Câu 299
. Bằng cách đổi biến số
x sint
2
thì tích phân
dx
1
2
0
2
4
là:
A.
dt
3
0
2 . B.
6
0
2 C.
dt
6
0
2 . D.
dt
t
3
0
2 .
Câu 300. Biết rằng thể tích vật tròn xoay khi quay hình phẳng giới hạn bởi các đường
y tanx
,
y
0
,
x ,x
0
3
có dạng
b
V a
3
3
(đvtt)
a,b
0
. Tổng giá trị của
a b
3 2
có giá trị gần với giá trị
nào nhất sau đây ?
A.
,
6 25
. B.
,
8 24
. C.
,
7 65
. D.
,
9 41
.
Câu 301. Cho hình phẳng
H
giới hạn bởi các đường
y x mx m ,x ,x
4 2 2
2 0 1
(m là tham số thức).
Biết rằng
m ,m m m
1 2 1 2
là hai giá trị để diện tích hình phẳng
H
bằng
28
15
(đvdt). Khi đó Tổng
m m
1 2
3
bằng:
A.
4
. B.
3
. C.
3
. D.
4
.
Câu 302. Anh An muốn làm cửa rào sắt có hình dạng và kích thước
giống như hình vẽ kế bên, biết đường cong phía trên là một
parabol. Giá
m
2
1
cửa rào sắt có giá là 700.000 đồng. Vậy anh An
phải trả bao nhiêu tiền để làm cài cửa rào sắt như vậy. (làm tròn
đến hàng chục nghìn) ?
A.
. .
6 420 000
đồng. B.
. .
6 320 000
đồng.
C.
. .
6 520 000
đồng. D.
. .
6 620 000
đồng.
Câu 303. Tính tích phân
1
2
0
3 2
x x
dx
A.
4 10 3
ln3 ln6 2ln2
B.
4 10 3
ln3 ln6 2ln2
C
C.
4 10 3
ln3 ln6 2ln2
D.
4 10 3
ln3 ln6 ln4
Câu 304. Tích phân
1
0
ln 1 2ln 1
I x dx a
vậy kết luận nào sau đây là đúng
A.
2
a
B.
1
2
a
C.
4
a
D.
3
a
Câu 305. Một hình phẳng H đươc giới hạn bởi một Parapol và một đường thẳng như hình bên ( miền
gạch ca rô ) có dienj tích là bao nhiêu
A.
9
2
B.
9
2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
34
C.
9
D.
9
Câu 306. Cho hình phẳng
: ln ; 0; 1;
H y x y x x e
Tính thể tích tạo thành khi cho hình phẳng
trên quay quanh trục Ox
A.
1
ox
V
B.
ox
V
C.
2
ox
V
D.
2
ox
V
Câu 307. Tính nguyên hàm :
x
I dx
x x
2
3 9 1
A.
I ( x ) x
3
2 3
2
1
9 1
27
B.
I x x C
3
2 3
1
9 1
27
C.
I x x C
3
2 3
27 9 1 D.
I x x C
3
2 3
9 1
Câu 308.
x x
I dx
x x
2
1
, có bao nhiêu kết quả đúng ?
i.
I x x C
3
4
1
9
ii.
I x x
3
4
1
9
iii.
I x x C
3
2
4
1
9
A. 0 B. 1 C. 2 D. 3
Câu 309. Cho
x
I dx a lna;a Q
x
4
0
2 1
1 2 1
.Phát biểu nào sai ?
A.
a
2
3
B.
a a
2
2
C.
a
2
D.
a
2
Câu 310. Cho
dx a
I ln , a;b Q
b
x x
a.b
6
2
2
1
2 1 4 1
, Chọn phát biểu đúng ?
A.
a b
0
B.
b a
2
1
C.
b a a b
2 2
2 2
D.
a b
2 2
Câu 311. Tính
I x x dx
1
3 2
0
1
Có bao nhiêu phát biểu sai trong các phát biểu sau?
i. Đặt:
t x
2
1
I t t dt
1
2 4
0
. ii. I
2
15
iii. Đặt:
t x
2
1
I t t dt
0
4 2
1
. 4i. I
1
12
A. 0 B. 1 C. 2 D. 4
Câu 312. Cho
x a
I dx cln ; a;b;c
b
x
1
0
1
2
1
, hãy tính
P a b c
2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
35
A.
P
20
B.
P
16
C.
P
10
D.
15
Câu 313. Cho
x a
I dx a aln , a;b
b
x x
3
0
3
2
3 1 3
, Hãy tính
P a b ab
3 3
2
A.
P ab
B.
P ba
C.
P ba
2
D.
P a b
2
Câu 314. Cho
I x. x dx
0
3
1
1
, chọn phát biểu sai
A. Đặt
t x t ;
3
1 0 1
B.
t t
I
1
7 4
0
9
3
7 4 28
C. Đặt
t x dx t dt I (t )dt
0
2 33
1
1 3 3 1
D.Đặt
t x dx t dt I (t )dt
1
2 33
0
1 3 3 1
Câu 315.
Tinh
x a b
I dx ln ,voi : a;b P a b
a
x x
b

5
2 2 2
2
3
1
1 4
2
3 1
A.
P
26
B.
P
31
C.
P
41
D.
P
52
Câu 316.
x x
I dx
x
3
2
0
2 1
1
, Bạn Tiên giải như sau
Đặt x t x t
2
1 1
dx tdt
2
(t ) (t ) t
I tdt ( t t )dt t
t
2
2 2
2 2 2 5
4 2 3
1
1 1
2 1 1 1 4 54
2 2 2 3 2
5 5
Bạn Nhi với sự cố vấn của bạn Linh đã giải như sau
Đặt x t x t
2
1 1
dx tdt
2
(t ) (t ) x
I tdt ( x x )dx x
t
2
2 2
2 2 2 5
4 2 3
1
1 1
2 1 1 1 4 54
2 2 2 3 2
5 5
Em hãy cho biết, trong lời giải trên của hai bạn ai giải sai
A. Tiên giải sai B. Nhi giải sai C. Cả hai đều sai D. Cả hai đều đúng
Câu 317. Cho
Tinh
x dx a b c
I ;a,b,c,d P a b c d
d
(x ) x

1
2 2
0
2
1 1
A.
P
32
B.
P
20
C.
P
31
D.
P
18 2
Câu 318.
x
I dx
x
4
2
0
1
1 1 2
, Bạn Hô Nam đã giải như sau
Bước 1
Đặt
dx
t x dt dx (t )dt
x
1 1 2 1
1 2
và
t t
x
2
2
2
Bước 2. Ta có: I =
(t t )(t ) t t t
dt dt t dt
t
t t t
4 4 4
2 3 2
2 2 2
2 2 2
1 2 2 1 1 3 4 2 1 4 2
3
2 2 2
Nguyễn Tiến Chinh – Vinastudy.vn Trắc nghiệm nguyên hàm – Tích Phân
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN
36
Bước 3 I =
t
t ln t
t
2
1 2
3 4
2 2
= ln
1
2 2
4
Hãy cho biết , bài giải của bạn Nam đúng hay sai , nếu sai thì sai ở bước giải thứ mấy
A. Không sai B. Bước 1 C. Bước 2 D. Bước 3
Câu 319
. Tính
x
I dx
x
8
2
3
1
1
, có bao nhiêu phát biểu đúng
i.
x
I dx
x x
8
2 2
3
1
1 1
=
x ln x x
8
2 2
3
1 1
ii.
I ln ln
1 3 2 8 3
iii.
I ln
3 2
1
8 3
iii.
e e
I log log
1 3 2 8 3
A. 1 B. 2 C. 3 D. 4
Câu 320. Tính
I (x ) x x dx
1
3 2
0
1 2
, chọn phát biểu đúng ?
A. I
2
15
B. I
2
15
C. I
1
15
D. I
1
15
Câu 321. Tính
x x x
I dx
x x
2
3 2
2
0
2 3
1
, chọn phát biểu đúng?
A.
4
3
B.
2
3
C.
4
3
D.
3 3 2
3
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

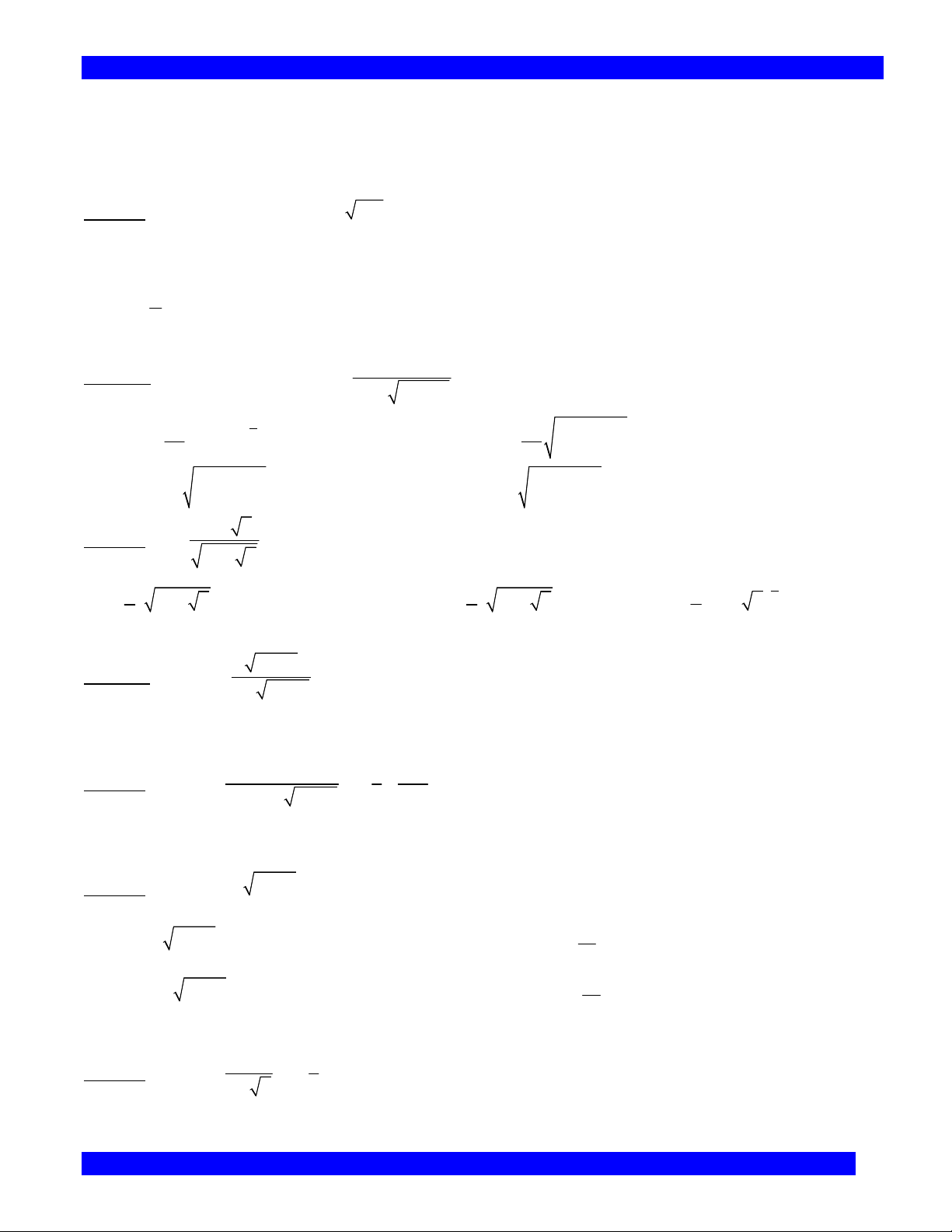
Preview text:

Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Chuyên đề 5 – Nguyên Hàm – Tích phân
Câu 1: Biết F(x) là một nguyên hàm của hàm số: f (x) sin2 x x3  2. Giá trị của // F   là?  2  2 3 2 3 2 3 2 3 A. 1  B. 1  C.  D. 4 4 4 4
Câu 2: Nguyên hàm của hàm số: f (x) xx2 1 là? 3 1 3 1 A. F(x)  
1 x2  C B. F(x)
1 x2 C 3 3 3 1 C. F(x)   x2 1  C D. F(x)
1 x2 C 2
Câu 3: Nguyên hàm của hàm số: x f (x) xe2  là? 1 A. 2x
F(x) (2x ) 1 eC B. 2x
F(x) (2x ) 1 eC 4 C. 2x
F(x) ( x ) 1 eC D. 2x
F(x) ( x ) 1 eC 2 x2  3x
Câu 4: Giá trị của dx  là? x 1 3 3 A.  B. C. 3 D. –2 2 2
Câu 5: Diện tích hình phẳng giới hạn bởi (C): y = x3 –3x2 +1 và (D): y = 1 là? 13 27 A. 3 B. C. 9 D. 2 4
Câu 6: Thể tích của khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi hai đường: y = x2 –x, y = 0 quanh trục Ox là? 1 1 1 A.  B. C. D. 6 6 30 30
Câu 7: Một chiếc xe ô tô sẽ chạy trên đường với vận tốc tăng dần đều với vận tốc v = 10t (m/s) t là khoảng
thời gian tính bằng giây, kể từ lúc bắt đầu chạy. Hỏi quảng đường xe phải đi là bao nhiêu từ lúc xe bắt
đầu chạy đến khi đạt vận tốc 20 (m/s)? A. 10m B. 20m C. 30m D. 40m 7 x3dx a
Câu 8. Giá trị của tích phân I  
được viết dưới dạng . Khi đó giá trị của a-7b bằng 3  x2 0 1 b A. 2 B. 0 C. 1 D. -1
Câu 9. Cho hình phẳng giới hạn bởi các đường y x , y x . Quay xung quanh trục ox. Thể tích khối
tròn xoay tạo thành bằng A. B. C. D. 6 3 4
Câu 10. Công thức nào sau đây đúng với k là hằng số b a b b
A. k. f (x)dx f (x) kdx  
B. k. f ( x)dx  k f ( x)dx   a b a a
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 1
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân b a b b
C. k. f ( x)dx k f (x)dx  
D. k. f ( x)dx k f (x)dx   a b a a
Câu 11. Diện tích hình phẳng giới hạn bởi các đường cong y=x+sinx và y=x 0  x  2A. 5 B. 3 C. 4 D. 4
Câu 12. Cho M x2 .x3 4 dx  chọn câu đúng 3 2 3 A. M
4  x3 C B. M    x3 2 4  C 9 3 1 C. 3 M   x3 2 4  C D. M
4 x  C 9 1 dx A Câu 13. Cho
x(x )1 . Kết quả nào sau đây đúng 1 2
A. 0B. 1C. A<0 D. 2ln m x e dx Câu 14. Biết  ln 2  Khi đó giá trị m là x 0 e  2 A. 1 B. 2 C. 3 D. 4 x
Câu 15. Gọi F(x) là nguyên hàm của hàm số f (x)
thỏa mãn F(2)=0. Khi đó phương trình F(x)=x  x2 8 có nghiệm là A. 1  3 B. 1 C. -1 D. 0 2x4  3
Câu 16: Tìm nguyên hàm của hàm số f(x) = x2 2x4  3 2x3 3 2x4  3 2x3 3 A. dx    C  B. dx    Cx2 3 x x2 3 x 2x4  3 2x 3 2x4  3 2x 3 C. dx    C  D. dx    Cx2 3 x3 x2 3 x3 e ln x
Câu 17: Tính tích phân I dxx(lnx )2 1 2 1 3 1 3 1 3 1 3 A. I   l n
B. I    l n
C. I    l n D. I   l n 3 2 3 2 3 2 3 2 2
Câu 18: Tính tích phân s inx I (ecos x)cos xdx.  0
A. I  e   1 B. I e   1 C. I e   1
D. I  e   1 4 4 4 4
Câu 19:Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x) liên tục trên đoạn a;b   ,trục hoành, hai
đường thẳng x a,x b có công thức là:
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 2
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân b b b a A.S f (x) dx  B. S f (x)dx  C. S [ f (x)]2  dx  D.S f (x) dxa a a b
Câu 20: Diện tích hình phẳng giới hạn bởi đồ hai thị hàm số y x2  x  2 ,y x  2 và hai đường thẳng x  1  , x  3 . 20 34 20 34 A. B.  C.  D. 3 3 3 3
Câu 21: Cho hình (H) giới hạn bởi : y sin x cos x,y  0 ,x  0 ,x
. Thể tích khối tròn xoay khi cho hình 2 (H) quay quanh trục Ox . 2 2 2 2 A. B. C. D. 8 2 16 4
Câu 22: Một vật chuyển động với gia tốc đầu bằng 0, vận tốc biến đổi theo quy luật a , (m / s2 0 3 ) .Xác
định quãng đường vật đó đi được trong 40 phút đầu tiên. A. 1200m B. 240m C. 3600m D.3200m
2 1  sin2x cos2x
Câu 23: Tích phân I dx  bằng: sin x cos x 0 A. I  2 B. I  1 C. I D. I  1  2 2
Câu 24: Tích phân I x.sin xdx.  bằng: 0 A. I  3 B. I  2 C. I  1 D. I  1 
Câu 25: Họ nguyên hàm của hàm số: x y xe dx  là: A. x xe C B. x x
xe e C C. x x
xe e C D. xxe C
Câu 26: Họ nguyên hàm của hàm số: y = cos2x.sinx là: 1 1 1
A. cos3 x C B. cos3  x C
C. sin3 x C
D.  cos3 x C 3 3 3
Câu 27: Họ nguyên hàm của hàm số: y ln xdx  là:
A. x ln x x C
B. x ln x C
C. x ln x x C
D. ln x x C
Câu 28: Diện tích hình phẳng được giới hạn bởi hai đường y x2  2 và y x là: 9 9 2 9 A. S = B. S= C. S= D. S = 3 4 9 3
Câu 29: Thể tích khối tròn xoay được tạo bởi phép quay quanh trục 0x hình phẳng giới hạn bởi hai đường y x2  và y2  x là: 3 7 A. V  B. V  C. V  D. V  10 5 10 10 dx
Câu 30: Biết I  
= a. 2x  1  b.ln 2x  1  4  C . Tính a + b 2x  1  4
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 3
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân A. -2 B. -3 C. 1 D. 2 Câu 31: Biết x L e cos xdx  = a.e + b. Tính a + b 0 A. 0 B. 1 C. -2 D. 3 1
Câu 32: Biết L x 1  x2 dx a. 2  b  . Tính a - b 0 A. 1 B. 1/3 C. 2 D. 3
Câu 33: Diện tích hình phẳng giới hạn bởi các đường y = x2 và y = x + 2 là A. 3/2 ; B. 9/2 ; C. 15/2 ; D. 21/2
Câu 34: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 2 – x2 , y  1 quanh trục Ox là: A. 56/15 ; B. 86/15 ; C. 16/15 ; D. 16/7 1
Câu 35: Diện tích hình phẳng giới hạn bởi các đường y = x – 1 + lnx, y = x – 1, x = e là : x 1 1 1 2 A. ; B. ; C. ; D. 2 3 8 3 1 dx
Câu 36: Giá trị của I   là: x2 0  5x  6 3 A. I = 1 B. I ln C. I = ln2 D. I = ln(4/3) 4
Câu 37: Cho hai hàm số y f (x), y g(x) liên tục trên đoạn a;b 
 . Diện tích hình phẳng giới hạn bởi đồ
thị hai hàm số đó và các đường thẳng x a, x b được tính theo công thức: b b
A. S  g(x) f (x) dx   
B. S   f (x) g( x) dx    a a b b
C. S   f (x) g(x) dx    D. S
f ( x) g(x)dxa a 1
Câu 38: Cho hàm số f (x)
. Khi đó F(x) f (x)dx  là 2x  1 1 A. F(x)  2x  1
B. F(x)  2x  1  C 2 1 C. F(x)  2x  1  C
D. F(x)  2x  1 2
Câu 39: Một hòn đá rơi tự do từ đỉnh của một vách núi thẳng đứng và chạm vào mặt đất với vận tốc 98
m/s. Hỏi đỉnh núi cao bao nhiêu mét so với mặt đất? (lấy gia tốc rơi tự do bằng 9,8 m/s2) A. 490 m B. 430 m C. 400 m D. 460 m 2
Câu 40: Giá trị tích phân I ( x ) 1 sin xdx  là 0 A. I  2  B. I  3 C. I  1 D. I  2
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 4
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân e
Câu 41: Giá trị tích phân I x2 lnxdx  là 1  e3 1 2 e3 2  1 e3 2  1 e3 2  1 A. I B. I C. I   D. I  9 9 9 9 2
Câu 42: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y x x2 6
và đồ thị hàm số y  x  6 là A. 10 B. 8 C. 7 D. 9
Câu 43: Kí hiệu (H) là hình phẳng giới hạn bởi hai đồ thị hàm số y   x2 2 1
và y  2(1  x) . Thể tích V
của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là 5 4 2 A. V B. V C. V D. V  3 3 3 3 0 dx
Câu 44: Tính tích phân I    x2 1  3x  2 5 3 3 2 A. ln B. ln C. ln D. ln 6 4 2 3 1 x
Câu 45: Tính tích phân I dx( x)3 0 1 2 1 1 1 1 A B. C. D. 18 15 11 8 1 x3dx
Câu 46: Tính tích phân I    2 x8 0  4 1 ln 3 1 ln3 1 ln3 1 ln3 A.  B.  C.  D.  2 2 6 12 9 28 96 128 2 2
Câu 47: Tính tích phân I  1  x2 dx  1 2 3  1 3  1 2  3 2  3 A.  B.  C.  D.  12 4 12 4 24 8 24 8 2
Câu 48: Tính tích phân I  4  x2 dx  1 1  3 16  3 3 3 3  1 6  2 2 A. B. C. D. 2 12 6 9 e
Câu 49: Tính tích phân I cos(ln x)dx  1 1 1 1 1 A. e 1 B. e 1 C. e 1 D.  e  1 4 2 2 2
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 5
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 50: Tính diện tích hình phẳng giới hạn bởi các đường thẳng x  0,x ,
1 y  0 và đồ thị hàm số x2  3x  1 y x  1 1 1 3 3 A.  ln 2 B.  ln 3 C.  ln 2 D.  ln 3 2 2 2 2
Câu 51: Tính diện tích hình phẳng giới hạn bởi các đồ thị y  x2  2x,y  3x 125 125 125 125 A. B. C. D. 2 3 6 8
Câu 52: Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số y sin3 x,y cos3   x và trục Oy với 0  x  4 A. 2  1 B. 2 2  1 C. 4 2  5 D. 5 2  4
Câu 53: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi: y x ln x, y  0,x , 1 x e e3 1 e3 1
e3  3 e3 5  3 A. B. C. D. 3 2 27 27
Câu 54: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi: y , y cos6 x sin6 0
x ,x  0,x  2 2 2 2 5 2 5 A. B. C. D. 3 2 6 16
Câu 55: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới hạn bởi: y x2  ,y x 3 2 A. B. C. D. 10 10 3 3
Câu 56: Tính thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với H là hình phẳng giới
hạn bởi: y x2  x ,y  x2 4 6  2x  6 A. B. 2 C. 3 D. 8
Câu 57: Công thức nào sau đây sai?
A. 1.dx  0  C  B.
dx x Cx a C. x a dx   C
D. cos xdx  s inx  C  ln a 1
Câu 58: Hàm số y  có nguyên hàm là: 2 sin x
A.  cot x C B. cot x C C. tan x C
D.  tan x C 2x x
Câu 59: Nguyên hàm của hàm số f (x)  là: x 3 4 3 3 A. 2
f (x)dx  .x x C  B. 2
f (x)dx  .x x C  3 4
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 6
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 3 3 4 C. 2 f (x)dx x   x C  D. 2
f (x)dx  .x C  3 2x  3
Câu 60: Nuyên hàm của hàm số f (x)  là: x 1 A.
f (x)dx 2x  5 ln x 1  C  B.
f (x)dx 2x  5ln x 1  C
C. f (x)dx x
  5ln x 1  C  D.
f (x)dx 2x  3  5 ln x 1  C
Câu 61: Nguyên hàm của hàm số f (x)  sin(3  5x) là: 1 1 A.
f (x)dx  o
c s(3  5x)  C  B.
f (x)dx   o
c s(3  5x)  C  5 5 C. f (x)dx 5  os
c (3  5x)  C  C.
f (x)dx   5 os
c (3  5x)  C   4  Câu 62: Nguyên hàm 3 2 x dx   là:  x  3 5 A. 3 5
x  4 ln x C B. 3 5
x  4 ln x C 5 3 C. 3 5
x  4 ln x C D. 3 5
x  4 ln x C  3  Câu 63: Nguyên hàm 2 x   2 x dx   là:  x  3 x 4 4 A. 3  3ln x x C B. 3 2x  3ln x x C 3 3 3 3 x 4 3 x 3 C. 3  3ln x x C D. 3  3ln x x C 3 3 3 4 1 Câu 64: Nguyên hàm dx  là: x(x  3) 1 x 1 x 1 x  3 1 x  3 A. ln  C B.  ln  C C. ln  C D.  ln  C 3 x  3 3 x  3 3 x 3 x Câu 65: Nguyên hàm 2 (1 sin x) dx  là: 3 1 3 1 A.
x  2 cos x  sin 2x C B.
x  2 cos x  sin 2x C 2 4 2 4 3 1 3 1 C.
x  2 cos x  sin x C C.
x  2 cos x  sin x C 2 4 2 4
Câu 66: Nguyên hàm ln xdx  là:
A. x ln x x C
B. x ln x x C
C. x ln x x C
D. x ln x x C
Câu 67: Theo định nghĩa tích phân thì: b b b b A.
f (x)dx F (x)  F (b)  F (a)  B.
f (x)dx F (x)  F (a)  F (b)  a a a a b b b b
C. f (x)dx F (x)  F (b)  F (a)  C.
f (x)dx F (x)  f (b)  f (a)  a a a a
Câu 68: Tính chất nào sau đây sai?
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 7
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân b c b b c b A.
f (x)dx
f (x)dx
f (x)dx, (a c b)   
B. f (x)dx
f (x)dx
f (x)dx, (a c b)    a a c a a c b b b b b
C. k. f (x)dx k f (x)d , x  
k là hằng số D.  f (x)  g(x)dx f (x)dx g(x)dx    a a a a a
Câu 69: Nếu u u(x) và v v(x) là hai hàm số có đạo hàm liên tục trên đoạn [ ; a b] thì: b b b b b b A.
u(x) v'(x)dx  (u(x) v(x))  u'(x) v(x)dx  
B. u(x) v'(x)dx  (u'(x) v'(x))  u'(x) v(x)dx   a a a a a a b b b b b b C.
u(x) v'(x)dx  (u(x) v'(x))  u'(x) v(x)dx   D.
u(x) v'(x)dx  (u(x) v(x))  u'(x) v(x)dx   a a a a a a 1
Câu 70: Giá trị của tích phân 3x 1 I e   dx  là: 0 1 1 A. 4 I  (e e) B. 4 I  (e e) C. 4 I  3(e  ) e D. 4
I  3(e e) 3 3 3 2 2x  3x  1
Câu 71: Cho I dx
. Kết quả nào sau đây sai? x  2 1 3 5 A. I  6  3ln B. I  6  3ln 5 3
C. I  6  3ln 5  3ln 3 D.
I  (9  3  3ln 5)  (11 3ln 3) 2
Câu 72: Giá trị của tích phân I  sin 3x cos 5xdx  là:  2 A. I  0 B. I  1 C. I  2 D. I  3 1
Câu 73: Giá trị của tích phân 3
I x 1 xdx  là: 0 9 28 A. I  B. I  C. I  0 D. I  1 28 9 2
Câu 74: Giá trị của tích phân 5 I  sin xdx  là: 0 8 2 A. I  B. I  C. I  1 D. I  1 15 9 2
Câu 75: Giá trị của tích phân I  (2x 1) os c xdx  là: 0
A. I 1
B. I  1 C. I D. I  2 2
Câu 76: Giá trị của tích phân 2
I x ln xdx  là: 1
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 8
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 1 1 8 8 1 8 8 1 A. (24 ln 2  7) B.  (24 ln 2  7) C. ln 2   D.  ln 2   9 9 3 9 9 3 9 9
Câu 77: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số f (x) liên tục, trục hoành và hai đường thẳng x  ,
a x b được tính theo công thức: b b A. S f ( ) x dx  B. S f ( ) x dxa a b b 2 C. S f ( ) x dx  D. S
f (a) f (b)dxa a
Câu 78: Cho hàm số y f x liên tục trên đoạn [ ;
a b] . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y f x , trục hoành và hai đường thẳng x = a, x = b. Khi D quay xung quanh Ox ta được một khối tròn xoay có thể tích là: b b b b A. 2
V   f (x)dx
B. V   f (x)dx  C. 2 V f (x)dx  D. V f (x)dxa a a a
Câu 79: Diện tích hình phẳng giới hạn bởi các đường sau y  s inx , trục hoành, trục tung và đường
thẳng x là: A. S 2 B. S  2  C. S  2 D. S  2
Câu 80: Diện tích hình phẳng giới hạn bởi các đường sau 3
y x  3x , y x là: A. S 8 B. S  8  C. S 4 D. S  4 
Câu 81: Diện tích hình phẳng giới hạn bởi các đường sau 3 2
y x  3x , y  2
x , được tính bằng tích phân sau 2 2 3 2 3 2 A. S x 3  x 2xdx  B. S x 3  x 2xdx  0 1  2 2 3 2 3 2 C. S  (x 3  x 2 ) x dx  D. S  (x 3  x 2 ) x dx  0 1 
Câu 82: Diện tích hình phẳng giới hạn bởi các đường sau y  cos ,
x y  0, x  0, x  , được tính bằng 4 tích phân sau 4 4 2 x 4 2 A. S  cosxdx
B. S cosxdx  C. S  cos dxS  cos xdx  2 D. 0 0 0 0
Câu 83: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau: Trục Ox,
y  s inx, (0  x ) , quay xung quanh trục Ox là:
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 9
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 2 2 2 2 A. V  B. V  C. V  D. V  2 4 2 4
Câu 84: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau: 2
y  2x x , y  0 ,
quay xung quanh trục Ox là: 16 15 16 15 2 2 A. V B. V C. V D. V 15 16 15 16
Câu 85: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau: 2
y x 1, y  0 , quay
xung quanh trục Ox được tính bởi: 1 1 2 2 2 2 2
A. V (x 1  ) dx  B. V (x 1  ) dx  1  1  1 1 2 2 2
C. V  (x 1  ) dx
D. V (x 1  )dx  1  1 
Câu 86: Thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường sau:
y  s inx, y  0, x  0, x
, quay xung quanh trục Ox được tính bởi: 4 4 4 4 4 2 2 2 2
A. V sin xdx  B. V sin xdx
C. V sinxdx  D. V sinxdx  0 0 0 0 1 1
Câu 88. Họ nguyên hàm của hàm số f (x)   là: 2 x x 1 1 1 A. 2
ln x  ln x C B. lnx – + C C. ln|x| + + C D. lnx + + C x x x
Câu 89. Họ nguyên hàm của hàm số f x  1 cos3x là: 1 1
A. x  sin 3x C
B. x  sin 3x C
C. x  sin 3x C
D. x  sin 3x C 3 3 x e
Câu 90. Họ nguyên hàm của hàm số: y = là: x e  2 A. 2ln( x e  2)  C B. ln( x e  2) + C C. exln( x e  2) + C D. 2x e + C. dx
Câu 91. Kết quả của  là: 2
x  3x  2 x 1 x 1 2  x A.  ln  C B. ln  C C. ln  C D.  ln  x  
1 2  x  C 2  x 2  x x 1
Câu 92. Họ nguyên hàm của hàm số: y  sin x.cos x là: 1 1 1 A.  cos 2x +C
B.  cos 2x C
C.  sin 2x C
D.  cos 2x C 2 4 4 1 
Câu 93. Kết quả của dx  là: 1 2x
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 10
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 1 1 1 A. ln 1 2x C
B. ln 1 2x C
C.  ln 1 2x C
D. ln 1 2x  C 2 2 2
Câu 94. Họ nguyên hàm của hàm số 2
y  (t anx  cot x) là: 1 A. 3
(t anx  cot x)  C
B. tan x  cot x C 3
C. t anx  cot x  2x C
D. tan x  cot x  2x C 1 2
Câu 95. Tích phân I = 1 . x x e dx  có giá trị là: 0 2 e e 2 e e 2 e e 2 e e A. B. C. D. 2 3 2 3 3 x 2 Câu 96. Biến đổi dx
= f tdt
, với t  1 x . Khi đó f(t) là hàm nào trong các hàm số sau: 1 1 x 0 1 A. f t  2  2t  2t B.   2
f t t t C.   2
f t t t D. f t  2  2t  2t
Câu 97 .Diện tích hình phẳng được giới hạn bởi các đường 2
y  2x x và đường thẳng x y  2 là: 1 5 6 1 A. dvdt  B. dvdt C. dvdt  D. dvdt 6 2 5 2
Câu 98. Diện tích hình phẳng giới hạn bởi 3
y x , y  0, x  1
 , x  2 có kết quả là: 17 15 14 A. B. 4 C. D. 4 4 4
Câu 99. Cho hình (H) giới hạn bởi các đường y
x ; x  4 ; trục hoành. Quay hình (H) quanh trục Ox
ta được khối tròn xoay có thể tích là: 15 14 16 A. B. C. 8 D. 2 3 3 2
Câu 100. Tìm nguyên hàm của hàm số f(x) = x 2xe . 2 2 A. 2 x f ( x)dx x eC  . B. x f ( x)dx eC  . 2 C. 2 x
f (x)dx  2x e C  . D. x f ( x)dx  2eC  .
Câu 101. Cho hàm số f(x) = 2x + sinx + 2cosx. Một nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 là: A. F(x) = x2 + cosx – 2sinx.
B. F(x) = x2 – cosx + 2sinx – 2.
C. F(x) = x2 + cosx – 2sinx + 2.
D. F(x) = x2 – cosx + 2sinx + 2. 1 x e
Câu 102. Tính tích phân I = dx  . x 0 e  1 1  1  e   2  A. I = 1.
B. I = ln(1  e) . C. I = ln  . D. I = ln  . 2  2  1   e 2
Câu 103. Tính tích phân I =   sinx e
cos xcosxdx . 0 A. I = + e – 1. B. I = + 1. C. I = e – 1. D. I = – 1. 4 4 4
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 11
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 2 x
Câu 104. Tính tích phân I = dx  . 2  sin x 4 1 A. I = + ln2. B. I =  ln2 . C. I = – 2ln2. D. I = + 2ln2. 4 4 2 4 4 4 Câu 105. Đặt In = n tan xdx
. Mệnh đề nào sau đây là đúng: 0 1 1 1 1 A. In + In + 1 = . B. In – In + 1 = . C. In – In + 2 = . D. In + In + 2 = . n n  1 n n  1
Câu 106. Diện tích hình phẳng giới hạn bởi hai đường y = x3 và y = x được tính bởi công thức nào sau đây: 1 1 1 1
A.  x3  xdx .
B. 2  x x3 dx .
C.  x3  xdx .
D.  x x3 dx . 1  0 1 1 2 1
Câu 107. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x3  x2  và trục Ox là: 3 3 9 32 9 12 A. . B. . C. . D. . 32 9 13 11
Câu 108. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị các hàm số y = x xe , y = 0,
x = 0 và x = 1 quanh trục Ox là: A. . B. e2 4  1 . C. e2 1 . D. e2 . e2  1 4 4
Câu 109 .Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị các hàm số y = 1 – x2, y = 0 a
quanh trục Ox có kết quả dạng . Khi đó a + b bằng: b A. 17. B. 11. C. 25. D. 31.
Câu 110: Hàm số F(X) ln x x2  1  2016 là một nguyên hàm của hàm số 1 x A. f (x) B. f (x)
C. f (x) x2  1 D. f (x) x2  1  2016 1  x2  x2 1 2 Câu 111: Hàm số sin x F(X) e
là một nguyên hàm của hàm số 2 2 2 2 A. sin x sin 2x.e B. 2 sin x sin x.e 1 C. sin x cos 2x.e D. sin x e
Câu 112: Hàm số F(X) ln 1  ln x C là họ nguyên hàm của hàm số 1 1 1 1 A. C. D. x(1  ln x) B. xlnx x ln(1  x) 1  ln x cos x
Câu 113: Tích phân 2 e sinxdx 0  bằng e  1 A. e  1 B. e  1 C. D. e2  1 2
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 12
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân e2 dx
Câu 114: Tích phân ex(lnx)2 bằng 2 e2 e2 e e2 1 1 x3 1 A. B. C. D. ln x x 3 ln x e e e e 3
Câu 115: Cho I
( 3 x x ) 1 dx 1  thì I bằng 3 3 4 3  4 3 3 2   3 2  A. x3 x2 x     3 2 1    4 3  B. x x  4 3    1   1 3 3 4 3   4 3  3 2  C. x3 x 2 x    D. x3 x2 x       4 3    1   1 e Câu 116: Tích phân x ln xdx 1  bằng: e e ex2 x   x2 x (ln x)2 A.    e x lnx xlnx   C. ln x   D. 1 B.  2 2      2 2 2 1   1 1 1
Câu 117: Tích phân 2 2x d 1 x 0  bằng 2 1 1 1 A. ( 8  1) 3 4  1 C. ( 8  1)
D. ( 8  ) 1 3 B. ( ) 3 2 3
Câu 118: Diện tích hình phẳng giới hạn bởi các đường y x x2 2
, x y  0 là 9 5 7 11 A. C. D. 2 B. 2 2 2
Câu 119: Diện tích hình phẳng giới hạn bởi các đường x
y  2 , y  2 , x  0 được tính bởi công thức 1 1 2 2 A. 2  2 x 2  2 dx C. 2  2 D. 2  2 0   xdx 0   x dx 0   x dx B. 0   
Câu 120: Diện tích hình phẳng (H) giới hạn bởi các đường y ln x , y  1 , x e2 
được tính bởi công thức e2 e2 e2 e2
A.  lnx  1dx lnx  1 dx
C.  1  lnxdx
D.  lnx  1dx e B.    1 e 0  
Câu 121: Tìm nguyên hàm của hàm số x2 3   2 x dx    xx3 4 x3 4 A.  3ln x x3  C B.  3 ln x x3 3 3 3 3 x3 4 x3 4 C.  3ln x x3  C D.  3ln x x3  C 3 3 3 3
Câu 122: Giá trị m để hàm số F(x) mx3  ( m )x2 3 2
 4x  3 là một nguyên hàm của hàm số f (x) x2 3  10x  4 là: A. m  3 B. m  0 C. m  1 D. m  2
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 13
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 4 1  sin3 x
Câu 123: Tính tích phân dx  2 sin x 6 3  2 3  2  2 3  2 3  2 2  2 A. B. C. D. 2 2 2 2 e
Câu 124: Tính tích phân x.ln xdx  1 1 1 1 1 A. e2  1 B. e2 C. e2  1 D. e  1 4 4 4 4
Câu 125: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y   x2 2 và y x 9 11 A. 5 B. 7 C. D. 2 2
Câu 126: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y x x2 2
và y  0 . Tính thể tích vật thể
tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox 16 17 18 19 A. B. C. D. 15 15 15 15
Câu 127 : Tìm họ nguyên hàm của hàm số f (x) x( x)20 1 ( x )22 ( x )21 1 1 ( x )22 ( x )21 1 1 A. f ( x)dx    Cf ( x)dx    C  22 21 B. 23 22 ( x )21 1 (x )22 1 C. f ( x)dx   Cf ( x)dx   C  22 D. 23 2 x2  2lnx
Câu 128: Tính tích phân I dx  . x 1 3 3
A. I ln2 2 B. I   ln 2 C. I   ln2 2
D. I ln2 2 2
Câu 129 : Gọi (D) là miền giới hạn bởi y x x2 2
và trục hoành. Tính thể tích của vật thể tròn xoay
sinh ra bởi hình (D) khi nó quay xung quanh trục Ox . 16 1 16
A. V  16 B. V C. V D. V 25 25 5 (ln x)4
Câu 130 : Tìm họ nguyên hàm của hàm số f (x) x 1 5 1 4
A. f ( x)dx (ln x) C     5 B. f ( x)dx (lnx) C 4 1 5 1 4
C. f ( x)dx (lnx) C     4 D. f ( x)dx (ln x) C 5
Câu 131 : Tính diện tích hình phẳng giới hạn bởi trục hoành, y x2  2x và đường thẳng x  1,x  2 8 A. 16 B. 0 C. 8 D. 3
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 14
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 132 : Cho hình phẳng (D) giới hạn bởi các đường y ( x )2
2 và y  4 . Tính thể tích của vật thể
tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox . 16 26 256 16 A. V B. V C. V D. V  25 25 5 25
Câu 133 : Gọi (D) là miền giới hạn bởi y x sin x cos2  
x , trục hoành và đường thẳng x  0,x  . 2
Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox . A. V ( 2 4 ) B. V (4  ) C. V ( 2 4 ) D. V (4  ) 4 4 4 4
2 x2  3x  1
Câu 134 : Tính tích phân I dx  . x2 1  x
A. I ln3  1
B. I ln3
C. I  1  ln3
D. I  1  ln3 1
Câu 135 : Tính tích phân I x 2  x2 dx  . 0 1   2 2 2 2  1 2 2  1 A. I B. I C. I D. I  2 2 3 3 3 e dx
Câu 136 : Tính tích phân I   . 1 x 1  ln x A. I  1
B. I  1  ln3
C. I  2 2  2
D. I ln2
Câu 137: Tính thể tích V khối tròn xoay tạo thành khi quay hình phẳng được giới hạn bởi các đường 1 y
, y  0, x  0 và x  1 xung quanh trục hoành. 1  4  3x  3   3  1  3  1  3  A. V  6ln  1   B. V  6 ln  1   C. V  6 ln  1   D. V  6 ln  1   9  2  9  2  9  2  9  2   2 1 x  1
Câu 138 : Tính tích phân I dx  . x2 0  1
A. I ln2  1
B. I  1  ln2
C. I ln2
D. I  1  ln2 ln 2 2
Câu 139 : Tính tích phân    x 1 x I e e dx . 0 1
A. I e2 1 
B. I e2 1  C. I
D. I e 3 3 3 4
Câu 140 : Tính tích phân I   x  1sin2xdx . 0 3 3 A. I
B. I
C. I  2 D. I  4 2 2
Câu 141 : Tính tích phân I cos2 x sin2xdx  . 0
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 15
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 1 2 A. I 2  B. I C. I  0 D. I  2 2
Câu 142 : Tính diện tích hình phẳng giới hạn bởi hai đường cong y x3  và y x2   1 A. 12 B. 1 C. 0 D. 12
Câu 143 : Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x2  x  3 và đồ thị hàm số
y  2x  1 . 1 1 A. I B. I  6 C. I  36 D. I  36 6 4
Câu 144 : Tính tích phân I x
 1  sin2xdx . 0 2 1 2 1 A. I   B. I C. I D. I   32 4 32 32 32 4
x4  2x2  x  2
Câu 145 : Tìm họ nguyên hàm của hàm số f (x) x2  x  1 x3 x2 x3 x2 A. f ( x)dx    x Cf ( x)dx    2x C  3 2 B. 3 2 x3 2 2 3 x C. f ( x)dx
x  2x C
f ( x)dx x   2x C  3 D. 2 2 1
Câu 146 : Tính tích phân x x I (2ee )xdx 0  . . A. I e3  B. I = e
C. I  1  e D. I e2 
Câu 147 : Hàm số F x  ln sinx cosx là một nguyên hàm của hàm số: s inx cos x sinx- cos x 1 1 A. B. C. D. sinx cos x sinx+ cos x sinx+ cos x sinx cos x 1
Câu 148 : Nguyên hàm của f x  là: x2  3x  2 x  2 x  1 2x  3
A. ln ( x  1)(x  2) C B. lnC C. lnC D. lnC x  1 x  2
x2  3x  2
Câu 149: Thể tích của vật thể được tạo ra khi quay hình phẳng giới hạn bởi hai đường y x2  1 và y = 0 quanh trục Ox là : 15 15 8 8 A. B. C. D. 6 6 15 15
Câu 150: Diện tích hình phẳng giới hạn bởi hai đường y x2 
và y   x2 2 là: 8 8 4 A. B. C. D. 2 15 3 3
Câu 151: Thể tích của vật thể được tạo ra khi quay hình phẳng giới hạn bởi hai đường y x x2   và y =
0 quanh trục Ox là :
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 16
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân A. B. C. D. 4 5 6 3
C©u 152 : Cho ha hàm số y f x và y f x liên tục trên đoạn a;b 2  1  
 . Gọi D là hình phẳng giới hạn bởi
đồ thị hai hàm số đó và các đường thẳng x=a, x=b. Giả sử f x  f x, x   a; b 1 2   . Khi đó diện tích của hình D là : b b A. f
x. f xdx 1 2 B. f
x  f xdx 1 2 a a b b C. f
x  f xdx 1 2 D. f
x  f xdx 1 2 a a
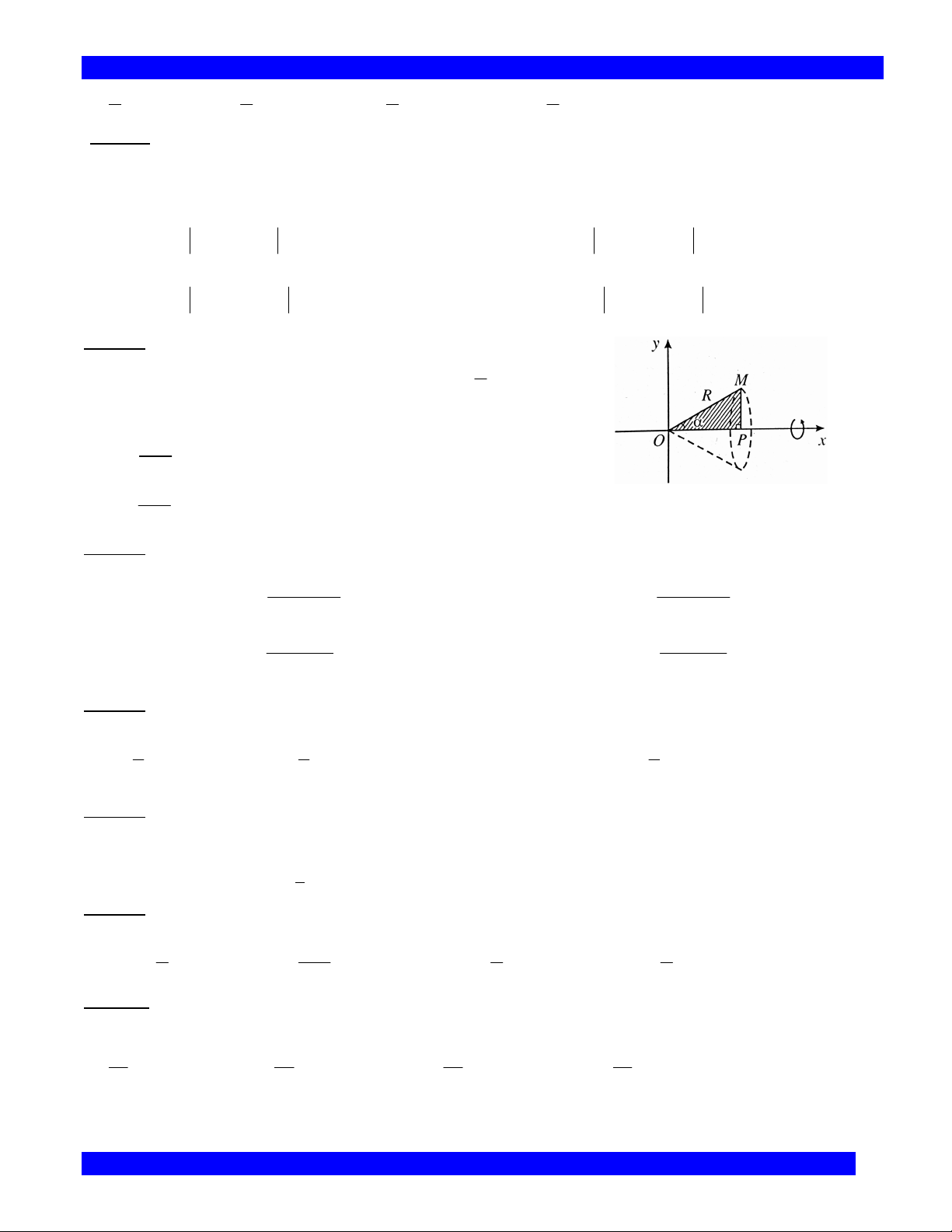
Câu 153: Cho tam giác vuông OPM có cạnh OP nằm trên  
Trục Ox (Hình bên). Đặt POM , OM R 0  , R  0 .    3 
Tính thể tích của V theo và R. R3 A. V
(cos cos3 ) . B. V
R3(cos cos3   ) . 3 R3 C. V
(cos cos2 ) . D. V
R3(cos cos2   ) . 3 9
Câu 154. Tìm nguyên hàm của hàm số f (x)  4x  2 dx .  10 10 9 4x  2 9 4x  2
A. f (x)  4x  2 dx   C .
B. f (x)  4x  2 dx   C . 4 8  9 9 9 4x  2 9 4x  2
C. f (x)  4x  2 dx   C .
D. f (x)  4x  2 dx   C . 4 8
Câu 155. Tính tích phân I sin2 x cos x dx  . 0 1 1 2
A. I .
B. I 3 . C. I  0 . D. I   . 2 4 3 1
Câu 156. Tính tích phân    1 x I x e dx . 0
A. I  2  e .
B. I e .
C. I  2  e .
D. I  2e  1 . 2
Câu 157. Tính tích phân    sinx I e
cos xcosxdx . 0 e  1
A. I e   1 . B. I  .
C. I e  .
D. I e   1 . 2 2 4 4
Câu 158. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x3  x2 5
 1 và đồ thị hàm số y  8  x  3 . 95 28 17 1 A. . B. . C. . D. . 12 3 12 12
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 17
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân x2 1
Câu 159. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y
, trục tung. Tính thể tích V của x  2
khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V  4 ln3  4 .
B. V  4(ln 3  ) 1 .
C. V  4 ln3  4 .
D. V  4(ln 3  ) 1 . 3x e  1
Câu 160: Tính nguyên hàm dxx e  1 1 1 1 A. 2x x e
e x C
B. x C C. 2x x e
e x C D. 2x ex C 2 2 2 ln 2
Câu 161: Tính tích phân x xe dx  0 A. 2 ln 2  1 B. ln2  1 C. 2 ln 2  1 D. 1  2 ln2 x  3
Câu 162: Tính diện tích hình phẳng giới hạn bởi đồ thị (C) y  , trục tung, trục hoành. x  1 A. 4 ln 4  3 B. 4 ln 4  4 C. 3  4ln4
D. 4 ln 4  3 .
Câu 163: Xét hình phẳng giới hạn bởi y   x2 2 1 , y (
2 1  x) . Tính diện tích hình phẳng. A. B. 1 C.  1 D.  1 2 2 2
Câu 164: Cho hình phẳng giới hạn bởi đường cong y = sinx, trục Ox, x = 0, x = .
Tính thể tích khối tròn xoay thu được khi quay hình này xung quanh trục Ox. 3 2 A.  1 B. C. D. 2 2 2 2 2 x
Câu 165: Tính tích phân I dx.x2 0  1 2  4 2 1  4 2 1  4 2  4
A. I ln
B. I ln
C. I ln
D. I ln 2 2 4 2 2 4
Câu 166: Xét hình phẳng giới hạn bởi y   x2 2 1 , y (
2 1  x) . Tính thể tích khối tròn xoay tạo thành khi
quay hình phẳng quanh trục Ox. 4 A.  1 B. C. 1 D. 2 3 2 1 1
Câu 167: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y x 2 .e 2  ,x=1, x=2, y=0 quanh trục Ox là: A. (  e2  e) B. (  e2  e) C. e2 D. 3 e 2 4
Câu 168: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y  , y=0, x=1, x=4 x quanh trục Ox là: A. 6 B. 4 C. 12 D. 8
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 18
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 4 1
Câu 169: Giá trị của (1  tanx)4 . dx  bằng : cos2 0 x 1 1 1 1 A. B. C. D. 5 3 2 4 x
Câu 170: Kết quả của dx  là: x2 1  1  1 A. x2 1   C B.C C.C D. - x2 1   C 1  x2 1  x2
Câu 171: diện tích hình phẳng giới hạn bởi đồ thị hàm số y x2 
và đường thẳng y=2x là: 4 3 5 23 A. B. C. D. 3 2 3 15
Câu 172. Tìm nguyên hàm của hàm số f x   x  10 ( ) 3 1 dx  .  x  11 10 3 1  x  10 10 3 1
A. f (x)  3x   1 dx   C
B. f (x)  3x   1 dx   C  3 33  x  11 10 3 1  x  11 10 3 1
C. f (x)  3x   1 dx   C
D. f (x)  3x   1 dx   C  11 33 2
Câu 173. Tính tích phân 2
I  sin x cos x dx  . 0 1 1 1 2 A. 3 I
B. I 3 C. I D. I   12 4 3 3 1
Câu 174. Tính tích phân x I xe dx  . 0
A. I  2e 1 B. I  1 C. I  1 
D. I  2e  1
Câu 175. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  5 và đồ thị hàm số y  x  3. 10 9 27 7 A. B. C. D. 3 2 2 3
Câu 176. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số 3 y
x  8 , trục tung và truch hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V  12 B. V  12
C. V  20
D. V  4
Câu 177: Một nguyên hàm của hàm   x f x e là: A. x x.e B. 2 x x .e 1 C. x e D. x e 1 1
Câu 178: Một nguyên hàm của hàm f x  là: sin x
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 19
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân x 1 x A. ln tan B. C. ln sin D. ln tan x 2 sin x 2 1 4x  11
Câu 179: Tính tích phân: I dxx2 0  5x  6 9 11 A. ln B. ln9 C. ln6 D. ln 2 2 4 2
Câu 180: Tính tích phân: I   x  1 dx 1 9 7 7 11 A. B. C. ln D. 2 6 6 2
Câu 181: Tính diện tích hình phẳng giới hạn bởi y x2  2x và y  x2  4x A. 3 B. 6 C. 9 D. 12 dx
Câu 182 : Tìm họ nguyên hàm F(x) =  8  x  1 1 A. F(x) = ln|1-8x| +C
B. F(x) =  ln|1  8x| 8 1 C. F(x) =- ln|1-8x| + C
D.F(x) =  ln|1  8x| C  8
Câu 183 :Gọi F(x) = ( x )11 2 1 dx
. F(x) bằng biểu thức nào sau đây 1 1 1 1 A.
(2x  1)12  C B.
(2x  1)12  C C.
(2x )12 1  C D.
ln(2x  1)12  C 24 22 12 12 1
Câu 184: Tính tích phân I= 2x x.e dx  0 1 1 1 1 A. (e2  ) 1 B. (e2  1) C. (e2  ) 1 D. (e2  1) 4 4 2 2 1
Câu 185: Tính tích phân I = 1  x2 dx  2 2 1 3 1 3 A.  B.  C.  D.  8 4 2 4 8 4 2 4 2
Câu 186: Tính tích phân I = (1sin x) cos x.e dx  0 1 A. 2e-1 B.e2 – 1 C. e2 –e D. e 2 3x  5
Câu 187: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=
, trục hoành và các đường thẳng 2x  2 x = 0 ; x= 2 A. S = ln3 + 3 B. S = ln3 C.S= ln2+ 3 D. S = ln3-2
Câu 188: Tính diện tích hình phẳng giới hạn bởi các đường y +x2 -5 = 0; x + y – 3 = 0
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 20
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 9 11 7 A. S = 9 B. S= C. S = D. 2 2 2
Câu189 : Tính thể tích vật thể giới hạn bởi các đường y = -x2 + 5 và y = 3 – x khi quay quanh trục Ox 53 153 31 A. 2 B. C. D. 15 5 13
Câu 190: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi 1
y= 2x  13 ,x = 0 , y = 3, quay quanh trục oy 480 460 450 490 A. V = B.V = C. D. V = 7 5 3 9
Câu 191: Viết công thức thể tích khối tròn xoay tạo thành khi quay hình thang cong , giới hạn bởi đồ thị
hàm số x = g(y) , trục oy và 2 đường thẳng y = a; y = b (a < b) , xung quanh trục Oy. b b b b A. V  g2  ( y)dy  B. V g2  ( y)dy
C. V  g ( y)dy
D. V  |g( y)|dya a a a Câu 192. Hàm số x
f (x)  2 có nguyên hàm là : x 2 x 2 A. x 2 .ln2  C B.  C C. x 2 .ln x C D.  C ln 2 lnx
Câu 193. Hàm số f (x) ( x)5 1 có nguyên hàm là: 1 1 A. (1  x)6
B.  (1  x)6 C. ( x)6 1  D. (   x)6 1 6 6 1 Câu 194. Tích phân x x (x e )e dx  bằng : 0 1 A.0 B.1 C. e2  1 D. (e2  1) 2 2 Câu 195. Tích phân 4  x2 dx  bằng : 0 3 A. B. 2 C. D. 2 2 2 sin2x Câu 196. Tích phân dx  bằng : 4  cos2 0 x A .2ln2 + ln3 B.ln3 – 2ln2 C. 2ln2-ln3 D.ln2 – ln3
Câu 197. Diện tích giới hạn bởi y x2  , y  2
x  3 và hai đường thẳng x =0, x=2. A.1 B. 2 C. 3 D. 4
Câu 198. Tính thể tích vật thể tròn xoay sinh ra khi quay hình (D) quanh trục Ox biết (D) giới hạn bởi y   x2 1 và y = 0
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 21
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 3 16 1 5 A. V  B. V  C. V  D. V  2 2 15 16
Câu 199: Nguyên hàm của hàm số x 2x
f (x) e (1  3e ) bằng: A. xx
F(x) e  3eC B. xx
F(x) e  3eC C. x 2x
F(x) e  3eC D. x 3  x
F(x) e  3eC
Câu 200: Cho M x2  x3 4 dx
. Chọn câu đúng trong các câu sau: 2 A. 3 3 2 M  4  x C
B. M  2 (4  x ) C 9 2 1 C. 3 3 3 2 M
(4  x ) C D. M
(4  x ) C 9 9 x
Câu 201: Gọi F(x) là nguyên hàm của hàm số f (x)
thỏa mãn F(2)  0 .Khi đó phương trình  x2 8
F(x) x có nghiệm là: A. x  0 B. x  1 C. x  1  D. x  1  3 4 dx
Câu 202: Cho M .
Bất đẳng thức nào sau đây là đúng? x(x ) 1 1 A. 0  M  1 B. 1  M  2 C. M  0 D. 2  M  3 2 x2dx
Câu 203: Cho P .
Giá trị của P là: x  1 1 1 1 1 A. ln2  B. ln2  C. 2 D.  ln 2 2 2 2 t dx 1
Câu 204: Với t (1; ) 1 ta có   ln 3.
Khi đó giá trị của t là: x2  1 2 0 1 1 1 A.  B. C. 0 D. 3 2 3
Câu 205: Các đường cong y sinx, y cos x với 0  x
và trục Ox tạo thành một hình phẳng. Diện 2
tích của hình phẳng này là: A. 2 2 B. 2  2 C. 2 D. Đáp số khác.
Câu 206: Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số y ln x và các đường thẳng y  0,
x  1, x e2  là: A. e2 3  1 B. e2 2  1 C. e2 2  1 D. e2  1
Câu 207: Cho đồ thị hàm số y x3  x2 3
 9x. Diện tích của hình phẳng giới hạn bởi đồ thị, tiếp tuyến của
nó tại điểm (2;2) và trục tung là: A. 30 B. 24 C. 28 D. 20
Câu 208: Diện tích của hình phẳng giới hạn bởi y   x2 4
và y  3 x là: 5 13 17 3 A. B. C. D. 2 3 6 2
Câu 209. Tìm nguyên hàm của hàm số f (x) cos(4x ) 1
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 22
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 1 1
A. cos(4x ) 1 dx
sin(4x  1) C
B. cos(4x )
1 dx   sin(4x ) 1  C  4 4 1 1
C. cos(4x )
1 dx cos(4x ) 1  C
D. cos(4x ) 1 dx
sin(4x  1) C  2 2
Câu 210. Tính I x3( x4 )3 5 dx  : 1 1 A. I  
(5  x4 )4  C B. I
(5  x4 )4  C 16 16 1 1
C. I (5  x4 )4  C
D. I   (5  x4 )4  C 4 4
Câu 211. Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y  0 và y x x2 2 khi
nó quay quanh trục Ox bằng bao nhiêu? 3 8 1 5 16 A. V  B. V  C. V  D. V  8 3 16 15 1 x  1
Câu 212. Tính I dxx 1 0 A. I ln4
B. I  1  ln4
C. I ln4  1
D. I  1  ln4 1 Câu 213. Tính 2x I xe dx  0 e2  1 e2  1 A. I
B. I e2  1 C. I
D. I e2  1 4 4
Câu 215. Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số y ln x , trục hoành và các đường 1
thẳng x  , x e là: e 2 2 A.0 B. -2e C. -2e D. e e 1
Câu 216: Nguyên hàm của y là x( x  3) 2 x 1 x 1 x  3 1 x A. lnC B. lnC C. lnC D. lnC 3 x  3 3 x  3 3 x 3 x  3
Câu 217: Nguyên hàm của hàm số x
y e x2 1 3  là. x A. x e x3   ln x c B. x e x3   ln x c C. x e x3   ln x c D. x e x3   ln x c
Câu 218: Cho hàm y f (x) và y g(x) liên tục trên a : b 
 khi đó diện tích hình phẳng giới hạn bởi hàm
số y f (x) và y g(x) và 2 đường thẳng x a,x b,(a b) là. b b b b A. S
f (x) g( x) .dx  B. S
f (x) g( x) .dx  C. S f (x) .dx
D. S g(x) .dxa a a a
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 23
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 6
Câu 219: Tính tích phân I (1  cos3x) sin 3xdx  0 1 1 1 1 A. I   B. I   C. I  D. I  3 6 3 6 2
Câu 220: Tính tích phân I (2x ) 1 cos xdx  0
A. I  3
B. I  3 C. I
D. I  3  1 4x  2
Câu 221: Tính tích phân I dxx2 0  x  1 A. I ln2 B. I  2 ln3 C. I  3ln2 D. I  2 ln2
Câu 222: Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đường y x x2 2 và y  0 khi
quay xung quanh trục ox bằng. 16 15 5 6 A. ( đvdt) B. ( đvdt) C. ( đvdt) D. ( đvdt) 15 16 6 5
Câu 223. Diện tích hình phẳng giới hạn bởi các đường cong y f (x), y g( x) và các đường thẳng
x a,x b là: b b A. S
f (x) g(x) dx S
f (x) g(x) dx a  B.    a b b
C. S    f (x) g(x)dx
D. S    f (x) g(x) dx a a
Câu 224. Trong các công thức sau đây, công thức nào sai: b b b b b b A.  f ( x).g(x) dx f (x)dx. g(x)dx
f ( x) g(x) dx f (x)dx g(x)dx a    aa  B. a   aab b b b c b C.
f ( x) g(x) dx f (x)dx g( x)dx f (x)dx f ( x)dx f (x)dx
(a c b) a    aa  D. aac  2 
Câu 225. Nguyên hàm của hàm f (x)  2x  1 là: 1  1 A. f ( x)dx   c  B. f ( x)dx   c( 2 2x ) 1 ( 2 2x ) 1 2  2 C. f ( x)dx   c  D. f ( x)dx   c(2x ) 1 (2x ) 1 1 
Câu 226. Nguyên hàm của hàm f (x)  1  2x là: 1 1
A. f ( x)dx   ln 1  2x c
B. f ( x)dx ln(1  2x) c  2 2 1 1
C. f ( x)dx   ln(1  2x) c  D. f (x)dx    c  2 ( 2 2x )2 1
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 24
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 227. Tính tích phân I
2 sin 2x(1  cos2 2 x)dx 0  A. 1 B. -1 C. 2 D. -2
Câu 228. Tính tích phân I
2x(1  sin x)dx 0  A. 2  2 B. 2  2 C. 2 2  D. 2 2 
Câu 229. Tính tích phân I
2 sin 2x(1  sin2 2 x)dx 0  A. 1 B. -1 C. 2 D. -2 e
Câu 230. Tính tích phân I  2x(1  ln x)dx 1  e2 3 1 e2 5 3 e2 3 1 e2 5 3 A.  B.  C.  D.  2 2 2 2 2 2 2 2 3
2a x  2x  3 1
Câu 231. Tìm a>0, biết: I dx   3ln 2 ax 3 A. 1 B. 2 C. e D. 2e a 1 8
Câu 232. Tìm a>0, biết: I dx lna x(x )1 5 4 A. 4 B. 3 C. 3e D. 4e
Câu 233. Hình phẳng giới hạn bởi các đường cong: f (x) x2  2x và g(x) x  2 có diện tích là: 9 19 7 17 A. B. C. D. 2 2 2 2
Câu 234. Hình phẳng giới hạn bởi các đường cong: f (x) x2  2x  1 , g(x) x  1 và các đường thẳng: x  1
, x  1 có diện tích là: 2 3 1 A. 3 B. C. D. 3 2 3
Câu 235. Khối tròn xoay sinh ra khi xoay quanh trục hoành phần hình phẳng giới hạn bởi các đường :
y cos x,y  0,x  0,x có thể tích là: 2 2 2 3 2 3 A. B. C. D. 2 4 2 4
Câu 236. Khối tròn xoay sinh ra khi xoay quanh trục hoành phần hình phẳng giới hạn bởi các đường :
y x2  1,y x  1 có thể tích là: 7 28 2 7 2 28 A. B. C. D. 15 15 15 15
Một vật chuyển động với biểu thức vận tốc vxQuang.duong.di.duoc t
trong thời gian từ t t  S v 1 2  2 xdx t1
Câu 237. Một ô tô đang chuyển động với vận tốc 12m / s thì người lái xe bất ngờ tăng tốc cho xe chạy
nhanh dần đều , sau 15s thì xe đạt vận tốc 15m / s .Tính quãng đường xe đi được sau 30s kể từ khi tăng tốc A. 270m B. 450m C. 360m D. 540m
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 25
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 238. Một lực có độ lớn 40 N (newton) cần thiết để kéo căng một chiếc lò xo có độ dài tự nhiên 10 cm
lên 15 cm. Biết rằng theo định luật Hooke trong Vật lý, khi một chiếc lò xo bị kéo căng thêm x (đơn vị độ
dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho bởi công thức
f x  kx N , trong đó k là hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo lò xo
có độ dài từ 15 cm đến 18 cm ? (kí hiệu J Jun là đơn vị của công) A. , 1 56 J . B. 0,94 J . C. 1,78 J . D. 2, 03 J .
Câu 239. Một vật chuyển động chậm dần với vận tốc v t   160 10t m/s . Hỏi rằng trong 3s trước khi dừng hẳn
vật di chuyển được bao nhiêu mét ? A. 16 m. B. 130 m. C. 435 m. D. 170 m.
Câu 240: Bạn Nhớ đang chở hai người bạn gái của mình là Ty và Sương trên chiếc xe thể thao hiệu
Lamborghini Aventador chạy trên một đường đua thẳng có độ dài 4km. Xe tăng tốc từ 0km/h đến
100km/h trong 3 giây đầu tiên đi hết 260m và sau đó xe chuyển động nhanh dần đều với gia tốc 20m / s .
Tính thời gian để xe hoàn thành đường đua biết vận tốc của chuyển động nhanh dần đều có công thức
v at v với a,v là gia tốc và vận tốc đầu. o o A. 21s B. 11s C. 14s D. 18s
Câu 241. Một vật đang chuyển động thẳng nhanh dần đều có vận tốc là 18km / h . Trong giây thứ 5 mật
đi được quãng đường là 5,9m > tính quãng đường vật đi được sau 10s kể từ lúc bắt đầu chuyển động 132 A. m B. 103,6m C. 60m D. đáp án khác 5
Câu 242. Bạn Phương vừa nhai quần đùi vừa thả một hòn bi chuyển động trên một rãnh nằm ngang để 
tạo một dao động điều hòa với phương trình chuyển động là x  4cos 4 t  
cm , cùng lúc đó ở máng  3 
bên cạnh bạn Hợp cũng đang điều khiển chiếc xe hơi đồ chơi mới mượn được của bạn Nhớ và cũng 
đang dao động điều hòa với phương trình dao động là x  2cos 2 t  
 cm .Nếu gọi S1 là quãng  2 
đường hòn bi của Phương đi được trong khoảng thời gian là 0,2 s
5 kể từ lúc xuất phát và S2 là quãng
đường chiếc siêu xe của bạn hợp chạy được trong khoảng thời gian 2,87 s
5 kể từ lúc xuất phát. Khi đó i. S S 12 1 2 ii. S S 1 2 iii. S S 1 2 4i.S S  2 1
Có bao nhiêu khẳng định đúng A. 1 B. 2 C. 3 D. 0 b b b b
Câu 243. Cho  f
x  2gx 19   3  30   và f  5 x
g xdx    khi đó f
 xdx A; g
 xdx B thì a a a a
A và B có giá trị là bao nhiêu b b b
Câu 244. Cho  f
x  2gx 1   3  30   12    và f  x
g xdx    khi đó f  11 x
g xdx ?   a a a b b b b
Câu 245. Cho  f
x  gx 10    15 2016 2017   và f
 3 xgxdx    khi đó f  xdx g  xdx a a a a 3 3
Câu 246. Cho f xdx  2 
15 . Hãy tính x  5x f xdx 0 0
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 26
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 4 4 Câu 247. Cho
f xdx  
, Hãy tính  sin2x  3 f xdx 4 0 0  5  2  1  Câu 248: Cho   x ; khi:x 0 f x   Hãy tính tích f  xdx5x+1;khi:x<0  3
x  6; Khi:x<-1 2 
Câu 249. Cho f x   Hãy tính tích f  xdx 2
x x  5; Khi : x    1 3 2x ; 1 khi : x  1  0
Câu 250. Cho Cho f x   , Hãy tính tích f  xdx 2 x ; 1 khi : x   0 1 2 x2
Câu 251.Cho I
dx  1  a2 lnc b2 ln
c  1 ;a;b;c Q , Khi đó , hãy tính kết quả của P a b c
1 x2  7x  12 A. P  43 B. P  11 C. P  3 D. P  3 2 dx a a b a
Câu 252.Cho I    lnb ln
a b  ,a;b Q hãy chọn phát biểu sai 4 1 x5  x3 b b b A. a b B. a b  1
C. a2  b2  5
D. a  2b  10 5 3x2  1
Câu 253. Cho I dx
, Chọn phát biểu đúng ?
4 x3  2x2  5x  6 2 4 13 7 14 2 4 13 7 14
A. I   ln ln ln 2
B. I   ln ln ln2  C 3 3 15 6 5 3 3 15 6 5 2 4 13 7 14 2 4 13 7 14
C. I   ln ln ln2 D. I ln ln ln 2 3 3 15 6 5 3 3 15 6 5 1 xdx
Câu 254. Tính I  
, Chọn phát biểu đúng ? 0 (x )3 1 1 1 2 A. 1 B. C. D. 3 8 3 ( x )2 1
Câu 255. Cho I dx
, Phát biểu nào sau đây là sai
(2x )4 1 3 2 1  x  1  1  x  1   x  1  A. I   C   B. I d     9 2x   1  3 2x  1 2x     1  ' 2 ' 1 (x )2 1  x  1 
x  1   x  1  C. I . dx    D. I . dx    
3 (2x )2 1  2x  1  2x  1 2x     1  1  99 7x  1
Câu 256. Tính I dx  , chọn kết quả đúng  101 0 2x  1
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 27
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 1 1 1 A. I   100 2   1 B. I   100 2   1 C. I   100 2   1 D. kết quả khác 900 700 100 1 5x
Câu 257. Tính I dx  , chọn phát biểu sai (x2  4)2 0 1 A. I
B.  Đặt t x2  4 , t   ; 1 5 8   5 1 2 dt 5 5 2 dt
C.  Đặt t x  4  I  
D. .  Đặt t x  4  I  0  2 t2 1 2 t2 1 x7
Câu 258. Cho I dx
, Bạn Phương đã giải bài toán như sau
( x2 )5 0 1
Bước 1. t   x2 1  dt  2xdx 2 3 1 (t ) 1 Bước 2. I dx  2 t5 1 1 1
Bước 3. I . 5 4 2
Hãy cho biết lời giải trên đúng hay sai , nếu sai thì sai ở bước nào? A. Bước 1 B. Bước 2 C. Bước 3 D. Không sai 1 1
Câu 259. Cho I x5(1  x3 )6dx ; a,b,c Q
.Hãy tính P a  2b c 3 abc 0 A. 35 B. 36 C. 37 D. 38 4 3 1 1 b
Câu 260. Cho I
dx ln ,a;b;c Q
, Chọn phát biểu sai? 1 x( x4  ) 1 a c
A. b2  2b c 5
B. a b c
C. a2  b2  c2  1
D. a b c 2 1  x7
2 (1  x7 ).x6 128 1 1  t
Câu 261. Tính I dx I dx
. Đặt t x7  I dtx(1  x7 7 7 7 t(1  t) 1 ) 1 x .(1  x ) 1 1 2
Câu 262. Khi tính I  x   1 dx
một học sinh đã thực hiện các bước như sau: 0 1 1 2 Bước I. I  x   1 dx  x2  2x   1 0   0 1  x3  Bước II. I  2   x x     3  0  13  2 7 Bước III. I  1     1  0   3  3  
Lời giải trên đã đúng chưa ? Nếu sai thì sai từ bước nào ? A. Sai từ bước I. B. Sai từ bước II. C. Sai từ bước III. D. Lời giải đúng
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 28
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 263. Tính thể tích khối cầu bán kính R là khối tròn xoay thu đc khi quay nửa hình tròn giới hạn bởi đường  2  2 y R
x R x R và đường thẳng y  0 xung quanh trục Ox 3 3 4 4 A. 3 R . B. 3  R . C. 3 R . D. 3  R . 4 4 3 3 3 x
Câu 264. Tích phân I dx a
b ln 2,a; b  
. Khi đó tổng a b gần với gía trị nào nhất sau cos2 x 3 0 đây ? A. 3 . B. 3 . C. 1 . D. 1 . 16 0
Câu 265. Cho f x là hàm số liên tục và lẻ trên  , biết rằng f xdx   3 . Khi đó tích phân
f xdx  0 16 bằng A. -3. B. 2016. C. 3. D. -2016.
Câu 267. Vòm cửa lớn của trường Đại Học Bôn Ba có dạng hình Parabol. Người ta dự định lắp cửa kính
cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp biết rằng vòm cửa cao 8 m và rộng 8 m ? 128 64 32 16 A. m2 . B. m2 . C. m2 . D. m2 . 3 3 3 3
Câu 268. Tính diện tích hình phẳng giới hạn bởi đường cong 2
y x x  2 , trục Oy và đường thẳng x  3 . 15 59 15 A. S  B. S   C. S   B. 2 6 2
Câu 269. Kí hiệu (H) là hình phẳng giới hạn bởi hai đường cong x
y e trục Oy và đường thẳng x  ln 4 .
Tính thể tích khối tròn xoay thu được khi cho (H) xoay quanh trục Oy. 3 A. V e B. V  C. V  2 D. V  4 2 1 (3x 1 d ) x a 5 Câu 270. I   3 ln  
vậy phát biểu nào sau là đúng x2  6x  9 b 6 0
1. a b  7
2. a b  7
3. a b
4. a b A. chỉ 1 và 3 đúng
B. chỉ 2 và 3 đúng C. Chỉ 1 và 4 đúng
D. không đáp án nào đúng 3 4 2 3x x  2
Câu 271. Chọn đáp án đúng khi tính tích phân I dx 2 2 x  1 3 3
A. I  23  ln B. I  23  ln 2 2 3 C. I  ln D. I  23 2  2 Câu 272. Cho I 5  cos xdx
, Đâu là kết quả của tích phân trên trong các số dưới đây 0 8 8  8  A.  8 B. C.  D.  15 15 15 4 15 2
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 29
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 273. Thể tích vật thể khối tròn xoay giới hạn bởi các đường 2
y x ln x , trục hoành, x e khi xoay
quanh trục hoành được tính bới công thức nào dưới đây? e A. Vx lnx e dx  1 2 B. Vox x ln xdx  2 0x 0 1 e e 2
C. Vox   x2 lnxdx D. Vox   x lnxdx  2 1 1
Câu 274. Diện tích hình phẳng giới hạn bởi các đường y x2  2x và y  x2  4x có kết quả nào dưới đây A. 81 B. 9 C. 9 D. 81
Câu 275. Cho hình phẳng H được giới hạn bởi các đường y x2  4x  6; y  0; x  2; x  4 .Diện tích
hình phẳng H có giá trị là A. 36 B. 36 C. 9 D. 9
Câu 276. Cho hình phẳng giới hạn bởi đường cong y sin x , trục hoành và hai đường thẳng x  0,x .
Thể tích của khối tròn xoay thu được khi quay hình này quanh trục Ox:
A. V  sin xdx  3 . B. V sin xdx  2 . 0 0
C. V  sin xdx  2 . D. V sin xdx  2 . 0 0
Câu 277. Cho hình phẳng (H) giới hạn bởi trục hoành và Parabol C: y ax x2 a  0 . Thể tích tính theo
a sinh ra khi quay hình phẳng (H) quanh trục Ox là:  a3  a5  a5  a5 A. (đvtt). B. (đvtt). C. (đvtt). D. (đvtt). 30 20 15 30 5 2x  1 3
Câu 278. Biết rằng tích phân
dx a b ln
c ln 2, a; b; c    . Khi đó giá trị
2x  3 2x  1  1 5 1
A a b  2c là A. 8 B. 0 C. 4 D. 7
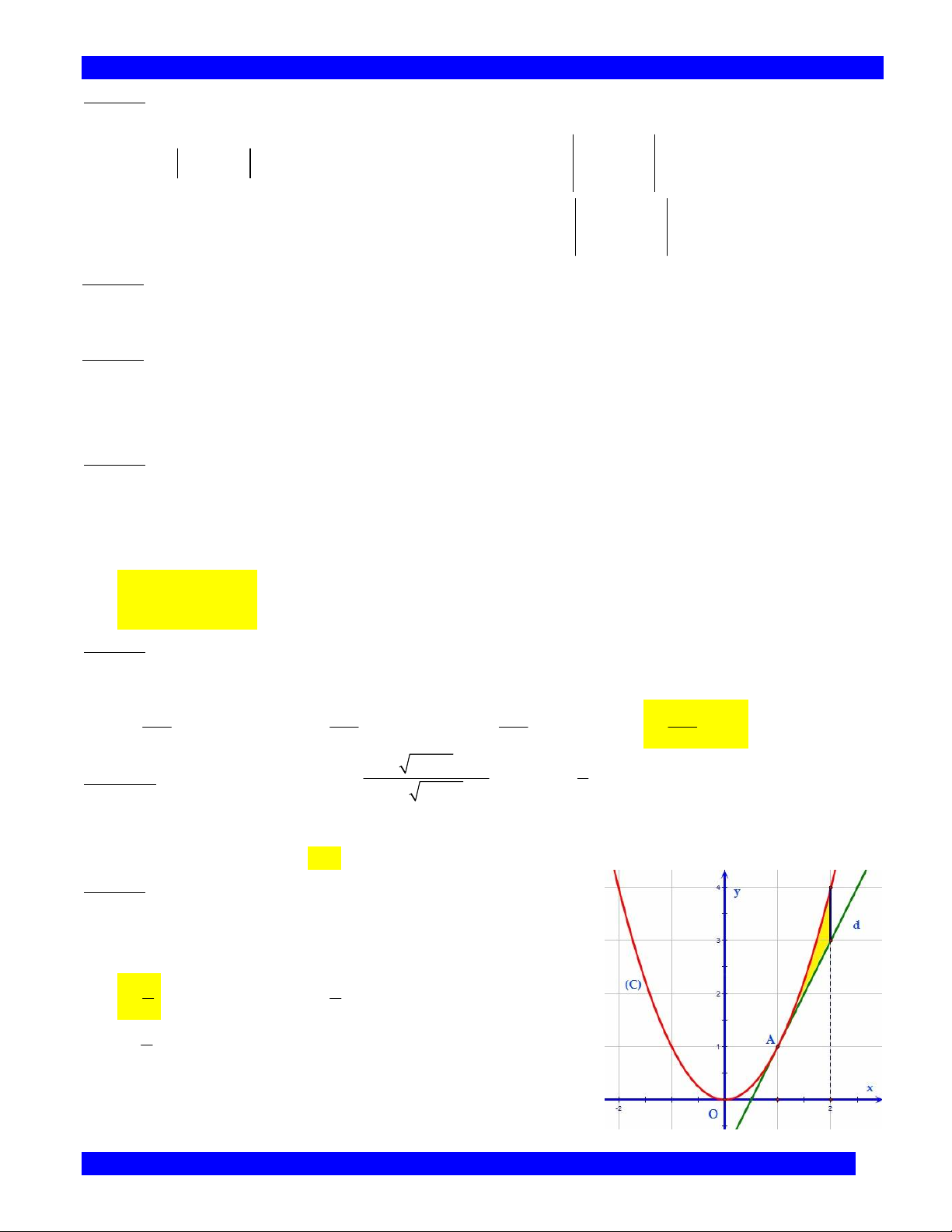
Câu 279. Trong hệ tọa độ Oxy, cho Parabol C và d là tiếp tuyến
của C tại điểm A 1;
1 như hình vẽ. Diện tích của phần tô vàng như hình vẽ là: 1 2 A. . B. . 3 3 4 C. . D. 1 . 3
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 30
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 280. Tính diện tích hình phẳng giới hạn bởi hai đường thẳng x  0, x và đồ thị hai hàm số
y  sin x, y  cos x. A. 2. B. 2 2 . C. 2 3 . D. 1.
Câu 281. Tính diện tích hình phẳng giới hạn bởi đường cong có phương trình 2
y x 1 , tiếp tuyến với
đường này tại điểm M 2;  5 và trục tung. 5 8 A. 3. B. . C. . D. 6. 3 3
Câu 282. Tính thể tích vật thể nằm giữa hai mặt phẳng có phương trình x  0 và x  2 , biết rằng thiết
diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0;2 là một phần tư đường tròn bán kính 2
2x , ta được kết quả nào sau đây? 16 A. V  32 . B. V  64 . C. V  . D. V  8 . 5 1 2x
Câu 283 . Tính tích phân I  dx  . 2 x 1 0 A. I  1 . B. I  ln 2 . C. I  1 . D. I  ln 2 . 2 2
Câu 284. Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y  2
x  4 , trục hoành và hai đường thẳng
x  1, x  1 . A. S  406 . B. S  22 . C. S  22 . D. S  11 . 15 3 3 3
Câu 285. Cho hình  được giới hạn bởi đồ thị C : y  2x  
1 .ln x , trục hoành và đường thẳng x  2 . Tính
thể tích khối tròn xoay được tạo thành khi quay  quanh trục hoành. 5
A. V   5 .
B. V   ln 64 . C. V  ln 64  4. D. V  143 . 2 2 9
Câu 286. Tìm nguyên hàm của hàm số y  2 sin x . x x
A. F x  2  cos x C . B. F x  2 sin 2  C . 4 1 C.
F x   x  cos 2x C .
D. F x    C . 2 cot x ln x ln x
Câu 287 F x  là một nguyên hàm của hàm số y  . Nếu F  2 e   4 thì dx  bằng: x x 2 ln x 2 ln x
A. F x   C . B. F x    2 . 2 2 2 ln x 2 ln x
C. F x   2 .
D. F x    x C . 2 2
Câu 288. Trong giải tích, với hàm số y f x  liên tục trên miền D   ,
a b có đồ thị là một đường cong C , người ta b
có thể tính độ dài của C bằng công thức L
  f x 2 1 '  dx   
. Với thông tin đó, hãy tính độ dài của đường cong a 2 x
C cho bởi hàm số y
ln x trên 1;2 . 8
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 31
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân 38 ln 2 31 3  8 ln 2 31 A. . B. ln 4 . C. . D.  ln 4 . 8 24 8 24 b b c
Câu 289 . Giá trị của
f x dx  12  và
f x dx  8  . Khi đó I
f x dx  có giá trị bằng : a c a A. I  20 . B. I  20 . C. I  4 . D. I  4 . ln m x e dx
Câu 290. Cho I   ln 2 
. Khi đó, giá trị của số thực m bằng : x e 2 0 m  0 A.    . B. m  2 . C. m  4 . D. m e . m  4 
Câu 291. Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  6x  9x và trục Ox . Tìm số nguyên
lớn nhất không vượt quá giá trị của S . A. 10 . B. 6 . C. 7 . D. 27 .
Câu 292 Sơ đồ ở bên phải phác thảo của một khung cửa sổ. y
Diện tích của cửa sổ được tính bằng công thức nào sau đây? 5 2 y   2x 2 1 1 2 5  2 5 A. 2 S  
  4x dx 2   . B. S  2x dx   . 2  2 1  1  2 2 1 1 2 2 2 x y  2x C. 2 S  2x dx  . D. S    2 1 4x dx . 1 O 1 1  1   2 2 2 2
Câu 293. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol 2
y  4  x và 2
y  2  x quay
quanh trục Ox là kết quả nào sau đây? A. V  10 . B. V  12 . C. V  14 . D. V  16 . 1
Câu 294. Tính tích phân    1 2x I x e dx 0 3 2 3e  1 2 3e  1 1 A. I   2 e  1 B. I  C. I  D. I   2 e  1 4 4 4 4
Câu 295: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x x  2 và đồ thị hàm số 2
y x  3x . 27 21 9 A. B. C. 0 D. 4 4 2
Câu 296: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y  3x  2 ln x và trục
hoành. Tính thể tích khối tròn xoay thu được khi cho hình (H) xoay quanh trục Ox. A.
V  8ln2 16
B. V  24ln2 16 C.
V  24ln2 16 D. V  8ln2 16 2
Câu 297. Giá trị của : 3x2  2x   3dx bằng : 1 A.6. B. 7. C. 8 . D. 9.
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 32
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân
Câu 298. Diện tích hình phẳng giới hạn bởi các đường y x2 , trục Ox và đường thẳng x  2 là 8 16 A. 8 . B. C. 16 . D. . 3 3 1 2dx
Câu 299. Bằng cách đổi biến số x  2 sint thì tích phân  là: 4  x2 0 3 6 6 3 dt A. 2 dt  . B. 2 tdt  C. 2 dt  . D. 2 . t 0 0 0 0
Câu 300. Biết rằng thể tích vật tròn xoay khi quay hình phẳng giới hạn bởi các đường y tan x , y  0 , b x
, x  0 có dạng V  a 3  
 (đvtt) a, b  0 . Tổng giá trị của a
3  2b có giá trị gần với giá trị 3  3 
nào nhất sau đây ? A. 6, 25 . B. 8, 24 . C. 7,65 . D. 9,41 .
Câu 301. Cho hình phẳng H giới hạn bởi các đường y x4  mx2  m2 2
, x  0, x  1 (m là tham số thức). 28 Biết rằng m , m
là hai giá trị để diện tích hình phẳng H bằng (đvdt). Khi đó Tổng 1 2  m m 1 2  15 m m 3 bằng: 1 2 A. 4 . B. 3 . C. 3 . D. 4 .
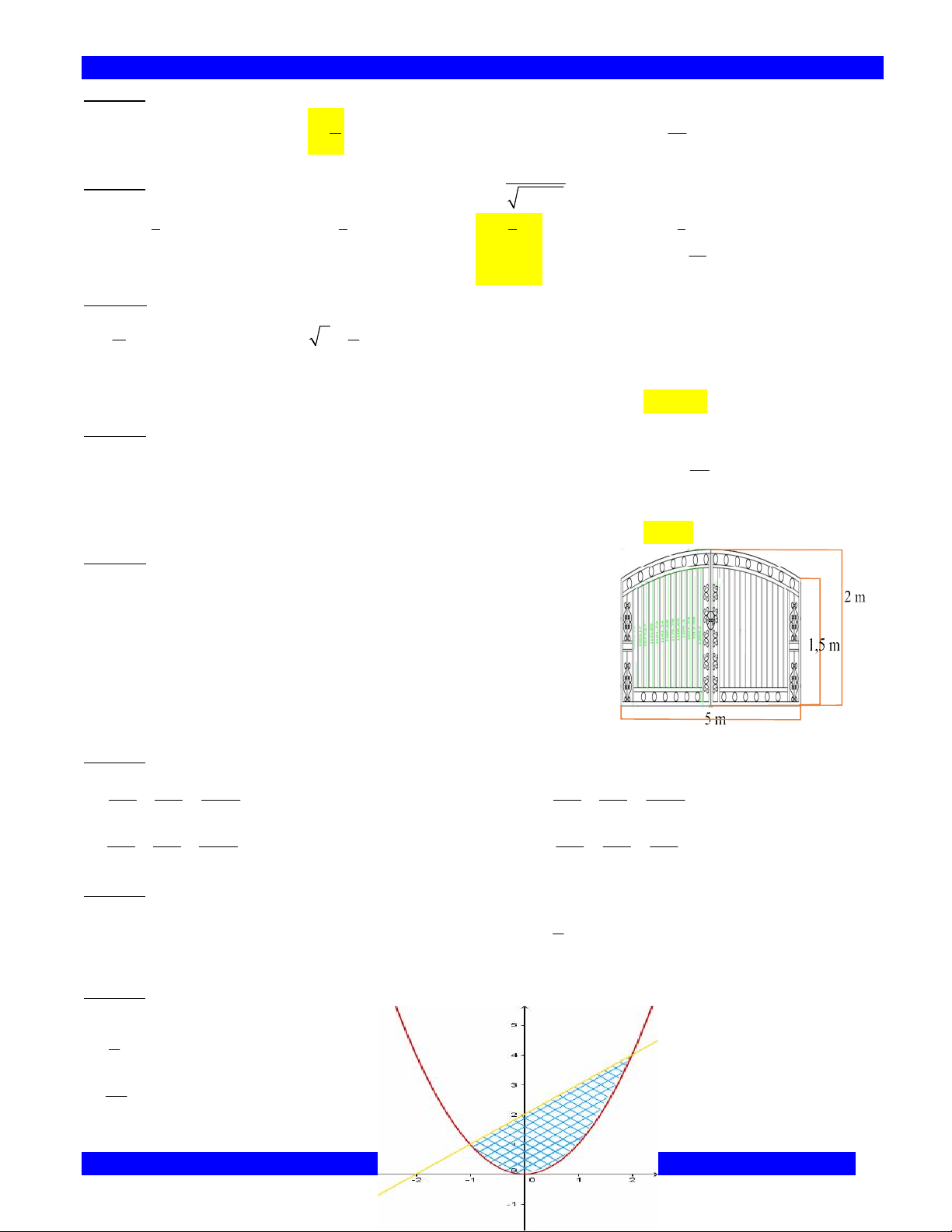
Câu 302. Anh An muốn làm cửa rào sắt có hình dạng và kích thước
giống như hình vẽ kế bên, biết đường cong phía trên là một parabol. Giá m2 1
cửa rào sắt có giá là 700.000 đồng. Vậy anh An
phải trả bao nhiêu tiền để làm cài cửa rào sắt như vậy. (làm tròn đến hàng chục nghìn) ?
A. 6.420.000 đồng. B. . 6 32 . 0 000 đồng. C. . 6 52 . 0 000 đồng. D. . 6 62 . 0 000 đồng. 1 2
Câu 303. Tính tích phân 3 
x 2xdx 0 4 10 3 4 10 3 A.   B.    C ln 3 ln 6 2 ln 2 ln 3 ln 6 2 ln 2 4 10 3 4 10 3 C.   D.   ln 3 ln 6 2 ln 2 ln 3 ln 6 ln 4 1
Câu 304. Tích phân I  lnx  
1 dx  2 ln a  
1 vậy kết luận nào sau đây là đúng 0 1 A. a  2 B. a  2
C. a  4 D. a  3
Câu 305. Một hình phẳng H đươc giới hạn bởi một Parapol và một đường thẳng như hình bên ( miền
gạch ca rô ) có dienj tích là bao nhiêu 9 A. 2 9 B. 2
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 33
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân C. 9 D. 9
Câu 306. Cho hình phẳng H : y  ln x; y  0; x  1; x e Tính thể tích tạo thành khi cho hình phẳng trên quay quanh trục Ox A. V  1 B. V ox ox C. V  D. 2 V ox 2 ox x
Câu 307. Tính nguyên hàm : I dxxx2 3 9  1 3 1 3 1 A. I
(9x2  ) 1  x3 2 B. I
9x2 1  x3 C 27 27 3 3 C. I
x2    x3 27 9 1  C 2 3 D. I
9x 1  x C x2  x Câu 308. I dx
, có bao nhiêu kết quả đúng ? 1  x x 3 3 4 3 4 4
i. I   1  x x   C
ii. I   1  x x
iii. I  1 x x 2  C 9 9 9 A. 0 B. 1 C. 2 D. 3 4 2x  1
Câu 309. Cho I
dx a lna;a Q
.Phát biểu nào sai ? 1  0 2x  1 A. a2  3 B. a2  2a C. a  2 D. a  2 6 dx a 1
Câu 310. Cho I   ln ,  a;bQ
, Chọn phát biểu đúng ?
2x  1  4x  1 b a.b2 2 A. a b  0
B. b2  a  1
C. b2  a a2 2
 2b D. a2  b2 1
Câu 311. Tính I x3 1  x2 dx
Có bao nhiêu phát biểu sai trong các phát biểu sau? 0 1 2 i. Đặt: t   x2 1
 I   t2  t4 . ii. I  0 dt 15 0 1 iii. Đặt: t   x2 1
  4  2  I t t dt. 4i. I  12 1 A. 0 B. 1 C. 2 D. 4 1 1  x a
Câu 312. Cho I
dx   c ln 2; 2 
a;b;c  , hãy tính P a b c 1  0 x b
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 34
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân A. P  20 B. P  16 C. P  10 D. 15 3 x  3 a
Câu 313. Cho I
dx  a  2a ln , 3 3 
a;b , Hãy tính P a b  2ab
0 3 x  1  x  3 b A. P ab B. P ba C. P ba2
D. P a2b 0
Câu 314. Cho I x.3 x d 1 x  , chọn phát biểu sai 1 1  7 4  A. Đặt 9
t  3 x  1  t  0;    1 B. t t I  3      7 4  0 28 0 1
C. Đặt t  3 x  1  dx t2 3 dt I ( 3 t3  ) 1 dt
D.Đặt t  3 x  1  dx t2 3 dt I ( 3 t3  ) 1 dt  1 0 5 x2  1 4a2 b2 Câu 315. Tinh I dx   ln
,voi : a;b   
P a2  b  2 1 x 3x  1 b3 a A. P  26 B. P  31 C. P  41 D. P  52
3 2x2  x  1 Câu 316. I dx
, Bạn Tiên giải như sau 0 x  1  Đặt
x   t x t2 1
 1  dx  2tdt 2 2 ( 2 t2 )2 1 (t2 ) 2  1 1 4 2 4t5      54  I
2tdt  2 (2t t 3 )dt    2t3     t  5  5 1 1 1
Bạn Nhi với sự cố vấn của bạn Linh đã giải như sau
 Đặt x   t x t2 1
 1  dx  2tdt 2 2 ( 2 t2 )2 1 (t2 ) 2  1 1 4 2 4x5      54  I
2tdt  2 (2x  3x )dx    2x3     t  5  5 1 1 1
Em hãy cho biết, trong lời giải trên của hai bạn ai giải sai A. Tiên giải sai B. Nhi giải sai C. Cả hai đều sai D. Cả hai đều đúng 1 x2dx a2  b c Câu 317. Cho Tinh I  2 
; a,b,c,d   
P a b c d  0 ( x ) 1 x  1 d A. P  32 B. P  20 C. P  31 D. P  18  2 4 x  1 Câu 318. I dx
, Bạn Hô Nam đã giải như sau  2 0 1  1  2x dx t2  2t
Bước 1 Đặt t  1  1  2x dt
dx (t ) 1 dt và x  1  2x 2 4
1 (t2  2t  2)(t ) 4 1 1 t3  t2 3  4t  4 2 1  4 2  Bước 2. Ta có: I = dt dt t  3   dt  2  2    2 2 2 2 t 2 tt 2 t2 
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 35
Nguyễn Tiến Chinh – Vinastudy.vn
Trắc nghiệm nguyên hàm – Tích Phân  1 t2  2 1 Bước 3 I =   t
3  4 ln t   = 2 ln2   2 2 t    4
Hãy cho biết , bài giải của bạn Nam đúng hay sai , nếu sai thì sai ở bước giải thứ mấy A. Không sai B. Bước 1 C. Bước 2 D. Bước 3 8 x  1
Câu 319. Tính I dx
, có bao nhiêu phát biểu đúng x2 3  1 8 8  x 1   2 2  i. I   dx   
=  x  1  lnx x  1  2 2  3 3  x  1 x  1 
ii. I  1  ln 3  2  ln 8  3   3  2
iii. I  1 ln    8   3 
iii. I  1 log 3  2  log 8  3 e e   A. 1 B. 2 C. 3 D. 4 1
Câu 320. Tính I ( x )3 1
2x x2 dx
, chọn phát biểu đúng ? 0 2 2 1 1 A. I   B. I  C. I   D. I  15 15 15 15
2 2x3  3x2  x
Câu 321. Tính I dx  , chọn phát biểu đúng? x2 0  x  1 4 2 4 3 3  2 A.  B. C. D. 3 3 3 3
15 Phó Đức Chính hoặc 135 Nguyễn Chí Thanh - ĐN 36