350 câu hỏi trắc nghiệm chuyên đề hàm số và các vấn đề liên quan – Nhóm Toán

350 câu hỏi trắc nghiệm chuyên đề hàm số và các vấn đề liên quan – Nhóm Toán được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
48 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

350 câu hỏi trắc nghiệm chuyên đề hàm số và các vấn đề liên quan – Nhóm Toán

350 câu hỏi trắc nghiệm chuyên đề hàm số và các vấn đề liên quan – Nhóm Toán được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

69 35 lượt tải Tải xuống

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

48 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 001-KSHS)
C©u 1 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
y x 3x 9x 35
trên đoạn
4;4
lần lượt
là:
A.
20; 2
10; 11
C.
40; 41
D.
40; 31
C©u 2 :
Cho hàm số y = x
4
+ 2x
2
– 2017. Trong các mệnh đề sau , mệnh đề nào sai ?
A.
Đồ thị của hàm số f(x) có đúng 1 điểm uốn
B.
lim va lim
xx
f x f x
 
 
C.
Đồ thị hàm số qua A(0;-2017)
D.
Hàm số y = f(x) có 1 cực tiểu
C©u 3 :
Hàm số
42
y x 2x 1
đồng biến trên các khoảng nào?
A.
1;0
1;0
và
1;
C.
1;
D.
x
C©u 4 :
Tìm m lớn nhất để hàm số
32
1
(4 3) 2016
3
y x mx m x
đồng biến trên tập xác định của nó.
A.
Đáp án khác.
m 3
C.
m 1
D.
m 2
C©u 5 :
Xác định m để phương trình
3
x 3mx 2 0
có một nghiệm duy nhất:
A.
m1
m2
C.
m1
D.
m2
C©u 6 :
Tìm giá trị lớn nhất của hàm số
2
4y x x
.
A.
1
;3
3
1
f 4 ln2
2



Max x f
B.
1
;3
3
1
f 1 ln2
2



Max x f
C.
1
;3
3
193
f2
100



Max x f
D.
1
;3
3
1
f1
5



Max x f
C©u 7 :
Cho các dạng đồ thị của hàm số
32
y ax bx cx d
như sau:
2
A B
C D
Và các điều kiện:
1.
2
a0
b 3ac 0

2.
2
a0
b 3ac 0

3.
2
a0
b 3ac 0

4.
2
a0
b 3ac 0

Hãy chọn sự tương ứng đúng giữa các dạng đồ thị và điều kiện.
A.
A 2;B 4;C 1;D 3
B.
A 3;B 4;C 2;D 1
C.
A 1;B 3;C 2;D 4
D.
A 1;B 2;C 3;D 4
C©u 8 :
Tìm
m
để đường thẳng
:d y x m
cắt đồ thị hàm số
2
1
x
y
x
tại hai điểm phân biệt.
A.
3 3 2
3 3 2
m
m
3 2 2
3 2 2
m
m
C.
1 2 3
1 2 3
m
m
D.
4 2 2
4 2 2
m
m
C©u 9 :
Tìm GTLN của hàm số
2
2 5 y x x
A.
5
25
C.
6
D.
Đáp án khác
C©u 10 :
Cho hàm số
32
12
33
y x mx x m
(C
m
). Tìm m để (C
m
) cắt trục Ox tại ba điểm phân biệt có
4
2
2
4
2
2
4
6
4
2
2
2
4
6
3
hoành độ x
1
; x
2
; x
3
thỏa x
1
2
+ x
2
2
+ x
3
2
> 15?
A.
m < -1 hoặc m > 1
m < -1
C.
m > 0
D.
m > 1
C©u 11 :
Tìm các giá trị của tham số m để hàm số
4 2 2
2( 1) 1 y x m x
có 3 điểm cực trị thỏa mãn
giá trị cực tiểu đạt giá trị lớn nhất.
A.
m 1
m 0
C.
m 3
D.
m 1
C©u 12 :
Họ đường cong (C
m
) : y = mx
3
– 3mx
2
+ 2(m-1)x + 1 đi qua những điểm cố định nào?
A.
A(0;1) ; B(1;-1) ; C(2;-3)
B.
A(0;1) ; B(1;-1) ; C(-2;3)
C.
A(-1;1) ; B(2;0) ; C(3;-2)
D.
Đáp án khác
C©u 13 :
Hàm số
32
xy ax b cx d
đạt cực trị tại
12
x,x
nằm hai phía trục tung khi và chỉ khi:
A.
a 0, 0,c 0b
2
12a 0bc
C.
a
và
c
trái dấu
D.
2
12a 0bc
C©u 14 :
Hàm số
mx 1
y
xm
đồng biến trên khoảng
(1; )
khi:
A.
1 m 1
m1
C.
m \[ 1;1]
D.
m1
C©u 15 :
Hàm số
3
1
y x m 1 x 7
3
nghịch biến trên thì điều kiện của m là:
A.
m1
m1
C.
m2
D.
m2
C©u 16 :
Đồ thị của hàm số
2
2x 1
1
y
xx

có bao nhiêu đường tiệm cận:
A.
0
1
C.
2
D.
3
C©u 17 :
Hàm số
42
y ax bx c
đạt cực đại tại
(0; 3)A
và đạt cực tiểu tại
( 1; 5)B 
Khi đó giá trị của a, b, c lần lượt là:
A.
2; 4; -3
-3; -1; -5
C.
-2; 4; -3
D.
2; -4; -3
C©u 18 :
Cho đồ thị (C) : y = ax
4
+ bx
2
+ c . Xác định dấu của a ; b ; c biết hình dạng đồ thị như sau :
4
A.
a > 0 và b < 0 và c > 0
B.
a > 0 và b > 0 và c > 0
C.
Đáp án khác
D.
a > 0 và b > 0 và c < 0
C©u 19 :
Tìm tất cả các giá trị của tham số k để phương trình sau có bốn nghiệm thực phân biệt
22
4 1 1x x k
.
A.
02k
01k
C.
11 k
D.
3k
C©u 20 :
Viết phương trình tiếp tuyến d của đồ thị hàm số
32
( ) 2 4f x x x x
tại giao điểm của đồ thị
hàm số với trục hoành.
A.
21yx
88yx
C.
1y
D.
7yx
C©u 21 :
Tìm giá trị nhỏ nhất của hàm số:
1 3 1. 3y x x x x
A.
2 2 1
Min
y
2 2 2
Min
y
C.
9
10
Min
y
D.
8
10
Min
y
C©u 22 :
Hàm số
3
2
3 5 2
3
x
y x x
nghịch biến trên khoảng nào trong các khoảng sau đây?
A.
2;3
R
C.
;1 v 5;a
D.
1;6
C©u 23 :
Chọn đáp án đúng. Cho hàm số
2x 1
2
y
x
, khi đó hàm số:
A.
Nghịch biến trên
2; 
B.
Đồng biến trên
\2R
C.
Đồng biến trên
2; 
D.
Nghịch biến trên
\2R
C©u 24 :
Cho hàm số
()
f x x x

32
3
, tiếp tuyến của đồ thị có hệ số góc k= -3 là
10
8
6
4
2
2
4
6
5
5
10
15
20
5
A.
()
yx
2 3 1 0
()
yx
3 1 2
C.
()
yx
2 3 1
D.
()
yx
2 3 1
C©u 25 :
Tìm cận ngang của đồ thị hàm số
2
x3
y
x1
A.
y3
y2
C.
y 1;y 1
D.
y1
C©u 26 :
Đồ thị hàm số
2x 1
y
x1
là
C
. Viết phương trình tiếp tuyết của
C
biết tiếp tuyến đó song
song với đường thẳng
d : y 3x 15
A.
y 3x 1
B.
y 3x 11
C.
y 3x 11; y 3x 1
D.
y 3x 11
C©u 27 :
Cho hàm số
21
()
1
x
yC
x
. Tìm các điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến hai
đường tiệm cận là nhỏ nhất
A.
M(0;1) ; M(-2;3)
Đáp án khác
C.
M(3;2) ; M(1;-1)
D.
M(0;1)
C©u 28 :
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của
42
23y x x
trên
0;2
:
A.
11, 2Mm
3, 2Mm
C.
5, 2Mm
D.
11, 3Mm
C©u 29 :
Tìm các giá trị của tham số m để hàm số
3
2
15
3
x
y m x mx
có 2 điểm cực trị.
A.
m
1
3
m
1
2
C.
m32
D.
m 1
C©u 30 :
Cho hàm số y = 2x
3
– 3x
2
+ 5 (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến qua
19
( ;4)
12
A
và tiếp xúc với (C) tại điểm có hoành độ lớn hơn 1
A.
y = 12x - 15
y = 4
C.
y =
21 645
32 128
x
D.
Cả ba đáp án trên
C©u 31 :
Tâm đối xứng của đồ thị hàm số
32
3x 9x 1yx
là :
A.
( 1;6)I
(3;28)I
C.
(1; 4)I
D.
( 1;12)I
C©u 32 :
Định m để hàm số
32
1
3 2 3
x mx
y
đạt cực tiểu tại
2x
.
A.
m 3
m 2
C.
Đáp án khác.
D.
m 1
6
C©u 33 :
Tìm số cực trị của hàm số sau:
()
f x x x
42
21
A.
Cả ba đáp án A, B,
C
y=1; y= 0
C.
x=0; x=1; x= -1
D.
3
C©u 34 :
Với giá trị nào của m thì hàm số
y sin3x msin x
đạt cực đại tại điểm
x
3
?
A.
m5
6
C.
6
D.
5
C©u 35 :
Tiệm cận ngang của đồ thị hàm số
2x 1
1
y
x
là:
A.
y3
x1
C.
1
x
2

D.
y2
C©u 36 :
Tìm tiêm cận đứng của đồ thị hàm số sau:
()
xx
fx
xx

2
2
52
43
A.
y= -1
y=1; x=3
C.
x=1; x= 3
D.
;
xx
13
C©u 37 :
Điều kiện cần và đủ để
2
43y x x m
xác định với mọi
:x
A.
7m
7m
C.
7m
D.
7m
C©u 38 :
Phát biểu nào sau đây là đúng:
1. Hàm số
()y f x
đạt cực đại tại
0
x
khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua
0
x
.
2. Hàm số
()y f x
đạt cực trị tại
0
x
khi và chỉ khi
0
x
là nghiệm của đạo hàm.
3. Nếu
'( ) 0
o
fx
và
0
'' 0fx
thì
0
x
không phải là cực trị của hàm số
()y f x
đã cho.
Nếu
'( ) 0
o
fx
và
0
'' 0fx
thì hàm số đạt cực đại tại
0
x
.
A.
1,3,4 .
1, 2, 4
C.
1
D.
Tất cả đều đúng
C©u 39 :
Tìm số tiệm cận của hàm số sau:
()
xx
fx
xx


2
2
31
34
A.
4
2
C.
1
D.
3
C©u 40 :
Cho hàm số
24
42 xxy
. Hãy chọn mệnh đề sai trong bốn phát biểu sau:
A.
Hàm số nghịch biến trên mỗi khoảng
1;
và
1;0
.
B.
Trên các khoảng
1;
và
1;0
,
0'y
nên hàm số nghịch biến.
7
C.
Hàm số đồng biến trên mỗi khoảng
1;
và
;1
.
D.
Trên các khoảng
0;1
và
;1
,
0'y
nên hàm số đồng biến.
C©u 41 :
Xác định k để phương trình
32
31
2 3 1
2 2 2
k
x x x
có 4 nghiệm phân biệt.
A.
3 19
2; ;7
44
k
B.
3 19
2; ;6
44
k
C.
3 19
5; ;6
44
k
D.
3; 1 1;2 k
C©u 42 :
Hàm số
3
y x 3mx 5
nghịch biến trong khoảng
1;1
thì m bằng:
A.
3
1
C.
2
D.
1
C©u 43 :
Cho hàm số
32
11
32
y x x mx
. Định m để hàm số đạt cực đại và cực tiểu tại các điểm có hoành
độ lớn hơn m?
A.
2m 
m > 2
C.
m = 2
D.
2m 
C©u 44 :
Cho hàm số
x8
x-2m
m
y
, hàm số đồng biến trên
3; 
khi:
A.
22m
22m
C.
3
2
2
m
D.
3
2
2
m
C©u 45 :
Tìm tất cả các đường tiệm cận của đồ thị hàm số
2
3
1
x
y
x
A.
1y 
y = -1
C.
x = 1
D.
y = 1
C©u 46 :
Từ đồ thị
C
của hàm số
3
y x 3x 2
. Xác định m để phương trình
3
x 3x 1 m
có 3
nghiệm thực phân biệt.
A.
0 m 4
1 m 2
C.
1 m 3
D.
1 m 7
C©u 47 :
Tìm khoảng đồng biến của hàm số sau:
()
y f x x x
42
18 8
A.
;; 3 0 3
B.
;; 3 3 3
C.
;; 30
D.
;; 3 0 3
C©u 48 :
Cho hàm số
42
11
22
y x x
. Khi đó:
8
A.
Hàm số đạt cực tiểu tại điểm
0x
, giá trị cực tiểu của hàm số là
0)0( y
.
B.
Hàm số đạt cực tiểu tại các điểm
1x
, giá trị cực tiểu của hàm số là
1)1( y
.
C.
Hàm số đạt cực đại tại các điểm
1x
, giá trị cực đại của hàm số là
1)1( y
D.
Hàm số đạt cực đại tại điểm
0x
, giá trị cực đại của hàm số là
2
1
)0( y
.
C©u 49 :
Cho hàm số
x2
y
x2
có I là giao điểm của hai tiệm cận. Giả sử điểm M thuộc đồ thị sao cho tiếp
tuyến tại M vuông góc với IM. Khi đó điểm M có tọa độ là:
A.
M(0; 1);M( 4;3)
M( 1; 2);M( 3;5)
C.
M(0; 1)
D.
M(0;1);M( 4;3)
C©u 50 :
Cho hàm số
32
y 2x 3 m 1 x 6 m 2 x 1
. Xác định m để hàm số có điểm cực đại và
cực tiểu nằm trong khoảng
2;3
A.
m 1;3
m 3;4
C.
m 1;3 3;4
D.
m 1;4
……….HẾT………
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 002-KSHS)
C©u 1 :
Đồ thị hàm số nào sau đây không có điểm uốn
A.
3
y x x

4
( 1)
yx

C.
42
y x x

D.
3
( 1)
yx

C©u 2 :
Miền giá trị của
2
61y x x
là:
A.
10;T
; 10T
C.
; 10T
D.
10;T 
C©u 3 :
Với giá trị m là bao nhiêu thì hàm số
3 2 2
( ) 3 3 2 5f x x x m m x
đồng biến trên (0; 2)
A.
12m
12mm
C.
12m
D.
12mm
C©u 4 :
Số giao điểm của đồ thị hàm số
42
2x
y x m
với trục hoành là 02 khi và chỉ khi
A.
0
m
0
m
C.
0
1
m
m
D.
0
1
m
m

C©u 5 :
Cho hàm số
3
52
63
xm
y mx
(C). Định m để từ
2
,0
3
A



kẻ đến đồ thị hàm số (C) hai tiếp tuyến
vuông góc nhau.
A.
1
2
m 
hoặc
2m
B.
1
2
m
hoặc
2m
C.
1
2
m
hoặc
2m 
D.
1
2
m 
hoặc
2m 
C©u 6 :
Tiếp tuyến của đồ thị hàm số
x+2
1
y
x
tại giao điểm với trục tung cắt trục hoành tại điểm có hoành
độ là
A.
2
x

2
x
C.
1
x
D.
1
x

C©u 7 :
Tìm m để f(x) có ba cực trị biết
()
f x x mx
42
21
A.
m
0
m > 0
C.
m < 0
D.
m
0
2
C©u 8 :
Với giá trị m là bao nhiêu thì hàm số
4 2 2
( ) 1 2f x mx m x m
đạt cực tiểu tại
x =1.
A.
1
3
m 
1m 
C.
1m
D.
1
3
m
C©u 9 :
Tìm giá trị lớn nhất của hàm số sau:
()
f x x x x x
22
2 8 4 2
A.
2
- 1
C.
1
D.
0
C©u 10 :
Cho
432
4 6 1 ( )y x x x C
. Mệnh đề nào sau đây đúng?
A.
(C) luôn lõm
B.
(C) có điểm uốn
1;4
C.
(C) luôn lồi
D.
(C) có 1 khoảng lồi và 2 khoảng lõm
C©u 11 :
Tìm điểm cực đại của đồ thị hàm số
32
36y x x
A.
0
1x
0
3x
C.
0
2x
D.
0
0x
C©u 12 :
Cho hàm số
26
4
x
y
x
có đồ thị (C). Phương trình đường thẳng qua
0,1M
cắt đồ thị hàm số tại
A và B sao cho độ dài AB là ngắn nhất. Hãy tìm độ dài AB.
A.
2
3
C.
4
D.
5
C©u 13 :
Giá trị lớn nhất của hàm số
2
+6x
yx
trên đoạn
[ 4;1]
là
A.
7
8
C.
9
D.
12
C©u 14 :
Cho hàm số
32
y x 3x 4
có hai cực trị là A và B. Khi đó diện tích tam giác OAB là :
A.
2
4
C.
25
D.
8
C©u 15 :
Đường thẳng qua hai cực trị của hàm số
2
31
()
2
xx
fx
x

song song với:
A.
23yx
1
2
2
yx
C.
22yx
D.
11
22
yx
C©u 16 :
Tìm m để f(x) có một cực trị biết
()
f x x mx
42
1
A.
m < 0
m
0
C.
m > 0
D.
m
0
C©u 17 :
Với giá trị a bao nhiêu thì
2
2 1 0 1x a x a x
.
A.
Không tồn tại a thỏa mãn điều kiện trên
B.
a tùy ý.
3
C.
4 2 2a 
D.
4 2 2a 
C©u 18 :
Đạo hàm của hàm số
yx
tại điểm
0
x
là
A.
0
Không tồn tại
C.
1
D.
1
C©u 19 :
Đồ thị f(x) có bao nhiêu điểm có tọa độ là cặp số nguyên
()
xx
fx
x

2
2
1
A.
3
6
C.
Không có
D.
Vô số
C©u 20 :
Cho hàm số
2x m
y (C)
x1
và đường thẳng
y x 1(d)
. Đường thẳng d cắt đồ thị (C) khi:
A.
m2
m2
C.
m2
D.
m 2;m 1
C©u 21 :
Cho đồ thị (C):
3
3y x x
. Tiếp tuyến tại N(1; 3) cắt (C) tại điểm thứ 2 là M (M ≠ N). Tọa độ M
là:
A.
1;3M
1;3M
C.
2;9M
D.
2; 3M 
C©u 22 :
Điểm cực đại của hàm số
3
( ) 3 2f x x x
là:
A.
1;0
1;0
C.
1;4
D.
1;4
C©u 23 :
Gọi M, m lần lượt là GTLN và GTNN của hàm số
3
( ) sin 3sin 1f x x x
trên
0;
. Khi
đó giá trị M và m là:
A.
3, 2Mm
3, 1Mm
C.
1, 2Mm
D.
1, 3Mm
C©u 24 :
Hàm số
32
x 2017
3
m
y x x
có cực trị khi và chỉ khi
A.
1
0
m
m
1
m
C.
1
m
D.
1
0
m
m
C©u 25 :
Cho
32
3 2 ( ), ( )
mm
y x mx C C
nhận
(1;0)I
làm tâm đối xứng khi:
A.
1m
1m 
C.
0m
D.
Các kết quả a, b, c
đều sai
C©u 26 :
Cho hàm số
42
43y x x
có đồ thị (C). Tìm điểm A trên đồ thị hàm số sao cho tiếp tuyến tại A
cắt đồ thị tại hai điểm B, C (khác A) thỏa
222
8
A B C
xxx
A.
1,0A
1,0A
C.
2,3A
D.
0,3A
C©u 27 :
Tất cả các điểm cực đại của hàm số
cos
yx
là
4
A.
2 ( )
x k k
2 ( )
x k k

C.
()
x k k

D.
()
2
x k k
C©u 28 :
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của
42
23y x x
trên
0;2
:
A.
11, 2Mm
3, 2Mm
C.
5, 2Mm
D.
11, 3Mm
C©u 29 :
Cho hàm số
3
32y x x
có đồ thị (C). Tìm m biết đường thẳng (d):
3y mx
cắt đồ thị tại hai
điểm phân biệt có tung độ lớn hơn 3.
A.
0m
64m
C.
9
6
2
m
D.
9
4
2
m
C©u 30 :
Giá trị nhỏ nhất của hàm số
2
4
y x x
là
A.
22
2
C.
-2
D.
22
C©u 31 :
Viết phương trình tiếp tuyến d với đồ thị (C):
2
,
2
x
y
x
biết d đi qua điểm
( 6,5)A
A.
7
1,
42
x
y x y
B.
7
1,
22
x
y x y
C.
7
1,
42
x
y x y
D.
5
1,
42
x
y x y
C©u 32 :
Hàm số
1
x
y
xm
nghịch biến trên khoảng
( ;2)
khi và chỉ khi
A.
1
m
2
m
C.
2
m
D.
1
m
C©u 33 :
Cho các đồ thị hàm số
2x 1
1
y
x
,
1
y
x
,
2x-1
y
,
2
y
. Số đồ thị có tiệm cận ngang là
A.
1
3
C.
2
D.
4
C©u 34 :
Hàm số
3 2 2
y x 3(m 1)x 3(m 1) x
. Hàm số đạt cực trị tại điểm có hoành độ
x1
khi:
A.
m2
m 0;m 1
C.
m1
D.
m 0;m 2
C©u 35 :
Cho hàm số
42
2 1 2y x m x m
. Tìm m để hàm số đồng biến trên
1,3
A.
,5m
2,m 
C.
5,2m
D.
,2m
C©u 36 :
Cho hàm số:
32
1
( ) 2 1 5
3
f x x x m x
. Với m là bao nhiêu thì hàm số đã cho đồng biến trên
R.
A.
3m
3m
C.
3m
D.
3m
5
C©u 37 :
Cho
2
( 1) 2 1
.
x m x m
y
xm
Để y tăng trên từng khoảng xác định thì:
A.
1m
1m
C.
1m
D.
1m
C©u 38 :
Có bao nhiêu tiếp tuyến của đồ thị hàm số (C):
3
62y x x
qua
M(1; -3).
A.
2.
3.
C.
1.
D.
0.
C©u 39 :
Cho hàm số
27
2
x
y
x
có đồ thị (C). Tìm điểm M trên (C) sao cho khoảng cách từ M đến gốc tọa
độ là ngắn nhất.
A.
1
2
3, 1
1
4,
2
M
M



1
2
13
3,
5
1,3
M
M



C.
1
2
1,5
3, 1
M
M
D.
1
2
3, 1
1,3
M
M
C©u 40 :
Hàm số
22
3
y (x 2x)
đạt cực trị tại điểm có hoành độ là:
A.
x 1;x 0;x 2
x 1;x 0
C.
x1
D.
Hàm số không có
cực trị
C©u 41 :
Cho hàm số
32
(2 1) 2 2y x m x m x
. Tìm m để đồ thị hàm số có cực đại và cực tiểu.
A.
1,m 
5
1,
4
m




C.
,1m 
D.
5
, 1 ,
4
m
 
C©u 42 :
2
3
.
2
xx
Cho y
x

Các mệnh đề sau đây, mệnh đề nào đúng?
A.
y không có cực trị
B.
y có một cực trị
C.
y có hai cực trị
D.
y tăng trên
C©u 43 :
Hàm số
32
y ax bx cx d
đồng biến trên R khi:
A.
2
a b 0,c 0
a 0;b 3ac 0
B.
2
a b 0,c 0
a 0;b 3ac 0
C.
2
a b 0,c 0
b 3ac 0

D.
2
a b c 0
a 0;b 3ac 0
C©u 44 :
Cho hàm số
3
2
59
3
mx
y x mx
có đồ thị hàm số là (C). Xác định m để (C) có điểm cực trị nằm
trên Ox.
6
A.
3m
2m 
C.
2m 
D.
3m 
C©u 45 :
Tìm giá trị nhỏ nhất của hàm số sau:
()
f x x x x x
22
2 4 2 2
A.
0
-2
C.
Không có
D.
2
C©u 46 :
Cho
36
()
2
x
yC
x

. Kết luận nào sau đây đúng?
A.
(C) không có tiệm cận
B.
(C) có tiệm cận ngang
3y 
C.
(C) có tiệm cận đứng
2x
D.
(C) là một đường thẳng
C©u 47 :
Cho hàm số
2x 1
y
x1
. Tiếp tuyến tại điểm M thuộc đồ thị cắt Ox và Oy lần lượt tại hai điểm A và
B thỏa mãn
OB 3OA
. Khi đó điểm M có tọa độ là:
A.
M(0; 1);M(2;5)
M(0; 1)
C.
M(2;5);M( 2;1)
D.
M(0; 1);M(1;2)
C©u 48 :
Cho hàm số sau:
1
()
1
x
fx
x
A.
Hàm số đồng biến trên
( ;1) (1; )
.
B.
Hàm số nghịch biến trên
\{1}
.
C.
Hàm số nghịch biến trên
( ;1),(1; )
.
D.
Hàm số đồng biến trên
\{1}
.
C©u 49 :
Phương trình
32
x x x m 0
có hai nghiệm phân biệt thuộc
[ 1;1]
khi:
A.
5
m1
27
5
m1
27
C.
5
m1
27
D.
5
1m
27
C©u 50 :
Cho hàm số
3
32y x x
có đồ thị (C). Tìm trên đồ thị hàm số (C) điểm M cắt trục Ox, Oy tại A,
B sao cho
3MA MB
A.
1,0M
0,2M
C.
1,4M
D.
Không có điểm M.
………HẾT……….
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 003-KSHS)
C©u 1 :
Hm s
2sin 1
sin 2
x
y
x
c GTLN l
A.
3
1
C.
1
D.
1
3
C©u 2 :
Với giá trị nào của m thì phường trình
42
23x x m
có 4 nghiệm phân biệt (m là tham s).
A.
( 4; 3)m
3m 
hoặc
4m 
C.
( 3; )m 
D.
( ; 4)m
C©u 3 :
Hm s
32
2 4 5y x x
đng bin trên khong no?
A.
4
0;
3



;0
;
4
;
3



C.
;0
;
4
;
3




D.
4
0;
3



C©u 4 :
Tìm m để hàm s:
3
22
( 2) ( 2) ( 8) 1
3
x
y m m x m x m
nghịch bin trên
A.
2m 
2m 
C.
2m 
D.
2m 
C©u 5 :
Cho hàm s
1
2
x
y
x
c đ thị là
()H
. Chọn đáp án sai.
A.
Tip tuyn với
()H
tại giao điểm của
()H
với trục honh c phương trình :
1
( 1)
3
yx
B.
Có hai tip tuyn của
()H
đi qua điểm
( 2;1)I
C.
Đường cong
()H
có vô s cặp điểm mà tip tuyn tại các cặp điểm đ song song với nhau
D.
Không có tip tuyn của
()H
đi qua điểm
( 2;1)I
C©u 6 :
Giá trị nhỏ nhất của hàm s
2
3 10y x x
là:
A.
3 10
3 10
C.
10
D.
Không xác định.
2
C©u 7 :
Cho hm s
2
1x mx
y
xm

. Định mđể hm s đạt cc trị tại
2x
A.
13mm
1m 
C.
2m 
D.
3m 
C©u 8 :
Cho hàm s
32
2 3 2 1 6 1 2y x a x a a x
. Nu gọi
12
, xx
lần lượt l honh độ các điểm
cc trị của hàm s thì giá trị
21
xx
là:
A.
1.a
.a
C.
1.
D.
1.a
C©u 9 :
Trong các hàm s sau, hàm s no đơn điệu trên tập xác định của chúng.
A.
21
()
1
x
fx
x
B.
32
'( ) 4 2 8 2f x x x x
C.
42
( ) 2 4 1f x x x
D.
42
(x) 2f x x
C©u 10 :
Cho hàm s:
32
9 15 13
4 4 4
y x x x
, phát biểu no sau đây l đúng:
A.
Đ thị hàm s có tiệm cận ngang và tiệm cận
đứng.
B.
Đ thị hàm s cắt trục hoành tại 1 điểm.
C.
Hàm s có cc trị.
D.
Hàm s nghịch bin trên tập xác định.
C©u 11 :
Với giá trị no của tham s m thì hm s
3
2
3 2 3y m mx
không c cc trị
A.
3m
B.
Không c m thỏa yêu cầu bi toán.
C.
30mm
D.
0m
C©u 12 :
Tìm m để hàm s sau gim tên từng khong xác định
A.
1
2
2
m
2m 
hay
1
2
m
C.
1
2
m
hay
2m
D.
1
2
2
m
C©u 13 :
Cho hàm s
3 2 2
3 3( 1) 2 3y x mx m x m
, m là tham s. Hàm s nghịch bin trong
khong(1;2) khi m bằng:
A.
12m
1m
C.
2m
D.
mR
C©u 14 :
Cho
2
7 4 5
:
23
xx
Cy
x

.
C
c tiệm cận đứng l
A.
3
2
y
2
3
y
C.
3
2
x
D.
2
3
x
C©u 15 :
Cho hàm s
32
1
(2 1) 2
3
y x mx m x m
. Giá trị
m
để hàm s đng bin trên là :
3
A.
Không có
m
1m
C.
1m
D.
1m
C©u 16 :
Cho đường cong
()C
c phương trình
2
1yx
. Tịnh tin
()C
sang phi
2
đơn vị, ta được đường
cong c phương trình no sau đây ?
A.
2
12yx
2
43y x x
C.
2
12yx
D.
2
43y x x
C©u 17 :
Hàm s no sau đây nghịch bin trên các khong xác định của nó:
A.
2
2
x
y
x
2
2
x
y
x
C.
2
2
x
y
x
D.
Không c đáp án
no đúng.
C©u 18 :
Vit phương trình đường thng đi qua 2 điểm cc trị của đ thị hm s
32
23y x x
A.
yx
1yx
C.
1yx
D.
yx
C©u 19 :
Tìm m để hàm s
4 2 2
25y x m x
đạt cc tiểu tại
1x 
A.
1m
1m 
C.
1m 
D.
m
C©u 20 :
Tìm khong đng bin của hàm s
42
2x 3yx
A.
(-1;0)
0;
C.
(0;1)
D.
;0
C©u 21 :
Cho hàm s
23
1
x
x
c đ thị (C). Điểm M thuộc (C) thì tip tuyn của đ thị (C) tại M vuông góc
với đường y= 4x+7. Tất c điểm M có tọa độ thỏa mãn điều kiện trên là:
A.
5
1;
2
M



hoặc
3
3;
2
M



.
B.
5
1;
2
M



.
C.
3
3;
2
M



.
D.
5
1;
2
M



hoăc
3
3;
2
M



.
C©u 22 :
Tìm m để hàm s đng bin trên tập xách định
3 2 2
3 x (3 1) 5y x m m m x m
A.
m>1
m<1
C.
1m 
D.
1m 
C©u 23 :
Tìm m để hàm s:
42
2(2 1) 3y x m x
c đúng 1 cc trị:
A.
1
2
m
1
2
m
C.
1
2
m
D.
1
2
m
C©u 24 :
Hm s
23
32y x x
đạt cc trị tại
A.
0; 1
CÐ CT
xx
B.
0; 1
CÐ CT
xx
C.
1; 0
CÐ CT
xx
D.
1; 0
CÐ CT
xx
4
C©u 25 :
Với những giá trị nào của
m
thì đ thị
()C
của hàm s
2
2x x m
y
xm
không có tiệm cận đứng ?
A.
1; 2mm
0; 1mm
C.
0m
D.
0; 2mm
C©u 26 :
Cho hàm s
1
2
mx
y
x
c đ thị C
m
(m là tham s). Với giá trị nào của m thì đường thng
21yx
cắt đ thị C
m
tại 2 điểm phân biệt A, B sao cho AB=
10
.
A.
3m
3m
C.
1
2
m 
D.
1
2
m
C©u 27 :
Đ thị hàm s
2016
21
x
y
x
cắt trục tung tại điểm
M
có tọa độ ?
A.
2016; 2016 .
2016;0 .M
C.
0; 2016 .M
D.
0;0 .M
C©u 28 :
Cho hàm s
2
1
x ax b
y
x
. Đặt
,2A a b B a b
. Để hàm s đạt cc đại tại điểm
(0; 1)A
thì tổng giá
trị của
2AB
là :
A.
6
1
C.
3
D.
0
C©u 29 :
Hàm s no sau đây nghịch bin trên toàn trục s ?
A.
32
3 3 1y x x x
32
31y x x
C.
3
32y x x
D.
3
3yx
C©u 30 :
S điểm chung của đ thị hàm s
32
2x 12y x x
với trục Ox là:
A.
0
1
C.
2
D.
3
C©u 31 :
Cho hàm s
2
1
( ) ln tan
2sin
y g x x
x
. Giá trị đúng của
6
g
là:
A.
8
3
12
3
C.
16
3
D.
32
3
C©u 32 :
Hàm s
4
2
2x 1
2
x
y
đạt cc đại tại:
A.
2; 3xy
0; 1xy
C.
2; 3xy
D.
2; 3xy
C©u 33 :
Dùng định nghĩa, tính đạo hàm của hàm s sau:
2
2
2 3 4
1
xx
y
x

A.
2
2
2
3 4 3
'
1
xx
y
x
B.
2
2
2
3 8 3
'
1
xx
y
x

5
C.
2
2
2
3 4 3
'
1
xx
y
x

D.
2
2
2
3 4 3
'
1
xx
y
x

C©u 34 :
Đ thị hàm s
2
3 4 1
1
xx
y
x
A.
Có tiệm cận đứng.
B.
Có tiệm cận đứng và tiệm cận xiên.
C.
Không có tiệm cận.
D.
Có tiệm cận ngang.
C©u 35 :
Trên đoạn
1;1
, hàm s
32
4
23
3
y x x x
A.
Có giá trị nhỏ nhất tại
1
và giá trị lớn nhất tại
1
.
B.
Không có giá trị nhỏ nhất và có giá trị lớn nhất tại
1
.
C.
Có giá trị nhỏ nhất tại
1
và giá trị lớn nhất tại
1
.
D.
Có giá trị nhỏ nhất tại
1
và không có giá trị lớn nhất.
C©u 36 :
Đường thng
1yx
cắt đ thị hàm s
21
1
x
y
x
tại các điểm có tọa độ là:
A.
(0;-1) và (2;1)
(-1;0) và (2;1)
C.
(0;2)
D.
(1;2)
C©u 37 :
Cho hàm s
2
yx
x
. Khng định no sau đây sai
A.
Đạo hàm của hàm s đổi dấu khi đi qua
2x
và
2.x
B.
Hàm s có giá trị cc tiểu là
22
, giá trị cc đại là
22
.
C.
Hàm s có GTNN là
22
, GTLN là
2 2.
D.
Đ thị của hàm s c điểm cc tiểu là
2;2 2
v điểm cc đại là
2; 2 2 .
C©u 38 :
Phương trình đường thng vuông góc với
1
9
x
y 
và tip xúc với (C):
32
3x 1yx
là
A.
9x+14y
9x+4; 9x 26yy
C.
9x+14; 9x-26yy
D.
9x 4y 
C©u 39 :
Cho hàm s
3 2 2
3 ( 1) 2y x mx m x
, m là tham s. Hàm s đạt cc tiểu tại x =2 khi m bằng:
A.
1m
2m
C.
1m
D.
1m
C©u 40 :
Cho
31
:
32
x
Cy
x
.
C
c tiệm cận ngang l
6
A.
1y
3x
C.
1x
D.
3y
C©u 41 :
Đạo hàm của hàm s
cos tanyx
bằng:
A.
sin tan .x
sin tan .x
C.
2
1
sin tan . .
cos
x
x
D.
2
1
sin tan .
cos
x
x
C©u 42 :
Tìm m để hàm s
x2m
y
mx
đng bin trên các khong xác định:
A.
2m 
2
2
m
m

C.
2
2
m
m

D.
m
C©u 43 :
Cho hàm s
2
3
ax
y
bx
c đ thị là
C
. Tại điểm
2; 4M
thuộc
C
, tip tuyn của
C
song
song với đường thng
7 5 0xy
. Các giá trị thích hợp của
a
và
b
là:
A.
1; 2.ab
2; 1.ab
C.
3; 1.ab
D.
1; 3.ab
C©u 44 :
Trong các hàm s sau, hàm s no đng bin trên R.
A.
32
( ) 3f x x x x
B.
32
( ) 2 3 1f x x x
C.
1
()
32
x
fx
x
D.
42
( ) 4 1f x x x
C©u 45 :
Tiệm cận đứng và tiệm cận ngang của hàm s
2x 1
2
y
x
là:
A.
2; 2xy
2; 2xy
C.
2; 2xy
D.
2; 2xy
C©u 46 :
Cho hm s
32
: 6 9 6C y x x x
. Định m để đường thng
: 2 4d y mx m
cắt đ thị
C
tại ba điểm phân biệt.
A.
3m
3m 
C.
3m
D.
3m 
C©u 47 :
Nu hàm s
11
2
mx
y
xm
nghịch bin trên từng khong xác định thì giá trị của
m
là:
A.
2.m
2.m
C.
1 2.m
D.
2.m
C©u 48 :
Cho hàm s
cos x
ye
. Hãy chọn hệ thức đúng:
A.
'.cos .sin '' 0y x y x y
B.
'.sin ''.cos ' 0y x y x y
C.
'.sin .cos '' 0y x y x y
D.
'.cos .sin '' 0y x y x y
7
C©u 49 :
Tip tuyn của đ thị hàm s
32
32y x x
tại điềm M(-1;-2) là
A.
97yx
92yx
C.
24 2yx
D.
24 22yx
C©u 50 :
Cho hàm s
32
3 9 4y x x x
. Nu hàm s đạt cc đại
1
x
và cc tiểu
2
x
thì tích
12
( ). ( )y x y x
bằng :
A.
207
302
C.
82
D.
25
………HẾT……….
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 004-KSHS)
C©u 1 :
Giá trị nhỏ nhất của hàm số
46
y x x
đạt tại
0
x
, tìm
0
x
:
A.
0
1
x

0
4
x
C.
0
6
x

D.
0
1
x
C©u 2 :
Tìm m để pt sau có nghiệm
2
31x m x
A.
1 10m
-1<m<
10
C.
10m
D.
m>-1
C©u 3 :
Cho hàm số
42
25y x x
và
[ 1;2]D 
;
max( )
D
My
,
min( )
D
my
. Tìm câu đúng?
A.
M = 13 và m = 4
M = 5 và m = 0
C.
M = 5 và m = 4
D.
M = 13 và m = 5
C©u 4 :
Hãy xác định
,ab
để hàm số
2ax
y
xb
có đồ thị như hình vẽ
A.
a = 1; b = -2
a = b = 1
C.
a = 1; b = 2
D.
a = b = 2
C©u 5 :
Cho
32
( ) : 2 3 4C y x x x
và đường thẳng
:4d y mx
. Giả sử
d
cắt
()C
tại ba điểm phân
biệt
(0; 4)A
,
,BC
. Khi đó giá trị của
m
là:
A.
3m
Một kết quả khác
C.
2m
D.
2m
2
C©u 6 :
Cho hàm số
32
34y x x C
. Gọi d là đường thẳng đi qua điểm A(- 1; 0) với hệ số góc là k (
k thuộc R). Tìm k để đường thẳng d cắt (C) tại ba điểm phân biệt và hai giao điểm B, C ( B, C khác
A ) cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 1.
A.
3
1
4
k 
Đáp án khác
C.
3
1
4
k 
D.
3
1
4
k
C©u 7 :
Giá trị lớn nhất của hàm số 𝑦 = 4𝑦
3
− 3𝑦
4
là:
A.
3
4
C.
8
D.
6
C©u 8 :
Đồ thị hàm số
22
29y x mx m
cắt trục hoành tại hai điểm M và N thì
A.
4MN
6MN
C.
6MN m
D.
4MN m
C©u 9 :
Cho hàm số
21
2
x
y
x
. Mệnh đế nào sau đây sai?
A.
Đồ thị tồn tại một cặp tiếp tuyến vuông góc với nhau
B.
Tại giao điểm của đồ thị và
Oy
, tiếp tuyến song song với đường thẳng
51
44
yx
C.
Tại
3
2;
4
A



, tiếp tuyến của đồ thị có hệ số góc
5
16
k
D.
Lấy
,MN
thuộc đồ thị với
0, 4
MN
xx
thì tiếp tuyến tại
,MN
song song với nhau
C©u 10 :
Xác định tiệm cận của đồ thị hàm số
85
3
x
y
x
A.
Tiệm cận đứng:
3
x
; Tiệm cận ngang:
8
3
y
B.
Tiệm cận đứng:
3
x
; Tiệm cận ngang:
8
y

C.
Tiệm cận đứng:
3
x
; Tiệm cận ngang:
5
y

D.
Tiệm cận đứng:
3
x
; Tiệm cận ngang:
5
3
y
C©u 11 :
Tìm cực trị của hàm số sau
2
1y x x
A.
Điểm CT
13
( ; )
22
Điểm CT(-1:3)
C.
Không có
D.
Điểm CĐ (1;3)
C©u 12 :
Cho hàm số
32
2 3 4
m
y x mx m x C
(1). Tìm m để đường thẳng d : y = x + 4 cắt đồ thị
hàm số (1) tại ba điểm phân biệt A, B, C sao cho tam giác MBC có diện tích bằng 4 . ( Điểm B, C có
3
hoành độ khác không ; M(1;3) ).
A.
23mm
23mm
C.
23mm
D.
3m
C©u 13 :
Cho hàm số
2
m
mx
yH
x
. Tìm m để đường thẳng d : 2x + 2y - 1= 0 cắt
m
H
tại hai điểm
phân biệt A, B sao cho tam giác OAB có diện tích bằng
8
3
.
A.
3 10m
2 10m
C.
2 10m 
D.
2 10m 
C©u 14 :
Tìm m để hàm số
32
( 3) 1y x m x m
đạt cực đại tại x=-1
A.
3
2
m
m=1
C.
3
2
m
D.
m=-3
C©u 15 :
Tìm giá trị LN và NN của hàm số
4
6 , 1
1
y x x
x
A.
m=-3
M=-2
C.
m=1;M=2
D.
m=-1;M=5
C©u 16 :
Cho hàm số
32
3y x x a
. Trên
[ 1;1]
, hàm số có giá trị nhỏ nhất bằng 0. Tính a?
A.
0a
4a
C.
2a
D.
6a
C©u 17 :
Tìm m để hàm số
42
1 2 1y mx m x m
có ba cực trị.
A.
0m
1
0
m
m

C.
1
0
m
m

D.
10m
C©u 18 :
Cho hàm số
1
23
xxy
có đồ thị (C). Phương trình tiếp tuyến của (C), biết tiếp tuyến cắt trục
Ox, Oy lần lượt tại A, B và tam giác OAB cân tại O là :
A.
32
:
27
d y x
32
:
27
d y x
C.
32
:
27
d y x
D.
32
:
27
d y x
C©u 19 :
Cho hàm số
32
32y x x
, gọi A là điểm cực đại của hàm số trên. A có tọa độ:
A.
A(0,0)
A(2,-2)
C.
A(0,2)
D.
A(-2,-2)
C©u 20 :
Cho hàm số
32
4 3 7
y x x x
đạt cực tiểu tại
CT
x
. Kết luận nào sau đây đúng?
A.
3
CT
x

1
3
CT
x
C.
1
3
CT
x

D.
1
CT
x
C©u 21 :
Xác định m để hàm số
3 2 2
3
( ) 2
2
y x mx m m x
đạt cực tiểu tại
1x 
A.
1m
3m
C.
{1; 3}m
D.
2m
4
C©u 22 :
Tìm giá trị lớn nhất M của hàm số
32
3 9 1
y x x x
trên
2;4


A.
21
M
5
M
C.
4
M
D.
3
M
C©u 23 :
Hàm số
32
1
1
32
m
y x x m x
đạt cực đại tại
1
x
khi
A.
2
m
2
m
C.
2
m
D.
2
m
C©u 24 :
Với giá trị nào của m thì tiếp tuyến của đồ thị hàm số
3
1
3
3
y x x
tại điểm có hoành độ bằng
1
song song với đường thẳng
2
( 1) 2
y m x
?
A.
5
m

3
m

C.
5
m
D.
3
m
C©u 25 :
Cho hàm số
3 2 2 2
3 3 1 3 1 1y x x m x m
. Tìm m để hàm số (1) có cực đại , cực tiểu ,
đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O.
A.
6
1;
2
mm
6
1;
2
mm
C.
6
1;
2
mm
D.
6
1;
2
mm
C©u 26 :
Cho hàm số
4 2 2
21
m
y x m x C
(1). Tìm m dể hàm số (1) có ba điểm cực trị là ba đỉnh của
một tam giác vuông cân
A.
1m 
1m
C.
2m 
D.
1m 
C©u 27 :
Cho hàm số
2
3
2
mx m
y
x

, tìm m để hàm số đồng biến trên từng khoảng xác định.
A.
31m
2m 
C.
3
1
m
m

D.
31m
C©u 28 :
Tìm m để đường thẳng
ym
cắt đồ thị hàm số
42
23y x x
tại bốn điểm phân biệt.
A.
01m
11m
C.
43m
D.
40m
C©u 29 :
Cho hàm số
2
1
x
yC
x
. Tìm tọa độ điểm M thuộc (C) , biết tiếp tuyến tại M cắt hai trục Ox, Oy
tại hai điểm A, B sao cho tam giác OAB có diện tích bằng
4
1
.
A.
12
1
1;1 ; ;2
2
MM



B.
12
1
1;1 ; ; 2
2
MM



C.
12
1
1; 1 ; ; 2
2
MM



D.
12
1
1;1 ; ; 2
2
MM




5
C©u 30 :
Tìm GTNN của hàm số
2
2 5 4
2
xx
y
x

trên [0,1]
A.
-7
11
3
C.
2
D.
1
C©u 31 :
Tìm m để hàm số
3 2 2
2 2 1y x mx m x m
đạt cực tiểu tại
1x
.
A.
3m 
3
2
m 
C.
1m 
D.
1m
C©u 32 :
Cho hàm số
32
3 3 1 1 3
m
y x x m x m C
.Tìm m để hàm số có cực đại , cực tiểu ,
đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác có diện tích
bằng 4 .
A.
1m 
1m 
C.
2m 
D.
1m
C©u 33 :
Tìm tập xác định D của hàm số sau:
31
3 2 5
x
y
xx

A.
D =
3,
D =
5
,
2



C.
D =
5
, \ 3
2




D.
D =
3,
C©u 34 :
Hình vẽ này là đồ thị của hàm số nào sau đây
A.
3
1yx
3
31y x x
C.
3
1yx
D.
3
31y x x
C©u 35 :
Tìm m để hàm số
3 2 2
3 x 3( 1) 2 3y x m m x m
ngịch biến trên khoảng (1;3)
A.
12m
m>-1
C.
m>1
D.
m<2
C©u 36 :
Cho hàm số
42
4 10
y x x
và các khoảng sau:
(I).
;2
; (II).
2;0
; (III).
0; 2
.
Hãy tìm các khoảng đồng biến của hàm số trên?
A.
(I) và (II)
(I) và (III)
C.
(II) và (III)
D.
Chỉ (I).
6
C©u 37 :
Cho hàm số
23
1
x
y
x
, tiệm cận ngang của hàm số trên là:
A.
1x 
1y 
C.
2y
D.
2x
C©u 38 :
Cho hàm số
sin cosy x x
. Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số đã cho.
Khi đó: hiệu
Mm
bằng
A.
22
2
C.
2
D.
4
C©u 39 :
Cho hàm số
4
2
1
2
x
yx
, hàm số đồng biến trên:
A.
,0 ; 1, 
, 1 ; 0,1
C.
1,0 ; 1,
D.
, 
C©u 40 :
Tìm giá trị LN và NN của hàm số
2
sinx 2 sinyx
A.
m=0;M=2
m=0;M=-2
C.
m=-1;M=4
D.
m=1;M=4
C©u 41 :
Cho hàm số
1
ax b
y
x
có đồ thị cắt trục tung tại
(0;1)
A
, tiếp tuyến tại A có hệ số góc
3
. Tìm các
giá trị a, b:
A.
2; 1
ab
2; 1
ab

C.
4; 1
ab
D.
1; 1
ab
C©u 42 :
Cho hàm số
3
52
y x x
có đồ thị (C) và đường thẳng (d):
2
y
. Trong các điểm:
(I).
(0;2) ;
(II).
( 5;2) ;
(III).
( 5;2) ,
điểm nào là giao điểm của (C) và (d)?
A.
Chỉ II, III.
B.
Cả I, II, III.
C.
Chỉ I, II.
D.
Chỉ III, I.
C©u 43 :
Cho hàm số
32
2 3( 1) 2y x mx m x
(1), m là tham số thực.
Tìm m để đồ thị hàm số cắt đường thẳng
:2yx
tại 3 điểm phân biệt
(0;2)A
; B; C sao cho
tam giác
MBC
có diện tích
22
, với
(3;1).M
A.
0m
3m 
C.
3m
D.
03mm
C©u 44 :
Tìm cực trị của hàm số y=sinx-cosx
A.
;2
4
CT CT
x k y
và
DD
3
2 ;y 2
4
CC
xk
B.
DD
;2
4
CC
x k y
7
C.
3
;2
4
CT CT
x k y
D.
;2
4
CD CD
x k y
và
3
2 ;y 2
4
CT CT
xk
C©u 45 :
Cho hàm số
12
24
mxxy
(1) .Tìm các giá trị của tham số m để đồ thi hàm số (1) có ba điểm
cực trị và đường tròn đi qua ba điểm này có bán kính bằng 1.
A.
15
1;
2
mm


15
1;
2
mm

C.
15
1;
2
mm


D.
15
1;
2
mm


C©u 46 :
Giá trị cực đại của hàm số
2cosy x x
trên khoảng
(0; )
là:
A.
3
6
5
3
6
C.
5
3
6
D.
3
6
C©u 47 :
Tìm tập xác định D của hàm số sau:
2
1
23
x
y
xx

A.
D = R\{3}
D = R
C.
D = R\{-1,3}
D.
D = R\{-1}
C©u 48 :
Với giá trị nào của m thì hàm số
32
1
(2 3) 2
3
y x mx m x m
nghịch biến trên tập xác định?
A.
31
m
31
m
C.
1
m
D.
3
m

hay
1
m
C©u 49 :
Tìm m để đồ thị hàm số
22
1 2 2 2
y x x mx m m
cắt trục hoành tại ba điểm phân biệt.
A.
13
m

1, 3
mm

C.
1
m
D.
0
m
C©u 50 :
Cho hàm số
43
34
y x x

. Khẳng định nào sau đây đúng
A.
Hàm số đạt cực đại tại gốc tọa độ
B.
Hàm số không có cực trị
C.
Hàm số đạt cực tiểu tại gốc tọa độ
D.
Điểm
11;
A
là điểm cực tiểu
……….HẾT……….
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 005-KSHS)
C©u 1 :
Hàm số
1
)(
2
x
x
xf
có tập xác định là
A.
1;1
;1
C.
1;
D.
 ;11;
C©u 2 :
Với giá trị nào của m thì đồ thị hàm số :
2
4)6(2
2
mx
xmx
y
đi qua điểm M(1; -1)
A.
m = 3
m = 2
C.
m = 1
D.
Không có m
C©u 3 :
Cho đường cong
3
y x x

(C). Phương trình tiếp tuyến của (C) tại điểm
10;
A
là
A.
22
yx

22
yx

C.
22
yx
D.
22
yx
C©u 4 :
Tìm khoảng nghịch biến của hàm số
2
32
)(
x
x
xf
A.
2;
;2
C.
 ;22;
D.
2;
và
;2
C©u 5 :
Cho đồ thị (H) của hm số
24
3
x
y
x
. Phương trình tiếp tuyến của (H) tại giao điểm của (H) v Ox
A.
Y= 2x-4
Y = -2x+ 4
C.
Y = - 2x-4
D.
Y= 2x+4
C©u 6 :
Cho hàm số :
3
31y x mx m
.Tìm
m
để hàm số cắt trục hoành tại ba điểm phân biệt
A.
1m
1m
C.
1m
D.
01m
C©u 7 :
Cho hàm số
42
23y x x
xác định trên đoạn
0,2
.Gọi M và N lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của hàm số thì
MN
bằng bao nhiêu ?
A.
15
5
C.
13
D.
14
C©u 8 :
Tiệm cận ngang của đồ thị hàm số
2
32x
x
y
là
A.
1
3
y
1
3
y

C.
1
3
x

D.
1
3
x
2
C©u 9 :
Cho hàm số sau:
1
3
2
x
xx
y
. Đường thẳng d: y = - x +m cắt đồ thị hàm số tại mấy điểm ?
A.
1
3
C.
0
D.
2
C©u 10 :
Giá trị lớn nhất của hàm số
xxf 34)(
là:
A.
-3
-4
C.
3
D.
0
C©u 11 :
Giá trị lớn nhất của hàm số
44
( ) 1f x x x
là
A.
4
6
4
8
C.
4
10
D.
2
C©u 12 :
Đồ thị hàm số
2
21
32
x
y
xx

có
A.
Hai đường tiệm cận
B.
Không có tiệm cận
C.
Một đường tiệm cận
D.
Ba đường tiệm cận
C©u 13 :
Giá trị nhỏ nhất của hàm số :
3
25
x
xy
trên (3; +) là:
A.
8
10
C.
11
D.
13
C©u 14 :
Cho hàm số
42
: 2 3 4
m
C y x mx m
.Tìm
m
để hàm số tiếp xúc với trục hoành
A.
3
4, , 1
4
m m m
B.
3
;1
4
mm
C.
3
4;
4
mm
D.
4, 1mm
C©u 15 :
Cho hàm số
m
C
32
2( 1) 2 3 5y x m x m x
v đường thẳng
:5d y x
.Tìm
m
để
d
cắt
đồ thị
m
C
tại ba điểm phân biệt
A.
15m
15mm
C.
2m
D.
mR
C©u 16 :
Cho hàm số
2
( ) 2 2f x mx x x
. Mệnh đề no sau đây đúng
A.
Hàm số không có cực tiểu với mọi m thuộc R
B.
Cả 3 mệnh đề A, B, C đều sai
C.
Hàm số không có cực đại với mọi m thuộc R
D.
Hàm số có cực trị khi m > 100
C©u 17 :
Cho hàm số :
32
: 2 6 3C y x x
Phương trình tiếp tuyến với đồ thị
C
có hệ số góc nhỏ nhất là
:
A.
63yx
67yx
C.
65yx
D.
65yx
3
C©u 18 :
Hàm số 𝑦 3𝑦
4
𝑦
3
15 có bao nhiêm điểm cực trị
A.
Không có
Có 3
C.
Có 1
D.
Có 2
C©u 19 :
Đồ thị hm số
32
31y x x m
cắt trục honh tại 3 điểm phân biệt khi v ch khi
A.
1<m<3
-1< m<3
C.
-3<m<1
D.
-3< m <-1
C©u 20 :
Giá trị lớn nhất của hàm số
46
( ) Sin .Cosf x x x
là
A.
107
3125
108
3125
C.
109
3125
D.
106
3125
C©u 21 :
Cho các hàm số :
32
1
34
3
y x x x
;
1
1
x
y
x
;
2
4yx
;
3
4 siny x x x
;
42
2y x x
.Có bao nhiêu hàm số đồng biến trên tập xác định của chúng
A.
2
4
C.
3
D.
Kết quả khác
C©u 22 :
Cho hàm số :
44
( ) sin cosy f x x x
.Tính giá trị :
1
'( ) ''( )
4 4 4
ff

A.
-1
0
C.
1
D.
Kết quả khác
C©u 23 :
Cho hàm số
2
1
1
xx
y
x
có đồ thị (C). Tiếp tuyến với 󰇛𝑦󰇜 song song với đường thẳng
3
: 1
4
d y x
là
A.
33
44
yx
3
2
4
yx
C.
33
44
yx
D.
Không có
C©u 24 :
Hệ số góc tiếp tuyến của đồ thị (C):
13
2
2
x
x
y
tại điểm có honh độ x
0
= 1 bằng:
A.
3
2
4
3
C.
1
D.
8
5
C©u 25 :
Đồ thị sau đây l đồ thị của hàm số nào?
8
6
4
2
-2
-4
-6
-8
-10
-5
5
10
4
A.
43
2x
yx

2
1
x
y
x
C.
32
2
y x x

D.
42
2
y x x

C©u 26 :
TXĐ của hàm số
11
()
Sin2 Cos2
fx
xx

A.
4
xk
xk
C.
2xk
D.
2
xk
C©u 27 :
Cho hàm số
3 2 2
1
1 (2 1) 3
3
y x m x m x
.Tìm
m
để hàm số có hai điểm cực trị cách đều
trục tung
A.
2m
1m
C.
1m 
D.
1m 
C©u 28 :
Cho hàm số
432
1 4 7
( ) 2 1
4 3 2
f x x x x x
. Khẳng định no sau đây đúng?:
A.
Hàm số có 1 cực đại và 2 cực tiểu
B.
Hàm số ch có 1 cực tiểu và không có cực đại
C.
Hàm số có 1 cực tiểu và 2 cực đại
D.
Hàm số không có cực trị
C©u 29 :
Đường thẳng
ym
cắt đồ thị hàm số
42
y x x

tại bốn điểm phân biệt khi và ch khi
A.
1
0
4
m
0
m
C.
1
0
4
m

D.
1
4
m

C©u 30 :
Đồ thị hàm số no sau đây không có điểm uốn
A.
2
31
y x x
32
y x x

C.
32
33
y x x
D.
32
14
3
33
y x x x
C©u 31 :
Cho hàm số f có đạo hm l f’(x) = x
2
(x-1)(x-2) với mọi xR
A.
0
3
C.
1
D.
2
C©u 32 :
Để hàm
1
1
2
x
mxx
y
có cực đại và cực tiểu thì các giá trị của m là:
A.
m = 0
m R
C.
m < 0
D.
m > 0
C©u 33 :
Hàm số
Cos2
()
Sin
x
fx
x
A.
Chẵn
Lẻ
C.
Không chẵn,
không lẻ
D.
Vừa chẵn, vừa lẻ
C©u 34 :
Hàm số
32
( ) 3 3f x x mx mx
có 1 cực trị tại điểm x=-1. Khi đó hm số đạt cực trị tại điểm
khác có honh độ là
5
A.
1
3
1
4
C.
1
3
D.
Đáp số khác
C©u 35 :
Tìm điểm M thuộc
2
: ( ) 3 8 9P y f x x x
v điểm N thuộc
2
' : 8 13P y x x
sao cho
MN nhỏ nhất
A.
(0, 9);N 3, 2M
B.
(1,4);N 3, 2M
C.
(1,4);N 3, 2M 
D.
(3, 12);N 1,6M 
C©u 36 :
Giá trị lớn nhất, nhỏ nhất của hàm số 𝑦
𝑦
2
2𝑦3
𝑦1
trên đoạn [2;4] là
A.
2;4 2;4
11
min 2; max
3
f x f x
B.
2;4 2;4
11
min 2 2;max
3
f x f x
C.
2;4 2;4
min 2; max 3f x f x
D.
2;4 2;4
min 2 2;max 3f x f x
C©u 37 :
Tâm đối xứng của đồ thị hàm số
21
1
x
y
x
là
A.
21;
12;
C.
12;
D.
21;
C©u 38 :
Cho hàm số
32
12
( ) 4 12
33
f x x x x
.Tổng các giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên
[0;5] là
A.
16
3
Đáp số khác
C.
7
D.
7
3
C©u 39 :
Xác định tất cả các giá trị của m để đồ thị hm số
4 2 2
(3 4)y x m x m
cắt trục honh tại 4 điểm
phân biệt
A.
m>0
4
0
5
m
C.
m<2
D.
4
5
m 
C©u 40 :
Cho hàm số
( ) Sin2 3f x x x
. Mệnh đề no sau đây đúng
A.
Hàm số nhận
6
x
lm điểm cực tiểu
B.
Hàm số nhận
6
x
lm điểm cực đại
C.
Hàm số nhận
2
x
lm điểm cực đại
D.
Hàm số nhận
2
x
lm điểm cực tiểu
C©u 41 :
Tìm giá trị lớn nhất của hàm số 𝑦 2
𝑦 1
6 𝑦
A.
2.
5
C.
3
D.
4
6
C©u 42 :
Cho hàm số
:2C y x
.Phương trình tiếp tuyến với đồ thị
C
tại điểm có tung độ bằng 2 là
A.
4 3 0xy
4 2 0xy
C.
4 6 0xy
D.
4 1 0xy
C©u 43 :
Cho hàm số sau:
mx
mxm
y
22)1(
Với tất cả các giá trị nào của m thì hàm số nghịch biến trên
(-1;+)
A.
m <1 v m > 2
m > 2
C.
m < 1
D.
1 m < 2
C©u 44 :
Tiếp tuyến của parabol
2
4 xy
tại điểm (1; 3) tạo với hai trục tọa độ một tam giác vuông. Diện
tích tam giác vuông đó l
A.
4
5
2
25
C.
2
5
D.
4
25
C©u 45 :
Cho hàm số
32
2 2 1y x x x
có đồ thị 󰇛𝑦󰇜. Số tiếp tuyến với đồ thị song song với đường
thẳng
1yx
là
A.
0.
1.
C.
2.
D.
3.
C©u 46 :
Hàm số no sau đây có cực đại
A.
2
2
2
x
y
x

2
2
x
y
x

C.
2
2
x
y
x
D.
2
2
x
y
x

C©u 47 :
Xác định tất cả các giá trị của m để hm số có cực đại v cực tiêu
32
1
( 6) 1
3
y x mx m x
A.
m>3
3
2
m
m

C.
m< -2
D.
-2<m<3
C©u 48 :
Tìm tất cả các giá trị của m để hm số
2
1x mx
y
xm

đạt cực trị tại x=2
A.
m=-3
3
1
m
m


C.
m=-1
D.
Đáp số khác
C©u 49 :
Với giá trị nào của m thì đồ thị (C):
mx
mx
y
2
1
có tiệm cận đứng đi qua điểm M(-1;
2
) ?
A.
2
1
0
C.
2
2
D.
2
C©u 50 :
Gọi D1 l TXĐ của hàm số
( ) an
2
x
f x t
v D2 l TXĐ của hàm số
1
()
1 Cos
fx
x
. Khi đó D1
D2 là
7
A.
\ 2 |kk
B.
\ 2 1 |kk

C.
\ 2 1 |
2
kk




D.
\|kk
……….HẾT……….
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 006-KSHS)
C©u 1 :
Tiệm cận xiên của
82
3
53
x
xy
là
A.
53 xy
82 xy
C.
4x
D.
Không có tiệm cận
xiên
C©u 2 :
Hàm số
32
3y x x
nghịch biến trên khoảng:
A.
( 2;0)
(0; )
C.
[ 2;0]
D.
( ; 2)
C©u 3 :
Hàm số
2
4yx
có mấy điểm cực tiểu ?
A.
3
2
C.
1
D.
0
C©u 4 :
Cho hàm số
32
1, ( 0)y x mx m
có đồ thị
()
m
C
. Tập hợp các điểm cực tiểu của
()
m
C
khi
m
thay đổi là đồ thị có phương trình:
A.
3
1
2
x
y
2
1yx
C.
3
yx
D.
3
2
x
y 
C©u 5 :
Cho hàm số
432
1 4 7
( ) 2 1
4 3 2
f x x x x x
. Khẳng định nào sau đây đúng?:
A.
Hàm số không có cực trị
B.
Hàm số chỉ có 1 cực tiểu và không có cực đại
C.
Hàm số có 1 cực đại và 2 cực tiểu
D.
Hàm số có 1 cực tiểu và 2 cực đại
C©u 6 :
Cho hàm số
2
( ) 2 2f x mx x x
. Mệnh đề nào sau đây đúng
A.
Hàm số không có cực đại với mọi m thuộc R
B.
Hàm số có cực trị khi m > 100
C.
Cả 3 mệnh đề A, B, C đều sai
D.
Hàm số không có cực tiểu với mọi m thuộc R
C©u 7 :
Giá trị lớn nhất của hàm số
44
( ) 1f x x x
là
A.
4
6
4
10
C.
4
8
D.
2
C©u 8 :
Với giá trị nào của b thì
1
1
:)(
x
x
yC
luôn cắt
bxyd :)(
2
A.
Mọi b là số thực
Không có giá trị
nào của b
C.
b > 1
D.
b < 1
C©u 9 :
Tìm m để hàm số sau đồng biến trên từng khoảng xác định
xm
mmx
y
910
A.
m < 1 hoặc m > 9
91 m
C.
1 < m < 9
D.
1m
hoặc
9m
C©u 10 :
Cho x, y là các số thực thỏa:
2
0, 12.y x x y
GTLN, GTNN của biểu thức
2 17P xy x y
lần lượt bằng:
A.
10 ;-6
5 ;-3
C.
20 ;-12
D.
8 ;-5
C©u 11 :
Dùng định nghĩa, tính đạo hàm của hàm số sau:
)1ln()(
2
xxxf
A.
1
1
)('
2
x
xf
2ln)(' xf
C.
0)(' xf
D.
1
1
)('
2
xx
xf
C©u 12 :
Để hàm số
3
35y x mx
nghịch biến trong khoảng (-1;1) thì
m
bằng:
A.
1
2
C.
3
D.
4
C©u 13 :
Với giá trị nào của m thì hàm số
3 2 2 2
3 3 1 3 5y x mx m x m
đạt cực đại tại
1x
.
A.
1m
0m
C.
0; 2mm
D.
2m
C©u 14 :
Giá trị cực đại của hàm số
32
1
2 3 1
3
y x x x
là
A.
1
3
C.
1
D.
1
3
C©u 15 :
Hàm số
2
1
1
xx
y
x

đồng biến trên khoảng:
A.
(1; )
( ;0)
C.
(0;1)
D.
(0;2)
C©u 16 :
GTLN của hàm số
sin (1 cos )y x x
trên đoạn
[0; ]
là:
A.
33
33
4
C.
33
2
D.
3
C©u 17 :
Giá trị lớn nhất của hàm số
46
( ) Sin .Cosf x x x
là
A.
106
3125
107
3125
C.
108
3125
D.
109
3125
C©u 18 :
Cho hình chữ nhật có chu vi là 16 cm, hình chữ nhật có diện tích lớn nhất bằng
3
A.
2
36 cm
2
16 cm
C.
2
20 cm
D.
2
30 cm
C©u 19 :
Hàm số nào sau đây đồng biến trên R ?
A.
3
1yx
42
1y x x
C.
2
( 1)yx
D.
tanyx
C©u 20 :
Giá trị cực đại của hàm số
103632
23
xxxy
là
A.
71
2
C.
-3
D.
-54
C©u 21 :
Gọi D1 là TXĐ của hàm số
( ) Tan
2
x
fx
và D2 là TXĐ của hàm số
1
()
1 Cos
fx
x
. Khi đó D1
D2 là
A.
\ 2 1 |
2
kk




B.
\ 2 1 |kk

C.
\ 2 |kk
D.
\|kk
C©u 22 :
Cho hai số x, y không âm có tổng bằng 1. GTLN, GTNN của
33
P x y
là :
A.
-1;-2
1;-1
C.
1
1;
4
D.
0;-1
C©u 23 :
Hàm số
mx
mxx
y
1
2
đạt cực tiểu tại x = 2 khi
A.
m = - 1
m = - 3
C.
m = 0
D.
Không có giá trị
của m
C©u 24 :
TXĐ của hàm số
11
()
Sin2 Cos2
fx
xx

A.
2
xk
xk
C.
4
xk
D.
2xk
C©u 25 :
Giá trị lớn nhất của hàm số
32yx
trên đoạn
[ 1;1]
bằng:
A.
1
5
C.
3
D.
3
C©u 26 :
Giá trị nhỏ nhất của hàm số
32
( ) 3 9 1f x x x x
trên đoạn
[0;2]
là
A.
1
28
C.
3
D.
4
C©u 27 :
Cực trị của hàm số
sin2y x x
là:
A.
; ( )
66
CD CT
x k x k k


B.
()
3
CT
x k k
4
C.
2 ( )
6
CD
x k k
D.
()
3
CD
x k k
C©u 28 :
Hàm số
3
31yx
x
đồng biến trên khoảng:
A.
( 1;2)
( 1;0)
C.
( 1;1)
D.
( ;0)
C©u 29 :
Hàm số
32
35y x x
nghịch biến các khoảng:
A.
( ;0) [2; ) 
( ;0) (2; )
C.
( ;0] [2; ) 
D.
( ;0] (2; )
C©u 30 :
Hàm số nào sau đây nghịch biến trên R ?
A.
2
x
y
3y 
C.
1
2
x
y
x
D.
4
1yx
C©u 31 :
Hàm số
42
23y x x
nghịch biến trên khoảng:
A.
( 1;1)
(1;2)
C.
(0;1)
D.
( ; 1)
C©u 32 :
Hàm số
2
32y x x
nghịch biến trên khoảng:
A.
(1;2)
3
(1; )
2
C.
3
( ;2)
2
D.
( ;1)
C©u 33 :
Hàm số
42
1
23
2
y x x
có mấy điểm cực đại ?
A.
3
1
C.
0
D.
2
C©u 34 :
Điểm cực đại của hàm số
32
24y x x x
là
A.
4
1
3
C.
104
27
D.
1
C©u 35 :
Hàm số
32
( ) 3 3f x x mx mx
có 1 cực trị tại điểm x=-1. Khi đó hàm số đạt cực trị tại điểm
khác có hoành độ là
A.
1
4
1
3
C.
1
3
D.
Đáp số khác
C©u 36 :
Cho hàm số
( ) Sin2 3f x x x
. Mệnh đề nào sau đây đúng
A.
Hàm số nhận
6
x
làm điểm cực tiểu
B.
Hàm số nhận
2
x
làm điểm cực đại
C.
Hàm số nhận
6
x
làm điểm cực đại
D.
Hàm số nhận
2
x
làm điểm cực tiểu
5
C©u 37 :
Hàm số nào sau đây nghịch biến trên khoảng (-1 ;1) ?
A.
1
y
x
3
32y x x
C.
3yx
D.
1
1
y
x
C©u 38 :
Giá trị nhỏ nhất của hàm số
4
1
yx
x

trên đoạn
[0;4]
là
A.
4
24
5
C.
5
D.
3
C©u 39 :
Cho hàm số
32
12
( ) 4 12
33
f x x x x
.Tổng các giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên
[0;5] là
A.
16
3
7
C.
Đáp số khác
D.
7
3
C©u 40 :
Hàm số nào sau đây đồng biến trên khoảng (1 ;2) ?
A.
2
2yx
2
23y x x
C.
1
1
y
x
D.
3
1yx
C©u 41 :
Hàm số
42
22y x x
nghịch biến các khoảng:
A.
( ; 1) (0;1)
( 1;0) (1; )
C.
( ; 1) (1; ) 
D.
( 1;0) (0;1)
C©u 42 :
Cho hàm số
2
()
1
x
fx
x
.Mệnh đề nào sau đây sai ?
A.
Hàm số
()fx
đồng biến trên các khoảng (-∞ ;0)
(2;+∞)
B.
Hàm số
()fx
nghịch biến trên các khoảng (0 ;1)
(1;2)
C.
Hàm số
()fx
có tập xác định là R\{1}
D.
Hàm số
()fx
đồng biến trên R.
C©u 43 :
GTLN và GTNN của hàm số
sin cosyxx
lần lượt là:
A.
2;-2
2; 2
C.
-1;1
D.
1;-1
C©u 44 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
42
41y x x
trên đoạn
[ 1; 5]
lần lượt là:
A.
4 và 1
4 và
4
C.
5 và 1
D.
5 và
4
C©u 45 :
Tìm m để phương trình
03
23
mxx
có ba nghiệm phân biệt
A.
40 m
Không có m
C.
0m
D.
4m
6
C©u 46 :
GTLN của hàm số
53
3
xxy
trên đoạn
2
3
;0
là
A.
8
31
3
C.
5
D.
7
C©u 47 :
Hàm số
Cos2
()
Sin
x
fx
x
A.
Vừa chẵn, vừa lẻ
Lẻ
C.
Chẵn
D.
Không chẵn,
không lẻ
C©u 48 :
Giá trị cực tiểu của hàm số
3
2
22
3
y x x
là
A.
1
1
C.
10
3
D.
2
3
C©u 49 :
Cho hàm số
32
( ) 3 2f x x x
.Mệnh đề nào sau đây sai ?
A.
Hàm số
()fx
đồng biến trên khoảng (-∞ ;0) .
B.
Hàm số
()fx
đồng biến trên khoảng (2 ;+∞) .
C.
Hàm số
()fx
nghịch biến trên khoảng (0;2)
D.
Hàm số
()fx
nghịch biến trên khoảng (0 ;+∞)
C©u 50 :
Điểm cực tiểu của hàm số
32
31y x x
là
A.
0
3
C.
1
D.
2
……….HẾT……….
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 007-KSHS)
C©u 1 :
Phương trình tiếp tuyến của đồ thị (C)
3
31y x x
và vuông góc với đường thẳng
1
9
x
y
là:
A.
9 8, 9 8y x y x
B.
9 8, 9 12y x y x
C.
9 8, 9 24y x y x
D.
9 15, 9 17y x y x
C©u 2 :
GTLN của hàm số
sin (1 cos )y x x
trên đoạn
[0; ]
là:
A.
33
4
33
2
C.
33
D.
3
C©u 3 :
Với giá trị nào của m, hàm số
2
( 1) 1
2
x m x
y
x
nghịch biến trên mỗi khoảng xác định của
nó?
A.
1m 
1m
C.
1;1m
D.
5
2
m 
C©u 4 :
Cho phương trình
2
1 (2 )x x k
. Giá trị nào của k để phương trình có 3 nghiệm
A.
03k
9
0
2
k
C.
05k
D.
04k
C©u 5 :
Phát biểu nào sau đây đúng
A.
X
0
điểm cực đại của hàm số
0
'( ) 0fx
B.
X
0
là điểm cực tiểu của hàm số khi
00
'( ) 0, ''( ) 0f x f x
C.
X
0
là điểm cực đại của hàm số khi
00
'( ) 0, ''( ) 0f x f x
D.
Nếu tồn tại h>0 sao cho f(x) <
0
()fx
00
( ; )x x h x h
và
0
xx
thì ta nói hàm số f(x) đạt cực
2
tiểu tại điểm x
0
C©u 6 :
GTLN và GTNN của hàm số
sin cosyxx
lần lượt là:
A.
2; 2
-1;1
C.
1;-1
D.
2;-2
C©u 7 :
Hàm số nào sau đây đồng biến trên tập xác định của nó
A.
2
2
x
y
x

2
2
x
y
x
C.
2
2
x
y
x

D.
2
2
x
y
x

C©u 8 :
Cho hàm số
1
()
1
x
fx
x
.Mệnh đề nào sau đây đúng ?
A.
Hàm số
()fx
đồng biến trên R.
B.
Hàm số
()fx
đồng biến trên các khoảng (-∞ ;-1)
(-1;+∞)
C.
Hàm số
()fx
nghịch biến trên R
D.
Hàm số
()fx
nghịch biến trên các khoảng (-∞ ;-1)
(-1;+∞)
C©u 9 :
Hàm số nào sau đây nghịch biến trên R ?
A.
2
x
y
4
1yx
C.
1
2
x
y
x
D.
3y 
C©u 10 :
Tìm m để hàm số
32
3 3(2 1) 1y x mx m x
đồng biến trên R
A.
1m
m = 1
C.
luôn thỏa với mọi
giá trị m
D.
Không có giá trị m
C©u 11 :
Cho hàm số
32
( ) 3 2f x x x
.Mệnh đề nào sau đây sai ?
A.
Hàm số
()fx
nghịch biến trên khoảng (0 ;+∞)
B.
Hàm số
()fx
nghịch biến trên khoảng (0;2)
C.
Hàm số
()fx
đồng biến trên khoảng (2 ;+∞) .
D.
Hàm số
()fx
đồng biến trên khoảng (-∞ ;0) .
C©u 12 :
GTNN của hàm số
32
2 3 12 10y x x x
trên đoạn [-3; 3] là:
A.
-10
1
C.
17
D.
-35
C©u 13 :
Số đường tiệm cận của hàm số
2
21
23
xx
y
x

A.
0
1
C.
2
D.
3
3
C©u 14 :
Cho hàm số
4
2
9
2
44
x
yx
(C), phương trình tiếp tuyến của (C) tại các giao điểm của (C) với
trục Ox là:
A.
15( 3), 15( 3)y x y x
B.
15( 3), 15( 3)y x y x
C.
15( 3), 15( 3)y x y x
D.
15( 3), 15( 3)y x y x
C©u 15 :
Hàm số nào sau đây có cực trị
A.
32
( ) 3 3 5f x x x x
B.
32
4
( ) 6 9 1
3
f x x x x
C.
2
2
( 4)
()
25
x
fx
xx

D.
2
89
()
5
xx
fx
x

C©u 16 :
Các tiếp tuyến của đường cong (C ): y = x
3
- 2x - 1 song song với đường thẳng d :y = x + 2 có
phương trình là:
A.
y = x - 3 và y = x + 1
B.
y = x - 1 và y = x + 3
C.
y = x - 1 và y = x + 4
D.
y = x - 1 và y = x - 2
C©u 17 :
Cho hàm số
32
2
5
3
y x mx m x



. Với giá trị nào của m hàm số đạt cực tiểu tại x=1
A.
4
3
m
3
4
m
C.
m= 1
D.
7
3
m
C©u 18 :
Hàm số
Cos2
()
Sin
x
fx
x
A.
Chẵn
Lẻ
C.
Không chẵn,
không lẻ
D.
Vừa chẵn, vừa lẻ
C©u 19 :
Hàm số nào sau đây có cực đại và cực tiểu
A.
2
( ) 2 1 2 8f x x x
B.
2
( ) 8f x x
C.
3
2
()
6
x
fx
x
D.
2
()
10
x
fx
x
C©u 20 :
Số điểm cực đại của hàm số y = x
4
+ 100 là
A.
1
0
C.
2
D.
3
C©u 21 :
Cho hình chữ nhật có chu vi là 16 cm, hình chữ nhật có diện tích lớn nhất bằng
A.
2
16 cm
2
30 cm
C.
2
20 cm
D.
2
36 cm
4
C©u 22 :
Các tiếp tuyến của đường cong
1
2
:)(
x
x
yC
vuông góc với đường thẳng d :y = -3x + 2 có
phương trình là:
A.
6
3
1
3
2
3
1
xyxy vaø
B.
3
10
3
1
3
2
3
1
xyxy vaø
C.
102 xyxy vaø
D.
3
10
3
1
2
3
1
xyxy vaø
C©u 23 :
Hàm số
4
2
x
y 
đồng biến trên khoảng:
A.
1; 
3;4
C.
;1
D.
;0
C©u 24 :
Giá trị nhỏ nhất của hàm số
4
1
yx
x

trên đoạn
[0;4]
là
A.
3
24
5
C.
4
D.
5
C©u 25 :
Hàm số
32
2 3( 1) 6x m x mx
có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc
với đường thẳng d: y=x+2. Giá trị của m là
A.
2m
B.
0m
C.
Cả hai đáp án A và B đều sai
D.
Hai đáp án A và B đều đúng
C©u 26 :
Cho đường cong (C ) : y = x
3
- 2x
2
- 2x -3 .Tiếp tuyến của đường cong (C) tại điểm có hoành độ
bằng -1 có phương trình là:
A.
y = 5x + 5
y = 5x + 1
C.
y = - 3x - 7
D.
y = - x - 5
C©u 27 :
Cho hàm số
42
( ) 2 3f x x x
.Mệnh đề nào sau đây đúng ?
A.
Hàm số
()fx
nghịch biến trên khoảng (1;+∞)
B.
Hàm số
()fx
đồng biến trên khoảng (-∞ ;0)
C.
Hàm số
()fx
nghịch biến trên khoảng (-1 ;1)
D.
Hàm số
()fx
đồng biến trên khoảng (-1;0) .
C©u 28 :
Hàm số nào sau đây không có cực trị
A.
32
1
x
y
x
31
1
x
y
x
C.
2
1
8
x
y
x
D.
2
5
1
xx
y
x

C©u 29 :
Hàm số nào sau đây chỉ có cực tiểu không có cực đại
5
A.
1
()f x x
x

B.
( ) 3 cos cos2f x x x
C.
2
( ) 1f x x x
D.
'( ) ( 3)f x x x
C©u 30 :
32
3 3 2y x x x
có hai điểm cực trị A và B. Đường thẳng AB song song với đường thẳng nào
sau đây
A.
14yx
3 2 7 0xy
C.
38yx
D.
4 3 0xy
C©u 31 :
Tìm m để hàm số:
32
3
2
m
y x x m
có hai điểm cực trị
A.
m
0m
C.
0m
D.
0m
C©u 32 :
Hàm số
2
1yx
A.
Đồng biến trên [0; 1]
B.
Nghịch biến trên [0; 1]
C.
Nghịch biến trên (0; 1)
D.
Đồng biến trên (0; 1)
C©u 33 :
Hàm số
2
4yx
có mấy điểm cực tiểu ?
A.
0
1
C.
2
D.
3
C©u 34 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
42
41y x x
trên đoạn
[ 1; 5]
lần lượt là:
A.
5 và
4
4 và 1
C.
4 và
4
D.
5 và 1
C©u 35 :
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
32
1
2 3 5
3
y x x x
A.
Song song với đường thẳng x = 1
B.
Có hệ số góc bằng - 1
C.
Song song với trục hoành
D.
Có hệ số góc dương
C©u 36 :
Hàm số nào sau đây không nhận O(0,0) làm điểm cực trị
A.
32
( ) 3f x x x
3
2
( ) 6f x x x
C.
3
( ) (7 ) 5f x x x
D.
()f x x
C©u 37 :
Hàm số
3
31yx
x
đồng biến trên khoảng:
A.
( 1;0)
( ;0)
C.
( 1;2)
D.
( 1;1)
C©u 38 :
Hàm số
42
23y x x
có bao nhiêu điểm cực trị?
A.
0
1
C.
2
D.
3
6
C©u 39 :
Cho hàm số
4
()
1
f x x
x
.Mệnh đề nào sau đây sai ?
A.
Hàm số
()fx
đồng biến trên các khoảng (-1 ;1)
(1;3)
B.
Hàm số
()fx
nghịch biến trên các khoảng (-∞ ;1)
(1;+∞)
C.
Hàm số
()fx
có tập xác định là R\{1}
D.
Hàm số
()fx
nghịch biến trên các khoảng (-∞ ;-1)
(3;+∞)
C©u 40 :
Hàm số nào sau đây đạt cực đại tại
2
4
xk

A.
( ) sin2f x x
B.
( ) cos sinf x x x
C.
'( ) sinx cosf x x
D.
( ) sin2 2f x x x
C©u 41 :
Cho x, y là các số thực thỏa:
2
0, 12.y x x y
GTLN, GTNN của biểu thức
2 17P xy x y
lần lượt bằng:
A.
20 ;-12
5 ;-3
C.
10 ;-6
D.
8 ;-5
C©u 42 :
Tìm m để hàm số đồng biến trên khoảng (2,+∞ )
A.
1m
1m
C.
1m
D.
1m
C©u 43 :
Tọa độ giao điểm của đồ thị hàm số
2
23
2
xx
y
x

và đường thẳng
1yx
là:
A.
3,2
2, 1
C.
3;4
D.
1;0
C©u 44 :
Tìm m để phương trình
03
23
mxx
có ba nghiệm phân biệt
A.
40 m
0m
C.
4m
D.
Không có m
C©u 45 :
Các điểm cực tiểu của hàm số
42
32y x x
là:
A.
1x 
1, 2xx
C.
5x
D.
0x
C©u 46 :
Tìm m để đồ thị hàm sô
42
2( 1)y x m x m
có 3 điểm cực trị tạo thành 3 đỉnh của 1 tam giác
vuông
A.
m = 1
m = 0
C.
m = 3
D.
m = 2
C©u 47 :
Hàm số
3
32y x x
có bao nhiêu điểm cực trị?
A.
2
0
C.
1
D.
3
7
C©u 48 :
Cho hàm số
42
5y x mx m
. Giá trị m để hàm số có 3 cực trị là:
A.
3m
3m
C.
0m
D.
0m
C©u 49 :
Với giá trị nào của k thì phương trình
3
3 2 0x x k
có 3 nghiệm phân biệt
A.
-1 < k < 1
04k
C.
0 < k < 4
D.
Không có giá trị
nào của k
C©u 50 :
Tìm GTLN của hàm số
2
22
1
xx
y
x

trên
1
;2
2



A.
8
3
3
C.
10
3
D.
Hàm số không có
GTLN
.........HẾT……….
| 1/48

Tài liệu khác của Toán 12

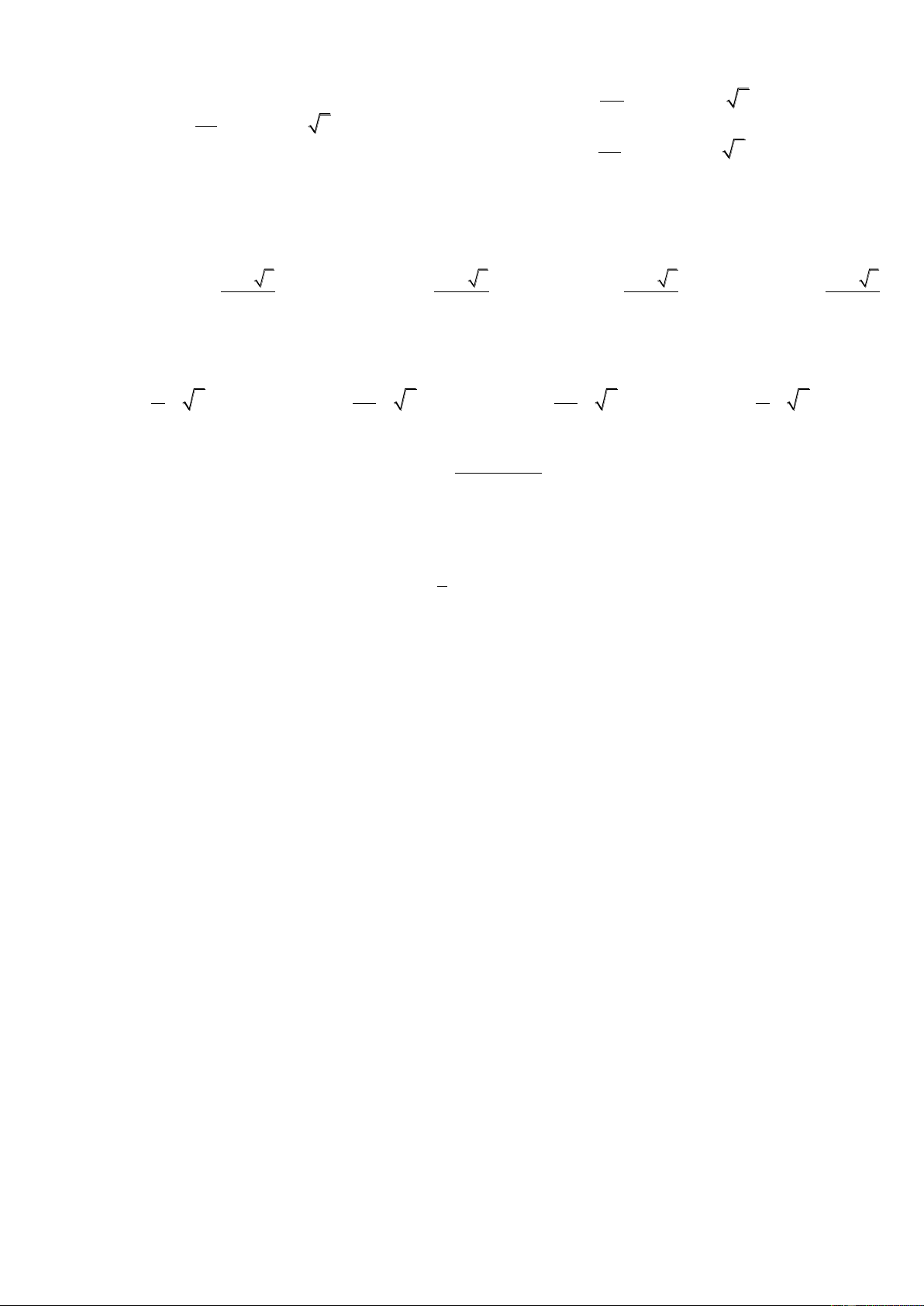
Preview text:

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 001-KSHS) C©u 1 : 3 2
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y x 3x 9x
35 trên đoạn 4;4 lần lượt là: A. 20; 2 B. 10; 11 C. 40; 41 D. 40; 31
C©u 2 : Cho hàm số y = x4 + 2x2 – 2017. Trong các mệnh đề sau , mệnh đề nào sai ?
A. Đồ thị của hàm số f(x) có đúng 1 điểm uốn
lim f x   va lim f x   B. x x
C. Đồ thị hàm số qua A(0;-2017)
D. Hàm số y = f(x) có 1 cực tiểu C©u 3 : 4 2 Hàm số y x 2x
1 đồng biến trên các khoảng nào? 1;0 và A. 1;0 B. C. 1; D. x 1; C©u 4 : 1
Tìm m lớn nhất để hàm số 3 2 y
x mx  (4m  3)x  2016 đồng biến trên tập xác định của nó. 3 A. Đáp án khác. B. m  3 C. m  1 D. m  2
C©u 5 : Xác định m để phương trình 3 x 3mx 2
0 có một nghiệm duy nhất: A. m 1 B. m 2 C. m 1 D. m 2
C©u 6 : Tìm giá trị lớn nhất của hàm số 2
y  4  x x . 1 Ma f
x x  f 4 1   Ma f
x x  f     A. ln 2 1 ln 2  B. 1    1  ;3 2  2   ;3    3   3  1 Ma f
x x  f 2 193  Ma f
x x  f    C. 1  D. 1    1  ;3 100  5   ;3    3   3 
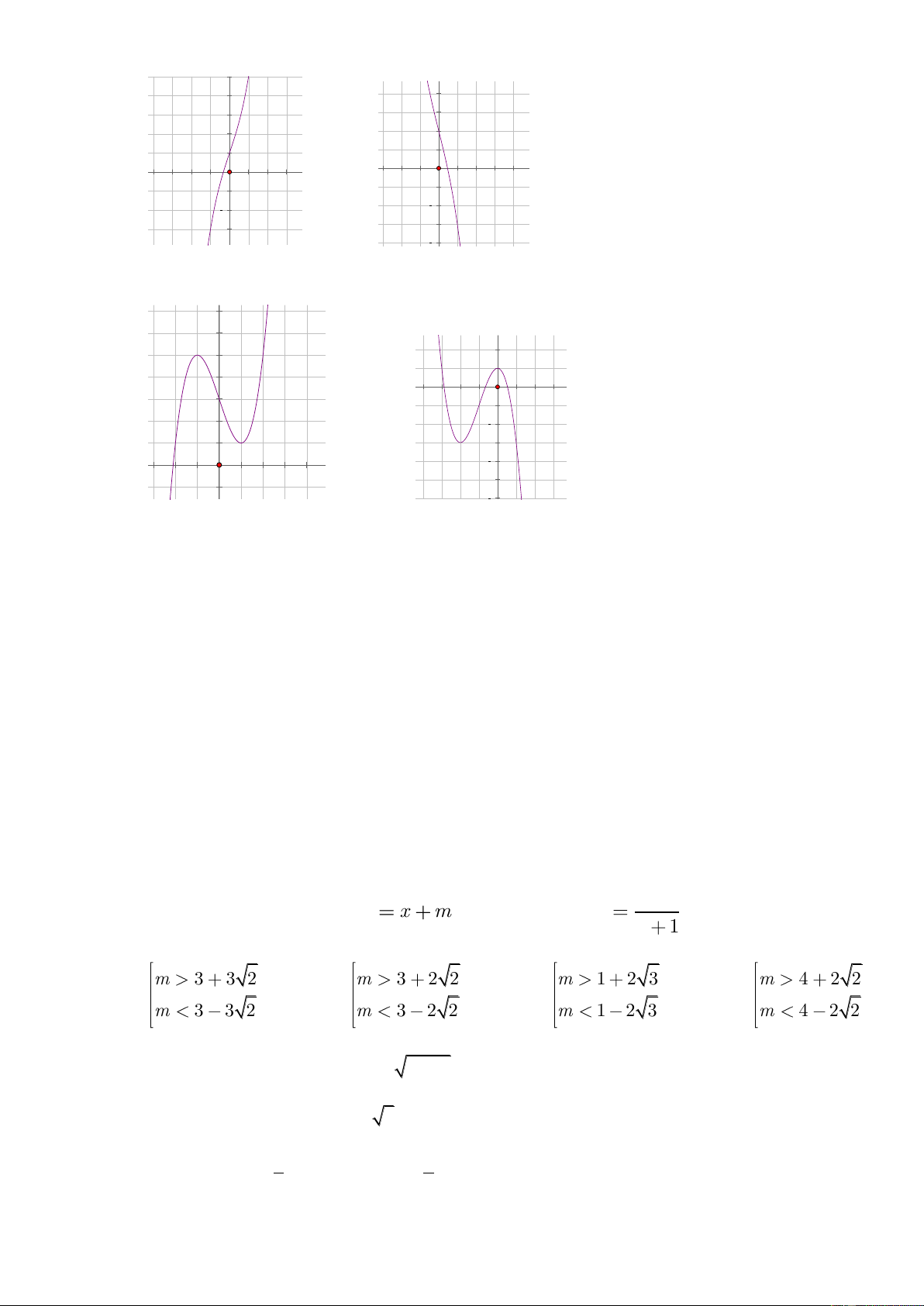
C©u 7 : Cho các dạng đồ thị của hàm số 3 2
y  ax  bx  cx  d như sau: 1 4 4 2 2 2 2 4 A B 6 2 4 2 2 4 6 C D Và các điều kiện: a  0 a  0 1.  2.  2 b  3ac  0 2 b  3ac  0 a  0 a  0 3.  4.  2 b  3ac  0 2 b  3ac  0
Hãy chọn sự tương ứng đúng giữa các dạng đồ thị và điều kiện.
A. A  2; B  4;C 1; D  3
B. A  3; B  4;C  2; D 1
C. A 1; B  3;C  2; D  4
D. A 1; B  2;C  3; D  4 C©u 8 : 2x
Tìm m để đường thẳng d : y x
m cắt đồ thị hàm số y
tại hai điểm phân biệt. x 1 m 3 3 2 m 3 2 2 m 1 2 3 m 4 2 2 A. B. C. D. m 3 3 2 m 3 2 2 m 1 2 3 m 4 2 2
C©u 9 : Tìm GTLN của hàm số 2
y  2x  5  x A. 5 B. 2  5 C. 6 D. Đáp án khác C©u 10 : 1 2 Cho hàm số 3 2 y
x mx x m  (C ). Tìm m để m
(Cm) cắt trục Ox tại ba điểm phân biệt có 3 3 2 hoành độ x 2 2 2
1 ; x2 ; x3 thỏa x1 + x2 + x3 > 15?
A. m < -1 hoặc m > 1 B. m < -1 C. m > 0 D. m > 1
C©u 11 : Tìm các giá trị của tham số m để hàm số 4 2 2
y x  2(m 1)x 1 có 3 điểm cực trị thỏa mãn
giá trị cực tiểu đạt giá trị lớn nhất. A. m  1 B. m  0 C. m  3 D. m  1
C©u 12 : Họ đường cong (Cm) : y = mx3 – 3mx2 + 2(m-1)x + 1 đi qua những điểm cố định nào?
A. A(0;1) ; B(1;-1) ; C(2;-3)
B. A(0;1) ; B(1;-1) ; C(-2;3)
C. A(-1;1) ; B(2;0) ; C(3;-2) D. Đáp án khác C©u 13 : 3 2
Hàm số y ax  x b
cx d đạt cực trị tại x ,x nằm hai phía trục tung khi và chỉ khi: 1 2
A. a  0,b  0,c  0 B. 2 b 12ac  0
C. a và c trái dấu D. 2 b 12ac  0 C©u 14 : mx 1 Hàm số y 
đồng biến trên khoảng (1; )  khi: x  m A. 1   m 1 B. m  1 C. m  \ [ 1;1] D. m  1 C©u 15 : 1 Hàm số 3 y x m 1 x
7 nghịch biến trên thì điều kiện của m là: 3 A. m 1 B. m 1 C. m 2 D. m 2 C©u 16 :  Đồ 2x 1
thị của hàm số y
có bao nhiêu đường tiệm cận: 2 x x  1 A. 0 B. 1 C. 2 D. 3 C©u 17 : Hàm số 4 2
y ax bx c đạt cực đại tại ( A 0; 3
 )và đạt cực tiểu tại ( B 1  ; 5  )
Khi đó giá trị của a, b, c lần lượt là: A. 2; 4; -3 B. -3; -1; -5 C. -2; 4; -3 D. 2; -4; -3
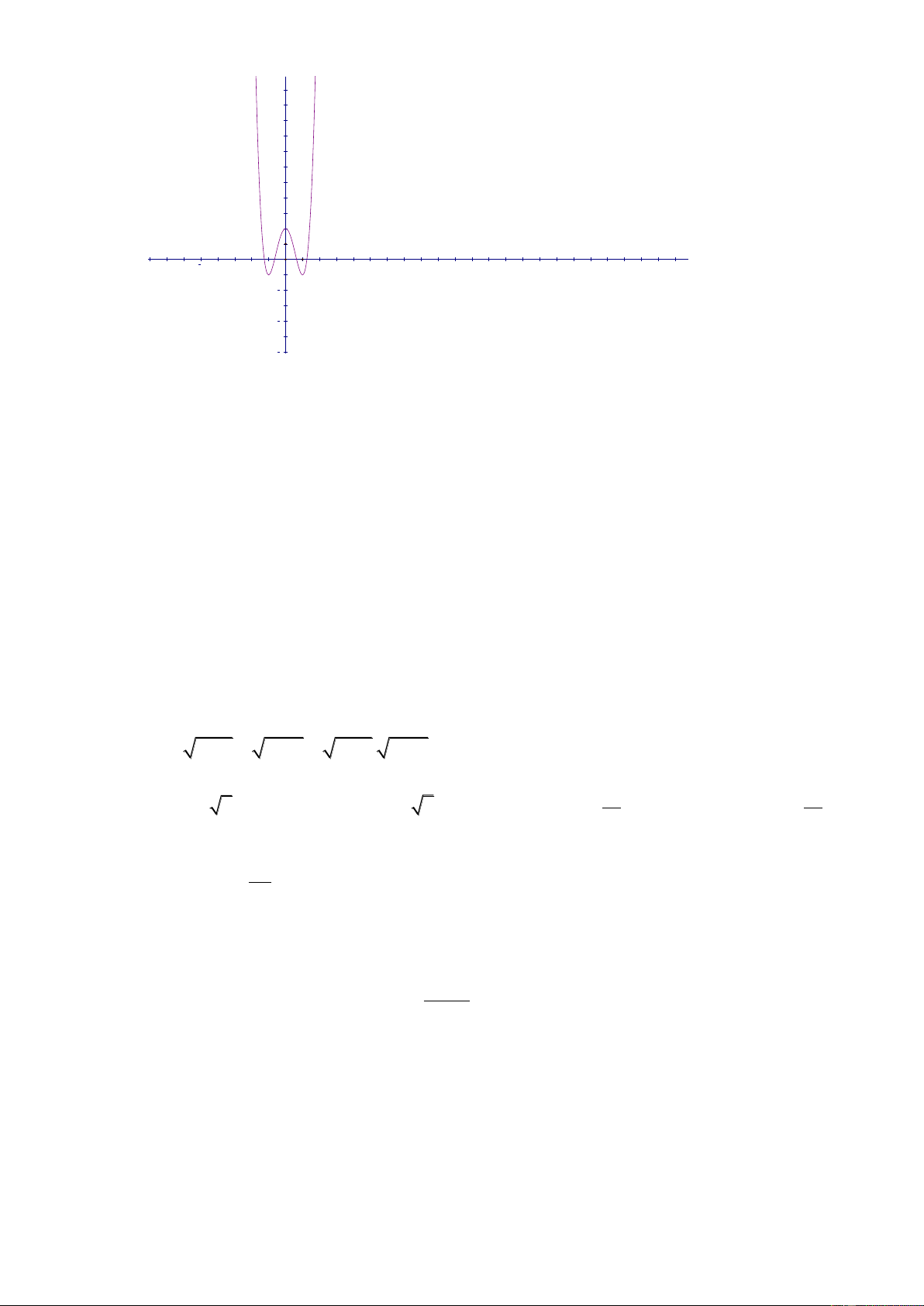
C©u 18 : Cho đồ thị (C) : y = ax4 + bx2 + c . Xác định dấu của a ; b ; c biết hình dạng đồ thị như sau : 3 10 8 6 4 2 5 5 10 15 20 2 4 6
A. a > 0 và b < 0 và c > 0
B. a > 0 và b > 0 và c > 0 C. Đáp án khác
D. a > 0 và b > 0 và c < 0
C©u 19 : Tìm tất cả các giá trị của tham số k để phương trình sau có bốn nghiệm thực phân biệt 2 x  2 4
1 x  1 k .
A. 0  k  2
B. 0  k  1 C. 1   k 1 D. k  3
C©u 20 : Viết phương trình tiếp tuyến d của đồ thị hàm số 3 2
f (x)  x  2x x  4 tại giao điểm của đồ thị
hàm số với trục hoành.
A. y  2x 1 B. y  8x  8 C. y  1
D. y x  7
C©u 21 : Tìm giá trị nhỏ nhất của hàm số:
y  1 x  3  x x 1. 3  x 9 8 A. y  2 2 1 B. y  2 2  2 C. yD. yMin Min Min 10 Min 10 C©u 22 : 3 x 2 Hàm số y
3x  5x  2 nghịch biến trên khoảng nào trong các khoảng sau đây? 3 A. 2;3 B. R C.  ;  
1 va 5;  D. 1;6 C©u 23 : 2x  1
Chọn đáp án đúng. Cho hàm số y  2 , khi đó hàm số: x
A. Nghịch biến trên 2; 
B. Đồng biến trên R  \  2
C. Đồng biến trên 2; 
D. Nghịch biến trên R  \  2
C©u 24 : Cho hàm số f (x)  x3  x2
3 , tiếp tuyến của đồ thị có hệ số góc k= -3 là 4 A. y  2  ( 3 x  ) 1 0 B. y   ( 3 x  ) 1 2
C. y  2   ( 3 x  ) 1
D. y  2   ( 3 x  ) 1 C©u 25 : x 3
Tìm cận ngang của đồ thị hàm số y 2 x 1 A. y 3 B. y 2 C. y 1;y 1 D. y 1 C©u 26 : 2x 1 Đồ thị hàm số y
là C . Viết phương trình tiếp tuyết của C biết tiếp tuyến đó song x 1
song với đường thẳng d : y 3x 15 A. y 3x 1 B. y 3x 11 C. y 3x 11; y 3x 1 D. y 3x 11 C©u 27 : 2x 1 Cho hàm số y
(C) . Tìm các điểm M trên đồ thị (C) sao cho tổng khoảng cách từ M đến hai x 1
đường tiệm cận là nhỏ nhất A. M(0;1) ; M(-2;3) B. Đáp án khác C. M(3;2) ; M(1;-1) D. M(0;1)
C©u 28 : Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của 4 2
y x  2x  3 trên 0;2 :
A. M  11, m  2
B. M  3, m  2
C. M  5, m  2
D. M  11, m  3 C©u 29 : 3 x
Tìm các giá trị của tham số m để hàm số y   m   2
1 x mx  5 có 2 điểm cực trị. 3 A. m  1 B. m  1
C. 3  m  2 D. m  1 3 2
C©u 30 : Cho hàm số y = 2x3 – 3x2 + 5 (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến qua 19 ( A
; 4) và tiếp xúc với (C) tại điểm có hoành độ lớn hơn 1 12 21 645 A. y = 12x - 15 B. y = 4 C.   y = x
D. Cả ba đáp án trên 32 128
C©u 31 : Tâm đối xứng của đồ thị hàm số 3 2
y x  3x  9x  1 là : A. I( 1  ;6) B. I(3; 28) C. I(1; 4) D. I( 1  ;12) C©u 32 : 3 2 x mx 1
Định m để hàm số y  
 đạt cực tiểu tại x  2. 3 2 3 A. m  3 B. m  2 C. Đáp án khác. D. m  1 5
C©u 33 : Tìm số cực trị của hàm số sau: f (x)  x4  x2 21 Cả ba đáp án A, B, A. C. x=0; x=1; x= -1 D. 3 C B. y=1; y= 0 C©u 34 :
Với giá trị nào của m thì hàm số y sin 3x
msin x đạt cực đại tại điểm x ? 3 A. m 5 B. 6 C. 6 D. 5 C©u 35 : 2x  1
Tiệm cận ngang của đồ thị hàm số y  là: x  1 1 A. y  3  B. x  1 C. x   D. y  2 2 C©u 36 :
x2 5x  2
Tìm tiêm cận đứng của đồ thị hàm số sau: f (x)  
x2 4 x  3 A. y= -1 B. y=1; x=3 C. x=1; x= 3 D. x   ; 1 x  3
C©u 37 : Điều kiện cần và đủ để 2 y
x  4x m  3 xác định với mọi x  : A. m  7 B. m  7 C. m  7 D. m  7
C©u 38 : Phát biểu nào sau đây là đúng:
1. Hàm số y f ( )
x đạt cực đại tại x khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua 0 x . 0
2. Hàm số y f ( )
x đạt cực trị tại x khi và chỉ khi x là nghiệm của đạo hàm. 0 0
3. Nếu f '(x )  0 và f ''x  0 thì x không phải là cực trị của hàm số y f ( ) x đã cho. 0  o 0
Nếu f '(x )  0 và f ''x  0 thì hàm số đạt cực đại tại x . 0  o 0 A. 1,3,4 . B. 1, 2, 4 C. 1
D. Tất cả đều đúng C©u 39 :
x2 3x  1
Tìm số tiệm cận của hàm số sau: f (x) 
x2 3x  4 A. 4 B. 2 C. 1 D. 3 C©u 40 : 4 2   Cho hàm số y 2x
4x . Hãy chọn mệnh đề sai trong bốn phát biểu sau:  ;     
A. Hàm số nghịch biến trên mỗi khoảng 1 và 1 ; 0 .  ;     
B. Trên các khoảng 1 và 1 ; 0
, y'  0 nên hàm số nghịch biến. 6  ;     ;1  C. 
Hàm số đồng biến trên mỗi khoảng 1 và .  0; 1   ;1  D.  Trên các khoảng và
, y'  0 nên hàm số đồng biến. C©u 41 : 3 1 k
Xác định k để phương trình 3 2 2x x  3x  
1 có 4 nghiệm phân biệt. 2 2 2  3  19   3  19  A. k  2  ;  ; 7     B. k  2  ;  ; 6      4   4   4   4   3  19  C. k  5  ;  ; 6     D. k  3  ;  1  1;2  4   4  C©u 42 : 3 Hàm số y x 3mx
5 nghịch biến trong khoảng 1;1 thì m bằng: A. 3 B. 1 C. 2 D. 1 C©u 43 : 1 1 Cho hàm số 3 2 y x
x mx . Định m để hàm số đạt cực đại và cực tiểu tại các điểm có hoành 3 2 độ lớn hơn m? A. m  2  B. m > 2 C. m = 2 D. m  2  C©u 44 : x m  8 Cho hàm số y
, hàm số đồng biến trên 3;  khi: x-2m 3 3 A. 2   m  2 B. 2   m  2 C. 2   m D. 2   m  2 2 C©u 45 : x  3
Tìm tất cả các đường tiệm cận của đồ thị hàm số y  2 x 1 A. y  1  B. y = -1 C. x = 1 D. y = 1 C©u 46 : 3
Từ đồ thị C của hàm số y x 3x
2 . Xác định m để phương trình 3 x 3x 1 m có 3 nghiệm thực phân biệt. A. 0 m 4 B. 1 m 2 C. 1 m 3 D. 1 m 7
C©u 47 : Tìm khoảng đồng biến của hàm số sau: y  f (x)  x4  x2 188 A.   ; 3 0  ; 3  B.   ;  3  ; 3 3C.   ;  3  ; 0  D.   ;  3  ; 0 3 C©u 48 : 1 1 Cho hàm số 4 2
y   x x  . Khi đó: 2 2 7
A. Hàm số đạt cực tiểu tại điểm x  0 , giá trị cực tiểu của hàm số là y ) 0 (  0 . B. y  
Hàm số đạt cực tiểu tại các điểm x  1
 , giá trị cực tiểu của hàm số là ( ) 1 1. C. y  
Hàm số đạt cực đại tại các điểm x  1
 , giá trị cực đại của hàm số là ( ) 1 1 1 D. y( ) 0 
Hàm số đạt cực đại tại điểm x  0 , giá trị cực đại của hàm số là 2 . C©u 49 : x  2 Cho hàm số y 
có I là giao điểm của hai tiệm cận. Giả sử điểm M thuộc đồ thị sao cho tiếp x  2
tuyến tại M vuông góc với IM. Khi đó điểm M có tọa độ là: M( 1  ; 2  );M( 3  ;5) A. M(0; 1  );M( 4  ;3) B. C. M(0; 1  ) D. M(0;1); M( 4  ;3) C©u 50 : Cho hàm số 3 2 y 2x 3 m 1 x
6 m 2 x 1 . Xác định m để hàm số có điểm cực đại và
cực tiểu nằm trong khoảng 2;3 m 1;3 3;4 A. m 1;3 B. m 3;4 C. D. m 1;4
……….HẾT……… 8 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 002-KSHS)
C©u 1 : Đồ thị hàm số nào sau đây không có điểm uốn A. 3 y  x  x B. 4 y  (x 1) C. 4 2 y  x  x D. 3 y  (x 1)
C©u 2 : Miền giá trị của 2
y x  6x 1 là: A. T   1  0;
B. T   ;  1  0
C. T   ;  1  0 D. T   1  0;
C©u 3 : Với giá trị m là bao nhiêu thì hàm số 3 2
f x x x   2 ( ) 3
m  3m  2 x  5 đồng biến trên (0; 2)
A. 1  m  2
B. m  1 m  2
C. 1  m  2
D. m  1 m  2
C©u 4 : Số giao điểm của đồ thị hàm số 4 2
y  x  2x  m với trục hoành là 02 khi và chỉ khi m  0 m  0 A. m0 B. m  0 C. D.  m  1 m  1  C©u 5 : 3 5x 2m  2  Cho hàm số y   mx
(C). Định m để từ A , 0 
 kẻ đến đồ thị hàm số (C) hai tiếp tuyến 6 3  3  vuông góc nhau. 1 A. m   hoặc m  2 B. 2 1 m  hoặc m  2 2 1 1 C. m  hoặc m  2  D. m   hoặc m  2  2 2 C©u 6 : x+2
Tiếp tuyến của đồ thị hàm số y 
tại giao điểm với trục tung cắt trục hoành tại điểm có hoành x 1 độ là A. x  2  B. x  2 C. x  1 D. x  1 
C©u 7 : Tìm m để f(x) có ba cực trị biết f (x)  x4  mx2 21 A. m  0 B. m > 0 C. m < 0 D. m  0 1
C©u 8 : Với giá trị m là bao nhiêu thì hàm số 4
f x mx  m   2 2 ( )
1 x m  2 đạt cực tiểu tại x =1. 1 1 A. m   B. m  1  C. m  1 D. m  3 3
C©u 9 : Tìm giá trị lớn nhất của hàm số sau: f (x)  x2  x  x  x2 2 8 42 A. 2 B. - 1 C. 1 D. 0 C©u 10 : Cho 4 3 2
y x  4x  6x 1 (C) . Mệnh đề nào sau đây đúng?
A. (C) luôn lõm
B. (C) có điểm uốn 1; 4
C. (C) luôn lồi
D. (C) có 1 khoảng lồi và 2 khoảng lõm
C©u 11 : Tìm điểm cực đại của đồ thị hàm số 3 2
y x  3x  6 A. x  1 x  3 x  2 x  0 0 B. 0 C. 0 D. 0 C©u 12 : 2x  6 Cho hàm số y
có đồ thị (C). Phương trình đường thẳng qua M 0, 
1 cắt đồ thị hàm số tại x  4
A và B sao cho độ dài AB là ngắn nhất. Hãy tìm độ dài AB. A. 2 B. 3 C. 4 D. 5
C©u 13 : Giá trị lớn nhất của hàm số 2
y  x +6x trên đoạn [  4;1] là A. 7 B. 8 C. 9 D. 12 C©u 14 : Cho hàm số 3 2
y  x  3x  4 có hai cực trị là A và B. Khi đó diện tích tam giác OAB là : A. 2 B. 4 C. 2 5 D. 8 C©u 15 : 2   Đườ x 3x 1
ng thẳng qua hai cực trị của hàm số f (x)  song song với: 2  x 1 1 1 A. y  2  x  3 B. y x  2 C. y  2  x  2 D. y x  2 2 2
C©u 16 : Tìm m để f(x) có một cực trị biết f (x)  x4  mx2 1 A. m < 0 B. m  0 C. m > 0 D. m  0
C©u 17 : Với giá trị a bao nhiêu thì 2
x  2  ax 1 a  0 x  1.
A. Không tồn tại a thỏa mãn điều kiện trên B. a tùy ý. 2
C. a  4  2 2
D. a  4  2 2
C©u 18 : Đạo hàm của hàm số y  x tại điểm x  0 là A. 0 B. Không tồn tại C. 1  D. 1 C©u 19 : 2   2 Đồ x x
thị f(x) có bao nhiêu điểm có tọa độ là cặp số nguyên f (x)  x  1 A. 3 B. 6 C. Không có D. Vô số C©u 20 : 2x  m Cho hàm số y 
(C) và đường thẳng y  x 1(d) . Đường thẳng d cắt đồ thị (C) khi: x 1 A. m  2  B. m  2  C. m  2 D. m  2  ;m  1 
C©u 21 : Cho đồ thị (C): 3
y x x  3 . Tiếp tuyến tại N(1; 3) cắt (C) tại điểm thứ 2 là M (M ≠ N). Tọa độ M là: A. M  1  ;3 B. M 1;3 C. M 2;9 D. M  2  ; 3  
C©u 22 : Điểm cực đại của hàm số 3
f (x)  x  3x  2 là: A.  1  ;0 B. 1;0 C.  1  ;4 D. 1; 4 C©u 23 :
Gọi M, m lần lượt là GTLN và GTNN của hàm số 3
f (x)  sin x  3sin x 1 trên 0;  . Khi đó giá trị M và m là:
A. M  3, m  2 
B. M  3, m  1
C. M  1, m  2 
D. M  1, m  3  C©u 24 : m Hàm số 3 2 y 
x  x  x  2017 có cực trị khi và chỉ khi 3 m  1 m  1 A. B. m  1 C. m  1 D.  m  0 m  0 C©u 25 : Cho 3 2
y  x  3mx  2 (C ), (C ) nhận I (1;0) làm tâm đối xứng khi: m m
Các kết quả a, b, c A. m  1 B. m  1  C. m  0 D. đều sai C©u 26 : Cho hàm số 4 2
y x  4x  3 có đồ thị (C). Tìm điểm A trên đồ thị hàm số sao cho tiếp tuyến tại A
cắt đồ thị tại hai điểm B, C (khác A) thỏa 2 2 2
x x x  8 A B C A. A 1  ,0 B. A1, 0 C. A2,3 D. A0,3
C©u 27 : Tất cả các điểm cực đại của hàm số y  cos x là 3  A. x    2 k  (k ) B. x  2 k  (k ) C. x  k (k ) D. x   k (k ) 2
C©u 28 : Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của 4 2
y x  2x  3 trên 0;2 :
A. M  11, m  2
B. M  3, m  2
C. M  5, m  2
D. M  11, m  3 C©u 29 : Cho hàm số 3
y x  3x  2 có đồ thị (C). Tìm m biết đường thẳng (d): y mx  3 cắt đồ thị tại hai
điểm phân biệt có tung độ lớn hơn 3. 9 9 A. m  0 B. 6   m  4  C. 6   m   D.   m  4  2 2
C©u 30 : Giá trị nhỏ nhất của hàm số 2 y  x  4  x là A. 2  2 B. 2 C. -2 D. 2 2 C©u 31 : x  2
Viết phương trình tiếp tuyến d với đồ thị (C): y  , biết d đi qua điểm ( A 6  ,5) x  2 x 7 x 7
A. y  x 1, y   
B. y x 1, y    4 2 2 2 x 7 x 5
C. y x 1, y  
D. y  x 1, y    4 2 4 2 C©u 32 : x 1 Hàm số y 
nghịch biến trên khoảng ( ;  2) khi và chỉ khi x  m A. m  1 B. m  2 C. m  2 D. m  1 C©u 33 :  Cho các đồ 2x 1 1 thị hàm số y  , y 
, y  2x-1, y  2 . Số đồ thị có tiệm cận ngang là x 1 x A. 1 B. 3 C. 2 D. 4 C©u 34 : Hàm số 3 2 2
y  x  3(m 1)x  3(m 1) x . Hàm số đạt cực trị tại điểm có hoành độ x  1 khi: A. m  2 B. m  0; m  1 C. m  1 D. m  0; m  2 C©u 35 : Cho hàm số 4
y x  m   2 2
1 x m  2 . Tìm m để hàm số đồng biến trên 1,3 A. m  ,  5  
B. m 2,  C. m  5  ,2 D. m  ,  2 C©u 36 : 1 Cho hàm số: 3 2 f (x) 
x  2x  m  
1 x  5 . Với m là bao nhiêu thì hàm số đã cho đồng biến trên 3 R. A. m  3 B. m  3 C. m  3 D. m  3 4 C©u 37 : 2
x  (m 1)x  2m 1 Cho y
. Để y tăng trên từng khoảng xác định thì: x m A. m  1 B. m  1 C. m  1 D. m  1
C©u 38 : Có bao nhiêu tiếp tuyến của đồ thị hàm số (C): 3
y x  6x  2 qua M(1; -3). A. 2. B. 3. C. 1. D. 0. C©u 39 : 2x  7 Cho hàm số y
có đồ thị (C). Tìm điểm M trên (C) sao cho khoảng cách từ M đến gốc tọa x  2 độ là ngắn nhất. M 3, 1   13  1   M 3,  M 1, 5 M 3, 1  1   1   1   A.  1  B.  5  C. D. M 4, M 3, 1  M 1  ,3 2   2   2    2  M 1  ,3 2   C©u 40 : Hàm số 2 2 3
y  (x  2x) đạt cực trị tại điểm có hoành độ là: Hàm số không có
A. x  1; x  0; x  2 B. x  1; x  0 C. x  1 D. cực trị C©u 41 : Cho hàm số 3 2
y  x  (2m 1)x  2  mx  2 . Tìm m để đồ thị hàm số có cực đại và cực tiểu.    5  m    5 , 1  ,    A. m  1  , B. m  1  ,   C. m  ,    1 D.   4  4  C©u 42 : 2 x x  3 Cho y
. Các mệnh đề sau đây, mệnh đề nào đúng? x  2
A. y không có cực trị
B. y có một cực trị
C. y có hai cực trị
D. y tăng trên C©u 43 : Hàm số 3 2
y  ax  bx  cx  d đồng biến trên R khi: a  b  0,c  0 a  b  0,c  0 A. B.  2 a  0;b  3ac  0 2 a  0;b  3ac  0 a  b  0,c  0 a  b  c  0 C. D.  2 b  3ac  0 2 a  0;b  3ac  0 C©u 44 : 3 mx Cho hàm số 2 y
 5x mx  9 có đồ thị hàm số là (C). Xác định m để (C) có điểm cực trị nằm 3 trên Ox. 5 A. m  3 B. m  2  C. m  2  D. m  3 
C©u 45 : Tìm giá trị nhỏ nhất của hàm số sau: f (x)  x  x2  x  x2 2 4 22 A. 0 B. -2 C. Không có D. 2 C©u 46 : 3  x  6 Cho y
(C) . Kết luận nào sau đây đúng? x  2
A. (C) không có tiệm cận
B. (C) có tiệm cận ngang y  3 
C. (C) có tiệm cận đứng x  2
D. (C) là một đường thẳng C©u 47 : 2x 1 Cho hàm số y 
. Tiếp tuyến tại điểm M thuộc đồ thị cắt Ox và Oy lần lượt tại hai điểm A và x 1
B thỏa mãn OB  3OA . Khi đó điểm M có tọa độ là: A. M(0; 1  );M(2;5) B. M(0; 1  ) C. M(2;5); M( 2  ;1) D. M(0; 1  );M(1;2) C©u 48 : x 1
Cho hàm số sau: f (x)  x 1
A. Hàm số đồng biến trên ( ;  1) (1; )  .
B. Hàm số nghịch biến trên \{1} .
C. Hàm số nghịch biến trên ( ;  1),(1; )  .
D. Hàm số đồng biến trên \{1} . C©u 49 : Phương trình 3 2
x  x  x  m  0 có hai nghiệm phân biệt thuộc [ 1;1] khi: 5 5 5 5 A.   m 1 B.   m 1 C.   m 1 D. 1   m  27 27 27 27 C©u 50 : Cho hàm số 3
y x  3x  2 có đồ thị (C). Tìm trên đồ thị hàm số (C) điểm M cắt trục Ox, Oy tại A,
B sao cho MA  3MB A. M 1, 0 B. M 0, 2 C. M  1  ,4
D. Không có điểm M.
………HẾT………. 6 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 003-KSHS) C©u 1 : 2sin x 1 Hàm số y  có GTLN là sin x  2 1 A. 3  B. 1  C. 1 D. 3
C©u 2 : Với giá trị nào của m thì phường trình 4 2
x  2x m  3 có 4 nghiệm phân biệt (m là tham số). m  3  hoặc A. m( 4  ; 3  ) B. C. m( 3  ; )  D. m( ;  4  ) m  4  C©u 3 : Hàm số 3 2 y  2
x  4x  5 đồng biến trên khoảng nào?  ;0    ; 4  4   4  A. 0;   B.  ;0   ;    D. 0;     4  3  ; 3  C. ;     3   3  C©u 4 : 3 Tìm m để x hàm số: 2 2 y  (m  2)
 (m  2)x  (m 8)x m 1 nghịch biến trên 3 A. m  2  B. m  2  C. m  2  D. m  2  C©u 5 : Cho hàm số x 1 y
có đồ thị là (H) . Chọn đáp án sai. x 2 1
A. Tiếp tuyến với (H) tại giao điểm của (H) với trục hoành có phương trình : y (x 1) 3
B. Có hai tiếp tuyến của (H) đi qua điểm I( 2;1)
C. Đường cong (H) có vô số cặp điểm mà tiếp tuyến tại các cặp điểm đó song song với nhau
D. Không có tiếp tuyến của (H) đi qua điểm I( 2;1)
C©u 6 : Giá trị nhỏ nhất của hàm số 2
y  3x  10  x là: A. 3  10 B. 3 10 C. 10
D. Không xác định. 1 C©u 7 : 2 x mx 1 Cho hàm số y
. Định mđể hàm số đạt cực trị tại x  2 x m A. m  1   m  3  B. m  1  C. m  2  D. m  3  C©u 8 : Cho hàm số 3 2 y 2x 3 2a 1 x
6a a 1 x 2 . Nếu gọi x , x 1
2 lần lượt là hoành độ các điểm
cực trị của hàm số thì giá trị x x 2 1 là: A. a 1. B. . a C. 1. D. a 1.
C©u 9 : Trong các hàm số sau, hàm số nào đơn điệu trên tập xác định của chúng. 2x 1 A. f (x)  B. 3 2
f '(x)  4x  2x  8x  2 x 1 C. 4 2
f (x)  2x  4x 1 D. 4 2
f (x)  x  2x C©u 10 : 9 15 13 Cho hàm số: 3 2 y x x x
, phát biểu nào sau đây là đúng: 4 4 4
A. Đồ thị hàm số có tiệm cận ngang và tiệm cận
B. Đồ thị hàm số cắt trục hoành tại 1 điểm. đứng.
C. Hàm số có cực trị.
D. Hàm số nghịch biến trên tập xác định.
C©u 11 : Với giá trị nào của tham số m thì hàm số y  m  3 2
3  2mx  3 không có cực trị A. m  3
B. Không có m thỏa yêu cầu bài toán.
C. m  3  m  0 D. m  0
C©u 12 : Tìm m để hàm số sau giảm tên từng khoảng xác định 1  1 1 1 A. 2   m B. m  2
 hay m C. m  hay m  2 D. m  2 2 2 2 2 C©u 13 : Cho hàm số 3 2 2
y x  3mx  3(m 1)x  2m  3 , m là tham số. Hàm số nghịch biến trong khoảng(1;2) khi m bằng:
A. 1  m  2 B. m  1 C. m  2 D. m   R C©u 14 : x x  Cho C  2 7 4 5 : y
C có tiệm cận đứng là 2  .   3x 3 2 3 2 A. y B. y C. x D. x  2 3 2 3 C©u 15 : 1 Cho hàm số 3 2 y x mx (2m 1)x m
2 . Giá trị m để hàm số đồng biến trên là : 3 2
A. Không có m B. m 1 C. m 1 D. m 1
C©u 16 : Cho đường cong (C) có phương trình 2 y
1 x . Tịnh tiến (C) sang phải 2 đơn vị, ta được đường
cong có phương trình nào sau đây ? A. 2 y 1 x 2 B. 2 y x 4x 3 C. 2 y 1 x 2 D. 2 y x 4x 3
C©u 17 : Hàm số nào sau đây nghịch biến trên các khoảng xác định của nó: x  2 2  x 2  x Không có đáp án A. y B. y C. y D. x  2 2  x 2  x nào đúng.
C©u 18 : Viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3 2 y  2  x  3x A. y  x B. y x 1 C. y x 1
D. y x C©u 19 : 4 2 2 Tìm m để     hàm số y x 2m x
5 đạt cực tiểu tại x  1 A. m  1 B. m  1  C. m  1  D. m
C©u 20 : Tìm khoảng đồng biến của hàm số 4 2
y  x  2x  3 A. (-1;0) B. 0;   C. (0;1) D.  ; 0 C©u 21 : 2x  3 Cho hàm số
có đồ thị (C). Điểm M thuộc (C) thì tiếp tuyến của đồ thị (C) tại M vuông góc x 1
với đường y= 4x+7. Tất cả điểm M có tọa độ thỏa mãn điều kiện trên là:  5   3   5  A. M 1;   hoặc M 3;    . B. M 1  ;   .  2   2   2   3   5    C. M 3;    . D. M 1  ;   hoăc 3 M 3;   .  2   2   2 
C©u 22 : Tìm m để hàm số đồng biến trên tập xách định 3 2 2 y x 3 x
m  (3m m 1)x 5m A. m>1 B. m<1 C. m  1   D. m  1
C©u 23 : Tìm m để hàm số: 4 2
y  x  2(2m 1)x  3 có đúng 1 cực trị: 1 1 1 1 A. m B. m C. m D. m  2 2 2 2 C©u 24 : Hàm số 2 3
y  3x  2x đạt cực trị tại A. x  0; x 1 xx   CÐ CT B. 0; 1 CÐ CT C. x  1  ; x  0 xxCÐ CT D. 1; 0 CÐ CT 3 C©u 25 : 2
Với những giá trị nào của x 2x m
m thì đồ thị (C) của hàm số y
không có tiệm cận đứng ? x m
A. m 1;m 2
B. m 0;m 1 C. m 0
D. m 0;m 2 C©u 26 : mx  Cho hàm số 1 y  có đồ thị C  
m (m là tham số). Với giá trị nào của m thì đường thẳng y 2x 1 x  2
cắt đồ thị Cm tại 2 điểm phân biệt A, B sao cho AB= 10 . 1 1  A. m  3 B. m  3 C. m   D. m  2 2 C©u 27 : x 2016
Đồ thị hàm số y
cắt trục tung tại điểm M có tọa độ ? 2x 1 A. 2016; 2016 . B. M 2016;0 . C. M 0; 2016 . D. M 0;0 . C©u 28 : 2 x ax b Cho hàm số y
. Đặt A a b,B a 2b . Để hàm số đạt cực đại tại điểm (
A 0; 1) thì tổng giá x 1
trị của A 2B là : A. 6 B. 1 C. 3 D. 0
C©u 29 : Hàm số nào sau đây nghịch biến trên toàn trục số ? A. 3 2 y x 3x 3x 1 B. 3 2 y x 3x 1 C. 3 y x 3x 2 D. 3 y x 3
C©u 30 : Số điểm chung của đồ thị hàm số 3 2
y x  2x  x 12 với trục Ox là: A. 0 B. 1 C. 2 D. 3 C©u 31 : 1 Cho hàm số y g(x)
ln tan x . Giá trị đúng của g là: 2 2 sin x 6 8 12 16 32 A. B. C. D. 3 3 3 3 C©u 32 : 4 x Hàm số 2 y
 2x 1 đạt cực đại tại: 2
A. x  2; y  3 
B. x  0; y  1 
C. x   2; y  3 
D. x   2; y  3  C©u 33 : 2 2x  3x  4
Dùng định nghĩa, tính đạo hàm của hàm số sau: y  2 x 1 2 3
x  4x  3 2    3x 8x 3  A. y '  B. y ' 2 x  2 2 1  2x  1 4 2 3x  4x  3 2    3x 4x 3  C. y '  D. y ' 2 x  2 2 1  2x  1 C©u 34 : 2 3x 4x 1
Đồ thị hàm số y x 1
A. Có tiệm cận đứng.
B. Có tiệm cận đứng và tiệm cận xiên.
C. Không có tiệm cận.
D. Có tiệm cận ngang. C©u 35 : 4 Trên đoạn 1;1 , hàm số 3 2 y x 2x x 3 3
A. Có giá trị nhỏ nhất tại 1 và giá trị lớn nhất tại 1 .
B. Không có giá trị nhỏ nhất và có giá trị lớn nhất tại 1 .
C. Có giá trị nhỏ nhất tại 1 và giá trị lớn nhất tại 1 .
D. Có giá trị nhỏ nhất tại 1 và không có giá trị lớn nhất. C©u 36 :  Đườ 2x 1
ng thẳng y x 1cắt đồ thị hàm số y
tại các điểm có tọa độ là: x 1 A. (0;-1) và (2;1) B. (-1;0) và (2;1) C. (0;2) D. (1;2) C©u 37 : 2 Cho hàm số y x
. Khẳng định nào sau đây sai x
A. Đạo hàm của hàm số đổi dấu khi đi qua x 2 và x 2.
B. Hàm số có giá trị cực tiểu là 2 2 , giá trị cực đại là 2 2 .
C. Hàm số có GTNN là 2 2 , GTLN là 2 2.
D. Đồ thị của hàm số có điểm cực tiểu là
2;2 2 và điểm cực đại là 2; 2 2 .
C©u 38 : Phương trình đườ x
ng thẳng vuông góc với y
1 và tiếp xúc với (C): 3 2
y  x  3x 1 là 9
y  9x+4; y  9x  26
y  9x+14; y  9x-26 A. y  9x+14 B. C.
D. y  9x  4 C©u 39 : Cho hàm số 3 2 2
y x  3mx  (m 1)x  2 , m là tham số. Hàm số đạt cực tiểu tại x =2 khi m bằng: A. m  1 B. m  2 C. m  1 D. m  1 C©u 40 : x  Cho C  3 1 : y
C có tiệm cận ngang là 3x  .   2 5 A. y  1 B. x  3 C. x  1 D. y  3
C©u 41 : Đạo hàm của hàm số y cos tan x bằng: 1 1 sin tan x . A. sin tan x . B. sin tan x . C. sin tan x . . 2 D. 2 cos x cos x C©u 42 :  Tìm m để x m 2 hàm số y
đồng biến trên các khoảng xác định: m xm  2 m  2 A. m   2 B. C. D. m  m   2 m   2 C©u 43 : ax 2 Cho hàm số y
có đồ thị là C . Tại điểm M
2; 4 thuộc C , tiếp tuyến của C song bx 3
song với đường thẳng 7x y 5
0 . Các giá trị thích hợp của a và b là: A. a 1; b 2. B. a 2; b 1. C. a 3; b 1. D. a 1; b 3.
C©u 44 : Trong các hàm số sau, hàm số nào đồng biến trên R. A. 3 2
f (x)  3x x x B. 3 2
f (x)  2x  3x 1 x 1 C. f (x)  D. 4 2
f (x)  x  4x 1 3x  2 C©u 45 : 2x 1 
Tiệm cận đứng và tiệm cận ngang của hàm số y x  2 là:
A. x  2; y  2  B. x  2  ; y  2 C. x  2  ; y  2 
D. x  2; y  2
C©u 46 : Cho hàm số C 3 2
: y x  6x  9x  6 . Định m để đường thẳng d  : y mx  2m  4 cắt đồ thị
C tại ba điểm phân biệt. A. m  3 B. m  3  C. m  3 D. m  3  C©u 47 : m 1 x 1 Nếu hàm số y
nghịch biến trên từng khoảng xác định thì giá trị của m là: 2x m A. m 2. B. m 2. C. 1 m 2. D. m 2. C©u 48 : Cho hàm số cos x y e
. Hãy chọn hệ thức đúng:
A. y '.cos x . y sin x y ' 0
B. y '.sin x y ' .cos x y ' 0
C. y '.sin x . y cos x y ' 0
D. y '.cos x . y sin x y ' 0 6
C©u 49 : Tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 tại điềm M(-1;-2) là
A. y  9x  7 B. y  9x  2
C. y  24x  2
D. y  24x  22 C©u 50 : Cho hàm số 3 2 y x 3x 9x
4 . Nếu hàm số đạt cực đại x và cực tiểu x thì tích ( y x ). ( y x ) bằng : 1 2 1 2 A. 207 B. 302 C. 82 D. 25 ………HẾT………. 7 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 004-KSHS)
C©u 1 : Giá trị nhỏ nhất của hàm số y  4  x  x 6 đạt tại x x 0 , tìm 0 : A. x  1  x  4 x  6  x 1 0 B. 0 C. 0 D. 0
C©u 2 : Tìm m để pt sau có nghiệm 2
x  3  m x 1 A. 1   m  10
B. -1C. m  10 D. m>-1 C©u 3 : Cho hàm số 4 2
y x  2x  5 và D  [ 1
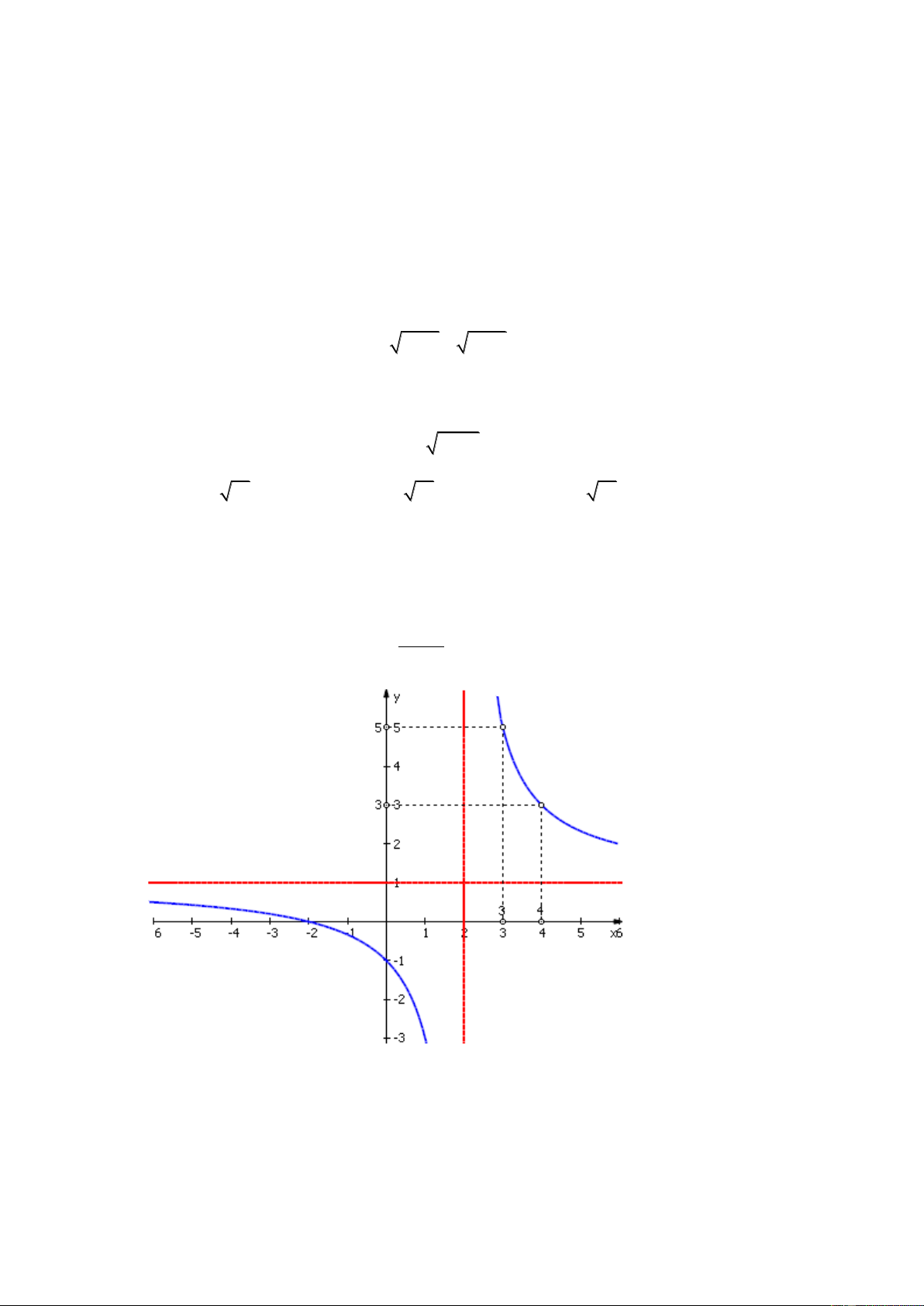
 ; 2]; M  max(y) , m  min(y). Tìm câu đúng? D D A. M = 13 và m = 4 B. M = 5 và m = 0 C. M = 5 và m = 4 D. M = 13 và m = 5 C©u 4 :  Hãy xác đị ax 2
nh a,b để hàm số y
có đồ thị như hình vẽ x b A. a = 1; b = -2 B. a = b = 1 C. a = 1; b = 2 D. a = b = 2 C©u 5 : Cho 3 2
(C) : y x  2x  3x  4 và đường thẳng d : y mx  4 . Giả sử d cắt (C) tại ba điểm phân biệt (
A 0; 4) , B,C . Khi đó giá trị của m là: A. m  3
B. Một kết quả khác C. m  2 D. m  2 1 C©u 6 : 3 2
Cho hàm số y x  3x  4
C. Gọi d là đường thẳng đi qua điểm A(- 1; 0) với hệ số góc là k (
k thuộc R). Tìm k để đường thẳng d cắt (C) tại ba điểm phân biệt và hai giao điểm B, C ( B, C khác
A ) cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 1. 1 1 1 A. k   B. Đáp án khác C. k   D. k  3 4 3 4 3 4
C©u 7 : Giá trị lớn nhất của hàm số 𝑦 = 4𝑦3 − 3𝑦4 là: A. 3 B. 4 C. 8 D. 6
C©u 8 : Đồ thị hàm số 2 2
y x  2mx m  9 cắt trục hoành tại hai điểm M và N thì A. MN  4 B. MN  6
C. MN  6m
D. MN  4m C©u 9 : 2x  1 Cho hàm số y
. Mệnh đế nào sau đây sai? x  2
A. Đồ thị tồn tại một cặp tiếp tuyến vuông góc với nhau 5 1 B. Oy y x
Tại giao điểm của đồ thị và
, tiếp tuyến song song với đường thẳng 4 4  3  5
C. Tại A 2;  k
 4  , tiếp tuyến của đồ thị có hệ số góc 16 D.   
Lấy M, N thuộc đồ thị với x 0, x 4 M N M N thì tiếp tuyến tại , song song với nhau C©u 10 : 8x  5
Xác định tiệm cận của đồ thị hàm số y  3  x 8
A. Tiệm cận đứng: x  3 ; Tiệm cận ngang: y  3
B. Tiệm cận đứng: x  3 ; Tiệm cận ngang: y  8 
C. Tiệm cận đứng: x  3 ; Tiệm cận ngang: y  5  5
D. Tiệm cận đứng: x  3 ; Tiệm cận ngang: y  3
C©u 11 : Tìm cực trị của hàm số sau 2 y x x 1 1 3 A. Điểm CT ( ; ) B. Điểm CT(-1:3) C. Không có D. Điểm CĐ (1;3) 2 2 C©u 12 : Cho hàm số 3 2
y x  2mx  m  
3 x  4 C (1). Tìm m để đường thẳng d : y = x + 4 cắt đồ thị m
hàm số (1) tại ba điểm phân biệt A, B, C sao cho tam giác MBC có diện tích bằng 4 . ( Điểm B, C có 2
hoành độ khác không ; M(1;3) ). A. m  2   m  3 B. m  2   m  3  C. m  2   m  3  D. m  3 C©u 13 : m x Cho hàm số y
H  . Tìm m để đường thẳng d : 2x + 2y - 1= 0 cắt H tại hai điểm m x  2 m 3
phân biệt A, B sao cho tam giác OAB có diện tích bằng . 8 A. m  3 10 B. m  2 10 C. m  2  10 D. m  2  10
C©u 14 : Tìm m để hàm số 3 2
y x  (m  3)x 1 m đạt cực đại tại x=-1 3  3 A. m C. m  2 B. m=1 2 D. m=-3 C©u 15 : 4
Tìm giá trị LN và NN của hàm số y x  6  , x  1  x 1 A. m=-3 B. M=-2 C. m=1;M=2 D. m=-1;M=5 C©u 16 : Cho hàm số 3 2
y  x  3x a . Trên [ 1
 ;1], hàm số có giá trị nhỏ nhất bằng 0. Tính a? A. a  0 B. a  4 C. a  2 D. a  6
C©u 17 : Tìm m để hàm số 4
y mx  m   2
1 x  2m 1 có ba cực trị. m  1  m  1  A. m  0 B. C. D. 1   m  0 m  0 m  0 C©u 18 : 3 2
Cho hàm số y x x  1 có đồ thị (C). Phương trình tiếp tuyến của (C), biết tiếp tuyến cắt trục
Ox, Oy lần lượt tại A, B và tam giác OAB cân tại O là : 32 32 32 32
A. d : y x
B. d : y  x
C. d : y  x
D. d : y x  27 27 27 27 C©u 19 : Cho hàm số 3 2
y x  3x  2 , gọi A là điểm cực đại của hàm số trên. A có tọa độ: A. A(0,0) B. A(2,-2) C. A(0,2) D. A(-2,-2) C©u 20 : Cho hàm số 3 2
y  x  4x 3x 7 đạt cực tiểu tại xCT . Kết luận nào sau đây đúng? 1 1 A. x  3  x x x  CT B.    CT 3 C. CT 3 D. 1 CT C©u 21 : Xác định m để 3 hàm số 3 2 2
y x mx  (m  )
m x  2 đạt cực tiểu tại x  1  2 A. m  1 mB. m  3 C. {1; 3} D. m  2 3
C©u 22 : Tìm giá trị lớn nhất M của hàm số 3 2 y  x 3x 9x 1   trên 2;4   A. M  21 B. M  5 C. M  4 D. M  3 C©u 23 : 1 m Hàm số 3 2 y  x  x  m 
1 x đạt cực đại tại x  1 khi 3 2 A. m  2 B. m  2 C. m  2 D. m  2 C©u 24 : 1
Với giá trị nào của m thì tiếp tuyến của đồ thị hàm số 3 y   x  3x 3
tại điểm có hoành độ bằng 1 
song song với đường thẳng 2 y  (m 1)x 2 ? A. m   5 B. m   3 C. m  5 D. m  3 C©u 25 : Cho hàm số 3 2
y  x x   2 m   2 3 3
1 x  3m 1  
1 . Tìm m để hàm số (1) có cực đại , cực tiểu ,
đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O. 6 6 6 6 A. m  1  ;m
B. m  1; m C. m  1  ;m   D. m  1  ;m   2 2 2 2 C©u 26 : Cho hàm số 4 2 2
y x  2m x 1 C (1). Tìm m dể hàm số (1) có ba điểm cực trị là ba đỉnh của m  một tam giác vuông cân A. m  1  B. m  1 C. m  2  D. m  1  C©u 27 : 2 mx m  3 Cho hàm số y
, tìm m để hàm số đồng biến trên từng khoảng xác định. x  2 m  3  A. 3   m 1 B. m  2  C. D. 3   m 1 m  1
C©u 28 : Tìm m để đường thẳng y m cắt đồ thị hàm số 4 2
y x  2x  3 tại bốn điểm phân biệt.
A. 0  m  1 B. 1   m 1 C. 4   m  3  D. 4   m  0 C©u 29 : 2x Cho hàm số y
C. Tìm tọa độ điểm M thuộc (C) , biết tiếp tuyến tại M cắt hai trục Ox, Oy x 1 1
tại hai điểm A, B sao cho tam giác OAB có diện tích bằng . 4  1   1 
A. M 1;1 ; M  ;2 M 1;1 ; M ; 2  1   2   B. 1      2  2  2   1   1  C. M 1; 1  ; M  ; 2  M 1;1 ; M  ; 2  1   2   D. 1      2  2  2  4 C©u 30 : 2 2x  5x  4
Tìm GTNN của hàm số y x  trên [0,1] 2 11 A. -7 B. C. 2 D. 1 3
C©u 31 : Tìm m để hàm số 3 2 2
y x  2mx m x  2m 1 đạt cực tiểu tại x  1. 3 A. m  3  B. m   C. m  1  D. m  1 2 C©u 32 : 3 2
Cho hàm số y x  3x  31 mx 1 3m C
.Tìm m để hàm số có cực đại , cực tiểu , m
đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 4 . A. m  1  B. m  1  C. m  2  D. m 1 C©u 33 : 3x 1
Tìm tập xác định D của hàm số sau: y  
x  3 2x  5    5 5  D = ,  \     3 A. D = 3,  B. D = ,    C.   D. D = 3,   2 2 
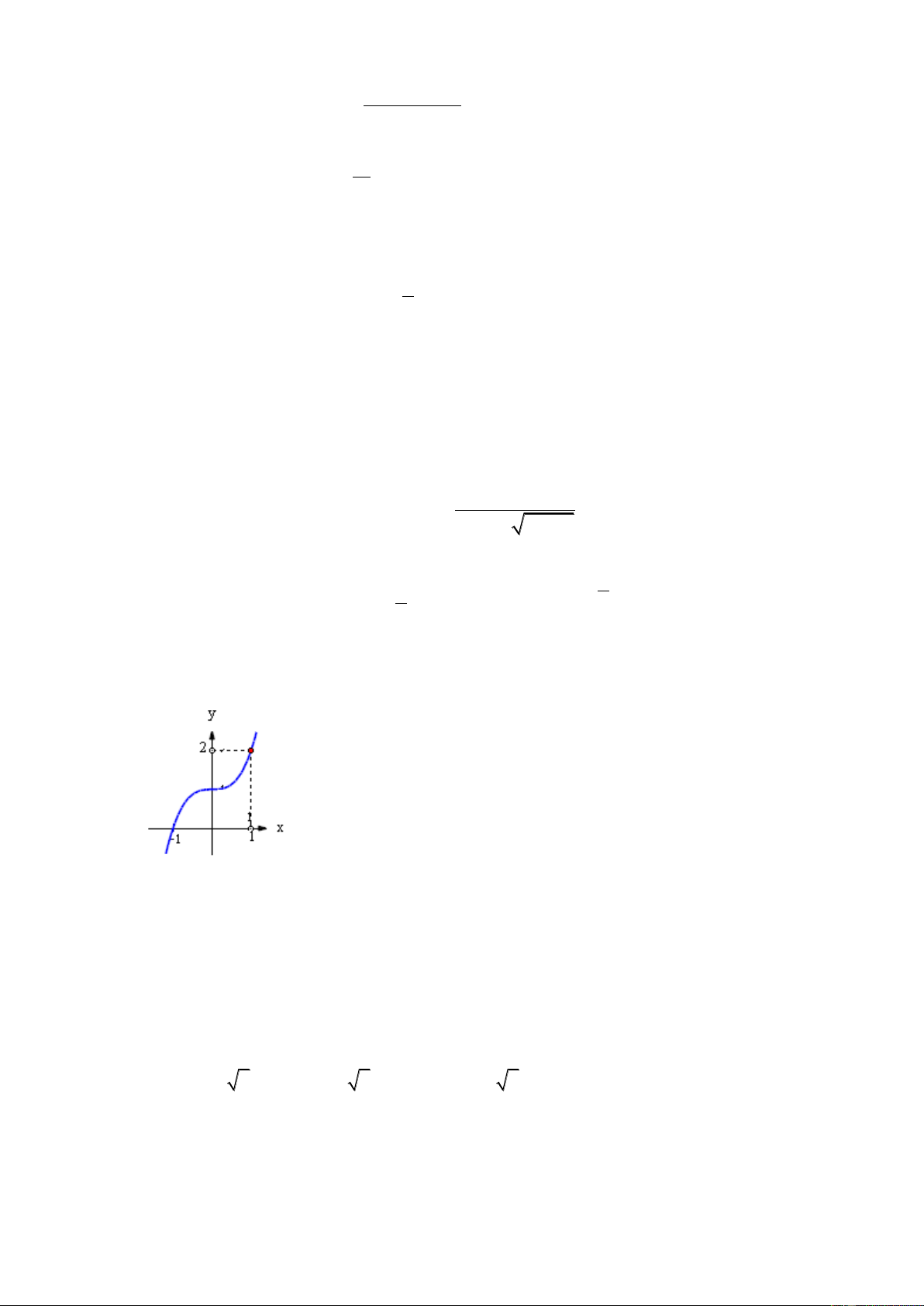
C©u 34 : Hình vẽ này là đồ thị của hàm số nào sau đây A. 3 y x  1 B. 3
y  x  3x  1 C. 3
y  x  1 D. 3
y x  3x  1
C©u 35 : Tìm m để hàm số 3 2 2 y x  3 x m
 3(m 1)x  2m  3 ngịch biến trên khoảng (1;3)
A. 1  m  2 B. m>-1 C. m>1 D. m<2 C©u 36 : Cho hàm số 4 2
y  x  4x 10 và các khoảng sau: (I).  ;   2   2;0 0; 2 ; (II).   ; (III).  .
Hãy tìm các khoảng đồng biến của hàm số trên? A. (I) và (II) B. (I) và (III) C. (II) và (III) D. Chỉ (I). 5 C©u 37 : 2x  3 Cho hàm số y
, tiệm cận ngang của hàm số trên là: x 1 A. x  1  B. y  1  C. y  2 D. x  2
C©u 38 : Cho hàm số y  sin x  cos x . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho.
Khi đó: hiệu M m bằng A. 2 2 B. 2 C. 2 D. 4 C©u 39 : 4 x Cho hàm số 2 y
x 1, hàm số đồng biến trên: 2 A.  ,  0;1, B.  ,    1 ;0,  1 C.  1  ,0;1, D.  ,  
C©u 40 : Tìm giá trị LN và NN của hàm số 2
y  s inx  2  sin x A. m=0;M=2 B. m=0;M=-2 C. m=-1;M=4 D. m=1;M=4 C©u 41 : ax  b Cho hàm số y  A
x 1 có đồ thị cắt trục tung tại (0;1), tiếp tuyến tại A có hệ số góc 3  . Tìm các giá trị a, b: A. a  2; b  1  B. a  2; b  1 C. a  4; b  1  D. a  1; b  1  C©u 42 : Cho hàm số 3
y  x 5x  2 có đồ thị (C) và đường thẳng (d): y  2 . Trong các điểm: (I). (0;2) ;  (II). ( 5; 2) ; (III). ( 5;2) ,
điểm nào là giao điểm của (C) và (d)? A. Chỉ II, III. B. Cả I, II, III. C. Chỉ I, II. D. Chỉ III, I. C©u 43 : Cho hàm số 3 2
y x  2mx  3(m 1)x  2 (1), m là tham số thực.
Tìm m để đồ thị hàm số cắt đường thẳng  : y  x  2 tại 3 điểm phân biệt (0 A ; 2) ; B; C sao cho
tam giác MBC có diện tích 2 2 , với M (3;1). A. m  0 B. m  3  C. m  3
D. m  0  m  3
C©u 44 : Tìm cực trị của hàm số y=sinx-cosx   x
k; y   2 và CT 4 CT   A. B. x
k; y   2 3 D C D 4 C x   k2; y  2 D C D 4 C 6   x
k; y   2 và 3 CD 4 CD C. x
k; y  2 D. CT 4 CT 3 x   k2; y  2 CT 4 CT C©u 45 : Cho hàm số 4 y x  2 2
mx 1 (1) .Tìm các giá trị của tham số m để đồ thi hàm số (1) có ba điểm
cực trị và đường tròn đi qua ba điểm này có bán kính bằng 1. 1   5 1   5 1   5 1   5
A. m  1;m B. m  1  ;m
C. m  1;m
D. m  1;m  2 2 2 2
C©u 46 : Giá trị cực đại của hàm số y x  2cos x trên khoảng (0; ) là:  5 5  A.  3 B.  3 C.  3 D.  3 6 6 6 6 C©u 47 : x 1
Tìm tập xác định D của hàm số sau: y  2 x  2x  3 A. D = R\{3} B. D = R C. D = R\{-1,3} D. D = R\{-1} C©u 48 : 1 3 2
Với giá trị nào của m thì hàm số y   x  mx  (2m  3)x  m  2 3
nghịch biến trên tập xác định? A. 3   m 1 B. 3   m 1 C. m  1 D. m  3  hay m 1 C©u 49 : 2 2
Tìm m để đồ thị hàm số y   x  
1 x 2mx m 2m2 cắt trục hoành tại ba điểm phân biệt. A. 1  m  3 B. m  1, m  3 C. m  1 D. m  0 C©u 50 : Cho hàm số 4 3
y  3x  4x . Khẳng định nào sau đây đúng
A. Hàm số đạt cực đại tại gốc tọa độ
B. Hàm số không có cực trị
C. Hàm số đạt cực tiểu tại gốc tọa độ D. Điểm  A 1;  1 là điểm cực tiểu ……….HẾT………. 7 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 005-KSHS) C©u 1 : x
Hàm số f (x)  có tập xác định là 2 x 1 A.  1 ; 1 B.    ; 1 C.  ;    1 D.    ;  1   ; 1   C©u 2 : 2 2 x  (6  ) m x  4
Với giá trị nào của m thì đồ thị hàm số : y  đi qua điểm M(1; -1) mx  2 A. m = 3 B. m = 2 C. m = 1 D. Không có m C©u 3 : Cho đường cong 3
y  x  x (C). Phương trình tiếp tuyến của (C) tại điểm  A 1;0 là A. y  2x  2 B. y  2x  2 C. y  2  x  2 D. y  2  x  2 C©u 4 : 2x  3
Tìm khoảng nghịch biến của hàm số f (x)  x  2 A.  2 ;   B.    ; 2 C.   2 ;   ; 2   D.  2 ;   và    ; 2 C©u 5 : 
Cho đồ thị (H) của hàm số 2x 4 y
. Phương trình tiếp tuyến của (H) tại giao điểm của (H) và Ox x  3 A. Y= 2x-4 B. Y = -2x+ 4 C. Y = - 2x-4 D. Y= 2x+4 C©u 6 : Cho hàm số : 3
y x  3mx m 1 .Tìm m để hàm số cắt trục hoành tại ba điểm phân biệt A. m  1 B. m  1 C. m  1
D. 0  m  1 C©u 7 : Cho hàm số 4 2
y x  2x  3 xác định trên đoạn 0, 2 .Gọi M và N lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của hàm số thì M N bằng bao nhiêu ? A. 15 B. 5 C. 13 D. 14 C©u 8 : x 2
Tiệm cận ngang của đồ thị hàm số y   là 3x  2 1 1 1 1 A. y  B. y   C. x   D. x  3 3 3 3 1 C©u 9 : 2 x  3x
Cho hàm số sau: y
. Đường thẳng d: y = - x +m cắt đồ thị hàm số tại mấy điểm ? x 1 A. 1 B. 3 C. 0 D. 2
C©u 10 : Giá trị lớn nhất của hàm số f (x)  4 3  x là: A. -3 B. -4 C. 3 D. 0
C©u 11 : Giá trị lớn nhất của hàm số 4 4 f (x) 
x  1 x là A. 4 6 B. 4 8 C. 4 10 D. 2 C©u 12 : 2x 1 Đồ thị hàm số y  có 2 x  3x  2
A. Hai đường tiệm cận
B. Không có tiệm cận
C. Một đường tiệm cận
D. Ba đường tiệm cận C©u 13 : 25
Giá trị nhỏ nhất của hàm số : y x  trên (3; +) là: x  3 A. 8 B. 10 C. 11 D. 13
C©u 14 : Cho hàm số C  4 2
: y x  2mx  3m  4 .Tìm m để hàm số tiếp xúc với trục hoành m 3 3
A. m  4, m   , m  1 
B. m   ; m  1  4 4 3
C. m  4; m  
D. m  4, m  1  4
C©u 15 : Cho hàm số C 3 2
y x  2(m 1)x  2m  3 x  5 và đường thẳng d : y x  5 .Tìm m để d cắt m
đồ thị C tại ba điểm phân biệt m
A. 1  m  5
B. m  1 m  5 C. m  2 D. m   R C©u 16 : Cho hàm số 2
f (x)  mx x  2x  2 . Mệnh đề nào sau đây đúng
A. Hàm số không có cực tiểu với mọi m thuộc R
B. Cả 3 mệnh đề A, B, C đều sai
C. Hàm số không có cực đại với mọi m thuộc R
D. Hàm số có cực trị khi m > 100
C©u 17 : Cho hàm số : C 3 2
: y  2x  6x  3 Phương trình tiếp tuyến với đồ thị C  có hệ số góc nhỏ nhất là :
A. y  6x  3 B. y  6  x  7 C. y  6  x  5
D. y  6x  5 2
C©u 18 : Hàm số 𝑦 = 3𝑦4 − 𝑦3 + 15 có bao nhiêm điểm cực trị A. Không có B. Có 3 C. Có 1 D. Có 2
C©u 19 : Đồ thị hàm số 3 2
y x  3x m 1 cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi
A. 1B. -1< m<3
C. -3D. -3< m <-1
C©u 20 : Giá trị lớn nhất của hàm số 4 6 f (x)  Sin . x Cos x là 107 108 109 106 A. B. C. D. 3125 3125 3125 3125 C©u 21 : 1 x 1 Cho các hàm số : 3 2 y
x x  3x  4 ; y  ; 2 y x  4 ; 3
y x  4x  sin x ; 4 2
y x x  2 3 x 1
.Có bao nhiêu hàm số đồng biến trên tập xác định của chúng A. 2 B. 4 C. 3 D. Kết quả khác C©u 22 :  1  Cho hàm số : 4 4
y f (x)  sin x  cos x .Tính giá trị : f '( )  f ' ( ) 4 4 4 A. -1 B. 0 C. 1 D. Kết quả khác C©u 23 : 2 x x 1 Cho hàm số y
có đồ thị (C). Tiếp tuyến với (𝑦) song song với đường thẳng x 1 3 d : y x 1 là 4 3 3 3 3 3 A. y x B. y x 2 C. y x D. Không có 4 4 4 4 4 C©u 24 : 2 x
Hệ số góc tiếp tuyến của đồ thị (C): y
tại điểm có hoành độ x0 = 1 bằng: 3 2 x  1 2 3 5 A. B. C. 1 D. 3 4 8
C©u 25 : Đồ thị sau đây là đồ thị của hàm số nào? 8 6 4 2 -10 -5 5 10 -2 -4 -6 -8 3 x  2 A. 4 3 y  x  2x B. y  y  x  x y  x  x x C. 3 2 2 D. 4 2 2 1 C©u 26 : TXĐ củ 1 1
a hàm số f (x)   Sin 2x Cos 2x  
A. x k
B. x k
C. x k2
D. x k 4 2 C©u 27 : 1 Cho hàm số 3 y x   2 m   2
1 x  (2m 1)x  3 .Tìm m để hàm số có hai điểm cực trị cách đều 3 trục tung A. m  2 B. m  1 C. m  1  D. m  1  C©u 28 : 1 4 7 Cho hàm số 4 3 2 f (x)  x x
x  2x 1. Khẳng định nào sau đây đúng?: 4 3 2
A. Hàm số có 1 cực đại và 2 cực tiểu
B. Hàm số chỉ có 1 cực tiểu và không có cực đại
C. Hàm số có 1 cực tiểu và 2 cực đại
D. Hàm số không có cực trị
C©u 29 : Đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  x tại bốn điểm phân biệt khi và chỉ khi 1 1 1 A.   m  0 B. m  0 C. 0  m  D. m   4 4 4
C©u 30 : Đồ thị hàm số nào sau đây không có điểm uốn 1 4 3 2 y   x  x  3x  A. 2 y  x 3x 1 B. 3 2 y  x  x C. 3 2 y  3x  x  3 D. 3 3
C©u 31 : Cho hàm số f có đạo hàm là f’(x) = x2(x-1)(x-2) với mọi xR A. 0 B. 3 C. 1 D. 2 C©u 32 : 2 x mx  Để 1 hàm y
có cực đại và cực tiểu thì các giá trị của m là: x 1 A. m = 0 B. m  R C. m < 0 D. m > 0 C©u 33 : Cos 2x
Hàm số f (x)  Sin x Không chẵn, A. Chẵn B. Lẻ C. không lẻ
D. Vừa chẵn, vừa lẻ C©u 34 : Hàm số 3 2
f (x)  3x mx mx  3 có 1 cực trị tại điểm x=-1. Khi đó hàm số đạt cực trị tại điểm khác có hoành độ là 4 1 1 1 A. B. C. D. Đáp số khác 3 4 3
C©u 35 : Tìm điểm M thuộc P 2
: y f (x)  3
x 8x 9 và điểm N thuộc P  2
' : y x  8x 13 sao cho MN nhỏ nhất A. M (0, 9  ); N 3  , 2  
B. M (1, 4); N 3, 2  
C. M (1, 4); N  3  , 2   D. M (3, 1  2); N 1  ,6
C©u 36 : Giá trị lớn nhất, nhỏ nhất của hàm số 𝑦 = 𝑦2−2𝑦+3 trên đoạn [2;4] là 𝑦−1 11 11 A. min f x 2;max f x B. min f x 2 2;max f x 2;4 2;4 3 2;4 2;4 3 min f x 2;max f x 3 C. D. min f x 2 2;max f x 3 2;4 2;4 2;4 2;4 C©u 37 : x  Tâm đố 2 1
i xứng của đồ thị hàm số y  x là 1 A. 2  1 ; B. 1; 2 C.  1  ;2 D. 2;   1 C©u 38 : 1 2 Cho hàm số 3 2 f (x) 
x  4x 12x
.Tổng các giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 3 3 [0;5] là 16 7 A. B. Đáp số khác C. 7 D. 3 3
C©u 39 : Xác định tất cả các giá trị của m để đồ thị hàm số 4 2 2
y x  (3m  4)x m cắt trục hoành tại 4 điểm phân biệt 4 4 A. m>0 B.   m  0 C. m<2 D. m   5 5
C©u 40 : Cho hàm số f (x)  x Sin 2x  3. Mệnh đề nào sau đây đúng    
A. Hàm số nhận x  làm điểm cực tiểu
B. Hàm số nhận x  làm điểm cực đại 6 6   
C. Hàm số nhận x  làm điểm cực đại
D. Hàm số nhận x  làm điểm cực tiểu 2 2
C©u 41 : Tìm giá trị lớn nhất của hàm số 𝑦 = 2√𝑦 − 1 + √6 − 𝑦 A. 2. B. 5 C. 3 D. 4 5
C©u 42 : Cho hàm số C: y x  2 .Phương trình tiếp tuyến với đồ thị C tại điểm có tung độ bằng 2 là
A. x  4y  3  0
B. x  4y  2  0
C. x  4y  6  0
D. 4x y 1  0 C©u 43 : (m  ) 1 x  2m
Cho hàm số sau: y
2 Với tất cả các giá trị nào của m thì hàm số nghịch biến trên x m (-1;+) A. m <1 v m > 2 B. m > 2 C. m < 1 D. 1  m < 2
C©u 44 : Tiếp tuyến của parabol 2
y  4  x tại điểm (1; 3) tạo với hai trục tọa độ một tam giác vuông. Diện
tích tam giác vuông đó là 5 25 5 25 A. B. C. D. 4 2 2 4 C©u 45 : Cho hàm số 3 2 y x 2x 2x
1có đồ thị (𝑦). Số tiếp tuyến với đồ thị song song với đường thẳng y x 1 là A. 0. B. 1. C. 2. D. 3.
C©u 46 : Hàm số nào sau đây có cực đại x  2 x  2 x  2 x  2 A. y  B. y  C. y  D. y  2 x  2 x  2 x  2 x  2
C©u 47 : Xác định tất cả các giá trị của m để hàm số có cực đại và cực tiêu 1 3 2 y
x mx  (m  6)x 1 3 m  3 A. m>3 B. C. m< -2 D. -2m  2  C©u 48 : 2  
Tìm tất cả các giá trị của m để hàm số x mx 1 y  đạt cực trị tại x=2 x mm  3  A. m=-3 B. m  1  C. m=-1 D. Đáp số khác C©u 49 : mx 1
Với giá trị nào của m thì đồ thị (C): y
có tiệm cận đứng đi qua điểm M(-1; 2 ) ? 2x m 1 2 A. B. 0 C. D. 2 2 2 C©u 50 : x
Gọi D1 là TXĐ của hàm số f (x)  t an
và D2 là TXĐ của hàm số 1 f (x)  . Khi đó D1  2 1 Cos x D2 là 6 A.
\ k2 | k   B. \ 
 2k  1 | k     C. \   2k   1 | k   D.
\ k | k    2  ……….HẾT………. 7 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 006-KSHS) C©u 1 : 3
Tiệm cận xiên của y  3x  5  là 2x  8 Không có tiệm cận
A. y  3x  5 B. y  2x  8 C. x  4 D. xiên C©u 2 : Hàm số 3 2
y x  3x nghịch biến trên khoảng: A. ( 2  ;0) B. (0; )  C. [ 2  ;0] D. ( ;  2  ) C©u 3 : Hàm số 2
y  4  x có mấy điểm cực tiểu ? A. 3 B. 2 C. 1 D. 0 C©u 4 : Cho hàm số 3 2
y x mx 1, (m  0) có đồ thị (C ) . Tập hợp các điểm cực tiểu của (C ) khi m m m
thay đổi là đồ thị có phương trình: 3 x 3 x A. y   1 B. 2 y x 1 C. 3 y x D. y   2 2 C©u 5 : 1 4 7 Cho hàm số 4 3 2 f (x)  x x
x  2x 1. Khẳng định nào sau đây đúng?: 4 3 2
A. Hàm số không có cực trị
B. Hàm số chỉ có 1 cực tiểu và không có cực đại
C. Hàm số có 1 cực đại và 2 cực tiểu
D. Hàm số có 1 cực tiểu và 2 cực đại C©u 6 : Cho hàm số 2
f (x)  mx x  2x  2 . Mệnh đề nào sau đây đúng
A. Hàm số không có cực đại với mọi m thuộc R
B. Hàm số có cực trị khi m > 100
C. Cả 3 mệnh đề A, B, C đều sai
D. Hàm số không có cực tiểu với mọi m thuộc R
C©u 7 : Giá trị lớn nhất của hàm số 4 4 f (x) 
x  1 x là A. 4 6 B. 4 10 C. 4 8 D. 2 C©u 8 : x  1
Với giá trị nào của b thì (C) : y
luôn cắt (d) : y x b x 1 1 Không có giá trị
A. Mọi b là số thực B. D. b < 1 nào của b C. b > 1 C©u 9 :  10  Tìm m để mx m
hàm số sau đồng biến trên từng khoảng xác định y  9 m x
A. m < 1 hoặc m > 9
B. 1  m  9 C. 1 < m < 9
D. m  1 hoặc m  9
C©u 10 : Cho x, y là các số thực thỏa: 2
y  0, x x y 12.
GTLN, GTNN của biểu thức P xy x  2y 17 lần lượt bằng: A. 10 ;-6 B. 5 ;-3 C. 20 ;-12 D. 8 ;-5
C©u 11 : Dùng định nghĩa, tính đạo hàm của hàm số sau: f (x)  ln( 2 x x  ) 1 1 1 f '(x)  A. f '(x)  B. f '(x)  ln 2 C. f '(x)  0 D. 2 x x  2 1 x  1 C©u 12 : Để hàm số 3
y x  3mx  5 nghịch biến trong khoảng (-1;1) thì m bằng: A. 1 B. 2 C. 3 D. 4
C©u 13 : Với giá trị nào của m thì hàm số 3 2
y x mx   2 m   2 3 3
1 x  3m  5 đạt cực đại tại x  1 . A. m  1 B. m  0
C. m  0; m  2 D. m  2 C©u 14 : 1
Giá trị cực đại của hàm số 3 2 y
x  2x  3x 1 là 3 1 A. 1  B. 3 C. 1 D. 3 C©u 15 : 2 x x  1 Hàm số y
đồng biến trên khoảng: x 1 A. (1; )  B. ( ;  0) C. (0;1) D. (0; 2)
C©u 16 : GTLN của hàm số y  sin x(1 cos )
x trên đoạn [0; ] là: 3 3 3 3 A. 3 3 B. C. D. 3 4 2
C©u 17 : Giá trị lớn nhất của hàm số 4 6 f (x)  Sin . x Cos x là 106 107 108 109 A. B. C. D. 3125 3125 3125 3125
C©u 18 : Cho hình chữ nhật có chu vi là 16 cm, hình chữ nhật có diện tích lớn nhất bằng 2 A. 2 36 cm B. 2 16 cm C. 2 20 cm D. 2 30 cm
C©u 19 : Hàm số nào sau đây đồng biến trên R ? A. 3 y x 1 B. 4 2
y x x 1 C. 2 y  (x 1)
D. y  tan x
C©u 20 : Giá trị cực đại của hàm số y  2 3 x  3 2
x  36x 10 là A. 71 B. 2 C. -3 D. -54 C©u 21 : x
Gọi D1 là TXĐ của hàm số f (x)  Tan
và D2 là TXĐ của hàm số 1 f (x)  . Khi đó D1  2 1 Cos x D2 là    A. \   2k   1 | k   B. \ 
 2k  1 | k   2  C.
\ k2 | k   D.
\ k | k  
C©u 22 : Cho hai số x, y không âm có tổng bằng 1. GTLN, GTNN của 3 3
P x y là : 1 A. -1;-2 B. 1;-1 C. 1; D. 0;-1 4 C©u 23 : x2  mx  Hàm số y
1 đạt cực tiểu tại x = 2 khi x m Không có giá trị A. m = - 1 B. m = - 3 C. m = 0 D. của m C©u 24 : TXĐ củ 1 1
a hàm số f (x)   Sin 2x Cos 2x  
A. x k
B. x k
C. x k
D. x k2 2 4
C©u 25 : Giá trị lớn nhất của hàm số y  3 2x trên đoạn [ 1  ;1] bằng: A. 1 B. 5 C. 3 D. 3
C©u 26 : Giá trị nhỏ nhất của hàm số 3 2
f (x)  x  3x  9x 1 trên đoạn [0; 2] là A. 1 B. 28 C. 3 D. 4 
C©u 27 : Cực trị của hàm số y  sin 2x x là:    A. x
  k; x    k (k  ) B. x
   k (k  ) CD 6 CT 6 CT 3 3   C. x
  k2 (k  ) D. x
  k (k  ) CD 6 CD 3 C©u 28 : 3 Hàm số y  3
x 1 đồng biến trên khoảng: x A. ( 1  ;2) B. ( 1  ;0) C. ( 1  ;1) D. ( ;  0) C©u 29 : Hàm số 3 2
y  x  3x  5 nghịch biến các khoảng: A. ( ;  0) [2; )  B. ( ;  0)  (2; )  C. ( ;  0][2; )  D. ( ;  0] (2; ) 
C©u 30 : Hàm số nào sau đây nghịch biến trên R ? x 1 A. 2 x y   B. y  3  C. y y  x x D. 4 1 2 C©u 31 : Hàm số 4 2
y  x  2x  3 nghịch biến trên khoảng: A. ( 1  ;1) B. (1; 2) C. (0;1) D. ( ;  1  ) C©u 32 : Hàm số 2 y
x  3x  2 nghịch biến trên khoảng: 3 3 A. (1; 2) B. (1; ) C. ( ; 2) D. ( ;  1) 2 2 C©u 33 : 1 Hàm số 4 2 y  
x  2x  3 có mấy điểm cực đại ? 2 A. 3 B. 1 C. 0 D. 2
C©u 34 : Điểm cực đại của hàm số 3 2
y  x  2x x  4 là 1 104 A. 4 B. C. D. 1 3 27 C©u 35 : Hàm số 3 2
f (x)  3x mx mx  3 có 1 cực trị tại điểm x=-1. Khi đó hàm số đạt cực trị tại điểm khác có hoành độ là 1 1 1 A. B. C. D. Đáp số khác 4 3 3
C©u 36 : Cho hàm số f (x)  x Sin 2x  3. Mệnh đề nào sau đây đúng   
A. Hàm số nhận x  làm điểm cực tiểu
B. Hàm số nhận x  làm điểm cực đại 6 2    
C. Hàm số nhận x  làm điểm cực đại
D. Hàm số nhận x  làm điểm cực tiểu 6 2 4
C©u 37 : Hàm số nào sau đây nghịch biến trên khoảng (-1 ;1) ? 1 1  A. y B. 3
y x  3x  2
C. y x  3 D. y x x  1 C©u 38 : 4
Giá trị nhỏ nhất của hàm số y x  trên đoạn [0; 4] là x 1 24 A. 4 B. C. 5  D. 3 5 C©u 39 : 1 2 Cho hàm số 3 2 f (x) 
x  4x 12x
.Tổng các giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 3 3 [0;5] là 16 7 A. B. 7 C. Đáp số khác D. 3 3
C©u 40 : Hàm số nào sau đây đồng biến trên khoảng (1 ;2) ? 1 A. 2
y  x  2 B. 2
y x  2x  3 C. y y   x x D. 3 1 1 C©u 41 : Hàm số 4 2
y  x  2x  2 nghịch biến các khoảng: A. ( ;  1  )  (0;1) B. ( 1  ;0)  (1; )  C. ( ;  1  )  (1; )  D. ( 1  ;0)  (0;1) C©u 42 : 2 x
Cho hàm số f (x) 
.Mệnh đề nào sau đây sai ? x 1
A. Hàm số f (x) đồng biến trên các khoảng (-∞ ;0)  (2;+∞)
B. Hàm số f (x) nghịch biến trên các khoảng (0 ;1)  (1;2)
C. Hàm số f (x) có tập xác định là R\{1}
D. Hàm số f (x) đồng biến trên R.
C©u 43 : GTLN và GTNN của hàm số y  sin x  cos x lần lượt là: A. 2;-2 B. 2;  2 C. -1;1 D. 1;-1
C©u 44 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2
y  x  4x 1 trên đoạn [ 1  ; 5] lần lượt là: A. 4 và 1 B. 4 và 4  C. 5 và 1 D. 5 và 4 
C©u 45 : Tìm m để phương trình 3 x  3 2
x m  0 có ba nghiệm phân biệt
A. 0  m  4 B. Không có m C. m  0 D. m  4 5 C©u 46 :  3 GTLN của hàm số 3
y x  3x  5 trên đoạn  ; 0  là  2 31 A. B. 3 C. 5 D. 7 8 C©u 47 : Cos 2x
Hàm số f (x)  Sin x Không chẵn,
A. Vừa chẵn, vừa lẻ B. Lẻ C. Chẵn D. không lẻ C©u 48 : 2
Giá trị cực tiểu của hàm số 3 y  
x  2x  2 là 3 10 2 A. 1  B. 1 C. D. 3 3 C©u 49 : Cho hàm số 3 2
f (x)  x  3x  2 .Mệnh đề nào sau đây sai ?
A. Hàm số f (x) đồng biến trên khoảng (-∞ ;0) .
B. Hàm số f (x) đồng biến trên khoảng (2 ;+∞) .
C. Hàm số f (x) nghịch biến trên khoảng (0;2)
D. Hàm số f (x) nghịch biến trên khoảng (0 ;+∞)
C©u 50 : Điểm cực tiểu của hàm số 3 2
y x  3x 1 là A. 0 B. 3  C. 1 D. 2 ……….HẾT………. 6 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN (ĐỀ 007-KSHS) C©u 1 : x Phương trình tiế 3
p tuyến của đồ thị (C) y x  3x  1 và vuông góc với đường thẳng y   1 9 là: A.
y  9x  8, y  9x  8 B.
y  9x  8, y  9x 12 C.
y  9x  8, y  9x  24 D.
y  9x 15, y  9x 17
C©u 2 : GTLN của hàm số y  sin x(1 cos )
x trên đoạn [0; ] là: 3 3 3 3 A. B. C. 3 3 D. 3 4 2 C©u 3 : 2
x  (m 1)x 1
Với giá trị nào của m, hàm số y  2 
nghịch biến trên mỗi khoảng xác định của x nó? 5 A. m  1  B. m  1 C. m  1  ;  1 D. m   2
C©u 4 : Cho phương trình x  2
1 (2  x)  k . Giá trị nào của k để phương trình có 3 nghiệm 9
A. 0  k  3 B. 0  k
C. 0  k  5
D. 0  k  4 2
C©u 5 : Phát biểu nào sau đây đúng
f '(x )  0 A. 0
X0 điểm cực đại của hàm số
f '(x )  0, f ' (x )  0 B. 0 0
X0 là điểm cực tiểu của hàm số khi
f '(x )  0, f ' (x )  0 C. 0 0
X0 là điểm cực đại của hàm số khi D.     
Nếu tồn tại h>0 sao cho f(x) < f (x ) x (x ; h x ) h x x 0 0 0 và
0 thì ta nói hàm số f(x) đạt cực 1 tiểu tại điểm x 0
C©u 6 : GTLN và GTNN của hàm số y  sin x  cos x lần lượt là: A. 2;  2 B. -1;1 C. 1;-1 D. 2;-2
C©u 7 : Hàm số nào sau đây đồng biến trên tập xác định của nó x  2 x  2 x  2 x  2 A. y B. y C. y D. y x  2 x  2 x  2 x  2 C©u 8 : x 1
Cho hàm số f (x)  x  .Mệnh đề nào sau đây đúng ? 1
A. Hàm số f (x) đồng biến trên R.
B. Hàm số f (x) đồng biến trên các khoảng (-∞ ;-1)  (-1;+∞)
C. Hàm số f (x) nghịch biến trên R
D. Hàm số f (x) nghịch biến trên các khoảng (-∞ ;-1)  (-1;+∞)
C©u 9 : Hàm số nào sau đây nghịch biến trên R ? x 1 A. 2 x y   B. 4 y  x 1 C. y y   x D. 3 2
C©u 10 : Tìm m để hàm số 3 2
y x  3mx  3(2m 1)x 1 đồng biến trên R luôn thỏa với mọi A. m  1 B. m = 1 C. giá trị m
D. Không có giá trị m C©u 11 : Cho hàm số 3 2
f (x)  x  3x  2 .Mệnh đề nào sau đây sai ?
A. Hàm số f (x) nghịch biến trên khoảng (0 ;+∞)
B. Hàm số f (x) nghịch biến trên khoảng (0;2)
C. Hàm số f (x) đồng biến trên khoảng (2 ;+∞) .
D. Hàm số f (x) đồng biến trên khoảng (-∞ ;0) . C©u 12 : 3 2
GTNN của hàm số y  2x  3x 12x 10 trên đoạn [-3; 3] là: A. -10 B. 1 C. 17 D. -35 C©u 13 : 2 2x x 1
Số đường tiệm cận của hàm số y  2x  3 A. 0 B. 1 C. 2 D. 3 2 C©u 14 : 4 x 2 9 Cho hàm số y
 2x  (C), phương trình tiếp tuyến của (C) tại các giao điểm của (C) với 4 4 trục Ox là: A.
y 15(x  3), y 15(x  3) B. y  1
 5(x  3), y  1  5(x  3) C. y  1
 5(x  3), y 15(x  3) D.
y 15(x  3), y  1  5(x  3)
C©u 15 : Hàm số nào sau đây có cực trị 4 A. 3 2
f (x)  x  3x  3x  5 B. 3 2 f (x) 
x  6x  9x 1 3 2 (x  4) 2 x  8x  9 C. f (x)  D. f (x)  2 x  2x  5 x  5
C©u 16 : Các tiếp tuyến của đường cong (C ): y = x3 - 2x - 1 song song với đường thẳng d :y = x + 2 có phương trình là:
A. y = x - 3 và y = x + 1
B. y = x - 1 và y = x + 3
C. y = x - 1 và y = x + 4
D. y = x - 1 và y = x - 2 C©u 17 : 3 2  2 
Cho hàm số y x mx m x  5  
. Với giá trị nào của m hàm số đạt cực tiểu tại x=1  3  4 3 7 A. m B. m C. m= 1 D. m  3 4 3 C©u 18 : Cos 2x
Hàm số f (x)  Sin x Không chẵn, A. Chẵn B. Lẻ C. không lẻ
D. Vừa chẵn, vừa lẻ
C©u 19 : Hàm số nào sau đây có cực đại và cực tiểu A. 2
f (x)  2x 1 2x  8 B. 2
f (x)  8  x 3 x x C. f (x)  D. f (x)  2 x  6 2 10  x
C©u 20 : Số điểm cực đại của hàm số y = x4 + 100 là A. 1 B. 0 C. 2 D. 3
C©u 21 : Cho hình chữ nhật có chu vi là 16 cm, hình chữ nhật có diện tích lớn nhất bằng A. 2 16 cm B. 2 30 cm C. 2 20 cm D. 2 36 cm 3 C©u 22 : x  2
Các tiếp tuyến của đường cong (C) : y
vuông góc với đường thẳng d :y = -3x + 2 có x  1 phương trình là: 1 2 1 1 2 1 10 A. y x  v
aø y x  6 B. y x  v aø y x  3 3 3 3 3 3 3 1 1 10
C. y x  2 v
aø y x 10 D. y x  2 v aø y x  3 3 3 C©u 23 : 4 x Hàm số y  
đồng biến trên khoảng: 2 A. 1; B.  3  ;4 C.   ;1  D.  ;0   C©u 24 : 4
Giá trị nhỏ nhất của hàm số y x  trên đoạn [0; 4] là x 1 24 A. 3 B. C. 4 D. 5  5 C©u 25 : Hàm số 3 2
2x  3(m 1)x  6mx có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc
với đường thẳng d: y=x+2. Giá trị của m là A. m  2 B. m  0
C. Cả hai đáp án A và B đều sai
D. Hai đáp án A và B đều đúng
C©u 26 : Cho đường cong (C ) : y = x3 - 2x2 - 2x -3 .Tiếp tuyến của đường cong (C) tại điểm có hoành độ
bằng -1 có phương trình là: A. y = 5x + 5 B. y = 5x + 1 C. y = - 3x - 7 D. y = - x - 5 C©u 27 : Cho hàm số 4 2
f (x)  x  2x  3 .Mệnh đề nào sau đây đúng ?
A. Hàm số f (x) nghịch biến trên khoảng (1;+∞)
B. Hàm số f (x) đồng biến trên khoảng (-∞ ;0)
C. Hàm số f (x) nghịch biến trên khoảng (-1 ;1)
D. Hàm số f (x) đồng biến trên khoảng (-1;0) .
C©u 28 : Hàm số nào sau đây không có cực trị 3  2x 3x 1 x 1 2 x x  5 A. y B. y C. y D. y x 1 1 x 2 x  8 x 1
C©u 29 : Hàm số nào sau đây chỉ có cực tiểu không có cực đại 4 1 A.
f (x)  x B. f ( )
x  3  cos x  cos 2x x C. 2 f (x)  x x 1 D.
f '(x)  (x  3) x C©u 30 : 3 2
y x  3x  3x  2 có hai điểm cực trị A và B. Đường thẳng AB song song với đường thẳng nào sau đây
A. y  1 4x
B. 3x  2y  7  0 C. y  3  x 8
D. 4x y  3  0 C©u 31 : Tìm m để 3m hàm số: 3 2 y x
x m có hai điểm cực trị 2 A. m B. m  0 C. m  0 D. m  0 C©u 32 : Hàm số 2 y  1 x
A. Đồng biến trên [0; 1]
B. Nghịch biến trên [0; 1]
C. Nghịch biến trên (0; 1)
D. Đồng biến trên (0; 1) C©u 33 : Hàm số 2
y  4  x có mấy điểm cực tiểu ? A. 0 B. 1 C. 2 D. 3
C©u 34 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2
y  x  4x 1 trên đoạn [ 1  ; 5] lần lượt là: A. 5 và 4  B. 4 và 1 C. 4 và 4  D. 5 và 1 C©u 35 : 1
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 3 2 y
x  2x  3x  5 3
A. Song song với đường thẳng x = 1
B. Có hệ số góc bằng - 1
C. Song song với trục hoành
D. Có hệ số góc dương
C©u 36 : Hàm số nào sau đây không nhận O(0,0) làm điểm cực trị 3
f (x)  (7  x) x  5 A. 3 2
f (x)  x  3x B. 3 2
f (x)  x  6 x C. D.
f (x)  x C©u 37 : 3 Hàm số y  3
x 1 đồng biến trên khoảng: x A. ( 1  ;0) B. ( ;  0) C. ( 1  ;2) D. ( 1  ;1) C©u 38 : Hàm số 4 2
y  x  2x  3 có bao nhiêu điểm cực trị? A. 0 B. 1 C. 2 D. 3 5 C©u 39 : 4
Cho hàm số f (x)  x x  .Mệnh đề nào sau đây sai ? 1
A. Hàm số f (x) đồng biến trên các khoảng (-1 ;1)  (1;3)
B. Hàm số f (x) nghịch biến trên các khoảng (-∞ ;1)  (1;+∞)
C. Hàm số f (x) có tập xác định là R\{1}
D. Hàm số f (x) nghịch biến trên các khoảng (-∞ ;-1)  (3;+∞) C©u 40 : 
Hàm số nào sau đây đạt cực đại tại x   k2 4 A.
f (x)  sin 2x B. f ( )
x  cos x sin x C.
f '(x)  s inx  cos x D.
f (x)  x  sin 2x  2
C©u 41 : Cho x, y là các số thực thỏa: 2
y  0, x x y 12.
GTLN, GTNN của biểu thức P xy x  2y 17 lần lượt bằng: A. 20 ;-12 B. 5 ;-3 C. 10 ;-6 D. 8 ;-5
C©u 42 : Tìm m để hàm số đồng biến trên khoảng (2,+∞ ) A. m  1 B. m  1 C. m  1 D. m  1 C©u 43 : 2 x  2x  3
Tọa độ giao điểm của đồ thị hàm số y
y x  là: x  và đường thẳng 1 2 A. 3, 2 B.  2  ,  1 C. 3;4 D.  1  ;0
C©u 44 : Tìm m để phương trình 3 x  3 2
x m  0 có ba nghiệm phân biệt
A. 0  m  4 B. m  0 C. m  4 D. Không có m C©u 45 : Các điể 4 2
m cực tiểu của hàm số y x  3x  2 là: A. x  1 
B. x  1, x  2 C. x  5 D. x  0
C©u 46 : Tìm m để đồ thị hàm sô 4 2
y x  2(m 1)x m có 3 điểm cực trị tạo thành 3 đỉnh của 1 tam giác vuông A. m = 1 B. m = 0 C. m = 3 D. m = 2 C©u 47 : Hàm số 3
y  x  3x  2 có bao nhiêu điểm cực trị? A. 2 B. 0 C. 1 D. 3 6 C©u 48 : 4 2
Cho hàm số y x mx m  5. Giá trị m để hàm số có 3 cực trị là: A. m  3 B. m  3 C. m  0 D. m  0
C©u 49 : Với giá trị nào của k thì phương trình 3
x  3x  2  k  0 có 3 nghiệm phân biệt Không có giá trị A. -1 < k < 1
B. 0  k  4 C. 0 < k < 4 D. nào của k C©u 50 : 2 x  2x  2  1  
Tìm GTLN của hàm số y  trên ; 2   x 1  2  8 10 Hàm số không có A. B. 3 C. D. 3 3 GTLN .........HẾT………. 7
Document Outline

  • DE-O1
  • DE-02
  • DE-03
  • DE-04
  • DE-05
  • DE-06
  • DE-07