38 bài toán đường tiệm cận của đồ thị hàm số trong đề thi THPT môn Toán (2016 – 2021)
38 bài toán đường tiệm cận của đồ thị hàm số trong đề thi THPT môn Toán (2016 – 2021) được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 BÀI TOÁN NG TI M C N C A L uy TH HÀM S en th TRONG THI BGD i tra c 2016 - 2021 n ghi
Câu 1: (Câu 4 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Tiệm cận đứng của đồ thị hàm số em x −1 . = v y
là đường thẳng có phương trình: n x + 2 Ⓐ. x = 2 . Ⓑ. x = −1 . Ⓒ. x = −2 . Ⓓ. x = 1 . Lời giải Chọn C x −1 Ta có lim
= −∞ nên đồ thị hàm số có đường tiệm cận đứng là x = −2 . x 2+ →− x + 2
Câu 2: (Câu 24 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Tiệm cận đứng của đồ thị hàm số 2x +1 y =
là đường thẳng có phương trình x −1 − Ⓐ. x = 2. Ⓑ. x =1. Ⓒ. 1 x = . Ⓓ. −1. 2 N gu Lời giải y0 Chọn B n H 2x +1 2x +1 lim = +∞ ; lim = −∞ o + − x 1 → x 1 → à x −1 x −1 ng
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x =1. Vi4
Câu 3: (Câu 23 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Tiệm cận đứng của đồ thị hàm số t x + 1 y =
là đường thẳng có phương trình: x − 2 Ⓐ. x = 1 − . Ⓑ. x = 2 − . Ⓒ. x = 2. Ⓓ. x =1. Lời giải Chọn C TXĐ: D = ℝ \ { } 2 . Ta có: lim y = − ; ∞ lim y = +∞ . − + x→2 x→2
Vậy đường thẳng x = 2 là TCĐ của đồ thị hàm số đã cho.
Câu 4: (Câu 20 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Tiệm cận đứng của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: x − 1
https://www.facebook.com/vietgold Trang 1
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 Ⓐ. x = 1. Ⓑ. x = 1 − . Ⓒ. x = 2. Ⓓ. 1 x = . 2 Lời giải Luy Chọn A en 2x −1 2x −1 t Ta có lim
= +∞ nên đồ thị hàm số y =
có tiệm cận đứng là x = 1 . h + x 1 → x −1 x − 1 itra
Câu 5: (Câu 6 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Tiệm cận đứng của đồ thị hàm số cn + g 2x 4 h y = i x −1 em .v Ⓐ. x = 1. Ⓑ. x = −1. Ⓒ. x = 2 . Ⓓ. x = 2 − . n Lời giải Chọn A
Tập xác định D = ℝ \{ } 1 2x + 4 2x + 4 Ta có lim = −∞ ; lim = +∞ − + x 1 → x −1 x 1 → x −1
Vậy tiệm cận đứng của đồ thị hàm số là x = 1
Câu 6: (Câu 3 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tiệm cận đứng của đồ thị hàm số x + 1 y = là x + 3 N gu Ⓐ. x = 1 − . Ⓑ. x =1. Ⓒ. x = 3 − . Ⓓ. x = 3. y0n Lời giải Ho Chọn C àng x +1 x +1 V Ta có lim = −∞; lim = +∞ nên x = 3
− là tiệm cận của đồ thị hàm số. i + − → − + → − 4 x ( 3) x 3 x ( 3) x + 3 t
Câu 7: (Câu 9 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tiệm cận đứng của đồ thị hàm số 2x − 2 y = là x +1 Ⓐ. x = 2 − . Ⓑ. x =1. Ⓒ. x = 1 − . Ⓓ. x = 2. Lời giải Chọn C 2x − 2 2x − 2 Ta có lim y = lim
= −∞ và lim y = lim
= +∞ nên đường thẳng x = 1 − là x 1+ x 1+ →− →− x +1 x 1− x 1− →− →− x +1
tiệm cận đứng của đồ thị hàm số.
https://www.facebook.com/vietgold Trang 2
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021
Câu 8: (Câu 12 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tiệm cận đứng của đồ thị hàm số x −1 y = là x − 3 Lu Ⓐ. x = 3 − . Ⓑ. x = −1. Ⓒ. x = 1. Ⓓ. x = 3. yen Lời giải thit Chọn D racn x −1 x −1 Ta có g lim = −∞; lim = +∞ − + h x→3 x→3 x − 3 x − 3 iem x −1 .
Vậy tiệm cận đứng của đồ thị hàm số y = là x = 3 v x − 3 n
Câu 9: (Câu 20 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tiệm cận đứng của đồ thị hàm số 2x + 2 y = là x −1 Ⓐ. x = 2 . Ⓑ. x = −2. Ⓒ. x =1. Ⓓ. x = 1 − . Lời giải Chọn C
Tập xác định: D = ℝ \ { } 1 . 2x + 2 Ta có lim
= +∞ ⇒ x = 1 là tiệm cận đứng của đồ thị hàm số. + x 1 → x −1 N g
Câu 10: (Câu 6 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tiệm cận ngang của đồ thị hàm số uy 3x +1 0 y = . n x −1 Hoàn Ⓐ. 1 y = . Ⓑ. y = 3. Ⓒ. y = 1 − . Ⓓ. y =1. g 3 Vi Lời giải 4 t Chọn B 3x +1 Ta có: lim y = lim = 3 x→±∞ x→±∞ x −1
Do đó đường thẳng y = 3 là đường tiệm cận ngang của đồ thị hàm số.
Câu 11: (Câu 18 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tiệm cận ngang của đồ thị hàm số 2x +1 y = là x −1 Ⓐ. 1 y = . Ⓑ. y = −1. Ⓒ. y = 1. Ⓓ. y = 2 . 2 Lời giải Chọn D
https://www.facebook.com/vietgold Trang 3
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 2x +1 Ta có: lim y = lim
= 2 . Nên đường thẳng y = 2 là một tiệm cận ngang của đồ thị hàm x→±∞ x→±∞ x −1 số. L
Câu 12: (Câu 9 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tiệm cận ngang của đồ thị hàm số uye 5x +1 n y = là t x −1 hitra Ⓐ. y = 1. Ⓑ. 1 y = . Ⓒ. y = 1 − . Ⓓ. = 5 y . cn 5 gh Lời giải iem Chọn D .vn
Theo công thức ta có tiệm cận ngang của dồ thị hàm số là = 5 y .
Câu 13: (Câu 11 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tiệm cận ngang của đồ thị hàm số 4x +1 y = là x −1 Ⓐ. 1 y = . Ⓑ. y = 4 . Ⓓ. y =1. Ⓓ. y = 1 − . 4 Lời giải Chọn B 4x +1 4x +1 Ta có lim = 4 (hoặc lim
= 4 ) nên đồ thị hàm số có tiệm cận ngang y = 4 . x→−∞ x −1 x→+∞ x −1 N gu
Câu 14: (Câu 15 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Tiệm cận ngang của đồ thị hàm số y0 x − 2 n y = là H x +1 oàn Ⓐ. y = −2 . Ⓑ. y = 1. Ⓒ. x = 1 − . Ⓓ. x = 2. g Vi Lời giải 4t Chọn B Ta thấy x − 2 lim = 1 x→+∞ x + 1
⇒ Vậy đồ thị hàm số có tiệm cận ngang là y = 1. x − 2 lim 1 = x→−∞ x + 1
Câu 15: (Câu 27 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Đồ thị của hàm số nào trong các hàm số
dưới đây có tiệm cận đứng? 1 1 1 Ⓐ. 1 y = . Ⓑ. y = . Ⓒ. y = . Ⓓ. y = . 2 4 2 x x + x +1 x +1 x +1 Lời giải
https://www.facebook.com/vietgold Trang 4
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 Chọn A 1
Đồ thị hàm số y =
có tiệm cận đứng là x = 0 . x Lu
Đồ thị các hàm số ở các đáp án B,C, D đều không có tiệm cận đứng do mẫu vô nghiệm. yenth
Câu 16: (Câu 1 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Đường thẳng nào dưới đây là tiệm cận đứng it 2x +1 ra
của đồ thị hàm số y = ? c x +1 ngh x = y = − y = x = − i Ⓐ. 1 Ⓑ. 1 Ⓒ. 2 Ⓓ. 1 em Lời giải . vn Chọn D
Xét phương trình x +1 = 0 ⇔ x = −1 và lim y = +∞ nên x = −1 là tiệm cận đứng. + x→ 1 −
Câu 17: (Câu 2 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f (x) có lim f (x) = 1và x→+∞ lim f (x) = 1
− . Khẳng định nào sau đây là khẳng định đúng? x→−∞
Ⓐ. Đồ thị hàm số đã cho không có tiệm cận ngang.
Ⓑ. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Ⓒ. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y =1 và y = 1 − . N gu
Ⓓ. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x =1 và x = 1 − . y0n Lời giải H oà Chọn C ng
Dựa vào định nghĩa đường tiệm cận ngang của đồ thị hàm số ta chọn đáp án C Vi4t
Câu 18: (Câu 27 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Tổng số tiệm cận đứng và tiệm cận 2 5x − 4x −1
ngang của đồ thị hàm số y = là 2 x −1 Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 3 . Lời giải Chọn C
Tập xác định D = ℝ \{1; −1} 2
5x − 4x −1 5x −1 Ta có: y = = 2 x −1 x +1 5x −1 5x −1 lim = − ; ∞ lim
= +∞ ⇒ đồ thị hàm số có một tiệm cận đứng x = −1 . + − x→−1 x→−1 x +1 x +1
https://www.facebook.com/vietgold Trang 5
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 5x −1 5x −1 lim = 5 và lim = 5 x→+∞ x +1 x→−∞ x +1
⇒ đồ thị hàm số có một đường tiệm cận ngang y = 5 . Lu
Vậy tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là 2. yenth
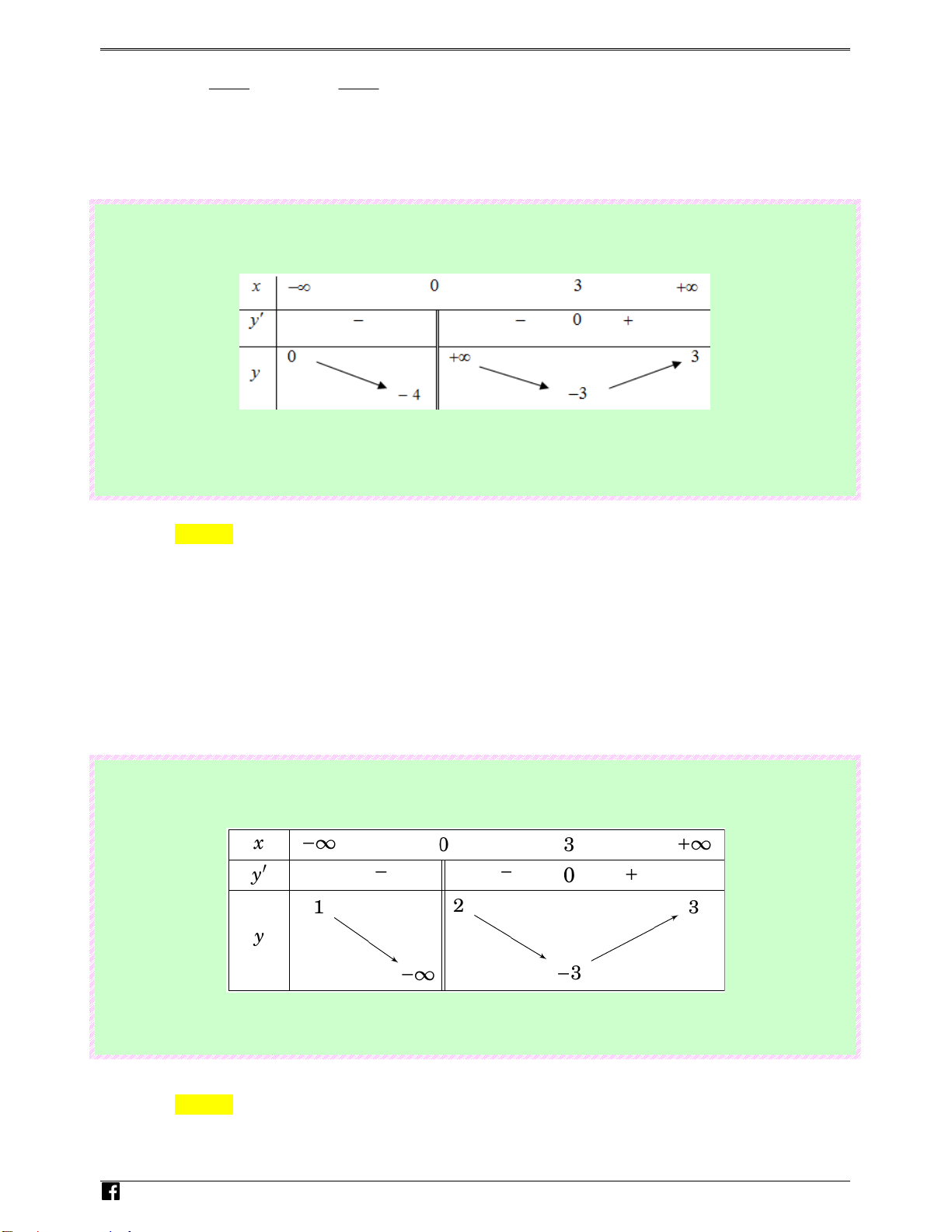
Câu 19: (Câu 23 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có bảng biến thiên itr như sau: acnghiem.vn
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là Ⓐ. 2 . Ⓑ. 1 . Ⓒ. 3 . Ⓓ. 4 . Lời giải Chọn C
Dựa vào bản biến thiên ta có
lim y = +∞ ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số. x 0+ →
lim y = 0 ⇒ y = 0 là tiệm cận ngang của đồ thị hàm số. x→ −∞ N g
lim y = 3 ⇒ y = 3 là tiệm cận ngang của đồ thị hàm số. u x→+∞ y0n
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 3 Hoà
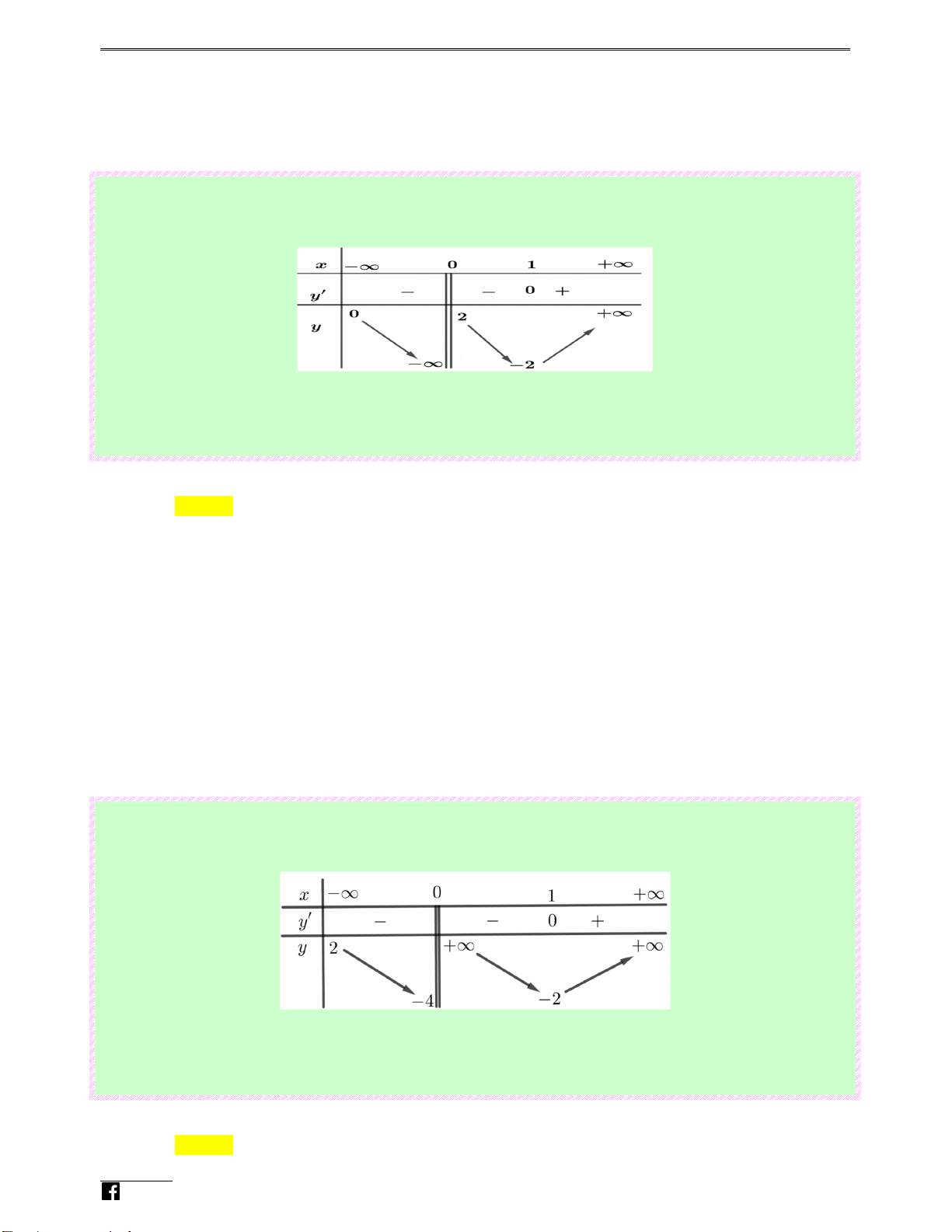
Câu 20: (Câu 28 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số
có bảng biến thiên như n f ( x) g V sau: i4t
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là Ⓐ. 1. Ⓑ. 2. Ⓒ. 3. Ⓓ. 4. Lời giải Chọn C
https://www.facebook.com/vietgold Trang 6
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021
Quan sát bảng biến thiên ta có lim y = 3 và lim y = 1 nên đồ thị hàm số có hai tiệm cận ngang x→+∞ x→−∞
y =1, y = 3 . Mặt khác lim y = −∞ nên đồ thị hàm số có tiệm cận đứng x = 0 . Vậy đồ thị hàm − x→0
số có tổng cộng ba đường tiệm cận. Luye
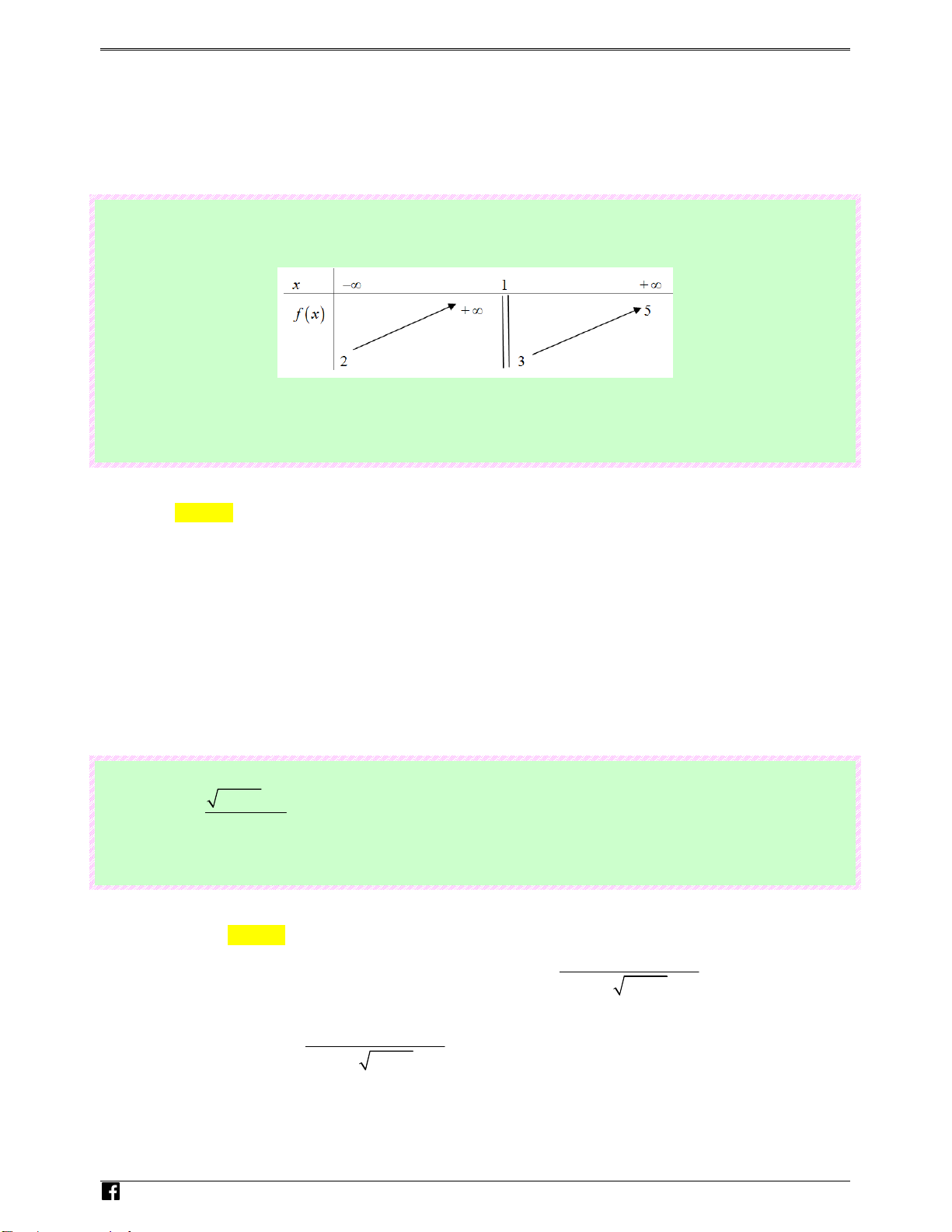
Câu 21: (Câu 24 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có bảng biến thiên nth như sau: itracnghiem.vn
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: Ⓐ. 3. Ⓑ. 1. Ⓒ. 2. Ⓓ. 4. Lời giải Chọn C
Hàm số y = f ( x) có tập xác định: D = ℝ\{ } 0 . Ta có:
lim f ( x ) = +∞ đồ thị hàm số không tồn tại tiệm cận ngang khi x→+ . ∞ x → +∞ N
lim f x = 0 Vậy đồ thị hàm số y = f ( x) có tiệm cận ngang y = 0. g ( ) x→−∞ uy0n
lim f ( x) = 2 ; lim f ( x ) = −∞. Đồ thị hàm số y = f ( x) có tiệm cận đứng x = 0. + − H x→0 x → 0 oà
Vậy tổng số tiệm cận đứng và ngang là 2. ng Vi
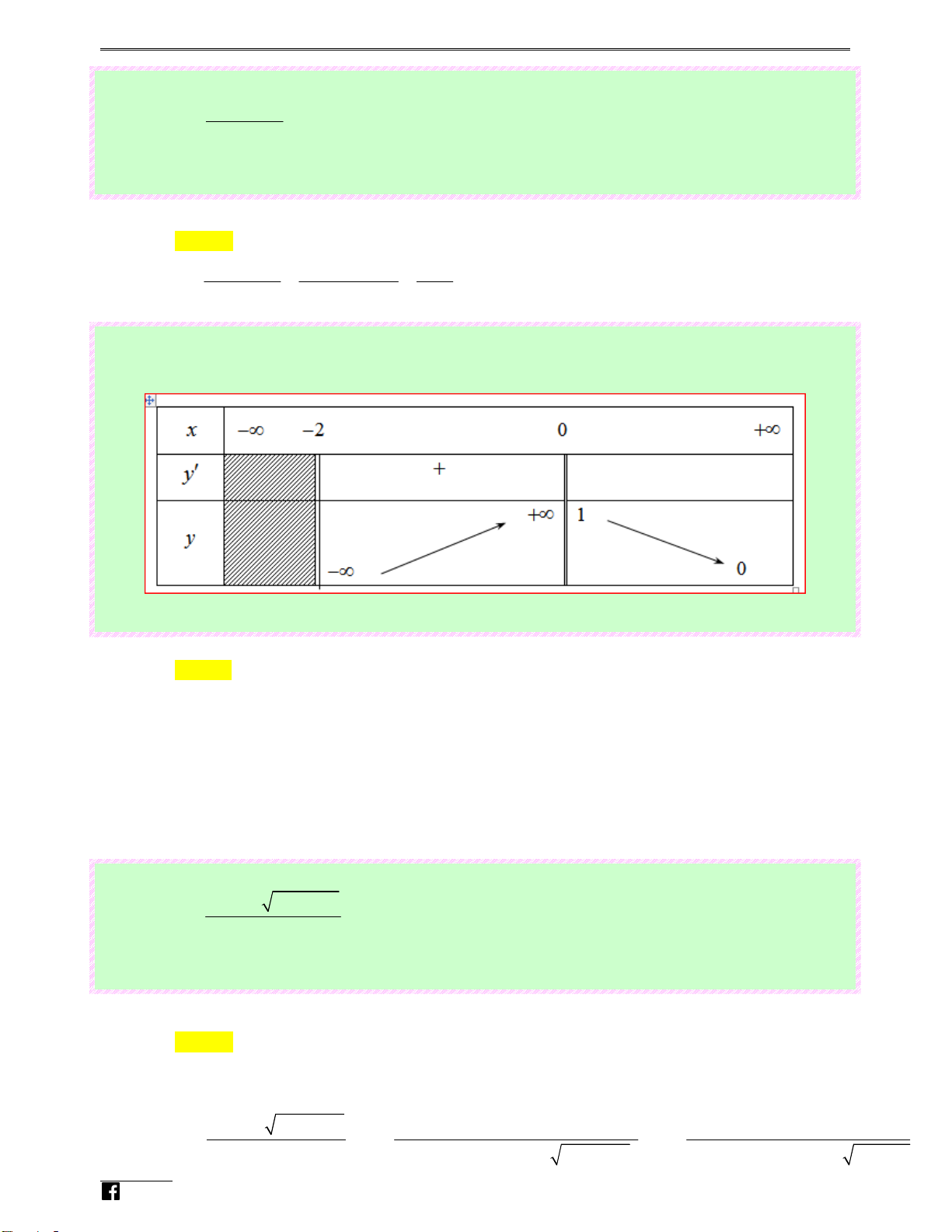
Câu 22: (Câu 28 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có bảng biến thiên 4t như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là Ⓐ. 4. Ⓑ. 1 . Ⓒ. 3. Ⓓ. 2. Lời giải Chọn D
Dựa vào bản biến thiên ta có
https://www.facebook.com/vietgold Trang 7
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021
lim y = +∞ ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số. + x→0
lim y = 2 ⇒ y = 2 là tiệm cận ngang của đồ thị hàm số. x→−∞ Lu
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 2 yent
Câu 23: (Câu 26 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có bảng biến thiên như hit sau racnghiem.vn
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là Ⓐ. 4 . Ⓑ. 1. Ⓒ. 3 . Ⓓ. 2 . Lời giải Chọn C
Nhìn bảng biến thiên ta có: +) lim = 2 y ⇒ = 2 y
là đường tiệm cận ngang của đồ thị hàm số đã cho. x→−∞ + lim = 5 y ⇒ = 5 y
là đường tiệm cận ngang của đồ thị hàm số đã cho. x →+∞ N g +) lim y = +∞ ⇒ = 1 x
là đường tiệm cận đứng của đồ thị hàm số đã cho. u − 1 x→ y0n
Vậy tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số đã cho là 3 . Hoà
Câu 24: (Câu 18 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Số tiệm cận đứng của đồ thị hàm số ng x + 25 − 5 V y = là i 2 4 x + x t Ⓐ. 2 . Ⓑ. 0 . Ⓒ. 1. Ⓓ. 3 Lời giải Chọn C 1
Tập xác định D = [−25;+∞) \{−1; }
0 . Biến đổi f (x) = . (x + ) 1 ( x + 25 +5) 1 Vì lim y = lim
= +∞ nên đồ thị hàm số đã cho có 1 tiệm cận đứng + + x ( → − ) 1 x ( → − ) 1 (x + ) 1 ( x + 25 +5) x = 1 − .
https://www.facebook.com/vietgold Trang 8
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021
Câu 25: (Câu 22 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Số tiệm cận đứng của đồ thị hàm số x + 4 − 2 y = là 2 x + x Lu Ⓐ. 3. Ⓑ. 0 . Ⓒ. 2 . Ⓓ. 1 yenth Lời giải itra Chọn D cn
Tập xác định của hàm số: D = [−4;+∞) \ {0; − } 1 ghi 1 e Ta có: lim y = . m x→0 4 .vn x + 4 − 2 x + 4 − 2 lim y = lim = +∞ và lim y = lim = −∞ + + − − x→(− ) x→(− ) 2 1 1 x + x x→(− ) x→(− ) 2 1 1 x + x ⇒ TCĐ: x = 1 − .
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 26: (Câu 18 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Số tiệm cận đứng của đồ thị hàm số x + 9 − 3 y = là 2 x + x Ⓐ. 3 Ⓑ. 2 Ⓒ. 0 Ⓓ. 1 Lời giải Chọn D N
Tập xác định của hàm số: D = [ 9 − ;+∞) \{0;− } 1 gu x + 9 − 3 x + 9 − 3 y0 Ta có: lim y = lim = +∞ và lim y = lim = −∞ . + + − − n x→(− ) 1 x→(− ) 2 1 x + x x→(− ) 1 x→(− ) 2 1 x + x H ⇒ TCĐ: x = −1 . oàn x + 9 − 3 x 1 1 g lim y = lim = lim = lim = . + + 2 + + x→0 x→0 + 2 x→0 x→0 6 V x x
(x + x)( x+9 +3) (x + ) 1 ( x + 9 + 3) i4t x + 9 − 3 1 1 lim x y = lim = lim = lim = . − − 2 − − x→0 x→0 x + x x→ ( 2 0
x + x)( x + 9 + 3) x→0 ( x + ) 1 ( x +9 +3) 6
⇒ x = 0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 27: (Câu 16 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 x − 3x + 2 2 x Ⓐ. x y = Ⓑ. y = Ⓒ. 2 y = x −1 Ⓓ. y = x −1 2 x +1 x + 1 Lời giải Chọn D
https://www.facebook.com/vietgold Trang 9
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021
Ta có lim x = +∞, lim x = −∞ nên đường thẳng x = −1 là tiệm cận đứng của đồ thị x 1− x 1 x +1 + →− →− x + 1 hàm số. L x − 2 u
Câu 28: (Câu 16 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Đồ thị hàm số y = có mấy tiệm y 2 e x − 4 nt cận. hitra Ⓐ. 1 Ⓑ. 3 Ⓒ. 0 Ⓓ. 2 cng Lời giải hi Chọn D em Ta có 2
x − 4 = 0 ⇔ x = ±2 .vn x − 2 1 lim =
nên đường thẳng x = 2 không phải là tiệm cân đứng của đồ thị hàm số. 2
x→2 x − 4 4 x − 2 1 x − 2 1 lim = lim = +∞, lim = lim = −∞,
nên đườngthẳng x = 2 − là + 2 + − 2 − x→ 2 − x→−2 x − 4 x + 2 x ( → −2) x − 4 x ( → −2) x + 2
tiệm cân đứng của đồ thị hàm số. x − 2 lim = 0
nên đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. 2
x→±∞ x − 4
Vậy có đồ thị có hai đường tiệm cận.
Câu 29: (Câu 15 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Tìm số tiệm cận của đồ thị hàm số 2 x − 5x + 4 y = . 2 x −1 N Ⓐ. 3 Ⓑ. 1 Ⓒ. 0 Ⓓ. 2 guy0 Lời giải n Chọn D H oàn
Tập xác định: D = ℝ \{± } 1 g V 5 4 i 2 1− + 4 2 x − 5x + 4 t x x Ta có: lim y = lim = lim
=1 ⇒ y =1 là đường tiệm cận ngang. 2 x→±∞ x→±∞ x −1 x→±∞ 1 1− 2 x Mặc khác: 2 x − 5x + 4 (x − ) 1 ( x − 4) (x − 4) 3 lim y = lim = lim = lim = − 2 x 1 → x 1 → x 1 x −1 → ( x − ) 1 ( x + ) x 1 1 → ( x + ) 1 2
⇒ x =1 không là đường tiệm cận đứng. 2 x − 5x + 4 (x − ) 1 ( x − 4) (x − 4) lim y = lim = lim = lim = −∞ + + + + x→(− ) 1 x→(− ) 2 1 x 1 x −1 → (x − ) 1 ( x + ) 1 x→(− ) 1 (x + ) 1 2 x − 5x + 4 (x − ) 1 ( x − 4) (x − 4) lim y = lim = lim = lim = +∞ − − − − x→(− ) x→(− ) 2 1 1 x −1 x→(− ) 1 (x − ) 1 ( x + ) 1 x→(− ) 1 (x + ) 1 ⇒ x = 1
− là đường tiệm cận đứng.
Vậy đồ thị hàm số có 2 đường tiệm cận
https://www.facebook.com/vietgold Trang 10
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021
Câu 30: (Câu 12 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Tìm số tiệm cận đứng của đồ thị hàm số 2 x − 3x − 4 y = . 2 x − 16 Lu Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0. yenth Lời giải it Chọn C ra 2 c − 3 − 4 x x (x + ) 1 ( − 4 x ) +1 x n y = = = có TCĐ: 4 x = − g 2 −16 x ( + 4 x )( − 4 x ) + 4 x hiem
Câu 31: (Câu 11 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Cho hàm số y = f ( x) có bảng biến thiên như .vn
hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận? Ⓐ. 1 Ⓑ. 3 Ⓒ. 2 Ⓓ. 4 Lời giải N Chọn B guy
Dựa vào bảng biến thiên ta có : 0n
lim f x = −∞ , suy ra đường thẳng x = −2 là tiệm cận đứng của đồ thị hàm số. ( ) H + x→ 2 − oà
lim f ( x) = +∞ , suy ra đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số. − n x→0 g V
lim f ( x) = 0 , suy ra đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số. →+∞ i x 4t
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 32: (Câu 8 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Tìm tất cả các tiệm cận đứng của đồ thị hàm số 2
2x −1− x + x + 3 y = . 2 x − 5x + 6 Ⓐ. x = 3 − và x = 2 − . Ⓑ. x = 3 − .
Ⓒ. x = 3 và x = 2. Ⓓ. x = 3. Lời giải Chọn D
Tập xác định D = ℝ\{2; } 3 x − − x + x + (2x − )2
1 − (x + x + 3) (2x − )2 2 1 − ( 2 2 x + x + 3 2 1 3 ) lim = lim = lim + 2 x 2 x 2 x − 5x + 6 + ( 2 x − 5x + 6)( 2
2x −1+ x + x + 3) x 2+ → → → ( 2x −5x + 6)( 2
2x −1+ x + x + 3
https://www.facebook.com/vietgold Trang 11
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 (3x + 1) 7 = lim = − x 2+ → (x − )( 2 x − + x + x + ) 6 3 2 1 3 2 L
2x −1− x + x + 3 7 Tương tự lim
= − . Suy ra đường thẳng x = 2 không là tiệm cận đứng của u − 2 x→2 y x − 5x + 6 6 en
đồ thị hàm số đã cho. thi 2 2 t
2x −1− x + x + 3
2x −1− x + x + 3 r lim = + ; ∞ lim
= −∞ . Suy ra đường thẳng x = 3 là tiệm a + 2 − 2 x→3 x→3 c x − 5x + 6 x − 5x + 6 ng
cận đứng của đồ thị hàm số đã cho. hie
Câu 33: (Câu 19 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Số tiệm cận đứng của đồ thị hàm số m .v x + 16 − 4 n y = là 2 x + x Ⓐ. 0 Ⓑ. 3 Ⓒ. 2 Ⓓ. 1 Lời giải Chọn D
Tập xác định hàm số D = [ 1 − 6; +∞) \{−1; } 0 . Ta có x +16 − 4 x 1 1 lim y = lim = lim = lim = . x→0 x→0 (x + ) x→0 1 x x ( x + )
1 ( x +16 + 4) x→0 (x + ) 1 ( x +16 + 4) 8 x +16 − 4 1 lim y = lim = lim = +∞ . + + + x→(− ) 1 x→(− ) 1 (x + ) 1 x x→(− ) 1 x +1 x +16 + 4 N ( )( ) gu + y vì lim + + = + > , lim ( x + ) 1 = 0 và x → (− ) 1 thì x > 1 − ⇒ x +1 > 0 . + ( x 16 4) 15 4 0 + 0 x→(− ) 1 x ( → − ) 1 n H 1 o lim y = lim = −∞ à Tương tự . − − n x→(− ) 1 x→(− ) 1 (x + ) 1 ( x +16 + 4) g Vi
Vậy đồ thị hàm số đã cho có tiệm cận đứng là x = 1 − . 4t x − 2
Câu 34: (Câu 40 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y =
có đồ thị (C). Gọi x + 2
I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh ,
A B thuộc (C),
đoạn thẳng AB có độ dài bằng Ⓐ. 2 2.. Ⓑ. 4.. Ⓒ. 2.. Ⓓ. 2 3. Lời giải Chọn B
TXĐ: D = ℝ \{ − 2}. x − 2 4 Ta có: y = = 1− . x + 2 x + 2
Đồ thị (C) có hai đường tiệm cận là x = −2 và y =1. Suy ra I ( 2 − ;1).
https://www.facebook.com/vietgold Trang 12
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 4 4 Gọi A a − 2;1−
, B = b − 2;1−
với a,b ≠ 0, a ≠ . b a b
Tam giác IAB đều ⇔ IA = IB = A . B L 16 16 b = ±a (1) u Ta có: 2 2
IA = IB ⇔ a + = b + 2 2 2 2
⇔ (a − b )(a b −16) = 0 ⇔ . 2 2 2 2 y a b a b = 16 (2) e nt
sẽ dẫn tới A ≡ B hoặc I là trung điểm AB nên loại. hi 2 t 16 ( − ) r 2 2 a Vậy 2 2 a b = 16. Lại có: = ⇒ + = ( − ) +16 a b IA AB a a b 2 2 2 c a a b n g ab = 4 h 2 2 2
⇒ a + b = 2(a − b) 2 2
⇒ a + b = 4ab ⇒ i 2 2 e a + b = 16 m . 2 2 2 v
⇒ (a − b) = 8 ⇒ AB = 2(a − b) =16 ⇒ AB = 4 . n
Câu 35: (Câu 9 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Tìm tất cả các giá trị thực của tham số m sao x +1
cho đồ thị của hàm số y = có hai tiệm cận ngang 2 mx +1
Ⓐ. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài Ⓑ. m < 0 Ⓒ. m = 0 Ⓓ. m > 0 Lời giải Chọn D
Xét các trường hơp sau:
Với m = 0 : hàm số trở thành y = x +1 nên không có tiệm cận ngang. N Với m < 0 : gu + + 1 1 y x 1 x 1 = − 0 hàm số y = =
có tập xác định là D ; suy ra không tồn tại n 2 2 mx +1 1− m x m m H o
giới hạn lim y hay hàm số không có tiệm cận ngang. à x→±∞ ng Với m > 0 : Vi4 1 t − 1+ x +1 x +1 x +1 x 1 Ta có: lim y = lim = lim = lim = lim = − . x→−∞ x→−∞ 2 mx +1 x→−∞ 1 x→−∞ 1 x→−∞ 1 m x m + −x m + m + 2 2 2 x x x 1 1+ x +1 x +1 x +1 x 1 và lim y = lim = lim = lim = lim = . x→+∞ x→+∞ 2 mx +1 x→+∞ 1 x→+∞ 1 x→+∞ 1 m x m + x m + m + 2 2 2 x x x 1 1
Vậy hàm số có hai tiệm cận ngang là : y = ; y = − khi m > 0 . m m
https://www.facebook.com/vietgold Trang 13
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 x − 2
Câu 36: (Câu 43 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y =
có đồ thị (C ) . Gọi x + 1
I là giao điểm của hai tiệm cận của (C ) . Xét tam giác đều ABI có hai đỉnh A , B thuộc (C ) , L
đoạn thẳng AB có độ dài bằng uyen Ⓐ. 2 3 Ⓑ. 2 2 Ⓒ. 3 Ⓓ. 6 thit Lời giải ra Chọn A cn − g − h
Tịnh tiến hệ trục theo vecto OI = ( 1; )
1 → I (0;0) và (C) 3 :Y = . i X em 3 − 3 − . Gọi A a; , B ; b
∈ (C ) , điều kiện: (a ≠ b) . v n a b 9 9 2 2 a + = b + 1 2 2 ( ) IA = IB a b Theo đề bài, ta có: ( ⇔ IA IB) 9 cos ; = 60° ab + 1 ab = 2 2 ( ) AB 2
Từ (2) → ab > 0 , do đó: ( ) ↔ ( 2 2 a − b )( 2 2 1 a b − 9) ab>0 = 0 →ab = 3 . 9 Suy ra: 2 AB = 2 3 + = 12 → AB = 2 3 . 3 x −1
Câu 37: (Câu 48 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y =
có đồ thị (C ) . Gọi x +1
I là giao điểm của hai tiệm cận của (C ) . Xét tam giác đều IAB có hai đỉnh ,
A B thuộc (C ) , N g
đoạn thẳng AB có độ dài bằng uy0n Ⓐ. 3. Ⓑ. 2 . Ⓒ. 2 2 . Ⓓ. 2 3 Ho Lời giải à n Chọn C g V x −1 2 i4 Ta có y = = 1− . t x +1 x +1
Đồ thị (C ) có hai đường tiệm cận là x = 1
− và y = 1. Do đó I (−1;1) . Giả sử ,
A B có hoành độ lần lượt là x , 1 2 x . Ta có: 2 4 IA = ( x + )2 4 2 1 + ; 2 IB = ( x +1 + ; 2 ) 1 ( 2 x + )2 1 (x +1 2 ) 1 2 2 2
4 x +1 − x +1 2 2 ( 2 2 ) ( 1 ) 2
AB = ( x − x + −
= x +1 − x +1 + 2 1 ) ( 2 ) ( 1 ) x +1 x +1 (x + )2 1 .( x + )2 2 1 1 2 1
Do tam giác IAB đều nên ta có:
4 ( x +1 − x +1 2 )2 ( 1 )2 x +1 − x +1 = 0 2 2 ( 2 )2 ( 1 )2 2 2
IA = IB ⇔ ( x +1 − x +1 = ⇔ 2 ) ( 1 ) (x + )2 1 ( x + )2 1 (x + )2 1 ( x + )2 2 1 1 = 4 2 1
https://www.facebook.com/vietgold Trang 14
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 (x + )2 1 − ( x + )2
1 = 0 ⇒ AB = 0 ⇒ Loại. 2 1 2 x +1 = 2 ( x +1 x +1 x +1 = 4 ⇔ 2 )2 ( 1 )2 1 L 2 u x +1 = − y 2 e x +1 1 nth 2 i + x +1 = : 2 tr x +1 1 ac 2 n 2 2 2 2 2 g
Khi đó AB = 2 (x +1 − x +1 = 2 x +1 − = x +1 − 2 2 ) ( 1 ) ( 2 ) 2 ( 2 ) h (x +1 2 ) i (x +1 2 ) em 2 2 2 2 4 2 2 . = ⇔ + − v Lại có AB IB x 1 2 = x +1 + 2 ( 2 ) ( 2 ) 2 n ( x +1 x +1 2 ) ( 2 ) 2 2 − 2 3 2 2 ( )2
(x +1 = 4 − 2 3 ⇒ AB = = 8 2 ) ( −
⇔ x + )4 − ( x + )2 4 2 3 1 8 1 + 4 = 0 ⇔ 2 2 2 2 − − 2 3 2 2 ( )2
(x +1 = 4 + 2 3 ⇒ AB = = 8 2 ) 4 + 2 3 2 + x +1 = − : 2 x +1 1 2 2 2 2
Khi đó AB = 2 (x + ) 1 − ( x + ) 1 = 2 ( x + ) 1 + = x +1 + 2 2 ( 2 )2 2 2 1 2 (x +1 2 ) (x +1 2 ) 2 2 4
Lại có AB = IB ⇔
x +1 + 2 = x +1 + 2 ( 2 )2 ( 2 )2 2 2 N 2 x +1 x +1 g ( 2 ) ( 2 ) uy 2 0 x +1 = 4 − − 2 3 < 0 4 2 ( 2 ) n
⇔ ( x +1 + 8 x +1 + 4 = 0 ⇔ ⇒ Loại 2 ) ( 2 ) 2 H (x +1 = 4 − + 2 3 < 0 2 ) oàn Vậy AB = 2 2 . g Vi4 x −1 t
Câu 38: (Câu 45 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y =
có đồ thị (C ) . Gọi x + 2
I là giao điểm của hai đường tiệm cận của (C ) . Xét tam giác đều ABI có hai đỉnh A , B thuộc
(C ), đoạn thẳng AB có độ dài bằng: Ⓐ. 6 Ⓑ. 2 3 Ⓒ. 2 Ⓓ. 2 2 Lời giải Chọn B Cách 1: a −1 b −1 Giả sử A ; a , B ; b , I ( 2 − ; ) 1 . a + 2 b + 2 3 3 3 3 IA = a + 2; −
, IB = b + 2;−
⇒ IA = a ;−
, IB = b ; − . 1 1 a + 2 b + 2 1 a 1 b
https://www.facebook.com/vietgold Trang 15
Luyenthitracnghiem.vn 38 BTOÁN TI M C N C A Đ TH" HÀM S% TRONG Đ( THI BGD T* 2016 - 2021 9 9 2 2 2 2 2
IA = IB = AB = + = + 1 a b 2 1 2 Do tam giác a b ABI đều nên 1 1 (IA IB) 1 cos , = L 2 uy 9 2 2 e
(a −b 1− = 0 1 1 1 ) 2 2 ( ) n a b t 1 1 h ⇒ it 9 1 9 r 2 a a b + = a + 2 1 1 1 2 ( ) c a b 2 1 1 1 a ngh = − 1 a 1 b ie m ( ) = 1 a 1 b 1 ⇔ .v a b = 3 1 1 n a b = 3 − 1 1 Nếu = − thì (2) vô lý. 1 a 1 b Nếu = thì ≡ ⇒ Loại. 1 a 1 b A B Nếu a b = 3 − thì (2) vô lý. 1 1 9 Nếu a b = 3 thì (2) 2 ⇒ a + =12 ⇒ AB = 2 3 . 1 1 1 2 1 a Vậy AB = 2 3 .
Cách 2: I (−2; ) 1 ( − IXY C ) x 1 : y = ⇒ (C) 3 :Y = − . x + 2 X N
Trong hệ trục toạn độ IXY (C ) nhận đường thẳng Y = − X làm trục đối xứng. guy
∆ABI đều nên IA tạo với IX một góc 15° ⇒ A∈ d :Y = − tan15 .
° X ⇒ A∈ d :Y = ( 3 − 2) X 0n . H o ⇒ A X ; 3 − 2 . à ( ( ) X ) ng 3 2 V
Mà A∈ (C ) ⇒ ( − ) 3 3 2 X = − ⇒ X = = 3(2+ 3) . i4 X 2 − 3 t
⇒ AB = IA = X + ( − ) 2 2 2 2
3 2 X =12 ⇒ AB = 2 3.
https://www.facebook.com/vietgold Trang 16