50 bài tập trắc nghiệm tính đơn điệu của hàm hợp có đáp án và lời giải Toán 12

50 bài tập trắc nghiệm tính đơn điệu của hàm hợp có đáp án và lời giải Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Strong Team Toán VD – VDC Trang 1/50

BÀI TẬP TRẮC NGHIỆM TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP

ĐỀ BÀI

Câu 1. Cho đồ thị hàm số

 

 y f x

như hình vẽ:

Hàm số

 

3 

y f x

nghịch biến trên khoảng nào dưới đây?

 

0;1

. B.

 

1;3

. C.

 

; 1 

. D.

 

1;0



Câu 2. Cho hàm số

 

f x

có bảng xét dấu đạo hàm

 

f x



như sau:

Hàm số

 

2y f x x

 

nghịch biến trên khoảng nào dưới đây?

 

2;1



. B.

 

4; 3 

. C.

 

0;1

. D.

 

2; 1 

Câu 3. Cho hàm số

 



y f x

liên tục trên



và hàm số

 

y f x





có đồ thị như hình vẽ. Hàm số

 

1 2 2020

y g x f x x    

đồng biến trên khoảng nào dưới đây?

 

1;0



. B.

 

0;1

. C.

 

2;3

. D.

 

3;5

Câu 4. Cho hàm số

 



y f x

có đạo hàm

     

2 3

. 2 5

f x x x x



  

. Hàm số

   

10 5g x f x

 

đồng biến trên khoảng nào dưới đây?

 

;1

. B.

 

1;2

. C.

 



. D.

 

1;3

Câu 5. Cho hàm số

( )y f x

có đạo hàm

( ) ( 1) ( 2)



  

f x x x x

với mọi giá trị thực của

. Xét hàm

số

( )

 



 



 

g x f

. Trong các khẳng định sau khẳng định nào đúng?

A. Hàm số đồng biến trên khoảng

(0;1)

. B. Hàm số nghịch biến trên khoảng

(0;4)

C. Hàm số đạt cực đại tại

0

. D. Hàm số đạt giá trị nhỏ nhất tại

1x

Strong Team Toán VD – VDC Trang 2/50

Câu 6. Cho hàm số

 

f x

. Hàm số

 

y f x





có đồ thị như hình bên.

Hỏi hàm số

 

2 2

2 6 3g x f x x x x   

đồng biến trên khoảng nào dưới đây?

 



 

 

. B.

 

 

 

 

0;1

. D.

 



Câu 7. Cho hàm số

 

y f x



có đạo hàm

     

2 2

' (3 ) 10 3 2

f x x x x   

với mọi

 

Hàm số

   

2 3

3 ( 1)

g x f x x

   

đồng biến trên khoảng nào trong các khoảng sau?

 

;0 .



 

0;1 .

 

1; .

; .

 

 

 

 

Câu 8. Cho hàm số

 

f x

có bảng biến thiên như sau:

Hàm số

 

3 2

y f x f x

 

nghịch biến trên khoảng nào dưới đây?

 

2;3

. B.

 

1;2

. C.

 

3;4

. D.

 

; 1 

Câu 9. Cho hàm số

 

y f x



, hàm số

   

3 2

, ,f x x ax bx c a b c



    



có đồ thị như hình vẽ

Hàm số

   

 

g x f f x





nghịch biến trên khoảng nào dưới đây?

 



. B.

 

; 2 

. C.

 

1;0



. D.

3 3

;

3 3

 



 

 

Strong Team Toán VD – VDC Trang 3/50

Câu 10. Cho hàm số

 

y f x

liên tục có đạo hàm trên



. Biết hàm số

 

'f x

có đồ thị cho như hình

vẽ. Có bao nhiêu giá trị nguyên của

thuộc

 

2019;2019

để hàm số

 

2019 2

g x f mx  

đồng biến trên

 

0;1

2028

. B.

2019

2011

. D.

2020

Câu 11. Cho hàm số

 

y f x

có đạo hàm trên



và có đồ thị hàm

 

f x



như hình vẽ dưới đây. Hàm

số

 

g x f x x 

đồng biến trên khoảng nào?

 

 

 

. B.

 

1; 2

 



 

 

. D.

 

; 1 

Câu 12. Cho hàm số

 

y f x

có đạo hàm trên



. Biết hàm số

 

y f x





liên tục trên



và có đồ thị

như hình vẽ. Hàm số





1y f x 

đồng biến trong khoảng nào dưới đây?

Strong Team Toán VD – VDC Trang 4/50

   

; 3 , 0; 3

 

. B.

   

; 3 , 3;

  

   

3;0 , 3;

 

. D.

 

; 3 , 0;

  

Câu 13. Cho hàm số

 

y f x



. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

y f x x

 

nghịch biến trên khoảng nào dưới đây.

;

 

 

 

 

. B.

;

 

 

 

 

. C.

;

 



 

 

. D.

;

 



 

 

Câu 14. Cho hàm số

 

y f x



có đạo hàm trên



. Đường cong trong hình vẽ bên là đồ thị của hàm số

 

y f x





(

 

y f x





liên tục trên



). Xét hàm số

 

g x f x

 

. Mệnh đề nào dưới đây

sai?

A. Hàm số

 

g x

đồng biến trên

 

1;0



. B. Hàm số

 

g x

nghịch biến trên

 

; 1 

C. Hàm số

 

g x

nghịch biến trên

 

1; 2

. D. Hàm số

 

g x

đồng biến trên

 



Câu 15. Cho hàm số

 

y f x



có đồ thị nằm trên trục hoành và có đạo hàm trên



, bảng xét dấu của

biểu thức

 

f x



như bảng dưới đây:

Hàm số

 

2 1

f x x

y g x

f x x



 

 

nghịch biến trên khoảng nào dưới đây?

 

;1

. B.

 



 

 

. C.

 

1;3

. D.

 



Câu 16. Cho hàm số

 

f x

có bảng biến thiên như sau:

2

1

Strong Team Toán VD – VDC Trang 5/50

Hàm số

 

3 2

y f x f x

 

nghịch biến trên khoảng nào dưới đây?

 

1; 2

. B.

 

3 ; 4

. C.

 

; 1



. D.

 

2 ; 3

Câu 17. Cho hàm số

 

y f x



đạo hàm liên tục trên



có đồ thị hàm số

 

f x



như hình vẽ

Hỏi hàm số

 

2y f x x

 

đồng biến trên khoảng nào sau đây?

 

1;0



. B.

 

0;1

. C.

 

1;3

. D.

 



Câu 18. Cho hàm số

 

f x

có đạo hàm, liên tục trên



, có đồ thị như hình vẽ

Hỏi hàm số

 

y f x



 

 

nghịch biến trên khoảng nào sau đây?

 

1;1



. B.

 

 

 

. C.

 

 

 

. D.

 

2; 1 

Câu 19. Cho hàm số

 

y f x

có bảng biến thiên như sau:

Có bao nhiêu số nguyên

2019



để hàm số

 

g x f x x m  

đồng biến trên khoảng

 



A. 2016. B. 2015. C. 2017. D. 2018.

Câu 20. Cho hàm số

( )y f x

có bảng biến thiên như sau:

Hàm số

 

( ) (3 )g x f x

 

nghịch biến trên khoảng nào trong các khoảng sau?

( 2;5)

. B.

(1;2)

. C.

(2;5)

. D.

(5; )

Strong Team Toán VD – VDC Trang 6/50

Câu 21. Cho hàm số

 

y f x

có đồ thị như hình vẽ. Hàm số đồng biến trong khoảng nào

dưới đây?

 

0;1

. B.

 

1;1

 

0;2

. D.

 

1;2

Câu 22. Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên dưới:

Hàm số

 

3g x f x 

đồng biến trên khoảng nào trong các khoảng sau?

 

; 1 . 

 

1;2 .

 

2;3 .

 

4;7 .

Câu 23. Cho hàm số bậc ba

 

y f x

, hàm số

 

y f x





có đồ thị như hình vẽ. Hỏi hàm số

 

1g x f x 

nghịch biến trên khoảng nào dưới đây?

 

1, 

. B.

 

1,0

 

1,2

. D.

 

,1

Câu 24. Có bao nhiêu giá trị nguyên của tham số

nhỏ hơn 10 để hàm số

4 3 2

3 4 12y x x x m   

nghịch biến trến khoảng

 

; 1 

. B.

. C.

. D.

Câu 25. Cho hàm số

 

y f x

. Đồ thị hàm số

 

y f x





như hình vẽ sau:

 

y f x



Strong Team Toán VD – VDC Trang 7/50

Hàm số

 

4 2g x f x

 

nghịch biến trên khoảng nào sau đây?

1 3

;

2 2

 

 

 

. B.

 

; 2



 

. C.

 

 

 

. D.

3 5

;

2 2

 

 

 

Câu 26. Cho hàm số

 

y f x



có đạo hàm

   

 

1 2f x x x x



  

, với

 

. Số giá trị nguyên

của tham số

để hàm số

 

3 2

g x f x x m

  

có

điểm cực trị là

. B.

. C.

. D.

Câu 27. Cho hàm số

 

y f x



xác định trên R và hàm số

 

'y f x



có đồ thị như hình bên dưới và

 

' 0

f x



với mọi

   

; 3, 4 9;x

    

. Đặt

   

5g x f x mx  

. Có bao nhiêu giá trị

dương của tham số

để hàm số

 

g x

có đúng hai điểm cực trị?

A. 4. B. 7. C. 8. D. 9.

Câu 28. Cho hàm số đa thức bậc bốn

 



y f x

, biết hàm số có ba điểm cực trị

3, 3, 5   

x x x

. Có

tất cả bao nhiêu giá trị nguyên của tham số

sao cho hàm số

 

3 2

3

 

x x

g x f e m

có đúng

điểm cực trị

Câu 29. Cho hàm số

)(xfy



có đạo hàm

 

  





xxxxxf

 

. Tính tổng tất cả các giá

trị nguyên của tham số m để hàm số

 

mxfxg 

có 3 cực trị.

A. 0. B. 6. C. 3. D. 2.

Câu 30. Cho hàm số

 

y f x



liên tục trên



và có đồ thị như hình vẽ .

Strong Team Toán VD – VDC Trang 8/50

Xét hàm số

 

2 1 .g x f x x m   

Tìm

để

 

 

0;1

max 10.

g x

 



. B.

 

. C.

 

. D.



Câu 31. Cho hàm số

 

f x

có đạo hàm trên



là

    

1 3

f x x x



  

. Có bao nhiêu giá trị nguyên

của tham số

thuộc đoạn

 

10;20



để hàm số

 

y f x x m

  

đồng biến trên khoảng

 

0;2

. B.

. C.

. D.

Câu 32. Cho các hàm số

 

f x x x m  

và

 

    

2 3

2 2 2

2018 2019 2020

g x x x x    . Có bao

nhiêu giá trị nguyên của tham số

 

2020;2020

m 

để hàm số

 

g f x

đồng biến trên

 



2005

. B.

2037

. C.

4016

. D.

4041

Câu 33. Cho hàm số

 

y f x

có đạo hàm

   

 

1 2 1

f x x x x mx



   

với mọi

 

Có bao nhiêu số

nguyên âm

để hàm số

   

2 1

g x f x

 

đồng biến trên khoảng

 

3;5

Câu 34. Cho hàm số

 

f x

xác định và liên tục trên

. Hàm số

 

y f x





liên tục trên



và có đồ thị

như hình vẽ.

Xét hàm số

     

2 2 2020

g x f x m m x    

, với

là tham số thực. Gọi

là tập hợp

các giá trị nguyên dương của

để hàm số

 



y g x

nghịch biến trên khoảng

 

3;4

. Hỏi số

phần tử của

bằng bao nhiêu?

. B.

. C.

. D. Vô số.

Câu 35. Cho hàm số

 

f x

liên tục trên



và có đạo hàm

   

 

2 2

2 6

f x x x x x m



   

với mọi

 

. Có bao nhiêu số nguyên

thuộc đoạn

 

2020;2020



để hàm số

   

g x f x 

nghịch biến trên khoảng

 

; 1 

2016

. B.

2014

. C.

2012

. D.

2010

Câu 36. Cho hàm số

( )y f x

có đồ thị

( )f x



như hình vẽ. Có bao nhiêu giá trị nguyên

 

2020;2020

m 

để hàm số

   

 

2 3 ln 1 2g x f x x mx

    

đồng biến trên

 

 

 

Strong Team Toán VD – VDC Trang 9/50

2020

. B.

2019

2021

. D.

2018

Câu 37. Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ.

Hàm số

 

2 3 2

4 3 6 2020

g x f x x x x x     

đồng biến trên khoảng nào sau đây?

 



 

 

. B.

 

2;0

 

1;

. D.

 

0;1

Câu 38. Cho hàm số

 

y f x

xác định trên



và có bảng xét dấu đạo hàm như sau:

Biết

 

2,f x x  

. Xét hàm số

   

 

3 2

3 2 3 2020g x f f x x x    

. Khẳng định nào

sau đây đúng?

A. Hàm số

 

g x

đồng biến trên khoảng

 

2; 1 

B. Hàm số

 

g x

nghịch biến trên khoảng

 

0;1

C. Hàm số

 

g x

đồng biến trên khoảng

 

3;4

Hàm số

 

g x

nghịch biến trên khoảng

 

2;3

Câu 39. Cho hàm số

( )y f x

xác định trên



. Hàm số

 

( ) ' 2 3 2y g x f x   

có đồ thị là một

parabol với tọa độ đỉnh

 

2; 1I 

và đi qua điểm

 

1;2A

. Hỏi hàm số

( )y f x

nghịch biến

trên khoảng nào dưới đây?

 

5;9

. B.

 

1;2

. C.

 

;9

. D.

 

1;3

Câu 40. Cho hàm số

 

y f x

có đạo hàm cấp

liên tục trên



và thỏa mãn

       

2 3

. 1 4f x f x x x x



  

với mọi

x 

và

       

2 .g x f x f x f x

 

 

 

 

. Hàm số

 

2h x g x x 

đồng biến trên khoảng nào dưới đây?

-2 -1

Strong Team Toán VD – VDC Trang 10/50

 

;1

. B.

 

2;

. C.

 

0;1

. D.

 

1; 2

Câu 41. Cho hàm số

( )y f x

liên tục trên



. Biết rằng hàm số

'( )y f x

có đồ thị như hình vẽ. Hàm

số

( 5)y f x 

nghịch biến trên khoảng nào sau đây ?

( 1;0)

. B.

(1;2)

. C.

( 1;1)

. D.

(0;1)

Câu 42. Cho hàm số

( )y f x

. Hàm số

'( )y f x

có đồ thị như hình vẽ bên.

Hàm số

( )y f x

đồng biến trên khoảng

1 1

;

2 2

 















 

 

0;2

 















 

 

2; 1 

Câu 43. Cho hàm số

 

.y f x

Hàm số

 

y f x





có đồ thị như hình bên.

Hàm số

 

3 2y f x 

nghịch biến trên khoảng

 

1; 

 

0;2

 

; 1 

 

1;3

Câu 44. Cho hàmsố

( )y f x

có đạo hàm trên



. Đường cong trong hình vẽ dưới là đồ thị của hàm số

'( )y f x

. Xét hàm số

( ) (3 )g x f x 

Mệnh đề nào dưới đây là đúng?

A. Hàm số

( )g x

đồng biến trên

( ;1)

B. Hàm số

( )g x

đồng biến trên

(0;3)

C. Hàm số

( )g x

nghịch biến trên

( 1; ) 

-4 -3 -2 -1 1 2 3 4 5 6 7

O-1

'( )y f x

1

Strong Team Toán VD – VDC Trang 11/50

D. Hàm số

( )g x

nghịch biến trên

( ; 2) 

và

(0;2)

Câu 45. Cho hàm số

 

y f x



. Hàm số

 

y f x





có đồ thị như hình vẽ. Hàm số

 

y f e

 

nghịch

biến trên khoảng nào sau đây?

-4

 



. B.

 



. C.

 

1;3



. D.

 

2;1



Câu 46. Cho hàm số

 

f x

có đạo hàm liên tục trên



và có đồ thị của hàm

 





y f x

như hình vẽ.

Xét hàm số

 

( ) 2 

g x f x

. Mệnh đề nào dưới đây sai?

A. Hàm số

( )g x

đồng biến trên

 

2; .

B. Hàm số

( )g x

nghịch biến trên

 

0;2 .

C. Hàm số

( )g x

nghịch biến trên

 

1;0 .



D. Hàm số

( )g x

nghịch biến trên

 

; 2 . 

Câu 47. Cho hàm số

 

y f x



. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

y f x 

đồng

biến trên khoảng:

 

1;3

. B.

 



. C.

 

2;1



. D.

 



Câu 48. Cho hàm số

 

y f x



có đạo hàm là hàm số

 

f x



trên



. Biết rằng hàm số

 

2 2

y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

f x

nghịch biến trên khoảng nào?

1

4

2

Strong Team Toán VD – VDC Trang 12/50

 

;2

. B.

 

1;1

. C.

3 5

;

2 2

 

 

 

. D.

 

2;

Câu 49. Cho hàm số

 

y f x

có đạo hàm là hàm số

 

f x



trên



. Biết rằng hàm số

 

2 2y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

f x

đồng biến trên khoảng nào?

   

;3 , 5; 

. B.

   

; 1 , 1;  

. C.

 

1;1

. D.

 

3;5

Câu 50. Cho hàm số

 

y f x

có đạo hàm là hàm số

 

f x



trên



. Biết rằng hàm số

 

2 2y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

f x

nghịch biến trên khoảng nào?

   

3; 1 , 1;3 

. B.

   

1;1 , 3;5

. C.

   

; 2 , 0;2 

. D.

   

5; 3 , 1;1  

-------------------- HẾT --------------------

Strong Team Toán VD – VDC Trang 13/50

BẢNG ĐÁP ÁN

1.A

2.D

3.B

4.B

5.C

6.A

7.D

8.A

9.B

10.D

11.C

12.C

13.D

14.C

15.C

16.D

17.A

18.C

19.A

20.C

21.D

22.B

23.B

24.D

25.A

26.C

27.C

28.D

29.C

30.C

31.A

32.B

33.A

34.B

35.C

36.B

37.D

38.D

39.A

40.D

41.D

42.C

43.C

44.D

45.B

46.C

47.C

48.B

49.B

50.B

LỜI GIẢI CHI TIẾT

Câu 1. Cho đồ thị hàm số

 

 y f x

như hình vẽ

Hàm số

 

3 

y f x

nghịch biến trên khoảng nào dưới đây?

 

0;1

. B.

 

1;3

. C.

 

; 1 

. D.

 

1;0



Lời giải

Chọn A

Gọi

 

là đồ thị hàm số

   

  y g x f x

Tịnh tiến

 

sang trái 2 đơn vị ta được đồ thị hàm số

   

   y g x f x

Lấy đối xứng đồ thị hàm số

 

 y f x

qua Oy ta được đồ thị hàm số

 



y f x

Strong Team Toán VD – VDC Trang 14/50

Ta có

   

2 2

3 2 . 3

 

    

y f x y x f x

 

0 3 0 3

3 0

3 3

















       





 







 

 



y x x

f x

Bảng xét dấu



Vậy hàm số

 

3 

y f x

nghịch biến trên khoảng

 

0;1

Câu 2. Cho hàm số

 

f x

có bảng xét dấu đạo hàm

 

f x



như sau:

Hàm số

 

2y f x x

 

nghịch biến trên khoảng nào dưới đây?

 

2;1



. B.

 

4; 3 

. C.

 

0;1

. D.

 

2; 1 

Lời giải

Chọn D

Đặt:

 

2y g x f x x

  

;

 

g x f x x



 

 

2 2 . 2x f x x



  

 

g x





 

2 2 . 2 0

x f x x



   

 

2 2 0

2 0

f x x

 









 





 

2 2

2 1

2 3

x x

 





  







 



 



vo ânghieäm

Strong Team Toán VD – VDC Trang 15/50

1 2

 





  



   







 





. (

1 2

x   

là các nghiệm bội chẵn của phương trình:

2 1x x 

Ta có bảng biến thiên:

Dựa vào bảng biến thiên, suy ra hàm số

 

2y f x x

 

nghịch biến trên khoảng

 

2; 1 

Chú ý: Cách xét dấu

 

g x



Chọn giá trị

 

0 1; 1 2

x     

2 0

x x

  

   

0 0 0

g f

 

  

(dựa theo bảng xét dấu

của hàm

 

f x



). Suy ra

 

g x





 

1; 1 2

x     . Sử dụng quy tắc xét dấu đa thức “lẻ

đổi, chẵn không” suy ra dấu của

 

g x



trên các khoảng còn lại.

Câu 3. Cho hàm số

 



y f x

liên tục trên



và hàm số

 

y f x





có đồ thị như hình vẽ.

Hàm số

 

1 2 2020

y g x f x x    

đồng biến trên khoảng nào dưới đây?

 

1;0



. B.

 

0;1

. C.

 

2;3

. D.

 

3;5

Lời giải

Chọn B

Ta có

   

 

2 2 . 1 2

g x x f x x

 

   

Strong Team Toán VD – VDC Trang 16/50

 

2 2 0

1 2 0

g x

f x x

 





 





  





1 2 2

1 2 1

x x







    



   









 



 



 



 



1 3

Bảng biến thiên:

Dựa vào bảng biến thiên hàm số

 

g x

đồng biến trên khoảng

 

; 1 

và

 

1 3;1 và

 

1 3;3 .

Mà

(0;1) (1 3;1) 

nên hàm số

 

1 2 2020y g x f x x    

đồng biến trên

(0;1)

Câu 4. Cho hàm số

 

y f x

có đạo hàm

     

2 3

. 2 5f x x x x



  

. Hàm số

   

10 5g x f x 

đồng biến trên khoảng nào dưới đây?

 

;1

. B.

 

1;2

. C.

 

2;

. D.

 

1;3

Lời giải

Chọn B

Ta có

       



  

     g x x f x f x10 5 . 10 5 5. 10 5

   

10 5 0

0 10 5 0 10 5 2

10 5 5

g x f x x x





  



 

         



 









Bảng xét dấu

( )g x



Vậy hàm số

 

g x

đồng biến trên khoảng

 

1;2

Strong Team Toán VD – VDC Trang 17/50

Câu 5. Cho hàm số

( )y f x

có đạo hàm

( ) ( 1) ( 2)



  

f x x x x

với mọi giá trị thực của

. Xét hàm

số

( )

 



 



 

g x f

. Trong các khẳng định sau khẳng định nào đúng?

A. Hàm số đồng biến trên khoảng

(0;1)

. B. Hàm số nghịch biến trên khoảng

(0;4)

C. Hàm số đạt cực đại tại

0

. D. Hàm số đạt giá trị nhỏ nhất tại

1x

Lời giải

Chọn C

Ta có:

 

2 2

5 5

4 4

x x

g x f

x x



   

 



   

 

   

 

2 2 2

20 5 5 5 5

1 2 ,

4 4 4

x x x x

x x x



    

    

    

  

    





 

20 5

( ) 0

g x













 















 





















Bảng biến thiên của hàm số

( )y g x

Vậy hàm số

( )y g x

đạt cực đại tại

0

x .

Câu 6. Cho hàm số

 

f x

. Hàm số

 

y f x





có đồ thị như hình bên.

Strong Team Toán VD – VDC Trang 18/50

Hỏi hàm số

 

2 2

2 6 3g x f x x x x   

đồng biến trên khoảng nào dưới đây?

 



 

 

. B.

 

 

 

. C.

 

0;1

. D.

 



Lời giải

Chọn A

Ta có:

 

2 2

2 6 3g x f x x x x   

   

 

4 1 2 12 3g x x f x x x

 

     

 

4 1 2 3

x f x x

 



   

 

 

4 1 0

2 3

g x

f x x

 





 





  





 







  





 



 



 



2 1 voânghieäm

2 1

2 0

2 2 nghieäm keùp

x x

 











 































1 17

nghieäm keùp

1 17

nghieäm keùp

Ta có :

   

   ' 2 9 '(10) 3

g f

dựa vào đồ thì

 

'f x

ta thấy

   

    ' 10 3 ' 10 3 0

f f

 

  ' 2 0

Ta có bảng xét dấu như sau:

Strong Team Toán VD – VDC Trang 19/50

Xét dấu

 

g x



ta được

 

1 1 1 1 17 1 17

0, ;0 ; 1; ;

2 4 2 4 4

g x x

   

 

   



       

   

   

Suy ra

 

g x

đồng biến trên các khoảng

 



 

 

và

1 1

;

4 2

 

 

 

và

1 17

 



 

 

và

1 17

;

 





 

 

Mà

1 1

;0 ;0

4 2

   

  

   

   

nên hàm số

 

2 2

2 6 3g x f x x x x   

đồng biến trên khoảng

 



 

 

Câu 7. Cho hàm số

 

y f x

có đạo hàm

     

2 2

' (3 ) 10 3 2f x x x x   

với mọi

.x  

Hàm số

   

2 3

3 ( 1)

g x f x x   

đồng biến trên khoảng nào trong các khoảng sau?

 

;0 .

 

0;1 .

 

1; .

; .

 

 

 

 

Lời giải

Chọn D

Ta có

   

2 2

' ' 3 ( 1)g x f x x x    

Theo giả thiết

     

2 2

' (3 ) 10 3 2f x x x x   

nên

     

2 2

' 3 3 1 1f x x x x   

Từ đó suy ra

     

2 2

' 3 1 1 ( 1)g x x x x x x     

2 2 2 2 2

( 1) (3 1) ( 1) ( 1) ( 8 4 )

 

         

 

x x x x x x x x

2 2

( 1) ( 8 4)   x x x

Khi đó

 









  



 





0( )

' 0 1( )

x nghiÖm kÐp

g x x nghiÖm kÐp

Bảng biến thiên

Khi đó hàm số đồng biến trên

; .

 

 

 

 

Strong Team Toán VD – VDC Trang 20/50

Câu 8. Cho hàm số

 

f x

có bảng biến thiên như sau

Hàm số

 

3 2

y f x f x

 

nghịch biến trên khoảng nào dưới đây?

 

2;3

. B.

 

1;2

. C.

 

3;4

. D.

 

; 1 

Lời giải

Chọn A

Ta có

 

     

3 . 6 .

y f x f x f x f x

  

 

     

3 . 2

y f x f x f x

 

 

 

 

 

0 0

f x

y f x

f x











  







 

f x













 











;

 

x x

f x

 



 







;

 

2 1

1;2

x x x

x x

f x

x x

  



 



 



 







+ Bảng xét dấu của



Từ bảng xét dấu suy ra hàm số

 

3 2

y f x f x

 

nghịch biến trên khoảng

 

2;3

Câu 9. Cho hàm số

 

y f x



, hàm số

   

3 2

, ,f x x ax bx c a b c



    



có đồ thị như hình vẽ

Strong Team Toán VD – VDC Trang 21/50

Hàm số

   

 

g x f f x





nghịch biến trên khoảng nào dưới đây?

 



. B.

 

; 2 

. C.

 

1;0



. D.

3 3

;

3 3

 



 

 

Lời giải

Chọn B

Vì các điểm

     

1;0 , 0;0 , 1;0



thuộc đồ thị hàm số

 

y f x





nên ta có hệ:

   

3 2

1 0 0

0 1 '' 3 1

1 0 0

a b c a

c b f x x x f x x

a b c c

     

 

 



         

 

 

    

 

Ta có:

   

 

   

 

. ''g x f f x g x f f x f x

   

  

Xét

     

 

  

3 2

0 ' . 0 3 1 0

3 1 0

x x

g x g x f f x f x f x x x

x x



 



 



    

        



  



 



1 1

2 2

( 1,325 )

( 1,325)

x x x





 







  



  



 





Bảng biến thiên

Dựa vào bảng biến thiên ta có

 

g x

nghịch biến trên

 

; 2 

Strong Team Toán VD – VDC Trang 22/50

Câu 10. Cho hàm số

 

y f x



liên tục có đạo hàm trên



. Biết hàm số

 

'f x

có đồ thị cho như hình

vẽ. Có bao nhiêu giá trị nguyên của

thuộc

 

2019;2019



để hàm só

 

2019 2

g x f mx

  

đồng biến trên

 

0;1

2028

. B.

2019

. C.

2011

. D.

2020

Lời giải

Chọn D

Ta có

 

' 2019 ln 2019. ' 2019

x x

g x f m 

Ta lại có hàm số

2019

y 

đồng biến trên

 

0;1

Với

 

0;1

x 

thì

 

2019 1;2019



mà hàm

 

'y f x



đồng biến trên

 



nên hàm

 

' 2019

y f

đồng biến trên

 

0;1

Mà

 

 

2019 1; ' 2019 0 0;1

x x

f x   

nên hàm

 

2019 ln 2019. ' 2019

x x

h x f

đồng biến

trên

 

0;1

Hay

   

 

0 0, 0;1

h x h x   

Do vậy hàm số

 

g x

đồng biến trên đoạn

 

0;1

 

 

' 0, 0;1

g x x   

 

 

2019 ln 2019. ' 2019 , 0;1

x x

m f x   

 

   

0;1

min 0 0

m h x h



   

Vì

nguyên và

 

2019;2019m

  

có

2020

giá trị

thỏa mãn yêu cầu bài toán.

Câu 11. Cho hàm số

 

y f x



có đạo hàm trên



và có đồ thị hàm

 

f x



như hình vẽ dưới đây. Hàm

số

 

g x f x x 

đồng biến trên khoảng nào?

 

 

 

. B.

 

1; 2

. C.

 



 

 

. D.

 

; 1 

Strong Team Toán VD – VDC Trang 23/50

Lời giải

Chọn C

 

g x f x x 

   

 

2 1g x x f x x

 

   

 

2 1 0

0 0 1

g x x x x

f x x

x x



















 







      



 

 





 

 











Từ đồ thị

 

f x



ta có

 

2 2

0 2

f x x x x







     



 



Xét dấu

 

g x



Từ bảng xét dấu ta có hàm số

 

g x

đồng biến trên khoảng

 



 

 

Câu 12. Cho hàm số

 

y f x

có đạo hàm trên



. Biết hàm số

 

y f x





liên tục trên



và có đồ thị

như hình vẽ. Hàm số





1y f x 

đồng biến trong khoảng nào dưới đây?

   

; 3 , 0; 3 

. B.

   

; 3 , 3;  

Strong Team Toán VD – VDC Trang 24/50

   

3;0 , 3; 

. D.

 

; 3 , 0;  

Lời giải

Chọn C

Xét hàm số





1y f x 





y f x

 

  







1 0

f x









 



 





1 1

1 0

1 1

1 2







  



  



 



 



1 1

1 2







  



 





1 1

1 4







  



 









  







Bảng biến thiên

Vậy hàm số





1y f x 

đồng biến trên các khoảng

   

3;0 , 3; 

Câu 13. Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

y f x x 

nghịch biến trên khoảng nào dưới đây.

;

 

 

 

 

. B.

;

 

 

 

 

. C.

;

 



 

 

. D.

;

 



 

 

Lời giải

Chọn D

Đặt

 

y g x f x x  

 

   

 

2 2 2

. 1 2g x f x x x x x f x x



  

      

Cho

 

0g x





 

1 2 0

f x x

 









 





 

1 2 0

1 ptvn

2 ptvn

x x



 



  



 



x 

Strong Team Toán VD – VDC Trang 25/50

Ta có

 

1 1

' 0 0

x x x

f x f x x

x x



  



     





 



( Luôn đúng với mọi



)

Vậy

 

' 0 1 2 0

g x x x

     

Hay hàm số

 

g x f x x

 

nghịch biến trên khoảng

;

 



 

 

Câu 14. Cho hàm số

 

y f x



có đạo hàm trên



. Đường cong trong hình vẽ bên là đồ thị của hàm số

 

y f x





(

 

y f x





liên tục trên



). Xét hàm số

 

g x f x

 

. Mệnh đề nào dưới đây

sai?

A. Hàm số

 

g x

đồng biến trên

 

1;0



. B. Hàm số

 

g x

nghịch biến trên

 

; 1 

C. Hàm số

 

g x

nghịch biến trên

 

1; 2

. D. Hàm số

 

g x

đồng biến trên

 



Lời giải

Chọn C

 

g x f x



 

   

2 2

3 3

x f x



  

 

2 3

xf x



 

Ta có

 

f x





  

nên

f '(x

 3)  0

3 2

   

 

1 1x   

Ta có bảng xét dấu:



2

1



f '(x

 3)

- | -

g '(x)

Từ bảng xét dấu ta thấy đáp án C đúng

Câu 15. Cho hàm số

 

y f x



có đồ thị nằm trên trục hoành và có đạo hàm trên



, bảng xét dấu của

biểu thức

 

f x



như bảng dưới đây.

Hàm số

 

2 1

f x x

y g x

f x x



 

 

nghịch biến trên khoảng nào dưới đây?

2

1

Strong Team Toán VD – VDC Trang 26/50

 

;1

. B.

 



 

 

. C.

 

1;3

. D.

 



Lời giải

Chọn C

 

   

 

2 2 2

2 2

2 . 2 2 2 . 2

2 1 2 1

x x f x x x f x x

g x

f x x f x x



 

   



 

   

 

2 2 0

2 2

0 1

2 0

2 1

2 3

x x

g x x

f x x

x x









 





  



     





 

  











 



Ta có bảng xét dấu của

 

g x



Dựa vào bảng xét dấu ta có hàm số

 

y g x



nghịch biến trên các khoảng

 

; 1 

và

 

1;3

Câu 16. Cho hàm số

 

f x

có bảng biến thiên như sau:

Hàm số

 

3 2

y f x f x

 

nghịch biến trên khoảng nào dưới đây?

 

1; 2

. B.

 

3 ; 4

. C.

 

; 1



. D.

 

2 ; 3

Lời giải

Chọn D

Ta có

 

     

3. . 6. .

y f x f x f x f x

  

 

     

= 3 . . 2

f x f x f x





 

 

   

1 1

2 3 4 1 2 3 4

0 ,4 | 1

0 2 , ,3, | 1 2;4

' 0 1,2,3,4

f x x x x

y f x x x x x x x x x

f x x

   







         



  



Strong Team Toán VD – VDC Trang 27/50

Lập bảng xét dấu ta có

Do đó ta có hàm số nghịch biến trên khoảng

 

2 ; 3

Câu 17. Cho hàm số

 

y f x

đạo hàm liên tục trên



có đồ thị hàm số

 

f x



như hình vẽ

Hỏi hàm số

 

2y f x x 

đồng biến trên khoảng nào sau đây?

 

1;0

. B.

 

0;1

. C.

 

1;3

. D.

 

2;

Lời giải

Chọn A

Có

 

2 2 2y x f x x

 

  

Do đó





 

2 0

f x x











 





2 2

2 0

2 3

x x







  







 



  













 



 







Ta có bảng xét dấu đạo hàm như sau

Dựa vào bảng xét dấu đạo hàm, hàm số

 

2y f x x 

đồng biến trên các khoảng

     

1;0 , 1;2 , 3; 

Câu 18. Cho hàm số

 

f x

có đạo hàm, liên tục trên



, có đồ thị như hình vẽ

Strong Team Toán VD – VDC Trang 28/50

Hỏi hàm số

 

y f x

 

 

nghịch biến trên khoảng nào sau đây?

 

1;1

. B.

 

 

 

. C.

 

 

 

. D.

 

2; 1 

Lời giải

Chọn C

Có

   

2y f x f x

 



. Do đó





 

f x

















 









 







 



Ta có bảng xét dấu đạo hàm như sau

Dựa vào bảng xét dấu đạo hàm, hàm số

 

y f x

 

 

nghịch biến trên các khoảng

   

; 2 , 1;0 , ;4

 

  

 

 

Câu 19. Cho hàm số

 

y f x

có bảng biến thiên như sau

Có bao nhiêu số nguyên

2019m 

để hàm số

 

2g x f x x m  

đồng biến trên khoảng

 

1;

A. 2016. B. 2015. C. 2017. D. 2018.

Lời giải

Chọn A

Strong Team Toán VD – VDC Trang 29/50

Ta có

 

   

 

2 2 2

2 2 2 1 2

g x x x m f x x m x f x x m



  

        

Hàm số

 

y g x

đồng biến trên khoảng

 



khi và chỉ khi

   

0, 1;g x x



   

và

 

g x





tại hữu hạn điểm

 

2 1 2 0, 1;x f x x m x



       

 

2 0, 1;f x x m x



      

 

2 2, 1;

2 0, 1;

x x m x



     







     





Xét hàm số

y x x m  

, ta có bảng biến thiên

Dựa vào bảng biến thiên ta có

TH1:

 

2 2, 1; 1 2 3

x x m x m m

          

TH2:

 

2 0, 1;x x m x

     

: Không có giá trị

thỏa mãn.

Vậy có 2016 số nguyên

2019



thỏa mãn yêu cầu bài toán.

Câu 20. Cho hàm số

( )y f x

có bảng biến thiên như sau:

Hàm số

 

( ) (3 )g x f x

 

nghịch biến trên khoảng nào trong các khoảng sau?

( 2;5)

. B.

(1;2)

. C.

(2;5)

. D.

(5; )

Lời giải

Chọn C

Từ bảng biến thiên suy ra

( ) 0, (3 ) 0,f x x f x x

        

Ta có

'( ) 2 '(3 ). (3 )g x f x f x   

Xét

 

     

2 3 1 2 5

0 2 3 . 3 0 3 0

3 2 1

x x

g x f x f x f x

x x

 

 

 

     

  

          

  

Suy ra hàm số

 

g x

nghịch biến trên các khoảng

( ;1)

và

(2;5)

Strong Team Toán VD – VDC Trang 30/50

Câu 21. Cho hàm số

 

y f x

có đồ thị như hình vẽ. Hàm số đồng biến trong khoảng nào

dưới đây ?

 

0;1

. B.

 

1;1

. C.

 

0;2

. D.

 

1; 2

Lời giải

Chọn D

Thực hiện liên hoàn biến đổi đồ thị

 

y f x

thành đồ thị

 

y f x

, sau đó biến đổi

đồ thị

 

y f x

thành đồ thị

 

y f x

Dựa vào đồ thị hàm số

 

y f x

ta suy ra hàm số đồng biến trên khoảng

 

1; 2

Câu 22. Cho hàm số

 

.y f x

Đồ thị hàm số

 

y f x





như hình bên dưới

Hàm số

 

3g x f x 

đồng biến trên khoảng nào trong các khoảng sau ?

 

; 1 . 

 

1;2 .

 

2;3 .

 

4;7 .

Lời giải

 

y f x



Strong Team Toán VD – VDC Trang 31/50

Chọn B

Dựa vào đồ thị, suy ra

 

1 1

f x

  





 







và

 

0 .

1 4

f x

 





 



 



Với



khi đó

   

3g x f x

  

   

3 0

g x f x

 

  

1 3 1

3 4

   







 



2 4

 











Do đó hàm số

 

g x

đồng biến trên các khoảng

 

3;4 ,

 

7; .

Với



khi đó

         

3 3 0 3 0

g x f x g x f x f x

  

         

 

3 1

1 3 4

1 2

x loai



  



 



  

  



. Do đó hàm số

 

g x

đồng biến trên khoảng

 

1;2 .



Câu 23. Cho hàm số bậc ba

 

y f x



, hàm số

 

y f x





có đồ thị như hình vẽ. Hỏi hàm số

 

g x f x

 

nghịch biến trên khoảng nào dưới đây?

 



. B.

 

1,0



. C.

 

1,2



. D.

 

,1

Lời giải

Chọn B

Ta có:

 

g x f x

 

 

Xét

 

1 ( )

1 0

0 1 0

1 0

1 2

x L

g x f x

f x









  

  

 

      





 















 









Ta có bảng biến thiên:

Strong Team Toán VD – VDC Trang 32/50

Từ bảng biến thiên thì ta có

 

g x f x

 

nghịch biến trên khoảng

 

1,1



và đồng biến trên

khoảng

   

, 1 1,

   

Câu 24. Có bao nhiêu giá trị nguyên của tham số

nhỏ hơn 10 để hàm số

4 3 2

3 4 12

y x x x m   

nghịch biến trến khoảng

 

; 1 

. B.

. C.

. D.

Lời giải

Chọn D

Xét hàm số

   

4 3 2 3 2

3 4 12 12 12 24f x x x x m f x x x x



       

 

f x x



 





  







BBT:

Để hàm số

 

y f x

nghịch biến trên

 

; 1 5 0 5

m m

      

Do yêu cầu

là số nguyên nhỏ hơn

nên ta có

 

5;6;7;8;9



Vậy có 5 giá trị m thỏa yêu cầu..

Câu 25. Cho hàm số

 

y f x



. Đồ thị hàm số

 

y f x





như hình vẽ sau:

Strong Team Toán VD – VDC Trang 33/50

Hàm số

 

4 2g x f x

 

nghịch biến trên khoảng nào sau đây?

1 3

;

2 2

 

 

 

. B.

 

; 2



 

. C.

 

 

 

. D.

3 5

;

2 2

 

 

 

Lời giải

Chọn A

Trường hợp 1:



. Khi đó

   

4 2g x f x

 

Ta có

   

2 4 2g x f x

 

  

   

4 2 2

4 2 0

1 3

1 4 2 3

2 2

fg x x





  







    





  







So điều kiện



ta được

 

g x

nghịch biến trên

1 3

;

2 2

 

 

 

Trường hợp 2:



Khi đó

   

2 4

g x f x

 

Ta có

   

2 2 4

g x f x

 

 

   

2 2 4 1

2 4 00

2 4 3 7

f x

g x



 



   





    



 















So điều kiện



ta được

 

g x

nghịch biến trên

; ;

;







  



  

   

Câu 26. Cho hàm số

 

y f x



có đạo hàm

   

 

1 2f x x x x



  

, với

 

. Số giá trị nguyên

của tham số

để hàm số

 

3 2

g x f x x m

  

có

điểm cực trị là

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

 

   

2 3 2

3 6 . 3

g x x x f x x m

 

   

Strong Team Toán VD – VDC Trang 34/50

 

3 2

3 6 0

3 1

0 3 1

3 0

3 2

x x

x x m

g x x x m

x x m







 







  





     



  



  



  





  



Vì khi đi qua các nghiệm của phương trình

3 2

3 1

x x m

  

(nếu có) dấu của

 

3 2

f x x m



 

không đổi nên dấu của

 

g x



chỉ phụ thuộc các nghiệm của hai phương trình còn lại.

Vậy hàm số

 

y g x



có 8 điểm cực trị khi và chỉ khi mỗi phương trình

3 2

3 0

x x m

  

và

3 2

x x m

  

phải có ba nghiệm phân biệt (khác

và khác

Xét hàm số

 

3 2

3h x x x

  

, ta có

 

3 6h x x x



  

;

 

h x







 







Bảng biến thiên của hàm số

 

y h x



Dựa vào bảng biến thiên, ta thấy điều kiện để mỗi phương trình

3 2

x x m  

và

3 2

x x m

   

phải có ba nghiệm phân biệt (khác

và khác

) là

0 2 4 2 4

m m m

      

Vậy chỉ có một giá trị nguyên của

thỏa mãn là



Câu 27. Cho hàm số

 

y f x



xác định trên R và hàm số

 

'y f x



có đồ thị như hình bên dưới và

 

' 0

f x



với mọi

   

; 3, 4 9;x

    

. Đặt

   

5g x f x mx  

. Có bao nhiêu giá trị

dương của tham số

để hàm số

 

g x

có đúng hai điểm cực trị?

A. 4. B. 7. C. 8. D. 9.

Lời giải

Chọn C

















Strong Team Toán VD – VDC Trang 35/50

Ta có

   

g x f x m

 

 

;

   

0 0

g x f x m

 

   

 

f x m



 

. Để hàm số

 

y g x



có

đúng hai điểm cực trị khi và chỉ khi phương trình

 

g x





có hai nghiệm bội lẻ phân biệt

10 13









 



. Khi đó

 

1,2,3,4,5,10,11,12

m

. Vậy có

giá trị của

thỏa mãn yêu cầu đề

bài.

Câu 28. Cho hàm số đa thức bậc bốn

 



y f x

, biết hàm số có ba điểm cực trị

3, 3, 5   

x x x

. Có

tất cả bao nhiêu giá trị nguyên của tham số

sao cho hàm số

 

3 2

3

 

x x

g x f e m

có đúng

điểm cực trị

Lời giải

Chọn D

Ta có:

 

3 2 3 2

2 3 3

3 6 .

 



 





x x x x

g x x x e f e m

 

3 2 3 2

2 3 3

0 3 6 . 0

 

 

    

x x x x

g x x x e f e m

3 2









 

   

 







x x

e m

 

3 2

3 1

3 2

5 3

x x

e m









 



  



 



 





Hàm số

 

g x

có

điểm cực trị khi và chỉ khi tổng số nghiệm đơn và bội lẻ, khác

và

2

của

các phương trình

     

1 , 2 , 3

là

Xét hàm số

 

3 2





x x

h x e

có

 

3 2

2 3

3 6





 

x x

h x x x e

Ta có

 





 







 

h x

Bảng biến thiên:

Khi đó có

trường hợp sau:

Trường hợp 1:

Strong Team Toán VD – VDC Trang 36/50

Khi đó:

4 4

3 3 51,6

1 3 4 3 57,6

 

    



 

      

 

m e m e

nguyên nên

 

52;53;54;55;56;57

m

Trường hợp 2:

Khi đó:

4 4

5 5 49,6

1 3 2 3

0 3 1 3 4

 

    

 

         

 

 

    

 

m e m e

m e m e m

m m

Trường hợp 3:

Khi đó:

1 5

3 1

3 0



  



 





 



m e

4 5 49,6



    



    









m e

m m

Vậy có

giá trị nguyên của tham số

thỏa yêu cầu bài toán.

Câu 29. Cho hàm số

)(xfy



có đạo hàm

 

  





xxxxxf

  

. Tính tổng tất cả các giá

trị nguyên của tham số m để hàm số

 

mxfxg 

có 3 cực trị.

Strong Team Toán VD – VDC Trang 37/50

A. 0. B. 6. C. 3. D. 2.

Lời giải

Chọn C

Ta có

     













031

xxxxf

Lại có

 













































3 3

2 1

0.2

mxf

mxfxxg

 

có nghiệm luôn là nghiệm bội chẵn ; các phương trình

 

có nghiệm không chung

nhau và



nên:

Hàm số

 

có 3 cực trị

 

0



 xg

có 3 nghiệm bội lẻ













 m

Vì



 

2;1;0 m

. Vậy tổng các giá trị nguyên bằng 3.

Câu 30. Cho hàm số

 

y f x



liên tục trên



và có đồ thị như hình vẽ .

Xét hàm số

 

2 1 .g x f x x m   

Tìm

để

 

 

0;1

max 10.

g x

 



. B.

 

. C.

 

. D.



Lời giải

Chọn C

Đặt

 

2 1t x x x  

với

 

0;1 .

x 

Ta có

 

 

6 1 0, 0;1 .

t x x x



    

Suy ra hàm số

 

t x

đồng biến nên

   

0;1 1;2 .

x t   

Từ đồ thị hàm số ta có

 

 

 

 

1;2 1;2

max 3 max 3 .f t f t m m

 

    

 

 

Theo yêu cầu bài toán ta cần có:

3 10 13.

m m

     

Câu 31. Cho hàm số

 

f x

có đạo hàm trên



là

    

1 3

f x x x



  

. Có bao nhiêu giá trị nguyên

của tham số

thuộc đoạn

 

10;20



để hàm số

 

y f x x m

  

đồng biến trên khoảng

 

0;2

Strong Team Toán VD – VDC Trang 38/50

. B.

. C.

. D.

Lời giải

Chọn A

Ta có

 

2 2

3 2 3 3

y f x x m x f x x m

  

      

Theo đề bài ta có:

    

1 3

f x x x



  

suy ra

 

f x

 





 







và

 

0 3 1f x x



    

Hàm số đồng biến trên khoảng

 

0;2

khi

 

0, 0;2

y x



  

 

2 3 3 0, 0;2

x f x x m x



      

 

0;2

x 

nên

 

2 3 0, 0;2

x x   

. Do đó, ta có:

 

2 2

3 3 3 3

0, 0;2 3 0

3 1 3 1

x x m m x x

y x f x x m

x x m m x x

 

      

 

        

 

     

 

 

 

 

 

0;2

max 3 3

min 3 1

m x x



  







 



 

  







 

10;20

m 



nên có

giá trị nguyên của

thỏa yêu cầu đề bài.

Câu 32. Cho các hàm số

 

f x x x m  

và

 

    

2 3

2 2 2

2018 2019 2020

g x x x x    . Có bao

nhiêu giá trị nguyên của tham số

 

2020;2020

m 

để hàm số

 

g f x

đồng biến trên

 



2005

. B.

2037

. C.

4016

. D.

4041

Lời giải

Chọn B

Ta có

 

f x x x m  

 

    

2 3

2 2 2 12 10 2

12 10 2 0

2018 2019 2020 ...

g x x x x a x a x a x a        

Suy ra

 

3 4

f x x



 

 

11 9

12 10 2

12 10 ... 2

g x a x a x a x



   

Và

 

   

 

11 9

12 10 2

12 10 ... 2

g f x f x a f x a f x a f x



 



   

 

     

 





10 8

12 10 2

12 10 ... 2f x f x a f x a f x a



   

Dễ thấy

12 10 2 0

; ;...; ; 0

a a a a



và

 

3 4 0

f x x



  

 

Do đó

   

 





10 8

12 10 2

12 10 ... 2 0

f x a f x a f x a



   

 

Strong Team Toán VD – VDC Trang 39/50

Hàm số

 

g f x

đồng biến trên

 



khi

 

g f x



 



 

 



 

f x



 



4 0

x x m

  

 



4m x x  

 







 

max 4 16

m x x



    

Vì

 

2020;2020

m 

và



nên có 2037 giá trị thỏa mãn

Câu 33. Cho hàm số

 

y f x

có đạo hàm

   

 

1 2 1

f x x x x mx



   

với mọi

 

Có bao nhiêu số

nguyên âm

để hàm số

   

2 1

g x f x

 

đồng biến trên khoảng

 

3;5

Lời giải

Chọn A

Ta có:

 

2 2

2 '(2 1) 2(2 1)(2 2) [(2 1) 2 (2 1) 1]

g x f x x x x m x



        

Đặt

2 1t x 

Để hàm số

 

g x

đồng biến trên khoảng

 

3;5

khi và chỉ khi

   

0, 3;5

g x x



  

     

2 2

( 2 1) 0, 7;11 2 1 0, 7;11 2 , 7;11

t t mt t t mt t m t

 

               

Xét hàm số

( )

h t

 



trên

 

7;11

, có

'( )

h t

 



BBT:

Dựa vào BBT ta có

 

 

 

7;11

1 50

2 , 7;11 2 max

m t m h t m

 

       

Vì

{ 3; 2; 1}

m m



     

Câu 34. Cho hàm số

 

f x

xác định và liên tục trên

. Hàm số

 

y f x





liên tục trên



và có đồ thị

như hình vẽ.

Strong Team Toán VD – VDC Trang 40/50

Xét hàm số

     

2 2 2020

g x f x m m x    

, với

là tham số thực. Gọi

là tập hợp

các giá trị nguyên dương của

để hàm số

 



y g x

nghịch biến trên khoảng

 

3;4

. Hỏi số

phần tử của

bằng bao nhiêu?

. B.

. C.

. D. Vô số.

Lời giải

Chọn B

Ta có

     

' ' 2 2

g x f x m m x   

Đặt

     

h x f x x  

. Từ đồ thị hàm số

 

'y f x



và đồ thị hàm số

y x 

trên hình vẽ

suy ra:

   

3 1

0 '

h x f x x

  



    







Ta có

   

3 2 1 2 3 2 1

' 2 0

2 3 2 3

x m m x m

g x h x m

x m x m

       

 

    

 

   

 

Suy ra hàm số

 



y g x

nghịch biến trên các khoảng

 

2 3;2 1

m m

 

và

 

2 3;m

 

Strong Team Toán VD – VDC Trang 41/50

Do đó hàm số

 



y g x

nghịch biến trên khoảng

 

3;4

2 3 3

2 1 4

2 3 3

  





 





 

 











 



Mặt khác, do

nguyên dương nên

   

2;3 2;3

m S  

. Vậy số phần tử của

bằng 2.

Câu 35. Cho hàm số

 

f x

liên tục trên



và có đạo hàm

   

 

2 2

2 6

f x x x x x m



   

với mọi

 

. Có bao nhiêu số nguyên

thuộc đoạn

 

2020;2020



để hàm số

   

g x f x 

nghịch biến trên khoảng

 

; 1 

2016

. B.

2014

. C.

2012

. D.

2010

Lời giải

Chọn C

Ta có:

           

2 2

1 1 1 1 6 1

g x f x x x x x m

 

 

          

 

   

 

1 1 4 5

x x x x m

     

Hàm số

 

g x

nghịch biến trên khoảng

 

; 1 

 

0, 1

g x x



    

 

, (dấu

" "

xảy ra tại hữu hạn điểm).

Với

 

thì

 

1 0

 

và

1 0

 

nên

 

4 5 0, 1

x x m x

      

4 5, 1

m x x x

      

Xét hàm số

4 5

y x x

   

trên khoảng

 

; 1 

, ta có bảng biến thiên:

Từ bảng biến thiên suy ra



Kết hợp với

thuộc đoạn

 

2020;2020



và

nguyên nên

 

9;10;11;...;2020

m

Vậy có

2012

số nguyên

thỏa mãn đề bài.

Câu 36. Cho hàm số

( )y f x

có đồ thị

( )f x



như hình vẽ. Có bao nhiêu giá trị nguyên

 

2020;2020

m 

để hàm số

   

 

2 3 ln 1 2g x f x x mx

    

đồng biến trên

 

 

 

Strong Team Toán VD – VDC Trang 42/50

2020

. B.

2019

. C.

2021

. D.

2018

Lời giải

Chọn B

+ Ta có

   

2 2 3 2

g x f x m

 

   



Hàm số

 

g x

đồng biến trên

 

 

 

khi và chỉ khi

     

0, 1;2 2 3 , ;2

1 2

g x x m f x x

 

 

         

 



 

 

min 2 3

m f x

 



 

 

 



   

 



 

 

+ Đặt

2 3t x 

, khi đó

 

;2 2;1

x t

 

   

 

 

Từ đồ thị hàm

 

f x



suy ra

   

0, 2;1

f t t



   

và

 

f t





khi

 

Tức là

 

2 3 0, ;2

f x x

 



   

 

 

 

min 2 3 0

f x

 



 

 



  

khi

1x 

 

+ Xét hàm số

 

h x

 



trên khoảng

 

 

 

. Ta có

 

h x









và

 

0 1 0 1

h x x x



      

Bảng biến thiên của hàm số

 

h x

trên

 

 

 

như sau:

-2 -1

Strong Team Toán VD – VDC Trang 43/50

Từ bảng biến thiên suy ra

 

h x  

 

min

h x

 



 

 

  

khi

1x 

 

Từ

 

và

 

suy ra

m  

Kết hợp với

m 

 

2020;2020m  

thì

 

2019; 2018;....; 2; 1m    

Vậy có tất cả

2019

giá trị

cần tìm.

Câu 37. Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ.

Hàm số

 

2 3 2

4 3 6 2020g x f x x x x x     

đồng biến trên khoảng nào sau đây ?

 



 

 

. B.

 

2;0

. C.

 

1;

. D.

 

0;1

Lời giải

Chọn D

Ta có

   

 

2 2

2 1 12 6 6g x x f x x x x

 

     

Từ đồ thị hàm số

 

y f x



suy ra

 

0 1 2

f x x



    

. Do đó

 

2 2

1 1 0;

0 2 1

2 2 0

x x x x x

f x x x

x x x x

 

       

 



       

 

    

 

 



Ta có bảng xét dấu

 

g x



Vậy hàm số

 

g x

đồng biến trên khoảng

 



 

 

Strong Team Toán VD – VDC Trang 44/50

Câu 38. Cho hàm số

 

y f x



xác định trên



và có bảng xét dấu đạo hàm như sau:

Biết

 

2,f x x

  

. Xét hàm số

   

 

3 2

3 2 3 2020

g x f f x x x    

. Khẳng định nào

sau đây đúng?

A. Hàm số

 

g x

đồng biến trên khoảng

 

2; 1 

B. Hàm số

 

g x

nghịch biến trên khoảng

 

0;1

C. Hàm số

 

g x

đồng biến trên khoảng

 

3;4

Hàm số

 

g x

nghịch biến trên khoảng

 

2;3

Lời giải

Chọn D

Ta có:

     

 

' 2 ' ' 3 2 3 6g x f x f f x x x    

Vì

 

2,f x x

  

nên

 

3 2 1

f x

  

 

Từ bảng xét dấu

 

'f x

suy ra

 

' 3 2 0,f f x x

   

Từ đó ta có bảng xét dấu sau:

Từ bảng xét dấu trên, loại trừ đáp án suy ra hàm số

 

g x

nghịch biến trên khoảng

 

2;3

Câu 39. Cho hàm số

( )y f x

xác định trên



. Hàm số

 

( ) ' 2 3 2

y g x f x

   

có đồ thị là một

parabol với tọa độ đỉnh

 

2; 1



và đi qua điểm

 

1;2

. Hỏi hàm số

( )y f x

nghịch biến

trên khoảng nào dưới đây?

 

5;9

. B.

 

1; 2

. C.

 



. D.

 

1;3

Lời giải

Chọn A

Xét hàm số

 

( ) ' 2 3 2

g x f x

  

có đồ thị là một Parabol nên có phương trình dạng:

 

( )

y g x ax bx c P

   

Vì

 

có đỉnh

 

2; 1



nên

 

4 4 0

4 2 1 4 2 1

2 1

b a a b

a b c a b c







   

 



 

  

       

 



 



Strong Team Toán VD – VDC Trang 45/50

 

đi qua điểm

 

1;2

nên

 

1 2 2

g a b c

    

Ta có hệ phương trình

4 0 3

4 2 1 12

2 11

a b a

a b c b

a b c c

  

 

 

      

 

 

   

 

nên

 

3 12 11

g x x x

  

Đồ thị của hàm

( )y g x

là

Theo đồ thị ta thấy

'(2 3) 0 '(2 3) 2 2 1 3

f x f x x

        

Đặt

2 3

t x x



   

khi đó

'( ) 0 1 3 5 9

f t t



      

Vậy

( )y f x

nghịch biến trên khoảng

 

5;9

Câu 40. Cho hàm số

 

y f x



có đạo hàm cấp

liên tục trên



và thỏa mãn

       

2 3

. 1 4

f x f x x x x



  

với mọi



và

       

2 .

g x f x f x f x

 

 

 

 

. Hàm số

 

2h x g x x

 

đồng biến trên khoảng nào dưới đây?

 

;1

. B.

 



. C.

 

0;1

. D.

 

1; 2

Lời giải

Chọn D

Ta có

                 

2 2 . 2 . 2 . ;g x f x f x f x f x f x f x f x f x

      

    

Khi đó

 

    

2 3

2 2 2 2

2 2 2 2 2 2 2 2 1 2 4

h x x g x x x x x x x x x



          

 

1 2

h x













 







 





Ta có bảng xét dấu của

 

h x



5 5

Strong Team Toán VD – VDC Trang 46/50

Suy ra hàm số

 

2h x g x x 

đồng biến trên khoảng

 

1; 2

Câu 41. Cho hàm số

( )y f x

liên tục trên



. Biết rằng hàm số

'( )y f x

có đồ thị như hình vẽ. Hàm

số

( 5)y f x 

nghịch biến trên khoảng nào sau đây ?

( 1;0)

. B.

(1;2)

. C.

( 1;1)

. D.

(0;1)

Lời giải

Chọn D.

+ Đặt

2 2

( ) ( 5) ( ), 5g x f x f u u x    

2 2

'( ) ( 5)' '( ) 2 '( 5)g x x f u xf x   

+ Hàm số

( )y g x

nghịch biến khi

'( ) 0g x 

và dấu bằng xảy ra tại hữu hạn điểm

( )

'( 5) 0

2 '( 5) 0

( )

'( 5) 0

f x

xf x

f x











 





   













 





Giải (I): Từ đồ thị hàm số

'( )y f x

ta có

( )

5 2

2 1

4 5 1

1 2 1

x x

 





  





















 





  

 









   



 





     

     



















Strong Team Toán VD – VDC Trang 47/50

Xét (II): Từ đồ thị

'( )y f x

ta có

2 2

5 4 1 1 1

( )

4 2 2

1 5 2 7 2 2 7

7 7 7

0 1

1 1

2 7

7 2 2 7

x x x

x x









        











     





            







    









 



  





  

















  





      







Vậy hàm số đồng biến trên mỗi khoảng:

 

   

 

; 7 ; 2; 1 ; 0;1 ; 2; 7   

. Chọn đáp án D.

Câu 42. Cho hàm số

( )y f x

. Hàm số

'( )y f x

có đồ thị như hình vẽ bên.

Hàm số

( )y f x

đồng biến trên khoảng

1 1

;

2 2

 















 

 

0;2

 















 

 

2; 1 

Lời giải

Chọn C

Xét hàm '( ) ( 1)( 1)( 4)f x x x x     . Đặt

 

( )g x f x

Có

2 2 2 2

'( ) 2 '( ) 2 ( 1)( 1)( 4)g x xf x x x x x     

. Suy ra

'( ) 0 1

g x x







   



 



Xét dấu

'( )g x

Câu 43. Cho hàm số

 

.y f x

Hàm số

 

y f x





có đồ thị như hình bên.

'( )y f x

1

Strong Team Toán VD – VDC Trang 48/50

Hàm số

 

3 2y f x

 

nghịch biến trên khoảng

 

 

 

0;2

 

; 1 

 

1;3

Lời giải

Chọn C

Ta có

   

1 5

2 3 2 2

2. 3 2 ; 0 3 2 0

2 2

3 2 5

y f x y f x



   

 





   

        



 



 



Vậy hàm số

 

3 2y f x

 

nghịch biến trên các khoảng

 

; 1 

và

1 5

; .

2 2

 

 

 

Câu 44. Cho hàmsố

( )y f x

có đạo hàm trên



. Đường cong trong hình vẽ dưới là đồ thị của hàm số

'( )y f x

. Xét hàm số

( ) (3 )g x f x

 

Mệnh đề nào dưới đây là đúng?

A. Hàm số

( )g x

đồng biến trên

( ;1)

B. Hàm số

( )g x

đồng biến trên

(0;3)

C. Hàm số

( )g x

nghịch biến trên

( 1; ) 

D. Hàm số

( )g x

nghịch biến trên

( ; 2) 

và

(0;2)

Lời giải

Chọn D

Ta có

 

' 2 ' 3

g x xf x

  

 

3 1 2

' 3 0

3 3

x x

f x



    



   





 



-4 -3 -2 -1 1 2 3 4 5 6 7

O-1

Strong Team Toán VD – VDC Trang 49/50

Ta có bảng xét dấu:

Hàm số

( )g x

nghịch biến trên

( ; 2) 

và

(0;2)

Câu 45. Cho hàm số

 

y f x



. Hàm số

 

y f x





có đồ thị như hình vẽ. Hàm số

 

y f e

 

nghịch

biến trên khoảng nào sau đây?

-4

 



. B.

 



. C.

 

1;3



. D.

 

2;1



Lời giải

Phân tích

Dựa vào đồ thị hàm

 

y f x





, suy ra nghiệm

 

f x





và dấu của

 

f x



Dùng tính chất hàm hợp xét dấu

 

f e





, suy ra dấu của

 

. 2

x x

e f e





. Từ đó chọn đáp án.

Chọn B

Ta có

 

f x







 







Xét

 

y f e

 

, có

 

. 2

x x

y e f e

 

 

;

 

0 . 2 0

x x

y e f e

 

   

2 0

2 3



 

  



 



Mặt khác,

 

0 . 2 0

x x

y e f e

 

   

2 3 0

e x

    

Do đó hàm số

 

y f e

 

nghịch biến trên

 



Câu 46. Cho hàm số

 

f x

có đạo hàm liên tục trên



và có đồ thị của hàm

 





y f x

như hình vẽ.

Xét hàm số

 

( ) 2 

g x f x

. Mệnh đề nào dưới đây sai?

g'(x)

∞

(3-

)

Strong Team Toán VD – VDC Trang 50/50

A. Hàm số

( )g x

đồng biến trên

 

2; .

B. Hàm số

( )g x

nghịch biến trên

 

0;2 .

C. Hàm số

( )g x

nghịch biến trên

 

1;0 .



D. Hàm số

( )g x

nghịch biến trên

 

; 2 . 

Lời giải

Chọn C

Dựa vào đồ thị hàm số

 

 





 







f x

và

 

0 2



  

f x x

Xét

 

2 

g x f x

có tập xác định



   

' 2 .





g x x f t

với

2 

t x

 

' 0 2 1 1

2 2











        



 

  



g x t x x

t x

Lại có

 

0 2 2







     



 



f t t x

Do đó, ta có bảng xét dấu

 

'g x



2

1



 



g x









Từ bảng xét dấu ta chọn phát biểu sai là C

Câu 47. Cho hàm số

 

y f x



. Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

y f x 

đồng

biến trên khoảng:

 

1;3

. B.

 



. C.

 

2;1



. D.

 



1

4

2

Strong Team Toán VD – VDC Trang 51/50

Lời giải

Chọn C.

Ta có:

 

     

2 2 . 2 2

f x x f x f x



 

      

Hàm số đồng biến khi

 

2 1 3

2 0 2 0

1 2 4 2 1

x x

f x f x

x x

   

 



      

 

     

 

Câu 48. Cho hàm số

 

y f x



có đạo hàm là hàm số

 

f x



trên



. Biết rằng hàm số

 

2 2

y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

f x

nghịch biến trên khoảng nào?

 



. B.

 

1;1



. C.

3 5

;

2 2

 

 

 

. D.

 



Lời giải.

Chọn B

Hàm số

 

2 2

y f x



  

có đồ thị

 

như sau:

Dựa vào đồ thị

 

ta có:

       

2 2 2, 1;3 2 0, 1;3

f x x f x x

 

         

Đặt

* 2x x 

thì

   

* 0, * 1;1



   f x x

Vậy: Hàm số

 

f x

nghịch biến trên khoảng

 

1;1



Cách khác:

Tịnh tiến sang trái hai đơn vị và xuống dưới 2 đơn vị thì từ đồ thị

 

sẽ thành đồ thị của hàm

 





y f x

. Khi đó:

   

0, 1;1

f x x



   

Vậy: Hàm số

 

f x

nghịch biến trên khoảng

 

1;1



Phân tích: Cho biết đồ thị của hàm số

 

f x



sau khi đã tịnh tiến và dựa vào đó để xét sự đồng

biến của hàm số

 

f x

Strong Team Toán VD – VDC Trang 52/50

Câu 49. Cho hàm số

 

y f x

có đạo hàm là hàm số

 

f x



trên



. Biết rằng hàm số

 

2 2y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

f x

đồng biến trên khoảng nào?

   

;3 , 5; 

. B.

   

; 1 , 1;  

. C.

 

1;1

. D.

 

3;5

Lời giải.

Chọn B

Hàm số

 

2 2y f x



  

có đồ thị

 

như sau:

Dựa vào đồ thị

 

ta có:

           

2 2 2, ;1 3; 2 0, ;1 3;f x x f x x

 

              

Đặt

* 2x x 

suy ra:

     

* 0, * ; 1 1;f x x



     

Vậy: Hàm số

 

f x

đồng biến trên khoảng

   

; 1 , 1;  

Câu 50. Cho hàm số

 

y f x

có đạo hàm là hàm số

 

f x



trên



. Biết rằng hàm số

 

2 2y f x



  

có đồ thị như hình vẽ bên dưới. Hàm số

 

f x

nghịch biến trên khoảng nào?

   

3; 1 , 1;3 

. B.

   

1;1 , 3;5

. C.

   

; 2 , 0;2 

. D.

   

5; 3 , 1;1  

Lời giải

Chọn B

Hàm số

 

2 2y f x



  

có đồ thị

 

như sau:

Strong Team Toán VD – VDC Trang 53/50

Dựa vào đồ thị

 

ta có:

           

2 2 2, 3; 1 1;3 2 0, 3; 1 1;3f x x f x x

 

               

Đặt

* 2x x 

suy ra:

     

* 0, * 1;1 3;5f x x



    

Vậy: Hàm số

 

f x

đồng biến trên khoảng

   

1;1 , 3;5

-------------------- HẾT --------------------

Bấm Tải xuống để xem toàn bộ.

| 1/53

| | Tải xuống

Preview text:

BÀI TẬP TRẮC NGHIỆM TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP ĐỀ BÀI Câu 1.
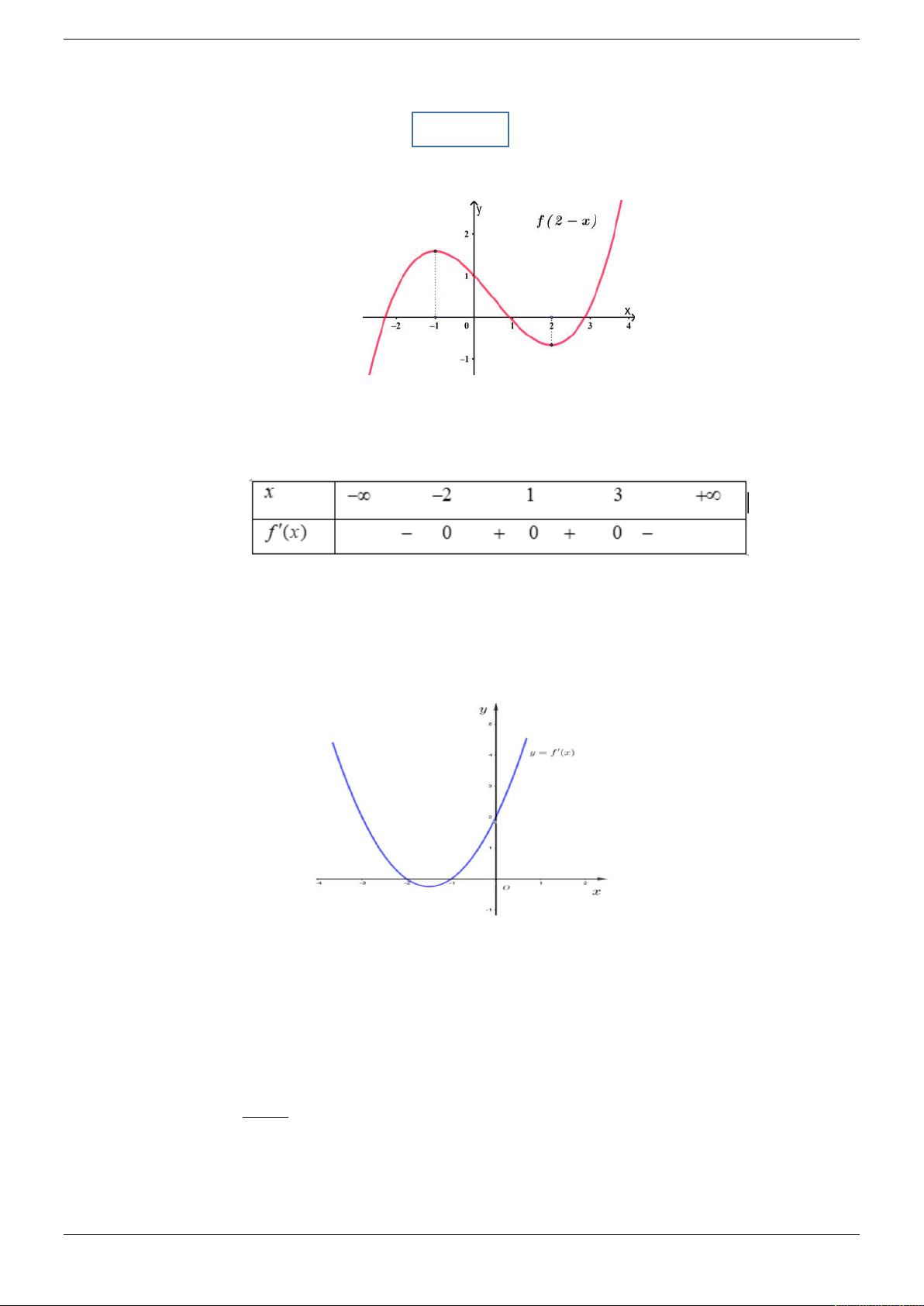
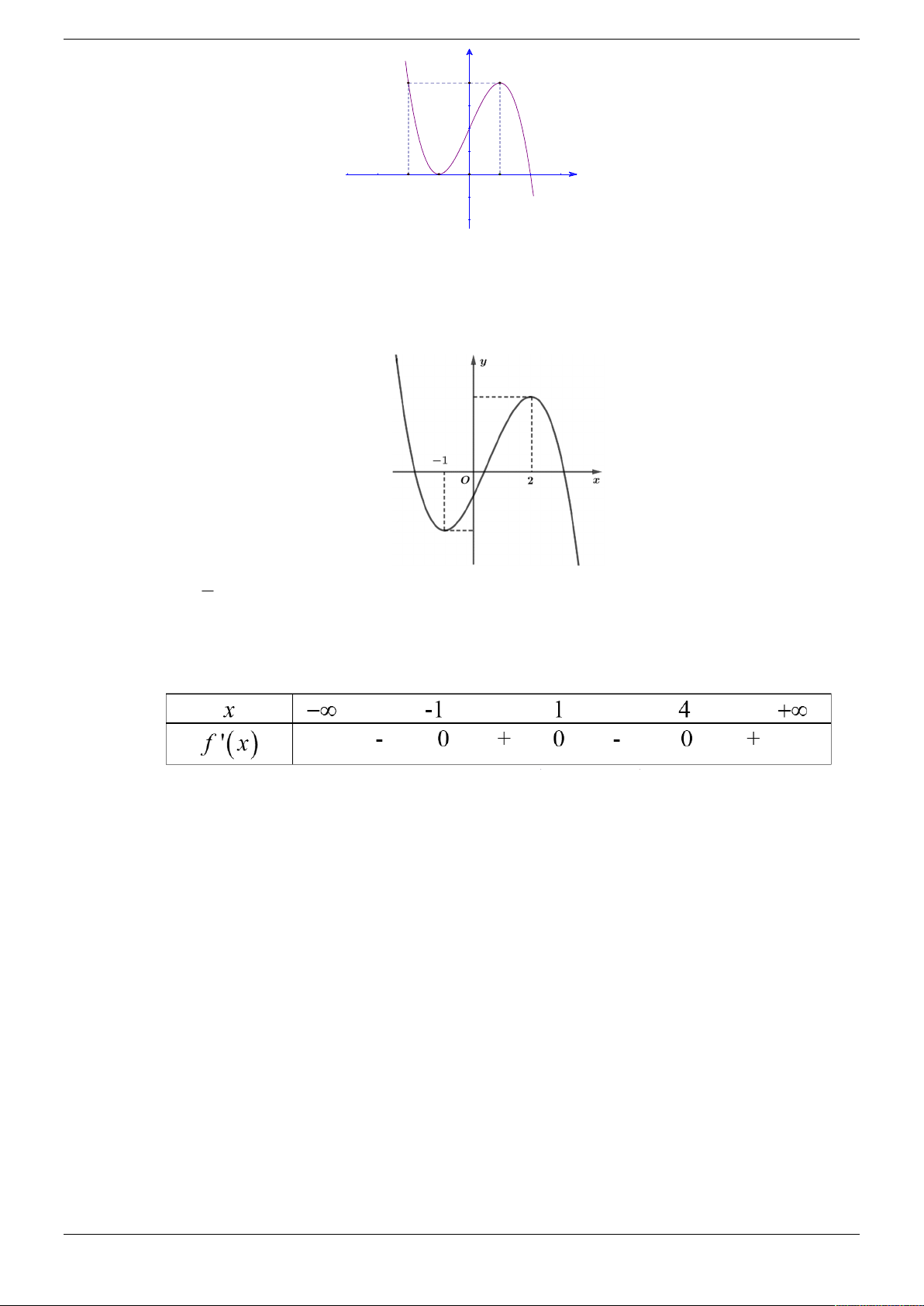
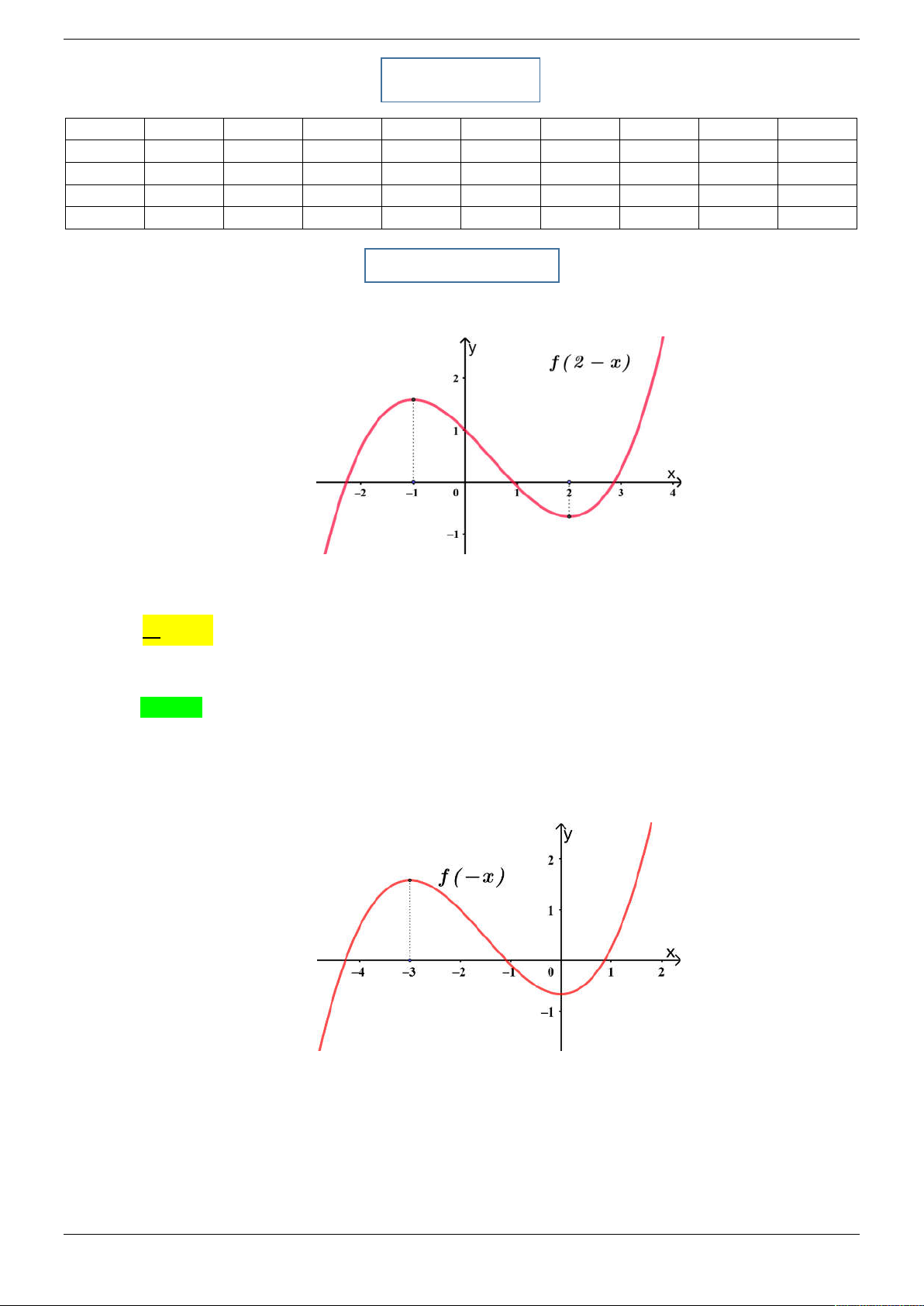
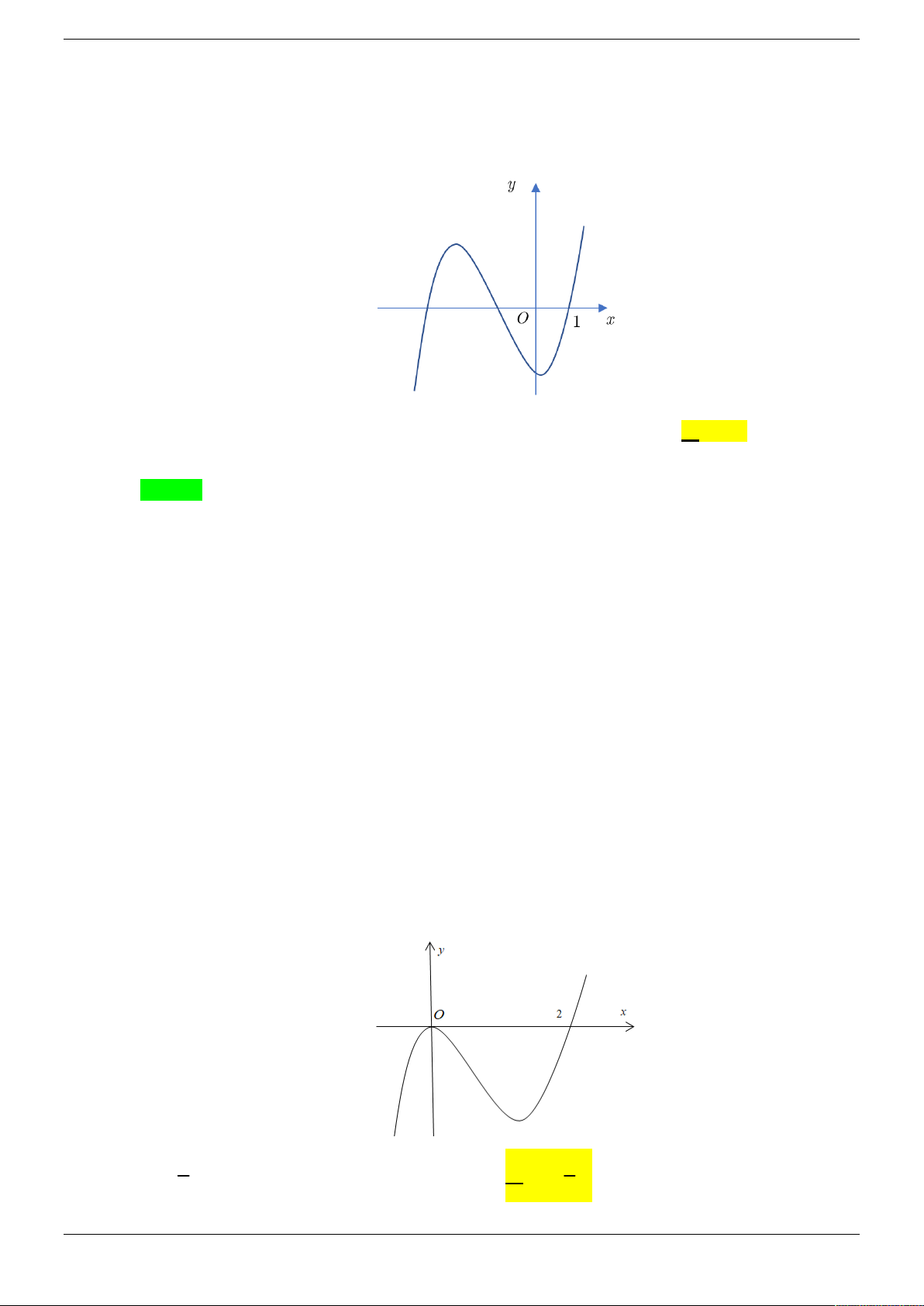
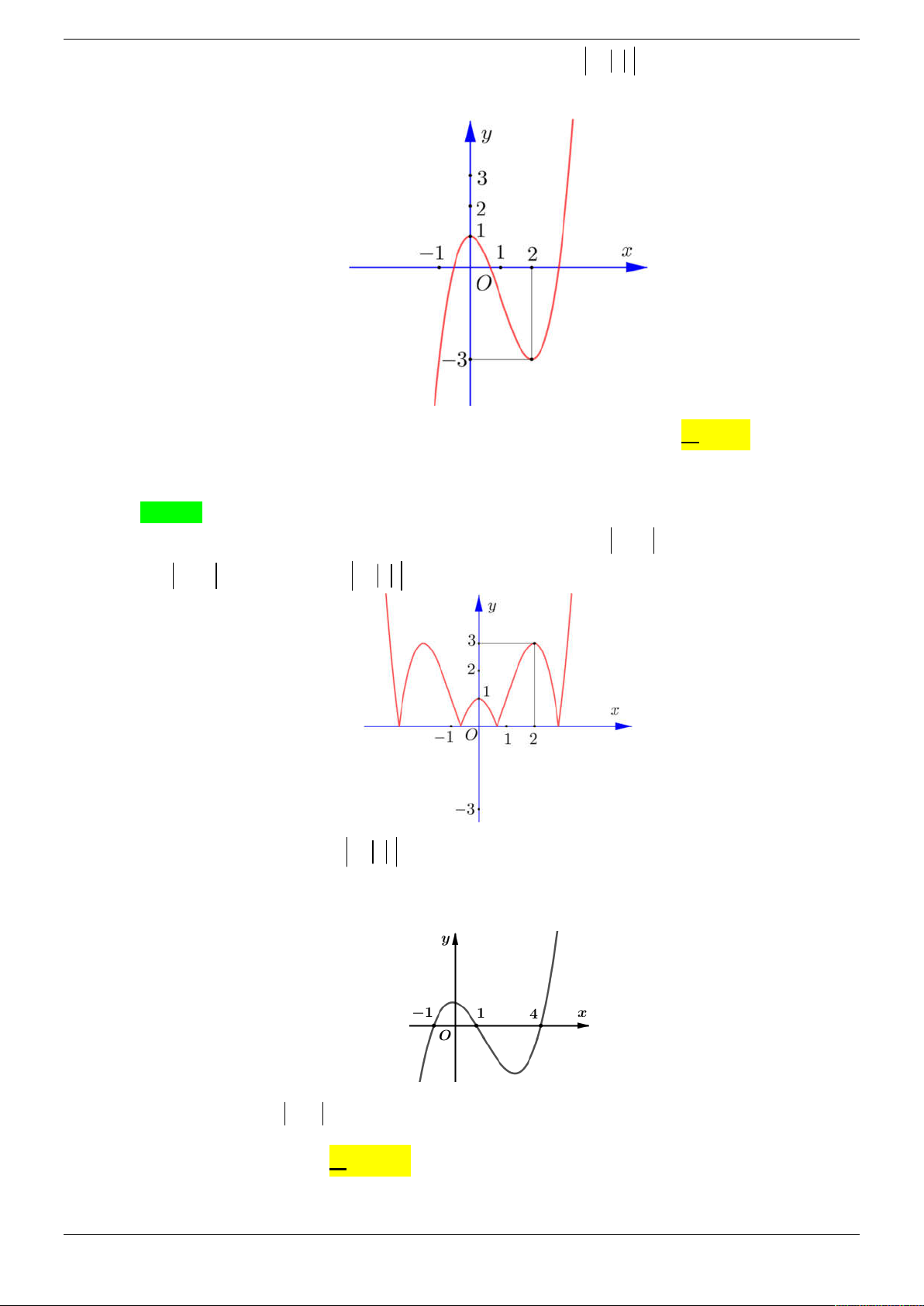
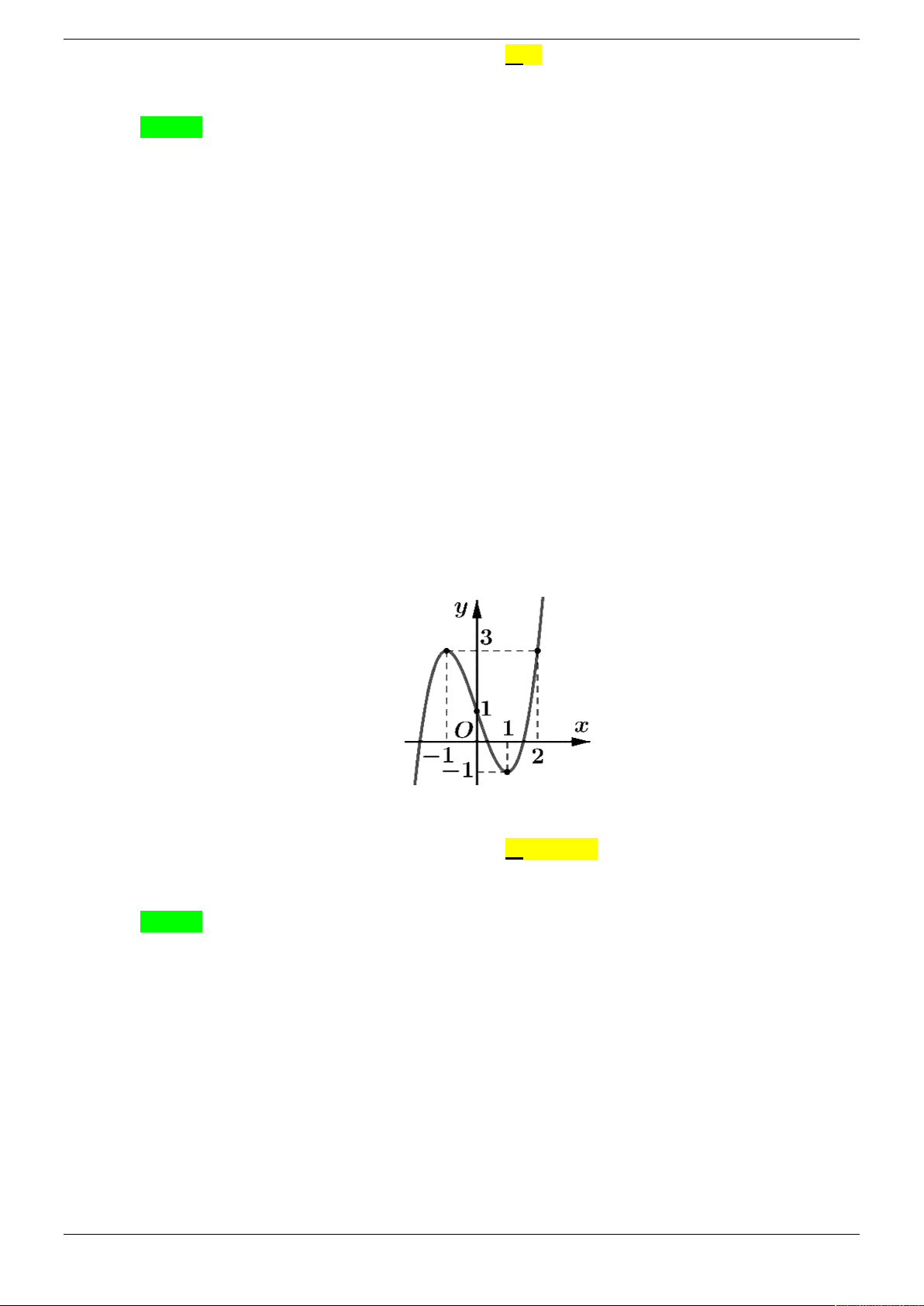
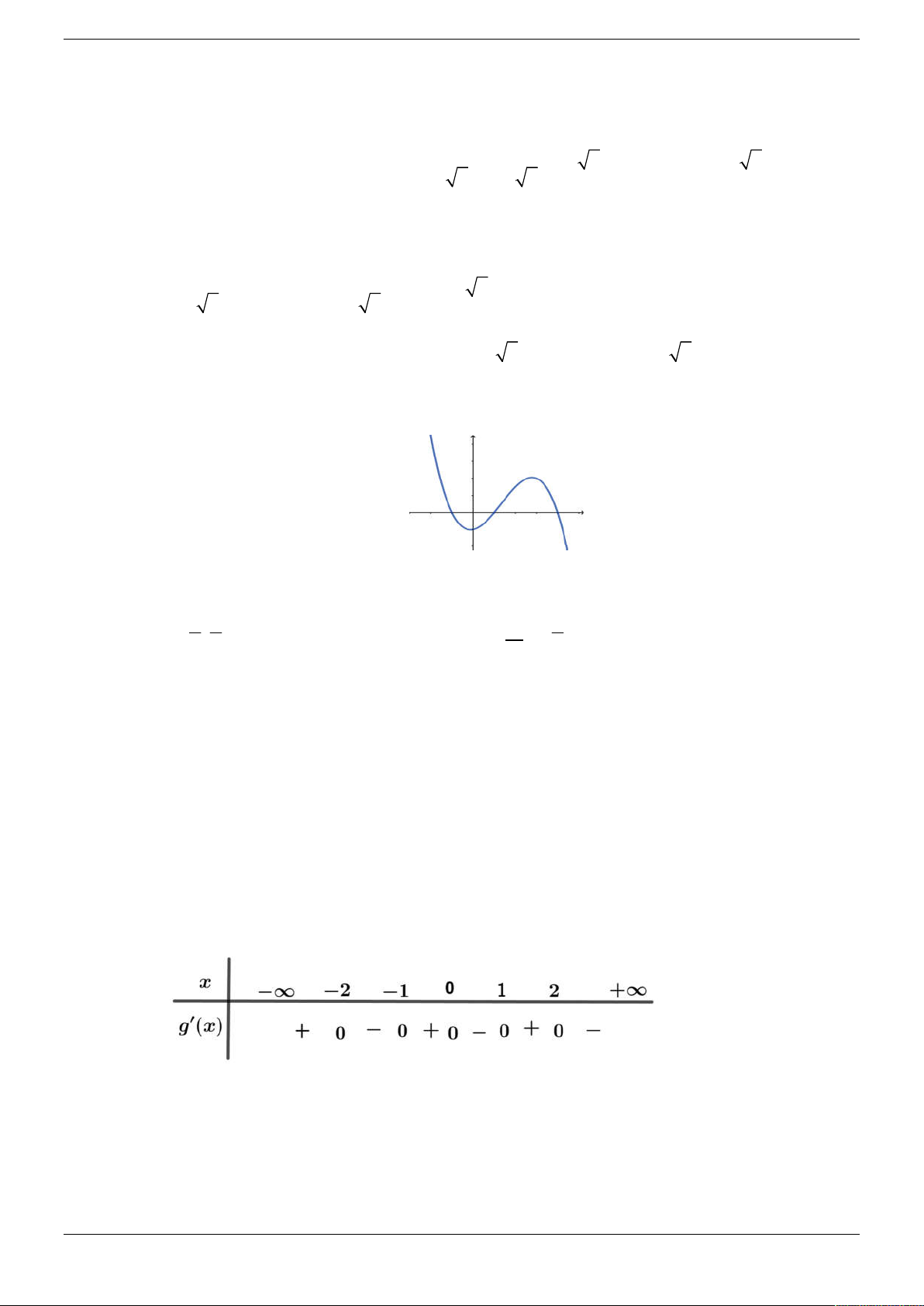
Cho đồ thị hàm số y  f 2  x như hình vẽ:
Hàm số y  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. 0  ;1 . B. 1;3 . C. ;   1 . D. 1;0 . Câu 2.
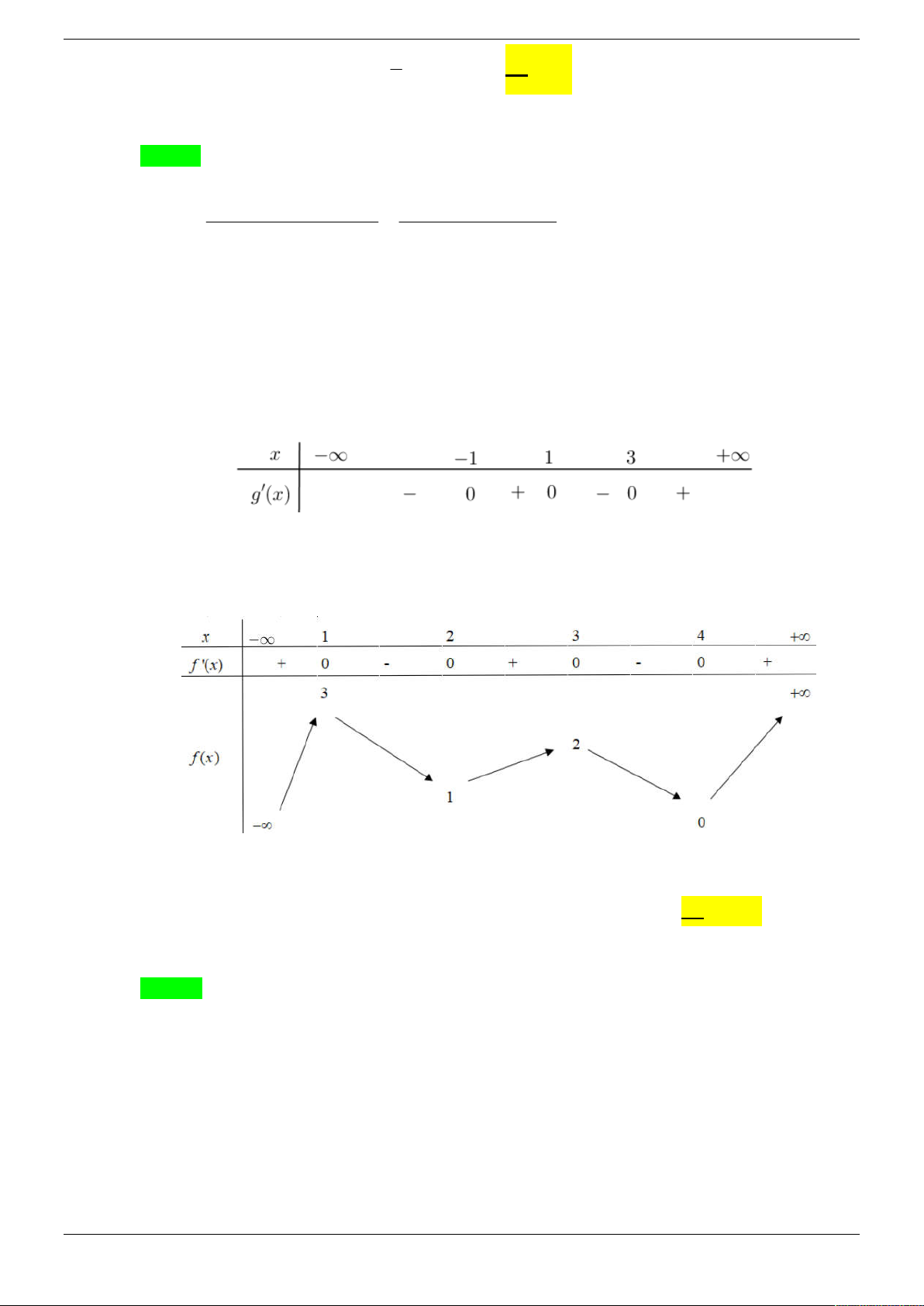
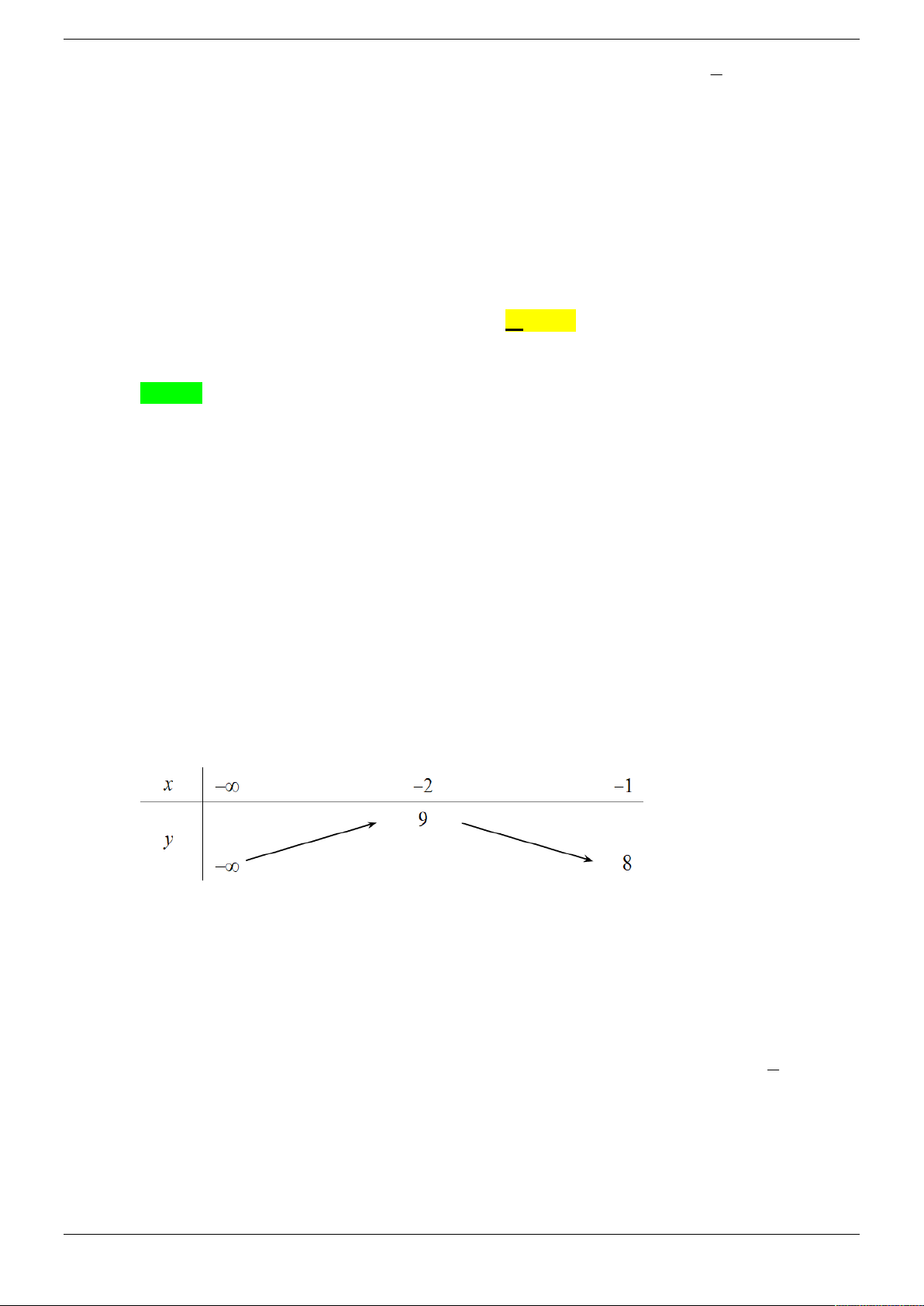
Cho hàm số f  x có bảng xét dấu đạo hàm f  x như sau:
Hàm số y  f  2
x  2x nghịch biến trên khoảng nào dưới đây? A. 2  ;1 . B.  4  ;  3 . C. 0  ;1 . D. 2;   1 . Câu 3.
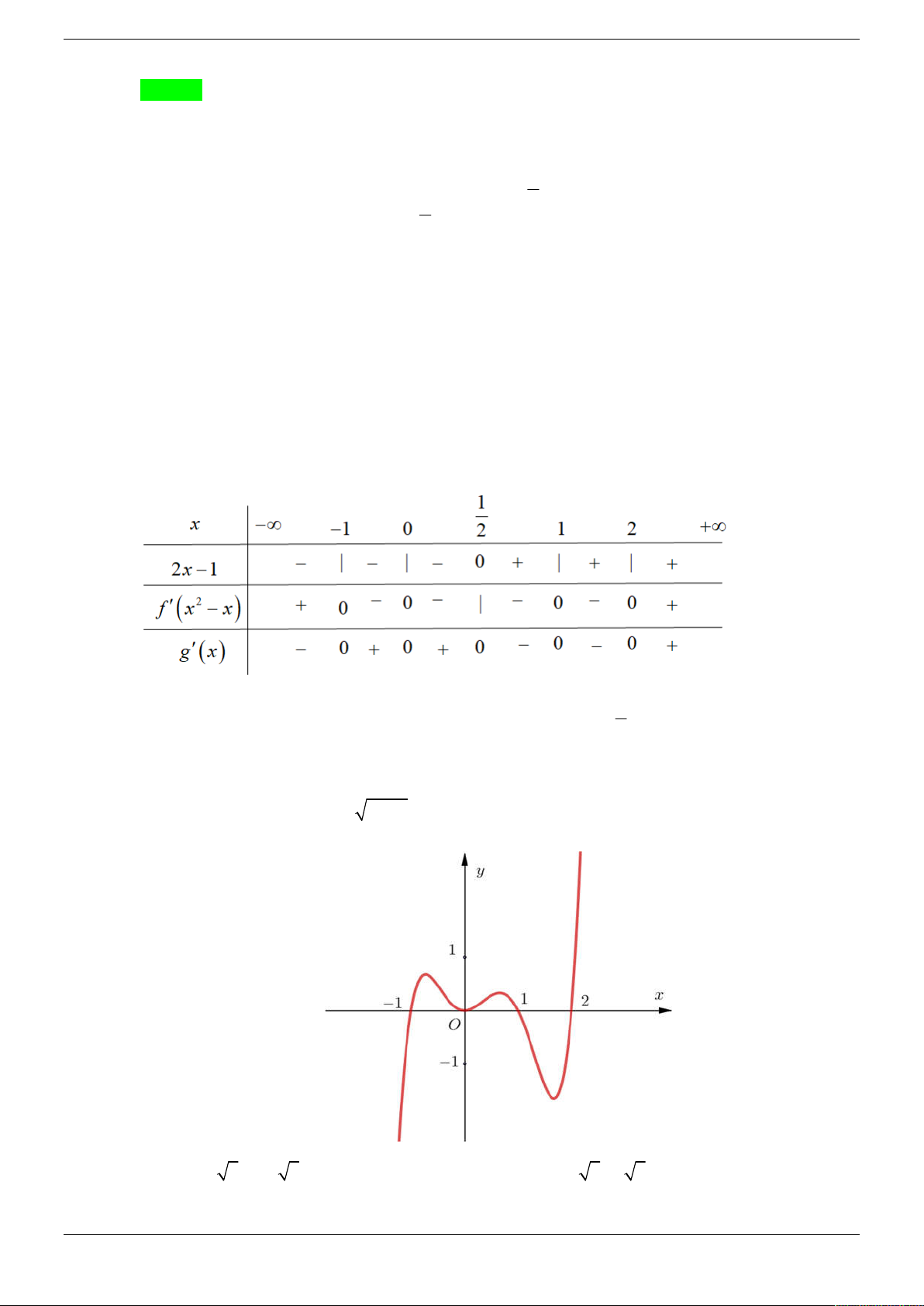
Cho hàm số y  f  x liên tục trên  và hàm số y  f  x có đồ thị như hình vẽ. Hàm số
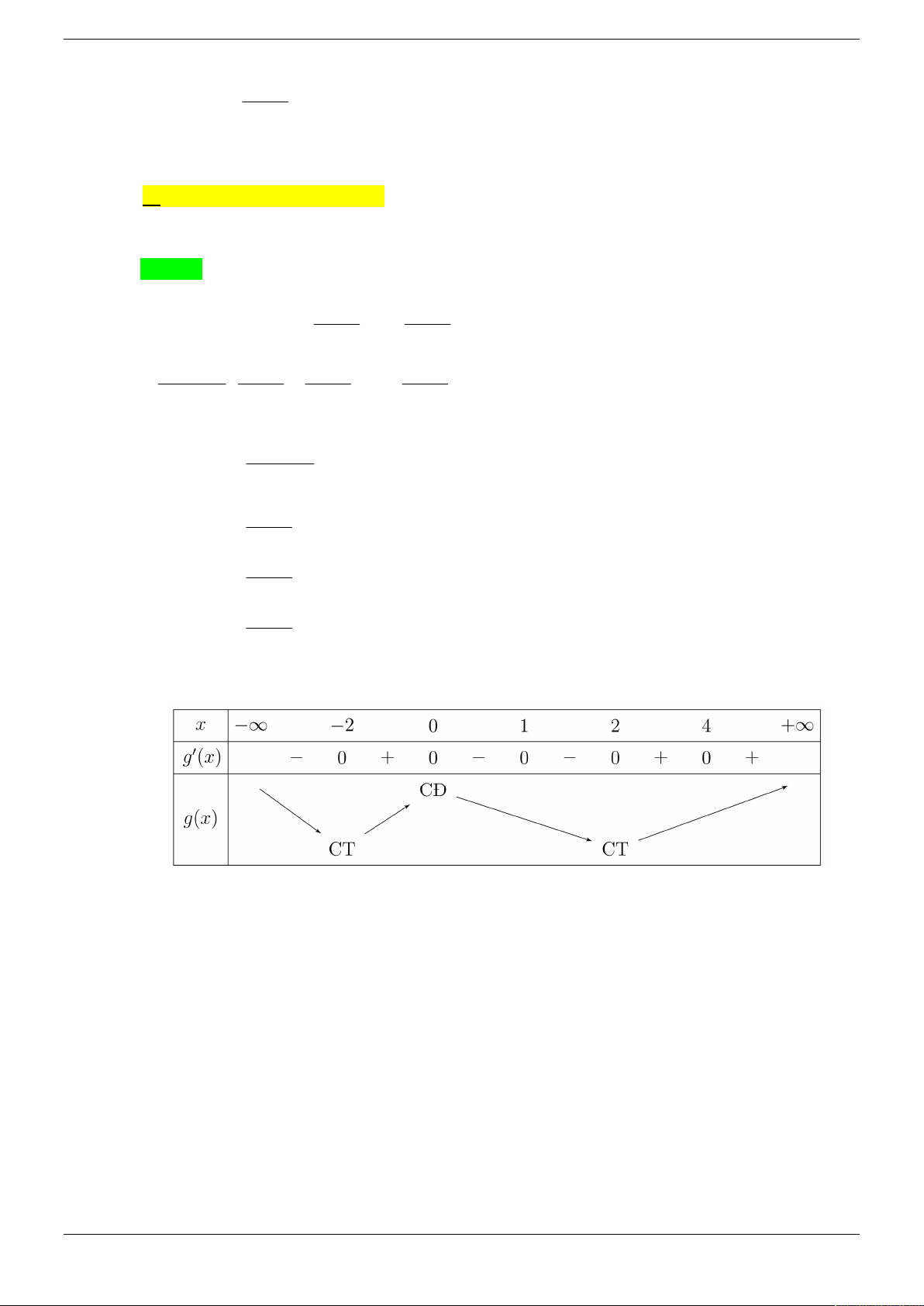
y  g  x  f  2
1 2x  x   2020 đồng biến trên khoảng nào dưới đây? A. 1; 0 . B. 0;1 . C. 2;3 . D. 3;5 . 2 3 Câu 4.
Cho hàm số y  f  x  có đạo hàm f  x  x. x  2  x  5 . Hàm số g x  f 10  5x
đồng biến trên khoảng nào dưới đây? ;  1 1;2 2; 1;3 A. . B. . C. . D. . Câu 5.
Cho hàm số y  f (x) có đạo hàm 2 f (
 x)  x(x 1) (x  2) với mọi giá trị thực của x . Xét hàm  5x 
số g(x)  f 
. Trong các khẳng định sau khẳng định nào đúng? 2   x  4 
A. Hàm số đồng biến trên khoảng (0;1) .
B. Hàm số nghịch biến trên khoảng (0; 4) .
C. Hàm số đạt cực đại tại x  0 .
D. Hàm số đạt giá trị nhỏ nhất tại x  1 . Strong Team Toán VD – VDC Trang 1/50 Câu 6.
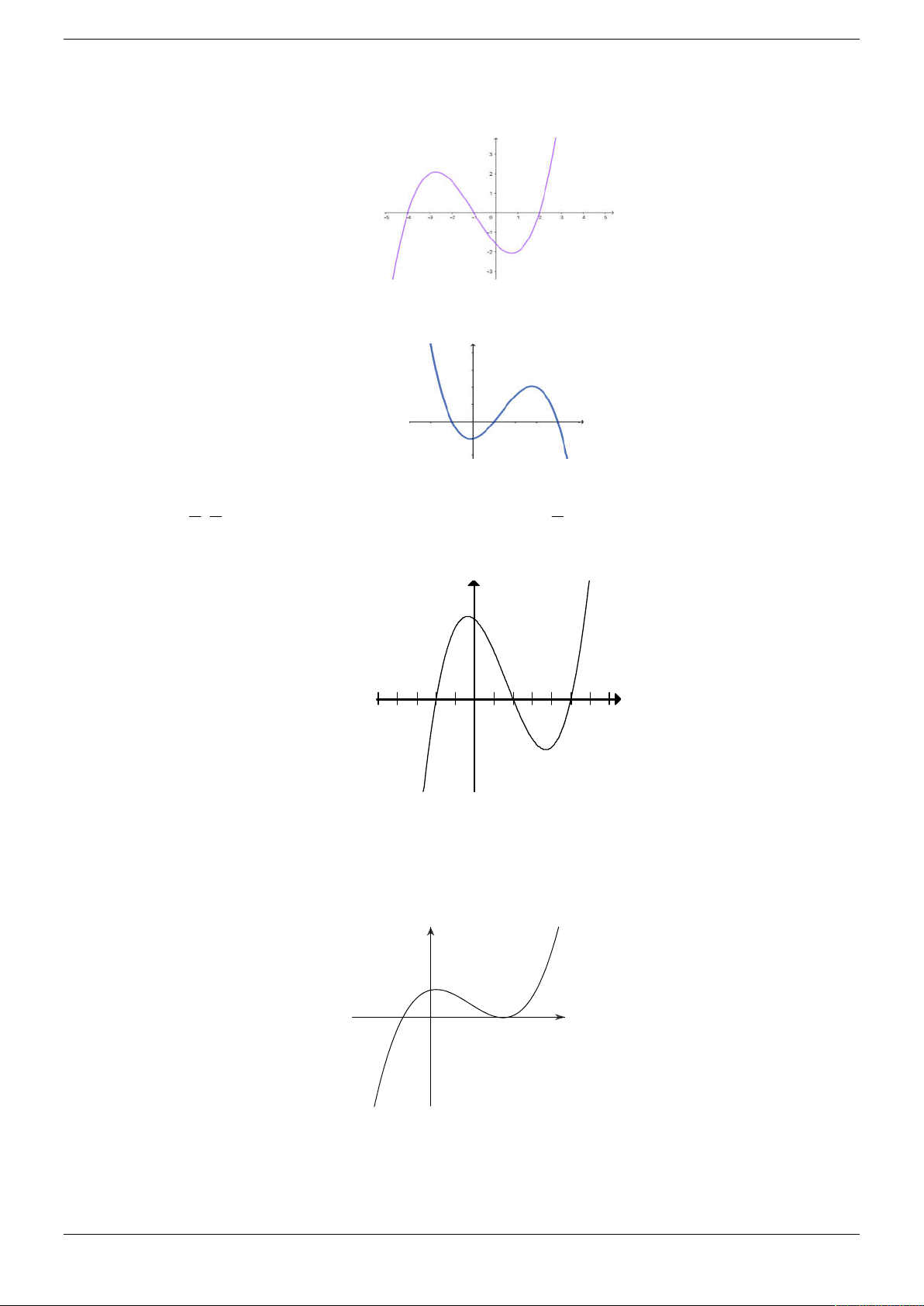
Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình bên.
Hỏi hàm số g  x  f  2 x  x 2 2
 6x  3x đồng biến trên khoảng nào dưới đây?  1   1  A.  ; 0   . B. ;1   .  4   4  C. 0;  1 . D. ;0 . 2 2 Câu 7.
Cho hàm số y  f  x có đạo hàm f ' x  (3  x)10  3x  x  2 với mọi x  . Hàm số 1
g  x  f 3  x 2 3 
(x 1) đồng biến trên khoảng nào trong các khoảng sau? 6  1  A.  ;  0. B. 0;  1 . C. 1;. D. ;  .    2  Câu 8.
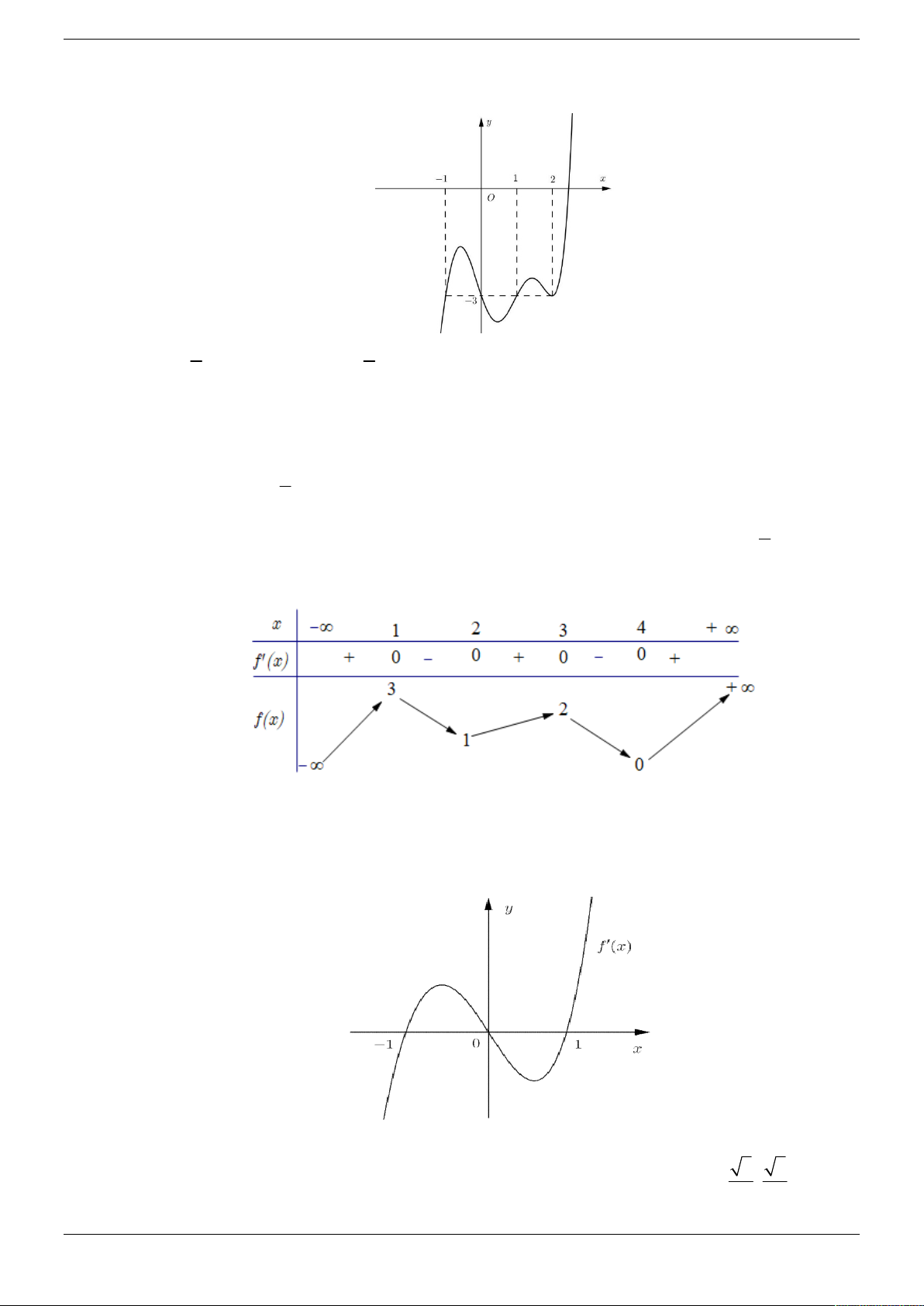
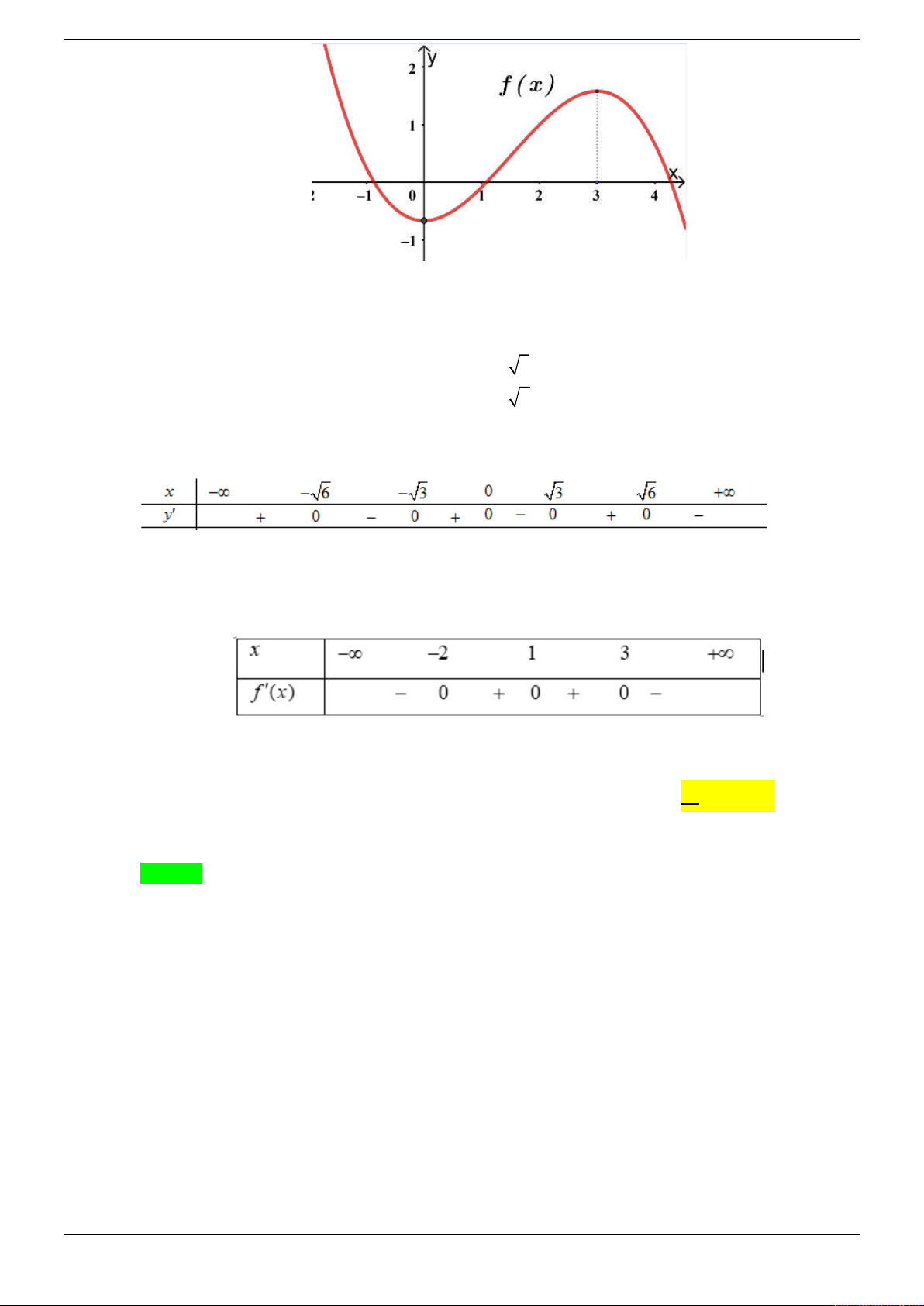
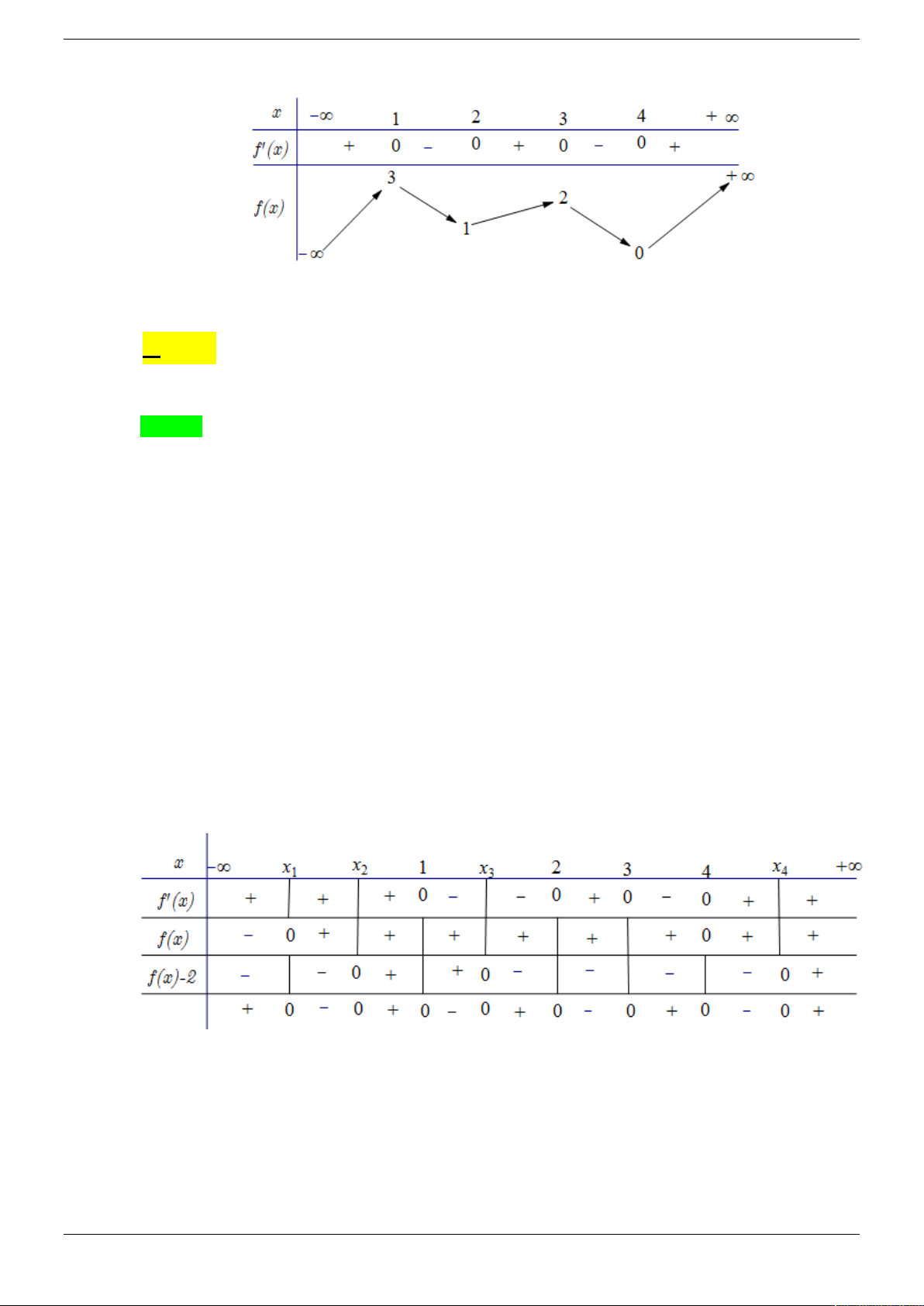
Cho hàm số f  x có bảng biến thiên như sau: 3 2
Hàm số y   f  x  3 f  x nghịch biến trên khoảng nào dưới đây? A. 2;  3 . B. 1;2 . C. 3;4 . D. ;  1 . Câu 9.
Cho hàm số y  f  x , hàm số f  x 3 2
 x  ax  bx  c a, ,
b c   có đồ thị như hình vẽ
Hàm số g  x  f  f  x nghịch biến trên khoảng nào dưới đây?  3 3  A. 1;  . B.  ;  2   . C.  1  ; 0 . D.   ;  .  3 3    Strong Team Toán VD – VDC Trang 2/50
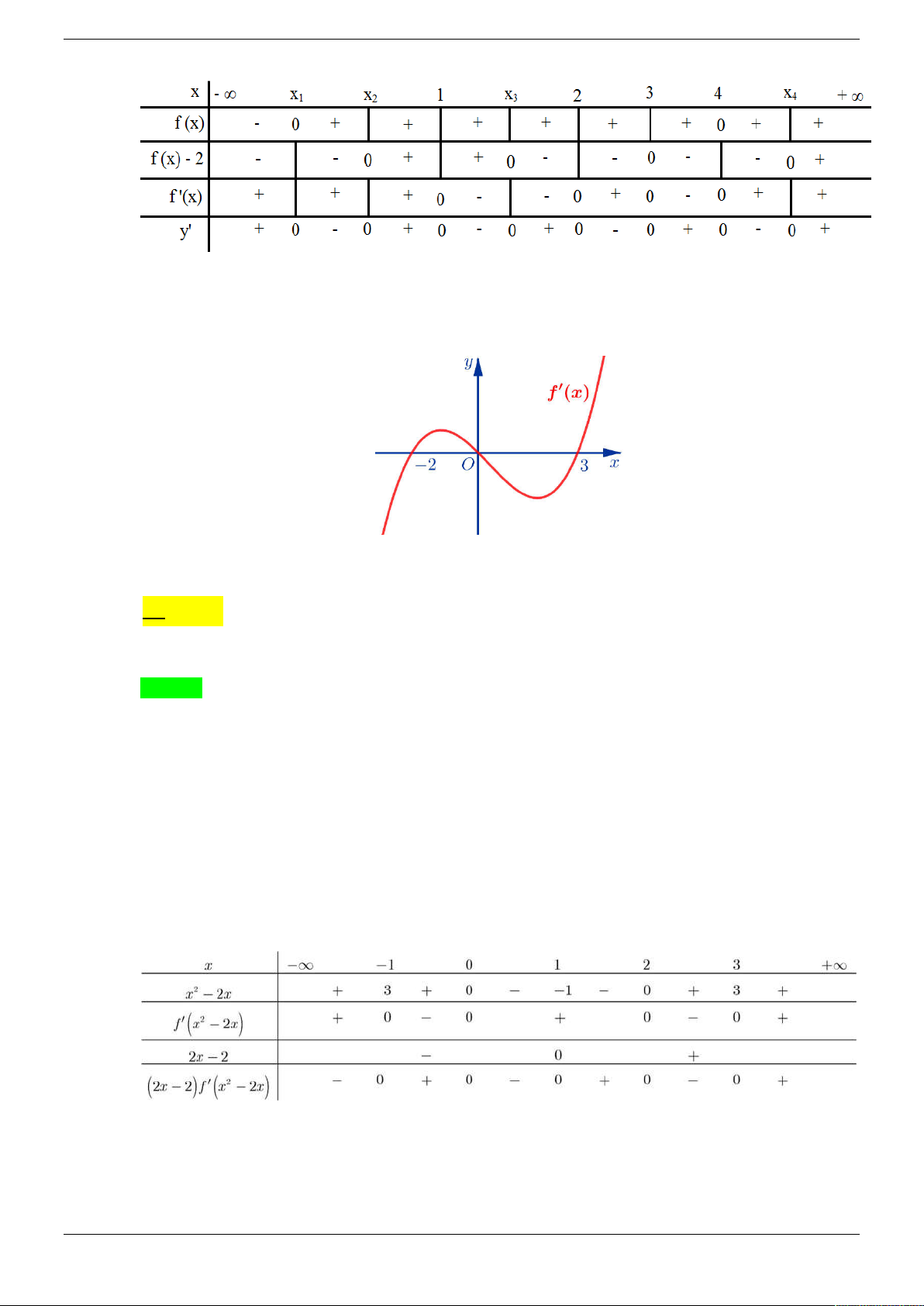
Câu 10. Cho hàm số y  f  x liên tục có đạo hàm trên  . Biết hàm số f ' x có đồ thị cho như hình
vẽ. Có bao nhiêu giá trị nguyên của m thuộc  2
 019; 2019 để hàm số    2019x g x f
  mx  2 đồng biến trên 0  ;1 ? A. 2028 . B. 2019 . C. 2011 . D. 2020
Câu 11. Cho hàm số y  f  x có đạo hàm trên  và có đồ thị hàm f  x như hình vẽ dưới đây. Hàm số     2 g x
f x  x  đồng biến trên khoảng nào?  1  A. ;1   . B. 1; 2 .  2   1  C. 1  ;   . D. ;   1 .  2 
Câu 12. Cho hàm số y  f  x có đạo hàm trên  . Biết hàm số y  f  x  liên tục trên  và có đồ thị
như hình vẽ. Hàm số y  f  2
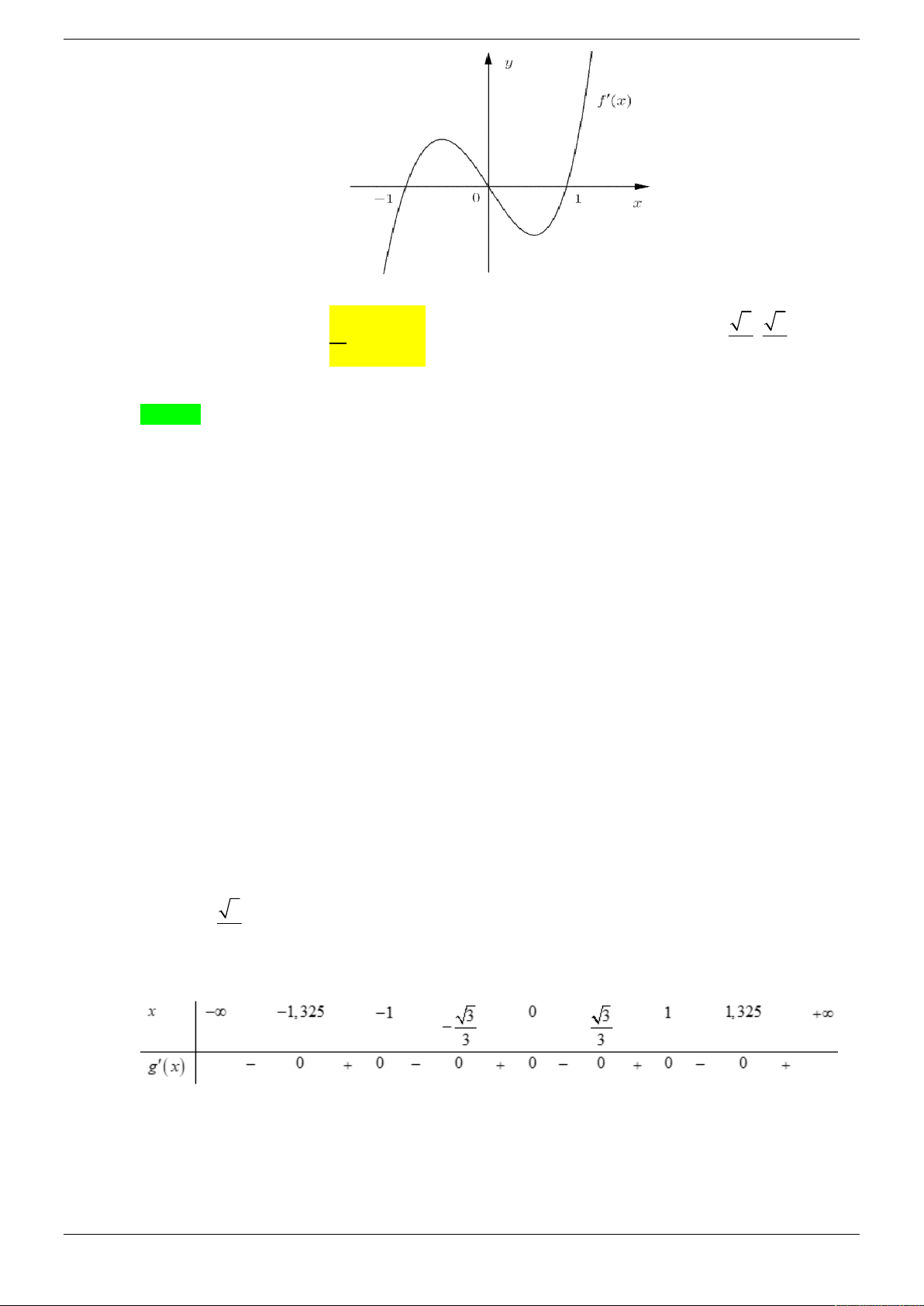
x 1 đồng biến trong khoảng nào dưới đây? Strong Team Toán VD – VDC Trang 3/50
A. ; 3,0; 3 .
B. ;  3, 3; .
C.  3;0, 3; .
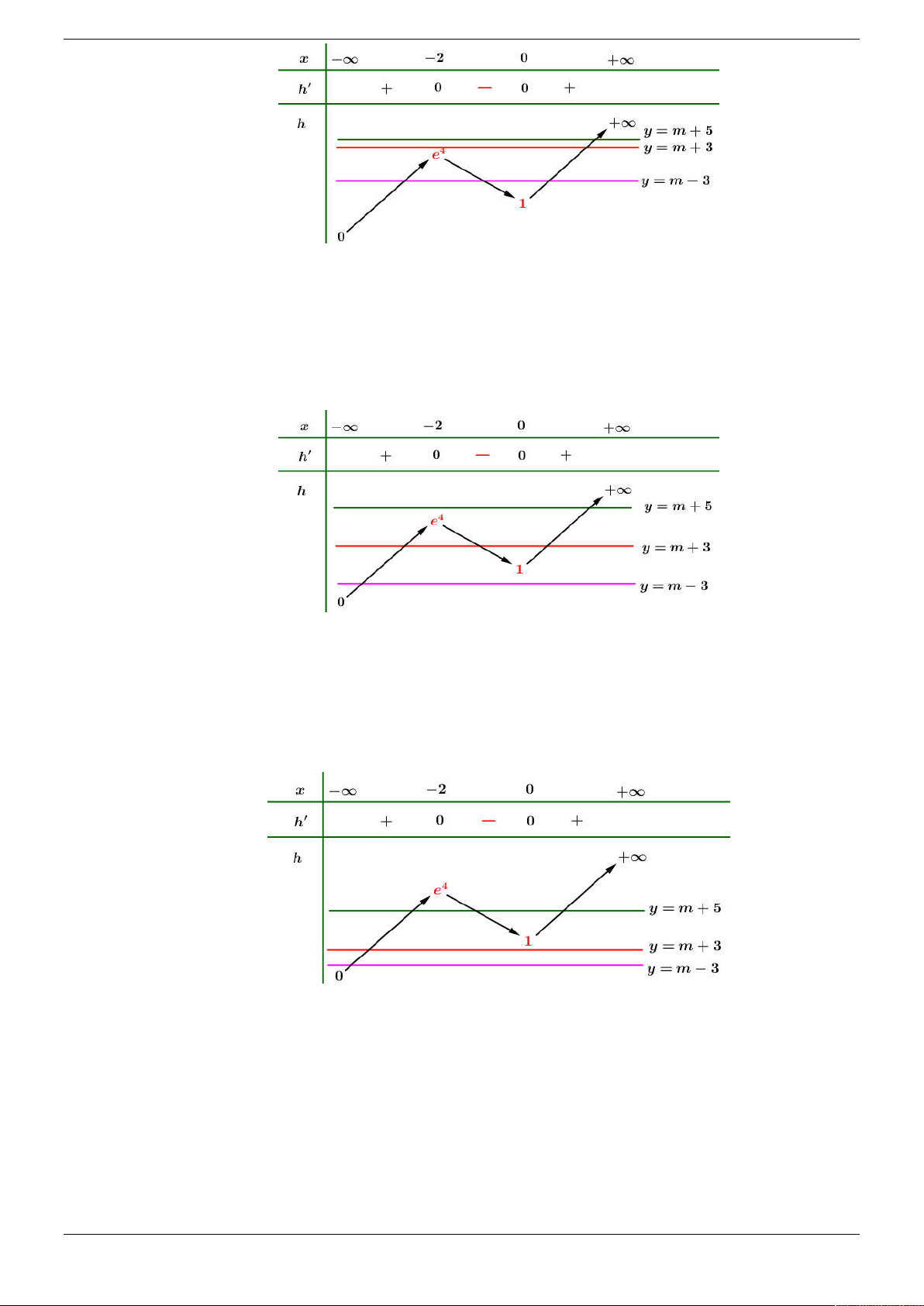
D. ; 3,0; .
Câu 13. Cho hàm số y  f  x . Hàm số y  f  x  có đồ thị như hình bên. Hàm số   2 y f x  x 
nghịch biến trên khoảng nào dưới đây. y 2 O 1 2 x  1   3   3   1  A.  ;    . B.  ;    . C.  ;    . D. ;    .  2   2   2   2 
Câu 14. Cho hàm số y  f  x có đạo hàm trên  . Đường cong trong hình vẽ bên là đồ thị của hàm số
y  f   x  ( y  f  x  liên tục trên  ). Xét hàm số g  x  f  2
x  3 . Mệnh đề nào dưới đây sai? y 4 2 2 1 O 1 x
A. Hàm số g  x đồng biến trên 1; 0 .
B. Hàm số g  x nghịch biến trên ;   1 .
C. Hàm số g  x nghịch biến trên 1; 2 .
D. Hàm số g  x đồng biến trên 2;  .
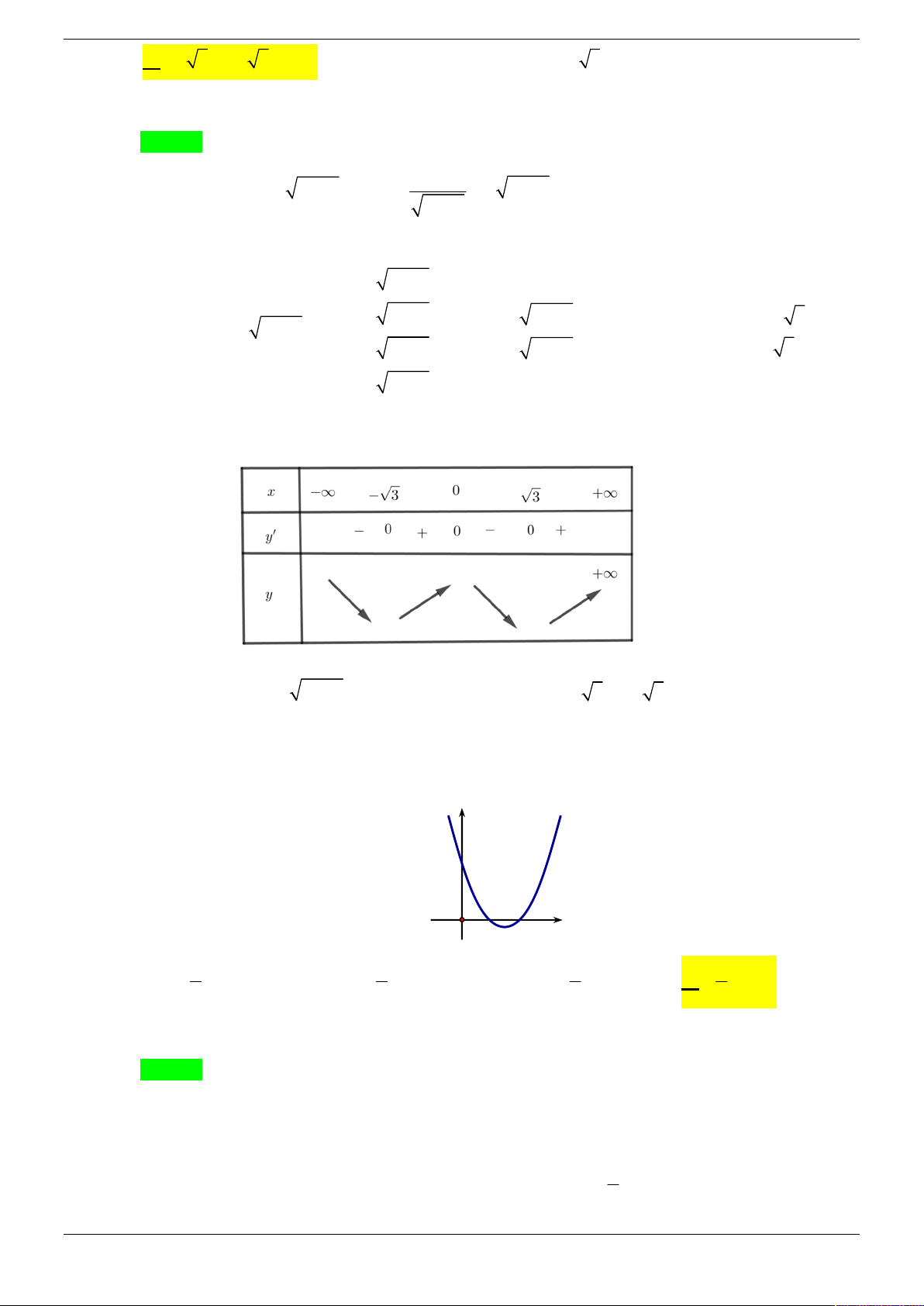
Câu 15. Cho hàm số y  f  x có đồ thị nằm trên trục hoành và có đạo hàm trên , bảng xét dấu của
biểu thức f   x như bảng dưới đây: f  2 x  2x
Hàm số y  g  x 
nghịch biến trên khoảng nào dưới đây? f  2 x  2x 1  5 
A. ;1 . B. 2;   . C. 1; 3 . D. 2;   .  2 
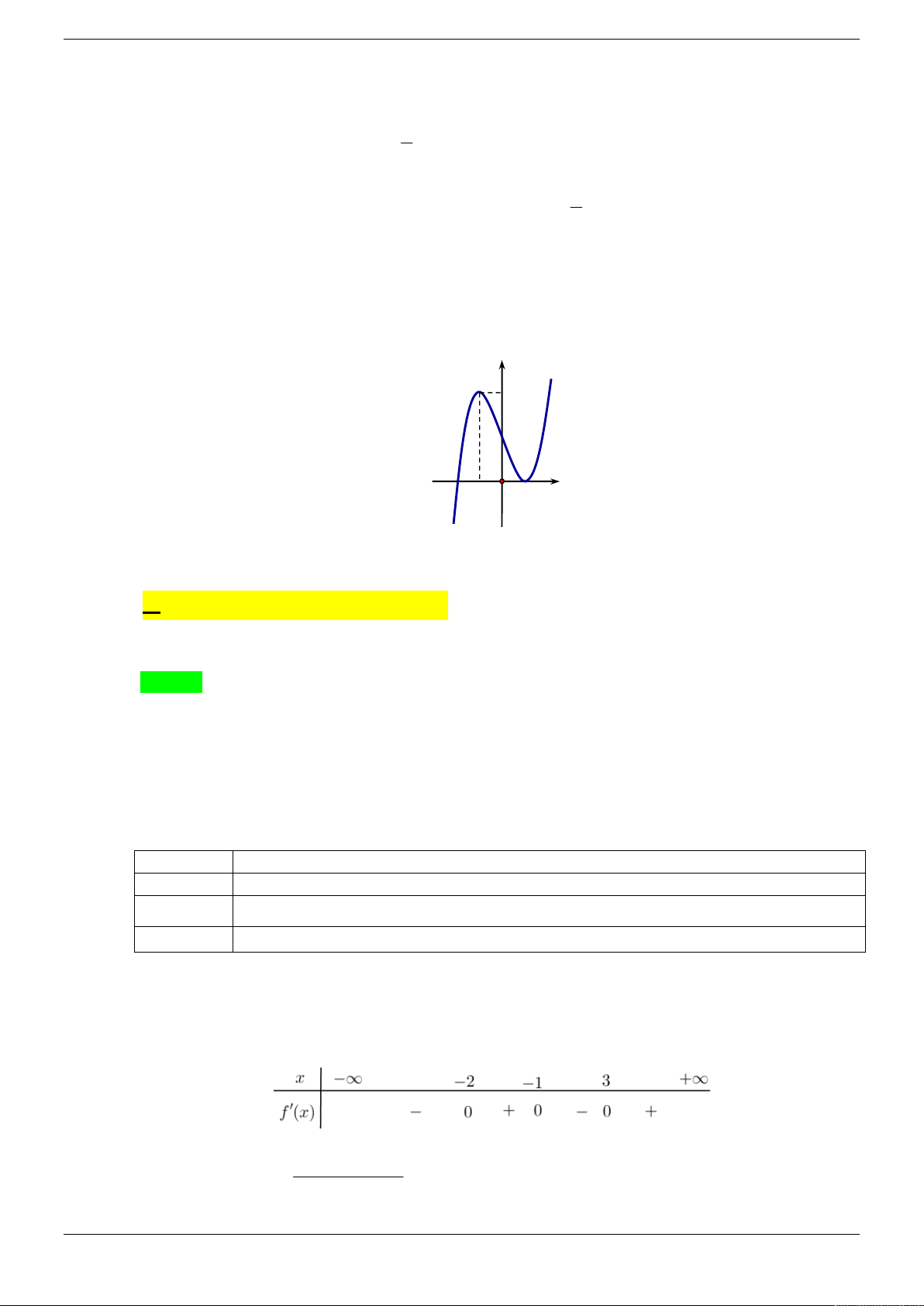
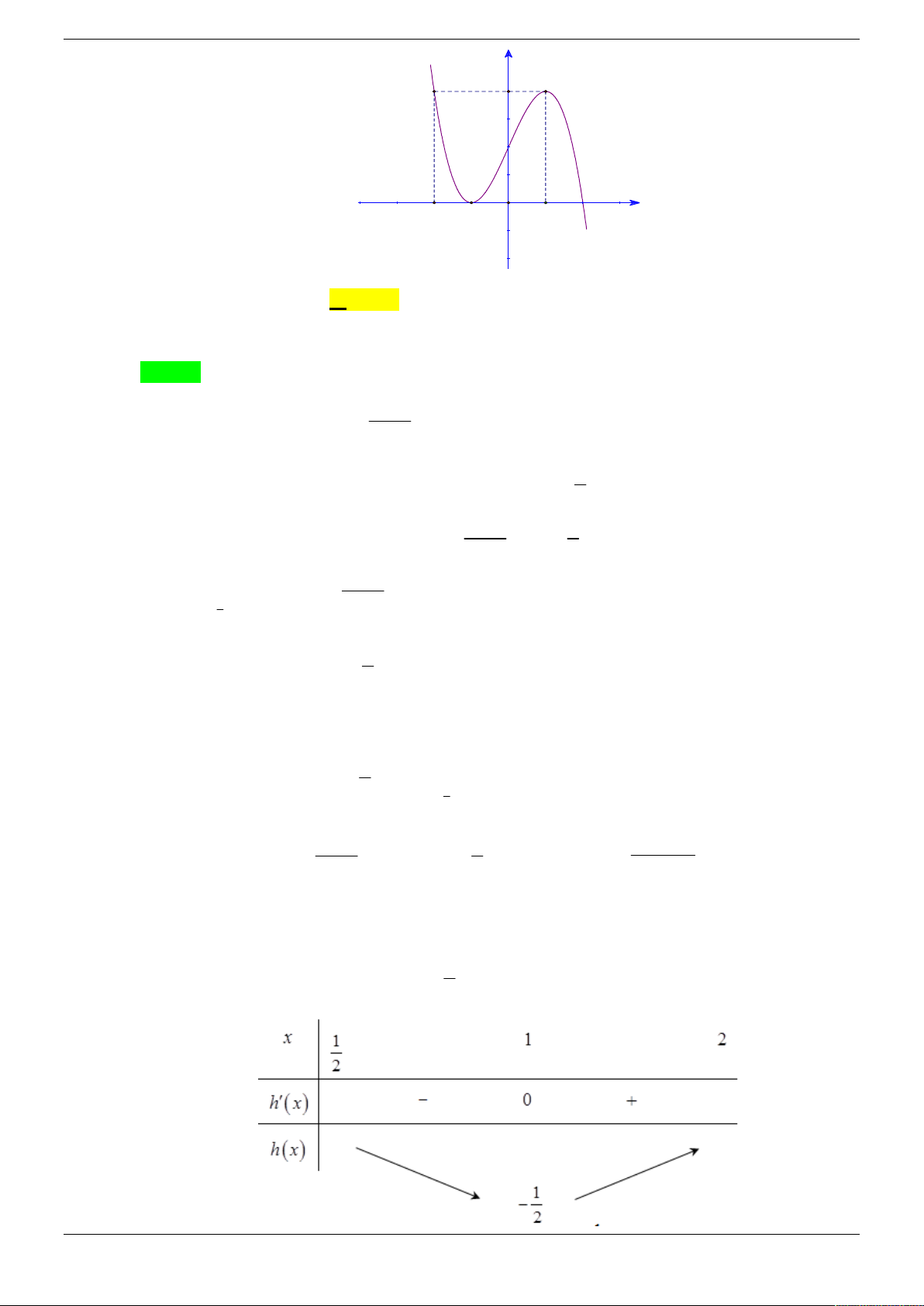
Câu 16. Cho hàm số f  x  có bảng biến thiên như sau: Strong Team Toán VD – VDC Trang 4/50 3 2
Hàm số y   f  x  3. f  x nghịch biến trên khoảng nào dưới đây? A. 1; 2 .
B. 3 ; 4 . C.  ;  1 . D. 2 ; 3 .
Câu 17. Cho hàm số y  f  x đạo hàm liên tục trên  có đồ thị hàm số f  x như hình vẽ
Hỏi hàm số y  f  2
x  2x đồng biến trên khoảng nào sau đây? A.  1  ; 0 . B. 0  ;1 . C. 1;3 . D. 2;  .
Câu 18. Cho hàm số f  x có đạo hàm, liên tục trên , có đồ thị như hình vẽ Hỏi hàm số     2 y f x  
 nghịch biến trên khoảng nào sau đây?  5   5  A. 1  ;1 . B. 0;   . C. ; 4   . D. 2;   1 .  2   2 
Câu 19. Cho hàm số y  f x có bảng biến thiên như sau:
Có bao nhiêu số nguyên m  2019 để hàm số g x  f  2
x  2x  m đồng biến trên khoảng 1; ? A. 2016. B. 2015. C. 2017. D. 2018.
Câu 20. Cho hàm số y  f (x) có bảng biến thiên như sau:
Hàm số g x   f  x 2 ( ) (3
) nghịch biến trên khoảng nào trong các khoảng sau? A. ( 2  ;5) . B. (1; 2) . C. (2;5) . D. (5;  )  . Strong Team Toán VD – VDC Trang 5/50
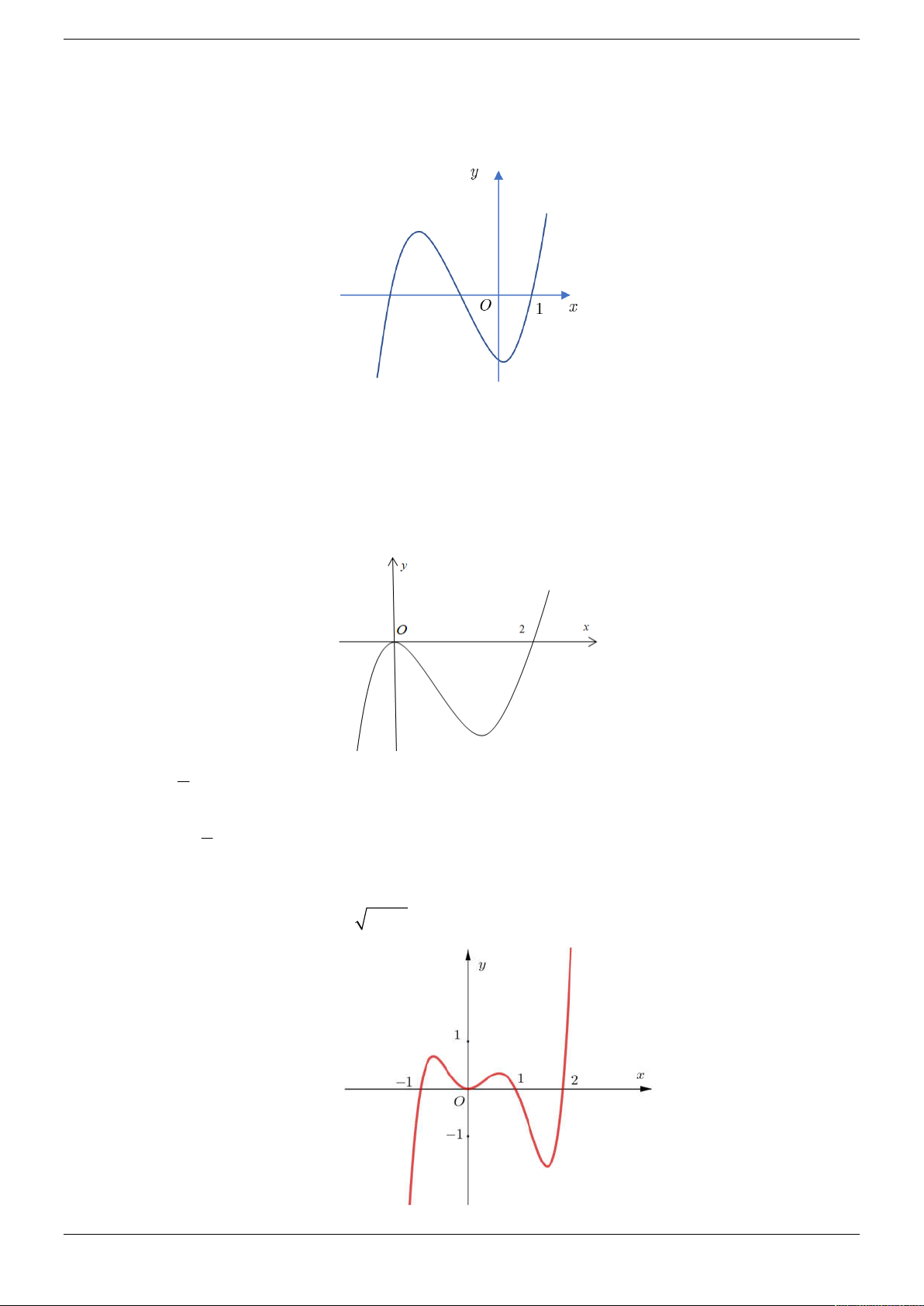
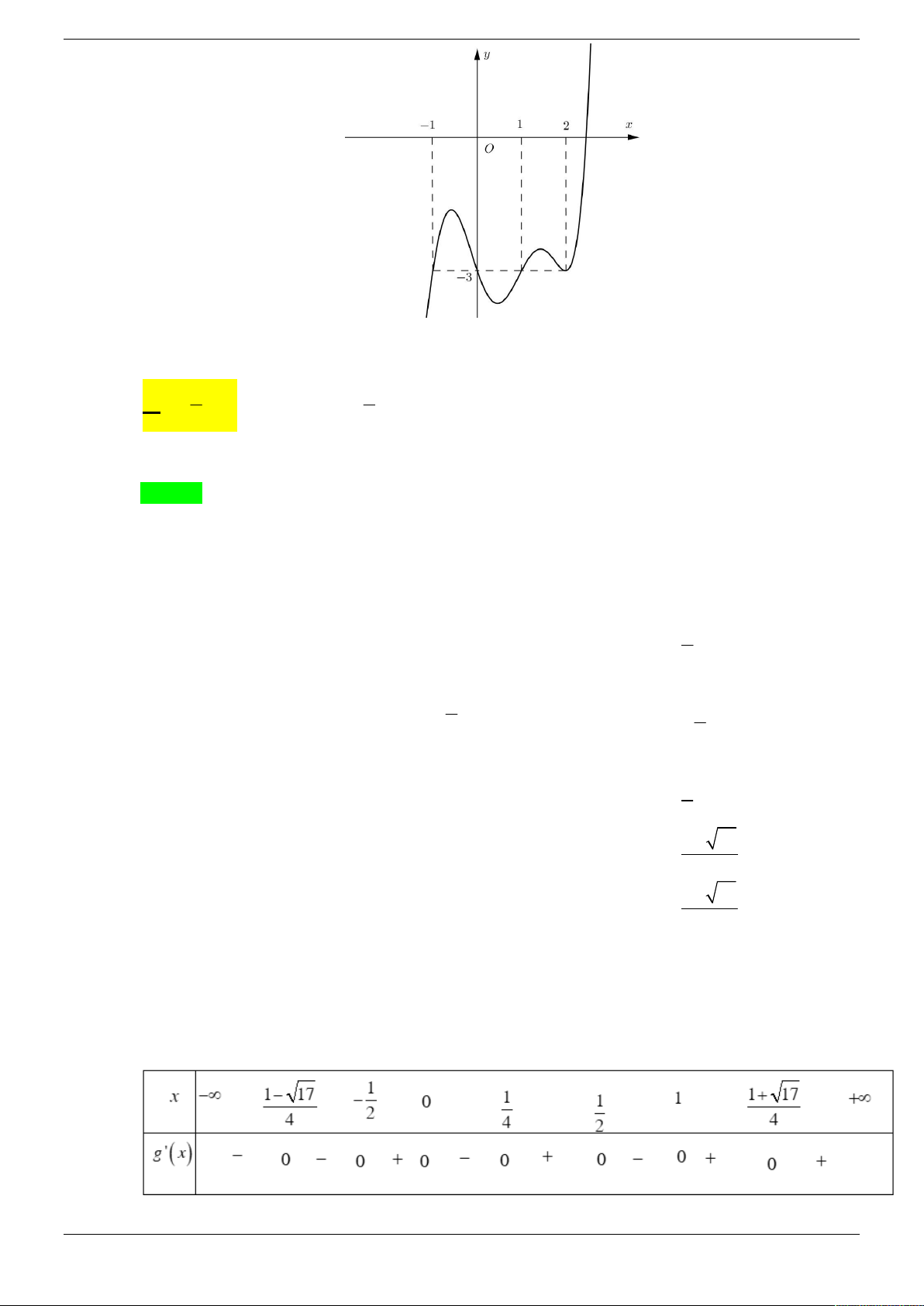
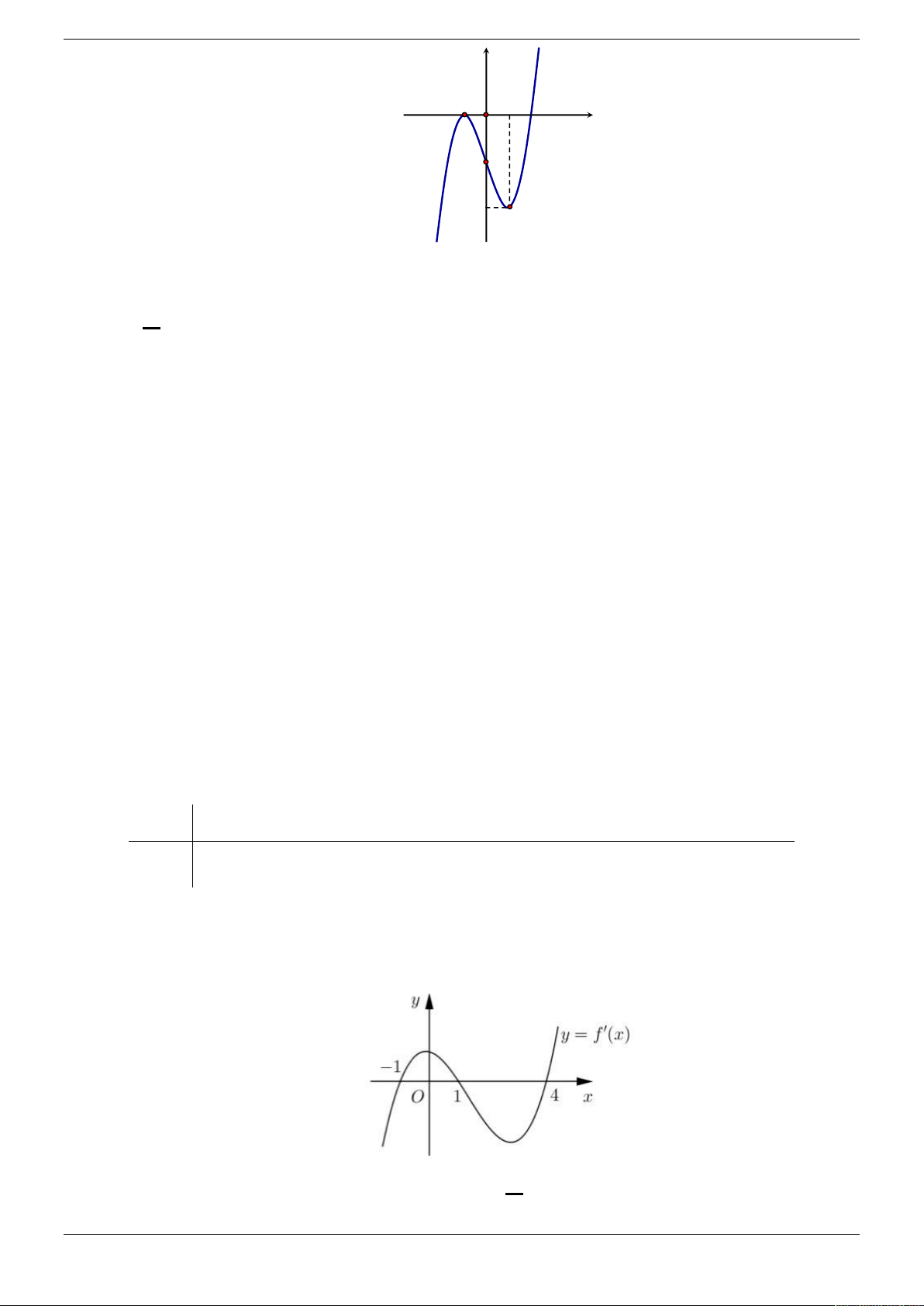
Câu 21. Cho hàm số y  f  x có đồ thị như hình vẽ. Hàm số y  f  x  đồng biến trong khoảng nào dưới đây? A. 0  ;1 . B.  1   ;1 . C. 0; 2 . D. 1; 2 .
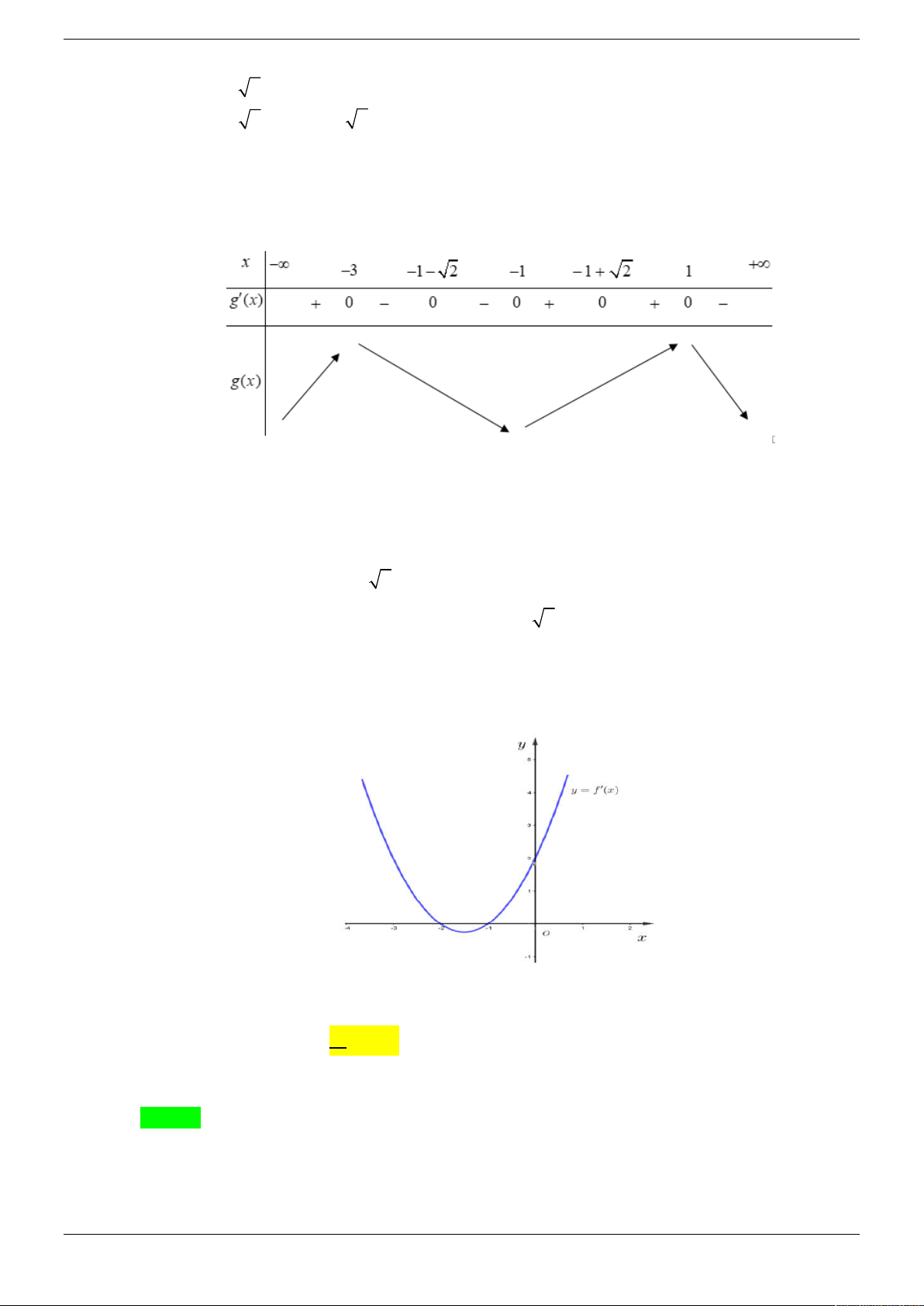
Câu 22. Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới:
Hàm số g  x  f  3  x  đồng biến trên khoảng nào trong các khoảng sau? A.  ;    1 . B.  1  ; 2. C. 2;3. D. 4;7.
Câu 23. Cho hàm số bậc ba y  f  x , hàm số y  f  x có đồ thị như hình vẽ. Hỏi hàm số
g  x  f  x  
1 nghịch biến trên khoảng nào dưới đây? A. 1,  . B.  1  , 0 . C.  1  , 2 . D. ,  1 .
Câu 24. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số 4 3 2
y  3x  4x 12x  m
nghịch biến trến khoảng  ;    1 ? A. 4 . B. 6 . C. 3 . D. 5 .
Câu 25. Cho hàm số y  f  x . Đồ thị hàm số y  f  x như hình vẽ sau: Strong Team Toán VD – VDC Trang 6/50
Hàm số g  x  f  4  2x  nghịch biến trên khoảng nào sau đây?  1 3   5   3 5  A. ;   . B.  ;  2   . C. ; 7   . D. ;   .  2 2   2   2 2  2
Câu 26. Cho hàm số y  f  x có đạo hàm f  x   x    2 1
x  2x  , với x
   . Số giá trị nguyên
của tham số m để hàm số g  x  f  3 2
x  3x  m có 8 điểm cực trị là A. 2 . B. 3. C. 1. D. 4 .
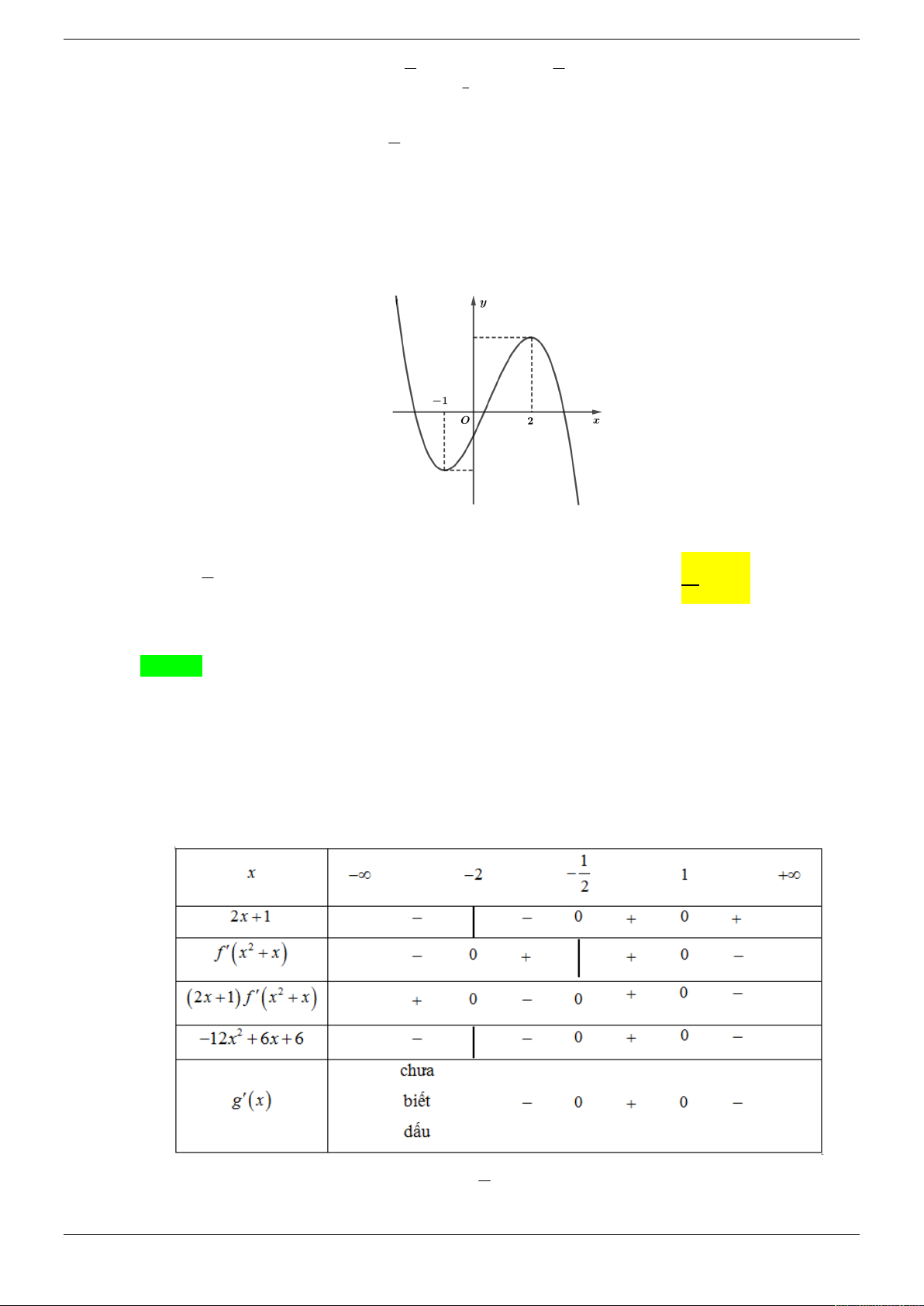
Câu 27. Cho hàm số y  f  x xác định trên R và hàm số y  f ' x có đồ thị như hình bên dưới và
f ' x  0 với mọi x  ; 3, 4  9;  . Đặt g  x  f  x  mx  5. Có bao nhiêu giá trị
dương của tham số m để hàm số g  x có đúng hai điểm cực trị? A. 4. B. 7. C. 8. D. 9.
Câu 28. Cho hàm số đa thức bậc bốn y  f  x , biết hàm số có ba điểm cực trị x  3
 , x  3, x  5 . Có 3 2
tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số     x 3x g x f e  m có đúng 7 điểm cực trị A. 3 B. 4 C. 5 D. 6
Câu 29. Cho hàm số y  f (x) có đạo hàm f   x   2 x  x 2 x  4x   3 , x
   . Tính tổng tất cả các giá
trị nguyên của tham số m để hàm số gx  f x2  m có 3 cực trị. A. 0. B. 6. C. 3. D. 2.
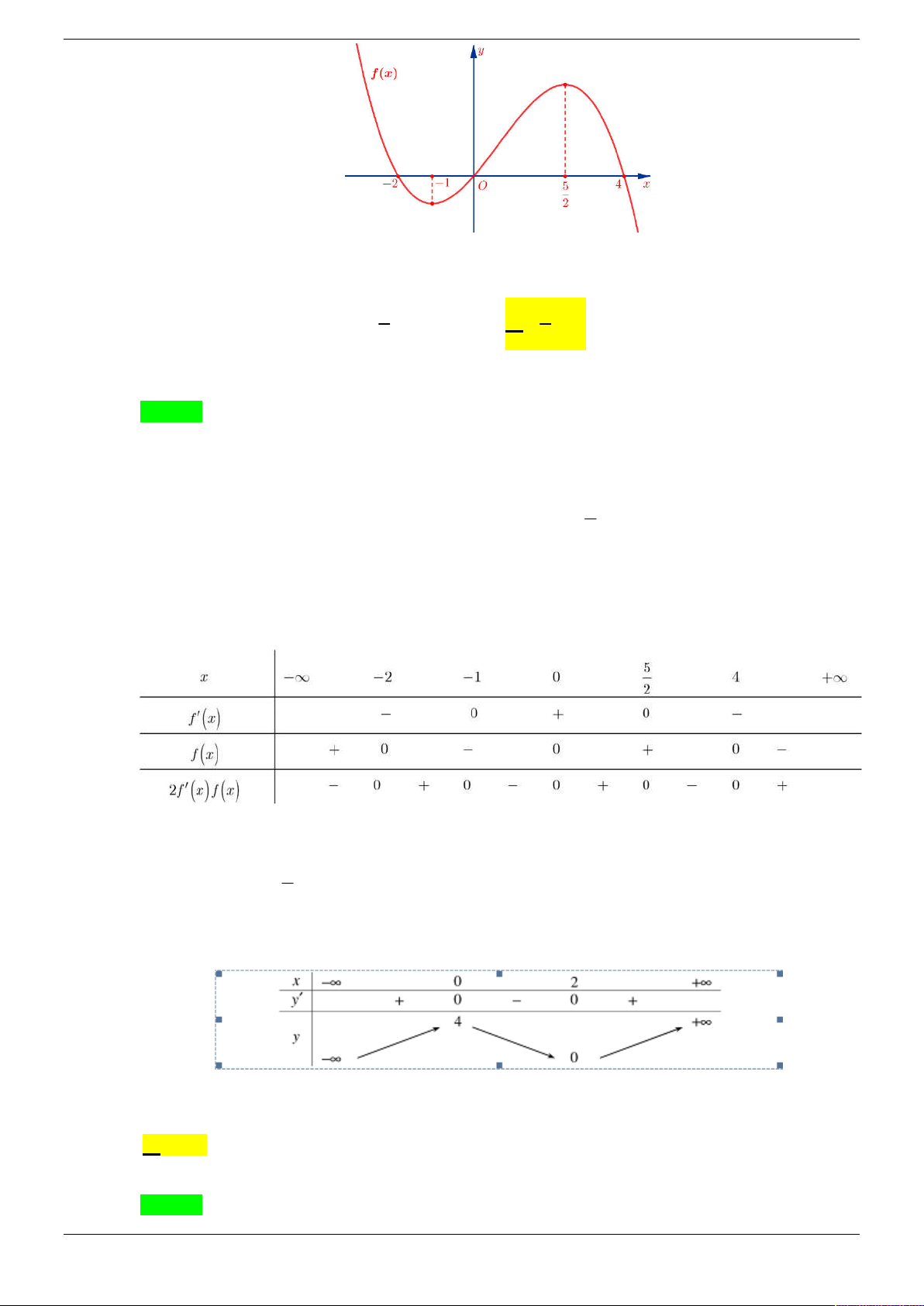
Câu 30. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ . Strong Team Toán VD – VDC Trang 7/50
Xét hàm số g  x  f  3 2x  x   1  .
m Tìm m để max g  x  10. 0;  1
A. m  3 . B. m  1  2 . C. m  1  3 . D. m  6 .
Câu 31. Cho hàm số f  x có đạo hàm trên  là f  x   x  
1  x  3 . Có bao nhiêu giá trị nguyên
của tham số m thuộc đoạn  10 
; 20 để hàm số y  f  2
x  3x  m đồng biến trên khoảng 0;2 ? A. 18 . B. 17 . C. 16 . D. 20 . 2 3
Câu 32. Cho các hàm số f  x 3
 x  4x  m và g  x   2 x   2 x    2 2018 2019
x  2020 . Có bao
nhiêu giá trị nguyên của tham số m  20 
20; 2020 để hàm số g  f  x đồng biến trên 2; ? A. 2005 . B. 2037 . C. 4016 . D. 4041 . Câu 33. Cho hàm số 2
y  f x  có đạo hàm f x   x x    2 1
x  2mx   1 với mọi x  .  Có bao nhiêu số
nguyên âm m để hàm số g x  f 2x  
1 đồng biến trên khoảng 3;  5 ? A. 3 B. 2 C. 4 D. 6
Câu 34. Cho hàm số f  x xác định và liên tục trên R . Hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ. 1
Xét hàm số g  x  f  x  2m  2m  x2  2020 , với m là tham số thực. Gọi S là tập hợp 2
các giá trị nguyên dương của m để hàm số y  g  x nghịch biến trên khoảng 3; 4 . Hỏi số
phần tử của S bằng bao nhiêu? A. 4 . B. 2 . C. 3 . D. Vô số.
Câu 35. Cho hàm số f  x liên tục trên  và có đạo hàm f  x 2
 x  x   2 2
x  6x  m với mọi
x   . Có bao nhiêu số nguyên m thuộc đoạn  20 
20; 2020 để hàm số g x  f 1 x
nghịch biến trên khoảng  ;    1 ? A. 2016 . B. 2014 . C. 2012 . D. 2010 .
Câu 36. Cho hàm số y  f (x) có đồ thị f (
 x) như hình vẽ. Có bao nhiêu giá trị nguyên  1  m  20  20; 2020 2
để hàm số g  x  f 2x  3  ln 1 x   2mx đồng biến trên ; 2   ?  2  Strong Team Toán VD – VDC Trang 8/50 y 4 -2 -1 0 1 x A. 2020 . B. 2019 . C. 2021 . D. 2018 .
Câu 37. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.
Hàm số g  x  f  2 x  x 3 2
 4x  3x  6x  2020 đồng biến trên khoảng nào sau đây?  1  A. 1  ;   . B.  2  ; 0 .  2  C. 1;  . D. 0  ;1 .
Câu 38. Cho hàm số y  f  x xác định trên  và có bảng xét dấu đạo hàm như sau:
Biết f  x  2, x
   . Xét hàm số g  x  f   f  x 3 2 3 2
 x  3x  2020 . Khẳng định nào sau đây đúng?
A. Hàm số g  x đồng biến trên khoảng  2  ;   1 .
B. Hàm số g  x nghịch biến trên khoảng 0  ;1 .
C. Hàm số g  x đồng biến trên khoảng 3;4 .
D. Hàm số g  x nghịch biến trên khoảng 2;3 .
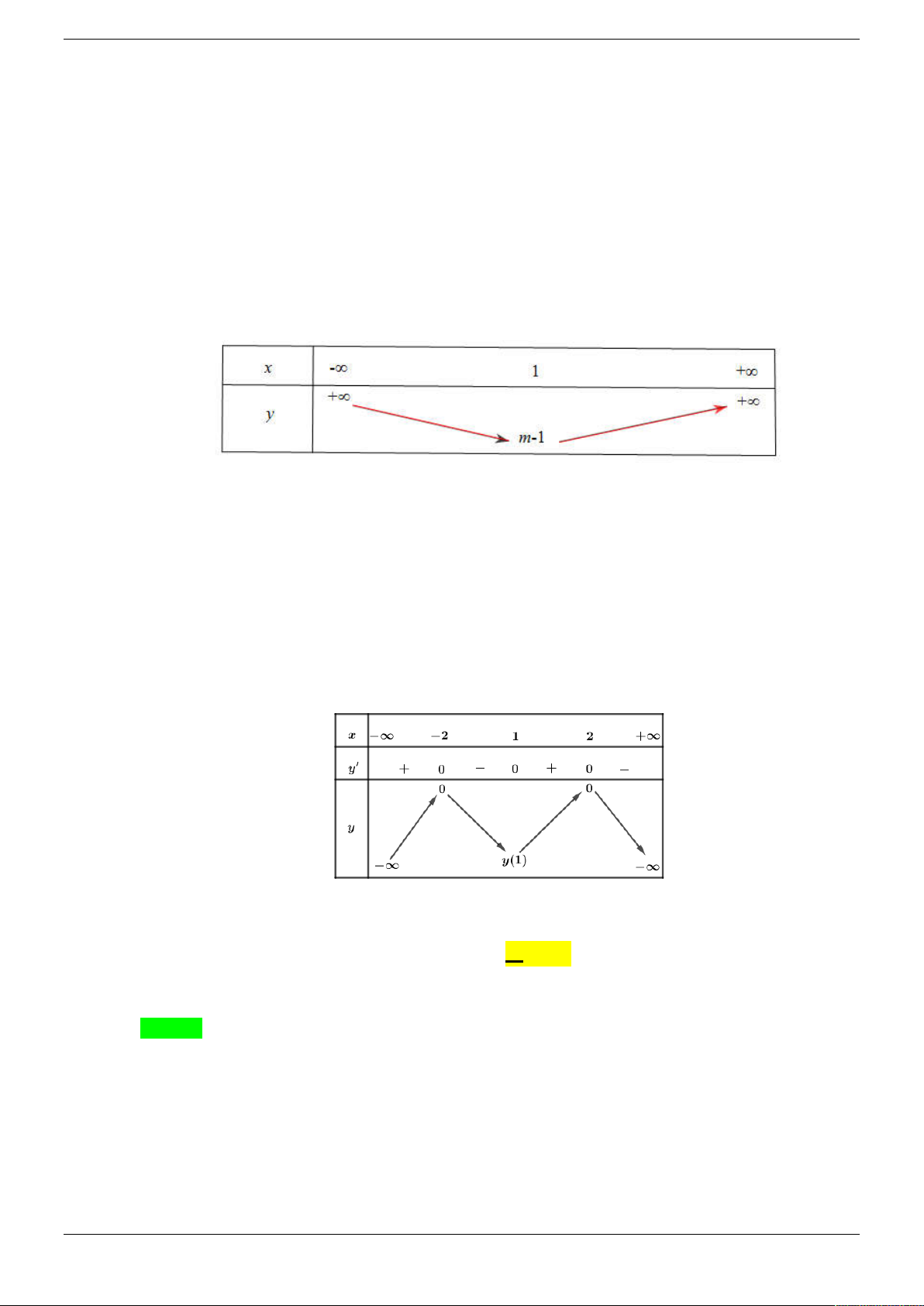
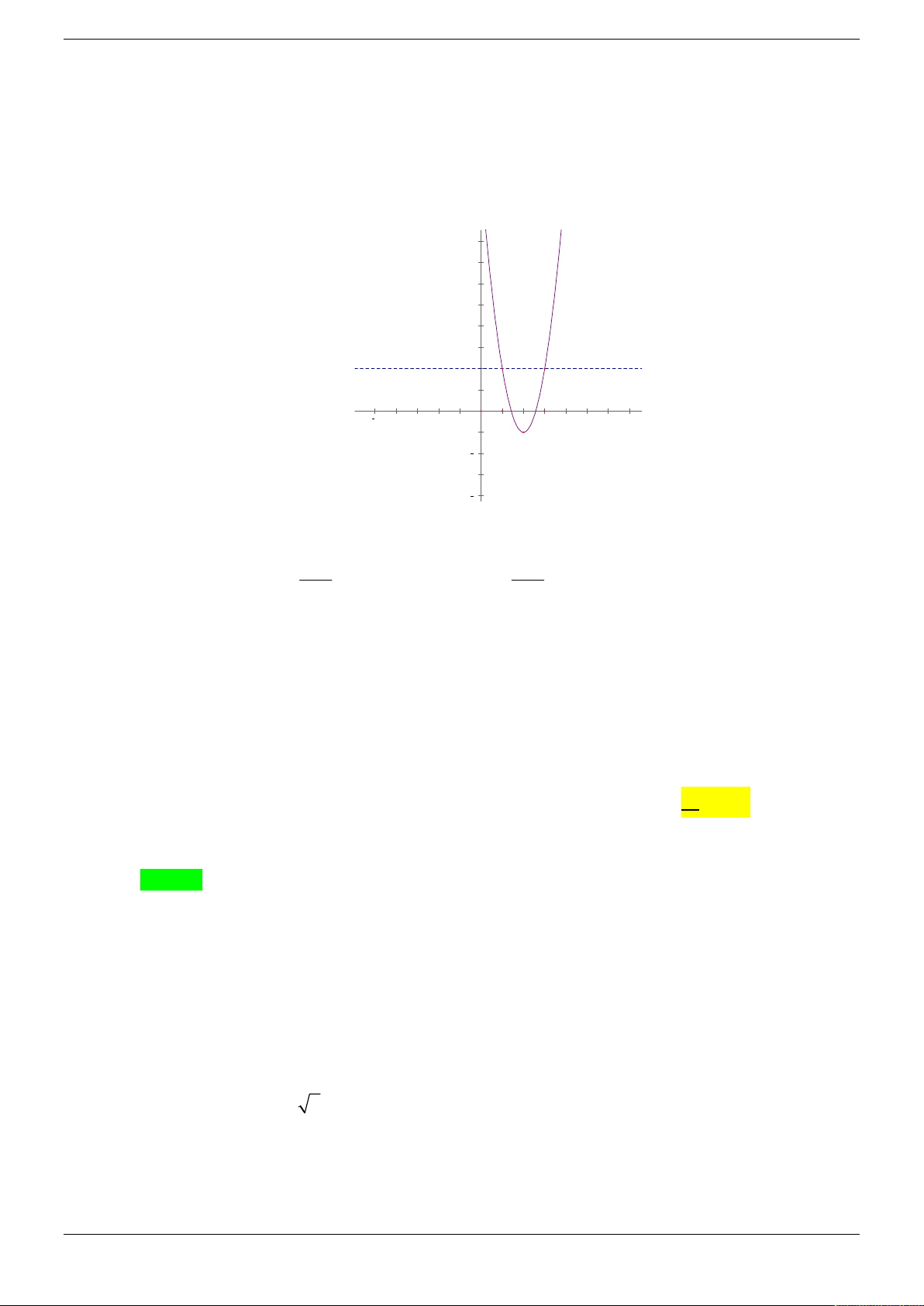
Câu 39. Cho hàm số y  f (x) xác định trên  . Hàm số y  g(x)  f '2x  3  2 có đồ thị là một
parabol với tọa độ đỉnh I 2;  
1 và đi qua điểm A1; 2 . Hỏi hàm số y  f (x) nghịch biến
trên khoảng nào dưới đây? A. 5;9 . B. 1; 2 . C.  ;  9 . D. 1;3 . Câu 40. Cho hàm số
y  f  x có đạo hàm cấp 3 liên tục trên  và thỏa mãn 2
f  x f  x  x  x  2  x  3 . 1
4 với mọi x   và g  x   f  x  2 f  x. f   x   . Hàm số
h  x  g  2
x  2x đồng biến trên khoảng nào dưới đây? Strong Team Toán VD – VDC Trang 9/50 A.   ;1  .
B. 2;  . C. 0  ;1 . D. 1; 2 .
Câu 41. Cho hàm số y  f (x) liên tục trên  . Biết rằng hàm số y  f '(x) có đồ thị như hình vẽ. Hàm số 2
y  f (x 5
 ) nghịch biến trên khoảng nào sau đây ? A. ( 1  ;0) . B. (1; 2) . C. ( 1  ;1) . D. (0;1)
Câu 42. Cho hàm số y  f (x ) . Hàm số y  f '(x) có đồ thị như hình vẽ bên. y
y  f '(x ) O 1 1 4 x Hàm số 2
y  f (x ) đồng biến trên khoảng  1 1  1  A.   ;     B. 0;2 C.   ;0 D.  2;    1  2 2  2 
Câu 43. Cho hàm số y  f  x. Hàm số y  f  x có đồ thị như hình bên. y x -4 -3 -2 -1 1 2 3 4 5 6 7
Hàm số y  f 3  2x nghịch biến trên khoảng A.  1  ;  B. 0; 2 C.  ;    1 D. 1;3
Câu 44. Cho hàmsố y  f (x) có đạo hàm trên  . Đường cong trong hình vẽ dưới là đồ thị của hàm số
y  f '( x) . Xét hàm số 2
g(x)  f (3  x ) . y -1 O 3 x
Mệnh đề nào dưới đây là đúng?
A. Hàm số g(x) đồng biến trên (;1) .
B. Hàm số g(x) đồng biến trên (0; 3) .
C. Hàm số g(x) nghịch biến trên (1; ) . Strong Team Toán VD – VDC Trang 10/50
D. Hàm số g(x) nghịch biến trên ( ;  2) và (0; 2) .
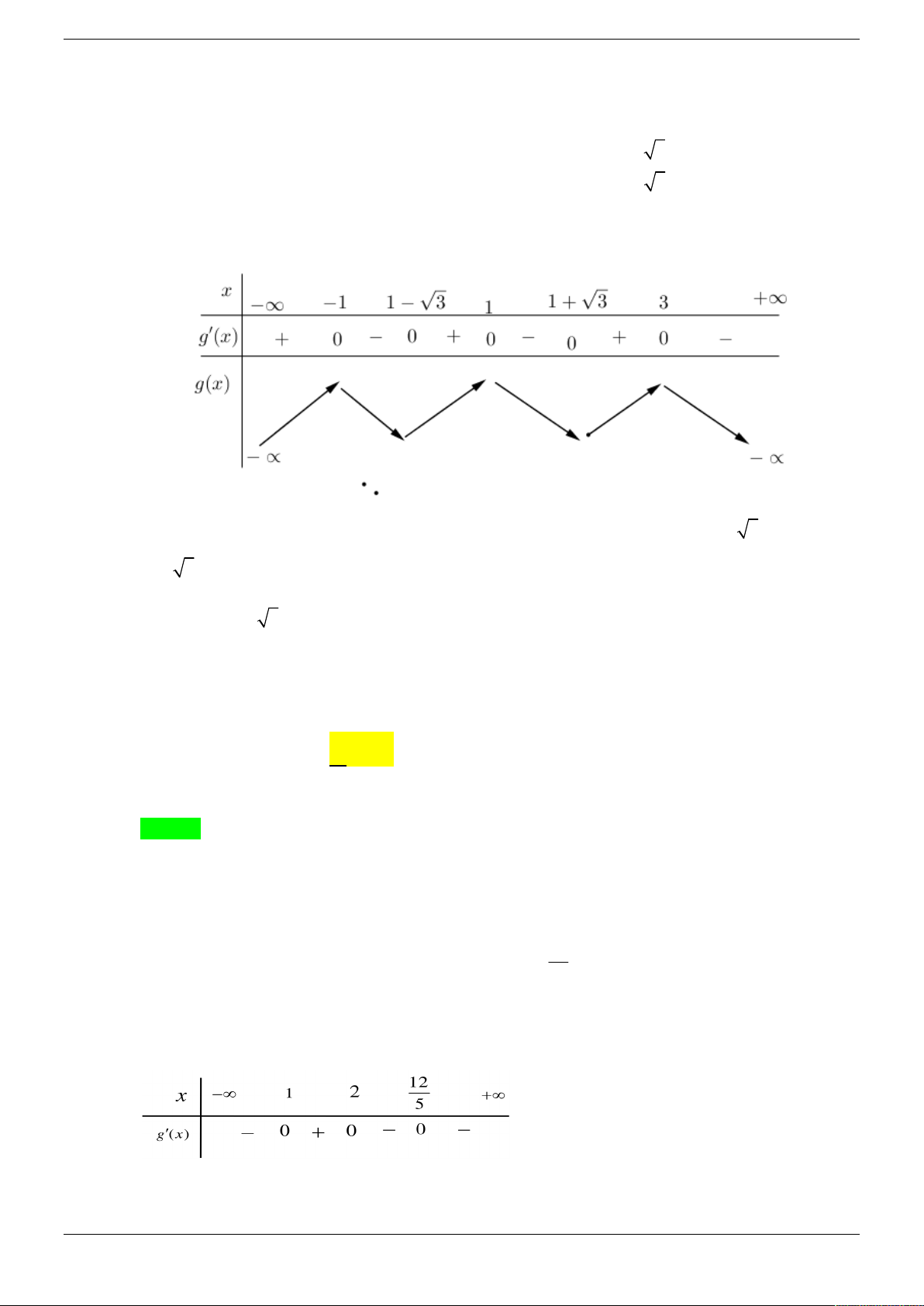
Câu 45. Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ. Hàm số  2 x y f
 e  nghịch
biến trên khoảng nào sau đây? y x 0 1 2 3 -4 A. 0;  . B.  ;  0 . C.  1  ;3 . D.  2   ;1 .
Câu 46. Cho hàm số f  x có đạo hàm liên tục trên  và có đồ thị của hàm y  f  x như hình vẽ.
Xét hàm số g x  f  2 ( )
x  2 . Mệnh đề nào dưới đây sai? y O 1 2 x 1 2 4
A. Hàm số g(x) đồng biến trên 2; .
B. Hàm số g(x) nghịch biến trên 0; 2.
C. Hàm số g(x) nghịch biến trên  1  ; 0.
D. Hàm số g(x) nghịch biến trên  ;  2  .
Câu 47. Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình bên. Hàm số y  f 2  x đồng biến trên khoảng: A. 1;3 . B. 2;  . C.  2   ;1 . D.  ;  2 .
Câu 48. Cho hàm số y  f  x có đạo hàm là hàm số f  x trên  . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x nghịch biến trên khoảng nào? Strong Team Toán VD – VDC Trang 11/50  3 5  A. ; 2 . B. 1;  1 . C. ;   . D. 2;  .  2 2 
Câu 49. Cho hàm số y  f  x có đạo hàm là hàm số f  x trên  . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x đồng biến trên khoảng nào?
A. ;3, 5;  . B. ;  
1 , 1;  . C. 1;  1 . D. 3;5 .
Câu 50. Cho hàm số y  f  x có đạo hàm là hàm số f  x trên  . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x nghịch biến trên khoảng nào? A. 3;   1 , 1;3 . B. 1;  1 , 3;5 .
C. ; 2, 0; 2 .
D. 5; 3, 1;  1 .
-------------------- HẾT -------------------- Strong Team Toán VD – VDC Trang 12/50 BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.B 5.C 6.A 7.D 8.A 9.B 10.D 11.C 12.C 13.D 14.C 15.C 16.D 17.A 18.C 19.A 20.C 21.D 22.B 23.B 24.D 25.A 26.C 27.C 28.D 29.C 30.C 31.A 32.B 33.A 34.B 35.C 36.B 37.D 38.D 39.A 40.D 41.D 42.C 43.C 44.D 45.B 46.C 47.C 48.B 49.B 50.B
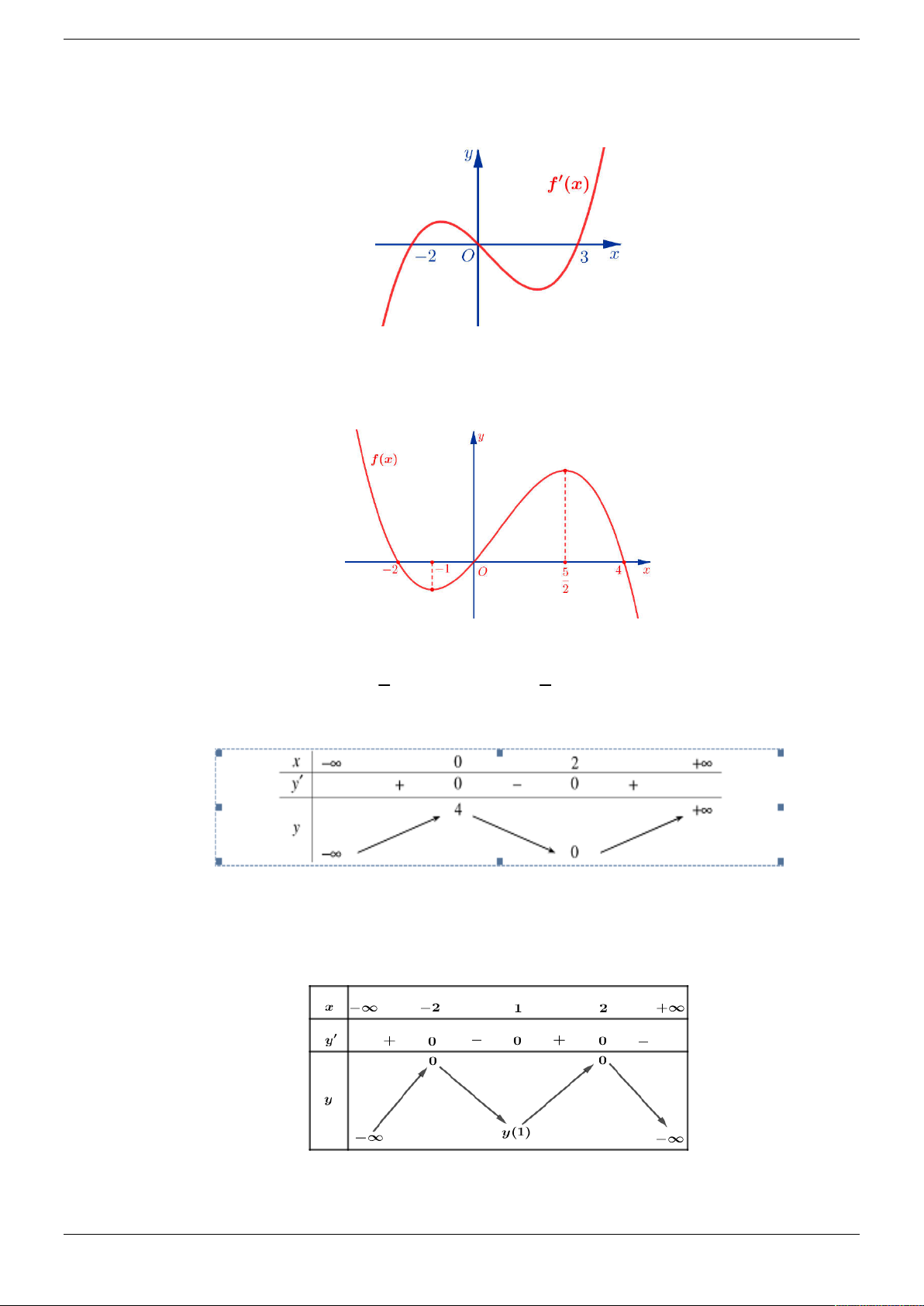
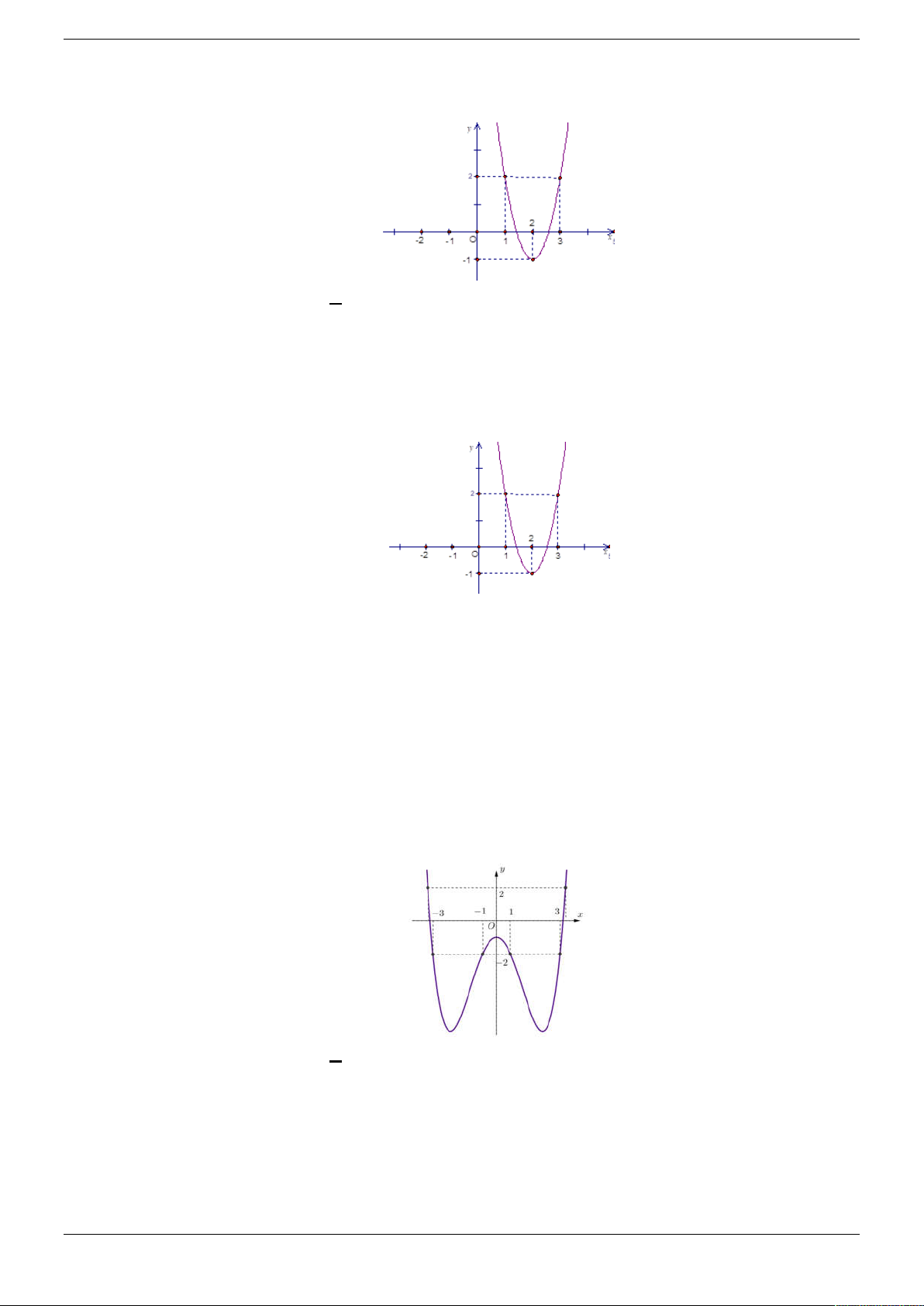
LỜI GIẢI CHI TIẾT Câu 1.
Cho đồ thị hàm số y  f 2  x như hình vẽ
Hàm số y  f  2
x  3 nghịch biến trên khoảng nào dưới đây? A. 0;1 . B. 1;3 . C. ;   1 . D.  1  ; 0 . Lời giải Chọn A
Gọi C là đồ thị hàm số y  g  x  f 2  x .
Tịnh tiến C sang trái 2 đơn vị ta được đồ thị hàm số y  g  x  2  f x .
Lấy đối xứng đồ thị hàm số y  f  x qua Oy ta được đồ thị hàm số y  f  x . Strong Team Toán VD – VDC Trang 13/50
Ta có y  f  2
x    y  x f  2 3 2 . x  3 .  x  0 x  0  x  0   2 y  0  
 x  3  0  x   3 . f    2   x  3  0  2  x  3  3   x   6  Bảng xét dấu y
Vậy hàm số y  f  2
x  3 nghịch biến trên khoảng 0;1 . Câu 2.
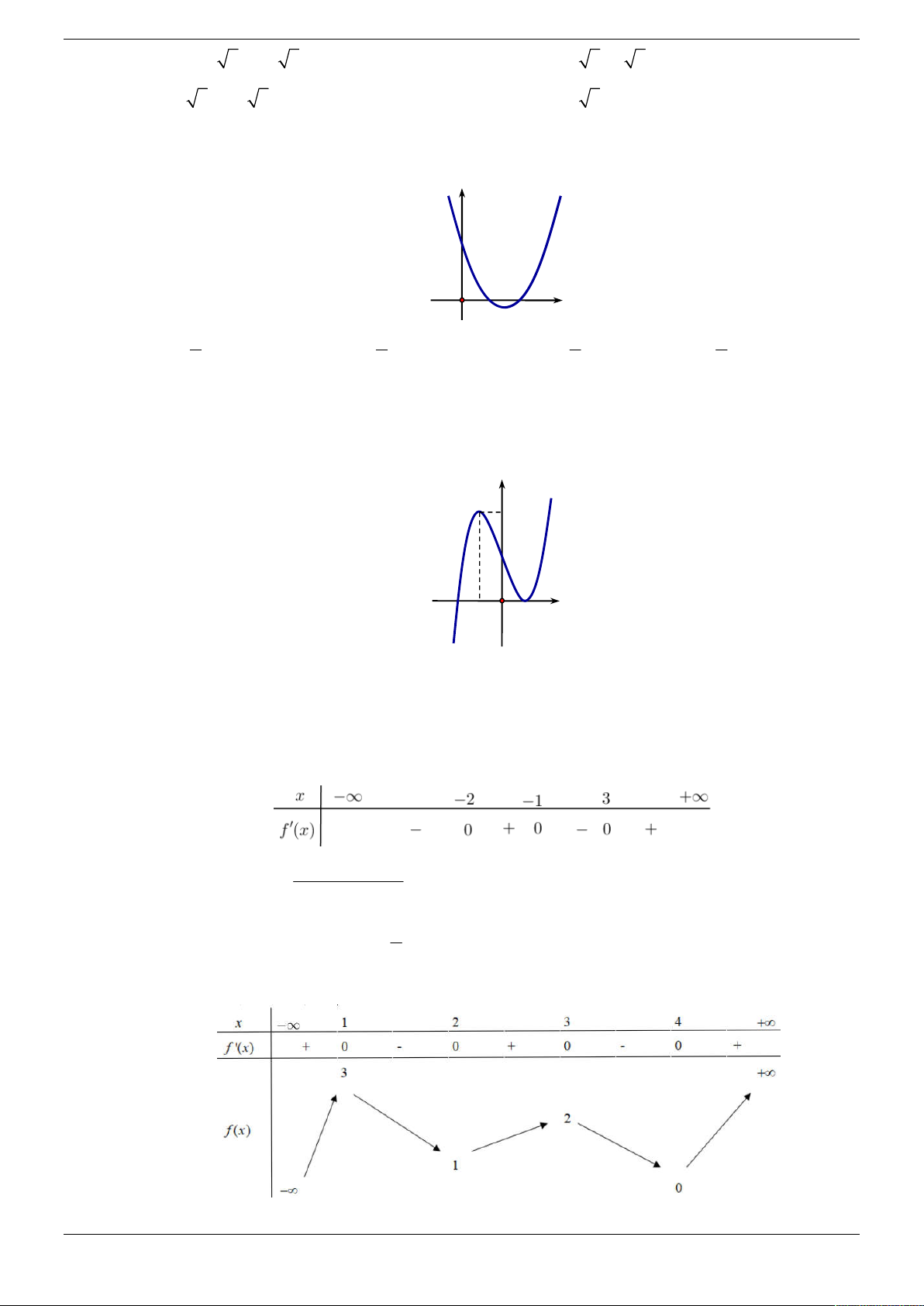
Cho hàm số f  x có bảng xét dấu đạo hàm f  x như sau:
Hàm số y  f  2
x  2x nghịch biến trên khoảng nào dưới đây? A.  2   ;1 . B.  4  ;  3 . C. 0  ;1 . D.  2  ;   1 . Lời giải Chọn D
Đặt: y  g  x  f  2
x  2x ; g x   f  2
x  2x    x   f  2 2 2 . x  2x .  x  1  2x  2  0 2 x  2x  2  vo ânghieäm g x 
 0   x   f  2 2 2 .
x  2x  0    f   2   2
x  2x  0  x  2x  1  2
 x  2x  3  Strong Team Toán VD – VDC Trang 14/50 x  1  x  1   2    x  1   2 . ( x  1
  2 là các nghiệm bội chẵn của phương trình: 2
x  2x  1 ).  x  1 x  3   Ta có bảng biến thiên:
Dựa vào bảng biến thiên, suy ra hàm số y  f  2
x  2x nghịch biến trên khoảng  2  ;   1 .
Chú ý: Cách xét dấu g x :
Chọn giá trị x  0   1;  1 2  2
 x  2x  0  g0  f 0  0 (dựa theo bảng xét dấu
của hàm f  x ). Suy ra g x  0 , x    1;
 1 2  . Sử dụng quy tắc xét dấu đa thức “lẻ
đổi, chẵn không” suy ra dấu của g x trên các khoảng còn lại. Câu 3.
Cho hàm số y  f  x liên tục trên  và hàm số y  f  x có đồ thị như hình vẽ.
Hàm số y  g  x  f  2
1 2x  x   2020 đồng biến trên khoảng nào dưới đây? A. 1; 0 . B. 0;1 . C. 2;3 . D. 3;5 . Lời giải Chọn B
Ta có g x    x f  2 2 2 .
1 2x  x  . Strong Team Toán VD – VDC Trang 15/50  x  1   x  1  x  1 2  2x  0 
g x  0   2
 1 2x  x  2   x  3 . f      2
1 2x  x   0  2 1
  2x  x  1   x  1 3   x  1   3 Bảng biến thiên:
Dựa vào bảng biến thiên hàm số g  x đồng biến trên khoảng ;   1 và 1 3;  1 và 1 3;3.
Mà (0;1)  (1 3;1) nên hàm số y  g  x  f  2
1 2x  x   2020 đồng biến trên (0;1) . 2 3 Câu 4.
Cho hàm số y  f x  có đạo hàm f  x  x. x  2  x  5 . Hàm số g x  f 10  5x
đồng biến trên khoảng nào dưới đây? ;  1 1;2 2; 1;3 A. . B. . C. . D. . Lời giải Chọn B
Ta có g  x   10  5x  
. f 10  5x   5. f 10  5x  .  x  2 10   5x  0 
gx   f   x  12 0 10 5
 0  10  5x  2   x   .  5 10   5x  5   x  1  Bảng xét dấu g (  x)
Vậy hàm số g  x đồng biến trên khoảng 1;2 . Strong Team Toán VD – VDC Trang 16/50 Câu 5.
Cho hàm số y  f (x) có đạo hàm 2 f (
 x)  x(x 1) (x  2) với mọi giá trị thực của x . Xét hàm  5x 
số g(x)  f 
. Trong các khẳng định sau khẳng định nào đúng? 2   x  4 
A. Hàm số đồng biến trên khoảng (0;1) .
B. Hàm số nghịch biến trên khoảng (0; 4) .
C. Hàm số đạt cực đại tại x  0 .
D. Hàm số đạt giá trị nhỏ nhất tại x  1 . Lời giải Chọn C   5x   5x  Ta có: g x  f   2   2   x  4   x  4  2 2
20  5x  5x   5x   5x   1  2 , x          . x  2 2 2 2 2
 x  4   x  4   x  4 4  2  20  5x  0    x  42 2  x  2 5x   0 x  0 2 g (
 x)  0   x  4   .   5x x  1   1  2  x  4 x  4   5x   2 2  x  4
Bảng biến thiên của hàm số y  g(x) :
Vậy hàm số y  g(x) đạt cực đại tại x  0 . Câu 6.
Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình bên. Strong Team Toán VD – VDC Trang 17/50
Hỏi hàm số g  x  f  2 x  x 2 2
 6x  3x đồng biến trên khoảng nào dưới đây?  1   1  A.  ; 0   . B. ;1   . C. 0;  1 . D. ;0 .  4   4  Lời giải Chọn A
Ta có: g  x  f  2 x  x 2 2  6x  3x
 g x   x   f  2 4 1
2x  x 12x  3   x    f  2 4 1
2x  x  3 .    1 x   4   x  1  1 x   1  4  x     2 2 4x 1  0
2x  x  1voânghieäm  x  0
g x  0     2   . f  2
2x  x  3   2x  x  1 1    x   2 2x  x  0  2    2
2x  x  2nghieäm keùp 1 17   x  nghieäm keùp  4  1  17 x  nghieäm keùp  4
Ta có : g '2  9 f '(10)  3 dựa vào đồ thì f ' x ta thấy f '10  3  f '10  3  0
 g '2  0 .
Ta có bảng xét dấu như sau: Strong Team Toán VD – VDC Trang 18/50  1   1 1   1 17   1 17 
Xét dấu g x ta được g x  0, x    ;0  ;      1;    ;   . 2 4 2  4   4           1   1 1   1 17 
Suy ra g  x đồng biến trên các khoảng  ;0   và ;   và 1;  và  2   4 2   4     1 17   ;   .  4     1   1  Mà  ; 0   ; 0 2 2   
 nên hàm số g  x  f 2x  x  6x  3x đồng biến trên khoảng  4   2   1   ; 0   .  4  2 2 Câu 7.
Cho hàm số y  f  x có đạo hàm f ' x  (3  x)10  3x  x  2 với mọi x  . Hàm số 1
g  x  f 3  x 2 3 
(x 1) đồng biến trên khoảng nào trong các khoảng sau? 6  1  A.  ;  0. B. 0;  1 . C. 1;. D. ;  .    2  Lời giải Chọn D
Ta có g  x   f   x 2 2 ' ' 3  x(x 1) . 2 2 2 2
Theo giả thiết f ' x  (3  x)10  3x  x  2 nên f '3  x  x 3x   1 1 x 2 2
Từ đó suy ra g  x  x x     x 2 2 ' 3 1 1  x(x 1) 2 2 2 2 2
 x(x 1) (3x 1)  (x 1)   x(x 1) ( 8  x  4x) 2 2  
 x (x 1) ( 8  x  4) 
 x  0 (nghiÖm kÐp) 
Khi đó g ' x   0  x   1(nghiÖm kÐp)  1  x    2 Bảng biến thiên  1 
Khi đó hàm số đồng biến trên ;  .    2  Strong Team Toán VD – VDC Trang 19/50 Câu 8.
Cho hàm số f  x có bảng biến thiên như sau 3 2
Hàm số y   f  x  3 f  x nghịch biến trên khoảng nào dưới đây? A. 2;  3 . B. 1;2 . C. 3;4 . D. ;  1 . Lời giải Chọn A 2
Ta có y  3 f  x . f  x  6 f  x. f  x .
y  3 f   x. f  x  f  x  2   .
 f  x  0  y  0  f   x  0 .
 f x  2  x  1
 x  x  x ;1 2  1    x  2 x  x  1 x  x  1; 2  3  
+ f  x  0   ; f  x 1  0 
; f  x  2  .   x  3 x  4   x  x  4  4  x  4   x  3 
+ Bảng xét dấu của y 3 2
Từ bảng xét dấu suy ra hàm số y   f  x  3 f  x nghịch biến trên khoảng 2;  3 . Câu 9.
Cho hàm số y  f  x , hàm số f  x 3 2
 x  ax  bx  c a, ,
b c   có đồ thị như hình vẽ Strong Team Toán VD – VDC Trang 20/50
Hàm số g  x  f  f  x nghịch biến trên khoảng nào dưới đây?  3 3  A. 1;  . B.  ;  2   . C.  1  ; 0 . D.   ;  .  3 3    Lời giải Chọn B Vì các điểm  1
 ; 0,0;0,1;0 thuộc đồ thị hàm số y  f  x nên ta có hệ:  1
  a  b  c  0 a  0   c  0  b   1
  f  x 3
 x  x  f '  x 2  3x 1 1  a b c 0      c  0  
Ta có: g  x  f  f  x  g x  f  f  x. f '  x 3 x  x  0  3 x  x  1 
Xét g x  0  g x  f  f ' x. f  x  0  f  3 x  x 2 3x   1  0   3 x  x  1  2 3x 1  0    x  1   x  0 
 x  x (x  1,325 ) 1 1 
 x  x (x  1  ,325) 2 2   3 x    3 Bảng biến thiên
Dựa vào bảng biến thiên ta có g  x nghịch biến trên  ;  2   Strong Team Toán VD – VDC Trang 21/50
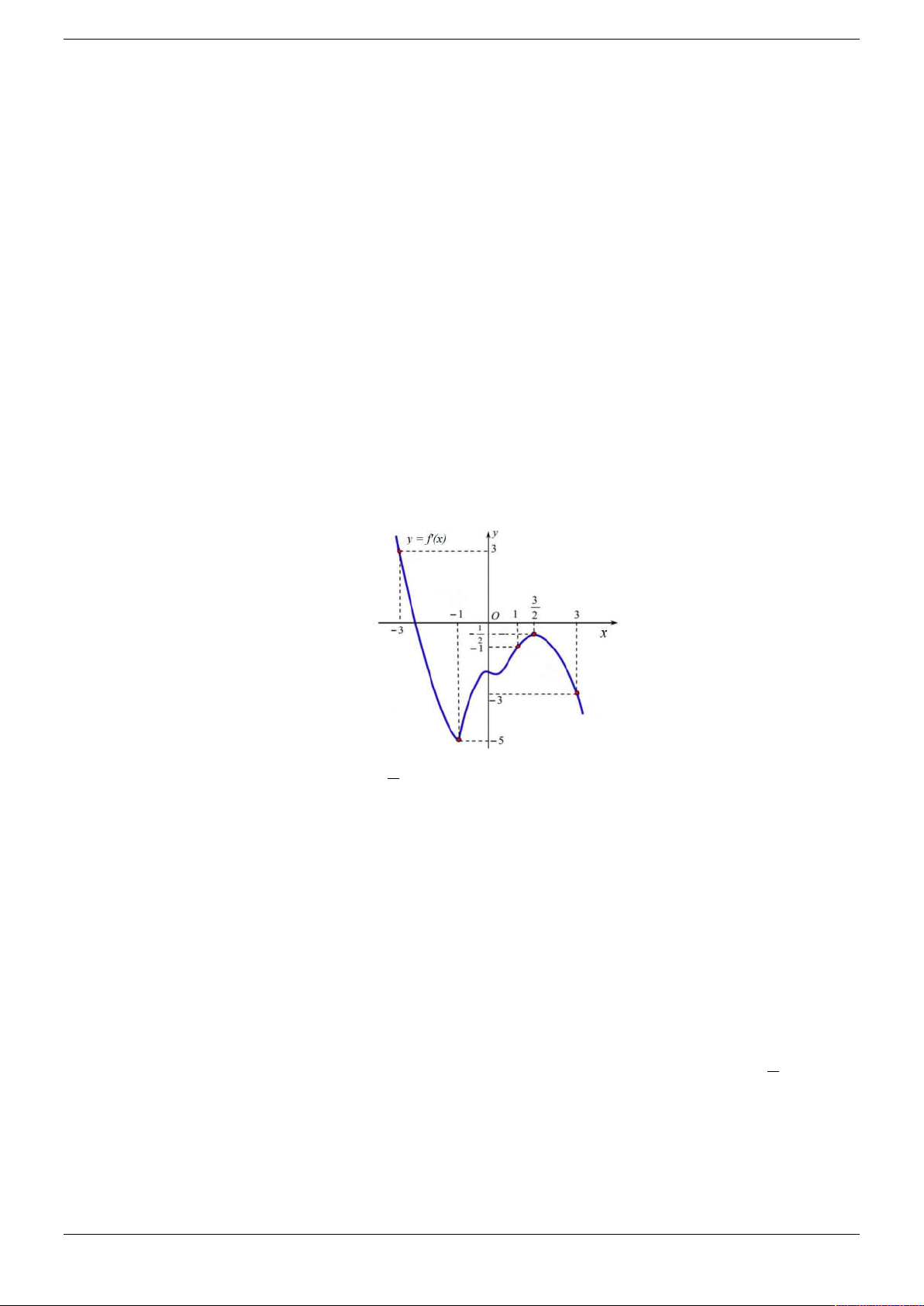
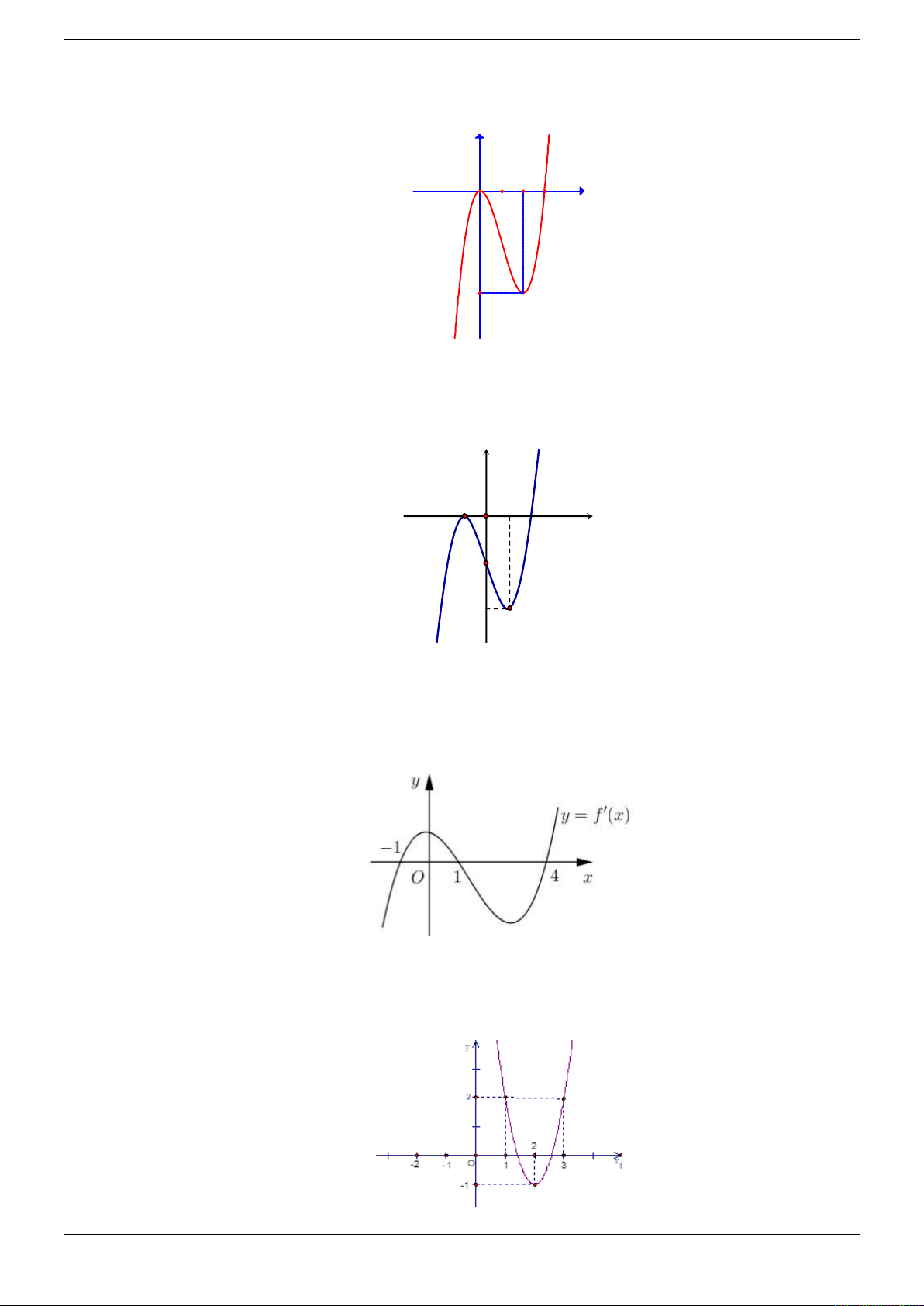
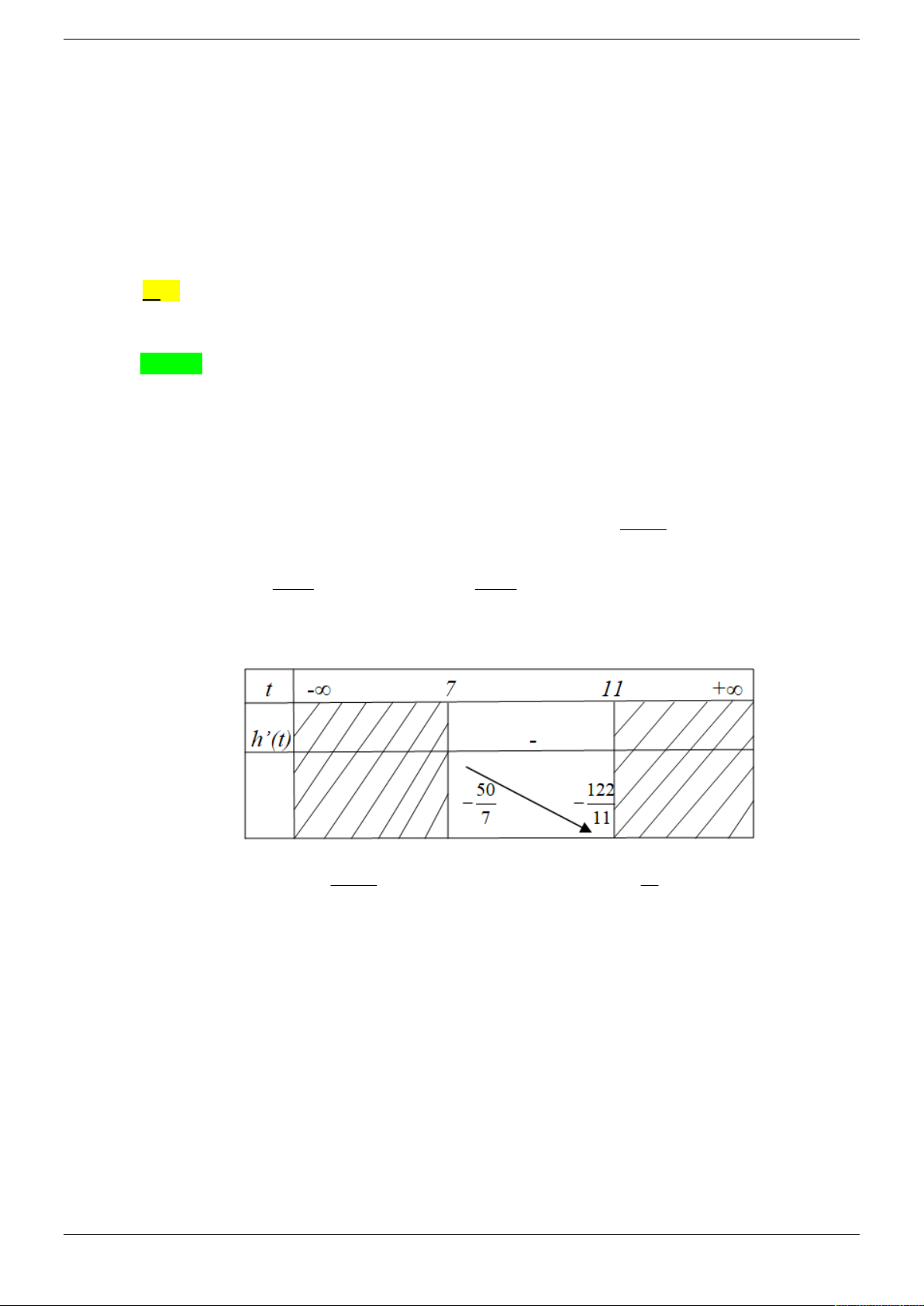
Câu 10. Cho hàm số y  f  x liên tục có đạo hàm trên  . Biết hàm số f ' x có đồ thị cho như hình
vẽ. Có bao nhiêu giá trị nguyên của m thuộc  2
 019; 2019 để hàm só    2019x g x f
  mx  2 đồng biến trên 0  ;1 A. 2028 . B. 2019 . C. 2011 . D. 2020 Lời giải Chọn D
Ta có '   2019x ln 2019. '2019x g x f   m. Ta lại có hàm số 2019x y  đồng biến trên 0  ;1 . Với x 0; 
1 thì 2019x 1; 2019 mà hàm y  f ' x đồng biến trên 1;  nên hàm  '2019x y f
 đồng biến trên 0  ;1 Mà 2019x  1; '2019x f
  0 x0 
;1 nên hàm    2019x ln 2019. '2019x h x f  đồng biến trên 0  ;1
Hay h  x  h 0  0, x 0  ;1
Do vậy hàm số g  x đồng biến trên đoạn0 
;1  g ' x  0, x 0  ;1 
 2019x ln 2019. '2019x m f , x0 
;1  m  min h  x  h 0  0 x   0;  1
Vì m nguyên và m  20 
19; 2019  có 2020 giá trị m thỏa mãn yêu cầu bài toán.
Câu 11. Cho hàm số y  f  x có đạo hàm trên  và có đồ thị hàm f  x như hình vẽ dưới đây. Hàm số     2 g x
f x  x  đồng biến trên khoảng nào?  1   1  A. ;1   . B. 1; 2 . C. 1  ;   . D. ;   1 .  2   2  Strong Team Toán VD – VDC Trang 22/50 Lời giải Chọn C     2 g x
f x  x   g x   x   f  2 2 1 x  x .  1 x  1   2 x    2 x  0 2x 1 0     g  x 2 0  x x 0         x  1 . f    2 x  x  0    2 x  x  2  x  1     x  2    x  2
Từ đồ thị f   x ta có f  2 x  x 2
 0  x  x  2   , x  1  
Xét dấu g x :  1 
Từ bảng xét dấu ta có hàm số g  x đồng biến trên khoảng 1  ;   .  2 
Câu 12. Cho hàm số y  f  x có đạo hàm trên  . Biết hàm số y  f  x  liên tục trên  và có đồ thị
như hình vẽ. Hàm số y  f  2
x 1 đồng biến trong khoảng nào dưới đây?
A. ; 3,0; 3 .
B. ;  3, 3; . Strong Team Toán VD – VDC Trang 23/50
C.  3;0, 3; .
D. ; 3,0; . Lời giải Chọn C x
Xét hàm số y  f  2
x 1  y  f  2 x 1 . 2  x 1  x  0  2  x 1  1   x  0  x  0 x  0  x  0     y  0   2  x 1  0 2 2 
  x 1  1  x 1  1  x   3   f  2 x 1  0     2 2   x 1  1 2 x 1  4   x 1  2   x  3   2 x 1  2  Bảng biến thiên
Vậy hàm số y  f  2
x 1 đồng biến trên các khoảng  3;0, 3; .
Câu 13. Cho hàm số y  f  x . Hàm số y  f  x  có đồ thị như hình bên. Hàm số   2 y f x  x 
nghịch biến trên khoảng nào dưới đây. y 2 O 1 2 x  1   3   3   1  A.  ;    . B.  ;    . C.  ;    . D. ;    .  2   2   2   2  Lời giải Chọn D  Đặt      2 y g x
f x  x   g x  f  2 x  x   2
x  x     x f  2 . 1 2 x  x  1   2x  0 1   2x  0  1
Cho g x  0   2
 x  x  1  ptvn  x  . f    2
x  x   0   2 2
x  x  2 ptvn   Strong Team Toán VD – VDC Trang 24/50 2  x  1
 x  x  1
Ta có f ' x  0   f   2
x  x   0  
( Luôn đúng với mọi x   ) 2 x  2  x  x  2  1
Vậy g ' x  0  1 2x  0  x  . 2  1  Hay hàm số     2 g x
f x  x  nghịch biến trên khoảng ;    .  2 
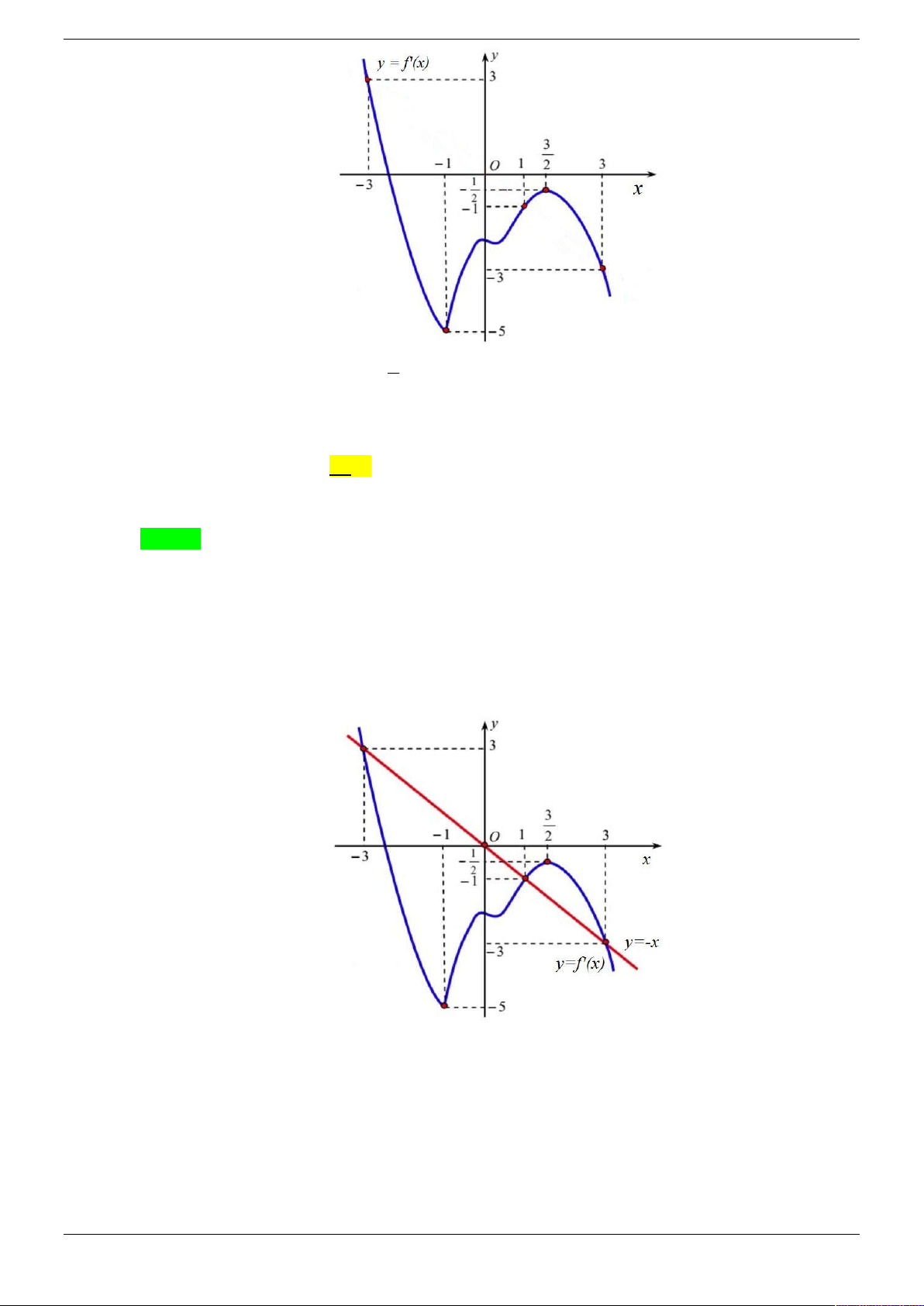
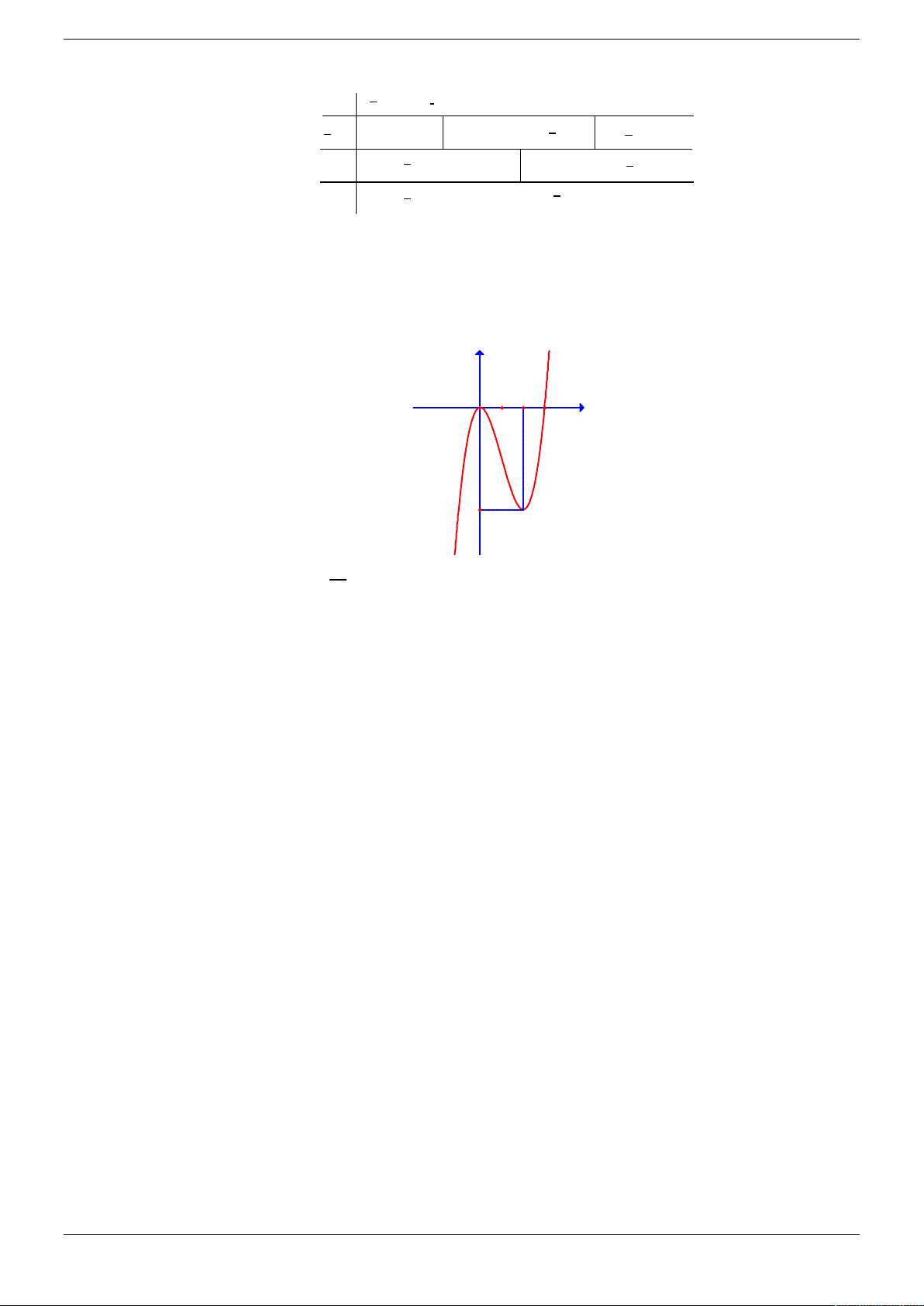
Câu 14. Cho hàm số y  f  x có đạo hàm trên  . Đường cong trong hình vẽ bên là đồ thị của hàm số
y  f   x  ( y  f  x  liên tục trên  ). Xét hàm số g  x  f  2
x  3 . Mệnh đề nào dưới đây sai? y 4 2 2  1  O 1 x
A. Hàm số g  x đồng biến trên 1; 0 .
B. Hàm số g  x nghịch biến trên ;   1 .
C. Hàm số g  x nghịch biến trên 1; 2 .
D. Hàm số g  x đồng biến trên 2;  . Lời giải Chọn C 
g x   f  2 x  3   2 
x   f  2 3
x  3  xf  2 2 x  3
Ta có f  x  0  x  2
 nên f '(x2  3)  0 2  x  3  2  2  x  1  1   x  1. Ta có bảng xét dấu: x  2 1  0 1 2  2x - | - | - 0 + | + | + f '(x2  3) + 0 + 0 - | - 0 + 0 + g '(x) - 0 - 0 + 0 - 0 + 0 +
Từ bảng xét dấu ta thấy đáp án C đúng
Câu 15. Cho hàm số y  f  x có đồ thị nằm trên trục hoành và có đạo hàm trên , bảng xét dấu của
biểu thức f   x như bảng dưới đây. f  2 x  2x
Hàm số y  g  x 
nghịch biến trên khoảng nào dưới đây? f  2 x  2x 1 Strong Team Toán VD – VDC Trang 25/50  5 
A. ;1 . B. 2;   . C. 1; 3 . D. 2;   .  2  Lời giải Chọn C  2 
x  2x . f  2 x  2x
2x  2. f  2 x  2x
g  x   .
 f x  2x  2 1
 f x  2x  2 2 2 1  x  1 2  x  1 2x  2  0     g  x x 2x 2  0        f  2 x  x 2 x 1 2  0
 x  2x  1   x  3  2 x  2x  3  
Ta có bảng xét dấu của g  x :
Dựa vào bảng xét dấu ta có hàm số y  g  x nghịch biến trên các khoảng  ;   1 và 1;3 .
Câu 16. Cho hàm số f  x  có bảng biến thiên như sau: 3 2
Hàm số y   f  x  3. f  x nghịch biến trên khoảng nào dưới đây? A. 1; 2 .
B. 3 ; 4 . C.  ;  1 . D. 2 ; 3 . Lời giải Chọn D 2
Ta có y  3. f  x . f  x  6. f  x. f  x
= 3f  x. f  x. f  x  2  
 f  x  0  x x , 4 | x  1 1 1   y  0  f
  x  2  x x , x , 3, x | x  x  1  x  2; 4  x 2 3 4 1 2 3 4 
 f 'x  0  x1,2,3,  4  Strong Team Toán VD – VDC Trang 26/50
Lập bảng xét dấu ta có
Do đó ta có hàm số nghịch biến trên khoảng 2 ; 3 .
Câu 17. Cho hàm số y  f  x đạo hàm liên tục trên  có đồ thị hàm số f  x như hình vẽ
Hỏi hàm số y  f  2
x  2x đồng biến trên khoảng nào sau đây? A.  1  ; 0 . B. 0  ;1 . C. 1;3 . D. 2;  . Lời giải Chọn A
Có y   x   f  2 2 2 x  2x  .  x  1 x  1   x  0 x  1 2 x  2x  2   Do đó y  0       x  2 . f  2    2
x  2x  0  x  2x  0   x  1 2 
x  2x  3   x  3 
Ta có bảng xét dấu đạo hàm như sau
Dựa vào bảng xét dấu đạo hàm, hàm số y  f  2
x  2x đồng biến trên các khoảng
1;0,1; 2,3;  .
Câu 18. Cho hàm số f  x có đạo hàm, liên tục trên , có đồ thị như hình vẽ Strong Team Toán VD – VDC Trang 27/50 Hỏi hàm số     2 y f x  
 nghịch biến trên khoảng nào sau đây?  5   5  A. 1  ;1 . B. 0;   . C. ; 4   . D. 2;   1 .  2   2  Lời giải Chọn C x  2 x  0 
 f  x  0  5
Có y  2 f  x f  x . Do đó y  0    x   .
 f  x  0  2  x  4 x  1 
Ta có bảng xét dấu đạo hàm như sau
Dựa vào bảng xét dấu đạo hàm, hàm số     2 y f x  
 nghịch biến trên các khoảng  5    ;  2  ,1;0, ; 4   .  2 
Câu 19. Cho hàm số y  f x có bảng biến thiên như sau
Có bao nhiêu số nguyên m  2019 để hàm số g x  f  2
x  2x  m đồng biến trên khoảng 1; ? A. 2016. B. 2015. C. 2017. D. 2018. Lời giải Chọn A Strong Team Toán VD – VDC Trang 28/50 
Ta có gx   2
x  x  m f  2
x  x  m  x   f  2 2 2 2 1
x  2x  m .
Hàm số y  g x đồng biến trên khoảng 1; khi và chỉ khi gx 0, x  1; và
g x  0 tại hữu hạn điểm  x   f  2 2 1
x  2x  m  0, x  1; 2
x 2x  m  2,x 1;   f  2
x  2x  m  0, x  1;   2
x  2x  m  0, x  1;    Xét hàm số 2
y  x 2x  m , ta có bảng biến thiên
Dựa vào bảng biến thiên ta có TH1: 2
x  2x  m  2, x  1;  m 1 2  m  3 . TH2: 2
x  2x  m  0, x  1; : Không có giá trị m thỏa mãn.
Vậy có 2016 số nguyên m  2019 thỏa mãn yêu cầu bài toán.
Câu 20. Cho hàm số y  f (x) có bảng biến thiên như sau:
Hàm số g x   f  x 2 ( ) (3
) nghịch biến trên khoảng nào trong các khoảng sau? A. ( 2  ;5) . B. (1; 2) . C. (2;5) . D. (5;  )  . Lời giải Chọn C
Từ bảng biến thiên suy ra f (x)  0, x
    f (3  x)  0, x    .
Ta có g '(x)  2
 f '(3  x). f (3  x) .   x    x 
Xét gx    f  x f  x   f  x 2 3 1 2 5 0 2 3 . 3 0 3 0     3x 2 x  . 1  
Suy ra hàm số g x  nghịch biến trên các khoảng ( ;  1) và (2;5) Strong Team Toán VD – VDC Trang 29/50
Câu 21. Cho hàm số y  f  x có đồ thị như hình vẽ. Hàm số y  f  x  đồng biến trong khoảng nào dưới đây ? A. 0  ;1 . B.  1   ;1 . C. 0; 2 . D. 1; 2 . Lời giải Chọn D
Thực hiện liên hoàn biến đổi đồ thị y  f  x thành đồ thị y  f  x , sau đó biến đổi đồ thị
y  f  x thành đồ thị y  f  x  .
Dựa vào đồ thị hàm số y  f  x  ta suy ra hàm số đồng biến trên khoảng 1; 2 .
Câu 22. Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới
Hàm số g  x  f  3  x  đồng biến trên khoảng nào trong các khoảng sau ? A.  ;    1 . B.  1  ; 2. C. 2;3. D. 4;7. Lời giải Strong Team Toán VD – VDC Trang 30/50 Chọn B  1   x  1 x  1 
Dựa vào đồ thị, suy ra f  x  0  
và f  x  0  .  x  4  1  x  4   1   x  3  1 2  x  4
Với x  3 khi đó g  x  f  x  3 
 g x  f  x  3  0     . x  3  4  x  7 
Do đó hàm số g  x đồng biến trên các khoảng 3; 4, 7;.
Với x  3 khi đó g  x  f 3 x 
 g x   f 3 x  0  f 3 x  0 3  x  1
 x  4 loai    
. Do đó hàm số g  x đồng biến trên khoảng  1  ; 2. 1  3  x  4  1  x  2 
Câu 23. Cho hàm số bậc ba y  f  x , hàm số y  f  x có đồ thị như hình vẽ. Hỏi hàm số
g  x  f  x  
1 nghịch biến trên khoảng nào dưới đây? A. 1,  . B.  1  , 0 . C.  1  , 2 . D. ,  1 . Lời giải Chọn B x
Ta có: g x 
f  x   1 . x  x  x  0 x  0  0 x   
Xét g x  0 
f  x   1  0 x 
  x 1  0   x  1  (L)    . x  
 f  x   1  0    x 1  2    x  1   x  0   x  1   .   x  1  Ta có bảng biến thiên: Strong Team Toán VD – VDC Trang 31/50
Từ bảng biến thiên thì ta có g  x  f  x  
1 nghịch biến trên khoảng  1  ,  1 và đồng biến trên khoảng ,   1  1,  .
Câu 24. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số 4 3 2
y  3x  4x 12x  m
nghịch biến trến khoảng  ;    1 ? A. 4 . B. 6 . C. 3 . D. 5 . Lời giải Chọn D
Xét hàm số f x 4 3 2
 x  x  x  m  f x 3 2 3 4 12 12x 12  x 24x x  1    f x 1  0  x   2  x  2  BBT:
Để hàm số y  f x nghịch biến trên  ;   
1  m 5  0  m  5
Do yêu cầu m là số nguyên nhỏ hơn 10 nên ta có m  5;6;7;8;  9
Vậy có 5 giá trị m thỏa yêu cầu..
Câu 25. Cho hàm số y  f  x . Đồ thị hàm số y  f  x như hình vẽ sau: Strong Team Toán VD – VDC Trang 32/50
Hàm số g  x  f  4  2x  nghịch biến trên khoảng nào sau đây?  1 3   5   3 5  A. ;   . B.  ;  2   . C. ; 7   . D. ;   .  2 2   2   2 2  Lời giải Chọn A
Trường hợp 1: x  2 . Khi đó g  x  f 4  2x .  x  3 4  2x  2 
Ta có g x  2
 f 4  2x , g x  0  f 4  2x  0      1 3 1  4  2x  3   x    2 2  1 3 
So điều kiện x  2 ta được g  x nghịch biến trên ;   .  2 2 
Trường hợp 2: x  2. Khi đó g  x  f 2x  4 .  5 1  x   2   2x  4  1  2
Ta có g x  2 f 2x  4 , g x  0  f 2x  4  0     2x  4  3 7  x   2  5   7 
So điều kiện x  2 ta được g  x nghịch biến trên 2; ; ;      .  2   2  2
Câu 26. Cho hàm số y  f  x có đạo hàm f  x   x    2 1
x  2x  , với x
   . Số giá trị nguyên
của tham số m để hàm số g  x  f  3 2
x  3x  m có 8 điểm cực trị là A. 2 . B. 3. C. 1. D. 4 . Lời giải Chọn C
Ta có g x   2
x  x f  3 2 3 6 .
x  3x  m . Strong Team Toán VD – VDC Trang 33/50  x  0 2
3x  6x  0   x  2 3 2 
x  3x  m  1  g  x 3 2 0    
 x  3x  m  1 .  3 2 x 3x m 0     3 2 
 x  3x  m  0 3 2
x  3x  m  2   3 2
x  3x  m  2 
Vì khi đi qua các nghiệm của phương trình 3 2
x  3x  m  1 (nếu có) dấu của f  3 2
x  3x  m
không đổi nên dấu của g x chỉ phụ thuộc các nghiệm của hai phương trình còn lại.
Vậy hàm số y  g  x có 8 điểm cực trị khi và chỉ khi mỗi phương trình 3 2
x  3x  m  0 và 3 2
x  3x  m  2 phải có ba nghiệm phân biệt (khác 0 và khác 2 ).  x  0
Xét hàm số h x 3 2
 x  3x , ta có h x 2  3
 x  6x ; h x  0   . x  2 
Bảng biến thiên của hàm số y  h  x x  0 2  y  0  0   y 4 0 
Dựa vào bảng biến thiên, ta thấy điều kiện để mỗi phương trình 3 2
x  3x  m và 3 2
 x  3x  m  2 phải có ba nghiệm phân biệt (khác 0 và khác 2 ) là
0  m  2  m  4  2  m  4 .
Vậy chỉ có một giá trị nguyên của m thỏa mãn là m  3 .
Câu 27. Cho hàm số y  f  x xác định trên R và hàm số y  f ' x có đồ thị như hình bên dưới và
f ' x  0 với mọi x  ; 3, 4  9;  . Đặt g  x  f  x  mx  5. Có bao nhiêu giá trị
dương của tham số m để hàm số g  x có đúng hai điểm cực trị? A. 4. B. 7. C. 8. D. 9. Lời giải Chọn C Strong Team Toán VD – VDC Trang 34/50
Ta có g x  f  x  m ; g x  0  f  x  m  0  f  x  m . Để hàm số y  g  x có
đúng hai điểm cực trị khi và chỉ khi phương trình g x  0 có hai nghiệm bội lẻ phân biệt m  5  
. Khi đó m 1, 2,3, 4,5,10,11, 
12 . Vậy có 8 giá trị của m thỏa mãn yêu cầu đề 10  m 13  bài.
Câu 28. Cho hàm số đa thức bậc bốn y  f  x , biết hàm số có ba điểm cực trị x  3
 , x  3, x  5 . Có 3 2
tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số     x 3x g x f e  m có đúng 7 điểm cực trị A. 3 B. 4 C. 5 D. 6 Lời giải Chọn D 3 2 3 2
Ta có:     2 
 x 3x  x 3 3 6 . x g x x x e f e  m   x  0 x  0   x  2  x  2   3 2 3 2         3 2 x  x  3 2 2 3 x 3 0 3 6 . x g x x x e f e  m  0 x 3  x e  m  3 x 3x   e  m  3   1 3 2   x 3 x e  m  3 3 2 x 3x e  m  3 2  3 2 x 3  x  e  m 5 3 2   x 3x e  m  5  3 
Hàm số g  x có 7 điểm cực trị khi và chỉ khi tổng số nghiệm đơn và bội lẻ, khác 0 và 2 của các phương trình   1 , 2,3 là 5 . Xét hàm số   3 2 3  x x h x e có     3 2 2 3 3 6     x x h x x x e .  x  0 Ta có 
h  x  0   . x  2   Bảng biến thiên:
Khi đó có 3 trường hợp sau: Trường hợp 1: Strong Team Toán VD – VDC Trang 35/50 4 4
m  3  e
m  e  3  51, 6 Khi đó:    4 4
1  m  3  e
4  m  e  3  57, 6  
Do m nguyên nên m 52;53;54;55;56;5  7 . Trường hợp 2: 4 4 m  5  e
m  e  5  49, 6   Khi đó: 4 4 1
  m  3  e   2
  m  e  3  m   . 0 m 3 1 3      m  4   Trường hợp 3: 4
 1  m  5  e 4  4
  m  e  5  49, 6  
Khi đó: m  3 1  m  2   m   . m 3  0   m  3 
Vậy có 6 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 29. Cho hàm số y  f (x) có đạo hàm f   x   2 x  x 2 x  4x   3 , x
   . Tính tổng tất cả các giá
trị nguyên của tham số m để hàm số gx  f x2  m có 3 cực trị. Strong Team Toán VD – VDC Trang 36/50 A. 0. B. 6. C. 3. D. 2. Lời giải Chọn C x  0  Ta có f 
 x  xx  
1 2 x  3  0  x  1  x  3 x  0 x  0  2  x  0 x  m  0 2 x  m   1 Lại có g   x  2 . x f   2 x  m    0   2 2 2  f   x  m      0 x  m  1 x  1 m  2    2 x  m  3  2 
x  3  m  3
Do 2 có nghiệm luôn là nghiệm bội chẵn ; các phương trình  
1 , 3 có nghiệm không chung
nhau và  m  3  m nên: 3   m  0
Hàm số gx có 3 cực trị  g 
 x  0 có 3 nghiệm bội lẻ    0  m  3  m  0 
Vì m    m  ; 1 ; 0 
2 . Vậy tổng các giá trị nguyên bằng 3.
Câu 30. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ .
Xét hàm số g  x  f  3 2x  x   1  .
m Tìm m để max g  x  10. 0;  1
A. m  3 . B. m  1  2 . C. m  1  3 . D. m  6 . Lời giải Chọn C
Đặt t  x 3
 2x  x 1 với x 0 
;1 . Ta có t x 2
 6x 1  0, x  0  ;1 .
Suy ra hàm số t  x đồng biến nên x 0  ;1  t  1  ; 2.
Từ đồ thị hàm số ta có max f t   3  max  f t   m  3  . m   1;2  1  ;2
Theo yêu cầu bài toán ta cần có: 3  m  1  0  m  1  3.
Câu 31. Cho hàm số f  x có đạo hàm trên  là f  x   x  
1  x  3 . Có bao nhiêu giá trị nguyên
của tham số m thuộc đoạn  10 
; 20 để hàm số y  f  2
x  3x  m đồng biến trên khoảng 0;2 ? Strong Team Toán VD – VDC Trang 37/50 A. 18 . B. 17 . C. 16 . D. 20 . Lời giải Chọn A
Ta có y  f  2
x  x  m   x   f  2 3 2 3
x  3x  m .
Theo đề bài ta có: f  x   x   1  x  3  x  3 
suy ra f  x  0  
và f  x  0  3   x  1. x  1 
Hàm số đồng biến trên khoảng 0; 2 khi y  0, x  0; 2
  x   f  2 2 3
x  3x  m  0, x   0; 2 .
Do x  0; 2 nên 2x  3  0, x
  0; 2 . Do đó, ta có: 2 2
 x  3x  m  3
m  x  3x  3 y  0, x
  0; 2  f  2
x  3x  m  0     2 2
x  3x  m  1
m  x  3x 1   m  max  2
x  3x  3 0;2 m  13     . m   2 x  x   m  1 min 3 1   0;2  Do m  10 
; 20 , m   nên có 18 giá trị nguyên của m thỏa yêu cầu đề bài. 2 3
Câu 32. Cho các hàm số f  x 3
 x  4x  m và g  x   2 x   2 x    2 2018 2019
x  2020 . Có bao
nhiêu giá trị nguyên của tham số m  20 
20; 2020 để hàm số g  f  x đồng biến trên 2; ? A. 2005 . B. 2037 . C. 4016 . D. 4041 . Lời giải Chọn B
Ta có f  x 3
 x  4x  m , 2 3
g  x   2 x  2018 2 x  2019  2 x  2020 12 10 2
 a x  a x  ...  a x  a . 12 10 2 0
Suy ra f  x 2
 3x  4 , g x 11 9
 12a x 10a x  ...  2a x . 12 10 2 11 9 
Và g  f  x  f  x 1  2a f x 10a f x  ...  2a f x     12    10    2      
 f  x f  x12a  f x10 10a  f x8 ... 2a . 12 10 2 
Dễ thấy a ; a ;...; a ; a  0 và f  x 2
 3x  4  0 , x   2 . 12 10 2 0 10 8
Do đó f  x12a f x 10a f x  ...  2a  0 , x   2 . 12    10    2  Strong Team Toán VD – VDC Trang 38/50 
Hàm số g  f  x đồng biến trên 2; khi g  f  x  0   , x
  2  f  x  0 , x   2 .  3
x  4x  m  0 , x   3  3
m   x  4x , x
  2  m  max  3
x  4x  16  . 2; Vì m  20 
20; 2020 và m  nên có 2037 giá trị thỏa mãn m . Câu 33. Cho hàm số 2
y  f x  có đạo hàm f x   x x    2 1
x  2mx   1 với mọi x  .  Có bao nhiêu số
nguyên âm m để hàm số g x  f 2x  
1 đồng biến trên khoảng 3;  5 ? A. 3 B. 2 C. 4 D. 6 Lời giải Chọn A
Ta có: g x 2 2
 2 f '(2x  1)  2(2x 1)(2x  2) [(2x 1)  2m(2x  1) 1]
Đặt t  2x 1
Để hàm số g x đồng biến trên khoảng 3; 
5 khi và chỉ khi g x   0, x  3;5 2 t  1 2
 t(t  2mt 1)  0, t  7;  2
11  t  2mt 1  0, t  7;1  1  2m  , t   7;  11 t 2 t  1 2 t  1
Xét hàm số h(t)  trên 7;1 
1 , có h '(t)  t 2 t BBT: 2 t  1 50
Dựa vào BBT ta có 2m  , t  7; 
11  2m  max ht   m   7;1  1 t 14 Vì m 
   m {  3; 2  ; 1  } .
Câu 34. Cho hàm số f  x xác định và liên tục trên R . Hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ. Strong Team Toán VD – VDC Trang 39/50 1
Xét hàm số g  x  f  x  2m  2m  x2  2020 , với m là tham số thực. Gọi S là tập hợp 2
các giá trị nguyên dương của m để hàm số y  g  x nghịch biến trên khoảng 3; 4 . Hỏi số
phần tử của S bằng bao nhiêu? A. 4 . B. 2 . C. 3 . D. Vô số. Lời giải Chọn B
Ta có g ' x  f ' x  2m  2m  x .
Đặt h  x  f ' x  x . Từ đồ thị hàm số y  f ' x và đồ thị hàm số y   x trên hình vẽ  3   x  1
suy ra: h  x  0  f ' x  x   . x  3   3
  x  2m  1
2m  3  x  2m 1
Ta có g ' x  h  x  2m  0     . x  2m  3 x  2m  3  
Suy ra hàm số y  g  x nghịch biến trên các khoảng 2m  3; 2m  
1 và 2m  3;  . Strong Team Toán VD – VDC Trang 40/50 2m  3  3  3   m  3
Do đó hàm số y  g  x nghịch biến trên khoảng 3; 4 2m 1  4     2  .   m  0 2m  3  3  
Mặt khác, do m nguyên dương nên m 2;  3  S  2; 
3 . Vậy số phần tử của S bằng 2.
Câu 35. Cho hàm số f  x liên tục trên  và có đạo hàm f  x 2
 x  x   2 2
x  6x  m với mọi
x   . Có bao nhiêu số nguyên m thuộc đoạn  20 
20; 2020 để hàm số g x  f 1 x
nghịch biến trên khoảng  ;    1 ? A. 2016 . B. 2014 . C. 2012 . D. 2010 . Lời giải Chọn C 2 2
Ta có: g x  f 1 x   1 x x  
1 1 x  61 x  m  
 x 2 x   2 1
1 x  4x  m   5
Hàm số g  x nghịch biến trên khoảng  ;    1
 g x  0, x   1   
* , (dấu "  " xảy ra tại hữu hạn điểm).
Với x  1 thì  x  2 1
 0 và x 1  0 nên   * 2
 x  4x  m5  0, x 1 2
 m x  4x  5, x  1  . Xét hàm số 2
y  x  4x  5 trên khoảng  ;   
1 , ta có bảng biến thiên:
Từ bảng biến thiên suy ra m  9 .
Kết hợp với m thuộc đoạn  20 
20; 2020 và m nguyên nên m 9;10;11;...; 20  20 .
Vậy có 2012 số nguyên m thỏa mãn đề bài.
Câu 36. Cho hàm số y  f (x) có đồ thị f (
 x) như hình vẽ. Có bao nhiêu giá trị nguyên  1  m  20  20; 2020 2
để hàm số g  x  f 2x  3  ln 1 x   2mx đồng biến trên ; 2   ?  2  Strong Team Toán VD – VDC Trang 41/50 y 4 -2 -1 0 1 x A. 2020 . B. 2019 . C. 2021 . D. 2018 . Lời giải Chọn B 2x
+ Ta có g x  2 f 2x  3   2m . 2 1 x  1  Hàm số g  x đồng biến trên ; 2   khi và chỉ khi  2  x  1 
g x  0, x
  1; 2  m  f 2x  3  , x  ; 2 2   1 x  2   x   m  min
f 2x  3     1 2   1  x ;2  1 x     2   1 
+ Đặt t  2x  3 , khi đó x  ; 2  t    2  ;1 .  2 
Từ đồ thị hàm f   x suy ra f t   0, t   2  
;1 và f t   0 khi t  1  .  1 
Tức là f 2x  3  0, x  ; 2 
  min f 2x  3  0 khi x  1 . 2  2   1  x ;2    2  x 2  1  x 1
+ Xét hàm số h  x   trên khoảng
; 2 . Ta có h x  và 2   1 x 2  2   2 1 x  h x 2
 0  x 1  0  x  1  .  1 
Bảng biến thiên của hàm số h  x trên ; 2   như sau:  2  Strong Team Toán VD – VDC Trang 42/50 1 1
Từ bảng biến thiên suy ra h  x  
 min h  x   khi x  1. 3 2  1  x ;2 2    2  1 Từ  
1 , 2 và 3 suy ra m   . 2
Kết hợp với m   , m  20 
20; 2020 thì m  20  19;  2018;....; 2  ;   1 .
Vậy có tất cả 2019 giá trị m cần tìm.
Câu 37. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.
Hàm số g  x  f  2 x  x 3 2
 4x  3x  6x  2020 đồng biến trên khoảng nào sau đây ?  1  A. 1  ;   . B.  2  ; 0 . C. 1;  . D. 0  ;1 .  2  Lời giải Chọn D
Ta có g x   x   f  2 x  x 2 2 1
12x  6x  6 .
Từ đồ thị hàm số y  f  x suy ra f  x  0  1
  x  2 . Do đó 2 2 
x  x  1 
x  x 1  0; x    f  2
x  x  0      2  x  1. 2 2 x  x  2 
x  x  2  0 
Ta có bảng xét dấu g x :  1 
Vậy hàm số g  x đồng biến trên khoảng  ;1   .  2  Strong Team Toán VD – VDC Trang 43/50
Câu 38. Cho hàm số y  f  x xác định trên  và có bảng xét dấu đạo hàm như sau:
Biết f  x  2, x
   . Xét hàm số g  x  f   f  x 3 2 3 2
 x  3x  2020 . Khẳng định nào sau đây đúng?
A. Hàm số g  x đồng biến trên khoảng  2  ;   1 .
B. Hàm số g  x nghịch biến trên khoảng 0  ;1 .
C. Hàm số g  x đồng biến trên khoảng 3;4 .
D. Hàm số g  x nghịch biến trên khoảng 2;3 . Lời giải Chọn D
Ta có: g  x   f  x f   f  x 2 ' 2 ' ' 3 2  3x  6x .
Vì f  x  2, x
   nên 3  2 f  x  1  x   
Từ bảng xét dấu f ' x suy ra f '3  2 f  x  0, x   
Từ đó ta có bảng xét dấu sau:
Từ bảng xét dấu trên, loại trừ đáp án suy ra hàm số g  x nghịch biến trên khoảng 2;3 .
Câu 39. Cho hàm số y  f (x) xác định trên  . Hàm số y  g(x)  f '2x  3  2 có đồ thị là một
parabol với tọa độ đỉnh I 2;  
1 và đi qua điểm A1; 2 . Hỏi hàm số y  f (x) nghịch biến
trên khoảng nào dưới đây? A. 5;9 . B. 1; 2 . C.  ;  9 . D. 1;3 . Lời giải Chọn A
Xét hàm số g(x)  f '2x  3  2 có đồ thị là một Parabol nên có phương trình dạng: 2
y  g(x)  ax  bx  c  P  b  2   b   4a
4a  b  0
Vì  P có đỉnh I 2;   1 nên 2a      .         g   4a 2b c 1 4a 2b c 1 2  1     Strong Team Toán VD – VDC Trang 44/50
P đi qua điểm A1;2 nên g  
1  2  a  b  c  2
4a  b  0 a  3  
Ta có hệ phương trình 4a  2b  c  1   b  12  nên g  x 2
 3x 12x 11 . a b c 2     c  11  
Đồ thị của hàm y  g(x) là 8 6 4 2 5 5 2 4
Theo đồ thị ta thấy f '(2x  3)  0  f '(2x  3)  2  2  1  x  3 . t  3 t  3
Đặt t  2x  3  x 
khi đó f '(t)  0  1 
 3  5  t  9 . 2 2
Vậy y  f (x) nghịch biến trên khoảng 5;9 . Câu 40. Cho hàm số
y  f  x có đạo hàm cấp 3 liên tục trên  và thỏa mãn 2
f  x f  x  x  x  2  x  3 . 1
4 với mọi x   và g  x   f  x  2 f  x. f   x   . Hàm số
h  x  g  2
x  2x đồng biến trên khoảng nào dưới đây? A.   ;1  .
B. 2;  . C. 0  ;1 . D. 1; 2 . Lời giải Chọn D
Ta có g x  2 f   x f  x  2 f  x. f   x  2 f  x. f  x  2
 f  x. f  x; 2 3
Khi đó h x   x   g 2
x  x    x   2 x  x 2
x  x    2 2 2 2 2 2 2 2 2 1
x  2x  4  x  0 x 1 h  x 0     x  2  x  1 2 
Ta có bảng xét dấu của h x Strong Team Toán VD – VDC Trang 45/50
Suy ra hàm số h  x  g  2
x  2x đồng biến trên khoảng 1; 2 .
Câu 41. Cho hàm số y  f (x) liên tục trên  . Biết rằng hàm số y  f '(x) có đồ thị như hình vẽ. Hàm số 2
y  f (x 5
 ) nghịch biến trên khoảng nào sau đây ? A. ( 1  ;0) . B. (1; 2) . C. ( 1  ;1) . D. (0;1) Lời giải Chọn D. + Đặt 2 2
g(x)  f (x  5)  f (u),u  x  5 + 2 2
g '(x)  (x  5) ' f '(u)  2xf '(x  5)
+ Hàm số y  g(x) nghịch biến khi g '(x)  0 và dấu bằng xảy ra tại hữu hạn điểm x  0  (I ) 2
f '(x  5)  0 2 
 2xf '(x  5)  0   x  0  (II ) 2
 f '(x  5)  0 
Giải (I): Từ đồ thị hàm số y  f '(x) ta có x  0    x   7 2 x  0 x  7   x   7 2
(I )   x  5  2    x  0     2  x  1  2  2 
 4  x  5  1  
x  1  2  x  1  2  x  4  Strong Team Toán VD – VDC Trang 46/50
Xét (II): Từ đồ thị y  f '(x) ta có x  0  2 2
 x  5  4  x  1  1   x  1  (II )   2  
x  4  x  2  x  2 2  1
  x  5  2      7  x  2   2  x  7 2
x  7   7  x  7   x  0   0  x  1 1   x  1   x  0    2  x  7
 7  x  2  2  x  7 
Vậy hàm số đồng biến trên mỗi khoảng:  ;   7 ; 2  ;   1 ;0 
;1 ;2; 7  . Chọn đáp án D.
Câu 42. Cho hàm số y  f (x ) . Hàm số y  f '(x) có đồ thị như hình vẽ bên. y
y  f '(x ) O 1 1 4 x Hàm số 2
y  f (x ) đồng biến trên khoảng  1 1  1  A.   ;     B. 0;2 C.   ;0 D.  2;    1  2 2  2  Lời giải Chọn C
Xét hàm f '(x )  (
 x 1)(x 1)(x 4) . Đặt g x  f  2 ( ) x  x  0  Có 2 2 2 2
g '(x)  2xf '(x )  2x (x 1)(x 1)(x  4) . Suy ra g '(x )  0  x  1  x  2 
Xét dấu g '(x )
Câu 43. Cho hàm số y  f  x. Hàm số y  f  x có đồ thị như hình bên. Strong Team Toán VD – VDC Trang 47/50 y x -4 -3 -2 -1 1 2 3 4 5 6 7
Hàm số y  f 3  2x nghịch biến trên khoảng A.  1  ;  B. 0; 2 C.  ;    1 D. 1;3 Lời giải Chọn C  1 5  2   3  2x  2  x  Ta có y  2
 . f 3  2x; y  0  f 3  2x  0        2 2  3  2x  5   x  1    1 5 
Vậy hàm số y  f 3  2x nghịch biến trên các khoảng  ;    1 và ; .    2 2 
Câu 44. Cho hàmsố y  f (x) có đạo hàm trên  . Đường cong trong hình vẽ dưới là đồ thị của hàm số
y  f '( x) . Xét hàm số 2
g(x)  f (3  x ) . y -1 O 3 x
Mệnh đề nào dưới đây là đúng?
A. Hàm số g(x) đồng biến trên (;1) .
B. Hàm số g(x) đồng biến trên (0; 3) .
C. Hàm số g(x) nghịch biến trên (1; ) .
D. Hàm số g(x) nghịch biến trên ( ;  2) và (0; 2) . Lời giải Chọn D
Ta có g  x   xf  2 ' 2 ' 3  x  2 3  x  1 x  2 f ' 2 3  x   0    2  3  x  3 x  0   Strong Team Toán VD – VDC Trang 48/50 Ta có bảng xét dấu: x ∞ 2 0 2 + ∞ x + + 0 f(3-x2) 0 + + 0 g'(x) + 0 0 0 +
Hàm số g(x) nghịch biến trên ( ;  2) và (0; 2) .
Câu 45. Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ. Hàm số  2 x y f
 e  nghịch
biến trên khoảng nào sau đây? y x 0 1 2 3 -4 A. 0;  . B.  ;  0 . C.  1  ;3 . D.  2   ;1 . Lời giải Phân tích
Dựa vào đồ thị hàm y  f  x , suy ra nghiệm f  x  0 và dấu của f  x .
Dùng tính chất hàm hợp xét dấu  2 x f
 e  , suy ra dấu của x. 2 x e f
 e  . Từ đó chọn đáp án. Chọn B x  0
Ta có f  x  0   . x  3  2 x  e  0 Xét  2 x y f  e  , có x   .  2 x y e f
 e  ;   0 x  . 2 x y e f  e   0   x  0  . 2 x  e  3  Mặt khác,   0 x  . 2 x y e f  e   0  2 x
 e  3  x  0 . Do đó hàm số  2 x y f
 e  nghịch biến trên  ;  0 .
Câu 46. Cho hàm số f  x có đạo hàm liên tục trên  và có đồ thị của hàm y  f  x như hình vẽ.
Xét hàm số g x  f  2 ( )
x  2 . Mệnh đề nào dưới đây sai? Strong Team Toán VD – VDC Trang 49/50 y O 1 2 x 1 2 4
A. Hàm số g(x) đồng biến trên 2; .
B. Hàm số g(x) nghịch biến trên 0; 2.
C. Hàm số g(x) nghịch biến trên  1  ; 0.
D. Hàm số g(x) nghịch biến trên  ;  2  . Lời giải Chọn C  x  1 
Dựa vào đồ thị hàm số f  x  0  
và f  x  0  x  2 x  2 
Xét g  x  f  2
x  2 có tập xác định 
g ' x  2 .
x f t  với 2 t  x  2  x  0  x  0   g ' x 2
 0  t  x  2  1  x  1   2
t  x  2  2  x  2    x  2
Lại có f t  2
 0  t  x  2  2   x  2  
Do đó, ta có bảng xét dấu g ' x x  2 1 0 1 2  g x  0  0  0  0  0 
Từ bảng xét dấu ta chọn phát biểu sai là C
Câu 47. Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình bên. Hàm số y  f 2  x đồng biến trên khoảng: A. 1;3 . B. 2;  . C.  2   ;1 . D.  ;  2 . Strong Team Toán VD – VDC Trang 50/50 Lời giải Chọn C.
Ta có:  f 2  x  2  x . f 2  x   f 2  x 2  x  1   x  3
Hàm số đồng biến khi  f 2  x  0  f 2  x  0     . 1  2  x  4 2   x  1  
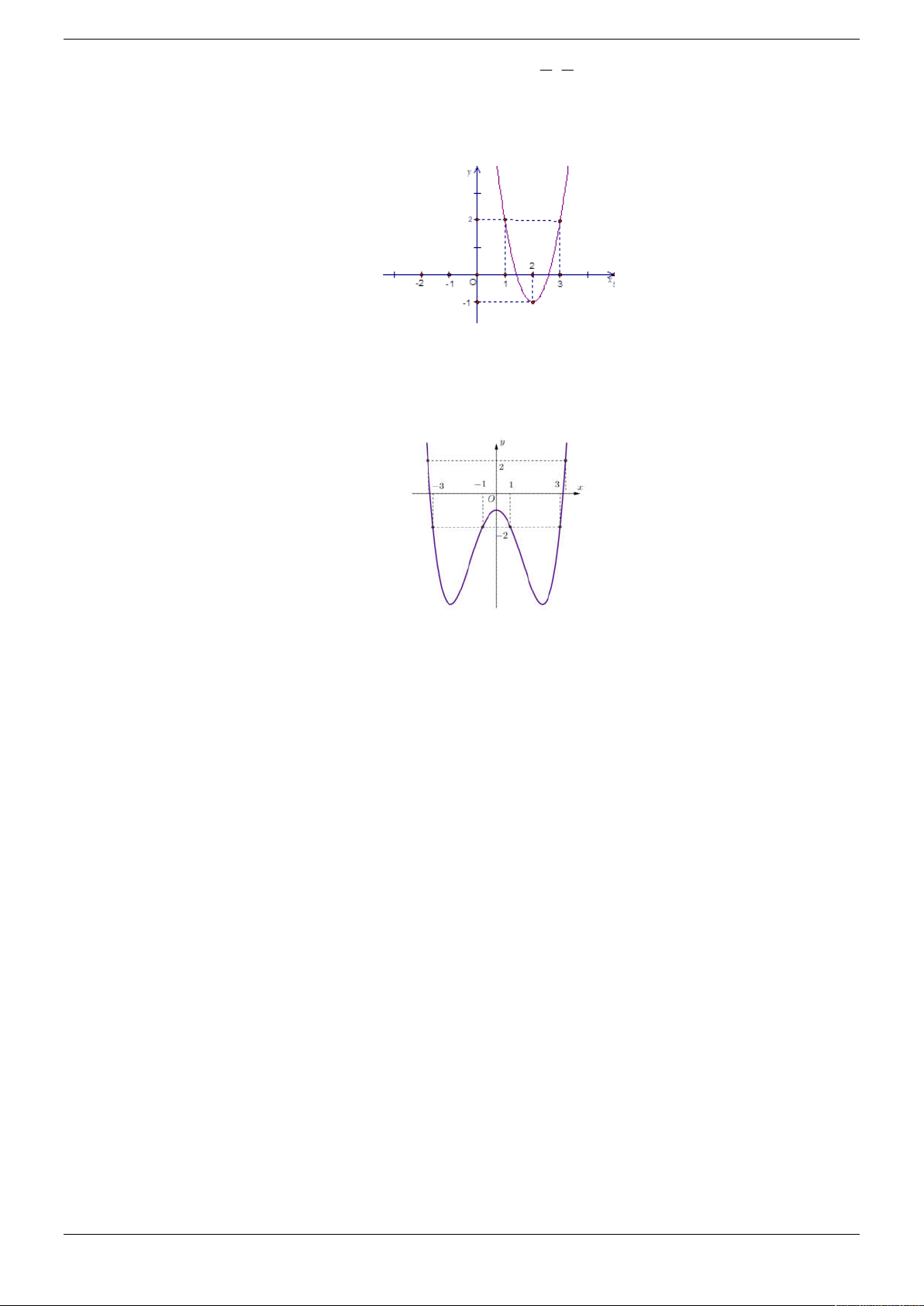
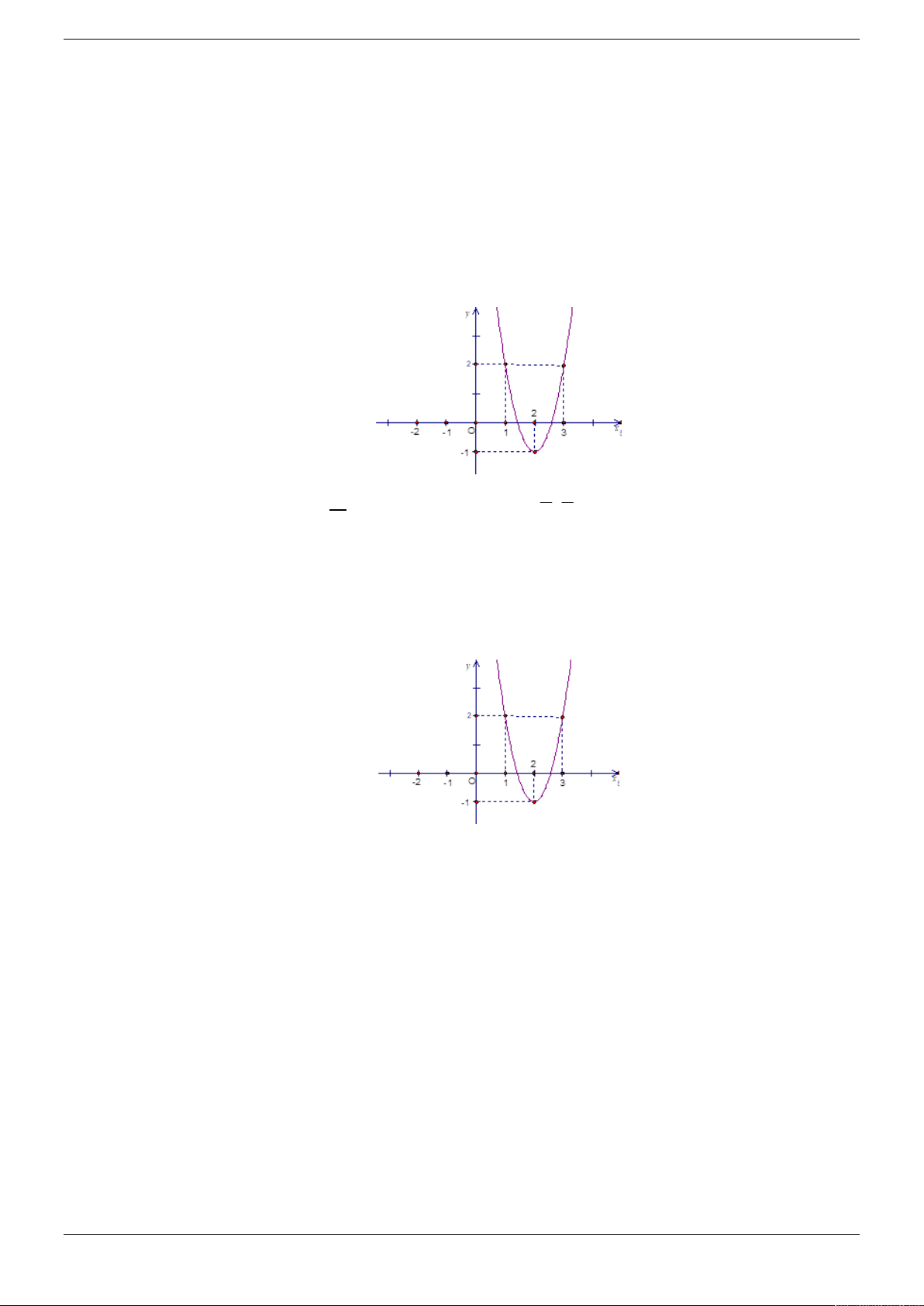
Câu 48. Cho hàm số y  f  x có đạo hàm là hàm số f  x trên  . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x nghịch biến trên khoảng nào?  3 5  A. ; 2 . B. 1;  1 . C. ;   . D. 2;  .  2 2  Lời giải. Chọn B
Hàm số y  f  x  2  2 có đồ thị C  như sau:
Dựa vào đồ thị C  ta có: f  x  2  2  2, x  1;3  f  x  2  0,x  1;3 . Đặt *
x  x  2 thì f  x *  0, * x  1;  1 .
Vậy: Hàm số f  x nghịch biến trên khoảng 1;  1 . Cách khác:
Tịnh tiến sang trái hai đơn vị và xuống dưới 2 đơn vị thì từ đồ thị C  sẽ thành đồ thị của hàm
y  f   x . Khi đó: f  x  0,x  1;  1 .
Vậy: Hàm số f  x nghịch biến trên khoảng 1;  1 .
Phân tích: Cho biết đồ thị của hàm số f   x sau khi đã tịnh tiến và dựa vào đó để xét sự đồng
biến của hàm số f  x . Strong Team Toán VD – VDC Trang 51/50
Câu 49. Cho hàm số y  f  x có đạo hàm là hàm số f  x trên  . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x đồng biến trên khoảng nào?
A. ;3, 5;  . B. ;  
1 , 1;  . C. 1;  1 . D. 3;5 . Lời giải. Chọn B
Hàm số y  f  x  2  2 có đồ thị C  như sau:
Dựa vào đồ thị C  ta có:
f  x  2  2  2,x   
;1  3;   f  x  2  0,x  ;  1  3;  . Đặt *
x  x  2 suy ra: f   x *  0, *
x  ;   1  1;  .
Vậy: Hàm số f  x đồng biến trên khoảng ;   1 , 1;  .
Câu 50. Cho hàm số y  f  x có đạo hàm là hàm số f  x trên  . Biết rằng hàm số
y  f  x  2  2 có đồ thị như hình vẽ bên dưới. Hàm số f  x nghịch biến trên khoảng nào? A. 3;   1 , 1;3 . B. 1;  1 , 3;5 .
C. ; 2, 0; 2 .
D. 5; 3, 1;  1 . Lời giải Chọn B
Hàm số y  f  x  2  2 có đồ thị C  như sau: Strong Team Toán VD – VDC Trang 52/50
Dựa vào đồ thị C  ta có:
f  x  2  2  2,x  3;  
1  1;3  f  x  2  0,x  3;   1  1;3 . Đặt *
x  x  2 suy ra: f  x *  0, * x  1;  1  3;5 .
Vậy: Hàm số f  x đồng biến trên khoảng 1;  1 , 3;5 .
-------------------- HẾT -------------------- Strong Team Toán VD – VDC Trang 53/50

50 bài tập trắc nghiệm tính đơn điệu của hàm hợp có đáp án và lời giải Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số