











Preview text:
Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 BÀI TOÁN GTLN - GTNN L uy TRONG THI BGD en thi 2016 - 2021 tra cng
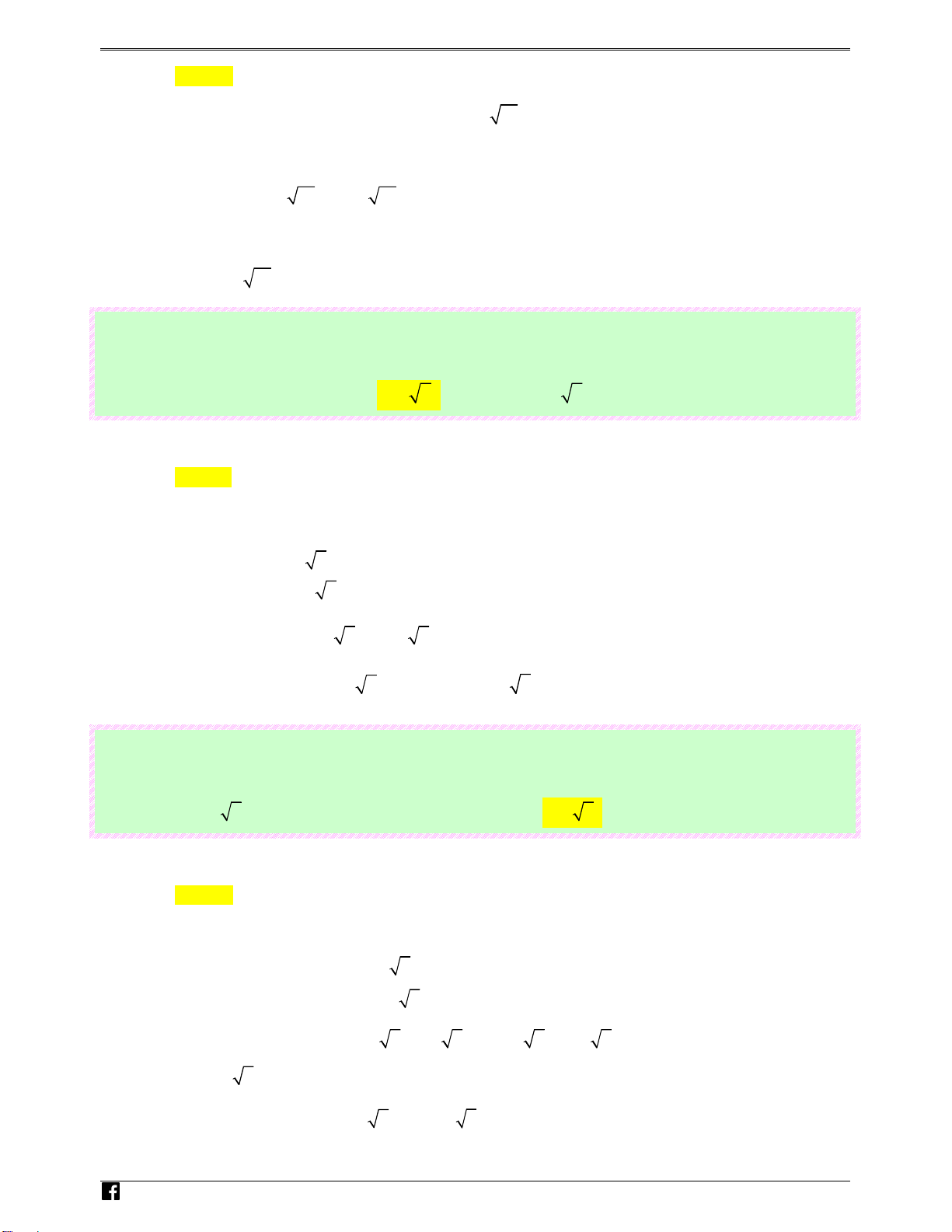
Câu 1: (Câu 32 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số hi 4 2 e
f (x) = x −10x − 2 trên đoạn [0;9] bằng m .vn Ⓐ. 2 − . Ⓑ. 1 − 1. Ⓒ. 2 − 6. Ⓓ. 2 − 7 . Lời giải Chọn D Hàm số 4 2
f (x) = x −10x − 2 xác định và liên tục trên đoạn [0;9] . Ta có 3
f '(x) = 4x − 20x x = 0 ∈[0;9] 3
f '(x) = 0 ⇔ 4x − 20x = 0 ⇔ x = 5 ∈[0;9] x = − 5 ∉ [0;9] N guy f (0) = −2;
f ( 5) = −27; f (9) = 5749 . %n H
So sánh 3 giá trị trên và kết luận min f (x) = −27 . o x [ ∈ 0;9] àng V
Câu 2: (Câu 21 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3 = x −3x i)t trên đoạn [ 3 − ; ] 3 bằng Ⓐ. 18. Ⓑ. 1 − 8. Ⓒ. −2 . Ⓓ. 2 . Lời giải Chọn B
Ta có: f ′( x) 2 = 3x −3 x = −1∈[−3;3]
Có: f ′( x) = 0 ⇔ x = 1∈ [−3;3] Mặt khác: f (− ) 3 = 1 − 8; f ( ) 3 =18; f (− ) 1 = 2; f ( ) 1 = 2 − .
Vậy min f ( x) = f (−3) = −18 . [−3;3]
https://www.facebook.com/vietgold Trang 1 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Câu 3: (Câu 19 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Giá trị lớn nhất của hàm số f ( x) 3 = x −3x trên đoạn [ 3 − ; ] 3 bằng L − . u Ⓐ. 18. Ⓑ. 2. Ⓒ. 18 Ⓓ. 2 − . yen Lời giải thi Chọn A tra f ( x) 3
= x −3x xác định trên đoạn [ 3 − ; ] 3 . cng ′ = − h f ( x) 2 3x 3. iem x = 1∈[−3;3] Cho 2 ′ .
f ( x) = 0 ⇔ 3x − 3 = 0 ⇔ v = − ∈ − n x 1 [ 3;3] Ta có f (− ) 3 = 1 − 8; f (− ) 1 = 2; f ( ) 1 = 2 − ; f ( ) 3 =18.
Vậy max y = f (3) = 18 . [−3; ] 3
Câu 4: (Câu 21 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Giá trị nhỏ nhất của hàm số 3 2
y = x + 3x trên đoạn [−4;− ] 1 bằng Ⓐ. 4 − . Ⓑ. −16 . Ⓒ. 0 . Ⓓ. 4 Lời giải Chọn B N x = 0 ∉ 4 − ; −1 2 [ ] ′ ′ g Ta có 2
y = 3x + 6x ; y = 0 ⇒ 3x + 6x = 0 ⇔ . u x = −2 ∈ [ 4 − ; − ] 1 y%n
Khi đó y (−4) = −16 ; y (−2) = 4 ; y (−1) = 2 . H oàn Nên min y = −16 . [−4;− ] 1 g Vi)
Câu 5: (Câu 18 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Giá trị nhỏ nhất của hàm số t 3 2
y = x + 2x − 7x trên đoạn [0;4] bằng Ⓐ. 2 − 59. Ⓑ. 68. Ⓒ. 0 . Ⓓ. 4 − Lời giải Chọn D TXĐ D = . ℝ
Hàm số liên tục trên đoạn [0;4] . Ta có 2
y′ = 3x + 4x − 7
https://www.facebook.com/vietgold Trang 2 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 x = 1∈[0;4] y′ = 0 ⇔ 7 x = − ∉[0;4] 3 Lu y (0) = 0; y ( ) 1 = 4 − ; y(4) = 68. yent Vậy min y = −4 . h [0;4] itrac 2 n
Câu 6: (Câu 20 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Tìm giá trị nhỏ nhất m của hàm số 2 y = x + gh x ie 1 m trên đoạn ;2 . . 2 vn Ⓐ. 17 m = . Ⓑ. m =10. Ⓒ. m = 5 . Ⓓ. m = 3 4 Lời giải Chọn D 2
Đặt y = f ( x) 2 = x + x 3 2 2 − 2 1 Ta có ′ = 2 x y x − =
, y′ = 0 ⇒ x = 1∈ ; 2 2 2 x x 2 1 17 Khi đó f ( ) 1 = 3, f = , f (2) = 5 2 4
Vậy m = min f ( x) = f ( ) 1 = 3 . N 1;2 g 2 uy
Câu 7: (Câu 37 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Trên đoạn [ 1 − ;2] , hàm số %n 3 2
y = x + 3x +1 đạt giá trị nhỏ nhất tại điểm H oàn Ⓐ. x = 2. Ⓑ. x = 0 . Ⓒ. x = 1 − . Ⓓ. x 1 = . g Vi Lời giải )t Chọn B 3 2
y = x + 3x +1 x = 0 2
y′ = 3x + 6x = 0 ⇔ . x = 2 − ∉ [ 1 − ;2] y (− )
1 = 3; y (0) = 1; y (2) = 21. Vậy GTNN trên đoạn [ 1
− ;2] của hàm số bằng 1 tại x = 0 .
Câu 8: (Câu 36 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Trên đoạn [0; ] 3 , hàm số 3
y = x − 3x + 4
đạt giá trị nhỏ nhất tại điểm Ⓐ. x =1. Ⓑ. x = 0 . Ⓒ. x = 3. Ⓓ. x = 2. Lời giải Chọn A
https://www.facebook.com/vietgold Trang 3 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 x = 1 Ta có 2
y′ = 3x − 3 ⇒ y ' = 0 ⇔ . x = 1 − ∉ [0; ] 3
Ta có: y (0) = 4, y (3) = 22, y ( ) 1 = 2 Lu Vậy hàm số 3
y = x − 3x + 4 đạt giá trị nhỏ nhất trên đoạn [0;3] tại điểm x =1. yent
Câu 9: (Câu 35 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Trên đoạn [−2; ] 1 , hàm số hit 3 2 r
y = x − 3x −1 đạt giá trị lớn nhất tại điểm acng Ⓐ. x = 2 − . Ⓑ. x = 0 . Ⓒ. x = 1 − . Ⓓ. x =1. hiem Lời giải .v Chọn B n
Tập xác định D = ℝ . x = 0 2
y′ = 3x − 6x = 0 ⇔ x = 2 ∉ [ 2 − ; ] 1 Ta có y ( 2
− ) = −21, y (0) = −1, y ( ) 1 = −3 . Vậy max y = 1 − tại x = 0 . [ 2 − ; ] 1
Câu 10: (Câu 31 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Trên đoạn [0; ] 3 , hàm số 3
y = −x + 3x
đạt giá trị lớn nhất tại điểm Ⓐ. x = 0. Ⓑ. x = 3. Ⓒ. x =1. Ⓓ. x = 2. N Lời giải gu Chọn C y% = = − + ⇒ ′ n Ta có: y f ( x) 3 2 x 3x f (x) = 3 − x + 3 H x = 1 oà y′ = 0 ⇔ . n x = 1 − ∉ [0; ] 3 g V
Ta có f (0) = 0; f ( ) 1 = 2; f (3) = 1 − 8 . i)t Vậy hàm số 3
y = −x + 3x đạt giá trị lớn nhất tại điểm x = 1 .
Câu 11: (Câu 31 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Gọi M, m lần lượt là giá trị lớn
nhất, giá trị nhỏ nhất của hàm số f ( x) 4 2
= x − 2x + 3 trên đoạn [0;2] . Tổng M + m bằng Ⓐ. 11. Ⓑ. 14. Ⓒ. 5. Ⓓ. 13. Lời giải Chọn D
Tập xác định: D = ℝ f ′( x) 3 = 4x − 4x
https://www.facebook.com/vietgold Trang 4 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 x = 0 ∈[0;2] f ′( x) 3
= 0 ⇔ 4x − 4x = 0 ⇔ x = −1∉[0;2] x =1 ∈ [0;2] Lu f (0) = 3; f ( ) 1 = 2; f (2) = 11 yen M =11 t ⇒
⇒ M + m = 13 . hi m = 2 tracn
Câu 12: (Câu 31 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số gh f ( x) 4 2
= x −12x −1 trên đoạn [0;9] bằng iem. − − − v Ⓐ. 28. Ⓑ. −1. Ⓒ. 36. Ⓓ. 37. n Lời giải Chọn D x = 0 f ′( x) 3
= 4x − 24x ; f ′( x) = 0 ⇔ x = 6 x = − 6 ∉ [0;9]
f (0) = −1; f ( 6 ) = −37; f (9) = 5588
Vậy min f ( x) = −37 [0;9] N
Câu 13: (Câu 32 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số g 4 2 u
f (x) = x −12x − 4 trên đoạn [0;9] bằng y%n H Ⓐ. 3 − 9 . Ⓑ. 4 − 0 . Ⓒ. 3 − 6 . Ⓓ. −4. oàn Lời giải g Vi Chọn B )t +) Ta có 3 f (
′ x) = 4x − 24x . 3 f ′ x = ⇔ x − x = ⇔ x ( 2 ( ) 0 4 24 0 4 x − 6) = 0. x = 0
⇔ x = − 6 ∉(0;9). x = 6 ∈ (0;9) +) Ta có:
f (0) = −4; f ( 6 ) = −40; f (9) = 5585 .
Vậy min f (x) = f ( 6) = 4 − 0 . [0;9]
https://www.facebook.com/vietgold Trang 5 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Câu 14: (Câu 31 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −10x − 4 trên đoạn [0;9] bằng L Ⓐ. 2 − 8. Ⓑ. 4 − . Ⓒ. 1 − 3. Ⓓ. 2 − 9. uyen Lời giải thi Chọn D tra x = 0 cn g Ta có f ′( x) 3
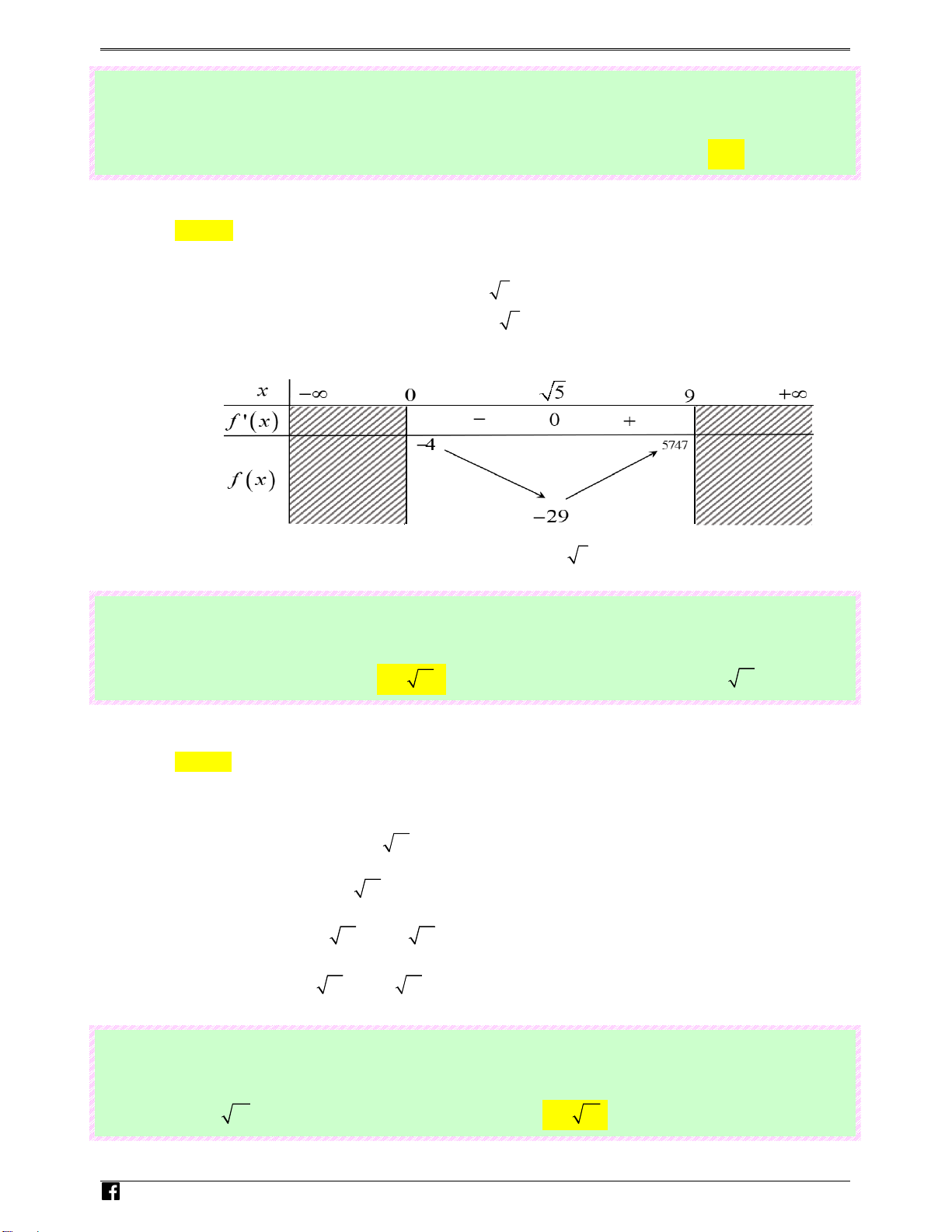
= 4x − 20x ; f ′( x) = 0 ⇔ x = 5 . h i e x = − 5 m .v Bảng biến thiên n
Dựa vào bảng biến thiên ta có min f ( x) = −29 khi x = 5 . [0;9]
Câu 15: (Câu 29 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số f ( x) 3
= x − 33x trên đoạn [2;19] bằng N g Ⓐ. 7 − 2 . Ⓑ. 2 − 2 11 . Ⓒ. 5 − 8 . Ⓓ. 22 11 . uy%n Lời giải Ho Chọn B àng Ta có f ′( x) 2 = 3x − 33 Vi)t f ′( x) 2
= 0 ⇔ x =11 ⇔ x = ± 11
Xét trên [2;19] ta có x = 11∈[2;19]
Ta có f (2) = −58; f ( 11) = −22 11; f (19) = 6232 .
Vậy min f ( x) = f ( 11) = −22 11 [2;19]
Câu 16: (Câu 35 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số f ( x) 3
= x −30x trên đoạn [2;1 ] 9 bằng Ⓐ. 20 10 . Ⓑ. 6 − 3 . Ⓒ. 2 − 0 10 . Ⓓ. 5 − 2 . Lời giải
https://www.facebook.com/vietgold Trang 6 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Chọn C Ta có f ′( x) 2
= 3x − 30 ; f ′(x) = 0 ⇔ x = ± 10 . L Hàm số f ( x) 3
= x −30x liên tục trên đoạn [2;1 ] 9 và uye f (2) = −52; f
10 = −20 10; f 19 = 6289 . n ( ) ( ) thitr
So sánh các giá trị trên, ta có giá trị nhỏ nhất của hàm số f ( x) 3
= x −30x trên đoạn [2;1 ] 9 acn bằng 2 − 0 10 ghie
Câu 17: (Câu 26 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số m .v f ( x) 3
= x − 21x trên đoạn [2; 19] bằng n Ⓐ. 3 − 6. Ⓑ. 1 − 4 7 . Ⓒ. 14 7 . Ⓓ. 3 − 4. Lời giải Chọn B
Đạo hàm f ′( x) 2
= 3x − 21, x ∈(2; 19). = f ′( x) x 7 (T / m) = 0 ⇔ . x = − 7 (L)
Ta có f (2) = −34; f ( 7 ) = −14 7; f (19) = 6460 . N g
Do vậy Min f ( x) = 1
− 4 7 , đạt được khi x = 7 . u x [ ∈ 2; 19] y%n H
Câu 18: (Câu 36 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số oà f ( x) 3
= x − 24x trên đoạn [2;19] bằng ng V − − − i Ⓐ. 32 2 . Ⓑ. 40 . Ⓒ. 32 2 . Ⓓ. 45 . )t Lời giải Chọn C Ta có: f ( x) 3 = x − 24x x = 2 2 ∈[2;19] f ′( x) 2 = 3x − 24 = 0 ⇔ . x = 2 − 2 ∉ [2;19] f ( ) 3 2 = 2 − 24.2 = 4 − 0 ; f ( ) =( )3 2 2
2 2 − 24.2 2 = −32 2 ; f ( ) 3
19 = 19 − 24.19 = 6403 . Mà 3
− 2 2 < − 40 < 6403.
Kết luận: min f ( x) = 3
− 2 2 tại x = 2 2 . x [ ∈ 2;19]
https://www.facebook.com/vietgold Trang 7 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Câu 19: (Câu 28 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Giá trị nhỏ nhất của hàm số 4 2
y = x −10x + 2 trên đoạn [ 1 − ; ] 2 bằng: L Ⓐ. 2. Ⓑ. −23 . Ⓒ. −22 . Ⓓ. 7 − . uye Lời giải nth Chọn C itra 4 2 3 2 = − + ⇒ ′ . c y x 10x 2
y = 4x − 20 x = 4x ( x − 5) ngh x = 0 iem
y′ = 0 ⇔ x = 5 . .vn x = − 5
Các giá trị x = − 5 và x = 5 không thuộc đoạn [ 1 − ; ] 2 nên ta không tính. Có f (− ) 1 = 7
− ; f (0) = 2; f (2) = 2 − 2.
Nên giá trị nhỏ nhất của hàm số trên đoạn [ 1 − ; ] 2 là −22 .
Câu 20: (Câu 19 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Giá trị lớn nhất của hàm số f ( x) 4 2
= −x +12x +1 trên đoạn [ 1 − ; ] 2 bằng Ⓐ. 1 Ⓑ. 37 . Ⓒ. 33 . Ⓓ. 12 . Lời giải N gu Chọn C y%n
Hàm số liên tục và xác định trên [ 1 − ; ] 2 . Ho x = 0 à n Ta có f ′( x) 3 = 4 − x + 24x 3
⇒ f ′ x = 0 ⇔ −4x + 24x = 0 ⇔ x = 6 ∉ −1;2 . g ( ) [ ] V i x = − 6 ∉ [−1;2] )t
Ta có f (0) =1; f (− ) 1 =12 ; f (2) = 33
Vậy max f ( x) = 33. [−1;2]
Câu 21: (Câu 17 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x − 3x + 2 trên [ − 3;3] bằng Ⓐ. 20. Ⓑ. 4. Ⓒ. 0. Ⓓ. –16. Lời giải Chọn D
Ta có: f ′( x) 2
= 3x − 3 ⇒ f ′(x) = 0 ⇔ x = 1 ± .
https://www.facebook.com/vietgold Trang 8 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Ta có: f (− ) 3 = 1 − 6; f (− ) 1 = 4; f ( ) 1 = 0; f ( ) 3 = 20.
Do hàm số f ( x) liên tục trên [ − 3;3] nên giá trị nhỏ nhất của hàm số bằng –16. Luy
Câu 22: (Câu 20 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Giá trị lớn nhất của hàm số 3 f ( )
x = x −3x+2 en
trên đoạn [ − 3; 3] bằng thitra Ⓐ. 1 − 6. Ⓑ. 20. Ⓒ. 0. Ⓓ. 4. cng Lời giải hie Chọn B m 3 2 .
f x = x − 3x + 2 ⇒ f ′ x = 3x −3 v Ta có: ( ) ( ) n x = 1 Có: f ′( x) 2
= 0 ⇔ 3x − 3 = 0 ⇔ x = 1 − Mặt khác: f (− ) 3 = 1 − 6, f (− ) 1 = 4, f ( ) 1 = 0, f ( ) 3 = 20.
Vậy max f ( x) = 20 . [ 3 − ; ] 3
Câu 23: (Câu 22 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Giá trị lớn nhất của hàm số 4 2
y = x − x +13
trên đoạn [−1; 2] bằng Ⓐ. 25 Ⓑ. 51 Ⓒ. 13 Ⓓ. 85 4 N gu Lời giải y%n Chọn A H oà
y = f ( x) 4 2
= x − x +13 ng V 3 i
y ' = 4x − 2x )t x = 0∈[ −1;2] 1 3
4x − 2x = 0 ⇔ x = − ∈[ −1;2] 2 1 x = ∈[ −1; 2] 2 1 51 1 51 f ( 1
− ) = 13; f (2) = 25; f (0) = 13; f − = ; f = 2 4 2 4
Giá trị lớn nhất của hàm số 4 2
y = x − x +13 trên đoạn [−1; 2] bằng 25.
https://www.facebook.com/vietgold Trang 9 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Câu 24: (Câu 23 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Giá trị lớn nhất của hàm số 4 2
y = x − 4x + 9 trên đoạn [ 2 − ; ] 3 bằng L Ⓐ. 201 Ⓑ. 2 Ⓒ. 9 Ⓓ. 54 uyen Lời giải t hitr Chọn D ac x = 0 n 3 g
y′ = 4x − 8x ; y′ = 0 ⇔ . h x = ± 2 iem. Ta có y( 2 − ) = 9 ; y( )
3 = 54 ; y(0) = 9 ; y ± 2 = 5 . v ( ) n
Vậy max y = 54 . [ 2 − ; ] 3
Câu 25: (Câu 18 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Giá trị lớn nhất của hàm số f ( x) 4 2 = x − 4x +5 trêm đoạn [ 2 − ; ] 3 bằng Ⓐ. 50 Ⓑ. 5 Ⓒ. 1 Ⓓ. 122 Lời giải Chọn A x = 0 3
f '(x) = 4x − 8x = 0 ⇔ ∈[ 2 − ; ] 3 ; N x = ± 2 guy%
f (0) = 5; f (± 2 ) = 1; f ( 2
− ) = 5; f (3) = 50 n Ho Vậy Max y = 50 à [ 2 − ; ] 3 ng V
Câu 26: (Câu 15 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Tìm giá trị nhỏ nhất i m của hàm số )t 4 2
y = x − x +13 trên đoạn [ 2 − ; ] 3 . Ⓐ. 51 m = . Ⓑ. 49 m = . Ⓒ. m =13. Ⓓ. 51 m = . 4 4 2 Lời giải Chọn A Ta có: 3
y′ = 4x − 2 . x x = 0 1 51 y′ = 0 ⇔ 1 ; y (0) = 13, ± = , y ( 2
− ) = 25 , y (3) = 85 . y x = ± 2 4 2
https://www.facebook.com/vietgold Trang 10 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 51 Vậy: m = . 4
Câu 27: (Câu 24 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Tìm giá trị lớn nhất M của hàm số L 4 2 u
y = x − 2x + 3 trên đoạn 0; 3 y . enth Ⓐ. M = 9 Ⓑ. M = 8 3 Ⓒ. M = 1 Ⓓ. M = 6 itra Lời giải cn Chọn D g 3 2 h
Ta có: y′ = 4x − 4x = 4x(x − ) 1 iem x = 0 .v 2 n
y′ = 0 ⇔ 4x ( x − ) 1 = 0 ⇔ x = 1 x = 1 − (l)
Ta có : y (0) = 3 ; y( ) 1 = 2 ; y ( 3) = 6
Vậy giá trị lớn nhất của hàm số 4 2
y = x − 2x + 3 trên đoạn 0; 3
là M = y ( 3) = 6
Câu 28: (Câu 23 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Tìm giá trị nhỏ nhất m của hàm số 3 2
y = x − 7 x + 11x − 2 trên đoạn [0; 2] Ⓐ. m = 11 Ⓑ. m = 0 Ⓒ. m = 2 − Ⓓ. m = 3 Lời giải Chọn C 11 N x = ∉(0;2) 2 g ′
y = 3x −14x +11 y ' = 0 ⇔ 3 u y x = 1∈ (0;2) %n f 0 = −2; f 1 = 3;
f 2 = 0 ⇒ min y = −2 H ( ) ( ) ( ) [0;2] oàn 2 g x + 3
Câu 29: (Câu 6 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Tìm giá trị nhỏ nhất của hàm số y = trên Vi x −1 )t đoạn [2;4] . 19 Ⓐ. min y = 6 Ⓑ. min y= 2 −
Ⓒ. min y = −3 Ⓓ. min y = [2;4] [2;4] [2;4] [2;4] 3 Lời giải Chọn A
Tập xác định: D = ℝ \{ } 1 2 x + 3 Hàm số y =
xác định và liên tục trên đoạn [2;4] x −1 2 x − 2x − 3 Ta có 2 y′ =
;y′ = 0 ⇔ x − 2x − 3 = 0 ⇔ x = 3 hoặc x = 1 − (loại) (x − )2 1
https://www.facebook.com/vietgold Trang 11 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Suy ra y ( ) = y ( ) = y ( ) 19 2 7; 3 6; 4 =
. Vậy min y= 6 tại x = 3. 3 [2;4]
Câu 30: (Câu 19 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Tính giá trị nhỏ nhất của hàm số L 4 u y = 3x + trên khoảng (0; +∞ ) . 2 y x ent 3 h
Ⓐ. min y = 3 9 Ⓑ. min y = 7 i (0;+∞) (0;+∞) tra 33 c = 3 min y = 2 9 n Ⓒ. min y Ⓓ. (0;+∞) (0;+∞) g 5 hie Lời giải m .v Chọn A n Cách 1: 4 3x 3x 4 3x 3x 4 3 3 y = 3x + = + + ≥ 3 . . = 3 9 2 2 2 x 2 2 x 2 2 x 3x 4 8 Dấu " = " xảy ra khi 3 = ⇔ x = . 2 2 x 3 Vậy 3 min y = 3 9 (0;+∞) Cách 2: 4
Xét hàm số y = 3x + trên khoảng (0; +∞ ) 2 x N gu 4 8 y Ta có y = 3x + ⇒ y ' = 3 − 2 3 % x x n H 8 8 8 o Cho 3 3 y ' = 0 ⇔
= 3 ⇔ x = ⇔ x = à 3 n x 3 3 g Vi 8 ) 3 t x 0 +∞ 3 y ' − 0 + y 3 3 9 8 3 3 ⇒ min y = y = 3 9 (0;+∞) 3
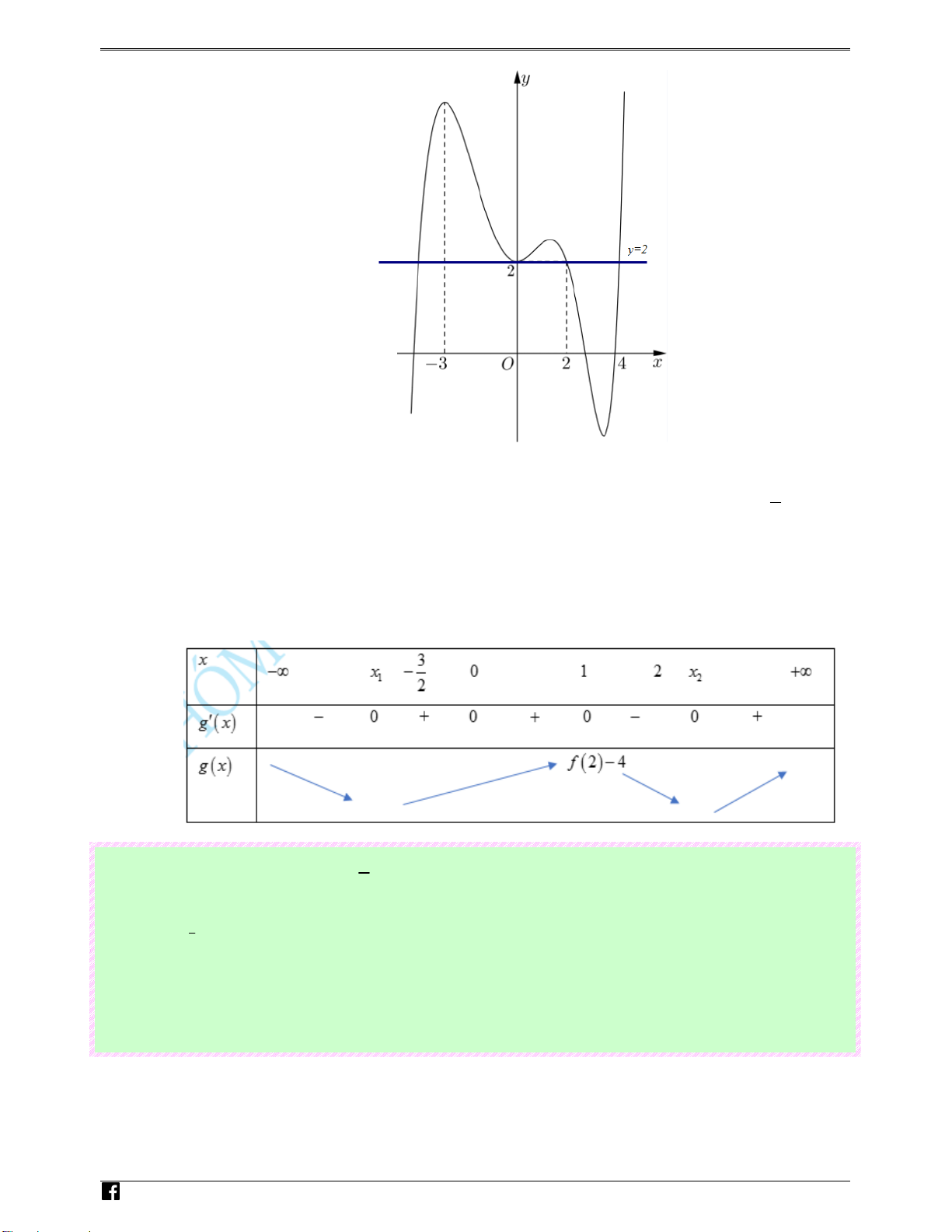
Câu 31: (Câu 16 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) liên tục trên
đoạn (-1;3) và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn [ 1 − ; ]
3 . Giá trị của M − m bằng
https://www.facebook.com/vietgold Trang 12 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Luyenthitracnghi em .v Ⓐ. 0. Ⓑ. 1. Ⓒ. 4. Ⓓ. 5. n Lời giải Chọn D
Căn cứ vào đồ thị ta có M = max y = 3 , m = min y = −2 [ 1 − ;3] [ 1 − ;3]
Vậy M − m = 5 .
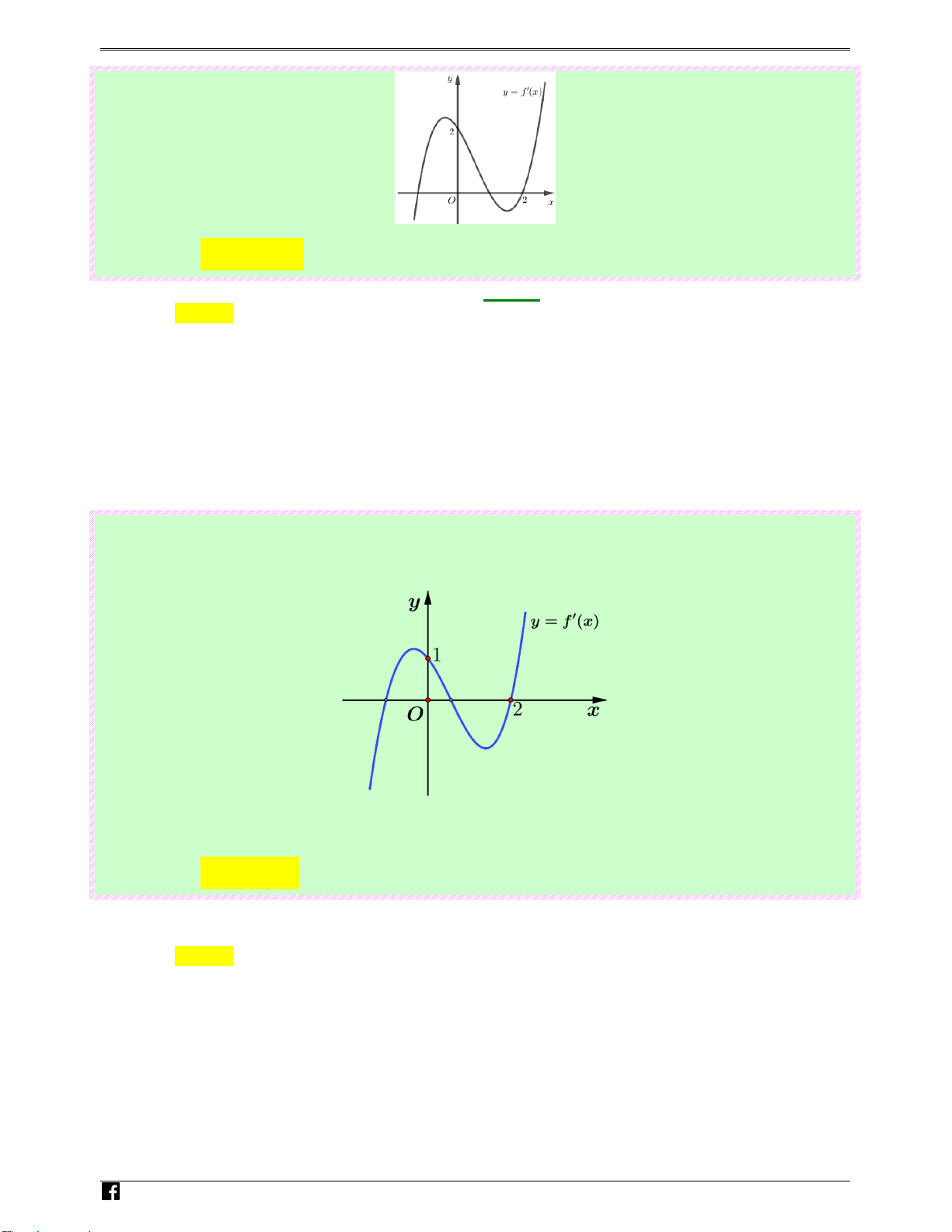
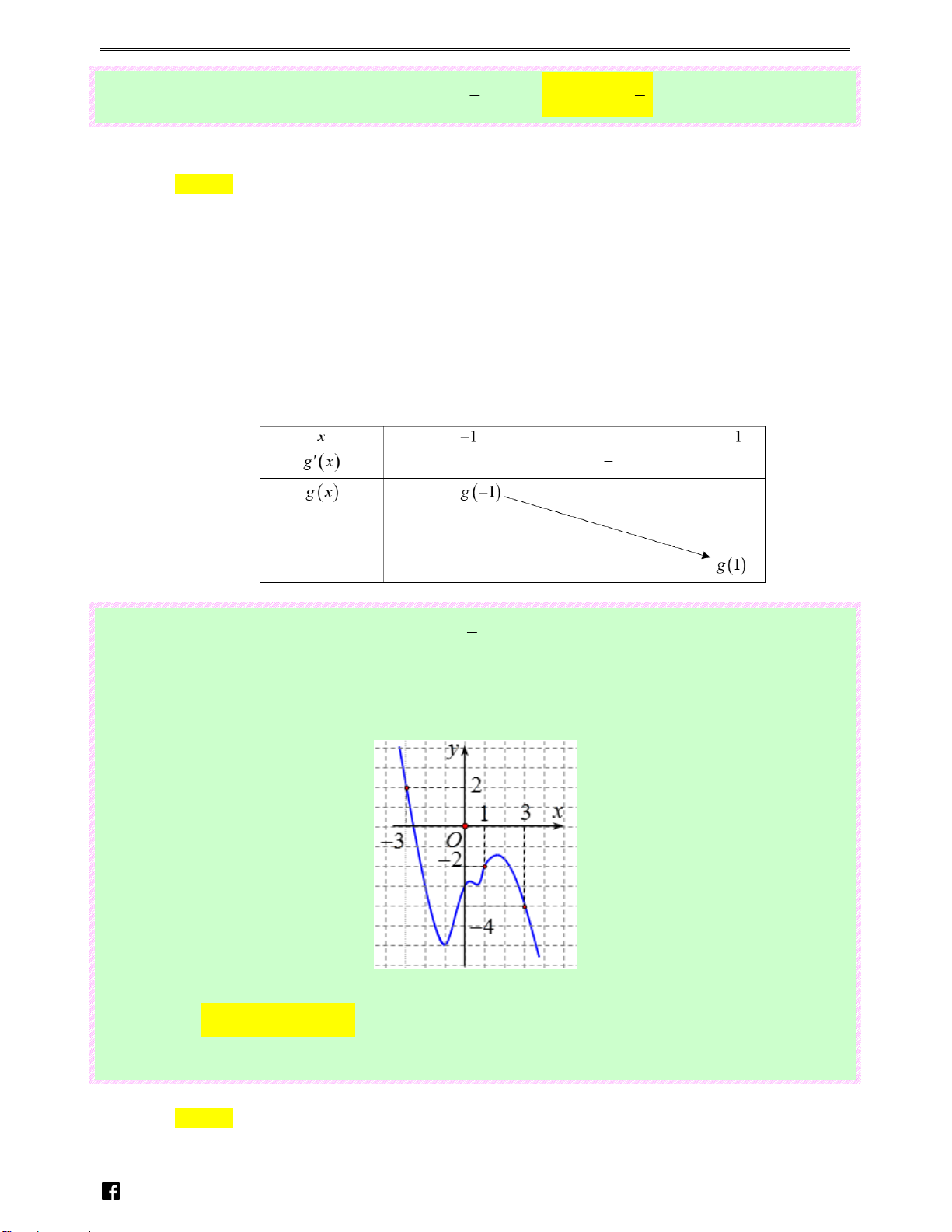
Câu 32: (Câu 39 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Cho hàm số f ( x) , đồ thị
của hàm số y = f ′( x) là đường cong trong hình bên. N guy%n Hoàng Vi)t 3
Giá trị lớn nhất của hàm số g ( x) = f (2x) − 4x trên đoạn − ;2 bằng 2 Ⓐ. f (0) .
Ⓑ. f (−3) + 6 .
Ⓒ. f (2) − 4 . Ⓓ. f (4) −8 . Lời giải Chọn C
https://www.facebook.com/vietgold Trang 13 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Luyenthitracnghiem.vn
Ta có: g′( x) = 2 f ′(2x) − 4 . 3
2x = x < −3 = < − 1 x 1 x 2 = g′( x) x
= 0 ⇔ 2 f ′(2x) − 4 = 0 ⇔ f ′(2x) 2 0 = 2 ⇔ ⇔ x = 0 2x = 2 x =1
2x = x > 4 2 x > 2 2
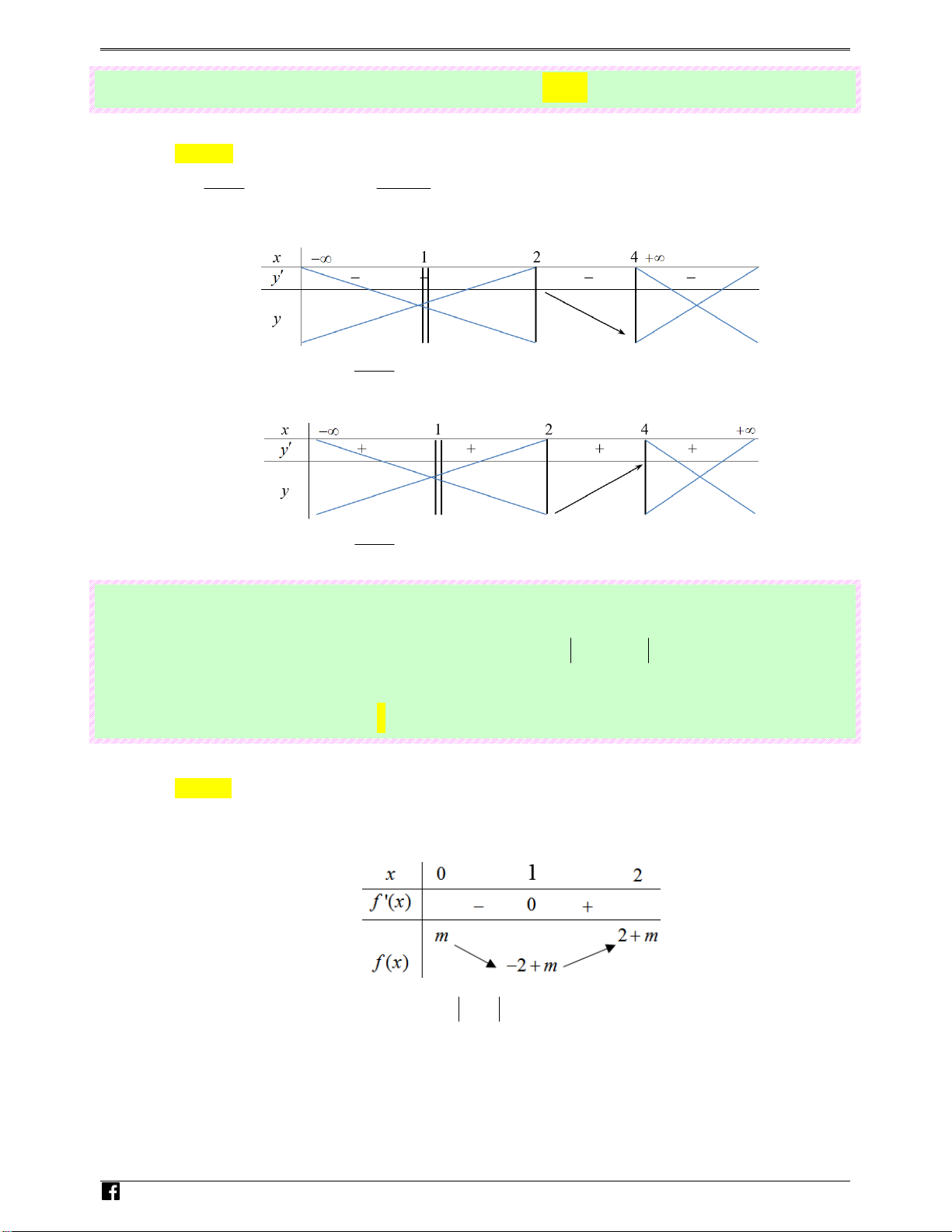
Ta có bảng biến thiên của hàm số y = g ( x) : N guy%n Hoàng Vi) t 3
Từ bảng biến thiên ta có: trên − ; 2
hàm số g ( x) = f (2x) − 4x đạt giá trị lớn nhất tại x = 1 và 2
max y = f (2) − 4 . 3;1 − 2
Câu 33: (Câu 37 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , hàm số
y = f ′ ( x ) liên tục trên R và có đồ thị như hình vẽ bên. Bất phương trình f ( x ) > 2x + m ( m là
tham số thực) nghiệm đúng với mọi x ∈ (0;2) khi và chỉ khi
https://www.facebook.com/vietgold Trang 14 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Luyenth itra
Ⓐ. m ≤ f (2) − 4 .
Ⓑ. m ≤ f (0) .
Ⓒ. m < f (0) .
Ⓓ. m < f (2) − 4 . cng Lời giải hi Chọn A em
Ta có f ( x) > 2x + m nghiệm đúng với mọi x ∈ (0;2) .vn
⇒ m < f ( x) − 2x nghiệm đúng với mọi x ∈ (0;2)
Xét hàm số g ( x) = f ( x) − 2x với x ∈(0; 2)
⇒ g′( x) = f ′( x) − 2 ≤ 0 với mọi x ∈(0;2)
⇒ hàm số nghịch biến trên (0;2) .
Để m < f ( x) − 2x nghiệm đúng với mọi x ∈(0;2) thì m ≤ g (2) = f (2) − 4
Câu 34: (Câu 38 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , hàm số y = f ′( x) liên
tục trên ℝ và có đồ thị như hình vẽ bên N guy%n Hoàng Vi)
Bất phương trình f (x) > x+m ( m là tham số thực) nghiệm đúng với mọi x∈(0;2) khi và chỉ khi t Ⓐ. m≤ f ( ) 2 −2.
Ⓑ. m < f (2) −2.
Ⓒ. m ≤ f (0) .
Ⓓ. m < f (0). Lời giải Chọn A
Bất phương trình f ( x) > x+m nghiệm đúng với mọi x∈(0;2)
⇔m< f (x) −x nghiệm đúng với mọi x∈(0;2) (1)
Xét hàm số g( x) = f ( x) − x trên khoảng (0; ) 2
Có g′( x) = f ′( x) −1< 0, x ∀ ∈(0;2)
https://www.facebook.com/vietgold Trang 15 Luyenthitracnghiem.vn
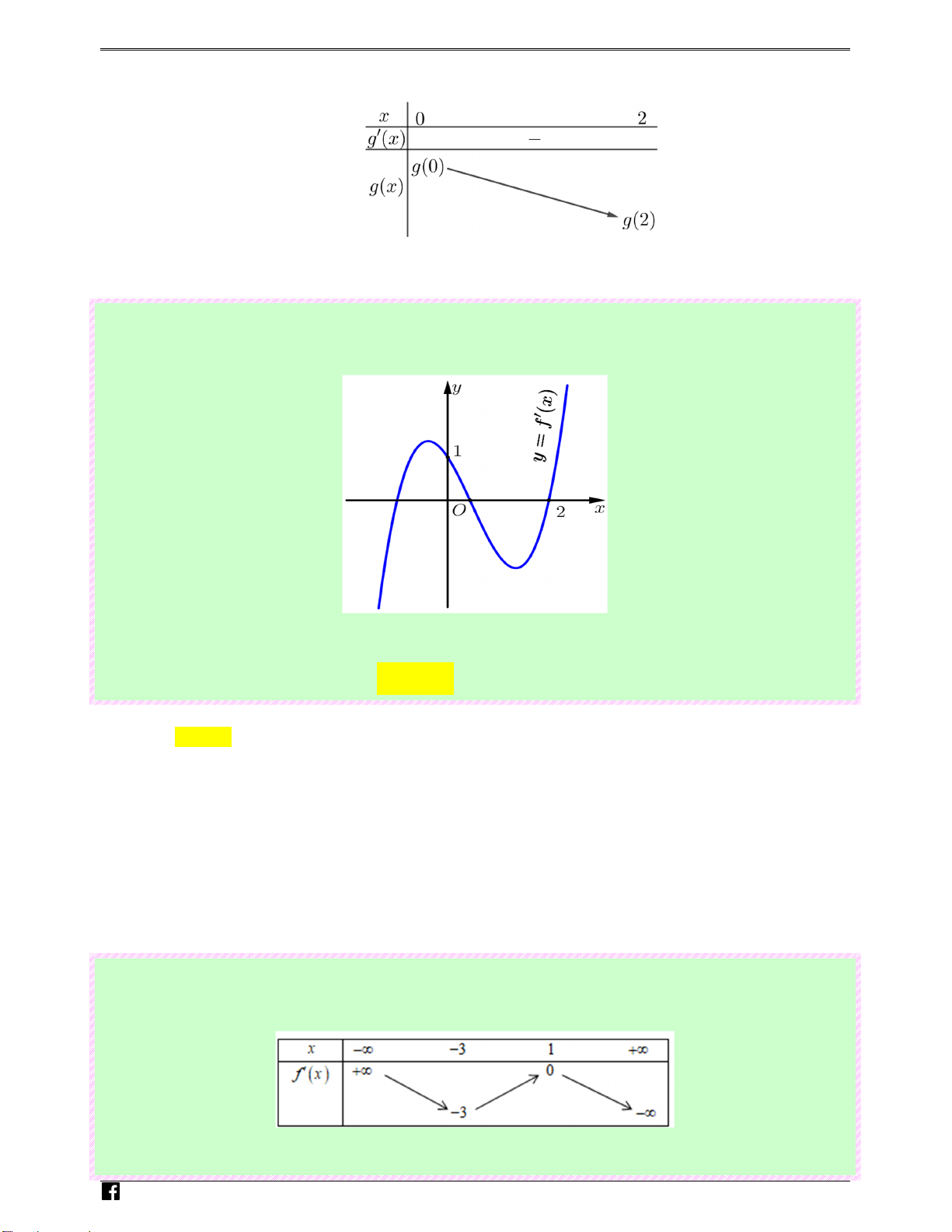
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Bảng biến thiên Luyenthi trac
Vậy (1) ⇔ m ≤ g (2) ⇔m≤ f ( ) 2 −2 . nghie
Câu 35: (Câu 36 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , hàm số y = f ′( x) liên m .v
tục trên ℝ và có đồ thị như hình vẽ bên. n
Bất phương trình f (x) < x + m ( m là tham số thực) nghiệm đúng với mọi x ∈(0; 2) khi và chỉ khi N g
Ⓐ. m ≥ f (2) −2.
Ⓑ. m ≥ f (0).
Ⓒ. m > f (2) −2.
Ⓓ. m > f (0). uy% Lời giải n Chọn B H o
Ta có f ( x) < x + ,
m ∀x ∈(0;2) ⇔ m > f ( x) − ,
x ∀x ∈(0;2)( ) * . àng
Dựa vào đồ thị của hàm số y = f ′( x) ta có với x ∈ (0; 2) thì f ′( x) < 1. Vi)
Xét hàm số g ( x) = f ( x) − x trên khoảng (0;2) . t
g′( x) = f ′( x) −1< 0,∀x∈(0;2) .
Suy ra hàm số g ( x) nghịch biến trên khoảng (0;2) . Do đó ( )
* ⇔ m ≥ g(0) = f ( ) 0 .
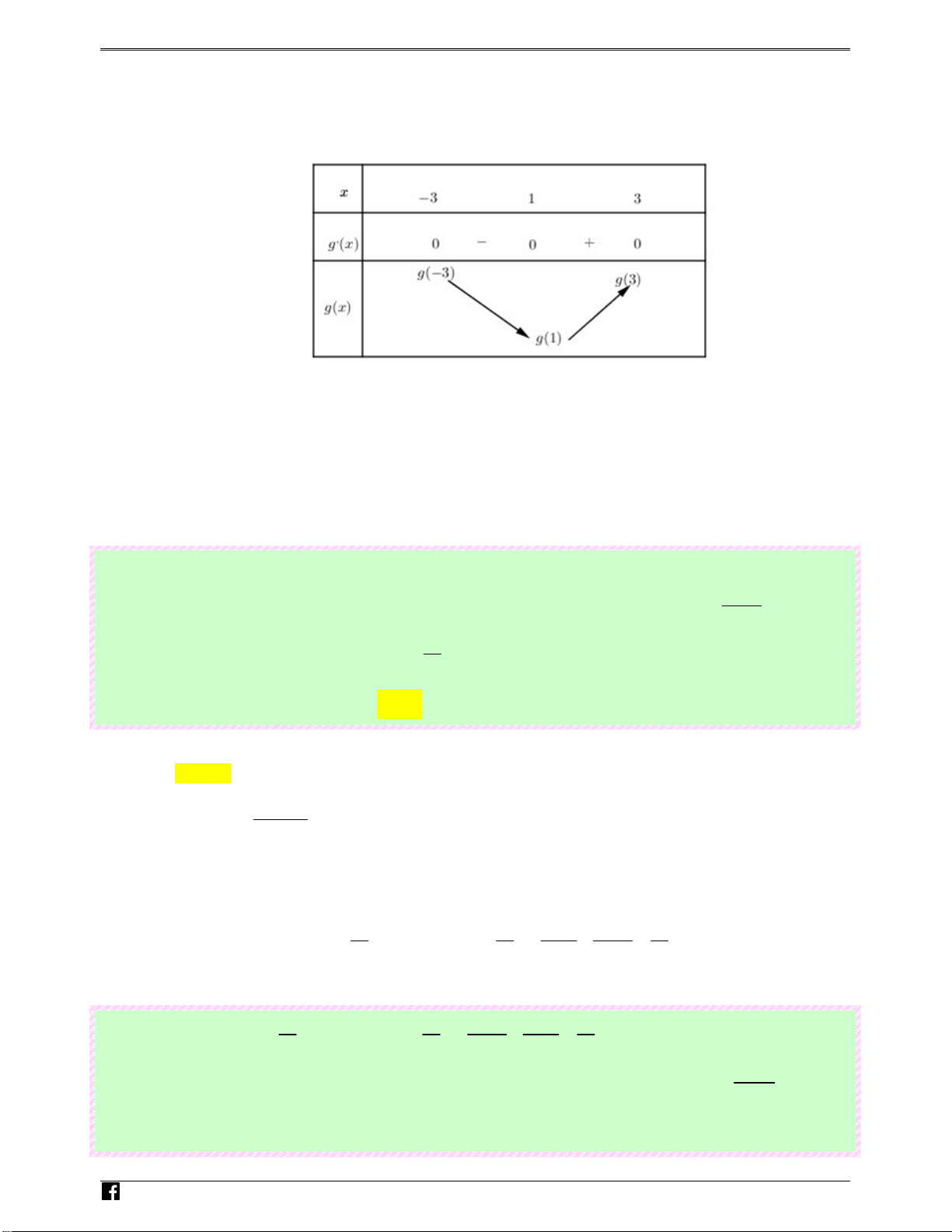
Câu 36: (Câu 39 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) . Hàm số y = f ′( x) có bảng biến thiên như sau
Bất phương trình ( ) < ex f x
+ m đúng với mọi x ∈( 1 − ; ) 1 khi và chỉ khi
https://www.facebook.com/vietgold Trang 16 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Ⓐ. m ≥ f ( ) 1 − e .
Ⓑ. m > f (− ) 1 1 − .
Ⓒ. m ≥ f (− ) 1 1 − .
Ⓓ. m > f ( ) 1 − e . e e Lời giải Luy Chọn C enth Ta có: ( ) < ex f x + m , x ∀ ∈( 1 − ; ) 1 ⇔ ( ) − ex f x < m , x ∀ ∈( 1 − ; ) 1 (*) . itrac = − n Xét hàm số ( ) ( ) ex g x f x ghi Ta có: ( ′ ) = (′ ) − ex g x f x . em . x x v Ta thấy với x ∀ ∈ ( 1 − ; ) 1 thì f ( ′ x) < 0 , e
− < 0 nên g (′x) = f (′x) − e < 0 , x ∀ ∈(−1; ) 1 . n Bảng biến thiên 1
Từ bảng biến thiên ta có m ≥ g( 1
− ) ⇔ m ≥ f (−1) − . e N
Câu 37: (Câu 48 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số y = f ( x) . Đồ thị guy%
của hàm số y = f ′( x) như hình bên. Đặt g ( x) = f ( x) + ( x + )2 2 1 . n Hoàng Vi)t
Mệnh đề nào dưới đây đúng? Ⓐ. g ( )
1 < g (3) < g (−3) .
Ⓑ. g (1) < g (−3) < g (3) .
Ⓒ. g (3) = g (−3) < g ( ) 1 .
Ⓓ. g (3) = g (−3) > g ( ) 1 . Lời giải Chọn A Ta có
https://www.facebook.com/vietgold Trang 17 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
g ′( x ) = 2 f ′( x) + 2 ( x + )
1 ⇒ g′(−3) = 2 f ′(−3) − 4, g′( ) 1 = 2 f ′( )
1 + 4, g′(3) = 2 f ′(3) + 8
Lại có nhìn đồ thị ta thấy f ′(−3) = 2, f ′(1) = −2, f ′(3) = −4 ⇒ g′(−3) = g′( ) 1 = g′(3) = 0
Hay phương trình g′( x) = 0 ⇔ f ′( x) = −x −1 có 3 nghiệm Luyenthitracnghiem.v n
Nhìn đồ thị ta có bảng biến thiên, suy ra g (3) > g ( )
1 , g (−3) > g ( ) 1 .
Mặt khác diện tích hình phẳng giới hạn bởi đường thẳng y = −x −1 và đồ thị hàm số 1 3 , y = f ( )
x trên 2 miền [−3; ]
1 và [1;3] , ta có (−x −1− f ′( x))dx > ( f ′( x) + x + ∫ ∫ )1dx 3 − 1 1 3
⇔ − g (′x)dx > g′ ∫
∫ (x)dx ⇔ −g ( )1+ g( 3 − ) g > (3) − g ( ) 1 ⇔ g ( 3 − ) > g (3) . 3 − 1 Vậy g ( )
1 < g (3) < g (−3) . +
Câu 38: (Câu 35 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Cho hàm số x m y = ( m là tham x +1 16
số thực) thoả mãn min y + max y =
. Mệnh đề nào dưới đây đúng? [1;2] 1;2 N [ ] 3 guy Ⓐ. m ≤ 0 Ⓑ. m > 4
Ⓒ. 0 < m ≤ 2 Ⓓ. 2 < m ≤ 4 %n H Lời giải oà Chọn B ng V 1− m i Ta có y′ = . )t (x + )2 1
Nếu m = 1⇒ y = 1, x ∀ ≠ 1
− . Không thỏa mãn yêu cầu đề bài.
Nếu m <1 ⇒ Hàm số đồng biến trên đoạn [1; ] 2 . 16 + + Khi đó: min m m y + max y =
⇔ y ( ) + y ( ) 16 1 2 16 1 2 = ⇔ + = ⇔ m = 5 . [1;2] [1;2] 3 3 2 3 3
Nếu m >1 ⇒ Hàm số nghịch biến trên đoạn [1; ] 2 . 16 16 2 + m 1+ m 16
Khi đó: min y + max y =
⇔ y (2) + y ( ) 1 = ⇔ + = ⇔ m = 5 [1;2] [1;2] 3 3 3 2 3 +
Câu 39: (Câu 33 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Cho hàm số x m y = thỏa mãn x − 1
min y = 3. Mệnh đề nào sau dưới đây đúng? [2;4]
https://www.facebook.com/vietgold Trang 18 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Ⓐ. m < 1 −
Ⓑ. 3 < m ≤ 4 Ⓒ. m > 4 Ⓓ. 1≤ m < 3 Lời giải Chọn C Lu x + m −1− m y y = , D = ℝ \ { } 1 , y′ = e 2 n x −1 (x − ) 1 thi TH1: ′
y < 0 ⇔ m > −1 tracnghiem .vn 4 + m
min y = 3 ⇔ f 4 = 3 ⇔ = 3 ⇔ m = 5 ( ) (n) [2;4] 3 TH2: ′
y > 0 ⇔ m < −1 + y = ⇔ f ( ) 2 m min 3 2 = 3 ⇔
= 3 ⇔ m =1 (l) [2;4] 1 Vậy m = 5
Câu 40: (Câu 36 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Gọi S là tập hợp tất cả các giá trị của
tham số thực m sao cho giá trị lớn nhất của hàm số 3
y = x − 3x + m trên đoạn [0; ] 2 bằng 3. S ố Ng phần tử của S là uy% n Ⓐ. 1 Ⓑ. 2 Ⓒ. 0 Ⓓ. 6 Ho Lời giải àng Chọn B Vi)
Xét hàm số f ( x) 3
= x −3x+m , ta có f ′(x) 2 =3x −3 f x : t
. Ta có bảng biến thiên của ( )
TH 1 : 2 + m < 0 ⇔ m < − 2 . Khi đó max f ( x) = −(− 2 + m) = 2 − m [0;2]
2 − m = 3 ⇔ m = −1 .
https://www.facebook.com/vietgold Trang 19 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 2 + m > 0
TH 2 :
⇔ − 2< m <0 . Khi đó : m−2 =2−m>2>2+m m < 0
⇒ max f (x) = −(− 2+ m)= 2−m [0;2] Luye
2 − m = 3 ⇔ m = −1 . nth m >0 it
TH 3 :
⇔ 0< m < 2 . Khi đó : m−2 =2−m<2<2+m ⇒max f (x) =2+ m ra − 2 + m <0 [0;2] cngh
2 + m = 3⇔ m =1 . iem
TH 4: − 2 + m > 0 ⇔ m > 2 . Khi đó max f ( x) = 2 + m .v [0;2] n
2 + m = 3⇔ m =1 . +
Câu 41: (Câu 48 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Cho hàm số ( ) x m f x = ( x +1
m là tham số thực). Gọi S là tập hợp tất cả các giá trị của S sao cho max f ( x) + min f ( x) = 2 [0; ] 1 [0; ] 1
. Số phần tử của S là Ⓐ. 6. Ⓑ. 2. Ⓒ. 1. Ⓓ. 4. Lời giải Chọn B N
a/ Xét m =1, ta có f ( x) = 1 ∀x ≠ −1 guy
Dễ thấy max f ( x) =1, min f ( x) =1 suy ra max f ( x) + min f ( x) = 2 . % [0; ]1 [0; ]1 [0; ] 1 [0; ] 1 n H
Tức là m =1 thỏa mãn yêu cầu. oà 1− m n
b/ Xét m ≠1 ta có f '( x) = không đổi dấu x ∀ ∈ ℝ \{− } 1 g (x + )2 1 Vi)
Suy ra f (x) đơn điệu trên đoạn [0; ] 1 t + Ta có ( ) = ( ) 1 0 ; 1 m f m f = 2 min f (x) = 0 [0; ]1 1+ m Trường hợp 1: . m < 0 ⇔ 1
− < m < 0 ⇒ m +1 2
max f (x) = max m ; < 1 [0; ]1 2
Suy ra không thỏa mãn điều kiện max f ( x) + min f ( x) = 2 [0; ] 1 [0; ] 1 1+ m
m ≥ 0(m ≠ ) 1 Trường hợp 2: . m ≥ 0 ⇔ 2 m ≤ 1 − m = 1(KTM ) m +1 3m +1
Suy ra min f (x) max f (x) m 2 + = + = = ⇔ 5 [0; ]1 [0; ]1 2 2 m = − (TM ) 3
https://www.facebook.com/vietgold Trang 20 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 5 Vậy S = 1 ; − . 3
Câu 42: (Câu 42 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Gọi S là tập hợp tất cả các giá trị thực Lu
của tham số thực m sao cho giá trị lớn nhất của hàm số 3
y = x − 3x + m trên đoạn [0; ] 3 bằng yent
16 . Tính tổng các phần tử của S bằng hitr Ⓐ. −16 . Ⓑ. 16. Ⓒ. −12. Ⓓ. −2. acng Lời giải hiem Chọn A .v
Nhận xét: Hàm số 3
g(x) = x − 3x + m là hàm số bậc ba không đơn điệu trên đoạn [0; ] 3 nên ta n
sẽ đưa hàm số này về hàm bậc nhất để sử dụng các tính chất cho bài tập này. Đặt 3
t = x − 3x , do [0; ]
3 nên ta tìm được miền giá trị t ∈[ 2 − ;1 ]
8 . Khi đó y = t + m đơn điệu trên [ 2 − ;1 ] 8 . Ta có
m − 2 + m +18 + m − 2 − m −18
max y = max t + m = max{ m − 2 ; m +18} = . = m+8 +10 x [ ∈ 0; ] 3 t [ ∈ −2;18] 2 m = 2 −
Từ giả thiết ta có max y = 16 ⇔ m + 8 +10 =16 ⇔ m + 8 = 6 ⇔ . x [ ∈ 0;2] m = 1 − 4 N
Chú ý: Cách giải trên ta đã sử dụng tính chất của hàm số bậc nhất là gu
a + b + a −b y max a ; b = 1 . % { } ( ) n 2 Ho
Tuy nhiên có thể trình bày phần sau bài toán như sau mà không cần công thức ( ) 1 . àng Ta có Vi)t
max y = max t + m = max{ m − 2 ; m +18} x [ ∈ 0; ] 3 t [ ∈ −2;18] m +18 = 16
+ Trường hợp 1:
max y = m +18 = 16 ⇔ ⇔ m = −2 . x [ ∈ 0; ] 3 m − 2 < 16 m − 2 = 16 +
Trường hợp 2: max y = m − 2 = 16 ⇔ ⇔ m = −14 . x [ ∈ 0;3] m +18 < 16 Cách 2 Xét 3
u = x −3x + m trên đoạn [0;3]có 2
u ′ = 0 ⇔ 3x − 3 = 0 ⇔ x = 1 ∈ [0;3] .
https://www.facebook.com/vietgold Trang 21 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 max u = max {u(0),u( ) 1 ,u( ) 3 } = max {m, m−2,m+1 } 8 = m +18 Khi đó [0; ] 3 . min u = min {u(0),u( ) 1 ,u( ) 3 } = min {m, m−2,m+1 } 8 = m −2 [0;3] Lu m +18 =16 y e n m +18 ≥ m − 2 m = −2 t h
Suy ra M ax f (x)= max{ m−2 , m +18 } =16 ⇔ ⇔ . 0;3 i [ ] m− 2 =16 m = −14 t r a c m − 2 ≥ m +18 n ghie
Do đó tổng tất cả các phần tử của S bằng −16 . m
Câu 43: (Câu 47 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Xét các số thực không .vn
âm x và y thỏa mãn 1 2 .4x y 3 x y + − +
≥ . Giá trị nhỏ nhất của biểu thức = 2 + 2 + 4 + 2 P x y x y bằng Ⓐ. 33 . Ⓑ. 9 . Ⓒ. 21 . Ⓓ. 41 . 8 8 4 8 Lời giải Chọn D Ta có : 1 2 y− 3−2 2 .4x y 3 x y + − + ≥ ( x) ⇔ 2 . y 2 ≥ 3− 2x 2 y ( ) 3 2 2 .2 3 2 .2 x y x − ⇔ ≥ − (*) .
Xét hàm số ( ) = .2t f t t
có ′( ) = 2t + .2t f t t .ln 2 . N 3 g
Trường hợp 1 : Với x ≥ ⇒ (*) luôn đúng ∀y ≥ 0 . u 2 y%n 2 2 2 3 2 33 H
Ta có : P = ( x + 2) + ( y + ) 1 − 5 ≥ + 2 + (0 + ) 1 − 5 = . o 2 4 àng 3 V x = i) Dấu bằng xảy ra ⇔ 2 . t y = 0 3
Trường hợp 2 : 0 ≤ x < suy ra t ≥ 0 ⇒ f ′(t ) > 0 hay hàm số y = f (t) luôn đồng biến nên 2 ( 3 − 2 *) ⇔ 2 x
y ≥ 3 − 2x ⇔ y ≥ . 2 2 3 − 2 Ta có : 2 2 2 = + + 4 + 2 x P x y x y ≥ x + + 4x + 3 − 2x 2 1 2 = 21 x 1 41 41 2 = 2 4 x − x + = 2 x − + ≥ dấu bằng xảy ra ⇔ . 4 4 8 8 5 y = 4
https://www.facebook.com/vietgold Trang 22 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Câu 44: (Câu 45 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Xét các số thực không âm , x y thỏa mãn x+ y 1 2x y.4 − +
≥ 3 . Tìm giá trị nhỏ nhất của biểu thức 2 2
P = x + 2x + y + 4 y . Lu Ⓐ. 33 . Ⓑ. 9 . Ⓒ. 21 . Ⓓ. 41 . y 8 8 4 8 enth Lời giải itra Chọn D cng
Cách 1 (Thầy Nguyễn Duy Hiếu). hie + − + − m Ta có x y 1 2x + . y 4 ≥ 3 ⇔ 2x 2 y 3 2x − 3 + 2 . y 2
≥ 0 ⇔ x + y − + y ( 2x+2y−3 2 2 3 2 . 2 − ) 1 ≥ 0 (1) .vn 3
Nếu 2x + 2 y − 3 < 0 thì VT(1) < 0, vô lý, nên từ (1) suy ra 2x + 2 y − 3 ≥ 0 ⇔ x + y ≥ 2
P = ( x + )2 + ( y + )2 1 1 2 − 5 = (1+ ) 1 ( x + )2 1 + ( y + 2)2 − 5 2 2 1 ( ≥ x + + y + )2 1 3 41 1 2 − 5 ≥ 3 + − 5 = . 2 2 2 8 5 1 41
Dấu “=” xảy ra ⇔ x = , y = . Vậy min P = . 4 4 8
Cách 2 (Trần Văn Trưởng). x+ y− y x− 2 y 2−2x N Ta có 1 1 2x + . y 4 ≥ 3 ⇔ . y 4 .4 ≥ 3 − 2x ⇔ . y 2 ≥ (3− 2x).2 guy% 2 y 3 2 2 .2 3 2 .2 x y x − ⇔ ≥ − n ( ) . (*) Ho 3 3 à
Nếu 3 − 2x ≤ 0 ⇔ x ≥ thì với mọi x ≥ , y ≥ 0 đều thỏa mãn (*) và khi đó ng 2 2 Vi 2 2 21 )
P = x + y + 2x + 4 y ≥ . t 4
Nếu 3 − 2x > 0 .
Xét hàm số ( ) = .2t f t t
với t ∈ (0; +∞) .
Ta có '( ) = 2t + .2t f t
t .ln 2 > 0, t ∀ ( ∈ 0;+ ) ∞ .
Do đó hàm số f (t) đồng biến trên (0;+∞) . Từ (*) suy ra 2y ≥ 3− 2x ⇔ 2x + 2y ≥ 3. Xét 2 2
P = ( x + )2 + ( y + )2 1 2 − 5 ⇔ ( x + )
1 + ( y + 2) = P + 5 .
https://www.facebook.com/vietgold Trang 23 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 3 0 ≤ x < ( ) 1 2
Ta có hệ điều kiện sau: y ≥ 0 (2) L
2x + 2y − 3 ≥ 0 (3) u 2 2 y e (x + )
1 + ( y + 2) = P + 5 (4) nthit
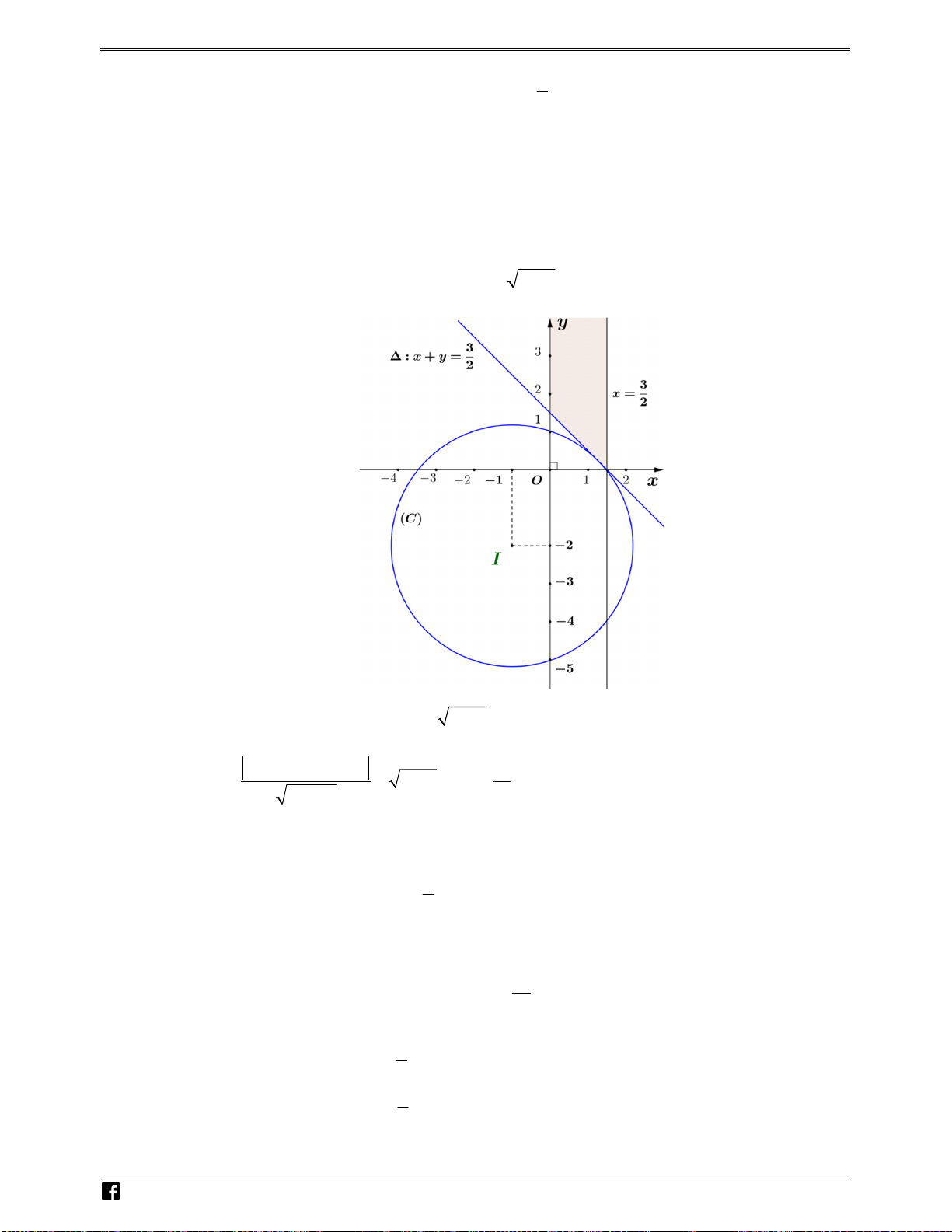
Hệ điều kiện (1), (2), (3) là phần tô màu trên hình vẽ. racn
(4) coi như là đường tròn tâm I ( 1 − ; 2
− ), R = P + 5 . ghiem.vn N g uy%
Để hệ có nghiệm thì d (I;∆) ≤ R = P + 5 , ở đó ∆ : 2x + 2y − 3 = 0 . n Hoà 2(− ) 1 + 2( 2 − ) −3 41 n Suy ra
≤ P + 5 ⇔ P ≥ . g 2 2 2 + 2 8 Vi)t
Dấu bằng xảy ra khi hệ sau có nghiệm: 3 0 ≤ x < 2 y ≥ 0
2x + 2 y − 3 = 0
( x + )2 + ( y + )2 41 1 2 = + 5 8 5 x =
Giải hệ này ta tìm được 4 . 1 y = 4
https://www.facebook.com/vietgold Trang 24 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 41 5 1 Vậy Min P =
khi x = , y = . 8 4 4
Câu 45: Cách 3 (Nguyễn Kim Duyên) Luy x+ y 1 2x . y 4 − + ≥ 3 1 2 x+2 y−2 e
Câu 46: Giả thiết
( ) ⇔ 2x − 2 + y.2 ≥ 1. nthi a − b tr
Đặt a = 2x + 2y − 2 ; b = 2x − 2 ⇒ a ≥ b và y = . a 2 cng a − b h ( )1 viết lại: b +
.2a ≥ 1 ⇔ 2(b − a) + (a − b) 2a ≥ 2 − 2a ⇔ ( − )(2a a b
− 2) ≥ 2 − 2a ( ) * ie 2 m .v
VT * ≤ 0 < VP * n
• Nếu a < 1 thì ( )
( ) . Vậy không xảy ra a < 1. x ≥ 0
• Nếu a ≥ 1 thì y ≥ 0 (D) . 2x + 2y ≥ 3
Biểu diễn được P + = ( x + )2 + ( y + )2 5 1
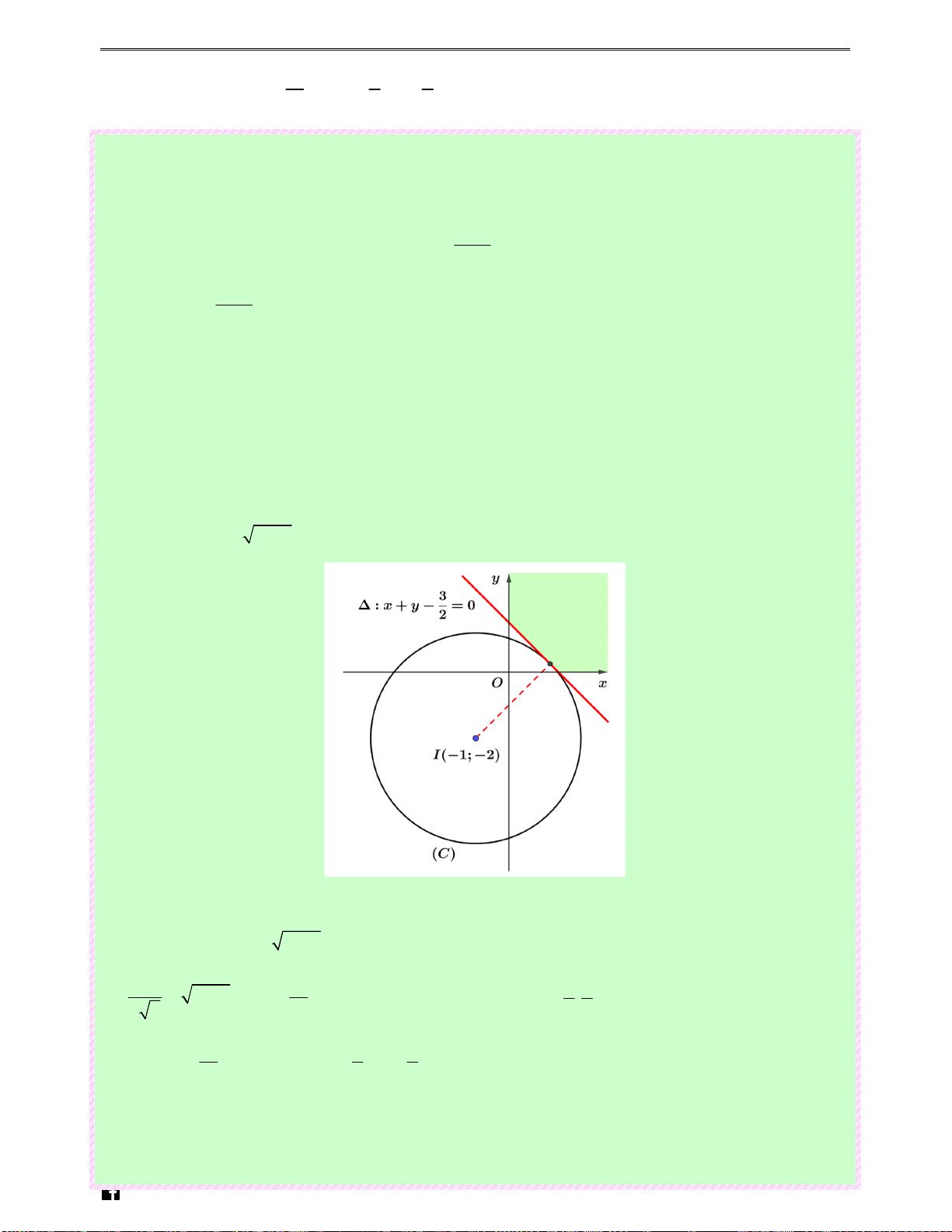
2 , xem như là phương trình đường tròn (C) có tâm I ( 1 − ; 2 − ) , bán kính P + 5 . N guy%n Hoàng Vi)t
Ta cần tìm min P trên miền (D) . Khi đó (C) là đường tròn có bán kính nhỏ nhất chạm miền (D)
⇔ d (I,∆) = P + 5 (trong đó, ∆ : 2x + 2y − 3 = 0 ). 9 41 ⇔ = 5 1 P + 5 ⇔ P =
. Khi đó ∆ tiếp xúc (C) tại điểm ; . 2 2 8 4 4 41 5 1 Vậy min P =
, đạt được khi x = , y = . 8 4 4
Cách 4 ( NT AG). Ta có x + y 1 − 2 x+2 y−3 2x + y.4
≥ 3⇔ 2x + 2 y.2 ≥ 3 .
Nếu 2x + 2y − 3 < 0 thì 2 x+2 y−3 0 3 ≤ 2x + 2 y.2
< 2x + 2 y.2 = 2x + 2 y . Suy ra 2x + 2y − 3 > 0 . Mâu thuẫn.
https://www.facebook.com/vietgold Trang 25 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 3 5 5
Nếu 2x + 2y − 3 ≥ 0 (1). Ta có (1) ⇔ x + y ≥
⇔ x + ( y + 1) ≥ . Đặt t = y +1 ( t ≥ 1). Ta có x + t≥ . 2 2 2 Khi đó, L 2 2 2 2 2 2 u
P = x + 2x + y + 4 y = x + ( y + 1) + 2x + 2 y + 2 − 3 = x + t + 2(x + t) − 3 yen 2 th 1 1 5 5 41 2 i
≥ (x + t) + 2(x + t) − 3 ≥ . + 2. − 3 = . tr 2 2 2 2 8 acng 5 5 1 h
Dấu đẳng thức xảy ra khi và chỉ khi x = t = hay x = , y = . i 4 4 4 em .
Câu 47: (Câu 48 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Xét các số thực không âm x và y vn thỏa mãn x+ y 1 2x y.4 − +
≥ 3 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 6x + 4 y bằng Ⓐ. 65 . Ⓑ. 33 . Ⓒ. 49 . Ⓓ. 57 . 8 4 8 8 Lời giải Chọn A Ta có x+ y 1 − 2 x+2 y−2 2x + y.4 ≥ 3 ⇔ y.2 ≥ 3 − 2x 2 y ( ) 3 2 2 .2 3 2 .2 x y x − ⇔ ≥ − (*) Hàm số ( ) = .2t f t t
đồng biến trên R , nên từ (*) ta suy ra 2y ≥ 3 − 2x ⇔ 2x + 2y − 3 ≥ 0 ( ) 1 Ta thấy ( )
1 bất phương trình bậc nhất có miền nghiệm là nửa mặt phẳng có bờ là đường thẳng
d : 2x + 2 y − 3 = 0 (phần không chứa gốc tọa độ O ), kể cả các điểm thuộc đường thẳng d . N
Xét biểu thức P = x + y + x + y ⇔ ( x + )2 + ( y + )2 2 2 6 4 3 2 = P +13 (2) guy
Để P tồn tại thì ta phải có P +13 ≥ 0 ⇔ P ≥ 1 − 3 . %n
Trường hợp 1: Nếu P = 1
− 3 thì x = −3; y = −2 không thỏa ( )
1 . Do đó, trường hợp này không H oà thể xảy r Ⓐ. ng
Trường hợp 2: Với P > 1
− 3, ta thấy 2 là đường tròn có tâm I 3 − ; 2 − và bán kính V ( ) (C) ( ) i)t R = P + 13 .
Để d và (C ) có điểm chung thì d (I d ) 13 65 ; ≤ R ⇔
≤ P +13 ⇔ P ≥ . 2 2 8 65 1 5 Khi P =
đường tròn (C ) tiếp xúc đường thẳng d tại N ;
(thỏa mãn vì N thuộc (T ) 8 4 4 ). 65 Vậy min P = . 8
Câu 48: (Câu 48 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Xét các số thực không âm x và y thỏa mãn x+ y 1 2x . y 4 − +
≥ 3. Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 4x + 6y bằng
https://www.facebook.com/vietgold Trang 26 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021
Ⓐ. 33 . Ⓑ. 65 . Ⓒ. 49 . Ⓓ. 57 . 4 8 8 8 Lời giải Luy Chọn B ent x+ y 1 − h
Nhận xét: Giá trị của ,
x y thỏa mãn phương trình 2x + y ⋅ 4 = 3( )
1 sẽ làm cho biểu thức P itra nhỏ nhất. Khi đó cngh x+ y− x+ y− 2 3 1 1 i
(1) : 2x + y ⋅ 4 = 3 ⇔ 4
+ (x + y) − 2 − = 0 em y y .vn
Đặt a = x + y , từ ( ) 1 ta được phương trình a− 2 3 1 4 + .a − 2 − = 0 ( ) * . y y a− 2 a− 2 3
Xét hàm số f (a) 1
= 4 + .a − 2 − . Ta có f '(a) 1 = 4 .ln 4 + > 0, y
∀ > 0 nên f (a) hàm y y y số đồng biến.
Mặt khác, lim f (a) = −∞ , lim f (a) = +∞ . x→−∞ x→+∞ 3 3
Do đó, phương trình (*) có nghiệm duy nhất a = ⇒ x + y = . 2 2 N 2 1 1 65 65 g
Ta viết lại biểu thức P = ( x + y) + 4( x + y) + 2 y − − = . Vậy m P = . in u 4 8 8 8 y%n Cách khác: H oà Với mọi , x y không âm ta có ng 3 3 V x+ y− + − x+ y− 3 3 x y i 1 2 2 ) 2x + y.4
≥ 3 ⇔ x + y.4 ≥ ⇔ x + y − + y. 4 − 1 ≥ 0 (1) t 2 2 3 3 + − Nếu 3 x y x + y −
< 0 thì x + y − + y. 4 − 1 < 0 + y.( 0 2 4 − ) 1 = 0 (vô lí) 2 2 3
Vậy x + y ≥ . 2
Áp dụng bất đẳng thức Bunhyakovski ta được
P = x + y + x + y = ( x + )2 + ( y + )2 2 2 4 6 3 2 −13 2 1 ( ≥ x + y + )2 1 3 65 5 −13 ≥ + 5 −13 = 2 2 2 8
https://www.facebook.com/vietgold Trang 27 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 5 3 y = x + y = Đẳng thức xảy ra khi 4 2 ⇔ . 1 x + 3 = y + 2 x = 4 Luye 65 n Vậy min P = . t 8 hit
Câu 49: (Câu 41 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Một vật chuyển động theo quy rac 1 n luật 3 2
s = − t + 6t với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s g 2 hie
(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian m .
6 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? vn
Ⓐ. 24(m / s).
Ⓑ. 108(m / s).
Ⓒ. 18(m / s).
Ⓓ. 64(m / s). Lời giải Chọn A 2 3 Ta có ( ) = ′( ) t v t s t = − +12t ; 2 v′(t ) = 3
− t +12 ; v′(t ) = 0 ⇔ t = 4 .
v (0) = 0 ; v (4) = 24 ; v (6) = 18 . Suy ra vận tốc lớn nhất của vật đạt được trong 6 giây đầu là 24(m / s). 1
Câu 50: (Câu 7 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Một vật chuyển động theo quy luật 3
s = − t + 9t 2 N 2 gu
với t (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và s (mét) là quãng đường vật y%n
đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển H
động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? oàng
Ⓐ. 216 (m/s)
Ⓑ. 30 (m/s)
Ⓒ. 400 (m/s) Ⓓ. 54 (m/s) Vi) Lời giải t Chọn D 3
Vận tốc tại thời điểm t là 2
v(t) = s (
′ t) = − t +18t với t ∈ [0;10]. 2
Ta có : v (′t) = −3t +18 = 0 ⇔ t = 6 .
Suy ra: v (0) = 0;v (10) = 30;v (6) = 54 . Vậy vận tốc lớn nhất của vật đạt được bằng 54 (m/s) .
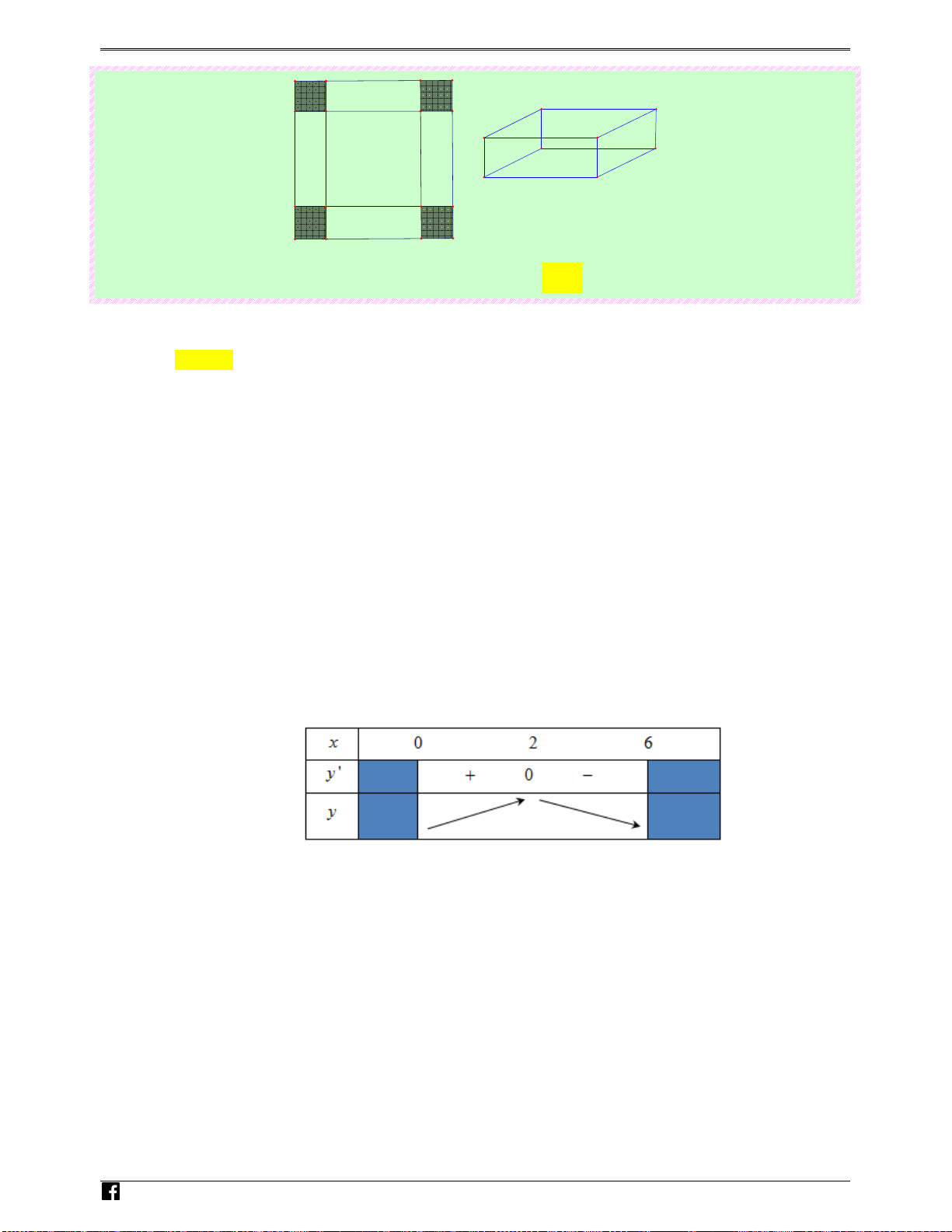
Câu 51: (Câu 10 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Cho một tấm nhôm hình vuông cạnh 12 cm.
Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh
bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x để hộp nhận được có thể tích lớn nhất.
https://www.facebook.com/vietgold Trang 28 Luyenthitracnghiem.vn
51 BÀI TOÁN GTLN - GTNN TRONG Đ THI BGD T! 2016 - 2021 Luyenthit racn Ⓐ. x = 6 Ⓑ. x = 3 Ⓒ. x = 2 Ⓓ. x = 4 ghiem Lời giải .vn Chọn C
Ta có : h = x (cm) là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 12 − 2x (cm) x > 0 x > 0
Vậy diện tích đáy hình hộp S = ( − x)2 ( 2 12 2 cm ). Ta có: ⇔ ⇔ x ∈(0;6) 12 − 2x > 0 x < 6
Thể tích của hình hộp là: V = S.h = x ( 2 − 2x)2 . 1
Xét hàm số: y = x ( − x)2 . 12 2 x ∀ ∈(0;6)
Ta có : y = ( − x)2 ' 12 2
− 4x (12 − 2x) = (12 − 2x)(12 − 6x) ; N gu
y ' = 0 ⇔ (12 − 2x ).(12 − 6x ) = 0 ⇔ x = 2 hoặc x = 6 (loại). y%n Hoàng Vi)t
Suy ra với x = 2 thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là y (2) = 128 .
https://www.facebook.com/vietgold Trang 29




