55 câu trắc nghiệm nguyên hàm, tích phân và ứng dụng – Đoàn Trí Dũng Toán 12

Chuyên đề NGUYÊN HÀM – TÍCH PHÂN
§ BÀI 1: NGUYÊN HÀM – TÍCH PHÂN CƠ BẢN 
Câu 1: Trong các mệnh đề sau, có bao nhiêu mệnh đề sai: (1)  f
 xdx' f x
(2) af  xdx  a f  xdx, a    (3)  f
 x gx dx  f 
 xdx g
 xdx (4) f
 xgxdx  f  xdx g
 xdx A. 1 B. 2 C. 3 D. 4
Câu 2: Trong các mệnh đề sau, có bao nhiêu mệnh đề sai: (1) F '
 xdx  FxC (2) f
 xdx  g
 xdx  f x  gx
(3) f ' x  g ' x  f  x  g  x
(4) F  x là một nguyên hàm của f  x  f
 xdx  FxC A. 1 B. 2 C. 3 D. 4
Câu 3: Tìm mệnh đề sai trong các mệnh đề sau:
A. Nếu f  x liên tục trên  ;
a b thì f  x có nguyên hàm trên  ; a b .
B. Nếu f  x và g  x có nguyên hàm trên  ;
a b thì f  x.g  x có nguyên hàm trên  ; a b . f  x
C. Nếu f  x và g  x có nguyên hàm trên  ; a b thì có nguyên hàm trên  ; a b . g  x
D. Nếu f  x có nguyên hàm trên  ; a b thì 2
f  x có nguyên hàm trên  ; a b .
Câu 4: Tìm mệnh đề sai trong các mệnh đề sau: 1 4 x  C A. x x
dx  ln x  C  B. 2e dx  2 
e C C. sinxdx C cosx  D. 3 x dx   x 4
Câu 5: Tìm mệnh đề sai trong các mệnh đề sau: A. 2
tan xdx  tan x  x  C  B. 2
cot xdx  cot x  x  C  1 1 2 C.  dx   C  D. 2
dx  ln x  C  2 x x x
Câu 6: Họ nguyên hàm của  x   2 2 1 dx bằng:  x  3 2 1  C  x  3 2 1  C 4 A. B. C. 3 2
x  2x  x  C D. Đáp án khác 2 3 3 3 2 x  2x  5
Câu 7: Họ nguyên hàm của dx  bằng: 2 x 5 5 5 2 x 5 A. 2 x  x   C B. 2
 x   C C. 2 x  2x   C D.
 2x   C x x x 2 x x
Câu 8: Họ nguyên hàm của 2 2sin dx  bằng: 2
A. x  sin x  C
B. x  sin x  C
C. sin x  C
D. sin 2x  C 1
Câu 9: Họ nguyên hàm của dx  bằng: 1  cos 2x tan 2x tan x  C 1 sin x  C A.  C B. C.  C D. 2 2 2 2sin x 2 cos x 1 1
Câu 10: Tìm nguyên hàm F  x của hàm số f  x  
biết rằng F   1  1. 3 x x 3 1 1 3 1 1 A. 3 2 2 x  x  B. 3 2 2  x  x  C. 3 2 2 x  x  D. 3 2 2 x  x  2 2 2 2 2 2
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389 x
Câu 11: Họ nguyên hàm của hàm số f  x cos 2  bằng: sin x  cos x
A. sin x  cos x
B. sin x  cos x
C. 2sin x  1
D. sin 2x 1
Câu 12: Tích phân  4 x   1dx bằng? 0 2 4 6 8 A. B. C. D. 5 5 5 5 8
Câu 13: Tích phân 3 xdx  bằng? 1 45 47 25 A. B. C. D. 2 4 4 4 4 Câu 14: Tích phân xdx  bằng? 1 14 16 7 5 A. B. C. D. 3 3 3 3
Câu 15: Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng: b b b (1) Ta luôn có: f
 xdx  0 (2) Ta luôn có: f
 xdx  f  xdx a a a b
(3) Nếu f  x  0 trên a;b và f
 xdx  0 thì f x  0 trên a;b. a A. 0 B. 1 C. 2 D. 3
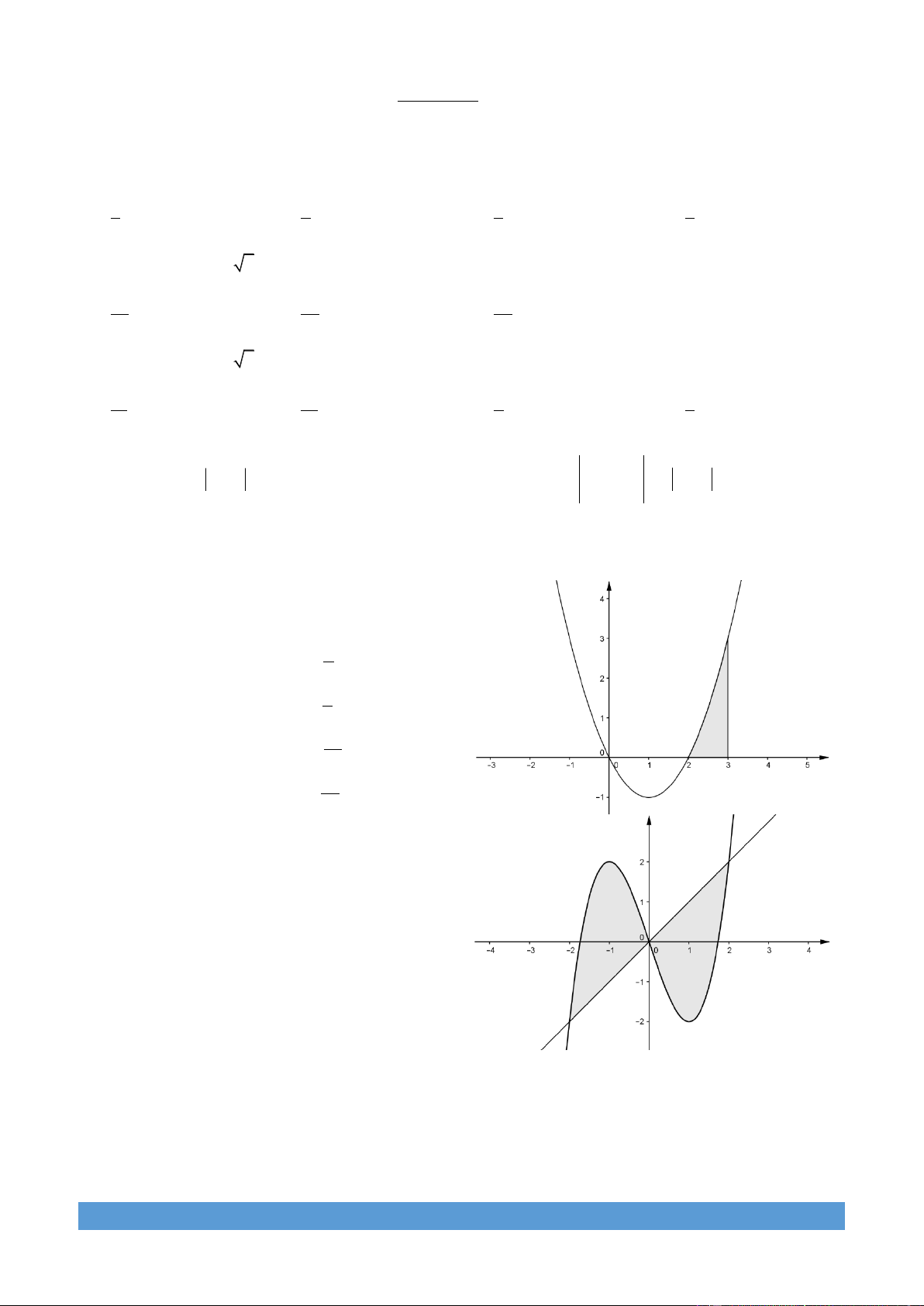
Câu 16: Miền diện tích ở trong hình vẽ bên được giới
hạn bởi các đường cong nào dưới đây, và diện tích của miền đó là bao nhiêu? 4 A. 2
y  x  2x,Ox, x  2, x  3, S  . 3 2 B. 2
y  x  2x,Ox, x  2, x  3, S  . 3 34 C. 2
y  x  2x,Ox, x  2, x  3, S  . 3 50 D. 2
y  x  2x,Ox, x  1, x  3, S  . 3
Câu 17: Miền diện tích ở trong hình vẽ bên được giới
hạn bởi các đường cong nào dưới đây, và diện tích của miền đó là bao nhiêu? A. 3
y  x  3x, y  x, S  16 . B. 3
y  x  3x, y  x, S  4 . C. 3
y  x  3x, y  2x, S  12 . D. 3
y  x  3x, y  x, S  8 .
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389
Câu 18: Miền diện tích ở trong hình vẽ bên được giới
hạn bởi các đường cong nào dưới đây, và diện tích của miền đó là bao nhiêu? 8 A. 2
y  x , y  x  2, y  x, S  . 3 8 B. 2
y  x , y  x  2, y  x, S  . 3 13 C. 2
y  x , y  x  2, y  x, S  . 3 11 D. 2
y  x , y  x  2, y  x, S  . 3
Câu 19: Miền diện tích ở trong hình vẽ bên được giới
hạn bởi các đường cong nào dưới đây, và diện tích của miền đó là bao nhiêu?
A. y  sin x  cos x,Ox,Oy, x   , S  2 .
B. y  sin x  cos , x O ,
x Oy, x   , S  2 2 .
C. y  sin x  3 cos , x O ,
x Oy, x   , S  2 .
D. y  3 sin x  cos , x O ,
x Oy, x   , S  2 .
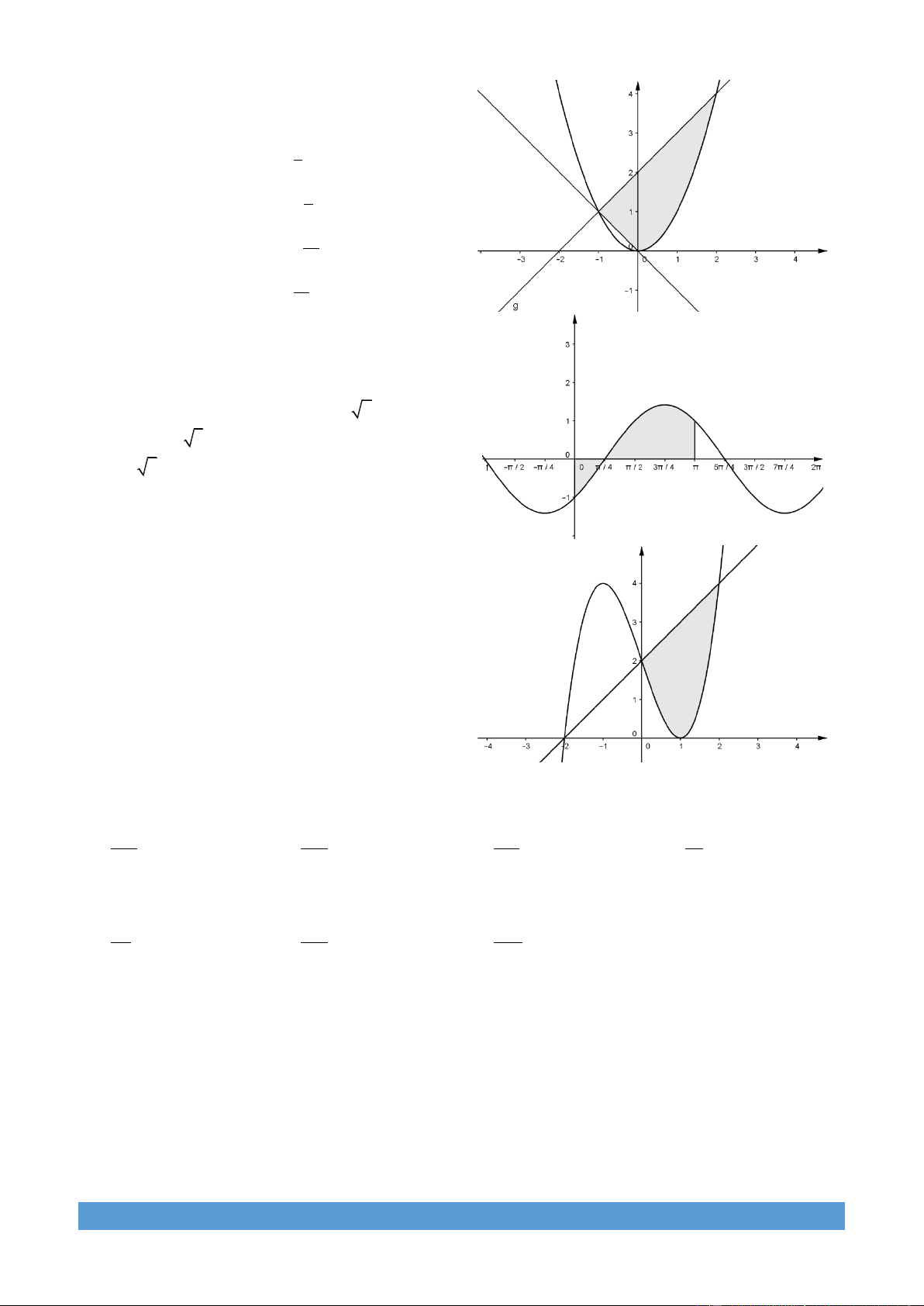
Câu 20: Hình phẳng được tô màu ở trong hình vẽ bên
được giới hạn bởi một đồ thị hàm số bậc ba với một
đường thẳng d  cùng với trục hoành và trục tung.
Cho hình phẳng đó quay quanh trục hoành. Thể tích
của khối tròn xoay thu được có giá trị gần với giá trị nào nhất sau đây? A. 51.22 B. 48.02 C. 46.44 D. 42.18
Câu 21: Cho đồ thị hàm số C 4 2
: y  x  7x và điểm A0; 2
 0 . Tính diện tích hình phẳng được giới hạn
bởi đồ thị C  và các tiếp tuyến qua A kẻ tới C  . 296 296 592 74 A. B. C. D. 15 5 15 3
Câu 22: Thể tích vật thể tròn xoay sinh ra bởi hình giới hạn Parabol  P 2
: y  x 1 và trục hoành khi quay
xung quanh trục Ox bằng bao nhiêu đơn vị thể tích? 3 13 16 A. B. C. D. Đáp án khác 5 10 15
Câu 23: Cho hình phẳng  H  giới hạn bởi Parabol  P 2
: y  4x và một đường thẳng d  như hình vẽ dưới
đây. Thể tích vật thể tròn xoay được tạo thành bởi việc cho hình H  xoay xung quanh trục hoành có thể tích bằng bao nhiêu?
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389 16 23 32 35 A. B. C. D. 3 4 3 4
Câu 24: Tìm m để diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 2
y  3x  2mx  m  1 , trục hoành, trục
tung và đường thẳng x  2 đạt giá trị nhỏ nhất là: A. m  2  B. m  1 
C. m  1 D. Đáp án khác
Câu 25: Cho Parabol  P 2
: y  x 1 và đường thẳng y  mx  2 thay đổi nhưng luôn cắt đường tròn C 2 2
: x  y  1. Khi m thay đổi, hãy tìm giá trị nhỏ nhất của diện tích hình phẳng tạo bởi đường thẳng và
Parabol  P . 2 6 4 3 4 7 7 A. B. C. D. 3 3 3 6
Câu 26: Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc vt   5
 t 10 m/s, trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi đến khi dừng hẳn, ô tô đã đi được quãng đường là bao nhiêu mét?
A. 0, 2m B. 2m C. 10m D. 20m
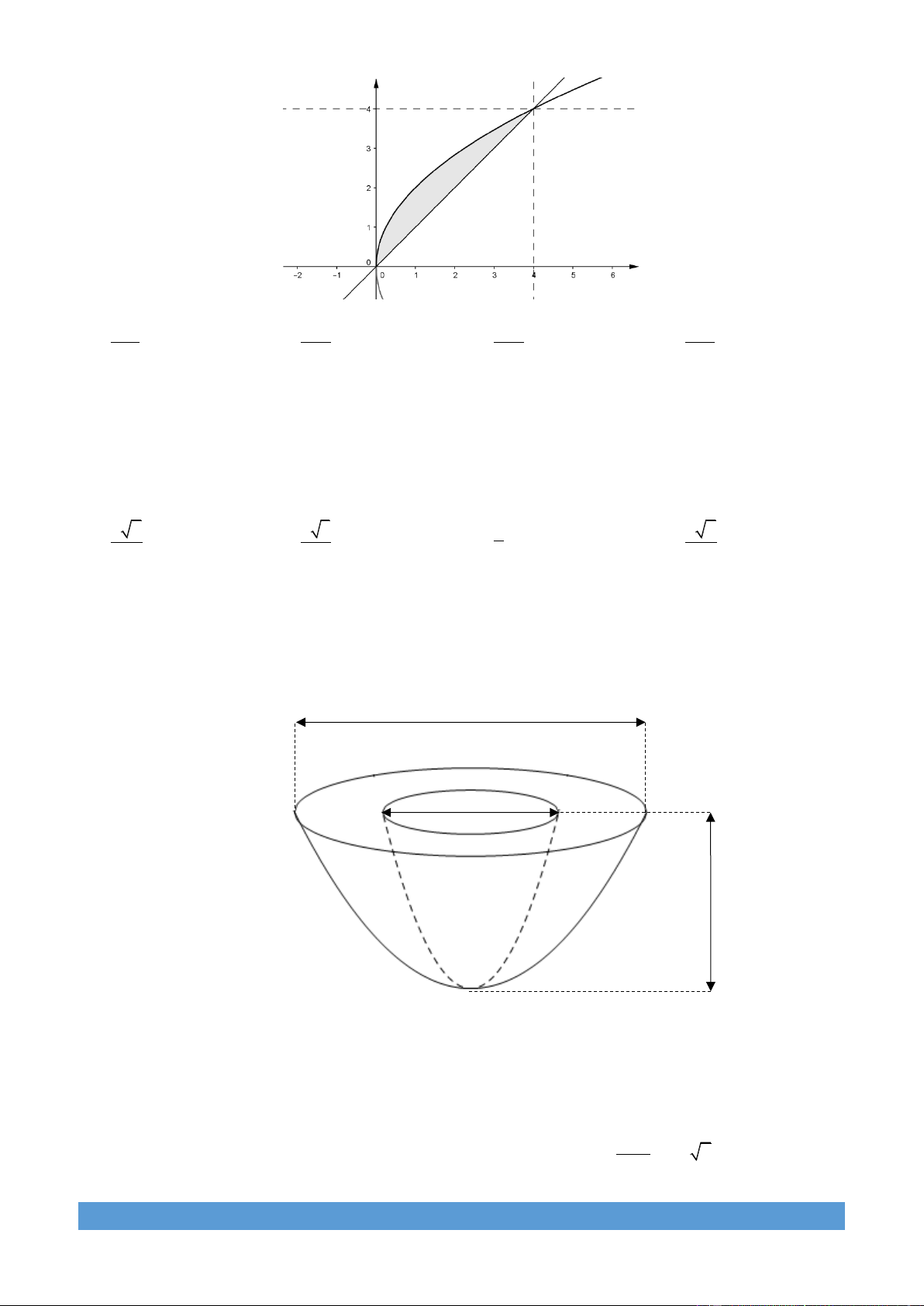
Câu 27: Người ta thiết kế đầu đạn của một quả bom là một khối tròn xoay đặc, được khoét vào trong. Biết
rằng thiết diện qua trục đối xứng của đầu đạn là hai Parabol với các kích thước như hình vẽ dưới đây. Tính thể
tích của đầu đạn đó? 8cm 4cm 4cm 3 2
x 1 khi x  0
Bài 28: Tính tích phân f
 xdx biết rằng: f x   . 1   x khi x  0 2  ax   1 khi x  0  1
Bài 29: Cho hàm số: f  x  
. Xác định các giá trị của a,b sao cho f
 xdx 1. b   2
1 x  khi x  0 1  x f t 
Bài 30: Tìm hàm số f  x và số thực a  0 thỏa mãn với mọi x  0 ta có: dt  2 x  6  . 2 t a
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389
BÀI TẬP TỰ LUYỆN
Câu 1: Hàm số nào sau đây là một nguyên hàm của hàm 5 y  x ? 6 x A. 6 y  x B. 4 y  5x C. y  D. 5 y  6x 6
Câu 2: Hàm số nào sau đây không là nguyên hàm của hàm 3 y  x ? 4 x 4 x 4 x A. y  1 B. y   2 C. y   3 D. 2
y  3x 4 4 4
Câu 3: Phát biểu nào sau đây là đúng?
A. sin xdx  cos x  C 
B. sin xdx  cos x  C 
C. sin xdx  sin x  C 
D. sin xdx  sin x  C 
Câu 4: Phát biểu nào sau đây là đúng?
A. cos xdx  sin x  C 
B. cos xdx  sin x  C 
C. cos xdx  cos x  C 
D. cos xdx  cos x  C 
Câu 5: Phát biểu nào sau đây là đúng? 1 1 A.
dx  cot x  C  B.
dx   tan x  C  2 cos x 2 cos x 1 1 C.
dx  cot x  C  D.
dx  tan x  C  2 cos x 2 cos x
Câu 6: Phát biểu nào sau đây là đúng? 1 1 A.
dx  cot x  C  B.
dx  cot x  C  2 sin x 2 sin x 1 1 C.
dx  tan x  C  D.
dx   tan x  C  2 sin x 2 sin x
Câu 7: Phát biểu nào sau đây là đúng?  A. x x e dx  e  C  B. x x
e dx  e  C   C. x x
e dx  e  C  D. x x e dx  e  C 
Câu 8: Cho a là số dương khác 1. Hàm số nào sau đây là một nguyên hàm của hàm số x y  a ? x a A. x  y  a B. x 1 y  a C. y  D. x
y  a ln a ln a
Câu 9: Cho a là số dương khác 1. Hàm số y  log
là một nguyên hàm của hàm số: a x 1 1 1 ln a A. y  B. y  C. y  D. y  x ln e x ln a x x 
Câu 10: Cho số thực   1
 . Hàm số nào sau đây là một nguyên hàm của hàm số y  x ?   1     x x A. 1 y  x
B. y     1 1 x C. y    D. y 1  1
Câu 11: Phát biểu nào sau đây là đúng? 1 1 A.
dx  ln x  C  B.
dx  ln x  C 
C. ln xdx  x  C 
D. ln x dx  ln x  C  x x
Câu 12: Phát biểu nào sau đây là đúng? dx 1 dx 2 dx 1  dx 2  A.   C  B.   C  C.   C  D.   C  3 2 x x 3 2 x x 3 2 x 2x 3 2 x x
Câu 13: Cho m, n là các số nguyên dương lớn hơn 1. Hàm số nào sau đây là một nguyên hàm của hàm số m n y  x ?
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389 m n  x n m m n m 1   n x A. y  C. m n m y  x B. m y  x D. y  n  1 m  n m  n
Câu 14: Hàm số nào sau đây là một nguyên hàm của hàm số 2 y  tan x ? 3 tan x A. y 
B. y  tan x  x
C. y   tan x  x
D. y  tan x 3
Câu 15: Phát biểu nào sau đây là đúng? 2 3  2 1  1  1   1   1  A. x  dx  x   C     B. x  dx  2 x   C      x  3  x   x   x  2  2 1  1 1  1  1 1 C. 3 x  dx  x  2x   C   D. 3 x  dx  x  2x   C    x  3 x  x  3 x
Câu 16: Phát biểu nào sau đây là đúng? 2  x x  A. sin  cos
dx  x  2 cos x  C    2 2  2  x x  B. sin  cos
dx  x  cos x  C    2 2  2 3  x x  1  x x  C. sin  cos dx  sin  cos  C      2 2  3  2 2  2  x x  D. sin  cos
dx  x  cos x  C    2 2 
Câu 17: Phát biểu nào sau đây là đúng? A. 2
cot xdx   cot x  x  C  B. 2
cot xdx  cot x  x  C  C. 2
cot xdx   cot x  x  C  D. 2
cot xdx  cot x  x  C 
Câu 18: Phát biểu nào sau đây là đúng? 2 2 x x A. dx 
 2x  ln x  2  C  x  2 2 2 2 x x B. dx 
 2x  4ln x  2  C  x  2 2 2 2 x x C. dx 
 2x  4ln x  2  C  x  2 2 2 x D. 2
dx  x  2x  4ln x  2  C  x  2
Câu 19: Phát biểu nào sau đây là đúng? x 1  x2 x x 3  4  3   4  A. dx  3 16  C      5x  5   5  x 1  x2 x 1  x2 3  4 1  3  1  4  B. dx    C      x 3 5  5 4   5  ln ln 5 5 x 1  x2 x2 x3 3  4  3   4  C. dx  3 16  C      5x  5   5  x 1  x2 x x 3  4 3  3  16  4  D. dx    C      5x ln 3  ln 5  5  ln 4  ln 5  5 
Câu 20: Cho hàm số y  f  x có đạo hàm là hàm liên tục trên tập hợp
. Phát biểu nào sau đây là đúng? A. f
 xdx  f 'xC B. f '
 xdx  f x
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389 C. f '
 xdx  f xC D. f
 xdx  f 'x
Câu 21: Cho các hàm số y  f  x, y  g  x có đạo hàm trên
. Phát biểu nào sau đây là đúng? A. Nếu f '
 xdx  g'
 xdx thì f x  gx x   B. Nếu f
 xdx  g
 xdx thì f x  gx x   C. Nếu f
 xdx  g
 xdx thì f x  gx x  
D. Nếu f  x  g  x 1 x   thì f '
 xdx  g'  xdx
Câu 22: Diện tích hình phẳng giới hạn bởi hai Parabol 2 y  x và 2
y  x  2x bằng bao nhiêu? 1 1 A. 1 B. 3 C. D. 2 3
Câu 23: Miền diện tích ở trong hình vẽ bên được giới 2  x 
hạn bởi đường cong C  : y  1    và trục hoành.  
Diện tích của miền đó là bao nhiêu? 4 A. . 3 B. 3 . 3 C. . 2 D.  .
Câu 24: Miền diện tích ở trong hình vẽ bên được giới
hạn bởi đường cong  P 2
: y  x 1 và đường thẳng
d  . Diện tích của miền đó là bao nhiêu? A. 2 . 10 B. . 3 9 C. . 2 D. 5 .
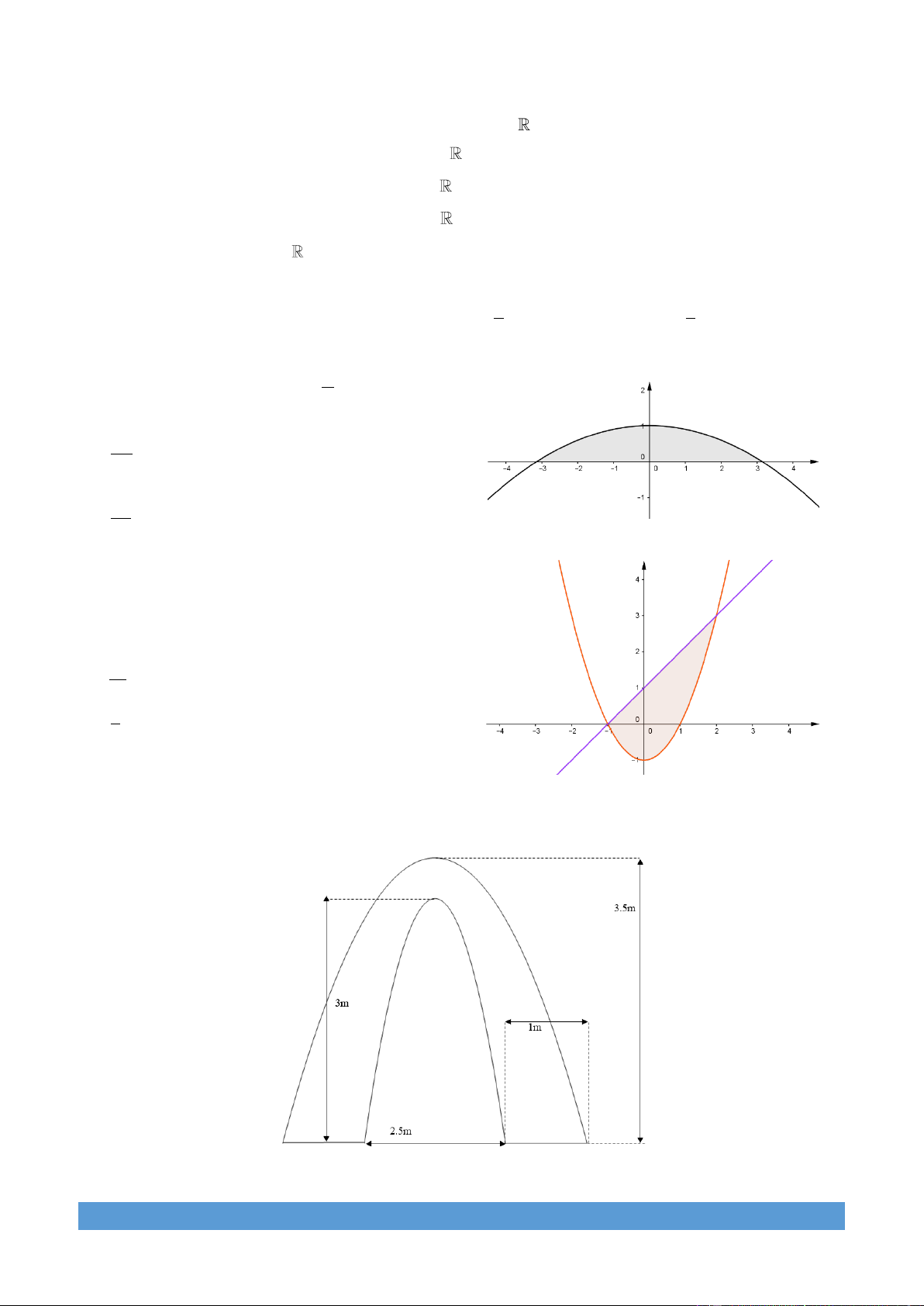
Câu 25: Một chiếc cổng Parabol có các kích thước như hình vẽ. Giả sử chi phí vật liệu là 1.500.000 đồng mỗi
mét vuông và giả thiết độ dày không đáng kể. Tính số tiền cần chi trả để hoàn thành chiếc cổng đó.
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389 ĐÁP ÁN Câu 1: C Câu 2: D Câu 3: A Câu 4: B Câu 5: D Câu 6: A Câu 7: B Câu 8: C Câu 9: B Câu 10: D Câu 11: B Câu 12: C Câu 13: C Câu 14: B Câu 15: D Câu 16: B Câu 17: A Câu 18: B Câu 19: D Câu 20: C Câu 21: D Câu 22: D Câu 23: A Câu 24: C
NGUYÊN HÀM – TÍCH PHÂN
ĐOÀN TRÍ DŨNG – 0902.920.389