600 câu hỏi trắc nghiệm chuyên đề tích phân và ứng dụng – Nhóm Toán 12

600 câu hỏi trắc nghiệm chuyên đề tích phân và ứng dụng – Nhóm Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

96 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 01
C©u 1 :
Hàm số nào dưới đây không là nguyên hàm của hàm số
2
(2 )
()
( 1)
xx
fx
x
A.
2
1
1
xx
x

B.
2
1
1
xx
x

2
1
1
xx
x

2
1
x
x
C©u 2 :
Cho đồ thị hàm số
()y f x
. Diện tích hình phẳng (phần gạch trong hình) là:
A.
00
34
( ) ( )f x dx f x dx

14
31
( ) ( )f x dx f x dx

C.
34
00
( ) ( )f x dx f x dx

4
3
()f x dx
C©u 3 :
Diện tích hình phẳng giới hạn bởi các đồ thị:
2
2y x x
và
2
y x x
có kết quả là:
A.
12
B.
10
3
9
6
C©u 4 :
Kết quả nào sai trong các kết quả sao?
A.
11
2 5 1 2
10 5.2 .ln 2 5 .ln 5
xx
x x x
dx C

44
34
21
ln
4
xx
dx x C
xx

C.
2
2
11
ln
21
1
xx
dx x C
x
x
2
tan tanxdx x x C
C©u 5 :
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
1x
22
y x .e , x 1, x 2 , y 0
quanh trục ox là:
2
A.
2
(e )e
B.
2
(e )e
2
e
e
C©u 6 :
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
4
y , y 0 , x 1, x 4
x
quanh trục ox là:
A.
6
B.
4
12
8
C©u 7 :
Giá trị của
4
4
2
0
1
(1 tan ) .
cos
x dx
x
bằng:
A.
1
5
B.
1
3
1
2
1
4
C©u 8 :
Nếu
( ) 5
d
a
f x dx
;
( ) 2
d
b
f x dx
, với
a d b
thì
()
b
a
f x dx
bằng:
A.
2
B.
3
8
0
C©u 9 :
Hàm số
2
( ) ln
x
x
e
e
f x t tdt
đạt cực đại tại
?x
A.
ln2
B.
0
ln 2
ln4
C©u 10 :
Cho tích phân
2
2
sin 3
0
.sin cos
x
I e x xdx
. Nếu đổi biến số
2
sintx
thì
A.
1
0
1
(1 )
2
t
I e t dt
11
00
2
tt
I e dt te dt





C.
1
0
2 (1 )
t
I e t dt
11
00
1
2
tt
I e dt te dt





C©u 11 :
Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0,
x
và đồ thị của hai hàm số y =
cosx, y = sinx là:
A.
22
B.
2
2
22
C©u 12 :
Diện tích hình phẳng giới hạn bởi các đường
2
yx
,trục Ox và đường thẳng
x2
là:
A.
8
B.
8
3
16
16
3
3
C©u 13 :
Cho hình phẳng
H
giới hạn bởi các đường
y sinx
;
x0
;
y0
và
x 
. Thể tích vật thể
tròn xoay sinh bởi hình
H
quay quanh Ox bằng
A.
2
B.
2
2
2
4
2
C©u 14 :
Cho tích phân
3
2
2
1
1 x
I dx
x
. Nếu đổi biến số
2
1x
t
x
thì
A.
2
3
2
2
2
1
t dt
I
t

B.
3
2
2
2
1
t dt
I
t
2
3
2
2
1
tdt
I
t
3
2
2
1
tdt
I
t
C©u 15 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
1y x x
và trục ox và đường thẳng x=1
là:
A.
3 2 2
3
B.
3 2 1
3
2 2 1
3
32
3
C©u 16 :
Tìm nguyên hàm:
3
2
4
()x dx
x
A.
3
5
5
4ln
3
x x C
3
5
3
4ln
5
x x C
C.
3
5
3
4ln
5
x x C
3
5
3
4ln
5
x x C
C©u 17 :
Tích phân
2
0
cos sinx xdx
bằng:
A.
2
3
B.
2
3
3
2
0
C©u 18 :
Hàm số nào sau đây không là nguyên hàm của hàm số
2
(2 )
()
( 1)
xx
fx
x
A.
2
1
1
xx
x

B.
2
1
1
xx
x

2
1
x
x
2
1
1
xx
x

C©u 19 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
45y x x
và hai tiếp tuyến với đồ thị
hàm số tai A(1;2) và B(4;5) có kết quả dạng
a
b
khi đó: a+b bằng
A.
12
B.
13
12
13
4
5
4
C©u 20 :
Giá trị của tích phân
2
2
1
I x 1 ln xdx
là:
A.
2ln2 6
9
B.
6ln2 2
9
2ln2 6
9
6ln2 2
9
C©u 21 :
Kết quả của
2
1
x
dx
x
là:
A.
2
1 xC
B.
2
1
1
C
x
2
1
1
C
x
2
1 xC
C©u 22 :
Hàm số
( ) ln sin 3cosF x x x
là một nguyên hàm của hàm số nào trong các hàm số sau
đây:
A.
cos 3sin
()
sin 3cos
xx
fx
xx
( ) cos 3sinf x x x
C.
cos 3sin
()
sin 3cos
xx
fx
xx

sin 3cos
()
cos 3sin
xx
fx
xx
C©u 23 :
Giá trị của tích phân
e
2
1
x 2lnx
I dx
x
là:
A.
2
e1
2
B.
2
e1
2
2
e1
2
e
C©u 24 :
Giả sử
4
0
2
I sin3xsin2xdx a b
2
, khi đó, giá trị của
ab
là:
A.
1
6
B.
3
10
3
10
1
5
C©u 25 :
Tìm nguyên hàm:
2
3
( 2 )x x dx
x

A.
3
3
4
3ln
33
x
x x C
3
3
4
3ln
33
x
Xx
C.
3
3
4
3ln
33
x
x x C
3
3
4
3ln
33
x
x x C
C©u 26 :
Tìm nguyên hàm:
1
( 3)
dx
xx
5
A.
2
ln
33
x
C
x
B.
1
ln
33
x
C
x

13
ln
3
x
C
x
1
ln
33
x
C
x
C©u 27 :
Diện tích hình phẳng giới hạn bởi các đường (P): y=2x
2
, (C): y=
2
x1
và Ox là:
A.
3 2 2
B.
22
2
23
28
42
C©u 28 :
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
2
2
x 27
y=x ; y= ; y=
8x
là:
A.
27ln2-3
B.
63
8
27ln2
27ln2+1
C©u 29 :
Tìm nguyên hàm:
2
(1 sin )x dx
A.
21
2cos sin2
34
x x x C
;
21
2cos sin2
34
x x x C
;
C.
21
2cos2 sin2
34
x x x C
;
21
2cos sin2
34
x x x C
;
C©u 30 :
Cho
2
2
1
21I x x dx
và
2
1ux
. Chọn khẳng định sai trong các khẳng định sau:
A.
2
1
I udu
B.
3
0
I udu
2
27
3
I
3
3
2
0
2
3
Iu
C©u 31 :
Cho biết
5
2
f x dx 3
,
5
2
g t dt 9
. Giá trị của
5
2
A f x g x dx


là:
A.
Chưa xác định
được
B.
12
3
6
C©u 32 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx
và đường thẳng
2yx
là:
A.
4
3
B.
3
2
5
3
23
15
C©u 33 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y = 2 x - 4x - 6
2
trục hoành và hai đường
thẳng x=-2 , x=-4 là
A.
12
B.
40
3
92
3
50
3
6
C©u 34 :
Giả sử rằng
0
2
1
3x 5x 1 2
I dx aln b
x 2 3

. Khi đó, giá trị của
a 2b
là:
A.
30
B.
40
50
60
C©u 35 :
Kết quả của
ln xdx
là:
A.
lnx x x C
B.
Đáp án khác
lnx x C
lnx x x C
C©u 36 :
Tìm nguyên hàm:
3
5
()x dx
x
A.
5
2
5ln
5
x x C
5
2
5ln
5
x x C
C.
5
2
5ln
5
x x C
5
2
5ln
5
x x C
C©u 37 :
Tìm nguyên hàm:
1
( 3)
dx
xx
.
A.
1
ln
33
x
C
x
B.
13
ln
3
x
C
x
1
ln
33
x
C
x
13
ln
3
x
C
x
C©u 38 :
Diện tích hình phẳng giới hạn bởi các đường cong
3
yx
và
5
yx
bằng:
A.
4
B.
1
6
0
2
C©u 39 :
Cho hai tích phân
2
2
0
sin xdx
và
2
2
0
cos xdx
, hãy chỉ ra khẳng định đúng:
A.
22
22
00
sin cosxdx xdx


Không so sánh được
C.
22
22
00
sin cosxdx xdx


22
22
00
sin = cosxdx xdx


C©u 40 :
Cho hai tích phân
2
2
0
sinI xdx
và
2
2
0
cosJ xdx
. Hãy chỉ ra khẳng định đúng:
A.
IJ
B.
IJ
IJ
Không so sánh
được
7
C©u 41 :
Hàm số
2
()
x
F x e
là nguyên hàm của hàm số
A.
2
( ) 2
x
f x xe
B.
2
()
x
f x e
2
()
2
x
e
fx
x
2
2
( ) 1
x
f x x e
C©u 42 :
Tính
ln 2
2
x
dx
x
, kết quả sai là:
A.
2 2 1
x
C
B.
2
x
C
1
2
x
C
2 2 1
x
C
C©u 43 :
Cho tích phân
2
0
sin
1 2 cos
x
I
x


, với
1
thì
I
bằng:
A.
2
B.
2
2
2
C©u 44 :
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
2
1, 5y x y x
có kết quả là
A.
35
12
B.
10
3
73
3
73
6
C©u 45 :
Nếu
( ) 5
d
a
f x dx
,
( ) 2
d
b
f x dx
với a < d < b thì
()
b
a
f x dx
bằng
A.
-2
B.
0
8
3
C©u 46 :
Kết quả nào sai trong các kết quả sao?
A.
1
tan
1 cos 2 2
dx x
C
x

2
22
1 1 1
ln
2
1 1 1
dx x
C
x x x


C.
ln(ln(ln ))
ln .ln(ln )
dx
xC
x x x

2
2
1
ln 3 2
4
32
xdx
xC
x
C©u 47 :
Diện tích hình phẳng giới hạn bởi hai đường cong y = x
3
– x và
y = x – x
2
là :
A.
Đáp án khác
B.
37
6
33
12
37
12
C©u 48 :
Tìm nguyên hàm:
3
2
()x x dx
x

8
A.
43
12
2ln
43
x x x C
43
12
2ln
43
x x x C
C.
43
12
2ln
43
x x x C
43
12
2ln
43
x x x C
C©u 49 :
Cho hình phẳng giới hạn bởi các đường
yx
và
yx
quay xung quanh trục
Ox
. Thể tích
khối tròn xoay tạo thành bằng:
A.
B.
6
0
C©u 50 :
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
2x y x y , y 0 ,
quanh trục ox là:
A.
7
12
B.
6
35
12
6
5
C©u 51 :
Biến đổi
3
0
11
x
dx
x
thành
2
1
()f t dt
, với
1tx
. Khi đó
()ft
là hàm nào trong các hàm
số sau?
A.
2
( ) 2 2f t t t
B.
2
()f t t t
2
()f t t t
2
( ) 2 2f t t t
C©u 52 :
Cho
2
0
cos
x
I e xdx
;
2
0
sin
x
J e xdx
và
0
cos 2
x
K e xdx
. Khẳng định nào đúng trong các
khẳng định sau?
(I)
I J e

(II)
I J K
(III)
1
5
e
K
A.
Chỉ (II)
B.
Chỉ (III)
Chỉ (I)
Chỉ (I) và (II)
C©u 53 :
Hàm số
2
y tan 2x
nhận hàm số nào dưới đây là nguyên hàm?
A.
2tan2x x
B.
1
tan2x x
2
tan2x x
1
tan2x x
2
C©u 54 :
Thể tích vật thể tròn xoang khi quay hình phẳng giới hạn bởi đồ thị hàm số
y = x
22
;xy
quanh trục ox là
9
A.
2
10
B.
4
3
3
10
10
C©u 55 :
Cho
6
0
1
sin cos
64
n
I x xdx

. Khi đó
n
bằng:
A.
3
B.
4
6
5
C©u 56 :
Tìm nguyên hàm:
32
(2 )
x
e dx
A.
36
41
3
36
xx
x e e C
36
45
4
36
xx
x e e C
C.
36
41
4
36
xx
x e e C
36
41
4
36
xx
x e e C
C©u 57 :
Giả sử
5
1
ln
21
dx
K
x
. Giá trị của
K
là:
A.
3
B.
8
81
9
C©u 58 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y = x +11x - 6,
3
y = 6x
2
, 0, 2xx
có
kết quả dạng
a
b
khi đó a-b bằng
A.
2
B.
-3
3
59
C©u 59 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y = -x + 4x
2
và các tiếp tuyến với đồ thị
hàm số biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng
a
b
khi đó a-b bằng
A.
12
11
B.
14
5
-5
C©u 60 :
Diện tích hình phẳng giới hạn bởi (C): y= x
2
+3x2, d
1
:y = x1 và d
2
:y=x+2 có kết quả là
A.
1
8
B.
2
7
12
1
1
6
C©u 61 :
Diện tích hình phẳng giới hạn bởi đường cong y = x
2
+ 1, tiếp tuyến với đường này tại điểm
M(2; 5) và trục Oy là:
A.
7
3
B.
5
3
2
8
3
10
C©u 62 :
Giá trị của
1
x
0
I x.e dx
là:
A.
1
B.
2
1
e
2
e
2e 1
C©u 63 :
Tính
1
dx
x
, kết quả là:
A.
1
C
x
B.
21 xC
2
1
C
x
1Cx
C©u 64 :
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
y=( 1)ex
và
(1 )
x
y e x
là:
A.
2
2
e
B.
2
1
2
e
3
1
e
C©u 65 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
23y x x
và trục hoành là:
A.
125
24
B.
125
34
125
14
125
44
C©u 66 :
Diện tích hình phẳng giới hạn bởi đường thẳng
4yx
và patabol
2
2
x
y
bằng:
A.
28
3
B.
25
3
22
3
26
3
C©u 67 :
Diện tích hình phẳng giới hạn bởi các đồ thị:
2
43y x x
và y=x+3 có kết quả là:
A.
55
6
B.
205
6
109
6
126
5
C©u 68 :
Tìm nguyên hàm:
2
3
( 2 )x x dx
x

11
A.
31
2sinx sin2
24
x x C
31
2sinx- sin2
24
x x C
C.
31
2cosx sin2
24
x x C
31
2sinx sin2
24
x x C
C©u 69 :
Diện tích hình phẳng giới hạn bởi các đường cong
siny x x
và
yx
, với
02x

bằng:
A.
4
B.
4
0
1
C©u 70 :
Cho
Fx
là một nguyên hàm của hàm số
2
1
y
cos x

và
F 0 1
. Khi đó, ta có
Fx
là:
A.
tanx
B.
tanx 1
tanx 1
tanx 1
C©u 71 :
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đồ thị hàm số
y = 8
2
x
và
x=2 quanh trục ox là:
A.
12
B.
4
16
8
C©u 72 :
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
1 , 0xy y
quanh
trục ox có kết quả dạng
a
b
khi đó a+b có kết quả là:
A.
11
B.
17
31
25
C©u 73 :
Nguyên hàm
()Fx
của hàm số
2
2
1
()
x
fx
x



là hàm số nào trong các hàm số sau?
A.
3
1
( ) 2
3
x
F x x C
x
3
1
( ) 2
3
x
F x x C
x
C.
3
2
3
()
2
x
x
F x C
x

3
3
2
3
()
2
x
x
F x C
x







C©u 74 :
Diện tích hình phẳng giới hạn bởi các đường (P): y =x
2
-2x+2 và các tiếp tuyến bới (P) biết
tiếp tuyến đi qua A(2;-2) là:
A.
8
3
B.
64
3
16
3
40
3
C©u 75 :
Thể tích khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y
=(1- x)
2
, y = 0, x = 0 và x = 2 bằng:
12
A.
2
B.
82
3
5
2
2
5
C©u 76 :
Thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các
đường y = x
2
và x = y
2
bằng:
A.
10
B.
10
3
3
3
10
C©u 77 :
Giá trị của
2
2
0
2
x
e dx
bằng:
A.
4
1e
B.
4
4e
4
e
4
3e
C©u 78 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y = - x + 3x +1
và đường thẳng y=3 là
A.
57
4
B.
45
4
27
4
21
4
C©u 79 :
Tìm khẳng định sai trong các khẳng định sau:
A.
2
00
sin 2 sin
2
x
dx xdx

1
0
(1 ) 0
x
x dx
C.
11
00
sin(1 ) sinx dx xdx

1
2007
1
2
(1 )
2009
x x dx

13
ĐÁP ÁN
01
{ ) } ~
28
{ | ) ~
55
) | } ~
02
) | } ~
29
{ | } )
56
{ | } )
03
{ | ) ~
30
) | } ~
57
) | } ~
04
) | } ~
31
{ ) } ~
58
{ | ) ~
05
{ | ) ~
32
) | } ~
59
{ | ) ~
06
{ | ) ~
33
{ | ) ~
60
{ | ) ~
07
) | } ~
34
{ ) } ~
61
{ | } )
08
{ ) } ~
35
{ | } )
62
{ ) } ~
09
) | } ~
36
{ | } )
63
{ ) } ~
10
) | } ~
37
{ | } )
64
{ | ) ~
11
{ | } )
38
{ ) } ~
65
) | } ~
12
{ ) } ~
39
{ | } )
66
) | } ~
13
{ ) } ~
40
{ ) } ~
67
{ | ) ~
14
) | } ~
41
) | } ~
68
{ | } )
15
{ | ) ~
42
{ ) } ~
69
{ ) } ~
16
{ | } )
43
) | } ~
70
{ ) } ~
17
{ ) } ~
44
{ | ) ~
71
{ | ) ~
18
{ | } )
45
{ | } )
72
{ | ) ~
19
{ | ) ~
46
) | } ~
73
) | } ~
20
{ ) } ~
47
{ | } )
74
{ | ) ~
21
{ | } )
48
{ | } )
75
{ | } )
22
) | } ~
49
{ ) } ~
76
{ | } )
23
{ ) } ~
50
{ | ) ~
77
) | } ~
24
{ ) } ~
51
) | } ~
78
{ | ) ~
25
{ | } )
52
) | } ~
79
{ ) } ~
26
{ | } )
53
{ ) } ~
27
{ | ) ~
54
{ | ) ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 02
C©u 1 :
Tính
dxex
x 1
2
.
A.
2
1x
eC
B.
2
1
2
x
eC
2
1
1
2
x
eC
2
1
1
2
x
eC
3
C©u 2 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường
1yx
, trục hoành,
2, 5xx
quanh trục Ox bằng:
A.
d
5
2
1xx
B.
d
5
2
1xx
d
2
2
2
1
1yx
d
5
2
1xx
C©u 3 :
Giá trị của
d
2
2
0
2
x
ex
là:
A.
4
e
B.
4
1e
4
4e
4
31e
C©u 4 :
Cho tích phân
4
2
0
6tan
cos 3tan 1
x
I dx
xx
. Giả sử đặt
3tan 1ux
thì ta được:
A.
2
2
1
4
21
3
I u du
.
2
2
1
4
1
3
I u du
.
C.
2
2
1
4
1
3
I u du
.
2
2
1
4
21
3
I u du
.
C©u 5 :
Nếu
6
0
( ) 10f x dx
và
4
0
( ) 7f x dx
, thì
6
4
()f x dx
bằng :
A.
3
B.
17
170
3
C©u 6 :
Họ nguyên hàm của hàm số
3
2
1
x
fx
x
là:
A.
22
1
21
3
x x C
22
1
11
3
x x C
2
C.
22
1
11
3
x x C
22
1
21
3
x x C
C©u 7 :
Giả sử
d
5
1
ln
21
x
c
x
. Giá trị đúng của
c
là:
A.
9
B.
3
81
8
C©u 8 :
Tính diện tích
S
hình phẳng được giới hạn bởi các đường:
22
4;
4
42
xx
yy
.
A.
2
2
3
S

.
B.
5
2
3
S

.
4
2
3
S

.
1
2
3
S

.
C©u 9 :
Nếu
(1) 12, '( )f f x
liên tục và
4
1
'( ) 17f x dx
, giá trị của
(4)f
bằng:
A.
29
B.
5
19
9
C©u 10 :
Nếu
()fx
liên tục và
4
0
( ) 10f x dx
, thì
2
0
(2 )f x dx
bằng :
A.
5
B.
29
19
9
C©u 11 :
Biết
0
2 4 0
b
x dx
, khi đó b nhận giá trị bằng:
A.
1b
hoặc
4b
0b
hoặc
2b
C.
1b
hoặc
2b
0b
hoặc
4b
C©u 12 :
Cho
d
6
0
1
sin cos
64
n
I x x x
. Khi đó
n
bằng:
A.
5
B.
3
4
6
C©u 13 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx
và đường thẳng
2yx
bằng:
A.
23
15
B.
4
3
3
2
5
3
C©u 14 :
Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường
2
2yx
;
1y
và trục Ox khí quay xung quanh Ox là
3
A.
11
22
11
( 1)x dx dx



11
22
11
( 2)x dx dx



C.
11
22
11
( 2)x dx dx



1
22
1
( 2)x dx

C©u 15 :
Cho
2
4
( ) sin
m
f x x

. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và
48
F




A.
B.
C©u 16 :
Khẳng định nào sau đây đúng về kết quả
3
1
31
ln
e
a
e
x xdx
b
?
A.
. 64ab
B.
. 46ab
12ab
4ab
C©u 17 :
Khẳng định nào sau đây đúng về kết quả
1
3
4
0
1
ln 2
1
x
dx
a
x
?
A.
2a
B.
4a
4a
2a
C©u 18 :
Cho các hàm số:
2
20 30 7
()
23
xx
fx
x

;
2
23F x ax bx x x
với
3
2
x
. Để hàm số
Fx
là một nguyên hàm của hàm số
()fx
thì giá trị của
,,abc
là:
A.
4; 2; 1abc
4; 2; 1a b c
C.
4; 2; 1a b c
.
4; 2; 1abc
C©u 19 :
Tính tích phân
1
2
0
(3 1)
69
x dx
I
xx

A.
45
3ln
36
B.
45
3ln
36
47
3ln
36
C©u 20 :
Một nguyên hàm
( )cos3 1
( 2) sin3 sin3 2017
x a x
x xdx x
bc
thì tổng
.S a b c
bằng :
A.
14S
B.
15S
3S
10S
C©u 21 :
Tìm họ nguyên hàm:
()
2ln 1
dx
Fx
xx
A.
( ) 2 2ln 1F x x C
( ) 2ln 1F x x C
C.
1
( ) 2ln 1
4
F x x C
1
( ) 2ln 1
2
F x x C
4
3
m 
3
4
m
3
4
m 
4
3
m
35
3ln
46
4
C©u 22 :
Nguyên hàm của hàm số
2
– 3
1
f x x x
x

là
A.
F(x) =
32
3
ln
32
xx
xC
F(x) =
Cx
xx
ln
2
3
3
23
C.
F(x) =
32
3
ln
32
xx
xC
F(x) =
32
3
ln
32
xx
xC
C©u 23 :
Thể tích của khối tròn xoay sinh ra khi quay quanh trục Oy hình phẳng giới hạn bởi các
đường:
2
y x 4x 3
và Ox bằng:
A.
16
5
B.
5
5
16
3
C©u 24 :
Cho
2
2
1
x
fx
x
. Khi đó:
A.
2
2ln 1f x dx x C
2
3ln 1f x dx x C
C.
2
4ln 1f x dx x C
2
ln 1f x dx x C
C©u 25 :
Cho hai hàm số y = f(x), y = g(x) có đồ thị (C
1
) và (C
2
) liên tục trên [a;b] thì công thức tính
diện tích hình phẳng giới hạn bởi (C
1
), (C
2
) và hai đường thẳng x = a, x = b là:
A.
b
a
S f(x) g(x) dx
b
a
S g(x) f(x) dx
C.
bb
aa
S f(x)dx g(x)dx

b
a
S f(x) g(x) dx
C©u 26 :
Khẳng định nào sau đây sai về kết quả
0
1
1
ln 1
2
xb
dx a
xc
?
A.
. 3( 1)a b c
B.
3ac b
2 10a b c
1ab c
C©u 27 :
Tính tích phân
1
2
0
( 4)
32
x dx
I
xx

A.
5ln2 3ln2
B.
5ln2 2ln3
5ln2 2ln3
2ln5 2ln3
C©u 28 :
Cho hàm
4
sin 2f x x
. Khi đó:
A.
11
3 sin4 sin8
88
f x dx x x x C



11
3 cos4 sin8
88
f x dx x x x C



5
C.
11
3 cos4 sin8
88
f x dx x x x C



11
3 sin4 sin8
88
f x dx x x x C



C©u 29 :
Cho hàm số y = f(x) liên tục và chỉ triệt tiêu khi x = c trên [a; b]. Các kết quả sau, câu nào
đúng?
A.
bb
aa
f(x) dx f(x)dx

b c b
a a c
f(x) dx f(x) dx f(x) dx
C.
b c b
a a a
f(x) dx f(x) dx f(x)dx
A, B, C đều đúng
C©u 30 :
Diện tích phẳng giới hạn bởi:
2
1; 2; 0; 2x x y y x x
A.
4
3
B.
1
0
8
3
C©u 31 :
Tìm một nguyên hàm F(x) của hàm số
32
2
x 3x 3x 1
f(x)
x 2x 1

biết
1
F(1)
3
A.
2
2
F(x) x x 6
x1
2
2 13
F(x) x x
x 1 6
C.
2
x 2 13
F(x) x
2 x 1 6
2
x2
F(x) x 6
2 x 1
C©u 32 :
Tính diện tích
S
hình phẳng được giới hạn bởi các đường:
2
1
; ln ; 1
1
y x y x
x
A.
8 31
ln2
3 18
S
B.
8 23
ln2
3 18
S 
8 17
ln2
3 18
S 
8 23
ln2
3 18
S 
C©u 33 :
Gọi
2008
x
dx F x C
, với C là hằng số. Khi đó hàm số
Fx
bằng
A.
2008 ln2008
x
B.
1
2008
x
2008
x
2008
ln2008
x
C©u 34 :
Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường
ln , 0,y x x y x e
có giá trị bằng:
3
(b 2)e
a
trong đó a,b là hai số thực nào dưới đây?
A.
a=27; b=5
B.
a=24; b=6
a=27; b=6
a=24; b=5
C©u 35 :
Cho đồ thị hàm số
y f x
. Diện tích hình phẳng (phần tô đậm trong hình) là:
6
A.
d
4
3
f x x
dd
00
34
f x x f x x
C.
dd
14
31
f x x f x x
dd
34
00
f x x f x x
C©u 36 :
Diện tích hình phẳng giới hạn bởi hai đường cong
(1 )
x
y e x
và
( 1)y e x
là?
A.
1
2
e
( đvdt)
B.
2
2
e
( đvdt)
2
2
e
( đvdt)
1
2
e
( đvdt)
C©u 37 :
Tích phân
d
2
0
cos . sinx x x
bằng:
A.
2
3
B.
2
3
3
2
0
C©u 38 :
Cho tích phân
sin
2
0
sin2 .
x
I x e dx
: .một học sinh giải như sau:
Bước 1: Đặt
sin cost x dt xdx
. Đổi cận:
00
1
2
xt
xt
1
0
2.
t
I t e dt
.
Bước 2: chọn
tt
u t du dt
dv e dt v e





11
11
00
00
. . 1
t t t t
t e dt t e e dt e e

Bước 3:
1
0
2 . 2
t
I t e dt
.
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A.
Bài giải trên sai từ bước 1.
Bài giải trên sai từ bước 2 .
C.
Bài giải trên hoàn toàn đúng.
Bài gaiir trên sai ở bước 3.
C©u 39 :
Cho hình phẳng giới hạn bởi:
tan ; 0; ; 0
3
D y x x x y



7
Thể tích vật tròn xoay khi D quay quanh Ox:
A.
3
3



B.
3
3
3
3
3
3



C©u 40 :
Nguyên hàm của hàm số
31yx
trên
1
;
3
là:
A.
2
3
2
x x C
3
2
31
9
xC
C.
3
2
31
9
xC
2
3
2
x x C
C©u 41 :
Cho tích phân
1
2
2
0
1 x dx
bằng:
A.
3
64




B.
13
2 6 4




3
64




13
2 6 4




C©u 42 :
Tính diện tích hình phẳng tạo bởi các đường: Parabol
2
: 4 5P y x x
và 2 tiếp tuyến tại
các điểm
1;2 , 4;5AB
nằm trên
P
.
A.
7
2
S
B.
11
6
S
9
4
S
13
8
S
C©u 43 :
Tìm hàm số F(x) biết rằng F’(x) = 4x
3
– 3x
2
+ 2 và F(-1) = 3
A.
F(x) = x
4
– x
3
- 2x -3
F(x) = x
4
– x
3
- 2x + 3
C.
F(x) = x
4
– x
3
+ 2x + 3
F(x) = x
4
+ x
3
+ 2x + 3
C©u 44 :
0
I 1 cos2x dx

bằng:
A.
2
B.
0
2
22
C©u 45 :
Tìm họ nguyên hàm:
3
4
()
1
x
F x dx
x
A.
4
( ) ln 1F x x C
4
1
( ) ln 1
4
F x x C
C.
4
1
( ) ln 1
2
F x x C
4
1
( ) ln 1
3
F x x C
8
C©u 46 :
Nếu
9
0
( ) 37f x dx
và
9
0
g( ) 16x dx
thì
9
0
2 ( ) 3 g( )f x x dx
bằng :
A.
122
B.
74
48
53
C©u 47 :
Biết rằng
x;
43





thì
3 cotx 4
.
x


Gọi
3
4
cot x
I dx.
x
Kết luận nào sau đây là đúng ?
A.
31
I
12 4

B.
11
I
43

11
I
54

31
I
12 3

C©u 48 :
Giá trị của tích phân
1
3
34
0
1.x x dx
bằng?
A.
3
16
B.
2
6
13
Đáp án khác
C©u 49 :
Tính
d
ln 2
2
x
x
x
, kết quả là:
A.
2 2 1
x
C
B.
2
x
C
2 2 1
x
C
1
2
x
C
C©u 50 :
Tính
d
1
x
x
, kết quả là:
A.
1
C
x
B.
21 xC
2
1
C
x
1Cx
C©u 51 :
Diện tích hình phẳng giới hạn bởi
2
xln(x 2)
y
4x
và trục hoành là:
A.
23
3

B.
2ln2 2
4

ln2 2 3
3
2ln 2 2 3
3
C©u 52 :
Một nguyên hàm của
2
2
xln x x 1
f(x)
x1

là:
A.
2
xln x x 1 x C
2
ln x x 1 x C
C.
2
xln x 1 x C
22
x 1ln x x 1 x C
C©u 53 :
Cho hình phẳng giới hạn bởi các đường y = 2x – x
2
và y = 0. Thì thể tích vật thể tròn xoay
9
được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox có giá trị bằng?
A.
16
15
(đvtt)
B.
15
16
(đvtt)
5
6
(đvtt)
6
5
(đvtt)
C©u 54 :
Khẳng định nào sau đây sai về kết quả
2
0
1
(2 1 sin ) 1x x dx
ab
?
A.
28ab
B.
5ab
2 3 2ab
2ab
C©u 55 :
Một nguyên hàm của hàm số
sin3yx
A.
1
os3
3
cx
B.
3 os3cx
3 os3cx
1
os3
3
cx
C©u 56 :
Nếu
2
()
6 2 , 0
x
a
ft
dt x x
t
thì hệ số
a
bằng :
A.
9
B.
19
5
29
C©u 57 :
Biết tích phân
1
0
23
2
x
dx
x
=aln2 +b . Thì giá trị của a là:
A.
7
B.
2
3
1
C©u 58 :
Thể tích hình khối do hình phẳng giới hạn bởi các đường
2
y x 4,
y 2x 4,x 0,x 2
quay quanh trục Ox bằng:
A.
32
5
B.
6
6
32
5
C©u 59 :
Nguyên hàm của hàm số
4
2
23x
y
x
là:
A.
C
x
x
3
3
2
3
B.
3
3
3xC
x

3
23
3
x
C
x

3
3
3
x
C
x

C©u 60 :
Biết tích phân
3
2
0
1
9
dx
x
=
a
thì giá trị của a là
A.
1
12
B.
1
6
6
12
C©u 61 :
Cho
2
2
sin
()
sin
a b x b
fx
x

với a,b là các số thực. Tìm nguyên hàm F(x) của f(x) biết
1
; 0; 1
4 2 6 3
F F F
10
A.
31
tanx-cotx
42
Fx
31
tanx+cotx
42
Fx
C.
31
tanx-cotx
42
Fx
31
tanx+cotx
42
Fx
C©u 62 :
Cho hàm
2
1
32
fx
xx

.Khi đó:
A.
1
ln
2
x
f x dx C
x

1
ln
2
x
f x dx C
x

C.
2
ln
1
x
f x dx C
x

2
ln
1
x
f x dx C
x

C©u 63 :
Tính
ln x
A.
lnx x x C
B.
ln x x C
lnx x x C
lnx x x C
C©u 64 :
Cho hàm
2
1
sin
y
x
.Nếu
Fx
là nguyên hàm của hàm số và đồ thị hàm số
y F x
đi qua
điểm
;0
6
M



thì
Fx
là:
A.
3
cot
3
x
B.
3
cot
3
x
3 cot x
3 cot x
C©u 65 :
Nếu
10
0
( ) 17f x dx
và
8
0
( ) 12f x dx
thì
10
8
()f x dx
bằng :
A.
5
B.
29
5
15
C©u 66 :
Nguyên hàm của hàm số
2
2 ()
cos
x
x
e
f x e
x

là:
A.
2
x
F x e tanx
- 2
x
F x e tanx C
C.
2
x
F x e tanx C
Đáp án khác
C©u 67 :
Cho
f(x)dx F(x) C.
Khi đó với a 0, ta có
f(ax b)dx
bằng:
A.
1
F(a x b) C
2a

B.
aF(a x b) C
1
F(a x b) C
a

F(ax b) C
C©u 68 :
Thể tích của vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường y = x
2
–
2x, y = 0, x = 0, x = 1 quanh trục hoành Ox có giá trị bằng?
11
A.
8
15
(đvtt)
B.
7
8
(đvtt)
8
15
(đvtt)
8
7
(đvtt)
C©u 69 :
Tìm nguyên hàm của:
35
()
dx
Fx
xx
A.
2
2
11
( ) ln ln 1
22
F x x x C
x
2
2
11
( ) ln ln 1
22
F x x x C
x
C.
2
2
11
( ) ln ln 1
22
F x x x C
x
2
2
11
( ) ln ln 1
22
F x x x C
x
C©u 70 :
BIết :
4
4
0
1
3
a
dx
cos x
. Mệnh đề nào sau đây đúng?
A.
a là một số chẵn
a là số lớn hơn 5
C.
a là số nhỏ hơn 3
a là một số lẻ
C©u 71 :
Cho hình phẳng
H
được giới hạn bởi các đường:
ln , 0,y x x y x e
. Tính thể tích khối
tròn xoay tạo thành khi hình
H
quay quanh trục
Ox
.
A.
3
52
25
Ox
e
V
B.
3
52
27
Ox
e
V
3
52
27
Ox
e
V
3
52
25
Ox
e
V
C©u 72 :
Khẳng định nào sau đây đúng ?
A.
Nếu
'( )wt
là tốc độ tăng trưởng cân nặng/năm của một đứa trẻ, thì
10
5
'( )w t dt
là sự cân
nặng của đứa trẻ giữa
5
và
10
tuổi.
B.
Nếu dầu rò rỉ từ
1
cái thùng với tốc độ
()rt
tính bằng galông/phút tại thời gian
t
, thì
120
0
()r t dt
biểu thị lượng galông dầu rò rỉ trong
2
giờ đầu tiên.
C.
Nếu
()rt
là tốc độ tiêu thụ dầu của thế giới, trong đó
t
được bằng năm, bắt đầu tại
0t
vào ngày
1
tháng
1
năm
2000
và
()rt
được tính bằng thùng/năm,
17
0
()r t dt
biểu thị
số lượng thùng dầu tiêu thụ từ ngày
1
tháng
1
năm
2000
đến ngày
1
tháng
1
năm
2017
.
D.
Cả
,,A B C
đều đúng.
12
ĐÁP ÁN
01
{ | ) ~
28
{ | } )
55
) | } ~
02
{ ) } ~
29
{ | } )
56
) | } ~
03
{ ) } ~
30
{ | } )
57
) | } ~
04
{ | ) ~
31
{ | ) ~
58
{ | } )
05
) | } ~
32
{ ) } ~
59
) | } ~
06
{ | } )
33
{ | } )
60
) | } ~
07
{ ) } ~
34
) | } ~
61
{ | ) ~
08
{ | ) ~
35
{ ) } ~
62
{ | } )
09
) | } ~
36
) | } ~
63
{ | ) ~
10
) | } ~
37
{ ) } ~
64
{ | } )
11
{ | } )
38
{ | ) ~
65
) | } ~
12
{ ) } ~
39
{ | } )
66
{ | ) ~
13
{ ) } ~
40
{ ) } ~
67
{ | ) ~
14
{ | ) ~
41
{ | } )
68
) | } ~
15
{ | ) ~
42
{ | ) ~
69
{ ) } ~
16
) | } ~
43
{ | ) ~
70
) | } ~
17
{ ) } ~
44
{ | } )
71
{ | ) ~
18
{ | ) ~
45
{ ) } ~
72
{ | } )
19
{ | ) ~
46
) | } ~
20
{ ) } ~
47
{ | } )
21
{ ) } ~
48
) | } ~
22
{ | ) ~
49
{ ) } ~
23
{ | } )
50
{ ) } ~
24
{ | } )
51
{ | } )
25
{ | } )
52
{ | } )
26
{ | } )
53
) | } ~
27
{ | ) ~
54
{ ) } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 03
C©u 1 :
Cho
1
53
0
d
ln 2 ln 5
x
a b c
xx
. Khi đó
24a b c
bằng
A.
2
B.
3
0
1
C©u 2 :
Một nguyên hàm của
1
2x 1
x
f x e

là
A.
1
.
x
xe
B.
1
2
1
x
xe
1
2
x
xe
1
x
e
C©u 3 :
Tính tích phân:
5
1
31
dx
I
xx
được kết quả
ln3 ln5I a b
. Giá trị
22
3a ab b
là:
A.
4
B.
1
0
5
C©u 4 :
Tích phân
2
0
1 cos sinx
n
I x dx

bằng
A.
1
1n
B.
1
1n
1
2n
1
n
C©u 5 :
Hình phẳng giới hạn bởi
2
,y x y x
có diện tích là:
A.
1
2
B.
1
6
1
3
1
C©u 6 :
1
dx
e
e
I
x
có giá trị
2
A.
0
B.
-2
2
e
C©u 7 :
Cho
()fx
liên tục trên [0; 10] thỏa mãn:
10 6
02
( ) 7, ( ) 3f x dx f x dx

Khi đó, giá trị của P =
2 10
06
( ) ( )f x dx f x dx

có giá trị là:
A.
1
B.
4
3
2
C©u 8 :
Thể tích của vật thể giới hạn bởi 2 mặt trụ:
2 2 2
x z a
và
2 2 2
y z a
là
2
3
V
(đvtt). Tính
giá trị của a?
A.
1
B.
1
2
2
1
4
C©u 9 :
Tính
1
2
2
ln2
2
x
dx
x
, kết quả sai là:
A.
1
2
2 2 2
x
C





B.
1
1
2
2
x
C
1
2
2
x
C
1
2
2 2 2
x
C





C©u 10 :
Tính:
1
22
0
x
K x e dx
A.
2
1
4
e
K
B.
2
1
4
e
K
2
4
e
K
1
4
K
C©u 11 :
Diện tích hình giới hạn bởi
3
3
P y x

, tiếp tuyến của (P) tại
2
x
và trục Oy là
A.
2
3
B.
8
8
3
4
3
C©u 12 :
Nguyên hàm của hàm số: y = sin
3
x.cosx là:
A.
4
1
sin
4
xC
B.
3
1
cos
3
xC
3
1
sin
3
xC
4
sin
xC
C©u 13 :
Cho
()fx
là hàm số lẻ và liên tục trên . Khi đó giá trị tích phân
1
1
()f x dx
là:
A.
2
B.
0
1
-2
C©u 14 :
Thể tích của khối tròn xoay do hình phẳng (H) giới hạn bởi các đường
y sinx;y 0 ;x 0;x
khi quay xung quanh Ox là :
3
A.
2
3
B.
2
2
2
4
2
2
3
C©u 15 :
Tích phân
1
3
0
x 1 x
I xd

A.
28
9
B.
9
28
9
28
3
28
C©u 16 :
Cho
()fx
là hàm số chẵn và liên tục trên thỏa mãn
1
1
( ) 2f x dx
. Khi đó giá trị tích phân
1
0
()f x dx
là:
A.
2
B.
1
1
2
1
4
C©u 17 :
Cho
( ) 3 5sinf x x

và
(0) 10f
. Trong các khẳng định sau khẳng định nào đúng?
A.
( ) 3 5cos 2f x x x
B.
3
22
f



3f
3 5 cosf x x x
C©u 18 :
Cho hàm số
y f x
thỏa mãn
2
'.y x y
và f(-1)=1 thì f(2) bằng bao nhiêu:
A.
3
e
B.
2
e
2e
1e
C©u 19 :
Một nguyên hàm của hàm số:
2
( ) 1f x x x
là:
A.
3
2
1
( ) 1
3
F x x
2
2
1
( ) 1
3
F x x
C.
2
2
2
( ) 1
2

x
F x x
2
2
1
( ) 1
2
F x x
C©u 20 :
Tính:
1
2
0
ln 1K x x dx
A.
Ln2 -1/2
B.
Ln2- 1/4
Ln2 +1/2
-ln2 +1/2
C©u 21 :
Cho hình phẳng (S) giới hạn bởi Ox, Oy, y = cosx và
2
1yx

. Diện tích hình phẳng (S)
là:
A.
2
B.
3
2
2
3
1
4
4
C©u 22 :
Tính tích phân
1
2
0
d
12
x
xx
A.
9
ln
16
B.
19
ln
4 16
19
ln
7 16
19
ln
7 16
C©u 23 :
Biết F(x) là nguyên hàm của hàm số
1
1x
và F(2)=1. Khi đó F(3) bằng bao nhiêu:
A.
ln2 1
B.
1
2
3
ln
2
ln2
C©u 24 :
2
x
1
d
xx
A.
2
ln 1
x x C

B.
2
ln 1
x x C

2
ln
1
x
C
x
2
ln
1
x
C
x
C©u 25 :
Cho hàm số
fx
và
gx
liên tục trên
a;b
và thỏa mãn
f x g x 0
với mọi
x a;b
.
Gọi V là thể tích khối tròn xoay sinh ra khi quay quanh Ox hình phẳng giới hạn đồ thị
C : y f x ;
C' : y g x
; đường thẳng
x a;x b
. V được tính bởi công thức nào sau
đây ?
A.
2
b
a
V f x g x dx







b
22
a
V f (x) g (x) dx


C.
b
a
V f x g x dx
b
2
a
V f x g x dx


C©u 26 :
Cho parabôn
2
:1Pyx
và đường thẳng
:2d y mx
. Tìm m để diện tích hình phẳng
giới hạn bởi
P
và
d
đạt giá trị nhỏ nhất?
A.
1
2
B.
3
4
1
0
C©u 27 :
Tính nguyên hàm
2
dx
xa
?
A.
2
ln x x a C
2
ln 2x x a C
C.
2
ln 2x x a C
2
ln x x a C
5
C©u 28 :
Tính
1
2
0
I x x 1dx
, kết quả là :
A.
2
I
3
B.
2 2 1
I
3
22
I
3
2
I
3
C©u 29 :
Đổi biến x=2sint tích phân
1
2
0
4
dx
I
x
trở thành
A.
6
0
dt
B.
6
0
tdt
6
0
1
dt
t
3
0
dt
C©u 30 :
Họ các nguyên hàm của hàm số
sin2yx
là:
A.
cos2xC
.
B.
1
cos2
2
xC
.
cos2xC
.
1
cos2
2
xC
.
C©u 31 :
Cho
3
4
2
4
1
2
cos
xx
I dx
x

. Tính
2
I
A.
5
B.
2
3
4
C©u 32 :
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
: sinC y x
và
:D y x
là:
2
S a b
. Giá trị
3
2ab
là:
A.
24
B.
33
8
9
8
9
C©u 33 :
Tính:
23
2
2
3
dx
I
xx
A.
Đáp án khác
B.
3
I
I =
6
I
C©u 34 :
Cho
2
5
1
( 1)I x x dx
và
1ux
. Chọn khẳng định sai trong các khẳng định sau:
A.
1
5
2
(1 )I x x dx
B.
13
42
I
1
65
0
65
uu
I




1
5
0
( 1)I u u du
6
C©u 35 :
Nguyên hàm của hàm số
2
1
21x
là
A.
1
24
C
x
B.
3
1
21
C
x
1
42
C
x
1
21
C
x
C©u 36 :
Giả sử
2
1
ln
3
dx a
xb
(với
,ab
là các số tự nhiên và ước chung lớn nhất của bằng 1).
Chọn khẳng định sai trong các khẳng định sau:
A.
3 12ab
B.
2 13ab
2ab
22
41ab
C©u 37 :
Họ nguyên hàm
Fx
của hàm số
2
cosx
fx
1 cos x
là:
A.
cosx
F x C
sinx
1
F x C
sinx
C.
1
F x C
sinx

2
1
F x C
sin x

C©u 38 :
Cho hình phẳng (S) giới hạn bởi Ox, Oy, y = 3x + 2. Thể tích cuaa3 khối tròn xoay khi quay
(S) quanh Oy là:
A.
8
3
B.
4
3
2
3
16
3
C©u 39 :
Cho hình phẳng (S) giới hạn bởi Ox và
2
1yx
. Thể tích của khối tròn xoay khi quay (S)
quanh Ox là
A.
3
2
B.
4
3
3
4
2
3
C©u 40 :
Nguyên hàm F(x) của hàm số
( ) sinf x x x
thỏa mãn
F(0) 19
là:
A.
2
F( ) os
2
x
x c x
2
F( ) os 2
2
x
x c x
C.
2
F( ) os 20
2
x
x c x
2
F( ) os 20
2
x
x c x
C©u 41 :
Tính:
0
sinL x xdx
A.
L =
B.
L = 
L = 2
Đáp án khác
,ab
7
C©u 42 :
Tìm nguyên hàm của hàm số
fx
thỏa mãn điều kiện:
2 3cos , 3
2
f x x x F


A.
2
2
( ) 3sin 6
4
F x x x
2
2
( ) 3sin
4
F x x x
C.
2
2
( ) 3sin
4
F x x x
2
2
( ) 3sin 6
4
F x x x
C©u 43 :
Cho hình phẳng giới hạn bởi các đường
3
1yx
,
0y
,
0x
và
1x
quay quanh trục
Ox
. Thể tích của khối tròn xoay tạo thành bằng
A.
3
B.
9
23
14
13
7
C©u 44 :
Diện tích hình phẳng được giới hạn bởi hai đường
2
3y x x
và
yx
bằng (đvdt)
A.
32
3
B.
16
3
8
3
2
C©u 45 :
Họ các nguyên hàm của hàm số
3
tanyx
là:
A.
2
tan ln cosxx
.
2
1
tan ln cos
2
xx
C.
2
1
tan ln cos
2
xx
2
1
tan ln cos
2
xx
C©u 46 :
Nguyên hàm F(x) của hàm số
2
1
( ) 2
sin
f x x
x
thỏa mãn
F( ) 1
4
là:
A.
2
2
F( ) ot
4
x c x x
2
2
F( ) ot
16
x c x x
C.
2
F( ) otx c x x
2
2
F( ) ot
16
x c x x
C©u 47 :
Cho hàm số
f x cos3x.cosx
. Nguyên hàm của hàm số
fx
bằng 0 khi
x0
là hàm số
nào trong các hàm số sau ?
A.
3sin3x sinx
B.
sin4x sin2x
84
sin4x sin2x
24
cos4x cos2x
84
C©u 48 :
Họ nguyên hàm của
cosxcos3x
fx
là
8
A.
sin3x
sinx
3
C

2sin4x sin2x
C

C.
sin 4x sin2x
84
C

sin4x sin2x
84
C
C©u 49 :
Diện tích hình phẳng giởi hạn bởi các đường cong
2
2y x x
và
6yx
A.
95
6
B.
265
6
125
6
65
6
C©u 50 :
Nguyên hàm F(x) của hàm số
32
( ) 4 3 2 2f x x x x
thỏa mãn
F(1) 9
là:
A.
4 3 2
F( ) 2x x x x
4 3 2
F( ) 10x x x x
C.
4 3 2
F( ) 2x x x x x
4 3 2
F( ) 2 10x x x x x
C©u 51 :
Nguyên hàm của hàm số
xx
xx
ee
fx
ee
A.
ln
xx
e e C

B.
1
xx
C
ee
ln
xx
e e C

1
xx
C
ee
C©u 52 :
Tính:
2
1
(2 1)lnK x xdx
A.
1
2ln 2
2
K 
B.
1
2
K
1
2ln 2
2
K 
K = 2ln2
C©u 53 :
Tính
2
1
dx
x 4x 3
, kết quả là :
A.
1 x 1
ln C
2 x 3
B.
1 x 3
ln C
2 x 1
2
ln x 4x 3 C
x3
ln C
x1
C©u 54 :
Tích phân
2
2
4
sin
dx
I
x
bằng
A.
1
B.
3
4
2
C©u 55 :
Tích phân
1
0
x
I xe dx
bằng
A.
1
B.
2
3
4
9
C©u 56 :
Cho
sinx
cosxe ; 0
1
;0
1
x
fx
x
x


. Nhận xét nào sau đây đúng?
A.
cosx
;0
2 1 1 ; 0
ex
Fx
xx

là một nguyên hàm của
fx
B.
sinx
;0
21
0 ;
ex
Fx
xx

là một nguyên hàm của
fx
C.
cosx
;0
21
;0
ex
Fx
xx

là một nguyên hàm của
fx
D.
sinx
;0
2 1 1 ; 0
ex
Fx
xx

là một nguyên hàm của
fx
C©u 57 :
Tính
23
2
2
3
I dx
x x 3
, kết quả là :
A.
I 
B.
I
6
I
3
I
2
C©u 58 :
Tính:
2
2
0
( 1)
43
x
K dx
xx

= a.ln5+ b.ln3 thì giá trị của a và b là
A.
A=2; b=-3
B.
A=3; b=2
A=2; b=3
A=3; b=-2
C©u 59 :
Nếu
2
1
( ) 3f x dx
và
3
2
( ) 4f x dx
thì
3
1
()f x dx
có giá trị bằng
A.
1
B.
1
7
12
C©u 60 :
Họ nguyên hàm
Fx
của hàm số
2
f x cot x
là :
A.
cotx x C
B.
cotx x C
cotx x C
tanx x C
C©u 61 :
Nguyên hàm của hàm số: y = sin
2
x.cos
3
x là:
A.
35
11
sin sin
35
x x C

sin
3
x + sin
5
x + C
C.
35
11
sin sin
35
x x C
sin
3
x sin
5
x + C
C©u 62 :
Gọi S là diện tích hình phẳng giới hạn bởi các đường
3
y x 3x ;
y x;x 2 ; x 2
. Vậy
10
S bằng bao nhiêu ?
A.
4
B.
8
2
16
C©u 63 :
Cho
1
3
0
1
d
a
x
e
ex
b
. Khi đó khẳng định nào sau đây là đúng
A.
ab
B.
ab
ab
ab
C©u 64 :
Trong các khẳng định sau khẳng định nào sai?
A.
0dx C
(
C
là hằng số)
1
lndx x C
x

(
C
là hằng số)
C.
1
1
1
x dx x C

(
C
là hằng số)
dx x C
(
C
là hằng số)
C©u 65 :
Tính tích phân
2
2
6
sin
sin 3
x
I dx
x
được kết quả
1
ln 3I b c
a

với
;;a b c
. Giá trị của
23a b c
là:
A.
2
B.
3
8
5
C©u 66 :
Hàm số
()
xx
F x e e x
là nguyên hàm của hàm số
A.
( ) 1
xx
f x e e
2
1
()
2
xx
f x e e x
C.
( ) 1
xx
f x e e
2
1
()
2
xx
f x e e x
C©u 67 :
Một nguyên hàm của
2
2x 3
1
x
fx
x

là
A.
2
3x 6 ln 1
2
x
x
2
3x-6 ln 1
2
x
x

C.
2
3x+6ln 1
2
x
x

2
3x+6ln 1
2
x
x

C©u 68 :
Tính nguyên hàm
cos
dx
I
x
được kết quả
2
ln tan
x
IC
a
b


với
;;a b c
. Giá trị của
2
ab
là:
A.
8
B.
4
0
2
11
C©u 69 :
Cho
1
1
a
x
dx e
x
. Khi đó, giá trị của a là:
A.
2
1 e
B.
e
2
e
2
1 e
C©u 70 :
Diện tích hình phẳng giới hạn bởi
2
43y x x
,
0, 3xx
và trục Ox là
A.
1
3
B.
2
3
10
3
8
3
C©u 71 :
2
2 .3 .7
x x x
dx
là
A.
84
ln84
x
C
B.
2
2 .3 .7
ln4.ln3.ln7
x x x
C
84
x
C
84 ln84
x
C
C©u 72 :
Cho (H) là hình phẳng giới hạn bởi
2
4x+4,y=0,x=0,x=3
P y x

Thể tích V khi quay (H) quanh trục Ox là
A.
33
B.
33
5
33
5
33
C©u 73 :
Tính:
6
0
tg
I xdx
A.
23
ln
3
B.
-
23
ln
3
3
ln
2
1
ln
2
C©u 74 :
Một nguyên hàm của
2
cos
x
fx
x
là
A.
tan ln cosx
xx
tan ln cosx
xx
C.
tan ln cosx
xx
tan ln sin
x x x
C©u 75 :
Cho
2
0
1
sin d
a
x
e
e x x
b
. Khi đó
sin os2a c a
bằng
A.
1
B.
2
4
0
C©u 76 :
Diện tích hình phẳng giới hạn bởi
3
;4y x y x
,
0, 3xx
là :
12
A.
5
B.
4
1
8
C©u 77 :
Tích phân
1
ln
e
x xdx
bằng
A.
2
4
e
B.
2
1
4
e
2
1
4
e
2
1
24
e
C©u 78 :
Tính
2
1
11
dx
x

?
A.
2ln3
B.
ln3
ln2
ln6
C©u 79 :
Cho
1
2
0
( 1)d
22
xx
ab
xx
. Khi
ab
bằng:
A.
5
B.
1
2
3
C©u 80 :
Cho
2
e
1
cos ln x
I dx
x
, ta tính được :
A.
I cos1
B.
I1
I sin1
Một kết quả khác
13
ĐÁP ÁN
01
{ | } )
28
{ ) } ~
55
) | } ~
02
{ | ) ~
29
) | } ~
56
{ | } )
03
{ | } )
30
{ ) } ~
57
{ ) } ~
04
) | } ~
31
{ | ) ~
58
) | } ~
05
{ ) } ~
32
{ | } )
59
{ | ) ~
06
{ | ) ~
33
) | } ~
60
{ ) } ~
07
{ ) } ~
34
{ | ) ~
61
) | } ~
08
{ | } )
35
) | } ~
62
{ ) } ~
09
{ | ) ~
36
{ | ) ~
63
{ | } )
10
) | } ~
37
{ ) } ~
64
{ | ) ~
11
{ | ) ~
38
{ ) } ~
65
{ | } )
12
) | } ~
39
{ ) } ~
66
{ | ) ~
13
{ ) } ~
40
{ | } )
67
{ | ) ~
14
{ ) } ~
41
) | } ~
68
{ | } )
15
{ | ) ~
42
{ | } )
69
{ ) } ~
16
{ ) } ~
43
{ | ) ~
70
{ | } )
17
{ | ) ~
44
) | } ~
71
) | } ~
18
) | } ~
45
{ ) } ~
72
{ | ) ~
19
) | } ~
46
{ | } )
73
) | } ~
20
) | } ~
47
{ ) } ~
74
{ | ) ~
21
{ ) } ~
48
{ | ) ~
75
{ | } )
22
{ | } )
49
{ | ) ~
76
{ | } )
23
) | } ~
50
{ | } )
77
{ | ) ~
24
{ | ) ~
51
) | } ~
78
{ | } )
25
{ ) } ~
52
) | } ~
79
{ | } )
26
{ | } )
53
{ ) } ~
80
{ ) } ~
27
{ | } )
54
) | } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 04
C©u 1 :
Giả sử
0k
và
3
2
0
ln(2 3)
dx
xk

. Giá trị của
k
là
A.
3
B.
2
23
1
C©u 2 :
Hàm số
10
)1()( xxxf
có nguyên hàm là:
A.
C
xx
xF
11
)1(
12
)1(
)(
1112
C
xx
xF
11
)1(
12
)1(
)(
1112
C.
)(xF
C
xx
10
)1(
11
)1(
1011
C
xx
xF
10
)1(
11
)1(
)(
1011
C©u 3 :
Cho tích phân
2
2
0
sin 2 1x x m dx
. Giá trị của tham số m là:
A.
5
B.
3
4
6
C©u 4 :
Tính
cos5 .cos3x xdx
A.
11
sin8 sin2
82
x x C
11
sin8 sin2
22
xx
C.
11
sin8 sin2
16 4
xx
11
sin8 sin2
16 4
xx
C©u 5 :
Diện tích hình phẳng giới hạn bởi các đường:
xxyyxx 2;0;2;1
2
là:
A.
0
B.
3
8
3
8
3
2
C©u 6 :
Nguyên hm của hm số
2
cos .sin .x x dx
bng:
:
A.
3sin sin3
12
xx
C
B.
3cos cos3
12
xx
C
3
sin xC
.
2
sinx.cos xC
2
C©u 7 :
Tính
.ln
dx
xx
A.
ln xC
B.
ln | |xC
ln(lnx) C
ln | lnx | C
C©u 8 :
Diện tích hình phẳng giới hạn bởi:
xxyxxy 4;2
22
là:
A.
-9
B.
9
3
20
3
16
C©u 9 :
Họ nguyên hàm của hàm số
2
cosf x x
là :
A.
cos2
24
xx
C
B.
cos2
24
xx
C
sin2
24
xx
C
sin2
24
xx
C
C©u 10 :
Cho hm số
11
25
()
10
xx
x
fx

. Khi đ:
A.
21
( ).
5 .ln5 5.2 .ln 2
xx
f x dx C
.
21
( ).
5 ln5 5.2 .ln2
xx
f x dx C
C.
5 5.2
( ).
2ln5 ln2
xx
f x dx C
5 5.2
( ).
2ln5 ln2
xx
f x dx C
C©u 11 :
Tch phân
cos(ln ).
2016
1
x dx
e
=
2016
1
.e
2
m
. Khi đ giá trị m:
A.
1
2
m 
B.
1m
2m
1m 
C©u 12 :
Th tch khối trn xoay khi cho Elip
22
2
1
3
xy
b

quay quanh trc Ox, c kt quả bng:
A.
2
43
3
b
B.
2 b
4 b
2
23
3
b
C©u 13 :
Tìm a thỏa mãn:
0
4
0
2
a
x
dx
A.
a=ln2
B.
a=0
a=ln3
a=1
C©u 14 :
Cho
x
ln2
I2
x
. Khi đó kết quả nào sau đây là sai :
A.
x
I 2 C
B.
x1
I 2 C

x
I 2(2 1) C
x
I 2(2 1) C
C©u 15 :
Th tích khối trn xoay giơi han bởi các đường
2
2 ; 0y x x y
khi quay quanh trc Ox là:
3
A.
4
15
V
B.
18
15
V
16
15
V
12
15
V
C©u 16 :
Trong các khẳng định sau, khẳng định nào sai?
A.
1 tanF x x
là một nguyên hàm của hàm số
2
1 tanf x x
B.
Nêu F(x) là một nguyên hàm của hàm số f(x) thì mọi nguyên hàm của f(x) đều có dạng
F x C
(C là hng số)
C.
'
lg
ux
dx u x C
ux

D.
5 cosF x x
là một nguyên hàm của
sinf x x
C©u 17 :
Tích phân:
x
I xe dx
bng:
A.
e
B.
1e
1
1
1
2
e
C©u 18 :
Tính diện tích hình phẳng giới hạn bởi
2
3x 2
1
0, 2
yx
yx
xx


A.
8
3
B.
2
3
4
3
2
C©u 19 :
Cho hình phẳng D giới hạn bởi:
0;
3
;0;tan yxxxy
gọi S là diện tích hình phẳng
giới hạn bởi D. gọi V là th tích vật tròn xoay khi D quay quanh ox. Chọn mệnh đề đúng.
A.
S=ln2,
)
3
3(
V
S=ln2;
)
3
3(
V
C.
S=ln3;
)
3
3(
V
S=ln3;
)
3
3(
V
C©u 20 :
(H) giới hạn bởi các đường:
2
0
2x
y
yx

. Tính th tích vật tròn xoay khi quay (H) quanh Ox
4
A.
4
3
B.
16
15
4
3
16
15
C©u 21 :
Cho
0
( ) cos
x
g x tdt
. Hãy chọn câu khẳng định đúng trong 4 câu khẳng định sau:
A.
'( ) sin(2 )g x x
B.
'( ) cosg x x
'( ) sing x x
cos
'( )
2
x
gx
x
C©u 22 :
Cho
)(xf
là hàm số chẵn và
adxxf
0
3
)(
chọn mệnh đề đúng
A.
adxxf
3
0
)(
B.
adxxf 2)(
3
3
adxxf
3
3
)(
adxxf
0
3
)(
C©u 23 :
Giả sử
2
0
( ) cos( )
x
f t dt x x
. Giá trị của
(4)f
là
A.
1
B.
1
2
Một đáp số khác.
1
4
C©u 24 :
Một nguyên hàm của hàm số:
f(x) cos5x.cosx
là:
A.
1 sin6 sin4
()
2 6 4



xx
Fx
F(x) sin6x
C.
F(x) cos6x
1 1 1
( ) sin6 sin4
2 6 4




F x x x
C©u 25 :
Trong các mệnh đề sau, mệnh đề nào sai:
A.
42
3
42
xx
x x dx C
2
1
2
xx
e dx e C
C.
sin cosxdx x C
2
2
1
4
ln
3
dx
xx
C©u 26 :
Tính
2
x
2x 3
d
x 
A.
11
ln
43
x
C
x

B.
13
ln
41
x
C
x

13
ln
41
x
C
x
11
ln
43
x
C
x
C©u 27 :
Tính
2
3x x dx
5
A.
2
3xC
B.
22
( 3)xC
22
( 3)
4
x
C
2
4
x
C
C©u 28 :
Tính diện tích hình phẳng giới hạn bởi các đường:
22
, 4x , 4y x y y
A.
8
B.
4
4
3
8
3
C©u 29 :
Trong các khẳng định sau, khăng định nào sai?
A.
1 2 1 2
f x f x dx f x dx f x dx
B.
Nu
Fx
và
Gx
đều là nguyên hàm cùa hàm số
fx
thì
F x G x C
là hng số
C.
F x x
là một nguyên hàm của
2f x x
D.
2
F x x
là một nguyên hàm của
2f x x
C©u 30 :
Trong các khẳng định sau khẳng định nào sai?
A.
2
7 sinF x x
là một nguyên hàm của hàm số
sin2f x x
B.
Nu
Fx
và
Gx
đều là nguyên hàm của hàm số f(x) thì
F x G x dx
có dạng
h x Cx D
(C,D là các hng số,
0C
)
C.
'ux
u x C
ux

D.
Nu
f t dt F t C
thì
f u x dt F u x C
C©u 31 :
Diện tch hnh phẳng giới hạn bởi
2
x
y
a
v
2
y
x
a
( với
0a
) c kt quả bng:
A.
2
3
a
B.
2
a
2
2
a
2
4
a
C©u 32 :
Cho
1
3
42
0
4
2 3. . 0
( 2)
x
m dx
x

. Khi đ
2
144. 1m
bng:
A.
2
3
B.
4 3 1
23
3
Kt quả khác..
6
C©u 33 :
Thể tích vật giới hạn bởi miền hình phẳng tạo bởi các đường
2
yx
và
y4
khi quay
quanh trục Ox là :
A.
64
5
B.
152
5
128
5
256
5
C©u 34 :
Tính
1
0
23
2
842
)252(
xxx
dxxx
I
A.
12ln
6
1
I
B.
4
3
ln
6
1
I
2ln23ln
6
1
I
2ln23ln
6
1
I
C©u 35 :
Tính
2
1
( 3 )x x dx
x

A.
32
3 lnx x x C
3
2
3
ln
32
x
x x C
C.
3
2
2
31
32
x
xC
x
3
2
3
ln | |
32
x
x x C
C©u 36 :
Cho hàm số
y f(x)
có nguyên hàm trên (a ;b) đồng thời thỏa mãn
f(a) f(b)
. Lựa chọn
phương án đúng :
A.
b
f (x)
a
f '(x).e dx 0
b
f (x)
a
f '(x).e dx 1
C.
b
f (x)
a
f '(x).e dx 1
b
f (x)
a
f '(x).e dx 2
C©u 37 :
Cho hm số
4
2
52
()
x
fx
x
. Khi đ:
A.
3
25
()
3
x
f x dx C
x
3
5
( ) 2f x dx x C
x
C.
3
25
()
3
x
f x dx C
x
3
2
2
( ) 5ln
3
x
f x dx x C
.
C©u 38 :
Cho
2
2
1
21I x x dx
. Khẳng định no sau đây sai:
A.
3
0
I udx
B.
2
27
3
I
33I
3
2
3
2
0
3
It
7
C©u 39 :
Biết
b
a
f(x)dx 10
và
b
a
g(x)dx 5
. Khi đó giá trị của tích phân :
b
a
I (3f(x) 5g(x))dx
là :
A.
I5
B.
I5
I 10
I 15
C©u 40 :
Diện tch hnh phẳng giới hạn bởi
yx
v
2
33
22
y x x
bng:
A.
23
3
B.
3
2
55
12
1
4
C©u 41 :
Cho hàm số
4
2
1f x x x
. Biết F(x) là một nguyên hàm của f(x); đồ thị hàm số
y F x
đi
qua điểm
1;6M
. Nguyên hàm F(x) là.
A.
4
2
1
2
45
x
Fx
5
2
1
2
55
x
Fx
C.
5
2
1
2
55
x
Fx
4
2
1
2
45
x
Fx
C©u 42 :
Kết quả
dx
I
x1
là :
A.
2 x 2ln( x 1) C
2 2ln( x 1) C
C.
2 x 2ln( x 1) C
2 x 2ln( x 1) C
C©u 43 :
Tính:
x
dx
cos1
A.
C
x
2
tan2
B.
C
x
2
tan
C
x
2
tan
2
1
C
x
2
tan
4
1
C©u 44 :
Hình phẳng (H) giới hạn bởi các đường
,6y x y x
và trc hoành thì diện tích của hình
phẳng (H) là:
A.
20
3
B.
25
3
16
3
22
3
C©u 45 :
Th tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đường
44
3
sin cos , 0, 0,
4 12
y x x y x x
quay quanh trc hoành
Ox
là
A.
3
16
B.
3
32
3
24
3
32
8
C©u 46 :
Bit
a
dxx
0
4
0)
2
3
sin4(
giá trị của
);0(
a
là:
A.
4
a
B.
2
a
8
a
3
a
C©u 47 :
Giá trị của
1
ln 1
e
x
dx
x
là :
A.
2
e
B.
3
2
1
2
2
2
ee
C©u 48 :
ln 2sin cosF x x x x
là một nguyên hàm của:
A.
sinx cosx
3 cos sinxx
B.
2 cos sin
2 sin cos
xx
xx
3 sin cos
2 sin cos
xx
xx
sin cos
3 cos sin
xx
xx
C©u 49 :
Tính th tích vật th tròn xoay sinh ra khi quay (H) quanh trc Ox, bit (H) là hình phẳng
giới hạn bởi (C):
tan
cos
x
e
y
x
, trc Ox, trc Oy v đường thẳng
3
x
A.
2
3
( 1)
2
e
B.
23
( 1)e
2
3
( 1)e
23
( 1)
2
e
C©u 50 :
Cho hàm số
sin2 .cosf x x x
và các mệnh đề sau:
i) Họ nguyên hàm của hàm số là
3
2
cos
3
xC
ii) Họ nguyên hàm của hàm số là
11
cos3 cos
62
x x C
ii) Họ nguyên hàm của hàm số là
3
2
cos
3
xC
A.
Chỉ có duy nhất một mệnh đề đúng.
Có hai mệnh đề đúng.
C.
Không có mệnh đề nào đúng.
Cả ba mệnh đều đều đúng.
C©u 51 :
Khẳng định no sau đây l đúng:
(a) Một nguyên hàm của hàm số
cos x
ye
là
cos
sin .
x
xe
.
(b) Hai hàm số
22
6 1 10
( ) ; ( )
2 3 2 3
x x x
f x g x
xx


đều là nguyên hàm của một hàm số.
(c)
11
( 1)
xx
xe dx x e C

.
9
23
11
00
xx
e dx e dx


A.
(a)
B.
(c)
(d)
(b)
C©u 52 :
Th tch khối trn xoay tạo nên khi quay hnh H quanh trc Ox, với
ln ; y 0; x 1; x eH y x x
bng:
A.
3
(5 3)
27
e
B.
3
( 1)
2
e
3
( 3)
27
e
3
( 1)
3
e
C©u 53 :
Diện tích hình phẳng giới hạn bởi parabol
2
yx
và đường thẳng
32yx
là :
A.
1
4
B.
1
6
1
5
1
3
C©u 54 :
Cho hình phẳng (H) giới hạn bởi đường thẳng
yx
; trục hoành và đường thẳng
,0x m m
.
Thể tích khối tròn xoay tạo bởi khi quay (H) quanh trục hoành là
9
(đvtt). Giá trị của tham số m
là :
A.
9
B.
3
3
3
3
33
C©u 55 :
Tìm 1 nguyên hàm F(x) của
3
2
1
()
x
fx
x
bit F(1) = 0
A.
2
11
()
22
x
Fx
x
2
13
()
22
x
Fx
x
C.
2
11
()
22
x
Fx
x
2
13
(x)
22
x
F
x
C©u 56 :
Nguyên hàm của
sin cos
sin cos
xx
xx
là:
A.
ln sin cosx x C
1
ln sin cos
C
xx
C.
ln sin cosx x C
1
sin cos
C
xx
C©u 57 :
Giả sử hình phẳng tạo bởi các đường cong
y f(x);y 0;x a;x b
có diện tích là
1
S
còn
hình phẳng tạo bởi đường cong
y |f(x)|;y 0;x a;x b
có diện tích là
2
S
, còn hình
phẳng tạo bởi đường cong
y f(x);y 0;x a;x b
có diện tích là S
3
. Lựa chọn phương
án đúng:
10
A.
13
SS
B.
13
SS
13
SS
21
SS
C©u 58 :
Cho
n
và
2
1
0
4 ( 1)( 1)
nx
e xdx e e
. Giá trị của
n
là
A.
1
B.
3
4
2
C©u 59 :
Giá trị của
5
1
21
2 3 2 1 1
x
E dx
xx
là:
A.
2 4ln15 ln2E
5
2 4ln ln4
3
E
C.
3
2 4ln ln2
5
E
5
2 4ln ln4
3
E
C©u 60 :
Một nguyên hàm của hàm số
f(x) 1 2x
là :
A.
3
(2x 1) 1 2x
4

3
(2x 1) 1 2x
2

C.
3
(1 2x) 1 2x
2
3
(1 2x) 1 2x
4

C©u 61 :
Cho
2
0
1f x dx
và
fx
là hàm số chẵn. Giá trị tích phân
0
2
f x dx
là :
A.
-2
B.
1
-1
2
C©u 62 :
Họ nguyên hàm của hàm số
2
32
26
()
7 14 8
xx
fx
x x x

là
A.
3ln 1 7ln 2 5ln 4x x x C
3ln 1 7ln 2 5ln 4x x x C
C.
3ln 1 7ln 2 5ln 4x x x C
3ln 1 7ln 2 5ln 4x x x C
C©u 63 :
Giá trị của
1
2
0
ln 1K x x dx
là:
A.
52
2 ln
22
K
52
2 ln
22
K
C.
52
2 ln
22
K
52
2 ln
22
K
C©u 64 :
Xác định a,b,c đ hàm số
x
ecbxaxxF
)()(
2
là một nguyên hàm của hàm số
11
x
exxxf
)23()(
2
A.
1,1,1 cba
B.
1,1,1 cba
1,1,1 cba
1,1,1 cba
C©u 65 :
Họ nguyên hàm
3
1x x dx
là :
A.
54
11
54
xx
C
54
11
54
xx
C
C.
5 4 2
3
3
5 4 2
x x x
xC
5 4 2
3
3
5 4 2
x x x
xC
C©u 66 :
Diện tích hình phẳng (H) giới hạn bởi đường cong
2yx
; đường thẳng
yx
và trục
hoành là :
A.
8
3
B.
7
3
10
3
3
C©u 67 :
Tch phân:
4
4
0
(3 ).
x
x e dx
= a + b.e. Khi đ a + 5b bng
A.
8
B.
18
13
23.
C©u 68 :
Diện tích hình phẳng giới hạn bởi các đường
2
2y x x
và
24yx
là:
A.
7
2
B.
5
2
9
2
11
2
C©u 69 :
Biết
22
1
2 ln ln 2
3
2
a
xx
dx
x
, a là tham số. Giá trị của tham số a là.
A.
4
B.
2
-1
3
C©u 70 :
Giả sử A, B là các hng số của hàm số
2
( ) sin( )f x A x Bx

. Bit
'(1) 2f
và
2
0
( ) 4f x dx
.
Giá trị của B là
A.
1
B.
Một đáp số khác
2
3
2
C©u 71 :
Hàm số
( ) 1f x x x
có một nguyên hàm là
()Fx
. Nu
(0) 2F
thì giá trị của
(3)F
là
A.
116
15
B.
Một đáp số khác
146
15
886
105
12
C©u 72 :
Trong các khẳng định sau, khẳng định no đúng?
A.
2
2
21
1
dx
xC
x
B.
Nu
0
b
a
f x dx
thì
0, x ;f x a b


C.
b c b
a a c
f x dx g x dx f x dx
với mọi
,,a b c
thuộc TXĐ của
fx
D.
Nu F(x) là nguyên hàm của f(x) thì
Fx
là nguyên hàm của hàm số
fx
13
ĐÁP ÁN
01
{ | } )
28
{ | } )
55
{ | } )
02
{ ) } ~
29
{ | ) ~
56
{ | ) ~
03
{ | ) ~
30
{ | ) ~
57
) | } ~
04
{ | ) ~
31
) | } ~
58
{ | } )
05
{ ) } ~
32
) | } ~
59
{ ) } ~
06
) | } ~
33
{ ) } ~
60
) | } ~
07
{ | } )
34
{ ) } ~
61
{ | ) ~
08
{ ) } ~
35
{ | } )
62
{ | } )
09
{ | ) ~
36
) | } ~
63
) | } ~
10
) | } ~
37
) | } ~
64
{ ) } ~
11
) | } ~
38
{ | ) ~
65
{ ) } ~
12
) | } ~
39
) | } ~
66
{ | ) ~
13
{ ) } ~
40
) | } ~
67
) | } ~
14
) | } ~
41
{ ) } ~
68
{ | ) ~
15
{ | ) ~
42
) | } ~
69
{ ) } ~
16
{ | ) ~
43
{ ) } ~
70
{ | } )
17
{ | ) ~
44
{ | } )
71
{ | } )
18
{ | } )
45
{ | } )
72
{ | ) ~
19
{ ) } ~
46
{ ) } ~
20
{ | } )
47
{ ) } ~
21
{ | } )
48
{ | ) ~
22
{ ) } ~
49
{ | } )
23
{ | } )
50
{ ) } ~
24
) | } ~
51
{ | } )
25
{ | ) ~
52
) | } ~
26
{ | } )
53
{ ) } ~
27
{ | ) ~
54
{ | ) ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 05
C©u 1 :
Hàm số
2
( ) e
x
fx
là nguyên hàm của hàm số nào ?
A.
2
e
()
2
x
fx
x
B.
2
( ) e
x
fx
2
( ) 2 e
x
f x x
2
2
( ) e 1
x
f x x
C©u 2 :
Tìm khẳng định đúng trong các khẳng định sau
A.
31
02
21x dx x dx
33
00
22x dx x dx
C.
3 3 2
0 2 0
222x dx x dx x dx
3 2 3
0 0 2
2 2 2x dx x dx x dx
C©u 3 :
Giá trị trung bình của hàm số
y f x
trên
;ab
, kí hiệu là
mf
được tính theo công thức
1
b
a
m f f x dx
ba
. Giá trị trung bình của hàm số
sinxfx
trên
0;
là:
A.
2
B.
3
1
4
C©u 4 :
22
d
sin cos
x
xx
A.
1 C
B.
tan cotx x C
tan cotx x C
11
cos sin
C
xx
C©u 5 :
Tích phân:
3
2
0
cos
x
dx
x
A.
3
ln2
3
B.
3
ln2
3

3
ln2
3

3
ln2
3
C©u 6 :
Diện tích hình phẳng giới hạn bởi các đường thẳng
3 , 4
x
y y x
và trục trung bằng
A.
71
2 ln3
(đvdt)
B.
72
2 ln3
(đvdt)
52
2 ln3
(đvdt)
2
1
ln3
(đvdt)
2
C©u 7 :
Tìm khẳng định sai trong các khẳng định sau
A.
2
00
sin 2 sin
2
x
dx xdx
1
0
1
1
x
e dx
e
C.
00
sin cos
44
x dx x dx
11
00
sin(1 ) sinx dx xdx
C©u 8 :
Tính thể tích khối tròn xoay tạo bởi quay quanh trục Ox và hình phẳng giới hạn bởi
21
: , 0, 1
1
x
C y y x
x
A.
3
2
B.
7
2
1
2
5
2
C©u 9 :
Cho
1
44
4
00
d
, sin cos d
31
x
I J x x x
x

và
2
2
1
3 1 dK x x x
. Tích phân nào có giá trị
bằng
63
6
?
A.
I
B.
K
J
J và K
C©u 10 :
Giá trị của
2
2
0
2
x
e dx
bằng ?
A.
4
e
B.
e
4
4
4
1e
e
4
3
C©u 11 :
Diện tích hình phẳng giới hạn bởi
2
45y x x
và hai tiếp tuyến tại A(1; 2) và B(4; 5) là:
A.
13
4
B.
9
4
15
4
11
4
C©u 12 :
4
2
2
d
9
x
x
x
A.
5
2
1
59
C
x

B.
3
2
1
39
C
x

5
2
4
9
C
x

3
2
1
9
C
x

C©u 13 :
Tích phân:
2
2
0
2
x
e dx
A.
4
e
B.
4
3e
4
4e
4
1e
C©u 14 :
Họ nguyên hàm của hàm số: y = sin
3
x.cosx là:
3
A.
tg
3
x + C
B.
cos
2
x + C
3
1
cos
3
xC
4
1
sin
4
xC
C©u 15 :
sin cos2 dx x x
A.
11
cos3 cos
22
x x C
11
cos3 cos
62
x x C
C.
11
sin3 sin
62
x x C
11
cos3 cos
22
x x C
C©u 16 :
Với
0a
. Giá trị của tích phân
2
0
sin
a
x ax dx
là
A.
2
a
B.
2
1
2
a
2
1
a
2
2a
a
C©u 17 :
Nguyên hàm
cosx xdx
A.
sin cosx x x C
B.
sin cosx x x C
sin cosx x x
sin cosx x x
C©u 18 :
Nguyên hàm của (với C hằng số) là
2
2
1
x
dx
x
A.
1
1
x
C
x
B.
1
x
C
x
1
1
C
x
2
ln 1 xC
C©u 19 :
Diện tích hình phẳng giới hạn bởi trục hoành, đường cong (C)
2
23y x x
, tiếp tuyến
với (C) tại A(1; 6) và x= -2 là:
A.
7
2
B.
9
2
5
2
11
2
C©u 20 :
Tích phân
3
2
sin 2
0
3 cos
xx
e x x dx

A.
3
1
8
1e
B.
3
1
8
eC
3
1
8
1e
3
1
8
eC
C©u 21 :
Họ nguyên hàm của hàm số
sin2f x x
là
A.
1
cos2
2
F x x C
cos2F x x C
C.
1
cos2
2
F x x C
cos2F x x C
4
C©u 22 :
Cho
0
sin
sin cos 4
a
x
dx
xx
. Giá trị của a là
A.
3
B.
4
2
6
C©u 23 :
Tính:
0
cos
x
L e xdx
A.
1Le

B.
1Le
1
( 1)
2
Le
1
( 1)
2
Le

C©u 24 :
Trong các mệnh đề sau, mệnh đề nào sai?
3
2
sin
( ): sin d
3
x
I x x C
2
2
42
( ): d 2ln 3
3
x
II x x x C
xx

6
( ): 3 2 3 d
ln6
x
x x x
III x x C
A.
()III
B.
()I
Cả 3 đều sai.
()II
C©u 25 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx
và đường thẳng
2yx
là
A.
5
3
B.
3
2
23
15
4
3
C©u 26 :
Tính
4
2
0
tgI xdx
A.
I = 2
B.
3
I
ln2
1
4
I

C©u 27 :
Nguyên hàm của hàm số: y = sin
3
x.cosx là:
A.
4
1
cos
4
xC
B.
4
1
sin
4
xC
cos
2
x + C
3
1
sin
3
xC
C©u 28 :
Diện tích hình phẳng giới hạn bởi đồ thị
2
( ): 2 3P y x x
và hai tiếp tuyến của
()P
tại
(0;3)A
và
(3;6)B
bằng:
A.
7
2
(đvdt)
B.
9
4
(đvdt)
9
2
(đvdt)
17
4
(đvdt)
5
C©u 29 :
Tính:
2
1
(2 1)lnK x xdx
A.
1
3ln2
2
K 
B.
1
2
K
K = 3ln2
1
3ln2
2
K 
C©u 30 :
Nguyên hàm
()Fx
của hàm số
2
sin2
sin 3
x
y
x
khi
(0) 0F
là
A.
2
ln 1 sin x
B.
2
ln 2 sin
3
x
2
ln cos x
2
sin
ln 1
3
x
C©u 31 :
Tính:
1
22
0
x
K x e dx
A.
2
1
4
e
K
B.
2
1
4
e
K
2
4
e
K
1
4
K
C©u 32 :
Nguyên hàm
ln xdx
A.
ln x x C
B.
ln xx
ln x x C
ln xx
C©u 33 :
Nếu
2
( ) d sin
x
f x x e x C
thì
()fx
bằng:
A.
2sin
x
ex
B.
sin2
x
ex
2
cos
x
ex
2sin
x
ex
C©u 34 :
Tính:
2
1
ln
e
x
J dx
x
A.
1
2
J
B.
3
2
J
1
4
J
1
3
J
C©u 35 :
Tính:
2
1
1
x
P dx
x
A.
2
1 P x x x C
22
1 ln 1P x x x C
C.
2
2
11
1 ln

x
P x C
x
Đáp án khác.
C©u 36 :
Với
2a
, giá trị của tích phân sau
2
0
32
a
dx
xx
là
6
A.
2
ln
21
a
a
B.
2
ln
1
a
a
2
ln
21
a
a
2
ln
21
a
a
C©u 37 :
ln5
ln3
d
23
xx
x
ee

A.
7
ln
2
B.
3
ln
2
2
ln
3
2
ln
7
C©u 38 :
Cho
2
2
1
21I x x dx
và
2
1ux
. Chọn khẳng định sai trong các khẳng định sau:
A.
3
0
I udu
B.
2
1
I udu
3
3
2
0
2
3
Iu
2
27
3
I
C©u 39 :
Tính diện tích hình phẳng được giới hạn bởi
32
4 3 1, 2 1y x x x y x
A.
1
12
B.
3
1
2
C©u 40 :
Cho
0a
, diện tích giới hạn bởi các đường có phương trình
22
1
4
23
:
1
x ax a
Cy
a
và
2
2
4
:
1
a ax
Cy
a
là
A.
3
4
1
a
a
B.
3
4
31
a
a
3
4
61
a
a
3
4
6
1
a
a
C©u 41 :
Tính diện tích hình phẳng được giới hạn bởi
2
2 , 0, 1, 2y x x y x x
A.
8
3
B.
2
7
3
3
C©u 42 :
Nguyên hàm của hàm số: y = sin
2
x.cos
3
x là:
A.
sin
3
x + sin
5
x + C
35
11
sin sin
35
x x C

C.
sin
3
x sin
5
x + C
35
11
sin sin
35
x x C
C©u 43 :
Cho
6
0
1
sin .cos .
64
n
x x dx
, giá trị của n là
A.
3
B.
5
4
6
7
C©u 44 :
Nếu
()Fx
là một nguyên hàm của hàm
2
3
( ) , (0) 0
23
x
f x F
xx


thì hằng số C bằng
A.
2
ln 3
3
B.
3
ln 3
2
2
ln 3
3
3
ln 3
2
C©u 45 :
Cho đồ thị hàm số
y f x
.Diện tích hình phẳng (phần gạch chéo trong Hình 1) là :
A.
2
2
f x dx
22
00
f x dx f x dx
C.
00
22
f x dx f x dx
12
21
f x dx f x dx
C©u 46 :
Nếu
()Fx
là một nguyên hàm của hàm số
1
1
y
x
và
(2) 1F
thì
(3)F
bằng
A.
1
2
B.
3
ln
2
ln2
ln2 1
C©u 47 :
Cho
22
12
: 4 ; : 3 0C y x C x y
. Tính diện tích hình phẳng tạo bởi
1
C
và
2
C
.
A.
23
33
B.
43
53
43
33
3
33
C©u 48 :
Tính:
0
sinL x xdx
A.
L =
B.
L = 2
L = 0
L = 
C©u 49 :
Hàm số nào dưới đây là một nguyên hàm của hàm số:
2
1
4
y
x
8
A.
2
( ) 2 4F x x
2
( ) 2 4 F x x x
C.
2
( ) ln 4 F x x x
2
( ) ln 4 F x x x
C©u 50 :
Gọi S là miền giới hạn bởi
2
:;C y x Ox
và hai đường thẳng
1; 2xx
. Tính thể tích
vật thể tròn xoay khi S quay quanh trục Ox.
A.
31 1
53
B.
31 1
53
31
5
31
1
5
C©u 51 :
Thể tích khối tròn xoay có được khi cho miền phẳng giới hạn bởi các đường
ln ; 0; 2y x y x
quay xing quanh trục hoành là
A.
2ln2 1
B.
2 ln2 1
2 ln2
ln2 1
C©u 52 :
Giả sử
5
1
lnb
21
dx
a
x
. Giá trị của a,b là ?
A.
0; 81ab
B.
1; 9ab
0; 3ab
1; 8ab
C©u 53 :
Công thức nguyên hàm nào sau đây không đúng?
A.
ln
dx
xC
x

1
1
1
x
x dx C
C.
01
ln
x
x
a
a dx C a
a
tan
cos
dx
xC
x

C©u 54 :
Tích phân
2
2
0
sin2
1 sin
x
dx
x
A.
ln2
B.
0
ln3
2
C©u 55 :
Tích phân:
0
1
2
21
1
x
dx
x
A.
1 ln2
B.
1
ln2
2
1
ln 2
2
1 ln2
C©u 56 :
Giả sử
1 4 4
0 1 0
( ) 2, ( ) 3, g( ) 4f x dx f x dx x dx
khẳng định nào sau đây là sai ?
9
A.
4
0
( ) g 1f x x dx
44
00
( ) g( )f x dx x dx
C.
44
00
( ) g( )f x dx x dx
4
0
( ) 5f x dx
C©u 57 :
Tính:
1
2
0
56
dx
I
xx

A.
I = ln2
B.
4
ln
3
I
3
ln
4
I
I = ln2
C©u 58 :
Biết
0
1
sin cos
4
a
x xdx
. Khi đó giá trị của a là
A.
2
B.
2
3
4
3
C©u 59 :
Họ nguyên hàm của hàm số
cos
x
f x e x
là
A.
1
sin cos
2
x
F x e x x C
1
sin cos
2
x
F x e x x C
C.
1
sin cos
2
x
F x e x x C
1
sin cos
2
x
F x e x x C
C©u 60 :
Cho
16
1
dI x x
và
4
0
cos2 d .J x x
Chọn khẳng định đúng.
A.
IJ
B.
IJ
IJ
1IJ
C©u 61 :
Tính:
1
2
0
56
dx
I
xx

A.
I = 1
B.
I = ln2
I = ln2
4
ln
3
I
C©u 62 :
Vận tốc của một vật chuyển động là
sin
1
/
2
t
v t m s


. Quãng đường di chuyển của
vật đó trong khoảng thời gian 1,5 giây chính xác đến 0,01m là
A.
0,34m
B.
0,32m
0,33m
0,31m
C©u 63 :
Tích phân:
4
0
2x dx
10
A.
0
B.
2
8
4
C©u 64 :
Hàm số
2
()
x
F x e
là nguyên hàm của hàm số
A.
2
()
x
f x e
B.
2
2
( ) 1
x
f x x e
2
()
2
x
e
fx
x
2
( ) 2
x
f x xe
C©u 65 :
Nguyên hàm
2.
x
x e dx
A.
22
xx
xe e C
B.
22
xx
xe e
22
xx
xe e
22
xx
xe e C
C©u 66 :
Trong các đẳng thức sau, đẳng thức nào sai?
A.
1
2
00
sinxdx dx
.
22
00
sin cosxdx tdt
C.
22
00
1
sin sin 2 1 sin 2 1
8
xdx x d x
.
2
0
2
sin sinxdx tdt
.
C©u 67 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx
và đường thẳng
2yx
là ?
A.
5
3
B.
23
15
4
3
3
2
C©u 68 :
Một nguyên hàm của hàm số:
2
( ) sin 1f x x x
là:
A.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
2 2 2
( ) 1 cos 1 sin 1 F x x x x
C.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
2 2 2
( ) 1 cos 1 sin 1 F x x x x
C©u 69 :
Một nguyên hàm của hàm số: y = cos5x.cosx là:
A.
F(x) = cos6x
B.
F(x) = sin6x
1 sin6 sin4
2 6 4




xx
1 1 1
sin6 sin4
2 6 4



xx
C©u 70 :
Cho biết
1
2
0
4 11
ln
56
xa
I dx
x x b


, với
,ab
là các số nguyên dương. Giá trị của
ab
là
A.
11
B.
12
10
13
C©u 71 :
Với
0a
. Tích phân
1
2
2
2
a
x
dx
ax
có giá trị là
11
A.
1
a
B.
2
1
1
a
aa
1
1
a
aa
1
1
a
a
C©u 72 :
Tính diện tích hình phẳng được giới hạn bởi
32
12
, 0, 2, 0
33
y x x y x x
A.
5
6
B.
1
12
2
3
Tất cả đều sai.
C©u 73 :
Tính
3
2
2
1
x
K dx
x
A.
K = ln2
B.
8
ln
3
K
K = 2ln2
18
ln
23
K
C©u 74 :
Tích phân
2
2
0
x x dx
bằng
A.
2
3
B.
0
1
3
2
C©u 75 :
Tính:
23
2
2
3
dx
I
xx
A.
I =
B.
6
I
Đáp án khác
3
I
C©u 76 :
Thể tích của khối tròn xoay tạo nên do quay quanh trục
Ox
hình phẳng giới hạn bởi các
đường
2
(1 ), 0, 0y x y x
và
2x
bằng :
A.
82
3
B.
2
2
5
5
2
C©u 77 :
Một nguyên hàm của hàm số: y = cos5x.cosx là:
A.
cos6x
B.
1 1 1
sin6 sin4
2 6 4



xx
sin6x
1 sin6 sin4
2 6 4




xx
C©u 78 :
Diện tích của hình phăng giới hạn bởi các đồ thị hàm số
2
2;y x y x
, trục hoành trong
miền
0x
là
A.
5
6
B.
6
7
7
8
8
9
12
C©u 79 :
Tích phân
0
2 cos2x xdx

A.
0
B.
1
4
1
4
1
2
C©u 80 :
Giả sử
( ) 2, ( ) 3
bb
ac
f x dx f x dx
với
a b c
thì
()
c
a
f x dx
bằng?
A.
5
B.
1
1
5
13
ĐÁP ÁN
01
{ | ) ~
28
{ ) } ~
55
{ | } )
02
{ | ) ~
29
{ | } )
56
{ | ) ~
03
) | } ~
30
{ | } )
57
{ ) } ~
04
{ ) } ~
31
{ ) } ~
58
{ | ) ~
05
{ | } )
32
) | } ~
59
) | } ~
06
{ ) } ~
33
{ ) } ~
60
{ ) } ~
07
{ | ) ~
34
{ | } )
61
{ | } )
08
) | } ~
35
{ ) } ~
62
) | } ~
09
{ ) } ~
36
{ | ) ~
63
{ | } )
10
{ | ) ~
37
{ ) } ~
64
{ | } )
11
{ ) } ~
38
) | } ~
65
) | } ~
12
{ ) } ~
39
) | } ~
66
{ | ) ~
13
{ | } )
40
{ | ) ~
67
{ | ) ~
14
{ | } )
41
) | } ~
68
{ ) } ~
15
{ ) } ~
42
{ ) } ~
69
{ | } )
16
{ | ) ~
43
) | } ~
70
) | } ~
17
) | } ~
44
{ | } )
71
{ | ) ~
18
{ | } )
45
{ | ) ~
72
) | } ~
19
{ ) } ~
46
{ | } )
73
{ | } )
20
) | } ~
47
{ | ) ~
74
{ | ) ~
21
) | } ~
48
{ | } )
75
{ ) } ~
22
{ | ) ~
49
{ | } )
76
{ | ) ~
23
{ | } )
50
{ | ) ~
77
{ ) } ~
24
{ ) } ~
51
) | } ~
78
) | } ~
25
{ | } )
52
{ | ) ~
79
) | } ~
26
{ | } )
53
) | } ~
80
{ | ) ~
27
{ ) } ~
54
) | } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 06
C©u 1 :
Tìm diện tích hình phẳng giới hạn bởi các đường
2
44
3
xx
y
x

;
1; 2; 0y x x x
2yx
A.
3
ln
2
B.
1
ln3
2
ln3
1
ln3
4
C©u 2 :
Tìm
m
biết
0
2 5 . 6
m
x dx
A.
1, 6mm
B.
1, 6mm
1, 6mm
1, 6mm
C©u 3 :
Tìm nguyên hàm của hàm số f(x) biết
xxf
2
tan)(
A.
C
x
3
tan
3
B.
Đáp án khác
Tanx-1+C
C
x
xxx
cos
cossin
C©u 4 :
Tính diện tích hình phẳng giới hạn bởi
 và hai tiếp tuyến tại 󰇛󰇜 và
󰇛󰇜
A.
B.
C©u 5 :
Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức:
2
A.
( ) ( )
bc
ab
S f x dx f x dx

.
( ) ( )
cb
ba
S f x dx f x dx

.
C.
()
c
a
S f x dx
.
()
c
a
S f x dx
C©u 6 :
Tính tích phân
2
2
0
sin cosx xdx
A.
1
4
B.
1
1
3
1
2
C©u 7 :
Nếu
Fx
là một nguyên hàm của
( ) (1 )
xx
f x e e

và
(0) 3F
thì
()Fx
là ?
A.
x
ex
B.
2
x
ex
x
e x C
1
x
ex
C©u 8 :
Diện tích hình phẳng giới hạn bởi
2
32y x x
và trục Ox là:
A.
6
B.
3
4
729
35
27
4
C©u 9 :
Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi
2
2y x x
và trục Ox quanh
trục Ox là:
A.
16
15
B.
4
3
3
16
15
72
5
C©u 10 :
Tính diện tích hình phẳng giới hạn bởi đường cong
󰇛
󰇜

và
A.

B.



C©u 11 :
Họ nguyên hàm của tanx là:
A.
ln
Cx cos
B.
-ln
Cx cos
C
x
2
tan
2
ln(cosx) + C
C©u 12 :
xx
dx
)1(
2
bằng:
A.
ln
C
x
x
2
1
B.
ln
C
x
x
2
1
ln
Cxx 1
2
ln
Cxx )1(
2
C©u 13 :
Xét các mệnh đề:
3
31
46
31
1. 1.I x dx x dx

3 1 1
4 4 4
0 0 3
1. 1. 1.II x dx x dx x dx
A.
(I) đúng, (II) sai
(I) sai, (II) đúng
C.
Cả (I) và (II) đều đúng
Cả (I) và (II) đều sai
C©u 14 :
Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi
2
yx
và
2yx
quanh trục
Ox là:
A.
72
5
B.
138
5
9
2
72
5
C©u 15 :
Một nguyên hàm của
2
()
1
x
fx
x
là:
A.
1
ln( 1)
2
x
B.
2
2 ln( 1)x
2
1
ln( 1)
2
x
2
ln( 1)x
C©u 16 :
Họ nguyên hàm của hàm số
5
(2 1)yx
là:
A.
6
1
(2 1)
12
xC
B.
6
1
(2 1)
6
xC
6
1
(2 1)
2
xC
.
4
10(2 1)xC
C©u 17 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x
3
, trục hoành và các đường thẳng x= -1,
x=3 là
A.
2
45
(đvdt)
B.
2
27
(đvdt)
3
17
(đvdt)
2
41
(đvdt)
C©u 18 :
Hàm số nào là nguyên hàm của f(x) =
5.
2
xx
:
A.
F(x) =
2
3
2
)5( x
F(x) =
2
3
2
)5(
3
1
x
C.
F(x) =
2
3
2
)5(
2
1
x
2
3
2
)5(3)( xxF
C©u 19 :
Tìm nguyên hàm của hàm số f(x) biết
xx
xf
9
1
)(
A.
Cxx
3
3
9
27
2
Đáp án khác
4
C.
C
xx
)9(3
2
3
3
Cxx
3
3
9
27
2
C©u 20 :
Nguyên hàm của hàm số
2ln
,0
xx
f x x
x

là:
A.
2
ln x
C
x
B.
2ln 1xC
2
2ln lnx x x C
2
ln x
xC
x

C©u 21 :
Họ nguyên hàm của
1
2
x
x
e
e
là:
A.
2
1
x
ln e C
B.
11
21
x
x
e
ln C
e
ln
1
1
x
x
e
C
e
11
21
x
x
e
ln C
e
C©u 22 :
Diện tích giới hạn bởi đồ thị hàm
32
34y x x
và đường thẳng
10xy
A.
10
B.
8
6
4
C©u 23 :
Cho
2
2
2
1
2
.
2
x
M dx
x
. Giá trị của
M
là:
A.
2
B.
5
2
1
11
2
C©u 24 :
Thể tích khối tròn xoay trong không gian Oxyz giới hạn bởi hai mặt phẳng
0;x x
và có
thiết diện cắt bởi mặt phẳng vuông góc với Ox tại điểm
( ;0;0)x
bất kỳ là đường tròn bán kính
sin x
là:
A.
2
.
B.
.
2
.
4
.
C©u 25 :
Thể tích khối tròn xoay tạo thành khi cho đường x
2
+(y-1)
2
=1 quay quanh trục hoành là
A.
2
6
(đvtt)
B.
2
8
(đvtt)
2
4
(đvtt)
2
2
(đvtt)
C©u 26 :
Tính tích phân sau:
 


A.

B.



C©u 27 :
Cho hàm số
󰇛
󰇜

󰇛󰇜
󰉨
󰇛
󰇜

󰇛󰇜


và tính
󰇛
󰇜

A.
  
  
C.
  
  
5
C©u 28 :
Diện tích hình phẳng giới hạn bởi đường thẳng
2
2yx
và đường thẳng
yx
bằng:
A.
9
2
B.
10
3
11
2
17
3
C©u 29 :
Tính tích phân
1
3
2
0
1
x
dx
x
A.
5
16
B.
3
8
3
16
5
8
C©u 30 :
Mệnh đề nào sau đây sai?
A.
Nếu
()Fx
là một nguyên hàm của
()fx
trên
;ab
và C là hằng số thì
( ) ( )f x dx F x C
.
B.
Mọi hàm số liên tục trên
;ab
đều có nguyên hàm trên
;ab
.
C.
()Fx
là một nguyên hàm của
()fx
trên
; ( ) ( ), ; .a b F x f x x a b
D.
( ) ( )f x dx f x
C©u 31 :
2
0
1 cos
dx
I
x
A.
1
4
B.
1
2
1
2
C©u 32 :
Tìm một nguyên hàm
Fx
của hàm số
2
2f x x
biết
7
2
3
F
A.
3
1
2
33
x
F x x
3
19
2
3
F x x x
C.
3
21
3
x
F x x
3
23
3
x
F x x
C©u 33 :
Tính diện tích hình phẳng giới hạn bởi các đường
󰇛
󰇜
󰇛
󰇜
󰇛
󰇜
và
󰇛
󰇜
󰇛
󰇜
󰇛
󰇜
A.
B.
6
C©u 34 :
3
3
0
cosI xdx
bằng:
A.
33
2
B.
33
4
33
8
33
C©u 35 :
Nguyên hàm của hàm số
x
f x xe
là:
A.
xx
xe e C
B.
x
eC
2
2
x
x
eC
xx
xe e C
C©u 36 :
Gọi
()Fx
là một nguyên hàm của hàm
cos.y xx
mà
(0) 1F
. Phát biểu nào sau đây là
đúng:
A.
()Fx
là hàm chẵn
()Fx
là hàm lẻ
C.
()Fx
là hàm tuần hoàn chu kỳ
2
()Fx
không là hàm chẵn cũng không là
hàm lẻ
C©u 37 :
Tính tích phân sau:
dx
x
x
I
1
1
2
22
A.
I=4
B.
I=2
I=0
Đáp án khác
C©u 38 :
Gọi
()Fx
là một nguyên hàm của hàm
2
ln
ln 1.
x
xy
x
mà
1
(1)
3
F
. Giá trị
2
()Fe
bằng:
A.
8
9
B.
1
9
.
8
3
.
1
3
.
C©u 39 :
Cho
4
0
3
( ) 4sin
2
t
f x x dx




.Giải phương trình
( ) 0fx
A.
2,k k Z
B.
,
2
k
kZ
,k k Z
,
2
k k Z

C©u 40 :
Diện tích hình phẳng giới hạn bởi
2
yx
và
23yx
là:
A.
512
15
B.
88
3
32
3
32
3
C©u 41 :
Cho hai hàm số
( ), ( )f x g x
là hàm số liên tục ,có
( ), ( )F x G x
lần lượt là nguyên hàm của
( ), ( )f x g x
.Xét các mệnh đề sau :
(I):
( ) ( )F x G x
là một nguyên hàm của
( ) ( )f x g x
7
(II):
.Fkx
là một nguyên hàm của
kf x
kR
(III):
( ). ( )F x G x
là một nguyên hàm của
( ). ( )f x g x
Mệnh đề nào là mệnh đề đúng ?
A.
I
B.
I và II
I,II,III
II
C©u 42 :
1
2
x
dx
bằng
A.
1
2
ln 2
x
B.
1
2
x
C
1
2
ln 2
x
C
1
2 .ln2
x
C
C©u 43 :
Biết rằng tích phân
1
0
(2 1) .
x
x e dx a b e
, tích
ab
bằng:
A.
1
B.
-1
-15
5
C©u 44 :
Tính tích phân sau:

A.
Cả 3 đáp án trên
B.



C©u 45 :
Hàm số nào là nguyên hàm của f(x) =
xsin1
1
:
A.
F(x) = 1 + cot
42
x
F(x) =
2
tan1
2
x
C.
F(x) = ln(1 + sinx)
F(x) = 2tan
2
x
C©u 46 :
Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các
đường
3
3
x
y
và y=x
2
là
A.
35
436
(đvtt)
B.
2
9
(đvtt)
35
468
(đvtt)
35
486
(đvtt)
C©u 47 :
Tính diện tích hình phẳng giới hạn bởi
󰇛
󰇜
 và
A.
9
B.
3
7
5
C©u 48 :
Một nguyên hàm của
1
( ) (2 1).
x
f x x e
là:
A.
1
( ) .
x
F x x e
B.
1
()
x
F x e
1
2
( ) .
x
F x x e
1
2
( ) 1 .
x
F x x e
8
C©u 49 :
Tìm diện tích hình phẳng giới hạn bởi các đường
2
yx
và
2yx
A.
9
B.
9
8
9
2
9
4
C©u 50 :
Hàm số
CxexF
x
tan)(
là nguyên hàm của hàm số f(x) nào
A.
x
exf
x
2
sin
1
)(
Đáp án khác
C.
x
exf
x
2
sin
1
)(
x
e
exf
x
x
2
cos
1)(
C©u 51 :
2
2
0
4
dx
I
x
bằng:
A.
B.
3
2
6
C©u 52 :
Nếu
2
( ) sin
x
f x dx e x C
thì
()fx
là hàm nào ?
A.
2
cos
x
ex
B.
sin2
x
ex
cos2
x
ex
2sin
x
ex
C©u 53 :
1
2
0
1
dx
I
x
bằng:
A.
6
B.
3
4
2
C©u 54 :
Họ nguyên hàm của
xsin
1
là:
A.
ln
cot
2
x
C
B.
ln
C
x
2
tan
-ln
C
x
2
tan
ln
Cx sin
C©u 55 :
Họ nguyên hàm của f(x) = sin
x
3
A.
C
x
x
3
cos
cos
3
B.
C
x
x
3
cos
cos
3
c
x
x
cos
1
cos
C
x
4
sin
4
C©u 56 :
Cho
2
0
5f x dx
. Khi đó
2
0
2sin .f x x dx


bằng:
9
A.
5
B.
5
2
7
3
C©u 57 :
Cho hình phẳng (H) giới hạn bởi các đường
4 2 2
2 , 0,y x mx m x
1x
. TÌm m để diện
tích hình phẳng đó bằng
1
5
A.
1, 2mm
B.
0; 2/ 3mm
2/3, 1mm
0, 2/3mm
C©u 58 :
xdxx
3
sin.cos
bằng:
A.
C
x
4
cos
4
B.
C
x
4
sin
4
Cx
4
sin
Cx
4
cos
C©u 59 :
Tính tích phân sau:

A.
1
B.
11
6
3
C©u 60 :
Cho hàm số
2
2sin
2
x
fx
Khi đó
()f x dx
bằng ?
A.
sinx x C
B.
sinx x C
cosx x C
cosx x C
C©u 61 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
4yx x
và trục hoành bằng:
A.
4
B.
0
2
8
C©u 62 :
Hàm nào không phải nguyên hàm của hàm số
2
2
( 1)
y
x
:
A.
1
1
x
x

B.
2
1
x
x
2
1x
1
1
x
x
C©u 63 :
Gọi S là diện tích giới hạn bởi đồ thị hàm số
2
2 5 3
2
xx
y
x

,tiệm cận xiên của đồ thi và các
đường thẳng
1, 1x x m m
.Tìm giá trị
m
để
6S
A.
6
4e
B.
6
2e
6
1e
6
3e
C©u 64 :
Tìm nguyên hàm của hàm số f(x) biết
x
x
xf
ln1
)(
A.
Đáp án khác
B.
Cxx ln
Cxx
2
ln
2
1
ln
Cxx
2
ln
4
1
ln
C©u 65 :
Để
1
4 3 1 0
k
k x dx k
thì giá trị của
k
là bao nhiêu ?
10
A.
1
B.
3
2
4
C©u 66 :
Cho hình phẳng trong hình (phần tô đậm ) quay quanh trục hoành .Thể tích khối tròn xoay
tạo thành được tính theo công thức nào ?
A.
2
( ) ( )
b
a
V f x g x dx
22
( ) g ( )
b
a
V f x x dx



C.
2
( ) ( )
b
a
V f x g x dx

( ) ( )
b
a
V f x g x dx

C©u 67 :
Họ nguyên hàm của
2
( ) .cosf x x x
là:
A.
2
cos xC
B.
2
sin xC
2
1
sin
2
xC
2
2sin xC
C©u 68 :
Đặt
0
cos .
m
f m x dx
.
Nghiệm của phương trình
0fm
là
A.
2,m k k

B.
,
2
m k k
,m k k

2,
2
m k k
C©u 69 :
Nguyên hàm của hàm số
2sin cosf x x x
là:
A.
2cos sinxxC
2cos sinxxC
C.
2cos sinxxC
2cos sinxxC
11
C©u 70 :
Họ nguyên hàm của
2
sin x
là:
A.
1
2cos2
2
x x C
1 sin 2
22
x
x
C.
sin 2
24
xx
C
1
2cos2
2
x x C
C©u 71 :
Họ nguyên hàm của f(x) =
)1(
1
xx
là:
A.
F(x) = ln
C
x
x
1
F(x) = ln
1
x
C
x
C.
F(x) =
1
ln
21
x
C
x
F(x) = ln
Cxx )1(
C©u 72 :
Tính tích phân sau:
󰇻

󰇡
󰇢
󰇛
󰇜
󰇻




A.

B.



C©u 73 :
Một nguyên hàm của f(x) = xe
2
x
là:
A.
2
x
e
B.
2
2
1
x
e
2
x
e
2
2
1
x
e
C©u 74 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x
2
và đường thẳng y= - x+2 là
A.
2
13
(đvdt)
B.
11 (đvdt)
7 (đvdt)
Một kết quả khác
C©u 75 :
Tính diện tích hình phẳng được giới hạn bởi đường cong
󰇛
󰇜
󰇛
󰇜


và hai trục tọa độ.
A.
 
B.
 
 
 
C©u 76 :
Tìm nguyên hàm của hàm số f(x) biết
34
32
)(
2
xx
x
xf
A.
C
xx
xx
2
2
2
34
3
Cxxx 34ln)32(
2
C.
C
xx
xx
34
3
2
2
Cxx 3ln31ln
2
1
12
C©u 77 :
Cho
1
ln
e
k
I dx
x
.Xác định
k
để
2Ie
A.
2ke
B.
ke
1ke
1ke
C©u 78 :
Tích phân
3
1
l
21
n
1
2
x
dx a b
x

. Tổng của
ab
bằng:
A.
1.
B.
7
-3
2
C©u 79 :
Tính
0
1
21
1
x
dx
x
bằng:
A.
ln2 2
B.
ln2 2
ln2 2
ln2 2
C©u 80 :
Tìm công thức sai:
A.
Cedxe
xx
10
ln
aC
a
a
dxa
x
x
C.
Cxxdx
sincos
sin cosxdx x C
13
ĐÁP ÁN
01
{ | ) ~
28
) | } ~
55
{ ) } ~
02
{ | ) ~
29
{ | ) ~
56
{ | ) ~
03
{ | } )
30
{ | ) ~
57
{ | } )
04
) | } ~
31
{ | ) ~
58
{ ) } ~
05
) | } ~
32
{ | ) ~
59
) | } ~
06
{ | ) ~
33
) | } ~
60
{ ) } ~
07
{ ) } ~
34
{ | ) ~
61
) | } ~
08
{ | } )
35
{ | } )
62
) | } ~
09
{ | } )
36
) | } ~
63
{ ) } ~
10
) | } ~
37
{ | } )
64
{ | } )
11
{ ) } ~
38
) | } ~
65
{ ) } ~
12
{ ) } ~
39
{ ) } ~
66
{ ) } ~
13
{ | ) ~
40
{ | } )
67
{ | ) ~
14
{ | } )
41
{ ) } ~
68
{ | ) ~
15
{ | ) ~
42
{ | ) ~
69
{ | } )
16
) | } ~
43
) | } ~
70
{ | ) ~
17
{ | } )
44
) | } ~
71
{ ) } ~
18
{ ) } ~
45
{ ) } ~
72
) | } ~
19
{ | } )
46
{ | } )
73
{ ) } ~
20
{ | } )
47
) | } ~
74
{ | } )
21
{ ) } ~
48
{ | ) ~
75
) | } ~
22
{ ) } ~
49
{ | ) ~
76
{ | } )
23
{ | ) ~
50
{ | } )
77
{ ) } ~
24
) | } ~
51
{ | ) ~
78
) | } ~
25
{ | } )
52
{ ) } ~
79
{ | } )
26
) | } ~
53
{ | ) ~
80
{ | } )
27
) | } ~
54
{ ) } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 07
C©u 1 :
Tìm d để diện tích hình phẳng giới hạn bởi đường cong
2
y
x
, Ox, x=1, x=d (d>1) bằng 2:
A.
2
e
B.
e
2e
e+1
C©u 2 :
Tính các hằng số A và B để hàm số
( ) sinf x A x B
thỏa mãn đồng thời các điều
kiện
'(1) 2f
và
2
0
( ) 4f x dx
A.
2
,2AB
B.

2
,2AB
2, 2AB
2, 2AB
C©u 3 :
Cho hình phẳng giới hạn bởi các đường
2
; 0; 0; 1
x
y xe y x x
. Thể tích của khối tròn xoay
sinh bởi hình phẳng trên khi quay quanh trục hoành là
A.
2
2e
B.
2
2e
2e
2e
C©u 4 :
Diện tích hình phẳng giới hạn bởi đường cong
32
C : y x 3x 2
, hai trục tọa
độ và đường thẳng
x2
là:
y = 2/x
O
y
x
1
d
2
A.
3
2
(đvdt)
B.
7
2
(đvdt)
4 (đvdt)
5
2
(đvdt)
C©u 5 :
Nguyên hàm
Fx
của hàm số
23
24f x x x
thỏa mãn điều kiện
00F
là
A.
4
B.
34
24xx
4
3
2
4
34
x
xx
34
2x x x
C©u 6 :
Gọi F(x) là nguyên hàm của hàm số
2
1
()
32

fx
xx
thỏa mãn F(3/2) =0. Khi đó F(3)
bằng:
A.
2ln2
B.
ln2
-2ln2
–ln2
C©u 7 :
Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn
lại?
A.
sin2x
và
2
cos x
2
tan x
và
22
1
cos x
C.
x
e
và
x
e
sin2 x
và
2
sin x
C©u 8 :
Nguyên hàm của hàm số
3
f x x
trên là
A.
4
x
xC
4
B.
2
3x C
2
3x x C
4
x
C
4
C©u 9 :
Tìm họ nguyên hàm
2
()
x
F x x e dx
?
A.
2
( ) ( 2 2)
x
F x x x e C
2
( ) (2 2)
x
F x x x e C
C.
2
( ) ( 2 2)
x
F x x x e C
2
( ) ( 2 2)
x
F x x x e C
C©u 10 :
Để tìm nguyên hàm của
45
f x sin x cos x
thì nên:
A.
Dùng phương pháp đổi biến số, đặt
t cosx
B.
Dùng phương pháp lấy nguyên hàm từng phần, đặt
44
u cos x
dv sin x cos xdx
C.
Dùng phương pháp lấy nguyên hàm từng phần, đặt
4
5
u sin x
dv cos xdx
D.
Dùng phương pháp đổi biến số, đặt
t sinx
3
C©u 11 :
Cho hình phẳng giới hạn bởi các đường
y 1 x, Ox, x=0, x=4
quay xung quanh trục
Ox. Thể tích của khối tròn xoay tạo thành bằng:
A.
2
28
3
B.
68
.
3
28
3
2
68
.
3
C©u 12 :
Giá trị của
2
2
2
1x dx
là
A.
2
B.
3
4
5
C©u 13 :
Họ nguyên hàm của hàm số
cos3 tanf x x x
là
A.
3
4
cos 3cos
3
x x C
3
1
sin 3sin
3
x x C
C.
3
4
cos 3cos
3
x x C
3
1
cos 3cos
3
x x C
C©u 14 :
Tính
2
0
cosI x xdx
A.
I =
2
B.
I =
2
+ 1
I =
3
I =
1
32
C©u 15 :
Tính
5
3
x1
dx
x
ta được kết quả nào sau đây?
A.
Một kết quả
khác
B.
32
xx
C
32
6
4
x
x
6
C
x
4
3
2
x1
C
3
2x
C©u 16 :
Thể tích vật thể tròn xoay sinh ra bởi hình phẳng giới hạn parabol
2
:1P y x
và trục
hoành khi quay xung quanh trục Ox bằng bao nhiêu đơn vị thể tích?
A.
7
2
B.
5
2
8
3
3
C©u 17 :
Gọi F
1
(x) là nguyên hàm của hàm số
2
1
( ) sinf x x
thỏa mãn F
1
(0) =0 và F
2
(x) là nguyên hàm
của hàm số
2
2
( ) cosf x x
thỏa mãn F
2
(0)=0.
Khi đó phương trình F
1
(x) = F
2
(x) có nghiệm là:
A.
2
xk
B.
xk
2
xk
2
k
x
4
C©u 18 :
Diện tích hình phẳng giới hạn bởi
2
20 y y x
, x + y = 0 là:
A.
Đáp số khác
B.
11
2
5
9
2
C©u 19 :
Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng (H) giới hạn bởi
các đường cong
2
yx
và
yx
quanh trục Ox.
A.
3
10
V
B.
13
15
V
13
5
V
3
5
V
C©u 20 :
Cho tích phân

3
0
24
x
I dx
, trong các kết quả sau:
(I).

32
20
2 4 2 4
xx
I dx dx
(II).

32
20
2 4 2 4
xx
I dx dx
(III).

3
2
2 2 4
x
I dx
kết quả nào đúng?
A.
Chỉ II.
B.
Chỉ III.
Cả I, II, III.
Chỉ I.
C©u 21 :
Tính tích phân


A.

B.



C©u 22 :
Tính
󰇛

󰇜


.
Lời giải sau sai từ bước nào:
Bước 1: Đặt   
Bước 2: Ta có   
Bước 3:
󰇛

󰇜


󰇛

󰇜



Bước 4: Vậy 
5
A.
Bước 4
B.
Bước 3
Bước 2
Bước 1
C©u 23 :
Nguyên hàm
Fx
của hàm số
4
sin 2f x x
thỏa mãn điều kiện
3
0
8
F
là
A.
3 1 1 3
sin2 sin4
8 8 64 8
x x x
3 1 1
sin4 sin8
8 8 64
x x x
C.
3 1 1
1 sin4 sin8
8 8 64
x x x
3
sin4 sin6x
8
xx
C©u 24 :
Họ nguyên hàm của hàm số
3
2ln 3x
fx
x
là
A.
2
2ln 3
2
x
C
B.
2ln 3
8
x
C
4
2ln 3
8
x
C
4
2ln 3
2
x
C
C©u 25 :
Hình phẳng D giới hạn bởi y = 2x
2
và y = 2x + 4 khi quay D xung quanh trục hoành thì thể
tích khối tròn xoay tạo thành là:
A.
V =
288
5
(đvtt)
V =
2
(đvtt)
C.
V = 72
(đvtt)
V =
4
5
(đvtt)
C©u 26 :
Các đường cong y = sinx, y=cosx với 0 ≤ x ≤
2
và trục Ox tạo thành một hình phẳng. Diện
tích của hình phẳng là:
A.
2 - 2
B.
2
22
Đáp số khác.
C©u 27 :
Một nguyên hàm của hàm số
2
4
()
cos
fx
x
là:
A.
2
4
sin
x
x
B.
4tan x
4 tanx
3
4
4 tan
3
xx
C©u 28 :
Tính tích phân


ta được kết quả:
A.
B.
C©u 29 :
Một nguyên hàm của
3
1
()
1
x
x
e
fx
e
là:
A.
2
1
()
2
xx
F x e e x
2
1
()
2
xx
F x e e
6
C.
2
1
()
2
xx
F x e e
2
1
( ) 1
2
xx
F x e e
C©u 30 :
Gọi F(x) là nguyên hàm của hàm số
2
()
8
x
fx
x
thỏa mãn F(2) =0. Khi đó phương trình
F(x) = x có nghiệm là:
A.
x = 0
B.
x = 1
x = -1
13x
C©u 31 :
Giả sử
5
1
ln
21
dx
c
x
. Giá trị của
c
là
A.
9
B.
8
3
81
C©u 32 :
Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi đường thẳng
4yx
và đồ
thị hàm số
3
yx
là
A.
5
B.
3
4
7
2
C©u 33 :
Giá trị của
2
2
0
2
x
e dx
là
A.
4
4e
B.
4
e
4
1e
4
31e
C©u 34 :
Biểu thức nào sau đây bằng với
2
sin 3xdx
?
A.
11
(x sin6x) C
26

11
(x sin6x) C
26

C.
11
(x sin3x) C
23

11
(x sin3x) C
23

C©u 35 :
Cho hình phẳng giới hạn bởi các đường
y cos4x, Ox, x=0, x=
8
quay xung quanh trục
Ox. Thể tích của khối tròn xoay tạo thành bằng:
A.
2
2
B.
2
16
4
3
C©u 36 :
Tính
1
2
0
1I x dx
A.
I =
4
B.
I =
1
2
I = 2
I =
3
C©u 37 :
Tính tích phân

7
A.
ln2
B.
6
1
ln8
C©u 38 :
Cho đồ thị hàm số y=f(x) trên đoạn [0;6] như hình vẽ.
Biểu thức nào dưới đây có giá trị lớn nhất:
A.
1
0
f(x)dx
B.
2
0
f(x)dx
3
0
f(x)dx
6
0
f(x)dx
C©u 39 :
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số

là:
A.
2
B.
5/3
7/3
3
C©u 40 :
Biết rằng


33
12
( ) 5; ( ) 3f x dx f x dx
. Tính
2
1
()f x dx
?
A.
2
B.
2
1
5
C©u 41 :
Họ nguyên hàm của hàm số
1
18
x
fx
là
A.
18
ln
ln12 1 8
x
x
F x C
18
ln
12 1 8
x
x
F x C
C.
18
ln
ln8 1 8
x
x
F x C
8
ln
18
x
x
F x C
C©u 42 :
Diện tích hình phẳng giới hạn bởi các đường
2
y 4x x
và
y 2x
là:
O
2
x
4
6
y=f(x)
y
8
A.
4
2
0
(2x x )dx
B.
2
2
0
(x 2x)dx
2
2
0
(2x x )dx
4
2
0
(x 2x)dx
C©u 43 :
Một nguyên hàm F(x) của
2
( ) 3 1f x x
thỏa F(1) = 0 là:
A.
3
1x
B.
3
2xx
3
4x
3
22x
C©u 44 :
Diện tích hình phẳng giới hạn bởi
2
4yx
và y=3|x| là:
A.
17
6
B.
3
2
5
2
13
3
C©u 45 :
Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bới các đường
yx
,
y x 2
,
y0
quay quanh trục Oy, có giá trị là kết quả nào sau đây ?
A.
1
3
(đvtt)
B.
3
2
(đvtt)
11
6
(đvtt)
32
15
(đvtt)
C©u 46 :
Biểu thức nào sau đây bằng với
tanxdx
?
A.
1
ln( tanx) C
sinx

B.
ln(cosx) C
2
tan x
C
2
2
1
C
cos x
C©u 47 :
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
  là:
A.
B.
C©u 48 :
Tính diện tích hình phẳng giới hạn bởi các đường
32
2y x x x
và
4yx
.
A.
71
6
B.
2
3
24
53
7
C©u 49 :
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) = cos3x và
󰇡
󰇢
=

thì
4
(2;4)
O
y
x
9
A.
󰇛
󰇜


󰇛
󰇜

C.
󰇛
󰇜

󰇛
󰇜


C©u 50 :
Vận tốc của một vật chuyển động là
2
v t 3t 5 m / s
. Quãng đường vật đó đi
được từ giây thứ 4 đến giây thứ 10 là :
A.
36m
B.
252m
1200m
1014m
C©u 51 :
Nếu
4
3
1
ln
12
dx m
xx

thì m bằng
A.
12
B.
4
3
1
3
4
C©u 52 :
Gọi (H) là đồ thị của hàm số
1
()
x
fx
x
. Diện tích giới hạn bởi (H), trục hoành và hai
đường thẳng có phương trình x=1, x=2 bằng bao nhiêu đơn vị diện tích?
A.
1e
B.
2e
2e
1e
C©u 53 :
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
3 3 1y x x x
và tiếp
tuyến của đồ thị tại giao điểm của đồ thị và trục tung.
A.
27
4
S
B.
5
3
S
23
4
S
4
7
S
C©u 54 :
Diện tích hình phẳng giới hạn bởi đồ thị có phương trình
  là:
A.
8
B.
11/2
9/2
7/2
C©u 55 :
Một nguyên hàm của
( ) cos3 cos2f x x x
bằng
A.
11
sin sin5
22
xx
11
sin sin5
2 10
xx
C.
11
cos cos5
2 10
xc
1
sin3 sin2
6
xx
C©u 56 :
Một học sinh tính tích phân
1
0
1
x
dx
I
e
tuần tự như sau:
10
(I). Ta viết lại
1
0
1
x
xx
e dx
I
ee
(II). Đặt
x
ue
thì

1 1 1
ln ln 1
1
(1 ) 1
e e e
e
du du du
I u u
u u u u
(III).
ln ln( 1) ln1 ln 1 1 ln
1
e
I e e
e
Lý luận trên, nếu sai thì sai từ giai đoạn nào?
A.
III
B.
I
II
Lý luận đúng.
C©u 57 :
Tính
1
4
1
21
x
x
I dx
A.
I =
1
5
B.
I =
5
7
I =
7
5
I = 5
C©u 58 :
Diện tích hình phẳng giới hạn bởi các đường
yx
và
1
yx
2
là:
A.
2
B.
4
3
16
3
5
12
C©u 59 :
Nguyên hàm của hàm số
2
( ) (1 3 )

xx
f x e e
bằng:
A.
( ) 3
xx
F x e e C
3
( ) 3
xx
F x e e C
C.
2
( ) 3
xx
F x e e C
( ) 3
xx
F x e e C
C©u 60 :
Diện tích hình phẳng giới hạn bởi hai parabol (P):
2
yx
và
2
:2q y x x
là bao nhiêu
đơn vị diện tích?
A.
1
B.
1
3
1
2
3
C©u 61 :
Hàm số
fx
có nguyên hàm trên K nếu
A.
fx
xác định trên K
fx
có giá trị lớn nhất trên K
C.
fx
có giá trị nhỏ nhất trên K
fx
liên tục trên K
11
C©u 62 :
Tích phân
1
x
dx
e
bằng
A.
ln
22
e
e
B.
2
ln
1
e
e
ln
21
e
e
ln 1 ln2e 
C©u 63 :
Biểu thức nào sau đây bằng với
2
x sinxdx
?
A.
2
2xcosx x cosxdx
2
x cosx 2xcosxdx
C.
2
x cosx 2xcosxdx
2
2xcosx x cosxdx
C©u 64 :
Cho hàm số F(x) là một nguyên hàm của hàm số
󰇛
󰇜

và
󰇛
󰇜
thì
A.
󰇛
󰇜


󰇛
󰇜


C.
󰇛
󰇜


󰇛
󰇜


C©u 65 :
Tìm họ nguyên hàm của hàm số
3
4
()f x x x x
?
A.
4
35
3
24
2 3 4
()
3 4 5
F x x x x C
24
5
33
4
2 3 4
()
3 4 5
F x x x x C
C.
24
5
33
4
2 4 5
()
3 3 4
F x x x x C
1
35
3
24
2 1 4
()
3 3 5
F x x x x C
C©u 66 :
Giá trị của tích phân


 là
A.

B.

Không tồn tại

C©u 67 :
Cho (H) là hình phẳng giới hạn bởi đường cong (L):

3
ln 1y x x
, trục Ox và
đường thẳng
1x
. Tính thể tích của vật thể tròn xoay tạo ra khi cho (H) quay
quanh trục Ox.
A.
ln 4 1
3
V

B.
ln 4 2
3
V

ln3 2
3
V

ln3
3
V
C©u 68 :
Diện tích hình phẳng giới hạn bởi hai parabol
22
y x 2x;y x 4x
là giá trị nào
sau đây ?
12
A.
12 (đvdt)
B.
27 (đvdt)
4 (đvdt)
9 (đvdt)
C©u 69 :
Tính
1
2
0
2
dx
I
xx

A.
I =
2
ln2
3
I 
B.
I = - 3ln2
1
ln3
2
I
I = 2ln3
C©u 70 :
Bằng cách đổi biến số
2sinxt
thì tích phân
1
0
2
4
dx
x
là:
A.
1
0
dt
B.
6
0
dt
6
0
tdt
3
0
dt
t
C©u 71 :
Diện tích hình phẳng giới hạn bởi hai đường y = x, y = x + sin
2
x và hai đường thẳng x = 0,
x =
là:
A.
S =
2
(đvdt)
B.
S =
1
2
(đvdt)
S =
1
2
(đvdt)
S =
(đvdt)
C©u 72 :
Với giá trị nào của m > 0 thì diện tích hình phẳng giới hạn bởi hai đường y = x
2
và y = mx
bằng
4
3
đơn vị diện tích ?
A.
m = 2
B.
m = 1
m = 3
m = 4
C©u 73 :
Cho hàm số
32
( ) 2 1f x x x x
. Gọi F(x) là một nguyên hàm của f(x), biết rằng F(1) = 4
thì
A.
43
2
49
()
4 3 12
xx
F x x x
43
2
( ) 1
43
xx
F x x x
C.
43
2
( ) 2
43
xx
F x x x
43
2
()
43
xx
F x x x
C©u 74 :
Tích phân
4
0
cos2xdx
bằng:
A.
1
B.
1
2
2
0
C©u 75 :
Tích phân
2
0
a
x
dx
ax
bằng
A.
1
2
a




B.
2
4
a




1
2
a




2
4
a




13
C©u 76 :
Với t thuộc (-1;1) ta có
2
0
1
ln3
12

t
dx
x
. Khi đó giá trị t là:
A.
1/3
B.
1
3
0
1/2
C©u 77 :
Tìm a sao cho
2
23
1
[a +(4 - a)x + 4x ]dx = 12I
A.
Đáp án khác
B.
a = - 3
a = 5
a = 3
C©u 78 :
Tính
3
cos xdx
ta được kết quả là :
A.
4
cos x
C
x
1 3 sin x
sin3x C
12 4
C.
4
cos x.sin x
C
4
1 sin 3x
3sin x C
43
C©u 79 :
Cho
ln
0
ln2
2

m
x
x
e dx
A
e
. Khi đó giá trị của m là:
A.
m=0; m=4
B.
Kết quả khác
m=2
m=4
C©u 80 :
Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
69 y x x x
và trục Ox. Số
nguyên lớn nhất không vượt quá S là:
A.
10
B.
7
27
6
14
ĐÁP ÁN
01
{ ) } ~
28
{ | ) ~
55
{ ) } ~
02
) | } ~
29
) | } ~
56
) | } ~
03
{ | ) ~
30
{ | } )
57
) | } ~
04
{ | } )
31
{ | ) ~
58
{ ) } ~
05
{ | ) ~
32
{ | ) ~
59
{ | } )
06
{ | } )
33
{ | ) ~
60
{ ) } ~
07
{ | } )
34
{ ) } ~
61
{ | } )
08
{ | } )
35
{ ) } ~
62
{ ) } ~
09
) | } ~
36
) | } ~
63
{ ) } ~
10
{ | } )
37
{ | ) ~
64
{ | ) ~
11
{ ) } ~
38
{ ) } ~
65
) | } ~
12
{ | ) ~
39
{ | ) ~
66
{ | ) ~
13
{ | ) ~
40
) | } ~
67
) | } ~
14
) | } ~
41
{ | ) ~
68
{ | } )
15
{ | } )
42
{ ) } ~
69
) | } ~
16
{ ) } ~
43
{ ) } ~
70
{ ) } ~
17
{ | } )
44
{ | } )
71
) | } ~
18
{ | } )
45
{ | } )
72
) | } ~
19
) | } ~
46
{ ) } ~
73
) | } ~
20
) | } ~
47
{ | ) ~
74
{ ) } ~
21
{ | ) ~
48
) | } ~
75
{ ) } ~
22
{ | ) ~
49
{ | ) ~
76
{ | } )
23
{ | ) ~
50
{ | } )
77
) | } ~
24
{ | ) ~
51
{ ) } ~
78
{ | } )
25
) | } ~
52
{ ) } ~
79
{ | } )
26
{ | } )
53
) | } ~
80
{ | } )
27
{ ) } ~
54
{ | ) ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 08
C©u 1 :
Tnh A =
23
sin cosx xdx
, ta c
A.
35
sin sin
35
xx
AC
35
sin sinA x x C
C.
35
sin sin
35
xx
AC
Đp n khc
C©u 2 :
Nguyên hm ca hm s
3
(x) tan
fx
l:
A.
Đp n khc
B.
2
tan 1
x
4
tan
4
x
C
2
1
tan ln cos
2
x x C

C©u 3 :
Kt qu ca tch phân:
1
0
76
32
x
I dx
x
A.
15
ln
22
B.
5
ln
2
2+
5
ln
2
5
3 2 ln
2
C©u 4 :
H nguyên hm F(x) ca hm s
2
1
()
( 2)
fx
x
l:
A.
1
()
2
F x C
x

Đp s khc
C.
1
()
2
F x C
x

3
1
()
( 2)
F x C
x

C©u 5 :
H nguyên hm F(x) ca hm s
4
( ) sin cosf x x x
A.
5
1
( ) sin
5
F x x C
5
( ) cosF x x C
2
C.
5
( ) sinF x x C
5
1
( ) sin
5
F x x C
C©u 6 :
H nguyên hm F(x) ca hm s
2
( ) sinf x x
l
A.
1
( ) (2 sin2 )
4
F x x x C
C (A), (B) v (C) đu đng
C.
1
( ) ( sinx.cosx)
2
F x x C
1 sin2
( ) ( )
22
x
F x x C
C©u 7 :
Tnh din tch S ca hnh phng đưc gii hn bi cc đưng
2
4y x x
v y = 0, ta c
A.
3
(đvdt)
23
S
B.
32
(đvdt)
3
S
23
(đvdt)
3
S
1(đvdt)S
C©u 8 :
Kt qu ca tch phân
1
1
( ) ln
e
I x xdx
x

l:
A.
2
4
e
B.
2
1
24
e
2
1
44
e
2
3
44
e
C©u 9 :
Cho
2
3
1
2 (2 ln )dx
I x x

. Tm I?
A.
1 2ln2
B.
13
2 ln 2
2
13
ln 2
4
1
ln 2
2
C©u 10 :
Bit
3
2
1
2 ln 1
ln 2
2
a
xx
I dx
x
. Gi tr ca a l:
A.
4
B.
ln2
2
3
C©u 11 :
Tnh din tch S ca hnh phng đưc gii hn bi cc đưng
2
yx
v
2
2yx
, ta c
A.
3
(đvdt)
8
S
B.
8
(đvdt)
3
S
8(đvdt)S
Đp s khc
C©u 12 :
H nguyên hm F(x) ca hm s
2
1
()
43
fx
xx

l
A.
13
( ) ln | |
21
x
F x C
x

11
( ) ln | |
23
x
F x C
x

C.
2
( ) ln| 4 3|F x x x C
3
( ) ln | |
1
x
F x C
x

C©u 13 :
Tm nguyên hm
( cos )
I x x xdx

3
A.
3
sin cos
3
x
x x x c
Đp n khc
C.
3
sin cos
3
x
x x x c
3
sin cos
3
x
x x x c
C©u 14 :
Kt qu ca tch phân
4
0
1
1 2 2 1
I dx
x

l:
A.
15
1 ln
23
B.
1
1 ln 2
4
17
1 ln
33
17
1 ln
43
C©u 15 :
Tch phân
2
2
0
3
( 1)
4
a
x
e
x e dx

. Gi tr ca a l:
A.
2
B.
3
1
4
C©u 16 :
Tnh
2
1
0
(2 )
xx
I e e dx

?
A.
2
e
B.
1
e
1
e
C©u 17 :
H nguyên hm F(x) ca hm s
2
1
()
1
xx
fx
x

l
A.
2
( ) ln | 1|
2
x
F x x C
2
( ) ln| 1|F x x x C
C.
1
()
1
F x x C
x
Đp s khc
C©u 18 :
H nguyên hm F(x) ca hm s
2
2
()
43
x
fx
xx

l
A.
2
1
( ) ln | 4 3|
2
F x x x C
2
1
( ) ln| 4 3|
2
F x x x C
C.
2
( ) ln| 4 3|F x x x C
2
( ) 2ln | 4 3|F x x x C
C©u 19 :
Cho
2
1
0
cos 3sin 1
I x x dx

2
2
2
0
sin 2
(sinx 2)
x
I dx
Pht biu no sau đây sai?
A.
1
14
9
I
B.
12
II
2
33
2 ln
22
I

Đp n khc
C©u 20 :
Tnh th tch V ca khi trn xoay to thnh khi ta cho min phng D gii hn bi cc
4
đưng
x
ye
, y = 0, x = 0, x = 1 quay quanh trc ox . Ta c
A.
(đvtt)V
B.
2
( 1)
(đvtt)
2
e
V
2
(đvtt)
2
e
V
2
(đvtt)V
5
ĐÁP ÁN
01
) | } ~
02
{ | } )
03
{ | ) ~
04
) | } ~
05
) | } ~
06
{ ) } ~
07
{ ) } ~
08
{ | } )
09
{ | ) ~
10
{ | ) ~
11
{ ) } ~
12
) | } ~
13
{ | } )
14
{ | } )
15
{ | ) ~
16
{ | } )
17
) | } ~
18
{ ) } ~
19
{ | ) ~
20
{ ) } ~
| 1/96
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 01 C©u 1 : ( x 2  x)
Hàm số nào dưới đây không là nguyên hàm của hàm số f (x)  2 (x  1) 2 x x  1 2 x x  1 2 x x  1 2 x A. B. C. D. x  1 x  1 x  1 x  1
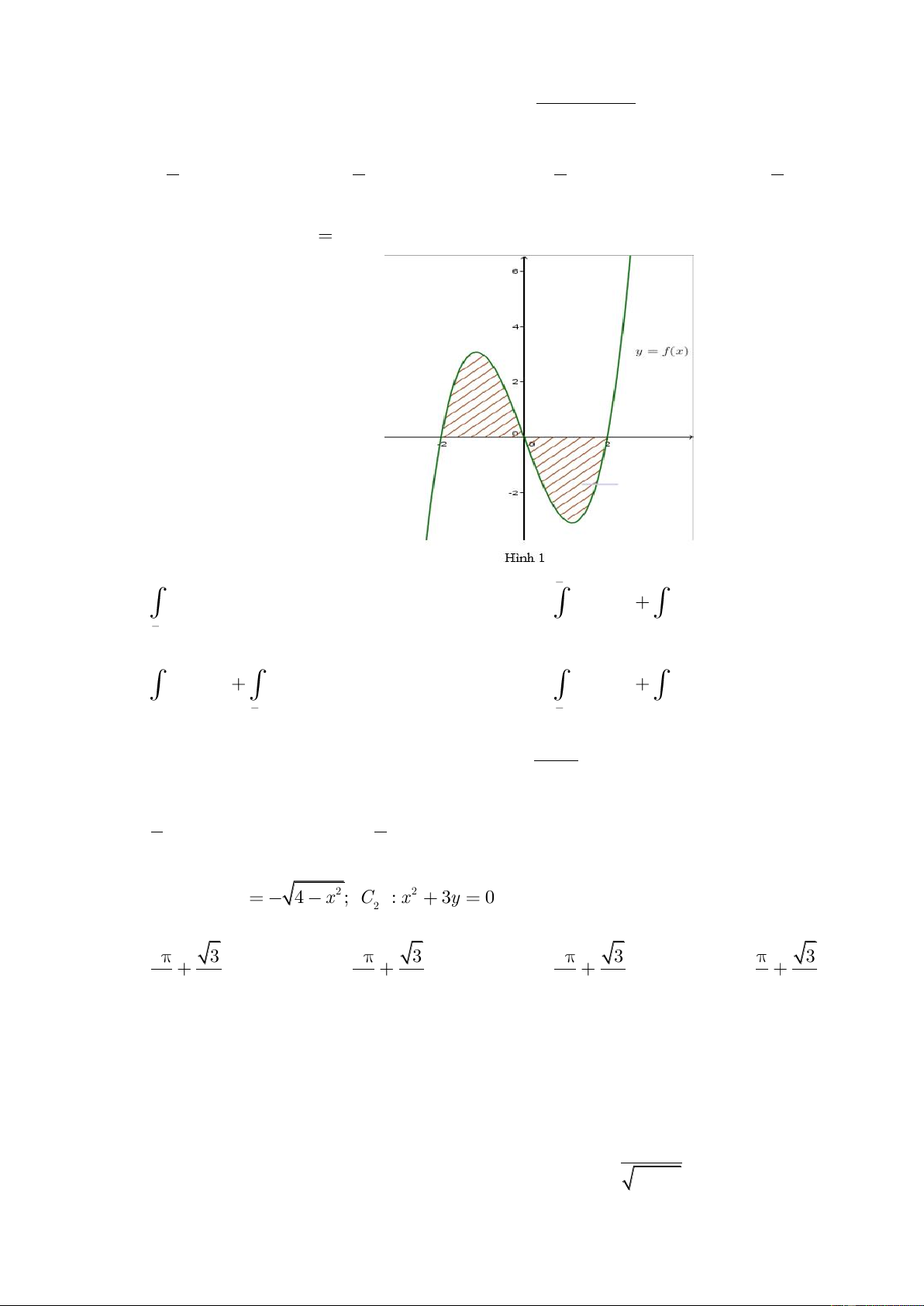
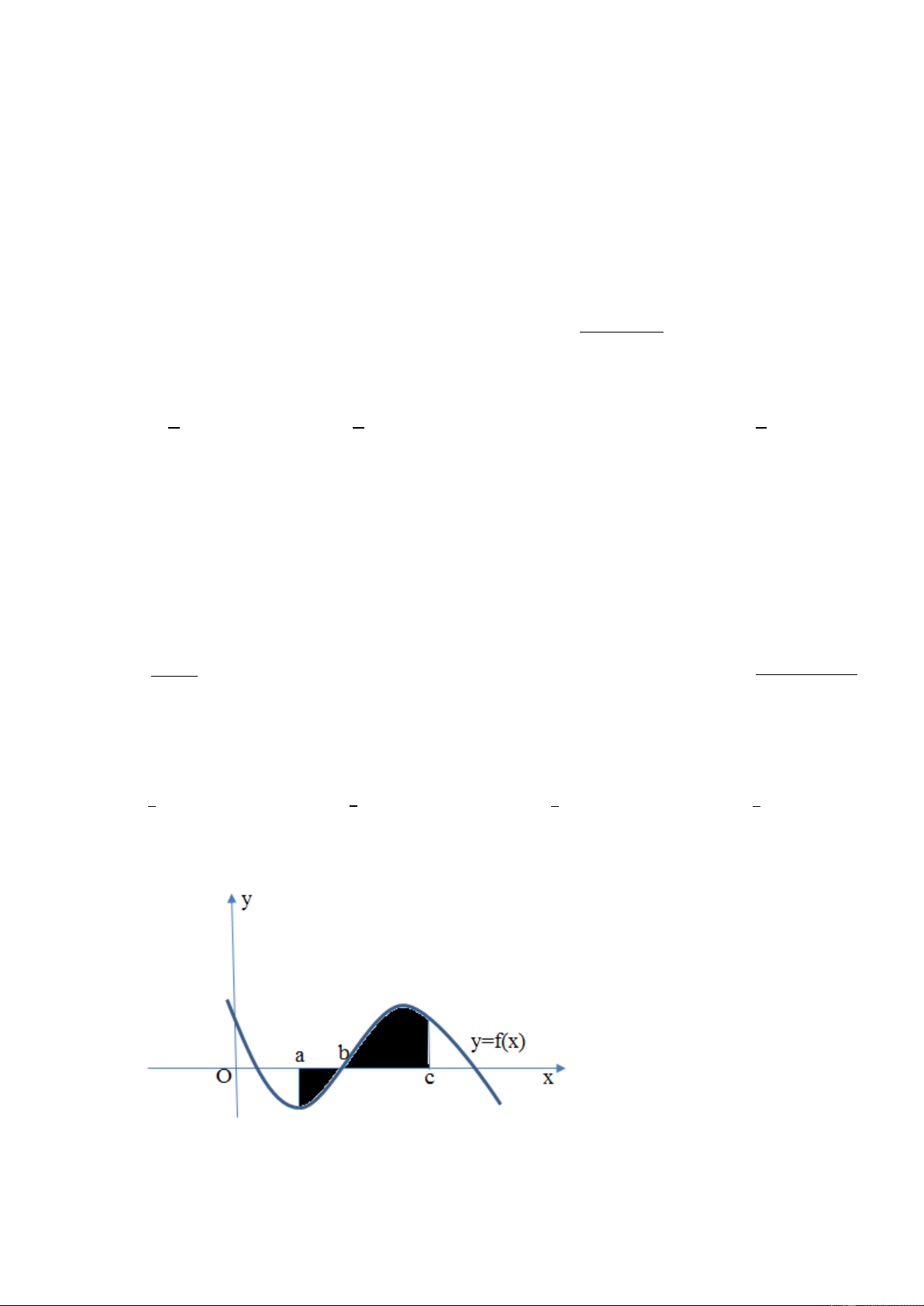
C©u 2 : Cho đồ thị hàm số y f ( )
x . Diện tích hình phẳng (phần gạch trong hình) là: 0 0 1 4 A.
f (x)dx f (x)dx   B.
f (x)dx f (x)dx   3  4 3  1 3  4 4 C.
f (x)dx f (x)dx   D. f (x)dx  0 0 3 
C©u 3 : Diện tích hình phẳng giới hạn bởi các đồ thị: 2
y x  2x và 2
y  x x có kết quả là: 10 A. 12 B. C. 9 D. 6 3
C©u 4 : Kết quả nào sai trong các kết quả sao? x1 x 1 2 5   1 2 4 4 x x   2 1 A. dx    CB. dx  ln x   C  10x 5.2x.ln 2 5x.ln 5 3 4 x 4x 2 x 1 x  1 C. dx  ln  x CD. 2
tan xdx  tan x x C  2 1 x 2 x  1
C©u 5 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 1 x  2 2
y x .e , x 1, x  2 , y  0 quanh trục ox là: 1 A. 2  (e  ) e B. 2  (e  ) e C. 2 e D.  e
C©u 6 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 4
y  , y  0 , x 1, x  4 quanh trục ox là: x A. 6 B. 4 C. 12 D. 8 C©u 7 :  4 1 Giá trị của 4 (1  tan x) . dx  bằng: 2 cos x 0 1 1 1 1 A. B. C. D. 5 3 2 4 C©u 8 : d d b
Nếu f (x)dx  5 
; f (x)dx  2 
, với a d b thì f (x)dx  bằng: a b a A. 2  B. 3 C. 8 D. 0 C©u 9 : 2 x e
Hàm số f (x)  t ln tdt
đạt cực đại tại x  ? x e A. ln 2 B. 0 C. ln 2 D. ln 4 C©u 10 :  2 2 Cho tích phân sin x 3 I e .sin x cos xdx  . Nếu đổi biến số 2
t  sin x thì 0 1 1 1 1   A. t I
e (1 t)dtB.  2 t t I
e dt te dt    2 0 0 0  1 1 1 1   C.  2 t I
e (1  t)dtD. t t I
e dt te dt    2 0 0 0 
C©u 11 : Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x   và đồ thị của hai hàm số y = cosx, y = sinx là: A. 2  2 B. 2 C. 2 D. 2 2
C©u 12 : Diện tích hình phẳng giới hạn bởi các đường 2
y  x ,trục Ox và đường thẳng x  2 là: 8 16 A. 8 B. C. 16 D. 3 3 2
C©u 13 : Cho hình phẳng H giới hạn bởi các đường y  sin x ; x  0; y  0 và x   . Thể tích vật thể
tròn xoay sinh bởi hình H quay quanh Ox bằng 2  2   A. 2 B. C. D. 2 4 2 C©u 14 : 3 2 1 x 2 x  1 Cho tích phân I dx
. Nếu đổi biến số t  thì 2 x x 1 2 2 3 2 3 3 2 t dt 3 tdt A. t dttdtI    B. IC. I  2 I   D. 2 2   t  1 t 1 2 t 1 2 t  1 2 2 2
C©u 15 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x x 1 và trục ox và đường thẳng x=1 là: 3  2 2 3 2 1 2 2 1 3  2 A. B. C. D. 3 3 3 3 C©u 16 : 4 Tìm nguyên hàm: 3 2 ( x  )dxx 5 3 A. 3 5
x  4 ln x C B. 3 5 
x  4 ln x C 3 5 3 3 C. 3 5
x  4 ln x C D. 3 5
x  4 ln x C 5 5 C©u 17 :  Tích phân 2 cos x sin xdx  bằng: 0 2 2 3 A. B. C. D. 0 3 3 2 C©u 18 : x(2  x)
Hàm số nào sau đây không là nguyên hàm của hàm số f (x)  2 (x 1) 2 x x 1 2 x x 1 2 x 2 x x 1 A. B. C. D. x 1 x 1 x 1 x 1
C©u 19 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  5 và hai tiếp tuyến với đồ thị a
hàm số tai A(1;2) và B(4;5) có kết quả dạng khi đó: a+b bằng b 13 4 A. 12 B. C. 13 D. 12 5 3 C©u 20 : 2
Giá trị của tích phân I   2 x   1lnxdx là: 1 2 ln 2  6 6 ln 2  2 2 ln 2  6 6 ln 2  2 A. B. C. D. 9 9 9 9 C©u 21 : x Kết quả của dx  là: 2 1 x 1  1 A. 2   1 x C B. C C. C D. 2
 1 x C 2 1 x 2 1 x
C©u 22 : Hàm số F( )
x  ln sin x  3cos x là một nguyên hàm của hàm số nào trong các hàm số sau đây: cos x  3sin x
A. f (x)  B. f ( )
x  cos x  3sin x sin x  3cos x
cos x  3sin x sin x  3cos x
C. f (x) 
D. f (x)  sin x  3cos x cos x  3sin x C©u 23 : e 2 x  2 ln x
Giá trị của tích phân I  dx  là: x 1 2 e 1 2 e 1 A. B. C. 2 e 1 D. 2 e 2 2 C©u 24 :  4 2
Giả sử I  sin 3x sin 2xdx  a  b 
, khi đó, giá trị của a  b là: 2 0 1 3 3 1 A. B. C. D. 6 10 10 5 C©u 25 : 3 Tìm nguyên hàm: 2 (x   2 x)dxx 3 x 4 3 x 4 A. 3  3ln x x C B. 3  3ln X x 3 3 3 3 3 x 4 3 x 4 C. 3  3ln x x C D. 3  3ln x x C 3 3 3 3 C©u 26 : 1 Tìm nguyên hàm: dxx(x  3) 4 2 x 1 x 1 x  3 1 x A. ln  C B.  ln  C C. ln  C D. ln  C 3 x  3 3 x  3 3 x 3 x  3
C©u 27 : Diện tích hình phẳng giới hạn bởi các đường (P): y=2x2 , (C): y= 2 1 x và Ox là:  8 2  A. 3 2  2 B. 2 2  C. D. 4 2  2 3 2 C©u 28 : 2
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 x 27 y=x ; y= ; y= là: 8 x 63 A. 27ln2-3 B. C. 27ln2 D. 27ln2+1 8 C©u 29 : Tìm nguyên hàm: 2 (1 sin x) dx  2 1 2 1 A.
x  2 cos x  sin 2x C ; B.
x  2 cos x  sin 2x C ; 3 4 3 4 2 1 2 1 C.
x  2 cos 2x  sin 2x C ; D.
x  2 cos x  sin 2x C ; 3 4 3 4 C©u 30 : 2 Cho 2
I  2x x  1dx  và 2
u x 1. Chọn khẳng định sai trong các khẳng định sau: 1 2 3 3 2 3 2 A. I uduB. I uduC. I  27 D. 2 I u 3 3 1 0 0 C©u 31 : 5 5 5 Cho biết f  xdx  3, g
 tdt  9. Giá trị của A  f  xgxdx  là: 2 2 2 Chưa xác định A. đượ B. 12 C. 3 D. 6 c
C©u 32 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y  2x là: 4 3 5 23 A. B. C. D. 3 2 3 15
C©u 33 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 x2 - 4x - 6 trục hoành và hai đường thẳng x=-2 , x=-4 là 40 92 50 A. 12 B. C. D. 3 3 3 5 C©u 34 : 0 2 3x  5x 1 2 Giả sử rằng I  dx  a ln  b 
. Khi đó, giá trị của a  2b là: x  2 3 1  A. 30 B. 40 C. 50 D. 60
C©u 35 : Kết quả của ln xdx  là:
A. x ln x x C B. Đáp án khác
C. x ln x C
D. x ln x x C C©u 36 : 5 Tìm nguyên hàm: 3 (  x )dxx 2 2 A. 5 5ln x x C B. 5 5  ln x x C 5 5 2 2 C. 5 5  ln x x C D. 5 5ln x x C 5 5 C©u 37 : 1 Tìm nguyên hàm: dx  . x(x  3) 1 x 1 x  3 1 x 1 x  3 A. ln  C B. ln  C C. ln  C D. ln  C 3 x  3 3 x 3 x  3 3 x
C©u 38 : Diện tích hình phẳng giới hạn bởi các đường cong 3 y x và 5
y x bằng: 1 A. 4  B. C. 0 D. 2 6 C©u 39 :   2 2 Cho hai tích phân 2 sin xdx  và 2 cos xdx
, hãy chỉ ra khẳng định đúng: 0 0  
B. Không so sánh được 2 2 A. 2 2
sin xdx  cos xdx   0 0     2 2 2 2 C. 2 2
sin xdx  cos xdx   D. 2 2
sin xdx = cos xdx   0 0 0 0 C©u 40 :   2 2 Cho hai tích phân 2 I  sin xdx  và 2 J  cos xdx
. Hãy chỉ ra khẳng định đúng: 0 0 Không so sánh
A. I J
B. I J
C. I J D. được 6 C©u 41 : 2 Hàm số ( ) x
F x e là nguyên hàm của hàm số 2 x 2 e 2 A. ( )  2 x f x xe B. 2 ( ) x f x e
C. f (x)  D. 2 ( ) x
f x x e 1 2x C©u 42 : ln 2 Tính 2 x dx  , kết quả sai là: x
A. 2 2 x   1  C B. x 2 x C C. 1 2 x C D. 22   1  C C©u 43 :  sin x
Cho tích phân I  
, với   1 thì I bằng: 2    0 1 2 cos x 2  A. B. 2 C. 2 D. 2
C©u 44 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2
y x 1 , y x  5 có kết quả là 35 10 73 73 A. B. C. D. 12 3 3 6 C©u 45 : d d b
Nếu f (x)dx  5 
, f (x)dx  2 
với a < d < b thì f (x)dx  bằng a b a A. -2 B. 0 C. 8 D. 3
C©u 46 : Kết quả nào sai trong các kết quả sao? dx 1 x 2 dx 1 x  1  1 A.  tan CB.  ln  C  1 cos x 2 2 2 2  2 x x 1 x  1  1 dx xdx 1 C.
 ln(ln(ln x)) CD. 2
  ln 3  2x Cx ln . x ln(ln x) 2 3  2x 4
C©u 47 : Diện tích hình phẳng giới hạn bởi hai đường cong y = x3 – x và y = x – x2 là : 37 33 37 A. Đáp án khác B. C. D. 6 12 12 C©u 48 : 2 Tìm nguyên hàm: 3 (x   x)dxx 7 1 2 1 2 A. 4 3 x  2 ln x x C B. 4 3 x  2 ln x x C 4 3 4 3 1 2 1 2 C. 4 3 x  2 ln x x C D. 4 3 x  2 ln x x C 4 3 4 3
C©u 49 : Cho hình phẳng giới hạn bởi các đường y x và y x quay xung quanh trục Ox . Thể tích
khối tròn xoay tạo thành bằng:  A. B. C. 0 D.   6
C©u 50 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
y  x , y  0 , y  2  x quanh trục ox là: 7 35 6 A. B. 6 C. D. 12 12 5 C©u 51 : 3 x 2 Biến đổi dx
thành f (t)dt
, với t  1 x . Khi đó f (t) là hàm nào trong các hàm   0 1 1 x 1 số sau? A. 2
f (t)  2t  2t B. 2
f (t)  t t C. 2
f (t)  t t D. 2
f (t)  2t  2t C©u 52 :    Cho x 2
I e cos xdx  ; x 2
J e sin xdx  và x
K e cos 2xdx
. Khẳng định nào đúng trong các 0 0 0 khẳng định sau? (I) I J e  
(II) I J K e  1 (III) K  5 A. Chỉ (II) B. Chỉ (III) C. Chỉ (I) D. Chỉ (I) và (II) C©u 53 : Hàm số 2
y  tan 2x nhận hàm số nào dưới đây là nguyên hàm? 1 1 A. 2 tan 2x  x B. tan 2x  x C. tan 2x  x D. tan 2x  x 2 2
C©u 54 : Thể tích vật thể tròn xoang khi quay hình phẳng giới hạn bởi đồ thị hàm số y = x2 2 ;x y quanh trục ox là 8  2 4 3  A. B. C. D. 10 3 10 10 C©u 55 :  6 n 1
Cho I  sin x cos xdx   . Khi đó n bằng: 64 0 A. 3 B. 4 C. 6 D. 5 C©u 56 : Tìm nguyên hàm: 3x 2 (2  e ) dx  4 4 x 5 x 1 A. 3 6 3 x x e eC B. 3 6 4 x x e eC 3 6 3 6 4 4 x 1 x 1 C. 3 6 4 x x e eC D. 3 6 4 x x e eC 3 6 3 6 C©u 57 : 5 dx Giả sử  ln K
. Giá trị của K là: 2x  1 1 A. 3 B. 8 C. 81 D. 9 C©u 58 : 3
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x + 11x - 6, y = 6x2,x 0,x 2 có a kết quả dạng khi đó a-b bằng b A. 2 B. -3 C. 3 D. 59
C©u 59 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = -x2 + 4x và các tiếp tuyến với đồ thị a
hàm số biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng khi đó a-b bằng b 12 A. B. 14 C. 5 D. -5 11
C©u 60 : Diện tích hình phẳng giới hạn bởi (C): y= x2+3x2, d1:y = x1 và d2:y=x+2 có kết quả là 1 2 1 1 A. B. C. D. 8 7 12 6
C©u 61 : Diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1, tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy là: 7 5 8 A. B. C. 2 D. 3 3 3 9 C©u 62 : 1 Giá trị của x I  x.e dx  là: 0 2 2 A. 1 B. 1 C. D. 2e 1 e e C©u 63 : dx Tính  , kết quả là: 1  x C 2 A. B. 2
 1 x C C. C
D. C 1 x 1  x 1  x
C©u 64 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = (e 1)x và (1 x y e )x là: e e 3 A. 2  B. 2 C. 1 D. 1 2 2 e
C©u 65 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y  2
x x  3 và trục hoành là: 125 125 125 125 A. B. C. D. 24 34 14 44 C©u 66 : 2 x
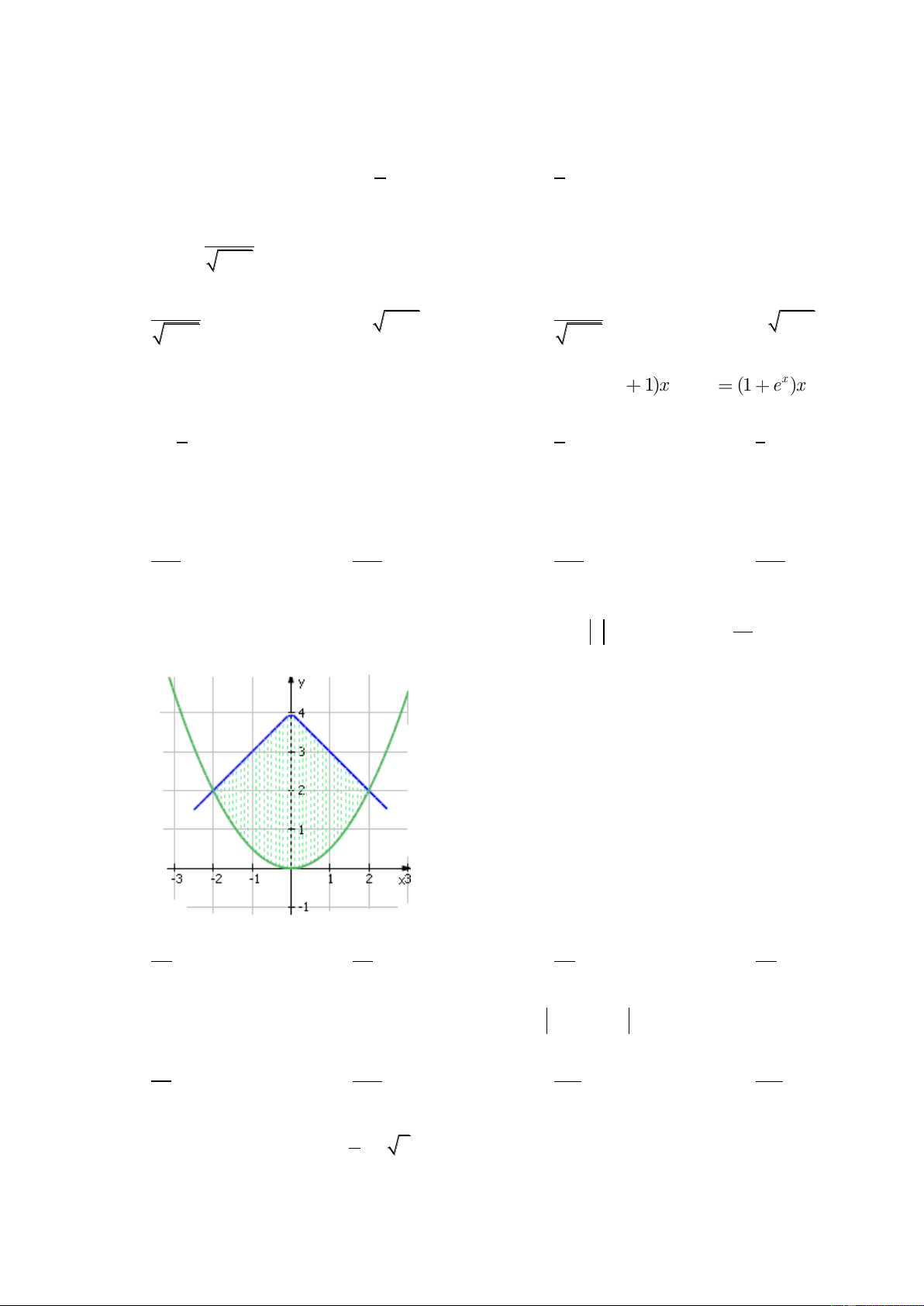
Diện tích hình phẳng giới hạn bởi đường thẳng y  4  x và patabol y  bằng: 2 28 25 22 26 A. B. C. D. 3 3 3 3
C©u 67 : Diện tích hình phẳng giới hạn bởi các đồ thị: 2
y x  4x  3 và y=x+3 có kết quả là: 55 205 109 126 A. B. C. D. 6 6 6 5 C©u 68 : 3 Tìm nguyên hàm: 2 (x   2 x)dxx 10 3 1 3 1 A. x  2s inx  sin 2x C B.
x  2s inx- sin 2x C 2 4 2 4 3 1 3 1 C. x  2 cos x  sin 2x C D. x  2s inx  sin 2x C 2 4 2 4
C©u 69 : Diện tích hình phẳng giới hạn bởi các đường cong y x  sin x và y x , với 0  x  2 bằng: A. 4  B. 4 C. 0 D. 1 C©u 70 : 1
Cho Fx là một nguyên hàm của hàm số y  
và F0 1. Khi đó, ta có Fx là: 2 cos x A.  tan x B.  tan x 1 C. tan x 1 D. tan x 1
C©u 71 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đồ thị hàm số y2 = 8x và x=2 quanh trục ox là: A. 12 B. 4 C. 16 D. 8
C©u 72 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y 1 x , y  0 quanh a
trục ox có kết quả dạng
khi đó a+b có kết quả là: b A. 11 B. 17 C. 31 D. 25 C©u 73 : 2 2  x 1
Nguyên hàm F(x) của hàm số f (x)  
 là hàm số nào trong các hàm số sau?  x  3 x 1 3 x 1
A. F(x) 
  2x C
B. F(x) 
  2x C 3 x 3 x 3 3 x 3    x x   x  3
C. F(x)   C D. 3 F(x)     C 2 x 2  x    2  2 
C©u 74 : Diện tích hình phẳng giới hạn bởi các đường (P): y =x2-2x+2 và các tiếp tuyến bới (P) biết
tiếp tuyến đi qua A(2;-2) là: 8 64 16 40 A. B. C. D. 3 3 3 3
C©u 75 : Thể tích khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y
=(1- x)2, y = 0, x = 0 và x = 2 bằng: 11  5 2 A. 2 B. 8 2 C. D. 3 2 5
C©u 76 : Thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các
đường y = x2 và x = y2 bằng: 10 3 A. 10 B. C. 3 D. 3 10 C©u 77 : 2 Giá trị của 2 2 x e dx  bằng: 0 A. 4 e  1 B. 4 4e C. 4 e D. 4 3e
C©u 78 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = - x + 3x + 1 và đường thẳng y=3 là 57 45 27 21 A. B. C. D. 4 4 4 4
C©u 79 : Tìm khẳng định sai trong các khẳng định sau:   1 2 A. x x  
sin dx  2 sin xdx   B. (1 x) dx 0  2 0 0 0 1 1 1 2 C.
sin(1 x)dx  sin xdx   D. 2007 x (1 x)dx    2009 0 0 1 12 ĐÁP ÁN 01 { ) } ~ 28 { | ) ~ 55 ) | } ~ 02 ) | } ~ 29 { | } ) 56 { | } ) 03 { | ) ~ 30 ) | } ~ 57 ) | } ~ 04 ) | } ~ 31 { ) } ~ 58 { | ) ~ 05 { | ) ~ 32 ) | } ~ 59 { | ) ~ 06 { | ) ~ 33 { | ) ~ 60 { | ) ~ 07 ) | } ~ 34 { ) } ~ 61 { | } ) 08 { ) } ~ 35 { | } ) 62 { ) } ~ 09 ) | } ~ 36 { | } ) 63 { ) } ~ 10 ) | } ~ 37 { | } ) 64 { | ) ~ 11 { | } ) 38 { ) } ~ 65 ) | } ~ 12 { ) } ~ 39 { | } ) 66 ) | } ~ 13 { ) } ~ 40 { ) } ~ 67 { | ) ~ 14 ) | } ~ 41 ) | } ~ 68 { | } ) 15 { | ) ~ 42 { ) } ~ 69 { ) } ~ 16 { | } ) 43 ) | } ~ 70 { ) } ~ 17 { ) } ~ 44 { | ) ~ 71 { | ) ~ 18 { | } ) 45 { | } ) 72 { | ) ~ 19 { | ) ~ 46 ) | } ~ 73 ) | } ~ 20 { ) } ~ 47 { | } ) 74 { | ) ~ 21 { | } ) 48 { | } ) 75 { | } ) 22 ) | } ~ 49 { ) } ~ 76 { | } ) 23 { ) } ~ 50 { | ) ~ 77 ) | } ~ 24 { ) } ~ 51 ) | } ~ 78 { | ) ~ 25 { | } ) 52 ) | } ~ 79 { ) } ~ 26 { | } ) 53 { ) } ~ 27 { | ) ~ 54 { | ) ~ 13 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 02 C©u 1 : 2 Tính  x x e 1 . dx 2 1 2 1 2 1 A. 2   x 1 x x 1 x 1 e   C B. eC C. eC D. eC 3 2 2 2
C©u 2 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường y x 1 , trục hoành, x 2,x 5 quanh trục Ox bằng: 5 5 2 5 2 2 A. x d 1 x B. x 1 dx C. y 1 dx D. x 1 dx 2 2 1 2 C©u 3 : 2 Giá trị của 2 2 x e dx là: 0 A. 4 e B. 4 e 1 C. 4 4e D. 4 3e 1 C©u 4 :  6 tan x Cho tích phân 4 I dx
. Giả sử đặt u  3tan x 1 thì ta được: 2 0
cos x 3 tan x 1 2 4 2 4 A. I   2 2u   1du . B. I   2u   1du. 1 3 1 3 2 4 2 4 C. I   2u   1du. D. I   2 2u   1du. 1 3 1 3 C©u 5 : 6 4 6 Nếu f (x)dx 10 và f (x)dx 7 , thì
f (x)dx bằng : 0 0 4 A. 3 B. 17 C. 170 D. 3 C©u 6 : x
Họ nguyên hàm của hàm số f x 3  là: 2 1 x 1 1 A.  2x 2 2 1 x C B.   2 x   2 1 1 x C 3 3 1 1 1 C.  2x   2 1 1 x C D.   2 x  2 2 1 x C 3 3 C©u 7 : 5 dx Giả sử
lnc . Giá trị đúng của c là: 2x 1 1 A. 9 B. 3 C. 81 D. 8
C©u 8 : Tính diện tích S  hình phẳng được giới hạn bởi các đường: 2 2 x x y  4  ; y  . 4 4 2 2 5 4 1
A. S  2  .
B. S  2  .
C. S  2  .
D. S  2  . 3 3 3 3 C©u 9 : 4
Nếu f (1) 12, f '(x) liên tục và f '(x)dx
17 , giá trị của f (4) bằng: 1 A. 29 B. 5 C. 19 D. 9 C©u 10 : 4 2
Nếu f (x) liên tục và f (x)dx 10 , thì
f (2x)dx bằng : 0 0 A. 5 B. 29 C. 19 D. 9 C©u 11 : b
Biết 2x  4dx  0 , khi đó b nhận giá trị bằng: 0
A. b  1 hoặc b  4
B. b  0 hoặc b  2
C. b  1 hoặc b  2
D. b  0 hoặc b  4 C©u 12 : 6 n 1 Cho I
sin x cos xdx . Khi đó n bằng: 64 0 A. 5 B. 3 C. 4 D. 6
C©u 13 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y
x và đường thẳng y 2x bằng: 23 4 3 5 A. B. C. D. 15 3 2 3
C©u 14 : Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường 2
y  x  2
; y 1và trục Ox khí quay xung quanh Ox là 2 1 1 1 1 A. 2 2
 (x 1) dx   dx   B. 2 2
 (x  2) dx   dx   1  1  1  1  1 1 1 C. 2 2
 (x  2) dx  dx   D. 2 2
 (x  2) dx  1  1  1  C©u 15 : 4m     Cho 2 f (x)   sin x  
. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và F    4  8 4 A. m   3 B. m  3 C. m   4 D. m  3 4 4 3 C©u 16 : e 3 a e 1
Khẳng định nào sau đây đúng về kết quả 3 x ln xdx ? b 1 A. . a b 64 B. . a b 46 C. a b 12 D. a b 4 C©u 17 : 1 3 x 1
Khẳng định nào sau đây đúng về kết quả dx ln 2 ? 4 x 1 a 0 A. a 2 B. a 4 C. a 4 D. a 2 C©u 18 : 2
20x  30x  7 3
Cho các hàm số: f (x) 
; F x   2
ax bx x 2x  3 với x  . Để hàm số 2x  3 2
F x là một nguyên hàm của hàm số f (x) thì giá trị của a, , b c là:
A. a  4;b  2;c 1
B. a  4;b  2  ;c  1 
C. a  4;b  2  ;c 1.
D. a  4;b  2;c  1  C©u 19 : 1 (3x 1)dx
Tính tích phân I   2 x  6x  9 0 4 5 3 5 4 5 4 7 A. 3ln  B. 3ln  C. 3ln  D. 3ln  3 6 4 6 3 6 3 6 C©u 20 : (x a) cos3x 1
Một nguyên hàm (x 2)sin3xdx
sin 3x 2017 thì tổng S . a b c bằng : b c A. S 14 B. S 15 C. S 3 D. S 10 C©u 21 : dx
Tìm họ nguyên hàm: F(x)   x 2 ln x 1
A. F(x)  2 2ln x 1  C
B. F(x)  2ln x 1  C 1 1
C. F(x) 
2 ln x 1  C
D. F(x) 
2 ln x 1  C 4 2 3
C©u 22 : Nguyên hàm của hàm số f x 2
x – 3x  1 là x 3 2 x 3x x3 3x2 A. F(x) =   ln x C B. F(x) =   ln x C 3 2 3 2 3 2 x 3x 3 2 x 3x C. F(x) =   ln x C D. F(x) =   ln x C 3 2 3 2
C©u 23 : Thể tích của khối tròn xoay sinh ra khi quay quanh trục Oy hình phẳng giới hạn bởi các đường: 2
y  x  4x  3 và Ox bằng: 16  16 A. B. 5 C. D. 5 5 3 C©u 24 : 2x
Cho f x  . Khi đó: 2 x 1 A. f
 xdx   2
2 ln 1 x   C B. f
 xdx   2
3ln 1 x   C C. f
 xdx   2
4 ln 1 x   C D. f
 xdx   2
ln 1 x   C
C©u 25 : Cho hai hàm số y = f(x), y = g(x) có đồ thị (C1) và (C2) liên tục trên [a;b] thì công thức tính
diện tích hình phẳng giới hạn bởi (C1), (C2) và hai đường thẳng x = a, x = b là: b b
A. S  f (x)  g(x)dx
B. S  g(x)  f (x)dx a a b b b
C. S  f (x)dx  g(x)dx  
D. S  f (x)  g(x) dx  a a a C©u 26 : 0 x 1 b
Khẳng định nào sau đây sai về kết quả dx a ln 1 ? x 2 c 1 A. . a b 3(c 1) B. ac b 3 C. a b 2c 10 D. ab c 1 C©u 27 : 1 (x  4)dx
Tính tích phân I   2 x  3x  2 0 A. 5ln 2  3ln 2 B. 5ln 2  2ln3 C. 5ln 2  2ln3 D. 2ln5  2ln3
C©u 28 : Cho hàm f x 4
 sin 2x . Khi đó:     A. f  x 1 1 dx
3x  sin 4x  sin 8x C   B. f  x 1 1 dx
3x  cos 4x  sin 8x C   8  8  8  8  4     C. f  x 1 1 dx
3x  cos 4x  sin 8x C   D. f  x 1 1 dx
3x  sin 4x  sin 8x C   8  8  8  8 
C©u 29 : Cho hàm số y = f(x) liên tục và chỉ triệt tiêu khi x = c trên [a; b]. Các kết quả sau, câu nào đúng? b b b c b A. f (x) dx  f(x)dx   B. f (x) dx  f(x) dx  f(x) dx    a a a a c b c b
D. A, B, C đều đúng C. f (x) dx  f(x) dx  f (x)dx    a a a
C©u 30 : Diện tích phẳng giới hạn bởi: 2 x  1
 ; x  2; y  0; y x  2x 4 8 A. B. 1 C. 0 D. 3 3 C©u 31 : 3 2 x  3x  3x 1 1
Tìm một nguyên hàm F(x) của hàm số f (x)  biết F(1)  2 x  2x 1 3 2 2 13 A. 2 F(x)  x  x   6 B. 2 F(x)  x  x   x 1 x 1 6 2 x 2 13 2 x 2 C. F(x)   x   D. F(x)   x   6 2 x 1 6 2 x 1 C©u 32 : 1
Tính diện tích S  hình phẳng được giới hạn bởi các đường: 2
y x ; y  ln ; x  1 x 1 8 31 8 23 8 17 8 23
A. S   ln 2 
B. S  ln 2 
C. S  ln 2 
D. S  ln 2  3 18 3 18 3 18 3 18
C©u 33 : Gọi 2008xdx F
xC , với C là hằng số. Khi đó hàm số F x bằng 2008x
A. 2008x ln 2008 B. 1 2008xC. 2008x D. ln2008
C©u 34 : Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường  y x ln ,
x y  0, x e có giá trị bằng: 3
(b e  2) trong đó a,b là hai số thực nào dưới đây? a A. a=27; b=5 B. a=24; b=6 C. a=27; b=6 D. a=24; b=5
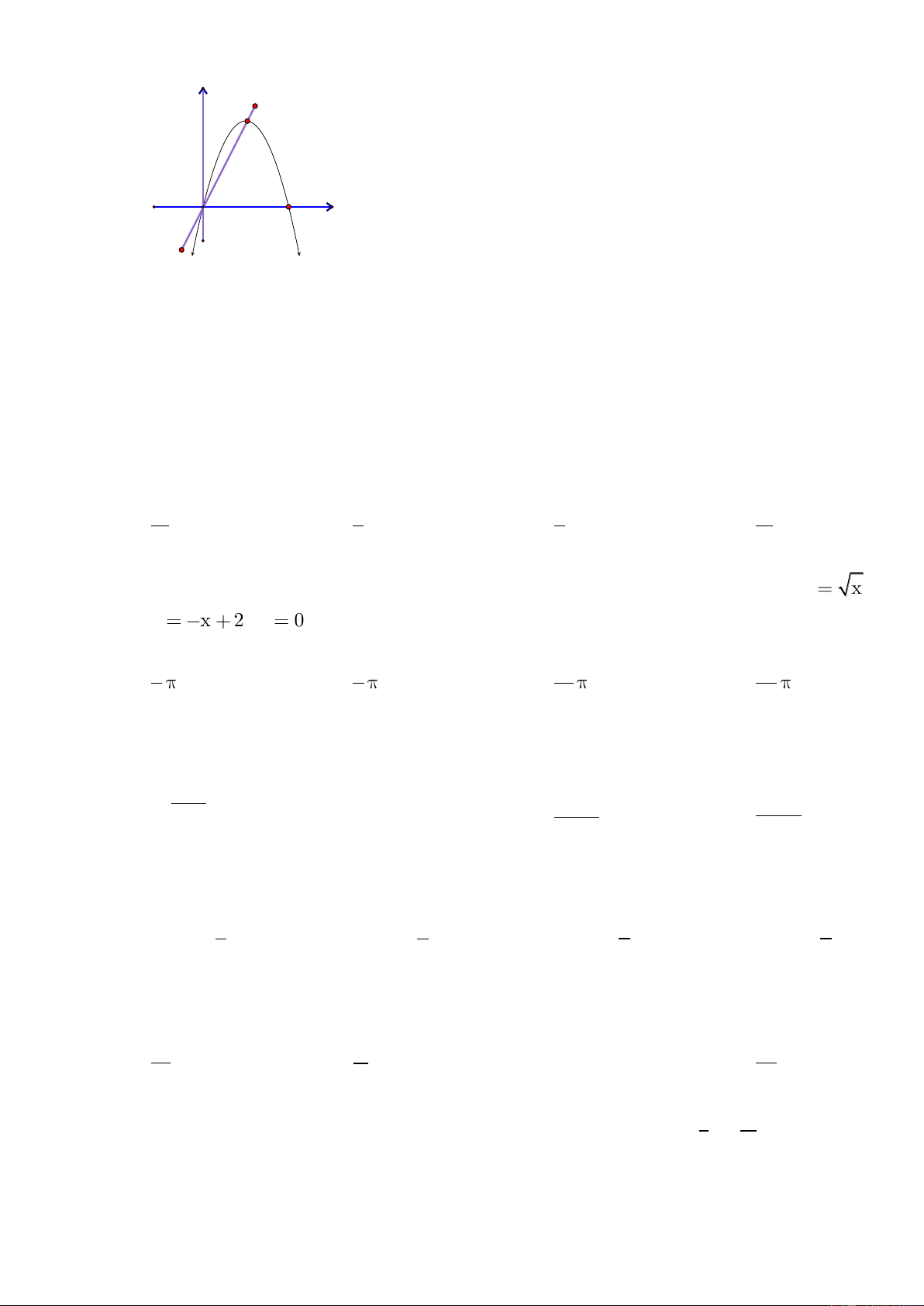
C©u 35 : Cho đồ thị hàm số y
f x . Diện tích hình phẳng (phần tô đậm trong hình) là: 5 4 0 0 A. f x dx B. f x dx f x dx 3 3 4 1 4 3 4 C. f x dx f x dx D. f x dx f x dx 3 1 0 0
C©u 36 : Diện tích hình phẳng giới hạn bởi hai đường cong  (1 x y
e )x và y  (e 1)x là? e e e e A. 1( đvdt) B.  2 ( đvdt) C.  2 ( đvdt) D. 1 ( đvdt) 2 2 2 2 C©u 37 : Tích phân 2
cos x.sin xdx bằng: 0 2 2 3 A. B. C. D. 0 3 3 2 C©u 38 :  Cho tích phân sin 2  sin 2 . x I x e dx
: .một học sinh giải như sau: 0
x  0  t  0 Bước 1: Đặ 1
t t  sin x dt  cos xdx . Đổi cận:    2 . t I t e dt  . x   t 1 0 2  u tdu dt Bước 2: chọn    t tdv e dtv e 1 1 1 1  . t  . t t t t e dt t e
e dt e e 1   0 0 0 0 Bướ 1 c 3:  2 . t I t e dt  2  . 0
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Bài giải trên sai từ bước 1.
B. Bài giải trên sai từ bước 2 .
C. Bài giải trên hoàn toàn đúng.
D. Bài gaiir trên sai ở bước 3. C©u 39 :   
Cho hình phẳng giới hạn bởi: D  y  tan ; x x  0; x  ; y  0  3  6
Thể tích vật tròn xoay khi D quay quanh Ox:     A.    3    B. 3  C. 3  D.    3     3  3 3  3  C©u 40 : 1
Nguyên hàm của hàm số y 3x 1 trên ; là: 3 3 2 3 A. 2 x x C B. 3x 1 C 2 9 2 3 3 C. 3x 1 C D. 2 x x C 9 2 C©u 41 : 12 Cho tích phân 2 1 x dx  bằng: 0   3  1   3    3  1   3  A.      B.      C.      D.      6 4   2 6 4   6 4   2 6 4  
C©u 42 : Tính diện tích hình phẳng tạo bởi các đường: Parabol P 2
: y x  4x  5 và 2 tiếp tuyến tại
các điểm A1;2, B4;5 nằm trên P . 7 11 9 13 A. S B. S C. S D. S  2 6 4 8
C©u 43 : Tìm hàm số F(x) biết rằng F’(x) = 4x3 – 3x2 + 2 và F(-1) = 3
A. F(x) = x4 – x3 - 2x -3
B. F(x) = x4 – x3 - 2x + 3
C. F(x) = x4 – x3 + 2x + 3
D. F(x) = x4 + x3 + 2x + 3 C©u 44 :  I  1 cos 2x dx  bằng: 0 A. 2 B. 0 C. 2 D. 2 2 C©u 45 : 3 x
Tìm họ nguyên hàm: F(x)  dx  4 x 1 1 A. 4
F(x)  ln x 1  C B. 4 F (x) 
ln x 1  C 4 1 1 C. 4 F (x) 
ln x 1  C D. 4 F (x) 
ln x 1  C 2 3 7 C©u 46 : 9 9 9 Nếu f (x)dx
37 và g(x)dx 16 thì
2 f (x) 3g(x) dx bằng : 0 0 0 A. 122 B. 74 C. 48 D. 53 C©u 47 :    3 cot x 4 3 cot x Biết rằng x   ;   thì   . Gọi I  dx. 
Kết luận nào sau đây là đúng ?  4 3   x   x 4 3 1 1 1 1 1 A.  I  B.  I  C.  I  D. 3 1  I  12 4 4 3 5 4 12 3 C©u 48 : 1 Giá trị của tích phân 3 3 4 x 1 x d . x  bằng? 0 3 6 A. B. 2 C. D. Đáp án khác 16 13 C©u 49 : ln 2 Tính 2 x dx , kết quả là: x x x A. 2 2 1 C B. 2x C C. 2 2 1 C D. 1 2 x C C©u 50 : dx Tính , kết quả là: 1 x C 2 A. B. 2 1 x C C. C
D. C 1 x 1 x 1 x C©u 51 : x ln(x  2)
Diện tích hình phẳng giới hạn bởi y  và trục hoành là: 2 4  x     A. 2   3 B. 2ln 2  2  C. ln 2  2   3
D. 2ln 2  2   3 3 4 3 3 C©u 52 : x ln  2 x  x 1
Một nguyên hàm của f (x)  là: 2 x 1 A.  2
x ln x  x 1  x  C B.  2
ln x  x 1  x  C C. 2 2 2      x ln x 1  x  C D. x 1 ln x x 1 x C
C©u 53 : Cho hình phẳng giới hạn bởi các đường y = 2x – x2 và y = 0. Thì thể tích vật thể tròn xoay 8
được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox có giá trị bằng? 16 15 5 6 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 15 16 6 5 C©u 54 : 2 1
Khẳng định nào sau đây sai về kết quả (2x 1 sin x)dx 1 ? a b 0 A. a 2b 8 B. a b 5 C. 2a 3b 2 D. a b 2
C©u 55 : Một nguyên hàm của hàm số y  sin 3x 1 1 A.  o c s3x B. 3  o c s3x C. 3 o c s3x D. o c s3x 3 3 C©u 56 : x f (t) Nếu dt 6 2 x , x
0 thì hệ số a bằng : 2 t a A. 9 B. 19 C. 5 D. 29 C©u 57 : 1 2x  3 Biết tích phân dx
=aln2 +b . Thì giá trị của a là: 2  x 0 A. 7 B. 2 C. 3 D. 1
C©u 58 : Thể tích hình khối do hình phẳng giới hạn bởi các đường 2
y  x  4, y  2x  4, x  0, x  2 quay quanh trục Ox bằng: 32 32 A. B. 6 C. 6   D. 5 5 C©u 59 : 4 2x  3
Nguyên hàm của hàm số y  là: 2 x 2x3 3 3 2x 3 3 x 3 A.  3  C B. 3 3  xC C.   C D.   C 3 x x 3 x 3 x C©u 60 : 3 1 Biết tích phân dx
= a thì giá trị của a là 2 9  x 0 1 1 A. B. C. 6 D. 12 12 6 C©u 61 : a b 2 sin x b Cho f (x) 
với a,b là các số thực. Tìm nguyên hàm F(x) của f(x) biết 2 sin x    1       F  ;F  0;F 1        4  2  6   3  9 3 1 3 1
A. F x  tanx-cotx 
B. F x  tanx+cotx  4 2 4 2 3 1 3 1
C. F x  tanx-cotx 
D. F x  tanx+cotx  4 2 4 2 C©u 62 : 1
Cho hàm f x  .Khi đó: 2 x  3x  2 x x A. f  x 1 dx  ln  C B. f  x 1 dx  ln  C x  2 x  2 x x C. f  x 2 dx  ln  C D. f  x 2 dx  ln  C x 1 x 1 C©u 63 : Tính ln x
A. xln x x C
B. ln x x C
C. xln x x C
D. xln x x C C©u 64 : 1 Cho hàm y
.Nếu F x là nguyên hàm của hàm số và đồ thị hàm số y F x đi qua 2 sin x   điể  m M ; 0 
 thì F x là:  6  3 3 A.  cot x B.   cot x   D. 3  cot x 3 3 C. 3 cot x C©u 65 : 10 8 10 Nếu f (x)dx 17 và f (x)dx 12 thì
f (x)dx bằng : 0 0 8 A. 5 B. 29 C. 5 D. 15 C©u 66 : x e
Nguyên hàm của hàm số f x  x e (2  ) là: 2 cos x A.    2 x F x e tanx B.    2 x F x
e - tanxC C.    2 x F x
e tanxC D. Đáp án khác
C©u 67 : Cho f (x)dx  F(x)  C. 
Khi đó với a  0, ta có f (a x  b)dx  bằng: 1 1 A. F(a x  b)  C B. aF(a x  b)  C C. F(a x  b)  C D. F(a x  b)  C 2a a
C©u 68 : Thể tích của vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường y = x2 –
2x, y = 0, x = 0, x = 1 quanh trục hoành Ox có giá trị bằng? 10 8 8 15 7 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 15 7 8 8 C©u 69 : dx
Tìm nguyên hàm của: F(x)   3 5 x x 1 1 1 1
A. F(x)   ln x  ln  2 1 xC
B. F(x)    ln x  ln  2 1 xC 2  2  2x 2 2x 2 1 1 1 1
C. F(x)    ln x  ln  2 1 xC
D. F(x)    ln x  ln  2 1 xC 2  2  2x 2 2x 2 C©u 70 :  4 1 a BIết : dx  
. Mệnh đề nào sau đây đúng? 4 cos x 3 0
A. a là một số chẵn
B. a là số lớn hơn 5
C. a là số nhỏ hơn 3
D. a là một số lẻ
C©u 71 : Cho hình phẳng H  được giới hạn bởi các đường: y xln ,
x y  0, x e . Tính thể tích khối
tròn xoay tạo thành khi hình  H  quay quanh trục Ox .   3 5e  2   3 5e  2   3 5e  2   3 5e  2 A. V B. V C. V D. V Ox 25 Ox 27 Ox 27 Ox 25
C©u 72 : Khẳng định nào sau đây đúng ? 10
Nếu w '(t) là tốc độ tăng trưởng cân nặng/năm của một đứa trẻ, thì w '(t)dt là sự cân A. 5
nặng của đứa trẻ giữa 5 và 10 tuổi.
Nếu dầu rò rỉ từ 1 cái thùng với tốc độ r(t) tính bằng galông/phút tại thời gian t , thì
B. 120 r(t)dt biểu thị lượng galông dầu rò rỉ trong 2 giờ đầu tiên. 0
Nếu r(t) là tốc độ tiêu thụ dầu của thế giới, trong đó t được bằng năm, bắt đầu tại 17 t
0 vào ngày 1 tháng 1 năm 2000 và r(t) được tính bằng thùng/năm, r(t)dt biểu thị C. 0
số lượng thùng dầu tiêu thụ từ ngày 1 tháng 1 năm 2000 đến ngày 1 tháng 1 năm 2017 . D. Cả , A , B C đều đúng. 11 ĐÁP ÁN 01 { | ) ~ 28 { | } ) 55 ) | } ~ 02 { ) } ~ 29 { | } ) 56 ) | } ~ 03 { ) } ~ 30 { | } ) 57 ) | } ~ 04 { | ) ~ 31 { | ) ~ 58 { | } ) 05 ) | } ~ 32 { ) } ~ 59 ) | } ~ 06 { | } ) 33 { | } ) 60 ) | } ~ 07 { ) } ~ 34 ) | } ~ 61 { | ) ~ 08 { | ) ~ 35 { ) } ~ 62 { | } ) 09 ) | } ~ 36 ) | } ~ 63 { | ) ~ 10 ) | } ~ 37 { ) } ~ 64 { | } ) 11 { | } ) 38 { | ) ~ 65 ) | } ~ 12 { ) } ~ 39 { | } ) 66 { | ) ~ 13 { ) } ~ 40 { ) } ~ 67 { | ) ~ 14 { | ) ~ 41 { | } ) 68 ) | } ~ 15 { | ) ~ 42 { | ) ~ 69 { ) } ~ 16 ) | } ~ 43 { | ) ~ 70 ) | } ~ 17 { ) } ~ 44 { | } ) 71 { | ) ~ 18 { | ) ~ 45 { ) } ~ 72 { | } ) 19 { | ) ~ 46 ) | } ~ 20 { ) } ~ 47 { | } ) 21 { ) } ~ 48 ) | } ~ 22 { | ) ~ 49 { ) } ~ 23 { | } ) 50 { ) } ~ 24 { | } ) 51 { | } ) 25 { | } ) 52 { | } ) 26 { | } ) 53 ) | } ~ 27 { | ) ~ 54 { ) } ~ 12 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 03 C©u 1 : 1 d x Cho
a ln 2 b ln 5 c . Khi đó a 2b 4c bằng 5 3 x x 0 A. 2 B. 3 C. 0 D. 1 C©u 2 :
Một nguyên hàm của       1 2x 1 x f x e là 1 1 1 A. . x x e B.    1 2 1 x x e C. 2 x x e D. x e C©u 3 : 5 dx
Tính tích phân: I  
được kết quả I aln 3  bln 5 . Giá trị 2 2
a ab  3b là:  1 x 3x 1 A. 4 B. 1 C. 0 D. 5 C©u 4 :  2 n
Tích phân I  1 cos x sin xdx bằng 0 1 1 1 1 A. B. D. n  1 n C. 1 2n n
C©u 5 : Hình phẳng giới hạn bởi 2 y  ,
x y x có diện tích là: 1 1 1 A. B. C. D. 1 2 6 3 C©u 6 : e dx I   có giá trị x 1 e 1 A. 0 B. -2 C. 2 D. e C©u 7 : 10 6
Cho f (x) liên tục trên [0; 10] thỏa mãn:
f (x)dx  7,
f (x)dx  3  
Khi đó, giá trị của P = 0 2 2 10
f (x)dx f (x)dx   có giá trị là: 0 6 A. 1 B. 4 C. 3 D. 2 C©u 8 : 2
Thể tích của vật thể giới hạn bởi 2 mặt trụ: 2 2 2
x z a và 2 2 2
y z a là V  (đvtt). Tính 3 giá trị của a? 1 1 A. 1 B. C. 2 D. 2 4 C©u 9 : 1 ln 2 Tính 2 2 x dx  , kết quả sai là: 2 x 1   1   1 1 A. 2
2 2 x  2  C 2x   B. 1  2 2  2  C 2 2     2 xC
C. 2 x C D.   C©u 10 : 1 Tính: 2 2 x K x e dx  0 2 e 1 2 e  1 2 e 1 A. K B. K C. K D. K  4 4 4 4
C©u 11 : Diện tích hình giới hạn bởi P  3
y  x  3 , tiếp tuyến của (P) tại x  2 và trục Oy là 2 8 4 A. B. 8 C. D. 3 3 3
C©u 12 : Nguyên hàm của hàm số: y = sin3x.cosx là: 1 1 1 A. 4 sin x  C B. 3 cos x  C C. 3 sin x  C D. 4 sin x  C 4 3 3 C©u 13 : 1
Cho f (x) là hàm số lẻ và liên tục trên
. Khi đó giá trị tích phân f (x)dx  là: 1  A. 2 B. 0 C. 1 D. -2
C©u 14 : Thể tích của khối tròn xoay do hình phẳng (H) giới hạn bởi các đường
y  sin x ; y  0 ; x  0; x   khi quay xung quanh Ox là : 2 2  2  2  2 2 A. B. C. D. 3 2 4 3 C©u 15 : 1 Tích phân 3 I  x 1 x xd  0 28 9 9 3 A. B. C. D. 9 28 28 28 C©u 16 : 1
Cho f (x) là hàm số chẵn và liên tục trên thỏa mãn
f (x)dx  2 
. Khi đó giá trị tích phân 1  1 f (x)dx  là: 0 1 1 A. 2 B. 1 C. D. 2 4 C©u 17 : Cho f (
x)  3  5sinx và f(0)  10 . Trong các khẳng định sau khẳng định nào đúng?
f (x)  3x  5 cosx  2   3
f x   3x  5cosx A. B. f   
C. f    3 D. 2 2  
C©u 18 : Cho hàm số y f x thỏa mãn 2
y '  x .y và f(-1)=1 thì f(2) bằng bao nhiêu: A. 3 e B. 2 e C. 2e D. e  1
C©u 19 : Một nguyên hàm của hàm số: 2
f (x)  x 1  x là: 1 1
A. F(x)   1 x 3 2
B. F(x)   1 x 2 2 3 3 2 2 x 1 C. F x   2 ( ) 1  x
D. F(x)   1x 22 2 2 C©u 20 : 1
Tính: K x ln   2 1  x dx 0 A. Ln2 -1/2 B. Ln2- 1/4 C. Ln2 +1/2 D. -ln2 +1/2 C©u 21 : 2 
Cho hình phẳng (S) giới hạn bởi Ox, Oy, y = cosx và y x 1 
. Diện tích hình phẳng (S) là: 3 3 A. 2 B. 2  C. D. 1 2 4 3 C©u 22 : 1 d x Tính tích phân 2 x x 12 0 9 1 9 1 9 1 9 A. ln B. ln C. ln D. ln 16 4 16 7 16 7 16 C©u 23 : 1
Biết F(x) là nguyên hàm của hàm số x  và F(2)=1. Khi đó F(3) bằng bao nhiêu: 1 1 3 A. ln 2  1 B. C. ln D. ln 2 2 2 C©u 24 : x d    2 1 x  x x x A. x  2 ln x   1  C B. 2 ln x 1 x  C C. ln  C D. ln  C 2 2 1 x 1 x
C©u 25 : Cho hàm số f x và gx liên tục trên a;b và thỏa mãn f x  gx  0 với mọi x a;b .
Gọi V là thể tích khối tròn xoay sinh ra khi quay quanh Ox hình phẳng giới hạn đồ thị
C: y  f x; C': y  gx; đường thẳng x  a;x  b . V được tính bởi công thức nào sau đây ? 2 b   b A. V   f  2 2  x  gx d  x  
B. V   f (x)  g (x) d  x     a  a b b 2 C. V  f  xgxdx D. V   f
 xgx dx  a a
C©u 26 : Cho parabôn P 2
: y x  1và đường thẳng d : y mx  2 . Tìm m để diện tích hình phẳng
giới hạn bởi P và d đạt giá trị nhỏ nhất? 1 3 A. B. C. 1 D. 0 2 4 C©u 27 : dx Tính nguyên hàm  ? 2 x a A. 2
ln x x a C B. 2
ln 2x x a C C. 2
ln 2x x a C D. 2
ln x x a C 4 C©u 28 : 1 Tính 2 I  x x 1dx  , kết quả là : 0 2 2 2 1 2 2 2 A. I  B. I  C. I  D. I  3 3 3 3 C©u 29 : 1 dx
Đổi biến x=2sint tích phân I   trở thành 2  0 4 x     6 6 6 3 A. 1 dtB. tdtC. dtD. dtt 0 0 0 0
C©u 30 : Họ các nguyên hàm của hàm số y  sin 2x là: 1 1
A. cos 2x C .
B.  cos 2x C .
C. cos 2x C . D. cos 2x C . 2 2 C©u 31 :  4 3 x  x 1 Cho 2I  dx  . Tính I  2 2  cos x 4 A. 5 B. 2 C. 3 D. 4
C©u 32 : Diện tích hình phẳng giới hạn bởi đồ thị các hàm số C : y  sin x và D : y x   là: 2
S a b . Giá trị 3 2a b là: 33 9 A. 24 B. C. D. 9 8 8 C©u 33 : 2 3 dx Tính: I   2  2 x x 3   A. Đáp án khác B. I C. I = D. I  3 6 C©u 34 : 2 Cho 5
I x(x  1) dx
và u x  1. Chọn khẳng định sai trong các khẳng định sau: 1 1 1 6 5   1 5 13 u u 5
A. I x(1  x) dxB. I C. I    
D. I  (u  1)u du  42 6 5 2   0 0 5 C©u 35 : 1
Nguyên hàm của hàm số  là 2x  2 1 1 1   1 1  A. C C C. CC 2  B. 4x 2x  3 1 4x D. 2 2x  1 C©u 36 : 2 dx a Giả sử  ln 
(với a,b là các số tự nhiên và ước chung lớn nhất của a,b bằng 1). x  3 b 1
Chọn khẳng định sai trong các khẳng định sau:
A. 3a b  12
B. a  2b  13
C. a b  2 D. 2 2 a b  41 C©u 37 : cos x
Họ nguyên hàm Fx của hàm số f x  là: 2 1 cos x A.   cos x F x    C B.   1 F x    C sin x sin x 1 C.   1 F x   C D. Fx   C sin x 2 sin x
C©u 38 : Cho hình phẳng (S) giới hạn bởi Ox, Oy, y = 3x + 2. Thể tích cuaa3 khối tròn xoay khi quay (S) quanh Oy là: 8 4 2 16 A. B. C. D.  3 3 3 3
C©u 39 : Cho hình phẳng (S) giới hạn bởi Ox và 2
y  1 x . Thể tích của khối tròn xoay khi quay (S) quanh Ox là 3 4 3 2 A. B. C. D.  2 3 4 3
C©u 40 : Nguyên hàm F(x) của hàm số f (x) x sin x thỏa mãn F(0) 19 là: 2 x 2 x A. F(x) o c sx B. F(x) o c sx 2 2 2 2 x 2 x C. F(x) o c sx 20 D. F(x) o c sx 20 2 2 C©u 41 : 
Tính: L x sin xdx  0 A. L =  B. L =  C. L = 2
D. Đáp án khác 6
C©u 42 : Tìm nguyên hàm của hàm số f xthỏa mãn điều kiện:   
f x  2x  3cos x, F    3  2  2  2  A. 2 F( )
x x  3sin x  6  B. 2 F( )
x x  3sin x  4 4 2  2  C. 2 F( )
x x  3sin x D. 2 F( )
x x  3sin x  6  4 4
C©u 43 : Cho hình phẳng giới hạn bởi các đường 3
y x  1, y  0 , x  0 và x  1 quay quanh trục
Ox . Thể tích của khối tròn xoay tạo thành bằng 23 13 A. B. C. D. 3 9 14 7 C©u 44 : 2
y x  3x
Diện tích hình phẳng được giới hạn bởi hai đường
và y x bằng (đvdt) 32 16 8 A. C. D. 2 3 B. 3 3
C©u 45 : Họ các nguyên hàm của hàm số 3
y  tan x là: 1 A. 2
tan x  ln cos x . B. 2
tan x  ln cos x 2 1 1 C.  2
tan x  ln cos x D. 2
 tan x  ln cos x 2 2 C©u 46 : 1
Nguyên hàm F(x) của hàm số f (x) 2x thỏa mãn F( ) 1 2 sin x 4 là: 2 2 A. 2 F(x) o c tx x B. 2 F(x) o c tx x 4 16 2 C. 2 F(x) o c tx x D. 2 F(x) o c tx x 16
C©u 47 : Cho hàm số f x  cos3x.cos x . Nguyên hàm của hàm số f x bằng 0 khi x  0 là hàm số
nào trong các hàm số sau ? sin 4x sin 2x sin 4x sin 2x cos 4x cos 2x A. 3sin 3x  sin x B. C. D.  8 4 2 4 8 4
C©u 48 : Họ nguyên hàm của f x  cosxcos3x là 7 sin 3x A. sinx  C
B. 2sin 4x  sin2x  C 3 sin 4x sin 2x sin 4x sin 2x C.   C D.    C 8 4 8 4
C©u 49 : Diện tích hình phẳng giởi hạn bởi các đường cong 2
y x  2x và y x  6 95 265 125 65 A. B. C. D. 6 6 6 6
C©u 50 : Nguyên hàm F(x) của hàm số 3 2 f (x) 4x 3x 2x 2 thỏa mãn F(1) 9 là: A. 4 3 2 F(x) x x x 2 B. 4 3 2 F(x) x x x 10 C. 4 3 2 F(x) x x x 2x D. 4 3 2 F(x) x x x 2x 10 C©u 51 : e e
Nguyên hàm của hàm số f xx x  x x ee  1  1 A. ln x x e eC B. C   D. C x x e C. ln x x e e C ex x e e C©u 52 : 2
Tính: K  (2x 1) ln xdx  1 1 1 1
A. K  2 ln 2  B. K
C. K  2 ln 2  D. K = 2ln2 2 2 2 C©u 53 : 1 Tính dx  , kết quả là : 2 x  4x  3 1 x 1 1 x  3 x  3 A. ln  C B. ln  C C. 2 ln x  4x  3  C D. ln  C 2 x  3 2 x 1 x 1 C©u 54 :  2 dx Tích phân I   bằng 2  sin x 4 A. 1 B. 3 C. 4 D. 2 C©u 55 : 1 Tích phân x I xe dx  bằng 0 A. 1 B. 2 C. 3 D. 4 8 C©u 56 : sinx cosxe ; x   0 
Cho f x   1
. Nhận xét nào sau đây đúng? ; x   0   1 x e x  
A. F x cosx ; 0  
là một nguyên hàm của f x 2 1 x  1 ; x   0 e x  
B. F x sinx ; 0  
là một nguyên hàm của f x 2 1 x ; x   0 e x  
C. F x cosx ; 0  
là một nguyên hàm của f x
2 1 x ; x   0 e x  
D. F x sinx ; 0  
là một nguyên hàm của f x 2 1 x  1 ; x   0 C©u 57 : 2 3 3 Tính I  dx  , kết quả là : 2  2 x x 3    A. I   B. I  C. I  D. I  6 3 2 C©u 58 : 2 (x 1) Tính: K dx
= a.ln5+ b.ln3 thì giá trị của a và b là 2 x  4x  3 0 A. A=2; b=-3 B. A=3; b=2 C. A=2; b=3 D. A=3; b=-2 C©u 59 : 2 3 3
Nếu f (x)dx  3 
và f (x)dx  4 
thì f (x)dx  có giá trị bằng 1 2 1 A. 1  B. 1 C. 7 D. 12
C©u 60 : Họ nguyên hàm Fx của hàm số   2 f x  cot x là : A. cot x  x  C
B. cot x  x  C C. cot x  x  C D. tan x  x  C
C©u 61 : Nguyên hàm của hàm số: y = sin2x.cos3x là: 1 1 A. 3 5 sin x  sin x  C
B. sin3x + sin5x + C 3 5 1 1 C. 3 5  sin x  sin x  C
D. sin3x  sin5x + C 3 5
C©u 62 : Gọi S là diện tích hình phẳng giới hạn bởi các đường 3
y  x  3x ; y  x ; x  2  ; x  2 . Vậy 9 S bằng bao nhiêu ? A. 4 B. 8 C. 2 D. 16 C©u 63 : 1 a e x 1 Cho 3 e d x
. Khi đó khẳng định nào sau đây là đúng b 0 A. a b B. a b C. a b D. a b
C©u 64 : Trong các khẳng định sau khẳng định nào sai? 1 A. 0dx C  (C là hằng số) B.
dx  ln x C  (C là hằng số) x 1 C. 1 x dx x    C  (C là hằng số) D.
dx x C  (C là hằng số)  1 C©u 65 :  2 2 s in x 1 Tính tích phân I dx
được kết quả I  ln b  3c với ; a ;
b c  . Giá trị của  sin 3x a 6
a  2b  3c là: A. 2 B. 3 C. 8 D. 5 C©u 66 : Hàm số ( ) xx
F x e e
x là nguyên hàm của hàm số xx 1 A. ( ) x x
f x e e  1 B. 2
f (x)  e e x 2 xx 1 C. ( ) x x f x e e    1 D. 2
f (x)  e e x 2 C©u 67 : x  
Một nguyên hàm của f  x 2 2x 3  là x 1 2 x 2 x A.  3x  6ln x 1 B.  3x-6ln x 1 2 2 2 x 2 x C.  3x+6ln x 1 D.  3x+6ln x 1 2 2 C©u 68 : dxx  
Tính nguyên hàm I  
được kết quả I  ln tan     C với ; a ;
b c  . Giá trị của cosx 2  a b  2 a b là: A. 8 B. 4 C. 0 D. 2 10 C©u 69 : a x 1 Cho dx e
. Khi đó, giá trị của a là: x 1 2 e 2 A. B. e C. D. 1 e 2 1 e
C©u 70 : Diện tích hình phẳng giới hạn bởi 2 y x 4x 3 , x 0,x 3 và trục Ox là 1 2 10 8 A. B. C. D. 3 3 3 3 C©u 71 : 2
2 x.3x.7x dx  là 2 2 x.3x.7x 84xC A. C B. x ln 4.ln 3.ln 7
C. 84x C
D. 84 ln84  C ln 84
C©u 72 : Cho (H) là hình phẳng giới hạn bởi P 2 y  x  4x+4,y=0,x=0,x=3
Thể tích V khi quay (H) quanh trục Ox là 33 33 A. 33 B. C. D. 33 5 5 C©u 73 :  6 Tính: I  tg  xdx 0 2 3 2 3 3 1 A. ln B. - ln C. ln D. ln 3 3 2 2 C©u 74 : x
Một nguyên hàm của f  x  là 2 cos x A. xtan x  ln cosx
B. xtan x  lncosx C. xtan x  ln cosx D. xtan x  ln sin x C©u 75 : 2 a e x 1 Cho
e sin x d x . Khi đó sina o c s2a bằng b 0 A. 1 B. 2 C. 4 D. 0
C©u 76 : Diện tích hình phẳng giới hạn bởi 3 y x ;y 4x , x 0,x 3 là : 11 A. 5 B. 4 C. 1 D. 8 C©u 77 : e
Tích phân x ln xdx  bằng 1 2 e 2 e 2 e  1 2 1 e A. B.  1 C. D.  4 4 4 2 4 C©u 78 : 2 Tính dx  ?    1 1 x 1 A. 2ln3 B. ln3 C. ln2 D. ln6 C©u 79 : 1 (x 1)d x Cho a
b . Khi a b bằng: 2 0 x 2x 2 A. 5 B. 1 C. 2 D. 3 C©u 80 :  2 e cos ln x Cho I  dx  , ta tính được : x 1 A. I  cos1 B. I 1 C. I  sin1
D. Một kết quả khác 12 ĐÁP ÁN 01 { | } ) 28 { ) } ~ 55 ) | } ~ 02 { | ) ~ 29 ) | } ~ 56 { | } ) 03 { | } ) 30 { ) } ~ 57 { ) } ~ 04 ) | } ~ 31 { | ) ~ 58 ) | } ~ 05 { ) } ~ 32 { | } ) 59 { | ) ~ 06 { | ) ~ 33 ) | } ~ 60 { ) } ~ 07 { ) } ~ 34 { | ) ~ 61 ) | } ~ 08 { | } ) 35 ) | } ~ 62 { ) } ~ 09 { | ) ~ 36 { | ) ~ 63 { | } ) 10 ) | } ~ 37 { ) } ~ 64 { | ) ~ 11 { | ) ~ 38 { ) } ~ 65 { | } ) 12 ) | } ~ 39 { ) } ~ 66 { | ) ~ 13 { ) } ~ 40 { | } ) 67 { | ) ~ 14 { ) } ~ 41 ) | } ~ 68 { | } ) 15 { | ) ~ 42 { | } ) 69 { ) } ~ 16 { ) } ~ 43 { | ) ~ 70 { | } ) 17 { | ) ~ 44 ) | } ~ 71 ) | } ~ 18 ) | } ~ 45 { ) } ~ 72 { | ) ~ 19 ) | } ~ 46 { | } ) 73 ) | } ~ 20 ) | } ~ 47 { ) } ~ 74 { | ) ~ 21 { ) } ~ 48 { | ) ~ 75 { | } ) 22 { | } ) 49 { | ) ~ 76 { | } ) 23 ) | } ~ 50 { | } ) 77 { | ) ~ 24 { | ) ~ 51 ) | } ~ 78 { | } ) 25 { ) } ~ 52 ) | } ~ 79 { | } ) 26 { | } ) 53 { ) } ~ 80 { ) } ~ 27 { | } ) 54 ) | } ~ 13 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 04 C©u 1 : 3 dx Giả sử k  0 và  ln(2  3) 
. Giá trị của k là 2  0 x k A. 3 B. 2 C. 2 3 D. 1 C©u 2 : Hàm số 10
f (x)  x 1
(  x) có nguyên hàm là: (x  ) 1 12 (x  ) 1 11 (x  ) 1 12 (x  ) 1 11
A. F(x)    C
B. F(x)    C 12 11 12 11 (x  ) 1 11 (x  ) 1 10 (x  ) 1 11 (x  ) 1 10
C. F(x)    C
D. F(x)    C 11 10 11 10 C©u 3 : 2 Cho tích phân 2 x sin x 2m dx 1
. Giá trị của tham số m là: 0 A. 5 B. 3 C. 4 D. 6 C©u 4 : Tính cos5 . x cos 3xdx  1 1 1 1 A. sin 8x  sin 2x C B. sin 8x  sin 2x 8 2 2 2 1 1 1  1 C. sin 8x  sin 2x D. sin 8x  sin 2x 16 4 16 4
C©u 5 : Diện tích hình phẳng giới hạn bởi các đường: x   ; 1 x  ; 2 y  ;
0 y x2  2x là: 8 8 2 A. 0 B. C. D. 3 3 3
C©u 6 : Nguyên hàm của hàm số 2 cos . x sin . x dx  bằng::
3cos x  cos 3x
3sin x  sin 3xC 3 A. C B. 12
C. sin x C . D. 2 sinx.cos x C 12 1 C©u 7 : dx Tính  . x ln x
A. ln x C
B. ln | x | CC. ln(lnx)  C D. ln | lnx |  C
C©u 8 : Diện tích hình phẳng giới hạn bởi: y x2  2x; y  x2  4x là: 20 16 A. -9 B. 9 C. D. 3 3
C©u 9 : Họ nguyên hàm của hàm số 2 f x cos x là : x cos 2x x cos 2x x sin 2x x sin 2x A. C B. C C. C D. C 2 4 2 4 2 4 2 4 C©u 10 : x 1  x 1   Cho hàm số 2 5 f (x)  . Khi đó: 10x 2 1 2 1 A.
f (x).dx     C  . B.
f (x).dx    C  5 .
x ln 5 5.2 .xln 2 5x ln 5 5.2 . x ln 2 5x 5.2x 5x 5.2x C.
f (x).dx    CD.
f (x).dx     C  2 ln 5 ln 2 2 ln 5 ln 2 C©u 11 : 2016 e Tích phân  1 cos(ln x).dx = 2016   .e m . Khi đó giá trị m: 1 2 1 A. m   B. m  1 C. m  2 m   2 D. 1 C©u 12 : 2 2
Thể tích khối tròn xoay khi cho Elip x y
1 quay quanh trục Ox, có kết quả bằng: 2 3 b 4 3 2 3 A. 2 bC. 4b D. 2 b 3 B. 2 b 3 C©u 13 : a dx Tìm a thỏa mãn:  0  4 2  x 0 A. a=ln2 B. a=0 C. a=ln3 D. a=1 C©u 14 : ln 2 Cho x I  2 
. Khi đó kết quả nào sau đây là sai : x A. x I  2  C B. x 1 I 2    C C. x I  2(2 1)  C D. x I  2(2 1)  C
C©u 15 : Thể tích khối tròn xoay giơi han bởi các đường 2
y  2x x ;y  0 khi quay quanh trục Ox là: 2 4 18 16 12 A. V V V D. V  15 B. 15 C. 15 15
C©u 16 : Trong các khẳng định sau, khẳng định nào sai?
F x   1  tanx f x  2  1  tan x A.
là một nguyên hàm của hàm số
Nêu F(x) là một nguyên hàm của hàm số f(x) thì mọi nguyên hàm của f(x) đều có dạng
B. F x  C (C là hằng số) u ' x
   dx  lg ux C u x C.
F x   5  cosx
f x   sinx D. là một nguyên hàm của C©u 17 : Tích phân: x I xe dx  bằng: 1 A. e B. e  1 C. 1 e  1 D. 2 C©u 18 : 2
y x  3x  2 
Tính diện tích hình phẳng giới hạn bởi  y x 1
x  0, x  2  8 2 4 A. B. 3 3 C. 3 D. 2 C©u 19 : 
Cho hình phẳng D giới hạn bởi: y  tan ; x x  ; 0 x
; y  0 gọi S là diện tích hình phẳng 3
giới hạn bởi D. gọi V là thể tích vật tròn xoay khi D quay quanh ox. Chọn mệnh đề đúng.  
A. S=ln2, V   ( 3  )
B. S=ln2; V   ( 3  ) 3 3  
C. S=ln3; V   ( 3  )
D. S=ln3; V   ( 3  ) 3 3 C©u 20 : y  0
(H) giới hạn bởi các đường: 
. Tính thể tích vật tròn xoay khi quay (H) quanh Ox 2
y  2x  x 3 4 16 4 16 A. B. C. D. 3 15 3 15 C©u 21 : x Cho g(x)  cos tdt
. Hãy chọn câu khẳng định đúng trong 4 câu khẳng định sau: 0 cos x
A. g '(x)  sin(2 x)
B. g '(x)  cos x
C. g '(x)  sin x
D. g '(x)  2 x C©u 22 : 0
Cho f (x) là hàm số chẵn và f (x)dx a
 chọn mệnh đề đúng 3 3 3 3 0 A.
f (x)dx   aB.
f (x)dx 2aC. f (x)dx a   D. f (x)dx a   0 3 3 3 C©u 23 : 2 x Giả sử
f (t)dt x cos( x) 
. Giá trị của f (4) là 0 1 1 A. 1 B.
C. Một đáp số khác. D. 2 4
C©u 24 : Một nguyên hàm của hàm số: f (x)  cos5x.cosx là: 1  sin 6x sin 4x
A. F(x)      B. F(x)  sin 6x 2  6 4  1  1 1  C. F(x)  cos 6x
D. F(x)  sin 6x  sin 4  x  2  6 4 
C©u 25 : Trong các mệnh đề sau, mệnh đề nào sai: 4 2 x x x 1 A. 3 x x dx C B. 2 x e dx e C 4 2 2 2 dx 4 C. sin xdx cos x C D. ln 2 x x 3 1 C©u 26 : x d Tính  2 x  2x  3 1  x 1 1  x  3 1 x  3 1 x 1 A. ln  C B. ln  C C. ln  C D. ln  C 4 x  3 4 x 1 4 x 1 4 x  3 C©u 27 : Tính 2 x x  3dx  4 2 2 (x  3) 2 x A. 2 x  3  C B. 2 2
(x  3)  C C. C D. C 4 4
C©u 28 : Tính diện tích hình phẳng giới hạn bởi các đường: 2 2
y x , y  4x , y  4 4 8 A. 8 B. 4 C. D. 3 3
C©u 29 : Trong các khẳng định sau, khăng định nào sai?
A.  f x f x dx f x dx f x dx   1   2   1   2   F x G x B.
đều là nguyên hàm cùa hàm số f x  thì F x  G x   C là hằng số Nếu và
C. F x   x
f x   2 x là một nguyên hàm của   2 F x x
f x   2x D. là một nguyên hàm của
C©u 30 : Trong các khẳng định sau khẳng định nào sai? F x  2  7  sin x
f x   sin2x A.
là một nguyên hàm của hàm số F x G x
F x G xdx Nếu và
đều là nguyên hàm của hàm số f(x) thì có dạng
B. hx Cx D(C,D là các hằng số, C  0) u ' x
C.     ux C u x f
 tdt F t  f
 uxdt F u x  D. C C Nếu thì C©u 31 : 2 2
Diện tích hình phẳng giới hạn bởi x y y  và x
( với a  0 ) có kết quả bằng: a a 2 a 2 a 2 a A. C. D. 3 B. 2 a 2 4 C©u 32 : 1 3 4x Cho 2 3.m  .dx  0  . Khi đó 2 144.m 1 bằng: 4 2 (x  2) 0 2 2 3 A. B. 4 3 1
D. Kết quả khác.. 3 C. 3 5
C©u 33 : Thể tích vật giới hạn bởi miền hình phẳng tạo bởi các đường 2 y  x và y  4 khi quay quanh trục Ox là : 64 152 128 256 A. B. C. D. 5 5 5 5 C©u 34 : 1 2 (2x  5x  ) 2 dx Tính I   3 x  2 2x  4x  8 0 1 1 3 1 1 A. I   ln12 B. I   ln C. I
 ln 3  2ln 2 D. I   ln 3  2ln 2 6 6 4 6 6 C©u 35 : 1 Tính 2
(x  3x  )dxx 3 x 3 A. 3 2
x  3x  ln x C B. 2
x  ln x C 3 2 3 x 3 1 3 x 3 C. 2  x   C D. 2
x  ln | x | C 2 3 2 x 3 2
C©u 36 : Cho hàm số y  f (x) có nguyên hàm trên (a ;b) đồng thời thỏa mãn f (a)  f (b) . Lựa chọn phương án đúng : b b f ( x ) f ( x ) A. f '(x).e dx  0  B. f '(x).e dx  1  a a b b f ( x ) f ( x ) C. f '(x).e dx  1   D. f '(x).e dx  2  a a C©u 37 : 4  Cho hàm số 5 2x f (x)  . Khi đó: 2 x 3 2x 5 5 A.
f (x)dx    CB. 3
f (x)dx  2x   C  3 x x 3 2x 5 3 2x C.
f (x)dx    CD. 2
f (x)dx   5lnx C  3 x 3 . C©u 38 : 2 Cho 2 I  2x x  1dx
. Khẳng định nào sau đây sai: 1 3 3 2 2 3 A. I udx  2 I  27 C. I  3 3 D. I t 0 B. 3 3 0 6 C©u 39 : b b b Biết f (x)dx  10  và g(x)dx  5 
. Khi đó giá trị của tích phân : I  (3f (x)  5g(x))dx  là : a a a A. I  5 B. I  5  C. I  10 D. I  15
C©u 40 : Diện tích hình phẳng giới hạn bởi 3 3 y x và 2 y x x  bằng: 2 2 23 3 55 1 A. B. C. D. 3 2 12 4 C©u 41 : 4 Cho hàm số 2 f x x x
1 . Biết F(x) là một nguyên hàm của f(x); đồ thị hàm số y F x đi
qua điểm M 1;6 . Nguyên hàm F(x) là. 4 5 2 x 1 2 x 1 A. 2 2 F x B. F x 4 5 5 5 5 4 2 x 1 2 x 1 C. 2 2 F x D. F x 5 5 4 5 C©u 42 : dx Kết quả I   là : x 1
A. 2 x  2ln( x 1)  C
B. 2  2ln( x 1)  C
C. 2 x  2ln( x 1)  C
D. 2 x  2ln( x 1)  C C©u 43 : dx Tính:  1  cos x x x 1 x 1 x A. 2 tan  C B. tan  C C. tan  C D. tan  C 2 2 2 2 4 2
C©u 44 : Hình phẳng (H) giới hạn bởi các đường y x, y  6  x và trục hoành thì diện tích của hình phẳng (H) là: 20 25 16 22 A. B. C. D. 3 3 3 3
C©u 45 : Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đường  4 4 3
y  sin x  cos x
, y  0, x  0, x
quay quanh trục hoành Ox là 4 12  3 3  3  3 A. B. C. D. 16 32 24 32 7 C©u 46 : a 3 Biết  4
(4sin x  )dx  0 giá trị của a  ; 0 (  ) là: 2 0     A. a B. a C. a D. a  4 2 8 3 C©u 47 : e ln x 1 Giá trị của dx là : x 1 e 3 1 2 e e A. B. C. D. 2 2 2 2
C©u 48 : F x  x  ln 2sinx  cosx là một nguyên hàm của: sinx cosx
2 cos x  sin x
3 sin x  cos x sin x  cos x
A. 3cosx  sinx
B. 2sinx  cosx
C. 2sinx  cosx
D. 3cosx  sinx
C©u 49 : Tính thể tích vật thể tròn xoay sinh ra khi quay (H) quanh trục Ox, biết (H) là hình phẳng tan x e   
giới hạn bởi (C): y x
cos x , trục Ox, trục Oy và đường thẳng 3 2  2  A. 3 (e 1) B. 2 3  (e 1) C.  3  (e 1) D. 2 3 (e 1) 2 2
C©u 50 : Cho hàm số f x sin 2 .
x cos x và các mệnh đề sau: 2
i) Họ nguyên hàm của hàm số là 3 cos x C 3 1 1
ii) Họ nguyên hàm của hàm số là cos3x cos x C 6 2 2
ii) Họ nguyên hàm của hàm số là 3 cos x C 3
A. Chỉ có duy nhất một mệnh đề đúng.
B. Có hai mệnh đề đúng.
C. Không có mệnh đề nào đúng.
D. Cả ba mệnh đều đều đúng.
C©u 51 : Khẳng định nào sau đây là đúng:
(a) Một nguyên hàm của hàm số cos x y e là cos sin . x x e . 2 2 x  6x 1 x 10
(b) Hai hàm số f (x)  ; g(x) 
đều là nguyên hàm của một hàm số. 2x  3 2x  3   (c) 1 x 1  (  1) x xe dx x eC  . 8 1 1 2 3 xx e dx e dx   0 0 A. (a) B. (c) C. (d) D. (b)
C©u 52 : Thể tích khối tròn xoay tạo nên khi quay hình H quanh trục Ox, với
H  y x ln ;
x y  0; x 1; x   e bằng: 3  (5e  3) 3  (e 1) 3  (e  3) 3  (e 1) A. B. C. D. 27 2 27 3
C©u 53 : Diện tích hình phẳng giới hạn bởi parabol 2 y
x và đường thẳng y 3x 2 là : 1 1 1 1 A. B. C. D. 4 6 5 3
C©u 54 : Cho hình phẳng (H) giới hạn bởi đường thẳng y
x ; trục hoành và đường thẳng x , m m 0 .
Thể tích khối tròn xoay tạo bởi khi quay (H) quanh trục hoành là 9 (đvtt). Giá trị của tham số m là : A. 9 B. 3 3 C. 3 D. 3 3 3 C©u 55 : 3 x 1
Tìm 1 nguyên hàm F(x) của f (x)  biết F(1) = 0 2 x 2 x 1 1 2 x 1 3
A. F(x)    F (x)    2 x 2 B. 2 x 2 2 x 1 1 2 x 1 3
C. F(x)    D. F(x)    2 x 2 2 x 2 C©u 56 : sin x  cos x Nguyên hàm của là: sin x  cos x 1
A. ln sin x  cos x CC
B. ln sinx  cosx 1
C. ln sin x  cos x C D. C sin x  cos x
C©u 57 : Giả sử hình phẳng tạo bởi các đường cong y  f (x); y  0;x  a; x  b có diện tích là S còn 1
hình phẳng tạo bởi đường cong y |
 f (x) |;y  0;x  a;x  bcó diện tích làS , còn hình 2
phẳng tạo bởi đường cong y  f
 (x);y  0;x  a;x  bcó diện tích là S3. Lựa chọn phương án đúng: 9 A. S  S B. S  S  S  S D. S  S 1 3 1 3 C. 1 3 2 1 C©u 58 : 1 2 Cho n  và nx e
4xdx  (e 1)(e 1) 
. Giá trị của n là 0 A. 1 B. 3 C. 4 D. 2 C©u 59 : 5 2x 1 Giá trị của E dx  là:
2x  3 2x 1  1 1 5
A. E  2  4ln15  ln 2
B. E  2  4ln  ln 4 3 3 5
C. E  2  4ln  ln 2
D. E  2  4ln  ln 4 5 3
C©u 60 : Một nguyên hàm của hàm số f (x)  1 2x là : 3 3 A. (2x 1) 1 2x B. (2x 1) 1 2x 4 2 3 3
C.  (1 2x) 1 2x D. (1 2x) 1 2x 2 4 C©u 61 : 2 0 Cho f x dx
1 và f x là hàm số chẵn. Giá trị tích phân f x dx là : 0 2 A. -2 B. 1 C. -1 D. 2 C©u 62 : 2 x  2x  6
Họ nguyên hàm của hàm số f (x)  là 3 2
x  7x 14x  8
A. 3ln x 1  7ln x  2  5ln x  4  C
B. 3ln x 1  7ln x  2  5ln x  4  C
C. 3ln x 1  7ln x  2  5ln x  4  C
D. 3ln x 1  7ln x  2  5ln x  4  C C©u 63 : 1
Giá trị của K x ln   2
1  x dx là: 0 5 2 5 2 A. K   2  ln B. K   2  ln 2 2 2 2 5 2 5 2 C. K   2  ln D. K   2  ln 2 2 2 2
C©u 64 : Xác định a,b,c để hàm số 2 x
F(x)  (ax bx c e )
là một nguyên hàm của hàm số 10 2 x
f (x)  (x  3x e ) 2 a   , 1 b  , 1 c  1  A. a  , 1 b  , 1 c  1  B. a   , 1 b  , 1 c  1 C. D. a  , 1 b  , 1 c  1 C©u 65 : Họ nguyên hàm 3 x x 1 dx là : 5 4 5 4 x 1 x 1 x 1 x 1 A. C B. C 5 4 5 4 5 4 2 x 3x x 5 4 2 x 3x x C. 3 x C D. 3 x C 5 4 2 5 4 2
C©u 66 : Diện tích hình phẳng (H) giới hạn bởi đường cong y x 2 ; đường thẳng y x và trục hoành là : 8 7 10 A. B. C. D. 3 3 3 3 C©u 67 : 4 x Tích phân: 4
(3x e ).dx
= a + b.e. Khi đó a + 5b bằng 0 A. 8 B. 18 C. 13 D. 23.
C©u 68 : Diện tích hình phẳng giới hạn bởi các đường 2
y x x  2 và y  2x  4 là: 7 5 9 11 A. 2 B. 2 C. 2 D. 2 C©u 69 : a 2 2 2x ln x ln 2 Biết dx 3
, a là tham số. Giá trị của tham số a là. x 2 1 A. 4 B. 2 C. -1 D. 3 C©u 70 : 2
Giả sử A, B là các hằng số của hàm số 2
f (x)  Asin( x)  Bx . Biết f '(1)  2 và f (x)dx  4  . 0 Giá trị của B là 3 A. 1
B. Một đáp số khác C. 2 D. 2
C©u 71 : Hàm số f (x)  x x 1có một nguyên hàm là F(x) . Nếu F(0)  2 thì giá trị của F(3) là 116 146 886 A.
B. Một đáp số khác C. D. 15 15 105 11
C©u 72 : Trong các khẳng định sau, khẳng định nào đúng? dx 2 A.
 2 1  x C  2 1  x b B. Nếu f
 xdx  0 thì f x  0,x  a;b   a b c b C. f
 xdx g
 xdx f  xdx , a , b c f x  với mọi thuộc TXĐ của a a c D. F x f x
Nếu F(x) là nguyên hàm của f(x) thì
là nguyên hàm của hàm số 12 ĐÁP ÁN 01 { | } ) 28 { | } ) 55 { | } ) 02 { ) } ~ 29 { | ) ~ 56 { | ) ~ 03 { | ) ~ 30 { | ) ~ 57 ) | } ~ 04 { | ) ~ 31 ) | } ~ 58 { | } ) 05 { ) } ~ 32 ) | } ~ 59 { ) } ~ 06 ) | } ~ 33 { ) } ~ 60 ) | } ~ 07 { | } ) 34 { ) } ~ 61 { | ) ~ 08 { ) } ~ 35 { | } ) 62 { | } ) 09 { | ) ~ 36 ) | } ~ 63 ) | } ~ 10 ) | } ~ 37 ) | } ~ 64 { ) } ~ 11 ) | } ~ 38 { | ) ~ 65 { ) } ~ 12 ) | } ~ 39 ) | } ~ 66 { | ) ~ 13 { ) } ~ 40 ) | } ~ 67 ) | } ~ 14 ) | } ~ 41 { ) } ~ 68 { | ) ~ 15 { | ) ~ 42 ) | } ~ 69 { ) } ~ 16 { | ) ~ 43 { ) } ~ 70 { | } ) 17 { | ) ~ 44 { | } ) 71 { | } ) 18 { | } ) 45 { | } ) 72 { | ) ~ 19 { ) } ~ 46 { ) } ~ 20 { | } ) 47 { ) } ~ 21 { | } ) 48 { | ) ~ 22 { ) } ~ 49 { | } ) 23 { | } ) 50 { ) } ~ 24 ) | } ~ 51 { | } ) 25 { | ) ~ 52 ) | } ~ 26 { | } ) 53 { ) } ~ 27 { | ) ~ 54 { | ) ~ 13 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 05 C©u 1 : 2 Hàm số ( ) ex f x
là nguyên hàm của hàm số nào ? 2 ex 2 A. f (x) B. 2 ( ) e x f x C. ( ) 2 ex f x x D. 2 2 ( ) ex f x x 1 2x
C©u 2 : Tìm khẳng định đúng trong các khẳng định sau 3 1 3 3 A. x 2 dx x 1 dx B. x 2 dx x 2 dx 0 2 0 0 3 3 2 3 2 3 C. x 2 dx x 2 dx x 2 dx D. x 2 dx x 2 dx x 2 dx 0 2 0 0 0 2
C©u 3 : Giá trị trung bình của hàm số y f x trên  ;
a b , kí hiệu là mf  được tính theo công thức mf  1 bf
 xdx . Giá trị trung bình của hàm số f x  sinx trên 0;  là: b a a 2 3 1 4 A. B. C. D.  C©u 4 : dx   2 2 sin x cos x 1 1 A. 1   C
B. tan x  cot x C
C.  tan x  cot x C D.    C cos x sin x C©u 5 : 3 x Tích phân: dx  2 cos x 0 3 3 3 A.   ln 2 B.    ln 2 C.    ln 2 D. 3  ln 2 3 3 3 3
C©u 6 : Diện tích hình phẳng giới hạn bởi các đường thẳng  3x y
, y  4  x và trục trung bằng 7 1 7 2 5 2 2 A.  (đvdt) B.  (đvdt) C.  (đvdt) D. 1 (đvdt) 2 ln 3 2 ln 3 2 ln 3 ln 3 1
C©u 7 : Tìm khẳng định sai trong các khẳng định sau 1 2 x x 1 A. sin dx 2 sin xdx B. e dx 1 2 e 0 0 0 1 1 C. sin x dx cos x dx D. sin(1 x)dx sin xdx 4 4 0 0 0 0
C©u 8 : Tính thể tích khối tròn xoay tạo bởi quay quanh trục Ox và hình phẳng giới hạn bởi   C  2x 1 : y
, y  0, x  1  x 1 3 7 1 5 A. B. C. D. 2 2 2 2 C©u 9 :  1 dx 2 Cho I  , J     4 4 4
sin x  cos x dx và K   2x 3x 
1 dx. Tích phân nào có giá trị 0 0 3x 1 1  63 bằng ? 6 A. I B. K C. J D. J và K C©u 10 : 2 Giá trị của 2 2 x e dx bằng ? 0 A. 4 e B. e4 4 C. 4 e 1 D. e4 3 C©u 11 : 2
Diện tích hình phẳng giới hạn bởi y x  4x  5 và hai tiếp tuyến tại A(1; 2) và B(4; 5) là: 13 9 15 11 A. B. C. D. 4 4 4 4 C©u 12 : 2x   x x  9 d 4 2 1   1 4 1       A. C B. C C. C D. C 5 x  95 2 3 x  93 2 x 95 2 x 93 2 C©u 13 : 2 Tích phân: 2 2 x e dx  0 A. 4 e B. 4 3e C. 4 4e D. 4 e  1
C©u 14 : Họ nguyên hàm của hàm số: y = sin3x.cosx là: 2 1 1 A. tg3x + C B. cos2x + C C. 3 cos x  C D. 4 sin x  C 3 4 C©u 15 :
sinx cos 2x dx   1 1 1 1
A.  cos 3x  cos x C
B.  cos 3x  cos x C 2 2 6 2 1 1 1 1 C. sin 3x  sin x C D. cos 3x  cos x C 6 2 2 2 C©u 16 : 2a Với a
0 . Giá trị của tích phân
x sin ax dx là 0 1 1 A. B. C. D. 2 a 2 2 a 2 a 2 a 2a
C©u 17 : Nguyên hàm xcos xdx  
A. xsin x  cos x C B. xsin x  cos x C C. xsin x  cos x
D. xsin x  cos x C©u 18 : 2  x
Nguyên hàm của (với C hằng số) là dx  2 1  x 1  x x 1 2 A. C B. C C. C
D. ln 1  x C 1  x 1  x 1  x C©u 19 : 2
Diện tích hình phẳng giới hạn bởi trục hoành, đường cong (C) y x  2x  3, tiếp tuyến
với (C) tại A(1; 6) và x= -2 là: 7 9 5 11 A. B. C. D. 2 2 2 2 C©u 20 :  2 3  Tích phân x sin x e  2
3x  cos xdx   0 3  3  3  3  A. 1  1  1  1  8 e 1 B. 8 eC C. 8 e 1 D. 8 eC
C©u 21 : Họ nguyên hàm của hàm số f x  sin 2x là
A. F x 1
  cos2x C
B. F x  cos 2x C 2
C. F x 1
 cos2x C
D. F x  cos2x C 2 3 C©u 22 : a sin x Cho dx . Giá trị của a là sin x cos x 4 0 A. B. C. D. 3 4 2 6 C©u 23 :  Tính: x
L e cos xdx  0 1  1  A.   L e 1
B. L e  1
C. L   (e 1)
D. L  (e 1) 2 2
C©u 24 : Trong các mệnh đề sau, mệnh đề nào sai? 3 sin x 2
(I ) : sin x dx   C  3 4x  2 (II ) : dx  2 ln 
 2x x3 C 2  x x  3 x   x x III   6x ( ) : 3 2 3 dx   x C ln 6 A. (III ) B. (I ) C. Cả 3 đều sai. D. (II )
C©u 25 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y  2x là 5 3 23 4 A. B. C. D. 3 2 15 3 C©u 26 :  4 Tính 2 I  tg xdx  0   A. I = 2 B. I C. ln2 D. I  1 3 4
C©u 27 : Nguyên hàm của hàm số: y = sin3x.cosx là: 1 1 1 A. 4 cos x  C B. 4 sin x  C C. cos2x + C D. 3 sin x  C 4 4 3
C©u 28 : Diện tích hình phẳng giới hạn bởi đồ thị 2
(P) : y x  2x  3 và hai tiếp tuyến của (P) tại (0
A ;3) và B(3;6) bằng: 7 9 9 17 A. (đvdt) B. (đvdt) C. (đvdt) D. (đvdt) 2 4 2 4 4 C©u 29 : 2
Tính: K  (2x 1) ln xdx  1 1 1 1
A. K  3ln 2  B. K C. K = 3ln2
D. K  3ln 2  2 2 2 C©u 30 : sin 2x
Nguyên hàm F(x) của hàm số y  khi F(0)  0 là 2 sin x  3 2 2 sin x 2 ln 2  sin x 2
A. ln 1  sin x B. C. ln cos x D. ln 1  3 3 C©u 31 : 1 Tính: 2 2 x K x e dx  0 2 e  1 2 e 1 2 e 1 A. K B. K C. K D. K  4 4 4 4
C©u 32 : Nguyên hàm ln xdx  
A. ln x x C
B. ln x x
C. ln x x C
D. ln x x C©u 33 : Nếu x 2
f (x) dx e  sin x C
thì f (x) bằng: A. x e  2sin x B. x e  sin 2x C. x 2 e  cos x D. x e  2sin x C©u 34 : e 2 ln x Tính: J dxx 1 1 3 1 1 A. J B. J C. J D. J  2 2 4 3 C©u 35 : x 1 Tính: P dx  2 x 1 2 2 A. 2
P x x 1  x C
B. P x 1  ln x x 1  C 2  D. Đáp án khác. x  2 1 1 C. P x  1  ln  C x C©u 36 : a dx Với a
2 , giá trị của tích phân sau là 2 x 3x 2 0 5 a 2 a 2 a 2 a 2 A. ln B. ln C. ln D. ln 2a 1 a 1 2 a 1 2a 1 C©u 37 : ln 5 dx   ln 3 x e  2 x e  3 7 3 2 2 A. ln B. ln C. ln D. ln 2 2 3 7 C©u 38 : 2 Cho 2
I  2x x 1dx  và 2
u x 1 . Chọn khẳng định sai trong các khẳng định sau: 1 3 2 3 3 2 2 A. I uduB. I uduC. 2 I u D. I  27 0 1 3 3 0
C©u 39 : Tính diện tích hình phẳng được giới hạn bởi 3 2
y x  4x  3x 1, y  2  x 1 1 A. B. 3 C. 1 D. 2 12 C©u 40 : Cho a
0 , diện tích giới hạn bởi các đường có phương trình 2 2 x 2ax 3a 2 a ax C : y và C : y là 1 4 1 a 2 4 1 a 3 3 3 a a a 3 6a A. B. C. D. 4 1 a 4 3 1 a 4 6 1 a 4 1 a
C©u 41 : Tính diện tích hình phẳng được giới hạn bởi 2 y x  2 ,
x y  0, x  1  , x  2 8 7 A. B. 2 C. D. 3 3 3
C©u 42 : Nguyên hàm của hàm số: y = sin2x.cos3x là:
A. sin3x + sin5x + C 1 1 B. 3 5 sin x  sin x  C 3 5
C. sin3x  sin5x + C 1 1 D. 3 5  sin x  sin x  C 3 5 C©u 43 :  6 n 1 Cho sin . x cos . x dx   , giá trị của n là 64 0 A. 3 B. 5 C. 4 D. 6 6 C©u 44 : x  3
Nếu F(x) là một nguyên hàm của hàm f (x) 
,F(0)  0 thì hằng số C bằng 2 x  2x  3 2 3 2 3 A.  ln 3 B. ln 3 C. ln 3 D.  ln 3 3 2 3 2
C©u 45 : Cho đồ thị hàm số y
f x .Diện tích hình phẳng (phần gạch chéo trong Hình 1) là : 2 2 2 A. f x dx B. f x dx f x dx 2 0 0 0 0 1 2 C. f x dx f x dx D. f x dx f x dx 2 2 2 1 C©u 46 : 1
Nếu F(x) là một nguyên hàm của hàm số y
và F(2)  1 thì F(3) bằng x  1 1 3 A. B. ln C. ln 2  2 2 D. ln2 1 C©u 47 : Cho 2 2 C : y 4 x ; C : x 3y
0 . Tính diện tích hình phẳng tạo bởi C và C . 1 2 1 2 2 3 4 3 4 3 3 A. B. C. D. 3 3 5 3 3 3 3 3 C©u 48 : 
Tính: L x sin xdx  0 A. L =  B. L = 2 C. L = 0 D. L =  C©u 49 : 1
Hàm số nào dưới đây là một nguyên hàm của hàm số: y  2 4  x 7 A. 2
F(x)  2 4  x B. 2
F(x)  x  2 4  x 2 2
C. F(x)  ln x  4  x
D. F(x)  ln x  4  x
C©u 50 : Gọi S là miền giới hạn bởi 2 C : y
x ; Ox và hai đường thẳng x 1; x 2. Tính thể tích
vật thể tròn xoay khi S quay quanh trục Ox. 31 1 31 1 31 31 A. B. C. D. 1 5 3 5 3 5 5
C©u 51 : Thể tích khối tròn xoay có được khi cho miền phẳng giới hạn bởi các đường
y  ln x; y  0; x  2 quay xing quanh trục hoành là A.  2ln 2   1 B. 2 ln 2   1 C. 2 ln 2 D.  ln 2   1 C©u 52 : 5 dx Giả sử a
lnb . Giá trị của a,b là ? 2x 1 1 A. a 0;b 81 B. a 1;b 9 C. a 0;b 3 D. a 1;b 8
C©u 53 : Công thức nguyên hàm nào sau đây không đúng? dx  1   x A.  ln x CB. x dx   C      1 x  1 x a dx C. x a dx
C 0  a    1 D.  tan x C  ln a cos x C©u 54 :  2 sin 2x Tích phân dx   2 1 sin x 0  A. ln 2 B. 0 C. ln 3 D. 2 C©u 55 : 0 2x  1 Tích phân: dx   1 x 1 2 1 1 A. 1  ln 2 B.  ln 2 C. ln 2 D. 1  ln2 2 2 C©u 56 : 1 4 4 Giả sử f (x)dx 2, f (x)dx 3, g(x)dx
4 khẳng định nào sau đây là sai ? 0 1 0 8 4 4 4 A. f (x) g x dx 1 B. f (x)dx g(x)dx 0 0 0 4 4 4 C. f (x)dx g(x)dx D. f (x)dx 5 0 0 0 C©u 57 : 1 dx Tính: I   2 x  5x  6 0 4 3 A. I = ln2 B. I  ln C. I  ln D. I = ln2 3 4 C©u 58 : a 1 Biết sin x cos xdx
. Khi đó giá trị của a là 4 0 2 A. B. C. D. 2 3 4 3
C©u 59 : Họ nguyên hàm của hàm số    x
f x e cos x là 1 1 A.    x F x
e sin x  cos x  C B.    x F x
e sin x  cos x  C 2 2 1 1 C.    x
F x   e sin x  cos x  C D.    x
F x   e sin x  cos x  C 2 2 C©u 60 :  16 Cho I x dx  và 4 J  cos2x d . x
Chọn khẳng định đúng. 1 0
A. I J
B. I J
C. I J
D. I J 1 C©u 61 : 1 dx Tính: I   2 x  5x  6 0 4 A. I = 1 B. I = ln2 C. I = ln2 D. I  ln 3 C©u 62 : 1 sin  t
Vận tốc của một vật chuyển động là vt    
m / s . Quãng đường di chuyển của 2 
vật đó trong khoảng thời gian 1,5 giây chính xác đến 0,01m là A. 0,34m B. 0,32m C. 0,33m D. 0,31m C©u 63 : 4 Tích phân: x  2 dx  0 9 A. 0 B. 2 C. 8 D. 4 C©u 64 : 2 Hàm số ( ) x
F x e là nguyên hàm của hàm số 2 x 2 2 e 2 A. ( ) x f x e B. 2 ( ) x
f x x e  1 C. f (x)  D. ( )  2 x f x xe 2x
C©u 65 : Nguyên hàm 2 . x x e dx   A. 2 x  2 x xe e C
B. 2 x  2 x xe e C. 2 x  2 x xe e
D. 2 x  2 x xe e C
C©u 66 : Trong các đẳng thức sau, đẳng thức nào sai? 2 1 2 2 A. sin xdx dx . B. sin xdx costdt 0 0 0 0 2 2 2 C. 1 sin xdx sin 2x 1 d sin 2x 1 . D. sin xdx sintdt . 8 0 0 0 2
C©u 67 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y
x và đường thẳng y 2x là ? 5 23 4 3 A. B. C. D. 3 15 3 2
C©u 68 : Một nguyên hàm của hàm số: 2
f (x)  x sin 1  x là: A. 2 2 2
F(x)   1 x cos 1  x  sin 1  x B. 2 2 2
F(x)   1 x cos 1  x  sin 1  x C. 2 2 2
F(x)  1 x cos 1  x  sin 1  x D. 2 2 2
F(x)  1  x cos 1  x  sin 1  x
C©u 69 : Một nguyên hàm của hàm số: y = cos5x.cosx là: 1  sin 6x sin 4x    1  1 1    sin 6x  sin 4  x
A. F(x) = cos6x
B. F(x) = sin6x C. 2  6 4  D. 2  6 4  C©u 70 : 1 4x 11 a Cho biết I dx  ln 
, với a,b là các số nguyên dương. Giá trị của a b là 2 x  5x  6 b 0 A. 11 B. 12 C. 10 D. 13 C©u 71 : 1 2x Với a 0 . Tích phân dx có giá trị là 2 2 a a x 10 2 1 a 1 a 1 a 1 A. B. C. D. a a a 1 a a 1 a 1 C©u 72 : 1 2
Tính diện tích hình phẳng được giới hạn bởi 3 2
y   x x
, y  0, x  2, x  0 3 3 5 1 2 A. B. C.
D. Tất cả đều sai. 6 12 3 C©u 73 : 3 x Tính K dx  2 x 1 2 8 1 8 A. K = ln2 B. K  ln C. K = 2ln2 D. K  ln 3 2 3 C©u 74 : 2 Tích phân 2 x x dx bằng 0 2 3 A. B. 0 C. 1 D. 3 2 C©u 75 : 2 3 dx Tính: I   2  2 x x 3   A. I = B. I C. Đáp án khác D. I  6 3
C©u 76 : Thể tích của khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường 2 y (1 x ),y 0,x 0 và x 2 bằng : 8 2 2 5 A. B. 2 C. D. 3 5 2
C©u 77 : Một nguyên hàm của hàm số: y = cos5x.cosx là: 1  1 1  1  sin 6x sin 4x  sin 6x  sin 4  x      A. cos6x B. 2  6 4 C. sin6x D. 2  6 4 
C©u 78 : Diện tích của hình phăng giới hạn bởi các đồ thị hàm số 2 y  2  ;
x y x , trục hoành trong miền x  0 là 5 6 7 8 A. B. C. D. 6 7 8 9 11 C©u 79 : 
Tích phân  x  2cos 2xdx   0 1 1 1 A. 0 B. C. D. 4 4 2 C©u 80 : b b c Giả sử f (x)dx 2, f (x)dx 3 với a b c thì
f (x)dx bằng? a c a A. 5 B. 1 C. 1 D. 5 12 ĐÁP ÁN 01 { | ) ~ 28 { ) } ~ 55 { | } ) 02 { | ) ~ 29 { | } ) 56 { | ) ~ 03 ) | } ~ 30 { | } ) 57 { ) } ~ 04 { ) } ~ 31 { ) } ~ 58 { | ) ~ 05 { | } ) 32 ) | } ~ 59 ) | } ~ 06 { ) } ~ 33 { ) } ~ 60 { ) } ~ 07 { | ) ~ 34 { | } ) 61 { | } ) 08 ) | } ~ 35 { ) } ~ 62 ) | } ~ 09 { ) } ~ 36 { | ) ~ 63 { | } ) 10 { | ) ~ 37 { ) } ~ 64 { | } ) 11 { ) } ~ 38 ) | } ~ 65 ) | } ~ 12 { ) } ~ 39 ) | } ~ 66 { | ) ~ 13 { | } ) 40 { | ) ~ 67 { | ) ~ 14 { | } ) 41 ) | } ~ 68 { ) } ~ 15 { ) } ~ 42 { ) } ~ 69 { | } ) 16 { | ) ~ 43 ) | } ~ 70 ) | } ~ 17 ) | } ~ 44 { | } ) 71 { | ) ~ 18 { | } ) 45 { | ) ~ 72 ) | } ~ 19 { ) } ~ 46 { | } ) 73 { | } ) 20 ) | } ~ 47 { | ) ~ 74 { | ) ~ 21 ) | } ~ 48 { | } ) 75 { ) } ~ 22 { | ) ~ 49 { | } ) 76 { | ) ~ 23 { | } ) 50 { | ) ~ 77 { ) } ~ 24 { ) } ~ 51 ) | } ~ 78 ) | } ~ 25 { | } ) 52 { | ) ~ 79 ) | } ~ 26 { | } ) 53 ) | } ~ 80 { | ) ~ 27 { ) } ~ 54 ) | } ~ 13 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 06 C©u 1 : 2 x  4x  4
Tìm diện tích hình phẳng giới hạn bởi các đường y
; y x 1; x  2  ; x  0 x  3 y x  2 3 1 1 A. ln B. ln 3 C. ln3 D. ln 3 2 2 4 C©u 2 : m
Tìm m biết  2x 5.dx  6 0 A. m  1  ,m  6 B. m  1  ,m  6 
C. m 1, m  6 
D. m 1, m  6
C©u 3 : Tìm nguyên hàm của hàm số f(x) biết f (x 2 )  tan x tan3 x
sin x x cos x A. C B. Đáp án khác C. Tanx-1+C D. C 3 cos x
C©u 4 : Tính diện tích hình phẳng giới hạn bởi 𝑦 = 𝑥2 − 4𝑥 + 5 và hai tiếp tuyến tại 𝐴(1; 2) và 𝐵(4; 5) 9 7 3 5 A. B. C. D. 4 4 4 4
C©u 5 : Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức: 1 b c c b A. S
f (x)dx f (x)dx   . B. S
f (x)dx f (x)dx   . a b b a c c C. S f (x)dx  . D. S f (x)dxa a C©u 6 :  2 Tính tích phân 2 sin x cos xdx  0 1 1 1 A. B. 1 C. D. 4 3 2
C©u 7 : Nếu F x là một nguyên hàm của ( ) x (1 x f x e e  
) và F(0)  3 thì F (x) là ? A. x e x B. x e x  2 C. x
e x C D. x e x 1
C©u 8 : Diện tích hình phẳng giới hạn bởi 2
y x  3x  2 và trục Ox là: 3 729 27 A. 6 B. C. D. 4 35 4
C©u 9 : Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi 2
y  x  2x và trục Ox quanh trục Ox là: 16 4 3 16 72 A. B. C. D. 15 3 15 5
C©u 10 : Tính diện tích hình phẳng giới hạn bởi đường cong
(𝐶): 𝑦 = |𝑥2 − 4𝑥 + 3| và 𝑑: 𝑥 + 3 109 105 107 103 A. B. C. D. 6 6 6 6
C©u 11 : Họ nguyên hàm của tanx là: tan2 x
A. ln cos x C
B. -ln cos x C C. C D. ln(cosx) + C 2
C©u 12 :  dx bằng: 1 (  x2 )x x x A. ln  C  2  2 1  x (x  ) 1   B. ln C C. ln x x C D. ln C x2 1  x2 1
C©u 13 : Xét các mệnh đề: 2 3 1 I  4 6 x 1.dx x 1.dx   3 1 3 1 1 II  4 4 4 x 1.dx x 1.dx x 1.dx    0 0 3
A. (I) đúng, (II) sai
B. (I) sai, (II) đúng
C. Cả (I) và (II) đều đúng
D. Cả (I) và (II) đều sai
C©u 14 : Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi 2
y x và y x  2 quanh trục Ox là: 72 138 9 72 A. B. C. 5 5 2 D. 5 C©u 15 : x
Một nguyên hàm của f (x) là: 2 x 1 1 1 2 A. ln(x 1) x C. ln(x 1) x 2 B. 2 2 ln( 1) 2 D. 2 ln( 1)
C©u 16 : Họ nguyên hàm của hàm số 5
y  (2x 1) là: 1 1 1 A. 6
(2x 1)  C B. 6
(2x 1)  C C. 6
(2x 1)  C . D. 4
10(2x 1)  C 12 6 2
C©u 17 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x3 , trục hoành và các đường thẳng x= -1, x=3 là 45 27 17 41 A. (đvdt) B. (đvdt) C. (đvdt) D. (đvdt) 2 2 3 2
C©u 18 : Hàm số nào là nguyên hàm của f(x) = . 2 x x  5 : 3 3 1 A. 2 F(x) = 2 2 x  (x  ) 5 B. F(x) = 2 ( ) 5 3 3 1 3 C. F(x) = 2 2 (x  ) 5 D. 2 2 F(x)  ( 3 x  ) 5 2 C©u 19 : 1
Tìm nguyên hàm của hàm số f(x) biết f (x)  x  9  x 2  3 3  A.
 x  9  x   C B. Đáp án khác 27   3 2  2  3 3  C. D.
 x  9  x   C ( 3 x  9 C 3  x3 ) 27   C©u 20 : x x
Nguyên hàm của hàm số f x 2ln  , x  0 là: x 2  2 2 ln x x ln x ln x C 2 ln x A. C
B. 2ln x 1 C C. D. x C x x C©u 21 : x e Họ nguyên hàm của là: 2 x e 1 1 x e 1 x  1 x e 1 2 x e 1
A. ln e 1  C B. lnC C. lnC D. lnC 2 x e 1 x e 1 2 x e 1
C©u 22 : Diện tích giới hạn bởi đồ thị hàm 3 2
y x  3x  4 và đường thẳng x y 1  0 A. 10 B. 8 C. 6 D. 4 C©u 23 : 2 2 x  2 Cho M  .dx
. Giá trị của M là: 2 2x 1 5 11 A. 2 B. C. 1 D. 2 2
C©u 24 : Thể tích khối tròn xoay trong không gian Oxyz giới hạn bởi hai mặt phẳng x  0; x   và có
thiết diện cắt bởi mặt phẳng vuông góc với Ox tại điểm ( ;
x 0;0) bất kỳ là đường tròn bán kính sin x là: A. 2 . B.  . C. 2 . D. 4 .
C©u 25 : Thể tích khối tròn xoay tạo thành khi cho đường x2+(y-1)2=1 quay quanh trục hoành là A. 2 6 (đvtt) B. 2 8 (đvtt) C. 2 4 (đvtt) D. 2 2 (đvtt) C©u 26 : 3𝜋
Tính tích phân sau: 𝐼 = ∫ 8
𝜋 |𝑐𝑜𝑡𝑥 − 𝑡𝑎𝑛𝑥|𝑑𝑥 8 A. 𝑙𝑛2 B. 𝑙𝑛3 C. 𝑙𝑛√2 D. 𝑙𝑛√3 C©u 27 : 0 Cho hàm số ℎ(𝑥) = 𝑠𝑖𝑛2𝑥
. 𝑇ì𝑚 𝑎, 𝑏 để ℎ(𝑥) = 𝑎𝑐𝑜𝑠𝑥 + 𝑏𝑐𝑜𝑠𝑥 và tính 𝐼 = ∫ ℎ(𝑥)𝑑𝑥 (2+𝑠𝑖𝑛𝑥)2 (2+𝑠𝑖𝑛𝑥)2 2+𝑠𝑖𝑛𝑥 −𝜋2
A. 𝑎 = −4 𝑣à 𝑏 = 2; 𝐼 = 2𝑙𝑛2 − 2
B. 𝑎 = 4 𝑣à 𝑏 = −2; 𝐼 = 𝑙𝑛2 − 2
C. 𝑎 = 2 𝑣à 𝑏 = 4; 𝐼 = 2𝑙𝑛2 − 2
D. 𝑎 = −2 𝑣à 𝑏 = 4; 𝐼 = 𝑙𝑛2 − 2 4
C©u 28 : Diện tích hình phẳng giới hạn bởi đường thẳng 2
y  x  2 và đường thẳng y x bằng: 9 10 11 17 A. B. C. D. 2 3 2 3 C©u 29 : 1 x Tính tích phân    x dx 3 2 0 1 5 3 3 5 A. B. C. D. 16 8 16 8
C©u 30 : Mệnh đề nào sau đây sai?
Nếu F (x) là một nguyên hàm của f (x) trên a;b và C là hằng số thì A. f (x)dx
F (x) C .
B. Mọi hàm số liên tục trên a;b đều có nguyên hàm trên a;b .
C. F (x) là một nguyên hàm của f (x) trên ; a b F (x) f (x), x ; a b . D. f (x)dx f (x) C©u 31 : 2 dx I 1 cos x 0 1 1 A. 4 B. 2 C. 1 D. 2 C©u 32 :
Tìm một nguyên hàm F x của hàm số f x 2
 2  x biết F   7 2  3 3 x 1
A. F x  2x  
B. F x 3 19  2x x  3 3 3 3 x 3 x
C. F x  2x  1
D. F x  2x   3 3 3
C©u 33 : Tính diện tích hình phẳng giới hạn bởi các đường
(𝐶1): 𝑓(𝑥) = (𝑒 + 1)𝑥 và (𝐶2): 𝑔(𝑥) = (1 + 𝑒𝑥)𝑥 𝑒 𝑒2 A. − 1 B. 𝑒2 − 2 − 2 2 C. 𝑒3 − 3 D. 2 5 C©u 34 : 3 3 I cos xdx bằng: 0 3 3 3 3 3 3 A. B. C. D. 3 3 2 4 8
C©u 35 : Nguyên hàm của hàm số   x f x xe là: 2 x A. x x x
xe e C B. x e C C. e C D. x x
xe e C 2
C©u 36 : Gọi F(x) là một nguyên hàm của hàm y  .
x cos x mà F(0)  1. Phát biểu nào sau đây là đúng:
A. F(x) là hàm chẵn
B. F(x) là hàm lẻ
F (x) không là hàm chẵn cũng không là
F (x) là hàm tuần hoàn chu kỳ 2 C. D. hàm lẻ C©u 37 : 1 2x2  2
Tính tích phân sau: I dxx 1 A. I=4 B. I=2 C. I=0 D. Đáp án khác C©u 38 : ln x 1
Gọi F(x) là một nguyên hàm của hàm 2 y  ln x 1. mà F (1)  . Giá trị 2 F ( ) e bằng: x 3 8 1 8 1 A. B. . C. . D. . 9 9 3 3 C©u 39 : t  3  Cho 4 f (x)  4sin x dx 
 .Giải phương trình f (x)  0  2  0 k 
A. k2 , k Z B. , k Z
C. k , k Z D.
k ,k Z 2 2
C©u 40 : Diện tích hình phẳng giới hạn bởi 2
y x và y  2x  3 là: 512 88 32 32 A. B. C. D. 15 3 3 3
C©u 41 : Cho hai hàm số f (x), g(x) là hàm số liên tục ,có F(x),G(x) lần lượt là nguyên hàm của
f (x), g(x) .Xét các mệnh đề sau :
(I): F(x)  G(x) là một nguyên hàm của f (x)  g(x) 6
(II): k.F x là một nguyên hàm của kf x k R
(III): F(x).G(x) là một nguyên hàm của f (x).g(x)
Mệnh đề nào là mệnh đề đúng ? A. I B. I và II C. I,II,III D. II C©u 42 : 1 2x dx bằng x 1 2 x 1 2 A. B. 1 2x C C. C D. x 1 2 .ln 2 C ln 2 ln 2 C©u 43 : 1
Biết rằng tích phân (2 1) x x e dx a  . b e  , tích ab bằng: 0 A. 1 B. -1 C. -15 D. 5 C©u 44 : 2
Tính tích phân sau: 𝐼 = ∫ 𝑥|𝑎 − 𝑥|𝑑𝑥 0 1 8
A. Cả 3 đáp án trên B. 2𝑎 − 8 C. 𝑎3 + 8 − 2𝑎 D. − 2𝑎 3 3 3 3 C©u 45 : 1
Hàm số nào là nguyên hàm của f(x) = : 1  sin x  2 x   F(x) =  A. F(x) = 1 + cot    xB. 2 4  1  tan 2 C. F(x) = ln(1 + sinx) x D. F(x) = 2tan 2
C©u 46 : Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các 3 đườ x ng y  và y=x2 là 3 436 9 468 486 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 35 2 35 35
C©u 47 : Tính diện tích hình phẳng giới hạn bởi (𝑃): 𝑦2 = 4𝑥 và 𝑑: 𝑦 = 2𝑥 − 4 A. 9 B. 3 C. 7 D. 5 C©u 48 : 1 Một nguyên hàm của ( ) (2 1). x f x x e là: 1 1 1 1 A. ( ) . x F x x e B. ( ) x F x e C. 2 ( ) . x F x x e D. 2 ( ) 1 . x F x x e 7
C©u 49 : Tìm diện tích hình phẳng giới hạn bởi các đường 2
y x và y x  2 9 9 9 A. 9 B. C. D. 8 2 4
C©u 50 : Hàm số F(x)  ex  tan x C là nguyên hàm của hàm số f(x) nào 1
A. f (x)  ex B. Đáp án khác 2 sin x  1  x e x
C. f (x)  ex
D. f (x)  e 1 2  2 sin x  cos x  C©u 51 : 2 dx I bằng: 2 4 0 x A. B. C. 3 2 D. 6 C©u 52 : Nếu x 2
f (x)dx e  sin x C
thì f (x) là hàm nào ? A. x 2 e  cos x B. x e  sin 2x C. x e  cos 2x D. x e  2sin x C©u 53 : 1 dx I bằng: 2 1 x 0 A. C. 6 B. 3 4 D. 2 C©u 54 : 1 Họ nguyên hàm của là: sin x x x x A. ln cot  C B. ln tan  C C. -ln tan  C
D. ln sin x C 2 2 2
C©u 55 : Họ nguyên hàm của f(x) = sin 3 x cos3 x cos3 x  cos x   C 1 sin4 x A. cos x   C B. 3 C.  cos x   c D. C 3 cos x 4 C©u 56 :   2 2 Cho f
 xdx  5. Khi đó  f
  x2sin x .dx  bằng: 0 0 8  A. 5   B. 5  C. 7 D. 3 2
C©u 57 : Cho hình phẳng (H) giới hạn bởi các đường 4 2 2
y x  2mx m , x  0, x  1 . TÌm m để diện 1
tích hình phẳng đó bằng 5
A. m 1, m  2
B. m  0;m  2 / 3
C. m  2 / 3, m 1
D. m  0, m  2  / 3 C©u 58 : cos x 3
.sin xdx bằng: cos4 x sin4 x A. C B. C C. 4 sin x C D. 4 cos x C 4 4 C©u 59 : 2
Tính tích phân sau: 𝐼 = ∫ |𝑥 − 1| 𝑑𝑥 0 A. 1 B. 11 C. 6 D. 3 C©u 60 : x
Cho hàm số f x 2  2sin
Khi đó f (x)dx  bằng ? 2
A. x  sin x C
B. x  sin x C
C. x  cos x C
D. x  cos x C
C©u 61 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x  4x và trục hoành bằng: A. 4 B. 0 C. 2 D. 8 C©u 62 : 2
Hàm nào không phải nguyên hàm của hàm số y  : 2 (x 1) x 1 2x 2 x 1 A. B. C. D. x 1 x 1 x 1 x 1 C©u 63 : 2 2x  5x  3
Gọi S là diện tích giới hạn bởi đồ thị hàm số y
,tiệm cận xiên của đồ thi và các x  2
đường thẳng x  1
 , x mm   
1 .Tìm giá trị m để S  6 A. 6 e  4 B. 6 e  2 C. 6 e 1 D. 6 e  3 C©u 64 : 1  ln x
Tìm nguyên hàm của hàm số f(x) biết f (x)  x 1 1 A. Đáp án khác
B. x  ln x C C. ln x  2 ln x C D. ln x  2 ln x C 2 4 C©u 65 : k
Để k 4xdx 3k 1 0 thì giá trị của k là bao nhiêu ? 1 9 A. 1 B. 3 C. 2 D. 4 C©u 66 :
Cho hình phẳng trong hình (phần tô đậm ) quay quanh trục hoành .Thể tích khối tròn xoay
tạo thành được tính theo công thức nào ? b b 2 2
A. V   f x g x 2 ( ) ( ) dx
B. V    f (x)  g (x) dx   a a b b
C. V    f x g x 2 ( ) ( ) dx
D. V    f (x)  g(x)dx a a
C©u 67 : Họ nguyên hàm của 2 f (x) x.cos x là: 1 2 A. 2 cos x C B. 2 sin x C C. sin x C 2 D. 2 2sin x C C©u 68 : m
Đặt f m  cos . x dx  . 0
Nghiệm của phương trình f m  0 là   m   k2 ,k
A. m k2 , k B. m
k ,k C. m k,k D. 2 2
C©u 69 : Nguyên hàm của hàm số f x  2sin x  cos x là:
A. 2cos x  sinx  C
B. 2cos x  sinx  C C. 2
 cos x sinx  C D. 2
 cos x sinx C 10
C©u 70 : Họ nguyên hàm của 2 sin x là: 1 1 sin 2x A. x 2 cos 2x C B. x 2 2 2 x sin 2x 1 C. C D. x 2 cos 2x C 2 4 2 C©u 71 : 1
Họ nguyên hàm của f(x) = là: x( x  ) 1 x  1 x A. F(x) = ln  C B. F(x) = ln  C x x 1 1 x C. F(x) = ln  C
D. F(x) = ln x(x  ) 1  C 2 x 1 𝜋
C©u 72 : Tính tích phân sau: 𝐼 = ∫12
−𝜋 |𝑡𝑎𝑛𝑥. tan (𝜋 − 𝑥) tan (𝜋 + 𝑥)| 𝑑𝑥 3 3 12 1 2 2 1 A. 𝑙𝑛2 B. 𝑙𝑛√2 C. 𝑙𝑛√3 D. 𝑙𝑛3 3 3 3 3 C©u 73 : 2
Một nguyên hàm của f(x) = xe x là: 2 1 2 1 A. 2 x x x eB. e  C. 2 x e  D. e 2 2
C©u 74 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x2 và đường thẳng y= - x+2 là 13 A. (đvdt) B. 11 (đvdt) C. 7 (đvdt)
D. Một kết quả khác 2
C©u 75 : Tính diện tích hình phẳng được giới hạn bởi đường cong
(𝐶): 𝑓(𝑥) = −3𝑥−1 và hai trục tọa độ. 𝑥−1 A. −1 + 𝑙𝑛 4 B. −1 + 𝑙𝑛7 C. −1 + 2𝑙𝑛2 D. −1 + 𝑙𝑛 5 3 3 C©u 76 : 2x  3
Tìm nguyên hàm của hàm số f(x) biết f (x)  2 x  4x  3 x2  3x A.    (2x  )
3 ln x2  4x  3  2 B. C x2  4   C x 3 x2  3x 1 C. C D.
ln x 1 3ln x 3C x2  4x  3 2 11 C©u 77 : e k Cho I  ln dx
.Xác định k để I e  2 1 x
A. k e  2
B. k e
C. k e 1
D. k e 1 C©u 78 : 3 2x 1 Tích phân
dx a b ln 2 
. Tổng của a b bằng: x 1 1 A. 1. B. 7 C. -3 D. 2 C©u 79 : 0 2x 1 Tính dx  bằng: 1 x 1  A. ln 2  2 B. ln 2  2 C. ln 2  2 D. ln 2  2
C©u 80 : Tìm công thức sai: x x x x a A.
e dx e CB. a dx   C 0    1  a ln a C. cos xdx x C  sin D.
sin xdx  cos x C  12 ĐÁP ÁN 01 { | ) ~ 28 ) | } ~ 55 { ) } ~ 02 { | ) ~ 29 { | ) ~ 56 { | ) ~ 03 { | } ) 30 { | ) ~ 57 { | } ) 04 ) | } ~ 31 { | ) ~ 58 { ) } ~ 05 ) | } ~ 32 { | ) ~ 59 ) | } ~ 06 { | ) ~ 33 ) | } ~ 60 { ) } ~ 07 { ) } ~ 34 { | ) ~ 61 ) | } ~ 08 { | } ) 35 { | } ) 62 ) | } ~ 09 { | } ) 36 ) | } ~ 63 { ) } ~ 10 ) | } ~ 37 { | } ) 64 { | } ) 11 { ) } ~ 38 ) | } ~ 65 { ) } ~ 12 { ) } ~ 39 { ) } ~ 66 { ) } ~ 13 { | ) ~ 40 { | } ) 67 { | ) ~ 14 { | } ) 41 { ) } ~ 68 { | ) ~ 15 { | ) ~ 42 { | ) ~ 69 { | } ) 16 ) | } ~ 43 ) | } ~ 70 { | ) ~ 17 { | } ) 44 ) | } ~ 71 { ) } ~ 18 { ) } ~ 45 { ) } ~ 72 ) | } ~ 19 { | } ) 46 { | } ) 73 { ) } ~ 20 { | } ) 47 ) | } ~ 74 { | } ) 21 { ) } ~ 48 { | ) ~ 75 ) | } ~ 22 { ) } ~ 49 { | ) ~ 76 { | } ) 23 { | ) ~ 50 { | } ) 77 { ) } ~ 24 ) | } ~ 51 { | ) ~ 78 ) | } ~ 25 { | } ) 52 { ) } ~ 79 { | } ) 26 ) | } ~ 53 { | ) ~ 80 { | } ) 27 ) | } ~ 54 { ) } ~ 13 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 07 C©u 1 : Tìm d để 2
diện tích hình phẳng giới hạn bởi đường cong y 
, Ox, x=1, x=d (d>1) bằng 2: x y y = 2/x x O 1 d A. 2 e B. e C. 2e D. e+1
C©u 2 : Tính các hằng số A và B để hàm số f ( )
x Asin x B thỏa mãn đồng thời các điều 2
kiện f '(1)  2 và f (x)dx   4 0 2 2 A. A   , B A  , B A 2, B 2 A 2, B 2  2 B.  2 C.     D.   C©u 3 : x
Cho hình phẳng giới hạn bởi các đường 2
y xe ; y  0; x  0; x  1. Thể tích của khối tròn xoay
sinh bởi hình phẳng trên khi quay quanh trục hoành là A. 2  e  2 B. 2  e  2
C.  e  2
D.  e  2
C©u 4 : Diện tích hình phẳng giới hạn bởi đường cong 3 2 C : y x 3x 2 , hai trục tọa độ và đường thẳng x 2 là: 1 3 7 5 A. (đvdt) B. (đvdt) C. 4 (đvdt) D. (đvdt) 2 2 2
C©u 5 : Nguyên hàm F x của hàm số f x 2 3
 2x x  4 thỏa mãn điều kiện F 0  0 là 4 2 x A. 4 B. 3 4 2x  4x C. 3 x   4x D. 3 4
x x  2x 3 4 C©u 6 : 1
Gọi F(x) là nguyên hàm của hàm số f (x) 
thỏa mãn F(3/2) =0. Khi đó F(3) 2 x  3x  2 bằng: A. 2ln2 B. ln2 C. -2ln2 D. –ln2
C©u 7 : Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại? 1 A. sin2x và 2 cos x B. 2 tan x và 2 2 cos x C. x e và x e D. sin2 x và 2 sin x
C©u 8 : Nguyên hàm của hàm số 3 f x x trên là 4 x 4 x A. x C B. 2 3x C C. 2 3x x C D. C 4 4
C©u 9 : Tìm họ nguyên hàm   2 ( ) x F x x e dx ? 2 2 A. ( )  ( 2  2) x F x x x e C B. ( )  (2   2) x F x x x e C C. 2 ( )  (  2  2) x F x x x e C D. 2 ( )  ( 2 2) x F x x x e C
C©u 10 : Để tìm nguyên hàm của 4 5 f x sin x cos x thì nên:
A. Dùng phương pháp đổi biến số, đặt t cos x u cos x
B. Dùng phương pháp lấy nguyên hàm từng phần, đặt 4 4 dv sin x cos xdx 4 u sin x
C. Dùng phương pháp lấy nguyên hàm từng phần, đặt 5 dv cos xdx
D. Dùng phương pháp đổi biến số, đặt t sin x 2
C©u 11 : Cho hình phẳng giới hạn bởi các đường y 1 x, Ox, x=0, x=4 quay xung quanh trục
Ox. Thể tích của khối tròn xoay tạo thành bằng: 28 68 28 68 A. 2  B.  . C. D. 2  . 3 3 3 3 C©u 12 : 2 Giá trị của 2 x 1 dx  là 2  A. 2 B. 3 C. 4 D. 5
C©u 13 : Họ nguyên hàm của hàm số f x  cos3x tan x là 4 1 A. 3
 cos x  3cos x C B. 3
sin x  3sin x C 3 3 4 1 C. 3
 cos x  3cos x C D. 3
cos x  3cos x C 3 3 C©u 14 :  2
Tính I x cos xdx  0     1 A. I = B. I = + 1 C. I = D. I =  2 2 3 3 2 C©u 15 : 5 x 1 Tính
dx ta được kết quả nào sau đây? 3 x 6 x x Một kết quả 3 2 x x 6 3 x 1 A. B. C C. C D. C khác 3 2 4 x 2 3 2x 4
C©u 16 : Thể tích vật thể tròn xoay sinh ra bởi hình phẳng giới hạn parabol P 2
: y x 1 và trục
hoành khi quay xung quanh trục Ox bằng bao nhiêu đơn vị thể tích? 7 5 8 A. B. C. D. 3 2 2 3 C©u 17 : Gọi F f x
1(x) là nguyên hàm của hàm số 2 ( ) sin x thỏa mãn F 1
1(0) =0 và F2(x) là nguyên hàm của hàm số 2
f (x)  cos x thỏa mãn F 2 2(0)=0.
Khi đó phương trình F1(x) = F2(x) có nghiệm là:  
A. x k2 B. x   k C. x   kD. k x 2 2 3
C©u 18 : Diện tích hình phẳng giới hạn bởi 2
y  2y x  0 , x + y = 0 là: 11 9 A. Đáp số khác B. C. 5 D. 2 2
C©u 19 : Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng (H) giới hạn bởi các đường cong  2
y x và y x quanh trục Ox. 3 13 13 3 A. V   V   V   V   10 B. 15 C. 5 D. 5 C©u 20 : 3 Cho tích phân  2x I  
4 dx , trong các kết quả sau: 0 3 2 (I).  2x  4  2x I dx    4dx 2 0 3 2
(II).  2x  4  2x I dx    4dx 2 0 3 (III).  2 2x I   4dx 2 kết quả nào đúng? A. Chỉ II. B. Chỉ III. C. Cả I, II, III. D. Chỉ I. C©u 21 : 2√3 Tính tích phân 𝐼 = ∫ 𝑑𝑥 √5 𝑥√𝑥2+4 3 5 1 5 1 3 A. 3𝑙𝑛 𝑙𝑛 𝑙𝑛 4 B. 2𝑙𝑛 3 C. 4 3 D. 2 5 C©u 22 : 𝜋/2 Tính 𝐼 = ∫
(2𝑥 + 1)𝑠𝑖𝑛2𝑥𝑑𝑥 0 .
Lời giải sau sai từ bước nào:
Bước 1: Đặt 𝑢 = 2𝑥 + 1; 𝑑𝑣 = 𝑠𝑖𝑛2𝑥𝑑𝑥
Bước 2: Ta có 𝑑𝑢 = 2 𝑑𝑥; 𝑣 = 𝑐𝑜𝑠2𝑥 𝜋 𝜋 𝜋 Bướ 𝜋/2
c 3: 𝐼 = (2𝑥 + 1)𝑐𝑜𝑠2𝑥|2 − 2
= (2𝑥 + 1)𝑐𝑜𝑠2𝑥|2 − 2𝑠𝑖𝑛2𝑥| 0 ∫ 2𝑐𝑜𝑠2𝑥𝑑𝑥 0 0 0
Bước 4: Vậy 𝐼 = −𝜋 − 2 4 A. Bước 4 B. Bước 3 C. Bước 2 D. Bước 1
C©u 23 : Nguyên hàm F x của hàm số f x 4
 sin 2x thỏa mãn điều kiện F   3 0  là 8 3 1 1 3 3 1 1 A. x  sin 2x  sin 4x B. x  sin 4x  sin 8x 8 8 64 8 8 8 64 3 1 1 3 C. x   1  sin 4x  sin 8x
D. x  sin 4x  sin 6 x 8 8 64 8 C©u 24 : x
Họ nguyên hàm của hàm số f x  3 2 ln 3  là xx  2 2 ln 3 2 ln x  3  x  4 2 ln 3  x  4 2 ln 3 A. C B. C C. C D. C 2 8 8 2
C©u 25 : Hình phẳng D giới hạn bởi y = 2x2 và y = 2x + 4 khi quay D xung quanh trục hoành thì thể
tích khối tròn xoay tạo thành là: 288 A. V = (đvtt)
B. V = 2   (đvtt) 5 4 C. V = 72  (đvtt) D. V = (đvtt) 5 C©u 26 : 
Các đường cong y = sinx, y=cosx với 0 ≤ x ≤
và trục Ox tạo thành một hình phẳng. Diện 2
tích của hình phẳng là: A. 2 - 2 B. 2 C. 2 2 D. Đáp số khác. C©u 27 : 4
Một nguyên hàm của hàm số f (x)  là: 2 cos x 4x 4 3 A. B. 4 tan x C. 4  tan x D. 4x  tan x 2 sin x 3 C©u 28 : 2 Tính tích phân 𝐼 = ∫ 1 𝑑𝑥 0 ta được kết quả: 𝑥2−2𝑥+2 𝜋 𝜋 𝜋 𝜋 A. − 4 B. 2 C. 4 D. 3 C©u 29 : 3x e 1
Một nguyên hàm của f (x)  là: x e 1 1 1 A. 2 ( ) x x F x ee x B. 2 ( ) x x F x ee 2 2 5 1 1 C. 2 ( ) x x F x ee D. 2 ( ) x x F x ee 1 2 2 C©u 30 : x
Gọi F(x) là nguyên hàm của hàm số f (x) 
thỏa mãn F(2) =0. Khi đó phương trình 2 8  x
F(x) = x có nghiệm là: A. x = 0 B. x = 1 C. x = -1 D. x  1 3 C©u 31 : 5 dx Giả sử  ln c
. Giá trị của c là 1 2x 1 A. 9 B. 8 C. 3 D. 81
C©u 32 : Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi đường thẳng y  4x và đồ thị hàm số 3 y x là 7 A. 5 B. 3 C. 4 D. 2 C©u 33 : 2 Giá trị của 2 2 x e dx  là 0 A. 4 4e B. 4 e C. 4 e 1 D. 4 3e 1
C©u 34 : Biểu thức nào sau đây bằng với 2 sin 3xdx  ? 1 1 1 1 A. (x  sin 6x)  C B. (x  sin 6x)  C 2 6 2 6 1 1 1 1 C. (x  sin 3x)  C D. (x  sin 3x)  C 2 3 2 3 C©u 35 : 
Cho hình phẳng giới hạn bởi các đường y  cos 4x, Ox, x=0, x= quay xung quanh trục 8
Ox. Thể tích của khối tròn xoay tạo thành bằng: 2  2    A. B. C. D. 2 16 4 3 C©u 36 : 1 Tính 2 I  1 x dx  0  1  A. I = B. I = C. I = 2 D. I = 4 2 3 C©u 37 : 2
Tính tích phân 𝐼 = ∫ |𝑥2 − 𝑥|𝑑𝑥 0 6 A. ln2 B. 6 C. 1 D. ln8
C©u 38 : Cho đồ thị hàm số y=f(x) trên đoạn [0;6] như hình vẽ. y y=f(x) O 2 4 6 x
Biểu thức nào dưới đây có giá trị lớn nhất: 1 2 3 6 A. f (x)dx  B. f (x)dx  C. f (x)dx  D. f (x)dx  0 0 0 0
C©u 39 : Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 𝑦 = |𝑥| ; 𝑦 = 2 − 𝑥2 là: A. 2 B. 5/3 C. 7/3 D. 3 C©u 40 : 3 3 2
Biết rằng f (x)dx  5; f ( ) x dx   
3 . Tính  f(x)dx ? 1 2 1 A. 2 B. 2  C. 1 D. 5
C©u 41 : Họ nguyên hàm của hàm số f x 1  là 1 8x x x
A. F x 1 8  ln  C
B. F x 1 8  ln  C ln12 1 8x 12 1 8x x x
C. F x 1 8  ln  C
D. F x 8  ln  C ln 8 1 8x 1 8x
C©u 42 : Diện tích hình phẳng giới hạn bởi các đường 2
y  4x  x và y  2x là: 7 y (2;4) x O 4 4 2 2 4 A. 2 (2x  x )dx  B. 2 (x  2x)dx  C. 2 (2x  x )dx  D. 2 (x  2x)dx  0 0 0 0
C©u 43 : Một nguyên hàm F(x) của 2
f (x)  3x 1 thỏa F(1) = 0 là: A. 3 x 1 B. 3 x x  2 C. 3 x  4 D. 3 2x  2
C©u 44 : Diện tích hình phẳng giới hạn bởi 2
y  4  x và y=3|x| là: 17 3 5 13 A. B. C. D. 6 2 2 3
C©u 45 : Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bới các đường y x , y x 2, y
0 quay quanh trục Oy, có giá trị là kết quả nào sau đây ? 1 3 11 32 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 3 2 6 15
C©u 46 : Biểu thức nào sau đây bằng với tan xdx  ? 1 ln(  tan x)  C 2 tan x 1 A. sinx B. ln(cos x)  C C.  C D.  C 2 cos x 2
C©u 47 : Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 𝑦 = 𝑥2 + 2 ; 𝑦 = 3𝑥 là: 1 1 1 1 A. 2 B. 4 C. 6 D. 3
C©u 48 : Tính diện tích hình phẳng giới hạn bởi các đường y  3 x  2
2x x và y  4x . 71 2 53 A. B. 6 C. 24 D. 3 7 C©u 49 : 14
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) = cos3x và 𝐹 (𝜋) = thì 2 3 8 A. 1 13 1
𝐹(𝑥) = 𝑠𝑖𝑛3𝑥 + B.
𝐹(𝑥) = − 𝑠𝑖𝑛3𝑥 + 5 3 3 3 C. 1 1 13
𝐹(𝑥) = 𝑠𝑖𝑛3𝑥 + 5 D.
𝐹(𝑥) = − 𝑠𝑖𝑛3𝑥 + 3 3 3
C©u 50 : Vận tốc của một vật chuyển động là 2 v t 3t
5 m / s . Quãng đường vật đó đi
được từ giây thứ 4 đến giây thứ 10 là : A. 36m B. 252m C. 1200m D. 1014m C©u 51 : 4 1 Nếu dx  ln m  thì m bằng 3  x   1  x  2   4 3 A. 12 B. C. 1 D. 3 4 C©u 52 : x 1
Gọi (H) là đồ thị của hàm số f (x) 
. Diện tích giới hạn bởi (H), trục hoành và hai x
đường thẳng có phương trình x=1, x=2 bằng bao nhiêu đơn vị diện tích? A. e 1 B. e  2 C. e  2 D. e 1
C©u 53 : Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y   3 x  2
3x  3x  1và tiếp
tuyến của đồ thị tại giao điểm của đồ thị và trục tung. 27 5 23 4 A. S  S  S  S  4 B. 3 C. 4 D. 7
C©u 54 : Diện tích hình phẳng giới hạn bởi đồ thị có phương trình 𝑥2 − 2𝑥 + 𝑦 = 0 ; 𝑥 + 𝑦 = 0 là: A. 8 B. 11/2 C. 9/2 D. 7/2
C©u 55 : Một nguyên hàm của f (x)  cos3xcos 2x bằng 1 1 1 1 A. sin x  sin 5x B. sin x  sin 5x 2 2 2 10 1 1 1 C. cos x  cos5c D. sin 3xsin 2x 2 10 6 C©u 56 : 1 dx
Một học sinh tính tích phân I   tuần tự như sau: 1  x e 0 9 1 x e dx
(I). Ta viết lại I   x x
0 e 1  e e e e du du du e (II). Đặt  x u e thì I       
ln u ln 1u ( u 1  ) u u 1  u 1 1 1 1 e
(III). I  ln e  ln(e  1)  ln1  ln 1  1  ln e 1
Lý luận trên, nếu sai thì sai từ giai đoạn nào? A. III B. I C. II D. Lý luận đúng. C©u 57 : 1 4 x Tính I dx  2x 1 1  1 5 7 A. I = B. I = C. I = D. I = 5 5 7 5 C©u 58 : 1
Diện tích hình phẳng giới hạn bởi các đường y  x và y  x là: 2 4 16 5 A. 2 B. C. D. 3 3 12
C©u 59 : Nguyên hàm của hàm số x 2 ( ) (1 3    x f x e e ) bằng: A. ( ) x 3    x F x e eC B. x 3 ( ) 3    x F x e eC C. x 2 ( ) 3    x F x e eC D. ( ) x 3    x F x e eC C©u 60 : 2
Diện tích hình phẳng giới hạn bởi hai parabol (P): y x và q 2
: y  x  2x là bao nhiêu đơn vị diện tích? 1 1 A. 1 B. C. D. 3 3 2
C©u 61 : Hàm số f x có nguyên hàm trên K nếu
A. f x xác định trên K
B. f x có giá trị lớn nhất trên K
C. f x có giá trị nhỏ nhất trên K
D. f x liên tục trên K 10 C©u 62 : dx Tích phân  bằng x e  1 e 2e e A. ln ln ln
D. ln e   1  ln 2 2e B. 2 e C. 1 2e   1
C©u 63 : Biểu thức nào sau đây bằng với 2 x sin xdx  ? A. 2 2  xcos x  x cos xdx  B. 2 x cos x  2xcos xdx  C. 2 x cos x  2xcos xdx  D. 2 2  xcos x  x cos xdx 
C©u 64 : Cho hàm số F(x) là một nguyên hàm của hàm số 𝑓(𝑥) = 1 và 𝐹(3) = 0 thì 𝑥2−3𝑥+2 A. 𝑥 − 1 𝑥 − 2 𝐹(𝑥) = 𝑙𝑛 | | − 𝑙𝑛2 B. 𝐹(𝑥) = 𝑙𝑛 | | − 𝑙𝑛2 𝑥 − 2 𝑥 − 1 C. 𝑥 − 2 𝑥 − 1 𝐹(𝑥) = 𝑙𝑛 | | + 𝑙𝑛2 D. 𝐹(𝑥) = 𝑙𝑛 | | + 𝑙𝑛2 𝑥 − 1 𝑥 − 2
C©u 65 : Tìm họ nguyên hàm của hàm số f x x  3 x  4 ( ) x ? 3 4 5 2 3 4 2 4 5 2 3 4 A. 2 3 4 F( ) x  x  x  x C 3 3 4 F( ) x  x  x  x C 3 4 5 B. 3 4 5 2 4 5 2 4 5 3 1 5 2 1 4 C. 3 3 4 F( ) x  x  x  x C 2 3 4 F( ) x  x  x  x C 3 3 4 D. 3 3 5 C©u 66 : 4
Giá trị của tích phân 𝐼 = ∫ 1 𝑑𝑥 −2 là 2𝑥−1 1 7 1 7 7 A. 𝑙𝑛 𝑙𝑛 2 5 B. − 2 5 C. Không tồn tại D. 2𝑙𝑛 5
C©u 67 : Cho (H) là hình phẳng giới hạn bởi đường cong (L): y x   3
ln 1 x  , trục Ox và
đường thẳng x  1 . Tính thể tích của vật thể tròn xoay tạo ra khi cho (H) quay quanh trục Ox. A. V   ln4   1 V   ln 4  2 V   ln3  2 V   3 B.   3 C.   3 D. ln3 3
C©u 68 : Diện tích hình phẳng giới hạn bởi hai parabol 2 2 y x 2x;y x 4x là giá trị nào sau đây ? 11 A. 12 (đvdt) B. 27 (đvdt) C. 4 (đvdt) D. 9 (đvdt) C©u 69 : 1 dx Tính I   2 x x  2 0 2 1
A. I = I   ln 2 B. I = - 3ln2 C. I  ln 3 D. I = 2ln3 3 2 C©u 70 : 1 dx
Bằng cách đổi biến số x  2sin t thì tích phân  là: 0 2 4  x    1 dt A. dtB. 6  0 dtC. 6 tdtD. 3 0 0 0 t
C©u 71 : Diện tích hình phẳng giới hạn bởi hai đường y = x, y = x + sin2x và hai đường thẳng x = 0, x =  là:   1 A. S = (đvdt) B. S = 1 (đvdt) C. S = (đvdt) D. S =  (đvdt) 2 2 2
C©u 72 : Với giá trị nào của m > 0 thì diện tích hình phẳng giới hạn bởi hai đường y = x2 và y = mx 4 bằng đơn vị diện tích ? 3 A. m = 2 B. m = 1 C. m = 3 D. m = 4 C©u 73 : Cho hàm số 3 2
f (x)  x x  2x 1. Gọi F(x) là một nguyên hàm của f(x), biết rằng F(1) = 4 thì 4 3 x x 49 4 3 x x A. 2 F (x)    x x B. 2 F (x)  
x x 1 4 3 12 4 3 4 3 x x 4 3 x x C. 2 F (x)  
x x  2 D. 2 F (x)    x x 4 3 4 3 C©u 74 :  Tích phân 4 cos 2xdx  bằng: 0 1 A. 1 B. C. 2 D. 0 2 C©u 75 : a x Tích phân 2 dx  bằng 0 a x  1     2   1     2  A. a     B. a   C. a     D. a    2   4   2   4  12 C©u 76 : t dx 1
Với t thuộc (-1;1) ta có   ln 3 
. Khi đó giá trị t là: 2 x 1 2 0 1 A. 1/3 B. C. 0 D. 1/2 3 C©u 77 : 2 Tìm a sao cho 2 3
I  [a +(4 - a)x + 4x ]dx = 12  1 A. Đáp án khác B. a = - 3 C. a = 5 D. a = 3 C©u 78 : Tính 3
cos xdx ta được kết quả là : 4 cos x 1 3 sin x A. C B. sin 3x C x 12 4 4 cos x.sin x 1 sin 3x C. C D. 3 sin x C 4 4 3 C©u 79 : ln m x e dx Cho A   ln 2 
. Khi đó giá trị của m là: x e  2 0
A. m=0; m=4
B. Kết quả khác C. m=2 D. m=4
C©u 80 : Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  6x  9x và trục Ox. Số
nguyên lớn nhất không vượt quá S là: A. 10 B. 7 C. 27 D. 6 13 ĐÁP ÁN 01 { ) } ~ 28 { | ) ~ 55 { ) } ~ 02 ) | } ~ 29 ) | } ~ 56 ) | } ~ 03 { | ) ~ 30 { | } ) 57 ) | } ~ 04 { | } ) 31 { | ) ~ 58 { ) } ~ 05 { | ) ~ 32 { | ) ~ 59 { | } ) 06 { | } ) 33 { | ) ~ 60 { ) } ~ 07 { | } ) 34 { ) } ~ 61 { | } ) 08 { | } ) 35 { ) } ~ 62 { ) } ~ 09 ) | } ~ 36 ) | } ~ 63 { ) } ~ 10 { | } ) 37 { | ) ~ 64 { | ) ~ 11 { ) } ~ 38 { ) } ~ 65 ) | } ~ 12 { | ) ~ 39 { | ) ~ 66 { | ) ~ 13 { | ) ~ 40 ) | } ~ 67 ) | } ~ 14 ) | } ~ 41 { | ) ~ 68 { | } ) 15 { | } ) 42 { ) } ~ 69 ) | } ~ 16 { ) } ~ 43 { ) } ~ 70 { ) } ~ 17 { | } ) 44 { | } ) 71 ) | } ~ 18 { | } ) 45 { | } ) 72 ) | } ~ 19 ) | } ~ 46 { ) } ~ 73 ) | } ~ 20 ) | } ~ 47 { | ) ~ 74 { ) } ~ 21 { | ) ~ 48 ) | } ~ 75 { ) } ~ 22 { | ) ~ 49 { | ) ~ 76 { | } ) 23 { | ) ~ 50 { | } ) 77 ) | } ~ 24 { | ) ~ 51 { ) } ~ 78 { | } ) 25 ) | } ~ 52 { ) } ~ 79 { | } ) 26 { | } ) 53 ) | } ~ 80 { | } ) 27 { ) } ~ 54 { | ) ~ 14 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG ĐỀ SỐ 08 C©u 1 : Tính A = 2 3 sin x cos x dx  , ta có 3 5 sin x sin x A. A    C B. 3 5
A  sin x  sin x C 3 5 D. Đáp án khác C. 3 5 sin x sin x A     C 3 5
C©u 2 : Nguyên hàm của hàm số 3 f (x)  tan x là: 1 4 tan x 2 tan x  ln cos x  C A. Đáp án khác B. 2 tan x 1 C.  C D. 2 4 C©u 3 : 
Kết quả của tích phân: 1 7 6x I  dx  0 3x  2 1 5 5 5 5 A.  ln B. ln C. 2+ ln D. 3  2 ln 2 2 2 2 2 C©u 4 : 
Họ nguyên hàm F(x) của hàm số 1 f (x)  là: 2 (x  2) 1
A. F(x)   C B. Đáp số khác x  2 1  1 
C. F(x)   C
D. F(x)   C x  2 3 (x  2)
C©u 5 : Họ nguyên hàm F(x) của hàm số 4
f (x)  sin x cos x 1 A. 5 F (x)  sin x C B. 5
F(x)  cos x C 5 1 1 C. 5
F(x)  sin x C D. 5
F (x)   sin x C 5
C©u 6 : Họ nguyên hàm F(x) của hàm số 2
f (x)  sin x là 1
A. F(x) 
(2x  sin 2x)  C
B. Cả (A), (B) và (C) đều đúng 4 1 1 sin 2x
C. F(x) 
(x  sinx .cosx)  C
D. F(x)  (x  )  C 2 2 2
C©u 7 : Tính diện tích S của hình phẳng được giới hạn bởi các đường 2
y  4x x và y = 0, ta có 3 32 23 A. S  (đvdt) B. S  (đvdt) S  (đvdt)
D. S 1(đvdt) 23 3 C. 3
C©u 8 : Kết quả của tích phân e 1 I  (x  ) ln xdx  là: 1 x 2 e 2 1 e 2 1 e 2 3 e A. B. C. D.  4 2 4 4 4 4 4 C©u 9 : 2 Cho 3 2I  (2x  ln ) x dx  . Tìm I? 1 13 13 1 A. 1 2 ln 2 B.  2 ln 2 C.  ln 2 D.  ln 2 2 4 2 C©u 10 : 3  Biết a x 2 ln x 1 I  dx   ln 2  . Giá trị của a là: 2 1 x 2  A. B. ln2 C. 2 D. 3 4
C©u 11 : Tính diện tích S của hình phẳng được giới hạn bởi các đường 2 y x và 2
y  2  x , ta có 3 8
A. S  (đvdt)
B. S  (đvdt)
C. S  8(đvdt) D. Đáp số khác 8 3
C©u 12 : Họ nguyên hàm F(x) của hàm số 1 f (x)  là 2 x  4x  3 1 x  3 1 x 1
A. F(x)  ln | | C
B. F(x)  ln | | C 2 x 1 2 x  3 x  3 C. 2
F(x)  ln | x  4x  3 | C
D. F(x)  ln | | Cx 1
C©u 13 : Tìm nguyên hàm I  (x  cos ) x xdx  2 3 x B. Đáp án khác A.  xsin x  cos x  c 3 3 x 3 x C.  sin x  xcos x  c D.  xsin x  cos x  c 3 3
C©u 14 : Kết quả của tích phân 4 1 I  dx  là: 0 1 2 2x 1 1 5 1 1 7 1 7 A. 1 ln B. 1 ln 2 C. 1 ln D. 1 ln 2 3 4 3 3 4 3 C©u 15 : 2  Tích phân a e x 3 2 (x 1)e dx   . Giá trị của a là: 0 4 A. 2 B. 3 C. 1 D. 4 C©u 16 : Tính 1 2  (2 x x I e  e )dx  ? 0 1 A. 2 e B. C. 1 D. e e C©u 17 : 2  
Họ nguyên hàm F(x) của hàm số x x 1 f (x)  là x 1 2 x
A. F(x) 
 ln | x 1| CB. 2
F(x)  x  ln | x 1| C  2 1
C. F(x)  x   C D. Đáp số khác x 1 C©u 18 : 
Họ nguyên hàm F(x) của hàm số x 2 f (x)  là 2 x  4x  3 1 1 A. 2 F (x)  
ln | x  4x  3 | CB. 2 F (x) 
ln | x  4x  3 | C  2 2 C. 2
F(x)  ln | x  4x  3 | C      D. 2 F(x) 2ln | x 4x 3 | C C©u 19 :   sin 2x Cho 2 I  cos x 3sin x 1dx  2 I  dx  1 2 0 2 0 (sinx 2)
Phát biểu nào sau đây sai? 14 3 3 A. I  B. I  I C. I  2 ln  D. Đáp án khác 1 1 2 9 2 2 2
C©u 20 : Tính thể tích V của khối tròn xoay tạo thành khi ta cho miền phẳng D giới hạn bởi các 3 đường x
y e , y = 0, x = 0, x = 1 quay quanh trục ox . Ta có 2 (e 1) 2 e
A. V   (đvtt) B. V  (đvtt) C. V  (đvtt) D. 2 V   (đvtt) 2 2 4 ĐÁP ÁN 01 ) | } ~ 02 { | } ) 03 { | ) ~ 04 ) | } ~ 05 ) | } ~ 06 { ) } ~ 07 { ) } ~ 08 { | } ) 09 { | ) ~ 10 { | ) ~ 11 { ) } ~ 12 ) | } ~ 13 { | } ) 14 { | } ) 15 { | ) ~ 16 { | } ) 17 ) | } ~ 18 { ) } ~ 19 { | ) ~ 20 { ) } ~ 5