





































Preview text:
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
“Nơi nào có ý chí, nơi đó có con đường.” BÀI TOÁN CỰC TRỊ h t HÀM SỐ HỢP t 73 p s: TRONG CÁC THI TH 20-21 // lu ye n thi tracng
Ngày đã r ng, bình minh đang t nh gi c! h iem
“Khi nào em c m th y mu n phê phán và chê bai m t ai đó, .vn
hãy nh r ng không ph i ai trên th# gi i này c$ng có nh%ng
thu&n l(i trong cu c s ng mà em có đư(c."
Họ và Tên học sinh: …………
…………………….................. ht tps:
Trường:………………………… ………………. Lớp: ………. //w w w.f ace boo k.com/vietgold 0
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
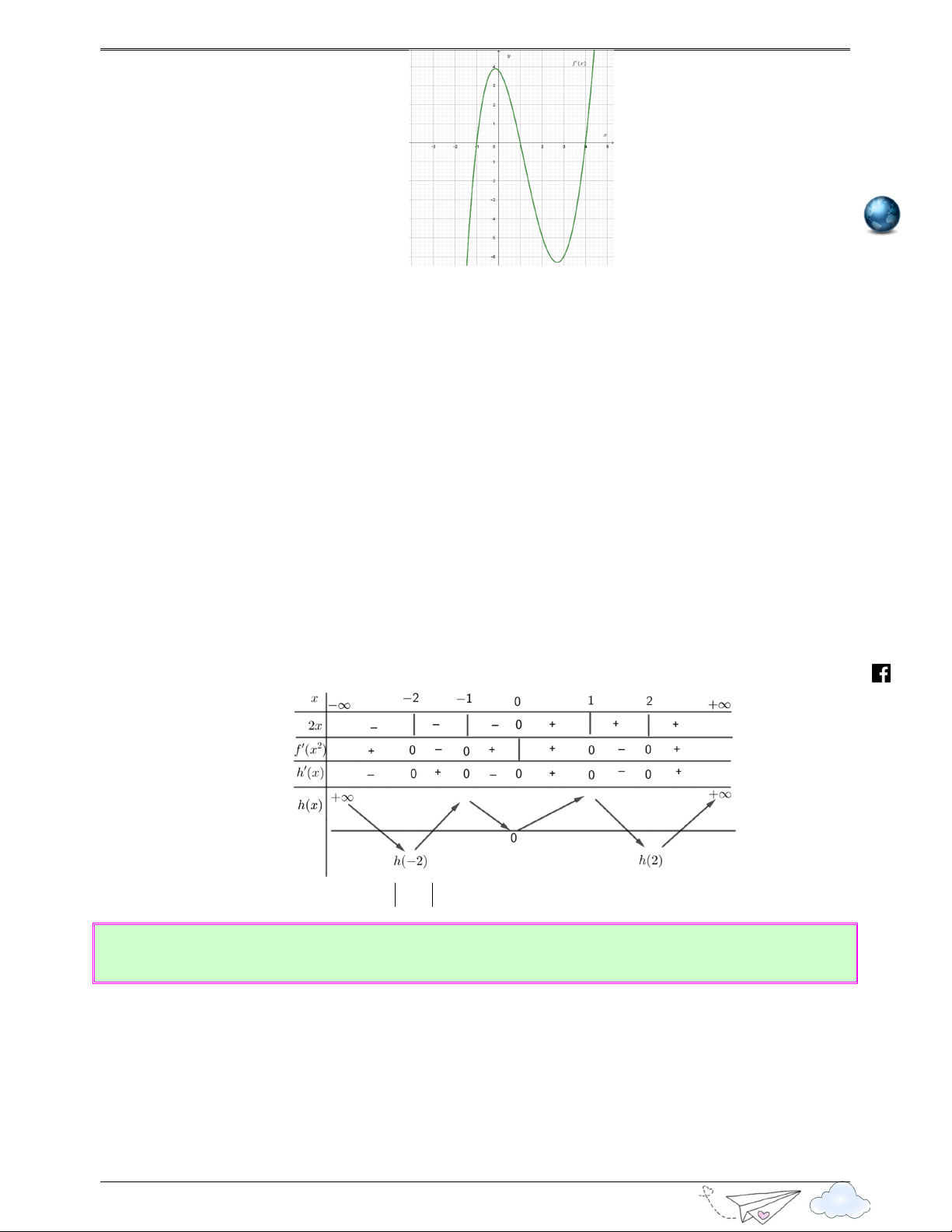
Câu 1: (Câu 31 - Chuyên Lê Hồng Phong - Nam Định - Năm 2020 - 2021) Cho hàm số f ( x) thỏa mãn f ′( x) 2
= x (1− x), x
∀ ∈ ℝ . Hỏi hàm số = ( 2 y
f x ) có bao nhiêu điểm cực tiểu? Ⓐ. 3 . Ⓑ. 2 . Ⓒ. 0 . Ⓓ. 1. Lời giải .vn Chọn D 2 iem
Xét hàm số y = f (x ) . gh
Tập xác định: D = ℝ . y ' = f ( 2 x ) ' = 2 . x f ' ( 2x) 4 = 2 . x x ( 2 1− x ) 5 = 2x ( 2 1− x ) itracn x = 0 th 5 y ' = 0 ⇔ 2x ( 2
1− x ) = 0 ⇔ x =1 yen x = −1 Bảng biến thiên: s://lu ttp h
Vậy hàm số có 1 điểm cực tiểu.
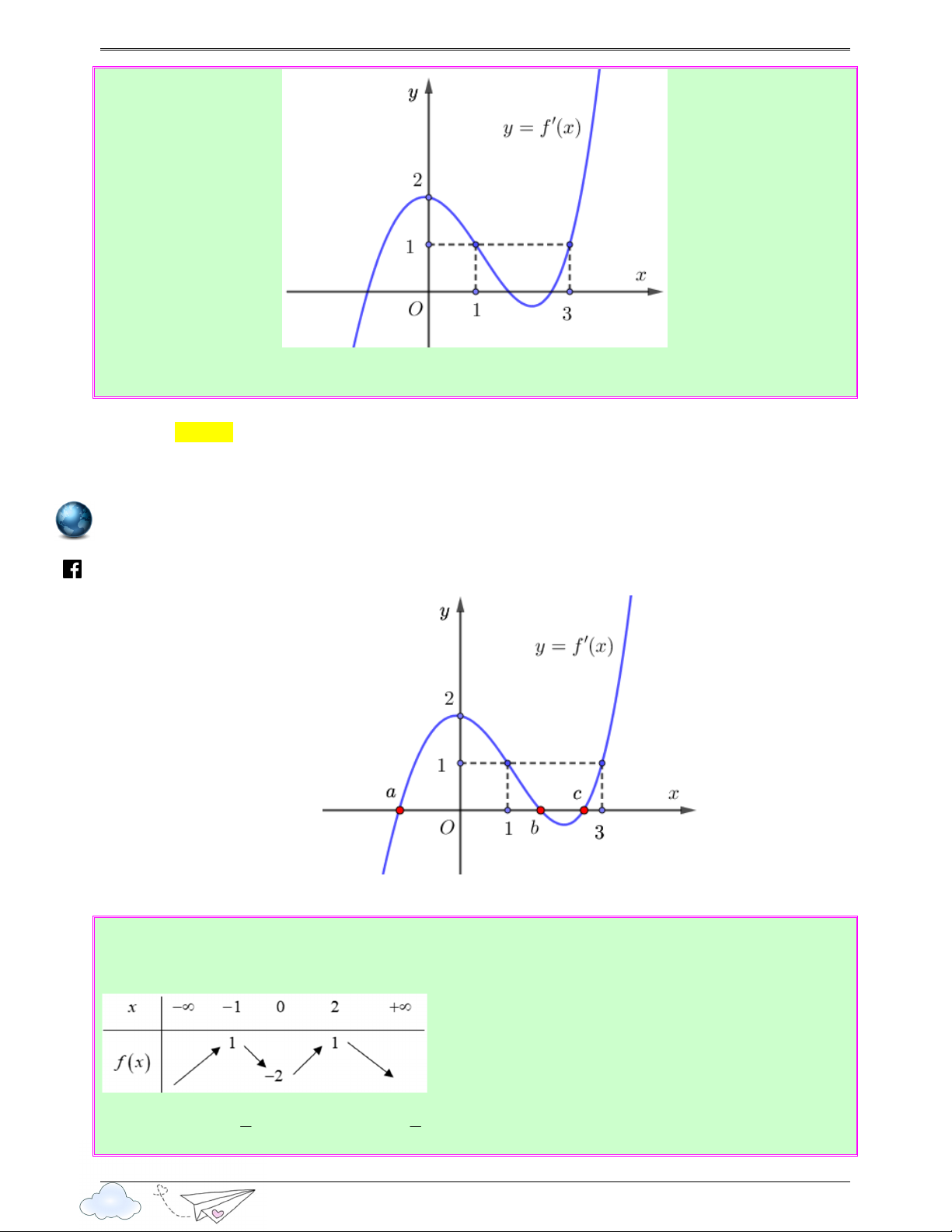
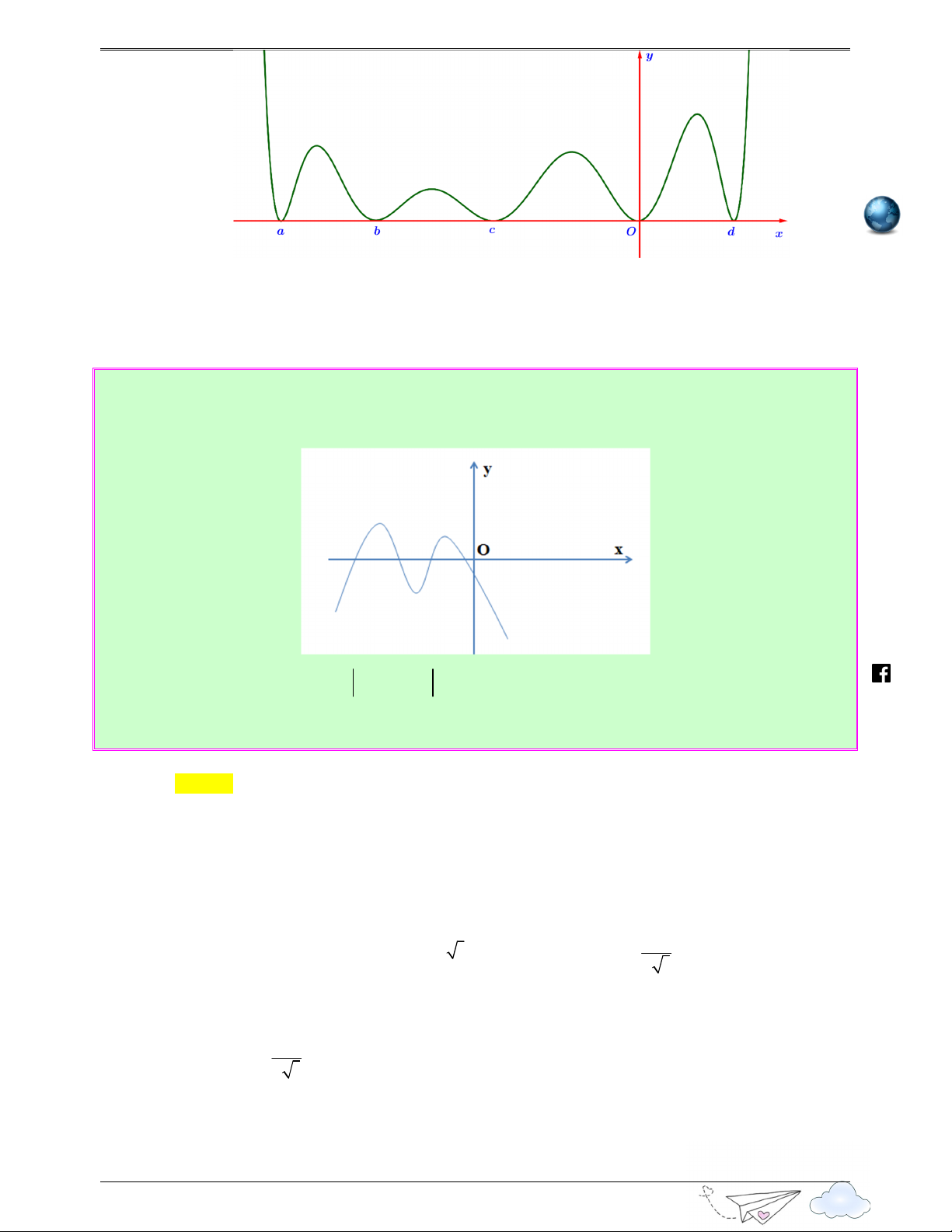
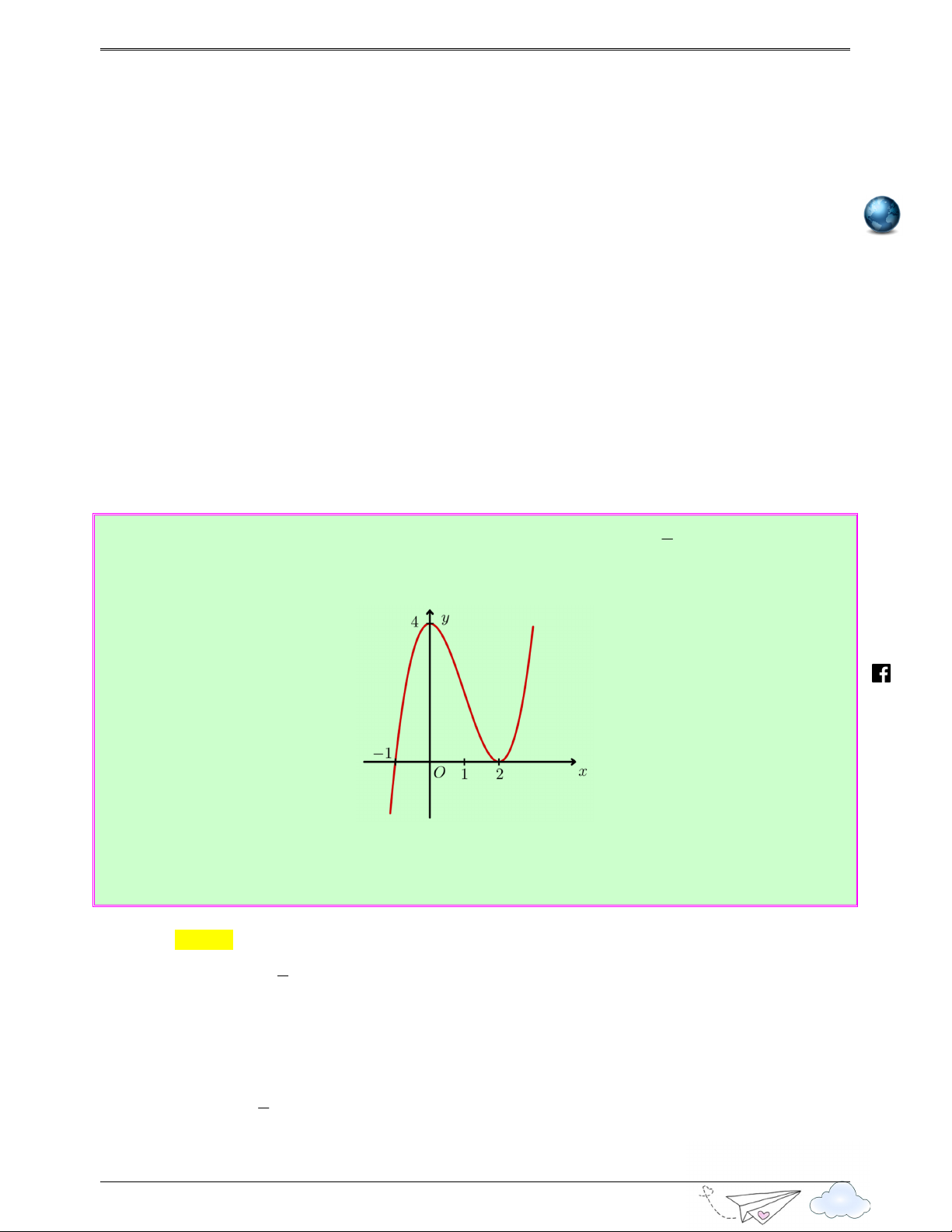
Câu 2: (Câu 18 - THPT Lê Lợi - Thanh Hóa - Năm 2020 - 2021) Cho hàm số bậc bốn y = f (x) . Hàm
số y = f '(x) có đồ thị như hình vẽ. /vietgold
Số điểm cực đại của hàm số y = f ( 2 x + ) 1 là
htps://www.facebook.com Ⓐ. 2. Ⓑ. 1. Ⓒ. 4. Ⓓ. 3. Lời giải Chọn B Ta có: 2 y ' = 2 . x f '(x +1) . x = 0 x = 0 x = 0 2 y ' = 0 ⇔
⇔ x + = ⇔ x = . f ' ( 1 1 2 2 x + ) 1 = 0 2 x +1 = 3 x = − 2 1
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Ta có bảng biến thiên sau:
Hàm số đạt cực đại tại điểm x khi đạo hàm của hàm số đó đổi dấu dương (+) sang âm (-) khi đi 0 qua điểm x . 0
Vậy hàm số y = f ( 2 x + ) 1 có 1 cực đại. h ttp
Câu 3: (Câu 4 - THPT Quế Võ 1 - Bắc Ninh - Lần 02 - Năm 2020 - 2021) Cho hàm số có đạo s f ( x) ://l hàm trên
f ′ x như sau u ℝ và có dấu của ( ) yenthit rac
Hàm số y = f (2 − x) có bao nhiêu điểm cực trị? n ghi e Ⓐ. 1. Ⓑ. 4 . Ⓒ. 3. Ⓓ. 2. m . Lời giải vn Chọn C Cách 1
Ta có y = f (2 − x) ⇒ y′ = − f ′(2 − x) . 2 − x = 1 − x = 3 2 − x = 1 x = 1
Ta có y′ = 0 ⇔ f ′(2 − x) = 0 ⇔ ⇔ 2 − x = 2 x = 0 2 − x = 3 x = 1 − . htt 2 − x < 1 − x > 3 p
y′ < 0 ⇔ f ′ 2 − x > 0 ⇔ ⇔ s ( ) : 2 < 2 − x < 3 1 − < x < 0 / /w Mặt khác 1 − < 2 − x <1 1 < x < 3 ww
y′ > 0 ⇔ f ′ 2 − x < 0 ⇔ 1 < 2 − x < 2 ⇔ 0 < x < 1 . ( ) f ac 2 − x > 3 x < 1 − . e boo
Ta có bảng xét dấu của y′ = − f ′(2 − x) k.com/v iet ′ = − ′ − = − g
Từ bảng xét dấu của y
f (2 x) ta thấy hàm số y
f (2 x) có 3 điểm cực trị. old Cách 2
Số điểm cực trị của hàm số f (2 − x) bằng số điểm cực trị của hàm số f ( x) .
Từ bảng xét dấu của f ′( x) ta thấy hàm số f (x) có 3 điểm cực trị.
Câu 4: (Câu 44 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số f (x) bậc 4 có bảng biến thiên như sau: 2
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
.vn Số điểm cực trị của hàm số g (x) = x f (x + ) 2 4 1 là iem Ⓐ. 11. Ⓑ. 9 . Ⓒ. 7 . Ⓓ. 5. gh Lời giải Chọn B itracn th Ta chọn hàm bậc bốn 4 2 y = f ( )
x = 5x −10x + 3 có bảng biến thiên như đề cho. 2 3 4 yen
Ta có g '(x) = 4x f ( x + ) 1 + x .2. f (x + ) 1 f '( x + ) 1 = 0 3
⇔ 2x . f (x + ) 1 .2 f (x + ) 1 + xf '( x + ) 1 = 0 s://lu 3 ttp x = 0 (1) h
⇔ f ( x + ) 1 = 0 (2) 2 f (x + ) 1 + xf '( x + ) 1 = 0 (3)
+ Phương trình (1) có nghiệm bội x = 0 .
+ Từ bảng biến thiên của hàm số y = f ( x) , ta có phương trình f ( x) = 0 có 4 nghiệm phân biệt
x ≠1 ⇒ Phương trình (2): f ( x + )
1 = 0 có 4 nghiệm phân biệt x ≠ 0.
+ Giải (3): Đặt x +1= t ⇒ x = t −1, phương trình (3) trở thành:
2 f (t) + (t − )
1 . f '(t) = 0 ⇔ 2( 4 2
5t −10t + 3) + (t − ) 1 ( 3
20t − 20t ) = 0 4 3 2
⇔ 30t −20t − 40t + 20t + 6 = 0 (3') /vietgold
Bấm MTCT thấy phương trình (3’) có 4 nghiệm phân biệt t ≠1.
⇒ Phương trình (3) có 4 nghiệm phân biệt x ≠ 0.
Ngoài ra, nghiệm của phương trình (2) không phải là nghiệm của phương trình (3) vì những giá
trị x thỏa mãn f (x + )
1 = 0 không thỏa mãn phương trình (3).
Do đó phương trình g '( x) = 0 có 9 nghiệm phân biệt nên hàm số g ( x) = x f ( x + ) 2 4 1 có 9 điểm cực trị.
Câu 5: (Câu 44) (MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc 4 có bảng biến htps://www.facebook.com thiên như hình vẽ
Số điểm cực trị của hàm số g ( x) = x f ( x − ) 2 4 1 là 3
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 Ⓐ. 7 . Ⓑ. 5. Ⓒ. 9 . Ⓓ. 11. Lời giải Chọn C
Cách 1. Từ giả thiết đề bài đã cho ta thấy rằng hàm số f ( x) có dạng ( ) 4 2
f x = ax + bx + c .
Sử dụng giả thiết ta được
f ( x) = x − x + ⇒ f ( x − ) = (x − )3 4 2 4 8 3 ' 1 16 1 −16( x − )
1 = 16x ( x − ) 1 ( x − 2) Ta có h t 2 t 3 4 p
g′( x) = 0 ⇔ 4x f ( x − ) 1 + 2x . f (x − )
1 . f ′( x − ) 1 = 0 s:// x = 0 lu y ⇔ f ( x − ) 1 = 0 en t 2 f (x − ) 1 + . x f ′( x − ) 1 = 0 ( ) * h itr x x 2 a
Xét phương trình (*) ⇔ f ( x − )
1 = − . f ′( x − )
1 , ta có − . f ′( x − )
1 = −8x ( x − ) 1 ( x − 2) . c 2 2 n g x h
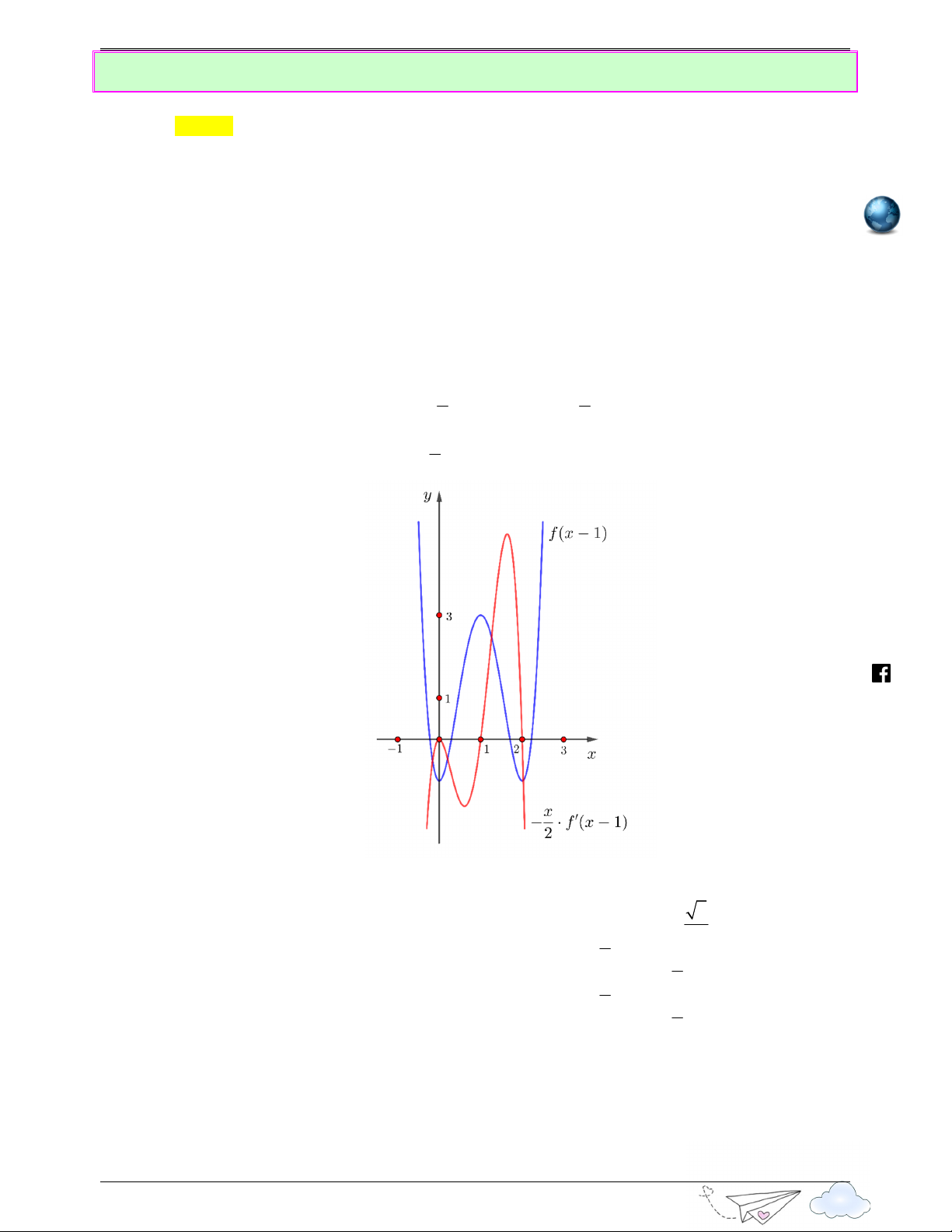
Biểu diễn hai hàm số f ( x − )
1 và − . f ′( x − )
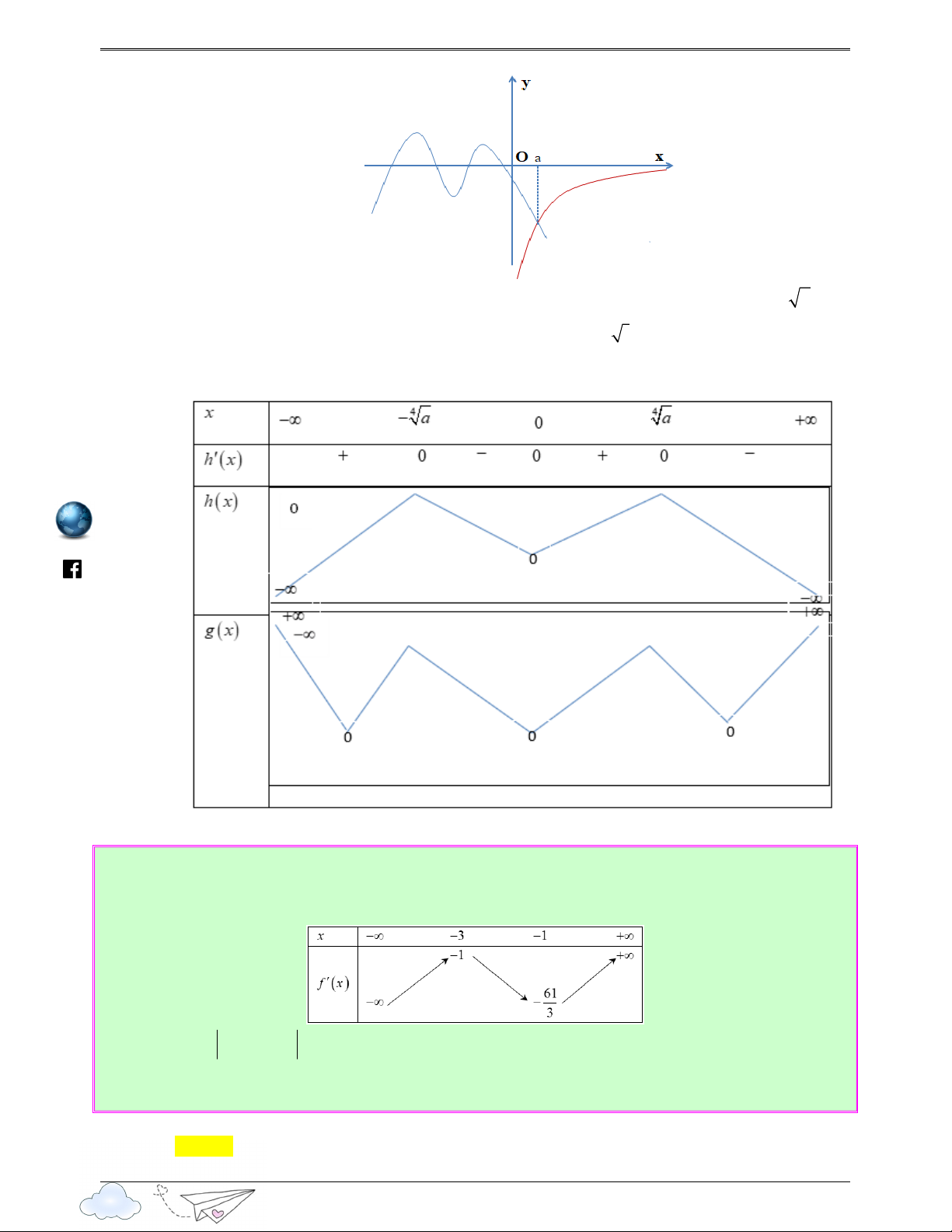
1 trên cùng một đồ thị đồ thị ta có ie 2 m .vn https://www.faceboo k.co Như vậy phương trình ( )
* có 4 nghiệm phân biệt. m /v 6 ie x = ± +1 tg 2 3 2 o (x ) 1 − = l d 2 5
Xét phương trình f ( x − ) 1 = 0 ⇔ ⇔ x = . (x − )2 1 4 1 = 2 3 x = 4
Thay 4 nghiệm này vào phương trình ( )
* thì ta thấy rằng các nghiệm của phương trình này không
phải là nghiệm của phương trình ( ) * .
Vậy hàm số đã cho có tất cả 9 điểm cực trị. Cách 2. 4
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
Từ bảng biến thiên, ta nhận thấy rằng phương trình f ( x − )
1 = 0 có 4 nghiệm phân biệt khác 0,
suy ra phương trình g ( x) = x f ( x − ) 2 4 1 = 0
có tất cả 5 nghiệm bội chẵn, khi đó đồ thị hàm số
g ( x) sẽ có dạng như sau .vn iem gh
Như vậy hàm g ( x) có 9 điểm cực trị.
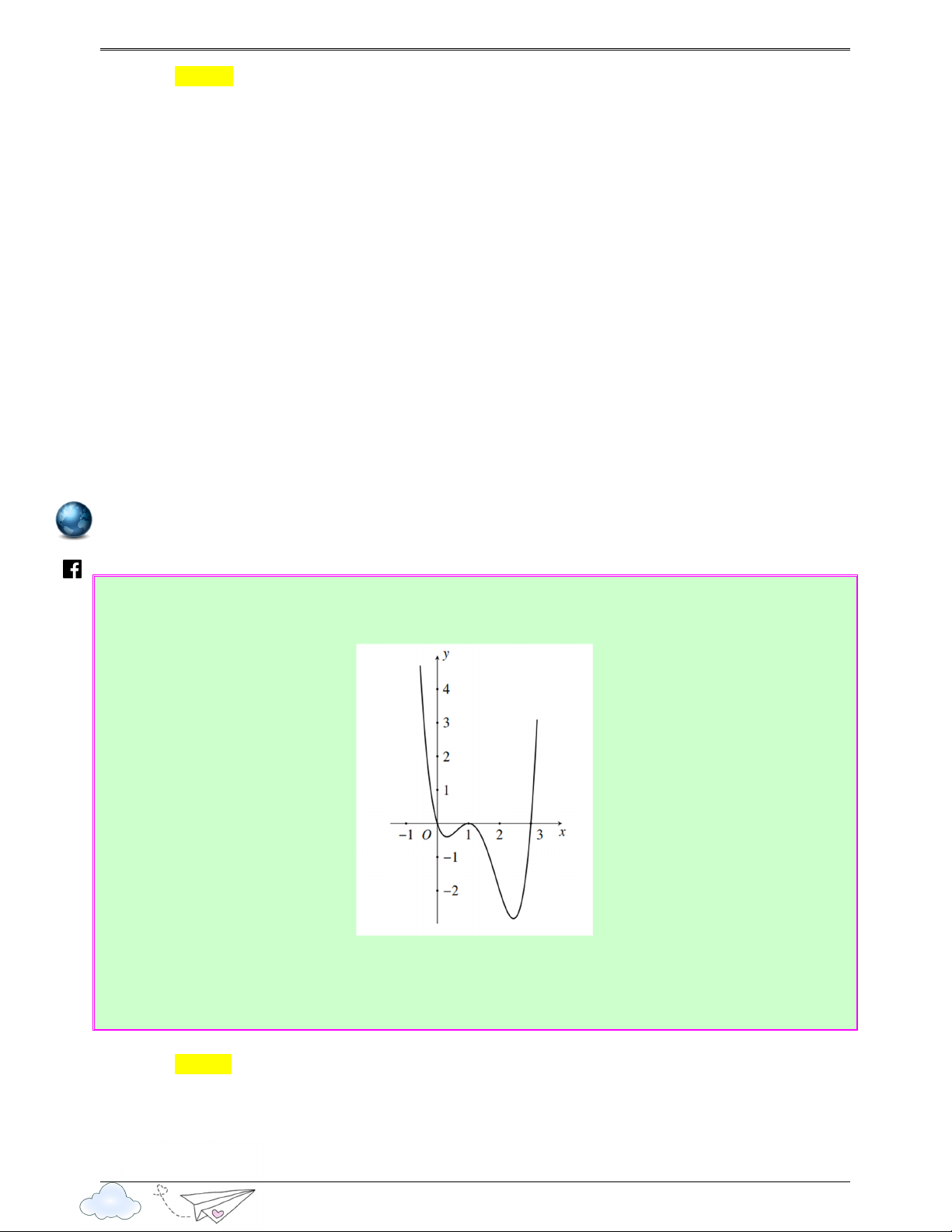
itracn Câu 6: (Câu 38 - SGD Cần Thơ - Mã đề 102 - Năm 2020 - 2021) Cho hàm số bậc bốn y = f (x) và th
có đồ thị f ′ ( x ) như sau: yen s://lu ttp h /vietgold
Số điểm cực trị của hàm số g ( x) = f ( 2 x − ) 1 là Ⓐ. 1. Ⓑ. 3. Ⓒ. 2. Ⓓ. 4. Lời giải Chọn B
Ta có g′( x) = x f ′( 2 2 . x − ) 1 htps://www.facebook.com x = 0 x = 0 x = 0
Xét g′( x) = 0 ⇔ ⇔ ⇔ f ′ ( 2 x − ) 2 1 = 0 x −1 = 2 x = ± 3
g ′ (2) = 4. f ′ (3) > 0
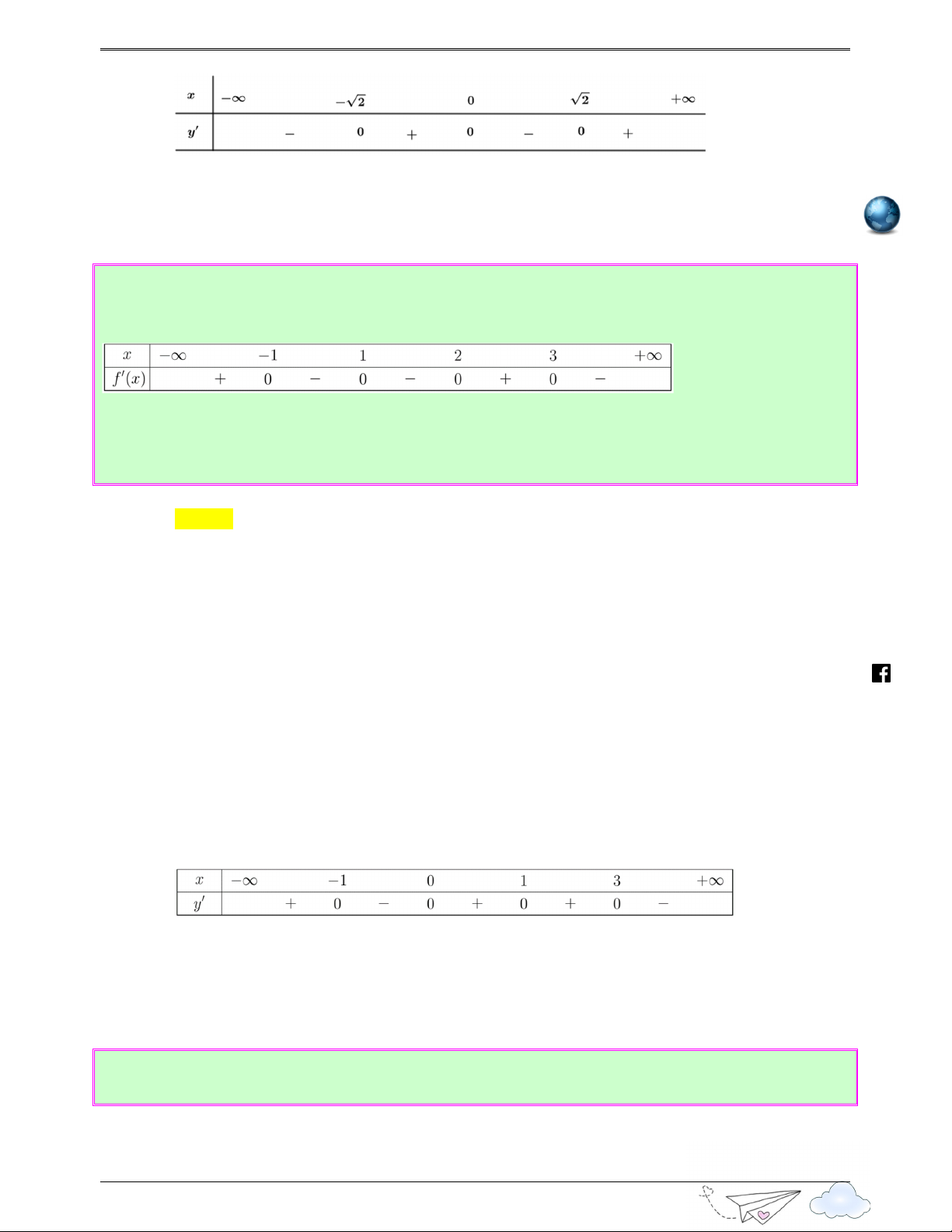
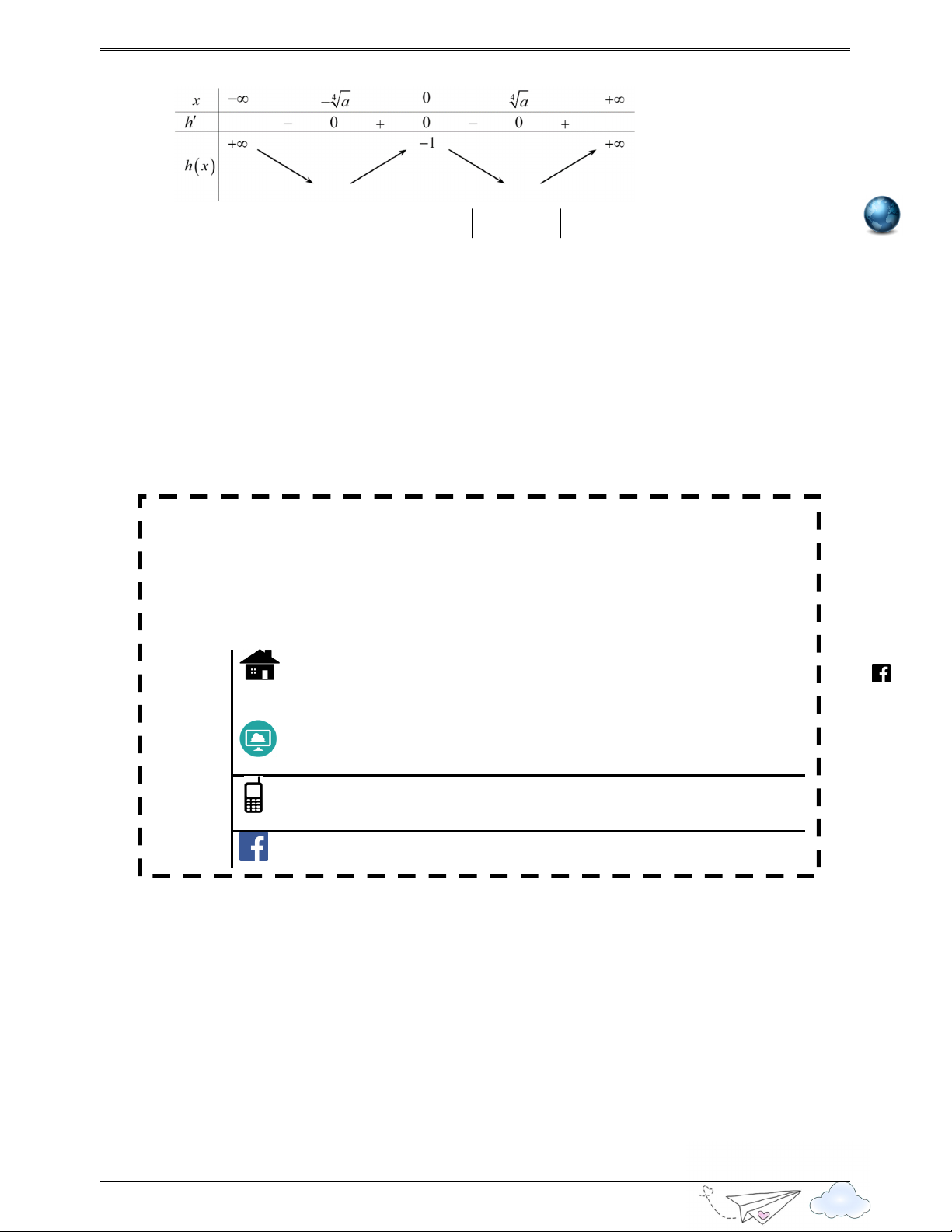
Ta có bảng xét dấu g ′( x) : x −∞ − 3 0 3 +∞ g ′ ( x ) − 0 + 0 − 0 +
Vậy số điểm cực trị của hàm số là 3 điểm. 5
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
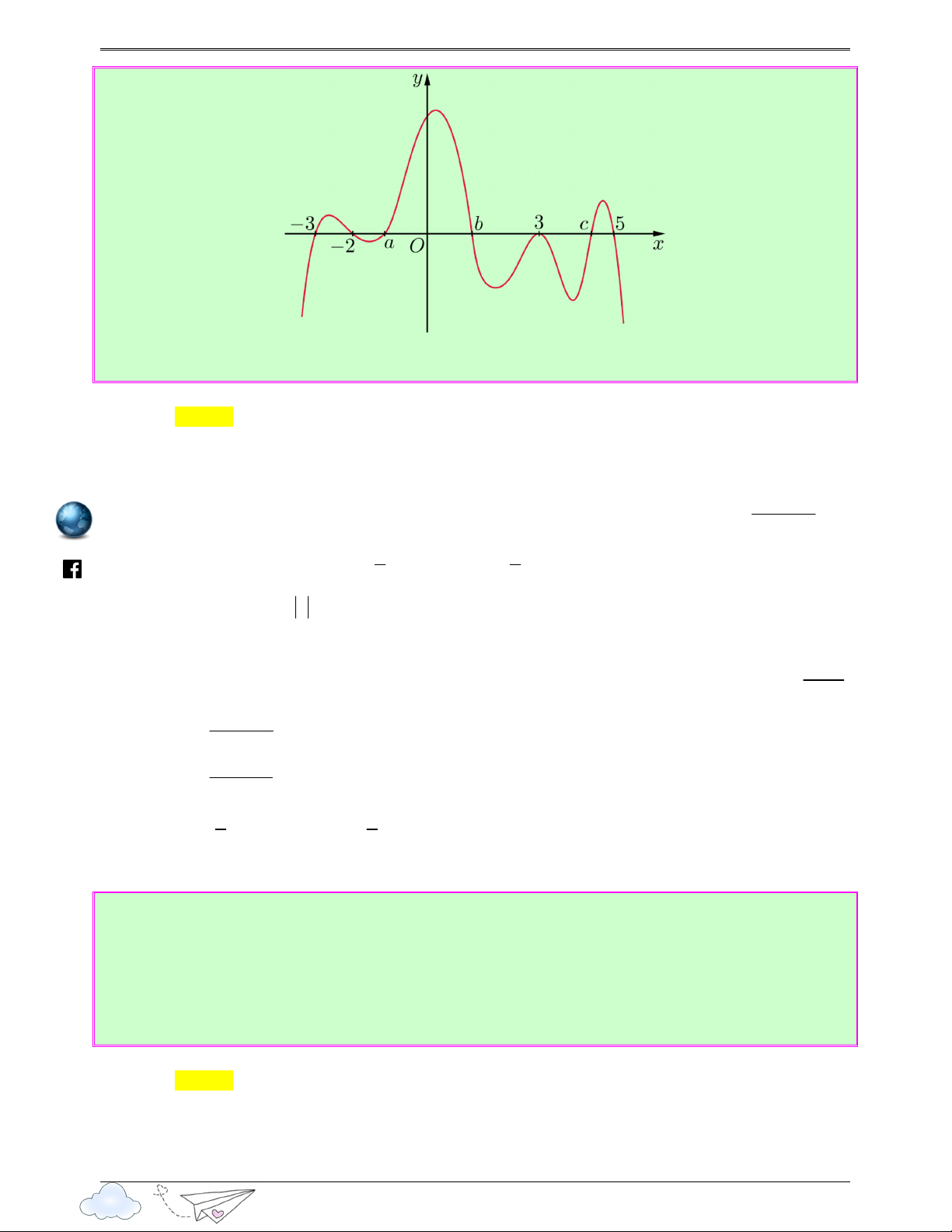
Câu 7: (Câu 41 - SGD Quảng Nam - Lần 2 - Năm 2020 - 2021) Biết hàm số f (x) có đồ thị được cho
như hình vẽ bên. Tìm số điểm cực đại của hàm số 2
y = f f ( x) h ttps://lu yen Ⓐ. 3. Ⓑ. 4. Ⓒ. 2. Ⓓ. 1. thi Lời giải tra Chọn C cn Ta có: gh
y′ = 2 f f x . f ′ f x . f ′ x ; i ( ) ( ) ( ) em ′ . f ( x) = 0 ( ) 1 v n
y′ = 0 ⇔ f ′ f ( x) = 0 (2). f f ( x) = 0 (3) x = Giải ( ) 1 : f ′( x) 0 = 0 ⇔ x = 2 x = 0(kep) f (x) = 0
Giải (2) : f ′ f ( x) = 0 ⇔ ⇔ x = x > 2 1 f x = 2 h ( ) t
x = x > x t 2 1 ps:/ x = 0(kep) /w f ( x) = 0 w
Giải (3) : f f ( x) = 0 ⇔ ⇔ x = x > 2 1 w f
( x) = x x > 2 1 ( 1 ) . = > f x 3 x 2 x a ceb
Vậy phương trình y′ = 0 có nghiệm x = 0 (bội 5 ), x = 2 , x = (kép), = , = Phương 1 x x 2 x x 3 x ook
trình (1) có 4 nghiệm làm đổi dấu y′ nên hàm số đã cho có hai điểm cực đại, hai điểm cực tiểu. .com/
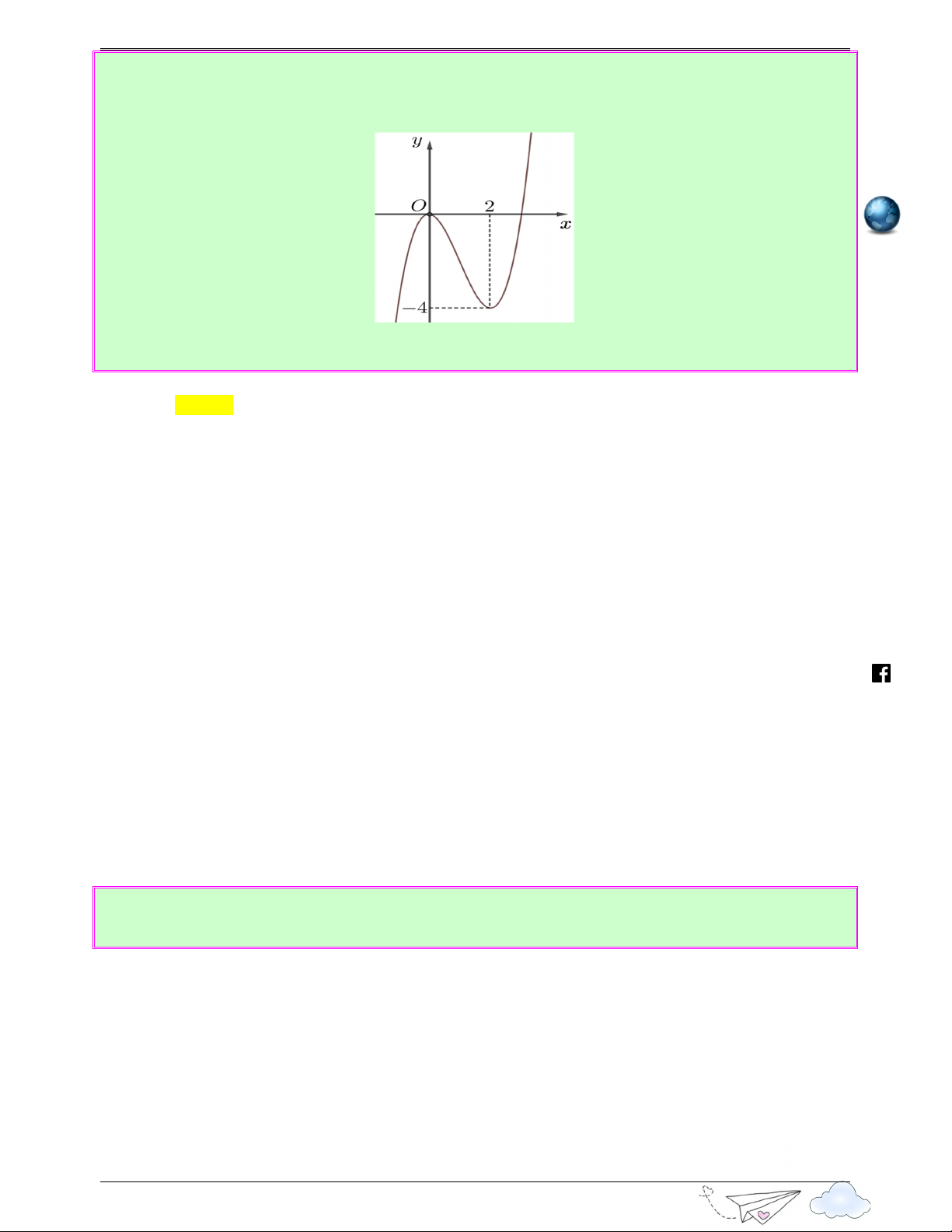
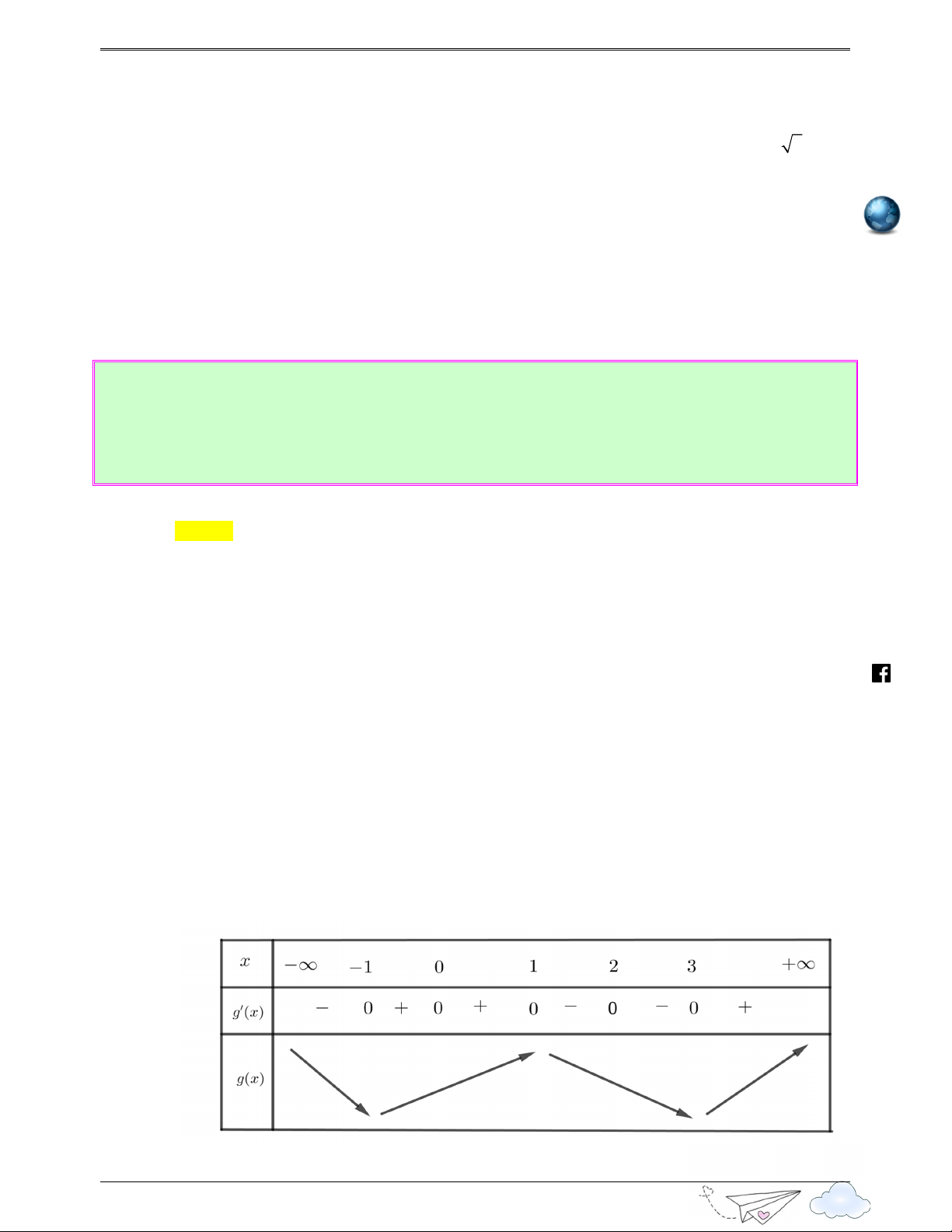
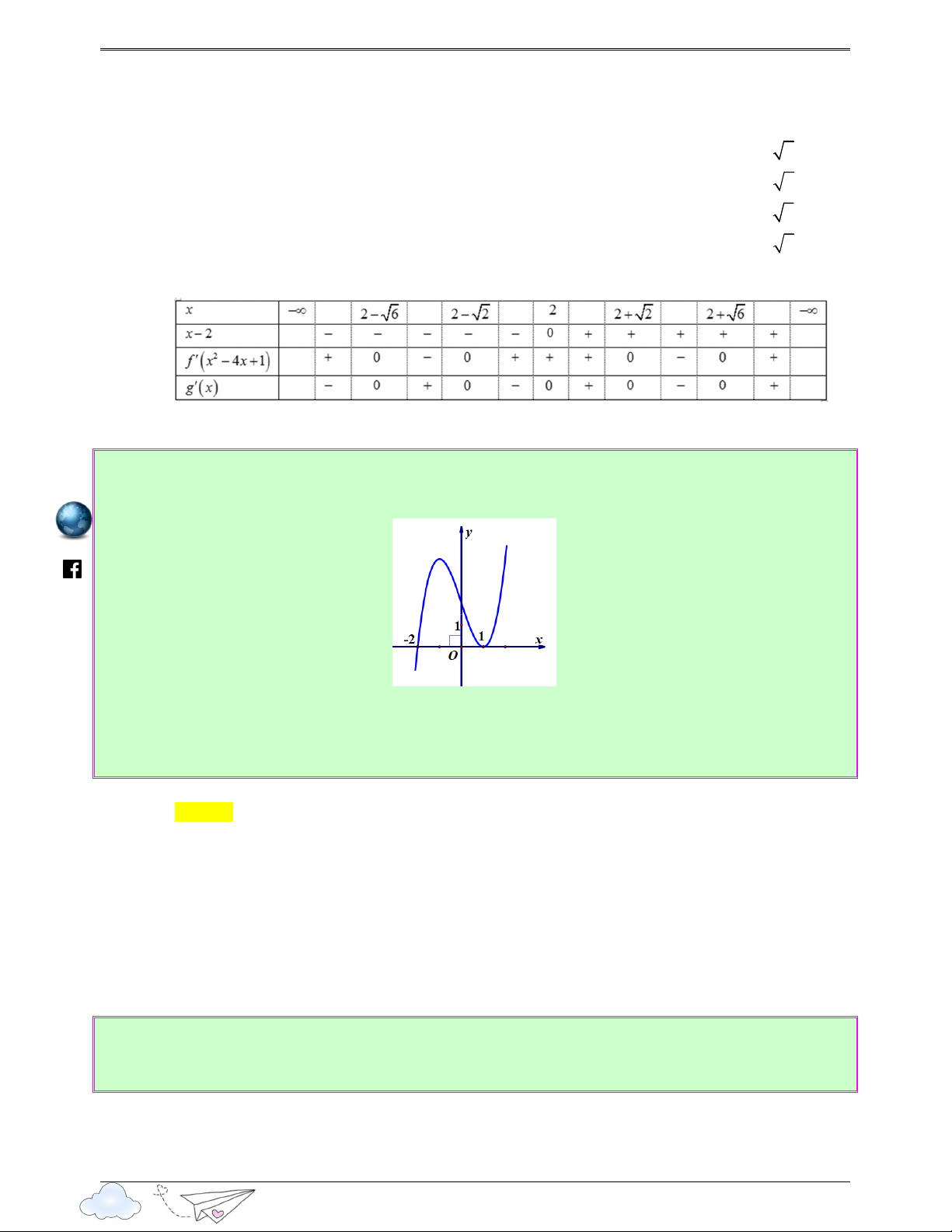
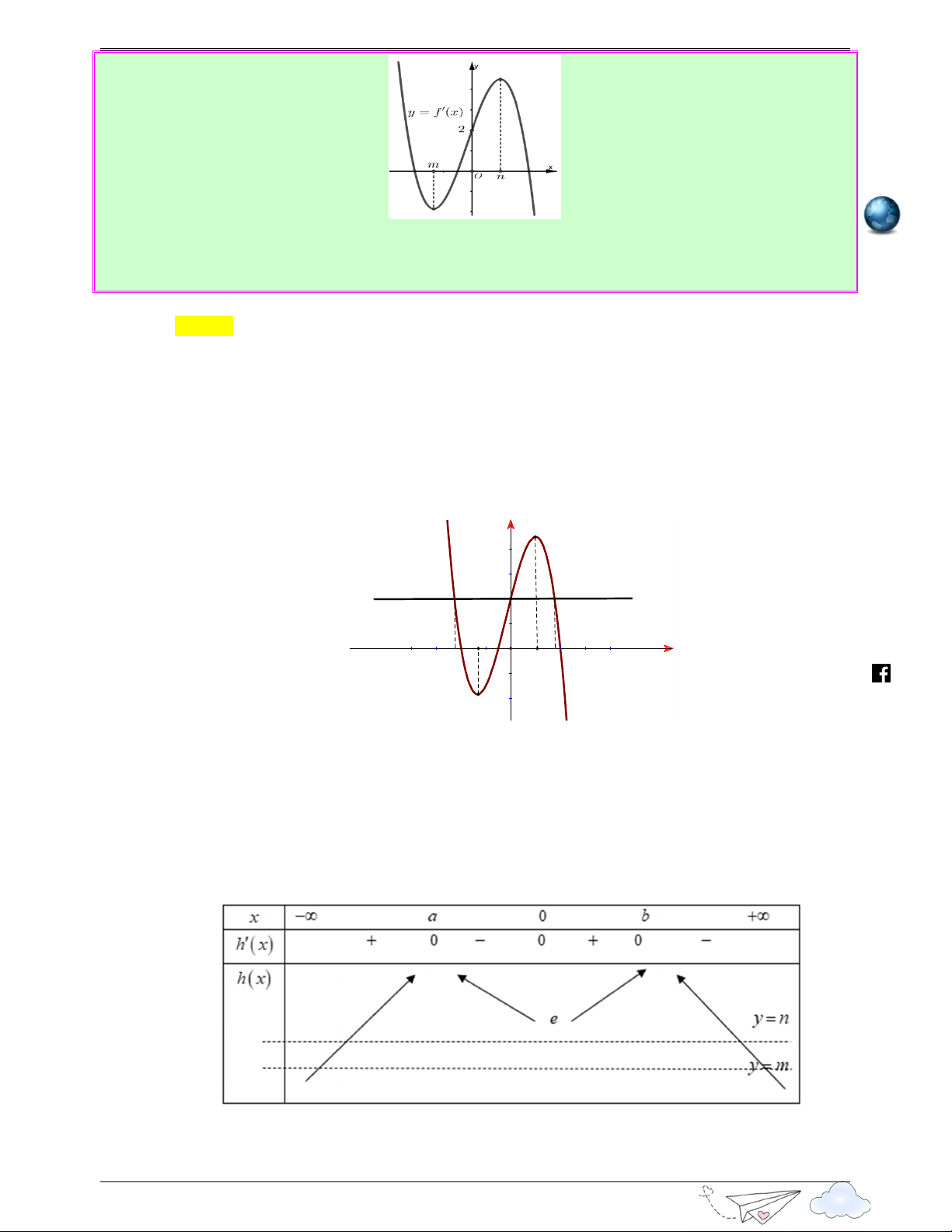
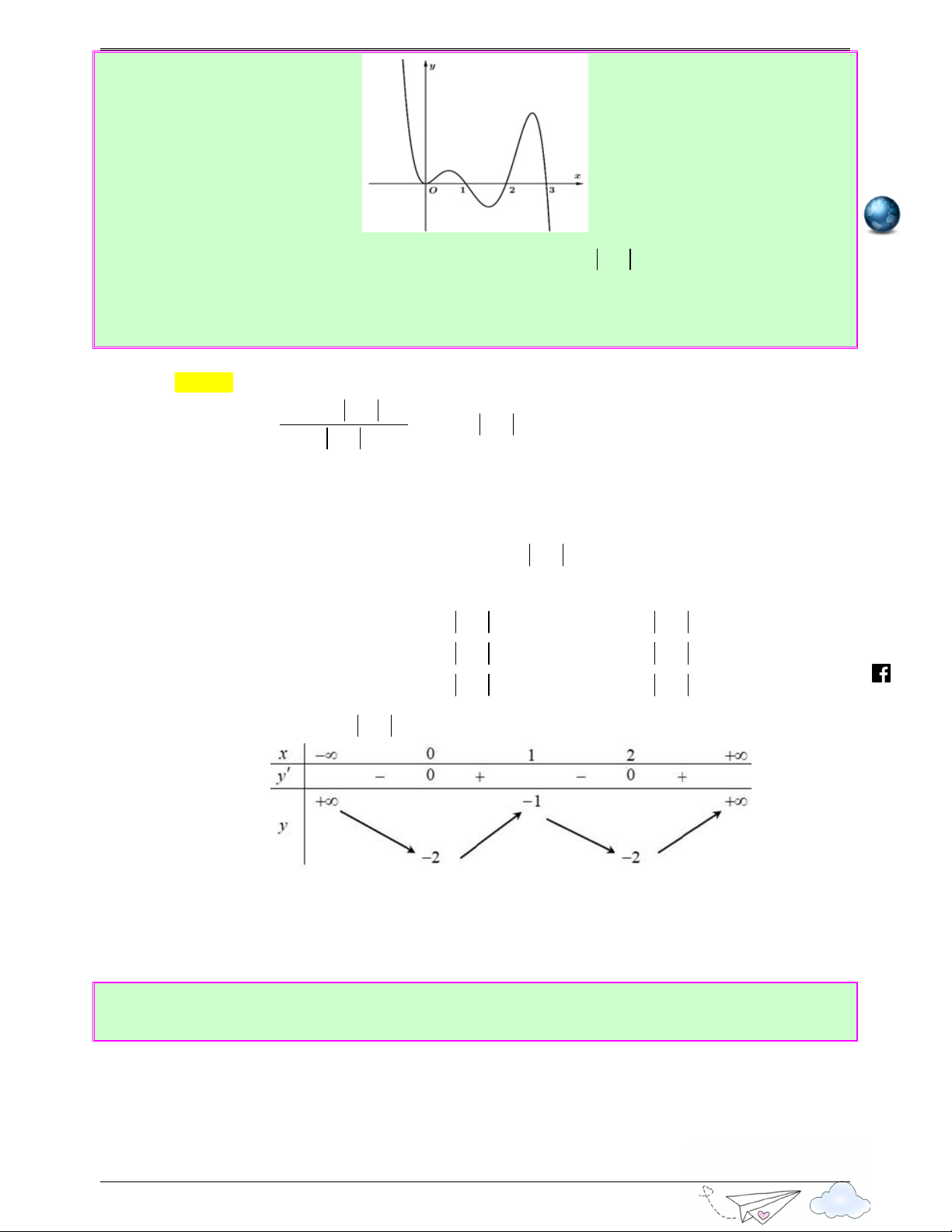
Câu 8: (Câu 47 - SGD Quảng Nam - Lần 2 - Năm 2020 - 2021) Cho hàm số bậc ba y = f ( x) có đồ viet thị như hình vẽ bên gold 6
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh itracn
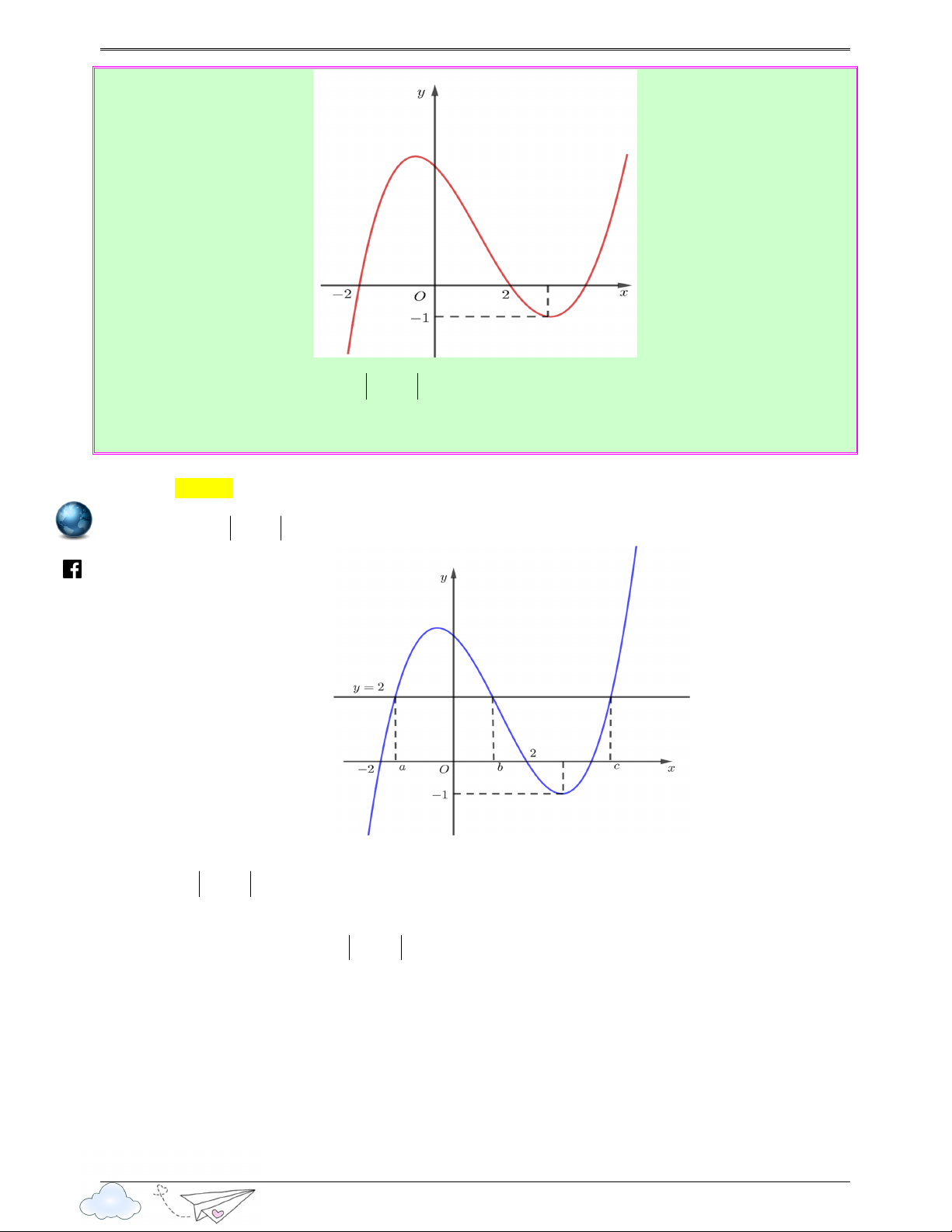
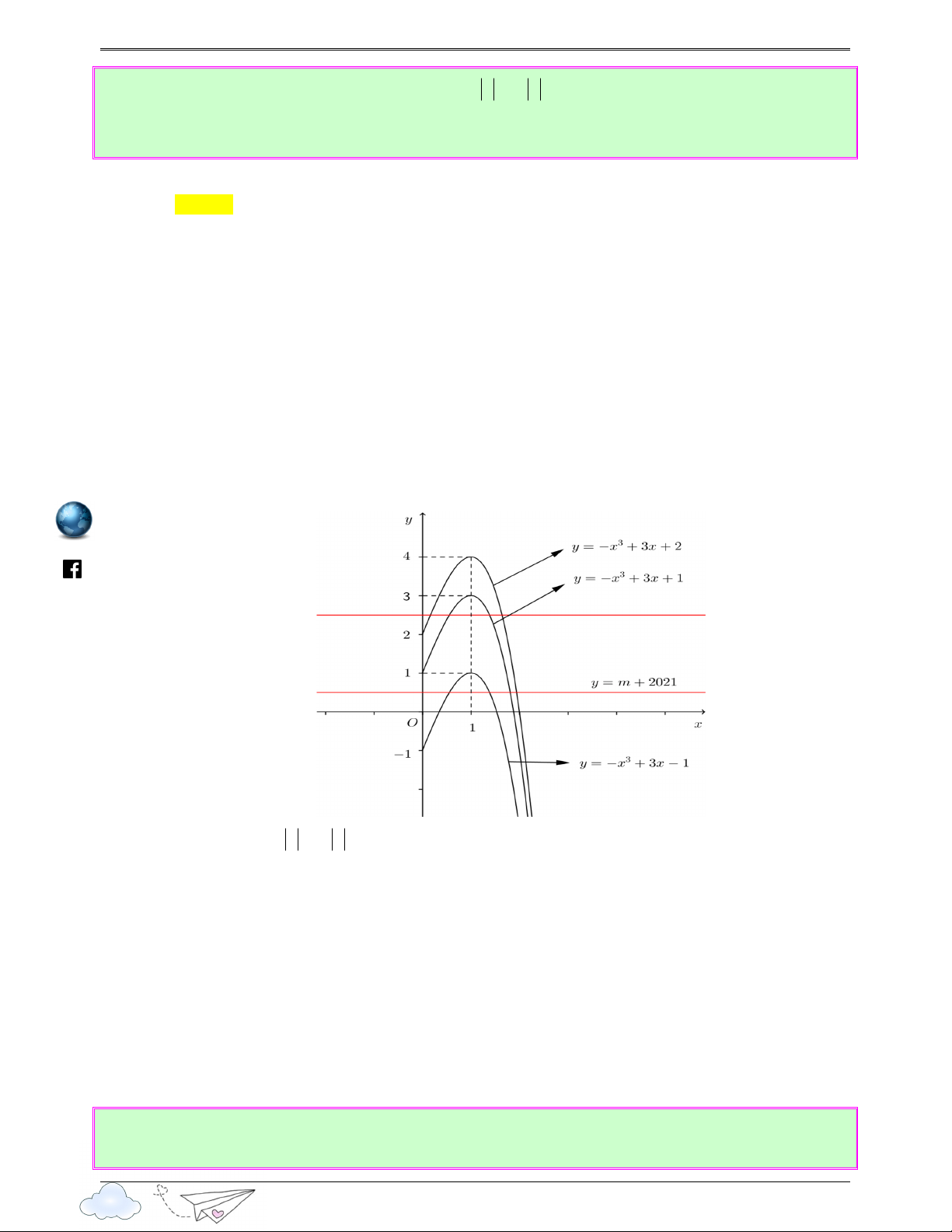
th Số nghiệm thực của phương trình f ( 3x−3x)=2 là yen Ⓐ. 9 . Ⓑ. 10. Ⓒ. 8 . Ⓓ. 6 . s://lu ttp Lời giải h Chọn C Đặt 3
t = x − 3x (t ≥ 0) /vietgold
t = a (−2 < a < 0) f ( 3
x − 3x ) = 2 ⇔ f (t) = 2 ⇔ t = b (0 < b < 2) t = c (c > 2) htps://www.facebook.com Ta có đồ thị hàm số 3
y = x − 3x (là phần nằm phía trên trục hoành trong hình vẽ dưới đây) 7
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h ttps://luy en
Dựa vào đồ thị của hàm số 3
y = x − 3x ta có thi
Với t = a ta có 3
x − 3x = a phương trình vô nghiệm trac
Với t = b ta có 3
x − 3x = b phương trình có 6 nghiệm thực phân biệt n gh
Với t = c ta có 3
x − 3x = c phương trình có 2 nghiệm thực phân biệt iem
Vậy số nghiệm thực của phương trình 3 f
x − 3x = 2 là 8 . . ( ) vn
Câu 9: (Câu 38 - SGD Sơn La - Lần 2 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đạo hàm
f ′( x) = ( x − )2
1 ( x − 2) . Số điểm cực trị của hàm số g ( x) = f ( 2x + 2x + 5) là Ⓐ. 3. Ⓑ. 0 . Ⓒ. 1. Ⓓ. 2 . Lời giải Chọn C htt 2 x =1 p
Ta có: f ′ x = 0 ⇔ x −1 x − 2 = 0 ⇔ . s ( ) ( ) ( ) : x = 2 / /w x + 1 w g′ ( x) = f ′ ( 2 x + 2x + 5 . 2 ) w x + 2x + 5 .fac x + 1 2 e g′( x) = 0 ⇔ f ′ x + 2x + 5 = 0 b 2 ( ) o x + 2x + 5 ok. x = 1 − co m 2 / ⇔
x + 2x + 5 = 1 VN . 2 v f ′
x + 2x + 5 = 0 ⇔ i ( ) ( ) e 2 2 t g
x + 2x + 5 = 2 ⇔ x + 2x +1 = 0 ⇔ x = −1 old ′
Bảng xét dấu g ( x) : Suy ra: Chọn C
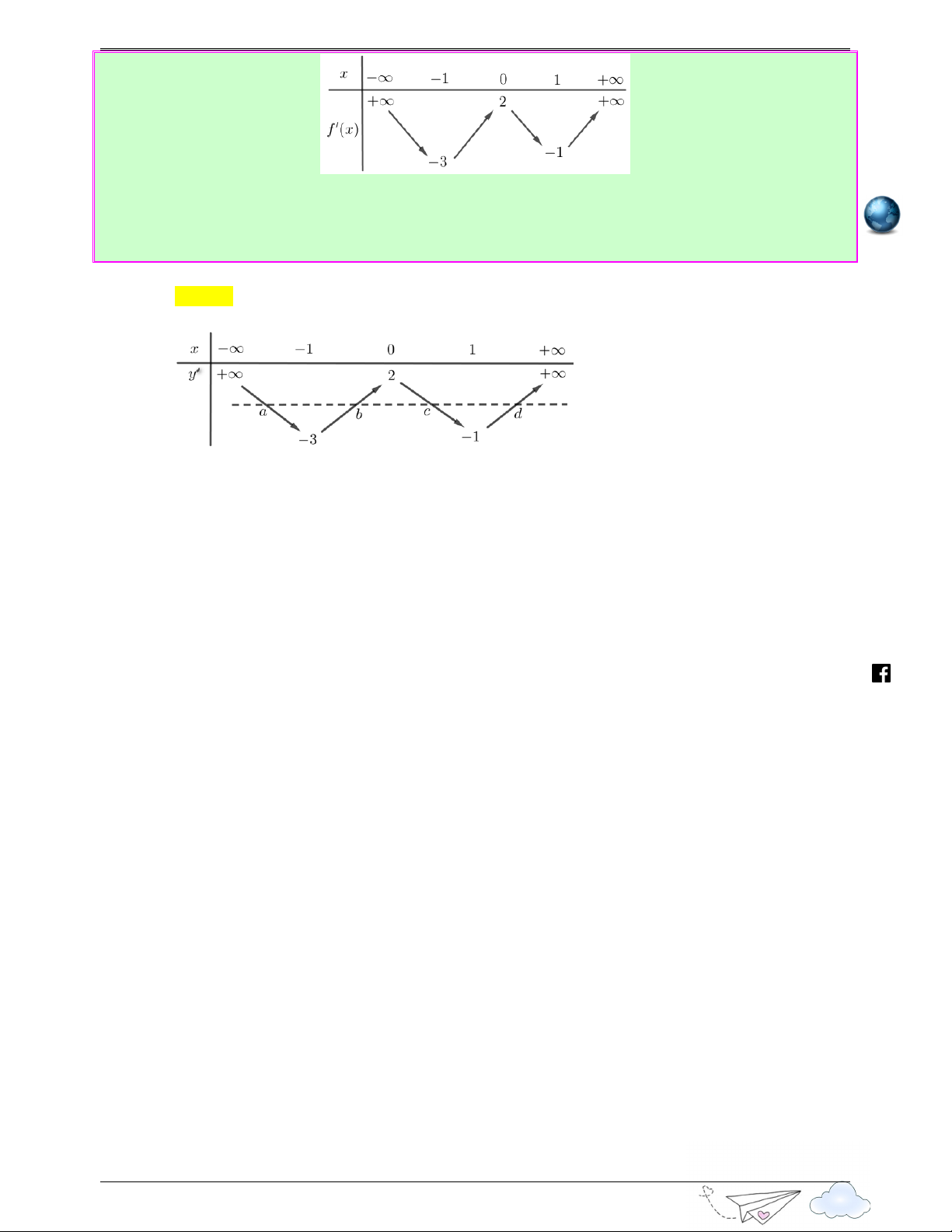
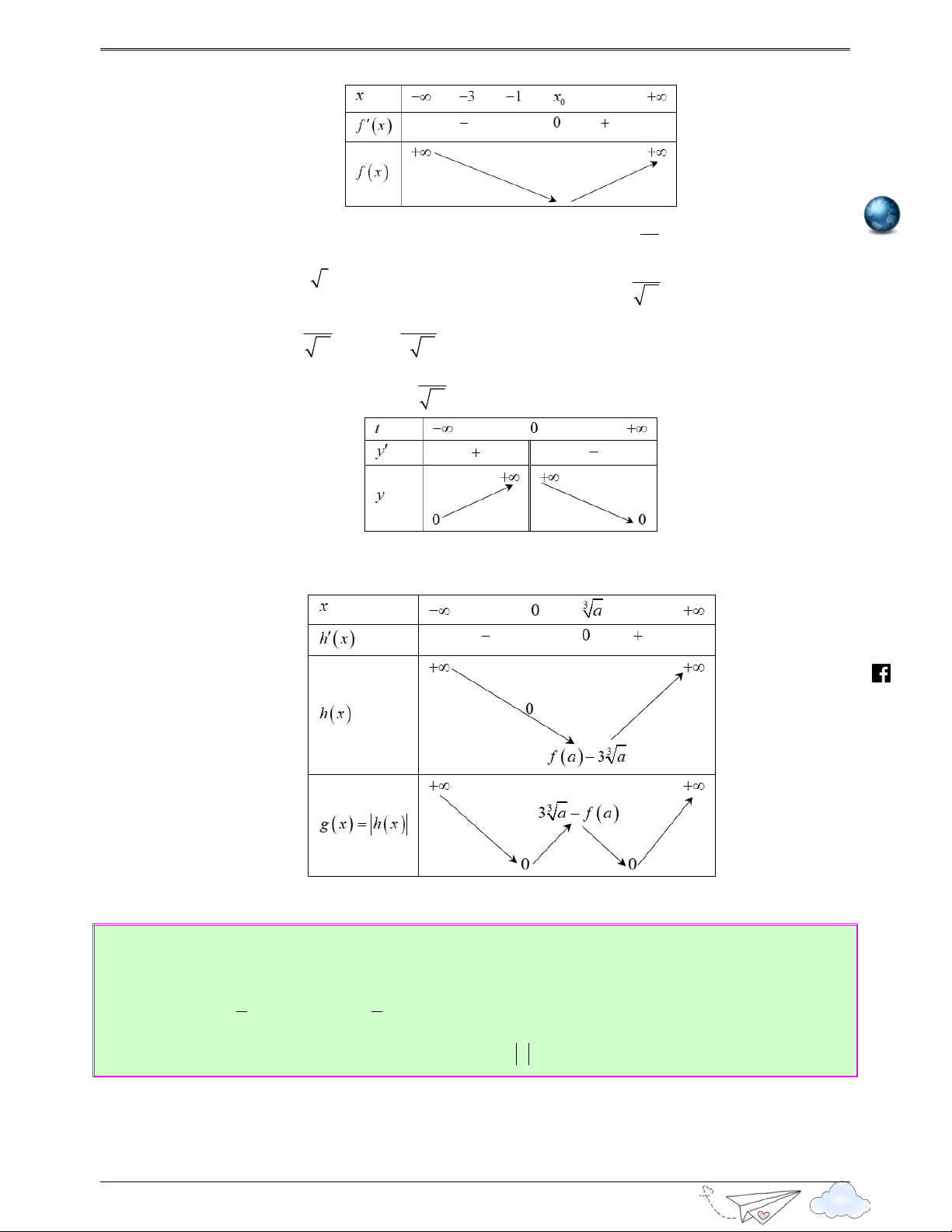
Câu 10: (Câu 39 - THPT Chuyên Bắc Ninh - Lần 3 - Năm 2020 - 2021) Cho hàm số y = f ( x) . Biết
hàm số y = f '( x) có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số f ( x ) f ( x) y = 2021 + 2020 là 8
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh itracn th Ⓐ. 2. Ⓑ. 5 . Ⓒ. 3 . Ⓓ. 4 . yen Lời giải Chọn C s://lu
Ta có y = f ( x) f ( x) + f ( x) f ( x) ' ' .2021 .ln 2021 ' .2020 .ln 2020. ttp h = f ( x) f ( x ) f ( x ) ' . 2021 .ln 2021 + 2020 .ln 2020 . = 1 x a Do f ( x) f ( x) 2021 .ln 2021 2020 .ln 2020 0, +
> ∀x ⇒ y ' = 0 ⇔ f '( x) = 0 ⇔ x = b. 2 = 3 x c /vietgold Vậy hàm số f ( x) f ( x) y = 2021 + 2020 có ba điểm cực trị.
htps://www.facebook.com Câu 11: (Câu 24 - Chuyên Vinh- Nghệ An – Lần 1 – Năm 2020 - 2021) Cho hàm số y = f (x) có đạo
hàm trên ℝ và có bảng biến thiên như hình vẽ. Hàm số y = f (1− 2x) đạt cực tiểu tại 1 1
Ⓐ. x = − .
Ⓑ. x = .
Ⓒ. x =1. Ⓓ. x = 0 2 2 Lời giải 9
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 Chọn B x =1 1 − 2x = 1 −
g′( x) = − f ′( − x) = ⇔⇒ − f ′( − x) 1 2 1 2 0 2 1 2 = 0 ⇔ 1− 2x = 0 ⇔ x = 2 1 − 2x = 2 1 x = − 2 Ta có bảng biến thiên h ttps://luyenth itr
Ta xét dấu bằng cách thay số acn
Với x = 2 ⇒ g′(2) = −2 f ′(−3) < 0 gh 3 3 1 ie
Với x = ⇒ g′ = 2 − f ′ − > 0 m 4 4 2 .v 1 1 1 n
Với x = ⇒ g′ = 2 − f ′ < 0 4 4 2
Với x = −1 ⇒ g′(− )
1 = −2 f ′(3) > 0 1
Vậy hàm số y = f (1− 2x) đạt cực tiểu tại x = . 2
Câu 12: (Câu 24 - Chuyên Hạ Long - Quảng Ninh - Lần 02 - Năm 2020 - 2021) Cho hàm số y = f (x)
có bảng biến thiên như sau:
https://www.facebook.com/v ietg
Điểm cực tiểu của hàm số y = f (3x) là old 2 2 Ⓐ. y = 3 −
Ⓑ. x = .
Ⓒ. x = 2 . Ⓓ. x = − . 3 3 Lời giải Chọn B Ta có:
y′ = 3 f ′(3x)
Từ BBT của hàm số y = f (x) ta có: 10
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” 1 3 x = − x = 1 − 3
y′ = 0 ⇔ f ′(3x) = 0 ⇔ ⇔ 3 x = 2 2 x = 3 1 x < − 3x < 1 − 3 y′ > 0 ⇔ ⇔ 3 x > 2 2 .vn x > 3 iem 1 2 gh y′ <0 ⇔ 1
− < 3x < 2 ⇔ − < x < 3 3 2
Do đó, điểm cực tiểu của hàm số là x = . itracn 3
th Câu 13: (Câu 47 - Chuyên Lam Sơn - Thanh Hóa - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f (x), yen
có đạo hàm f ′( x) = ( x + )2
1 ( x − 3). Tìm số điểm cực trị của hàm số g ( x) = f ( 2x + 2x + 6) s://lu ttp h Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 5. Lời giải Chọn C x + = x = − Ta có f ′( x) 1 0 1 = 0 ⇔ ⇔ . x − 3 = 0 x = 3 Bảng xét dấu /vietgold x +1
Xét hàm số g ( x) = f ( 2x + 2x + 6) có g′(x) = f ′( 2
x + 2x + 6 2 ) x + 2x + 6 x +1 = 0 x = 1 −
g′( x) = 0 ⇔ ⇔
f ′( 2x + 2x + 6) 2 = 0
x + 2x + 6 = 3 x = −1 x = 1 − ⇔ ⇔ x = −3 2 x 2x 3 0 + − = x = 1 Bảng xét dấu htps://www.facebook.com
Từ bảng biến thiên. Ta thấy hàm số g ( x) có 3 điểm cực trị.
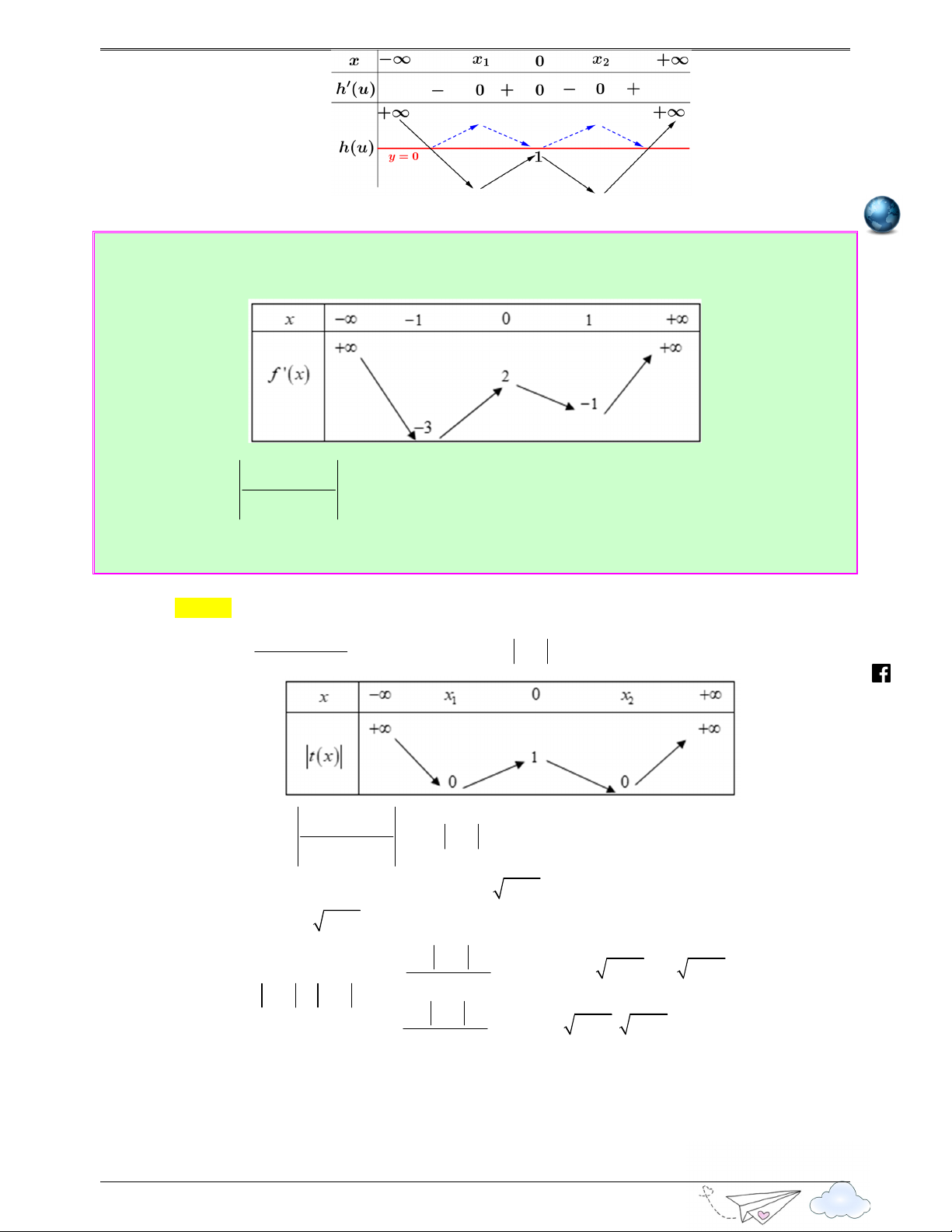
Câu 14: (Câu 45 - Chuyên Lam Sơn - Thanh Hóa - Lần 3 - Năm 2020 - 2021) Cho hàm số y = f ( x)
có đạo hàm liên tục trên ℝ và có đồ thị hàm số y = f ′( x) như hình dưới đây: 11
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 Hàm số = ( 2 y
f x + x) có bao nhiêu điểm cực đại? h Ⓐ. 1. Ⓑ. 0 . Ⓒ. 3. Ⓓ. 2 . ttp Lời giải s:/ Chọn D /lu Bảng xét dấu của ′ : y f ( x) enthitr ac 2 2 n
Đặt g ( x) = f (x + x) , ta có g′(x) = (2x + )
1 f ′(x + x) , ghi 1 − e x = m 2x +1 = 0 2 . v 2 x + x = 1 − 1 − ± 5 n g′( x) = 0 ⇔ ⇔ x = 2 x + x = 1 2 2 x + x = 4 1 − ± 17 x = 2 −1− 17 1 − − 5 1 − + 5 −1+ 17 Đặt a = , b = , c = , d =
; Ta có bảng xét dấu của g′( x) 2 2 2 2 https:/ /w
Từ bảng xét dấu của g′( x) ta có hàm số ( ) = ( 2 g x
f x + x) có 2 điểm cực đại. ww.fa
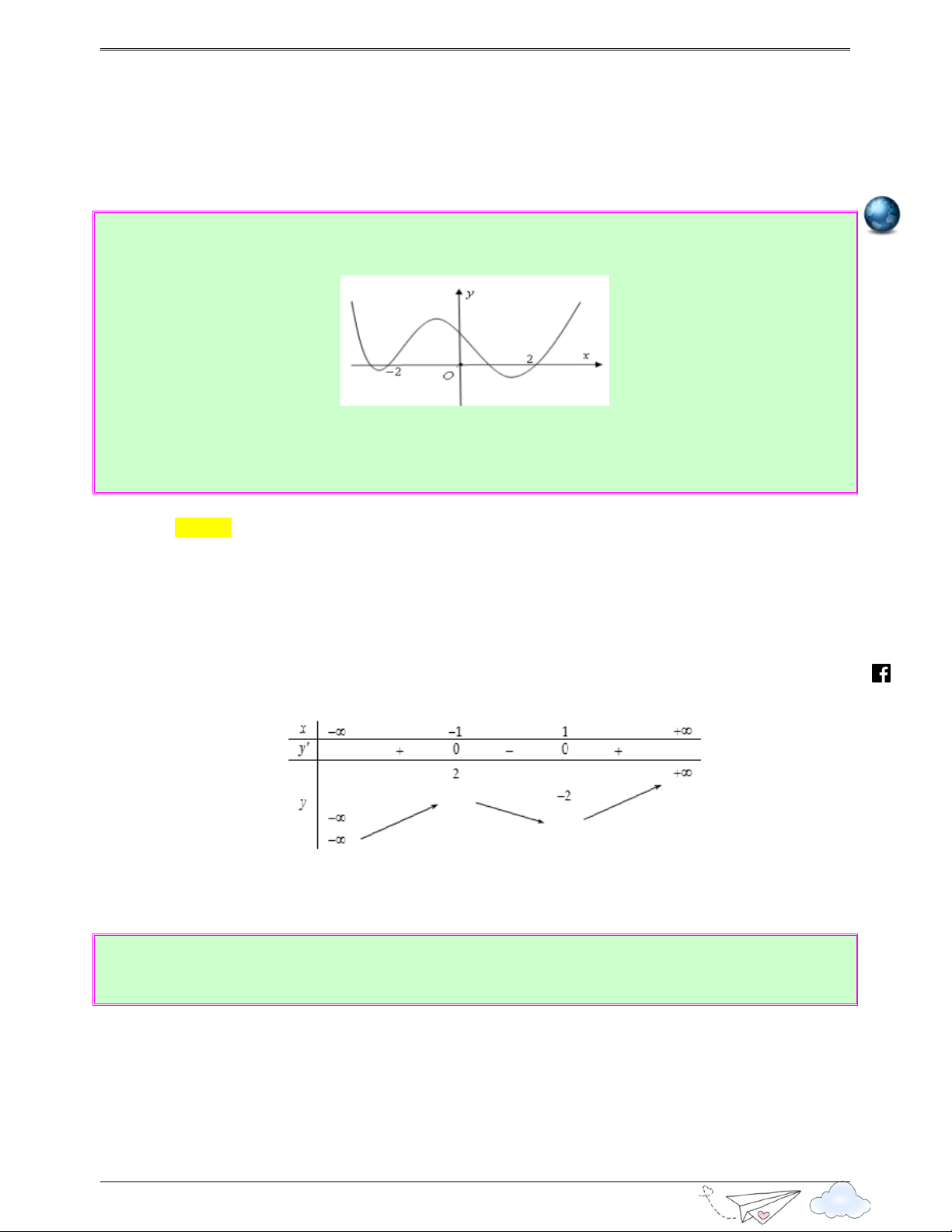
Câu 15: (Câu 13 - Chuyên Quang Trung - Bình Phước - Lần 1 - Năm 2020 - 2021) Cho hàm số bậc ceb
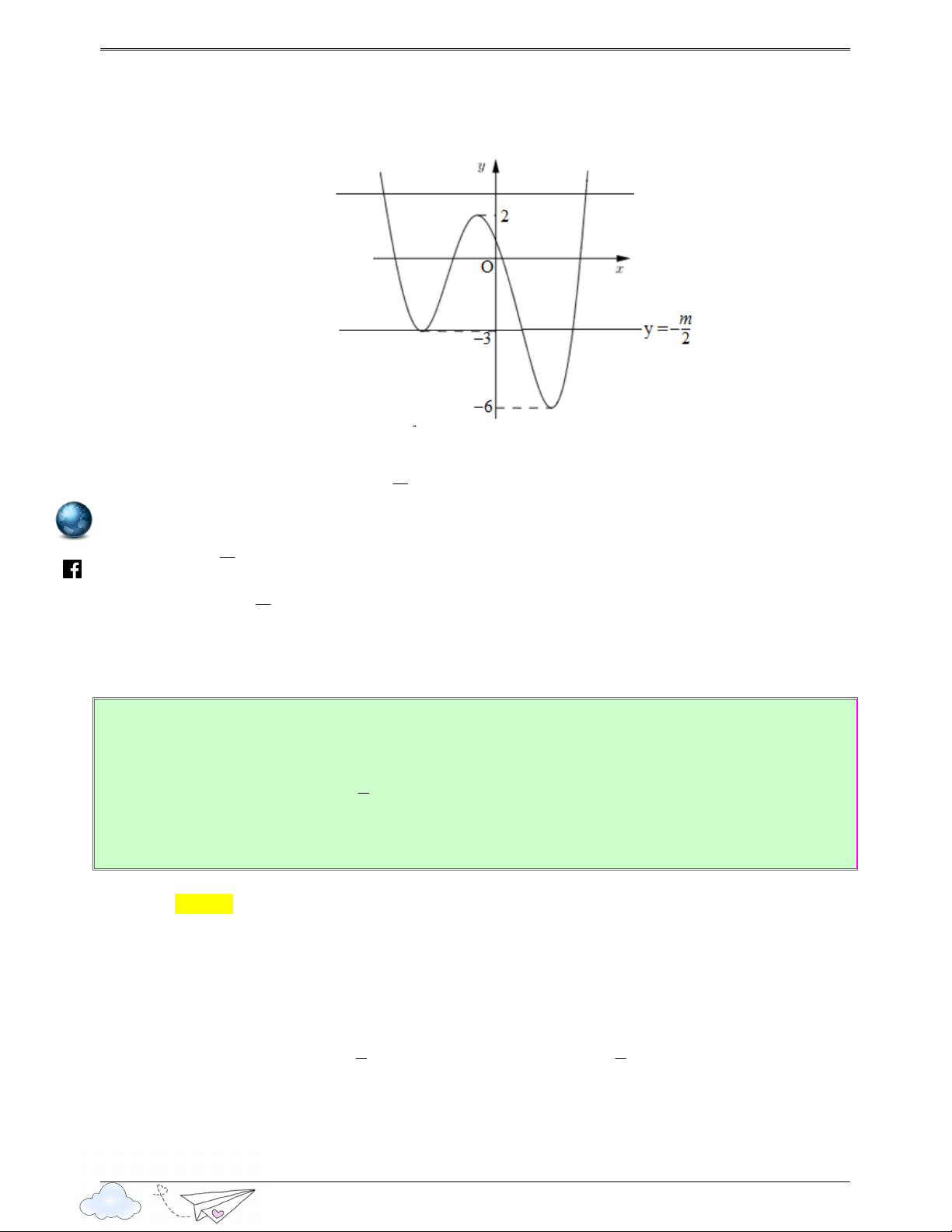
ba y = f ( x) có đồ thị như hình vẽ: ook.com/vietgold Gọi 2
S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = f ( x − )
1 + m) có 3 điểm cực trị.
Tổng các phần tử của S là: Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 8 . Ⓓ. 10 . Lời giải 12
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” Chọn A
Ta có y = ( x − ) f ( x − )2 ' 2 1 ' 1 + m) . x = 1 x = 1 x = 1 y ' = 0 ⇔ ⇔ − + = − ⇔ − = − − . f ( 2 2 (x − )2 + m) (x ) 1 m 1 (x ) 1 1 m( ) 1 ' 1 = 0 ( x − )2 1 + m = 3 ( x − )2 1 = 3 − m(2) .vn +) Nếu 1
− − m = 0 ⇔ m = 1
− khi đó phương trình ( ) ⇔ (x − )2 2
1 = 4 có hai nghiệm phân biệt iem khác 1 nên m = 1 − thỏa mãn. gh
+) Nếu 3 − m = 0 ⇔ m = 3 khi đó phương trình ( ) ⇔ ( x − )2 1
1 = −4 vô nghiệm. Do đó, m = 3 không thỏa mãn. itracn th
+) Để hàm số y = f ( x − )2
1 + m) có 3 điểm cực trị thì phương ( )
1 có hai nghiệm phân biệt và yen (2) vô nghiệm; hoặc ( )
1 vô nghiệm và (2) có hai nghiệm phân biệt. −1− m > 0 m < 1 − s://lu 3 − m < 0 m > 3 ttp ⇔ ⇔
⇔ −1 < m < 3. h 1 m 0 − − < m > −1 3 − m > 0 m < 3 Vậy 1 3 m m ∈ − ≤ <
ℤ→ m ∈{−1;0;1; } 2 . Chọn A .
Câu 16: (Câu 45 - Chuyên Quang Trung - Bình Phước - Lần 2 - Năm 2020 - 2021) Cho hàm số
y = f ( x) (với f (x) là đa thức bậc 5). Đồ thị hàm y = f '( x ) hình vẽ sau /vietgold
htps://www.facebook.com Hỏi hàm số y= f ( 2x−2x)có bao nhiêu điểm cực tiểu? Ⓐ. 1. Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 0 . Lời giải Chọn B
Ta có: y = ( x − ) f ( 2 ' 2 2 ' x − 2x) 13
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 x = 1 2 x − 2 = 0 x = 0 2 2x − 2 = 0 x − 2x = 0 x = 2
y ' = 0 ⇔ (2x − 2) f '( 2
x − 2x) = 0 ⇔ ⇔ ⇔ f ' ( 2 x − 2x) 2 = 0 x − 2x =1 x = 1± 2 . 2 x − 2x = 3 x = 3 x = 1 −
Dựa vào đồ thị ta suy ra y ' = 0 có đúng 5 nghiệm bội lẻ là: x = 1
− ; x = 0; x = 1; x = 2; x = 3 nên h 2 t
hàm số y = f (x − 2x) có 5 điểm cực trị. tps 2 :
Từ giả thiết đồ thị hàm số y = f '
và hàm số y = f x − 2x có 5 điểm cực trị suy ra hàm số / (x) ( ) /lu 2 y
y = f ( x − 2x) có 3 điểm cực tiểu enth
Câu 17: (Câu 44 - Chuyên Quốc Học Huế - Huế - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) itra 2 2 c
có đạo hàm f ′( x) = x ( x + 2)( x − 3) . Điểm cực đại của hàm số g(x) = f (x −2x) là n ghi x = x = − x = x = e Ⓐ. 0. Ⓑ. 1. Ⓒ. 3. Ⓓ. 1. m .v Lời giải n Chọn D x = 0
Theo giả thiết : f ′( x) = 0 ⇔ x = −2
(trong đó x = 0 là nghiệm kép). x = 3 2x − 2 = 0 2 2x − 2 = 0 x − 2x = 0 2
g′ x = 0 ⇔ ⇔ h
Ta có g′( x) = (2x −2) f ′(x −2x) , có ( ) 2 2 t
f ′ x − 2x = 0 t ( ) x − 2x = 2 − (vn) p s: 2 / x − 2x = 3 /ww x = 1 w .f x = 0 a ce
⇔ x = 2 (trong đó x = 0 và x = 2 là nghiệm kép). bo o x = − 1 k.c x = 3 o m /
Bảng biến thiên của hàm số g(x) vietgold
Dựa vào BBT, hàm số g(x) đạt cực đại tại x =1. 14
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
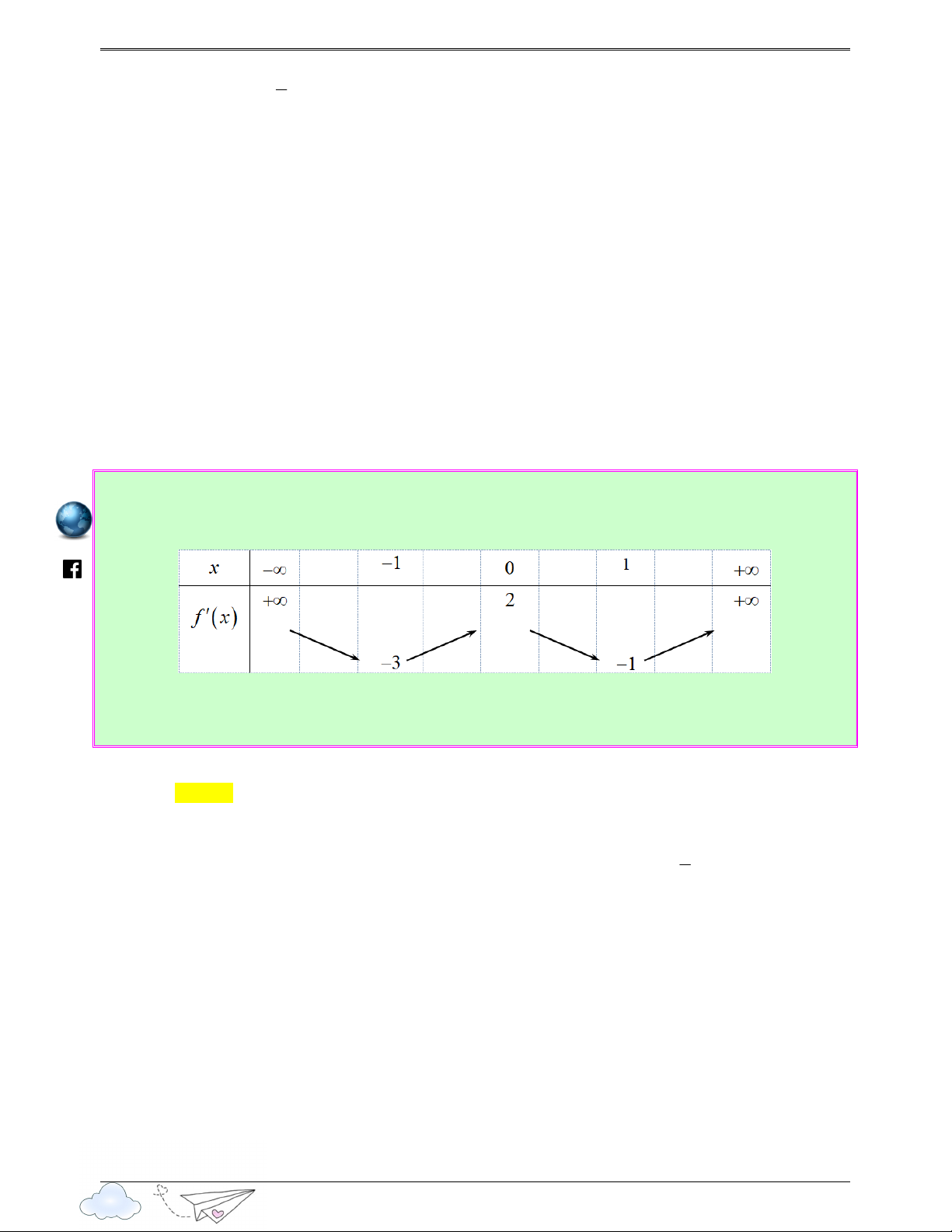
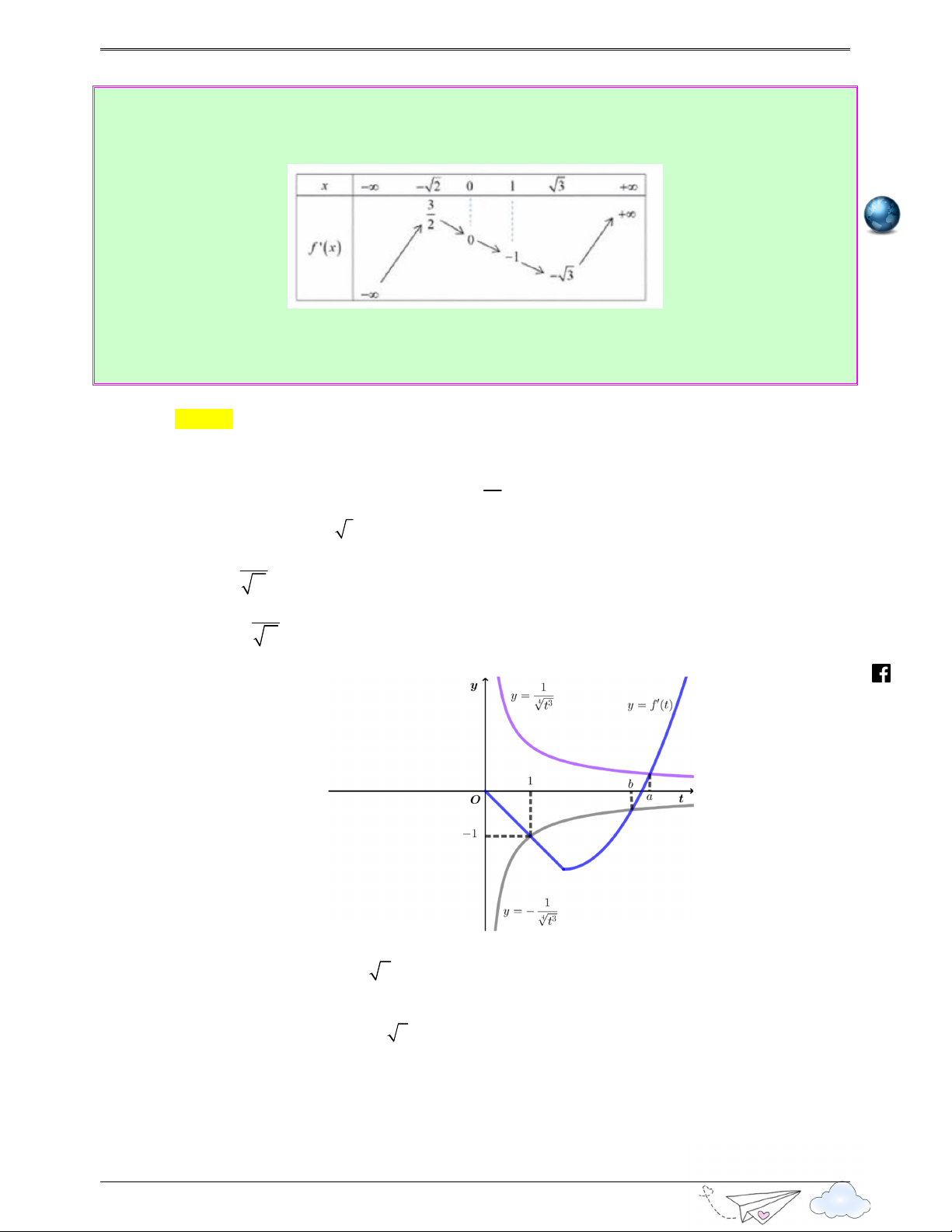
Câu 18: (Câu 48 - Chuyên Thái Bình - Thái Bình - Lần 4 - Năm 2020 - 2021 ) Cho hàm số f ( x) ,
bảng biến thiên của hàm số f ′( x) như sau: x ∞ 1 0 1 +∞ +∞ +∞ 2 f'(x) .vn 1 3 iem
gh Số điểm cực trị của hàm số y = f ( 2
3x − 6x + 2) là: itracn Ⓐ. 3 . Ⓑ. 5 . Ⓒ. 7 . Ⓓ. 9 . th Lời giải yen Chọn C
Ta có: y′ = ( x − ) f ′( 2 6 6 3x − 6x + 2) s://lu x = 1 ttp
y′ = 0 ⇔ (6x − 6) f ′( 2
3x − 6x + 2) = 0 ⇔ h f ′ ( 2
3x − 6x + 2) = 0 ( ) 1 BBT: /vietgold 2
3x − 6x + 2 = a ∈ − ; ∞ 1 − : 1 ( ) (vn) 2
3x − 6x + 2 = a ∈ 1 − ;0 2 2 ( ) ( 0n ) ( ) 1 ⇔ 2
3x − 6x + 2 = a ∈ 0;1 2 3 ( ) ( 0n ) 2
3x − 6x + 2 = a ∈ 1;+∞ 2 4 ( ) ( 0n ) 2 htps://www.facebook.com
Vì phưưng trình y′ =0 có 7 nghiưm đưn phân biưt nên hàm sư y = f (3x −6x + 2) có 7 cưc trư.
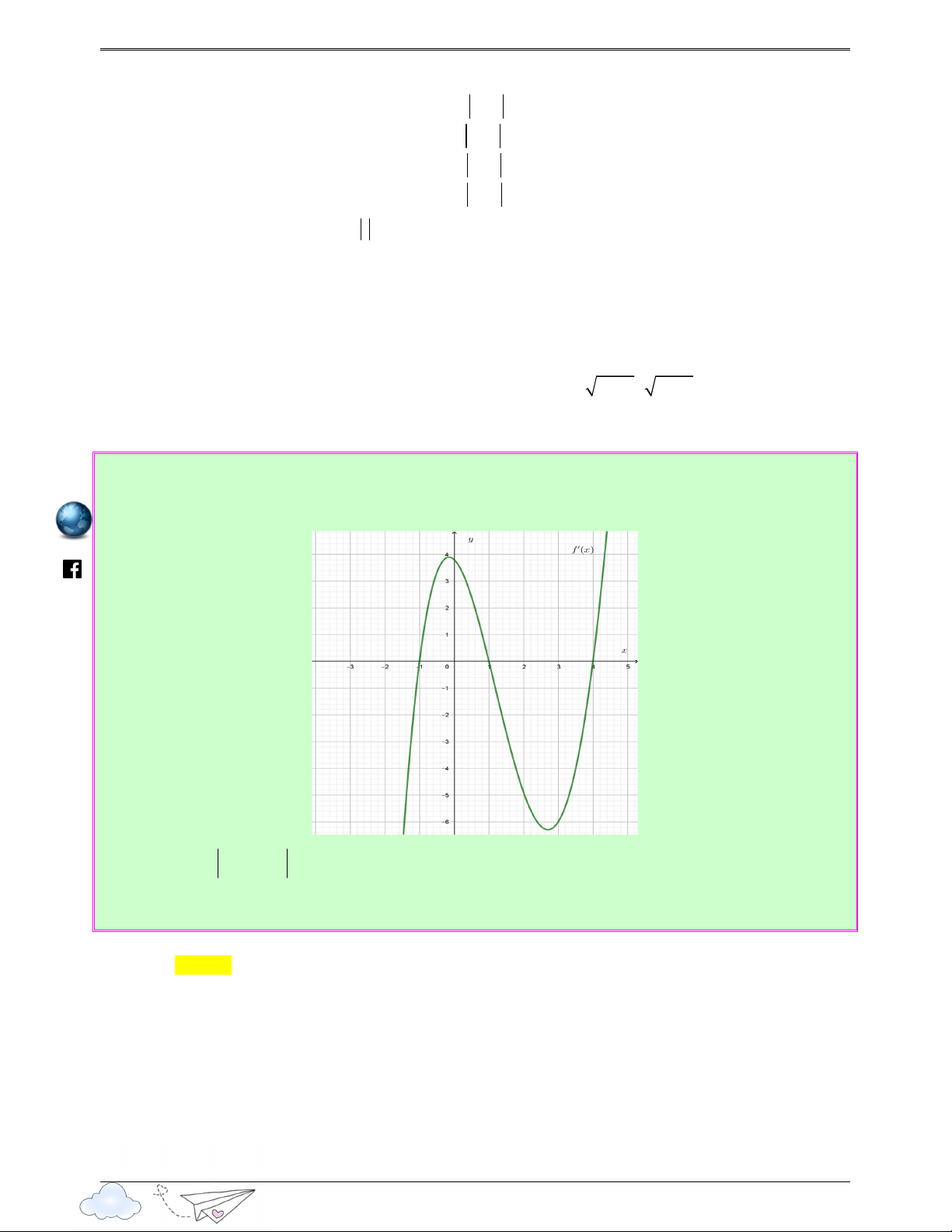
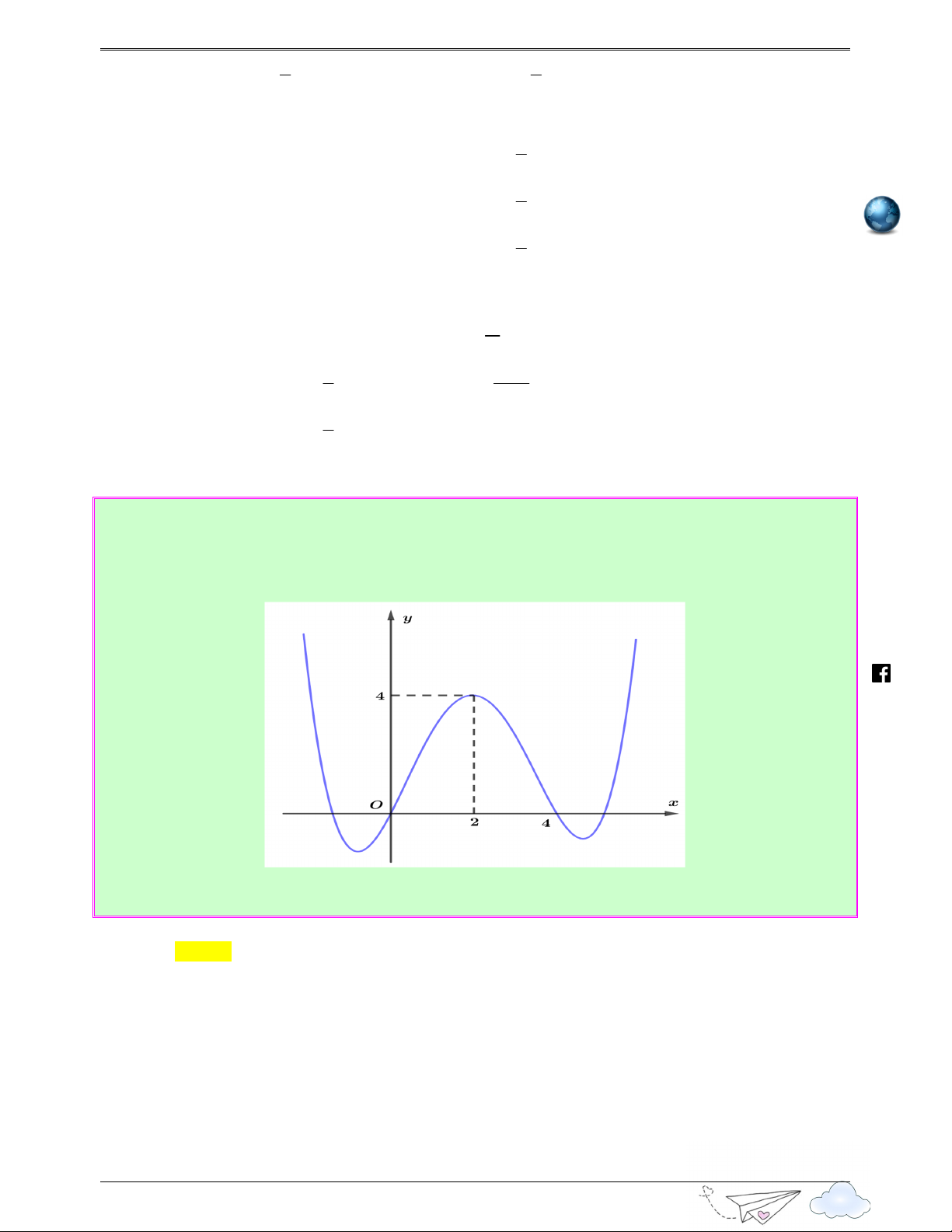
Câu 19: (Câu 50 - THPT Cẩm Bình - Hà Tĩnh - Lần 1 - Năm 2020 - 2021) Cho hàm số bậc ba y = f ( x)
có đồ thị như hình vẽ. 15
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h ttp s:/ 2 /
Số điểm cực tiểu của hàm số y = f −x + x bằng l ( ) u yen Ⓐ. 1. Ⓑ. 5. Ⓒ. 3. Ⓓ. 2 . thi Lời giải tra Chọn C cng
Từ đồ thị ta có hàm số bậc ba y = f ( x) có hai điểm cực trị x = 2 − ; x = 0 h ie 1 m Đặt 2
u = −x + x . Ta có u ' = 2
− x +1 = 0 ⇔ x = 2 .vn
Bảng biến thiên của hàm số = ( 2 y
f −x + x ) ht tps: 2 /
Câu 20: Vậy hàm số = − +
có 3 điểm cực tiểu.(Câu 46 - THPT Cẩm Bình - Hà Tĩnh - Lần / y f ( x x) ww
2 - Năm 2020 - 2021) Cho hàm số
có bảng biến thiên như hình dưới w y = f ( ) x .facebook.com/vietgo ld
Số điểm cực trị của hàm số y = f ( 2 x − 4x + ) 1 là Ⓐ. 1. Ⓑ. 5. Ⓒ. 3. Ⓓ. 2 . Lời giải Chọn B
Xét hàm số: y = g ( x) = f ( 2 x − 4x + ) 1
y ' = g '( x) = (2x − 4) f '( 2 x − 4x + ) 1 16
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” x = 2 2x − 4 = 0 x = 2 x = 2 + 2 2 x − 4 = 0
g '( x) = 0 ⇔ 2
⇔ x − 4x +1 = −1 2
⇔ x − 4x + 2 = 0 ⇔ x = 2 − 2 f ' ( 2 x − 4x + ) 1 = 0 2
x − 4x +1 = 3 2
x − 4x − 2 = 0 x = 2 + 6 x = 2 − 6 .vn
Suy ra g '(x) bị đổi dấu 5 lần, nên hàm số y = f ( 2 x − 4x + ) 1 có 5 điểm cực trị.
iem Câu 21: (Câu 18 - THPT Đào Duy Từ - Hà Nội - Lần 1 - Năm 2020 - 2021) Cho hàm số gh
f ( x) . Bảng biến thiên của hàm số f ′( x) như sau: itracn th yen s://lu ttp
h Số điểm cực trị của hàm số y = f ( 2x − 2x) là Ⓐ. 7 . Ⓑ. 9 . Ⓒ. 3. Ⓓ. 6 . Lời giải Chọn A
Có y′ = ( x − ) f ′( 2 2 2 x − 2x) . 2x − 2 = 0 x = 1
Xét phương trình y′ = 0 ⇔ ⇔ f ′ ( 2 x − 2x) = 0 f ′ ( 2 x − 2x) = 0 /vietgold
Dựa vào bảng biến thiên của hàm số f ′(x) , ta có 2
x − 2x = a (a < − ) 1 ( ) 1 2 − = − < < f ′( x 2x b 1 b 0 2 2 x − 2x) ( ) ( ) = 0 ⇔ 2
x − 2x = c (0 < c < ) 1 (3) 2
x − 2x = d (d > ) 1 (4)
Xét hàm số g (x) 2
= x − 2x , có bảng biến thiên như sau htps://www.facebook.com
Dựa vào bảng biến thiên của hàm số g (x) 2
= x − 2x , suy ra:
+ Phương trình (1) vô nghiệm. 17
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
+ Phương trình (2) có hai nghiệm phân biệt x ,1 2 x khác 1.
+ Phương trình (3) có hai nghiệm phân biệt x , x , x ,1 . 3 4
x khác các nghiệm: 1 2
+ Phương trình (4) có hai nghiệm phân biệt x ,
x , x , x , x ,1. 5 6
x khác các nghiệm: 1 2 3 4
Vậy phương trình y′ = 0 có 7 nghiệm phân biệt nên hàm số đã cho có 7 điểm cực trị.
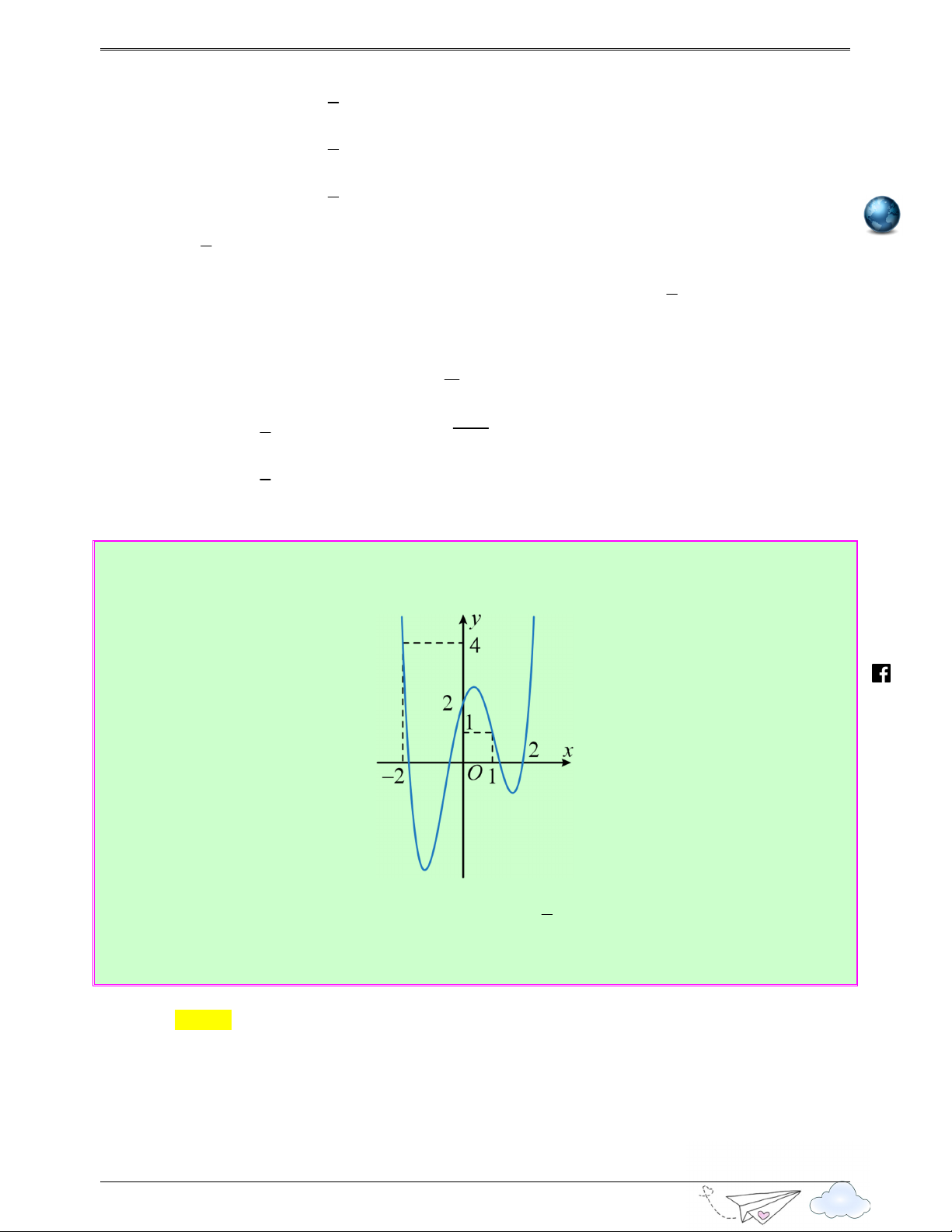
Câu 22: (Câu 27 - THPT Đội Cấn - Vĩnh Phúc - Lần 01 - Năm 2020 - 2021) Cho hàm số bậc bốn h
y = f(x) có đồ thị hình vẽ bên? ttps://luyenthitr acn
Số điểm cực trị của hàm số 3
g(x) = f (x − 3x) là ghie Ⓐ. 7 . Ⓑ. 9. Ⓒ. 11. Ⓓ. 5. m .v Lời giải n Chọn B x = 1 ± Ta có 2 3
g '(x) = (3x − 3) f '(x − 3x) = 0 ⇔ 3
f '(x − 3x) = 0 3
x − 3x = t(−2 > t) Dựa vào đồ thị ta có 3 3
f '( x − 3x) = 0 ⇔ x − 3x = u(−2 < u < 0) (*) 3
x − 3x = v(0 < v < 2) ht Xét 3 2 ( h )
x = x −3x ⇒ h'( )
x = 3x −3 = 0 ⇔ x = 1 ± t
ta có bảng biến thiên sau: ps://www.faceboo k.co
Dựa vào bảng biến thiên ta được (*) có 7 nghiệm phân biệt khác ± 1 nên g '(x) = 0 có 9 nghiệm m /v
đơn phân biệt. Vậy hàm số 3
g(x) = f (x − 3x) có 9 cực trị. ietgo
Câu 23: (Câu 37 - THPT Kinh Môn - Hải Dương - Lần 02 - Năm 2020 - 2021) Cho hàm số y = f x l ( ) d
. Đồ thị của hàm số y = f ′(x) như hình bên. 18
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn
iem Hàm số g (x) = f ( x ) + 2021 có bao nhiêu điểm cực trị? gh Ⓐ. 5 . Ⓑ. 7. Ⓒ. 3. Ⓓ. 2. itracn Lời giải th Chọn A yen
Từ hình vẽ ta thấy đồ thị của y = f ′( x) cắt trục hoành tại 2 điểm có hoành độ dương (và 1 điểm có hoành độ âm). s://lu
Suy ra hàm số f ( x) có 2 điểm cực trị dương. ttp h
Suy ra hàm số f ( x ) có 5 điểm cực trị.
Suy ra hàm số g ( x) = f ( x ) + 2021 có 5 điểm cực trị (vì tịnh tiến đồ thị lên trên hay xuống
dưới không ảnh hưởng đến số điểm cực trị của hàm số).
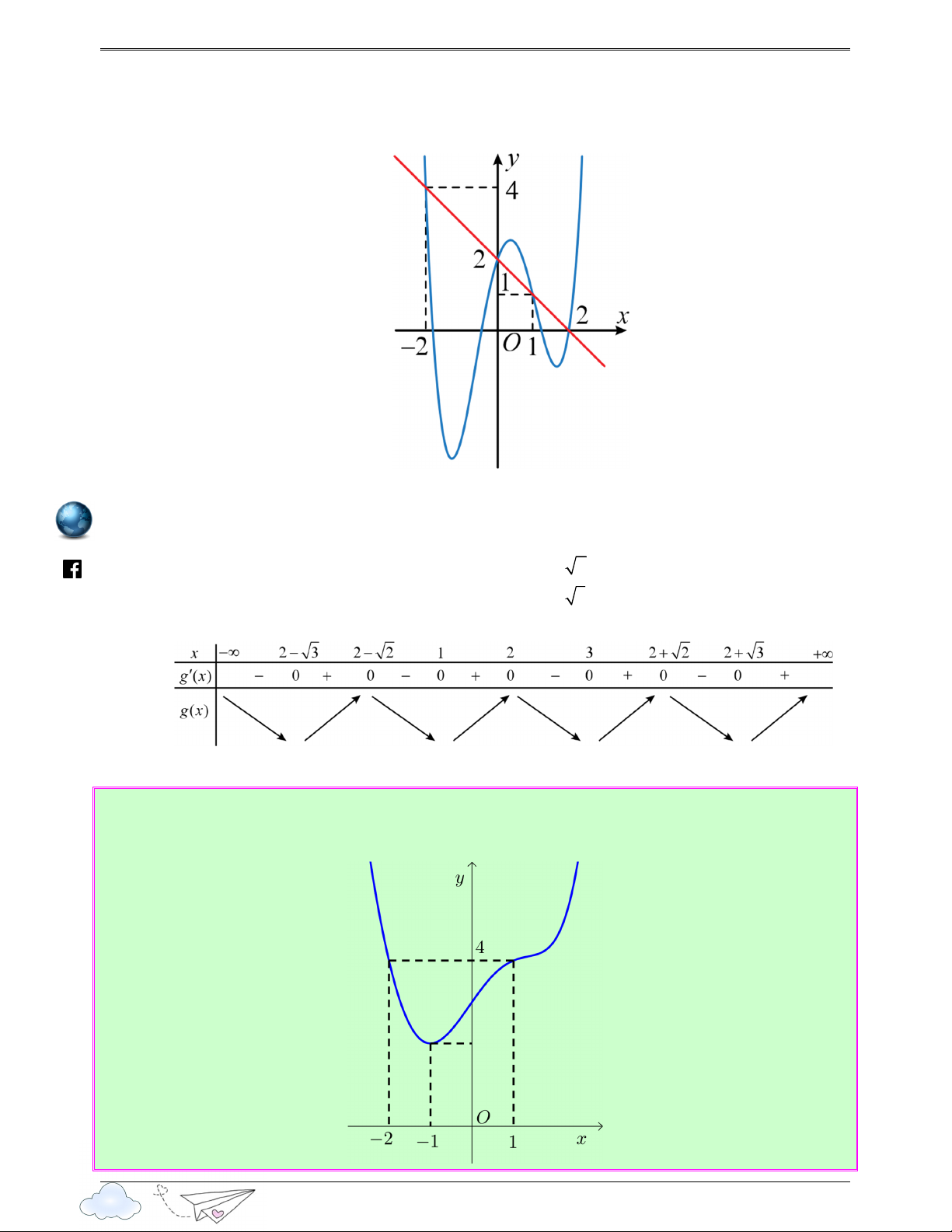
Câu 24: (Câu 36 - THPT Lý Thái Tổ - Bắc Ninh - Lần 2 - Năm 2020 - 2021) Cho hàm số bậc bốn
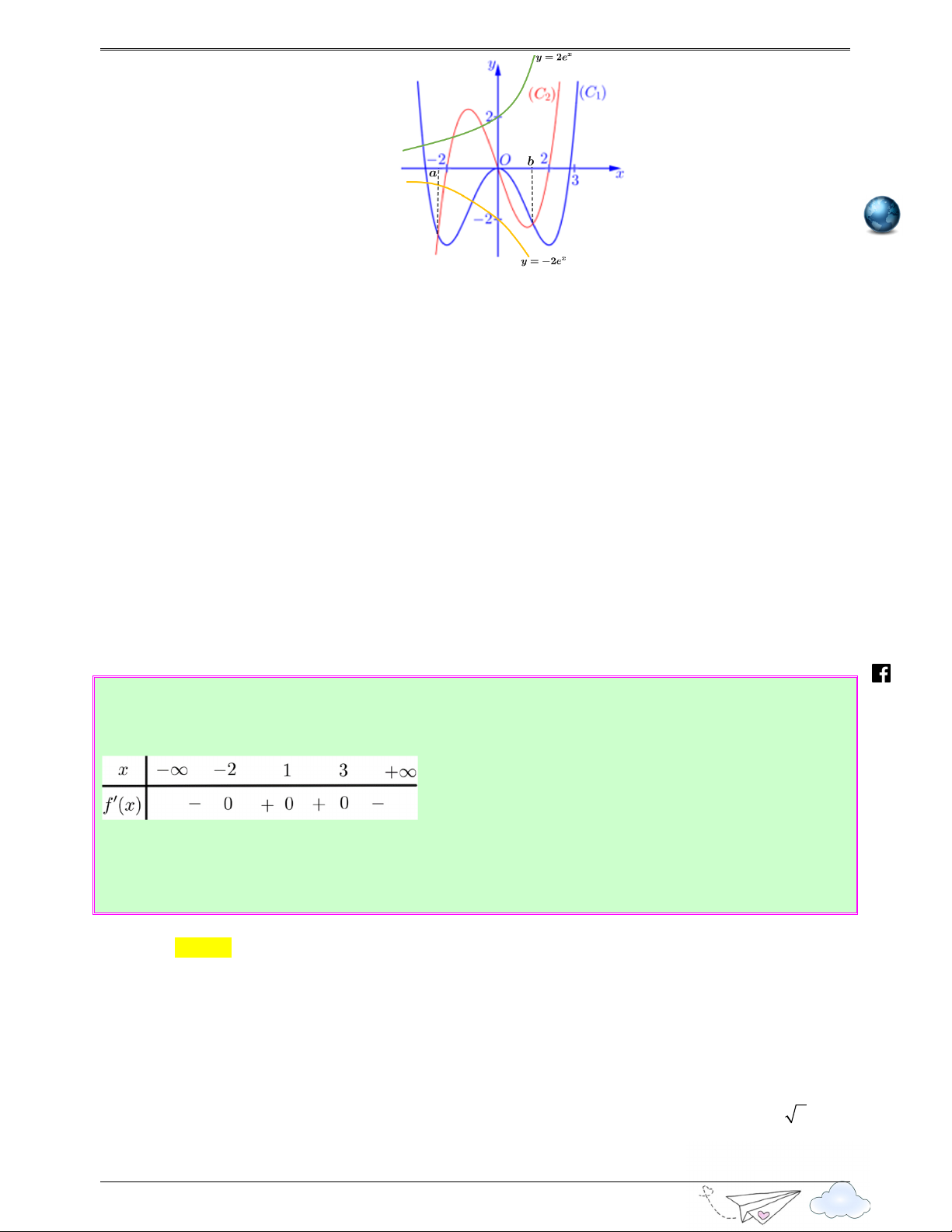
y = f ( x) có đồ thị (
và hàm số y = f ′( x) có đồ thị (C như hình vẽ 2 ) 1 C )
bên. Số điểm cực trị của đồ thị hàm số ( ) = e−x g x f . f ( x) trên khoảng (− ; ∞ 3) là /vietgold Ⓐ. 9. Ⓑ. 6. Ⓒ. 7. Ⓓ. 8. Lời giải htps://www.facebook.com Chọn D
Ta có ′( ) = e−x. ′ ( ) − ( ). ′ (e−x g x f x f x f − f ( x)) . 19
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h tt p s
f ′(x) − f ( x) = 0
f ′( x) = f (x) :/ ′ /
Xét g ( x) = 0 ⇔ ⇔ . l − x − x u f
(e . f ( x)) = 0 f
(e . f ( x)) = 0 yen x = a x = a th x = 0 x = 0 it ra x = b x = b c ⇔ n ⇔ e− x . f x = 2 −x − g ( ) f ( x) = 2e h − x i e . f x = 0 f x = 0 e ( ) ( ) m −x x . e . f (x) = 2 f ( x) = 2e vn
Từ đồ thị ta suy ra được: Phương trình ( ) 2ex f x = − có nghiệm đơn.
Phương trình f ( x) = 0 có 2 nghiệm đơn và 1 nghiệm bội chẵn ( x = 0) . Phương tridnh ( ) 2ex f x = có 1 nghiệm đơn.
Vậy g′( x) = 0 có 8 nghiệm đơn nên hàm số g ( x) có 8 điểm cực trị. h
Câu 25: (Câu 45 - THPT Ngọc Tảo - Hà Nội - Năm 2020 - 2021) Cho hàm số y = f (x) có đạo hàm ttps
trên ℝ và có bảng xét dấu của f ′( x) như sau ://www.fac ebo 2 o
Hỏi hàm số g ( x) = f (x − 2x) có bao nhiêu điểm cực tiểu? k.com Ⓐ. 4 . Ⓑ. 1. Ⓒ. 3. Ⓓ. 2 . /vie Lời giải tgo Chọn B ld
Ta có g′( x) = ( x − ) f ′( 2 2 2 x − 2x) . Suy ra x = 1 x = 1 2 2 x − 2 = 0 − = x = 3 ′( ) x x
g x = 0 ⇔ (2x − 2) f ′( 2 3 2
x − 2x) = 0 ⇔ ⇔ ⇔ . f ′ x = 1 − ( 2 x − 2x) 2 = 0
x − 2x = −2 2 x − 2x = 1 x = 1± 2 20
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” x ≥1 2x − 2 ≥ 0 2 2
− ≤ x − 2x ≤ 3 f ′ ( 2 x − 2x) ≥ 0 Xét
g′( x) ≥ 0 ⇔ ( x − ) f ′( 2 2 2
x − 2x) ≥ 0 ⇔ ⇔ x ≤1 2 x − 2 ≤ 0 2
x − 2x ≥ 3 f ′ ( 2 x − 2x) ≤ 0 2
x − 2x ≤ 2 − .vn x ≥1 2 x ≥1 iem
x − 2x + 2 ≥ 0 1 − ≤ x ≤ 3 gh 2
x − 2x − 3 ≤ 0 1 ≤ x ≤ 3 ⇔ ⇔ x ≤1 ⇔ . x ≤ 1 x ≤ 1 − x ≥ 3 itracn 2
x − 2x − 3 ≥ 0 th x ≤ 1 − 2
x − 2x + 2 ≤ 0 yen Bảng biến thiên s://lu ttp h
Từ bảng biến thiên suy ra hàm số g ( x) = f ( 2
x − 2x) có 1 điểm cực tiểu. Cách khác: /vietgold
Từ BBT hàm f ( 2
x − 2x) được mô tả ở dưới ta suy ra hàm có 1 điểm cực tiểu. htps://www.facebook.com
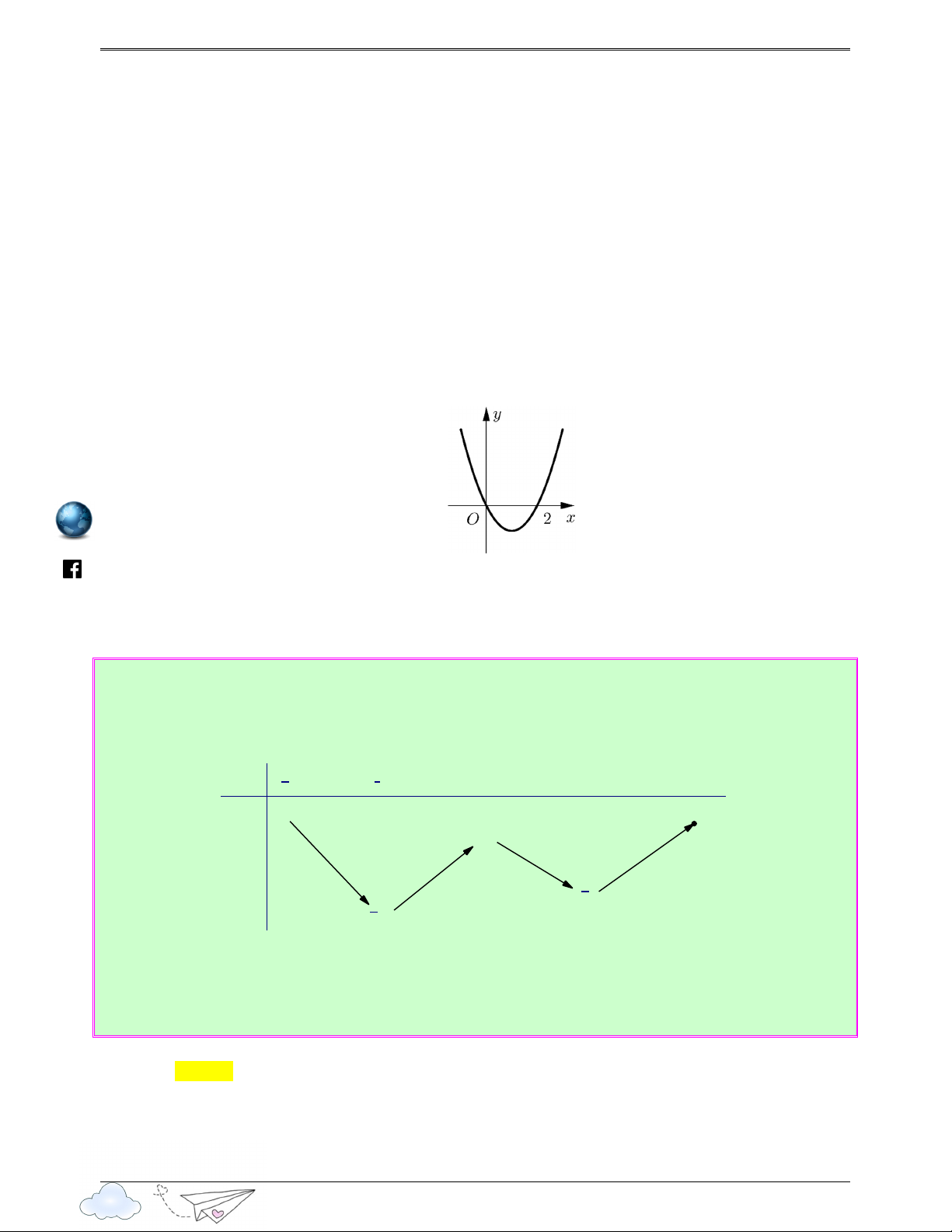
Câu 26: (Câu 45 - THPT Phụ Dực - Thái Bình - Năm 2020 - 2021) Cho hàm số = ( ) 3 2 y
f x = ax + bx + cx + d với a ≠ 0 có đồ thị hàm số như hình bên. Điểm cực đại của đồ thị
hàm số y = f (2 − x) + 3 là 21
↸ Quảng Thuận – Ba Đồn – Quảng Bình
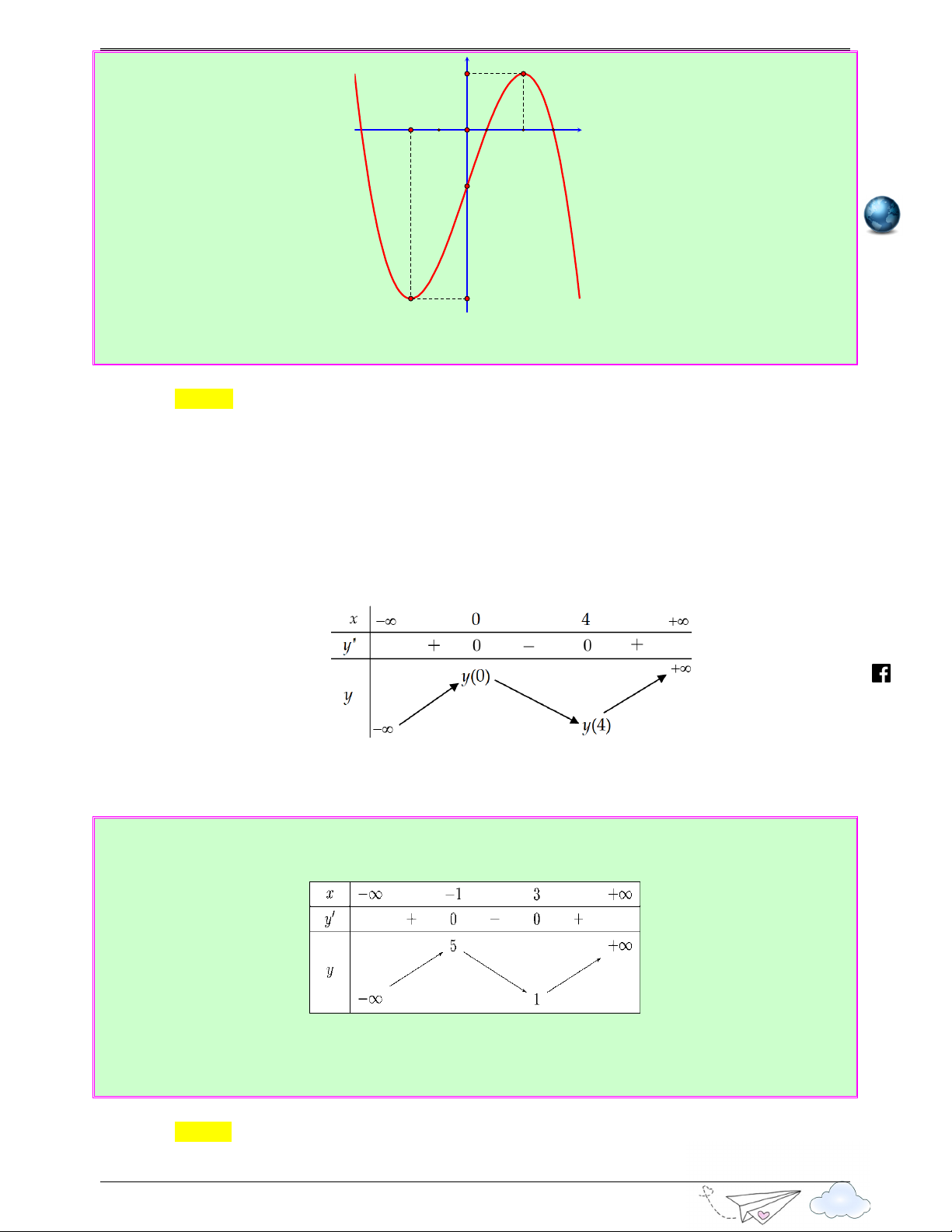
C c tr hàm s h p trong các đ thi 2020 - 2021 y 2 x -2 O 2 -2 h ttps 6 ://l u ye Ⓐ. (0;5) . Ⓑ. (0;2) . Ⓒ. (5;−6) . Ⓓ. (5; ) 3 . n th Lời giải itr Chọn A acn x = x < − g
Dựa vào đồ thị hàm số đã cho ta có f ′( x) 2 = 0 ⇔ và f ′( x) 2 < 0 ⇔ . h x = 2 − x > 2 iem 2 − x = 2 − x = 0 .
Ta có y′ = − f ′(2 − x) . Cho y′ = 0 ⇔ ⇔ . v 2 − x = 2 x = 4 n − x < x >
Giả sử y′ > ⇔ − f ′( − x) > ⇔ f ′( − x) 2 2 4 0 2 0 2 < 0 ⇔ ⇔ . 2 − x > 2 x < 0
Do đó ta có bảng biến thiên sau: https: //w
Vậy hàm số y = f (2 − x) + 3 đặt cực tại tại x = 0 khi y(0) = f (2) + 3 = 2 + 3 = 5 . ww
Vậy tọa độ điểm cực đại là (0;5) . .faceb
Câu 27: (Câu 46 - THPT Tam Dương - Vĩnh Phúc - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f (x) ook
có bảng biến thiên như hình dưới: .com/vietgold
Số điểm cực trị của hàm số y = f ( 2 x − 4x + ) 1 là: Ⓐ. 1. Ⓑ. 5. Ⓒ. 3 . Ⓓ. 2 . Lời giải Chọn B
Ta có g ( x) = f ( 2 x − 4x + ) 1 . 22
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” ⇒ ′ g′( x) = ( 2 x − 4x + ) 1 . f ′( 2 x − 4x + )
1 = 2( x − 2). f ′( 2 x − 4x + ) 1 . x = 2 x = 2 x = 2 − 2
Ta có g′( x) = 0 ⇔ 2( x − 2). f ′( 2 x − 4x + ) 2
1 = 0 ⇔ x − 4x +1 = 1 − ⇔ x = 2 + 2 . 2
x − 4x +1= 3 x = 2 − 6 .vn x = 2 + 6 iem
Ta có bảng xét dấu của g′( x) . gh itracn th yen
Dựavào bảng biến thiên ta thấy hàm số g ( x) = f ( 2 x − 4x + ) 1 có 5 điểm cực trị. s://lu
ttp Câu 28: (Câu 47 - THPT Yên Hòa - Hà Nội - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f (x) có đạo h
hàm trên R . Biết hàm số y = f (′x) có đồ thị như hình vẽ.
Sô điểm cực trị của hàm số y = f ( 2 x − 3) là /vietgold Ⓐ. 5. Ⓑ. 4. Ⓒ. 2. Ⓓ. 3. Lời giải Chọn D
Đặt g x = f ( 2 ( )
x − 3) ta có g′ x = x f ′( 2 ( ) 2 . x − 3) . 2x = 0 x = 0 Từ đồ thị của y = f ( ′ x) ta có 2 g (
′ x) = 0 ⇔ x − 3 = 1 ⇔ x = 2 ± . 2 x −3 = −2 x = 1 ± htps://www.facebook.com
Cũng từ đồ thị ta thấy x = 2
± là nghiệm kép của phương trình, nên ta có x = 0, x = 1 ± là các
nghiệm đơn của g (
′ x) = 0. Vậy hàm số y = g x = f ( 2 ( )
x − 3) có tất cả là 3 cực trị.
Câu 29: (Câu 46 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , bảng biến thiên của hàm số f ′( ) x như sau 23
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Số điểm cực trị của hàm số y = f ( 2 x − 2 x ) là Ⓐ. 9. Ⓑ. 3. Ⓒ. 7. Ⓓ. 5. h ttp Lời giải s:/ Chọn C /lu Cách 1 yenthitracng h ie
x = a, a ∈(− ; ∞ − ) 1 m . x = , b b ∈ (−1;0) v
Từ bảng biến thiên ta có phương trình f ′( x) = 0 có các nghiệm tương ứng là n
x = c, c ∈ (0; ) 1
x = d,d ∈(1;+∞ ) .
Xét hàm số y = f ( 2
x − x) ⇒ y′ = ( x − ) f ′( 2 2 2 1 x − 2x) . x = 1 2
x − 2x = a ( ) 1 x −1 = 0 h Giải phương trình 2 2
y′ = 0 ⇔ 2 x −1 f ′ x − 2x = 0 ⇔
⇔ x − 2x = b 2 . t ( ) ( ) 2 ( ) t p f ′
( x − 2x) = 0 s 2 :
x − 2x = c (3) / /w 2
x − 2x = d (4) ww.
Xét hàm số h x = x − x ta có = − = − + − ≥ − ∀ ∈ f ( ) 2 2 h ( x) x x (x )2 2 2 1 1 1, x ℝ do đó ace 2 b
Phương trình x − 2x = , a (a < − ) 1 vô nghiệm. ook 2 .
Phương trình x − 2x = , b ( 1
− < b < 0) có hai nghiệm phân biệt x ; x không trùng với nghiệm c 1 2 om/ của phương trình ( ) 1 . vie 2 tg
Phương trình x − 2x = ,
c (0 < c < )
1 có hai nghiệm phân biệt x ; 3 4
x không trùng với nghiệm của old phương trình ( ) 1 và phương trình (2) . Phương trình 2
x − 2x = d,(d > )
1 có hai nghiệm phân biệt x ; 5 6
x không trùng với nghiệm của phương trình ( )
1 và phương trình (2) và phương trình (3) . Vậy phương trình 2
y′ = 0 có 7 nghiệm phân biệt nên hàm số y = f ( x − 2x) có 7 điểm cực trị. Cách 2 24
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
x = a, a ∈(− ; ∞ − ) 1 x = ,bb∈ ( 1 − ;0)
Từ bảng biến thiên ta có phương trình f ′( x) = 0 có các nghiệm tương ứng là
x = c, c ∈ (0; ) 1
x = d,d ∈(1;+∞ )
Xét hàm số y = f ( 2
x − x) ⇒ y′ = ( x − ) f ′( 2 2 2 1 x − 2x) . .vn x = 1 2 iem
x − 2x = a ( ) 1 x −1 = 0 gh
y′ = 0 ⇔ 2 ( x − ) 1 f ′( 2 x − 2x ) 2 = 0 ⇔ ⇔ − = . f ′ ( x 2x b 2 2 x − 2x ) ( ) = 0 2
x − 2x = c (3) itracn 2
x − 2x = d (4) th
Vẽ đồ thị hàm số h( x) 2 = x −2x yen s://lu ttp h
Dựa vào đồ thị ta thấy: phương trình (1) vô nghiệm. Các phương trình (2);(3);(4) mỗi
phương trình có 2 nghiệm. Các nghiệm đều phân biệt nhau. Vậy phương trình 2
y′ = 0 có 7 nghiệm phân biệt nên hàm số y = f ( x − 2x) có 7 điểm cực trị.
Câu 30: (Câu 48 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f (x), bảng biến thiên của
hàm số f '( x) như sau: /vietgold x ∞ 1 0 1 +∞ +∞ +∞ 2 f'(x) 1 3 htps://www.facebook.com
Số điểm cực trị của hàm số y = f ( 2
x + 2 x ) là Ⓐ. 3. Ⓑ. 9. Ⓒ. 5. Ⓓ. 7. Lời giải Chọn D
Xét hàm số y = f ( 2
x + 2 x ) trên ℝ .
Ta có y = ( x + ) f ( 2 ' 2 2 ' x + 2x) . 25
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Dựa vào bảng biến thiên của hàm f '( ) x ta được x = 1 − x = 1 −
x + x = a (x+ )2 2 1 = a +1 ( ) 1 2 y ' 0
= ⇔ x + 2x = b ⇔ ( x + )2 2 1 = b +1 (2)
< − < < < < < , trong đó a
1 b 0 c 1 d . 2
x + 2x = c ( x + )2 1 = c +1 (3) 2 x 2x d + = (x + )2 1 = d +1 (4) h ttp a +1 < 0 s : b +1 > 0 //
< − < < < < < l Do a
1 b 0 c 1 d nên . u c + 1 > 0 y e d +1 > 0 n th 2 , 3 , 4 i Khi đó phương trình ( )
1 vô nghiệm. Các phương trình ( ) ( ) ( ) mỗi phương trình đều có 2 trac
nghiệm phân biệt và khác nhau, cùng khác 1
− . Suy ra phương trình y' = 0 có 7 nghiệm đơn. n g Vậy hàm số 2
y = f x + 2 x có 7 điểm cực trị. h ( ) iem
Câu 31: (Câu 48 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , bảng biến thiên của .vn ′
hàm số f ( x) như sau: ht 2 t
Số điểm cực trị của hàm số y = f (4x − 4x) là ps://w Ⓐ. 9. Ⓑ. 5. Ⓒ. 7. Ⓓ. 3. ww.f Lời giải ace Chọn C boo
x = a ∈(− ; ∞ − ) 1 k. co x = b ∈ ( 1 − ;0) m
Dựa vào bảng biến thiên ta có: f ′( x) = 0 ⇔ . / v x = c ∈(0; ) 1 i etg
x = d ∈(1;+ ∞ ) old 1 x = 2 2
4x − 4x = a ∈(− ; ∞ − ) 1 8 x − 4 = 0
Ta có: y′ = ( x − ) f ′( 2 8 4
4x − 4x) , y′ = 0 ⇔ 2
⇔ 4x − 4x = b ∈ (−1;0) . f ′ ( 2 4x − 4x) = 0 2
4x − 4x = c ∈ (0; ) 1 2
4x − 4x = d ∈(1;+ ∞) 26
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” 1 Ta có khi 2 x =
⇒ 4x − 4x = −1 và f ′(− ) 1 = −3 ≠ 0 2
Mặt khác: x − x = ( x − )2 2 4 4 2 1 −1 ≥ −1 nên: 2
4x − 4x = a vô nghiệm. 2
4x − 4x = b có 2 nghiệm phân biệt 1 x , 2 x . 2
4x − 4x = c có 2 nghiệm phân biệt .vn 3 x , 4 x . 2
4x − 4x = d có 2 nghiệm phân biệt 5 x , 6 x . iem
Vậy phương trình y′ = 0 có 7 nghiệm bội lẻ phân biệt nên hàm số có 7 điểm cực trị. gh Cách 2:
Gọi m đại diện cho các tham số ta xét phương trình 2
4x − 4x − m = 0 có ∆ ' = 4(m + ) 1 , itracn th ′ ∆ > 0 ⇒ m > 1 − .
Vậy với mỗi giá trị b, c, 2
f ′ 4x − 4x = 0 có 6 nghiệm phân yen
d thuộc khoảng đã cho phương trình ( ) biệt. s://lu
Vậy phương trình y′ = 0 có 7 nghiệm bội lẻ phân biệt nên hàm số có 7 điểm cực trị. ttp
h Câu 32: (Câu 50 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f (x) , bảng biến thiên của
hàm số f ′( x) như sau:
Số điểm cực trị của hàm số y = f ( 2
4x + 4x) là /vietgold Ⓐ. 5. Ⓑ. 9 . Ⓒ. 7 . Ⓓ. 3. Lời giải Chọn C ′ + =
f ′( x + x) f ( 2 2 4x 4x) 0 4 4 = 0 Ta có
y′ = ( x + ) f ′( 2 8 4
4x + 4x); y′ = 0 ⇔ ⇔ 1 . 8 x + 4 = 0 = − 1 x 2
x = a ∈(− ; ∞ − ) 1 htps://www.facebook.com x = b ∈ (−1;0)
Dựa vào bảng biến thiên của f ′( x) nhận thấy f ′( x) = 0 ⇔ . x = c ∈ (0; ) 1
x = d ∈(1;+∞ ) 2
4x + 4x = a ∈(− ; ∞ − ) 1 2
4x + 4x = b ∈(−1;0) Do đó f ′( 2
4x + 4x) = 0 ⇔ (*) . Lại có 2
4x + 4x = c ∈ (0; ) 1 2
4x + 4x = d ∈(1;+∞ ) 2
4x + 4x = a vô nghiệm vì x + x = ( x + )2 2 4 4 2 1 −1 ≥ −1,∀x ; 27
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 x = x 2 2
4x + 4x = b ⇔ ; x = 3 x x = x 2 4
4x + 4x = c ⇔ ; x = 5 x x = x 2 6
4x + 4x = d ⇔ . x = 7 x
Vì ≠ ≠ do thuộc các khoảng khác nhau (như * ) nên các nghiệm x , x , x , x , x , h b c d ( ) 2 3 4 5 6 7 x đều ttp 1 s khác nhau và khác
có 7 nghiệm đơn phân biệt nên 1 x = − . Do đó y′ = 0
y′ đổi dấu 7 lần suy :/ 2 /lu
ra hàm số có 7 điểm cực trị. yen
Câu 33: (Câu 45 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc bốn f ( x) có bảng thi biế thiên như sau: tracnghiem.vn
Số điểm cực trị của hàm số g ( x) = x f ( x − ) 4 2 1 là Ⓐ. 7 . Ⓑ. 8 . Ⓒ. 5. Ⓓ. 9. Lời giải htt Chọn D ps:
Ta có hàm số g (x) liên tục và có đạo hàm là //w 4 3 3 2 w g ' ( x ) = 2 . x f
( x − 1) + 4.x . f ' (x − ) 1 . f
( x − 1) = 2x f ( x − ) 1 .
( f ( x − )
1 + 2xf '( x − ) 1 ) w.f a x = x = 0 1 c e Cho . b g ( x ) = 0 ⇔ f ( x − 1) = 0 oo k f
( x − 1) + 2x. f '( x − 1) = 0 .com
* Với phương trình f ( x − ) 1 = 0 . /vie
Vì f ( x) là hàm bậc bốn và có bảng biến thiên như trên ta thấy phương trình f ( x − ) 1 = 0 có tgo
bốn nghiệm đơn phân biệt x , x , x , x khác l 2 3 4 5 1 x . d
* Với phương trình f ( x − )
1 + 2xf '( x − ) 1 = 0
Ta thấy phương trình không nhận các số x , x , x , x , 1 2 3 4 5 x làm nghiệm. Gọi ( ) 4 2
f x = ax + bx + c , vì f '( x) = 0 có 3 nghiệm phân biệt −1; 0;1 và f (0) = −1, f ( ) 1 = 3
nên c = −1, a = −4,b = 8 , suy ra f ( x) 4 2
= −4x + 8x −1 .
Đặt t = x − 1, phương trình f ( x − )
1 + 2xf '( x − )
1 = 0 trở thành f (t ) + 2(t + ) 1 f '(t ) = 0 4 2
⇔ − t + t − + (t + )( 3 − t + t ) 4 3 2 4 8 1 2 1 16
16 = 0 ⇔ −36t − 32t + 40t + 32t − 1 = 0 . 28
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
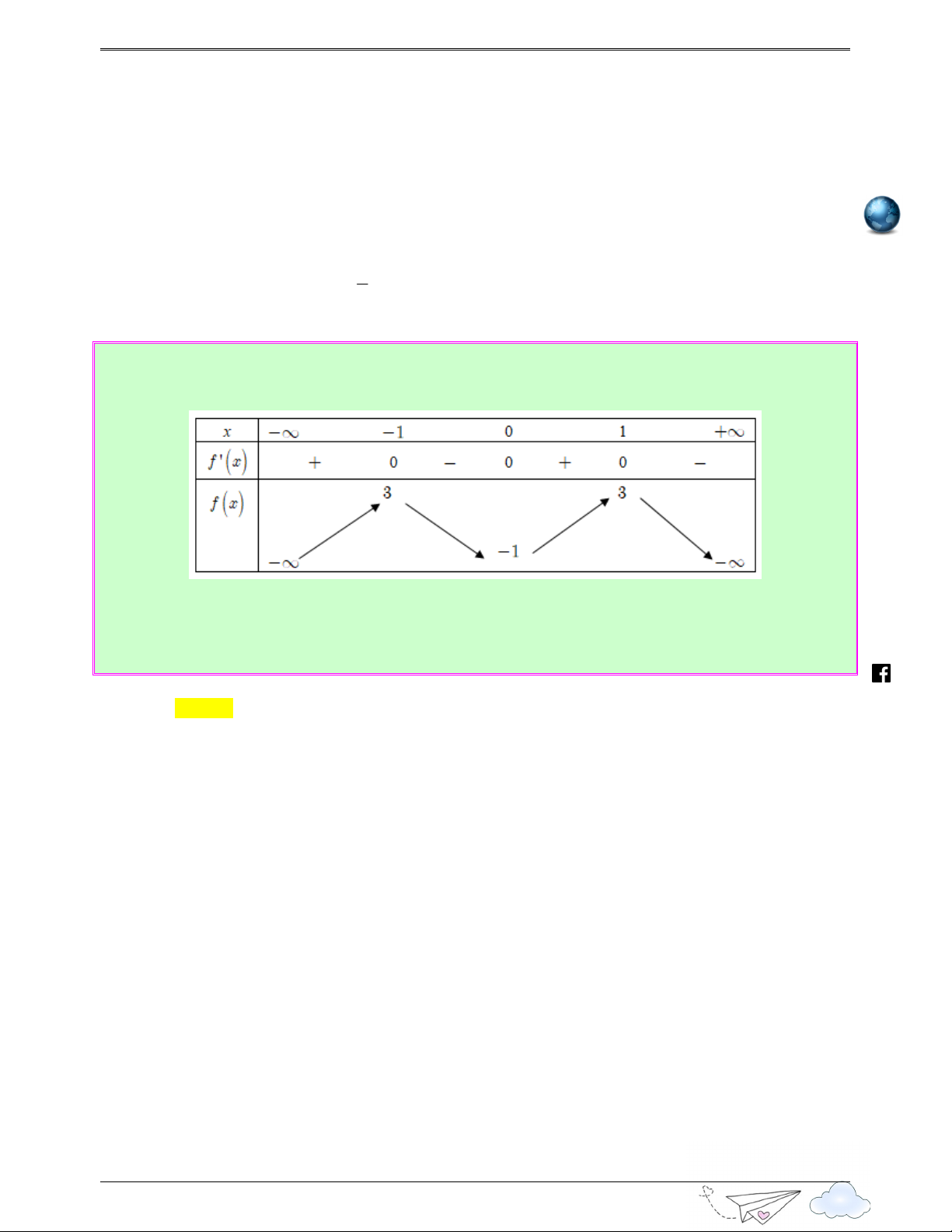
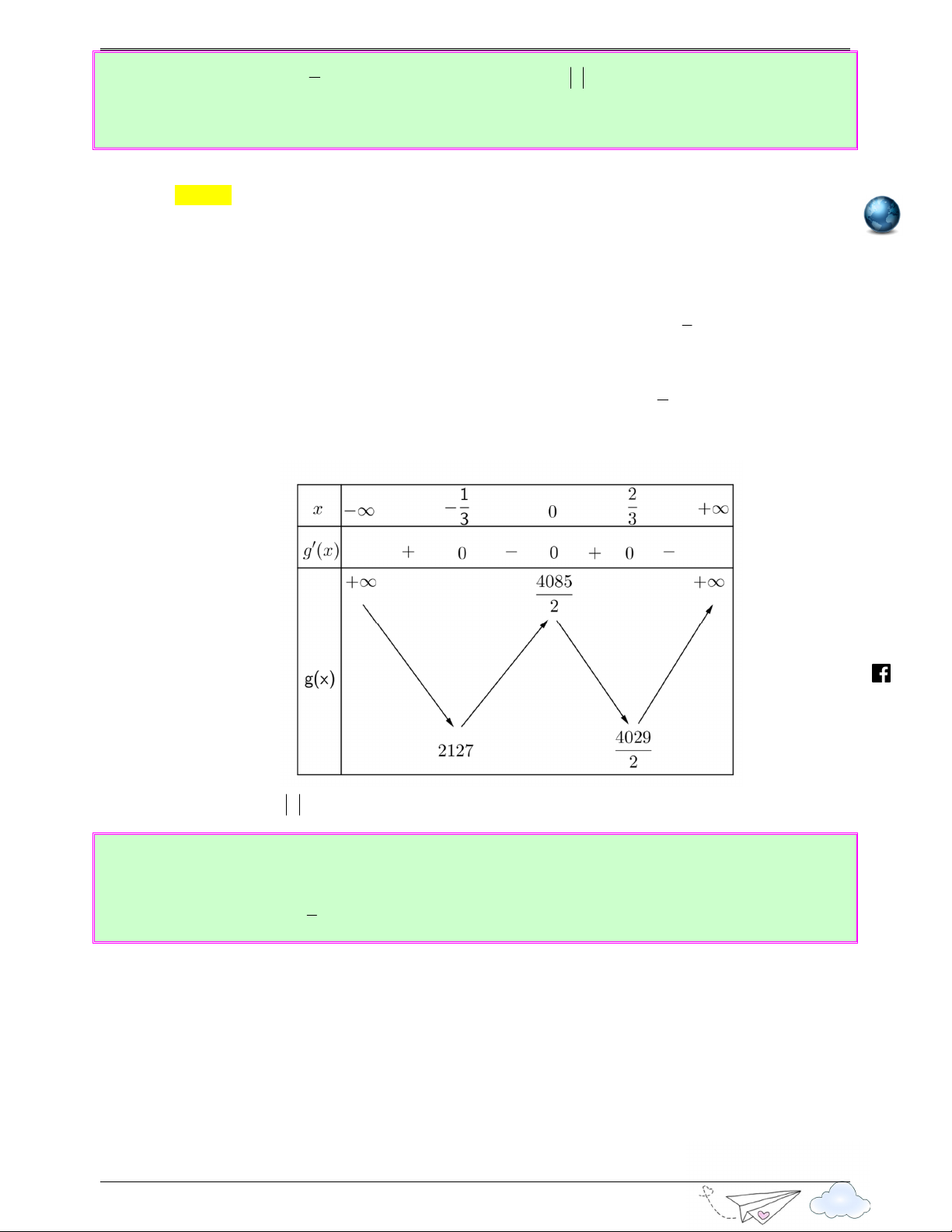
Xét hàm số h (t ) 4 3 2
= −36t − 32t + 40t + 32t −1 có h (t ) 3 2 '
= −144t − 96t + 80t + 32 , cho h ( x) 1 2 '
= 0 ⇔ x = −1; x = − , x = . 3 3 Ta có bảng biến thiên .vn iem gh itracn th
Do đó phương trình h (t ) = 0 có 4 nghiệm đơn phân biệt hay phương trình yen f ( x − )
1 + 2xf '( x − )
1 = 0 có 4 nghiệm đơn phân biệt x , x , x , có 9 điểm 6 7 8 9
x . Hay hàm số g ( x) s://lu
cực trị là x , x , x , x , x , x , x , x , 1 2 3 4 5 6 7 8 9 x . ttp
h Câu 34: (Câu 46 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số bậc bốn f (x) có bảng biến thiên sau:
/vietgold Số điểm cực trị của hàm số g(x) = x f (x+ ) 4 2 1 là Ⓐ. 7 . Ⓑ. 8 . Ⓒ. 9 . Ⓓ. 5. Lời giải Chọn C
g (x) ≥ 0, x ∀ Nhận xét ,
lim g ( x) = +∞ x→±∞ htps://www.facebook.com 2 x = 0 x = 0
Cho g ( x) = 0 ⇔ ⇔ f ( x + )
f ( x + ) 4 1 = 0 1 = 0
Nhận thấy: Tịnh tiến đồ thị f ( x) sang trái 1 đơn vị ta thu được đồ thị của f ( x + ) 1
x = a, a < 2 −
x = ,b − 2 < b < 1 −
Do đó f ( x + ) 1 = 0 ⇔
x = c, −1 < c < 0
x = d, d > 0 29
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h ttp
Vì thế g ( x) = 0 có 5 nghiệm phân biệt s://l
Hay đồ thị g ( x) có 5 điểm tiếp xúc với trục hoành u ye
Vậy hàm số g ( x) có 9 cực trị. n thi
Câu 35: (Câu 45 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số y = f ( x) với f (0) = 0 trac
. Biết y = f ′( x) là một hàm số bậc bốn và có đồ thị là đường cong như hình dưới đây n ghiem.vn
Số điểm cực trị của hàm số ( ) = ( 4 ) 2 g x f x + x là https : Ⓐ. 3. Ⓑ. 6. Ⓒ. 5. Ⓓ. 4 . //w Lời giải ww Chọn C .fa 4 2 2 4 = + ⇒ ′ = ′ c
Xét hàm số h ( x) f (x ) x
h ( x) 2x (2x . f ( x ) + ) 1 eboo x = 0 k h′ x = 0 ⇔ . ( ) c 2 4 ′ o 2x f (x )+1= 0(1) m /v Giải phương trình ( ) 1 ietg 1 o Đặt 4
x = t t ≥ 0 , ta có phương trình ′ + = ⇔ ′
(Vì t = 0 không thỏa l ( ) 2 t f (t ) 1 0 f (t ) = − (2) d 2 t mãn)
Số nghiệm của phương trình (2) chính là số giao điểm của đồ thị hàm số y = f ′(t ) và đồ thị 1 hàm số y = − 2 t
Ta có các đồ thị như sau 30
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh
Căn cứ đồ thị, suy ra phương trình (2) có nghiệm duy nhất 4 4
t = a > 0 ⇒ x = a ⇔ x = ± a
Căn cứ đồ thị hàm số y = f ′(t) ⇒ lim ( f ′(t )) = −∞ ⇒ lim (2 t f ′(t) + ) 1 = −∞ itracn t →+∞ t →+∞ th
Ta có bảng biến thiên của hàm số y = h( x) và y = g ( x) như sau: yen s://lu ttp h /vietgold
Câu 36: (Câu 46 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Cho hàm số f ( x) là hàm số bậc
bốn thoả mãn f (0) = 0. Hàm số f ′( x) có bảng biến thiên như sau: htps://www.facebook.com
Hàm số g ( x) = f ( 3
x ) − 3x có bao nhiêu điểm cực trị? Ⓐ. 3 . Ⓑ. 5. Ⓒ. 4. Ⓓ. 2 . Lời giải Chọn A 31
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Bảng biến thiên hàm số f ( x) 1
Đặt h ( x) = f ( 3
x ) − 3x ⇒ h′( x) 2 = 3x f ′( 3
x ) − 3 = 0 ⇔ f ′( 3 x ) = 2 h x ttp 1 Đặt 3 3 = ⇒ =
thế vào phương trình trên ta được ′ s t x x t f (t ) = ( ) 1 : 3 2 / t /lu 1 2 y Xét hàm số y = ⇒ y′ = − , lim y = 0 . e 3 2 3 5 t →±∞ n t 3 t th 1 i
Bảng biến thiên của hàm số y = tr 3 2 a t cnghiem.vn
Dựa vào bảng biến thiên ta thấy phương trình ( )
1 có một nghiệm t = a > 0 . Bảng biến thiên https://www.facebook.c om
Vậy hàm số g ( x) có 3 cực trị. /vietg
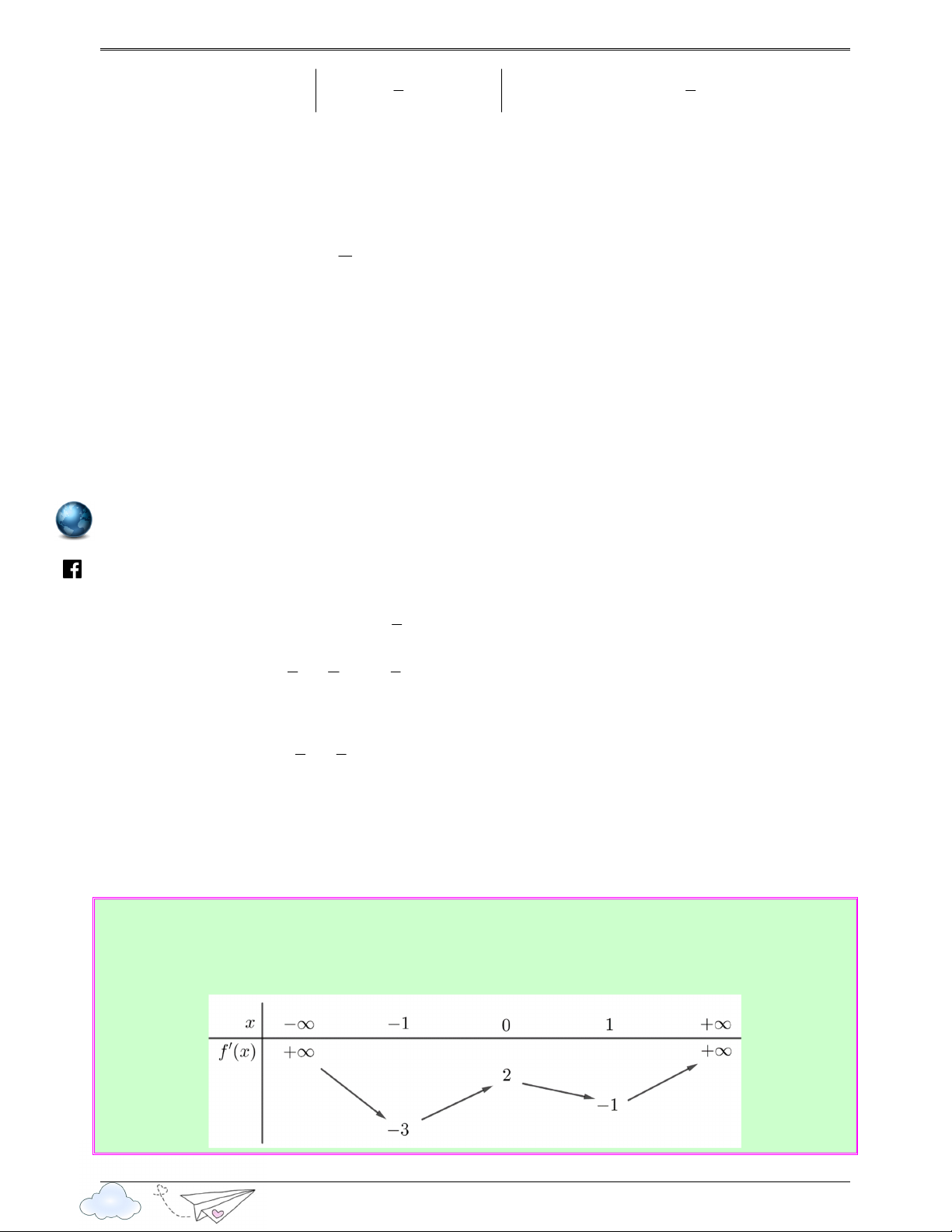
Câu 37: (Câu 41 - SGD Bắc Giang - lần 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đạo hàm trên old
ℝ và đồ thị hàm số y = f ′( x ) cắt trục hoành tại các điểm có hoành độ −3 ; −2 ; a ; b ; 3; c ; 4 4
5 với − < a < 1
− ; 1< b < ; 4 < c < 5 (có dạng như hình vẽ bên dưới). Có bao nhiêu giá trị 3 3
nguyên của tham số thực m để hàm số y = f (2 x + m −3) có 7 điểm cực trị? 32
↸ Quảng Thuận – Ba Đồn – Quảng Bình
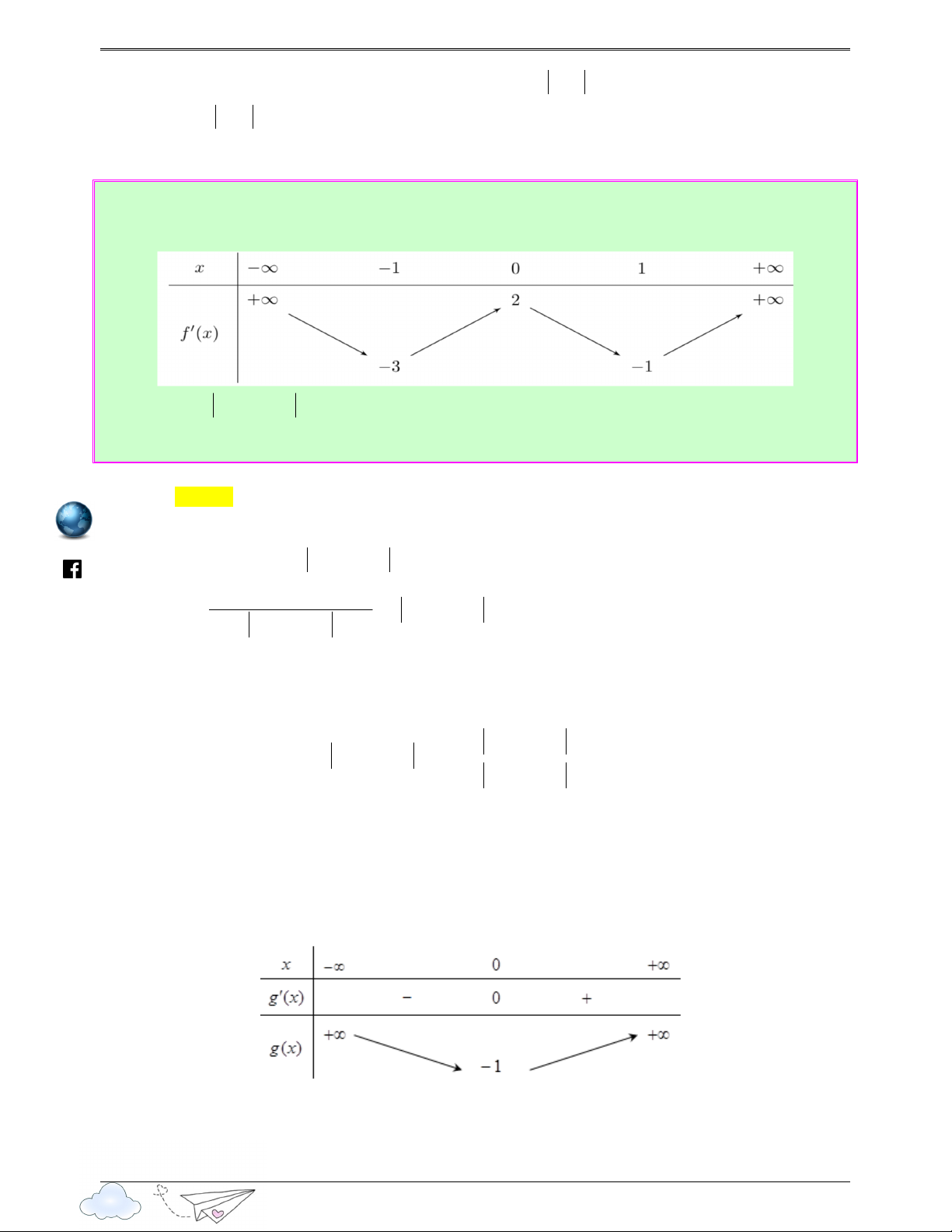
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh itracn th Ⓐ. 3 . Ⓑ. 2 . Ⓒ. 4 . Ⓓ. Vô số. yen Lời giải Chọn A s://lu
Xét hàm số h ( x) = f (2x + m − 3) ttp
Ta có: h′( x) = 2 f ′(2x + m − 3) = 0 ⇔ f ′(2x + m − 3) = 0 h k + 3 − m
Từ đồ thị của hàm số f ′( x ) suy ra f ′(2x + m − 3) = 0 ⇔ 2x + m − 3 = k ⇔ x = với 2 4 4
k ∈ {−3; − 2 ; a ; b ; 3; c ; } 5 ( − < a < 1
− ; 1< b < ; 4 < c < 5 ) 3 3
Hàm số y = f (2 x + m − )
3 có 7 điểm cực trị ⇔ hàm số h (x) = f (2x + m − 3) có 3 cực trị có
hoành độ dương, mà 3 là nghiệm bội chẵn của f ′( x) nên hàm số h ( x) = f (2x + m − 3) có 3 6 −
cực trị có hoành độ dương ⇔ phương trình m
h′ ( x ) = 0 có 3 nghiệm dương phân biệt khác 2 /vietgold
a + 3 − m < 0 2
a + 3 − m < 0 m > a + 3 ⇔ ⇔ ⇔
⇔ a + 3 < m < b + 3 b + 3 − m
b + 3 − m > 0 m < b + 3 > 0 2 4 4 Do − < a < 1
− và 1< b < nên −1+ 3 ≤ m ≤ 1+ 3 hay 2 ≤ m ≤ 4 3 3
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán là 2 ; 3 ; 4 .
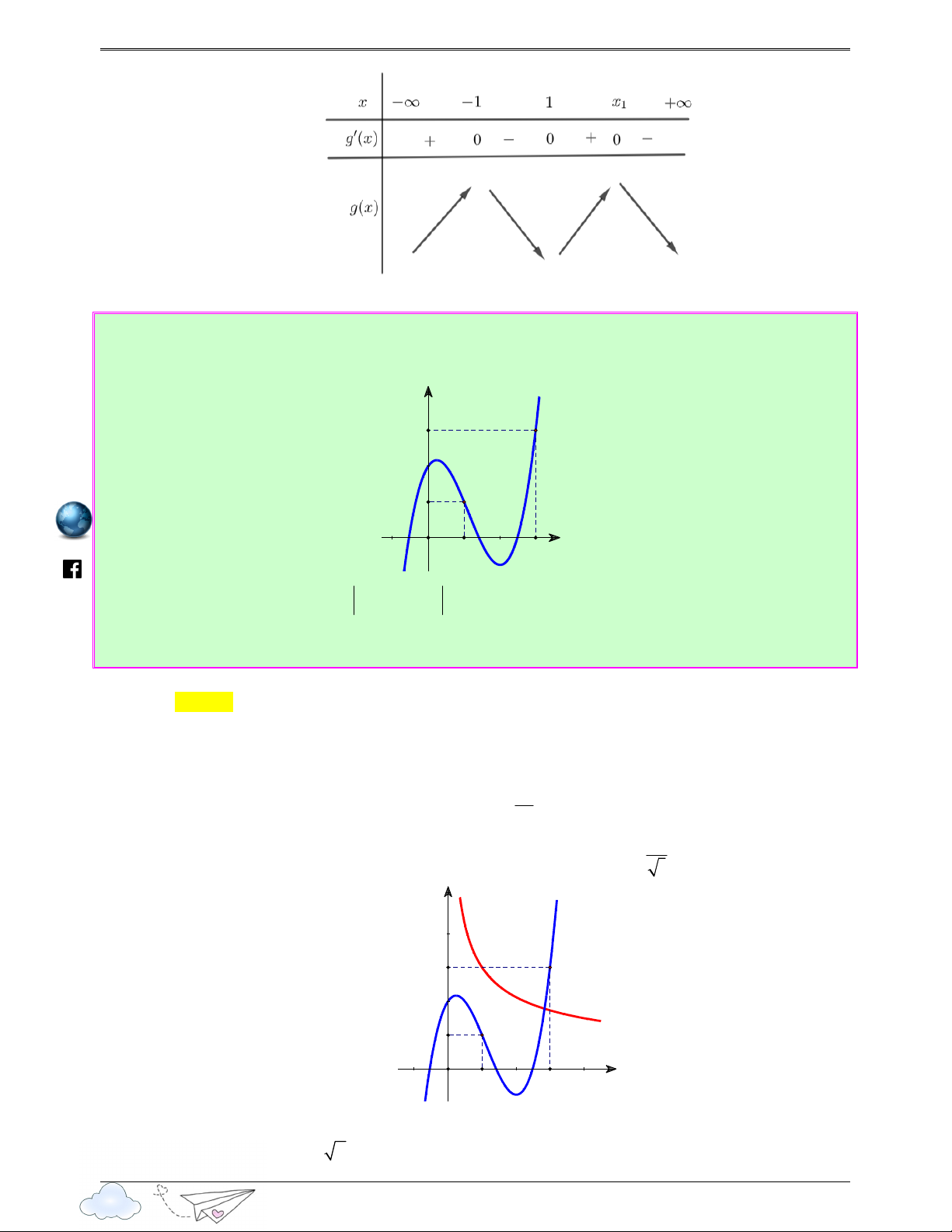
Câu 38: (Câu 46 - SGD Hải Phòng - Năm 2020 - 2021) Cho hàm số f ( x) có htps://www.facebook.com f ′( x) = ( 2 x − )(x + )( 2 16
1 x − 4x + m − 4). Có bao nhiêu giá trị nguyên của tham số m thuộc [ 2 − 021;202 ] 1 sao cho hàm số ( ) = ( 2 g x
f x ) có 5 điểm cực trị? Ⓐ. 2025. Ⓑ. 2026. Ⓒ. 2021. Ⓓ. 4043. Lời giải Chọn A
Ta có: g ( x) = x f ′( 2 x ) = x ( 4 x − )( 2x + )( 4 2 ' 2 . 2 16
1 x − 4x + m − 4). 33
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 x = 0 x = 0 x = 2 g '( x) 4 = 0 ⇔ x −16 = 0 ⇔ . x = 2 − 4 2
x − 4x + m − 4 = 0 4 2
x − 4x + m − 4 = 0 (*)
TH1: Phương trình ( * ) có nghiệm x = 0 ⇒ m − 4 = 0 ⇒ m = 4. x = 0
Thay m = 4 vào phương trình ( * ) ta có: 4 2
x − 4x = 0 ⇔ x = 2 . h t x = −2 tps
Khi đó g′( x) = 0 có 3 nghiệm bội chẵn nên hàm số g (x) không thể có 5 điểm cực trị nên m = 4 : //lu loại. ye
TH2: Phương trình ( * ) có nghiệm x = ±2 ⇒ m−4 = 0 ⇒ m = 4 n (loại). th
TH3: Phương trình ( * ) có 2 nghiệm đơn phân biệt, khác 0 và khác ±2 hay it 2 ra
t − 4t + m− 4 = 0 phải có hai nghiệm trái dấu (với 2
t = x ) ⇔ m − 4 < 0 ⇔ m < 4 . cn
Khi đó g′( x) = 0 có 5 nghiệm phân biệt nên hàm số g (x) có 5 điểm cực trị. ghi
Kết hợp điều kiện m thuộc [ 2 − 021;202 ] 1 suy ra 2
− 021≤ m < 4,m∈ℤ e nên có 2025 giá trị m
nguyên của tham số m thỏa mãn yêu cầu. .vn 1
Câu 39: (Câu 48 - Sở GD Lào Cai - Năm 2020 - 2021) Cho hàm số 4 3 2 f (x) =
x + ax + bx + cx có đồ 4
thị (C) của hàm y = f '(x) như hình vẽ sau: https://www.fac ebo
Đặt g(x) = f ( f '(x)), h
(x) = f '( f (x)). Tổng số điểm cực trị của g(x) và h(x) là: ok.com Ⓐ. 12. Ⓑ. 11. Ⓒ. 8. Ⓓ. 13. /vi Lời giải etg Chọn C old 1 Ta có: 4 3 2 3 2 f (x) =
x + ax + bx + cx ⇒ f '( x) = x + 3ax + 2bx + c 4 f '(0) = 4 c = 4 c = 4 a = 1 −
Ta lại có: f '(−1) = 0 ⇔ 1
− + 3a − 2b + 4 = 0 ⇔ 3 a − 2b = 3 − ⇔ b = 0 f '(2) = 0
8 +12a + 4b + 4 = 0 12a + 4b = 1 − 2 c = 4 1 hay 4 3 3 2 2 f (x) =
x − x + 4x, f '(x) = x − 3x + 4 → f ' (x) = 3x − 6x 4 34
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” x = 0 2
f '(x) = 3x − 6x = 0 ⇔ x = 2
● Tìm số cực trị của hàm số: g(x) = f ( f '(x)) x = 0 x = 0 x = 2 f '(x) = 0 x = 2 x = x .vn Ta có: 1 g '(x)
f ' (x). f '( f '(x)) 0 = = ⇔ ⇔ ⇔
f '( f '(x)) = 0 f '(x) = 1 − x = 2 x iem f '(x) = 2 x = 3 x gh x = 4 x với f x = − itracn 1
x là nghiệm của phương trình '( ) 1 th và x , x ,
= , x < x < 0 < x < 2 < 2 3 4
x là ba nghiệm của phương trình f '(x) 2 1 2 3 4 x yen
Bảng xét dấu y = g '(x) s://lu ttp h
nhìn vào bảng trên, hàm số g(x) = f ( f '(x)) có 3 cực trị
●Tìm số cực trị của hàm số h(x) = f '( f (x))
BBT của hàm số y = f (x) /vietgold x = 1 − x = 2 f '(x) 0 = x = x Ta có: 1
h '(x) = f '(x). f ' ( f (x)) = 0 ⇔ f (x) = 0 ⇔ x = 2 x f (x) = 2 x = 3x x = 4 x htps://www.facebook.com Với x , = x , = 1 2
x là nghiệm của phương trình f (x) 0, 3 4
x là nghiệm của phương trình f (x) 2
và x < x < 1
− < x < x < 2 3 1 2 4
Bảng xét dấu y = h '(x)
nhìn vào bảng trên, hàm số h(x) = f '( f (x)) có 5 cực trị 35
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Vậy tổng có 8 cực trị.
Câu 40: (Câu 49 - SGD Nam Định - Online - Lần 01 - Năm 2020 - 2021) Cho hàm số f ( x) có đạo
hàm liên tục trên ℝ và bảng biến thiên của f ′( x) như sau: h ttps:// lu Hỏi hàm số 4
có mấy điểm cực tiểu? y
g ( x) = f ( x ) − 4x ent Ⓐ. 3 . Ⓑ. 1. Ⓒ. 4 . Ⓓ. 2 . h itr Lời giải ac Chọn D n g 3 4 h
Có g '( x) = 4x f '(x ) − 4 . iem g′( x) 1 3 = 0 ⇔ 4x f ′( 4
x ) − 4 = 0 ⇔ f ′( 4 x ) = x ≠ 0 1 . 3 ( ) ( ) .v x n Đặt 4 4
t = x > 0 ⇒ x = ± t phương trình trở thành: f ′(t) 1 = (2) 4 3 t . f ′(t) 1 = − (3) 4 3 t
Mô phỏng bằng đồ thị https://www.facebook.com/vie tgo
Dựa vào đồ thị ta có: ld (2) có nghiệm 4
t = a ⇒ x = a (
t = 1 ⇒ x = −1 3) có nghiệm 4
t = b ⇒ x = − b Bảng biến thiên 36
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
Vậy hàm số g ( x) có 2 điểm cực tiểu.
.vn Câu 41: (Câu 46 - SGD Quảng Bình - Năm 2020 - 2021) Cho y = f (x) là hàm số đa thức bậc bốn thỏa iem mãn f ( )
1 ≤ 0 và hàm số y = f ′( x) có bảng biến thiên như sau gh itracn th yen s://lu 2 2
ttp Hàm số g (x) = f ( x +1) + x có mấy điểm cực trị? h Ⓐ. 1. Ⓑ. 3. Ⓒ. 5. Ⓓ. 2. Lời giải Chọn C
Ta có f ′ ( x) = a ( 2
x − ) ⇒ f ′( x) a 3 1
= x − ax + C 3 2 ′ (− ) 1 = 1 a = − f − 3 ⇔ ⇒ f ′( x) 2 2 2 3 = − − − ′ ( ) x x f 1 = 3 − 2 9 3 9 C = − /vietgold 9 Xét hàm số 2 x u = x +1 có u′ =
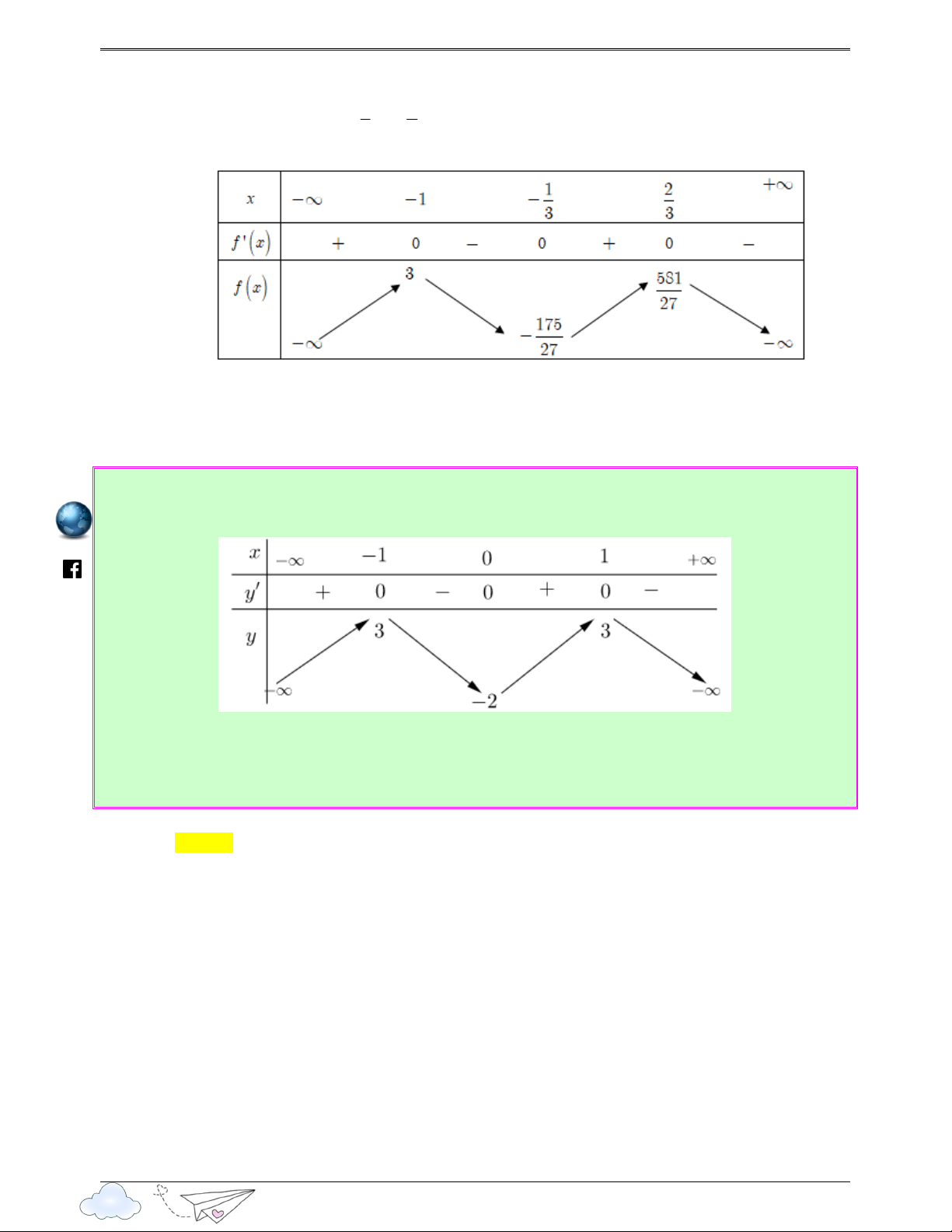
,u′ = 0 ⇔ x = 0 2 x +1 Bảng biến thiên htps://www.facebook.com
Xét hàm số h(u) = f (u) 2
+ u −1 có h′(u) = u f′ ′(u) + 2u.u′ = u′ f ′(u) + 2u u′ = 0
h′(u) = 0 ⇔ f ′ (u) = 2 − u
u′ = 0 ⇔ x = 0
f ′(u) = − u ⇔ u = a ∈( ) 2 2
1;2 ⇒ x +1 = a có 2 nghiệm trái dấu x , 1 2 x Do f ( )
1 ≤ 0 nên ta có bảng biến thiên 37
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Dựa vào bảng biến thiên, ta thấy hàm số đã cho có 5 điểm cực trị. h
Câu 42: (Câu 29 - SGD Quảng Trị - Năm 2020 - 2021) Cho hàm số f ( x) liên tục trên ℝ và có bảng ttp
biến thiên của đạo hàm như sau: s://luyenthitracng h ie 2 ln x +1 − 2 m ( )
Hàm số g ( x) = f
có bao nhiêu điểm cực trị? .v 2 n Ⓐ. 5 . Ⓑ. 9 . Ⓒ. 11. Ⓓ. 7 . Lời giải Chọn B ( 2 ln x + ) 1 − 2 Xét t ( x) =
, ta có bảng giá trị của t ( x) 2 https://www. fac 2 + − e ln (x )1 2 b
Ta có g ( x) = f
= f ( t(x) o ) o 2 k .com
Hàm số không có đạo hàm tại hai điểm 2 x = ± e −1 . /vie Tại mọi điểm 2
x ≠ ± e −1 , ta có: tgol f ' t x . d ( ( ) ) x 2 2 khi x ∈ − ; ∞ − e −1 ∪ e −1; +∞ 2 ( ) ( ) +
g ( x) = f ( t ( x) ) ( t ( x) ) x 1 ' ' . ' = (*)
f '( t (x) ).x − khi x ∈ ( 2 2
− e −1; e −1 2 ) x +1 38
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” x = 0
t (x) = t t < 1 − (1) 1 ( 1 )
g '( x) = 0 ⇔ t ( x) = t 1 − < t < 0 (2) 2 ( 2 )
t ( x) = t 0 < t < 1 3 3 ( 3 ) ( )
t(x) = t t > 1 4 4 ( 4 ) ( ) .vn
Dựa vào bảng giá trị hàm t , suy ra:
+) Phương trình (1) , (2) vô nghiệm. iem gh
+) Phương trình (3) có 4 nghiệm phân biệt khác 0 .
+) Phương trình (4) có 2 nghiệm phân biệt khác 0 và khác các nghiệm của phương trình (3) . itracn
⇒ g '( x) = 0 có 7 nghiệm và qua các nghiệm này g '( x) đều đổi dấu. th
Từ (*) , ta thấy g '( x) cũng đổi dấu khi x đi qua 2 điểm 2 2
− e −1, e −1 . yen
Vậy hàm số g ( x) có 9 cực trị. s://lu
ttp Câu 43: (Câu 48 - SGD Sóc Trăng - Lần 2 - Năm 2020 - 2021) Cho hàm số bậc bốn y = f (x) có đồ h
thị của đạo hàm f ′( x) là đường cong như hình vẽ bên dưới và f (0) = −1. /vietgold
Hàm số g ( x) = f ( 2
x ) +1 có bao nhiêu điểm cực tiểu? Ⓐ. 7 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 3 . htps://www.facebook.com Lời giải Chọn B 39
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h t tp 2 2 s
Xét h ( x) = f (x ) +1⇒ h′(x) = 2xf ′(x ) . ://lu −1 < x < 1 2 y 0 ≤ t < 1 0 ≤ x < 1 e Đặt 2
x = t,t ≥ 0 ta có hàm f ′(t ) > 0 ⇔ ⇒ ⇔ x > 2 . n 2 t 4 > x > 4 t h x < −2 itr −1 < x < 1 ac 2 n
Vậy f ′( x ) > 0 ⇔ x > 2 . g h x < −2 iem
Ta có f ′( x) là hàm bậc ba có hệ số của 3
x dương suy ra f ( x) là hàm bậc bốn có hệ số của 4 x .vn dương. Suy ra ( ) = ( 2 h x
f x ) là hàm bậc tám có hệ số của 8
x dương. Vậy lim h ( x) = +∞ . x→±∞
h (0) = f (0) +1 = 1 − +1 = 0 , h( 2
− ) = h(2) = f (4) +1 1 4
Từ đồ thị hàm f ′( x) ta có f ′
∫ (x)dx < − f ′
∫ (x)dx ⇒ f (4) < f (0) = 1
− ⇒ f (4) < −1. 0 1
Suy ra h(−2) = h(2) < 0 . Vậy ta có bảng sau https://www.facebook.c om
Từ bảng suy ra hàm số g ( x) = h ( x) có 5 điểm cực tiểu. /vietg
Câu 44: (Câu 50 - SGD Vĩnh Phúc - Lần 2 - Năm 2020 - 2021) Cho hàm số f (x) . Biết f '( x) là hàm old
bậc 3. Có đồ thị như hình vẽ sau 40
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh
itracn Có bao nhiêu giá trị nguyên m ∈[−10,10] để hàm số g (x) = f (x) + mx + 2021 có đúng 1 cực trị? th Ⓐ. 20 . Ⓑ. 16. Ⓒ. 15. Ⓓ. 18. yen Lời giải s://lu Chọn D ttp
Ta có g '( x) = f '( x) + m ⇔ g '( x) = 0 ⇔ g '( x) = −m ( ) 1 h
Số nghiệm của (1) là số giao điểm của 2 đồ thị hàm số y = f '( x) và đường d : y = −m /vietgold
Dựa vào đồ thị trên. Để g (x) có đúng 1 cực trị thì điều kiện là m ∈[ 1 − 0,10] m < 1 −
⇔ m ∈{4,5,6,7,8,9,10, 1 − 0, 9 − , 8 − , 7 − , 6 − , 5 − , 4 − , 3 − , − } 2 m > 3 htps://www.facebook.com
Số giá trị của m là 16 .
Câu 45: (Câu 48 - Chuyên Vinh- Nghệ An – Lần 1 – Năm 2020 - 2021) Cho hàm số 4 3 2
f (x) = ax + bx + cx + dx + e ( ae < 0 ). Đồ thị hàm số y = f (
′ x) như hình bên. Hàm số 2
y = 4 f (x) − x có bao nhiêu điểm cực tiểu 41
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h ttps Ⓐ. 3. Ⓑ. 5. Ⓒ. 4 . Ⓓ. 2 . ://lu Lời giải ye Chọn A n th Đặt 2
g(x) = 4 f (x) − x . Ta có g (
′ x) = 4 f (′x) − 2x = 2(2 f (′x) − x). itracnghiem.vn Ta có (′ ) = 0 ⇔ ( ′ ) x x g x f x =
. Dựa vào đồ thị hàm số y = f (
′ x) và đường thẳng y = suy ra 2 2 x = 1 − x f (
′ x) = ⇔ x = 0 . h t 2 tp x = 2 s ://
Theo hình vẽ ta có a < 0 , mà ae < 0 ⇒ e > 0 suy ra g(0) = 4 f (0) = 4e > 0 . www
Bảng biến thiên của y = g(x) như sau: .facebook.com/vietgold
Dựa vào đồ thị y = g(x) suy ra hàm số 2
y = 4 f (x) − x có 3 điểm cực tiểu.
Câu 46: (Câu 43 - Chuyên Hạ Long - Quảng Ninh - Lần 02 - Năm 2020 - 2021) Cho hàm số y = f (x)
có bảng biến thiên như sau: 42
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn 2 2
iem Số điểm cực đại của hàm số g(x)= f (2x + x) là gh Ⓐ. 3. Ⓑ. 2. Ⓒ. 1. Ⓓ. 4. Lời giải itracn th Chọn B 2 yen
Ta có: g (x) f ( 2 2x x) = + 2 2
; g′(x)= 2 f (2x + x). f ′(2x + x).(4x + ) 1 . s://lu 4x +1 = 0 ttp
g ′(x) = 0 ⇔ f ( 2 2x + x)= 0 h f ′( 2 2x + x)= 0 1
4x +1= 0 ⇔ x = − . 4 2 x = 1 2 − x + x = 2 − VN 2 ( )
Từ bảng biến thiên ta có: f (2x x) 0 ′ + = ⇔ ⇔ 1 . 2 2x + x = 1 x = 2
Dựa vào bảng biến thiên ta có phương trình f (x)= 0 chỉ có 1 nghiệm x >1 (Vì đồ thị hàm số 0
y = f (x) cắt trục Ox tại một điểm có hoành độ lớn hơn 1). Khi đó /vietgold
x = x ∈ − ; ∞ −1 1 ( ) f ( 2 2x + x) 2 = 0 ⇔ 2x + x = ⇔ . 0 x 1
x = x ∈ ; 2 +∞ 2
Do lim g (x)= lim g (x)= +∞ nên ta có bảng biến thiên: x→+∞ x→−∞ htps://www.facebook.com 2
Từ bảng biến thiên của hàm số y = g (x) ta có số điểm cực đại của hàm số g (x) f ( 2 2x x) = + là 2.
Câu 47: (Câu 50 - Chuyên Hưng Yên - Lần 1 - Năm 2020 - 2021) Cho hàm số f ( x) 4 3 2
= ax + bx + cx + dx + e,(a ≠ 0) có đồ thị hàm số f ′( x) như hình vẽ. Biết rằng e > n 43
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Số điểm cực trị của hàm số y = f ′( f ( x) − 2x) là h ttp Ⓐ. 7 . Ⓑ. 6 . Ⓒ. 10 Ⓓ. 14 . s://lu Lời giải ye Chọn A n th
f ′( x) = 2 it
Xét y = f ′( f (x) − 2x) ⇒ y′ = ( f ′(x) − 2). f ′ ( f ( x) − 2x) = 0 ⇔ . ra f ′
( f (x)− 2x) = 0 cngh
Với f ′( x) = 2 . Đường thẳng y = 2 cắt đồ thị f ′( x) tại 3 điểm phân biệt. iem
f x − 2x = m, m < 0 1 . ′ v
Với f ( f (x) − 2x) ( ) ( ) ( ) = 0 ⇔ n f
( x) − 2x = n,(n < e) (2)
Đặt h ( x) = f ( x) − 2x ⇒ h′( x) = f ′( x) − 2 = 0 ⇔ f ′( x) = 2 .
Bảng biến thiên của h ( x) : https:// ww Vậy các phương trình ( )
1 và (2) cho 4 nghiệm phân biệt. w.fac
Câu 48: Vậy số điểm cực trị của hàm số y = f ′( f (x) − 2x) là 7.(Câu 47 - Chuyên Lê Khiết - Quảng eboo
Ngãi - Lần 3 - Năm 2020 - 2021) Cho hàm số f ( x) có đạo hàm liên tục trên ℝ , đồ thị hàm số k.co
y = f ′( x) có đúng 4 điểm chung với trục hoành như hình vẽ bên dưới: m /vietgold 44
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
Có bao nhiêu giá trị nguyên của 3
m để hàm số y = f ( x −3 x + m + 202 )
1 có đúng 11 điểm cực trị? Ⓐ. 0 . Ⓑ. 2 . Ⓒ. 5 . Ⓓ. 1. Lời giải Chọn D .vn
Xét x > 0 : Hàm số có dạng y = f ( 3
x − 3x + m + 202 ) 1 iem y′ = ( 2 x − ) f ′( 3 3 3
x − 3x + m + 202 ) 1 gh
Do nghiệm của phương trình 3
x − 3x + m + 2021 = 4 là các nghiệm bội bậc chẵn của phương trình y′ = 0 nên ta có: itracn
x = 1 (do x > 0)
x = 1 (do x > 0) th 2 3x − 3 = 0 3
x − 3x + m + 2021 = 1 − 3
m + 2021 = −x + 3x −1 yen y′ = 0 ⇔ ⇔ ⇔ f ′ 3 3 ( 3
x − 3x + m + 202 ) 1 = 0
x − 3x + m + 2021 = 1
m + 2021 = −x + 3x +1 3 3 s://lu
x − 3x + m + 2021 = 2
m + 2021 = −x + 3x + 2 ttp Vẽ đồ thị ba hàm số 3
y = −x + 3x −1; 3
y = −x + 3x +1; 3
y = −x + 3x + 2 với x > 0 trên cùng một h hệ trục. /vietgold
Hàm số y = f ( 3
x − 3 x + m + 202 )
1 có đúng 11 điểm cực trị
⇔ Hàm số y = f ( 3
x − 3x + m + 202 )
1 có đúng 5 điểm cực trị dương
⇔ Phương trình f ′( 3
x − 3x + m + 202 )
1 = 0 có đúng 4 nghiệm bội lẻ dương khác 1 htps://www.facebook.com
⇔ Đường thẳng y = m + 2021 cắt đồ thị ba hàm số 3
y = −x + 3x −1; 3
y = −x + 3x +1; 3
y = −x + 3x + 2 tại 4 điểm phân biệt có hoành độ dương khác 1 1
− < m + 2021 < 1
−2022 < m < 2 − 020 ⇔ ⇔ 2 < m + 2021 < 3 −2019 < m < 2 − 018
Do m nguyên nên m = 2 − 021.
Vậy chỉ có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 49: (Câu 4 - Chuyên Lê Quý Đôn - Điện Biên - Lần 3 - Năm 2020 - 2021) Cho hàm số f ( x) 4 3 2
= ax + bx + cx + dx + ,
e (a ≠ 0) có đồ thị của đạo hàm f ′( x) như hình vẽ. 45
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Biết rằng e > n. Số điểm cực trị của hàm số y = f ′( f ( x) − 2x) bằng h ttp Ⓐ. 7 . Ⓑ. 10. Ⓒ. 14. Ⓓ. 6 . s:// Lời giải lu Chọn A yen
f ′( x) = 2 th
g(x) = f ′( f ( x) − 2x) ⇒ g (
′ x) = f ′( x) − 2. f ′ ( f (x) − 2x) = 0 ⇔ i f ′
( f (x)−2x) = 0 t racng
x = a < m h i e + f (
′ x) = 2 ⇔ x = 0 m , ( có 3 nghiệm đơn) = > . x b n vn y
y=f ' (x) 2 y=2 m a O n b x http s:/ x = m /w
+ Từ đồ thị hàm số y = f ( ′ )
x ta suy ra f ′ ( ′ x) = 0 ⇔ w x = n w.f
f x − x = m a ′ c
Do đó f ( f x − x) ( ) 2 , (1) ( ) 2 = 0 ⇔ e
f (x) − 2x = n , (2) b ook Lập BBT cho hàm số ( h ) x = f ( )
x − 2x , với h ( ′ ) x = f ( ′ ) x − 2. .co = = > > m Ta có ( h 0) f (0) , e e n m /vietgold
Do đó phương trình (1) và (2) có 4 nghiệm đơn.
Suy ra phương trình g ( ′ )
x = 0 có 7 nghiệm đơn 46
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
nên hàm số g(x) = f ′( f ( x) − 2x) có 7 cực trị.
Câu 50: (Câu 49 - Chuyên Lê Thánh Tông - Quảng Nam - Lần 1 - Năm 2020 - 2021) Cho hàm số
y = f ( x) có đồ thị y = f ′( x − ) 1 như hình vẽ .vn iem gh itracn th yen f x x
s://lu Khi đó hàm số ( ) 2 y e + =
đạt cực tiểu tại điểm 0
x . Mệnh đề nào dưới đây đúng? ttp h
Ⓐ. x ∈ −1;0 . Ⓑ. x ∈ 4 − ; 2 − .
Ⓒ. x ∈ 0;1 . Ⓓ. x ∈ 2 − ; 1 − . 0 ( ) 0 ( ) 0 ( ) 0 ( ) Lời giải Chọn A f (x)+2 x y′ = e (. f ′(x)+ ) 2 Ta có:
y′(x) = 0 ⇔ f ′(x)+ 2 = 0 ⇔ f ′(x) = −2
Đồ thị y = f ′(x − )
1 dời sang phải 1 đơn vị theo trục Ox ta được đồ thị y = f ′(x). Khi đó
đường thẳng y = 2 cắt đồ thị y = f ′(x) tại 2 điểm có hoành độ là 1 và a với 1 − < a <0 nên
phương trình y′(x)= 0 có 2 nghiệm là 1 (nghiệm kép) và 1 − < a <0 /vietgold Bảng biến thiên x – ∞ a 1 + ∞ y' – 0 + 0 + y f(1) f(a)
Vậy hàm số đạt tiểu tại điểm x = a ∈ −1;0 . 0 ( )
htps://www.facebook.com Câu 51: (Câu 40 - Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - Lần 1 - Năm 2020 - 2021) Cho hàm
số y = f ( x) có đồ thị như hình vẽ. 47
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 y 4 -2 O 2 x h ttps ://
Mệnh đề nào sau đây đúng: lu 1 y
Ⓐ. Hàm số y = f ln đạt cực tiểu tại = . e ( x) x n e thi
Ⓑ. Hàm số y = f (ln x) đạt cực tiểu tại 2 x = e . trac
Ⓒ. Hàm số y = f (ln x) đạt cực tiểu tại x = 0 . n gh
Ⓓ. Hàm số y = f ln đạt cực tiểu tại x = 2 . i ( x) em .v Lời giải n Chọn B
y = g ( x) = f (ln x); TXĐ: x > 0 ln x = 0 x = 1 g′( x) 1
= . f ′(ln x) ; g′( x) = 0 ⇔ ⇔ x ln x = 2 2 x = e BBT: x 0 1 2 e +∞ h g′ ( x) + 0 − 0 + ttps:/ g ( x) 4 +∞ /ww −∞ 0 w.fa
Từ BBT, ta thấy: hàm số y = g ( x) = f (ln x) đạt cực tiểu tại 2 x = e . cebook
Câu 52: (Câu 50 - Chuyên Nguyễn Trãi - Hải Dương - Lần 1 - Năm 2020 - 2021) Cho hàm số F ( x) .com
có F (0) = 0 . Biết y = F ( x) là một nguyên hàm của hàm số y = f ( x) có đồ thị như hình vẽ. /vietgold 48
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
Số điểm cực trị của hàm số ( ) = ( 6 ) 3 G x F x − x là Ⓐ. 4 . Ⓑ. 5 . Ⓒ. 6 . Ⓓ. 3 . Lời giải Chọn D
Xét g ( x) = F ( 6 x ) 3
− x ⇒ g ( x) 5 = x F ( 6 x ) 2 2 3
− x = x x f ( 6 ' 6 ' 3 3 2 x ) −1 .vn . Xét hàm số iem h ( x) 3 = x f ( 6
x ) − ⇒ h ( x) 2 = x f ( 6 x ) 8 + x f ( 6 x ) 2 = x f ( 6x) 6 + x f ( 6 2 1 ' 6 12 . ' 3 2 4 . ' x ) gh .
Từ đồ thị của y = f ( x) suy ra dấu của f '( x) itracn th yen f ( 6 x ) s://lu > 0 nên
⇒ h '( x) > 0 ∀x nên hàm số y = h ( x) đồng biến trên ℝ và vì lim h( x) = ±∞ ttp f ' x→±∞ ( 6 x ) > 0 h
nên phương trình h ( x) = 0 có 1 nghiệm duy nhất =
đổi dấu từ âm sang dương khi 0 x và y h ( x) qua g '
đổi dấu từ âm sang dương khi qua 0 x . Suy ra (x) 0 x nên 0
x là điểm cực tiểu. Bảng biến thiên /vietgold
Câu 53: Từ bảng biến thiên suy ra hàm số y = G ( x) có 3 cực trị.(Câu 40 - Chuyên PTNK - HCM - Lần
1 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đạo hàm là f ′ ( x) 2 = x − ( 2 (
2) x − x), x ∈ ℝ . Gói htps://www.facebook.com 1
S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 2 f
x − 6x + m có 5 2
điểm cực trị. Tính tổng tất cả các phần tử của S. Ⓐ. 154. Ⓑ. 17 . Ⓒ. 213. Ⓓ. 153. Lời giải Chọn D
Ta có. Với x = 2 là nghiệm kép, x = 0, x =1 là nghiệm đơn. Dó đó hàm số f ( x) có hai điểm
cực trị là x = 0, x =1. 49
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 1 1 Đặt 2 2 g(x) = f
x − 6x + m ⇒ g (
′ x) = (x − 6) f ′
x − 6x + m . 2 2 x = 6 1 2
x − 6x + m = 2 2 Khi đó g ( ′ x) = 0 ⇔ 1 . 2
x − 6x + m = 0(1) 2 1 2 h
x − 6x + m = 1(2) t 2 tps
Để hàm số có 5 điểm cực trị thì ( )
1 & (2) có hai nghiệm phân biệt không trùng nhau và khác ://lu ∆ > 0 1 m y 9 − > 0 e ∆ > 0 2 n 2 th 1 m −1 2 i
6 Suy ra ⋅6 − 6.6 + m ≠ 0 9 −
> 0 ⇔ m < 18 ⇒ m ∈{1, 2,…,17}. t r 2 2 a c 1 n 2
m ≠ 18, m ≠ 19 ⋅6 − 6.6 + m ≠ 1 g 2 h iem
Vậy Tổng các giá trị của m là 1+ 2 +…+17 = 153. .vn
Câu 54: (Câu 49 - Đề thi thử cụm trường THPT - Hải Dương - Lần 4 - năm 2021) Cho hàm số bậc
năm y = f ( x) có đồ thị y = f ′( x) như hình bên. Số điểm cực trị của hàm số
g ( x) = f ( 3 2 x + x ) 3 2 3
− 2x − 6x là https://www.facebook .com Ⓐ. 7. Ⓑ. 10. Ⓒ. 5. Ⓓ. 11. /viet Lời giải gol Chọn B d
Xét hàm số g ( x) = f ( 3 2 x + x ) 3 2 3 − 2x − 6x
Ta có g′( x) = ( 2
x + x) f ′( 3 2 x + x ) 2
− x − x = x(x + ) f ′ ( 3 2 3 6 3 6 12 3 2
x + 3x ) − 2 . 50
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh itracn x = 0 th x = −2 x = 0 3 2 yen
x + 3x = c c < 0 1 1 ( 1 ) ( )
Cho g′( x) = 0 ⇔ x = 2 − ⇔ . 3 2
x + 3x = c 0 < c < 2 2 2 ( 2 ) ( ) s://lu f ′ ( 3 2 x + 3x ) = 2 3 2
x + 3x = c 2 < c < 4 3 3 ( 3 ) ( ) ttp h 3 2
x + 3x = c c > 4 4 4 ( 4 ) ( )
Xét hàm số h( x) 3 2
= x + 3x , ta có h′( x) 2 = 3x + 6x .
Bảng biến thiên h( x) : /vietgold
Vẽ đồ thị của các hàm số y = h ( x) , y = , = , = , = trên cùng một mặt phẳng tọa 1 c y 2 c y 3 c y 4 c độ ta được htps://www.facebook.com 51
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h
ttps://luyenthitracnghiem.vn x = = 2 x x 3 x ( ) 1 ⇔ x = ; (2) ⇔ = ; (3) ⇔ = ; (4) ⇔ = 1 x x 5 x x 4 x x 8 x x = = 6 x x 7 x
Trong đó x < x < x < 2
− < x < x < 0 < < < . 1 2 3 4 5 6 x 7 x 8 x
Bảng xét dấu g′( x) : https://www .fa
Từ bảng xét dấu ta kết luận được hàm số g ( x) có 10 điểm cực trị. ceboo
Câu 55: (Câu 44 - THPT Gia Bình - Bắc Ninh - Lần 1- Nưm 2020 - 2021) Cho hàm số k.c = = + + o ( ) 4 2 y f x ax bx
c có đồ thị như hình vẽ bên dưới. m /vietgold 52
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh itracn th
yen Số điểm cực trị của hàm số ( ) = ( 3 g x
f x + f ( x)) là s://lu Ⓐ. 11. Ⓑ. 9. Ⓒ. 8. Ⓓ. 10. ttp h Lời giải Chọn B
Từ đồ thị ta thấy hàm số trên có phương trình là 4 2
y = x − 2x . Vậy ta có: f ( x) 4 2
= x − 2x và f ′( x) 3 = 4x − 4x ′ ′
g′( x) = ( f ( 3
x + f ( x))) = ( 3
x + f ( x)) f ′( 3
x + f ( x)) = ( 2
x + f ′( x)) f ( 3 3
x + f ( x)) .
Suy ra g′( x) = ( 2
x + f ′( x)) f ′( 3
x + f ( x)) = ( 2 3
x + x − x) f ′( 3 4 2 3 3 4 4
x + x − 2x ) .
g′( x) = 0 ⇔ ( 2 3
3x + 4x − 4x) f ′( 3 4 2
x + x − 2x ) = 0 x = 0 /vietgold x ≈ 0,6930 x ≈ 1 − , 4430 3 2 3 2
4x + 3x − 4x = 0
4x + 3x − 4x = 0 x ≈ 1, 21195 4 3 2 4 3 2
x + x − 2x = 1
x + x − 2x −1 = 0 . ⇔ ⇔ ⇒ x ≈ 2 − ,0754 4 3 2 4 3 2
x + x − 2x = −1
x + x − 2x +1 = 0 x ≈ 0 − ,6710 4 3 2 4 3 2
x + x − 2x = 0
x + x − 2x = 0 x ≈ 1 − ,9051 x = 1 x = 2 − htps://www.facebook.com
Phương trình g′( x) = 0 có đúng 8 nghiệm đơn và 1 nghiệm bội lẻ x = 0(nghiệm bội ba).
Vậy hàm số g ( x) có 9 điểm cực trị.
Câu 56: (Câu 42 - THPT Hàn Thuyên - Bắc Ninh - Lần 1 - Năm 2020 - 2021) Cho hàm đa thức
y = f (x) . Hàm số y = f '(x) có đồ thị như hình vẽ sau 53
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h 2 t
Có bao nhiêu giá trị của m ∈[0;6];2m ∈ ℤ để hàm số g(x) = f (x − 2 x −1 − 2x + m) có đúng 9 điểm cực tps trị? ://luy Ⓐ. 7 . Ⓑ. 5. Ⓒ. 3. Ⓓ. 6. en Lời giải thi Chọn C tra 2( x − ) 1 ( x −1 − ) 1 c 2 n Ta có: g ( ′ x) =
f '( x − 2 x −1 − 2x + m) g x −1 h ie x =1 m . x = 0 v n g ( ′ x) = 0 ⇔ x = 2 f ' ( 2
x − 2 x −1 − 2x + m) = 0
Dựa vào đồ thị hàm số x = 0 2 2
x − 2 x −1 − 2x + m =1
x − 2 x −1 − 2x =1− m =
f ′( x) ⇒ f ′( x) x 1 2 2 = 0 ⇔
⇒ x − 2 x −1 − 2x + m = 2 ⇒ x − 2 x −1 − 2x = 2 − m x = 2 2 2
x − 2 x −1 − 2x + m = 3 =
x − 2 x −1 − 2x = 3− m h x 3 ttps
Xét hàm số h ( x) 2
= x − 2 x −1 − 2x .Ta có ://www.facebook. co
Để hàm số có 9 cực trị thì m /v TH1: 2 − < 2−m< 1 − ⇔3< m< 4 ietg TH2: 1−m ≥ 1 − ⇔m≤ 2. old
Vậy có ba giá trị của m.
Câu 57: (Câu 50 - THPT Hậu Lộc 4 - Thanh Hóa - Lần 1 - Năm 2020 - 2021) Cho hàm số f ( x ) có
đạo hàm trên ℝ và có bảng biến thiên như sau 54
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
.vn Số điểm cực đại của hàm số g (x) = f ( 2 2
x − 8x + 7 + x − 3) là iem Ⓐ. 6 . Ⓑ. 8. Ⓒ. 7 . Ⓓ. 9. gh Lời giải Chọn C itracn th 2 Đặt
2 x − 8x + 4 khi x ≤ 1 ∨ x ≥ 7 u( x) 2 2
= x −8x + 7 + x −3, ta có u (x) = . 8x − 10
khi1 < x < 7 yen − < ∨ > ⇒ u′( x)
4x 8 khi x 1 x 7 = . s://lu 8
khi 1 < x < 7 ttp Ta có bảng biến thiên h
Đặt h ( x) = f (u (x)) , ta có h′(x) = u′(x). f ′(u (x)) .
Ta có: u′( x ) chỉ đổi dấu qua . x = 1 u ( x) = 3 u(x) = 2 /vietgold
f ′(u ( x)) = 0 ⇔ u ( x) = 1 . u(x) = 1 − u ( x) = 3 −
Từ bảng biến thiên của u(x) ta có
u ( x ) = 3 có hai nghiệm phân biệt x , 1 8 x .
u ( x ) = 2 có hai nghiệm phân biệt x , 2 7 x
u ( x ) = 1 có hai nghiệm phân biệt x , 3 6 x htps://www.facebook.com
u ( x) = −1 có hai nghiệm x , 4 5 x
u ( x) = −3 vô nghiệm Ta có bảng biến thiên 55
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 2 2 h
Câu 58: Từ bảng, dễ dàng suy ra hàm số g (x) = f ( x − 8x + 7 + x − 3) = h(x) có 7 điểm cực đại.(Câu ttp
48 - THPT Hồng Quang - Hải Dương - Lần 3 - Năm 2020 - 2021) Cho hàm số bậc bốn trùng s://
phương y = f ( x) có bảng biến thiên sau luyenthitracnghiem .vn 1
Số điểm cực trị của hàm số g (x) =
( f (x)− 6)4 là 2 x Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 5. Ⓓ. 3. Lời giải Chọn B Theo giả thiết ta có ( ) 4 2
f x = ax + bx + c ⇒ f ′( x) 3 = 4ax + 2bx .
Từ bảng biến thiên ta có hàm số f ( x) đi qua A( 2
− ;2), B(0;6),C (2;2) và có ba điểm cực trị http 1 s: a = / 1
6a + 4b + c = 2 / 4 w 1 w ⇒ c = 6 ⇔ b = 2
− . Vậy f (x) 4 2
= x − 2x + 6 , f ′( x) 3 = x − 4x w 4 . 32a + 4b = 0 c = 6 f a ce boo 1 k
Ta có Hàm số g ( x) =
( f (x)− 6)4 xác định trên D = ℝ \{ } 0 . 2 .c x om 2 4 1 3 / g′ ( x) = − f x − 6 +
.4 f x − 6 . f ′ x 3 ( ( ) ) 2 ( ( ) ) ( ) vi x x etg 3 o ( f (x)−6) ld ⇒ g′( x) = 4 .
x f ′ x − 2 f x +12 3 ( ( ) ( ) ) x f ( x) − 6 = 0 ( ) 1
g′( x) = 0 ⇔ 4xf ′
(x) − 2 f (x) +12 = 0 (2) 1 x = 0 Ta có ( ) 4 2 1 ⇔
x − 2x + 6 = 6 ⇔ . 4 x = ±2 2 56
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” x = 0 ( 2) 4 . ⇔ x ( 1 7 3 x − 4x) 4 2 4 2 − 2
x − 2x + 6 +12 = 0 ⇔ x −12x = 0 2 42 . 4 2 x = ± 7 x = ±2 2 Vì
x ≠ 0 nên có g′( x) = 0 ⇔
và các nghiệm đó đều là nghiệm bội lẻ. 2 42 x = ± 7 .vn
Do đó hàm số g (x) có 4 điểm cực trị. iem
gh Câu 59: (Câu 49 - THPT Kim Liên - Hà Nội - Lần 2 - Năm 2020 - 2021) Cho hàm số y = f (x) liên
tục trên ℝ có bảng biến thiên như hình vẽ: itracn th yen s://lu ttp h
Số điểm cực đại của hàm số y = f ( f (x) ) là Ⓐ. 2. Ⓑ. 3. Ⓒ. 0. Ⓓ. 1. Lời giải Chọn A
f ′ x . f x
Đặt g ( x) = f ( f (x) ) ⇒ g′(x) = f ′( f (x) ) ( ) ( ) . f ( x) /vietgold
Do đó g′( x) không xác định khi f ( x) = 0 hay x = 0 . f ′(x) = f ′( x) 0 = 0 x = 1 ±
g′( x) = 0 ⇔ ⇔ = ⇔ ⇔ = ± . f ′ ( f ( x) 1 x 1 f ( x) ) = 0 f ( x) = 1 ±
f ( x) = −1
Từ bảng biến thiên của f ( x) ta có: f ( x) ∈[0; ] 1 , x
∀ ∈ ℝ . Suy ra f ′( f (x) ) ≥ 0, x ∀ ∈ ℝ .
Ta có bảng xét dấu g′( x) như sau: htps://www.facebook.com
Từ bảng biến thiên suy ra số điểm cực đại của hàm số y = f ( f (x) ) là 2..
Câu 60: (Câu 41 - THPT Kim Sơn A- Ninh Bình - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f (x)
có đạo hàm liên tục trên R và bảng biến thiên của hàm số f '(x) như sau: 57
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h ttp Hỏi hàm số s: 2 / ln(x +1) − 2 /l g ( x) = f
có bao nhiêu điểm cực tiểu? u 2 y enth Ⓐ. 9. Ⓑ. 4. Ⓒ. 7 . Ⓓ. 5. itra Lời giải cn Chọn B gh 2 2 ln(x +1) − 2 i
+) Do x ≥ 0 với ∀x ∈ nên
≥ −1 với ∀x ∈ . e ℝ ℝ m 2 .v +) Bảng biến thiên n http s:/
x = a ∈ (1; +∞) /w w x = b ∈ (0; ) 1 w
Suy ra f '(x) = 0 ⇔ . .f
x = c ∈ (−1;0) a ce
x = d ∈ −∞;−1 b ( ) oo 2 k ln(x +1)−2 .c
+) Xét hàm số trên y = f trên +∞ o 0; ) m 2 /vi 2 e ln(x +1)−2 tg =a o 2 l d 2
ln(x +1)−2 =b 2 + a 2 2 x + − x = e −1 ln( 1) 2 2 f ' 0 2 = 2 2 + ln(x +1)−2 b 2 x 2 ln(x +1)−2 x = e −1 y' = f ' . =0⇔ ⇔ =c ⇔ 2 2 x +1 2 2 + x c 2 x = e − = 1 0 2 2 ln(x +1)−2 x +1 = ( d VN) x = 0 2 x= 0 Suy ra bảng biến thiên 58
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh 2 ln(x +1) − 2
Mặt khác đồ thị hàm số g(x) = f được vẽ như sau: itracn 2 th 2 ln(x +1)−2 yen
- Giữ phần đồ thị hàm số y = f trên +∞ 0; ). 2 s://lu 2 ln(x +1)−2
- Lấy đối xứng phần đồ thị hàm số y = f trên +∞ 0; ) qua Ox. ttp 2 h 2 ln(x +1) − 2
Vậy hàm số g(x) = f có 4 điểm cực tiểu. 2
Câu 61: (Câu 50 - THPT Lê Hồng Phong - Nam Định - Năm 2020 - 2021) Cho f ( x) là hàm số có đạo
hàm liên tục trên ℝ và có bảng biến thiên của f ′( x) như sau: /vietgold
Tìm số điểm cực tiểu của hàm số g ( x) = f ( 3 x ) −3 x . Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3. Ⓓ. 0. Lời giải htps://www.facebook.com Chọn C
Xét hàm số h ( x) = f ( 3 x ) − 3x . h′( x) 2 = x f ′( 3 3 . x ) − 3. h′( x) 2 = ⇔ x f ′( 3 0 3 . x ) − 3 = 0 (1). 1
Dễ thấy x = 0 không là nghiệm của (1) nên ( ) 1 ⇔ f ′( 3 x ) = (2). 2 x 1 Đặt 3
t = x thì (2) trở thành f ′(t ) = ( t ≠ 0 - 3). 3 2 t 59
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 Xét hàm số 1 y = 3 2 t 2 5 − 2 − + t > 0 thì 3 y = t là hàm số lũy thừa, 3 y′ = − t
< 0 nên y nghịch biến trên (0;+ ∞) và đồ thị 3
của y nhận hai trục tọa độ làm hai tiệm cận.
+ y (t ) = y (−t ) nên y là hàm số chẵn. Do đó đồ thị của y nhận Oy làm trục đối xứng. Vẽ đồ thị của 1
f ′ (t ) và y =
trên cùng hệ trục tọa độ ta có: 3 2 h t
ttps://luyenthitracnghiem.vn
Từ đồ thị ta có (3) ⇔ t = a > 0 . Suy ra 3 x = a > 0
Bảng biến thiên của h( x) : https://www .fac
Ta thấy hàm số g ( x) = h( x ) là hàm số chẵn nên đồ thị của g ( x) nhận Oy làm trục đối xứng. eboo
Do đó ta có bảng biến thiên của g (x) như sau: k.com/vietgold (Để ý ( 3 − ) = (3 g a g a ) )
Vậy hàm số g ( x) có hai điểm cực tiểu và một điểm cực đại.
Câu 62: --- HẾT ---(Câu 48 - THPT Ngô Quyền - Ba Vì - Hà Nội - Lần 2 - Năm 2020 - 2021) Cho
hàm số y = f ( x) xác định và liên tục trên ℝ , có đồ thị hàm số f ′( x) như hình vẽ. Số điểm cực
tiểu của hàm số g ( x) = f ( x) + x là 60
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 0 . itracn th Lời giải Chọn A yen
Ta có: g′( x) = f ′( x) +1; g′( x) = 0 ⇔ f ′( x) = 1 − (*). s://lu
Phương trình chính là phương trình hoành độ giao điểm của đồ thị hàm số f ′( x) và đường thẳng ttp − h y = 1. /vietgold
Dựa vào đồ thị, ta thấy có nghiệm x = 0 , x = 1 và x = 2 .
Bảng biến thiên của hàm số g ( x) : htps://www.facebook.com
Dựa vào BBT, hàm số g ( x) = f ( x) + x có một điểm cực tiểu x = 1.
Câu 63: (Câu 44 - THPT Nguyễn Đăng Đạo - Thanh Hóa - Lần 2 - Năm 2020 - 2021) Cho hàm số
y = f ( x) liên tục trên R và có bảng biến thiên như sau: 61
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Số điểm cực tiểu của hàm số f ( x) f ( x) y = 2021 − 2020 là Ⓐ. 1. Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 4 . h ttp Lời giải s:/ Chọn B /lu
Xét hàm số y = g ( x) f ( x) f ( x ) = 2021 − 2020 yen Ta có: ' g ( x) ' = f ( x) f ( x) f ( x) (2021 ln2021−2020 ln2020). thi ' t f
x = 0 ⇔ x = 0; x = ±2 r ' ( ) a y = 0 ⇔ . c f ( x) f ( x) n log 2021 ln 2021 2020 ln 2020 0(*) − = gh f ( x) 2021
x = a ∈ (0;2) i e Ta có: (*) ⇔ = log 2020 ⇔ f x = log log 2020 ⇒ 2021 ( ) 2021 ( 2021 ) m 2020
x = b ∈ (2; +∞ ) 2020 . vn
Vậy, từ bảng xét dấu ta thấy số điểm cực tiểu của hàm số y = g ( x) là 3. ht
Câu 64: (Câu 49 - THPT Nguyễn Huệ - Đắk Lắk - Lần 1 - Năm 2020 - 2021) Cho y = f ( x) là hàm đa tp s:/
thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 1 − 2;12] / ww
để hàm số g (x) = 2 f ( x − )
1 + m có 5 điểm cực trị? w.facebook.com/vietgold Ⓐ. 12 . Ⓑ. 14 . Ⓒ. 15 . Ⓓ. 13. Lời giải Chọn C 62
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
Nhận xét: Số điểm cực trị của hàm số y = f ( x − )
1 bằng số điểm cực trị của hàm số y = f ( x) trên tập xác định ℝ
Dựa vào đồ thị, hàm số y = f ( x) có 3 điểm cực trị .vn iem gh itracn th yen s://lu
Để hàm số g ( x) có 5 điểm cực trị ttp m h
⇔ 2 f ( x) + m = 0 ⇔ f ( x) = − có 2 ngiệm phân biệt hoặc 3 nghiệm trong đó có 1 nghiệm bội 2 chẵn và 2 nghiệm đơn m − ≥ 2 m ≤ 4 2 − ⇔ ⇔ m 6 ≤ m < 12 6 − < − ≤ 3 − 2
Mà m là giá trị nguyên thuộc [ 1 − 2;12] nên m∈{ 1 − 2;−11;...; 4 − ;6;7;...;1 } 1
Vậy có 15 giá trị nguyên m thỏa yêu cầu bài toán.
Câu 65: (Câu 40 - PTNK Cơ Sở 2 - TPHCM - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đạo /vietgold
hàm f ( x) = ( x − )2 ( 2 ' 2
x − x) với x
∀ ∈ℝ . Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số 1 m để hàm số 2 f
x − 6x + m
có 5 điểm cực trị. Tính tổng các phần tử của S ? 2 Ⓐ. 154. Ⓑ. 17 . Ⓒ. 213. Ⓓ. 153. Lời giải Chọn D x = 2 htps://www.facebook.com Ta có
f '( x) = ( x − 2)2 ( 2
x − x) ⇒ f '( x) = 0 ⇔ x = 1
. Với x = 2 là nghiệm kép, x = 1, x = 0 là x = 0
nghiệm đơn. Do đó hàm số f = f ( x) đạt cực trị tại x = 1, x = 0 . Đặt g ( x) 1 1 2 = f
x − 6x + m ⇒ g ' (x) = (x − 6) 2 f '
x − 6x + m . Khi đó 2 2 63
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 x = 6 1 2
x − 6x + m = 2 2
g '( x) = 0 ⇔ 1 . Giả sử 2 0
x là nghiệm của phương trình ( ) 1 thì
x − 6x + m = 0( ) 1 2 1 2
x − 6x + m = 1 (2) 2 1 2 h
x − 6x + m = 0 do đó 2 hay nói cách khác 0 0 0
x không thể là nghiệm của phương trình ( ) t 2 tps 1 : phương trình ( )
1 ,(2) không có nghiệm chung. Vì vậy, để hàm số 2 f
x − 6x + m có 5 điểm / / 2 l u y
cực trị thì phương trình ( )
1 ,(2) có hai nghiệm phân biệt khác 6 hay ent ∆ > 0 h 1 9 m − > 0 i t ∆ > 0 2 r 2 a c m −1 1 m + ∈ n 2 ⇔ 9 − + ≠ −
> 0 ⇔ m < 18 ℤ → m m ∈ {1,2,...,1 } 7 .6 6.6 0 . g 2 h 2 ie 1
m ≠ 18,m ≠ 19 2 m
.6 − 6.6 + m ≠ 1 2 .vn
Vậy tổng các giá trị của m là: 1+ 2 +...+17 =153.
Câu 66: (Câu 49 - THPT Quảng Xương - Thanh Hóa - Năm 2020 - 2021) Cho hàm số y = f (x) . Hàm
số y = f ′( x) có đồ thị như hình vẽ. https://www.facebook.c om/ 1 v
Số điểm cực đại của hàm số 2 2 4
g (x) = f (x − 4x + 3) − 3( x − 2) + (x − 2) là ie 2 tgold Ⓐ. 7. Ⓑ. 3. Ⓒ. 4. Ⓓ. 5. Lời giải Chọn B Ta có: 2 3 2 2 g (
′ x) = (2x − 4) f (′x − 4x + 3) − 6(x − 2) + 2(x − 2) = (2x − 4) f (′x − 4x + 3) − 3 + (x − 2) 2x − 4 = 0 Ta có: g ( ′ x) = 0 ⇔ 2 2 f (
′ x − 4x + 3) − 3+ (x − 2) = 0 64
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” x = 2 ⇔ 2 2 f (
′ x − 4x + 3) = 2 − (x − 4x + 3) (*) Đặt 2
x − 4x + 3 = t , ta có: (*) ⇔ f ′(t ) = 2 − t . .vn iem gh itracn th yen s://lu ttp h
Từ đồ thị hàm số y = f ′(t) và y = 2 − t ta có: 2 t = −2
x − 4x + 3 = −2 x = 1 2 t = x − x + = x = 3 0 4 3 0 f ( ′ t) = 2 − t ⇔ ⇔ ⇔ 2 t = 1 x − 4x + 3 = 1 x = 2 ± 2 2 t = 2
x − 4x + 3 = 2 x = 2 ± 3
Ta có bảng biến thiên hàm số y = g (x) như sau: /vietgold
Vậy hàm số y = g(x) có 3 điểm cực đại.
Câu 67: (Câu 47 - THPT Quảng Xương 1 - Thanh Hóa - Lần 1 - Năm 2020 - 2021) Cho hàm số f ( x) 5 4 3 2
= ax + bx + cx + dx + ex + f (a ≠ 0) và hàm số y = f ′(x) có hình vẽ dưới đây htps://www.facebook.com 65
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 9
Đặt g ( x) = f (3x − ) 3 2
1 − 9x + x − 6x + 2021. Hòi hàm số f = g ( x ) có bao nhiêu điểm cực trị ? 2 Ⓐ. 7 . Ⓑ. 3. Ⓒ. 9. Ⓓ. 5. Lời giải Chọn B
g′( x) = f ′( x − ) 2 3 3
1 − 27x + 9x − 6 h
Đặt t = 3x −1⇒ 3x = t +1 ttp ′ = ′ − − − s g (t) f (t) 2 3 3t 3t 6 ://l 1 u t = 2 − ⇒ x = − y e 3 n ′ = ⇔ ′ t * g (t) 0 f (t ) 2
= t + t + 2 ⇔ t = 1 − ⇒ x = 0 h i t 2 r t =1⇒ x = ac 3 n g
Bảng biến thiên của g ( x) h iem.vn https://www .fa
Vậy hàm số g ( x ) có ba điểm cực trị ceboo
Câu 68: (Câu 50 - THPT Thăng Long - Hà Nội - Lần 2 - Năm 2020 - 2021) Cho hàm số bậc năm k.c
y = f ( x) có đồ thị hàm số y = f ′( x) như hình vẽ dưới đây. Số điểm cực trị của hàm số om/ 8 2 3 2 v
y = f 4x − 4x −
x + 6x − 4x +1 là i ( ) et 3 gold 66
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh itracn Ⓐ. 4. Ⓑ. 5. Ⓒ. 9 . Ⓓ. 7. th Lời giải yen Chọn B
Ta có y′ = ( x − ) f ′( 2 4 2 1
4x − 4x) − 4(2x − ) 1 ( x − ) 1 s://lu 2 ⇒ ′ = − ′ − − − ttp y 4(2x ) 1 f (4x 4x) (x ) 1 . h 1 x =
y′ = 0 ⇔ y′ = 4(2x − ) 1 f ′ ( 2
4x − 4x) − (x − ) 1 = 0 ⇔ 2 f ′ ( 2
4x − 4x) = x −1
Xét phương trình: f ′( 2
4x − 4x) = x −1 ( ) 1 Đặt 2 2
t = 4x − 4x ⇒ 4x − 4x − t = 0 ′
∆ = 4 + 4t ≥ 0 ⇔ t ≥ 1 − . 1− 1+ t −1− 1+ = −1 t x x = Khi đó: 2 2 2
4x − 4x − t = 0 ⇔ ⇒ 1+ 1+ t −1+ 1+ = −1 t x x = /vietgold 2 2 ′ ( ) −1− 1+ t f t = Phương trình ( ) 1 trở thành: 2 ′( ) −1+ 1+ t f t = 2 −1− 1+ x −1+ 1+
Vẽ đồ thị 3 hàm số = ′( ), = (C , x y f x y =
trên cùng hệ trục tọa độ 1 ) y (C2 ) 2 2 ta thấy đồ thị (
cắt đồ thị y = f ′( x) tại 3 điểm, đồ thị (C cắt đồ thị y = f ′( x) tại 1 điểm. 2 ) 1 C ) htps://www.facebook.com 67
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 h ttps://luy en 1 th
Với mỗi nhánh, mỗi giao điểm t sẽ tương ứng với một giá trị duy nhất của x khác . i 2 trac 8 2 3 2 n
Vậy hàm số y = f (4x − 4x) − x + 6x − 4x +1 có 5 điểm cực trị. g 3 h iem
Câu 69: (Câu 50 - THPT Thanh Chương 1 – Nghệ An – Lần 2 – Năm 2020 - 2021) Cho f (x) là một .v
hàm đa thức bậc năm thoả mãn f (0) = 0. Hàm số f '( x) có đồ thị như hình vẽ bên n y x h -1 O 1 t tps 1 : Hàm số
có bao nhiêu điểm cực trị trên khoảng 0;3π ? /
g ( x) = f (sin x) 3 2
+ sin x − sin x ( ) / 3 www Ⓐ. 15 . Ⓑ. 11. Ⓒ. 9. Ⓓ. 13. .fac Lời giải ebo Chọn D ok ′ .
Do f (x) là một hàm đa thức bậc năm nên f ( x) là một hàm đa thức bậc bốn. com
Dựa vào đồ thị hình vẽ ta nhận thấy f ′( x) có dạng ′( ) 4 2 f
x = ax + bx + c , đồ thị đi qua các điểm /viet (
A 0;1), B(1; 0) và có điểm cực tiểu x = 1. Từ đó ta có: g CT old f ′(0) =1 c =1 c =1 f ′( ) 4 2
1 = 0 ⇒ a + b + c = 0 ⇒ a =1 ⇒ f (′x) = x − 2x +1 f ′ ( ) 1 = 0 4a + 2b = 0 b = 2 − 5 3 x 2 ⇒ ( ) x f x = − + x + c 5 3 5 3 x 2 Do (0) = 0 ⇒ = 0 ⇒ ( ) x f c f x = − + x . 5 3 68
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” 1 1
Xét hàm số g ( x) = f (sin x) 3 2
+ sin x − sin x , ta đặt h ( x) = f (sin x) 3 2
+ sin x − sin x 3 3
Tìm số cực trị của hàm số y = h(x) . 2 h ( ′ x) = cos .
x f '(sin x) + sin .
x cos x − 2 sin . x cos x cos x = 0 h ( ′ x) = 0 ⇔ 2
f '(sin x) = − sin x + 2 sin x .vn π
+)Với cos x = 0 ⇔ x =
+ kπ , k ∈ Z . iem 2 gh
Vậy phương trình cos x = 0 có 3 nghiệm đơn thuộc khoảng (0;3π ) . ( ) 1 +)Với 2 f (
′ sin x) = −sin x + 2sin x itracn th Đặt t =
x t ∈[− ] ⇒ f (t) 2 sin , 1;1 ' = t − + 2t Xét phương trình hoành độ giao điểm: yen t
= α (α ≈1,3864) (l) 2 4 2 4 2 t
− + 2t = t − 2t +1 ⇔ t −t − 2t +1 = 0 ⇔ s://lu t = β (β ≈ 0,4257) (n) ttp Với t = β ∈(0; )
1 thì sin x = β , khi đó 2
f '(sin x) = − sin x + 2sin x có 4 nghiệm đơn thuộc h khoảng (0;3π ) .(2) Từ ( )
1 ,(2)suy ra hàm số y = h(x) có 7 cực trị trên khoảng (0;3π ) (*)
Tìm số nghiệm của phương trình h(x) = 0 . 1 3 2
t = sin x ⇒ f (t) + t − t = 0 3 1 2 1 5 3 3 2
⇒ t − t + t + t − t = 0 5 3 3 t = 0 t = 0 /vietgold sin x = 0 ⇒ 1 1
⇒ t = a a ≈ 1,69 (l) ⇒ 4 2 ( )
t − t − t +1 = 0 sin x = b (b ≈ 0,86) 5 3 t = b (b ≈ 0,86)
+ sin x = 0 ⇔ x = kπ , k ∈ Z ⇒ phương trình h(x) = 0 có 2 nghiệm thuộc khoảng (0;3π ) .(3)
+ sin x = b (b ≈ 0,86) ⇒phương trình h(x) = 0 có 4 nghiệm thuộc khoảng (0;3π ) .(4) Từ ( )
3 ,(4) , suy ra h(x) = 0 có 6 nghiệm đơn trên khoảng (0;3π ) (**)
Câu 70: Từ (*), (**) ta kết luận được hàm số y = g(x) đã cho có 13 điểm cực trị.(Câu 40 - TX Quảng htps://www.facebook.com
Trị - Lần 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) liên tục trên ℝ và có bảng biến thiên của đạo hàm như sau: 69
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021 ( 2 ln x + ) 1 − 2
Hàm số g ( x) = f
có bao nhiêu điểm cực trị? 2 Ⓐ. 7. Ⓑ. 11. Ⓒ. 5. Ⓓ. 9. Lời giải Chọn D ( 2 ln x + ) 1 − 2 h Đặt x h( x) = ⇒ h′( x) = t 2 t 2 x + 1 p s:
Cho h′( x) = 0 ⇒ x = 0 //lu BBT ( ) 1 yenthitracnghiem.vn h x
Ta có: g ( x) = f ( h(x) ) ⇒ g′(x) = h′(x) ( ) ⋅
f ′( h( x) ) h( x) h′(x) = 0 h
Cho g′(x) = 0 ⇒ h( x) = 0 tt ps ′ = : f ( h ( x) ) 0 //w ′ w
Với h ( x) = 0 ⇔ x = 0 w.f
x = a (a < 0) ac
Với h ( x) = 0 ⇔ eb x = b (b > 0) ook.
Với f ′( h(x) ) = 0, ta có: com/vietgold
h(x) = c(c < − ) 1 (l)
h( x) = d ( 1
− < d < 0)(l)
⇒ f ′( h(x) ) = 0 ⇔
h( x) = e(0 < e < ) 1
h( x) = f ( f > ) 1 70
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng”
Dựa vào bảng biến thiên ( )
1 ta có được phương trình h ( x) = e có 4 nghiệm phân biệt và phương
trình h ( x) = f có hai nghiệm phân biệt, tất cả đều khác 0,a và b .
Vậy phương trình g′( x) = 0 có tổng cộng 9 nghiệm bội lẻ ⇒ hàm số g ( x) có 9 cực trị.
Câu 71: (Câu 40 - THPT – Thuận Thành 01 – Bắc Ninh – Lần 1 – Năm 2020 - 2021) Cho hàm số
y = f ( x) có đạo hàm trên ℝ và có bảng biến thiên f ′( x) như hình vẽ: .vn iem gh itracn th
yen Hàm số = ( 2x y f e
− 2x − 2 ) có bao nhiêu điểm cực trị? s://lu Ⓐ. 9. Ⓑ. 7. Ⓒ. 11. Ⓓ. 5. ttp Lời giải h Chọn A
Ta có: f ′( x) = 0 tại x ; x ; x ;
x < −1 < x < 0 < x < 1 < 1 2 3 4 x trong đó 1 2 3 4 x Xét hàm số = ( 2x y f e
− 2x − 2 ) có tập xác định là ℝ 2( 2x e − ) 1 ( 2x e − 2x − 2) y′ = f ′ e − x − x ( 2x 2 2 2 ) e − 2x − 2 Với 2x e − 2x − 2 ≠ 0 x = 0 2 x = 0 x e − 2x − 2 = x (1) /vietgold 2 x − = 3 e 1 0 2x ′ = ⇔ ⇔ 2 y 0 − − = ⇔ − − = f ′ ( e 2x 2 x x e 2x 2 x (2) 2x e − 2x − 2 ) 3 4 = 0 2 2 x x
e − 2x − 2 = −x (3) e − 2x − 2 = x 3 4 2x
e − 2x − 2 = −x (4) 4 Xét hàm số ( ) 2x
g x = e − 2x − 2 có tập xác định là ℝ . ′( ) 2 = 2 x g x e − 2
g′( x) = 0 ⇔ x = 0
Ta có bảng biến thiên của hàm số htps://www.facebook.com
Dựa vào bảng biến thiên của hàm số ta có: phương trình (1), (2), (3) có hai nghiệm phân biệt
khác 0, phương trình (4) vô nghiệm vì vậy phương trình y′ = 0 có 7 nghiệm phân biệt.
Mặt khác hàm số đạt cực trị tại các điểm thỏa mãn: 2x
e − 2x − 2 = 0 (5) . 71
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Dựa vào bảng biến thiên hàm g ( x) suy ra phương trình (5) có hai nghiệm phân biệt khác 7
nghiệm của phương trình y′ = 0 .
Vậy hàm số đã cho có 9 điểm cực trị.
Câu 72: (Câu 42 - THPT Trần Phú - Đà Nẵng - Năm 2020 - 2021) Cho hàm số f ( )
x , bảng biến thiên của hàm số f ( ′ ) x như sau: h ttps://luyenthitr acn Hàm số 3
g(x) = f (x − 3x) có bao nhiêu điểm cực đại? ghie m Ⓐ. 1. Ⓑ. 4. Ⓒ. 2. Ⓓ. 3. .v Lời giải n Chọn C Ta có: 3 2 3
g(x) = f (x − 3x) ⇒ g (
′ x) = (3x − 3). f (′x − 3x) x = 1 ⇒ g (
′ x) = 0 ⇔ x = −1 3
x − 3x = x (x > 3) 0 0 x =1 Xét hàm: 3 2
h(x) = x − 3x ⇒ h (
′ x) = 3x −3 = 0 ⇔ h x = 1 − ttps BBT: ://www.facebook.com/vietgo ld
Từ BBT suy ra phương trình 3
x − 3x = x (x > 3) có 1 nghiệm đơn x = x (x > 1) 0 0 1 1
Vậy phương trình g ( ′ )
x = 0 có 3 nghiệm đơn x = 1
− ; x =1; x = x (x >1) và 1 1 g ( ′ 0) = 3
− . f (′0) < 0 (Do f (′0)∈(3;5)) nên ta có BBT của hàm g(x) như sau: 72
↸ Quảng Thuận – Ba Đồn – Quảng Bình
“Thành công là nói không v!i lư#i bi%ng” .vn iem gh
Từ BBT ta có hàm số đã cho có 2 điểm cực đại.
Câu 73: (Câu 48 - THPT Triệu Sơn 1 - Thanh Hóa - Lần 1 - Năm 2020 - 2021) [ Mức độ 4] Cho hàm itracn
số f ( x) có f (0) = 1
− . Biết y = f ′( x) là hàm số bậc ba có đồ thị là đường cong dưới đây. th yen y 3 s://lu 2 ttp h 1 x O 1 3
Số điểm cực trị của hàm số g ( x) = f ( 4 x ) 2 − 6x là Ⓐ. 3. Ⓑ. 6 . Ⓒ. 5. Ⓓ. 4 . Lời giải Chọn C /vietgold
Xét hàm số h( x) = f ( 4 x ) 2
− 6x có h′(x) 3 = x f ′( 4 x ) 2
− x = x x f ′ ( 4 4 12 4 x ) − 3 . x = 0 h′( x) 2
= 0 ⇔ 4x x f ′( 4 x ) − 3 = 0 ⇔ . f ′( 3 4 x ) = x ≠ 0 1 2 ( ) ( ) x Xét phương trình ( ) 1 : đặt 4
t = x thì phương trình có dạng ′( ) 3 f t = với t > 0 (2) . t y htps://www.facebook.com 3 2 1 x O 1 3
Dựa vào đồ thị, phương trình (2) có một nghiệm duy nhất a > 0 . Khi đó ta được 4 x = ± a . 73
↸ Quảng Thuận – Ba Đồn – Quảng Bình
C c tr hàm s h p trong các đ thi 2020 - 2021
Bảng biến thiên của hàm số h( x) = f ( 4 x ) 2 − 6x
Số điểm cực trị của hàm số g ( x) = f ( 4 x ) 2
− 6x bằng số điểm cực trị của hàm số h 4 2 t
h( x) = f x − 6x cộng với số nghiệm đơn hoặc nghiệm bội lẻ của phương trình h ( x) = 0 . t ( ) p s:
Do đó hàm số g ( x) có 5 cực trị. //lu ye n th it rac n gh iem .vn
THAM GIA LỚP LUYỆN THI CHẤT LƯỢNG CAO MR.VIỆT MATH CLASS
82 Võ Thị Sáu - TDP Bến Chợ – Phường Q.Thuận - T.xã Ba h
Đồn –Tỉnh Quảng Bình ttps:// LIÊN w
http://luyenthitracnghiem.vn w HỆ w.fa
0905 193 688 (Điện thoại hoặc nhắn tin) cebook
Facebook: https://www.facebook.com/vietgold .com/vietgold 74




