8 kỹ thuật đạt điểm tối đa nguyên hàm – tích phân – Nguyễn Tiến Đạt Toán 12

8 kỹ thuật đạt điểm tối đa nguyên hàm – tích phân – Nguyễn Tiến Đạt Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

86 43 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

http://hoc24h.vn - LỜI NÓI ĐẦU

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

LỜI NÓI ĐẦU

Khi các em cầm trên tay cuốn sách này tức là các em đang rất quan tâm đến việc học của

mình, chúc mừng tinh thần học tập đó của em!

Có thể em chưa biết, tích phân là một mảng rất rộng và bao hàm nhiều dạng bài và

phương pháp xử lý khác nhau. Đặc biệt khi lên đại học, những nghành liên quan đến kỹ thuật,

chúng ta sẽ tiếp cận Nguyên Hàm – Tích Phân ở mức độ cao hơn.

Tuy nhiên trong khuôn khổ kỳ thi THPT Quốc gia 2017, thầy đã chắt lọc cho các em trong cuốn

sách này:

 Đầy đủ những phương pháp chắc chắn có trong đề thi, bám sát cấu trúc đề của Bộ Giáo

Dục

 Nhiều ví dụ đa dạng và giải chi tiết theo hướng Step by Step (từng bước), dù là học sinh

mất gốc vẫn có thể sử dụng cuốn sách này.

 Đề trắc nghiệm theo mọi hướng để các em tiếp cận được rộng nhất.

 Kết hợp các phương pháp sử dụng máy tính Casio, Vinacal.

Thầy tự tin khẳng định rằng, khi các em sử dụng thành thạo 8 kỹ thuật trong cuốn sách này,

việc đạt điểm tối đa chuyên đề Nguyên Hàm – Tích Phân là cực kỳ đơn giản!

Cách sử dụng sách

Bước 1: Đọc kỹ và hiểu phương pháp.

Bước 2: Đọc ví dụ rồi đóng sách làm lại

Bước 3: Làm đề trắc nghiệm bên cạnh đồng hồ (Cố làm nhanh nhất có thể).

Chú ý: Không được đọc phần bấm máy trước! Hãy nhuần nhuyễn giải tay trước, vì nhiều bài

có khả năng bấm máy lâu hơn tính tay rất nhiều.

Mặc dù thầy đã cố gắng hết sức, nhưng không tránh khỏi sai sót, mong các em đóng góp

ý kiến chân thành.

Giáo viên

Nguyễn Tiến Đạt

Mọi góp ý gửi về: “Trung tâm luyện thi Đại Học Tiến Đạt”

 Số 8 ngõ 17 Tạ Quang Bửu, HBT, Hà Nội | Liên hệ: 090.32888.66

Email: tiendatnguyen2510@gmail.com | Facebook: Đạt Nguyễn Tiến

“Tri thức không vô tình mà đạt được. Chúng ta phải tìm kiếm nó với sự nhiệt tình và đạt

được nó bằng sự chăm chỉ.”

LỜI NÓI ĐẦU - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

MỤC LỤC

Nguyên Hàm .................................................................................................................................. 5

A. Định Nghĩa Và Tính Chất ...................................................................................................... 5

B. Bảng Các Nguyên Hàm, Đạo Hàm Cơ Bản ........................................................................... 6

Trắc Nghiệm Lý Thuyết .............................................................................................................. 8

Đáp Án Trắc Nghiệm Lý Thuyết .............................................................................................. 11

Kỹ Thuật 1: Sử Dung Bảng Nguyên Hàm Cơ Bản ..................................................................... 12

Trắc Nghiệm Kỹ Thuật 1 – Dạng 1 ........................................................................................... 13

Đáp Án Trắc Nghiệm Kỹ Thuật 1 – Dạng 1 ............................................................................. 14

Trắc Nghiệm Kỹ Thuật 1 – Dạng 2 ........................................................................................... 15

Đáp Án Trắc Nghiệm Kỹ Thuật 1 – Dạng 2 ............................................................................. 15

Kỹ Thuật 2: Tính Nguyên Hàm Của Hàm Số Hữu Tỷ ............................................................... 16

Trắc Nghiệm Kỹ Thuật 2 .......................................................................................................... 22

Đáp Án Trắc Nghiệm Kỹ Thuật 2 ............................................................................................. 23

Kỹ Thuật 3: Đổi Biến Dạng 1 ..................................................................................................... 24

1. Các Dạng Đổi Biến Số Thường Gặp ..................................................................................... 24

Trắc Nghiệm Đổi Biến Số Dạng 1 ............................................................................................ 26

Đáp Án Trắc Nghiệm Đổi Biến Dạng 1 .................................................................................... 28

Tích Phân ..................................................................................................................................... 30

Trắc Nghiệm Lý Thuyết Tích Phân........................................................................................... 31

Đáp Án Trắc Nghiệm Lý Thuyết Tích Phân ............................................................................. 33

Tích Phân Đổi Biến Dạng 1 .......................................................................................................... 37

Dạng





       



 



        

 





 



       







2 2

( ) .

1 ( 1) .

( ) 2 .

n n

I f ax b xdx t ax b dt a dx

I dx t x dt n x dx

I f ax b xdx t ax b dt ax dx

................................... 37

Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P1) ........................................................................ 43

Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P1) ........................................................... 45

Dạng: ......................................................................................................................................... 46

Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P2) ........................................................................ 47

Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P2) ........................................................... 48

http://hoc24h.vn - LỜI NÓI ĐẦU

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Dạng .......................................................................................................................................... 49

Trắc Nghiệm Dạng

(ln )

I f x dx

  



.................................................................................... 50

Đáp Án Trắc Nghiệm Dạng

(ln )

I f x dx

  



...................................................................... 51

Kỹ Thuật 4: Tích Phân Lượng Giác ............................................................................................ 51

1.Công Thức Lượng Giác Thường Sử Dụng: ........................................................................... 51

Dạng 4.1. Sử Dụng Công Thức Nguyên Hàm Cơ Bản ............................................................. 53

Dạng 4.2: Dùng Công Thức Hạ Bậc ......................................................................................... 55

Dạng 4.3: Dùng Công Thức Biến Đổi Tích Thành Tổng .......................................................... 57

Dạng 4.4: Đổi Biến Số .............................................................................................................. 59

Dạng 4.4.1. Kết Hợp 1 Trong 4 Dạng A,B,C,D Với D(Sinx)=Cosx, D(Cosx)=-Sinx .......... 59

Dạng 4.4.2. Kết Hợp 1 Trong 4 Dạng A,B,C,D Và









2 2

sin sin 2 ; cos sin 2

d x xdx d x xdx

   ......................................................................... 66

Dạng 4.4.3 Kết Hợp 1 Trong 4 Dạng A,B,C,D Và............................................................... 67

 

tan 1 tan

cos

d x dx x dx

   ;

 

cot 1 cot

sin

d x dx x dx

     ................. 67

Dạng 4.4.4 Kết Hợp 1 Trong 4 Dạng A,B,C,D Và









sin cos cos sin

d x x x x dx

 



..... 70

Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P3) ........................................................................ 72

Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P3) ........................................................... 75

Kỹ Thuật 5: Đổi Biến Số Dạng 2 ................................................................................................ 76

Trắc Nghiệm Tích Phân Đổi Biến Dạng 2 ................................................................................ 85

Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 2................................................................... 86

Kỹ Thuật 6: Tích Phân Từng Phần .............................................................................................. 87

Trắc Nghiệm Tích Phân Từng Phần .......................................................................................... 93

Đáp Án Trắc Nghiệm Tích Phân Từng Phần ............................................................................ 97

Kỹ Thuật 7: Tích Phân Chứa Giá Trị Tuyệt Đối ......................................................................... 98

Ứng Dụng Tích Phân .................................................................................................................. 102

1. Tính Diện Tích Hình Phẳng ................................................................................................ 102

1.1 Diện Tích Hình Thang Cong ......................................................................................... 102

1.2. Diện Tích Hình Phẳng .................................................................................................. 103

LỜI NÓI ĐẦU - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2. Tính Thể Tích Khối Tròn Xoay .......................................................................................... 107

3. Bài Toán Chuyển Động ....................................................................................................... 111

Trắc Nghiệm Ứng Dụng Tích Phân ........................................................................................ 113

Đáp Án Trắc Nghiệm Ứng Dụng Tích Phân ........................................................................... 117

Kỹ Thuật 8: Sử Dụng Máy Tính Casio ..................................................................................... 118

Dạng: Tìm Nguyên Hàm F X  Của Hàm Số F X ............................................................... 118

Dạng: Tìm Nguyên Hàm F(X) Của F(X) Khi Biết ( )

F x M



............................................. 120

Dạng: Tính Tích Phân ............................................................................................................. 122

Dạng: Tìm A, B Sao Cho ( ).

f x dx A





................................................................................. 122

Dạng: Tính Diện Tích, Thể Tích ............................................................................................. 123

Dạng: Mối Liên Hệ Giữa A, B,C… ........................................................................................ 125

Phụ Lục: ..................................................................................................................................... 127

A. Đề Tổng Hợp Nguyên Hàm – Tích Phân ............................................................................ 127

Đáp Án Đề Tổng Hợp ............................................................................................................. 139

B .Tích Phân Trong Đề Thi Đại Học 10 Năm Gần Đây ............................................................. 140

http://hoc24h.vn - NGUYÊN HÀM

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

NGUYÊN HÀM

A. ĐỊNH NGHĨA VÀ TÍNH CHẤT

1. Định nghĩa

Ta gọi





F x

là một nguyên hàm của





f x

. Vì với

là một hằng số bất kỳ, ta có

 





   

F x C F x f x

   nên nếu





F x

là nguyên hàm của





f x

thì





F x C



cũng là một

nguyên hàm của





f x

. Ta gọi





F x C



(c là hằng số (constant) là Họ nguyên hàm của





f x

Ký hiệu:









f x dx F x C

 



Hay đơn giản cho dễ hiểu nhé mấy đứa: NGUYÊN HÀM LÀ NGƯỢC LẠI CỦA

ĐẠO HÀM.

VÍ DỤ :

đạo hàm là gì?

( )' 2

x x



chuẩn chưa?

Thì

xdx x C

 



. Tại sao phải cộng thêm C? Vì đạo hàm của hằng số luôn là 0.

Nên

( )' 2

x C x

 

. Người ta ghi thêm C vào cho đầy đủ?

Oke? Vậy tạm hiểu nguyên hàm là gì rồi nhé!!

2. Tính chất

•

 





 

f x dx f x





•









kf x dx k f x dx



 

, .

. là hằng số

•

















f x g x dx f x dx g x dx

  

 

 

  

•

















f x g x dx f x dx g x dx

  

 

 

  

3. Sự tồn tại nguyên hàm

Mọi hàm số liên tục trên đoạn





;

a b

đều có nguyên hàm trên đoạn





;

a b

NGUYÊN HÀM - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

B. BẢNG CÁC NGUYÊN HÀM, ĐẠO HÀM CƠ BẢN

Bảng đạo hàm

(u là hàm số hợp)

Bảng nguyên hàm





' 1



kdx kx c

 



, k là hằng số









1 1

' ; ' . '.

x x u u u

   

 

 

 

 

x dx c





 



 



 

ax b

ax b dx c





  





 

ln ' , 0

u u

 

dx x c

 



1 1

dx ax b c

ax b a

  









' '.

u u

e u e



x x

e dx e c

 



ax b ax b

e dx e c

 

 







' '. .ln , 0 1

u u

a u a a a

  

a dx c

 



.ln

mx n

a dx c

m a



 







sin ' '.cos

u u u



cos sin

xdx x c

 



   

cos sin

ax b dx ax b c

   







cos ' '.sin

u u u

 

sin cos

xdx x c

  



   

sin cos

ax b dx ax b c

    



 

tan ' '. 1 tan

cos

u u u

  

tan

cos

dx x c

 



 

1 1

tan

cos

dx ax b c

ax b a

  





 

cot ' '. 1 cot

sin

u u u



   

cot

sin

dx x c

  



 

1 1

cot

sin

dx ax b c

ax b a

   





Một số lưu ý

1. Cần nắm vững bảng nguyên hàm.

2. Nguyên hàm của một tích (thương) của nhiều hàm hàm số không bao giờ bằng tích (thương) của

các nguyên hàm của những hàm thành phần.

3. Muốn tìm nguyên hàm của một hàm số, ta phải biến đổi hàm số này thành một tổng hoặc hiệu

của những hàm số tìm được nguyên hàm (dựa vào bảng nguyên hàm).

http://hoc24h.vn - NGUYÊN HÀM

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

* Lưu ý: do









f x dx F x c

 



thì









F x f x

 nên khi quên công thức nguyên hàm, ta cần

liên tưởng đến đạo hàm. Cụ thể như sau:

VÍ DỤ ta cần tìm





f x dx



(mà quên công thức) ta có thể tự đặt câu hỏi : “ hàm số nào

mà lấy đạo hàm ra là f(x)?”. Với cách hỏi như thế, kết hợp với việc nắm vững công thức đạo

hàm, ta có thể nhớ lại công thức nguyên hàm một cách dễ dàng.

I. BẢNG CÔNG THỨC MỞ RỘNG (LÀM NHANH TRẮC NGHIỆM)

Chú ý: Những công thức không có trong SGK, nếu khi các em dùng cho làm tự

luận, phải chứng minh lại! (Cách chứng minh đơn giản nhất: Đạo hàm lại kết

quả. Hehe.

ax b ax b

e e c

 

 



   

tg dx ln cos

ax b ax b c

    



ax b ax b

m m c

a m

 

 



   

cotg dx ln sin

ax b ax b c

   



2 2

dx 1

arctg

a x a a

 





 

dx 1

cotg

sin

ax b c

ax b a



  





2 2

dx 1

a x

a x a a x



 

 



 

dx 1

cos

ax b c

ax b a

  









2 2

x x a c

x a

   





2 2

arcsin

a x

 





NGUYÊN HÀM - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM LÝ THUYẾT

Câu 1. Hàm số





f x

có nguyên hàm trên

nếu:





f x

xác định trên

. B.





f x

có giá trị lớn nhất trên





f x

có giá trị nhỏ nhất trên

. D.





f x

liên tục trên

Câu 2. Mệnh đề nào sau đây sai?

A. Nếu





F x

là một nguyên hàm của





f x

trên





;

a b

và

là hằng số thì









f x x F x C

 



B. Mọi hàm số liên tục trên





;

a b

đều có nguyên hàm trên





;

a b





F x

là một nguyên hàm của





f x

trên

















; , ;

a b F x f x x a b

    .

 





 

f x x f x





Câu 3. Xét hai khẳng định sau:

(I) Mọi hàm số





f x

liên tục trên đoạn





;

a b

đều có đạo hàm trên đoạn đó.

(II) Mọi hàm số





f x

liên tục trên đoạn





;

a b

đều có nguyên hàm trên đoạn đó.

Trong hai khẳng định trên:

A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.

C. Cả hai đều đúng. D. Cả hai đều sai.

Câu 4. Hàm số





F x

được gọi là nguyên hàm của hàm số





f x

trên đoạn





;

a b

nếu:

A. Với mọi





;

x a b

 , ta có









F x f x

 .

B. Với mọi





;

x a b

 , ta có









f x F x

 .

C. Với mọi





;

x a b

 , ta có









F x f x

 .

D. Với mọi





;

x a b

 , ta có









F x f x

 , ngoài ra









F a f a



 và









F b f b



 .

Câu 5. Trong các câu sau đây, nói về nguyên hàm của một hàm số

xác định trên khoảng

câu nào là sai?

http://hoc24h.vn - NGUYÊN HÀM

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

(I)

là nguyên hàm của

trên

nếu và chỉ nếu









: '

x D F x f x

   .

(II) Nếu

liên tục trên

thì .

. có nguyên hàm trên

(III) Hai nguyên hàm trên

của cùng một hàm số thì sai khác nhau một hằng số.

A. Không có câu nào sai. B. Câu (I) sai.

C. Câu (II) sai. D. Câu (III) sai.

Câu 6. Giả sử





F x

là một nguyên hàm của hàm số





f x

trên khoảng





;

a b

. Giả sử





G x

cũng là

một nguyên hàm của





f x

trên khoảng





;

a b

. Khi đó:









F x G x

 trên khoảng





;

a b









G x F x C

 

trên khoảng





;

a b

, với

là hằng số.









F x G x C

 

với mọi

thuộc giao của hai miền xác định,

là hằng số.

D. Cả ba câu trên đều sai.

Câu 7. Xét hai câu sau:

(I)





























d d d

f x g x x f x x g x x F x G x C

     

  

trong đó





F x

và





G x

tương ứng là nguyên hàm của









f x g x

(II) Mỗi nguyên hàm của





a f x

là tích của

với một nguyên hàm của





f x

Trong hai câu trên:

A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.

C. Cả hai câu đều đúng. D. Cả hai câu đều sai.

Câu 8. Các khẳng định nào sau đây là sai?

















d d

f x x F x C f t t F t C

    

 

   

f x x f x

 



 



















d d

f x x F x C f u x F u C

    

 









d d

kf x x k f x x



 

(

là hằng số).

NGUYÊN HÀM - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 9. Trong các khẳng định sau, khẳng định nào sai?





F x x



là một nguyên hàm của





f x x







F x x



là một nguyên hàm của





f x x

 .

C. Nếu





F x

và





G x

đều là nguyên hàm của hàm số





f x

thì









F x G x C

 

(hằng số).

D. Cả 3 đáp án trên

Câu 10. Trong các khẳng định sau, khẳng định nào sai?

A. Nếu





F x

là một nguyên hàm của hàm số





f x

thì mọi nguyên hàm của





f x

đều có

dạng





F x C



(

là hằng số).





 

d log

u x

x u x C

u x

 







1 tan

F x x

  là một nguyên hàm của hàm số





1 tan

f x x

  .





5 cos

F x x

  là một nguyên hàm của hàm số





sin

f x x

 .

Câu 11. Trong các khẳng định sau, khẳng định nào sai?

A. 0d

x C





(

là hằng số). B.

d ln

x x C

 



(

là hằng số).

x x C





 





(

là hằng số). D. d

x x C

 



(

là hằng số).

http://hoc24h.vn - NGUYÊN HÀM

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN TRẮC NGHIỆM LÝ THUYẾT

Câu 1. Để hàm số





f x

có nguyên hàm trên

khi và chỉ khi





f x

liên tục trên

. Chọn D.

Câu 2. Sửa lại cho đúng là

Tất cả các nguyên hàm của





f x

trên





;

a b

đều có đạo hàm bằng





f x

. Chọn C.

Câu 3. Vì hàm số có đạo hàm tại

thì liên tục tại

, nhưng nếu hàm số liên tục tại

thì chưa

chắc đã có đạo hàm tại

. Chẳng hạn xét hàm số





f x x



tại điểm



. Chọn B.

Câu 4. Với mọi





;

x a b

 , ta có









F x f x

 , ngoài ra









F a f a



 và









F b f b



 .Chọn D.

Câu 5. Chọn A.

Câu 6. Vì hai nguyên hàm trên

của cùng một hàm số thì sai khác nhau một hằng số. Chọn B.

Câu 7. Chọn C.

Câu 8. Vì

















f x dx F x C f u du F u C

    

 

. Chọn C.

Câu 9. Vì

       

1 2

x x F x f x F x x

     

không phải là nguyên hàm của hàm số





f x x

 . Chọn B.

Câu 10. Vì





 









 

d u x

u x

dx u x C

u x u x

  

 

. Chọn B.

Câu 11. Vì kết quả này không đúng với trường hợp



 

. Chọn C.

CÂU ĐÁP ÁN

10.

11.

KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM CƠ BẢN -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM CƠ BẢN



1. Tích của đa thức hoặc lũy thừa



khai triển.

2. Tích các hàm mũ



khai triển theo công thức mũ.

3. Chứa căn



chuyển về lũy thừa.

4. Tích lượng giác bậc một của sin và cosin



khai triễn theo công thức tích thành tổng.



 

sin .cos sin( ) sin( )

ax bx a b x a b x

   



 

sin .sin cos( ) cos( )

ax bx a b x a b x

   



 

cos .cos cos( ) cos( )

ax bx a b x a b x

   

5. Bậc chẵn của sin và cosin



Hạ bậc.

Bài 1. Tìm các nguyên hàm:

http://hoc24h.vn - KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM

CƠ BẢN

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 1

Câu 12. Tìm nguyên hàm

( ) 3

f x x

  

( ) .

F x x C

  

( ) .

F x x C

  

( ) .

F x x C

  

( ) 5 .

F x x C

  

Câu 13. Tìm nguyên hàm

( ) 2 5 7.

f x x x

  

4 2

( ) 7 .

2 3

x x

F x x C

   

4 2

( ) 7 .

2 2

x x

F x x C

   

4 2

3 5

( ) 7 .

2 2

x x

F x x C

   

4 2

( ) 8 .

2 2

x x

F x x C

   

Câu 14. Tìm nguyên hàm

5 3 2

( ) 6 12 8.

f x x x x

   

6 4

( ) 3 8 .

F x x x x C

    

6 4

( ) 3 8 .

F x x x x C

    

6 4

( ) 3 8 .

F x x x x C

    

6 4

( ) 8 .

F x x x x C

    

Câu 15. Tìm nguyên hàm

( ) ( 3 ) ( 1)

f x x x x

    

4 3 2

2 3

( ) .

4 3 2

x x x

F x C

   

4 3 2

2 3

( ) .

2 3 2

x x x

F x C

   

4 3 2

2 3

( ) .

4 5 2

x x x

F x C

   

4 3 2

2 3

( ) .

4 3 7

x x x

F x C

   

Câu 16.

( ) (3 ) .

f x x

  Biết nguyên hàm của f(x) là

(3 )

( ) .

F x C



  

Tìm

A. 4

B. 16

C. 32

D. 9

Câu 17.

1 1

( )

f x x

   

Biết nguyên hàm của f(x) là

( ) .

x x

F x C

x a b

    

Tính a-b?

A. 0

B. 1

C. 2

D. 3

Câu 18.

( ) 10 .

f x  Biết nguyên hàm của f(x) là

( ) .

2ln10

F x C

 

Tìm a?

KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM CƠ BẢN -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

A. 10

B. 100

C. 5

D. 20

Câu 19.

( ) 4f x x x

   

Biết nguyên hàm của f(x) là

( ) .ln .

F x bx c x C

   

Tính a-b+c

A. 5

B. 1

C. 4

D. 7

Câu 20.

3 2

I x dx

 

  

 

 



3 .

x x C

  

Tính a-b?

A. 0

B. 1

C. 2

D. 3

ĐÁP ÁN TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 1

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

20. A

http://hoc24h.vn - KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM

CƠ BẢN

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bài 2. Tìm nguyên hàm của các hàm số thỏa mãn điều kiện cho trước trong các trường hợp sau:

Phương pháp: Tìm nguyên hàm của hàm số

( ),

f x

tức đi tính

( ) ( ) .

f x dx F x C

  



Rồi sau đó thế ( )

F x C

  

để tìm hằng số

VÍ DỤ :

( ) 4 5, (1) 3.

f x x x F

   

Ta có

3 2

( 4 5) 5

x x dx x x c

      



Mà

(1) 3.





1 5.1 3

   

 c=



. Kết luận:

( ) 5

4 4

F x x x

    

TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 2

Tìm F(x) biết:

Câu 21.

( ) 3 5cos , ( ) 2.

f x x F



  

( ) 3 5sin

F x x x

 

( ) 3 5sin 2 2 .

F x x x



   

( ) 3 5sin 2

F x x x

  

( ) 3 5sin 2 3 .

F x x x



   

Câu 22.

3 5

( ) , ( ) 1.

f x F e



 

Biết

2 2

5 5

( ) 3ln .

2 2

x e

F x x c

   

c chia hết cho mấy?

A. 2

B. 3

C. 6

D. 7

Câu 23.

1 3

( ) , (1)

f x F



  

Biết

( ) ln .

F x b x c

  

Kết quả của a-b-c là?

A. 4

B. 3

C. 8

D. 0

Câu 24.

4 3

3 2 5

x x

I dx

 

 



biết

(1) 2.



ĐS:

3 2

( ) . .

F x x c x b

   

Tính a+b+c?

A. 1

B. 2

C. 3

D. 4

ĐÁP ÁN TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 2

CÂU ĐÁP ÁN CÂU ĐÁP ÁN

Câu 21 D Câu 23 D

Câu 22 A Câu 24 A

KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ



Bài toán tổng quát: Tính nguyên hàm

( )

P x

I dx

Q x

 



với

( )

P x

và

( )

Q x

là các đa thức không

căn.

Phương pháp giải:

Nếu bậc của tử số

( )

P x



bậc của mẫu số

( )

Q x



Chia đa thức.

Nếu bậc của tử số

( )

P x



bậc của mẫu số

( )

Q x



Xem xét mẫu số và khi đó:

+ Nếu mẫu số phân tích được thành tích số, ta sẽ sử dụng đồng nhất thức để đưa về dạng tổng

của các phân số.

Một số trường hợp đồng nhất thức thường gặp:

1 1

( ) ( )

a b

ax m bx n an bm ax m bx n

 

    

 

     

 

( ) ( )

( ) ( ) ( ) ( )

A B m

mx n A B A B x Ab Ba

Ab Ba n

x a x b x a x b x a x b

 



    

     



  

       



2 2

( ) ( )

A Bx C

x m ax bx c x m ax bx c



  

      

với

4 0.

b ac

   

2 2 2 2

( ) ( ) ( ) ( )

A B C D

x a x b x a x a x b x b

     

      

+ Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về dạng lượng giác).

Mẹo sử dụng Casio

( ) ( )

mx n A B

x a x b x a x b



  

    

(Ta muốn tìm hệ số nào, ta xóa nghiệm dưới mẫu của thằng đó đi trong

( ) ( )

mx n

x a x b



  

. Và

Calc đúng nghiệm dưới mẫu của nó)

Để tìm A. Ta nhập vào máy tính

( )

mx n

x b





. Calc x = a

Để tìm B. Ta nhập vào máy tính

( )

mx n

x a





. Calc x = b

http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM

SỐ HỮU TỶ

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

BÀI TẬP VẬN DỤNG

VÍ DỤ 1. Tìm nguyên hàm

2 1

I dx



  





Ta thấy bậc tử bằng bậc mẫu: Chia đa thức

2 1 3

(2 ) 2 3.ln | 1|

1 1

I dx dx x x c

x x



       

 

 

VÍ DỤ 2. Tìm nguyên hàm

x x

I dx

 

  





Ta thấy bậc tử lớn hơn bậc mẫu: Chia đa thức

2 2

1 3

( 1 ) 3ln 2 .

2 2 2

x x x

I dx I x dx x x C

x x

 

           

 

 

VÍ DỤ3. Tìm nguyên hàm

2 7 5

x x

 

 



( )

2 7 5 ( 1)(2 5) 1 2 5

dx dx A B

I dx

x x x x x x

   

     

  

Ta có:

( 1) (2 5) 1

(2 ) 5 1

2 0

5 1 2

B x A x

x A B A B

A B

   

    









 





 

 

  











1 2

1 2 ln | 2 5 | 1 1

3 3

( ) ln | 1| ln | 1| ln | 2 5 |

1 2 5 3 3 2 3 3

I dx x C x x C

x x



  

          

 



Mẹo sử dụng máy tính:

Tìm A: Nhập vào máy

(2 5)



Calc X = 1. Thu được





Tìm B: Nhập vào máy



Calc X =

. Thu được B =

VÍ DỤ 4. Tìm nguyên hàm

3 2

6 10 2

3 2

x x

I dx

x x x

 



 



  

2 2

3 2

6 10 2 6 10 2

3 2 1 2

x x x x

I dx dx

x x x x x x

   

 

   

 

KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Xét:

  

6 10 2

1 2 1 2

x x A B C

x x x x x x

 

  

   

















6 10 2 1 2 2 1

x x A x x Bx x Cx x

         









2 2

6 10 2 3 2 2

x x A B C x A B C x A

         

  

6 1

6 10 2 1 2 3

10 3 2 2

1 2 1 2

2 2 3

A B C A

x x

A B C B

x x x x x x

A C

   

 

 

 

         

 

   

 

 

 

Từ đó:

1 2 3

ln 2ln 1 3ln 2

1 2

I dx x x x C

x x x

 

        

 

 

 



Mẹo sử dụng máy tính

Tìm A: Ta nhập vào máy

  

6 10 2

1 2

x x

 

Calc X=0. Thu được A = 1

Tìm B: Ta nhập vào máy

 

6 10 2

x x

 



Calc X=-1. Thu được B = 2

Tìm C: Ta nhập vào máy

 

6 10 2

x x

 



Calc X=-2. Thu được C = 3

  

6 10 2 1 2 3

1 2 1 2

x x

x x x x x x

 

   

   

VÍ DỤ 5. Tìm nguyên hàm

3 2

6 26 26

6 11 6

x x

J dx

x x x

 



  



   

2 2

3 2

6 26 26 6 26 26

6 11 6 1 2 3

x x x x

J dx dx

x x x x x x

   

 

     

 

Ta tìm

, ,

A B C

sao cho:

http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM

SỐ HỮU TỶ

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

   

6 26 26

1 2 3 1 2 3

x x A B C

x x x x x x

 

  

     

























6 26 26 2 3 1 3 1 2

x x A x x B x x C x x

           

Cho

giá trị lần lượt bằng 1, 2, 3 ta tìm được

3; 2; 1

A B C

  

Từ đó:

3 2 1

3ln 1 2ln 2 ln 3

1 2 3

J dx x x x C

x x x

 

         

 

  

 



•

  

8 8 2 1

2ln 2 ln 3

6 2 3 2 3

x x

K dx dx dx x x C

x x x x x x

 

 

        

 

     

 

  

VÍ DỤ 6 .Tìm nguyên hàm

3 2

3 13 11

5 8 4

x x

L dx

x x x

 



  



  

2 2

3 2

3 13 11 3 13 11

5 8 4

1 2

x x x x

L dx dx

x x x

x x

   

 

  

 

 

Ta tìm

, ,

A B C

sao cho:

    

2 2

3 13 11

1 2

1 2 2

x x A B C

x x

x x x

 

  

 

  

      

3 13 11 2 1 2 1

x x A x B x x C x

         













2 2

3 13 11 4 3 4 2

x x A B x A B C x A B C

          

3 1

13 4 3 2

11 4 2 3

A B A

A B C B

A B C C

  

 

 

     

 

 

   

 

Từ đó:

 

1 2 3 3

ln 1 2ln 2

1 2 2

L dx x x C

x x x

 

        

 

  



 



KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 7. Tìm nguyên hàm

3 2

2 6 4 1

3 2

x x x

M dx

x x

  



 



  

3 2

2 2

2 6 4 1 1 1

2 2

3 2 3 2 1 2

x x x

M dx x dx x dx

x x x x x x

 

  

 

    

 

     

 

  

1 1

2 ln 2 ln 1

2 1

x dx x x x C

x x

 

        

 

 

 



VÍ DỤ 8. Tìm nguyên hàm

3 2

3 4 2

2 2 5

x x

N dx

x x x

 



  







3 2

3 2 3 2

2 2 5

3 4 2

ln 2 2 5

2 2 5 2 2 5

d x x x

x x

N dx x x x C

x x x x x x

  

 

      

     

 

VÍ DỤ 9. Tìm nguyên hàm

   

2 2

3 1

x x



 



Ta phân tích:

   

  

2 2

3 1

1 1 1 1 1

4 3 1 4 1 3

3 1

x x

x x x x

x x

 

  

 

  

 

 

   

 

 

 

   

  

   

2 2 2 2

1 1 1 2 1 1 1 1 1

4 1 3 4 3 1

1 3 1 3

x x x x

   

      

   

   

   

   

Từ đó:

   

2 2

1 1 1 1

3 1

1 3

I dx

x x

 

   

 

 

 

 



1 1 1 1 1 1

. . ln 3 ln 1

4 1 4 3 4 4

x x C

x x

       

 

VÍ DỤ 10. Tìm nguyên hàm .

   

2 2

3 4

x x



 



Ta phân tích:

http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM

SỐ HỮU TỶ

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

   

  

 

  

 

2 2 2 2

4 3

1 1 1 1 2 1

49 3 4 49 3 4

3 4 3 4

x x

x x x x

 

  

   

 

   

 

 

Từ đó:

 

  

 

2 2

1 1 1 2 1 1

49 49 3 4 49

3 4

J dx dx dx

x x

  

 

  

1 1 1 1 1 1 1

. .

49 3 49 4 343 3 4

x x x x

 

    

 

   

 



1 1 1 1 1 3

. . ln

49 3 49 4 343 4

x x x



    

  

KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM KỸ THUẬT 2

Câu 25.

4 6 1

2 1

x x

 





là

. . .ln 2 1

I a x b x c x C

    

. Tính a-b-c ?



Câu 26.

3 2

4 4 1

2 1

x x

 





có dạng





3 2

. . . .ln 2 1

F x a x b x c x d x C

     

. Tính





a b c d

 

C. 3 D. 2

Câu 27.

2 1







có dạng . .ln 1

I a x b x C

   

. Tính a.b ?

A. 4 B. 5 C. 6 D. 7

Câu 28.

3 1







có dạng . .ln 2

I a x b x C

   

. Tính b-a ?

A. 2 B. 3 C. 4 D. 5

Câu 29. Nguyên hàm của

 

2 3

f x







có dạng





. .ln 2 3

F x a x b x C

   

. Tính a.b ?



B. 4 C. 2 D. -6

Câu 30.

x x

 





có dạng

. . .ln 2

I a x b x c x C

    

. Tính b+c ?

A. 8 B. 6 C. 4 D. 2

Câu 31.

6 9

x x

 

 



I C

 



I C

  



I C

  



I C

  



Câu 32.

I dx



  





ĐS:

ln .

I x C



  



2 1

ln .

I x C



  



ln .

I x C



  



ln .

I x C



  



ln .

I C



 



Câu 33.

3 2

4 4 1

I dx

x x



 

 



ln 2 1 .

4(2 1)

x C

b x

   



. Tính b – a ?

A. 0 B. 1

http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM

SỐ HỮU TỶ

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

C. 2 D. 3

Câu 34.

( 2)

x x

I dx



 





ln 2 .

ax b x C

    



Tính a + b – c?

A. 0

B. 1

C. 2

D. 3

ĐÁP ÁN TRẮC NGHIỆM KỸ THUẬT 2

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

25 C

KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1

1. CÁC DẠNG ĐỔI BIẾN SỐ THƯỜNG GẶP

DẠNG CÁCH ĐỔI BIẾN





ax b dx





Đặt

t ax b

 

n n

x x dx





Đặt

t x









f x



Đặt

t x







sin cos

f x xdx



Đặt

sin

t x







cos sin

f x xdx



Đặt

cos

t x



 

tan

cos

f x



Đặt

tan

t x



 

cot

sin

f x



Đặt

cot

t x







x x

f e e dx



Đặt

t e



 

f x



Đặt

t x



1 1

f x x dx

x x

   

 

   

   



Đặt

t x

 

Các bước để đổi biến:

Bước 1: Đặt v(x) = t

Bước 2: vi phân: d(v(x)) = d(t) (Vi phân như đạo hàm thôi, nhưng đạo hàm theo biến x, nhân thêm dx,

đạo hàm theo biến t thì nhân thêm dt)

Bước 3: Chuyển hết f(x) về f(t).

Ví dụ về vi phân:

2 2

( 2 1) ( 2 1)'. (2 2)

d x x x x dx x dx

      

VÍ DỤ : Tìm nguyên hàm các hàm số sau

2004 2003

I x x dx

 



Đặt

2004 2004 2003 2003

1 ( ) ( 1) 2004

2004

t x d t d x dt x dx x dx dt

         . Từ đó ta được:

1 3

2 2

1 1 1 2

2004 2004 2004 3

I tdt t dt t C

   

 

 

3 2004

1 1

3006 3006

t C x C

    

http://hoc24h.vn - KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2•

1 1

x x

e x e x

I e dx e e dx

  

 

 

Đặt

x x

e t e dx dt

  

. Thay vào ta được:

 

1 1 1 1

t t t e

L e dt e d t e C e C

   

      

 

I dx







Đặt

10 9

1 1 10

x t x t dx t dt

       . Từ đó ta được:

   

9 10 8 18 8 19 9

1 10 10

.10 10 1 10

19 9

N t dt t t dt t t dt t t C



       

  

   

19 9

10 10

1 1

19 9

x x C

    

 

I x x dx

 



Đặt 1

x t dx dt

    

. Từ đó ta được:

   





10 2 10 10 11 12

1 1 2 . 2

O t t dt t t t dt t dt t dt t dt

          

    

     

11 12 13

1 1 1 1 1 1

1 1 1

11 6 13 11 6 13

t t t C x x x C

            

KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM ĐỔI BIẾN SỐ DẠNG 1

Câu 34. Câu nào sau đây sai?

A. Nếu









F t f t

 thì

















F u x f u x

 .





























d ' d

f t t F t C f u x u x x F u x C

    

 

C. Nếu





G t

là một nguyên hàm của hàm số





g t

thì









G u x

là một nguyên hàm của hàm số













g u x u x

















d d

f t t F t C f u u F u C

    

 

với





u u x

 .

Câu 35. Trong các khẳng định sau, khẳng định nào sai?

A. Nếu









f t t F t C

 



thì





















. d

f u x u x x F u x C

 



B. Nếu





F x

và





G x

đều là nguyên hàm của hàm số





f x

thì









F x G x x



 

 



có dạng





h x Cx D

 

(

C D

là các hằng số và







7 sin

F x x

  là một nguyên hàm của





sin 2

f x x

 .





 

u x

x u x C

u x

 



Câu 36. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Tìm nguyên hàm của hàm số





2 1.

f x x

 

   

d 2 1 2 1 .

f x x x x C

   



   

d 2 1 2 1 .

f x x x x C

   



 

d 2 1 .

f x x x C

   



 

d 2 1 .

f x x x C

  



Câu 37. Để tính



theo phương pháp đổi biến số, ta đặt:

t e

 B.

ln .

t x



t x



Câu 38.





F x

là một nguyên hàm của hàm số

y xe

 .

Hàm số nào sau đây không phải là





F x

http://hoc24h.vn - KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

 

F x e

 

. B.

 





F x e

 

 

F x e C

  

. D.

 





F x e

   .

Câu 39.





F x

là một nguyên hàm của hàm số

 .

Nếu





F e



thì



bằng:

 

F x C

 

. B.

 

F x

 

 

F x

 

. D.

 

F x x C

  

Câu 40.





F x

là một nguyên hàm của hàm số

sin

cos

y e x

 .

Nếu









thì

sin

cos d

e x x



bằng:





sin

F x e

 

. B.





sin x

F x e C

 





cos

F x e

 

. D.





cosx

F x e C

 

Câu 41.





F x

là nguyên hàm của hàm số

sin cos

y x x

 .





F x

là hàm số nào sau đây?

 

cos

F x C

 

. B.

 

cos

F x C

 

 

sin

F x C

 

. D.

 

sin

F x C

 

Câu 42. Xét các mệnh đề sau, với

là hằng số:

(I)





tan d ln cos

x x x C

  



(II)

3cos 3cos

sin d

x x

e x x e C

  



KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

(III)

cos sin

d 2 sin cos

sin cos

x x

x x x C

x x



  





Số mệnh đề đúng là:

. B.

. C.

. D.

ĐÁP ÁN TRẮC NGHIỆM ĐỔI BIẾN DẠNG 1

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

Câu 34. Chọn A. Vì nếu

















F t f t F t f t dt

  



. Đặt









t u x dt u x dx

   .

Suy ra





















F u x f u x u x dx





hay





















/ /

F u x f u x u x

 .

Câu 35. Chọn D. Vì





 









 

d u x

u x

dx u x C

u x u x

  

 

Câu 36. Ta có





2 1 .

I f x dx x dx

  

 

Đặt

2 1

x t x



   

 

2 3

1 1

2 1 2 1 .

2 3 3

t t

I td t dt C x x C

 



        

 

 

 

Chọn B.

Câu 37. Đặt

t x dt dx

   . Khi đó

ln x

dx e dt



 

. Chọn B.

Câu 38. Đặt

t x dt xdx

   .

Suy ra

 

1 1 1 1

2 2 2 2

t t t x

I e dt d e e C e C

     

 

. Chọn C.

Câu 39. Đặt ln

x t dt

   . Suy ra

 

2 2

t x

F x tdt C C

    



http://hoc24h.vn -

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Vì

 





2 2

4 4 2

F e C C

     

. Chọn B.

Câu 40. Đặt sin cos

t x dt xdx

  

. Suy ra

sint t x

I e dt e C e C

    



Vì





sin

5 5 1 5 4

F e C C C



        

. Suy ra





sin

F x e

 

. Chọn A.

Câu 41. Đặt

sin

t x



, suy ra cos

dt xdx



Khi đó

5 5

sin

5 5

t x

I t dt C C

    



. Chọn D.

Câu 42. Xét (I): Ta có

sin

tan

cos

x dx dx



 

. Đặt cos sin

t x dt xdx

   

Khi đó

sin

ln ln cos

cos

x dt

dx t C x C

x t

       

 

. Do đó (I) đúng.

Xét (II): Đặt

3cos 3sin sin

t x dt xdx xdx dt

       .

Khi đó

3cos 3cos

1 1 1

sin

3 3 3

x t t x

e x dx e dt e C e C

       

 

. Do đó (II) đúng.

Xét (III): Đặt





sin cos sin cos 2 cos sin

t x x t x x tdt x x dx

        .

Khi đó

2 2 2 sin cos

tdt

dt t C x x C

     

 

. Do đó (III) đúng.

Chọn D.

TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TÍCH PHÂN

Khái niệm tích phân

— Cho hàm số

( )

f x

liên tục trên

và

, .

a b K



Hàm số

( )

F x

được gọi là nguyên hàm của

( )

f x

trên

thì

( ) ( )

F b F a



được gọi là tích phân của

( )

f x

từ

đến

và được kí hiệu

là

( )

f x dx



. Khi đó:

( ) ( ) ( ) ( ) ,

I f x dx F x F b F a

    



với

gọi là cận dưới,

là

cận trên.

— Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác nhau thay cho

, nghĩa là:

( ) ( ) ( ) ( ) ( ).

b b b

a a a

I f x dx f t dt f u du F b F a

         

  

— Nếu hàm số

( )

y f x



liên tục và không âm trên đoạn





;

a b

thì diện tích

của hình thang

cong giới hạn bởi đồ thị của

( ),

y f x



trục

và hai đường thẳng ,

x a x b

 

là:

( )

S f x dx

  



Tính chất của tích phân



( ) ( )

b a

a b

f x dx f x dx

   

 

và

( ) 0.

f x dx

 





( ) ( ) ,

b b

a a

k f x dx k f x dx

    

 

với

( 0).





 

( ) ( ) ( ) ( )

b b b

a a a

f x g x dx f x dx g x dx

      

  

 ( ) ( ) ( )

b c b

a a c

f x dx f x dx f x dx

     

  

http://hoc24h.vn - TÍCH PHÂN

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM LÝ THUYẾT TÍCH PHÂN

Câu 1. Cho hàm số





f x

liên tục trên đoạn





;

a b

. Hãy chọn mệnh đề sai dưới đây:

   

d d

b a

a b

f x x f x x

 

 

 

.d ,

k x k b a k

   





     

d d d

b c b

a a c

f x x f x x f x x

 

  

với





;

c a b

 .

   

b a

a b

f x dx f x x



 

Câu 2. Giả sử hàm số





f x

liên tục trên khoảng

và

a b

là hai điểm của

, ngoài ra

là một số thực

tùy ý. Khi đó:

(I)

 

d 0

f x x





.(II)

   

d d

a b

b a

f x x f x x



 

.(II)

   

. d d

b b

a a

k f x x k f x x



 

Trong ba công thức trên:

A. Chỉ có (I) sai. B. Chỉ có (II) sai.

C. Chỉ có (I) và (II) sai. D. Cả ba đều đúng.

Câu 3. Trong các khẳng định sau, khẳng định nào đúng?

d 1







       

1 2 1 2

. d d . d

b b b

a a a

f x f x x f x x f x x



  

C. Nếu





f x

liên tục và không âm trên đoạn





;

a b

thì

 

d 0

f x x





D. Nếu

 

d 0

f x x





thì





f x

là hàm số lẻ.

TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 4. Trong các khẳng định sau, khẳng định nào đúng?

     

d d d

b c b

a a c

f x x f x x f x x

 

  

với mọi

, ,

a b c

thuộc tập xác định của





f x

B. Nếu

 

d 0

f x x





thì









0, ;

f x x a b

   .

2 1

x C

  





D. Nếu





F x

là nguyên hàm của hàm số





f x

thì

 

F x

là nguyên hàm của hàm số

 

f x

Câu 5. Đặt

 

1 d

F x t t

 



. Đạo hàm





F x

là hàm số nào dưới đây?

 

F x





. B.

 

/ 2

F x x

 

 

F x





. D.

 





/ 2 2

1 1 .

F x x x

  

Câu 6. Cho

 

F x t t t

 



. Giá trị nhỏ nhất của





F x

trên đoạn





1;1

 là:



Câu 7. Cho

 

F x t









. Xét các mệnh đề:

 

F x







II. Hàm số





F x

đạt cực tiểu tại

x 

II. Hàm số





F x

đạt cực đại tại

x 

Mệnh đề nào đúng?

A. Chỉ I. B. Chỉ II. C. I và II. D. I và III.

http://hoc24h.vn - TÍCH PHÂN

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 8. Hãy chọn mệnh đề sai dưới đây:

1 1

2 3

0 0

d d

x x x x



 

B. Đạo hàm của

 

F x







là

   

F x x

 



C. Hàm số





f x

liên tục trên





;

a a

 thì

   

d 2 d

a a

f x x f x x





 

D. Nếu





f x

liên tục trên



thì

     

d d d

b c c

a b a

f x x f x x f x x

 

  

Câu 9. Cho





f x

là hàm số chẵn và

 

f x x a







. Chọn mệnh đề đúng:

 

f x x a

 



. B.

 

d 2

f x x a







 

f x x a







. D.

 

f x x a





Câu 10. Nếu









1 12, '

f f x

 liên tục và

 

' d 17

f x x





. Giá trị của





f bằng:

A. 29. B. 5. C. 19. D. 9.

ĐÁP ÁN TRẮC NGHIỆM LÝ THUYẾT TÍCH PHÂN

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 1. Sửa lại cho đúng là:

   

b a

a b

f x dx f x dx

 

 

. Chọn D.

Câu 2. Công thức (2) sai, sửa lại cho đúng là

   

a b

b a

f x dx f x dx

 

 

Hai công thức (1) và (3) đều đúng. Chọn B.

Câu 3. Ta có

dx x



 



Do đó A sai.

Theo tính chất tích phân thì B sai (vì không có tính chất này).

Xét câu C. Giả sử





F x

là một nguyên hàm của hàm số





f x

trên đoạn





;

a b

Suy ra













0, ;

F x f x x a b

    .

●









0, ;

F x x a b

   , suy ra





F x

là hàm hằng nên

   

f x dx F x

 



●









0, ;

F x x a b

   , suy ra





F x

đồng biến trên đoạn





;

a b

nên









F b F a

 .

Do đó

       

f x dx F x F b F a

   



. Do đó C đúng.

Chọn





f x



thì

0 0

dx C

 



nhưng





f x



không phải là hàm số lẻ.

Do đó D sai. Chọn C.

Câu 4. Theo tính chất tích phân, suy ra A đúng. Chọn





f x x



và









; 1;2

a b   .

Khi đó

   

1 1

4 1 0

2 2

f x dx xdx x



    

 

nhưng hàm





f x x



không thỏa mãn không âm trên





1;2

 . Do đó B sai.

Vì





2 2

2 1

1 1

x C

x x

   

 

nên C sai.

Ta có

là một nguyên hàm của

nhưng

không là nguyên hàm của

http://hoc24h.vn - TÍCH PHÂN

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Do đó D sai. Chọn A.

Câu 5. Áp dụng tính chất

   

F x f t dt





là một nguyên hàm của





f x

. Chọn B.

Câu 6. Ta có

 

3 2 3 2

3 2 3 2 6

t t x x

F x t t dt

 

      

 

 



Xét hàm số

 

3 2

3 2 6

x x

F x

  

trên đoạn





1;1



Đạo hàm

   

/ 2 /

; 0

F x x x F x

 



   







Suy ra

     

2 5

1 ; 0 ; 1 0

3 6

F F F

     

Do hàm số liên tục trên





1;1

 nên

 

   

1;1

min 0

F x F



  

. Chọn C.

Câu 7. Áp dụng tính chất

   

F x f t dt





là một nguyên hàm của





f x

Suy ra

 

F x







. Do đó I đúng. Lại có

 

0 0 3

F x x



    



Qua điểm

x  ta thấy





F x

đổi dấu từ âm sang dương.

Suy ra hàm số đạt cực tiểu tại

x  . Khi đó, mệnh đề II đúng, mệnh đề III sai. Chọn C.

Câu 8. Do

 

1 1

2 3 2 3

0 0

0;1

x x x x dx x dx

    

 

. Do đó A đúng.

Áp dụng tính chất

   

F x f t dt





là một nguyên hàm của





f x

Suy ra

 

F x





. Do đó B đúng.

Mệnh đề C sai vì tính chất này chỉ đúng nếu





f x

là hàm chẵn hoặc ta có thể lấy VÍ DỤ cụ thể cho

hàm





f x x



và



chẳng hạn.

TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Khi đó

 

1 1

4 4 0

2 2

xdx x



   



nhưng

2 4

xdx x

 



Mệnh đề D đúng theo tính chất tích phân. Chọn C.

Câu 9. Áp dụng tính chất

Nếu





f x

là hàm số chẵn thì

     

2 2

a a

f x dx f x dx f x dx

 

 

  

. Chọn B.

Câu 10. Ta có

       

' 4 1

f x dx f x f f

  



Theo bài ra ta có

         

' 17 4 1 17 4 17 1 17 12 29

f x dx f f f f

         



. Chọn A.

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TÍCH PHÂN ĐỔI BIẾN DẠNG 1



       

( ) ( ) ( ) ( ) ( )

f x u x dx F u x F u b F u a



     



–Bước 1. Biến đổi để chọn phép đặt

( ) ( )

t u x dt u x dx



   

(xem lại các phương pháp đổi

biến số trong phần nguyên hàm)

–Bước 2. Đổi cận:

( )

x b t u b

x a t u a

 

 



 

 

 

(nhớ: đổi biến phải đổi cận)

–Bước 3. Đưa về dạng

( )

u b

u a

I f t dt

 



đơn giản hơn và dễ tính toán.

DẠNG





       



 



        

 





 



       







2 2

( ) .

1 ( 1) .

( ) 2 .

n n

I f ax b xdx t ax b dt a dx

I dx t x dt n x dx

I f ax b xdx t ax b dt ax dx

VÍ DỤ 1: Tính tích phân I =

3 1





Lời Giải:

Đặt t =

3 1





= 3x + 1



x =



dx = t

Do đó: I =

2 2

1 1

( 1)

2 1

( )

3 3

t dt

t t dt





 

 

2 2

1 1

2 1 1 31 46

. . 1

3 2 3 5 15 15

t   

VÍ DỤ 2: Tính tích phân I =

3 2

x



TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Lời giải:

Đặt t =





= 1+x



dt = 2xdx



xdx =

t dt

Khi x = 0 thì t = 1

Khi x =

thì t = 2

Do đó:

I =

2 2

3 2

1 1

3 ( 1) 3

( )

2 2

t t dt



 

 

5 2

3 141

( )

2 5 2 20

t t

 

VÍ DỤ 3: Tính tích phân I =

x dx





Lời giải:

Đặt t =





= 1- x



2tdt = -2xdx



-xdx = tdt

Khi x = 0 thì t = 1

Khi x =

thì t =

Do đó:

I =

2 2

2 3

2 2

1 1

(1 )( )

( 1) ( )

t tdt t

t dt t

 

   

 

2 5 2

3 12



VÍ DỤ 4: Tính tích phân I =

x x 



Lời giải:

Đặt t =





=x + 2



2tdt = dx

Khi x= 2 thì t = 2

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Khi x = 7 thì t = 3

Do đó:

I =

3 3 3

2 2 2

2 2 2 2 1

( )

2 ( 1)( 2) 3 2 1

tdt tdt

t t t t t t

  

     

  

2 2 5

(2ln 2 ln 1) (2ln ln 2)

3 3 4

t t    

VÍ DỤ 5: Tính tích phân I =

3 2

x x dx





(Đề thi ĐH Ngoại Thương 1996)

Lời giải:

Đặt t =





= 1 – x



xdx = -tdt

Khi x = 0 thì t=1

Khi x= 1thì t = 0

Do đó:

I =

0 1

3 5

2 2 4

1 0

1 1 2

(1 )( ) ( ) ( )

3 5 3 5 15

t t

t t tdt t t dt        

 

VÍ DỤ 6: Tính tích phân I =

x xdx





(Đề thi ĐH Y TPHCM 1997 – 1998)

Lời giải:

Đặt t = 1





= 1 – x



dx = -2tdt

Khi x = 0 thì t=1

Khi x= 1thì t = 0

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Do đó:

I =

0 1

3 5

2 2 4

1 0

1 1 4

(1 )( 2 ) 2 ( ) 2( ) 2( )

3 5 3 5 15

t t

t t tdt t t dt

        

 

VÍ DỤ 7: Tính tích phân I =





ĐH Cần Thơ khối D 1998

Lời giải:

Đặt t =





= x+1



x = t

-1



dx = 2tdt

Khi x = 0 thì t= 1

Khi x = 3 thì t = 2

Do đó:

I =

2 2

4 2

1 1

( 1) 1

.2 2 ( 2 2)

tdt t t dt

 

  

 

=2(

2 53

2 )

5 3 15

t t  

VÍ DỤ 8: Tính tích phân I =

3 2

x x dx





(ĐH Quốc Gia HN– khối B - 1998)

Lời giải:

Đặt t =





= 1 + x



xdx = tdt

Khi x = 0 thì t=1

Khi x= 1 thì t =

Do đó:

I =

2 2

5 3

2 4 2

1 1

4 2 2 2 1 1 2( 2 1)

( 1) . ( ) ( ) ( )

5 3 5 3 5 3 15

t t

t t tdt t t dt



         

 

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 9:Tính tích phân I =

2 1

xdx





(ĐH Quốc Gia TPHCM khối A – 1998)

Lời giải:

Đặt t =

2 1





= 2x+1



x =





dx = tdt

Khi x=0 thì t = 1

Khi x = 1 thì t =

Do đó:

I =

3 3

1 1

( 1)

1 1 1

( 1) ( )

2 2 3 3

tdt

t dt t



    

 

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P1)

1. Tìm a thỏa mãn

 

1 .

x x dx





120



D. 3

2. Tìm a thỏa mãn

 

1 .

x x dx





168

C. -

3. Tìm a,b,c:

x



1 1

.ln

a b



n 4

4. Tính

 

1 3 . 1 2 3

x x x dx

  



6 2



6 2



6 1



5. Tính

1 .

x x dx





B. -

D. 5

6. Tính

x 



? ( đề thi dự bị THPT Quốc Gia 2015 )

A. 8 B. 3 C.

7. Tính

2 . ?

x x dx





( đề thi Đại học khối B 2013 )

2 2 1



2 2

2 2 1

3 3



2 1



8. Tính

5 .

x x dx





5 5 8



5 5 8



5 8



5 5

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

9. Tính

. 1 .

x x dx





468



259

D. 4

10. Tính

3 2

. 1.

x x dx





14 3

B. 1 C.

D. 9

11. Tính

3 2

. 1 .

x x dx





(đề thi học kì II năm 2014-THPT Nguyễn Khuyến-TP.HCM)

12. Tính

3 2

x dx





13. Tính

e dx

 



 



 



? ( đề thi thử THPT QG 2015-THPT Hàn Thuyên-Bắc Ninh-Lần 3 )



912

e  D.



14. Tính

2 1

x x





 







2 3 1







2 3 2







4 3 1







2 2 3 1



15. Tính

 

1 . 2 .

x x x dx

 





D. 15

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P1)

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

DẠNG:

( ). .

x x

I f e e dx







Đặt

x x

t e dt e dx

   

VÍ DỤ 1. Tính tích phân I =

ln3





Lời giải:

Đặt t =





2tdt =

e dx



dx =



Khi x = 0 thì t =

Khi x = ln3 thì t = 2

Do đó:

I =

2 2 2

2 2

2 2 2

2 2 1 1

( )

( 1) 1 1 1

tdt dt

t t t t t

  

   

  

=ln

1 1 2 1 3 2 2

ln ln ln

1 3 3

2 1

  

  



VÍ DỤ 2: Tính tích phân I =

ln 2

e 



Lời giải:

Đặt t =









e dx tdt



Khi x = 0 thì t =

Khi x = ln2 thì t =

Do đó:I =

3 3

2 3

2 2

( 1)2 2 2

2 ( 1) 2( )

3 3

t tdt t

t dt t



    

 

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P2)

Câu 1: Tìm a biết:

ln 2

. .

x x

e a e dx





2 3



Câu 2: Tính

 

e dx

e 



3 2 3

 B.

2 1



Câu 3: Tính

ln5

ln 2

e dx





Câu 4: Tính

ln6





 

ln 2 3

 B.

 

ln 2 3

 C.





ln 2 3

 D.





ln 2 3



Câu 5: Tính

ln 2

e dx





A. A.

3 2 3

 B.

2 1



2 2

Câu 6: Tính

ln 2

e dx





2 3



2 3



Câu 7: Tính

ln6

3 3 2 7

x x

e dx

e e

  



ln 4

800

Câu 8: Tính

ln16





ln 4

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P2)

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

DẠNG

(ln )

I f x dx

  





Đặt

t x dt dx

    

Nếu

(ln )

f x

có chứa

.ln

m n x



với m, n là hằng số thì ta đặt luôn

.ln .

t m n x

 

Bởi

lẻ khi vi phân

dt n dx

  

sẽ không bị mất tính tổng quát so với khi đặt

t x



và

làm cho việc xử lý bài toán sau khi đặt ẩn phụ sẽ đơn hơn. Ngoài ra, khi gặp căn thức,

ta cũng đặt

(ln )

t f x

 

Nếu có chứa

log

thì ta chuyển về

bằng công thức:

log log .log

a a e

x e x

  

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM DẠNG

(ln )

I f x dx

  



Câu 1: Tính

ln .

1 ln

x dx

x x





4 2 2



4 2



5 2 2



5 2 2



Câu 2: Tính

1 3ln .ln

x x





270

478

178

116

135

Câu 3: Tính

3 2

ln . 2 ln

x x





9 3 6 2



3 2



9 3 6 2



3 2



Câu 4: Tính

. 1 ln

x x





3. 4 3



3. 4

4 3



3. 3 3



Câu 5: Tính

3 2ln

1 2ln

e e

x x









Câu 6: Tính

ln .

ln 1

x dx

x x





105

270

Câu 7: Tính

ln .

1 3

x dx

x ln x





http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN TRẮC NGHIỆM DẠNG

(ln )

I f x dx

  



CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

KỸ THUẬT 4: TÍCH PHÂN LƯỢNG GIÁC

1.CÔNG THỨC LƯỢNG GIÁC THƯỜNG SỬ DỤNG:

a. Hệ thức cơ bản:

sin

a + cos

a = 1; tana.cota = 1

2 2

1 1

1 tan ; 1 cot

cos sin

a a

   

b. Công thức nhân đôi

sin2a = 2sina.cosa

2 2 2 2

cos2 cos sin 2cos 1 1 2sin

a a a a a

     

2 tan cot 1

tan 2 ; cot 2

1 tan 2cot

a a



 



c.Công thức hạ bậc

1 cos 2

sin





1 cos2

cos





1 cos 2

tan

1 cos 2







d.Công thức biến tích thành tổng

 

cos .cos cos( ) cos( )

a b a b a b

   

 

sin .sin cos( ) cos( )

a b a b a b

   

 

sin .cos sin( ) sin( )

a b a b a b

   

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Nhắc lại công thức nguyên hàm lượng giác:

Nguyên hàm số sơ cấp Nguyên hàm hàm mở rộng

cos sin

xdx x C

 



   

cos sin

ax b dx ax b C

   



sin cos

xdx x C

  



   

sin cos

ax b dx ax b C

    



tan

cos

dx x C

 



 

1 1

tan

cos

dx ax b C

ax b a

  





cot

sin

dx x C

  



 

1 1

cot

sin

dx ax b C

ax b a

   





Công thức Walliss (dùng cho trắc nghiệm)

2 2

0 0

( 1)!!

(1)

cos sin

( 1)!!

. (2)

!! 2

n n

xdx xdx

 









 









 

(Nếu n lẻ : Dùng ct (1) ; Nếu n chẵn: Dùng ct (2) )

Trong đó

n!! đọc là n walliss và được định nghĩa dựa vào n lẻ hay chẵn. Chẳng hạn:

0!! 1; 1!! 1; 2!! 2; 3!! 1.3; 4!! 2.4; 5!! 1.3

.5;

     

6!! 2.4.6; 7!! 1.3.5.7; 8!! 2.4.6.8; 9!! 1.3

.5.7.9; 10!! 2.4.6.8.10

    

VÍ DỤ 1.

10!! 2.4.6.8.10 256

cos

11!! 1.3.5.7.9.11 693

xdx



  



VÍ DỤ 2.

9!! 1.3.5.7.9 63

sin . .

10!! 2 2.4.6.8.10 2 512

xdx



  

  



http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

DẠNG 4.1. SỬ DỤNG CÔNG THỨC NGUYÊN HÀM CƠ BẢN

VÍ DỤ 1: Tính

1 sin

sin

I dx









Bài giải:

Ta thấy đề bài biểu thức dưới dấu tích phân ở dạng thương nên phải biến đổi để không còn dạng thương,

mặt khác

sin

, sinx có công thức nguyên hàm nên

 

4 4

2 2

6 6

1 sin 1

sin

sin sin

2 3

cot cos 1

2 2

I dx x dx

x x

 





 

  

 

 

      

 

Vậy

2 3

2 2

I    

VÍ DỤ 2: Tính

3cos

1 sin

I dx









Bài giải:

Ta thấy biểu thức dưới dấu tích phân ở dạng thương nên phải biến đổi để không còn dạng thương, tử thức

là cosx, mẫu là biểu thức theo sinx nên ta biến đổi tử theo sinx để rút gọn

 

2 2

0 0

1 sin cos

3cos

1 sin 1 sin

x x

I dx dx

x x

 



 

 

 

 

3 1 sin cos 3sin cos 2

x xdx x x



 

   

 

 





Vậy



TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 3: Tính

2 2

sin cos

I dx

x x







Bài giải:

Ta có công thức nguyên hàm

2 2

1 1

sin cos

x x

nhưng nếu tách

2 2 2 2

1 1 1

sin cos sin cos

x x x x

 được biểu thức

dưới dấu tích phân là tích hai hàm nên

Cách 1:

2 2

3 3

2 2 2 2

4 4

1 sin cos

sin cos sin cos

x x

I dx dx

x x x x

 



 

 

 

2 2

1 1

tan cot

cos sin

dx x x

x x



 

   

 

 



2 3



Vậy

2 3

I 

Cách 2:

3 3

2 2 2

4 4

1 1

sin cos (sin cos )

I dx dx

x x x x

 

 

 

2cot 2

sin 2

dx x



  



2 3



Vậy

2 3

I 

VÍ DỤ 4: Tính

cot

I xdx







http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bài giải:

Ta không có công thức nguyên hàm của

cot

nên cần phải biến đổi. Có hai cách.

Cách1:

 

4 4

2 2

6 6

cot cot 1 1

I xdx x dx

 

   

 

 

cot 1 3 1 3

4 6 12

x x



  

           

Cách 2:

4 4

6 6

cos

cot

sin

I xdx dx

 

 

 

4 4

2 2

6 6

1 sin 1

sin sin

dx dx

x x

 



 

  

 

 

 

 

cot 1 3 1 3

4 6 12

x x



  

           

Bài tập tự luyện

Tính : a.

3 2cot

cos







4sin

1 cos







tan

xdx





cos 2

cos





sin

cos





Đáp án:

11 3

. 5







. 1





5 3

4 8





DẠNG 4.2: DÙNG CÔNG THỨC HẠ BẬC

VÍ DỤ 1: Tính

cos

J xdx







TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bài giải:

Ta không có công thức nguyên hàm của cos

x nên phải dùng công thức hạ bậc

2 2

0 0

1 cos 2 1 1

cos sin 2

2 2 4 4

J xdx dx x x

 





 

    

 

 

 

Vậy





VÍ DỤ 2: Tính

sin cos 2

J x xdx







Bài giải:

2 2

0 0

1 cos 2

sin cos 2 cos2

J x xdx xdx

 



 

 

 

2 2

0 0

1 1 1 cos4

cos 2 cos 2 cos 2

2 2 2

x x dx x dx

 



 

   

 

 

 

1 1 1 1

sin 2 sin8

2 2 2 8 4

x x x



 

     

 

 

Vậy



 

VÍ DỤ 3:

 

4 4

cos 2 sin cos

J x x x dx



 



Bài giải:

   

2 2

4 4 2 2

0 0

cos 2 sin cos cos 2 1 2sin cos

J x x x dx x x x dx

 

   

 

2 2

0 0

1 1 1 cos 4

cos2 1 sin 2 cos2 1 .

2 2 2

x x dx x dx

 



   

   

   

   

 

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2 2

0 0

1 1

3cos 2 cos 4 cos2

4 4

xdx x xdx

 

 

 

 

2 2

0 0

1 1

3cos 2 cos6 cos 2

4 8

xdx x x dx

 

  

 

2 2 2

0 0 0

3 1 1

sin 2 sin 6 sin 2 0

8 64 12

x x x

  

   

Vậy J

= 0

Bài tập tự luyện

Tính các tích phân

2 2

cos sin

x dx



 



 

 



2 4

cos .sin

x xdx





sin 5

xdx





 

2 2

2sin sin cos cos

x x x x dx



 



sin

xdx





cos

xdx





Đáp án:

3 1

3 8 2



 

1 3

16 6 4



 



 

 

40 20





4 2





1 3

. 1

4 8



 



 

 

1 3

. 1

4 8



 



 

 

DẠNG 4.3: DÙNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG

VÍ DỤ 1: Tính tích phân:

sin 2 cos6

K x xdx







Bài giải:

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Biểu thức dưới dấu tích phân là tích của hai hàm nên ta dùng công thức biến đổi tích thành tổng

 

3 3

6 6

sin 2 cos6 sin8 sin 4

K x xdx x x dx

 

  

 

1 1 1

cos8 cos 4

2 8 4

x x



 

  

 

 

= 0

Vậy



VÍ DỤ 2: Tính tích phân:

cos cos2 cos3

K x x xdx







Bài giải:

Ta có:

cos cos 2 cos3 cos 2 cos3 cos

x x x x x x



 

cos 2 cos 4 cos 2

x x x

 

 

cos 4 cos 2 cos 2

x x x

 

 

cos6 cos2 1 cos4

x x x

   

Do đó

 

cos6 cos 2 1 cos 4

K x x x dx



   



1 1 1 1

sin 6 sin 2 sin 4

24 8 4 16

x x x x



 

   

 

 





Vậy





Bài tập tự luyện:

. sin 5 sin 3

a x xdx





sin sin 2 cos5

x x xdx





 

. sin 6 sin 2 6

c x x dx







http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đáp án:



3 3





DẠNG 4.4: ĐỔI BIẾN SỐ

Các dạng thường gặp khi đổi biến

a. Chứa biểu thức mang mũ

b. Chứa mẫu

c. Chứa căn

d. Chứa mũ

Dạng





sinx .cos

f x



đặt

sin

t x



hoặc

.sin

t a b x

 

Dạng





cos sin

f x x



đặt

cos

t x



hoặc

cos

t a b x

 

Dạng

 

tan

cos

f x



đặt

tan

t x



Dạng

 

cot

sin

f x



đặt

cot

t x



Dạng









sinx cos . sin cosf x x x

  

đặt

sin cos

t x x

 

Dạng 4.4.1. Kết hợp 1 trong 4 dạng a,b,c,d với d(sinx)=cosx, d(cosx)=-sinx

VÍ DỤ 1: Tính:

 

1 2sin cos

L x xdx



 



Bài giải:

Biểu thức dưới dấu tích phân chứa biểu thức mang mũ và d(sinx) = cosxdx. Nên

Đặt: 1 2sin , 2cos cos

t x dt xdx xdx

    

Đổi cận: khi x = 0 thì t = 1; x =



thì t =3

Do đó

 

0 1

1 2sin cos 10

2 8

dt t

L x xdx t



 

    

 

 

 

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 2: Tính L

cos

xdx





Bài giải:

-Mặc dù chứa biểu thức mang mũ nhưng ta không đặt t = cosx được vì tích phân mới không chuyển hoàn

toàn về theo biến t.

 

2 2

3 2

0 0

cos cos 1 sin

xdx x x dx

 

 

 

Đặt sin , cos cos

t x dt xdx xdx dt

   

Đổi cận: khi x = 0 thì t = 0; x =



thì t =1

Do đó:

 

3 3

L t dt t

 

    

 

 



Rút kinh nghiệm:

- Dạng tổng quát

2 1 2 2

sin sin sin (1 cos ) sin

n n n

xdx x xdx x xdx



  

  

Đặt t = cosx ( chứa sinx mũ lẻ ta đặt t = cosx)

- Dạng tổng quát

2 1 2 2

cos cos cos (1 sin ) cos

n n n

xdx x xdx x xdx



  

  

Đặt t = sinx ( chứa cosx mũ lẻ ta đặt t = sinx).

- Áp dụng được đối với biểu thức dưới dấu tích phân là tích của sinx và cosx

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 3: Tính L

3 2

sin cos

x xdx





Bài giải:

3 2

sin cos

x xdx





 

2 2

1 cos cos sin

x x xdx







Đặt t = cosx, dt = - sinxdx sin

xdx dt

  

Đổi cận: x =



 

; x =



 

Do đó L

   

2 2 2 4

1 ( )

t t dt t t dt

   

 

3 5

3 5 480

t t

 

  

 

 

Vậy L

480

VÍ DỤ 4: Tính

3 3

sin cos

L x xdx







Bài giải: Cả sin và cosx đều mũ lẻ nên ta có thể giải bằng các cách sau:

Cách 1:

 

6 6 6

3 3 2

0 0 0

1 1

(sin cos ) sin 2 1 cos 2 sin 2

8 8

L x x dx xdx x xdx

  

   

  

Đặt t = cos2x, dt = - 2sin2xdx

sin 2

xdx dt

  

Đổi cận: x =



 

; x = 0

 

Do đó

1 1 1 11 5

(1 )

16 16 3 24 384 384

L t dt t

 

      

 

 



TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Cách 2:

 

2 3

sin 1 cos cos

L x x xdx



 



Đặt t = cosx, dt = - sinxdx sin

xdx dt

  

Đổi cận: x =



t  ; x = 0

 

Do đó

1 1

4 6

2 3 3 5

3 3

2 2

(1 ) ( )

4 6 384

t t

L t t dt t t dt

 

      

 

 

 

Vậy

384

L 

Ta có thể tách cos

x = (1 – sin

x)cosx

VÍ DỤ 5: Tính

1 2sin

1 sin 2

L dx











( ĐHKB - 2003)

Bài giải:

Đề bài dạng phân thức hơn nữa

(1 2sin ) cos 2

x dx xdx

 

Đặt t = 1 + sin2x, dt = 2cos2xdx



cos2

xdx



Đổi cận: khi x = 0 thì t = 1; x =



thì t = 2

Do đó:

0 1

1 2sin 1 1

ln ln 2

1 sin 2 2 2 2

x dt

L dx t

x t





   



 

Vậy

ln 2

L 

VÍ DỤ 6: Tính

 

sin 2

2 sin

L dx











http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bài giải:

Đề bài chứa biểu thức mang mũ nên đặt t = 2 + sinx nhưng dt = cosxdx nên ta phải dùng công thức nhân

đôi tách sin2x

   

0 0

2 2

sin 2 2sin cos

2 sin 2 sin

x x x

L dx dx

x x

 

 

 

 

 

Đặt

2 sin sin 2

t x x t

    

Ta có cos

dt xdx



Đổi cận khi



 

thì t = 1;



thì t = 2

Do đó





2 2

1 1

2 2

2 4 4

2ln 2ln 2 2

L dt dt t

t t t t



   

      

   

   

 

Vậy L

= 2ln2 - 2

VÍ DỤ 7: Tính L

sin 2 sin

1 3cos

x x







Bài giải:

Đề bài chứa căn thức và d(cosx) = - sinxdx nên

Đặt

1 3cos 1 3cos

t x t x

    

2 3sin sin

tdt

tdt xdx xdx     

Đổi cận khi x = 0 thì t = 2; x =



thì t = 1

Do đó

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

 

2 2

0 0

2cos 1 sin

sin 2 sin

1 3cos 1 3cos

x x

dx dx

x x

 





 

 

 

2 2

1 1

2 1

2 2 2 2 44 10 34

2 1

3 9 9 3 27 27 27

tdt t dt t

 





 

 

 

       

 

 

 

Vậy L

VÍ DỤ 8: Tính

cos2

sin 2

L e xdx







Bài giải:

Đề bài chứa mũ nên

Đặt t = cos2x, dt = -2sin2xdx

sin 2

xdx dt

  

Đổi cận: x =



 

; x = 0

 

Do đó:

1 1 1 1

2 2 2 2

t t

L e dt e e

   



Vậy

1 1

2 2

L e

 

VÍ DỤ 9: Tính

sin tan

L x xdx







( Dự bị A – 2005)

Bài giải:

 

3 3

2 2

0 0

sin

sin tan 1 cos

cos

L x xdx x dx

 

  

 

Đặt t = cosx, dt = -sinxdx sin

xdx dt

  

Đổi cận: khi x = 0 thì t = 1; khi x =



thì



http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Do đó:

 

1 ln ln 2

2 8

dt t

L t t

 

       

 

 



Vậy

ln 2

 

Bài tập tự luyện: Tính các tích phân

cos

2sin 1

xdx







cos

sin

b dx





 

2 2

cos

1 sin sin

c dx

x x







sin 4

3 cos 2

d dx







. tan

f xdx





sin 2 cos

1 cos

x x

g dx







(ĐHKB- 2005)

Đáp án:

. ln 2

9 2 7 3



1 3 2 2

. ln 2 2

2 3



 

.1 3ln

d 

1 2

. ln

2 2

f 

.2ln 2 1



TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Dạng 4.4.2. Kết hợp 1 trong 4 dạng a,b,c,d và









2 2

sin sin 2 ; cos sin 2

d x xdx d x xdx

  

VÍ DỤ 1: Tính

2 3

sin 2 (1 sin )

M x x dx



 



Bài giải:

Đề bài chứa biểu thức mang mũ và





sin sin 2

d x xdx

 nên

Đặt

1 sin sin 2

t x dt xdx

   

Đổi cận khi x = 0 thì t = 1; khi x =



thì t = 2

Do đó:

4 4

M t dt  



Vậy



VÍ DỤ 2: Tính

sin 4

1 cos

M dx









Bài giải:

Đề bài chứa mẫu và





1 cos sin 2

d x xdx

   ; sin4x = 2 sin2xcos2x. Nên

Đặt

1 cos sin 2

t x dt xdx

    

Đổi cận khi x = 0 thì t = 2; khi x =



thì t =

Do đó:

 

2 2 3

2sin 2 cos2 4

4 6ln 2 6ln

1 cos 3

x x

M dx dt t t

x t





     



 

Vậy

2 6 ln

M  

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 3:

2 2

sin 2

cos 4sin

M dx

x x









Bài giải:

Đề bài chứa căn thức nên

Đặt

2 2

cos 4sin 2 3sin 2

t x x tdt xdx

   

Đổi cận khi x = 0 thì t = 1; khi x =



thì t = 2

Do đó

2 2

3 3

tdt

M t

  



Vậy M

Bài tập tự luyện: Tính các tích phân:

sin 2

1 cos

a dx







sin cos

4 3sin

x x

b dx







Đáp án:

.ln 2

7 2



Dạng 4.4.3 Kết hợp 1 trong 4 dạng a,b,c,d và

 

tan 1 tan

cos

d x dx x dx

   ;

 

cot 1 cot

sin

d x dx x dx

    

VÍ DỤ 1: Tính

 

tan tan

N x x dx



 



Bài giải:

   

3 3

3 2

4 4

tan tan tan 1 tan

N x x dx x x dx

 

   

 

Đặt t = tanx





1 tan

dt x dx

  

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đổi cận: Khi x =



thì t =1; x =



thì t =

Do đó:

N tdt

  



Vậy



VÍ DỤ 2: Tính

tan

cos 2

N dx







Bài giải:

4 4

6 6 6

2 2 2

0 0 0

tan .

tan tan

cos

cos 2 cos sin 1 tan

x x

N dx dx dx

x x x x

  

  

 

  

Đặt t = tanx

cos

dt dx

 

Đổi cận: Khi x = 0 thì t = 0; x =



thì t =

Dođó:

3 3

4 4

3 3

2 2

0 0

t t 1 1

1 1

N dt dt

t t

 

 

 

 

   

3 3

2 2

0 0

1 1 1 1

1 1

1 2 1 1

t dt t dt

t t t

 

   

        

 

 

  

   

 

 

 

1 1 1 10

ln ln 2 3

3 2 1 2

9 3

t t

 

 



      

 

 



 

 

Vậy N





1 10

ln 2 3

9 3

 

VÍ DỤ 3: Tính

sin cot

N dx

x x







Bài giải:

Đề bài chứa căn thức và d(cotx) =

sin

 nên

Đặt

cot cot 2

sin

t x t x tdt dx

     

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đổi cận: Khi x =



thì t =

;khi





thì t =1

Do đó

2 2 2 3 2

N dt t

     



Vậy

2 3 2

 

VÍ DỤ 4: Tính

sin

N dx







Bài giải:

Đề bài chứa biểu thức mang mũ là sinx nhưng ta không đặt t = sinx vì d(sinx) = cosxdx không có ở đề

bài mà phải xem

4 2 2

1 1 1

sin sin sin

x x x



Ta có

 

2 2

4 2

4 4

1 1

1 cot .

sin sin

N dx x dx

x x

 

  

 

Đặt

cot

sin

t x dt dx

   

Đổi cận: Khi x =



thì t = 1;khi





thì t = 0

Do đó

 

3 3

N t dt t

 

    

 

 



Vậy



Bài tập tự luyện: Tính các tích phân:

cos

a dx





 

. cot cot

b x x dx







Đáp án

.2 3



TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Dạng 4.4.4 Kết hợp 1 trong 4 dạng a,b,c,d và









sin cos cos sin

d x x x x dx

 



VÍ DỤ 1: Tính

cos sin

sin cos

x x

P dx

x x











Bài giải:

Đặt





sin cos cos sin

t x x dt x x dx

    

Đổi cận khi x = 0 thì t = 1;

x t



  

Do đó:

ln ln 2

P dt t

  



Vậy:

ln 2

P 

VÍ DỤ 2: Tính

 

cos 2

sin cos 3

P dx

x x





 



Bài giải:

Đặt t = sinx – cosx + 3





cos sin

dt x x dx

  

Đổi cận khi x = 0 thì t = 2;

x t



  

Do đó:

  

 

cos sin cos sin

sin cos 3

x x x x

P dx

x x



 



 



3 3 3

ln ln 2

dt t

t t

 

 

     

 

 



Vậy P

ln 2



VÍ DỤ 3: Tính

cos

sin cos

P dx

x x









Bài giải:

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Ta không tính P

độc lập được mà phải dựa vào

sin

sin cos

Q dx

x x









bằng cách tính

3 3 3 3

;

P Q P Q

 

đó giải hệ để tính P

Tính

3 3

cos sin

sin cos

x x

P Q dx

x x





 





1 1 1

1 sin 2 cos2

2 4 2 2

x dx x x



   

     

   

   



Tính

  

3 3

2 2

3 3

0 0

cos sin 1 sin cos

cos sin

sin cos sin cos

x x x x

x x

P Q dx dx

x x x x

 

 



  

 

 

Đặt t = sinx + cosx





cos sin

dt x x dx

  

Đổi cận khi x = 0 thì t = 1; khi x =



thì t= 1

Do đó

3 3

P Q dt

 





 

 

  



Giải hệ ta được

4 4



 

Vậy

4 4



 

Bài tập tự luyện: Tính các tích phân:

cos 2

sin cos 2

a dx

x x



 



cos

sin cos

b dx

x x







 

sin

sin cos

c dx

x x







sin

sin 2 2(1 sin cos )

x x x



 



 

 

  



(ĐHKB–2008)

Hướng dẫn giải câu d. đặt t = 1 + sinx + cosx

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đáp án:

2 2

. 2 1 2ln



 

. ln 2





4 3 2



TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P3)

Tính các tích phân sau (không dùng máy tính)

( dạng





sinx .cos

f x



đặt

sin

t x



hoặc

.sin

t a b x

 

)

Câu 1: Tính

sin .cos .

x x dx





? (đề HK II 2014- THPT Lương Văn Can- TP.HCM )



Câu 2: Tính

 

1 3sin .cos .

x x dx







? (đề HK II 2014- THPT Quốc Trí- TP.HCM )



Câu 3: Tính

cos

1 sin







? (đề HK II 2014- THPT Marie Curie- TP.HCM )

A. ln4 B. ln5 C. ln3 D. ln2

Câu 4: Tính

cos

5 2sin







1 5

3 2

  B.

1 5

2 3

1 3

3 2

 D.

1 5

3 2



Câu 5: Tính

sin 2 .

1 sin

x dx







? (đề HK II 2014-THCS & THPT Bắc Mỹ- TP.HCM )

A. 1-ln4 B. 4ln5 C. 3-ln3 D. 2-2ln2

Câu 6: Tính

 

1 sinx .cos .

x dx







A. 8 B. 3 C.

http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 7: Tính

 

1 2sin .cos .

x x dx







A. 5 B. 10 C. 15 D. 20

Tính các tích phân sau ( dạng





cos sin

f x x



đặt

cos

t x



hoặc

cos

t a b x

 

)

Câu 8: Tính

sinx.cos .

x dx





? ( đề thi HK II-THPT Lê Thánh Tôn- TP.HCM )

105

160

270

Câu 9: Tính

sinx

cos





? ( đề thi HK II-THPT Việt Mỹ Anh- TP.HCM )

C. 2 D. 1

Câu 10: Tính

sin 2 .cos .

x x dx





?(đề thi thử THPT QG 2015-THPT Nguyễn Văn Trỗi- Hà Tĩnh-Lần1)

A. 0 B. 2 C.4 D.6

Câu 11: Tính

 

sin .cos 1 cos .

x x x dx







105

160

270

Câu 12: Tính

4sin

1 cos







A. 0 B. 2 C.4 D.6

Tính các tích phân sau ( dạng

 

tan

cos

f x



đặt

tan

t x



)

Câu 13: Tính

 

1 tan .

cos

x dx







D. 3

TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 14: Tính

2 3tan

1 cos 2







? ( đề thi thử THPT QG 2015-THPT Chuyên Lam Sơn-Thanh Hóa )

5 5 2 2



5 5 2



5 2 2



5 2 2



Câu 15: Tính

 

tan

cos .sin .

cos

x e x dx







A. 2 B. 1 C.

D. 3

Câu 16: Tính

tan

cos 2





? ( đề thi Đại Học khối A năm 2008 )

 

10 3 1

ln 2 3

27 2

   B.

 

10 3 1

ln 2 3

27 2

 

 

10 3 1

ln 2 3

27 2

   D.

 

10 3 1

ln 2 3

27 2

  

Tính các tích phân sau ( dạng









sinx cos . sin cosf x x x

  

đặt

sin cos

t x x

 

)

Câu 17: Tính

sin cos

x x









ln 2

ln 4

ln 2

Câu 18: Tính

sin cos

sin cos 3

x x





 



3 2



 B.

3 2



3 2



 D.

3 2





Câu 19: Tính

cos 2

sin cos 2

x x



 



2 1 2ln

2 2

 



2 1 2ln

2 2

 



2 1 2ln

2 2

 



2 1 2ln

2 2

 



Câu 20: Tính

 

cos2

sin cos 3

x x



 



http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

D. 3

Câu 21: Tính

1 sin 2 cos2

sin cos

x x



 





A. 3 B. 2 C. 1 D. -1

ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P3)

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

Câu 1.

Câu 7.

B Câu 13.

B Câu 19.

Câu 2.

Câu 8.

B Câu 14.

A Câu 20.

Câu 3.

Câu 9.

D Câu 15.

C Câu 21.

Câu 4.

Câu 10.

A Câu 16.

Câu 5.

Câu 11.

C Câu 17.

Câu 6.

Câu 12.

B Câu 18.

KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2

DẤU HIỆU CÁCH CHỌN

2 2

a x



sin

cos

x a t

 









2 2

x a



sin

cos













2 2

a x



cot

x a tgt

x a gt

 









a x





cos

x a t



a x





cos

x a t



2 2 2

a b x



sin

x t



2 2 2

( )

a b x



, n=1, 2, …

x tgt



http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 1: Tính tích phân(với a>0)

2 2

a x





Lời giải:

Đặt t= asint, t



;

2 2

 

 



 

 



dx= acostdt

Với x = 0 thì t=0

Với x=

thì t=



Do đó: I =

6 6

2 2 2

0 0

cos

6 6

sin

a tdt

a a t

 

   



 

VÍ DỤ 2: Tính tích phân(với a >0)

2 2

a x





Lời giải:

Đặt x = tgt , t



;

2 2

 

 



 

 



dx = a(tg

t + 1)dt.

Với x = 0 thì t=0

Với x= a thì t =



Do đó:

I =

4 4

2 2 2

0 0

( 1) 1

( 0)

4 4

a tg t dt dt

a a tg t a a a

 



   



 

KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 3 : Tính tích phân:

1 x

I dx







Lời giải:

Đặt x = sint,



dx = costdt

Khi x =

thì t =



Khi x = 1 thì t =



Do đó:

I =

2 2

2 2 2

4 4 4

cos 1 sin 1

( 1)

sin sin sin

t t

dt dt dt

t t t

  



  

  

=-(cotgt+t)



=1-



VÍ DỤ 4: Tính tích phân

I =

x



Lời giải:

Đặt x = 2cost,



dx = -2sintdt

Khi x = 0 thì t =



Khi x = 1 thì t =



Do đó:

http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

I =

3 3

2 2

4cos .2sin 1 3

2 (1 2cos ) 2 sin 2

2sin 2 3 2

t tdt

t dt t t

 



 



 

        

 

 

 

VÍ DỤ 5: Tính tích phân

I =

2 2

x x dx





Lời giải:

Đặt x = 2sint,



dx = 2cosdt

Khi x = 0 thì t = 0

Khi x = 2 thì t =



2 2

4sin

x t



Do đó: I =

2 2 2

0 0 0

16sin cos 4 sin 2 2 (1 cos 4 )

t tdt tdt t dt

  

  

  

sin 4 2( 0)

4 2

t t



 

   

 

 

VÍ DỤ 6: Tính tích phân

I =

x dx





Lời giải:

Đặt x = sint,



dx = cosdt

Khi x = 0 thì t = 0

Khi x =

thì t =



KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Do đó:

I =

4 4 4

2 2

0 0 0

sin .cos

sin .sin (1 cos ) (cos )

sin

cos

t t

t tdt t d t

dt tdt



  

  

 



  

= (-cost +

cos



2 5 2

3 12



VÍ DỤ 7: Tính tích phân

I =

x dx





Lời giải:

Đặt x = sint,



dx = cosdt

Khi x = 0 thì t = 0

Khi x =

thì t =



Do đó: I =

4 4 4

0 0 0

sin .cos 1 1 1 1

sin (1 cos 2 ) sin 2

cos 2 2 2 8 4

t tdt

tdt t dt t t

  



 

      

 

 

  

VÍ DỤ 8: Tính tích phân

I =

x x





Lời giải:

Đặt x =

cos



dx =

sin

cos

tdt

Khi x =

thì t =



http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Khi x =

thì t =



Do đó: I =

4 4 4

2 2

6 6 6

sin sin

cos cos

sin

1 1

cos cos

t t

dt dt dt t

t t

  



  



   



  

VÍ DỤ 9: Tính tích phân

I =

2 2

4 3

x x dx





Lời giải:

Đặt x =

sin



dx =

cos

tdt

Khi x = 0 thì t = 0

Khi x = 1 thì t =



Do đó:

I =

3 3 3

2 2 2

0 0 0

4 2 4 2

sin 4 4sin . cos sin 2 (1 cos 4 )

3 3 3 3 3

t t tdt tdt t dt

  

   

  

2 1 2 3

sin 4 ( )

4 3 8

3 3 3 3

t t



 

  

 

 

VÍ DỤ 10: Tính tích phân

I =







Lời giải:

Đặt x=cost,



dx = -sintdt

KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Khi x=0 thì t =



Khi x =

thì t =



Do đó:

I =

4 2 2 2

2 4 4 4

2cos cos cos

1 cos

2 2 2

.sin .sin .sin .2sin cos

1 cos 2 2

2sin sin sin

2 2 2

t t t

tdt tdt tdt dt

t t t

   



   



   

2 2

4 4

2cos (1 cos ) ( sin ) 1

2 4 2

dt t dt t t

 



 



      

 

VÍ DỤ 11: Tính tính phân

I =

x x





Lời giải:

Đặt x = tgt,



dx =

cos

Khi x=1 thì t =



Khi x =

thì t =



cos

 

Do đó:

I =

3 3

4 4

cos

. (ln ) ln( ) ln( )

. cos sin 2 6 8

dt dt t

tg tg tg

tgt t t

 



 

   

 

http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 12: Tính tích phân

I =

2 2

(1 3 )





Lời giải:

Đặt x =

tgt



dx =

1 1

(1 )

cos

3 3

tg t dt

 

Khi x=0 thì t = 0

Khi x = 1 thì t =



1+3x

=1+tg

Do đó:

I =

3 3 3

0 0 0

1 1 1 1 1

cos (1 cos 2 ) sin 2

1 2

3 3 2 3 2 3

tdt t dt t t

tg t

  



 

    

 



 

  

1 3

( )

3 4

2 3





VÍ DỤ 13: Tính tích phân

I =

9 2x





Lời giải:

Đặt x=

tgt



dx =

cos

Khi x=

thì t =



;

KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Khi x =

thì t =



2 2

9 2 3 1 3.

cos

x tg t

   

Do đó:

I =

4 4 4 4

3 2 2 2 2

6 6 6 6

3 1 1

.3.

sin

cos cos

2 2 2

cos . cos .sin (1 sin ).sin

dt dt d t

t t

t tg t t t t t

tg t

   

  



   

Đặt: v=sint thì

I =

2 2

2 2 2 2

1 1

2 2

1 1 1 1 1

2 2 ( ) 2 ln

(1 ) 1 2 1

dv v

v v v v v v

  

    

 

  

 

 

2 2 2 2 ln( 6 3)

  

VÍ DỤ 14: Tính tích phân

I =

x dx





(Đại học Y HN 1998)

Lời giải:

Đặt x = sint,



dx=costdt.

Khi x =



thì t =





Khi x = 1 thì t=



2 2

1 1 sin cos

x t t

   

Do đó: I =

2 2

6 6

1 1 1 3

cos (1 cos 2 ) sin 2

2 2 2 3 8

tdt t dt t t

 



 





 

 

     

 

 

 

http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 2

Câu 1: Tính

 

2 2

, 0

x a











ln 1 2 2

 B.





ln 1 2

 C.





ln 1 2 2

 D.





ln 2 2

Câu 2: Tính

2 2

a x dx





 

2 ln 2 1

 

 

 

 

2 ln 2 1

 

 

 

 

2 ln 2 1

 

 

 

 

1 ln 2 1

 

 

 

Câu 3: Tính

 

2 2 2

. , 0

x x a dx a

 



 

3 2 ln 2 1

 

 

 

 

2 ln 2 1

 

 

 

 

3 ln 2 1

 

 

 

 

3 2 ln 2 1

 

 

 

Câu 4: Tính







Câu 5: Tính

x





Câu 6: Tính









ln 1 2 2

 B.





ln 1 2

 C.





ln 1 2 2

 D.





ln 2 2

Câu 7: Tính

x dx









1 1

ln 1 2

  B.





1 1

ln 1 2

  C.





1 1

ln 1 2

  D.





ln 1 2



Câu 8: Tính

 

2 2

, 0

x a







KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ln 2





ln 1 3

 C.





ln 2 3

 D.





ln 1 2 3



Câu 9: Tính

 

2 2

. , 0

x a dx a

 



 

3 ln 2 3

 

 

 

 

 

3 ln 2 3

 

 

 

 





3 ln 1 3

 

 

 





3 2ln 2 2

 

 

 

Câu 10: Tính

x dx





 

5 2 1

ln 1 2

2 2

  B.





5 1

ln 1 2

2 2

 

 

5 2

ln 1 2

  D.

 

5 2 1

ln 4 2

2 2

 

Câu 11: Tính

x dx





10 ln3

 B.

10 ln 3

 C.

10 ln 3



10 ln3



Câu 12: Tính









ln 1 2 2

 B.





ln 1 2

 C.





ln 1 2 2

 D.





ln 2 2

ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 2

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

87 KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN



Định lý: Nếu

( )

u u x



và

( )

v v x



là hai hàm số có đạo hàm và liên tục trên đoạn





;

a b

thì:

 

( ) ( ) ( ) ( ) ( ) ( )

b b

a a

I u x v x dx u x v x u x v x dx

 

       

 

hay

. .

b b

a a

I udv u v vdu

  

 

Thực hành:

— Nhận dạng: Tích 2 hàm khác loại nhân nhau, chẳng hạn: mũ nhân lượng giác,…

— Đặt:

Vi phân

Nguyên ha m

u du dx

dv dx v



    







    







Suy ra:

. .

b b

a a

I udv u v vdu

  

 

— Thứ tự ưu tiên chọn u: log – đa – lượng – mũ và



phần còn lại. Nghĩa là nếu có ln hay

log

thì chọn



hay

log .ln

u x x

  và



còn lại. Nếu không có

ln; log

thì chọn



đa

thức và



còn lại. Nếu không có log, đa thức, ta chọn



lượng giác,….

— Lưu ý rằng bậc của đa thức và bậc của ln tương ứng với số lần lấy nguyên hàm.

— Dạng mũ nhân lượng giác là dạng nguyên hàm từng phần luân hồi.

Tìm các nguyên hàm:

VÍ DỤ 1. sin2

I x xdx





Theo thứ tự ưu tiên ở trên, với nguyên hàm này là tích của Hàm đa thức với Hàm lượng giác, nên ta ưu tiên

đặt

u x



Đặt

sin 2

cos 2

du dx

u x

dv xdx

v x













 



 







1 1 1 1

cos2 cos 2 cos2 sin 2

2 2 2 4

I x x xdx x x x C

       



VÍ DỤ 2.

2 2x

I x e dx





Đặt

du xdx

u x

v e

dv e dx







 



 











2 2 2 2 2

1 1

2 2

x x x

I x e xe dx x e I

    



Tính

I xe dx





KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đặt

2 2 2 2

1 1 1 1

2 2 2 4

x x x x

du dx

u x

I xe e dx xe e C

v e

dv e dx











      

 











Từ đó:





2 2

2 2 2 2

2 2 1

1 1 1

2 2 4 4

x x x

x x e

I x e xe e C C

 

     

VÍ DỤ 3.

cos 2

I x xdx





2 2

1 cos 4 1 1 1

cos 2 . cos 4

2 2 2 4

I x xdx x dx xdx x xdx x I



     

   

Tính

cos 4

I x xdx





. Đặt

cos4

sin 4

du dx

u x

dv xdx

v x











 



 

 









1 1 1 1

sin 4 sin 4 sin 4 cos 4

8 8 8 32

I x x xdx x x x C

     



Từ đó:

1 1 1

sin 4 cos 4

4 8 32

I x x x x C

   

VÍ DỤ 4.





2 1

I x x e dx

  



-Với VÍ DỤ này, khi mà bậc của





P x



, sử dụng phương pháp Nguyên hàm từng phần ta phải tiến

hành hai lần. Tuy nhiên, trong trường hợp này, ta cũng có thể sử dụng một cách khác được chỉ ra ở đây!

Đặt:





 

4 1

2 1

2 1 4 1

x x

du x dx

u x x

I x x e x e dx

dv e dx

v e

  



  

 

      

 









Tính





4 1

I x e dx

 



. Đặt

4 1 4

x x

u x du dx

dv e dx v e

  

 



 

 

 













4 1 4 4 1 4 4 3

x x x x x

I x e e dx x e e C x e C

          



89 KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến













2 2

2 1 4 3 2 3 4

x x x

I x x e x e C x x e C

          

VÍ DỤ 5.

cos3

I e xdx





Đặt

cos3

sin 3

du e dx

u e

dv xdx

v x













 









2 2 2

1 2 1 2

sin 3 sin 3 sin 3

3 3 3 3

x x x

I e x e xdx e x I

    



Đặt

sin 3

cos3

du e dx

u e

dv xdx

v x













 



 







2 2 2

1 2 1 2

cos3 cos3 cos3

3 3 3 3

x x x

I e x e x e x M

      



Từ đó:

2 2 2 2

1 1

1 2 1 2 1 2 1 2

sin 3 sin 3 sin 3 cos3

3 3 3 3 3 3 3 3

x x x x

I e x M e x I e x e x I

 

       

 

 

2 2 2 2

1 2 4 13 1 2

sin 3 cos3 sin 3 cos3

3 9 9 9 3 9

x x x x

e x e x I I e x e x C

      





3sin 3 2cos3

x x e

I C



  

VÍ DỤ 6.





ln 1

x x x

I dx

 







Đặt





ln 1

u x x

dv dx

v x



  









 



 

 









Ta được





2 2

1ln 1

I x x x x C

     

KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 7.





2 2

ln 1

I x x dx

  



Đặt:









2 2

2ln 1 .

ln 1

du x x

u x x

dv dx

v x



  

 





 

 

















2 2 2

.ln 1 2 ln 1 .

xdx

I x x x x x

      













2 2 2 2

ln 1 2 1.ln 1 2

x x x x x x x C

        

VÍ DỤ 8.

ln x

I dx

 



 

 



Ta có

I dx





. Đặt

2ln .

du x

u x







 



 



 

 







Ta được

1 1

I x C

x x

   

VÍ DỤ 9.

1 1

ln ln

I dx

x x

 

 

 

 



1 2

2 2

1 1

ln ln ln ln

dx dx

I dx I I

x x x x

 

     

 

 

  

Tính

. Đặt

ln ln

u du

x x x

dv dx v x

 

  

 



 

 

 

 

Từ đó

1 2

I I

 

. Từ đó

I C

 

VÍ DỤ 10.

I x dx









91 KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đặt

dv xdx

x x













 







 

 









. Từ đó

1 1

2 1

I x C



  



VÍ DỤ 11.





3 2 2

2 5 2 4

I x x x e dx

   



Giả sử:









3 2 2 3 2 2

2 5 2 4

x x

Q x x x e dx ax bx cx d e C

        















3 2 2 2 2 3 2 2

2 5 2 4 3 2 2

x x x

x x x e ax bx c e ax bx cx d e

          









3 2 3 2

2 5 2 4 2 3 2 2 2 2

x x x ax a b x b c x c d

          

 

3 2 2

2 2 1

5 3 2 1

2 3

2 2 2 2

4 2 3

a a

a b b

Q x x x e C

b c c

c d d

 

 

 

  

 

       

 

    

 

  

 









2 2

2 1 ... 2 3 4

x x

R x x e dx x x e C

       



IV. PHƯƠNG PHÁP 4. PHỐI HỢP ĐỔI BIẾN SỐ VÀ PHƯƠNG PHÁP TÍCH PHÂN TỪNG

PHẦN

VÍ DỤ 1. sin

I xdx





Đặt





2 sin . 2 2 sin

x t x t dx tdt I t tdt t tdt

       

 

Đặt

2 2

2 cos 2 cos 2 cos 2sin

sin cos

u t du dt

I t t tdt t t t C

dv tdt v t

 

 

        

 

  

 



Vậy 2sin 2 cos

I x x x C

  

VÍ DỤ 2: Tính tích phân

ln d .

I t t





KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đặt

u t

dv dt

v t











 











. Khi đó

2 2 2

1 1 1

ln ln 2ln 2 1.

I t t dt t t t

     



VÍ DỤ 3: Biết

ln 1 1

d ln 2

2 2

I x

  



. Giá trị của

bằng:

Đặt

u x









 



 



 

 







Khi đó

ln ln 1 ln 1

x dx a a

x x a x a a

 

         

 

 



. Suy ra



VÍ DỤ 4: Kết quả của tích phân

 

ln d

I x x x

 



được viết ở dạng

ln3

I a b

 

với

a b

là các số

nguyên. Khi đó

a b



nhận giá trị?

Đặt

 

2 1 2 1

x x

du dx dx

u x x

x x x x

dv dx

v x

 



 

 

 

 



 











Khi đó

   

3 3

2 2

2 1 1

ln ln 2

1 1

I x x x dx x x x dx

x x



 

      

 

 

 

 

 

3 3

2 2

ln 2 ln 1 3ln 3 2.

x x x x x

      

Suy ra

3, 2

a b

 

93 KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM TÍCH PHÂN TỪNG PHẦN

Câu 1. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Tính tích phân

ln d .

I x x x









 C.



 D.





Câu 2. Khẳng định nào sau đây đúng về kết quả

3 1

ln d

x x x









. B.



. C.

a b

 

a b

 

Câu 3. Kết quả của tích phân

 

ln 2 d

I x x x

 



được viết ở dạng ln3 ln 2

I a b c

  

với

, ,

a b c

là các

số hữu tỉ. Hỏi tổng

a b c

 

bằng bao nhiêu?

Câu 4. Cho

ln d

I x





. Xác định

để

I e

 

k e

 

. B.

k e



. C.

k e

 

. D.

k e

 

Câu 5. Tính tích phân

2 d

I x x





2ln 2 1

ln 2



 B.

2ln 2 1

ln 2



 C.

2ln 2 1

ln 2



 D.

2ln 2 1

ln 2





Câu 6. Kết quả tích phân

 

2 3 d

I x e x

 



được viết dưới dạng

I ae b

 

với , a b





. Khẳng định nào

sau đây là đúng?

a b

 

. B.

3 3

a b

 

. C.



2 1

a b

 

Câu 7. Cho tích phân

sin

sin 2 . d

I x e x







. Một học sinh giải như sau:

KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bước 1: Đặt

sin d cos d

t x t x x

  

. Đổi cận

0 0

2 d .

x t

I te t

x t



  





 



  







Bước 2: Chọn

d d

t t

u t u t

v e t v e

 

 



 

 

 

. Suy ra

1 1

0 00 0

d d 1

t t t t

te t te e t e e

    

 

Bước 3:

2 d 2

I te t

 



Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?

A. Bài giải trên sai từ Bước 1. B. Bài giải trên sai từ Bước 2.

C. Bài giải trên hoàn toàn đúng. D. Bài giải trên sai từ Bước 3.

Câu 8. Cho

2 2

0 0

cos d , sin d

x x

I e x x J e x x

 

 

 

và

cos 2 d

K e x x







. Khẳng định nào đúng trong các

khẳng định sau?

(I).

I J e



 

.(II).

I J K

 

.(III).





 .

A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Cả (II) và (III).

Câu 9. Cho

I x







với n





. Giá trị của

0 1

I I



là:

A. 0. B. 1. C. 2. D. 3.

Câu 10: Tính

2 .cos .

x x dx





? (đề thi HK II 2014-THPT Nguyễn Hữu Thọ-TP.HCM)

2 2



 



 C. 1 D.

2 2



Câu 11: Tính

.ln .

x x dx



? (đề thi HK II 2014-THPT Văn Lang-TP.HCM)

2ln 2 4



2ln 2



2ln 2



2ln 2

Câu 12: Tính

.cos .

e x dx





? (đề thi HK II 2014-THPT Trần Quang Khải-TP.HCM)

95 KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến









Câu 13: Tính

.cos .

x x dx





















Câu 14: Tính

ln .

x dx





? ( đề thi Đại Học khối A, A1 năm 2013 )

5 3

ln 2

2 2



ln 2

5 3

ln 2

2 2



ln 2



Câu 15: Tính

3 1





5 11

4 4

 B.

5 11

2 2

 C.

5 1

4 4

 D.

Tính các tích phân sau (tách thành 2 tích phân A, B với A: dạng cơ bản và B: tích phân từng phần )

Câu 16: Tính a-b biết:

 

3 1

1 ln .

x x dx

a b

  



Câu 17: Biết

 

1 . 2 .

e c

x e dx



  



. Tính



Câu 18: Tính

 

sinx

x x dx







? ( đề thi thử THPT QG 2015- THPT Chu Văn An- HN)















Câu 19: Tính

 

2 ln .

x x dx





? ( đề minh họa 2015- Bộ GD & ĐT )

ln 2

 B.

2ln 2

 C.

3ln 2

 D.

4ln 2



Tính các tích phân sau ( sử dụng đổi biến trước rồi tính tích phân từng phần sau )

KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 20: Tính

cos .

x dx a



 



Tìm a?

A. 0 B.



Câu 21: Tính

sin .

x dx





. Tìm a

A. 2 B.







Câu 22: Tính

 

sin 2 .ln 1 cos .

x x dx







? (đề thi thử THPT QG 2015-THPT Phan Đình Phùng-HN )

A. -



Câu 23: Tính

. .

x e dx



A. -



Câu 24: Tính

 

3 .

8 2 . .

x x e dx





A. e B. 5-e C. e+4 D. 1

97 KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN TỪNG PHẦN

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

19 C

20 B

21 A

22 A

23 C

6 D 12

18 C 24 B

KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

1. Dạng 1

Giả sử cần tính tích phân

( )

I f x dx





, ta thực hiện các bước sau

Bước 1. Lập bảng xét dấu (BXD) của hàm số f(x) trên đoạn [a; b], giả sử f(x) có BXD:

( )

f x







Bước 2. Tính

1 2

( ) ( ) ( ) ( )

x x

b b

a a x x

I f x dx f x dx f x dx f x dx

   

   

KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI

VÍ DỤ 1. Tính tích phân

3 2

I x x dx



  



Giải

Bảng xét dấu



3 2

x x

 





   

1 2

2 2

3 1

3 2 3 2

I x x dx x x dx



      

 

Vậy

I  .

VÍ DỤ 2. Tính tích phân

5 4cos 4sin

I x xdx



  



99 KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2. Dạng 2

Giả sử cần tính tích phân ( ) ( )

I f x g x dx

   

 



, ta thực hiện

Cách 1.

Tách

( ) ( ) ( ) ( )

b b b

a a a

I f x g x dx f x dx g x dx

     

 

  

rồi sử dụng dạng 1 ở trên.

Cách 2.

Bước 1. Lập bảng xét dấu chung của hàm số f(x) và g(x) trên đoạn [a; b].

Bước 2. Dựa vào bảng xét dấu ta bỏ giá trị tuyệt đối của f(x) và g(x).

ĐS: 2 3 2



  

VÍ DỤ 3. Tính tích phân

 

I x x dx



  



Giải

Cách 1.

 

2 2 2

1 1 1

1 1

I x x dx x dx x dx

  

     

  

0 2 1 2

1 0 1 1

( 1) ( 1)

xdx xdx x dx x dx

 

      

   

1 2

0 2

2 2 2 2

1 0

1 1

2 2 2 2

x x x x

x x



   

       

   

   

100

KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Cách 2.

Bảng xét dấu

x –1 0 1 2

– 0 +



x – 1 – – 0 +

     

0 1 2

1 0 1

1 1 1

I x x dx x x dx x x dx



         

  





0 2

1 1

x x x x



     

Vậy



3. Dạng 3

Để tính các tích phân

 

max ( ), ( )

I f x g x dx





và

 

min ( ), ( )

J f x g x dx





, ta thực hiện các bước sau:

Bước 1. Lập bảng xét dấu hàm số

( ) ( ) ( )

h x f x g x

 

trên đoạn [a; b].

Bước 2.

+ Nếu

( ) 0

h x



thì





max ( ), ( ) ( )

f x g x f x

 và





min ( ), ( ) ( )

f x g x g x

 .

+ Nếu

( ) 0

h x



thì





max ( ), ( ) ( )

f x g x g x

 và





min ( ), ( ) ( )

f x g x f x

 .

101 KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 4. Tính tích phân

 

max 1, 4 2

I x x dx

  



Giải

Đặt









2 2

( ) 1 4 2 4 3

h x x x x x

      

Bảng xét dấu

X 0 1 3 4

h(x) + 0 – 0 +

 

1 3 4

2 2

0 1 3

1 4 2 1

I x dx x dx x dx      

  

Vậy

I  .

VÍ DỤ 5. Tính tích phân

 

min 3 , 4

I x dx

 



Giải

Đặt





( ) 3 4 3 4

x x

h x x x

     

Bảng xét dấu

x 0 1 2

h(x) – 0 +

 

1 2

0 1

3 2 5

3 4 4

ln3 2 ln 3 2

I dx x dx x

 

       

 

 

 

Vậy

2 5

ln3 2

 

102

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ỨNG DỤNG TÍCH PHÂN

1. TÍNH DIỆN TÍCH HÌNH PHẲNG

1.1 Diện tích hình thang cong

Cho hàm số

( )

f x

liên tục trên đoạn [a; b]. Diện tích hình thang cong giới hạn bởi các đường

( ), ,

y f x x a x b

  

và trục hoành là

( )

S f x dx





Phương pháp giải toán

Bước 1. Lập bảng xét dấu hàm số f(x) trên đoạn [a; b].

Bước 2. Dựa vào bảng xét dấu tính tích phân

( )

f x dx



VÍ DỤ 1. Tính diện tích hình phẳng giới hạn bởi ln , 1,

y x x x e

  

và Ox.

Giải





ln 0 1;

x x e

   nên

 

1 1

ln ln ln 1 1

e e

S x dx xdx x x

    

 

Vậy



(đvdt).

VÍ DỤ 2. Tính diện tích hình phẳng giới hạn bởi

4 3, 0, 3

y x x x x

     

và Ox.

Giải

Bảng xét dấu

0 1 3

– 0 + 0

   

1 3

2 2

0 1

4 3 4 3

S x x dx x x dx

        

 

1 3

3 3

2 2

0 1

2 3 2 3

3 3 3

x x

x x x x

   

         

   

   

.(ĐVDT)

103 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

1.2. Diện tích hình phẳng

1.2.1. Trường hợp 1.

Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các

đường ( ), ( ), ,

y f x y g x x a x b

   

là

( ) ( )

S f x g x dx

 



Phương pháp giải toán

Bước 1. Lập bảng xét dấu hàm số

( ) ( )

f x g x



trên đoạn [a; b].

Bước 2. Dựa vào bảng xét dấu tính tích phân

( ) ( )

f x g x dx





1.2.2. Trường hợp 2.

Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các đường

( ), ( )

y f x y g x

 

là

( ) ( )

S f x g x dx





 



. Trong đó

 

là nghiệm nhỏ nhất và lớn nhất của phương

trình

( ) ( )

f x g x







a b

 

  

Phương pháp giải toán

Bước 1. Giải phương trình

( ) ( )

f x g x



Bước 2. Lập bảng xét dấu hàm số

( ) ( )

f x g x



trên đoạn





;

 

Bước 3. Dựa vào bảng xét dấu tính tích phân

( ) ( )

f x g x dx









VÍ DỤ 3. Tính diện tích hình phẳng giới hạn bởi các đường

3 2

11 6, 6

y x x y x

    ,

0, 2

x x

 

Giải

Đặt

3 2 3 2

( ) ( 11 6) 6 6 11 6

h x x x x x x x

       

( ) 0 1 2 3

h x x x x

      

(loại).

104

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bảng xét dấu

0 1 2

h(x)

– 0 + 0

   

1 2

3 2 3 2

0 1

6 11 6 6 11 6

S x x x dx x x x dx

        

 

1 2

4 2 4 2

3 3

0 1

11 11 5

2 6 2 6

4 2 4 2 2

x x x x

   

         

   

   

Vậy



(đvdt).

VÍ DỤ 4. Tính diện tích hình phẳng giới hạn bởi các đường

3 2

11 6, 6

y x x y x

    .

Giải

Đặt

3 2 3 2

( ) ( 11 6) 6 6 11 6

h x x x x x x x

       

( ) 0 1 2 3

h x x x x

      

Bảng xét dấu

1 2 3

h(x)

0 + 0 – 0

   

2 3

3 2 3 2

1 2

6 11 6 6 11 6

S x x x dx x x x dx

       

 

2 3

4 2 4 2

3 3

1 2

11 11 1

2 6 2 6

4 2 4 2 2

x x x x

   

        

   

   

Vậy



(đvdt).

Chú ý:Nếu trong đoạn





;

 

phương trình

( ) ( )

f x g x



không còn nghiệm nào nữa thì ta có thể dùng

công thức

 

( ) ( ) ( ) ( )

f x g x dx f x g x dx

 

 

  

 

105 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ 5.Tính diện tích hình phẳng giới hạn bởi

, 4

y x y x

 

Giải

Ta có

4 2 0 2

x x x x x

       

   

0 2

3 3

2 0

4 4

S x x dx x x dx



    

 

0 2

4 4

2 2

2 0

2 2 8

4 4

x x



   

    

   

   

Vậy



(đvdt).

VÍ DỤ 6. Tính diện tích hình phẳng giới hạn bởi

4 3

y x x

  

và trục hoành.

Giải

Ta có

2 2

4 3 0 4 3 0, 0

x x t t t x

        

1 1

3 3

t x

 

  

 

  



 

  



 





3 3

2 2

3 0

4 3 2 4 3

S x x dx x x dx



      

 

   

1 3

2 2

0 1

2 4 3 4 3

x x dx x x dx

 

     

 

 

 

1 3

3 3

2 2

0 1

2 2 3 2 3

3 3 3

x x

x x x x

 

   

 

      

   

 

   

 

Vậy

S  (đvdt).

VÍ DỤ 7. Tính diện tích hình phẳng giới hạn bởi

4 3

y x x

  

và

y x

 

Giải

Phương trình hoành độ giao điểm

4 3 3

x x x

   

106

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

3 0

4 3 3

x x x

 











 

   













    





Bảng xét dấu

x 0 1 3 5

4 3

x x

 

+ 0 – 0 +

     

1 3 5

2 2 2

0 1 3

5 3 6 5

S x x dx x x dx x x dx

        

  

1 3 5

3 2 3 2 3 2

0 1 3

5 3 5 109

3 2 3 2 3 2 6

x x x x x x

     



       

     

     

Vậy

109

S  (đvdt).

VÍ DỤ 8. Tính diện tích hình phẳng giới hạn bởi

1 , 5

y x y x

   

Giải

Phương trình hoành độ giao điểm

2 2

1 5 1 5, 0

x x t t t x

        

1 5

t x

t t

  



    



  

 











   





 

3 3

2 2

3 0

1 5 2 1 5

S x x dx x x dx



        

 

Bảng xét dấu

x 0 1 3



– 0 +

   

1 3

2 2

0 1

2 4 6

S x x dx x x dx

       

 

107 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

1 3

3 2 3 2

0 1

2 4 6

3 2 3 2 3

x x x x

x x

   



      

   

   

Vậy

S  (đvdt).

Chú ý:

Nếu hình phẳng được giới hạn từ 3 đường trở lên thì vẽ hình (tuy nhiên thi ĐH thì không có).

2. TÍNH THỂ TÍCH KHỐI TRÒN XOAY

2.1. Trường hợp 1.

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường





( ) 0 ;

y f x x a b

    ,



x a



và

( )

x b a b

 

quay quanh trục Ox là

( )

V f x dx







VÍ DỤ 9. Tính thể tích hình cầu do hình tròn

2 2 2

( ) :

C x y R

 

quay quanh Ox.

Giải

Hoành độ giao điểm của (C) và Ox là

2 2

x R x R

   

Phương trình

2 2 2 2 2 2

( ) :

C x y R y R x

    

   

2 2 2 2

R R

V R x dx R x dx

 



    

 

3 3

x R

R x



 

  

 

 

(dvtt)

108

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2. Trường hợp 2.

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường





( ) 0 ;

x g y y c d

    ,



y c



và

( )

y d c d

 

quay quanh trục Oy là

( )

V g y dy







VÍ DỤ 10. Tính thể tích hình khối do ellipse

2 2

( ) : 1

x y

a b

 

quay quanh Oy.

Giải

Tung độ giao điểm của (E) và Oy là

y b

   

Phương trình

2 2 2 2

2 2

2 2 2

( ) : 1

x y a y

E x a

a b b

    

2 2 2 2

2 2

b b

a y a y

V a dy a dy

b b

 



   

    

   

   

 

2 3 2

3 3

a y a b

a y



 

  

 

 

Vậy

a b



 (đvtt).

3. Trường hợp 3.

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường

( ), ( )

y f x y g x

 

x a



và





( , ( ) 0, ( ) 0 ; )

x b a b f x g x x a b

      quay quanh trục Ox là

2 2

( ) ( )

V f x g x dx



 



VÍ DỤ 11. Tính thể tích hình khối do hình phẳng giới hạn bởi các đường

y x



y x



quay quanh Ox.

Giải

Hoành độ giao điểm

x x





















109 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

 

1 1

4 4

0 0

V x x dx x x dx

 

    

 

5 2

1 1 3

5 2 10

x x



 

  

 

 

Vậy



 (đvtt).

(ĐỀ MINH HỌA QUỐC GIA NĂM 2017)

Viết Kí hiệu





là hình phẳng giới hạn bởi đồ thị hàm số





2 1 ,

y x e

  trục tung và trục hoành.

Tính thể tích

của khối tròn xoay thu được khi quay hình





xung quanh trục

4 2 .

V e

 





4 2 .

V e



  C.

V e

 





5 .

V e



 

Ta có

 

1 1

2 2

0 0

2 1 4 2 1 4

x x

V x e dx x x e dx I

  

 

     

 

 

Đặt

 

2 2

2 1

2 1 1

du x

u x x

I x x x e dx

dv e dv

 



  

 

      

 





 





  

Đặt

 

1 1 1

2 2 2

0 0

1 1 3

2 2 2 4 4 4

x x

du dx

u x

e e e

I x e dx

dv e dx





 





        

 











Do vậy



 suy ra





5 .

V e



  Chọn D.

110

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

4. Trường hợp 4.

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường

( ), ( )

x f y x g y

 

y c



và





( , ( ) 0, ( ) 0 ; d )

y d c d f y g y y c      quay quanh trục Oy là

2 2

( ) ( )

V f y g y dy



 



VÍ DỤ 12. Tính thể tích hình khối do hình phẳng giới hạn bởi các đường

x y

  

, 3

x y

 

quay

quanh Oy.

Giải

Tung độ giao điểm

5 3

y y

 



    







 

5 3

V y y dy





     



 

4 2

11 6 16

y y y dy





   



5 3

11 153

3 16

5 3 5

y y





 

    

 

 

Vậy

153



 (đvtt).

111 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

3. BÀI TOÁN CHUYỂN ĐỘNG

Quãng đường đi được từ thời điểm a đến thời điểm b (Mối liên hệ quãng đường và vận tốc):

( )

S v t dt







Mối liên hệ giữa vận tốc v và gia tốc a:

( ) ( ).

v t a t dt





VÍ DỤ 1. Một ô tô đang chạy với vận tốc 20m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động

chậm dần đều với vận tốc





40 20( / )

v t t m s

   ,trong đó t là khoảng thời gian tính bằng giây, kể từ lúc

bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ?

A. 0,2 m. B. 5 m. C. 10 m. D. 20 m.

Giải:

Lấy mốc thời gian là lúc ô tô bắt đầu đạp phanh. Gọi T là thời điểm ô tô dừng. Ta có v(T)=0

0 = -40T+20

 T = 0,5.

Như vậy khoảng thời gian từ lúc đạp phanh đến khi ô tô dừng hẳn là 0.5s. Trong khoảng thời gian 0.5s đó,

ô tô đi được quãng đường là:

0.5

(20 40 ) 5( )

S t dt m



  



Chọn đáp án B.

VÍ DỤ 2. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc





2 2

3 ( / )

a t t t m s

  .

Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu ?

4000

m B.

4300

m C.

1900

m D.

2200

Giải

2 3

(3 ) 3

2 3

t t

v t t dt c

    



112

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Lấy mốc thời gian là lúc bắt đầu tăng tốc

(0) 10



Vận tốc tại thời điểm T

2 3

( ) 3 10

2 3

t t

v T

   

 Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng:

2 3

4300

(3 10) ( )

2 3 3

t t

S dt m

   



Chọn đáp án B

VÍ DỤ 4. Một đám vi trùng ngày thứ t có số lượng là N(t). Biết rằng

 

4000

1 0,5

N t





và lúc đầu đám vi

trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ hang đơn vị):

A. 264.334 con. B. 257.167 con. C. 258.959 con. D. 253.584 con.

Giải

Số vi trùng ở ngày thứ t

N(t) =

4000

8000.ln |1 0,5 |

1 0,5

dt t C

  





Số vi trùng ở thời điểm ban đầu là 250.000

N(0)=

8000.ln |1 0,5.0 |

 

=250000

 C = 2500000

 Số vi khuẩn sau 10 ngày là : N(10) =

8000.ln |1 0,5.10 | 250000 264334

  

(con)

Chọn đáp án A.

113 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TRẮC NGHIỆM ỨNG DỤNG TÍCH PHÂN

Câu 1:(ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Viết công thức tính thể tích

của khối tròn xoay

được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số





y f x

 trục

và hai đường

thẳng





, ,

x a x b a b

   xung quanh trục

 

d .

V f x x







 

d .

V f x x





 

d .

V f x x







 

d .

V f x x





Câu 2. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành

được tính theo công thức nào?

   

V f x g x x

  

 



   

2 2

V f x g x x



 

 

 



   

V f x g x x



  

 



   

V f x g x x



 

 

 



Câu 3. Viết công thức tính thể tích

của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục

tại các điểm





, ,

x a x b a b

   có thiết diện bị cắt bởi mặt phẳng vuông góc với trục

tại điểm có

hoành độ





x a x b

 

là





S x

 

d .

V S x x







 

d .

V S x x







 

d .

V S x x





 

d .

V S x x







Câu 4. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Viết Kí hiệu





là hình phẳng giới hạn bởi đồ thị

hàm số





2 1 ,

y x e

  trục tung và trục hoành. Tính thể tích

của khối tròn xoay thu được khi quay

hình





xung quanh trục

114

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

4 2 .

V e

 





4 2 .

V e



  C.

V e

 





5 .

V e



 

Câu 5. Thể tích của phần vật thể giới hạn bởi hai mặt phẳng



và



, có thiết diện bị cắt bởi mặt

phẳng vuông góc với trục

tại điểm có hoành độ





0 3

x x

 

là một hình chữ nhật có hai kích thước

bằng

và

2 9



, bằng:



. B.

18.



20.



22.



Câu 6. Tính thể tích vật thể nằm giữa hai mặt phẳng có phương trình



và



, biết rằng thiết diện của

vật thể bị cắt bởi mặt phẳng vuông góc với trục

tại điểm có hoành độ





0;2

x là một phần tư đường

tròn bán kính

, ta được kết quả nào sau đây?

32 .





64 .







 D.

8 .





Câu 7. Hình phẳng

giới hạn bởi các đường

y x

 

, trục tung và tiếp tuyến của đồ thị hàm số

y x

 

tại điểm





1;2

, khi quay quanh trục

tạo thành khối tròn xoay có thể tích bằng:



 B.



 C.



 D.





Câu 8. Khối tròn xoay tạo nên khi ta quay quanh trục

hình phẳng

giới hạn bởi đồ thị





: 2

P y x x

 

và trục

sẽ có thể tích là:



 B.



 C.



 D.





Câu 9. Hình phẳng giới hạn bởi đồ thị hai hàm số

y x x

 

và

y x



khi quay quanh trục

tạo thành

khối tròn xoay có thể tích bằng:



 B.



 C.



 D.





Câu 10. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol

y x

 

và

y x

 

quay quanh trục

là kết quả nào sau đây?

10 .





12 .





14 .





16 .





Câu 11. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x



y x



qua

quanh trục hoành bằng bao nhiêu?

115 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

124



 B.

126



 C.

128



 D.

131





Câu 12. Cho hình phẳng





giới hạn bởi các đường

y x

 ,

y x

 

và



. Tính thể tích của khối

tròn xoay tạo thành khi quay hình





quanh trục hoành nhận giá trị nào sau đây:



 B.



 C.



 D.





Câu 13. Thể tích của khối tròn xoay tạo nên khi quay quanh trục

hình phẳng giới hạn bởi





: ln

C y x

 , trục

và đường thẳng

x e



là:





2 .

V e



  B.





1 .

V e



 

V e









1 .

V e



 

Câu 14. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x

 ,

y x

  



quay quanh trục

, có giá trị là kêt quả nào sau đây?



 B.



 C.



 D.





Câu 15. Một vật chuyển động với vận tốc

   

1,2 m/s

v t



 



. Quãng đường vật đó đi được trong 4

giây đầu tiên bằng bao nhiêu ? (Làm tròn kết quả đến hàng phần trăm).

18,82

m. B.

11,81

m. C.

4,06

m. D.

7,28

Câu 16. Bạn Nam ngồi trên máy bay đi du lịch thế giới và vận tốc chuyển động của máy bay là









3 5 m/s

v t t  . Quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 là :

A. 36m. B. 252m. C. 1134m. D. 966m.

Câu 17. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Một ô tô đang chạy với vận tốc 10m/s thì người lái

đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc





5 10

v t t

  

(m/s), trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô

còn di chuyển bao nhiêu mét ?

A. 0,2 m. B. 2 m. C. 10 m. D. 20 m.

Câu 18. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc





a t t t

 

(m/s

). Quãng đường vật

đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu ?

4000

. B.

4300

. C.

1900

. D.

2200

116

ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 19. Một vật chuyển động với vận tốc









m/s

v t , có gia tốc

 

' m/s

v t





. Vận tốc ban đầu của

vật là

6m/s

. Vận tốc của vật sau 10 giây là (làm tròn kết quả đến hàng đơn vị):

14m/s

. B.

13m/s

. C.

11m/s

. D.

12m/s

Câu 20. Một đám vi trùng ngày thứ

có số lượng là





N t

. Biết rằng

 

4000

1 0,5

N t





và lúc đầu đám vi

trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ hang đơn vị):

A. 264.334 con. B. 257.167 con. C. 258.959 con. D. 253.584 con.

Câu 21. Gọi









h t là mực nước ở bồn chứa sau khi bơm nước được

giây. Biết rằng

 

' 8

h t t

 

và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn kết quả

đến hàng phần trăm):

A. 2,33 cm. B. 5,06 cm. C. 2,66 cm. D. 3,33 cm.

Câu 22. Khẳng định nào sau đây đúng ?

A. Nếu





w t

là tốc độ tăng trưởng cân nặng/năm của một đứa trẻ, thì

 

' d

w t t



là sự cân nặng của đứa

trẻ giữa

và

tuổi.

B. Nếu dầu rò rỉ từ một cái thùng với tốc độ





r t

tính bằng galông/phút tại thời gian

, thì

 

120

r t t



biểu thị lượng galông dầu rò rỉ trong

giờ đầu tiên.

C. Nếu





r t

là tốc độ tiêu thụ dầu của thế giới, trong đó

được bằng năm, bắt đầu tại



vào ngày

tháng

năm

2000

và





r t

được tính bằng thùng/năm,

 

r t t



biểu thị số lượng thùng dầu tiêu thụ

từ ngày

tháng

năm

2000

đến ngày

tháng

năm

2017

D. Cả A, B, C đều đúng.

117 ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN TRẮC NGHIỆM ỨNG DỤNG TÍCH PHÂN

CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN

118

KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO

Các bạn chú ý: Khi dùng casio cho nguyên hàm, tích phân. Nhớ phải chuyển hết sang Radian

(qw4)

DẠNG: Tìm nguyên hàm F x  của hàm số f x

PHƯƠNG PHÁP:

Bước 1. Tính f(a) (Với a là 1 giá trị bất kỳ nằm trong TXĐ). Chú ý: Chọn a sao cho kết quả của f(a) thật

xấu.

Bước 2. Tính F’(a) của các đáp án.

Bước 3. So sánh Bước 1 và Bước 2. Nếu giống nhau thì chọn.

VÍ DỤ . (Trích đề minh họa 2017 BGD) Tìm nguyên hàm của hàm số

( ) 2 1.

f x x

 

( ) (2 1) 2 1 .

f x dx x x C

   



( ) (2 1) 2 1 .

f x dx x x C

   



( ) 2 1 .

f x dx x C

   



( ) 2 1 .

f x dx x C

  



Giải

 Bước 1. Chọn a = 2

Tính f(2). Nhập

( ) 2 1.

f x x

 

r2 ’

 Bước 2.

Thử từng đáp án

119 KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Đáp án A. => Không giống Kết quả Bước 1=> LOẠI A

Đáp án B (Giống kết quả bước 1)

 Chọn B

VÍ DỤ Hàm số





ln sin 3cos

F x x x

  là một nguyên hàm của hàm số nào trong các hàm số sau đây:





cos 3sin

f x x x

 

 

cos 3sin

sin 3cos

x x

f x

x x







 

cos 3sin

sin 3cos

x x

f x

x x

 





 

sin 3cos

cos 3sin

x x

f x

x x







 Bước 1:

 Bước 2: Thử từng đáp án

Đáp án A. (Ấn Calc x=1) => Không giống kết quả Bước 1. Loại A

Đáp án B (Ấn Calc x=1) => Giống kết quả Bước 1. Chọn B

120

KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Dạng: Tìm nguyên hàm F(x) của f(x) khi biết ( )

F x M



Phương pháp: Ta nhập:

( ). ( )

f x dx F A





. Với A là 1 số bất kỳ thuộc tập xác định. Thử từng đáp án, đến

khi ra Kết quả là M thì chọn đáp án đó.

VÍ DỤ : Tìm Nguyên hàm F(x) của hàm số: f(x) =

2 2

cos2

sin .cos

x x

. Biết

( )





-2

A. tanx - cotx -2

B. tanx - cotx

C. tanx + cotx -4

D. cotx tanx -2

Giải

 Thử đáp án A: Nhập vào máy tính

2 2

cos 2 1

(tan 2)

sin .cos tan

x x A



  



. Ấn, Calc X=1 (x giá trị gì

cũng được); Calc A=1

r = =

Không bằng -2 => Loại đáp án A

 Thử đáp án B:

r = =

Chọn đáp án B.

121 KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ . Tìm nguyên hàm F(x) của hàm số

3 2

3 3 1

( )

2 1

x x x

f x

x x

  



 

(1)



2 7

( )

2 1 6

F x

  



2 13

( )

2 1 6

F x x

   



2 13

( ) 2

2 1 6

F x x

   



( )

F x x

 



Giải



Thử đáp án A: Nhập vào máy tính

3 2 2

3 3 1 2 7

( )

2 1 2 1 6

x x x A

x x A

  

  



. Ấn Calc A = 0 (A bất

kỳ, các em có thể lấy số khác)

Không bằng

. Loại đáp án A

 Thử đáp án B:

3 2 2

3 3 1 2 13

( )

2 1 2 1 6

x x x A

dx A

x x A

  

   

  



. Ấn Calc A = 0 (A bất kỳ, các em có

thể lấy số khác)

. Chọn đáp án B

122

KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Dạng: Tính tích phân

Ấn nút y Nhập tích phân cần tính.

VÍ DỤ : Tính:

I xdx





A. I = 1 B. I = e C. I = e  1 D. I = 1  e

Nói chung thì cái này Easy rồi nhé ^^!

Dạng: Tìm a, b sao cho ( ).

f x dx A





VÍ DỤ . Tìm a sao cho

2 1 2

x x



 



A. a = 0 B. a=3 C. a=6 D. a=4

Nhập vào như màn hình. Ấn Calc thay từng giá trị các đáp án. Thấy Calc A = 3 thỏa mãn.

Chọn B

VÍ DỤ . Tìm a và b sao cho

1 8

1 2 3







A. a = 3; b = 2 B. a = 2; b =3 C.a=1; b =3 D. a = 0; b = 1

. Ấn Calc A = 2; B = 3. Ta thấy kết quả =

1 8

2 3

. Chọn B.

123 KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

DẠNG: TÍNH DIỆN TÍCH, THỂ TÍCH

Nhập trị tuyệt đối trong máy tính:

VÍ DỤ . Tính diện tích hình phẳng giới hạn bởi ln , 1,

y x x x e

  

và Ox.

Giải

VÍ DỤ . Tính diện tích hình phẳng giới hạn bởi

, 4

y x y x

 

Giải

Ta có

4 2 0 2

x x x x x

       

Lấy giá trị cận là lớn nhất và bé nhất

VÍ DỤ . Tính diện tích hình phẳng giới hạn bởi

4 3

y x x

  

và

y x

 

Giải

Phương trình hoành độ giao điểm

4 3 3

x x x

   

3 0

4 3 3

x x x

 











 

   













    





124

KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ : Tính thể tích hình khối do hình phẳng giới hạn bởi các đường

y x



y x



quay quanh Ox.

Giải

Hoành độ giao điểm

x x





















V x x dx



   



VÍ DỤ . Tính thể tích hình khối do hình phẳng giới hạn bởi các đường

x y

  

, 3

x y

 

quay quanh

Oy.

Giải

Tung độ giao điểm

5 3

y y

 



    







 

153

5 3

V y y dy





      



125 KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Dạng: mối liên hệ giữa a, b,c…

VÍ DỤ : Nguyên hàm của hàm số: y =

cos



 



 

 

là: . tan

a e b x C

 

. Tính a+b

A.2 B. 3 C. 4 D. 5

Lấy 2 cận bất kỳ (Giả sử lấy 0 và 1)

Ta lưu KQ vào biến A.

qJz

Ta có

1 0

. tan1 ( . tan 0)

.( ) (tan1 tan 0)

a e b a e b A

a b CacDapAn

a e e b A

a b CacDapAn



   



 





   





 



 Thử đáp án A:

1 0

.( ) (tan1 tan 0)

a e e b A

a b



   



 



Nghiệm Lẻ => Loại đáp án A

 Thử đáp án B:

1 0

.( ) (tan1 tan 0)

a e e b A

a b



   



 





 Số đẹp. Chọn Đáp án B

126

KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

VÍ DỤ :

2 2

K x e dx





e a



. Tính a+2b

A. 2 B. 3 C. 9 D. 1

Lưu vào biến A

Ta có

e a

A a Ab e



     

Ta giải hệ sau để tìm a và b.

a A b e

a b CacDapAn



   



 



 Thử đáp án A

Số xấu => Loại A

 Thử đáp án B.

Số xấu => Loại B

 Thử đáp án C.

=> Số đẹp. Chọn C

127 PHỤ LỤC: - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

PHỤ LỤC:

A. ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN

Câu 1 :

Hàm số nào dưới đây không là nguyên hàm của hàm số

(2 )

( )

( 1)

x x

f x







x x

 



x x

 



x x

 



Câu 2 :

Cho đồ thị hàm số

( )

y f x



. Diện tích hình phẳng (phần gạch trong hình) là:

0 0

3 4

( ) ( )

f x dx f x dx





 

1 4

3 1

( ) ( )

f x dx f x dx





 

3 4

0 0

( ) ( )

f x dx f x dx





 

( )

f x dx





Câu 3 :

Diện tích hình phẳng giới hạn bởi các đồ thị:

y x x

 

và

y x x

  

có kết quả là:

Câu 4 :

Kết quả nào sai trong các kết quả sao?

1 1

2 5 1 2

10 5.2 .ln 2 5 .ln 5

x x

x x x

dx C

 



  



4 4

3 4

2 1

x x

dx x C

x x



 

  



1 1

2 1

x x

dx x C



  





tan tan

xdx x x C

  



Câu 5 :

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các

128

ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

đường

   

1 x

2 2

y x .e , x 1, x 2 , y 0

quanh trục ox là:

(e )





(e )







Câu 6 :

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các

đường

   

y , y 0 , x 1, x 4

quanh trục ox là:



Câu 7 :

Giá trị của

(1 tan ) .

cos

x dx







bằng:

Câu 8 :

Nếu

( ) 5

f x dx





;

( ) 2

f x dx





, với

a d b

 

thì

( )

f x dx



bằng:



Câu 9 :

Hàm số

( ) ln

f x t tdt





đạt cực đại tại



ln 2



ln 2

ln 4



Câu 10 :

Cho tích phân

sin 3

.sin cos

I e x xdx







. Nếu đổi biến số

sin

t x

 thì

(1 )

I e t dt

 



1 1

0 0

t t

I e dt te dt

 

 

 

 

 

2 (1 )

I e t dt

 



1 1

0 0

t t

I e dt te dt

 

 

 

 

 

Câu 11 :

Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0,





và đồ thị của hai hàm số

y =

cosx, y = sinx là:

129 ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2 2



2 2

Câu 12 :

Diện tích hình phẳng giới hạn bởi các đường

y x



,trục Ox và đường thẳng

x 2



là:

Câu 13 :

Cho hình phẳng





giới hạn bởi các đường

y sin x



;

x 0



;

y 0



và

 

. Thể tích vật th

ể

tròn xoay sinh bởi hình





quay quanh Ox bằng



Câu 14 :

Cho tích phân

1 x

I dx







. Nếu đổi biến số



 thì

t dt

 





t dt







tdt







tdt







Câu 15 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y x x

 

và trục ox và đường thẳ

ng x=1

là:

3 2 2



3 2 1



2 2 1



3 2



Câu 16 :

Tìm nguyên hàm:

( )

x dx





4ln

x x C

 

4ln

x x C

  

4ln

x x C

 

4ln

x x C

 

Câu 17 :

Tích phân

cos sin

x xdx





bằng:

130

ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến



Câu 18 :

Hàm số nào sau đây không là nguyên hàm của hàm số

(2 )

( )

( 1)

x x

f x







x x

 



x x

 



x x

 



Câu 19 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

4 5

y x x

  

và hai tiếp tuyến với đồ thị

hàm số tai A(1;2) và B(4;5) có kết quả dạng

khi đó: a+b bằng

Câu 20 :

Giá trị của tích phân

 

I x 1 ln xdx

 



là:

2ln 2 6



6ln 2 2



2ln 2 6



6ln 2 2



Câu 21 :

Kết quả của





là:

x C

 











x C

  

Câu 22 :

Hàm số

( ) ln sin 3cos

F x x x

 

là một nguyên hàm của hàm số nào trong các hàm số sau

đây:

cos 3sin

( )

sin 3cos

x x

f x

x x







( ) cos 3sin

f x x x

 

cos 3sin

( )

sin 3cos

x x

f x

x x

 





sin 3cos

( )

cos 3sin

x x

f x

x x







Câu 23 :

Giá trị của tích phân

x 2ln x

I dx







là:

131 ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

e 1



e 1



e 1



Câu 24 :

Giả sử

I sin3xsin 2xdx a b



  



, khi đó, giá trị của

a b



là:



Câu 25 :

Tìm nguyên hàm:

( 2 )

x x dx

 



3ln

3 3

x x C

  

3ln

3 3

X x

 

3ln

3 3

x x C

  

3ln

3 3

x x C

  

Câu 26 :

Tìm nguyên hàm:

( 3)

x x 



3 3



3 3

 



1 3



3 3



Câu 27 :

Diện tích hình phẳng giới hạn bởi các đường (P): y=2x

, (C): y=

x1 và Ox là:

3 2 2





2 2





28 



4 2





Câu 28 :

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

x 27

y=x ; y= ; y=

8 x

là:

27ln2-3

27ln2

27ln2+1

Câu 29 :

Tìm nguyên hàm:

(1 sin )

x dx





2 1

2cos sin 2

3 4

x x x C

  

;

2 1

2cos sin 2

3 4

x x x C

  

;

132

ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

2 1

2cos 2 sin 2

3 4

x x x C

  

;

2 1

2cos sin 2

3 4

x x x C

  

;

Câu 30 :

Cho

2 1

I x x dx

 



và

u x

 

. Chọn khẳng định sai trong các khẳng định sau:

I udu





I udu





I 

I u



Câu 31 :

Cho biết

 

f x dx 3





 

g t dt 9





. Giá trị của

   

A f x g x dx

 

 

 



là:

Chưa xác định

được

Câu 32 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y x



và đường thẳng

y x



là:

Câu 33 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y = 2 x - 4x - 6

trục hoành và hai đường

thẳng x=-2 , x=-4 là

Câu 34 :

Giả sử rằng

3x 5x 1 2

I dx a ln b

x 2 3



 

  





. Khi đó, giá trị của

a 2b



là:

Câu 35 :

Kết quả của

xdx



là:

x x x C

 

Đáp án khác

x x C



x x x C

 

Câu 36 :

Tìm nguyên hàm:

( )

x dx





5ln

x x C

 

5ln

x x C

  

133 ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

5ln

x x C

  

5ln

x x C

 

Câu 37 :

Tìm nguyên hàm:

( 3)

x x 



3 3





1 3



3 3



1 3





Câu 38 :

Diện tích hình phẳng giới hạn bởi các đường cong

y x



và

y x



bằng:



Câu 39 :

Cho hai tích phân

sin

xdx





và

cos

xdx





, hãy chỉ ra khẳng định đúng:

2 2

0 0

sin cos

xdx xdx

 



 

Không so sánh được

2 2

0 0

sin cos

xdx xdx

 



 

2 2

0 0

sin = cos

xdx xdx

 

 

Câu 40 :

Cho hai tích phân

sin

I xdx







và

cos

J xdx







. Hãy chỉ ra khẳng định đúng:

I J



I J



I J



Không so sánh

được

Câu 41 :

Hàm số

( )

F x e



là nguyên hàm của hàm số

( ) 2

f x xe



( )

f x e



( )

f x



( ) 1

f x x e

 

Câu 42 :

Tính

ln 2



, kết quả sai là:

134

ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến





2 2 1

 







2 2 1

 

Câu 43 :

Cho tích phân

sin

1 2 cos



 



 



, với





thì

bằng:



Câu 44 :

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

1 , 5

y x y x

   

có kết quả là

Câu 45 :

Nếu

( ) 5

f x dx





( ) 2

f x dx





với a < d < b thì

( )

f x dx



bằng

-2

Câu 46 :

Kết quả nào sai trong các kết quả sao?

tan

1 cos 2 2

dx x

 





2 2

1 1 1

dx x

x x x

 

 

  



ln(ln(ln ))

ln .ln(ln )

x C

x x x

 



ln 3 2

3 2

xdx

x C

   





Câu 47 :

Diện tích hình phẳng giới hạn bởi hai đường cong y = x

– x và

y = x – x

là :

Đáp án khác

Câu 48 :

Tìm nguyên hàm:

( )

x x dx

 



4 3

1 2

2ln

4 3

x x x C

  

4 3

1 2

2ln

4 3

x x x C

  

135 ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

4 3

1 2

2ln

4 3

x x x C

  

4 3

1 2

2ln

4 3

x x x C

  

Câu 49 :

Cho hình phẳng giới hạn bởi các đường

y x

 và

y x



quay xung quanh trục

. Thể

tích

khối tròn xoay tạo thành bằng:





Câu 50 :

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các

đường

x y x

   

y , y 0 ,

quanh trục ox là:



Câu 51 :

Biến đổi

1 1

 



thành

( )

f t dt



, với

t x

 

. Khi đó

( )

f t

là hàm nào trong các hà

số sau?

( ) 2 2

f t t t

 

( )

f t t t

 

( )

f t t t

 

( ) 2 2

f t t t

 

Câu 52 :

Cho

cos

I e xdx







;

sin

J e xdx







và

cos 2

K e xdx







. Khẳng định nào đúng trong các

khẳng định sau?

(I)

I J e



 

(II)

I J K

 

(III)







Chỉ (II)

Chỉ (III)

Chỉ (I)

Chỉ (I) và (II)

Câu 53 :

Hàm số

y tan 2x

 nhận hàm số nào dưới đây là nguyên hàm?

2 tan 2x x



tan 2x x



tan 2x x



tan 2x x



Câu 54 :

Thể tích vật thể tròn xoang khi quay hình phẳng giới hạn bởi đồ thị hàm số

136

ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

y = x

2 2

;

x y



quanh trục ox là



Câu 55 :

Cho

sin cos

I x xdx



 



. Khi đó

bằng:

Câu 56 :

Tìm nguyên hàm:

3 2

(2 )

e dx





3 6

4 1

3 6

x x

x e e C

  

3 6

4 5

3 6

x x

x e e C

  

3 6

4 1

3 6

x x

x e e C

  

3 6

4 1

3 6

x x

x e e C

  

Câu 57 :

Giả sử

2 1







. Giá trị của

là:

Câu 58 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y = x + 11x - 6,

y = 6x

, 0, 2

x x

 

có

kết quả dạng

khi đó a-b bằng

-3

Câu 59 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y = -x + 4x

và các tiếp tuyến với đồ thị

hàm số biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng

khi đó a-b bằng

-5

Câu 60 :

Diện tích hình phẳng giới hạn bởi (C): y=



+3x



2, d

:y = x



1 và d

:y=



x+2 có kết quả là

137 ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 61 :

Diện tích hình phẳng giới hạn bởi đường cong y = x

+ 1, tiếp tuyến với đường này tại điể

M(2; 5) và trục Oy là:

Câu 62 :

Giá trị của

I x.e dx







là:



2e 1



Câu 63 :

Tính





, kết quả là:



2 1

x C

  





C x



Câu 64 :

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

y =

( 1)

e x



và

(1 )

y e x

 

là:



Câu 65 :

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

2 3

y x x

   

và trục hoành là:

125

Câu 66 :

Diện tích hình phẳng giới hạn bởi đường thẳng

y x

 

và patabol

y  bằng:

138

ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Câu 67 :

Diện tích hình phẳng giới hạn bởi các đồ thị:

4 3

y x x

  

và y=x+3 có kết quả là:

205

109

126

Câu 68 :

Tìm nguyên hàm:

( 2 )

x x dx

 



3 1

2sinx sin 2

2 4

x x C

  

3 1

2sinx- sin 2

2 4

x x C

 

3 1

2cos x sin 2

2 4

x x C

  

3 1

2sinx sin 2

2 4

x x C

  

Câu 69. Gọi









h t

là mực nước ở bồn chứa sau khi bơm nước được

giây. Biết rằng

 

' 8

h t t

 

và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn kết quả

đến hàng phần trăm):

A. 2,33 cm. B. 5,06 cm. C. 2,66 cm. D. 3,33 cm.

Câu 70. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động

chậm dần đều với vận tốc





5 10

v t t

  

(m/s), trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt

đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ?

A. 0,2 m. B. 2 m. C. 10 m. D. 20 m.

139 ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

ĐÁP ÁN ĐỀ TỔNG HỢP

140

B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY

Bài 1. (THPT QG 2016): Tính tích phân I=

3 ( 16)

x x x dx

 



ĐS: I = 88

Bài 2. (THPT QG 2015): Tính tích phân:

( 3)

x e dx





ĐS: I = 4-3e

Bài 3. (ĐH A2014): Tính diện tích hình phẳng giới hạn bởi:

y x x

  

và

2 1

y x

 

ĐS: I = 1/6

Bài 4. (ĐH B2014) : Tính tích phân :

3 1

x x

I dx

x x

 







ĐS :

1 ln 3

 

Bài 5. (ĐH D2014) : Tính tích phân :

 

1 sin 2

I x xdx



 



ĐS :



Bài 6. (ĐH A2013) : Tính tích phân :

I x dx







ĐS :

5 3

ln 2

2 2

 

Bài 7. (ĐH B2013) : Tính tích phân :

I x x dx

 



ĐS :

2 2 1





Bài 8. (ĐH D2013) : Tính tích phân :

( 1)

I dx









ĐS :

1 ln 2

 

Bài 9. (ĐH A2012) : Tính tích phân :

141 B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY -

http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

1 ln( 1)

I dx

 





ĐS :

2 2

n 3 ln 2

3 3

I l  

Bài 10. (ĐH B2012) : Tính tích phân :

4 2

3 2

I dx

x x



 



ĐS :

n 3 ln 2

I l 

Bài 11. (ĐH D2012) : Tính tích phân :

(1 sin 2 )

I x x dx



 



ĐS :

32 4



 

Bài 12. (ĐH A2011) : Tính tích phân :

sin ( 1) cos

sin cos

x x x x

I dx

x x x



 







ĐS :

n 1

4 2 4

I l

 

 

  

 

 

Bài 13. (ĐH B2011) : Tính tích phân :

1 sin

x x

I dx

c x









ĐS :





3 n 2 3

I l



   

Bài 14. (ĐH D2011) : Tính tích phân :

4 1

2 1 2

I dx





 



ĐS :

34 3

10 n

3 5

I l

 

 

 

 

Bài 15. (ĐH A2010) : Tính tích phân :

2 2

2 1

x x

x e x e

I dx

 







ĐS :

1 1 1 2

3 2 3

I l



 

Bài 16. (ĐH B2010) : Tính tích phân :

(ln 2)

I dx

x x







ĐS :

1 3

3 2

I l

  

142

B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY -

http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

Bài 17. (ĐH D2010) : Tính tích phân :

(2 )ln

I x xdx

 



ĐS :

 

Bài 18. (ĐH A2009) : Tính tích phân :

3 2

( os 1) os

I c c xdx



 



ĐS :

15 4



 

Bài 19. (ĐH B2009) : Tính tích phân :

3 ln

( 1)

I dx









ĐS :

1 27

(3 ln )

4 16

I  

Bài 20. (ĐH D2009) : Tính tích phân :







ĐS :

ln( 1) 2

I e e

   

Bài 21. (ĐH A2008) : Tính tích phân :

tan

os2

I dx

c x







. ĐS :

1 10

ln(2 3)

9 3

I   

Bài 22. (ĐH B2008) : Tính tích phân :

sin( )

sin2 2(1 sinx cos )

x dx

I dx

x x







  



. ĐS :

4 3 2





Bài 23. (ĐH D2008) : Tính tích phân :

I dx





ĐS :

3 2ln 2





Bài 24. (ĐH A2007) : Tính diện tích hình phẳng giới hạn bởi các đường:

143 B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY -

http://hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

( 1)

y e x

 

(1 )

y e x

  . ĐS :

 

Bài 25. (ĐH B2007) : Cho hình phẳng H giới hạn bởi các đường .

y x x



x e



. Tính thể

tích của khối tròn xoay tọa thành khi quay hình H quanh trục Ox.

ĐS :

(5 2)







Bài 26. (ĐH D2007) : Tính tích phân :

3 2

I x xdx





. ĐS :

5 1





Bài 27. (ĐH A2006) : Tính tích phân :

2 2

sin 2

os 4sin

I dx

c x x









ĐS :



Bài 28. (ĐH B2006) : Tính tích phân :

ln5

ln3

2 3

x x

e e





 



ĐS :

I 

Bài 29. (ĐH D2006) : Tính tích phân :

( 2) .

I x e dx

 



ĐS :

5 3





144

TÀI LIỆU THAM KHẢO - http://Hoc24h.vn

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến

TÀI LIỆU THAM KHẢO

1. Giải tích 12 Nâng Cao (Nhà xuất bản giáo dục)

2. Sách Bài tập Giải tích 12 (Nhà xuất bản giáo dục)

3. Câu hỏi và bài tập trắc nghiệm Toán 12 – Nguyễn Phú Khánh – Huỳnh Đức

Khánh. (Nhà xuất bản ĐHQG Hà Nội)

4. Tuyển tập các chuyên đề và kỳ thuật tính Tích Phân – Trần Phương (Nhà xuất

bản ĐHQG Hà Nội)

5. Group Toán - http://nhomtoan.net/

Bấm Tải xuống để xem toàn bộ.

| 1/145

| | Tải xuống

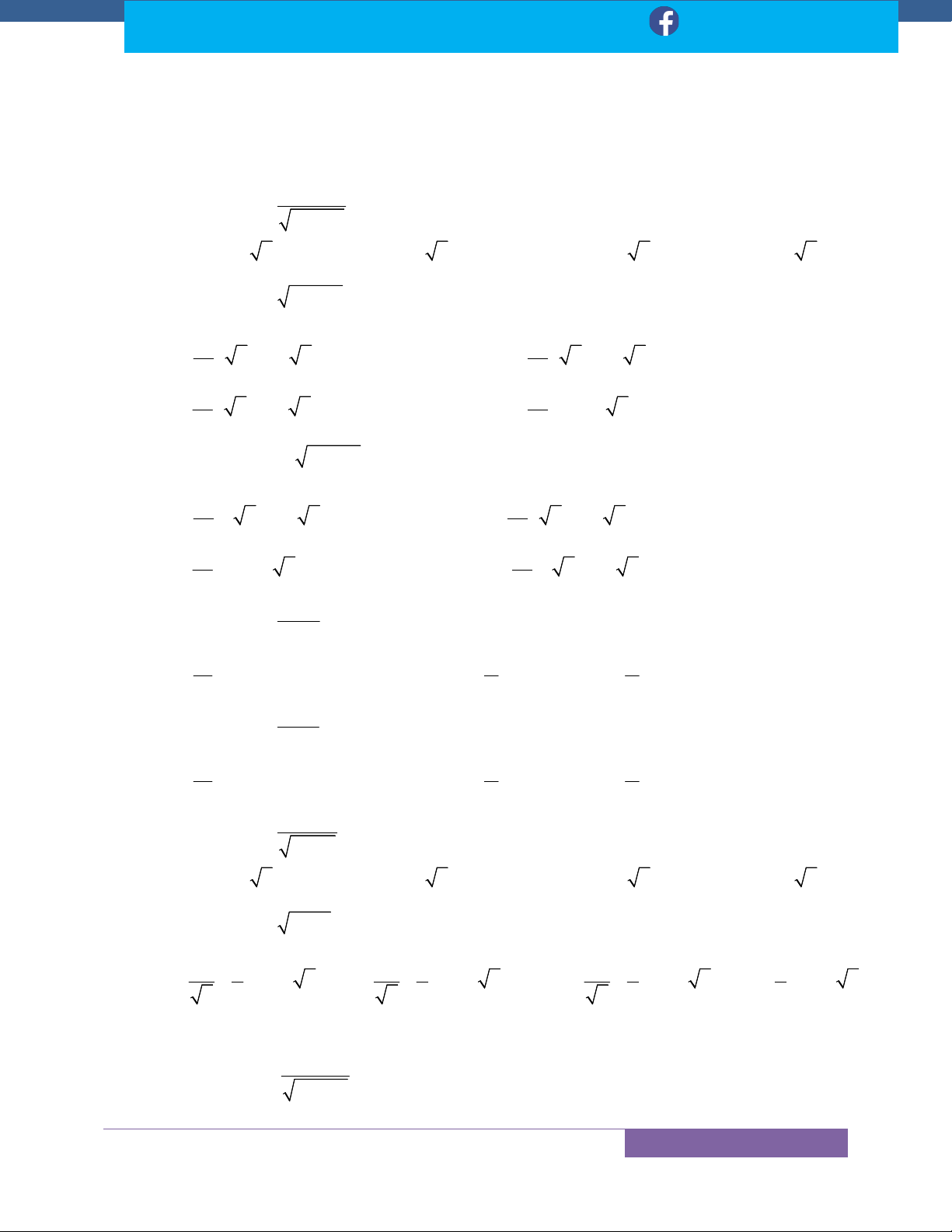
Preview text:

8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến LỜI NÓI ĐẦU
Khi các em cầm trên tay cuốn sách này tức là các em đang rất quan tâm đến việc học của
mình, chúc mừng tinh thần học tập đó của em!
Có thể em chưa biết, tích phân là một mảng rất rộng và bao hàm nhiều dạng bài và
phương pháp xử lý khác nhau. Đặc biệt khi lên đại học, những nghành liên quan đến kỹ thuật,
chúng ta sẽ tiếp cận Nguyên Hàm – Tích Phân ở mức độ cao hơn.
Tuy nhiên trong khuôn khổ kỳ thi THPT Quốc gia 2017, thầy đã chắt lọc cho các em trong cuốn sách này:
 Đầy đủ những phương pháp chắc chắn có trong đề thi, bám sát cấu trúc đề của Bộ Giáo Dục
 Nhiều ví dụ đa dạng và giải chi tiết theo hướng Step by Step (từng bước), dù là học sinh
mất gốc vẫn có thể sử dụng cuốn sách này.
 Đề trắc nghiệm theo mọi hướng để các em tiếp cận được rộng nhất.
 Kết hợp các phương pháp sử dụng máy tính Casio, Vinacal.
Thầy tự tin khẳng định rằng, khi các em sử dụng thành thạo 8 kỹ thuật trong cuốn sách này,
việc đạt điểm tối đa chuyên đề Nguyên Hàm – Tích Phân là cực kỳ đơn giản! Cách sử dụng sách
Bước 1: Đọc kỹ và hiểu phương pháp.
Bước 2: Đọc ví dụ rồi đóng sách làm lại
Bước 3: Làm đề trắc nghiệm bên cạnh đồng hồ (Cố làm nhanh nhất có thể).
Chú ý: Không được đọc phần bấm máy trước! Hãy nhuần nhuyễn giải tay trước, vì nhiều bài
có khả năng bấm máy lâu hơn tính tay rất nhiều.
Mặc dù thầy đã cố gắng hết sức, nhưng không tránh khỏi sai sót, mong các em đóng góp ý kiến chân thành. Giáo viên Nguyễn Tiến Đạt
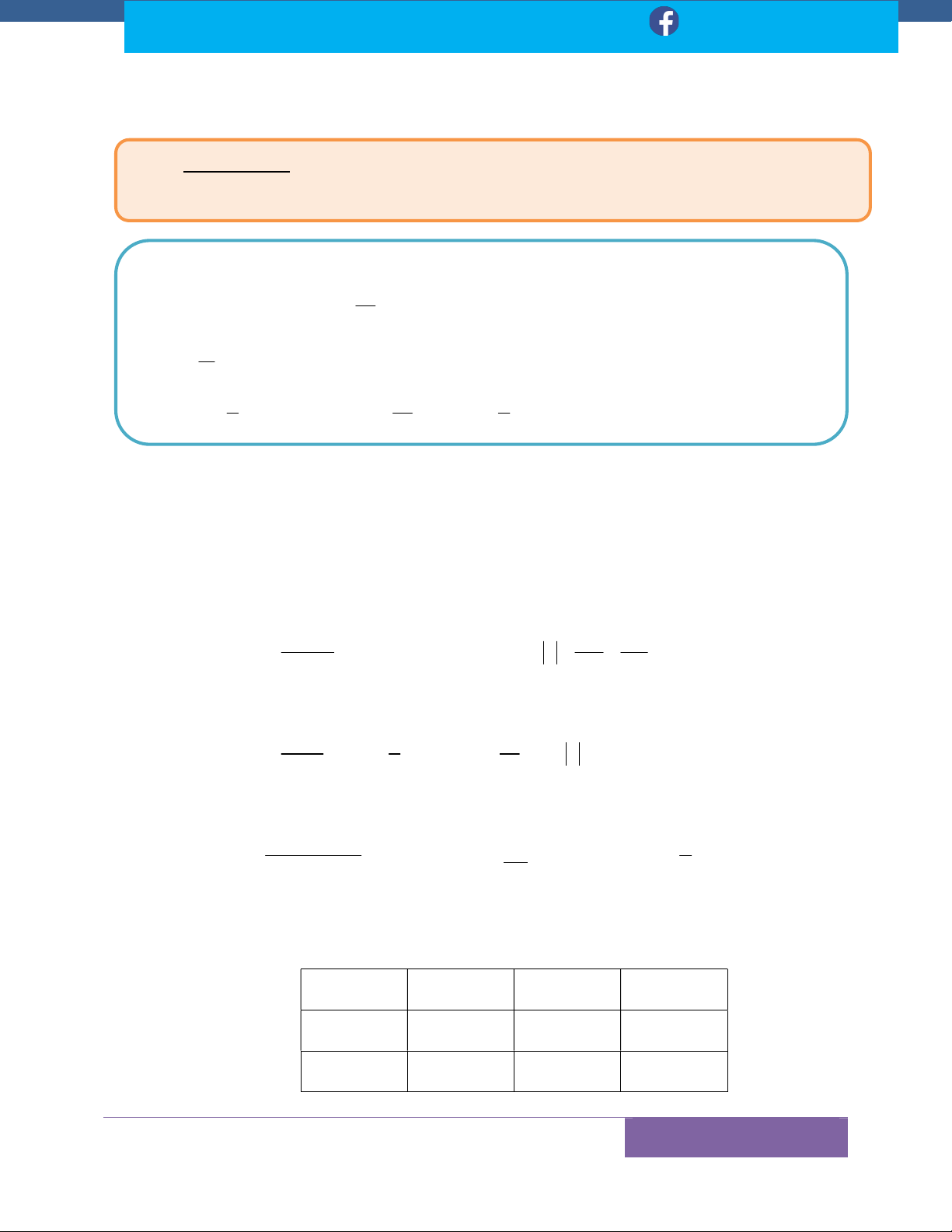
Mọi góp ý gửi về: “Trung tâm luyện thi Đại Học Tiến Đạt”
 Số 8 ngõ 17 Tạ Quang Bửu, HBT, Hà Nội | Liên hệ: 090.32888.66
Email: tiendatnguyen2510@gmail.com | Facebook: Đạt Nguyễn Tiến
“Tri thức không vô tình mà đạt được. Chúng ta phải tìm kiếm nó với sự nhiệt tình và đạt
được nó bằng sự chăm chỉ.”
http://hoc24h.vn - LỜI NÓI ĐẦU 1
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến MỤC LỤC
Nguyên Hàm .................................................................................................................................. 5
A. Định Nghĩa Và Tính Chất ...................................................................................................... 5
B. Bảng Các Nguyên Hàm, Đạo Hàm Cơ Bản ........................................................................... 6
Trắc Nghiệm Lý Thuyết .............................................................................................................. 8
Đáp Án Trắc Nghiệm Lý Thuyết .............................................................................................. 11
Kỹ Thuật 1: Sử Dung Bảng Nguyên Hàm Cơ Bản ..................................................................... 12
Trắc Nghiệm Kỹ Thuật 1 – Dạng 1 ........................................................................................... 13
Đáp Án Trắc Nghiệm Kỹ Thuật 1 – Dạng 1 ............................................................................. 14
Trắc Nghiệm Kỹ Thuật 1 – Dạng 2 ........................................................................................... 15
Đáp Án Trắc Nghiệm Kỹ Thuật 1 – Dạng 2 ............................................................................. 15
Kỹ Thuật 2: Tính Nguyên Hàm Của Hàm Số Hữu Tỷ ............................................................... 16
Trắc Nghiệm Kỹ Thuật 2 .......................................................................................................... 22
Đáp Án Trắc Nghiệm Kỹ Thuật 2 ............................................................................................. 23
Kỹ Thuật 3: Đổi Biến Dạng 1 ..................................................................................................... 24
1. Các Dạng Đổi Biến Số Thường Gặp ..................................................................................... 24
Trắc Nghiệm Đổi Biến Số Dạng 1 ............................................................................................ 26
Đáp Án Trắc Nghiệm Đổi Biến Dạng 1 .................................................................................... 28
Tích Phân ..................................................................................................................................... 30
Trắc Nghiệm Lý Thuyết Tích Phân........................................................................................... 31
Đáp Án Trắc Nghiệm Lý Thuyết Tích Phân ............................................................................. 33
Tích Phân Đổi Biến Dạng 1 .......................................................................................................... 37
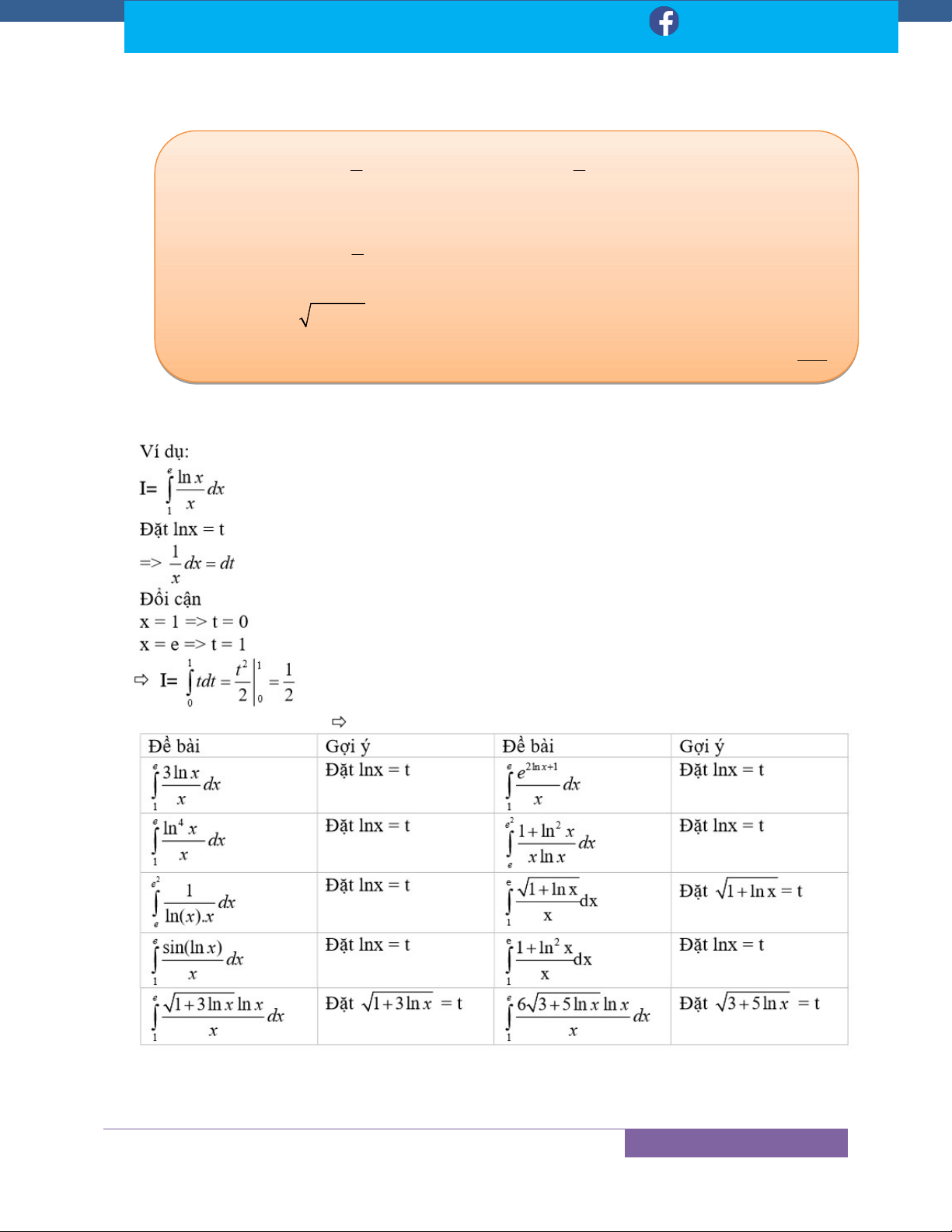
I  f (ax b)n xdx  t  ax b  dt  a.dx 1     x m n Dạng n I  dx t x 1 dt (n 1) n
x .dx ................................... 37 2  n 1     1        ax   1  I  2
f (ax b)n  xdx  t  2 ax b  dt   2ax.dx  3 
Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P1) ........................................................................ 43
Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P1) ........................................................... 45
Dạng: ......................................................................................................................................... 46
Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P2) ........................................................................ 47
Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P2) ........................................................... 48 2
LỜI NÓI ĐẦU - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
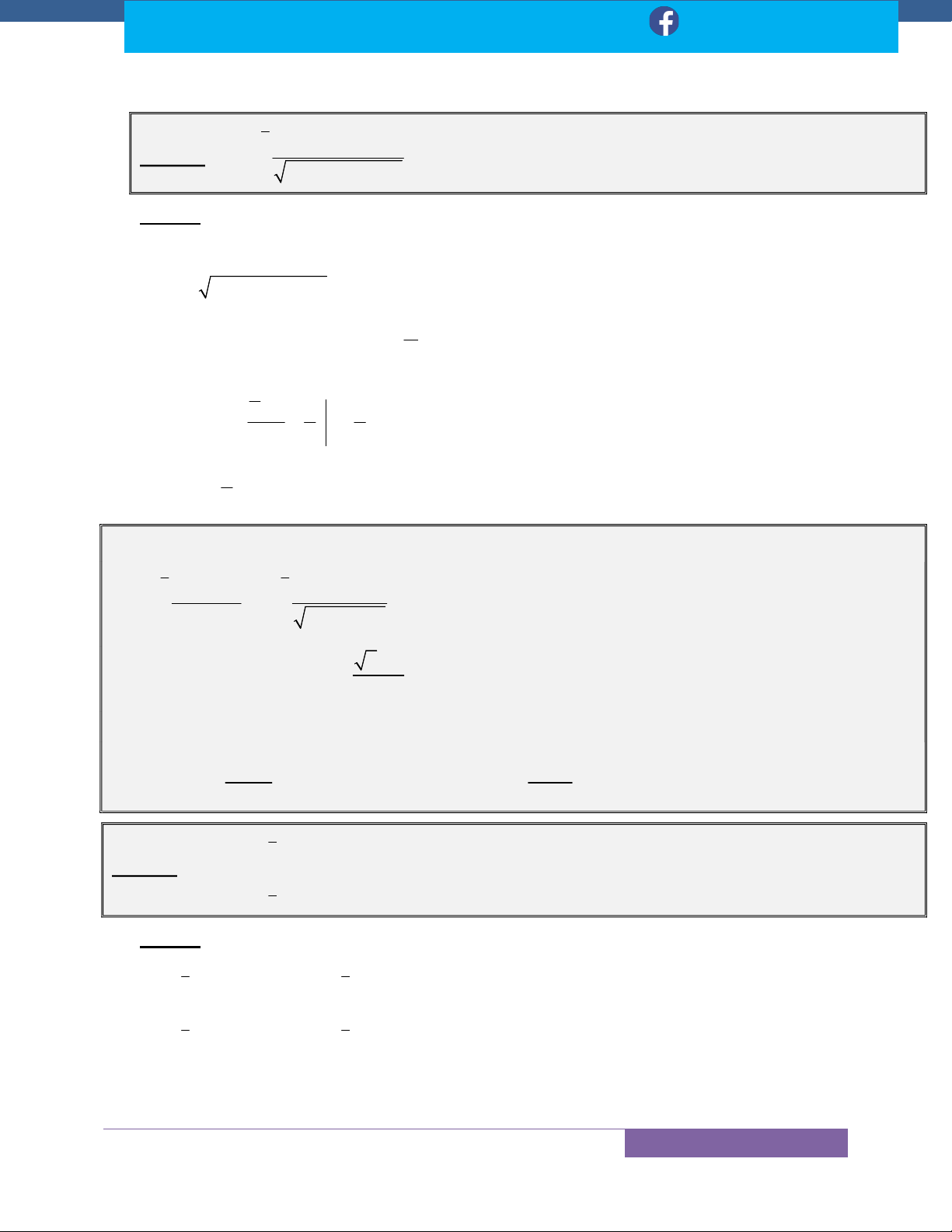
Dạng .......................................................................................................................................... 49 b 1
Trắc Nghiệm Dạng I  f (ln x)   dx 
.................................................................................... 50 x a b 1
Đáp Án Trắc Nghiệm Dạng I  f (ln x)   dx 
...................................................................... 51 x a
Kỹ Thuật 4: Tích Phân Lượng Giác ............................................................................................ 51
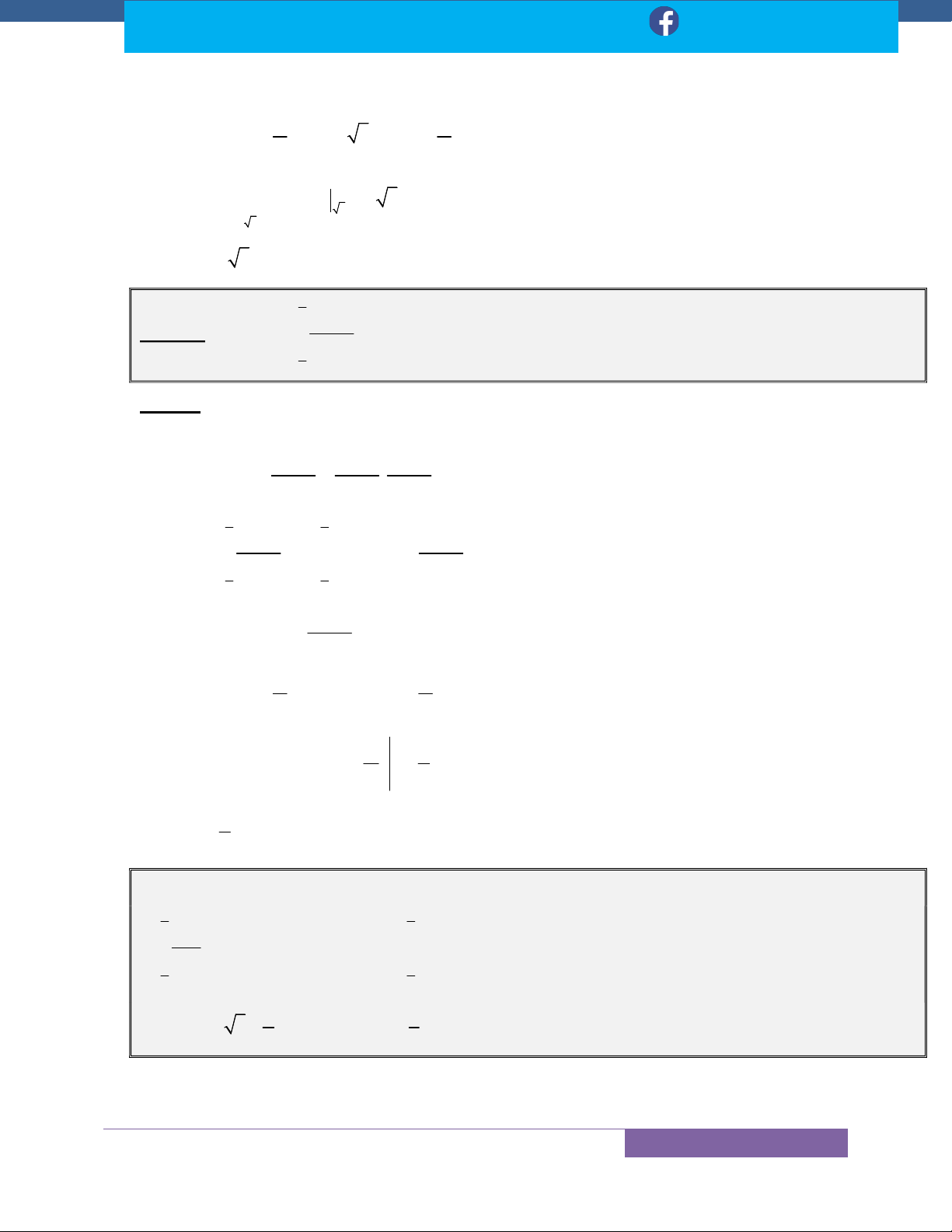
1.Công Thức Lượng Giác Thường Sử Dụng: ........................................................................... 51
Dạng 4.1. Sử Dụng Công Thức Nguyên Hàm Cơ Bản ............................................................. 53
Dạng 4.2: Dùng Công Thức Hạ Bậc ......................................................................................... 55
Dạng 4.3: Dùng Công Thức Biến Đổi Tích Thành Tổng .......................................................... 57
Dạng 4.4: Đổi Biến Số .............................................................................................................. 59
Dạng 4.4.1. Kết Hợp 1 Trong 4 Dạng A,B,C,D Với D(Sinx)=Cosx, D(Cosx)=-Sinx .......... 59
Dạng 4.4.2. Kết Hợp 1 Trong 4 Dạng A,B,C,D Và d  2 x  xdx d  2 sin sin 2 ;
cos x  sin 2xdx ......................................................................... 66
Dạng 4.4.3 Kết Hợp 1 Trong 4 Dạng A,B,C,D Và............................................................... 67 1 d  x 1 tan  dx   2
1 tan x dx ; d cot x   dx    2
1 cot x dx ................. 67 2  2  cos x sin x
Dạng 4.4.4 Kết Hợp 1 Trong 4 Dạng A,B,C,D Và d sin x  cos x  cos x  sin x dx ..... 70
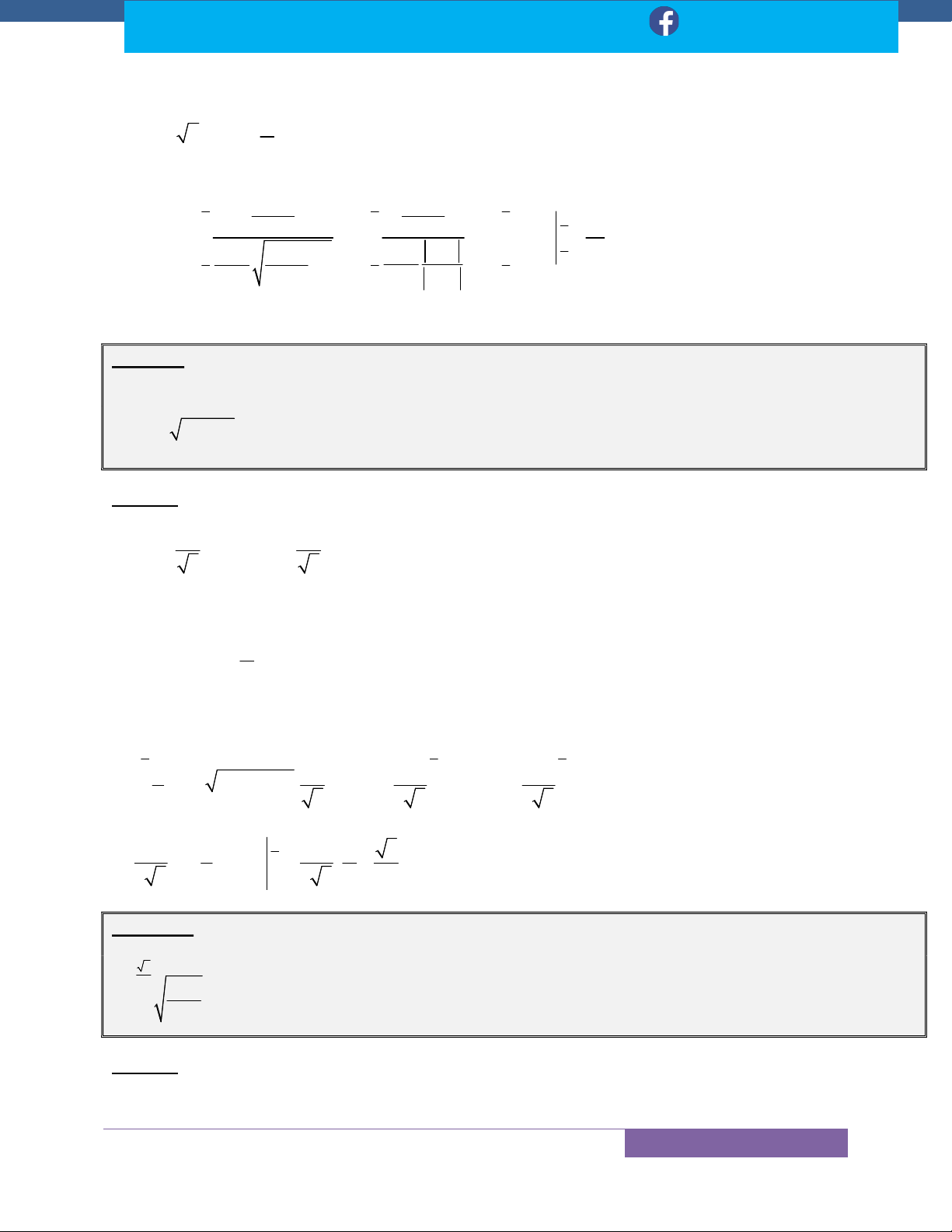
Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P3) ........................................................................ 72
Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 1 (P3) ........................................................... 75
Kỹ Thuật 5: Đổi Biến Số Dạng 2 ................................................................................................ 76
Trắc Nghiệm Tích Phân Đổi Biến Dạng 2 ................................................................................ 85
Đáp Án Trắc Nghiệm Tích Phân Đổi Biến Dạng 2................................................................... 86
Kỹ Thuật 6: Tích Phân Từng Phần .............................................................................................. 87
Trắc Nghiệm Tích Phân Từng Phần .......................................................................................... 93
Đáp Án Trắc Nghiệm Tích Phân Từng Phần ............................................................................ 97
Kỹ Thuật 7: Tích Phân Chứa Giá Trị Tuyệt Đối ......................................................................... 98
Ứng Dụng Tích Phân .................................................................................................................. 102
1. Tính Diện Tích Hình Phẳng ................................................................................................ 102
1.1 Diện Tích Hình Thang Cong ......................................................................................... 102
1.2. Diện Tích Hình Phẳng .................................................................................................. 103
http://hoc24h.vn - LỜI NÓI ĐẦU 3
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
2. Tính Thể Tích Khối Tròn Xoay .......................................................................................... 107
3. Bài Toán Chuyển Động ....................................................................................................... 111
Trắc Nghiệm Ứng Dụng Tích Phân ........................................................................................ 113
Đáp Án Trắc Nghiệm Ứng Dụng Tích Phân ........................................................................... 117
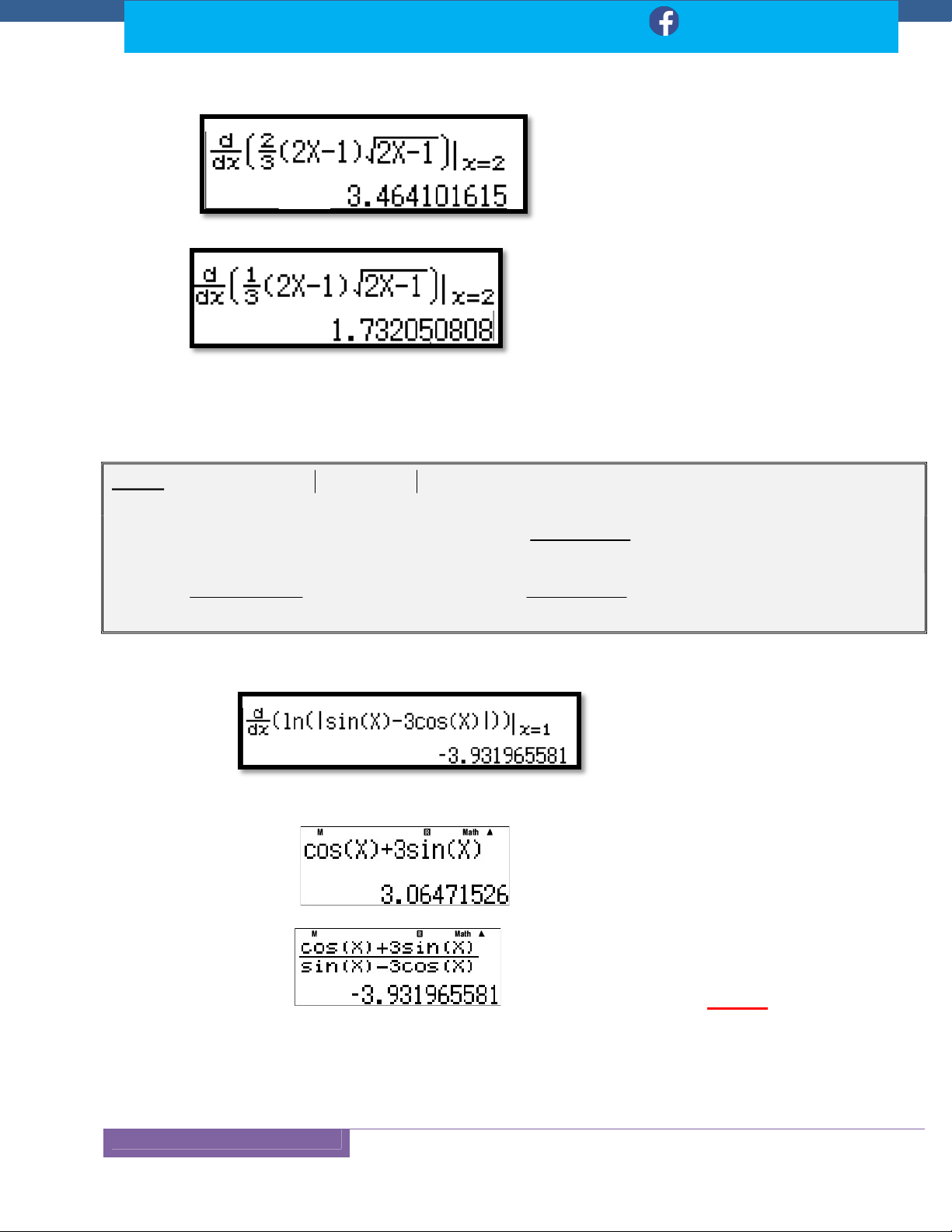
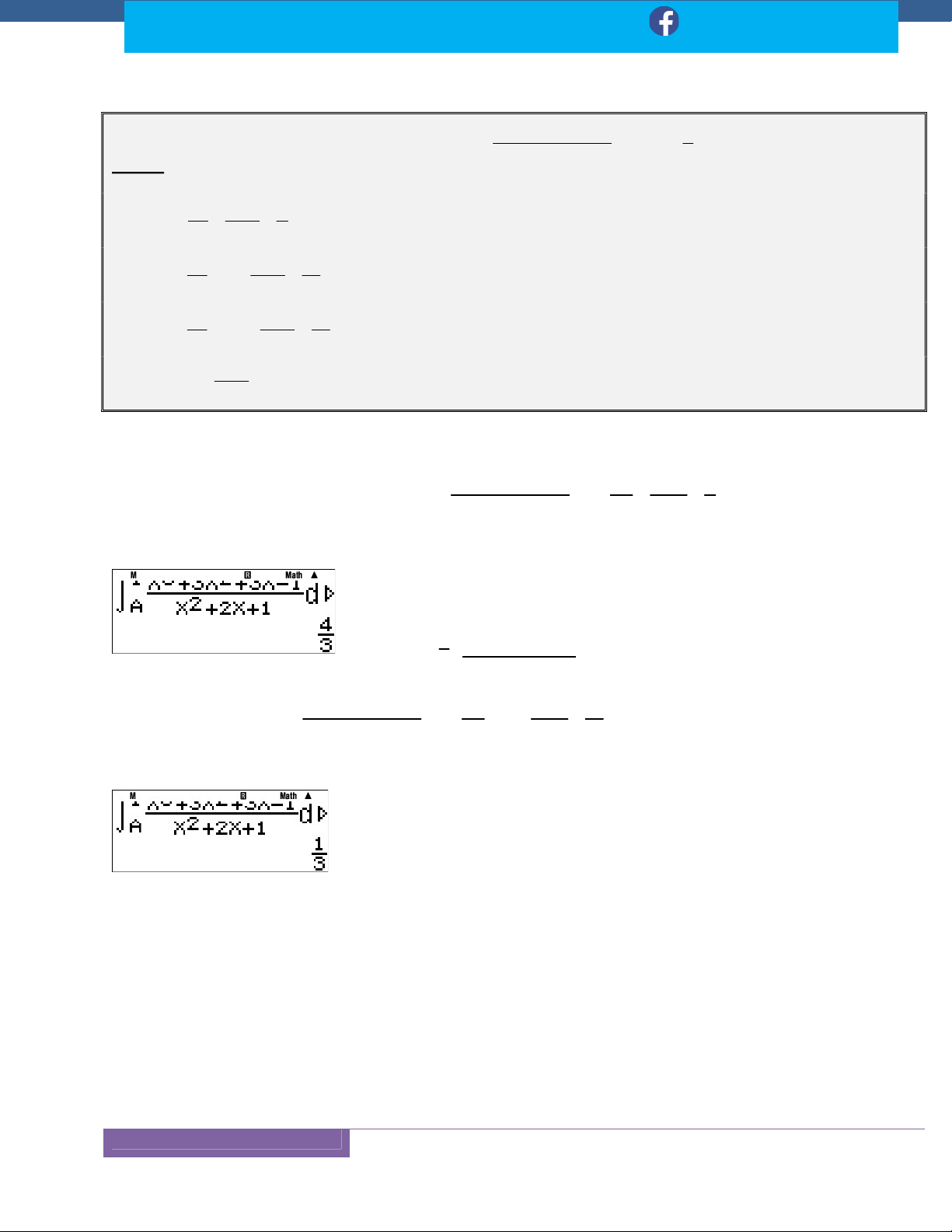
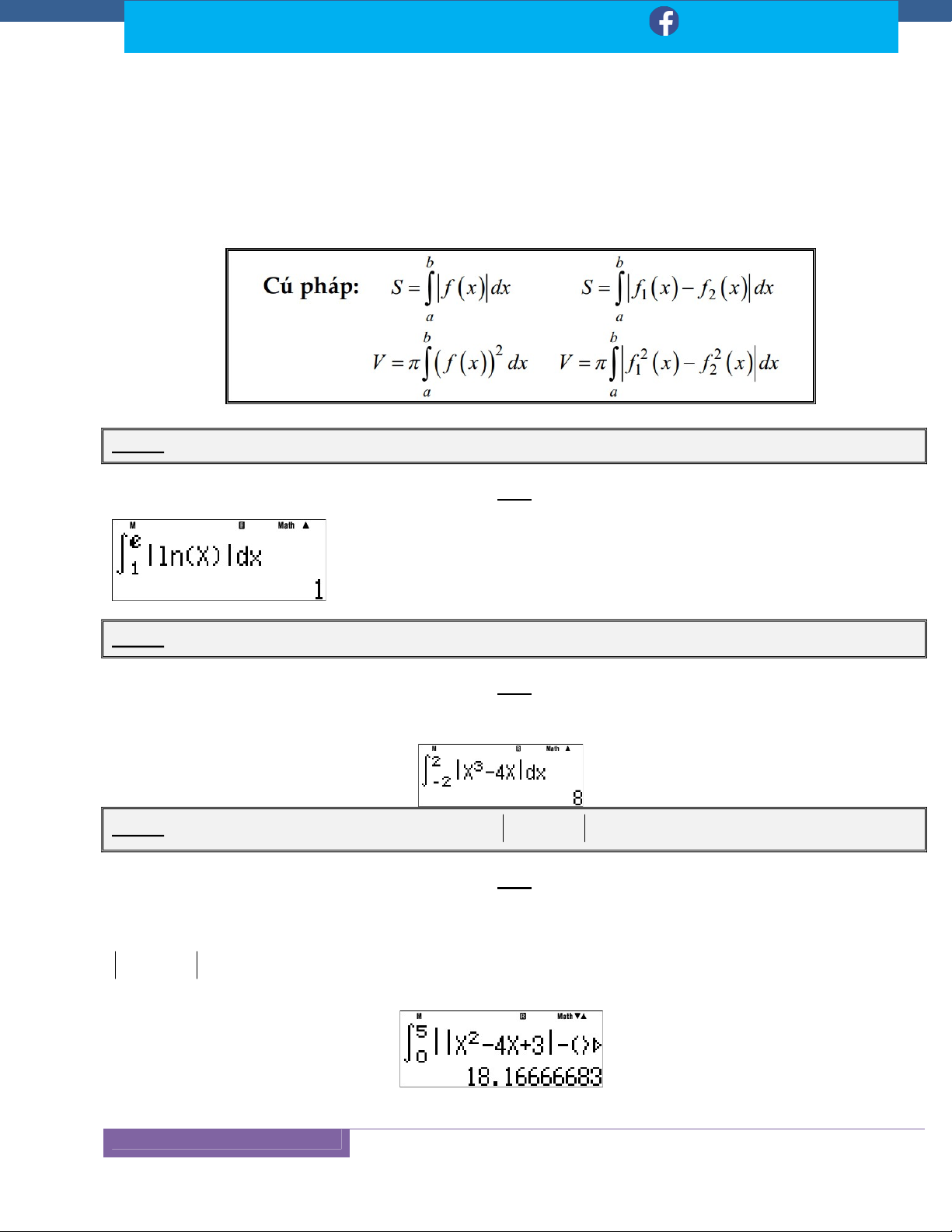
Kỹ Thuật 8: Sử Dụng Máy Tính Casio ..................................................................................... 118
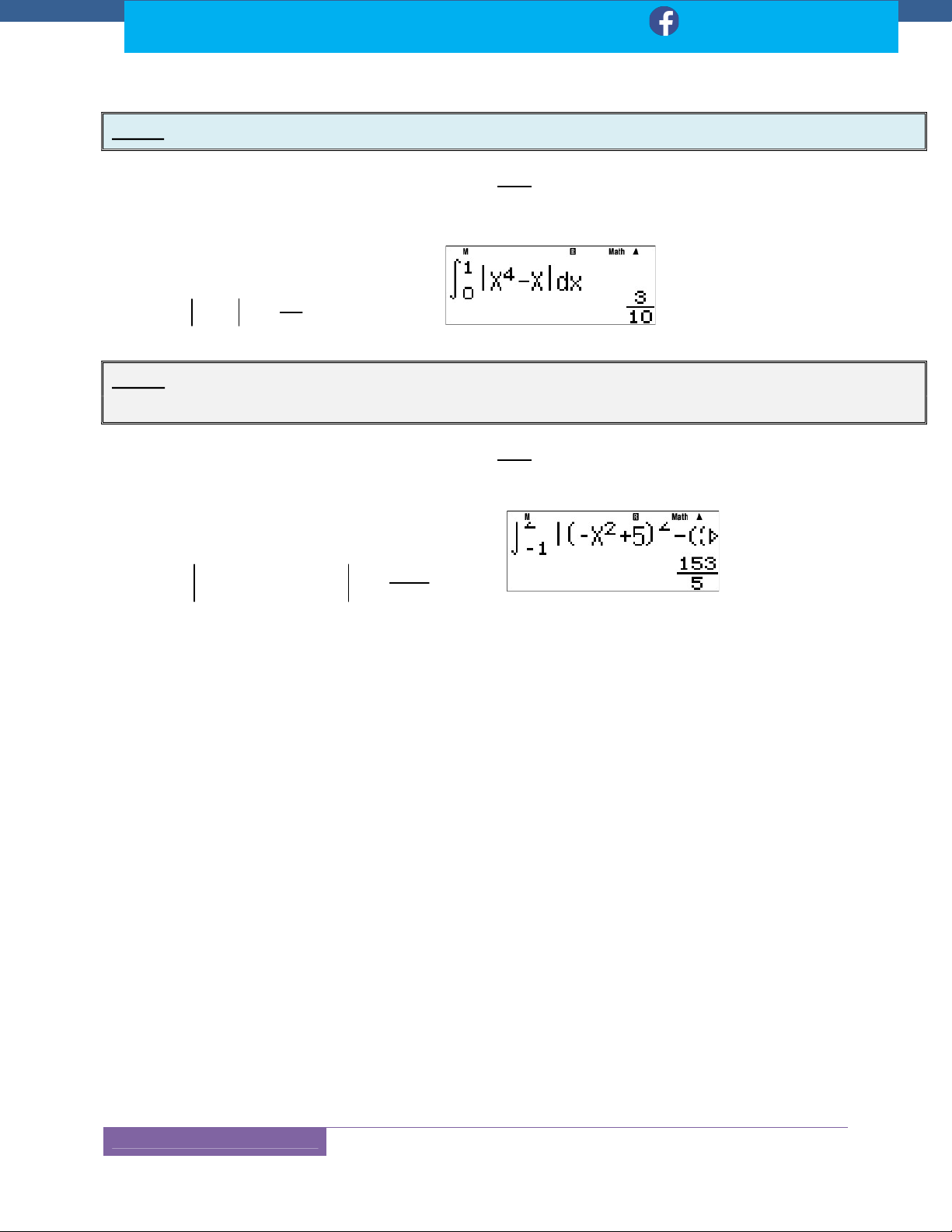
Dạng: Tìm Nguyên Hàm F X  Của Hàm Số F X ............................................................... 118
Dạng: Tìm Nguyên Hàm F(X) Của F(X) Khi Biết F (x )  M ............................................. 120 o
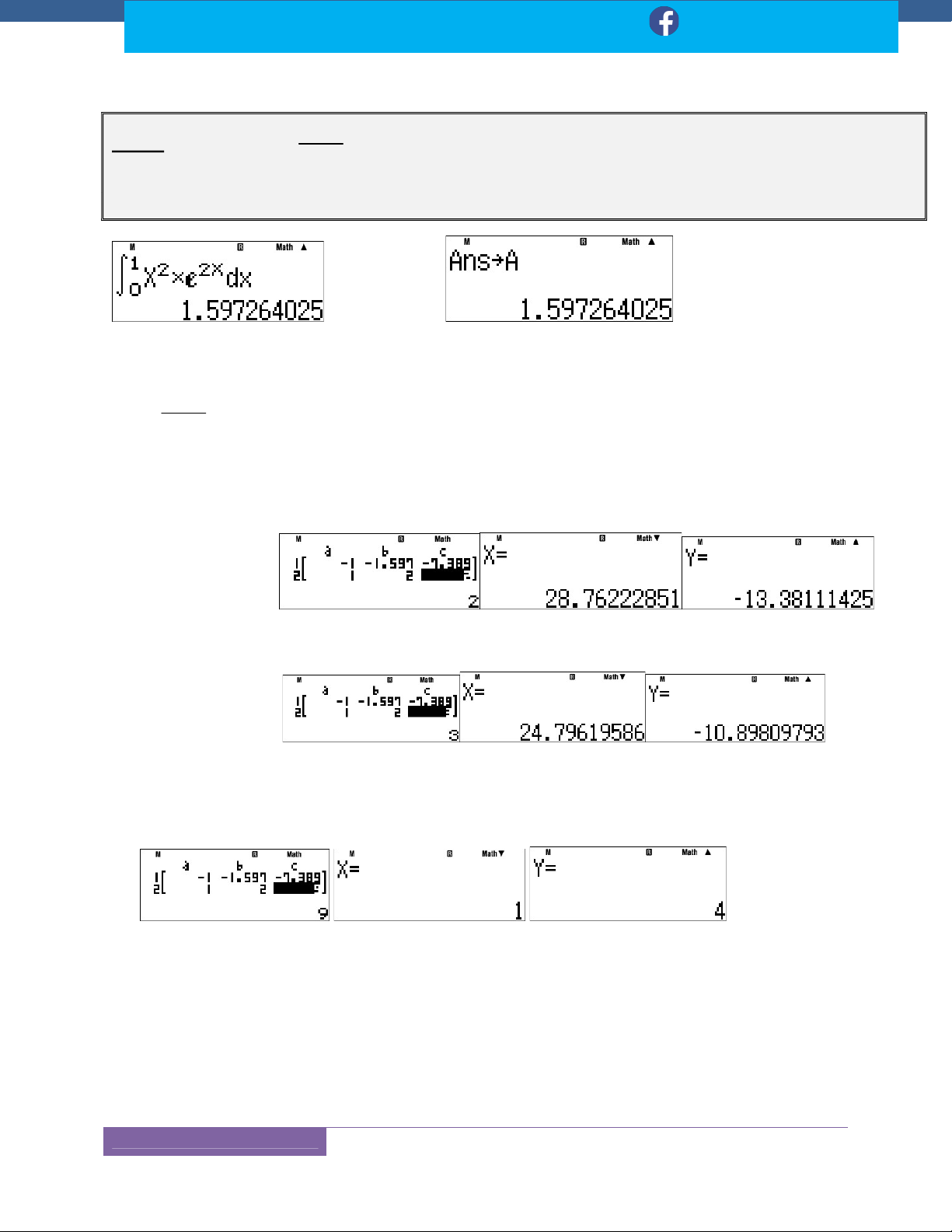
Dạng: Tính Tích Phân ............................................................................................................. 122 a
Dạng: Tìm A, B Sao Cho f (x).dx  A 
................................................................................. 122 b
Dạng: Tính Diện Tích, Thể Tích ............................................................................................. 123
Dạng: Mối Liên Hệ Giữa A, B,C… ........................................................................................ 125
Phụ Lục: ..................................................................................................................................... 127
A. Đề Tổng Hợp Nguyên Hàm – Tích Phân ............................................................................ 127
Đáp Án Đề Tổng Hợp ............................................................................................................. 139
B .Tích Phân Trong Đề Thi Đại Học 10 Năm Gần Đây ............................................................. 140 4
LỜI NÓI ĐẦU - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến NGUYÊN HÀM
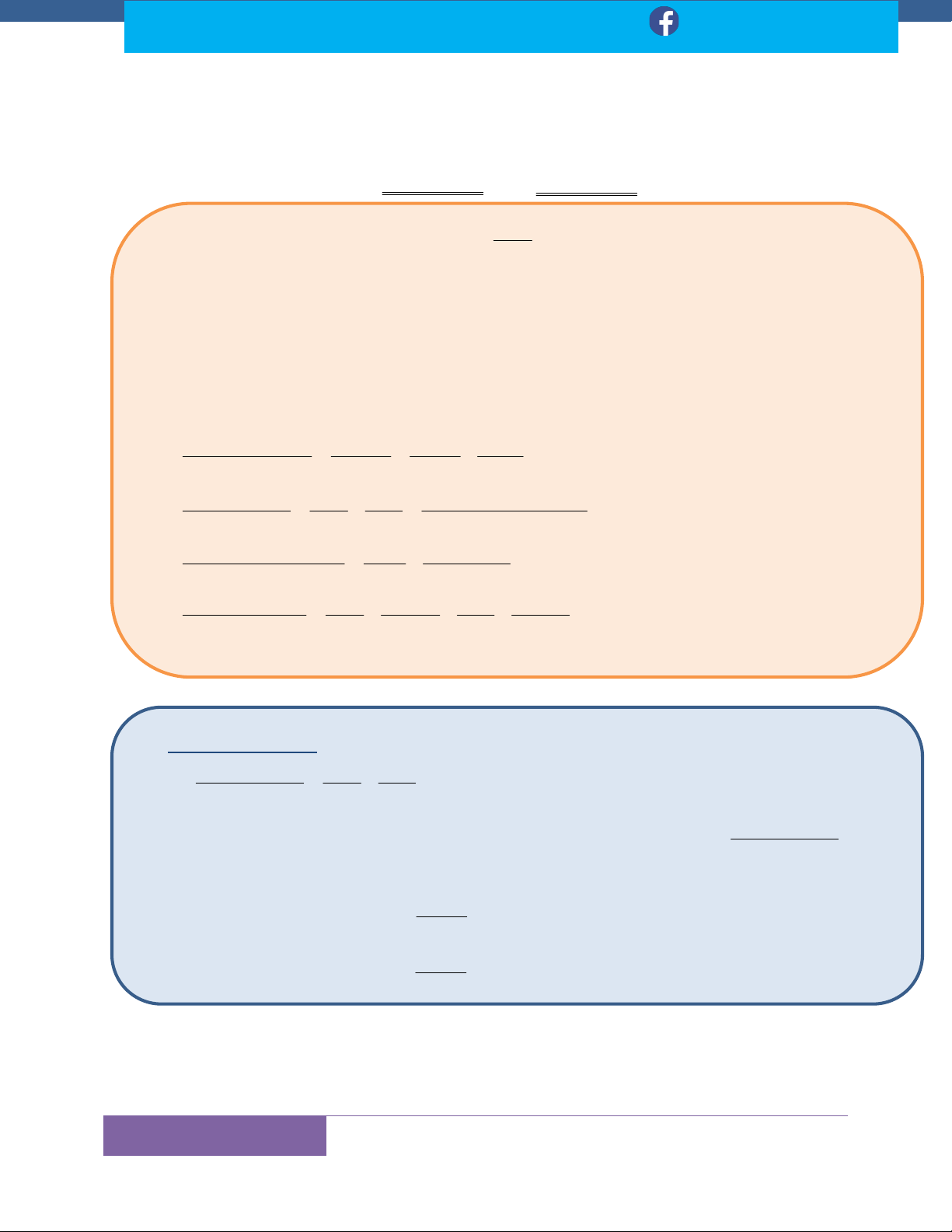
A. ĐỊNH NGHĨA VÀ TÍNH CHẤT 1. Định nghĩa
Ta gọi F  x là một nguyên hàm của f  x . Vì với C là một hằng số bất kỳ, ta có
F xC'  F 'x  f x nên nếu F x là nguyên hàm của f x thì F xC cũng là một
nguyên hàm của f  x . Ta gọi F  x  C, (c là hằng số (constant) là Họ nguyên hàm của f  x . Ký hiệu: f
 xdx  F xC
Hay đơn giản cho dễ hiểu nhé mấy đứa: NGUYÊN HÀM LÀ NGƯỢC LẠI CỦA ĐẠO HÀM. VÍ DỤ : 2 x đạo hàm là gì? 2 (x ) '  2x chuẩn chưa? Thì 2 2xdx  x  C 
. Tại sao phải cộng thêm C? Vì đạo hàm của hằng số luôn là 0. Nên 2
(x  C) '  2x . Người ta ghi thêm C vào cho đầy đủ?
Oke? Vậy tạm hiểu nguyên hàm là gì rồi nhé!! 2. Tính chất ' •  f
 xdx  f x • kf  xdx  k f
 xdx, .k . là hằng số •  f
 x gxdx  f   xdx  g  xdx •  f
 x gxdx  f   xdx g  xdx
3. Sự tồn tại nguyên hàm
Mọi hàm số liên tục trên đoạn  ;
a b đều có nguyên hàm trên đoạn  ; a b .
http://hoc24h.vn - NGUYÊN HÀM 5
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
B. BẢNG CÁC NGUYÊN HÀM, ĐẠO HÀM CƠ BẢN Bảng đạo hàm Bảng nguyên hàm (u là hàm số hợp) x' 1 kdx  kx  c  , k là hằng số x   1  x  u   1 ' ; ' .u '.u     1     x x dx   c,  ax  b  1  ax b   1 1 dx  .  c a  1     1  1 1 1 u u ' ln '  , u  0 dx  ln x  c  dx  ln ax  b  c  u x ax  b a  u '  '. u e u e x x e dx  e  c  axb 1 axb e dx  e  c  a  u' '. u a u a .ln a , 0  a  1 x a mxn  a x a dx   c  mx n a dx   c  ln a . m ln a sinu'  u'.cosu cos xdx  sin x  c   ax b 1 cos
dx  sin ax  b  c a cosu'  u'.sinu sin xdx   cos x  c   ax b 1 sin
dx   cos ax  b  c a  1 1 1 u u ' tan '   u '. 2 1 tan u dx  tan x  c  dx  tan ax  b  c  2  cos u 2 cos x 2 cos ax  b   a   1 1 1 u u ' cot '   u '. 2 1 cot u dx   cot x  c  dx   cot ax  b  c  2  sin u 2 sin x 2 sin ax  b   a Một số lưu ý
1. Cần nắm vững bảng nguyên hàm.
2. Nguyên hàm của một tích (thương) của nhiều hàm hàm số không bao giờ bằng tích (thương) của
các nguyên hàm của những hàm thành phần.
3. Muốn tìm nguyên hàm của một hàm số, ta phải biến đổi hàm số này thành một tổng hoặc hiệu
của những hàm số tìm được nguyên hàm (dựa vào bảng nguyên hàm). 6
NGUYÊN HÀM - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến * Lưu ý: do f
 xdx  F xc thì F 'x  f x nên khi quên công thức nguyên hàm, ta cần
liên tưởng đến đạo hàm. Cụ thể như sau:
VÍ DỤ ta cần tìm f  x dx 
(mà quên công thức) ta có thể tự đặt câu hỏi : “ hàm số nào
mà lấy đạo hàm ra là f(x)?”. Với cách hỏi như thế, kết hợp với việc nắm vững công thức đạo
hàm, ta có thể nhớ lại công thức nguyên hàm một cách dễ dàng.
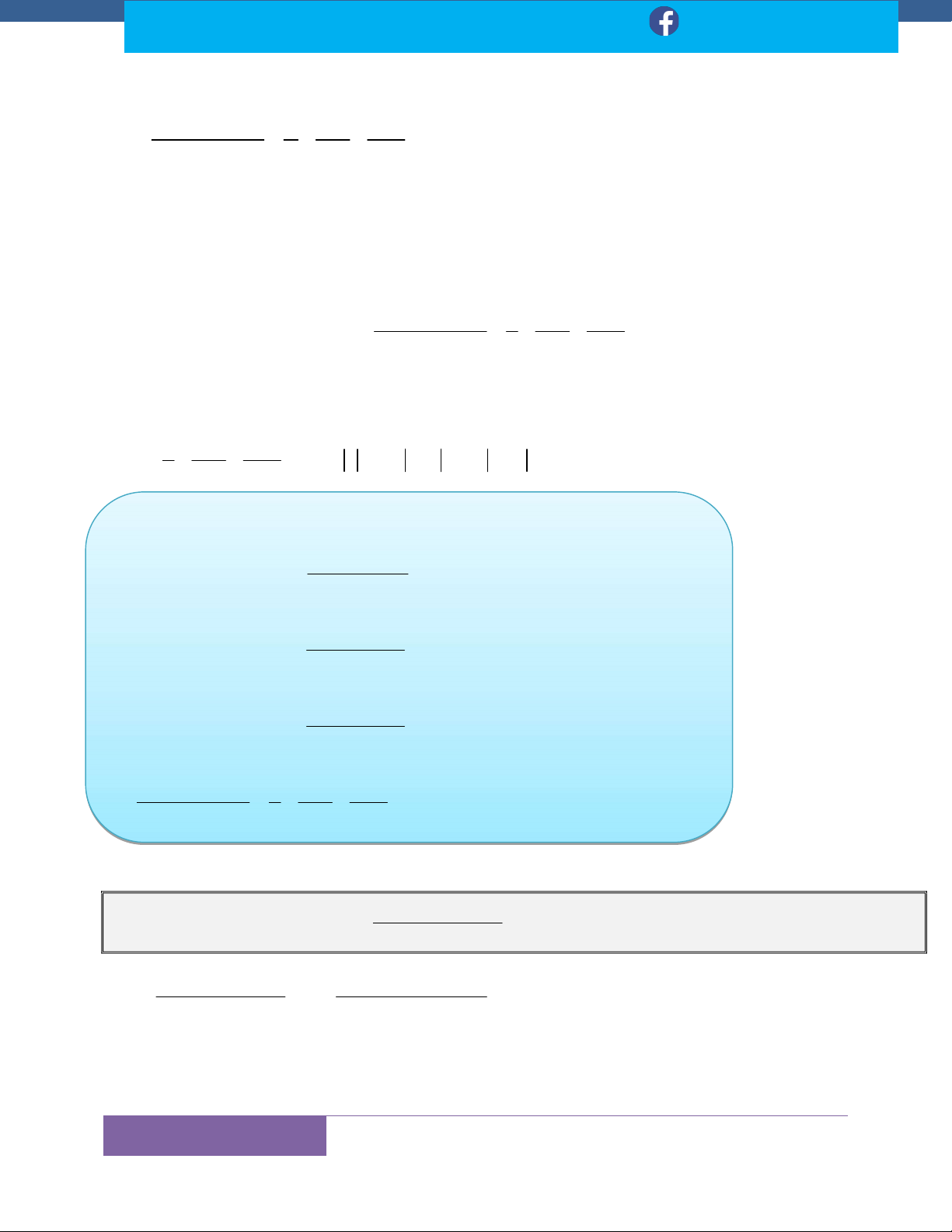
I. BẢNG CÔNG THỨC MỞ RỘNG (LÀM NHANH TRẮC NGHIỆM)
Chú ý: Những công thức không có trong SGK, nếu khi các em dùng cho làm tự
luận, phải chứng minh lại! (Cách chứng minh đơn giản nhất: Đạo hàm lại kết quả. Hehe. 1 axb 1 dx axb e  e  c 
tg ax  bdx   ln cos ax  b  c  a a 1 axb 1 dx axb m  m  c 
cotg ax  bdx  ln sin ax  b  c  a ln m a dx 1 x dx 1  arctg  c   cotg ax  b  c  2 2 a  x a a 2 sin ax  b a dx 1 a  x dx 1  ln  c   tg ax  b  c  2 2 a  x 2a a  x 2 cos ax  b a dx  dx x ln  2 2 x  x  a   c   arcsin  c  2 2 x  a 2 2 a  x a
http://hoc24h.vn - NGUYÊN HÀM 7
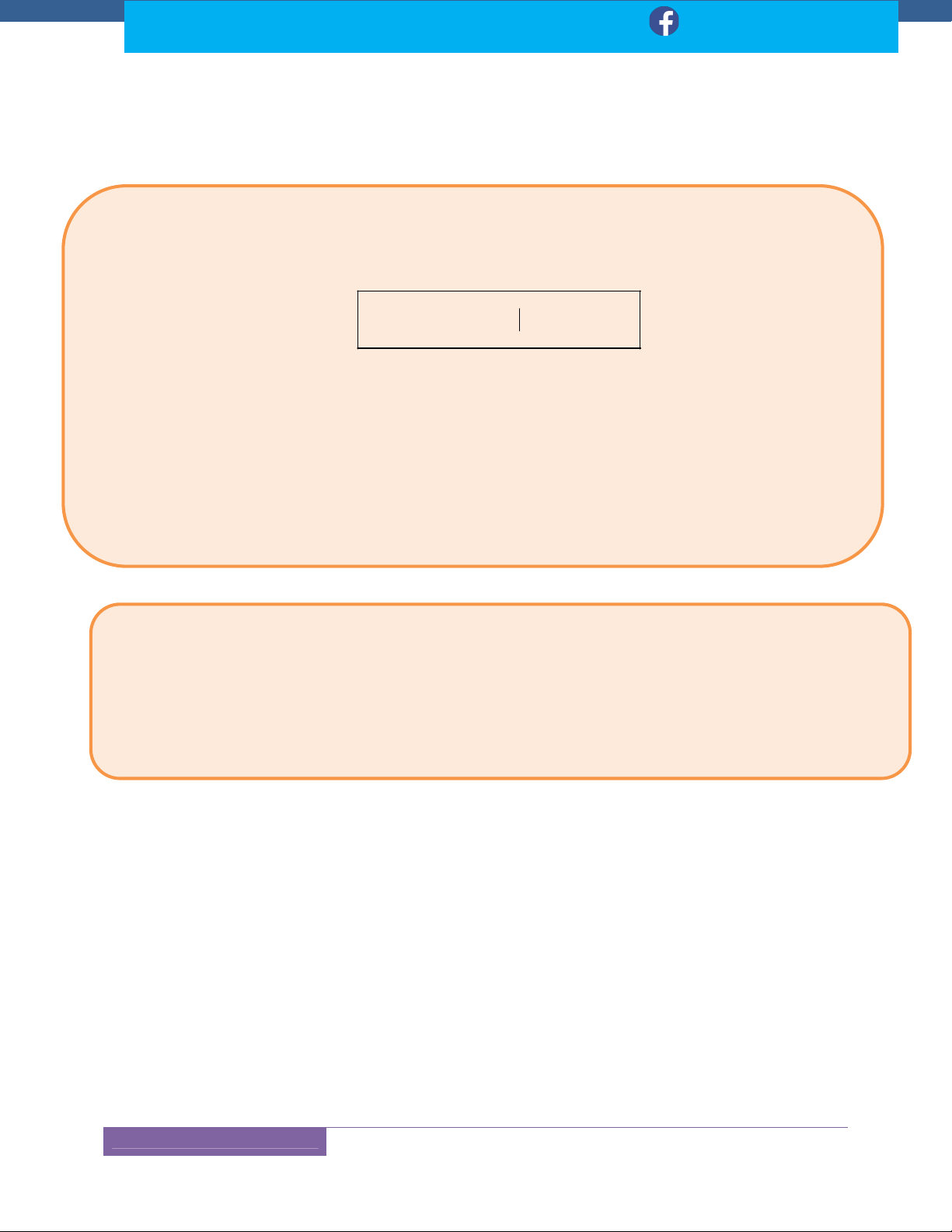
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến TRẮC NGHIỆM LÝ THUYẾT
Câu 1. Hàm số f  x có nguyên hàm trên K nếu:
A. f  x xác định trên K .
B. f  x có giá trị lớn nhất trên K .
C. f  x có giá trị nhỏ nhất trên K .
D. f  x liên tục trên K .
Câu 2. Mệnh đề nào sau đây sai?
A. Nếu F  x là một nguyên hàm của f  x trên a;b và C là hằng số thì f
 xdx  F xC .
B. Mọi hàm số liên tục trên a;b đều có nguyên hàm trên a;b .
C. F  x là một nguyên hàm của f  x trên a b / ;  F x  f x, x   ; a b . / D.  f
 xdx  f x.
Câu 3. Xét hai khẳng định sau:
(I) Mọi hàm số f  x liên tục trên đoạn  ;
a b đều có đạo hàm trên đoạn đó.
(II) Mọi hàm số f  x liên tục trên đoạn  ;
a b đều có nguyên hàm trên đoạn đó.
Trong hai khẳng định trên: A. Chỉ có (I) đúng. B. Chỉ có (II) đúng. C. Cả hai đều đúng. D. Cả hai đều sai.
Câu 4. Hàm số F  x được gọi là nguyên hàm của hàm số f  x trên đoạn  ; a b nếu:
A. Với mọi x a;b , ta có / F  x  f  x .
B. Với mọi x a;b , ta có / f  x  F  x . C. Với mọi x  ; a b , ta có / F  x  f  x .
D. Với mọi x a;b , ta có /
F  x  f  x , ngoài ra /
F a   f a và / F b   f b .
Câu 5. Trong các câu sau đây, nói về nguyên hàm của một hàm số f xác định trên khoảng D , câu nào là sai? 8
NGUYÊN HÀM - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
(I) F là nguyên hàm của f trên D nếu và chỉ nếu x
  D : F 'x  f x .
(II) Nếu f liên tục trên D thì . f . có nguyên hàm trên D .
(III) Hai nguyên hàm trên D của cùng một hàm số thì sai khác nhau một hằng số. A. Không có câu nào sai. B. Câu (I) sai. C. Câu (II) sai. D. Câu (III) sai.
Câu 6. Giả sử F  x là một nguyên hàm của hàm số f  x trên khoảng a;b . Giả sử G  x cũng là
một nguyên hàm của f  x trên khoảng a;b . Khi đó:
A. F  x  G  x trên khoảng a;b .
B. G  x  F  x  C trên khoảng a;b , với C là hằng số.
C. F  x  G  x  C với mọi x thuộc giao của hai miền xác định, C là hằng số.
D. Cả ba câu trên đều sai. Câu 7. Xét hai câu sau:
(I)  f x g xdx  f  xdx  g
 xdx  F xGxC ,
trong đó F  x và G  x tương ứng là nguyên hàm của f  x, g  x .
(II) Mỗi nguyên hàm của .
a f  x là tích của a với một nguyên hàm của f  x . Trong hai câu trên: A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.
C. Cả hai câu đều đúng. D. Cả hai câu đều sai.
Câu 8. Các khẳng định nào sau đây là sai? A. f
 xdx  F xC  f
 tdt  F tC . / B.  f  xdx  f x   . C. f
 xdx  F xC  f
 udx  F uC . D. kf  xdx  k f
 xdx (k là hằng số).
http://hoc24h.vn - NGUYÊN HÀM 9
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Câu 9. Trong các khẳng định sau, khẳng định nào sai? A.   2
F x  x là một nguyên hàm của f  x  2x .
B. F  x  x là một nguyên hàm của f  x  2 x .
C. Nếu F  x và G  x đều là nguyên hàm của hàm số f  x thì F  x  G  x  C (hằng số). D. Cả 3 đáp án trên
Câu 10. Trong các khẳng định sau, khẳng định nào sai?
A. Nếu F  x là một nguyên hàm của hàm số f  x thì mọi nguyên hàm của f  x đều có
dạng F  x  C ( C là hằng số). / u  x
B.    dx  log ux C . u x
C. F  x 1 tan x là một nguyên hàm của hàm số f  x 2 1 tan x .
D. F  x  5  cos x là một nguyên hàm của hàm số f  x  sin x .
Câu 11. Trong các khẳng định sau, khẳng định nào sai? 1 A. 0dx  C  ( C là hằng số). B. dx  ln x  C  ( C là hằng số). x  1   x C. x dx   C  ( C là hằng số). D. dx  x  C   ( C là hằng số). 1 10
NGUYÊN HÀM - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
ĐÁP ÁN TRẮC NGHIỆM LÝ THUYẾT CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1. D 5. A 9. B 2. C 6. B 10. B 3. B 7. C 11. C 4. D 8. C
Câu 1. Để hàm số f  x có nguyên hàm trên K khi và chỉ khi f  x liên tục trên K . Chọn D.
Câu 2. Sửa lại cho đúng là ' Tất cả các nguyên hàm của f  x trên a;b đều có đạo hàm bằng f  x' . Chọn C.
Câu 3. Vì hàm số có đạo hàm tại x thì liên tục tại x , nhưng nếu hàm số liên tục tại x thì chưa 0 0 0
chắc đã có đạo hàm tại x . Chẳng hạn xét hàm số f  x  x tại điểm x  0 . Chọn B. 0
Câu 4. Với mọi x a;b , ta có /
F  x  f  x , ngoài ra /
F a   f a và /
F b   f b .Chọn D. Câu 5. Chọn A.
Câu 6. Vì hai nguyên hàm trên D của cùng một hàm số thì sai khác nhau một hằng số. Chọn B. Câu 7. Chọn C. Câu 8. Vì f
 xdx  F xC  f
 udu  F uC . Chọn C. Câu 9. Vì  x/ /
 1  2 x  F x  f x  F x  x không phải là nguyên hàm của hàm số
f  x  2 x . Chọn B. / u  x d u x
Câu 10. Vì    dx      ln ux C . Chọn B. u x u x
Câu 11. Vì kết quả này không đúng với trường hợp   1  . Chọn C.
http://hoc24h.vn - NGUYÊN HÀM 11
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM CƠ BẢN 
1. Tích của đa thức hoặc lũy thừa PP  khai triển. 2. Tích các hàm mũ PP
 khai triển theo công thức mũ. 3. Chứa căn PP
 chuyển về lũy thừa.
4. Tích lượng giác bậc một của sin và cosin PP
 khai triễn theo công thức tích thành tổng.  1 sin a .
x cosbx  sin(a  b)x  sin(a  b)x 2  1 sin a .
x sin bx  cos(a  b)x  cos(a  b)x 2  1 cos a .
x cos bx  cos(a  b)x  cos(a  b)x 2
5. Bậc chẵn của sin và cosin PP  Hạ bậc.
Bài 1. Tìm các nguyên hàm: 12
KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM CƠ BẢN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 1 x Câu 12. Tìm nguyên hàm 2 f (x)  3x   2 2 x 2 7x A. 3 F (x)  x   C. C. 3 F (x)  x   C. 4 4 2 x 2 x B. 3 F (x)  x   C. D. 3 F (x)  5x   C. 4 4 Câu 13. Tìm nguyên hàm 3 f (x)  2x  5x  7. 4 2 x 5x 4 2 3x 5x A. F (x)    7x  C. C. F (x)    7x  C. 2 3 2 2 4 2 x 5x 4 2 x 5x B. F (x)    7x  C. F (x)    8x  C. 2 2 D. 2 2 Câu 14. Tìm nguyên hàm 5 3 2
f (x)  6x 12x  x  8. 3 x 3 x A. 6 4 F (x)  x  3x   8x  C. C. 6 4 F (x)  x  3x   8x  C. 3 3 3 x 3 x B. 6 4 F (x)  x  3x   8x  C. 6 4 F (x)  x  x  8x  C. 3 D. 3 Câu 15. Tìm nguyên hàm 2
f (x)  (x  3x) (x 1)  4 3 2 x 2x 3x 4 3 2 x 2x 3x A. F(x)     C. C. F(x)     C. 4 3 2 4 5 2 4 3 2 x 2x 3x 4 3 2 x 2x 3x B. F(x)     C. F (x)     C. 2 3 2 D. 4 3 7 (3  )a x Câu 16. 3
f (x)  (3  x) . Biết nguyên hàm của f(x) là F (x)    C. Tìm 2 a a A. 4 C. 32 B. 16 D. 9 1 1 3 1 x x Câu 17. 2 f (x) 
 x   Biết nguyên hàm của f(x) là F(x)      C. Tính a-b? 2 x 3 x a b A. 0 C. 2 B. 1 D. 3 x a Câu 18. 2 ( ) 10 x f x 
. Biết nguyên hàm của f(x) là F (x)   C.Tìm a? 2ln10
http://hoc24h.vn - KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM 13 CƠ BẢN
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến A. 10 C. 5 B. 100 D. 20 3 4 x Câu 19. 3
f (x)  x  4x   Biết nguyên hàm của f(x) là 2 F (x)   bx  . c ln x  C.Tính a-b+c x a A. 5 C. 4 B. 1 D. 7  1  2 Câu 20. 2 I  2x   dx 3   3b x x  C. Tính a-b? 3 2  x  a A. 0 C. 2 B. 1 D. 3
ĐÁP ÁN TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 1 CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 12 A 16 B 20. A 13 B 17 A 14 C 18 B 15 A 19 A 14
KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM CƠ BẢN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Bài 2. Tìm nguyên hàm của các hàm số thỏa mãn điều kiện cho trước trong các trường hợp sau:
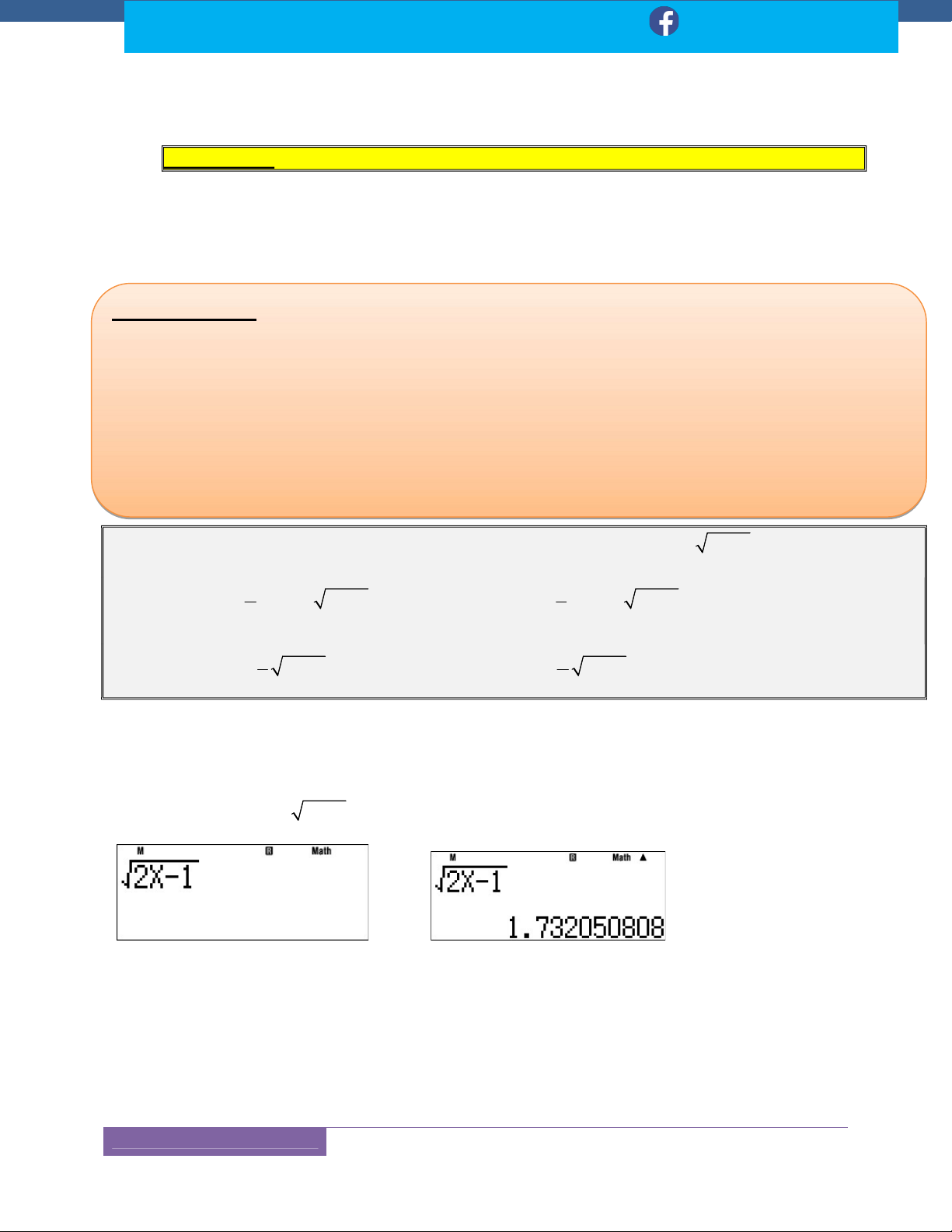
Phương pháp: Tìm nguyên hàm của hàm số f (x), tức đi tính f (x)  dx  F (x)  C. 
Rồi sau đó thế F (x )  C   để tìm hằng số C. o VÍ DỤ : 3
f (x)  x  4x  5, F(1)  3. 4 x Ta có 3 2 (x  4x  5)dx   x  5x  c   Mà F (1)  3. 4 4 1  2 1  5.1 c  3 4 5 4 x 5  c=  . Kết luận: 2 F (x)   x  5x   4 4 4
TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 2 Tìm F(x) biết:
Câu 21. f (x)  3  5cos x, F ( )  2. A. F(x)  3x  5sin x
C. F(x)  3x  5sin x  2
B. F(x)  3x  5sin x  2  2.
D. F(x)  3x  5sin x  2  3. 2 3  5x 2 2 5x 5e Câu 22. f (x) 
, F (e)  1. Biết F (x)  3ln x    . c c chia hết cho mấy? x 2 2 A. 2 C. 6 B. 3 D. 7 2 x 1 3 2 x Câu 23. f (x) 
, F (1)   Biết F (x)   bln x  .
c Kết quả của a-b-c là? x 2 a A. 4 C. 8 B. 3 D. 0 4 3 3x  2x  5 a Câu 24. I  dx,  biết F (1)  2.ĐS: 3 2 F (x)  x  . c x   . b Tính a+b+c? 2 x x A. 1 C. 3 B. 2 D. 4
ĐÁP ÁN TRẮC NGHIỆM KỸ THUẬT 1 – DẠNG 2 CÂU ĐÁP ÁN CÂU ĐÁP ÁN Câu 21 D Câu 23 D Câu 22 A Câu 24 A
http://hoc24h.vn - KỸ THUẬT 1: SỬ DUNG BẢNG NGUYÊN HÀM 15 CƠ BẢN
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ  P(x)
Bài toán tổng quát: Tính nguyên hàm I  dx, 
với P(x) và Q(x) là các đa thức không Q(x) căn. Phương pháp giải:
Nếu bậc của tử số P(x)  bậc của mẫu số Q(x) PP  Chia đa thức.
Nếu bậc của tử số P(x)  bậc của mẫu số Q(x) PP
 Xem xét mẫu số và khi đó:
+ Nếu mẫu số phân tích được thành tích số, ta sẽ sử dụng đồng nhất thức để đưa về dạng tổng của các phân số.
Một số trường hợp đồng nhất thức thường gặp: 1 1  a b         (ax  m) (bx  n)
an  bm  ax  m bx  n  mx  n A B
(A  B)  x  (Ab  Ba) A  B  m        (x  a)  (x  b) x  a x  b (x  a) (x  b) Ab  Ba  n 1 A Bx  C    , với 2   b  4ac  0. 2 2
(x  m)  (ax  bx  c) x  m ax  bx  c 1 A B C D       2 2 2 2 (x  a)  (x  b) x  a (x  a) x  b (x  b)
+ Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về dạng lượng giác). Mẹo sử dụng Casio mx  n A B    (x  a)  (x  b) x  a x  b mx  n
(Ta muốn tìm hệ số nào, ta xóa nghiệm dưới mẫu của thằng đó đi trong . Và (x  a)  (x  b)
Calc đúng nghiệm dưới mẫu của nó) mx  n
Để tìm A. Ta nhập vào máy tính . Calc x = a (x  b) mx  n
Để tìm B. Ta nhập vào máy tính . Calc x = b (x  a) 16
KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến BÀI TẬP VẬN DỤNG 2x 1
VÍ DỤ 1. Tìm nguyên hàm I   dx   x 1
Ta thấy bậc tử bằng bậc mẫu: Chia đa thức 2x 1 3 I   dx  (2 
)dx  2x  3.ln | x 1| c   x 1 x 1 2 x  x 1
VÍ DỤ 2. Tìm nguyên hàm I   dx   x  2
Ta thấy bậc tử lớn hơn bậc mẫu: Chia đa thức 2 2 x  x 1 3 x I  dx  I  (x 1 )  dx   x  3ln x  2  C.   x  2 x  2 2 dx
VÍ DỤ3. Tìm nguyên hàm I    2 2x  7x  5 dx dx A B I    (  )dx    2 2x  7x  5 (x 1)(2x  5) x 1 2x  5 Ta có: B(x 1)  ( A 2x  5)  1
 x(2A  B)  5A  B 1  1  A   2A  B  0  3     5A  B  1 2  B   3 1  2 1 2 ln | 2x  5 | 1  1 3 3 I  (  )dx  ln | x 1|   C 
ln | x 1|  ln | 2x  5 | C  x1 2x5 3 3 2 3 3 Mẹo sử dụng máy tính: Tìm A: Nhập vào máy 1 Calc X = 1. Thu được 1  A  (2x  5) 3
Tìm B: Nhập vào máy 1 Calc X = 5 . Thu được B = 2 x 1 2 3 2 6x 10x  2
VÍ DỤ 4. Tìm nguyên hàm I  dx  3 2 x  3x  2x 2 2 6x 10x  2 6x 10x  2 I  dx  dx   3 2 x  3x  2x x  1x  2 x
http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM 17 SỐ HỮU TỶ
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 6x 10x  2 A B C Xét:    x  x   1  x  2 x x 1 x  2 2
 6x 10x  2  Ax  
1  x  2  Bx  x  2  Cx x   1 2
 x  x    A  B  C 2 6 10 2
x  3A  2B  C x  2A 6  A  B  C A 1 2   6x 10x  2 1 2 3  1
 0  3A  2B  C  B  2     x   x  
1  x  2 x x 1 x  2 2  2A C  3   Từ đó:  1 2 3  I   
dx  ln x  2ln x 1  3ln x  2  C    x x 1 x  2  Mẹo sử dụng máy tính 2 6x 10x  2
Tìm A: Ta nhập vào máy  Calc X=0. Thu được A = 1 x   1  x  2 2 6x 10x  2 Tìm B: Ta nhập vào máy
Calc X=-1. Thu được B = 2 x  x  2 2 6x 10x  2 Tìm C: Ta nhập vào máy
Calc X=-2. Thu được C = 3 x  x   1 2 6x 10x  2 1 2 3     x  x  
1  x  2 x x 1 x  2 2 6x  26x  26
VÍ DỤ 5. Tìm nguyên hàm J  dx  3 2 x  6x 11x  6 2 2 6x  26x  26 6x  26x  26 J  dx  dx   3 2 x  6x 11x  6
x  1x  2x 3 Ta tìm , A B,C sao cho: 18
KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 6x  26x  26 A B C     x  
1  x  2 x  3 x 1 x  2 x  3 2
 6x  26x  26  Ax  2x  3  B x  
1  x  3  C  x   1  x  2
Cho x giá trị lần lượt bằng 1, 2, 3 ta tìm được A  3; B  2;C  1 Từ đó:  3 2 1  J   
dx  3ln x 1  2 ln x  2  ln x  3  C    x 1 x  2 x  3  x  8 x  8  2 1  • K  dx  dx  
dx  2ln x  2  ln x  3  C    2   x  x  6 x  2x 3  x  2 x  3  2 3x 13x 11
VÍ DỤ 6 .Tìm nguyên hàm L  dx  3 2 x  5x  8x  4 2 2 3x 13x 11 3x 13x 11 L  dx  dx   3 2 x  5x  8x  4 x   1  x  22 Ta tìm , A B,C sao cho: 2 3x 13x 11 A B C   
x  1x  22 x 1 x  2 x  22  x  x   Ax  2 2 3 13 11 2  B  x  
1  x  2  C  x   1 2
 x  x    A  B 2 3 13 11
x  4A  3B  C x  4A  2B  C 3   A  B A 1    1
 3  4A  3B  C  B  2 1  1 4A 2B C C      3   Từ đó:  1 2 3  3 L     d
 x  ln x 1  2ln x  2   C  x 1 x  2  x  22  x  2 
http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM 19 SỐ HỮU TỶ
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 3 2 2x  6x  4x 1
VÍ DỤ 7. Tìm nguyên hàm M  dx  2 x  3x  2 3 2 2x  6x  4x 1  1   1  M  dx  2x  dx     2x  dx 2 2 x 3x 2  x 3x 2    x  1  x 2          1 1  2  2x  
dx  x  ln x  2  ln x 1  C    x  2 x 1 2 3x  4x  2
VÍ DỤ 8. Tìm nguyên hàm N  dx  3 2 x  2x  2x  5 3x  4x  2 d  3 2 2 x  2x  2x  5 3 2 N  dx 
 ln x  2x  2x  5  C   3 2 3 2 x  2x  2x  5 x  2x  2x  5 dx
VÍ DỤ 9. Tìm nguyên hàm I   x  2 x  2 3 1 Ta phân tích: 1
1  x  3   x   2 2 1  1  1 1          x  32  x  2 1
4  x  3x   1 4   x 1 x  3  1  1 1 2  1  1 1 1 1             4 x  2 1
x 32 x  1x  3 4 x  2 1
x 32 x  3 x 1     Từ đó:  1 1 1 1  1 1 1 1 1 1 I      d  x    .  .
 ln x  3  ln x 1  C  x  2 1
x  32 x 3 x 1   4 x 1 4 x  3 4 4 dx
VÍ DỤ 10. Tìm nguyên hàm . J   . x  2 x  2 3 4 Ta phân tích: 20
KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1
1  x  4   x  3 2  1  1 2 1   .      
x 32 x  42 49  x 3x  4 49 
x 32 x 3x  4 x  42  Từ đó: 1 1 1 2 1 1 J  dx  dx  dx    49 x 32
49  x  3 x  4 49 x  42 1 1 1 1 1  1 1    .  .   dx  
49 x  3 49 x  4 343  x  3 x  4  1 1 1 1 1 x  3   .  .  ln  C 49 x  3 49 x  4 343 x  4
http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM 21 SỐ HỮU TỶ
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM KỸ THUẬT 2 2 4x  6x 1 Câu 25. .dx  là 2 I  . a x  . b x  .
c ln 2x 1  C . Tính a-b-c ? 2x 1 1 3 1 3 A. B. C.  D.  2 2 2 2 3 2 4x  4x 1 Câu 26. .dx  có dạng F  x 3 2  . a x  . b x  .
c x  d.ln 2x 1  C . Tính . a b  c  d  ? 2x 1 1 3 A. B. C. 3 D. 2 3 2 2x 1 Câu 27. .dx  có dạng I  . a x  .
b ln x 1  C . Tính a.b ? x 1 A. 4 B. 5 C. 6 D. 7 3x 1 Câu 28. .dx  có dạng I  . a x  .
b ln x  2  C . Tính b-a ? x  2 A. 2 B. 3 C. 4 D. 5 x 
Câu 29. Nguyên hàm của f  x 1  có dạng F  x  . a x  .
b ln 2x  3  C . Tính a.b ? 2x  3 1 A.  B. 4 C. 2 D. -6 8 2 x  x 1 Câu 30. .dx  có dạng 2 I  . a x  . b x  .
c ln x  2  C . Tính b+c ? x  2 A. 8 B. 6 C. 4 D. 2 dx I    Câu 31. 2 x  6x  9 1 1 A. I   C. C. I    C. x  3 x  3 1 2 B. I    C. D. I    C. x  3 x  3 2 x 1 x 1 Câu 32. I   dx   ĐS: I  x  ln  C. 2 x 1 x 1 2x 1 x 1 A. I  x  ln  C. C. I  x  ln  C. x 1 x 1 x 1 x 1 B. I  x  ln  C. D. I  ln  C. x 1 x 1 3x  2 a Câu 33. I  dx  7  ln 2x 1   C.. Tính b – a ? 2 4x  4x 1 b 4(2x 1) A. 0 B. 1 22
KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM SỐ HỮU TỶ - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến C. 2 D. 3 2 x  x c Câu 34. I  dx   ax  b ln x  2   C. Tính a + b – c? 2 (x  2) x  2 A. 0 C. 2 B. 1 D. 3
ĐÁP ÁN TRẮC NGHIỆM KỸ THUẬT 2 CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 25 C 29 A 33 B 26 A 30 D 34 B 27 C 31 C 28 C 32 B
http://hoc24h.vn - KỸ THUẬT 2. TÍNH NGUYÊN HÀM CỦA HÀM 23 SỐ HỮU TỶ
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1
1. CÁC DẠNG ĐỔI BIẾN SỐ THƯỜNG GẶP DẠNG CÁCH ĐỔI BIẾN axbdx Đặt t  ax  b n 1  . n x x dx  Đặt n 1 t x      dx f x . Đặt t  x 2 x f sin xcos xdx  Đặt t  sin x f cos xsin xdx  Đặt t  cos x   dx Đặt t  tan x f tan x 2 cos x   dx Đặt t  cot x f cot x 2 sin x  x. x f e e dx  Đặt x t  e   dx Đặt t  ln x f ln x x  1   1  1 f x  . x  dx      Đặt t  x   x   x  x
Các bước để đổi biến: Bước 1: Đặt v(x) = t
Bước 2: vi phân: d(v(x)) = d(t) (Vi phân như đạo hàm thôi, nhưng đạo hàm theo biến x, nhân thêm dx,
đạo hàm theo biến t thì nhân thêm dt)
Bước 3: Chuyển hết f(x) về f(t). Ví dụ về vi phân: 2 2
d (x  2x 1)  (x  2x 1) '.dx  (2x  2)dx
VÍ DỤ : Tìm nguyên hàm các hàm số sau 1. 2004 2003 I  x 1.x dx  1 Đặt 2004 2004 2003 2003 t  x 1 d(t)  d(x 1)  dt  2004x dx  x dx  dt . Từ đó ta được: 2004 1 3 1 1 1 2 1 1 2 2 I  tdt  t dt  . t  C    t  C  x  3 3 2004 1  C 2004 2004 2004 3 3006 3006 24
KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2• x  1 x e x e 1    . x I e dx e e dx   Đặt x x
e  t  e dx  dt . Thay vào ta được: 1  1      1  1 1 x t t t e L e dt e d t e C e         C x 3. I  dx  10 x 1 Đặt 10 10 9
x 1  t  x 1  t  dx  10t dt . Từ đó ta được: 10 t 1 10 10 9 N  .10t dt  10   10t   8 1 t dt  10 18 8 t  t  19 9 dt  t  t  C t 19 9 10  x  19 10 1  x  9 10 10 1  C 19 9 4. I  x    x10 2 1 dx
Đặt 1 x  t  dx  dt . Từ đó ta được: O   t2 10 t dt   2  t  t  10 10 11 12 1 1 2
.t dt   t dt  2 t dt  t dt    1 1 1 1   t  t  t  C     x11 1    x12 1 1 1  1 x13 11 12 13  C 11 6 13 11 6 13
http://hoc24h.vn - KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 25
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM ĐỔI BIẾN SỐ DẠNG 1
Câu 34. Câu nào sau đây sai?
A. Nếu F 't  f t thì /
F u  x  f u  x . B. f
 tdt  F tC  f
 uxu'xdx  F uxC .
C. Nếu G t là một nguyên hàm của hàm số g t thì G u  x là một nguyên hàm của hàm số g u  x / .u  x . D. f
 tdt  F tC  f
 udu  F uC với u  ux.
Câu 35. Trong các khẳng định sau, khẳng định nào sai? A. Nếu f
 tdt  F tC thì f  ux /
.u  xdx  F u  x  C .
B. Nếu F  x và G  x đều là nguyên hàm của hàm số f  x thì F  xGxdx  có dạng
h x  Cx  D (C, D là các hằng số và C  0 ). C. F  x 2
 7  sin x là một nguyên hàm của f x  sin 2x . / u  x
D.    dx  ux C . u x
Câu 36. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Tìm nguyên hàm của hàm số f  x  2x 1. 2 1 A. f
 xdx  2x  1 2x1C. B. f
 xdx  2x  1 2x1C. 3 3 C. f  x 1 dx   2x 1  C. D. f  x 1 dx  2x 1  C. 3 2 ln x e Câu 37. Để tính dx 
theo phương pháp đổi biến số, ta đặt: x 1 A. ln x t  e . B. t  ln . x C. t  . x D. t  . x
Câu 38. F  x là một nguyên hàm của hàm số 2 x y  xe .
Hàm số nào sau đây không phải là F  x : 26
KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 1 A.   2 x F x  e  2 . B.     2x F x e  5 . 2 2 1 1 C.   2 x F x   e  C . D.      2 2 x F x  e  . 2 2 ln x
Câu 39. F  x là một nguyên hàm của hàm số y  . x ln x Nếu F  2 e   4 thì dx  bằng: x 2 ln x 2 ln x A. F  x   C . B. F  x   2 . 2 2 2 ln x 2 ln x C. F  x   2 . D. F  x   x  C . 2 2
Câu 40. F  x là một nguyên hàm của hàm số sin x y  e cos x .
Nếu F    5 thì sinx e cos xdx  bằng: A.   sin x F x  e  4 . B.   sin x F x  e  C . C.   cos x F x  e  4 . D.   cosx F x  e  C .
Câu 41. F  x là nguyên hàm của hàm số 4 y  sin x cos x .
F  x là hàm số nào sau đây? 5 cos x 4 cos x A. F  x   C . B. F  x   C . 5 4 4 sin x 5 sin x C. F  x   C . D. F  x   C . 4 5
Câu 42. Xét các mệnh đề sau, với C là hằng số: (I) tan x dx   ln  cos x C . x 1 (II) 3cos 3cos sin d x e x x   e  C  . 3
http://hoc24h.vn - KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 27
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến cos x  sin x (III) dx  2 sin x  cos x  C  . sin x  cos x Số mệnh đề đúng là: A. 0 . B. 1. C. 2 . D. 3 .
ĐÁP ÁN TRẮC NGHIỆM ĐỔI BIẾN DẠNG 1 CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 34 A 37 B 40 A 35 D 38 C 41 D 36 B 39 B 42 D
Câu 34. Chọn A. Vì nếu F 't  f t  F t  f
 tdt . Đặt    /
t u x  dt  u  x dx .
Suy ra F u  x  f  ux / .u  xdx hay /
F u  x  f u  x / .u  x . / u  x d u x
Câu 35. Chọn D. Vì    dx      ln ux C . u x u x Câu 36. Ta có I  f  xdx  2x1d .x  2 t 1 Đặt 2x 1  t  x  2 2 3  t 1 t 1 2  I  td     t dt   C   2x   1 2x 1  C. Chọn B.  2  3 3 1 ln x e
Câu 37. Đặt t  ln x  dt  dx . Khi đó t dx  e dt   . Chọn B. x x Câu 38. Đặt 2 t  x  dt  2xdx . 1 t 1 t 1 t 1 Suy ra       2 x I e dt
d e  e  C  e  C . Chọn C. 2 2 2 2 dx 2 2 t ln x
Câu 39. Đặt ln x  t  dt 
. Suy ra F  x  tdt   C   C  . x 2 2 28
KỸ THUẬT 3. ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 2 ln e Vì F  2 e     4 
 C  4  C  2 . Chọn B. 2
Câu 40. Đặt t  sin x  dt  cos xdx . Suy ra t t sin x I  e dt  e  C  e  C  . Vì F   sin 5 e    
 C  5  1 C  5  C  4 . Suy ra   sin x F x  e  4 . Chọn A.
Câu 41. Đặt t  sin x , suy ra dt  cos xdx . 5 5 t sin x Khi đó 4 I  t dt   C   C  . Chọn D. 5 5 sin x
Câu 42. Xét (I): Ta có tan x dx  dx  
. Đặt t  cos x  dt   sin xdx . cos x sin x dt Khi đó dx  
  ln t  C   ln cos x  C   . Do đó (I) đúng. cos x t 1
Xét (II): Đặt t  3cos x  dt  3
 sin xdx  sin xdx   dt . 3 x 1 t 1 t 1 Khi đó 3cos 3cos sin x e x dx   e dt   e  C   e  C   . Do đó (II) đúng. 3 3 3 Xét (III): Đặt 2
t  sin x  cos x  t  sin x  cos x  2tdt  cos x  sin xdx . 2tdt Khi đó
 2 dt  2t  C  2 sin x  cos x  C   . Do đó (III) đúng. t Chọn D. http://hoc24h.vn - 29
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến TÍCH PHÂN Khái niệm tích phân
— Cho hàm số f (x) liên tục trên K và a, b  K. Hàm số F (x) được gọi là nguyên hàm của
f (x) trên K thì F (b)  F (a) được gọi là tích phân của f (x) từ a đến b và được kí hiệu b b là f (x)dx 
. Khi đó: I  f (x)  dx  F(x) b  F (b)  F (a) , 
với a gọi là cận dưới, b là a a a cận trên.
— Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác nhau thay cho x , nghĩa là: b b b
I  f (x)  dx  f (t) dt  f (u)  du    F (b)  F (a).    a a a
— Nếu hàm số y  f (x) liên tục và không âm trên đoạn  ;
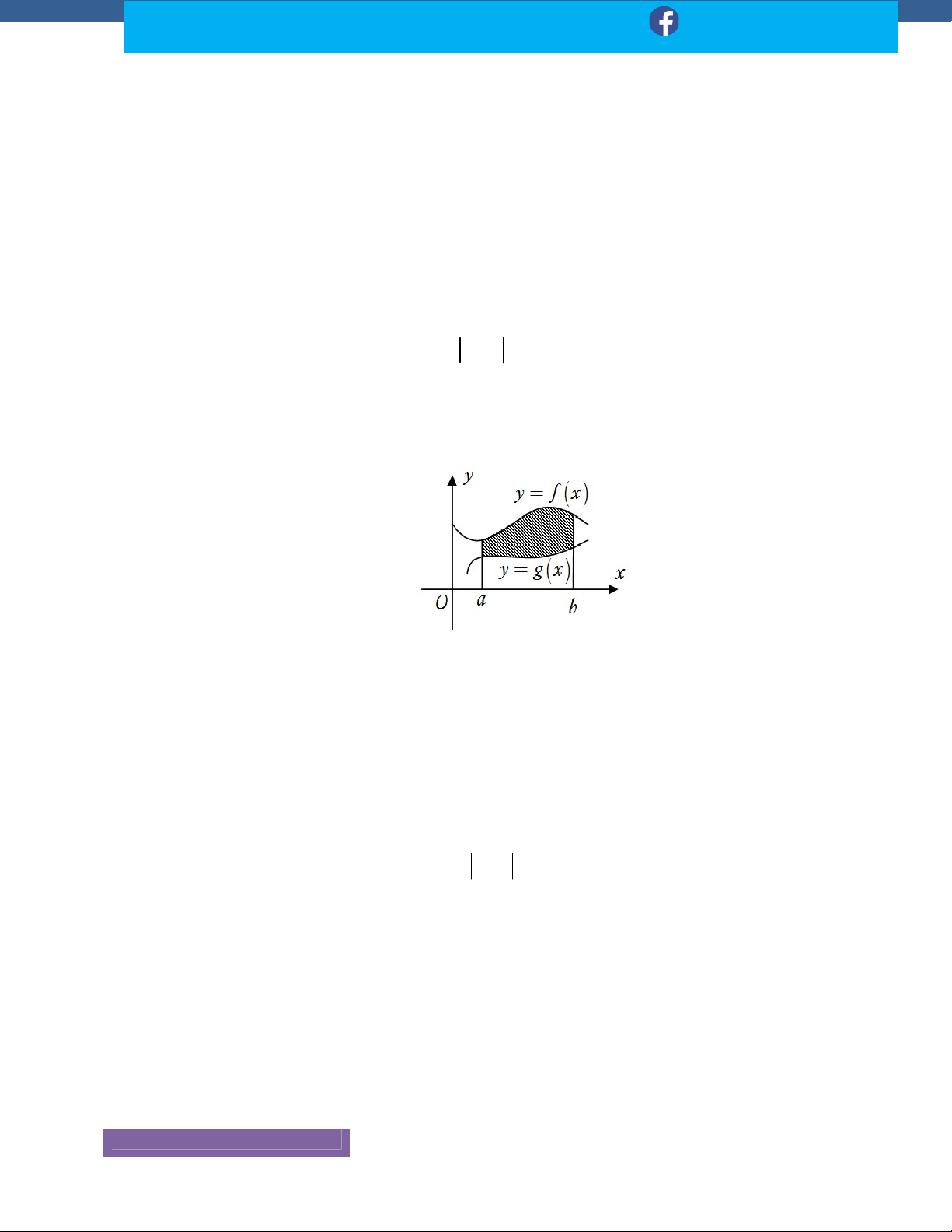
a b thì diện tích S của hình thang
cong giới hạn bởi đồ thị của y  f (x), trục Ox và hai đường thẳng x  a, x  b là: b S  f (x)  dx   a
Tính chất của tích phân b a a b b
 f (x)  dx   f (x)  dx   và f (x)  dx  0. 
 k  f (x)  dx  k  f (x)  dx,   với a b a a a (k  0). b b b b c b
  f (x)  g(x)dx  f (x)dx  g(x)dx    
 f (x)  dx  f (x) dx  f (x)  dx     a a a a a c 30
TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM LÝ THUYẾT TÍCH PHÂN
Câu 1. Cho hàm số f  x liên tục trên đoạn  ;
a b . Hãy chọn mệnh đề sai dưới đây: b a A. f  xdx   f  xdx. a b b
B. k.dx  k b  a, k    . a b c b C. f  xdx  f  xdx f
 xdx với c ;ab. a a c b a D. f  xdx  f  xdx. a b
Câu 2. Giả sử hàm số f  x liên tục trên khoảng K và a, b là hai điểm của K , ngoài ra k là một số thực tùy ý. Khi đó: a a b b b (I) f  xdx  0.(II) f  xdx  f  xdx.(II) k.f  xdx  k f  xdx. a b a a a Trong ba công thức trên: A. Chỉ có (I) sai. B. Chỉ có (II) sai.
C. Chỉ có (I) và (II) sai. D. Cả ba đều đúng.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng? 1 A. dx  1  . 1  b b b B. f x . f x dx  f x d . x f x dx  1  2    1   . 2   a a a b
C. Nếu f  x liên tục và không âm trên đoạn  ; a b thì f  xdx  0 . a a D. Nếu f
 xdx  0 thì f x là hàm số lẻ. 0
http://hoc24h.vn - TÍCH PHÂN 31
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Câu 4. Trong các khẳng định sau, khẳng định nào đúng? b c b A. f  xdx  f  xdx f
 xdx với mọi a, b, c thuộc tập xác định của f x. a a c b B. Nếu f
 xdx  0 thì f x  0, x   ; a b. a dx C. 2  2 1 x  C  . 2 1 x
D. Nếu F  x là nguyên hàm của hàm số f  x thì F  x là nguyên hàm của hàm số f  x . x Câu 5. Đặt F  x 2  1 t dt  . Đạo hàm /
F  x là hàm số nào dưới đây? 1 x A. / F  x  . B. / F  x 2  1 x . 2 1 x 1 C. / F  x  . D. / F  x   2 x   2 1 1 x . 2 1 x x
Câu 6. Cho F  x   2t tdt . Giá trị nhỏ nhất của F x trên đoạn 1; 1 là: 1 1 5 5 A. . B. 2. C.  . D. . 6 6 6 x t  3 Câu 7. Cho F  x  dt  . Xét các mệnh đề: 2 t 1 0 x  3 I. F ' x  . 2 x 1
II. Hàm số F  x đạt cực tiểu tại x  3.
II. Hàm số F  x đạt cực đại tại x  3. Mệnh đề nào đúng? A. Chỉ I. B. Chỉ II. C. I và II. D. I và III. 32
TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Câu 8. Hãy chọn mệnh đề sai dưới đây: 1 1 A. 2 3 x dx  x dx   . 0 0 x dt 1
B. Đạo hàm của F  x   là / F  x  x  0 . 1 t 1 x 1 a a
C. Hàm số f  x liên tục trên  ; a a thì f  xdx  2 f  xdx. a 0 b c c
D. Nếu f  x liên tục trên  thì f  xdx f  xdx  f  xdx. a b a 0
Câu 9. Cho f  x là hàm số chẵn và f
 xdx  a. Chọn mệnh đề đúng: 3  3 3 A. f  xdx  a. B. f  xdx  2a. 0 3  3 0 C. f  xdx  a. D. f  xdx  a. 3  3 4 Câu 10. Nếu f  
1  12, f ' x liên tục và f '
 xdx 17. Giá trị của f 4 bằng: 1 A. 29. B. 5. C. 19. D. 9.
ĐÁP ÁN TRẮC NGHIỆM LÝ THUYẾT TÍCH PHÂN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 D 5 B 9 B 2 B 6 C 10 A 3 C 7 C 4 A 8 C
http://hoc24h.vn - TÍCH PHÂN 33
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến b a
Câu 1. Sửa lại cho đúng là: f  xdx   f  xdx . Chọn D. a b a b
Câu 2. Công thức (2) sai, sửa lại cho đúng là f  xdx   f  xdx . b a
Hai công thức (1) và (3) đều đúng. Chọn B. 1 1 Câu 3. Ta có dx  x  2.  Do đó A sai. 1 1  
Theo tính chất tích phân thì B sai (vì không có tính chất này).
Xét câu C. Giả sử F  x là một nguyên hàm của hàm số f  x trên đoạn  ; a b . Suy ra /
F  x  f  x  0, x   ; a b . b ● / F  x  0, x   ;
a b , suy ra F  x là hàm hằng nên f
 xdx  F xb  0. a a ● / F  x  0, x   ;
a b , suy ra F  x đồng biến trên đoạn  ;
a b nên F b  F a . b Do đó f
 xdx  F xb  F b F a  0. Do đó C đúng. a a a a
Chọn f  x  0 thì 0dx  C  0 
nhưng f  x  0 không phải là hàm số lẻ. 0 0 Do đó D sai. Chọn C.
Câu 4. Theo tính chất tích phân, suy ra A đúng. Chọn f  x  x và  ; a b  1;2. b 2 2 1 1 Khi đó f  x 2 dx  xdx  x  
4  1  0 nhưng hàm f x  x không thỏa mãn không âm trên 2 1  2 a 1  1;2. Do đó B sai. x 1 Vì  2 2 1 x  C    nên C sai. 2 2 1 x 1 x 2 x x Ta có
là một nguyên hàm của x nhưng
không là nguyên hàm của x . 2 2 34
TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Do đó D sai. Chọn A. x
Câu 5. Áp dụng tính chất F ' x  f
 tdt là một nguyên hàm của f x. Chọn B. a x x  t t  x x 5
Câu 6. Ta có F  x  t t 3 2 3 2 2 dt         3 2  3 2 6 1 1 3 2 x x 5 Xét hàm số F  x    trên đoạn 1;  1 3 2 6 x  1 Đạo hàm / F  x 2 /  x  ; x F  x  0   x  0 2 5 Suy ra F  
1   ; F 0   ; F   1  0 . 3 6 5
Do hàm số liên tục trên 1; 
1 nên min F  x  F 0   . Chọn C. 1; 1 6 x
Câu 7. Áp dụng tính chất F ' x  f
 tdt là một nguyên hàm của f x. a x  3 x  3 Suy ra / F  x 
. Do đó I đúng. Lại có / F  x  0   0  x  3 . 2 x 1 2 x 1
Qua điểm x  3 ta thấy /
F  x đổi dấu từ âm sang dương.
Suy ra hàm số đạt cực tiểu tại x  3 . Khi đó, mệnh đề II đúng, mệnh đề III sai. Chọn C. 1 1 Câu 8. Do x 0;  2 3 2 3
1  x  x  x dx  x dx   . Do đó A đúng. 0 0 x
Áp dụng tính chất F ' x  f
 tdt là một nguyên hàm của f x. a 1 Suy ra / F  x  . Do đó B đúng. 1 x
Mệnh đề C sai vì tính chất này chỉ đúng nếu f  x là hàm chẵn hoặc ta có thể lấy VÍ DỤ cụ thể cho
hàm f  x  x và a  2 chẳng hạn.
http://hoc24h.vn - TÍCH PHÂN 35
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 2 1 1 2 2 Khi đó 2 xdx  x   4 4  0 nhưng 2 2 xdx  x  4  . 2 2 2 2  0 0
Mệnh đề D đúng theo tính chất tích phân. Chọn C.
Câu 9. Áp dụng tính chất a 0 a
' Nếu f  x là hàm số chẵn thì f  xdx  2 f  xdx  2 f  xdx ' . Chọn B. a a 0 4 4 Câu 10. Ta có f '
 xdx  f x  f 4 f  1. 1 1 Theo bài ra ta có 4 f '
 xdx 17  f 4 f  1 17  f 4 17 f  1 1712  29. Chọn A. 1 36
TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TÍCH PHÂN ĐỔI BIẾN DẠNG 1  b  b
f (x)u (x)dx  F u(x)  F u(b) F u(a)  a a
–Bước 1. Biến đổi để chọn phép đặt t  u(x)  dt  u (
 x) dx (xem lại các phương pháp đổi
biến số trong phần nguyên hàm) x  b t   u(b)
–Bước 2. Đổi cận:   
(nhớ: đổi biến phải đổi cận) x  a t   u(a) u(b)
–Bước 3. Đưa về dạng I  f (t)  dt 
đơn giản hơn và dễ tính toán. u (a)
I  f (ax b)n xdx  t  ax b  dt  a.dx 1     x m n DẠNG n I  dx t x 1 dt (n 1) n x .dx 2  n 1     1        ax   1  I  2
f (ax b)n  xdx  t  2 ax b  dt   2ax.dx  3  7 3 x 1
VÍ DỤ 1: Tính tích phân I = dx  3 3x 1 0 Lời Giải: 3 t 1
Đặt t = 3 3x 1  t3 = 3x + 1  x = 3 dx = t2dt 3 t 1 2 2 ( 1)t dt 2 2 1 2 2 2 2 t 1 1 31 46 Do đó: I = 3 4  ( t  t )dt   = 5 .  . t 1  t 3 3 3 2 3 5 15 15 1 1 1 1 7 3 x
VÍ DỤ 2: Tính tích phân I = dx  3 2 0 1 x
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 37
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Lời giải: 3 Đặt t = 3 2
1 x ,  t3 = 1+x2  3t2dt = 2xdx  xdx = 2 t dt 2 Khi x = 0 thì t = 1 Khi x = 7 thì t = 2 Do đó: 2 3 2 2 3 (t 1)t dt 3 5 2 2 3 t t 141 I = 4  (t  t)dt   = (  )  2 t 2 2 5 2 20 1 1 1 2 2 3 x dx
VÍ DỤ 3: Tính tích phân I =  2 0 1 x Lời giải: Đặt t = 2
1 x  t2 = 1- x2  2tdt = -2xdx  -xdx = tdt Khi x = 0 thì t = 1 2 2 Khi x = thì t = 2 2 Do đó: 2 2 2 2 2 2 3 2 (1 t )( t  dt) t 2 5 2 I = 2  (t 1)dt  (  t)   =  t 3 1 3 12 1 1 7 1
VÍ DỤ 4: Tính tích phân I = dx  x  x  2 2 Lời giải:
Đặt t = x  2  t2=x + 2  2tdt = dx Khi x= 2 thì t = 2 38
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Khi x = 7 thì t = 3 Do đó: 3 3 3 2tdt 2tdt 2 2 1 I =   (  )dt    2 t  t  2 (t 1)(t  2) 3 t  2 t 1 2 2 2 3 2 2 5
= (2ln t  2  ln t 1)  (2ln  ln 2) 3 2 3 4 1
VÍ DỤ 5: Tính tích phân I = 3 2 x 1 x dx 0
(Đề thi ĐH Ngoại Thương 1996) Lời giải: Đặt t = 2
1 x  t2 = 1 – x2  xdx = -tdt Khi x = 0 thì t=1 Khi x= 1thì t = 0 Do đó: 0 1 3 5 1 t t 1 1 2 I = 2 2 4 t(1 t )( t
 dt)  (t  t )dt  (  )      3 5 0 3 5 15 1 0 1
VÍ DỤ 6: Tính tích phân I = x 1 xdx  0
(Đề thi ĐH Y TPHCM 1997 – 1998) Lời giải:
Đặt t = 1 x  t2 = 1 – x  dx = -2tdt Khi x = 0 thì t=1 Khi x= 1thì t = 0
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 39
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Do đó: 0 1 3 5 1 t t 1 1 4 I = 2 2 4
t(1 t )(2tdt)  2 (t  t )dt  2(  )  2(  )    3 5 0 3 5 15 1 0 3 2 x 1
VÍ DỤ 7: Tính tích phân I = dx  x 1 0 ĐH Cần Thơ khối D 1998 Lời giải:
Đặt t = x 1  t2 = x+1  x = t2 -1  dx = 2tdt Khi x = 0 thì t= 1 Khi x = 3 thì t = 2 Do đó: 2 2 2 2 (t 1) 1 5 2 t 2 53 I = 4 2 .2tdt  2 (t  2t  2)dt   =2( 3  t  2t)  t 5 3 15 1 1 1 1
VÍ DỤ 8: Tính tích phân I = 3 2 x 1 x dx  0
(ĐH Quốc Gia HN– khối B - 1998) Lời giải: Đặt t = 2
1 x  t2 = 1 + x2  xdx = tdt Khi x = 0 thì t=1 Khi x= 1 thì t = 2 Do đó: 2 2 5 3 2 t t 4 2 2 2 1 1 2( 2 1) I = 2 4 2
(t 1)t.tdt  (t  t )dt  (  )    (  )    5 3 1 5 3 5 3 15 1 1 40
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 xdx
VÍ DỤ 9:Tính tích phân I =  2x 1 0
(ĐH Quốc Gia TPHCM khối A – 1998) Lời giải: 2 t 1
Đặt t = 2x 1  t2 = 2x+1  x =  dx = tdt 2 Khi x=0 thì t = 1 Khi x = 1 thì t = 3 Do đó: 2 (t 1) 3 .tdt 3 3 3 1 1 t 1 I = 2 2  (t 1)dt  (  t)    t 2 2 3 1 3 1 1
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 41
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 42
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P1) a 1 1. Tìm a thỏa mãn x  1 x19.dx = 120 0 3 A. 1 B. 1 C. D. 3 20 1 6 1 2. Tìm a thỏa mãn a x   3 1 x  .dx = 168 0 1 A. 5 B. 3 C. -1 D. 20 1 3 x 1 1 3. Tìm a,b,c: .dx  =  .ln c 2 1 x a b 0 1 A.8 B. 1 C. D. l n 4 4 10 1 4. Tính 13x. 2 1 2x  3x  dx ? 0 11 6  2 11 6  2 11 6 11 6 1 A. B. C. D. 22 2 22 22 1 5. Tính x 1 x.dx  ? 0 1 1 4 A. B. - C. D. 5 4 4 15 3 x 6. Tính .dx 
? ( đề thi dự bị THPT Quốc Gia 2015 ) x 1 0 8 3 A. 8 B. 3 C. D. 3 8 1 7. Tính 2 x 2  x .dx ? 
( đề thi Đại học khối B 2013 ) 0 2 2 1 2 2 2 2 1 2 1 A. B. C. D. 3 3 3 3 3 1 8. Tính 2 x 5  x .dx  ? 0 5 5  8 5 5  8 5  8 5 5 A. B. C. D. 6 3 6 6
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 43
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 9 9. Tính 3 . x 1 x.dx  ? 1 468 1 259 A. B. C. D. 4 7 2 6 3 10. Tính 3 2 . x x 1.dx  ? 1 14 3 3 A. B. 1 C. D. 9 5 5 7 11. Tính 3 2 . x 1 x .dx 
(đề thi học kì II năm 2014-THPT Nguyễn Khuyến-TP.HCM) 0 45 3 8 46 A. B. C. D. 8 5 3 15 7 3 x .dx 12. Tính  ? 3 2 0 x 1 45 93 8 46 A. B. C. D. 8 10 3 15 3 2  x  13. Tính x e  .
 dx ? ( đề thi thử THPT QG 2015-THPT Hàn Thuyên-Bắc Ninh-Lần 3 )  x 1 0  91 9 912 91 A. 3 e  B. 3 e  C. 3 e  D. 2 e  15 5 15 15 1 2x 1 14. Tính .dx  ? 2 1  x  x 1 A. 2 3   1
B. 2 3  2 C. 4 3   1 D. 22 3   1 1 15. Tính x  3 2 1 . 2x  x .dx ? 0 2 1 2 A. B.  C.  D. 15 15 15 15 44
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P1) CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 B 5 C 9 A 13 A 2 B 6 C 10 A 14 A 3 A 7 A 11 D 15 C 4 D 8 B 12 B
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 45
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến b DẠNG: I  f ( x e ). x e .dx   Đặt x x t  e  dt  e .dx  a ln 3 dx
VÍ DỤ 1. Tính tích phân I =  x 0 e 1 Lời giải: 2t Đặt t = x e 1  t2 = x e +1  2tdt = x e dx  dx = dt 2 t 1 Khi x = 0 thì t = 2 Khi x = ln3 thì t = 2 Do đó: 2 2 2 2tdt 2dt 1 1 I =   (  )dt    2 2 t(t 1) t 1 t 1 t 1 2 2 2 2 t 1 1 2 1 3  2 2 =ln  ln  ln  ln t 1 2 3 2 1 3 ln 2 2 x e
VÍ DỤ 2: Tính tích phân I = dx  x 0 e 1 Lời giải: Đặt t = x e 1  t2 = x e 1  x e dx  2tdt Khi x = 0 thì t = 2 Khi x = ln2 thì t = 3 3 2 3 3 3 (t 1)2tdt t 2 2 Do đó:I = 2  2 (t 1)dt  2(  t)    t 3 2 3 2 2 46
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P2) ln 2 16 Câu 1: Tìm a biết: x . x e a  e .dx  =  2 3 3 0 . A. 3 B. 2 C. 5 D. 1 3 x e .dx Câu 2: Tính  ?  xe  3 0 1 2 A. 3  2 3 B. C. 2 1 D. 2 3 ln5 2 x e .dx Câu 3: Tính  ? x ln 2 e 1 45 20 8 46 A. B. C. D. 8 3 3 15 ln 6 dx Câu 4: Tính  ? x 0 e  3 3 2 1 A. ln 2  3 B. ln 2  3
C. ln 2  3 D. ln2  3 3 3 3 ln 2 2 x e .dx Câu 5: Tính  ? x 0 e 1 2 2 2 A. A. 3  2 3 B. C. 2 1 D. 3 3 ln 2 2x e .dx Câu 6: Tính  ? x 0 e  2 8 8 2 A. B. 2 3  C. 2 3 D. 2 3  3 3 3 ln 6 x e .dx Câu 7: Tính  ? x x 0 3 3  e  2e  7 80 8 800 A. ln 4 B. ln C. ln D. ln 3 3 3 ln16 dx Câu 8: Tính  ? 4 x 0 e  4 80 8 3 A. ln 4 B. ln C. ln D. ln 3 3 5
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 47
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P2) CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 C 4 A 7 B 2 C 5 D 8 D 3 B 6 B 9 48
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến b 1 1
DẠNG I  f (ln x)   dx 
 Đặt t  ln x  dt   dx  x x a
Nếu f (ln x) có chứa m  .
n ln x với m, n là hằng số thì ta đặt luôn t  m  . n ln . x Bởi 1
lẻ khi vi phân dt  n   dx sẽ không bị mất tính tổng quát so với khi đặt t  ln x và x
làm cho việc xử lý bài toán sau khi đặt ẩn phụ sẽ đơn hơn. Ngoài ra, khi gặp căn thức, ta cũng đặt n t  f (ln x)  ln x
Nếu có chứa log x thì ta chuyển về ln x bằng công thức: log x  log . e log x   a a a e ln a
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 49
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến b 1
TRẮC NGHIỆM DẠNG I  f (ln x)   dx  x a e ln . x dx Câu 1: Tính  ? x 1 ln x 1 4  2 2 4  2 5  2 2 5  2 2 A. B. C. D. 3 3 3 3 e 1 3ln x.ln x Câu 2: Tính .dx  ? x 1 29 478 13 116 A. B. C. D. 270 15 178 135 e 3 2 ln . x 2  ln x Câu 3: Tính .dx  ? x 1 3 3 9 3  6 2 3 3 3  2 3 3 9 3  6 2 3 3 3  2 A. B. C. D. 8 8 7 7 e dx Câu 4: Tính  ? 3 . x 1 ln x 1 3 3. 4  3 3 3. 4 3 4  3 3 3. 3  3 A. B. C. D. 2 2 2 5 e e 3  2ln x Câu 5: Tính .dx  x 1 2ln x 1 1 3 1 5 A. B. C.  D. 2 2 2 3 3 e ln . x dx Câu 6: Tính  x ln x 1 1 64 76 46 29 A. B. C. D. 105 15 15 270 e 3 ln . x dx Câu 7: Tính  ? 2 1 x 1  3ln x 45 4 8 46 A. B. C. D. 8 27 3 15 50
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến b 1
ĐÁP ÁN TRẮC NGHIỆM DẠNG I  f (ln x)   dx  x a CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 A 4 A 7 B 2 D 5 D 3 A 6 B
KỸ THUẬT 4: TÍCH PHÂN LƯỢNG GIÁC
1.CÔNG THỨC LƯỢNG GIÁC THƯỜNG SỬ DỤNG: a. Hệ thức cơ bản:
sin2a + cos2a = 1; tana.cota = 1 1 1 2 2 1 tan a  ; 1 cot a  2 2 cos a sin a b. Công thức nhân đôi sin2a = 2sina.cosa 2 2 2 2
cos 2a  cos a  sin a  2cos a 1  1 2sin a 2 2 tan a cot a 1 tan 2a  ; cot 2a  2 1 tan a 2cot a c.Công thức hạ bậc 1 cos 2a 1 cos 2a 1 cos 2a 2 sin a  2 cos a  2 tan a  2 2 1 cos 2a
d.Công thức biến tích thành tổng 1 cos . a cos b 
cos(a b)  cos(a b) 2 1 sin . a sin b 
cos(a b) cos(a b) 2 1 sin . a cos b 
sin(a b) sin(a b)  2
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 51
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Nhắc lại công thức nguyên hàm lượng giác: Nguyên hàm số sơ cấp Nguyên hàm hàm mở rộng cos xdx  sin x  C   ax b 1 cos
dx  sin ax  b  C a sin xdx   cos x  C   ax b 1 sin
dx   cos ax  b  C a 1 1 1 dx  tan x  C  dx  tan ax  b  C  2 cos x 2 cos ax  b   a 1 1 1 dx   cot x  C  dx   cot ax  b  C  2 sin x 2 sin ax  b   a
Công thức Walliss (dùng cho trắc nghiệm)   (n 1)!! (1) 2 2  n n n!! cos xdx  sin xdx     . (n 1)!!  0 0  . (2)  n!! 2
(Nếu n lẻ : Dùng ct (1) ; Nếu n chẵn: Dùng ct (2) ) Trong đó
n!! đọc là n walliss và được định nghĩa dựa vào n lẻ hay chẵn. Chẳng hạn:
0!!  1; 1!!  1; 2!!  2; 3!!  1.3; 4!!  2.4; 5!!  1.3.5;
6!!  2.4.6; 7!!  1.3.5.7; 8!!  2.4.6.8; 9!!  1.3.5.7.9; 10!!  2.4.6.8.10 .  2 10!! 2.4.6.8.10 256 VÍ DỤ 1. 11 cos xdx     . 11!! 1.3.5.7.9.11 693 0  2 9!!  1.3.5.7.9  63 VÍ DỤ 2. 10 sin xdx  .  .   . 10!! 2 2.4.6.8.10 2 512 0 52
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
DẠNG 4.1. SỬ DỤNG CÔNG THỨC NGUYÊN HÀM CƠ BẢN  4 3 1 sin x VÍ DỤ 1: Tính I  dx 1  2  sin x 6 Bài giải:
Ta thấy đề bài biểu thức dưới dấu tích phân ở dạng thương nên phải biến đổi để không còn dạng thương, 1 mặt khác
, sinx có công thức nguyên hàm nên 2 sin x   4 3 4 1 sin x  1  I  dx   sin x dx 1   2  2   sin x   sin x  6 6   cot x  cos x 2 3 4  1     2 2 6 2 3 Vậy I  1    1 2 2  2 3 3cos x VÍ DỤ 2: Tính I  dx 2  1 sin x 0 Bài giải:
Ta thấy biểu thức dưới dấu tích phân ở dạng thương nên phải biến đổi để không còn dạng thương, tử thức
là cosx, mẫu là biểu thức theo sinx nên ta biến đổi tử theo sinx để rút gọn   2 2 3cos x  2 3 1 sin xcos x I  dx  3 dx 2   1 sin x 1 sin x 0 0   2      3 x 2 3 3 1 sin cos xdx  3sin x  cos 2x     4  2 0 0 3 Vậy I  2 2
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 53
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  3 1 VÍ DỤ 3: Tính I  dx 3  2 2  sin x cos x 4 Bài giải: 1 1 1 1 1
Ta có công thức nguyên hàm , nhưng nếu tách  . được biểu thức 2 2 sin x cos x 2 2 2 2 sin x cos x sin x cos x
dưới dấu tích phân là tích hai hàm nên Cách 1:   3 3 2 2 1 sin x  cos x I  dx  dx 3   2 2 2 2  sin x cos x  sin x cos x 4 4  3  1 1     dx   2 3   tan x  cot x 3  2 2  cos x sin x    3 4 4 2 3 Vậy I  3 3 Cách 2:   3 3 1 1 I  dx  dx 3   2 2 2  sin x cos x  (sin x cos x) 4 4  3 4  3  dx  2cot 2x  2 3  2 sin 2x   3 4 4 2 3 Vậy I  3 3  4 VÍ DỤ 4: Tính 2 I  cot xdx 4   6 54
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Bài giải:
Ta không có công thức nguyên hàm của 2
cot x nên cần phải biến đổi. Có hai cách. Cách1:   4 4 2 I  cot xdx    2 cot x 11 dx 4    6 6     
  cot x  x 4  1  3   1    3  4 6 12 6 Cách 2:     4 4 2 cos x 4 2 4 1 sin x  1 2  I  cot xdx  dx  dx  1 dx 4     2 2  2    sin x  sin x   sin x  6 6 6 6     
  cot x  x 4  1  3   1    3  4 6 12 6 Bài tập tự luyện    3 2 3  2cot x 2 3 4sin x 4 Tính : a. dx  b. dx  c. 2 tan xdx  2  cos x 1 cos x 0 0 4   4 cos 2x 4 4 sin x d. dx  e. dx  2 cos x 2 cos x 0 0 11 3   5 3 Đáp án: . a  5 . b 2 . c 1 d. 1 . e  3 4 2 4 8
DẠNG 4.2: DÙNG CÔNG THỨC HẠ BẬC  2 VÍ DỤ 1: Tính 2 J  cos xdx 1  0
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 55
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Bài giải:
Ta không có công thức nguyên hàm của cos2x nên phải dùng công thức hạ bậc    2 2  2 1 cos 2x  1 1   2 J  cos xdx  dx  x  sin 2x  1     2  2 4  4 0 0 0  Vậy J  1 4  2 VÍ DỤ 2: Tính 2 J  sin x cos 2xdx 2  0 Bài giải:     2 2 1 cos 2x 2 2 1 1  1 cos 4x 2  J  sin x cos 2xdx  cos 2xdx 2  cos 2x  cos 2x dx  cos 2x  dx 2       2 2 2  2  0 0 0 0  2 1  1 1 1     x  sin 2x  sin8x     2  2 2 8  4 0  Vậy J   2 4  2 VÍ DỤ 3: J  cos 2x   4 4 sin x  cos x dx 3  0 Bài giải:   2 J  cos 2x  sin xcos x 2 4 4 dx  cos 2x   2 2 1 2sin x cos x dx 3  0 0   2 2  1   1 1 cos 4x 2 
 cos 2x 1 sin 2x dx  cos 2x 1 . dx        2   2 2  0 0 56
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến     2 2 1 1 2 2  1 1 3cos 2xdx  cos 4x cos 2xdx    3cos 2xdx    cos6xcos2xdx 4 4 4 8 0 0 0 0    2 2 2 3 1 1  sin 2x  sin 6x  sin 2x  0 8 64 12 0 0 0 Vậy J3 = 0 Bài tập tự luyện Tính các tích phân   3  x  3 a. 2 2 cos x  sin dx   b. 2 4 cos . x sin xdx   4  0  6   20 2 c. 2 sin 5xdx  d.  2 2
2sin x  sin x cos x  cos xdx 0 0   4 4 e. 4 sin xdx  f. 4 cos xdx  0 0  3 1 1   3   1 Đáp án: . a   . b    . c  3 8 2 16  6 4    40 20  1 1  3  1  3  d.  . e 1   f . 1   4 2 4  8  4  8 
DẠNG 4.3: DÙNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG  3
VÍ DỤ 1: Tính tích phân: K  sin 2x cos 6xdx 1   6 Bài giải:
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 57
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Biểu thức dưới dấu tích phân là tích của hai hàm nên ta dùng công thức biến đổi tích thành tổng    3 3 1 3 1  1 1  K  sin 2x cos 6xdx  sin 8x  sin 4x dx   cos8x  cos 4x = 0 1       2  2  8 4   6 6 6 Vậy K  0 1  2
VÍ DỤ 2: Tính tích phân: K  cos x cos 2x cos3xdx 2  0 Bài giải:
Ta có: cos x cos 2x cos 3x  cos 2x cos3x cos x 1
 cos 2xcos 4x  cos 2x 2 1   2 cos 4x cos 2x  cos 2x 2 1
 cos6x  cos 2x 1 cos 4x 4  2 1 Do đó K 
cos 6x  cos 2x 1 cos 4x dx 2   4 0  2  1 1 1 1    sin 6x  sin 2x  x  sin 4x     24 8 4 16  8 0  Vậy K  2 8 Bài tập tự luyện:    4 4 6 . a sin 5x sin 3xdx  b. sin x sin 2x cos 5xdx  . c sin6xsin 2x 6dx 0 0 0 58
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 1 3 3 Đáp án: . a . b  . c  4 6 32
DẠNG 4.4: ĐỔI BIẾN SỐ
Các dạng thường gặp khi đổi biến
a. Chứa biểu thức mang mũ b. Chứa mẫu c. Chứa căn d. Chứa mũ
Dạng f sinx.cos x  đặt t  sin x hoặc t  a  . b sin x
Dạng f cos xsin x  đặt t  cos x hoặc t  a  b cos x 1 Dạng f tan x  đặt t  tan x 2 cos x 1 Dạng f cot x  đặt t  cot x 2 sin x
Dạng f sinx  cos x.sin x  cos x  đặt t  sin x  cos x
Dạng 4.4.1. Kết hợp 1 trong 4 dạng a,b,c,d với d(sinx)=cosx, d(cosx)=-sinx  2
VÍ DỤ 1: Tính: L  1 2sin x3 cos xdx 1 0 Bài giải:
Biểu thức dưới dấu tích phân chứa biểu thức mang mũ và d(sinx) = cosxdx. Nên dt
Đặt: t  1 2sin x, dt  2cos xdx  cos xdx  2 
Đổi cận: khi x = 0 thì t = 1; x = thì t =3 2  3 2 3 4 dt  t 
Do đó L  1 2sin x3 3 cos xdx  t     10 1 2  8 0 1  1
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 59
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  2 VÍ DỤ 2: Tính L 3 2 = cos xdx  0 Bài giải:
-Mặc dù chứa biểu thức mang mũ nhưng ta không đặt t = cosx được vì tích phân mới không chuyển hoàn toàn về theo biến t.   2 2 L 3 2 2 = cos xdx  cos x   1sin xdx 0 0
Đặt t  sin x, dt  cos xdx  cos xdx  dt 
Đổi cận: khi x = 0 thì t = 0; x = thì t =1 2 1 1 3  t  2 Do đó: L   2 1 t dt  t   2     3  3 0 0 Rút kinh nghiệm: - Dạng tổng quát 2n 1  2n 2 sin  sin sin  (1 cos )n xdx x xdx x sin xdx    .
Đặt t = cosx ( chứa sinx mũ lẻ ta đặt t = cosx) - Dạng tổng quát 2n 1  2n 2 cos  cos cos  (1 sin )n xdx x xdx x cos xdx    .
Đặt t = sinx ( chứa cosx mũ lẻ ta đặt t = sinx).
- Áp dụng được đối với biểu thức dưới dấu tích phân là tích của sinx và cosx 60
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  2 VÍ DỤ 3: Tính L 3 2 3 = sin x cos xdx   3 Bài giải:   2 2 L 3 2 2 2 3 = sin x cos xdx 
= 1cos xcos xsin xdx   3 3
Đặt t = cosx, dt = - sinxdx  sin xdx  dt  1  Đổi cận: x =  t  ; x =  t  0 3 2 2 1 1 0 2 3 5 2  t t  17 Do đó L 2 2 2 4
3 =  1 t t (dt)   t  t  dt       3 5  480 1 0 0 2 17 Vậy L3 = 480  6 VÍ DỤ 4: Tính 3 3 L  sin x cos xdx 4  0
Bài giải: Cả sin và cosx đều mũ lẻ nên ta có thể giải bằng các cách sau: Cách 1:    6 6 6 1 1 3 3 L  (sin x cos x) dx  sin 2xdx     2 1 cos 2x sin 2xdx 4  8 8 0 0 0 1
Đặt t = cos2x, dt = - 2sin2xdx  sin 2xdx   dt 2  1 Đổi cận: x =  t  ; x = 0 t  1 6 2 Do đó 1 1 3 1 1  t  1 11 5 2 L  (1 t )dt   t      4 16 16  3 1  24 384 384 1 2 2
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 61
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Cách 2:  6 L  sin x   2 1 cos x 3 cos xdx 4 0
Đặt t = cosx, dt = - sinxdx  sin xdx  dt  3 Đổi cận: x =  t  ; x = 0  t  1 6 2 Do đó 1 1 1 4 6  t t  5 2 3 3 5 L  (1 t )t dt  (t  t )dt    4      4 6 3  384 3 3 2 2 2 5 Vậy L  4 384
Ta có thể tách cos3x = (1 – sin2x)cosx  4 2 1 2sin x VÍ DỤ 5: Tính L  dx 5  ( ĐHKB - 2003) 1 sin 2x 0 Bài giải:
Đề bài dạng phân thức hơn nữa 2 (1 2sin x)dx  cos 2xdx dt
Đặt t = 1 + sin2x, dt = 2cos2xdx  cos 2xdx  2 
Đổi cận: khi x = 0 thì t = 1; x = thì t = 2 4  4 2 2 2 1 2sin x dt 1 1 Do đó: L  dx   ln t  ln 2 5   1 sin 2x 2t 2 2 0 1 1 1 Vậy L  ln 2 5 2 0 sin 2x VÍ DỤ 6: Tính L  dx 6   2  sin x2  2 62
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Bài giải:
Đề bài chứa biểu thức mang mũ nên đặt t = 2 + sinx nhưng dt = cosxdx nên ta phải dùng công thức nhân đôi tách sin2x 0 0 sin 2x 2sin x cos x L  dx  dx 6    2  sin x2   2  sin x2   2 2
Đặt t  2  sin x  sin x  t  2 Ta có dt  cos xdx  Đổi cận khi x  
thì t = 1; x  0 thì t = 2 2 2t  2 2 2 2  2 4   4  Do đó L  dt   dt  2ln t   2ln 2  2 6   2  2    t  t t   t  1 1 1 Vậy L6 = 2ln2 - 2  2 sin 2x  sin x VÍ DỤ 7: Tính L7 = dx  1 3cos x 0 Bài giải:
Đề bài chứa căn thức và d(cosx) = - sinxdx nên Đặt 2
t  1 3cos x  t  1 3cos x 2tdt
 2tdt  3sin xdx  sin xdx   3 
Đổi cận khi x = 0 thì t = 2; x = thì t = 1 2 Do đó
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 63
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến   2 2 sin 2x  sin x 2cos x   1 sin x L7= dx  dx   1 3cos x 1 3cos x 0 0 2  t 1  2 1 2 2   2 2  3  2      t  tdt 2t   3 2 2 44 10 34 2 1 dt    t     3 t 9 9  3  27 27 27 1 1 1 34 Vậy L7 = 27  4 VÍ DỤ 8: Tính cos 2 x L  e sin 2xdx 8  0 Bài giải: Đề bài chứa mũ nên 1
Đặt t = cos2x, dt = -2sin2xdx  sin 2xdx   dt 2  Đổi cận: x =
 t  0 ; x = 0 t  1 4 1 1 t 1 1 t 1 1 Do đó: L  e dt  e  e  8  0 2 2 2 2 0 1 1 Vậy L  e  8 2 2  3 VÍ DỤ 9: Tính 2 L  sin x tan xdx 9  ( Dự bị A – 2005) 0 Bài giải:   3 3 sin x 2 L  sin x tan xdx    2 1 cos x dx 9 cosx 0 0
Đặt t = cosx, dt = -sinxdx  sin xdx  dt  1
Đổi cận: khi x = 0 thì t = 1; khi x = thì t  3 2 64
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 1 2 2 2 dt  t  3 Do đó: L   2 1 t
 lnt    ln 2  9  t  2  8 1 1 3 Vậy L  ln 2  9 8
Bài tập tự luyện: Tính các tích phân    6 cos xdx 3 3 cos x 4 cos x . a  . b dx  . c dx  2sin x 1 2   2 1 sin x 2  sin x sin x 0 4 6    4 sin 4x 4 2 sin 2x cos x d. dx  3 f . tan xdx  g. dx  (ĐHKB- 2005) 3  cos 2x 1 cos x 0 0 0 Đáp án: 1 9 2  7 3 1 3  2 2 . a ln 2 . b . c ln  2  2 2 6 2 3 3 1 2 d.1 3ln f .  ln g.2ln 2 1 4 2 2
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 65
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Dạng 4.4.2. Kết hợp 1 trong 4 dạng a,b,c,d và d  2 x  xdx d  2 sin sin 2 ; cos x  sin 2xdx  2 VÍ DỤ 1: Tính 2 3 M  sin 2x(1 sin x) dx 1  0 Bài giải:
Đề bài chứa biểu thức mang mũ và d  2 sin x  sin 2xdx nên Đặt 2
t  1 sin x  dt  sin 2xdx 
Đổi cận khi x = 0 thì t = 1; khi x = thì t = 2 2 2 2 4 t 15 Do đó: 3 M  t dt   1  4 4 1 1 15 Vậy M  1 4  4 sin 4x VÍ DỤ 2: Tính M  dx 2  2 1 cos x 0 Bài giải:
Đề bài chứa mẫu và d  2
1 cos x  sin 2xdx ; sin4x = 2 sin2xcos2x. Nên Đặt 2
t  1 cos x  dt   sin 2xdx  3
Đổi cận khi x = 0 thì t = 2; khi x = thì t = 4 2  4 2 2sin 2x cos 2x 22t  3 4 Do đó: M  dx  dt   
4t  6lnt 23  26ln 2 2 1 cos x t 3 0 3 2 2 4 Vậy M  2  6 ln 2 3 66
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  2 sin 2x VÍ DỤ 3: M  dx 3  2 2 0 cos x  4sin x Bài giải:
Đề bài chứa căn thức nên Đặt 2 2
t  cos x  4sin x  2tdt  3sin 2xdx 
Đổi cận khi x = 0 thì t = 1; khi x = thì t = 2 2 2 2 tdt 2 2 2 Do đó 3 M   t  3  t 3 3 1 1 2 Vậy M3 = 3
Bài tập tự luyện: Tính các tích phân:   2 sin 2x 2 sin x cos x . a dx  . b dx  2 1 cos x 2 0 0 4  3sin x 7  2 Đáp án: . a ln 2 . b 3
Dạng 4.4.3 Kết hợp 1 trong 4 dạng a,b,c,d và 1 d  x 1 tan  dx   2
1 tan x dx ; d cot x   dx    2 1 cot x dx 2  2  cos x sin x  3 VÍ DỤ 1: Tính N   3 tan x  tan x dx 1   4 Bài giải:   3 N  tan x  tan x 3 3 dx  tan x   2 1 tan x dx 1    4 4 Đặt t = tanx  dt   2 1 tan xdx
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 67
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  
Đổi cận: Khi x = thì t =1; x = thì t = 3 4 3 3 3 2 t Do đó: N  tdt  1 1  2 1 1 Vậy N  1 1  6 4 tan x VÍ DỤ 2: Tính N  dx 2  cos 2x 0 Bài giải:    4 1 6 4 6 4 6 tan . x 2 tan x tan x cos x N  dx  dx  dx 2    2 2 2 cos 2x cos x  sin x 1 tan x 0 0 0 1 Đặt t = tanx  dt  dx 2 cos x  3
Đổi cận: Khi x = 0 thì t = 0; x = thì t = 6 3 3 3 3 3 3 4 3 4 t t 11 3 3  1   1  1 1  Dođó: N  dt  dt 2 2   t 1  dt   t 1   dt 2        2     2 2   1 t 1 t  1 t   2  t 1 t 1   0 0 0 0  3 3 3   t 1 t 1  1    t       10 ln ln 2 3    3 2 t 1  2  9 3 0 1 10
Vậy N2 = ln 2  3  2 9 3  4 1 VÍ DỤ 3: Tính N  dx 3  2  sin x cot x 6 Bài giải: 1
Đề bài chứa căn thức và d(cotx) =  dx nên 2 sin x 1 Đặt 2
t  cot x  t  cot x  2tdt   dx 2 sin x 68
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  
Đổi cận: Khi x = thì t = 4 3 ;khi x  thì t =1 6 4 1 Do đó 1 4 N   2dt  2t  2 3  2 3  4 3 4 3 Vậy 4 N  2 3  2 3  2 1 VÍ DỤ 4: Tính N  dx 4  4  sin x 4 Bài giải:
Đề bài chứa biểu thức mang mũ là sinx nhưng ta không đặt t = sinx vì d(sinx) = cosxdx không có ở đề 1 1 1 bài mà phải xem  . 4 2 2 sin x sin x sin x   2 2 1 1 Ta có N  dx    2 1 cot x . dx 4 4  2  sin x  sin x 4 4 1
Đặt t  cot x  dt   dx 2 sin x  
Đổi cận: Khi x = thì t = 1;khi x  thì t = 0 4 2 1 1 3  t  4 Do đó N   2 1 t dt  t   4     3  3 0 0 4 Vậy N  4 3
Bài tập tự luyện: Tính các tích phân:   3 3 1 . a dx  . b  3 cot x  cot xdx 4 cos x   4 4 4 1 Đáp án . a 2 3  . b 3 3
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 69
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Dạng 4.4.4 Kết hợp 1 trong 4 dạng a,b,c,d và d sin x  cos x  cos x  sin x dx  4 cos x  sin x VÍ DỤ 1: Tính P  dx 1  sin x  cos x 0 Bài giải:
Đặt t  sin x  cos x  dt  cos x  sin xdx 
Đổi cận khi x = 0 thì t = 1; x   t  2 4 2 1 Do đó: 2 P  dt  ln t  ln 2 1  1 t 1 Vậy: P  ln 2 1  2 cos 2x VÍ DỤ 2: Tính P  dx 2  sin x cos x 32 0 Bài giải:
Đặt t = sinx – cosx + 3  dt  cos x  sin xdx 
Đổi cận khi x = 0 thì t = 2; x   t  4 2 Do đó: 
2 cos x  sin xcos x  sin x P  dx 2  sin x cos x 32 0 4 4 t   3  3  3  dt   ln t    ln 2  2   t  t  4 2 2 3 Vậy P2 =  ln 2 4  2 3 cos x VÍ DỤ 3: Tính P  dx 3  sin x  cos x 0 Bài giải: 70
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  2 3 sin x
Ta không tính P3 độc lập được mà phải dựa vào Q  dx P  Q ; P  Q sau 3  bằng cách tính sin x  cos x 3 3 3 3 0
đó giải hệ để tính P3  2 3 3 cos x  sin x Tính P  Q  dx 3 3  sin x  cos x 0   2 2  1   1   1 
1 sin 2x dx  x  cos 2x        2   4  2 2 0 0   2 3 3 2 cos x  sin x
cos x sin x1sin xcos x Tính P  Q  dx  dx 3 3   sin x  cos x sin x  cos x 0 0
Đặt t = sinx + cosx  dt  cos x  sin xdx 
Đổi cận khi x = 0 thì t = 1; khi x = thì t= 1 2 2  t 1 1 1    2 Do đó P Q    dt  0 3 3  t 1  1 Giải hệ ta được P   3 4 4  1 Vậy P   3 4 4
Bài tập tự luyện: Tính các tích phân:   4 cos 2x 4 cos x . a dx  . b dx  sin x  cos x  2 sin x  cos x 0 0      sin x  2 sin x 4    4 . c dx  d.  dx   (ĐHKB–2008) sin x  cos x3
sin 2x  2(1 sin x  cos x) 0 0
Hướng dẫn giải câu d. đặt t = 1 + sinx + cosx
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 71
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Đáp án: 2  2 1 1 4  3 2 . a 2 1 2ln . b ln 2   . c d. 3 8 2 2 4
TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P3)
Tính các tích phân sau (không dùng máy tính)
( dạng f sinx.cos x  đặt t  sin x hoặc t  a  . b sin x )  2 Câu 1: Tính 2 sin . x cos . x dx 
? (đề HK II 2014- THPT Lương Văn Can- TP.HCM ) 0 1 3 1 3 A. B. C.  D.  2 2 2 2  2 Câu 2:
Tính 13sin x.cos .xdx ? (đề HK II 2014- THPT Quốc Trí- TP.HCM ) 0 1 3 1 3 A. B. C.  D.  2 2 2 2  2 cos x Câu 3: Tính .dx 
? (đề HK II 2014- THPT Marie Curie- TP.HCM ) 1 sin x 0 A. ln4 B. ln5 C. ln3 D. ln2  2 cos x Câu 4: Tính .dx  ? 5  2sin x 0 1 5 1 5 1 3 1 5
A.   ln B. ln C.  ln D.  ln 3 2 2 3 3 2 3 2  2 sin 2 . x dx Câu 5: Tính 
? (đề HK II 2014-THCS & THPT Bắc Mỹ- TP.HCM ) 1 sin x 0 A. 1-ln4 B. 4ln5 C. 3-ln3 D. 2-2ln2  2 Câu 6:
Tính 1 sinx2.cos .xdx ? 0 7 3 A. 8 B. 3 C. D. 3 8 72
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  2 Câu 7:
Tính 1 2sin x3.cos .xdx ? 0 A. 5 B. 10 C. 15 D. 20
Tính các tích phân sau ( dạng f cos xsin x  đặt t  cos x hoặc t  a  b cos x )  3 Câu 8: Tính 4 s inx.cos . x dx 
? ( đề thi HK II-THPT Lê Thánh Tôn- TP.HCM ) 0 64 31 46 29 A. B. C. D. 105 160 15 270  3 sinx Câu 9: Tính .dx 
? ( đề thi HK II-THPT Việt Mỹ Anh- TP.HCM ) 2 cos x 0 1 1 A. B. C. 2 D. 1 2 4  Câu 10: Tính 2 sin 2 . x cos . x dx 
?(đề thi thử THPT QG 2015-THPT Nguyễn Văn Trỗi- Hà Tĩnh-Lần1) 0 A. 0 B. 2 C.4 D.6  2 Câu 11: Tính sin . x cos x  1 cos x2 .dx ? 0 64 31 17 29 A. B. C. D. 105 160 12 270  2 3 4sin x Câu 12: Tính .dx  ? 1 cos x 0 A. 0 B. 2 C.4 D.6 1
Tính các tích phân sau ( dạng f tan x  đặt t  tan x ) 2 cos x  1tan x2 4 .dx Câu 13: Tính  ? 2 cos x 0 11 7 5 A. B. C. D. 3 6 3 2
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 73
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  4 2  3 tan x Câu 14: Tính .dx 
? ( đề thi thử THPT QG 2015-THPT Chuyên Lam Sơn-Thanh Hóa ) 1 cos 2x 0 5 5  2 2 5 5  2 5  2 2 5  2 2 A. B. C. D. 9 9 9 9   tan 4 cos x x  e .sin .xdx Câu 15: Tính  ? 3 cos x 0 A. 2 B. 1 C. 2 D. 3  6 4 tan x Câu 16: Tính .dx 
? ( đề thi Đại Học khối A năm 2008 ) cos 2x 0 10 3 1 10 3 1 A.   ln 2  3 B.  ln 2  3 27 2 27 2 10 3 1 10 3 1 C.   ln 2  3 D.   ln 2  3 27 2 27 2
Tính các tích phân sau ( dạng f sinx  cos x.sin x  cos x  đặt t  sin x  cos x )  2 sin x  cos x Câu 17: Tính .dx  ?  sin x  cos x 4 1 1 A. ln 2 B. ln 4 C. ln 4 D. ln 2 2 2  4 sin x  cos x Câu 18: Tính .dx  ? sin x  cos x  3 0 3  2 3  2 3  2 3  2 A.  ln B. ln C.  ln D.  ln 4 4 4 2  4 cos 2x Câu 19: Tính .dx  ? sin x  cos x  2 0 3 1 A. 2 1 2ln B. 2 1 2ln 2  2 2  2 3 3 C. 2 1 2ln D. 2 1 2ln 2  2 2  2  2 cos 2x Câu 20: Tính .dx  ? sin x cos x 33 0 74
TÍCH PHÂN ĐỔI BIẾN DẠNG 1 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 11 1 5 A. B. C. D. 3 6 32 2  2 1 sin 2x  cos 2x Câu 21: Tính .dx   sin x  cos x 4 A. 3 B. 2 C. 1 D. -1
ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 1 (P3) CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN Câu 1. A Câu 7. B Câu 13. B Câu 19. A Câu 2. C Câu 8. B Câu 14. A Câu 20. B Câu 3. D Câu 9. D Câu 15. C Câu 21. C Câu 4. B Câu 10. A Câu 16. A Câu 5. D Câu 11. C Câu 17. D Câu 6. C Câu 12. B Câu 18. A
http://hoc24h.vn - TÍCH PHÂN ĐỔI BIẾN DẠNG 1 75
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 DẤU HIỆU CÁCH CHỌN x  a sin t 2 2 a  x  x  a cost   a x  sint 2 2 x  a   a x   cost x  a tgt 2 2 a  x  x  a cot gt  a  x x  a cos t a  x a  x x  a cos t a  x a 2 2 2 a  b x x  sin t b 1 , n=1, 2, … a x  tgt 2 2 2 (  )n a b x b 76
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
VÍ DỤ 1: Tính tích phân(với a>0) a 2 dx I=  2 2 0 a  x Lời giải:     Đặt t= asint, t   ;  ,  dx= acostdt 2 2    Với x = 0 thì t=0 a  Với x= thì t= 2 6   6 6 a cos tdt   Do đó: I =  dt   0    2 2 2 a  a sin t 6 6 0 0
VÍ DỤ 2: Tính tích phân(với a >0) a dx I=  2 2 a  x 0 Lời giải:     Đặt x = tgt , t   ;   ,  dx = a(tg2t + 1)dt.  2 2  Với x = 0 thì t=0  Với x= a thì t = 4 Do đó:   4 2 4 a(tg t 1)dt dt 1   I =   (  0)    2 2 2 a  a tg t a a 4 4a 0 0
http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 77
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
VÍ DỤ 3 : Tính tích phân: 1 2 1 x I  dx  2 x 2 2 Lời giải:
Đặt x = sint,  dx = costdt 2  Khi x = thì t = 2 4  Khi x = 1 thì t = 2 Do đó:    2 2 2 2 2 cos t 1 sin t 1 I = dt  dt  ( 1)dt    2 2 2  sin t  sin t  sin t 4 4 4   =-(cotgt+t) 2 =1- 4 4 VÍ DỤ 4: Tính tích phân 1 2 x I = dx  2 0 4  x Lời giải:
Đặt x = 2cost,  dx = -2sintdt  Khi x = 0 thì t = 2  Khi x = 1 thì t = 3 Do đó: 78
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến   3 2 3 4cos t.2sin tdt  1    3 I = 3   2  (1 2cost)dt  2  t  sin 2t     2sin t  2      3 2 2 2 2 VÍ DỤ 5: Tính tích phân 2 I = 2 2 x 4  x dx  0 Lời giải:
Đặt x = 2sint,  dx = 2cosdt Khi x = 0 thì t = 0  Khi x = 2 thì t = 2 2 2 x  4sin t    2 2 2 Do đó: I = 2 2 2
16sin t cos tdt  4 sin 2tdt  2 (1 cos 4t)dt    0 0 0  1    =2 2 t  sin 4t  2(  0)    4    0 2 VÍ DỤ 6: Tính tích phân 2 2 3 x dx I =  2 0 1 x Lời giải:
Đặt x = sint,  dx = cosdt Khi x = 0 thì t = 0 2  Khi x = thì t = 2 4
http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 79
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Do đó:     4 4 3 4 4 2 2 sin t.cos t I = 3
sin t.sin tdt   (1 cos t)d(cos t) dt  sin tdt      cos t 0 0 0 0 1  2 5 2 = (-cost + cos3t) 4 =  3 0 3 12 VÍ DỤ 7: Tính tích phân 2 2 2 x dx I =  2 0 1 x Lời giải:
Đặt x = sint,  dx = cosdt Khi x = 0 thì t = 0 2  Khi x = thì t = 2 4    4 2 4 4 sin t.cos tdt 1 1  1    1 Do đó: I = 2 4  sin tdt  (1 cos 2t)dt  t  sin 2t      cos t 2 2  2    0 8 4 0 0 0 VÍ DỤ 8: Tính tích phân 2 dx I =  2 2 x x 1 3 Lời giải: 1 sin tdt Đặt x = ,  dx = cos t 2 cos t 2  Khi x = thì t = 3 6 80
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  Khi x = 2 thì t = 4  sin t  sin t  4 4 4 2 2   Do đó: I = cos t cos t 4 dt  dt  dt  t     1 1 1 sin t     12 6 1 6 2 6 6 cost cos t cost cost VÍ DỤ 9: Tính tích phân 1 I = 2 2 x 4  3x dx  0 Lời giải: 2 2 Đặt x = sin t  dx = costdt 3 3 Khi x = 0 thì t = 0  Khi x = 1 thì t = 3 Do đó:    3 3 3 4 2 4 2 I = 2 2 2 sin t 4  4sin t. costdt  sin 2tdt  (1 cos 4t)dt    3 3 3 3 3 3 0 0 0 2  1   2  3 = 3 t  sin 4t  (  ) 3 3  4    0 3 3 3 8
VÍ DỤ 10: Tính tích phân 2 2 1 x I = dx  1 x 0 Lời giải:
Đặt x=cost,  dx = -sintdt
http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 81
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  Khi x=0 thì t = 2 2  Khi x = thì t = 2 4 Do đó:     2 t t t 4 2 2cos 2 cos 2 cos 1 cos t t t I = 2 2 2  .sin tdt  .sin tdt  .sin tdt  .2sin cos dt      1 cos t 2 t t t    2 2 2sin sin sin 2 4 4 4 2 2 2   2 2 t   2 = 2 2 2cos
dt  (1 cost)dt  (t  sin t)  1   2    4 2 4 4 4
VÍ DỤ 11: Tính tính phân 3 dx I =  2 1 x 1  x Lời giải: dt Đặt x = tgt,  dx = 2 cos t  Khi x=1 thì t = 4  Khi x = 3 thì t = 3 1 2 1 x  cos t Do đó:   3 3 cost dt dt t    I = 3 . 
 (ln tg )  ln(tg )  ln(tg )   2 tgt. cos t sin t 2    6 8 4 4 4 82
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
VÍ DỤ 12: Tính tích phân 1 dx I =  2 2 (1 3x ) 0 Lời giải: 1 1 dt 1 Đặt x = tgt ,  dx = 2  (1 tg t)dt 3 2 3 cos t 3 Khi x=0 thì t = 0  Khi x = 1 thì t = 3 1+3x2=1+tg2t Do đó:    3 3 3 1 dt 1 1 1 1    1  3 I = 2 3  cos tdt  (1 cos 2t)dt  t  sin 2t    = (  ) 2 3 1 tg t 3 2 3 2 3  2     0 2 3 3 4 0 0 0
VÍ DỤ 13: Tính tích phân 3 2 2 9  2x I = dx  2 x 3 2 Lời giải: 3 3 dt Đặt x= tgt ,  dx = 2 2 2 cos t 3  Khi x= thì t = ; 2 6
http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 83
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 3  Khi x = thì t = 2 4 1 2 2
9  2x  3 1 tg t  3. cos t Do đó:  3 1 1 .3.    4 2 4 4 4 2 cos t cost dt dt d sin t I = dt  2  2  2     3 2 2 2 2 9 2   cos t.tg t  cos t.sin t  (1  sin t).sin t tg t 6 6 6 6 2 Đặt: v=sint thì 2 2 2 2 2 dv 1 1 1 v 1 1 I = 2 2  2 (  )dv   2 ln   
= 2 2  2  2 ln( 6  3) 2 2 2 2   1 v (1 v ) v 1 v  2 v 1 v 1 1  2 2 2
VÍ DỤ 14: Tính tích phân 1 I = 2 1 x dx  (Đại học Y HN 1998) 1  2 Lời giải:
Đặt x = sint,  dx=costdt. 1  Khi x =  thì t =  2 6  Khi x = 1 thì t= . 2 ` 2 2
1 x  1 sin t  cost   2 2 1 1  1    3 Do đó: I = 2 2 cos tdt  (1 cos 2t)dt  t  sin 2t     2 2  2       3 8 6   6 6 84
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 2 a dx Câu 1: Tính ,  a  0 ? 2 2 0 x  a
A. ln 1 2 2 B. ln1 2 C. ln1 2 2 D. ln2 2 a Câu 2: Tính 2 2 a  x .dx  ? 0 2 a 2 a A.  2  ln 2       1 2 ln 2 1 2  B.    2  2 a 2 a C.  2  ln 2       1 1 ln 2 1 2  D.    2  a Câu 3: Tính 2 2 2 x x  a .dx,  a  0 0 4 a 4 a A. 3 2  ln 2       1 2 ln 2 1 8  B.    8  4 a 4 a C. 3 ln  2       1 3 2 ln 2 1 8  D.    2  1 dx Câu 4: Tính  ? 2 1 x 0    A. B.  C. D. 16 2 4 1 3 x Câu 5: Tính .dx  8 1 x 0    A. B.  C. D. 16 2 4 2 dx Câu 6: Tính  ? 2 0 x  4
A. ln 1 2 2 B. ln1 2 C. ln1 2 2 D. ln2 2 1 Câu 7: Tính 2 x 1.dx  ? 0 1 1 1 1 1 1 1 A.  ln 1 2 B.  ln 1 2 C.
 ln 1 2 D. ln1 2 2 2 2 2 2 2 2 2a dx Câu 8: Tính ,  a  0 ? 2 2 a x  a
http://hoc24h.vn - KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 85
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
A. ln 2 B. ln 1 3 C. ln2  3 D. ln1 2 3 2a Câu 9: Tính 2 2 x  a .dx,  a  0 ? a  1   1  A. 2 a 3  ln 2  2 3 B. a 3 ln  2 3 2    2    C. 2 a  3  ln 2    
1 3 D. a  3 2ln  2 2 3 Câu 10: Tính 2 x 1.dx  ? 2 5 2 1 5 1 A.
 ln 1 2 B.  ln1 2 2 2 2 2 5 2 5 2 1 C.  ln 1 2 D.  ln 4  2 2 2 2 5 Câu 11: Tính 2 x  9.dx  ? 3 9 9 9
A. 10  ln 3 B. 10  ln 3 C. 10  ln 3 C. 10  ln 3 3 2 3 3 dx Câu 12: Tính  ? 2 2 x 1
A. ln 1 2 2 B. ln1 2 C. ln1 2 2 D. ln2 2
ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN ĐỔI BIẾN DẠNG 2 CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 B 5 A 9 B 2 A 6 B 10 A 3 A 7 A 11 B 4 D 8 C 12 B 86
KỸ THUẬT 5: ĐỔI BIẾN SỐ DẠNG 2 - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN 
Định lý: Nếu u  u(x) và v  v(x) là hai hàm số có đạo hàm và liên tục trên đoạn  ; a b thì: b b b b I  u(x) v (  x)dx  
u(x)v(x)b  u (x)v(x)dx  hay I  udv  u. b v  vdu.   a a a a a a Thực hành:
— Nhận dạng: Tích 2 hàm khác loại nhân nhau, chẳng hạn: mũ nhân lượng giác,… Vi u
   phân
 du   dx b b — Đặt:   Suy ra: I  udv  u. b v  vdu.   Nguyên
dv  dx ham 
 v   a a a
— Thứ tự ưu tiên chọn u: log – đa – lượng – mũ và dv  phần còn lại. Nghĩa là nếu có ln hay log x a 1
thì chọn u  ln hay u  log x 
.ln x và dv  còn lại. Nếu không có ln; log thì chọn u  đa a ln a
thức và dv  còn lại. Nếu không có log, đa thức, ta chọn u  lượng giác,….
— Lưu ý rằng bậc của đa thức và bậc của ln tương ứng với số lần lấy nguyên hàm.
— Dạng mũ nhân lượng giác là dạng nguyên hàm từng phần luân hồi. Tìm các nguyên hàm: VÍ DỤ 1. I  s x in2xdx 
Theo thứ tự ưu tiên ở trên, với nguyên hàm này là tích của Hàm đa thức với Hàm lượng giác, nên ta ưu tiên đặt u  x du  dx u   x  Đặt    1 dv  sin 2xdx v   cos 2x  2 1 1 1 1  I   x cos 2x 
cos 2xdx   x cos 2x  sin 2x  C  2 2 2 4 VÍ DỤ 2. 2 2x I  x e dx    2 du 2xdx u   x  1 x x 1 Đặt    1 2 2 2 2 2 x
 I  x e  xe dx  x e  I  2x 2 x  1 dv  e dx v  e  2 2  2 Tính 2 x I  xe dx 1  87
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến du  dx u   x  1 x 1 x 1 x 1 Đặt 2 2 2 2     I  xe  e dx  xe  e  C  x 1 x 2 2x 1 dv  e dx v  e 2 2 2 4  2 Từ đó: 1 x  x  e x 1 x 1 x  2 2 2  2 1 x 2 2 2 2
I  x e  xe  e  C   C 2 2 4 4 VÍ DỤ 3. 2 I  x cos 2xdx  1 cos 4x 1 1 1 2 2 I  x cos 2xdx  . x dx  xdx  x cos 4xdx  x  I     1 2 2 2 4  1  1 du  dx 1 u   x  Tính I  x cos 4xdx 2   1  . Đặt 2  2 1
dv  cos4xdx v  sin 4x  4 1 1 1 1  I  xsin 4x  sin 4xdx  x sin 4x  cos 4x  C 1  8 8 8 32 1 1 1 Từ đó: 2 I  x  x sin 4x  cos 4x  C 4 8 32 VÍ DỤ 4.   2 2    1 x I x x e dx
-Với VÍ DỤ này, khi mà bậc của P  x  2 , sử dụng phương pháp Nguyên hàm từng phần ta phải tiến
hành hai lần. Tuy nhiên, trong trường hợp này, ta cũng có thể sử dụng một cách khác được chỉ ra ở đây! Đặt: 2 u
  2x  x 1 du  4x   1 dx     I   2 2x  x   1 x e  4x   1 x e dx x x dv  e dx v  e u   4x 1 du  4dx Tính  4 1 x I x e dx . Đặt   1    x x dv  e dx v  e   4 1 x  4 x
 4 1 x  4 x   4  3 x I x e e dx x e e C x e  C 1        88
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
   2    x    x    2 2 1 4 3 2  3  4 x I x x e x e C x x e  C VÍ DỤ 5. 2 x I  e cos3xdx  2 x   2x du 2e dx u   e  Đặt    1 dv  cos3xdx v  sin 3x  3 1 x 2 x 1 x 2 2 2 2  I  e sin 3x  e sin 3xdx  e sin 3x  I  1 3 3 3 3 2x   2x du 2e dx u   e  Đặt    1 dv  sin 3xdx v   cos 3x  3 1 x 2 x 1 x 2 2 2 2  I   e cos3x  e cos 3x   e cos3x  M 1  3 3 3 3 Từ đó: 1 x 2 1 x 2 1 x 2  1 x 2 2 2 2 2 
I  e sin 3x  M  e sin 3x  I  e sin 3x   e cos3x  I 1 1   3 3 3 3 3 3  3 3  1 x 2 x 4 13 1 x 2 2 2 2 2  sin 3  cos 3    sin 3 x e x e x I I e x  e cos3x  C 1 3 9 9 9 3 9    2 3sin 3 2 cos 3 x x x e  I   C 13 x ln  2 x  x 1 VÍ DỤ 6. I  dx  2 x 1 u   ln   2 x  x 1  dx du    Đặt 2    x 1 x . dv  dx  2 2   v  x 1 x 1 Ta được 2 I  x   2
1ln x  x 1 x  C 89
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến VÍ DỤ 7. 2 I    2 ln x  x 1dx  dx  2 u   ln  2 x  x 1 du  2ln   2 x  x 1. Đặt: 2    x 1 dv  dx v  x xdx 2  I  . x ln  2 x  x 1  2 ln   2 x  x 1. 2x 1 2  x  2 x  x   2  x   2 ln 1 2
1.ln x  x 1  2x C 2  ln x  VÍ DỤ 8. I  dx   .  x   dx 2 u   ln x du  2ln . x 2 ln x    Ta có I  dx  . Đặt x    . 2 x dx dv  1  2 v x     x 1 1
Ta được I   ln x   C x x  1 1  VÍ DỤ 9. I   dx  2   ln x ln x   1 1  dx dx I   dx    I  I    . 2  2 1 2  ln x ln x  ln x ln x  1  dx u   du   Tính I . Đặt 2   . 1 ln x  x ln x dv  dx v  x x x Từ đó I   I . Từ đó I   C 1 2 ln x ln x x 1 VÍ DỤ 10. I  x ln dx  . x 1 90
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  2dx  x 1 du     2 u ln   1 x 1 Đặt x 1  x 1   . Từ đó I  x  ln  C 1  2  2 x 1 dv  xdx x  x  2 VÍ DỤ 11.   3 2      2 2 5 2 4 x I x x x e dx Giả sử:   3 2     2   3 2     2 2 5 2 4 x x Q x x x e dx ax bx cx d e  C   3 2     2x   2    2x   3 2     2 2 5 2 4 3 2 2 x x x x e ax bx c e ax bx cx d e 3 2 3
 x  x  x   ax   a  b 2 2 5 2 4 2 3
2 x  2b  2c x  c  2d 2  2a a  1 5   3a 2b    b  1      Q   3 2 x  x  2x  3 2x e  C 2  2b  2c c  2   4  c  2d d  3
  2    x    2 2 1 ... 2  3  4 x R x x e dx x x e  C
IV. PHƯƠNG PHÁP 4. PHỐI HỢP ĐỔI BIẾN SỐ VÀ PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN VÍ DỤ 1. I  sin xdx  Đặt 2
x  t  x  t  dx  2tdt  I  sin t.  2tdt  2tsintdt  u   2t du  2dt Đặt     I  2  t cost  2 costdt  2  t cost  2sin t  C  dv  sin tdt v  cost
Vậy I  2sin x  2 x cos x  C 2
VÍ DỤ 2: Tính tích phân I  ln d t t.  1 91
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  dt u   ln t du  2 2 2 2 Đặt   
t . Khi đó I  t ln t  dt  t ln t  t  2ln 2 1.  dv  dt v  t 1 1 1 1 a ln x 1 1 VÍ DỤ 3: Biết I  dx   ln 2  . Giá trị của a bằng: 2 x 2 2 1  dx u   ln x du     Đặt x  dx   . dv  1  2  x v    x  ln a a x  dx ln a 1 a ln a 1 Khi đó I          1    . Suy ra a  2 . 2  x  x a x a a 1 1 1 3
VÍ DỤ 4: Kết quả của tích phân I  ln
  2x  xdx được viết ở dạng I  aln3b với a, b là các số 2
nguyên. Khi đó a  b nhận giá trị?  x  x  u   ln 2 1 2 1 2 x  x du  dx  dx  Đặt 2   x  x x  x  1 . dv  dx  v  x 3 3 3 3 2x 1  1  Khi đó I  x ln  2 x  x  dx  x ln   2x  x  2 dx   2 x 1 2  x 1 2 2 3 3  x ln  2
x  x  2x  ln x 1   3ln 3 2. Suy ra a  3, b  2 . 2 2 92
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM TÍCH PHÂN TỪNG PHẦN e
Câu 1. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Tính tích phân I  x ln d x . x  1 1 2 e  2 2 e 1 2 e 1 A. I  . B. I  . C. I  . D. I  . 2 2 4 4 e 3 a e 1
Câu 2. Khẳng định nào sau đây đúng về kết quả 3 x ln d x x   ? b 1 A. ab  64 . B. ab  46 . C. a  b  12 D. a  b  4 . 1
Câu 3. Kết quả của tích phân I  x ln   2
2  x dx được viết ở dạng I  a ln 3 bln 2  c với a, b, c là các 0
số hữu tỉ. Hỏi tổng a  b  c bằng bao nhiêu? 3 A. 0. B. 1. C. . D. 2. 2 e k Câu 4. Cho I  ln dx 
. Xác định k để I  e  2 . x 1 A. k  e  2 . B. k  e . C. k  e 1. D. k  e 1. 1 Câu 5. Tính tích phân  2x I x dx  . 0 2ln 2 1 2ln 2 1 2ln 2 1 2ln 2 1 A. I  . B. I  . C. I  . D. I  . 2 ln 2 ln 2 2 ln 2 ln 2 1
Câu 6. Kết quả tích phân  2  3 x I x
e dx được viết dưới dạng I  ae  b với a, b   . Khẳng định nào 0 sau đây là đúng? A. a  b  2 . B. 3 3 a  b  28 . C. ab  3. D. a  2b  1 .  2 Câu 7. Cho tích phân sin  sin 2 . x I x e dx 
. Một học sinh giải như sau: 0 93
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  x  0  t  0 1 
Bước 1: Đặt t  sin x  dt  cos xdx . Đổi cận    I  2 t te dt.  x   t  1  0  2 u   t du  dt 1 1 1 1 Bước 2: Chọn    . Suy ra t d t t   d t te t te e t  e  e 1   . d t v  e d t t v  e 0 0 0 0 1 Bước 3:  2 t I te dt  2  . 0
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Bài giải trên sai từ Bước 1.
B. Bài giải trên sai từ Bước 2.
C. Bài giải trên hoàn toàn đúng.
D. Bài giải trên sai từ Bước 3.    Câu 8. Cho x 2 x 2 I  e cos d x , x J  e sin d x x   và x K  e cos 2 d x x 
. Khẳng định nào đúng trong các 0 0 0 khẳng định sau? e 1 (I). I J e  
.(II). I  J  K .(III). K  . 5 A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Cả (II) và (III). 1 nx e Câu 9. Cho I  dx I  I là: n 
với n   . Giá trị của 1 x  e 0 1 0 A. 0. B. 1. C. 2. D. 3.  4 Câu 10: Tính 2 . x cos . x dx 
? (đề thi HK II 2014-THPT Nguyễn Hữu Thọ-TP.HCM) 0  2  2 A.  2  2 B.  2 C. 1 D. 2  2 4 4 2 Câu 11: Tính . x ln . x dx 
? (đề thi HK II 2014-THPT Văn Lang-TP.HCM) 1 3 4
A. 2ln 2  4 B. 2ln 2  C. 2ln 2  D. 2ln 2 4 3  Câu 12: Tính x e .cos . x dx 
? (đề thi HK II 2014-THPT Trần Quang Khải-TP.HCM) 0 94
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 e  e 3e 5 e  A. B. C. D. 2 2 2 2  2 Câu 13: Tính . x cos . x dx  ? 0     A. 1 B. 1 C. 1 D. 1 3 6 2 4 2 2 x 1 Câu 14: Tính ln . x dx 
? ( đề thi Đại Học khối A, A1 năm 2013 ) 2 x 1 5 3 5 5 3 3 A. ln 2  B. ln 2 C. ln 2  D. ln 2  2 2 2 2 2 2 1 3x 1 Câu 15: Tính .dx  ? 2 x e 0 5 11 5 11 5 1 11 A.  B.  C.  D. 2 4 4e 2 2 2e 2 4 4e 2 4e
Tính các tích phân sau (tách thành 2 tích phân A, B với A: dạng cơ bản và B: tích phân từng phần ) e 2 3e 1
Câu 16: Tính a-b biết: x 1 ln x.dx    a b 1 2 3e 1 A. 0 B. C. 1 D. e 4 4 1 b e  c a
Câu 17: Biết 1 x. 2 2 x  e .dx   . Tính  c ? a b 0 A. 1 B. 2 C. 3 D. 5  Câu 18: Tính x
 xsinxdx ? ( đề thi thử THPT QG 2015- THPT Chu Văn An- HN) o  3  3  3  A. 2  B. 2  C.  D. 3 3 3 3 2 Câu 19: Tính  3
2x  ln x.dx ? ( đề minh họa 2015- Bộ GD & ĐT ) 1 13 13 13 13 A.  ln 2 B.  2ln 2 C.  3ln 2 D.  4ln 2 2 2 2 2
Tính các tích phân sau ( sử dụng đổi biến trước rồi tính tích phân từng phần sau ) 95
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2  4
Câu 20: Tính cos x.dx    a  Tìm a? 0 A. 0 B.  C. 2 D. 4 2 a Câu 21: Tính sin x.dx  = 2 . Tìm a 0 A. 2 B. 2 C.   2 D.   2 Câu 22: Tính sin 2 . x ln 
1 cos x.dx ? (đề thi thử THPT QG 2015-THPT Phan Đình Phùng-HN ) 0 1 3 1 3 A. - B. C. D.  2 2 2 2 1 Câu 23: Tính 2 3. x x e .dx  ? 0 1 3 1 3 A. - B. C. D.  2 2 2 2 1 Câu 24: Tính  3 8x  2x 2x. .e .dx ? 0 A. e B. 5-e C. e+4 D. 1 96
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
ĐÁP ÁN TRẮC NGHIỆM TÍCH PHÂN TỪNG PHẦN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 C 7 C 13 C 19 C 2 A 8 D 14 A 20 B 3 C 9 B 15 A 21 A 4 D 10 A 16 C 22 A 5 A 11 B 17 D 23 C 6 D 12 A 18 C 24 B 97
KỸ THUẬT 6: TÍCH PHÂN TỪNG PHẦN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI 1. Dạng 1 b
Giả sử cần tính tích phân I  f (x) dx 
, ta thực hiện các bước sau a Bư
ớc 1. Lập bảng xét dấu (BXD) của hàm số f(x) trên đoạn [a; b], giả sử f(x) có BXD: x a x x b 1 2 f (x)  0  0  b 1 x 2 x b Bước 2. Tính I 
f (x) dx  f (x)dx  f (x)dx  f (x)dx     . a a 1 x 2 x 2 VÍ DỤ 1. Tính tích phân 2 I  x  3x  2 dx  . 3 Giải Bảng xét dấu x 3 1 2 2 x  3x  2  0  0 1 I  x  3x  2 2 59 2 dx   2 x  3x  2dx    . 2 3 1 59 Vậy I  . 2  2 VÍ DỤ 2. Tính tích phân 2 I  5  4 cos x  4sin xdx  . 0 98
KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến  ĐS: I  2 3  2  . 6 2. Dạng 2 b
Giả sử cần tính tích phân I   f (x)  g(x) dx   , ta thực hiện a Cách 1. b b b
T ách I   f (x)  g(x)  dx  f (x) dx  g(x) dx    
rồi sử dụng dạng 1 ở trên. a a a Cách 2.
Bước 1. Lập bảng xét dấu chung của hàm số f(x) và g(x) trên đoạn [a; b].
Bước 2. Dựa vào bảng xét dấu ta bỏ giá trị tuyệt đối của f(x) và g(x). 2
VÍ DỤ 3. Tính tích phân I    x  x 1dx . 1 Giải Cách 1. 2 I    x  x 1 2 2 dx  x dx  x 1 dx   1 1 1 0 2 1 2
  xdx  xdx  (x 1)dx  (x 1)dx     1  0 1 1 0 2 1 2 2 2 2 2 x x  x   x       x   x  0     . 2 2  2   2 1 0  1  1 99
KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Cách 2. Bảng xét dấu x –1 0 1 2 x – 0 +  + x – 1 – – 0 + 0 1 2 I  x  x   1 dx   x  x   1 dx   x  x     1dx 1 0 1  x     .  x x1 0 2 2 x 0 1 1 0 Vậy I  0 . 3. Dạng 3 b b
Để tính các tích phân I  max 
 f (x), g(x )dx và J  min
  f (x), g(x )dx , ta thực hiện các bước sau: a a
Bước 1. Lập bảng xét dấu hàm số h(x)  f (x)  g(x) trên đoạn [a; b]. Bước 2.
+ Nếu h(x)  0 thì max f (x), g(x 
)  f (x) và min f (x), g(x  )  g(x) .
+ Nếu h(x)  0 thì max f (x), g(x 
)  g(x) và min f (x), g(x  )  f (x) . 100
KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 4
VÍ DỤ 4. Tính tích phân I  max 2 x 1, 4x   2dx . 0 Giải Đặt h x   2 x     x   2 ( ) 1 4 2  x  4x  3 . Bảng xét dấu X 0 1 3 4 h(x) + 0 – 0 + 1 I  x   3 4 80 2
1 dx  4x  2dx   2 x   1 dx     . 3 0 1 3 80 Vậy I  . 3 2
VÍ DỤ 5. Tính tích phân  min3x I , 4   xdx. 0 Giải
Đặt ( )  3x  4    3x h x x  x  4 . Bảng xét dấu x 0 1 2 h(x) – 0 + 1 2 1 2 x 2  x  x I  dx     x 3 2 5 3 4 dx   4x      . ln 3  2  ln 3 2 0 1 0 1 2 5 Vậy I   . ln 3 2 101
KỸ THUẬT 7: TÍCH PHÂN CHỨA GIÁ TRỊ TUYỆT ĐỐI - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến ỨNG DỤNG TÍCH PHÂN
1. TÍNH DIỆN TÍCH HÌNH PHẲNG
1.1 Diện tích hình thang cong
Cho hàm số f (x) liên tục trên đoạn [a; b]. Diện tích hình thang cong giới hạn bởi các đường b
y  f (x), x  a, x  b và trục hoành là S  f (x) dx  . a Phương pháp giải toán
Bước 1. Lập bảng xét dấu hàm số f(x) trên đoạn [a; b]. b
Bước 2. Dựa vào bảng xét dấu tính tích phân f (x) dx  . a
VÍ DỤ 1. Tính diện tích hình phẳng giới hạn bởi y  ln x, x  1, x  e và Ox. Giải Do ln x  0 x  1; e nên e e  ln  ln    ln   1 e S x dx xdx x x  1. 1 1 1 Vậy S  1 (đvdt).
VÍ DỤ 2. Tính diện tích hình phẳng giới hạn bởi 2
y  x  4x  3, x  0, x  3 và Ox. Giải Bảng xét dấu x 0 1 3 y – 0 + 0 1 1 3 3 3  x   x  8
S  x  4x 3 3 2 dx   2 x  4x  3dx 2 2     2x  3x    2x  3x      .(ĐVDT)  3   3  3 0 1 0 1 102
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
1.2. Diện tích hình phẳng 1.2.1. Trường hợp 1.
Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các b
đường y  f (x), y  g(x), x  a, x  b là S  f (x)  g(x) dx  . a Phương pháp giải toán
Bước 1. Lập bảng xét dấu hàm số f (x)  g(x) trên đoạn [a; b]. b
Bước 2. Dựa vào bảng xét dấu tính tích phân f (x)  g(x) dx  . a 1.2.2. Trường hợp 2.
Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các đường 
y  f (x), y  g(x) là S  f (x)  g(x) dx 
. Trong đó  ,  là nghiệm nhỏ nhất và lớn nhất của phương 
trình f (x)  g(x) a      b . Phương pháp giải toán
Bước 1. Giải phương trình f (x)  g(x) .
Bước 2. Lập bảng xét dấu hàm số f (x)  g(x) trên đoạn ;  . 
Bước 3. Dựa vào bảng xét dấu tính tích phân f (x)  g(x) dx  . 
VÍ DỤ 3. Tính diện tích hình phẳng giới hạn bởi các đường 3 2
y  x 11x  6, y  6x , x  0, x  2 . Giải Đặt 3 2 3 2
h(x)  (x 11x  6)  6x  x  6x 11x  6
h(x)  0  x  1 x  2  x  3 (loại). 103
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Bảng xét dấu x 0 1 2 h(x) – 0 + 0 1
S  x 6x 11x 6 2 3 2 dx   3 2 x  6x 11x  6dx 0 1 1 2 4 2 4 2  x 11x   x 11x  5 3 3    2x   6x   2x   6x      .  4 2   4 2  2 0 1 5 Vậy S  (đvdt). 2
VÍ DỤ 4. Tính diện tích hình phẳng giới hạn bởi các đường 3 2
y  x 11x  6, y  6x . Giải Đặt 3 2 3 2
h(x)  (x 11x  6)  6x  x  6x 11x  6
h(x)  0  x  1 x  2  x  3 . Bảng xét dấu x 1 2 3 h(x) 0 + 0 – 0 2
S  x 6x 11x  6 3 3 2 dx   3 2 x  6x 11x  6dx 1 2 2 3 4 2 4 2  x 11x   x 11x  1 3 3   2x   6x   2x   6x      .  4 2   4 2  2 1 2 1 Vậy S  (đvdt). 2
Chú ý:Nếu trong đoạn ;   phương trình f (x)  g(x) không còn nghiệm nào nữa thì ta có thể dùng  
công thức f (x)  g(x) dx    f (x) g(x)dx .   104
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
VÍ DỤ 5.Tính diện tích hình phẳng giới hạn bởi 3 y  x , y  4x . Giải Ta có 3 x  4x  x  2   x  0  x  2 0 0 2 4 4      x x S   x  4x 2 3 dx   3x  4xdx 2 2
   2x     2x   8.  4   4 2  0  2 0 Vậy S  8 (đvdt).
VÍ DỤ 6. Tính diện tích hình phẳng giới hạn bởi 2
y  x  4 x  3 và trục hoành. Giải Ta có 2 2
x  4 x  3  0  t  4t  3  0, t  x  0 t  1  x  1 x  1      t 3    x  3  x  3 3 3 1 3   2 2
 S  x  4 x  3 dx  2 x  4x  3 dx  
 2   2x 4x 3dx   2x  4x 3dx  3  0  0 1  1 3  3 3 x x      16 2 2
 2    2x  3x    2x  3x    .   3   3   3 0 1   16 Vậy S  (đvdt). 3
VÍ DỤ 7. Tính diện tích hình phẳng giới hạn bởi 2
y  x  4x  3 và y  x  3 . Giải
Phương trình hoành độ giao điểm 2 x  4x  3  x  3 105
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến x  3  0  x  0 2
 x  4x  3  x  3   .  x  5 2
x  4x  3  x  3 Bảng xét dấu x 0 1 3 5 2 x  4x  3 + 0 – 0 + 1  S  x 5x 3
dx  x 3x 6 5 2 2 dx   2x 5xdx 0 1 3 1 3 5 3 2 3 2 3 2  x 5x   x 3x   x 5x  109         6x       .  3 2   3 2   3 2  6 0 1 3 109 Vậy S  (đvdt). 6
VÍ DỤ 8. Tính diện tích hình phẳng giới hạn bởi 2
y  x 1 , y  x  5 . Giải
Phương trình hoành độ giao điểm 2 2
x 1  x  5  t 1  t  5, t  x  0 t   x  0  t   x  0 2
 t 1 t  5    x  3   t   3 2 t 1  t   5 3  S  x 1    x 5 3 2 2 dx  2 x 1   x 5 dx 3  0 Bảng xét dấu x 0 1 3 2 x 1 – 0 + 1
 S  2 x  x 4 3 2
dx   2x  x 6dx 0 1 106
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 3 3 2 3 2  x x   x x  73  2  
 4x      6x  .  3 2   3 2  3 0 1 73 Vậy S  (đvdt). 3 Chú ý:
Nếu hình phẳng được giới hạn từ 3 đường trở lên thì vẽ hình (tuy nhiên thi ĐH thì không có).
2. TÍNH THỂ TÍCH KHỐI TRÒN XOAY 2.1. Trường hợp 1.
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y  f (x)  0 x   ; a b , y  0, x  a và b
x  b (a  b) quay quanh trục Ox là 2 V   f (x)dx  . a
VÍ DỤ 9. Tính thể tích hình cầu do hình tròn 2 2 2
(C) : x  y  R quay quanh Ox. Giải
Hoành độ giao điểm của (C) và Ox là 2 2 x  R  x  R . Phương trình 2 2 2 2 2 2
(C) : x  y  R  y  R  x R  V     R 2 2
R  x dx  2  2 2 R  x dx  R 0 R 3 3  x  4 R 2  2 R x     (dvtt)  3  3 0 107
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2. Trường hợp 2.
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường x  g( y)  0 y   ;
c d  , x  0 , y  c và d
y  d (c  d) quay quanh trục Oy là 2 V   g ( y)dy  . c 2 2 x y
VÍ DỤ 10. Tính thể tích hình khối do ellipse (E) :   1 quay quanh Oy. 2 2 a b Giải 2 y
Tung độ giao điểm của (E) và Oy là  1  y  b . 2 b 2 2 2 2 x y a y Phương trình 2 2 (E) :   1  x  a  2 2 2 a b b b 2 2 b 2 2  a y   a y  2 2  V    a   dy  2 a   dy 2 2  b   b b 0  R 2 3 2  a y  4 a b 2  2 a y    . 2   3b  3 0 2 4 a b Vậy V  (đvtt). 3 3. Trường hợp 3.
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y  f (x), y  g(x) , x  a và b x  b (a  , b f (x)  0, g(x)  0 x   ;
a b) quay quanh trục Ox là 2 2 V   f (x)  g (x) dx  . a
VÍ DỤ 11. Tính thể tích hình khối do hình phẳng giới hạn bởi các đường 2 y  x , 2 y  x quay quanh Ox. Giải x  0 x  0 Hoành độ giao điểm   . 4  x  x x  1 108
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 1 4
 V   x  x dx     4x  xdx 0 0 1 1 1 3 5 2     x  x    .  5 2  10 0 3 Vậy V  (đvtt). 10
(ĐỀ MINH HỌA QUỐC GIA NĂM 2017)
Viết Kí hiệu H  là hình phẳng giới hạn bởi đồ thị hàm số  2   1 x y x
e , trục tung và trục hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình H  xung quanh trục O . x A. V  4  2 . e B. V  4  2e. C. 2 V  e  5. D. V   2 e  5. 1 1 2 Ta có   2    1 x  4    2 2   2 1 x V x e dx x x e dx  4 I 1 0 0 du  2x  2 2 2 x 1 1 u   x  2x 1  e 1 Đặt     I  x  x   x  e dx e     I x  2 2 1   2 2 1 x x 2  2 dv  e dv v  2  2 0 0  2 du  dx 1 2 x 1 1 2 x 1 2 u   x 1  e 1 e e x 1 3 Đặt 1 x     I   x   2 2 1  e dx e     1  2 x dv  e dx  v  2 2 2 4 4 4 1  1 0 0 0  2 2 e  5 Do vậy I  suy ra V   2 e  5. Chọn D. 1 4 109
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 4. Trường hợp 4.
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường x  f ( y), x  g( y) , y  c và d
y  d (c  d, f ( y)  0, g( y)  0 y   ;
c d) quay quanh trục Oy là 2 2 V   f ( y)  g ( y) dy  . c
VÍ DỤ 12. Tính thể tích hình khối do hình phẳng giới hạn bởi các đường 2
x   y  5 , x  3  y quay quanh Oy. Giải  y  1  Tung độ giao điểm 2
 y  5  3  y   .  y  2 2
 V    y 52 3 y2 2 dy 1 2 2 5 3        4 2 y 11y 153 y 11y  6y 16dy 2      3y 16y   .  5 3  5 1  1 153 Vậy V  (đvtt). 5 110
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
3. BÀI TOÁN CHUYỂN ĐỘNG b
Quãng đường đi được từ thời điểm a đến thời điểm b (Mối liên hệ quãng đường và vận tốc): S   v(t)dt a
Mối liên hệ giữa vận tốc v và gia tốc a: v(t)  a(t).dt 
VÍ DỤ 1. Một ô tô đang chạy với vận tốc 20m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc v t  4
 0t  20(m / s) ,trong đó t là khoảng thời gian tính bằng giây, kể từ lúc
bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ?
A. 0,2 m. B. 5 m. C. 10 m. D. 20 m. Giải:
Lấy mốc thời gian là lúc ô tô bắt đầu đạp phanh. Gọi T là thời điểm ô tô dừng. Ta có v(T)=0 0 = -40T+20  T = 0,5.
Như vậy khoảng thời gian từ lúc đạp phanh đến khi ô tô dừng hẳn là 0.5s. Trong khoảng thời gian 0.5s đó,
ô tô đi được quãng đường là: 0.5
S   (20  40t)dt  5(m) 0 Chọn đáp án B.
VÍ DỤ 2. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a t 2 2  3t  t (m / s ) .
Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu ? 4000 4300 1900 2200 A. m B. m C. m D. m 3 3 3 3 Giải 2 3 t t 2 v  (3t  t )dt  3   c  2 3 111
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Lấy mốc thời gian là lúc bắt đầu tăng tốc v(0)  10
Vận tốc tại thời điểm T 2 3 t t  v(T )  3  10 2 3
 Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng: 10 2 3 t t 4300 S  (3  10)dt  (m)  2 3 3 0 Chọn đáp án B
VÍ DỤ 4. Một đám vi trùng ngày thứ t có số lượng là N(t). Biết rằng N t 4000 '  và lúc đầu đám vi 1 0,5t
trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ hang đơn vị):
A. 264.334 con. B. 257.167 con. C. 258.959 con. D. 253.584 con. Giải
Số vi trùng ở ngày thứ t 4000 N(t) =
dt  8000.ln |1 0,5t | C  1 0,5t
Số vi trùng ở thời điểm ban đầu là 250.000
N(0)=8000.ln |1 0,5.0 | C =250000  C = 2500000
 Số vi khuẩn sau 10 ngày là : N(10) = 8000.ln |1 0,5.10 | 2  50000  264334 (con) Chọn đáp án A. 112
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
TRẮC NGHIỆM ỨNG DỤNG TÍCH PHÂN
Câu 1:(ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Viết công thức tính thể tích V của khối tròn xoay
được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số y  f  x, trục Ox và hai đường
thẳng x  a, x  b a  b, xung quanh trục O . x b b A. 2 V   f  xd .x B. 2 V  f  xd .x a a b b C. V   f  xd .x D. V  f  x d .x a a
Câu 2. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành
được tính theo công thức nào? b A. V   f
 x gx 2 dx  . a b B. 2 V    f  x 2  g  x dx   . a b C. V    f
 x gx 2 dx  . a b D. V    f
 x gxdx  . a
Câu 3. Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox
tại các điểm x  a, x  b a  b, có thiết diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có
hoành độ x a  x  b là S  x . b b A. V   S  xd .x B. V   S  x d .x a a b b C. V  S  xd .x D. 2 V   S  xd .x a a
Câu 4. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Viết Kí hiệu H  là hình phẳng giới hạn bởi đồ thị hàm số  2   1 x y x
e , trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay
hình H  xung quanh trục O . x 113
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến A. V  4  2 . e B. V  4  2e. C. 2 V  e  5. D. V   2 e  5.
Câu 5. Thể tích của phần vật thể giới hạn bởi hai mặt phẳng x  0 và x  3 , có thiết diện bị cắt bởi mặt
phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x  3 là một hình chữ nhật có hai kích thước bằng x và 2 2 9  x , bằng: A. V  3 . B. V  18. C. V  20. D. V  22.
Câu 6. Tính thể tích vật thể nằm giữa hai mặt phẳng có phương trình x  0 và x  2 , biết rằng thiết diện của
vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0;2 là một phần tư đường tròn bán kính 2
2x , ta được kết quả nào sau đây? 16 A. V  32. B. V  64 . C. V  . D. V  8 . 5
Câu 7. Hình phẳng C giới hạn bởi các đường 2
y  x 1, trục tung và tiếp tuyến của đồ thị hàm số 2
y  x 1 tại điểm 1;2 , khi quay quanh trục Ox tạo thành khối tròn xoay có thể tích bằng: 4 28 8 A. V   . B. V  . C. V  . D. V   . 5 15 15
Câu 8. Khối tròn xoay tạo nên khi ta quay quanh trục Ox hình phẳng D giới hạn bởi đồ thị P 2
: y  2x  x và trục Ox sẽ có thể tích là: 16 11 12 4 A. V  . B. V  . C. V  . D. V  . 15 15 15 15
Câu 9. Hình phẳng giới hạn bởi đồ thị hai hàm số 2
y  2x  x và y  x khi quay quanh trục Ox tạo thành
khối tròn xoay có thể tích bằng:    A. V  . B. V  . C. V  . D. V   . 3 4 5
Câu 10. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol 2 y  4  x và 2 y  2  x
quay quanh trục Ox là kết quả nào sau đây? A. V  10 . B. V  12 . C. V  14 . D. V  16 .
Câu 11. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 2 4 y  x , y  x qua
quanh trục hoành bằng bao nhiêu? 114
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 124 126 128 131 A. V  . B. V  . C. V  . D. V  . 15 15 15 15
Câu 12. Cho hình phẳng H  giới hạn bởi các đường y  x , y  x và x  4 . Tính thể tích của khối
tròn xoay tạo thành khi quay hình H  quanh trục hoành nhận giá trị nào sau đây: 41 40 38 41 A. V  . B. V  . C. V  . D. V  . 3 3 3 2
Câu 13. Thể tích của khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi
C: y  ln x, trục Ox và đường thẳng x  e là:
A. V   e  2. B. V   e   1 . C. V   . e D. V   e   1 .
Câu 14. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường y  x , y  x  2 ,
y  0 quay quanh trục Oy , có giá trị là kêt quả nào sau đây? 1 3 32 11 A. V   . B. V   . C. V  . D. V  . 3 2 15 6 2 t  4
Câu 15. Một vật chuyển động với vận tốc v t 1,2 
m/s . Quãng đường vật đó đi được trong 4 t  3
giây đầu tiên bằng bao nhiêu ? (Làm tròn kết quả đến hàng phần trăm). A. 18,82 m. B. 11,81m. C. 4,06 m. D. 7, 28 m.
Câu 16. Bạn Nam ngồi trên máy bay đi du lịch thế giới và vận tốc chuyển động của máy bay là v t 2
 3t  5m/s . Quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 là : A. 36m. B. 252m. C. 1134m. D. 966m.
Câu 17. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Một ô tô đang chạy với vận tốc 10m/s thì người lái
đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v t  5
 t 10 (m/s), trong đó t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô
còn di chuyển bao nhiêu mét ? A. 0,2 m. B. 2 m. C. 10 m. D. 20 m.
Câu 18. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a t 2
 3t  t (m/s2). Quãng đường vật
đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu ? 4000 4300 1900 2200 A. m . B. m . C. m . D. m . 3 3 3 3 115
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 3
Câu 19. Một vật chuyển động với vận tốc v tm/s , có gia tốc v 't   2
m/s  . Vận tốc ban đầu của t 1
vật là 6 m/s . Vận tốc của vật sau 10 giây là (làm tròn kết quả đến hàng đơn vị): A. 14 m/s . B. 13m/s . C. 11m/s . D. 12 m/s .
Câu 20. Một đám vi trùng ngày thứ t có số lượng là N t . Biết rằng N t 4000 '  và lúc đầu đám vi 1 0,5t
trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ hang đơn vị): A. 264.334 con. B. 257.167 con. C. 258.959 con. D. 253.584 con. 1
Câu 21. Gọi htcm là mực nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng h 't  3  t  8 5
và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn kết quả đến hàng phần trăm): A. 2,33 cm. B. 5,06 cm. C. 2,66 cm. D. 3,33 cm.
Câu 22. Khẳng định nào sau đây đúng ? 10
A. Nếu w't là tốc độ tăng trưởng cân nặng/năm của một đứa trẻ, thì w't dt 
là sự cân nặng của đứa 5 trẻ giữa 5 và 10 tuổi. 120
B. Nếu dầu rò rỉ từ một cái thùng với tốc độ r t tính bằng galông/phút tại thời gian t , thì r tdt  0
biểu thị lượng galông dầu rò rỉ trong 2 giờ đầu tiên.
C. Nếu r t là tốc độ tiêu thụ dầu của thế giới, trong đó t được bằng năm, bắt đầu tại t  0 vào ngày 1 17
tháng 1 năm 2000 và r t được tính bằng thùng/năm, r tdt 
biểu thị số lượng thùng dầu tiêu thụ 0
từ ngày 1 tháng 1 năm 2000 đến ngày 1 tháng 1 năm 2017 .
D. Cả A, B, C đều đúng. 116
ỨNG DỤNG TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
ĐÁP ÁN TRẮC NGHIỆM ỨNG DỤNG TÍCH PHÂN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 A 7 C 13 C 19 B 2 B 8 A 14 C 20 A 3 A 9 C 15 B 21 C 4 D 10 D 16 D 22 D 5 B 11 C 17 C 6 C 12 B 18 B 117
ỨNG DỤNG TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO
Các bạn chú ý: Khi dùng casio cho nguyên hàm, tích phân. Nhớ phải chuyển hết sang Radian (qw4)
DẠNG: Tìm nguyên hàm F x  của hàm số f x PHƯƠNG PHÁP:
Bước 1. Tính f(a) (Với a là 1 giá trị bất kỳ nằm trong TXĐ). Chú ý: Chọn a sao cho kết quả của f(a) thật xấu.
Bước 2. Tính F’(a) của các đáp án.
Bước 3. So sánh Bước 1 và Bước 2. Nếu giống nhau thì chọn.
VÍ DỤ . (Trích đề minh họa 2017 BGD) Tìm nguyên hàm của hàm số f (x)  2x 1. 2 1
A. f (x)dx  (2x 1) 2x 1  C. 
B. f (x)dx  (2x 1) 2x 1  C.  3 3 1 1 C. f (x)dx   2x 1  C.  D. f (x)dx  2x 1  C.  3 2 Giải  Bước 1. Chọn a = 2
Tính f(2). Nhập f (x)  2x 1. r2 ’  Bước 2. Thử từng đáp án 118
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Đáp án A.
=> Không giống Kết quả Bước 1=> LOẠI A Đáp án B
(Giống kết quả bước 1)  Chọn B
VÍ DỤ Hàm số F  x  ln sin x  3cos x là một nguyên hàm của hàm số nào trong các hàm số sau đây: x  x
f  x  cos x  3sin x f  x cos 3sin  A. B. sin x  3cos x   cos x 3sin x x  x f x  f  x sin 3cos  C. sin x  3cos x D. cos x  3sin x  Bước 1:
 Bước 2: Thử từng đáp án Đáp án A. (Ấn Calc x=1)
=> Không giống kết quả Bước 1. Loại A Đáp án B (Ấn Calc x=1)
=> Giống kết quả Bước 1. Chọn B 119
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Dạng: Tìm nguyên hàm F(x) của f(x) khi biết F (x )  M o o x
Phương pháp: Ta nhập: f (x).dx  F ( ) A 
. Với A là 1 số bất kỳ thuộc tập xác định. Thử từng đáp án, đến A
khi ra Kết quả là M thì chọn đáp án đó. cos 2x 
VÍ DỤ : Tìm Nguyên hàm F(x) của hàm số: f(x) = . Biết F ( )  -2 2 2 sin . x cos x 4 A. tanx - cotx -2 B. tanx - cotx C. tanx + cotx -4 D. cotx tanx -2 Giải  4  cos 2x 1
Thử đáp án A: Nhập vào máy tính  (tan A   2) 
. Ấn, Calc X=1 (x giá trị gì 2 2 sin . x cos x tan A A cũng được); Calc A=1 r = =
Không bằng -2 => Loại đáp án A  Thử đáp án B: r = = Chọn đáp án B. 120
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 3 2 x  3x  3x 1 1 f (x)  F (1)  2
VÍ DỤ . Tìm nguyên hàm F(x) của hàm số x  2x 1 , 3 2 x 2 7 A. F (x)    2 x 1 6 2 x 2 13 B. F (x)   x   2 x 1 6 2 x 2 13 C. F (x)   2x   2 x 1 6 2 D. F (x)  x  x1 Giải 1 3 2 2     x 3x 3x 1 A 2 7 dx  (   )  . Ấn Calc A = 0 (A bất 2
Thử đáp án A: Nhập vào máy tính x  2x 1 2 A 1 6 A
kỳ, các em có thể lấy số khác) 1
Không bằng . Loại đáp án A 3 1 3 2 2     x 3x 3x 1 A 2 13 Thử đáp án B: dx  (  A   ) 
. Ấn Calc A = 0 (A bất kỳ, các em có 2 x  2x 1 2 A 1 6 A thể lấy số khác) . Chọn đáp án B 121
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến Dạng: Tính tích phân
Ấn nút y Nhập tích phân cần tính. e VÍ DỤ : Tính: I  ln xdx  1 A. I = 1 B. I = e C. I = e  1 D. I = 1  e
Nói chung thì cái này Easy rồi nhé ^^! a
Dạng: Tìm a, b sao cho f (x).dx  A  b a dx 1 VÍ DỤ . Tìm a sao cho   2 x  2x 1 2 2 A. a = 0 B. a=3 C. a=6 D. a=4
Nhập vào như màn hình. Ấn Calc thay từng giá trị các đáp án. Thấy Calc A = 3 thỏa mãn. Chọn B b x 1 8
VÍ DỤ . Tìm a và b sao cho dx  ln  2 x 1 2 3 a A. a = 3; b = 2 B. a = 2; b =3 C.a=1; b =3 D. a = 0; b = 1 1 8
. Ấn Calc A = 2; B = 3. Ta thấy kết quả = ln . Chọn B. 2 3 122
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
DẠNG: TÍNH DIỆN TÍCH, THỂ TÍCH
Nhập trị tuyệt đối trong máy tính: qc
VÍ DỤ . Tính diện tích hình phẳng giới hạn bởi y  ln x, x  1, x  e và Ox. Giải
VÍ DỤ . Tính diện tích hình phẳng giới hạn bởi 3 y  x , y  4x . Giải Ta có 3 x  4x  x  2   x  0  x  2
Lấy giá trị cận là lớn nhất và bé nhất
VÍ DỤ . Tính diện tích hình phẳng giới hạn bởi 2
y  x  4x  3 và y  x  3 . Giải
Phương trình hoành độ giao điểm 2 x  4x  3  x  3 x  3  0  x  0 2
 x  4x  3  x  3   .  x  5 2
x  4x  3  x  3 123
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
VÍ DỤ : Tính thể tích hình khối do hình phẳng giới hạn bởi các đường 2 y  x , 2 y  x quay quanh Ox. Giải x  0 x  0 Hoành độ giao điểm   . 4  x  x x  1 1 3 4  V   x  x dx   10 0
VÍ DỤ . Tính thể tích hình khối do hình phẳng giới hạn bởi các đường 2
x   y  5 , x  3  y quay quanh Oy. Giải  y  1  Tung độ giao điểm 2
 y  5  3  y   .  y  2 2 
 V   y  52 3 y2 153 2 dy   5 1  124
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Dạng: mối liên hệ giữa a, b,c…  x  e 
VÍ DỤ : Nguyên hàm của hàm số: y = x e  2  là: . x
a e  b tan x  C . Tính a+b 2   cos x  A.2 B. 3 C. 4 D. 5 qJz
Lấy 2 cận bất kỳ (Giả sử lấy 0 và 1) Ta lưu KQ vào biến A. Ta có 1 0  . a e  b tan1 ( . a e  b tan 0)  A   a  b  CacDapAn 1 0  .
a (e  e )  b(tan1 tan 0)  A   a  b  CacDapAn 1 0  .
a (e  e )  b(tan1 tan 0)  A  Thử đáp án A:   a  b  2
Nghiệm Lẻ => Loại đáp án A 1 0  .
a (e  e )  b(tan1 tan 0)  A  Thử đáp án B:   a  b  3 
 Số đẹp. Chọn Đáp án B 125
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 2 e  a VÍ DỤ : 2 2 x K  x e dx  = . Tính a+2b b 0 A. 2 B. 3 C. 9 D. 1 Lưu vào biến A 2 e  a Ta có 2  A  a  . A b  e b 2 a  . A b  e
Ta giải hệ sau để tìm a và b.  a  2b  CacDapAn  Thử đáp án A Số xấu => Loại A  Thử đáp án B. Số xấu => Loại B  Thử đáp án C. => Số đẹp. Chọn C 126
KỸ THUẬT 8: SỬ DỤNG MÁY TÍNH CASIO - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến PHỤ LỤC:
A. ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN Câu 1 : ( x 2  x)
Hàm số nào dưới đây không là nguyên hàm của hàm số f (x)  2 (x  1) 2 x  x 1 2 x  x 1 2 x  x  1 2 x A. B. C. D. x 1 x 1 x 1 x 1
Câu 2 : Cho đồ thị hàm số y  f (x). Diện tích hình phẳng (phần gạch trong hình) là: 0 0 1 4 A. f (x)dx  f (x)dx   B. f (x)dx  f (x)dx   3  4 3  1 3  4 4 C. f (x)dx  f (x)dx   D. f (x)dx  0 0 3 
Câu 3 : Diện tích hình phẳng giới hạn bởi các đồ thị: 2 y  x  2x và 2
y  x  x có kết quả là: 10 A. 12 B. C. 9 D. 6 3
Câu 4 : Kết quả nào sai trong các kết quả sao? x1 x1 2  5 1 2 4 4 A. dx    C  B. x  x  2 1 dx  ln x   C 10x 5.2x.ln 2 5x.ln 5  3 4 x 4x 2 x 1 x  1 C. dx  ln  x  C  xdx  x  x C 2 1 D. 2 tan tan   x 2 x  1
Câu 5 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các 127
PHỤ LỤC: - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 x đường  2 2
y x .e , x  1, x  2 , y  0 quanh trục ox là: A. 2  (e  e) B. 2  (e  e) C. 2  e D. e
Câu 6 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các 4
đường y  , y  0 , x  1, x  4 quanh trục ox là: x A. 6 B. 4 C. 12 D. 8 Câu 7 :  4 1 Giá trị của 4 (1 tan x) . dx  bằng: 2 cos x 0 1 1 1 1 A. B. C. D. 5 3 2 4 Câu 8 : d d b Nếu f (x)dx  5  ; f (x)dx  2 
, với a  d  b thì f (x)dx  bằng: a b a A. 2  B. 3 C. 8 D. 0 Câu 9 : 2 x e Hàm số f (x)  t lntdt 
đạt cực đại tại x  ? x e A.  ln 2 B. 0 C. ln 2 D.  ln 4 Câu 10 :  2 Cho tích phân 2 sin x 3 I  e .sin x cos xdx  . Nếu đổi biến số 2 t  sin x thì 0 1 1 1 1   A. t I  e (1t)dt  2 t t I  e dt  te dt 2  B.    0 0 0  1 1 1 1   C.  2 t I e (1 t)dt  D. t t I   e dt  te dt 2    0 0 0 
Câu 11 : Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x   và đồ thị của hai hàm số y = cosx, y = sinx là: 128
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến A. 2  2 B. 2 C. 2 D. 2 2
Câu 12 : Diện tích hình phẳng giới hạn bởi các đường 2
y  x ,trục Ox và đường thẳng x  2 là: 8 16 A. 8 B. C. 16 D. 3 3
Câu 13 : Cho hình phẳng H giới hạn bởi các đường y  sin x ; x  0; y  0 và x   . Thể tích vật thể
tròn xoay sinh bởi hình H quay quanh Ox bằng 2  2   A. 2 B. C. D. 2 4 2 Câu 14 : 3 2 1 x 2 x  1 Cho tích phân I  dx 
. Nếu đổi biến số t  thì 2 x x 1 2 2 3 3 3 2 2 t dt 3 tdt A. t dt I tdt    B. I   C. I  I   2 t 2  D. 2  1 t  1 t  1 2 2 t 1 2 2 2
Câu 15 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x x 1 và trục ox và đường thẳng x=1 là:     A. 3 2 2 B. 3 2 1 C. 2 2 1 D. 3 2 3 3 3 3 Câu 16 : Tìm nguyên hàm: 4 3 2 ( x  )dx  x 5 3 A. 3 5 x  4ln x  C B. 3 5  x  4 ln x  C 3 5 3 3 C. 3 5 x  4 ln x  C D. 3 5 x  4ln x  C 5 5 Câu 17 :  Tích phân 2 cos xsin xdx  bằng: 0 129
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 2 3 A.  B. C. D. 0 3 3 2 Câu 18 : x(2  x)
Hàm số nào sau đây không là nguyên hàm của hàm số f (x)  2 (x 1) 2 x  x 1 2 x  x 1 2 x 2 x  x 1 A. B. C. D. x 1 x 1 x 1 x 1
Câu 19 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  4x  5 và hai tiếp tuyến với đồ thị
hàm số tai A(1;2) và B(4;5) có kết quả dạng a khi đó: a+b bằng b 13 4 A. 12 B. C. 13 D. 12 5 Câu 20 : 2
Giá trị của tích phân I   2 x   1lnxdx là: 1 2ln 2  6 6 ln 2  2 2 ln 2  6 6 ln 2  2 A. B. C. D. 9 9 9 9
Câu 21 : Kết quả của x dx  là: 2 1 x 1 1 A. 2 1 x  C B.  C C.  C D. 2  1 x  C 2 1 x 2 1 x Câu 22 : Hàm số F( )
x  ln sin x  3cos x là một nguyên hàm của hàm số nào trong các hàm số sau đây: cos x  3sin x A. f (x)  B. f (x)  cos x  3sin x sin x  3cos x cos x  3sin x sin x  3cos x C. f (x)  D. f (x)  sin x  3cos x cos x  3sin x Câu 23 : e 2 x  2ln x
Giá trị của tích phân I  dx  là: x 1 130
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 e 1 2 e 1 A. B. C. 2 e 1 D. 2 e 2 2 Câu 24 :  4 2
Giả sử I  sin 3x sin 2xdx  a  b 
, khi đó, giá trị của a  b là: 2 0 1 3 3 1 A.  B. C.  D. 6 10 10 5 Câu 25 : Tìm nguyên hàm: 3 2 (x   2 x )dx  x 3 x 4 3 x 4 A. 3  3ln x  x  C B. 3  3ln X  x 3 3 3 3 3 x 4 3 x 4 C. 3  3ln x  x  C D. 3  3ln x  x  C 3 3 3 3 Câu 26 : 1 Tìm nguyên hàm: dx  x(x  3) 2 x 1 x 1 x  3 1 x A. ln  C B.  ln  C C. ln  C D. ln  C 3 x  3 3 x  3 3 x 3 x  3
Câu 27 : Diện tích hình phẳng giới hạn bởi các đường (P): y=2x2 , (C): y= 2 1 x và Ox là:  A. 8 2  3 2  2 B. 2 2  C.  D. 4 2  2 3 2 Câu 28 : 2
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 x 27 y=x ; y= ; y= là: 8 x 63 A. 27ln2-3 B. C. 27ln2 D. 27ln2+1 8 Câu 29 : Tìm nguyên hàm: 2 (1 sin x) dx  2 1 2 1 A.
x  2 cos x  sin 2x  C ; B.
x  2 cos x  sin 2x  C ; 3 4 3 4 131
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 1 2 1 C.
x  2 cos 2x  sin 2x  C ; D.
x  2 cos x  sin 2x  C ; 3 4 3 4 Câu 30 : 2 Cho 2 I  2x x 1dx  và 2
u  x 1. Chọn khẳng định sai trong các khẳng định sau: 1 2 3 2 3 3 2 A. I  udu  B. I  udu  C. I  27 D. 2 I  u 3 1 0 3 0 Câu 31 : 5 5 5 Cho biết f  xdx  3, g
 tdt  9 . Giá trị của A  f  xgxdx  là: 2 2 2 Chưa xác định A. B. 12 C. 3 D. 6 được
Câu 32 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x và đường thẳng y  2x là: 4 3 5 23 A. B. C. D. 3 2 3 15
Câu 33 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 x2 - 4x - 6 trục hoành và hai đường thẳng x=-2 , x=-4 là 40 92 50 A. 12 B. C. D. 3 3 3 Câu 34 : 0 2 3x  5x 1 2 Giả sử rằng I  dx  a ln  b 
. Khi đó, giá trị của a  2b là: x  2 3 1  A. 30 B. 40 C. 50 D. 60
Câu 35 : Kết quả của ln xdx  là: A. x ln x  x  C B. Đáp án khác C. x ln x  C D. x ln x  x  C Câu 36 : Tìm nguyên hàm: 5 3 (  x )dx  x 2 2 A. 5 5ln x  x  C B. 5 5ln x  x  C 5 5 132
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 2 2 C. 5 5ln x  x  C D. 5 5ln x  x  C 5 5 Câu 37 : 1 Tìm nguyên hàm: dx  . x(x  3) 1 x 1 x  3 1 x 1 x  3 A. ln  C B. ln  C C. ln  C D. ln  C 3 x  3 3 x 3 x  3 3 x
Câu 38 : Diện tích hình phẳng giới hạn bởi các đường cong 3 y  x và 5 y  x bằng: 1 A. 4  B. C. 0 D. 6 2 Câu 39 :   2 2 Cho hai tích phân 2 sin xdx  và 2 cos xdx 
, hãy chỉ ra khẳng định đúng: 0 0   B. Không so sánh được 2 2 A. 2 2 sin xdx  cos xdx   0 0     2 2 2 2 C. 2 2 sin xdx  cos xdx   D. 2 2 sin xdx = cos xdx   0 0 0 0 Câu 40 :   2 2 Cho hai tích phân 2 I  sin xdx  và 2 J  cos xdx 
. Hãy chỉ ra khẳng định đúng: 0 0 Không so sánh A. I  J B. I  J C. I  J D. được Câu 41 : Hàm số 2 ( ) x
F x  e là nguyên hàm của hàm số 2 x A. 2 ( )  2 x f x xe B. 2 ( ) x f x  e C. ( ) e f x  D. 2 2 ( ) x f x  x e 1 2x Câu 42 : ln 2 Tính 2 x dx  , kết quả sai là: x 133
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến A. 22 x   1 C B. 2 x  C C. 1 2 x C D. 22 x   1 C Câu 43 :  sin x Cho tích phân I  
, với   1 thì I bằng: 2 0 1 2 cos x  2  A. B. 2 C.  2 D. 2
Câu 44 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2
y  x 1 , y  x  5 có kết quả là 35 10 73 73 A. B. C. D. 12 3 3 6 Câu 45 : d d b Nếu f (x)dx  5  , f (x)dx  2 
với a < d < b thì f (x)dx  bằng a b a A. -2 B. 0 C. 8 D. 3
Câu 46 : Kết quả nào sai trong các kết quả sao? dx 1 x 2 dx 1 x  1 1 A.  tan  C  B.  ln  C  1 cos x 2 2 2 2 x x  1 2 x  1 1 dx xdx 1 C.  ln(ln(ln x))  C      xln . x ln(ln x) D. 2 ln 3 2x C  2 3  2x 4
Câu 47 : Diện tích hình phẳng giới hạn bởi hai đường cong y = x3 – x và y = x – x2 là : 37 33 37 A. Đáp án khác B. C. D. 6 12 12 Câu 48 : Tìm nguyên hàm: 2 3 (x   x )dx  x 1 2 1 2 A. 4 3 x  2 ln x  x  C B. 4 3 x  2 ln x  x  C 4 3 4 3 134
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 2 1 2 C. 4 3 x  2 ln x  x  C D. 4 3 x  2 ln x  x  C 4 3 4 3
Câu 49 : Cho hình phẳng giới hạn bởi các đường y  x và y  x quay xung quanh trục Ox . Thể tích
khối tròn xoay tạo thành bằng:  A.  B. C. 0 D.   6
Câu 50 : Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các
đường y  x , y  0 , y  2  x quanh trục ox là: 7 35 6 A. B. 6 C. D. 12 12 5 Câu 51 : 3 x 2 Biến đổi dx  thành f (t)dt 
, với t  1 x . Khi đó f (t) là hàm nào trong các hàm 0 1  1 x 1 số sau? A. 2 f(t)  2t  2t B. 2 f(t)  t t C. 2 f(t)  t t D. 2 f(t)  2t  2t Câu 52 :    Cho x 2 I  e cos xdx  ; x 2 J  e sin xdx  và x K  e cos 2xdx 
. Khẳng định nào đúng trong các 0 0 0 khẳng định sau? (I) I J e   (II) I  J  K e 1 (III) K  5 A. Chỉ (II) B. Chỉ (III) C. Chỉ (I) D. Chỉ (I) và (II) Câu 53 : Hàm số 2
y  tan 2x nhận hàm số nào dưới đây là nguyên hàm? 1 1 A. 2 tan 2x  x B. tan 2x  x C. tan 2x  x D. tan 2x  x 2 2
Câu 54 : Thể tích vật thể tròn xoang khi quay hình phẳng giới hạn bởi đồ thị hàm số 135
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến y = x2 2 ;x  y quanh trục ox là  4 3  A. 2 B. C. D. 10 3 10 10 Câu 55 :  6 n 1 Cho I  sin x cos xdx   . Khi đó n bằng: 64 0 A. 3 B. 4 C. 6 D. 5 Câu 56 : Tìm nguyên hàm: 3x 2 (2  e ) dx  4 4 x 5 x 1 A. 3 6 3 x x  e  e  C B. 3 6 4 x x  e  e  C 3 6 3 6 4 4 x 1 x 1 C. 3 6 4 x x  e  e  C D. 3 6 4 x x  e  e  C 3 6 3 6 Câu 57 : 5 dx Giả sử  ln K  . Giá trị của K là: 2x  1 1 A. 3 B. 8 C. 81 D. 9
Câu 58 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x3 + 11x - 6, y = 6x2,x  0,x  2 có
kết quả dạng a khi đó a-b bằng b A. 2 B. -3 C. 3 D. 59
Câu 59 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = -x2 + 4x và các tiếp tuyến với đồ thị
hàm số biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng a khi đó a-b bằng b 12 A. B. 14 C. 5 D. -5 11
Câu 60 : Diện tích hình phẳng giới hạn bởi (C): y= x2+3x2, d1:y = x1 và d2:y=x+2 có kết quả là 136
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 1 2 1 A. B. C. 1 D. 8 7 12 6
Câu 61 : Diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1, tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy là: 7 5 8 A. B. C. 2 D. 3 3 3 Câu 62 : 1 Giá trị của x I  x.e dx  là: 0 2 2 A. 1 B. 1 C. D. 2e 1 e e Câu 63 : dx Tính  , kết quả là: 1 x C 2 A. B. 2  1 x C  C D. C 1 x 1 C.  x 1 x
Câu 64 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = (e  1)x và  (1 x y e )x là: e e 3 A. 2  B. 2 C. 1 D. 1 2 2 e
Câu 65 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y  2
 x  x  3 và trục hoành là: 125 125 125 125 A. B. C. D. 24 34 14 44 Câu 66 : 2 x
Diện tích hình phẳng giới hạn bởi đường thẳng y  4  x và patabol y  bằng: 2 137
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 28 25 22 26 A. B. C. D. 3 3 3 3
Câu 67 : Diện tích hình phẳng giới hạn bởi các đồ thị: 2
y  x  4x  3 và y=x+3 có kết quả là: 55 205 109 126 A. B. C. D. 6 6 6 5 Câu 68 : Tìm nguyên hàm: 3 2 (x   2 x )dx  x 3 1 3 1 A. x  2s inx  sin 2x  C B. x  2sinx- sin 2x  C 2 4 2 4 3 1 3 1 C.
x  2 cos x  sin 2x  C D. x  2s inx  sin 2x  C 2 4 2 4 1
Câu 69. Gọi h t cm là mực nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng h 't  3  t  8 5
và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn kết quả đến hàng phần trăm): A. 2,33 cm. B. 5,06 cm. C. 2,66 cm. D. 3,33 cm.
Câu 70. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc v t  5
 t 10(m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ? A. 0,2 m. B. 2 m. C. 10 m. D. 20 m. 138
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến ĐÁP ÁN ĐỀ TỔNG HỢP 01 B 28 C 55 A 02 A 29 D 56 D 03 C 30 A 57 A 04 A 31 B 58 C 05 C 32 A 59 C 06 C 33 C 60 C 07 A 34 B 61 D 08 B 35 D 62 B 09 A 36 D 63 B 10 A 37 D 64 C 11 D 38 B 65 A 12 B 39 D 66 A 13 B 40 B 67 C 14 A 41 A 68 D 15 C 42 B 69 C 16 D 43 A 70 C 17 B 44 C 18 D 45 D 19 C 46 A 20 B 47 D 21 D 48 D 22 A 49 B 23 B 50 C 24 B 51 A 25 D 52 A 26 D 53 B 27 C 54 C 139
ĐỀ TỔNG HỢP NGUYÊN HÀM – TÍCH PHÂN - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY 3
Bài 1. (THPT QG 2016): Tính tích phân I= 2 3x(x  x 16)dx  ĐS: I = 88 0 1
Bài 2. (THPT QG 2015): Tính tích phân: (  3) x x e dx  ĐS: I = 4-3e 0
Bài 3. (ĐH A2014): Tính diện tích hình phẳng giới hạn bởi: 2
y  x  x  3 và y  2x 1 ĐS: I = 1/6
Bài 4. (ĐH B2014) : Tính tích phân : 2 2 x  3x 1 I  dx  ĐS : I  1 ln 3 2 x  x 1
Bài 5. (ĐH D2014) : Tính tích phân :  4 3 I   x    1 sin 2xdx ĐS : I  4 0
Bài 6. (ĐH A2013) : Tính tích phân : 2 2 x 1 5 3 I  ln x dx  ĐS : I  ln 2  2 x 2 2 1
Bài 7. (ĐH B2013) : Tính tích phân : 1 2 2 1 2 I  x 2  x dx  ĐS : I  3 0
Bài 8. (ĐH D2013) : Tính tích phân : 1 2 (x 1) I  dx  ĐS : I  1 ln 2 2 x 1 0
Bài 9. (ĐH A2012) : Tính tích phân : 140
B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến 3 1 ln(x 1) 2 2 I  dx 
ĐS : I   l n 3  ln 2 2 x 3 3 1
Bài 10. (ĐH B2012) : Tính tích phân : 1 3 x 3 I  d . x  ĐS : I  l n 3  ln 2 4 2 x  3x  2 2 0
Bài 11. (ĐH D2012) : Tính tích phân :  /4 2  1 I  x(1 sin 2x)dx  ĐS : I   32 4 0
Bài 12. (ĐH A2011) : Tính tích phân :  4 x sin x  (x 1) cos x   2    I  dx  ĐS : I   l n  1    x sin x  cos x 4 2 4     0 
Bài 13. (ĐH B2011) : Tính tích phân :  3 1 x sin x 2 I  dx  ĐS : I  3   l n 2 3 2 o c s x 3 0
Bài 14. (ĐH D2011) : Tính tích phân : 4 4x 1 34  3  I  dx  ĐS : I  10l n   2x 1  2 3  5  0
Bài 15. (ĐH A2010) : Tính tích phân : 1 2 x 2 x  e  2 x x e 1 1 1 2e I  dx  ĐS : I   l n 2 x e 1 3 2 3 0
Bài 16. (ĐH B2010) : Tính tích phân : e ln x 1 3 I  dx  ĐS : I    l n 2 x(ln x  2) 3 2 1 141
B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến
Bài 17. (ĐH D2010) : Tính tích phân : e 3 2 e I  (2x  ) ln xdx  ĐS : I  1 x 2 1
Bài 18. (ĐH A2009) : Tính tích phân :  2 8  3 2 I  ( o c s 1) o c s xdx  ĐS : I   15 4 0
Bài 19. (ĐH B2009) : Tính tích phân : 3 3 ln x 1 27 I  dx  ĐS : I  (3  ln ) 2 (x 1) 4 16 1
Bài 20. (ĐH D2009) : Tính tích phân : 3 dx I   ĐS : 2 I  ln(e  e 1)  2 x e 1 1
Bài 21. (ĐH A2008) : Tính tích phân :  6 4 tan x 1 10 I  dx  . ĐS : I  ln(2  3)  o c s2x 2 9 3 0
Bài 22. (ĐH B2008) : Tính tích phân :   4 sin(x  )dx 4  3 2 4 I  dx  . ĐS : I 
sin2x  2(1 s inx  cos x) 4 0
Bài 23. (ĐH D2008) : Tính tích phân : 2 ln x 3  2 ln 2 I  dx  ĐS : I  3 x 16 1
Bài 24. (ĐH A2007) : Tính diện tích hình phẳng giới hạn bởi các đường: 142
B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY - http://Hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến e y  (e 1)x ,  (1 x y  e )x . ĐS : S  1 2
Bài 25. (ĐH B2007) : Cho hình phẳng H giới hạn bởi các đường . y  xln x , y  0 , x  e . Tính thể
tích của khối tròn xoay tọa thành khi quay hình H quanh trục Ox. 3  (5e  2) ĐS : V  27
Bài 26. (ĐH D2007) : Tính tích phân : e 4 5e 1 3 2 I  x ln xdx  . ĐS : I  32 1
Bài 27. (ĐH A2006) : Tính tích phân :  2 sin 2x 2 I  dx  ĐS : I  2 2 3 0 o c s x  4sin x
Bài 28. (ĐH B2006) : Tính tích phân : ln5 dx 3 I  .  ĐS : I  ln x x   e 2e 3 2 ln 3
Bài 29. (ĐH D2006) : Tính tích phân : 1 2 5  3e 2  (  2) x I x e d . x  ĐS : I  4 0 143
B .TÍCH PHÂN TRONG ĐỀ THI ĐẠI HỌC 10 NĂM GẦN ĐÂY - http://hoc24h.vn
8 Kỹ thuật đạt điểm tối đa Nguyên hàm - Tích phân 2017 | : Đạt Nguyễn Tiến TÀI LIỆU THAM KHẢO
1. Giải tích 12 Nâng Cao (Nhà xuất bản giáo dục)
2. Sách Bài tập Giải tích 12 (Nhà xuất bản giáo dục)
3. Câu hỏi và bài tập trắc nghiệm Toán 12 – Nguyễn Phú Khánh – Huỳnh Đức
Khánh. (Nhà xuất bản ĐHQG Hà Nội)
4. Tuyển tập các chuyên đề và kỳ thuật tính Tích Phân – Trần Phương (Nhà xuất bản ĐHQG Hà Nội)
5. Group Toán - http://nhomtoan.net/ 144
TÀI LIỆU THAM KHẢO - http://Hoc24h.vn

8 kỹ thuật đạt điểm tối đa nguyên hàm – tích phân – Nguyễn Tiến Đạt Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề nguyên hàm – tích phân Toán 12

Gắn hệ tọa độ Oxyz để giải các bài toán hình học không gian – Phương Nguyễn Toán 12

20 kĩ thuật chinh phục vận dụng cao số phức – Hoàng Xuân Nhàn Toán 12

Phân dạng bài tập và lời giải chi tiết chuyên đề Tích phân – Lưu Huy Thưởng Toán 12

Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12