

Preview text:
Microeconomics ASSIGNMENT 8 Group 8 – EBBA 13.2 Nguyen Khanh Hang Truong Van Phuc Tran Quynh Chi Le Phuc Anh Tuan Ha Anh Nguyet Problem 1. Th
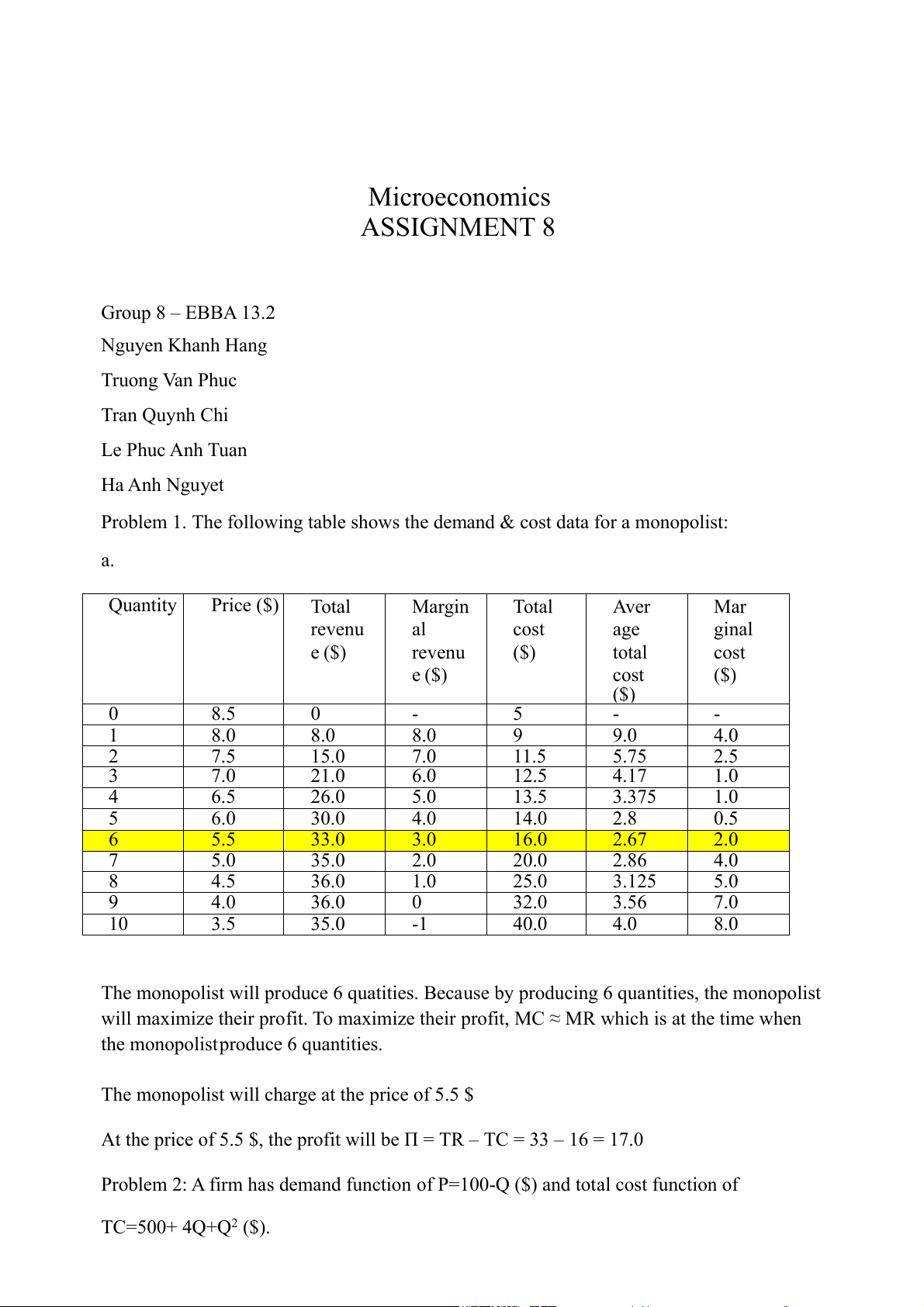
e following table shows the demand & cost data for a monopolist: a. Quantity Price ($) Total Margin Total Aver Mar revenu al cost age ginal e ($) revenu ($) total cost e ($) cost ($) ($) 0 8.5 0 - 5 - - 1 8.0 8.0 8.0 9 9.0 4.0 2 7.5 15.0 7.0 11.5 5.75 2.5 3 7.0 21.0 6.0 12.5 4.17 1.0 4 6.5 26.0 5.0 13.5 3.375 1.0 5 6.0 30.0 4.0 14.0 2.8 0.5 6 5.5 33.0 3.0 16.0 2.67 2.0 7 5.0 35.0 2.0 20.0 2.86 4.0 8 4.5 36.0 1.0 25.0 3.125 5.0 9 4.0 36.0 0 32.0 3.56 7.0 10 3.5 35.0 -1 40.0 4.0 8.0
The monopolist will produce 6 quatities. Because by producing 6 quantities, the monopolist
will maximize their profit. To maximize their profit, MC ≈ MR which is at the time when
the monopolist produce 6 quantities.
The monopolist will charge at the price of 5.5 $
At the price of 5.5 $, the profit will be Π = TR – TC = 33 – 16 = 17.0
Problem 2: A firm has demand function of P=100-Q ($) and total cost function of TC=500+ 4Q+Q2 ($).
TR = P x Q = (100 – Q)xQ = -Q2 + 100Q
→ MR = (TR)’ = 100 - 2Q < 100 – Q = P ↔ MR < P
→ This firm is not a perfect competitive firm. MR = 100 – 2Q
To maximize the total revenue ↔ MR = 0 ↔ 100 – 2Q = 0 ↔ Q = 50.
At the point Q = 50 → P = 50, TC = 500 + 4.50+502 = 3200 ($).
And the maximum total revenue is
TRMax = - 502 +100.50 = 2500 ($). c. MC = (TC)’ = 2Q +4
To maximize profit ↔ MC = MR ↔ 2Q + 4 = 100 - 2Q ↔ Q = 24. At Q = 24 the price i s P = 100 – 24 = 76 ($).
And the maximum total profit i s
ΠMax = TR* - TC* = - 242 +100.24 – (500 + 4.24 + 242) = 652 ($)
If the government imposes a tax of 8 $ per unit of good sold we will have:
TC1 = 500 +4Q + Q2 + 8Q = 500 + 12Q + Q2 → MC1 = (TC1)’ = 2Q + 12
To maximize the firm profit ↔ MC1 = MR ↔ 2Q + 12 = 100 – 2Q ↔ Q = 22
So at Q = 22 we will have the price P1= 100 – 22 = 78 ($).
And the maximum total profit i s
ΠMax = TR* - TC1*= -222 +100.22 – (500 +12.22 + 222) = 468 ($).
Asume government imposes a fixed tax of 100 $ then we will have:
TC2 = 500 + 4Q + Q2 + 100 = 600 + 4Q + Q2 → MC2 = (TC2)’ = 2Q + 4
To maximize the firm profit ↔ MC2 = MR ↔ 2Q + 4 = 100 – 2Q ↔ Q = 24.
So at Q = 24 we will have the pric e P2= 100 – 22 = 76 ($).
And the maximum total profit i s
ΠMax = TR* - TC2*= -242 +100.24 – (600 + 4.24 +242) = 552 ($).




