Assignment 7: Analyzing Firm Profits and Production Decisions | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

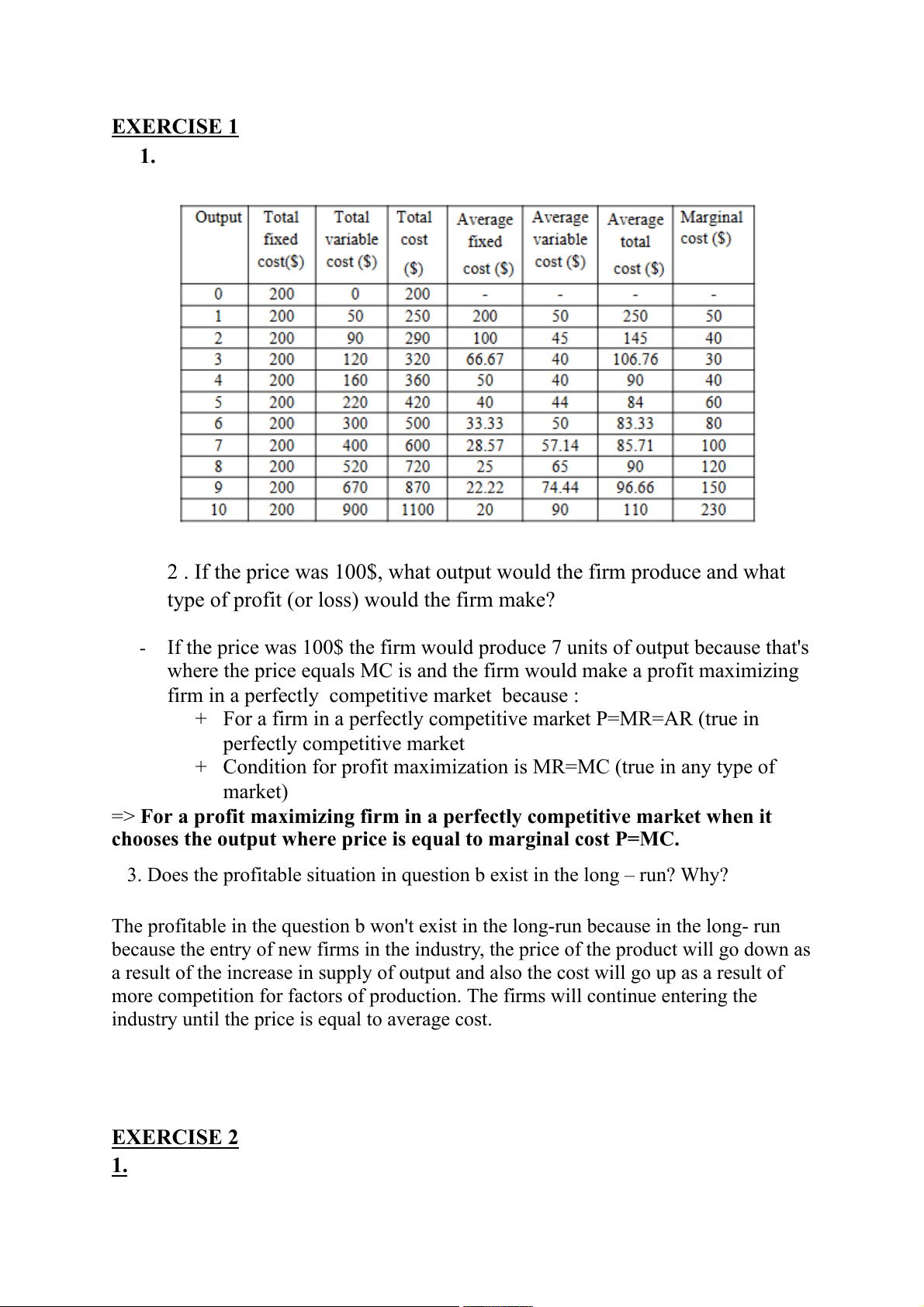
EXERCISE 1 1.
2 . If the price was 100$, what output would the firm produce and what
type of profit (or loss) would the firm make? -
If the price was 100$ the firm would produce 7 units of output because that's
where the price equals MC is and the firm would make a profit maximizing
firm in a perfectly competitive market because :
+ For a firm in a perfectly competitive market P=MR=AR (true in perfectly competitive market
+ Condition for profit maximization is MR=MC (true in any type of market)
=> For a profit maximizing firm in a perfectly competitive market when it
chooses the output where price is equal to marginal cost P=MC.
3. Does the profitable situation in question b exist in the long – run? Why?
The profitable in the question b won't exist in the long-run because in the long- run
because the entry of new firms in the industry, the price of the product will go down as
a result of the increase in supply of output and also the cost will go up as a result of
more competition for factors of production. The firms will continue entering the
industry until the price is equal to average cost. EXERCISE 2 1. Q 0 1 2 3 4 5 6 7 8 TC($) 50 55 62 75 96 125 162 203 248 TR 0 21 42 63 84 105 126 147 168 MC - 5 7 13 21 29 3750 41 45 FC 50 50 50 50 50 50 50 50 50 VC 0- 5 12 25 46 75 112 153 198 AVC - 5 6 8.33 11.5 15 18.67 21.86 24.75 AFC - 50 25 16.67 12.5 10 8.33 7.14 6.25 ATC - 55 31 25 24 25 27 29 31 2. Q 0 1 2 3 4 5 6 7 8 TR 0 21 42 63 84 105 126 147 168 TC($) 50 55 62 75 96 125 162 203 248 Profit -50 -34 -20 -12 -12 -20 -36 -56 -80 3. -
With the above profit in question 2, the firm should continue production to minimize total loss -
Because the price >= AVC, the firm can cover its variable costs => it is
better to continue producing in the short run to minimize losses. EXERCISE 3
3. Optimal Output Level (Q*) and Maximum Profit -
In a perfectly competitive market, a firm maximizes its profit by
producing the output level where marginal cost (MC) = market
price (P), as the demand (price) curve is flat at P = 8. -
1. Total Cost (TC): TC = Q^2 + 2Q + 4 - 2. Marginal Cost (MC):
To find the MC, take the derivative of the TC function with respect to Q. MC = d(TC)/dQ = 2Q + 2
3. Set MC equal to the market price to find the optimal output Q∗: 2Q + 2 = 8 Solving for Q:
1. 2Q = 6 ⇒ Q∗ = 3 Maximum Profit: Profit (π ) is defined as Total
Revenue (TR) minus Total Cost (TC). a. Total Revenue (TR) = P × Q
b. At P = 8 and Q = 3: TR = 8 × 3 = 24
c. Total Cost at Q = 3: TC = 3^2 + 2 × 3 + 4 = 9 + 6 + 4 = 19
=> Therefore, Maximum Profit:
Π = TR − TC = 24 − 19 = 5
So, the optimal output level Q∗ is 3, and the maximum profit is 5.
4. Break-even Price and Break-even Quantity -
The break-even point occurs where Total Revenue (TR) = Total
Cost (TC), meaning the firm earns zero profit. -
1. Break-even Price: To find the break-even price, first set TR
equal to TC: TR = P × Q = Q^2 + 2Q + 4
+ a. Dividing both sides by Q (assuming Q>0) gives the average total cost (ATC):
ATC = TC/Q = Q + 2 + 4/Q
b. For the firm to break even, Price (P) must equal ATC: P = Q + 2 + 4/Q
c. To solve for the break-even Q, set P = ATC and solve for both Q and P simultaneously. -
2. By solving the above equation, we can find the break-even values for price and quantity.
5. Should the Firm Continue Production if Price Decreases to P=4? -
In a perfectly competitive market, the firm should only produce if the
price covers the average variable cost (AVC) in the short run. At P = 4,
we need to determine if producing at this price still covers the AVC or if
the firm incurs a loss that it can’t sustain in the short term. -
If the market price P = 4 is lower than the break-even price and doesn't
cover AVC, the firm should consider shutting down. If it covers AVC but
not ATC, the firm may continue in the short term, but in the long run, it
would need to exit the market if prices don’t rise.