Assignment on Consumer Choice & Utility Theory | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Name: Vũ Việt Anh Class: E-BDB 4 Student ID: 11220700
TOPIC 5: CONSUMER CHOICE USING UTILITY THEORY
Group assignment presentation 5
Problem solving Exercise
Problem 1: Suppose that a consumer who uses $60 to buy 2 goods: X and Y. Given that
price of the good X is $3 per unit and price of the good Y is $1 per unit. Suppose that the
utility function of this consumer is TU=XY
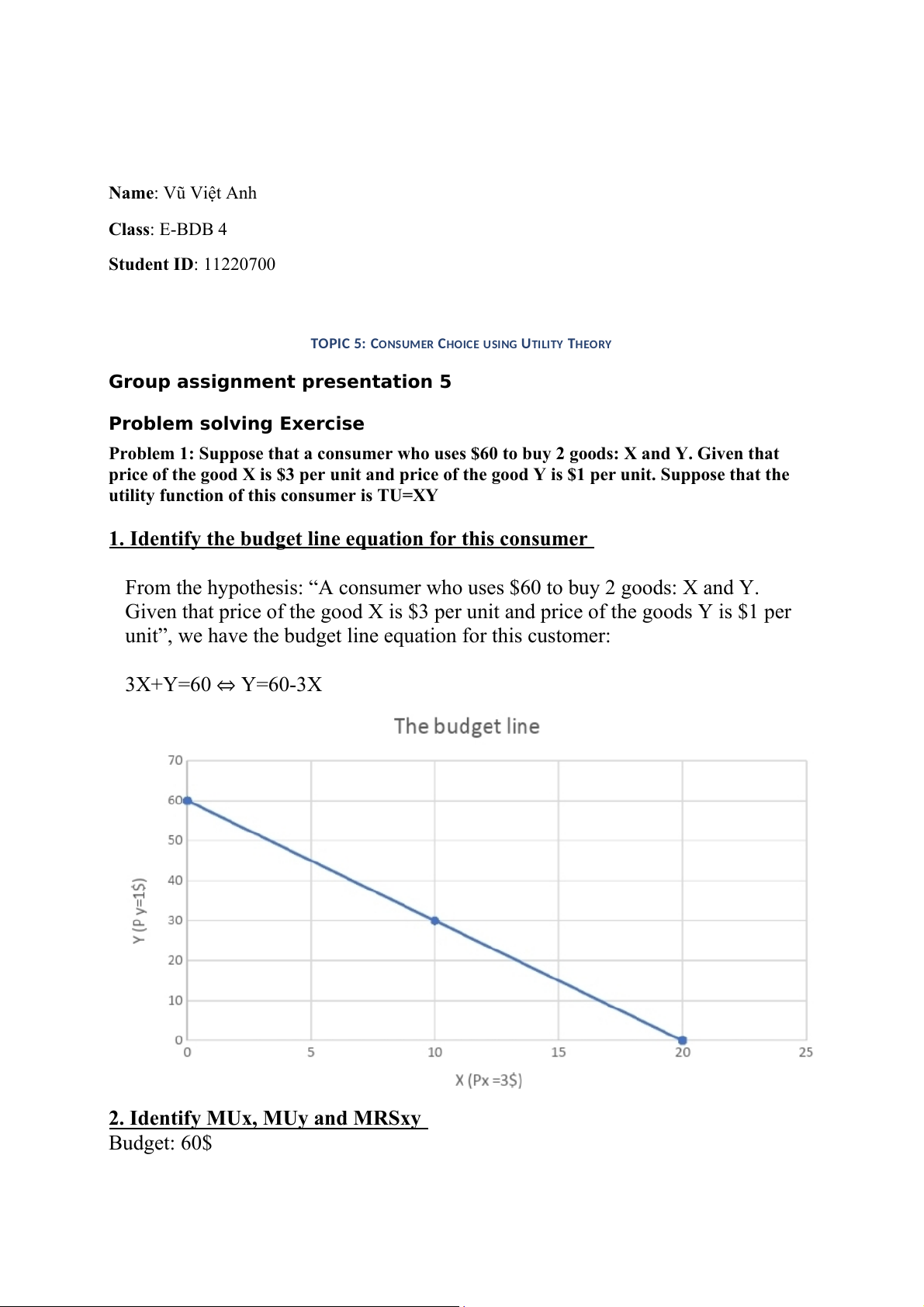
1. Identify the budget line equation for this consumer
From the hypothesis: “A consumer who uses $60 to buy 2 goods: X and Y.
Given that price of the good X is $3 per unit and price of the goods Y is $1 per
unit”, we have the budget line equation for this customer: 3X+Y=60 ⇔ Y=60-3X 2.
Identify MUx, MUy and MRSxy Budget: 60$ Price of X: 3$/unit Price of Y: 1$/unit
The utility function of this consumer is TU=X.Y → MUx = ▲TUx/ ▲Qx → MUy = ▲TUy/ ▲Qy
We have a function: 3X + Y = 60 (1) => Y = 60 - 3X
→ TU = X.(60 - 3X) = -3X² + 60X
→ MUx = (TU)’x = 60 - 6X
=> X = 20 - 13Y
→ TU = (20 - 13Y).Y = 20Y - 13Y²
→ MUy = (TU)’y = 20 - 23Y
→ MRSxy = MUxMUy = 60 - 6X20 - 23Y
3. What are optimal quantity of good X (X*) and optimal quantity of good Y
(Y*) that he should buy to maximize his utility.
To maximize consumer’s utility, we base on the equilibrium of marginal utility:
MUxPx = MUyPy ⇔
⇔ 60 - 6X3 = 20 - 23Y1 ⇔ -2X + 23Y = 0 (2) ⇔ FROM (1) AND (2) → 3X + Y = 60 -2X + 23Y = 0 → X = 10, Y = 30
So, he should buy 10 units of X and 30 units of Y to maximize his utility.
Problem 2: Monthly, Ms. Lan spends 1 million VND for buying meat (X) and
potato (Y). Price of meat is 20,000 dong/kg and price of potato is 5000 dong/kg.
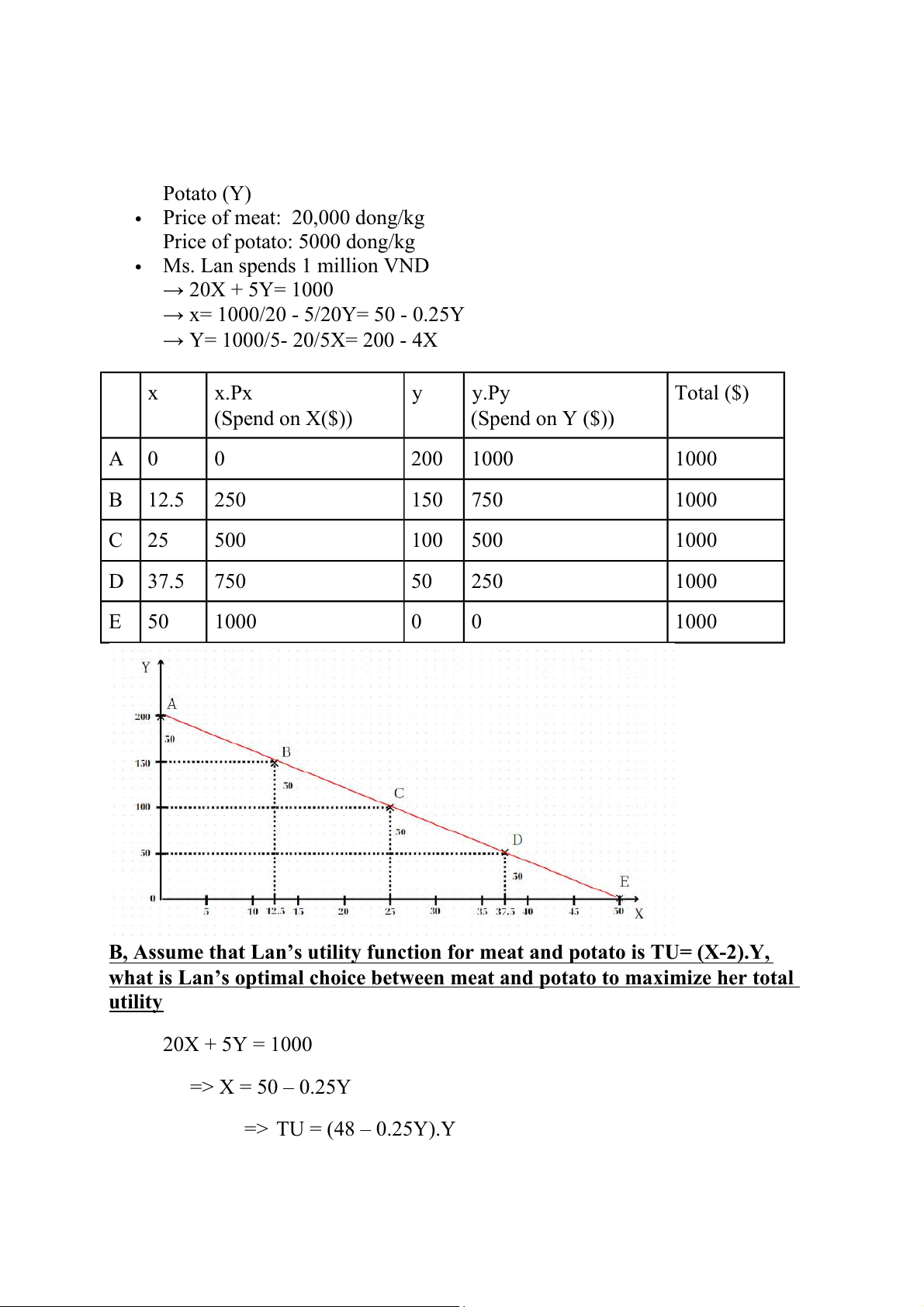
A, Identify Lan’s budget line equation and draw that BL curve  Meat (X) Potato (Y)  Price of meat: 20,000 dong/kg Price of potato: 5000 dong/kg  Ms. Lan spends 1 million VND → 20X + 5Y= 1000
→ x= 1000/20 - 5/20Y= 50 - 0.25Y → Y= 1000/5- 20/5X= 200 - 4X x x.Px y y.Py Total ($) (Spend on X($)) (Spend on Y ($)) A 0 0 200 1000 1000 B 12.5 250 150 750 1000 C 25 500 100 500 1000 D 37.5 750 50 250 1000 E 50 1000 0 0 1000 B,
Assume that Lan’s utility function for meat and po tato is TU= (X-2).Y,
what is Lan’s optimal choice between meat and potato to maximize her total utility 20X + 5Y = 1000 => X = 50 – 0.25Y => TU = (48 – 0.25Y).Y
=> MUy = TU’Y = 48 – 0.5Y => Y = 200 – 4X
=> TU = (X – 2) (200 – 4X) => TU = -400 + 208X – 4X2
=> MUx = TU’X = 208 – 8X
We have the utility maximum point is: MUx/Px = MUy/Py ⇔ 4X – Y = 8 (*) AND: 20X + 5Y = 1000 (**) FROM (*) (**) => X* = 26 => Y* = 96