




























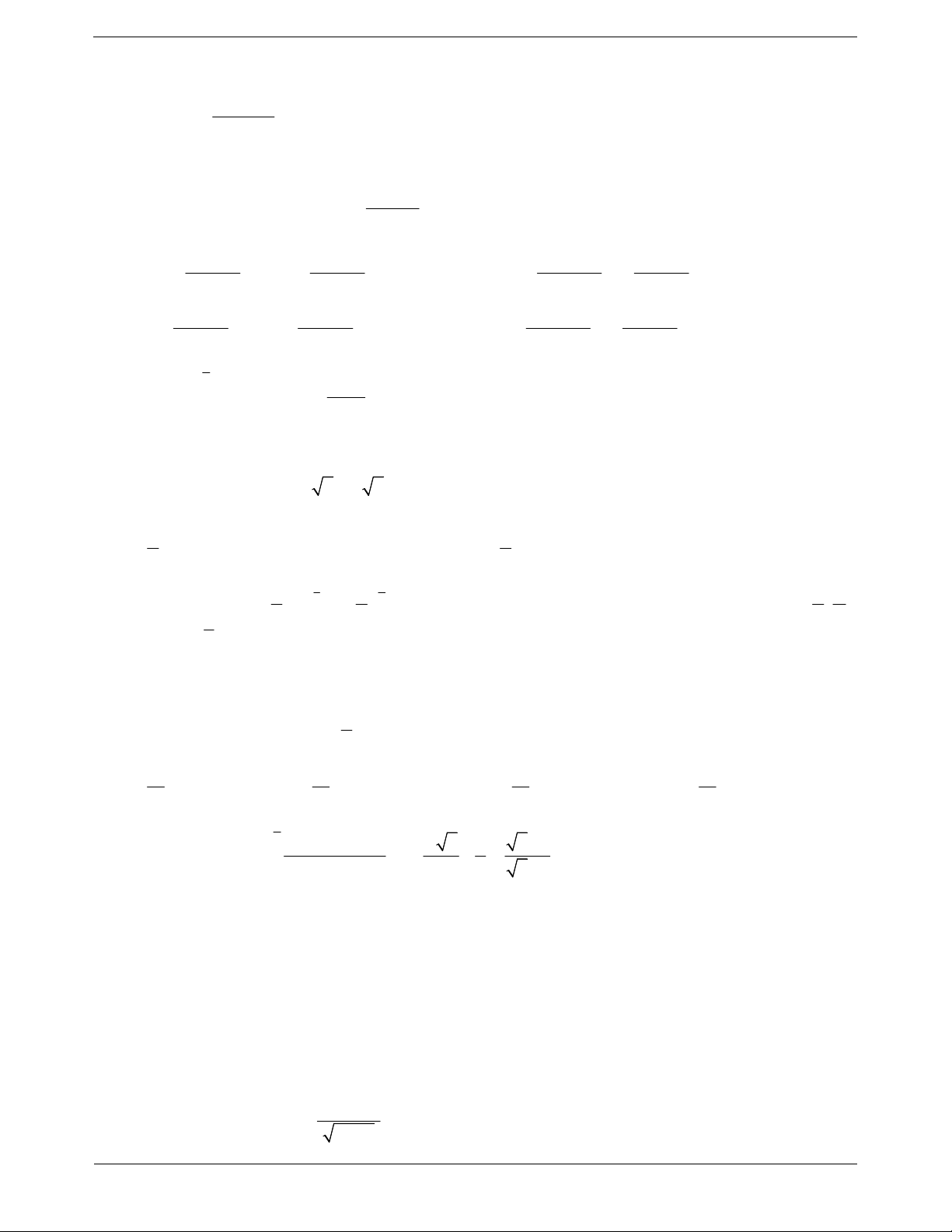





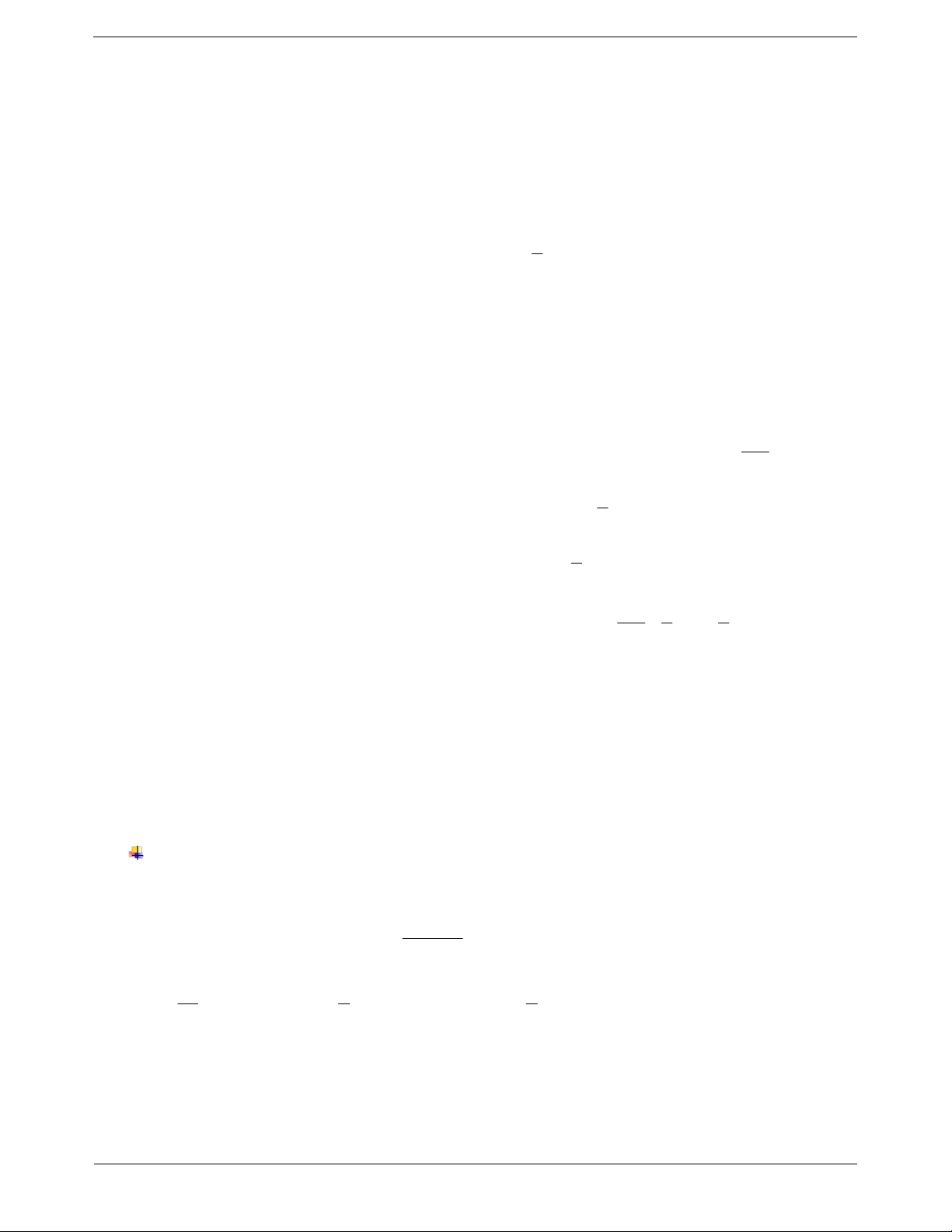
















Preview text:
CHUYÊN ĐỀ 3 NGUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG BÀI 2: TÍCH PHÂN Mục tiêu Kiến thức
+ Nắm được định nghĩa và các tính chất của tích phân.
+ Nắm vững các phương pháp tính nguyên hàm và bảng nguyên hàm cơ bản để áp dụng tính tích phân.
+ Nắm vững các tính chất tích phân của các hàm số chẵn, hàm số lẻ và các quy tắc đạo hàm của hàm số hợp.
+ Nắm vững các ý nghĩa vật lí của đạo hàm, từ dó giải quyết các bài toán thực tế sử dụng tích phân. Kĩ năng
+ Hiểu rõ định nghĩa và tính chất của tích phân để vận dụng vào việc tính tích phân.
+ Sử dụng thành thạo bảng nguyên hàm và các phương pháp tính tích phân.
+ Vận dụng tích phân vào các bài toán thực tế. TOANMATH.com Trang 1 I. LÍ THUYẾT TRỌNG TÂM
I. ĐỊNH NGHĨA VÀ TÍNH CHẤT CỦA TÍCH PHÂN 1. Định nghĩa tích phân Định nghĩa Chẳng hạn: 3
F x x C là một nguyên
Cho hàm số f x liên tục trên đoạn ; a b , với a . b
hàm của hàm số f x 2 3x nên tích phân
Nếu F x là nguyên hàm của hàm số f x trên đoạn 1 f xdxFx 1 F 1F0
;ab thì giá trị F b F a được gọi là tích phân của 0 0
hàm số f x trên đoạn ; a b . 3 C 3 1 0 C 1. b
Lưu ý: Giá trị của tích phân không phụ thuộc b Kí hiệu f
xdx F x F b F a (1) vào hằng số C. a a
Trong tính toán, ta thường chọn C 0.
Công thức (1) còn được gọi là công thức Newton –
Leibnitz; a và b được gọi là cận dưới và cận trên của tích phân.
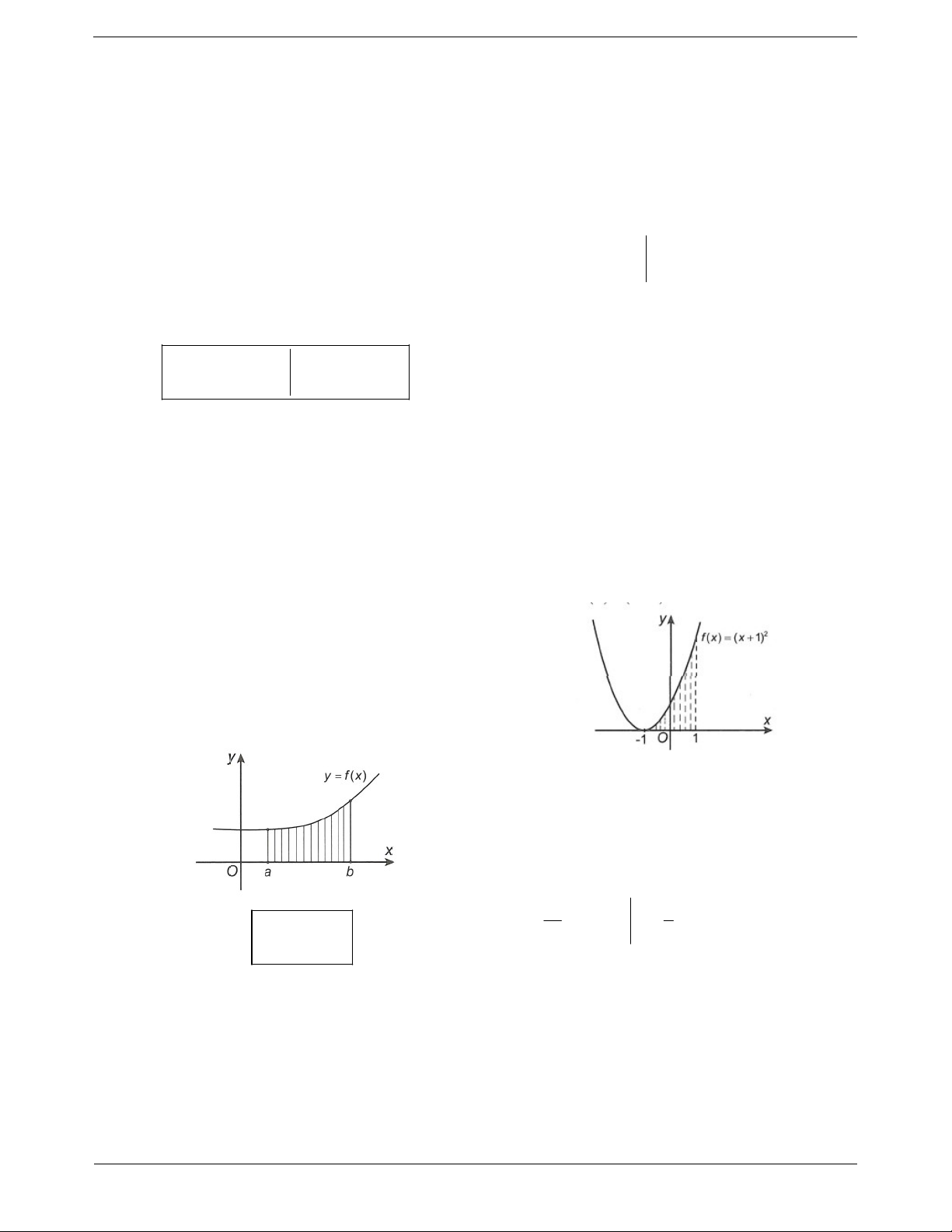
Ý nghĩa hình học của tích phân
Chẳng hạn: Hàm số f x 2 x 2x 1 có đồ
Giả sử hàm số y f x là hàm số liên tục và không âm b
thị C và f x x 2 1 0 , với x . trên đoạn ;
a b . Khi đó, tích phân f xdx chính là a
diện tích hình phẳng giới hạn bởi đường cong y f x ,
trục hoành Ox và hai đường thẳng x a, x , b với a . b
Diện tích “tam giác cong” giới hạn bởi C ,
trục Ox và hai đường thẳng x 1 và x 1 1 1 là S f x dx 2 x 2x 1dx 1 1 3 1 x 8 b 2 x x . S f xdx 3 1 3 a
Lưu ý: Ta còn gọi hình phẳng trên là “hình thang cong”.
2. Tính chất cơ bản của tích phân
Cho hàm số f x và g x là hai hàm số liên tục trên
khoảng K, trong đó K có thể là khoảng, nửa khoảng TOANMATH.com Trang 2 hoặc đoạn và a, , b c K, khi đó: a a. Nếu b a thì f xdx 0
Chẳng hạn: Cho hàm số f x liên tục, có a
b. Nếu f x có đạo hàm liên tục trên đoạn ;
a b thì đạo hàm trên đoạn 1;2 thỏa mãn ta có: f
1 8 và f 2 1. b Khi đó f
xdx f x b f b f a a 2 2 a f
xdx f x f 2 f 1 9 1 1
Lưu ý: Từ đó ta cũng có b
f b f a f xdx a b
và f a f b f xdx a c. Tính chất tuyến tính b b b k. f
x .hgxdx k f xdx .h g xdx a a a Với mọi k, h . d. Tính chất trung cận b c b f xdx f xdx f
xdx , với c ;ab a a c e. Đảo cận tích phân a b f xdx f xdx b a b f. Nếu f x 0, x a;b thì f xdx 0 và a b f
xdx 0 khi f x 0. a
g. Nếu f x g x, x a;b thì b b f xdx g xdx a a
h. Nếu m min f x và M max f x thì a;b a;b TOANMATH.com Trang 3 b mb a f
xdx M ba a
i. Tích phân không phụ thuộc vào biến, tức là ta luôn có b b b b f xdx f tdt f udu f ydy ... a a a a
II. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
1. Phương pháp đổi biến số Đổi biến dạng 1 b
Bài toán: Giả sử ta cần tính tích phân I f xdx, trong đó a
ta có thể phân tích f x g u xu x thì ta thực hiện Lưu ý: Phương pháp đổi biến số trong phép đổi biến số.
tích phân cơ bản giống như đổi biến số Phương pháp:
trong nguyên hàm, ở đây chỉ thêm bước
+ Đặt u u x , suy ra du u x d . x đổi cận. + Đổi cận: x a b u u a u b b ub ub + Khi đó I f xdx g udu Gu , với G u ua a u a
là nguyên hàm của g u. Đổi biến dạng 2 Dấu hiệu Cách đặt 2 2 a x x a sin t;t ; 2 2 2 2 x a a x ; t ; \ 0 sin t 2 2 2 2 a x x a tan t;t ; 2 2 a x x . a cos 2t;t 0; a x 2 a x x . a cos 2t;t 0; a x 2 TOANMATH.com Trang 4 x ab x x a b a 2 sin t;t 0; 2
2. Phương pháp tích phân từng phần b
Chú ý: Cần phải lựa chọn u và dv hợp lí sao
Bài toán: Tính tích phân I u x.vxdx b a
cho ta dễ dàng tìm được v và tích phân vdu Hướng dẫn giải a b u u x du u xdx dễ tính hơn udv Đặt . dv v xdx v v x a b
Khi đó I u.v b . v du a
(công thức tích phân từng a phần)
III. TÍCH PHÂN CÁC HÀM SỐ ĐẶC BIỆT
1. Cho hàm số f x liên tục trên ; a a. Khi đó a a Đặc biệt f xdx f
x f xdx (1) a 0 a
+ Nếu f x là hàm số lẻ thì ta có f xdx 0 (1.1) a a a
+ Nếu f x là hàm số chẵn thì ta có f xdx 2 f xdx (1.2) a 0 a f x 1 a và dx f x dx 0 b 1 (1.3) x 1 b 2 a 0 b b
2. Nếu f x liên tục trên đoạn ; a b thì f xdx f a b xdx a a 2 2
Hệ quả: Hàm số f x liên tục trên 0; 1 , khi đó: f sin xdx f cos xdx 0 0 b b a b
3. Nếu f x liên tục trên đoạn ;
a b và f a b x f x thì xf xdx f xdx 2 a a TOANMATH.com Trang 5 SƠ ĐỒ HỆ THỐNG HÓA Định nghĩa
Cho hàm số f x liên tục trên đoạn ;
a b , với a b . Nếu F x là nguyên hàm của hàm số f x trên đoạn ;
a b thì giá trị F b F a được gọi là tích phân của hàm số f x trên đoạn ; a b . b b Kí hiệu f
xdx F x F b F a a a
Ý nghĩa hình học của tích phân b
Giả sử hàm số y f x là hàm số liên tục và không âm trên đoạn ;
a b. Khi đó, tích phân f x dx a
chính là diện tích hình phẳng giới hạn bởi đường cong y f x , trục hoành và hai đường thẳng
x a, x b a b . b S f xdx a
Tính chất cơ bản của tích phân
Cho hàm số f x và g x là hai hàm số liên tục trên khoảng K, trong đó K có thể là khoảng, nửa
khoảng hoặc đoạn và a, ,
b c K , khi đó ta có các tính chất sau b b b f xdx 0 ; f
xdx f x f b f a ; a a a b b b k. f
x .hgxdx k f xdx .h g
xdx , với k,h a a a b c b a b f xdx f xdx f
xdx , với c ;ab; f xdx f xdx ; a a c b a b f xdx 0 b b f x 0, x ; a b a ; f x g x, x ; a b f xdx g xdx b f
xdx 0 f x 0 a a a m min f x b b b b b a;b mb a f
xdx M b a ; f xdx f tdt f udu f ydy .... M max f x a a a a a a;b TOANMATH.com Trang 6 II. CÁC DẠNG BÀI TẬP
Dạng 1: Tính tích phân bằng cách sử dụng định nghĩa, tính chất Phương pháp giải
Ví dụ: Cho hàm số f x có đạo hàm trên đoạn 1;2 , f 1 1 và f 2 2 . Tích phân 2 I f xdx bằng 1 A. 3. B. 2. C. 1. D. 0. Hướng dẫn giải
Sử dụng các tính chất của tích phân. 2 2
Sử dụng bảng nguyên hàm và định nghĩa tích phân I f
xdx f x f 2 f 1 211. 1 để tính tích phân. 1 Chọn C. Ví dụ mẫu 3
Ví dụ 1: Giá trị của dx bằng 0 A. 3. B. 2. C. 0. D. 1. Hướng dẫn giải 3 Ta có 3 dx x 3 0 3. 0 0 Chọn A. 2
Ví dụ 2: Giá trị của sin xdx bằng 0 A. 0. B. 1. C. 1 . D. . 2 Hướng dẫn giải 2 Ta có 2 sin xdx cos x 1. 0 0 Chọn B.
Ví dụ 3: Cho hàm số 3
f x x có một nguyên hàm là F x . Khẳng định nào sau đây đúng?
A. F 2 F 0 16. B. F 2 F 0 1.
C. F 2 F 0 8.
D. F 2 F 0 4. Hướng dẫn giải TOANMATH.com Trang 7 2 4 2 x Ta có 3 x dx 4 F 2 F 0 4 0 0 Chọn D. 2 1
Ví dụ 4: Giá trị của I dx là 2x 1 1 A. I ln 3 1. B. I ln 3. C. I ln 2 1. D. I ln 2 1. Hướng dẫn giải 2 2 1 1 I dx ln 2x 1 2x 1 2 1 1 1 1 ln 3 ln1 ln 3 ln 3. 2 2 Chọn B. 1 1 1 Ví dụ 5: Cho f xdx 2 và g
xdx 5. Giá trị của I f
x 2gxdx là 0 0 0 A. 5. B. 7. C. 9. D. 12. Hướng dẫn giải 1 1 I f xdx 2 g xdx 12. 0 0 Chọn D. 2 2 5 Ví dụ 6: Cho f xdx 3 và f
xdx 1. Giá trị của I f xdx là 1 5 1 A. 2. B. 4. C. 3. D. 2 . Hướng dẫn giải 5 2 5 I f xdx f xdx f xdx 1 1 2 3 1 2. Chọn A. 2 2 2 Ví dụ 7: Cho f
xdx 2, gxdx 1 . Khi đó I x 2 f x 3g x d x bằng 1 1 1 17 15 1 A. I 17. B. I . C. I . D. I . 2 2 2 Hướng dẫn giải 2 2 2 2 2 x Ta có I x 2 f x 3g x d x 2 f xdx 3 g xdx 2 1 1 1 1 TOANMATH.com Trang 8 3 17 2.2 3 1 . 2 2 Chọn B. 2 2 Ví dụ 8: Cho f
xdx 5 . Giá trị của I f x 2sin xdx là bao nhiêu? 0 0 A. I 3. B. I 5. C. I 6. D. I 7. Hướng dẫn giải 2 2 2 I f
x 2sin xdx f x 2
dx 2 sin xdx 5 2cos x 7. 0 0 0 0 Chọn D.
Ví dụ 9: Cho F x là nguyên hàm của hàm số ln x f x
. Giá trị của F e F 1 bằng x 1 3 1 A. I 0. B. I . C. I . D. I . 2 2 2 Hướng dẫn giải e e 2 ln ln e x x 1 Ta có F e F 1 dx ln xd ln x . x 2 1 2 1 1 Chọn D. 1 1 Ví dụ 10: Tích phân I dx bằng 2 x 3x 2 0 4 3 1 3 A. I ln . B. I ln . C. I ln . D. I ln . 3 2 2 4 Hướng dẫn giải 1 x 2 x 1 1 1 Ta có 2 x 3x 2 x 1 x 2 x 1 x 2 1 1 1 1 1 Suy ra I dx dx
ln x1 ln x 2 2ln2ln3. x 1 x 2 0 0 0 Chọn A. Ví dụ 11: Tích phân 3 I cos x sin xdx bằng 0 A. I 1. B. I 0. C. I 3. D. I 1 . Hướng dẫn giải 1 1 1 Ta có 3 I cos xd cos x 4 cos x 0. 4 0 4 4 0 Chọn B. TOANMATH.com Trang 9
Ta có cos x sin x nên sin xdx d cos x 2 dx
Ví dụ 12: Biết tích phân I a 2 b 3 c , với a, ,
b c . Giá trị biểu thức x 1 x x x 1 1 P a b c là A. P 8. B. P 0. C. P 2. D. P 6. Hướng dẫn giải Ta có x 1 x 0, x 1;2 nên 2 2 2 x 1 x 1 1 I dx dx dx 2 x 2 x1 2 x. x 1 x x 1 1 1 1 1
4 2 2 3 2. Suy ra a 4,b c 2
nên P a b c 0. Chọn B.
Nhân liên hợp x 1 x.
Ví dụ 13: Cho hàm số f x thỏa mãn f 1
2 và 2 f x x f x f 3
với mọi x . Giá trị 1 bằng A. f 2 1 . B. f 3 1 . C. f 2 1 . D. f 1 1 . 3 2 3 3 Hướng dẫn giải
Từ 2 f x x f x
(1), suy ra f x 0 với mọi x 1;2.
Suy ra f x là hàm không giảm trên đoạn 1;2 nên f x f 2 0 , x 1;2 . f x
Chia 2 vế hệ thức (1) cho 2 f x ta được x,x 1; 2 . (2) 2 f x
Lấy tích phân 2 vế trên đoạn 1;2 hệ thức (2), ta được 2 f x 2 2 2 2 1 x 1 1 3 dx xdx . f x 2 f x 1 2 1 f 1 f 2 2 1 1 Do f 1
2 nên suy ra f 2 1 . 3 3 Chọn C.
Chú ý rằng đề bài cho f 2 , yêu cầu tính f
1 , ta có thể sử dụng nguyên hàm để tìm hằng số C.
Tuy nhiên ta cũng có thể dựa vào định nghĩa của tích phân để xử lí. TOANMATH.com Trang 10 1
Ví dụ 14: Cho hàm số f x xác định trên \ thỏa mãn f x 2
và f 0 1, f 1 2 . Khi 2 2x 1 đó f 1 f 3 bằng A. 1 ln15. B. 3 ln 5. C. 2 ln 3. D. 1 ln15. Hướng dẫn giải 0 0
Ta có f xdx f 0 f 1 nên suy ra f 1 f 0 f xd .x 1 1 0 1 f xd .x 1 Tương tự ta cũng có 3 f 3 f 1 f xdx 1 3 2 f xdx. 1 0 3 0 3 Vậy f 1 f 3 1 f xdx f xdx 1 ln 2x 1 ln 2x 1 . 1 1 1 1 Vậy f 1 f 3 1 ln15. Chọn A. 1
Ví dụ 15: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 1 thỏa mãn f 1 0 , f x 2 dx 7 0 1 1 và 3 x . f
xdx 1. Giá trị I f xdx là 0 0 7 7 A. 1. B. . C. . D. 4. 4 5 Hướng dẫn giải 1 Ta có f x 2 dx 7 (1). 0 1 1 1 6 6 x dx 49x dx 7 (2). 7 0 0 1 và 3 14x . f xdx 1 4 (3). 0
Cộng hai vế (1), (2) và (3) suy ra 1 f x 2 3 7x dx 0 mà f x 2 3 7x 0 0 TOANMATH.com Trang 11 f x 3 7x . 4 7x Hay f x C. 4 f 7 7
1 0 C 0 C . 4 4 4 7x 7 Do đó f x . 4 4 1 1 4 7x 7 7 Vậy f xdx dx . 4 4 5 0 0 Chọn C.
Ví dụ 16: Cho f x, g x là hai hàm số liên tục trên đoạn 1;
1 và f x là hàm số chẵn, g x là hàm 1 1 số lẻ. Biết f xdx 5; g xdx 7. 0 0 1 1 Giá trị của A f xdx g xdx là 1 1 A. 12. B. 24. C. 0. D. 10. Hướng dẫn giải 1 1
Vì f x là hàm số chẵn nên f xdx 2 f xdx 2.5 10 1 0 1
Vì g x là hàm số lẻ nên g xdx 0 . 1 Vậy A 10. Chọn D. 1 xdx Ví dụ 17: Cho a b ln 3
với a, b là các số hữu tỉ. Giá trị của a b bằng 2x 2 0 1 5 1 1 1 A. . B. . C. . D. . 12 3 4 12 Hướng dẫn giải 1 1 1 xdx 1 2x 1 1 1 1 1 Ta có dx dx 2x 2 1 2 2x 2 1 2 2x 1 2x 2 0 0 0 1 1 1 1 1 x ln 2x 1 1 ln 3. 4 2 1 4 0 6 4 1 1 1
Vậy a ,b a b . 6 4 12 Chọn D. TOANMATH.com Trang 12 2 x Ví dụ 18: Cho dx a . b ln 2 . c ln 3 , với a, ,
b c là các số hữu tỷ. Giá trị của 6a b c bằng x 2 1 1 A. 2 . B. 1. C. 2. D. 1 . Hướng dẫn giải 2 2 2 x 1 1 1 1 Ta có dx dx ln x 1 ln 2 ln 3 x 2 1 x 1 x 2 1 x 1 1 6 1 1 1
a ,b 1,c 1 nên 6a b c 1 . 6 Chọn D. 1
Kĩ thuật tích phân hữu tỉ, ở đây ta tách x 2x 1 1 . 2 3 2x 3 Ví dụ 19: Cho dx a ln 2 b ln 3,
với a,b . Giá trị biểu thức 2 a ab b là 2 x x 2 A. 11. B. 21. C. 31. D. 41. Hướng dẫn giải 3 3 3 2x 3 2x 1 2 2x 1 2 Ta có dx dx dx 2 2 2 2 x x x x x x x x 2 2 2 3 2x 1 2 2 dx
ln x x 2ln x 2ln x1 3 2 5 ln 2 4ln 3 2 x x x x 1 2 2 a 5 2 a ab b 41. b 4 Chọn D. 2 5x 6
Ví dụ 20. Biết rằng tích phân
dx a ln 2 b ln 3 c ln 5,
với a,b, c là các số nguyên. Giá trị 2 x 5x 6 1
biểu thức S a bc là bao nhiêu? A. S 6 2. B. S 10. C. S 20. D. S 1 0. Hướng dẫn giải 2 2 2 5x 6 5x 6 9 4 Ta có dx dx dx 2 x 5x 6 x 2 x 3 x 3 x 2 1 1 1
9ln x 3 4ln x 2 2 9ln5 4ln 3 26ln 2. 1
Suy ra a 26,b 4,c 9. Vậy S a bc 2 6 4.9 10. Chọn B. TOANMATH.com Trang 13 2 sin x Ví dụ 21: Tích phân A dx bằng sin x cos x 0 A. . B. . C. . D. . 2 16 4 8 Hướng dẫn giải 2 cos x Xét B dx ta có sin x cos x 0 2 A B dx . 2 0 2 sin x cos x A B dx sin x cos x 0
ln sin x cos x 2 0 ln1 ln1 0.
Từ đó, ta có hệ phương trình A B 2 A B . 4 A B 0 Chọn C. 3 2 cos x sin . x cos x 1 Ví dụ 22: Cho
dx a b ln 2 c ln 1 3
, với a,b,c là các số hữu tỉ. Giá trị abc 4 3 cos x sin . x cos x 4 bằng A. 0. B. 2 . C. 4 . D. 6 . Hướng dẫn giải 3 2 3 2 2 cos x sin . x cos x 1 2cos x sin . x cos x sin x Ta có dx dx 4 3 2 cos x sin . x cos x cos x 2 cos x sin . x cos x 4 4 3 2 3 2 2 tan x tan x 2 tan x tan x dx d tan x 2 cos x 1 tan x 1 tan x 4 4 3 2 3 2 tan x 3 tan x x d tan x 2ln tan x 1 1 tan 2 4 4 4 TOANMATH.com Trang 14
1 2ln 2 2ln 3 1. Suy ra a 1,b 2 ,c 2 nên abc 4 . Chọn C. x e m, khi x 0
Ví dụ 23: Cho hàm số f x liên tục trên . 2 2x 3 x , khi x 0 1 Biết
f xdx ae b 3 ca, , b c
. Tổng T a b 3c bằng 1 A. 15. B. 1 0. C. 1 9. D. 1 7. Hướng dẫn giải
Do hàm số liên tục trên nên hàm số liên tục tại x 0
lim f x lim f x f 0 1 m 0 m 1. x 0 x 0 1 0 1 Ta có f xdx f xdx f xdx I I 1 2 1 1 0 I 2x 3 x dx
3 x 1 d 3 x 2 3 x 0 0 0 16 2 2 2 2 2 2 3 x 2 3 . 1 1 1 3 1 3
x 1 x I e dx e x 1 1 e 2. 2 0 0 1 22 22 Suy ra f
xdx I I e 2 3 . Suy ra a 1;b 2;c . 1 2 1 3 3
Vậy T a b 3c 1 2 22 1 9. Chọn C. 2 cos x 2 cos x Ví dụ 24: Biết dx m . Giá trị của dx bằng 1 3x 1 3x A. . m B. . m C. . m D. . m 4 4 Hướng dẫn giải 2 2 cos x cos x 1 Ta có 2 dx dx cos xdx x dx x x 1 cos2 . 1 3 1 3 2 2 cos x Suy ra dx . m 1 3x Chọn A.
Bài tập tự luyện dạng 1
Câu 1: Giả sử f x là một hàm số liên tục trên khoảng ; và a,b,c,b c ; . Mệnh đề nào sau đây sai? b c b b bc c A. f xdx f xdx f xd .x B. f xdx f xdx f xd .x a a c a a a TOANMATH.com Trang 15 b bc b b c c C. f xdx f xdx f xd .x D. f xdx f xdx f xd .x a a bc a a b Câu 2: Cho hàm số 3
y x có một nguyên hàm là F x . Khẳng định nào sau đây đúng?
A. F 2 F 0 16. B. F 2 F 0 1.
C. F 2 F 0 8.
D. F 2 F 0 4. e Câu 3: Tích phân cos xdx bằng 0 A. sin . e B. cos . e C. sin . e D. cos . e 2
Câu 4: Tích phân I 2x 1 dx bằng 0 A. I 5. B. I 6. C. I 2. D. I 4. 0 3 3 Câu 5: Cho f xdx 1; f
xdx 3. Tích phân f xdx bằng 1 0 1 A. 6. B. 4. C. 2. D. 0. 2 4 4 Câu 6: Cho f
xdx 1, f tdt 4 . Giá trị của I f ydy là 2 2 2 A. I 5. B. I 3. C. I 3 . D. I 5 . c c a Câu 7: Cho f xdx 50 và f
xdx 20. Giá trị f xdx bằng a b b A. 3 0. B. 0. C. 70. D. 30. 1 1 1 Câu 8: Cho f
x2gxdx 12 và g
xdx 5, khi đó f xdx bằng 0 0 0 A. 2 . B. 12. C. 22. D. 2. 5 5 5 Câu 9: Cho f xdx 4 và g
xdx 3, khi đó 2 f
x3gx dx bằng 2 2 2 A. 1. B. 12. C. 7. D. 1 . 2 4 4 4 Câu 10: Cho f xdx 3; f xdx 6 và g
xdx 8. Khi đó 3f
x gxdx bằng 0 2 0 0 A. 14. B. 3. C. 17. D. 1 . 2 2 2 Câu 11: Cho f
x 2gxdx 5 và 2 f
x3gx dx 4 . Khi đó f
x gxdx bằng 1 1 1 A. 14. B. 3. C. 17. D. 1 . 6 10 6
Câu 12: Cho hàm số f x liên tục trên thỏa mãn f xdx 7, f xdx 8 và f xdx 9. Giá 0 3 3 10
trị của tích phân I f xdx bằng 0 A. I 5. B. I 6. C. I 7. D. I 8. TOANMATH.com Trang 16 3
Câu 13: Cho hàm số f x có đạo hàm trên đoạn 1; 3 , f 3 4 và f
xdx 7 . Khi đó f 1 bằng 1 A. 3. B. 11. C. 3 . D. 1 1. e 1 1
Câu 14: Giá trị của I dx là 2 x x 1 1 1 A. I . B. I 1. C. I 1. D. I . e e e 2 Câu 15: Cho 3x 1 p q e
dx m e e với m, p,q và là các phân số tối giản. Giá trị m p q bằng 1 22 A. 10. B. 6. C. . D. 8. 3 3 3 3 3 Câu 16: Cho f xdx 1, g
xdx 5. Để a 2ax3f x dx
a2g xdx 10 thì 2 2 2 2 A. a 2. B. a 3 . C. a 1. D. a 3. 1
Câu 17: Cho f x, g x là các hàm số có đạo hàm liên tục trên 0; 1 và g
x.f xdx 1, 0 1 1 g
x.f xdx 2. Khi đó I f x.gx dx có giá trị là 0 0 A. I 3. B. I 1. C. I 2. D. I 1 .
Câu 18: Cho hàm số y f x có đạo hàm là hàm liên tục trên thỏa mãn f 0 2, f 1 6 . Khẳng
định nào sau đây là đúng? 1 1 1 1 A. f xdx 8. B. f xdx 4. C. f xdx 3. D. f xdx 12. 0 0 0 0 2 2 Câu 19: Cho 4 f x2xdx 1 . Khi đó f x dx bằng 1 1 A. 1. B. 3 . C. 3. D. 1 . 4 4 3
Câu 20: Cho hàm số f x liên tục trên và f xdx 10, f
xdx 4. Tích phân f xdx bằng 0 3 0 A. 4. B. 7. C. 3. D. 6. b
Câu 21: Với a, b là các tham số thực. Giá trị tích phân 2 3x 2ax 1dx bằng 0 A. 3 2 b b a . b B. 3 2 b b a . b C. 3 2 b ba . b D. 2 3b 2ab 1. 1
Câu 22: Tích phân 3x 1 x 3 dx bằng 0 A. 12. B. 9. C. 5. D. 6. 3 x 2 Câu 23: Biết dx a b ln c , với a, ,
b c ,c 9. Tổng S a b c là x 1 TOANMATH.com Trang 17 A. S 7. B. S 5. C. S 8. D. S 6. 1 1 Câu 24: Tích phân I dx có giá trị bằng x 1 0 A. ln 2 1. B. ln 2. C. ln 2. D. 1 ln 2. m
Câu 25: Cho số thực m 1 thỏa mãn 2mx 1 dx 1.
Khẳng định nào sau đây đúng? 1 A. m 4;6. B. m 2;4. C. m 3;5. D. m 1;3. 1 1 a ln 2
Câu 26: Biết rằng tích phân I dx
, với a,b . Biểu thức P a b có giá trị bằng 2 x x 2 b 0 A. 5 . B. 3. C. 1. D. 1 . 2 2 Câu 27: Cho hai tích phân 2 A sin xdx và 2 B cos xd . x
Trong các khẳng định sau, khẳng định đúng 0 0 là A. A 2 . B B. A . B C. A . B D. A B 1. 5 x 2 Câu 28: Cho tích phân
dx a b ln 2 c ln 3, với a, ,
b c là các số nguyên. Tích P abc là x 1 1 A. P 3 6. B. P 0. C. P 1 8. D. P 18. 1 2
Câu 29: Biết rằng hàm số f x mx n thỏa mãn f xdx 3, f
xdx 8. Khẳng định nào dưới 0 0 đây là đúng? A. m n 4. B. m n 4. C. m n 2. D. m n 2 . 2 2 x 5x 2 Câu 30: Biết
dx a b ln 3 c ln 5, a,b,c
. Giá trị của abc bằng 2 x 4x 3 0 A. 8 . B. 1 0. C. 1 2. D. 16. a
Câu 31: Cho a là số thực dương, tính tích phân I x dx theo a. 1 2 a 1 2 a 2 2 2 a 1 2 3a 1 A. I . B. I . C. I . D. I . 2 2 2 2 2 dx Câu 32: Biết
a ln 2 bln 3 c ln 5.
Khi đó giá trị a b c bằng x 1 2x 1 1 A. 3 . B. 2. C. 1. D. 0. 0 2 3x 5x 1 2 Câu 33: Biết I dx a ln , b
a,b. Khi đó giá trị của a 4b bằng x 2 3 1 A. 50. B. 60. C. 59. D. 40. 4 5 8 Câu 34: Cho ln 3 ln 2 ln 5, x dx a b c
với a,b, c là các số hữu tỉ. 2 x 3x 2 3 TOANMATH.com Trang 18 Giá trị của 3 2a bc bằng A. 12. B. 6. C. 1. D. 64. 1 dx 8 2 Câu 35: Cho a b a *
a,b . Giá trị của a 2b là bao nhiêu? x 2 x 1 3 3 0 A. a 2b 7. B. a 2b 5. C. a 2b 1 . D. a 2b 8. 2 1 x 2 1 Câu 36: Biết dx n ln 2, với ,
m n là các số nguyên. Tổng S m n là 0 x 1 m A. S 1. B. S 4. C. S 5 . D. S 1 . 2 x 10 a Câu 37: Cho 2 x dx ln , với a,b . Tổng P a b là x 1 b b 1 A. P 1. B. P 5. C. P 7. D. P 2. 3 1 5x Câu 38: Cho dx a ln b c,
với a,b, c là các số hữu tỷ. Giá trị của 9a 11b 22c bằng 2 9x 24x 16 2 A. 15. B. 1 0. C. 7. D. 9. 0 2 3x 5x 1 2 Câu 39: Cho dx a ln b
với a, b là các số hữu tỉ. Giá tị của a 2b bằng x 2 3 1 A. 60. B. 50. C. 30. D. 40. 1 2 4x 15x 11 Câu 40: Cho dx a b ln 2 c ln 3
với a,b,c là các số hữu tỷ. Biểu thức T . a c b bằng 2 2x 5x 2 0 1 1 A. 4. B. 6. C. . D. . 2 2 2 2x 1 1 Câu 41: Cho dx ln a ln b c
, với a,b, c là các số hữu tỷ. Giá trị của 3a b 10c 2 4x 4x 1 2 0 bằng A. 15. B. 1 5. C. 14. D. 9. 1 2 x 3 Câu 42: Cho dx a b ln 2 c ln 3
với a,b, c là các số nguyên. Giá trị của a b c bằng 2 x 3x 2 0 A. 2 . B. 1 . C. 2. D. 1. 1a dx
Câu 43: Có bao nhiêu giá trị nguyên của tham số a để tích phân tồn tại? x x 5 x 4 1 A. 3. B. 5. C. Vô số. D. 0. 1 3 1
Câu 44: Cho hàm số f x liên tục trên , có f xdx 2 và f
xdx 6. Tính I f 2x 1d .x 0 0 1 3 A. I 8. B. I 16. C. I . D. I 4. 2
Câu 45: Khẳng định nào sau đây đúng? 1 1 2019 2019 A. 3 3 x dx x dx . B. 4 2 x x 1 dx 4 2 x x 1d .x 1 1 1 1 TOANMATH.com Trang 19 3 3 C. x 1 x e x dx e x 1d .x D. 2 2 2 1 cos xdx sin xd . x 2 2 2 2 4 1 1 a 1 a Câu 46: Cho dx ln , với a, ,
b c là các số nguyên dương và tối giản. Giá trị của 2 x x 2 4 b c b 3 a b c bằng A. 7. B. 5 . C. 14. D. 9 4 dx Câu 47: Cho I a b 3
với a,b là số thực. Giá trị của a b bằng 2 2 cos . x sin x 6 1 2 1 2 A. . B. . C. . D. . 3 3 3 3 a b
Câu 48: Cho hàm số f x
2, với a,b là các số hữu tỉ thỏa mãn điều kiện 2 x x 1 f
xdx 23ln2. Tổng T a b là 1 2 A. T 1 . B. T 2. C. T 2 . D. T 0. a 2 2 x 2x 2 a
Câu 49: Xác định số a dương sao cho dx a ln 3 . Giá trị của a là x 1 2 0 A. a 1. B. a 2. C. a 3. D. a 4 . 1 2 2x 1 Câu 50: Cho dx a b ln 2,
với a,b là các số hữu tỉ. Giá trị của 2a b bằng x 1 0 A. 1 . B. 6. C. 5. D. 4. 3 2 6x x 2 3 5 Câu 51: Cho
với a,b, c là các số hữu tỷ. x dx 2ln a ln b ln c, 2 x 1 2 2 2
Giá trị của 2a 3b 5c bằng A. 10. B. 1 0. C. 8. D. 9. 2 3x khi 0 x 1 2
Câu 52: Cho hàm số y f x . Tích phân f xdx bằng 4 x khi 1 x 2 0 7 5 3 A. . B. 1. C. . D. . 2 2 2 0
Câu 53: Cho tích phân cos 2x cos 4xdx a b 3
, trong đó a, b là các hằng số hữu tỉ. 3 Giá trị a e log b bằng 2 1 A. 2 . B. 3 . C. . D. 0. 8 TOANMATH.com Trang 20 2
Câu 54: Giá trị của tích phân max sin x,cos x dx bằng 0 1 A. 0. B. 1. C. 2. D. . 2 3 2 x x 1 a 4 b Câu 55: Biết rằng dx
, với a, b, c là các số nguyên dương. x x 1 c 2
Tổng T a b c bằng A. 31. B. 29. C. 33. D. 27. 1 3 x 3x Câu 56: Biết
dx a b ln 2 c ln 3,
với a,b,c là các số hữu tỉ. Giá trị của biểu thức 2 x 3x 2 0 2 2 S 2a b c bằng A. S 515. B. S 164. C. S 436. D. S 9 .
Câu 57: Cho M, N là các số thực. Xét hàm số f x M.sin x N.cos x thỏa mãn f 1 3 và 1 2 1 f x 1
dx . Giá trị của f bằng 4 0 5 2 5 2 2 2 A. . B. . C. . D. . 2 2 2 2 2 2019. k e kx 2019
Câu 58: Gọi S là tập hợp tất cả các số nguyên dương k thỏa mãn e dx . Số phần tử k 1 của tập hợp S bằng. A. 7. B. 8. C. Vô số. D. 6. 2 3 2 x x cos x sin x b b Câu 59: Biết I dx . Trong đó a, ,
b c là các số nguyên dương. Phân số 1 cos x a c c 0
tối giản. Giá trị của 2 2 2 T a b c là A. T 16. B. T 59. C. T 69. D. T 50. 4 1 x x e Câu 60: Biết b c dx a e e
với a, b, c là các số nguyên. 2 4 x x xe 1
Giá trị của T a b c bằng A. T 3 . B. T 3. C. T 4 . D. T 5 .
Dạng 2: Tính tích phân bằng phương pháp đổi biến Phương pháp giải
Nắm vững phương pháp đổi biến số dạng 1 và dạng 2, cụ thể: Đổi biến dạng 1 TOANMATH.com Trang 21 b
Bài toán: Giả sử ta cần tính I f
xdx, trong đó ta Ví dụ 1: Giá trị của 2 I cos . x sin xdx là a 0
có thể phân tích f x g uxu x. A. . B. 0. 1 2 C. . D. . 3 3 Hướng dẫn giải
Bước 1: Đặt u u x, suy ra du u x d . x
Đặt u cos x du sin . x dx sin . x dx du. Bước 2: Đổi cận x 0 u 1 Đổi cận x a B x u 1 u u a u b Bước 3: Tính 1 1 3 1 2 Khi đó 2 2 . u I u du u du 3 3 b ub 1 ub 1 1 I f x dx g u du G u Chọn D. ua a u a
Với G u là một nguyên hàm của g u . Đổi biến dạng 2 b
Bài toán: Giả sử ta cần tính I f xdx, ta có thể 1 a 2 2 đổi biến như sau:
Ví dụ 2: Giá trị của I 1 x dx là 0 3 3 A. . B. . 12 8 12 8 3 3 C. . D. . 6 4 6 4 Hướng dẫn giải
Bước 1: Đặt x t, ta có dx t dt.
Đặt x sin t dx costdt. Bước 2: Đổi cận x 0 t 0 x a b Đổi cận 1 x t t 2 6 Bước 3: 6 Khi đó 2 I 1 sin t.cos tdt 0 Tính I f
t.tdt g tdt Gt 6 6 1 2 cos t.dt 1cos2t.dt
Với G t là một nguyên hàm của g t . 2 0 0 TOANMATH.com Trang 22 Dấu hiệu Cách đặt 1 1 1 3 6 t sin 2t . 2 2 a x 2 2 0 2 6 4 x a sin t,t ; 2 2 Chọn A. 2 2 x a a x ,t ; \ 0 sin t 2 2 2 2 a x x a tan t,t ; 2 2 a x x . a cos 2t,t 0; a x 2 a x x . a cos 2t,t 0; a x 2 x ab x x a b a 2 sin t,t 0; 2 Ví dụ mẫu 2 3 1
Ví dụ 1: Giá trị của I dx là 2 5 x x 4 1 3 1 5 1 5 1 3 A. I ln . B. I ln . C. I ln . D. I ln . 4 5 4 3 2 3 2 5 Hướng dẫn giải Đặt 2 2 2
u x 4 x u 4 nên xdx udu Đổi cận x 5 2 3 u 3 4 2 3 1 4 4 1 1 Khi đó I .xdx nên I .udu d . u 2 2 2u 4 u u 4 3 2 5 x x 4 3 4 4 1 1 1 1 1 5 Suy ra I du
ln u 2 ln u 2 ln . 4 u 2 u 2 4 3 4 3 3 Chọn B. + Đặt 2 u x 4 . + Rút 2 2 x u 4 . + Đổi cận.
+ Phương pháp tách phân thức hữu tỉ. TOANMATH.com Trang 23 2 x
Ví dụ 2: Giá trị của I dx là 1 x 1 1 11 1 11 11 A. I ln 2. B. I 2ln 2. C. I 4ln 2. D. I 11 4ln 2. 3 2 3 3 Hướng dẫn giải Đặt 2
u x 1 x u 1 nên dx 2udu. Đổi cận x 1 2 u 0 1 1 2 1 u 1 4 Khi đó 2 I .2udu 2u 2u 4 du 1 u u 1 0 0 3 1 2u 11 2 u 4u 4ln u 1 4ln 2. 3 0 3 Chọn C. Đổi biến số dạng 1. Đặt u x 1. e 1 3ln x.ln x
Ví dụ 3: Giá trị của I dx là x 1 116 116 153 161 A. I . B. I . C. I . D. I . 135 153 116 135 Hướng dẫn giải 2 u 1 1 2
Đặt u 1 3ln x ln x nên dx udu . 3 x 3 Đổi cận x 1 e u 1 2 u. 2 2 u 2 5 3 2 1 2 2 2 u u 116 Khi đó I . udu 4 2 u u du . 3 3 9 9 5 3 1 135 1 1 Chọn A. 2 sin 2x sin x
Ví dụ 4: Giá trị của I dx là 1 3cos x 0 16 43 11 34 A. I . B. I . C. I . D. I . 27 27 27 27 Hướng dẫn giải TOANMATH.com Trang 24 2 u 1 2
Đặt u 1 3cos x cos x nên sin xdx udu . 3 3 Đổi cận x 0 2 u 2 1 2 sin x 2cos x 2 1 2 cos x 1 Ta viết I dx sin xd . x 1 3cos x 1 3cos x 0 0 2 u 1 2 1 1 2 3 2 3 2 4 4 2u 34 Khi đó I . udu 2 2u 1 du u . u 3 9 9 3 1 27 2 1 Chọn D. 2 2 2 x
Ví dụ 5: Giá trị của I dx là 2 0 1 x 1 1 1 1 A. I . B. I . C. I . D. I . 8 4 4 8 3 4 8 2 Hướng dẫn giải
Đặt x sin t dx costdt . Đổi cận x 0 2 2 u 0 4 4 2 4 4 sin t.cos t 1 Khi đó 2 I dt sin tdt 1cos2tdt 2 1 sin t 2 0 0 0 1 1 1 4 t sin 2t . 2 2 0 8 4 Chọn A. Đổi biến số dạng 2: x sin t, với t ; . 2 2 6 1
Ví dụ 6: Giá trị của I dx là 2 3 2 x x 9 TOANMATH.com Trang 25 A. I . B. I . C. I . D. I . 8 36 6 24 Hướng dẫn giải 3 3cost Đặt x dx dt 2 sin t sin t Đổi cận x 3 2 6 u 4 6 6 4 3 cost 1 1 Khi đó I dt dt . 3 9 3 3 4 6 36 2 sin t. 9 4 2 6 sin t sin t Chọn B. 1 x
Ví dụ 7: Giá trị của I dx là 4 2 x x 1 0 3 3 3 3 A. I . B. I . C. I . D. I . 4 6 18 12 Hướng dẫn giải
Đột biến lần 1: (Dạng 1) 1 Đặt 2 u x xdx du. 2 Đổi cận x 0 1 u 0 1 1 1 1 1 1 1 Suy ra I du du. 2 2 2 u u 1 2 0 0 1 3 u 2 4
Đổi biến lần 2: (Dạng 2) 1 3 3 Đặt u tan t. Ta có du 2 1 tan t dt 2 2 2 Đổi cận x 0 1 u 6 3 TOANMATH.com Trang 26 3 3 3 3 Khi đó I dt . 3 3 3 6 18 6 Chọn C. 2 cos x Ví dụ 8: Biết dx a ln 2 b ln 3,
với a,b là các số nguyên. 2 sin x 3sin x 2 0
Giá trị của P 2a b là A. 3. B. 7. C. 5. D. 1. Hướng dẫn giải 2 2 cos x 1 Ta có dx d sin x 2 sin x 3sin x 2 sin x 1 sin x 2 0 0 2 1 1 d
sin x ln sin x 1 ln sin x 2 2 sin x 1 sin x 2 0 0
ln 2 ln1 ln 3 ln 2 2ln 2 ln 3 Suy ra a 2,b 1 2a b 3. Chọn A. ln 2 dx 1 Ví dụ 9: Biết I a b c , với a, ,
b c là các số nguyên tố. x x ln ln ln 0 e 3e 4 c
Giá trị của P 2a b c là A. P 3 . B. P 1 . C. P 4. D. P 3. Hướng dẫn giải x ln 2 dx ln 2 e dx Ta có I . x x 2 0 0 e 3e 4 x e 4 x e 3 Đặt x x t e dt e d . x
Đổi cận x 0 t 1, x ln 2 t 2. Khi đó 2 2 1 1 2 1 1 1 t 1 1 I dt dt ln ln 3 ln 5 ln 2 . 2 1 1 t 4t 3 2 t 1 t 3 2 t 3 1 2
Suy ra a 3,b 5, c 2 . Vậy P 2a b c 3. Chọn D. 6 dx a 3 b Ví dụ 10: Biết , với a,b ,c
và a, b, c là các số nguyên tố cùng nhau. Giá trị 1 sin x c 0
của tổng a b c bằng TOANMATH.com Trang 27 A. 5. B. 12. C. 7. D. 1 . Hướng dẫn giải 1 x 2 x 2 cos 1 tan 6 6 6 6 dx dx 2 2 Ta có I dx d . x 2 2 2 1 sin x 0 0 x x 0 x 0 x cos sin 1 tan 1 tan 2 2 2 2 x x Đặt 2
t 1 tan 2dt 1 tan d . x 2 2
Đổi cận x 0 t 1; x t 3 3. 6 3 3 3 3 2dt 2 3 3 I . 2 t t 1 3 1 Suy ra a 1
,b 3,c 3 nên a b c 5. Chọn A. Lưu ý: 2 x x x 1 sin x sin cos . Chia tử và mẫu cho 2 cos . 2 2 2 1
Ví dụ 11: Cho hàm số y f x liên tục trên và f 2xdx 8. 0 2 Giá trị của I xf 2xdx là 0 A. 4. B. 8. C. 16. D. 64. Hướng dẫn giải Đặt 2
x 2u 2xdx 2du xdx du.
Đổi cận x 0 u 0, x 2 u 1. 1 1 Khi đó I f 2udu f 2xdx 8. 0 0 Chọn B.
Ví dụ 12: Cho hàm số y f x xác định và liên tục trên 0; sao cho 2 x x x xf e f e 1; với e f x.ln x
mọi x 0; . Giá trị của I dx là x e 1 2 1 3 A. I . B. I . C. I . D. I . 8 3 12 8 Hướng dẫn giải TOANMATH.com Trang 28 x x x x 1
Với x 0; ta có x xf e f e 1 f e 2 2 1 . x 1 x dx Đặt ln t x t x e dt . x 1
Đổi cận x e t ; x e t 1. 2 1 1 t 1 Khi đó I t. f
e dt t1tdt . 12 1 1 2 2 Chọn C. 2 3sin x cos x 11 b Ví dụ 13: Biết dx ln 2 b ln 3 c ,
b,c. Giá trị của là 2sin x 3cos x 13 c 0 22 22 22 22 A. . B. . C. . D. . 3 3 3 13 Hướng dẫn giải 3sin x cos x
m 2sin x 3cos x n2cos x 3sin x Phân tích 2sin x 3cos x 2sin x 3cos x
2m 3nsin x 3m 2ncos x 2sin x 3cos x 2m 3n 3 3 11
Đồng nhất hệ số ta có m ; n . 3 m 2n 1 13 13 3 11 2 2
2sin x 3cos x 2cos x 3sin x 3sin x cos x Suy ra 13 13 dx d . x 2sin x 3cos x 2sin x 3cos x 0 0 2 2 3 11 2cos x 3sin x 3 x x . dx x 11 2 cos 3sin 2 d . x 13 13 2sin x 3cos x 13 0 13 2sin x 3cos x 0 0 2 3 11 d 2sin x 3cos x 3 11 2 dx ln 2sin x 3cos x 26 13 2sin x 3cos x 26 13 0 0 11 b 3 11 11 13 b 11 26 22 ln 2 ln 3. Do đó . 26 13 13 3 c 13 3 3 c 26 Chọn A. TOANMATH.com Trang 29 4 2 e f 2 ln x
Ví dụ 14: Cho hàm số f x liên tục trên và thỏa mãn tan . x f 2 cos xdx 2 và dx 2 . x ln x 0 e 2 f 2x Giá trị của I dx là x 1 4 A. 0. B. 1. C. 4. D. 8. Hướng dẫn giải 4 4 sin . x cos x Đặt A tan . x f 2 cos xdx 2 .f 2 cos x dx 2. 2 cos x 0 0. 1 Đặt 2
t cos x dt 2sin x cos xdx dt sin x cos xd . x 2 1 1 f t
Đổi cận x 0 t 1 và x t . Khi đó A dt 4. 4 2 t 1 2 2 e f ln x 2 2 e ln . x f 2 ln x Đặt B dx 2 dx 2. 2 x ln x x ln x e e 4 f t Tương tự ta có B dt 4. t 1 2 f 2x 1 Giá trị của I d . x
Đặt t 2x dx dt. x 2 1 4 1 1
Đổi cận x t và x 2 t 4. 4 2 4 f t 1 f t 4 f t Khi đó I dt dt dt 4 4 8 t t t 1 1 1 2 2 Chọn D. 1 1 Ví dụ 15: Cho dx a b;
với a,b là các số nguyên. x 3x 3 0 1
Giá trị của biểu thức b a a b bằng A. 17. B. 57. C. 145. D. 32. Hướng dẫn giải 1 1 1 1 dx Giá trị của I dx . x 3x x 3 1 x 2 3 0 0 1 x 1 TOANMATH.com Trang 30 x 3 2 dx Đặt t 2tdt dx tdt. x 1 x 2 1 x 2 1
Đổi cận x 0 t 3, x 1 t 2. 1 2 3 3 1 dx 1 Ta có I t dt dt t 3 2. 2 x 3 x t 0 1 2 3 2 x 1 1 1 Mà dx a b nên suy ra a 3,b 2. x 3x 3 0 1 Từ đó ta có giá trị b a 2 3 a b 3 2 17. Chọn A. 1 x 1 a Ví dụ 16: Cho dx ln b
, với a,b là các số nguyên tố. Giá trị của biểu thức 3 x 1 a b 1 2 P 2a b bằng A. 12. B. 10. C. 18. D. 15. Hướng dẫn giải 1 1 1 1 3 x x 1 x 1 Biến đổi I dx dx dx . dx . 3 4 x 1 1 x 1 1 3 1 1 1 1 x 1 3 . x 1 1 2 2 2 3 2 3 x x x 1 1 3 1 Đặt 2 u 1 u 1 2udu dx và 3 x . 3 3 4 x x x 2 u 1 1
Đổi cận x u 3; x 1 u 2. 2 2udu 3 3 3 2 du 1 u 1 1 3 Ta có 3 I ln ln 2 . 2 u 2 1 .u 3 u 1 3 u 1 3 2 2 2 2
Suy ra a 3,b 2. Vậy P 2a b 10. Chọn B.
Bài tập tự luyện dạng 2 4 2 Câu 1: Cho f
xdx 2019. Giá trị của I f
2x f 42x dx là 0 0 A. I 0. B. I 2019. C. I 4038. D. I 2020. 1 2 3
Câu 2: Cho hàm số f x liên tục trên có 2 f xdx 2và f
x 1dx 4.Giá trị của I f xdx là 0 0 0 A. I 5. B. I 4. C. I 6. D. I 7. TOANMATH.com Trang 31 4 5 2 ln 2 Câu 3: Biết f xdx 5 và f
xdx 20. Giá trị của 4 3 2x 2x I f x dx f e e dx là 1 4 1 0 15 5 A. I . B. I 15. C. I . D. I 25. 4 2 4 e 1 4 Câu 4: Biết f
ln x dx 4. Giá trị của I f xdx là x e 1 A. I 8. B. I 16. C. I 2. D. I 4. 8 1 Câu 5: Cho f
x 1dx 10. Giá rị của J f 5x 4dx là 3 0 A. J 4. B. J 10. C. J 32. D. J 2. 9 0 Câu 6: Cho f
xdx 27. Giá trị của f 3 xdx là 0 3 A. I 27. B. I 3 . C. I 9. D. I 3. 1
Câu 7: Cho hàm số f x liên tục trên thỏa mãn f x 4 tan cos x, x
. Giá trị của I f xdx 0 là 2 2 A. . B. 1. C. . D. . 8 4 4 1 4
Câu 8: Giá trị của I x 2 1 x dx là 0 31 30 31 32 A. . B. . C. . D. . 10 10 10 10 11 2 Câu 9: Biết f
xdx 18. Giá trị của I x2 f 2 3x 1 dx là 1 0 A. I 5. B. I 7. C. I 8. D. I 10. 2 Câu 10: Giá trị của 2 I sin . x cos xdx là 0 1 3 A. I 0. B. I 1. C. I . D. I . 3 24 b b 1 e 1 Câu 11: Biết dx 2,
trong đó a,b là các hằng số dương. Giá trị của dx là x x x a ln a e 1 1 A. I ln 2. B. I 2. C. I . D. I . ln 2 2 5 1
Câu 12: Giả sử tích phân I dx a b ln 3 c ln 5
a,b,c . Giá trị của giá trị biểu thức 1 3x 1 1 P a b c là TOANMATH.com Trang 32 8 4 5 7 A. P . B. P . C. P . D. P . 3 3 3 3 e ln x c Câu 13: Biết rằng I dx a ln 3 bln 2 , với a, ,
b c . Giá trị của giá trị biểu thức x ln x 22 3 1 2 2 2 P a b c là A. P 1. B. P 11. C. P 9. D. P 3. 1 dx Câu 14: Biết rằng
a ln 2 bln 3 c ln 5, với a, , b c là các số hữu tỉ. 3x 5 3x 1 7 0
Giá trị của a b c bằng 10 5 10 5 A. . B. . C. . D. . 3 3 3 3 a 2
Câu 15: Có bao nhiêu số a 0;20 sao cho 5 sin x sin 2xdx . 7 0 A. 10. B. 9. C. 20. D. 19. 1 3 x 3 x 2 ex 2x 1 1 e Câu 16: Biết dx .ln p , với , m ,
n p là các số nguyên dương. x . e 2 m e ln n e 0
Giá trị của tổng T m n p là A. T 5. B. T 6. C. T 8. D. T 7. ln 6 x e Câu 17: Biết dx a b ln 2 c ln 3 , với a, ,
b c là các số nguyên. Giá trị của T a b c là x 0 1 e 3 A. T 1 . B. T 0. C. T 2. D. T 1. e 3 3x 2 1 ln x 3x 1 Câu 18: Cho 3 dx . a e b . c ln
e 1 , với a,b,c là các số nguyên. Giá trị của 1 x ln x 1 2 2 2 P a b c là A. P 9. B. P 14. C. P 10. D. P 3.
Câu 19: Cho hàm số y f x liên tục trên đoạn 1;
3 , thỏa mãn f 4 x f x, x 1; 3 và 3 3 xf xdx 2 . Giá trị 2 f xdx bằng 1 1 A. 1. B. 2. C. 1 . D. 2 .
Câu 20: Cho hàm số f x luôn nhận giá trị âm và có đạo hàm liên tục trên thỏa mãn 1
f x x f x 2 2 1 , x
và f 0 1. Giá trị của tích phân f xdx bằng 0 1 3 2 3 A. . B. ln 2. C. . D. . 6 9 9 2 2 sin xf 3cos x 1 Câu 21: Cho I f
xdx 2. Giá trị của dx bằng 3cos x 1 1 0 TOANMATH.com Trang 33 4 4 A. 2. B. . C. . D. 2 . 3 3 3 x 3 Câu 22: Cho dx a ln 3 b ln 2 c với a, ,
b c là các số hữu tỉ. Giá trị của 2 2 2 a b c 3 x 1 x 3 0 bằng A. 3. B. 63. C. 81. D. 9. 4 2 3tan x Câu 23: Cho dx a 5 b 2,
với a,b . Giá trị của giá trị biểu thức A a b là 1 cos 2x 0 1 7 2 4 A. . B. . C. . D. . 3 12 3 3 2 x 3 khi x 1 2 1
Câu 24: Cho hàm số y f x . Giá trị của I 2 f sin xcos xdx 3 f 32xdx 5 x khi x 1 0 0 là 71 32 A. I . B. I 31. C. I 32. D. I . 6 3 x khi x
Câu 25: Cho hàm số y f x 4 2 . 2 x 12 khi x 2 . x f 2 3 x 1 ln 3 Giá trị của 2 I dx 4 x e . f 2 1 x e dx là 2 0 x 1 ln 2 309 3 A. I 309. B. I 159. C. I . D. I 9 150 ln . 2 2 1 x 2 Câu 26: Biết dx a ln 12 b ln 7,
với a,b là các số nguyên. Giá trị của tổng a b bằng 2 x 4x 7 0 1 A. 1 . B. 1. C. . D. 0. 2 2 2x 1 1 Câu 27: Cho dx ln a ln b c , với a, ,
b c là các số hữu tỷ. Giá trị của 3a b 10c 2 4x 4x 1 2 1 bằng A. 15. B. 1 5. C. 14. D. 9. e x 1 ln x 2 e 1 a Câu 28: Biết dx ae b ln
trong đó a,b là các số nguyên. Khi đó tỉ số là 1 x ln x e b 1 1 A. . B. 1. C. 3. D. 2. 2 e x 1 Câu 29: Biết dx ln ae b ,
với a,b là các số nguyên dương. Giá trị của biểu thức 2 x x ln x 1 2 2 T a ab b là A. 3. B. 1. C. 0. D. 8. TOANMATH.com Trang 34 2 3 cos x sin x Câu 30: Biết rằng dx . a b . c ln 2,a, , b c
. Giá trị của tổng S a b c là sin x 6 13 23 7 A. S 1. B. S . C. S . D. S . 24 24 24 x ln m e Câu 31: Cho dx ln 2.
Khi đó giá trị của m là 0 x e 2 1 A. m . B. m 2. C. m 4. D. m 0, m 4. 2 6 n 1 Câu 32: Biết sin . x cos xdx và *
n . Giá trị của n bằng 64 0 A. 3. B. 4. C. 5. D. 6. 2 Câu 33: Cho tích phân I 2 cos x.sin xd . x
Nếu đặt t 2 cos x thì kết quả nào sau đây đúng? 0 2 3 2 2 A. I tdt. B. I tdt. C. I 2 tdt. D. I tdt. 3 2 3 0
Câu 34: Cho hàm số f x liên tục trên thỏa điều kiện f x f x 2 2cos . x 2 Giá trị của I f xdx 2 A. 0. B. . C. 1. D. 1 . 2 5 dx Câu 35: Giá trị của
được kết quả I a ln 3 b ln 5, với a,b . Giá trị 2 2 a ab 3b là x 3x 1 1 A. 4. B. 5. C. 1. D. 0. 9 3 4 3 Câu 36: Giá trị I x sin x cos 2 3 x e
dx gần bằng giá trị nào nhất trong các số sau đây? 1 3 6 A. 0,046. B. 0,036. C. 0,037. D. 0,038. 2 x 1 Câu 37: Biết dx ln ln a b
với a, b là các số nguyên dương. Giá trị của 2 2 P a b ab 2 x x ln x 1 là A. 10. B. 8. C. 12. D. 6. 2 x Câu 38: Biết dx a b 2 c 35
với a, b, c là các số hữu tỷ. 2 1 3x 9x 1
Giá trị của P a 2b c 7 là TOANMATH.com Trang 35 1 86 67 A. . B. . C. 2 . D. . 9 27 27 2 3x 1 ln b Câu 39: Biết dx ln a
với a,b,c là các số nguyên dương và c 4. 2 3x x ln x c 1 Tổng a b c bằng A. 6. B. 9. C. 7. D. 8. m sin x 1
Câu 40: Có bao nhiêu giá trị của tham số m trong khoảng 0;6 thỏa mãn dx ? 5 4cos x 2 0 A. 6. B. 12. C. 8. D. 4. 1 dx 2 a Câu 41: Biết rằng 2ln
với a, b là các số nguyên dương. 2 x 4x 3 1 b 0
Giá trị của a b bằng A. 3. B. 5. C. 9. D. 7. 2019
Câu 42: Cho hàm số f x liên tục trên thỏa f
xdx 2. Khi đó tích phân 0 2019 e 1 x f ln 2x 1 dx bằng 2 x 1 0 A. 4. B. 1. C. 2. D.3. 2 2
x 2x cos xcos x 1 sin x c Câu 43: Cho tích phân 2 I dx a b ln với a, , b c là các số hữu x cos x 0
tỉ. Giá trị của biểu thức 3 P ac b là 5 3 A. P 3. B. P . C. P . D. P 2. 4 2 6
Câu 44: Cho hàm số f x liên tục trên 0; 1 thỏa mãn f x 2 6x f 3 x . Giá trị của 3x 1 1 f xdx là 0 A. 2. B. 4. C. 1 . D. 6. 2 1 x x x e Câu 45: Cho dx . a e b ln e c với a, ,
b c . Giá trị của P a 2b c là x x e 0 A. P 1. B. P 1 . C. P 0. D. P 2 . 1
Câu 46: Cho hàm số f x liên tục trên thỏa mãn f 2x 3 f x , x . Biết rằng f xdx 1. 0 2
Giá trị của tích phân I f xdx bằng 1 A. I 5. B. I 3. C. I 8. D. I 2. TOANMATH.com Trang 36 3 a a Câu 47: Giá trị của 2 9 x dx
trong đó a,b và là phân số tối giản. Giá trị của biểu thức b b 0 T ab là A. T 35. B. T 24. C.T 12. D. T 36. n 1 dx
Câu 48: Giá trị của lim bằng 1 x n e n A. 1 . B. 1. C. e. D. 0. ln 6 dx Câu 49: Biết I 3ln a ln b
với a,b là các số nguyên dương. Giá trị của P ab là x e 2 x e 3 ln3 A. P 10. B. P 1 0. C. P 15. D. P 20. f 2 x 1 ln x
Câu 50: Cho hàm số f x liên tục trên đoạn 1;4 và thỏa mãn f x . Giá trị của x x 4 I f xdx là 3 A. 2 I 3 2 ln 2. B. 2 I 2 ln 2. C. 2 I ln 2. D. I 2ln 2.
Câu 51: Cho hai hàm số f x và g x có đạo hàm trên đoạn 1;4 và thỏa mãn hệ thức f 1 g 1 4 4 Giá trị của I f
x gxdx là g
x x f x f x x g x. . ; . 1 A. 8ln 2. B. 3ln 2. C. 6ln 2. D. 4 ln 2. 3
Câu 52: Giá trị của max 2 4, x dx là 0 43 A. 12. B. 21. C. . D. 9. 3 2 2 1 x 1 b Câu 53: Giả sử dx a a b với a, , b c ; 1 a, ,
b c 9. Giá trị của biểu thức 4 x c b c 1 b a C là 2ac A. 165. B. 715. C. 5456. D. 35. 6 2 2 4 2 4 3 2 Câu 54: Tính tích phân 3 4, x x dx a b c với a, , b c là các số nguyên. 4 x 1 8 1 Khi đó biểu thức 2 4
a b c có giá trị bằng A. 20. B. 241. C. 196. D. 48.
Dạng 3: Tính tích phân bằng phương pháp tích phân từng phần Phương pháp giải TOANMATH.com Trang 37 b 2
Bài toán: Tính tích phân I u x.vxd .x Ví dụ: Biết 2x ln
1 xdx .aln ,b với * a,b , a 0
b là số nguyên tố. Giá trị của 3a 4b bằng A. 42. B. 21. C. 12. D. 32. Hướng dẫn giải 2 Xét I 2x ln 1 xd .x u u x du u xdx 0 Đặt dv v xdx v v x u x 1 ln 1 du dx Đặt 1 x . Khi đó dv 2xdx 2 v x 1 b b I . u v vdu 2 2 2 x 1 2 a Ta có I x 1 ln x 1 dx a 0 x 1 0 2 2 2 x
3ln 3 x 1dx 3ln3 x 3ln 3. 2 0 0
Vậy a 3,b 3 3a 4b 21. Chọn B.
Chú ý: Cần phải lựa chọn u và dv hợp lí sao cho b
ta dễ dàng tìm được v và tích phân vdu dễ tính a b hơn ud . v a Ví dụ mẫu 2 e dx
Ví dụ 1: Giá trị của tích phân I là x ln x e A. 1. B. 0. C. ln 2. D. 4. Hướng dẫn giải dx Đặt u ln x du . x x e u 1 Đổi cận . 2 x e u 2 2 2 du Do đó I
ln u ln 2 ln1 ln 2. u 1 1 Chọn C. TOANMATH.com Trang 38 1
Ví dụ 2: Giá trị của tích phân 2 2 I x 1 x dx là 0 A. . B. . C. . D. . 2 16 4 8 Hướng dẫn giải
Đặt x sin t dx costdt. x 0 t 0 Đổi cận . x 1 t 2 /2 2 2 I sin t. 1 sin t costdt 0 /2 2 2 sin t cos tdt 0 /2 1 1 cos 4t dt . 8 16 0 Chọn B. 1
Ví dụ 3: Giá trị của tích phân 2 I x tan xdx là 0 A. 1 tan1 ln cos1 . B. 1 tan1 ln cos1 . 2 2 C. 1 cot1 ln cos1 . D. 1 cot1 ln cos1 . 2 2 Hướng dẫn giải u x du dx Đặt . 2 dv tan xdx v tan x x x I x tan x x 1 1 2 tan x x 1 2
dx tan11 ln cos x 0 2 0 0 1 tan1 ln cos1 . 2 Chọn A. 2 ln x b b
Ví dụ 4. Cho tích phân I dx a ln 2
với a là số thực b và c là các số dương, đồng thời là x c c 1
phân số tối giản. Giá trị của biểu thức P 2a 3b c là A. P 6. B. P 5. C. P 6 . D. P 4. Hướng dẫn giải TOANMATH.com Trang 39 dx u ln x du Đặt x dx . dv 1 2 x v x 2 2 2 ln x 1 ln x 1 1 ln 2 Khi đó I dx . 2 x 1 x x x 1 2 2 1 1 Suy ra b 1, c 2, a
. Do đó P 2a 3b c 4. 2 Chọn D. + Ưu tiên logarit. u ln x + Đặt dx . dv 2 x 4 x Ví dụ 5: Biết dx a b ln 2,
với a,b là các số hũu tỉ. 1 cos 2x 0
Giá trị của T 16a 8b là A. T 4. B. T 5. C. T 2. D. T 2 . Hướng dẫn giải 4 4 4 x x 1 x Đặt A dx dx d . x 2 2 1 cos 2x 2 cos x 2 cos x 0 0 0 u x du dx Đặt 1 dv dx v tan x 2 cos x Khi đó 4 1 1 4 A x tan x tan xdx
xtan xln cos x 4 2 0 2 0 0 1 2 1 1 1 ln ln 2 ln 2. 2 4 2 2 4 2 8 4 1 1 Vậy a ,b
do đó 16a 8b 2 2 4. 8 4 Chọn A. + Biến đổi 2 1 cos 2x 2 cos . x + Ưu tiên đa thức. TOANMATH.com Trang 40 u x + Đặt 1 . dv dx 2 cos x 1 Ví dụ 6: Cho 2x 2 I xe dx . a e b
với a,b . Giá trị của tổng a b là 0 1 1 A. . B. . C. 0. D. 1. 2 4 Hướng dẫn giải
Sử dụng phương pháp từng phần. du dx u x Đặt x 1 . 2 2 x dv e dx v e 2 1 1 1 1 1 1 1 x 1 x 1 x 1 x 1 1 Khi đó 2 2 2 2 2 I u.v . v du . x e e dx . x e e e . 0 2 0 2 2 0 4 0 4 4 0 0 1 1 Suy ra 2 2 . a e b e . 4 4 1 1 1
Đồng nhất hệ số hai vế ta có a ,b . Vậy a b . 4 4 2 Chọn A. + Ưu tiên đa thức. u x + Đặt . 2x dv e dx 2
Ví dụ 7: Cho hàm số f x liên tục, có đạo hàm trên , f 2 16 và f
xdx 4. Tích phân 0 4 x xf dx bằng 2 0 A. 112. B. 12. C. 56. D. 144. Hướng dẫn giải x
Đặt t x 2t dx 2dt. 2 x 0 t 0 4 2 2 x Đổi cận . Do đó xf dx 4tf tdt 4xf xd .x x 4 t 2 2 0 0 0 u 4x du 4dx Đặt dv f xdx v f x. Suy ra TOANMATH.com Trang 41 2 2 2 2 4xf xdx 4xf x 4 f
xdx 8f 24 f
xdx 8.164.4 112. 0 0 0 0 Chọn A. 4 ln sin x 2cos x Ví dụ 8. Cho
dx a ln 3 b ln 2 c với a, , b c là các số hữu tỉ. 2 cos x 0 Giá trị của abc bằng 15 5 5 17 A. . B. . C. . D. . 8 8 4 8 Hướng dẫn giải u
ln sin x 2cos x cos x 2sin x du dx Đặt dx sin x 2cos x . dv 2 v tan x 2 cos x Khi đó 4 ln sin x 2cos x 4 x x dx
tan x 2ln sin x 2cos x cos 2sin 4 dx 2 cos x 0 cos x 0 0 4 3 2 3ln
2ln 2 1 2tan xdx 2 0 7
3ln 3 ln 2 x 2ln cos x 4 2 0 7 2 5 3ln 3 ln 2 2ln 3ln 3 ln 2 . 2 4 2 2 4 5 1
Suy ra a 3,b ,c . Vậy abc 18. 2 4 Chọn A. 2 1 p x p
Ví dụ 9. Biết x 2 1 x q e dx me n, trong đó , m ,
n p, q là các số nguyên dương và là phân số tối q 1
giản. Giá trị của T m n p q là A. T 11. B. T 10. C. T 7. D. T 8. Hướng dẫn giải Ta có 2 1 2 1 2 1 2 1 2 x x x x 1 x
2 2 1 x 2 1 x 2 x I x e dx x x e dx x e dx xe d . x 1 1 1 1 2 1 2 1 2 2 1 2 1 x x x 1 x 1 x Xét I 2 x 2 2 2 1 x e dx x . x e . dx x . x e d x x x d e 1 2 x x 1 1 1 1 TOANMATH.com Trang 42 1 2 2 1 2 x x 2 1 2 2 1 2 x x x x x 2 x x e e d x x e xe dx 1 1 1 1 2 1 1 2 1 2 3 x 2 x 2 x x x x 2 I 2xe dx x e I x e 4e 1 1 1 1 1
m 4, n 1, p 3, q 2.
Khi đó T m n p q 4 1 3 2 10. Chọn B.
Bài tập tự luyện dạng 3 1
Câu 1: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 1 thỏa mãn f 1 5, f xdx 12. 0 1 Giá trị của J xf xdx là 0 A. J 1 7. B. J 17. C. J 7. D. J 7 . 1
Câu 2: Cho hàm số f x có đạo hàm liên tục trên 0; 1 thỏa mãn x f
x2 dx f 1. Giá trị của 0 1 I f xdx bằng 0 A. 2 . B. 2. C. 1 . D. 1. 1
Câu 3: Cho hàm số f x có đạo hàm f x và thỏa 2x
1 f xdx 10 , 3 f
1 f 0 12. Giá trị 0 1 của I f xdx là 0 A. I 2. B. I 1. C. I 1 . D. I 2 .
Câu 4: Cho hai hàm số liên tục f x và g x có nguyên hàm lần lượt là F x và G x trên đọan 2 3 67
1; 2. Biết rằng F
1 1, F 2 4,G 1 ,G 2 2 và f
xGxdx . Giá trị của 2 12 1 2 F x g xdx là 1 11 145 11 145 A. . B. . C. . D. . 12 12 12 12 2 Câu 5: Tích phân 3 x I xe dx
nhận giá trị nào sau đây? 1 3 3e 6 3 3e 6 3 3e 6 3 3e 6 A. I . B. I . C. I . D. I . 1 e 1 e e e TOANMATH.com Trang 43 1
Câu 6: Giá trị của tích phân 2 1 x I x e dx là 0 A. 5e 3. B. e 1. C. e 1. D. 5e 1. e
Câu 7: Giá trị của I x ln xdx là 1 1 1 1 A. I . B. I 2 e 2. C. I 2. D. I 2 e 1 . 2 2 4 4 Câu 8: Biết x ln
2x 9dx aln5bln3 ,c trong đó a, b, c là các số nguyên. Giá trị của biểu thức 0 T a b c là A. T 10. B. T 9. C. T 8. D. T 11. 2
Câu 9: Giá trị của tích phân 2 I x cos xdx
được biểu diễn dưới dạng 2 .
a ba,b . Khi đó tích 0 . a b bằng 1 1 1 A. 0. B. . C. . D. . 32 16 64 2
Câu 10: Giá trị của tích phân 2 I x ln xdx là 1 8 7 8 7 7 A. ln 2 . B. ln 2 . C. 24 ln 2 7. D. 8ln 2 . 3 9 3 3 3 4 1
Câu 11: Biết 1 xcos 2xdx * a,b
. Giá trị của tích ab bằng a b 0 A. 32. B. 2. C. 4. D. 12. 4
Câu 12: Biết x cos 2xdx a b ,
với a, b là các số hữu tỉ. Giá trị của S a 2b là 0 1 3 A. S 0. B. S 1. C. S . D. S . 2 8 5
Câu 13: Giá trị của tích phân I x 1 ln x 3dx là 4 19 19 19 A. 10ln 2 . B. 10ln 2 . C. 10 ln 2. D. 10ln 2. 4 4 4 e4
Câu 14: Giá trị K x 4lnx 4dx là 3 2 e 1 2 e 2 1 2 e 1 A. K . B. K . C. K . D. K . 4 2 2 4 e
Câu 15: Giá trị của tích phân x 1ln xdx là 1 TOANMATH.com Trang 44 2 e 5 2 e 5 2 e 5 2 e 5 A. . B. . C. . D. . 4 2 2 4 e Câu 16: Cho tích phân 2 I x ln xd . x
Mệnh đề nào dưới đây đúng? 1 1 e e e e A. 2 2 I x ln x x ln xd . x B. 2 2 I x ln x 2 x ln xd . x 2 1 1 1 1 e e 1 e e C. 2 2 I x ln x x ln xd . x D. 2 2 I x ln x x ln xd . x 1 2 1 1 1 3 Câu 17: Biết ln
2x xdx aln3b với a,b là các số nguyên. Khi đó a b bằng 2 A. 1. B. 2. C. 0. D. 1 . 1
Câu 18: Giá trị của . . x x e dx là 0 1 A. . B. . . e C. . D. . 3 3 e 2ln x 3 a Câu 19: Biết dx b
với a,b . Giá trị của a b bằng 2 x e 1 A. 2 . B. 8 . C. 2. D. 8. 4 a
Câu 20: Biết 1 xsin 2xdx * a,b
. Giá trị của tích ab bằng 2b 0 A. 6. B. 2. C. 4. D. 12. m Câu 21: Cho 2 2 1 x I x e d .
x Tập hợp tất cả các giá trị của tham số m để I m là khoảng a;b . Giá 0
trị của P a 3b là A. P 3 . B. P 2 . C. P 4 . D. P 1 . 1 f x e Câu 22: Cho F x
là một nguyên hàm của hàm số . Giá trị của f xln xdx bằng 2 2x x 1 2 e 3 2 2 e 2 e 2 2 3 e A. I . B. I . C. I . D. I . 2 2e 2 e 2 e 2 2e 2
Câu 23: Cho hàm số f x có đạo hàm và liên tục trên 0; 2 , thỏa mãn f xcos xdx 10 và 2 0 2 f 0 3. Tích phân f xsin2xdx bằng 0 A. 1 3. B. 13. C. 7. D. 7 . 4 a a
Câu 24: Biết J x log xdx 16 với *
a,b , là phân số tối giản. Giá trị của T a b là 2 b ln 2 b 1 TOANMATH.com Trang 45 A. T 11. B. T 19. C. T 17. D. T 13. 2 ln 1 Câu 25: Cho ln 2 ln 3, x dx a b
với a,b là các số hữu tỉ. Giá trị của P a 4b là 2 x 1 A. P 0. B. P 1. C. P 3. D. P 3 . 2019 2 ln x
Câu 26: Giá trị của tích phân I dx là x 2 1 1 2019 ln 2 2 2019 2019ln 2 2 A. I 2020ln . B. I ln . 2019 2019 1 2 1 2 2019 2019 1 2 1 2 2019 ln 2 2 2019 2019ln 2 2 C. I 2020ln . D. I ln . 2019 2019 1 2 1 2 2019 2019 1 2 1 2 2 a Câu 27: Biết x 1 cos xdx với ; a b . Khi đó 2 2 a b bằng b 0 A. 14. B. 12. C. 8. D. 4. 2 Câu 28: Cho tích phân 2 I
x.sin xdx a ba,b
. Mệnh đề nào sau đây đúng? 0 a a A. 3. B. 2 a b 4 . C. 1;0. D. a b 6. b b 12 1 1 c x a a c Câu 29: Biết 1 x d x e dx e trong đó a, ,
b c, d là các số nguyên dương và các phân số , x b b d 1 12
là tối giản. Giá trị của bc ad là A. 12. B. 1. C. 24. D. 64. e 1 Câu 30: Cho tích phân 2 I x ln xdx . a e , b
a và b là các số hữu tỉ. Giá trị của 4a 3b là x 1 13 13 13 13 A. . B. . C. . D. . 2 4 4 2 4 sin 2x x sin x 2 1 2 1 Câu 31: Cho tích phân dx ln c ln 2
(với a, b, c là các số nguyên). Khi 2 cos x a b 2 1 0 đó a b c bằng A. 2. B. 4. C. 1 . D. 1. 1
Câu 32: Cho các hàm số f x có đạo hàm f x và thỏa mãn 2x 1 f x dx 10 , 0 1 3 f
1 f 0 12. Giá trị của f x dx là 0 A. I 1. B. I 2. C. I 2. D. I 1. 4 1 x x e
Câu 33: Biết rằng tích phân 4 dx ae . b Giá trị của 2 2 T a b là 2x 1 0 TOANMATH.com Trang 46 3 5 A. T 1. B. T 2. C. T . D. T . 2 2 1 n I
Câu 34: Với mỗi số nguyên dương n ta kí hiệu 2 I x x dx Giá trị của 1 lim n là n 2 1 . n I 0 n A. 1. B. 2. C. 3. D. 5. 1
Câu 35: Cho hàm số y f x với f 0 f 1 1. Biết rằng x e f
x f xdx .aeb . Giá trị 0 của 2019 2020 Q a b là A. 2019 Q 2 1. B. Q 0. C. Q 2. D. 2019 Q 2 1. e 2ln x 3 a Câu 36: Biết dx b
với a,b . Giá trị của a b bằng 2 x e 1 A. 2. B. 8. C. 2. D. 8. 2
Câu 37: Cho hàm số f x liên tục trên và f 2 16, f xdx 4. 0 1
Giá trị của tích phân I . x f 2xdx là 0 A. I 13. B. I 12. C. I 20. D. I 7. e k Câu 38: Đặt I ln dx
I e thì khẳng định nào sau đây là đúng? k
, với k nguyên dương. Nếu 2 1 x k A. k 1; 2 . B. k 2; 3 . C. k 4; 1 . D. k 3; 4 . 1 2 1 a ln 2 bc ln 3 c Câu 39: Cho x ln x 2 dx với a, ,
b c . Giá trị của T a b c là x 2 4 0 A. T 13. B. T 15. C. T 17. D. T 11. 6 2 x cos x 3 Câu 40: Biết dx a
với a, b, c là các số nguyên. Giá trị của M a b c là 2 1 x x b c 6 A. M 35. B. M 41. C. M 37. D. M 35.
Dạng 4: Tính tích phân các hàm đặc biệt, hàm ẩn Phương pháp giải
a. Cho hàm số f x liên tục trên ; a a. Khi đó 1 2 x
Ví dụ 1: Tích phân I cos . x ln dx bằng 2 x a a 1 f xdx f
x f xdx (1) A. 1 . B. 2. a 0 C. 0. D. 1. Chứng minh Hướng dẫn giải TOANMATH.com Trang 47 a 0 a Ta có f xdx f xdx f xd .x a a 0 0 Xét I f
xd .x Đổi biến x t dx dt. a
Đổi cận x a t a; x 0 t 0 Khi đó 0 a a I f
tdt f tdt f xdx a 0 0
Do đó (1) được chứng minh. Đặc biệt x
+ Nếu f x là hàm số lẻ thì ta có Hàm số f x 2 cos . x ln xác định và liên tục 2 x a trên đoạn 1; 1 . f xdx 0 (1.1). a
Mặt khác, với x 1 ; 1 x 1; 1 và x 2 x 2 x f x cos .ln cos . x ln f x. 2 x 2 x x Do đó hàm số f x 2 cos . x ln là hàm số lẻ. 2 x 1 2 x Vậy I cos . x ln dx 0 . 2 x 1 Chọn C.
Ví dụ 2: Cho y f x là hàm số chẵn, liên tục trên đoạn 6;6. 2 3 Biết rằng f xdx 8 và f 2xdx 3. 1 1 6 Tính f xd .x 1 A. I 11. B. I 5. C. I 2. D. I 14. Hướng dẫn giải
+ Nếu f x là hàm số chẵn thì ta có
Gọi F x là một nguyên hàm của hàm số f x trên a a f xdx 2 f xdx (1.2) đoạn 6;6 ta có a 0 3 3 f 2xdx 3 f 2xdx 3 1 1 TOANMATH.com Trang 48 1 F 2x 3 3. 2 1 6
Do đó F 6 F 2 6 hay f xdx 6. 2 6 2 6
Vậy I f xdx f xdx f xdx 14. 1 1 2 Chọn D. 1 2020 x Ví dụ 3: Tích phân I dx có giá trị là x e 1 1 2020 2 A. I 0. B. I . 2019 2021 2 2019 2 C. I . D. I . 2021 2019 Hướng dẫn giải
+ Nếu f x là hàm số chẵn thì ta cũng có
Áp dụng bài toán (1.3) ở cột bên trái cho hàm số f x 2020 a x và ta có f x b e 1 a dx f x dx 0 b 1 (1.3). x 1 b 2 Ta có a a 1 2021 1 2021 2021 Chứng minh (1.3): 1 x 2.2 2 2020 I x dx I . 2 2021 2021 2021 a f x 1 1 Đặt A dx (*). 1 x b Chọn C. a Đổi biến x t dx dt.
Đổi cận x a t a; x a t a a f 1 a t b . f t Khi đó A dt dt t . 1 b 1 t b a a a x b . f x Hay A dx (**). 1 x b a a 1 a Suy ra 2A f xdx A f xd .x 2 a a
b. Nếu f x liên tục trên đoạn ; a b thì
Ví dụ 4: Cho hàm số f x liên tục trên thỏa điều b b
kiện f x f x 2cos x, với x . f xdx f a b xdx a a 2
Hệ quả: hàm số f x liên tục trên 0; 1 , khi Giá trị của N f xdx là 2 TOANMATH.com Trang 49 đó: A. N 1. B. N 0. C. N 1. D. N 2. 2 2 f sin xdx f cos xdx Hướng dẫn giải 0 0 2 2 Ta có N f xdx f xdx 2 2 2 2 Suy ra 2N f
x f xdx 2cos xd .x 2 2 2 Vậy 2
N 2 cos xdx 2sin x 2. 0 0 Chọn D.
Ví dụ 5: Cho hàm số f x liên tục trên và thỏa
mãn f x f 2 x x2 x, x . 2 Giá trị tích phân G f xdx là 0 1 A. G 2. B. G . 2 2 1 C. G . D. G . 3 3 Hướng dẫn giải 2 2 Ta có G f xdx f 2 xdx
c. Nếu f x liên tục trên đoạn a;b và 0 0 2 2
f a b x f x thì Suy ra 2G f
x f xdx x 2 xdx 0 0 b b a b xf x dx f xdx 2 1 2 2 Vậy G x 2 xdx . a a 2 3 0 Chọn C.
Ví dụ 6: Cho hàm số f x có đạo hàm liên tục trên 1 đoạn 0; 1 thỏa mãn f 1 0, f x 2 dx 7 và 0 1 1 1 2 x f
xdx . Tích phân f xdx bằng 3 0 0 TOANMATH.com Trang 50 7 A. . B. 1. 5 7 C. . D. 4. 4 Hướng dẫn giải du f x dx u f x Đặt 3 x
d. Nếu f x liên tục trên đoạn a;b và 2 dv x dx v 3 b f x 0 với x ; a b thì f xdx 0 và 1 3 1 1 x f x 1 Ta có 2 x f x 3 dx x f xdx a 3 0 3 0 0 b f
xdx 0 khi f x 0. 1 1 1 1 3 x . f x 3 dx x . f x x d 1 . a 3 3 0 0 1 2 Cách 1: Ta có f x dx 7 (1). 0 1 7 1 1 x 1 1 6 6 x dx 49x dx .49 7 (2). 7 0 7 7 0 0 1 1 3 x . f x 3 dx 1 14x . f xdx 1 4 (3). 0 0
Cộng hai vế (1), (2) và (3) suy ra 1 1 1 f ' x 2 6 3
dx 49x dx 14x . f xdx 0 0 0 0 1 f x 2 3 7x dx 0. 0 1 2 2 Do f x 3 7x 0 f x 3 7x dx 0 . Mà 0 1 f x 2 3
7x dx 0 f x 3 7 x . 0 4 7x f x C. 4 Mà f 7 7
1 0 C 0 C . 4 4 4 7x 7 Do đó f x . 4 4 1 1 4 7x 7 7 Vậy f xdx dx . 4 4 5 0 0 TOANMATH.com Trang 51 1
Cách 2: Tương tự như trên ta có 3 x . f xdx 1
e. Bất đẳng thức Cauchy-Schwarz 0
Cho hàm số f x và g x liên tục trên đoạn Áp dụng BĐT Cauchy-Schwarz, ta có 2 ; a b . Khi đó, ta có 1 1 1 7 7 x f
xdx 7x 2 dx. f x 2 3 3 dx 2 0 0 0 b b b f xg x 2 dx f x 2 dx . g xdx 1 1 1 2 2 a a a 7 7. . f
x dx f x d .x 7 Chứng minh 0 0
Dấu bằng xảy ra khi và chỉ khi f x 3 ax , với
Với mọi , ta có f
x g x 2 0 . a . 2 2
f x f x g x 2 2 g x 0 1 1 Ta có 3 x . f x 3 3 dx 1 x .ax dx 1 a 7 . Suy ra 0 0 b b b 2 2 f xdx f xgx 2 2 dx g xdx 0 4 7x Suy ra f x 3 7 x f x C , mà a a a 4 (*) 7
Coi (*) là tam thức bậc hai theo biến , và vì (*) f 1 0 nên C . 4
đúng với mọi nên ta có 0 khi và chỉ 7 Do đó f x 4 1 x , x 0; 1 . khi 4 2 b b b 1 1 4 7x 7 7 2 f x 2 dx f x 2 dx g xdx 0 Vậy f xdx dx . 4 4 5 a a a 0 0 2 b b b Chọn A. 2 f x 2 dx f x 2 dx g xdx. a a a
Dấu “=” xảy ra khi và chỉ khi f x 0 hoặc
g x f x, với . Ví dụ mẫu
Ví dụ 1: Cho số thực a 0. Giả sử hàm số f x liên tục và luôn dương trên đoạn 0;a thỏa mãn a 1
f x. f a x 1. Giá trị tích phân I dx là 1 f x 0 2a a a A. I . B. I . C. I . D. I . a 3 2 3 Hướng dẫn giải
Đặt t a x dt d .
x Đổi cận x 0 t a; x a t 0. TOANMATH.com Trang 52 a 1 a 1 a 1 a f x Khi đó I dt dx dx d . x 1 f a t 1 f a x 1 1 f x 0 0 0 0 1 f x a 1 a a f x a 2I dx dx 1.dx . a Vậy I . 1 f x 1 f x 2 0 0 0 Chọn B.
Ta có thể chọn hàm số f x 1, với mọi x 0;a thỏa mãn yêu cầu đề bài. a 1 a 1 a Khi đó I dx dx . 1 f x 2 2 0 0
Ví dụ 2: Cho hàm số f x liên tục trên 1; 1 và 2019 x f x f x e , x 1 ; 1 . Tích phân 1 M f xdx bằng 1 2 e 1 2 e 1 2 e 1 A. . B. . C. . D. 0. 2019e e 2020e Hướng dẫn giải 1 1 Ta có M f xdx f xd .x 1 1 1 1 1 Do đó 2020M 2019 f xdx f xdx f
x2019 f xd .x 1 1 1 1 2 1 e x 1 Suy ra M e dx . 2020 2020e 1 Chọn C. b
Nếu f x liên tục trên đoạn ; a b thì f x dx a b f a b xdx a
Ví dụ 3. Cho f x là một hàm số liên tục trên thỏa mãn f x f x 2 2cos 2x . 3 2 Giá trị tích phân P f xdx là 3 2 A. P 3. B. P 4. C. P 6. D. P 8. Hướng dẫn giải TOANMATH.com Trang 53 3 3 2 2 Ta có P f x dx f x dx 3 3 2 2 3 3 3 2 2 2 2P f
x f xdx
2 2cos 2xdx 4 sin x d . x 3 3 0 2 2 3 2 3 Hay 2
P 2 sin xdx 2 sin xdx 2 cosx 2cos x 6. 0 0 Chọn C.
Ví dụ 4: Cho f x là hàm số liên tục trên thỏa mãn f x f x sin x với mọi x và f 0 1.
Tích phân e . f bằng e 1 e 1 e 3 1 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải
Ta có f x f x sin x nên x x x e f x e f x e .sin , x x . x x e f x e .sin x x x hay e f x dx e .sin xdx 0 0 x 1 x e f x e x
x e f f 1 sin cos 0 e 1 0 2 0 2 e f e 3 . 2 Chọn C. Để ý rằng x x e
e nên nếu nhân thêm hai vế của f x f x sin x với x e thì ta sẽ có ngay x. x e f x e .sin . x
Ví dụ 4: Cho hàm số f x tuần hoàn với chu kì và có đạo hàm liên tục thỏa mãn f 0 , 2 2 f x 2 dx và f
x.cos xdx . Giá trị của f 2019 . 4 4 2 2 1 A. 1. B. 0. C. . D. 1. 2 Hướng dẫn giải
Bằng phương pháp tích phân từng phần ta có TOANMATH.com Trang 54 f
x.cos xdx f x.sin x f x.sin xd .x Suy ra f x.sin xdx . 4 2 2 2 2 1 cos 2x 2x sin 2x Mặt khác 2 sin xdx dx . 2 4 4 2 2 2 Suy ra 2 2 2 2 f
x 2 dx 2 sin xf
xdx sin xdx 0 f x 2 2 sin x dx 0. 0 0 0 0 f x sin .
x Do đó f x cos x C. Vì f 0 nên C 0. 2
Ta được f x cos x f 2019 cos 2019 1 . Chọn A.
Ví dụ 5: Cho hàm số f x có đạo hàm liên tục trên đoạn 0;
1 , và f f 14 1 0 . Biết rằng 2 1
0 f x 2 2x,x 0;
1 . Khi đó, giá trị của tích phân f x 2 dx thuộc khoảng nà o sau 0 đây? 13 14 10 13 A. 2;4 . B. ; . C. ; . D. 1;3. 3 3 3 3 Hướng dẫn giải
Do 0 f x 2 2x, x 0;
1 nên f x2 0 8x, x 0; 1 . 1 1 1 Suy ra f 2 x 2 dx 8xdx hay f x dx 4 (1). 0 0 0
Mặt khác, áp dụng BĐT Cauchy-Schwarz, ta có: 2 1 1 1 1 f
xdx 1 d .x f
x 2 dx f 1 f 0 2 f x 2 2 dx 0 0 0 0 1 7 f x 2 dx 2 0 1 7 Vậy f x 2 dx 4. 2 0 Chọn C.
Bài tập tự luyện dạng 4 TOANMATH.com Trang 55
Câu 1: Cho hàm số f x liên tục trên và f x f x 2 3 2 tan x, với x
k , k . Giá trị 2 4 của f xdx là 4 A. 1 . B. 1. C. 1 . D. 2 . 2 2 4 2 Câu 2: Biết f
sin xdx 1. Giá trị của xf sin xdx là 0 0 1 A. . B. . C. . D. 0. 2 2
Câu 3: Cho hàm số f x liên tục trên đoạn 1;
1 và f x 0 với mọi x 1 ; 1 . Đặt g x f x f x
, với mọi x 1;
1 . Mệnh đề nào sau đây đúng? f x. f x 1 1 1 A. g xdx 2 g xd .x B. g xdx 0. 1 0 1 1 1 1 C. g xdx 2 g xd .x D. g xdx 0. 1 0 0 4 1 2 x f x
Câu 4: Cho hàm số f x liên tục trên và các tích phân f tan xdx 4 và dx 2. Giá trị 2 x 1 0 0 1 của tích phân I f xdx là 0 A. 2. B. 6. C. 3. D. 1.
Câu 5: Cho hàm số f x và g x liên tục, có đạo hàm trên và thỏa mãn f 0. f 2 0 và 2
' 2 x g x f x x x
e . Giá trị của giá trị của tích phân I f x.gxdx là 0 A. 4. B. e 2. C. 4. D. 2 . e
Câu 6: Cho hàm số f x liên tục và nhận giá trị dương trên 0;
1 . Biết f x. f 1 x 1 với 1 dx x 0;
1 . Giá trị của tích phân I ta được kết quả là 1 f x 0 3 1 A. . B. . C. 1. D. 2. 2 2
Câu 7: Xét hàm số f x liên tục trên đoạn 0;
1 và thỏa f x f x 2 2 3 1 1 x . 1 Giá trị của f x dx bằng 0 TOANMATH.com Trang 56 A. . B. . C. . D. . 4 6 20 16
Câu 8: Xét hàm số f x liên tục trên 0;
1 và thỏa mãn điều kiện x f 2 x f x 2 4 . 3 1 1 x . Tích 1 phân I f xdx là 0 A. I . B. I . C. I . D. I . 4 6 20 16 1
Câu 9: Cho hàm số f x liên tục trên và thỏa mãn 2 f x 3 f x . 2 4 x 2 Giá trị của I f xdx là 2 A. I . B. I . C. I . D. I . 20 20 10 10 Câu 10: Cho hàm số
f x liên tục thỏa mãn điều kiện f x 1 , f 0 0 và f x 2
x 1 2x f x 1. Giá trị của f 3 là A. 0. B. 3. C. 7. D. 9.
Câu 11: Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;4, đồng biến trên đoạn 1;4 và thỏa 4
mãn đẳng thức x x f x f x 2 2 . , x
1;4. Biết rằng f 3
1 , giá trị của I f xdx là 2 1 1186 1174 1222 1201 A. I . B. I . C. I . D. I . 45 45 45 45
Câu 12: Cho hàm số f x có đạo hàm liên tục trên thỏa mãn f x f x 1, x
và f 0 0.
Giá trị lớn nhất của f 1 là bao nhiêu? 2e 1 e 1 A. . B. . C. e 1. D. 2e 1. e e
Câu 13: Cho hàm số f x có đạo hàm xác định, liên tục và khác 0 trên đoạn 0;
1 thỏa mãn f 0 1 và f x 2 f
x. Đặt T f 1 f 0 , khẳng định nào sau đây đúng? A. 2 T 1. B. 1 T 0. C. 0 T 1. D. 1 T 2.
Câu 14: Giả sử hàm số y f x liên tục nhận giá trị dương trên 0; và thỏa mãn f 1 1,
f x f x. 3x 1, với mọi x 0. Mệnh đề nào sau đây đúng? A. 3 f 5 4. B. 1 f 5 2. C. 4 f 5 5. D. 2 f 5 3.
Câu 15: Cho hàm số y f x liên tục trên 0; thỏa mãn điều kiện f 1 2 ln 2 và
x x f x f x 2 1 .
x x, với mọi x 0;. Giá trị f 2 a bln 3, với a,b . Giá trị của 2 2 a b là TOANMATH.com Trang 57 25 9 5 13 A. . B. . C. . D. . 4 2 2 4
Câu 16: Cho hàm số f x có đạo hàm liên tục trên đoạn 0;
1 , f x và f x đều nhận giá trị dương 1 1 trên đoạn 0;
1 và thỏa mãn f 0 2, f
x. f x 2 1 dx 2 f x. f xd .x Giá trị của 0 0 1 f x 3 dx là 0 15 15 17 19 A. . B. . C. . D. . 4 2 2 2 1
Câu 17: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 1 thỏa mãn f 1 1, f x 2 dx 9 và 0 1 1 1 3 x f
xdx . Tích phân f xdx bằng 2 0 0 2 5 7 6 A. . B. . C. . D. . 3 2 4 5
Câu 18: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0; và f 0. Biết 4 4 4 4 8 2 f xdx , f
xsin2xdx . Giá trị của tích phân I f 2xdx là 8 4 0 0 0 1 1 A. I 1. B. I . C. I 2. D. I . 2 4
Câu 19: Cho hàm số f x liên tục và có đạo hàm tại mọi x 0; đồng thời thỏa mãn điều kiện 3 2
f x xsin x f x cos x và f xsin xdx 4
. Khi đó f nằm trong khoảng nào? 2 A. 6;7. B. 5;6. C. 12;13. D. 11;12.
Câu 20: Cho hàm số f x xác định và có đạo hàm liên tục trên 0; thỏa mãn f xcos xdx ,A 0 2A 4 f 0 và f x 2 2 dx
, với A là hằng số. Giá trị của f 2xdx theo A là 2 0 0 A A A. 4A. B. . C. . D. 2 . A 2 1 2
Câu 21: Cho hàm số f x có đạo hàm f x liên tục trên đoạn 0; 1 thỏa f
1 0, f x2 dx 8 0 1 1 1 và cos x f
xdx . Giá trị của f xdx là 2 2 0 0 TOANMATH.com Trang 58 1 A. . B. . C. . D. . 2 2 2
Câu 22: Cho hàm số f x có đạo hàm liên tục trên 0; 2
thỏa mãn f 0 0, f x dx và 2 4 0 2 2 sin . x f
xdx . Tích phân I f xdx bằng 4 0 0 A. 1. B. . C. 2. D. . 2 4
Câu 23: Cho hàm số f x xác định và liên tục trên 0; thỏa mãn 2 2 2 2 2 f
x2 2 f xsin x dx . Tích phân f xdx bằng 4 2 0 0 A. . B. 0. C. 1. D. . 4 2
Câu 24: Cho hàm số f x có đạo hàm liên tục trên khoảng 0;
1 và f x 0 , x 0; 1 . Biết rằng 1 3 f a, f b và
x xf x 2 f x 4, x 0; 1 . Giá trị của tích phân 2 2 3 2 sin . x cos x 2sin 2x I dx theo a và b là 2 f sin x 6 3a b 3b a 3b a 3a b A. I . B. I . C. I . D. I . 4ab 4ab 4ab 4ab
Câu 25: Cho hàm số f x có đọa hàm dương, liên tục trên đoạn 0;
1 thỏa mãn f 0 1 và 1 1 1 f x f 3 x 2 1 3 dx 2 f
x f xd .x Giá trị của tích phân f x dx là 9 0 0 0 3 5 5 7 A. . B. . C. . D. . 2 4 6 6 1 9
Câu 26: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 1 thỏa mãn f 1 1, f x 2 dx và 5 0 1 1 f x 2
dx . Giá trị của tích phân I f xdx là 5 0 0 3 1 3 1 A. I . B. I . C. I . D. I . 5 4 4 5
Câu 27: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;
1 và thỏa mãn f 0 0. Biết 1 9 1 x 3 1 2 f x dx và f
xcos dx . Tích phân của f xdx bằng 2 2 4 0 0 0 TOANMATH.com Trang 59 1 4 6 2 A. . B. . C. . D. . x
Câu 28: Cho hàm số y f x 2020 2020ln e
e . Giá trị của giá trị biểu thức T f
1 f 2 ... f 2019 là 2019 2021 A. T . B. T 1009. C. T . D. T 1010. 2 2 0 1 2 3 2017 2018 C C C C C C
Câu 29: Giá trị của tổng 2018 2018 2018 2018 2018 2018 T ... là 3 4 5 6 2020 2021 1 1 1 1 A. . B. . C. . D. . 4121202989 4121202990 4121202992 4121202991 1
Câu 30: Cho hàm số y f x liên tục trên 0; 1 thỏa mãn xf
xdx 0 và max f x 1. Tích phân 0; 1 0 1 x I e f
xdx thuộc khoảng nào trong các khoảng sau đây? 0 5 3 5 3 A. ; . B. ;e 1 . C. ; . D. e 1;. 4 2 4 2 4 f x
Câu 31: Cho hàm số y f x có đạo hàm và liên tục trên 0; thỏa mãn f 3, dx 1 và 4 4 cos x 0 4 4 sin . x tan . x f x dx 2. Tích phân sin . x f xdx bằng 0 0 2 3 2 1 3 2 A. 4. B. . C. . D. 6. 2 2
Câu 32: Cho hàm số y f x biết f x 0 với mọi x 1
, f 0 1 và f x x 1. f x với mọi
x 1 . Mệnh đề nào dưới đây đúng? A. 4 f 3 6. B. f 3 2. C. 2 f 3 4. D. f 3 6.
Câu 33: Cho hàm số f x có f x2 f x f x 3 . x 2x, x 0;
1 , f 0 f 0 1. Giá trị của 2 T f 2 là 43 16 43 26 A. . B. . C. . D. . 30 35 15 15
Câu 34: Cho hàm số y f x liên tục trên thỏa mãn f x f x x 2x 2x 1 3 2 2 1 e 4. 2
Giá trị của tích phân I f
xdx ta được kết quả là 0 A. I e 4. B. I 8. C. I 2. D. I e 2. TOANMATH.com Trang 60
Câu 35: Cho hàm số f x có đạo hàm trên 0; thỏa mãn 2 1 x x f x x f x e , với mọi x 0 và f 1
0 . Giá trị của f 2 là 2 e e 2 e 2 e A. f 2 . B. f 2 . C. f 2 . D. f 2 . 3 6 3 6
Câu 36: Cho hàm số y f x có f x liên tục trên nửa khoảng 0; thỏa mãn 2 3 1 3. x f x f x e . Khi đó 1 1 1 1 A. 3 e f 1 f 0 . B. 3 e f 1 f 0 . 2 e 3 2 2 2 e 3 4 e 3 e 3 8 3 2 2 C. e f 1 f 0 . D. 3
e f f 2 e 2 1 0 3 e 3 8. 3 3 2 f x x 2x
Câu 37: Cho hàm số y f x có đạo hàm trên thỏa mãn 3 f x 1 .e 0 và f 0 1. 2 f x 7 Tích phân . x f x dx bằng 0 2 7 15 45 5 7 A. . B. . C. . D. . 3 4 8 4 1 2 1
Câu 38: Cho y f x là hàm số chẵn và liên tục trên . Biết f xdx f
xdx 1. Giá trị của 2 0 1 2 f x dx bằng 3x 1 2 A. 1. B. 6. C. 4. D. 3. 3 e f ln x 2
Câu 39: Cho hàm số f x liên tục trên . Biết dx 7 , f
cos x.sin xdx 3. Giá trị của x 1 0 3
f x 2xdx là 1 A. 12. B. 15. C. 10. D. 1 0. x f t
Câu 40: Hàm số f x liên tục trên 0; . Biết rằng tồn tại hằng số a 0 để dt 2 x 6, 4 t a a x
0. Giá trị của tích phân f xdx là 1 21869 39364 40 A. . B. . C. 4374. D. . 5 9 3
Câu 41: Cho hàm số f x liên tục trên , có đạo hàm đến cấp hai trên và thỏa mãn 5ln 2 2 3 . 4. . x f x f x f x f x e , x 5
, biết f 0 0. Khi đó f x.dx bằng 0 TOANMATH.com Trang 61 2 25ln 2 1 355ln 2 A. 531 5ln 2. B. 31 . 2 5 2 2 1 25ln 2 355ln 2 C. 31 5ln 2. D. 5 31 . 5 2 2 1 1
Câu 42: Cho hàm số f x có đạo hàm liên tục trên 0;
1 thỏa mãn f 0 1, f x 2 dx , 30 0 1 1 x f x 1 2 1 dx . Tích phân f xdx bằng 30 0 0 11 11 1 11 A. . B. . C. . D. . 12 4 30 30
Câu 43: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0; 1 và thỏa mãn f 1 0. 1 1 2 1 f x 2 dx x e x e f x 1 1 dx
. Giá trị của f x dx là 4 0 0 0 e 2 e A. . B. 2 . e C. . D. e 2. 2 4
Câu 44: Cho hàm số f x liên tục trên đoạn 1;
1 và 2019 2x f x f x ,x 1; 1 . Giá trị của 1 f xdx bằng 1 1 3 5 A. . B. . C. 0. D. . 2019ln 2 4040ln 2 2018ln 2 6 e f ln x 2
Câu 45: Cho hàm số f x liên tục trên biết dx 6 và f 2
cos xsin 2xdx 2. Giá trị x 1 0 3
của f x 2dx bằng 1 A. 10. B. 16. C. 9. D. 5. Câu 46: Cho hàm số
y f x xác định và liên tục trên \ 0 thỏa mãn: 2 2 2
x . f x 2x 1 . f x .
x f x 1 với x \ 0 đồng thời f
1 2 . Giá trị của f xdx là 1 ln 2 3 1 ln 2 3 A. . B. ln 2 . C. 1. D. ln 2 . 2 2 2 2 2
Câu 47: Cho hàm số f x liên tục và dương trên 0; thỏa mãn f x x 2 2 4 f x 0 và a a f 1
0 . Giá trị của tổng S f 0 f
1 f 2 ... f 2018 với a ,b , tối giản. Khi 3 b b đó b a bằng 1 2020 1009 A. . B. 1011. C. 1. D. 2018. 2 2021 2020 TOANMATH.com Trang 62
Dạng 5: Một số bài toán thực tế ứng dụng tích phân Phương pháp giải
5.1.1. Một vật chuyển động có phương trình vận Ví dụ 1: Một vật chuyển động chậm dần đều với
tốc v t trong khoảng thời gian từ t a đến vận tốc vt 160 10t m / s . Quãng đường mà
t ba b sẽ di chuyển được quãng đường là:
vật chuyển động từ thời điểm t 0s đến thời b
điểm mà vật dừng lại là S v tdt A. 1028m. B. 1280m. a C. 1308m. D. 1380m. Hướng dẫn giải
Khi vật dừng lại thì v t 160 10t 0 t 16 16 16 Do đó S v
tdt 16010tdt 0 0 160t 5t 16 2 1280m . 0 Chọn B.
5.1.2. Một vật chuyển động có phương trình gia Ví dụ 2: Một chiếc ô tô chuyển động với vận tốc
tốc a t thì vận tốc của vật đó sau khoảng thời 3
v t m / s , có gia tốc a t vt 2 m / s . 2t 1 gian t ;t là: 1 2
Vận tốc của ô tô sau 10 giây (làm tròn đến hàng đơn t2 vị) là v a tdt A. 4,6 m/s. B. 7,2 m/s. 1 t C. 1,5 m/s. D. 2,2 m/s. Hướng dẫn giải
Vận tốc của ô tô sau 10 giây là 10 10 3 3 3 v dt ln 2t 1 ln 21 4,6 m / s. 2t 1 2 0 2 0 Chọn A.
5.1.4. Điện lượng chuyển qua tiết diện của dây dẫn
của đoạn mạch trong thời gian từ t đến t là: 1 2 t2 Q I tdt 1 t TOANMATH.com Trang 63 Ví dụ mẫu
Ví dụ 1: Một vật chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc a t 2 3t t . Tính quãng
đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. 4300 430 A. . m B. 4300 m. C. 430 m. D. . m 3 3 Hướng dẫn giải 3t t
Hàm vận tốc v t a
tdt 3t t 2 3 2 dt C. 2 3
Lấy mốc thời gian lúc tăng tốc v 0 10 C 10. 2 3 3t t Ta được v t 10. 2 3
Sau 10 giây, quãng đường vật đi được là 10 2 3 3 4 10 3t t t t 4300 S 10 d t 10t m 2 3 2 12 0 3 0 Chọn A. v t a tdt
Ví dụ 2: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức cường độ là i t I cos t
. Biết i q với q là điện tích tức thời ở tụ điện. Tính từ lúc t 0 , điện lượng 0 2
chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian từ 0 đến là 2I 2I I A. 0 . B. 0. C. 0 . D. 0 . 2 Hướng dẫn giải
Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ 0 đến là Q I t I 2I 0 0 dt I cos t dt sin t . 0 2 2 0 0 0 Chọn C. Q t I tdt 1
Ví dụ 3: Gọi h tcm là mức nước trong bồn chứa sau khi bơm được t giây. Biết rằng ht 3 t 8 5
và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (chính xác đến 0,01cm) TOANMATH.com Trang 64 A. 2,67 cm. B. 2,66 cm. C. 2,65 cm. D. 2,68 cm. Hướng dẫn giải
Mức nước ở bồn sau khi bơm nước được 6 giây là 6 6 h t 1 3 dt t 8dt t 8 6 3 3 t 8 2,66cm 5 20 0 0 0 Chọn B.
Bài tập tự luyện dạng 5
Câu 1: Một vật chuyển động chậm dần với vận tốc v t 160 10t m / s . Tìm quãng đường S mà vật di
chuyển trong khoảng thời gian từ thời điểm t 0s đến thời điểm vật dừng lại. A. S 2560 . m B. S 1280 . m C. S 2480 . m D. S 3840 . m
Câu 2: Một ô tô chuyển động nhanh dần đều với vận tốc v t 7t m / s . Đi được 5s người lái xe
phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a 2
70 m / s . Quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là bao nhiêu? A.87,50 m. B. 94,00 m. C. 97,50 m. D. 96,25 m.
Câu 3: Một ô tô đang đi với vận tốc 60 km/h thì tăng tốc với gia tốc a t t 2
2 6 km / h . Quãng đường
ô tô đi được trong vòng 1h kể từ khi tăng tốc. A. 26 km. B. 62 km. C. 60 km. D. 63 km.
Câu 4: Một ô tô đang chạy với vận tốc 20 m/s thì người lái xe phát hiện có hàng rào chắn ngang đường ở
phía trước cách xe 45 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe
chuyển động chậm dần đều với vận tốc v t 5
t 20m / s, trong đó t là thời gian được tính từ lúc
người lái đạp phanh. Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là bao nhiêu? A. 4 m. B. 5 m. C. 3 m. D. 6 m.
Câu 5: Cho hai chất điểm A và B cùng bắt đầu chuyển động trên trục Ox từ thời điểm t 0. Tại thời điểm 1
t, vị trí của chất điểm A được cho bởi x f t 2
6 2t t và vị trí của chất điểm B được cho bởi 2
x g t 4sin t. Gọi t là thời điểm đầu tiên và t là thời điểm thứ hai mà hai chất điểm có vận tốc bằng 1 2
nhau. Tính theo t và t độ dài quãng đường mà chất điểm A đã di chuyển từ thời điểm t đến thời điểm 1 2 1 t . 2 1 1
A. 4 2t t 2 2 t t .
B. 4 2t t 2 2 t t . 1 2 1 2 1 2 1 2 2 2 1 1 C. 2t t 2 2 t t . D. 2t t 2 2 t t . 1 2 1 2 2 1 2 1 2 2
Câu 6: Một tia lửa được bắn thẳng đứng từ mặt đất với vận tốc 15 m/s. Hỏi sau 2,5 giây, tia lửa ấy cách
mặt đất bao nhiêu mét, biết gia tốc là 2 9,8 m / s ? A. 30,625m. B. 37,5m. C. 68,125m. D. 6,875m. TOANMATH.com Trang 65 20
Câu 7: Một hạt proton di chuyển trong điện trường có biểu thức gia tốc (theo 2 cm / s ) là a t 1 2t2
(với t tính bằng giây). Tìm hàm vận tốc v theo t, biết rằng khi t 0 thì v 30cm / s. Hàm vận tốc đó là 10 10 20 A. . B. 20. C. t 3 1 2 30. D. 30. 1 2t 1 2t 1 2t2
Câu 8: Một ô tô đang chạy với vận tốc 18 m/s thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc v t 36t 18m / s trong đó t là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu hãm phanh. Quãng đường ô tô di chuyển được kể từ lúc hãm phanh đến khi dừng hẳn là bao nhiêu mét? A. 5,5 m. B. 3,5 m. C. 6,5 m. D. 4,5 m.
Câu 9: Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy 1 11 luật v t 2 t
t m / s , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. 180 18
Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng
chậm hơn 5 giây so với A và có gia tốc bằng a 2
m / s (a là hằng số). Sau khi B xuất phát được 10 giây
thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng A. 22 m / . s B. 15 m / . s C.10 m / . s D. 7 m / . s
Câu 10: Một ô tô đang chạy với vận tốc 19 m/s thì người lái hãm phanh, ô tô chuyển động chậm dần đều
với vận tốc v t 38t 19m / s trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu hãm
phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 4,75m. B. 4,5m. C. 4,25m. D. 5 m.
Câu 11: Một ô tô đang chạy với tốc độ 10 m/s thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động
chậm dần đều với v t 5t 10m / s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2 m. B. 2 m. C. 10 m. D. 20 m.
Câu 12: Một vật chuyển động trong 3 giờ với vận tốc v
(km/h) phụ thuộc vào thời gian t h có đồ thị là một phần
của đường parabol có đỉnh I 2;9 và trục đối xứng song
song với trục tung như hình bên. Quãng đường s mà vật di
chuyển được trong 3 giờ đó là A. s 24, 25 k . m B. s 26,75 k . m C. s 24,75 k . m D. s 25, 25 k . m TOANMATH.com Trang 66
Câu 13: Một vật chuyển động trong 3 giờ với vận tốc v
(km/h) phụ thuộc vào thời gian t h có đồ thị như hình
bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu
chuyển động, đồ thị đó là một phần của đường parabol có
đỉnh I 2;9 và trục đối xứng song song với trục tung.
Khoảng thời gian còn lại đồ thị là một đoạn thẳng song
song với trục hoành. Tính quãng đường s mà vật di
chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm). A. s 23, 25 k . m B. s 21,58 k . m C. s 15,50 k . m D. s 13,83 k . m
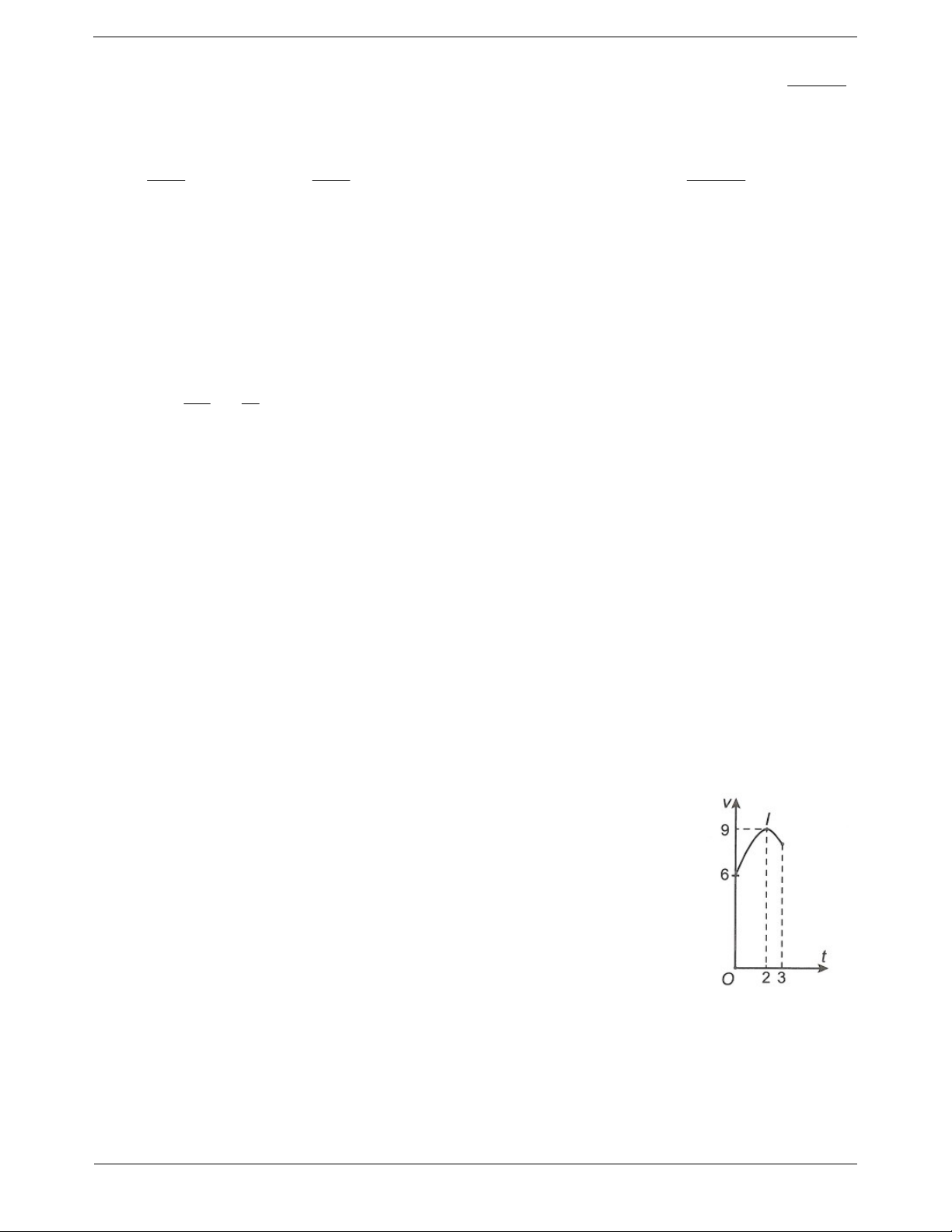
Câu 14: Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu
phóng nhanh với vận tốc tăng liên tục được biểu thị bằng
đồ thị là đường cong parabol có hình bên. Biết rằng sau
10s thì xe đạt đến vận tốc cao nhất 50m/s và bắt đầu giảm
tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì xe
đã đi được quãng đường bao nhiêu mét? 1000 1100 A. . m B. . m 3 3 1400 C. . m D. 300m. 3
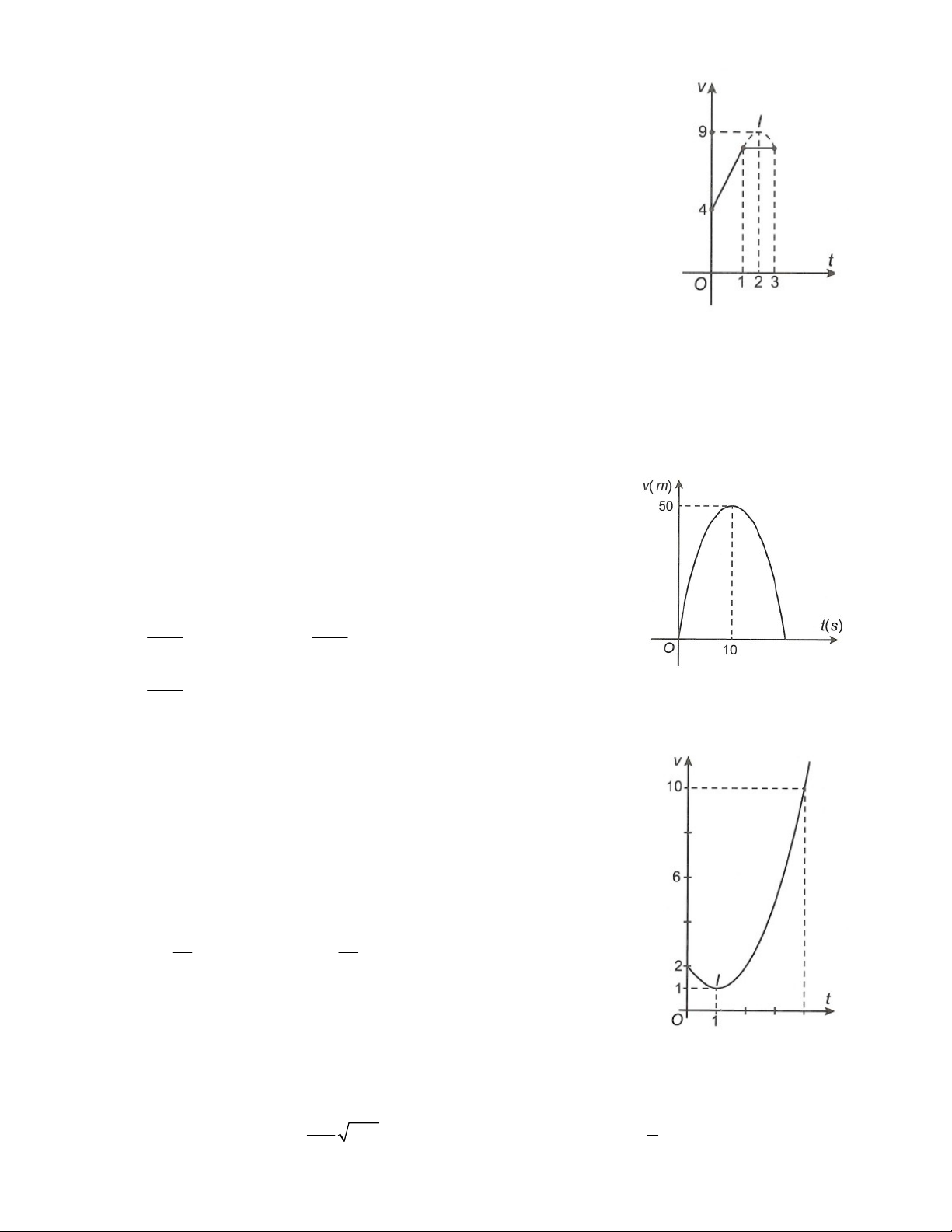
Câu 15: Một vật chuyển động trong 4 giờ với vận tốc v
(km/h) phụ thuộc thời gian t h có đồ thị là một phần của
đường parabol cố định I 1;
1 và trục đối xứng song song
với trục tung như hình bên. Tính quãng đường s mà vật di
chuyển được trong 4 giờ kể từ lúc xuất phát. A. s 6 k . m B. s 8 k . m 40 46 C. s k . m D. s k . m 3 3
Câu 16: Người ta thay nước mới cho một bể bơi dạng hình hộp chữ nhật có độ sâu h 280 cm . Giả sử 1
h t cm là chiều cao của mực nước bơm được tại thời điểm t giây, biết rằng tốc độ tăng của chiều cao 1 3
nước tại giây thứ t là ht 3
t 3 . Hỏi sau bao lâu thì nước bơm được độ sâu của hồ bơi? 500 4 TOANMATH.com Trang 67 A. 7545,2 giây. B. 7234,8 giây. C. 7200,7 giây. D. 7560,5 giây.
Câu 17: Một vật chuyển động chậm dần đều với vận tốc v t 30 5t m / s . Quãng đường vật di
chuyển từ thời điểm t 2s đến khi dừng hẳn là A. 50m. B. 30m. C. 90m. D. 40m.
Câu 18: Một vật đang chuyển động với vận tốc v 20m / s thì thay đổi vận tốc với gia tốc được tính
theo thời gian t là a t t 2
4 2 m / s . Tính quãng đường vật đi được kể từ thời điểm thay đổi gia tốc
đến lúc vật đạt vận tốc bé nhất 104 104 A. . m B. 104 . m C. 208m. D. . m 3 6
Câu 19: Một chất điểm đang chuyển động với vận tốc v 15m / s thì tăng vận tốc với gia tốc 0 a t 2 t t 2
4 m / s . Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc
bắt đầu tăng vận tốc. A. 68,25m. B. 70,25m. C. 69,75m. D. 67,25m.
Câu 20: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v t 4t m / s . Đi được 6s, người 1
lái xe phát hiện chướng ngại vật và phanh gấp, ô tiếp tục chuyển động chậm dần đều với gia tốc 2
12 m / s . Tính quãng đường S m đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn A. S 456 . m B. S 240 . m C. S 72 . m D. 96 . m
Câu 21: Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối
thiểu 1m. Một ô tô A đang chạy với vận tốc 16m/s bỗng gặp ô tô B đang dừng đèn đỏ nên ô tô A hãm
phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức v t 16 4t (đơn vị tính A
bằng m/s), thời gian tính bằng giây. Hỏi rằng để 2 ô tô A và B đạt khoảng cách an toàn khi dừng lại thì ô
tô A phải hãm phanh khi cách ô tô B một khoảng ít nhất là bao nhiêu? A. 33 m. B. 12 m. C. 31 m. D. 32 m.
Câu 22: Một chiếc xe đua đang chạy 180 km/h. Tay đua nhấn ga để về đích kể từ đó xe chạy với gia tốc a t t 2 2
1 m / s . Hỏi rằng 5 s sau khi nhấn ga thì xe chạy với vận tốc bao nhiêu km/h? A. 200. B. 243. C. 288. D. 300.
Câu 23: Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc được tính theo thời gian là a t 2
t 3t. Tính quãng đường vật đi được trong khoảng thời gian 6 giây kể từ khi vật bắt đầu tăng tốc. A. 136m. B. 126m. C. 276m. D. 216m.
Câu 24: Một chiếc máy bay chuyển động trên đường băng với vận tốc v t 2
t 10t m / s với t là thời
gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc
200m / s thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là 4000 2500 A. 500 . m B. 2000 . m C. . m D. . m 3 3
Câu 25: Tốc độ phát triển của số lượng vi khuẩn trong hồ bơi được mô hình bởi hàm số Bt 1000
,t 0 , trong đó B t là số lượng vi khuẩn trên mỗi ml nước tại ngày thứ t. Số lượng vi 1 0,3t2 TOANMATH.com Trang 68
khuẩn ban đầu là 500 con trên một ml nước. Biết rằng mức độ an toàn cho người sử dụng hồ bơi là số vi
khuẩn phải dưới 3000 con trên mỗi ml nước. Hỏi vào ngày thứ bao nhiêu thì nước trong hồ không còn an toàn nữa? A. 9. B. 10. C. 11. D. 12.
Câu 26: Một ô tô đang chạy đều với vận tốc 15m/s thì phía trước xuất hiện chướng ngại vật nên người lái
đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc 2 a m / s . Biết ô tô
chuyển động thêm được 20 m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây? A. 3;4. B. 4;5. C. 5;6. D. 6;7.
Câu 27: Tại một nơi không có gió, một chiếc khinh khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt
đất đã được phi công cài đặt cho chế độ chuyển động đi xuống. Biết rằng, khinh khí cầu đã chuyển động
theo phương thẳng đứng với vận tốc tuân theo quy luật v t 2
10t t , trong đó t (phút) là thời gian tính
từ lúc bắt đầu chuyển động, v (t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp
đất vận tốc v của khinh khí cầu là A. v 5m / . p B. v 7 m / . p C. v 9 m / . p D. v 3m / . p
Câu 28: Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy 1 59 luật v t 2 t
t m / s , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. 150 75
Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng
chậm hơn 3 giây so với A và có gia tốc bằng a 2
m / s (a là hằng số). Sau khi B xuất phát được 12 giây
thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng A. 20 m/s. B. 16 m/s. C. 13 m/s. D. 15 m/s. Đáp án và lời giải
Dạng 1. Tính tích phân bằng cách sử dụng định nghĩa, tính chất 1 – B 2 – D 3 – C 4 – B 5 – B 6 – D 7 – A 8 – C 9 – D 10 – B 11 – B 12 – B 13 – C 14 – A 15 – C 16 – B 17 – A 18 – B 19 – A 20 – D 21 – A 22 – B 23 – A 24 – C 25 – D 26 – C 27 – B 28 – A 29 – A 30 – C 31 – A 32 – D 33 – C 34 – D 35 – D 36 – A 37 – B 38 – B 39 – D 40 – B 41 – C 42 – B 43 – A 44 – D 45 – B 46 – B 47 – D 48 – C 49 – B 50 – C 51 – D 52 – A 53 – A 54 – C 55 – C 56 – A 57 – A 58 – A 59 – C 60 – C
Dạng 2. Tính bằng phương pháp đổi biến 1 – B 2 – A 3 – A 4 – D 5 – D 6 – C 7 – A 8 – C 9 – B 10 – C 11 – B 12 – B 13 – D 14 – A 15 – A 16 – D 17 – B 18 – D 19 – D 20 – C 21 – C 22 – D 23 – A 24 – B 25 – A 26 – D 27 – C 28 – B 29 – B 30 – C 31 – C 32 – A 33 – B 34 – B 35 – B 36 – C 37 – C 38 – A 39 – C 40 – A TOANMATH.com Trang 69 41 – B 42 – B 43 – D 44- B 45 – D 46 – A 47 – D 48 – D 49 – A 50 – B 51 – A 52 – C 53 – D 54 – B
Dạng 3. Giá trị của tích phân bằng phương pháp tích phân từng phần 1 - D 2 – C 3 – B 4 – A 5 – C 6 – C 7 – D 8 – C 9 – D 10 – A 11 – A 12 – A 13 – A 14 – D 15 – A 16 – D 17 – A 18 – A 19 – A 20 – A 21 – A 22 – A 23 – B 24 – B 25 – D 26 – A 27 – B 28 – C 29 – C 30 – B 31 – C 32 – A 33 – B 34 – A 35 – C 36 – A 37 – D 38 – A 39 – A 40 – A
Dạng 4. Tính tích phân các hàm đặc biệt, hàm ẩn 1 – D 2 – B 3 – C 4 – B 5 – C 6 – B 7 – A 8 – C 9 – B 10 – B 11 – A 12 – B 13 – A 14 – A 15 – B 16 – D 17 – B 18 – D 19 – B 20 – C 21 – D 22 – A 23 – B 24 – D 25 – D 26 – B 27 – C 28 – A 29 – B 30 – C 31 – B 32 – D 33 – C 34 – C 35 – D 36 – C 37 – C 38 – D 39 – A 40 – B 41 – A 42 – A 43 – D 44 – B 45 – D 46 – B 47 – A
Dạng 5. Các bài toán thực tế của tích phân 1 – B 2 – D 3 – B 4 – B 5 – A 6 – C 7 – B 8 – D 9 – B 10 – A 11 – C 12 – C 13 – B 14 – A 15 – C 16 – B 17 – D 18 – A 19 – C 20 – D 21 – A 22 – C 23 – C 24 – D 25 – B 26 – C 27 – C 28 – B TOANMATH.com Trang 70




