Bài tập Báo cáo cuối kỳ môn Đầu tư và tài trợ bất động sản | Đại học Kinh tế Thành phố Hồ Chí Minh

lOMoAR cPSD| 58457166 – – MỤC LỤC
MỤC LỤC ..................................................................................................................... 1
LỜI MỞ ĐẦU ............................................................................................................... 1
PHÂN CHIA CÔNG VIỆC NHÓM............................................................................ 2
1. Nam gửi tiết kiệm ngân hàng 3 tỷ ồng với lãi suất kép hàng năm là 6% ............... 4
2. Quyết ịnh ầu tư theo các phương án sau: ................................................................ 7
7. Một khoản ầu tư vào một dự án bất ộng sản sẽ mang lại lợi nhuận vào cuối 4 năm
tiếp theo như sau: năm 1 ược 100 triệu ồng; năm 2 ược 150 triệu ồng; năm 3 ược
180 triệu ồng; và năm 4 ược 250 triệu ồng ............................................................... 10
13. Lâm muốn mua một bất ộng sản với giá 2,625 tỷ ồng và muốn vay 80%. Một
bên cho vay chỉ ra rằng có thể vay một khoản vay trả góp toàn bộ khoản thanh toán
cố ịnh (F.A) trong 20 năm với lãi suất 8%; tuy nhiên, Lâm cũng cần phải trả phí
phát sinh khoản vay là 87,500,000 ồng ể có ược khoản vay .................................... 13
14. Một khoản vay thế chấp với số tiền là 100.000 ô la ược thực hiện với lãi suất
12% trong 20 năm. Các khoản thanh toán sẽ ược thực hiện hàng tháng .................. 17
15. Thế chấp iều chỉnh theo mức giá (PLAM) giải quyết vấn ề bất ổn trong kỳ vọng
lạm phát như thế nào? Một số hạn chế thực tế trong việc triển khai chương trình
PLAM là gì?.............................................................................................................. 26
17. Khoản vay ARM 3/1 ược lập cho 3,750,000,000 ồng với lãi suất 7% và kỳ hạn
30 năm ....................................................................................................................... 28
18. Một người vay ang phân tích các phương án vay ARM ể mua một căn nhà mới.
Người vay dự trù sẽ sở hữu căn nhà trong 5 năm. Người cho vay ưa ra khoản ...... 33
vay ARM ầu tiên là 1,875,000,000 ồng, thời hạn 15 năm với các iều khoản sau: .. 33 LỜI MỞ ĐẦU
Trước hết, chúng em xin gửi lời cảm ơn chân thành ến Cô Nguyễn Thị Hồng Thu
vì ã tận tình giảng dạy và hướng dẫn chúng em trong suốt môn học Đầu tư và Tài trợ
Bất ộng sản. Những kiến thức và kinh nghiệm quý báu mà cô ã truyền ạt không chỉ
giúp chúng em hiểu sâu hơn về lĩnh vực bất ộng sản, mà còn mở ra những góc nhìn mới
mẻ về các cơ hội ầu tư và các hình thức tài trợ hiệu quả trong thực tiễn.
Đặc biệt, chúng em rất biết ơn cô vì ã cung cấp những công cụ hữu ích thông qua
các bài tập tính toán phức tạp liên quan ến hàm số trên Excel, các phương thức tính lãi
suất, lãi kép và dòng tiền trong lĩnh vực bất ộng sản. Những kỹ năng này không chỉ giúp
chúng em nắm bắt ược cách tính toán tài chính chi tiết và chính xác, mà còn giúp chúng
em hiểu rõ hơn về các mô hình ầu tư, ánh giá hiệu quả tài trợ và quản lý rủi ro trong
thực tế. Việc áp dụng các phương pháp tính toán cụ thể vào các tình huống giả ịnh ã
giúp chúng em củng cố kiến thức và nâng cao khả năng phân tích.
Chúng em xin chân thành cảm ơn cô ã luôn tận tụy và hỗ trợ chúng em trong quá
trình học tập. Hy vọng rằng những kiến thức ã học ược sẽ là hành trang quý giá giúp
chúng em trong con ường sự nghiệp sắp tới.
PHÂN CHIA CÔNG VIỆC NHÓM Thành Tiến ộ Bài tập Lý do phân chia Ghi chú viên hoàn thành Bài 1 về lãi suất kép Chú ý ến chi Bài 1: Tính toán và bài 13, 15 liên tiết về lãi suất lãi suất kép và so quan ến vay thế hàng quý và sánh lợi suấ
chấp, lãi suất thực tế hàng năm Bài 13: Phân tích và so sánh các Xem xét lãi khoản vay bất Tô Tuyết phương thức thanh suất, phí phát ộng sản và tính 100% Sương toán khác nhau. Các sinh và phạt trả lãi suất thực tế bài này có mức ộ trước Bài 15: So sánh khó tương ương, Tập trung vào
các phương án thế phù hợp với khả năng hạn chế thực tế chấp PLAM và tính toán và phân tích và giải pháp ARM tài chính của Sương. thay thế Bài 2 về quyết ịnh ầu tư với các Bài 2: Quyết ịnh phương án lãi suất So sánh lãi ầu tư với các lãi khác nhau, bài 14 và suất hàng suất khác nhau 17 liên quan ến các tháng và hàng Bài 14: Tính toán tính toán cụ thể về năm Bao gồm các khoản vay và Từ Ngọc khoản vay, phân tích các phương 100% Khả Tú thanh toán hàng thanh toán theo nhiều thức tháng
phương thức. Các bài F.A, P.A, N.A
Bài 17: Tính toán này cần sự phân tích và trả trước
khoản vay ARM kỹ lưỡng và tính toán Lưu ý ến thay với các lãi suất
chi tiết, phù hợp với ổi lãi suất vào thay ổi năm thứ 4 khả năng xử lý thông tin của Tú.
Bài 7 về lợi nhuận từ ầu tư dự án và bài Tập trung vào Bài 7: Đánh giá
18 về các khoản vay dòng tiền và tỷ
lợi nhuận từ dự án ARM, lãi suất thay suất sinh lợi kỳ bất ộng sản ổi và các iều kiện Lý Thảo vọng
Bài 18: Phân tích vay phức tạp. Các bài 100% Vi Tính toán các phương án này có tính toán cụ CAM, dư nợ, vay ARM cho căn
thể về dòng tiền và và lợi suất theo nhà mớ lãi suất biến ộng, các iều kiện vay phù hợp với kỹ năng phân tích của Vi. Cách thực hiện:
• Mỗi thành viên tự nghiên cứu và hoàn thành bài tập ược giao, ảm bảo tính chính
xác trong các bước tính toán và trình bày rõ ràng kết quả.
• Từ Ngọc Khả Tú và Tô Tuyết Sương cần gửi phần tính toán của mình cho Sương
trước deadline ể có thời gian tổng hợp và kiểm tra lại.
• Lý Thảo Vi sẽ chịu trách nhiệm tổng hợp, kiểm tra và chuẩn bị file Excel chung
cho nhóm, ồng thời là người cuối cùng kiểm tra lại toàn bộ nội dung trước khi
nộp ể ảm bảo sự thống nhất và logic.
1. Nam gửi tiết kiệm ngân hàng 3 tỷ ồng với lãi suất kép hàng năm là 6%.
• Nam sẽ có bao nhiêu tiền sau 7 năm?
• Giả sử khoản tiền gửi với lãi suất kép hàng quý là 9%, Nam sẽ có bao nhiêu tiền sau 7 năm?
• So sánh lợi suất hiệu quả hàng năm của 2 phương án (a) và (b), lựa chọn
phương án nào tốt hơn? 1. Giới thiệu
Nam gửi tiết kiệm ngân hàng 3 tỷ ồng với lãi suất kép. Chúng ta sẽ tính toán số tiền mà
Nam sẽ có sau 7 năm với hai phương án lãi suất khác nhau: lãi suất hàng năm là 6% và
lãi suất hàng quý là 9%.
2. Tính toán số tiền với lãi suất hàng năm (6%) 2.1. Thông tin •
Số tiền gửi ban ầu (PV): 3.000.000.000 VNĐ •
Lãi suất hàng năm (rate): 6% • Số năm (nper): 7 năm •
Khoản thanh toán ịnh kỳ (PMT): 0 (không có thêm tiền gửi hàng năm)
2.2. Công thức sử dụng hàm FV trong Excel
Cú pháp của hàm FV là: =FV (rate, nper, pmt, [pv], [type])
Công thức cụ thể cho trường hợp này sẽ là: =FV (0.06, 7, 0, -3000000000) 2.3. Kết quả
Sau khi nhập công thức vào Excel, số tiền Nam sẽ có sau 7 năm với lãi suất 6% là: 4.510.890.776,97 ₫
3. Tính toán số tiền với lãi suất hàng quý (9%) 3.1. Thông tin •
Lãi suất hàng quý: 9%/5 = 2.25% •
Số kỳ (nper): 7 năm × 4 quý/năm = 28 quý •
Khoản thanh toán ịnh kỳ (PMT): 0 (không có thêm tiền gửi hàng quý)
3.2. Công thức sử dụng hàm FV trong Excel
Công thức cho trường hợp này sẽ là: =FV (0.0225, 28, 0, -3000000000) 3.3. Kết quả
Sau khi nhập công thức vào Excel, số tiền Nam sẽ có sau 7 năm với lãi suất 9% là: 5.593.634.970,20 ₫
4 . So sánh lợi suất hiệu quả hàng năm Trong ó: r: lãi suất hàng năm q: số kỳ trong năm
Lãi suất 6% ghép lãi hàng năm: (1+𝟔% )1 – 1 = 6% 𝟏
Lãi suất 9% ghép lãi hàng quý: (1+𝟗% )4 – 1 = 9.31% 𝟒
=>Phương án b tốt hơn vì lợi suất hiệu quả hàng năm cao hơn.
2. Quyết ịnh ầu tư theo các phương án sau:
a) Bạn thích ầu tư 500 triệu ồng sẽ kiếm ược lãi suất kép hàng tháng là 6%
hay ầu tư 500 triệu ồng với lãi suất kép hàng năm là 7%?
b) Bạn sẽ có bao nhiêu vào cuối 5 năm nếu bạn gửi 700 triệu vào cuối mỗi quý
trong một tài khoản sẽ hưởng lãi suất hàng năm là 10% ược tính gộp theo quý? 1. Giới thiệu
Bài toán ặt ra vấn ề bạn có 500 triệu ồng và muốn bắt ầu tư theo hai phương án lãi suất
khác nhau. Phương án thứ hai có lãi kép hàng tháng là 6% và phương án thứ hai có lãi
kép hàng năm là 7%. Sau ó, chúng tôi cũng sẽ tính toán số tiền bạn có thể nhận ược nếu
gửi 700 triệu vào cuối mỗi quý với lãi suất hàng năm là 10% (tính gộp theo quý). Chúng
ta sẽ sử dụng hàm FV trong Excel ể tính số tiền sau khi bắt ầu tư theo cả hai phương án,
từ ó so sánh và ưa ra quyết ịnh ầu tư.
2. So sánh hai phương án ầu:
a) Cú pháp của hàm FV là: =FV (rate, nper, pmt, [pv], [type])
 Xét trường hợp trong dài hạn (ví dụ: Ví dụ: bạn ầu tư trong 5 năm)
Phương án 1: Đầu tư 500 triệu với lãi
Phương án 2: Đầu tư 500 triệu với lãi
suất kép hàng tháng 6%
suất kép hàng năm 7% Thông tin: Thông tin:
• Số tiền ầu tư bản ầu (PV): 500
• Số tiền ầu tư bản ầu (PV): 500 triệu triệu
• Lãi suất hàng tháng (tỷ lệ): 6%/12
• Lãi suất hàng tháng (tỷ lệ): 7%/1 = 0.5% = 7%
• Số tháng (nper): 5 năm × 12 tháng
• Số tháng (nper): 5 năm × 1 năm= = 60 kỳ 5 kỳ
• Tiền thanh toán ịnh kỳ (PMT): 0
• Tiền thanh toán ịnh kỳ (PMT): 0
(không có thêm tiền ầu tư) Công
(không có thêm tiền ầu tư)
thức tính số tiền cuối kỳ
Công thức tính số tiền cuối kỳ
Công thức trong Excel: =FV (0.005, 60, Công thức trong Excel: =FV (0.07, 5, 0,
0, -500000000) Kết quả: -500000000)
Lựa chọn 1 (lãi suất hàng tháng 6%): Kết quả: 674.425.076,27 ₫
Lựa chọn 2 (lãi suất hàng năm 7%): 701.275.865,35 ₫
 Xét trường hợp trong ngắn hạn (dưới 1 năm) (ví dụ: Ví dụ: bạn ầu tư chỉ trong 6 tháng)
Phương án 1: Đầu tư 500 triệu với lãi
Phương án 2: Đầu tư 500 triệu với lãi
suất kép hàng tháng 6%
suất kép hàng năm 7% Thông tin: Thông tin:
• Số tiền ầu tư bản ầu (PV): 500
• Số tiền ầu tư bản ầu (PV): 500 triệu triệu
• Lãi suất hàng tháng (tỷ lệ): 7%/1 =
• Lãi suất hàng tháng (tỷ lệ): 6%/12 7% = 0.5%
• Số tháng (nper): 0,5 năm × 1 năm=
• Số tháng (nper): 6 tháng = 6 kỳ 0,5 kỳ
• Tiền thanh toán ịnh kỳ (PMT): 0
• Tiền thanh toán ịnh kỳ (PMT): 0
(không có thêm tiền ầu tư)
(không có thêm tiền ầu tư)
Công thức tính số tiền cuối kỳ
Công thức tính số tiền cuối kỳ
Công thức trong Excel: =FV (0.005, 6, 0,
Công thức trong Excel: =FV (0.07, 0,5, 0,
-500000000) Kết quả: -500000000)
Lựa chọn 1 (lãi suất hàng tháng 6%): Kết quả: 515.188.754,70 ₫
Lựa chọn 2 (lãi suất hàng năm 7%): 517.204.021,64 ₫  Kết luận:
• Trong thời hạn ngắn, cả hai phương án ều có sự khác biệt không vì hiệu suất tăng
trưởng ều ược tính theo lãi suất kép, nhưng phương án 2 với lãi suất hàng năm
cao hơn cho kết quả tốt hơn so với phương án 1.
• Trong thời gian dài, chênh lệch giữa lãi kép hàng tháng và hàng năm càng trở
nên rõ ràng. Phương án 2 với lãi suất 7% hàng năm cho giá trị tương lai cao hơn
áng kể so với phương án 1. Điều này cho thấy phương án 2 là ơn vị tốt hơn về
lâu dài, vì nó mang lại lợi nhuận nhuận cao hơn cho cùng một tài khoản ban ầu.
b) Số tiền bạn sẽ có sau 5 năm khi gửi 700 triệu vào cuối mỗi quý với lãi suất hàng
năm là 10%, ược tính toán theo quý: b)
Bước 1: Nhập dữ liệu vào Excel
• Số tiền gửi mỗi kỳ (pmt): 700 triệu (70
• Lãi suất mỗi kỳ (theo quý): 10%/4 = 2,5%
• Số kỳ (nper) (theo quý): 5 năm x 4 quý = 20 kỳ
• Hiện tại giá trị (pv): Không có tài khoản ầu tư ban ầu, nên pv = 0.
• Thời iểm thanh toán (loại): Vì gửi tiền vào cuối kỳ nên type = 0
Bước 2: Sử dụng hàm FV ể tính giá trị tươnng lai của khoảng ầu tư (FV)
Công thức trong Excel: =FV (0.025, 20, -700000000, 0, 0)
Bước 3: Kết quả nhận ược
Kết quả là 17.881.260.328,13 ₫. Điều này phản ánh úng số tiền bạn sẽ có sau 5 năm với iều kiện ã ề ra.
7. Một khoản ầu tư vào một dự án bất ộng sản sẽ mang lại lợi nhuận vào cuối 4 năm
tiếp theo như sau: năm 1 ược 100 triệu ồng; năm 2 ược 150 triệu ồng; năm 3 ược 180
triệu ồng; và năm 4 ược 250 triệu ồng.
a . Nếu nhà ầu tư kỳ vọng tỷ suất sinh lợi 12% tính theo năm thì nên bỏ ra
bao nhiêu cho khoản ầu tư này.
b. Nếu nhà ầu tư kỳ vọng tỷ suất sinh lợi 12% tính theo tháng thì nên bỏ ra
bao nhiêu cho khoản ầu tư này.
c. Giải thích sự khác nhau giữa (a) và (b) 1. Giới thiệu:
Trình bày cách tính toán giá trị hiện tại của một khoản ầu tư vào một dự án bất ộng sản,
với lợi nhuận dự kiến trong 4 năm. Chúng tôi sẽ xem xét hai trường hợp kỳ vọng tỷ suất
sinh lợi: 12% theo năm và 12% theo tháng, sử dụng hàm FV trong Excel.
2. Thông tin dự án: • Lợi nhuận dự kiến: o Năm 1: 100 triệu ồng o Năm 2: 150 triệu ồng o Năm 3: 180 triệu ồng o Năm 4: 250 triệu ồng
3. Phương pháp và cách tính toán: Chúng tôi sử dụng hàm FV trong Excel ể tính giá
trị hiện tại của các khoản ầu tư. Cú pháp của hàm FV trong Excel là: Trong ó: •
r: Tỷ suất sinh lợi (lãi suất) •
n: Tổng số kỳ (thời gian) •
pmt: Khoản thanh toán ịnh kỳ (ở ây là 0 vì chúng ta không có khoản thanh toán ịnh kỳ) •
pv: Giá trị hiện tại (giá trị mà bạn cần tính toán, sẽ là âm khi nhập vào hàm) •
type: Tùy chọn (0 hoặc 1, mặc ịnh là 0 nghĩa là cuối kỳ)
a. Tính toán với tỷ suất sinh lợi 12% theo năm
Bước 1: Nhập dữ liệu vào Excel Mở
Excel và tạo bảng như sau: Tỷ suất sinh lợi
Giá trị hiện tại Kỳ
Dòng tiền tương lai hàng năm (PV) 1 100.000.000,00 12% 2 150.000.000,00 12% 3 180.000.000,00 12% 4 250.000.000,00 12% Tổng
Bước 2: Sử dụng hàm FV ể tính giá trị hiện tại cho từng năm
Năm 1: Nhập công thức vào ô ể tính giá trị hiện tại cho năm 1 = 89.285.714,29 ₫ Năm
2: Nhập công thức vào ô ể tính giá trị hiện tại cho năm 2 = 119.579.081,63 ₫ Năm 3:
Nhập công thức vào ô ể tính giá trị hiện tại cho năm 3 = 128.120.444,61 ₫ Năm 4:
Nhập công thức vào ô ể tính giá trị hiện tại cho năm 4 = 158.879.519,60 ₫
Bước 3: Tính tổng giá trị hiện tại: Sử dụng hàm SUM
Tổng giá trị hiện tại (12%/năm) = 495.864.760,13 ₫
b. Tính toán với tỷ suất sinh lợi 12% theo tháng
Bước 1: Chuyển ổi tỷ suất sinh lợi từ năm sang tháng: (12%/12 = 1%)
Bước 2: Tạo bảng dữ liệu cho tỷ suất sinh lợi hàng tháng Tỷ suất sinh lợi
Giá trị hiện tại Kỳ
Dòng tiền tương lai hàng năm (PV) 12 100.000.000,00 1% 24 150.000.000,00 1% 36 180.000.000,00 1% 48 250.000.000,00 1% Tổng
Bước 3: Sử dụng hàm FV ể tính giá trị hiện tại cho từng năm (tháng)
Năm 1: Nhập công thức vào ô ể tính giá trị hiện tại cho năm 1 = 88.744.922,53 ₫ Năm
2: Nhập công thức vào ô ể tính giá trị hiện tại cho năm 2 = 118.134.919,11 ₫ Năm 3:
Nhập công thức vào ô ể tính giá trị hiện tại cho năm 3 = 125.806.490,93 ₫ Năm 4:
Nhập công thức vào ô ể tính giá trị hiện tại cho năm 4 = 155.065.101,27 ₫
Bước 4: Tính tổng giá trị hiện tại: Sử dụng hàm SUM
Tổng giá trị hiện tại (1%/tháng) = 487.751.433,84 ₫ Kết quả
Tổng giá trị hiện tại với tỷ suất sinh lợi 12% theo năm: 495.864.760,13 ₫
Tổng giá trị hiện tại với tỷ suất sinh lợi 12% theo tháng: 487.751.433,84 ₫
c. Giải thích sự khác nhau giữa (a) và (b)
Sự khác biệt giữa kết quả của (a) và (b) có thể ược giải th ch;
• Hiệu ứng lãi kép: Khi tính lãi suất hàng tháng, lãi ược tính trên cả gốc và lªi của
các kỳ trước ó. Điều này tạo ra hiệu ứng lãi kép, khiến cho số tiền tích lũy ược
tăng lên nhanh hơn so với việc chỉ tính lãi trên gốc ban ầu (như trong trường hợp
tính lãi suất hàng năm).
• Chiết khấu nhiều lần hơn: Để so sánh giá trị của các dòng tiền trong tương lai
với hiện tại, chúng ta cần chiết khấu chúng về thời iểm hiện tại. Khi tính theo lãi
suất hàng tháng, việc chiết khấu ược thực hiện nhiều lần hơn (12 lần/năm), dẫn
ến giá trị hiện tại của mỗi dòng tiền giảm i nhiều hơn so với trường hợp chỉ chiết khấu một lần/năm.
• Tỷ suất sinh lợi hiệu quả hàng năm (EAR): Do hiệu ứng lãi kép, tỷ suất sinh
lợi thực tế mà nhà ầu tư nhận ược khi tính lãi hàng tháng (EAR) sẽ cao hơn so
với tỷ suất sinh lợi danh nghĩa hàng năm. Điều này cũng góp phần làm giảm giá
trị hiện tại của các dòng tiền trong tương lai.
Như vậy, với cùng một tỷ suất sinh lợi danh nghĩa 12%, nhưng khi tính lãi hàng tháng,
số tiền bạn nhận ược sau 1 năm sẽ lớn hơn so với trường hợp tính lãi hàng năm. Điều
này cũng ồng nghĩa với việc ể ạt ược một mục tiêu tài chính nhất ịnh, bạn sẽ cần phải
bỏ ra một số tiền gốc nhỏ hơn khi tính lãi hàng tháng. Hiểu rõ về khái niệm này giúp
chúng ta ưa ra quyết ịnh ầu tư chính xác hơn, ặc biệt là khi so sánh các sản phẩm tài
chính có kỳ hạn và lãi suất khác nhau. Điều này minh họa vai trò quan trọng của tần
suất tính lãi trong các phép tính tài chính và giá trị thời gian của tiền.
13. Lâm muốn mua một bất ộng sản với giá 2,625 tỷ ồng và muốn vay 80%. Một
bên cho vay chỉ ra rằng có thể vay một khoản vay trả góp toàn bộ khoản thanh
toán cố ịnh (F.A) trong 20 năm với lãi suất 8%; tuy nhiên, Lâm cũng cần phải trả
phí phát sinh khoản vay là 87,500,000 ồng ể có ược khoản vay.
a) Người cho vay thực sự sẽ giải ngân bao nhiêu?
b) Lãi suất thực tế cho người vay là bao nhiêu, giả sử khoản thế chấp ược trả hết sau 20 năm?
c) Nếu Lâm trả hết khoản vay sau 5 năm, lãi suất thực tế là bao nhiêu? Tại
sao lại khác so với lãi suất thực tế trong (b)?
d) Giả sử người cho vay cũng áp dụng hình phạt trả trước là 2% số dư nợ
chưa thanh toán nếu khoản vay ược trả trong vòng 8 năm kể từ ngày óng.
Nếu Lâm trả hết khoản vay sau 5 năm với hình phạt trả trước, lãi suất thực tế là bao nhiêu? Thông tin ề bài: •
Giá trị bất ộng sản: 2,625,000,000 ồng •
Vay 80% giá trị: 80% × 2,625,000,000 = 2,100,000,000 ồng (khoản vay gốc) • Thời gian vay: 20 năm • Lãi suất: 8%/năm •
Phí phát sinh khoản vay: 87,500,000 ồng
a) Người cho vay thực sự sẽ giải ngân bao nhiêu?
Số tiền vay gốc là 80% giá trị bất ộng sản:
Phí phát sinh khoản vay là 87,500,000 ồng, vì vậy số tiền thực sự mà Lâm nhận ược sẽ là:
b) Lãi suất thực tế nếu Lâm trả hết khoản vay sau 20 năm
Lãi suất thực tế phản ánh tổng chi phí vay thực tế khi tính cả các khoản phí phát sinh.
Chúng ta sử dụng hàm RATE ể tính lãi suất thực tế hàng tháng, dựa trên các thông tin:
Bước 1: Tính khoản thanh toán hàng năm (PMT)
Khoản thanh toán hàng năm của khoản vay ược tính bằng công thức PMT ể tính khoản
thanh toán hàng tháng dựa trên lãi suất 8%/năm và khoản vay trong 20 năm (240 tháng).
Sử dụng hàm PMT ể tính khoản thanh toán hàng tháng. Công thức trong Excel:
Cụ thể: =PMT(0, 67%, 240, -2100000000)
• Lãi suất hàng năm là 8%, do ó lãi suất hàng tháng là: 8%/12 = 0, 67% • Số tháng:
20 năm × 12 tháng = 240 tháng
• Khoản vay: 2,100,000,000 ồng.
Kết quả là 17.565.241,45 ₫ sẽ khoản thanh toán hàng tháng.
Bước 2: Sử dụng hàm RATE ể tính lãi suất thực tế
Sau khi ã biết khoản thanh toán hàng tháng và số tiền giải ngân thực sự (2,012,500,000
ồng), dùng hàm RATE ể tính lãi suất thực tế.
Sử dụng hàm RATE ể tính khoản thanh toán hàng tháng. Công thức trong Excel:
Cụ thể: =RATE(240, 17804361, -2012500000, 0, 0, 0.67%)
• Nper (số tháng): 240 tháng (20 năm)
• Pmt (khoản thanh toán hàng tháng): kết quả từ PMT (17,804,361 ồng)
• Pv (số tiền giải ngân thực tế): -2,012,500,000 ồng (số tiền ã nhận thực tế sau khi trừ phí phát sinh)
• Fv (giá trị tương lai): 0 (vì Lâm trả hết khoản vay)
• Guess (ước oán): Có thể ể trống hoặc nhập giá trị 0.0066667 (lãi suất tháng ban ầu).
Bước 3: Kết quả
Excel sẽ trả về lãi suất thực tế theo tháng là 0,71%. Để chuyển ổi kết quả thành lãi suất
thực tế theo năm, rồi nhân kết quả với 12, ta ược là 8,58%. c) Lãi suất thực tế nếu trả hết sau 5 năm
Lâm chỉ thanh toán trong 5 năm (tức là 60 tháng), sau ó tất toán toàn bộ khoản vay.
Chúng ta cần tính số dư nợ còn lại sau 60 tháng và tính lãi suất thực tế dựa trên dòng tiền này.
Bước 1: Tính số dư nợ sau 5 năm (60 tháng)
Sử dụng hàm PV ể tính số dư nợ còn lại sau 5 năm. Công thức Excel:
Cụ thể: =PV(0.67%, 180, -17565241.45, 0, 0)
• Lãi suất hàng tháng (rate): 0.0066667
• Số tháng còn lại (nper): 240 -60 = 180 tháng
• Khoản thanh toán hàng tháng (pmt): 17,565,241.45 ồng
• Giá trị tương lai (fv): 0 (vì bạn muốn tất toán khoản vay)
• Thời iểm thanh toán (type): Thanh toán vào cuối kỳ (0)
Bước 2: Tạo dòng tiền trong Excel
• Năm 0: -2,012,500,000 ồng (số tiền giải ngân thực tế)
• Tháng 1-60: Các khoản thanh toán hàng tháng (kết quả từ hàm PMT).
• Tháng 60: Số dư nợ còn lại (kết quả từ hàm PV).
Bước 3: Tính lãi suất thực tế
Sử dụng hàm IRR trong Excel ể tính lãi suất thực tế dựa trên dòng tiền. Công thức:
Excel sẽ trả về lãi suất thực tế theo tháng là 0,75%. Để chuyển ổi kết quả thành lãi suất
thực tế theo năm, rồi nhân kết quả với 12, ta ược là 8,99%.
Tại sao lại khác so với lãi suất thực tế trong (b)?
Khi trả hết khoản vay sớm (trong 5 năm thay vì 20 năm), lãi suất thực tế khác biệt so
với khi trả hết sau 20 năm, chủ yếu do hai yếu tố chính:
1. Tác ộng của phí phát sinh
Phí phát sinh khoản vay (87,500,000 ồng) ược trả ngay khi vay, nhưng nó không giảm
theo thời gian hay thay ổi dựa trên số năm trả nợ. Khi trả nợ úng hạn trong 20 năm
(phần b), phí này sẽ ược "trải ều" ra trong suốt 240 tháng, khiến chi phí thực tế mỗi
tháng giảm i và tác ộng của phí phát sinh lên tổng chi phí vay nhỏ hơn. Ví dụ: •
Khi trả nợ sau 20 năm (240 tháng), phí 87,500,000 ồng ược "phân bổ" trong toàn
bộ thời gian, dẫn ến chi phí thêm hàng tháng khá thấp so với khoản thanh toán hàng tháng (PMT) ã tính. •
Khi trả nợ sớm sau 5 năm (60 tháng), cùng một khoản phí phát sinh này ược trải
ra trong thời gian ngắn hơn (chỉ 60 tháng), khiến chi phí hàng tháng thực sự tăng
lên áng kể khi tính trên tổng số tiền ã vay.
Khi tính lãi suất thực tế, phí phát sinh chiếm tỷ lệ lớn hơn so với tổng số tiền ã trả khi
bạn trả nợ sớm, khiến lãi suất thực tế cao hơn.
2. Chi phí lãi chưa ược trả ầy ủ
Trong một khoản vay dài hạn với lãi suất cố ịnh, phần lớn các khoản thanh toán trong
giai oạn ầu là ể trả lãi suất, trong khi phần gốc giảm rất chậm. Điều này có nghĩa là
trong 5 năm ầu tiên, phần lớn khoản thanh toán hàng tháng của Lâm chỉ là trả lãi, còn
phần nợ gốc giảm rất ít.
Khi Lâm trả nợ sau 5 năm, chưa có ủ thời gian ể trả phần lớn nợ gốc. Điều này làm tăng
tổng chi phí thực tế cho khoản vay, vì tổng số tiền lãi và phần phí phát sinh vẫn còn cao
hơn so với trường hợp trả nợ trong 20 năm.
d) Lãi suất thực tế nếu có hình phạt trả trước 2% sau 5 năm
Nếu có hình phạt trả trước 2% số dư nợ còn lại, chúng ta sẽ thêm khoản phạt này vào
dòng tiền cuối cùng (tháng 60).
Bước 1: Tính hình phạt trả trước
Hình phạt trả trước là 2% của số dư nợ còn lại (kết quả từ hàm PV ở trên).
Kết quả là phí phạt do trả trước 5 năm là 36.760.745,33 ₫. Bước
2: Tạo dòng tiền trong Excel • Năm 0: -2,012,500,000 ồng •
Tháng 1-60: Các khoản thanh toán hàng tháng •
Tháng 60: Số dư nợ còn lại + Hình phạt (2% của số dư nợ).
Bước 3: Tính lãi suất thực tế
Sử dụng hàm IRR trong Excel với dòng tiền mới ể tính lãi suất thực tế (tương tự như câu c).
Excel sẽ trả về lãi suất thực tế theo tháng là 0,77%. Để chuyển ổi kết quả thành lãi suất
thực tế theo năm, rồi nhân kết quả với 12, ta ược là 9,28%.
14. Một khoản vay thế chấp với số tiền là 100.000 ô la ược thực hiện với lãi suất 12%
trong 20 năm. Các khoản thanh toán sẽ ược thực hiện hàng tháng.
a. Các khoản thanh toán hàng tháng sẽ như thế nào nếu:
(1) Khoản vay theo phương thức thanh toán toàn bộ gốc và lãi cố ịnh (F.A)?
(2) Khoản vay theo phương thức thanh toán một phần gốc và lãi cố ịnh (P.A)
và số dư khoản vay là 50.000 ô la vào cuối năm 20?
(3) Khoản vay trả góp âm (N.A) và số dư khoản vay sẽ là 150.000 ô la vào cuối năm 20?
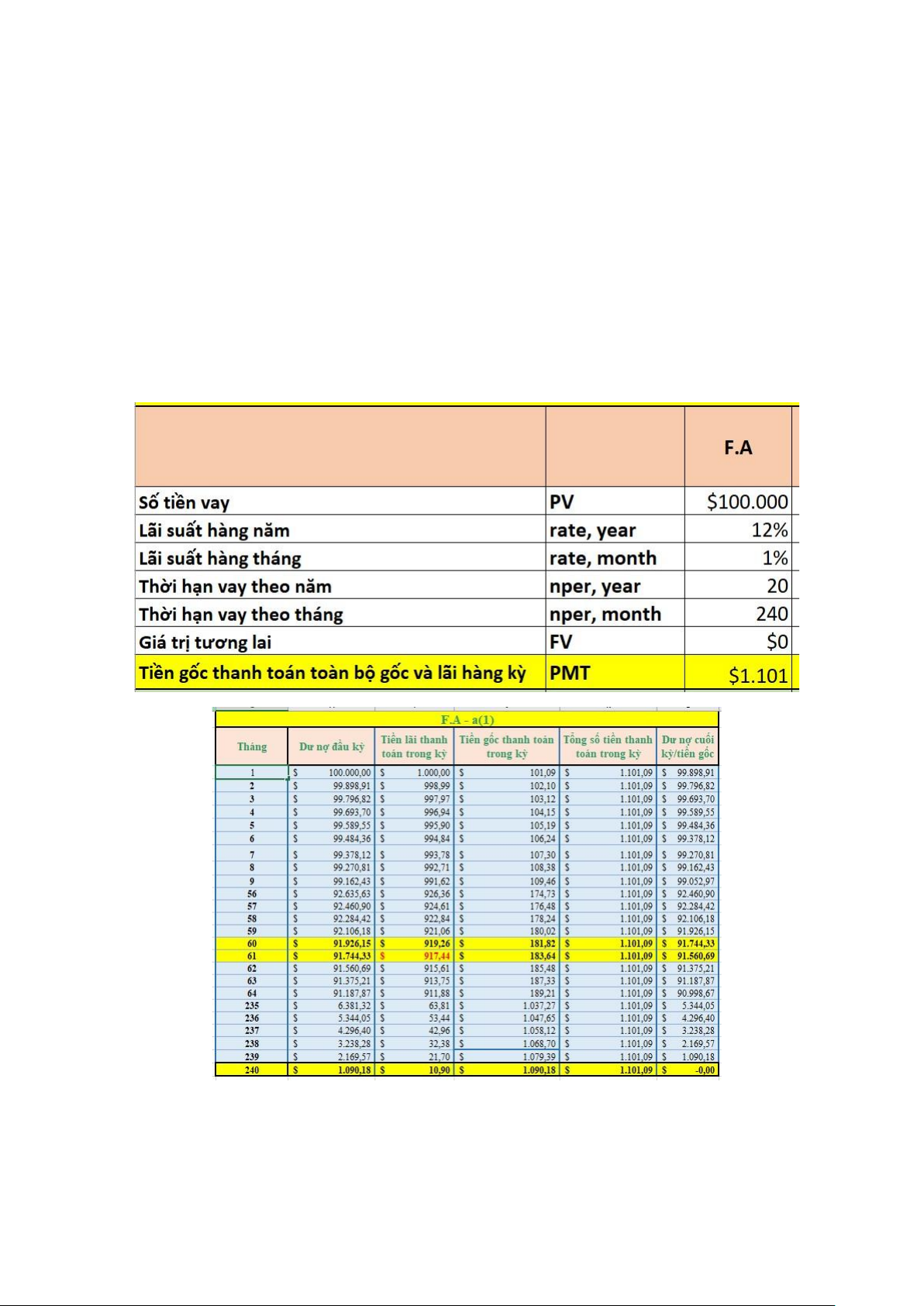
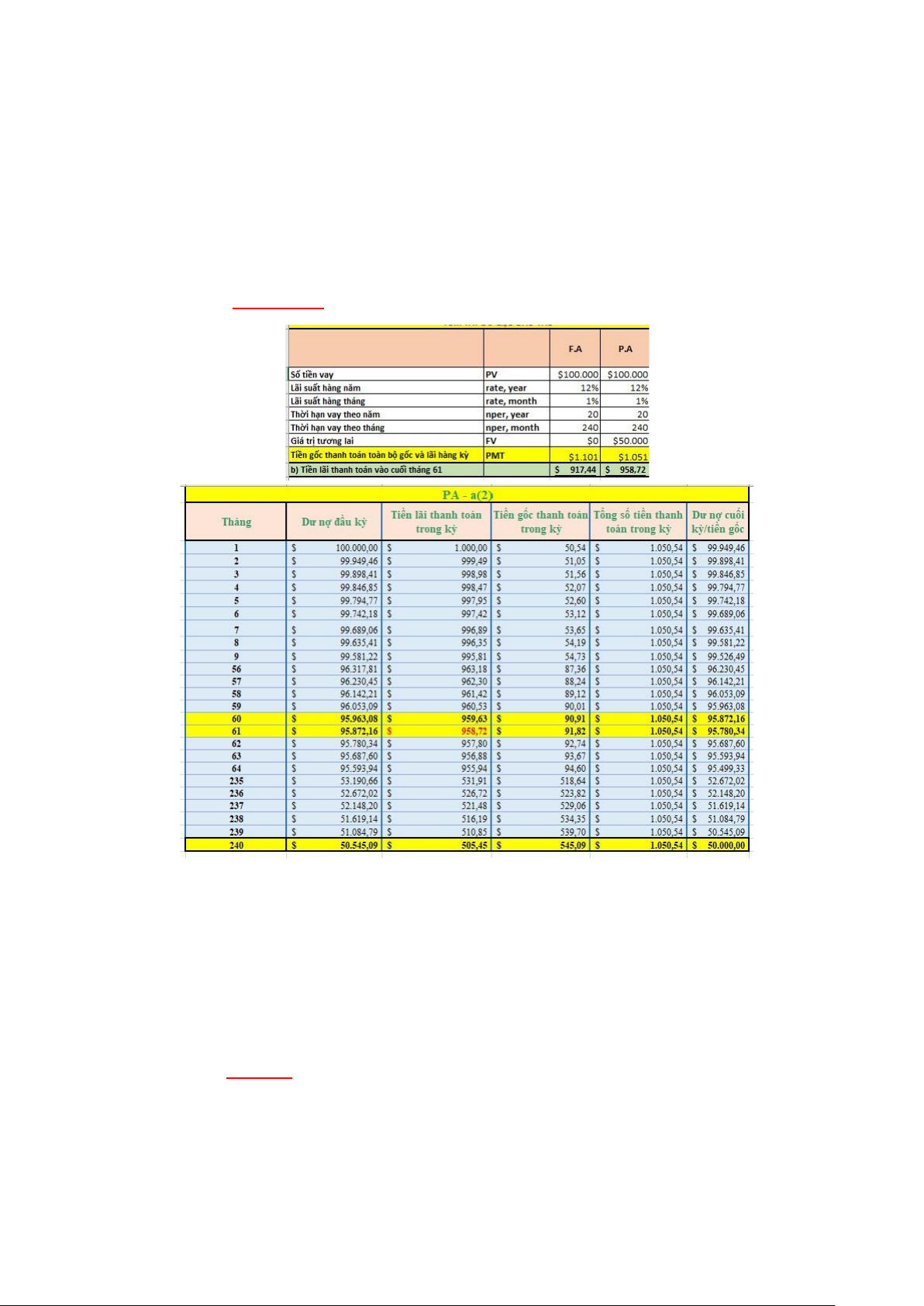
b. Tiền lãi của khoản thanh toán ược lên lịch thanh toán vào cuối tháng 61
cho mỗi trường hợp (1) ến (3) ở trên sẽ là bao nhiêu?
c. Nếu khoản vay ược trả trước vào cuối năm 5, thì lãi suất thực tế cho mỗi
khoản vay trong phần a (1) - a (3) sẽ là bao nhiêu?
d. Giả sử các iều kiện trong a (1) thay ổi phương thức chỉ trả lãi (I.O)
trong 3 năm ầu tiên (36 tháng). Nếu khoản vay thanh toán theo dư nợ giảm
dần ều hoàn toàn (F.A) trong 17 năm còn lại, thì các khoản thanh toán hàng
tháng phải là bao nhiêu từ năm 4 ến năm 20?
e. Dựa vào a (3) ở trên, trong ó người vay và bên cho vay ồng ý rằng số dư
khoản vay là 150.000 ô la sẽ ược thanh toán vào cuối năm 20:
• Tổng số tiền lãi sẽ ược thanh toán từ tất cả các khoản thanh toán là
bao nhiêu? Tổng số tiền gốc sẽ ược thanh toán là bao nhiêu?
• Số dư khoản vay vào cuối năm thứ 3 sẽ là bao nhiêu?
• Nếu khoản vay ược trả hết vào cuối năm thứ 3, lãi suất thực tế sẽ là bao nhiêu? Thông tin chung:
• Số tiền vay (P): 100.000 ô la
• Lãi suất hàng năm (r): 12% (0.12)
• Thời gian vay: 20 năm (240 tháng)
• Số lần thanh toán hàng tháng: 240 kỳ
a. Các khoản thanh toán hàng tháng:
(1) Khoản vay theo phương thức thanh toán toàn bộ gốc và lãi cố ịnh (Fully Amortizing - F.A):
Công thứ hàm PMT excel tính khoản thanh toán hàng tháng cho khoản vay F.A:
=PMT(1%, 240, -100000)
• Số tiền vay (P): 100,000 USD
• Lãi suất hàng tháng (r/12): 12%/12 = 1% (12% hàng năm chia cho 12 tháng)
• Số tháng thanh toán (n): 240 tháng
Kết quả là 1,101 ô la sẽ khoản thanh toán hàng tháng theo phương thức F.A.
(2) Khoản vay theo phương thức thanh toán một phần gốc và lãi cố ịnh (Partially Amortizing - P.A):
Ở ây, bạn thanh toán một phần gốc và lãi hàng tháng, và cuối kỳ vẫn còn dư nợ là 50.000 ô la.
Công thức Hàm Excel: =PMT(1%, 240, -100000, 50000) Trong ó:
• FV=50. 000 ô la (số dư khoản vay cuối kỳ).
Kết quả là 1,1051 ô la sẽ khoản thanh toán hàng tháng theo phương thức F.A.
(3) Khoản vay trả góp âm (Negative Amortizing - N.A):
Trong trường hợp trả góp âm, số dư khoản vay cuối kỳ sẽ tăng lên thành 150.000 ô la.
Công thức tương tự như P.A, nhưng với số dư lớn hơn: Công thức Hàm Excel:
=PMT(1%, 240, -100000, 150000) Trong ó:
• FV=50. 000 ô la (số dư khoản vay cuối kỳ).
Kết quả là 949 ô la sẽ khoản thanh toán hàng tháng theo phương thức F.A.