









































Preview text:
CHƯƠNG II:
THU THẬP VÀ TRÌNH BÀY DỮ LIỆU THỐNG KÊ Bài 2.1:
Phân tổ công nhân theo bậc thợ: 1. Ta có: 1 1 3 3 n ( 2*k) ( 2*84) 6 X X (n 1) 7 1 (6 1) 1 Khoảng cách tổ: max min d n 6 6
Kết quả phân tổ công nhân theo bậc thợ: Bậc thợ Số CN Tần suất f / f x f i i i i 1 13 0,15 2 13 0,15 3 23 0,27 4 18 0,21 5 9 0,1 6 6 0,07 7 2 0,02 Tổng 84 1 2.
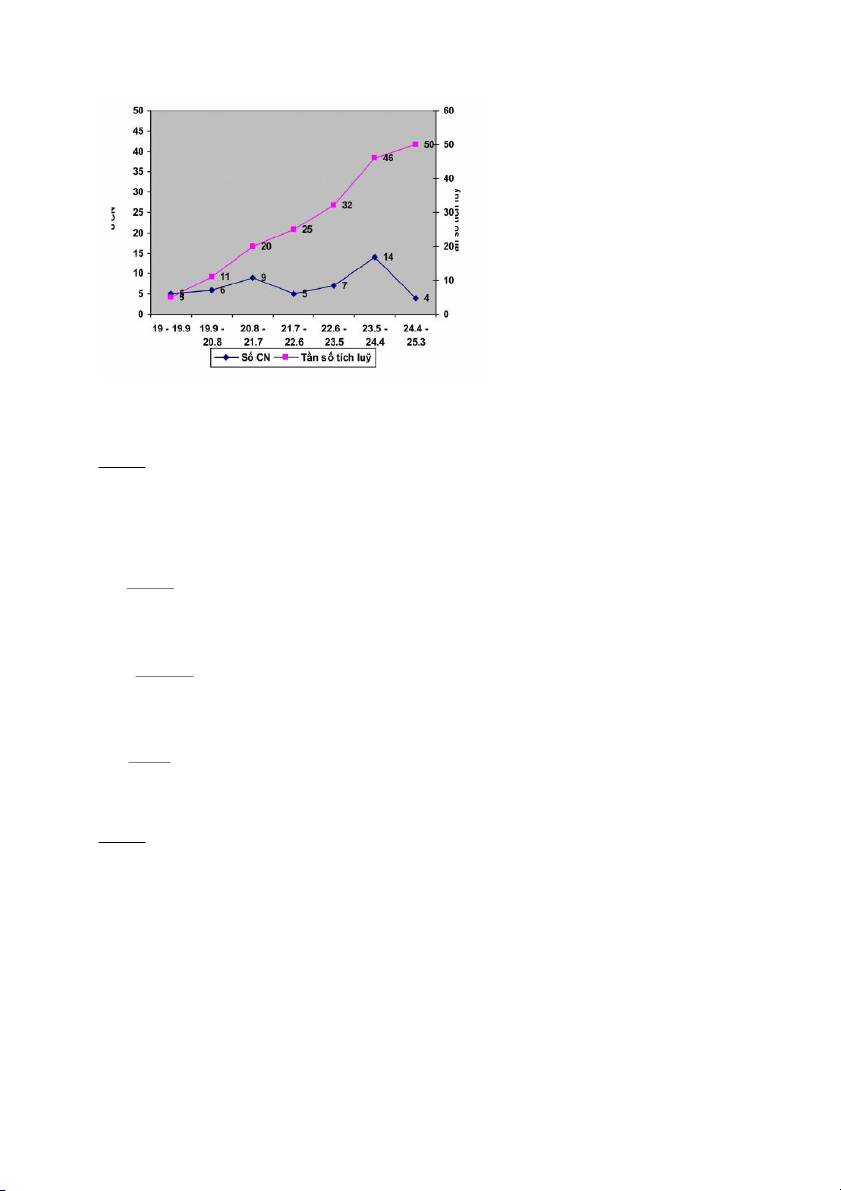
Biểu diễn kết quả lên đồ thị: Bài 2.2: Khoảng cách tổ: X X (n 1) 25 1 (5 1) max min d 4 n 5 Ta có kết quả phân tổ: f Số nhân viên Số cửa hàng i g i f d i i 1-5 7 17.5 1.75 6-10 9 22.5 2.25 11-15 10 25 2.5 16-20 8 20 2 21-25 6 15 1.5 Tổng 40 100 Bài 2.3: Khoảng cách tổ: X X 25,3 19 max min d 0 ,9 n 7 Kết quả phân tổ: Thời gian Số CN Tần suất Tần số tích luỹ 19 -19.9 5 0.1 5 19.9 - 20.8 6 0.12 11 20.8 - 21.7 9 0.18 20 21.7 - 22.6 5 0.1 25 22.6 - 23.5 7 0.14 32 23.5 - 24.4 14 0.28 46 24.4 - 25.3 4 0.08 50 Tổng 50 1
Vẽ đồ thị tần số và tần số tích luỹ: CHƯƠNG III:
MÔ TẢ DỮ LIỆU BẰNG CÁC ĐẶC TRƯNG THỐNG KÊ Bài 3.1: 1
Các số tương đối có thể tính toán là: tđt : số tương đối động thái, t : số tương đối kết cấu, t : số tương kc KG đối không gian. 2 Ví dụ minh hoạ: 15959,1 t 100% 124, 6% dt 12806,3
=> Tốc độ tăng trương về chỉ tiêu vốn đầu tư xây dựng cơ bản của địa phương đó năm 2007 là 124.6%. 8195.9 t 1 x 00% 6 4% kc 12806.3
=> Chỉ tiêu về vốn đầu tư xâu dựng của bộ phận xâu lắp chiếm 64% tổng vốn dầu tư xây dựng. 8195,9 t 100% 227, 4% kg 3603,5
=> Chỉ tiêu về vốn đầu tư xây dựng của bộ phận xây lắp so với chỉ tiêu của bộ phận thiết bị là 227.4% Bài 3.2:
Tính các số tương đối thích hợp nhằm đánh giá kế hoạch doanh thu của từng cửa hàng và cả công ty.
Các số tương đối có thể tính được: tđt , tnv , tht
Theo yêu cầu của bài toán, chúng ta chỉ tính: t , t nv ht Thực tế quý Kế hoạch Thực tế quý
Số tương đối Số tương đối Tên cửa I quý II II NVKH HTKH hàng y / 1 0 y 1 900 1000 1000 1,1 1 2 1300 1500 1800 1.15 1,2 3 1600 2500 2075 1.5625 0,83 Công ty 3800 5000 4875 1,31 0,975 Ta có y 5000 kh t 1 ,31 nv y 3800 0
Nhiệm vụ đặt ra cho quý 2 về doanh thu phải tăng so với quý 1 là 31%. y 4875 1 t 0, 975 ht y 5000 KH
Như vậy, thực tế quý 2 đã không hoàn thành kế hoạch đặt ra là 2,5% Bài 3.3: 1
Tính số tương đối giảm giá thành: Ta có: yKH t 0 ,95 nv 0 y 1 y t 0,93 dt 0 y Ta có: t t .t dt ht nv t 0,93 dt t ht 0,98 t 0,95 nv
Vậy, chỉ tiêu về giá thành đối với sản phẩm của kỳ nghiên cứu hoàn thành vượt mức kế hoạch là 3% ( vì chênh
lệch giữa số tương đối nhiệm vụ và kế hoạch là 3%). 2 t 0 ,96 nv t 1 , 02 dt t 1, 02 dt t 1 ,0625 ht t 0,96 nv
Vậy, chỉ tiêu về thời gian lao động hao phí của kỳ nghiên cứu không hoàn thành so với kế hoạch đặt ra. 3 t 1 ,08 nv t 1 ,12 dt t 1,12 dt t 1 .03 ht t 1,08 nv
Vậy trong kỳ nghiên cứu xí nghiệp đã không hoàn thành kế hoạch đặt ra về chỉ tiêu số lượng là 3%. Bài 3.4: Vụ hè thu Vụ đông xuân Tên Năng suất Diện tích Năng suất Diện tích Hợp tác xã (tạ/ha) (ha) (tạ/ha) (ha) A 33 100 40 120 B 35 120 38 140 C 37 180 36 140 1.
Tính năng suất lúa bình quân vụ hè thu, vụ đông xuân của toàn xã? x f i i 33 100 35 120 37 180 x 35 ,5 1
Năng suất lúa bình quân vụ hè thu f 400 i x f i i 40 120 38 140 36 140 x 37, 9 2
Năng suất lúa bình quân vụ đông xuân. f 400 i 2.
Tính năng suất lúa bình quân mỗi vụ trong năm của toàn xã? x f i i 35, 4 400 37,9 400 x 3 6, 65 f 800 i Bài 3.5:
Tình hình thu hoạch lúa trong năm của 3 hợp tác xã thuộc một xã như sau: Tỷ trọng diện tích thu Năng suất Hợp tác xã hoạch( %) (tạ/ha) A 33 20 B 35 35 C 37 45
Năng suất lúa bình quân trong năm của toàn xã: x d i i 33 20 35 35 37 45 x 3 5,5 d 100 i Bài 3.6:
Có tài liệu về tình hình sản xuất lúa vụ mùa năm báo cáo của 3 hợp tác xã trong cùng một huyện như sau: Hợp tác xã Diện tích Lượng phân hoá Năng suất lúa Giá thành gieo cây học bón cho bình quân 1 tạ lúa (ha) 1 ha (tạ/ha) (1000đ) (kg/ha) Số 1 120 180 36 74 Số 2 180 160 35 76 Số 3 250 200 40 70 1.
Lượng phân hoá học bình quân cho một ha: x fii 180 120 160 180 200 250 x 182 ,5(kg ) 1 550 fi
Vậy, lượng phân hoá học bình quân cho 1 ha lúa là: 182,5 (kg) 2.
Năng suất thu hoạch lúa bình quân: x f i i 36 120 35 180 40 250 x 37,5 2 (tạ/ha) f 550 i
Vậy, năng suất thu hoạch lúa bình quân của 3 hợp tác xã trong cùng một huyện là: 37,5 (tạ/ha) 3.
Giá thành bình quân một tạ lúa:
Ta có: Sản lượng lúa thu được = năng suất x diện tích SL 3 6 1 20 4 320 1 SL 3 5 1 80 6 300 2 SL 4 0 2 50 1 0000 3
Giá thành bình quân một tạ lúa là: 74 4 320 76 6 3000 70 1 0000 Ta có : X 7 2,6 3 20620
Vậy, giá thành bình quân 1 tạ lúa là: 72,6 (1000đ/tạ) Bài 3.8:
Có tài liệu về phân tổ các hợp tác xã thuộc một huyện theo năng suất thu hoạch lúa vụ mùa năm báo cáo như sau: Năng suất lúa (tạ/ha) Số hợp tác xã 30-35 10 35-40 20 40-45 40 45-50 25 50-55 5 1.
Có thể tính năng suất thu hoạch lúa bình quân của toàn huyện hay không?
Trả lời: không thể tính năng suất thu hoạch lúa bình quân của toàn huyện. 2.
Điều kiện để tính được năng suất bình quân: trước tiên cần phải tính trị số giữa của mỗi tổ. Năng suất lúa bình quân: 32,5 1 0 37,5 2 0 42,5 4 0 47,5 2 5 52,5 5 X 4 2,25 100
Vậy, năng suất bình quân lúa của các hợp tác xã năm báo cáo là: 42,25 (tạ/ha) Bài 3.9: 1.
Tốc độ bình quân của xe trong tất cả lượt đi và về, biết rằng quảng đường từ nhà ga đến nông trường là 120 km M i 4 120 x 43, 26 M 120 120 120 120 i (km/h) x 40 35 45 60 i
Vậy, tốc độ bình quân của xe trong tất cả lượt đi và về với quảng quảng đường bằng 120 là: 43,26 (km/h) 2.
Nếu không biết quảng đường từ nhà ga đến nông trường, trong trường hợp này vẫn tính được vận tốc
bình quân. Vì quảng đường là một (như nhau) nên ta có thể áp dụng công thức: n 4 x 43, 26 1 1 1 1 1 x 40 35 45 60 i
Vậy, tốc độ bình quân của xe trong tất cả lượt đi và về là 43,26 (km/h)
Bài 3.10: Có tài liệu về 2 xí nghiệp chế biến thuộc Công ty K cùng sản xuất một loại sản phẩm trong kỳ nghiên cứu như sau: Quý Xí nghiệp X Xí nghiệp Y Giá thành Tỷ trọng sản lượng Giá thành Tỷ trọng sản lượng đơn vị sản của từng quý trong đơn vị sản của từng quý trong phẩm năm (%) phẩm năm (%) (1000đ) (1000đ) I 19,5 16 20,0 18 II 20,2 35 21,4 36 III 20,4 30 19,2 29 IV 19,8 19 18,5 17 1.
Giá thành bình quân đơn vị sản phẩm của xí nghiệp X: x d i i
19,5 16 20,2 35 20,4 30 19,8 19 x 1 7,307 di 100
Vậy, giá thành bình quân đơn vị sản phẩm của xí nghiệp X là: 17,307 nghìn đồng 2.
Giá thành bình quân đơn vị sản phẩm của xí nghiệp Y: d i 100 x 1 9,95 d 18 36 29 17 i (nghìn đồng) x 20 21, 4 19,2 18,5 i
Vậy, giá thành bình quân đơn vị sản phẩm của xí nghiệp Y là 19,95 nghìn đồng.
Bài 3.11: Có tình hình sản xuật tại 2 xí nghiệp Dệt trong 6 tháng của một năm như sau: Xí Quý I Quý II nghiệp Sản lượng vải Tỷ trọng vải Sản lượng vải Tỷ trọng vải (1000m) loại I (1000m) loại I A 240 90 250 92 B 360 92 350 94 1.
Tỷ trọng vải loại I bình quân mỗi quý của từng xí nghiệp trong 6 tháng: x f i i 90 240 92 250 x 245,05 A f 182 i x f i i 360 92 350 94 x 354, 9 B f 186 i 2.
Tỷ trọng vải loại I bình quân chung cho cả 2 xí nghiệp trong quý III, IV, và trong 6 tháng cuối năm: - Quý III: x f i i 240 90 360 92 x 300, 6 1 f 182 i - Quý IV: x f i i 250 92 350 94 x 300,5 2 f 186 i - 6 tháng cuối năm: x f i i 300, 6 182 300,5 186 x 3 00,54 f 368 i Bài 3.12:
Có tài liệu về tuổi nghề của công nhân 3 tổ trong một xí nghiệp cơ khí như sau: Tổ I 2 2 5 7 9 9 9 10 10 11 12 Tổ II 3 5 8 10 12 15 16 Tổ III 2 3 4 4 4 5 5 7 7 8
Trong mỗi tổ, tính tuổi nghề bình quân, số mốt và số trung vị? * Tổ I: - Tuổi nghề bình quân: x
i 2 2 5 7 9 9 9 10 10 11 12 x 7, 81 1 n 11 - Số mốt: Mode = 9
- Số trung vị: 11=2 x 5 + 1 Vị trí chứa Med là vị trí của x => Me =9 6 * Tổ II: - Tuối nghề bình quân: x i 3 5 8 10 12 15 16 x 9 ,85 1 n 7 - Số mốt : Mode = không tồn tại
- Số trung vị : 7 = 2 x 3 + 1 Vị trí chứa Me là vị trí của x => Me = 10 4 * Tổ III: - Tuổi nghề bình quân: x
i 2 3 4 4 4 5 5 7 7 8 x 4,9 1 n 10 - Số mốt : Mode = 4
- Số trung vị: 10 = 2 x 5 => Me = (4 + 5) / 2 = 4,5 Bài 3.13:
Ta có cột trị số giữa như sau: Phân tổ CN theo Trị số giữa Số CN f i R năng suất lao động i di ngày (kg) 400 – 450 425 10 0,2 450 – 500 475 15 0,3 500 – 600 550 15 0,15 600 – 800 700 30 0,15 800 – 1200 1000 5 0,125 Tổng 75 1.
Năng suất lao động bành quân: x f i i
425 10 475 15 550 15 700 30 1000 5 x 6 08,3 f 75 i
Vậy năng suất lao động bình quân của các công nhân trong mỏ than là 608,3 (kg/CN) 2.
Mốt về năng suất lao động ngày của công nhân: f
Trước hết, do khoảng cách tổ không đều nhau nên ta phải tính i R
. Qua đó ta thấy, tổ chứa tổ Mode là tổ 2. i di
Trị số gần đúng của Mode: R R M M (0,3 0,2) 0 01 M x i 450 50 470 0 M 0 M 0 (R R ) (R R ) (0,3 0,2) (0,3 0,15) M 0 M 01 M 0 M 0 1
(Ta thấy: 450 < 470 <500 =>đúng) 3.
Số trung vị về năng suất lao động ngày của công nhân: Tổ có số Me là tổ 3
Trị số gần đúng của Me: f i 75 S (10 15) (Me 1) 2 2 Me x h Me(min) 500 100 583,3 Me f 15 Me Bài 3.14:
Có tài liệu về tuổi nghề (TN) và tiền lương (TL) của các công nhân như sau: TN(năm) 2 2 5 7 9 9 10 11 12 TL (10.000đ) 633 655 780 810 820 815 850 900 940 1.
Tính khoảng biến thiên, độ lệch chuẩn, độ lệch tuyệt đối bình phương, phương sai, độ lệch chuẩn của từng tiêu thức?
Về tuổi nghề: x 7 1 R 1 2 2 1 0 1 x x
2 7 2 7 5 7 7 7 9 7 9 7 10 7 11 7 12 7 i d 3,11 n 9 2 ( x ) 2 2 2 2 2 2 2 2 2
(2 7) (2 7) (5 7) (7 7) (9 7) (9 7) (10 7) (11 7) (12 7) 2 x i n 9 =12,44 2 12, 44 3 ,52 3,52 => V 1 00% 1 00% 5 0,28% 1 x 7 1
Về tiền lương: x 8 00,3 2 R 9 40 633 3 07 2 x x
633 800,3 655 800,3 ............ 940 800,3 i d 74 n 9 2 ( x ) 2 2 2
(633 800,3) (655 800,3) ....... (940 800,3) 2 x i 9126 ,4 n 9 2 9126,4 9 5,5 95,5 => V 1 00% 1 00% 1 1,9% 2 x 800,3 2 => Ta thấy, 1 R 2
R độ biến thiên về tuổi nghề nhỏ hơn độ biến thiên về tiền lương à
tính chất đại biểu của à
số bình quân về tuổi nghề cao hơn tính chất đại biểu của số bình quân về tiền lương. Bài 3.15: Năng suất lao động Trị số giữa Số CN 30 – 40 35 10 40 – 50 45 30 50 – 75 62,5 40 75 – 100 87,5 15 100 – 125 112,5 5 a.
Năng suất lao động ngày bình quân: x f i i
35 10 45 30 62,5 40 87,5 15 112,5 5 x 6 0,75 f 10 30 40 15 5 i b.
Độ lệch tuyệt đối bình quân: x x f
35 60,75 10 45 60,75 30 ....... 112,5 60,75 5 i i d 14,6 f 100 i c.
Độ lệch chuẩn về NSLĐ: 2 2 2 2
(x x) f 2 i i
(30 60,75) 10 (45 60,75) 30 ....... (112,5 60,75) 5 3 83,18 f 100 i 2 1 0,5 d.
Hệ số biến thiên về năng suất lao động ngày của công nhân: 10,5 V 100% 100 % 32,09% x 60,75 Bài 3.16:
Có tài liệu về tiền lương của các công nhân trong một doanh nghiệp như sau: Loại công nhân Số công nhân
Mức lương tháng mỗi công nhân (người) (10.000đ) Thợ rèn 2 170; 180 Thợ nguội 3 160; 180; 200 Thợ tiện 5 170; 190; 200; 210; 230 1.
Tiền lương bình quân của công nhân mỗi loại và toàn thể công nhân:
- Tiền lương bình quân của công nhân mỗi loại: Ký hiệu: Thợ rèn: x1 Thợ nguội: x2 Thợ tiện: x3 x i 170 180 x 1
75lương bình quân của thợ rèn là 1,75 triệu đồng. 1 n 2 x i 160 180 200 x 1
80 lương bình quân của thợ nguội là 1,8 triệu đồng. 2 n 3 x i 170 190 200 210 230 x 2
00 lương bình quân của thợ tiện là 2 triệu đồng. 3 n 5
- Tiền lương bình quân của toàn thể CN: x f i i 175 2 180 3 200 5 x 189 f 10 i 2.
Phương sai chung và các phương sai tổ về tiền lương: - Phương sai chung: 2 2 2 2 2 (x x) 2 i (170 189) (180 189) (160 189) ....... (230 189) 4 09 n 10
- Các phương sai tổ về tiền lương: 2 2 2 (x x) 2 i (170 175) (180 175) 2 5 1 n 2 2 2 2 2 (x x ) 2 i (160 180) (180 180) (200 180) 266, 66 2 n 3 2 2 2 2 2 (x x) 2 i (170 200) (190 200) (210 200) (230 200) 400 3 n 5 3.
Phương sai các số bình quân tổ: 2 2 2 2 ( x x) 2 f i i
(175 189) 2 (180 189) 3 (200 189) 5 124 f 10 i 4.
Bình quân của các phương sai tổ: 2 f i i 25 2 266, 66 3 400 5 2 2 85 f 10 i 5.
Dùng quy tắc cộng phương sai để kiểm tra lại kết quả tính toán: 2 2 2 i => 409 2 85 124 => Đúng Bài 3.17:
Trong tổng số 10000 bóng đèn của Xí nghiệp bóng đèn-phích phích nước sản xuất ra, người ta
điều tra thấy có 200 phế phẩm. Tính phương sai của tiêu thức phẩm chất bóng đèn sản xuất?
Ta có: Tỷ lệ bóng đèn phế phẩm (xác suất) 200 p 0 ,02 10000
à Tỷ lệ bóng đèn đạt tiêu chuẩn: q 1 p 1 0,02 0 ,98
Vậy tỷ lệ bóng đèn đạt tiêu chuẩn là 98%
Phương sai của tiêu thức phẩm chất bóng đèn là: 2 p q 0 ,02 0 ,98 0 ,0196
Chương 4: DÃY SỐ THỜI GIAN Bài 4.1
a. Đây là dãy số thời kỳ vì ta thấy số liệu nói về chỉ tiêu kết quả, có thể cộng dồn. b. Đồ thị
c. Doanh thu bình quân trong một ngày của tuần 1( đơn vị tính: triệu đồng)
Y = 140/2145134126/ 2 137.33 1 Y i 3 n Tương tự : 2 Y =21.28 3 Y =22.85 4 Y =28.28
Doanh thu bình quân trong cả tháng:
20.14 21.28 22.85 28.28 Y = 23.14 4 Bài 4.2
a. Đây là dãy số thời điểm.
b. Giá trị hàng hoá tồn kho bình quân trong mỗi tháng:( Đơn vị tính: triệu đồng) 122 120 Tháng 1: 121 Tháng 7: 1 Y = 2 7 Y =147
Tháng 2: Y =124 Tháng 8: Y = 146 2 8
Tháng 3: Y = 127 Tháng 9: Y = 142 3 9
Tháng 4: Y =131 Tháng 10: Y = 142.5 4 10
Tháng 5: Y =137 Tháng 11:Y = 130.5 5 11 Tháng 6: 6 Y =143 Tháng 12: 1 Y = 130 2
Giá trị hàng hoá tồn kho bình quân mỗi quý( triệu đồng):
120 / 2 122 126 128/ 2 Quý 1: Y = 124 ! 3 128/ 2134140146 / 2 Quý 2: Y = 137 II 3
146 / 2 148144 140 / 2 Quý 3: Y = = 145 III 3 140 / 2145134 126 / 2 Quý 4: Y = = 137.33 IV 3
Giá trị hàng tồn kho bình quân 6 tháng đầu năm( triệu đồng): 124 137 Y = =130.5 2
Giá trị hàng tồn kho bình quân cho cả năm( triệu đồng): 124 137 145 137.33 Y = = 135.83. 4 Bài 4.3
a. Dãy số về giá trị hàng tồn kho của công ty trong tháng 1( Đơn vị tính: triệu đồng) Ngày 1 5 10 20 25 30 Giá trị hàng hoá 320 370 310 410 346 346 tồn kho
b.Giá trị hàng hoá tồn kho bình quân tại kho trong tháng 1:
320*4 370*5 310*10 410*5 346*6 Y = = 345.2 (triệu đồng) 30 Bài 4.4
a. Dãy số thời gian về số công nhân trong danh sách của xí nghiệp năm N ( đơn vị tính: người) Ngày 1.1 14.1 28.2 16.4 17.8 21.10 31.12 Số CN 146 149 156 161 159 162 162
Đây là dãy số thời điểm.
b. Số công nhân bình quân trong danh sách của xí nghiệp: 146*13 149*15 156 *48 161 *123 159 *65 162 *72 Y = = 158.17 (người) 366
( Trong năm có các tháng có 31 ngày là: 1, 3, 5, 7, 8, 10, 12 và tháng 2 có 29 ngày vì năm đó là năm nhuần). Bài 4.5
a. Giá trị sản xuất thực tế bình quân mỗi tháng (triệu đồng): 316 336 338 Y = = 330 3
b. Số công nhân bình quân mổi tháng: 300 304 Tháng 1: = 302 1 Y = 2 304 304 Tháng 2: = 304 2 Y = 2 304 308 Tháng 3: = 306 3 Y = 2
Số công nhân bình quân của quý:
300 / 2 304 304 308/ 2 Y = = 304 3
c. Năng suất lao động bình quân của mỗi công nhân quý 1( triệu đồng/ người)
Năng suất = Giá trị sản xuất/ lao động = Tổng giá trị sản xuất/ Số lao động bình quân. 316 336 338 f = = 3.25 i 304
d. Tỉ lệ % hoàn thành kế hoạch bình quân trong quý 1 y i
Theo công thức: t = 1 và ht y x = kh i xi 316 336 338
Nên ta có: y = 316 336 338 = 103.68 102 105 104
Như vậy, tỉ lệ hoàn thành vượt mức sản xuất là 3.68%.
e. Dãy số thời gian về năng suất lao động bình quân tháng. Tháng 1 2 3
Giá trị sản xuất thực tế 316 336 338 ( triệu đồng) Số công nhân bình quân 302 304 306 tháng (người) Năng suất lao động bình quân tháng (triệu đồng/ 1.046 1.105 1.104 người) Bài 4.6
a. Lượng tăng tuyệt đối liên hoàn qua các năm: y y 2 200 2000 2 00 2 2 1
( giá trị sản xuất năm 2003 cao hơn năm 2002 là 200 triệu đồng). y y 2 442 2200 242 3 3 2
( giá trị sản xuất năm 2004 cao hơn năm 2003 là 242 triệu đồng). y y 2 704 2442 2 62 4 4 3
( giá trị sản xuất năm 2005 cao hơn năm 2004 là 262 triệu đồng). y y 3 040 2704 3 36 5 5 4
( giá trị sản xuất năm 2006 cao hơn năm 2005 là 336 triệu đồng).
Lượng tăng tuyệt đối định gốc: y y 0 1 1 0
( vì năm 2002 lấy làm gốc).
y y 200 2 2 0
( giá trị sản xuất năm 2003 cao hơn so với 2002 là 200 triệu đồng).
y y 442 3 3 0
(giá trị sản xuất năm 2004 cao hơn so với 2002 là 442 triệu đồng). y y 7 04 4 4 0
(giá trị sản xuất năm 2005 cao hơn so với 2002 là 704 triệu đồng). y y 1 040 5 5 0
(giá trị sản xuất năm 2006 cao hơn so với 2002 là 1040 triệu đồng).
b. Tốc độ phát triển qua các năm: * Giá trị liên hoàn: y 2200 2 t 1.1 2
( tốc độ phát triển của năm 2003 so với năm 2002 là 10%). y 2000 1 3 y t 1.11 3
(tốc độ phát triển của năm 2004 so với năm 2003 là 11%). 2 y y4 t 1.108 4
(tốc độ phát triển của năm 2005 so với năm 2004 là 10.8%). 3 y 5 y t 1.124 5
(tốc độ phát triển của năm 2006 so với năm 2005 là 12.4%). 4 y Giá trị định gốc: T 1 1
(vì lấy năm 2002 làm gốc) 2 y T 1.1 2 1 y 3 y T 1.221 3
( tốc độ phát triển năm 2004 so với năm gốc tăng 22.1%) 1 y 4 y T 1.352 4
(tốc độ phát triển năm 2005 so với năm gốc tăng 35.2%) 1 y 5 y T 1.52 5
(tốc độ phát triển năm 2006 so với năm gốc tăng 52%). 1 y
Tốc độ phát triển bình quân: t = n1 t = 4 4 1.1*1.11*1.108*1.12 1.52 1 .109 i
Tốc độ phát triển bình quân qua các năm là 10.9%.
c. Tốc độ tăng qua các năm: *Giá trị liên hoàn: a t 1 1 .1 1 0 .1 2 2
( năm 2003 so với năm 2002). a t 1 1 .11 1 0 .11 3 3
(năm 2004 so với năm 2003). a t 1 1 .108 1 0
.108 (năm 2005 so với năm 2004). 4 4 a t 1 1 .124 1 0 .124 5 5
( năm 2006 so với năm 2005). *Giá trị định gốc: b T 1 0 1 1
( lấy năm 2002 làm gốc). b T 1 0 .11 2 2 b T 1 0 .221 3 3 b T 1 0 .352 4 4 b T 10.52 5 5 Tốc độ tăng bình quân: a t 1 1 .109 1 0
.109 như vậy tốc độ tăng bình quân qua các năm là 10.9%.
d. Giá trị tuyệt đối của 1% tăng qua các năm( 1% tăng ứng với sự tăng lên một lượng tuyệt đối). 2000 2 c 20 2 a (%) 0.1*100 2 y 2200 2 c 22 3 100 100 y 2442 3 c 24.42 4 100 100 y 2709 4 c 27.09 5 100 100 Bài 4.7
a. Chỉ tiêu lượng tuyệt đối là lượng tăng tuyệt đối liên hoàn( sản lượng qua các năm đều tăng).
b. Bảng tình hình sản xuất của một xí nghiệp: Căn cứ lập bảng 9 G 7 9 G 6 a G G .a G 0,16 78 78 90 ,48 97 97 96 97 96 9 G 6 G G G G 9 0,48 13 1 03,48 98 98 97 98 97 98 9 G 9 c 1 ,13 G 113 00 99 100 G G .t 113 106 00 99 00 t 100 G 119, 78 00 00 G 100 100 99 G G 1 19,78 9 1 28,78 01 00 01 t .G 128,78 105 02 01 G 135 , 22 02 100 100
Và áp dụng các công thức: G G i i i 1 Gi t i Gi 1 a t 100 i i i c i ai Chỉ tiêu 96 97 98 99 00 01 02
1.Giá trị sản xuất( G-triệu đồng) 78 90,48 103,48 113 119,78 128,78 135,22
2.Lượng tuyệt đối tăng( -triệu đồng) - 12,48 13 9,52 6,78 9 6,44
3.Tốc độ phát triển liên hoàn(t- %) - 116 114,38 109,2 106 107,5 105 4.Tốc độ tăng(a- %) - 16 14,38 9,2 6 7,5 5
5.Giá trị tuyệt đối của 1% tăng(c- triệu đồng) - 0,78 0,9 1,03 1,13 1,2 1,29
c. Tốc độ phát triển bình quân hằng năm chỉ tiêu giá trị sản xuất của xí nghiệp: y 135, 22 1 t
t n 1 n n 6 109.59 i y 78 1
Như vậy, từ năm 1996 đến năm 2002 tốc độ phát triển bình quân của xí nghiệp là 9.59%/năm. Bài 4.8
Tốc độ phát triển định gốc của chỉ tiêu lợi nhuận của xí nghiệp: (2001 = 100 % ) Năm 2001 2002 2003 2004
Tốc độ phát triển định gốc(%) 100 112 134 146
b. Tốc độ phát triển liên hoàn qua các năm: y y 112 2 2 1 112 1 12 y T y y t 112 2 2 1 2
( năm 2002 so với năm 2001). 1 y 1 y 1 y 134 T t .t 134 t 1 19.6% 3 3 2 3
(năm 2003 so với năm 2002). 112 146 T t .t .t 146 t 108.9% 4 4 3 2 3
(năm 2004 so với năm 2003). 112*119.6
c. Tốc độ tăng bình quân lợi nhuận trong ca giai đoạn 2001- 2004: Ta có: 3
t t .t .t 1 13.4 2 3 4 nên a t 100 1 3.4%
Như vậy, tốc độ tăng bình quân trong giai đoạn này của xí nghiệp là 13.4%. Bài 4.9
a. Đây là dãy số thời kì.
b. Ta có bản kết quả sản xuất từng tuần của xí nghiệp tron tháng Hai: Tuần
GT sản lượng(triệu đồng) I 1409 II 1508 III 1547 IV 1694
Nhận xét: Giá trị sản lượng tăng dần theo từng tuần.
c. Điều chỉnh doanh số bằng số bình quân di động với khoảng cách san bằng là 5: GT sản lượng Giá trị sản lượng Ngày Số BQDD Ngày Số BQDD ( triệu đồng) ( triệu đồng) 1 201 - 15 196 211.4 2 202 - 16 190 213.4 3 204 198.8 17 228 215.6 4 191 200.6 18 230 223 5 196 201.2 19 234 232.2 6 210 203 20 233 233.4 7 205 207.8 21 236 235 8 213 210.6 22 234 236 9 215 210.2 23 238 238.4 10 210 213 24 239 239.6 11 208 214.4 25 245 242 12 219 216 26 242 244.6 13 220 213.2 27 246 - 14 223 209.6 28 250 - Bài 4.10 Doanh thu Năm Thứ tự năm ( t ) (tỷ đồng) 1997 346 1 1998 369 2 1999 441 3 2000 354 4 2001 506 5 2002 516 6 2003 467 7 2004 521 8 2005 566 9 2006 648 10
a. Xây dựng đường hồi quy tuyến tính:
Phương trình tuyến tính: ˆY a bt i i Ta có: y n
a bt i i 2 y t a
t b t i i i i Mà 2 t 385 y 4734 y t 28460 i i i i 4734 1
0a 55b a 3 11.866 28460 5
5a 385b b 2 9.3696
Như vậy phương trình tuyến tính là: ˆY 3 11.886 29.3696t i i
b. Dự báo doanh thu của doanh nghiêp năm 2010:
Vào năm 2010 thì t =14, ta có doanh thu là: i DT 3 11.866 29.2696*14 7 23.04 ( tỷ đồng). Chương 5 : CHỈ SỐ Bài 5.1 Giá bán Lượng hàng bán ( 1000đ) (chiếc) p q p q p q Sản 1 1 0 1 0 0 Kỳ báo Kỳ báo Kỳ gốc Kỳ gốc phẩm cáo cáo (5)=(2) (6)=(1) (1) (2) (3) (4) (7)=(1)(3) (4) (4) A 300 320 4000 4200 1344000 1260000 1200000 B 175 180 3100 3120 561600 546000 542500 C 140 150 200 210 31500 29400 28000 Tổng 1037100 1835400 1770500
a. Chỉ số phản ánh tình hình biến động về giá bán riêng cho từng loại sản phẩm: * Sản phẩm A: p 320 1 i 1.066 a p p 300 0 p p 3 20 300 2 0 p 1 0
Giá của sản phẩm A vào kỳ báo cáo tăng 6.6% so với kỳ gốc, tương ứng một sự tăng về lượng là 20000đồng. Sản phẩm B: p 180 1 i 1.028 p p 175 0 p p 1 80 175 5 p 1 0
Giá của sản phẩm B vào kỳ báo cáo tăng 2.8% so với kỳ gốc, tương ứng một sự tăng về lượng là 5000đồng. Sản phẩm C: p 150 1 i 1.071 p p 140 0 p p 1 50 140 1 0 p 1 0
Giá của sản phẩm C vào kỳ báo cáo tăng 7.1% so với kỳ gốc, tương ứng một sự tăng về lượng là 10000đồng.
Chỉ số chung về giá bán:
1p 1q 1937100 I 1.055 p p q 1835400 0 1
p q p q 1 937100 1835400 1 01700 pq p 1 1 0 1
Như vậy, ở kỳ báo cáo giá chung cho tất cả các sản phẩm tăng 5.5% tương ứng với lượng tăng về giá là 101700000đồng.
b. Chỉ số phản ánh tình hình biến động về lượng bán riêng cho từng loại sản phẩm: * Sản phẩm A: q q 4 200 4000 2 00 q 1 0 q 4200 1 i 1 .05 q q 4000 0
Lượng bán của sản phẩm A vào kỳ báo cáo tăng 5% so với kỳ gốc, tương ứng một sự tăng về lượng là 200 chiếc. Sản phẩm B: q 3120 1 i 1.006 q q 3100 0 q
q 3120 3100 20 q 1 0
Lượng bán của sản phẩm B vào kỳ báo cáo tăng 0.6% so với kỳ gốc, tương ứng một sự tăng về lượng là 20 chiếc. Sản phẩm C: q 210 1 i 1.05 q q 200 0 q q 2 10 200 1 0 q 1 0
Lượng bán của sản phẩm C vào kỳ báo cáo tăng 5% so với kỳ gốc, tương ứng một sự tăng về lượng là 10 chiếc.
Chỉ số chung về lượng bán:
0p 1q 1835400 I 1.036 q p q 1770500 0 0 p q p q 1 835400 1770500 6 4900 pq q 0 1 0 0
Như vậy, ở kỳ báo cáo lượng bán chung cho tất cả các sản phẩm tăng 3.6% tương ứng với lượng tăng về lượng bán là 64900000chiếc.
c. Bảng thống kê các chỉ số: Sản phẩm Chỉ số về giá bán Chỉ số về lượng bán A 1.066 1.05 B 1.028 1.006 C 1.071 1.05 Chỉ số chung 1.055 1.036 Bài 5.2 Giá thành Sản lượng (kg) Tên (1000 đ) Z1Q1 Z0Q1 Z Tên xí 0Q0 T1 T2 T1 T sản 2 nghiệp Z0 Z1 Q phẩm 0 Q2 (5)=(2) (1) (2) (3) (4) (6)=(1)(4) (7)=(1)(3) (4) A 20 19 5000 6000 114000 120000 100000 X B 210 205 80 100 20500 21000 16800 Tổng 134500 141000 116800 A 20 19 7000 8000 152000 160000 140000 Y B 220 210 50 60 12600 13200 11000 Tổng 164600 173200 151000
Tổng của tất cả chỉ tiêu 299100 314200 267800
a. Chỉ số phản ánh biến động về chỉ tiêu giá thành đơn vị sản phẩm của toàn bộ sản phẩm mỗi xí nghiệp: 1z 1q 134500 I 0,95395,3% P X z q 141000 1 0 z 1 1q 164600 I 0 ,95 95% P Y z q 173200 1 0 z 0 1q 141000 I 1 ,207 120, 7% q X z q 116800 0 0 z 0 1q 173200 I 1 ,147 114, 7% q Y z q 151000 0 0
Giá thành sản phẩm của xí nghiệp X giảm 4,7%; của xí nghiệp Y giảm 5%.
Sản lượng sản phẩm của xí nghiệp X tăng 20,7%; của xí nghiệp Y tăng 14,7%.
b. Chỉ số phản ánh các chỉ tiêu về giá thành và sản lượng toàn bộ sản phẩm của công ty: 1z 1q 299100 I 0,9519 95 ,19% p z q 314200 0 0 z 0 1q 314200 Iq 1,173117,3% z q 267800 0 0
→ giá thành sản phẩm của công ty giảm 4,81%
Số lượng sản phẩm của công ty tăng 17,3%.
c.Tính chỉ số chung về giá thành, số lượng của mỗi sản phẩm công ty Giá thành Số lượng T1 T2 T1 T2 Z1q1 Zoq1 Zoqo (1) (2) (3) (4) (5) = (1) (6)= (1) (7)= (1) (4) (4) (3) X 20 19 5000 6000 114000 120000 100000 Y 21 19 7000 8000 152000 168000 147000 266000 288000 247000 X 210 205 80 100 20500 21000 16800 Y 220 210 50 60 12600 13200 11000 Tổng 33100 34200 27800 z1q1 266000 IpA 0, 923 92, 3% z q 288000 0 1 288000 IqA 1 ,165 116, 5% 247000 33100 IpB 0,967 96, 7% 34200 0z 1q 34200 IqB 1, 23123% z q 27800 0 0
→ giá thành sản phẩm A của cả công ty giảm 7,7%, sản phẩm B của công ty giảm 3,3%.
Số lượng sản phẩm A củâ công ty tăng 16,5%, sản phẩm B tăng 23%.
3. phân tích các yếu tố ảnh hưởng đến sự biến động tổng hi phí sản xuất toàn bộ sản phẩm của công ty: z 1q1 1 z 1 q z 0 1 q . 0 z 0 q 0 z 1 q 0 z 0 q
-khi chi phí sản xuất tăng 11,68% thì giá thành ( z q z q ) ( z q z q ) ( z q z q ) 1 1 0 0 1 1 0 0 0 1 0 0
sản phẩm giảm 4,9% và sản lượng tăng 17,3%. 299100 299100 314200
-chi phí sản xuất tăng 31300(nghìn đồng) thì giá . 267800 314200 267800
thành sản phẩm giảm 15100(nghìn đồng) và sản (299100 267800) (
299100 314200) (314200 267800) lượng tăng 46400(nghìn đồng). 1,1468 0, 951.1,173 31300 15100 46400 Bài 5.3 Nhóm hàng Mức tiêu thụ(1000đ)
Tốc độ phát triển (%) về 2007 2008 Giá bán Số lượng A 3000 3000 100 100 B 2500 4200 93,3 180 C 4500 7800 86,6 200 Poqo P1q1 ip Iq
a.tính chỉ số chung về giá cả. 1 p 1 q 300 4200 7800 15000 I 0, 908 90, 8% p p q 300 4200 7800 1 1 16508,5 ip 100% 93,3% 86,6% p q p q 1508,53 pq ( p ) 1 1 0 0
b.Chỉ số chung về lượng hàng hoá tiêu thụ. iqp 0q0 100.300 180.2500 200.4500 Iq 1 65% p q 3000 2500 4500 0 0
c.Phân tích ảnh hưởng của sự thay đổi giá cả và lượng hàng hoá tiêu thụ đối với sự thay đổi mức tiêu thụ hàng hoá.
Ta có: phương trình kinh tế: M pq 1 p 1 q 1 p 1 q 0 p 1 q 0 p q0 p0 1 q p0q0 15000 15000 16508,5 10000 16508,5 10000 1,5 = 0,9 . 1,65
( p q p q ) (
p q p q ) ( p q p q ) 1 1 0 0 1 1 0 1 0 1 0 0 (15000 10000) (
15000 16508,5) (16508,5 10000) 5000 = ( -1508,5 ) + 6508,5
Nhận xét: Mức tiêu thụ hàng hoá qua 2 năm tăng 50% tương ứng một sự tăng về lượng là 5 triệu đồng, do ảnh hưởng của 2 nhân tố: -
Do giá bán giảm 10%, tương ứng làm múc tiêu thu hàng hoá giảm 1,508 triệu đồng. -
Do lượng hàng hoá tăng 65%, tương ứng làm mức tiêu thụ hàng hoá tăng 6,5 triệu đồng. Bài 5.4 Tỉ trọng mức tiêu thụ hàng hoá kỳ báo cáo Chỉ số giá Tên hàng 1 p 1 q (i ) p 1 p 1 q A 30 120 B 45 105 C 25 100
Theo giả thuyết: mức tiêu thụ hàng hoá chung cho cả 3 mặt hàng kỳ báo cáo so với kỳ gốc tăng 25% 1p 1q 125 0pq0
Và giá trị tuyệt đối của một phần trăm tăng là 1,2 tỷ đồng p q 1 , 2 0 0 p q 1 ,2 1 00 1 20(ty) 0 0 p q 1 , 25 1 20 1 50(ty) (4) 1 1 p q ( ) 1 1 A 30% p q ( ) A 45 1 1 1p 1q
Tương tự: p q (B) 1 1 = 67,5 p q (C) 1 1 = 37,5 1.
Chỉ số chung về giá cả: 1p 1q 150 Ip 1 ,0769 p q 45 67,5 37,5 1 1 ip 1, 2 1,05 1
tiền chi thêm của người mua do tăng giá 45 67,5 37,5 pq (P) 150 10, 714(ty) 1,2 1,05 1
2. Chỉ số chung về lượng hàng hóa tiêu thụ: 1 p 1 q 1 p 1 q Ip 1 ,0769 1 poq 1 p 1 q ip 1 p 1 0 1 q p q 139, 285 ip 0 p 1 q 139,285 Iq 1 ,1607 p0q0 120
→ tiên chi thêm của người mua do mua thêm hàng hoá p q(P) 1 39,285 120 1 9,285(ty)
c. phân tích ảnh hưởng của các nhân tố đến biến động của mức tiêu thụ hàng hoá 2 kỳ 1 p 1 q 1 p 1 q p0 1 q 0 p 0 q 0 p 1 q p0qo 1 p 1 q p0q0 p1q1 p0 1 q p0q1 p0q0 150 150 139,285 (ty) 120 139,285 120
(150-120) =(150− 139.285) + (139,285− 120) 1,25 =1,0769 1,1607 30= 10,715+ 19,285
Nhận xét: Mức tiêu thụ hàng hóa 2 kỳ tăng 25%, tương ứng một sự tăng về lượng 30 tỷ, do ảnh hưởng của 2 nhân tố:
-Do giá cả của 3 loại hàng hóa tăng 7,69%, làm giá cả bình quân 10,715 (tỷ đồng).
-Do có sự thay đổi về kết cấu lượng hàng hóa mua của 2 kỳ làm giá cả bình quân tăng 19,285 tỷ đồng. Bài 5.5 Giá trị sản xuất Tốc độ tăng sản Tốc độ phát triển Sản phẩm Q1 lượng quý II so với Q2 q1/qo=iq quý I A 105 110 15 115 B 620 650 5 105 (zoqo) (z1q1)
1.Tính các chỉ số chung theo thứ tự *chỉ số sản lượng: iqz
0q0 1,15.105 1,05.620 Iq 1,0644 z q 105 620 0 0
*chỉ số tổng chi phí sản xuất:
1z 1q 110 650 Izq 1 ,0482 z q 105 620 0 0 *chỉ số giá thành: Izq 1, 0482 Iz 0,9847 Iq 1, 0644
2.Tính các chỉ số chung theo thứ tự:
*Chỉ số tổng chi phí sản xuất: 1z 1q I 1 , 0482 ZQ z0q0 *chỉ số giá thành: z1 1q I Z z0 1q Mà: 1 . q z q iq z q . 0 1 0 0 z0q0 q 0 1
,15.105 1,05.620 771, 75 1 z 1 q 110 650 Iz 0, 9847 z q 771,75 0 1 *chỉ số sản lượng: Izq Iq 1 , 0644 Iz Bài 5.6
a.Chỉ số chung về lượng hàng hóa tiêu thụ: i p q q 0 0
1, 05 0,3 1,04 0,25 ... 1,12 0,07 I 1 ,055 q hay 105,5% p q
0,3 0,25 0,23 0,15 0,07 0 0
b.Bảng tình hình mức tiêu thụ hàng hóa và lượng hàng hóa tại một thị trường: Tên hàng
Tỉ trọng mức tiêu thụ hàng hóa iq kỳ gốc(%) A 30 1,05 B 25 1,04 C 23 1,045 D 15 1,08 E 7 1,12
Ta có mức tiêu thụ hàng hóa chung kì báo cáo tăng so với kì gốc là 10% nên I 1 10% I pq hay 1,1 pq 1p 1q I pq p0q0 Ipq 1,1 Mà I I I I 1 ,047 pq p q p I 1, 05 q Bài 5.7 z q q Sản phẩm 0 0 (%) 1 i z q z q 0 0 0 0 q q0 A 27 1,05 238,999 B 15 1,07 132,777 C 58 1,2 513,4073 Theo giả thuyết: z q 956 1 1 1z 1q Izq 1 , 08 z0q0 zoqo 8 85,185 →
a.Chỉ số chung về khối lượng sản phẩm: i z q q 0 0
105.238,999 1,07.132,777 1,2.513, 4073 I 1 ,13999 q z q 885,185 0 0
b.Chỉ số chung về giá thành: Izq 1, 08 I 0, 9473 z I 1,3999 q
c.phân tích các nhân tố ảnh hưởng đên sự thay đổi của tổng chi phí sản xuất qua 2 kì. Ta có: n! 1 q z q .z q i . q z q 1 009,1091 0 1 r ! n r 0 0 0 0 ! 0 q z q z q z q 1 1 1 1 0 1 . z 0q0 z0 1 q z0q0 1 z 1 q 0 z 0 q 1 z 1 q 0 z 1 q 0 z 1 q 0 z 0 q 1,08 0 ,9473.1,13999
70,815 53,1094 123, 9241
Nhận xét:Tổng chi phí sản xuất tăng 8% tương ứng với một lượng tăng tuyệt đối 70,815 triệu đồng, do ảnh hưởng của 2 nhân tố:
-Giá thành giảm 5,37%, làm tổng chi phí sản xuất giảm 53,1094( đơn vị)
-Do có sự thay đổi kết cấu về khối lượng 3 sản phẩm làm cho tổng chi phí sản xuất tăng 123,92 triệu đồng. Bài 5.8.
aTtính giá bán bình quân 1gói hàng hóa trên cho từng tháng. *tháng 6: 0 p 0 q 5,5.5000 5,6.5000 p 5 ,55(ngdong) 0 q 10000 0 *tháng 7: 1 p 1 q 6,5.7000 6, 25.6000 p 6,3846(ngdong) 1 q 13000 0
b.lập hệ thống chỉ số phân tích sự biến động giá bình quân nói trên: ta có:
0p 1q 5,5.7000 5,6.6000 p 5, 5461( ) 01 ngdong q 13000 1 p1 p1 0 p 1 . p0 p01 p0 1 p
p0 p1 p01 p01 p0 6,3846 6,3846 5,5461 . 5,55 5,5461 5,55
6,3846 5,55 6,3846 5,5461 5,5461 5,55 1,15 1 ,151187.0,99 0,8346 0, 8385 0,0039
Giá bán bình quân tăng 15% tương ứng với tăng 1lượng tuyệt đối là 0,8346(ngàn đồng).
Do giá bán của 2 khu vực tăng15,12% làm giá bán bình quân tăng 0,8385(ngàn đồng).
Do có sự thay đổi về kết cấu lượng hàng bán ra của 2 kì làm giá bán bình quân giảm 0,0039( ngàn đồng).
c.phân tích biến động của doanh số bán ra theo nhân tố: giá bán, kết cấu lượng hàng, khối lượng hàng bán ra. p q 55500 0 0 p q 83000 1 1 q 10000 0 q 13000 1 p q
p . p p . p p . p 1 1 1 1 01 1 0 1 . . p q p q p . p p . 0 0 p 01 1 0 1 0 0
p q p q p p .q p p .q p p . 1 1 0 0
1 01 1 01 0 1 1 0 p0 82999,8
6,3846.13000 5,54651.13000 5,55.13000 . . 55500 5,5461.13000 5,55.13000 5,55.10000
304599,810900,5 ( 50,7) 10650 1,5 1 ,15.0,819.1,3 27499,8 10900, 5 50,7 16650
Nhận xét: Doanh số bán ra tăng 50%, tương ứng một sự tăng về lượng là 27,499 triệu đồng, do ảnh hưởng của 3 nhân tố:
-Giá bán tăng 15%, làm giá bán bình quân 2 tháng tăng 10,9 triệu đồng.
-Do có sự thay đổi về kết cấu lượng hàng bán ra làm cho doanh số bán ra giảm 50,7 nghìn đồng.
-Do khối lượng hàng bán ra tăng 30% làm cho doanh số bán ra tăng 16650 nghìn đồng. Bài 5.9.
a.Phân tích các nhân tố ảnh hưởng đến sự biến động năng suất lao động bình quân toàn địa phương:
Ta có: Năng suất= Giá trị sản xuất/ số lao động 1 T 140 317 W T . 0 0 15000. 8000. W01 0 T 200 200 W01 50 ,7721 T T 140 317 1 1 W 1 W 1 W 01 . W 0 W 01 W 0
W1 W 0 W 1 W 01 W 01 W 0 1,3319 1 ,5099.0,88211 19,086 25,8639 6,7779
- Năng suất lao động bình quân qua 2 năm tăng 33,19%, tương ứng tăng 1 lượng tuyệt đối là 19,086(tỷ người).
- Do năng suất lao động của 2 nghành tăng 50,99%, làm năng suất lao động bình quân tăng 25,8639(tỷ người).
-Do có sự thay đổi về kết cấu lao động làm năng suất lao động bình quân giảm 6,7779( tỷ đồng/ người)
b. phân tich sự biến động giá trị sản xuất theo 3 nhân tố : năng suất lao động, kết cấu lao động, số lượng lao động. W 1. T
W 1.T W 01.T W 0. 1 1 1 1 T . . W 0 .T
W 01.T W 0 .T W 0 . 0 1 1 0 T
W1.T W0.T W1.T W01.T W01.T W0.T W0.T W0. 1 0 1 1 1 1 T 1 0 76,586.457
76,586.457 50,7221.457 57,5.457 . . 57,5.400 50,7221.457 57,5.457 57,5.400 11999,8 1 1819,8 3097,5 3277,5 1,52 1 ,5.0,882.1,14 11999,8 1 1819,8 3097,5 3 277,5 Nhận xét:
Gía trị sản xuất tăng 52% tương ứng 1lượng tăng tuyệt đối là 11999,8 tỷ đồng.
-Do năng suất lao động của 2 nghành tăng 50% làm giá trị sản xuất tăng 11819,8 tỷ đồng.
-Do có sự thay đổi về kết cấu lao động làm giá trị sản xuât giảm 3097,5 tỷ đồng.
-Do số lượng lao động tăng 14% làm giá trị sản xuất tăng 3277,5 tỷ đồng. Bài 5.10.
a. Tính giá thành bình quân đơn vị sản phẩm các quý của cả xí nghiệp. Z 0 Z 0 d0 11, 05 12,03 13,02 11, 7 Z1 Z d 10,
23.0,25 11, 25.0, 25 13,11.0,511,92 1 1
b.Dùng phương pháp chỉ số để phân tích các nhân tố ảnh hưởng đến sự thay đổi giá trị bình quân. Z 1 Z 1 Z 01 . Z 0 Z 01 Z 0 Với: Z 01 Z d 11
, 25 12,025 13,05 12, 25 0 1
Z0 Z0
Z1 Z01 Z01 Z0 1,02 0, 97.1,047 0,225 0,325 0,55
Giá thành bình quân tăng 2% tương ứng tăng 1 lượng tuyệt đối là 0,225 (ngàn đồng)
-Do giá thành giảm 3%làm giá thành bình quân giảm 0,325ngàn đồng.
-Do có sự thay đổi về kêt cấu sản lượng làm giá thành bình quân tăng 0,55 ngìn đồng.
CHƯƠNG 6: ĐIỀU TRA CHỌN MẪU VÀ ƯỚC LƯỢNG Bài 6.1
a. Năng suất lao động bình quân của số công nhân đã được điều tra x .f i i 450.15 550.60 650.25 x 560 ( kg/ngày) fi 100 b.
phương sai mẫu về năng suất lao động 2 2 2 2
( x x) f 2 i i (450 560) 15 (550 560) 60 (650 560) 25 ˆ S f 100 =3900 i
c.Sai số bình quân chọn mẫu khi suy rộng năng suất lao động bình quân chung cho cả xí nghiệp: 2 2 ˆ S 3900 6,276 n X n n 1 100 1
d.Tỉ lệ số công nhân bình quân có năng suất lao động từ 600 trở lên: 25 w= 0 , 25 100
Phương sai mẫu về số công nhân có năng suất lao động từ 600 trở lên: 2
ˆS w(1-w)=0,25(1-0,25)=0,1875
e.Sai số bình quân chọn mẫu khi suy rộng ra tỉ lệ chung của cả xí nghiệp về số công nhân có năng suất lao động từ 600 trở lên: 2 ˆS 0,1875 0 ,0435 F n n 1 100 1 Bài 6.2
a.Phạm vi sai số chọn mẫu khi suy rộng
x z . x n; x z . x / 2 / 2 n Ta có: x f i . i x 995, 75 fi Phương sai mẫu: 2 2 2
(x x) f 2 i i (350 995,75) 20 ... (1650 995,75) 23 ˆs 14104 4,4375 fi 200 2 ˆS N n 141044,4375 2000 200 25 , 25 n X n 1 N 200 1 2000 Tra bảng:Z 1 ,96 / 2 → phạm vi sai số:
z . x n 1,96.25, 25 49,49 / 2
b.tỷ lệ mẫu về số công nhân có năng suất lao động từ 1200 kg trở lên: 37 23 w 0, 3 200 c. Với = 13,16 → Z 1 ,51 / 2
Phạm vi sai số chọn mẫu khi năng suất lao động từ 1200kg trở lên: Z . / 2 Fn Với: 2 N n
W (1 W ) N n 0.3(1 0,3) 2000 200 Fn . . . 0,0308 n 1 N n 1 N 200 1 2000 → phạm vi sai số: Z . 1 ,51.0, 0308 0 ,046508 / 2 Fn Bài 6.3
Tỷ lệ phế phẩm của toàn kho là: w= 20/400=0,05 ( w 1 ) w 0,05(1 0,05) 0, 0109 Fn n 1 400 1 Z . 0,02 / 2 Fn
Suy rộng tỷ lệ phế phẩm của toàn kho : w Z . p w Z Fn . / 2 / 2 Fn
0,05 0,02 p 0, 05 0,02 0,03 p 0, 07
Tỷ lệ phế phẩm toàn kho nằm trong khoảng 0,03 và 0,07
*Sự suy rộng này đảm bảo độ tin cậy là: Z . Fn 0,02 / 2 Z .0.0109 0,02 Z 1,83 / 2 / 2 Tra bảng: Z 1 ,83 / 2 Z 0,4664 1 2 0, 4664
Vậy độ tin cậy là: 93,28% Bài 6.4 Phân tổ theo số Số công Số xí lượng công nhân N n 1 0%N W nghiệp i i i i nhân(người) (người) Dưới 500 10000 5 2000 1000 0,02 500-700 40000 8 5000 4000 0,03 700-900 29400 6 4900 2940 0,05 900 trở lên 30600 6 5100 3060 0,07 N 110000 Với độ tin cậy 95% Z 1 ,96 / 2
Tỷ lệ công nhân đang theo học tại lớp tại chức là: w Z . p w Z . / 2 Fn / 2 Fn Trước hêt ta tính: 2 k w (1 w ) . N N n i i . i . i i Fn 2 n N N i 1 1 i i 2 2
0,02.(1 0,02) 10000 10000 1000 0,07(1 0,07) 30600 30600 3060 . . ... . . 2 2 1000 1 110000 10000 3060 1 110000 30600 7 7 6 6 3
1, 46.10 8,66.10 1.04.10 1, 48.10 1 ,87.10 w n i i
0,02.1000 0,03.4000 0,05.2940 0, 07.3060 w 0,0455 n 11000 i
tỷ lệ công nhân đang theo học lớp tại chức là: w Z . P w Z Fn . / 2 / 2 Fn 3 3
0,0455 1,96.1,87.10 P 0,04551,96.1,87.10 0,042 P 0, 049
Vậy tỷ lệ công nhân đang theo học lớp tại chức nằm trong khoảng: 0,042 đến 0,049 Bài 6.5
a.Ước lượng trọng lượng bình quân mỗi chi tiết máy sản xuất trong tháng x x kx 52 n
x xkx n i 2 5 . i 2 i 1 S 5 kx n i i 1
50 522 .400 49 522 .400 53 522 .400 55 522 .400 2000 4, 8 Xác suất = 0,4595 Z 2 / 2 k 2 2 k ni s K k k x i 1 . . xn 2 k 1 n K 2 4,8 5.5.400 100 5 . . 1 ,0677 2 5 1 2000 100
Trọng lượng bình quân mỗi chi tiếy máy sản xuất trong tháng là: x Z . X x Z . / 2 / 2 xn xn 52 2 1 ,0677 52 2 1 , 0677 49,8646 X 54 ,1354
Vậy trọng lượng bình quân mỗi chi tiết máy trong tháng nằm trong khoảng từ: 49,8646 đến 54,1354 (g) b. phạm vi sai số Z . 3 / 2 xn Tính xác suất: Z .1, 0677 3 Z 2, 809 / 2 / 2 Z 0,005 1 0, 01 (1 2.0 ,005) Vậy xác suất là 99%
c.Tính số hòm cần chọn ra để điều tra biết xác suất: 0,6833 Z 1 / 2 2 2 2 Z . 1 .4,8 / 2
0,7(g ) n 9,8 2 2 0,7 x
Vậy số hòm cần điều tra là 10 hòm. Bài 6.6
a.Tuổi nghề bình quân của số công nhân được điều tra: x i 5 7 ... 13 x 9, 33 n 15
b. Phương sai về tuổi nghề: 2 (x x f i ) 2 ˆ i S f i 2 2 (5 9,33) 1 ... (13 9,33) 1 29, 42 15
c.Ước lượng tuổi nghề bình quân số công nhân: Ta có:1 0 ,935 Z 1 ,84 / 2
Sai số bình quân chọn mẫu: 2 N n 29,42 300 15 1 ,365 n X n N 15 300
Khoảng ước lượng tuổi nghề bình quân của số công nhân trong cả xí nghiệp: x Z . X x Z . / 2 X / 2 n X n 9,33 1,84 1 ,365 X 9, 331,84 1 ,365 6,82 X 11 ,84
Như vậy tuổi nghề bình quân của công nhân nằm trong khoảng 6,82 đến 11,84. Bài 6.7
a. Dữ liệu này được thu thập theo phương pháp chọn mẫu phân loại.
b. Ước lượng chỉ tiêu trung bình của 1 hộ ở thành phố (1-=0,95) Ta có: x i x n
Trung bình chi tiêu của hộ ở ngoại ô: 0,81,09 ..... 2,6 x 1 ,49 1 10
Trung bình chi tiêu của hộ ở ven đô: (2,2 2,2 ... 8) x 4, 735 2 20
Trung bình chi tiêu của hộ ở trung tâm: 3,4 3,5 ... 9,3 x 6 ,65 30 Ước lượng điểm: x .N i i 1, 49.500 4,735.1000 6,65.1500 x 5,151 Ni 3000 2 2
(x x ).n i i
(0,8 1, 49) .1 .... (2,6 1, 49) .1 2 1 1 1 S 0 ,3149 1 n 10 1i 2 S 3 ,1163 2 2 S 3, 28 3 3 2 2 S N N n i . i . i i X 2 n i 1 n 1 N N i 2 2 2 0,3149 500
500 10 3,1163 1000 1000 200 3, 28 1500 1500 30 . . . . . 2 2 2 10 1 3000 500 20 1 3000 1000 30 1 3000 1500 4
9,52.10 0,0178 0,0277 0, 216
ước lượng chỉ tiêu trung bình của 1hộ ở thành phố: Z 1,96 / 2 x Z . X x Z . / 2 / 2 xn xn
5,1516 1,96.0,216 X 5 ,1516 1,96.0, 216 4,72824 X 5 ,57496
Vậy chỉ tiêu trung bình của 1 hộ ở thành phố nằm trong khoảng từ
4,72884 đến 5,57496 (triệu đồng)
c. Ước lượng tỷ lệ hộ của thành phố có tổng chi tiêu từ 5 triêu đồng trở lên độ tin câỵ 99% Z 2 ,5 / 2
Tỷ lệ hộ có chi tiêu lớn hơn hoặc bằng 5 triệu đồng là: W= 33/60 =0,55 Phương sai mẫu: 2 S w (1 w) 0 , 2475
Sai số bình quân chọn mẫu: 2 S 0,2475 0, 065 Fn n 1 60 1
ước lượng tỉ lệ hộ ở thành phố có tổng chi tiêu từ 5 triệu đồng trở lên: w Z . P w Z . / 2 Fn / 2 Fn
0,55 2,5.0,065 P 0, 55 2,5.0,065 0,382 P 0 ,717
Vậy tỷ lệ hộ ở thành phố có chi tiêu từ 5 triệu đồng trở lên nằm trong khoảng từ 0,382 đến 0,717.
d.Xác định kích thước mẫu cần điều tra nếu cần ước lượng chi tiêu trung bình, độ dài khoảng tin cậy 1,1 triệu đồng/hộ: 1- =99% 2 2
D (x Z . ) (x Z . ) 2.Z . 1,1 x / 2 xn / 2 xn / 2 xn
Kích thướt mẫu cần điều tra: 2 2 2 2 Z . Z . / 2 / 2 n 4. 2 2 D x x Với: 2 (x x) 2 n i i ni 2 2 2 (1, 49 5,15) 500 (4,735 5,15) 1000 (6,65 5,15) 1500 3000 3 , 415 2 N i . 2 i
0,3149 500 0,1163 1000 3, 28 1500 2, 73 N 3000 i 2 2 2 S 2, 73 3, 415 6,145 2 2 2 Z 2,58 6,145 Như vậy: / 2 n 4 4 135 2 2 D 1,1 x
f.Xác định kích thức mẫu cần điều tra ứơc lượng tỷ lệ hộ có tổng chi tiêu từ 5 triệu đồng trở lên: D=4,5% 1 9 5% Với độ tin cậy 95% Z 1 ,96 / 2 2 2 Z p(1 p) Z p(1 p) / 2 / 2 n 4 2 2 D p p 2 1,96 0 ,55(1 0,55) 4 1878 2 0,045
Vậy kích thước mẫu cần điều tra ở đây là 1787 hộ. Bài 6.8
a.Việc lấy mẫu trên của doanh nghiệp thuộc loại lấy mẫu phân loại.
b. Ước lượng trọng lượng bình quân một bao bột mỳ trong từng kho với độ tin cậy 95%: * Kho 1: Giá trị trung bình: x f i i 30 2 31 3 32 4 33 1 x 31 , 4 1 f 10 (kg) i Khoảng ước lượng:
(x Z ; x Z ) 1 / 2 X 1 / 2 n X n 2 (x x ) 2 1 f i 1 ˆ i S f Với: i 2 2 (30 31, 4) 2 ... (33 31, 4) 1 0, 84 10 2 ˆ S N n 0,84 500 10 Ta có: 1 0 , 287 X 1 n n N 10 500 1 1 0 ,95 0 ,05 Z 1 ,96 / 2 Khoảng ước lượng: x Z . X x Z . 1 / 2 X 1 1 / 2 1 n X 1 n 31, 4 1,96 0, 287 X 31 , 4 1,96 0 ,287 1 30,83 X 31 ,96 1
Như vậy trọng lượng bình quân của một bao gạo trong kho một nằm trong khoảng 30,83 đến 31,96 kg. *Kho 2: Giá trị trung bình: x f i i 31 3 32 4 ... 35 3 x 33 ,05 1 (kg) f 20 i Khoảng ước lượng:
(x Z ; x Z ) 1 / 2 X 1 / 2 n X n 2 (x x ) 2 1 f i 1 ˆ i S f Với: i 2 2 (31 33,05) 3 ... (35 33,05) 3 1 ,6475 20 2 ˆS N n 1, 6475 1000 20 Ta có: 2 0, 284 X 2 n n N 20 1000 2 1 0 ,95 0 ,05 Z 1 ,96 / 2 Khoảng ước lượng: x Z . X x Z . 2 / 2 X 2 2 / 2 2 n X 2 n 33,05 1,96 0,
284 X 33,051,96 0, 284 2 32.49 X 33 ,6 2
Như vậy trọng lượng bình quân của một bao gạo trong kho 2 nằm trong khoảng 32,49 đến 33,6 kg. *Kho 3: Giá trị trung bình: x f i i 31 3 32 5 ... 36 2 x 33,73 3 (kg) f 40 i Khoảng ước lượng:
(x Z ; x Z ) 1 / 2 X 1 / 2 n X n 2 (x x f i ) 2 2 1 ˆ i S f Với: i 2 2 (31 33,73) 3 ... (36 33,73) 2 1 ,8 40 2 ˆS N n 1,8 2000 40 Ta có: 3 0, 21 X 3 n n N 40 2000 3 1 0 ,95 0 ,05 Z 1 ,96 / 2 Khoảng ước lượng: x Z . X x Z . 3 / 2 X 3 3 / 2 n 3 n X 3 33,73 1,96 0, 21X 33 ,73 1,96 0, 21 3 33,31 X 34,137 3
Như vậy trọng lượng bình quân của một bao gạo trong kho3 nằm trong khoảng 33,31 đến 34,137 kg.
c.ước lượng trọng lượng bình quân một bao bột mỳ của doanh nghiệp: x 1N 1
x 2N 2 x3N 3 x N 31, 4 500 33, 05 1000 33,73 2000 33 , 2 3500 3 2 2 ˆS N N n i i i i X 2 n i n 1 1 N N i i 2 2 0,84 500 500 10 1,8 2000 2000 40 ... 2 2 10 1 3500 500 40 1 3500 2000 3 3
1,866.10 6,93.10 0,01477 0,1535 Khoảng ước lượng: x Z . X x Z . / 2 X / 2 n X n 33, 2 1,96 0,1535
X 33,21,96 0,1535 32,9 X 33 ,5
Vậy trọng lượng bình quân của một bao bột mỳ của doanh nghiệp nằm trong khoảng giữa 32,9 và 33,5 kg.
d.Ước lượng tỉ lệ số bao bột mỳ có trọng lượng từ 32 kg trở xuống ở kho 3:
Tỉ lệ bao bột mỳ có trọng lượng từ 32 kg trở xuống: 8 w 0,2 3 40
Sai số bình quân chọn mẫu: ( w 1 ) w N n F n n 1 N 0,2(1 0,2) 2000 40 0,063 40 1 2000 Khoảng ước lượng: 3 w Z /2 p w Z F 3 / 2 n n F
0,2 1,96.0,063 p 0 ,2 1 ,96.0,063 0,076 p 0, 323
Vậy tỉ lệ số bao bột mỳ có trọng lượng từ 32 kg trong kho 3 nằm trong khoảng từ 0,075 đến 0,325.
e.Ước lượng tỉ lệ số bao bột mỳ có trọng lượng từ 32 kg trở xuống của doanh nghiệp:
Tỉ lệ số bao bột mỳ có trọng lượng từ 32 kg trở xuống của từng kho: 9 Kho 1: w 0, 9 1 10 7 Kho 2: w 0 ,35 2 20 8 Kho 3: w 0,2 3 40 Của cả 3 kho: 9 8 7 w 0,34 10 20 40 Ta có: 3 2 w (1 w ) N N n i i i i i F 2 n i 1 n N N i 1 i 2 2 0,9(1 0,9) 500 500 10 0,2(1 0,2) 2000 2000 40 ... 2 2 10 1 3500 500 40 1 3500 2000 4 4 3 2 10 9,57 10 1 ,31 10 0, 05 Khoảng ước lượng: w Z . p w Z . / 2 F / 2 n n F 0,34 1,96 0, 05 p 0, 34 1,96 0, 05 0,242 p0,438
Như vậy, tỉ lệ số bao bột mỳ có trọng lượng từ 32 kg trở xuống của doanh nghiệp nằm trong khoảng 0,242 đến 0,438.
f.Xác định số bao bột mỳ cần điều tra để ước lượng trọng lượng trung bình một bao bột mỳ của doanh nghiệp với
độ dài khoang tin cậy là 0,6 kg và độ tin cậy 99%: D 0, 6 x Áp dụng công thức : 2 2 2 2 4 Z / 2 Z /2 n 2 2 D x x Ta có: 2 2 2 S 2 N i i 0,84 500 1,6475 1000 1,8 2000 2 Với: Ni 3500 1 , 62 2
(x x) N 2 i i S N i 2 2 (31, 4 33, 2) 50
0 ... (33,725 33, 2) 2000 3500 0, 6267 2 1 ,62 0,6267 2 ,2467
Số bao bột mỳ cần điều tra là: 2 2,58 2, 2467 n 4 166 (bao). 2 0,6
g. Xác định số bao bột mỳ cần điều tra nếu ước lượng tỉ lệ số bao bột mỳ có trọng lượng từ 32 kg trở xuống của doanh nghiệp với D 0 ,05 x Z 2 ,58 / 2 Áp dụng công thức: 2 2 Z p(1 p) Z p(1 p) / 2 / 2 n 4 2 2 D p p 2 2,58 0, 34(1 0,34) 4 1577 2 0,05
Vậy số bao bột mỳ cần điều tra là 1577 (bao).
Chương 7: KIỂM ĐỊNH GIẢ THUYẾT Bài 7.1: Giả thuyết: H : 5 0 0 ( Với 0 mm ) 1 H 0 x n i i 4.9 2 5 4 ... 5.3 3 x 5.12 n 20 Ta có: i 2 2 2 2 2 (x )x i (4.9 5.12) 2 (5 5.12) 4 ...(5.3 5.12) 3 ˆ S 0.0146 n 20 i Tiêu chuẩn kiểm định: x 5.12 5 0 t 4.329 2 0.0146 ˆS 19 n 1 Tra bảng: T T 2.861 19,0.005 n 1, 2
Ta thấy: t T
Bác bỏ H chấp nhận H n 1, 2 0 1
Như vậy doanh nghiệp không cam kết như đã hứa, chiều dài trung bình của sản phẩm không đúng bằng 5mm với 0.01 Bài 7.2:
Giả thuyết: H : 5 000 0 0 (với 0 giờ) H 1 0 n x i i 4800 2 4850 3 ... 5100 2 x 4940 n 20 Ta có: i 2 2 (x x n i ) i S 9400 n i Tiêu chuẩn kiểm định: x 4940 5000 0 t 2.6975 2 9400 ˆ S 19 n 1 Tra bảng: T T 2.539 n 1, 19,0.01
Ta thấy: t T H H n 1, Bác bỏ 0 chấp nhận 1
Như vậy với mức ý nghĩa 0.01 tuổi thọ trung bình của sản phẩm nhỏ hơn 5000 giờ, sản phẩm không đạt chỉ tiêu về chất lượng. Bài 7.3:
Giả thuyết: H : D D 3 0 (Với nghìn đồng/sp) y X 0 0
H : D 1 y X 0 Ta có: KH 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 x
50 48 52 49 51 53 47 52 50 48 50 49 48 51 49 49 50 51 53 47 i y
55 50 58 51 55 56 50 56 52 52 54 58 51 49 57 54 56 51 50 53 i k 5 2 6 2 4 3 3 4 2 4 4 9 3 -2 8 5 6 0 -3 6 i KH 21 22 23 24 25 26 27 28 29 30 x 46 51 54 48 49 52 45 49 52 51 i y 48 53 54 49 56 58 48 52 54 55 i k 2 2 0 1 7 6 3 3 2 4 i k k 3.37
(k y x ) i i i n x : Giá mua BBC i y : Giá mua BBM i 2 2 (k k ) ˆ i S k 7.03 n Tiêu chuẩn kiểm định: k D 3.37 3 0 Z 0.75 2 7.03 ˆ S k 29 n 1
Tra bảng ta thấy: Z Z 2 .327 0.01
. Ta thấy: Z < Z Chấp nhận H0 .
Như vậy, với 0.01 thì chi phí thêm cho bao bì 1000d/sp thì có thể bán hàng giá cao hơn giá cũ 3000d/sp. Bài 7.4:
Gỉa thuyết: H D (D 0 .05 0 nghìn đồng/sp) X y 0 0
H : D 1 X y 0 Ta có bảng sau: CN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 x 5.1 6.0 5.8 5.4 5.8 5.0 5.2 5.5 5.8 6.1 6.3 5.2 5.6 5.9 6.2 6.0 i y 5.0 5.8 5.5 5.3 5.9 5.1 5.0 5.3 5.5 5.9 6.1 5.4 5.2 5.7 6.0 5.7 i k 0.1 0.2 0.3 0.1 -0.1 -0.1 0.2 0.2 0.3 0.2 0.2 -0.2 0.4 0.2 0.2 0.3 i
(k x y ) x : Chi phí lương theo phương pháp X i i i i
y : Chi phí lương theo phương pháp Y i k k 0.15625 n 2 2 (k k) ˆ i S k 0.025 n k k 0.15625 0.05 0 t 2.603 Tiêu chuẩn kiểm định: 2 0.025 ˆ S k 15 n 1 T T n 2.262 1, 15,0.01 Tra bảng Chấp nhận H t T 0 n 1 ,
Như vậy với 0.01 phương pháp sản xuất X có chi phí tiền lương cao hơn phương pháp sản xuất Y từ 50 nghìn đồng/sp trở lên. 3 3 Bài 7.5: 3 3 w 3.10 ; w 2.10
w : tỉ lệ sai hỏng của máy A A 1000 B 1500 A
w : tỉ lệ sai hỏng của máy B B Gỉa thuyết:
H : P P 0.01 0 B A
H :P P B A 0.01 1 3 3 w n w n 3x10 1000 2 10 1500 A A B B 3 w 2.10 n n A B 1000 1500 Tiêu chuẩn kiểm định: w B -w A 0.002 0.003 t 0.548 w(1 w) w(1 w)
0.002(1 0.002) 0.002(1 0.002) n n 1000 1500 A B
Tra bảng Z Z 2.326 0.01 . Ta thấy Z > Z Chấp nhận H 0
Như vậy với mức ý nghĩa 0.01 , tỉ lệ thành phẩm của máy A lớn hơn máy B từ 1% trở lên. Bài 7.6:
Gỉa thuyết: H D 0 .1 0 D X y 0 (Với 0 nghìn đồng)
H : D 1 X y 0 x ni ix x 5.084 n ix y niyi y 4.868 ny Ta có: i 2 2 (x x n i ) ˆ xi S x 0.0165 n ix 2 2
(y y) ˆ n i y i S y 0.0174 n iy 2 2 2 S n S n x x y y S 0.0177 n n x y 2 Tiêu chuẩn kiểm định:
(x y) D (5.084 4.868) 0.1 0 t 3.038 2 2 S S 0.0177 0.0177 n n 25 25 x y Tra bảng: T T 1.677 t T H n n 2; 48;0.05 . Ta thấy: n n 2; Chấp nhận 0 x y x y
Như vậy đối với 0.05 , chi phí điện năng cho một sản phẩm của máy X lớn hơn máy Y từ 100d/sp trở lên.
Bài 7.7: Gỉa thuyết: H : D 0 .1kg) 0 1 2 0 D ( Với 0 H : 1 1 2 0
D Kiểm định về mức hao phí nguyên vật liệu x n Ta có: 1i 1i x 12.26 1 n
Mức hao phí bình quân của máy 1 1i x n 2i 2i x 12.307 2 n
Mức hao phí bình quân của máy 2 2i 2
(x x ) xn 1i 1 1 ˆ i S1 0.0234 n 1i 2
( x x ) n 2i 2 2 ˆ i S2 0.0173 n 2i 2 2 S n S n 2 1 1 2 2 S 0.0206 n n 2 1 2 Tiêu chuẩn kiểm định:
(x x ) D (12.26 12.307) 0.1 1 2 0 t 3.548 2 2 S S 0.0206 0.0206 n n 20 30 1 2 Tra bảng: T T 1.677 . Ta thấy t T Chấp nhận H n 1 n 2 2; 48;0.05 1 n 2 n 2; 0
Như vậy 0.05 , máy 1 có mức hao phí nguyên liệu nhỏ hơn máy 2 ít nhất là 0.1kg nguyên liệu hay máy 1 tiết
kiệm nguyên liệu hơn máy hơn so với máy 2 từ 0.1kg nguyên liệu trở lên. Bài 7.8:
Dùng phương pháp kiểm định dấu:
Giả thuyết: H : p 0 .5 0
( p là sản xuất sản phẩm A được ưa thích hơn sản phẩm B) H : 1 p 0.5 Khách hàng Điểm sp A Điểm sp B Dấu(A-B) 1 8 9 - 2 9 8 + 3 7 7 0 4 6 4 + 5 10 9 + 6 6 5 + 7 8 7 + 8 7 5 + 9 9 7 + 10 9 9 0 11 10 8 + 12 8 6 +
Tổng số dấu n = 10 ; số dấu cộng c = 9 Tra bảng B(10;5)
p p(k 0) p (k 1) p(k 2) ... p(k 9) 0 0.001
0,0098 0.0439 0.1172 0.2051 0.2461 0.2051 0.1172 0.0439 0.0098 0.999 1
p 0.9991 0.005 0 Chấp nhận H0
Như vậy với 0.05 sản phẩm A được ưa thích hơn hoặc bằng sản phẩm B
Bài 7.9: Dùng phương pháp kiểm định dấu: Giả thuyết: H : p 0 .5 0
( p là sác xuất cách trả lương cũ được hài lòng hơn cách trả lương mới) H : p 0.5 1 CN
Điểm cho cách trả lương Dấu (A-B) A B 1 53 80 - 2 63 75 - 3 45 50 - 4 37 30 + 5 74 65 + 6 37 85 - 7 55 66 - 8 65 70 - 9 32 75 - 10 15 15 0
Tổng số dấu n = 9, số dấu cộng c = 2
Sác xuất tích lũy các khả năng k lây từ 2 đến 9 dấu cộng là p p k
p k p k n ( 2) ( 3) ... ( 9) 0.0703
0.1641 0.24610.16410.0703 0.0176 0.002 0.998 Ta thấy p 0
.05 Chấp nhận H n 0
Như vậy với 0.05 ; cách trả lương cũ ít được hài lòng hơn so với cách trả lương mới. Bài 7.10: Ta có: KH 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Điểm 53 63 45 37 74 37 55 65 32 15 30 67 90 45 75 56 80 59 70 25 cách trả lương cũ Điểm 80 75 50 30 65 85 66 80 75 15 25 46 80 70 66 85 90 70 56 30 cách trả lương mới Dấu - - - + + - - - - 0 + + + - + - - - + - Giả thuyết: H : p 0 .05 0
( Với p là sác xuất cách trả lương cũ được hài lòng hơn cách trả lương mới)
H : p 0.5 1
Tổng số dấu n= 19; tổng số dấu cộng c = 7
Sác xuất tích lũy các khả năng k lấy từ 7 đến 19 dấu cộng là: p p k
p k p k n ( 7) ( 8) ... ( 19) 1
[p(k 0) p(k 1
) ... p(k 8)] 1
[0 0 0.0003 0.0018 0.0074 0.0222 0.0518 0.0961 0.1442] 0.6765 Ta thấy p 0
.05 chấp nhận H n 0
Như vậy 0.05 cách trả lương cũ ít được hài lòng so với cách trả lương mới. Bài 7.1
1 : Phương pháp kiểm định khi bình phương với 0.05 Cặp giả thuyết: H :
0 Quy mô và tỉ suất lợi nhuận là độc lập H : 1
Quy mô và tỉ suất lợi nhuận có quan hệ phụ thuộc
Bảng quy mô là tỉ suất lợi nhuận của 140 doanh nghiệp: Quy mô
Tỉ suất lợi nhuận trên vốn(%) 5->10 10->15 15->20 Cộng Vừa 20 60 6 86 (15,35) (55,29) (15,36) Nhỏ 5 30 19 54 (9,64) (34,71) (9,64) Cộng 25 90 25 140 n xn (Với ix iy là số trong ngoặc) 0 n ij n 2 k m (n n ) Ta có ij 0ij k Với k=2;m=3 k 1 j 1 0 n ij 2 2 2 (20 15.36) (60 55.29) (19 9.64) ... 19.46 15.36 55.29 9.64 2 2 X X 5.991 (k 1)(m 1); 2;0.05 Tra bảng
bác bỏ H chấp nhận H 2 0 1 k X
(k 1)(m 1);
Như vậy với 0.05 quy mô và tỷ suất lợi nhuận có quan hệ phụ thuộc.




