12 trang 94 lượt tải

Bài tập cuối chương 2 | Bài giảng PowerPoint Toán 8 | Kết nối tri thức

188

Bài giảng điện tử Toán lớp 8 Kết nối tri thức được biên soạn kỹ càng, tính toán chi tiết về thời gian, các hoạt động dạy và học sẽ đảm bảo giờ học đi theo trình tự, diễn ra thành công. Giúp người giảng dạy trình bày bài giảng sinh động, thu hút hơn. Đồng thời học sinh dễ dàng học tập, từ đó trình bày ý tưởng, báo cáo của mình với thầy cô và bạn bè. Vậy dưới đây là trọn bộ Giáo án PowerPoint Toán 8 Kết nối tri thức mời các bạn cùng theo dõi và tải tại đây.

Chủ đề: Giáo án Toán 8 61 tài liệu

Môn: Toán 8 1.9 K tài liệu

Sách: Kết nối tri thức

Tác giả:

Profile

M. Hậu

1 năm trước
Danh sách Quiz
/12
BÀI TẬP CUỐI CHƯƠNG II
BÀI TẬP CUỐI CHƯƠNG II
Đại số 8 – sách KNTTVCS
KHỞI ĐỘNG
KHỞI ĐỘNG
(
𝑥 − 𝑦
)
(
𝑥
2
+𝑥𝑦 + 𝑦
2
)
(
𝑥+ 𝑦
) (
𝑥 − 𝑦
)
𝑥
2
−2 𝑥𝑦 +𝑦
2
(
𝑥+ 𝑦
)
2
(
𝑥+ 𝑦
)
(
𝑥
2
− 𝑥𝑦 + 𝑦
2
)
(
𝑥 − 𝑦
)
3
𝑥
3
+ 𝑦
3
𝑥
3
− 𝑦
3
𝑥
2
+2 𝑥𝑦 +𝑦
2
𝑥
2
− 𝑦
2
(
𝑦 − 𝑥
)
2
𝑥
3
−3 𝑥
2
𝑦 +3 𝑥 𝑦
2
− 𝑦
3
(
𝑥+ 𝑦
)
3
Bài 2.29 – SGK tr47
Khẳng định nào sau đây là đúng ?
2 2
. 2 .A A B A B A AB B
2 2
. 2 .B A B A B A AB B
2 2
. .C A B A B A B
2 2
. .D A B A B A B
Đáp án D
Bài 2.30 – SGK tr47
Biểu thức : viết dưới dạng bình phương của một tổng :
Đáp án D
2
. 5 2A x y
2
. 2 5B x y
2 2
25 20 4x xy y
II. Luyện tập
1. Vận dụng hằng đẳng thức để tính nhanh , tính giá trị biểu thức
a)
, tại x = 102
, tại x = 999
Lời giải
a)
Thay x = 102 vào biểu thức trên ta có:
Vậy giá trị của biểu thức trên là 10000 tại x=102.
b)
Thay x = 999 vào biểu thức trên ta có:
Vậy giá trị của biểu thức trên là 1000000000 tại x=999.
Bài 2.32-sgk/tr47 . Tính nhanh giá trị của các biểu thức sau :
2
) 4 4a x x
3 2
) 3 3 1b x x x
2
2
4 4 2x x x
2
2
102 2 100 10000
3
3 2
3 3 1 1x x x x
3
3
999 1 1000 1000000000
II. Luyện tập
1. Vận dụng hằng đẳng thức để tính nhanh , tính giá trị biểu thức
Bài 2.31-sgk/tr47 . Hãy chọn phương án đúng :
Rút gọn biểu thức :
ta được
3
. 1B x
3
.8 1C x
3
A= 2 1 6 2 1x x x
II. Luyện tập
1. Vận dụng hằng đẳng thức để tính nhanh , tính giá trị biểu thức
Bài 2.33-sgk/tr47 . Rút gọn biểu thức :
a)
Lời giải
2
a) 2 5 (2 5 ) 2 5x y x y x y
2 2 2 2
b) 2 2 4 2 4 2x y x xy y x y x xy y
2
2 2 2 2
2
a) 2 5 (2 5 ) 2 5
4 25 4 20 25
8 20
x y x y x y
x y x xy y
x xy
2 2 2 2
3 3 3 3
3 3
b) 2 2 4 2 4 2
8 8
9 7
x y x xy y x y x xy y
x y x y
x y
z
II. Luyện tập
Bài 2.28-sgk/tr47 . Hãy chọn phương án đúng :
a)
A. x-1 và x+8
B. x-1 và x-8
2. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử.
Đa thức :
2
9 8x x
được phân tích thành tích của 2 đa thức
C. x-2 và x-4
D. x-2 và x+4
II. Luyện tập
Bài 2.34-sgk/tr47 . Phân tích các đa thức sau thành nhân tử :
a)
2. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử.
2 2
a)6 24x y
3 3
b)64 27x y
4 3 2
c) 2x x x
3
3
d) 8x y y
Lời giải
2 2 2 2
a)6 24 6 4
6 2 2
x y x y
x y x y
b )64 𝑥
3
− 27 𝑦
3
=
(
4 𝑥
)
3
−
(
3 𝑦
)
3
¿
(
4 𝑥 −3 𝑦
)
(
16 𝑥
2
+12 𝑥𝑦 +9 𝑦
2
)
4 3 2 2 2
2
2
c) 2 ( 2 1)
1
x x x x x x
x x
3 2
3 2
2 2 2 2
2 2
d) 8 2 2 4
2 2 2 4
4 7
x y y x y y x y y x y y
x y x xy y xy y y
x y x xy y
z
II. Luyện tập
3. Chứng minh hằng đẳng thức
a)
Lời giải
Diện tích của hình vuông ABCD là
2
a b
Diện tích hình vuông P là
2
a
Diện tích hình vuông S là
2
b
Diện tích của hình chữ nhật Q và R lần lượt là ab và ba.
Suyra
2
2 2 2 2
2a b a ab ba b a ab b
z
Hướng dẫn về nhà
- Đọc lại toàn bộ các dạng bài đã chữa .
a)
BT: Bác Ngọc dự định gấp một khối lập phương có cạnh là 5cm. Sau khi xem xét
lại, bác Ngọc quyết định tăng độ dài của khối lập phương thêm x (cm ). Viết đa thức
biểu thị phần thể tích tăng thêm của khối lập phương mới so với khối lập phương dự
định gấp ban đầu theo x.

Tài liệu khác của Toán 8

Preview text:

BÀI BÀ I TẬP P CUỐI CH UỐI CHƯƠNG II
Đại số 8 – sách KNTTVCS KHỞI ĐỘNG
( 𝑥 − 𝑦 )( 𝑥2+ 𝑥𝑦 + 𝑦2) 𝑥3 + 𝑦3
( 𝑥+ 𝑦 ) ( 𝑥 − 𝑦 ) 𝑥3 − 𝑦3
𝑥2 −2 𝑥𝑦 + 𝑦 2
𝑥2+2 𝑥𝑦 + 𝑦 2 ( 𝑥 + 𝑦 )2 𝑥2 − 𝑦2
( 𝑥 + 𝑦 ) ( 𝑥2 − 𝑥𝑦 + 𝑦 2 ) ( 𝑦 − 𝑥 )2
𝑦3+ 3 𝑥 𝑦2+3 𝑥 𝑦2+ 𝑥3
𝑥3 −3 𝑥2 𝑦 +3 𝑥 𝑦2− 𝑦3 ( 𝑥 − 𝑦 )3 ( 𝑥 + 𝑦 )3 Bài 2.29 – SGK tr47
Khẳng định nào sau đây là đúng ?
A A B  A B 2 2 .
A  2AB B .
B A B  A B 2 2 .
A  2AB B .
C AB  AB 2 2 . A B .
D AB  AB 2 2 . A B . Đáp án D Bài 2.30 – SGK tr47 Biểu thức : 2 x xy  vi 2 25 20
4y ết dưới dạng bình phương của một tổng : 2 2 . A .
B  2x   5y
 5x    2 y         Đáp án D a) II. Luyện tập
1. Vận dụng hằng đẳng thức để tính nhanh , tính giá trị biểu thức
Bài 2.32-sgk/tr47 . Tính nhanh giá trị của các biểu thức sau : 2 a)x 3 2
 4x  4 , tại x = 102
b)x  3x  3x 1 , tại x = 999 Lời giải
a) x x   x  b)   2 2 4 4 2
x x x    x   3 3 2 3 3 1 1
Thay x = 102 vào biểu thức trên ta có:
Thay x = 999 vào biểu thức trên ta có:    2 2 102 2 1  00 1  0000    3 3 999 1 1000  1000  000000
Vậy giá trị của biểu thức trên là 10000 tại x=102. Vậy giá trị của biểu thức trên là 1000000000 tại x=999. II. Luyện tập
1. Vận dụng hằng đẳng thức để tính nhanh , tính giá trị biểu thức
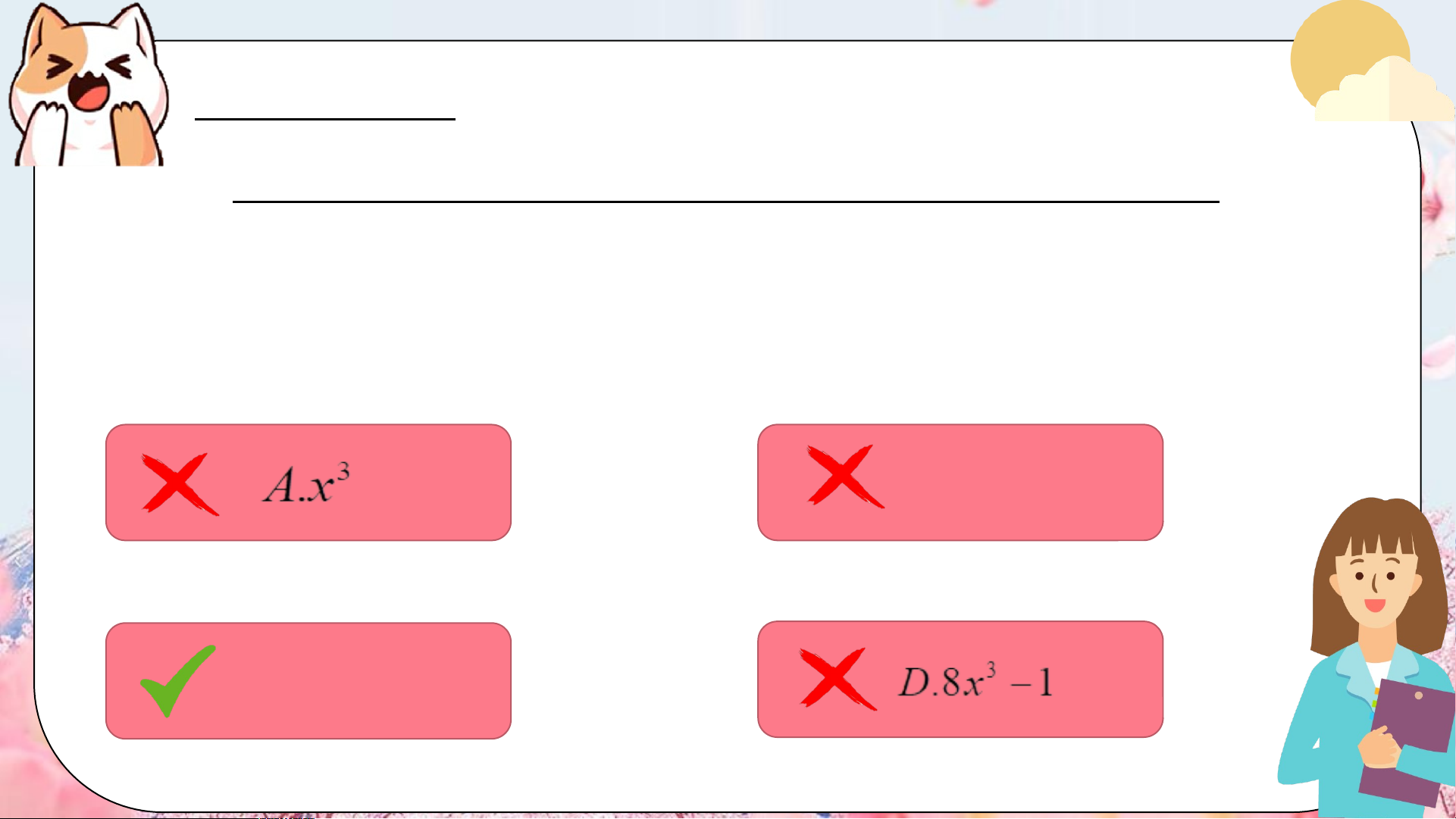
Bài 2.31-sgk/tr47 . Hãy chọn phương án đúng : Rút gọn biểu thức 3 : A=  2x  
1  6x  2x   1 ta được 3 . B x 1 3 C.8x 1 a) II. Luyện tập
1. Vận dụng hằng đẳng thức để tính nhanh , tính giá trị biểu thức
Bài 2.33-sgk/tr47 . Rút gọn biểu thức :  x 2 2 2 2 
yx y   x y 2 a) 2 5 (2 5 ) 2 5
b) x  2y  x  2xy  4y   2x y  4x  2xy y  Lời giải
a)2x 5y(2x5y)2x5y2
b)x2y 2 2
x  2xy4y 2xy 2 2
4x 2xyy  2 2 2 2 4
x  25y 4x 20xy 25y 3 3 3 3
x 8y 8x y 2 8  x 20xy 3 3 9  x 7y a) II. Luyện tập
2. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử.
Bài 2.28-sgk/tr47 . Hãy chọn phương án đúng : Đa thức : 2
x  9x 8 được phân tích thành tích của 2 đa thức z A. x-1 và x+8 B. x-1 và x-8 C. x-2 và x-4 D. x-2 và x+4 a) II. Luyện tập
2. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử.
Bài 2.34-sgk/tr47 . Phân tích các đa thức sau thành nhân tử : 2 2 a)6x 3 3  24 y b)64x  27 y 4 3 2
c)x  2x xx y3 3 d)  8 y Lời giải 2 2 x y   2 2 a)6 24 6 x  4 y
b )64 𝑥3− 27 𝑦3=( 4 𝑥)3− (3 𝑦)3 6
  x  2 y  x  2 y
¿ (4 𝑥 −3 𝑦 )( 16 𝑥2+12 𝑥𝑦 +9 𝑦 2) 4 3 2 2 2 c)x 3 2
 2x x x (x  2x 1) d) x y 3 8y
x y 2y  x y 2y x y 2 4y               x y  2 2 2 2
x  2xy y  2xy  2 y  4 y
x x   2 2 1   
x y   2 2
x  4xy  7 y  a) II. Luyện tập
3. Chứng minh hằng đẳng thức z Lời giải
Diện tích của hình vuông ABCD là    2 a b
Diện tích hình vuông P là 2 a
Diện tích hình vuông S là 2 b
Diện tích của hình chữ nhật Q và R lần lượt là ab và ba.
Suyra  a b2 2 2 2 2 a
ab ba b a   2ab b a) Hướng dẫn về nhà
- Đọc lại toàn bộ các dạng bài đã chữa .
BT: Bác Ngọc dự định gấp một khối lập phương có cạnh là 5cm. Sau khi xem xét
lại, bác Ngọc quyết định tăng độ dài của khối lập phương thêm x (cm ). Viết đa thức z
biểu thị phần thể tích tăng thêm của khối lập phương mới so với khối lập phương dự
định gấp ban đầu theo x.
Document Outline

  • Slide 1
  • KHỞI ĐỘNG
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12

Tài liệu liên quan: