Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số – Lê Bá Bảo Toán 12

Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số – Lê Bá Bảo Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

71 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
G
G
i
i
á
á
o
o
v
v
i
i
ê
ê
n
n
:
:
L
L
Ê
Ê
B
B
Á
Á
B
B
Ả
Ả
O
O
_
_
T
T
r
r
ư
ư
ờ
ờ
n
n
g
g
T
T
H
H
P
P
T
T
Đ
Đ
ặ
ặ
n
n
g
g
H
H
u
u
y
y
T
T
r
r
ứ
ứ
,
,
H
H
u
u
ế
ế
S
S
Đ
Đ
T
T
:
:
0
0
9
9
3
3
5
5
.
.
7
7
8
8
5
5
.
.
1
1
1
1
5
5
Đ
Đ
ă
ă
n
n
g
g
k
k
í
í
h
h
ọ
ọ
c
c
t
t
h
h
e
e
o
o
đ
đ
ị
ị
a
a
c
c
h
h
ỉ
ỉ
:
:
1
1
1
1
6
6
/
/
0
0
4
4
N
N
g
g
u
u
y
y
ễ
ễ
n
n
L
L
ộ
ộ
T
T
r
r
ạ
ạ
c
c
h
h
,
,
T
T
P
P
H
H
u
u
ế
ế
H
H
o
o
ặ
ặ
c
c
T
T
r
r
u
u
n
n
g
g
t
t
â
â
m
m
K
K
m
m
1
1
0
0
H
H
ư
ư
ơ
ơ
n
n
g
g
T
T
r
r
à
à
Chuyªn ®Ò:
KH¶O S¸T HµM Sè
Chñ ®Ò:
GI¸ TRÞ LíN NHÊT - GI¸
TRÞ NHá NHÊT CñA HµM Sè
HuÕ, th¸ng 6/2019
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------1
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
CHUY£N §Ò: KH¶O S¸T HµM Sè
Chñ ®Ò 3:
GI¸ TRÞ LíN NHÊT Vµ
GI¸ TRÞ NHá NHÊT CñA HµM Sè
Trong quá trình sưu tầm, biên soạn lời giải, có sai sót gì kính mong quý thầy cô và các em học sinh góp
ý để đề kiểm tra được hoàn chỉnh hơn! Xin chân thành cảm ơn!
NỘI DUNG ĐỀ BÀI
DẠNG TOÁN 1: GTLN - GTNN TRÊN KHOẢNG (NỬA KHOẢNG - ĐOẠN)
Câu 1: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
()fx
liên tục trên


;ab
. Khẳng định nào sau đây đúng?
A. Hàm số không có giá trị lớn nhất trên đoạn


;ab
.
B. Hàm số luôn có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn


;ab
.
C. Hàm số không có giá trị nhỏ nhất trên đoạn


;ab
.
D. Hàm số luôn có cực đại và cực tiểu trên đoạn


;ab
.
Câu 2: (THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số
y f x
liên tục trên
thỏa mãn giá trị nhỏ nhất của hàm số trên là
. Khẳng định nào sau đây là đúng?
A.
0fx
x
,
0
x
,
0
0fx
. B.
0fx
x
.
C.
0fx
x
,
0
x
,
0
0fx
. D.
0fx
x
.
Câu 3: (THPT CẦU GIẤY HÀ NỘI NĂM 2018-2019 LẦN 01) Cho
,ab
,
0 ab
, hàm số
()y f x
có đạo hàm trên thỏa mãn
0fx
,
 ;x a b
. Giá trị nhỏ nhất của hàm số đã cho trên
đoạn


;ab
bằng
A.
fb
. B.



2
ab
f
. C.
fa
. D.
f ab
.
Câu 4: (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số
()y f x
liên tục và có bảng biến thiên trên đoạn


1;3
như hình vẽ. Khẳng định nào sau đây đúng?
A.
1;3
max ( ) (0).f x f


B.


1;3
max 3f x f
. C.


1;3
max 2f x f
. D.



1;3
max 1f x f
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------2
Câu 5: (THPT CỔ LOA HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
xác định, liên tục trên và
có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số
y f x
trên đoạn


0;2
bằng
A.
1
. B.
3
. C.
. D.
2
.
Câu 6: (THPT NGUYỄN DU - DAK LAC - NĂM 2018-2019) Cho hàm số
y f x
xác định, liên tục
trên và có bảng biến thiên như sau
Khẳng định nào sau đây sai?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x
.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
1
.
D. Hàm số có đúng hai cực trị.
Câu 7: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số
y f x
xác định, liên tục trên và có
bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng
1
.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
1
.
D. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x
.
Câu 8: (Đề minh họa) Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới
đây đúng ?
x

1

y
y


Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------3
A.
5.
CĐ
y
B.
0.
CT
y
C.
min 4.y
D.
max 5.y
Câu 9: (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên trên
5;7
như sau:
Mệnh đề nào dưới đây đúng?
A.
min

5;7
6fx
. B.
min

5;7
2fx
. C.
-5;7
max
9fx
. D.
max

5;7
6fx
.
Câu 10: (SỞ GD&ĐT KIÊN GIANG NĂM 2018-2019) Hàm số
y f x
liên tục trên và có bảng biến
thiên như hình bên dưới.
Biết
48ff
,
khi đó giá trị nhỏ nhất của hàm số đã cho trên bằng
A.
9
. B.
4f
. C.
8f
. D.
4
.
Câu 11: (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
xác định và liên tục trên có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn
nhất
M
của hàm số
y f x
trên đoạn


2;2
.
A.
5; 1mM
. B.
2; 2mM
. C.
1; 0mM
. D.
5; 0mM
.
Câu 12: (THPT THÁI PHIÊN HẢI PHÒNG NĂM 2018-2019) Cho hàm số
fx
lên tục trên đoạn


1;3
và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số

2
3sin 1y f x
bằng
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------4
A.
. B.
2
. C.
. D.
1
.
Câu 13: Cho hàm số
()y f x
có đồ thị như hình dưới. Gọi
,mM
lần lượt là
giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( 2 )y f x
trên
1
1; .
2



Giá trị
mM
bằng
A.
0.
B.
4.
C.
19
8
D.
4.
Câu 14: (THPT HOÀNG VĂN THỤ - HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có đạo hàm cấp
2 trên , hàm số
y f x
có đồ thị như hình vẽ bên.
Giá trị lớn nhất của hàm số




sin 3cos
2
xx
yf
trên đoạn




5
;
66
bằng
A.



5
6
f
. B.



3
f
. C.
0f
. D.



6
f
.
Câu 15: Cho hàm số
y f x
liên tục, đồng biến trên đoạn


;ab
. Khẳng định nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn


;ab
.
B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng
;ab
.
C. Phương trình
0fx
có nghiệm duy nhất thuộc đoạn


;ab
.
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn


;ab
.
Câu 16: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số
fx
xác định,liên tục trên và có
bảng biến thiên sau:
Phát biểu nào sau đây đúng?
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 2.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------5
B. Hàm số nhận giá trị dương với mọi
x
.
C. Trên


2;8
hàm số có giá trị lớn nhất là
M
, giá trị nhỏ nhất là
m
. Giá trị biểu thức
36mM
.
D. Hàm số có đúng một cực trị.
Câu 17: Cho hàm số
y f x
liên tục trên đoạn (-1;3) và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn


1;3
. Giá trị của
Mm
bằng
A. 0. B. 1. C. 4. D. 5.
Câu 18: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
max 2.
x
fx
B.


1;1
max 1.
x
fx
C.


1;1
max 0.
x
fx
D.



1;1
max 3.
x
fx
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
min 2.
x
fx
B.


1;1
min 1.
x
fx
C.


1;1
min 0.
x
fx
D.



1;1
min 3.
x
fx
Câu 20: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------6
A.



0;1
min 3.
x
fx
B.


0;1
min 2.
x
fx
C.


0;1
min 0.
x
fx
D.


0;1
min 1.
x
fx
Câu 21: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


5;15
max 5 .
x
f x f
B.


5;15
max 15 .
x
f x f
C.


x
fx
5;15
max 2.
D.


5;15
max 10 .
x
f x f
Câu 22: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.



15; 5
max 5 .
x
f x f
B.



15; 5
max 15 .
x
f x f
C.


15; 5
max 2.
x
fx
D.



15; 5
max 10 .
x
f x f
Câu 23: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
2 1.g x f x
Khẳng định nào sau đây đúng?
A.


1;1
max 2.
x
gx
B.


1;1
max 5.
x
gx
C.


1;1
max 1.
x
gx
D.



1;1
max 5.
x
gx
Câu 24: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
3 4 .g x f x
Khẳng định nào sau đây đúng?
A.


1;1
min 15.
x
gx
B.



1;1
min 5.
x
gx
C.



1;1
min 15.
x
gx
D.



1;1
max 3.
x
gx
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------7
Câu 25: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
max 2.
x
fx
B.


1;1
max 1.
x
fx
C.


1;1
max 0.
x
fx
D.


1;1
max 3.
x
fx
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
min 2.
x
fx
B.


1;1
min 1.
x
fx
C.


1;1
min 0.
x
fx
D.


1;1
min 3.
x
fx
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
sin .g x f x
Khẳng định nào sau đây đúng?
A.
max 2.gx
B.
max 1.gx
C.
max 3.gx
D.
max 4.gx
Câu 28: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
cos .g x f x
Khẳng định nào sau đây đúng?
A.



0;
2
min 1.gx
B.



0;
2
min 2.gx
C.




0;
2
min 3.gx
D.



0;
2
min 0.gx
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------8
Câu 29: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt

32
3.g x f x f x
Khẳng định nào sau đây đúng?
A.


1;1
max 4.gx
B.


1;1
max 4.gx
C.


1;1
max 0.gx
D.


1;1
max 2.gx
Câu 30: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Giá trị lớn nhất của hàm số
3
x
fx
x
trên đoạn


2;3
bằng
A.
3.
B.
2.
C.
1
.
2
D.
2.
Câu 31: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số

1
()f x x
x
trên nửa khoảng

2;
là
A.
. B.
5
2
. C.
. D.
7
2
.
Câu 32: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn


2;4
.
A.


2;4
min 6.y
B.



2;4
min 2.y
C.



2;4
min 3.y
D.


2;4
19
min .
3
y
Câu 33: Tìm giá trị nhỏ nhất của hàm số

9
yx
x
trên đoạn
[2;4]
.
A.
[
2;4]
13
min .
2
y
B.
[
2;4]
25
min .
4
y
C.
[
2;4]
min 6.y
D.
[

2;4]
min 6.y
Câu 34: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Tìm giá trị lớn nhất của hàm số
15y f x x x
trên đoạn


1;5
.
A.


1;5
max 3 2fx
. B.


1;5
max 2fx
. C.


1;5
max 2 2fx
. D.


1;5
max 2fx
.
Câu 35: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
17y x x
. Khi đó
có bao nhiêu số nguyên dương nằm giữa
m
và
M
?
A.
1
. B.
5
. C.
. D.
0
.
Câu 36: (THPT THĂNG LONG HÀ NỘI NĂM 2018-2019 LẦN 02) Hàm số

8
10
yx
x
đạt giá trị nhỏ
nhất trên đoạn


39
10 ;10
tại
x
bằng
A.
4
10
. B.
3
10
. C.
5
10
. D.
6
10
.
Câu 37: (SỞ GD&ĐT BÌNH THUẬN NĂM 2018-2019) Giá trị lớn nhất của hàm số
2
5y x x
bằng
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------9
A.
. B.
5
2
. C.
6
. D.
2
.
Câu 38: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Tìm giá trị nhỏ nhất của hàm số
2
sin 4sin 5y x x
.
A.
20
. B.
8
. C.
9
. D.
0
.
Câu 39: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
2sin 3
sin 1
x
y
x
trên đoạn



0;
2
là
A.
. B.
2
. C.
. D.
5
2
.
Câu 40: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số
3
sin 3sin 2f x x x
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó
2Mm
là
A.
. B. 1. C. 4. D. 5.
Lời giải
Đặt
sinxt



1; 1t
. Ta có
3
3 2.f t t t
Xét hàm số
3
32f t t t
với



1; 1 ;t
2
' 3 3 0f t t
1t
hoặc
1.t
Ta có
14f
,
1 0 .f
Suy ra, giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là 4 và 0 hay
4 ; m 0.M
Giá trị
2 4 2.0 4Mm
.
Câu 41: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
cos2 cos 1f x x x
. Giá trị nhỏ nhất của hàm số trên là
A.

1
min
8
fx
. B.

1
min
4
fx
. C.
1
min
8
fx
. D.
1
min
4
fx
.
Câu 42: (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Giá trị lớn nhất của hàm số

2
2sin cosy x x
là phân số tối giản có dạng với
,ab
là các số nguyên dương. Tìm
–ab
.
A.
. B.
9
. C.
. D.
10
.
Câu 43: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
3cos2 4siny x x
là
A.
1
. B.
7
. C.
5
. D.
11
3
.
Câu 44: (MĐ 102 BGD&ĐT NĂM 2016-2017) Tìm giá trị lớn nhất
M
của hàm số
42
23y x x
trên
đoạn


0; 3
.
A.
9M
. B.
83M
. C.
1M
. D.
6M
.
Câu 45: (MĐ 104 BGD&ĐT NĂM 2018-2019) Giá trị nhỏ nhất của hàm số

3
3f x x x
trên đoạn


3;3
bằng
A.
18
. B.
18
. C.
2
. D.
2
.
Câu 46: (MĐ 104 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số

2
2
yx
x
trên đoạn



1
;2
2
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------10
A.
17
4
m
. B.
10m
. C.
5m
. D.
3m
.
Câu 47: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Gọi
M
và
m
lầ lượt là giá trị lớn
nhất và giá trị nhỏ nhất của hàm số
2 4 6f x x x
trên


3;6
. Tổng
Mm
có giá trị là:
A.
12
. B.
6
. C.
18
. D.
4
.
Câu 48: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
M
là giá trị lớn nhất của hàm số
22
4 4 6 4 1f x x x x x
. Tính tích các nghiệm của phương trình
f x M
.
A.
. B.
4
. C.
2
. D.
4
.
Câu 49: (MĐ 103 BGD&ĐT NĂM 2016-2017) Tìm giá trị nhỏ nhất
m
của hàm số
42
13y x x
trên
đoạn


2;3 .
A.
51
.
4
m
B.
49
.
4
m
C.
13.m
D.
51
.
2
m
Câu 50: (SỞ GD&ĐT LẠNG SƠN NĂM 2018-2019) Tìm x để hàm số
2
4y x x
đạt giá trị lớn
nhất.
A.
2x
. B.
22x
. C.
1x
. D.
2.x
Câu 51: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2016-2017) Tính giá trị nhỏ nhất của hàm số

2
4
3yx
x
trên khoảng
0;
.
A.

3
0;
min 3 9.y
B.

0;
min 7.y
C.

0;
33
min .
5
y
D.

3
0;
min 2 9.y
Câu 52: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Gọi M, m lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của hàm số
f x x x
trên đoạn


0;3
. Giá trị của biểu thức
2Mm
gần với số
nào nhất trong các số dưới đây?
A.
1,768
. B.
0,767
. C.
1,767
. D.
0,768
.
Câu 53:
Câu 54:
(THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 02) Giá trị nhỏ nhất của hàm số
1 2 3 4 2019f x x x x x
là
A.
2017.
B.
2020.
C.
2018.
D.
2019.
Câu 55: (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Tổng giá trị lớn nhất
M
và giá trị nhỏ
nhất
m
của hàm số
2
64f x x x
trên đoạn


0;3
có dạng
a b c
với
a
là số nguyên
và
,bc
là các số nguyên dương. Tnh
S a b c
.
A.
. B.
2
. C.
22
. D.
5
.
Câu 56: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 02) Cho hàm số
fx
có đạo hàm
2
23f x x x x
,
x
. Giá trị lớn nhất của hàm số đã cho trên đoạn


0;4
bằng
A.
0f
. B.
2f
. C.
3f
. D.
4f
.
Câu 57: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
xác định
và liên tục trên , đồ thị của hàm số
y f x
như hình vẽ sau:
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------11
Giá trị lớn nhất của hàm số
y f x
trên đoạn


1;2
là
A.
1f
. B.
1f
. C.
2f
. D.
0f
.
Câu 58: (THPT YÊN MÔ A-NINH BÌNH NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
liên tục trên



7
0;
2
có đồ thị hàm số
y f x
như hình vẽ sau:
Hàm số
y f x
đạt giá trị nhỏ nhất trên



7
0;
2
tại điểm
0
x
nào dưới đây?
A.
0
0x
. B.
0
7
2
x
. C.
0
3x
. D.
0
1x
.
Câu 59: (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
fx
có đạo hàm
là
fx
. Đồ thị của hàm số
y f x
được cho như hình vẽ bên. Biết rằng
0 1 2 3 5 4f f f f f
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
fx
trên
đoạn


0;5
.
A.
5 , 3 .m f M f
B.
5 , 1 .m f M f
C.
0 , 3 .m f M f
D.
1 , 3 .m f M f
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------12
Câu 60: (THPT LÝ NHÂN TÔNG LẦN 1 NĂM 2018-2019) Cho hàm số có
fx
có đạo hàm là hàm
'fx
. Đồ thị hàm số
'fx
như hình vẽ bên. Biết rằng
0 1 2 2 4 3f f f f f
. Tìm
giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
fx
trên đoạn


0;4
.
A.
4 , 2m f M f
. B.
1 , 2 .m f M f
C.
4 , 1m f M f
. D.
0 , 2m f M f
.
Câu 61: (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Cho hàm số
fx
có đồ thị của hàm
số
fx
như hình vẽ. Biết
0 1 2 2 4 3f f f f f
. Giá trị nhỏ nhất
m
, giá trị lớn nhất
M
của hàm số
fx
trên đoạn


0;4
là
A.
4mf
,
1Mf
. B.
4mf
,
2Mf
.
C.
1mf
,
2Mf
. D.
0mf
,
2Mf
.
Câu 62: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số
y f x
có
bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
11
4 3 8
33
g x f x x x x x
trên đoạn


1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Câu 63: (THPT KINH MÔN HAI DƯƠNG NĂM 2018-2019 LẦN 03) Cho hàm số
y f x
có đạo
hàm
fx
. Hàm số
y f x
liên tục trên tập số thực và có bảng biến thiên như sau:
O
2
4
x
y
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------13
Biết rằng

10
1
3
f
,
26f
. Giá trị nhỏ nhất của hàm số

3
3g x f x f x
trên đoạn


1;2
bằng
A.
10
3
. B.
820
27
. C.
730
27
. D.
198
.
DẠNG TOÁN 2: MAX MIN HÀM NHIỀU BIẾN
Câu 64: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
22
2x xy y
. Giá trị nhỏ nhất
của
22
P x xy y
bằng
A.
2
3
. B.
1
6
. C.
1
2
. D.
2
.
Câu 65: (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019)Cho hai số thực
,xy
thay đổi thỏa mãn
điều kiện

22
2xy
. Gọi
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của biểu
thức
33
2( ) 3P x y xy
. Giá trị của
Mn
bằng:
A.
4.
B.
1
.
2
C.
6.
D.
1 4 2.
Câu 66: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Cho
,xy
thỏa mãn
1xy
và
22
1x y xy x y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
1
xy
P
xy
. Tính
Mm
.
A.
1
3
. B.
2
3
. C.
1
2
. D.
1
3
.
Câu 67: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho
,xy
thỏa mãn
22
5 6 5 16x xy y
và hàm số
bậc ba
y f x
có đồ thị như hình vẽ. Gọi
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của





22
22
2
24
xy
Pf
x y xy
. Tính
22
Mm
10
8
6
4
2
2
4
6
8
10
x
7
6
5
4
3
2
1
1
2
3
0
1
-1
A.

22
4Mm
. B.

22
1Mm
. C.

22
25Mm
. D.

22
2Mm
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------14
Câu 68: (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Cho các số thực
,xy
thay đổi
nhưng luôn thỏa mãn
22
3 2 5x xy y
. Giá trị nhỏ nhất của biểu thức
22
2P x xy y
thuộc
khoảng nào sau đây?
A.
4;7
. B.
2;1
. C.
1;4
. D.
7;10
.
Câu 69: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
x
,
y
là các số thực thỏa mãn
1 2 2x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
22
2 1 1 8 4P x y x y x y
. Tính giá trị
Mm
A.
42
. B.
41
. C.
43
. D.
44
.
DẠNG TOÁN 3: BÀI TOÁN THỰC TẾ - TỐI ƯU
Câu 70: (ĐỀ THỬ NGHIỆM BGD&ĐT NĂM 2016-2017) Một vật chuyển động theo quy luật
32
1
9
2
s t t
với
t
(giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và
s
(mét) là
quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian
10
giây, kể
từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A.
/216 ms
. B.
/30 ms
. C.
/400 ms
. D.
/54 ms
.
Câu 71: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để
hộp nhận được có thể tích lớn nhất.
A.
6x
. B.
3x
. C.
2x
. D.
4x
.
Câu 72: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông
A
dự định dùng hết
2
6,5m
knh để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không
đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 .m
B.
3
1,61 .m
C.
3
1,33 .m
D.
3
1,50 .m
Câu 73: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Bác Bính có một tấm thép mỏng hình
tròn, tâm O, bán kính
dm4
. Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai
mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình
vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (bỏ qua phần
mối hàn và độ dày của tấm thép).
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------15
A.
3
dm
128 3
27
. B.
3
dm
128 3
81
. C.
3
dm
16 3
27
. D.
3
dm
64 3
27
.
Câu 74: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một chất điểm chuyển động theo
phương trình
32
9 21 9S t t t
trong đó
t
tính bằng giây
()s
và
tính bằng mét
()m
. Tính
thời điểm
()ts
mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất.
A.
4( ).ts
B.
5( ).ts
C.
3( ).ts
D.
7( ).ts
Câu 75: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một công ty bất động sản có 40 căn hộ
cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 3.000.000 đồng một tháng thì mọi căn hộ
đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100.000 đồng một tháng (theo qui
định trong hợp đồng) thì sẽ có một căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì
công ty đó phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng?
A.
3.700.000
đồng. B.
3.500.000
đồng. C.
3.900.000
đồng. D.
4.000.000
đồng.
Câu 76: (SỞ GD QUẢNG NAM 2019) Cho nửa đường tròn đường kính
AB
và hai điểm
,CD
thay đổi
trên nửa đường tròn đó sao cho
ABCD
là hình thang. Diện tích lớn nhất của hình thang
ABCD
bằng
A.
1
2
B.
33
4
C.
1
D.
33
2
Câu 77: (SỞ GD&ĐT CÀ MAU NĂM 2018-2019) Người ta muốn xây một cái bể hình hộp đứng có
thể tích
3
18Vm
, biết đáy bể là hình chữ nhật có chiều dài gấp
lần chiều rộng và bể
không có nắp. Hỏi cần xây bể có chiều cao
h
bằng bao nhiêu mét để nguyên vật liệu xây dựng
là ít nhất (biết nguyên vật liệu xây dựng các mặt là như nhau)?
A.
2 m
. B.
5
2
m
. C.
1 m
. D.
3
2
m
.
Câu 78: (CỤM 1 SỞ GD&ĐT BẠC LIÊU NĂM 2018-2019 LẦN 01) Người ta muốn xây một bể chứa
nước dạng hình hộp chữ nhật không nắp có thể tích 200m
3
. Đáy bể là hình chữ nhật có chiều
dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m
2
. Chi phí thuê công nhân
thấp nhất là
A. 51 triệu đồng . B. 75 triệu đồng. C. 46 triệu đồng. D. 36 triệu đồng.
DẠNG TOÁN 4: PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH
Câu 79: (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên
Tìm tất cả các giá trị của
m
để bất phương trình
11f x m
có nghiệm?
A.
4.m
B.
1m
. C.
2m
. D.
5m
.
Câu 80: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho hàm số
fx
, hàm số
y f x
liên tục trên và có
đồ thị như hình vẽ bên.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------16
Bất phương trình
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
0;2x
khi và chỉ
khi
A.
22mf
. B.
0mf
. C.
22mf
. D.
0mf
.
Câu 81: (MĐ 102 BGD&ĐT NĂM 2018-2019) Cho hàm số
fx
, hàm số
y f x
liên tục trên và có
đồ thị như hình vẽ sau:
Bất phương trình
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
0;2x
khi và chỉ
khi
A.
22mf
. B.
22mf
. C.
0mf
. D.
0mf
.
Câu 82: (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 04) Cho hàm số
y f x
và hàm số
y g x
có đạo hàm xác định trên và có đồ thị như hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số m để phương trình
fx
m
gx
có nghiệm thuộc


2;3
?
A. 4. B. 5. C. 7. D. 6.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------17
Câu 83: (MĐ 103 BGD&ĐT NĂM 2018-2019) Cho hàm số
fx
, hàm số
y f x
liên tục trên và có
đồ thị như hình vẽ bên.
Bất phương trình
2f x x m
(
m
là tham số thực) nghiệm đúng với mọi
0;2x
khi và chỉ
khi
A.
0mf
. B.
24mf
. C.
0mf
. D.
24mf
.
Câu 84: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số
y f x
. Hàm số
y f x
có bảng
biến thiên như sau:
x

2
1


0
y
2

Bất phương trình

3
f x x m
đúng với mọi
1;1x
khi và chỉ khi
A.
1m f x
. B.
11mf
. C.
11mf
. D.
11mf
.
Câu 85: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Số các giá trị nguyên của tham số
m
thuộc đoạn


2019;2019
để phương trình
23
2 4 1 4x m x m x x
có nghiệm là
A.
2011
. B.
2012
. C.
2013
. D.
2014
.
Câu 86: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số
m
để
bất phương trình
2
6 2 8 1x x x x m
nghiệm đúng với mọi



2;8 .x
A.
16m
. B.
15m
. C.
8m
. D.
2 16m
.
Câu 87: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số giá trị nguyên của tham số
m
nằm
trong khoảng
0;2020
để phương trình
1 2019 2020x x m
có nghiệm là
A.
2020
. B.
2021
. C.
2019
. D.
2018
.
Câu 88: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Gọi
S
là tập tất cả các giá trị của tham số
m
để bất
phương trình
4
2 4 2
1 4 5 6x x x m m m
thỏa mãn với mọi giá trị của
x
. Tính tổng
các giá trị của
.S
A.
1
. B.
3
. C.
5.
D.
2
.
Câu 89: (SỞ GD&ĐT QUẢNG BÌNH NĂM 2018-2019) Gọi
S
là tập hợp tất cả các giá trị nguyên
dương của tham số
m
để bất phương trình sau
6 4 3 3 2
3 4 2 0x x m x x mx
nghiệm đúng
với mọi


1;3x
. Tổng tất cả các phần tử của
bằng:
A.
. B.
2
. C.
1
. D.
4
.
Câu 90: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Giá trị lớn nhất của hàm
số

32
1
x x m
y
x
trên


0; 2
bằng
5
. Tham số
m
nhận giá trị là
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------18
A.
5
. B.
1
. C.
3
. D.
8
.
Câu 91: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi
s
là tập hợp các giá trị
nguyên của tham số


0;2019m
để bất phương trình
3
22
10x m x
đúng với mọi



1;1x
. Số phần tử của tập
s
bằng
A.
1
. B.
2020
. C.
2019
. D.
2
.
Câu 92: (CHUYÊN ĐẠI HỌC VINH LẦN 03 NĂM 2018 - 2019) Cho
()fx
mà đồ thị hàm số
'( )y f x
như hình vẽ sau:
Bất phương trình
( ) sin
2
x
f x m
nghiệm đúng với mọi



1;3x
khi và chỉ khi
A.
(0)mf
. B.
(1) 1mf
. C.
( 1) 1mf
. D.
(2)mf
.
Câu 93: (CHUYÊN QUỐC HỌC HUẾ LẦN 3 2018-2019) Cho phương trình
22
2 2 1 2 0m x x x x
(
m
là tham số). Biết rằng tập hợp các giá trị của tham số
m
để
phương trình có nghiệm thuộc đoạn


0 ; 1 2 2
là đoạn


;ab
. Tính giá trị của biểu thức
2T b a
.
A.
4T
. B.
7
2
T
. C.
3T
. D.
1
2
T
.
Câu 94: (THPT CHUYÊN HOÀNG VĂN THỤ HÒA BÌNH NĂM 2018-2019 LẦN 04) Tổng các giá trị
nguyên dương của m để tập nghiệm của bất phương trình

2
1
72
m
xx
có chứa đúng hai số
nguyên là
A.
27
. B.
29
. C.
28
. D.
30
.
DẠNG TOÁN 5: BÀI TOÁN THAM SỐ
Câu 95: (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
32
23y x x m
.
Trên


1;1
hàm số có giá trị nhỏ nhất là
1
. Tính
.m
A.
6m
. B.
3m
. C.
4.m 
D.
5m
.
Câu 96: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số
2
1y x m x
có giá trị lớn nhất bằng
22
thì giá trị của
m
là
A.
2
2
. B.
2
. C.
2
. D.
2
2
.
Câu 97: (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Có một giá trị
0
m
của tham số
m
để hàm số
3 2 2
11y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn


0;1
. Khi đó
mệnh đề nào sau đây đúng ?
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------19
A.
2
00
2018 0.mm
B.
0
2 1 0.m 
C.
2
00
6 0.mm
D.
0
2 1 0.m 
Câu 98: (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị của tham số
m
để giá
trị lớn nhất của hàm số

2
2xm
y
xm
trên đoạn


0;4
bằng
1
.
A.
. B.
2
. C.
. D.
1
.
Câu 99: Cho hàm số
2
8
xm
fx
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn


0;3
bằng
3
. Giá trị
0
m
thuộc khoảng nào trong các
khoảng cho dưới đây?
A.
20;25
. B.
5;6
. C.
6;9
. D.
2;5
.
Câu 100: (MĐ 101 BGD&ĐT NĂM 2016-2017) Cho hàm số
1
xm
y
x
(
m
là tham số thực) thỏa mãn
[
2;4]
min 3y
. Khẳng định nào sau dưới đây đúng?
A.
1.m
B.
3 4.m
C.
4.m
D.
1 3.m
Câu 101: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho hàm số
1
xm
y
x
(
m
là tham số thực) thoả mãn





1;2
1;2
16
min max
3
yy
. Khẳng định nào dưới đây đúng?
A.
0m
B.
4m
C.
02m
D.
24m
Câu 102: (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm
số
1
xm
y
x
trên


1;2
bằng
8
(
m
là tham số thực). Khẳng định nào sau đây đúng?
A.
10m
. B.
8 10m
. C.
04m
. D.
48m
.
Câu 103: (THPT HUỲNH MẪN ĐẠT NĂM 2018-2019 LẦN 01) Cho hàm số
2sin cos
sin cos
x m x
y
xx
đạt giá
trị lớn nhất trên



0;
4
bằng
1
. Khẳng định nào sau đây đúng?
A.

1;0m
. B.
0;1m
. C.
1;2m
. D.
2;3m
.
Câu 104: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
,AB
lần lượt là giá trị nhỏ nhất, giá trị
lớn nhất của hàm số

2
1
x m m
y
x
trên đoạn


2;3
. Tìm tất cả các giá trị thực của tham số
m
để

13
2
AB
.
A.
1; 2mm
. B.
2m
. C.
2m
. D.
1; 2mm
.
Câu 105: (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Gọi
T
là tập hợp tất cả giá trị của tham số
m để hàm số
2
1mx
y
xm
có giá trị lớn nhất trên đoạn


2;3
bằng
5
6
. Tính tổng của các phần tử
trong
T
.
A.
17
5
. B.
16
5
. C.
2
. D.
6
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------20
Câu 106: (THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số
x
2
3
3y x m
.
Tổng tất cả các giá trị của tham số
m
sao cho giá trị nhỏ nhất của hàm số trên đoạn


1;1
bằng 1 là
A.
1
. B.
4
. C.
. D.
4
.
Câu 107: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số
sin
sin 1
xm
fx
x
. Tìm giá trị
của
m
để giá trị lớn nhất của hàm số
()fx
trên đoạn



2
0;
3
bằng
2.
A.
5.m
B.
5
.
2
m
m
C.
2.m
D.
3.m
Câu 108: Có bao nhiêu giá trị nguyên dương của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
xm
y
x
trên đoạn


2; 3
bằng 14?
A.
. B.
1
. C.
. D. 4.
Câu 109: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
2y x x m
trên đoạn


1;2
bằng
5
.
A.
1
. B.
2
. C.
2
. D.
1
.
Câu 110: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017-2018) Gọi S là tập hợp tất cả các giá trị của tham số
thực m sao cho giá trị lớn nhất của hàm số
3
3y x x m
trên đoạn


0;2
bằng 3. Số phần tử
của S là
A. 1. B. 2. C. 0. D. 6.
Câu 111: (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số
m
để hàm số

2
1x mx
y
xm
liên tục và đạt giá trị nhỏ nhất trên đoạn


0;2
tại một điểm
0
0;2x
.
A.
01m
. B.
1m
. C.
2m
. D.
11m
.
Câu 112: (THPT Phụ Dực - Thái Bình - 2019) Gọi
là tập hợp các giá trị của
m
để hàm số
32
3y x x m
đạt giá trị lớn nhất bằng
50
trên
[ 2;4]
. Tổng các phần tử thuộc
là
A.
. B.
36
. C.
140
. D.
0
.
Câu 113: (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số

2
2
2
x mx m
y
x
trên đoạn


1;1
bằng
3
. Tính tổng tất cả các
phần tử của
S
.
A.
8
3
. B.
5
. C.
5
3
. D.
1
.
Câu 114: (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực
m
để giá trị nhỏ nhất
của hàm số
2
4 3 4y x x m x
bằng
5
.
A.
. B.
3
. C.
. D.
1
.
HẾT
HUẾ...16h00 Ngày 08 tháng 8 năm 2020
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------21
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
CHUY£N §Ò: KH¶O S¸T HµM Sè
Chñ ®Ò 3:
GI¸ TRÞ LíN NHÊT Vµ
GI¸ TRÞ NHá NHÊT CñA HµM Sè
LỜI GIẢI CHI TIẾT
DẠNG TOÁN 1: GTLN - GTNN TRÊN KHOẢNG (NỬA KHOẢNG - ĐOẠN)
Câu 1: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
()fx
liên tục trên


;ab
. Khẳng định nào sau đây đúng?
A. Hàm số không có giá trị lớn nhất trên đoạn


;ab
.
B. Hàm số luôn có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn


;ab
.
C. Hàm số không có giá trị nhỏ nhất trên đoạn


;ab
.
D. Hàm số luôn có cực đại và cực tiểu trên đoạn


;ab
.
Lời giải
Theo định lý về giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn.
Câu 2: (THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số
y f x
liên tục trên
thỏa mãn giá trị nhỏ nhất của hàm số trên là
. Khẳng định nào sau đây là đúng?
A.
0fx
x
,
0
x
,
0
0fx
. B.
0fx
x
.
C.
0fx
x
,
0
x
,
0
0fx
. D.
0fx
x
.
Lời giải
Ta có định nghĩa giá trị nhỏ nhất của hàm số: Cho hàm số
y f x
xác định trên tập
D
. Số
m
được gọi là giá trị nhỏ nhất của hàm số
y f x
trên tập
D
nếu
f x m
với mọi
x
thuộc
D
và tồn tại
0
xD
sao cho
0
f x m
.
Câu 3: (THPT CẦU GIẤY HÀ NỘI NĂM 2018-2019 LẦN 01) Cho
,ab
,
0 ab
, hàm số
()y f x
có đạo hàm trên thỏa mãn
0fx
,
 ;x a b
. Giá trị nhỏ nhất của hàm số đã cho trên
đoạn


;ab
bằng
A.
fb
. B.



2
ab
f
. C.
fa
. D.
f ab
.
Lời giải
Hàm số
()y f x
thỏa mãn
0fx
 ;x a b
nên hàm số nghịch biến trên
;ab
.
Do đó


;
min
ab
f x f b
.
Câu 4: (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số
()y f x
liên tục và có bảng biến thiên trên đoạn


1;3
như hình vẽ. Khẳng định nào sau đây đúng?
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------22
A.

1;3
max ( ) (0)f x f
. B.


1;3
max 3f x f
. C.


1;3
max 2f x f
. D.



1;3
max 1f x f
.
Lời giải
Nhìn vào bảng biến thiên ta thấy


1;3
max 0 .f x f
Câu 5: (THPT CỔ LOA HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
xác định, liên tục trên và
có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số
y f x
trên đoạn


0;2
bằng
A.
1
. B.
3
. C.
. D.
2
.
Lời giải
Dựa vào bảng biến thiên ta thấy trên đoạn


0;2
giá trị lớn nhất của hàm số
y f x
bằng
.
Câu 6: (THPT NGUYỄN DU - DAK LAC - NĂM 2018-2019) Cho hàm số
y f x
xác định, liên tục
trên và có bảng biến thiên như sau
Khẳng định nào sau đây sai?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x
.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
1
.
D. Hàm số có đúng hai cực trị.
Lời giải
Từ bảng biến thiên ta dễ thấy ý A, B, D đúng.
Do
 
 lim , lim
xx
f x f x
nên hàm số đã cho không có giá trị lớn nhất và không có giá
trị nhỏ nhất.
Câu 7: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số
y f x
xác định, liên tục trên và có
bảng biến thiên:
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------23
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng
1
.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
1
.
D. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x
.
Lời giải
Đáp án A sai vì hàm số có
điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu
1y
khi
0x
.
Đáp án C sai vì hàm số không có GTLN và GTNN trên .
Đáp án D đúng vì hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x
.
Câu 8: (Đề minh họa) Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới
đây đúng ?
x

1

y
y


A.
5.
CĐ
y
B.
0.
CT
y
C.
min 4.y
D.
max 5.y
Lời giải
Từ BBT suy ra hàm số đạt cực đại tại
1x
, giá trị cực đại
15
CĐ
y y
.
Câu 9: (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên trên
5;7
như sau:
Mệnh đề nào dưới đây đúng?
A.
min

5;7
6fx
. B.
min

5;7
2fx
. C.
-5;7
max
9fx
. D.
max

5;7
6fx
.
Lời giải
Dựa vào bảng biến thiên trên
5;7
, ta có:
min


5;7
12f x f
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------24
Câu 10: (SỞ GD&ĐT KIÊN GIANG NĂM 2018-2019) Hàm số
y f x
liên tục trên và có bảng biến
thiên như hình bên dưới.
Biết
48ff
,
khi đó giá trị nhỏ nhất của hàm số đã cho trên bằng
A.
9
. B.
4f
. C.
8f
. D.
4
.
Lời giải
Từ bảng biến thiên:
Ta có:
 ;( ) ( 4), ;0 ( ) (8), 0;f x f x f x f x
.
Mặt khác:
48ff
suy ra:
  ; : ( ) (8).x f x f
Vậy
()min (8).fx f
Câu 11: (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
xác định và liên tục trên có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn
nhất
M
của hàm số
y f x
trên đoạn


2;2
.
A.
5; 1mM
. B.
2; 2mM
. C.
1; 0mM
. D.
5; 0mM
.
Lời giải
Nhìn vào đồ thị ta thấy:


2;2
max 1M f x
khi
1x
hoặc
2x
;


2;2
min 5m f x
khi
2x
hoặc
1x
.
Câu 12: (THPT THÁI PHIÊN HẢI PHÒNG NĂM 2018-2019) Cho hàm số
fx
lên tục trên đoạn


1;3
và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số

2
3sin 1y f x
bằng
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------25
A.
. B.
2
. C.
. D.
1
.
Lời giải
Đặt


2
3sin 1 1;2t x t
Nhận xét: Giá trị lớn nhất của hàm số

2
3sin 1y f x
là giá trị lớn nhất của hàm số
y f t
trên


1;2
. Dựa vào đồ thị ta có:



1;2
max max 2y f t
.
Câu 13: Cho hàm số
()y f x
có đồ thị như hình dưới. Gọi
,mM
lần lượt là
giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( 2 )y f x
trên
1
1; .
2



Giá trị
mM
bằng
A.
0.
B.
4.
C.
19
8
D.
4.
Lời giải
Đặt
2,tx
vì
1
1; [ 1;2].
2
xt



Khi đó cần tìm GTNN, GTLN của hàm số
( ), [ 1;2].y f t t
Với
khi
khi
[ 1;2]
[ 1;2]
min ( ) 4 2
[ 1;2] .
max ( ) 0 0
m f t t
t
M f t t
Suy ra
4.mM
Câu 14: (THPT HOÀNG VĂN THỤ - HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có đạo hàm
cấp 2 trên , hàm số
y f x
có đồ thị như hình vẽ bên.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------26
Giá trị lớn nhất của hàm số




sin 3cos
2
xx
yf
trên đoạn




5
;
66
bằng
A.



5
6
f
. B.



3
f
. C.
0f
. D.



6
f
.
Lời giải
Đặt



sin 3 cos
sin
23
xx
tx
. Vì


5
; ; 1;1
6 6 3 2 2
x x t
.
Dựa vào đồ thị của hàm số
fx
, ta có bảng biến thiên
Ta có:








5 1;1
;
66
sin 3 cos
max max
2
xx
f f t




0 sin 0
33
t x x
.
Vậy












5
;
66
sin 3 cos
max
23
xx
ff
.
Câu 15: Cho hàm số
y f x
liên tục, đồng biến trên đoạn


;ab
. Khẳng định nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn


;ab
.
B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng
;ab
.
C. Phương trình
0fx
có nghiệm duy nhất thuộc đoạn


;ab
.
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn


;ab
.
Lời giải
Vì hàm số
y f x
liên tục, đồng biến trên đoạn


;ab
nên





;
;
min ;max
ab
ab
f x f a f x f b
Vậy hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn


;ab
.
Câu 16: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số
fx
xác định,liên tục trên và có
bảng biến thiên sau:
Phát biểu nào sau đây đúng?
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 2.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------27
B. Hàm số nhận giá trị dương với mọi
x
.
C. Trên


2;8
hàm số có giá trị lớn nhất là
M
, giá trị nhỏ nhất là
m
. Giá trị biểu thức
36mM
.
D. Hàm số có đúng một cực trị.
Lời giải
Dựa vào bảng biến thiên ta thấy:
Hàm số có giá trị nhỏ nhất bằng 0 và không có giá trị lớn nhất nên loại phương án A.
Hàm số nhận giá trị không âm với mọi
x
(
(2) 0f
) nên loại phương án B.
Hàm số có 3 cực trị nên loại phương án D.
Hàm số có giá trị lớn nhất trên


2;8
là
2M
và giá trị nhỏ nhất trên


2;8
là
0m
. Giá trị
biểu thức
3 0 3.2 6mM
. Vậy phát biểu đúng là C.
Câu 17: Cho hàm số
y f x
liên tục trên đoạn (-1;3) và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn


1;3
. Giá trị của
Mm
bằng
A. 0. B. 1. C. 4. D. 5.
Lời giải
Căn cứ vào đồ thị ta có
[ 1;3]
max 3My

,
[ 1;3]
min 2.my
Vậy
5Mm
.
Câu 18: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
max 2.
x
fx
B.


1;1
max 1.
x
fx
C.


1;1
max 0.
x
fx
D.



1;1
max 3.
x
fx
Lời giải
Chọn đáp án A.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------28
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
min 2.
x
fx
B.


1;1
min 1.
x
fx
C.


1;1
min 0.
x
fx
D.



1;1
min 3.
x
fx
Lời giải
Chọn đáp án D.
Câu 20: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.



0;1
min 3.
x
fx
B.


0;1
min 2.
x
fx
C.


0;1
min 0.
x
fx
D.


0;1
min 1.
x
fx
Lời giải
Chọn đáp án D.
Câu 21: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


5;15
max 5 .
x
f x f
B.


5;15
max 15 .
x
f x f
C.


x
fx
5;15
max 2.
D.


5;15
max 10 .
x
f x f
Lời giải
Dựa vào BBT ta thấy
fx
đồng biến trên





5;15
5;15 max 15 .
x
f x f
Câu 22: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.



15; 5
max 5 .
x
f x f
B.



15; 5
max 15 .
x
f x f
C.


15; 5
max 2.
x
fx
D.



15; 5
max 10 .
x
f x f
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------29
Lời giải
Dựa vào BBT ta thấy
fx
nghịch biến trên




15; 5
15; 5 max 15 .
x
f x f
Câu 23: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
2 1.g x f x
Khẳng định nào sau đây đúng?
A.


1;1
max 2.
x
gx
B.


1;1
max 5.
x
gx
C.


1;1
max 1.
x
gx
D.



1;1
max 5.
x
gx
Lời giải
Dựa vào BBT, ta có:


1;1 : 3 2 6 2 4 5 2 1 5.x f x f x f x
Câu 24: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
3 4 .g x f x
Khẳng định nào sau đây đúng?
A.


1;1
min 15.
x
gx
B.



1;1
min 5.
x
gx
C.



1;1
min 15.
x
gx
D.



1;1
max 3.
x
gx
Lời giải
Dựa vào BBT, ta có:


1;1 : 3 2 8 4 12 5 3 4 15.x f x f x f x
Câu 25: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
max 2.
x
fx
B.


1;1
max 1.
x
fx
C.


1;1
max 0.
x
fx
D.


1;1
max 3.
x
fx
Lời giải
BBT:
x

1
0
1

fx
0
0
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------30
fx

3
2
1

fx
0
0
2
1
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Khẳng định nào sau đây đúng?
A.


1;1
min 2.
x
fx
B.


1;1
min 1.
x
fx
C.


1;1
min 0.
x
fx
D.


1;1
min 3.
x
fx
Lời giải
BBT:
x

1
0
1

fx
0
0
fx

3
2
1

fx
0
0
2
1
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
sin .g x f x
Khẳng định nào sau đây đúng?
A.
max 2.gx
B.
max 1.gx
C.
max 3.gx
D.
max 4.gx
Lời giải:
Đặt
sin ; 1;1 .t x x t
Ta có:



1;1
max max 2g x f t
đạt được khi
sin 0 , .x x k k
Câu 28: Cho hàm số
y f x
có bảng biến thiên như sau:
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------31
x

1
0
1

fx
0
0
fx

3
2
1

Đặt
cos .g x f x
Khẳng định nào sau đây đúng?
A.



0;
2
min 1.gx
B.



0;
2
min 2.gx
C.




0;
2
min 3.gx
D.



0;
2
min 0.gx
Lời giải
Đặt





cos ; 0; 0;1 .
2
t x x t
Ta có:




0;1
0;
2
min min 1g x f t
đạt được khi
cos 1 2 , .x x k k
Câu 29: Cho hàm số
y f x
có bảng biến thiên như sau:
x

1
0
1

fx
0
0
fx

3
2
1

Đặt

32
3.g x f x f x
Khẳng định nào sau đây đúng?
A.


1;1
max 4.gx
B.


1;1
max 4.gx
C.


1;1
max 0.gx
D.


1;1
max 2.gx
Lời giải
Ta có:
1;1 3;2 .x f x
Đặt


3;2 .t f x
Xét hàm số






3 2 2
0 3;2
3 , 3;2 3 6 0 .
2 3;2
t
h t t t t h t t t
t
Ta có:
0 0; 2 4; 3 54.h h h
Câu 30: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Giá trị lớn nhất của hàm số
3
x
fx
x
trên đoạn


2;3
bằng
A.
3.
B.
2.
C.
1
.
2
D.
2.
Lời giải
Ta có:

2
3
'0
3
fx
x
,


2;3x
Do đó hàm số
fx
đồng biến trên


2;3 .
Suy ra:



2;3
1
max 3 .
2
f x f
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------32
Câu 31: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số

1
()f x x
x
trên nửa khoảng

2;
là
A.
. B.
5
2
. C.
. D.
7
2
.
Lời giải
Áp dụng bất đẳng thức Cô-si, ta được:
1 3 1 3.2 1 5
( ) 2 .
4 4 4 4 2
x x x
f x x
x x x
.
Dấu bằng xảy ra khi
2x
.
Câu 32: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn


2;4
.
A.


2;4
min 6.y
B.



2;4
min 2.y
C.



2;4
min 3.y
D.


2;4
19
min .
3
y
Lời giải
Tập xác định:
\ 1 .D
Hàm số
2
3
1
x
y
x
xác định và liên tục trên đoạn


2;4
Ta có


2
2
2
23
; 0 2 3 0 3
1
xx
y y x x x
x
hoặc
1x
(loại)
Suy ra

19
2 7; 3 6; 4
3
y y y
. Vậy


2;4
min 6y
tại
3x
.
Câu 33: Tìm giá trị nhỏ nhất của hàm số

9
yx
x
trên đoạn
[2;4]
.
A.
[
2;4]
13
min .
2
y
B.
[
2;4]
25
min .
4
y
C.
[
2;4]
min 6.y
D.
[

2;4]
min 6.y
Lời giải
Xét hàm số

9
yx
x
trên đoạn
[2;4]
;

2
3
9
1 ; 0
3 (2;4)
x
yy
x
x
Ta có:
13 25
(2) ; (3) 6; (4) .
24
y y y
Vậy
[
2;4]
min 6y
khi
3x
.
Câu 34: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Tìm giá trị lớn nhất của hàm số
15y f x x x
trên đoạn


1;5
.
A.


1;5
max 3 2fx
. B.


1;5
max 2fx
. C.


1;5
max 2 2fx
. D.


1;5
max 2fx
.
Lời giải
Áp dụng bất đẳng thức Bunyakovsky, ta có:
22
1 5 1 1 1 5 2 2y f x x x x x
.
Dấu bằng xảy ra khi

15
11
xx



3 1;5x
. Vậy
1;5
max 2 2fx
.
Câu 35: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
17y x x
. Khi đó
có bao nhiêu số nguyên dương nằm giữa
m
và
M
?
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------33
A.
1
. B.
5
. C.
. D.
0
.
Lời giải
Tập xác định


1;7D
. Ta có:


11
2 1 2 7
y
xx
;
04yx
.
Khi đó
1 7 6yy
,
4 2 3y
. Suy ra
 6 2 3 3
k
kk
.
Vậy có duy nhất một số nguyên dương thoả mãn.
Câu 36: (THPT THĂNG LONG HÀ NỘI NĂM 2018-2019 LẦN 02) Hàm số

8
10
yx
x
đạt giá trị nhỏ
nhất trên đoạn


39
10 ;10
tại
x
bằng
A.
4
10
. B.
3
10
. C.
5
10
. D.
6
10
.
Lời giải
Cách 1: Hàm số

8
10
yx
x
liên tục trên


39
10 ;10
. Ta có

8
2
10
1y
x
.





4 3 9
28
4 3 9
10 10 ;10
0 10
10 10 ;10
x
yx
x
.

3 3 5
10 10 10y
,
44
10 2.10y
,

9 9 1
10 10 10y
. Vậy


39
4
10 ;10
min 2.10y
khi
4
10x
.
Cách 2: Vì
0x
nên theo bất đẳng thức Côsi ta có
88
4
10 10
2 . 2.10y x x
xx
.
Dấu
""
xảy ra


8
4 3 9
10
10 10 ;10xx
x
. Vậy


39
4
10 ;10
min 2.10y
khi
4
10x
.
Câu 37: (SỞ GD&ĐT BÌNH THUẬN NĂM 2018-2019) Giá trị lớn nhất của hàm số
2
5y x x
bằng
A.
. B.
5
2
. C.
6
. D.
2
.
Lời giải
TXĐ:


0;5D
. Ta có:


2
25
'
25
x
y
xx
;
' 0 2 5 0yx
5
0;5 .
2
x


Ta có:
0 5 0yy
;



55
22
y
. Vậy




55
max
22
yy
.
Câu 38: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Tìm giá trị nhỏ nhất của hàm số
2
sin 4sin 5y x x
.
A.
20
. B.
8
. C.
9
. D.
0
.
Lời giải
Xét hàm số:
2
sin 4sin 5y x x
Txđ:
.D
Đặt
sintx
,
11t
. Ta có:
2
45y t t t
, hàm số liên tục trên


1;1
24y t t
,
02y t t
;
1 8, ( 1) 0yy
. Vậy
min 1 8yy
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------34
Câu 39: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
2sin 3
sin 1
x
y
x
trên đoạn



0;
2
là
A.
. B.
2
. C.
. D.
5
2
.
Lời giải
Đặt
sintx
. Với



0;
2
x
thì
0 sin 1x
01t
. Khi đó:

23
()
1
t
y f t
t
, với


0;1t
.
Có


1
'( ) 0, 0;1
( 1)
f t t
t
nên hàm số
()ft
nghịch biến trên đoạn


0;1
.
Suy ra



0;1
5
min ( ) (1)
2
f t f
. Vậy
5
min .
2
y
Câu 40: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số
3
sin 3sin 2f x x x
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó
2Mm
là
A.
. B. 1. C. 4. D. 5.
Lời giải
Đặt
sin xt



1; 1t
. Ta có
3
3 2.f t t t
Xét hàm số
3
32f t t t
với



1; 1 ;t
2
' 3 3 0f t t
1t
hoặc
1.t
Ta có
14f
,
1 0 .f
Suy ra, giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là 4 và 0 hay
4 ; m 0.M
Giá trị
2 4 2.0 4Mm
.
Câu 41: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
cos2 cos 1f x x x
. Giá trị nhỏ nhất của hàm số trên là
A.

1
min
8
fx
. B.

1
min
4
fx
. C.
1
min
8
fx
. D.
1
min
4
fx
.
Lời giải
Hàm số được viết lại
2
2cos cos .f x x x
Đặt
costx
. Với mọi
x
suy ra



1;1t
.
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số

2
2g t t t
trên


1;1
.
Ta có
' 4 1g t t
;
1
' 0 ;
4
g t t



11
1 3; 1 1;
48
g g g
. Vậy

1
min
8
fx
.
Câu 42: (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Giá trị lớn nhất của hàm số

2
2sin cosy x x
là phân số tối giản có dạng với
,ab
là các số nguyên dương. Tìm
–ab
.
A.
. B.
9
. C.
. D.
10
.
Lời giải
TXĐ:
.D
Ta có:
2 2 2
2sin cos 2(1 cos ) cos 2cos cos 2y x x x x x x
Đặt:
cost x
, với
11t
Như vậy ta đi tìm giá trị lớn nhất của hàm số
2
22y t t
trên đoạn


1;1
Ta có:


1
' 4 1 0 1;1 ;
4
y t t



1 17
( 1) 1; ; (1) 1
48
y y y
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------35
Vậy: Giá trị lớn nhất của hàm số là




1 17
48
y
suy ra
–9ab
Câu 43: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
3cos2 4siny x x
là
A.
1
. B.
7
. C.
5
. D.
11
3
.
Lời giải
Ta có
22
3 1 2sin 4sin 6sin 4sin 3y x x y x x
. Đặt
sin ,tx
11t
.
Khi đó
2
6 4 3y t t
với



1;1t
.

1
12 4, 0
3
y t y t
và



1 11
1 1, 1 7,
33
y y y
.
Vậy giá trị nhỏ nhất của hàm số là
7
đạt được khi
sin 1 2
2
x x k
Câu 44: (MĐ 102 BGD&ĐT NĂM 2016-2017) Tìm giá trị lớn nhất
M
của hàm số
42
23y x x
trên
đoạn


0; 3
.
A.
9M
. B.
83M
. C.
1M
. D.
6M
.
Lời giải
Ta có:
32
4 4 4 1y x x x x
;
0y

2
4 1 0xx


0
1
1( )
x
x
xl
Ta có :
03y
;
12y
;
3 6.y
Vậy giá trị lớn nhất của hàm số
42
23y x x
trên đoạn


0; 3
là
36My
Câu 45: (MĐ 104 BGD&ĐT NĂM 2018-2019) Giá trị nhỏ nhất của hàm số

3
3f x x x
trên đoạn


3;3
bằng
A.
18
. B.
18
. C.
2
. D.
2
.
Lời giải
Ta có:

2
3 3.f x x
Ta có:





1 3;3
0
1 3;3
x
fx
x
Mặt khác:
3 18; 3 18; 1 2; 1 2f f f f
. Vậy


3;3
min 3 18f x f
.
Câu 46: (MĐ 104 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất
m
của hàm số

2
2
yx
x
trên đoạn



1
;2
2
.
A.
17
4
m
. B.
10m
. C.
5m
. D.
3m
.
Lời giải
Đặt
2
2
.y f x x
x
Ta có
3
22
2 2 2
2
x
yx
xx
,



1
0 1 ;2
2
yx
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------36
Khi đó



1 17
1 3, , 2 5.
24
f f f
Vậy



1
;2
2
min 1 3m f x f
.
Câu 47: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Gọi
M
và
m
lầ lượt là giá trị lớn
nhất và giá trị nhỏ nhất của hàm số
2 4 6f x x x
trên


3;6
. Tổng
Mm
có giá trị là:
A.
12
. B.
6
. C.
18
. D.
4
.
Lời giải
Hàm số xác định liên tục trên
3;6 .


Ta có
2
2 0 3;6
6
f x x
x
, hàm số đồng biến trên
3;6


3;6
max 6 12M y f
;


3;6
min 3 18m y f
;
6.Mm
Câu 48: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
M
là giá trị lớn nhất của hàm số
22
4 4 6 4 1f x x x x x
. Tính tích các nghiệm của phương trình
f x M
.
A.
. B.
4
. C.
2
. D.
4
.
Lời giải
Đặt
2
2
4 6 2 2 2t x x x
.
Khi đó,


2;
max maxM f x g t
, với
2
47g t t t
trên

2;
.
Ta có:
2
2
4 7 11 2 11g t t t t
, dấu đẳng thức xảy ra khi
2
2 4 6 2t x x
2
4 2 0xx


22
22
x
x
.
Như vây,

2;
max max 11 2 2M f x g t x
, suy ra nghiệm của phương trình
f x M
là
22x
. Vậy tích các nghiệm của phương trình
f x M
bằng
2
.
Câu 49: (MĐ 103 BGD&ĐT NĂM 2016-2017) Tìm giá trị nhỏ nhất
m
của hàm số
42
13y x x
trên
đoạn


2;3 .
A.
51
.
4
m
B.
49
.
4
m
C.
13.m
D.
51
.
2
m
Lời giải
Ta có:

3
4 2 .y x x


0
0
1
2
x
y
x
;
0 13y
,




1 51
4
2
y
,
2 25y
,
3 85y
.
Vậy
51
4
m
.
Câu 50: (SỞ GD&ĐT LẠNG SƠN NĂM 2018-2019) Tìm x để hàm số
2
4y x x
đạt giá trị lớn
nhất.
A.
2x
. B.
22x
. C.
1x
. D.
2.x
Lời giải
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------37
Tập xác định



2;2D
. Ta có:
2
1.
4
x
y
x





2
22
2
0
0
2
0 1 0 4
4
4
2
x
x
x
xn
y x x
xx
x
xl
Ta có:
2 2; 2 2; 2 2 2.f f f
Vậy hàm số đạt giá trị lớn nhất là
22
khi
2x
Câu 51: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2016-2017) Tính giá trị nhỏ nhất của hàm số

2
4
3yx
x
trên khoảng
0;
.
A.

3
0;
min 3 9.y
B.

0;
min 7.y
C.

0;
33
min .
5
y
D.

3
0;
min 2 9.y
Lời giải
Cách 1:
3
3
2 2 2
4 3 3 4 3 3 4
3 3 . . 3 9
2 2 2 2
x x x x
yx
x x x
Dấu
""
xảy ra khi
3
2
3 4 8
23
x
x
x
. Vậy

3
0;
min 3 9y
Cách 2: Xét hàm số

2
4
3yx
x
trên khoảng
0;
Ta có
23
48
3 ' 3 .y x y
xx
Cho
3
3
3
8 8 8
' 0 3
33
y x x
x





3
3
0;
8
min 3 9.
3
yy
Lưu ý: Các em nếu có sử dụng MTCT thì bấm cẩn thận nhé!
Câu 52: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Gọi M, m lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của hàm số
f x x x
trên đoạn


0;3
. Giá trị của biểu thức
2Mm
gần với số
nào nhất trong các số dưới đây?
A.
1,768
. B.
0,767
. C.
1,767
. D.
0,768
.
Lời giải
Ta có

1
'1
2
fx
x
;
11
' 0 1 0 0;3
4
2
f x x
x
.



11
0 0, , 3 3 3
44
f f f
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------38
Suy ra,

1 5 2 3
3 3, 2 0,7679491924...
42
M m M m
Câu 53:
Câu 54:
(THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 02) Giá trị nhỏ nhất của hàm số
1 2 3 4 2019f x x x x x
là
A.
2017.
B.
2020.
C.
2018.
D.
2019.
Lời giải
Tập xác định:
D = .
Biến đổi :
22
1 2 3 4 2019 5 4 5 6 2019.f x x x x x x x x x
Đặt



2
2
5 9 9
5 4 .
2 4 4
t x x t x t x
Hàm số đã cho trở thành
2
2
9
2 2019 1 2018 2018 .
4
f t t t t t
Vậy giá trị nhỏ nhất của hàm số đã cho bằng
2018
tại


9
1 ; .
4
t
Câu 55: (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Tổng giá trị lớn nhất
M
và giá trị nhỏ
nhất
m
của hàm số
2
64f x x x
trên đoạn


0;3
có dạng
a b c
với
a
là số nguyên
và
,bc
là các số nguyên dương. Tnh
S a b c
.
A.
. B.
2
. C.
22
. D.
5
.
Lời giải
Hàm số
2
64f x x x
xác định và liên tục trên đoạn


0;3
.

2
2
2
2 2 2
46
2 6 4
4 6 .
4 4 4
x x x
x x x
f x x x
x x x
;







1 0;3
0
2 0;3
x
fx
x
0 12; 3 3 13 ; 1 5 5 ; 2 8 2f f f f
Suy ra
max


0;3
3 13yM
và


0;3
min 12ym
12 3 13M m a b c
với
a
là số nguyên và
,bc
là các số nguyên dương nên
12; 3; 13a b c
. Do đó
4S a b c
.
Câu 56: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 02) Cho hàm số
fx
có đạo hàm
2
23f x x x x
,
x
. Giá trị lớn nhất của hàm số đã cho trên đoạn


0;4
bằng
A.
0f
. B.
2f
. C.
3f
. D.
4f
.
Lời giải
Ta có
2
0
2 3 0 2
3
x
f x x x x x
x
.
Bảng biến thiên của hàm số
y f x
trên đoạn


0;4
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------39
Từ bảng biến thiên ta thấy giá trị lớn nhất của hàm số
fx
trên đoạn


0;4
là
3f
.
Câu 57: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
xác định
và liên tục trên , đồ thị của hàm số
y f x
như hình vẽ sau:
Giá trị lớn nhất của hàm số
y f x
trên đoạn


1;2
là
A.
1f
. B.
1f
. C.
2f
. D.
0f
.
Lời giải

1
01
2
x
f x x
x
.
Từ đồ thị hàm
y f x
ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên


1;2
là
1f
.
Câu 58: (THPT YÊN MÔ A-NINH BÌNH NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
liên tục trên



7
0;
2
có đồ thị hàm số
y f x
như hình vẽ sau:
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------40
Hàm số
y f x
đạt giá trị nhỏ nhất trên



7
0;
2
tại điểm
0
x
nào dưới đây?
A.
0
0x
. B.
0
7
2
x
. C.
0
3x
. D.
0
1x
.
Lời giải
Xét hàm số
y f x
trên đoạn



7
0;
2
. Dựa vào đồ thị ta có

1
0
3
x
fx
x
Bảng biến thiên:
Nhìn bảng biến thiên ta thấy hàm số
y f x
đạt giá trị nhỏ nhất trên



7
0;
2
tại điểm
0
3.x
Câu 59: (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số
fx
có đạo hàm
là
fx
. Đồ thị của hàm số
y f x
được cho như hình vẽ bên. Biết rằng
0 1 2 3 5 4f f f f f
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
fx
trên
đoạn


0;5
.
A.
5 , 3 .m f M f
B.
5 , 1 .m f M f
C.
0 , 3 .m f M f
D.
1 , 3 .m f M f
Lời giải
Từ đồ thị ta có bảng biến thiên của
fx
trên đoạn


0;5
3Mf
và
1 3 , 4 3f f f f
5 0 1 3 4 3 0 5 0 5f f f f f f f f m f
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------41
Câu 60: (THPT LÝ NHÂN TÔNG LẦN 1 NĂM 2018-2019) Cho hàm số có
fx
có đạo hàm là hàm
'fx
. Đồ thị hàm số
'fx
như hình vẽ bên. Biết rằng
0 1 2 2 4 3f f f f f
. Tìm
giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
fx
trên đoạn


0;4
.
A.
4 , 2m f M f
. B.
1 , 2 .m f M f
C.
4 , 1m f M f
. D.
0 , 2m f M f
.
Lời giải
Dựa vào đồ thị của hàm
'fx
ta có bảng biến thiên:
Vậy giá trị lớn nhất
2Mf
.
Hàm số đồng biến trên khoảng
0;2
nên
2 1 2 1 0f f f f
.
Hàm số nghịch biến trên khoảng
2;4
nên
2 3 2 3 0f f f f
.
Theo giả thuyết:
0 1 2 2 4 3f f f f f
0 4 2 1 2 3 0 0 4 .f f f f f f f f
Vậy giá trị nhỏ nhất
4mf
.
Câu 61: (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Cho hàm số
fx
có đồ thị của hàm
số
fx
như hình vẽ. Biết
0 1 2 2 4 3f f f f f
. Giá trị nhỏ nhất
m
, giá trị lớn nhất
M
của hàm số
fx
trên đoạn


0;4
là
A.
4mf
,
1Mf
. B.
4mf
,
2Mf
.
O
2
4
x
y
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------42
C.
1mf
,
2Mf
. D.
0mf
,
2Mf
.
Lời giải
Từ đồ thị của hàm số
fx
trên đoạn


0;4
ta có bảng biến thiên của hàm số trên đoạn


0;4
như sau:
Từ bảng biến thiên ta có
max



0;4
2M f x f
.
Mặt khác
0 1 2 2 4 3f f f f f
0 4 2 1 2 3 0f f f f f f
(do
2 1 ; 2 3f f f f
)
Suy ra
04ff
min


0;4
4m f x f
.
Câu 62: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số
y f x
có
bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
11
4 3 8
33
g x f x x x x x
trên đoạn


1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Lời giải

22
4 2 4 6 8g x x f x x x x


2
2 2 4 4x f x x x
.
Với


1;3x
thì
40x
;
2
3 4 4xx
nên

2
40f x x
.
Suy ra
2
2 4 4 0f x x x
,



1;3x
.
Bảng biến thiên:
Suy ra


1;3
max 2g x g
4 7 12f
.
Câu 63: (THPT KINH MÔN HAI DƯƠNG NĂM 2018-2019 LẦN 03) Cho hàm số
y f x
có đạo
hàm
fx
. Hàm số
y f x
liên tục trên tập số thực và có bảng biến thiên như sau:
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------43
Biết rằng

10
1
3
f
,
26f
. Giá trị nhỏ nhất của hàm số

3
3g x f x f x
trên đoạn


1;2
bằng
A.
10
3
. B.
820
27
. C.
730
27
. D.
198
.
Lời giải
Xét hàm số

3
3g x f x f x
trên đoạn


1;2



2
31g x f x f x
,
0gx
2
01
12
fx
fx
.
Từ bảng biến thiên, ta có:




1 1;2
1
2 1;2
x
x
Và
0fx
,


1;2x
nên
fx
đồng biến trên


1;2
10
1
3
f x f
1fx

2
1fx
,


1;2x
nên
2
vô nghiệm.
Do đó,
0gx
chỉ có
2
nghiệm là
1x
và
2x
.
Ta có
3
1 1 3 1g f f
3
10 10 730
3;
3 3 27

3
2 2 3 2g f f
3
6 3 6 198
.
Vậy


1;2
730
min 1
27
g x g
.
DẠNG TOÁN 2: MAX MIN HÀM NHIỀU BIẾN
Câu 64: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
22
2x xy y
. Giá trị nhỏ nhất
của
22
P x xy y
bằng
A.
2
3
. B.
1
6
. C.
1
2
. D.
2
.
Lời giải
Xét


2 2 2 2
22
22
x xy y x xy y
P
x xy y
+ Nếu
0y
thì
2
2x
. Do đó

2
2Px
suy ra
min 2P
+ Nếu
0y
ta chia tử mẫu cho
2
y
ta được:





2
22
2 2 2
1
2
1
xx
yy
x xy y
P
x xy y
xx
yy
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------44
Đặt
x
t
y
, khi đó


2
2
1
2
1
P t t
tt
. Xét


22
22
2
1 2 2
'
1
1
t t t
f t f t
tt
tt
;


1
'0
1
t
ft
t
Bảng biến thiên
Khi đó
1
min
23
P
do đó
2
min
3
P
.
Câu 65: (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019)Cho hai số thực
,xy
thay đổi thỏa mãn
điều kiện

22
2xy
. Gọi
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của biểu
thức
33
2( ) 3P x y xy
. Giá trị của
Mn
bằng:
A.
4.
B.
1
.
2
C.
6.
D.
1 4 2.
Lời giải
Ta có



3
33
2( ) 3 2 3 ( ) 3P x y xy x y xy x y xy
Từ
2
2 2 2
()
2 ( ) 2 2 1
2
xy
x y x y xy xy
, đặt
x y t
và thay vào
P
ta được




22
3 3 2
3
2 3 1 3 1 6 3
2 2 2
tt
P t t t t t
Mặt khác

22
2 2 2
( ) ( )
2 ( ) 2 ( ) ( ) 4 0
22
x y x y
x y xy x y x y


2 2 2;2x y t
Khảo sát hàm số
32
3
63
2
P t t t
trên



2;2t
ta được
max

2;2 2;2
13
min 7;
2
m P M P
Vậy
1
.
2
Mm
Câu 66: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Cho
,xy
thỏa mãn
1xy
và
22
1x y xy x y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
1
xy
P
xy
. Tính
Mm
.
A.
1
3
. B.
2
3
. C.
1
2
. D.
1
3
.
Lời giải
Cách 1: Với điều kiện
22
1; 1x y x y xy x y
ta có

22
xy
P
x y xy
.
Nếu
0y
thì


2
1
15
2
10
x
x
xx
. Khi đó
0P
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------45
Nếu
0y
thì




2
1
x
y
P
xx
yy
. Đặt
x
t
y
. Ta có

2
1
t
P
tt
,
t
.
Xét

2
1
t
ft
tt
,
t
.


2
2
2
1
1
t
ft
tt
;
01f t t
Từ bảng biến thiên:
1
3
M
tại



2
22
1
1
1
1
3 2 1 0
1
1
3
3
xy
x
xy
xy
x
y
xx
xy
x y xy x y
x
.
1m
tại










2
22
1
1
1
1
10
1
1
1
1
x
xy
x
y
xy
y
x
x
x
x y xy x y
x
y
Vậy
2
.
3
Mm
Cách 2: Với điều kiện
22
1; 1x y x y xy x y
ta có

22
xy
P
x y xy
.
22
1 0 (*)Px xy P Py
+) Nếu
0P
thì
0x
hoặc
0y
.
+) Nếu
0P
thì
0
0
x
y
.
Để phương trình (*) có nghiệm
x
thì
2
1
1 3 1 0 1
3
x
y P P P
.
Ta có:
1
3
M
tại





2
22
1
1
1
1
2
3 2 1 0
1
1
3
3
xy
yP
xy
xy
xy
x
P
xx
xy
x y xy x y
x
.
1m
tại










2
22
1
1
1
1
2
10
1
1
1
1
x
xy
yP
y
xy
xy
x
P
x
x
x y xy x y
x
y
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------46
Do đó
1
;m 1.
3
M
Vậy
2
.
3
Mm
Câu 67: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho
,xy
thỏa mãn
22
5 6 5 16x xy y
và hàm số
bậc ba
y f x
có đồ thị như hình vẽ. Gọi
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của





22
22
2
24
xy
Pf
x y xy
. Tính
22
Mm
10
8
6
4
2
2
4
6
8
10
x
7
6
5
4
3
2
1
1
2
3
0
1
-1
A.

22
4Mm
. B.

22
1Mm
. C.

22
25Mm
. D.

22
2Mm
.
Lời giải
Đặt

22
22
2
24
xy
t
x y xy
P f t
. Vì
22
5 6 5 16x xy y
nên



2 2 2 2
2
22
2 2 2
2
2 2 2 2
1
5 6 5
36
3
8
.
1
18 2 4
2 16
2 5 6 5
4
x y x xy y
x y xy
xy
t
x y xy
x y x
x y xy x xy y
Do đó
3
0
2
t P f t
với



3
0;
2
t
.
10
8
6
4
2
2
4
6
8
10
x
7
6
5
4
3
2
1
1
2
3
0
1
-1
Dựa vào đồ thị, ta có
33
0; 0;
22
0 0 ; 1 2.M MaxP f m MinP f
Suy ra

22
4Mm
.
Câu 68: (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Cho các số thực
,xy
thay đổi
nhưng luôn thỏa mãn
22
3 2 5x xy y
. Giá trị nhỏ nhất của biểu thức
22
2P x xy y
thuộc
khoảng nào sau đây?
A.
4;7
. B.
2;1
. C.
1;4
. D.
7;10
.
Lời giải
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------47
Xét
5
0
3
yP
loại phương án
A
và
.D
Xét



2
2
7
00
24
yy
y P x
khi đó ta có biểu thức


22
22
32
5
2
x xy y
P
x xy y
Chia cả tử và mẫu của vế phải cho
2
y
tâ được








2
2
3 2 1
5
2
xx
yy
P
xx
yy
.
Đặt

22
2 2 2
3
5 3 2 1 5 14 3
( ) ' , ' 0
1
2 ( 2)
5
t
x t t t t
t t R f t f t f t
yP
t t t t
t
Bảng biến thiên hàm số
ft
.
Từ bảng biến thiên ta có
55
44
4
f t P
P
.
Vậy
P
đạt giá trị nhỏ nhất bằng
5
4
, dấu bằng xảy ra khi
33t x y
.
Câu 69: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho
x
,
y
là các số thực thỏa mãn
1 2 2x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
22
2 1 1 8 4P x y x y x y
. Tính giá trị
Mm
A.
42
. B.
41
. C.
43
. D.
44
.
Lời giải
2
2
1 2 1 3 0 3x y x y x y x y
2
22
2 1 1 8 4 2 2 8 4P x y x y x y x y x y x y
Đặt


4 , 1;2t x y t
. Ta có:
2
2 2 4 2
4 2 4 2 8 10 8 26f t t t t t t t
.
3
4 20 8f t t t
;







2
2 1;2
2
0 1 2 1;2
2 1 0
1 2 1;2
t
t
f t t
tt
t
;
1 25; 2 18ff
.
Suy ra




1;2
1;2
min 2 18; max 1 25m f t f M f t f
. Vậy
43Mm
.
DẠNG TOÁN 3: BÀI TOÁN THỰC TẾ - TỐI ƯU
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------48
Câu 70: (ĐỀ THỬ NGHIỆM BGD&ĐT NĂM 2016-2017) Một vật chuyển động theo quy luật
32
1
9
2
s t t
với
t
(giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và
s
(mét) là
quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian
10
giây, kể
từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A.
/216 ms
. B.
/30 ms
. C.
/400 ms
. D.
/54 ms
.
Lời giải
Vận tốc tại thời điểm
t
là
2
3
( ) ( ) 18
2
v t s t t t
với


0;10t
.
Ta có :
( ) 3 18 0 6v t t t
.
Suy ra:
0 0; 10 30; 6 54v v v
. Vậy vận tốc lớn nhất của vật đạt được bằng
/54 ms
Câu 71: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để
hộp nhận được có thể tích lớn nhất.
A.
6x
. B.
3x
. C.
2x
. D.
4x
.
Lời giải
Ta có:
,0h x cm x
là đường cao hình hộp.
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
12 2x cm
Vậy diện tch đáy hình hộp

2
2
12 2S x cm
. Ta có:




00
0;6
12 2 0 6
xx
x
xx
Thể tích của hình hộp là:

2
.. 12 2 .V S h xx
Xét hàm số:
2
. 12 2 0;6y x x x
Ta có :
2
' 12 2 4 12 2 12 2 12 6y x x x x x
;
' 0 12 2 . 12 6 0 2y x x x
hoặc
6x
(loại).
Suy ra với
2x
thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là
2 128y
Câu 72: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông
A
dự định dùng hết
2
6,5m
knh để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không
đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 .m
B.
3
1,61 .m
C.
3
1,33 .m
D.
3
1,50 .m
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------49
Lời giải
c
b
a
Giả sử hình hộp chữ nhật có kch thước như hình vẽ. Ta có dung tích của bể cá:
V abc
Mặt khác theo giả thiết ta có:
2 2 6,5
2
ab bc ac
ab

2
2 6 6,5
2
b bc
ab
2
6,5 2
6
2
b
c
b
ab
Khi đó
2
2
6,5 2
2.
6
b
Vb
b

3
6,5 2
3
bb
V
. Xét hàm số:
3
6,5 2
3
bb
fb
.
BBT:
Vậy bể cá có dung tích lớn nhất là :




3
39
1,50
6
fm
.
Câu 73: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Bác Bính có một tấm thép mỏng hình
tròn, tâm O, bán kính
dm4
. Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai
mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình
vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (bỏ qua phần
mối hàn và độ dày của tấm thép).
A.
3
dm
128 3
27
. B.
3
dm
128 3
81
. C.
3
dm
16 3
27
. D.
3
dm
64 3
27
.
Lời giải
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------50
Khi hàn hai mép của hình quạt tròn, độ dài đường sinh của hình nón bằng bán kính của hình
quạt tròn, tức là
4AB
.
Thể tích của hình nón:

22
11
. . . 16 .
33
V r h h h
với
04h
.
2
1 4 3
16 3 0
33
V h h h
.
Dựa vào bảng biến thiên, suy ra thể tích lớn nhất của hình nón là
dm
3
128 3
27
.
Câu 74: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một chất điểm chuyển động theo
phương trình
32
9 21 9S t t t
trong đó
t
tính bằng giây
()s
và
tính bằng mét
()m
. Tính
thời điểm
()ts
mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất.
A.
4( ).ts
B.
5( ).ts
C.
3( ).ts
D.
7( ).ts
Lời giải
Ta có:
22
3 18 21 3( 3) 48 48S V t t t
max 48V
khi
3t
.
Vận tốc chuyển động đạt giá trị lớn nhất khi
3( ).ts
Câu 75: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một công ty bất động sản có 40 căn hộ
cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 3.000.000 đồng một tháng thì mọi căn hộ
đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100.000 đồng một tháng (theo qui
định trong hợp đồng) thì sẽ có một căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì
công ty đó phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng?
A.
3.700.000
đồng. B.
3.500.000
đồng. C.
3.900.000
đồng. D.
4.000.000
đồng.
Lời giải
Theo bài cứ tăng thêm 100.000 đồng trên một căn thì có 1 căn trống.
Do đó nếu tăng x đồng trên một căn thì có
100.000
x
căn trống.
Số tiền thu nhập một tháng khi cho thuê căn hộ là
x
2
(3000.000 )(40 ) 10 120.000.000 ( )
100.000 100.000
xx
x f x
Do
()fx
là một hàm bậc hai với hệ số số
0a
nên
()fx
đạt giá trị lớn nhất khi
500.000x
đ.
Vậy khi đó giá thuê mỗi căn là
3.500.000
đồng.
Câu 76: (SỞ GD QUẢNG NAM 2019) Cho nửa đường tròn đường kính
AB
và hai điểm
,CD
thay
đổi trên nửa đường tròn đó sao cho
ABCD
là hình thang. Diện tích lớn nhất của hình thang
ABCD
bằng
A.
1
2
B.
33
4
C.
1
D.
33
2
Lời giải
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------51
1
x
H
O
D
C
B
A
Gọi
H
là trung điểm của
CD
. Đặt
OH x
01x
. Ta có
2
2 2 1CD CH x
.
Diện tích hình thang
ABCD
là:
22
.
1.
2
AB CD OH
S x x x
Xét hàm số
2
1f x x x x
, với
0;1x
.
Ta có

2
2
12
'1
1
x
fx
x
;
22
3
'( ) 0 1 2 1
2
f x x x x
.
Bảng biến thiên:
Vậy diện tích lớn nhất của hình thang
ABCD
là
33
.
4
Câu 77: (SỞ GD&ĐT CÀ MAU NĂM 2018-2019) Người ta muốn xây một cái bể hình hộp đứng có thể
tích
3
18Vm
, biết đáy bể là hình chữ nhật có chiều dài gấp
3
lần chiều rộng và bể không có
nắp. Hỏi cần xây bể có chiều cao
h
bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất
(biết nguyên vật liệu xây dựng các mặt là như nhau)?
A.
2 m
. B.
5
2
m
. C.
1 m
. D.
3
2
m
.
Lời giải
Gọi
x
0x
là chiều rộng hình chữ nhật đáy bể, suy ra chiều dài hình chữ nhật đáy bể là
3.x
2
. .3 .3 18V h x x h x
0x
22
18 6
3
h
xx
,
Gọi
P
là diện tích xung quanh cộng với diện tích một đáy bể của hình hộp chữ nhật.
Nguyên vật liệu ít nhất khi
P
nhỏ nhất.
2 2 2
22
6 6 48
2 2. .3 3 2. . 2. .3 3 3 .P hx h x x x x x x
x
xx
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------52
Đặt

2
48
3f x x
x
,
0x
. Ta có

2
48
6f x x
x
,
2
48
0 6 0 2f x x x
x
.
Bảng biến thiên:
Suy ra vật liệu ít nhất khi
2
6 6 3
42
hm
x
.
Câu 78: (CỤM 1 SỞ GD&ĐT BẠC LIÊU NĂM 2018-2019 LẦN 01) Người ta muốn xây một bể chứa
nước dạng hình hộp chữ nhật không nắp có thể tích 200m
3
. Đáy bể là hình chữ nhật có chiều
dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m
2
. Chi phí thuê công nhân
thấp nhất là
A. 51 triệu đồng . B. 75 triệu đồng. C. 46 triệu đồng. D. 36 triệu đồng.
Lờigiải
Gọi chiều rộng, chiều dài của đáy lần lượt là x và 2x, chiều cao là y
Diện tích các mặt bên và mặt đáy là

2
62S xy x
Thể tích là
2
100
2 200 ;V x y xy
x
2 2 2
3
3
600 300 300 300 300
2 2 3 . .2 30 180S x x x
x x x x x
Vậy chi phí thấp nhất là
d
3
30 180.300000 51T
triệu
DẠNG TOÁN 4: PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH
Câu 79: (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số
y f x
có bảng biến thiên
Tìm tất cả các giá trị của
m
để bất phương trình
11f x m
có nghiệm?
A.
4.m
B.
1m
. C.
2m
. D.
5m
.
Lời giải
Đặt
1 1 1t x t
. Khi đó BPT
11f x m
trở thành
1f t m
Khi đó BPT
11f x m
có nghiệm khi và chỉ khi BPT
1f t m
có nghiệm
1t
1
min 4
t
m f t m
.
Câu 80: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho hàm số
fx
, hàm số
y f x
liên tục trên và có
đồ thị như hình vẽ bên.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------53
Bất phương trình
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
0;2x
khi và chỉ
khi
A.
22mf
. B.
0mf
. C.
22mf
. D.
0mf
.
Lời giải
Ta có
, 0;2 , 0;2 *f x x m x m f x x x
.
Dựa vào đồ thị của hàm số
y f x
ta có với
0;2x
thì
1fx
.
Xét hàm số
g x f x x
trên khoảng
0;2
;

1 0, 0;2g x f x x
.
Suy ra hàm số
gx
nghịch biến trên khoảng
0;2
. Do đó
* 0 0m g f
.
Câu 81: (MĐ 102 BGD&ĐT NĂM 2018-2019) Cho hàm số
fx
, hàm số
y f x
liên tục trên và
có đồ thị như hình vẽ sau:
Bất phương trình
f x x m
(
m
là tham số thực) nghiệm đúng với mọi
0;2x
khi và chỉ
khi
A.
22mf
. B.
22mf
. C.
0mf
. D.
0mf
.
Lời giải
Bất phương trình
f x x m
nghiệm đúng với mọi
0;2x
m f x x
nghiệm đúng với mọi
0;2x
(1)
Xét hàm số
g x f x x
trên khoảng
0;2
, có

1 0, 0;2g x f x x
Bảng biến thiên:
Vậy (1)
2mg
22mf
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------54
Câu 82: (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 04) Cho hàm số
y f x
và hàm số
y g x
có đạo hàm xác định trên và có đồ thị như hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số m để phương trình
fx
m
gx
có nghiệm thuộc


2;3
?
A. 4. B. 5. C. 7. D. 6.
Lời giải
Xét hàm số
fx
hx
gx
. Dựa vào đồ thị, ta thấy các hàm số
fx
và
gx
liên tục và nhận giá
trị dương trên


2;3
, do đó
hx
liên tục và nhận giá trị dương trên


2;3
.
Ngoài ra với



2;3x
, dễ thấy
6fx
,
1gx
nên
6
fx
hx
gx
, mà
0
6
06
1
0
f
h
g
nên


2;3
max 6hx
(1).
Lại có
0hx
với mọi



2;3x
và
21h
nên


2;3
0 min 1hx
(2).
Phương trình
fx
m
gx
có nghiệm trên


2;3
khi và chỉ khi





2;3
2;3
min maxh x m h x
(3).
Từ
1
,
2
và
3
, kết hợp với
m
, ta có
1;2;3;4;5;6m
. Chọn D.
Câu 83: (MĐ 103 BGD&ĐT NĂM 2018-2019) Cho hàm số
fx
, hàm số
y f x
liên tục trên và
có đồ thị như hình vẽ bên.
Bất phương trình
2f x x m
(
m
là tham số thực) nghiệm đúng với mọi
0;2x
khi và chỉ
khi
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------55
A.
0mf
. B.
24mf
. C.
0mf
. D.
24mf
.
Lời giải
Ta có
22f x x m m f x x
*
. Xét hàm số
2g x f x x
trên
0;2
.
Ta có

20g x f x
0;2x
nên hàm số
gx
nghịch biến trên
0;2
.
Do đó
2m f x x
nghiệm đúng với mọi
0;2x
khi
00m g f
.
Câu 84: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số
y f x
. Hàm số
y f x
có bảng
biến thiên như sau:
x

2
1


0
y
2

Bất phương trình

3
f x x m
đúng với mọi
1;1x
khi và chỉ khi
A.
1m f x
. B.
11mf
. C.
11mf
. D.
11mf
.
Lời giải
33
f x x m m f x x
1
. Xét

3
g x f x x
.

2
3 0, 1;1g x f x x x
vì

2
1 0, 1;1
3 0, 1;1
f x f x
xx
Hàm số
y g x
nghịch biến trên
1;1
11g g x g
,
1;1x
.
1
đúng với mọi
1;1x
1 1 1m g f
.
Câu 85: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Số các giá trị nguyên của tham số
m
thuộc đoạn


2019;2019
để phương trình
23
2 4 1 4x m x m x x
có nghiệm là
A.
2011
. B.
2012
. C.
2013
. D.
2014
.
Lời giải
Điều kiện :
3
4 0 0x x x
.
*) Nhận thấy
0x
không là nghiệm của phương trình.
*) Với
0x
chia cả hai vế của phương trình cho
3
4xx
ta được:
2
2
4
2 1. 1
4
xx
mm
x
x
Đặt
2
4 4 4
2. . 2
x
t x x
x x x
. Vậy
2t
với
0x
.
Phương trình
1
trở thành:


2
2
24
1 2 0 2 ( 2) 2
11
tt
t m t m m m t t
tt
.
Xét hàm số
4
2
1
f t t
t
trên

2;
.





2
22
3 2;
4 2 3
1 ; 0
1 2;
11
t
tt
f t f t
t
tt
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------56
Bảng biến thiên của hàm số
ft
:
Phương trình đã cho có nghiệm khi và chỉ khi phương trình
2
có nghiệm

2;t
.
Từ bảng biến thiên ta thấy
7m
. Kết hợp
m
và



2019;2019m
suy ra có 2013 giá trị
m
.
Câu 86: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số
m
để
bất phương trình
2
6 2 8 1x x x x m
nghiệm đúng với mọi



2;8 .x
A.
16m
. B.
15m
. C.
8m
. D.
2 16m
.
Lời giải
Xét bất phương trình:
2
6 2 8 1 1x x x x m
, điều kiện



2;8 .x
Đặt
28t x x
,



2;8 .x
Ta có:

3
'
28
x
t
xx
,
' 0 3tx
Bảng biến thiên:
Suy ra


0; 5t
. Khi đó
1
trở thành:
2
15 2t t m
. Xét hàm số
2
15f t t t
,
Bất phương trình
1
nghiệm đúng với mọi



2;8x
khi và chỉ khi
2
nghiệm đúng với mọi


0;5t


0;5
max
15f t m m
.
Câu 87: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số giá trị nguyên của tham số
m
nằm
trong khoảng
0;2020
để phương trình
1 2019 2020x x m
có nghiệm là
A.
2020
. B.
2021
. C.
2019
. D.
2018
.
Lời giải
Ta có





2018, 1;2019
1 2019
2 2020 , 1;2019
x
f x x x
xx
.
Vì hàm số
x( ) 2 2020hx
là hàm số đồng biến trên đoạn
[1;2019]
nên ta có
[1;2019] [1;2019]
max max min min ( ) (1), (2019) 2018, ( ) (1), (2019) 2018h x h h h x h h
Suy ra:


1;2019
min 0fx
và


1;2019
max 2018fx
. Do đó, ta có:
min 0fx
và
max 2018fx
.
Vì vậy, phương trình đã cho có nghiệm khi và chỉ khi:
0 2020 2018 2 2020mm
.
Suy ra có 2018 giá trị nguyên của
m
nằm trong khoảng
0;2020
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------57
Câu 88: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Gọi
S
là tập tất cả các giá trị của tham số
m
để
bất phương trình
4
2 4 2
1 4 5 6x x x m m m
thỏa mãn với mọi giá trị của
x
. Tính
tổng các giá trị của
.S
A.
1
. B.
3
. C.
5.
D.
2
.
Lời giải
Đặt
4
2
1 4 5f x x x x
.
3
32
4 1 2 4 4 12 14f x x x x x x



2
2 3 3xx
,
00f x x
f(x)
f '(x)
0
-
∞
+
∞
-
+
∞
0
-4
+
∞
+
x
Xét
4 2 3 2
6 4 2 6 2 1 2 2 3f m m m m f m m m m m m
0 1.f m m
f(m)
f '(m)
0
-
∞
+
∞
-
+
∞
1
-4
+
∞
+
m
Ycbt
4 2 4 2
min 6 6 4f x m m m m m m
1.m
Vậy tổng các giá trị của
S
là
1.
Câu 89: (SỞ GD&ĐT QUẢNG BÌNH NĂM 2018-2019) Gọi
S
là tập hợp tất cả các giá trị nguyên
dương của tham số
m
để bất phương trình sau
6 4 3 3 2
3 4 2 0x x m x x mx
nghiệm đúng
với mọi


1;3x
. Tổng tất cả các phần tử của
bằng:
A.
. B.
2
. C.
1
. D.
4
.
Lời giải
Ta có:
6 4 3 3 2 6 4 2 3 3
3 4 2 0 3 4 2x x m x x mx x x x m x mx
3
3
22
1 1 1x x mx mx
Xét hàm đặc trưng
32
' 3 1 0f t t t f t t
22
1 1 1f x f mx x mx
Bài toán trở thành tìm
m
để bất phương trình

2
1x mx
nghiệm đúng với mọi


1;3x


2
2
1
1 , 1;3
x
x mx m g x x
x
;




2
1;3
1
' 1 0 1;3 1 2
x
g x x Min g x g
x
Vậy để bất phương trình đã cho nghiệm đúng với mọi


1;3x
thì
2m
Vì
m
nguyên dương nên
1;2S
có
phần tử. Tổng các phần tử bằng
.
Câu 90: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Giá trị lớn nhất của hàm
số

32
1
x x m
y
x
trên


0; 2
bằng
5
. Tham số
m
nhận giá trị là
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------58
A.
5
. B.
1
. C.
3
. D.
8
.
Lời giải
Đặt

32
1
x x m
fx
x
.
Giá trị lớn nhất của
y f x
trên


0; 2
bằng




00
5, 0; 2
0;2 5
f x x
x f x
.
*


5, 0; 2f x x

32
5,
1
x x m
x



0; 2x
32
5 5,m x x x



0; 2x
0;2
max


m h x
, với
32
55h x x x x
.
+ Ta có:
2
3 2 5h x x x
,
0hx
2
3 2 5 0xx
L

1
5
3
x
x
.
Ta có:
05h
,
23h
,
18h
. Suy ra
0;2
max


3hx
,
0;2
min


8hx
.
Vậy
3m
.
1
*


00
0;2 5x f x


32
5
1
x x m
x
có nghiệm trên


0;2
.
32
55m x x x
có nghiệm trên


0;2
.
Theo phần trên, ta suy ra
83m
.
2
. Từ
1
và
2
suy ra
3m
.
Cách dùng casio: Kiểm tra từng giá tri của
m
từ các đáp án A, B, C, D như sau
Trường hợp 1:
5m
thì

32
5
1
xx
fx
x
.
Trước khi làm thì tắt hàm
gx
bằng lệnh “ SHIFT + MODE +
+ 5 + 1”.
Bước 1: Vào môi trường TABLE bằng lệnh “Mode + 7”.
Bước 2: Nhập hàm

32
5
1
xx
fx
x
.
Bước 3: Nhập
0Start
;
2End
;
20
29
Step
.
Quan sát bên cột
fx
có giá trị
5,67fx
nên loại
5m
. Ba trường hợp còn lại làm tương
tự như trên chỉ có
3m
thỏa mãn giá trị lớn nhất của
fx
là
5
.
Câu 91: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi
s
là tập hợp các giá trị
nguyên của tham số


0;2019m
để bất phương trình
3
22
10x m x
đúng với mọi



1;1x
. Số phần tử của tập
s
bằng
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------59
A.
1
. B.
2020
. C.
2019
. D.
2
.
Lời giải
Đặt

2
1tx
, với
1;1 0;1xt
. Bất phương trình
3
22
1 0 1x m x
trở thành
3 2 3 2
1 0 1 2t t m m t t
Bất phương trình
1
đúng với mọi



1;1x
khi và chỉ khi bất phương trình
2
nghiệm
đúng với mọi


0;1t
. Hay
ax


32
0;1
11m m t t m
.
Mặt khác, m là số nguyên thuộc


0;2019
nên
1;2;3;...;2019m
Vậy có 2019 giá trị của m thỏa mãn bài toán.
Câu 92: (CHUYÊN ĐẠI HỌC VINH LẦN 03 NĂM 2018 - 2019) Cho
()fx
mà đồ thị hàm số
'( )y f x
như hình vẽ sau:
Bất phương trình
( ) sin
2
x
f x m
nghiệm đúng với mọi



1;3x
khi và chỉ khi
A.
(0)mf
. B.
(1) 1mf
. C.
( 1) 1mf
. D.
(2)mf
.
Lời giải
Cách 1: Xét
sin
2
x
g x f x

' ' cos
22
x
g x f x
• Với


1;1 ; cos 0
2 2 2 2
xx
x
(1)
Đồng thời dựa vào đồ thị
'fx
ta thấy
' 0, 1;1f x x
(2)
Từ (1), (2) ta suy ra
' 0, 1;1g x x
.
• Với
1;3x


3
; cos 0
2 2 2 2
xx
(3)
Đồng thời dựa vào đồ thị ta thấy
' 0, 1;3f x x
(4)
Từ (3), (4) ta suy ra
'0gx
,

1;3x
.
Tại
' 1 0
1: ' 1 0
cos 0
2
f
xg
. Ta có bảng biến thiên của
gx
như sau:
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------60
Để bất phương trình
sin
2
gx
x
f x m
nghiệm đúng với mọi



1;3x


1;3
min 1 1 1m g x m g f
.
Cách 2: Xét bất phương trình
( ) sin
2
x
f x m
(1) với



1;3x
, ta có:

( ) sin ( ) sin
22
xx
f x m f x m
(2). Xét
( ) sin
2
x
fx
với



1;3x
+ Từ đồ thị của hàm số
'( )y f x
đã cho ta suy ra BBT của
()fx
như sau:
x
1
1
'( )fx
0
()fx
( 1)f
(3)f
(1)f
Từ BBT ta suy ra:


( ) (1), 1;3f x f x
(*)
+ Do



1;3x
nên:
3
1 3 .
2 2 2
x
x
Suy ra:
1 sin 1
2
x
1 sin 1
2
x
(**)
+ Từ (*) và (**) cho ta:


( ) sin (1) 1, 1;3
2
x
f x f x
. Dấu
""
xảy ra khi
1x
Do đó: Bất phương trình
( ) sin
2
x
f x m
nghiệm đúng với mọi



1;3x
(1) 1mf
.
Câu 93: (CHUYÊN QUỐC HỌC HUẾ LẦN 3 2018-2019) Cho phương trình
22
2 2 1 2 0m x x x x
(
m
là tham số). Biết rằng tập hợp các giá trị của tham số
m
để
phương trình có nghiệm thuộc đoạn


0 ; 1 2 2
là đoạn


;ab
. Tính giá trị của biểu thức
2T b a
.
A.
4T
. B.
7
2
T
. C.
3T
. D.
1
2
T
.
Lời giải
Đặt
2
22t x x
. Xét hàm số
2
( ) 2 2g x x x
trên đoạn


0 ; 1 2 2 .

2
1
'( )
22
x
gx
xx
;
'( ) 0 1;g x x


0 2, 1 1, 1 2 2 3 1; 3g g g t
.
Khi đó phương trình trở thành
2
2
2
12
1
t
m t t m
t
.
Xét hàm số
2
2
()
1
t
ft
t
trên đoạn


1;3
.



22
22
2 ( 1) 2 2 2
0 1; 3
( 1) ( 1)
t t t t t
f t t
tt
;
17
1 ; 3
24
ff
.
Để phương trình có nghiệm thì




1;3
1;3
17
min max .
24
x
x
f t m f t m
Vậy
17
; 4.
24
a b T
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------61
Câu 94: (THPT CHUYÊN HOÀNG VĂN THỤ HÒA BÌNH NĂM 2018-2019 LẦN 04) Tổng các giá trị
nguyên dương của m để tập nghiệm của bất phương trình

2
1
72
m
xx
có chứa đúng hai số
nguyên là
A.
27
. B.
29
. C.
28
. D.
30
.
Lời giải
ĐK:
0x
. Do
m
dương nên
2
1 0, .
72
m
xx
Ta có:

2
1
72
m
xx
2
1
72
m
xx
2
72 1mx x
1
Nhận thấy
0x
không là nghiệm của
1
nên

2
72 1
1
x
m
x
Xét hàm số

2
72 1
()
x
y f x
x
với
0x
;


3
72 2
( ) 0
x
y f x
x
2x
.
Bảng biến thiên của
fx
với
0x
:
Từ bảng biến thiên ta có
27
2 3 4 , \ 2,3,4
2
f f f f x x
, nên để tập nghiệm của
bất phương trình
2
72 1x
m
x
có chứa đúng hai số nguyên thì
27
4 3 16
2
f m f
. (tập
nghiệm chứa
2, 3xx
)
Với
*
m
thì
14,15 .m
Do vậy, tổng các giá trị nguyên dương của m là
14 15 29
.
DẠNG TOÁN 5: BÀI TOÁN THAM SỐ
Câu 95: (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số
32
23y x x m
.
Trên


1;1
hàm số có giá trị nhỏ nhất là
1
. Tính
.m
A.
6m
. B.
3m
. C.
4.m 
D.
5m
.
Lời giải
Xét
1;1
có

2
66y x x
;
0y
2
6 6 0xx




0 1;1
1 1;1
x
x
.
Khi đó:
15ym
;
0ym
;
11ym
Ta thấy
51m m m
nên

1;1
min 5ym
.
Theo bài ra ta có



1;1
min 1y
nên
51m
4m
.
Câu 96: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số
2
1y x m x
có giá trị lớn nhất bằng
22
thì giá trị của
m
là
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------62
A.
2
2
. B.
2
. C.
2
. D.
2
2
.
Lời giải
Xét hàm số
2
1.y x m x
Tập xác định:



1;1D
. Ta có:

2
1
1
x
y
x



2
2
1
0
10
xx
y
x


2
10
1
x
xx





2
10
1
10
1
2
21
2
1
2
x
x
x
x
x
x
.
Ta có:



1
1 1 , 1 1 , 2
2
y m y m y m
.
Do hàm số
2
1y x m x
liên tục trên


1;1
nên
1;1
max 2ym


.
Theo bài ra thì
1;1
max 2 2y


, suy ra
2 2 2 2mm
.
Câu 97: (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Có một giá trị
0
m
của tham số
m
để hàm số
3 2 2
11y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn


0;1
. Khi đó
mệnh đề nào sau đây đúng ?
A.
2
00
2018 0.mm
B.
0
2 1 0.m 
C.
2
00
6 0.mm
D.
0
2 1 0.m 
Lời giải
Ta có


22
' 3 2 1 0, 0;1y x m x x
nên hàm số đã cho đồng biến trên


0;1 .
Suy ra


0;1
min 0 1 5y y m
2
0 0 0
4 2018 0m m m
Câu 98: (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị của tham số
m
để giá
trị lớn nhất của hàm số

2
2xm
y
xm
trên đoạn


0;4
bằng
1
.
A.
. B.
2
. C.
. D.
1
.
Lời giải
Điều kiện:
xm
.
Hàm số đã cho xác định trên


0;4
khi


0;4m
(*).
Ta có






2
2
22
17
24
2
0
m
mm
y
x m x m
với



0;4x
.
Hàm số đồng biến trên đoạn


0;4
nên



2
0;4
2
max 4
4
m
yy
m
.



0;4
max 1y
2
2
1
4
m
m
2
60mm

2
3
m
m
.
Kết hợp với điều kiện (*) ta được
3m
. Do đó có một giá trị của
m
thỏa yêu cầu bài toán.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------63
Câu 99: Cho hàm số
2
8
xm
fx
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn


0;3
bằng
3
. Giá trị
0
m
thuộc khoảng nào trong các
khoảng cho dưới đây?
A.
20;25
. B.
5;6
. C.
6;9
. D.
2;5
.
Lời giải
Xét hàm số
2
8
xm
fx
x
trên đoạn


0;3
.
Ta có:


2
2
8
0, 0;3
8
m
yx
x
hàm số
2
8
xm
fx
x
đồng biến trên đoạn


0;3


2
0;3
min 0 .
8
m
f x f
Theo giả thiết, ta có:



2
2
0;3
26
min 3 3 24 .
8
26
m
m
f x m
m
Mà
0, 2 6 4,9 2;5m m m
.
Câu 100: (MĐ 101 BGD&ĐT NĂM 2016-2017) Cho hàm số
1
xm
y
x
(
m
là tham số thực) thỏa mãn
[
2;4]
min 3y
. Khẳng định nào sau dưới đây đúng?
A.
1.m
B.
3 4.m
C.
4.m
D.
1 3.m
Lời giải
Ta có

2
1
1
m
y
x
.
+) Nếu
2;4
1 0 1 1, 1 min 1 3m m y x f x


(loại).
+) Nếu
1 0 1mm
thì
lo¹i
2;4
min 2 2 3 1y y m m


.
+) Nếu
1 0 1mm
thì
nhËn)


2;4
4
min 4 3 5 (
3
m
y y m
Câu 101: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho hàm số
1
xm
y
x
(
m
là tham số thực) thoả mãn





1;2
1;2
16
min max
3
yy
. Khẳng định nào dưới đây đúng?
A.
0m
B.
4m
C.
02m
D.
24m
Lời giải
Ta có
2
1
1
m
y
x
.
Nếu
1 1, 1m y x
. Không thỏa mãn yêu cầu đề bài.
Nếu
1m
Hàm số đồng biến trên đoạn


1;2
.
Khi đó:





1;2
1;2
16
min max
3
yy

16 1 2 16
1 2 5
3 2 3 3
mm
y y m
(loại).
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------64
Nếu
1m
Hàm số nghịch biến trên đoạn


1;2
.
Khi đó:





1;2
1;2
16 16 2 1 16
min max 2 1 5
3 3 3 2 3
mm
y y y y m
( t/m).
Câu 102: (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm
số
1
xm
y
x
trên


1;2
bằng
8
(
m
là tham số thực). Khẳng định nào sau đây đúng?
A.
10m
. B.
8 10m
. C.
04m
. D.
48m
.
Lời giải
Nếu
1m
thì
1y
(không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu
1m
thì hàm số đã cho liên tục trên


1;2
và
2
1
'
1
m
y
x
.
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn


1;2
.
Do vậy





1;2
1;2
1 2 41
min max 1 2 8
2 3 5
x
x
mm
y y y y m
.
Câu 103: (THPT HUỲNH MẪN ĐẠT NĂM 2018-2019 LẦN 01) Cho hàm số
2sin cos
sin cos
x m x
y
xx
đạt giá
trị lớn nhất trên



0;
4
bằng
1
. Khẳng định nào sau đây đúng?
A.

1;0m
. B.
0;1m
. C.
1;2m
. D.
2;3m
.
Lời giải
Ta có:
2
2
.
sin cos
m
y
xx
TH1:
2
2
02
sin cos
m
ym
xx
hàm số luôn đồng biến trên



0;
4
Khi đó
π
0;
4
max






2
10
42
m
y y m
(thỏa mãn)
TH2:
2
2
02
sin cos
m
ym
xx
hàm số luôn nghịch biến trên



0;
4
Khi đó
max



0;
4
0 1 1y y m m
(loại)
TH3:
2
2
02
sin cos
m
ym
xx
2y
, khi đó
max



0;
4
2y
(loại)
Câu 104: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi
,AB
lần lượt là giá trị nhỏ nhất, giá trị
lớn nhất của hàm số

2
1
x m m
y
x
trên đoạn


2;3
. Tìm tất cả các giá trị thực của tham số
m
để

13
2
AB
.
A.
1; 2mm
. B.
2m
. C.
2m
. D.
1; 2mm
.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------65
Lời giải
Xét hàm số

2
1
x m m
y
x
trên đoạn


2;3
.


2 2 2
2
1 3 2
' 0 2;3 3 , 2
21
1
m m m m m m
y x A f B f
x
.

22
1
13 3 2 13
2
2 2 1 2
m
m m m m
AB
m
.
Câu 105: (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Gọi
T
là tập hợp tất cả giá trị của tham số
m để hàm số
2
1mx
y
xm
có giá trị lớn nhất trên đoạn


2;3
bằng
5
6
. Tính tổng của các phần tử
trong
T
.
A.
17
5
. B.
16
5
. C.
2
. D.
6
.
Lời giải
Ta có:
2
1mx
y
xm
. Điều kiện

2
xm
. Ta có:

3
22
2
11mx m
yy
xm
xm
.
- Nếu
1m
thì
1
1
x
y
x
. Khi đó
[2;3]
max 1y
, suy ra
1m
không thỏa mãn.
- Nếu
3
1 0 1mm
thì
0y
. Suy ra hàm số
2
1mx
y
xm
đồng biến trên đoạn
[2;3]
.
Khi đó
2
2
[2;3]
3
3 1 5
max 3 5 18 9 0
3
6
3
5
m
m
y y m m
m
m
.
Đối chiếu với điều kiện
1m
, ta có
3m
thỏa mãn yêu cầu bài toán.
- Nếu
3
1 0 1mm
thì
0y
. Suy ra hàm số
2
1mx
y
xm
nghịch biến trên đoạn
[2;3]
.
Khi đó
2
2
[2;3]
2
2 1 5
max 2 5 12 4 0
2
6
2
5
m
m
y y m m
m
m
.
Đối chiếu với điều kiện
1m
, ta có
2
5
m
thỏa mãn yêu cầu bài toán.
Vậy



2
3;
5
T
. Do đó tổng các phần tử của
T
là

2 17
3
55
.
Câu 106: (THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số
x
2
3
3y x m
.
Tổng tất cả các giá trị của tham số
m
sao cho giá trị nhỏ nhất của hàm số trên đoạn


1;1
bằng 1 là
A.
1
. B.
4
. C.
. D.
4
.
Lời giải
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------66
Xét hàm số
x
3
3f x x m
.
Để GTNN của hàm số
x
2
3
3y x m
trên đoạn


1;1
bằng
1
thì


1;1
min 1fx
hoặc


1;1
max 1fx
. Ta có
x

2
33fx
;


1
0
1
x
fx
x
fx
nghịch biến trên


1;1
.
Suy ra


1;1
max 1 2f x f m
và


1;1
min 1 2f x f m
.
Trường hợp 1:


1;1
min 1 2 1 3f x m m
.
Trường hợp 2:


1;1
max 1 2 1 3f x m m
.
Vậy tổng các giá trị của tham số
m
là
0
.
Câu 107: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số
sin
sin 1
xm
fx
x
. Tìm giá trị
của
m
để giá trị lớn nhất của hàm số
()fx
trên đoạn



2
0;
3
bằng
2.
A.
5.m
B.
5
.
2
m
m
C.
2.m
D.
3.m
Lời giải
Đặt
inx st
,






0;0
3
1
2
;xt
. Ta có hàm số



2
( ) , 0;
13
tm
g t t
t
. Ta có
2
1
'( )
1
m
gt
t
+) Với
1 0 1mm
. Ta có
'( ) 0gt
.
Suy ra


0;1
1
max ( ) 2 (1) 2 2 5
2
m
g t g m
(thỏa điều kiện)
+) Với
1 0 1mm
. Ta có
'( ) 0gt
.
Suy ra


0;1
max ( ) 2 (0) 2 2 2g t g m m
(không thỏa điều kiện). Vậy
5m
Câu 108: Có bao nhiêu giá trị nguyên dương của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
xm
y
x
trên đoạn


2; 3
bằng 14?
A.
. B.
1
. C.
. D. 4.
Lời giải
Tập xác định
\1D
. Ta có


2
2
1
0
1
m
y
x
,
xD
.
Do đó hàm số nghịch biến trên đoạn


2; 3
. Suy ra
min


2;3
3yy
2
3
31
m
14
5m
.
Vậy có 1 giá trị nguyên dương của
m
.
Câu 109: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
2y x x m
trên đoạn


1;2
bằng
5
.
A.
1
. B.
2
. C.
2
. D.
1
.
Lời giải
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------67
Ta có

2
22
2
x
y
x x m
,
01yx
. Do đó yêu cầu bài toán tương đương
max 1 , 2 , 1 5y y y
max 3 , , 1 5mmm
.
+ Trường hợp
1m
, ta có
max 3 , , 1 5 3 5 2m m m m m
.
+ Trường hợp
1m
ta có
max 3 , , 1 5 1 5 4m m m m m
.
Vậy tổng các giá trị
m
bằng
2
.
Câu 110: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017-2018) Gọi S là tập hợp tất cả các giá trị của tham số
thực m sao cho giá trị lớn nhất của hàm số
3
3y x x m
trên đoạn


0;2
bằng 3. Số phần tử
của S là
A. 1. B. 2. C. 0. D. 6.
Lời giải
Xét hàm số
3
3f x x x m
, ta có

2
33f x x
. Ta có bảng biến thiên của
fx
:
TH 1 :
2 0 2mm
. Khi đó


0;2
22max f x m m
2 3 1mm
(loại).
TH 2 :

20
20
0
m
m
m
. Khi đó :
2 2 2 2m m m


0;2
22max f x m m
2 3 1mm
(thỏa mãn).
TH 3 :
0
02
20
m
m
m
. Khi đó :
2 2 2 2m m m


0;2
2max f x m
2 3 1mm
(thỏa mãn).
TH 4:
2 0 2mm
. Khi đó



0;2
2max f x m
2 3 1mm
(loại).
Câu 111: (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số
m
để hàm số

2
1x mx
y
xm
liên tục và đạt giá trị nhỏ nhất trên đoạn


0;2
tại một điểm
0
0;2x
.
A.
01m
. B.
1m
. C.
2m
. D.
11m
.
Lời giải
Tập xác định:
\Dm
. Hàm số liên tục trên


0;2




00
22
mm
mm
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------68
Ta có



2
22
22
1
21
xm
x mx m
y
x m x m
. Cho

1
2
1
0
1
xm
y
xm
.
Ta có bảng biến thiên
Hàm số đạt giá trị nhỏ nhất tại
0
0;2x
nên
0 1 2 1 1mm
So với điều kiện hàm số liên tục trên đoạn


0;2
. Ta có
01m
.
CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định
xm
Hàm số liên tục trên đoạn


0;2
nên





00
0;2 *
22
mm
m
mm



2
22
22
1
21
'
xm
x mx m
y
x m x m
;
'0y
có hai nghiệm là
1
2
1
1
xm
xm
,

12
2xx
nên chỉ có nhiều nhất một nghiệm thuộc
0;2
Ta thấy
1 1,m m m
và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên


0;2
tại
một điểm
0
0;2x
thì
0 1 2 1 1 * *mm
. Từ
* , * *
ta có
0 1.m
Câu 112: (THPT Phụ Dực - Thái Bình - 2019) Gọi
là tập hợp các giá trị của
m
để hàm số
32
3y x x m
đạt giá trị lớn nhất bằng
50
trên
[ 2;4]
. Tổng các phần tử thuộc
là
A.
. B.
36
. C.
140
. D.
0
.
Lời giải
Xét hàm số
32
( ) 3g x x x m
có

2
36g x x x
. Xét

0
0
2
x
gx
x
.
Khi đó giá trị lớn nhất của hàm số
32
3y x x m
trên
[ 2;4]
là:



2;4
max max 0 ; 2 ; 2 ; 4
x
y y y y y
max ; 4 ; 20 ; 16m m m m
.
Trường hợp 1: Giả sử
max 50ym

50
50
m
m
.
Với
50m
thì
16 66 50m
( loại).
Với
50m
thì
20 70 50m
(loại).
Trường hợp 2: Giả sử
max 4 50ym

54
46
m
m
.
Với
54 54 50mm
(loại).
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------69
Với
46m
thì
20 66 50m
( loại).
Trường hợp 3: Giả sử
max 20 50ym

70
30
m
m
Với
70m
thì
16 86 50m
(loại).
Với
30m
thì
16 14 50m
,
30 50m
;
4 34 50m
(thỏa mãn).
Trường hợp 4: Giả sử
max 16 50ym

34
66
m
m
.
Với
34m
thì
34 50, 4 30 50, 20 14 50m m m
(thỏa mãn).
Với
66m
thì
66 50m
(loại).
Vậy
30;34S
. Do đó tổng các phẩn tử của
S
là:
30 34 4
.
Câu 113: (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số

2
2
2
x mx m
y
x
trên đoạn


1;1
bằng
3
. Tính tổng tất cả các
phần tử của
S
.
A.
8
3
. B.
5
. C.
5
3
. D.
1
.
Lời giải
Xét hàm số


2
2
2
x mx m
y f x
x
trên


1;1
có

2
4
1
2
fx
x
;



0
0
4 1;1
x
fx
x
;


3 1 1
1 ; 0 ; 1
31
mm
f f m f
.
Bảng biến thiên:
Trường hợp 1.
0 0 0fm
. Khi đó


1;1
3 max max 1 ; 1f x f f




31
3 max ; 1
3
m
m
1 3 2mm
.
Trường hợp 2.
0 0 0fm
.
Khả năng 1.

10
1
10
f
m
f
. Khi đó



1;1
3 max 0f x f
3m
.
Khả năng 2.
1
1
3
m
. Khi đó

10
10
f
f
.



1;1
3 max max 0 ; 1f x f f
3 max ; 1mm
: Trường hợp này vô nghiệm.
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------70
Khả năng 3.
1
0
3
m
. Khi đó


1;1
3 max max 0 ; 1 ; 1f x f f f
: Vô nghiệm.
Vậy có hai giá trị thỏa mãn là
12
3, 2mm
. Do đó tổng tất cả các phần tử của
S
là
1
.
Câu 114: (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực
m
để giá trị nhỏ nhất
của hàm số
2
4 3 4y x x m x
bằng
5
.
A.
. B.
3
. C.
. D.
1
.
Lời giải
Xét
2
43f x x x m
có
1 m
.
TH1.
1m
:
2
0 8 3f x x y x x m
.
min 5 8ym
(TM).
TH2.
1m
:
0fx
có hai nghiệm
1
21xm
;
2
21xm
.
Nếu
12
;x x x
:
2
3y x m
.
1
8 4 1 ;y x m
2
8 4 1y x m

12
y x y x
12
;
min 8 4 1 8
xx
ym
(Không
TM).
Nếu
12
;x x x
:
2
83y x x m
.
)
2
4 1 3xm
:
min 13 5 8y m m
(Loại).
)
2
43xm
:
min 8 4 1 8ym
(Không TM). Vậy có 1 giá trị của
m
.
HẾT
HUẾ ... 16h00 Ngày 08 tháng 8 năm 2020
| 1/71
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


Giáo viên: LÊ BÁ BẢO_ Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115
Đăng kí học theo địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Hoặc Trung tâm Km 10 Hương Trà Chuyªn ®Ò: KH¶O S¸T HµM Sè
Chñ ®Ò: GI¸ TRÞ LíN NHÊT - GI¸ TRÞ NHá NHÊT CñA HµM Sè HuÕ, th¸ng 6/2019
Lớp Toán thầy Lê Bá Bảo…0935.785.115…
Trường THPT Đặng Huy Trứ, Huế
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
CHUY£N §Ò: KH¶O S¸T HµM Sè
Chñ ®Ò 3: GI¸ TRÞ LíN NHÊT Vµ
GI¸ TRÞ NHá NHÊT CñA HµM Sè
Trong quá trình sưu tầm, biên soạn lời giải, có sai sót gì kính mong quý thầy cô và các em học sinh góp
ý để đề kiểm tra được hoàn chỉnh hơn! Xin chân thành cảm ơn! NỘI DUNG ĐỀ BÀI DẠNG TOÁN 1:
GTLN - GTNN TRÊN KHOẢNG (NỬA KHOẢNG - ĐOẠN) Câu 1:
(GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số f (x) liên tục trên a;b 
 . Khẳng định nào sau đây đúng?
A. Hàm số không có giá trị lớn nhất trên đoạn a; b   .
B. Hàm số luôn có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a; b   .
C. Hàm số không có giá trị nhỏ nhất trên đoạn a; b   .
D. Hàm số luôn có cực đại và cực tiểu trên đoạn a; b   . Câu 2:
(THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số y f x liên tục trên
thỏa mãn giá trị nhỏ nhất của hàm số trên
là 0 . Khẳng định nào sau đây là đúng?
A. f x  0 x  , x , f x 0 .
B. f x  0 x  . 0   0
C. f x  0 x  , x , f x 0 .
D. f x  0 x  . 0   0 Câu 3:
(THPT CẦU GIẤY HÀ NỘI NĂM 2018-2019 LẦN 01) Cho a,b  , 0  a b , hàm số y f (x) có đạo hàm trên
thỏa mãn f x  0 , xa;b . Giá trị nhỏ nhất của hàm số đã cho trên
đoạn a; b   bằng  a b  A. f b . B. f   . C. f a .
D. f ab .  2  Câu 4:
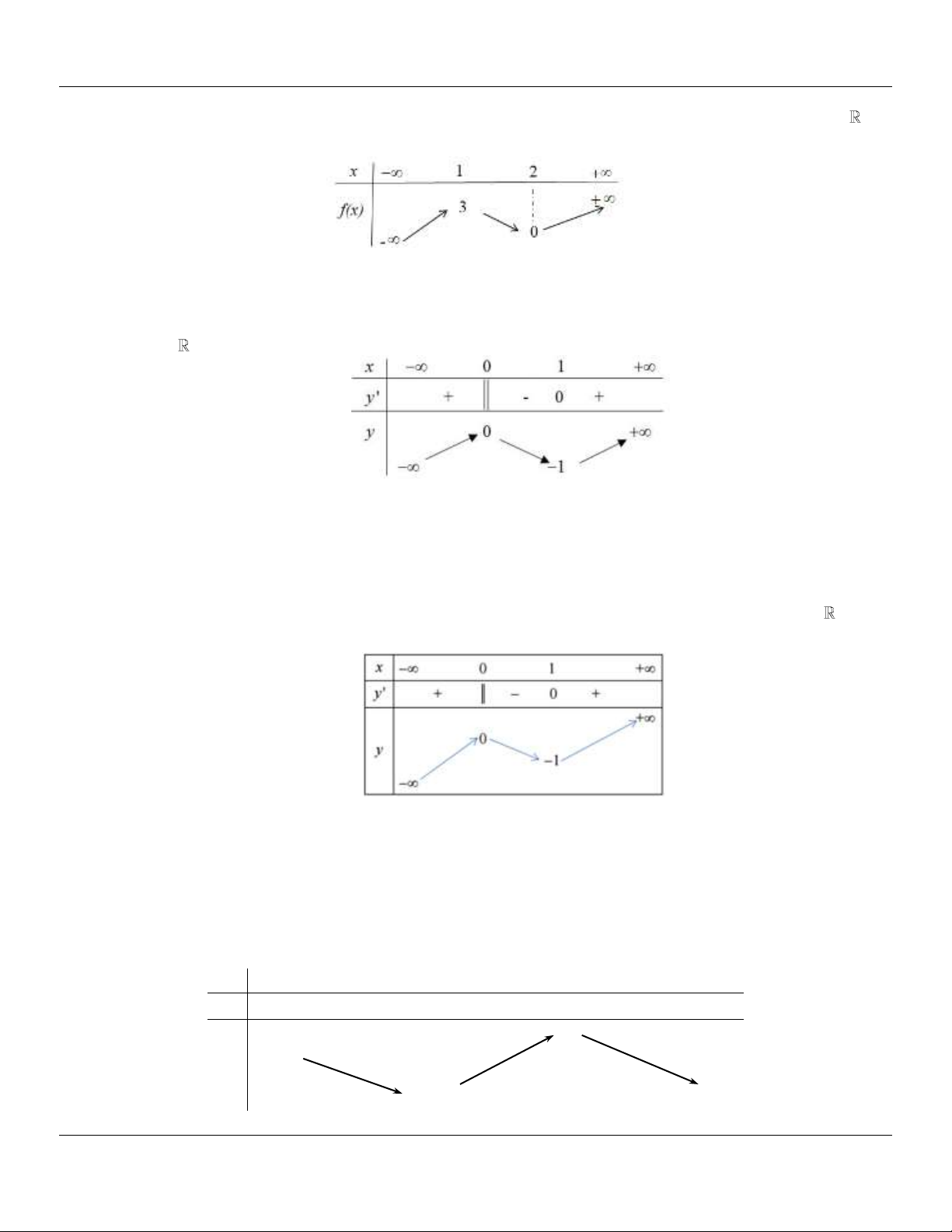
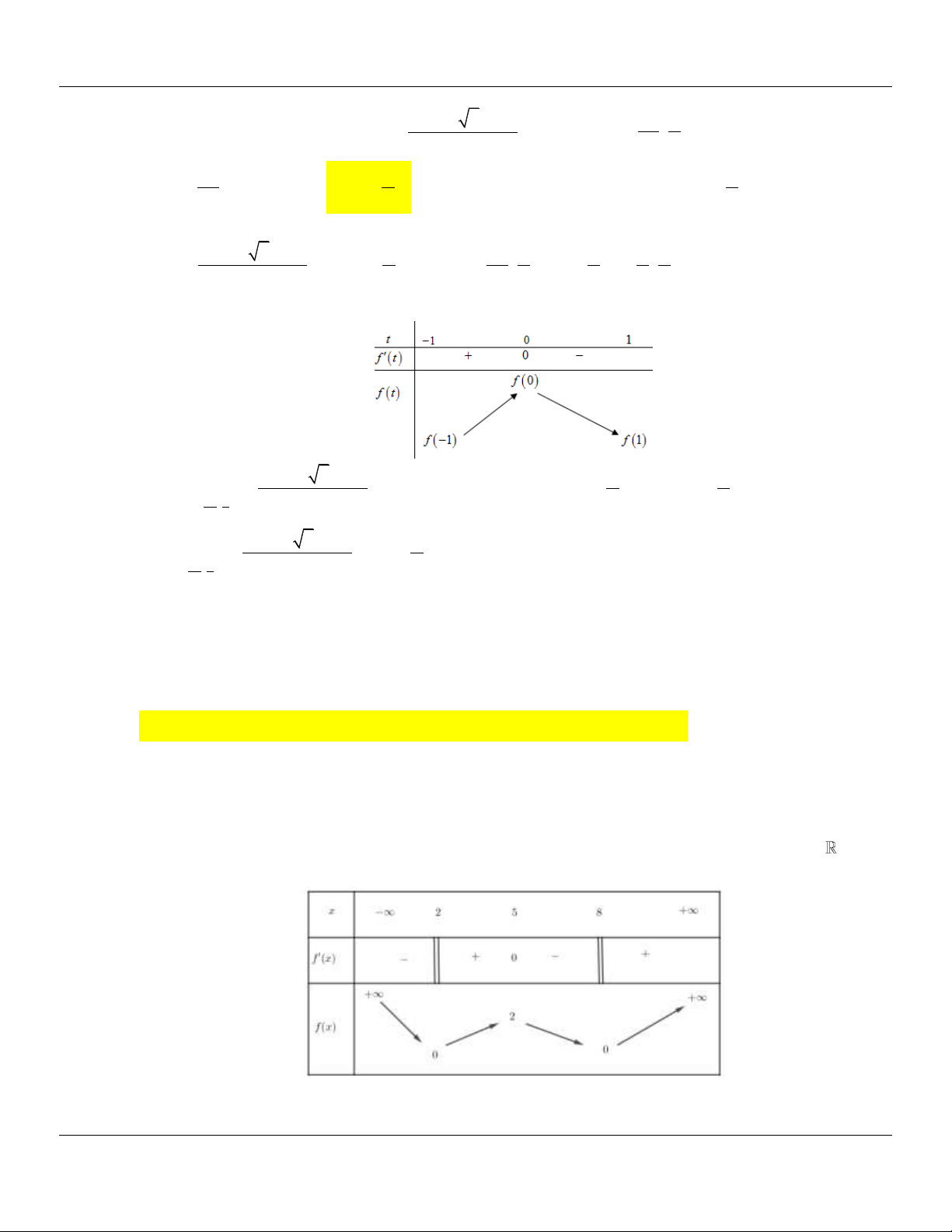
(CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số y f (x)
liên tục và có bảng biến thiên trên đoạn 1; 3 
 như hình vẽ. Khẳng định nào sau đây đúng?
A. max f (x)  f (0).
B. max f x  f 3 .
C. max f x  f 2 . D. max f x  f 1 .  1;  3   1;3   1;3   1;3  
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------1
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế Câu 5:
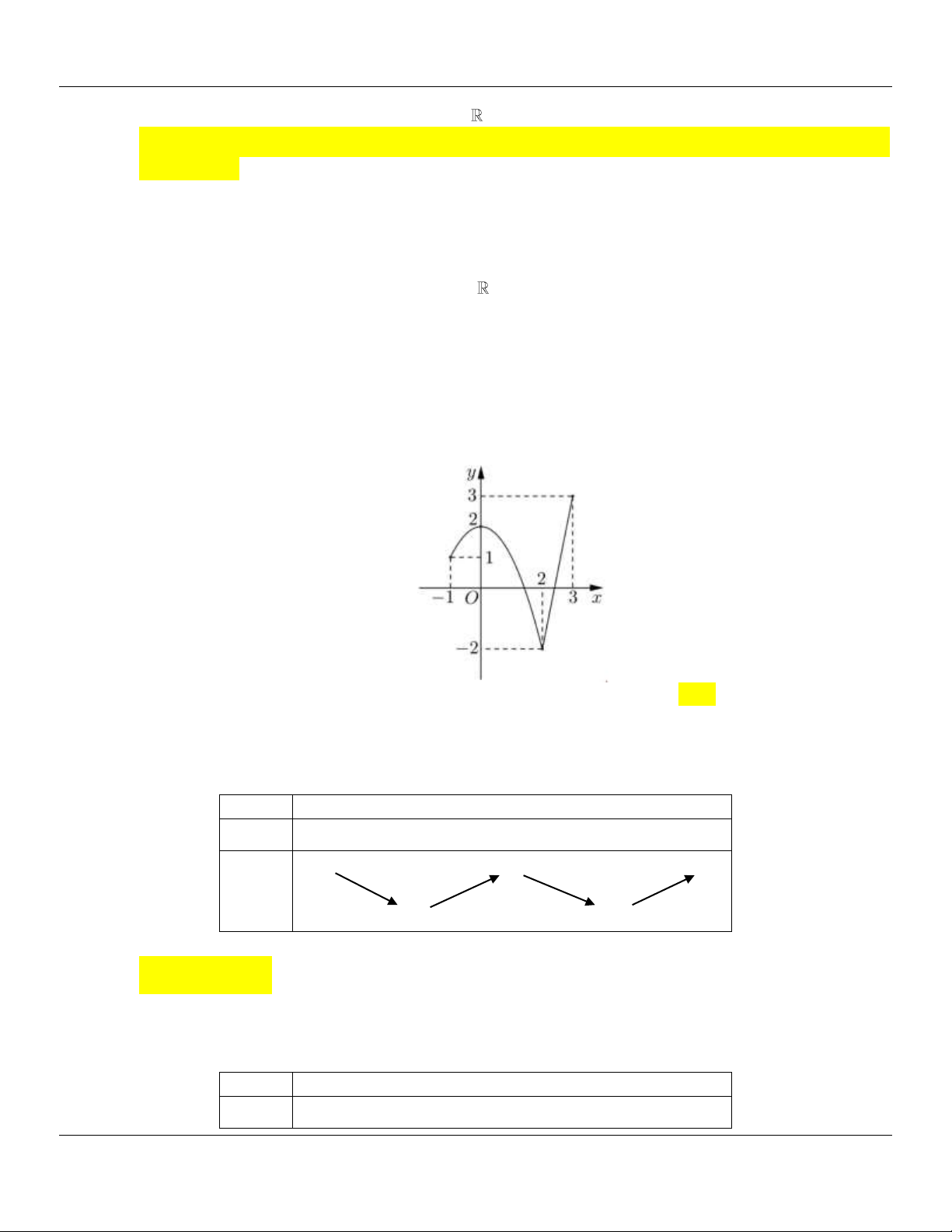
(THPT CỔ LOA HÀ NỘI NĂM 2018-2019) Cho hàm số y f x xác định, liên tục trên và
có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số y f x trên đoạn 0; 2   bằng A. 1 . B. 3 . C. 0 . D. 2 . Câu 6:
(THPT NGUYỄN DU - DAK LAC - NĂM 2018-2019) Cho hàm số y f x xác định, liên tục trên
và có bảng biến thiên như sau
Khẳng định nào sau đây sai?
A. Hàm số có giá trị cực tiểu bằng 1 .
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1 .
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1 .
D. Hàm số có đúng hai cực trị. Câu 7:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1 .
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1 .
D. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1 . Câu 8:
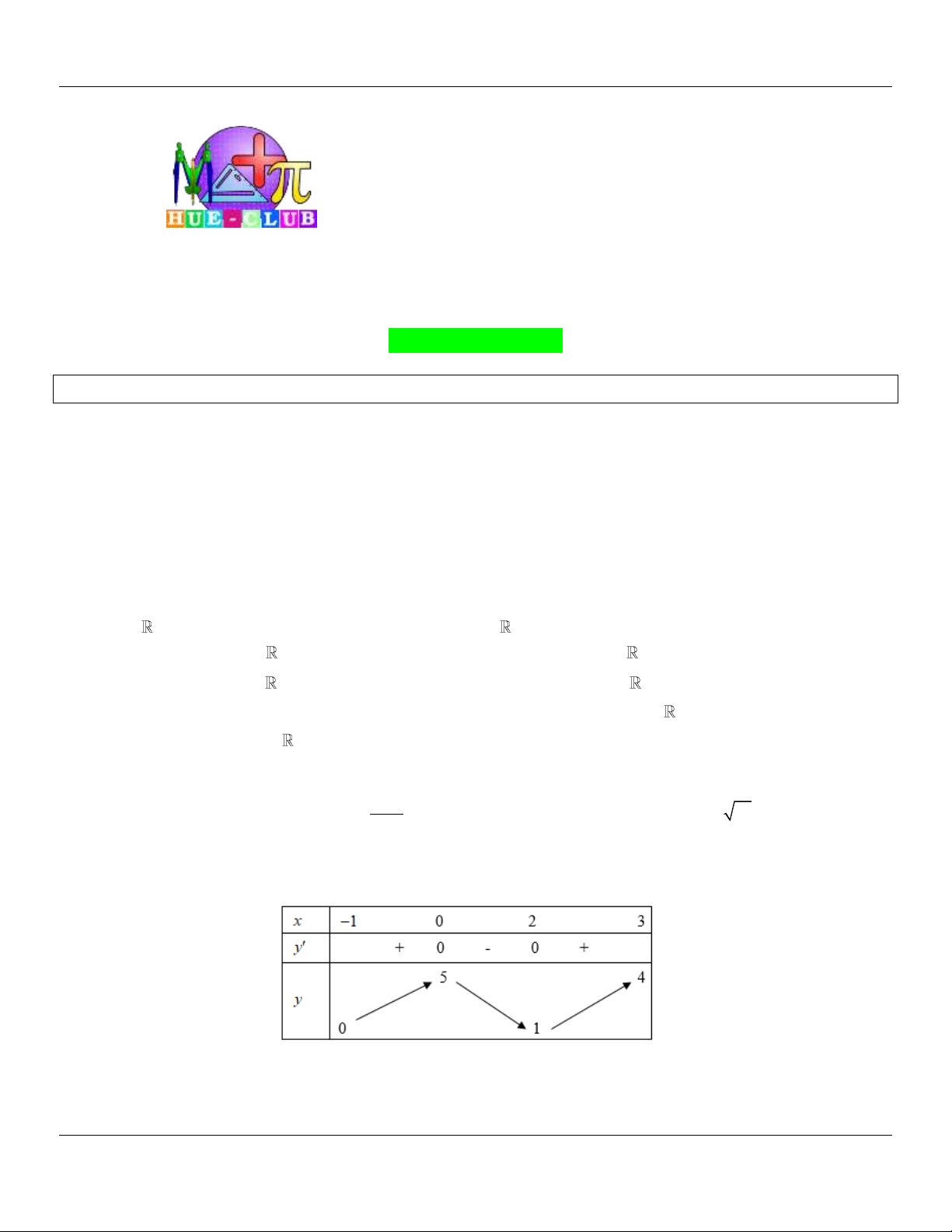
(Đề minh họa) Cho hàm số y f x có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng ? x  0 1  y  0  0   5 y 4 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------2
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. y  5. B. y  0. C. min y  4. D. max y  5. CĐ CT Câu 9:
(SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên trên   5;7 như sau:
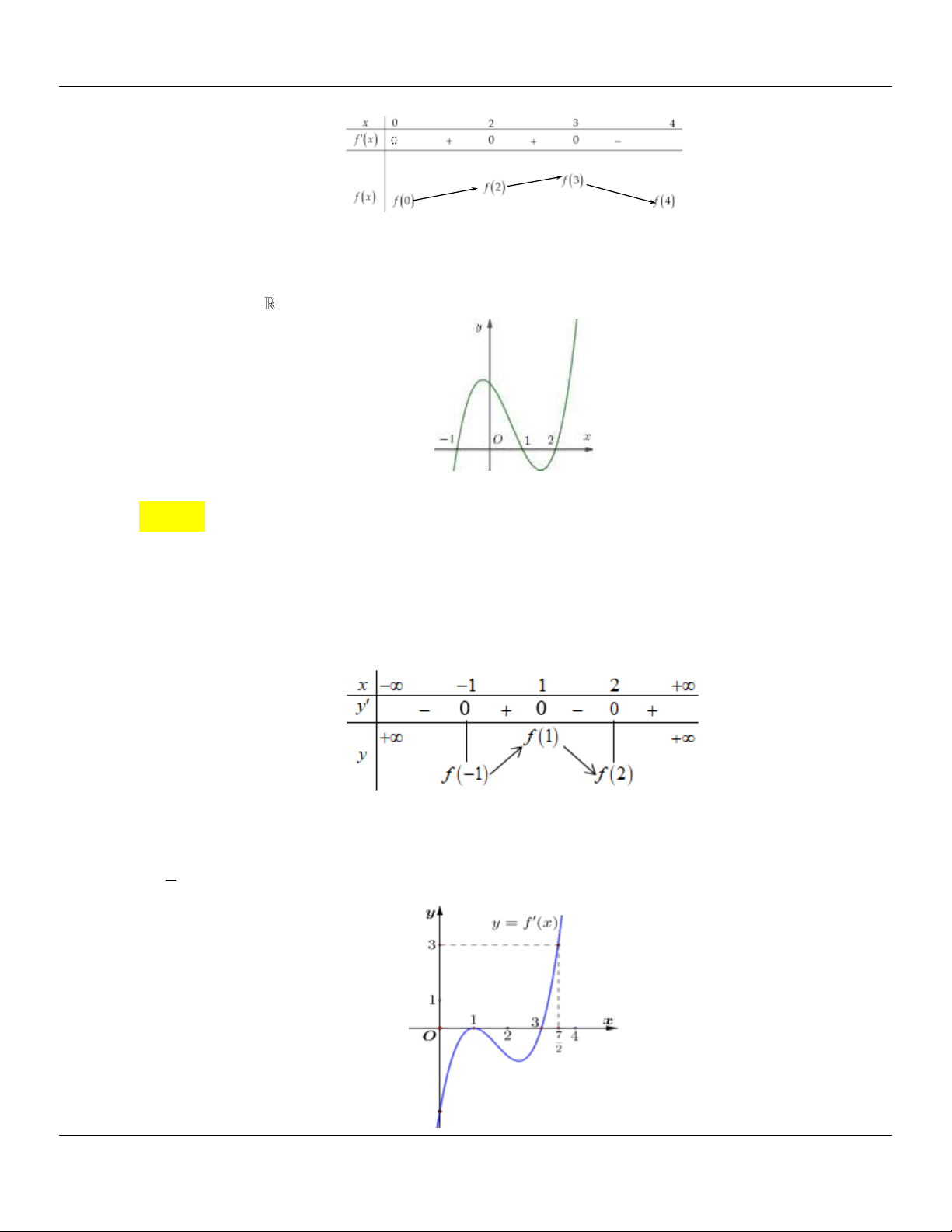
Mệnh đề nào dưới đây đúng?
A. min f x  6 .
B. min f x  2 .
C. max f x  9 .
D. max f x  6 .   5;7   5;7 -5;7     5;7
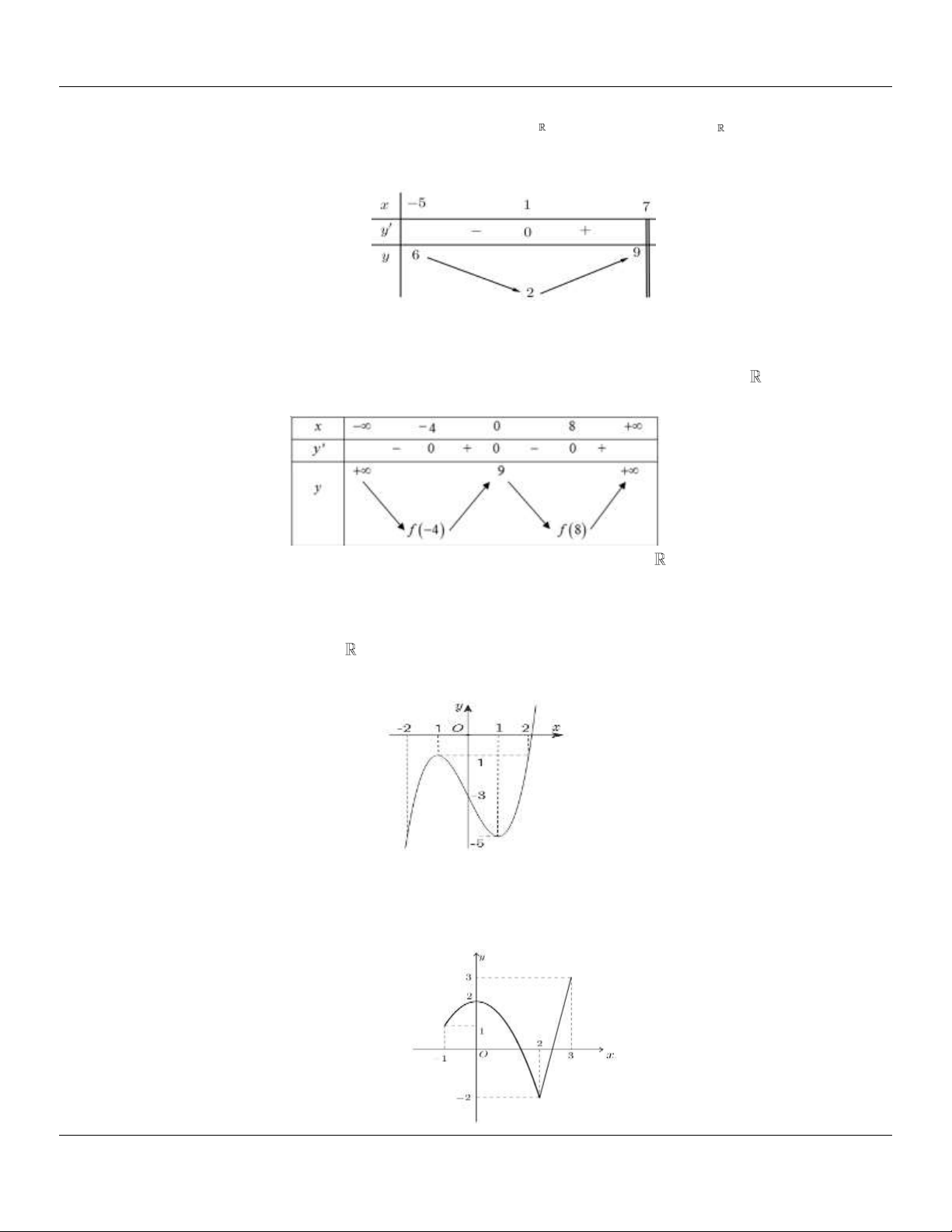
Câu 10: (SỞ GD&ĐT KIÊN GIANG NĂM 2018-2019) Hàm số y f x liên tục trên và có bảng biến
thiên như hình bên dưới.
Biết f 4  f 8 , khi đó giá trị nhỏ nhất của hàm số đã cho trên bằng A. 9 . B. f 4 . C. f 8 . D. 4 .
Câu 11: (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số y f x
xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn
nhất M của hàm số y f x trên đoạn 2; 2   .
A. m  5; M  1 .
B. m  2 ; M  2 .
C. m  1; M  0 .
D. m  5; M  0 .
Câu 12: (THPT THÁI PHIÊN HẢI PHÒNG NĂM 2018-2019) Cho hàm số f x lên tục trên đoạn 1;3 
 và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số y f  2 3sin x  1 bằng
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------3
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 3 . B. 2 . C. 0 . D. 1 .
Câu 13: Cho hàm số y f (x) có đồ thị như hình dưới. Gọi m, M lần lượt là  1 
giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f ( 2  x) trên 1  ; .    2 
Giá trị m M bằng A. 0. B. 4. 19 C.  D. 4. 8
Câu 14: (THPT HOÀNG VĂN THỤ - HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có đạo hàm cấp 2 trên
, hàm số y f x có đồ thị như hình vẽ bên.  sinx   3 cos x   5  
Giá trị lớn nhất của hàm số y f     trên đoạn   ;  bằng  2   6 6    5        A. f    . B. f    . C. f 0 . D. f   .  6   3   6 
Câu 15: Cho hàm số y f x liên tục, đồng biến trên đoạn a;b 
 . Khẳng định nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn a; b   .
B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng a;b .
C. Phương trình f x  0 có nghiệm duy nhất thuộc đoạn a;b   .
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a; b   .
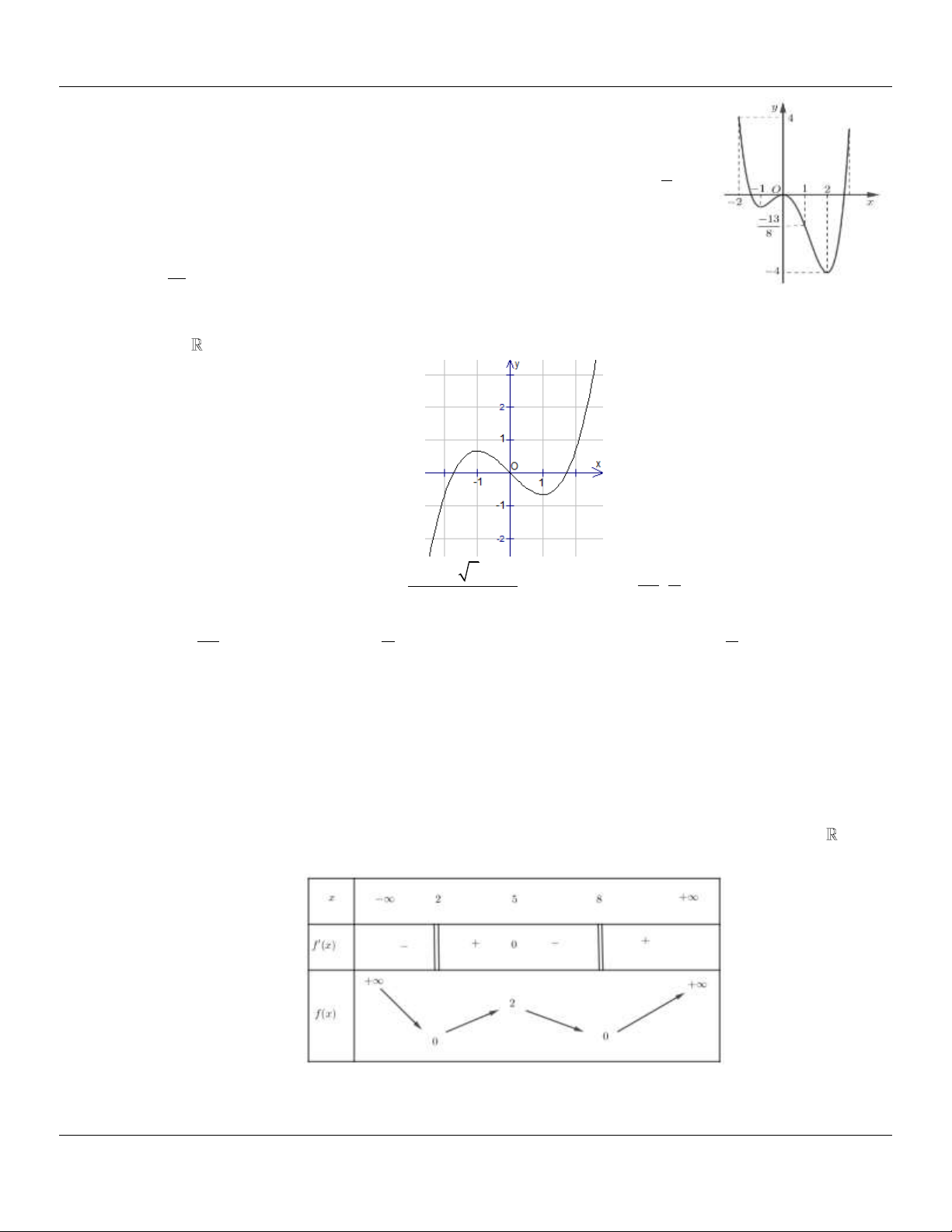
Câu 16: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số f x xác định,liên tục trên và có bảng biến thiên sau:
Phát biểu nào sau đây đúng?
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 2.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------4
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
B. Hàm số nhận giá trị dương với mọi x  . C. Trên 2; 8 
 hàm số có giá trị lớn nhất là M , giá trị nhỏ nhất là m . Giá trị biểu thức
m  3M  6 .
D. Hàm số có đúng một cực trị.
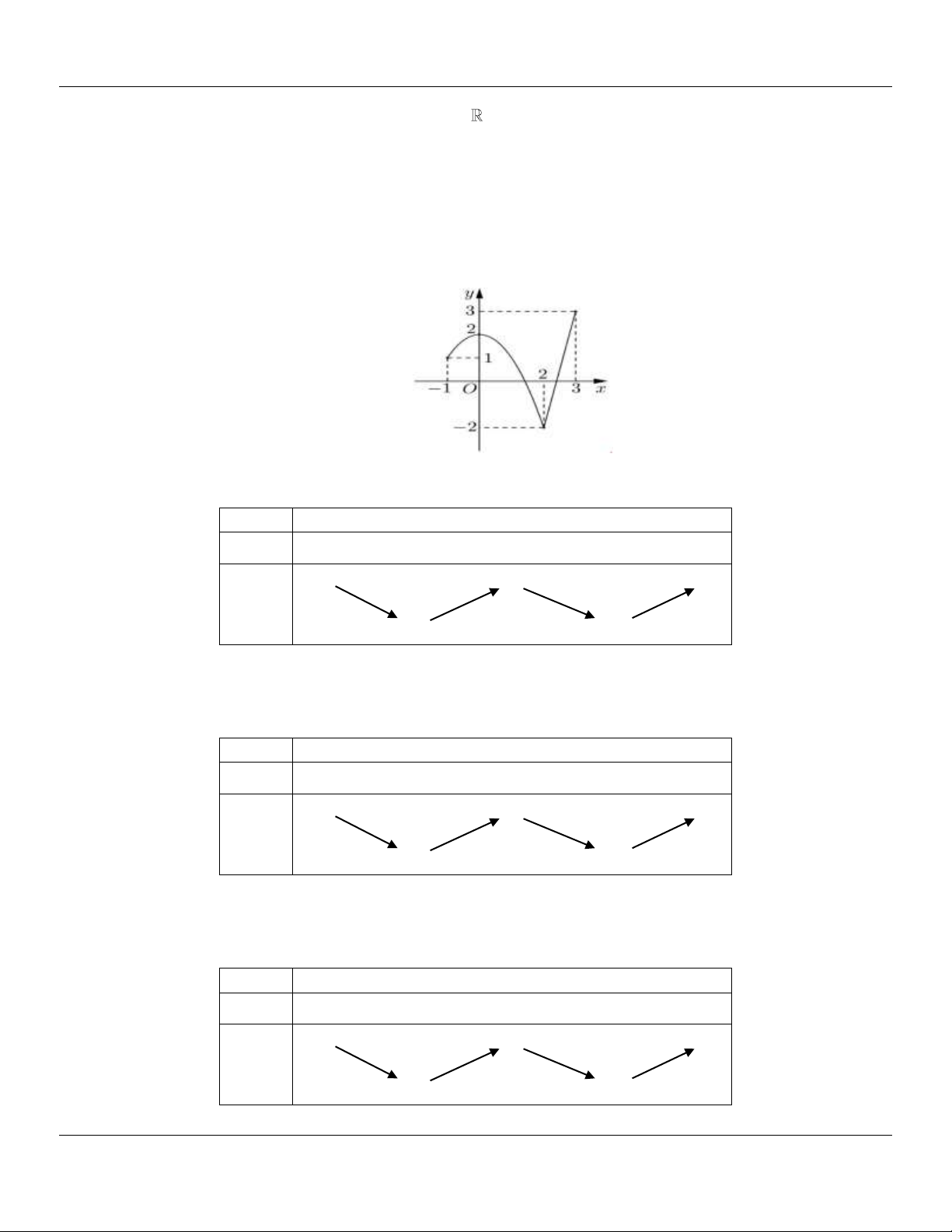
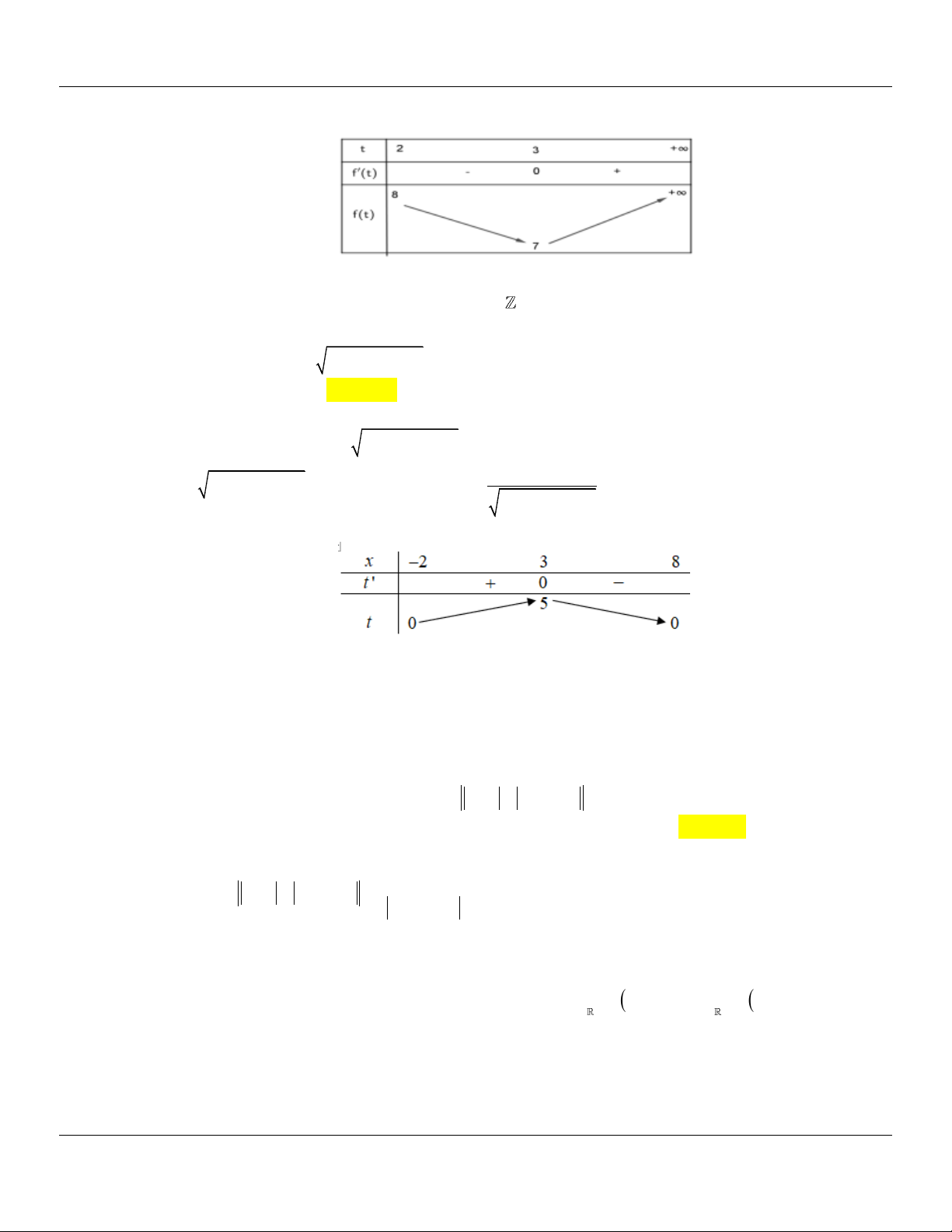
Câu 17: Cho hàm số y f x liên tục trên đoạn (-1;3) và có đồ thị như hình vẽ bên. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1; 3 
 . Giá trị của M m bằng A. 0. B. 1. C. 4. D. 5.
Câu 18: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. max f x  2.
B. max f x  1.
C. max f x  0.
D. max f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1
Câu 19: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. min f x  2.
B. min f x  1.
C. min f x  0.
D. min f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1
Câu 20: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------5
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
A. min f x  3.
B. min f x  2.
C. min f x  0.
D. min f x  1.  x 0;    1  x 0;    1  x 0;    1  x 0;    1
Câu 21: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    f x 2 3 1
Khẳng định nào sau đây đúng?
A. max f x  f 5. B. max f x  f 15. C. max f x  2.
D. max f x  f 10.  x 5;15    x 5;15    x 5;15    x 5;15  
Câu 22: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    f x 2 3 1
Khẳng định nào sau đây đúng?
A. max f x  f 5.
B. max f x  f 15.  x 15;5    x 15;5  
C. max f x  2.
D. max f x  f 10.  x 15;5    x 15;5  
Câu 23: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt gx  2 f x  1. Khẳng định nào sau đây đúng?
A. max gx  2.
B. max gx  5.
C. max gx  1.
D. max g x  5.  x 1;    1  x 1;    1  x 1;    1  x 1;    1
Câu 24: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt gx  3  4 f x. Khẳng định nào sau đây đúng?
A. min g x  15.
B. min g x  5.
C. min gx  15.
D. max g x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------6
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 25: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. max f x  2.
B. max f x  1.
C. max f x  0.
D. max f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1
Câu 26: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. min f x  2.
B. min f x  1.
C. min f x  0.
D. min f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1
Câu 27: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt g x  f sin x. Khẳng định nào sau đây đúng?
A. max g x  2.
B. max g x  1.
C. max g x  3.
D. max g x  4.
Câu 28: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt gx  f cos x. Khẳng định nào sau đây đúng?
A. min gx  1.
B. min gx  2.
C. min gx  3.
D. min gx  0.             0;  0;  0;  0;   2   2   2   2 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------7
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 29: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    f x 2 3 1 3 2
Đặt gx   f x  3 
f x . Khẳng định nào sau đây đúng?
A. max g x  4.
B. max gx  4.
C. max gx  0.
D. max gx  2. 1;    1 1;    1 1;    1 1;    1
Câu 30: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Giá trị lớn nhất của hàm số    x f x trên đoạn 2; 3   bằng x  3 1 A. 3. B. 2. C. . D. 2. 2
Câu 31: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số f x x  1 ( )
trên nửa khoảng   2;  là x 5 7 A. 2 . B. . C. 0 . D. . 2 2 2 x  3
Câu 32: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số y  trên đoạn x  1 2;4   . 19 A. miny  6. B. min y 2. C. miny  3. D. miny  . 2;4    2;4 2;4 2;4       3
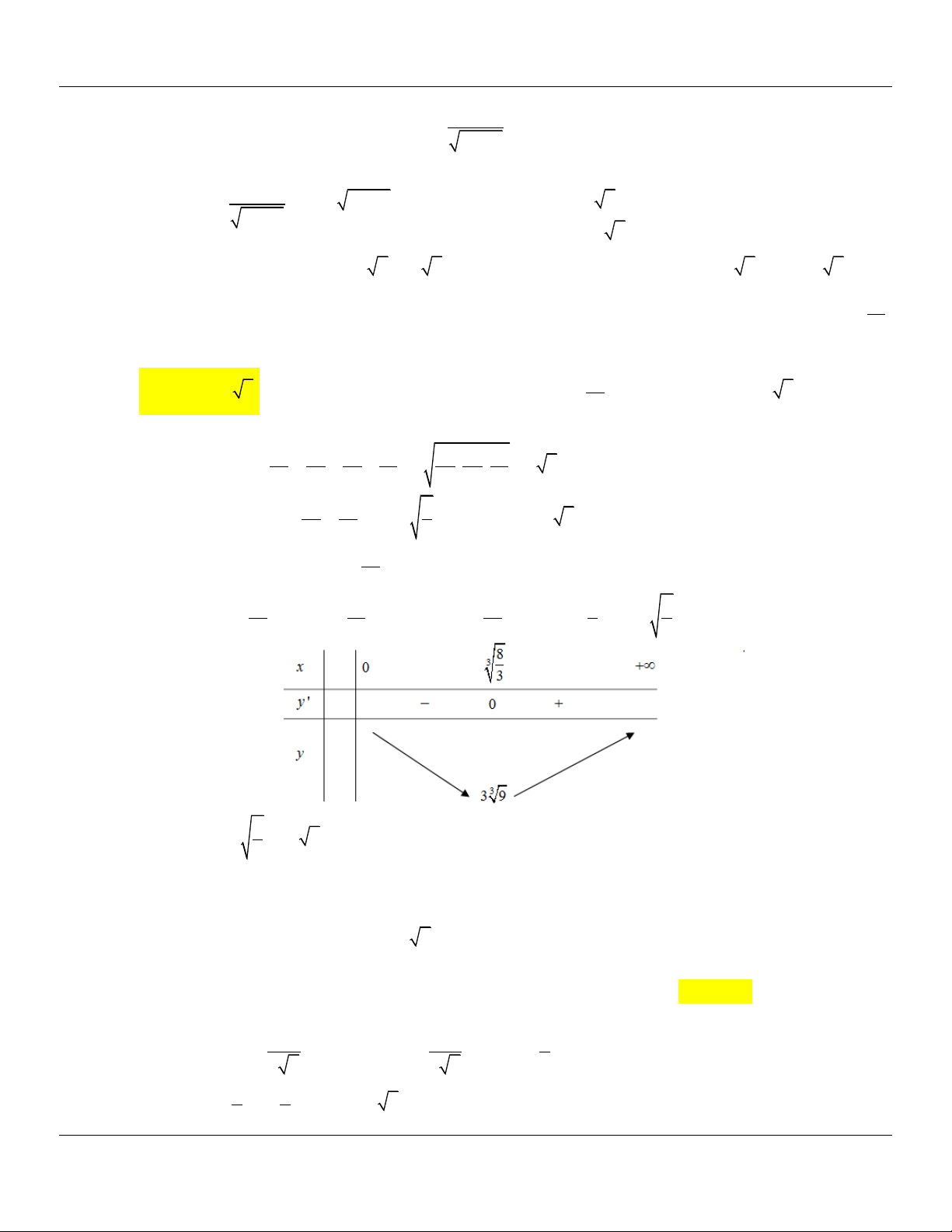
Câu 33: Tìm giá trị nhỏ nhất của hàm số   9 y x
trên đoạn [2 ; 4]. x 13 25 A. min y  . B. min y  . C. min y  6. D. min y  6. [2 ; 4] 2 [2 ; 4] 4 [2 ; 4] [2 ; 4]
Câu 34: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Tìm giá trị lớn nhất của hàm số
y f x  x  1  5  x trên đoạn 1; 5   .
A. max f x  3 2 .
B. max f x  2 .
C. max f x  2 2 .
D. max f x  2 . 1;5   1;5   1;5   1;5  
Câu 35: Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y x  1  7  x . Khi đó
có bao nhiêu số nguyên dương nằm giữa m và M ? A. 1 . B. 5 . C. 7 . D. 0 . 8 10
Câu 36: (THPT THĂNG LONG HÀ NỘI NĂM 2018-2019 LẦN 02) Hàm số y x  đạt giá trị nhỏ x nhất trên đoạn  3 9 10 ;10    tại x bằng A. 4 10 . B. 3 10 . C. 5 10 . D. 6 10 .
Câu 37: (SỞ GD&ĐT BÌNH THUẬN NĂM 2018-2019) Giá trị lớn nhất của hàm số y   2
x  5x bằng
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------8
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 5 A. 0 . B. . C. 6 . D. 2 . 2
Câu 38: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Tìm giá trị nhỏ nhất của hàm số y  2
sin x  4 sin x  5 . A. 20 . B. 8 . C. 9 . D. 0 .
Câu 39: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Giá trị nhỏ nhất của hàm số 2 sin x     y  3 trên đoạn 0;  là sin x  1  2  5 A. 5 . B. 2 . C. 3 . D. . 2
Câu 40: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số f x  3
sin x  3sin x  2 . Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó M  2m là A. 0 . B. 1. C. 4. D. 5. Lời giải
Đặt sin x t t  1; 1  
  . Ta có f t  3 t  3t  2.
Xét hàm số f t  3
t  3t  2 với t  1; 1  
 ; f t  2 '
3t  3  0  t   1 hoặc t  1 .
Ta có f 1  4 , f 1  0 . Suy ra, giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là 4 và 0 hay
M  4 ; m  0. Giá trị M  2m  4  2.0  4 .
Câu 41: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
f x  cos 2x  cos x  1 . Giá trị nhỏ nhất của hàm số trên là A.
f x   1 min . B.
f x   1 min . C. f x  1 min . D. f x  1 min . 8 4 8 4
Câu 42: (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Giá trị lớn nhất của hàm số y  2
2 sin x  cos x là phân số tối giản có dạng với a,b là các số nguyên dương. Tìm a – b . A. 8 . B. 9 . C. 7 . D. 10 .
Câu 43: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
y  3cos 2x  4 sin x là 11 A. 1 . B. 7 . C. 5 . D. . 3
Câu 44: (MĐ 102 BGD&ĐT NĂM 2016-2017) Tìm giá trị lớn nhất M của hàm số y  4 x  2 2x  3 trên đoạn   0; 3 . A. M  9 . B. M  8 3 . C. M  1 . D. M  6 .
Câu 45: (MĐ 104 BGD&ĐT NĂM 2018-2019) Giá trị nhỏ nhất của hàm số f x  3
x  3x trên đoạn 3;3   bằng A. 18 . B. 18 . C. 2 . D. 2 . 2  1 
Câu 46: (MĐ 104 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số y  2 x  trên đoạn  ;2 . x  2 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------9
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. m  17 . B. m  10 . C. m  5 . D. m  3 . 4
Câu 47: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Gọi M và m lầ lượt là giá trị lớn
nhất và giá trị nhỏ nhất của hàm số f x  2x  4 6  x trên 3;6 
 . Tổng M m có giá trị là: A. 12 . B. 6 . C. 18 . D. 4 .
Câu 48: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi M là giá trị lớn nhất của hàm số f x  2
x x   x  2 4 4 6 4
x  1 . Tính tích các nghiệm của phương trình f x  M . A. 2 . B. 4 . C. 2 . D. 4 .
Câu 49: (MĐ 103 BGD&ĐT NĂM 2016-2017) Tìm giá trị nhỏ nhất m của hàm số y  4 x  2 x  13 trên đoạn 2; 3  . A. m  51. B. m  49 . C. m  13. D. m  51. 4 4 2
Câu 50: (SỞ GD&ĐT LẠNG SƠN NĂM 2018-2019) Tìm x để hàm số y x   2
4 x đạt giá trị lớn nhất. A. x  2 . B. x  2 2 . C. x  1 . D. x  2. 4
Câu 51: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2016-2017) Tính giá trị nhỏ nhất của hàm số y  3x  2 x
trên khoảng 0;  . 33 A. min y  3 3 9. B. min y  7. C. min y  . D. min y  3 2 9. 0; 0; 0; 5 0;
Câu 52: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Gọi M, m lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của hàm số f x  x x trên đoạn 0; 3 
 . Giá trị của biểu thức M  2m gần với số
nào nhất trong các số dưới đây? A. 1,768 . B. 0,767 . C. 1,767 . D. 0,768 . Câu 53:
(THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 02) Giá trị nhỏ nhất của hàm số Câu 54:
f xx 1x  2x  3x  4 2019 là A. 2017. B. 2020. C. 2018. D. 2019.
Câu 55: (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Tổng giá trị lớn nhất M và giá trị nhỏ
nhất m của hàm số f x  x   2 6
x  4 trên đoạn 0 ; 3 
 có dạng a b c với a là số nguyên
và b ,c là các số nguyên dương. Tính S a b c . A. 4 . B. 2 . C. 22 . D. 5 .
Câu 56: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 02) Cho hàm số f x có đạo hàm
f x  xx  2
2 x  3 , x  . Giá trị lớn nhất của hàm số đã cho trên đoạn 0; 4   bằng A. f 0 . B. f 2 . C. f 3 . D. f 4 .
Câu 57: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y f x xác định và liên tục trên
, đồ thị của hàm số y f x như hình vẽ sau:
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------10
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Giá trị lớn nhất của hàm số y f x trên đoạn 1; 2   là A. f 1 . B. f 1 . C. f 2 . D. f 0 .
Câu 58: (THPT YÊN MÔ A-NINH BÌNH NĂM 2018-2019 LẦN 01) Cho hàm số y f x liên tục trên  7 
0;  có đồ thị hàm số y f x như hình vẽ sau:  2   7 
Hàm số y f x đạt giá trị nhỏ nhất trên 0;  tại điểm x nào dưới đây?  2  0 7 A. x  0 . B. x  . C. x  3 . D. x  1 . 0 0 2 0 0
Câu 59: (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm
là f x . Đồ thị của hàm số y f x được cho như hình vẽ bên. Biết rằng
f 0  f 1  2 f 3  f 5  f 4 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f x trên đoạn 0; 5   .
A. m f 5 , M f 3.
B. m f 5 , M f 1.
C. m f 0 , M f 3.
D. m f 1 , M f 3.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------11
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 60: (THPT LÝ NHÂN TÔNG LẦN 1 NĂM 2018-2019) Cho hàm số có f x có đạo hàm là hàm
f 'x . Đồ thị hàm số f 'x như hình vẽ bên. Biết rằng f 0  f 1  2 f 2  f 4  f 3 . Tìm
giá trị nhỏ nhất m và giá trị lớn nhất M của f x trên đoạn 0; 4   . y x 2 4 O
A. m f 4 , M f 2 .
B. m f 1 , M f 2.
C. m f 4 , M f 1 .
D. m f 0 , M f 2 .
Câu 61: (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Cho hàm số f x có đồ thị của hàm
số f x như hình vẽ. Biết f 0  f  
1  2 f 2  f 4  f  3 . Giá trị nhỏ nhất m , giá trị lớn nhất
M của hàm số f x trên đoạn 0; 4   là
A. m f 4 , M f 1 .
B. m f 4 , M f 2 .
C. m f 1 , M f 2 .
D. m f 0 , M f 2 .
Câu 62: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số y f x có
bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
gx  f x  2 x   1 3 x  2 x x  1 4 3 8 trên đoạn 1; 3   . 3 3 25 19 A. 15. B. . C. . D. 12. 3 3
Câu 63: (THPT KINH MÔN HAI DƯƠNG NĂM 2018-2019 LẦN 03) Cho hàm số y f x có đạo
hàm f x . Hàm số y f x liên tục trên tập số thực và có bảng biến thiên như sau:
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------12
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Biết rằng f    10 1
, f 2  6 . Giá trị nhỏ nhất của hàm số gx  3
f x  3 f x trên đoạn 3 1;2   bằng 10 820 730 A. . B. . C. . D. 198 . 3 27 27
DẠNG TOÁN 2: MAX MIN HÀM NHIỀU BIẾN
Câu 64: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho 2 x xy  2
y  2 . Giá trị nhỏ nhất của  2   2 P x xy y bằng 2 1 1 A. . B. . C. . D. 2 . 3 6 2
Câu 65: (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019)Cho hai số thực x, y thay đổi thỏa mãn điều kiện 2 x  2
y  2 . Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức P  3 x  3 2(
y )  3xy . Giá trị của M n bằng: 1 A. 4. B.  . C. 6. D. 1  4 2. 2
Câu 66: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Cho x, y  thỏa mãn
x y  1 và 2 x  2
y xy x y  1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức  xy P
. Tính M m . x y  1 1 1 A. . B.  2 . C. . D.  1 . 3 3 2 3
Câu 67: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho x , y thỏa mãn 2 x xy  2 5 6
5y  16 và hàm số
bậc ba y f x có đồ thị như hình vẽ. Gọi M ,7m lần lượt là giá trị lớn nhất và nhỏ nhất của  2 x  2 y  2  6 P f   2 2 
. Tính M m 2 2  5
x y  2xy   4  4 3 2 1 10 x 8 6 4 2 2 4 6 8 10 0 -1 1 1 2 3 A. 2 M  2 m  4 . B. 2 M  2 m  1 . C. 2 M  2 m  25 . D. 2 M  2 m  2 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------13
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 68: (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Cho các số thực x, y thay đổi nhưng luôn thỏa mãn 2 x xy  2 3 2
y  5 . Giá trị nhỏ nhất của biểu thức P  2 x xy  2 2y thuộc khoảng nào sau đây? A. 4;7 . B. 2;1 . C. 1; 4 . D. 7;10 .
Câu 69: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho x , y là các số thực thỏa mãn
x y x  1  2y  2 . Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của P  2 x  2
y  2x  1y  1 8 4 xy . Tính giá trị M m A. 42 . B. 41 . C. 43 . D. 44 .
DẠNG TOÁN 3: BÀI TOÁN THỰC TẾ - TỐI ƯU
Câu 70: (ĐỀ THỬ NGHIỆM BGD&ĐT NĂM 2016-2017) Một vật chuyển động theo quy luật s   1 3 t  2
9t với t (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và s (mét) là 2
quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể
từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 216 m/s .
B. 30 m/s .
C. 400 m/s .
D. 54 m/s .
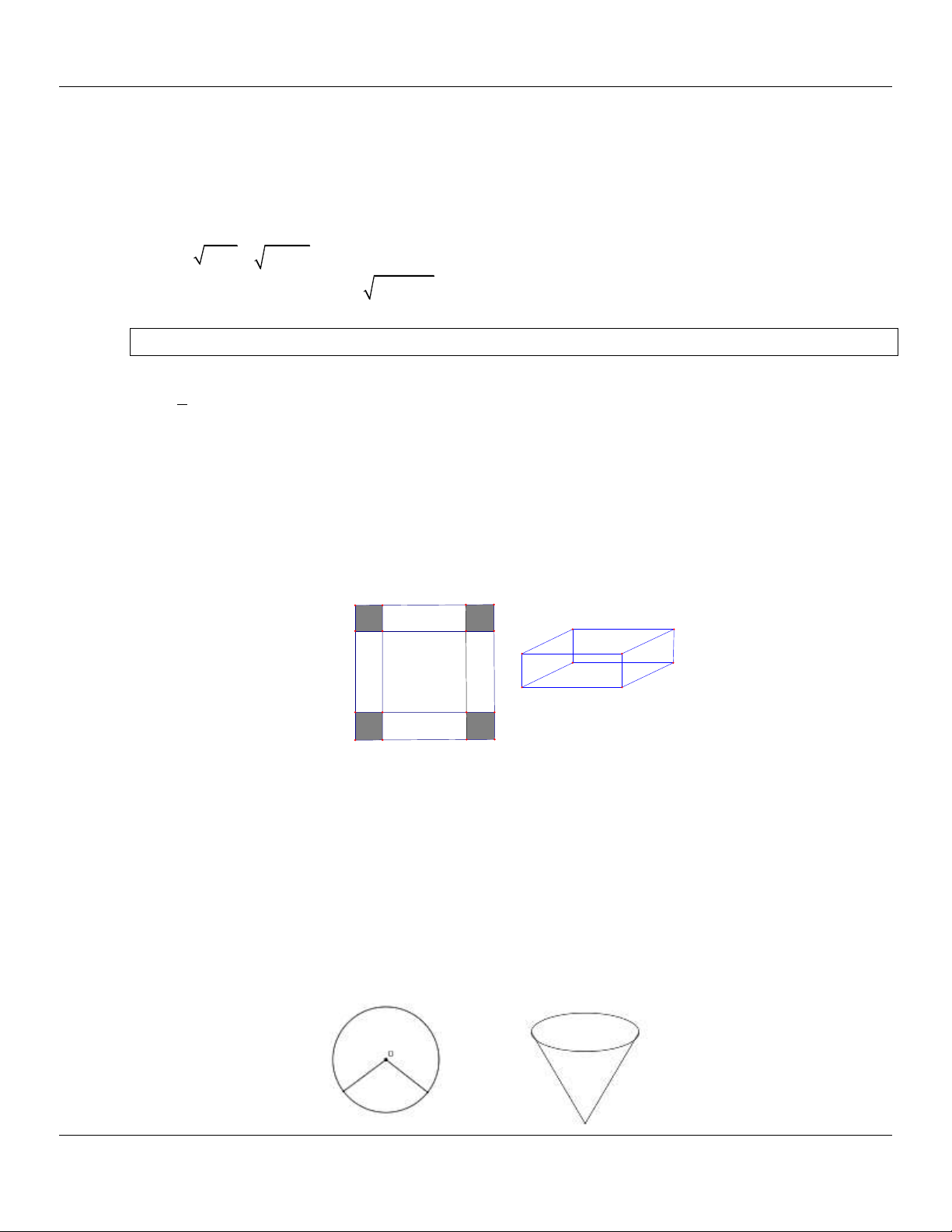
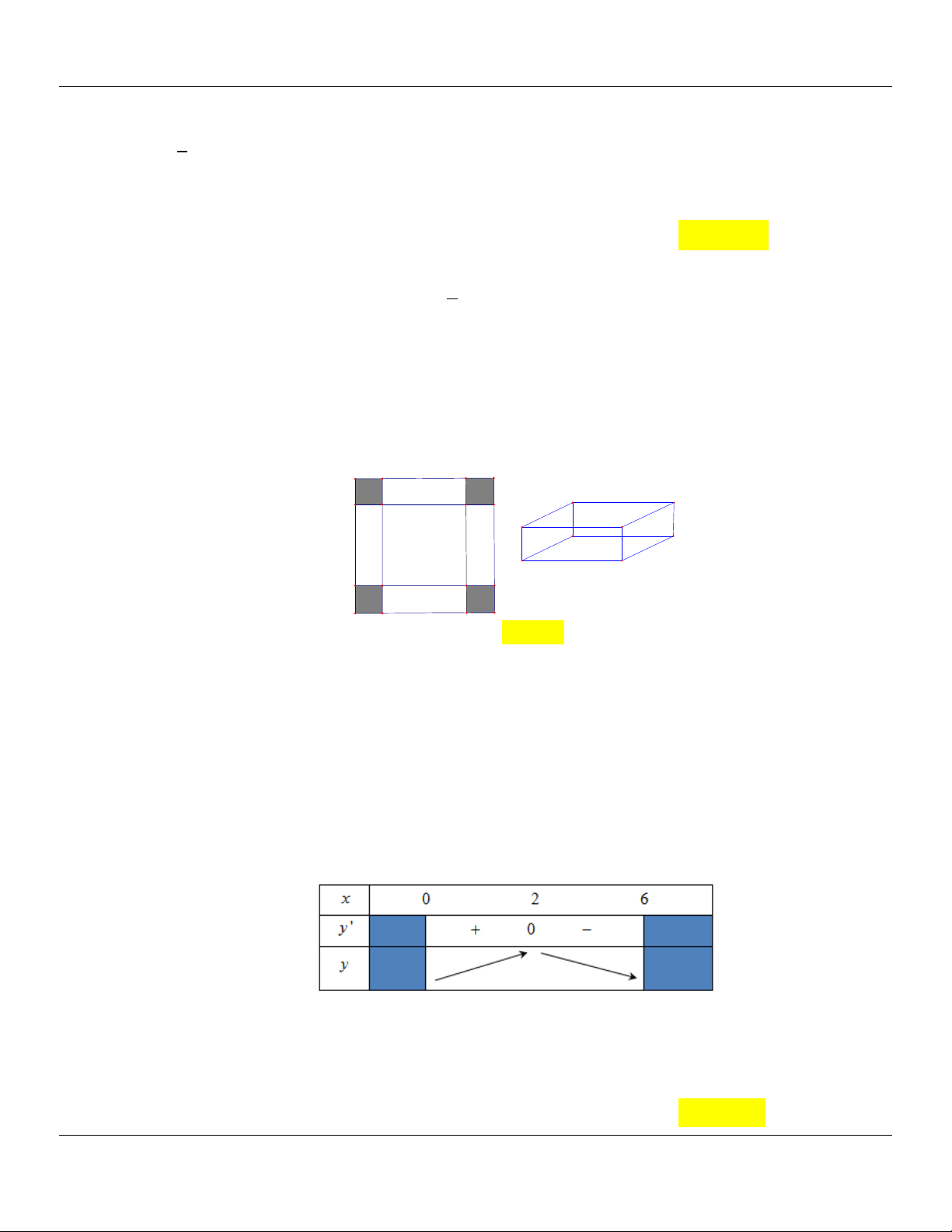
Câu 71: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để
hộp nhận được có thể tích lớn nhất. A. x  6 . B. x  3 . C. x  2 . D. x  4 .
Câu 72: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông A dự định dùng hết 2
6, 5m kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không
đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 2,26 m . B. 3 1,61 m . C. 3 1,33 m . D. 3 1,50 m .
Câu 73: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Bác Bính có một tấm thép mỏng hình
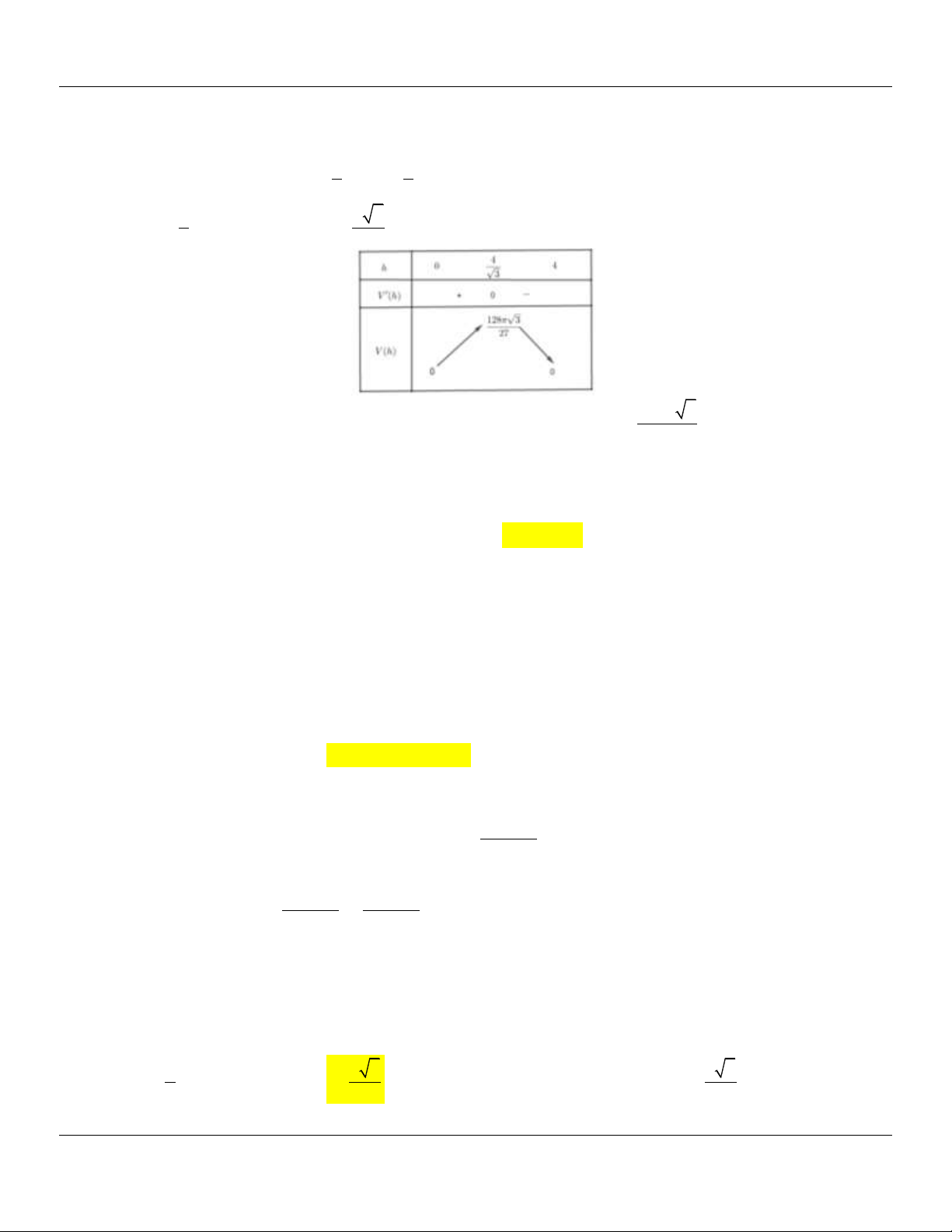
tròn, tâm O, bán kính 4 dm . Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai
mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình
vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (bỏ qua phần
mối hàn và độ dày của tấm thép).
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------14
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 12  8 3 12  8 3 1  6 3 6  4 3 A. 3 dm . B. 3 dm . C. 3 dm . D. 3 dm . 27 81 27 27
Câu 74: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một chất điểm chuyển động theo
phương trình S   3 t  2
9t  21t  9 trong đó t tính bằng giây (s) và S tính bằng mét (m) . Tính
thời điểm t(s) mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất.
A. t  4(s). B. t  5(s). C. t  3(s). D. t  7(s).
Câu 75: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một công ty bất động sản có 40 căn hộ
cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 3.000.000 đồng một tháng thì mọi căn hộ
đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100.000 đồng một tháng (theo qui
định trong hợp đồng) thì sẽ có một căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì
công ty đó phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng? A. 3.700.000 đồng. B. 3.500.000 đồng. C. 3.900.000 đồng. D. 4.000.000 đồng.
Câu 76: (SỞ GD QUẢNG NAM 2019) Cho nửa đường tròn đường kính AB và hai điểm C, D thay đổi
trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng 1 3 3 3 3 A. B. C. 1 D. 2 4 2
Câu 77: (SỞ GD&ĐT CÀ MAU NĂM 2018-2019) Người ta muốn xây một cái bể hình hộp đứng có thể tích V   3
18 m  , biết đáy bể là hình chữ nhật có chiều dài gấp 3 lần chiều rộng và bể
không có nắp. Hỏi cần xây bể có chiều cao h bằng bao nhiêu mét để nguyên vật liệu xây dựng
là ít nhất (biết nguyên vật liệu xây dựng các mặt là như nhau)? 5 3 A. 2m . B. m . C. 1 m . D. m . 2 2
Câu 78: (CỤM 1 SỞ GD&ĐT BẠC LIÊU NĂM 2018-2019 LẦN 01) Người ta muốn xây một bể chứa
nước dạng hình hộp chữ nhật không nắp có thể tích 200m3. Đáy bể là hình chữ nhật có chiều
dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m2. Chi phí thuê công nhân thấp nhất là A. 51 triệu đồng . B. 75 triệu đồng. C. 46 triệu đồng. D. 36 triệu đồng.
DẠNG TOÁN 4: PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH
Câu 79: (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên
Tìm tất cả các giá trị của m để bất phương trình f x  1   1  m có nghiệm? A. m  4. B. m  1. C. m  2 . D. m  5 .
Câu 80: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho hàm số f x , hàm số y f x liên tục trên và có
đồ thị như hình vẽ bên.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------15
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Bất phương trình f x  x m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m f 2  2 .
B. m f 0 .
C. m f 2  2 .
D. m f 0 .
Câu 81: (MĐ 102 BGD&ĐT NĂM 2018-2019) Cho hàm số f x , hàm số y f x liên tục trên và có
đồ thị như hình vẽ sau:
Bất phương trình f x  x m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m f 2  2 .
B. m f 2  2 .
C. m f 0 .
D. m f 0 .
Câu 82: (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 04) Cho hàm số y f x và hàm số
y g x có đạo hàm xác định trên và có đồ thị như hình vẽ dưới đây: f x
Có bao nhiêu giá trị nguyên của tham số m để phương trình    m có nghiệm thuộc g x 2;3   ? A. 4. B. 5. C. 7. D. 6.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------16
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 83: (MĐ 103 BGD&ĐT NĂM 2018-2019) Cho hàm số f x , hàm số y f x liên tục trên và có
đồ thị như hình vẽ bên.
Bất phương trình f x  2x m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m f 0 .
B. m f 2  4 .
C. m f 0 .
D. m f 2  4 .
Câu 84: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số y f x . Hàm số y f x có bảng
biến thiên như sau: x  2 1   0 y 2 
Bất phương trình    3 f x
x m đúng với mọi x 1;1 khi và chỉ khi
A. m f x  1.
B. m f 1  1 .
C. m f 1  1.
D. m f 1  1 .
Câu 85: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Số các giá trị nguyên của tham số m thuộc đoạn 2019;2019   để phương trình 2
x  m   x   m   3 2 4 1
x  4x có nghiệm là A. 2011 . B. 2012 . C. 2013 . D. 2014 .
Câu 86: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số m để
bất phương trình x    x  x  2 6 2 8
x m  1 nghiệm đúng với mọi x  2; 8  . A. m  16 . B. m  15 . C. m  8 . D. 2  m  16 .
Câu 87: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số giá trị nguyên của tham số m nằm
trong khoảng 0; 2020 để phương trình x  1  2019  x  2020  m có nghiệm là A. 2020 . B. 2021 . C. 2019 . D. 2018 .
Câu 88: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Gọi S là tập tất cả các giá trị của tham số m để bất 4
phương trình x    2 x x   4 m  2 1 4 5
m  6m thỏa mãn với mọi giá trị của x  . Tính tổng
các giá trị của S. A. 1 . B. 3 . C. 5. D. 2 .
Câu 89: (SỞ GD&ĐT QUẢNG BÌNH NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị nguyên
dương của tham số m để bất phương trình sau 6 x  4 x  3 3 m x  2 3
4x mx  2  0 nghiệm đúng
với mọi x  1; 3 
 . Tổng tất cả các phần tử của S bằng: A. 3 . B. 2 . C. 1 . D. 4 .
Câu 90: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Giá trị lớn nhất của hàm 3 x  2 x m số y  trên 0; 2 
 bằng 5 . Tham số m nhận giá trị là x  1
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------17
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 5 . B. 1 . C. 3 . D. 8 .
Câu 91: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi s là tập hợp các giá trị 3
nguyên của tham số m 0; 2019 
 để bất phương trình 2
x m    2 1 x   0 đúng với mọi x  1;   
1 . Số phần tử của tập s bằng A. 1 . B. 2020 . C. 2019 . D. 2 .
Câu 92: (CHUYÊN ĐẠI HỌC VINH LẦN 03 NĂM 2018 - 2019) Cho f (x) mà đồ thị hàm số y f '(x) như hình vẽ sau:  x
Bất phương trình f (x)  sin
m nghiệm đúng với mọi x 1;3   khi và chỉ khi 2
A. m f (0) .
B. m f (1)  1 .
C. m f (1)  1 .
D. m f (2) . Câu 93: (CHUYÊN QUỐC HỌC HUẾ LẦN 3 2018-2019) Cho phương trình m 2
x x     2 2 2 1
x  2x  0 ( m là tham số). Biết rằng tập hợp các giá trị của tham số m để
phương trình có nghiệm thuộc đoạn 0 ; 1   
2 2  là đoạn a ; b 
 . Tính giá trị của biểu thức
T  2b a . A. T  4 . B. T  7 . C.T  3 . D. T  1 . 2 2
Câu 94: (THPT CHUYÊN HOÀNG VĂN THỤ HÒA BÌNH NĂM 2018-2019 LẦN 04) Tổng các giá trị m
nguyên dương của m để tập nghiệm của bất phương trình 2
x  1  x có chứa đúng hai số 72 nguyên là A. 27 . B. 29 . C. 28 . D. 30 .
DẠNG TOÁN 5: BÀI TOÁN THAM SỐ
Câu 95: (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số y  3 x  2 2 3x m . Trên 1;   
1 hàm số có giá trị nhỏ nhất là 1 . Tính . m A. m  6 . B. m  3 . C. m  4. D. m  5 .
Câu 96: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số y x m   2 1 x
có giá trị lớn nhất bằng 2 2 thì giá trị của m là 2 A. . B.  2 . C. 2 . D.  2 . 2 2
Câu 97: (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Có một giá trị m của tham số 0
m để hàm số y  3 x   2 m   2
1 x m  1 đạt giá trị nhỏ nhất bằng 5 trên đoạn 0;    1 . Khi đó
mệnh đề nào sau đây đúng ?
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------18
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 2
2018m m  0. B. 2m  1  0. C. 2 6m m  0. D. 2m  1  0. 0 0 0 0 0 0
Câu 98: (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị của tham số m để giá x  2 m  2
trị lớn nhất của hàm số y  trên đoạn 0; 4   bằng 1 . x m A. 0 . B. 2 . C. 3 . D. 1 . 2 x m
Câu 99: Cho hàm số f x  
với m là tham số thực. Giả sử m là giá trị dương của tham số m để x  8 0
hàm số có giá trị nhỏ nhất trên đoạn 0 ; 3 
 bằng 3 . Giá trị m thuộc khoảng nào trong các 0 khoảng cho dưới đây? A. 20; 25. B. 5;6 . C. 6;9 . D. 2; 5 . x m
Câu 100: (MĐ 101 BGD&ĐT NĂM 2016-2017) Cho hàm số y
( m là tham số thực) thỏa mãn x  1
min y  3 . Khẳng định nào sau dưới đây đúng? [2;4] A. m  1. B. 3  m  4. C. m  4. D. 1  m  3. x m
Câu 101: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho hàm số y
( m là tham số thực) thoả mãn x  1 y y  16 min max
. Khẳng định nào dưới đây đúng? 1;2 1;2     3 A. m  0 B. m  4 C. 0  m  2 D. 2  m  4
Câu 102: (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm x m số y  trên 1; 2 
 bằng 8 ( m là tham số thực). Khẳng định nào sau đây đúng? x  1 A. m  10 . B. 8  m  10 . C. 0  m  4 . D. 4  m  8 .
2sin x mcos x
Câu 103: (THPT HUỲNH MẪN ĐẠT NĂM 2018-2019 LẦN 01) Cho hàm số y  đạt giá sin x  cos x   
trị lớn nhất trên 0;  bằng 1 . Khẳng định nào sau đây đúng?  4  A. m   1;0 .
B. m  0;1 .
C. m  1;2 . D. m 2;3 .
Câu 104: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi A, B lần lượt là giá trị nhỏ nhất, giá trị x  2 m m
lớn nhất của hàm số y  trên đoạn 2; 3 
 . Tìm tất cả các giá trị thực của tham số m x  1
để A B  13 . 2
A. m  1; m  2 . B. m  2 . C. m  2 .
D. m  1; m  2 .
Câu 105: (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Gọi T là tập hợp tất cả giá trị của tham số mx  1 5
m để hàm số y
có giá trị lớn nhất trên đoạn 2; 3 
 bằng . Tính tổng của các phần tử x  2 m 6 trong T . 17 16 A. . B. . C. 2 . D. 6 . 5 5
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------19
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 2
Câu 106: (THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số y   3 x  x 3  m .
Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn 1;    1 bằng 1 là A. 1 . B. 4 . C. 0 . D. 4 . x m
Câu 107: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số f x sin  . Tìm giá trị sin x  1   2 
của m để giá trị lớn nhất của hàm số f (x) trên đoạn 0;  bằng 2.  3  m  5 A. m  5. B.  . C. m  2. D. m  3. m   2 x  2 m
Câu 108: Có bao nhiêu giá trị nguyên dương của tham số m để giá trị nhỏ nhất của hàm số y x  1 trên đoạn 2; 3   bằng 14? A. 2 . B. 1 . C. 0 . D. 4.
Câu 109: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số m sao cho giá trị lớn nhất của hàm số y  2
x  2x m trên đoạn 1; 2   bằng 5 . A. 1 . B. 2 . C. 2 . D. 1 .
Câu 110: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017-2018) Gọi S là tập hợp tất cả các giá trị của tham số
thực m sao cho giá trị lớn nhất của hàm số y  3
x  3x m trên đoạn 0; 2 
 bằng 3. Số phần tử của S là A. 1. B. 2. C. 0. D. 6.
Câu 111: (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số m 2 x mx  1 để hàm số y
liên tục và đạt giá trị nhỏ nhất trên đoạn 0; 2   tại một điểm x m x  0; 2 . 0   A. 0  m  1 . B. m  1 . C. m  2 . D. 1  m  1 .
Câu 112: (THPT Phụ Dực - Thái Bình - 2019) Gọi S là tập hợp các giá trị của m để hàm số y  3 x  2
3x m đạt giá trị lớn nhất bằng 50 trên [  2; 4]. Tổng các phần tử thuộc S là A. 4 . B. 36 . C. 140 . D. 0 .
Câu 113: (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi S là tập hợp các giá trị của tham số m 2
x mx  2m
để giá trị lớn nhất của hàm số y  trên đoạn 1;   
1 bằng 3 . Tính tổng tất cả các x  2 phần tử của S . 5 A.  8 . B. 5 . C. . D. 1 . 3 3
Câu 114: (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực m để giá trị nhỏ nhất của hàm số y  2
x  4x m  3  4x bằng 5 . A. 2 . B. 3 . C. 0 . D. 1 . HẾT
HUẾ...16h00 Ngày 08 tháng 8 năm 2020
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------20
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
CHUY£N §Ò: KH¶O S¸T HµM Sè
Chñ ®Ò 3: GI¸ TRÞ LíN NHÊT Vµ
GI¸ TRÞ NHá NHÊT CñA HµM Sè
LỜI GIẢI CHI TIẾT
DẠNG TOÁN 1: GTLN - GTNN TRÊN KHOẢNG (NỬA KHOẢNG - ĐOẠN) Câu 1:
(GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số f (x) liên tục trên a;b 
 . Khẳng định nào sau đây đúng?
A. Hàm số không có giá trị lớn nhất trên đoạn a; b   .
B. Hàm số luôn có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a; b   .
C. Hàm số không có giá trị nhỏ nhất trên đoạn a; b   .
D. Hàm số luôn có cực đại và cực tiểu trên đoạn a; b   . Lời giải
Theo định lý về giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn. Câu 2:
(THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số y f x liên tục trên
thỏa mãn giá trị nhỏ nhất của hàm số trên
là 0 . Khẳng định nào sau đây là đúng?
A. f x  0 x  , x , f x 0 .
B. f x  0 x  . 0   0
C. f x  0 x  , x , f x 0 .
D. f x  0 x  . 0   0 Lời giải
Ta có định nghĩa giá trị nhỏ nhất của hàm số: Cho hàm số y f x xác định trên tập D . Số m
được gọi là giá trị nhỏ nhất của hàm số y f x trên tập D nếu f x  m với mọi x thuộc D
và tồn tại x D sao cho f x m . 0   0 Câu 3:
(THPT CẦU GIẤY HÀ NỘI NĂM 2018-2019 LẦN 01) Cho a,b  , 0  a b , hàm số y f (x) có đạo hàm trên
thỏa mãn f x  0 , xa;b . Giá trị nhỏ nhất của hàm số đã cho trên
đoạn a; b   bằng  a b  A. f b . B. f   . C. f a .
D. f ab .  2  Lời giải
Hàm số y f (x) f x
xa;b thỏa mãn   0
nên hàm số nghịch biến trên a;b .
Do đó min f x  f b . a;b   Câu 4:
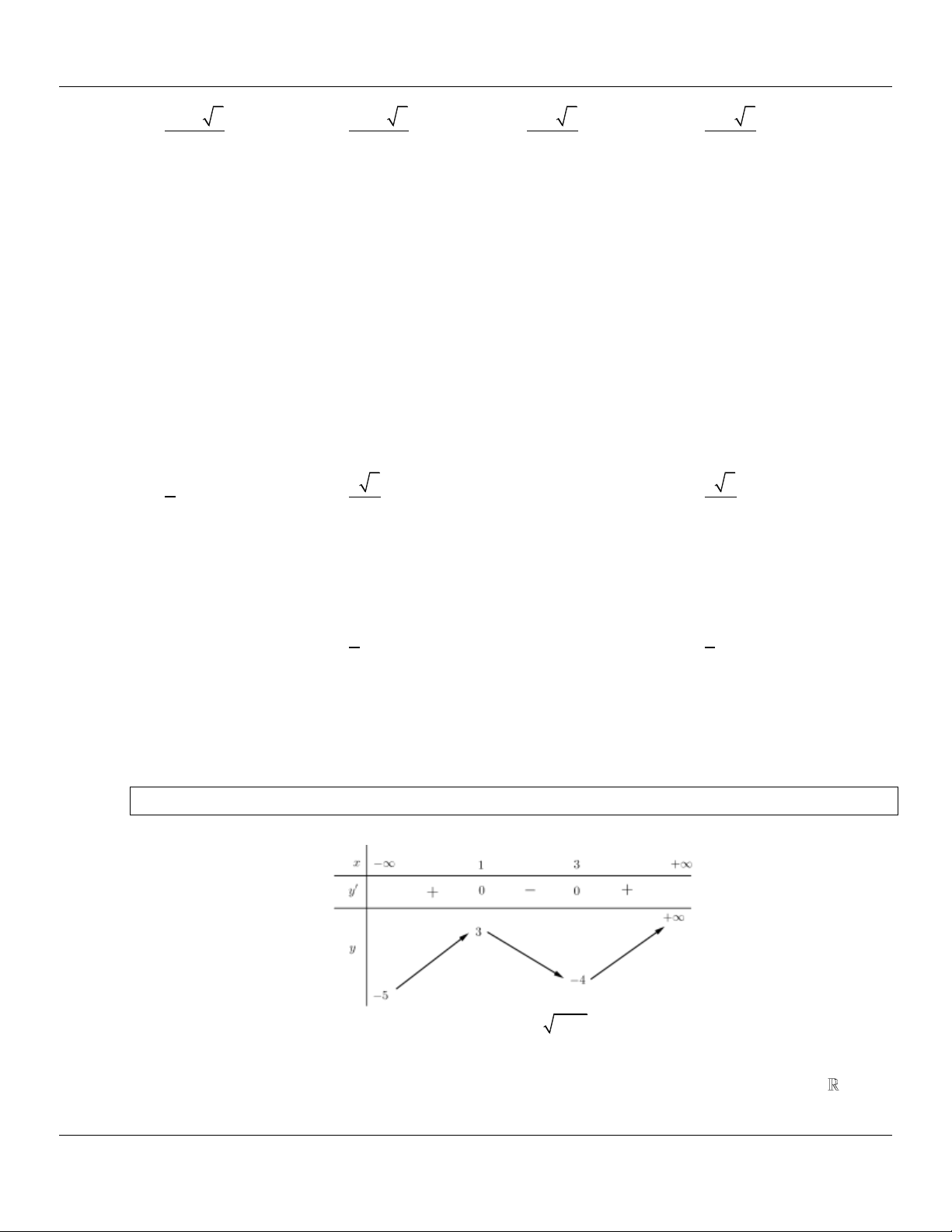
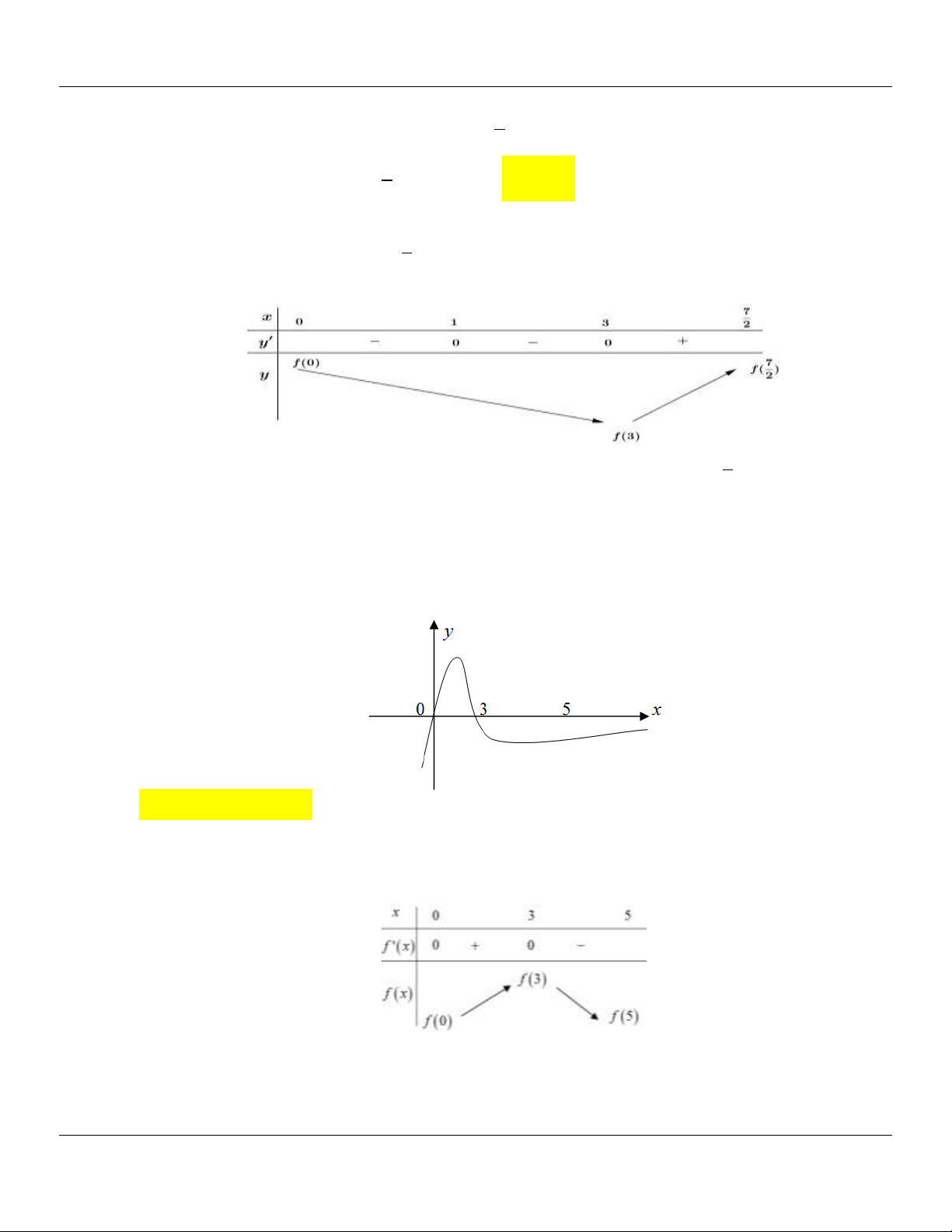
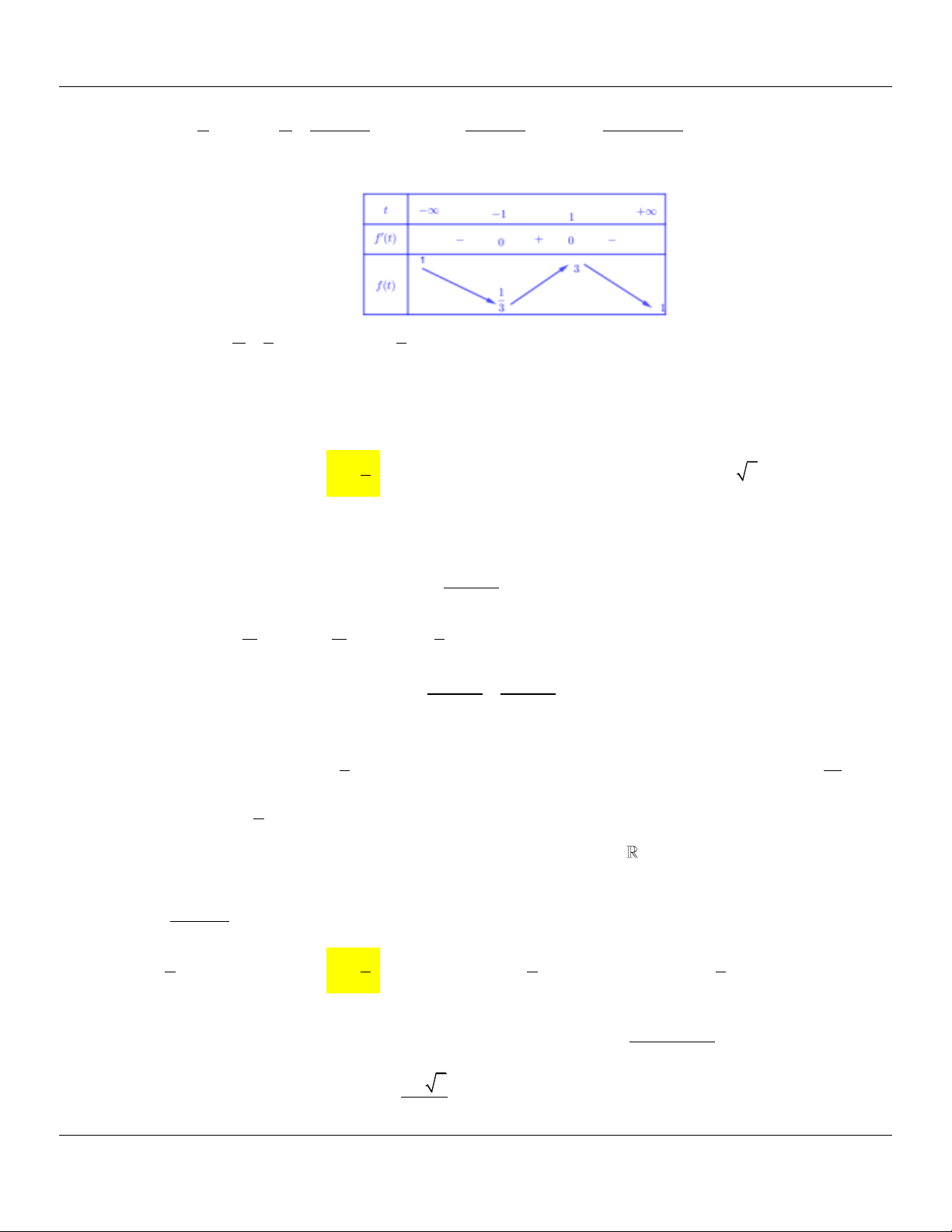
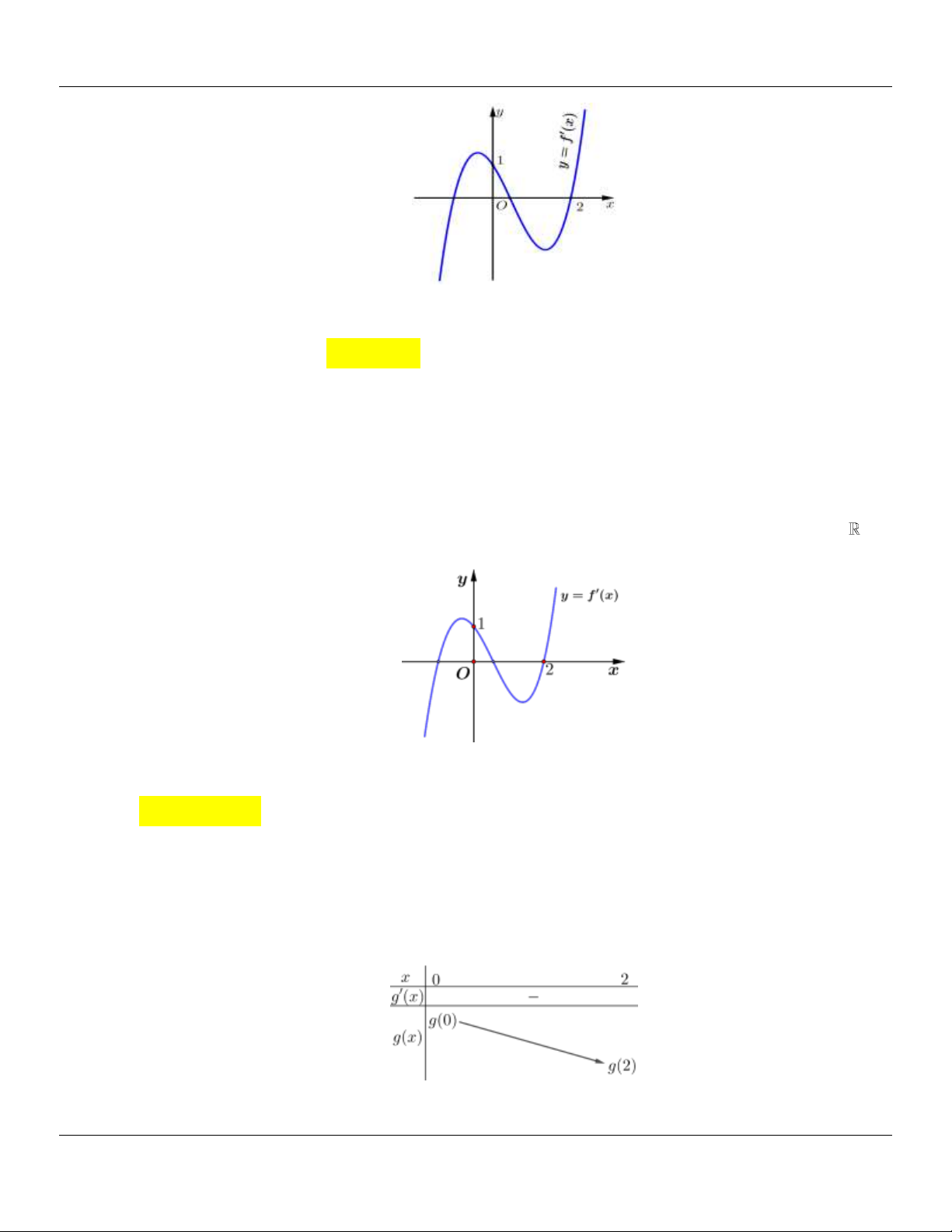
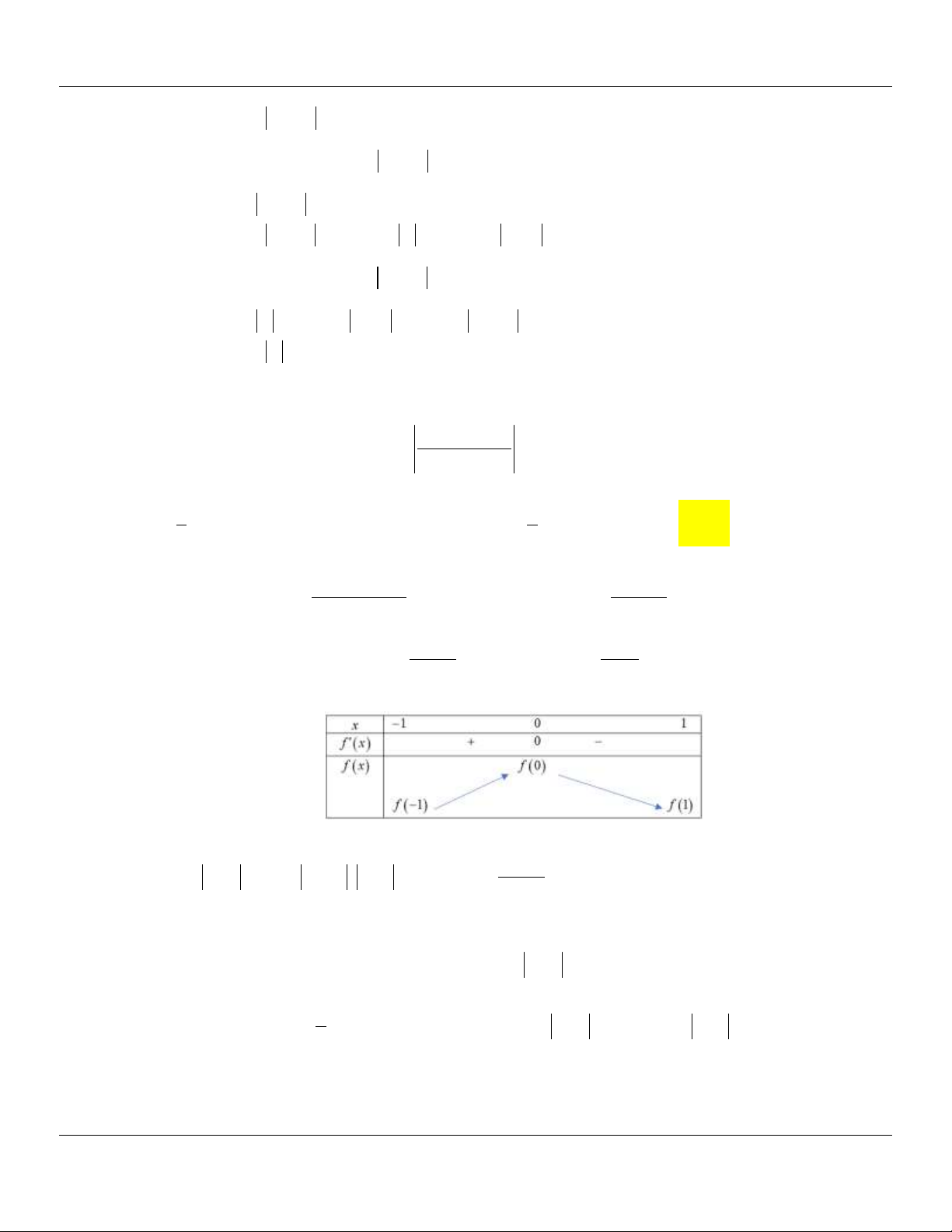
(CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho hàm số y f (x)
liên tục và có bảng biến thiên trên đoạn 1; 3 
 như hình vẽ. Khẳng định nào sau đây đúng?
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------21
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
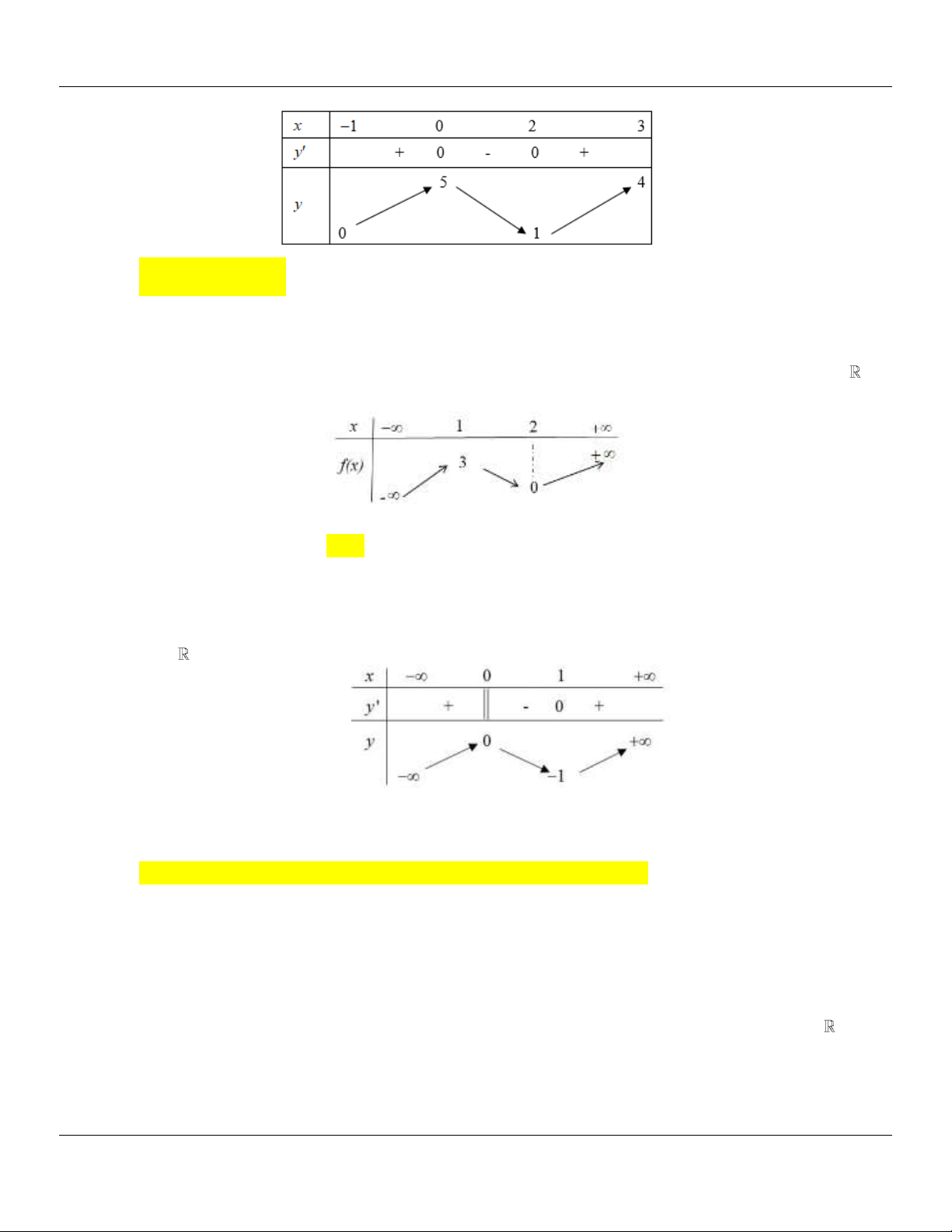
A. max f (x)  f (0) .
B. max f x  f 3 .
C. max f x  f 2 . D. max f x  f 1 . 1;3   1;3   1;3   1;3   Lời giải
Nhìn vào bảng biến thiên ta thấy max f x  f 0. 1;3   Câu 5:
(THPT CỔ LOA HÀ NỘI NĂM 2018-2019) Cho hàm số y f x xác định, liên tục trên và
có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số y f x trên đoạn 0; 2   bằng A. 1 . B. 3 . C. 0 . D. 2 . Lời giải
Dựa vào bảng biến thiên ta thấy trên đoạn 0; 2 
 giá trị lớn nhất của hàm số y f x bằng 3 . Câu 6:
(THPT NGUYỄN DU - DAK LAC - NĂM 2018-2019) Cho hàm số y f x xác định, liên tục trên
và có bảng biến thiên như sau
Khẳng định nào sau đây sai?
A. Hàm số có giá trị cực tiểu bằng 1 .
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1 .
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1 .
D. Hàm số có đúng hai cực trị. Lời giải
Từ bảng biến thiên ta dễ thấy ý A, B, D đúng.
Do lim f x  , lim f x   nên hàm số đã cho không có giá trị lớn nhất và không có giá x x trị nhỏ nhất. Câu 7:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên:
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------22
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1 .
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1 .
D. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1 . Lời giải
Đáp án A sai vì hàm số có 2 điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu y  1 khi x  0 .
Đáp án C sai vì hàm số không có GTLN và GTNN trên .
Đáp án D đúng vì hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1 . Câu 8:
(Đề minh họa) Cho hàm số y f x có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng ? x  0 1  y  0  0   5 y 4  A. y  5. B. y  0. C. min y  4. D. max y  5. CĐ CT Lời giải
Từ BBT suy ra hàm số đạt cực đại tại x  1 , giá trị cực đại yy1  5 . CĐ Câu 9:
(SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên trên   5;7 như sau:
Mệnh đề nào dưới đây đúng?
A. min f x  6 .
B. min f x  2 .
C. max f x  9 .
D. max f x  6 .   5;7   5;7 -5;7     5;7 Lời giải
Dựa vào bảng biến thiên trên 
 5;7 , ta có: min f x  f   1  2 .   5;7
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------23
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 10: (SỞ GD&ĐT KIÊN GIANG NĂM 2018-2019) Hàm số y f x liên tục trên và có bảng biến
thiên như hình bên dưới.
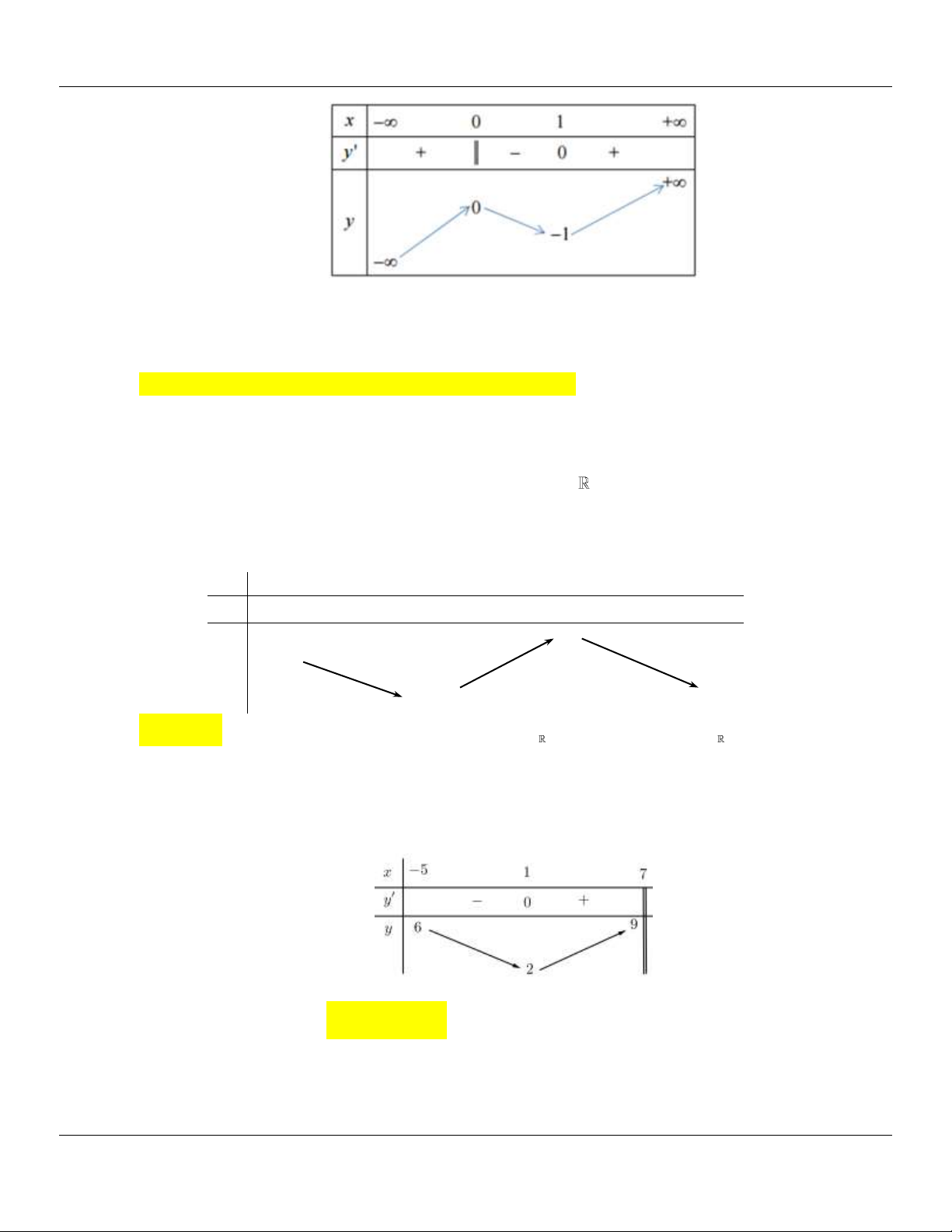
Biết f 4  f 8 , khi đó giá trị nhỏ nhất của hàm số đã cho trên bằng A. 9 . B. f 4 . C. f 8 . D. 4 . Lời giải
Từ bảng biến thiên:
Ta có: f (x)  f (4), x;0; f ( )
x f (8),x0; .
Mặt khác: f 4  f 8 suy ra:x; : f (x)  f (8). Vậy min f (x)  f (8).
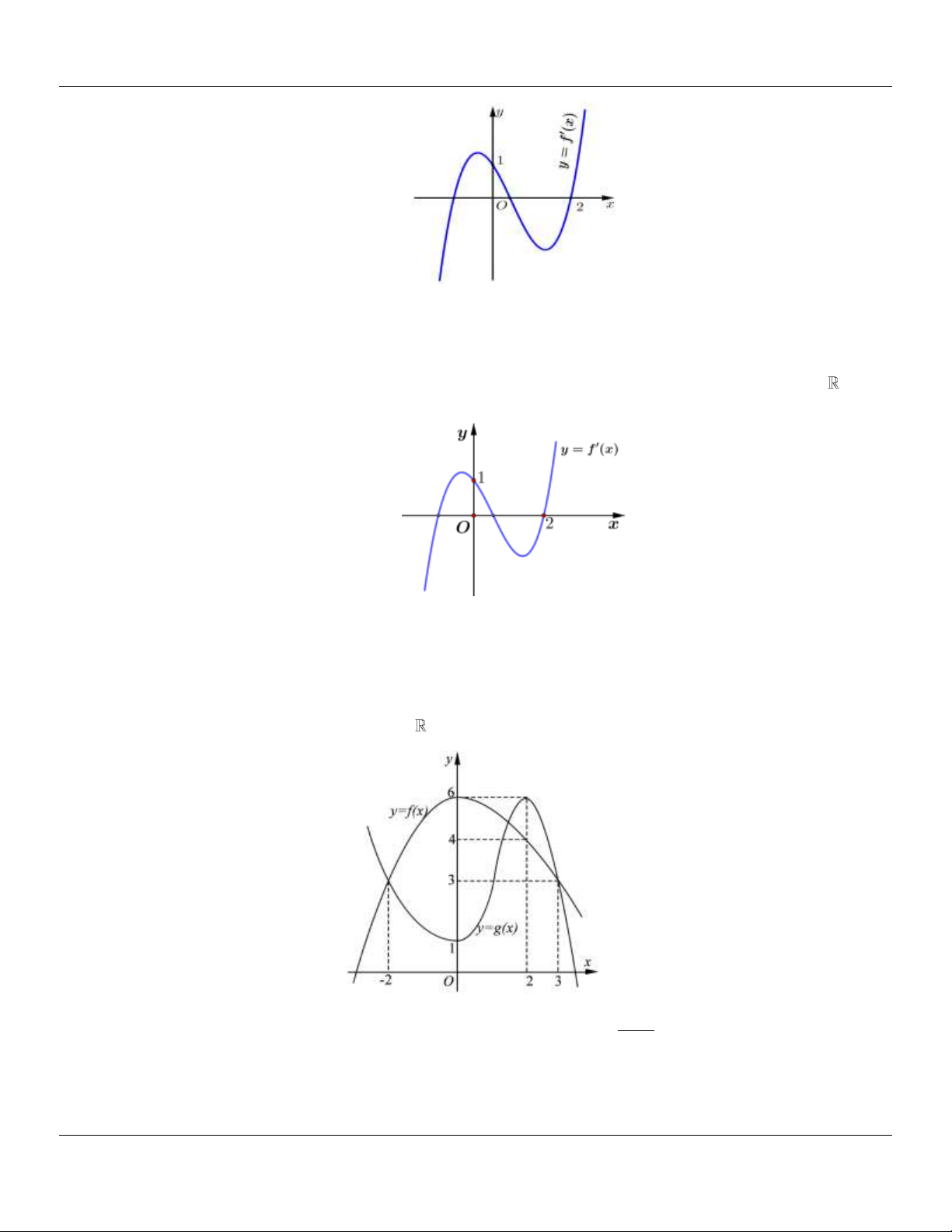
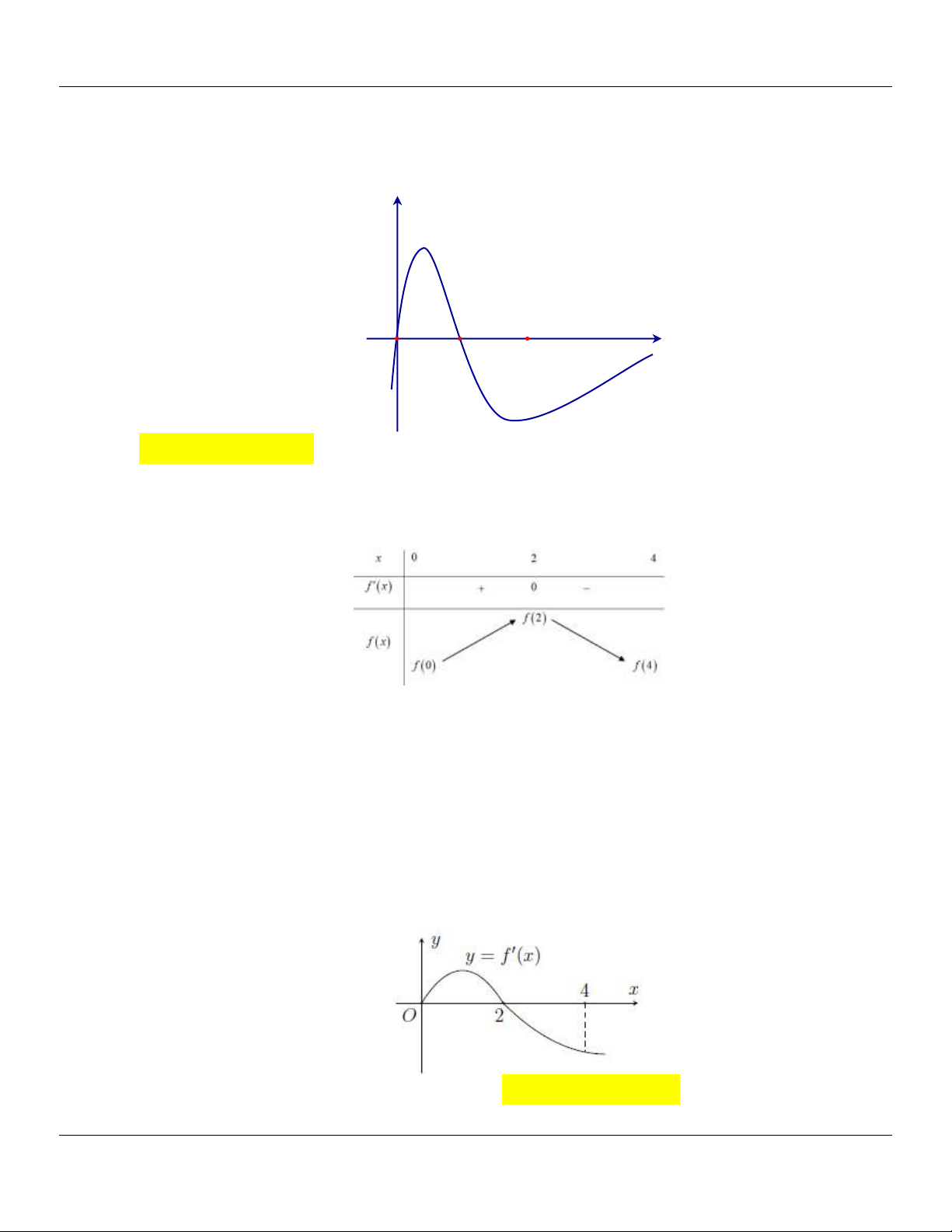
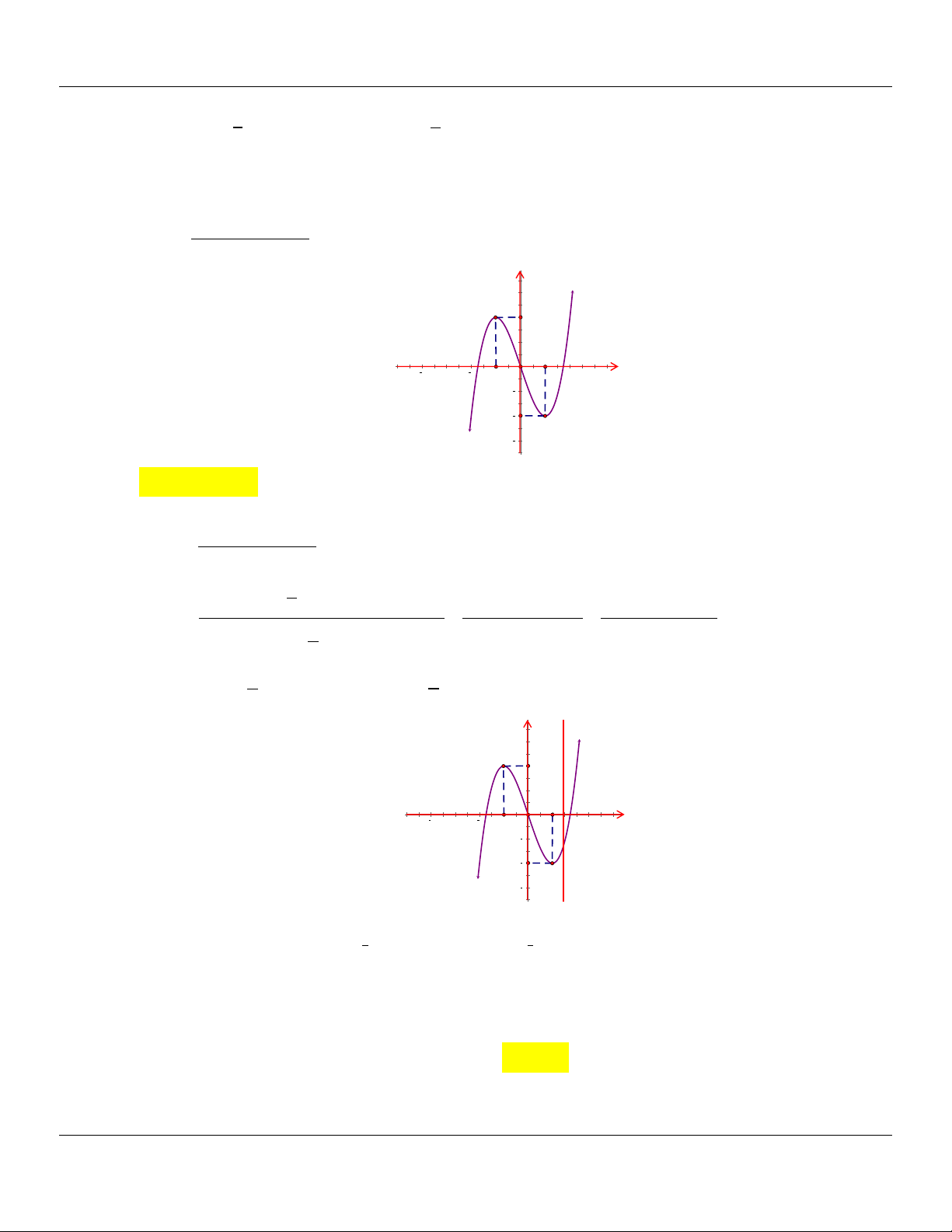
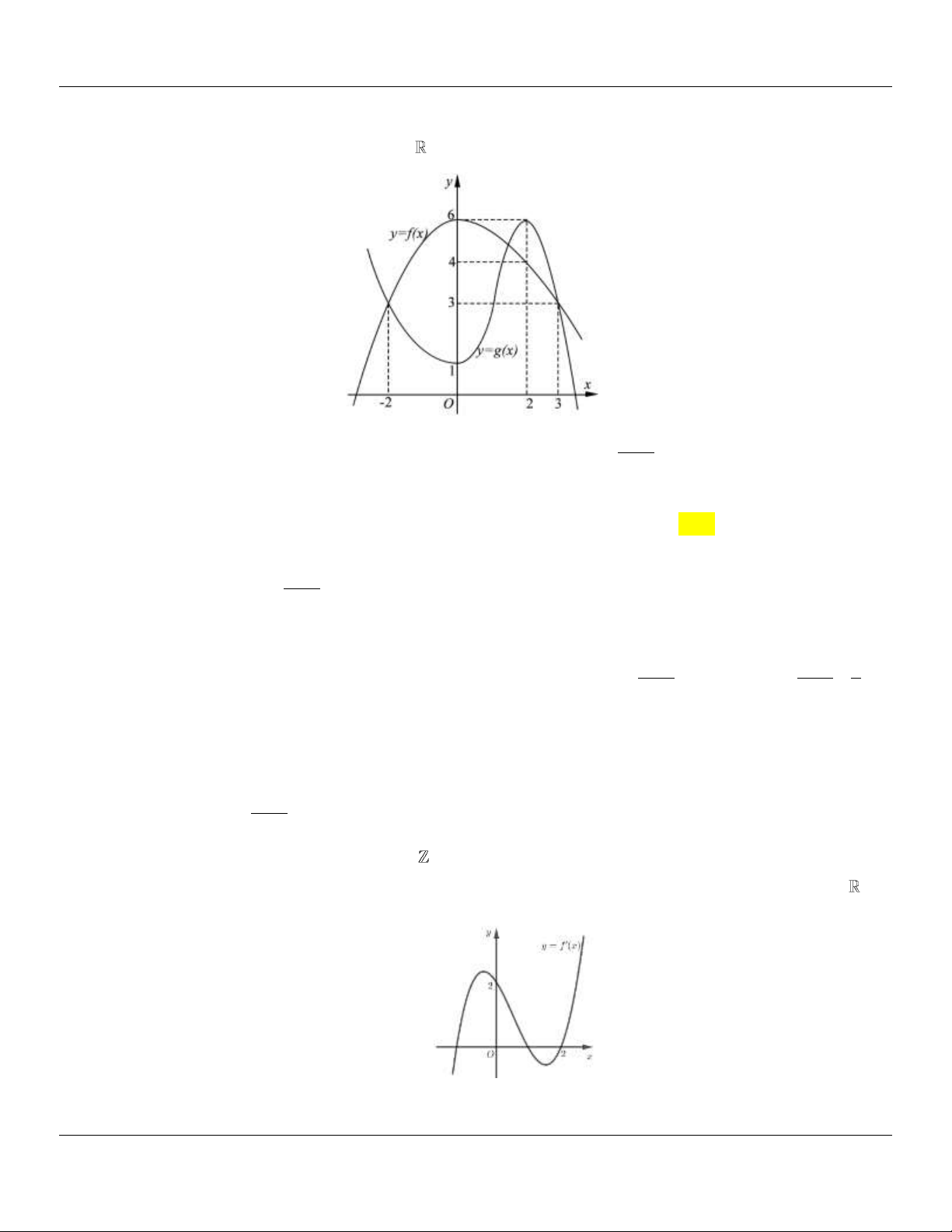
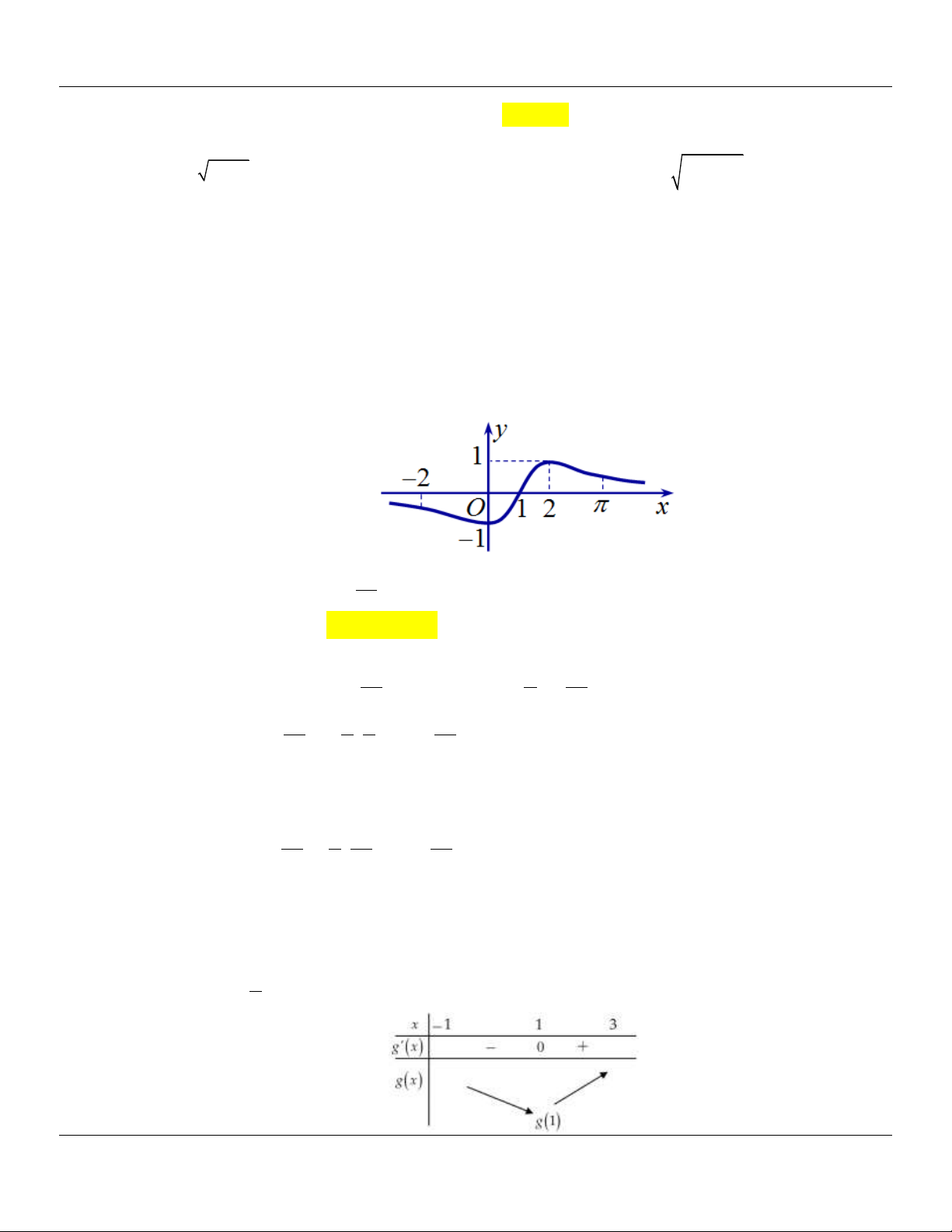
Câu 11: (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hàm số y f x
xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn
nhất M của hàm số y f x trên đoạn 2; 2   .
A. m  5; M  1 .
B. m  2 ; M  2 .
C. m  1; M  0 .
D. m  5; M  0 . Lời giải
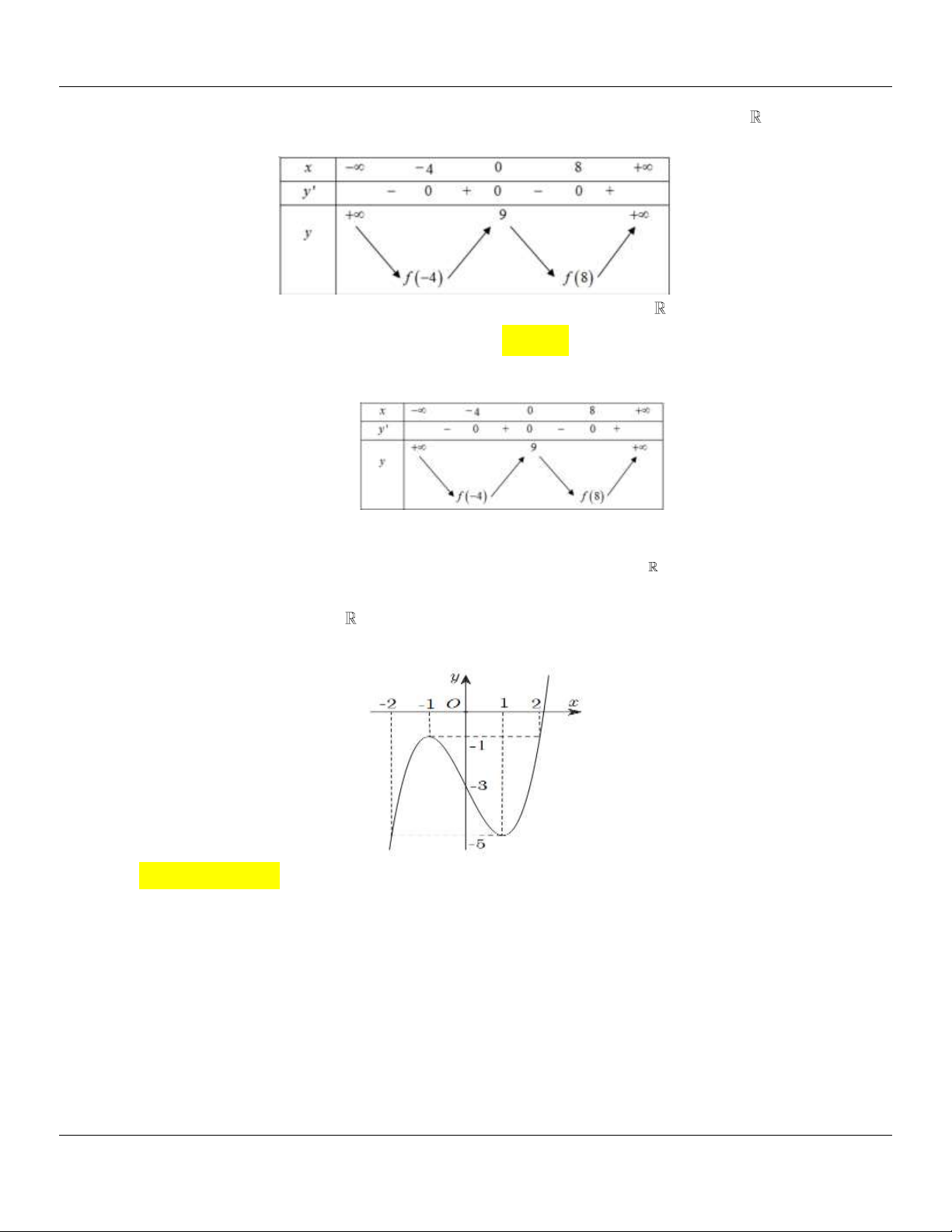
Nhìn vào đồ thị ta thấy:
M  max f x  1 khi x  1 hoặc x  2 ; m  min f x  5 khi x  2 hoặc x  1 . 2;2   2;2  
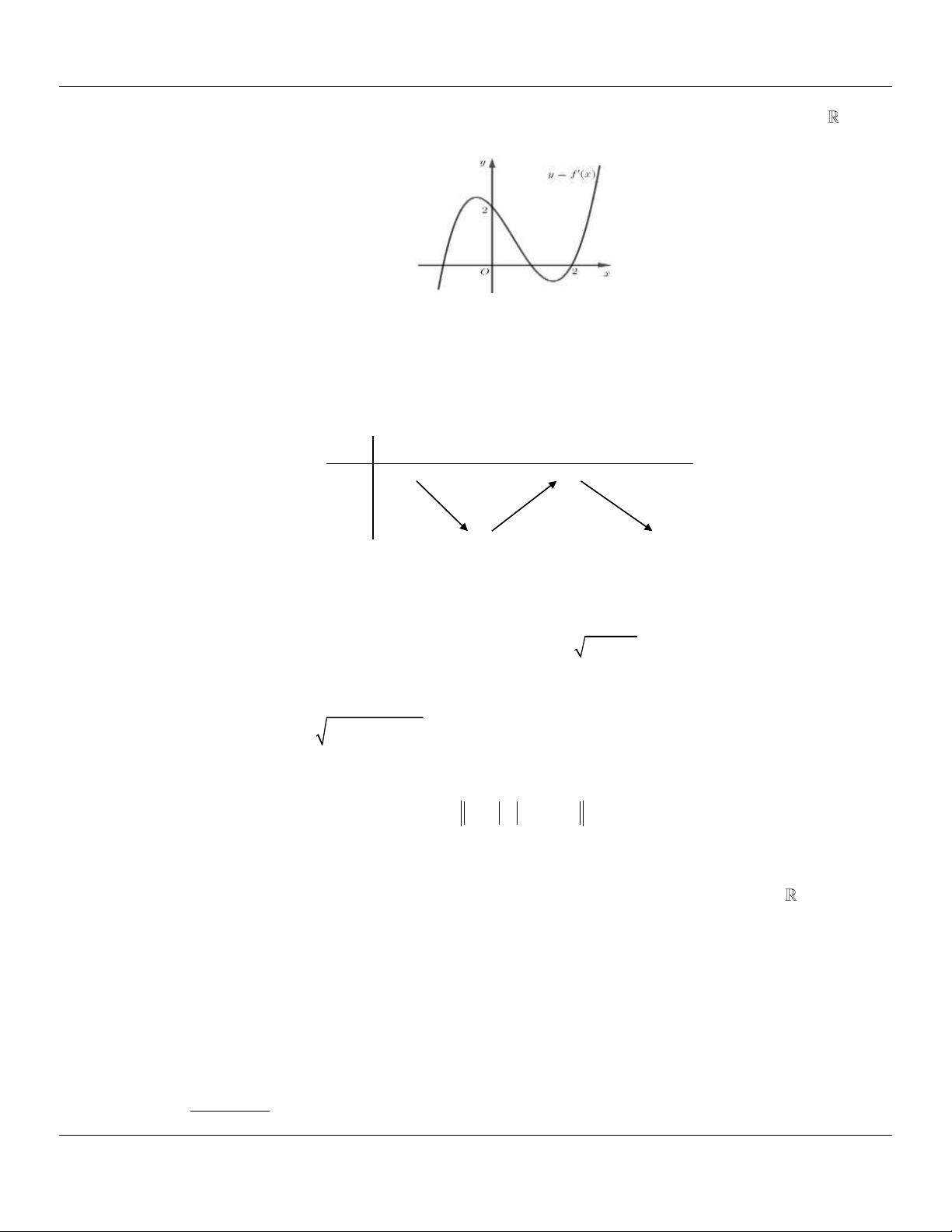
Câu 12: (THPT THÁI PHIÊN HẢI PHÒNG NĂM 2018-2019) Cho hàm số f x lên tục trên đoạn 1;3 
 và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số y f  2 3sin x  1 bằng
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------24
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 3 . B. 2 . C. 0 . D. 1 . Lời giải Đặt t  2
3sin x  1  t  1; 2  
Nhận xét: Giá trị lớn nhất của hàm số y f  2
3sin x  1 là giá trị lớn nhất của hàm số
y f t trên 1; 2 
 . Dựa vào đồ thị ta có: max y  max f t  2 . 1;2  
Câu 13: Cho hàm số y f (x) có đồ thị như hình dưới. Gọi m, M lần lượt là  1 
giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f ( 2  x) trên 1  ; .    2 
Giá trị m M bằng A. 0. B. 4. 19 C.  D. 4. 8 Lời giải  1 
Đặt t  2x, vì x  1  ;  t [ 1  ;2].    2 
Khi đó cần tìm GTNN, GTLN của hàm số y f (t), t [ 1  ;2].
m  min f (t)  4  khi t  2   Với [ 1;2] t [ 1  ;2] 
. Suy ra m M  4.
M  max f (t)  0 khi t  0  [ 1  ;2]
Câu 14: (THPT HOÀNG VĂN THỤ - HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có đạo hàm cấp 2 trên
, hàm số y f x có đồ thị như hình vẽ bên.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------25
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế  sinx   3 cos x   5  
Giá trị lớn nhất của hàm số y f     trên đoạn   ;  bằng  2   6 6    5        A. f    . B. f    . C. f 0 . D. f   .  6   3   6  Lời giải
sin x  3 cos x      5        Đặt t   sin x    . Vì x  ;  x    ;  t  1;        1 . 2  3   6 6  3  2 2 
Dựa vào đồ thị của hàm số f x , ta có bảng biến thiên  sin x   3 cos x     Ta có: max f
  max f t  t  0  sin x   0  x     .  5     1;  2    1  ;     3  3  6 6   sin x   3 cos x    Vậy max f    f    .  5      2 3  ;       6 6 
Câu 15: Cho hàm số y f x liên tục, đồng biến trên đoạn a;b 
 . Khẳng định nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn a; b   .
B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng a;b .
C. Phương trình f x  0 có nghiệm duy nhất thuộc đoạn a;b   .
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a; b   . Lời giải
Vì hàm số y f x liên tục, đồng biến trên đoạn a;b 
 nên min f x  f a;max f x  f b a;b a;b    
Vậy hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a; b   .
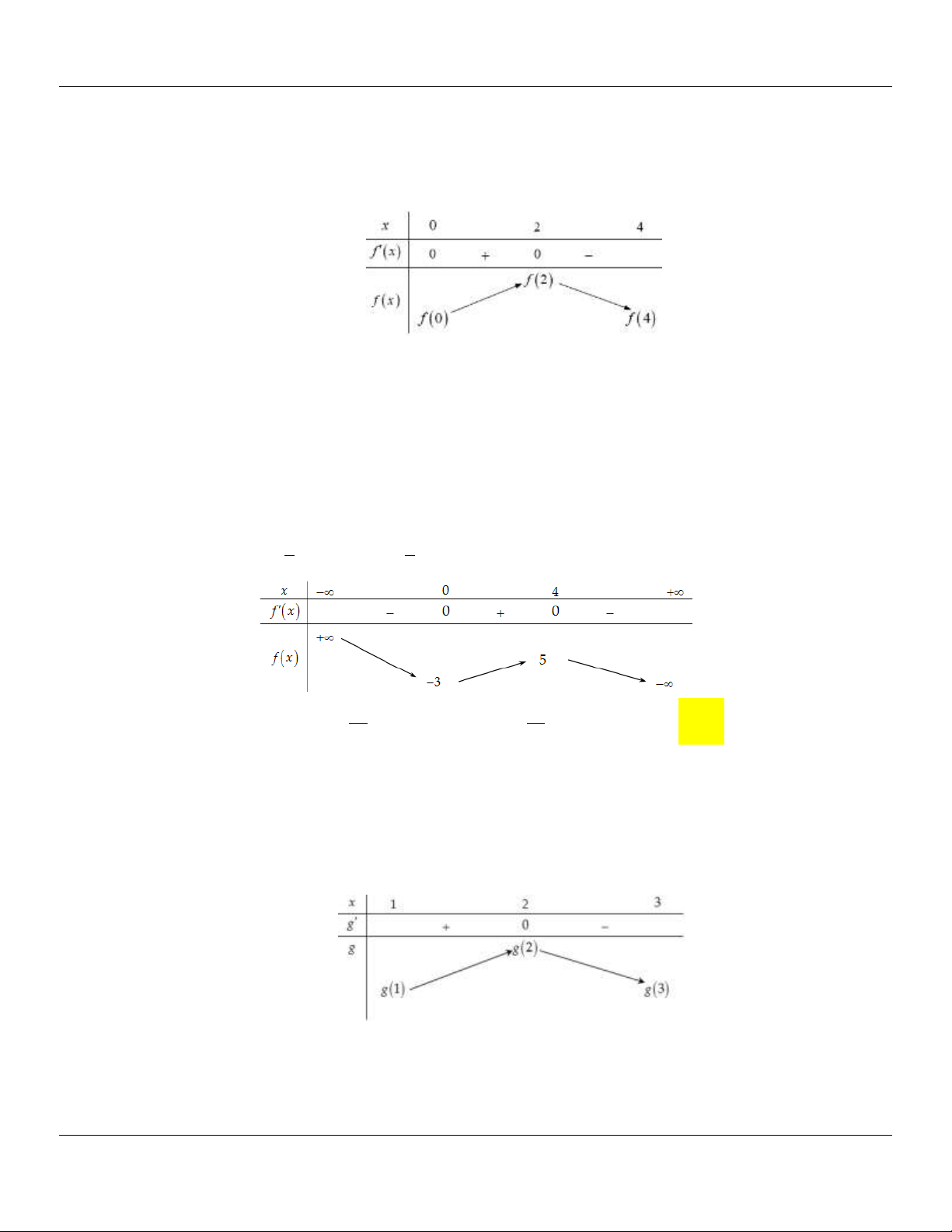
Câu 16: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số f x xác định,liên tục trên và có bảng biến thiên sau:
Phát biểu nào sau đây đúng?
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 2.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------26
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
B. Hàm số nhận giá trị dương với mọi x  . C. Trên 2; 8 
 hàm số có giá trị lớn nhất là M , giá trị nhỏ nhất là m . Giá trị biểu thức
m  3M  6 .
D. Hàm số có đúng một cực trị. Lời giải
Dựa vào bảng biến thiên ta thấy:
Hàm số có giá trị nhỏ nhất bằng 0 và không có giá trị lớn nhất nên loại phương án A.
Hàm số nhận giá trị không âm với mọi x  ( f (2)  0 ) nên loại phương án B.
Hàm số có 3 cực trị nên loại phương án D.
Hàm số có giá trị lớn nhất trên 2; 8 
 là M  2 và giá trị nhỏ nhất trên 2;8 
 là m  0 . Giá trị
biểu thức m  3M  0  3.2  6. Vậy phát biểu đúng là C.
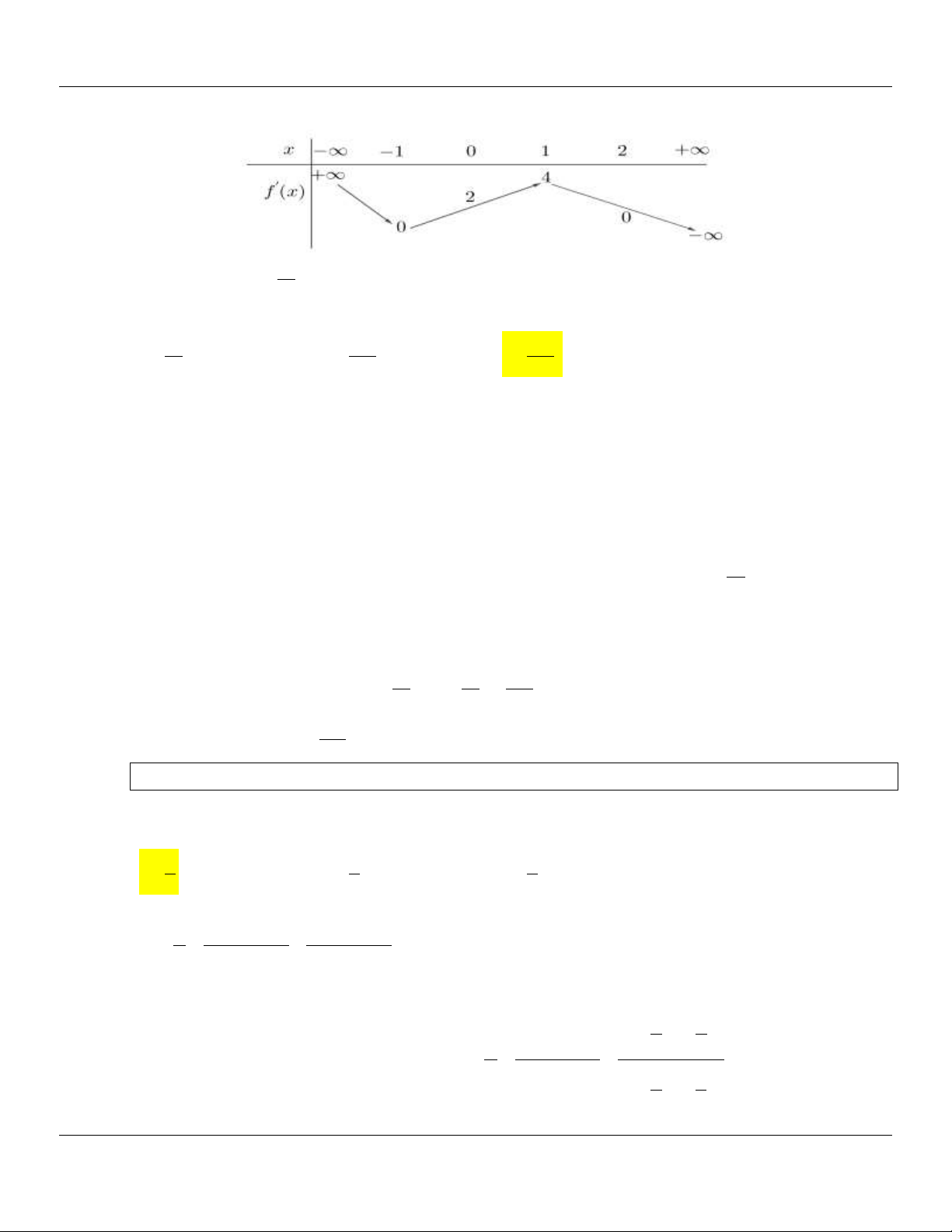
Câu 17: Cho hàm số y f x liên tục trên đoạn (-1;3) và có đồ thị như hình vẽ bên. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1; 3 
 . Giá trị của M m bằng A. 0. B. 1. C. 4. D. 5. Lời giải
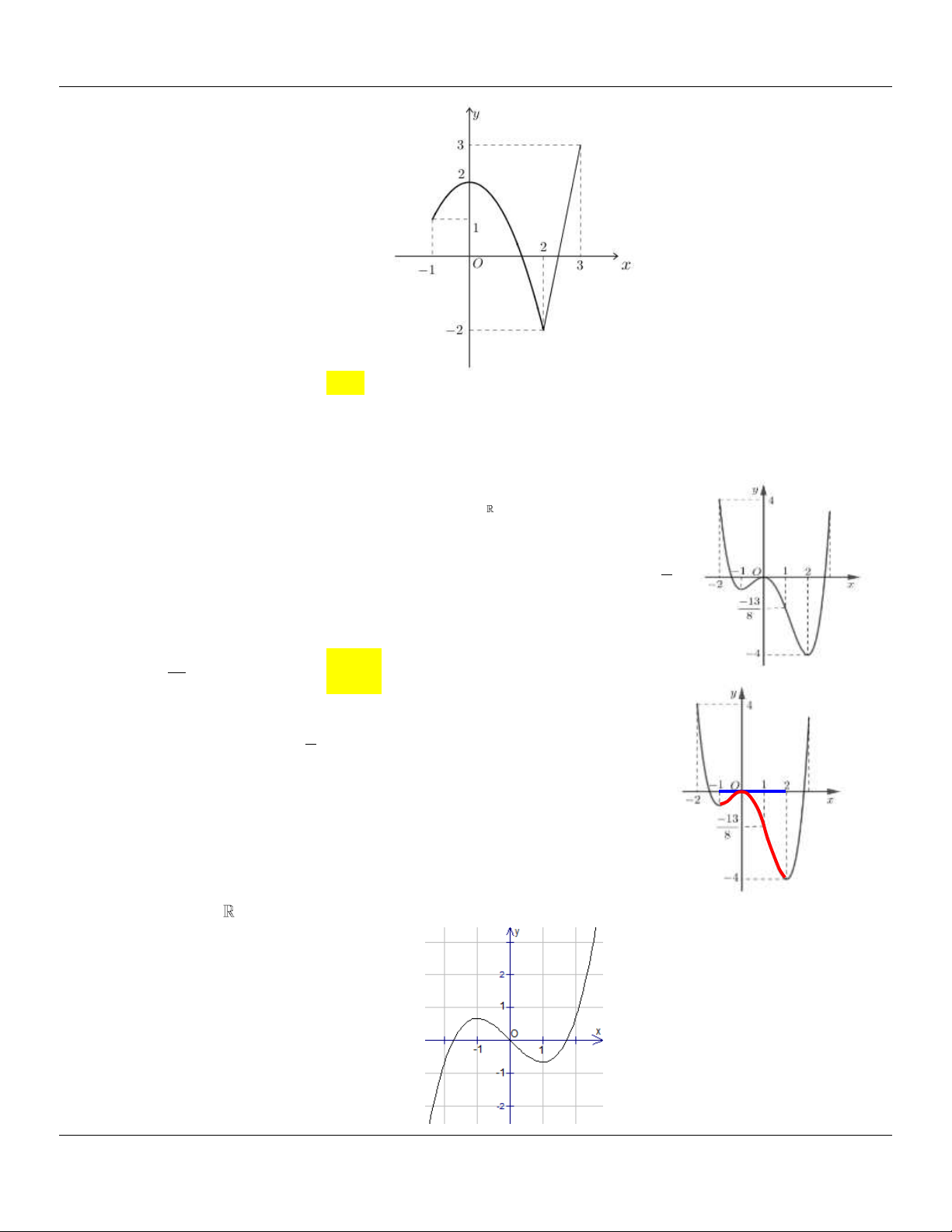
Căn cứ vào đồ thị ta có M  max y  3 , m  min y  2.
 Vậy M m  5 . [ 1  ;3] [ 1  ;3]
Câu 18: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. max f x  2.
B. max f x  1.
C. max f x  0.
D. max f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1 Lời giải
Chọn đáp án A.
Câu 19: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------27
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế   2 f x 3 1
Khẳng định nào sau đây đúng?
A. min f x  2.
B. min f x  1.
C. min f x  0.
D. min f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1 Lời giải
Chọn đáp án D.
Câu 20: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. min f x  3.
B. min f x  2.
C. min f x  0.
D. min f x  1.  x 0;    1  x 0;    1  x 0;    1  x 0;    1 Lời giải
Chọn đáp án D.
Câu 21: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    f x 2 3 1
Khẳng định nào sau đây đúng?
A. max f x  f 5. B. max f x  f 15. C. max f x  2.
D. max f x  f 10.  x 5;15    x 5;15    x 5;15    x 5;15   Lời giải
Dựa vào BBT ta thấy f x đồng biến trên 5;15  max f x    f 15.  x 5;15  
Câu 22: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    f x 2 3 1
Khẳng định nào sau đây đúng?
A. max f x  f 5.
B. max f x  f 15.  x 15;5    x 15;5  
C. max f x  2.
D. max f x  f 10.  x 15;5    x 15;5  
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------28
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế Lời giải
Dựa vào BBT ta thấy f x nghịch biến trên 15; 5  max f x  f    15.  x 15;5  
Câu 23: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt gx  2 f x  1. Khẳng định nào sau đây đúng?
A. max gx  2.
B. max gx  5.
C. max gx  1.
D. max g x  5.  x 1;    1  x 1;    1  x 1;    1  x 1;    1 Lời giải
Dựa vào BBT, ta có: x  1; 
1 :  3  f x  2  6  2 f x  4  5  2 f x  1    5.
Câu 24: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt gx  3  4 f x. Khẳng định nào sau đây đúng?
A. min g x  15.
B. min g x  5.
C. min gx  15.
D. max g x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1 Lời giải
Dựa vào BBT, ta có: x  1; 
1 :  3  f x  2  8  4 f x  12  5  3  4 f x    15.
Câu 25: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. max f x  2.
B. max f x  1.
C. max f x  0.
D. max f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1 Lời giải BBT: x  1 0 1  f x  0  0  0 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------29
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế   f x 2 3 1 3 f x 2 1 0 0
Câu 26: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Khẳng định nào sau đây đúng?
A. min f x  2.
B. min f x  1.
C. min f x  0.
D. min f x  3.  x 1;    1  x 1;    1  x 1;    1  x 1;    1 Lời giải BBT: x  1 0 1  f x  0  0  0    f x 2 3 1 3 f x 2 0 0 1
Câu 27: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt g x  f sin x. Khẳng định nào sau đây đúng?
A. max g x  2.
B. max g x  1.
C. max g x  3.
D. max g x  4. Lời giải:
Đặt t  sin x; x   t  1;    1 .
Ta có: max gx  max f t  2 đạt được khi sin x  0  x   k , k  . 1;    1
Câu 28: Cho hàm số y f x có bảng biến thiên như sau:
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------30
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế x  1 0 1  f x  0  0  0    2 f x 3 1
Đặt gx  f cos x. Khẳng định nào sau đây đúng?
A. min gx  1.
B. min gx  2.
C. min gx  3.
D. min gx  0.             0;  0;  0;  0;   2   2   2   2  Lời giải   
Đặt t  cos x; x 0;  t 0;      1 .  2 
Ta có: min gx  min f t  1 đạt được khi cos x  1  x k  2 , k  .    0;    1 0;   2 
Câu 29: Cho hàm số y f x có bảng biến thiên như sau: x  1 0 1  f x  0  0  0    f x 2 3 1 3 2
Đặt gx   f x  3 
f x . Khẳng định nào sau đây đúng?
A. max g x  4.
B. max gx  4.
C. max gx  0.
D. max gx  2. 1;    1 1;    1 1;    1 1;    1 Lời giải
Ta có: x  1;  1   
f x 3; 2 
. Đặt t f x 3; 2  . t  0  3; 2 3 2 2  
Xét hàm số ht  t  3t ,t  3;2  ht   
 3t  6t  0     .
t  23;2   
Ta có: h0  0; h2  4; h3  54.
Câu 30: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Giá trị lớn nhất của hàm số    x f x trên đoạn 2; 3   bằng x  3 1 A. 3. B. 2. C. . D. 2. 2 Lời giải 3
Ta có: f 'x   x   0 ,  2;3   x  32 1
Do đó hàm số f x đồng biến trên 2; 3 
. Suy ra: max f x  f 3  . 2;3   2
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------31
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 31: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Giá trị nhỏ nhất của hàm số f x x  1 ( )
trên nửa khoảng   2;  là x 5 7 A. 2 . B. . C. 0 . D. . 2 2 Lời giải 1 3x x 1 3.2 x 1 5
Áp dụng bất đẳng thức Cô-si, ta được: f (x)  x       2 .  . x 4 4 x 4 4 x 2
Dấu bằng xảy ra khi x  2 . 2 x  3
Câu 32: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất của hàm số y  trên đoạn x  1 2;4   . 19 A. miny  6. B. min y 2. C. miny  3. D. miny  . 2;4    2;4 2;4 2;4       3 Lời giải 2 x  3
Tập xác định: D   \  1 . Hàm số y
xác định và liên tục trên đoạn 2; 4   x  1 2 x  2x  3 Ta có y  ;y  0  2
x  2x  3  0  x  
3 hoặc x  1 (loại) x  2 1
Suy ra y   y   y   19 2 7; 3 6; 4
. Vậy min y 6 tại x  3 . 3 2;4  
Câu 33: Tìm giá trị nhỏ nhất của hàm số   9 y x
trên đoạn [2 ; 4]. x 13 25 A. min y  . B. min y  . C. min y  6. D. min y  6. [2 ; 4] 2 [2 ; 4] 4 [2 ; 4] [2 ; 4] Lời giải 9 x  3 Xét hàm số   9 y x trên đoạn [2 ; 4] y  1  ; y  0  2  x ; x x  3  (2; 4) 13 25 Ta có: ( y 2)  ; ( y 3)  6; ( y 4) 
. Vậy min y  6 khi x  3 . 2 4 [2 ; 4]
Câu 34: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Tìm giá trị lớn nhất của hàm số
y f x  x  1  5  x trên đoạn 1; 5   .
A. max f x  3 2 .
B. max f x  2 .
C. max f x  2 2 .
D. max f x  2 . 1;5   1;5   1;5   1;5   Lời giải
Áp dụng bất đẳng thức Bunyakovsky, ta có:
y f x  x    x   2  2 1 5 1
1 x  1 5  x  2 2 . x  1 5  x Dấu bằng xảy ra khi 
x  3 1;5 
 . Vậy max f x  2 2 . 1 1 1  ;5
Câu 35: Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y x  1  7  x . Khi đó
có bao nhiêu số nguyên dương nằm giữa m và M ?
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------32
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 1 . B. 5 . C. 7 . D. 0 . Lời giải 1 1
Tập xác định D  1;7   . Ta có: y  
; y  0  x  4 . 2 x  1 2 7  x
Khi đó y1  y7  6 , y4  2 3 . Suy ra  6   2 3  k k   k  3 .
Vậy có duy nhất một số nguyên dương thoả mãn. 8 10
Câu 36: (THPT THĂNG LONG HÀ NỘI NĂM 2018-2019 LẦN 02) Hàm số y x  đạt giá trị nhỏ x nhất trên đoạn  3 9 10 ;10    tại x bằng A. 4 10 . B. 3 10 . C. 5 10 . D. 6 10 . Lời giải 8 10 8 10
Cách 1: Hàm số y x  liên tục trên  3 9 10 ;10  
 . Ta có y  1  . x 2 xx  4 10   3 9 10 ;10  2 8  
y  0  x  10   . x   4 10   3 9 10 ;10     y  3   3  5 10 10 10 , y  4   4 10 2.10 , y  9  9    1 10 10 10 . Vậy min y  4 2.10 khi x  4 10 .  3 9  10 ;10  8 8 10 10
Cách 2: Vì x  0 nên theo bất đẳng thức Côsi ta có y x   2 . x  4 2.10 . x x 8 10
Dấu "  " xảy ra  x   x  4 10   3 9 10 ;10  4 
 . Vậy min y  2.10 khi x  4 10 . x  3 9  10 ;10 
Câu 37: (SỞ GD&ĐT BÌNH THUẬN NĂM 2018-2019) Giá trị lớn nhất của hàm số y   2
x  5x bằng 5 A. 0 . B. . C. 6 . D. 2 . 2 Lời giải 2x  5 5 TXĐ: D  0; 5   . Ta có: y' 
; y'  0  2x  5  0  x   0; 5.   2  2 x  5x 2  5  5  5  5
Ta có: y 0  y5  0 ; y   
. Vậy max y y    .  2  2  2  2
Câu 38: (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Tìm giá trị nhỏ nhất của hàm số y  2
sin x  4 sin x  5 . A. 20 . B. 8 . C. 9 . D. 0 . Lời giải Xét hàm số: y  2
sin x  4 sin x  5
Txđ: D  . Đặt t  sin x , 1  t  1. Ta có: yt  2
t  4t  5 , hàm số liên tục trên 1;    1
yt  2t  4 , yt  0  t  2 ; y1  8, (
y 1)  0 . Vậy min y y  1  8 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------33
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 39: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Giá trị nhỏ nhất của hàm số 2 sin x     y  3 trên đoạn 0;  là sin x  1  2  5 A. 5 . B. 2 . C. 3 . D. . 2 Lời giải    2t  3
Đặt t  sin x . Với x 0;  thì 0  sin x  1  0  t  1. Khi đó: y f (t)  , với t  0;    1 .  2  t  1 1 Có f '(t) 
 0, t  0;   
1 nên hàm số f (t) nghịch biến trên đoạn 0;    1 . (t  1) 5
Suy ra min f (t)  f (1)  . Vậy y  5 min . 0;    1 2 2
Câu 40: (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hàm số f x  3
sin x  3sin x  2 . Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó M  2m là A. 0 . B. 1. C. 4. D. 5. Lời giải
Đặt sin x t t  1; 1  
  . Ta có f t  3 t  3t  2.
Xét hàm số f t  3
t  3t  2 với t  1; 1  
 ; f t  2 '
3t  3  0  t   1 hoặc t  1 .
Ta có f 1  4 , f 1  0 . Suy ra, giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là 4 và 0 hay
M  4 ; m  0. Giá trị M  2m  4  2.0  4 .
Câu 41: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018-2019) Cho hàm số
f x  cos 2x  cos x  1 . Giá trị nhỏ nhất của hàm số trên là A.
f x   1 min . B.
f x   1 min . C. f x  1 min . D. f x  1 min . 8 4 8 4 Lời giải
Hàm số được viết lại f x 2  2cos x  cos .
x Đặt t  cos x . Với mọi x
suy ra t  1;    1 .
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số gt  2
2t t trên 1;    1 .  1  1
Ta có g't  4t  1; g t   t  1 ' 0 ; g  1  3; g  1  1; g     . Vậy
f x   1 min . 4  4  8 8
Câu 42: (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Giá trị lớn nhất của hàm số y  2
2 sin x  cos x là phân số tối giản có dạng với a,b là các số nguyên dương. Tìm a – b . A. 8 . B. 9 . C. 7 . D. 10 . Lời giải
TXĐ: D  . Ta có: y  2 x x   2 x x   2 2 sin cos 2(1 cos ) cos
2 cos x  cos x  2
Đặt: t  cos x , với 1  t  1
Như vậy ta đi tìm giá trị lớn nhất của hàm số y   2
2t t  2 trên đoạn 1;    1 1  1  17
Ta có: y'  4t  1  0  t    1;    1 ; (
y 1)  1; y   ; ( y 1)     1 4  4  8
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------34
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế  1  17
Vậy: Giá trị lớn nhất của hàm số là y    
suy ra a – b  9  4  8
Câu 43: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
y  3cos 2x  4 sin x là 11 A. 1 . B. 7 . C. 5 . D. . 3 Lời giải Ta có y    2 x  x y   2 3 1 2 sin 4 sin
6 sin x  4 sin x  3 . Đặt t  sin x, 1  t  1. Khi đó y   2
6t  4t  3 với t  1;    1 . 1 11
y   t
y   t   1 12 4, 0 và y  1 1, y1      7,y     . 3  3  3 
Vậy giá trị nhỏ nhất của hàm số là 7 đạt được khi sin x  1  x   k  2 2
Câu 44: (MĐ 102 BGD&ĐT NĂM 2016-2017) Tìm giá trị lớn nhất M của hàm số y  4 x  2 2x  3 trên đoạn   0; 3 . A. M  9 . B. M  8 3 . C. M  1 . D. M  6 . Lời giải x  0  Ta có: y  3
x x x 2 4 4 4
x  1 ; y  0  x 2 4 x  1  0  x   1 x    1(l)
Ta có : y 0  3 ; y1  2 ; y 3  6.
Vậy giá trị lớn nhất của hàm số y  4 x  2
2x  3 trên đoạn  
0; 3 là M y 3   6
Câu 45: (MĐ 104 BGD&ĐT NĂM 2018-2019) Giá trị nhỏ nhất của hàm số f x  3
x  3x trên đoạn 3;3   bằng A. 18 . B. 18 . C. 2 . D. 2 . Lời giải x  1   3;3
Ta có: f x  2
3x  3. Ta có: f x     0  
x  1 3;3   
Mặt khác: f 3  18; f 3  18; f 1  2; f 1  2 . Vậy min f x  f 3  18 . 3;3   2  1 
Câu 46: (MĐ 104 BGD&ĐT NĂM 2017) Tìm giá trị nhỏ nhất m của hàm số y  2 x  trên đoạn  ;2 . x  2  A. m  17 . B. m  10 . C. m  5 . D. m  3 . 4 Lời giải 2 3 2 2x  2  1 
Đặt y f x  2
x  . Ta có y  2x  
, y  0  x  1  ;2 x 2 2 x x 2 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------35
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế  1  17
Khi đó f 1  3, f  , f 2   
5. Vậy m  min f x  f   1  3 .  2  4  1   ;2 2 
Câu 47: (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Gọi M và m lầ lượt là giá trị lớn
nhất và giá trị nhỏ nhất của hàm số f x  2x  4 6  x trên 3;6 
 . Tổng M m có giá trị là: A. 12 . B. 6 . C. 18 . D. 4 . Lời giải
Hàm số xác định liên tục trên 3; 6.   2
Ta có f x  2 
 0 x3;6 , hàm số đồng biến trên 3;6 6  x
M  max y f 6  12 ; m  min y f 3  18 ; M m  6. 3;6   3;6  
Câu 48: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi M là giá trị lớn nhất của hàm số f x  2
x x   x  2 4 4 6 4
x  1 . Tính tích các nghiệm của phương trình f x  M . A. 2 . B. 4 . C. 2 . D. 4 . Lời giải 2 Đặt t  2
x  4x  6  x  2  2  2 .
Khi đó, M  max f x  max gt , với gt   2
t  4t  7 trên    2; .  2;   2
Ta có: gt   2
t  4t  7  11  t  2  11, dấu đẳng thức xảy ra khi x  2  2 t   2 2
x  4x  6  2  2
x  4x  2  0   . x  2   2
Như vây, M  max f x  max gt  11  x  2  2 , suy ra nghiệm của phương trình f x  M  2;  
là x  2  2 . Vậy tích các nghiệm của phương trình f x  M bằng 2 .
Câu 49: (MĐ 103 BGD&ĐT NĂM 2016-2017) Tìm giá trị nhỏ nhất m của hàm số y  4 x  2 x  13 trên đoạn 2; 3  . A. m  51. B. m  49 . C. m  13. D. m  51. 4 4 2 Lời giải x  0   1  51 Ta có: y  3 4x  2 .
x y  0  
; y 0  13 , y   
, y2  25 , y3  85 . x   1   2  4  2 Vậy m  51 . 4
Câu 50: (SỞ GD&ĐT LẠNG SƠN NĂM 2018-2019) Tìm x để hàm số y x   2
4 x đạt giá trị lớn nhất. A. x  2 . B. x  2 2 . C. x  1 . D. x  2. Lời giải
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------36
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế x
Tập xác định D  2; 2 
 . Ta có: y  1  . 2 4  xx  0  x x 0 2    y  0  1 
 0  4  x x    x   2 n 4  4  2 x  2 2   x x x    2 l
Ta có: f 2  2; f 2  2; f  2   2 2. Vậy hàm số đạt giá trị lớn nhất là 2 2 khi x  2 4
Câu 51: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2016-2017) Tính giá trị nhỏ nhất của hàm số y  3x  2 x
trên khoảng 0;  . 33 A. min y  3 3 9. B. min y  7. C. min y  . D. min y  3 2 9. 0; 0; 0; 5 0; Lời giải 4 3x 3x 4 3x 3x 4
Cách 1: y  3x      3 . .  3 3 3 9 2 2 2 x 2 2 x 2 2 x 3x 4 8 Dấu "  " xảy ra khi 
x  3 . Vậy min y  3 3 9 2 2 x 3 0; 4
Cách 2: Xét hàm số y  3x
trên khoảng 0;  2 x 4 8 8 8 8
Ta có y  3x   y'  3  . Cho y'  0   3  3 x   x  3 2 3 x x 3 x 3 3    y y 8 min   3 3 3 9. 0;    3 
Lưu ý: Các em nếu có sử dụng MTCT thì bấm cẩn thận nhé!
Câu 52: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Gọi M, m lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của hàm số f x  x x trên đoạn 0; 3 
 . Giá trị của biểu thức M  2m gần với số
nào nhất trong các số dưới đây? A. 1,768 . B. 0,767 . C. 1,767 . D. 0,768 . Lời giải 1 1
Ta có f x   1 ' 1
; f 'x  0  1 
 0  x  0;3 . 2 x 2 x 4 f    1   f   1 0 0, , f 3  3    3 .  4  4
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------37
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 1 5  2 3
Suy ra, M  3  3, m   M  2m   0,7679491924... 4 2 Câu 53:
(THPT SƠN TÂY HÀ NỘI NĂM 2018-2019 LẦN 02) Giá trị nhỏ nhất của hàm số Câu 54:
f xx 1x  2x  3x  4 2019 là A. 2017. B. 2020. C. 2018. D. 2019. Lời giải
Tập xác định: D = .
Biến đổi : f xx  x  x  x    2
x x   2 1 2 3 4 2019 5 4
x  5x  6 2019.  5 2 9 9 Đặt t  2
x  5x  4t x
 t  x   .  2  4 4 2 9
Hàm số đã cho trở thành f t 2
t  2t  2019 t 1  2018 2018 t  . 4  9 
Vậy giá trị nhỏ nhất của hàm số đã cho bằng 2018 tại t    1  ;  .  4 
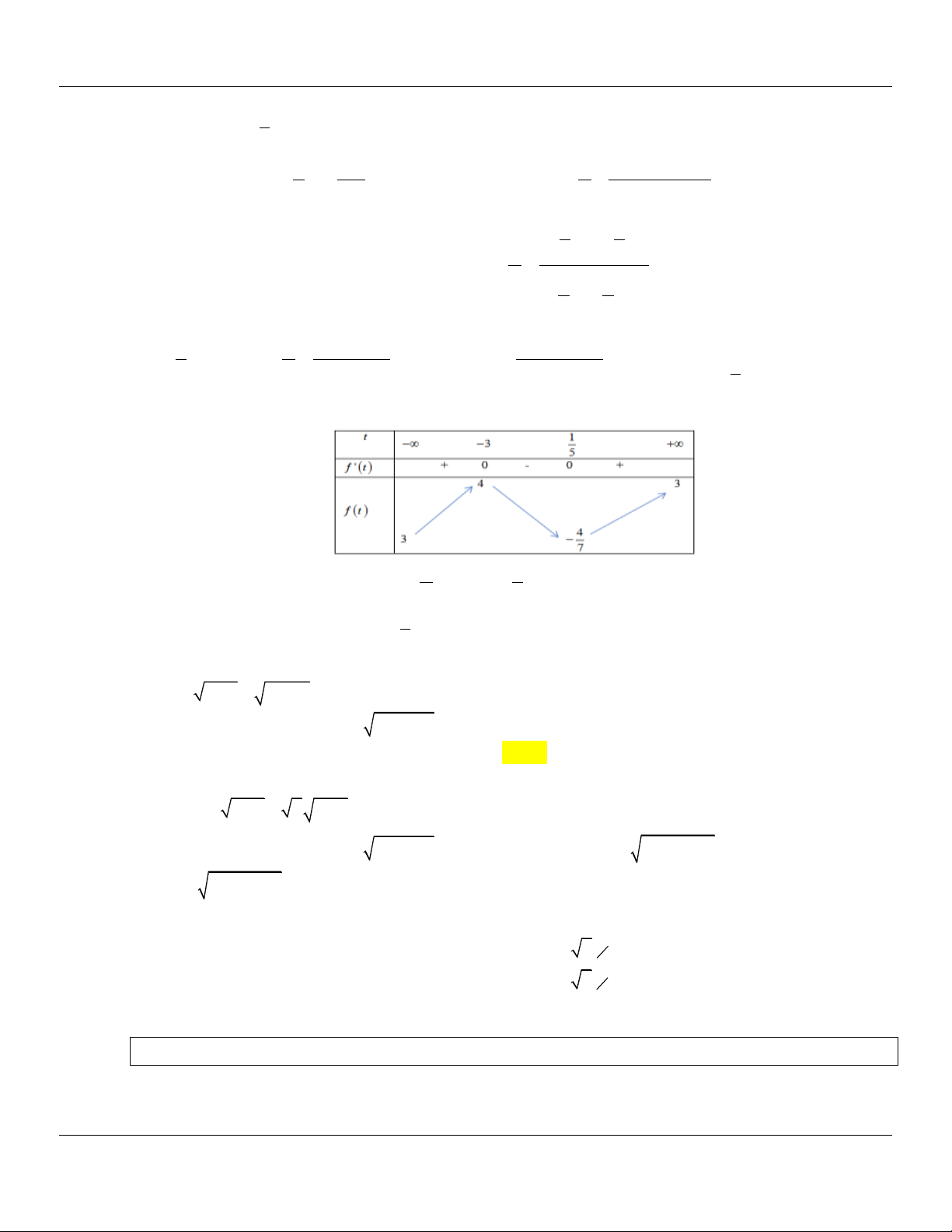
Câu 55: (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Tổng giá trị lớn nhất M và giá trị nhỏ
nhất m của hàm số f x  x   2 6
x  4 trên đoạn 0 ; 3 
 có dạng a b c với a là số nguyên
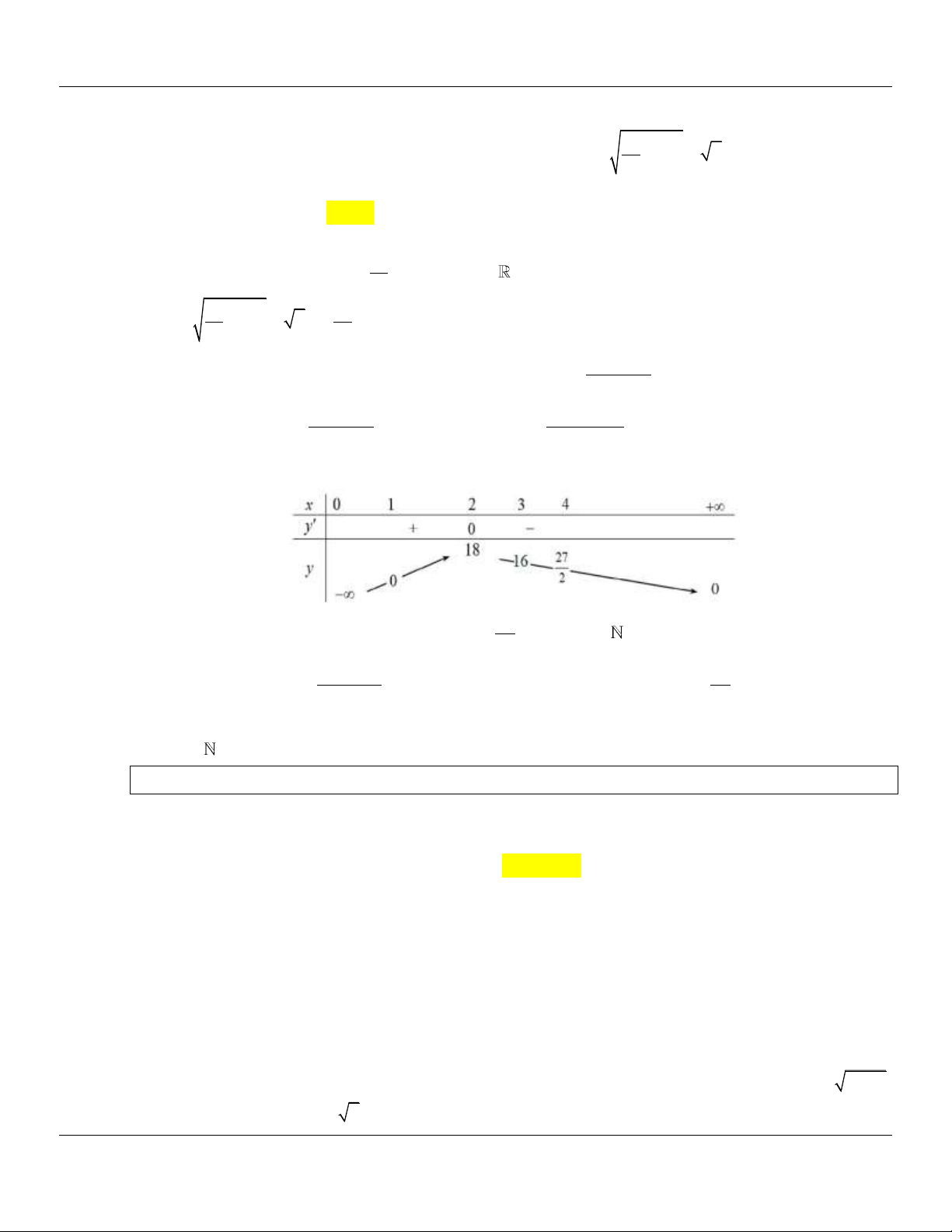
và b ,c là các số nguyên dương. Tính S a b c . A. 4 . B. 2 . C. 22 . D. 5 . Lời giải
Hàm số f x  x   2 6
x  4 xác định và liên tục trên đoạn 0 ; 3   . 2 x  1 0;3 f xx x 4 x 6 x 2 xx       2 2x  6x         4 4 6 . ; f x     0   2 x  2 4 x  2 4 x  4 x  20;3   
f 0  12; f 3  3 13 ; f 1  5 5 ; f 2  8 2
Suy ra max y M  3 13 và min y m  12 0;3   0;3  
M m  12  3 13  a b c với a là số nguyên và b ,c là các số nguyên dương nên
a  12 ; b  3; c  13 . Do đó S a b c  4 .
Câu 56: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 02) Cho hàm số f x có đạo hàm
f x  xx  2
2 x  3 , x  . Giá trị lớn nhất của hàm số đã cho trên đoạn 0; 4   bằng A. f 0 . B. f 2 . C. f 3 . D. f 4 . Lời giải x  0 2 
Ta có f x  xx  2 x  3  0  x   2 . x   3
Bảng biến thiên của hàm số y f x trên đoạn 0; 4  
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------38
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Từ bảng biến thiên ta thấy giá trị lớn nhất của hàm số f x trên đoạn 0; 4   là f 3 .
Câu 57: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y f x xác định và liên tục trên
, đồ thị của hàm số y f x như hình vẽ sau:
Giá trị lớn nhất của hàm số y f x trên đoạn 1; 2   là A. f 1 . B. f 1 . C. f 2 . D. f 0 . Lời giải x  1 f x    0  x   1 . x   2
Từ đồ thị hàm y f x ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên 1; 2   là f 1 .
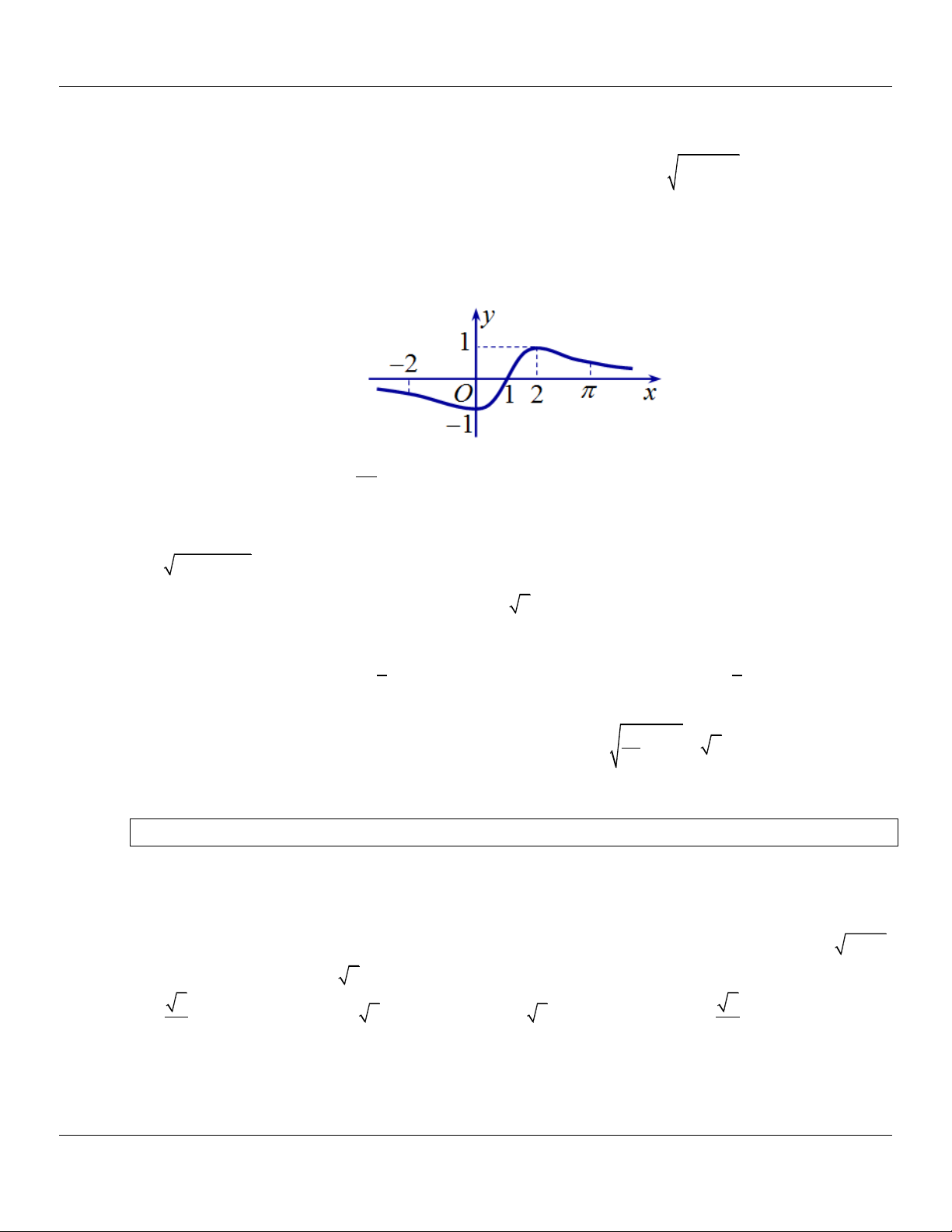
Câu 58: (THPT YÊN MÔ A-NINH BÌNH NĂM 2018-2019 LẦN 01) Cho hàm số y f x liên tục trên  7 
0;  có đồ thị hàm số y f x như hình vẽ sau:  2 
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------39
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế  7 
Hàm số y f x đạt giá trị nhỏ nhất trên 0;  tại điểm x nào dưới đây?  2  0 7 A. x  0 . B. x  . C. x  3 . D. x  1 . 0 0 2 0 0 Lời giải  7  x 1
Xét hàm số y f x trên đoạn
0;  . Dựa vào đồ thị ta có f x     0    2  x   3 Bảng biến thiên:  7 
Nhìn bảng biến thiên ta thấy hàm số y f x đạt giá trị nhỏ nhất trên
0;  tại điểm x  3.  2  0
Câu 59: (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hàm số f x có đạo hàm
là f x . Đồ thị của hàm số y f x được cho như hình vẽ bên. Biết rằng
f 0  f 1  2 f 3  f 5  f 4 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f x trên đoạn 0; 5   .
A. m f 5 , M f 3.
B. m f 5 , M f 1.
C. m f 0 , M f 3.
D. m f 1 , M f 3. Lời giải
Từ đồ thị ta có bảng biến thiên của f x trên đoạn 0; 5  
M f 3 và f 1  f 3, f 4  f 3
f 5  f 0  f 1  f 3  f 4  f 3  0  f 5  f 0  m f 5 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------40
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 60: (THPT LÝ NHÂN TÔNG LẦN 1 NĂM 2018-2019) Cho hàm số có f x có đạo hàm là hàm
f 'x . Đồ thị hàm số f 'x như hình vẽ bên. Biết rằng f 0  f 1  2 f 2  f 4  f 3 . Tìm
giá trị nhỏ nhất m và giá trị lớn nhất M của f x trên đoạn 0; 4   . y x 2 4 O
A. m f 4 , M f 2 .
B. m f 1 , M f 2.
C. m f 4 , M f 1 .
D. m f 0 , M f 2 . Lời giải
Dựa vào đồ thị của hàm f 'x ta có bảng biến thiên:
Vậy giá trị lớn nhất M f 2 .
Hàm số đồng biến trên khoảng 0; 2 nên f 2  f 1  f 2  f 1  0 .
Hàm số nghịch biến trên khoảng 2; 4 nên f 2  f 3  f 2  f 3  0 .
Theo giả thuyết: f 0  f 1  2 f 2  f 4  f 3
f 0  f 4  f 2  f 1  f 2  f 3  0  f 0  f 4. Vậy giá trị nhỏ nhất m f 4.
Câu 61: (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Cho hàm số f x có đồ thị của hàm
số f x như hình vẽ. Biết f 0  f  
1  2 f 2  f 4  f  3 . Giá trị nhỏ nhất m , giá trị lớn nhất
M của hàm số f x trên đoạn 0; 4   là
A. m f 4 , M f 1 .
B. m f 4 , M f 2 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------41
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
C. m f 1 , M f 2 .
D. m f 0 , M f 2 . Lời giải
Từ đồ thị của hàm số f x trên đoạn 0; 4 
 ta có bảng biến thiên của hàm số trên đoạn 0; 4   như sau:
Từ bảng biến thiên ta có M  max f x  f 2 . 0;4  
Mặt khác f 0  f 1  2 f 2  f 4  f 3
f 0  f 4   f 2  f 1   f 2  f 3    
 0 (do f 2  f 1; f 2  f 3 )
Suy ra f 0  f 4  m  min f x  f 4 . 0;4  
Câu 62: (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hàm số y f x có
bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
gx  f x  2 x   1 3 x  2 x x  1 4 3 8 trên đoạn 1; 3   . 3 3 25 19 A. 15. B. . C. . D. 12. 3 3 Lời giải
gx    xf  x  2 x   2 4 2 4
x  6x  8    x 2 f  2 2 
4xx 4 x . Với x  1; 3 
 thì 4  x  0 ;  x  2 3 4
x  4 nên f  x  2 4 x   0 .
Suy ra f  x  2 2 4
x   4  x  0 , x 1;3 .   Bảng biến thiên:
Suy ra max gx  g2  f 4  7  12 . 1;3  
Câu 63: (THPT KINH MÔN HAI DƯƠNG NĂM 2018-2019 LẦN 03) Cho hàm số y f x có đạo
hàm f x . Hàm số y f x liên tục trên tập số thực và có bảng biến thiên như sau:
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------42
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Biết rằng f    10 1
, f 2  6 . Giá trị nhỏ nhất của hàm số gx  3
f x  3 f x trên đoạn 3 1;2   bằng 10 820 730 A. . B. . C. . D. 198 . 3 27 27 Lời giải
Xét hàm số gx  3
f x  3 f x trên đoạn 1; 2  
f x  0   1
gx   2
3  f x   1  f  
x , gx  0   .  2
f x  1 2 x    1   1;2
Từ bảng biến thiên, ta có:      1  
x  2  1;2   
Và f x  0 , x 1; 2 
 nên f x đồng biến trên 1; 2 
  f x  f    10 1 3
f x  1  2
f x  1, x 1; 2 
 nên 2 vô nghiệm.
Do đó, gx  0 chỉ có 2 nghiệm là x  1 và x  2 .  3 10  10  730 3
Ta có g   3 1
f 1  3 f 1   3      ; g    3 2
f 2  3 f 2  6  36  198 .  3   3  27 730
Vậy min gx  g  1  . 1;2   27
DẠNG TOÁN 2: MAX MIN HÀM NHIỀU BIẾN
Câu 64: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho 2 x xy  2
y  2 . Giá trị nhỏ nhất của  2   2 P x xy y bằng 2 1 1 A. . B. . C. . D. 2 . 3 6 2 Lời giải 2 P x xy  2 2 y x xy  2 y Xét   2 x xy  2 2 2 y + Nếu y  0 thì 2
x  2 . Do đó P  2
x  2 suy ra min P  2
x   x 2 1       2 P x xy  2 y
y   y
+ Nếu y  0 ta chia tử mẫu cho 2 y ta được:   2 2 x xy  2 y
x   x 2 1      
y   y
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------43
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế P 1  t  2 t 1  t  2 t  2 2t  2 t 1 Đặt  x t , khi đó 
. Xét f t   f ' t ; f 't    0   2    y 2 1  t  2 t 1  t tt  
1  t t 2 2  1 Bảng biến thiên P Khi đó  1 min do đó P  2 min . 2 3 3
Câu 65: (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019)Cho hai số thực x, y thay đổi thỏa mãn điều kiện 2 x  2
y  2 . Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức P  3 x  3 2(
y )  3xy . Giá trị của M n bằng: 1 A. 4. B.  . C. 6. D. 1  4 2. 2 Lời giải 3 Ta có 3 3  P 2(x
y ) 3xy 2 x y        3x ( y x y)    3xy (x  2 y) Từ 2 x  2
y  2  (x  2
y)  2xy  2  xy
 1, đặt x y t và thay vào P ta được 2   2 t   2 tP   3 t  3 2 3t
 1  3 1   3t  2t  6t  3   2   2  2 (x  2 y) (x  2 y)
Mặt khác 2  (x  2
y)  2xy  (x  2 y)    (x  2 y)  4  0 2 2
2  x y  2  t  2;2   3 13
Khảo sát hàm số P   3 t  2
t  6t  3 trên t  2; 2 
 ta được m  min P  7; M  maxP  2 2;2 2;2     2
Vậy M m   1 . 2
Câu 66: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Cho x, y  thỏa mãn
x y  1 và 2 x  2
y xy x y  1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức  xy P
. Tính M m . x y  1 1 1 A. . B.  2 . C. . D.  1 . 3 3 2 3 Lời giải xy
Cách 1: Với điều kiện x y   2 x  2 1;
y xy x y  1 ta có P  . 2 x  2 y xy x  1 1  5 Nếu y  0 thì   x  . Khi đó P  0 .
x x  1   2 0 2
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------44
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế x y t
Nếu y  0 thì P  . Đặt  x t . Ta có P  , t  .  2 x 2 x y t t  1     1  y y t  2 t  1
Xét f t 
, t  . f t 
; f t  0  t  1 2 t t  1
t t 12 2 Từ bảng biến thiên: x   y x  x y    x y x  1 1 1 
M  1 tại  y      . 2  1 3  3x 2x 1 0 x y 2 2      1     
x y xy x y    1 x     3  3 x  1  xx  y     1 x  yy    1
m  1 tại  y    x  1  2   x 1 0 x 1 2 2        
x y xy x y  1 x  1      y   1
Vậy M m   2 . 3 xy
Cách 2: Với điều kiện x y   2 x  2 1;
y xy x y  1 ta có P  . 2 x  2 y xy  2
Px xy P    2 1 Py  0 (*)
+) Nếu P  0 thì x  0 hoặc y  0 . x  0
+) Nếu P  0 thì  . y   0 1
Để phương trình (*) có nghiệm x thì    2 y P P P . x
  13  1  0  1  3  x y y P 1       x y  x    yx y x  1 Ta có: 1  M  1 tại   2P     . 2  1 3  3x 2x 1 0 x y 2 2      1     
x y xy x y    1 x     3  3  x 1 
yP  1   x  y  x     yx  yy    1 m  1 tại   2P   x  1  2   x 1 0 x 1 2 2        
x y xy x y  1 x  1      y   1
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------45
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 1
Do đó M  ; m  1.
 Vậy M m   2 . 3 3
Câu 67: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho x , y thỏa mãn 2 x xy  2 5 6
5y  16 và hàm số
bậc ba y f x có đồ thị như hình vẽ. Gọi M ,7m lần lượt là giá trị lớn nhất và nhỏ nhất của  2 x  2 y  2  6 P f   2 2 
. Tính M m 2 2  5
x y  2xy   4  4 3 2 1 10 x 8 6 4 2 2 4 6 8 10 0 -1 1 1 2 3 A. 2 M  2 m  4 . B. 2 M  2 m  1 . C. 2 M  2 m  25 . D. 2 M  2 m  2 . Lời giải 2 x  2 y  2 Đặt t
P f t . Vì 2 x xy  2 5 6 5y  16 2 x  2 y  2xy  4 2 x  2 y  1  2 5x  6xy  2 5y
3x y   6xy 3x y2 2 2 nên t  8   . 1   2 18x  2 2y  4xy 2 7
x y2       2 2 2 2 2 16 2 5 6 5 x x y xy x xy y 4 6 3  3 Do đó 0  t
P f t với t 0;  . 5 2  2  4 3 2 1 10 x 8 6 4 2 2 4 6 8 10 0 -1 1 1 2 3
Dựa vào đồ thị, ta có M Max P f 0  0 ; m MinP f   1  2. Suy ra 2 M  2 m  4 .  3  3 0;  0;   2  2
Câu 68: (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Cho các số thực x, y thay đổi nhưng luôn thỏa mãn 2 x xy  2 3 2
y  5 . Giá trị nhỏ nhất của biểu thức P  2 x xy  2 2y thuộc khoảng nào sau đây? A. 4;7 . B. 2;1 . C. 1; 4 . D. 7;10 . Lời giải
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------46
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Xét y   P  5 0
loại phương án A và . D 3  y 2 2 7y 2 5 3x  2xy  2 y
Xét y  0  P   x   
 0 khi đó ta có biểu thức   2  4 2 P x xy  2 2yx 2 x 3   2  1 5  y y
Chia cả tử và mẫu của vế phải cho 2 y tâ được  . Px 2 x     2  y yt  3 2 x 5 3t  2t  2 1 5t  14t  3 Đặt t (t R) f t f ' t , f ' t 0 2     2 2             y P t t t t  t  1 2 ( 2)  5
Bảng biến thiên hàm số f t . 5 5
Từ bảng biến thiên ta có f t  4   4  P  . P 4 5
Vậy P đạt giá trị nhỏ nhất bằng , dấu bằng xảy ra khi t  3  x  3y . 4
Câu 69: (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho x , y là các số thực thỏa mãn
x y x  1  2y  2 . Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của P  2 x  2
y  2x  1y  1 8 4 xy . Tính giá trị M m A. 42 . B. 41 . C. 43 . D. 44 . Lời giải  2
x y2   x  1  2 y  1  3x y  0  x y  3
P x y  x  y   
x y  x y2 2 2 2 1 1 8 4
 2x y  2  8 4  x y 2
Đặt t  4  x y,t  1; 2 
 . Ta có: f t    2 t     2
t    t  4 t  2 4 2 4 2 8
10t  8t  26 . t  21;2   t   2
f t  3
4t  20t  8 ; f t  0  
 t  1 2  1;2 ; f 1  25; f 2  18 . 2  
t  2t  1   0 
t  1  2  1;2   
Suy ra m  min f t  f 2  18; M  max f t  f 1  25 . Vậy M m  43 . 1;2 1;2    
DẠNG TOÁN 3: BÀI TOÁN THỰC TẾ - TỐI ƯU
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------47
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 70: (ĐỀ THỬ NGHIỆM BGD&ĐT NĂM 2016-2017) Một vật chuyển động theo quy luật s   1 3 t  2
9t với t (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và s (mét) là 2
quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể
từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 216 m/s .
B. 30 m/s .
C. 400 m/s .
D. 54 m/s . Lời giải 3
Vận tốc tại thời điểm t là ( v t)   s (t)   2
t  18t với t  0;10   . 2
Ta có : v(t)  3t  18  0  t  6 .
Suy ra: v0  0; v10  30; v6  54 . Vậy vận tốc lớn nhất của vật đạt được bằng 54 m/s
Câu 71: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để
hộp nhận được có thể tích lớn nhất. A. x  6 . B. x  3 . C. x  2 . D. x  4 . Lời giải
Ta có: h x cm ,x  0 là đường cao hình hộp.
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 12  2x cm 2 x  0 x  0
Vậy diện tích đáy hình hộp S    x  2 12 2 cm  . Ta có:     x0;6 12  2x  0 x    6 2 2
Thể tích của hình hộp là: V  . S h  .
x 12  2x . Xét hàm số: y  .
x 12  2x x0;6 2
Ta có : y'  12  2x  4x12  2x  12  2x12  6x ;
y'  0  12  2x.12  6x  0  x  2 hoặc x  6 (loại).
Suy ra với x  2 thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là y2  128
Câu 72: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông A dự định dùng hết 2
6, 5m kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không
đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 2,26 m . B. 3 1,61 m . C. 3 1,33 m . D. 3 1,50 m .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------48
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế Lời giải a c b
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá: V abc  2  6,5  2b
ab  2bc  2ac  6,5  2
2b  6bc  6,5 c
Mặt khác theo giả thiết ta có:      6b a   2ba   2ba   2b  2 b b  3 6,5 2b 3 6,5b 2b Khi đó V  2 6, 5 2 2b .  V
. Xét hàm số: f b   . 6b 3 3 BBT:   39
Vậy bể cá có dung tích lớn nhất là : f    3   1,50 m .  6 
Câu 73: (SỞ GD&ĐT NINH BÌNH NĂM 2018-2019 LẦN 02) Bác Bính có một tấm thép mỏng hình
tròn, tâm O, bán kính 4 dm . Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai
mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình
vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (bỏ qua phần
mối hàn và độ dày của tấm thép). 12  8 3 12  8 3 1  6 3 6  4 3 A. 3 dm . B. 3 dm . C. 3 dm . D. 3 dm . 27 81 27 27 Lời giải
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------49
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Khi hàn hai mép của hình quạt tròn, độ dài đường sinh của hình nón bằng bán kính của hình
quạt tròn, tức là AB  4 . 1 1
Thể tích của hình nón: V   2
.r .h   .16  2
h .h với 0  h  4 . 3 3
V h  1    2
h    h  4 3 16 3 0 . 3 3 12  8 3
Dựa vào bảng biến thiên, suy ra thể tích lớn nhất của hình nón là dm3 . 27
Câu 74: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một chất điểm chuyển động theo
phương trình S   3 t  2
9t  21t  9 trong đó t tính bằng giây (s) và S tính bằng mét (m) . Tính
thời điểm t(s) mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất.
A. t  4(s). B. t  5(s). C. t  3(s). D. t  7(s). Lời giải Ta có: 
S V   2 t t    t  2 3 18 21 3(
3)  48  48  max V  48 khi t  3 .
Vận tốc chuyển động đạt giá trị lớn nhất khi t  3(s).
Câu 75: (SỞ GD&ĐT BÀ RỊA VŨNG TÀU NĂM 2018-2019) Một công ty bất động sản có 40 căn hộ
cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 3.000.000 đồng một tháng thì mọi căn hộ
đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100.000 đồng một tháng (theo qui
định trong hợp đồng) thì sẽ có một căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì
công ty đó phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng? A. 3.700.000 đồng. B. 3.500.000 đồng. C. 3.900.000 đồng. D. 4.000.000 đồng. Lời giải
Theo bài cứ tăng thêm 100.000 đồng trên một căn thì có 1 căn trống. x
Do đó nếu tăng x đồng trên một căn thì có căn trống. 100.000
Số tiền thu nhập một tháng khi cho thuê căn hộ là x  2 x (3000.000  ) x (40  ) 
 10x  120.000.000  f( ) x 100.000 100.000
Do f (x) là một hàm bậc hai với hệ số số a  0 nên f (x) đạt giá trị lớn nhất khi x  500.000 đ.
Vậy khi đó giá thuê mỗi căn là 3.500.000 đồng.
Câu 76: (SỞ GD QUẢNG NAM 2019) Cho nửa đường tròn đường kính AB và hai điểm C, D thay
đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng 1 3 3 3 3 A. B. C. 1 D. 2 4 2 Lời giải
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------50
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế H D C x 1 A O B
Gọi H là trung điểm của CD . Đặt OH x 0  x  1 . Ta có CD CH   2 2 2 1 x .
ABCD.OH
Diện tích hình thang ABCD là: S   2 x x 1  2 x . 2
Xét hàm số f x  x x  2
1 x , với x 0;1 . 2 1 2x 3
Ta có f 'x   1
; f '(x)  0  1  2 x  2
2x  1  x  . 1  2 x 2 Bảng biến thiên: 3 3
Vậy diện tích lớn nhất của hình thang ABCD là . 4
Câu 77: (SỞ GD&ĐT CÀ MAU NĂM 2018-2019) Người ta muốn xây một cái bể hình hộp đứng có thể tích V   3
18 m  , biết đáy bể là hình chữ nhật có chiều dài gấp 3 lần chiều rộng và bể không có
nắp. Hỏi cần xây bể có chiều cao h bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất
(biết nguyên vật liệu xây dựng các mặt là như nhau)? 5 3 A. 2m . B. m . C. 1 m . D. m . 2 2 Lời giải
Gọi x x  0 là chiều rộng hình chữ nhật đáy bể, suy ra chiều dài hình chữ nhật đáy bể là 3 . x 18 6 V h x x  2 . .3 .3
h x  18 x  0  h   , 2 2 3x x
Gọi P là diện tích xung quanh cộng với diện tích một đáy bể của hình hộp chữ nhật.
Nguyên vật liệu ít nhất khi P nhỏ nhất.
P hx h x  2 x
6 x  6 x  2 x  48 2 2. .3 3 2. . 2. .3 3  2 3x . 2 2 x x x
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------51
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 48 48 48
Đặt f x   2
3x , x  0 . Ta có f x   
 6x , f x    0 
 6x  0  x  2 . x 2 x 2 x Bảng biến thiên: 6 6 3
Suy ra vật liệu ít nhất khi h    m . 2   x 4 2
Câu 78: (CỤM 1 SỞ GD&ĐT BẠC LIÊU NĂM 2018-2019 LẦN 01) Người ta muốn xây một bể chứa
nước dạng hình hộp chữ nhật không nắp có thể tích 200m3. Đáy bể là hình chữ nhật có chiều
dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m2. Chi phí thuê công nhân thấp nhất là A. 51 triệu đồng . B. 75 triệu đồng. C. 46 triệu đồng. D. 36 triệu đồng. Lờigiải
Gọi chiều rộng, chiều dài của đáy lần lượt là x và 2x, chiều cao là y
Diện tích các mặt bên và mặt đáy là S xy  2 6 2x 100 600 300 300 300 300 Thể tích là V  2
2x y  200  xy  ; S   2 2x    2 2x  2 3 . .2x  3 3 30 180 x x x x x x
Vậy chi phí thấp nhất là T  3 30 180.300000d  51 triệu
DẠNG TOÁN 4: PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH
Câu 79: (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hàm số y f x có bảng biến thiên
Tìm tất cả các giá trị của m để bất phương trình f x  1   1  m có nghiệm? A. m  4. B. m  1. C. m  2 . D. m  5 . Lời giải
Đặt t x  1  1  t  1. Khi đó BPT f x  1  
1  m trở thành f t  m 1
Khi đó BPT f x  1  
1  m có nghiệm khi và chỉ khi BPT f t  m 1 có nghiệm
t  1  m  min f t  m  4 . t1
Câu 80: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho hàm số f x , hàm số y f x liên tục trên và có
đồ thị như hình vẽ bên.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------52
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Bất phương trình f x  x m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m f 2  2 .
B. m f 0 .
C. m f 2  2 .
D. m f 0 . Lời giải
Ta có f x  x m, x
 0;2  m f x  x, x  0;2 * .
Dựa vào đồ thị của hàm số y f x ta có với x 0; 2 thì f x  1 .
Xét hàm số g x  f x  x trên khoảng 0; 2 ; gx  f x  1  0,x0; 2 .
Suy ra hàm số g x nghịch biến trên khoảng 0; 2 . Do đó *  m g0  f 0 .
Câu 81: (MĐ 102 BGD&ĐT NĂM 2018-2019) Cho hàm số f x , hàm số y f x liên tục trên và
có đồ thị như hình vẽ sau:
Bất phương trình f x  x m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
A. m f 2  2 .
B. m f 2  2 .
C. m f 0 .
D. m f 0 . Lời giải
Bất phương trình f x  x m nghiệm đúng với mọi x 0; 2
m f x  x nghiệm đúng với mọi x0;2 (1)
Xét hàm số g x  f x  x trên khoảng 0; 2 , có gx  f x  1  0 , x0; 2 Bảng biến thiên:
Vậy (1)  m g2  m f 2  2 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------53
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 82: (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 04) Cho hàm số y f x và hàm số
y g x có đạo hàm xác định trên và có đồ thị như hình vẽ dưới đây: f x
Có bao nhiêu giá trị nguyên của tham số m để phương trình    m có nghiệm thuộc g x 2;3   ? A. 4. B. 5. C. 7. D. 6. Lời giải f x
Xét hàm số hx   
. Dựa vào đồ thị, ta thấy các hàm số f x và gx liên tục và nhận giá gx
trị dương trên 2 ; 3 
 , do đó hx liên tục và nhận giá trị dương trên 2; 3   . f x f 0 6
Ngoài ra với x  2; 3 
 , dễ thấy f x  6 , gx  1 nên hx    , mà h0      6 g x  6 g0 1
nên max hx  6 (1). 2;3  
Lại có hx  0 với mọi x 2; 3 
 và h2  1 nên 0  min hx  1 (2). 2;3   f x
Phương trình    m có nghiệm trên 2;3 
 khi và chỉ khi min hx  m  maxhx (3). g x 2;3 2;3    
Từ 1 , 2 và 3 , kết hợp với m  , ta có m1; 2; 3; 4; 5;  6 . Chọn D.
Câu 83: (MĐ 103 BGD&ĐT NĂM 2018-2019) Cho hàm số f x , hàm số y f x liên tục trên và
có đồ thị như hình vẽ bên.
Bất phương trình f x  2x m ( m là tham số thực) nghiệm đúng với mọi x 0; 2 khi và chỉ khi
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------54
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
A. m f 0 .
B. m f 2  4 .
C. m f 0 .
D. m f 2  4 . Lời giải
Ta có f x  2x m m f x  2x * . Xét hàm số gx  f x  2x trên 0; 2 .
Ta có gx  f x  2  0 x0; 2 nên hàm số gx nghịch biến trên 0; 2 .
Do đó m f x  2x nghiệm đúng với mọi x 0; 2 khi m g0  f 0 .
Câu 84: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Cho hàm số y f x . Hàm số y f x có bảng
biến thiên như sau: x  2 1   0 y 2 
Bất phương trình    3 f x
x m đúng với mọi x 1;1 khi và chỉ khi
A. m f x  1.
B. m f 1  1 .
C. m f 1  1.
D. m f 1  1 . Lời giải
   3      3 f x x m m f x
x 1 . Xét       3 g x f x x .
f x  f   1  0 ,x   1;  1
gx  f x  2
3x  0,x 1;1 vì 
3x  0 ,x  2 1;  1
 Hàm số y gx nghịch biến trên 1;1  g1  gx  g1, x1;1 .
1 đúng với mọi x1;1  m g1  f 11.
Câu 85: (SỞ GD&ĐT NAM ĐỊNH 2018-2019) Số các giá trị nguyên của tham số m thuộc đoạn 2019;2019   để phương trình 2
x  m   x   m   3 2 4 1
x  4x có nghiệm là A. 2011 . B. 2012 . C. 2013 . D. 2014 . Lời giải Điều kiện : 3
x  4x  0  x  0 .
*) Nhận thấy x  0 không là nghiệm của phương trình.
*) Với x  0 chia cả hai vế của phương trình cho 3
x  4x ta được: 2 x  4    x m 2  m  1. 1 2   x x  4 2 x  4 4 4 Đặt t   x   2. . x
 2 . Vậy t  2 với x  0 . x x x 2 t t  2 4
Phương trình 1 trở thành: 2
t  m  
1 t m  2  0  m
m t  2  (t  2) 2. t  1 t  1 4
Xét hàm số f t  t  2  trên   2;  . t  1 2 t 3 2; f t 4 t  2t     3 1 ; f t 0 2 2             t 1 t 1
t  1 2;    
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------55
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Bảng biến thiên của hàm số f t :
Phương trình đã cho có nghiệm khi và chỉ khi phương trình 2 có nghiệm t    2;  .
Từ bảng biến thiên ta thấy m  7 . Kết hợp m  và m 2019; 2019 
 suy ra có 2013 giá trị m .
Câu 86: (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tìm tất cả các giá trị tham số m để
bất phương trình x    x  x  2 6 2 8
x m  1 nghiệm đúng với mọi x  2; 8  . A. m  16 . B. m  15 . C. m  8 . D. 2  m  16 . Lời giải
Xét bất phương trình: x    x  x  2 6 2 8
x m  1 1 , điều kiện x 2;8  . 3  x
Đặt t  2  x8  x , x 2;8  . Ta có: t'  
, t'  0  x  3
2  x8  x Bảng biến thiên: Suy ra t  0; 5 
 . Khi đó 1 trở thành: 2
t t  15  m 2 . Xét hàm số f t  2
t t  15 ,
Bất phương trình 1 nghiệm đúng với mọi x 2;8 
 khi và chỉ khi 2 nghiệm đúng với mọi t  0 ; 5 
  max f t  m m  15 . 0;5  
Câu 87: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số giá trị nguyên của tham số m nằm
trong khoảng 0; 2020 để phương trình x  1  2019  x  2020  m có nghiệm là A. 2020 . B. 2021 . C. 2019 . D. 2018 . Lời giải 2018, x   1;2019 Ta có f x   
x  1  2019  x   .
2x  2020 , x  1; 2019    Vì hàm số (
h x)  2x  2020 là hàm số đồng biến trên đoạn [1; 2019] nên ta có max ( h x)  max ( h 1), ( h 2019  )  2018, min ( h x)  min ( h 1), ( h 2019  )  2018 [1;2019] [1;2019]
Suy ra: min f x  0 và max f x  2018 . Do đó, ta có: min f x  0 và max f x  2018 . 1;2019   1;2019  
Vì vậy, phương trình đã cho có nghiệm khi và chỉ khi: 0  2020  m  2018  2  m  2020 .
Suy ra có 2018 giá trị nguyên của m nằm trong khoảng 0; 2020 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------56
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 88: (SỞ GD&ĐT ĐIỆN BIÊN NĂM 2018-2019) Gọi S là tập tất cả các giá trị của tham số m để 4
bất phương trình x    2 x x   4 m  2 1 4 5
m  6m thỏa mãn với mọi giá trị của x  . Tính
tổng các giá trị của S. A. 1 . B. 3 . C. 5. D. 2 . Lời giải 4
Đặt f x  x    2 1
x  4x  5 .  2
f x  x  3  x   3 x  2 4 1 2 4 4 12x  14xx 2x 3     
f x  0  x   3 ,   0 x -∞ 0 +∞ f '(x) - 0 + +∞ +∞ f(x) -4
Xét f m  4 m  2
m m f m  3
m m   m   2 6 4 2 6 2
1 2m  2m  3  f m  0  m  1. m -∞ 1 +∞ f '(m) - 0 + +∞ +∞ f(m) -4 Ycbt  f x  4 m  2 m m  4 m  2 min 6
m  6m  4  m  1. Vậy tổng các giá trị của S là 1.
Câu 89: (SỞ GD&ĐT QUẢNG BÌNH NĂM 2018-2019) Gọi S là tập hợp tất cả các giá trị nguyên
dương của tham số m để bất phương trình sau 6 x  4 x  3 3 m x  2 3
4x mx  2  0 nghiệm đúng
với mọi x  1; 3 
 . Tổng tất cả các phần tử của S bằng: A. 3 . B. 2 . C. 1 . D. 4 . Lời giải Ta có: 6 x  4 x  3 3 m x  2
x mx    6 x  4 x  2 x   3 3 3 4 2 0 3 4 2 m x mx
 x  3  x    mx3 2 2 1 1  mx 1
Xét hàm đặc trưng f t  3
t t f t  2 ' 3t  1  0
   f  2x   f mx  2 1 1 x  1  mx
Bài toán trở thành tìm m để bất phương trình 2
x  1  mx nghiệm đúng với mọi x  1; 3   2 x  2 1
x   mx m  1 1
gx ,x1;3 
g'x  1 
 0x 1;3  Min g x g 1 2 2         x ;  x 1; 3 x   x  1; 3 m
Vậy để bất phương trình đã cho nghiệm đúng với mọi   thì 2 S  1; 
Vì m nguyên dương nên
2 có 2 phần tử. Tổng các phần tử bằng 3 .
Câu 90: (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Giá trị lớn nhất của hàm 3 x  2 x m số y  trên 0; 2 
 bằng 5 . Tham số m nhận giá trị là x  1
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------57
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 5 . B. 1 . C. 3 . D. 8 . Lời giải 3 2 x x m Đặt f x    . x  1
 f x  5, x0; 2  
Giá trị lớn nhất của y f x trên 0; 2   bằng 5   .
x  0;2 f x 5 0    0   3 x  2 x m
* f x  5, x 0; 2   
 5, x 0; 2   x  1  m  3 x  2
x  5x  5, x  0; 2 
  m  max hx , với hx  3 x  2
x  5x  5 . 0;2   x  1 + Ta có:  hx  2
3x  2x  5 , hx  0  2
3x  2x  5  0   . x   5 L  3
Ta có: h0  5 , h2  3 , h1  8 . Suy ra max hx  3 , min hx  8 . 0;2   0;2  
Vậy m  3 . 1 3 x  2 x m
* x  0; 2 f x 5 
 5 có nghiệm trên 0;2 . 0  0      x  1  m  3 x  2
x  5x  5 có nghiệm trên 0; 2   .
Theo phần trên, ta suy ra 8  m  3 . 2 . Từ 1 và 2 suy ra m  3 .
Cách dùng casio: Kiểm tra từng giá tri của m từ các đáp án A, B, C, D như sau 3 2 x x 5
Trường hợp 1: m  5 thì f x    . x  1
Trước khi làm thì tắt hàm g x bằng lệnh “ SHIFT + MODE +  + 5 + 1”.
Bước 1: Vào môi trường TABLE bằng lệnh “Mode + 7”. 3 2 x x 5
Bước 2: Nhập hàm f x    . x  1 
Bước 3: Nhập Start  0 ; End  2 ; Step  2 0 . 29
Quan sát bên cột f x có giá trị f x  5,67 nên loại m  5 . Ba trường hợp còn lại làm tương
tự như trên chỉ có m  3 thỏa mãn giá trị lớn nhất của f x là 5 .
Câu 91: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Gọi s là tập hợp các giá trị 3
nguyên của tham số m 0; 2019 
 để bất phương trình 2
x m    2 1 x   0 đúng với mọi x  1;   
1 . Số phần tử của tập s bằng
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------58
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế A. 1 . B. 2020 . C. 2019 . D. 2 . Lời giải 3 Đặt t   2
1 x , với x  1;  1  t  0;      1 . Bất phương trình 2
x m    2
1 x   0 1 trở thành 3 t  2
t   m   m  3 t  2 1 0 t  1 2
Bất phương trình 1 đúng với mọi x 1;   
1 khi và chỉ khi bất phương trình 2 nghiệm
đúng với mọi t  0;    1 . Hay m  ax m  3 t  2
t  1  m  1 . 0;    1
Mặt khác, m là số nguyên thuộc 0; 2019 
 nên m1; 2; 3;...; 201  9
Vậy có 2019 giá trị của m thỏa mãn bài toán.
Câu 92: (CHUYÊN ĐẠI HỌC VINH LẦN 03 NĂM 2018 - 2019) Cho f (x) mà đồ thị hàm số y f '(x) như hình vẽ sau:  x
Bất phương trình f (x)  sin
m nghiệm đúng với mọi x 1;3   khi và chỉ khi 2
A. m f (0) .
B. m f (1)  1 .
C. m f (1)  1 .
D. m f (2) . Lời giải x x
Cách 1: Xét gxf x    sin
g'xf 'x      cos 2 2 2 x   x • Với x    1;      1    ;  cos    0 (1) 2  2 2  2
Đồng thời dựa vào đồ thị f 'x ta thấy f 'x  0,x   1;  1 (2)
Từ (1), (2) ta suy ra g'x  0,x   1;1 .  x    3   x
• Với x 1; 3   ;  cos    0 (3) 2  2 2  2
Đồng thời dựa vào đồ thị ta thấy f 'x  0,x1; 3 (4)
Từ (3), (4) ta suy ra g'x  0 , x1; 3 .  f '1   0 Tại x  1 :  
g'1  0 . Ta có bảng biến thiên của gx như sau: cos  0  2
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------59
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huếx
Để bất phương trình f x  sin
m nghiệm đúng với mọi x1;3   2 gx
m  min gx  m g  1  f   1  1. 1;3    x
Cách 2: Xét bất phương trình f (x)  sin
m (1) với x 1;3   , ta có: 2  xxx f (x)  sin
m f (x)  sin
m (2). Xét f (x)  sin
với x  1; 3   2 2 2
+ Từ đồ thị của hàm số y f '(x) đã cho ta suy ra BBT của f (x) như sau: x 1 1 3 f '(x)  0  f (x) f (1) f (3) f (1)
Từ BBT ta suy ra: f (x)  f (1),x  1; 3   (*)   x 3  xx
+ Do x  1; 3   nên: 1
  x  3     . Suy ra: 1  sin  1  1  sin  1 (**) 2 2 2 2 2  x
+ Từ (*) và (**) cho ta: f (x)  sin
f (1)  1,x1;3 
 . Dấu "  " xảy ra khi x  1 2 x
Do đó: Bất phương trình f (x)  sin
m nghiệm đúng với mọi x 1;3 
  m f (1)  1 . 2 Câu 93: (CHUYÊN QUỐC HỌC HUẾ LẦN 3 2018-2019) Cho phương trình m 2
x x     2 2 2 1
x  2x  0 ( m là tham số). Biết rằng tập hợp các giá trị của tham số m để
phương trình có nghiệm thuộc đoạn 0 ; 1   
2 2  là đoạn a ; b 
 . Tính giá trị của biểu thức
T  2b a . A. T  4 . B. T  7 . C.T  3 . D. T  1 . 2 2 Lời giải Đặt t  2
x  2x  2 . Xét hàm số g x  2 ( )
x  2x  2 trên đoạn 0 ; 1    2 2 . x g x  1 '( )
; g'(x)  0  x  1; g0  2 , g1  1, g1 2 2   3  t1; 3   . 2 x  2x  2 2 t 2
Khi đó phương trình trở thành mt    1  2
t  2  m  . t  1 2 t  2
Xét hàm số f (t)  trên đoạn 1; 3   . t  1 1 7
f t 2t(t  1)  2 t  2 2 t  2t    
2  0 t1; 3 ; f  1   ; f 3  . 2 2   (t  1) (t  1) 2 4 1 7 1 7
Để phương trình có nghiệm thì min f t  m  max f t    m  . Vậy a   ;b   T  4.  x 1;3  x 1;3     2 4 2 4
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------60
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Câu 94: (THPT CHUYÊN HOÀNG VĂN THỤ HÒA BÌNH NĂM 2018-2019 LẦN 04) Tổng các giá trị m
nguyên dương của m để tập nghiệm của bất phương trình 2
x  1  x có chứa đúng hai số 72 nguyên là A. 27 . B. 29 . C. 28 . D. 30 . Lời giải m
ĐK: x  0 . Do m dương nên 2
x  1  0,x  . 72 m m Ta có: 2
x  1  x  2
x  1  x  2
mx  72x  1 1 72 72 72 x  1
Nhận thấy x  0 không là nghiệm của 1 nên     1  m  2 x 72x   1 72x  2
Xét hàm số y f (x) 
với x  0 ; y  f (x)   0  x  2 . 2 x 3 x
Bảng biến thiên của f x với x  0 : 27
Từ bảng biến thiên ta có f 2  f 3  f 4 
f x,x  \ 2 ,3 , 
4 , nên để tập nghiệm của 2 72x  1 27
bất phương trình m
có chứa đúng hai số nguyên thì f 4 
m f 3  16 . (tập 2 x 2
nghiệm chứa x  2, x  3 ) Với  * m thì m14 , 
15 . Do vậy, tổng các giá trị nguyên dương của m là 14  15  29 .
DẠNG TOÁN 5: BÀI TOÁN THAM SỐ
Câu 95: (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số y  3 x  2 2 3x m . Trên 1;   
1 hàm số có giá trị nhỏ nhất là 1 . Tính . m A. m  6 . B. m  3 . C. m  4. D. m  5 . Lời giải
x  01;    1 Xét 1;  1 có y  2
6x  6x ; y  0  2
6x  6x  0   .
x  11;     1
Khi đó: y 1  5  m ; y0  m ; y1  1  m
Ta thấy 5  m  1  m  m nên min y  5  m . 1;    1
Theo bài ra ta có min y  1 nên 5  m  1  m  4 . 1;    1
Câu 96: (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Nếu hàm số y x m   2 1 x
có giá trị lớn nhất bằng 2 2 thì giá trị của m là
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------61
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 2 A. . B.  2 . C. 2 . D.  2 . 2 2 Lời giải x Xét hàm số 2
y x m  1  x . Tập xác định: D  1;   
1 . Ta có: y  1  1  2 x 1  x  0   1  1  x  0  x    1 1  2 x  1  x  0   x       x y 0     2  2x  2  1  2 . 1  2 x   0  1  x   2 x   x   1   2 1 Ta có: y  1 1 m, y1        1 m, y   2  m .  2 
Do hàm số y x m   2
1 x liên tục trên 1;   
1 nên max y m  2 .  1  ;1  
Theo bài ra thì max y  2 2 , suy ra m  2  2 2  m  2 .  1  ;1  
Câu 97: (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Có một giá trị m của tham số 0
m để hàm số y  3 x   2 m   2
1 x m  1 đạt giá trị nhỏ nhất bằng 5 trên đoạn 0;    1 . Khi đó
mệnh đề nào sau đây đúng ? A. 2
2018m m  0. B. 2m  1  0. C. 2 6m m  0. D. 2m  1  0. 0 0 0 0 0 0 Lời giải Ta có y  2 x   2 ' 3
2 m  1x  0,x 0;   
1 nên hàm số đã cho đồng biến trên 0;    1 .
Suy ra min y y0  m  1  5  m  4  2018m  2 m  0 0 0 0 0;    1
Câu 98: (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Có bao nhiêu giá trị của tham số m để giá x  2 m  2
trị lớn nhất của hàm số y  trên đoạn 0; 4   bằng 1 . x m A. 0 . B. 2 . C. 3 . D. 1 . Lời giải
Điều kiện: x m .
Hàm số đã cho xác định trên 0 ; 4   khi m 0; 4   (*).  1 2 m   7 2   m m  2  2  4 Ta có y    x  0 với 0;4   . x m2 x m2 2  2 m
Hàm số đồng biến trên đoạn 0; 4 
 nên max y y4  . 0;4   4  m  2 2 mm  2 max y  1   1  2
m m  6  0   . 0;4   4  m m    3
Kết hợp với điều kiện (*) ta được m  3 . Do đó có một giá trị của m thỏa yêu cầu bài toán.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------62
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 2 x m
Câu 99: Cho hàm số f x  
với m là tham số thực. Giả sử m là giá trị dương của tham số m để x  8 0
hàm số có giá trị nhỏ nhất trên đoạn 0 ; 3 
 bằng 3 . Giá trị m thuộc khoảng nào trong các 0 khoảng cho dưới đây? A. 20; 25. B. 5;6 . C. 6;9 . D. 2; 5 . Lời giải 2 x m
Xét hàm số f x   trên đoạn 0 ; 3   . x  8 8  2 m 2 x m Ta có: y 
 0,x0;3  
hàm số f x  
đồng biến trên đoạn 0 ; 3   x 82    x  8 m
min f xf 0  2    . 0;3   8 2  m m  2 6
Theo giả thiết, ta có: min f x  3   3  2 m  24   . 0; 3   8 m    2 6
Mà m  0 , m  m  2 6  4,9 2; 5 . x m
Câu 100: (MĐ 101 BGD&ĐT NĂM 2016-2017) Cho hàm số y
( m là tham số thực) thỏa mãn x  1
min y  3 . Khẳng định nào sau dưới đây đúng? [2;4] A. m  1. B. 3  m  4. C. m  4. D. 1  m  3. Lời giải 1 m Ta có y   . x  2 1 +) Nếu 1
  m  0  m  1
  y  1, x
  1 min f x  1  3 (loại). 2;4  
+) Nếu 1  m  0  m  1 thì min y y2  2  m  3  m  1 lo¹i . 2;4   4  m
+) Nếu 1  m  0  m  1 thì min y y4 
 3  m  5 (nhËn) 2;4   3 x m
Câu 101: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho hàm số y
( m là tham số thực) thoả mãn x  1 y y  16 min max
. Khẳng định nào dưới đây đúng? 1;2 1;2     3 A. m  0 B. m  4 C. 0  m  2 D. 2  m  4 Lời giải 1  m Ta có y   . x  2 1
 Nếu m  1  y  1, x  1 . Không thỏa mãn yêu cầu đề bài.
 Nếu m  1 Hàm số đồng biến trên đoạn 1; 2   . 16 16 m 1 m 2 16
Khi đó: min y  max y y   1 y 2          m  5 (loại). 1;2 1;2     3 3 2 3 3
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------63
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
 Nếu m  1 Hàm số nghịch biến trên đoạn 1; 2   . 16 16 2  m 1  m 16
Khi đó: min y  max y
y2  y1      m  5 ( t/m). 1;2 1;2     3 3 3 2 3
Câu 102: (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm x m số y  trên 1; 2 
 bằng 8 ( m là tham số thực). Khẳng định nào sau đây đúng? x  1 A. m  10 . B. 8  m  10 . C. 0  m  4 . D. 4  m  8 . Lời giải
Nếu m  1 thì y  1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8) 1  m
Nếu m  1 thì hàm số đã cho liên tục trên 1; 2   và y'   . x  2 1
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn 1; 2   . m  1 m  2 41
Do vậy min y  max y y1  y2    8  m  .  x 1;2  x 1;2     2 3 5
2sin x mcos x
Câu 103: (THPT HUỲNH MẪN ĐẠT NĂM 2018-2019 LẦN 01) Cho hàm số y  đạt giá sin x  cos x   
trị lớn nhất trên 0;  bằng 1 . Khẳng định nào sau đây đúng?  4  A. m   1;0 .
B. m  0;1 .
C. m  1;2 . D. m 2;3 . Lời giải 2  m Ta có: y  
sin x  cos x . 2 2  m    TH1: y   0  m   
2 hàm số luôn đồng biến trên 0; 
sin x  cos x2  4     2  m
Khi đó max y y   1  m    0 (thỏa mãn)  π  4 2 0;      4  2  m    TH2: y   0  m   
2 hàm số luôn nghịch biến trên 0; 
sin x  cos x2  4 
Khi đó max y y0  m  1  m  1 (loại)    0;   4  2  m TH3: y 
 0  m    y y   2 2 , khi đó max 2 (loại)
sin x  cos x2    0;   4 
Câu 104: (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Gọi A, B lần lượt là giá trị nhỏ nhất, giá trị x  2 m m
lớn nhất của hàm số y  trên đoạn 2; 3 
 . Tìm tất cả các giá trị thực của tham số m x  1
để A B  13 . 2
A. m  1; m  2 . B. m  2 . C. m  2 .
D. m  1; m  2 .
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------64
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế Lời giải x  2 m m Xét hàm số y  trên đoạn 2; 3   . x  1  2 m m  2 2 y  1  x  A m m 3 m m 2 ' 0 2; 3 f 3 , B f 2 . 2                x   2 1 1 2 13 m m  2 3 m m  2 13 m A B      1  . 2 2 1 2 m    2
Câu 105: (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Gọi T là tập hợp tất cả giá trị của tham số mx  1 5
m để hàm số y
có giá trị lớn nhất trên đoạn 2; 3 
 bằng . Tính tổng của các phần tử x  2 m 6 trong T . 17 16 A. . B. . C. 2 . D. 6 . 5 5 Lời giải mx  1 mx  3 1 m  1 Ta có: y  . Điều kiện   2 x
m . Ta có: y   y  . x  2 m x  2 mxm 2 2 x  1
- Nếu m  1 thì y
. Khi đó max y  1 , suy ra m  1 không thỏa mãn. x  1 [2;3] mx  1 - Nếu 3
m  1  0  m  1 thì y  0 . Suy ra hàm số y
đồng biến trên đoạn [2; 3] . x  2 mm m  3 3 1 5
Khi đó max y y 3 2   
  5m  18m  9  0  . 3  2 3 [2;3]  m 6 m   5
Đối chiếu với điều kiện m  1 , ta có m  3 thỏa mãn yêu cầu bài toán. mx  1 - Nếu 3
m  1  0  m  1 thì y  0 . Suy ra hàm số y
nghịch biến trên đoạn [2; 3] . x  2 mm m  2 2 1 5
Khi đó max y y 2 2   
  5m  12m  4  0  . 2  2 2 [2;3]  m 6 m   5
Đối chiếu với điều kiện m  1, ta có m  2 thỏa mãn yêu cầu bài toán. 5  2 2 17
Vậy T  3;  . Do đó tổng các phần tử của T là 3   .  5 5 5 2
Câu 106: (THPT CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 03) Cho hàm số y   3 x  x 3  m .
Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn 1;    1 bằng 1 là A. 1 . B. 4 . C. 0 . D. 4 . Lời giải
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------65
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Xét hàm số f x  3 x  x 3  m . 2
Để GTNN của hàm số y   3 x  x
3  m trên đoạn 1;   
1 bằng 1 thì min f x  1 hoặc 1;    1 x 1
max f x  1. Ta có f x  x2 3
 3 ; f x      0  
f x nghịch biến trên 1;    1 . 1;1   x   1
Suy ra max f x  f 1  2  m và min f x  f 1  2  m . 1;    1 1;    1
Trường hợp 1: min f x  1  2  m  1  m  3 . 1;    1
Trường hợp 2: max f x  1  2  m  1  m  3 . 1;    1
Vậy tổng các giá trị của tham số m là 0 . x m
Câu 107: (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số f x sin  . Tìm giá trị sin x  1   2 
của m để giá trị lớn nhất của hàm số f (x) trên đoạn 0;  bằng 2.  3  m  5 A. m  5. B.  . C. m  2. D. m  3. m   2 Lời giải   2  t m    1  m
Đặt t  s inx , x  0;    t  0;   
1 . Ta có hàm số g t t  2 ( ) , 0;
 . Ta có g'(t)   3  t  1  3  t  2 1
+) Với m  1  0  m  1 . Ta có g'(t)  0 . 1  m Suy ra max ( g t)  2  ( g 1)  2 
 2  m  5 (thỏa điều kiện) 0;    1 2
+) Với m  1  0  m  1 . Ta có g'(t)  0 . Suy ra max ( g t)  2  (
g 0)  2  m  2  m  2 (không thỏa điều kiện). Vậy m  5 0;    1 x  2 m
Câu 108: Có bao nhiêu giá trị nguyên dương của tham số m để giá trị nhỏ nhất của hàm số y x  1 trên đoạn 2; 3   bằng 14? A. 2 . B. 1 . C. 0 . D. 4. Lời giải 1 2 m
Tập xác định D   \  1 . Ta có y   
0 , x D . x  12  2 3 m
Do đó hàm số nghịch biến trên đoạn 2; 3 
 . Suy ra min y y3 
 14  m  5 . 2;3   3  1
Vậy có 1 giá trị nguyên dương của m .
Câu 109: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tính tổng tất cả các giá
trị của tham số m sao cho giá trị lớn nhất của hàm số y  2
x  2x m trên đoạn 1; 2   bằng 5 . A. 1 . B. 2 . C. 2 . D. 1 . Lời giải
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------66
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế 2x  2 Ta có y 
, y  0  x  1 . Do đó yêu cầu bài toán tương đương 2
x  2x m
maxy1,y2,y1  5  max 3  m , m , m  1  5 .
+ Trường hợp m  1 , ta có max 3  m , m , m  1  5  3  m  5  m  2 .
+ Trường hợp m  1 ta có max 3  m , m , m  1  5  m  1  5  m  4 .
Vậy tổng các giá trị m bằng 2 .
Câu 110: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017-2018) Gọi S là tập hợp tất cả các giá trị của tham số
thực m sao cho giá trị lớn nhất của hàm số y  3
x  3x m trên đoạn 0; 2 
 bằng 3. Số phần tử của S là A. 1. B. 2. C. 0. D. 6. Lời giải
Xét hàm số f x 3
x  3x m , ta có f x 2
3x  3 . Ta có bảng biến thiên của f x :
TH 1 : 2  m0  m  2 . Khi đó max f x 2 m 2m 0;2  
2  m  3  m  1 (loại). 2 m0 TH 2 : 
 2m . Khi đó : m2 2m22 mmax f x 2m2m m 0  0 0;2  
2  m  3  m  1 (thỏa mãn). m0 TH 3 : 
0m . Khi đó : m2 2m22 m max f x 2m 2 m 2  0 0;2  
2  m  3  m 1 (thỏa mãn).
TH 4:  2  m 0  m  2 . Khi đó max f x 2 m 0;2  
2  m  3  m 1 (loại).
Câu 111: (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Tìm tất cả giá trị thực của tham số m 2 x mx  1 để hàm số y
liên tục và đạt giá trị nhỏ nhất trên đoạn 0; 2   tại một điểm x m x  0; 2 . 0   A. 0  m  1 . B. m  1 . C. m  2 . D. 1  m  1 . Lời giải m  0 m  0
Tập xác định: D  \  
m . Hàm số liên tục trên 0; 2       m  2 m     2
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------67
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
x  2mx m  1 x m2 2 2  1
x  m  1 Ta có y   y  0  1  . Cho  . x m2 x m2 x  m   1 2 Ta có bảng biến thiên
Hàm số đạt giá trị nhỏ nhất tại x  0; 2 nên 0  m  1  2  1  m  1 0  
So với điều kiện hàm số liên tục trên đoạn 0; 2 
 . Ta có 0  m  1 . CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định x  m m  0 m  0
Hàm số liên tục trên đoạn 0; 2 
 nên m  0;2       * m  2 m     2
x  2mx m  1 x m2 2 2  1
x  m  1 y'   1 
; y'  0 có hai nghiệm là  , x m2 x m2 x  m   1 2
x x  2 nên chỉ có nhiều nhất một nghiệm thuộc 0; 2 1 2
Ta thấy m  1  m  1,m và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên 0; 2   tại
một điểm x  0; 2 thì 0  m  1  2  1  m  1 * * . Từ * ,* * ta có 0  m  1. 0  
Câu 112: (THPT Phụ Dực - Thái Bình - 2019) Gọi S là tập hợp các giá trị của m để hàm số y  3 x  2
3x m đạt giá trị lớn nhất bằng 50 trên [  2; 4]. Tổng các phần tử thuộc S là A. 4 . B. 36 . C. 140 . D. 0 . Lời giải x 0
Xét hàm số g x  3 x  2 ( ) 3 x m gx  2 3 x  có  
6 x . Xét g x     0   . x   2
Khi đó giá trị lớn nhất của hàm số y  3 x  2
3x m trên [  2; 4] là:
max y  maxy0; y2; y2; y4  max m ; m  4 ; m  20 ; m  16  .  x 2;4   m  50
Trường hợp 1: Giả sử max y m  50   . m    50
Với m  50 thì m  16  66  50 ( loại).
Với m  50 thì m  20  70  50 (loại). m  54
Trường hợp 2: Giả sử max y m  4  50   . m    46
Với m  54  m  54  50 (loại).
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------68
Lớp Toán thầy Lê Bá Bảo…0935.785.115… Trường THPT Đặng Huy Trứ, Huế
Với m  46 thì m  20  66  50 ( loại). m  70
Trường hợp 3: Giả sử max y m  20  50   m    30
Với m  70 thì m  16  86  50 (loại).
Với m  30 thì m  16  14  50 , m  30  50 ; m  4  34  50 (thỏa mãn). m  34
Trường hợp 4: Giả sử max y m  16  50   . m    66
Với m  34 thì m  34  50, m  4  30  50, m  20  14  50 (thỏa mãn).
Với m  66 thì m  66  50 (loại). Vậy S30; 
34 . Do đó tổng các phẩn tử của S là: 30  34  4 .
Câu 113: (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Gọi S là tập hợp các giá trị của tham số m 2
x mx  2m
để giá trị lớn nhất của hàm số y  trên đoạn 1;   
1 bằng 3 . Tính tổng tất cả các x  2 phần tử của S . 5 A.  8 . B. 5 . C. . D. 1 . 3 3 Lời giải 2 x mx 2m 4 Xét hàm số y f x     trên 1;   
1 có f x  1  ; x  2 x 22 3m  1 m  1 f x x   0  0   ; f   1  ; f 0   ; m f   1  .
x  4  1;     1 3 1 Bảng biến thiên:
Trường hợp 1. f 0  0  m  0 . Khi đó 3m  1 
3  max f x  max f 1 ; f 1  3  max ; m  
1  m  1  3  m  2 . 1;    1  3 
Trường hợp 2. f 0  0  m  0 .  f   1   0 Khả năng 1. 
. Khi đó 3  max f x  f 0  m  3 . f    m  1 1   0 1;    1  f 1   0
Khả năng 2.   m   1 1 . Khi đó 
. 3  max f x  max f 0; f 1 3 f 1   0 1;    1  3  max ; m m  
1 : Trường hợp này vô nghiệm.
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------69
Lớp Toán thầy Lê Bá Bảo…0935.785.115…
Trường THPT Đặng Huy Trứ, Huế 1
Khả năng 3.   m  0 . Khi đó 3  max f x  max f 0; f 1 ; f 1 : Vô nghiệm. 3 1;    1
Vậy có hai giá trị thỏa mãn là m  3, m  2 . Do đó tổng tất cả các phần tử của S là 1 . 1 2
Câu 114: (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Có bao nhiêu số thực m để giá trị nhỏ nhất của hàm số y  2
x  4x m  3  4x bằng 5 . A. 2 . B. 3 . C. 0 . D. 1 . Lời giải
Xét f x  2
x  4x m  3 có   1  m .
TH1. m  1: f x  x y  2 0
x  8x m  3 .
min y  5  m  8 (TM).
TH2. m  1: f x  0 có hai nghiệm x  2  1  m ; x  2  1  m . 1 2
Nếu x x ; x : y   2 x  3  m . 1 2 
y x   8  4 1  m; yx
8 4 1 m y x   y x  min y  8  4 1  m  8 (Không 1  2 2      1 x ;x 1 2  TM).
Nếu x x ; x : y  2
x  8x  3  m . 1 2 
) x  4  1  m  3 : 2
min y m  13  5  m  8 (Loại).
) x  4  m  3 : 2
 min y  8  4 1  m  8 (Không TM). Vậy có 1 giá trị của m. HẾT
HUẾ ... 16h00 Ngày 08 tháng 8 năm 2020
Địa chỉ lớp học: Số 4 Kiệt 116 Nguyễn Lộ Trạch TP Huế ---- Trung tâm KM10 Hương Trà------70