Bài tập max – min hàm số chứa dấu giá trị tuyệt đối Toán 12

Bài tập max – min hàm số chứa dấu giá trị tuyệt đối Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

24 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
1
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Câu 1. Có bao nhiêu giá trị nguyên của
x
để hàm số
13y x x
đạt giá trị nhỏ nhất.
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải: Chọn B
Ta có
2 2, 1
4, 3 1
2 2, 3
xx
x
xx
.
Trên
1;
, ta có
4y
và dấu bằng xảy ra khi
1x
.
Trên
3;1
, ta có
4y
và có bốn giá trị nguyên của
x
thuộc khoảng này.
Trên
;3
, ta có
2 2 4yx
.
Vậy
min
4y
và có
5
giá trị nguyên của
x
để
min
4y
.
Câu 2. Cho hàm số
1 2 5 10f x x x x x
và hàm số
3
31g x x x m
. Khi hàm
số
fx
đạt giá trị nhỏ nhất thì
gx
đạt giá lớn nhất bằng
8
. Hỏi tổng tất cả các giá trị tuyệt đối
của tham số thực
m
thỏa mãn bài toán bằng bao nhiêu?
A. 12 B. 2 C. 8 D. 7
Lời giải: Chọn A
Xét hàm số
1 2 5 10 1 2 5 10f x x x x x x x x x
1 2 5 10 4x x x x
, dấu bằng xảy ra khi
1; 2 ; 5 ; 10x x x x
có cùng
dấu hay
21x
. Vậy yêu cầu bài toán là hàm số
3
31g x x x m
đạt giá trị lớn nhất bằng 8 với
21x
. Lập bảng biến thiên, suy ra các
trường hợp sau:
Th1:
30m
. Khi đó,
2;1
max 1 1 8
x
g x g m

hay
7m
.
Th2:
3 0 1mm
. Khi đó,
2;1
max max 1 , 2 1 max 3 , 1 8
x
g x g g g m m

.
Th3:
10m
. Khi đó,
2;1
max 1 1 3 8
x
g x g g m

hay
5m 
.
Câu 3. Giá trị nhỏ nhất của hàm số
2 1 3 2 7 4y x x x
là
a
b
với
,ab
nguyên dương, phân
số
a
b
tối giản. Khi đó
ab
bằng
A.
5
. B.
34
. C.
12
. D.
41
.
Lời giải: Chọn B
Ta có:
2
3 12
3
21
76
32
2 1 3 2 7 4
14
52
27
4
12 3
7
x khi x
x khi x
y x x x
x khi x
x khi x

Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
2
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
BBT:
Từ BBT suy ra giá trị nhỏ nhất của hàm số là
27
27
34
7
7
a
a
ab
b
b
Câu 4. Giá trị nhỏ nhất của hàm số
2
49yx
trên đoạn
2;2
bằng
A.
0
. B.
6
. C.
7
. D.
9
.
Lời giải: Chọn C
Xét hàm số
2
49y f x x
, có
2
00
4
x
yx
x
.
Ta có bảng biến thiên của hàm số
y f x
và
y f x
trên
2;2
như sau:
Từ đó ta có giá trị nhỏ nhất của hàm số
2
49yx
trên
2;2
là 7 khi
0x
.
Câu 5. Cho hàm số
4 3 2
44f x x x x a
. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số trên đoạn
0;2
. Có bao nhiêu số nguyên
a
thuộc đoạn
3;2
sao cho
2Mm
?
A. 7. B. 5. C. 6. D. 4.
Lời giải: Chọn D
9
9
7
-7
-9
-9
-
+
0
(f(x))'
0
2
-2
|f(x)|
f(x)
x
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
3
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Đặt
4 3 2
44g x x x x a
32
0
4 12 8 0 1
2
x
g x x x x x
x
.
Ta có
0 ; 1 1; 2 .g a g a g a
0; 2
0; 2
max max 0 ; 1 ; 2 1.
min min 0 ; 1 ; 2 .
g x g g g a
g x g g g a
Trường hợp 1:
1
0
Ma
a
ma


.
Khi đó
2 1 2M m a a
1a
,
3;2a
1;2a
.
Trường hợp 2:
1 0 1
1
Ma
aa
ma

.
Khi đó
2 2 2M m a a
2a
,
3;2a 
3; 2a
.
Trường hợp 3:
1 0 1 0a a a
Khi đó
11
1
max 1, max 1 , 0
2 2 2
a a a a
M a a a a m
.
Như vậy có tất cả 4 giá trị của
a
thỏa mãn yêu cầu.
Câu 6. Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
24f x x x m
trên đoạn
2;1
bằng
5
?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải: Chọn A
Đặt
2
24t x x
,
2;1 5; 1xt
Ta có:
y t m
max
15
15
6
max 1; 5 5
0
55
15
m
mm
m
y m m
m
m
mm
.
Câu 7. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số
42
38 120 4y x x x m
trên
đoạn
0;2
đạt giá trị nhỏ nhất.
A. 26. B. 13. C. 14. D. 27.
Lời giải: Chọn D
Xét
42
38 120 4u x x x m
trên đoạn
0;2
ta có
3
5
' 0 4 76 120 0 2
3
x
u x x x
x

Vậy
0;2
0;2
max max 0 , 2 max 4 ,4 104 4 104
min min 0 , 2 min 4 ,4 104 4
u u u m m m
u u u m m m
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
4
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
Khi đó
0;2
min min 0 4 4 104 0 26 0.y m m m
có 27 số nguyên thỏa mãn.
*Chú ý ôn tập lại kiến thức đã học:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y u x
và
2
.
n
u u x
Gọi
;
;
min ; max .
ab
ab
m u x M u x
Khi đó
;
max max ,
2
ab
M m M m
y M m

.
Giá trị nhỏ nhất không có công thức nhanh mà phụ thuộc và dấu của M và m
;
0 min
ab
m y m
;
0 min
ab
M y m
00
;
. 0 ; 0 min 0
ab
M m x a b y x y
Câu 8. Cho hàm số
32
23f x x x m
có bao nhiêu số nguyên
m
để
1;3
min 3fx
.
A.
4
. B.
8
. C.
31
. D.
39
.
Lời giải: Chọn D
Xét
3 2 ' 2
0
2 3 6 6 0
1
x
t x x m t x x
x
.
Do đó:
1;3
min 5t x m

;
1;3
max 27t x m

.
Nếu
1;3
5 0 min 5 3 5 8 5;6;7;8m f x m m m
.
Nếu
1;3
27 0 min 27 3 30 27 30; 29; 28; 27m f x m m m
.
Nếu
1;3
5 27 0 min 0m m f x
.
Vậy,
30; 29;...8m
có tất cả 39 số nguyên thỏa mãn.
Câu 9. Có bao nhiêu giá trị nguyên của tham số m để
2
0;3
ax 2 5?m x x m
A.
5.
B.
6.
C.
7.
D.
8.
Lời giải: Chọn B
Đặt
2
2.f x x x m
là hàm số xác định và liên tục trên đoạn
0;3
Ta có:
' 2 2.f x x
Với mọi
0;3x
ta có
' 0 2 2 0 1.f x x x
Mặt khác:


0
11
33
fm
fm
fm
.
Ta có:
[0;3]
max max 0 ; 1 ; 3 .f x f f f
Theo bài:


[0;3]
05
5
55
max 5 1 5 1 5 5 1 5 .
5 3 5
35
35
f
m
m
f x f m m
m
m
f
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
5
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
55
4 6 4 2.
82
m
mm
m
Do
4; 3; 2; 1;0;1 .m Z m S
Vậy có tất cả 6 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 10. Có bao nhiêu giá trị nguyên của tham số để giá trị lớn nhất của hàm số
trên đoạn không lớn hơn ?
A. . B. . C. . D. .
Lời giải: Chọn D
Xét hàm số liên tục trên đoạn có .
.
.
Các giá trị nguyên thỏa mãn yêu cầu bài toán của tham số là .
Câu 11. Có bao nhiêu số nguyên
5;5m
để
32
1;3
min 3 2x x m
.
A.
6
. B.
4
. C.
3
. D.
5
.
Lời giải: Chọn B
Ta có
32
1;3
min 3 2x x m
32
3 2; 1;3 1x x m x
.
Giải
1
:
32
3 2; 1;3x x m x
32
32
3 2; 1;3
3 2; 1;3
x x m x
x x m x
32
32
3 2 ; 1;3
3 2 ; 1;3
x x m x
x x m x
32
1;3
32
1;3
2 min 3
*
2 max 3
m x x
m x x
.
Xét hàm số
32
3f x x x
trên
1;3
. Hàm số xác định và liên tục trên
1;3
mà
2
3 6 0f x x x
0
2
x
x
. Ta có:
1 2; 3 0; 2 4f f f
.
Do đó
1;3
1;3
max 0;min 4f x f x
. Từ
*
suy ra
2 4 6
2 0 2
mm
mm
.
Vì
5;5m
m
nên
5; 4; 3; 2m
.
Vậy có 4 giá trị
m
thỏa mãn yêu cầu bài toán.
Cách 2:
Đặt
32
3t x x
, với
1;3 4;0xt
. Khi đó bài toán trở thành
4;0
min 2tm
.
TH1:
4m
4;0
min 4 4 2t m m m
6m
.
TH2:
0m
4;0
min 2t m m m
2m
.
m
2
2f x x x m
0;3
3
4
5
6
3
2
2g x x x m
0;3
2 2 0 1g x x x
0;3
Max Max 0 , 3 , 1f x g g g
Max , 3 , 1 Max 3 , 1m m m m m
0;3
Max 3fx
33
13
m
m

3 3 3
3 1 3
m
m
20m
m
2, 1,0
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
6
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
Kết hợp với điều kiện
5;5m
m
suy ra
5; 4; 3; 2m
.
Vậy có 4 giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 12. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để
2
0;3
Max 2 4x x m
. Tổng
giá trị các phần tử của
S
bằng
A.
2
. B.
2
. C.
4
. D.
4
.
Lời giải: Chọn A
Đặt
2
2t x x
. Với
0;3 1; 3xt
.
Nên
2
0;3 1;3
Max 2 Max ax 1; 3 .x x m t m M m m
2
0;3
14
5
31
3
Max 2 4 .
1
34
7
13
m
ml
mm
m
x x m
m
m
ml
mm


3;1S
.
Vậy tổng giá trị các phần tử của
S
bằng
2
.
Câu 13. Có bao nhiêu giá trị nguyên của tham số m để
32
1;3
max 3 4?x x m
A. Vô số. B. 4. C. 6. D. 5.
Lời giải: Chọn D
Đặt
3 2 2
( ) 3 ( ) 3 6 .f x x x m f x x x
0
( ) 0 .
2
x
fx
x

Bảng biến thiên
Ta thấy
[1;3]
max ( ) (3)f x f m
và
[1;3]
min ( ) (2) 4.f x f m
Ta có
32
1;3
max 3 max ; 4 .x x m m m
Trường hợp 1:
22
4
2
8 16
0 2,
08
4 4 4
max ; 4 4 4
mm
m
m m m
m
m
m
m m m

mà
m
nên
0;1;2 .m
Trường hợp 2:
22
4
2
8 16
2 4,
44
44
max ; 4 4
mm
m
m m m
m
m
m
m m m
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
7
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
mà
m
nên
3;4 .m
Vậy, có 5 giá trị nguyên của tham số m.
Vậy Chọn D
Câu 14. Có bao nhiêu số thực
m
để giá trị nhỏ nhất của hàm số
2
24y x x m x
bằng
1
?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải: Chọn A
Ta có ycbt
2
2
0 0 0
2 4 1
1
2
: 2 4 1
x x m x
x x x m x
2
1 2 4 1x x m x
Nếu
4 1 0x
2
không thỏa mãn.
Nếu
1
4 1 0
4
xx
.
Khi đó
2
2
2 4 1
2 4 1
x x m x
x x m x
2
2
2 1 3
6 1 4
x x m
x x m
. Giả sử
12
,SS
lần lượt là tập nghiệm của
3 , 4
. Xét
2
1
1
: 2 1,
4
C y x x x
và
2
2
1
: 6 1,
4
C y x x x
.
+
0m
2
không thỏa mãn.
+
0m
0m
thỏa mãn.
+
9
0;
16
m



thì
1 1 2
1
;;
4
S x x



,
2
S 
12
1
;
4
SS



+ Tương tự
9
;
16
m




thì
12
1
;
4
SS



.
Vậy
0m
là giá trị cần tìm.
Câu 15. Biết rằng giá trị lớn nhất của hàm số
2
24y x x m
trên đoạn
2;1
đạt giá trị nhỏ
nhất, giá trị của tham số
m
bằng
A.
1
. B.
3
. C.
4
. D.
5
Lời giải: Chọn B
Cách 1:
Xét hàm số
2
24y f x x x m
trên
1;2
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
8
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
22f x x

0 1 1;2f x x
2 4; 1 1; 1 5f m f m f m
Vậy
2;1
1; 4 ; 5Max y Max m m m
Biện luận:
TH1:
4 0 4mm
2;1
1; 4 ; 5 1 3Max y Max m m m m
1
TH2:
1 0 1mm
2;1
1; 4 ; 5 5 4Max y Max m m m m
2
TH3:
10
14
40
m
m
m


2;1
1;5Max y Max m m
i) Xét
34m
15mm
Do đó
2;1
1;5 1 2Max y Max m m m
3
ii) Xét
13m
51mm
Do đó
2;1
1;5 5 2Max y Max m m m
4
Từ
1 , 2 , 3
và
4
Giá trị lớn nhất của hàm số
2
24y x x m
trên đoạn
2;1
đạt giá trị nhỏ nhất bằng
2
khi
giá trị của tham số
3m
.
Cách 2: Thừ với
1,3,4,5m
rút ra kết luận.
Câu 16. Tìm
m
để giá trị lớn nhất của hàm số
2
24 f x x x m
trên đoạn
2;1
đạt giá trị
nhỏ nhất.
A.
1.m
B.
2.m
C.
3.m
D.
4.m
Lời giải: Chọn C
Xét
2
24 g x x x m
trên đoạn
2;1 .
Đạo hàm
2 2; 0 1 2;1 .

g x x g x x
Ta có
2;1
2;1
24
max 1
1 5 .
min 5
11






gm
g x m
gm
g x m
gm
Cách 1. Suy ra
2;1
15
max max 1 , 5 2.
2
mm
f x m m
Dấu
'' ''
xảy ra
1 5 3. m m m
Cách 2. • Nếu
1 5 0 3 m m m
thì
2;1
max 1 2.
f x m
Dấu
'' ''
xảy ra
3.m
• Nếu
1 5 0 3 m m m
thì
2;1
max 5 2.
f x m
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
9
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Dấu
'' ''
xảy ra
3.m
.
Câu 17. Gọi
S
là tập hợp các giá trị của tham số
m
sao cho giá trị lớn nhất của hàm số
3
3y x x m
trên đoạn
0;2
bằng
10
. Số phần tử của
S
là:
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải: Chọn B
Xét hàm số
3
3y x x m
trên đoạn
0;2
2
3 3 0, 0;2y x x
.
Vậy:
0;2 0;2
max maxy f x
max 0 ; 2ff
max 14 ;mm
TH1. Với
0;2
max 14ym
, ta có
14
14 10
mm
m

14
4
14
mm
m
m


4m
TH2. Với
1;2
max ym
, ta được
14
10
mm
m
14
10
10
mm
m
m

10m
Vậy có 2 giá trị của m thỏa yêu cầu
Câu 18. Có bao nhiêu giá trị
m
để hàm số
2
( ) 4f x x x m
đạt giá trị nhỏ nhất trên đoạn
1 ; 4
bằng 6?
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải: Chọn B
Đặt
2
4t x x
.
Vì
1;4 4;0xt
. Ta được hàm số:
()f t t m
,
4;0t 
.
Vì hàm số
()g t t m
là hàm số bậc nhất nên
()f t t m
đạt giá trị nhỏ nhất tại một trong 2
điểm mút
4
hay
0
và
4;0m
.
Do đó:
1;4 4;0
min ( ) min (t) min 4 ; .f x f m m
Yêu cầu bài toán
4
6
4;0
6
.
10
4
46
4;0
mm
m
m
m
m
mm
m
m


Chọn B
Câu 19. Tính tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số
y x x m
2
2
trên đoạn
;12
bằng 5.
A.
1
. B.
2
. C.
2
. D.
1
.
Lời giải: Chọn B
+) Đặt
(x )t
2
1
, với
;x 12
thì
;t 04
, hàm số trở thành:
y t m 1
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
10
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
+) Hàm số
y t m 1
luôn đồng biến trên đoạn
;04
nên
;
max max ;y m m
04
13
Nếu
m m m1 3 1
thì
(ktm)
( )
m
m
m tm
6
15
4
Nếu
m m m1 3 1
thì
(ktm)
( )
m
m
m tm
8
35
2
Đáp số: có 2 giá trị của tham số m
Câu 20. Cho hàm số
2
24y x x a
. Tìm
a
để giá trị lớn nhất của hàm số trên đoạn
2;1
đạt
giá trị nhỏ nhất.
A.
1a
. B.
2a
. C. Một giá trị khác. D.
3a
.
Lời giải: Chọn D
Xét
2
2 4 ' 2 2y x x a y x
' 0 1yx
Ta có
2
1 5 5x a a
Vì
22
1 5 12; 1 5 11 x a ax a
Ta có
[ 2;1]
| 5|;| 1|M max y max a a
Lại có
2 | 5| | 1| 5 1 4 2M a a a a M
Dấu
""
xảy ra khi và chỉ khi
| 5| | 1|
3
5 1 0
aa
a
aa

, Chọn D
Câu 21. Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn nhất của hàm số
42
1
14 48 30
4
f x x x x m
trên đoạn
0;2
không vượt quá
30.
Tổng các phần tử của
S
bằng
Câu 22. A.
108.
B.
120.
C.
210.
D.
136.
Lời giải: Chọn D
Xét hàm số
42
1
14 48 30
4
g x x x x m
trên đoạn
0;2
.
Ta có
3
' 28 48;g x x x
6 0;2
' 0 2
4 0;2
x
g x x
x

Bảng biến thiên:
Dựa vào BBT, để
0;2
0 30
30 30
max 30 0 16
14 30
2 30
g
m
g x m
m
g



0;1;2;...;15;16
m
m
tổng các phần tử của
S
là
136.
Câu 23. Tìm
m
để giá trị lớn nhất của hàm số
3
3 2 1y x x m
trên đoạn
0;2
là nhỏ nhất.
Giá trị của
m
thuộc khoảng?
A.
0;1
. B.
1;0
. C.
2
;2
3



. D.
3
;1
2




.
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
11
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Lời giải: Chọn A
Xét hàm số
3
3 2 1g x x x m
,
2
33g x x

,
1
0
1
x
gx
x


.
Trên
0;2
ta có
0 2 1gm
;
1 2 3gm
;
2 1 2gm
.
Khi đó
0;2
max max 2 3 ; 2 1y m m
2 3 2 1
2 3 2 1
22
mm
mm

2 1 1 1m
Suy ra để giá trị lớn nhất của hàm số
3
3 2 1y x x m
trên đoạn
0;2
là nhỏ nhất thì
1
2
m
.
Câu 24. Cho hàm số
4
1
x ax a
y
x

. Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
hàm số đã cho trên đoạn
1;2
. Có bao nhiêu giá trị nguyên của
a
để
2.Mm
A.
15
. B.
14
. C.
15
. D.
16
.
Lời giải: Chọn A
Xét hàm số
4
1
x ax a
fx
x

. Ta có
43
2
34
0, 1;2
1
xx
f x x
x
Do đó
1 2 , 1;2f f x f x
hay
1 16
, 1;2
23
a f x a x
Ta xét các trường hợp sau:
Th1: Nếu
11
0
22
aa
thì
16 1
;
32
M a m a
Theo đề bài
16 1 13
2
3 2 3
a a a



Do
a
nguyên nên
0;1;2;3;4a
.
Th2: Nếu
16 16
0
33
aa
thì
16 1
;
32
m a M a
Theo đề bài
1 16 61
2
2 3 6
a a a
Do
a
nguyên nên
10; 9;...; 6a
.
Th3: Nếu
1 16 16 1
0
2 3 3 2
a a a
thì
0; 0Mm
Do
a
nguyên nên
5; 4;...; 1a
Vậy có
15
gái trị của
a
thỏa mãn yêu cầu bài toán.
Câu 25. Cho biết
M
là giá trị lớn nhất của hàm số
2
2f x x ax b
trên đoạn
1;2
. Khi
M
đạt giá trị nhỏ nhất có thể thì giá trị của biểu thức
3M a b
bằng:
A.
9
8
. B.
2
. C.
3
. D.
1
.
Lời giải: Chọn D
Ta có:
1;2x
M max f x

nên suy ra:
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
12
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
+
1 2 1 1M f a b
+
2 4 4 2M f a b
+
11
24
M f a b



1
2 2 2 3
2
M a b
Cộng các bất đẳng thức
1 , 2 , 3
theo vế ta có:
1
4 2 1 4 4 2 2
2
M a b a b a b
19
2 1 4 4 2 2
22
a b a b a b
9
8
M
*
.
Dấu
'' ''
xảy ra khi dấu
'' ''
ở
1 , 2 , 3
cùng đồng thời xảy ra và sao cho các giá trị
1
1 2 , 4 4 , 2 2
2
a b a b a b



cùng dấu với nhau.
Tức điều kiện dấu
'' ''
xảy ra khi:
9
12
1
8
9
2
44
7
8
19
8
22
28
9
12
8
9
44
8
19
22
28
a b M
a
a b M
b
a b M
a b M
a b M VN
a b M




Khi đó:
2
7
8
f x x x
.
Suy ra giá trị nhỏ nhất của
M
là:
9
8
khi
1
2
a
,
7
8
b 
Vậy
31M a b
.
Câu 26. Cho hàm số
6 3 3
2f x x x m x
. Gọi
S
là tập tất cả các giá trị thực của tham số
m
để
Giá trị nhỏ nhất của hàm số
fx
bằng
1
. Tổng tất cả các phần tử của
S
bằng
A.
1
4
. B.
5
4
. C.
2
. D.
0
.
Lời giải: Chọn B
Tập xác định:
6 3 3
( ) 2y f x x x m x
.
Đặt
3
tx
hàm số ban đầu trở thành hàm số
2
( ) 2y g t t t m t
.
Tam thức bậc hai
2
()h t t t m
có biệt thức
14m
. Ta xét 2 trường hợp sau:
Trường hợp 1:
1
1 4 0
4
mm
2
()h t t t m
có 2 nghiệm phân biệt
1
t
,
2
t
12
tt
.
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
13
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Vì
12
10tt
nên
12
0tt
hoặc
12
0tt
.
+) Nếu
12
0tt
thì
12
0P t t m
kết hợp với
1
4
m
ta có
1
0
4
m
. Khi đó.
13
( ) 1 0
24
gm
.
+) Nếu
12
0tt
thì
22
( ) 2 0g t t
.
Suy ra trong trường hợp này hàm số
()y g t
không thể có giá trị nhỏ nhất bằng 1 trên
.
Trường hợp 2:
1
1 4 0
4
mm
2
( ) 0, t .h t t t m
Khi đó,
2
22
1 1 1
( ) 2 , t .
2 4 4
y g t t t m t t t m t m m



11
min ( ) min ( ) ( ) .
24
xt
f x g t g m
Theo đề
11
5
44
min ( ) 1 .
15
4
1
44
x
mm
f x m
mm








Câu 27. Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
1
x mx m
fx
x

trên đoạn
1;2
bằng 2?
A. 3 B. 4 C. 1 D. 2
Lời giải: Chọn D
Đặt
2
1
x mx m
gx
x

.
Ta có:
2
22
22
21
2
1
11
x m x x mx m
x mx m x x
gx
x
xx




2
2
0
2
00
2
1
x
xx
gx
x
x

Dễ thấy trên đoạn
1;2
thì
gx
đồng biến và
1 2 4 3
1 ; 2
23
mm
gg


Ta xét 3 trường hợp
TH1: Đồ thị của hàm số
gx
trên
1;2
nằm phía trên trục hoành
Suy ra
4
1 2 4 3
3
1 . 2 0 . 0
1
23
2
m
mm
gg
m

Khi đó
4 3 2
max 2 2 2 2
33
m
f x g g m
TH2: Đồ thị của hàm số
gx
trên
1;2
nằm phía dưới trục hoành
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
14
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
Suy ra
4
1 2 4 3
3
1 . 2 0 . 0
1
23
2
m
mm
gg
m

Khi đó
1 2 5
max 1 1 2 2
22
m
f x g g m

TH3: Đồ thị của hàm số
gx
trên
1;2
cắt trục hoành
Suy ra
1 2 4 3 4 1
1 . 2 0 . 0
2 3 3 2
mm
g g m
Khi đó
max 2f x g
hoặc
max 1f x g
2
max 2
3
f x g m
5
max 1
2
f x g m
Vậy có 2 giá trị
m
thỏa yêu cầu bài toán.
Câu 28. Đồ thị của hàm số
42
f x ax bx c
có đúng ba điểm chung với trục hoành tại các
điểm
,,M N P
có hoành độ lần lượt là
,,m n p m n p
. Khi
3
1
4
f 
và
11f

thì
;
max
mp
fx
bằng
A.
1
4
. B.
4
. C.
0
. D.
1
.
Lời giải: Chọn D
3
42f x ax bx

Vì đồ thị của hàm số
42
f x ax bx c
có đúng ba điểm chung với trục hoành nên đồ thị
hàm số tiếp xúc với trục hoành tại gốc tọa độ suy ra
00f
.
Ta có
1
00
0
4
33
11
44
0
4 2 1
11
f
c
a
f a b c b
c
ab
f


.
Vậy
42
1
4
f x x x
.
42
0
1
0 0 2
4
2
x
f x x x x
x
suy ra
2, 0, 2m n p
.
Vậy
; 2;2
max max
mp
f x f x
.
Xét hàm số
42
1
4
g x f x x x
trên
2;2
.
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
15
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
3 4 2
42
1
2
4
1
4
x x x x
gx
xx




2
0
2
x
gx
x


và
gx
không xác định tại các điểm
0, 2xx
.
2 2 0 0, 2 2 1g g g g g
Suy ra
2;2
max 1gx
Vậy
;
max 1
mp
fx
.
Câu 29. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 3 2
3 4 12y x x x a
trên đoạn
3;2
. Có bao nhiêu số nguyên
2019;2019a
để
2.mM
A.
3209
. B.
3213
. C.
3215
. D.
3211
.
Lời giải: Chọn B
Cách 1
Xét
4 3 2
3 4 12g x x x x a
với
3;2x
.
3 2 2
12 12 24 12 2g x x x x x x x
;
0
01
2
x
g x x
x
.
0ga
;
15ga
;
2 32ga
;
3 243ga
.
Bảng biến thiên
gx
Có
[-3;2]
max max ( 3) , ( 1) , (0) , (2)g x g g g g
nên xảy ra các trường hợp sau:
Trường hợp 1:
32a
. Khi đó
243Ma
;
32ma
.
Ta có:
2 243 2( 32) 307M m a a a
. Với
2019;2019a
a

307;308;...;2017;2018a
. Vậy trong trường hợp này có
1712
giá trị a.
Trường hợp 2:
243 0 243aa
. Khi đó
32Ma
;
243ma
.
Ta có
2 32 2 243 518M m a a a
. Với
2019;2019a
a

2018; 2017;...; 519; 518a
. Vậy trong trường hợp này có
1501
giá trị a.
Trường hợp 3:
243 32a
. Khi đó
(243 )( 32) 0aa
nên
0; 0Mm
.Vậy trong trường
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
16
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
hợp này
0
có giá trị a để
2Mm
.
Tóm lại có
3213
giá trị
a
cần tìm.
Cách 2
Đặt
4 3 2
3 4 12t x x x
Ta xét hàm xét
4 3 2
3 4 12g x x x x
liên tục trên
3;2
. Có
3 2 2
12 12 24 12 2g x x x x x x x
;
0
01
2
x
g x x
x
.
00g
;
15g
;
2 32g 
;
3 243g 
. Suy ra
32;243t 
với
3;2x
.
Đặt
()f t t a
, khi
32;243t 
thì
()ft
liên tục trên
32;243
nên
[-32;243]
max max 32 , 243f t a a
.
Trường hợp 1:
32a
. Khi đó
243Ma
;
32ma
.
Ta có:
2 243 2( 32) 307M m a a a
. Với
2019;2019a
a

307;308;...;2017;2018a
. Vậy trong trường hợp này có
1712
giá trị a.
Trường hợp 2:
243 0 243aa
. Khi đó
32Ma
;
243ma
.
Ta có
2 32 2 243 518M m a a a
. Với
2019;2019a
a

2018; 2017;...; 519; 518a
. Vậy trong trường hợp này có
1501
giá trị a.
Trường hợp 3:
243 32a
. Khi đó
(243 )( 32) 0aa
nên
0; 0Mm
.Vậy trong trường
hợp này
0
có giá trị a để
2Mm
.
Tóm lại có
3213
giá trị
a
cần tìm.
Câu 30. Cho hàm số
43
44f x x x x a
. Gọi
,Mm
là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên
0;2
. Có bao nhiêu số nguyên
a
thuộc
4;4
sao cho
2Mm
?
A.
4
. B.
6
. C.
7
. D.
5
.
Lời giải: Chọn C
Đặt
4 3 2
44g x x x x
.
Vì
0;2
0;2
0;2 ; 1 max ,min ; 1x g x a a f x f x a a
.
TH1:
1 1;a a M a m a
.
Theo giả thiết, ta có:
2 1 2M m a a
.
Ta có hệ phương trình:
2
1
11
1
2 1 0
2
23
1
3 2 1 0
12
1
1
3
a
aa
a
a
aa
aa
a
aa




.
TH2:
1 ; 1a a M a m a
.
Theo giả thiết, ta có:
2 2 1M m a a
.
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
17
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Ta có hệ phương trình:
2
1
21
1
2 1 0
2
32
2
3 8 4 0
21
2
2
3
a
aa
a
a
aa
aa
a
aa





.
Kết hợp 2 TH
21
21
32
a a a
.
Mà
4; 3; 2;1;2;3;4
4;4
a
a
a

.
Câu 31. Xét tam thức bậc hai
2
()f x ax bx c
với
,,abc
, thỏa mãn điều kiện
( ) 1fx
,
1;1x
. Gọi
m
là số nguyên dương nhỏ nhất sao cho
2;2
max ( )
x
f x m
. Khi đó
m
bằng
A.
8
. B.
4
. C.
3
. D.
7
.
Lời giải: Chọn D
Đặt
2xt
.
Ta có
2;2 1;1xt
.
2 2 2 2
( ) 4 2 2 ( ) 2 2 ( ) (1) ( 1) 2f x at bt c f t at c f t f f t ct c
22
2 ( ) (1) ( 1) 2 (0) (0) 7f t f f t f t f
.
Suy ra
2;2
max ( ) 7
x
fx
.
Chọn
2
2() 1fx x
thì
( ) 1fx
,
1;1x
và
2;2
max ( ) 7
x
fx
.
Do đó
7m
.
Câu 32. Gọi
M
là giá trị lớn nhất của hàm số
2
f x x ax b
trên đoạn
1;3
. Khi
M
đạt giá
trị nhỏ nhất, tính
2ab
.
A.
7
. B.
5
. C.
4
. D.
6
.
Lời giải: Chọn C
Xét hàm số
2
f x x ax b
. Theo đề bài,
M
là giá trị lớn nhất của hàm số trên
1;3
.
Suy ra
1
3
1
Mf
Mf
Mf

1
93
1
M a b
M a b
M a b
4 1 9 3 2 1M a b a b a b
1 9 3 2( 1 )a b a b a b
48M
2M
.
Nếu
2M
thì điều kiện cần là
1 9 3 1 2a b a b a b
và
1 ab
,
93ab
,
1 ab
cùng dấu
1 9 3 1 2
1 9 3 1 2
a b a b a b
a b a b a b
2
1
a
b


.
Ngược lại, khi
2
1
a
b


ta có, hàm số
2
21f x x x
trên
1;3
.
Xét hàm số
2
21g x x x
xác định và liên tục trên
1;3
.
22g x x

;
0 1 1;3g x x
M
là giá trị lớn nhất của hàm số
fx
trên
1;3
max 1 ; 3 ; 1M g g g
=2
.
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
18
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
Vậy
2
1
a
b


. Ta có:
24ab
.
Câu 33. Cho hai số thực
,xy
thỏa mãn:
2
2
2
2 3 2
3
54
log 8 16 log 5 1 2log log 2 8
3
xx
y y x x y

.
Gọi
S
là tập các giá trị nguyên của tham số
m
để giá trị lớn nhất của biểu thức
22
P x y m
không vượt quá
10
. Hỏi
S
có bao nhiêu tập con không phải là tập rỗng?
A.
2047
. B.
16383
. C.
16384
. D.
32
.
Lời giải: Chọn B
Điều kiện:
4; 1 5.yx
Ta có:
2
2
2
2 3 2
3
45
log 8 16 log 5 1 2log log 2 8 (1)
3
xx
y y x x y
22
22
3 2 3 2
2log 4 log 4 5 2 log 4 5 1 log 4 4y x x x x y




22
22
3 2 3 2
2log 4 log 4 2log 4 5 log 4 5y y x x x x
.
Xét hàm số
32
( ) 2log log , 0f t t t t
, ta có:
2 1 1 2ln2 ln3
'( ) . 0, 0
ln3 ln2 ln2.ln3
f t t
t t t
Hàm số
()ft
đồng biến với
0t
, suy ra:
2 2 2
2
(2) 4 4 5 2 4 9y x x x y
Tập hợp các cặp số
( ; )xy
thỏa mãn là đường tròn
(C)
tâm là
(2; 4)I
và bán kính
3R
bỏ
bớt 2 điểm
1; 4 , 5; 4 .
Gọi
( ; )M x y
là điểm thuộc đường tròn
(C)
22
r x y
là khoảng cách từ
M
đến gốc
O
.
Vì
2 5 3IO 
nên
O
nằm ngoài
()C
và ta có:
2 5 3 2 5 3 2 5 3 2 5 3r m r m m
Với
P r m
,
2 5 3 , 2 5 3maxP max m m
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
19
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Để thỏa mãn bài toán ta phải có:
2 5 3 10
10 2 5 3 10
10 2 5 3 10
2 5 3 10
m
m
m
m


2 5 13 2 5 7
2 5 7 2 5 7
2 5 7 13 2 5
m
m
m
.
Ta có:
2 5 7 2,5;2 5 7 11,5 2; 1;0;...;11m
Tập
S
có 14 phần tử Số tập con
khác rỗng của tập
S
là:
14
2 1 16383.
Câu 34. Gọi
S
là tập hợp các giá trị của
m
để hàm số
32
3y x x m
đạt giá trị lớn nhất bằng
50
trên
[ 2;4]
. Tổng các phần tử thuộc
S
là
A.
4
. B.
36
. C.
140
. D.
0
.
Lời giải: Chọn A
Xét hàm số
32
( ) 3g x x x m
có
2
36g x x x

. Xét
0
0
2
x
gx
x

.
Khi đó giá trị lớn nhất của hàm số
32
3y x x m
trên
[ 2;4]
là:
2;4
max max 0 ; 2 ; 2 ; 4
x
y y y y y


max ; 4 ; 20 ; 16m m m m
.
Trường hợp 1: Giả sử
max 50ym
50
50
m
m

.
Với
50m
thì
16 66 50m
.
Với
50m 
thì
20 70 50m
.
Trường hợp 2: Giả sử
max 4 50ym
54
46
m
m

.
Với
54 54 50mm
.
Với
46m 
thì
20 66 50m
.
Trường hợp 3: Giả sử
max 20 50ym
70
30
m
m

Với
70m
thì
16 86 50m
.
Với
30m 
thì
16 14 50m
,
30 50m 
;
4 34 50m
.
Trường hợp 4: Giả sử
max 16 50ym
34
66
m
m

.
Với
34m
thì
34 50, 4 30 50, 20 14 50m m m
.
Với
66m 
thì
66 50m 
.
Vậy
30;34S 
. Do đó tổng các phẩn tử của
S
là:
30 34 4
.
Câu 35. Cho hàm số
32
3 9 12 2f x x x x m
. Có bao nhiêu giá trị nguyên của
20;20m
sao cho với mọi số thực
, , 1;3abc
thì
,,f a f b f c
là độ dài ba cạnh của một
tam giác.
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
20
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
A.
20
. B.
27
. C.
25
. D.
4
.
Lời giải: Chọn C
+ Xét hàm số
32
2 9 12 7y g x x x x m
2
6 12 12g x x x
1 1 2
0
2 2 3
x g m
gx
x g m
.
Bảng biến thiên
;;f a f b f c
là ba cạnh của một tam giác
, , , 1;3
f a f b f c
f b f c f a a b c
f a f c f b
1;3
1;3
2min maxf x f x
+ TH1:
3 0 3mm
* 2 3 2 8m m m
9;10;...;20m
có
12
giá trị của
m
.
+ TH2:
2 0 2mm
* 2 2 3 7m m m
8; 9;...; 20m
có
13
giá trị của
m
.
Vậy có tất cả
25
giá trị của
m
.
Câu 36. Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x

trên đoạn
1;1
bằng
3
. Tính tổng tất cả các phần tử của
S
.
A.
8
3
. B.
5
. C.
5
3
. D.
1
.
Lời giải: Chọn D
Xét hàm số
2
24
2
22
x mx m
f x x m
xx


trên đoạn
1;1
.
Có
2
4
1
2
fx
x

;
00f x x
.
Khi đó
1
1
3
fm
;
0fm
;
11fm
.
+ Nếu
10m
thì giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x

trên đoạn
1;1
bằng
m
.
Suy ra
33mm
.
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
21
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
+ Nếu
00
1
1 0 1 1
2
11
2
mm
m m m
mm
m



thì giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x

trên
đoạn
1;1
bằng
m
. Suy ra
33mm
.
+ Nếu
00
1
1 0 1 0
2
11
2
mm
m m m
mm
m



thì giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x

trên
đoạn
1;1
bằng
1 m
. Suy ra
1 3 2mm
.
+ Nếu
00mm
thì giá trị lớn nhất của hàm số
2
2
2
x mx m
y
x

trên đoạn
1;1
bằng
1 m
. Suy ra
1 3 2mm
.
Vậy
3
2
m
m

Câu 37. Xét hàm số
2
f x x ax b
, với
a
,
b
là tham số. Gọi
M
là giá trị lớn nhất của hàm số
trên
1;3 .
Khi
M
nhận giá trị nhỏ nhất có thể được, tính
2ab
.
A.
3
. B.
4
. C.
4
. D.
2
.
Lời giải: Chọn C
Ta có:
1 1; 3 3 9 1
1 1 2 2 2 2 2
M f b a M f b a
M f b a M b a
.
Từ
1
và
2
, kết hợp với
x y z x y z
, ta được:
4 1 3 9 2 2 2 1 3 9 2 2 2 8M b a b a b a b a b a b c
2M
. Vậy
2M
.
Dấu “
” xảy ra khi và chỉ khi
12
3 9 2
12
ba
ba
ba
và
1ba
;
39ba
;
2 2 2ba
cùng dấu.
Do đó:
2
1
a
b


24ab
.
Câu 38. Biết giá trị lớn nhất của hàm số
2
1
4
2
y x x m
là
18
. Mệnh đề nào sau đây đúng?
A.
5 10m
. B.
10 15m
. C.
15 20m
. D.
05m
.
Lời giải: Chọn C
Cách 1:
2
1
4
2
y x x m
, TXĐ:
2;2
. Đặt
2sinxt
,
;
22
t





.
Xét biểu thức
2
1
4 4sin 2sin
2
A t t
1
2cos 2sin
2
tt
1
2 2 sin
42
t



.
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
22
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
;
22
t





3
;
4 4 4
t


2
sin 1
24
t



5 1 1
2 2sin 2 2
2 4 2 2
t



nên
15
0 2 2sin
4 2 2
t



.
Dấu “=” xảy ra khi
2
t

Vậy giá trị lớn nhất của hàm số
2
1
4
2
y x x m
là
5
2
m
Theo giả thiết
5
18
2
m
nên
15,5m
.
Vậy
15 20m
.
Cách 2:
Xét
2
1
4
2
f x x x
, Tập xác định
2;2D 
.
2
1
4
x
fx
x

.
2
0 1 0
4
x
fx
x
2
4 , 0x x x
2x
.
Bảng biến thiên
Từ bảng biến thiên có
5
0
2
fx
.
5
2
y f x m m
.
2;2
5
max
2
x
ym

, khi
2x
, theo giả thiết có
2;2
max 18
x
y

.
5
18
2
m
31
15,5
2
m
. Vậy
15 20m
.
Câu 39. Cho hàm số
6 3 3
2f x x x m x
. Gọi
S
là tập tất cả các giá trị thực của tham số
m
để
Giá trị nhỏ nhất của hàm số
fx
bằng
1
. Tổng tất cả các phần tử của
S
bằng
A.
1
4
. B.
5
4
. C.
2
. D.
0
.
Lời giải: Chọn B
Tập xác định:
6 3 3
( ) 2y f x x x m x
.
+
0
x
f
/
(x)
f(x)
2
-2
_
-1+4
2
2
2
3
2
-5
2
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
23
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Đặt
3
tx
hàm số ban đầu trở thành hàm số
2
( ) 2y g t t t m t
.
Tam thức bậc hai
2
()h t t t m
có biệt thức
14m
. Ta xét 2 trường hợp sau:
Trường hợp 1:
1
1 4 0
4
mm
2
()h t t t m
có 2 nghiệm phân biệt
1
t
,
2
t
12
tt
.
Vì
12
10tt
nên
12
0tt
hoặc
12
0tt
.
+) Nếu
12
0tt
thì
12
0P t t m
kết hợp với
1
4
m
ta có
1
0
4
m
. Khi đó.
13
( ) 1 0
24
gm
.
+) Nếu
12
0tt
thì
22
( ) 2 0g t t
.
Suy ra trong trường hợp này hàm số
()y g t
không thể có giá trị nhỏ nhất bằng 1 trên
.
Trường hợp 2:
1
1 4 0
4
mm
2
( ) 0, t .h t t t m
Khi đó,
2
22
1 1 1
( ) 2 , t .
2 4 4
y g t t t m t t t m t m m



11
min ( ) min ( ) ( ) .
24
xt
f x g t g m
Theo đề
11
5
44
min ( ) 1 .
15
4
1
44
x
mm
f x m
mm








Câu 40. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm
số
2
1
x mx m
y
x

trên
1;2
bằng 2. Số phần tử của tập
S
là
A.
3.
B.
1.
C.
4.
D.
2.
Lời giải: Chọn D
Đặt
2
1
x mx m
fx
x

, ta có hàm số
fx
xác định và liên tục trên đoạn
1;2
.
Có:
2
2
2
0
1
xx
fx
x

,
1;2x
.
Suy ra:
1;2
43
max 2
3
m
f x f

;
1;2
12
min 1
2
m
f x f

.
Do đó
1;2
max max 2 ; 1f x f f
. Theo bài ta có:
22
12
f
f
12
22
f
f
Trường hợp 1:
Ta có:
22
12
f
f
43
2
3
12
2
2
m
m

2 10
33
53
22
mm
m
2
3
m
.
Trường hợp 2:
Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020
24
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
Ta có:
12
22
f
f
12
2
2
43
2
3
m
m

35
22
10 2
33
mm
m
5
3
m
.
Vậy có giá trị của tham số
m
thỏa yêu cầu bài toán. Do đó tập
S
có hai phần từ.
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 1. Có bao nhiêu giá trị nguyên của x để hàm số y x 1  x  3 đạt giá trị nhỏ nhất. A. 4 . B. 5 . C. 2 . D. 3 .
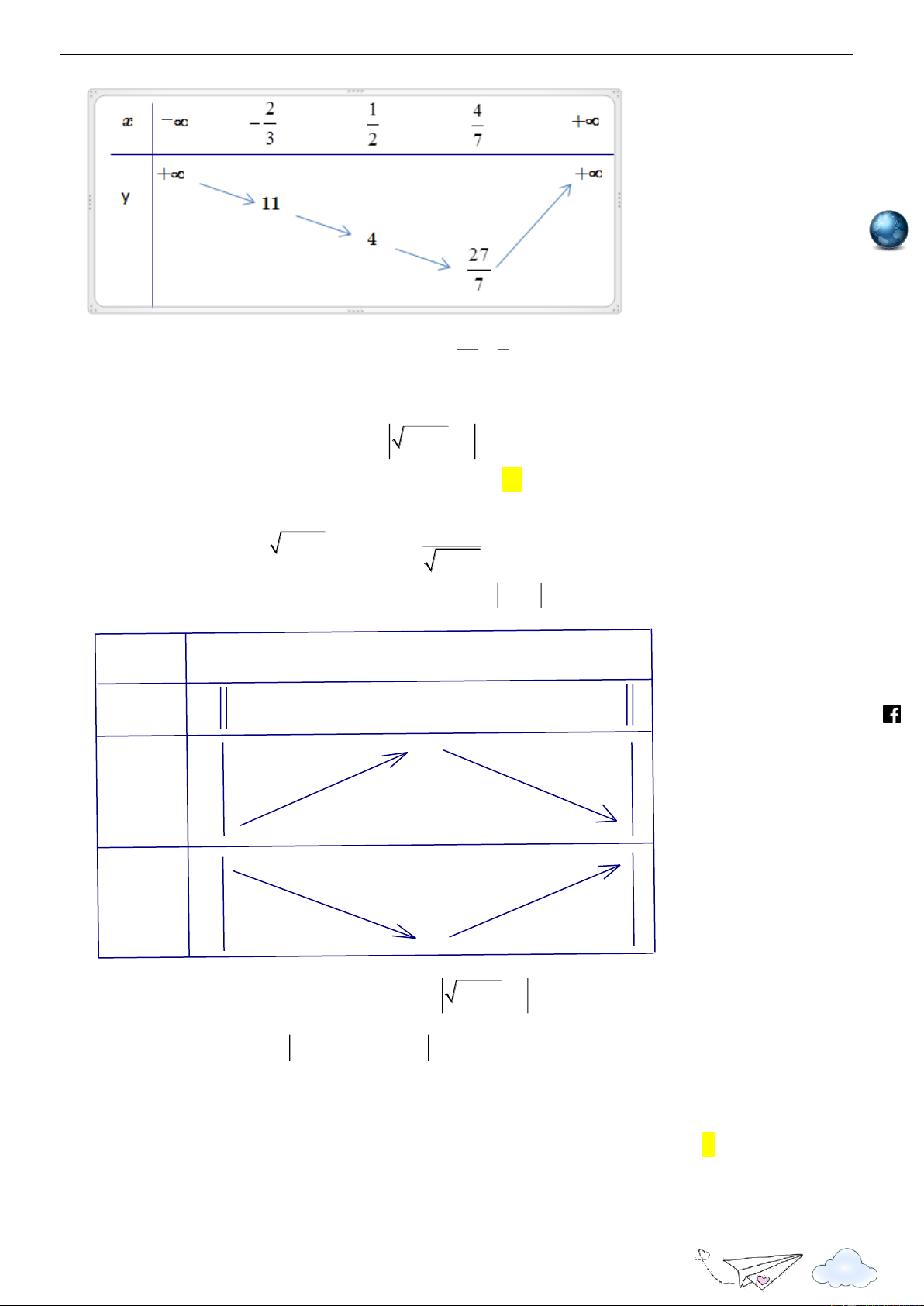
Lời giải: Chọn B 2x 2, x 1
Ta có y x 1  x  3 4, 3 x 1. 2x 2, x 3 m.vn ie Trên 1; , ta có y
4 và dấu bằng xảy ra khi x 1 . gh Trên 3;1 , ta có y
4 và có bốn giá trị nguyên của x thuộc khoảng này. racn Trên ; 3 , ta có y 2x 2 4 . it th Vậy y
4 và có 5 giá trị nguyên của x để y 4 . n min min
ye Câu 2. Cho hàm số f x  x 1  x  2  x 5  x 10 và hàm số g x 3
x 3x m 1 . Khi hàm lu
s:// số f x đạt giá trị nhỏ nhất thì g x đạt giá lớn nhất bằng 8 . Hỏi tổng tất cả các giá trị tuyệt đối
ttp của tham số thực m thỏa mãn bài toán bằng bao nhiêu? h A. 12 B. 2 C. 8 D. 7
Lời giải: Chọn A
Xét hàm số f x  x 1  x  2  x  5  x 10  x 1  2   x  5
  x x 10  x   1   2   x   5
  x  x 10  4 , dấu bằng xảy ra khi x 1; 2   ; x 5   ; x x 10 có cùng dấu hay 2
  x 1. Vậy yêu cầu bài toán là hàm số g x 3
x 3x m 1 đạt giá trị lớn nhất bằng 8 với 2
  x 1. Lập bảng biến thiên, suy ra các trường hợp sau:
/vietgold Th1:m30. Khi đó, max gx  g 1m18 haym7. x   2  ;  1
k.com Th2:m30m1. Khi đó, max gx maxg 1 , g 2  g 1max3 ,mm 18 . x   2  ;  1
ceboo Th3:m10. Khi đó, max gx  g 1  g 1 3m8 haym 5. .fa x   2  ;  1 a
Câu 3. Giá trị nhỏ nhất của hàm số y  2x 1  3x  2  7x  4 là với a,b nguyên dương, phân b a
số tối giản. Khi đó a b bằng
https://www bA. 5. B. 34 . C. 12 . D. 41.
Lời giải: Chọn B  2 3 12x khi x    3  2 1
7 6x khi   x   Ta có: 3 2
y  2x 1  3x  2  7x  4   1 4 5   2x khix   2 7  4 12  x  3 khi x   7 1
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 BBT: h ttp s:// lu 27 aa  27       ye
Từ BBT suy ra giá trị nhỏ nhất của hàm số là a b 34 7 b b   7 n th it rac
Câu 4. Giá trị nhỏ nhất của hàm số 2 y
4  x  9 trên đoạn  2  ;2 bằng n gh A. 0 . B. 6 . C. 7 . D. 9 . ie m.vn
Lời giải: Chọn C x
Xét hàm số y f x 2
 4  x  9 , có y   0  x  0 . 2 4  x
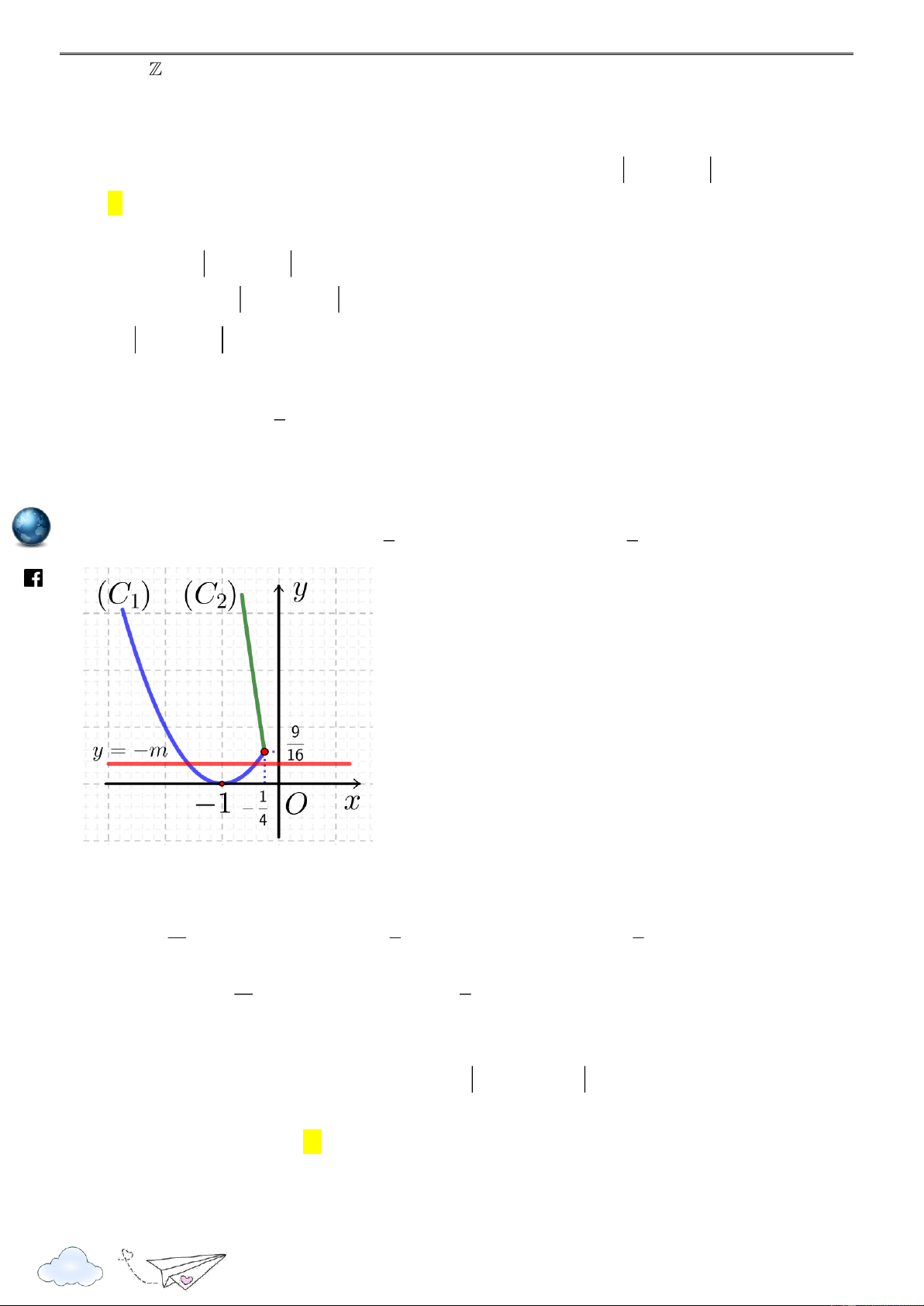
Ta có bảng biến thiên của hàm số y f x và y f x trên  2  ;2 như sau: x -2 0 2 + 0 - (f(x))' ht -7 tps://www f(x) -9 -9 .fa 9 ceboo 9 |f(x)| k.com 7 /v ietgold
Từ đó ta có giá trị nhỏ nhất của hàm số 2 y
4  x  9 trên  2
 ;2 là 7 khi x  0 .
Câu 5. Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số trên đoạn 0;2 . Có bao nhiêu số nguyên a thuộc đoạn  3
 ;2 sao cho M  2m ? A. 7. B. 5. C. 6. D. 4.
Lời giải: Chọn D 2
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” x  0 
Đặt g x 4 3 2
x  4x  4x a gx 3 2
 4x 12x  8x  0  x  1  . x  2 
Ta có g 0  a; g  
1  a 1; g 2  . a
  max g x  maxg 0; g  
1 ; g 2  a 1. 0; 2
  min g x  ming 0; g   1 ; g 2  m.vn . a 0; 2 ieM a 1 gh
Trường hợp 1: a  0   . m a racna 1;  it
Khi đó M  2m a 1  2a a  1, a  3  ;2 2 . th nM  a
Trường hợp 2: a 1  0  a  1    . ye
m  a 1 lu
Khi đó M  2m a   2
a  2  a  2  , a  3
 ;2  a  3  ;  2 . s://       ttp
Trường hợp 3: a a  1 0 1 a 0 h a   a a   a Khi đó M
a a  a  a 1 1 1 max 1 , max 1 ,     0  m . 2 2 2
Như vậy có tất cả 4 giá trị của a thỏa mãn yêu cầu.
Câu 6. Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số f x 2
x  2x m  4 trên đoạn  2   ;1 bằng 5 ? A. 2. B. 1. C. 3 . D. 4 .
Lời giải: Chọn A Đặt 2
t x  2x  4 , x  2  ;  1  t  5  ;  1
/vietgold Ta có: y tm k.com  m 1  5   ceboo
 m 1  m  5  m  6 .fa  y
 max m 1 ; m  5  5    . max     m  5  5  m  0 
 m 1  m  5 
Câu 7. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số 4 2
y x  38x 120x  4m trên
https://www đoạn 0;2đạt giá trị nhỏ nhất. A. 26. B. 13. C. 14. D. 27.
Lời giải: Chọn D x  5   Xét 4 2
u x  38x 120x  4m trên đoạn 0; 2 ta có 3
u '  0  4x  76x 120  0  x  2  x  3 
max u  maxu0,u2  max4 , m 4m 10  4  4m 104  0;2 Vậy 
min u  minu 0,u 2  min4 , m 4m 10  4  4m  0;2 3
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
Khi đó minmin y  0  4m 4m104  0  2
 6  m  0. có 27 số nguyên thỏa mãn. 0;2     
*Chú ý ôn tập lại kiến thức đã học: n
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y u x và u  u x2 .
M m M m
Gọi m  min u x; M  max u x. Khi đó max y  max M , m   . a;b a;b a;b 2
Giá trị nhỏ nhất không có công thức nhanh mà phụ thuộc và dấu của M và m h ttp
m  0  min y m a;bs://
M  0  min y  m lua;bye        n M .m 0 x ; a b y x 0 min y 0 0    0 a;bth it
Câu 8. Cho hàm số f x 3 2
 2x 3x m có bao nhiêu số nguyên m để min f x  3 . ra  1   ;3 cngh A. 4 . B. 8 . C. 31. D. 39 . ie
Lời giải: Chọn D m.vnx  0 Xét 3 2 ' 2
t  2x  3x m t  6x  6x  0   .  x 1
Do đó: min t x  m  5 ; max t x  m  27 .  1  ;  3  1  ;  3
Nếu m  5  0  min f x  m  5  3  5  m  8  m5;6;7;  8 .  1  ;  3
Nếu m  27  0  min f x  m  27  3  3  0  m  2  7  m 3  0; 2  9; 2  8; 2   7 .  1  ;  3
Nếu m  5m  27  0  min f x  0 . ht  1  ;  3 tps://www Vậy, m 3  0; 2  9;... 
8 có tất cả 39 số nguyên thỏa mãn.
Câu 9. Có bao nhiêu giá trị nguyên của tham số m để 2 a
m x x  2x m  5? 0; 3 .fa A. 5. B. 6. C. 7. D. 8. ceboo
Lời giải: Chọn B 2 k.com
Đặt f x  x  2x  .
m là hàm số xác định và liên tục trên đoạn 0;  3
Ta có: f ' x  2x  2. Với mọi x 0; 
3 ta có f ' x  0  2x  2  0  x  1. /viet f 0  m gold Mặt khác: f   1  m 1 .
f 3  m  3
Ta có: max f x  max f 0 ; f   1 ; f 3. [0;3]  f 0  5  m  5 5  m   5   
Theo bài: max f x  5   f  
1  5   m 1  5  5  m 1  5 . [0;3]   f 3    5 m  3  5  m  3  5  5   4
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 5  m  5 
 4  m  6  4  m  2. Do mZ mS 4;3;2;1;0;  1 . 8  m   2
Vậy có tất cả 6 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 10. Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số f x 2
x  2x m trên đoạn 0; 
3 không lớn hơn 3 ? m.vn ie A. 4 . B. 5 . C. 6 . D. 3 . gh
Lời giải: Chọn D g x 2    0;  g x      racn Xét hàm số x
2x m liên tục trên đoạn 3 có 2x 2 0 x 1 . it
Max f x  Max g 0 , g 3 , g  
1   Max m , m  3 , m 1  Max m  3 , m 1 th . n 0;  3 yem  3  3   3   m  3  3 lu
Max f x  3      2   m  0 . 0;  3  m 1  3   3   m 1 3 s://   ttp
Các giá trị nguyên thỏa mãn yêu cầu bài toán của tham số m là 2, 1,0 .
h Câu 11. Có bao nhiêu số nguyên m 5;5 để 3 2 min x 3x m 2 . 1;3 A. 6 . B. 4 . C. 3 . D. 5 .
Lời giải: Chọn B Ta có 3 2 min x 3x m 2 3 2 x 3x m 2; x 1;3 1 . 1;3 3 2 x 3x m 2; x 1;3 Giải 1 : 3 2 x 3x m 2; x 1;3 3 2 x 3x m 2; x 1;3 3 2 /vietgold 3 2 x 3x 2 ; m x 1;3 2 m min x 3x 1;3 * . 3 2 x 3x 2 ; m x 1;3 3 2 2 m max x 3x k.com 1;3 Xét hàm số 3 2 f x x
3x trên 1;3 . Hàm số xác định và liên tục trên 1;3 mà ceboo .fa x 0 2 f x 3x 6x 0 . Ta có: f 1 2; f 3 0; f 2 4 . x 2 2 m 4 m 6 Do đó max f x 0; min f x 4 . Từ * suy ra . 1;3 1;3 2 m 0 m 2 https://www m 5;5 Vì nên m 5; 4; 3; 2 . m
Vậy có 4 giá trị m thỏa mãn yêu cầu bài toán. Cách 2: Đặt 3 2 t x 3x , với x 1;3 t
4;0 . Khi đó bài toán trở thành min t m 2 . 4;0 TH1: m 4 min t m 4 m m 4 2 m 6 . 4;0 TH2: m 0 min t m m m 2 m 2 . 4;0 5
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 m 5;5
Kết hợp với điều kiện suy ra m 5; 4; 3; 2 . m
Vậy có 4 giá trị m thỏa mãn yêu cầu bài toán.
Câu 12. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để 2
Max x  2x m  4 . Tổng 0; 3
giá trị các phần tử của S bằng A. 2  . B. 2 . C. 4  . D. 4 . h ttp
Lời giải: Chọn A s:// Đặt 2
t x  2x . Với x 0;  3  t  1  ;  3 . lu Nên 2
Max x  2x m  Max t m  a
M x m 1 ; m  3. ye 0; 3  1  ;  3 n  m 1  4 th
m  5l  it
 m  3  m 1  m  3  r 2  a
Max x  2x m  4    . c   0;  3  m  3  4 m  1 n   gh      m  7 1 3   l m miem.vnS   3  ;  1 .
Vậy tổng giá trị các phần tử của S bằng 2  .
Câu 13. Có bao nhiêu giá trị nguyên của tham số m để 3 2
max x  3x m  4? 1;  3 A. Vô số. B. 4. C. 6. D. 5.
Lời giải: Chọn D Đặt 3 2 2
f (x)  x  3x m f (
x)  3x 6 . x x  0 ht f (  x)  0  .  tp x  2 s://www Bảng biến thiên .fa ceboo k.com
Ta thấy max f (x)  f (3)  m và min f (x)  f (2)  m  4. [1;3] [1;3] /v 3 2 iet
Ta có max x  3x m  max m ; m  4. 1;  3 gold Trường hợp 1: 2 2
m m  4 
m m 8m 16 m  2        m max  m ; m4 0 2,  m  4  4  4   m  4  4 0  m  8
mà m nên m0;1;  2 . Trường hợp 2: 2 2
m m  4 
m m 8m 16 m  2        m max  m ; m4 2 4,  m  4  4   m  4  4   m  4 6
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
mà m nên m3;  4 .
Vậy, có 5 giá trị nguyên của tham số m. Vậy Chọn D
Câu 14. Có bao nhiêu số thực m để giá trị nhỏ nhất của hàm số 2
y x  2x m  4x bằng 1  ? A. 1. B. 2 . C. 3 . D. 0 .
Lời giải: Chọn A m.vn ie 2
x  2x m  4x  1     1  gh Ta có ycbt  2  x
x x m x   2 : 2 4 1  0 0 0  racn   2 it
1  x  2x m  4  x 1 th n Nếu 4
x 1 0  2 không thỏa mãn. ye 1 lu Nếu 4
x 1 0  x   . 4 s:// 2
x  2x m  4  x 1 2
x  2x 1 m3 ttp Khi đó   
. Giả sử S , S lần lượt là tập nghiệm của h 2  1 2
x  2x m  4x 1 2
x  6x 1 m  4  1 1
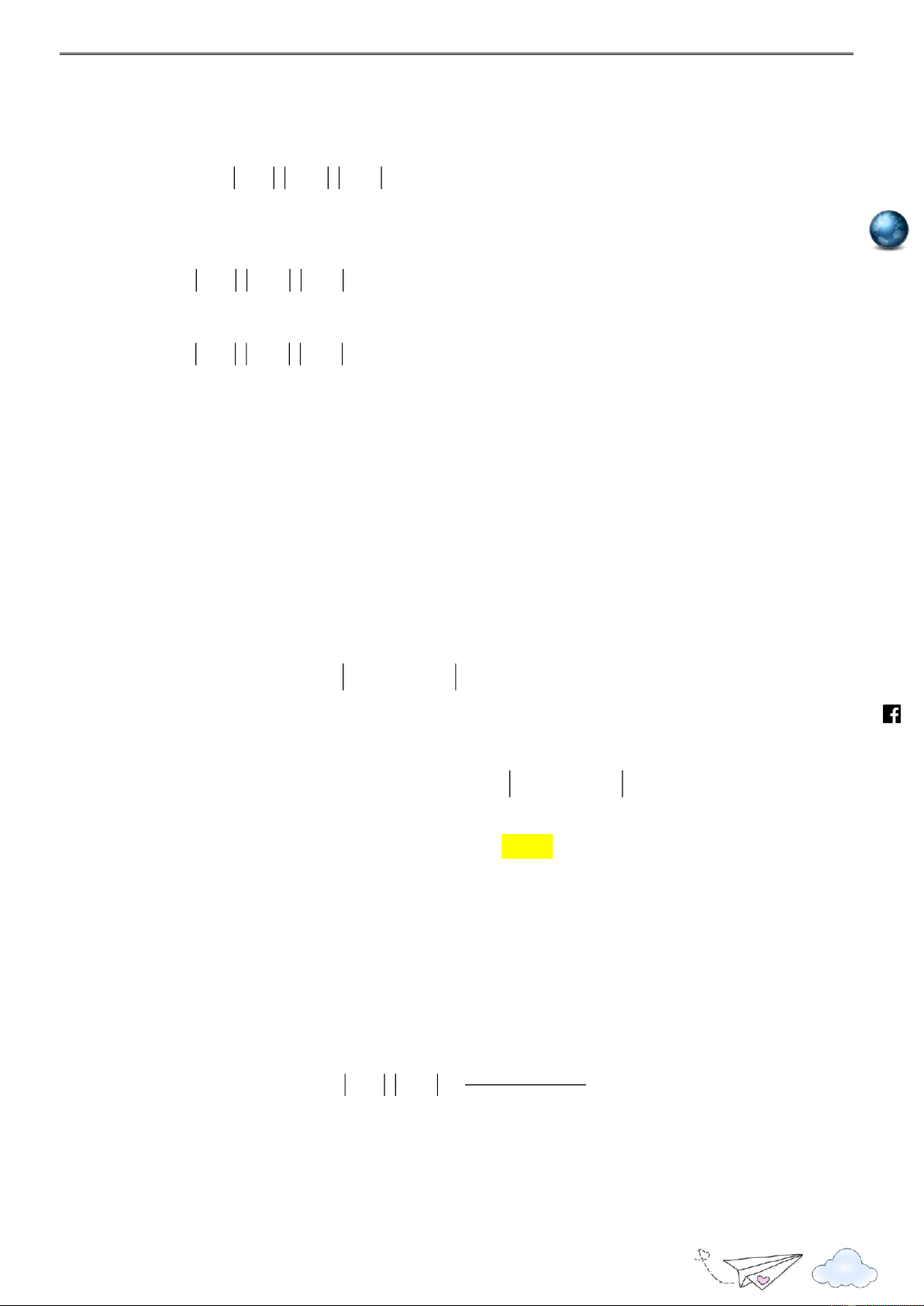
3,4 . Xét C  2
: y x  2x 1, x  
và C : y x  6x 1, x   . 2  2 1 4 4 /vietgold k.com ceboo .fa
+ m  0  2 không thỏa mãn.
+ m  0  m  0 thỏa mãn.  9   1   1  + m  0;   thì S   ;  x x ;
, S    S S   ;   1  1   2  2 1 2   https://www  16  4   4   9   1  + Tương tự m  ;  
 thì S S   ;    .   16  1 2  4 
Vậy m  0 là giá trị cần tìm.
Câu 15. Biết rằng giá trị lớn nhất của hàm số 2
y x  2x m  4 trên đoạn  2   ;1 đạt giá trị nhỏ
nhất, giá trị của tham số m bằng A. 1. B. 3 . C. 4 . D. 5
Lời giải: Chọn B Cách 1:
Xét hàm số y f x 2
x  2x m  4 trên  1  ;2 7
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
f  x  2x  2
f  x  0  x  1   1  ;2 f  2
   m 4; f  
1  m 1; f   1  m  5
Vậy Max y Maxm 1 ; m  4 ; m  5  2  ;  1 Biện luận:
TH1: m  4  0  m  4 h ttp
Max y Maxm 1 ; m  4 ; m  5  m 1 3   1  2  ;  1 s://
TH2: m 1 0  m 1 lu ye
Max y Maxm 1 ; m  4 ; m  5  5  m  4 2  2  ;  1 n thm 1 0 it TH3:   1 m  4 rm  4  0 acn
Max y Maxm 1;5  m gh  2  ;  1 ie
i) Xét 3  m  4  m 1 5  m m.vn
Do đó Max y Maxm 1;5  
m m 1  2 3  2  ;  1
ii) Xét 1 m  3  5  m m 1
Do đó Max y Maxm 1;5  
m  5  m  2 4  2  ;  1 Từ  
1 ,2,3 và 4
Giá trị lớn nhất của hàm số 2
y x  2x m  4 trên đoạn  2  
;1 đạt giá trị nhỏ nhất bằng 2 khi
giá trị của tham số m  3 . ht
Cách 2: Thừ với m 1,3, 4,5 rút ra kết luận. tps://www
Câu 16. Tìm m để giá trị lớn nhất của hàm số f x 2
x  2x m  4 trên đoạn  2   ;1 đạt giá trị nhỏ nhất. .fa A. m 1. B. m  2. C. m  3.
D. m  4. ceboo
Lời giải: Chọn C
Xét g x 2
x  2x m  4 trên đoạn  2   ;1 . k.com
Đạo hàm g x  2x  2; g x  0  x  1   2  ;  1 . /viet g  2    m  4
max g x  m 1 gold    2; 1 Ta có g   1  m  5     g x . min  m  5
g    m   2; 1 1 1
m 1  5  m
Cách 1. Suy ra max f x  max m 1 , m  5       2.  2  ;  1 2
Dấu '  ' xảy ra  m 1  5  m m  3.
Cách 2. • Nếu m  
1  m  5  0  m  3 thì max f x  m 1  2.  2  ;  1
Dấu '  ' xảy ra  m  3. • Nếu m  
1  m  5  0  m  3 thì max f x  m  5  2.  2  ;  1 8
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Dấu '  ' xảy ra  m  3..
Câu 17. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 3
y x  3x m trên đoạn 0; 2 bằng10 . Số phần tử của S là: A. 0 . B. 2 . C. 1. D. 3 .
Lời giải: Chọn B Xét hàm số 3
y x  3x m trên đoạn 0;2 m.vn ie 2
y  3x  3  0, x  0;2. gh
Vậy: max y  max f x  max f 0 ; f 2  max m 14 ; m 0;2 0;2 racn it       m 14 m th m 14 m   n
TH1. Với max y m 14 , ta có       m  4   m 4 0;2  m 14 10   ye m  14  lu
m m 14 s://
m m 14  
TH2. Với max y m , ta được   m  10   m  10  ttp  1  ;2  m 10 h   m 10
Vậy có 2 giá trị của m thỏa yêu cầu
Câu 18. Có bao nhiêu giá trị m để hàm số 2
f (x)  x  4x m đạt giá trị nhỏ nhất trên đoạn 1 ; 4 bằng 6? A. 4 . B. 2 . C. 1. D. 3 .
Lời giải: Chọn B Đặt 2
t x  4x .
Vì x 1;4  t  4
 ;0. Ta được hàm số: f (t)  t m ,t  4  ;0.
/vietgold Vì hàm số g(t)tm là hàm số bậc nhất nên f (t) tm đạt giá trị nhỏ nhất tại một trong 2
k.com điểm mút 4 hay 0và m 4;0.
ceboo Do đó: min f (x)min f (t)min 4m ; m. .fa 1;  4  4  ;0  4   m m   m  6 m   4  ;0 m  6   
https://www Yêu cầu bài toán .   Chọn B  4   m mm 10   4   m  6   m   4  ;0
Câu 19. Tính tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y x2 2x m trên đoạn ; 1 2 bằng 5. A. 1 . B. 2 . C. 2 . D. 1 .
Lời giải: Chọn B +) Đặt t (x )2 1 , với x ; 1 2 thì t ;
0 4 , hàm số trở thành: y t m 1 9
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 +) Hàm số y t m
1 luôn đồng biến trên đoạn ;
0 4 nên max y max m 1 ; m 3 0;4 m 6 (ktm) Nếu m 1 m 3 m 1 thì m 1 5 m 4 (t ) m m 8 (ktm) Nếu m 1 m 3 m 1 thì m 3 5 m 2 (t ) m
Đáp số: có 2 giá trị của tham số m h ttp Câu 20. Cho hàm số 2
y x  2x a  4 . Tìm a để giá trị lớn nhất của hàm số trên đoạn  2   ;1 đạt s:// giá trị nhỏ nhất. lu A. a  1. B. a  2 .
C. Một giá trị khác. D. a  3. ye
Lời giải: Chọn D n th Xét 2
y x  2x a  4  y '  2x  2 it r
y '  0  x  1  acn Ta có  x  2
1  a  5  a  5 gh 2 2 ie Vì x  2;   1   x  
1  a  5  1 
1  a  5  a 1 m.vn
Ta có M max y max| a  5 |;| a 1  | [2;1] Lại có 2M |
a 5|  | a 1| 5 a a 1  4  M  2 |  a  5 | |  a 1| 
Dấu "  " xảy ra khi và chỉ khi    , Chọn D   a  a   a 3 5 1  0
Câu 21. Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số f x 1 4 2
x 14x  48x m  30 trên đoạn 0;2 không vượt quá 30. Tổng các phần tử của S 4 http bằng s://www Câu 22. A. 108. B. 120. C. 210. D. 136.
Lời giải: Chọn D .fa 1 ceboo
Xét hàm số g x 4 2
x 14x  48x m  30 trên đoạn 0;2 . 4     k.com x 6 0; 2 
Ta có g x 3 '
x  28x  48; g 'x  0  x  2  /v x  4  0;2 ietgold Bảng biến thiên: g  0  3  0 m  30  3  0
Dựa vào BBT, để max g x  30      0  m 16 0;2 g  2  30 m 14  30 m 
m0;1;2;...;15;1  6 
 tổng các phần tử của S là 136.
Câu 23. Tìm m để giá trị lớn nhất của hàm số 3
y x  3x  2m 1 trên đoạn 0;2 là nhỏ nhất.
Giá trị của m thuộc khoảng?  2   3  A. 0;  1 . B.  1  ;0. C. ; 2   . D.  ; 1    .  3   2  10
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Lời giải: Chọn A x
Xét hàm số g x 3
x 3x  2m 1, gx 2
 3x 3 , gx 1  0   . x  1 
Trên 0;2 ta có g 0  2m 1; g  
1  2m  3; g 2 1 2m .
2m  3  2m 1
2m  3  2m   1
Khi đó max y  max 2m  3 ; 2m 1    2m 1 11 0;2 2 2 m.vn
Suy ra để giá trị lớn nhất của hàm số 3
y x  3x  2m 1 trên đoạn 0;2 là nhỏ nhất thì ie gh 1  m  . 2 racn it 4
x ax a
th Câu 24. Cho hàm số y
. Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của n x 1
ye hàm số đã cho trên đoạn 1;2. Có bao nhiêu giá trị nguyên của a để M  2 . m lu s:// A. 15 . B. 14 . C. 15 . D. 16 . ttp
Lời giải: Chọn A h
x ax a 4 3 3x  4x
Xét hàm số f x 4 
. Ta có f  x   0, x   1;2 2   x 1 x   1 1 16 Do đó f  
1  f x  f 2, x  1;  2 hay a
f x  a  , x  1;2 2 3
Ta xét các trường hợp sau: 1 1 16 1
Th1: Nếu a 0 a  thì M a ;ma 2 2 3 2 16  1  13 Theo đề bài a   2 a   a    /vietgold 3  2  3
Do a nguyên nên a 0;1;2;3;  4 . k.com 16 16  16   1  Th2: Nếu a   0  a  
thì m   a
; M   a          ceboo 3 3 3 2 .fa  1   16  61
Theo đề bài  a   2  a   a        2   3  6
Do a nguyên nên a  1  0; 9  ;...;  6 . 1 16 16 1 Th3: Nếu a   0  a   
a   thì M  0; m  0 https://www 2 3 3 2
Do a nguyên nên a  5  ; 4  ;...;  1
Vậy có 15 gái trị của a thỏa mãn yêu cầu bài toán.
Câu 25. Cho biết M là giá trị lớn nhất của hàm số f x 2
x  2ax b trên đoạn  1  ;2. Khi M
đạt giá trị nhỏ nhất có thể thì giá trị của biểu thức M a  3b bằng: 9 A. . B. 2  . C. 3 . D. 1  . 8
Lời giải: Chọn D
Ta có: M max f x nên suy ra: x   1  ;2 11
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
+ M f  
1  2a b 1   1
+ M f 2  4  4a b 2  1  1 1 + M f   a b  
 2M    2a  2b 3  2  4 2
Cộng các bất đẳng thức  
1 ,2,3 theo vế ta có: 1 1 9
4M  2a b 1  4  4a b  
 2a  2b  2a b 1 4  4a b   2a  2b  2 2 2 h ttp 9  M  * . s:// 8 lu
Dấu '  ' xảy ra khi dấu '  ' ở  
1 ,2,3 cùng đồng thời xảy ra và sao cho các giá trị ye n          tha b  a b 1 1 2 , 4 4 , 2a 2b   cùng dấu với nhau.  2  it ra  9 c
1 2a b M   n  8  1 gh  a   9    2 ie
4  4a b M     m.vn 8 7   b     1 9    8
  2a  2b M    2 8
Tức điều kiện dấu '  ' xảy ra khi:   9
1 2a b M    8  9
4 4a b M   VN   8   1 9
   2a  2b M     2 8 ht 7 tp
Khi đó: f x 2
x x  . s://www 8 9 1 7
Suy ra giá trị nhỏ nhất của M là: khi a  , b   8 2 8 .fa
Vậy M a  3b  1  . ceboo
Câu 26. Cho hàm số f x 6 3 3
x x m  2x . Gọi S là tập tất cả các giá trị thực của tham số m k.com để /v
Giá trị nhỏ nhất của hàm số f x bằng 1. Tổng tất cả các phần tử của S bằng ietgold 1 5 A. . B. . C. 2 . D. 0 . 4 4
Lời giải: Chọn B Tập xác định: 6 3 3
y f (x)  x x m  2x . Đặt 3
t x hàm số ban đầu trở thành hàm số 2
y g(t)  t t m  2t . Tam thức bậc hai 2 (
h t)  t t m có biệt thức  1 4m . Ta xét 2 trường hợp sau: 1
Trường hợp 1:   1 4m  0  m  2  (
h t)  t t m có 2 nghiệm phân biệt t , t t t . 1 2  4 1 2 12
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Vì t t  1
  0 nên t t  0 hoặc t  0  t . 1 2 1 2 1 2 1 1
+) Nếu t t  0 thì P t t m  0 kết hợp với m  ta có 0  m  . Khi đó. 1 2 1 2 4 4 1 3 g( )   m 1 0 . 2 4
+) Nếu t  0  t thì g(t )  2  t  0 . 1 2 2 2 m.vn
Suy ra trong trường hợp này hàm số y g(t) không thể có giá trị nhỏ nhất bằng 1 trên . ie 1 gh
Trường hợp 2:   1 4m  0  m  2  (
h t)  t t m  0, t   . 4 2 racn  1  1 1 2 2 it
Khi đó, y g(t)  t t m  2t t t m t
m   m  , t   .    2  4 4 th n 1 1     ye min f (x) min g(t) g( ) m . xt 2 4 lu  1  1 s:// m m     4  4 5 ttp
Theo đề min f (x)  1      m  . h x 1 5 4 m 1    m   4  4
Câu 27. Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số   2
x mx m f x
trên đoạn 1;2 bằng 2? x 1 A. 3 B. 4 C. 1 D. 2
Lời giải: Chọn D
x mx m
Đặt g x 2  . /vietgold x 1     
2x mx   1   2 2
x mx m x mx m  2x 2x
k.com Ta có: gx     x 1  x  2 1 x  2 1 ceboo    g x 2 x 2x x 0     .fa 0   x   0 2 1 x  2  1 2m 4  3m
Dễ thấy trên đoạn 1;2 thì g x đồng biến và g   1  ; g 2  2 3 Ta xét 3 trường hợp
https://www TH1: Đồ thị của hàm số gx trên 1;2 nằm phía trên trục hoành  4  m  1 2m 4 3m    3 Suy ra g   1 .g 2  0  .  0   2 3 1  m   2  m Khi đó
f x  g    g   4 3 2 max 2 2  2   2  m  3 3
TH2: Đồ thị của hàm số g x trên 1;2 nằm phía dưới trục hoành 13
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020  4  m  1 2m 4 3m    3 Suy ra g   1 .g 2  0  .  0   2 3 1  m   2  m  Khi đó
f x  g    g   1 2 5 max 1 1  2    2  m  2 2
TH3: Đồ thị của hàm số g x trên 1;2cắt trục hoành hm m   g g      m ttp Suy ra     1 2 4 3 4 1 1 . 2 0 . 0 2 3 3 2 s://
Khi đó max f x  g 2 hoặc max f x  g   1 lu ye
f x  g   2 max 2  m n 3 thit
f x  g   5 max 1  m r 2 a cn
Vậy có 2 giá trị m thỏa yêu cầu bài toán. gh ie
Câu 28. Đồ thị của hàm số   4 2
f x ax bx c có đúng ba điểm chung với trục hoành tại các m.vn
điểm M , N, P có hoành độ lần lượt là , m ,
n p m n p . Khi f   3 1   và f   1  1 thì 4
max f x bằng m;p 1 A. . B. 4 . C. 0 . D. 1 . 4
Lời giải: Chọn D f  x 3
 4ax  2bx ht
Vì đồ thị của hàm số   4 2
f x ax bx c có đúng ba điểm chung với trục hoành nên đồ thị tps://www
hàm số tiếp xúc với trục hoành tại gốc tọa độ suy ra f 0  0 .   f   1 0  0 c  0 a     4 .fa  3  3   Ta có  f   1  
 a b c   b   1. ceboo 4 4      f   c 0 1  1  4
a  2b 1    k.com  1   /v Vậy f x 4 2 x x . 4 ietgold x  0  f x 1 4 2
 0  x x  0  x  2  suy ra m  2
 ,n  0, p  2 . 4  x  2 
Vậy max f x  max f x . m;p  2  ;2 1
Xét hàm số g x  f x 4 2
x x trên  2  ;2. 4 14
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”   1  3 x  2x 4 2 x x     g x 4  1 4 2 x x 4   g xx 2  0  
và g x không xác định tại các điểm x  0, x  2  . x   2 m.vn g  2
   g 2  g 0  0, g  2  g 2 1 ie gh
Suy ra max g x  1  2  ; 2 racn
max f x  it Vậy 1. m;pth
n Câu 29. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số ye lu 4 3 2 y 3x 4x 12x a trên đoạn
3; 2 . Có bao nhiêu số nguyên a 2019; 2019 để 2m M. s:// A. 3209 . B. 3213 . C. 3215 . D. 3211. ttp h
Lời giải: Chọn B Cách 1 Xét g x 4 3 2
 3x  4x 12x a với x 3  ;2 . x  0  g x 3 2
x x x x 2 12 12 24 12
x x  2 ; g x  0  x  1   . x  2 
g 0  a ; g   1  5
  a ; g 2  3
 2  a ; g  3    243 a .
Bảng biến thiên g x /vietgold k.com ceboo .fa
Có max g x  max g( 3  ) , g( 1
 ) , g(0) , g(2)  nên xảy ra các trường hợp sau: [-3;2]
https://www Trường hợp 1: a32. Khi đó M 243a; m 32   a . a 2  019;2019 Ta có:
M  2m  243  a  2(a  32)  a  307 . Với  a
a307;308;...;2017;201 
8 . Vậy trong trường hợp này có 1712 giá trị a.
Trường hợp 2: a  243  0  a  2
 43 . Khi đó M  32  a; m  243 a . a 2  019;2019 Ta có
M  2m  32  a  2
 243 a  a  5  18 . Với  a  a 2  018; 2  017;...; 5  19; 5  1 
8 . Vậy trong trường hợp này có 1501 giá trị a. Trường hợp 3: 2
 43  a  32 . Khi đó (243 a)(a 32)  0 nên M  0;m  0 .Vậy trong trường 15
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
hợp này 0 có giá trị a để M  2m .
Tóm lại có 3213 giá trị a cần tìm. Cách 2 Đặt 4 3 2 t 3x 4x 12x
Ta xét hàm xét g x 4 3 2
 3x  4x 12x liên tục trên  3  ;2. Có x  0  g x 3 2
x x x x 2 12 12 24 12
x x  2 ; g x  0  x  1   . h ttpx  2  s://
g 0  0 ; g   1  5  ; g 2  3  2; g  3
   243. Suy ra t  3  2;24  3 với x  3  ;2 . lu
Đặt f (t)  t a , khi t  3  2;24 
3 thì f (t) liên tục trên  3  2;24  3 nên ye n
max f t  max 3
 2  a , 243 a . th [-32;243] it r
Trường hợp 1: a  32 . Khi đó M  243 a ; m  32   a . acn a 2  019;2019 gh Ta có:
M  2m  243  a  2(a  32)  a  307 . Với  aie m.vn
a307;308;...;2017;201 
8 . Vậy trong trường hợp này có 1712 giá trị a.
Trường hợp 2: a  243  0  a  2
 43 . Khi đó M  32  a; m  243 a . a 2  019;2019 Ta có
M  2m  32  a  2
 243 a  a  5  18 . Với  a  a 2  018; 2  017;...; 5  19; 5  1 
8 . Vậy trong trường hợp này có 1501 giá trị a. Trường hợp 3: 2
 43  a  32 . Khi đó (243 a)(a 32)  0 nên M  0;m  0 .Vậy trong trường
hợp này 0 có giá trị a để M  2m . ht
Tóm lại có 3213 giá trị a cần tìm. tps://www
Câu 30. Cho hàm số f x 4 3
x  4x  4x a . Gọi M ,m là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên 0;2 . Có bao nhiêu số nguyên a thuộc  4
 ;4 sao cho M  2m ? .fa A. 4 . B. 6 . C. 7 . D. 5 . ceboo
Lời giải: Chọn C k.com
Đặt g x 4 3 2
x  4x  4x .
Vì x 0;2  g xa;a  
1  max f x, min f x a ; a 1. /v 0;2 0;2 ietgold
TH1: a 1  a M a 1 ;m a .
Theo giả thiết, ta có: M  2m a 1  2 a .  1 a    1 1  a 1  a  2a 1 0  2   a   Ta có hệ phương trình:        2 3 . 2
a 1  2 a 3 
a  2a 1 0 1 
a    a 1 a 1  3
TH2: a 1  a M a ;m a 1 .
Theo giả thiết, ta có: M  2m a  2 a 1 . 16
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”  1 a    2 1  a 1  a  2a 1 0  2   a   Ta có hệ phương trình:        3 2 . 2
a  2 a 1 3 
a  8a  4  0 2  a  2   a   a  2   3 2 1
Kết hợp 2 TH  a  2
    a    a 1. 3 2 a   m.vn Mà   a  4  ; 3  ; 2;1;2;3;4 . iea    4  ;4  
gh Câu 31. Xét tam thức bậc hai 2 f (x) ax bx c với , a , b c
, thỏa mãn điều kiện f (x) 1 , racn it x
1;1 . Gọi m là số nguyên dương nhỏ nhất sao cho max f (x)
m . Khi đó m bằng x 2;2 th n A. 8 . B. 4 . C. 3 . D. 7 . ye
Lời giải: Chọn D lu Đặt x 2t . s:// Ta có x 2; 2 t 1;1 . ttp h 2 2 2 2 f (x) 4at 2bt c 2 f (t) 2at c 2 f (t) f (1) f ( 1) t 2ct c 2 2 2 f (t) f (1) f ( 1) t 2 f (0) t f (0) 7 . Suy ra max f (x) 7 . x 2;2 Chọn 2 f (x) 2x 1 thì f (x) 1, x
1;1 và max f (x) 7 . x 2;2 Do đó m 7.
Câu 32. Gọi M là giá trị lớn nhất của hàm số   2
f x x ax b trên đoạn  1  ;  3 . Khi M đạt giá
/vietgold trị nhỏ nhất, tính a2b.
A. 7 . B. 5  . C. 4  . D. 6  .
k.com Lời giải: Chọn C
ceboo Xét hàm số   2
f x x ax b . Theo đề bài, M là giá trị lớn nhất của hàm số trên  1  ;  3 . .fa
M f   1
M  1 a b  
Suy ra  M f 3  M  9  3a b  4M  1 a b  9  3a b  2 1   a b   M f    1
M  1 a b                https://www
1 a b 9 3a b 2( 1 a ) b 4M 8 M 2 .
Nếu M  2 thì điều kiện cần là 1 a b  9  3a b  1
  a b  2 và 1 a b , 93a b,
 1 a b  9  3a b  1
  a b  2 a  2  1
  a b cùng dấu     . 1
  a b  9  3a b  1
  a b  2  b  1  a  2  Ngược lại, khi 
ta có, hàm số f x 2
x  2x 1 trên  1  ;  3 . b  1 
Xét hàm số g x 2
x  2x 1 xác định và liên tục trên  1  ;  3 .
g x  2x  2 ; g x  0  x 1 1  ;  3
M là giá trị lớn nhất của hàm số f x trên  1  ; 
3  M  max g  
1 ; g 3 ; g   1  =2. 17
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 a  2  Vậy 
. Ta có: a  2b  4  . b  1  Câu 33. Cho hai số thực , x y thỏa mãn:    y y  
  x  x 2 5 4x x log 8 16 log 5 1  2log  log 2y  82 2 . 2 3 2 3 3
Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức 2 2 h P
x y m không vượt quá 10 . Hỏi S có bao nhiêu tập con không phải là tập rỗng? ttp s:// A. 2047 . B. 16383 . C. 16384 . D. 32 . lu
Lời giải: Chọn B ye Điều kiện: y  4  ;1 x  5. n 2 th
x  4x  5 2 Ta có: log
y  8y 16  log
5  x 1 x  2 log  log 2y 8 (1) 3  2  2    3 2   it 3 ra 2 2 2 2 c
 2log y  4  log x  4x  5  2 log x  4x  5 1  log 4 y  4  3   n 2   3    2      gh 2 2 2 2 ie
 2log y  4  log y  4  2log x  4x  5  log x  4x  5 . 3   2   3   2   m.vn 2 1 1 2 ln 2  ln 3
Xét hàm số f (t)  2log t  log t, t  0 , ta có: f '(t)    .  0, t   0 3 2 t ln 3 t ln 2 t ln 2.ln 3 Hàm số 2 2 2
f (t) đồng biến với t  0 , suy ra:   y   2 (2) 4
 x  4x  5  x  2  y  4  9
Tập hợp các cặp số ( ;
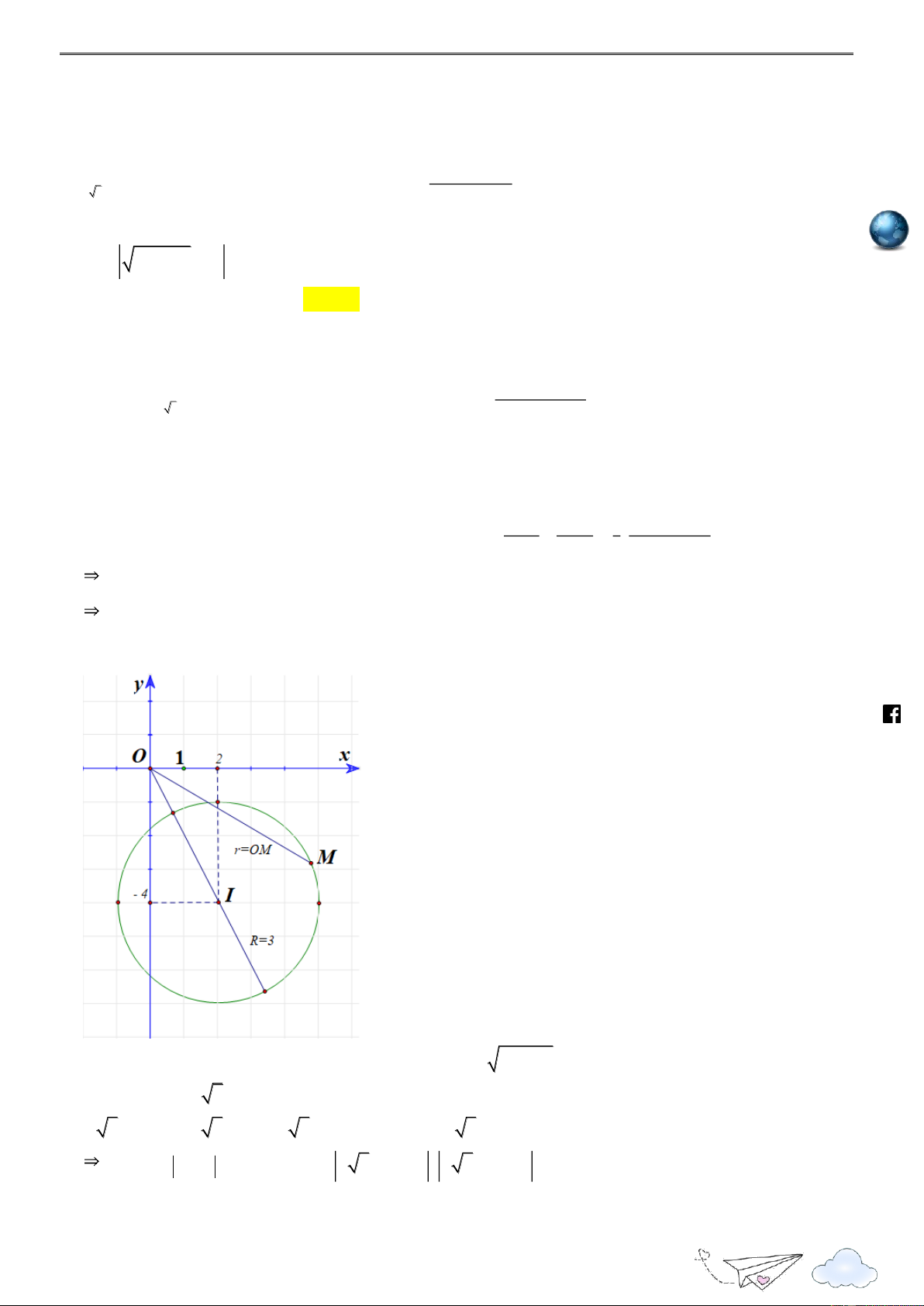
x y) thỏa mãn là đường tròn (C) tâm là I (2;  4) và bán kính R  3 bỏ bớt 2 điểm  1  ; 4, 5; 4. https://www .fa ceboo k.com /vietgold Gọi M ( ;
x y) là điểm thuộc đường tròn (C) 2 2
r x y là khoảng cách từ M đến gốc O . Vì IO  2 5  3 nên O nằm ngoài (C) và ta có:
2 5  3  r  2 5  3  2 5  3  m r m  2 5  3  m
Với P r m , maxP max 2 5  3  m , 2 5  3  m 18
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”  2 5 3 m 10    1
 0  2 5  3 m 10
Để thỏa mãn bài toán ta phải có:   
 2 5  3 m 10  1
 0  2 5  3 m 10 
2 5 13  m  2 5  7  
 2 5  7  m  2 5  7 .
2 5  7  m 13 2 5 Ta có: 2 5  7  2
 ,5;2 5  7 11,5  m 2  ;1;0;...;1 
1 Tập S có 14 phần tử Số tập con m.vn ie
khác rỗng của tập S là: 14 2 1  16383.
gh Câu 34. Gọi S là tập hợp các giá trị của m để hàm số 3 2
y x  3x m đạt giá trị lớn nhất bằng racn 50  it
trên [ 2; 4]. Tổng các phần tử thuộc S là th n A. 4 . B. 36 . C. 140 . D. 0 . ye
Lời giải: Chọn A lux  Xét hàm số 3 2
g(x)  x  3 x m
gx x x . Xét g x 0  0  . s:// có   2 3 6  x  2 ttp h
Khi đó giá trị lớn nhất của hàm số 3 2
y x  3x m trên [  2;4] là:
max y  maxy 0; y  2
 ; y2; y4  maxm ; m 4 ; m20 ; m16. x   2  ;4 m  50
Trường hợp 1: Giả sử max y m  50   . m  50 
Với m  50 thì m 16  66  50 . Với m 50
 thì m  20  70  50. m  54
Trường hợp 2: Giả sử max y m  4  50   . /vietgold m  46 
Với m  54  m  54  50 . k.com Với m 46
 thì m  20  66  50. ceboo m  70
.fa Trường hợp 3: Giả sử max y m20 50   m  30 
Với m  70 thì m 16  86  50 . Với m  30
 thì m 16 14  50 , m  30  50; m  4  34  50 . https://www m  34
Trường hợp 4: Giả sử max y m 16  50   . m  66 
Với m  34 thì m  34  50, m  4  30  50, m  20 14  50 . Với m  66
 thì m  66  50 . Vậy S  3  0;3 
4 . Do đó tổng các phẩn tử của S là: 3  0 34  4 . Câu 35. Cho hàm số 3 2 f x 3x 9x 12x m
2 . Có bao nhiêu giá trị nguyên của m
20; 20 sao cho với mọi số thực , a , b c
1;3 thì f a , f b , f c là độ dài ba cạnh của một tam giác. 19
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 A. 20 . B. 27 . C. 25 . D. 4 .
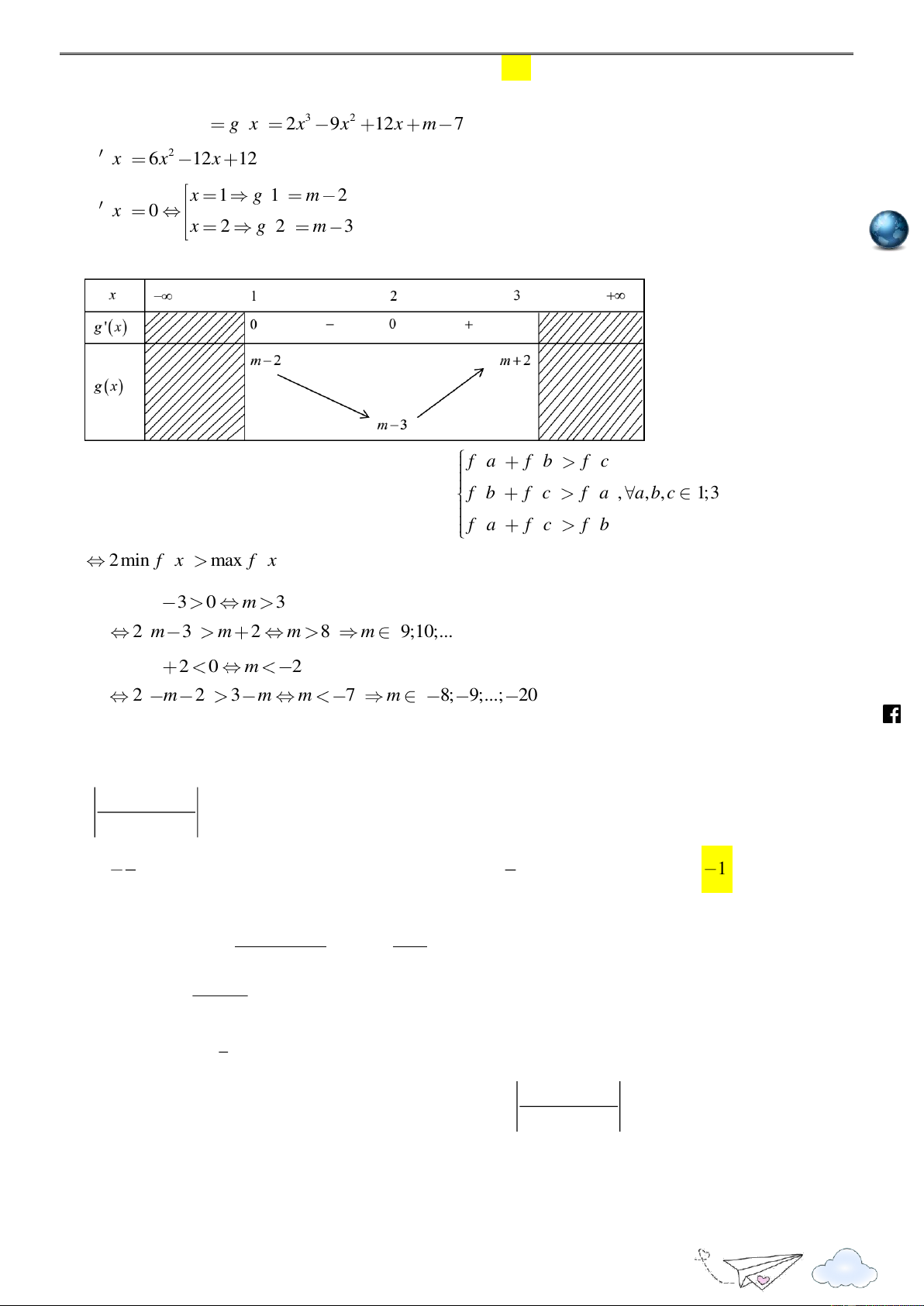
Lời giải: Chọn C + Xét hàm số 3 2 y g x 2x 9x 12x m 7 2 g x 6x 12x 12 x 1 g 1 m 2 g x 0 . x 2 g 2 m 3 h Bảng biến thiên ttp s:// lu ye n th it ra cngh f a f b f c ie
f a ; f b ; f c là ba cạnh của một tam giác f b f c
f a , a,b, c 1;3 m.vn f a f c f b 2 min f x max f x 1;3 1;3 + TH1: m 3 0 m 3 * 2 m 3 m 2 m 8 m
9;10;...; 20 có 12 giá trị của m . + TH2: m 2 0 m 2 * 2 m 2 3 m m 7 m
8; 9;...; 20 có 13 giá trị của m .
Vậy có tất cả 25 giá trị của m . https://www
Câu 36. Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số 2
x mx  2m y  1
 ;1 bằng 3 . Tính tổng tất cả các phần tử của S . x  trên đoạn   2 .fa 8 5 ceboo A. . B. 5 . C. . D. 1. 3 3 k.com
Lời giải: Chọn D
x mx m
Xét hàm số f x 2 2 4   x  2 
m trên đoạn  1   ;1 /v x  2 x  2 . iet 4 gold
Có f  x 1      ; f x 0 x 0 . x  22 Khi đó f   1
1    m ; f 0  m ; f   1  1   m . 3 2
x mx  2m + Nếu 1
  m  0 thì giá trị lớn nhất của hàm số y  1  ;1 bằng m . x  trên đoạn   2 Suy ra m   3  m  3  . 20
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”  m  0 m  0   2 1
x mx  2m + Nếu  1
  m  0  m  1   1
  m   thì giá trị lớn nhất của hàm số y  trên 2     x 2 m  1  m 1  m    2 đoạn  1  
;1 bằng m . Suy ra m   3  m  3  .  m.vn m  0 m  0 2 ie   1
x mx  2m + Nếu  1
  m  0  m  1
    m  0 thì giá trị lớn nhất của hàm số y  trên gh 2     x 2 m  1  m 1  m    2 racn it đoạn  1  
;1 bằng 1 m . Suy ra 1 m  3  m  2 . th n 2
x mx  2m ye + Nếu m
  0  m  0 thì giá trị lớn nhất của hàm số y  1  ;1 bằng x  trên đoạn   2 lu s://
1 m . Suy ra 1 m  3  m  2 . ttpm  3  h Vậy  m  2
Câu 37. Xét hàm số   2
f x x ax b , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên  1  ; 
3 . Khi M nhận giá trị nhỏ nhất có thể được, tính a  2b . A. 3 . B. 4 . C. 4  . D. 2 .
Lời giải: Chọn C M f   
1  b a 1 ; M f 3  b  3a  9   1 Ta có:  .
M f  
1  b a 1  2M  2
b  2a  2 2 
/vietgold Từ  1 và 2, kết hợp với x y z xyz , ta được:
4M b a 1  b  3a  9  2
b  2a  2  b a 1 b  3a  9 2b  2c  2  8 k.com
M  2. Vậy M  2 . ceboo
b a 1  2 .fa 
Dấu “  ” xảy ra khi và chỉ khi  b  3a  9  2 và b a 1; b  3a  9; 2
b  2a  2 cùng dấu.
ba 1  2  a  2  Do đó: 
a  2b  4 . https://www b   1  1
Câu 38. Biết giá trị lớn nhất của hàm số 2 y
4  x x
m là 18. Mệnh đề nào sau đây đúng? 2
A. 5  m 10 .
B. 10  m 15.
C. 15  m  20 .
D. 0  m  5.
Lời giải: Chọn C 1     Cách 1: 2 y
4  x x   m , TXĐ:  2
 ;2. Đặt x  2sint , t   ;   2  2 2  . 1    Xét biểu thức 2 A
4  4sin t  2sin t  1
 2cost  2sin t  1
 2 2 sin t    2 2  4  2 . 21
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020          3  2    5    1 1 t   ; 
  t    ;  
 sin t   1    2 2 sint     2 2     2 2   4   4 4  2  4  2  4  2 2    1 5
nên 0  2 2 sin t     .  4  2 2 
Dấu “=” xảy ra khi t   2 1 5
Vậy giá trị lớn nhất của hàm số 2 y
4  x x   m là m h 2 2 ttp 5 s:// Theo giả thiết m 18 nên m 15,5 . 2 lu
Vậy 15  m  20 . ye n Cách 2: th 1 it Xét f x 2
 4  x x  , Tập xác định D   2  ;2 . r 2 acnx gh
f  x  1. 2 4  x ie m.vn   x f x  0  1  0 2  4  x  ,
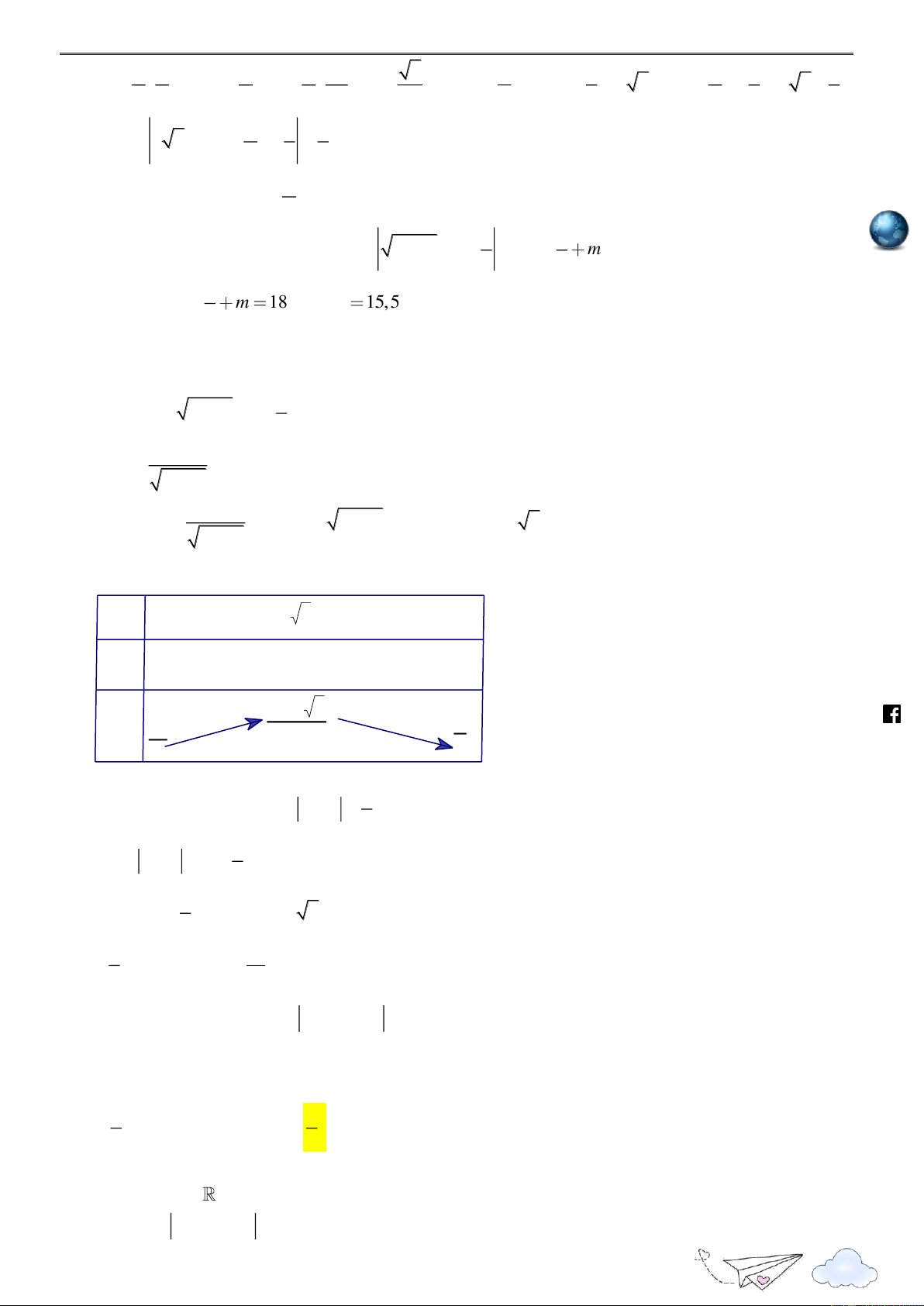
x x  0  x  2 . 2 4  x Bảng biến thiên x -2 2 2 + 0 _ f /(x) -1+4 2 f(x) 3 -5 ht 2 2 tp 2 s://www
Từ bảng biến thiên có  f x 5 0  . 2 .fa
y f x 5  m   m ceboo . 2 5 k.com
 max y   m , khi x  2 , theo giả thiết có max y 18. x   2  ;2 2 x   2  ;2 5 /v   m  31 18  m
15,5 . Vậy 15  m  20 . iet 2 2 gold
Câu 39. Cho hàm số f x 6 3 3
x x m  2x . Gọi S là tập tất cả các giá trị thực của tham số m để
Giá trị nhỏ nhất của hàm số f x bằng 1. Tổng tất cả các phần tử của S bằng 1 5 A. . B. . C. 2 . D. 0 . 4 4
Lời giải: Chọn B Tập xác định: 6 3 3
y f (x)  x x m  2x . 22
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Đặt 3
t x hàm số ban đầu trở thành hàm số 2
y g(t)  t t m  2t . Tam thức bậc hai 2 (
h t)  t t m có biệt thức   1 4m . Ta xét 2 trường hợp sau: 1
Trường hợp 1:   1 4m  0  m  2  (
h t)  t t m có 2 nghiệm phân biệt t , t t t . 1 2  4 1 2
Vì t t  1
  0 nên t t  0 hoặc t  0  t . 1 2 1 2 1 2 1 1
+) Nếu t t  0 thì P t t m  0 kết hợp với m  ta có 0  m  . Khi đó. m.vn 1 2 1 2 4 4 ie 1 3 gh g( )   m 1 0 . 2 4 racn
+) Nếu t  0  t thì g(t )  2  t  0 . it 1 2 2 2 th
Suy ra trong trường hợp này hàm số y g(t) không thể có giá trị nhỏ nhất bằng 1 trên . n ye 1
Trường hợp 2:   1 4m  0  m  2  (
h t)  t t m  0, t   . lu 4 s:// 2  1  1 1 Khi đó, 2 2
y g(t)  t t m  2t t t m t
m   m  , t   .   ttp  2  4 4 h 1 1
min f (x)  min g(t)  g( )  m  . xt 2 4  1  1 m m     4  4 5
Theo đề min f (x)  1      m  . x 1 5 4 m 1    m   4  4
Câu 40. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm 2
x mx m số y
trên 1;2 bằng 2. Số phần tử của tập S là /vietgold x 1 A. 3. B. 1. C. 4. D. 2.
k.com Lời giải: Chọn D ceboo
x mx m
.fa Đặt f x 2
f x xác định và liên tục trên đoạn 1; 2. x  , ta có hàm số   1 2 x  2x
Có: f  x    , x  1;2 . x   0 2 1  m 1 2m
max f x  f 2 4 3 
min f x  f    https://www Suy ra: ; 1 . 1;2 3 1;2 2  f  2  2  f    1  2
Do đó max f x  max f 2 ; f   1  . Theo bài ta có:    1;2  f   1  2   f 2  2  Trường hợp 1:  4  3m  2 10   2     f  2  2  m m 3  2 Ta có:    3 3    m  .  f   1  2  1 2m   5 3  3 2     m  2  2 2 Trường hợp 2: 23
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020  1 2m  3 5   2     f    1  2  m m 2  5 Ta có:    2 2    m   .  f 2  2  4  3m   10 2  3 2     m  3  3 3
Vậy có giá trị của tham số m thỏa yêu cầu bài toán. Do đó tập S có hai phần từ. h ttp s:// lu ye n th it racngh ie m.vn https://www .fa ceboo k.com /vietgold 24