Bài tập một số điểm đặc biệt của đồ thị hàm số – Diệp Tuân Toán 12

Bài tập một số điểm đặc biệt của đồ thị hàm số – Diệp Tuân Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

18 9 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

503

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

A. LÝ THUYẾT.

I. Tìm điểm cố định của họ đường cong

① Bài toán: Xét họ đường cong

()

có phương trình

( , )y f x m

, trong đó

là hàm đa thức theo

biến

với

là tham số sao cho bậc của

không quá 2. Hãy tìm những điểm cố định thuộc họ

đường cong khi

thay đổi?

② Phương pháp.

o Bước 1: Đưa phương trình

( , )y f x m

về dạng phương trình theo ẩn

có dạng sau:

0Am B

hoặc

0Am Bm C  

o Bước 2: Cho các hệ số bằng

, ta thu được hệ phương trình và giải hệ phương trình:











hoặc

















o Bước 3: Kết luận

 Nếu hệ vô nghiệm thì họ đường cong

()

không có điểm cố định.

 Nếu hệ có nghiệm thì nghiệm đó là điểm cố định của

()

③ Ví dụ minh họa.

Ví dụ 1.(THPT Chuyên Thái Bình 2020) Họ parabol

   

: 2 3 2

P y mx m x m    

 

0m 

luôn

tiếp xc với đường th󰉠ng

cố định khi

thay đổi. Đường th󰉠ng

đó đi qua điểm nào dưới đây?

 

0; 2 .

 

0;2 .

 

1;8 .

 

1; 8 .

Lời giải

................................................................................................

Ví dụ 2.(THPT Chuyên Lê Hồng Phong 2018)

Biết đồ thị hàm số

   

4 6 4 12 7 18y m x m x mx m      

(với

là tham số thực) có ba điểm

cố định th󰉠ng hàng. Viết phương trình đường th󰉠ng đi qua ba điểm cố định đó.

48 10yx  

. B.

31yx

. C.

2yx

. D.

21yx

Lời giải

................................................................................................

§BI 8. MỘT SỐ ĐIỂM ĐẶT BIỆT

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

504

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Ví dụ 3.Đồ thị của hàm số

3y x x mx m   

(

là tham số) luôn đi qua một điểm

cố định

có tọa độ là

 

1; 4M 

. B.

 

1; 4M 

. C.

 

1;2M 

. D.

 

1; 2M 

Lời giải

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 1. Đồ thị của hàm số

( 1) 3y m x m   

(

là tham số) luôn đi qua một điểm

cố định có

tọa độ là

(0;3)M

. B.

(1;2)M

. C.

( 1; 2)M

. D.

(0;1)M

Lời giải

................................................................................................

Câu 2. Đồ thị của hàm số

21y x mx m   

(

là tham số) luôn đi qua một điểm

cố định có

tọa độ là

 

0;1M

. B.

;







. C.

;







. D.

( 1;0)M

Lời giải

................................................................................................

Câu 3. Đồ thị của hàm số

3y x x mx m   

(

là tham số) luôn đi qua một điểm

cố định có

tọa độ là

 

1;2M

. B.

 

1; 4M

. C.

 

1; 2M

. D.

 

1; 4M

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

505

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Câu 4. Biết đồ thị

 

của hàm số

23y x mx  

luôn đi qua một điểm

cố định khi

thay

đổi, khi đó tọa độ của điểm

là

 

1;1M

. B.

 

1;4M

. C.

 

0; 2M

. D.

 

0;3M

Lời giải

................................................................................................

Câu 5. Biết đồ thị

 

của hàm số

 

( 1)

m x m







luôn đi qua một điểm

cố định khi

thay đổi. Tọa độ điểm

khi đó là









. B.

 

0;1M

. C.

 

1;1M

. D.

 

0; 1M

Lời giải

................................................................................................

Câu 6. Hỏi khi

thay đổi đồ thị

()

của hàm số

33   y x mx x m

đi qua bao nhiêu điểm cố

định ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 7. Hỏi khi

thay đổi đồ thị

()

của hàm số

(1 2 ) 3 1    y m x mx m

đi qua bao nhiêu

điểm cố định ?

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

506

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 8. Biết đồ thị

()

của hàm số

2016y x mx m   

luôn luôn đi qua hai điểm

và

cố

định khi

thay đổi. Tọa độ trung điểm

của đoạn th󰉠ng

là

( 1;0)I

. B.

(1;2016)I

. C.

(0;1)I

. D.

(0;2017)I

Lời giải

................................................................................................

Câu 9. Biết đồ thị

()

của hàm số

2 (1 ) 1

( 2)

x m x m

   

  



luôn luôn đi qua một điểm

 

;

M x y

cố định khi

thay đổi, khi đó



bằng

1

. B.

3

. C.

. D.

2

Lời giải

................................................................................................

Câu 10. Cho hàm số

4    y x mx x m

có đồ thị

()

và

là điểm cố định có hoành độ âm

của

()

. Giá trị của

để tiếp tuyến tại

của

()

vuông góc với đường phân giác góc phần tư

thứ nhất là

3m

. B.

6m

. C.

2m

. D.

m 

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

507

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 11. Cho hàm số

   

2 3 2 7y m x m x m     

có đồ thị

 

Kh󰉠ng định nào sau đây là kh󰉠ng định đng?

 

không đi qua điểm cố định nào. B.

 

có đng hai điểm cố định.

 

có đng ba điểm cố định. D.

 

có đng một điểm cố định.

Lời giải

................................................................................................

Câu 12. Cho hàm số

2 2 1    y x mx m

có đồ thị

()

. Gọi

là điểm cố định có hoành độ

dương của

()

. Khi tiếp tuyến tại

của

()

song song với đường th󰉠ng

: 16d y x

thì giá trị

của

là

5m

. B.

4m

. C.

1m

. D.

m

Lời giải

................................................................................................

II. Tìm điểm có tọa độ nguyên:

① Bài toán: Cho đường cong

()C

có phương trình

()y f x

(hàm phân thức). Hãy tìm những điểm

có tọa độ nguyên của đường cong?

Nhận xét: những điểm có tọa độ nguyên là những điểm sao cho cả hoành độ và tung độ của

điểm đó đều là số nguyên.

② Phương pháp.

o Bước 1: Thực hiện phép chia đa thức chia tử số cho mẫu số.

o Bước 2: Lí luận để giải bài toán.

③ Ví dụ minh họa.

Ví dụ 4. Trên đồ thị hàm số







có bao nhiêu điểm có tọa độ nguyên?

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

508

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Ví dụ 5. Số điểm có tọa độ là các số nguyên của đồ thị hàm số:







là:

. B.

. C.

. D.

Lời giải

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 13. Trên đồ thị

()C

của hàm số





có bao nhiêu điểm có tọa độ nguyên ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 14. Trên đồ thị

()C

của hàm số





có bao nhiêu điểm có tọa độ là các số nguyên dương

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 15. Trên đồ thị

()C

của hàm số





có bao nhiêu điểm có tọa độ nguyên ?

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

509

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 16. Trên đồ thị

()C

của hàm số





số điểm có tọa độ nguyên là

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 17. Trên đồ thị

()C

của hàm số







có bao nhiêu điểm có tọa độ nguyên ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 18. Trên đồ thị

()C

của hàm số







có bao nhiêu điểm có tọa độ nguyên ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 19. Trên đồ thị

()C

của hàm số







có bao nhiêu điểm có tọa độ nguyên ?

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

510

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 20. Trên đồ thị

()C

của hàm số

8 11







có bao nhiêu điểm có tọa độ nguyên ?

. B.

. C.

. D. 0.

Lời giải

................................................................................................

Câu 21. Trong tất cả các điểm có tọa độ nguyên thuộc đồ thị

()C

của hàm số







số điểm có

hoành độ lớn hơn tung độ là

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 22. Có bao nhiêu điểm thuộc đồ thị

()C

của hàm số





có tọa độ nguyên ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 23. Cho hàm số







có đồ thị

()C

. Hỏi trên

()C

có bao nhiêu điểm có hoành độ và

tung độ là các số tự nhiên.

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

511

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

III. Tìm điểm có tính chất đối xứng:

Bài toán: Cho đường cong

()C

có phương trình

()y f x

. Tìm những điểm đối xứng nhau qua một

điểm, qua đường th󰉠ng.

① Loại 1:

Cho đồ thị

 

:C y Ax Bx Cx D   

trên đồ thị

 

tìm những cặp điểm đối xứng nhau

qua điểm

( , )

I x y

② Phương pháp.

o Gọi

   

3 2 3 2

; , ;M a Aa Ba Ca D N b Ab Bb Cb D     

là hai điểm trên

 

đối xứng nhau

qua điểm

o Ta có

 

3 3 2 2

( ) 2 2

a b x

A a b B a b C a b D y









      





Giải hệ phương trình tìm được

,ab

từ đó tìm được toạ độ

,.MN

③ Ví dụ minh họa.

Ví dụ 6. Tìm tất cả các giá trị của tham số thực

để trên đồ thị hàm số

1y x x m   

có hai

điểm phân biệt đối xứng nhau qua điểm

 

0;1I

2m 

. B.

12m

. C.

1m 

. D.

1m 

Lời giải

Chọn A.

Giả sử

 

;M x y

là điểm thuộc đồ thị hàm số đã cho, ta được

 

0 0 0

11y x x m   

Khi đó nếu

 

;

N x y

là điểm đối xứng với

qua

thì

 

0 0 0

N x y

y y y y















   



  











Để

cũng thuộc đồ thị hàm số đã cho thì ta có phương trình

0 0 0

2 1 (2)y x x m     

Lấy

 

cộng

 

vế theo vế và biến đổi ta được phương trình

2xm

, phương trình này có

nghiệm khi và chỉ khi

2m 

Hơn nữa để

0 0 0

0M N x x x     

, ta chọn

2m 

Đặc biệt : Trên đồ thị

 

tìm những cặp điểm đối xứng nhau qua gốc tọa độ

 

0;0O

thì ta có

 

3 3 2 2

( ) 2 0

A a b B a b C a b D









      





Giải hệ phương trình tìm được

,ab

từ đó tìm được toạ độ

,MN

Ví dụ 7. Có bao nhiêu giá trị nguyên của

lớn hơn

2019

để đồ thị hàm số

 

3 2 2 2

3 3 1 1y x mx m x m     

có hai điểm phân biệt đối xứng nhau qua gốc tọa độ.

2017

. B. Vô số. C.

2019

. D.

2018

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

512

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 24. Tìm cặp điểm thuộc đồ thị

 

của hàm số







đối xứng nhau qua gốc tọa độ

 

2; 2

và

 

2; 2

. B.

 

3; 2

và

 

3; 2

 

2; 2

và

 

2; 2

. D.

 

2; 2

và

 

2;2

Lời giải

................................................................................................

Câu 25. Trên đồ thị

 

của hàm số

5 6 3y x x x   

có bao nhiêu cặp điểm đối xứng nhau qua

gốc tọa độ ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 26. Số cặp điểm thuộc đồ thị

 

của hàm số

32y x x  

đối xứng với nhau qua điểm

 

2;18I

là

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

513

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 27. Cặp điểm thuộc đồ thị

()C

của hàm số

32  y x x

đối xứng nhau qua điểm

(2;18)I

là

(1;2)

và

(3;34)

. B.

(3;2)

và

(1;34)

. C.

(0; 2)

và

(4;74)

. D.

(1;2)

và

( 1; 6)

Lời giải

................................................................................................

Câu 28. Cặp điểm thuộc đồ thị

()C

của hàm số

4 9 4   y x x x

đối xứng nhau qua gốc tọa

(3;22)

và

( 3; 22)

. B.

(2;14)

và

( 2; 14)

. C.

(1;10)

và

( 1; 10)

. D.

(0;4)

và

(4;40)

Lời giải

................................................................................................

Câu 29. Các giá trị thực của tham số

để đồ thị

()

của hàm số

3  y x x m

có hai điểm phân

biệt đối xứng nhau qua gốc tọa độ là

10  m

. B.

0m

. C.

3m

. D.

0m

Lời giải

................................................................................................

Câu 30. Tập hợp tất cả các giá trị thực của

để trên đồ thị

()

của hàm số







x mx m

có

hai điểm phân biệt đối xứng nhau qua gốc tọa độ là

 

0;

. B.

 

;0 \

2 13









. C.





1; 

. D.

 

1 4 4

;0 ; ;

2 3 3

   



   













Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

514

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Câu 31. Tọa độ hai điểm trên đồ thị

 

của hàm số

32y x x   

sao cho hai điểm đó đối xứng

nhau qua điểm

 

–1; 3M

là

   

1;0 ; 1;6

. B.

   

1;0 ; 1;6

. C.

 

0;2

;

 

2;4

   

1;0 ; 1;6

Lời giải

................................................................................................

① Loại 2: Cho đồ thị

 

:C y Ax Bx Cx D   

trên đồ thị

 

tìm những cặp điểm đối xứng nhau

qua đường th󰉠ng

:d y A x B

② Phương pháp.

o Gọi

   

3 2 3 2

; , ;M a Aa Ba Ca D N b Ab Bb Cb D     

là hai điểm trên

 

đối xứng nhau

qua đường th󰉠ng

o Ta có:

(1)

. 0 (2)

MN u















(với

là trung điểm của

và

là vectơ chỉ phương của

o Giải hệ phương trình tìm được

,.MN

③ Ví dụ minh họa.

Ví dụ 8. Tọa độ cặp điểm thuộc đồ thị

()C

của hàm số







đối xứng nhau qua đường th󰉠ng

: 2 6 0  d x y

là

 

4;4

và

 

1; 1

. B.

 

1; 5

và

 

1; 1

. C.

 

0; 2

và

 

3;7

. D.

 

1; 5

và

 

5;3

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

515

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 32. Tìm trên đồ thị hàm số

97y x x  

hai điểm phân biệt mà chng đối xứng với nhau qua

trục tung.

 

2; 3A 

 

2; 3B 

. B.

 

3;7A

 

3;7B 

 

4;4A

 

4; 4B 

. D. Không tồn tại.

Lời giải

................................................................................................

Câu 33. (THPT Nguyễn Huệ 2020)

Cặp điểm thuộc đồ thị

()C

của hàm số

y x x

đối xứng nhau qua đường th󰉠ng

d y x

là

 

1;2

và

 

2; 10

. B.

 

2; 1

và

 

2;1

. C.

 

1; 2

và

 

1;2

. D.

 

1;2

và

 

1; 2

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

516

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Câu 34. (THPT Hai Bà Trưng 2020)

Cặp điểm thuộc đồ thị

()C

của hàm số

1 11

    y x x x

mà chng đối xứng nhau qua trục

tung là









và









. B.







và















và









. D.









và









Lời giải

................................................................................................

Câu 35. Điều kiện của tham số

để trên đồ thị

 

của hàm số

 

3 1 2 1y x m x mx m     

có ít nhất hai điểm phân biệt đối xứng nhau qua trục

là

0m 

. B.

0m 

. C.

2m 

. D.

2m 

Lời giải

................................................................................................

IV. Tính chất các điểm liên quan đến khoảng cách:

1. Lí thuyết:

o Cho hai điểm

       

112 2 2 112

; ; ; PQP x y Q xyxy xy    

o Cho điểm

 

;M x y

và đường th󰉠ng

:0d Ax By C  

thì khoảng cách từ

đến

là

 

;

Ax By C

h M d







o Khoảng cách từ

 

;M x y

đến tiệm cận đứng

xa

là

h x a

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

517

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

o Khoảng cách từ

 

;M x y

đến tiệm cận ngang

yb

là

h y b

2. Các bài toán thường gặp:

① Bài toán 1:

Cho hàm số

 

0, 0

ax b

c ad bc



  





có đồ thị

 

. Hãy tìm trên

()C

hai điểm

và

thuộc hai nhánh đồ thị hàm số sao cho khoảng cách

ngắn nhất.

② Phương pháp.

 

có tiệm cận đứng



do tính chất của hàm phân thức, đồ thị nằm về hai phía của tiệm

cận đứng. Nên gọi hai số



là hai số dương.

o Nếu

thuộc nhánh trái thì

d d d

c c c



       

;

()

y f x

o Nếu

thuộc nhánh phải thì

d d d

c c c



       

;

()

y f x

o Sau đó tính

         

2 2 2

B A B A B A

AB x x y y a a y y



         





o Áp dụng bất đ󰉠ng thức Côsi (Cauchy), ta sẽ tìm ra kết quả.

③ Ví dụ minh họa.

Ví dụ 9.(THPT Chuyên Thái Bình 2018) Cho

là hai điểm di động và thuộc hai nhánh khác

nhau của đồ thị







. Khi đó khoảng cách

bé nhất là?

. B.

2 10

. C.

. D.

Lời giải

................................................................................................

Ví dụ 10.(Tạp chí THTT 2018)

và

là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số





. Khi đó độ dài đoạn

ngắn nhất bằng

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

518

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Ví dụ 11.(Sở GD & ĐT Hà Nam 2018) Biết

 

;

A x y

 

;

B x y

là hai điểm thuộc hai nhánh khác

nhau của đồ thị hàm số







sao cho độ dài đoạn th󰉠ng

nhỏ nhất. Tính

A B A B

P y y x x  

10P 

. B.

6P 

. C.

6 2 3P 

. D.

10 3P 

Lời giải

................................................................................................

Ví dụ 12.(THPT Chuyên Thái Bình 2018) Cho

là hai điểm di động và thuộc hai nhánh khác

nhau của đồ thị







. Khi đó khoảng cách

bé nhất là?

. B.

2 10

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

519

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 36. Gọi

A, B

là hai điểm thuộc hai nhánh khác nhau trên đồ thị

 

của hàm số







, độ

dài ngắn nhất của đoạn th󰉠ng

là

. B.

. C.

. D.

Lời giải

................................................................................................

① Bài toán 2:

Cho đồ thị hàm số

 

có phương trình

()y f x

. Tìm tọa độ điểm

thuộc

()C

để

tổng khoảng cách từ

đến hai trục tọa độ nhỏ nhất.

② Phương pháp.

o Gọi

 

;M x y

và tổng khoảng cách từ

đến hai trục tọa độ là

thì

d x y

o Xét các khoảng cách từ

đến hai trục tọa độ khi

nằm ở các vị trí đặc biệt: Trên trục hoành,

trên trục tung.

o Sau đó xét tổng quát, những điểm

có hoành độ, hoặc tung độ lớn hơn hoành độ hoặc tung độ

của

khi nằm trên hai trục thì loại đi không xét đến.

o Những điểm còn lại ta đưa về tìm giá trị nhỏ nhất của đồ thi hàm số dựa vào đạo hàm rồi tìm

được giá trị nhỏ nhất của

③ Ví dụ minh họa.

Ví dụ 13.(THPT Triệu Sơn 2018) Cho hàm số







 

và điểm

 

;M a b

thuộc đồ thị

 

. Đặt

 

32T a b ab  

, khi đó để tổng khoảng cách từ điểm

đến hai trục toạ độ là nhỏ nhất thì mệnh

đề nào sau đây là đng?

31T   

. B.

11T  

. C.

13T

. D.

24T

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

520

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

................................................................................................

Ví dụ 14.(THPT Chuyên Trần Phú 2018) Cho hàm số







có đồ thị

 

. Biết đồ thị

 

có

hai điểm phân biệt

và tổng khoảng cách từ

hoặc

tới hai tiệm cận là nhỏ nhất. Khi đó

có giá trị bằng

42MN 

. B.

6MN 

. C.

43MN 

. D.

62MN 

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

521

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Ví dụ 15.(THPT Kinh Môn 2018) Cho hàm số







có đồ thị

 

. Giả sử

là hai điểm thuộc

 

và đối xứng với nhau

qua giao điểm của hai đường tiệm cận. Dựng hình vuông

AEBF

. Tìm diện tích nhỏ nhất của hình vuông

AEBF

min

82S 

. B.

min

42S 

min

8S 

. D.

min

16S 

Lời giải

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 37. Tọa độ các điểm thuộc đồ thị

 

của hàm số







mà có tổng khoảng cách đến hai

đường tiệm cận của

 

bằng 4 là

A. . B. .

C. . D. .

Lời giải

................................................................................................

   

4;3 , 2;1

   

2;5 , 0; 1

       

2;5 , 0; 1 , 4;3 , 2;1

   

2;5 , 4;3

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

522

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 38. Tọa độ điểm

có hoành độ dương thuộc đồ thị hàm số







sao cho tổng khoảng

cách từ

đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là

(4;3)M

. B.

(3;5)M

. C.

(1; 3)M 

. D.

(0; 1)M 

Lời giải

................................................................................................

Câu 39. Cho hàm số







có đồ thị

 

. Gọi

là một điểm thuộc đồ thị

 

và

là tổng

khoảng cách từ

đến hai tiệm cận của

 

. Giá trị nhỏ nhất của

có thể đạt được là

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 40. Cho hàm số







có đồ thị

 

. Tổng khoảng cách từ một điểm

thuộc

 

đến hai

tiệm cận của

 

đạt giá trị nhỏ nhất bằng ?

. B.

. C.

. D.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

523

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 41. Cho hàm số







có đồ thị

 

. Tổng khoảng cách từ một điểm

thuộc

 

đến hai hai trục tọa độ đạt giá trị nhỏ nhất bằng ?

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 42. Cho hàm số







có đồ thị

 

. Tổng khoảng cách từ một điểm

thuộc

 

đến hai

tiệm cận của

 

đạt giá trị nhỏ nhất bằng

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 43. Tọa độ tất cả các điểm thuộc đồ thị

 

của hàm số







sao cho tổng khoảng cách từ

điểm đó đến 2 tiệm cận là nhỏ nhất là

 

1;1

. B. .

C. . D. và .

Lời giải

................................................................................................

 

1 3;1 3

 

1 3;1 3

 

2 3;1 3

 

2 3;1 3

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

524

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Câu 44. Cho hàm số







có đồ thị

 

. Tổng khoảng cách từ một điểm

thuộc

 

đến hai

hai trục tọa độ đạt giá trị nhỏ nhất bằng ?

. B.

. C.

. D.

Lời giải

................................................................................................

① Bài toán 3:

Cho đồ thị

()C

có phương trình

()y f x

. Tìm điểm

trên

()C

sao cho khoảng cách

từ

đến

bằng

lần khoảng cách từ

đến trục

② Phương pháp.

o Theo đầu bài ta có

 

f x kx

y kx

y k x

y kx

f x kx









  











③ Ví dụ minh họa.

Ví dụ 16. Cho điểm

thuộc đồ thị

 

của hàm số







, biết

có hoàng độ

và khoảng

cách từ

đến trục

bằng ba lần khoảng cách từ

đến trục

. Giá trị có thể có của

là

1a 

hoặc

a 

. B.

1a 

hoặc

x 

. C.

1a 

hoặc

a 

. D.

1a 

hoặc

a 

Lời giải

................................................................................................

Ví dụ 17. Có bao nhiêu điểm

thuộc đồ thị

 

của hàm số







sao cho khoảng cách từ

điểm

đến tiệm cận ngang bằng 5 lần khoảng cách từ

đến tiệm cận đứng?

. B.

. C.

. D.

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

525

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

................................................................................................

Ví dụ 18. Tọa độ các điểm thuộc đồ thị

 

của hàm số







cách đều tiệm cận đứng và trục

hoành là

   

2;1 , 4;3MM

. B.

   

0; 1 , 4;3MM

. C.

   

0; 1 , 3;2MM

. D.

   

2;1 , 3;2MM

Lời giải

................................................................................................

Ví dụ 19. Tọa độ các điểm thuộc đồ thị

 

của hàm số







cách đều hai tiệm cận của

 

   

1;1 ; 4; 6MN  

.B.

   

1;1 ; 3;4MN

. C.

   

1;3 ; 3;3MN

. D.

   

1;3 ; 3;3MN

Lời giải

................................................................................................

Ví dụ 20. Tọa độ điểm

 

MC

của hàm số







cách đều hai đường tiệm cận của

 

là

 

2;1M

. B.

   

0; 1 , 4;3MM

. C.

5; , 3;

   



   

   

. D.

 

2;2M 

Lời giải

................................................................................................

④ Câu hỏi trắc nghiệm.

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

526

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 45. Tọa độ điểm

thuộc đồ thị

 

của hàm số







cách đều hai trục tọa độ là

   

1; 1 , 3;3MM

. B.

 

1;3M 

. C.

 

1; 1M 

. D.

 

3;3M

Lời giải

................................................................................................

Câu 46. Đồ thị hàm số

2 12 13y x mx x   

có hai điểm cực trị cách đều trục tung khi và chỉ khi:

1m 

. B.

0m 

. C.

1; 2mm   

. D.

2m 

Lời giải

................................................................................................

Câu 47. Hỏi trên đồ thị

 

của hàm số







có bao nhiêu điểm cách đều hai trục tọa độ?

. B.

. C.

. D.

Lời giải

................................................................................................

① Bài toán 4:

Cho đồ thị hàm số

()C

có phương trình

 

( ) 0, 0

ax b

y f x c ad bc

cx d



    



. Tìm tọa

độ điểm

trên

()C

sao cho độ dài

ngắn nhất (với I là giao điểm hai tiệm cận).

② Phương pháp.

o Tiệm cận đứng





; tiệm cận ngang



o Ta tìm được tọa độ giao điểm

;









của hai tiệm cận.

o Gọi

 

;

Mx y

là điểm cần tìm. Khi đó:

 

M M M

IM x y g x

   

    

   

   

o Sử dụng phương pháp tìm GTLN - GTNN cho hàm số

để thu được kết quả.

③ Ví dụ minh họa.

Ví dụ 21. Cho hàm số







có đồ thị

 

. Gọi

là giao điểm hai đường tiệm cận của

 

. Biết

tọa độ điểm

 

;

M x y

có hoành độ dương thuộc đồ thị

 

sao cho

ngắn nhất. Khi đó giá trị

xy

bằng

. B.

. C.

. D.

2

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

527

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Ví dụ 22. Cho hàm số







có đồ thị

 

. Gọi

là khoảng cách từ một điểm

trên

 

đến

giao điểm của hai tiệm cận. Giá trị nhỏ nhất có thể có của

là

. B.

. C.

. D.

Lời giải

................................................................................................

Ví dụ 23. Khoảng cách ngắn nhất từ điểm

 

MC

của hàm số







đến

 

1,4I

. B.

. C.

2 2 2

. D.

2 2 2

Lời giải

................................................................................................

① Bài toán 5:

Cho đồ thị hàm số

()C

có phương trình

()y f x

và đường th󰉠ng

:0d Ax By C  

Tìm điểm

trên

()C

sao cho khoảng cách từ

đến

là ngắn nhất.

② Phương pháp.

o Gọi

thuộc

()C

 

0 0 0 0

; ; ( )I x y y f x

o Khoảng cách từ

đến

là

 

( ) ;

Ax By C

g x h I d







o Khảo sát hàm số

()y g x

để tìm ra điểm

thỏa mãn yêu cầu.

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

528

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

③ Ví dụ minh họa.

Ví dụ 24. Tọa độ điểm

thuộc đồ thị hàm số







cách đường tiệm cận đứng của đồ thị hàm

số một khoảng bằng

là

   

0; 1 ; 2;7

. B.

   

1;0 ; 2;7

. C.

   

0;1 ; 2; 7

. D.

   

0; 1 ; 2;7

Lời giải

................................................................................................

Ví dụ 25.(THPT Chuyên Bắc Ninh 2018) Gọi

 

; M a b

là điểm trên đồ thị hàm số







mà có

khoảng cách đến đường th󰉠ng

: 3 6d y x

nhỏ nhất. Khi đó

21ab

. B.

2ab

. C.

2ab  

. D.

23ab

Lời giải

................................................................................................

Ví dụ 26.(Đề Chính Thức 2018) Cho hàm số







có đồ thị

( ).C

Gọi

là giao điểm của hai tiệm

cận của

( ).C

Xét tam giác đều

ABI

có hai đỉnh

,AB

thuộc

( ),C

đoạn th󰉠ng

có độ dài bằng

2 2.

2 3.

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

529

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

④ Câu hỏi trắc nghiệm.

Câu 48. Tọa độ điểm

thuộc đồ thị

 

của hàm số







sao cho khoảng cách từ điểm

đến tiệm cận đứng bằng 1 là

   

0;1 , 2;3MM

. B.

 

2;1M

. C.









. D.







Lời giải

................................................................................................

Câu 49. Tọa độ điểm

thuộc đồ thị

 

của hàm số







mà có khoảng cách đến tiệm cận

ngang của

 

bằng 1 là

 

3;2M

. B.

 

5;2M

. C.

   

5;2 , 1;0MM

. D.

4; , 0;

   



   

   

Lời giải

................................................................................................

Câu 50. Tọa độ điểm

có hoành độ nguyên thuộc đồ thị

 

của hàm số







có khoảng

cách đến đường th󰉠ng

: 1 0xy   

bằng

là

 

2;0M 

. B.

 

2;4M

. C.

   

2;4 ; 2;0MM

. D.

 

2; 2M 

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

530

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Câu 51. Cho hàm số







có đồ thị

 

và

là giao điểm của hai đường tiệm cận của

 

. Tiếp

tuyến tại một điểm

bất kỳ của

 

cắt hai tiệm cận của

 

tại

và

. Diện tích của tam giác

ABI

bằng

. B.

. C.

. D.

Lời giải

................................................................................................

Câu 52. Tọa độ điểm

thuộc đồ thị

()C

của hàm số







sao cho khoảng cách từ điểm

)2;1(I

đến tiếp tuyến của

 

tại

là lớn nhất.là

   

1 3;2 3 , 1 3;2 3MM     

. B.

   

1 3;2 3 , 1 3;2 3MM     

   

1 3;2 3 , 1 3;2 3MM     

. D.

   

1 3;2 3 , 1 3; 2 3MM      

Lời giải

................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt

531

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................

Câu 53. Cho hàm số







có đồ thị

 

. Biết rằng tiếp tuyến tại một điểm

bất kỳ của

 

luôn cắt hai tiệm cận của

 

tại

và

. Độ dài ngắn nhất của đoạn th󰉠ng

là

. B.

. C.

. D.

Lời giải

................................................................................................

Bấm Tải xuống để xem toàn bộ.

| 1/29

| | Tải xuống

Preview text:

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt §BÀI 8.
MỘT SỐ ĐIỂM ĐẶT BIỆT A. LÝ THUYẾT.
I. Tìm điểm cố định của họ đường cong
① Bài toán: Xét họ đường cong (C ) có phương trình y  f (x, )
m , trong đó f là hàm đa thức theo m
biến x với m là tham số sao cho bậc của m không quá 2. Hãy tìm những điểm cố định thuộc họ
đường cong khi m thay đổi? ② Phương pháp.
o Bước 1: Đưa phương trình y  f (x, )
m về dạng phương trình theo ẩn m có dạng sau:
Am  B  0 hoặc 2
Am  Bm  C  0 .
o Bước 2: Cho các hệ số bằng 0 , ta thu được hệ phương trình và giải hệ phương trình:    A 0 A  0   hoặc B  0 . B  0 C  0  o Bước 3: Kết luận
 Nếu hệ vô nghiệm thì họ đường cong (C ) không có điểm cố định. m
 Nếu hệ có nghiệm thì nghiệm đó là điểm cố định của (C ) . m ③ Ví dụ minh họa.
Ví dụ 1.(THPT Chuyên Thái Bình 2020) Họ parabol P  2
: y  mx  2m  3 x  m  2 m  0 luôn m
tiếp xúc với đường thẳng d cố định khi m thay đổi. Đường thẳng d đó đi qua điểm nào dưới đây? A. 0; 2  . B. 0;2. C. 1;8. D. 1; 8  . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Ví dụ 2.(THPT Chuyên Lê Hồng Phong 2018)
Biết đồ thị hàm số y  m   3
x  m   2 4 6
4 x 12mx  7m 18 (với m là tham số thực) có ba điểm
cố định thẳng hàng. Viết phương trình đường thẳng đi qua ba điểm cố định đó. A. y  4  8x 10 .
B. y  3x 1.
C. y  x  2 .
D. y  2x 1. Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
503 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
Ví dụ 3.Đồ thị của hàm số 3 2
y  x  3x  mx  m ( m là tham số) luôn đi qua một điểm M cố định có tọa độ là A. M  1  ; 4  . B. M 1; 4  . C. M  1  ;2 . D. M 1; 2   . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm.
Câu 1. Đồ thị của hàm số y  (m 1)x  3  m ( m là tham số) luôn đi qua một điểm M cố định có tọa độ là A. M (0;3) . B. M (1; 2) . C. M ( 1  ; 2  ) . D. M (0;1) . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 2. Đồ thị của hàm số 2
y  x  2mx  m 1 ( m là tham số) luôn đi qua một điểm M cố định có tọa độ là  1 3   1 5  A. M 0  ;1 . B. M ;   . C. M ;   . D. M ( 1  ;0) .  2 2   2 4  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 3. Đồ thị của hàm số 3 2
y  x  3x  mx  m ( m là tham số) luôn đi qua một điểm M cố định có tọa độ là A. M  1  ;2 . B. M  1  ; 4   . C. M 1; 2  . D. M 1; 4   . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
504 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 4. Biết đồ thị C của hàm số 4 2
y  x  2mx  3 luôn đi qua một điểm M cố định khi m thay m 
đổi, khi đó tọa độ của điểm M là A. M  1   ;1 . B. M 1;4 . C. M 0; 2   . D. M 0;3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
(m 1)x  m
Câu 5. Biết đồ thị C của hàm số y 
m  0 luôn đi qua một điểm M cố định khi m  x  m
m thay đổi. Tọa độ điểm M khi đó là  1  A. M 1;    . B. M 0  ;1 . C. M  1   ;1 . D. M 0;  1  .  2  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 6. Hỏi khi m thay đổi đồ thị (C ) của hàm số 3 2
y  x  3mx  x  3m đi qua bao nhiêu điểm cố m định ? A. 1. B. 3 . C. 2 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 7. Hỏi khi m thay đổi đồ thị (C ) của hàm số 4 2
y  (1 2m)x  3mx  m 1 đi qua bao nhiêu m điểm cố định ? A. 3 . B. 4 . C. 1. D. 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
505 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
Câu 8. Biết đồ thị (C ) của hàm số 4 2
y  x  mx  m  2016 luôn luôn đi qua hai điểm M và N cố m
định khi m thay đổi. Tọa độ trung điểm I của đoạn thẳng MN là A. I ( 1  ;0) . B. I (1; 2016) . C. I (0;1) . D. I (0; 2017) . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2
2x  (1 m)x 1 m
Câu 9. Biết đồ thị (C ) của hàm số y  (m  2)
 luôn luôn đi qua một điểm m x  m
M  x ; y
cố định khi m thay đổi, khi đó x  y bằng M M  M M A. 1. B. 3  . C.1. D. 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ Câu 10. Cho hàm số 3 2
y  x  mx  x  4m có đồ thị (C ) và A là điểm cố định có hoành độ âm m
của (C ) . Giá trị của m để tiếp tuyến tại A của (C ) vuông góc với đường phân giác góc phần tư m m thứ nhất là 7 A. m  3  . B. m  6  . C. m  2 . D. m   . 2 Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
506 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
Câu 11. Cho hàm số y  m   3
2 x  3m  2 x  m  7 có đồ thị C . m 
Khẳng định nào sau đây là khẳng định đúng?
A. C không đi qua điểm cố định nào.
B. C có đúng hai điểm cố định. m  m 
C. C có đúng ba điểm cố định.
D. C có đúng một điểm cố định. m  m  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ Câu 12. Cho hàm số 4 2
y  x  2mx  2m 1 có đồ thị (C ) . Gọi A là điểm cố định có hoành độ m
dương của (C ) . Khi tiếp tuyến tại A của (C ) song song với đường thẳng d : y  16x thì giá trị m m của m là 63 A. m  5 . B. m  4 . C. m 1. D. m  . 64 Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
II. Tìm điểm có tọa độ nguyên:
① Bài toán: Cho đường cong (C) có phương trình y  f (x) (hàm phân thức). Hãy tìm những điểm
có tọa độ nguyên của đường cong?
Nhận xét: những điểm có tọa độ nguyên là những điểm sao cho cả hoành độ và tung độ của
điểm đó đều là số nguyên. ② Phương pháp.
o Bước 1: Thực hiện phép chia đa thức chia tử số cho mẫu số.
o Bước 2: Lí luận để giải bài toán. ③ Ví dụ minh họa. 2x 1
Ví dụ 4. Trên đồ thị hàm số y 
có bao nhiêu điểm có tọa độ nguyên? 3x  4 A. 1. B. 2 . C. 0 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
507 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x  3
Ví dụ 5. Số điểm có tọa độ là các số nguyên của đồ thị hàm số: y  là: x 1 A. 2 . B. 4 . C. 1. D. 3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm. 2
Câu 13. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ nguyên ? x  2 A. 4 . B. 1. C. 2 . D. 3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 3
Câu 14. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ là các số nguyên dương 2x 1 A. 4 . B. 3 . C. 1. D. 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 4
Câu 15. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ nguyên ? 3x  2 A. 6 . B. 2 . C. 3 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
508 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt 6
Câu 16. Trên đồ thị (C) của hàm số y 
số điểm có tọa độ nguyên là 4x 1 A. 4 . B. 8 . C. 3 . D. 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x 10
Câu 17. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ nguyên ? x 1 A. 4 . B. 2 . C. 10 . D. 6 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  2
Câu 18. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ nguyên ? 2x 1 A. 4 . B. 2 . C. 1. D. 6 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 5x  2
Câu 19. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ nguyên ? 3x 1 A. 4 . B. 2 . C. 1. D. 6 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
509 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt 8x 11
Câu 20. Trên đồ thị (C) của hàm số y 
có bao nhiêu điểm có tọa độ nguyên ? 4x  2 A. 6 . B. 2 . C. 1. D. 0. Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 3x  5
Câu 21. Trong tất cả các điểm có tọa độ nguyên thuộc đồ thị (C) của hàm số y  , số điểm có x 1
hoành độ lớn hơn tung độ là A. 2 . B. 8 . C. 6 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2
Câu 22. Có bao nhiêu điểm thuộc đồ thị (C) của hàm số y  có tọa độ nguyên ? 2 x  2x  2 A. 1. B. 8 . C. 3 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2 x  5x  2
Câu 23. Cho hàm số y 
có đồ thị (C) . Hỏi trên (C) có bao nhiêu điểm có hoành độ và 2x  2
tung độ là các số tự nhiên. A. 3 . B. 2 . C. 8 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
510 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
III. Tìm điểm có tính chất đối xứng:
Bài toán: Cho đường cong (C) có phương trình y  f (x) . Tìm những điểm đối xứng nhau qua một
điểm, qua đường thẳng.
① Loại 1: Cho đồ thị C  3 2
: y  Ax  Bx  Cx  D trên đồ thị C  tìm những cặp điểm đối xứng nhau
qua điểm I (x , y ) . I I ② Phương pháp. o Gọi M  3 2
a Aa  Ba  Ca  D N  3 2 ; , ;
b Ab  Bb  Cb  D là hai điểm trên C đối xứng nhau qua điểm I .
a  b  2x  I o Ta có  . 3 3 (
A a  b )  B   2 2
a  b   C a  b  2D  2yI
Giải hệ phương trình tìm được a,b từ đó tìm được toạ độ M , N. ③ Ví dụ minh họa.
Ví dụ 6. Tìm tất cả các giá trị của tham số thực m để trên đồ thị hàm số 3 2
y  x  x  m 1 có hai
điểm phân biệt đối xứng nhau qua điểm I 0  ;1 . A. m  2 . B. 1  m  2 . C. m 1. D. m 1. Lời giải Chọn A.
Giả sử M  x ; y là điểm thuộc đồ thị hàm số đã cho, ta được 3 2
y  x  x  m 1 1 . 0 0 0   0 0 
Khi đó nếu N  x ; y là điểm đối xứng với M qua I thì N N   x  x 0 N  0  2 x  x N 0   
 N x ;2  y . 0 0  y  y y  2  y  0 N  0 0  1  2
Để N cũng thuộc đồ thị hàm số đã cho thì ta có phương trình 3 2
2  y  x  x  m 1 (2) . 0 0 0 Lấy  
1 cộng 2 vế theo vế và biến đổi ta được phương trình 2 x
 m  2 , phương trình này có 0
nghiệm khi và chỉ khi m  2 .
Hơn nữa để M  N  x  x  x  0 , ta chọn m  2 . 0 0 0
Đặc biệt : Trên đồ thị C tìm những cặp điểm đối xứng nhau qua gốc tọa độ O0;0 a  b  0  thì ta có  . 3 3 (
A a  b )  B   2 2
a  b   C a  b  2D  0
Giải hệ phương trình tìm được a,b từ đó tìm được toạ độ M , N .
Ví dụ 7. Có bao nhiêu giá trị nguyên của m lớn hơn 2019  để đồ thị hàm số 3 2
y  x  mx   2 m   2 3 3
1 x 1 m có hai điểm phân biệt đối xứng nhau qua gốc tọa độ. A. 2017 . B. Vô số. C. 2019 . D. 2018 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
511 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm. x  2
Câu 24. Tìm cặp điểm thuộc đồ thị C  của hàm số y 
đối xứng nhau qua gốc tọa độ x 1
A.  2; 2 và  2; 2.
B.  3; 2 và  3; 2.
C.  2; 2 và  2; 2 . D. 2; 2   và  2  ;2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 25. Trên đồ thị C của hàm số 3 2
y  x  5x  6x  3 có bao nhiêu cặp điểm đối xứng nhau qua gốc tọa độ ? A. 2 . B. 1. C. 0 . D. 3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 26. Số cặp điểm thuộc đồ thị C của hàm số 3 2
y  x  3x  2 đối xứng với nhau qua điểm I 2;18 là A. 2 . B. 1. C. 3 . D. 4 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
512 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
Câu 27. Cặp điểm thuộc đồ thị (C) của hàm số 3
y  x  3x  2 đối xứng nhau qua điểm I (2;18) là A. (1; 2) và (3;34) . B. (3; 2) và (1;34) . C. (0; 2)
 và (4;74) . D. (1;2) và ( 1  ; 6)  . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 28. Cặp điểm thuộc đồ thị (C) của hàm số 3 2
y  x  4x  9x  4 đối xứng nhau qua gốc tọa O . A. (3; 22) và ( 3  ; 2  2) . B. (2;14) và ( 2  ; 1  4) . C. (1;10) và ( 1  ; 1  0). D. (0;4) và (4;40) . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 29. Các giá trị thực của tham số m để đồ thị (C ) của hàm số 3 2
y  x  3x  m có hai điểm phân m
biệt đối xứng nhau qua gốc tọa độ là A. 1   m  0 . B. m  0 . C. m  3  . D. m  0 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2
x  4mx  5m
Câu 30. Tập hợp tất cả các giá trị thực của m để trên đồ thị (C ) của hàm số y  có m x  2
hai điểm phân biệt đối xứng nhau qua gốc tọa độ là  1  4     A. 0;  . B.   ;0 \  . C. 1; . D.   1 4 4
; 0   ;    ;   .  2   13  2 3   3  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
513 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 31. Tọa độ hai điểm trên đồ thị C của hàm số 3
y  x  3x  2 sao cho hai điểm đó đối xứng
nhau qua điểm M –1; 3 là A.  1  ;0;1;6. B. 1;0;1;6 .
C. 0; 2 ; 2; 4 . D. 1;0; 1  ;6. Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
① Loại 2: Cho đồ thị C  3 2
: y  Ax  Bx  Cx  D trên đồ thị C  tìm những cặp điểm đối xứng nhau
qua đường thẳng d : y  A x  B . 1 1 ② Phương pháp. o Gọi M  3 2
a Aa  Ba  Ca  D N  3 2 ; , ;
b Ab  Bb  Cb  D là hai điểm trên C đối xứng nhau
qua đường thẳng d . I d (1)  o Ta có: 
(với I là trung điểm của MN và ud là vectơ chỉ phương của d ). MN.u  d 0 (2)
o Giải hệ phương trình tìm được M , N. ③ Ví dụ minh họa. x  4
Ví dụ 8. Tọa độ cặp điểm thuộc đồ thị (C) của hàm số y 
đối xứng nhau qua đường thẳng x  2
d : x  2 y  6  0 là A. 4;4 và  1  ;  1 . B. 1; 5   và  1  ;  1 . C. 0; 2   và 3;7. D. 1; 5   và 5;3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
514 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm.
Câu 32. Tìm trên đồ thị hàm số 3
y  x  9x  7 hai điểm phân biệt mà chúng đối xứng với nhau qua trục tung.
A. A2; 3 , B 2  ; 3 .
B. A3;7 , B  3  ;7 .
C. A4;4 , B4; 4 . D. Không tồn tại. Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 33. (THPT Nguyễn Huệ 2020) 1
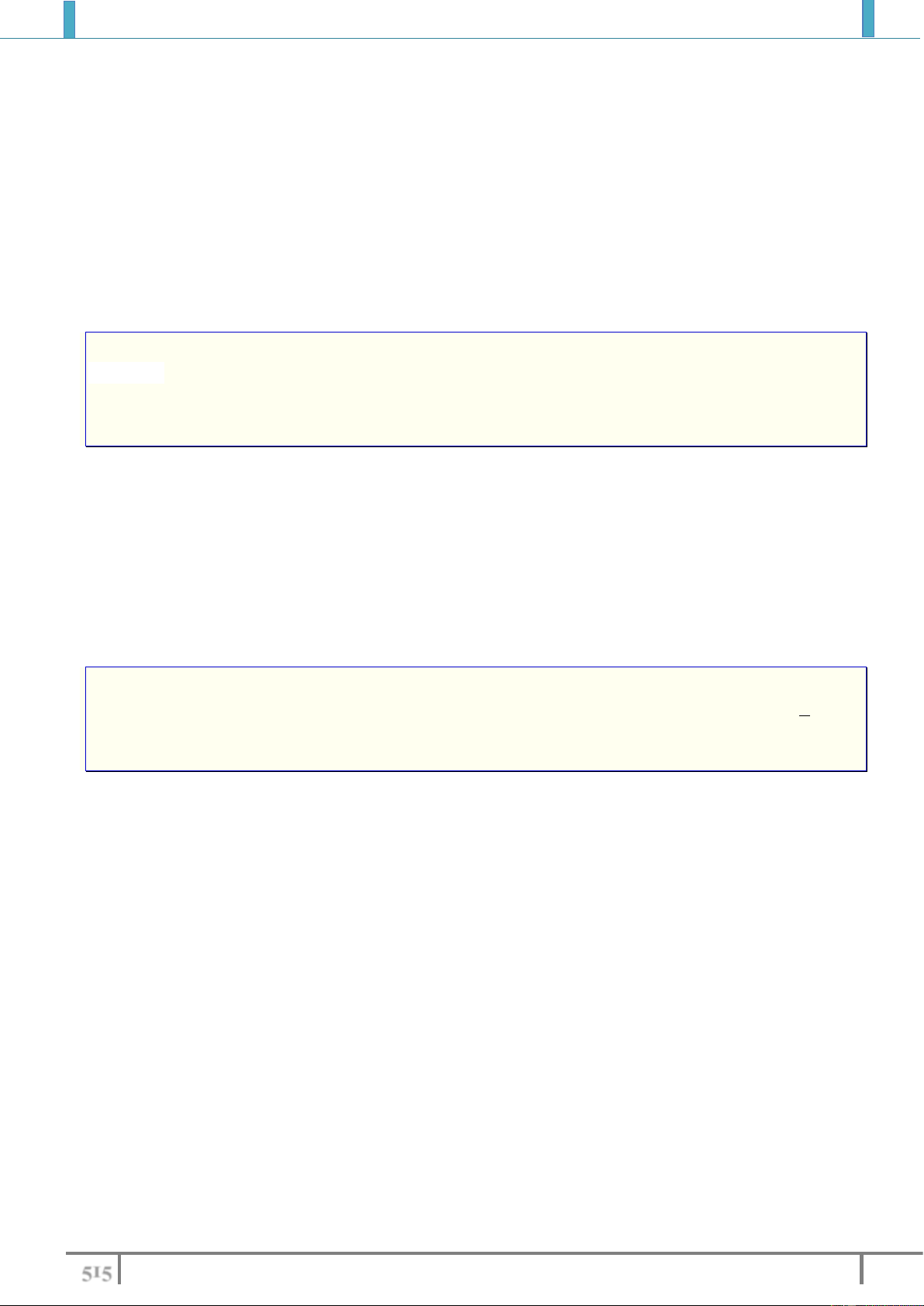
Cặp điểm thuộc đồ thị (C) của hàm số 3
y  x  x đối xứng nhau qua đường thẳng d : y   x là 2 A. 1;2 và  2  ; 1  0. B. 2;  1  và  2  ;  1 . C. 1; 2   và  1
 ;2 . D. 1;2 và  1  ; 2  . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
515 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 34. (THPT Hai Bà Trưng 2020) 1 11
Cặp điểm thuộc đồ thị (C) của hàm số 3 2
y   x  x  3x 
mà chúng đối xứng nhau qua trục 3 3 tung là  16   16   16   16  A. 3;    và 3;     . B. 3;   và 3;   .  3   3   3   3   11  11   11   11  C. 2;   và 2;    . D. 2;    và 2;   .  3   3   3   3  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 35. Điều kiện của tham số m để trên đồ thị C của hàm số 3
y  x   m   2 3
1 x  2mx  m 1 m 
có ít nhất hai điểm phân biệt đối xứng nhau qua trục Oy là A. m  0 . B. m  0 . C. m  2  . D. m  2  . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
IV. Tính chất các điểm liên quan đến khoảng cách: 1. Lí thuyết: o 2 2
Cho hai điểm P  x ; y ;Q x ; y  PQ  x  x  y  y . 1 1   2 2  2 1  2 1
o Cho điểm M  x ; y và đường thẳng d : Ax  By  C  0 thì khoảng cách từ M đến d là 0 0 
Ax  By  C
h M ; d  0 0  . 2 2 A  B
o Khoảng cách từ M  x ; y đến tiệm cận đứng x  a là h  x  a . 0 0  0
516 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
o Khoảng cách từ M  x ; y đến tiệm cận ngang y  b là h  y b . 0 0  0
2. Các bài toán thường gặp: ax  b
① Bài toán 1: Cho hàm số y 
c  0, ad bc  0 có đồ thị C. Hãy tìm trên (C) hai điểm cx  d
A và B thuộc hai nhánh đồ thị hàm số sao cho khoảng cách AB ngắn nhất. ② Phương pháp. d
o C có tiệm cận đứng x   do tính chất của hàm phân thức, đồ thị nằm về hai phía của tiệm c
cận đứng. Nên gọi hai số  ,  là hai số dương. d d d
o Nếu A thuộc nhánh trái thì x  
 x      ; y  f (x ) . A A c c c A A d d d
o Nếu B thuộc nhánh phải thì x  
 x       ; y  f (x ) . B B c c c B B o 2 2 2
Sau đó tính AB   x  x    y  y     a   
a    y  y 2 2 . B A B A B A
o Áp dụng bất đẳng thức Côsi (Cauchy), ta sẽ tìm ra kết quả. ③ Ví dụ minh họa.
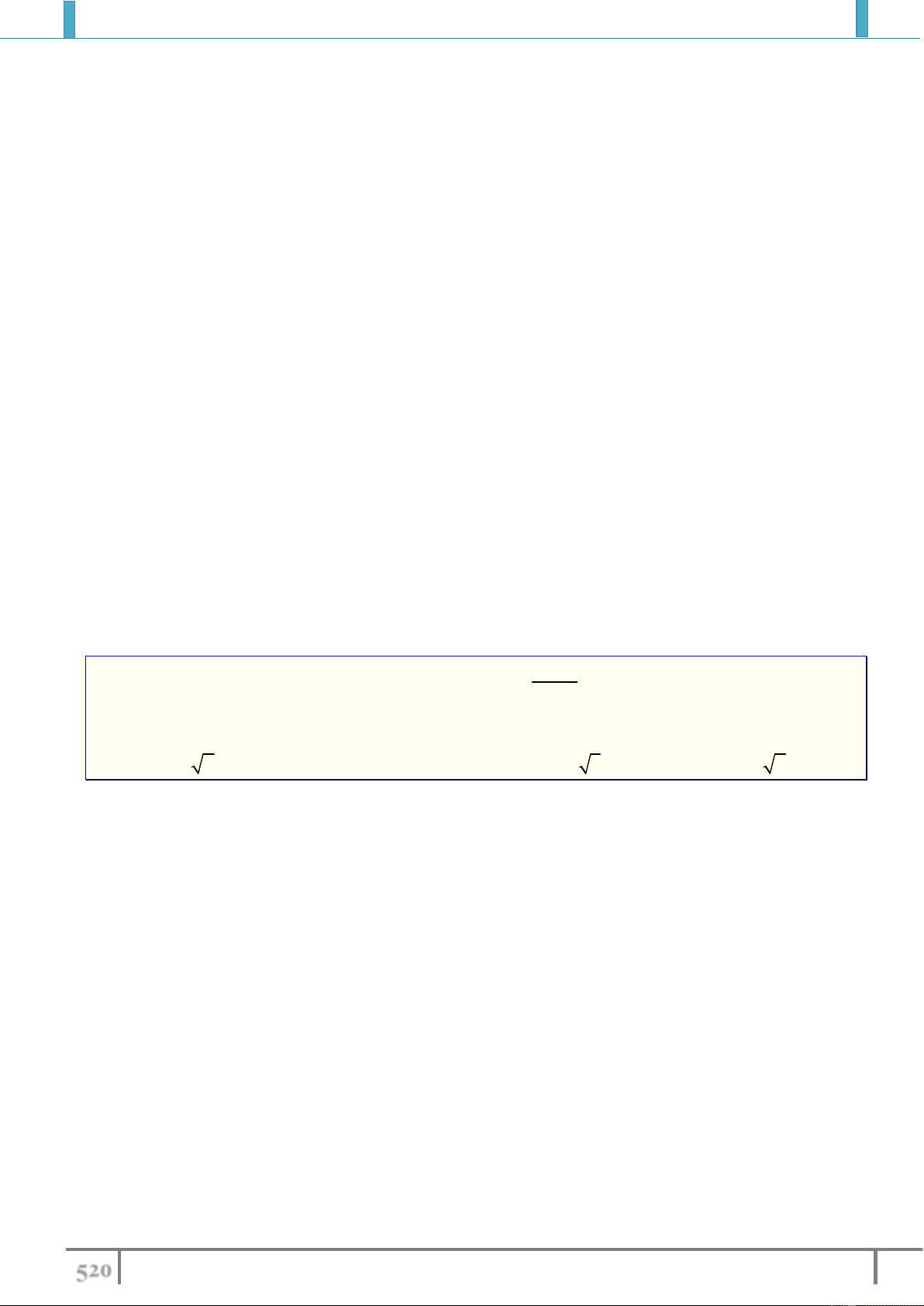
Ví dụ 9.(THPT Chuyên Thái Bình 2018) Cho A , B là hai điểm di động và thuộc hai nhánh khác 2x 1
nhau của đồ thị y 
. Khi đó khoảng cách AB bé nhất là? x  2 A. 10 . B. 2 10 . C. 5 . D. 2 5 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
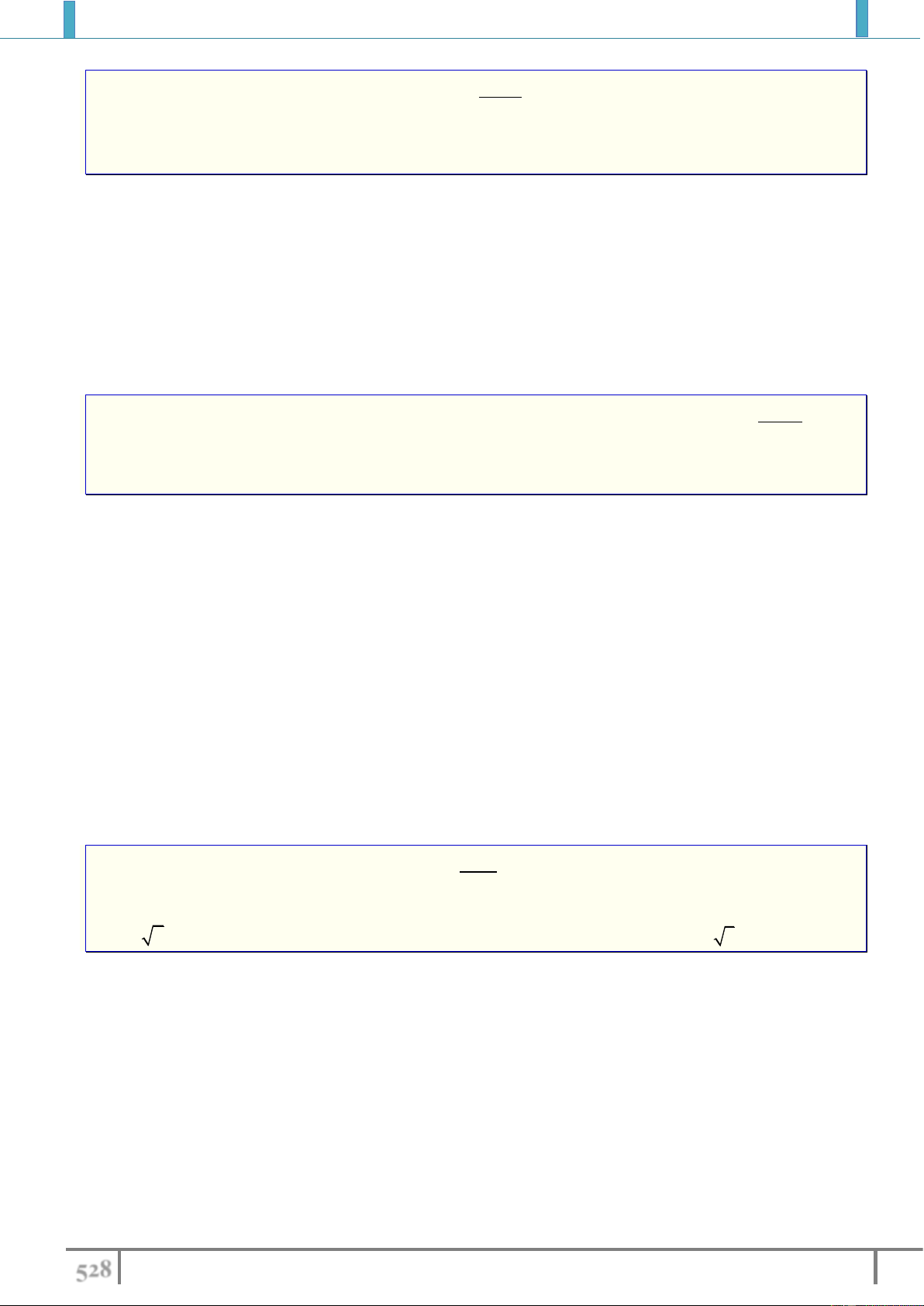
Ví dụ 10.(Tạp chí THTT 2018) A và B là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số x y 
. Khi đó độ dài đoạn AB ngắn nhất bằng x  2 A. 1. B. 2 . C. 4 . D. 8 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
517 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Ví dụ 11.(Sở GD & ĐT Hà Nam 2018) Biết A x ; y , B x ; y là hai điểm thuộc hai nhánh khác B B  A A  x  4
nhau của đồ thị hàm số y 
sao cho độ dài đoạn thẳng AB nhỏ nhất. Tính 2 2
P  y  y  x .x x 1 A B A B A. P 10 . B. P  6 . C. P  6  2 3 . D. P  10  3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Ví dụ 12.(THPT Chuyên Thái Bình 2018) Cho A , B là hai điểm di động và thuộc hai nhánh khác 2x 1
nhau của đồ thị y 
. Khi đó khoảng cách AB bé nhất là? x  2 A. 10 . B. 2 10 . C. 5 . D. 2 5 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
518 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm. x  3
Câu 36. Gọi A, B là hai điểm thuộc hai nhánh khác nhau trên đồ thị C của hàm số y  , độ x  3
dài ngắn nhất của đoạn thẳng AB là A. 4 3 . B. 2 3 . C. 4 . D. 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
① Bài toán 2: Cho đồ thị hàm số C  có phương trình y  f (x) . Tìm tọa độ điểm M thuộc (C) để
tổng khoảng cách từ M đến hai trục tọa độ nhỏ nhất. ② Phương pháp. o Gọi M  ;
x y và tổng khoảng cách từ M đến hai trục tọa độ là d thì d  x  y .
o Xét các khoảng cách từ M đến hai trục tọa độ khi M nằm ở các vị trí đặc biệt: Trên trục hoành, trên trục tung.
o Sau đó xét tổng quát, những điểm M có hoành độ, hoặc tung độ lớn hơn hoành độ hoặc tung độ
của M khi nằm trên hai trục thì loại đi không xét đến.
o Những điểm còn lại ta đưa về tìm giá trị nhỏ nhất của đồ thi hàm số dựa vào đạo hàm rồi tìm
được giá trị nhỏ nhất của d . ③ Ví dụ minh họa. x  3
Ví dụ 13.(THPT Triệu Sơn 2018) Cho hàm số y 
C và điểm M  ;
a b thuộc đồ thị C  . Đặt x 1
T  3a  b  2ab , khi đó để tổng khoảng cách từ điểm M đến hai trục toạ độ là nhỏ nhất thì mệnh
đề nào sau đây là đúng? A. 3   T  1  . B. 1  T  1. C. 1 T  3 . D. 2  T  4 .
519 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 4x  3
Ví dụ 14.(THPT Chuyên Trần Phú 2018) Cho hàm số y 
có đồ thị C . Biết đồ thị C có x  3
hai điểm phân biệt M , N và tổng khoảng cách từ M hoặc N tới hai tiệm cận là nhỏ nhất. Khi đó
MN có giá trị bằng A. MN  4 2 . B. MN  6 . C. MN  4 3 . D. MN  6 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
520 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt x 1
Ví dụ 15.(THPT Kinh Môn 2018) Cho hàm số y  có đồ thị x 1
C. Giả sử A , B là hai điểm thuộc C và đối xứng với nhau
qua giao điểm của hai đường tiệm cận. Dựng hình vuông AEBF
. Tìm diện tích nhỏ nhất của hình vuông AEBF . A. S  8 2 . B. S  4 2 . min min C. S  8 . D. S  16 . min min Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm. 2x 1
Câu 37. Tọa độ các điểm thuộc đồ thị C của hàm số y 
mà có tổng khoảng cách đến hai x 1
đường tiệm cận của C bằng 4 là A. 4;3, 2  ;  1 . B. 2;5,0;  1  . C. 2;5,0;  1 ,4;3, 2  ;  1 . D. 2;5,4;3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
521 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt x  2
Câu 38. Tọa độ điểm M có hoành độ dương thuộc đồ thị hàm số y  sao cho tổng khoảng x  2
cách từ M đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là A. M (4;3) . B. M (3;5) . C. M (1; 3  ) . D. M (0; 1  ) . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x  3
Câu 39. Cho hàm số y 
có đồ thị C . Gọi M là một điểm thuộc đồ thị C và d là tổng x  2
khoảng cách từ M đến hai tiệm cận của C . Giá trị nhỏ nhất của d có thể đạt được là A. 6 . B. 10 . C. 2 . D. 5 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x 1
Câu 40. Cho hàm số y 
có đồ thị C . Tổng khoảng cách từ một điểm M thuộc C đến hai x 1
tiệm cận của C đạt giá trị nhỏ nhất bằng ? 2 A. 3 . B. 2 . C. . D. 4 . 3 Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
522 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt 2 x  3x  3
Câu 41. Cho hàm số y 
có đồ thị C . Tổng khoảng cách từ một điểm M thuộc C x  2
đến hai hai trục tọa độ đạt giá trị nhỏ nhất bằng ? 1 3 A. 1. B. . C. 2 . D. . 2 2 Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x 1
Câu 42. Cho hàm số y 
có đồ thị C . Tổng khoảng cách từ một điểm M thuộc C đến hai x 1
tiệm cận của C đạt giá trị nhỏ nhất bằng A. 3 . B. 4 . C. 2 2 . D. 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x 1
Câu 43. Tọa độ tất cả các điểm thuộc đồ thị C  của hàm số y 
sao cho tổng khoảng cách từ x  2
điểm đó đến 2 tiệm cận là nhỏ nhất là A. 1;  1 . B. 1 3;1 3 .   C. 1 3;1 3 .
D. 2  3;1 3 và 2  3;1 3.   Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
523 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  2
Câu 44. Cho hàm số y 
có đồ thị C . Tổng khoảng cách từ một điểm M thuộc C đến hai x  3
hai trục tọa độ đạt giá trị nhỏ nhất bằng ? 2 1 A. 2 . B. . C. 1. D. . 3 6 Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
① Bài toán 3: Cho đồ thị (C) có phương trình y  f (x) . Tìm điểm M trên (C) sao cho khoảng cách
từ M đến Ox bằng k lần khoảng cách từ M đến trục Oy . ② Phương pháp.  y  kx
 f x  kx
o Theo đầu bài ta có y  k x     .  y  kx  f
  x  kx ③ Ví dụ minh họa. x  7
Ví dụ 16. Cho điểm M thuộc đồ thị C  của hàm số y 
, biết M có hoàng độ a và khoảng x 1
cách từ M đến trục Ox bằng ba lần khoảng cách từ M đến trục Oy . Giá trị có thể có của a là 7 7 7 7
A. a  1 hoặc a  . B. a  1  hoặc x  . C. a  1
 hoặc a   . D. a 1 hoặc a   . 3 3 3 3 Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  2
Ví dụ 17. Có bao nhiêu điểm M thuộc đồ thị C của hàm số y  sao cho khoảng cách từ x  2
điểm M đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng? A. 2 . B. 1. C. 3 . D. 4 .
524 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x 1
Ví dụ 18. Tọa độ các điểm thuộc đồ thị C  của hàm số y 
cách đều tiệm cận đứng và trục x 1 hoành là A. M 2;  1 , M 4;3 . B. M 0;  1 , M 4;3 . C. M 0; 
1 , M 3; 2 . D. M 2;  1 , M 3;2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 3x  5
Ví dụ 19. Tọa độ các điểm thuộc đồ thị C của hàm số y 
cách đều hai tiệm cận của C . x  2 A. M  1   ;1 ; N  4  ; 6   .B. M 1;  1 ; N 3;4 . C. M  1  ;3; N  3  ;3 . D. M  1  ;3; N  3  ;3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  2
Ví dụ 20. Tọa độ điểm M C của hàm số y 
cách đều hai đường tiệm cận của C là x  2  7   1  A. M 2  ;1 . B. M 0;  1 , M 4;3 . C. M 5; , M 3  ;     . D. M  2  ;2.  3   5  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm.
525 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt x  3
Câu 45. Tọa độ điểm M thuộc đồ thị C của hàm số y 
cách đều hai trục tọa độ là x 1 A. M  1  ; 
1 , M 3;3. B. M  1  ;3 . C. M  1  ;  1 . D. M 3;3 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
Câu 46. Đồ thị hàm số 3 2
y  2x  mx 12x 13 có hai điểm cực trị cách đều trục tung khi và chỉ khi: A. m  1  . B. m  0 . C. m  1  ;m  2  . D. m  2  . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x 1
Câu 47. Hỏi trên đồ thị C của hàm số y 
có bao nhiêu điểm cách đều hai trục tọa độ? x  2 A. 3 . B. 2 . C. 4 . D. 0 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ ax  b
① Bài toán 4: Cho đồ thị hàm số (C) có phương trình y  f (x) 
c  0, ad bc  0. Tìm tọa cx  d
độ điểm M trên (C) sao cho độ dài MI ngắn nhất (với I là giao điểm hai tiệm cận). ② Phương pháp. d a
o Tiệm cận đứng x 
; tiệm cận ngang y  . c c  d a 
o Ta tìm được tọa độ giao điểm I  ;  của hai tiệm cận.  c c 
o Gọi M x ; y
là điểm cần tìm. Khi đó: M M  2 2  d   a  2 IM  x   y   g x  M   M   M   c   c 
o Sử dụng phương pháp tìm GTLN - GTNN cho hàm số g để thu được kết quả. ③ Ví dụ minh họa. x  2
Ví dụ 21. Cho hàm số y 
có đồ thị C . Gọi I là giao điểm hai đường tiệm cận của C . Biết x 1
tọa độ điểm M  x ; y
có hoành độ dương thuộc đồ thị C sao cho MI ngắn nhất. Khi đó giá trị M M  x  y bằng M M A. 0 . B. 2 3 . C. 2 . D. 2 . Lời giải
526 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  3
Ví dụ 22. Cho hàm số y 
có đồ thị C . Gọi d là khoảng cách từ một điểm M trên C đến x 1
giao điểm của hai tiệm cận. Giá trị nhỏ nhất có thể có của d là A. 2 . B. 2 3 . C. 3 2 . D. 2 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2 x  2x  2
Ví dụ 23. Khoảng cách ngắn nhất từ điểm M C của hàm số y  đến I 1,4 x 1 A. 2 . B. 2 2 . C. 2  2 2 . D. 2 2  2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
① Bài toán 5: Cho đồ thị hàm số (C) có phương trình y  f (x) và đường thẳng d : Ax  By  C  0 .
Tìm điểm I trên (C) sao cho khoảng cách từ I đến d là ngắn nhất. ② Phương pháp.
o Gọi I thuộc (C)  I  x ; y ; y  f (x ) . 0 0  0 0
Ax  By  C
o Khoảng cách từ I đến d là g(x )  h I;d  0 0  0 2 2 A  B
o Khảo sát hàm số y  g(x) để tìm ra điểm I thỏa mãn yêu cầu.
527 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt ③ Ví dụ minh họa. 3x 1
Ví dụ 24. Tọa độ điểm M thuộc đồ thị hàm số y 
cách đường tiệm cận đứng của đồ thị hàm x 1
số một khoảng bằng 1 là A. 0;  1 ;  2  ;7 . B.  1  ;0; 2;7 . C. 0  ;1 ; 2; 7   . D. 0;  1 ; 2;7 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x 1
Ví dụ 25.(THPT Chuyên Bắc Ninh 2018) Gọi M  ;
a b là điểm trên đồ thị hàm số y  mà có x  2
khoảng cách đến đường thẳng d : y  3x  6 nhỏ nhất. Khi đó
A. a  2b 1 .
B. a  b  2 . C. a  b  2  .
D. a  2b  3. Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  2
Ví dụ 26.(Đề Chính Thức 2018) Cho hàm số y 
có đồ thị (C). Gọi I là giao điểm của hai tiệm x  2
cận của (C). Xét tam giác đều ABI có hai đỉnh ,
A B thuộc (C), đoạn thẳng AB có độ dài bằng A. 2 2. B. 4. C. 2. D. 2 3. Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
528 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
④ Câu hỏi trắc nghiệm. 2x 1
Câu 48. Tọa độ điểm M thuộc đồ thị C của hàm số y 
sao cho khoảng cách từ điểm M x 1
đến tiệm cận đứng bằng 1 là  3   5  A. M 0;  1 , M 2;3 . B. M 2  ;1 . C. M 1  ;   . D. M 3;   .  2   2  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x 1
Câu 49. Tọa độ điểm M thuộc đồ thị C của hàm số y 
mà có khoảng cách đến tiệm cận x  2
ngang của C bằng 1 là  5   1  A. M 3;2 . B. M 5;2 .
C. M 5;2, M  1
 ;0 . D. M 4; , M 0;     .  2   2  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x  2
Câu 50. Tọa độ điểm M có hoành độ nguyên thuộc đồ thị C của hàm số y  có khoảng x 1 1
cách đến đường thẳng  : x  y 1  0 bằng là 2 A. M  2  ;0. B. M 2;4 .
C. M 2;4; M  2  ;0 . D. M 2; 2  . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
529 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ x 1
Câu 51. Cho hàm số y 
có đồ thị C  và I là giao điểm của hai đường tiệm cận của C  . Tiếp x 1
tuyến tại một điểm M bất kỳ của C  cắt hai tiệm cận của C  tại A và B . Diện tích của tam giác ABI bằng A. 4 . B. 5 . C. 6 . D. 7 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x 1
Câu 52. Tọa độ điểm M thuộc đồ thị (C) của hàm số y 
sao cho khoảng cách từ điểm x 1 I ( ; 1 )
2 đến tiếp tuyến của C  tại M là lớn nhất.là A. M 1   3;2  3 , M 1   3;2  3 . B. M 1   3;2  3 , M 1   3;2  3 . 1   2  1   2  C. M 1   3;2  3 , M 1   3;2  3 . D. M 1   3;2  3 , M 1   3; 2   3 . 1   2  1   2  Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
530 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 8-Một Số Điểm Đặc Biệt
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................ 2x  3
Câu 53. Cho hàm số y 
có đồ thị C . Biết rằng tiếp tuyến tại một điểm M bất kỳ của C x  2
luôn cắt hai tiệm cận của C tại A và B . Độ dài ngắn nhất của đoạn thẳng AB là A. 4 . B. 2 . C. 2 . D. 2 2 . Lời giải
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
................................................................................................ ................................................................................................
531 Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập một số điểm đặc biệt của đồ thị hàm số – Diệp Tuân Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số