




Preview text:
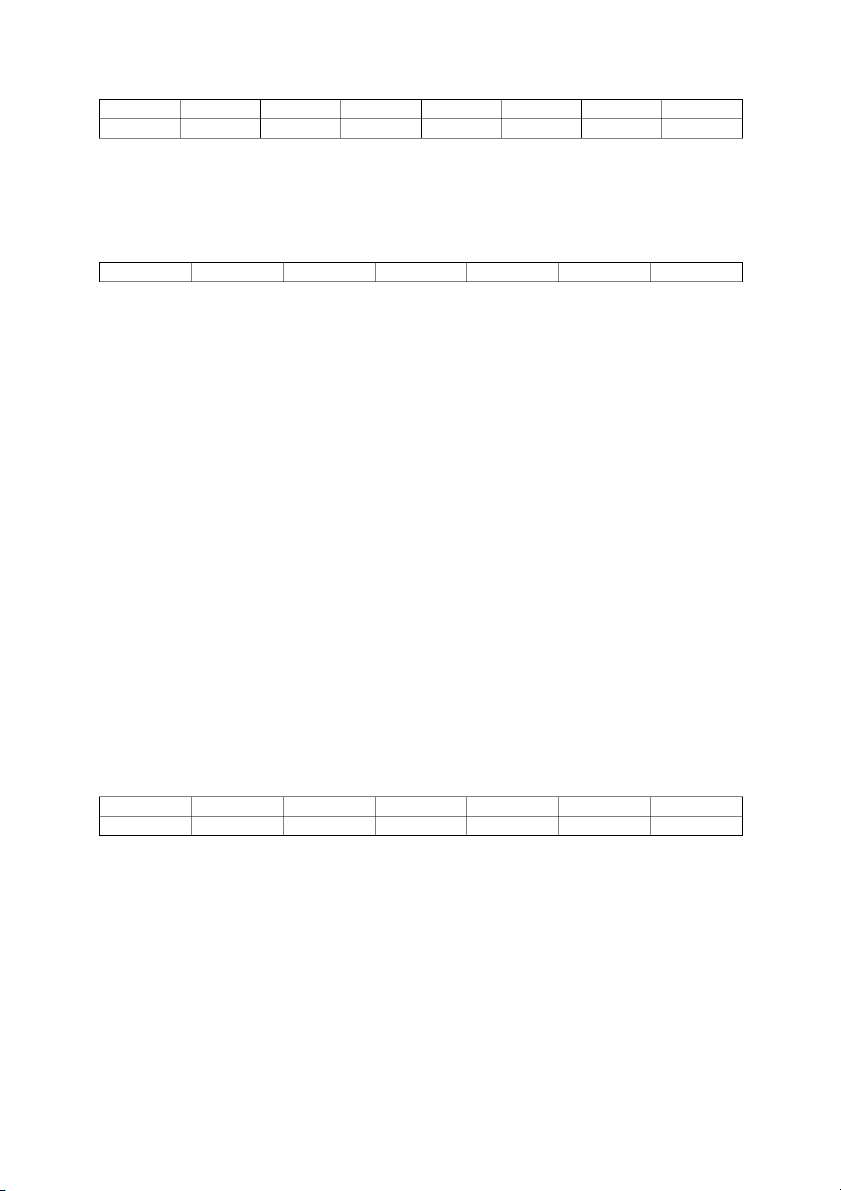
t (s) 0 0.51 1.03 1.74 2.36 3.24 3.82 x (m) 154 186 209 250 262 272 274
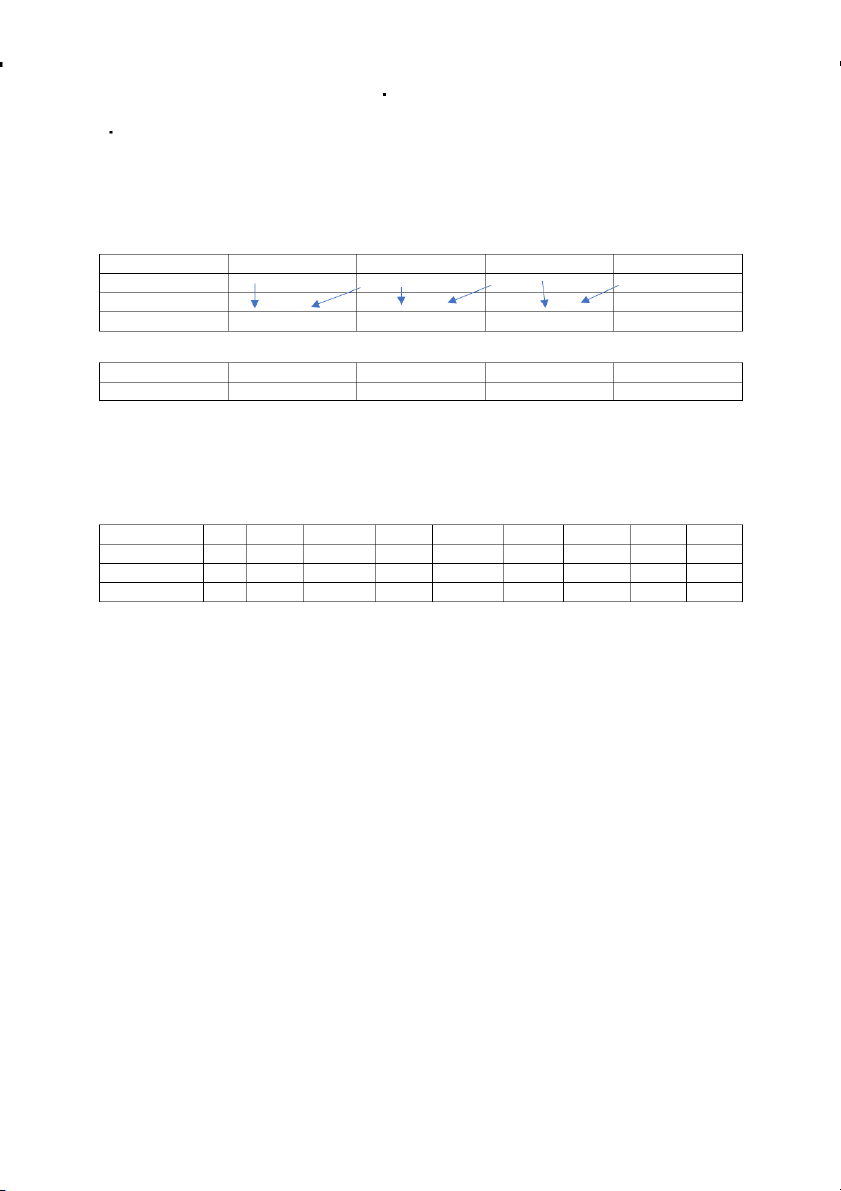
Tính vận tốc tính gia tốc Vận tốc f’() Gia tốc f”() h 0.51 0.52 0.71 0.62 0.88 0.58 Forward: f’(0) h =0.51 f’(x) = f(x0 +h) -f(x0) /h
f’(0) = f(0+0.51)-f(0)/0.51 = (186 – 154)/0.51 = 62.745 Backward: f’(3.82) h=0.58
f’(x) = f(x0) – f(x0 – h)/h
f’(3.82) = f(3.82) – f(3.82 – 0.58)/0.58 = 274 – 272 /0.58 = 3.4482 Central: h1 h2
f’’(x) = (h2*f(x0-h1) + h1*f(x0 +h2) – (h1+h2)*f(x0) )/ (h1^2*h2/2 + h2^2 * h1 /2)
. At t = 0.51 => h2 = 0.52, h1 = 0.51
f’’(0.51) = (0.52*154 + 0.51*209 –(0.51+0.52)*186)/(0.51^2*0.52/2 + 0.52^2*0.51/2) = -35.9501
.At t = 1.03 => h2 = 0.71, h1 = 0.52 x 0 2 4 6 8 10 y 0 14 20 49 16 23 h = 2 f’(2) hay f”(2) Central:
f’(x) = f(x0+h) – f(x0-h) /2h
f’’(x) = f(x0+h) -2f(x0) + f(x0-h)/h^2
f’(x) hoặc f”(x) từ những giá trị x, x+h, x-h, x+2h,….. or f(x), f(x+h), f(x-h),….
f’(x) = Af(x) + Bf(x-h) + Cf(x+h)
f’’(x) = Af(x) + Bf(x-h) + Cf(x+h) Taylor’s theorem gives:
f(x+h) = f(x) + hf’(x) + h^2/2!f”(x) + h^3/3! f”’(xi) + ….
f(x-h) = f(x) - hf’(x) + h^2/2!f”(x) - h^3/3! f”’(xi) + …. A+B+C = 0 Truncation error: o(h^n) Exercise:
f”(x) = Af(x) + Bf(x-h) + Cf(x-2h) (1) Taylor’s theorem gives:
f(x-h) = f(x) -hf’(x) + h^2/2!f”(x) - h^3/3!f”’(C1) (2)
f(x-2h) = f(x) -2hf’(x) + 4h^2/2! f”(x) - 8h^3/3!f”’(C2) (3)
f”(x) = (A+B+C)f(x) + (-Bh -2Ch)f’(x) +1/2*(Bh^2 + 4Ch^2)f”(x) + h^3/3!(-B f”’(C1) – 8C f”’(C2)) A+B+C =0 -Bh – 2Ch = 0 ½*Bh^2 + ½*4Ch^2 = 1 A = 1/h^2 B =-2/h^2 C = 1/h^2
f”(x) = 1/h^2f(x) -2/h^2f(x-h) + 1/h^2f(x-2h) + h/3(f”’(C1) – 4f”’(C2))
Truncation: h/3(f”’(C1) – 4f”’(C2)) Order: O(h) Middle-point:
Im = h*sigma(i:0->n) f(xi + xi+1/2)
Em = |I(f) -Im| = M/24 (b-a) *h^2 Order: O(h^2) i 0 1 2 3 xi 2 4 8 10 Xi + xi+1/2 3 6 9 f Xi 3 6 9 f(xi)
Exercise: f(x) = tp(0->1) e^-x^2 dx h = 0.25 => n = 4 f(x) = e^-x^2 i 0 1 2 3 4 Xi 0 0.25 0.5 0.75 1 Xi + xi+1/2 0.125 0.375 0.625 0.875 f 0.9844 0.8688 0.6766 0.465
Im = h*sigma(i:0->n) f(xi + xi+1/2)
= 0.25*(0.9844 + 0.8688 + 0.6766 + 0.465) = 0.7487 b. e = 10^-3
Em = M/24 (b-a) *h^2 <= 10^-3 f(x) = e^-x^2 f’(x) = -2x. e^-x^2 f’’(x) = M = max(0,1) |f”(x)| = 2
2/24 *1*(1/n)^2 <= 10^-3 n >= 9.1287 We choose n at least 10 Trapezoidal:
It = h/2 *(f(a) + f(b) + 2*sigma(i:1->n-1)f(xi))
Et = |I(f) – It| = M/12 (b-a) *h^2 Order: O(h^2) I 0 1 2 3 xi 0 0.25 0.5 0.75
It = h/2 *(f(0) + f(0.75) + 2*(f(x1) + f(x2)))
Exercise: f(x) = tp(0->1) e^-x^2 dx h = 0.25 => n = 4 I 0 1 2 3 4 xi 0 0.25 0.5 0.75 1 f 1 0.9394 0.7788 0.5697 0.3678
It = h/2 *(f(0) + f(0.75) + 2*(f(x1) + f(x2)+f(x3)))
= 0.25/2 * (1 + 0.3678 + 2*(0.9394 + 0.7788 + 0.5697 )) = 0.74295 e = 10^-3
Et = M/12 (b-a) *h^2 <= 10^-3 f(x) = e^-x^2 f’(x) = -2x. e^-x^2 f’’(x) = M = max(0,1) |f”(x)| = 2 2/12*(1/n)^2 <= 10^-3 n >= 12.9099 We chose n at least 13 Simpson’s 1/3:
Is1/3 = h/3*(f(a) + f(b) + 2sigma chẵn + 4 sigma lẻ)
Es1/3 = |I(f) – Is1/3| = M/180(b-a)*h^4 M = max|f””(x)|
Exercise: f(x) = tp(0->1) e^-x^2 dx h = 0.25 => n = 4 I 0 1 2 3 4 xi 0 0.25 0.5 0.75 1 f 1 0.9394 0.7788 0.5697 0.3678
It = h/3 *(f(0) + f(0.75) + 2*f(x2) + 4*(f(x1) + f(x3)))
= 0.25/3 * (1 + 0.3678 + 2*(0.7788) + 4*(0.9394+0.5697)) = 0.7468 e = 10^-3
Et = M/180 (b-a) *h^4 <= 10^-3 f(x) = e^-x^2 f’(x) = -2x. e^-x^2
f’’(x) = -2.e^-x^2 + 4x^2.e^-x^2
f”’(x) = -8x^3*e^-x^2 + 12xe^-x^2 M = max(0,1) |f””(x)| = 12 12/180*(1/n)^4 <= 10^-3 n >= 2.8574 We chose n at least 4 Euler: IVP Dy/dt = f(x,y(t)), t in [a,b] Y() = a
Let w = (w0, w1,…,wn) be a approx solution: W0 = a Wi+1 = wi +hf(ti, wi)
Error = sqrt( sigma Yexact – wi) Stepsize small h: M.h/2L * (e^(L(ti-a))-1) M = max|f”(y(t))| Y(t) 1. Exact 2. D^2y/dt^2 L = max|df/dy| F=dy/dt Exercise: (1)
Y’ + 4y/t = t^4 , 1<= t <=2 Y(1) = 1 F = t^4 – 4y/t h=0.25 => n = 4 i 0 1 2 3 4 ti 1 1.25 1.5 1.75 2
Let w = (w0, w1,…,w4) be approx solution of (1) w0 = 1 w1 = w0 +hf(t0,w0) = 0.25 w2 = 0.6603 w3 = 1.4857 w4 = 2.9814
Solution w = (0.25, 0.6603, 1.4857, 2.9814) Yexact(t) = 1/9 t^5 + 8/9t^-4
The error doesn’t exceed 10^-3 Df/dy = 4/t L = max|df/dy| = 4 Y(t) = 1/9 t^5 + 8/9t^-4 Y’(t) = 5/9 t^4 -32/9*t^-5 M = max|y”(t)| = 20
h.M/2L * (e^(L(ti-a))-1) <= 10^-3 N >= 133996,1677 We chose n at least 133997




