Bài tập Phân tích chi phí và doanh thu cho độc quyền | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Phạm Ánh Chinh MSV 11230035
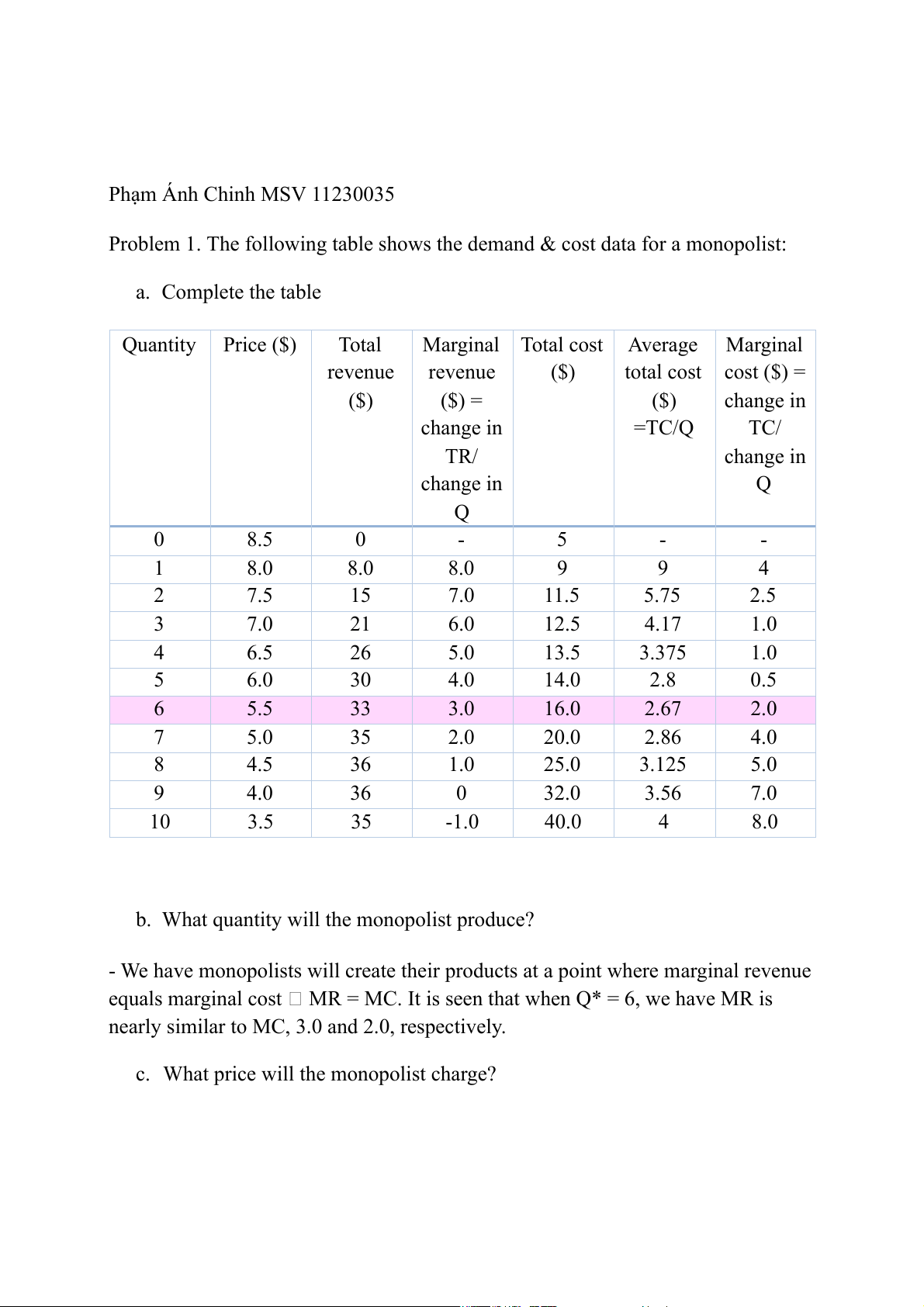
Problem 1. The following table shows the demand & cost data for a monopolist: a. Complete the table Quantity Price ($) Total Marginal Total cost Average Marginal revenue revenue ($) total cost cost ($) = ($) ($) = ($) change in change in =TC/Q TC/ TR/ change in change in Q Q 0 8.5 0 - 5 - - 1 8.0 8.0 8.0 9 9 4 2 7.5 15 7.0 11.5 5.75 2.5 3 7.0 21 6.0 12.5 4.17 1.0 4 6.5 26 5.0 13.5 3.375 1.0 5 6.0 30 4.0 14.0 2.8 0.5 6 5.5 33 3.0 16.0 2.67 2.0 7 5.0 35 2.0 20.0 2.86 4.0 8 4.5 36 1.0 25.0 3.125 5.0 9 4.0 36 0 32.0 3.56 7.0 10 3.5 35 -1.0 40.0 4 8.0
b. What quantity will the monopolist produce?
- We have monopolists will create their products at a point where marginal revenue
equals marginal cost MR = MC. It is seen that when Q* = 6, we have MR is
nearly similar to MC, 3.0 and 2.0, respectively.
c. What price will the monopolist charge?
- The price depends on Q and D. Therefore, the monopolist will charge depends on
Q*, so we have Q* = 6, they decide to produce with P = 5.5
d. What will the profit be at this price?
- It is observed that at Q* = 6, P* = 5.5 and ATC = 2.67
P max = Q* (P* - ATC*) = 6.(5.5 – 2,67) = 16.98
So the profit at this price will be $16.98 Problem 2:
A firm has demand function of P = 100 - Q ($) and total cost function of TC=500+ 4Q+Q2 ($).
a.Is this firm a perfect competitive firm? Why?
This firm isn’t a perfect competitive. Because if the firm is a perfect competitive,
D is perfect elastic. But D in this situation is P= 100 – Q Slope down D.
b. What is price and quantity to maximize total revenue ? What is that maximum total revenue ?
We have: TR = P.Q = (100 – Q).Q = 100Q – Q2
TR max = 2500 Q = 10 and P = 50.
c. What is price and optimal quantity (số lượng tối ưu) to maximize profit?
What is that maximum total profit ?
So we have MC = TC’ = (500+ 4Q+Q2)’ = 2Q + 4
And D: P = 100 – Q MR = 100 – 2Q
To maximize profit, we have MR=MC 100 – 2Q = 2Q + 4 Q = 24 P = 76 Profit = Q ( P – ATC) 500+4 Q+Q2 + + 2 And ATC = TC= = 500 4.24 24 = 48.83 C Q 24
So Profit = Q ( P – ATC). 24.( 76 – 48.83) = 652.08 ($)
d. Asume government imposes a tax of 8 $ per unit of good sold, what is price
and optimal quantity that gives the firm maximum profit? What is this maximum profit? Before 2 imposing a tax: TC=500+ 4Q+Q
After imposing a tax of $8: TC = 500 + 4Q + Q2 + 8Q = 500 + 12Q + Q2 MC = TC’ = 2Q +12
To maximize profit, we have MR=MC 100 – 2Q = 2Q + 12 Q = 22 P = 78 Profit = Q ( P – ATC) 500+12Q+Q2 + + 2 And ATC = TC= = 500 12.22 22 = 56.72 C Q 22
So Profit = Q ( P – ATC) = 22.( 78 – 56.72) = 468.16 ($)
e. Asume government imposes a fixed tax of 100 $, what is price and
optimal quantity that gives the firm maximum profit? Before 2 imposing a tax: TC=500+ 4Q+Q
After imposing a fixed tax of $100: TC = 500 + 4Q + Q2 + 100 = 600 + 4Q + Q2 MC = TC’ = 2Q + 4
To maximize profit, we have MR=MC 100 – 2Q = 2Q + 4 Q = 24 P = 76 Profit = Q ( P – ATC) 600+4 Q+Q2 +4.24 + 2 And ATC = TC= = 600 24 = 53 C Q 24
So Profit = Q ( P – ATC) = 24.( 76 – 53) = 552($)