BÀI TẬP
PHÉP TÍNH TÍCH PHÂN CỦA HÀM SỐ MỘT BIẾN
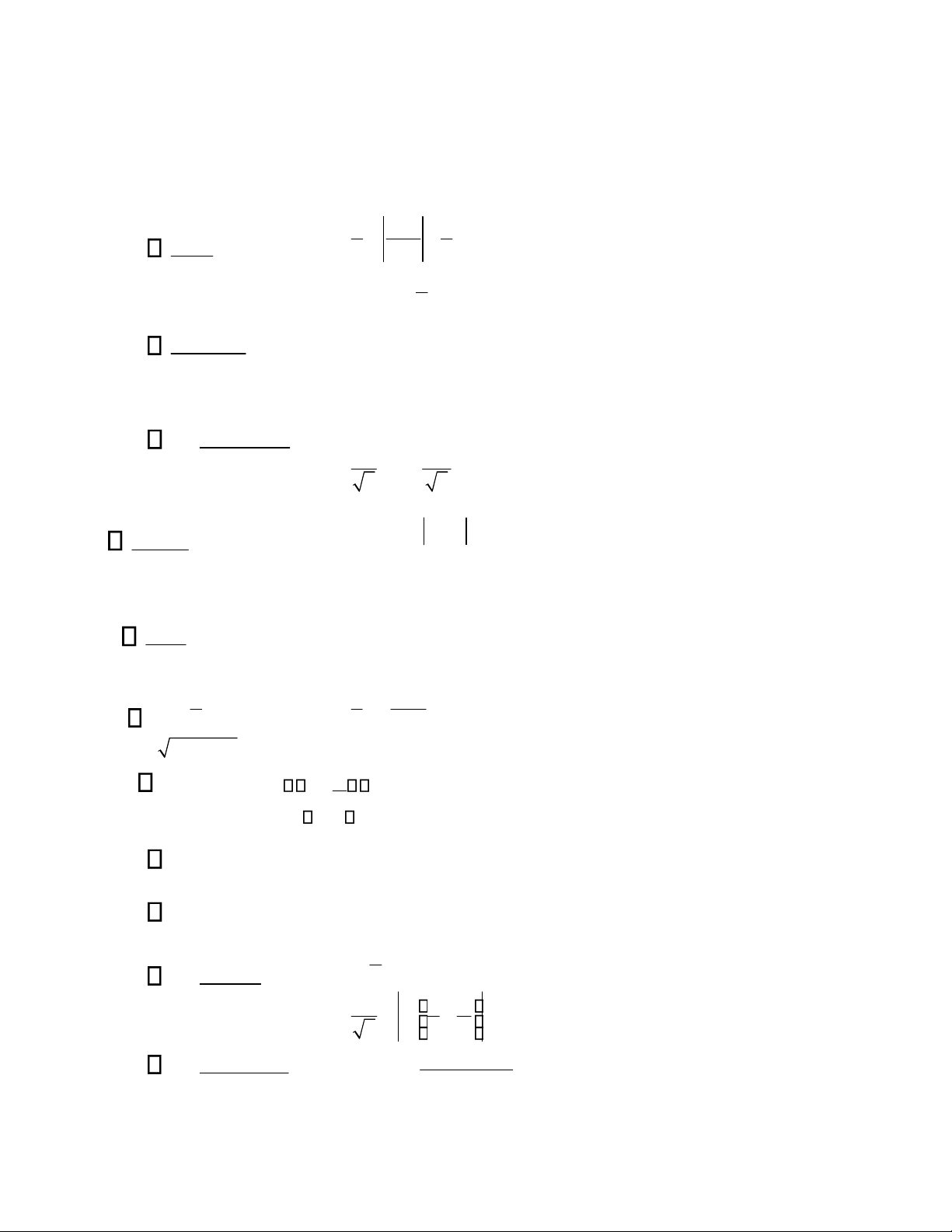
Bằng các phép biến đổi đồng nhất, hãy đưa các tích phân đã cho về tích phân bảng và tính các tích phân đó: 1. 4dx
(ĐS: 1 ln x −1 − 1 arctgx x −1 4 x +1 2 2. 1+ 2x2 dx (ĐS: arctgx− 1 ) x ( ) 2 1+ x2 x 3. dx (ĐS: 1 ln x arctg x(2+ln2 x) 2 2 x 2 x e 4. e ln 1 −
x +ex2x dx (ĐS: − −e 1−e 5. e ) x x dx (ĐS: ln 1( +ex 1+e 2 sin 6. x dx
(ĐS: 1 x− sin x 2 2 2
7. 1+sin 2xdx; x∈ 0,π
(ĐS: −cosx+sin x 2 8.
ecosx sin xdx (ĐS: −ecosx 9. e cosx e dxx (ĐS: sinex ) x ) 10. 1 dx 2 (ĐS: tg 1+cos x 1 x π ) 2 2 8 11. 2 dx (ĐS: ln tg + sin x+cos x 1 Dương T.T.Hương − 12. 1+cos x 3 dx (ĐS: 2 ) (x+sin x) 2(x+sin )x
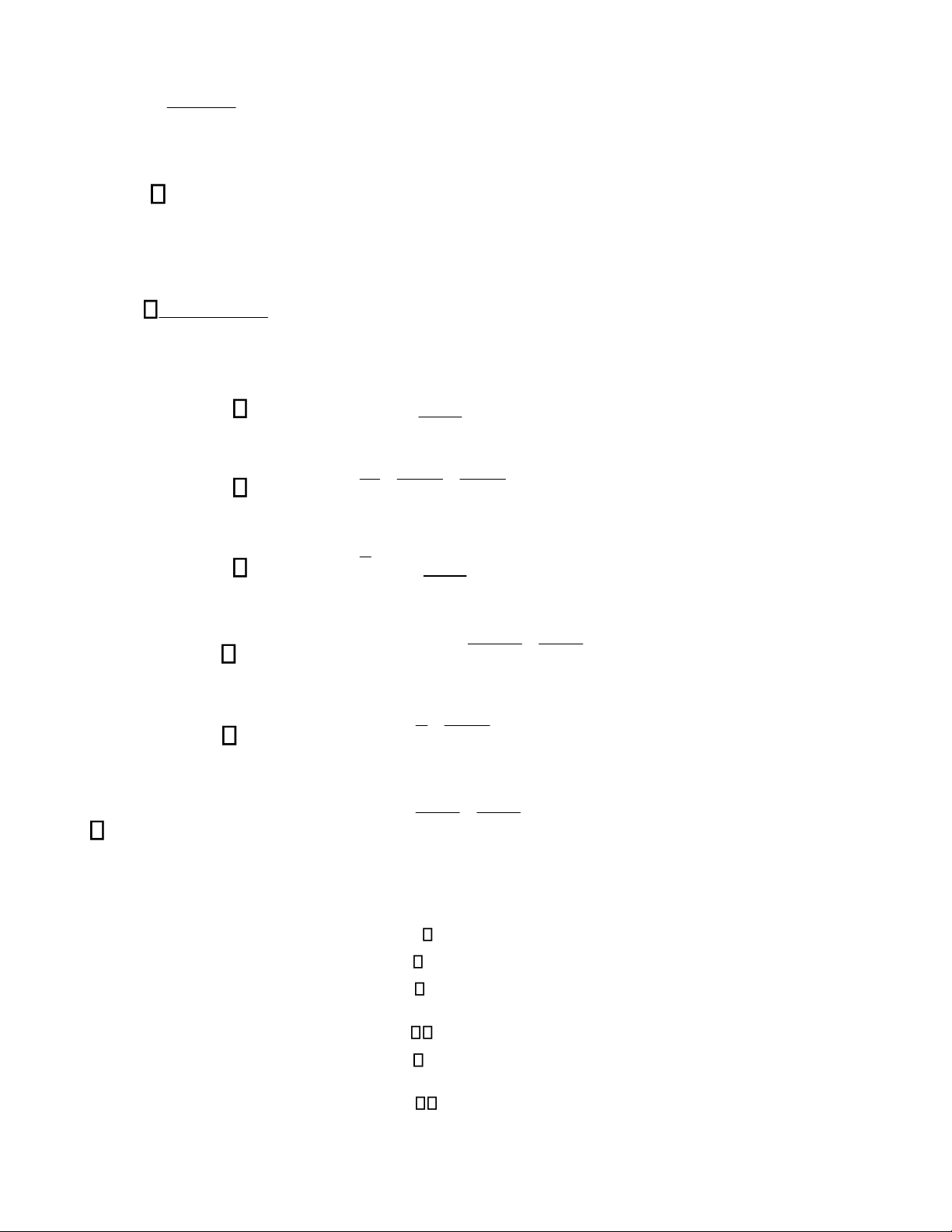
Tính các tích phân: (phương pháp đổi biến) 4 x x e − e + ) 4 x e 1 21 ( 3 4 3 4 ( 1) ) 13. e2x dx (ĐS: + HD: x
Đặt ex + =1 t4 dx 1 e +− 1 ) x e 1 + 1 x e ++ 1 2 x e dx ( x x Đ S: e x +ln e 1 − ) 14. (ĐS: ln e 1 − 1 +ln x 2 3 15. 1+ x ) ( ln ) x 3 ( Đ S: 21 +ln x +l nln x +2 ln 16. dx (ĐS: 17.
1+ln x dx 1+ln x −1 ) xln x 2 18.
e3x +e dx2x (ĐS: 3( ex +1)3/2 ) 1 19. e (
2x2+ −2 1x 2x+1)dx (ĐS: 2e 2x2+ −2x 1 ) 2 Dương T.T.Hương ( x Đ S: x 2 arctge 1 − ) 20. dx e 1 − 2 x edx 1 4 x ln e 1 + (2 x 4 x e + e 1 + ) ) 2 21. (ĐS: dx ( Đ S: 2 x 1 +− ln ) 1 ++x 1 ( 1 ++x 1) 2 2 2 2 2 a
x xa −x 22. HD:
a −x dx arc sin + 2 ) a 2 đặt x+1=t2 2 xdx 1 2 2 2 2 2 2 2 xa x +−
a ln( x + a +x ) ) ax + 2 2 2 23. (ĐS: HD: xdx a xx 2 2 arcsin 2 2 − a −x )
Đặt x = asint ax − aa dx 1 a arcsin ) 2 2 xx −a a x 24. (ĐS: dx 2 x −9 ) 2 2 x x 9 − 9x x 2 1 − dx 1 x − ( 1 arccos 2 Đ S: − ) 25. (ĐS: HD: Đặt x = x 1 + x x x dx asint ( Đ S: 2 arcsin x ) 2 2 x −x 2 x 2 1 + 2 1 + x 1 + ln x 26. (ĐS: − HD: Đặt x = 1 ax 1 hoac x = a t cost 27. (ĐS: 28. HD: Đặt x = 1 t 29.
HD: Đặt x =sin2t 30. dx (ĐS: x + −1 ) x dx 3 Dương T.T.Hương 31. 2 (ĐS: 3
arctg ax + x2 +a2 ) HD: Đặt x = atgt (x a ) 2 + 2 2a
Tính tích phân từng phần 32. x e dx2 −x
(ĐS: −x e2 −x −2xe−x − 2e−x ) 1 33. x e dx3 −x2 2
(ĐS: − ( x2 +1)e−x2 ) 3 31 x + x − 34. (
x3 + x e dx) 5x (ĐS: 5 25 125 1e5x x3 − 2 1 31 ) 2 x 1 −x ) 5 4 2 2 x 1 + 2 14 − x ) 35. xarcsin xdx (ĐS: 1 (2x2 −1)arcsin x+ 4 38. ln xdx
(ĐS: x(ln x−1) ) (
x3 +1)ln(x+1) x3 x2 x 39. x2 ln 1( + x dx) (ĐS: − + − ) 3 9 6 3 2 36. x2 arcsin 2xdx
(ĐS: x3 arcsin2x+ 3 36 1 37. arctgxdx
(ĐS: xarctgx −2ln(1 + x2 ) ) 1 2 − x x 40. x2 sin2xdx (ĐS: cos x2 + sin2x ) 4 2
ex (sin x −cos x) 41. ex sin xdx (ĐS: ) 2 sin x+(ln3)cosx 42. 3xcosxdx (ĐS: 23x ) 4 Dương T.T.Hương 1+ln 3
(x−1)2 sin x x+ −( 2 1)cosx (ĐS: ex ) 43.
x e2 x cos xdx 2
Tìm công thức truy hồi đối với mỗi tích phân In được cho dưới đây: 44. x e dx an ax ; ≠ 0
(ĐS: In = 1 x en ax − n In−1 ) a a 45. lnn xdx
(ĐS: In = xlnn x−nIn−1) 46.
xαlnn xdx; α≠−1
(ĐS: In = xα+1lnn x − n In−1) α+1 α+1 47. x dxn ; n > 2
(ĐS: In = xn−1 x2 +a − n−1aIn−2 ) 2 n n x +a
Tích phân các hàm hữu tỷ 1 2 ( ln x 1 +− ln ) 48. xdx Đ S: x 2 ++ x −3 4 5 20 3 2 x ( 2
x+1)(x+2)(x−3) ( Đ S: +ln x 1 − + ln2 x 2 x
+++ 1 arctg ( 2 x 1 + ) ) 2 ( ) 1 x 2 2 x 1 − 2 ( Đ S: arctg +ln x −x 1 ++ arctg ) 49. 3 3 ( ) 2x4 3+5x2 3 3 −2dx 2 x 1 21 21
ln x + ln x −2 + ln x +2 ) 2x − −x 1 2 4 8 8 3 1 50. 1 2x3 + + ln x 1 − + ln x 1 +− arctgx ) 4 4 + 2 x2 5x 1 dx x 1 + 1 ( + arctgx )
x2 +3)(x2 − +x x 1 − 2 4 1) +ln x ) 1 + x +2 51. x4 + +x2
1 dx (ĐS: − x x( −2)(x+2) 5 Dương T.T.Hương 52.
x3 + +4 x 1dx (ĐS: x −1 x4 4 dx (ĐS: − +x ln 53. 1− x 54. x22dx (ĐS: (x+ 2) (x+1)
Tính các tích phân bằng cách sử dụng các công thức lượng giác: cos x 1.
sin3 xdx (ĐS: −cosx+ 3 ) 3 2.
cos xdx4 (ĐS: 3x + sin2x + sin4x ) 8 4 32 5 3 2 − − cos x 3.
sin5 xdx (ĐS: cos x cosx) 3 5
4. cos xdx7 (ĐS: sin x−sin3 x+ 3sin5 x − sin7 x ) 5 7 x
5. cos x2 sin2 xdx (ĐS: − sin4x ) 8 32
sin3 xcos xdx2 (ĐS: cos x5 − cos x3 ) 6. 5 3
Ứng dụng của tích phân
y = − −6x x2 7
1. Tính diện tích hình phẳng giới hạn bởi y = −x 3 y= −4 x2
2. Tính diện tích hình phẳng giới hạn bởi 2 y x= −2x 6 Dương T.T.Hương : + =
3. Cho hình phẳng D giới hạn bởi D x22
y22 1 . Tính thể tích khối tròn xoay V được tạo thành khi a b
quay miền D quanh trục hoành Ox. (2014-2015) a x2 2 V =π x 1− 2 b dx= − a a
4. Cho hình phẳng D giới hạn bởi D ={(x y, ): y ≤ x y; ≥ x2} . Tính thể tích khối tròn xoay V được tạo
thành khi quay miền D quanh trục tung Oy. (2015-2016) 1 1 ) π V =π (( = = 6 =π ( y y)2 −y dy2 ... Vx x x dx2 − 4) = 00
5. Cho hình phẳng D giới hạn bởi {y = 2x y; = x2} . Tính thể tích khối tròn xoay V được tạo thành khi
quay miền D quanh trục tung Oy. (2016-2017) y V 4 ( 2 y =π 0 y)2 − 2 dy= =... 8π Vx =π ( − ) 4 ( ( 0
2x)2 x2)2 dx=... 3
6. Cho hình phẳng D giới hạn bởi {y
= x y; = x} . Tính thể tích khối tròn xoay V được tạo thành khi
quay miền D quanh trục hoành Ox. (2017-2018) 1 1 ( V =π ( =π x x)2 −x dx2 Vy 0 y2 −y dy4) 0
7. Cho hình phẳng D giới hạn bởi {y = −(x
2)2; y = 0;x = 0} . Tính thể tích khối tròn xoay V
được tạo thành khi quay miền D quanh trục tung Oy. (2017-2018) 7 Dương T.T.Hương 4 4 2
Vy =π x dy2 =π (2− y dy) 0 0 {
8. Cho hình phẳng D giới hạn bởi x= − + =(y 1)2
1;x 1; y= 0} . Tính thể tích khối tròn xoay V
được tạo thành khi quay miền D quanh trục hoành Ox. (2018-2019) π ( π Cách 1: Vx = 12 1− − −x 1)202 dx= 6
Cách 2: x= − +(y 1)2 1 dx= 2(y−1)dy . Khi x chạy từ 1 đến 2 thì y chạy từ 1 đến 0 2 0 π
Vx =π y dx2 =π y2.2(y−1)dy= 6 1 1
9. Cho hình phẳng D giới hạn bởi {y = −9 x2;x = 3} và tiếp tuyến tại đỉnh (P). Tính thể tích khối tròn
xoay V được tạo thành khi quay miền D quanh trục tung Oy. (2018-1019) π V 9 y = 0 9−( 9−y)2 dy= 812π {
10. . Tính thể tích khối tròn xoay V được tạo thành khi quay miền D x y= − =2 1; y 0;x= −2y 2} quanh trục hoành Ox. (2019-2020) 8 Dương T.T.Hương {
11. Cho hình phẳng D giới hạn bởi: x y= + = −2 1;x 3 y y2; = 0; y≥ 0} 2020-2021) a. Tính diện 4 tích miền D ĐS: 3
b. Tính thể tích khối tròn xoay V được tạo thành khi quay miền D quanh Ox. ĐS: π x2 12.
Tính thể tích vật thể tròn xoay tạo ra do quay miền giới hạn bởi các đường: y= −3, y x− =−3 3
quanh trục y = 1 (2021-2022-CLC) 13.
Tính thể tích khối tròn xoay xoay quanh Ox bởi phần hình phẳng giới hạn bởi 1 đường parabol và 2
đường thẳng x+ −(y 2)2 = 4, y x x= , = 0 . (2021-2022) 14.
Tính thể tích khối tròn xoay xoay quanh Oy bởi phần hình phẳng giới hạn bởi hai đường parabol 2 2
x −2x y= −2x x y, = và đường thẳng x=1 (2021-2022) 2 15.
Tính thể tích vật thể tròn xoay tạo ra do quay miền giới hạn bởi các đường: y x= +2 2x y x; + = 0
quanh trục y = -1 (2021-2022-CLC) 9 Dương T.T.Hương