Bài tập tích phân chống Casio – Nguyễn Tiến Chinh Toán 12

Bài tập tích phân chống Casio – Nguyễn Tiến Chinh Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

49 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

14 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
1
Câu 1: Biết
dx
I
2x 1 4
=
a. 2x 1 b.ln 2x 1 4 C
. Tính a + b
A. -2 B. -3 C. 1 D. 2
Câu 2: Biết
x
0
L e cosxdx
= a.e
+ b. Tính a + b
A. 0 B. 1 C. -2 D. 3
Câu 3: Biết
1
2
0
L x 1 x dx a. 2 b
. Tính a - b
A. 1 B. 1/3 C. 2 D. 3
Câu 4. Cho tích phân
2
2
1
I 2x x 1dx
, khẳng định nào sai ?
A.
3
0
I udu
B.
2
I 27
3
C.
3
2
3
0
2
I u
3
D.
I 3 3
Câu 5. Giá trị trung bình của hàm số
f x
trên
a;b
, kí hiệu là
m f
được tính theo công thức
b
a
1
m f f x dx
b a
. Giá trị trung bình của hàm số
f x sinx
trên
0;
A.
2
B.
3
C.
1
D.
4
Câu 6. Cho
2
0
f x dx 5
khi đó
2
0
f x 2sinx dx ?
A.
5
B.
5
2
C.
7
D. 3
Câu 7. Giả sử
1 4 4
0 0 0
f x dx 2, f x dx 3, g x dx 4
, khẳng định nào sai ?
A.
4
0
f x g x dx 1
B.
4 4
0 0
f x dx g x dx
C.
4 4
0 0
f x dx g x dx
D.
4
0
f x dx 5
Câu 8. Cho
2
1
0
I cosx 3sinx 1dx
và
2
2
2
0
sin2x
I
sinx 2
, phát biểu nào sai ?
A.
1
14
I
9
B.
1 2
I I
C.
2
3 3
I 2ln
2 2
D. Đáp án khác
Câu 9. Cho
3
2
0
sinx
I dx
cos2x 2
và đặt
t cosx
. Khẳng định nào sai ?
A.
3
2
0
1 sinx
I
4
cos x
B.
1
4
0.5
1 dt
I
4
t
C.
1
3
0,5
1
I t
12
D.
7
I
12
Câu 10. Cho
1
2
0
x 1
I dx a b a b ?
x 2x 2
A. 5 B. 1 C. 4 D. 3
Câu 11. Cho
a
1
x 1
dx e
x
, khi đó giá trị của a là ?
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
2
A.
2
1 e
B.
e
C.
e
2
D.
2
1 e
Câu 12. Cho tích phân
2
0
sinx
I dx,a 1
1 2acosx a
thì I bằng :
A.
2
a
B.
2a
C. 2 D.
a
2
Câu 13. Cho tích phân
a
0
sinx
I dx
sinx cosx 4
. Giá trị của a là :
A.
3
B.
4
C.
2
D.
6
Câu 14. Tính tích phân
5
1
dx
I aln3 bln5
x 3x 1
Tính giá trị của
2 2
a ab b
A. 4 B. 1 C. 0 D. 5
Câu 15. Tìm khẳng định đúng
3
1
4
0
x 1
I dx ln2
a
x 1
A.
a 2
B.
a 4
C.
a 4
D.
a 2
Câu 16. Cho
f x
là hàm số chẵn và liên tục trên R thỏa mãn
1
1
f x dx 2
khi đó giá trị tích phân
1
0
f x dx ?
A. 2 B. 1 C. 0.5 D. 0,25
Câu 17. Giả sử
5
1
dx
I a lnb
2x 1
giá trị của
a;b
là
A.
a 0;b 81
B.
a 1;b 9
C.
a 0;b 3
D.
a 1;b 8
Câu 18. Khẳng định nào sau đây là đúng
a
e
3
1
3e 1
I x lnxdx
b
A.
ab 64
B.
ab 46
C.
a b 12
D.
a b 4
Câu 19. Với
a 2
, giá trị của
a
2
0
dx
x 3x 2
là
A.
a 2
ln
2a 1
B.
a 2
ln
a 1
C.
a 2
ln
2(a 1)
D.
a 2
ln
2a 1
Câu 20. Cho
a
x
2
0
e 1
I e sinxdx
b
khi đó
sina cos2a ?
A. 1 B. 2 C. 4 D. 0
Câu 21. Cho
3
0
x
I dx
1 1 x
, nếu đặt
2
1
t x 1 I f t dt
, vậy :
A.
2
f t 2t 2t
B.
2
f t t t
C.
2
f t t t
D.
2
f t 2t 2t
Câu 22. Giả sử rằng
2
0
1
3x 5x 1 2
dx aln b
x 2 3
. Khi đó
a 2b ?
A. 30 B. 40 C. 50 D. 60
Câu 23. Cho

2
1
nx
0
n N,I e 4xdx e 1 e 1
, giá trị của n là
A. 1 B. 3 C. 4 D. 2
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
3
Câu 24. Biết
1
0
2x 3
I dx aln2 b
2 x
thì giá trị của a là
A. 7 B. 2 C. 3 D. 1
Câu 25. Biết
3 3 2
Tinh
1 2 1
f x dx 5; f x dx 3 f x dx ?
A. 2 B. – 2 C. 1 D. 5
Câu 26
. Tính tích phân sau
2
0
I x x a dx
A.
8
2a
3
B.
3
1 8
a 2a
3 3
C.
8
2a
3
D. Cả A, B, C
Câu 27. Biết
3
2
0
dx
a
9 x
thì giá trị của a là:
A.
1
12
B.
1
6
C.
6
D.
12
Câu 28. Nếu
4
3
1
dx lna
x 1 x 2
thì a bằng :
A.
12
B.
4
3
C.
1
D.
3
4
Câu 29. Bằng cách đổi biến
x 2sint
thì tích phân
1
2
0
dx
4 x
là :
A.
1
0
B.
6
0
C.
6
0
tdt
D.
3
0
t
Câu 30. Cho
x
lnm
x
0
e dx
A ln2
e 2
, khi đó giá trị của
m
là :
A.
m 0;m 4
B. Kết quả khác C.
m 2
D.
m 4
Câu 31. Tìm khẳng định sai trong các khẳng định sau
A.
2
0 0
x
sin dx 2 sinxdx
2
B.
1
x
0
1 x dx 0
C.
1 1
0 0
sin 1 x dx sinxdx
D.
1
2007
1
2
x 1 x dx
2009
Câu 32. Cho hàm số
f x
là hàm số chẵn và
0
3
f x dx a
, chọn mệnh đề đúng
A.
3
0
f x dx a
B.
3
3
f x dx 2a
C.
3
3
f x dx a
D.
0
3
f x dx a
Câu 33. Trong các đẳng thức sau , đẳng thức nào sai
A.
1
2
0 0
sinxdx dx
B .
2 2
0 0
sinxdx costdt
C.
2 2
0 0
1
sinxdx sin 2x 1 dsin 2x 1
8
D.
1
2
0 0
sinxdx dx
Câu 34. Tích phân
x
4
4
0
3x e dx a be
khi đó
a 5b
bằng :
A.
8
B. 18 C. 13 D. 23
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
4
Câu 35. Giả sử
5
1
dx
lnc
2x 1
. Giá trị của c là
A. 9 B. 8 C. 3 D. 81
Câu 36. Cho
n
6
0
1
I sin xcosxdx
64
. Khi đó giá trị của
n
bằng
A.
5 B. 3 C. 4 D. 6
Câu 37
. Biết
a
4
0
3
4sin x dx 0
2
, giá trị của
a 0;
là :
A.
4
B.
2
C.
8
D.
3
Câu 38. Cho
a
2
0
x
dx
a x
bằng
A.
1
a
2
B.
2
a
4
C.
1
a
2
D.
2
a
4
Câu 39. Cho tích phân
sinx
2
0
I sin2xe dx
, bạn Nhớ giải như sau
Bước 1. NHớ đặt
1
Doi.can t
0
x 0 t 0
t sinx dt cosxdx I 2 t.e dt
x t 1
2
Bước 2. Nhớ chọn
1
1
t t
t t
0
0
u t du dt
A t.e e dt 1
dv e dt v e
Bước 3.
I 2A 2
Bài giải của Nhớ đúng hay sai ? nếu sai thì sai ở bước nào?
A. Sai từ bước 1 B. Sai từ bước 2
C. Nhớ giải chính xác D. Sai từ bước 3
Câu 40. Nếu
f x
liên tục và
4
0
f x dx 10
thì
2
0
f 2x dx
bằng :
A. 5 B. 29 C. 19 D. 9
Câu 41. Cho
3
x
0
2 4 dx
, trong các kết quả sau
I .
3 2
x x
2 0
I 2 4 dx 2 4 dx
II.
3 2
x x
2 0
I 2 4 dx 2 4 dx
III.
3
x
2
I 2 2 4 dx
Kết quả nào đúng
A. Chỉ II B. Chỉ III C. Cả I, II, III D. Chỉ I
Câu 42
. Giả sử
4
0
2
I sin3xsin2xdx a b
2
, khi đó giá trị của
a b
là :
A.
1
6
B.
3
5
C.
3
10
D.
1
5
Câu 43. Cho hàm số
f x
liên tục và triệt tiêu khi
x c
trên
a;b
. Các kết quả sau , câu nào đúng ?
A.
b b
a a
f x dx f x dx
B.
b c b
a a c
f x dx f x dx f x dx
C.
b c b
a a a
f x dx f x dx f x dx
D. A,B,C đều đúng
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
5
Câu 44. Khẳng định nào sau đây sai về kết quả
2
0
1
2x 1 sinx dx 1
a b
A.
a 2b 8
B.
a b 5
C.
2a 3b 2
D.
a b 2
Câu 45. Biết
2 2
a
1
2x lnx ln 2
dx 3
x 2
, giá trị của a là
A. 4 B. 2 C. -1 D. 3
Câu 46. Biết
4
4
0
1 a
dx
3
cos x
A. a là một số chẵn B. A là số lớn hơn 5 C. A nhỏ hơn 3 D. A là số lẻ
Câu 47. Tìm khẳng định sai trong các khẳng định sau
A.
2
0 0
x
sin dx 2 sinxdx
2
B.
1
x
0
1
e dx 1
e
B.
0 0
sin x dx cos x dx
4 4
D.
1 1
0 0
sin 1 x dx sinxdx
Câu 48. Giả sử
5
1
dx
lnc
2x 1
, giá trị đúng của c là
A. 9 B. 3 C. 81 D. 8
Câu 49. Cho tích phân
2
3
2
1
1 x
I dx
x
, nếu đặt
2
1 x
t
x
thì
A.
2
2
3
2
2
t
I dt
t 1
B.
2
3
2
2
t
I dt
t 1
C.
2
2
3
2
2
t
I dt
t 1
D.
3
2
2
t
I dt
t 1
Câu 50. Cho
2
2 2
1
I 2x x 1dx;u x 1
, chọn khẳng định sai trong các khẳng định sau
A.
3
0
I udu
B.
2
1
I udu
C.
3
3
2
0
2
u
3
D.
2
I 27
3
Câu 51. Biết
a
0
1
sinxcosxdx
4
. Khi đó giá trị của a là
A.
2
B.
2
3
C.
4
D.
3
Câu 52. Một học sinh giải
1
x
0
dx
I
1 e
I Viết lại thành
x
1
x x
0
e dx
I
e 1 e
II .Đặt
e
e
x
1
1
du
u e I (ln u ln u 1)
u 1 u
III.
e
I ln
e 1
Lời giải trên nếu sai thì sai từ bước nào
A. III B. I C. II D. Giải đúng
Câu 53. Giả sử
b b
a c
f x dx 2; f x dx 3;a b c
thì
c
a
f x dx ?
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
6
A. 5 B. 1 C. -1 D. -5
Câu 54. Với
a 0
. Giá trị của tích phân
2a
0
I xsin ax dx
là
A.
2
a
B.
2
1
2
a
C.
2
1
a
D.
2
2a
a
Câu 55. Cho
a
1
3x
0
e 1
e dx
b
Khi đó khẳng định nào sau là đúng?
A.
a b
B.
a b
C.
a b
D.
a b
Câu 56. Với
t 1;1
ta có
t
2
0
dx 1
ln3
2
x 1
khi đó giá trị của t là
A.
1
3
B.
1
3
C.
0
D.
1
2
Câu 57. Cho
2
0
I 2x 1 sin2xdx
Lời giải sai từ bước nào
Bước 1. Đặt
u 2x 1;dv sin2xdx
Bước 2. Ta có
du 2dx;v cos2x
Bước 3.
2 2
2
2
0
0
0 0
I 2x 1 cos2x 2cos2xdx 2x 1 cos2x 2sin2x
Bước 4.
I 2
A. Bước 3 B. Bước 1 C. Bước 2 D. Không sai
Câu 58. Biết
b
0
2x 4 dx 0
Khi đó giá trị của b là :
A.
b 1 b 4
B.
b 0 b 2
C.
b 1 b 2
D.
b 0 b 4
Câu 59. Tích phân
3
1
2x 1
I dx a bln2
x 1
, khi đó tổng của
a b
là
A. 1 B. 7 C. 10 D. 2
Câu 60. Với
a 0
khi đó tích phân
1
2
2
a
2x
dx
a x
có giá trị là :
A.
1
a
B.
2
a 1
a a 1
C.
a 1
a a 1
D.
a 1
a 1
Câu 61. Trong các khẳng định sau , khẳng định nào đúng
A.
2
2
dx
2 1 x C
1 x
B.
b
a
f x dx 0 f x 0; x a;b
C.
c b c
a a b
f x dx g x dx f x dx;a b c
D. Nếu
F x
là nguyên hàm của
f x
thì
F x
cũng là nguyên hàm của
f x
Câu 62. Cho biết
1
2
0
4x 11 a
dx ln ;a,b N
b
x 5x 6
thì giá trị của
a b
bằng :
A. 11 B. 12 C. 10 D. 13
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
7
Câu 63. Cho
1 2
4
4 4 2
0 0 1
dx
I ;J sin x cos x dx;K x 3x 1 dx
3x 1
, tích phân nào có giá trị bằng
63
6
A. I B. J C. K D. J và K
Câu 64
. Nếu
2019 2019 2019
Tinh
0 0 0
f x dx 37; g x dx 16 2f x 3g x dx A
, giá trị của A là
A.
122 B. 74 C. 48 D. 53
Câu 65
. Nếu
201 203 203
Tinh
0 201 0
f x dx 201; f x dx 16 f x dx A
A.
A 215
B.
217
C.
219
D.
197
Câu 66. Cho
2
2
a b sin x b
f x ;a,b R
sin x
. Tìm nguyên hàm
F x
của
f x
biết
1
F ;F 0;
4 2 6
F 1
3
A.
3 1
F x tanx cotx
4 2
B.
3 1
F x tanx cotx
4 2
C.
3 1
F x tanx cotx
4 2
D.
3 1
F x tanx cotx
4 2
Câu 67. Cho
1
5 3
0
dx
aln2 bln5 c
x x
Khi đó
a 2b 4c
bằng
A. 2 B. 3 C . 0 D. 1
Câu 68. Tìm các hằng số A và B đê
Thoa.man
2
0
f' 1 2
f x Asin x B
f x dx 4
A.
2
A ;B 2
B.
2
A ;B 2
C.
A 2;B 2
D.
A 2;B 2
Câu 69. Tìm a sao cho
2
2 3
1
a 4 a x 4x dx 12
A.
a 3
B.
a 5
C.
a 3
D. Đáp án khác
Câu 70. Giả sử
k 0
và
3
2
0
dx
ln 2 3
x k
. giá trị của k là
A.
k 3
B.
k 2
C.
k 2 3
D.
k 1
Câu 71. Biết rằng
1
x
0
2x 1 e dx a b.e
, tích
ab ?
A.ab 1
B.
ab 1
C.
ab 15
D.
ab 5
Câu 72. Biết rằng
x ;
4 3
thì
3 cotx 4
x
. Gọi
3
4
cotx
I dx
x
thì
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
8
A.
3 1
I
12 4
B.
1 1
I
4 3
C.
1 1
I
5 4
D.
3 1
I
12 3
Câu 73. Tìm m biết
m
0
2x 5 dx 6
A.
m 1;m 6
B.
m 1;m 6
C.
m 1;m 6
D.
m 1;m 6
Câu 74. Nếu đặt
t cos2x
thì tích phân
4
4
2
0
I 2sin x 1 sin4xdx
A.
1
4
0
1
I t dt
2
B.
1
2
3
0
1
I t dt
2
C.
1
5
0
I t dt
D.
3
2
4
0
I t dt
Câu 75
. Nếu đặt
t 3tanx 1
thì tích phân
4
2
0
6tanx
I dx
cos x 3tanx 1
A.
2
2
1
4 t 1
I dt
3
B.
2
2
1
I t 1 dt
C.
2
2
1
4 t 1
I dt
3
D.
2
2
1
4 t 1
I dt
5
Câu 76. Tích phân
a
2
2x
0
3 e
x 1 e dx
4
,Giá trị của a là
A. 2 B. 1 C. 3 D. 4
Câu 77. Cho
e
1
k
I ln dx
x
, xác định
k
để
I e 2
A.
k e 2
B.
k e
C.
k e 1
D.
k e 1
Câu 78. Tính tích phân
2
2
6
sin x 1
I dx ln b 3c ;a,b,c Z
sin3x a
. Giá trị của
a 2b 3c
là :
A. 2 B. 3 C. 8 D. 5
Câu 79. Nếu đặt
1
2 3 2
0
u 1 x I x 1 x dx
trở thành:
A.
1
0
u 1 u du
B.
0
1
u 1 u du
C.
1
2
2
0
u 1 u du
D.
0
4 2
1
u u du
Câu 80. Để
k
1
k 4x dx 3k 1 0
thì giá trị của k là
A. 1 B. 3 C. 2 D. 4
Câu 81. Nếu
6 4
0 0
f x dx 10; f x dx 7
thì
6
4
f x dx ?
A. 3 B. 17 C. 170 D. -3
Câu 82. Cho tích phân
2
2
0
x sinx 2m dx 1
, giá trị của m là ?
A.
m 5
B.
m 3
C.
m 4
D.
m 6
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
9
Câu 83. Cho
x
0
g x costdt
, chọn khẳng định đúng
A.
g' x sin 2 x
B.
g' x cos x
C.
g' x sin x
D.
cos x
g' x
2 x
Câu 84. cho
f,g
là hai hàm số theo
x
.Biết rằng
x a;b ,f' x g' x
, Mệnh đề nào đúng?
I.
x a;b ,f' x g x
II.
b a
a b
f x dx g x dx
III.
f x f a g x g a
A. I B. II C. Không có D. III
Câu 85. Cho
t
4
0
3
f x 4sin x dx
2
. Giải Phương trình
f x 0
A.
k2 ;k z
B.
k
;k z
2
C.
k ;k z
D.
k ;k z
2
Câu 86. Giả sử
2
1
dx a
ln
x 3 b
với a, b là các số tự nhiên và ước chung lớn nhất của a, b bằng 1 . Khẳng định
nào sai ?
A.
3a b 12
B.
a 2b 13
C.
a b 2
D.
2 2
a b 41
Câu 87. Cho
2
5
1
I x x 1 dx
, nếu đặt
u x 1
, hãy chọn khẳng định sai trong các khẳng định sau
A.
1
5
2
I x 1 x dx
B.
13
I
42
C.
1
6 5
0
u u
I
6 5
D.
1
5
0
I u 1 u du
Câu 88. Cho
x 2 x 2 x
0 0 0
I e cos xdx;J e sin xdx;K e cos2xdx
. Khẳng định nào đúng trong các khẳng định
sau
I.
I J e
II .
I J K
III.
e 1
K
5
A. Chỉ II B. Chỉ III C. Chỉ I D. Cả I và II
Câu 89. Khẳng định nào sau đây là đúng?
I – Một nguyên hàm của hàm số
cosx
y e
là
cosx
sinxe
II – Hàm số
2 2
x 6x 1 x 10
f x ;g x
2x 3 2x 3
đều là một nguyên hàm của một hàm số
III -
1 x 1 x
xe dx x 1 e C
IV.
2 3
1 1
x x
0 0
e dx e dx
A. Chỉ I B. Chỉ III C. Chỉ IV D. Chỉ II
Câu 90. Nếu
d d
a b
f x dx 5, f x dx 2;a d b
thì
b
a
f x dx
bằng
A. -2 B. 0 C. 8 D. 3
Câu 91. Cho
1
3
2
4
0
4x
2 3m dx 0
x 2
Khi đó
2
144m 1
bằng :
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
10
A.
2
3
B.
4 3 1
C.
2 3
3
D. Đáp án khác
Câu 92. Nếu
10 8
0 0
f x dx 17; f x dx 12
thì
10
8
f x dx ?
A. 5 B. 29 C. -5 D. 15
Câu 93
. Tìm khẳng định đúng trong các khẳng định sau
A.
3 1
0 2
x 2 dx x 1 dx
B.
3 3
0 0
x 2 dx x 2 dx
C.
3 3 2
0 2 0
x 2 dx x 2 dx x 2 dx
D.
3 3 2
0 2 0
x 2 dx x 2 dx x 2 dx
Câu 94. Khẳng định nào là đúng
A. Nếu
w' t
là tốc độ tăng trưởng cân nặng / năm của một đứa trẻ thì
10
5
w' t dx
là sự cân nặng của đứa
trẻ giữa 5 đến 10 tuổi
B. Nếu dầu rò rỉ từ một cái thùng với tốc độ
r t
tính bằng galong/phút tại thời gian t thì
120
0
r t dt
biểu
thị lượng galong rò rỉ trong hai giờ đầu tiên
C. Nếu
r t
là tốc độ tiêu thụ dầu trên thế giới , trong đó t được tính bằng năm , bắt đầu tại
t 0
vào
ngày 1 tháng 1 năm 2000 và
r t
được tính bằng thùng/ năm thì
17
0
r t dt
biểu thị số dầu được tiêu thụ
từ 1/1/2000 đến 1/1/2017
D. Cả A,B,C đều đúng
Câu 95. Nếu
f 1 12;f' x
liên tục và
4
1
f' x dx 17
, giá trị của
f 4 ?
A. 29 B. 5 C. 19 D. 9
Câu 96. Cho
2
2
0
x 1
K dx aln5 bln3
x 4x 3
thì giá trị của
a;b
là
A.
a 2;b 3
B.
a 3;b 2
C.
a 2;b 3
D.
a 3;b 2
Câu 97. Biết
a
3
2
1
x 2lnx 1
dx ln2
2
x
thì giá trị của a là ?
A.
4
B.
ln2
C. 2 D. 3
Câu 98. Cho
2
2
sin x 3
0
I e sinxcos xdx
. Nếu đặt
2
t sin x
thì
A.
1
t
0
1
I e 1 t dt
2
B.
1 1
t t
0 0
I 2 e dt te dt
C.
1
t
0
I 2 e 1 t dt
D.
1 1
t t
0 0
1
I e dt te dt
2
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
11
Câu 99. Giả sử
2
x
0
f t dt xcos x
giá trị của
f 4
bằng:
A.
1
B.
1
2
C. Đáp án khác D.
1
4
A. 16 m. B. 130 m. C. 435 m. D. 170 m.
Câu 113: Bạn Nhớ đang chở hai người bạn gái của mình là Ty và Sương trên chiếc xe thể thao hiệu
Lamborghini Aventador chạy trên một đường đua thẳng có độ dài 4km. Xe tăng tốc từ 0km/h đến 100km/h
trong 3 giây đầu tiên đi hết 260m và sau đó xe chuyển động nhanh dần đều với gia tốc
20m / s
. Tính thời gian
để xe hoàn thành đường đua biết vận tốc của chuyển động nhanh dần đều có công thức
o
v at v
với
o
a,v
là gia tốc và vận tốc đầu.
A. 21s B. 11s C. 14s D. 18s
Câu 114. Một vật đang chuyển động thẳng nhanh dần đều có vận tốc là
18km / h
. Trong giây thứ 5 mật đi
được quãng đường là
5,9m
> tính quãng đường vật đi được sau
10s
kể từ lúc bắt đầu chuyển động
A.
132
m
5
B.
103,6m
C.
60m
D. đáp án khác
Câu 115. Bạn Phương vừa nhai quần đùi vừa thả một hòn bi chuyển động trên một rãnh nằm ngang để tạo
một dao động điều hòa với phương trình chuyển động là
x 4cos 4 t cm
3
, cùng lúc đó ở máng bên
cạnh bạn Hợp cũng đang điều khiển chiếc xe hơi đồ chơi mới mượn được của bạn Nhớ và cũng đang dao
động điều hòa với phương trình dao động là
x 2cos 2 t cm
2
.Nếu gọi
1
S
là quãng đường hòn bi của
Phương đi được trong khoảng thời gian là
0,25s
kể từ lúc xuất phát và
2
S
là quãng đường chiếc siêu xe của
bạn hợp chạy được trong khoảng thời gian
2,875s
kể từ lúc xuất phát. Khi đó
i.
1 2
S S
ii.
1 2
S S
iii.
1 2
S S
4i.
2 1
S S 12
Có bao nhiêu khẳng định đúng
A. 1 B. 2 C. 3 D. 0
Câu 116. Cho
b
a
f x 2g x 19
và
b
a
5f x 3g x dx 30
khi đó
b b
a a
f x dx A; g x dx B
thì
Câu 100. Một ô tô đang chuyển động với vận tốc 12m / s thì người lái xe bất ngờ tăng tốc cho xe chạy nhanh
dần đều , sau
15s
thì xe đạt vận tốc 15m / s .Tính quãng đường xe đi được sau
30s
kể từ khi tăng tốc
A. 270m B. 450m C. 360m D. 540m
Câu 111. Một lực có độ lớn 40 N (newton) cần thiết để kéo căng một chiếc lò xo có độ dài tự nhiên 10 cm lên 15
cm. Biết rằng theo định luật
Hooke
trong Vật lý, khi một chiếc lò xo bị kéo căng thêm x (đơn vị độ dài) so với
độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho bởi công thức f
x
kx
N
, trong đó
k
là
hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo lò xo có độ dài từ 15 cm đến 18 cm ? (kí
hiệu J
Jun
là đơn vị của công)
A. 1,56 J . B. 0,94 J . C. 1,78 J . D. 2,03 J .
Câu 112. Một vật chuyển động chậm dần với vận tốc v
t
16010t
m/s
. Hỏi rằng trong
3s
trước khi dừng hẳn vật
di chuyển được bao nhiêu mét ?
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
12
A và B có giá trị là bao nhiêu
Câu 117. Cho
b
a
f x 2g x 1
và
b
a
f x 3g x dx 30
khi đó
b
a
11f x 12g x dx ?
Câu 118. Cho
b
a
f x g x 10
và
b
a
3f x g x dx 15
khi đó
b b
a a
2016f x dx 2017g x dx
Câu 119. Cho
3
0
f x dx 15
. Hãy tính
3
2
0
x 5x f x dx
Câu 120. Cho
4
0
f x dx
4
, Hãy tính
4
0
sin2x 3f x dx
Câu 121: Cho
2
x 1;khi:x 0
f x
5x+1;khi:x<0
Hãy tính tích
5
3
f x dx
Câu 122. Cho
2
x 6;Khi:x<-1
f x
x x 5;Khi : x 1
Hãy tính tích
2
3
f x dx
Câu 123. Cho Cho
2
2x 1;khi : x 0
f x
x 1;khi: x 0
, Hãy tính tích
1
1
f x dx
Câu 124.Cho
2
2
2 2
2
1
x
I dx 1 a lnc b ln c 1 ;a;b;c Q
x 7x 12
, Khi đó , hãy tính kết quả của
P a b c
A.
P 43
B.
P 11
C.
P 3
D.
P 3
Câu 125.Cho
2
5 3
1
dx a a b a
I lnb ln a b ,a;b Q
b b 4b
x x
hãy chọn phát biểu sai
A.
a b
B.
a b 1
C.
2 2
a b 5
D.
a 2b 10
Câu 126. Tích phân
3
2
0
x
I dx a bln2, a;b
3
cos x
. Khi đó tổng
a b
gần với gía trị nào nhất sau đây
?
A.
3
. B.
3
. C.
1
. D. 1
Câu 127. Cho
f x
là hàm số liên tục và lẻ trên
, biết rằng
16
0
f x dx 3
. Khi đó tích phân
0
16
f x dx
bằng
A. -3 B. 2016. C. 3. D. -2016.
Câu 128. Vòm cửa lớn của trường Đại Học Bôn Ba có dạng hình Parabol. Người ta dự định lắp cửa kính cho
vòm cửa này. Hãy tính diện tích mặt kính cần lắp biết rằng vòm cửa cao 8 m và rộng 8 m ?
A.
2
128
m
3
B.
2
64
m
3
. C.
2
32
m
3
. D.
2
16
m
3
.
Câu 129. Trong hệ tọa độ
Oxy,
cho Parabol
C
và
d
là tiếp tuyến của
C
tại điểm
A 1;1
như hình vẽ. Diện tích của phần tô vàng như hình vẽ là:
A.
1
3
B.
2
3
.
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
13
C.
4
3
. D.
1
.
Câu 130
. Sơ đồ ở bên phải phác thảo của một khung cửa sổ. Diện tích của cửa sổ được tính bằng công thức nào sau đây?
A.
1
2
2
1
2
5
S 4x dx
2
. B.
1
2
2
1
2
5
S 2x dx
2
.
x
y
1
2
1
2
O
2
5
2
2
y x
2
2
y x
C.
1
2
2
1
2
S 2x dx
. D.
1
2
2
1
2
S 1 4x dx
.
Câu 131. Cho hình phẳng
H
giới hạn bởi các đường
4 2 2
y x 2mx m ,x 0,x 1
(m là tham số thức). Biết
rằng
1 2 1 2
m ,m m m
là hai giá trị để diện tích hình phẳng
H
bằng
28
15
(đvdt). Khi đó Tổng
1 2
m 3m
bằng:
A.
4
. B.
3
. C.
3
. D. -4
Câu 132. Anh An muốn làm cửa rào sắt có hình dạng và kích thước giống
như hình vẽ kế bên, biết đường cong phía trên là một parabol. Giá
2
1m
cửa rào sắt có giá là 700.000 đồng. Vậy anh An phải trả bao nhiêu tiền để
làm cài cửa rào sắt như vậy. (làm tròn đến hàng chục nghìn) ?
A.
6.420.000
đồng. B.
6.320.000
đồng.
C.
6.520.000
đồng. D.
6.620.000
đồng.
Câu 133. Một hình phẳng H đươc giới hạn bởi một Parapol và một đường
thẳng như hình bên ( miền gạch ca rô ) có dienj tích là bao nhiêu
A.
9
2
B.
9
2
C.
9
D.
9
Câu 134. Cho rằng
5 6
0 3
f x dx 5; f x 2 dx 7
. Hãy tính kết quả của
4
0
f 2x dx
Nguyễn Tiến Chinh – Vinastudy.vn Tích phân chống casio | 2017
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng
14
A. 5 B. 6 C. 7 D. 10
Câu 135. Giả sử
3
2
f x dx 2018
khi đó giá trị của
3
2
2
xf x dx
là:
A.
2018
B.
2
2018
C.
2.2018
D.
1009
Câu 136. Giả sử
3
2
f x dx 17
Khi đó
3
2
1
f 2x dx ?
A.
34
B.
17
C.
17
2
D.
19
Câu 137. Cho
3
x
2x
0
f t dt xe
, khi đó giá trị của
f 8
là:
A.
8
e
12
B.
4
e
12
C.
4
5e
12
D.
8
5e
12
Câu 138. Cho hàm số
f x
liên tục trên
R
, gọi
F x
là một nguyên hàm của
f x
và có đồ thị như hình bên .
Hãy cho biết tất cả các giá trị của
x
làm cho
f x 0
A.
S ;0 
B.
S 2;
C.
S 0;2
D.
S ;0 2;  
Câu 139
. Cho hàm số
f x liên tục trên R , gọi
F x là một nguyên
hàm của
f x và có đồ thị như hình bên . Hãy cho biết tất cả các giá trị của x làm cho
f x 0
A.
S ;0

B.
S 0;

C.
S R\ 0
D.
S
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 Câu 1: Biết   dx I
= a. 2x 1  b.ln 2x 1  4 C . Tính a + b 2x 1  4 A. -2 B. -3 C. 1 D. 2 
Câu 2: Biết L   x
e cos xdx = a.e + b. Tính a + b 0 A. 0 B. 1 C. -2 D. 3 1 Câu 3: Biết L  x 1 2 x dx  a. 2   b . Tính a - b 0 A. 1 B. 1/3 C. 2 D. 3 Câu 4. Cho tích phân I  2x x   2 2
1dx , khẳng định nào sai ? 1 3 2 2 A. I   3 udu B.  2 I 27 C. I  3 u D. I  3 3 0 3 3 0
Câu 5. Giá trị trung bình của hàm số fx trên  
a; b , kí hiệu là mf được tính theo công thức   1 m f
 bfxdx . Giá trị trung bình của hàm số fx sinx trên 0;   b  a a 2 3 1 4 A. B. C. D.       Câu 6. Cho fxdx   2 5 khi đó   2 fx   2sin x dx   ? 0   0  A. 5   B. 5  C. 7 D. 3 2 1 4 4 Câu 7. Giả sử fxdx  2, fxdx  3, gxdx    
4 , khẳng định nào sai ? 0 0 0 4 4 A.
fxgxdx   4 1 B. f   x dx    gxdx 0 0 0 4 4 C. f   x dx    gxdx D. fxdx   4 5 0 0 0   sin 2x Câu 8. Cho I  cosx 3 sin x   2 1dx và I  , phát biểu nào sai ? 2  2 1 0 sinx  22 0 14 3 3 A. I  B. I  I C. I  2 ln  D. Đáp án khác 1 9 1 2 2 2 2  sin x Câu 9. Cho I   3
dx và đặt t  cosx . Khẳng định nào sai ? cos2x  22 0  1 1 sinx 1 dt 1 A. I   3 B. I   1 C.  I   3 t D.  7 I 2 0 4 cos x 4 0.5 4 t 12 12 0 ,5 x  1 Câu 10. Cho I  dx  a  b  a  b   1 ? 0 2 x  2x  2 A. 5 B. 1 C. 4 D. 3 x  1 Câu 11. Cho dx   a
e , khi đó giá trị của a là ? 1 x
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 1
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 2 e 2 A. B. e C. D. 1 e 2 1 e  sinx
Câu 12. Cho tích phân I  dx,a   1 thì I bằng : 0 1 2acosx  2 a 2 a A. B. 2a C. 2 D. a 2 sinx 
Câu 13. Cho tích phân I  dx   a . Giá trị của a là : 0 s inx  cosx 4     A. B. C. D. 3 4 2 6 dx
Câu 14. Tính tích phân I   a ln 3   5
bln 5 Tính giá trị của 2   2 a ab b 1 x 3x  1 A. 4 B. 1 C. 0 D. 5 3 1 x 1
Câu 15. Tìm khẳng định đúng I  dx   ln 2 4 0 x  1 a
A. a  2 B. a  4 C. a  4 D. a  2
Câu 16. Cho fx là hàm số chẵn và liên tục trên R thỏa mãn f   x dx   1
2 khi đó giá trị tích phân 1 fxdx   1 ? 0 A. 2 B. 1 C. 0.5 D. 0,25 dx
Câu 17. Giả sử I   a   5
ln b giá trị của a; b là 1 2x 1 A. a  0; b  81 B. a  1; b  9 C. a  0; b  3 D. a  1; b  8 a e 3e  1
Câu 18. Khẳng định nào sau đây là đúng I  3 x ln xdx  1 b A. ab  64 B. ab  46 C. a  b  12 D. a  b  4 dx
Câu 19. Với a  2 , giá trị của  a là 2 0 x  3x  2 a  2 a  2 a  2 a  2 A. ln B. ln C. ln D. ln 2a 1 a 1 2(a 1) 2a  1  a e  1 Câu 20. Cho I  2 x e sinxdx  
khi đó sina  cos2a  ? 0 b A. 1 B. 2 C. 4 D. 0 x
Câu 21. Cho I   3
dx , nếu đặt t  x  1  I   2ftdt , vậy : 0 1  1 x 1 A.    2 f t 2t  2t B.    2 f t t  t C.    2 f t t  t D.    2 f t 2t  2t 2 0 3x  5x  1 2
Câu 22. Giả sử rằng dx  a ln   b . Khi đó a  2b  ? 1 x  2 3 A. 30 B. 40 C. 50 D. 60 1
Câu 23. Cho n  N,I  nx e 4xdx  e   1 e   2  1 , giá trị của n là 0 A. 1 B. 3 C. 4 D. 2
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 2
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 2x  3 Câu 24. Biết I  dx  a ln 2   1 b thì giá trị của a là 0 2  x A. 7 B. 2 C. 3 D. 1 3 3 2 Câu 25. Biết fxdx  5; fxdx  3  Tin  h fxdx     ? 1 2 1 A. 2 B. – 2 C. 1 D. 5
Câu 26. Tính tích phân sau I  x x   2 a dx 0 1 8 8 A.  8 2a B. 3 a   2a C.  2a D. Cả A, B, C 3 3 3 3 dx Câu 27. Biết  a  3 thì giá trị của a là: 9  2 0 x 1 1 A. B. C. 6 D. 12 12 6 1 Câu 28. Nếu dx   4 lna thì a bằng : 3 x   1 x  2 4 3 A. 12 B. C. 1 D. 3 4 dx
Câu 29. Bằng cách đổi biến x  2 sin t thì tích phân  1 là : 0 4  2 x    dt A.  1dt B.  6 dt C.  6 tdt D.  3 0 0 0 0 t x ln m e dx Câu 30. Cho A   
ln 2 , khi đó giá trị của m là : x 0 e  2
A. m  0; m  4 B. Kết quả khác C. m  2 D. m  4
Câu 31. Tìm khẳng định sai trong các khẳng định sau   x A. sin dx   2 2 sin xdx B. 1 x dx   1 x 0 0 0 2 0 1 1 2 C. sin1 xdx    sinxdx D. x 1 xdx   1 2007 0 0 1 2009
Câu 32. Cho hàm số fx là hàm số chẵn và fxdx   0
a , chọn mệnh đề đúng 3 A. fxdx    3 a B. fxdx   3 2a C. fxdx   3 a D. f xdx   0 a 0 3 3 3
Câu 33. Trong các đẳng thức sau , đẳng thức nào sai    A. sin xdx    1 2 dx B . 2 sin xdx    2costdt 0 0 0 0    1 C. 2 sin xdx  2 sin2x   1 d sin2x     1 D. sin xdx    1 2 dx 0 0 8 0 0  x 4    Câu 34. Tích phân 3x  4 e dx  a     be khi đó a  5b bằng : 0     A. 8 B. 18 C. 13 D. 23
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 3
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 dx Câu 35. Giả sử   5 ln c . Giá trị của c là 1 2x 1 A. 9 B. 8 C. 3 D. 81  1 Câu 36. Cho I  6 sin xcosxdx   n
. Khi đó giá trị của n bằng 0 64 A. 5 B. 3 C. 4 D. 6    4 3
Câu 37. Biết  a4sin x dx  0 , giá trị của a 0;   là : 0    2     A. B. C. D. 4 2 8 3 a x Câu 38. Cho  2 dx bằng 0 a  x    1    2    1     2 A. a       B. a  C. a     D. a         2   4    2  4  
Câu 39. Cho tích phân I   2 s inx sin 2xe
dx , bạn Nhớ giải như sau 0 x  0  t   0 
Bước 1. NHớ đặt t  sinx  dt  cosxdx    I   2 1 Doi.can t t.e dt x   t   0  1  2 u   t du    dt 1 Bước 2. Nhớ chọn     A  t t.e  t e dt   1 t t 0  1 dv   e dt v    0 e Bước 3. I  2A  2
Bài giải của Nhớ đúng hay sai ? nếu sai thì sai ở bước nào? A. Sai từ bước 1 B. Sai từ bước 2 C. Nhớ giải chính xác D. Sai từ bước 3
Câu 40. Nếu fx liên tục và f   x dx   4
10 thì  2f2xdx bằng : 0 0 A. 5 B. 29 C. 19 D. 9 Câu 41. Cho 2 
 3 x 4 dx , trong các kết quả sau 0 3 2 3 2 I . I   x2 4dx  x2    4dx II. I   x2 4dx  x2    4dx III. I  2 2   3 x 4dx 2 0 2 0 2 Kết quả nào đúng A. Chỉ II B. Chỉ III C. Cả I, II, III D. Chỉ I  2
Câu 42. Giả sử I  sin 3x sin 2xdx  a   4 b
, khi đó giá trị của a  b là : 0 2 3 1 A.  1 B. C.  3 D. 6 5 10 5
Câu 43. Cho hàm số fx liên tục và triệt tiêu khi x  c trên  
a; b . Các kết quả sau , câu nào đúng ? b b b c b A. fx dx    fxdx B. fx dx  fx dx     fx dx a a a a c b c b C. fx dx  fxdx     fxdx D. A,B,C đều đúng a a a
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 4
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017     1 
Câu 44. Khẳng định nào sau đây sai về kết quả  22x1sinxdx    1 0   a b A. a  2b  8 B. a  b  5 C. 2a  3b  2 D. a  b  2 2 2x  2 a ln x ln 2 Câu 45. Biết dx  3   , giá trị của a là 1 x 2 A. 4 B. 2 C. -1 D. 3  1 a Câu 46. Biết dx   4 4 0 cos x 3
A. a là một số chẵn B. A là số lớn hơn 5 C. A nhỏ hơn 3 D. A là số lẻ
Câu 47. Tìm khẳng định sai trong các khẳng định sau   x 1 A. sin dx   2 2 sin xdx B.  e dx  1  1 x 0 0 2 0 e       1 1 B.      sinx dx  cos x dx D. sin1 xdx    sinxdx 0         0   4   4 0 0 dx Câu 48. Giả sử   5
ln c , giá trị đúng của c là 1 2x 1 A. 9 B. 3 C. 81 D. 8 1 2 3 x  2 1 x
Câu 49. Cho tích phân I   dx , nếu đặt t  thì 2 1 x x 2 2 t 2 2 3 t 2 t t A. I   3 dt B. I   dt C. I   3 dt D. I   3 dt 2 2 t 1 2 2 t  1 2 2 t 1 2 2 t  1 Câu 50. Cho I  2x x 1dx; u  x   2 2 2
1 , chọn khẳng định sai trong các khẳng định sau 1 3 3 2 A. I   3 udu B. I   2 udu C. 2 u D.  2 I 27 0 1 3 3 0 1 Câu 51. Biết sin xcosxdx   a
. Khi đó giá trị của a là 0 4  2   A. B. C. D. 2 3 4 3 dx
Câu 52. Một học sinh giải I   11 x 0 e x 1 e dx
I Viết lại thành I   x e 1 x 0 e  du II .Đặt u  e  I   (ln u ln u   e e x 1 ) 1 u1  u 1 e III. I  ln e1
Lời giải trên nếu sai thì sai từ bước nào A. III B. I C. II D. Giải đúng b b Câu 53. Giả sử fxdx  2; f   x dx  3;a  b    c thì fxdx   c ? a c a
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 5
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 A. 5 B. 1 C. -1 D. -5 
Câu 54. Với a  0 . Giá trị của tích phân I   2a xsinaxdx là 0   1 1   A. B.  C. D.  2 a 2 2 a 2 a 2 a 2a a 1 e 1 Câu 55. Cho 3x e dx  
Khi đó khẳng định nào sau là đúng? 0 b A. a  b B. a  b C. a  b D. a  b dx 1
Câu 56. Với t 1;  1 ta có    t
ln 3 khi đó giá trị của t là 2 0 x  1 2 1 1 A. B.  1 C. 0 D. 3 3 2  Câu 57. Cho I  2x   2 
1 sin 2xdx Lời giải sai từ bước nào 0
Bước 1. Đặt u  2x  1;dv  sin 2xdx
Bước 2. Ta có du  2dx; v  cos2x     Bước 3. I  
 2x 1cos2x 2  2 2cos2xdx  2x 1cos2x 2   2sin2x 2 0 0 0 0 Bước 4. I    2 A. Bước 3 B. Bước 1 C. Bước 2 D. Không sai Câu 58. Biết 2x4dx   b
0 Khi đó giá trị của b là : 0 A. b  1 b  4 B. b  0  b  2 C. b  1 b  2 D. b  0  b  4 2x 1
Câu 59. Tích phân I  dx  a   3
b ln 2 , khi đó tổng của a  b là 1 x  1 A. 1 B. 7 C. 10 D. 2 1 2x
Câu 60. Với a  0 khi đó tích phân  dx có giá trị là : ax 2 2 a 1 2 a  1 a  1 a  1 A. B. C. D. a aa   1 aa   1 a 1
Câu 61. Trong các khẳng định sau , khẳng định nào đúng dx b A.  2 1 x   2 C
B.  fxdx  0  fx 0; x    a; b 1 2 x a c b c C. f xdx  gxdx  fxdx;a  b     c a a b
D. Nếu Fx là nguyên hàm của fx thì Fx cũng là nguyên hàm của fx 1 4x  11 a Câu 62. Cho biết  dx  ln ;a,b  
N thì giá trị của a  b bằng : 2 x  5x  6 b 0 A. 11 B. 12 C. 10 D. 13
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 6
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017  1 4 2 dx 63 Câu 63. Cho I  ; J     4 sin x  4 cos xdx; K    2 x  3x  
1 dx , tích phân nào có giá trị bằng 3x  1 6 0 0 1 A. I B. J C. K D. J và K 2019 2019 2019
Câu 64. Nếu  fxdx 37;  gx Tinh  dx 16  2fx 3gx      dx    A , giá trị của A là 0 0 0 A. 122 B. 74 C. 48 D. 53 201 203 203 Câu 65. Nếu fxdx  201; fxdx  16  Tin  h fxdx     A 0 201 0 A. A  215 B. 217 C. 219 D. 197 a  2 b sin x  b   1     
Câu 66. Cho fx 
;a, b  R . Tìm nguyên hàm Fx của fx biết F   ;F   0; 2     sin x  4 2 6     F     1  3 3 1 3 1 A. Fx  tanxcot x B. Fx  tanx cot  x  4 2 4 2 3 1 3 1 C. Fx  tanxcot x D. Fx  tanx cotx 4 2 4 2 1 dx Câu 67. Cho  aln 2  bln 5  
c Khi đó a  2b  4c bằng 5 x  3 x 0 A. 2 B. 3 C . 0 D. 1 f'  1   2 Thoa.man 
Câu 68. Tìm các hằng số A và B đê fx  A sin x  B   2  fxdx   4 0 2 2 A. A   ; B  2 B. A  ; B  2 C. A  2; B  2 D. A  2; B  2   2
Câu 69. Tìm a sao cho   2a 4 a 3    x  4x dx    12 1 A. a  3 B. a  5 C. a  3 D. Đáp án khác 3 dx
Câu 70. Giả sử k  0 và  
ln2  3 . giá trị của k là 2 0 x  k A. k  3 B. k  2 C. k  2 3 D. k  1 1 Câu 71. Biết rằng 2x   x 1 e dx  a   b.e , tích ab  ? 0 A.ab  1 B. ab  1 C. ab  15 D. ab  5    3 cot x 4 3 cot x
Câu 72. Biết rằng x   ;  I    thì   . Gọi  dx thì  4 3  x  x  4
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 7
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 3 1 1 1 1 1 3 1 A.  I  B.  I  C.  I  D.  I  12 4 4 3 5 4 12 3 m Câu 73. Tìm m biết 2x   5 dx   6 0 A. m  1; m  6 B. m  1; m  6 C. m  1; m  6 D. m  1; m  6  4 4
Câu 74. Nếu đặt t  cos2x thì tích phân I   2 2 sin x   1 sin4xdx 0 1 3 1 1 2 1 1 2 A. I   4tdt B. I   3tdt C. I   5tdt D. I   4tdt 2 2 0 0 0 0  4 6 tan x
Câu 75. Nếu đặt t  3 tan x  1 thì tích phân I   dx 2 cos x 3tan x  1 0 4 2 2 t   1 2 4 2 2 t   1 4 2 2 t   1 A. I   dt B. I   2t   1dt C. I   dt D. I   dt 3 3 5 1 1 1 1 a 2 3 e Câu 76. Tích phân x    2x 1 e dx   ,Giá trị của a là 4 0 A. 2 B. 1 C. 3 D. 4 e k
Câu 77. Cho I   ln dx , xác định k để I  e 2 x 1 A. k  e  2 B. k  e C. k  e  1 D. k  e 1  2 2 sin x 1
Câu 78. Tính tích phân I  dx  ln b  3c ;a,b,c  
Z . Giá trị của a  2b  3c là : sin 3x a  6 A. 2 B. 3 C. 8 D. 5 1
Câu 79. Nếu đặt u  1 2 x  I  3 x 1  2 x dx trở thành: 0 1 0 1 0 2 A. u1  udu B. u1  udu C. 2 u 1  u du D.  4 u   2 u du 0 1 0 1 k Câu 80. Để k4xdx  3k 1  0 thì giá trị của k là 1 A. 1 B. 3 C. 2 D. 4 6 4 6 Câu 81. Nếu f xdx  10; f   x dx    7 thì f xdx   ? 0 0 4 A. 3 B. 17 C. 170 D. -3  2
Câu 82. Cho tích phân
xsinx  2mdx  1    2 , giá trị của m là ? 0 A. m  5 B. m  3 C. m  4 D. m  6
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 8
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 x
Câu 83. Cho gx   costdt , chọn khẳng định đúng 0 A. g'x  sin2 x B. g'x  cos x C. g'x  sin x D.   cos x g' x 2 x
Câu 84. cho f,g là hai hàm số theo x .Biết rằng x    a; b ,f 'x  g'x   , Mệnh đề nào đúng? b a I. x    a; b ,f 'x  gx   II. fxdx    gxdx
III. fx fa  gxga a b A. I B. II C. Không có D. III t 3 Câu 85. Cho fx    4    4sin x  
dx . Giải Phương trình fx  0  2 0 k  A. k2; k  z B. ; k  z C.  k ; k  z D.  k;k  z 2 2 2 dx a Câu 86. Giả sử  
ln với a, b là các số tự nhiên và ước chung lớn nhất của a, b bằng 1 . Khẳng định x  3 b 1 nào sai ? A. 3a  b  12 B. a  2b  13 C. a  b  2 D. 2  2 a b  41 2 5 Câu 87. Cho I  xx   
1 dx , nếu đặt u  x 1 , hãy chọn khẳng định sai trong các khẳng định sau 1 1  1 6 5 1 5 u u  A. I  x1  x dx B.  13 I C. I     5   D. I  u    1 u du 42    6 5  2 0 0    Câu 88. Cho I  x 2 e cos xdx; J  x 2 e sin xdx;K   
 xecos2xdx . Khẳng định nào đúng trong các khẳng định 0 0 0 sau   I.  I  J  e II . I  J  K III.  e 1 K 5 A. Chỉ II B. Chỉ III C. Chỉ I D. Cả I và II
Câu 89. Khẳng định nào sau đây là đúng?
I – Một nguyên hàm của hàm số  cosx y e là  cosx sin xe 2   2 x 6x 1 x  10 II – Hàm số fx  ;gx 
đều là một nguyên hàm của một hàm số 2x  3 2x  3 1 1 2 3 III -          1 x 1 x xe dx x 1 e C IV. x  e dx    x e dx 0 0 A. Chỉ I B. Chỉ III C. Chỉ IV D. Chỉ II d d b Câu 90. Nếu fxdx  5, f   x dx  2;a  d    b thì  fxdx bằng a b a A. -2 B. 0 C. 8 D. 3 1 3 4x Câu 91. Cho 2 3m  dx   0 Khi đó 2 144m 1 bằng : x 22 4 0
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 9
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 2 3 A.  2 B. 4 3 1 C. D. Đáp án khác 3 3 10 8 10 Câu 92. Nếu fxdx  17; f xdx    12 thì f xdx   ? 0 0 8 A. 5 B. 29 C. -5 D. 15
Câu 93. Tìm khẳng định đúng trong các khẳng định sau 3 1 3 3 A. x  2 dx  x    1 dx B. x  2 dx  x   2dx 0 2 0 0 3 3 2 3 3 2 C. x  2 dx  x2dx x    2dx D. x  2 dx  x2dx  x    2dx 0 2 0 0 2 0
Câu 94. Khẳng định nào là đúng 10
A. Nếu w 't là tốc độ tăng trưởng cân nặng / năm của một đứa trẻ thì  w'tdx là sự cân nặng của đứa 5
trẻ giữa 5 đến 10 tuổi 120
B. Nếu dầu rò rỉ từ một cái thùng với tốc độ rt tính bằng galong/phút tại thời gian t thì  rtdt biểu 0
thị lượng galong rò rỉ trong hai giờ đầu tiên
C. Nếu rt là tốc độ tiêu thụ dầu trên thế giới , trong đó t được tính bằng năm , bắt đầu tại t  0 vào 17
ngày 1 tháng 1 năm 2000 và rt được tính bằng thùng/ năm thì  rtdt biểu thị số dầu được tiêu thụ 0 từ 1/1/2000 đến 1/1/2017 D. Cả A,B,C đều đúng 4 Câu 95. Nếu f  1  12;f '  x liên tục và f 'xdx  
17 , giá trị của f4  ? 1 A. 29 B. 5 C. 19 D. 9 2 x 1 Câu 96. Cho K  dx  a ln 5  
b ln 3 thì giá trị của a; b là 2 x  4x  3 0 A. a  2; b  3 B. a  3; b  2 C. a  2; b  3 D. a  3; b  2 a 3 x  2 ln x 1 Câu 97. Biết dx   
ln 2 thì giá trị của a là ? 2 x 2 1  A. B. ln 2 C. 2 D. 3 4  2 Câu 98. Cho I   2 sin x 3 e
sin xcos xdx . Nếu đặt  2 t sin x thì 0 1  1 1  1 1 A.  t t  I  t e 1  tdt B. I  2 e dt    te dt C. I  t 2 e 1  tdt D. 2  0 0  0   0  1 1  1  t t  I  e dt    te dt 2  0 0   
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 10
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 2 x Câu 99. Giả sử ftdt  xcos 
x giá trị của f4 bằng: 0 1 1 A. 1 B. C. Đáp án khác D. 2 4
Câu 100. Một ô tô đang chuyển động với vận tốc 12m / s thì người lái xe bất ngờ tăng tốc cho xe chạy nhanh
dần đều , sau 15s thì xe đạt vận tốc 15m / s .Tính quãng đường xe đi được sau 30s kể từ khi tăng tốc A. 270m B. 450m C. 360m D. 540m
Câu 111. Một lực có độ lớn 40 N (newton) cần thiết để kéo căng một chiếc lò xo có độ dài tự nhiên 10 cm lên 15
cm. Biết rằng theo định luật Hooke trong Vật lý, khi một chiếc lò xo bị kéo căng thêm x (đơn vị độ dài) so với
độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho bởi công thức fx  kx N, trong đó k là
hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo lò xo có độ dài từ 15 cm đến 18 cm ? (kí
hiệu J Jun là đơn vị của công) A. 1,56 J . B. 0,94 J . C. 1,78 J . D. 2,03 J .
Câu 112. Một vật chuyển động chậm dần với vận tốc vt  160 10t m/s . Hỏi rằng trong 3s trước khi dừng hẳn vật
di chuyển được bao nhiêu mét ? A. 16 m. B. 130 m. C. 435 m. D. 170 m.
Câu 113: Bạn Nhớ đang chở hai người bạn gái của mình là Ty và Sương trên chiếc xe thể thao hiệu
Lamborghini Aventador chạy trên một đường đua thẳng có độ dài 4km. Xe tăng tốc từ 0km/h đến 100km/h
trong 3 giây đầu tiên đi hết 260m và sau đó xe chuyển động nhanh dần đều với gia tốc 20m / s . Tính thời gian
để xe hoàn thành đường đua biết vận tốc của chuyển động nhanh dần đều có công thức v  at  v với a,v o o
là gia tốc và vận tốc đầu. A. 21s B. 11s C. 14s D. 18s
Câu 114. Một vật đang chuyển động thẳng nhanh dần đều có vận tốc là 18km / h . Trong giây thứ 5 mật đi
được quãng đường là 5,9m > tính quãng đường vật đi được sau 10s kể từ lúc bắt đầu chuyển động 132 A. m B. 103,6m C. 60m D. đáp án khác 5
Câu 115. Bạn Phương vừa nhai quần đùi vừa thả một hòn bi chuyển động trên một rãnh nằm ngang để tạo    
một dao động điều hòa với phương trình chuyển động là x  4cos4t  cm  
, cùng lúc đó ở máng bên  3
cạnh bạn Hợp cũng đang điều khiển chiếc xe hơi đồ chơi mới mượn được của bạn Nhớ và cũng đang dao    
động điều hòa với phương trình dao động là x  2cos2t  cm  
.Nếu gọi S là quãng đường hòn bi của  2  1
Phương đi được trong khoảng thời gian là 0,25s kể từ lúc xuất phát và S là quãng đường chiếc siêu xe của 2
bạn hợp chạy được trong khoảng thời gian 2,875s kể từ lúc xuất phát. Khi đó i. S  S ii. S  S iii. S  S 4i. S  S  12 1 2 1 2 1 2 2 1
Có bao nhiêu khẳng định đúng A. 1 B. 2 C. 3 D. 0 b b b b Câu 116. Cho   fx 2gx     
 19 và  5fx 3gxdx    30 khi đó f xdx  A; gxdx    B thì a a a a
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 11
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017
A và B có giá trị là bao nhiêu b b b Câu 117. Cho   fx 2gx       
 1 và  fx 3gxdx    30 khi đó  11f  x 12gx dx    ? a a a b b b b Câu 118. Cho   fx gx     
 10 và  3fx gxdx    15 khi đó 2016fxdx    2017gxdx a a a a 3 3 Câu 119. Cho f xdx   15 . Hãy tính  2x 5x  fxdx 0 0   4  4 Câu 120. Cho fxdx   , Hãy tính sin2x  3fxdx 4 0 0  2 x  1; khi:x  5  0
Câu 121: Cho fx  
Hãy tính tích  fxdx 5x+1;khi:x<0 3 x  2  6; Khi:x<-1
Câu 122. Cho fx  
Hãy tính tích  fxdx 2 x  x  5;Khi : x   1 3 2x 1;khi : x  1  0
Câu 123. Cho Cho fx  
, Hãy tính tích  fxdx 2 x  1; khi : x   0 1 2 2 x Câu 124.Cho I  dx  1 2 a ln c   2 b lnc  
1 ;a; b; c  Q , Khi đó , hãy tính kết quả của P  a  b  c 2 x 7x  12 1 A. P  43 B. P  11 C. P  3 D. P  3 2 dx a a  b a Câu 125.Cho I    ln b   lna   b  ,a; b  Q hãy chọn phát biểu sai 5 x  3 x b b 4b 1 A. a  b B. a  b  1 C. 2  2 a b  5 D. a  2b  10  3 x 
Câu 126. Tích phân I  dx  a  bln 2,a; b  
 . Khi đó tổng a  b gần với gía trị nào nhất sau đây 2 cos x 3 0 ? A. 3 . B. 3 . C. 1 . D. 1 16 0
Câu 127. Cho fx là hàm số liên tục và lẻ trên  , biết rằng f xdx  
3 . Khi đó tích phân  fxdx bằng 0 16 A. -3 B. 2016. C. 3. D. -2016.
Câu 128. Vòm cửa lớn của trường Đại Học Bôn Ba có dạng hình Parabol. Người ta dự định lắp cửa kính cho
vòm cửa này. Hãy tính diện tích mặt kính cần lắp biết rằng vòm cửa cao 8 m và rộng 8 m ? 128 64 32 16 A. 2 m B. 2 m . C. 2 m . D. 2 m . 3 3 3 3
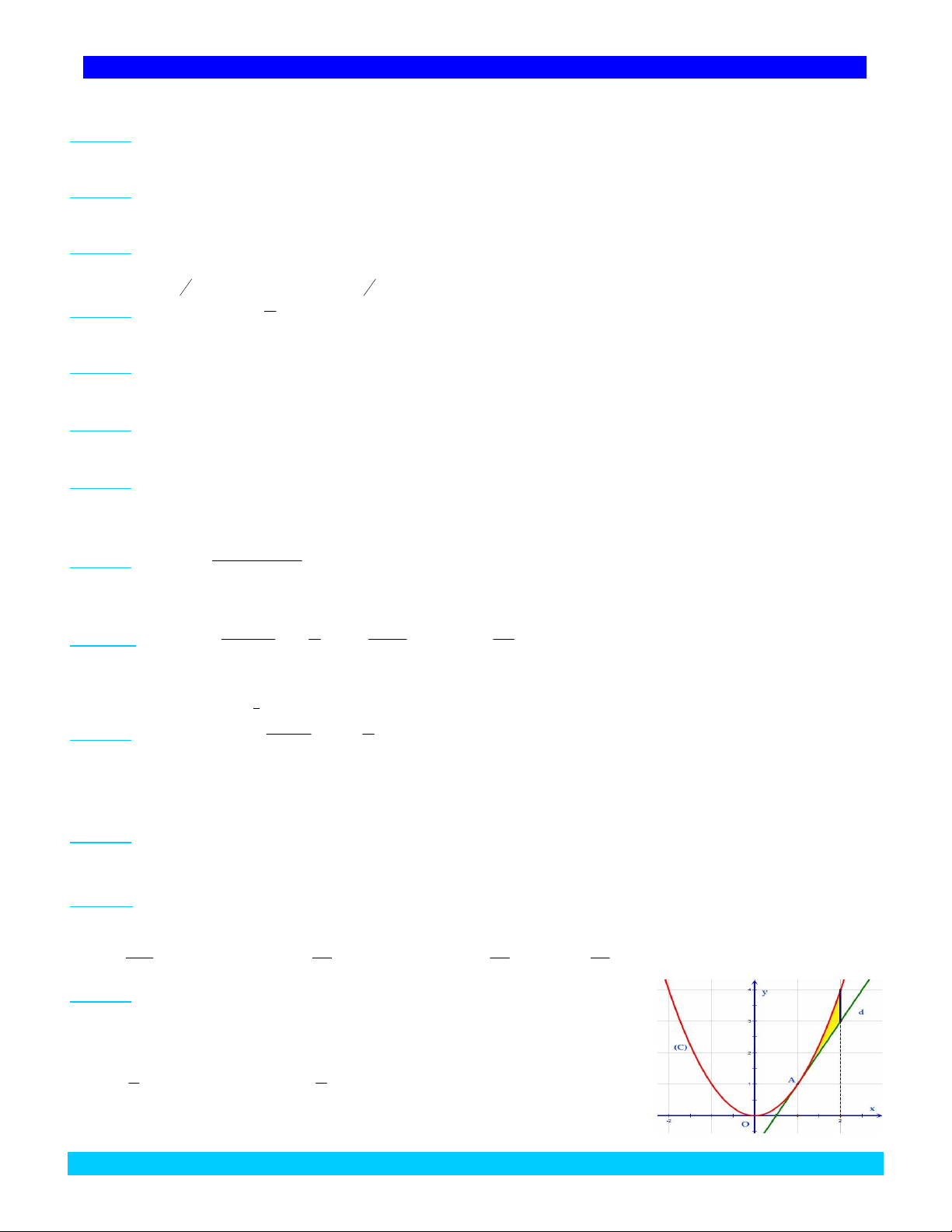
Câu 129. Trong hệ tọa độ Oxy, cho Parabol  
C và d là tiếp tuyến của   C tại điểm A1; 
1 như hình vẽ. Diện tích của phần tô vàng như hình vẽ là: 1 2 A. B. . 3 3
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 12
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 4 C. . D. 1 . 3
Câu 130. Sơ đồ ở bên phải phác thảo của một khung cửa sổ. Diện tích của cửa sổ được tính bằng công thức nào sau đây? y 5 2 y   2x 2 2 x y  2x 1 O 1 1 1  2   2 2 2 5 2  5
A. S     4x  2  dx . B. S    2x dx . 2  2 1 1 2 2 1 1 2 2 C. S   2 2x dx . D. S  1  2 4x dx .  1 1 2 2
Câu 131. Cho hình phẳng H giới hạn bởi các đường  4  2  2 y x 2mx
m ,x  0,x  1 (m là tham số thức). Biết 28
rằng m ,m m  m là hai giá trị để diện tích hình phẳng H bằng
(đvdt). Khi đó Tổng m  3m 1 2 1 2  15 1 2 bằng: A. 4 . B. 3 . C. 3 . D. -4
Câu 132. Anh An muốn làm cửa rào sắt có hình dạng và kích thước giống
như hình vẽ kế bên, biết đường cong phía trên là một parabol. Giá 2 1m
cửa rào sắt có giá là 700.000 đồng. Vậy anh An phải trả bao nhiêu tiền để
làm cài cửa rào sắt như vậy. (làm tròn đến hàng chục nghìn) ? A. 6.420.000 đồng. B. 6.320.000 đồng. C. 6.520.000 đồng. D. 6.620.000 đồng.
Câu 133. Một hình phẳng H đươc giới hạn bởi một Parapol và một đường
thẳng như hình bên ( miền gạch ca rô ) có dienj tích là bao nhiêu 9 A. 2 9 B. 2 C. 9 D. 9 5 6 4 Câu 134. Cho rằng f xdx  5; fx  2dx   
7 . Hãy tính kết quả của  f2xdx 0 3 0
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 13
Nguyễn Tiến Chinh – Vinastudy.vn
Tích phân chống casio | 2017 A. 5 B. 6 C. 7 D. 10 3 3 Câu 135. Giả sử f   x dx  
2018 khi đó giá trị của xf 2 x dx  là: 2 2 A. 2018 B. 2 2018 C. 2.2018 D. 1009 3 3 2 Câu 136. Giả sử f xdx   17 Khi đó f  2xdx ? 2 1 17 A. 34 B. 17 C. D. 19 2 3 x Câu 137. Cho f  t 2x
dt  xe , khi đó giá trị của f8 là: 0 8 e 4 e 4 5e 8 5e A. B. C. D. 12 12 12 12
Câu 138. Cho hàm số fx liên tục trên R , gọi Fx là một nguyên hàm của fx và có đồ thị như hình bên .
Hãy cho biết tất cả các giá trị của x làm cho fx 0 A. S  ;0 B. S  2;   C. S  0; 2
D. S  ;0 2;
Câu 139 . Cho hàm số fx liên tục trên R , gọi Fx là một nguyên
hàm của fx và có đồ thị như hình bên . Hãy cho biết tất cả các giá trị của x làm cho fx  0 A. S  ;0 B. S  0; C. S  R\0 D. S  
15 – Phó Đức Chính – 135 Nguyễn Chí Thanh – Đà Nẵng 14