Bài tập toán 9 tuần 1 (có đáp án và lời giải chi tiết)

BÀI TẬP TOÁN 9 TUẦN 1 Bài 1.
Thực hiện các phép tính sau a) 2 0  ,8 ( 0  ,125) b) 6 ( 2  ) c) 2 ( 3  2) 1 1 d) 2 (2 2  3) e) 2 (  ) f) 2 (0,1 0,1) 2 2 Bài 2.
Thực hiện các phép tính a) 2 2 (3  2 2)  (3  2 2) b) 2 2 (5  2 6)  (5  2 6) c) 2 2 (2  3)  (1  3) d) 2 2 (3  2)  (1  2) e) 2 2 ( 5  2)  ( 5  2) f) 2 2 ( 2  1)  ( 2  5) Bài 3.
Thực hiện các phép tính.       a) 5 2 6 5 2 6 b) 7 2 10 7 2 10 c). 4  2 3  4  2 3 d) 24  8 5  9  4 5 e). 17 12 2  9  4 2 f) 6  4 2  22 12 2 Bài 4.
Thực hiện các phép tính sau a)
5  3  29 12 5 c)  3  2  5  2 6 b)
13  30 2  9  4 2 d) 5  13  4 3  3  13  4 3
e) 1  3  13  4 3  1  3  13  4 3 Bài 5.
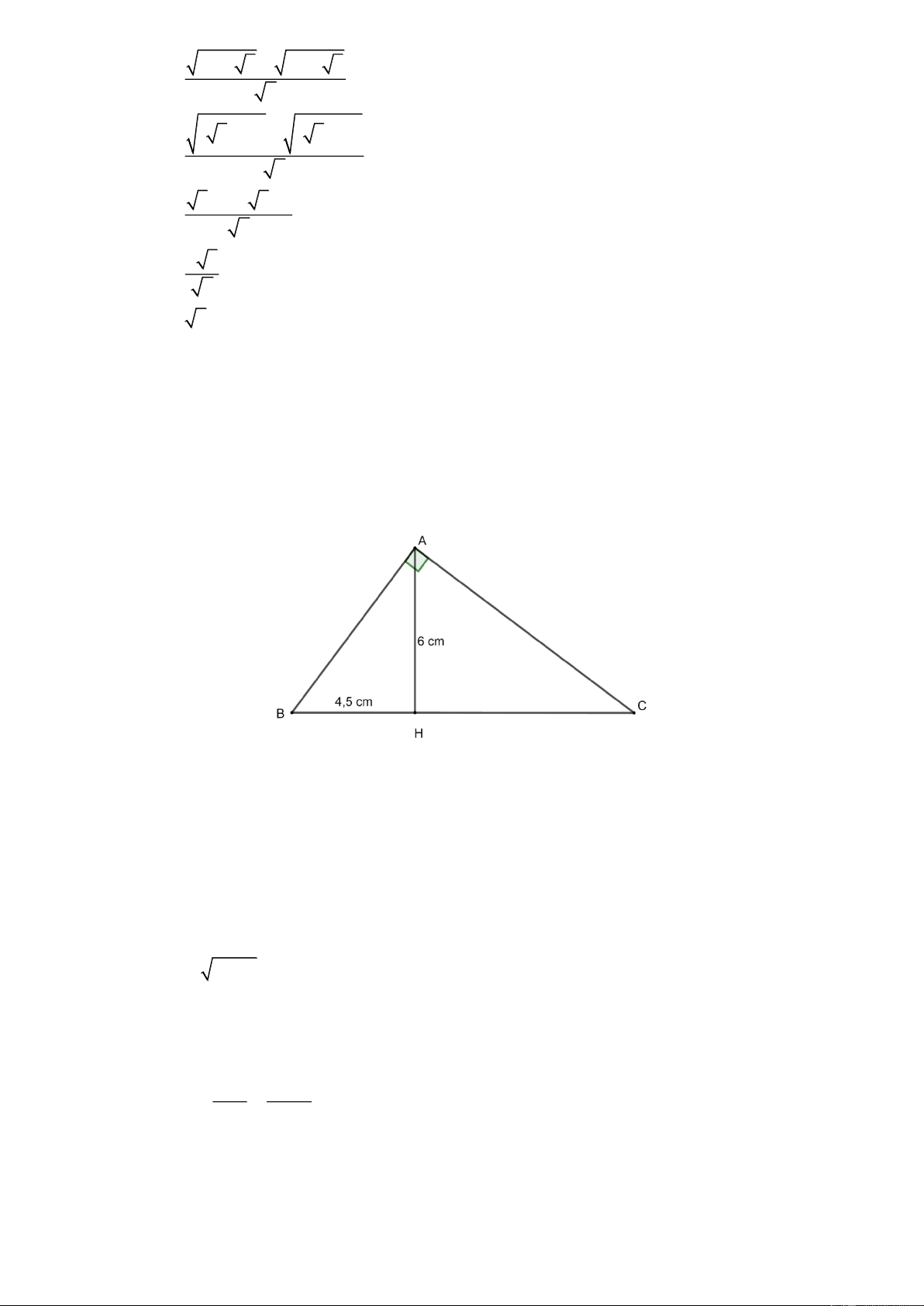
Cho tam giác ABC vuông ở A , đường cao AH .
a) Biết AH  6cm , BH  4,5cm. Tính AB, AC, BC, HC.
b) Biết AB  6cm BH  3cm . Tính AH, AC, CH. Bài 6.
Cho tam giác vuông ABC A  90, đường cao AH biết AB: AC  3: 4 và
BC  15cm . Tính BH và HC . Bài 7.
Cho hình vuông ABCD . Lấy điểm E trên cạnh BC . Tia AE cắt đường thẳng CD tại .
G .. Trên nửa mặt phẳng bờ là đường thẳng AE chứa tia AD , kẻ các tia AF vuông góc
AE và AF  AE .
a) Chứng minh ba điểm F , D, C thẳng hàng. 1 1 1 b) Chứng minh:   . 2 2 2 AD AE AG
c) Biết AD  13cm , AF : AG 10:13. Tính FG ? Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Thực hiện các phép tính sau a) 2 0  ,8 ( 0  ,125) b) 6 ( 2  ) c) 2 ( 3  2) 1 1 d) 2 (2 2  3) e) 2 (  ) f) 2 (0,1 0,1) 2 2 Lời giải a) 2 0  ,8 ( 0  ,125)  0  ,8. 0
 ,125  (0,8.0,125)  0,1. b) 6 ( 2  )  64  8 c) 2 ( 3  2)  3  2  2  3 d) 2
(2 2  3)  2 2  3  3  2 2 1 1 1 1 1 1 2 1 e) 2 (  )      2 2 2 2 2 2 2 1 10 10 1 f) 2
(0,1 0,1)  0,1 0,1    10 10 10 Bài 2.
Thực hiện các phép tính. a) 2 2 (3  2 2)  (3  2 2) b) 2 2 (5  2 6)  (5  2 6) c) 2 2 (2  3)  (1 3) d) 2 2 (3  2)  (1 2) e) 2 2 ( 5  2)  ( 5  2) f) 2 2 ( 2 1)  ( 2  5) Lời giải a) 2 2
(3  2 2)  (3  2 2)  3  2 2  3  2 2  (3  2 2)  (3  2 2)  6 b) 2 2
(5  2 6)  (5  2 6)  5  2 6  5  2 6  (5  2 6)  (5  2 6)  10 c) 2 2
(2  3)  (1 3)  2  3  1 3  (2  3)  ( 3 1)  1 d) 2 2
(3  2)  (1 2)  3  2  1 2  (3  2)  ( 2 1)  2 e) 2 2 ( 5  2)  ( 5  2)  5  2 
5  2  ( 5  2)  ( 5  2)  2 5 f) 2 2 ( 2 1)  ( 2  5)  2 1 
2  5  ( 2 1)  (5  2)  2 2  4 Bài 3.
Thực hiện các phép tính.       a) 5 2 6 5 2 6 b) 7 2 10 7 2 10 c). 4  2 3  4  2 3 d) 24  8 5  9  4 5 Trang 2 e). 17 12 2  9  4 2 f) 6  4 2  22 12 2 Lời giải a) 5  2 6  5  2 6 2 2
 ( 3  2)  ( 3  2)  3  2  3  2  ( 3  2)  ( 3  2)  2 2 b) 7  2 10  7  2 10 2 2
  5  2   5  2  5  2  5  2   5  2  5  2  2  2 c) 4  2 3  4  2 3
   2    2 3 1 3 1
 3 1  3 1   3   1   3   1  2 3 d) 24  8 5  9  4 5    2    2 2 5 2 5 2
 2 5  2  5  2  2 5  2   5 2  3 5    e) 17 12 2 9 4 2    2    2 3 2 2 2 2 1
 3 2 2  2 2 1  32 22 2   1  4    f) 6 4 2 22 12 2    2    2 2 2 3 2 2
 2  2  3 2  2  2 23 2 2  4 2 Bài 4.
Thực hiện các phép tính sau a)
5  3  29 12 5 c)  3  2  5  2 6 b)
13  30 2  9  4 2 d) 5  13  4 3  3  13  4 3
e) 1 3  13  4 3  1 3  13  4 3 Lời giải a) 5  3  29 12 5      2 5 3 2 5 3  5  3  2 5  3  5  6  2 5 2  5  ( 5 1)  5  ( 5 1)  1 1 Trang 3 b) 13  30 2  9  4 2      2 13 30 2 2 2 1  13 30 3 2 2     2 13 30 2 1  13 30( 2 1)  43  30 2    2 3 2 5  53 2 c)  3  2  5  2 6       2 3 2 3 2
  3  2 3  2  32 1 d)
5  13  4 3  3  13  4 3     2     2 5 2 3 1 3 2 3 1  5  2 3   1  3  2 3   1  4  2 3  4  2 3
   2    2 3 1 3 1  3 1 3 1  2 3 e)
1 3  13  4 3  1 3  13  4 3      2      2 1 3 2 3 1 1 3 2 3 1  1 3 2 3  
1  1 3  2 3   1
 1 4  2 3  1 4  2 3 
   2     2 1 3 1 1 3 1  1  3   1  1  3   1  2  3  2  3 Trang 4 4  2 3  4  2 3  2   2    2 3 1 3 1  2 3 1 3 1  2 2 3  2  6 Bài 5.
Cho tam giác ABC vuông ở A , đường cao AH .
a) Biết AH  6 cm , BH  4,5cm . Tính AB, AC, BC, HC.
b) Biết AB  6 cm BH  3cm . Tính AH , AC,CH. Lời giải a)
Xét tam giác ABH vuông tại H ta có : 2 2 2
AH  BH  AB   2 2 2 6 4,5  AB 2 36  20, 25  AB 2 56, 25  AB
 AB  56,25  7,5 (cm)
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có : 2
AB  BH .BC 2 AB 56, 25  BC   12,5 (cm) BH 4,5
Mà BH  HC  BC 4,5  HC  12,5
HC  12,5  4,5  8cm Trang 5 b) Ta có : 2
AC  CH .BC (hệ thức giữa cạnh góc vuông và hình chiếu của cạnh góc vuông trên cạnh huyền) 2 AC  8.12,5  100
AC  100  10 cm
Xét tam giác ABH vuông tại H ta có: 2 2 2
AB  AH  BH (Định lý pytago) 2 2 2 6  AH  3 2 2 2 AH  6  3  27
 AH  3 3 cm
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có : 2
AH  BH .HC 27  3.HC
 HC  27 :3  9cm . 2
AC  CH .BC 2
AC  9.(9  3)  108
AC  108  6 3 cm . Bài 6.
Cho tam giác vuông ABC A  90 , đường cao AH biết AB: AC  3: 4 và BC 15cm .
Tính BH và HC . Ta có: Trang 6 AB AC
AB : AC  3: 4   3 4 2 2 2 2 2 2 AB AC AB  AC BC 15       9 9 16 9 16 25 25 Do đó: 2
AB  81  AB  9 cm ; 2
AC  144  AC  12 cm .
Áp dụng hệ thức lượng trong tam giác vuông cho tam giác ABC A  90 , đường cao AH , ta có: 2
AB  BC.BH  81  15.BH  BH  5, 4 cm .
CH  BC  BH  9, 6 cm .
Vậy BH  5, 4 cm; CH  9, 6 cm . Bài 7.
Cho hình vuông ABCD . Lấy điểm E trên cạnh BC . Tia AE cắt đường thẳng CD tại
G . Trên nửa mặt phẳng bờ là đường thẳng AE chứa tia AD , kẻ các tia AF vuông góc
AE và AF  AE .
a) Chứng minh ba điểm F , D, C thẳng hàng. 1 1 1 b) Chứng minh:   . 2 2 2 AD AE AG
c) Biết AD  13cm , AF : AG 10:13. Tính FG ? Lời giải
a) Vì BAE  DAE  90 và DAE  DAF  90 nên BAE  DAF . Xét BAE  và D  AF có: AB  AD BAE  DAF AE  AF Trang 7 Do đó B  AE  D
 AF (c.g.c), suy ra ABE  ADF  90 hay DF  AD .   1
Ta cũng có DC  AD. 2 Từ  
1 và 2 suy ra ba điểm F, D,C thẳng hàng. b) Xét AFG 
vuông tại A có AD  FG .
Theo hệ thức lượng trong tam giác vuông AFG 
với đường cao AD , ta có: 1 1 1   2 2 2 AD AF AG Mà AE  AF . 1 1 1 Nên ta có:   . 2 2 2 AD AE AG
c) Ta có: AF : AG 10:13 AF AG  
 k, k  0. 10 13
Suy ra AF 10k , AG 13k . AFG  có: 2 2 2
FG  AF  AG 2 2  100k 169k 2
 269k  FG  k 269 .
Ta lại có: AF.AG  A .
D FG  10k.13k  269
13.k 269  k  . 10 269
Vậy FG  269.k.  26,9cm . 10  HẾT  Trang 8