Bài Tập Toán 9 Tuần 12 Có Lời Giải Chi Tiết

BÀI TẬP TOÁN 9 TUẦN 12
I. ĐẠI SỐ: ĐỒ THỊ HÀM SỐ BẬC NHẤT 1 Bài 3.
Cho hàm số y = −2x và y = x 2
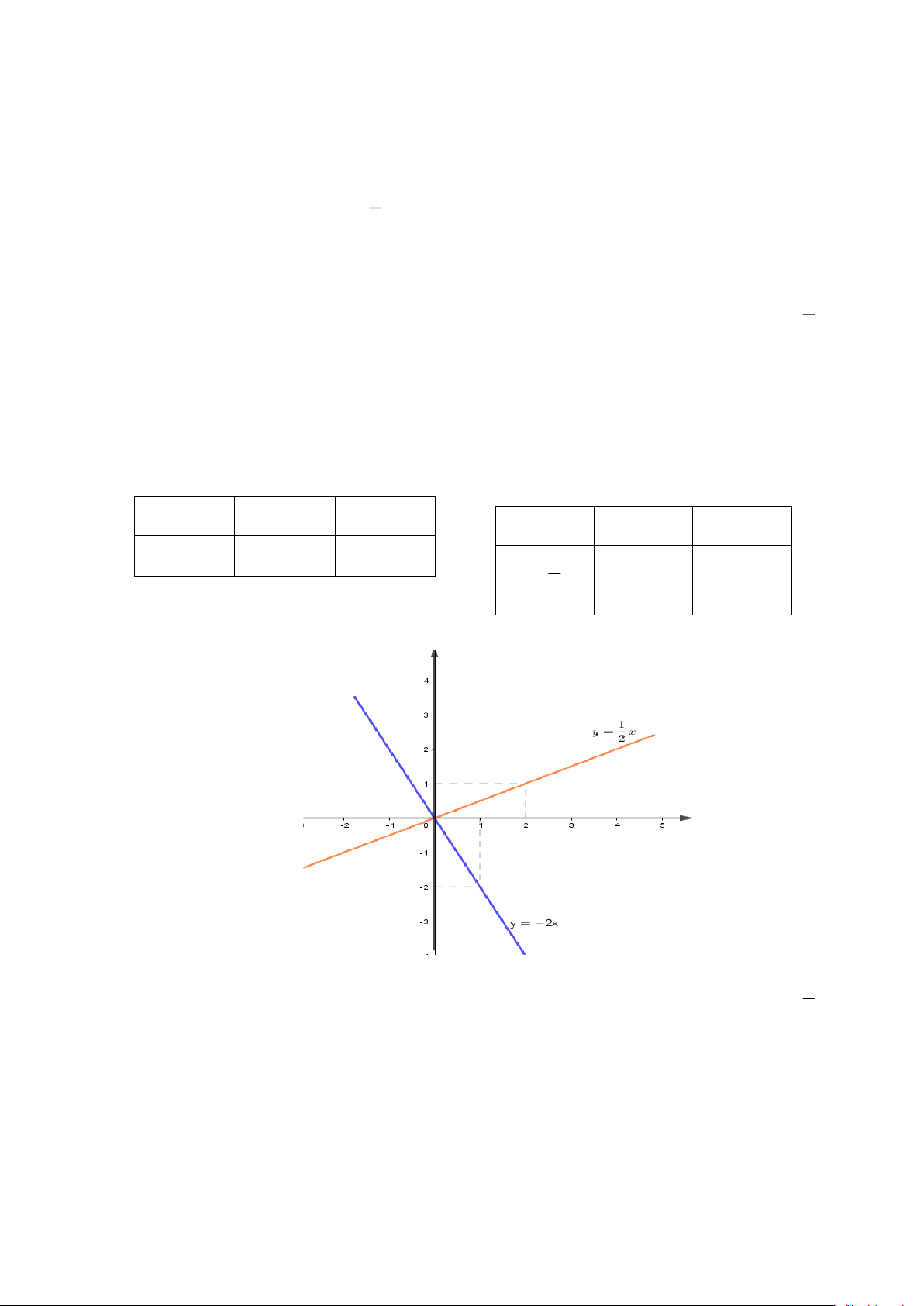
a) Vẽ trên cùng hệ trục tọa độ đồ thị hai hàm số trên cùng hệ trục tọa độ. 1
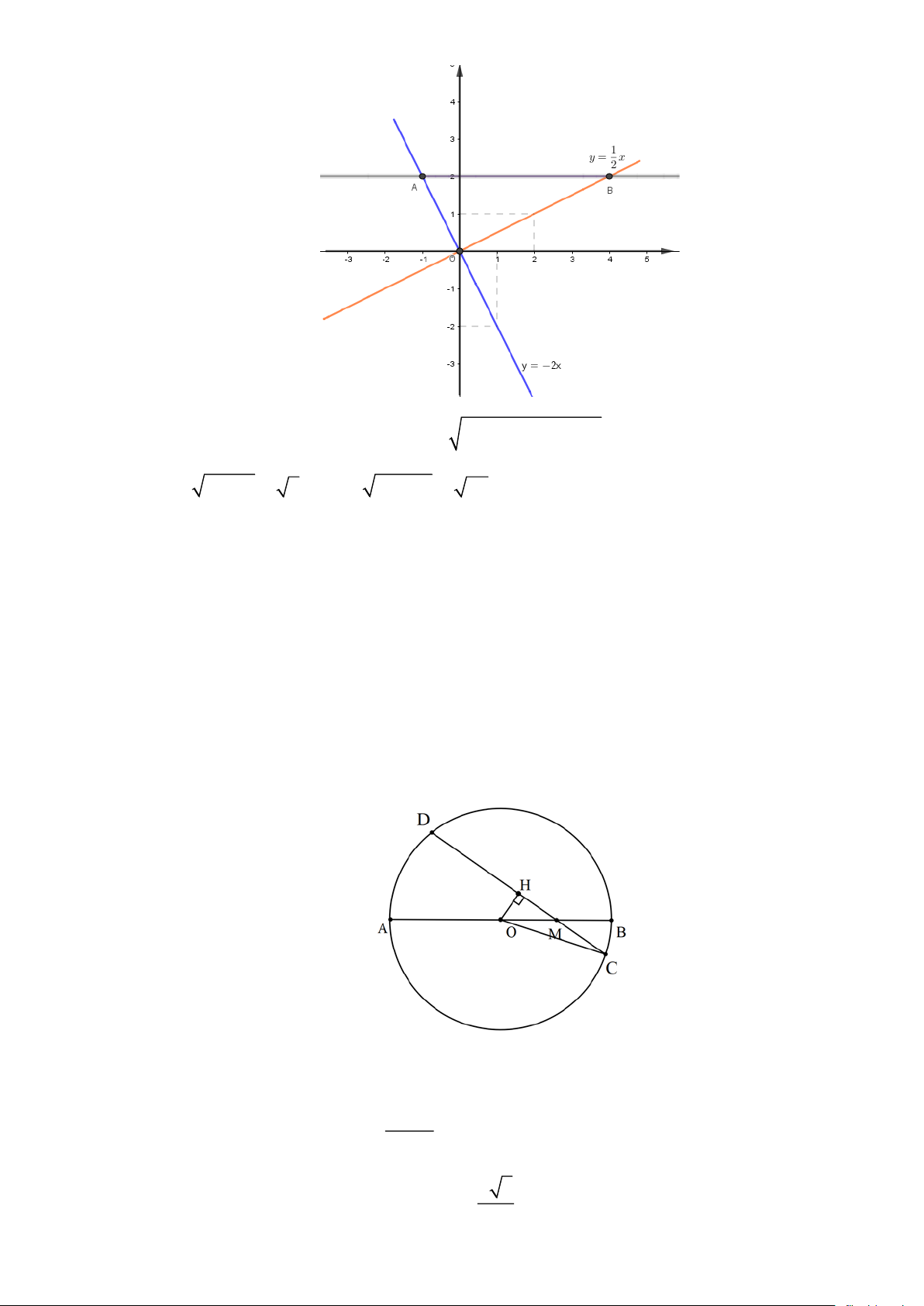
b) Qua điểm (0;2 ) vẽ đường thẳng song song với Ox cắt hai đường thẳng y = x và 2
y = −2x tại hai điểm A và B . Chứng minh tam giác AOB là tam giác vuông.
II. HÌNH HỌC: ÔN TẬP DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY Bài 1.
Cho đường tròn tâm (O; R) đường kính AB , dây cung CD cắt AB tại M , biết MC = 4c ,
m MD = 12cm và 30o AMD = .
a) Tính khoảng cách từ O đến CD .
b) Tính bán kính đường tròn tâm O . Bài 2.
Cho (O; R) đường kính AB . Dây cung CD vuông góc với OA tại M là trung điểm của OA .
a) Tứ giác ACOD là hình gì? Vì sao?
b) Tam giác BCD là tam giác gì? Bài 3.
Cho đường tròn (O; R) đường kính AB . Gọi M , N lần lượt là trung điểm của O , A OB . Qua
M , N lần lượt vẽ các dây CD và EF song song với nhau ( C và E cùng nằm trên một nửa
đường tròn đường kính AB ).
a) Chứng minh: tứ giác CDEF là hình chữ nhật.
b) Giả sử CD và EF cùng tạo với AB một góc nhọn 30 . Tính diện tích hình chữ nhật CDEF .
………………………………HẾT……………………………… Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: ĐỒ THỊ HÀM SỐ BẬC NHẤT 1 Bài 3.
Cho hàm số y = −2x và y = x 2
a) Vẽ trên cùng hệ trục tọa độ đồ thị hai hàm số trên cùng hệ trục tọa độ. 1
b) Qua điểm (0;2 ) vẽ đường thẳng song song với Ox cắt hai đường thẳng y = x và 2
y = −2x tại hai điểm A và B . Chứng minh tam giác AOB là tam giác vuông. Lời giải
a) Vẽ đồ thị hai hàm số trên cùng một hệ trục tọa độ + Bảng giá trị x 0 1 x 0 2
y = −2x 0 −2 1 0 1 y = x 2 + Hình vẽ 1
b) Qua điểm (0;2 ) vẽ đường thẳng song song với Ox cắt hai đường thẳng y = x và 2
y = −2x tại hai điểm A và B . Chứng minh tam giác AOB là tam giác vuông. Trang 2 Ta có: A( 1
− ;2); B(4;2), suy ra AB = ( + )2 + ( − )2 4 1 2 2 = 5 2 1 OA = 2 +1 = 5 2 2 ; OB = 2 + 4 = 20 Từ đó tính được 2 2 2
AB = OA + OB . Suy ra tam giác AOB là tam giác vuông.
II. HÌNH HỌC: ÔN TẬP DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY Bài 1.
Cho đường tròn tâm (O; R) đường kính AB , dây cung CD cắt AB tại M , biết MC = 4c ,
m MD = 12cm và 30o AMD = .
a) Tính khoảng cách từ O đến CD .
b) Tính bán kính đường tròn tâm O . Lời giải
a) Tính khoảng cách từ O đến CD . 12 + 4
Kẻ OH ⊥ CD  HC = HD =
= 8cm, MC = 4 cm  MH = CH − MC = 4 cm 2 o 4 3
Ta có: OH = HM .tan AMD = 4.tan 30 = cm 3 Trang 3
b) Tính bán kính đường tròn tâm O .
Ta có: OHC vuông tại H 2   2 2 2 2 4 3 208
CO = CH + OH = 8 +   = 3 3   4 39  4 39 CO = (cm) Hay R = (cm). 3 3 Bài 2.
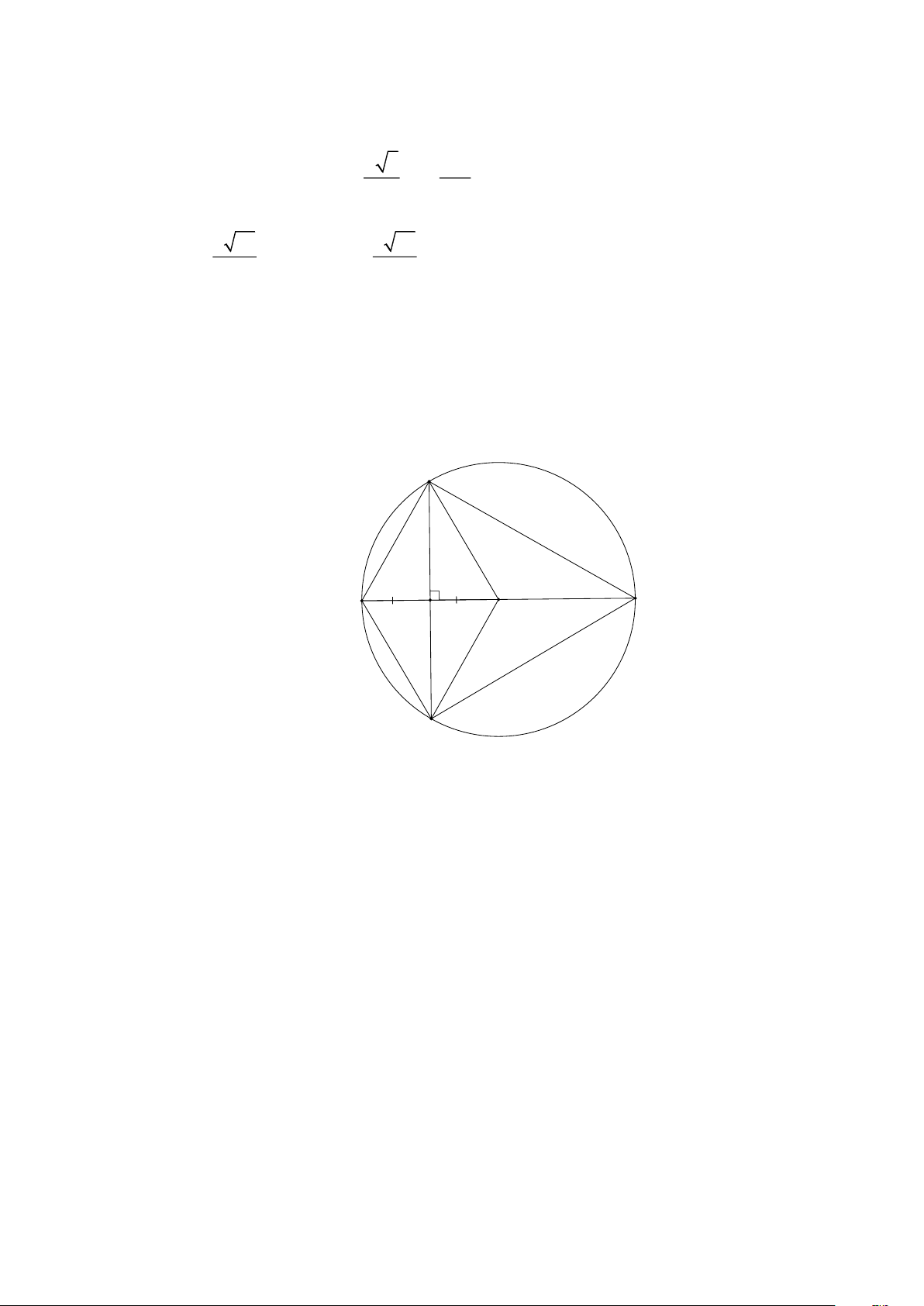
Cho (O; R) đường kính AB . Dây cung CD vuông góc với OA tại M là trung điểm của OA .
a) Tứ giác ACOD là hình gì? Vì sao?
b) Tam giác BCD là tam giác gì? Lời giải D A B M O C
a) Ta có AB ⊥ CD tại M
 M là trung điểm của CD (quan hệ vuông góc giữa đường kính và dây cung)
Tứ giác ACOD có hai đường chéo AO ⊥ DC tại M
MA = MO ( gt)
MC = MD (cmt)
 ACOD là hình thoi
b) Ta có AB ⊥ CD tại trung điểm M của CD nên AB là đường trung trực của đoạn thẳng CD  BC = BD  BC 
D cân tại B .
Mặt khác: tứ giác ACOD là hình thoi nên DA = DO
Lại có: OA = OD (bán kính của đường tròn (O) )
 OA = OD = DA Trang 4  ODA  là tam giác đều  DAB = 60 1
Xét DAB có trung tuyến OD = AO = AB 2  DAB 
là tam giác vuông tại D  ADB = 90
DAB là tam giác vuông tại D có DAB = 60  DBA = 30
BCD cân tại B có MB là đường cao  MB cũng là đường phân giác của DBC
 DBC = 2DBA = 2.30 = 60  BC 
D là tam giác đều (tam giác cân có góc ở đỉnh bằng 60 ). Bài 3.
Cho đường tròn (O; R) đường kính AB . Gọi M , N lần lượt là trung điểm của O , A OB . Qua
M , N lần lượt vẽ các dây CD và EF song song với nhau ( C và E cùng nằm trên một nửa
đường tròn đường kính AB ).
a) Chứng minh: tứ giác CDFE là hình chữ nhật.
b) Giả sử CD và EF cùng tạo với AB một góc nhọn 30 . Tính diện tích hình chữ nhật CDFE . Lời giải C E K N 30° 30° A B M O H D F
a) Qua O kẻ OH ,OK lần lượt vuông góc với EF và CD . vì EF
CD ( gt) nên suy ra O, H , K thẳng hàng. 1
Ta có: OM = OA 2 1 ON = OB 2
OA = OB = R Trang 5  OM = ON
Xét hai tam giác vuông OKM và OHN , ta có:
OKM = OHN = 90
OM = ON (cmt)
KOM = HON (2 góc đối đỉnh)
 OKM = OHN (cạnh huyền - góc nhọn)  OK = OH
 CD = EF (trong một đường tròn, hai dây cách đều tâm thì bằng nhau) Tứ giác CDFE có: CD FE ( gt)
CD = FE (cmt)
 CDFE là hình bình hành
 CE DF hay CDFE là hình thang có đáy là CE và DF
Mặt khác OK ⊥ CD tại K
 K là trung điểm của CD
Chứng minh tương tự ta có H là trung điểm của FE
 HK là đường trung bình của hình thang CDFE  HK CE Mà HK ⊥ EF
 CE ⊥ FE hay CFE = 90
Hình bình hành CDFE có CFE = 90  CDFE là hình chữ nhật.
b) Ta có: HK = DF = EC (vì CDFE là hình chữ nhật)
Xét tam giác vuông OKM có KMO = 30( gt) 1  OK = OM 2 1 R Mà OM = OA = 2 2 R  OK = 4 Trang 6 R  HK = 2OK = = EC 2
Xét tam giác vuông CKO có: 2 2 2  R  R 15R 2 2 2 2 2
CK = CO − OK = R − = R − =    4  16 16 R 15  CK = 4 R 15  CD = 2CK = 2 2 R 15 R R 15
Diện tích hình chữ nhật CDFE là S = C . D EC = . = (dvdt). 2 2 4  HẾT  Trang 7