Bài Tập Toán 9 Tuần 15 Có Lời Giải Chi Tiết

BÀI TẬP TOÁN 9 TUẦN 15
I. ĐẠI SỐ: ÔN TẬP VỀ HÀM SỐ y = ax + b(a  0) 2 Bài 1.
Viết phương trình đường thẳng d’ biết nó // với đường thẳng d có pt : y = x + 2 và đi qua 3 A(3;− ) 1 . 1 Bài 2.
Cho 2 đường thẳng: d : y = 3x + 4 và d : y = − x + 2 1 2 3
Cho d  Ox = A,d  Oy = B,d  Ox = C,d  Oy = D d  d = M 1 1 2 2 1 2
a) Chứng minh AMC vuông tại M
b) Tính diện tích cùa AM  C, AM  O, AB  O, BO  D . Bài 3.
Cho hàm số y = mx + m −1
a) Xác định m đồ thị hàm số cắt trục tung tại điểm có tung độ là 2
b) Xác định m đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 3
c) Vẽ đồ thị các hàm số vừa tìm được ở câu a và câu b trên cùng một hệ trục tọa độ . Tìm tọa
độ giao điểm của chúng và tính các góc của tam giác được tạo thành. Bài 4.
Cho hàm số y = (m + 4) x − m + 6
a) Tìm các giá trị của m để hàm số đồng biến ? Nghịch biến ?
b) Tìm các giá trị của m để đồ thị hàm số đi qua điểm A(−1;2)?
c) CMR: khi m thay đổi thì đường thẳng trên luôn đi qua một điểm cố định.
II. HÌNH HỌC: ÔN TẬP TÍNH CHẤT HAI TIẾP TUYẾN CẮT NHAU. Bài 1.
Cho (O;R) và một đường thẳng d cắt đường tròn (O) tại C và D. Một điểm M di động trên d
sao cho MC  MD và ở ngoài (O) . Qua điểm M kẻ các tiếp tuyến M ,
A MB với đường tròn
(A, B là các tiếp điểm). Gọi H là trung điểm của CD và giao điểm của AB với OM , OH lần
lượt E, F ở. Chứng minh rằng : a) 2
OE.OM = R .
b) Bốn điểm M , E, H , F cùng thuộc một đường tròn. Bài 2.
Cho đường tròn (O) đường kính AB . Một điểm M thay đổi trên đường tròn ( M khác , A B )
.Vẽ đường tròn tâm M tiếp xúc với AB tại H . Từ A và B kẻ các tiếp tuyến AC , BD với đường
tròn (M ) , (C, D là các tiếp điểm ).
a) Chứng minh CD là tiếp tuyến của (O) .
b) Chứng minh AC + BD có giá trị không đổi từ đó tính giá trị lớn nhất của AC.BD . Bài 3.
Cho đường tròn (O; R) hai tiếp tuyến MA, MB của đường tròn, AB cắt OM tại H.
a) Chứng minh AM .BM = MH.MO Trang 1 OA MB
b) Đường thẳng OA cắt MB tại N. Chứng minh = ON MN
c) Từ O kẻ OK // AM (K thuộc MB) chứng minh OK = MK
HƯỚNG DẪN GIẢI CHI TIẾT 2 Bài 1.
Viết phương trình đường thẳng d’ biết nó // với đường thẳng d có pt : y = x + 2 và đi qua 3 A(3;− ) 1 . Lời giải 2
Đường thẳng d’ song song với đường thẳng d nên đường thẳng d’ có dạng: y = x + b 3 2
Đường thẳng d’ đi qua điểm A(3;− )
1 , thay vào y = x + b ta được: 3 2 1
− = .3+ b  b = 3 − 3 2
Vậy phương trình đường thẳng d’ là: y = x − 3 3 1 Bài 2.
Cho 2 đường thẳng: d : y = 3x + 4 và d : y = − x + 2 1 2 3
Cho d  Ox = A,d  Oy = B,d  Ox = C,d  Oy = D d  d = M 1 1 2 2 1 2
a) Chứng minh AMC vuông tại M
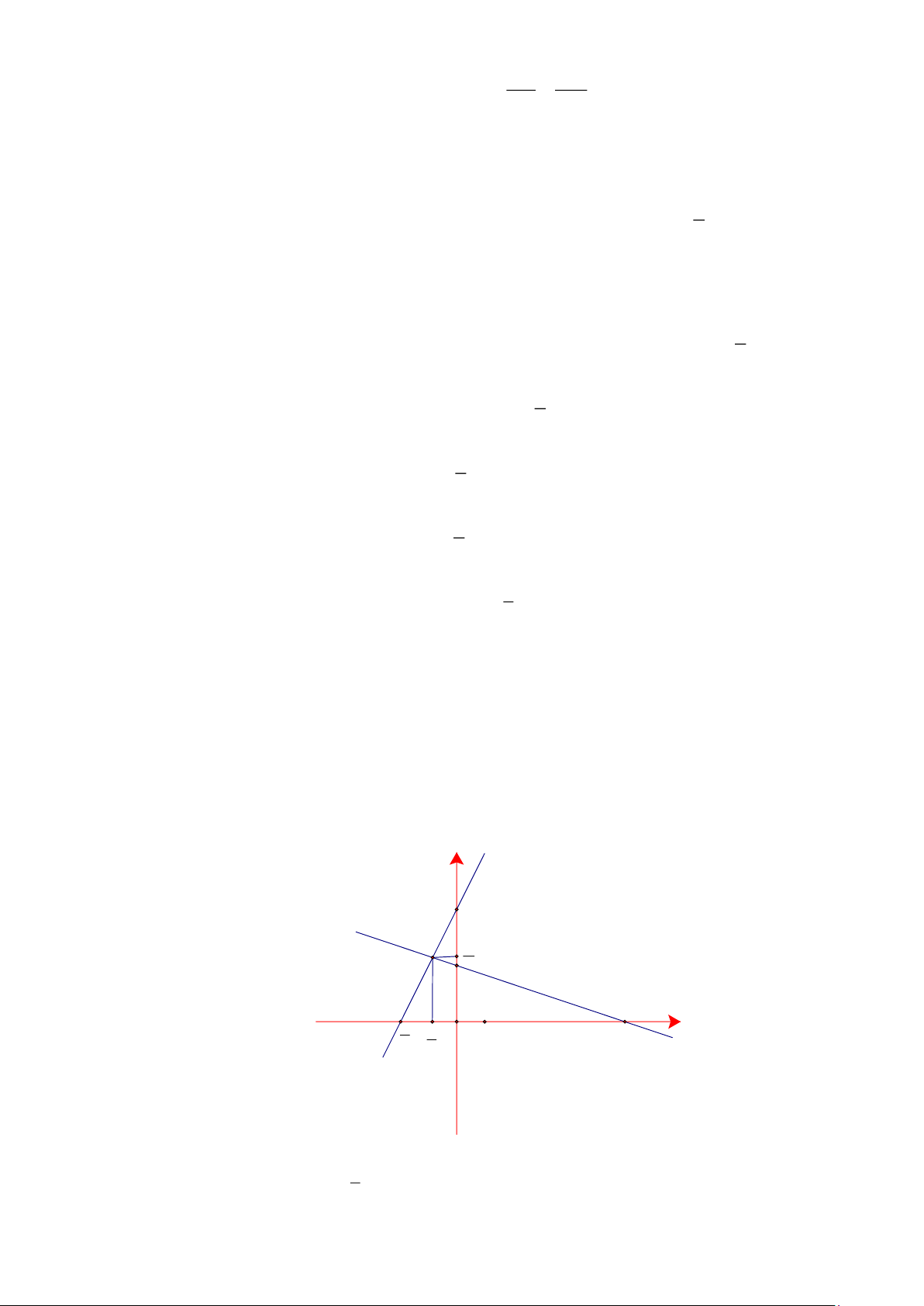
b) Tính diện tích cùa AM  C, AM  O, AB  O, BO  D . Lời giải a) y d1 4 B M D 11 5 2 A H C -4 -3 O 6 1 x 3 5 d2 1
d : y = 3x + 4 và d : y = − x + 2 1 2 3 Trang 2
+) Cho x = 0  y = 4  d  Oy tại B (0;4) 1 4 −  4 −  y = 0  x =
 d  Ox tại A ;0 1   3  3 
+) Cho x = 0  y = 2  d  Oy tại D (0;2) 2
y = 0  x = 6  d  Ox tại C (6;0) 2 Kẻ MH ⊥ Ox
Xét phương trình hoành độ giao điểm của d ; d ta có: 1 2 1 1 10 3 − 3 −
3x + 4 = − x + 2  3x + x = 2 − 4  x = 2 −  x = Thay x = vào phương trình 3 3 3 5 5 đường thẳng ( 11  3 − 11 11 d  y =  d  d = M ;  MH = 1 ) 1 2   5  5 5  5 3 − 3 4 3 11 OH =
=  AH = OA − OH = − = 5 5 3 5 5 3 33 4 22 C
H = OH + OC = 6 + = ; AC = A O + OC = + 6 = 5 5 3 3
Khi đó: Áp dụng định lý pytago vào các tam giác vuông A  HM ; M  HC ta có: 2 2 11  33  11 10 2 2
MC = MH + HC = + =      5   5  5 2 2 11  11 11 10 2 2
MA = MH + HA = + =      5  15  15 4 22
AC = OA + OC = + 6 = 3 3 2 2 11 10  11 10  484 Xét C có: 2 2 MA + MC =   +   =  5   15  9     2  22  484 2 AC = =    3  9 Do đó: 2 2 2
MA + MC = AC . Áp dụng định lý pytago đảo ta có AMC vuông tại M . b) Trang 3 y 4 B M D 11 5 2 A H C -4 -3 O 1 6 x 3 5 d2
Tính diện tích cùa AM  C, AM  O, AB  O, BO  D 1 1 11 10 11 10 121 Ta có: S = M . A MC = . . = (đvdt) AMC 2 2 15 5 15 1 1 11 4 22 S = MH.OA = . . = (đvdt) AMO 2 2 5 3 15 1 1 4 8 S = O . A OB = . .4 = (đvdt) ABO 2 2 3 3 1 1 3 6 S = M . D OB = . .4 = (đvdt) BOD 2 2 5 5 Bài 3.
Cho hàm số y = mx + m −1
a) Xác định m đồ thị hàm số cắt trục tung tại điểm có tung độ là 2
b) Xác định m đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 3
c) Vẽ đồ thị các hàm số vừa tìm được ở câu a và câu b trên cùng một hệ trục tọa độ . Tìm tọa
độ giao điểm của chúng và tính các góc của tam giác được tạo thành. Lời giải
a) Để đồ thị hàm số cắt trục tung tại điểm có tung độ là 2 ta có:
x = 0; y = 2  2 = .0
m + m −1  m = 3
Vậy m = 3 thì đồ thị hàm số cắt trục tung tại điểm có tung độ là 2
b) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 3 ta có: 1
y = 0; x = 3  0 = .3
m + m −1 4m = 1 m = 4 1
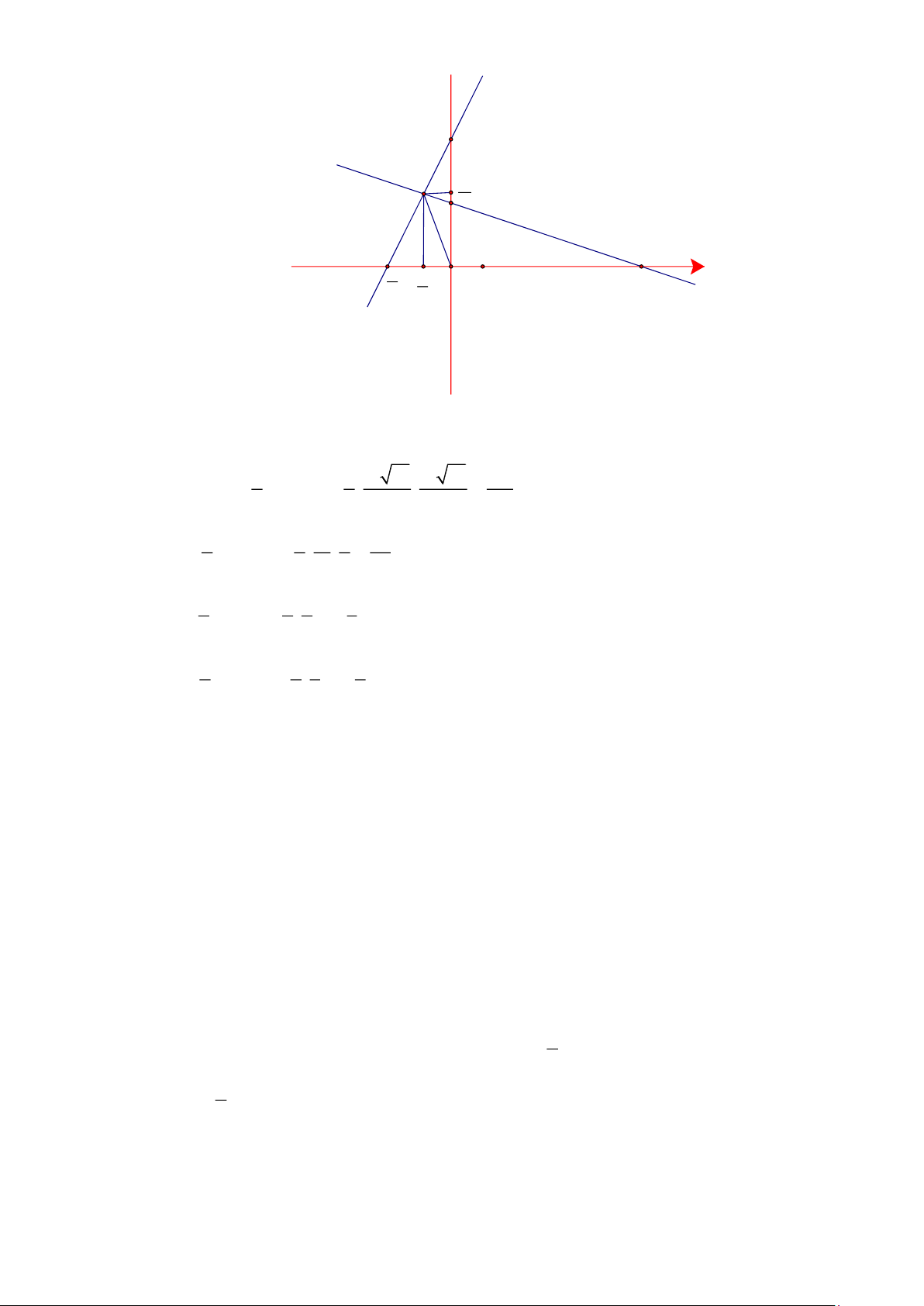
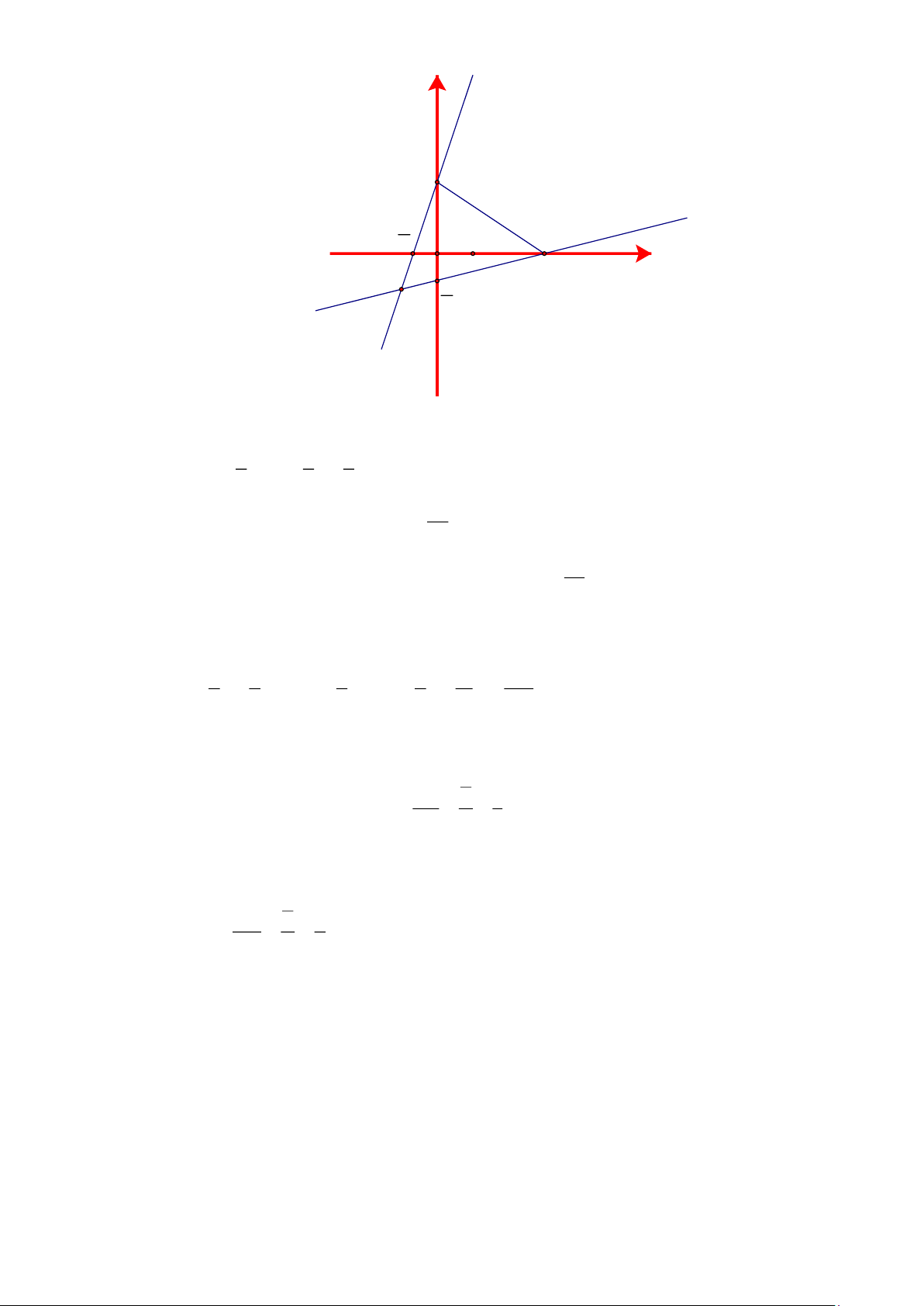
Vậy m = thì đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 3 . 4 c) Trang 4 y d1 2 B -2 3 D A O 3 E x -3 M 4 d2
+ Thay m = 3  y = 3x + 2 (d 1 ) 1 1 3
+ Thay m =  y = x − (d 2 ) 4 4 4  2 − 
Ta có đường thẳng (d cắt Ox tại A
;0 và cắt Oy tại B (0;2) 1 )    3   3 − 
Đường thẳng (d cắt Ox tại D (3;0) và cắt Oy tại E 0; 2 )    4 
Xét phương trình hoành độ giao điểm của d ; d ta có: 1 2 1 3 1 3 11 1 − 1 3x + 2 = x −  3x − x = 2 − −  x =  x = 1
− Thay x = −1 vào phương trình 4 4 4 4 4 4
đường thẳng d  y = 3. 1 − + 2 = 1 −  M 1 − ; 1 − 1 ( ) ( ) 2 OA 1
Xét AOB vuông tại O 3 tan ABO ABO 18 = = =   OB 2 3
Xét BOD vuông tại O 3 OE 1 4 tan ODE EDO 14 BDM BDO EDO 56 14 70 = = =    = + = + = OD 3 4
Do đó: ABD ABO DBO 18 56 74 = + = + =
Xét BDM có: BMD 180 (MBD MDB) 180 (74 70 ) 36 = − + = − + = Bài 4.
Cho hàm số y = (m + 4) x − m + 6
a) Tìm các giá trị của m để hàm số đồng biến ? Nghịch biến ?
b) Tìm các giá trị của m để đồ thị hàm số đi qua điểm A(−1;2)?
c) CMR: khi m thay đổi thì đường thẳng trên luôn đi qua một điểm cố định. Trang 5 Lời giải
a) Tìm các giá trị của m để hàm số đồng biến ? Nghịch biến ?
y = (m + 4) x − m + 6 đồng biến  (m + 4)  0  m  4 −
y = (m + 4) x − m + 6 nghịch biến  (m + 4)  0  m  4 −
b) Đồ thị hàm số y = (m + 4) x − m + 6 đi qua điểm A(−1;2), ta thay tọa độ vào phương trinh đường thẳng được: 2 = (m + 4)(− ) 1 − m + 6
 2 = −m − 4 − m + 6
 2m = −2 − 4 + 6 = 0  m = 0
Vậy m = 0 thì đường thẳng y = (m + 4) x − m + 6 đi qua A(−1;2).
c) CMR: khi m thay đổi thì đường thẳng trên luôn đi qua một điểm cố định.
Giả sử đường thẳng của đồ thị hàm số y = (m + 4) x − m + 6 luôn đi qua điểm cố định ( x ; y . 0 0 ) Ta được:
y = m + 4 x − m + 6 0 ( ) 0
 y = mx + 4x − m + 6 0 0 0
m( x −1 + 4x − y + 6 = 0 0 ) ( 0 0 )
Với mọi m để phương trinh bằng 0 thì x −1 = 0 x =1 x =1 0  0 0     4x − y + 6 = 0  4 − y + 6 = 0 y =10 0 0  0  0
Vậy đường thẳng trên luôn đi qua điểm cố định ( x ; y = 1;10 0 0 ) ( )
II. HÌNH HỌC: ÔN TẬP TÍNH CHẤT HAI TIẾP TUYẾN CẮT NHAU. Bài 1.
Cho (O;R) và một đường thẳng d cắt đường tròn (O) tại C và D. Một điểm M di động trên d
sao cho MC  MD và ở ngoài (O) . Qua điểm M kẻ các tiếp tuyến M ,
A MB với đường tròn
(A, B là các tiếp điểm). Gọi H là trung điểm của CD và giao điểm của AB với OM , OH lần
lượt E, F ở. Chứng minh rằng : a) 2
OE.OM = R .
b) Bốn điểm M , E, H , F cùng thuộc một đường tròn. Lời giải Trang 6 F A C H D O E M B a) Chứng minh 2
OE.OM = R .
Vì MB là tiếp tuyến của đường tròn nên MB ⊥ OB .
Ta có, MA = MB và ME là tia phân giác của góc AMB ( Tính chất hai tiếp tuyến cắt nhau
Suy ra, AB ⊥ MO tại E .
Xét MBO vuông tại B có BE là đường cao nên: 2
OE.OM = OB ( hệ thức lượng trong tam giác vuông ). Hay, 2
OE.OM = R .
b) Từ ý a ta có, AB ⊥ MO tại E.
Vì H là trung điểm của DC nên HO ⊥ CD tại H ( Liên hệ giữa đường kính và dây cung).
Xét tứ giác MEHF có E và H cùng nhìn MF dưới hai góc vuông.
Do đó, tứ giác MEHF là tứ giác nội tiếp.
Vậy bốn điểm M , E, H , F cùng thuộc một đường tròn. Bài 2.
Cho đường tròn (O) đường kính AB . Một điểm M thay đổi trên đường tròn ( M khác , A B ) .Vẽ
đường tròn tâm M tiếp xúc với AB tại H . Từ A và B kẻ các tiếp tuyến AC , BD với đường
tròn (M ) , (C, D là các tiếp điểm ).
a) Chứng minh CD là tiếp tuyến của (O) .
b) Chứng minh AC + BD có giá trị không đổi từ đó tính giá trị lớn nhất của AC.BD . Lời giải Trang 7 D M C A B H O
a) Trong đường tròn (M ; MH ) theo tính chất hai tiếp tuyến cắt nhau, ta có:
MA là tia phân giác của góc HMC và MB là tia phân giác của góc HMD .
Suy ra: CMA = HMA hay CMH = 2HMA .
HMB = DMB hay HMD = 2HMB
Tam giác ABM nội tiếp đường tròn (O) có AB là đường kính nên vuông tại M. Suy ra: 0 AMB = 90 . 0
 CMH + HMD = 2HMB + 2HMA = 180 0
 CMD = 180 . Hay C, M , D thẳng hàng.
Mặt khác, CMA đồng dạng với MBA ( vì 0
MCA = AMB = 90 , CAM = MAB ).
Suy ra, CMA = MBA . 0 0
MAB + MBA = 90  AMO + MBA = 90 (MAB = AMO) Mà . 0
 AMO + CMA = 90
Hay, CM ⊥ MO . Vậy CD là tiếp tuyến của (O) .
b) Trong đường tròn (M ; MH ) theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Suy ra: AC + BD = AH + BH = AB không đổi. 1 1 Ta có: 2 2
AC.BD = AH.BH  (AH + BH ) = AB . 4 4 1
Vậy giá trị lớn nhất của AC.BD là 2
AB  AH = BH . Hay M là điểm chính giữa cung AB. 4 Bài 3.
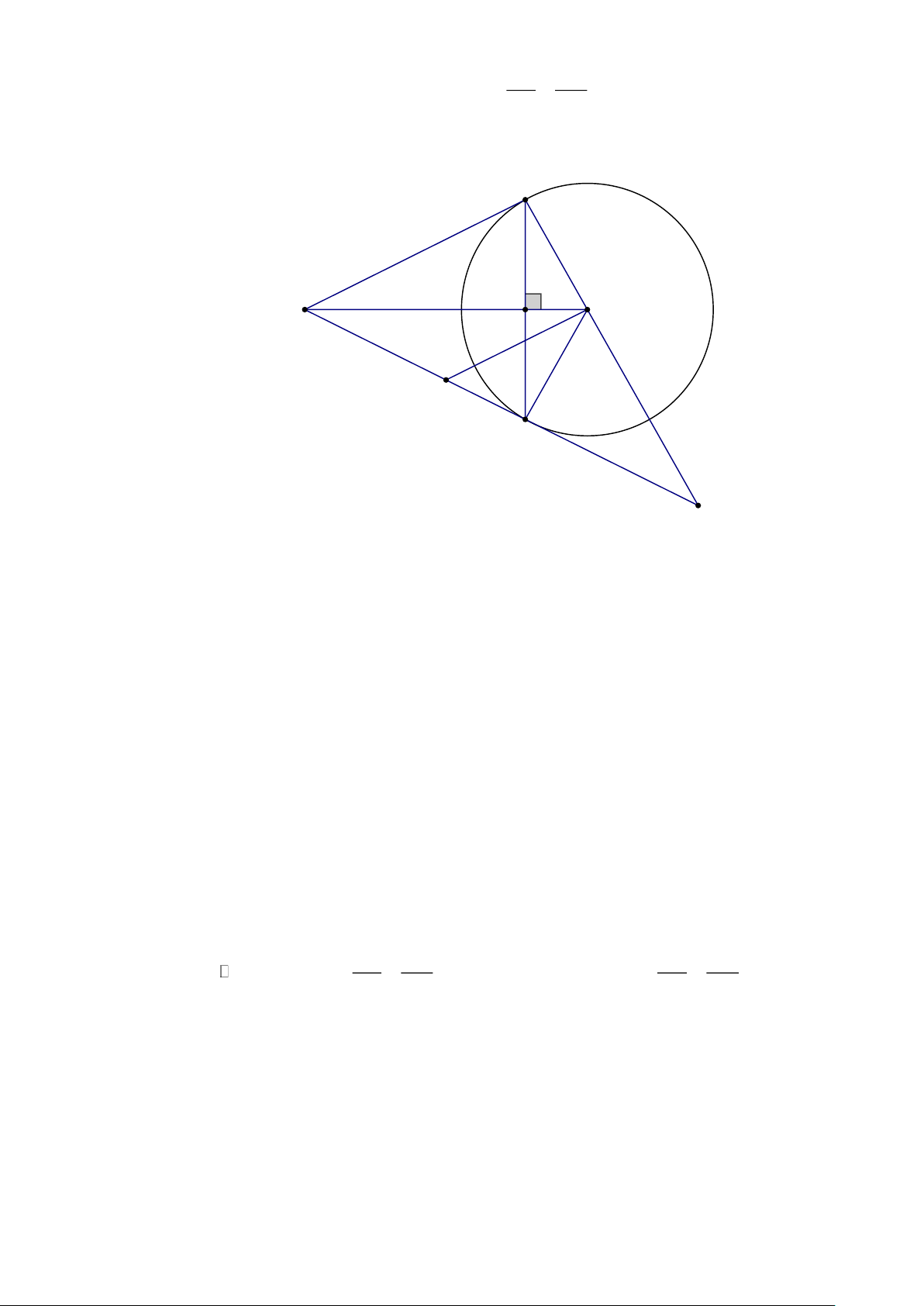
Cho đường tròn (O; R) hai tiếp tuyến MA, MB của đường tròn, AB cắt OM tại H.
a) Chứng minh AM .BM = MH.MO Trang 8 OA MB
b) Đường thẳng OA cắt MB tại N. Chứng minh = ON MN
c) Từ O kẻ OK // AM (K thuộc MB) chứng minh OK = MK Lời giải A O M H K B N
a) Xét (O; R) có MA, MB là hai tiếp tuyến, A, B là hai tiếp điểm OA  = OB = R MA = MB    MA ⊥ AO MB ⊥ BO 
MOlàtia phân giác cua góc AMB  AMO = BMO O
 A = OB = R *Vì  
 MO là đường trung trực của AB  AB ⊥ MO tại H MA = MB
* Xét tam giác AMO vuông tại A, đường cao AH 2
 MA = MH.MO (hệ thức lượng trong tam giác vuông), mà MA = MB  M .
A MB = MH.MO
b) Xét NBO và NAM có: 0
NBO = NAM = 90  N chung    ( ) BO MA OA MB NBO NAM gg  = , mà MA = MB, OB = OA  = ON MN ON MN OK ⊥ AO  c)
  MA // KO MOK = AMO(2 góc soletrong ) MO ⊥ AO
mà MOK = KMO  M
 OK cântai K  OK = MK HẾT Trang 9