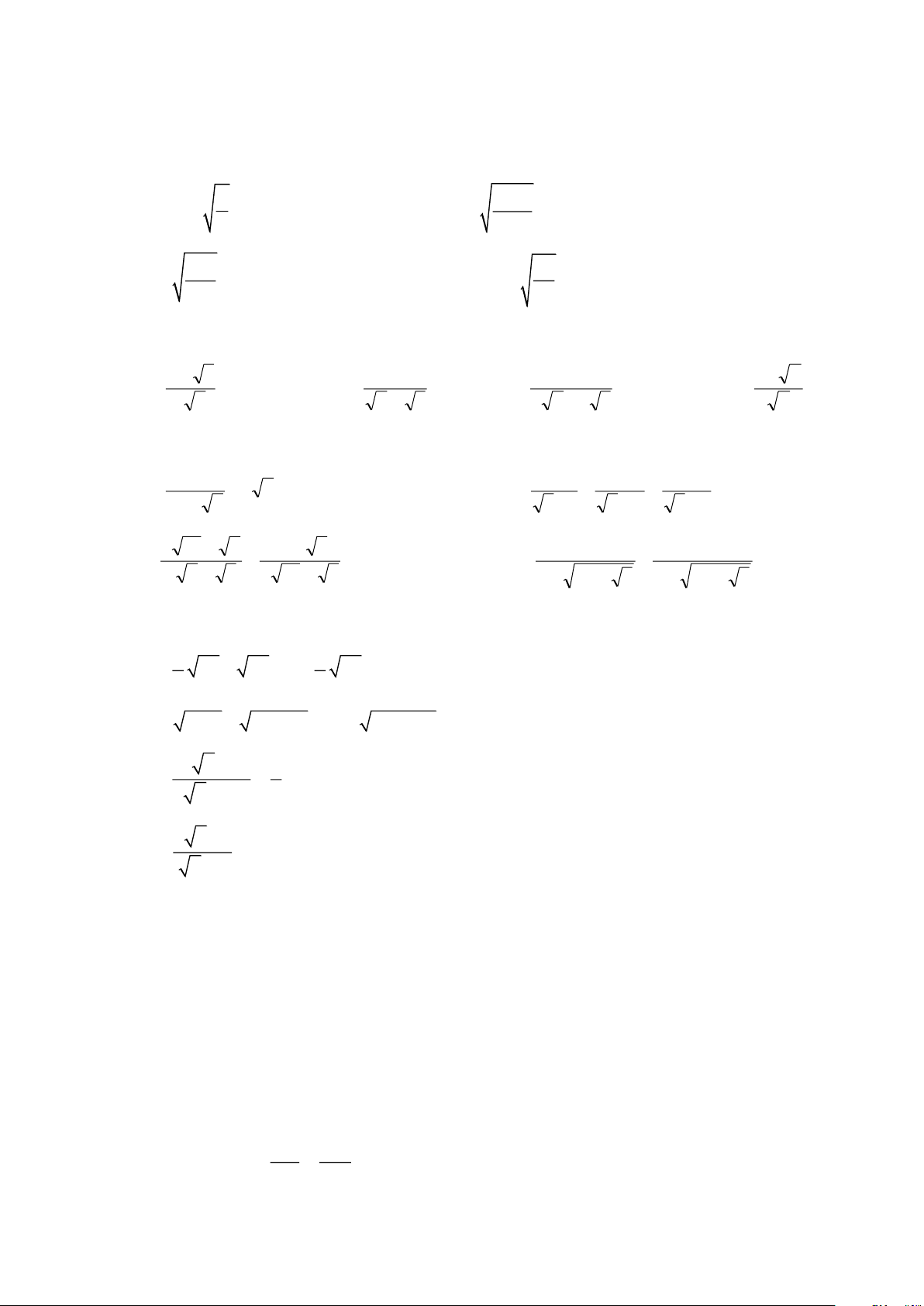
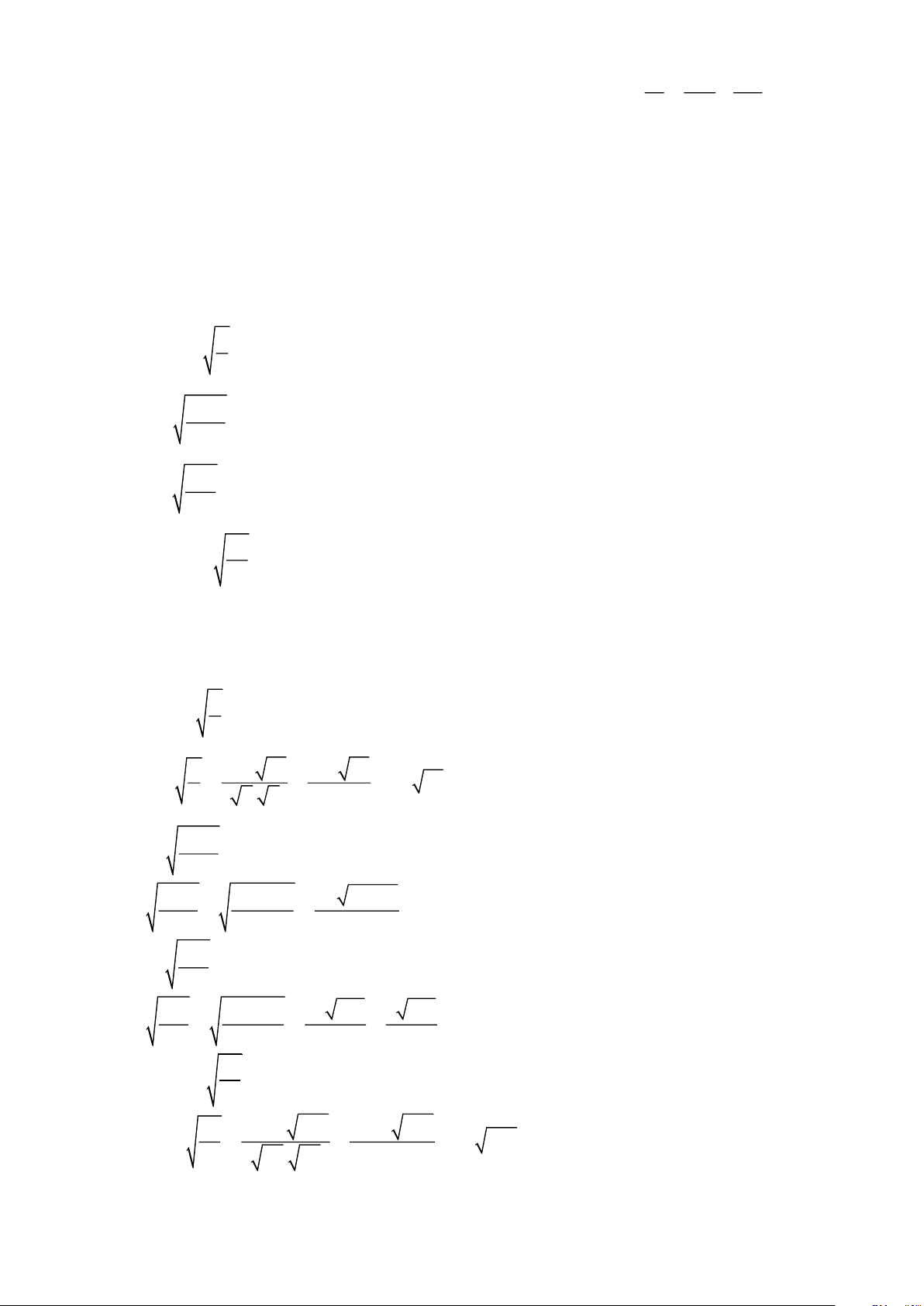


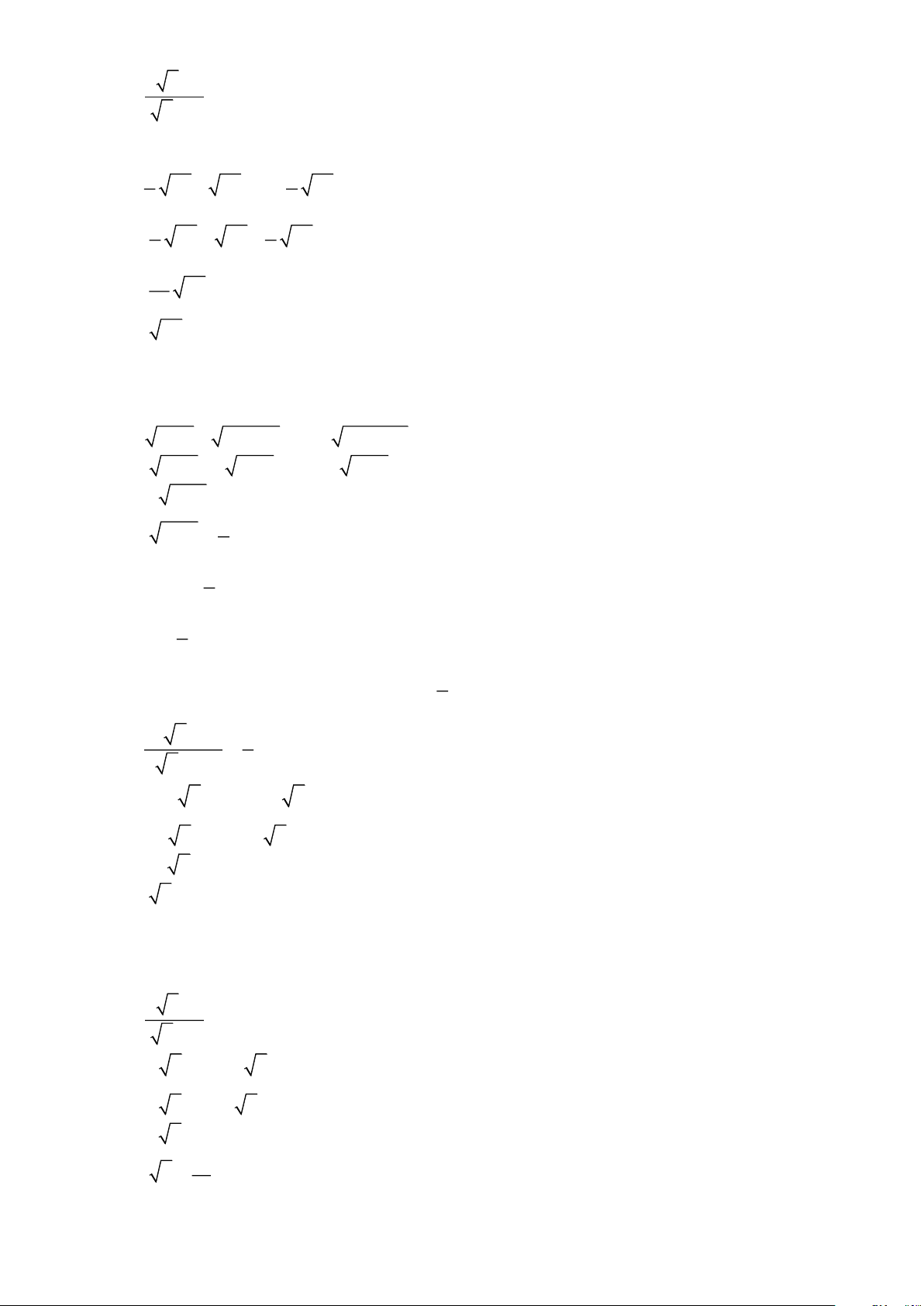


Preview text:
BÀI TẬP TOÁN 9 TUẦN 6
I. ĐẠI SỐ: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC BẬC HAI Bài 1.
Khử mẫu của biểu thức lấy căn 3 − a) y − 3x xy
với x 0, y 0 b) với x 0 x 35 3
c) 5a với a 0,b 0 d) 3 7 − xy
với x 0, y 0 49b xy Bài 2. Trục căn thức ở mẫu: 2 − 3 1 1 1+ a a) ; b) ; c) ; d) . 3 6 2 + 3 2 2 − 3 3 a Bài 3.
Rút gọn các biểu thức sau: 53 2 1 6 a) + 2 7 − 5 ; b) − + ; 9 − 2 6 3 +1 3 − 2 3 + 3 2 12 − 6 10 + 5 6 6 c) + ; d) − . 2 6 − 3 2 15 + 3 4 + 4 − 2 3 4 − 4 + 2 3 Bài 4. Giải phương trình 3 1 a) 4x − 4x + 5 =
4x (với x 0 ) 4 4
b) 3 − x − 27 − 9x + 1,25 48 − 16x = 6 (với x 3 ) − c) 5 x 2 2 = (với x 0 ) 8 x + 2, 5 7 +
d) 2 x 1 = 5 (với x 0; x 4 ) x − 2
II. HÌNH HỌC: HỆ THỨC GIỮA CẠNH VÀ GÓC, TỈ SỐ LƯỢNG GIÁC. Bài 1.
Cho ABC vuông tại A, 40o C = , BC = 20 . cm
a) Tính AB, AC.
b) Từ A kẻ AM , AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B.
Chứng minh MN // BC và MN = . AB
c) Chứng minh hai tam giác MAB và ABC đồng dạng. Tính tỉ số đồng dạng. Bài 2.
với AB tại H , DH cắt AI tại E . DE AD a) Chứng minh = . EH AH Trang 1 1 1 1
b) Gọi h là khoảng cách giữa hai cạnh DC và AB . Chứng minh = + . 2 2 2 h AI BI
c) Tính IA theo a biết góc ADC = 30 .
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC BẬC HAI Bài 1.
Khử mẫu của biểu thức lấy căn a) y −xy
với x 0, y 0 x 3 − b)
3x với x 0 35 3
c) 5a với a 0,b 0 49b d) 3 7 − xy
với x 0, y 0 xy Lời giải
Khử mẫu của biểu thức lấy căn a) y −xy
với x 0, y 0 x y −x . y xy −xy xy −xy = = = −y xy x x. x x 3 − b)
3x với x 0 35 3 3 3 − x 3 − .35x −x 1 − 05x = = 35 35.35 35 3
c) 5a với a 0,b 0 49b 3 3 5a 5a .49b 7a 5ab a 5ab = = = 49b 49 . b 49b 49b 7b d) 3 7 − xy
với x 0, y 0 xy 3 −7xy. 3xy 7 − xy 3xy 7 − xy = = = 7 − 3xy xy xy. xy xy Bài 2. Trục căn thức ở mẫu: Trang 2 2 − 3 1 1 1+ a a) ; b) ; c) ; d) . 3 6 2 + 3 2 2 − 3 3 a Lời giải: 2 − 3
(2− 3). 6 2 6 − .3 6 2 6 −3 2 a) = = = ; 3 6 3 6. 6 6 . 3 18 1 (.1 3− 2) 3 − 2 b) = = = − ; 2 + 3 ( 3+ 2)(. 3− 2) 3 2 2 2 3 − 2 1 (.12 2 +3 3) 2 2 + 3 3 2 2 + 3 3 c) = = = ; 2 2 − 3 3 (2 2 −3 3)(2 2 +3 3) ( 2 2 2 2) − (3 3) −19 1+ a
(1+ a). a a +a d) = = . a a. a a Bài 3.
Rút gọn các biểu thức sau: 53 2 1 6 a) + 2 7 − 5 ; b) − + ; 9 − 2 6 3 +1 3 − 2 3 + 3 2 12 − 6 10 + 5 6 6 c) + ; d) − 2 6 − 3 2 15 + 3 4 + 4 − 2 3 4 − 4 + 2 3 Lời giải: a) 53 + 2 7 − 5 9 − 2 7 53(9 + 2 7 ) = ( − )( + )+2 7 −5 9 2 7 9 2 7 53(9 + 2 7 ) = + 2 7 − 5 53 = 9 + 2 7 + 2 7 − 5 = 4 7 + 4 b) 2 1 6 − + 3 + 1 3 − 2 3 + 3 Trang 3 2 ( 3 −1) 6 + ( 3 −3 3 2 ) = ( − +
3 + 1)( 3 −1) ( 3 − 2)( 3 + 2) ( 3 + 3)( 3 − 3) 2 ( 3 −1) 6 + ( 3−3 3 2 ) = − + 2 1 − 6 − = 3 −1+ 3 + 2 − 3 + 3 = 4 + 3 c) 2 12 − 6 10 + 5 + 2 6 − 3 2 15 + 3 6 (2 2 −1) 5 (2 5 +1) = + 3 (2 2 −1) 3 (2 5 +1) 5 = 2 + 3 d) 6 6 − 4 + 4 − 2 3 4 − 4 + 2 3 6 6 = − 4 + ( 3 −1)2 4 − ( 3 +1)2 6 6 = − 4 + 3 − 1 4 − 3 − 1 6 6 = − 3 + 3 3 − 3 6 (3 − 3) 6 (3 + 3) = ( −
3 + 3 )(3 − 3) (3 − 3)(3 + 3) 6 (3 − 3) 6(3 + 3) = − 6 6 = 3 − 3 − 3 − 3 = 2 − 3 Bài 4. Giải phương trình 3 1 a) 4x − 4x + 5 =
4x (với x 0 ) 4 4
b) 3 − x − 27 − 9x + 1,25 48 − 16x = 6 (với x 3 ) − c) 5 x 2 2 = (với x 0 ) 8 x + 2, 5 7 Trang 4 +
d) 2 x 1 = 5 (với x 0; x 4 ) x − 2 Lời giải 3 1 a) 4x − 4x + 5 =
4x (với x 0 ) 4 4 3 1 4x − 4x − 4x = 5 − 4 4 1 − 4x = 5 − 2 4x = 10 4x = 100 x = 25 (TMĐK)
Vậy tập nghiệm của phương trình là S = 25
b) 3 − x − 27 − 9x + 1,25 48 − 16x = 6 (với x 3 )
3 − x − 3 3 − x + 1,25.4 3 − x = 6 4 3 − x = 6 3 3 − x = 2 9 3 − x = 4 3 x = (TMĐK) 4
Vậy tập nghiệm của phương trình là 3 S = 4 − c) 5 x 2 2 = (với x 0 ) 8 x + 2, 5 7
7(5 x −2) = 2(8 x + 2,5)
35 x −14 = 16 x + 5 19 x = 19 x = 1 x = 1 (TMĐK)
Vậy tập nghiệm của phương trình là S = 1 +
d) 2 x 1 = 5 (với x 0; x 4 ) x − 2
2 x +1 = 5( x −2)
2 x + 1 = 5 x −10 3 x = 11 11 x = 3 Trang 5 121 x = (TMĐK) 9
Vậy tập nghiệm của phương trình là 121 S = 9
II. HÌNH HỌC: HỆ THỨC GIỮA CẠNH VÀ GÓC, TỈ SỐ LƯỢNG GIÁC. Bài 1.
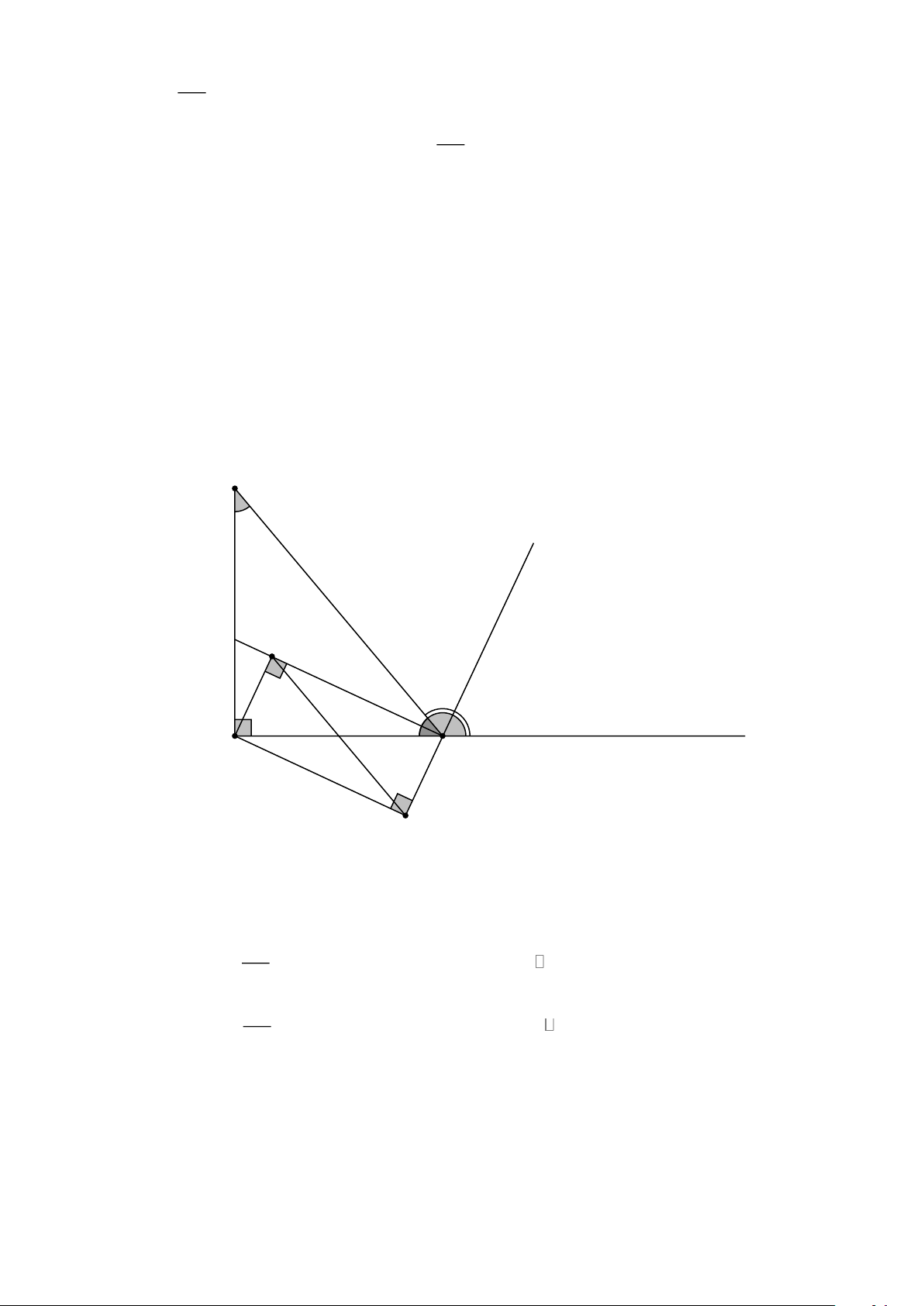
Cho ABC vuông tại A, 40o C = , BC = 20 . cm
a) Tính AB, AC.
b) Từ A kẻ AM , AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B.
Chứng minh MN // BC và MN = . AB
c) Chứng minh hai tam giác MAB và ABC đồng dạng. Tính tỉ số đồng dạng. Lời giải C 40° M A B N
a) Xét ABC vuông tại , A ta có: AB + sin ACB = = .sin = 20.sin 40o AB BC ACB 12,86 BC AC + cos ACB = = .cos = 20.cos 40o AC BC ACB 15,32 BC
Vậy AB = 12,86(cm) và AC =15,32(cm).
b) + Vì BN và BM là phân giác trong và ngoài của góc B
Nên BM ⊥ BN hay 90o MBN = ( ) 1 Trang 6
AM ⊥ BM (gt) = 90o AMB (2)
AN ⊥ BN (gt) = 90o ANB (3) Từ ( )
1 ,(2) và (3) ANBM là hình chữ nhật AB = MN
+ Vì ANBM là hình chữ nhật A MB = N
BM ( .cg.c)
ABM = NMB mà ABM = MBC (gt)
BMN = MBC mà hai góc ở vị trí so le trong MN // BC
c) ABC vuông tại A nên + = 90o ABC ACB mà 40o ACB =
= 90o − 40o = 50o ABC 1 1
Do BM là tia phân giác trong góc B nên = = .50o = 25o ABM ABC 2 2
Xét ACB và MAB có:
BAC = AMB = 90o
ACB = ABM = 90o A BC ∽ M
AB (g.g) AB 12,86 1286
Tỉ số đồng dạng: k = = = BC 15,32 1532 Bài 2.
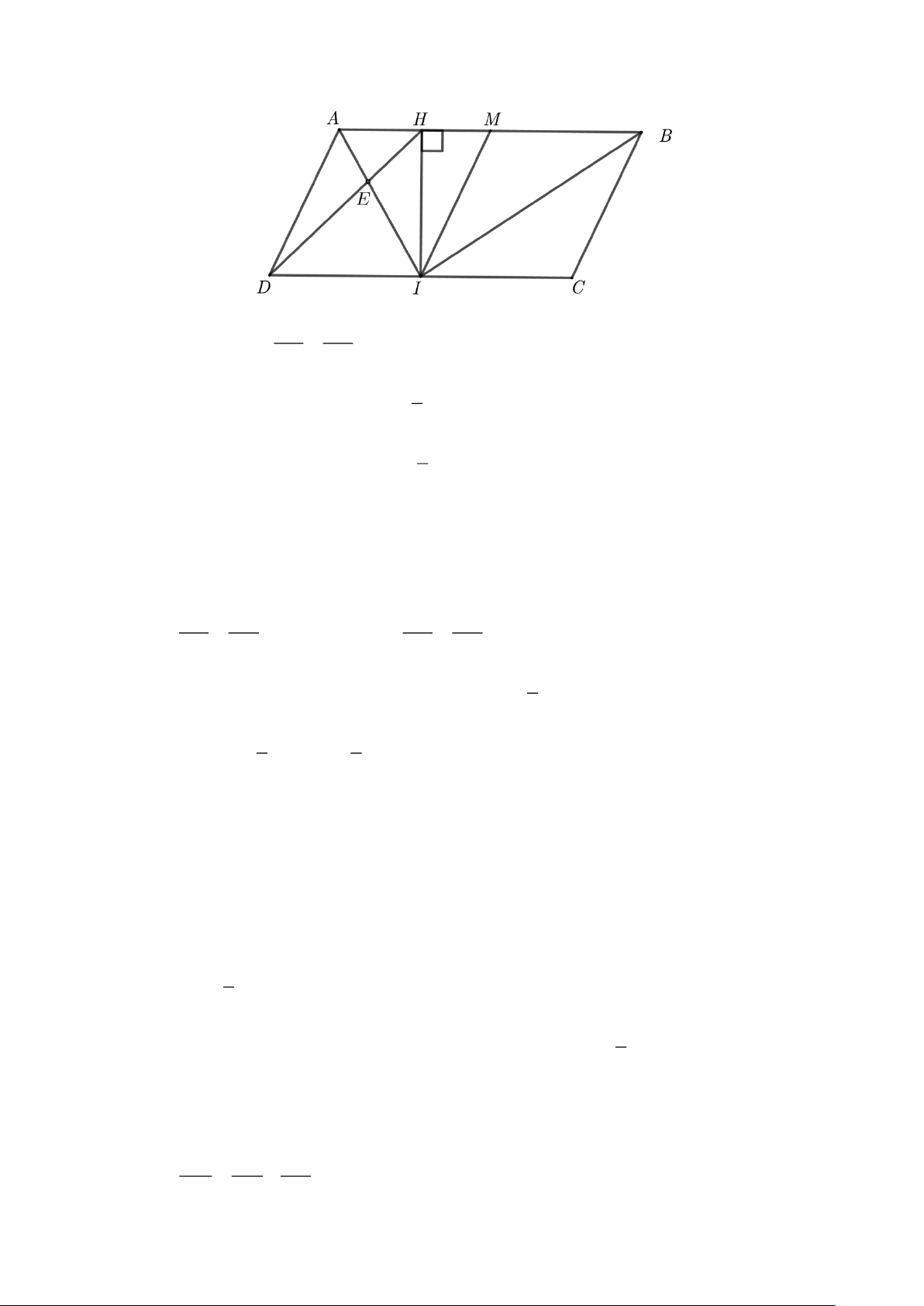
Cho hình bình hành ABCD có DC = 2AD = 2a . Từ trung điểm I của DC hạ IH vuông góc
với AB tại H , DH cắt AI tại E . DE AD a) Chứng minh = . EH AH 1 1 1
b) Gọi h là khoảng cách giữa hai cạnh DC và AB . Chứng minh = + . 2 2 2 h AI BI
c) Tính IA theo a biết góc ADC = 30 . Trang 7 Lời giải DE AD a) Chứng minh = . EH AH 1
I là trung điểm của DC DI = DC . 2 1
Có DC = 2AD (giả thiết) AD = DC . 2 DI = AD
Xét hình bình hành ABCD có AB // CD DI // AH .
Áp dụng hệ quả của định lí Talet cho DEI có: DI // AH . DE DI = DE AD
, mà DI = AD = . EH AH EH AH 1
b) Gọi M là trung điểm của AB AM = MB = AB = a . 2 1 1
Ta có: AM = AB , DI = DC , AB = DC ( ABCD là hình bình hành) 2 2 AM = DI
Xét tứ giác AMID có: AM = DI
AM // DI ( AB // CD )
AMID là hình bình hành
IM = AD = a 1 IM = AB . 2 1
Xét AIB có: IM là trung tuyến ứng với cạnh AB và IM = AB 2
AIB vuông tại I .
Áp dụng hệ thức lượng cho AIB vuông tại I có: 1 1 1 = + . 2 2 2 IH AI BI Trang 8 1 1 1 = + . 2 2 2 h AI BI
c) Vì AMID là hình bình hành nên AMI = ADC = 30 .
Áp dụng hệ thức lượng cho HMI vuông tại H có: HI IH sin HMI = sin 30 = 1 IH = a . IM a 2 HM HM a cosHMI = cos30 = 3 HM = . IM a 2 a − Có: AM = AH + 3
HM a = AH + 2 3 AH = a 0,13a . 2 2
Áp dụng định lý Pytago cho AHI vuông tại có: 2 2 2
AI = AH + IH AI = ( − ) 2 2 3 a 0,52a . Trang 9




