Bài tập toán 9 tuần 7 (có đáp án và lời giải chi tiết)

Tổng hợp Bài tập toán 9 tuần 7 (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc cùng theo dõi và đón xem.

48 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Minh Thư
Trang 1
BÀI TẬP TOÁN 9 TUẦN 7
I. ĐẠI SỐ: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC BẬC HAI
Bài 1.
1) Đơn giản biểu thức:
14 6 5 14 6 5P
.
2) Cho biểu thức:
2 2 1
1
21
x x x
Q
x
x x x





.
a) Rút gọn biểu thức
Q
.
b) Tìm
x
để
QQ
.
c) Tìm số nguyên
x
để
Q
nhận giá trị nguyên.
Bài 2. Cho biểu thức
1
1
x
P
x x x


.
a) Rút gọn biểu thức
P
.
b) Tính giá trị biểu thức
P
khi
.
Bài 3. Cho
11
1
1
x x x
A
x
x


.
a) Rút gọn biểu thức
A
.
b) Tính giá trị của biểu thức
A
khi
1
4
x
.
c) Tìm
x
để
0A
.
d) Tìm
x
để
AA
.
Bài 4. Cho
3 1 4 4
4
22
a a a
P
a
aa

0; 4aa
.
a) Rút gọn
P
.
b) Tính giá trị của
P
với
9a
.
II. HÌNH HỌC: HỆ THỨC GIỮA CẠNH VÀ GÓC, TỈ SỐ LƯỢNG GIÁC.
Bài 1. Cho tam giác nhọn
MNP
. Gọi
D
là chân đường cao của tam giác đó kẻ từ M . Chứng minh
rằng:
a)
1
. . .sin
2
MNP
S MP NP P
b)
.sin
tan
MN N
DP
P
c)
DNE
đồng dạng
MNP
trong đó
E
là chân đường cao của tam giác
MNP
kẻ từ
P
.
Trang 2
Bài 2. Cho tam giác
ABC
,
90A 
,
AB AC
, trung tuyến
AM
, góc
ACB
, góc
AMB
.
Chứng minh
2
sin os 1 sinc
.
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC BẬC HAI
Bài 1.
1) Đơn giản biểu thức:
14 6 5 14 6 5P
.
2) Cho biểu thức:
2 2 1
1
21
x x x
Q
x
x x x





.
a) Rút gọn biểu thức
Q
.
b) Tìm
x
để
QQ
.
c) Tìm số nguyên
x
để
Q
nhận giá trị nguyên.
Lời giải
1) Đơn giản biểu thức
P
.
2 2 2 2
22
14 6 5 14 6 5 3 2.3. 5 5 3 2.3 5 5 3 5 3 5P
3 5 3 5 6
.
2) Cho biểu thức:
2 2 1
1
21
x x x
Q
x
x x x





.
a) Rút gọn biểu thức
Q
.
Điều kiện:
0x
và
1x
.
2
2 2 1 2 2 1
.
11
21
1
x x x x x x
Q
xx
x x x x
x











2 2 2
2 . 1 2 . 1
2 2 1 1
..
11
1 1 . 1 1 . 1
x x x x
x x x x
xx
xx
x x x x x

22
22
1 2 1 2 2
..
1
11
1 . 1 1 . 1
x x x x
x x x
x
xx
xx
x x x x







.
b) Tìm
x
để
QQ
.
Điều kiện
1x
.
Nhận xét:
0Q
với mọi
1x
.
Trang 3
+ TH1:
2
0 0 1 0 1
1
Q x x
x
.
Vậy với
1x
0Q Q Q
.
+ TH2:
1
0 0 1 0 1
1
Q x x
x
.
Vậy với
1x
0Q Q Q
. Vậy bất phương trình
QQ
vô nghiệm.
Kết luận:
1x
.
c) Tìm số nguyên
x
để
Q
nhận giá trị nguyên.
Để
Q
thì:
21x
Vì
x
nên
1x 
Ư
2
2; 1;0;1;2
1;0;1;2;3x
.
Bài 2. Cho biểu thức
1
1
x
P
x x x


.
a) Rút gọn biểu thức
P
.
b) Tính giá trị biểu thức
P
khi
.
Lời giải
a) Rút gọn biểu thức
P
.
Điều kiện:
0x
và
1x
.
11
1 1 1
1 1 1 1
1 1 . 1
x x x
x x x
P
x x x x x x
x x x x
1
1
1
11
x
x
x
xx


.
b) Tính giá trị biểu thức
P
khi
.
2
1
1
2 1 2 1 2 1
1 2 1
2
3 2 2
1
11
12
2 1 2 1
1
2
x
P
x


.
Bài 3. Cho
11
1
1
x x x
A
x
x


.
a) Rút gọn biểu thức
A
.
b) Tính giá trị của biểu thức
A
khi
1
4
x
.
c) Tìm
x
để
0A
.
Trang 4
d) Tìm
x
để
AA
.
Lời giải
a) Rút gọn
A
.
ĐKXĐ:
0; 1xx
.
11
1
1
x x x
A
x
x


11
1
1
11
x x x
x
x
xx


11
11
x x x
xx


2
1
x
x
.
Vậy
2
1
x
A
x
với
0; 1xx
.
b) Tính giá trị của biểu thức
A
khi
1
4
x
.
Với
1
4
x
(tmđk) thay vào biểu thức
A
ta có:
1
2
5 2 5
2
.
1
2 3 3
1
2
A
Vậy
5
3
A
khi
1
4
x
.
c) Tìm
x
để
0A
.
ĐKXĐ:
0; 1xx
.
Để
0A
thì
2
0
1
x
x
.
Ta có
2 0,xx
ĐKXĐ,
1 0,xx
ĐKXĐ.
2
0
1
x
x

, x
ĐKXĐ.
Vậy
x
để
0A
.
Trang 5
d) Tìm
x
để
AA
.
ĐKXĐ:
0; 1xx
.
Để
AA
thì
0A
2
0
1
x
x

(luôn đúng
x
ĐKXĐ)
Vậy để
AA
thì
0; 1xx
.
Bài 4. Cho
3 1 4 4
4
22
a a a
P
a
aa

0; 4aa
.
a) Rút gọn
P
.
b) Tính giá trị của
P
với
9a
.
Lời giải
a) Rút gọn
P
.
ĐKXĐ:
0; 4aa
.
3 1 4 4
4
22
a a a
P
a
aa

3 1 4 4
4
22
a a a
P
a
aa

3 2 1 2
44
2 2 2 2 2 2
a a a a
a
P
a a a a a a
5 6 3 2 4 4
22
a a a a a
P
aa

48
22
a
P
aa

42
22
a
P
aa

4
2
P
a
Vậy
4
2
P
a
với
0; 4aa
.
b) Tính giá trị của
P
với
9a
.
Với
9a
(tmđk) thay vào biểu thức
P
ta được:
Trang 6
4
4
32
P 
Vậy
4P
khi
9a
.
II. HÌNH HỌC: HỆ THỨC GIỮA CẠNH VÀ GÓC, TỈ SỐ LƯỢNG GIÁC.
Bài 1. Cho tam giác nhọn
MNP
. Gọi
D
là chân đường cao của tam giác đó kẻ từ M . Chứng minh
rằng:
a)
1
. . .sin
2
MNP
S MP NP P
b)
.sin
tan
MN N
DP
P
c)
DNE
đồng dạng
MNP
trong đó
E
là chân đường cao của tam giác
MNP
kẻ từ
P
.
Lời giải
a) Có
1
..
2
MNP
S NP MD
Xét tam giác
MDP
vuông tại
D
có:
sin
MD
P
MP
sin .MD P MP
1
. . .sin
2
MNP
S MP NP P
b) Xét tam giác
MDN
vuông tại
D
có:
sin
MD
N
MN
.sinMD MN N
Xét tam giác
MDP
vuông tại
D
có:
tan
MD
P
DP
.sin
tan
MN N MD
DP
MD
P
DP
( đpcm )
c) Xét tam giác
MDN
vuông tại
D
có:
cos
DN
N
MN
(1)
Xét tam giác
PEN
vuông tại
E
có:
cos
NE
N
NP
(2)
E
D
P
N
M
Trang 7
Từ (1) (2)
DN NE
MN NP

Xét
DNE
và
MNP
có:
DN NE
MN NP
N
chung
DNE
đồng dạng
MNP
(c. g. c)
Bài 2. Cho tam giác
ABC
,
90A 
,
AB AC
, trung tuyến
AM
, góc
ACB
, góc
AMB
.
Chứng minh
2
sin os 1 sinc
.
Lời giải
Từ :
2
2
sin os
AH HC
c
AC AC




22
2 2 2 2
2. . 2. .
1
AH HC AH HC AH HC
AC AC AC AC
và
2
. 2. .AC CH HB CH AM
2
sin os 1 1 sin
AH
c
AM
HẾT
β
α
H
M
B
A
C
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

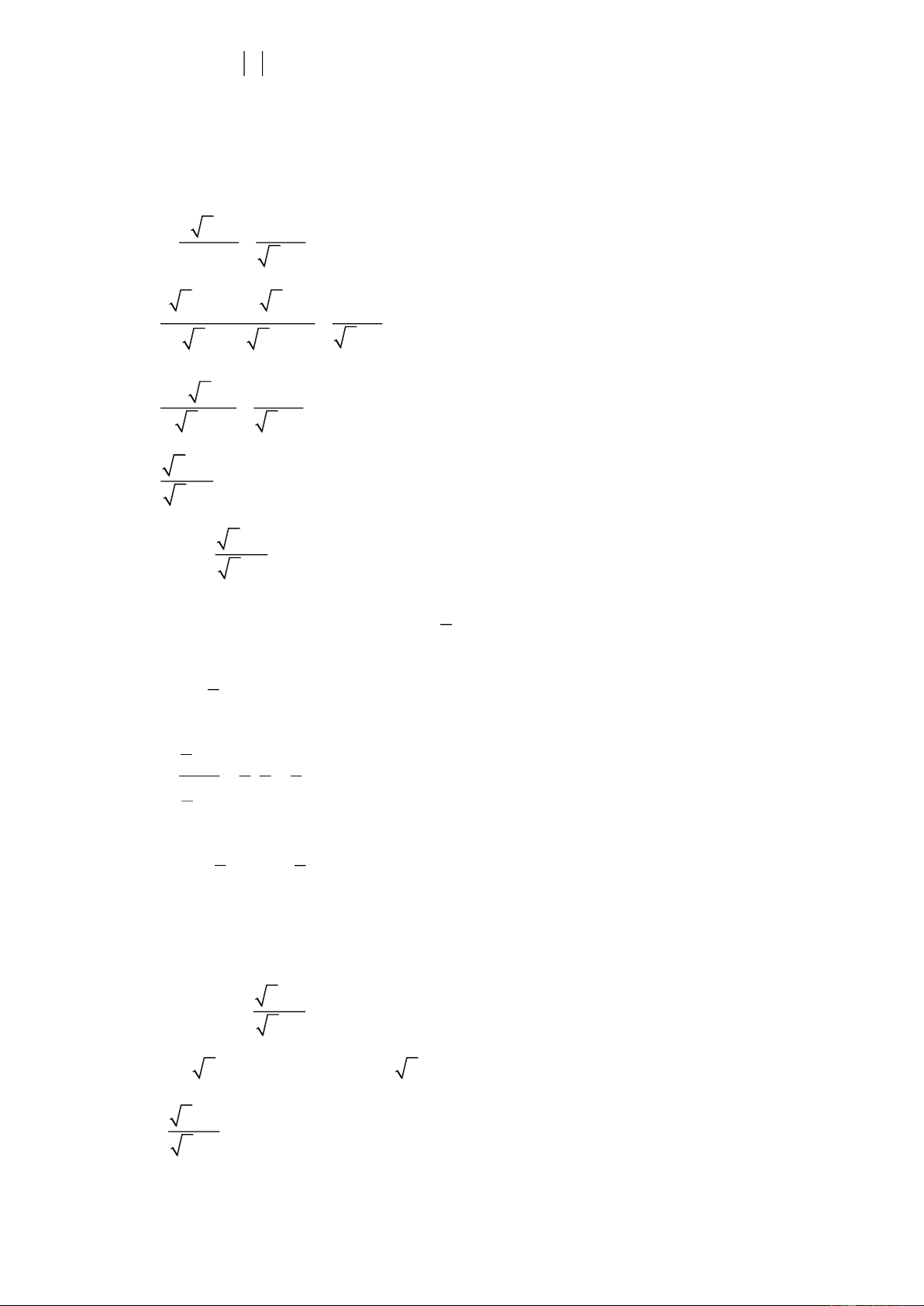
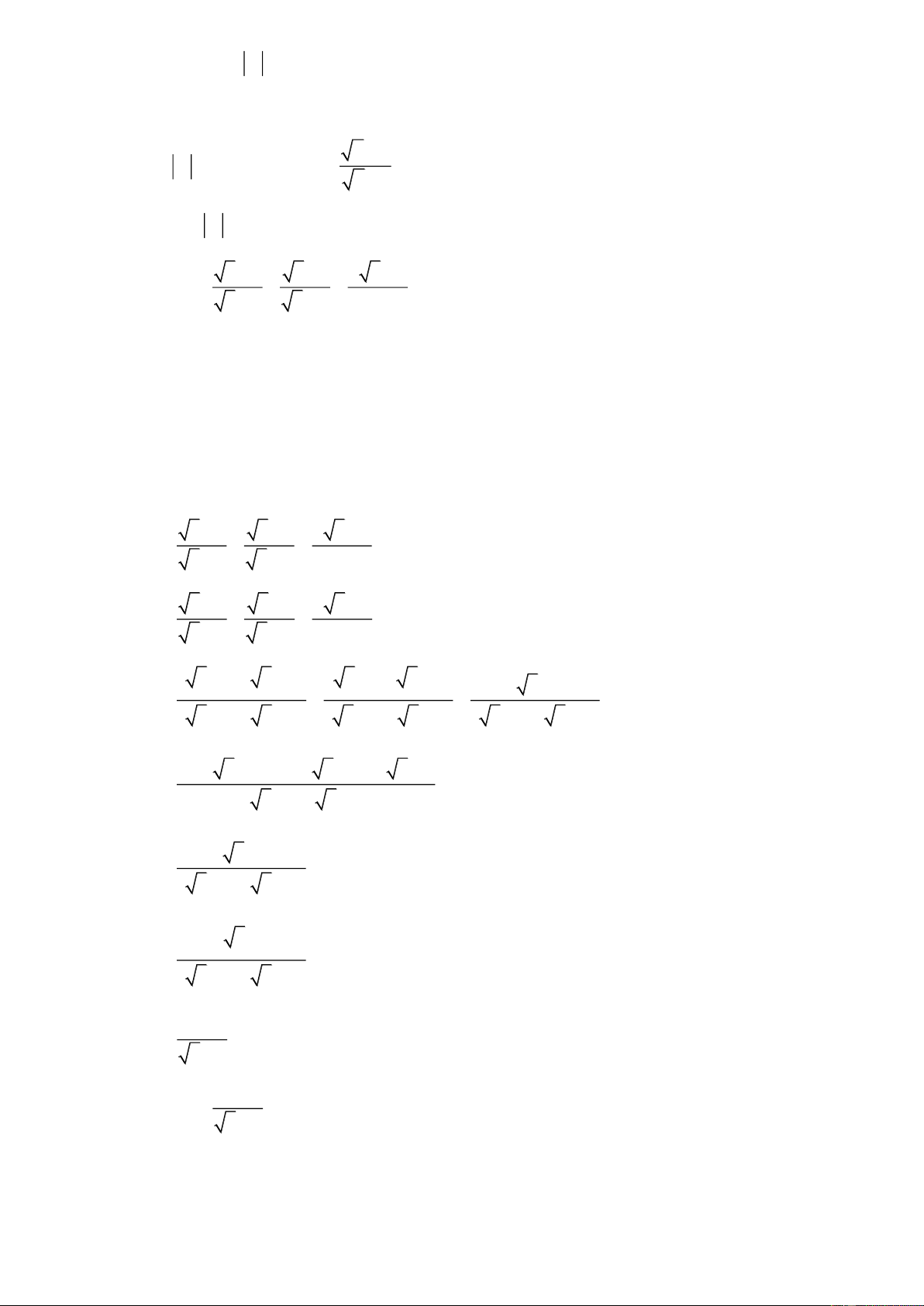
Preview text:

BÀI TẬP TOÁN 9 TUẦN 7
I. ĐẠI SỐ: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC BẬC HAI Bài 1.
1) Đơn giản biểu thức: P  14  6 5  14  6 5 .  x  2 x  2  x 1
2) Cho biểu thức: Q       . x  2 x 1 x 1 x  
a) Rút gọn biểu thức Q .
b) Tìm x để Q Q  .
c) Tìm số nguyên x để Q nhận giá trị nguyên. 1 x Bài 2. Cho biểu thức P   . x 1 x x
a) Rút gọn biểu thức P . 1
b) Tính giá trị biểu thức P khi x  . 2 x x  1 x  1 Bài 3. Cho A   . x  1 x  1
a) Rút gọn biểu thức A . 1
b) Tính giá trị của biểu thức A khi x  . 4
c) Tìm x để A  0 .
d) Tìm x để A A . a  3 a  1 4 a  4 Bài 4. Cho P   
a  0;a  4 . a  2 a  2 4  a a) Rút gọn P .
b) Tính giá trị của P với a  9 .
II. HÌNH HỌC: HỆ THỨC GIỮA CẠNH VÀ GÓC, TỈ SỐ LƯỢNG GIÁC. Bài 1.
Cho tam giác nhọn MNP . Gọi D là chân đường cao của tam giác đó kẻ từ M . Chứng minh rằng: 1 a) S  .M . P . NP sin P MNP 2 MN.sin N b) DP  tan P c) D
NE đồng dạng M
NP trong đó E là chân đường cao của tam giác MNP kẻ từ P . Trang 1 Bài 2.
Cho tam giác ABC , A  90 , AB AC , trung tuyến AM , góc ACB   , góc AMB   . Chứng minh    c  2 sin os 1 sin  .
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC BẬC HAI Bài 1.
1) Đơn giản biểu thức: P  14  6 5  14  6 5 .  x  2 x  2  x 1
2) Cho biểu thức: Q       . x  2 x 1 x 1 x  
a) Rút gọn biểu thức Q .
b) Tìm x để Q Q  .
c) Tìm số nguyên x để Q nhận giá trị nguyên. Lời giải
1) Đơn giản biểu thức P . P         2  
  2    2    2 2 2 14 6 5 14 6 5 3 2.3. 5 5 3 2.3 5 5 3 5 3 5  3 5  3 5  6.  x  2 x  2  x 1
2) Cho biểu thức: Q       . x  2 x 1 x 1 x  
a) Rút gọn biểu thức Q .
Điều kiện: x  0 và x 1.    x  2 x  2  x 1  x  2 x  2  x 1 Q           x  2 x 1 x 1 x        . 2 x 1 1  x x            
x  2. x   1
x 2. x x x x 1 2 2 1  x 1        .   . 2     x   1  x x   1 1  x   x  2 1 . x   1  x  2 1 . x     1 x      x
x  2   x x  2  x 1 2 x x 1 2 2   .      .  .   2         1 . 1 x   2 1 .
1 x x 1 x x x x x 1 x 1
b) Tìm x để Q Q  . Điều kiện x 1.
Nhận xét: Q  0 với mọi x 1. Trang 2 2 + TH1: Q  0 
 0  x 1  0  x  1. x 1
Vậy với x 1  Q
  0  Q Q  . 1 + TH2: Q  0 
 0  x 1  0  x  1. x 1
Vậy với x 1  Q
  0  Q Q
 . Vậy bất phương trình Q Q  vô nghiệm. Kết luận: x 1.
c) Tìm số nguyên x để Q nhận giá trị nguyên.
Để Q  thì: 2  x  
1 Vì x  nên  x   1 Ư 2   2  ; 1  ;0;1;  2  x  1  ;0;1;2;  3 . 1 x Bài 2. Cho biểu thức P   . x 1 x x
a) Rút gọn biểu thức P . 1
b) Tính giá trị biểu thức P khi x  . 2 Lời giải
a) Rút gọn biểu thức P .
Điều kiện: x  0 và x 1.
x 1 x x x x x 1 1 1 1 P        x 1 x x x 1 x 1 x x 1 x 1
x  1. x  1 1 x 1 x     . x   1  x   1 x 1 1
b) Tính giá trị biểu thức P khi x  . 2 1 1     x 2 
 2 1 2 1  2 2 1 1 2 1 P           . x 1 1 2   1  2 1 2  3 2 2 1 1 1 2 x x  1 x  1 Bài 3. Cho A   . x  1 x  1
a) Rút gọn biểu thức A . 1
b) Tính giá trị của biểu thức A khi x  . 4
c) Tìm x để A  0 . Trang 3
d) Tìm x để A A . Lời giải a) Rút gọn A .
ĐKXĐ: x  0; x  1. x x  1 x  1 A   x  1 x  1
x  1xx  1 x1    x   1  x 1 x  1 x x  1 x  1   x  1 x  1 x  2  . x  1 x  2 Vậy A
với x  0; x  1 . x  1 1
b) Tính giá trị của biểu thức A khi x  . 4 1 Với x
(tmđk) thay vào biểu thức A ta có: 4 1  2 5 2 5 2 A   .  1 2 3 3  1 2 5 1 Vậy A  khi x  . 3 4
c) Tìm x để A  0 .
ĐKXĐ: x  0; x  1.  Để x 2 A  0 thì  0 . x  1 Ta có x  2  0, x
  ĐKXĐ, x  1  0, x   ĐKXĐ. x  2   0 , x   ĐKXĐ. x  1
Vậy x để A  0 . Trang 4
d) Tìm x để A A .
ĐKXĐ: x  0; x  1.  Để x 2
A A thì A  0   0 (luôn đúng x   ĐKXĐ) x  1
Vậy để A A thì x  0; x  1 . a  3 a  1 4 a  4 Bài 4. Cho P   
a  0;a  4 . a  2 a  2 4  a a) Rút gọn P .
b) Tính giá trị của P với a  9 . Lời giải a) Rút gọn P .
ĐKXĐ: a  0; a  4. a  3 a  1 4 a  4 P    a  2 a  2 4  a a  3 a  1 4 a  4 P    a  2 a  2 a  4
a3 a2  a1 a2 4 a  4 P    
a  2 a  2  a  2 a  2  a  2 a  2
a  5 a  6  a  3 a  2  4 a  4 P  
a  2 a  2 4 a  8 P  
a  2 a  2 4 a  2 P  
a  2 a  2 4 P a  2 4 Vậy P
với a  0; a  4 . a  2
b) Tính giá trị của P với a  9 .
Với a  9 (tmđk) thay vào biểu thức P ta được: Trang 5 4 P   4 3  2
Vậy P  4 khi a  9 .
II. HÌNH HỌC: HỆ THỨC GIỮA CẠNH VÀ GÓC, TỈ SỐ LƯỢNG GIÁC. Bài 1.
Cho tam giác nhọn MNP . Gọi D là chân đường cao của tam giác đó kẻ từ M . Chứng minh rằng: 1 a) S  .M . P . NP sin P MNP 2 MN.sin N b) DP  tan P c) D
NE đồng dạng M
NP trong đó E là chân đường cao của tam giác MNP kẻ từ P . Lời giải M E P N D 1 a) Có S  .N . P MD MNP 2 MD
Xét tam giác MDP vuông tại D có: sin P   MD  sin . P MP MP  1 S  .M . P . NP sin P MNP 2 MD
b) Xét tam giác MDN vuông tại D có: sin N
MD MN.sin N MN MD
Xét tam giác MDP vuông tại D có: tan P DP MN.sin N MD    DP ( đpcm ) tan P MD DP DN
c) Xét tam giác MDN vuông tại D có: cos N  (1) MN NE
Xét tam giác PEN vuông tại E có: cos N  (2) NP Trang 6 DN NE Từ (1) (2)   MN NP Xét DNE và MNP có: DN NEMN NP N chung  D
NE đồng dạng MNP (c. g. c) Bài 2.
Cho tam giác ABC , A  90 , AB AC , trung tuyến AM , góc ACB   , góc AMB   . Chứng minh    c  2 sin os 1 sin  . Lời giải A β α B C H M 2 2 2 2  AH HC AH HC 2.AH.HC 2.AH.HC Từ : sin  o c s         1  AC AC  2 2 2 2 AC AC AC AC và 2
AC CH.HB  2.CH.AM
    c  2 AH sin os  1  1 sin  AM HẾT Trang 7