Bài tập trắc nghiệm chuyên đề hàm số – Trần Minh Tiến, Trần Thanh Phong Toán 12

Bài tập trắc nghiệm chuyên đề hàm số – Trần Minh Tiến, Trần Thanh Phong Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

76 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 1: Sự đồng biến, nghịch biến của hàm số” – P.1
Câu 01: Cho hàm s
42
y 3x 6x 13
. Hàm s nghch bin trên khong nào trong các kho

A.
1 2 3
;
42
. B.
;0
. C.
1;3
. D.
1;
.
Câu 02: Cho các kho  i, hàm s
2
3
y sin x x , x ;
2
nghch bin trên các
khong nào ?
53
1;
64
9
2;
10
4;
43
5 ;0
2
7
6;
4 12
A.
. B.
2 , 3 , 4
. C.
2 , 3 , 5
. D.
.
Câu 03: Cho hàm s
4 3 2
15
y x x 4x 4x 10
43
. Tìm khnh sai trong các khi ?
A. Hàm s ng bin trên
37
;
23
. B. o hàm ca hàm s i du hai ln.
C. Hàm s nghch bin trên
;0
. D. Khong bin dài nht là
1;
.
Câu 04: Cho hàm s
2
2
x
y
x1
 th hàm s i chiu my ln ?
A. 2. B. 4. C. 3. D. 1.
Câu 05: Hàm s ng bin là
2;5
?
A.
3x 1
y
x2
. B.
32
1
y x 2x 5x 3
3
.
C.
42
19
y x x 1
42
. D.
x5
y
x3
.
Câu 06: nh sai trong các kh
A. Hàm s
ng bin trên tng khonh.
B. Hàm s
2x
y
x5
luôn nghch bin trên tng khonh.
C. Hàm s
32
y x 3x 9x 5
nghch bin trên
;9
.
D. Hàm s
42
y x 2x 5
ng bin trên
9;
.
Câu 07: Xét các khnh sau:
I
. Hàm s
3
y x 1
nghch bin trên .
II
. Hàm s
x
y ln x 1
x1
ng bin trên tp
nh ca nó.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
III
. Hàm s
2
x
y
x1
ng bin trên .
Hi có bao nhiêu kh
A. 3. B. 2. C. 1. D. 0.
Câu 08: Cho hàm s
y x 1 x 2
. Khnh sai ?
A. Hàm s nghch bin trên khong
1
1;
2
. B. Hàm s nghch bin trên khong
;1
.
C. Hàm s ng bin trên các khong
;1
và
1
;
2
.
D. Hàm s nghch bin trên khong
1
1;
2
ng bin trên khong
1
;
2
.
Câu 09: Cho hàm s
y x 3 2 2 x
. Kh
A. Hàm s nghch bin trên khong
;2
ng bin trên khong
2;2
.
B. Hàm s ng bin trên khong
;2
và nghch bin trên khong
2;2
.
C. Hàm s ng bin trên khong
;1
và nghch bin trên khong
1;2
.
D. Hàm s nghch bin trên khong
;1
ng bin trên khong
1;2
.
Câu 10: Cho hàm s
y cos2x sin2x.tanx, x ;
22
. Khnh

A. Hàm s luôn gim trên
;
22
. B. Hàm s 
;
22
.
C. Hàm s i trên
;
22
. D. Hàm s luôn gim trên
;0
2
.
Câu 11:   sau ?
A. Hàm s
32
y x 6x 3x 4
có khong bin là
2 3;0
.
B. Hàm s
2
y x 5x 3
có khong nghch bin là
3;
.
C. Hàm s
có khong nghch bin dài nht là
2;
.
D. Hàm s
2
x 3x 2
y
x1
ng bin trên tng khonh.
Câu 12: Cho các hàm s sau:
4x 3
1y
2x 1
32
4
2 y x 3x 2x 1
3
42
3 y x 4x 3
32
5
4 y x 5x 6x 27
3
2
x4
5y
x 2x 4
4 3 2
11
6 y x x x 11
42
Tìm các hàm s  th i chiu bin thiên trên tng khonh ca chúng?
A.
2 , 3 , 5
. B.
. C.
. D.
2 , 5 , 6
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 13: Cho các phát biu sau:
1
Hàm s
32
y x 3x 12x 1
có khong nghch bin là
3;
.
2
Hàm s
y 2x 11 tanx
ng bin trên .
3
Hàm s
4 3 2
y 6x 8x 3x 1
 th i chiu bin thiên ba ln.
4
Hàm s
1 sinx
y , x 0;
1 sinx 2
luôn nghch bin trên khonh.
5
Hàm s
2
3x 1
y
x
có khong bin dài nht là
1
;
2
.
6
Hàm s
2
x 2x 3
y
x5
có 
y' 0
có nghim duy nht.
S phát bi
A. 5. B. 3. C.
1
. D. 0.
Câu 14: Cho hàm s
32
y 2x 3x 12x 10
. Khnhất ?
A. Hàm s gim trên
; 21
. B. Hàm s 
; 2 1;
.
C. Hàm s 
;2
và
1;
. D. Hàm s gim trên
2; 1
.
Câu 15: Cho hàm s
42
y 3x 6x 13
nh khong trong các khoi mà hàm
s nghch bin trên kho
A.
1 2 3
;
42
. B.
;0
. C.
1;3
. D.
1;
.
Câu 16: Hàm s
y f x
ng bin trên khong
a;b
. Khnh sai ?
A. Hàm s
y f x 1
ng bin trên
a;b
. B. Hàm s
y f x 1
nghch bin trên
a;b
.
C. Hàm s
y f x
nghch bin trên
a;b
. D. Hàm s
y f x 1
ng bin trên
a;b
.
Câu 17: Cho hàm s
3
y x 3x
. Nh
A. Tnh
D 3;0 3;
. B. Hàm s nghch bin trên
1;1
.
C. Hàm s nghch bin trên các khong
1;0
và
0;1
.
D. Hàm s ng bin trên các khong
;3
và
3;
.
Câu 18: Cho hàm s
2
y 2x x
. Hàm s nghch bin trên kho
A.
0;2
. B.
0;1
. C.
1;2
. D.
1;1
.
Câu 19: Cho hàm s
2
x 2x
y
x1
. Hãy ch
A. Hàm s nghch bin trên
\1
.
B. Hàm s nghch bin trên
;1
ng bin trên
1;
.
C. Hàm s ng bin trên
;1
và nghch bin trên
1;
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
D. Hàm s ng bin trên mi khong
;1
và
1;
.
Câu 20:  hàm s
32
y x 3x 3mx 1
nghch bin trên khong
0;
?
A.
m1
. B.
m1
. C.
m1
. D.
m1
.
Câu 21: Hi hàm s
2
x 3x 5
y
x1
nghch bin trên khong nào trong các kho
A.
;4
,
2;
. B.
4;2
,
2;
. C.
;1
,
1;
. D.
4; 1
,
1;2
.
Câu 22: Hi hàm s
3
2
x
y 3x 5x 2
3
nghch bin trên khong nào trong các kho
A.
5;
. B.
2;3
. C.
;1
. D.
1;5
.
Câu 23: Hi hàm s
5 4 3
3
y x 3x 4x 2
5
ng bin trên khong nào trong các kho
A.
;0
. B. . C.
0;2
. D.
2;
.
Câu 24: Cho hàm s
32
y ax bx cx d
. Hi hàm s ng bin trên khi nào ?
A.
2
a b 0, c 0
a 0, b 3ac 0
. B.
2
a b 0, c 0
a 0, b 3ac 0
. C.
2
a b 0, c 0
a 0, b 3ac 0
. D.
2
a b c 0
a 0, b 3ac 0
.
Câu 25: Cho hàm s
32
y x 3x 9x 15
. Khnh sai ?
A. Hàm s nghch bin trên khong
3;1
. B. Hàm s ng bin trên .
C. Hàm s ng bin trên
9; 5
. D. Hàm s ng bin trên khong
5;
.
Câu 26: Cho hàm s
32
4
y x 5x 6x 216
3
. Cho các phát biu sau, chn câu tr l
1
Hàm s 
3
1;
2
.
2
Hàm s gim trên
3
; 1 ;
2
.
3
Hàm s 
6
1;
5
,
63
;
52
.
4
x1
y' 0
3
x
2
.
A.
1
,
3
. B.
1
,
2
,
3
. C.
1
,
3
,
4
. D.
1
,
2
.
Câu 27: Cho hàm s
. M 
A. Hàm s ng bin trên
1
\
2
. B. Hàm s nghch bin trên
11
;;
22
. C. Hàm s nghch bin trên
1
;
2
và
1
;
2
.
D. Hàm s nghch bin trên
1
\
2
.
Câu 28: Cho hàm s
32
4
y x 2x x 7
3
. M 
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A. Hàm s ng bin trên
1
;
2
. B. Hàm s nghch bin trên
1
;
2
.
C. Hàm s nghch bin trên
1
;
2
. D. Hàm s nghch bin trên .
Câu 29: Cho hàm s
2
2x x 26
y
x2
. Có bao nhiêu khong bin ca hàm s 
1 ; 1 15
3 10;
4 1 15 ;
5 3;0
6 6; 3
5
7 ; 1 15
2
8 1 15 ; 1
A. 0. B. 1. C. 3. D. 2.
Câu 30: Cho hàm s
y 2x 5 x
. Hàm s ng bin trên khong nào trong các kho
?
A.
2;5
. B.
5
;3
2
. C.
4;5
. D.
2 15
2;
2
.
Câu 31: Hàm s
3
2
x
y mx 4x
3
ng bin trên khi:
A.
2 m 2
. B.
m2
m2
. C.
m2
. D.
m2
.
Câu 32: Hàm s
3
2
x
y mx 4x
3
nghch bin trên khi:
A.
2 m 2
. B.
m2
m2
. C.
m2
. D.
m2
.
Câu 33: Vi giá tr nào ca m thì hàm s
y 2m 1 x mcosx
ng bin trên ?
A.
m1
. B.
m1
. C.
1 m 1
. D.
m
.
Câu 34:  hàm s
32
y x 3x 4mx 2
nghch bin trên
;0
?
A.
3
m
4
. B.
3
m
4
. C.
3
m
4
. D.
3
m
4
.
Câu 35: Cho hàm s
3 2 2
y x m 1 x m 2 x m

A. Hàm s ng bin trên
2;4
. B. Hàm s luôn nghch bin trên .
C. Hàm s có c khong bin và khong nghch bin.
D. Hàm s luôn nghch bin trên
2
m;m 1
.
Câu 36: Cho hàm s
32
m m 3 3m 1
y x x x m
3 2 2
. Vi m nm trong tp h
 hàm s ng bin trên ?
A.
9
A x : x 1
5
. B.
5
B ; 1;
9
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
C.
5
C ;1
9
. D.
D x : x 0
.
Câu 37: Cho hàm s
32
m 2m 1
y x x 3m 2 x 7
32
 hàm s ng bin trên
?
A.
m1
. B.
m1
. C.
m1
. D. Không tìm c m.
Câu 38: Cho hàm s
32
m2
y x m 2 x m 1 x 3m
3
. Giá tr nguyên m là nh nh
hàm s ng bin trên trên ?
A. 2. B. 3. C. 4. D. 0.
Câu 39: Cho hàm s
mx 2m
y
xm
. Có bao nhiêu giá tr  hàm s luôn nghch bin
trên tng khonh ?
A.
1
. B. 2. C. 3. D. 4.
Câu 40:  hàm s
32
1
y x mx 4x
3
ng bin trên ?
A.
2 m 2
. B.
2 m 2
. C.
m2
. D.
m2
.
Câu 41: Cho hàm s
23
y 3x x
. Khhnh sai ?
A. Hàm s ng bin trên khong
0;2
.
B. Hàm s ng bin trên các khong
;0 , 2;3
.
C. Hàm s nghch bin trên các khong
;0 , 2;3
.
D. Hàm s nghch bin trên khong
2;3
.
Câu 42: Cho hàm s
2
x
y sin x,x 0;
2
. Hi hàm s ng bin trên các khong nào ?
A.
7 11
0; và ;
12 12
. B.
7 11
;
12 12
.
C.
7 7 11
0; và ;
12 12 12
. D.
7 11 11
; và ;
12 12 12
.
Câu 43: Cho hàm s
2
y x cos x
. Kh
A. Hàm s ng bin trên . B. Hàm s luôn nghch bin trên .
C. Hàm s ng bin trên
k;
4
và nghch bin trên khong
;k
4
.
D. Hàm s nghch bin trên
k;
4
ng bin trên khong
;k
4
.
Câu 44: Cho các hàm s sau:
32
1
I : y x x 3x 4
3
x1
II : y
x1
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
2
III : y x 4
3
IV : y x 4x sinx
42
V : y x x 2
Có bao nhiêu hàm s ng bin trên nhng khonh ?
A. 2. B. 4. C. 3. D. 5.
Câu 45: Cho các hàm s sau:
32
I : y x 3x 3x 1
II : y sinx 2x
3
III : y x 2
x2
IV : y
1x
Hi hàm s nào nghch bin trên toàn trc s ?
A.
I
,
II
. B.
II
,
I
,
III
. C.
II
,
I
,
IV
. D.
II
,
III
.
Câu 46: Cho hàm s
1
y 3x 5
x2
. Ch ra kho ng bi   dài ln nht trong các
kho
A.
13
;4
6
. B.
11
;6
2
. C.
3
;1
2
. D.
58
;
23
.
Câu 47: Cho hàm s
2x 3
y
2x 1
. Tìm ra khong nghch bi dài nh nht trong các khong

A.
1
;2
2
. B.
65
;
52
. C.
2 15 4 13
;
22
. D.
3 15 7
;
22
.
Câu 48: Cho hàm s
y 1 2x x 3
 th hàm s m gãy ?
A.
0
. B.
2
. C.
3
. D.
4
.
Câu 49: Trong các hàm s sau hàm s ng bin trên khonh ca chúng ?
A.
2x 3
y
x1
. B.
. C.
2x 3
y
x1
. D.
2x 3
y
x2
.
Câu 50: Cho hàm s
2
y 3 2x x
. Hàm s ng bi dài bé nht là:
A.
3; 1
. B.
1;0
. C.
1;1
. D.
1;2
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 1: Sự đồng biến, nghịch biến của hàm số” – P.2
Câu 01: Cho hàm s
32
1
y x m 3 x m 1 x 4
3
. Có bao nhiêu giá tr ca m sao cho hàm s
 dài b  hiu là khong bi dài bé nht bng
4).
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 02: Cho hàm s
32
y x 3mx 3mx 4
. Ti giá tr nào ca m thì hàm s cho gim trên
 dài b  hiu là khong nghch bi dài bé nht bng 1) ?
A.
12
m
2
. B.
2
m
23
. C.
5
m
3
. D.
23
m
3
.
Câu 03: Cho hàm s
3x m
y
2x 1
. Trong tt c các giá tr c  hàm s nghch bin trên
1
;
2
, thì m không th bng ?
A.
1
2
. B.
5
. C.
5
3
. D.
23
3
.
Câu 04: Cho hàm s
32
y mx 2x mx 1
. Giá tr nh nht c hàm s ng bin trên
1;2
là ?
A.
1
m
2
. B.
1
m
23
. C.
23
m
3
. D.
3
m
23
.
Câu 05: Cho hàm s
2
mx 6x 2
y
x2
. Tìm tt c các giá tr  hàm s ng bin trên
1;0
?
A.
1
m
2
. B.
1
m
23
. C.
m3
. D.
10
m
3
.
Câu 06: Cho hàm s
42
y x 2x
. Chsai:
A. Hàm s ng bin trên mi khong
1;0 , 1;
.
B. Hàm s ng bin trên mi khong
1;2 , 3;
.
C. Hàm s nghch bin trên mi khong
; 1 , 0;1
.
D. Hàm s ng bin trên
; 2 2;
.
Câu 07: Hàm s ng bin trên ?
A.
1
yx
x
. B.
4
yx
. C.
32
y x 6x 17x 4
. D.
x1
y
x1
.
Câu 08: Hàm s ng bin trên mi khonh ca nó ?
A.
x2
y
x2
. B.
x2
y
x2
. C.
x2
y
3x 2
. D.
x2
y
2x 2
.
Câu 09: Hàm s có chiu bin thiên khác vi chiu bin thiên ca các hàm s còn li trên
0;
?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
x2
fx
x2
. B.
32
f x x 6x 17x 4
.
C.
3
f x x x cosx 4
. D.
2
x 2x 3
fx
x1
.
Câu 10: Hàm s nào có chiu bin thiên khác vi chiu bin thiên ca các hàm s còn li trên ?
A.
3
f x x x cosx 4
. B.
f x sin2x 2x 3
.
C.
3
f x x x cosx 4
. D.
f x cos2x 2x 3
.
Câu 11: Cho hàm s
x1
y
1x
. Kh
A. Hàm s nghch bin trên khong
;1 1;
.
B. Hàm s ng bin trên khong
;1 1;
.
C. Hàm s nghch bin trên các khong
;1
và
1;
.
D. Hàm s ng bin trên các khong
;1
và
1;
.
Câu 12: Cho hàm s
32
y x 3x 3x 2
. Kh
A. Hàm s luôn nghch bin trên . B. Hàm s ng bin trên .
C. Hàm s nghch bin trên khong
;1 1;
.
D. Hàm s ng bin trên khong
;1
và nghch bin trên khong
1;
.
Câu 13: Cho hàm s
42
y x 4x 10
và các khong sau:
I : ; 2
II : 2;0
III : 0; 2
Hi hàm s ng bin trên các khong nào ?
A. Ch
I
. B.
I
và
II
. C.
II
và
III
. D.
I
và
III
.
Câu 14: Cho hàm s
3x 1
y
4 2x
. Kh ?
A. Hàm s luôn nghch bin trên .
B. Hàm s luôn nghch bin trên tng khonh.
C. Hàm s ng bin trên các khong
;2
và
2;
.
D. Hàm s nghch bin trên các khong
;2
và
2;
.
Câu 15: Hi hàm s ch bin trên ?
A.
42
h x x 4x 4
. B.
32
g x x 3x 10x 1
.
C.
53
44
f x x x x
53
. D.
32
k x x 10x cos x
.
Câu 16: Trong các phát biu sau, phát bi
A. Hàm s
y f x
ng bin trên
a;b
khi
f x 0, x a;b
.
B. Hàm s
y f x
nghch bin trên
a;b
khi
f x 0, x a; b
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
C. Hàm s
y f x
là hàm hng trên
a;b
khi
f x 0, x a;b
.
D. Hàm s
y f x
ng bin trên
a;b
khi
f x 0, x a;b
.
Câu 17: Cho hàm s
y f x
o hàm trên
a;b
vi
a ,b
là hai nghim phân bit c
trình
f x 0

f x 0
ch có 2 nghim). Khnh sai ?
A. Hàm s ng bin trên
a;b
khi
0
f' x 0,
vi
0
x a;b
.
B. Hàm s ng bin trên
a;b
khi
21
21
f x f x
0,
xx
vi
12
12
x ,x a; b
xx
.
C. Hàm s nghch bin trên
a;b
khi
0
f' x 0,
vi
0
x a;b
.
D. Hàm s là hàm hng trên
a;b
khi
21
21
f x f x
1,
xx
vi
12
12
x ,x a; b
xx
.
Câu 18: Trong các phát biu sau, phát biu nào sai ?
A. Hàm s
y f x
ng bin trên
c;d
khi
f x 0,
x c;d
.
B. Hàm s
m nx
y
px q
nghch bin trên tng khonnh khi
nq mp 0
.
C. Hàm s
y f x
ng bin trên
a;b
khi
21
21
f x f x
0,
xx
vi
12
12
x ,x a; b
xx
.
D. Hàm s
y f x
là hàm hng khi
f' x 0,
x c;d
.
Câu 19:  hàm s
32
2
y x m 1 x 2mx 5
3
ng bin trên
0;2
:
A.
2
m
3
. B.
2
m
3
. C.
2
m
3
. D.
2
m
3
.
Câu 20:  hàm s
32
11
y x mx m 2 x
33
ng bi dài bng 4.
A.
m2
m3
. B.
m2
. C.
m3
. D.
m2
m2
.
Câu 21:  hàm s
32
y x 6x mx 1
ng bin trên khong
0;
?
A.
m0
. B.
m 12
. C.
m0
. D.
m 12
.
Câu 22:  hàm s
x m 2
y
x1
gim trên mi khonh ca nó ?
A.
m1
. B.
m1
. C.
m3
. D.
m3
.
Câu 23: Tìm tt c các giá tr thc ca tham s
m
sao cho p
2
x mx 2 2x 1
có hai
nghim thc ?
A.
7
m
2
. B.
3
m
2
. C.
9
m
2
. D.
m
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 24: Tìm tt c các giá tr thc ca tham s
m
   
4
2
3 x 1 m x 1 2 x 1
có hai nghim thc ?
A.
1
m1
3
. B.
1
1m
4
. C.
1
2m
3
. D.
1
0m
3
.
Câu 25: Cho hàm s
32
y mx 2x mx 1
. Giá tr nh nht c hàm s ng bin trên
1;2
là ?
A.
1
m
2
. B.
1
m
23
. C.
23
m
3
. D.
3
m
23
.
Câu 26: Cho hàm s
32
1
y x mx m 2 x 5
3
. Vi
0 m 9
thì có bao nhiêu giá tr m là s t
nhiên sao cho hàm s ng bin trên
2;5
?
A. 0. B. 5. C. 3. D. 1.
Câu 27: Cho hàm s
mx 2
y
x 3m
. Vi m thuc tp h hàm s ng
;1
?
A.
12
A x : x
33
. B.
5
B ; 1;
9
.
C.
12
C x : x
33
. D.
D x : x 0
.
Câu 28: Cho hàm s
32
y x 3x 3mx m 1
. Hàm s nghch bin trên khong
1;1
thì mnh
 nào v 
A.
1 m 2
. B.
m ; 3 1;
.
C.
m1
. D.
m ; 1 1;
.
Câu 29: Cho hàm s
32
y x 3x m 1 x 1
 hàm s  cho nghch bin trên khong
0;
?
A.
m2
. B.
m2
. C.
m1
. D.
m1
.
Câu 30: Tìm tt c các giá tr thc ca tham s
m
sao cho b 
trình
2
1 2x 3 x m 2x 5x 3
nghii mi
?
A.
m1
. B.
m0
. C.
m1
. D.
m0
.
Câu 31: Tìm tt c các giá tr thc ca tham s
m
sao cho b 
trình
3 1 x 3 x 2 1 x 3 x m
nghii mi
x 1;3
?
A.
m6
. B.
m6
. C.
m 6 2 4
. D.
m 6 2 4
.
Câu 32: Tìm tt c các giá tr thc ca tham s
m
sao cho b  
22
3 x 6 x 18 3x x m m 1
nghi
x 3;6
?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m1
. B.
1 m 0
. C.
0 m 2
. D.
m1
m2
.
Câu 33: Tìm tt c các giá tr thc ca tham s
m
sao cho b  
x x 2
m.4 m 1 .2 m 1 0
nghi
x
?
A.
m3
. B.
m1
. C.
1 m 4
. D.
m0
.
Câu 34: Tìm tt c các giá tr thc ca tham s
m
sao cho b
3
3
1
x 3mx 2
x
nghi
x1
?
A.
2
m
3
. B.
2
m
3
. C.
3
m
2
. D.
13
m
32
.
Câu 35: Cho hàm s
32
1
y x m 3 x m 1 x 4
3
. Có bao nhiêu giá tr ca m sao cho hàm s
 dài b  hiu là khong bi dài bé nht bng
4).
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 36: Cho hàm s
32
y x 3mx 3mx 4
. Ti giá tr nào ca m thì hàm s m trên
 dài b  hiu là khong nghch bi dài bé nht bng 1) ?
A.
12
m
2
. B.
2
m
23
. C.
5
m
3
. D.
23
m
3
.
Câu 37: Cho hàm s
3x m
y
2x 1
. Trong tt c các giá tr c  hàm s nghch bin trên
1
;
2
, thì m không th bng ?
A.
1
2
. B.
5
. C.
5
3
. D.
23
3
.
Câu 38: Cho hàm s
32
y mx 2x mx 1
. Giá tr nh nht c hàm s ng bin trên
1;2
là ?
A.
1
m
2
. B.
1
m
23
. C.
23
m
3
. D.
3
m
23
.
Câu 39: Cho hàm s
2
mx 6x 2
y
x2
. Tìm tt c các giá tr  hàm s ng bin trên khong
1;0
?
A.
1
m
2
. B.
1
m
23
. C.
m3
. D.
10
m
3
.
Câu 40: Tìm giá tr ln nht ca tham s
m
sao cho b  
2 2 2
cos x sin x cos x
2 3 m.3
có
nghim ?
A.
m4
. B.
m8
. C.
m 12
. D.
m 16
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 41: B
32
2x 3x 6x 16 4 x 2 3
có tp nghim là
a; b
. Hi tng
ab
có giá tr là bao nhiêu ?
A.
2
. B. 4. C. 5. D. 3.
Câu 42: B  
22
x 2x 3 x 6x 11 3 x x 1
có tp nghim
a; b
. Hi
hiu
ba
có giá tr là bao nhiêu ?
A. 1. B. 2. C. 3. D.
1
.
Câu 43: Hàm s
y f x
ng bin trên khong
a;b
. M  sai ?
A. Hàm s
y f x 1
ng bin trên
a;b
. B. Hàm s
y f x 1
nghch bin trên
a;b
.
C. Hàm s
y f x
nghch bin trên
a;b
. D. Hàm s
y f x 1
ng bin trên
a;b
.
Câu 44: Tìm tt c các giá tr thc ca tham s
m
sao cho mi nghim ca b  
2
x 3x 2 0
m ca b
2
mx m 1 x m 1 0
?
A.
m1
. B.
3
m
7
. C.
3
m
7
. D.
m1
.
Câu 45: Tìm tt c các giá tr thc ca tham s
m
   
22
33
log x log x 1 2m 1 0
có ít nht mt nghin
3
1;3
?
A.
1 m 3
. B.
0 m 2
. C.
0 m 3
. D.
1 m 2
.
Câu 46: Cho hàm s
2
y m 1 x 3 m
vi
m
là tham s. Tp hp các giá tr ca
m
 hàm s
ng bin trên là ?
A.
1;1
. B.
1;
. C.
; 1 1;
. D.
;1
.
Câu 47: Tp hp các s thc
m
 hàm s
32
y x 5x 4mx 3
ng bin trên là ?
A.
25
;
12
. B.
25
;
12
. C.
25
;
2
. D.
25
;
12
.
Câu 48: 
2
x (m 1)x 1
y
2x
ên các kho

A.
m1
. B.
m1
. C.
m 1;1
. D.
5
m
2
.
Câu 49: Hàm s
mx 3
y
x m 2
ng bin trên tng khonh khi:
A.
m3
m1
. .B.
m3
. C.
3 m 1
. D.
m1
.
Câu 50: Hàm s
mx 3
y
x2
nghch bin trên tng khonh khi:
A.
3
m
2
. B.
3
m
2
. C.
3
m
2
. D.
3
m
2
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 1: Sự đồng biến, nghịch biến của hàm số” – P.3
Câu 01: Cho hàm s
32
y mx 2x mx 1
. Giá tr nh nht c hàm s ng bin trên
n
1;2
là ?
A.
1
m
2
. B.
1
m
23
. C.
23
m
3
. D.
3
m
23
.
Câu 02: Cho hàm s
32
1
y x mx m 2 x 5
3
. Vi
m 0;9
thì có bao nhiêu giá tr m là s t
nhiên sao cho hàm s ng bin
2;5
?
A. 0. B. 5. C. 3. D. 1.
Câu 03: Cho hàm s
mx 2
y
x 3m
. Vi m thuc tp h hàm s ng
;1
?
A.
22
A x : x
33
. B.
12
B x : x
33
.
C.
5
C ; 1;
9
. D.
D x : x 0
.
Câu 04: Cho hàm s
32
y x 3x 3mx m 1
. Hàm s nghch bin trên khong
1;1
thì mnh
 nào v úng ?
A.
1 m 2
. B.
m ; 3 1;
.
C.
m1
. D.
m ; 1 1;
.
Câu 05: Cho hàm s
32
y x 3x m 1 x 1
 hàm s ch bin trên khong
0;
?
A.
m2
. B.
m2
. C.
m1
. D.
m1
.
Câu 06: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
x m 2
y
x1
gim trên các
khonh ?
A.
m3
. B.
m3
. C.
m1
. D.
m1
.
Câu 07:  hàm s
mx 4
y
xm
gim trên khong
;1
?
A.
2 m 1
. B.
2 m 1
. C.
2 m 1
. D.
2 m 1
.
Câu 08:  hàm s
y 2m 1 sinx 3 m x
ng bin trên ?
A.
2
4m
3
. B.
2
4m
3
. C.
m4
. D.
2
m
3
.
Câu 09: Tìm GTNN c hàm s
3
2
x
y mx mx m
3
ng bin trên ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m0
. B.
m4
. C.
m4
. D.
m1
.
Câu 10: Vi giá tr nào ca a thì hàm s
3
y ax x
ng bin trên ?
A.
a0
. B.
a0
. C.
a0
. D.
a
.
Câu 11: Hàm s
32
1
y x m 2 x mx 3m
3
nghch bin trên khonh khi:
A.
m0
. B.
m4
. C.
1 m 4
. D.
m1
m4
.
Câu 12: Cho hàm s
3 2 2
1
y x m 1 x m m x 3
3
 hàm s nghch bin trên ?
A.
1;
. B.
;1
. C.
1;
. D.
;1
.
Câu 13: Cho hàm s
32
m 2 2m 7
y x x x 5
2 12
. Hàm s ng bin trên khi m nm trong
min giá tr nào ?
A.
1;3
. B.
1;3
.
C.
; 1 3;
. D. nh c m.
Câu 14: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
32
1
y x mx 2m 3 x m 2
3
luôn nghch bin trên ?
A.
3 m 1
. B.
m1
. C.
3 m 1
. D.
m3
m1
.
Câu 15: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
2
x m 1 2m 1
y
xm

tng khonh ca nó ?
A.
m1
. B.
m1
. C.
m1
. D.
m1
.
Câu 16: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y f x x mcosx
ng
bin trên ?
A.
m1
. B.
3
m
2
. C.
m1
. D.
1
m
2
.
Câu 17: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y m 3 x 2m 1 cosx
luôn
nghch bin trên ?
A.
2
4m
3
. B.
m2
. C.
m3
m1
. D.
m2
.
Câu 18: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
32
y 2x 3 m 2 x 6 m 1 x 3m 5
ng bin trên ?
A. 0. B. 1 . C. 2. D. 1.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 19: Cho hàm s
2
3x mx 2
y
2x 3
. Hãy cho bit có bao nhiêu giá tr  hàm
s luôn nghch bin trên tng khonh ca nó vi
m 0;10
?
A. 8. B. 6. C. 4. D.
2
.
Câu 20: Tìm giá tr nh nht ca tham s
m
sao cho hàm s
3
2
x
y mx mx m
3
ng bin
trên ?
A.
m5
. B.
m0
. C.
m1
. D.
m6
.
Câu 21: Tìm s nguyên
m
nh nht sao cho hàm s
m 3 x 2
y
xm
luôn nghch bin trên các
khonh ca nó ?
A.
m1
. B.
m2
. C.
m0
. D. Không có
m
tha
mãn.
Câu 22: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
mx 4
y
xm
gim trên khong
;1
?
A.
2 m 2
. B.
2 m 1
. C.
2 m 1
. D.
2 m 2
.
Câu 23: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
32
y x 6x mx 1
ng bin
trên khong
0;
?
A.
m0
. B.
m 12
. C.
m0
. D.
m 12
.
Câu 24: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
42
y x 2 m 1 x m 2
ng
bin trên khong
1;3
?
A.
m 5;2
. B.
m ;2
. C.
m 2,
. D.
m ; 5
.
Câu 25: Hàm s ch bin trên vi mi m ?
A.
23
y m x m
. B.
2 3 2
y m x mx 3x 1
.
C.
mx 1
y
xm
. D.
3
y x 2mx 1
.
Câu 26: Vi giá tr nào ca m thì hàm s
32
1
y x 2x mx 2
3
nghch bin trên các khong xác
nh ca nó ?
A.
m4
. B.
m4
. C.
m4
. D.
m4
.
Câu 27: Vu kin nào ca m thì hàm s
3 2 2
y x m 2 x m 4 x 9
ng bin trên ?
A.
m2
m1
. B.
m4
m2
. C.
m1
m0
. D.
m3
m3
.
Câu 28: Vi giá tr nào ca m thì hàm s
m 2 x m
y
xm
nghch bin trên mi khonh
ca nó ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m0
m2
. B.
m0
m3
. C.
m0
m2
. D.
0 m 3
.
Câu 29: Vi giá tr nào ca m thì hàm s
32
y x 3x mx 2
ng bin trên khong
0;
?
A.
m2
. B.
m3
. C.
m0
. D.
m4
.
Câu 30: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
32
11
y x mx 2mx 3m 4
32
nghch bin trên m dài là 3 ?
A.
m1
m9
. B.
m1
. C.
m9
. D.
m1
m9
.
Câu 31: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
tanx 2
y
tanx m
ng bin trên
khong
0;
4
?
A.
1 m 2
. B.
m0
1 m 2
. C.
m2
. D.
m0
.
Câu 32: Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
3
2
mx
y f x 7mx 14x m 2
3
gim trên na khong
1;
?
A.
14
;
15
. B.
14
;
15
. C.
14
2;
15
. D.
14
;
15
.
Câu 33: Tt c các giá tr thc ca tham s
m
sao cho hàm s
42
y x 2m 3 x m
nghch bin
trên khong
1;2
là
p
;
q

p
q
ti gin và
q0
. Hi tng
pq
là ?
A. 5. B. 9. C. 7. D. 3.
Câu 34: Hi có bao nhiêu giá tr nguyên ca tham s
m
sao cho hàm s
2
x 2mx m 2
y
xm
ng
bin trên tng khonh ca nó ?
A. 2. B. 4. C. Vô s. D. 0.
Câu 35: Cho hàm s
2
x m 2 x m 3
y
x1
. Vi giá tr nào ca m thì hàm s ng bin trên tng
khonh ca nó ?
A.
m2
. B.
m2
. C.
1 m 3
. D.
m1
.
Câu 36: Tt c các giá tr c hàm s
xm
y f x
x1
nghch bin trên tng khonh
ca nó là:
A.
m1
. B.
m1
. C.
m1
. D.
m1
.
Câu 37: Xét hai m sau:
I
Hàm s
3
y 1 x
ng bin trên .
II
Hàm s
4
y 1 x
ng bin trên .
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Hãy chn câu tr l
A. Ch
I
. B. Ch
II
. C. C . D. C hai sai.
Câu 38: Hàm s nào trong các hàm s sau ch có 1 chiu bin thiên trên tnh ca nó ?
A.
1
y
x
. B.
2
1
y
x
. C.
1
y
x
. D.
2
x
y
x
.
Câu 39: Tt c các giá tr c hàm s
3
2
x
y mx 4x
3
ng bin trên là:
A.
2 m 2
. B.
2 m 2
. C.
m2
. D.
m2
.
Câu 40: Hi có bao nhiêu giá tr   a tham s
m
sao cho hàm s
2
2x 1 m 1 m
y
xm
ng bin trên khong
1;
?
A. 3. B. 1. C. 2. D. 0.
Câu 41: Tìm tt c các giá tr thc ca tham s và sao cho hàm s
3
2
x 1 3
y f x sin cos x xsin cos 2
3 2 2
luôn gim trên ?
A.
kk
,k
12 4
2
. B.
5
kk
,k
12 12
2
.
C.
k
,k
4
2
. D.
5
k
,k
12
2
.
Câu 42: Tìm mi liên h gia các tham s
a
và
b
sao cho hàm s
y f x 2x asinx bcosx
 ?
A.
11
1
ab
. B.
a 2b 2 3
. C.
22
a b 4
. D.
12
a 2b
3
.
Câu 43: Tìm tt c các giá tr thc ca tham s
m

32
x 3x 9x m 0
có
m ?
A.
27 m 5
. B.
m5
m 27
. C.
m 27
m5
. D.
5 m 27
.
Câu 44: Tìm tt c các giá tr thc ca tham s
m

2 x 1 x m
có nghim
thc ?
A.
m2
. B.
m2
. C.
m3
. D.
m3
.
Câu 45: Cho hàm s
2x m
y
x3
. Có bao nhiêu giá tr nguyên m tha
m0
 hàm s ng
bin trên tng khonh ?
A. 4. B. 3. C. 2. D. 1.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 46: Cho hàm s
2
m 1 x 2x
y
mx 1
. Hãy cho bit có bao nhiêu giá tr m là s nguyên t sao cho
hàm s ng bin trên tng khonh ?
A. 1. B. 3. C. 2. D. 0.
Câu 47: Cho hàm s
y cosx 2ax
nh tham s  hàm s  ?
A.
1
a
2
. B.
1
a
2
. C.
1
a
2
. D.
1
a
2
.
Câu 48: Cho hàm s
y cos2x sin2x ax 4
. Phát bi a ?
A. Khi
a0
thì
1 y' 1
. B. Hàm s ng bin vi mi a.
C. Khi
a 2 2
thì hàm s ng bin trên .
D. Khi
a 2 2
thì hàm s luôn nghch bin trên .
Câu 49: Cho hàm s
2
y sin x sinx 3mx
. Phát bisai khi nói v m ?
A.
y y'' 3mx 3 0 , x
. B. Khi
m0
thì vi
x y' 1
2
.
C. Khi
3
m
2
thì hàm s ng bin trên .
D. Khi
2
m
3
thì hàm s luôn nghch bin trên .
Câu 50: Tìm tt c các giá tr thc ca tham s
m

22
x 4x 5 m 4x x

A.
1 m 3
. B.
3 m 5
. C.
5 m 3
. D.
3 m 3
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 2: Cực trị của hàm số” – P.1
Câu 01: Cho hàm s
32
y x x x 1
 th
C
. Khong cách t m cc tiu c th
hàm s là:
A.
2
. B. 2. C. 0. D. 1.
Câu 02: Tìm giá tr ci
CD
y
ca hàm s
3
y x 3x 2
?
A.
CD
y4
. B.
CD
y1
. C.
CD
y0
. D.
CD
y1
.
Câu 03: Cho hàm s
2
x x 1
y
x1
nh giá tr ci ca y ?
A.
2
. B.
3
. C. 0. D. 1.
Câu 04: Cho hàm s
y sinx cosx
, tìm khnh sai 
A.
x
4
là mt nghim ca y. B. Giá tr nh nht ca y là
2
2
.
C. Giá tr ln nht ca y là
2
2
. D. Hàm s c tr.
Câu 05: Hàm s  không có cc tr ?
A.
3
y x 5x
. B.
. C.
2
x 2x 4
y
x1
. D. C câu B và C.
Câu 06: Cho hàm s
y f x
 th i.  th hàm s
y f x
có mm cc tr ?
A. 2. B. 1. C. 0. D. 3.
Câu 07: Cho hàm s
y f x
có bng bin thiên:
x
2
4
y'
0
0
8
6
4
2
2
4
6
8
15
10
5
5
10
15
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
y
3
2
Kh
A. Hàm s t ci ti
x2
. B. Hàm s t ci ti
x3
.
C. Hàm s t ci ti
x4
. D. Hàm s t ci ti
x2
.
Câu 08: Cho hàm s
32
y x 3x 2
. Kh
A. Hàm s t ci ti
x2
t cc tiu ti
x0
.
B. Hàm s t cc tiu ti
x2
t ci
x0
.
C. Hàm s t ci ti
x2
và cc tiu ti
x0
.
D. Hàm s t ci ti
x0
và cc tiu ti
x2
.
Câu 09: Cho hàm s
42
y x 2x 3
. Kh
A. Hàm s m cc tr. B. Hàm s ch m cc tr.
C. Hàm s không có cc tr. D. Hàm s ch m cc tr.
Câu 10: Bi th hàm s
3
y x 3x 1
m cc tr
A,B
ng
thng
AB
là :
A.
y x 2.
B.
C.
y 2x 1.
D.
y x 2.
Câu 11: Cho hàm s
32
y 2x 5x 4x 1999
. Gi
1
x
và
2
x
(vi
12
xx
) l hai
m ci và cc tiu c th hàm s. Kt lu
A.
21
2
xx
3
. B.
21
1
2x x
3
. C.
12
1
2x x
3
. D.
12
1
xx
3
.
Câu 12: S m cc tr ca hàm s
32
y 2x 5x 4x 1999
là:
A. 1. B. 2. C. 3. D. 4.
Câu 13:  th hàm s
32
y 2x 3x 12x 2016
m cc tr lt là A và B vi
AB
xx
.
Kt lu
A.
A 2;2035
. B.
A 2;2008
. C.
A 2;2036
. D.
B 2;2009
.
Câu 14: Giá tr ci ca hàm s
2
y 2x 5x 4x 1999
là:
A.
54001
27
. B. 2. C.
54003
27
. D. 4.
Câu 15: Giá tr cc tiu ca hàm s
2
y 2x 3x 12x 2016
là:
A. 2006. B. 2007. C. 2008. D. 2009.
Câu 16: Cho hàm s
2
x 3x 5
y
x1
có 2 cc tr
12
x ,x
. Gi S là tng giá tr ca
12
x ,x
. Tính S ?
A.
S2
. B.
S2
. C.
S 2 3
. D.
S 2 3
.
Câu 17:    hàm s
3 2 2
23
y x mx 2 3m 1 x
32
có 2 cc tr
12
x ,x
tha mãn
1 2 1 2
x .x 2 x x 1
?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
2
m
3
. B.
3
m
2
. C.
2
m
3
. D. c m.
Câu 18: Cho hàm s
42
y x 5m 1 x 2
. Hàm s c tr vi giá tr nào ca m

A.
1
m
5
. B.
1
m
5
. C.
1
m
5
. D.
1
m
5
.
Câu 19: 
4 2 2
y x 2 m m 3 x m 5
. Vi giá tr nào ca m thì khong cách
gia 2 cc tr i xng qua trc tung là là nh nht và giá tr ng bao nhiêu ?
A.
1 11
m ,mind
24
. B.
1 11
m ,mind
22
.
C.
1
m ,mind 11
2
. D.
1
m 11,mind
2
.
Câu 20: Vi hàm s
yx
, phát bi
A. Hàm s o hàm. B. Hàm s không có cc tr.
C. Hàm s t cc tiu ti
x2
. D. Giá tr cc tiu là
CT
y0
.
Câu 21: Gi
M,n
lt là giá tr ci, giá tr cc tiu ca hàm s
2
x 3x 3
y
x2

ca biu thc
2
M 2n
bng:
A. 8. B. 7. C. 9. D. 6.
Câu 22: Cho hàm s
32
y x 17x 24x 8
. Kt lu
A.
CD
x 1.
B.
CD
2
x.
3
C.
CD
x 3.
D.
CD
x 12.
Câu 23: Cho hàm s
42
y 3x 6x 1
. Kt lu
A.
CD
y 2.
B.
CD
y 1.
C.
CD
y 1.
D.
CD
y 2.
Câu 24: Trong các hàm s sau, hàm s t ci ti
3
x
2
?
A.
4 3 2
1
y x x x 3x.
2
B.
2
y x 3x 2.
C.
2
y 4x 12x 8.
D.
x1
y.
x2
Câu 25: Trong các hàm s sau, hàm s nào ch có ci mà không có cc tiu ?
A.
42
y 10x 5x 7.
B.
32
y 17x 2x x 5.
C.
x2
y.
x1
D.
2
x x 1
y.
x1
Câu 26: Hàm s
32
y 3x 4x x 2016
t cc tiu ti:
A.
2
x
9
. B.
x1
. C.
1
x
9
. D.
x2
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 27: Cho hàm s
32
y x 3x 9x 2017
. Gi
1
x
và
2
x
l tm ci
và cc tiu c th hàm s. Kt lun 
A.
12
x x 4
. B.
21
x x 3
. C.
12
x x 3
. D.
2
12
x x 8
.
Câu 28: Hàm s
3
y x 8x 13x 1999
t ci ti:
A.
13
x
3
. B.
x1
. C.
13
x
3
. D.
x2
.
Câu 29: Hàm s
32
y x 10x 17x 25
t cc tiu ti:
A.
10
x
3
. B.
x 25
. C.
x 17
. D.
17
x
3
.
Câu 30: Cho hàm s
32
y 2x 3x 12x 2016
. Gi
1
x
và
2
x
l tm cc
i và cc tiu c th hàm s. Kt lu
A.
12
x x 4
. B.
21
x x 3
. C.
12
x x 3
. D.
2
12
x x 8
.
Câu 31: Cho hàm s
32
1
f x x mx 3m 4 x 3
3
, vi giá tr nào ca m thì hàm s có cc tiu,
ci ?
A.
4 m 1
. B.
4 m 1
. C.
m1
m4
. D.
m4
m1
.
Câu 32: Hàm s bc 3:
32
y ax bx cx d
vi
a0
có 2 cc tr khi nào ?
A.
y'
có nghim. B.
y'
có nghim kép.
C.
y'
có 2 nghim phân bit. D. hàm s luôn có 2 cc tr.
Câu 33: Cho bng bin thiên sau, phát bi
x
0
1
2
y'
0
y
1
3
A. Hàm s có cc tiu ti
x0
. B. Hàm s có ci ti
x2
.
C. Giá tr ci ca hàm s là
1
. D.
x1
là 2 cc tr ca hàm s .
Câu 34: Cho hàm s
3 2 2
y x m 1 x m 2m 3 x 4
nh tham s   th hàm s
m cc tr nm v 2 phía ca trc tung:
A. c giá tr m. B.
3 m 1
.
C.
3 m 1
. D. Vi mi giá tr m.
Câu 35: Giá tr cc tiu ca hàm s
1
yx
x
là giá tr 
A.
CT
y1
. B.
CT
y1
. C.
CT
y2
. D.
CT
y2
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 36: Cho hàm s
2
3x 13x 19
y
x3
ng thm cc tr c th hàm s có

A.
5x 2y 13 0.
B.
y 3x 13.
C.
y 6x 13.
D.
2x 4y 1 0.
.
Câu 37: Cho hàm s
2
y x 2x
. Kh
A. Hàm s m cc tr. B. Hàm s t cc tiu ti
x0
.
C. Hàm s t ci
x2
. D. Hàm s không có cc tr.
Câu 38: Cho hàm s
75
y x x
. Kh
A. Hàm s m cc tr. B. Hàm s m cc tr.
C. Hàm s m cc tr. D. Hàm s m cc tr.
Câu 39: Cho hàm s
y f x
o hàm
2 3 4
f x x 1 x 2 x 3 x 5
. Hi hàm s
y f x
có mm cc tr ?
A. 2. B. 3. C. 4. D. 5.
Câu 40: Cho hàm s
1
2
3
y x 2x
. Kh
A. Hàm s t cc tiu ti
x 1.
B. Hàm s t ci ti
x1
.
C. Hàm s m cc tr. D. Hàm s im cc tr.
Câu 41: Hàm s
32
y 3x 4x x 258
t ci ti:
A.
2
x
9
. B.
x1
. C.
1
x
9
. D.
x2
.
Câu 42: Hàm s
32
y x 8x 13x 1999
t cc tiu ti:
A.
x3
. B.
x1
. C.
1
x
3
. D.
x2
.
Câu 43: Bi th hàm s
32
y x 6x 9x 2
m cc tr là
11
A x ;y
và
22
B x ; y
. Nhn
không 
A.
12
x x 2
. B.
12
y y 4
. C.
12
yy
. D.
AB 2 6
.
Câu 44: Hàm s i ?
A.
42
y x x 1
. B.
x1
y
x2
. C. .
2
x2
y
x2
. D.
2
y x 2x
.
Câu 45: Tng s m ci ca hai hàm s
42
y f x x x 3
và
42
y g x x x 2
là:
A. 1. B. 2. C. 3. D. 4.
Câu 46: Cho hàm s
2
x 5x 3
y
x6
ng thm cc tr vuông góc vng thng

A.
y 5 2x
. B.
y 2x 5
. C.
1
y x 3
2
. D. M ng thng
khác.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 47: u kin c hàm s
4 2 2
y 2x 4 m 5 x m 4
có 3 cc tr ?
A.
m ; 5
. B.
m ; 5
. C.
m 5;
. D.
m 5;
.
Câu 48:   ng th    m cc tr (nu có) c  th hàm s
32
y f x x 2x
ng th
A.
8
yx
9
. B.
9
yx
8
. C.
9
yx
8
. D.
8
yx
9
.
Câu 49: Cho hàm s
43
11
y f x x x
43
, hàm s nhiêu cc tr ?
A. 1. B. 2. C. 3. D. 4 .
Câu 50: Cho hàm s
y x 3
, xét các kh
a) Hàm s không có cc tr. c) Giá tr cc tiu là 0.
b) Giá tr nh nht là 0. d) Hàm s t cc tiu ti
x3
.
S kh
A. 1. B. 2. C. 3. D. 4 .
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 2: Cực trị của hàm số” – P.2
Câu 01: Tng s m cc tiu ca hai hàm s
32
y f x x x 3
và
42
y g x x x 2
là:
A. 1. B. 2. C. 3. D. 4.
Câu 02: Cho hai hàm s
32
y f x x x 3
và
42
x 3x
y g x x 2
42
. Tng s m cc tr,
ci, cc tiu ca 2 hàm s lt là:
A. 5; 2; 3. B. 5; 3; 2. C. 4; 2; 2. D. 3; 1; 2.
Câu 03: Cho hàm s
32
y x 6x 9x 4
 th
C
. T m ci c th hàm s là:
A.
A 1; 8
. B.
A 3; 4
. C.
A 2; 2
. D.
A 1;10
.
Câu 04: Cho hàm s
32
y x 3x 4
 th
C
. Gm cc tr ca
C
. Din tích
tam giác OAB bng:
A. 4. B. 8. C. 2. D.
23
.
Câu 05:  th hàm s
32
y x 3x 9x 2
  th
C
  m c i, cc tiu l t là
11
x ;y
và
22
x ; y
vi
12
xx
. Tính
1 2 2 1
T x y x y
.
A. 4. B.
4
. C. 46. D.
46
.
Câu 06: Cho hàm s
32
y x 3x 6x
. Hàm s t cc tr tm
12
x ,x
 ca
biu thc
22
12
S x x
bng:
A.
10
. B.
8
. C. 10. D. 8.
Câu 07: Cho hàm s
y f x
o hàm trên . Kh
A. Ni du khi
x
chy qua
0
x
thì hàm s t cc tiu ti
0
x
.
B. Nu
0
f x 0
thì hàm s t cc tr ti
0
x
.
C. Nu hàm s t cc tr ti
0
x
i du khi
x
chy qua
0
x
.
D. Nu
00
f x f x 0
thì hàm s t cc tr ti
0
x
.
Câu 08: Cho hàm s
y f x
. Kh
A. Hàm s
y f x
t cc tr ti
0
x
thì
0
f x 0
.
B. Nu hàm s t cc tr ti
0
x
thì hàm s o hàm ti
0
x
hoc
0
f x 0
.
C. Hàm s
y f x
t cc tr ti
0
x
thì nó khôno hàm ti
0
x
.
D. Hàm s
y f x
t cc tr ti
0
x
thì
0
f x 0
hoc
0
f x 0
.
Câu 09: Cho hàm s
y f x
nh trên
a; b
và
0
x
thun
a; b
. Kh
kh
A. Hàm s
y f x
t cc tr ti
0
x
thì
0
f x 0
hoc
0
f x 0
.
B. Hàm s
y f x
t cc tr ti
0
x
thì
0
f x 0
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
C. Hàm s
y f x
t cc tr ti
0
x
o hàm ti
0
x
.
D. Nu hàm s t cc tr ti
0
x
thì hàm s o hàm ti
0
x
hoc
0
f x 0
.
Câu 10: Cho hàm s
y f x
. Khn
A. Nu hàm s
y f x
có giá tr ci là
M
, giá tr cc tiu là
m
thì
Mm
.
B. Nu hàm s
y f x
không có cc tr nh
0
f x 0
vô nghim.
C. Hàm s
y f x
m cc tr thì hàm s c ba.
D. Hàm s
42
y ax bx c
vi
a0
luôn có cc tr.
Câu 11: Cho hàm s
32
y f x ax bx cx d
 th hàm s có cc tr là
0;1 , 1; 1

nh hàm
fx
?
A.
3
f x x 3x 1
. B.
3
f x x 3x
. C.
3
f x x 3x
. D.
32
f x 4x 6x 1
.
Câu 12: Cho
x
f x e x
, tm
x0
thì hàm s 
A. nh. B. Là hàm hng. C. t cc tiu. D. t ci.
Câu 13: Cho các m sau:
a) Hàm s t cc tr ti
0
x
thì
0
f x 0
. b) Hàm s tha
0
f x 0
thì có cc tr ti
0
x
.
b) Hàm s t ci ti
0
x
thì giá tr ci là
0
fx
.
c) Hàm s t cc tiu ti
0
x
thì giá tr nh nht là
0
fx
.
S phát bi
A. 1. B. 2. C. 3. D. 4 .
Câu 14: Cho hàm hu t
có 2 cc trng thm cc tr là
ng th
A.
y x 2
. B.
y 2x 2
. C.
y x 2
. D.
y 2x
.
Câu 15: Cho hàm s
2
y x. 9 x
. Gm mà t th hàm s t cm
 ?
A.
39
;
2
2
. B.
29
;
2
3
. C.
39
;
2
2
. D.
39
;
2
2
.
Câu 16: Cho hàm s
32
y x x x 1
 th
C
. Khong cách t m cc tiu c th
hàm s là:
A.
2
. B. 2. C. 0. D. 1.
Câu 17: Khsai ?
A. Hàm s
32
y x 3x 2
có cc tr. B. Hàm s
32
y x 2x x
m cc tr.
C. Hàm s
32
y x 6x 12x 2
có cc tr. D. Hàm s
3
x1
không có cc tr.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 18: Gi s hàm s
32
y x 3x 3x 4
m cc tr, hàm s
42
y x 4x 2
m cc
tr và hàm s
2x 1
y
x1
m cc tr. Giá tr ca
T a b c
là:
A. 0. B. 3. C. 2. D. 1.
Câu 19: Hàm s
2
y f x x 2x
m cc tr ?
A. 0. B. 1. C. 2. D. 3.
Câu 20: Cho hàm s
42
y f x x 4x 2
. Chn phát bi
A. Hàm s m ci vm cc tiu.
B. Hàm s m cm cc tiu.
C. Hàm s m cc tr m ci . D. Hàm s m cc tr m cc tiu.
Câu 21: Hàm s bc ba dng
32
y ax bx cx d, a 0
có th m cc tr ?
A. 0 hoc 1 hoc 2. B. 1 hoc 2. C. 0 hoc 2. D. 0 hoc 1.
Câu 22: Cho hàm s
2
y f x x 2x 4
 th . Hàm s
y f x
có my cc tr ?
A. 4. B. 1. C. 3. D. 2.
Câu 23: Cho hàm s
y f x
. Hàm s
y f x
 th  i:
8
6
4
2
2
4
6
15
10
5
5
10
15
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Kh
A.  th hàm s
y f x
ct trc hoành tm phân bit.
B.  th hàm s
y f x
có m cc tr.
C.  th hàm s
y f x
m cc tr.
D.  th hàm s
y f x
có mm cc tr.
Câu 24: Cho hàm s
y f x
. Hàm s
y f x
 th  bi:
Kh
A. Hàm s
y f x
t ci ti
x1
. B.  th hàm s
y f x
có mm cc tiu.
8
6
4
2
2
4
6
15
10
5
5
10
15
8
6
4
2
2
4
6
8
15
10
5
5
10
15
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
C. Hàm s
y f x
ng bin trên
;1
. D.  th hàm s
y f x
m cc tr.
Câu 25: Cho hàm s
3
y x 3x 2
 th  i:
Kh
A.  th hàm s
y f x
ch m cc tim ci.
B.  th hàm s
y f x
có mm cc tiu và mm ci.
C.  th hàm s
y f x
có bm cc tr.
D.  th hàm s
y f x
có mm cm cc tiu.
Câu 26: Phát biu nào là chính xác v  th hàm s 
43
2
x 5x 1
y x 8x 10
4 3 7
?
A. Hàm s m cm cc tiu.
B. Hàm s trên có duy nhm cc tr.
C. Hàm s trên có m cc tim ci.
D. Hàm s m cc tr.
Câu 27: Nhng phát biu nào trong các phát bi
a) Hàm s
y f x
t cc tiu ti
0
x
khi và ch o hàm ca
y'
i du t sang 
qua
0
x
.
b) Nu
f x 0
và
f x 0
thì hàm s t cc tiu ti
0
x
.
c) Hàm s
y f x
t cc tiu khi và ch khi
0
x
là nghim c
f x 0
.
A. a. B. a,b,c. C. a,c. D. b,c.
Câu 28: Gi s m là s cc tr ca hàm
32
y ax bx
. Xét trên khong
1;
, m có th bng bao
nhiêu ?
10
8
6
4
2
2
4
15
10
5
5
10
15
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m1
. B.
m1
m2
. C.
m0
m2
. D.
m1
m0
.
Câu 29: Hàm s c tr ?
A.
32
y x 3x
. B.
x3
y
2x 4
. C.
1
yx
x
. D.
2
y x. 1 x
.
Câu 30:  th 
42
y x 2x 1
có tng giá tr ca
CD
y
và
CT
y
là bao nhiêu ?
A. 0. B. 5. C. 2. D. 3.
Câu 31: Cc tiu c th hàm s
2
2
3
y x 3x
c giá tr 
A.
CT
3
x 0; ;3
2
. B.
CT
3
x
2
. C.
CT
x 0;3
. D.
CT
3
x
2
.
Câu 32: Hàm s
32
y ax ax 2
t cc tiu ti
2
x
3
thì a thu kin gì ?
A.
a0
. B.
a0
. C.
a0
. D.
a0
.
Câu 33: 
42
y 2x 4 2m 1 x 1
, giá tr nh nht ca
CD
y
là bao nhiêu ?
A.
min 1
. B.
min 3
. C.
min 0
. D.
min 0
.
Câu 34:  hàm s
3
2
x
y 2mx 1
2
t cc tiu ti
x1
?
A.
1
m
4
. B.
1
m
2
. C. . D. c m.
Câu 35: Cho hàm s
32
11
y x m 1 x (m 2) 3
32
. nh giá tr  ci và cc tiu
nm trong khong
( 3;4)
:
A.
m 2;5
. B.
m 2;5 \ 3
. C.
m ;2
. D.
m 3;5
.
Câu 36:  th hàm s
2
y 9 x
có mm cc tiu ?
A. 0 . B. 1. C. 2. D. 3.
Câu 37: Hàm s
32
C : y x 2x x 1
t cc tr khi:
A.
x1
1
x
3
. B.
x1
1
x
3
. C.
x3
1
x
3
. D.
x3
10
x
3
.
Câu 38: Cho hàm s
3
y 2x 2x
. H thc liên h gia các giá tr ci
CD
y
và giá tr cc tiu
CT
y
ca hàm s 
A.
CT CD
y 2y
. B.
CT CD
2y 3y
. C.
CT CD
yy
. D.
CT CD
yy
.
Câu 39: Cho hàm s
2
y x x 1
. Hàm s t cc tr ti:
A.
x1
. B.
1
x
2
. C.
1
x
2
. D.
x1
.
Câu 40: Cho hàm s
2
2
y x 2 3
. Hàm s t ci khi:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
x2
. B.
x2
. C.
x1
. D.
x0
.
Câu 41: Cho hàm s
2
x 2x 1
y
x1
:
1:
Hàm s t ci ti
x1
.
2:
Hàm s có
CD CT
3x x
3
: Hàm s nghch bin trên
;1
4:
Hàm s ng bin trên
1;3
.
Các phát biu đúng là:
A.
1 , 4
. B.
1 , 2
. C.
1 , 3
. D.
2 , 3
.
Câu 42: Hàm s
32
y f x x x x 4
t cc tr khi:
A.
x1
x3
. B.
x0
2
x
3
. C.
x1
1
x
3
. D.
x1
1
x
3
.
Câu 43: Cho hàm s
42
y f x 3x 2x 2
. Chn phát biu sai:
A. Hàm s m cc tr.
B. Hàm s m cm cc tiu.
C. Hàm s m cm cc tiu.
D. Hàm s có ci, cc tiu.
Câu 44: Ving thm cc tr c th hàm s
3
y x 3x 1
.
A.
2x y 1 0
. B.
x 2y 1 0
. C.
2x y 1 0
. D.
x 2y 1 0
.
Câu 45: Hàm s m cc tr ?
A.
1
y x .
x1
B.
32
y x 3x 7x 2.
C.
42
y x 2x 3.
D.
2
y x .
x1
Câu 46: Hàm s c tr ?
A.
2
y 2x .
x1
B.
32
y x 3x .
C.
42
y x 2x 3.
D.
x1
y.
x2
Câu 47: Trong các khnh nào là khnh sai ?
A.  th hàm s
32
y ax bx cx d, a 0
luôn có cc tr.
B.  th hàm s
42
y ax bx c, a 0
luôn có ít nht mm cc tr.
C. Hàm s
ax b
y , ad bc 0
cx d
luôn không có cc tr.
D.  th hàm s
32
y ax bx cx d, a 0
có nhiu nhm cc tr.
Câu 48: m cc tiu ca hàm s
3
y x 3x 4
là:
A.
x 1.
B.
x 1.
C.
x 3.
D.
x 3.
Câu 49: Hàm s t ci ti
x1
?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
52
y x 5x 5x 13.
B.
4
y x 4x 3.
C.
1
y x .
x
D.
y 2 x x.
Câu 50: Cho hàm s
2
3
5x
y f x 2x x 4
2
t ci khi:
A.
x1
. B.
1
x
6
. C.
x1
. D.
x
6
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 2: Cực trị của hàm số” – P.3
Câu 01: Hàm s c tr ?
A.
B.
42
y x 3x 2.
C.
y 3x 4.
D.
2x 1
y.
3x 2
Câu 02:  th hàm s
42
y x 3x 5
m cc tiu ?
A.
1.
B.
0.
C.
2.
D.
3.
Câu 03: Tìm tt c các giá tr ca tham s
m
hàm s
32
y x mx 2m 3 x 3
t ci ti
x1
.
A.
m 3.
B.
m 3.
C.
m 3.
D.
m 3.
Câu 04:  th hàm s
x1
y
4x 7
m cc tr ?
A.
3.
B.
1.
C.
2.
D.
0.
Câu 05: o hàm hàm s
y f x
là
32
4
y' x x 1 x 1
, vy hàm s có bao nhiêu cc tr ?
A. 0. B. 1. C. 2. D. 3.
Câu 06: Cho hàm s
24
y 2x x
. Chn phát biu sai trong các phát bi
A. Hàm s t cc tiu ti
x0
. B. Hàm s có giá tr ci bng 1.
C. Hàm s có hai cc tr. D. m cc tiu c th hàm s là
A 0;0
.
Câu 07: Hàm s
42
y x 2mx 4
có 3 cc tr tng tròn ngoi tip
nh nht bng bao nhiêu ?
A.
1
m
2
. B.
3
1
m
2
. C.
m0
. D.
3
1
m
3
.
Câu 08: Cho hàm s
32
y x 3x x
. Giá tr nào c ng thc tr ca
hàm s o tip xúc vng tròn
22
1
C : x m 1 y m
25
?
A.
4
m
7
. B.
6
m
7
. C. C . D. C A và B sai.
Câu 09: Cho hàm s
2
x 2x 4
y
1 2x
m cc tr thung thng
y ux v
. Giá tr
uv
bng bao nhiêu ?
A.
0
. B.
1
. C.
1
. D.
2
.
Câu 10:  hàm s
42
y x 2 3m 4 x 3m 1
m cc tr ta thành tam giác có bán
ng tròn ni tip bng 1:
A.
m1
m2
. B.
m1
m2
. C.
m2
. D.
m2
.
Câu 11: ng thng
32
y x 3x 3x 1
m cc tr ng thng song song vi AB
có th ng th
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
4x y 2 0
. B.
4x y 1 0
. C.
4x 2y 1 0
. D.
1
y x 2
4
.
Câu 12: Hàm s
y 1 x x 5
, phát bi
A. Giá tr cc tiu là
23
. B. Giá tr ci là
23
.
C. m cc ti là
2.
D. m c là 2.
Câu 13: Cho hàm s
2
y x 6x 5
, chn phát bi
A. Hàm s t cc tiu ti
x 3.
B. Hàm s t cc tiu ti
x 1, x 5.
C. Hàm s t cc tr ti
x 1, x 3, x 5.
D. Hàm s không có cc tr .
Câu 14: Cho hàm s
22
y x 1 x 1
, phát bi
A.  th có 1 ci và 2 cc tiu. B.  th có 1 cc tiu và 2 ci.
C.  th có 1 ci . D.  th có 1 cc tiu.
Câu 15: Cho hàm s
32
1
y x m 2 x 2m 3
3
, phát bisai khi nói v  th
hàm s 
A. Hàm s luôn có ci cc tiu
m
. B. Hàm s luôn có c i cc tiu
m\ 1
.
C. Hàm s luôn có ci cc tiu
m 1;
.
D. Hàm s luôn có ci cc tiu
m ;1
.
Câu 16: ng thng thc tr ca hàm s
2
x 5x 2
y
3x
?
A.
y 2x 5
. B. Không tn ti. C.
y x 3
. D.
y 3 x
.
Câu 17: Cho hàm s
3
y x 3x 1
, khong cách gim cc tr c th hàm s bng bao
nhiêu ?
A. 2. B.
2
. C.
22
. D.
25
.
Câu 18: Cc tr ca hàm s
i kh
A. 0. B. 1. C. 2. D. Không tn ti cc tr.
Câu 19: Cho hàm s
4 2 2
m
y x 2m x 1 C
 hàm s m cc tr nh ca mt
tam giác vuông cân:
A. 0. B. 1. C. 2. D. 3.
Câu 20:  hàm s
2
x mx m 8
y
x1
có ci và cc tiu nm v 2 phía cng
thng
d : 9x 7y 1 0
:
A.
9
3m
7
. B.
9
3m
7
. C.
3
m9
7
. D.
3
m9
7
.
Câu 21:  hàm s
3 2 2 2
y x 3x 3 m 1 x 3m 1
có 2 cc tr
12
x ,x
thu kin cách
u gc t:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
11
m 0; ;
22
. B.
m0
. C.
1
m
2
. D.
1
m
2
.
Câu 22:  hàm s
3 2 2
y x m 2 x 3m 1 x m 5
có 2 cc tr
12
x ,x
tha
12
x .x 2
.
A.
5
m
3
. B.
7
m
3
. C.
7
m
3
. D. C u tha.
Câu 23:  hàm s
3 2 2 3
y x 3mx 3 m 1 x m 4m 1
có 3 cc tr to vi thành 1 tam
giác sao cho din nht và tìm giá tr 
A.
5
2
max
m 0,S 3
. B.
2
5
max
m 0,S 3
. C.
max
m 3,S 0
. D.
max
m 3,S 0
.
Câu 24:  th hàm s
4 2 2
y x 2mx m m 1
  th hàm s có 3 cc tr thành
ng tròn ngoi tip bng 1 ?
A.
15
m
2
m1
15
m
2
. B.
m1
15
m
2
. C.
15
m
2
15
m
2
. D.
m1
15
m
2
.
Câu 25: Vi giá tr nào ca m thì hàm s
3 2 2 3
y x 3mx 3 m 1 x m 4m 1
m cc tr
to vi gc t 1 tam giác vuông ti O ?
A.
m 1; 2
. B.
m 1;2
. C.
m 1;2
. D.
m 1; 2
.
Câu 26: Cho hàm s
42
11
y x mx n
42
t cc tr bng
11
4
ti
x1
 s
n
m
bng bao
nhiêu ?
A. 3. B.
1
3
. C.
1
. D.
1
9
.
Câu 27: Cho hàm s
4 3 2
y f x x x 3x x 5
  m cc tr tha mãn
1 2 3
x x x
 t
22
3 2 1 3 2 1
A x x x x x x
, giá tr ca
2A
bng giá tr  ?
A. 14 . B.
65
4
. C.
65
8
. D. 56.
Câu 28: Hàm s
3
y x 8x 13x 1999
t ci ti:
A.
13
x
3
. B.
x1
. C.
13
x
3
. D.
x2
.
Câu 29: Cho hàm s
4 3 2
y x x 3x x 5
, hi hàm s có mm ci, cc tiu ?
A. 2 cc tiu, 1 ci. B. 2 ci, 1 cc tiu.
C. Ch có cc tiu. D. Ch có ci .
Câu 30: Hàm s
42
y x 4mx 3 m 1 2
có duy nht 1 cc tr khi m tha giá tr nào ?
A.
m0
. B.
m0
. C.
m0
. D.
m0
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 31: Cho hàm s
32
11
y x m 1 x 3 m 2 x
33
 hàm s t ci, cc tiu ti
1 2 1` 2
x ,x x x
tha
2
12
x x 1
?
A.
m2
2
m
3
. B.
m2
2
m
3
. C.
1
m
2
3
m
2
. D.
1
m
2
2
m
3
.
Câu 32: Cho hàm s
4 3 2
y x mx 2x 3mx 1
 hàm s có hai cc tiu ?
A.
4
m
3
. B.
4
m
3
. C.
4
m
3
. D.
4
m
3
.
Câu 33:   th hàm s
2
mx 1
y
x
có hai cc tr ti A và B sao cho AB ngn nht.
A.
1
m
2
. B.
1
m
2
. C.
m2
. D.
m2
.
Câu 34: Cho hàm s
4 2 2
y x 2m x 1
. Tìm giá tr   th hàm s có 3 cc tr A,B,C và din tích
tam giác ABC bng 32:
A.
m1
. B.
1
m
2
. C.
m2
. D.
m3
.
Câu 35:  hàm s
4 2 2
y mx m 9 x 10
có 3 cc tr ?
A.
m3
0 m 3
. B.
3 m 3
. C.
0 m 3
. D.
m3
m0
.
Câu 36: Cho hàm s:
4 2 2
y x 5m 2 x m 3
, vi giá tr nào c hàm s có 3 cc
tr to thành tam giác có góc bng
30
?
A.
3
56 32 5
m
5
. B.
3
8
2
3
5
. C. C A và B. D. Không có m tha mãn.
Câu 37: Hàm s
32
y x 3x 1
t cc tiu ti:
A.
x0
. B.
x2
. C. Không có cc tiu. D.
x2
.
Câu 38: Khsai:
A.
3x 2
y
x1
t cc tiu ti -1. B.
3
2
x
y x 4x
3
không có cc tr.
C.
42
6y x x 2
t cc tiu là 0.
D. Ni dc tr.
Câu 39: m cc tr hàm s
2
3
3x
y 3x
2
là:
A.
CD CT
1
x 0,x
3
. B.
CD CT
x 3,x 3
. C.
CD CT
1
x ,x 0
3
. D. Không có cc tr.
Câu 40: Hàm s
42
y ax bx c
vi
a0
có tc tr ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A. 1. B. 2. C. 3. D. 4.
Câu 41: Cho hàm s
32
y 3x 4x 6x 2
, ving thm cc tr.
A.
8 92
yx
9 27
. B. Không tn ti. C.
92 8
yx
27 9
. D.
8 92
yx
9 27
.
Câu 42: Cho hàm s 
32
y x 3x 9x 11
, phát bi
?
A.  th hàm s nhm có
x1
m cc tiu.
B.  th hàm s nhm có
x3
m ci.
C.  th hàm s nhm có
x1
m ci.
D.  th hàm s nhm có
x3
im cc tiu .
Câu 43: 1 hàm s o hàm
2
2
f' x x x 1 2x 3
. S cc tr ca hàm
f(x)
là giá tr i

A. 1 . B. 2 . C. 3. D. 4 .
Câu 44: nh giá tr  hàm s
y sin4x 2mcosx
t cc tiu ti
x
3
?
A.
2
m
3
. B.
2
m
3
. C.
22
m
3
. D.
32
m
2
.
Câu 45: Cho hàm s
3
y m 2 x mx 2
  th hàm s không có ci và cc tiu ?
A.
0 m 2
. B.
0 m 2
. C.
2 m 0
. D. Không có m tho mãn.
Câu 46: Cho hàm s
y f x
nh, liên tc trên và có bng bin thiên:
x
0
1
y'
||
0
y
0
1
Kh
A. Hàm s c tr. B. Hàm s có giá tr cc tiu bng 1.
C. Hàm s có giá tr ln nht bng 0 và giá tr nh nht là
1
.
D. Hàm s t ci ti
x0
t cc tiu ti
x 1.
Câu 47: Cho hàm s
42
y 2x m 1 x 3
 hàm s m cc tr to thành tam
giác vuông cân ?
A.
3
m 16 1
. B.
3
m 16 1
. C.
3
m 16 1
. D.
m1
.
Câu 48: nh giá tr c hàm s
42
y x 3m 1 x 6
m cc tr to thành tam giác
cân có cnh bên gi c
A.
m3
. B.
m5
. C.
3
m
5
. D.
5
m
3
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 49: Cho hàm s
42
y x 2 m 1 x 3
 hàm s m cc tr to thành tam giác
có góc bng
120 :
A.
3
1
m1
3
. B.
3
1
m1
3
. C.
1
m
3
. D.
1
m
3
.
Câu 50: Hàm s c tr ?
A.
32
y x x 1
. B.
x1
y
x1
. C.
42
y x 3x 2
. D.
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số” – P.1
Câu 01: Giá tr ln nht, giá tr nh nht ca hàm s
1
y f x 3x 2
3x
trên tnh ca nó
lt là:
A. Không tn ti GTLN; GTNN. B.
0; 4
.
C. Không tn ti GTNN; 0. D.
;
.
Câu 02: Giá tr ln nht ca hàm s
y f x 4 3x 3x 16
n
0;1
là:
A.
6
. B.
25
. C.
2 10
. D.
1 19
.
Câu 03: Giá tr nh nht ca hàm s
32
y f x x 3x 6x 5
n
2; 1
là:
A.
13
. B.
13 6 3
. C.
21
. D.
13 6 3
.
Câu 04: Cho hàm s
1
y f x
4x 5
vi tnh
5
D\
4
. Giá tr
1;1
min y
bng:
A.
1
. B.
1
9
. C. Không tn ti GTNN. D.
0
.
Câu 05: Giá tr nh nht và giá tr ln nht ca hàm s
2x 1
y f x
3x 4
n
2;6
lt là:
A. Không tn ti GTNN, GTLN. B.
2
3
; không tn ti GTLN.
C. Không tn ti GTNN,
2
3
. D.
31
;
10 2
.
Câu 06: Giá tr nh nht ca hàm s
x1
y f x
x1
n
0;3
là:
A.
0;3
miny 3
. B.
0;3
1
min y
2
. C.
0;3
miny 1
. D.
0;3
miny 1
.
Câu 07: Giá tr nh nht ca hàm s
x
y f x x
9
n
2;4
là:
A.
2;4
20
min y
9
. B.
2;4
13
min y
2
. C.
2;4
miny 6
. D.
2;4
25
min y
4
.
Câu 08: Giá tr nh nht ca hàm s
2
x x 1
y f x
x1
trên khong
1;
là:
A.
1;
min y 1
. B.
1;
min y 3
. C.
1;
min y 5
. D.
1;
7
min y
3
.
Câu 09: Giá tr ln nht ca hàm s
2
2
x 8x 7
y f x
x1
là:
A.
maxy 1
. B.
maxy 1
. C.
maxy 9
. D.
maxy 10
.
Câu 10: Giá tr ln nht và giá tr nh nht ca hàm s
y f x 5 4x
n
1;1
là:
A.
1;1
maxy 5
và
1;1
miny 0
. B.
1;1
maxy 1
và
1;1
miny 3
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
C.
1;1
maxy 3
và
1;1
miny 1
. D.
1;1
maxy 0
và
1;1
miny 5
.
Câu 11: Giá tr ln nht ca hàm s
3
y f x x 12x 5
trên tn
4; 1 , 1; 4
lt là:
A.
21; 21
. B.
21; 11
. C.
21; 11
. D.
21; 11
.
Câu 12: Cho hàm s
2
y f x 16 x
vi tnh
D 4;4
. Giá tr ln nht và giá tr nh
nht trn
3;4
lt là:
A.
4; 0
. B.
0; 4
. C.
7; 4
. D.
4; 7
.
Câu 13: Cho hàm s
2
x x 1
y f x
x1
vi t  nh
D \ 1
 t
3; 2
a max f x ;
4 10;1
b min f x ;
5 53
;8
2
c min f x
. Các nghic 3 sau:
3
ax bx c 0
lt là ?
A.
1; 7; 6
. B.
1; 2; 3
. C.
1 71
1; ;
29
. D.
13
; 7; 6
2
.
Câu 14: Giá tr nh nht ca hàm s
2
1
4x m 3m
3
y f x
3x 2
n
0;2
bng
31
24
khi:
A.
3
m
2
. B.
m1
. C.
m 1; m 2
. D.
m2
.
Câu 15: Cho hàm s
23
y f x 3x 2x
. M  
A. Hàm s ng bin trên .
B. Ti
0
x1
, hàm s  t ct giá tr ln nht trên .
C. Ti
0
x0
, hàm s t cc tit giá tr nh nht trên .
D. Hàm s  ln nht và giá tr nh nht trên .
Câu 16: Hàm s
32
15
y f x x x 6x 1
32
t giá tr ln nht và giá tr nh nhn
1;3
t lt là
12
x ,x
ng
12
xx
bng:
A.
2
. B.
5
. C.
4
. D.
3
.
Câu 17: Hàm s
2
y f x 4 x
t giá tr nh nht ti x. Giá tr ca x là:
A.
x3
. B.
x0
x2
. C.
x0
. D.
x2
x2
.
Câu 18: Hàm s
22
y f x x 1 x 3
có giá tr nh nht bng:
A.
3
. B.
1
. C.
10
. D.
8
.
Câu 19: Giá tr nh nht ca hàm s
lnx
y f x
x
n
1;e
bng là:
A.
0
. B.
1
. C.
1
e
. D.
e
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 20: Hàm s
2
x1
y f x
x2
t giá tr ln nht và giá tr nh nhn
3;0
lt
ti
12
x ,x

12
xx
bng:
A.
2
. B.
0
. C.
6
. D.
2
.
Câu 21: Giá tr
2
là giá tr ln nht ca hàm s nào (xét trên 
A.
yx
. B.
y2
. C.
y cosx
. D.
y sinx
.
Câu 22: Cho hàm s
x 1 1
y f x x 2
2x 1 x
nh trên . Mt hc
tìm giá tr ln nht ca hàm s y trên
1;2

c 1: Tìm tnh ca hàm s y .
Tnh
1
D \ ;0
2
.
c 2: o hàm ca hàm s y.
2 2 2 2
2x 1 2 x 1
1 3 1
y 1 1 0, x D
xx
2x 1 2x 1
.
c 3: ng bing bin
1;2
.
c 4: Kt lun:
1;2
maxy y 1 2
.
Bn hu t c nào ?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 23: t
2;4
1;2
a maxf x ; b minf x
;
1;2
2; 1
c maxg x ; d ming x
  
f x 2 x
 nh
trên
0;
và
1
gx
x
nh trên
\0
. Xét h 
12
12
at bt 2
I
ct dt 0
vi
12
t ,t
là
các n ca h  s ca h m ca h
I
là:
A.
22
;
44
. B.
22
;
44
. C.
22
;
44
. D.
22
;
44
.
Câu 24: Cho hàm s
y f x 1 4x 8
nh trên
2;
và
2
g x x 3x 5
nh trên
t
5;6
3;4
a maxf x , b minf x
và
g b g a
A
ba
. Giá tr ca biu thc A bng:
A.
7
. B.
7
. C.
29
. D.
9
.
Câu 25: Cho hàm s
2
f x x 3x
 nh trên ,
2
gx
x1
 nh trên
\1
. Gi s
1;2
a maxf x
,
2;3
b ming x
. Va b
at b 2
là:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
1
t
2
. B.
4
t
9
. C.
t0
. D.
1
t
2
.
Câu 26: Hàm s
y f x cos2x 3
t giá tr nh nhn
0;
bng:
A.
4
. B.
3
. C.
2
. D.
0
.
Câu 27: Hàm s
y f x tanx x
t giá tr nh nhn
0;
4
tm
x?
A.
0
. B.
4
. C.
1
4
. D. 1.
Câu 28: Hàm s
y f x sinx cosx
có giá tr nh nht, giá tr ln nht lt là ?
A.
2; 2
. B.
2; 2
. C.
0; 1
. D.
1; 1
.
Câu 29: Hàm s
3
y f x 3sinx 4sin x
có giá tr ln nht, giá tr nh nht lt là:
A.
3; 4
. B.
1; 0
. C.
1; 1
. D.
0; 1
.
Câu 30: Hàm s
2
y f x sin x 2
có giá tr nh nht, giá tr ln nht lt bng:
A.
0; 2
. B.
1; 3
. C.
1; 2
. D.
2; 3
.
Câu 31: Cho hàm s
y f x 3x 4x 6
vi t  nh
3
D;
2
. Giá tr ca biu thc
2
2
3;6
3;6
A maxf x minf x
là:
A.
A 255 18 6 108 2.
B.
A 18 3 2
.
C.
A 9 6.
D.
9
A
2
.
Câu 32: Cho hàm s
y f x 4x 5x 7
vi t  nh
7
D;
5
. Giá tr ca biu thc
2
2
4;5
4;5
A maxf x minf x
là ?
A.
A 20 3 2
. B.
A 149 32 13 120 2.
C.
A 16 13.
D.
28
A
5
.
Câu 33: Cho hàm s
y f x 5x 6x 8
vi t  nh
4
D;
3
. Giá tr ca biu thc
2
2
5;6
5;6
A maxf x minf x
là:
A.
A 30 2 7
. B.
A 25 22
. C.
A 281 120 7 50 22
. D.
20
A
3
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 34: Cho hàm s
y f x 6x 7x 9
vi t  nh
9
D;
7
. Giá tr ca biu thc
2
2
3;4
3;4
A maxf x minf x
là:
A.
54
A
7
. B.
A 24 19
.
C.
A 18 2 3
. D.
A 259 48 19 72 3
.
Câu 35: Giá tr ln nht và giá tr nh nht ca hàm s
4x 3
y f x
5x 6
n
4;6
lt là:
A. Không tn ti GTLN, GTNN. B.
7
12
; không tn ti GTNN.
C. Không tn ti GTLN;
1
2
. . D.
71
;
12 2
.
Câu 36: Hàm s
y f x tanx cotx
t giá tr ln nhn
;
63
tm
x?
A.
4
. B.
9
. C.
6
. D.
5
.
Câu 37: Hàm s
y f x cosx sinx 1
có giá tr ln nhn
0;
là:
A.
1
. B.
2
. C.
33
4
. D.
0
.
Câu 38: Hàm s
33
y f x sin x cos x
có giá tr ln nht, giá tr nh nhn
0;
lt
là
12
y ,y
. hiu
12
yy
có giá tr bng:
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 39: Giá tr nh nht ca hàm s
x2
y f x e x x 1
n
0;2
là:
A.
0;2
miny 2e.
B.
2
0;2
miny e .
C.
0;2
miny 1.
D.
0;2
miny e.
Câu 40: Giá tr nh nht ca hàm s
x2
y f x e x -3
n
2;2
bng :
A.
2
2;2
miny e .
B.
2;2
miny 2e.
C.
2
2;2
miny e .
D.
2;2
miny 4e.
Câu 41: Giá tr ln nht ca hàm s
10 3sinx
y f x
2 sinx
là:
A.
13
3
. B.
7
. C.
5
. D.
1
.
Câu 42: Giá tr ln nht ca hàm s
7 2sinx
y f x
2 sinx
là:
A.
3
. B.
5
. C.
7
2
. D.
1
.
Câu 43: Giá tr ln nht ca hàm s
12 4sinx
y f x
2 sinx
là:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
16
3
. B.
8
. C.
6
. D.
1
.
Câu 44: Hai s có hiu
15
sao cho tích ca chúng là bé nht. S ln nht trong 2 s :
A.
15
2
. B.
15
2
. C.
225
4
. D. Không tn ti.
Câu 45: Hai s có hiu
10
sao cho tích ca chúng là bé nht. S ln nht trong 2 s :
A.
5
. B.
5
. C.
25
. D. Không tn ti.
Câu 46: Giá tr ln nht ca hàm s
1
y f x
cosx
trên khong
3
;
22
là:
A. Không tn ti. B. 1. C. . D. 1.
Câu 47: Giá tr nh nht ca hàm s
1
y f x
sinx
trên khong
0;
là:
A. 1. B. 1. C.
2
. D. Không tn ti.
Câu 48: Gi M là giá tr ln nht và m là giá tr nh nht ca hàm s
2
y f x x 1 x

Mm
bng:
A. 2. B. 1. C. 0. D.
1
.
Câu 49: Giá tr nh nht ca hàm s
2
y f x 3 x 2x 5
bng:
A.
miny 3.
B.
miny 5.
C.
miny 3 5.
D.
miny 0.
Câu 50: Giá tr nh nht ca hàm s
2
y f x x 2x 1
bng:
A.
1
min y .
2
B.
miny 0.
C.
miny 1.
D.
miny 2.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số” – P.2
Câu 01: Cho hàm s
2
y f x
4x 5 6
vi t  nh
5
D;
4
. Các giá tr
39
;
24
maxf x
;
39
;
24
minf x
lt là:
A.
1
;0
3
. B.
1
3
; không tn ti. C.
21
;
74
. D.
11
;
34
.
Câu 02: Cho hàm s
y f x 2x 3x 5
vi t  nh
5
D;
3
 t
2
2
2;7
2;7
A maxf x minf x
. Giá tr A bng ?
A.
299
. B.
299
. C.
18
. D.
5
.
Câu 03: Giá tr ln nht, giá tr nh nht ca hàm s
15 4sinx
y f x
5 2sinx
lt là ?
A.
3; 0
. B.
11 19
;
37
. C.
19 11
;
73
. D. Không tn ti.
Câu 04: Cho hàm s
2
2
2
cos x 1 sinx 2
y f x x
2 sinx
t
3
3
0;1
0;1
2
2
0;1
0;1
maxf x minf x
A
maxf x minf x
. Giá tr
A bng:
A.
0
. B.
35
13
. C.
1
. D.
91
75
.
Câu 05: Giá tr ln nht, giá tr nh nht ca hàm s
y sin 2x cos 2x
on
0;
2
lt
là:
A.
0;
0;
2
2
maxy 2; miny 1
. B.
0;
0;
2
2
maxy 2; miny 1
.
C.
0;
0;
2
2
maxy 2; min y 2
. D.
0;
0;
2
2
maxy 2; min y 2
.
Câu 06: Giá tr nh nht ca hàm s
3
y f x x 3x 5
n
0;2
là:
A.
2;4
miny 0
. B.
2;4
miny 3
. C.
2;4
miny 5
. D.
2;4
miny 7
.
Câu 07: Giá tr nh nht ca hàm s
32
y f x x 3x 9x 35
trên n
4;4
là:
A.
4;4
minf x 50
. B.
4;4
minf x 0
. C.
4;4
minf x 41
. D.
4;4
minf x 15
.
Câu 08: Giá tr ln nht ca hàm s
32
y f x x 8x 16x 9
n
1;3
là:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
1;3
maxf x 0
. B.
1;3
13
maxf x
27
. C.
1;3
maxf x 6
. D.
1;3
maxf x 5
.
Câu 09: Giá tr ln nht ca hàm s
42
y f x x 2x 1
n
0;2
là ?
A.
0;2
maxf x 64
. B.
0;2
maxf x 1
. C.
0;2
maxf x 0
. D.
0;2
maxf x 9
.
Câu 10: Giá tr nh nht ca hàm s
y f x x x 2 x 4 x 6
trên na khong
4;
là:
A.
4;
min y 8
. B.
4;
min y 16
. C.
4;
min y 17
. D.
4;
min y 9
.
Câu 11: Giá tr ln nht ca hàm s
32
1
y f x x 2x 3x 4
3
n
1;5
là ?
A.
8
3
. B.
10
3
. C.
4
. D.
10
3
.
Câu 12: Hàm s
42
y f x x 2x 1
có giá tr ln nht và giá tr nh nhn
0;2
lt
là ?
A.
9; 0
. B.
9; 1
. C.
2; 1
. D.
9; 2
.
Câu 13: Giá tr ln nht ca hàm s
x1
y f x
x2
n
0;2
là:
A.
1
4
. B.
2
. C.
1
2
. D.
0
.
Câu 14: Cho hàm s
2
x3
y f x
x2
. Kh giá tr ln nht và nh nht
ca hàm s n
3;4
?
A. Hàm s có giá tr nh nht bng
3
2
. B. Hàm s có giá tr ln nht bng 2.
C. Hàm s có giá tr ln nht bng 6.
D. Hàm s có giá tr ln nht bng
13
2
và giá tr nh nht bng
6
.
Câu 15: Hàm s
2
y x 2x 1
có giá tr ln nht và giá tr nh nhn
0;1
lt là
12
y ,y

12
y .y
bng:
A.
5
. B.
1
. C.
4
. D.
1
.
Câu 16: Cho hàm s
1
y f x 2x 1
2x 3
có tnh
3
D\
2
. M 

A. Không tn ti GTLN, GTNN trên D. B.
D
D
minf x 6; maxf x 2
.
C.
D
maxf x 2
; không tn ti GTNN. D.
D
maxf x 6
; không tn ti GTNN.
Câu 17: Cho hàm s
1
y f x 2x 1
3x 4
vi tnh
4
D;
3
. Ta xét các m

THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
1
Không tn ti
D
maxy
.
2
Không tn ti
D
min y
.
3
Hàm s ng bin trên .
4
Hàm s y nghch bin trên
D
.
5
11
y
3x 4
2x 1
.
6
11
y
2x 1 2 3x 4 3x 4
.
S m  ?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 18: Cho hàm s
2x 1
y f x
4x 5
vi tnh
5
D\
4
. Ta xét các kh
1
y 0, x
.
2
D
1
minf x
2
.
3
D
1
maxf x
2
.
4
1;2
3
maxf x
13
.
5
ng bin trên tng khong
5
;
4
và
5
;
4
ng bin trên .
S khnh sai là ?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 19: Cho
a
sao cho
2;4
2;4
a minf x maxg x
  
2
2
1
f x x , x \ 0
x
và
g x 0, x
. Trong s các m sau, m 
A.
a2
. B.
a2
. C.
a2
. D. Không tn ti
a
.
Câu 20: Cho các hàm s sau:
f x sinx cosx, x
;
g x sinx cosx, x
;
h x 1 2sinx, x
;
y 3cosx, x
. M  sau ?
A.
minf x 2
. B.
maxg x 2
. C.
minh x 1
. D.
max y 3
.
Câu 21: Hàm s
22
y f x x 1 x
có giá tr ln nht, giá tr nh nhn
1;1
lt
là:
A.
2 1; 0
. B.
2 1; 0
. C.
1; 1
. D.
1; 0
.
Câu 22: Giá tr ln nht ca hàm s
3
4
y f x 2sinx sin x
3
trên
0;
là ?
A.
0;
maxy 2
. B.
. C.
0;
maxy 0
. D.
0;
22
maxy
3
.
Câu 23: Giá tr nh nht ca hàm s
y f x 2 cos2x 4sinx
n
0;
2
là ?
A.
0;
2
min y 4 2
. B.
0;
2
min y 2 2
. C.
0;
2
min y 2
. D.
0;
2
min y 0
.
Câu 24: Giá tr nh nht ca hàm s
y f x 5cosx cos5x
vi
x;
44
là:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
;
44
min y 4
. B.
;
44
min y 3 2
. C.
;
44
min y 3 3
. D.
;
44
min y 1
.
Câu 25: Hàm s
y f x sinx 1
t giá tr ln nht trên n
;
22
bng ?
A.
2
. B.
2
. C.
0
. D.
1
.
Câu 26: Hàm s
y f x 9sinx sin3x
có giá tr ln nht và giá tr nh nht trên n
0;
ln
t là:
A.
8; 0
. B.
0; 8
. C.
1; 1
. D.
0; 1
.
Câu 27: Hàm s
y f x 3sinx cosx
có giá tr ln nht, giá tr nh nht lt là:
A.
0; 1
. B.
3; 0
. C.
3; 1
. D.
2; 2
.
Câu 28: Hàm s
2
y f x cos x 2cosx 1
có giá tr nh nht và giá tr ln nhn
0;
lt bng
12
y ,y
.  tích
12
y .y
có giá tr bng:
A.
3
4
. B.
4
. C.
3
8
. D.
1
.
Câu 29: Hàm s
y f x cos2x 2sinx
có giá tr ln nht, giá tr nh nhn
0;
2
ln
t là
12
y ,y
 tích
12
y .y
có giá tr bng ?
A.
5
. B.
1
. C.
1
4
. D.
0
.
Câu 30: Hàm s
y f x cos2x 4sinx 4
có giá tr ln nht, giá tr nh nhn
0;
2
là:
A.
;0
2
. B.
5; 1
. C.
5; 1
. D.
9; 1
.
Câu 31: Giá tr ln nht M, giá tr nh nht m ca hàm s
42
y f x sin x 4sin x 5
là:
A.
M 2; m 5
. B.
M 5; m 2
. C.
M 5; m 2
. D.
M 2; m 5
.
Câu 32: Giá tr ln nht M, giá tr nh nht m ca hàm s
42
y f x sin x cos x 2
là:
A.
11
M 3; m
4
. B.
11
M ; m 3
4
. C.
11
M 3; m
4
. D.
11
M ; m 3
4
.
Câu 33: Cho hàm s
2
2cos x cosx 1
y f x .
cosx 1
Gi M là giá tr ln nht và m là giá tr nh nht
ca hàm s 
Mm
bng:
A. 4. B. 5 . C. 6 . D. 3.
Câu 34: Cho hàm s
2
sinx 1
y f x .
sin x sinx 1
Gi M là giá tr ln nht và m là giá tr nh nht ca
hàm s n m 
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
2
Mm
3
. B.
M m 1
. C.
3
Mm
2
. D.
3
Mm
2
.
Câu 35: Giá tr ln nht ca hàm s
32
11
y f x x x 6x 3
32
on
0;4
là ?
A.
21
3
. B. 2. C. 1. D. 3.
Câu 36: Cho hàm s
2
y f x x 1 3
x
vi tnh
D 1;
. 3 là giá tr ca ?
A.
1;2
maxf x
. B.
2;3
maxf x
. C.
3;4
maxf x
. D.
4;5
maxf x
.
Câu 37: Cho hàm s
21
f x x x 2x 4
3 x 5
vi tnh
D 0;
. M  ?
A.
1;2 1;3
minf x minf x
. B.
1;2
3;4
minf x maxf x
. C.
2;3
0;1
maxf x minf x
. D.
5;6
3;4
maxf x minf x
.
Câu 38: Cho hàm s
y f x sinx
vi mi
x
. Giá tr
0;
4
maxf x
bng ?
A.
2
2
. B.
1
. C.
1
. D.
0
.
Câu 39: Giá tr nh nht ca hàm s
y f x cosx
n
;
42
bng ?
A.
2
2
. B.
0
. C.
1
. D.
1
.
Câu 40: Giá tr ln nht, giá tr nh nht ca hàm s
2
2x 3, khi x 2;1
y
31
x , khi x 1;5
44
n
2;5
lt là:
A.
4; 5
. B.
1; 5
. C.
4
, không tn ti GTNN . D.
4; 1
.
Câu 41: Giá tr ln nht ca hàm s
xx
y f x e 4e 3x
n
1;2
bng:
A.
2
2
1;2
4
maxy e 6.
e
B.
1;2
4
maxy e 3.
e
C.
1;2
max y 6e 3.
D.
1;2
maxy 5.
Câu 42: Giá tr ln nht ca hàm s
2x
y f x x.e
n
0;1
bng ?
A.
0;1
maxy 1.
B.
2
0;1
1
maxy .
e
C.
0;1
maxy 0.
D.
0;1
1
maxy .
2e
Câu 43: Gi M là giá tr ln nht và m là giá tr nh nht ca hàm s
2
y f x x ln 1 2x
trên
n
2;0
. 
Mm
bng :
A.
17
ln10
4
. B.
17
ln7
4
. C.
17 5
ln
42
. D.
15
ln10
4
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 44: Hàm s
1
y f x
sinx
n
5
;
36
có giá tr ln nht là M, giá tr nh nht là m. Khi

Mm
bng:
A.
2
2
3
. B. 1. C.
2
1
3
. D. 1.
Câu 45: Hàm s
y f x 2sinx sin2x
n
3
0;
2
có giá tr ln nht là M, giá tr nh nht
ng:
A.
33
. B.
33
. C.
33
4
. D.
33
4
.
Câu 46: Giá tr ln nht ca hàm s
y f x x 4 4 x 4 x 4 4 x 5
bng:
A.
4;4
maxy 10.
B.
4;4
maxy 5 2 2.
C.
4;4
maxy 7.
D.
4;4
maxy 5 2 2.
Câu 47: Giá tr ln nht ca hàm s
2
y f x 2sin x 2sinx 1
bng:
A.
maxy 4
. B.
3
maxy
2
. C.
maxy 3.
D.
max y 1.
Câu 48: Gi M là giá tr ln nht và m là giá tr nh nht ca hàm s
2
y f x x 1 x

Mm
bng:
A. 2. B. 1. C. 0. D.
1
.
Câu 49: Gi M là giá tr ln nht và m là giá tr nh nht ca hàm s
84
y f x 2sin x cos 2x
. Khi

Mm
bng ?
A.
28
27
. B. 4. C.
82
27
. D. 2.
Câu 50: Gi M là giá tr ln nht và m là giá tr nh nht ca hàm s
20 20
y f x sin x cos x
. Khi
ng ?
A.
1
512
. B. 1. C. 0. D.
513
512
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số” – P.3
Câu 01: Giá tr ln nht và giá tr nh nht ca hàm s
5x 4
y f x
6x 7
n
5;7
lt là:
A. Không tn ti GTLN, GTNN. B.
31
49
; không tn ti GTNN.
C. Không tn ti GTLN;
21
37
. D.
31 21
;
49 37
.
Câu 02: Giá tr ln nht và giá tr nh nht ca hàm s
6x 5
y f x
7x 8
n
6;8
lt là:
A. Không tn ti GTLN, GTNN. B.
43
64
; không tn ti GTNN.
C. Không tn ti GTLN;
31
50
. D.
43 31
;
64 50
.
Câu 03: Cho hàm s
2
y f x
6 5x 4
vi tnh
4
D;
5
. Giá tr
1;2
1;2
maxf x ; minf x
lt là:
A.
1
3
; không tn ti GTNN. B.
1 6 6
;
3 15
.
C.
2 6 6
;.
7 15
D.
2
7
; không tn ti GTNN.
Câu 04: Cho hàm s
1
y f x
5 4x 3
vi tnh
3
D;
4
. Giá tr
2;4
2;4
maxf x ;minf x
lt là:
A.
1
5
; không tn ti GTNN. B.
1 5 13
;.
5 12
C.
5 5 5 13
;.
20 12
D.
55
20
; không tn ti GTNN.
Câu 05: Cho hàm s
1
y f x
4 3x 3
vi tnh
D 1;
. Giá tr
2;4
2;4
maxf x ;minf x
lt là:
A.
1
4
; không tn ti GTNN. B.
11
;.
47
C.
4 3 1
;.
13 7
D.
43
13
; không tn ti giá tr nh nht.
Câu 06: Giá tr nh nht ca hàm s
y x 1
là ?
A. không có giá tr nh nht. B. có giá tr nh nht bng 1.
C. có giá tr nh nht bng 1. D. có giá tr nh nht bng 0.
Câu 07: Cho hàm s
2
y x x 1
. Kh
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A. Hàm s không có giá tr ln nht và giá tr nh nht.
B. Hàm s có giá tr nh nht bng
3
2
; không có giá tr ln nht.
C. Hàm s có giá tr ln nht bng
3
2
; giá tr nh nht bng
1
2
.
D. Hàm s có giá tr ln nht bng
3
2
; không có giá tr nh nht.
Câu 08: Hàm s
y 1 x 1 x
có giá tr ln nht, giá tr nh nht lt là ?
A.
2; 1
. B.
1; 0
. C.
2; 2
. D.
2; 1
.
Câu 09: Cho hàm s
y x 1 x 2
. Khnh sai ?
A. Hàm s không có giá tr nh nht. B. Hàm s có giá tr ln nht và giá tr nh nht.
C. Hàm s có giá tr ln nht bng
3
. D. Hàm s t giá tr ln nht ti
x2
.
Câu 10: Gi
12
y ,y
lt là giá tr ln nht, giá tr nh nht ca hàm s
11
y f x
x 1 x 2
n
3;4

12
y .y
là bao nhiêu ?
A.
3
2
. B.
5
6
. C.
5
4
. D.
7
3
.
Câu 11: Hàm s
1 1 1
y f x
x x 1 x 2
t giá tr ln nhn
5; 3
bng:
A.
13
12
. B.
11
6
. C.
47
60
. D.
11
6
.
Câu 12: Cho hàm s
y f x x x 1
. Kh
A. Hàm s có giá tr nh nht bng
3
4
và không có giá tr ln nht.
B. Hàm s có giá tr nh nht bng
3
4
và giá tr ln nht bng
1
.
C. Hàm s không có giá tr ln nht và giá tr nh nht.
D. Hàm s t giá tr ln nht t
x1
và giá tr ln nht bng
1
.
Câu 13: Hàm s
22
y f x 1 x 1 x
t giá tr nh nht lt tm
x
?
A.
0
. B.
1
. C.
2
. D.
2
.
Câu 14: Hàm s
44
y f x sin x cos x
có giá tr nh nht, giá tr ln nht lt là ?
A.
2; 1
. B.
0; 2
. C.
1
;1
2
. D.
0; 1
.
Câu 15: Hàm s
44
y f x sin x cos x
có giá tr ln nht bng:
A.
0
. B.
1
. C.
1
. D. Không tn ti.
Câu 16: Hai s có hiu
5
sao cho tích ca chúng là bé nht. S ln nht trong 2 s :
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
5
2
. B.
5
2
. C.
25
4
. D. Không tn ti.
Câu 17: Cho 3 s thc
a,b,c
tha mãn h 
a b c 15 0
a b c 15 0
và tích
ac
nh nht. S
ln nht trong 3 s
a,b,c
là:
A.
225
4
. B.
15
2
. C.
0
. D.
15
2
.
Câu 18: Trong các hình tr ni tip hình cu, bán kính
R2
th tích ln nht ca hình tr là:
A.
3
86
R
9
. B.
3
4 2R
. C.
3
43
R
9
. D.
0
.
Câu 19: Tng ca hai s
a,b
bng
24
, bit tích ca chúng là ln nht
2 2 2 2
32
a ab a b b
A
ab
,
giá tr ca biu thc
A
là:
A.
12
. B.
13
12
. C.
2
. D.
1
24
.
Câu 20: Hàm s
y f x 1 2sinx.cosx
t giá tr nh nhn
0;
2
ti:
A.
x
4
. B.
x
6
. C.
x0
và
x
2
. D.
x
3
.
Câu 21: Hàm s
66
y f x sin x cos x
có giá tr ln nht, giá tr nh nht lt là:
A.
1; 1
. B.
2; 0
. C.
1
;1
4
. D.
1
1;
4
.
Câu 22: Hàm s
22
y f x x 2x 3 x 2x 2
có giá tr ln nht là:
A. có giá tr ln nht là
0
. B. có giá tr ln nht là
8
.
C. có giá tr ln nht là
2
. D. không có giá tr ln nht.
Câu 23: Hàm s
2
2
x2
y f x
x1
có giá tr nh nht ti
x
?
A.
0
. B.
2
. C.
3
. D.
2
.
Câu 24: Hàm s
y x 1 x 2 x 3 x 4
có giá tr ln nht, giá tr nh nhn
1;3
là:
A.
9
10;
4
. B.
120; 1
. C.
10; 1
. D.
120; 1
.
Câu 25: Hàm s
y f x 1 x x 3 1 x. x 3
có giá tr ln nht, giá tr nh nht là ?
A.
2 2 2; 2
. B.
. C.
2 2; 2
. D.
2; 0
.
Câu 26: Hàm s
2
y f x x 2 2 x 2 4 x
t giá tr ln nht, giá tr nh nht ti
x
?
A.
2 2 4; 2
. B.
2 2 2; 2
. C.
2 2; 2
. D.
4; 2
.
Câu 27: Hàm s
3
y f x x 1 x 1
có giá tr nh nht, giá tr ln nhn
0;63
là:
A.
2; 12
. B.
1; 2
. C.
0; 2
. D.
0; 12
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 28: Hàm s
2
sinx 1
y
sin x 3
t giá tr ln nht, giá tr nh nhn
;
22
ti
x
?
A.
x,x
22
. B.
x,x
62
. C.
xx,
22
. D.
x 0,
2
x
.
Câu 29: Hàm s
2
2
11
y f x x x
x
x
có giá tr nh nht, giá tr ln nhn
1;3
là:
A.
112
3;
9
. B.
1; 4
. C.
112
1;
9
. D.
112
4;
9
.
Câu 30: Hàm s
2
84
y f x x x 1
t giá tr ln nht, giá tr nh nhn
1;2
lt
tm có hoà
12
x ;x

12
x .x
có giá tr bng:
A. 1. B. 2. C. 15. D. 0.
Câu 31: Hàm s
22
y f x x 3x x 3x 2
giá tr nh nht lt bng ?
A.
2
. B.
0
. C.
2
. D.
2
.
Câu 32: Hàm s
x
y f x x
x1
có giá tr ln nht và giá tr nh nhn
0;4
lt
là:
A.
8
;0
3
. B.
88
;
33
. C.
8
0;
3
. D.
24
;0
5
.
Câu 33: Trong s các hình ch nht có cùng chu vi 16 cm, hình ch nht có din tích ln nht bng ?
A. 64 cm
2
. B. 4 cm
2
. C. 16 cm
2
. D. 8 cm
2
.
Câu 34: Trong tt c các hình ch nht có cùng din tích 48 cm
2
, hình ch nht có chu vi nh nht
bng ?
A.
16 3
cm. B.
43
cm. C. 24 cm. D.
83
cm.
Câu 35: Tng ca hai s
a,b
bng
20
, bit tích ca chúng là ln nht
4 2 2 3
2
a ab a b b
A
ab
,
giá tr ca biu thc
A
là ?
A.
10
. B.
110
. C.
1300
11
. D.
400
.
Câu 36: Hia hai s không âm
a,b
bng
36
, bit tích ca chúng là nh nht.
t
3 2 2 2
32
a ab a b b
A
ab
, giá tr ca biu thc
A
là ?
A.
6
. B.
0
. C.
1
6
. D.
1
.
Câu 37: Cho 1 tam giác
ABC
vuông ti
A
, tam giác
ABC
có tng ca 1 cnh góc vuông và 1 cnh
huyn bng
3
. Din tích ln nht có th tn ti c
A.
1
. B.
2
. C.
3
. D.
3
2
.
Câu 38: Hai s có hiu là 13, tích ca chúng bé nht khi hai s ng ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A. 5; 8. B. 1; 12. C.
13 13
;
22
. D. 6; 7 .
Câu 39: Mt chm chuyng theo quy lut
23
S 6t t ,
vn tc
v m / s
ca chuyng
t giá tr ln nht ti thm
ts
bng ?
A.
2s
. B.
12 s
. C.
6s
. D.
4s
.
Câu 40: Tam giác vuông có din tích ln nht là bao nhiêu nu tng ca mt cnh góc vuông và cnh
huyn bng hng s
a a 0
?
A.
2
a
63
. B.
2
a
9
. C.
2
2a
9
. D.
2
a
33
.
Câu 41: Mt hp tác xã nuôi cá thí nghim trong hi ta thy rng nu trên m din
tích ca mt h có n con cá thì trung bình mi con cá sau mt v cân nng
P n 480 20n
(gam).
Hi phi th bao nhiêu cá trên m din tích ca mt h  sau mt v thu hoc nhiu
gam cá nht ?
A. 12. B. 24. C. 6. D. 32.
Câu 42:  gim huyt áp ca mt bc cho bi công thc
2
G x 0.025x 30 x ,
trong
ng thuc tiêm cho bc tính bng miligam). Ling thuc cn
tiêm cho b huyt áp gim nhiu nht bng ?
A. 100 mg. B. 20 mg. C. 30 mg. D. 0 mg.
Câu 43: Mt con cá h   t khong cách là 300 km. Vn t  c là
6 km / h
. Nu vn tng yên là
v km / h
ng tiêu hao ca cá
trong t gi c cho bi công thc
3
E v cv t,
ng s và E tính bng Jun. Vn t
c ng tiêu hao là ít nht bng:
A.
6 km / h
. B.
8 km / h
. C.
7 km / h
. D.
9 km / h
.
Câu 44: Sau khi phát hin mt bnh dch, các chuyên gia y t c tính s i nhim bnh k t
ngày xut hin bn ngày th t là
23
f t 45t t , t 0,1,2,...,25.
Nu coi
ft
là
hàm s n
0;25
o hàm
ft
c xem là t truyn bi/ngày) ti
thnh ngày mà t truyn bnh là ln nht ?
A. Ngày th 19. B. Ngày th 5. C. Ngày th 16. D. Ngày th 15.
Câu 45: Cho
ABC
u ci ta dng mt hình ch nht MNPQ có cnh MN nm trên BC,
nh P, Q theo th t nm trên hai cnh AC và AB ca nh v trí cm M sao
cho hình ch nht có din tích ln nht ?
A.
2a
BM
3
. B.
3a
BM
4
. C.
a
BM
3
. D.
a
BM
4
.
Câu 46: Mt hp không nc làm t mt mnh các tông theo m. H
mt hình vuông cnh x cm, chiu cao h cm và có th tích 500 cm
3
. Giá tr c din tích ca mnh
các tông nh nht bng:
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A. 100. B. 300. C. 10. D. 1000.
Câu 47: Trong các hình tr ni tip hình cu bán kính R, hình tr có th tích ln nht bng ?
A.
3
4R
3
. B.
3
4R
33
. C.
3
R
33
. D.
3
4R
3
.
Câu 48: Cho mt tm nhôm hình vuông ci ta ct 4 góc 4 hình vuông bng nhau, ri
gp tm nhôm l c mt cái hp không np. Tìm cnh ca hình vuông b ct sao cho th tích
ca khi hp là ln nht ?
A.
5a
6
. B.
a
6
. C.
a
12
. D.
a
9
.
Câu 49: Giá tr ln nht M, giá tr nh nht m ca hàm s:
2
y f x 2sin x 2sinx 1
là:
A.
3
M 1,m
2
. B.
M 3,m 1
. C.
3
M 3,m
2
. D.
3
M ,m 3
2
.
Câu 50: Giá tr ln nht M, giá tr nh nht m ca hàm s
y f x 2cos2x 2sinx
là:
A.
9
M ,m 4
4
. B.
M 4,m 0
. C.
9
M 0,m
4
. D.
9
M 4,m
4
.
x
x
h
h
h
h
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 4: Đƣờng tiệm cận” – P.1
Câu 01: Cho hàm s
mx 1
y f x C
x m 1
. Vi giá tr nào ca m thì tam giác to bng
tim cng thng
y 2x 1
có chu vi là
6 2 5
?
A.
5
. B.
5
. C.
9 3 5
. D.
3 5 9
.
Câu 02: Cho hàm s
2x 1
y f x C
3x 2
. Tính din tích tam giác to bng tim cn c th
hàm s ng thng
y 2x 1
?
A.
5
12
. B.
25
18
. C.
5
6
. D.
25
36
.
Câu 03: Cho
ax 2
C : y
2x 3a
i xng ca
C
m ca tim cng và
trc hoành, O là gc t, P là gm tim cn ngang và trc tung. Hình ch nht MNOP có
din tích là 4. Tìm tt c các giá tr ca
a?
A.
43
3
. B.
43
3
. C.
43
3
. D.
4
.
Câu 04: Vi giá tr nào ca m thì
1
2
x2
C : y f x
2mx m
và
2
2
x3
C : y g x
m x 2m
s có
i xng ?
A.
m2
. B.
m2
. C.
m0
. D. Không có m tha.
Câu 05: Cho hàm s
2
m 1 x 2
y f x C
m x 2m

C
có tim cn ngang trùng vi tim
cn ngang ca
1
2x 2
C : y
x1
?
A.
1
2
. B.
0
. C.
1
. D.
2
.
Câu 06:  th hàm s
2x 3
y f x
x1
ng tim cng và tim cn ngang lt là ?
A.
x1
và
y3
. B.
x2
và
y1
. C.
x1
và
y2
. D.
x1
và
y2
.
Câu 07:  th hàm s
1 3x
y f x
x2
ng tim cng và tim cn ngang lt là ?
A.
x2
và
y3
. B.
x2
và
y1
. C.
x2
và
y3
. D.
x2
và
y1
.
Câu 08:  th hàm s
2
2x 3
y f x
x 3x 2
ng tim cng và tim cn ngang lt
là:
A.
x 1, x 2
và
y0
. B.
x 1, x 2
và
y2
.
C.
x1
và
y0
. D.
x 1, x 2
và
y3
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 09:  th hàm s
2
2
1 3x
y f x
x 6x 9
ng tim cng và tim cn ngang lt
là ?
A.
x3
và
y3
. B.
x3
và
y0
. C.
x3
và
y1
. D.
y3
và
x3
.
Câu 10:  th hàm s
2
3
3x x 2
y f x
x8
ng tim cng và tim cn ngang lt
là ?
A.
y2
và
x0
. B.
x2
và
y0
. C.
x2
và
y3
. D.
y2
và
x3
.
Câu 11: S ng tim cn c th hàm s
1x
y f x
3 2x
là ?
A. 4. B. 1. C. 0. D. 2.
Câu 12: S ng tim cn c th hàm s
1
y f x
3x 2
là ?
A. 1. B. 3. C. 4. D. 2.
Câu 13: S ng tim cn c th hàm s
2
x1
y f x
x4
là ?
A. 4. B. 2. C. 1. D. 3.
Câu 14: S ng tim cn c th hàm s
2
x
y f x x
x 3x 4
là ?
A. 4. B. 3. C. 2. D. 5.
Câu 15: Cho hàm s
x2
y f x
x3
khây là khnh sai ?
A.  th hàm s có tim cng
x3
. B. Hàm s nghch bin trên
\3
.
C.  th hàm s có tim cn ngang là
y1
. D.  th hàm s i xng là
I 3;1
.
Câu 16: Cho hàm s
2
2
x2
y f x
2x 2mx m
  th hàm s có duy nht mt tim cn
ng và tim ct parabol
2
P : y x 2x 2
t là 2 ?
A.
m2
. B.
m0
. C.
m2
. D.
m1
.
Câu 17: Cho
2x 1
y f x
x3
 th hàm s
y f x
có:
A. ng thng
x3
là tim cng thng
y2
là tim cn ngang.
B. ng thng
x3
là tim cng thng
y2
là tim cn ngang.
C. ng thng
x3
là tim cng thng
y5
là tim cn ngang.
D. ng thng
x3
là tim cng thng
y0
là tim cn ngang.
Câu 18: Cho hàm s
y f x
tha
f 3 1
 th ca nó có hai tim ci xng qua gc
t, hàm s  là hàm s nào trong các hàm s c li
A.
2
x
y
x1
. B.
2
x2
y
x4
. C.
2
x6
y
x4
. D.
2
x3
y
x 2x 3
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 19:  th hàm s y có tim cng và tim cn ngang ?
A.
y ax b, a 0
. B.
42
y ax bx d, a 0
.
C.
32
y ax bx acx d, 0
. D.
ax b
y , c 0, ad bc 0
cx d
.
Câu 20: Trong các hàm s  th ca hàm nào có tim cng ?
A.
2
2
2x 3
y
x 2x 4
. B.
3
4
x 2x
y
x1
. C.
. D.
y sinx
.
Câu 21:  th hàm s nào trong các hàm s ng tim cn ?
A.
1 2x
y
1x
. B.
2
1
y
4x
. C.
x3
y
5x 1
. D.
2
x
y
x x 9
.
Câu 22: Cho hàm s
4
2
2
x 9x
y f x
3x 3
. Kh
A.  th hàm s có tim cng, không có tim cn ngang.
B.  th hàm s có 2 tim cng, có 1 tim cn ngang
y3
.
C.  th hàm s có 2 tim cng, có 1 tim cn ngang
y1
.
D.  th hàm s không có tim cng, có tim cn ngang.
Câu 23:  th hàm s m cng ?
A.
2
3x 1
y
x1
. B.
1
y
x
. C.
x3
y
x2
. D.
2
1
y
x 2x 1
.
Câu 24:  th hàm s m cn ngang ?
A.
. B.
42
x 3x 7
y
2x 1
. C.
2
3
y
x1
. D.
3
y1
x2
.
Câu 25:  th   th ca hàm s 
A.
x1
y
x1
. B.
3x
y
x1
. C.
x2
y
x1
. D.
x2
y
x1
.
Câu 26:  th hàm s
3x 1
y f x
3x 2

8
6
4
2
2
4
6
8
15
10
5
5
10
15
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
x3
. B.
x1
. C.
y3
. D.
y1
.
Câu 27:  th hàm s
2x 1
y f x
x2
ng tim cn ?
A. 1. B. 2. C. 3. D. 0.
Câu 28: S ng tim cn c th hàm s
2
2x 1
y f x
x 3x 2
là ?
A. 0. B. 1. C. 2. D. 3.
Câu 29: Cho hàm s
mx 9
y f x
xm
 th
C
. Kt lu ?
A. Khi
m3
thì
C
ng tim cn ngang.
B. Khi
m3
thì
C
ng tim cn ngang.
C. Khi
m3
thì
C
có tim cng
x m,
tim cn ngang
ym
.
D. Khi
m0
thì
C
không có tim cn ngang.
Câu 30: Tìm tt c ng tim cn c th hàm s
2
x3
y
x1
?
A.
y1
. B.
x1
. C.
y1
. D.
y1
.
Câu 31: Vi giá tr nào ca
m
  th
mx 1
C : y f x
2x m
có tim c    m
M 1; 2
?
A.
2
m
2
. B.
m0
. C.
1
m
2
. D.
m2
.
Câu 32: Cho hàm s
mx n
y f x
x1
  th
C
. Bit tim cn ngang ca
C
 m
A 1;2
ng thm
I 2;1
thuc
C
 ca
mn
là ?
A.
m n 1
. B.
m n 1
. C.
m n 3
. D.
m n 3
.
Câu 33: S tim cn ca hàm s
2
2
x 1 x
y f x
x 9 4
là ?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 34: Giá tr ca
m
  th hàm s
xm
y f x
mx 1
không có tim cng là ?
A.
m0
m1
. B.
m1
. C.
m1
. D.
m1
.
Câu 35: S tim cn ca hàm s
2 3 2
3
x 1 x 3x 1
y f x
x1
là ?
A. 3. B. 2. C. 1. D. 4.
Câu 36:  th hàm s
3x 1
y f x
2x 4
có tim cng là ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
3
x
2
. B.
x2
. C.
y2
. D.
3
y
2
.
Câu 37:  th hàm s nào không có tim cng ?
A.
. B.
. C.
2
x3
y
x
. D.
.
Câu 38: Tim cng c th hàm s
y f x
nu có thì luôn:
A. Song song vi trc tung. B. Song song vi trc hoành.
C. Vuông góc vi trc tung. D. Song song hoc trùng vi trc tung.
Câu 39:  th hàm s m cn ngang ?
A.
2
2x 4
y
x2
. B.
4
y 2x 5
3x 2
. C.
y tanx
. D.
2x 3
y
5x
.
Câu 40:  th hàm s
2x 4
y f x
x1
có tim cn ngang là ?
A.
x2
. B.
y1
. C.
x1
. D.
y2
.
Câu 41:  th hàm s
2
x 2x 2 mx
y f x
x2
ng tim cn ngang vi:
A.
m
. B.
m1
. C.
m0
m1
. D.
m0
.
Câu 42:  th hàm s
2
x x 1 mx
y f x
x1
ng tim cng khi:
A.
m0
. B.
mR
. C.
m1
. D.
m1
.
Câu 43: S ng tim cn c th hàm s
2
2
4x
y f x
x 3x 4
là ?
A. 1. B. 0. C. 2. D. 3.
Câu 44: S tim cn c th hàm s
2
x1
x 1
x
y f x
2x
x 1
x1
neáu
neáu
?
A. 1. B. 2. C. 3. D. 4.
Câu 45: Xác nh
m
  th hàm s
2
x 2m 3 x 2 m 1
y f x
x2
không có tim cng ?
A.
m2
. B.
m2
. C.
m3
. D.
m1
.
Câu 46: Xác nh
m
  th hàm s
22
3
y f x
4x 2 2m 3 x m 1
m cn
ng ?
A.
13
m
12
. B.
1 m 1
. C.
3
m
2
. D.
13
m
12
.
Câu 47: Xác nh
m
  th hàm s
22
x1
y
x 2 m 1 x m 2
m cng ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m1
3
m
2
m3
. B.
3
m
2
m1
. C.
3
m
2
. D.
3
m
2
.
Câu 48: Tìm tt c các giá tr thc ca tham s
m
  th hàm s
2
y f x x mx 1
có tim
cn ngang ?
A.
0 m 1
. B.
m1
. C.
m1
. D.
m1
.
Câu 49: Cho hàm s
2
32
x x 3 2x 1
y f x
x 2x x 2
. Trong các khnh sau, khnh nào là
kh
A.  th hàm s không có tim cng, không có tim cn ngang.
B.  th hàm s không có tim cm cn ngang.
C.  th hàm s m cng và 2 tim cn ngang.
D.  th hàm s m cng và 1 tim cn ngang.
Câu 50: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
2
x1
y f x
mx 1
có
hai tim cn ngang ?
A.
m0
. B.
m0
. C.
m0
. D. Không có
m
tha.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 4: Đƣờng tiệm cận” – P.2
Câu 01:  th hàm s nào trong các hàm s m cn ngang ?
A.
3
y 4 2x
x1
. B.
2
2
x 2x 3
y
x9
. C.
. D.
x
y2
.
Câu 02: N th hàm s
y f x
có tim cn ngang thì:
A. Tim cn ngang luôn trùng vi trc hoành. B. Tim cn ngang luôn song song vi trc hoành
C. Tim cn ngang luôn song song vi trc tung.
D. Tim cn ngang luôn vuông góc vi trc tung.
Câu 03: Tim cng và tim cn ngang c th hàm s nu có thì luôn:
A. Ct nhau ti gc t. B. Song song nhau.
C. Song song hoc trùng nhau. D. Vuông góc nhau.
Câu 04:  th hàm s nào trong các hàm s m cn ?
A.
4
y 2x 1
x1
. B.
y tanx
. C.
42
x 3x 2
y
6
. D.
x
ye
.
Câu 05: Cho hàm s
2
5
y f x
x2
và các m sau:
1
 th hàm s luôn ni trc hoành.
2
 th hàm s có tim cng là
x2
.
3
 th hàm s không có tim cn ngang.
4
: Hàm s o hàm
4
10x 2
y'
x2
.
5
: Hàm s luôn nghch bin trên tnh .
Các m không chính xác là ?
A.
3
. B.
5
. C.
1 , 2
. D.
3 , 4 , 5
.
Câu 06: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
1x
y f x
xm
có
tim cng ?
A.
m1
. B.
m1
. C.
m1
. D. Không có
m
tha.
Câu 07: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
32
x1
y f x
x 3x m
t tim cng ?
A.
m
. B.
m0
m4
. C.
m0
m4
. D.
m0
m4
.
Câu 08: Tìm tt c các giá tr thc ca tham s
m
   th ca hàm s
22
x mx 2m
y f x
x2
có tim cng ?
A. Không có
m
tha. B.
m2
m1
. C.
m
. D.
m2
m1
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 09: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
2
5x 3
y f x
x 2mx 1
không có tim cng ?
A.
m1
m1
. B.
1 m 1
. C.
m1
. D.
m1
.
Câu 10: Cho hàm s
2x 1
y f x
x1
 th
C
. Gi
M
là mm bt kì trên
C
. Tip tuyn
ca
C
ti
M
cng tim cn ca
C
ti
A
và
B
. Gi
I
m cng tim
cn ca
C
. Tính din tích ca tam giác
IAB
?
A.
2
. B.
12
. C.
4
. D.
6
.
Câu 11: S ng tim cn c th hàm s
2
x3
y f x
x1
là ?
A. 2. B. 0. C. 1. D. 3.
Câu 12: S ng tim cn c th hàm s
2
1x
y f x
x2
là ?
A. 0. B. 1. C. 3. D. 3.
Câu 13:  th hàm s
2
y f x x x 4x 2
có tim cn ngang là ?
A.
y2
. B.
y2
. C.
y2
. D.
x2
.
Câu 14: m M thu th hàm s
2x 1
y f x
x1
sao cho khong cách t n tim cn
ng bng khong cách t n trc hoành ?
A.
M 0; 1
M 3;2
. B.
M 2;1
M 4; 3
. C.
M 0; 1
M 4;3
. D.
M 2;1
M 3;2
.
Câu 15: S tim cn c th hàm s
2
x x 2
y f x
x2
là ?
A. 0. B. 1. C. 2. D. 3.
Câu 16: i xng c th hàm s
2x 1
y f x
5x
là ?
A.
2
5;
5
. B.
2
;5
5
. C.
5; 2
. D.
2;5
.
Câu 17:  th hàm s
2
x3
y f x
2 4x
có bao nhiêu tim cn ?
A. 2. B. 1. C. 0. D. 3.
Câu 18:  th hàm s
2
2
3x
y f x
2x 3x
có:
A. 1 tim cng và 1 tim cn ngang. B. 2 tim cng.
C. 2 tim cng, 1 tim ngang. D. Ít nht 3 tim cn.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 19:  th hàm s
3
y f x 2x
x5
có :
A. Tim cn ngang là
y 2x
. B. Tim cn ngang là
x5
.
C. Tim cng là
x5
. D. Tim cng là
y5
.
Câu 20: Tim cn c th hàm s
y f x
m
M(3,2)
và vuông góc trc hoành có th là
?
A. ng thng
y 3x 2
. B. Tim cn ngang
y2
.
C. Tim cng
x3
. D. u sai.
Câu 21: S tim cn c th hàm s
2
2
x x 2
y f x
x2
là ?
A. 0. B. 1. C. 2. D. 3.
Câu 22: S tim cn c th hàm s
2
x2
y f x
x1
là ?
A. 1. B. 0. C. 3. D. 2.
Câu 23: Cho hàm s
x2
y f x C
x3
. Có tt c m M thuc
C
sao cho khong
cách t n tim cn ngang bng 5 ln khong cách t n tim cng ?
A. 4. B. 3. C. 2. D. 1.
Câu 24:  th hàm s
x2
y f x
3x 9
ng tim cng là
xa
ng tim cn ngang
là
yb
. Giá tr ca s nguyên m nh nht tha mãn
m a b
là ?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 25: Cho hàm s
2x 3
y f x C
x2
. Gi
M
m bt k trên
C
, d là tng khong cách t
M
ng tim cn c th
C
. Giá tr nh nht ca d là ?
A. 5. B. 10. C. 6. D. 2.
Câu 26: Cho hàm s
2x 3
y f x C
x2
. Gi d là khong cách t m ca 2 tim cn ca
C
n mt tip tuyn bt k c th
C
. Giá tr ln nht ca d là:
A.
22
. B.
3
. C.
33
. D.
2
.
Câu 27: Cho hàm s
2x 3
y f x C
x2
. Gi d là tip tuyn bt kì ca
C
, d cng tim
cn c th
C
lt tng cách gia A và B ngn nht bng:
A.
4
. B.
32
. C.
22
. D.
33
.
Câu 28: Cho hàm s
mx 9
y f x
xm
 th
C
. Kt lu ?
A. Khi
m3
thì
C
ng tim cn ngang.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
B. Khi
m3
thì
C
ng tim cn ngang.
C. Khi
m3
thì
C
có tim cng
x m,
tim cn ngang
ym
.
D. Khi
m0
thì
C
không có tim cn ngang.
Câu 29: Tìm tt c ng tim cn c th hàm s
2
x3
y f x
x1
?
A.
y1
. B.
x1
. C.
y1
. D.
y1
.
Câu 30: S tim cn ca hàm s
2
2
x 1 x
y f x
x 9 4
là ?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 31: Giá tr ca
m
  th hàm s
xm
y f x
mx 1
không có tim cng là ?
A.
m0
m1
. B.
m1
. C.
m1
. D.
m1
.
Câu 32: S tim cn c th hàm s
2 3 2
3
x 1 x 3x 1
C : y f x
x1
là ?
A. 3. B. 2. C. 1. D. 4.
Câu 33:  th hàm s
2
x 2x 2 mx
y f x
x2
ng tim cn ngang vi:
A.
m
. B.
m1
. C.
m 0;m 1
. D.
m0
.
Câu 34:  th hàm s
2
x x 1 mx
y f x
x1
ng tim cng khi:
A.
m0
. B.
mR
. C.
m1
. D.
m1
.
Câu 35: S ng tim cn c th hàm s
2
2
x4
y f x
x 3x 4
là ?
A. 1. B. 0. C. 2. D. 3.
Câu 36:  th hàm s
2
x
y f x
x4
có ?
A. 1 tim cng, 1 tim cn ngang. B. 2 tim cng, 1 tim cn ngang.
C. 2 tim cng, 2 tim cn ngang. D. 1 tim cng, 2 tim cn ngang.
Câu 37:  th hàm s m cn ?
A.
. B.
3
y
15x 1
. C.
2
2
x1
y
x 5x 6
. D.
.
Câu 38: Cho hàm s
2
2
3x 4
y f x
x 5x 6
. Chn phát bi
A.
x0
không là tim cng c th hàm s.
B. Hàm s không xác nh trên
/ 2; 3
.
C.  th hàm s ng tim cng. D. Hàm s u trên toàn b .
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 39:  th hàm s
2x a
y f x
4x 9
m
A 2,0
. Tim cng c th hàm s này
là ?
A.
x1
. B.
9
x
4
. C.
1
x
2
. D.
x1
.
Câu 40:  th
C
ca hàm s
ax 3
y f x
2x 1

A 2,1
i xng ca
C
là ?
A.
2,1
. B.
1
,2
2
. C.
1
,1
2
. D.
11
,
22
.
Câu 41: S tim cn c th hàm s
2
x1
x 1
x
y f x
2x
x 1
x1
neáu
neáu
?
A. 1. B. 2. C. 3. D. 4.
Câu 42: Xác nh
m
  th hàm s
2
x 2m 3 x 2 m 1
y f x
x2
không có tim cng ?
A.
m2
. B.
m2
. C.
m3
. D.
m1
.
Câu 43: Xác nh
m
  th hàm s
22
3
y f x
4x 2 2m 3 x m 1
m cn
ng ?
A.
13
m
12
. B.
1 m 1
. C.
3
m
2
. D.
13
m
12
.
Câu 44: Xác nh
m
  th hàm s
22
x1
y f x
x 2 m 1 x m 2
m cng
?
A.
3
m
2
m 1,m 3
. B.
3
m ,m 1
2
. C.
3
m
2
. D.
3
m
2
.
Câu 45: Tìm tt c các giá tr thc ca tham s
m
  th hàm s
2
y f x x mx 1
có tim
cn ngang ?
A.
0 m 1
. B.
m1
. C.
m1
. D.
m1
.
Câu 46: Cho hàm s
2
32
x x 3 2x 1
y f x
x 2x x 2
. Trong các khnh sau, khnh nào là
kh ?
A.  th hàm s không có tim cng, không có tim cn ngang.
B.  th hàm s không có tim cm cn ngang.
C.  th hàm s m cng và 2 tim cn ngang.
D.  th hàm s m cng và 1 tim cn ngang.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 47: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
2
x1
y f x
mx 1
có
hai tim cn ngang ?
A.
m0
. B.
m0
. C.
m0
. D. Không có
m
tha.
Câu 48: Tìm tt c các giá tr thc ca tham s
m
sao cho  th ca hàm s
1x
y f x
xm
có
tim cng ?
A.
m1
. B.
m1
. C.
m1
. D. Không có
m
tha.
Câu 49: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
32
x1
y f x
x 3x m
t tim cng ?
A.
m
. B.
m0
m4
. C.
m0
m4
. D.
m0
m4
.
Câu 50: Tìm tt c các giá tr thc ca tham s
m
   th ca hàm s
22
x mx 2m
y f x
x2
có tim cng ?
A. Không có
m
tha. B.
m2
m1
. C.
m
. D.
m2
m1
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“Chuyên đề 4: Đƣờng tiệm cận” – P.3
Câu 01: nh hàm s
2x a
y f x
5x b
 th
C
ca hàm s m cng
x2

P 3;1
:
A.
2x 2
y
5x 10
. B.
2x 1
y
5x 10
. C.
2x 3
y
5x 10
. D.
2x
y
5x 10
.
Câu 02: Hàm s
y f x
tha mãn các tính cht sau:
1
ng bin trên các khonh.
2
nh ti
x2
.
3
Tim cn ngang c th hàm s nm trên trc hoành và cách trc hoành mn
d3
.
Hàm s  là ?
A.
2
3x
y
x2
. B.
. C.
2
3x 2
y
x2
. D.
2
2
3x 1
y
x4
.
Câu 03: Cho
32
2x 3
, x 2
C : y f x
4 2x
x 3x 1, x 2
. Kh
A.
C
không có tim cn. B.
C
có tim cng.
C.
C
có tim cn ngang. D.
C
có nhit tim cn.
Câu 04: Cho:
2
x 6x 5
y f x
2x 3
ng thng:
1
1
d : x
2
,
2
1
d : y
2
,
3
3
d : y
2
. Các
ng thng có th là tim cn c th là ?
A.
1
d
. B.
2
d
. C.
3
d
. D. C u sai.
Câu 05: Cho hàm s
2
2
1 x , 1 x 1
x2
y f x , x 1
x1
x , x 1
. Phát biu nào sau 
A.
D
là tnh ca hàm s
y f x
. B. Hàm s nhn giá tr 0 khi bin
x0
.
C.
x1
là tim cng c th hàm s
y f x
.
D.
y1
là tim cn ngang c th hàm s
y f x
.
Câu 06: Tìm tt c các giá tr thc ca tham s
m
 th ca hàm s
2
5x 3
y f x
x 2mx 1
không có tim cng ?
A.
m1
m1
. B.
1 m 1
. C.
m1
. D.
m1
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 07: Cho hàm s
2x 1
y f x
x1
 th
C
. Gi
M
là mt m bt kì trên
C
. Tip tuyn
ca
C
ti
M
cng tim cn ca
C
ti
A
và
B
. Gi
I
m cng tim
cn ca
C
. Tính din tích ca tam giác
IAB
?
A.
2
. B.
12
. C.
4
. D.
6
.
Câu 08:  th hàm s
2
y f x x x 4x 2
có tim cn ngang là ?
A.
y2
. B.
y2
. C.
y2
. D.
x2
.
Câu 09: m M thu th hàm s
2x 1
y f x
x1
sao cho khong cách t n tim cn
ng bng khong cách t n trc hoành ?
A.
M 0; 1 ; M 3;2
. B.
M 2;1 ; M 4;3
. C.
M 0; 1 ; M 4;3
. D.
M 2;1 ; M 3;2
.
Câu 10: Cho hàm s
x2
y f x C
x3
. Có tt c m M thuc
C
sao cho khong
cách t n tim cn ngang bng 5 ln khong cách t n tim cng ?
A. 4. B. 3. C. 2. D. 1.
Câu 11:  th hàm s
x2
y f x
3x 9
ng tim cng là
xa
ng tim cn ngang
là
yb
. Giá tr ca s nguyên m nh nht tha mãn
m a b
là ?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 12: Cho hàm s
2x 3
y f x C
x2
. Gi
M
m bt k trên
C
, d là tng khong cách t
M
ng tim cn c th
C
. Giá tr nh nht ca d là ?
A. 5. B. 10. C. 6. D. 2.
Câu 13: Cho hàm s
2x 3
y f x C
x2
. Gi d là khong cách t m ca 2 tim cn ca
C
n mt tip tuyn bt k c th
C
. Giá tr ln nht ca d là ?
A.
2
. B.
3
. C.
33
. D.
2
.
Câu 14: Cho hàm s
2x 3
y f x C
x2
. Gi d là tip tuyn bt kì ca
C
, d cng tim
cn c th
C
lt ti A, B. ng cách gia A và B ngn nht bng ?
A.
4
. B.
32
. C.
22
. D.
33
.
Câu 15:  th hàm s
2
2x
y f x
x 2x 1
ng tim cn ?
A. 3. B. 2. C. 1. D. 0.
Câu 16:  th hàm s
2
2
1
y f x
x 2 m 1 x m 1 4
có bao nhiêu tim cn ?
A.
2
. B.
3
. C.
1
. D. Không th nh.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 17: Cho
i, j
l t là tim c ng c  th ca hai hàm s
2x 5
y f x
x3
và
2
2
x2
y g x
x4
. Khnh 
A.
ij
. B.
ij
. C.
ij
. D.
i, j
không tn ti.
Câu 18: Vi giá tr nào ca
m
 th hàm s
2
mx 1
y f x
2x 3
có tim cn ngang ?
A.
0
. B.
2
. C.
3
2
. D.
1
.
Câu 19:  th hàm s
2
6
y f x
x 2ax 6a 7
có tim cng khi ?
A.
a7
. B.
a7
. C.
a7
a1
. D.
a1
.
Câu 20:  th hàm s có tim c
M 3;1
và có dng
x1
y f x
2x m
. Giá tr ca
m
là:
A.
2
. B.
3
. C.
1
2
. D.
23
.
Câu 21: ng tim cn c th hàm s
2
2
x x 1
y f x
x1
?
A.
y 1, x 1
. B.
y 1, x 1
. C.
yx
. D.
y1
.
Câu 22: ng tim cn c th hàm s
2
x 2x 5
y f x
x1
?
A.
y 1, x 1
. B.
y 1, x 1
.
C.
y 1, y 1, x 1
. D. Không tn ti tim cn.
Câu 23: ng tim cn c th hàm s
2
2
x 6x 3
y f x
x 3x 2
?
A.
y 1, x 1
. B.
y 1, x 2
.
C.
y 1, x 2, x 1
. D. Không tn ti tim cn.
Câu 24: Cho 3 hàm s
5x
1 y f x
2x
,
2
x
2 y g x
x1
,
2
x2
3 y h x
x 3x 2
. Hàm s
 th nhng thng
x2
làm tim cn ?
A.
1 , 3
. B.
1
. C.
1 , 2
. D.
3
.
Câu 25: ng thm cn c th hàm s
32
3
x 3x
y f x
x
?
A.
y1
. B.
y1
. C.
. D.
yx
.
Câu 26:  th hàm s
2
2
x
y f x
x 4x
ng tim cn ?
A. 2. B. 0. C. 3. D. 1.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
Câu 27: ng tim cn c th hàm s
3
y f x 1
2x 3
?
A.
3
y , 2x 3 0
2
. B.
y 1, 2x 3 0
.
C.
y 5x 1, 2x 3 0
. D.
y 2x 3, 2x 3 0
.
Câu 28:  th hàm s
3
3
x 2x
y f x
x
có tim cn là ?
A.
y x 1
. B.
yx
. C.
y 1, x 0
. D.
y 1, x 0
.
Câu 29: Vi giá tr nào ca
m
 th hàm s
2
2x 3x m
y f x
xm
không có tim cn ?
A.
m0
. B.
m1
m2
. C.
m0
m1
. D.
m1
.
Câu 30: Vi giá tr nào ca
m
 th hàm s
mx 1
y f x
2x m
có tim cm
?
A.
2
m
2
. B.
1
m
2
. C.
m0
. D.
m2
.
Câu 31: Có bao nhiêu giá tr
m
  th hàm s
2
2
mx 1
y f x
x 3x 2
ng têm cn ?
A. 3. B. 2. C. 1. D.
m
.
Câu 32: nh giá tr ca
m
  th hàm s
2
2x mx m
y f x
x1
c to  ?
A.
m1
. B.
m1
. C.
m2
. D.
m0
.
Câu 33: Bi th hàm s
2
2
2a b x ax 1
y f x
x ax a b 6
nhn trc hoành và trc tung làm tim cn.
Hãy tính tích
a.b
?
A. 8. B. 6. C. 4. D. 2.
Câu 34: ng cong
2
x 5x 6
C : y f x
x
. Tìm kh
A.
C
ch có tim cng. B.
C
có tim cn xiên.
C.
C
có hai tim cn. D.
C
có ba tim cn.
Câu 35:  th hàm s nào trong các hàm s m cn ngang ?
A.
2
2
x x 1
y
x1
. B.
1
y
x1
. C.
2
x1
y
x1
. D.
.
Câu 36: Gi
lt là tng s tim cng ca:
2
x 2x 3
y f x
x3
;
2x 2
y g x
x1
;
2
2
x 3x 1
y h x
x 4x 5
;
2
x
y u x
x4
;
 ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m n p q
. B.
q p n m
. C.
m n p q
. D.
m n p q
.
Câu 37:  th hàm s m cng tim cn là
21
;
33

A 3;1
. Hàm s
 là ?
A.
. B.
. C.
. D.
.
Câu 38: Cho hàm s
2
22
3mx 2m 9
y f x
3m 2 x 2
. Vi giá tr nào ca
m
 th hàm s có tim cn
ngang
y3
?
A.
1
. B.
1
3
. C.
2
3
. D.
3
.
Câu 39:  th hàm s a mãn khong cách t m ca nó vi trn
tim cn ngang ca nó bng
1
2
?
A.
. B.
x2
y
2x 1
. C.
. D.
.
Câu 40: ng thng
xa
và
yb
lt là tim cng và tim cn ngang c th
hàm s
22
2
m 2m 4 x 2m 1
y f x
3m 2 x 9
, vi
m
là nghi    
2
m 4 0,
a
và
b
lt có nhng giá tr ?
A.
4
a 1, b
9
. B.
4
a 1, b
9
. C.
4
a 1, b
9
. D.
3
a , b 1
2
.
Câu 41: Tim cn ngang c th hàm s
2
x x 1. x 1. 2x 1
y f x
x x 1
là ?
A.
y1
. B.
x 0, x 1
. C.
x2
. D.
y2
.
Câu 42: Cho hàm s
2mx 3
y f x
2 3x
, giá tr  ng tim cn to vi hai trc t mt
hình ch nht có din tích bng
1
3
là ?
A.
3
m
4
. B.
3
m
4
. C.
4
m
3
. D.
3
m
4
.
Câu 43:   th hàm s
2
3
y f x
x x m 2
m cng ?
A.
9
m
4
. B.
4
m
9
. C.
9
m
4
. D.
9
m
4
.
Câu 44:   th hàm s
2
1
y f x
x mx 3
m cng ?
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
A.
m 2 3
m 2 3
. B.
m2
. C.
m2
. D.
m2
.
Câu 45: Tìm   th hàm s
2
2
x x 3
y f x
x mx 3
t tim cn ?
A.
m3
m3
. B.
m 2 3
. C.
2 3 m 2 3
. D.
m 2 3
m 2 3
.
Câu 46:  th ca hàm s
mx 2
y f x
xn
có tim cn ngang là
y1
m
A 3; 1
thì hàm s là ?
A.
x2
y
x2
. B.
x2
y
x2
. C.
x2
y
x2
. D.
2
y
x2
.
Câu 47:  th ca hàm s
ax b
y f x
x1
có tim cn ngang là
y4
m
A 2;0
thì
tích
a.b
bng:
A. 32. B. 12. C. 8. D. 4.
Câu 48: Gi x, y, z lt là s ng tim cn ca các  th hàm s sau:
1 2x
y f x
x4
,
2
x2
y g x
x3
,
2
25
y h x
2x 3x 4
. Kh
A.
x y z
. B.
y x z
. C.
z x y
. D.
z y x
.
Câu 49: Cho hai hàm s
2
2x 1
y f x
m 8 x
và
5 2x
y g x
x4
. Tp hp các giá tr ca tham s
 ng tim cng c th hàm s trên trùng nhau là ?
A.
2;2
. B.
1;2
. C.
0
. D.
2;3
.
Câu 50: Cho hàm s
2
2
4x 15x 4
y
2x x 6
  ng thng:
33
x 4, x 2, x 2, x , x , y 2
22
ng thng nào là tim cn c th hàm s 
A.
3
x 4, x 2, x
2
. B.
3
x 2, x , y 2
2
.
C.
3
x 4, x , y 2
2
. D.
x 4, x 2, y 2
.
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 0975108292)
“BÀI GIẢNG VIDEO & PHƢƠNG PHÁP GIẢI chi tiết CHỈ CÓ TẠI KHÓA HỌC TP – 2K”
https://www.facebook.com/tranminhtien.hcmus
https://www.facebook.com/phongmath.casio
Mọi góp ý về đề thi, lời giải của các câu hỏi trắc nghiệm và lời phản biện của quý độc giả, quý thầy cô,
các bạn học sinh –– sinh viên vui lòng soạn thành các file PDF, file PPT và gửi trực tiếp qua các đƣờng
link FB – cá nhân trên để đƣợc đính chính các thắc mắc và giải đáp vƣớng mắc. Trân trọng và cảm ơn.
VIDEO KHAI GIẢNG KHÓA HỌC TP2K:
https://youtu.be/-2r7gGCpud0
LINK ĐĂNG KÝ HỌC LUYỆN THI 2018:
goo.gl/LdM2zn
| 1/76
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 1: Sự đồng biến, nghịch biến của hàm số” – P.1
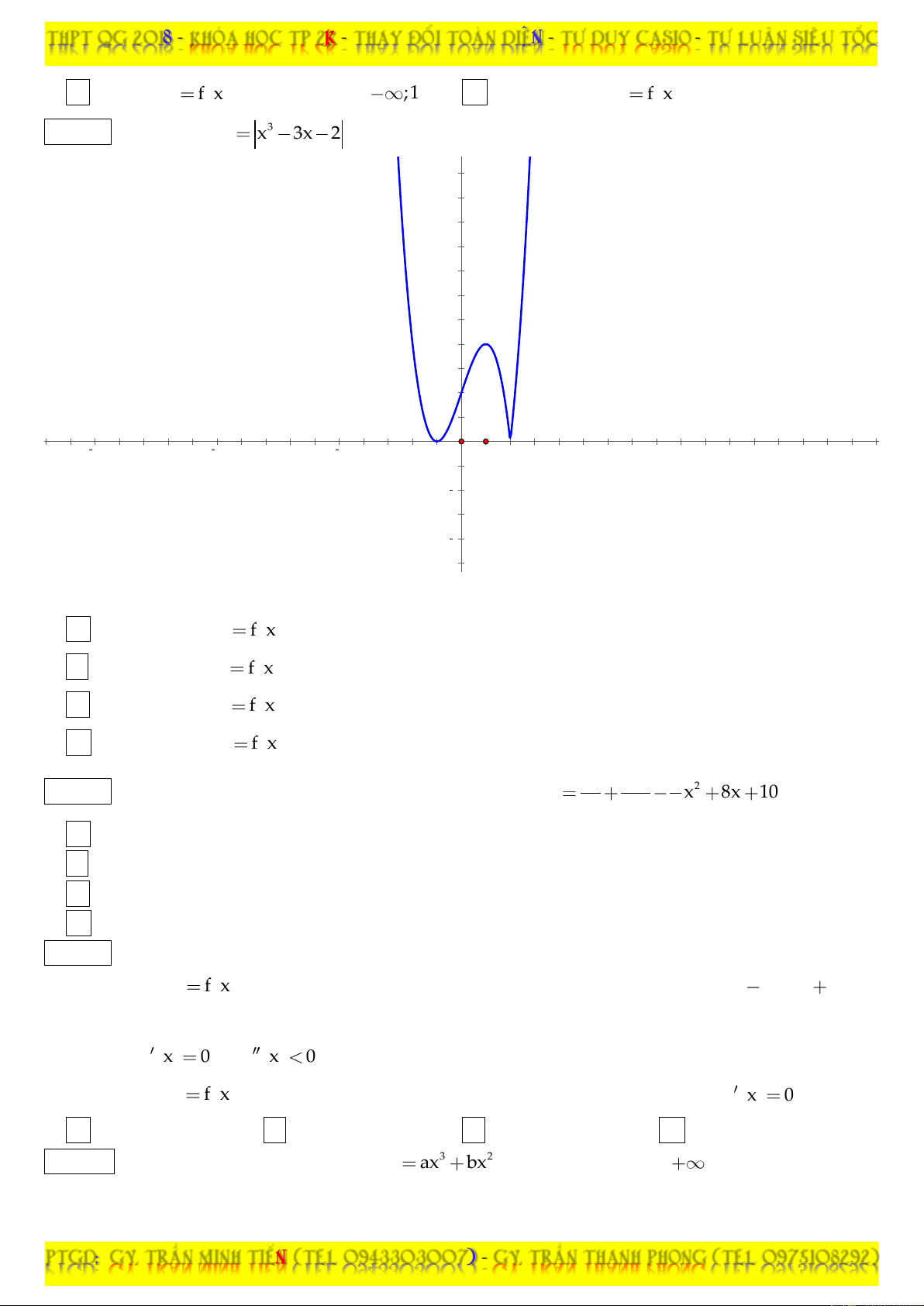
Câu 01: Cho hàm số 4 2 y 3x 6x
13 . Hàm số nghịch biến trên khoảng nào trong các khoảng đã cho dưới đây ? 1 2 3 A. ; . B. ; 0 . C. 1; 3 . D. 1; . 4 2
Câu 02: Cho các khoảng bên dưới, hàm số 2 3 y sin x x , x ; nghịch biến trên các 2 khoảng nào ? 5 3 9 1 ; 2 ; 3 0 ; 4 ; 6 4 10 12 4 3 7 5 ; 0 6 ; 2 4 12 A. 1 , 3 , 5 . B. 2 , 3 , 4 . C. 2 , 3 , 5 . D. 1 , 3 , 6 . 1 5
Câu 03: Cho hàm số 4 3 2 y x x 4x
4x 10 . Tìm khẳng định sai trong các khẳng định dưới ? 4 3 3 7
A. Hàm số đồng biến trên ; .
B. Đạo hàm của hàm số đổi dấu hai lần. 2 3
C. Hàm số nghịch biến trên ; 0 .
D. Khoảng đồng biến dài nhất là 1; . 2 x
Câu 04: Cho hàm số y
. Đồ thị hàm số đổi chiều mấy lần ? 2 x 1 A. 2. B. 4. C. 3. D. 1.
Câu 05: Hàm số nào sau đây có khoảng đồng biến là 2; 5 ? 3x 1 1 A. y . B. 3 2 y x 2x 5x 3 . x 2 3 1 9 x 5 C. 4 2 y x x 1 . D. y . 4 2 x 3
Câu 06: Đâu là khẳng định sai trong các khẳng định đã cho dưới đây ? 3x 2 A. Hàm số y
luôn đồng biến trên từng khoảng xác định. x 1 2 x B. Hàm số y
luôn nghịch biến trên từng khoảng xác định. x 5 C. Hàm số 3 2 y x 3x 9x
5 nghịch biến trên ; 9 . D. Hàm số 4 2 y x 2x 5 đồng biến trên 9; .
Câu 07: Xét các khẳng định sau: 3 x I . Hàm số y x 1 nghịch biến trên . II . Hàm số y ln x 1 đồng biến trên tập x 1
xác định của nó.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC x III . Hàm số y đồng biến trên . 2 x 1
Hỏi có bao nhiêu khẳng định đúng ? A. 3. B. 2. C. 1. D. 0.
Câu 08: Cho hàm số y
x 1 x 2 . Khẳng định nào sau đây là khẳng định sai ? 1
A. Hàm số nghịch biến trên khoảng 1; .
B. Hàm số nghịch biến trên khoảng ; 1 . 2 1
C. Hàm số đồng biến trên các khoảng ; 1 và ; . 2 1 1
D. Hàm số nghịch biến trên khoảng 1;
và đồng biến trên khoảng ; . 2 2
Câu 09: Cho hàm số y x
3 2 2 x . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng
; 2 và đồng biến trên khoảng 2; 2 .
B. Hàm số đồng biến trên khoảng
; 2 và nghịch biến trên khoảng 2; 2 .
C. Hàm số đồng biến trên khoảng
;1 và nghịch biến trên khoảng 1; 2 .
D. Hàm số nghịch biến trên khoảng
;1 và đồng biến trên khoảng 1; 2 .
Câu 10: Cho hàm số y cos 2x sin 2x.tan x, x ;
. Khẳng định nào sau đây là khẳng định 2 2 đúng ?
A. Hàm số luôn giảm trên ; .
B. Hàm số luôn tăng trên ; . 2 2 2 2
C. Hàm số không đổi trên ; .
D. Hàm số luôn giảm trên ; 0 . 2 2 2
Câu 11: Đâu là mệnh đề đúng trong các mệnh đề sau ? A. Hàm số 3 2 y x 6x
3x 4 có khoảng đồng biến là 2 3; 0 . B. Hàm số 2 y x 5x
3 có khoảng nghịch biến là 3; . 2x 5 C. Hàm số y
có khoảng nghịch biến dài nhất là 2 ; . x 3 2 x 3x 2 D. Hàm số y
luôn đồng biến trên từng khoảng xác định. x 1
Câu 12: Cho các hàm số sau: 4x 3 4 5 1 y 3 2 2 y x 3x 2x 1 4 2 3 y x 4x 3 3 2 4 y x 5x 6x 27 2x 1 3 3 x 4 1 1 5 y 4 3 2 6 y x x x 11 2 x 2x 4 4 2
Tìm các hàm số có đồ thị không đổi chiều biến thiên trên từng khoảng xác định của chúng? A. 2 , 3 , 5 . B. 1 , 4 , 5 . C. 1 , 3 , 6 . D. 2 , 5 , 6 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 13: Cho các phát biểu sau: 1 Hàm số 3 2 y x 3x
12x 1 có khoảng nghịch biến là 3; . 2 Hàm số y
2x 11 tan x luôn đồng biến trên . 3 Hàm số 4 3 2 y 6x 8x 3x
1 có đồ thị đổi chiều biến thiên ba lần. 1 sin x 4 Hàm số y , x 0 ;
luôn nghịch biến trên khoảng xác định. 1 sin x 2 3x 1 1 5 Hàm số y
có khoảng đồng biến dài nhất là ; . 2 x 2 2 x 2x 3 6 Hàm số y có phương trình y' 0 có nghiệm duy nhất. x 5 Số phát biểu đúng là: A. 5. B. 3. C. 1 . D. 0.
Câu 14: Cho hàm số 3 2 y 2x 3x
12x 10 . Khẳng định nào sau đây chính xác nhất ?
A. Hàm số giảm trên ; 21 .
B. Hàm số tăng trên ; 2 1; .
C. Hàm số tăng trên ; 2 và 1; .
D. Hàm số giảm trên 2 ; 1 .
Câu 15: Cho hàm số 4 2 y 3x 6x
13 . Xác định khoảng trong các khoảng đã cho bên dưới mà hàm
số nghịch biến trên khoảng đó: 1 2 3 A. ; . B. ; 0 . C. 1; 3 . D. 1; . 4 2 Câu 16: Hàm số y
f x đồng biến trên khoảng a; b . Khẳng định nào sau đây là khẳng định sai ? A. Hàm số y f x
1 đồng biến trên a; b . B. Hàm số y f x 1 nghịch biến trên a; b . C. Hàm số y
f x nghịch biến trên a; b . D. Hàm số y f x 1 đồng biến trên a; b .
Câu 17: Cho hàm số 3 y x
3x . Nhận định nào dưới đây là nhận định đúng ?
A. Tập xác định D 3; 0 3; .
B. Hàm số nghịch biến trên 1;1 .
C. Hàm số nghịch biến trên các khoảng 1; 0 và 0;1 .
D. Hàm số đồng biến trên các khoảng ; 3 và 3; .
Câu 18: Cho hàm số 2 y 2x
x . Hàm số nghịch biến trên khoảng nào dưới đây ? A. 0; 2 . B. 0;1 . C. 1; 2 . D. 1;1 . 2 x 2x
Câu 19: Cho hàm số y . Hãy chọn câu đúng ? x 1
A. Hàm số nghịch biến trên \ 1 .
B. Hàm số nghịch biến trên ;1 và đồng biến trên 1; .
C. Hàm số đồng biến trên
;1 và nghịch biến trên 1; .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
D. Hàm số đồng biến trên mỗi khoảng ;1 và 1; .
Câu 20: Tìm m để hàm số 3 2 y x 3x
3mx 1 nghịch biến trên khoảng 0; ? A. m 1. B. m 1. C. m 1. D. m 1. 2 x 3x 5
Câu 21: Hỏi hàm số y
nghịch biến trên khoảng nào trong các khoảng dưới đây ? x 1 A. ; 4 , 2; . B. 4; 2 , 2; . C. ; 1 , 1; . D. 4; 1 , 1; 2 . 3 x
Câu 22: Hỏi hàm số 2 y 3x 5x
2 nghịch biến trên khoảng nào trong các khoảng dưới đây ? 3 A. 5; . B. 2; 3 . C. ;1 . D. 1; 5 . 3
Câu 23: Hỏi hàm số 5 4 3 y x 3x 4x
2 đồng biến trên khoảng nào trong các khoảng dưới đây ? 5 A. ; 0 . B. . C. 0; 2 . D. 2; .
Câu 24: Cho hàm số 3 2 y ax bx
cx d . Hỏi hàm số luôn đồng biến trên khi nào ? a b 0, c 0 a b 0, c 0 a b 0, c 0 a b c 0 A. . B. . C. . D. . 2 a 0, b 3ac 0 2 a 0, b 3ac 0 2 a 0, b 3ac 0 2 a 0, b 3ac 0
Câu 25: Cho hàm số 3 2 y x 3x
9x 15 . Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số nghịch biến trên khoảng 3;1 .
B. Hàm số đồng biến trên .
C. Hàm số đồng biến trên 9; 5 .
D. Hàm số đồng biến trên khoảng 5; . 4
Câu 26: Cho hàm số 3 2 y x 5x 6x
216 . Cho các phát biểu sau, chọn câu trả lời đúng. 3 3 3 1 Hàm số tăng trên 1; . 2 Hàm số giảm trên ; 1 ; . 2 2 x 1 6 6 3 3 Hàm số tăng trên 1; , ; . 4 y' 0 3 . 5 5 2 x 2 A. 1 , 3 . B. 1 , 2 , 3 . C. 1 , 3 , 4 . D. 1 , 2 . 1 x
Câu 27: Cho hàm số y
. Mệnh đề nào sau đây là đúng: 2x 1 1 1 1
A. Hàm số đồng biến trên \ .
B. Hàm số nghịch biến trên ; ; 2 2 2 1 1
. C. Hàm số nghịch biến trên ; và ; . 2 2 1
D. Hàm số nghịch biến trên \ . 2 4
Câu 28: Cho hàm số 3 2 y x 2x x
7 . Mệnh đề nào sau đây là đúng ? 3
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 1 1
A. Hàm số đồng biến trên ; .
B. Hàm số nghịch biến trên ; . 2 2 1
C. Hàm số nghịch biến trên ; .
D. Hàm số nghịch biến trên . 2 2 2x x 26
Câu 29: Cho hàm số y
. Có bao nhiêu khoảng đồng biến của hàm số đã cho ? x 2 1 ; 1 15 2 1;1 3 10 ; 4 1 15 ; 5 5 3; 0 6 6 ; 3 7 ; 1 15 8 1 15 ; 1 2 A. 0. B. 1. C. 3. D. 2.
Câu 30: Cho hàm số y 2x 5
x . Hàm số đồng biến trên khoảng nào trong các khoảng dưới đây ? 5 2 15 A. 2 ; 5 . B. ; 3 . C. 4 ; 5 . D. 2 ; . 2 2 3 x Câu 31: Hàm số 2 y mx 4x đồng biến trên khi: 3 m 2 A. 2 m 2 . B. . C. m 2 . D. m 2 . m 2 3 x Câu 32: Hàm số 2 y mx 4x nghịch biến trên khi: 3 m 2 A. 2 m 2 . B. . C. m 2 . D. m 2 . m 2
Câu 33: Với giá trị nào của m thì hàm số y
2m 1 x mcos x đồng biến trên ? A. m 1. B. m 1. C. 1 m 1. D. m .
Câu 34: Tìm m để hàm số 3 2 y x 3x 4mx 2 nghịch biến trên ; 0 ? 3 3 3 3 A. m . B. m . C. m . D. m . 4 4 4 4
Câu 35: Cho hàm số 3 2 2 y x m 1 x m 2 x m . Tìm câu đúng.
A. Hàm số đồng biến trên 2; 4 .
B. Hàm số luôn nghịch biến trên .
C. Hàm số có cả khoảng đồng biến và khoảng nghịch biến.
D. Hàm số luôn nghịch biến trên 2 m; m 1 . m m 3 3m 1
Câu 36: Cho hàm số 3 2 y x x x
m . Với m nằm trong tập hợp nào sau đây 3 2 2
để hàm số đồng biến trên ? 9 5 A. A x : x 1 . B. B ; 1; . 5 9
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 5 C. C ;1 . D. D x : x 0 . 9 m 2m 1
Câu 37: Cho hàm số 3 2 y x x
3m 2 x 7 . Tìm m để hàm số luôn đồng biến trên 3 2 ? A. m 1. B. m 1 . C. m 1.
D. Không tìm được m. m 2
Câu 38: Cho hàm số 3 2 y x m 2 x m 1 x
3m . Giá trị nguyên m là nhỏ nhất để 3
hàm số luôn đồng biến trên trên ? A. 2. B. 3. C. 4. D. 0. mx 2m
Câu 39: Cho hàm số y
. Có bao nhiêu giá trị nguyên âm m để hàm số luôn nghịch biến x m
trên từng khoảng xác định ? A. 1 . B. 2. C. 3. D. 4. 1
Câu 40: Tìm m để hàm số 3 2 y x mx 4x đồng biến trên ? 3 A. 2 m 2 . B. 2 m 2 . C. m 2 . D. m 2 .
Câu 41: Cho hàm số 2 3 y 3x
x . Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số đồng biến trên khoảng 0; 2 .
B. Hàm số đồng biến trên các khoảng ; 0 , 2; 3 .
C. Hàm số nghịch biến trên các khoảng ; 0 , 2; 3 .
D. Hàm số nghịch biến trên khoảng 2; 3 . x
Câu 42: Cho hàm số 2 y sin x,x 0;
. Hỏi hàm số đồng biến trên các khoảng nào ? 2 7 11 7 11 A. 0; và ; . B. ; . 12 12 12 12 7 7 11 7 11 11 C. 0; và ; . D. ; và ; . 12 12 12 12 12 12
Câu 43: Cho hàm số 2 y
x cos x . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số luôn đồng biến trên .
B. Hàm số luôn nghịch biến trên .
C. Hàm số đồng biến trên k ;
và nghịch biến trên khoảng ; k . 4 4
D. Hàm số nghịch biến trên k ;
và đồng biến trên khoảng ; k . 4 4
Câu 44: Cho các hàm số sau: 1 x 1 3 2 I : y x x 3x 4 II : y 3 x 1
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 III : y x 4 3 IV : y x 4x sin x 4 2 V : y x x 2
Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định ? A. 2. B. 4. C. 3. D. 5.
Câu 45: Cho các hàm số sau: 3 2 I : y x 3x 3x 1 II : y sin x 2x x 2 3 III : y x 2 IV : y 1 x
Hỏi hàm số nào nghịch biến trên toàn trục số ? A. I , II .
B. II , I , III .
C. II , I , IV . D. II , III . 1
Câu 46: Cho hàm số y 3x 5
. Chỉ ra khoảng đồng biến có độ dài lớn nhất trong các x 2 khoảng dưới đây ? 13 11 3 5 8 A. ; 4 . B. ; 6 . C. ; 1 . D. ; . 6 2 2 2 3 2x 3
Câu 47: Cho hàm số y
. Tìm ra khoảng nghịch biến có độ dài nhỏ nhất trong các khoảng 2x 1 dưới đây ? 1 6 5 2 15 4 13 3 15 7 A. ; 2 . B. ; . C. ; . D. ; . 2 5 2 2 2 2 2
Câu 48: Cho hàm số y 1 2x
x 3 . Đồ thị hàm số đã cho có bao nhiêu điểm gãy ? A. 0 . B. 2 . C. 3 . D. 4 .
Câu 49: Trong các hàm số sau hàm số nào đồng biến trên khoảng xác định của chúng ? 2x 3 2x 3 2x 3 2x 3 A. y . B. y . C. y . D. y . x 1 x 1 x 1 x 2
Câu 50: Cho hàm số 2 y 3 2x
x . Hàm số đã cho có khoảng đồng biến có độ dài bé nhất là: A. 3; 1 . B. 1; 0 . C. 1;1 . D. 1; 2 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 1: Sự đồng biến, nghịch biến của hàm số” – P.2 1
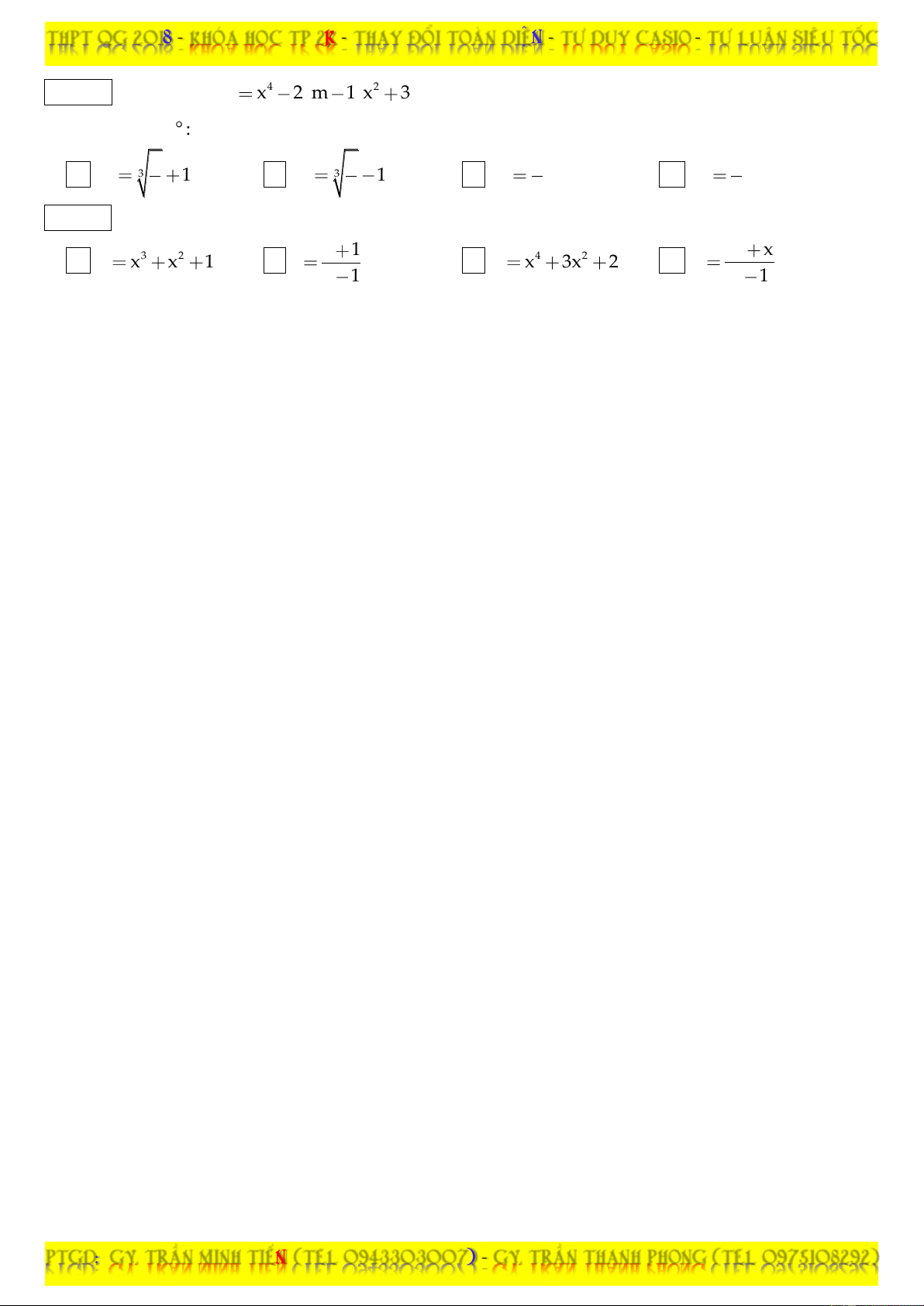
Câu 01: Cho hàm số 3 2 y x m 3 x m 1 x
4 . Có bao nhiêu giá trị của m sao cho hàm số 3
tăng trên đoạn có độ dài bằng 4 (để rõ hơn, có thể hiểu là khoảng đồng biến có độ dài bé nhất bằng 4). A. 5 . B. 3 . C. 4 . D. 2 .
Câu 02: Cho hàm số 3 2 y x 3mx 3mx
4 . Tại giá trị nào của m thì hàm số đã cho giảm trên
đoạn có độ dài bằng 1 (để rõ hơn, có thể hiểu là khoảng nghịch biến có độ dài bé nhất bằng 1) ? 1 2 2 5 2 3 A. m . B. m . C. m . D. m . 2 2 3 3 3 3x m
Câu 03: Cho hàm số y
. Trong tất cả các giá trị của m để hàm số nghịch biến trên 2x 1 1 ;
, thì m không thể bằng ? 2 1 5 2 3 A. . B. 5 . C. . D. . 2 3 3
Câu 04: Cho hàm số 3 2 y mx 2x
mx 1. Giá trị nhỏ nhất của m để hàm số đã cho đồng biến trên 1; 2 là ? 1 1 2 3 3 A. m . B. m . C. m . D. m . 2 2 3 3 2 3 2 mx 6x 2
Câu 05: Cho hàm số y
. Tìm tất cả các giá trị m để hàm số đồng biến trên 1; 0 ? x 2 1 1 10 A. m . B. m . C. m 3 . D. m . 2 2 3 3
Câu 06: Cho hàm số 4 2 y x
2x . Chọn phương án sai:
A. Hàm số đồng biến trên mỗi khoảng 1; 0 , 1; .
B. Hàm số đồng biến trên mỗi khoảng 1; 2 , 3; .
C. Hàm số nghịch biến trên mỗi khoảng ; 1 , 0;1 .
D. Hàm số đồng biến trên ; 2 2; .
Câu 07: Hàm số nào sau đây đồng biến trên ? 1 x 1 A. y x . B. 4 y x . C. 3 2 y x 6x 17x 4 . D. y . x x 1
Câu 08: Hàm số nào sau đây đồng biến trên mỗi khoảng xác định của nó ? x 2 x 2 x 2 x 2 A. y . B. y . C. y . D. y . x 2 x 2 3x 2 2x 2
Câu 09: Hàm số có chiều biến thiên khác với chiều biến thiên của các hàm số còn lại trên 0; ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC x 2 A. f x . B. 3 2 f x x 6x 17x 4 . x 2 2 x 2x 3 C. 3 f x x x cos x 4 . D. f x . x 1
Câu 10: Hàm số nào có chiều biến thiên khác với chiều biến thiên của các hàm số còn lại trên ? A. 3 f x x x cos x 4 . B. f x sin 2x 2x 3 . C. 3 f x x x cos x 4 . D. f x cos 2x 2x 3 . x 1
Câu 11: Cho hàm số y
. Khẳng định nào sao đây là khẳng định đúng ? 1 x
A. Hàm số nghịch biến trên khoảng ;1 1; .
B. Hàm số đồng biến trên khoảng ;1 1; .
C. Hàm số nghịch biến trên các khoảng ;1 và 1; .
D. Hàm số đồng biến trên các khoảng ;1 và 1; .
Câu 12: Cho hàm số 3 2 y x 3x 3x
2 . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số luôn nghịch biến trên .
B. Hàm số luôn đồng biến trên .
C. Hàm số nghịch biến trên khoảng ;1 1; .
D. Hàm số đồng biến trên khoảng
;1 và nghịch biến trên khoảng 1; .
Câu 13: Cho hàm số 4 2 y x 4x 10 và các khoảng sau: I : ; 2 II : 2; 0 III : 0; 2
Hỏi hàm số đồng biến trên các khoảng nào ? A. Chỉ I . B. I và II . C. II và III . D. I và III . 3x 1
Câu 14: Cho hàm số y
. Khẳng định nào sau đây là khẳng định đúng ? 4 2x
A. Hàm số luôn nghịch biến trên .
B. Hàm số luôn nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên các khoảng ; 2 và 2; .
D. Hàm số nghịch biến trên các khoảng ; 2 và 2; .
Câu 15: Hỏi hàm số nào sau đây luôn nghịch biến trên ? A. 4 2 h x x 4x 4 . B. 3 2 g x x 3x 10x 1. 4 4 C. 5 3 f x x x x . D. 3 2 k x x 10x cos x . 5 3
Câu 16: Trong các phát biểu sau, phát biểu nào đúng ? A. Hàm số y
f x đồng biến trên a ; b khi f x 0 , x a ; b . B. Hàm số y
f x nghịch biến trên a ; b khi f x 0 , x a ; b .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC C. Hàm số y
f x là hàm hằng trên a ; b khi f x 0 , x a ; b . D. Hàm số y
f x đồng biến trên a ; b khi f x 0 , x a ; b .
Câu 17: Cho hàm số y
f x có đạo hàm trên a ; b với a , b là hai nghiệm phân biệt của phương trình f x 0 (phương trình f x
0 chỉ có 2 nghiệm). Khẳng định sai ?
A. Hàm số đồng biến trên a ; b khi f ' x 0 , với x a ; b . 0 0 f x f x x , x a ; b
B. Hàm số đồng biến trên a ; b khi 2 1 0 , với 1 2 . x x 2 1 x x 1 2
C. Hàm số nghịch biến trên a ; b khi f ' x 0 , với x a ; b . 0 0 f x f x x , x a ; b
D. Hàm số là hàm hằng trên a ; b khi 2 1 1, với 1 2 . x x 2 1 x x 1 2
Câu 18: Trong các phát biểu sau, phát biểu nào sai ? A. Hàm số y
f x đồng biến trên c ; d khi f x 0 , x c ; d . m nx B. Hàm số y
nghịch biến trên từng khoảng xác định khi nq mp 0 . px q f x f x x , x a ; b C. Hàm số y
f x đồng biến trên a ; b khi 2 1 0 , với 1 2 . x x 2 1 x x 1 2 D. Hàm số y f x là hàm hằng khi f ' x 0 , x c ; d . 2
Câu 19: Tìm m để hàm số 3 2 y x m 1 x 2mx 5 đồng biến trên 0; 2 : 3 2 2 2 2 A. m . B. m . C. m . D. m . 3 3 3 3 1 1
Câu 20: Tìm m để hàm số 3 2 y x mx m 2 x
đồng biến trên đoạn có độ dài bằng 4. 3 3 m 2 m 2 A. . B. m 2 . C. m 3 . D. . m 3 m 2
Câu 21: Tìm m để hàm số 3 2 y x 6x
mx 1 đồng biến trên khoảng 0; ? A. m 0 . B. m 12 . C. m 0 . D. m 12 . x m 2
Câu 22: Tìm m để hàm số y
giảm trên mỗi khoảng xác định của nó ? x 1 A. m 1. B. m 1 . C. m 3 . D. m 3 .
Câu 23: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 x mx 2 2x 1 có hai nghiệm thực ? 7 3 9 A. m . B. m . C. m . D. m . 2 2 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 24: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 4 2 3 x 1 m x 1 2 x 1 có hai nghiệm thực ? 1 1 1 1 A. m 1. B. 1 m . C. 2 m . D. 0 m . 3 4 3 3
Câu 25: Cho hàm số 3 2 y mx 2x
mx 1. Giá trị nhỏ nhất của m để hàm số đã cho đồng biến trên 1; 2 là ? 1 1 2 3 3 A. m . B. m . C. m . D. m . 2 2 3 3 2 3 1
Câu 26: Cho hàm số 3 2 y x mx m 2 x 5 . Với 0 m
9 thì có bao nhiêu giá trị m là số tự 3
nhiên sao cho hàm số đồng biến trên 2 ; 5 ? A. 0. B. 5. C. 3. D. 1. mx 2
Câu 27: Cho hàm số y
. Với m thuộc tập hợp nào sau đây để hàm số tăng trên khoảng x 3m ; 1 ? 1 2 5 A. A x : x . B. B ; 1; . 3 3 9 1 2 C. C x : x . D. D x : x 0 . 3 3
Câu 28: Cho hàm số 3 2 y x 3x 3mx
m 1 . Hàm số nghịch biến trên khoảng 1;1 thì mệnh
đề nào về m là đúng ? A. 1 m 2 . B. m ; 3 1; . C. m 1. D. m ; 1 1; .
Câu 29: Cho hàm số 3 2 y x 3x
m 1 x 1 . Tìm m để hàm số đã cho nghịch biến trên khoảng 0; ? A. m 2 . B. m 2 . C. m 1. D. m 1.
Câu 30: Tìm tất cả các giá trị thực của tham số m sao cho bất phương 1 trình 2 1 2x 3 x m 2x
5x 3 nghiệm đúng với mọi x ; 3 ? 2 A. m 1. B. m 0 . C. m 1. D. m 0 .
Câu 31: Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 3 1 x 3 x 2 1 x 3 x
m nghiệm đúng với mọi x 1; 3 ? A. m 6 . B. m 6 . C. m 6 2 4 . D. m 6 2 4 .
Câu 32: Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 2 2 3 x 6 x 18 3x x m m 1 nghiệm đúng x 3; 6 ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC m 1 A. m 1. B. 1 m 0 . C. 0 m 2 . D. . m 2
Câu 33: Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình x x 2 m.4 m 1 .2 m 1 0 nghiệm đúng x ? A. m 3 . B. m 1. C. 1 m 4 . D. m 0 . 1
Câu 34: Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 3 x 3mx 2 3 x nghiệm đúng x 1 ? 2 2 3 1 3 A. m . B. m . C. m . D. m . 3 3 2 3 2 1
Câu 35: Cho hàm số 3 2 y x m 3 x m 1 x
4 . Có bao nhiêu giá trị của m sao cho hàm số 3
tăng trên đoạn có độ dài bằng 4 (để rõ hơn, có thể hiểu là khoảng đồng biến có độ dài bé nhất bằng 4). A. 5 . B. 3 . C. 4 . D. 2 .
Câu 36: Cho hàm số 3 2 y x 3mx 3mx
4 . Tại giá trị nào của m thì hàm số đã cho giảm trên
đoạn có độ dài bằng 1 (để rõ hơn, có thể hiểu là khoảng nghịch biến có độ dài bé nhất bằng 1) ? 1 2 2 5 2 3 A. m . B. m . C. m . D. m . 2 2 3 3 3 3x m
Câu 37: Cho hàm số y
. Trong tất cả các giá trị của m để hàm số nghịch biến trên 2x 1 1 ;
, thì m không thể bằng ? 2 1 5 2 3 A. . B. 5 . C. . D. . 2 3 3
Câu 38: Cho hàm số 3 2 y mx 2x
mx 1. Giá trị nhỏ nhất của m để hàm số đã cho đồng biến trên 1; 2 là ? 1 1 2 3 3 A. m . B. m . C. m . D. m . 2 2 3 3 2 3 2 mx 6x 2
Câu 39: Cho hàm số y
. Tìm tất cả các giá trị m để hàm số đồng biến trên khoảng x 2 1; 0 ? 1 1 10 A. m . B. m . C. m 3 . D. m . 2 2 3 3 2 2 2
Câu 40: Tìm giá trị lớn nhất của tham số m sao cho bất phương trình cos x sin x cos x 2 3 m.3 có nghiệm ? A. m 4 . B. m 8 . C. m 12 . D. m 16 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 41: Bất phương trình 3 2 2x 3x 6x 16 4 x
2 3 có tập nghiệm là a; b . Hỏi tổng a b
có giá trị là bao nhiêu ? A. 2 . B. 4. C. 5. D. 3.
Câu 42: Bất phương trình 2 2 x 2x 3 x 6x 11 3 x
x 1 có tập nghiệm a; b . Hỏi
hiệu b a có giá trị là bao nhiêu ? A. 1. B. 2. C. 3. D. 1 . Câu 43: Hàm số y
f x đồng biến trên khoảng a; b . Mệnh đề nào sau đây là sai ? A. Hàm số y
f x 1 đồng biến trên a; b . B. Hàm số y f x
1 nghịch biến trên a; b . C. Hàm số y
f x nghịch biến trên a; b . D. Hàm số y f x 1 đồng biến trên a; b .
Câu 44: Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: 2 x 3x 2
0 cũng là nghiệm của bất phương trình 2 mx m 1 x m 1 0 ? 3 3 A. m 1. B. m . C. m . D. m 1. 7 7
Câu 45: Tìm tất cả các giá trị thực của tham số m sao cho phương trình: 2 2 log x log x 1 2m 1
0 có ít nhất một nghiệm trên đoạn 3 1; 3 ? 3 3 A. 1 m 3. B. 0 m 2 . C. 0 m 3. D. 1 m 2 .
Câu 46: Cho hàm số 2 y m 1 x
3 m với m là tham số. Tập hợp các giá trị của m để hàm số đồng biến trên là ? A. 1;1 . B. 1; . C. ; 1 1; . D. ; 1 .
Câu 47: Tập hợp các số thực m để hàm số 3 2 y x 5x 4mx 3 đồng biến trên là ? 25 25 25 25 A. ; . B. ; . C. ; . D. ; . 12 12 2 12 2 x (m 1)x 1
Câu 48: ới giá trị nào của m, hàm số y
nghịch biến trên các khoảng xác định 2 x của nó ? 5 A. m 1 . B. m 1. C. m 1;1 . D. m . 2 mx 3 Câu 49: Hàm số y
đồng biến trên từng khoảng xác định khi: x m 2 m 3 A. . .B. m 3 . C. 3 m 1. D. m 1 . m 1 mx 3 Câu 50: Hàm số y
nghịch biến trên từng khoảng xác định khi: x 2 3 3 3 3 A. m . B. m . C. m . D. m . 2 2 2 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 1: Sự đồng biến, nghịch biến của hàm số” – P.3
Câu 01: Cho hàm số 3 2 y mx 2x
mx 1. Giá trị nhỏ nhất của m để hàm số đã cho đồng biến trên đoạn 1; 2 là ? 1 1 2 3 3 A. m . B. m . C. m . D. m . 2 2 3 3 2 3 1
Câu 02: Cho hàm số 3 2 y x mx m 2 x 5 . Với m
0; 9 thì có bao nhiêu giá trị m là số tự 3
nhiên sao cho hàm số đồng biến trên đoạn 2 ; 5 ? A. 0. B. 5. C. 3. D. 1. mx 2
Câu 03: Cho hàm số y
. Với m thuộc tập hợp nào sau đây để hàm số tăng trên khoảng x 3m ; 1 ? 2 2 1 2 A. A x : x . B. B x : x . 3 3 3 3 5 C. C ; 1; . D. D x : x 0 . 9
Câu 04: Cho hàm số 3 2 y x 3x 3mx
m 1 . Hàm số nghịch biến trên khoảng 1;1 thì mệnh
đề nào về m là đúng ? A. 1 m 2 . B. m ; 3 1; . C. m 1. D. m ; 1 1; .
Câu 05: Cho hàm số 3 2 y x 3x
m 1 x 1 . Tìm m để hàm số đã cho nghịch biến trên khoảng 0; ? A. m 2 . B. m 2 . C. m 1. D. m 1. x m 2
Câu 06: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y giảm trên các x 1
khoảng mà nó xác định ? A. m 3 . B. m 3 . C. m 1. D. m 1. mx 4
Câu 07: Tìm m để hàm số y giảm trên khoảng ;1 ? x m A. 2 m 1. B. 2 m 1. C. 2 m 1. D. 2 m 1.
Câu 08: Tìm m để hàm số y 2m 1 sin x 3 m x đồng biến trên ? 2 2 2 A. 4 m . B. 4 m . C. m 4 . D. m . 3 3 3 3 x
Câu 09: Tìm GTNN của m để hàm số 2 y mx mx m đồng biến trên ? 3
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. m 0 . B. m 4 . C. m 4 . D. m 1 .
Câu 10: Với giá trị nào của a thì hàm số 3 y ax x đồng biến trên ? A. a 0 . B. a 0 . C. a 0 . D. a . 1 Câu 11: Hàm số 3 2 y x m 2 x mx
3m nghịch biến trên khoảng xác định khi: 3 m 1 A. m 0 . B. m 4 . C. 1 m 4 . D. . m 4 1
Câu 12: Cho hàm số 3 2 2 y x m 1 x
m m x 3 . Tìm m để hàm số nghịch biến trên ? 3 A. 1; . B. ; 1 . C. 1; . D. ; 1 . m 2 2m 7
Câu 13: Cho hàm số 3 2 y x x x
5 . Hàm số đồng biến trên khi m nằm trong 2 12 miền giá trị nào ? A. 1; 3 . B. 1; 3 . C. ; 1 3; .
D. Không xác định được m.
Câu 14: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 1 3 2 y x mx 2m 3 x m 2 luôn nghịch biến trên ? 3 m 3 A. 3 m 1. B. m 1. C. 3 m 1. D. . m 1 2 x m 1 2m 1
Câu 15: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y tăng trên x m
từng khoảng xác định của nó ? A. m 1. B. m 1. C. m 1. D. m 1.
Câu 16: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y f x x m cos x luôn đồng biến trên ? 3 1 A. m 1 . B. m . C. m 1 . D. m . 2 2
Câu 17: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y m 3 x 2m 1 cos x luôn nghịch biến trên ? 2 m 3 A. 4 m . B. m 2 . C. . D. m 2 . 3 m 1
Câu 18: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y 2x 3 m 2 x 6 m 1 x 3m 5 luôn đồng biến trên ? A. 0. B. –1 . C. 2. D. 1.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 3x mx 2
Câu 19: Cho hàm số y
. Hãy cho biết có bao nhiêu giá trị nguyên dương m để hàm 2x 3
số luôn nghịch biến trên từng khoảng xác định của nó với m 0;10 ? A. 8. B. 6. C. 4. D. 2 . 3 x
Câu 20: Tìm giá trị nhỏ nhất của tham số m sao cho hàm số 2 y mx mx m luôn đồng biến 3 trên ? A. m 5 . B. m 0 . C. m 1 . D. m 6 . m 3 x 2
Câu 21: Tìm số nguyên m nhỏ nhất sao cho hàm số y
luôn nghịch biến trên các x m
khoảng xác định của nó ? A. m 1 . B. m 2 . C. m 0 . D. Không có m thỏa mãn. mx 4
Câu 22: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y giảm trên khoảng x m ;1 ? A. 2 m 2 . B. 2 m 1. C. 2 m 1. D. 2 m 2 .
Câu 23: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y x 6x mx 1 đồng biến trên khoảng 0; ? A. m 0 . B. m 12 . C. m 0 . D. m 12 .
Câu 24: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2 y x 2 m 1 x m 2 đồng biến trên khoảng 1; 3 ? A. m 5; 2 . B. m ; 2 . C. m 2, . D. m ; 5 .
Câu 25: Hàm số nào sau đây nghịch biến trên với mọi m ? A. 2 3 y m x m . B. 2 3 2 y m x mx 3x 1 . mx 1 C. y . D. 3 y x 2mx 1 . x m 1
Câu 26: Với giá trị nào của m thì hàm số 3 2 y x 2x mx
2 nghịch biến trên các khoảng xác 3 định của nó ? A. m 4 . B. m 4 . C. m 4 . D. m 4 .
Câu 27: Với điều kiện nào của m thì hàm số 3 2 2 y x m 2 x m 4 x 9 đồng biến trên ? m 2 m 4 m 1 m 3 A. . B. . C. . D. . m 1 m 2 m 0 m 3 m 2 x m
Câu 28: Với giá trị nào của m thì hàm số y
nghịch biến trên mỗi khoảng xác định x m của nó ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC m 0 m 0 m 0 A. . B. . C. . D. 0 m 3. m 2 m 3 m 2
Câu 29: Với giá trị nào của m thì hàm số 3 2 y x 3x mx
2 đồng biến trên khoảng 0; ? A. m 2 . B. m 3 . C. m 0 . D. m 4 . 1 1
Câu 30: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y x mx 2mx 3m 4 3 2
nghịch biến trên một đoạn có độ dài là 3 ? m 1 m 1 A. . B. m 1 . C. m 9 . D. . m 9 m 9 tan x 2
Câu 31: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y đồng biến trên tan x m khoảng 0; ? 4 m 0 A. 1 m 2 . B. . C. m 2 . D. m 0 . 1 m 2
Câu 32: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 mx 2 y f x 7mx 14x m
2 giảm trên nửa khoảng 1; ? 3 14 14 14 14 A. ; . B. ; . C. 2; . D. ; . 15 15 15 15
Câu 33: Tất cả các giá trị thực của tham số m sao cho hàm số 4 2 y x 2m 3 x m nghịch biến p p trên khoảng 1; 2 là ; , trong đó phân số tối giản và q 0 . Hỏi tổng p q là ? q q A. 5. B. 9. C. 7. D. 3. 2 x 2mx m 2
Câu 34: Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y đồng x m
biến trên từng khoảng xác định của nó ? A. 2. B. 4. C. Vô số. D. 0. 2 x m 2 x m 3
Câu 35: Cho hàm số y
. Với giá trị nào của m thì hàm số đồng biến trên từng x 1
khoảng xác định của nó ? A. m 2 . B. m 2 . C. 1 m 3 . D. m 1 . x m
Câu 36: Tất cả các giá trị của m để hàm số y f x
nghịch biến trên từng khoảng xác định x 1 của nó là: A. m 1. B. m 1. C. m 1. D. m 1 .
Câu 37: Xét hai mệnh đề sau: 3 4 I Hàm số y 1 x đồng biến trên . II Hàm số y 1 x đồng biến trên .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Hãy chọn câu trả lời đúng ?
A. Chỉ I đúng.
B. Chỉ II đúng.
C. Cả hai đúng.
D. Cả hai sai.
Câu 38: Hàm số nào trong các hàm số sau chỉ có 1 chiều biến thiên trên tập xác định của nó ? 1 1 1 2 x A. y . B. y . C. y . D. y . x 2 x x x 3 x
Câu 39: Tất cả các giá trị của m để hàm số 2 y mx 4x đồng biến trên là: 3 A. 2 m 2 . B. 2 m 2 . C. m 2 . D. m 2 .
Câu 40: Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số 2 2x 1 m 1 m y
đồng biến trên khoảng 1; ? x m A. 3. B. 1. C. 2. D. 0.
Câu 41: Tìm tất cả các giá trị thực của tham số và sao cho hàm số 3 x 1 2 3 y f x sin cos x x sin cos 2 luôn giảm trên ? 3 2 2 5 k k k k A. 12 4 , k . B. 12 12 , k . 2 2 5 k k C. 4 , k . D. 12 , k . 2 2
Câu 42: Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y f x 2x a sin x bcos x luôn tăng trên ? 1 1 1 2 A. 1 . B. a 2b 2 3 . C. 2 2 a b 4 . D. a 2b . a b 3
Câu 43: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 3 2 x 3x 9x m 0 có đúng 1 nghiệm ? m 5 m 27 A. 27 m 5 . B. . C. . D. 5 m 27 . m 27 m 5
Câu 44: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 x 1 x m có nghiệm thực ? A. m 2 . B. m 2 . C. m 3 . D. m 3 . 2x m
Câu 45: Cho hàm số y
. Có bao nhiêu giá trị nguyên m thỏa m
0 để hàm số luôn đồng x 3
biến trên từng khoảng xác định ? A. 4. B. 3. C. 2. D. 1.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 m 1 x 2x
Câu 46: Cho hàm số y
. Hãy cho biết có bao nhiêu giá trị m là số nguyên tố sao cho mx 1
hàm số luôn đồng biến trên từng khoảng xác định ? A. 1. B. 3. C. 2. D. 0.
Câu 47: Cho hàm số y
cos x 2ax . Xác định tham số a để hàm số tăng trên ? 1 1 1 1 A. a . B. a . C. a . D. a . 2 2 2 2
Câu 48: Cho hàm số y
cos 2x sin 2x ax 4 . Phát biểu nào sau đây là đúng khi nói về a ? A. Khi a 0 thì 1 y' 1 .
B. Hàm số luôn đồng biến với mọi a. C. Khi a
2 2 thì hàm số luôn đồng biến trên . D. Khi a
2 2 thì hàm số luôn nghịch biến trên .
Câu 49: Cho hàm số 2 y sin x sin x
3mx . Phát biểu nào sau đây là sai khi nói về m ? A. y y' 3mx 3 0 , x . B. Khi m 0 thì với x y' 1 . 2 3 C. Khi m
thì hàm số luôn đồng biến trên . 2 2 D. Khi m
thì hàm số luôn nghịch biến trên . 3
Câu 50: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 2 x 4x 5 m 4x x
có đúng 2 nghiệm dương ? A. 1 m 3 . B. 3 m 5 . C. 5 m 3 . D. 3 m 3 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 2: Cực trị của hàm số” – P.1
Câu 01: Cho hàm số 3 2 y x x
x 1 có đồ thị C . Khoảng cách từ O đến điểm cực tiểu của đồ thị hàm số là: A. 2 . B. 2. C. 0. D. 1.
Câu 02: Tìm giá trị cực đại y của hàm số 3 y x 3x 2 ? CD A. y 4 . B. y 1. C. y 0 . D. y 1 . CD CD CD CD 2 x x 1
Câu 03: Cho hàm số y
, xác định giá trị cực đại của y ? x 1 A. 2 . B. 3 . C. 0. D. 1.
Câu 04: Cho hàm số y
sinx cos x , tìm khẳng định sai trong các câu sau đây: 2 A. x
là một nghiệm của y.
B. Giá trị nhỏ nhất của y là . 4 2 2
C. Giá trị lớn nhất của y là .
D. Hàm số đã cho không có cực trị. 2
Câu 05: Hàm số nào sau đây không có cực trị ? 2x 5 2 x 2x 4 A. 3 y x 5x . B. y . C. y . D. Cả câu B và C. x 4 x 1
Câu 06: Cho hàm số y
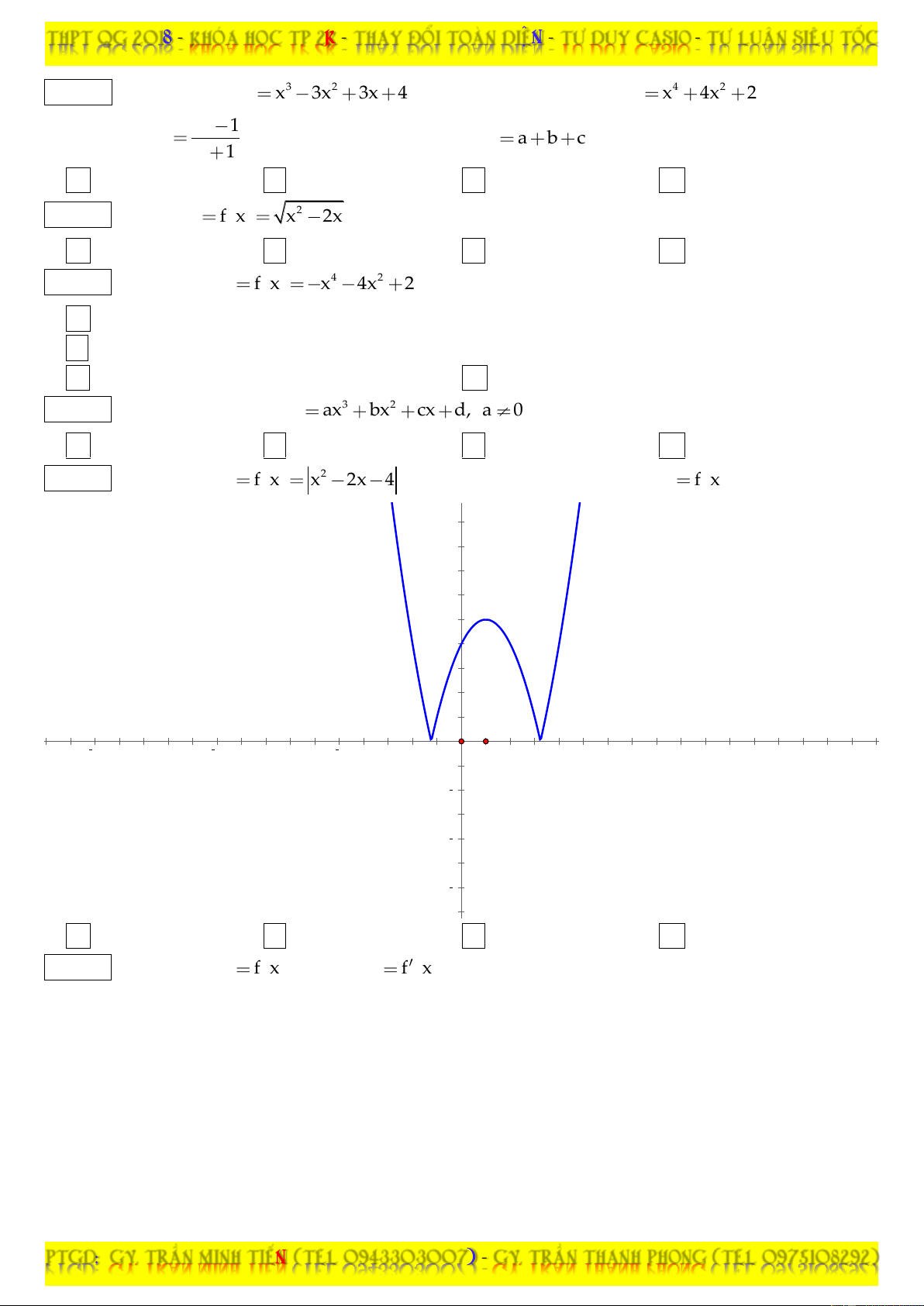
f x có đồ thị như hình dưới. Đồ thị hàm số y
f x có mấy điểm cực trị ? 8 6 4 2 15 10 5 5 10 15 2 4 6 8 A. 2. B. 1. C. 0. D. 3.
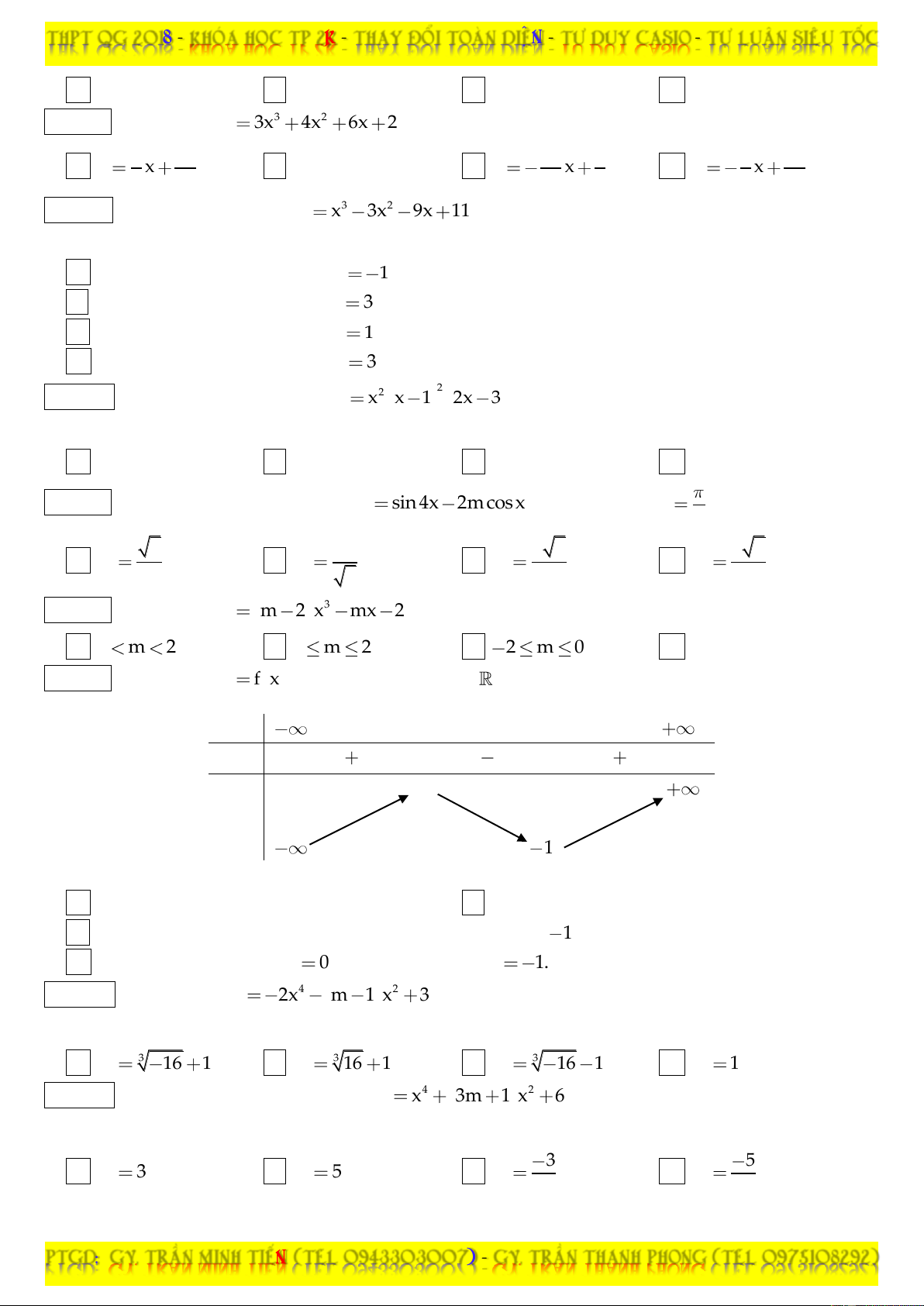
Câu 07: Cho hàm số y f x có bảng biến thiên: x 2 4 y ' 0 0
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 3 y 2
Khẳng định nào sau đây là đúng ?
A. Hàm số đạt cực đại tại x 2 .
B. Hàm số đạt cực đại tại x 3 .
C. Hàm số đạt cực đại tại x 4 .
D. Hàm số đạt cực đại tại x 2 .
Câu 08: Cho hàm số 3 2 y x 3x
2 . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đạt cực đại tại x
2 và đạt cực tiểu tại x 0 .
B. Hàm số đạt cực tiểu tại x 2 và đạt cực đại x 0 .
C. Hàm số đạt cực đại tại x 2 và cực tiểu tại x 0 .
D. Hàm số đạt cực đại tại x 0 và cực tiểu tại x 2 .
Câu 09: Cho hàm số 4 2 y x 2x
3 . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có ba điểm cực trị.
B. Hàm số chỉ có đúng 2 điểm cực trị.
C. Hàm số không có cực trị.
D. Hàm số chỉ có đúng một điểm cực trị.
Câu 10: Biết đồ thị hàm số 3 y x 3x
1 có hai điểm cực trị A, B . Khi đó phương trình đường thẳng AB là : A. y x 2. B. y 2x 1. C. y 2x 1. D. y x 2.
Câu 11: Cho hàm số 3 2 y 2x 5x
4x 1999 . Gọi x và x (với x
x ) lần lượt là hoành độ hai 1 2 1 2
điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng ? 2 1 1 1 A. x x . B. 2x x . C. 2x x . D. x x . 2 1 3 2 1 3 1 2 3 1 2 3
Câu 12: Số điểm cực trị của hàm số 3 2 y 2x 5x 4x 1999 là: A. 1. B. 2. C. 3. D. 4.
Câu 13: Đồ thị hàm số 3 2 y 2x 3x 12x
2016 có hai điểm cực trị lần lượt là A và B với x x . A B
Kết luận nào sau đây là đúng ? A. A 2; 2035 . B. A 2; 2008 . C. A 2; 2036 . D. B 2; 2009 .
Câu 14: Giá trị cực đại của hàm số 2 y 2x 5x 4x 1999 là: 54001 54003 A. . B. 2. C. . D. 4. 27 27
Câu 15: Giá trị cực tiểu của hàm số 2 y 2x 3x 12x 2016 là: A. 2006. B. 2007. C. 2008. D. 2009. 2 x 3x 5
Câu 16: Cho hàm số y
có 2 cực trị x , x . Gọi S là tổng giá trị của x , x . Tính S ? x 1 1 2 1 2 A. S 2 . B. S 2 . C. S 2 3 . D. S 2 3 . 2 3
Câu 17: Tìm m để hàm số 3 2 2 y x mx 2 3m 1 x
có 2 cực trị x , x thỏa mãn 3 2 1 2 x .x 2 x x 1 ? 1 2 1 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 3 2 A. m . B. m . C. m .
D. Không tìm được m. 3 2 3
Câu 18: Cho hàm số 4 2 y x 5m 1 x
2 . Hàm số đã cho có đúng 1 cực trị với giá trị nào của m sau đây ? 1 1 1 1 A. m . B. m . C. m . D. m . 5 5 5 5
Câu 19: Hàm trùng phương 4 2 2 y x 2 m m 3 x m
5 . Với giá trị nào của m thì khoảng cách
giữa 2 cực trị đối xứng qua trục tung là là nhỏ nhất và giá trị đó bằng bao nhiêu ? 1 11 1 11 A. m , min d . B. m , min d . 2 4 2 2 1 1 C. m , min d 11 . D. m 11, min d . 2 2
Câu 20: Với hàm số y
x , phát biểu nào sau đây là đúng ?
A. Hàm số đã cho không có đạo hàm.
B. Hàm số không có cực trị.
C. Hàm số đạt cực tiểu tại x 2 .
D. Giá trị cực tiểu là y 0 . CT 2 x 3x 3
Câu 21: Gọi M,n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số y . Khi đó giá trị x 2 của biểu thức 2 M 2n bằng: A. 8. B. 7. C. 9. D. 6.
Câu 22: Cho hàm số 3 2 y x 17x 24x
8 . Kết luận nào sau đây là đúng ? 2 A. x 1. B. x . C. x 3. D. x 12. CD CD 3 CD CD
Câu 23: Cho hàm số 4 2 y 3x 6x
1 . Kết luận nào sau đây là đúng ? A. y 2. B. y 1. C. y 1. D. y 2. CD CD CD CD 3
Câu 24: Trong các hàm số sau, hàm số nào đạt cực đại tại x ? 2 1 A. 4 3 2 y x x x 3x. B. 2 y x 3x 2. 2 x 1 C. 2 y 4x 12x 8. D. y . x 2
Câu 25: Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu ? A. 4 2 y 10x 5x 7. B. 3 2 y 17x 2x x 5. x 2 2 x x 1 C. y . D. y . x 1 x 1 Câu 26: Hàm số 3 2 y 3x 4x x
2016 đạt cực tiểu tại: 2 1 A. x . B. x 1. C. x . D. x 2 . 9 9
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 27: Cho hàm số 3 2 y x 3x 9x
2017 . Gọi x và x lần lượt có hoành độ tại hai điểm cực đại 1 2
và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng ? 2 A. x x 4 . B. x x 3 . C. x x 3 . D. x x 8 . 1 2 2 1 1 2 1 2 Câu 28: Hàm số 3 y x 8x
13x 1999 đạt cực đại tại: 13 13 A. x . B. x 1. C. x . D. x 2 . 3 3 Câu 29: Hàm số 3 2 y x 10x 17x 25 đạt cực tiểu tại: 10 17 A. x . B. x 25 . C. x 17 . D. x . 3 3
Câu 30: Cho hàm số 3 2 y 2x 3x 12x
2016 . Gọi x và x lần lượt có hoành độ tại hai điểm cực 1 2
đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng ? 2 A. x x 4 . B. x x 3 . C. x x 3 . D. x x 8 . 1 2 2 1 1 2 1 2 1
Câu 31: Cho hàm số 3 2 f x x mx 3m 4 x
3 , với giá trị nào của m thì hàm số có cực tiểu, 3 cực đại ? m 1 m 4 A. 4 m 1. B. 4 m 1. C. . D. . m 4 m 1
Câu 32: Hàm số bậc 3: 3 2 y ax bx cx d với a
0 có 2 cực trị khi nào ? A. y ' có nghiệm.
B. y ' có nghiệm kép.
C. y ' có 2 nghiệm phân biệt.
D. hàm số luôn có 2 cực trị.
Câu 33: Cho bảng biến thiên sau, phát biểu nào sau đây là đúng ? 0 1 2 x y ' 0 1 y 3
A. Hàm số có cực tiểu tại x 0 .
B. Hàm số có cực đại tại x 2 .
C. Giá trị cực đại của hàm số là 1 . D. x
1 là 2 cực trị của hàm số đã cho.
Câu 34: Cho hàm số 3 2 2 y x m 1 x m
2m 3 x 4 , xác định tham số m để đồ thị hàm số
y có 2 điểm cực trị nằm về 2 phía của trục tung:
A. Không tìm được giá trị m. B. 3 m 1. C. 3 m 1.
D. Với mọi giá trị m. 1
Câu 35: Giá trị cực tiểu của hàm số y x
là giá trị nào sau đây ? x A. y 1 . B. y 1. C. y 2 . D. y 2 . CT CT CT CT
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 3x 13x 19
Câu 36: Cho hàm số y
. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có x 3 phương trình là: A. 5x 2y 13 0. B. y 3x 13. C. y 6x 13. D. 2x 4y 1 0. .
Câu 37: Cho hàm số 2 y x
2x . Khẳng định nào sau đây là đúng ?
A. Hàm số có hai điểm cực trị.
B. Hàm số đạt cực tiểu tại x 0 .
C. Hàm số đạt cực đại x 2 .
D. Hàm số không có cực trị.
Câu 38: Cho hàm số 7 5 y x
x . Khẳng định nào sau đây là đúng ?
A. Hàm số có đúng 1 điểm cực trị.
B. Hàm số có đúng 3 điểm cực trị.
C. Hàm số có đúng hai điểm cực trị.
D. Hàm số có đúng 4 điểm cực trị. 2 3 4
Câu 39: Cho hàm số y f x có đạo hàm f x x 1 x 2 x 3 x 5 . Hỏi hàm số y f x
có mấy điểm cực trị ? A. 2. B. 3. C. 4. D. 5. 1
Câu 40: Cho hàm số 2 3 y x
2x . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đạt cực tiểu tại x 1.
B. Hàm số đạt cực đại tại x 1 .
C. Hàm số không có điểm cực trị.
D. Hàm số có đúng 2 điểm cực trị. Câu 41: Hàm số 3 2 y 3x 4x x
258 đạt cực đại tại: 2 1 A. x . B. x 1. C. x . D. x 2 . 9 9 Câu 42: Hàm số 3 2 y x 8x
13x 1999 đạt cực tiểu tại: 1 A. x 3 . B. x 1. C. x . D. x 2 . 3
Câu 43: Biết đồ thị hàm số 3 2 y x 6x
9x 2 có hai điểm cực trị là A x ; y và B x ; y . Nhận 1 1 2 2
định nào sau đây không đúng ? A. x x 2 . B. y y 4 . C. y y . D. AB 2 6 . 1 2 1 2 1 2
Câu 44: Hàm số nào dưới đây có cực đại ? x 1 x 2 A. 4 2 y x x 1. B. y . C. . y . D. 2 y x 2x . x 2 2 x 2
Câu 45: Tổng số điểm cực đại của hai hàm số 4 2 y f x x x 3 và 4 2 y g x x x 2 là: A. 1. B. 2. C. 3. D. 4. 2 x 5x 3
Câu 46: Cho hàm số y
, đường thẳng đi qua 2 điểm cực trị vuông góc với đường thẳng x 6 nào sau đây ? 1 A. y 5 2x . B. y 2x 5 . C. y x 3 .
D. Một đường thẳng 2 khác.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 47: Tìm điều kiện của m để hàm số 4 2 2 y 2x 4 m 5 x m 4 có 3 cực trị ? A. m ; 5 . B. m ; 5 . C. m 5; . D. m 5; .
Câu 48: Phương trình đường thẳng đi qua 2 điểm cực trị (nếu có) của đồ thị hàm số 3 2 y f x x
2x là đường thẳng nào dưới đây ? 8 9 9 8 A. y x . B. y x . C. y x . D. y x . 9 8 8 9 1 1
Câu 49: Cho hàm số 4 3 y f x x
x , hàm số đã cho có bao nhiêu cực trị ? 4 3 A. 1. B. 2. C. 3. D. 4 .
Câu 50: Cho hàm số y
x 3 , xét các khẳng định dưới đây:
a) Hàm số không có cực trị.
c) Giá trị cực tiểu là 0.
b) Giá trị nhỏ nhất là 0.
d) Hàm số đạt cực tiểu tại x 3 .
Số khẳng định đúng là ? A. 1. B. 2. C. 3. D. 4 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 2: Cực trị của hàm số” – P.2
Câu 01: Tổng số điểm cực tiểu của hai hàm số 3 2 y f x x x 3 và 4 2 y g x x x 2 là: A. 1. B. 2. C. 3. D. 4. 4 2 x 3x
Câu 02: Cho hai hàm số 3 2 y f x x x 3 và y g x x
2 . Tổng số điểm cực trị, 4 2
cực đại, cực tiểu của 2 hàm số lần lượt là: A. 5; 2; 3. B. 5; 3; 2. C. 4; 2; 2. D. 3; 1; 2.
Câu 03: Cho hàm số 3 2 y x 6x
9x 4 có đồ thị C . Tọa độ điểm cực đại của đồ thị hàm số là: A. A 1; 8 . B. A 3; 4 . C. A 2; 2 . D. A 1;10 .
Câu 04: Cho hàm số 3 2 y x 3x
4 có đồ thị C . Gọi A và B là 2 điểm cực trị của C . Diện tích tam giác OAB bằng: A. 4. B. 8. C. 2. D. 2 3 .
Câu 05: Đồ thị hàm số 3 2 y x 3x 9x
2 có đồ thị C , có điểm cực đại, cực tiểu lần lượt là x ; y và x ; y với x x . Tính T x y x y . 1 1 2 2 1 2 1 2 2 1 A. 4. B. 4 . C. 46. D. 46 .
Câu 06: Cho hàm số 3 2 y x 3x
6x . Hàm số đạt cực trị tại hai điểm x , x . Khi đó giá trị của 1 2 biểu thức 2 2 S x x bằng: 1 2 A. 10 . B. 8 . C. 10. D. 8.
Câu 07: Cho hàm số y f x có đạo hàm trên
. Khẳng định nào sau đây là đúng ?
A. Nếu đạo hàm đổi dấu khi x chạy qua x thì hàm số đạt cực tiểu tại x . 0 0 B. Nếu f x
0 thì hàm số đạt cực trị tại x . 0 0
C. Nếu hàm số đạt cực trị tại x thì đạo hàm đổi dấu khi x chạy qua x . 0 0 D. Nếu f x f x
0 thì hàm số không đạt cực trị tại x . 0 0 0
Câu 08: Cho hàm số y
f x . Khẳng định nào sau đây là khẳng định đúng ? A. Hàm số y
f x đạt cực trị tại x thì f x 0 . 0 0
B. Nếu hàm số đạt cực trị tại x thì hàm số không có đạo hàm tại x hoặc f x 0 . 0 0 0 C. Hàm số y
f x đạt cực trị tại x thì nó không có đạo hàm tại x . 0 0 D. Hàm số y
f x đạt cực trị tại x thì f x 0 hoặc f x 0 . 0 0 0
Câu 09: Cho hàm số y
f x xác định trên a; b và x thuộc đoạn a; b . Khẳng định nào sau đây là 0 khẳng định đúng ? A. Hàm số y
f x đạt cực trị tại x thì f x 0 hoặc f x 0 . 0 0 0 B. Hàm số y
f x đạt cực trị tại x thì f x 0 . 0 0
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC C. Hàm số y
f x đạt cực trị tại x thì nó không có đạo hàm tại x . 0 0
D. Nếu hàm số đạt cực trị tại x thì hàm số không có đạo hàm tại x hoặc f x 0 . 0 0 0
Câu 10: Cho hàm số y
f x . Khẳng định nào sau đây là khẳng định đúng ? A. Nếu hàm số y
f x có giá trị cực đại là M , giá trị cực tiểu là m thì M m . B. Nếu hàm số y
f x không có cực trị thì phương trình f x 0 vô nghiệm. 0 C. Hàm số y
f x có đúng hai điểm cực trị thì hàm số đó là hàm bậc ba. D. Hàm số 4 2 y ax bx c với a 0 luôn có cực trị.
Câu 11: Cho hàm số 3 2 y f x ax bx
cx d . Đồ thị hàm số có cực trị là 0;1 , 1; 1 . Khi đó xác định hàm f x ? A. 3 f x x 3x 1. B. 3 f x x 3x . C. 3 f x x 3x . D. 3 2 f x 4x 6x 1 . Câu 12: Cho x f x e x , tại điểm x 0 thì hàm số đã cho ?
A. Không xác định.
B. Là hàm hằng.
C. Đạt cực tiểu.
D. Đạt cực đại.
Câu 13: Cho các mệnh đề sau:
a) Hàm số đạt cực trị tại x thì f x 0 . b) Hàm số thỏa f x
0 thì có cực trị tại x . 0 0 0 0
b) Hàm số đạt cực đại tại x thì giá trị cực đại là f x . 0 0
c) Hàm số đạt cực tiểu tại x thì giá trị nhỏ nhất là f x . 0 0
Số phát biểu đúng là ? A. 1. B. 2. C. 3. D. 4 . 2 x 2
Câu 14: Cho hàm hữu tỉ y
có 2 cực trị. Phương trình đường thẳng qua 2 điểm cực trị là x 2
đường thẳng nào dưới đây ? A. y x 2 . B. y 2x 2 . C. y x 2 . D. y 2x .
Câu 15: Cho hàm số 2 y
x. 9 x . Gọi M là điểm mà tại đó đồ thị hàm số đạt cực đại. M là điểm nào sau đây ? 3 9 2 9 3 9 3 9 A. ; . B. ; . C. ; . D. ; . 2 2 3 2 2 2 2 2
Câu 16: Cho hàm số 3 2 y x x
x 1 có đồ thị C . Khoảng cách từ O đến điểm cực tiểu của đồ thị hàm số là: A. 2 . B. 2. C. 0. D. 1.
Câu 17: Khẳng định nào sau đây là sai ? A. Hàm số 3 2 y x 3x 2 có cực trị. B. Hàm số 3 2 y x 2x x có 2 điểm cực trị. C. Hàm số 3 2 y x 6x 12x 2 có cực trị. D. Hàm số 3 x 1 không có cực trị.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 18: Giả sử hàm số 3 2 y x 3x 3x
4 có a điểm cực trị, hàm số 4 2 y x 4x 2 có b điểm cực 2x 1 trị và hàm số y
có c điểm cực trị. Giá trị của T a b c là: x 1 A. 0. B. 3. C. 2. D. 1. Câu 19: Hàm số 2 y f x x
2x có bao nhiêu điểm cực trị ? A. 0. B. 1. C. 2. D. 3.
Câu 20: Cho hàm số 4 2 y f x x 4x
2 . Chọn phát biểu đúng:
A. Hàm số trên có 1 điểm cực đại và 2 điểm cực tiểu.
B. Hàm số trên có 2 điểm cực đại và 1 điểm cực tiểu.
C. Hàm số có 1 điểm cực trị là điểm cực đại .
D. Hàm số có 1 điểm cực trị là điểm cực tiểu.
Câu 21: Hàm số bậc ba dạng 3 2 y ax bx cx d, a
0 có thể có bao nhiêu điểm cực trị ?
A. 0 hoặc 1 hoặc 2. B. 1 hoặc 2. C. 0 hoặc 2. D. 0 hoặc 1.
Câu 22: Cho hàm số 2 y f x x
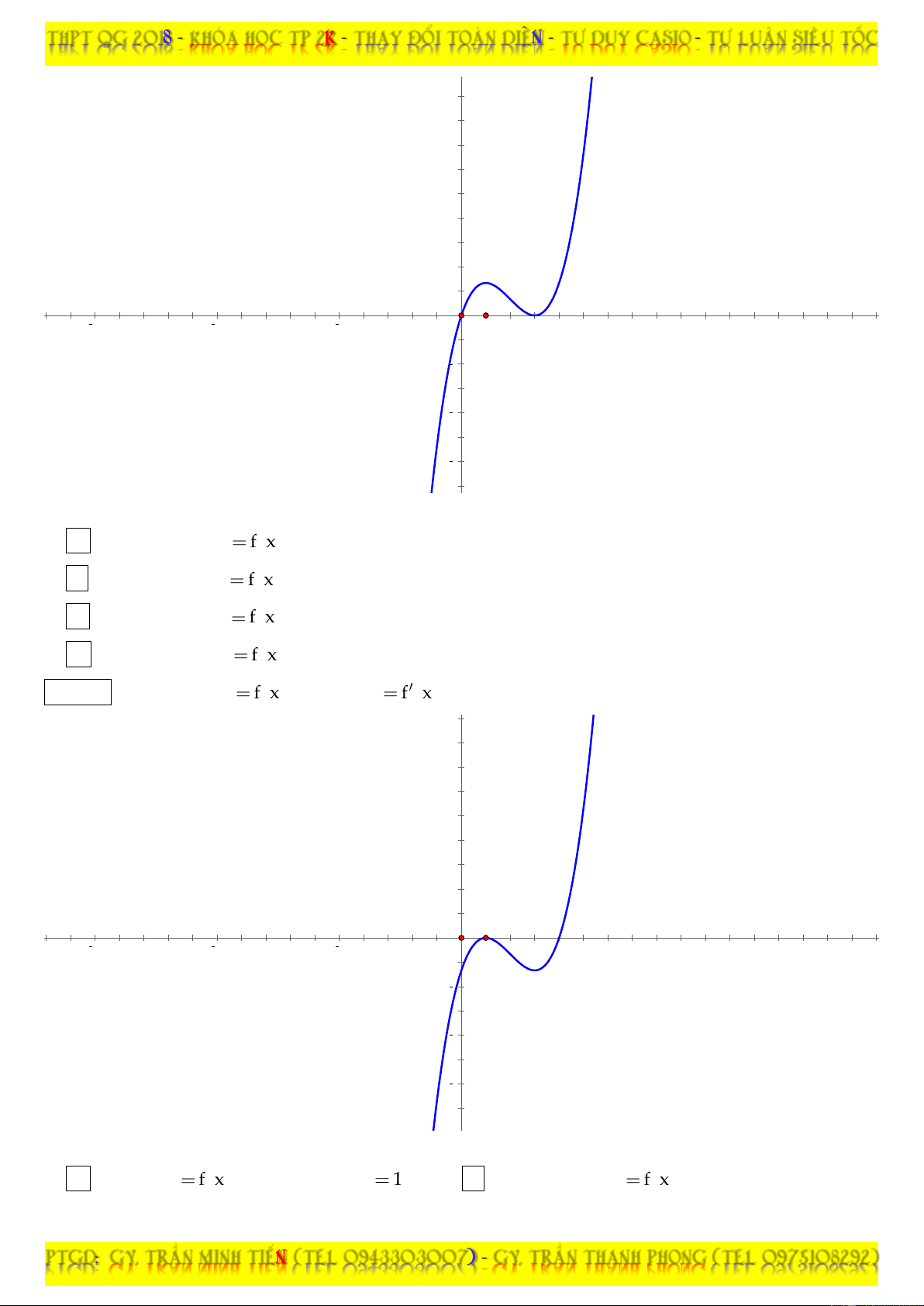
2x 4 có đồ thị như hình vẽ. Hàm số y f x có mấy cực trị ? 8 6 4 2 15 10 5 5 10 15 2 4 6 A. 4. B. 1. C. 3. D. 2.
Câu 23: Cho hàm số y f x . Hàm số y
f x có đồ thị như hình vẽ bên dưới:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 8 6 4 2 15 10 5 5 10 15 2 4 6
Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị hàm số y
f x cắt trục hoành tại ba điểm phân biệt.
B. Đồ thị hàm số y
f x có hai điểm cực trị.
C. Đồ thị hàm số y
f x có ba điểm cực trị.
D. Đồ thị hàm số y
f x có một điểm cực trị.
Câu 24: Cho hàm số y f x . Hàm số y
f x có đồ thị như hình vẽ bên dưới: 8 6 4 2 15 10 5 5 10 15 2 4 6 8
Khẳng định nào sau đây là khẳng định đúng ? A. Hàm số y
f x đạt cực đại tại x 1.
B. Đồ thị hàm số y
f x có một điểm cực tiểu.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC C. Hàm số y f x đồng biến trên ;1 .
D. Đồ thị hàm số y
f x có hai điểm cực trị.
Câu 25: Cho hàm số 3 y x
3x 2 có đồ thị như hình vẽ bên dưới: 10 8 6 4 2 15 10 5 5 10 15 2 4
Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị hàm số y
f x chỉ có điểm cực tiểu và không có điểm cực đại.
B. Đồ thị hàm số y
f x có một điểm cực tiểu và một điểm cực đại.
C. Đồ thị hàm số y
f x có bốn điểm cực trị.
D. Đồ thị hàm số y
f x có một điểm cực đại và hai điểm cực tiểu. 4 3 x 5x 1
Câu 26: Phát biểu nào là chính xác về đồ thị hàm số sau đây 2 y x 8x 10 ? 4 3 7
A. Hàm số trên có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số trên có duy nhất 1 điểm cực trị.
C. Hàm số trên có 2 điểm cực tiểu và 1 điểm cực đại.
D. Hàm số trên không có điểm cực trị.
Câu 27: Những phát biểu nào trong các phát biểu sau là đúng ? a) Hàm số y
f x đạt cực tiểu tại x khi và chỉ khi đạo hàm của y' đổi dấu từ sang khi đi 0 qua x . 0 b) Nếu f x 0 và f x
0 thì hàm số đạt cực tiểu tại x . 0 c) Hàm số y
f x đạt cực tiểu khi và chỉ khi x là nghiệm của phương trình f x 0 . 0 A. a. B. a,b,c. C. a,c. D. b,c.
Câu 28: Giả sử m là số cực trị của hàm 3 2 y ax bx . Xét trên khoảng 1; , m có thể bằng bao nhiêu ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC m 1 m 0 m 1 A. m 1 . B. . C. . D. . m 2 m 2 m 0
Câu 29: Hàm số nào sau đây không có cực trị ? x 3 1 A. 3 2 y x 3x . B. y . C. y x . D. 2 y x. 1 x . 2x 4 x
Câu 30: Đồ thị hàm trùng phương 4 2 y x 2x
1 có tổng giá trị của y và y là bao nhiêu ? CD CT A. 0. B. 5. C. 2. D. 3. 2
Câu 31: Cực tiểu của đồ thị hàm số 2 3 y x
3x có được ở giá trị nào sau đây ? 3 3 3 A. x 0; ; 3 . B. x . C. x 0; 3 . D. x . CT 2 CT 2 CT CT 2 2 Câu 32: Hàm số 3 2 y ax ax 2 đạt cực tiểu tại x
thì a thỏa điều kiện gì ? 3 A. a 0 . B. a 0 . C. a 0 . D. a 0 .
Câu 33: Cho hàm trùng phương 4 2 y 2x 4 2m 1 x
1, giá trị nhỏ nhất của y là bao nhiêu ? CD A. min 1. B. min 3 . C. min 0 . D. min 0 . 3 x
Câu 34: Định m để hàm số 2 y 2mx 1 đạt cực tiểu tại x 1 ? 2 1 1 A. m . B. m .
C. Đáp án khác.
D. Không tìm được m. 4 2 1 1
Câu 35: Cho hàm số 3 2 y x m 1 x (m 2)
3 . Xác định giá trị m để cực đại và cực tiểu 3 2
nằm trong khoảng ( 3; 4) : A. m 2; 5 . B. m 2; 5 \ 3 . C. m ; 2 . D. m 3; 5 .
Câu 36: Đồ thị hàm số 2 y
9 x có mấy điểm cực tiểu ? A. 0 . B. 1. C. 2. D. 3. Câu 37: Hàm số 3 2 C : y x 2x x 1 đạt cực trị khi: x 1 x 1 x 3 x 3 A. 1 . B. 1 . C. 1 . D. 10 . x x x x 3 3 3 3
Câu 38: Cho hàm số 3 y 2x
2x . Hệ thức liên hệ giữa các giá trị cực đại y và giá trị cực tiểu CD y
của hàm số đã cho là: CT A. y 2y . B. 2y 3y . C. y y . D. y y . CT CD CT CD CT CD CT CD
Câu 39: Cho hàm số 2 y x
x 1 . Hàm số đạt cực trị tại: 1 1 A. x 1. B. x . C. x . D. x 1. 2 2 2
Câu 40: Cho hàm số 2 y x 2
3 . Hàm số đạt cực đại khi:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. x 2 . B. x 2 . C. x 1. D. x 0 . 2 x 2x 1
Câu 41: Cho hàm số y : x 1
1 : Hàm số đạt cực đại tại x 1. 2 : Hàm số có 3x x CD CT
3 : Hàm số nghịch biến trên ; 1
4 : Hàm số đồng biến trên 1; 3 .
Các phát biểu đúng là: A. 1 , 4 . B. 1 , 2 . C. 1 , 3 . D. 2 , 3 . Câu 42: Hàm số 3 2 y f x x x x 4 đạt cực trị khi: x 0 x 1 x 1 x 1 A. . B. 2 . C. 1 . D. 1 . x 3 x x x 3 3 3
Câu 43: Cho hàm số 4 2 y f x 3x 2x
2 . Chọn phát biểu sai:
A. Hàm số trên có 3 điểm cực trị.
B. Hàm số trên có hai điểm cực đại và 1 điểm cực tiểu.
C. Hàm số trên có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số có cực đại, cực tiểu.
Câu 44: Viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3 y x 3x 1. A. 2x y 1 0 . B. x 2y 1 0 . C. 2x y 1 0 . D. x 2y 1 0 .
Câu 45: Hàm số nào sau đây có đúng hai điểm cực trị ? 1 A. y x . B. 3 2 y x 3x 7x 2. x 1 2 C. 4 2 y x 2x 3. D. y x . x 1
Câu 46: Hàm số nào sau đây không có cực trị ? 2 x 1 A. y 2x . B. 3 2 y x 3x . C. 4 2 y x 2x 3. D. y . x 1 x 2
Câu 47: Trong các khẳng định sau đây, khẳng định nào là khẳng định sai ?
A. Đồ thị hàm số 3 2 y ax bx cx d, a 0 luôn có cực trị.
B. Đồ thị hàm số 4 2 y ax bx c, a
0 luôn có ít nhất một điểm cực trị. ax b C. Hàm số y , ad bc
0 luôn không có cực trị. cx d
D. Đồ thị hàm số 3 2 y ax bx cx d, a
0 có nhiều nhất hai điểm cực trị.
Câu 48: Điểm cực tiểu của hàm số 3 y x 3x 4 là: A. x 1. B. x 1. C. x 3. D. x 3.
Câu 49: Hàm số nào sau đây đạt cực đại tại x 1 ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. 5 2 y x 5x 5x 13. B. 4 y x 4x 3. 1 C. y x . D. y 2 x x. x 2
Câu 50: Cho hàm số 3 5x y f x 2x x 4 đạt cực đại khi: 2 1 A. x 1. B. x . C. x 1. D. x . 6 6
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 2: Cực trị của hàm số” – P.3
Câu 01: Hàm số nào sau đây có cực trị ? 2x 1 A. 3 y x 1. B. 4 2 y x 3x 2. C. y 3x 4. D. y . 3x 2
Câu 02: Đồ thị hàm số 4 2 y x 3x
5 có bao nhiêu điểm cực tiểu ? A. 1. B. 0. C. 2. D. 3.
Câu 03: Tìm tất cả các giá trị của tham số m để hàm số 3 2 y x mx
2m 3 x 3 đạt cực đại tại x 1. A. m 3. B. m 3. C. m 3. D. m 3. x 1
Câu 04: Đồ thị hàm số y
có bao nhiêu điểm cực trị ? 4x 7 A. 3. B. 1. C. 2. D. 0. 3 2
Câu 05: Đạo hàm hàm số y f x là 4 y' x x 1
x 1 , vậy hàm số có bao nhiêu cực trị ? A. 0. B. 1. C. 2. D. 3.
Câu 06: Cho hàm số 2 4 y 2x
x . Chọn phát biểu sai trong các phát biểu dưới đây:
A. Hàm số đạt cực tiểu tại x 0 .
B. Hàm số có giá trị cực đại bằng 1.
C. Hàm số có hai cực trị.
D. Điểm cực tiểu của đồ thị hàm số là A 0; 0 . Câu 07: Hàm số 4 2 y x 2mx
4 có 3 cực trị tạo thành tam giác có bán kính đường tròn ngoại tiếp
nhỏ nhất bằng bao nhiêu ? 1 1 1 A. m . B. 3 m . C. m 0 . D. 3 m . 2 2 3
Câu 08: Cho hàm số 3 2 y x 3x
x . Giá trị nào của m dưới đây để đường thẳng đi qua 2 cực trị của 2 2 1
hàm số đã cho tiếp xúc với đường tròn C : x m 1 y m ? 25 4 6 A. m . B. m .
C. Cả A và B đúng. D. Cả A và B sai. 7 7 2 x 2x 4
Câu 09: Cho hàm số y
có 2 điểm cực trị thuộc đường thẳng y ux v . Giá trị u v 1 2x bằng bao nhiêu ? A. 0 . B. 1 . C. 1 . D. 2 .
Câu 10: Định m để hàm số 4 2 y x 2 3m 4 x
3m 1 có 3 điểm cực trị tọa thành tam giác có bán
kính đường tròn nội tiếp bằng 1: m 1 m 1 A. . B. . C. m 2 . D. m 2 . m 2 m 2
Câu 11: Đường thẳng 3 2 y x 3x
3x 1 có 2 điểm cực trị A và B. Đường thẳng song song với AB
có thể là đường nào trong các đường thẳng dưới đây ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 1 A. 4x y 2 0 . B. 4x y 1 0 . C. 4x 2y 1 0 . D. y x 2 . 4 Câu 12: Hàm số y 1 x x
5 , phát biểu nào sau đây là chính xác ?
A. Giá trị cực tiểu là 2 3 .
B. Giá trị cực đại là 2 3 .
C. Điểm cực tiểu có hoành độ là 2.
D. Điểm cực đại có hoành độ là 2.
Câu 13: Cho hàm số 2 y x 6x
5 , chọn phát biểu đúng ?
A. Hàm số đạt cực tiểu tại x 3.
B. Hàm số đạt cực tiểu tại x 1, x 5.
C. Hàm số đạt cực trị tại x 1, x 3, x 5.
D. Hàm số không có cực trị . 2 2
Câu 14: Cho hàm số y x 1
x 1 , phát biểu nào sau đây là đúng ?
A. Đồ thị có 1 cực đại và 2 cực tiểu.
B. Đồ thị có 1 cực tiểu và 2 cực đại.
C. Đồ thị có 1 cực đại .
D. Đồ thị có 1 cực tiểu. 1
Câu 15: Cho hàm số 3 2 y x m 2 x 2m
3 , phát biểu nào sau đây là sai khi nói về đồ thị 3 hàm số đã cho ?
A. Hàm số luôn có cực đại cực tiểu m .
B. Hàm số luôn có cực đại cực tiểu m\ 1 .
C. Hàm số luôn có cực đại cực tiểu m 1; .
D. Hàm số luôn có cực đại cực tiểu m ;1 . 2 x 5x 2
Câu 16: Đường thẳng nào sau đây là đường thẳng đi qua 2 cực trị của hàm số y ? 3 x A. y 2x 5 .
B. Không tồn tại. C. y x 3 . D. y 3 x .
Câu 17: Cho hàm số 3 y x
3x 1, khoảng cách giữa 2 điểm cực trị của đồ thị hàm số bằng bao nhiêu ? A. 2. B. 2 . C. 2 2 . D. 2 5 . 2x 1
Câu 18: Cực trị của hàm số y
đúng với khẳng định nào sau đây ? 3x 6 A. 0. B. 1. C. 2.
D. Không tồn tại cực trị.
Câu 19: Cho hàm số 4 2 2 y x 2m x 1 C
. Tìm m để hàm số có ba điểm cực trị là ba đỉnh của một m tam giác vuông cân: A. 0. B. 1. C. 2. D. 3. 2 x mx m 8
Câu 20: Xác định m để hàm số y
có cực đại và cực tiểu nằm về 2 phía của đường x 1 thẳng d : 9x 7y 1 0 : 9 9 3 3 A. 3 m . B. 3 m . C. m 9 . D. m 9 . 7 7 7 7
Câu 21: Tìm m để hàm số 3 2 2 2 y x 3x 3 m 1 x 3m
1 có 2 cực trị x , x thỏa điều kiện cách 1 2 điều gốc tọa độ:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 1 1 1 1 A. m 0; ; . B. m 0 . C. m . D. m . 2 2 2 2
Câu 22: Tìm m để hàm số 3 2 2 y x m 2 x 3m 1 x m
5 có 2 cực trị x ,x thỏa x .x 2 . 1 2 1 2 5 7 7 A. m . B. m . C. m .
D. Cả A và C đều thỏa. 3 3 3
Câu 23: Định m để hàm số 3 2 2 3 y x 3mx 3 m 1 x m
4m 1 có 3 cực trị tạo với thành 1 tam
giác sao cho diện tích tam giác đó lớn nhất và tìm giá trị đó ? 5 2 A. 2 m 0,S 3 . B. 5 m 0,S 3 . C. m 3,S 0 . D. m 3,S 0 . max max max max
Câu 24: Cho đồ thị hàm số 4 2 2 y x 2mx m
m 1 , tìm m để đồ thị hàm số có 3 cực trị thành
tam giác có bán kính đường tròn ngoại tiếp bằng 1 ? 1 5 m 1 5 2 m 1 m m 1 A. m 1 . B. 2 1 5 . C. . D. 1 5 . m 1 5 m 1 5 2 m 2 m 2 2
Câu 25: Với giá trị nào của m thì hàm số 3 2 2 3 y x 3mx 3 m 1 x m
4m 1 có 2 điểm cực trị
tạo với gốc tọa độ 1 tam giác vuông tại O ? A. m 1; 2 . B. m 1; 2 . C. m 1; 2 . D. m 1; 2 . 1 1 11 n
Câu 26: Cho hàm số 4 2 y x mx n đạt cực trị bằng tại x 1, khi đó tỉ số bằng bao 4 2 4 m nhiêu ? 1 1 A. 3. B. . C. 1 . D. . 3 9
Câu 27: Cho hàm số 4 3 2 y f x x x 3x
x 5 có 3 điểm cực trị thỏa mãn x x x . Đặt 1 2 3 2 2 A x x x x x x
, giá trị của 2A bằng giá trị nào dưới đây ? 3 2 1 3 2 1 65 65 A. 14 . B. . C. . D. 56. 4 8 Câu 28: Hàm số 3 y x 8x
13x 1999 đạt cực đại tại: 13 13 A. x . B. x 1. C. x . D. x 2 . 3 3
Câu 29: Cho hàm số 4 3 2 y x x 3x x
5 , hỏi hàm số có mấy điểm cực đại, cực tiểu ?
A. 2 cực tiểu, 1 cực đại.
B. 2 cực đại, 1 cực tiểu.
C. Chỉ có cực tiểu.
D. Chỉ có cực đại . Câu 30: Hàm số 4 2 y x 4mx 3 m 1
2 có duy nhất 1 cực trị khi m thỏa giá trị nào ? A. m 0 . B. m 0 . C. m 0 . D. m 0 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 1 1
Câu 31: Cho hàm số 3 2 y x m 1 x 3 m 2 x
. Tìm m để hàm số đạt cực đại, cực tiểu tại 3 3 2 x ,x x x thỏa x x 1 ? 1 2 1` 2 1 2 1 1 m 2 m 2 m m A. 2 2 2 . B. 2 . C. . D. . m m 3 2 3 3 m m 2 3
Câu 32: Cho hàm số 4 3 2 y x mx 2x
3mx 1. Xác định m để hàm số có hai cực tiểu ? 4 4 4 4 A. m . B. m . C. m . D. m . 3 3 3 3 2 mx 1
Câu 33: Tìm m để đồ thị hàm số y
có hai cực trị tại A và B sao cho AB ngắn nhất. x 1 1 A. m . B. m . C. m 2 . D. m 2 . 2 2
Câu 34: Cho hàm số 4 2 2 y x 2m x
1. Tìm giá trị m để đồ thị hàm số có 3 cực trị A,B,C và diện tích tam giác ABC bằng 32: 1 A. m 1. B. m . C. m 2 . D. m 3 . 2
Câu 35: Tìm m để hàm số 4 2 2 y mx m 9 x 10 có 3 cực trị ? m 3 m 3 A. . B. 3 m 3 . C. 0 m 3 . D. . 0 m 3 m 0
Câu 36: Cho hàm số: 4 2 2 y x 5m 2 x m
3 , với giá trị nào của m bên dưới để hàm số có 3 cực
trị tạo thành tam giác có góc bằng 30 ? 8 3 3 2 56 32 5 A. m . B. 3 .
C. Cả A và B.
D. Không có m thỏa mãn. 5 5 Câu 37: Hàm số 3 2 y x 3x 1 đạt cực tiểu tại: A. x 0 . B. x 2 .
C. Không có cực tiểu. D. x 2 .
Câu 38: Khẳng định nào sau đây là sai: 3x 2 3 x A. y
có đạt cực tiểu tại -1. B. 2 y x 4x x 1 3 không có cực trị. C. 4 2 y x 6x 2 đạt cực tiểu là 0.
D. Nếu đạo hàm không đổi dấu trên TXĐ D thì hàm không có cực trị. 2 3x
Câu 39: Điểm cực trị hàm số 3 y 3x là: 2 1 1 A. x 0, x . B. x 3,x 3 . C. x , x 0 .
D. Không có cực trị. CD CT 3 CD CT CD CT 3 Câu 40: Hàm số 4 2 y ax bx c với a
0 có tối đa bao nhiêu cực trị ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. 1. B. 2. C. 3. D. 4.
Câu 41: Cho hàm số 3 2 y 3x 4x 6x
2 , viết phương trình đường thẳng đi qua 2 điểm cực trị. 8 92 92 8 8 92 A. y x .
B. Không tồn tại. C. y x . D. y x . 9 27 27 9 9 27
Câu 42: Cho hàm số sau đây: 3 2 y x 3x
9x 11 , phát biểu nào đúng trong các phát biểu sau đây ?
A. Đồ thị hàm số nhận điểm có x 1 làm điểm cực tiểu.
B. Đồ thị hàm số nhận điểm có x 3 làm điểm cực đại.
C. Đồ thị hàm số nhận điểm có x 1 làm điểm cực đại.
D. Đồ thị hàm số nhận điểm có x 3 làm điểm cực tiểu . 2
Câu 43: 1 hàm số có đạo hàm 2 f ' x x x 1
2x 3 . Số cực trị của hàm f(x) là giá trị nào dưới đây ? A. 1 . B. 2 . C. 3. D. 4 .
Câu 44: Xác định giá trị m để hàm số y
sin 4x 2mcos x đạt cực tiểu tại x ? 3 2 2 2 2 3 2 A. m . B. m . C. m . D. m . 3 3 3 2
Câu 45: Cho hàm số 3 y m 2 x
mx 2 . Tìm m để đồ thị hàm số không có cực đại và cực tiểu ? A. 0 m 2 . B. 0 m 2 . C. 2 m 0 .
D. Không có m thoả mãn.
Câu 46: Cho hàm số y
f x xác định, liên tục trên
và có bảng biến thiên: x 0 1 y ' || 0 0 y 1
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng 1 cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất là 1 .
D. Hàm số đạt cực đại tại x
0 và đạt cực tiểu tại x 1.
Câu 47: Cho hàm số 4 2 y 2x m 1 x
3 . Tìm m để hàm số có ba điểm cực trị tạo thành tam giác vuông cân ? A. 3 m 16 1. B. 3 m 16 1 . C. 3 m 16 1. D. m 1 .
Câu 48: Định giá trị của m để hàm số 4 2 y x 3m 1 x
6 có 3 điểm cực trị tạo thành tam giác
cân có cạnh bên gấp rưỡi cạnh đáy. 3 5 A. m 3 . B. m 5 . C. m . D. m . 5 3
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 49: Cho hàm số 4 2 y x 2 m 1 x
3 . Tìm m để hàm số có ba điểm cực trị tạo thành tam giác có góc bằng 120 : 1 1 1 1 A. 3 m 1. B. 3 m 1. C. m . D. m . 3 3 3 3
Câu 50: Hàm số nào sau đây không có cực trị ? x 1 2 x x A. 3 2 y x x 1 . B. y . C. 4 2 y x 3x 2 . D. y . x 1 x 1
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số” – P.1 1
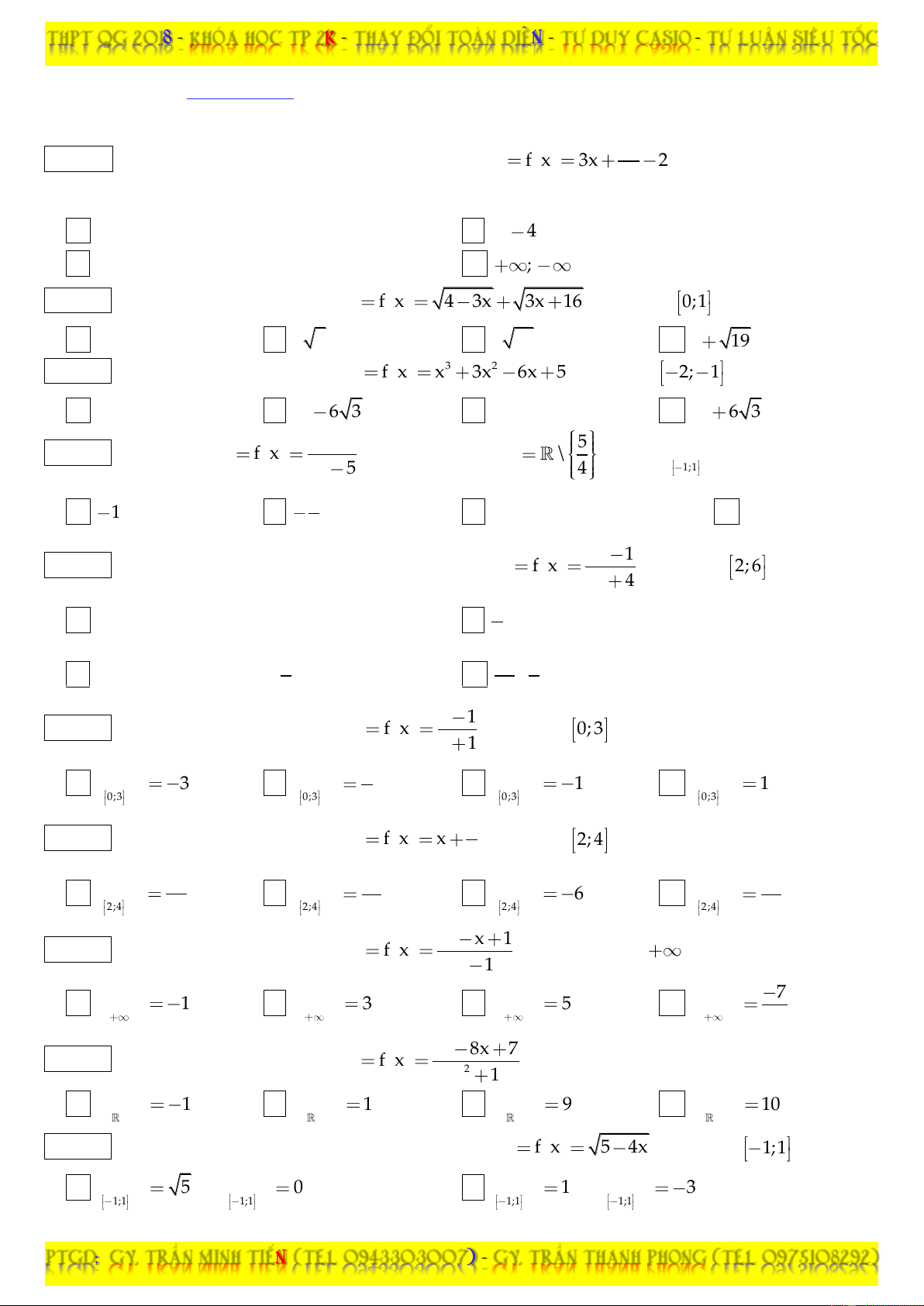
Câu 01: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x 3x
2 trên tập xác định của nó 3x lần lượt là:
A. Không tồn tại GTLN; GTNN. B. 0; 4 .
C. Không tồn tại GTNN; 0. D. ; .
Câu 02: Giá trị lớn nhất của hàm số y f x 4 3x 3x 16 trên đoạn 0;1 là: A. 6 . B. 2 5 . C. 2 10 . D. 1 19 .
Câu 03: Giá trị nhỏ nhất của hàm số 3 2 y f x x 3x 6x 5 trên đoạn 2; 1 là: A. 13 . B. 13 6 3 . C. 21. D. 13 6 3 . 1 5
Câu 04: Cho hàm số y f x với tập xác định D \ . Giá trị min y bằng: 4x 5 4 1;1 1 A. 1 . B. .
C. Không tồn tại GTNN. D. 0 . 9 2x 1
Câu 05: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f x
trên đoạn 2; 6 lần lượt là: 3x 4 2
A. Không tồn tại GTNN, GTLN.
B. ; không tồn tại GTLN. 3 2 3 1
C. Không tồn tại GTNN, . D. ; . 3 10 2 x 1
Câu 06: Giá trị nhỏ nhất của hàm số y f x trên đoạn 0; 3 là: x 1 1 A. min y 3 . B. min y . C. min y 1 . D. min y 1 . 0;3 0;3 2 0;3 0;3 x
Câu 07: Giá trị nhỏ nhất của hàm số y f x x trên đoạn 2; 4 9 là: 20 13 25 A. min y . B. min y . C. min y 6 . D. min y . 2;4 9 2;4 2 2;4 2;4 4 2 x x 1
Câu 08: Giá trị nhỏ nhất của hàm số y f x trên khoảng 1; là: x 1 7 A. min y 1 . B. min y 3 . C. min y 5 . D. min y . 1; 1; 1; 1; 3 2 x 8x 7
Câu 09: Giá trị lớn nhất của hàm số y f x là: 2 x 1 A. max y 1. B. max y 1. C. max y 9 . D. max y 10 .
Câu 10: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x 5 4x trên đoạn 1;1 là: A. max y 5 và min y 0 . B. max y 1 và min y 3 . 1;1 1;1 1;1 1;1
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC C. max y 3 và min y 1 . D. max y 0 và min y 5 . 1;1 1;1 1;1 1;1
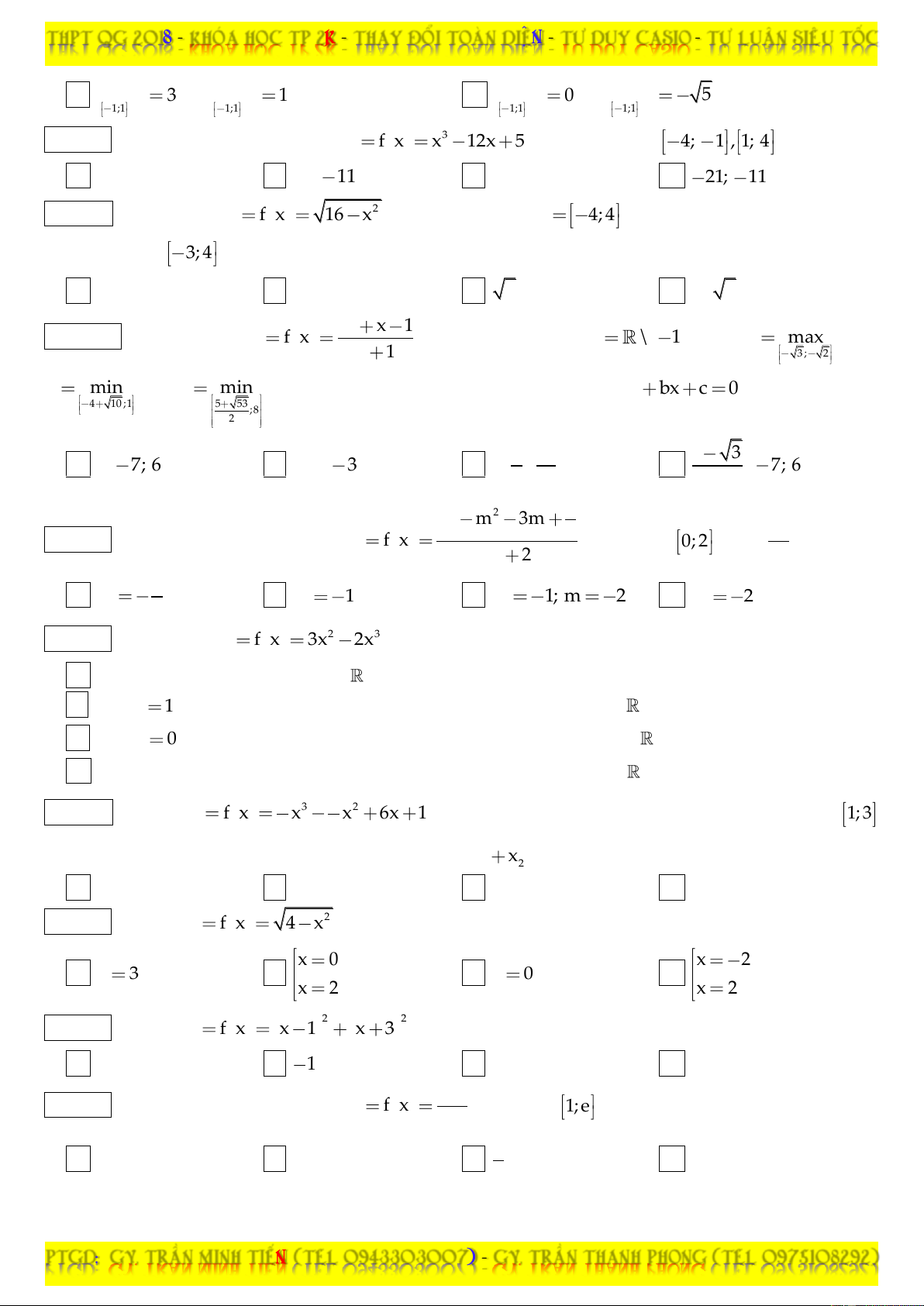
Câu 11: Giá trị lớn nhất của hàm số 3 y f x x 12x 5 trên từng đoạn 4; 1 , 1; 4 lần lượt là: A. 21; 21 . B. 21; 11. C. 21; 11. D. 21; 11 .
Câu 12: Cho hàm số 2 y f x
16 x với tập xác định D
4; 4 . Giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 3; 4 lần lượt là: A. 4; 0 . B. 0; 4 . C. 7 ; 4 . D. 4; 7 . 2 x x 1
Câu 13: Cho hàm số y f x với tập xác định D \ 1 . Đặt a max f x ; x 1 3 ; 2 b min f x ; c
min f x . Các nghiệm phương trình bậc 3 sau: 3 ax bx c 0 lần lượt là ? 4 10 ;1 5 53 ;8 2 1 71 1 3 A. 1; 7; 6 . B. 1; 2; 3 . C. 1; ; . D. ; 7; 6 . 2 9 2 2 1 4x m 3m 31
Câu 14: Giá trị nhỏ nhất của hàm số 3 y f x trên đoạn 0; 2 bằng khi: 3x 2 24 3 A. m . B. m 1 . C. m 1; m 2 . D. m 2 . 2
Câu 15: Cho hàm số 2 3 y f x 3x
2x . Mệnh đề nào sau đây là mệnh đề đúng ?
A. Hàm số đã cho đồng biến trên . B. Tại x
1, hàm số đã cho đạt cực đại và đạt giá trị lớn nhất trên . 0 C. Tại x
0 , hàm số đã cho đạt cực tiểu và đạt giá trị nhỏ nhất trên . 0
D. Hàm số đã cho không có giá trị lớn nhất và giá trị nhỏ nhất trên . 1 5 Câu 16: Hàm số 3 2 y f x x x
6x 1 đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 1; 3 3 2
tại điểm có hoành độ lần lượt là x , x . Khi đó tổng x x bằng: 1 2 1 2 A. 2 . B. 5 . C. 4 . D. 3 . Câu 17: Hàm số 2 y f x
4 x đạt giá trị nhỏ nhất tại x. Giá trị của x là: x 0 x 2 A. x 3 . B. . C. x 0 . D. . x 2 x 2 2 2 Câu 18: Hàm số y f x x 1 x
3 có giá trị nhỏ nhất bằng: A. 3 . B. 1 . C. 10 . D. 8 . ln x
Câu 19: Giá trị nhỏ nhất của hàm số y f x
trên đoạn 1; e bằng là: x 1 A. 0 . B. 1 . C. . D. e . e
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC x 1 Câu 20: Hàm số y f x
đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 3; 0 lần lượt 2 x 2 tại x , x . Khi đó x x 1 2 1 2 bằng: A. 2 . B. 0 . C. 6 . D. 2 .
Câu 21: Giá trị 2 là giá trị lớn nhất của hàm số nào (xét trên ) sau đây ? A. y x . B. y 2 . C. y cos x . D. y sin x . x 1 1
Câu 22: Cho hàm số y f x x 2 xác định trên
. Một học sinh trình bày các bước 2x 1 x
tìm giá trị lớn nhất của hàm số y trên 1; 2 như sau:
Bước 1: Tìm tập xác định của hàm số y . 1 Tập xác định D \ ; 0 . 2
Bước 2: Tìm đạo hàm của hàm số y. 2x 1 2 x 1 1 3 1 y 1 1 0, x D . 2 2 2 2 x x 2x 1 2x 1
Bước 3: Ta có: y đồng biến trên D suy ra y đồng biến trên đoạn 1; 2 . Bước 4: Kết luận: max y y 1 2 . 1; 2
Bạn học sinh đó trình bày sai bắt đầu từ bước nào ? A. 1 . B. 2 . C. 3 . D. 4 . Câu 23: Đặt a max f x ; b min f x ; c maxg x ; d ming x , trong đó f x 2 x xác định 1; 2 2; 4 2; 1 1; 2 1 at bt 2 trên 0; và g x xác định trên
\ 0 . Xét hệ phương trình 1 2 I với t , t là x ct dt 0 1 2 1 2
các ẩn của hệ phương trình và a, b, c, d là các hệ số của hệ được định nghĩa như trên. Nghiệm của hệ I là: 2 2 2 2 2 2 2 2 A. ; . B. ; . C. ; . D. ; . 4 4 4 4 4 4 4 4
Câu 24: Cho hàm số y f x 1 4x 8 xác định trên 2; và 2 g x x 3x 5 xác định trên g b g a . Đặt a max f x , b min f x và A
. Giá trị của biểu thức A bằng: 3; 4 5;6 b a A. 7 . B. 7 . C. 29 . D. 9 . 2
Câu 25: Cho hàm số 2 f x x 3x xác định trên , g x xác định trên \ 1 . Giả sử x 1 a max f x , b
min g x . Với a, b được định nghĩa như trên thì t thỏa bất phương trình at b 2 1; 2 2; 3 là:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 1 4 1 A. t . B. t . C. t 0 . D. t . 2 9 2 Câu 26: Hàm số y f x
cos 2x 3 đạt giá trị nhỏ nhất trên đoạn 0; bằng: A. 4 . B. 3 . C. 2 . D. 0 . Câu 27: Hàm số y f x tan x
x đạt giá trị nhỏ nhất trên đoạn 0; tại điểm x ? 4 A. 0 . B. . C. 1 . D. 1. 4 4 Câu 28: Hàm số y f x sin x
cos x có giá trị nhỏ nhất, giá trị lớn nhất lần lượt là ? A. 2; 2 . B. 2; 2 . C. 0; 1 . D. 1; 1 . Câu 29: Hàm số 3 y f x
3sin x 4 sin x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là: A. 3; 4 . B. 1; 0 . C. 1; 1. D. 0; 1. Câu 30: Hàm số 2 y f x sin x
2 có giá trị nhỏ nhất, giá trị lớn nhất lần lượt bằng: A. 0; 2 . B. 1; 3 . C. 1; 2 . D. 2; 3 . 3
Câu 31: Cho hàm số y f x 3x
4x 6 với tập xác định D ;
. Giá trị của biểu thức 2 2 2 A max f x min f x là: 3; 6 3; 6 A. A 255 18 6 108 2. B. A 18 3 2 . 9 C. A 9 6. D. A . 2 7
Câu 32: Cho hàm số y f x 4x
5x 7 với tập xác định D ;
. Giá trị của biểu thức 5 2 2 A max f x min f x là ? 4; 5 4; 5 A. A 20 3 2 . B. A 149 32 13 120 2. 28 C. A 16 13. D. A . 5 4
Câu 33: Cho hàm số y f x 5x
6x 8 với tập xác định D ;
. Giá trị của biểu thức 3 2 2 A max f x min f x là: 5; 6 5; 6 20 A. A 30 2 7 . B. A 25 22 . C. A 281 120 7 50 22 . D. A . 3
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 9
Câu 34: Cho hàm số y f x 6x
7x 9 với tập xác định D ;
. Giá trị của biểu thức 7 2 2 A max f x min f x là: 3; 4 3; 4 54 A. A . B. A 24 19 . 7 C. A 18 2 3 . D. A 259 48 19 72 3 . 4x 3
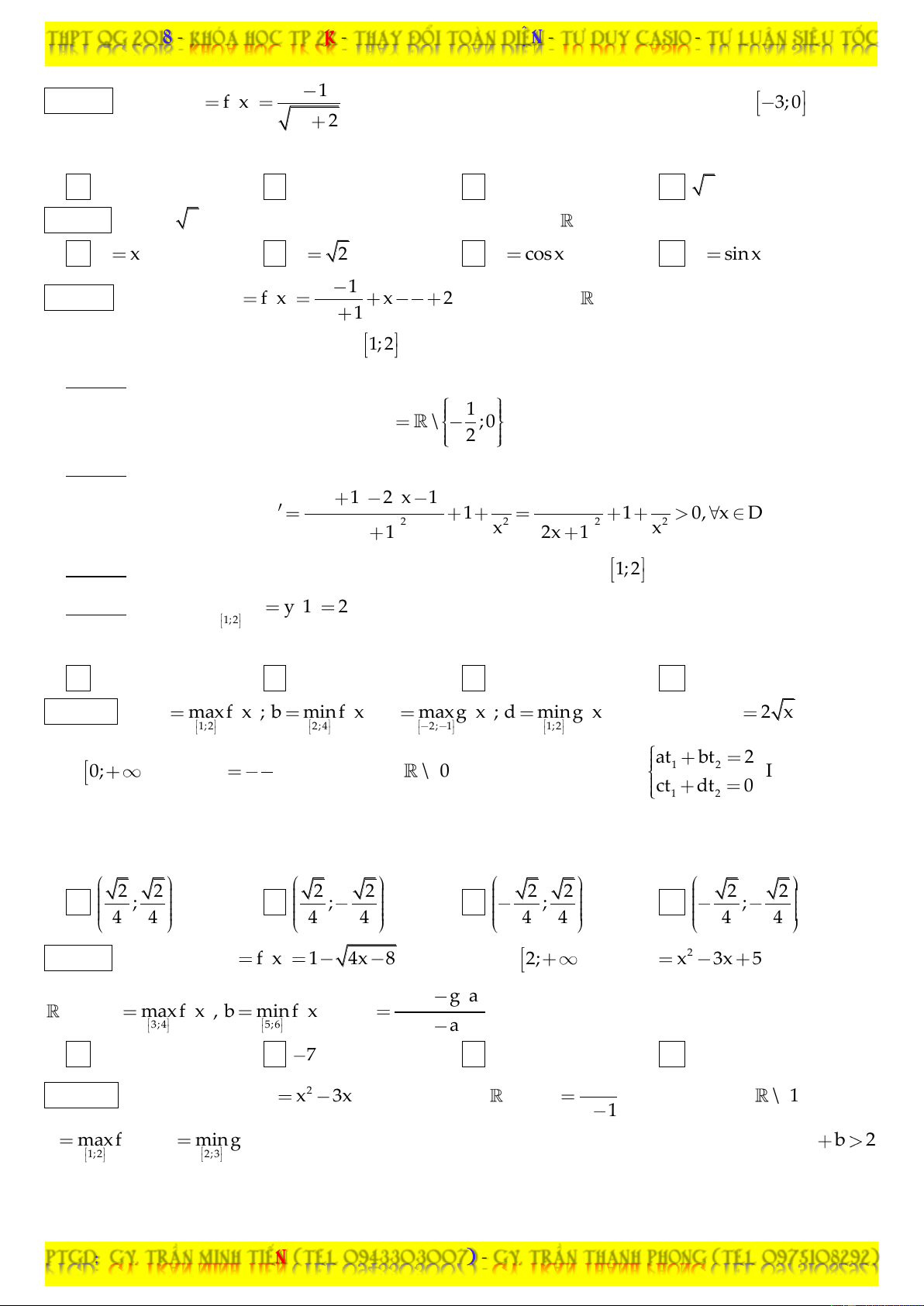
Câu 35: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x
trên đoạn 4; 6 lần lượt là: 5x 6 7
A. Không tồn tại GTLN, GTNN. B. ; không tồn tại GTNN. 12 1 7 1
C. Không tồn tại GTLN; . . D. ; . 2 12 2 Câu 36: Hàm số y f x tan x
cot x đạt giá trị lớn nhất trên đoạn ; tại điểm x ? 6 3 A. . B. . C. . D. . 4 9 6 5 Câu 37: Hàm số y f x
cos x sin x 1 có giá trị lớn nhất trên đoạn 0; là: 3 3 A. 1 . B. 2 . C. . D. 0 . 4 Câu 38: Hàm số 3 3 y f x sin x
cos x có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 0; lần lượt là y , y . Khi đó hiệu y y có giá trị bằng: 1 2 1 2 A. 4 . B. 1 . C. 3 . D. 2 .
Câu 39: Giá trị nhỏ nhất của hàm số x 2 y f x e x x 1 trên đoạn 0; 2 là: A. min y 2e. B. 2 min y e . C. min y 1. D. min y e. 0;2 0;2 0;2 0;2
Câu 40: Giá trị nhỏ nhất của hàm số x 2 y f x e x - 3 trên đoạn 2; 2 bằng : A. 2 min y e . B. min y 2e. C. 2 min y e . D. min y 4e. 2;2 2;2 2;2 2;2 10 3sin x
Câu 41: Giá trị lớn nhất của hàm số y f x là: 2 sin x 13 A. . B. 7 . C. 5 . D. 1 . 3 7 2 sin x
Câu 42: Giá trị lớn nhất của hàm số y f x là: 2 sin x 7 A. 3 . B. 5 . C. . D. 1 . 2 12 4 sin x
Câu 43: Giá trị lớn nhất của hàm số y f x là: 2 sin x
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 16 A. . B. 8 . C. 6 . D. 1 . 3
Câu 44: Hai số có hiệu 15 sao cho tích của chúng là bé nhất. Số lớn nhất trong 2 số đó là: 15 15 225 A. . B. . C. . D. Không tồn tại. 2 2 4
Câu 45: Hai số có hiệu 10 sao cho tích của chúng là bé nhất. Số lớn nhất trong 2 số đó là: A. 5 . B. 5 . C. 25 . D. Không tồn tại. 1 3
Câu 46: Giá trị lớn nhất của hàm số y f x trên khoảng ; là: cos x 2 2
A. Không tồn tại. B. 1. C. . D. – 1. 1
Câu 47: Giá trị nhỏ nhất của hàm số y f x trên khoảng 0; là: sin x A. – 1. B. 1. C. . D. Không tồn tại. 2
Câu 48: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 2 y f x x 1 x . Khi đó M m bằng: A. 2. B. 1. C. 0. D. 1 .
Câu 49: Giá trị nhỏ nhất của hàm số 2 y f x 3 x 2x 5 bằng: A. min y 3. B. min y 5. C. min y 3 5. D. min y 0.
Câu 50: Giá trị nhỏ nhất của hàm số 2 y f x x 2x 1 bằng: 1 A. min y . B. min y 0. C. min y 1. D. min y 2. 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số” – P.2 2 5
Câu 01: Cho hàm số y f x với tập xác định D ; . Các giá trị max f x ; 4x 5 6 4 3 9 ; 2 4 min f x lần lượt là: 3 9 ; 2 4 1 1 2 1 1 1 A. ; 0 .
B. ; không tồn tại. C. ; . D. ; . 3 3 7 4 3 4 5
Câu 02: Cho hàm số y f x 2x
3x 5 với tập xác định D ; . Đặt 3 2 2 A max f x min f x . Giá trị A bằng ? 2;7 2;7 A. 299 . B. 299 . C. 18 . D. 5 . 15 4 sin x
Câu 03: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x lần lượt là ? 5 2 sin x 11 19 19 11 A. 3; 0 . B. ; . C. ; . D. Không tồn tại. 3 7 7 3 3 3 2 2 cos x 1 sin x 2 max f x min f x 0;1 0;1
Câu 04: Cho hàm số 2 y f x x , đặt A . Giá trị 2 sin x 2 2 max f x min f x 0;1 0;1 A bằng: 35 91 A. 0 . B. . C. 1 . D. . 13 75
Câu 05: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y sin 2x cos 2x trên đoạn 0; lần lượt 2 là: A. max y 2; min y 1 . B. max y 2; min y 1. 0; 0; 0; 0; 2 2 2 2 C. max y 2; min y 2 . D. max y 2; min y 2 . 0; 0; 0; 2 2 0; 2 2
Câu 06: Giá trị nhỏ nhất của hàm số 3 y f x x 3x 5 trên đoạn 0; 2 là: A. min y 0 . B. min y 3 . C. min y 5 . D. min y 7 . 2;4 2;4 2;4 2;4
Câu 07: Giá trị nhỏ nhất của hàm số 3 2 y f x x 3x 9x 35 trên đoạn 4; 4 là: A. min f x 50 . B. min f x 0 . C. min f x 41. D. min f x 15 . 4;4 4;4 4;4 4;4
Câu 08: Giá trị lớn nhất của hàm số 3 2 y f x x 8x 16x 9 trên đoạn 1; 3 là:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 13 A. max f x 0 . B. max f x . C. max f x 6 . D. max f x 5 . 1;3 1;3 27 1;3 1;3
Câu 09: Giá trị lớn nhất của hàm số 4 2 y f x x 2x 1 trên đoạn 0; 2 là ? A. max f x 64 . B. max f x 1. C. max f x 0 . D. max f x 9 . 0;2 0;2 0;2 0;2
Câu 10: Giá trị nhỏ nhất của hàm số y f x x x 2 x 4 x 6 trên nữa khoảng 4; là: A. min y 8 . B. min y 16 . C. min y 17 . D. min y 9 . 4; 4; 4; 4; 1
Câu 11: Giá trị lớn nhất của hàm số 3 2 y f x x 2x 3x 4 trên đoạn 1; 5 là ? 3 8 10 10 A. . B. . C. 4 . D. . 3 3 3 Câu 12: Hàm số 4 2 y f x x 2x
1 có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 0; 2 lần lượt là ? A. 9; 0 . B. 9; 1 . C. 2; 1 . D. 9; 2 . x 1
Câu 13: Giá trị lớn nhất của hàm số y f x trên đoạn 0; 2 là: x 2 1 1 A. . B. 2 . C. . D. 0 . 4 2 2 x 3
Câu 14: Cho hàm số y f x
. Khẳng định nào sau đây đúng về giá trị lớn nhất và nhỏ nhất x 2
của hàm số trên đoạn 3; 4 ? 3
A. Hàm số có giá trị nhỏ nhất bằng .
B. Hàm số có giá trị lớn nhất bằng 2. 2
C. Hàm số có giá trị lớn nhất bằng 6. 13
D. Hàm số có giá trị lớn nhất bằng
và giá trị nhỏ nhất bằng 6 . 2 Câu 15: Hàm số 2 y x
2x 1 có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 0;1 lần lượt là y , y . Khi đó tích y .y 1 2 1 2 bằng: A. 5 . B. 1 . C. 4 . D. 1 . 1 3
Câu 16: Cho hàm số y f x 2x 1 có tập xác định D \
. Mệnh đề nào sau đây là 2x 3 2 đúng ?
A. Không tồn tại GTLN, GTNN trên D. B. min f x 6; max f x 2 . D D C. max f x
2 ; không tồn tại GTNN. D. max f x 6 ; không tồn tại GTNN. D D 1 4
Câu 17: Cho hàm số y f x 2x 1 với tập xác định D ; . Ta xét các mệnh đề 3x 4 3 sau đây:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
1 Không tồn tại max y .
2 Không tồn tại min y . D D
3 Hàm số y đồng biến trên .
4 Hàm số y nghịch biến trên D . 1 1 1 1 5 y . 6 y . 2x 1 3x 4 2x 1 2 3x 4 3x 4
Số mệnh đề đúng là ? A. 4 . B. 1 . C. 3 . D. 2 . 2x 1 5
Câu 18: Cho hàm số y f x với tập xác định D \
. Ta xét các khẳng định sau đây: 4x 5 4 1 1 3 1 y 0, x . 2 min f x . 3 max f x . 4 max f x . D 2 D 2 1; 2 13 5 5
5 ì f đồng biến trên từng khoảng ; và ; nên f đồng biến trên . 4 4
Số khẳng định sai là ? A. 2 . B. 1 . C. 4 . D. 3 . 1 Câu 19: Cho a sao cho a min f x maxg x , trong đó 2 f x x , x \ 0 và 2; 4 2; 4 2 x g x 0, x
. Trong số các mệnh đề sau, mệnh đề nào đúng: A. a 2 . B. a 2 . C. a 2 . D. Không tồn tại a .
Câu 20: Cho các hàm số sau: f x sin x cos x, x ; g x sin x cos x, x ; h x 1 2 sin x, x ; y 3cos x, x
. Mệnh đề nào đúng trong các mệnh đề sau ? A. min f x 2 . B. maxg x 2 . C. min h x 1 . D. max y 3 . Câu 21: Hàm số 2 2 y f x x 1
x có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 1;1 lần lượt là: A. 2 1; 0 . B. 2 1; 0 . C. 1; 1. D. 1; 0 . 4
Câu 22: Giá trị lớn nhất của hàm số 3 y f x 2 sin x sin x trên 0; là ? 3 2 2 2 A. max y 2 . B. max y . C. max y 0 . D. max y . 0; 0; 3 0; 0; 3
Câu 23: Giá trị nhỏ nhất của hàm số y f x 2 cos 2x 4 sin x trên đoạn 0; là ? 2 A. min y 4 2 . B. min y 2 2 . C. min y 2 . D. min y 0 . 0; 0; 0; 0; 2 2 2 2
Câu 24: Giá trị nhỏ nhất của hàm số y f x 5cos x cos 5x với x ; là: 4 4
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. min y 4 . B. min y 3 2 . C. min y 3 3 . D. min y 1 . ; ; ; ; 4 4 4 4 4 4 4 4 Câu 25: Hàm số y f x
sin x 1 đạt giá trị lớn nhất trên đoạn ; bằng ? 2 2 A. 2 . B. . C. 0 . D. 1 . 2 Câu 26: Hàm số y f x
9 sin x sin 3 x có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 0; lần lượt là: A. 8; 0 . B. 0; 8 . C. 1; 1. D. 0; 1. Câu 27: Hàm số y f x 3 sin x
cos x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là: A. 0; 1. B. 3; 0 . C. 3; 1 . D. 2; 2 . Câu 28: Hàm số 2 y f x
cos x 2 cos x 1 có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn 0;
lần lượt bằng y , y . Khi đó tích y .y có giá trị bằng: 1 2 1 2 3 3 A. . B. 4 . C. . D. 1 . 4 8 Câu 29: Hàm số y f x
cos 2x 2 sin x có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 0; lần 2
lượt là y , y . Khi đó tích y .y có giá trị bằng ? 1 2 1 2 1 A. 5 . B. 1 . C. . D. 0 . 4 Câu 30: Hàm số y f x
cos 2x 4 sin x 4 có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 0; là: 2 A. ; 0 . B. 5; 1 . C. 5; 1. D. 9; 1 . 2
Câu 31: Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số 4 2 y f x sin x 4 sin x 5 là: A. M 2; m 5 . B. M 5; m 2 . C. M 5; m 2 . D. M 2; m 5 .
Câu 32: Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số 4 2 y f x sin x cos x 2 là: 11 11 11 11 A. M 3; m . B. M ; m 3 . C. M 3; m . D. M ; m 3 . 4 4 4 4 2 2 cos x cos x 1
Câu 33: Cho hàm số y f x
. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất cos x 1
của hàm số đã cho. Khi đó M m bằng: A. –4. B. –5 . C. –6 . D. 3. sin x 1
Câu 34: Cho hàm số y f x
. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của 2 sin x sin x 1
hàm số đã cho. Chọn mệnh đề đúng.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 3 3 A. M m . B. M m 1 . C. M m . D. M m . 3 2 2 1 1
Câu 35: Giá trị lớn nhất của hàm số 3 2 y f x x x 6x 3 trên đoạn 0; 4 là ? 3 2 21 A. . B. 2. C. 1. D. 3. 3 2
Câu 36: Cho hàm số y f x x 1 3 với tập xác định D 1; . 3 là giá trị của ? x A. max f x . B. max f x . C. max f x . D. max f x . 1; 2 2; 3 3; 4 4; 5 2 1
Câu 37: Cho hàm số f x x x 2x 4 với tập xác định D 0; . Mệnh đề đúng là ? 3 x 5 A. min f x min f x . B. min f x max f x . C. max f x min f x . D. max f x min f x . 1; 2 1; 3 1; 2 3; 4 0;1 2; 3 3; 4 5;6
Câu 38: Cho hàm số y f x sin x với mọi x . Giá trị max f x bằng ? 0; 4 2 A. . B. 1 . C. 1 . D. 0 . 2
Câu 39: Giá trị nhỏ nhất của hàm số y f x cos x trên đoạn ; bằng ? 4 2 2 A. . B. 0 . C. 1 . D. 1 . 2 2 2x 3, khi x 2;1
Câu 40: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y 3 1 trên đoạn 2; 5 x , khi x 1; 5 4 4 lần lượt là: A. 4; 5 . B. 1; 5.
C. 4 , không tồn tại GTNN . D. 4; 1 .
Câu 41: Giá trị lớn nhất của hàm số x x y f x e 4e 3x trên đoạn 1; 2 bằng: 4 4 A. 2 max y e 6. B. max y e 3. 2 1;2 e 1;2 e C. max y 6e 3. D. max y 5. 1;2 1;2
Câu 42: Giá trị lớn nhất của hàm số 2x y f x x.e trên đoạn 0;1 bằng ? 1 1 A. max y 1. B. max y . C. max y 0. D. max y . 0;1 2 0;1 e 0;1 0;1 2e
Câu 43: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 2 y f x x ln 1 2x trên đoạn 2; 0 . Khi đó M m bằng : 17 17 17 5 15 A. ln10 . B. ln 7 . C. ln . D. ln10 . 4 4 4 2 4
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 1 5 Câu 44: Hàm số y f x trên đoạn ;
có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi sin x 3 6 đó giá trị M m bằng: 2 2 A. 2 . B. 1. C. 1. D. – 1. 3 3 3 Câu 45: Hàm số y f x 2 sin x sin 2x trên đoạn 0;
có giá trị lớn nhất là M, giá trị nhỏ nhất 2 là m. Khi đó M.m bằng: 3 3 3 3 A. 3 3 . B. 3 3 . C. . D. . 4 4
Câu 46: Giá trị lớn nhất của hàm số y f x x 4 4 x 4 x 4 4 x 5 bằng: A. max y 10. B. max y 5 2 2. C. max y 7. D. max y 5 2 2. 4;4 4;4 4;4 4;4
Câu 47: Giá trị lớn nhất của hàm số 2 y f x 2 sin x 2 sin x 1 bằng: 3 A. max y 4 . B. max y . C. max y 3. D. max y 1. 2
Câu 48: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 2 y f x x 1 x . Khi đó M m bằng: A. 2. B. 1. C. 0. D. 1 .
Câu 49: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 8 4 y f x 2 sin x cos 2x . Khi đó M m bằng ? 28 82 A. . B. 4. C. . D. 2. 27 27
Câu 50: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 20 20 y f x sin x cos x . Khi đó M.m bằng ? 1 513 A. . B. 1. C. 0. D. . 512 512
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số” – P.3 5x 4
Câu 01: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x
trên đoạn 5; 7 lần lượt là: 6x 7 31
A. Không tồn tại GTLN, GTNN. B. ; không tồn tại GTNN. 49 21 31 21
C. Không tồn tại GTLN; . D. ; . 37 49 37 6x 5
Câu 02: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x
trên đoạn 6; 8 lần lượt là: 7x 8 43
A. Không tồn tại GTLN, GTNN. B. ; không tồn tại GTNN. 64 31 43 31
C. Không tồn tại GTLN; . D. ; . 50 64 50 2 4
Câu 03: Cho hàm số y f x với tập xác định D ;
. Giá trị max f x ; min f x 6 5x 4 5 1; 2 1; 2 lần lượt là: 1 1 6 6
A. ; không tồn tại GTNN. B. ; . 3 3 15 2 6 6 2 C. ; .
D. ; không tồn tại GTNN. 7 15 7 1 3
Câu 04: Cho hàm số y f x với tập xác định D ;
. Giá trị max f x ; min f x 5 4x 3 4 2; 4 2; 4 lần lượt là: 1 1 5 13
A. ; không tồn tại GTNN. B. ; . 5 5 12 5 5 5 13 5 5 C. ; . D. ; không tồn tại GTNN. 20 12 20 1
Câu 05: Cho hàm số y f x với tập xác định D 1;
. Giá trị max f x ; min f x 4 3x 3 2; 4 2; 4 lần lượt là: 1 1 1
A. ; không tồn tại GTNN. B. ; . 4 4 7 4 3 1 4 3 C. ; . D.
; không tồn tại giá trị nhỏ nhất. 13 7 13
Câu 06: Giá trị nhỏ nhất của hàm số y x 1 là ?
A. không có giá trị nhỏ nhất.
B. có giá trị nhỏ nhất bằng 1.
C. có giá trị nhỏ nhất bằng –1.
D. có giá trị nhỏ nhất bằng 0.
Câu 07: Cho hàm số 2 y x
x 1 . Khẳng định nào sau đây là khẳng định đúng ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
A. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất. 3
B. Hàm số có giá trị nhỏ nhất bằng
; không có giá trị lớn nhất. 2 3 1
C. Hàm số có giá trị lớn nhất bằng
; giá trị nhỏ nhất bằng . 2 2 3
D. Hàm số có giá trị lớn nhất bằng
; không có giá trị nhỏ nhất. 2 Câu 08: Hàm số y 1 x
1 x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là ? A. 2; 1. B. 1; 0 . C. 2; 2 . D. 2; 1 .
Câu 09: Cho hàm số y x 1
x 2 . Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số không có giá trị nhỏ nhất.
B. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
C. Hàm số có giá trị lớn nhất bằng 3 .
D. Hàm số đạt giá trị lớn nhất tại x 2 . 1 1
Câu 10: Gọi y , y lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x 1 2 x 1 x 2
trên đoạn 3; 4 . Khi đó tích y .y là bao nhiêu ? 1 2 3 5 5 7 A. . B. . C. . D. . 2 6 4 3 1 1 1 Câu 11: Hàm số y f x
đạt giá trị lớn nhất trên đoạn 5; 3 bằng: x x 1 x 2 13 11 47 11 A. . B. . C. . D. . 12 6 60 6
Câu 12: Cho hàm số y f x x
x 1 . Khẳng định nào sau đây là khẳng định đúng ? 3
A. Hàm số có giá trị nhỏ nhất bằng và không có giá trị lớn nhất. 4 3
B. Hàm số có giá trị nhỏ nhất bằng và giá trị lớn nhất bằng 1 . 4
C. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số đạt giá trị lớn nhất tại điểm có hoành độ x
1 và giá trị lớn nhất bằng 1 . Câu 13: Hàm số 2 2 y f x 1 x
1 x đạt giá trị nhỏ nhất lần lượt tại hai điểm x ? A. 0 . B. 1. C. 2 . D. 2 . Câu 14: Hàm số 4 4 y f x sin x
cos x có giá trị nhỏ nhất, giá trị lớn nhất lần lượt là ? 1 A. 2; 1 . B. 0; 2 . C. ; 1. D. 0; 1 . 2 Câu 15: Hàm số 4 4 y f x
sin x cos x có giá trị lớn nhất bằng: A. 0 . B. 1 . C. 1 . D. Không tồn tại.
Câu 16: Hai số có hiệu 5 sao cho tích của chúng là bé nhất. Số lớn nhất trong 2 số đó là:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 5 5 25 A. . B. . C. . D. Không tồn tại. 2 2 4 a b c 15 0
Câu 17: Cho 3 số thực a, b,c thỏa mãn hệ phương trình
và tích ac nhỏ nhất. Số a b c 15 0
lớn nhất trong 3 số a, b,c là: 225 15 15 A. . B. . C. 0 . D. . 4 2 2
Câu 18: Trong các hình trụ nội tiếp hình cầu, bán kính R 2 thể tích lớn nhất của hình trụ là: 8 6 4 3 A. 3 R . B. 3 4 2R . C. 3 R . D. 0 . 9 9 2 2 2 2 a ab a b b
Câu 19: Tổng của hai số a, b bằng 24 , biết tích của chúng là lớn nhất. Đặt A , 3 2 a b
giá trị của biểu thức A là: 13 1 A. 12 . B. . C. 2 . D. . 12 24 Câu 20: Hàm số y f x
1 2 sin x.cos x đạt giá trị nhỏ nhất trên đoạn 0; tại: 2 A. x . B. x . C. x 0 và x . D. x . 4 6 2 3 Câu 21: Hàm số 6 6 y f x sin x
cos x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là: 1 1 A. 1; 1. B. 2; 0 . C. ; 1 . D. 1; . 4 4 Câu 22: Hàm số 2 2 y f x x 2x 3 x
2x 2 có giá trị lớn nhất là:
A. có giá trị lớn nhất là 0 .
B. có giá trị lớn nhất là 8 .
C. có giá trị lớn nhất là 2 .
D. không có giá trị lớn nhất. 2 x 2 Câu 23: Hàm số y f x
có giá trị nhỏ nhất tại x ? 2 x 1 A. 0 . B. 2 . C. 3 . D. 2 . Câu 24: Hàm số y
x 1 x 2 x 3 x 4 có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 1; 3 là: 9 A. 10; . B. 120; 1. C. 10; 1. D. 120; 1. 4 Câu 25: Hàm số y f x 1 x x 3 1 x. x
3 có giá trị lớn nhất, giá trị nhỏ nhất là ? A. 2 2 2; 2 . B. 2 2 2; 2 . C. 2 2; 2 . D. 2; 0 . Câu 26: Hàm số 2 y f x x 2 2 x
2 4 x đạt giá trị lớn nhất, giá trị nhỏ nhất tại x ? A. 2 2 4; 2 . B. 2 2 2; 2 . C. 2 2; 2 . D. 4; 2 . Câu 27: Hàm số 3 y f x x 1
x 1 có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn 0; 63 là: A. 2; 12 . B. 1; 2 . C. 0; 2 . D. 0; 12 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC sin x 1 Câu 28: Hàm số y
đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn ; tại x ? 2 sin x 3 2 2 A. x , x . B. x , x . C. x , x . D. x 0, x . 2 2 6 2 2 2 2 1 1 Câu 29: Hàm số 2 y f x x x
có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn 1; 3 là: 2 x x 112 112 112 A. 3; . B. 1; 4 . C. 1; . D. 4; . 9 9 9 2 Câu 30: Hàm số 8 4 y f x x x
1 đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 1; 2 lần lượt
tại hai điểm có hoành độ x ; x . Khi đó tích x .x có giá trị bằng: 1 2 1 2 A. 1. B. 2. C. 15. D. 0. Câu 31: Hàm số 2 2 y f x x 3x x 3x
2 giá trị nhỏ nhất lần lượt bằng ? A. 2 . B. 0 . C. 2 . D. 2 . x Câu 32: Hàm số y f x x
có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 0; 4 lần lượt x 1 là: 8 8 8 8 24 A. ; 0 . B. ; . C. 0; . D. ; 0 . 3 3 3 3 5
Câu 33: Trong số các hình chữ nhật có cùng chu vi 16 cm, hình chữ nhật có diện tích lớn nhất bằng ? A. 64 cm2. B. 4 cm2. C. 16 cm2. D. 8 cm2.
Câu 34: Trong tất cả các hình chữ nhật có cùng diện tích 48 cm2, hình chữ nhật có chu vi nhỏ nhất bằng ? A. 16 3 cm. B. 4 3 cm. C. 24 cm. D. 8 3 cm. 4 2 2 3 a ab a b b
Câu 35: Tổng của hai số a, b bằng 20 , biết tích của chúng là lớn nhất. Đặt A , 2 a b
giá trị của biểu thức A là ? 1300 A. 10 . B. 110 . C. . D. 400 . 11
Câu 36: Hiệu các bình phương của hai số không âm a, b bằng 36 , biết tích của chúng là nhỏ nhất. 3 2 2 2 a ab a b b Đặt A
, giá trị của biểu thức A là ? 3 2 a b 1 A. 6 . B. 0 . C. . D. 1 . 6
Câu 37: Cho 1 tam giác ABC vuông tại A , tam giác ABC có tổng của 1 cạnh góc vuông và 1 cạnh
huyền bằng 3 . Diện tích lớn nhất có thể tồn tại của tam giác đó là ? 3 A. 1 . B. 2 . C. 3 . D. . 2
Câu 38: Hai số có hiệu là 13, tích của chúng bé nhất khi hai số đó bằng ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 13 13 A. 5; –8. B. 1; –12. C. ; . D. 6; –7 . 2 2
Câu 39: Một chất điểm chuyển động theo quy luật 2 3 S 6t
t , vận tốc v m / s của chuyển động
đạt giá trị lớn nhất tại thời điểm t s bằng ? A. 2 s . B. 12 s . C. 6 s . D. 4 s .
Câu 40: Tam giác vuông có diện tích lớn nhất là bao nhiêu nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a a 0 ? 2 a 2 a 2 2a 2 a A. . B. . C. . D. . 6 3 9 9 3 3
Câu 41: Một hợp tác xã nuôi cá thí nghiệm trong hồ. Người ta thấy rằng nếu trên mỗi đơn vị diện
tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P n 480 20n (gam).
Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều gam cá nhất ? A. 12. B. 24. C. 6. D. 32.
Câu 42: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức 2 G x 0.025x 30 x , trong
đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng miligam). Liều lượng thuốc cần
tiêm cho bệnh nhân để huyết áp giảm nhiều nhất bằng ? A. 100 mg. B. 20 mg. C. 30 mg. D. 0 mg.
Câu 43: Một con cá hồi bơi ngược dòng để vượt khoảng cách là 300 km. Vận tốc dòng nước là
6 km / h . Nếu vận tốc bơi của cá khi nước đứng yên là v km / h thì năng lượng tiêu hao của cá
trong t giờ được cho bởi công thức 3 E v
cv t, trong đó c là hằng số và E tính bằng Jun. Vận tốc bơi
của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất bằng: A. 6 km / h . B. 8 km / h . C. 7 km / h . D. 9 km / h .
Câu 44: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ
ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là 2 3 f t 45t t , t
0,1,2,...,25.Nếu coi f t là
hàm số xác định trên đoạn 0; 25 thì đạo hàm f t được xem là tốc độ truyền bệnh (người/ngày) tại
thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất ?
A. Ngày thứ 19.
B. Ngày thứ 5.
C. Ngày thứ 16. D. Ngày thứ 15.
Câu 45: Cho ABC đều cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC,
hai đỉnh P, Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trí của điểm M sao
cho hình chữ nhật có diện tích lớn nhất ? 2a 3a a a A. BM . B. BM . C. BM . D. BM . 3 4 3 4
Câu 46: Một hộp không nắp được làm từ một mảnh các tông theo mẫu như hình vẽ. Hộp có đáy là
một hình vuông cạnh x cm, chiều cao h cm và có thể tích 500 cm3. Giá trị của x để diện tích của mảnh
các tông nhỏ nhất bằng:
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC h h x x h h A. 100. B. 300. C. 10. D. 1000.
Câu 47: Trong các hình trụ nội tiếp hình cầu bán kính R, hình trụ có thể tích lớn nhất bằng ? 3 4 R 3 4 R 3 R 3 4 R A. . B. . C. . D. . 3 3 3 3 3 3
Câu 48: Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi
gập tấm nhôm lại để được một cái hộp không nắp. Tìm cạnh của hình vuông bị cắt sao cho thể tích
của khối hộp là lớn nhất ? 5a a a a A. . B. . C. . D. . 6 6 12 9
Câu 49: Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số: 2 y f x 2 sin x 2 sin x 1 là: 3 3 3 A. M 1, m . B. M 3,m 1 . C. M 3, m . D. M , m 3 . 2 2 2
Câu 50: Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số y f x 2 cos 2x 2 sin x là: 9 9 9 A. M , m 4 . B. M 4,m 0 . C. M 0,m . D. M 4,m . 4 4 4
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 4: Đƣờng tiệm cận” – P.1 mx 1
Câu 01: Cho hàm số y f x
C . Với giá trị nào của m thì tam giác tạo bởi hai đường x m 1
tiệm cận và đường thẳng y 2x 1 có chu vi là 6 2 5 ? A. 5 . B. 5 . C. 9 3 5 . D. 3 5 9 . 2x 1
Câu 02: Cho hàm số y f x
C . Tính diện tích tam giác tạo bởi đường tiệm cận của đồ thị 3x 2
hàm số đã cho và đường thẳng y 2x 1 ? 5 25 5 25 A. . B. . C. . D. . 12 18 6 36 ax 2 Câu 03: Cho C : y
. Đặt M là tâm đối xứng của C , N là giao điểm của tiệm cận đứng và 2x 3a
trục hoành, O là gốc tọa độ, P là giao điểm tiệm cận ngang và trục tung. Hình chữ nhật MNOP có
diện tích là 4. Tìm tất cả các giá trị của a ? 4 3 4 3 4 3 A. . B. . C. . D. 4 . 3 3 3 x 2 x 3
Câu 04: Với giá trị nào của m thì C : y f x và C : y g x sẽ có 1 2 2mx m 2 2 m x 2m chung tâm đối xứng ? A. m 2. B. m 2 . C. m 0 .
D. Không có m thỏa. m 1 x 2
Câu 05: Cho hàm số y f x
C . Định m để C có tiệm cận ngang trùng với tiệm 2 m x 2m 2x 2 cận ngang của C : y ? 1 x 1 1 A. . B. 0 . C. 1 . D. 2 . 2 2x 3
Câu 06: Đồ thị hàm số y f x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là ? x 1 A. x 1 và y 3 . B. x 2 và y 1 . C. x 1 và y 2 . D. x 1 và y 2 . 1 3x
Câu 07: Đồ thị hàm số y f x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là ? x 2 A. x 2 và y 3 . B. x 2 và y 1 . C. x 2 và y 3 . D. x 2 và y 1 . 2x 3
Câu 08: Đồ thị hàm số y f x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt 2 x 3x 2 là: A. x 1, x 2 và y 0 . B. x 1, x 2 và y 2 . C. x 1 và y 0 . D. x 1, x 2 và y 3 .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2 1 3x
Câu 09: Đồ thị hàm số y f x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt 2 x 6x 9 là ? A. x 3 và y 3 . B. x 3 và y 0 . C. x 3 và y 1 . D. y 3 và x 3 . 2 3x x 2
Câu 10: Đồ thị hàm số y f x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt 3 x 8 là ? A. y 2 và x 0 . B. x 2 và y 0 . C. x 2 và y 3 . D. y 2 và x 3 . 1 x
Câu 11: Số đường tiệm cận của đồ thị hàm số y f x là ? 3 2x A. 4. B. 1. C. 0. D. 2. 1
Câu 12: Số đường tiệm cận của đồ thị hàm số y f x là ? 3x 2 A. 1. B. 3. C. 4. D. 2. x 1
Câu 13: Số đường tiệm cận của đồ thị hàm số y f x là ? 2 x 4 A. 4. B. 2. C. 1. D. 3. x
Câu 14: Số đường tiệm cận của đồ thị hàm số y f x x là ? 2 x 3x 4 A. 4. B. 3. C. 2. D. 5. x 2
Câu 15: Cho hàm số y f x
khẳng định nào sau đây là khẳng định sai ? x 3
A. Đồ thị hàm số có tiệm cận đứng x 3 .
B. Hàm số nghịch biến trên \ 3 .
C. Đồ thị hàm số có tiệm cận ngang là y
1 . D. Đồ thị hàm số có tâm đối xứng là I 3;1 . 2 x 2
Câu 16: Cho hàm số y f x
. Tìm m để đồ thị hàm số có duy nhất một tiệm cận 2 2x 2mx m
đứng và tiệm cận đứng đó cắt parabol 2 P : y x 2x
2 tại điểm có tung độ là 2 ? A. m 2 . B. m 0 . C. m 2 . D. m 1 . 2x 1 Câu 17: Cho y f x . Đồ thị hàm số y f x có: x 3 A. đường thẳng x
3 là tiệm cận đứng, đường thẳng y 2 là tiệm cận ngang. B. đường thẳng x
3 là tiệm cận đứng, đường thẳng y 2 là tiệm cận ngang. C. đường thẳng x
3 là tiệm cận đứng, đường thẳng y 5 là tiệm cận ngang. D. đường thẳng x
3 là tiệm cận đứng, đường thẳng y 0 là tiệm cận ngang.
Câu 18: Cho hàm số y f x thỏa f 3
1 và đồ thị của nó có hai tiệm cận đứng đối xứng qua gốc
tọa độ, hàm số đó có thể là hàm số nào trong các hàm số được liệt kê dưới đây ? x x 2 2 x 6 x 3 A. y . B. y . C. y . D. y . 2 x 1 2 x 4 x 4 2 x 2x 3
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
Câu 19: Đồ thị hàm số nào sau đây có tiệm cận đứng và tiệm cận ngang ? A. y ax b, a 0 . B. 4 2 y ax bx d, a 0 . ax b C. 3 2 y ax bx cx d, a 0 . D. y , c 0, ad bc 0 . cx d
Câu 20: Trong các hàm số dưới đây, đồ thị của hàm nào có tiệm cận đứng ? 2 2x 3 3 x 2x 3x 1 A. y . B. y . C. y . D. y sin x . 2 x 2x 4 4 x 1 2x 1
Câu 21: Đồ thị hàm số nào trong các hàm số sau đây có ba đường tiệm cận ? 1 2x 1 x 3 x A. y . B. y . C. y . D. y . 1 x 2 4 x 5x 1 2 x x 9 4 x 9x
Câu 22: Cho hàm số y f x
. Khẳng định nào sau đây là khẳng định đúng ? 2 2 3x 3
A. Đồ thị hàm số có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang y 3 .
C. Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang y 1 .
D. Đồ thị hàm số không có tiệm cận đứng, có tiệm cận ngang.
Câu 23: Đồ thị hàm số nào sau đây không có tiệm cận đứng ? 3x 1 1 x 3 1 A. y . B. y . C. y . D. y . 2 x 1 x x 2 2 x 2x 1
Câu 24: Đồ thị hàm số nào sau đây không có tiệm cận ngang ? 2x 3 4 2 x 3x 7 3 3 A. y . B. y . C. y . D. y 1. x 1 2x 1 2 x 1 x 2
Câu 25: Đồ thị như hình vẽ bên dưới là đồ thị của hàm số nào sau đây ? 8 6 4 2 15 10 5 5 10 15 2 4 6 8 x 1 3 x x 2 x 2 A. y . B. y . C. y . D. y . x 1 x 1 x 1 x 1 3x 1
Câu 26: Đồ thị hàm số y f x
có đường tiệm cận ngang là ? 3x 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. x 3 . B. x 1 . C. y 3 . D. y 1 . 2x 1
Câu 27: Đồ thị hàm số y f x
có bao nhiêu đường tiệm cận ? x 2 A. 1. B. 2. C. 3. D. 0. 2x 1
Câu 28: Số đường tiệm cận của đồ thị hàm số y f x là ? 2 x 3x 2 A. 0. B. 1. C. 2. D. 3. mx 9
Câu 29: Cho hàm số y f x
có đồ thị C . Kết luận nào sau đây đúng ? x m A. Khi m
3 thì C không có đường tiệm cận ngang. B. Khi m
3 thì C không có đường tiệm cận ngang. C. Khi m
3 thì C có tiệm cận đứng x m, tiệm cận ngang y m . D. Khi m
0 thì C không có tiệm cận ngang. x 3
Câu 30: Tìm tất cả các đường tiệm cận của đồ thị hàm số y ? 2 x 1 A. y 1. B. x 1 . C. y 1 . D. y 1 . mx 1
Câu 31: Với giá trị nào của m thì đồ thị C : y f x
có tiệm cận đứng đi qua điểm 2x m M 1; 2 ? 2 1 A. m . B. m 0 . C. m . D. m 2 . 2 2 mx n
Câu 32: Cho hàm số y f x
có đồ thị C . Biết tiệm cận ngang của C đi qua điểm x 1 A
1; 2 đồng thời điểm I 2;1 thuộc C . Khi đó giá trị của m n là ? A. m n 1 . B. m n 1. C. m n 3 . D. m n 3 . 2 x 1 x
Câu 33: Số tiệm cận của hàm số y f x là ? 2 x 9 4 A. 2 . B. 4 . C. 3 . D. 1 . x m
Câu 34: Giá trị của m để đồ thị hàm số y f x
không có tiệm cận đứng là ? mx 1 m 0 A. . B. m 1 . C. m 1. D. m 1 . m 1 2 3 3 2 x 1 x 3x 1
Câu 35: Số tiệm cận của hàm số y f x là ? x 1 A. 3. B. 2. C. 1. D. 4. 3x 1
Câu 36: Đồ thị hàm số y f x
có tiệm cận đứng là ? 2x 4
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 3 3 A. x . B. x 2 . C. y 2 . D. y . 2 2
Câu 37: Đồ thị hàm số nào không có tiệm cận đứng ? 2x 1 4x 1 x 3 2x 1 A. y . B. y . C. y . D. y . 2 x 1 1 x 2 x 2 x 1
Câu 38: Tiệm cận đứng của đồ thị hàm số y f x nếu có thì luôn:
A. Song song với trục tung.
B. Song song với trục hoành.
C. Vuông góc với trục tung.
D. Song song hoặc trùng với trục tung.
Câu 39: Đồ thị hàm số nào sau đây có tiệm cận ngang ? 2 2x 4 4 2x 3 A. y . B. y 2x 5 . C. y tan x . D. y . x 2 3x 2 5 x 2x 4
Câu 40: Đồ thị hàm số y f x có tiệm cận ngang là ? x 1 A. x 2 . B. y 1 . C. x 1. D. y 2 . 2 x 2x 2 mx
Câu 41: Đồ thị hàm số y f x
có hai đường tiệm cận ngang với: x 2 m 0 A. m . B. m 1 . C. . D. m 0 . m 1 2 x x 1 mx
Câu 42: Đồ thị hàm số y f x
có đường tiệm cận đứng khi: x 1 A. m 0 . B. m R . C. m 1 . D. m 1 . 2 4 x
Câu 43: Số đường tiệm cận của đồ thị hàm số y f x là ? 2 x 3x 4 A. 1. B. 0. C. 2. D. 3. 2 x 1 neáu x 1
Câu 44: Số tiệm cận của đồ thị hàm số x y f x ? 2x neáu x 1 x 1 A. 1. B. 2. C. 3. D. 4. 2 x 2m 3 x 2 m 1
Câu 45: Xác định m để đồ thị hàm số y f x
không có tiệm cận đứng ? x 2 A. m 2. B. m 2 . C. m 3 . D. m 1 . 3
Câu 46: Xác định m để đồ thị hàm số y f x có đúng hai tiệm cận 2 2 4x 2 2m 3 x m 1 đứng ? 13 3 13 A. m . B. 1 m 1. C. m . D. m . 12 2 12 x 1
Câu 47: Xác định m để đồ thị hàm số y
có đúng hai tiệm cận đứng ? 2 2 x 2 m 1 x m 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC m 1 3 3 m 3 3 A. m . B. 2 . C. m . D. m . 2 2 2 m 1 m 3
Câu 48: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 2 y f x x mx 1 có tiệm cận ngang ? A. 0 m 1. B. m 1 . C. m 1. D. m 1 . 2 x x 3 2x 1
Câu 49: Cho hàm số y f x
. Trong các khẳng định sau, khẳng định nào là 3 2 x 2x x 2 khẳng định đúng ?
A. Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số không có tiệm cận đứng và có đúng 1 tiệm cận ngang.
C. Đồ thị hàm số có đúng 3 tiệm cận đứng và 2 tiệm cận ngang.
D. Đồ thị hàm số có đúng 2 tiệm cận đứng và 1 tiệm cận ngang. x 1
Câu 50: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x có 2 mx 1 hai tiệm cận ngang ? A. m 0 . B. m 0 . C. m 0 .
D. Không có m thỏa.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 4: Đƣờng tiệm cận” – P.2
Câu 01: Đồ thị hàm số nào trong các hàm số sau đây không có tiệm cận ngang ? 3 2 x 2x 3 4x 2 A. y 4 2x . B. y . C. y . D. x y 2 . x 1 2 x 9 2x 1
Câu 02: Nếu đồ thị hàm số y
f x có tiệm cận ngang thì:
A. Tiệm cận ngang luôn trùng với trục hoành. B. Tiệm cận ngang luôn song song với trục hoành
C. Tiệm cận ngang luôn song song với trục tung.
D. Tiệm cận ngang luôn vuông góc với trục tung.
Câu 03: Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số nếu có thì luôn:
A. Cắt nhau tại gốc tọa độ. B. Song song nhau.
C. Song song hoặc trùng nhau. D. Vuông góc nhau.
Câu 04: Đồ thị hàm số nào trong các hàm số sau đây không có tiệm cận ? 4 4 2 x 3x 2 A. y 2x 1 . B. y tan x . C. y . D. x y e . x 1 6 5
Câu 05: Cho hàm số y f x và các mệnh đề sau: 2 x 2
1 : Đồ thị hàm số luôn nằm dưới trục hoành. 2 : Đồ thị hàm số có tiệm cận đứng là x 2 . 10x 2
3 : Đồ thị hàm số không có tiệm cận ngang.
4 : Hàm số có đạo hàm y' . 4 x 2
5 : Hàm số luôn nghịch biến trên tập xác định .
Các mệnh đề không chính xác là ? A. 3 . B. 5 . C. 1 , 2 . D. 3 , 4 , 5 . 1 x
Câu 06: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x có x m tiệm cận đứng ? A. m 1. B. m 1 . C. m 1.
D. Không có m thỏa. x 1
Câu 07: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x 3 2 x 3x m
có đúng một tiệm cận đứng ? m 0 m 0 m 0 A. m . B. . C. . D. . m 4 m 4 m 4
Câu 08: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 2 2 x mx 2m y f x có tiệm cận đứng ? x 2 m 2 m 2
A. Không có m thỏa. B. . C. m . D. . m 1 m 1
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 5x 3
Câu 09: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x 2 x 2mx 1
không có tiệm cận đứng ? m 1 A. . B. 1 m 1. C. m 1 . D. m 1 . m 1 2x 1
Câu 10: Cho hàm số y f x
có đồ thị C . Gọi M là một điểm bất kì trên C . Tiếp tuyến x 1
của C tại M cắt các đường tiệm cận của C tại A và B . Gọi I là giao điểm của các đường tiệm
cận của C . Tính diện tích của tam giác IAB ? A. 2 . B. 12 . C. 4 . D. 6 . x 3
Câu 11: Số đường tiệm cận của đồ thị hàm số y f x là ? 2 x 1 A. 2. B. 0. C. 1. D. 3. 2 1 x
Câu 12: Số đường tiệm cận của đồ thị hàm số y f x là ? x 2 A. 0. B. 1. C. 3. D. 3.
Câu 13: Đồ thị hàm số 2 y f x x x 4x
2 có tiệm cận ngang là ? A. y 2 . B. y 2 . C. y 2 . D. x 2 . 2x 1
Câu 14: Tìm điểm M thuộc đồ thị hàm số y f x
sao cho khoảng cách từ M đến tiệm cận x 1
đứng bằng khoảng cách từ M đến trục hoành ? M 0; 1 M 2;1 M 0; 1 M 2;1 A. . B. . C. . D. . M 3; 2 M 4; 3 M 4; 3 M 3; 2 2 x x 2
Câu 15: Số tiệm cận của đồ thị hàm số y f x là ? x 2 A. 0. B. 1. C. 2. D. 3. 2x 1
Câu 16: Tâm đối xứng của đồ thị hàm số y f x là ? 5 x 2 2 A. 5; . B. ; 5 . C. 5; 2 . D. 2; 5 . 5 5 x 3
Câu 17: Đồ thị hàm số y f x
có bao nhiêu tiệm cận ? 2 2 4x A. 2. B. 1. C. 0. D. 3. 2 3x
Câu 18: Đồ thị hàm số y f x có: 2 2x 3x
A. 1 tiệm cận đứng và 1 tiệm cận ngang.
B. 2 tiệm cận đứng.
C. 2 tiệm cận đứng, 1 tiệm ngang.
D. Ít nhất 3 tiệm cận.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 3
Câu 19: Đồ thị hàm số y f x 2x có : x 5
A. Tiệm cận ngang là y 2x .
B. Tiệm cận ngang là x 5 .
C. Tiệm cận đứng là x 5 .
D. Tiệm cận đứng là y 5 .
Câu 20: Tiệm cận của đồ thị hàm số y
f x đi qua điểm M(3,2) và vuông góc trục hoành có thể là ? A. Đường thẳng y 3x 2 . B. Tiệm cận ngang y 2 .
C. Tiệm cận đứng x 3 . D. A, B, C đều sai. 2 x x 2
Câu 21: Số tiệm cận của đồ thị hàm số y f x là ? 2 x 2 A. 0. B. 1. C. 2. D. 3. 2 x 2
Câu 22: Số tiệm cận của đồ thị hàm số y f x là ? x 1 A. 1. B. 0. C. 3. D. 2. x 2
Câu 23: Cho hàm số y f x
C . Có tất cả bao nhiêu điểm M thuộc C sao cho khoảng x 3
cách từ M đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm M đến tiệm cận đứng ? A. 4. B. 3. C. 2. D. 1. x 2
Câu 24: Đồ thị hàm số y f x
có đường tiệm cận đứng là x
a và đường tiệm cận ngang 3x 9 là y
b . Giá trị của số nguyên m nhỏ nhất thỏa mãn m a b là ? A. 0 . B. 3 . C. 1 . D. 2 . 2x 3
Câu 25: Cho hàm số y f x
C . Gọi M là điểm bất kỳ trên C , d là tổng khoảng cách từ x 2
M đến hai đường tiệm cận của đồ thị C . Giá trị nhỏ nhất của d là ? A. 5. B. 10. C. 6. D. 2. 2x 3
Câu 26: Cho hàm số y f x
C . Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của x 2
C đến một tiếp tuyến bất kỳ của đồ thị C . Giá trị lớn nhất của d là: A. 2 2 . B. 3 . C. 3 3 . D. 2 . 2x 3
Câu 27: Cho hàm số y f x
C . Gọi d là tiếp tuyến bất kì của C , d cắt hai đường tiệm x 2
cận của đồ thị C lần lượt tại A, B. Khi đó khoảng cách giữa A và B ngắn nhất bằng: A. 4 . B. 3 2 . C. 2 2 . D. 3 3 . mx 9
Câu 28: Cho hàm số y f x
có đồ thị C . Kết luận nào sau đây đúng ? x m A. Khi m
3 thì C không có đường tiệm cận ngang.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC B. Khi m
3 thì C không có đường tiệm cận ngang. C. Khi m
3 thì C có tiệm cận đứng x m, tiệm cận ngang y m . D. Khi m
0 thì C không có tiệm cận ngang. x 3
Câu 29: Tìm tất cả các đường tiệm cận của đồ thị hàm số y f x ? 2 x 1 A. y 1. B. x 1. C. y 1 . D. y 1 . 2 x 1 x
Câu 30: Số tiệm cận của hàm số y f x là ? 2 x 9 4 A. 2 . B. 4 . C. 3 . D. 1 . x m
Câu 31: Giá trị của m để đồ thị hàm số y f x
không có tiệm cận đứng là ? mx 1 m 0 A. . B. m 1. C. m 1. D. m 1 . m 1 2 3 3 2 x 1 x 3x 1
Câu 32: Số tiệm cận của đồ thị hàm số C : y f x là ? x 1 A. 3. B. 2. C. 1. D. 4. 2 x 2x 2 mx
Câu 33: Đồ thị hàm số y f x
có hai đường tiệm cận ngang với: x 2 A. m . B. m 1 . C. m 0; m 1. D. m 0 . 2 x x 1 mx
Câu 34: Đồ thị hàm số y f x
có đường tiệm cận đứng khi: x 1 A. m 0 . B. m R . C. m 1 . D. m 1 . 2 x 4
Câu 35: Số đường tiệm cận của đồ thị hàm số y f x là ? 2 x 3x 4 A. 1. B. 0. C. 2. D. 3. x
Câu 36: Đồ thị hàm số y f x có ? 2 x 4
A. 1 tiệm cận đứng, 1 tiệm cận ngang.
B. 2 tiệm cận đứng, 1 tiệm cận ngang.
C. 2 tiệm cận đứng, 2 tiệm cận ngang.
D. 1 tiệm cận đứng, 2 tiệm cận ngang.
Câu 37: Đồ thị hàm số nào sau đây có nhiều hơn hai tiệm cận ? 2x 1 3 2 x 1 2 x 6 A. y . B. y . C. y . D. y . x 2 15x 1 2 x 5x 6 2 x 2 2 3x 4
Câu 38: Cho hàm số y f x
. Chọn phát biểu đúng ? 2 x 5x 6 A. x
0 không là tiệm cận đứng của đồ thị hàm số.
B. Hàm số không xác định trên / 2; 3 .
C. Đồ thị hàm số có 3 đường tiệm cận đứng.
D. Hàm số đơn điệu trên toàn bộ .
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2x a
Câu 39: Đồ thị hàm số y f x
đi qua điểm A 2,0 . Tiệm cận đứng của đồ thị hàm số này 4x 9 là ? 9 1 A. x 1. B. x . C. x . D. x 1 . 4 2 ax 3
Câu 40: Đồ thị C của hàm số y f x
đi qua A 2,1 . Tâm đối xứng của C là ? 2x 1 1 1 1 1 A. 2,1 . B. , 2 . C. ,1 . D. , . 2 2 2 2 2 x 1 neáu x 1
Câu 41: Số tiệm cận của đồ thị hàm số x y f x ? 2x neáu x 1 x 1 A. 1. B. 2. C. 3. D. 4. 2 x 2m 3 x 2 m 1
Câu 42: Xác định m để đồ thị hàm số y f x
không có tiệm cận đứng ? x 2 A. m 2. B. m 2 . C. m 3 . D. m 1 . 3
Câu 43: Xác định m để đồ thị hàm số y f x có đúng hai tiệm cận 2 2 4x 2 2m 3 x m 1 đứng ? 13 3 13 A. m . B. 1 m 1. C. m . D. m . 12 2 12 x 1
Câu 44: Xác định m để đồ thị hàm số y f x
có đúng hai tiệm cận đứng 2 2 x 2 m 1 x m 2 ? 3 m 3 3 3 A. 2 . B. m ,m 1 . C. m . D. m . 2 2 2 m 1, m 3
Câu 45: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 2 y f x x mx 1 có tiệm cận ngang ? A. 0 m 1. B. m 1. C. m 1. D. m 1 . 2 x x 3 2x 1
Câu 46: Cho hàm số y f x
. Trong các khẳng định sau, khẳng định nào là 3 2 x 2x x 2 khẳng định đúng ?
A. Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số không có tiệm cận đứng và có đúng 1 tiệm cận ngang.
C. Đồ thị hàm số có đúng 3 tiệm cận đứng và 2 tiệm cận ngang.
D. Đồ thị hàm số có đúng 2 tiệm cận đứng và 1 tiệm cận ngang.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC x 1
Câu 47: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x có 2 mx 1 hai tiệm cận ngang ? A. m 0 . B. m 0 . C. m 0 .
D. Không có m thỏa. 1 x
Câu 48: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x có x m tiệm cận đứng ? A. m 1. B. m 1 . C. m 1.
D. Không có m thỏa. x 1
Câu 49: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x 3 2 x 3x m
có đúng một tiệm cận đứng ? m 0 m 0 m 0 A. m . B. . C. . D. . m 4 m 4 m 4
Câu 50: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 2 2 x mx 2m y f x có tiệm cận đứng ? x 2 m 2 m 2
A. Không có m thỏa. B. . C. m . D. . m 1 m 1
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“Chuyên đề 4: Đƣờng tiệm cận” – P.3 2x a
Câu 01: Xác định hàm số y f x
sao cho đồ thị C của hàm số đã cho có tiệm cận đứng 5x b x 2 và đi qua P 3;1 : 2x 2 2x 1 2x 3 2x A. y . B. y . C. y . D. y . 5x 10 5x 10 5x 10 5x 10 Câu 02: Hàm số y
f x thỏa mãn các tính chất sau:
1 Đồng biến trên các khoảng xác định. 2 Không xác định tại x 2 .
3 Tiệm cận ngang của đồ thị hàm số nằm trên trục hoành và cách trục hoành một đoạn d 3 .
Hàm số đó có thể là ? 3x 3x 7 2 3x 2 2 3x 1 A. y . B. y . C. y . D. y . 2 2 x 2 x 2 x 2 x 4 2x 3 , x 2 Câu 03: Cho C : y f x 4 2x
. Khẳng định nào sau đây là đúng ? 3 2 x 3x 1, x 2
A. C không có tiệm cận.
B. C có tiệm cận đứng.
C. C có tiệm cận ngang.
D. C có nhiều hơn một tiệm cận. 2 x 6x 5 1 1 3 Câu 04: Cho: y f x
và các đường thẳng: d : x , d : y , d : y . Các 2x 3 1 2 2 2 3 2
đường thẳng có thể là tiệm cận của đồ thị là ? A. d . B. d . C. d . D. Cả 3 đều sai. 1 2 3 2 1 x , 1 x 1 x 2
Câu 05: Cho hàm số y f x , x 1
. Phát biểu nào sau đây không chính xác? x 1 2 x , x 1 A. D
là tập xác định của hàm số y
f x . B. Hàm số nhận giá trị 0 khi biến x 0 . C. x
1 là tiệm cận đứng của đồ thị hàm số y f x . D. y
1 là tiệm cận ngang của đồ thị hàm số y f x . 5x 3
Câu 06: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y f x 2 x 2mx 1
không có tiệm cận đứng ? m 1 A. . B. 1 m 1. C. m 1 . D. m 1 . m 1
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2x 1
Câu 07: Cho hàm số y f x
có đồ thị C . Gọi M là một điểm bất kì trên C . Tiếp tuyến x 1
của C tại M cắt các đường tiệm cận của C tại A và B . Gọi I là giao điểm của các đường tiệm
cận của C . Tính diện tích của tam giác IAB ? A. 2 . B. 12 . C. 4 . D. 6 .
Câu 08: Đồ thị hàm số 2 y f x x x 4x
2 có tiệm cận ngang là ? A. y 2 . B. y 2 . C. y 2 . D. x 2 . 2x 1
Câu 09: Tìm điểm M thuộc đồ thị hàm số y f x
sao cho khoảng cách từ M đến tiệm cận x 1
đứng bằng khoảng cách từ M đến trục hoành ?
A. M 0; 1 ; M 3; 2 . B. M 2;1 ; M 4; 3 .
C. M 0; 1 ; M 4; 3 . D. M 2;1 ; M 3; 2 . x 2
Câu 10: Cho hàm số y f x
C . Có tất cả bao nhiêu điểm M thuộc C sao cho khoảng x 3
cách từ M đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm M đến tiệm cận đứng ? A. 4. B. 3. C. 2. D. 1. x 2
Câu 11: Đồ thị hàm số y f x
có đường tiệm cận đứng là x
a và đường tiệm cận ngang 3x 9 là y
b . Giá trị của số nguyên m nhỏ nhất thỏa mãn m a b là ? A. 0 . B. 3 . C. 1 . D. 2 . 2x 3
Câu 12: Cho hàm số y f x
C . Gọi M là điểm bất kỳ trên C , d là tổng khoảng cách từ x 2
M đến hai đường tiệm cận của đồ thị C . Giá trị nhỏ nhất của d là ? A. 5. B. 10. C. 6. D. 2. 2x 3
Câu 13: Cho hàm số y f x
C . Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của C x 2
đến một tiếp tuyến bất kỳ của đồ thị C . Giá trị lớn nhất của d là ? A. 2 . B. 3 . C. 3 3 . D. 2 . 2x 3
Câu 14: Cho hàm số y f x
C . Gọi d là tiếp tuyến bất kì của C , d cắt hai đường tiệm x 2
cận của đồ thị C lần lượt tại A, B. Khi đó khoảng cách giữa A và B ngắn nhất bằng ? A. 4 . B. 3 2 . C. 2 2 . D. 3 3 . 2x
Câu 15: Đồ thị hàm số y f x
có bao nhiêu đường tiệm cận ? 2 x 2x 1 A. 3. B. 2. C. 1. D. 0. 1
Câu 16: Đồ thị hàm số y f x
có bao nhiêu tiệm cận ? 2 2 x 2 m 1 x m 1 4 A. 2 . B. 3 . C. 1 .
D. Không thể xác định.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 2x 5
Câu 17: Cho i, j lần lượt là tiệm cận đứng của đồ thị của hai hàm số y f x và x 3 2 x 2 y g x
. Khẳng định nào sau đây là đúng ? 2 x 4 A. i j . B. i j . C. i j .
D. i, j không tồn tại. 2 mx 1
Câu 18: Với giá trị nào của m thì đồ thị hàm số y f x có tiệm cận ngang ? 2x 3 3 A. 0 . B. 2 . C. . D. 1 . 2 6
Câu 19: Đồ thị hàm số y f x
có tiệm cận đứng khi ? 2 x 2ax 6a 7 a 7 A. a 7 . B. a 7 . C. . D. a 1 . a 1 x 1
Câu 20: Đồ thị hàm số có tiệm cận đứng đi qua M 3;1 và có dạng y f x . Giá trị của 2x m m là: 1 A. 2 . B. 3 . C. . D. 2 3 . 2 2 x x 1
Câu 21: Xác định phương trình các đường tiệm cận của đồ thị hàm số y f x ? 2 x 1 A. y 1, x 1. B. y 1, x 1. C. y x . D. y 1 . 2 x 2x 5
Câu 22: Xác định phương trình các đường tiệm cận của đồ thị hàm số y f x ? x 1 A. y 1, x 1. B. y 1, x 1. C. y 1, y 1, x 1.
D. Không tồn tại tiệm cận. 2 x 6x 3
Câu 23: Xác định phương trình các đường tiệm cận của đồ thị hàm số y f x ? 2 x 3x 2 A. y 1, x 1 . B. y 1, x 2 . C. y 1, x 2, x 1.
D. Không tồn tại tiệm cận. 5x 2 x x 2
Câu 24: Cho 3 hàm số 1 y f x , 2 y g x , 3 y h x . Hàm số 2 x x 1 2 x 3x 2
nào có đồ thị nhận đường thẳng x 2 làm tiệm cận ? A. 1 , 3 . B. 1 . C. 1 , 2 . D. 3 . 3 3 2 x 3x
Câu 25: Đường thẳng nào dưới đây là tiệm cận của đồ thị hàm số y f x ? x A. y 1 . B. y 1 . C. y x 1 . D. y x . 2 x
Câu 26: Đồ thị hàm số y f x
có bao nhiêu đường tiệm cận ? 2 x 4x A. 2. B. 0. C. 3. D. 1.
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC 3
Câu 27: Tìm phương trình các đường tiệm cận của đồ thị hàm số y f x 1 ? 2x 3 3 A. y , 2x 3 0 . B. y 1, 2x 3 0 . 2 C. y 5x 1, 2x 3 0 . D. y 2x 3, 2x 3 0 . 3 3 x 2x
Câu 28: Đồ thị hàm số y f x có tiệm cận là ? x A. y x 1 . B. y x . C. y 1, x 0 . D. y 1, x 0 . 2 2x 3x m
Câu 29: Với giá trị nào của m thì đồ thị hàm số y f x không có tiệm cận ? x m m 1 m 0 A. m 0 . B. . C. . D. m 1 . m 2 m 1 mx 1
Câu 30: Với giá trị nào của m thì đồ thị hàm số y f x
có tiệm cận đứng đi qua điểm 2x m A 1; 2 ? 2 1 A. m . B. m . C. m 0 . D. m 2 . 2 2 2 mx 1
Câu 31: Có bao nhiêu giá trị m để đồ thị hàm số y f x
có đúng 2 đường tịêm cận ? 2 x 3x 2 A. 3. B. 2. C. 1. D. m . 2 2x mx m
Câu 32: Xác định giá trị của m để đồ thị hàm số y f x đi qua gốc toạ độ ? x 1 A. m 1 . B. m 1 . C. m 2 . D. m 0 . 2 2a b x ax 1
Câu 33: Biết đồ thị hàm số y f x
nhận trục hoành và trục tung làm tiệm cận. 2 x ax a b 6 Hãy tính tích a.b ? A. 8. B. 6. C. 4. D. 2. 2 x 5x 6
Câu 34: Cho đường cong C : y f x
. Tìm khẳng định đúng ? x
A. C chỉ có tiệm cận đứng.
B. C có tiệm cận xiên.
C. C có hai tiệm cận.
D. C có ba tiệm cận.
Câu 35: Đồ thị hàm số nào trong các hàm số sau đây không có tiệm cận ngang ? 2 x x 1 1 2 x 1 2x 2 A. y . B. y . C. y . D. y . 2 x 1 x 1 x 1 x
Câu 36: Gọi m, n, p, q lần lượt là tổng số tiệm cận ngang và đứng của: 2 x 2x 3 2x 2 2 x 3x 1 x y f x ; y g x ; y h x ; y u x ; x 3 x 1 2 x 4x 5 2 x 4
So sánh nào sau đây là đúng ?
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC A. m n p q . B. q p n m . C. m n p q . D. m n p q . 2 1
Câu 37: Cho đồ thị hàm số có giao điểm của hai đường tiệm cận là ;
và đi qua A 3;1 . Hàm số 3 3 đó có thể là ? x 4 2x 1 x 5 3x 2 A. y . B. y . C. y . D. y . 3x 2 x 3 3x 2 x 4 2 3mx 2m 9
Câu 38: Cho hàm số y f x
. Với giá trị nào của m thì đồ thị hàm số có tiệm cận 2 2 3m 2 x 2 ngang y 3 ? 1 2 A. 1 . B. . C. . D. 3 . 3 3
Câu 39: Đồ thị hàm số nào sau đây thỏa mãn khoảng cách từ giao điểm của nó với trục tung đến 1
tiệm cận ngang của nó bằng ? 2 x 2 x 2 x 2 x 2 A. y . B. y . C. y . D. y . 2x 2 2x 1 2x 1 2x 1
Câu 40: Cho các đường thẳng x a và y
b lần lượt là tiệm cận đứng và tiệm cận ngang của đồ thị 2 2 m 2m 4 x 2m 1 hàm số y f x
, với m là nghiệm nguyên dương của phương trình 2 3m 2 x 9 2 m 4
0, a và b lần lượt có những giá trị ? 4 4 4 3 A. a 1, b . B. a 1, b . C. a 1, b . D. a , b 1 . 9 9 9 2 2 x x 1. x 1. 2x 1
Câu 41: Tiệm cận ngang của đồ thị hàm số y f x là ? x x 1 A. y 1 . B. x 0, x 1. C. x 2 . D. y 2 . 2mx 3
Câu 42: Cho hàm số y f x
, giá trị m để hai đường tiệm cận tạo với hai trục tọa độ một 2 3x 1
hình chữ nhật có diện tích bằng là ? 3 3 3 4 3 A. m . B. m . C. m . D. m . 4 4 3 4 3
Câu 43: Tìm m để đồ thị hàm số y f x
có đúng hai tiệm cận đứng ? 2 x x m 2 9 4 9 9 A. m . B. m . C. m . D. m . 4 9 4 4 1
Câu 44: Tìm m để đồ thị hàm số y f x
có đúng hai tiệm cận đứng ? 2 x mx 3
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC m 2 3 A. . B. m 2 . C. m 2 . D. m 2 . m 2 3 2 x x 3
Câu 45: Tìm m để đồ thị hàm số y f x
có đúng một tiệm cận ? 2 x mx 3 m 3 m 2 3 A. . B. m 2 3 . C. 2 3 m 2 3 . D. . m 3 m 2 3 mx 2
Câu 46: Đồ thị của hàm số y f x có tiệm cận ngang là y 1 và đi qua điểm A 3; 1 x n thì hàm số là ? x 2 x 2 x 2 2 A. y . B. y . C. y . D. y . x 2 x 2 x 2 x 2 ax b
Câu 47: Đồ thị của hàm số y f x có tiệm cận ngang là y 4 và đi qua điểm A 2; 0 thì x 1 tích a.b bằng: A. 32. B. 12. C. 8. D. 4. 1 2x
Câu 48: Gọi x, y, z lần lượt là số các đường tiệm cận của các đồ thị hàm số sau: y f x , x 4 x 2 25 y g x , y h x
. Khẳng định nào sau đây đúng ? 2 x 3 2 2x 3x 4 A. x y z . B. y x z . C. z x y . D. z y x . 2x 1 5 2x
Câu 49: Cho hai hàm số y f x và y g x
. Tập hợp các giá trị của tham số 2 m 8 x x 4
m để hai đường tiệm cận đứng của hai đồ thị hàm số trên trùng nhau là ? A. 2; 2 . B. 1; 2 . C. 0 . D. 2; 3 . 2 4x 15x 4 Câu 50: Cho hàm số y và các đường thẳng: 2 2x x 6 3 3 x 4, x 2, x 2, x , x , y
2 . Đường thẳng nào là tiệm cận của đồ thị hàm số đã cho ? 2 2 3 3 A. x 4, x 2, x . B. x 2, x , y 2 . 2 2 3 C. x 4, x , y 2 . D. x 4, x 2, y 2 . 2
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)
THPT QG 2018 – KHOÙA HOÏC TP 2K – THAY ÑOÅI TOAØN DIEÄN – TÖ DUY CASIO – TÖÏ LUAÄN SIEÂU TOÁC
“BÀI GIẢNG VIDEO & PHƢƠNG PHÁP GIẢI chi tiết CHỈ CÓ TẠI KHÓA HỌC TP – 2K”
https://www.facebook.com/tranminhtien.hcmus
https://www.facebook.com/phongmath.casio
Mọi góp ý về đề thi, lời giải của các câu hỏi trắc nghiệm và lời phản biện của quý độc giả, quý thầy cô,
các bạn học sinh –– sinh viên vui lòng soạn thành các file PDF, file PPT và gửi trực tiếp qua các đƣờng
link FB – cá nhân trên để đƣợc đính chính các thắc mắc và giải đáp vƣớng mắc. Trân trọng và cảm ơn.
VIDEO KHAI GIẢNG KHÓA HỌC TP2K:
https://youtu.be/-2r7gGCpud0
LINK ĐĂNG KÝ HỌC LUYỆN THI 2018: goo.gl/LdM2zn
PTGD: GV. TRAÀN MINH TIEÁN (TEL 0943303007) – GV. TRAÀN THANH PHONG (TEL 097510 8292)