Bài tập trắc nghiệm cực trị của hàm số có lời giải chi tiết – Lê Bá Bảo Toán 12

Bài tập trắc nghiệm cực trị của hàm số có lời giải chi tiết – Lê Bá Bảo Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Ả

ờ

ặ

ứ

ế

ị

ỉ

ễ

ộ

ạ

ế

ị

ế

Bµi viÕt chuyªn ®Ò:

KH¶O S¸T HµM Sè

Cùc trÞ cña hµm sè

LuyÖn thi THPT 2017_2018

HuÕ, th¸ng 8/2017

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................1

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

CHUY£N §Ò TR¾C NGHIÖM

M«n: To¸n 12 CB

Chñ ®Ò:

Cùc trÞ cña hµm sè.

Dành tặng cho các em học sinh đang sợ Toán, yếu

Toán và đang loay hoay về Toán! Cố lên các em!

Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế

SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế

Dạng toán 1:

X¸c ®Þnh ®iÓm cùc trÞ, cùc trÞ cña hµm sè.

Phương pháp:

Lập bảng xét dấu

 



hoặc lập bảng biến thiên để đưa ra kết luận.

Câu 1. Tìm điểm cực đại của hàm số

3 2.y x x  

1.

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

    



   



  



Cách 1: (Dấu hiện I) Lập bảng biến thiên.



1



 









 





Dựa vào bảng biến thiên, điểm cực đại của hàm số là

C§

1.x 



Chọn đáp án B.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

3 3 0 ; 6 .

y x y x

    

 

    



  



Ta có:

 

1 6 0 1yx



   

là điểm cực tiểu của hàm số và

 

1 6 0 1yx



      

là

điểm cực đại của hàm số.

Câu 2. Tìm điểm cực tiểu của hàm số

3 2.y x x  

4.

Lời giải: TXĐ:

.D  

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................2

Ta có:

3 6 0 .

y x x

   



   



   



Cách 1: (Dấu hiện I) Lập bảng biến thiên.





 









 



4



Dựa vào bảng biến thiên, điểm cực tiểu của hàm số là

2.x 



Chọn đáp án B.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

3 6 0 ; 6 6.

y x x y x

    

 

     



  



Ta có:

 

2 6 0 2yx



   

là điểm cực tiểu của hàm số và

 

0 6 0 0yx



    

là điểm

cực đại của hàm số.

Câu 3. Tìm cực đại (giá trị cực đại)

C§

của hàm số

3 4.y x x   

C§

1.y 

C§

1.y 

C§

2.y 

C§

6.y 

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

     



    



   



Cách 1: (Dấu hiện I) Lập bảng biến thiên.



1



 









 



6

2



Dựa vào bảng biến thiên, cực đại của hàm số là

C§

2.y 



Chọn đáp án C.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

3 3 0 ; 6 .

y x y x

     

 

      



   



[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................3

Ta có:

 

1 6 0 1yx



    

là điểm cực đại của hàm số suy ra

 

C§

12yy  

và

 

1 6 0 1yx



     

là điểm cực tiểu của hàm số suy ra

 

1 6.yy   

Câu 4. Tìm cực tiểu giá trị cực tiểu)

của hàm số

3 4.y x x   

1.y 

1.y 

2.y 

6.y 

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

     



    



   



Cách 1: (Dấu hiện I) Lập bảng biến thiên.



1



 









 



6

2



Dựa vào bảng biến thiên, cực tiểu của hàm số là

6.y 



Chọn đáp án D.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

3 3 0 ; 6 .

y x y x

     

 

      



   



Ta có:

 

1 6 0 1yx



    

là điểm cực đại của hàm số suy ra

 

C§

12yy  

và

 

1 6 0 1yx



     

là điểm cực tiểu của hàm số suy ra

 

1 6.yy   

Câu 5. Tìm điểm cực đại của hàm số

2 2.y x x  

1.

Lời giải: TXĐ:

.D  

Ta có:

4 4 0 0 2 .

y x x x y

    





      



  



Cách 1: (Dấu hiện I) Lập bảng biến thiên.



1



 











 



[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................4

Dựa vào bảng biến thiên, điểm cực đại của hàm số

C§

0.x 



Chọn đáp án C.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

4 4 0 0 2 ; 12 4

y x x x y y x

    



 

        



  



Ta có:

     

1 8; 1 8 0; 0 4 0.y y y

  

      

Vậy hàm số đạt cực đại tại

0x 

và

 

C§

0 2;yy

hàm số đạt cực tiểu tại

1; 1xx  

và

   

1 1 1.y y y   

Câu 6. Tìm cực đại của hàm số

2 2.y x x  

1.

Lời giải: TXĐ:

.D  

Ta có:

4 4 0 0 2 .

y x x x y

    





      



  



Cách 1: (Dấu hiện I) Lập bảng biến thiên.



1



 











 



Dựa vào bảng biến thiên, điểm cực đại của hàm số

C§

0x 

và

 

C§

0 2.yy



Chọn đáp án D.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

4 4 0 0 2 ; 12 4

y x x x y y x

    



 

        



  



Ta có:

     

1 8; 1 8 0; 0 4 0.y y y

  

      

Vậy hàm số đạt cực đại tại

0x 

và

 

C§

0 2;yy

hàm số đạt cực tiểu tại

1; 1xx  

và

   

1 1 1.y y y   

Câu 7. Tìm cực tiểu của hàm số

2 2.y x x  

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................5

1.

Lời giải: TXĐ:

.D  

Ta có:

4 4 0 0 2 .

y x x x y

    





      



  



Cách 1: (Dấu hiện I) Lập bảng biến thiên.



1



 











 



Dựa vào bảng biến thiên, điểm cực đại của hàm số

CT CT

1; 1xx  

và

   

1 1 1.y y y   



Chọn đáp án A.

Cách 2: (Dấu hiện II) Xét dấu

 



với

là nghiệm phương trình

 

0.fx





Ta có:

4 4 0 0 2 ; 12 4

y x x x y y x

    



 

        



  



Ta có:

     

1 8; 1 8 0; 0 4 0.y y y

  

      

Vậy hàm số đạt cực đại tại

0x 

và

 

C§

0 2;yy

hàm số đạt cực tiểu tại

1; 1xx  

và

   

1 1 1.y y y   

Câu 8. Tìm điểm cực đại của đồ thị hàm số

3 2.y x x  

 

4; 1 .

 

1; 4 .

 

1; 0 .

 

0;1 .

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

    



   



  



Bảng biến thiên.



1



 









 





[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................6

Dựa vào bảng biến thiên, điểm cực đại của đồ thị hàm số là

 

1; 4 .



Chọn đáp án B.

Câu 9. Tìm điểm cực tiểu của đồ thị hàm số

3 2.y x x  

 

0; 2 .

 

2;0 .

 

2; 2 .

 

4; 2 .

Lời giải: TXĐ:

.D  

Ta có:

3 6 0 .

y x x

   



   



   



Bảng biến thiên.





 









 



2



Dựa vào bảng biến thiên, điểm cực tiểu của đồ thị hàm số là

 

2; 4 .



Chọn đáp án C.

Câu 10. Tìm điểm cực đại của hàm số





2.

4.

Lời giải: TXĐ:

 

\ 0 .D  

Ta có:

     





  



  



Bảng biến thiên:



2



 

'fx







 



4





Dựa vào bảng biến thiên, điểm cực đại của hàm số là

C§

2.x 



Chọn đáp án B.

Câu 11. Tìm cực tiểu của hàm số





2.

4.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................7

Lời giải: TXĐ:

 

\ 0 .D  

Ta có:

     





  



  



Bảng biến thiên:



2



 

'fx







 



4





Dựa vào bảng biến thiên, cực tiểu của hàm số là

4.y 



Chọn đáp án D.

Câu 12. Gọi

C§ CT

,xx

lần lượt là điểm cực đại và điểm cực tiểu của hàm số

3 2.y x x  

Tính

C§ CT

2.S x x

1.S 

0.S 

4.S 

1.S 

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

    



   



  



Bảng biến thiên.



1



 









 





Dựa vào bảng biến thiên, ta suy ra

C§ CT C§ CT

1, 1 2 1.x x S x x      



Chọn đáp án A.

Câu 13. Gọi

C§ CT

,xx

lần lượt là điểm cực đại và điểm cực tiểu của hàm số

3.y x x

Tính

C§ CT

.S x x

32.S 

0.S 

4.S 

2.S 

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

    



   



   



Bảng biến thiên.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................8



1



 









 



2



Dựa vào bảng biến thiên, ta suy ra

C§ CT C§ CT

1, 1 2.x x S x x      



Chọn đáp án D.

Câu 14. Gọi

C§ CT

,yy

lần lượt là cực đại và điểm cực tiểu của hàm số

3.y x x

Tính

C§ CT

2 3 1.S y y  

1.S 

0.S 

4.S 

2.S 

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

    



   



   



Bảng biến thiên.



1



 









 



2



Dựa vào bảng biến thiên, ta suy ra

C§ CT C§ CT

2, 2 2 3 1 1.y y S y y        



Chọn đáp án A.

Câu 15. Gọi

,AB

lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số

3.y x x

Tính độ dài đoạn thẳng

.AB

2 3.AB 

4.AB 

5.AB 

2 5.AB 

Lời giải: TXĐ:

.D  

Ta có:

3 3 0 .

    



   



   



Bảng biến thiên.



1



 









 



2



[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................9

Dựa vào bảng biến thiên, ta suy ra

     

1;2 , 1; 2 2; 4 2 5.A B AB AB      





Chọn đáp án D.

Câu 16. Gọi

,AB

lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số

3 2.y x x  

Trung điểm

của đoạn thẳng

có tọa độ nào dưới đây?

 

1;1 .

 

2;0 .

 

1; 0 .

 

1; 2 .

Lời giải: TXĐ:

.D  

Ta có:

3 6 0 .

y x x

   



   



   



Bảng biến thiên.





 









 



2



Dựa vào bảng biến thiên, ta suy ra

     

0;2 , 2; 2 1;0 .A B I  



Chọn đáp án C.

Câu 17. Gọi

,,A B C

là ba điểm cực trị của đồ thị hàm số

2 3.y x x  

Tìm tọa độ

trọng tâm của tam giác

.ABC

0; .







1; .







1; .









1; .







Lời giải: TXĐ:

.D  

Ta có:

4 4 0 0 3 .

y x x x y

    





      



  



Bảng biến thiên.



1



 











 



[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................10

Dựa vào bảng biến thiên, suy ra các điểm cực trị của đồ thị hàm số là

     

1; 2 , 0; 3 , 1; 2A B C

. Vậy tọa độ trọng tâm của tam giác

ABC

là

0; .









Chọn đáp án A.

Câu 18. Gọi

C§ CT

,yy

lần lượt là cực đại và cực tiểu của hàm số

2 2.y x x  

Tính

giá trị biểu thức

C§ CT C§ CT

..M y y y y  

3.M 

3.M 

1.M 

1.M 

Lời giải: TXĐ:

.D  

Ta có:

4 4 0 0 2 .

y x x x y

     





       



   



Bảng biến thiên.



1



 











 



3

2

3



Dựa vào bảng biến thiên, suy ra

C§ CT

2, 3.yy   

Vậy

C§ CT C§ CT

. 1.M y y y y   



Chọn đáp án C.

Câu 19. Gọi

C§ CT

,xx

lần lượt là điểm cực đại và điểm cực tiểu của hàm số





Tính

C§ CT

2 3 .S x x

4.S 

2.S 

1.S 

1.S 

Lời giải: TXĐ:

 

\ 0 .D  

Ta có:

     





  



  



Bảng biến thiên:



1



 

'fx







 



2





Dựa vào bảng biến thiên, suy ra

C§ CT C§ CT

1, 1 2 3 1.x x S x x      

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................11



Chọn đáp án D.

Câu 20. Gọi

C§ CT

,yy

lần lượt là cực đại và điểm cực tiểu của hàm số





Tính

C§ CT

2 3 .S y y

4.S 

2.S 

1.S 

1.S 

Lời giải: TXĐ:

 

\ 0 .D  

Ta có:

     





  



  



Bảng biến thiên:



1



 

'fx







 



2





Dựa vào bảng biến thiên, suy ra

C§ CT C§ CT

2, 2 2 3 2.y y S x x      



Chọn đáp án B.

Câu 21. Gọi

,PQ

lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số







Tính độ dài đoạn thẳng

.PQ

3 2.PQ 

2 5.PQ 

5.PQ 

4.PQ 

Lời giải: TXĐ:

 

\ 1 .D  

Ta có:

 

    





  



  





Bảng biến thiên:





 

'fx







 



2





Dựa vào bảng biến thiên, suy ra

     

0; 2 , 2;2 2;4 2 5.P Q PQ PQ    





Chọn đáp án B.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................12

SỬ DỤNG DẤU HIỆU 2 ĐỂ TÌM CỰC TRỊ CỦA HÀM SỐ

(Trong loạt bài tập này, tác giả quy ước

,km

Câu 22. Điểm nào sau đây là điểm cực đại của hàm số

2sin 1?yx







1.

Lời giải: TXĐ:

.D  

Ta có:

2cos 0 .

y x x k





    

Kiểm tra được:



   



  

   

   

Ta có:

 

2sin ,y x x











    





là điểm cực đại của hàm số và

C§

3;y 







     





là điểm cực tiểu của hàm số và

1.y 



Chọn đáp án B.

Kỹ thuật sử dụng MTCT:

Bước 1: Nhập biểu thức đạo hàm của hàm số vào máy tính:

qy2jQ))+1

Bước 2: Kiểm tra giá trị nào là nghiệm của đạo hàm:

Nhập





qKP2=

Nhập





pqKP2=

Nhập

3:x 

Nhập

1:x 

p1=

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................13

Vậy

;



  

là các nghiệm của

 

.fx



Bước 3: Nhập biểu thức đạo hàm cấp hai của hàm số vào máy tính:

Nhập

2cosyx





ô chứa đạo hàm trong phím đạo hàm.

qy2kQ))

Kiểm tra dấu của đạo hàm cấp hai tại các giá trị



  

+) qKP2= Vậy







    





là

điểm cực đại của hàm số.

*) Tính

C§

Nhập 2jQ))+1

rqKP2= Vậy

C§

3.y 

+) pqKP2= Vậy







     





là điểm cực tiểu của hàm số.

*) Tính

Nhập 2jQ))+1

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................14

rqpKP2= Vậy

1.y 

Câu 23. Điểm nào sau đây là điểm cực tiểu của hàm số

2sin 1?yx







1.

Lời giải: TXĐ:

.D  

Ta có:

2cos 0 .

y x x k





    

Kiểm tra được:



   



  

   

   

Ta có:

 

2sin ,y x x











    





là điểm cực đại của hàm số và

C§

3;y 







     





là điểm cực tiểu của hàm số và

1.y 



Chọn đáp án A.

Câu 24. Giá trị nào sau đây là cực đại của hàm số

2sin 1?yx







1.

Lời giải: TXĐ:

.D  

Ta có:

2cos 0 .

y x x k





    

Kiểm tra được:



   



  

   

   

Ta có:

 

2sin ,y x x











    





là điểm cực đại của hàm số và

C§

3;y 







     





là điểm cực tiểu của hàm số và

1.y 



Chọn đáp án C.

Câu 25. Giá trị nào sau đây là cực tiểu của hàm số

2sin 1?yx







1.

Lời giải: TXĐ:

.D  

Ta có:

2cos 0 .

y x x k





    

Kiểm tra được:



   



  

   

   

Ta có:

 

2sin ,y x x











    





là điểm cực đại của hàm số và

C§

3;y 

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................15







     





là điểm cực tiểu của hàm số và

1.y 



Chọn đáp án D.

Câu 26. Điểm nào sau đây là điểm cực đại của hàm số

cos2 1?yx



Lời giải: TXĐ:

.D  

Ta có:

2sin 2 0 .

y x x k





    

Kiểm tra được:

 

0 0.













Ta có:

 

4cos2 ,y x x











   





là điểm cực tiểu của hàm số và

0;y 

 

0 4 0 0yx



    

là điểm cực đại của hàm số và

C§

2.y 



Chọn đáp án A.

Câu 27. Điểm nào sau đây là điểm cực tiểu của hàm số

cos2 1?yx



Lời giải: TXĐ:

.D  

Ta có:

2sin 2 0 .

y x x k





    

Kiểm tra được:

 

0 0.













Ta có:

 

4cos2 ,y x x











   





là điểm cực tiểu của hàm số và

0;y 

 

0 4 0 0yx



    

là điểm cực đại của hàm số và

C§

2.y 



Chọn đáp án B.

Câu 28. Giá trị nào sau đây là cực tiểu của hàm số

cos2 1?yx



Lời giải: TXĐ:

.D  

Ta có:

2sin 2 0 .

y x x k





    

Kiểm tra được:

 

0 0.













Ta có:

 

4cos2 ,y x x











   





là điểm cực tiểu của hàm số và

0;y 

 

0 4 0 0yx



    

là điểm cực đại của hàm số và

C§

2.y 



Chọn đáp án A.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................16

Câu 29. Giá trị nào sau đây là cực đại của hàm số

cos2 1?yx



Lời giải: TXĐ:

.D  

Ta có:

2sin 2 0 .

y x x k





    

Kiểm tra được:

 

0 0.













Ta có:

 

4cos2 ,y x x











   





là điểm cực tiểu của hàm số và

0;y 

 

0 4 0 0yx



    

là điểm cực đại của hàm số và

C§

2.y 



Chọn đáp án D.

Câu 30. Tìm tất cả các điểm cực đại của hàm số

2sin 2 1.yx









1.

Lời giải: TXĐ:

.D  

Ta có:

4cos 2 0 .

x k x k





   





   



     





Ta có:

 

8sin2 ,y x x





y k x k







      





là các điểm cực đại của hàm số

và

C§

y y k





  





y k x k







       





là điểm cực tiểu của hàm số

và

y y k





    







Chọn đáp án B.

Câu 31. Tìm tất cả các điểm cực tiểu của hàm số

2sin 2 1.yx









1.

Lời giải: TXĐ:

.D  

Ta có:

4cos 2 0 .

x k x k





   





   



     





Ta có:

 

8sin2 ,y x x





y k x k







      





là các điểm cực đại của hàm số

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................17

và

C§

y y k





  





y k x k







       





là điểm cực tiểu của hàm số

và

y y k





    







Chọn đáp án A.

Câu 32. Tìm cực đại của hàm số

2sin 2 1.yx









Lời giải: TXĐ:

.D  

Ta có:

4cos 2 0 .

x k x k





   





   



     





Ta có:

 

8sin2 ,y x x





y k x k







      





là các điểm cực đại của hàm số

và

C§

y y k





  





y k x k







       





là điểm cực tiểu của hàm số

và

y y k





    







Chọn đáp án C.

Câu 33. Tìm cực tiểu của hàm số

2sin 2 1.yx









3.

1.

Lời giải: TXĐ:

.D  

Ta có:

4cos 2 0 .

x k x k





   





   



     





Ta có:

 

8sin2 ,y x x





y k x k







      





là các điểm cực đại của hàm số

và

C§

y y k





  





y k x k







       





là điểm cực tiểu của hàm số

và

y y k





    







Chọn đáp án D.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................18

Câu 34. Tìm tất cả các điểm cực đại của hàm số

2cos2 3.yx





Lời giải: TXĐ:

.D  

Ta có:

4sin 2 0 .













    











Ta có:

 

8cos2 ,y x x





 

80y k x k





    

là các điểm cực đại của hàm số và

 

C§

5;y y k





y k x k







     





là điểm cực tiểu của hàm số và

y y k





  







Chọn đáp án A.

Câu 35. Tìm tất cả các điểm cực tiểu của hàm số

2cos2 3.yx





Lời giải: TXĐ:

.D  

Ta có:

4sin 2 0 .













    











Ta có:

 

8cos2 ,y x x





 

80y k x k





    

là các điểm cực đại của hàm số và

 

C§

5;y y k





y k x k







     





là điểm cực tiểu của hàm số và

y y k





  







Chọn đáp án B.

Câu 36. Tìm cực đại của hàm số

2cos2 3.yx





Lời giải: TXĐ:

.D  

Ta có:

4sin 2 0 .













    











Ta có:

 

8cos2 ,y x x





 

80y k x k





    

là các điểm cực đại của hàm số và

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................19

 

C§

5;y y k





y k x k







     





là điểm cực tiểu của hàm số và

y y k





  







Chọn đáp án C.

Câu 37. Tìm cực tiểu của hàm số

2cos2 3.yx





3.

Lời giải: TXĐ:

.D  

Ta có:

4sin 2 0 .













    











Ta có:

 

8cos2 ,y x x





 

80y k x k





    

là các điểm cực đại của hàm số và

 

C§

5;y y k





y k x k







     





là điểm cực tiểu của hàm số và

y y k





  







Chọn đáp án D.

Câu 38. Tìm tất cả các điểm cực đại của hàm số

sin cos 2.y x x  









2 2.

2 2.

Lời giải: TXĐ:

.D  

Ta có:

cos sin 0 sin cos tan 1 .

y x x x x x x k











          









Ta có:

 

cos sin ;y x x x



  

2 2 0 2

y k x k







      





là các điểm cực đại

của hàm số và

C§

2 2 2;

y y k





   





2 2 0 2

y k x k







     





là

điểm cực tiểu của hàm số và

2 2 2.

y y k





   







Chọn đáp án B.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................20

Câu 39. Tìm tất cả các điểm cực tiểu của hàm số

sin cos 2.y x x  









2 2.

2 2.

Lời giải: TXĐ:

.D  

Ta có:

cos sin 0 sin cos tan 1 .

y x x x x x x k











          









Ta có:

 

cos sin ;y x x x



  

2 2 0 2

y k x k







      





là các điểm cực đại

của hàm số và

C§

2 2 2;

y y k





   





2 2 0 2

y k x k







     





là

điểm cực tiểu của hàm số và

2 2 2.

y y k





   







Chọn đáp án A.

Câu 40. Tìm cực đại của hàm số

sin cos 2.y x x  









2 2.

2 2 2.

Lời giải: TXĐ:

.D  

Ta có:

cos sin 0 sin cos tan 1 .

y x x x x x x k











          









Ta có:

 

cos sin ;y x x x



  

2 2 0 2

y k x k







      





là các điểm cực đại

của hàm số và

C§

2 2 2;

y y k





   





2 2 0 2

y k x k







     





là

điểm cực tiểu của hàm số và

2 2 2.

y y k





   







Chọn đáp án C.

Câu 41. Tìm cực tiểu của hàm số

sin cos 2.y x x  









2 4 2.

2 2.

Lời giải: TXĐ:

.D  

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................21

Ta có:

cos sin 0 sin cos tan 1 .

y x x x x x x k











          









Ta có:

 

cos sin ;y x x x



  

2 2 0 2

y k x k







      





là các điểm cực đại

của hàm số và

C§

2 2 2;

y y k





   





2 2 0 2

y k x k







     





là

điểm cực tiểu của hàm số và

2 2 2.

y y k





   







Chọn đáp án D.

Câu 42. Giá trị nào sau đây là điểm cực đại của hàm số

sin2 2sin ?y x x







  



Lời giải: TXĐ:

.D  

Ta có:

 

2cos 2 2cos 0 2 2cos 1 2cos 0 4cos 2cos 2 0y x x x x x x



          

cos 1

cos











  



   











  





Ta có:

 

4sin 2 2sin ;y x x x



  

2 3 3 0 2

y k x k







      





là các điểm cực

đại của hàm số và

C§

y y k





  





2 3 3 0 2

y k x k







       





là

điểm cực tiểu của hàm số và

y y k





    







Chọn đáp án A.

Câu 43. Giá trị nào sau đây là điểm cực tiểu của hàm số

sin2 2sin ?y x x







  



Lời giải: TXĐ:

.D  

Ta có:

 

2cos 2 2cos 0 2 2cos 1 2cos 0 4cos 2cos 2 0y x x x x x x



          

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................22

cos 1

cos











  



   











  





Ta có:

 

4sin2 2sin ;y x x x



  

2 3 3 0 2

y k x k







      





là các điểm cực

đại của hàm số và

C§

y y k





  





2 3 3 0 2

y k x k







       





là

điểm cực tiểu của hàm số và

y y k





    







Chọn đáp án B.

Câu 44. Giá trị nào sau đây là cực đại của hàm số

sin2 2sin ?y x x







  

Lời giải: TXĐ:

.D  

Ta có:

 

2cos 2 2cos 0 2 2cos 1 2cos 0 4cos 2cos 2 0y x x x x x x



          

cos 1

cos











  



   











  





Ta có:

 

4sin 2 2sin ;y x x x



  

2 3 3 0 2

y k x k







      





là các điểm cực

đại của hàm số và

C§

y y k





  





2 3 3 0 2

y k x k







       





là

điểm cực tiểu của hàm số và

y y k





    







Chọn đáp án C.

Câu 45. Giá trị nào sau đây là cực tiểu của hàm số

sin2 2sin ?y x x







  



Lời giải: TXĐ:

.D  

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................23

Ta có:

 

2cos 2 2cos 0 2 2cos 1 2cos 0 4cos 2cos 2 0y x x x x x x



          

cos 1

cos











  



   











  





Ta có:

 

4sin 2 2sin ;y x x x



  

2 3 3 0 2

y k x k







      





là các điểm cực

đại của hàm số và

C§

y y k





  





2 3 3 0 2

y k x k







       





là

điểm cực tiểu của hàm số và

y y k





    







Chọn đáp án C.

Câu 46. Giá trị nào sau đây là điểm cực đại của hàm số

cos2 2sin ?y x x







  





Lời giải: TXĐ:

.D  

Ta có:

 

cos 0

2sin 2 2cos 0 2 cos 1 2 sin 0

sin

y x x x x







       

















  

















Ta có:

 

4cos 2 2sin ;y x x x



  

2 3 0 2

y k x k







      





là

các điểm cực đại của hàm số và

C§

y y k





  







Chọn đáp án A.

Dạng toán 2:

X¸c ®Þnh sè ®iÓm cùc trÞ, cùc trÞ cña hµm sè.

Phương pháp:

Lập bảng xét dấu

 



hoặc lập bảng biến thiên để đưa ra kết luận.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................24

Câu 47. Tìm số điểm cực trị của hàm số





1.

Lời giải: TXĐ:

 

\ 1 .D  

Ta có:

 

0, .

y x D





   





không có nghiệm và không đổi dấu trên

nên

hàm số

không có cực trị.



Chọn đáp án C.

Kết quả: Hàm số

 

; ; ;

ax b

y a b c d

cx d









không có cực trị.

Câu 48. Hàm số nào sau đây không có cực trị?

 

.f x x

 

3.g x x x

 







 

.k x x

Lời giải:

Xét hàm số

 

h x h x D h x





      



không có cực trị.

Nhận xét: Dựa vào kết quả trên, trong một nốt nhạc, ta chọn đáp án C.



Chọn đáp án C.

Câu 49. Hàm số nào sau đây có cực trị?

 





 

3.g x x x

 







 

.k x x

Lời giải:

Dễ thấy

   

,f x h x

không có cực trị.

Xét

   

3 3 3 0,g x x x g x x g x



        

không có cực trị.

Cách khác: Xét

 

4 0 0.k x x k x x



     

Bảng xét dấu:





 







Dựa vào bảng xét dấu, suy ra hàm số đạt cực tiểu tại

0.x 



Chọn đáp án D.

Câu 50. Hàm số nào sau đây có số điểm cực trị khác với số điểm cực trị của các hàm số

còn lại?

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................25

 







 

3 1.g x x x  

 







 

.k x x

Lời giải: Dễ thấy

   

,f x h x

không có cực trị.

Xét

   

3 3 3 0,g x x x g x x g x



        

không có cực trị.

Cách khác: Xét

 

4 0 0.k x x k x x



     

Bảng xét dấu:





 







Dựa vào bảng xét dấu, suy ra hàm số đạt cực tiểu tại

0.x 



Chọn đáp án D.

Câu 51. Hàm số nào sau đây có số điểm cực trị khác với số điểm cực trị của các hàm số

còn lại?

 

.f x x

 

.g x x

 

.h x x

 

.k x x

Lời giải:

Dễ thấy

     

,,f x g x k x

đều có một điểm cực trị (Các em lập bảng xét dấu).

Xét

   

30h x x h x h x



    

không có điểm cực trị.



Chọn đáp án C.

Câu 52. Hàm số nào sau đây có số điểm cực trị nhiều nhất so với số điểm cực trị của

các hàm số còn lại?

 

1.f x x

 

2.g x x x

 





 

3.k x x x

Lời giải:

+) Ta có:

 

1 2 0 0f x x f x x



      

Bảng xét dấu:





 







Suy ra

 

có một điểm cực trị.

+) Ta có:

 

4 2 3

2 4 4 0 0 1 1.g x x x g x x x x x



            

Bảng xét dấu:



1



 











[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................26

Suy ra

 

có ba điểm cực trị.

+) Ta có:

 

h x h x D h x





      



không có cực trị.

+) Ta có:

 

3 3 3 0 1 1.k x x x k x x x



          

Bảng xét dấu:



1



 









Suy ra

 

có hai điểm cực trị.



Chọn đáp án B.

Câu 53. Hàm số nào sau đây có số điểm cực trị ít nhất so với số điểm cực trị của các

hàm số còn lại?

 

2.f x x

 

2.g x x x

 

3.h x x x

 

3.k x x x

Lời giải:

+) Ta có:

 

2 4 0 0f x x f x x



      

Bảng xét dấu:





 







Suy ra

 

có một điểm cực trị.

+) Ta có:

 

4 2 3

2 4 4 0 0 1 1.g x x x g x x x x x



            

Bảng xét dấu:



1



 











Suy ra

 

có ba điểm cực trị.

+) Ta có:

 

2 3 2

3 6 3 0 0 2.h x x x h x x x x



         

Bảng xét dấu:





 









Suy ra

 

có hai điểm cực trị.

+) Ta có:

 

3 3 3 0 1 1.k x x x k x x x



          

Bảng xét dấu:

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................27



1



 









Suy ra

 

có hai điểm cực trị.



Chọn đáp án A.

Câu 54. Cho hàm số

 

y f x

có đạo hàm

   

1f x x x





. Tìm số điểm cực trị của hàm số

 

.y f x

Lời giải:

Bảng xét dấu:



1



 







Suy ra

 

có một điểm cực trị (cực tiểu).



Chọn đáp án B.

Câu 55. Cho hàm số

 

y f x

có đạo hàm

   

1f x x x





. Tìm số điểm cực trị của hàm số

 

.y f x

Lời giải:

Bảng xét dấu:



1



 









Suy ra

 

có hai điểm cực trị.



Chọn đáp án C.

Câu 56. Cho hàm số

 

y f x

có đạo hàm

    

12f x x x x



  

. Tìm số điểm cực trị của

hàm số

 

.y f x

Lời giải:

Bảng xét dấu:



1



 









Suy ra

 

có hai điểm cực trị.



Chọn đáp án C.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................28

Câu 57. Cho hàm số

 

y f x

có đạo hàm

     

12f x x x x



  

. Tìm số điểm cực trị của

hàm số

 

.y f x

Lời giải:

Bảng xét dấu:



1



 







Suy ra

 

có một điểm cực trị.



Chọn đáp án B.

Dạng toán 2:

T×m ®iÒu kiÖn cña tham sè ®Ó hµm sè cã cùc trÞ vµ

tháa m·n c¸c yªu cÇu kh¸c.

Phương pháp:Xét các hàm số

 

có đạo hàm trên tập xác định của nó.

+) Kết quả 1:

 

có

 

nn

điểm cực trị khi và chỉ khi

 

0fx





có

nghiệm và

 



đổi dấu khi qua tất cả

nghiệm đó.

+) Kết quả 2: Tính chất của các điểm cực trị của hàm số được xử lí thông qua tính chất

nghiệm của phương trình

 



(khi đã thỏa mãn điều kiện có cực trị tương ứng).

+) Kết quả 3:

 

đạt cực trị (CĐ hoặc CT) tại

thì

 

0.fx





Đây là chiều suy ra,

nên khi thực hiện yêu cầu cụ thể là cực đại hay cực tiểu thì học sinh tiến hành kiểm tra lại các

trường hợp của tham số (bằng dấu hiệu 1 hay dấu hiệu 2) để đưa ra kết luận.

Câu 58. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

3y x x mx  

đạt

cực đại tại

1.x 

 

.

 

1, 3 .

Lời giải: TXĐ:

.D  

Ta có:

3 6 .y x x m



  

Hàm số đạt cực đại tại

 

1 1 0 3.x f m



    

+) Kiểm tra lại: Với

     

3 : 3 6 3 3 1 0m f x x x x f x



       

không có cực trị.



Chọn đáp án B.

Câu 59. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

3 12

y m m x x   

đạt cực đại tại

2.x 

 

.

 

1, 2 .

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................29

Lời giải: TXĐ:

.D  

Ta có:

 

2 3 12.y x m m x



   

Hàm số đạt cực đại tại

 

2 2 0 4 12 8 0 1 2.x f m m m m



           

+) Với

     

1: 4 12 0 2 6; 2 4 2 8 0m f x x x x x f x x f

  

               

Hàm số đạt cực tiểu tại

2x 

(không thỏa mãn).

+) Với

     

2 : 4 12 0 2 6; 2 4 2 8 0m f x x x x x f x x f

  

               

Hàm số đạt cực tiểu tại

2x 

(không thỏa mãn).



Chọn đáp án B.

Câu 60. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

3 12 1

y k k x x    

đạt cực tiểu tại

2.x 

 

.

 

1, 2 .

Lời giải: TXĐ:

.D  

Ta có:

 

2 3 12.y x k k x



   

Hàm số đạt cực tiểu tại

 

2 2 0 4 12 8 0 1 2.x f k k k k



           

+) Với

     

1: 4 12 0 2 6; 2 4 2 8 0k f x x x x x f x x f

  

               

Hàm số đạt cực tiểu tại

2x 

(thỏa mãn).

+) Với

     

2 : 4 12 0 2 6; 2 4 2 8 0k f x x x x x f x x f

  

               

Hàm số đạt cực tiểu tại

2x 

(thỏa mãn).



Chọn đáp án D.

Câu 61. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

5 2 2

k k x

y k x



    

đạt cực tiểu tại

1.x 

 

.

 

1, 6 .

Lời giải: TXĐ:

.D  

Ta có:

 

5 5 2 .y x k k x k



    

Hàm số đạt cực tiểu tại

 

1 1 0 7 6 0 1 6.x f k k k k



          

+) Với

     

1: 4 3 0 1 3; 2 4 1 2 0k f x x x x x f x x f

  

               

Hàm

số đạt cực đại tại

1x 

(không thỏa mãn).

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................30

+) Với

     

6 : 6 7 0 1 7; 2 6 1 8 0k f x x x x x f x x f

  

               

Hàm

số đạt cực tiểu tại

1x 

(thỏa mãn).



Chọn đáp án C.

Câu 62. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

a a x

y a x



   

đạt cực đại tại

1.x 

 

.

 

1, 6 .

Lời giải: TXĐ:

.D  

Ta có:

 

5 5 2 .y x a a x a



    

Hàm số đạt cực tiểu tại

 

1 1 0 7 6 0 1 6.x f a a a a



          

+) Với

     

1: 4 3 0 1 3; 2 4 1 2 0a f x x x x x f x x f

  

               

Hàm

số đạt cực đại tại

1x 

(thỏa mãn).

+) Với

     

6 : 6 7 0 1 7; 2 6 1 8 0a f x x x x x f x x f

  

               

Hàm

số đạt cực tiểu tại

1x 

(không thỏa mãn).



Chọn đáp án A.

Câu 63. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

y x x mx  

có

cực trị.



1; . 



 

;1 .

 

1; .



;1 . 



Lời giải: TXĐ:

.D  

Ta có:

2.y x x m



  

Để hàm số có cực trị (cụ thể là 2 cực trị) thì





có hai nghiệm

phân biệt và



đổi dấu khi qua hai nghiệm đó.

Yêu cầu bài toán

0 1.



    



Chọn đáp án B.

Nhận xét: Đối với hàm số bậc ba thì yêu cầu có cực trị tương đương với yêu cầu có 2 cực trị.

Câu 64. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

y mx x mx  

có

cực trị.



1; . 



   

1;1 \ 0 .

 

1;1 .



;1 . 



Lời giải: TXĐ:

.D  

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................31

Ta có:

2.y mx x m



  

Để hàm số có cực trị (cụ thể là 2 cực trị) thì





có hai nghiệm

phân biệt và



đổi dấu khi qua hai nghiệm đó.

+) TH 1: Xét

0 2 0 0.m y x x



      

Bảng xét dấu:





 







Trong trường hợp này, hàm số đạt CĐ tại

0x 

(thỏa mãn).

+) TH 2: Xét

0.m 

Yêu cầu bài toán

4 4 0 1 1.



        

Vậy

 

1;1 .m



Chọn đáp án C.

Câu 65. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

y mx mx x  

có

cực trị.

   

;0 1; .  

   

1;1 \ 0 .

 

1;1 .

0;1 .



Lời giải: TXĐ:

.D  

Ta có:

2 1.y mx mx



  

Để hàm số có cực trị (cụ thể là 2 cực trị) thì





có hai

nghiệm phân biệt và



đổi dấu khi qua hai nghiệm đó.

+) TH 1: Xét

0 1 0my



   

Trong trường hợp này, hàm số không có cực trị (không thỏa mãn).

+) TH 2: Xét

0.m 

Yêu cầu bài toán

   

4 4 0 ;0 1; .

m m m



         

Vậy

   

;0 1; .m   



Chọn đáp án A.

Câu 66. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

2y x mx  

có ba

điểm cực trị.



0; . 



 

;0 .

 

0; .



;0 . 



Lời giải: TXĐ:

.D  

Ta có:

 

(1)

4 4 4 0

y x mx x x m







     







Để hàm số có ba điểm cực trị thì





có ba nghiệm phân biệt và



đổi dấu khi qua ba

nghiệm đó.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................32

Yêu cầu bài toán







  











Chọn đáp án C.

Cách khác: Áp dụng công thức giải nhanh. Ta có

1;a b m  

Yêu cầu bài toán

 

0 1. 0 0.ab m m      

Lưu ý kết quả giải nhanh:

+) Đối với hàm số trùng phương

 

0.y ax bx c a   

Hàm số có ba cực trị

0.ab 

Hàm số có duy nhất một cực trị.

0.ab 

+) Đối với hàm số bậc ba

 

0.y ax bx cx d a    

Hàm số có cực trị (có 2 cực trị)





Hàm số không có cực trị.





Câu 67. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

1y mx m x  

có

ba điểm cực trị.



1; . 



 

0;1 .

   

;0 1; .  



;0 . 



Lời giải: TXĐ:

.D  

Ta có:

 

(1)

4 2 1 2 2 1 0

2 1 0

y mx m x x mx m

mx m







       



  



Để hàm số có ba điểm cực trị thì





có ba nghiệm phân biệt và



đổi dấu khi qua ba

nghiệm đó

 

1

có hai nghiệm phân biệt khác

Yêu cầu bài toán

     

0 0 8 1 0 ;0 1;

m m m

   







           

  

  

  







   

;0 1; .m    



Chọn đáp án C.

Cách khác: Áp dụng công thức giải nhanh. Ta có

;1a m b m  

Yêu cầu bài toán

     

0 . 1 0 ;0 1; .ab m m m         

Câu 68. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

4 2 2

9 10y mx m x   

có ba điểm cực trị.



3; . 



 

0; 3 .

   

; 3 3; .   

   

; 3 0; 3 .  

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................33

Lời giải: TXĐ:

.D  

Ta có:

   

3 2 2 2

4 2 9 2 2 9 .y mx m x x mx m



     

Ta có:

2 9 0

mx m











  



Hàm số có 3 điểm cực trị



Phương trình





có 3 nghiệm phân biệt (khi đó



đổi

dấu khi qua các nghiệm)



Phương trình

2 9 0mx m  

có 2 nghiệm phân biệt

0

Ta có:

2 9 0

mx m







   











. Yêu cầu bài toán



  











Vậy các giá trị

cần tìm là

   

; 3 0; 3 .m   



Chọn đáp án D.

Cách khác: Áp dụng công thức giải nhanh. Ta có

; 9.a m b m  

Yêu cầu bài toán

 

   

0 . 9 0 ; 3 0;3 .ab m m m         

Câu 69. Tìm tập hợp tất cả giá trị thực của tham số

để hàm số

 

3 2 2

2 3 1

y x mx m x    

có hai điểm cực trị

và

sao cho

 

1 2 1 2

2 1.x x x x  

0, .







 







.

Lời giải: TXĐ:

.D  

Ta có:

 

2 2 2 3 1 .y x mx m



   

Đồ thị hàm số có hai điểm cực trị khi và chỉ phương trình





có hai nghiệm phân

biệt

 

2 13 2 13

13 4 0 *

13 13

m m m       

. Ta có:

x x m

và

. 1 3x x m

Theo giả thiết:

 

1 2 1 2

2 1 1 3 2 1

x x x x m m





       









Kiểm tra điều kiện

 

, ta có

m 

là yêu cầu bài toán.



Chọn đáp án C.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................34

Câu 70. (NC) Tìm tập hợp tất cả giá trị thực của tham số

để đồ thị hàm số

3 2 2 3

3 3( 1) 3 1y x x m x m      

có các điểm cực trị cách đều gốc toạ độ.

, 1 .







, 1 .









 

1, 1 .









Lời giải: TXĐ:

.D  

Ta có:

 

(1)

2 2 2 2

3 6 3 1 , 0 2 1 0y x x m y x x m



           

Hàm số có cực trị



Phương trình (1) có 2 nghiệm phân biệt

0 0.mm



     

Gọi

,AB

là 2 điểm cực trị của đồ thị hàm số

   

1 ; 2 2 , 1 ; 2 2A m m B m m      

cách đều

và

OA OB m m







    









(thỏa mãn

0m 

)

Vậy các giá trị

cần tìm là

mm  



Chọn đáp án D.

Câu 71. (NC) Tìm tập hợp tất cả giá trị thực của tham số

để đồ thị hàm số

 

21y x m x m   

có ba điểm cực trị

,,A B C

sao cho

;OA BC

trong đó

là gốc

tọa độ,

là điểm cực trị thuộc trục tung,

và

là hai điểm cực trị còn lại.

 

2 2 2, 2 .

 

2 2 2, 2 .

 

2, 2 .

 

2 2 2, 2 2 2 .

Lời giải: TXĐ:

.D  

Ta có:

 

(1)

4 4 1 4 1 0

y x m x x x m







       







Đồ thị hàm số có ba điểm cực trị, khi chỉ khi (1) có 2 nghiệm phân biệt khác

(*)1m  

. Khi đó:

 

0; , 1; 1A m B m m m    

và

 

1; 1C m m m   

Suy ra:

 

2 2 2

4 1 4 4 0

2 2 2

OA BC m m m m





        







(thỏa (*)).

Vậy các giá trị

cần tìm là

2 2 2; 2 2 2.mm   

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................35



Chọn đáp án D.

Câu 72. (NC) Tìm tập hợp tất cả giá trị thực của tham số

để đồ thị hàm số

 

4 2 2

21y x m x m   

có ba điểm cực trị tạo thành một tam giác vuông.

 

0, 1 .

 

1.

.

Lời giải: TXĐ:

.D  

Ta có:

 

4 4 1 4 1y x m x x x m



     

Đồ thị có 3 điểm cực trị khi và chỉ khi

(*)1 0 1mm    

Các điểm cực trị của đồ thị là:

 

0; , 1; 2 1A m B m m   

và

 

1; 2 1C m m  

Suy ra:

 





1; 1AB m m    



và

 





1; 1AC m m   



Ta có:

AB AC

nên tam giác ABC vuông khi và chi khi

   

. 0 1 1 0.AB AC m m     

 

Kết hợp điều kiện (*), ta được

0m 



Chọn đáp án B.

Câu 73. (NC) Tìm tập hợp tất cả giá trị thực của tham số

để đồ thị hàm số

3 2 3

33y x mx m  

có hai điểm cực trị

và

sao cho tam giác

OAB

có diện tích bằng

(với

là gốc tọa độ).

, 2 .







, 2 .









 

2, 2 .









Lời giải: TXĐ:

.D  

Ta có:

3 6 0

y x mx





   







Đồ thị hàm số có 2 điểm cực trị khi và chỉ khi

0m 

(*).

Các điểm cực trị của đồ thị là

 

0; 3Am

và

 

2;B m m

Suy ra:

 

3 , , 2OA m d B OA m

Theo giả thiết:

 

48 , . 48 3 48

OAB

S d B OA OA m





     







(thỏa mãn).



Chọn đáp án C.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................36

Câu 74. (NC) Tìm tập hợp tất cả giá trị thực của tham số

để đồ thị hàm số

 

2 3 1 6y x m x mx   

có hai điểm cực trị

và

sao cho đường thẳng

vuông

góc với đường thẳng

2.yx

 

0, 2 .

 

0, 2 .

 

2, 2 .

2, .









Lời giải: TXĐ:

.D  

Ta có:

 

6 6 1 6y x m x m



   

;













Điều kiện để hàm số có cực trị

1m

Lúc đó:

 

1; 3 1 , ; 3A m B m m m  

. Hệ số góc của đường thẳng

là

 

1.km  

Đường thẳng

vuông góc với đường thẳng

2yx

1.k 

 



     







Vậy giá trị

cần tìm là

0m 

;

2m 



Chọn đáp án A.

Câu 75. (NC) Tìm tập hợp tất cả giá trị thực của tham số

để đồ thị hàm số

31y x mx  

có hai điểm cực trị

và

sao cho tam giác

ABC

cân tại

, với

 

2; 3 .A

0, .





















0, .









Lời giải: TXĐ:

.D  

Ta có

3 3 .y x m





Để hàm số có hai điểm cực trị



Phương trình





có hai

nghiệm phân biệt

0.m

(*)

Tọa độ các điểm cực trị là













3 3 3

; 2 1 , ; 2 1 2 ; 4B m m C m m BC m m      



Gọi

là trung điểm

,BC

suy ra

 

0;1I

. Ta có tam giác

ABC

cân tại

.0AI BC

 

4 8 0





    









[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................37

Đối chiếu điều kiện (*), ta có

m 

là yêu cầu bài toán.



Chọn đáp án B.

Kỹ năng 1:

§äc b¶ng biÕn thiªn (b¶ng xÐt dÊu).

Phương pháp:

Câu 76. Cho hàm số

 

y f x

xác định, liên tục trên



và có bảng biến thiên sau:





 









 



3



Khẳng định nào sau đây sai?

 

đồng biến trên

 

;0 .

 

đồng biến trên

 

2; 3 .

 

nghịch biến trên

 

0;1 .

 

đạt cực đại bằng

Lời giải:

Dựa vào bảng biến thiên ta có

       

0, ;0 1;f x x f x



      

đồng biến trên các

khoảng

 

;0

và

 

1; .

     

0, 0;1f x x f x



   

nghịch biến trên khoảng

 

0;1 .

Hàm số đạt cực đại tại

C§

0x 

và

C§

2;y 

hàm số đạt cực tiểu tại

1x 

và

3.y 



Chọn đáp án D.

Câu 77. Cho hàm số

 

y f x

xác định, liên tục trên



và có bảng biến thiên sau:





 









 



3



Khẳng định nào sau đây đúng?

A. Cực tiểu của

 

là

B. Điểm cực tiểu của

 

là

 

đạt cực đại tại

 

đạt cực đại bằng

Lời giải:

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................38

Hàm số đạt cực đại tại

C§

0x 

và

C§

2;y 

hàm số đạt cực tiểu tại

1x 

và

3.y 



Chọn đáp án B.

Câu 78. Cho hàm số

 

y f x

xác định, liên tục trên



và có bảng biến thiên sau:



1



 











 



2



Khẳng định nào sau đây đúng?

 

đồng biến trên

 

2; 3 .

 

đồng biến trên

   

1;0 1; .  

C. Cực đại của

 

bằng

 

đạt cực tiểu tại

2.

Lời giải:

Dựa vào bảng biến thiên ta có

       

0, 1;0 1;f x x f x



      

đồng biến trên các

khoảng

 

1; 0

và

 

1; .

       

0, ; 1 0;1f x x f x



      

nghịch biến trên các khoảng

 

;1 

và

 

0;1 .

Hàm số đạt cực đại tại

C§

0x 

và

C§

3;y 

hàm số đạt cực tiểu tại

CT CT

1; 1xx  

và

2.y 



Chọn đáp án C.

Câu 79. Cho hàm số

 

y f x

xác định, liên tục trên

 

\1

và có bảng biến thiên sau:



1













Khẳng định nào sau đây đúng?

 

đồng biến trên

 

;1 .

 

đồng biến trên

   

;1 \ 1 . 

C. Cực đại của hàm số bằng

D. Điểm

 

1; 4

là điểm cực đại của đồ thị hàm số.

Lời giải:

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................39

Dựa vào bảng biến thiên ta có

       

0, ; 1 1;1f x x f x



       

đồng biến trên các

khoảng

 

;1 

và

 

1;1 .

     

0, 1;f x x f x



    

nghịch biến trên khoảng

 

1; .

Hàm số đạt cực đại tại

C§

1x 

và

C§

4.y 



Chọn đáp án D.

Câu 80. Cho hàm số

 

y f x

có bảng xét dấu đạo hàm như sau:



2



 









Khẳng định nào sau đây đúng?

 

đồng biến trên

 

2;0 .

 

đồng biến trên

 

;0 .

 

đạt cực đại tại

2.x 

 

đạt cực đại tại

2.x 

Lời giải:

Dựa vào bảng xét dấu đạo hàm ta có

       

0, ; 2 2;f x x f x



       

đồng biến

trên các khoảng

 

;2 

và

 

2; .

       

0, 2;0 0;2f x x f x



     

nghịch biến trên các khoảng

 

2;0

và

 

0; 2 .

Hàm số đạt cực đại tại

C§

2x 

và hàm số đạt cực tiểu tại

2.x 



Chọn đáp án C.

Câu 81. Cho hàm số

 

y f x

có bảng xét dấu đạo hàm như sau:



1



 









Khẳng định nào sau đây sai?

 

đồng biến trên

 

1;0 .

 

nghịch biến trên

 

; 3 . 

 

có hai điểm cực trị. D.

 

có ba điểm cực trị.

Lời giải:

Dựa vào bảng xét dấu đạo hàm ta có

       

0, 1;0 0;1f x x f x



     

đồng biến

trên các khoảng

 

1; 0

và

 

0;1 .

       

0, ; 1 1;f x x f x



       

nghịch biến trên các khoảng

 

;1 

và

 

1; .

Qua các giá trị

1; 1

thì

 



đổi dấu nên

 

có hai điểm cực trị.



Chọn đáp án D.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................40

Kỹ năng 2:

§äc ®å thÞ hµm sè vµ sö dông c¸c phÐp biÕn ®æi ®å thÞ ®¬n gi¶n.

Phương pháp:

Dựa vào đồ thị, trên khoảng nào mà đồ thị

 

là đường đi lên (đi xuống) từ trái sang

phải thì khoảng đó hàm số

 

đồng biến (nghịch biến).

Câu 82. Cho hàm số

 

y f x

xác định, liên tục trên



và

có đồ thị như hình bên. Khẳng định nào sau đây đúng?

 

đồng biến trên

 

;0 .

 

nghịch biến trên

 

1; 2 .

 

đạt cực đại bằng

 

đạt cực tiểu tại

3.x 

-3

-1

Lời giải:

Dựa vào đồ thị ta có

 

đồng biến trên các khoảng

 

;1 

và

 

1; 

và

 

nghịch biến trên khoảng

 

1;1 .

Hàm số đạt cực đại tại

C§

1x 

và

C§

1;y 

hàm số đạt cực tiểu tại

1x 

và

3.y 



Chọn đáp án C.

Câu 83. Cho hàm số

 

y f x

xác định, liên tục trên



và có đồ thị như hình bên. Khẳng định nào sau đây

đúng?

 

đồng biến trên

 

;0 .

 

nghịch biến trên

 

\ 1 .

 

nghịch biến trên

 

0; 2 .

 

không có cực trị.

Lời giải:

Dựa vào đồ thị ta có

 

nghịch biến trên các khoảng

 

;1

và

 

1; .

Vậy

 

không có cực trị.



Chọn đáp án D.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................41

Câu 84. (Đề minh họa 2 2017) Cho hàm số

 

y f x

xác định, liên tục

trên đoạn

2;2 



và có đồ thị là đường cong trong hình vẽ bên. Hàm

số

 

đạt cực đại tại điểm nào dưới đây?

2x 

. B.

1x 

1x 

. D.

2x 

Lời giải:

Hàm số đạt cực đại tại

C§

1x 

và

C§

2;y 

hàm số đạt cực tiểu tại

1x 

và

2.y 



Chọn đáp án B.

Câu 85. Cho hàm số

 

y f x

xác định, liên tục trên đoạn

2;2 



và

có đồ thị là đường cong trong hình vẽ bên. Hàm số

 

đạt cực tiểu

tại điểm nào dưới đây?

2x 

. B.

1x 

1x 

. D.

2x 

Lời giải:

Hàm số đạt cực đại tại

C§

1x 

và

C§

2;y 

hàm số đạt cực tiểu tại

1x 

và

2.y 



Chọn đáp án C.

Câu 86. Cho hàm số

 

y f x

xác định, liên tục trên đoạn

2;2 



và

có đồ thị là đường cong trong hình vẽ bên. Cực đại của hàm số

 

là giá trị nào nào dưới đây?

2

. B.

1

. D.

Lời giải:

Hàm số đạt cực đại tại

C§

1x 

và

C§

2;y 

hàm số đạt cực tiểu tại

1x 

và

2.y 



Chọn đáp án D.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................42

Câu 87. Cho hàm số

 

y f x

xác định, liên tục trên đoạn

2;2 



và

có đồ thị là đường cong trong hình vẽ bên. Cực tiểu của hàm số

 

là giá trị nào nào dưới đây?

2

. B.

1

. D.

Lời giải:

Hàm số đạt cực đại tại

C§

1x 

và

C§

2;y 

hàm số đạt cực tiểu tại

1x 

và

2.y 



Chọn đáp án A.

Câu 88. (NC) Cho hàm số

 

y f x

xác định, liên tục trên



và hàm số đạo hàm

 



của

 

có đồ thị như hình bên.

Tìm số điểm cực trị của hàm số

 

.y f x

Lời giải:

Hàm số có

 

0, 1f x x



  

;

 

0, 1f x x



  

và

 

1 0.f





Vậy hàm số có duy nhất một

điểm cực trị và

1x 

là điểm cực tiểu của hàm số

 

.y f x



Chọn đáp án D.

Câu 89. (NC) Cho hàm số

 

y f x

xác định, liên tục

trên



và hàm số đạo hàm

 



của

 

có đồ thị như

hình bên. Tìm số điểm cực trị của hàm số

 

.y f x

Lời giải:

Hàm số có

 



có ba giao điểm với trục hoành (tức là phương trình

 



có ba

nghiệm) và

 



đổi dấu hai lần khi qua ba nghiệm đó. Vậy hàm số có hai điểm cực trị

(cụ thể là một điểm cực đại và một điểm cực tiểu).



Chọn đáp án B.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................43

Câu 90. (NC) Cho hàm số

 

y f x

xác định, liên tục trên



và hàm số đạo hàm

 



của

 

có đồ thị như hình

bên. Tìm số điểm cực trị của hàm số

 

.y f x

Lời giải:

Hàm số có

 



có ba giao điểm với trục hoành (tức là phương trình

 



có ba

nghiệm) và

 



không đổi dấu khi qua ba nghiệm đó. Vậy hàm số không có cực trị



Chọn đáp án D.

Câu 91. (NC) Cho hàm số

 

y f x

xác định, liên tục trên



và có đồ thị như hình bên. Tìm số điểm cực trị của hàm

số

 

.y f x

Lời giải:

Thực hiện phép biến đổi đồ thị:

+) Giữ phần đồ thị hàm số

 

phía trên trục

,Ox

bỏ phần đồ thị

 

phía dưới trục

.Ox

+) Lấy đối xứng phần đồ thị

 

phía dưới

trục

qua

.Ox

Dựa vào đồ thị

 

y f x

suy ra hàm số

 

y f x

có

điểm cực trị.



Chọn đáp án D.

Câu 92. (NC) Cho hàm số

 

y f x

xác định, liên tục

trên



và có đồ thị như hình bên. Tìm số điểm cực trị

của hàm số

 

.y f x

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................44

Lời giải:

Thực hiện phép biến đổi đồ thị:

+) Giữ phần đồ thị hàm số

 

phía bên phải

trục

,Oy

bỏ phần đồ thị

 

phía bên trái trục

.Oy

+) Lấy đối xứng phần đồ thị

 

phía bên

phải trục

qua

.Oy

Dựa vào đồ thị

 

y f x

suy ra hàm số

 

y f x

có

điểm cực trị.



Chọn đáp án C.

Câu 93. (NC) Cho hàm số

 

y f x

xác định, liên

tục trên



và có đồ thị như hình bên. Tìm số điểm

cực trị của hàm số

 

.y f x

Lời giải:

Thực hiện phép biến đổi đồ thị:

+) Giữ phần đồ thị hàm số

 

phía trên trục

,Ox

bỏ phần đồ thị

 

phía dưới trục

.Ox

+) Lấy đối xứng phần đồ thị

 

phía dưới

trục

qua

.Ox

Dựa vào đồ thị

 

y f x

suy ra hàm số

 

y f x

có

điểm cực trị.



Chọn đáp án D.

Câu 94. (NC) Cho hàm số

 

y f x

xác định, liên tục

trên



và có đồ thị như hình bên. Tìm số điểm cực trị

của hàm số

 

.y f x

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................45

Lời giải:

Thực hiện phép biến đổi đồ thị:

+) Giữ phần đồ thị hàm số

 

phía bên phải

trục

,Oy

bỏ phần đồ thị

 

phía bên trái trục

.Oy

+) Lấy đối xứng phần đồ thị

 

phía bên

phải trục

qua

.Oy

Dựa vào đồ thị

 

y f x

suy ra hàm số

 

y f x

có

điểm cực trị.



Chọn đáp án C.

Câu 95. (NC) Cho hàm số

 

y f x

xác định, liên tục

trên



và có đồ thị như hình bên. Tìm số điểm cực trị

của hàm số

 

.y f x

11.

10.

Lời giải:

Thực hiện hai phép biến đổi đồ thị:

Phép biến đổi 1: Từ đồ thị

 

y f x

suy ra

đồ thị

 

.y f x

(Kỹ năng câu 94).

Phép biến đổi 2: Từ đồ thị

 

y f x

suy ra

đồ thị

 

.y f x

(Kỹ năng câu 93).

Dựa vào đồ thị

 

y f x

sau phép biến đổi đồ thị số 2, suy ra hàm số

 

y f x

có

điểm cực trị.



Chọn đáp án B.

[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB

Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................46

SẼ CÒN UPDATE TIẾP......

Các em cùng thầy cô cố gắng nhé?! Thầy tin mọi việc rồi sẽ tốt đẹp thôi! À

quên, nếu có nhầm gì thì các em phản hồi giúp thầy nhé?! Hẹn gặp lại các em ở

những chủ đề sau!

Huế, ngày 29 tháng 8 năm 2017!

P/S: Trong quá trình biên soạn chắc chắn không tránh khỏi sai sót, rất mong nhận được

sự góp ý của quý thầy cô giáo và các em học sinh thân yêu để các bài viết tiếp theo được hoàn

thiên hơn. Xin chân thành cảm ơn!

CLB GIÁO VIÊN TRẺ TP HUẾ

Phụ trách chung: Giáo viên LÊ BÁ BẢO.

Đơn vị công tác: Trường THPT Đặng Huy Trứ, Thừa Thiên Huế.

Email: lebabaodanghuytru2016@gmail.com Facebook: Lê Bá Bảo

Số điện thoại: 0935.785.115

Bấm Tải xuống để xem toàn bộ.

| 1/47

| | Tải xuống

Preview text:

Giáo viên: LÊ BÁ BẢO_ Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Trung tâm BDKT 87 Bùi Thị Xuân, TP Huế Bµi viÕt chuyªn ®Ò: KH¶O S¸T HµM Sè Cùc trÞ cña hµm sè LuyÖn thi THPT 2017_2018 HuÕ, th¸ng 8/2017
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12 CB
Chñ ®Ò: Cùc trÞ cña hµm sè.
Dành tặng cho các em học sinh đang sợ Toán, yếu
Toán và đang loay hoay về Toán! Cố lên các em!
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Dạng toán 1: X¸c ®Þnh ®iÓm cùc trÞ, cùc trÞ cña hµm sè. Phương pháp:
Lập bảng xét dấu f x hoặc lập bảng biến thiên để đưa ra kết luận.
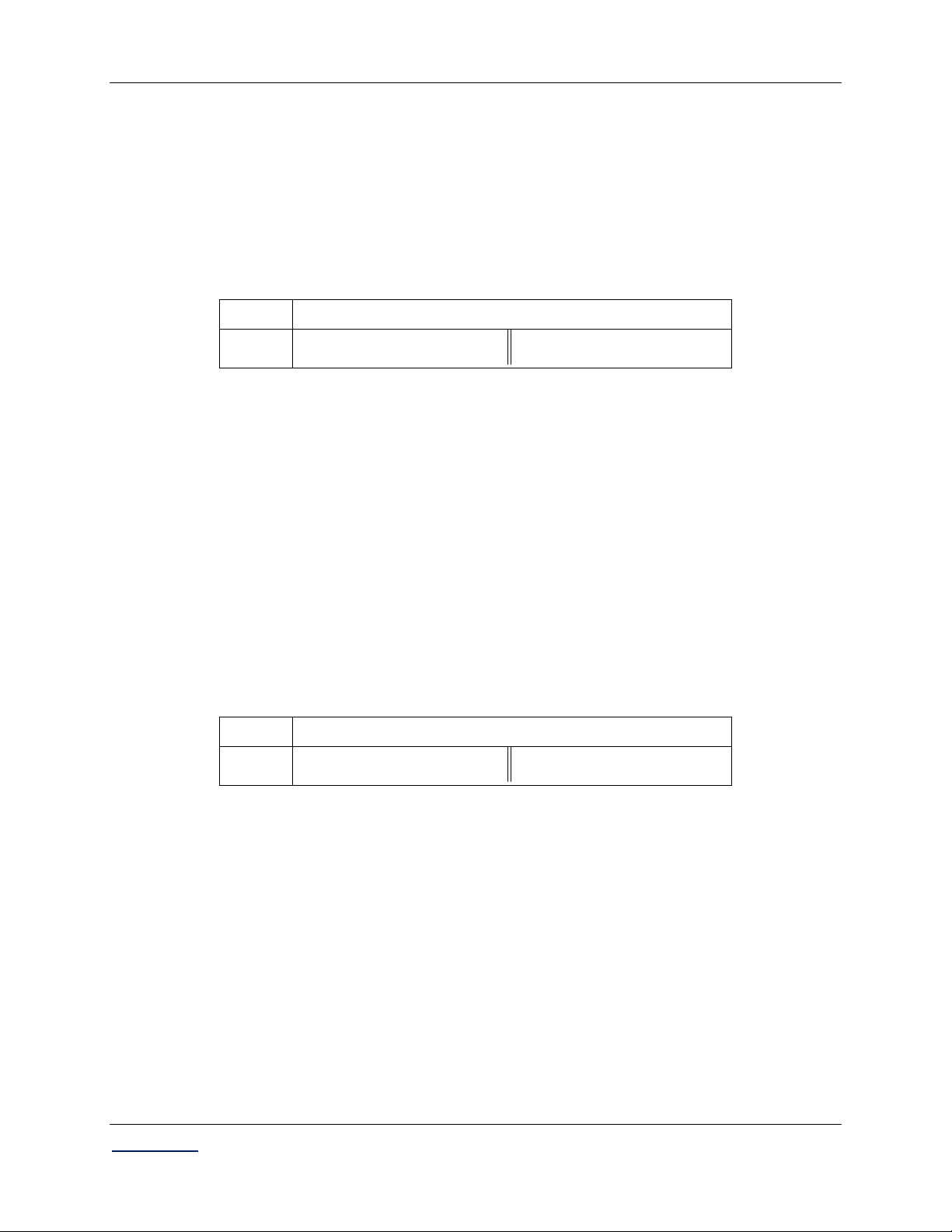
Câu 1. Tìm điểm cực đại của hàm số 3
y  x  3x  2. A. 1. B. 1.  C. 0. D. 4.
Lời giải: TXĐ: D  .  x  1   y  4 Ta có: 2
y  3x  3  0   .
x  1  y   0
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  1  1  f x  0  0  4  f x  0
Dựa vào bảng biến thiên, điểm cực đại của hàm số là x  1.  C§
 Chọn đáp án B.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0 x  1   y  4 Ta có: 2
y  3x  3  0   ; y  6 . x
x  1  y   0 Ta có: y  
1  6  0  x  1là điểm cực tiểu của hàm số và y   1  6   0  x  1  là
điểm cực đại của hàm số.
Câu 2. Tìm điểm cực tiểu của hàm số 3 2
y  x  3x  2. A. 0. B. 2. C. 4.  D. 1.
Lời giải: TXĐ: D  . 
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................1
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
x  0  y  2 Ta có: 2
y  3x  6x  0   .
x  2  y  2  
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  0 2  f x  0  0  2  f x  4 
Dựa vào bảng biến thiên, điểm cực tiểu của hàm số là x  2. CT
 Chọn đáp án B.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0
x  2  y  2  Ta có: 2
y  3x  6x  0  
; y  6x  6.
x  0  y   2
Ta có: y 2  6  0  x  2 là điểm cực tiểu của hàm số và y 0  6
  0  x  0 là điểm cực đại của hàm số.
Câu 3. Tìm cực đại (giá trị cực đại) y của hàm số 3
y  x  3x  4. C§ A. y  1. B. y  1.  C. y  2.  D. y  6.  C§ C§ C§ C§
Lời giải: TXĐ: D  .  x  1   y  6  Ta có: 2 y  3
 x  3  0   .
x  1  y  2  
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  1  1  f x  0  0   2  f x 6  
Dựa vào bảng biến thiên, cực đại của hàm số là y  2.  C§
 Chọn đáp án C.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0 x  1   y  6  Ta có: 2 y  3
 x  3  0   ; y  6  . x
x  1  y  2  
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................2
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB Ta có: y   1  6
  0  x  1 là điểm cực đại của hàm số suy ra y  y 1  2  và C§   y  
1  6  0  x  1
 là điểm cực tiểu của hàm số suy ra y  y 1   6  . CT  
Câu 4. Tìm cực tiểu giá trị cực tiểu) y của hàm số 3
y  x  3x  4. CT A. y  1. B. y  1.  C. y  2.  D. y  6.  CT CT CT CT
Lời giải: TXĐ: D  .  x  1   y  6  Ta có: 2 y  3
 x  3  0   .
x  1  y  2  
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  1  1  f x  0  0   2  f x 6  
Dựa vào bảng biến thiên, cực tiểu của hàm số là y  6.  CT
 Chọn đáp án D.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0 x  1   y  6  Ta có: 2 y  3
 x  3  0   ; y  6  . x
x  1  y  2   Ta có: y   1  6
  0  x  1 là điểm cực đại của hàm số suy ra y  y 1  2  và C§   y  
1  6  0  x  1
 là điểm cực tiểu của hàm số suy ra y  y 1   6  . CT  
Câu 5. Tìm điểm cực đại của hàm số 4 2
y  x  2x  2. A. 1. B. 1.  C. 0. D. 2.
Lời giải: TXĐ: D  .  x  1   y  1  Ta có: 3
y  4x  4x  0  x  0  y  2 . 
x  1 y  1 
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  1  0 1  f x  0  0  0   2  f x 1 1
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................3
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
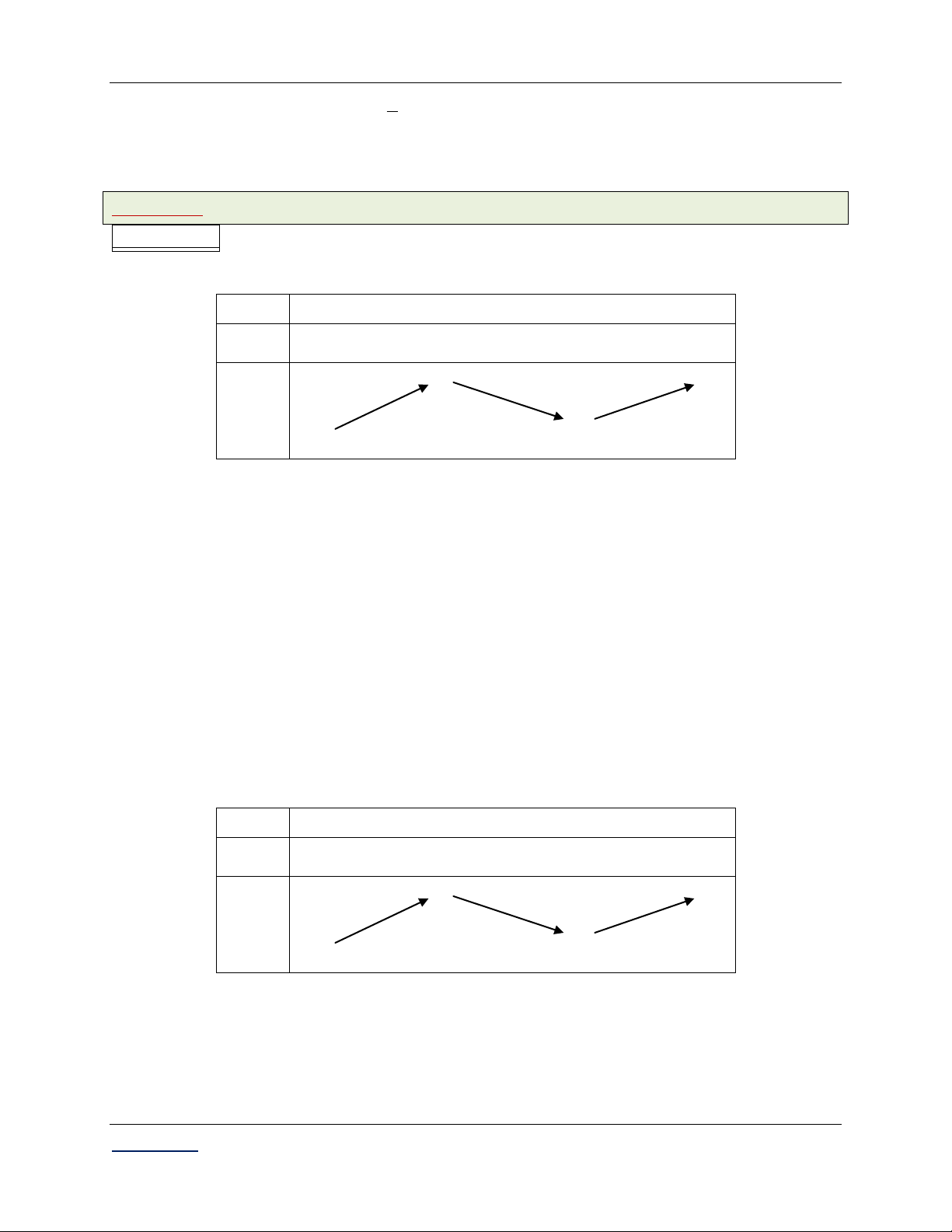
Dựa vào bảng biến thiên, điểm cực đại của hàm số x  0. C§
 Chọn đáp án C.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0 x  1   y  1  Ta có: 3 2
y  4x  4x  0  x  0  y  2 ; y  12x  4 
x  1 y  1  Ta có: y   1  8; y  
1  8  0; y 0  4   0.
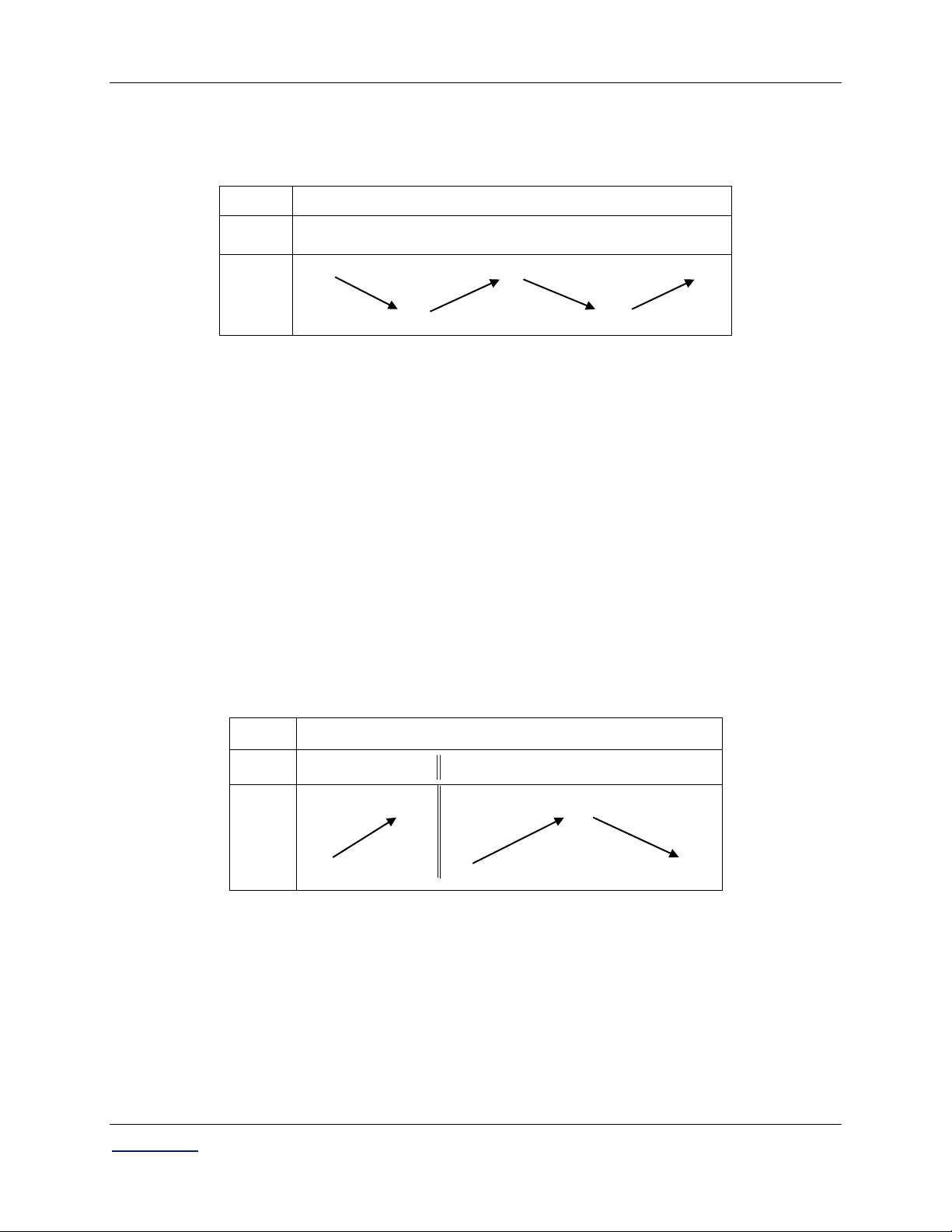
Vậy hàm số đạt cực đại tại x  0 và y
 y 0  2; hàm số đạt cực tiểu tại x  1  ; x  1 C§   và y  y 1   y 1  1. CT    
Câu 6. Tìm cực đại của hàm số 4 2
y  x  2x  2. A. 1. B. 1.  C. 0. D. 2.
Lời giải: TXĐ: D  .  x  1   y  1  Ta có: 3
y  4x  4x  0  x  0  y  2 . 
x  1 y  1 
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  1  0 1  f x  0  0  0   2  f x 1 1
Dựa vào bảng biến thiên, điểm cực đại của hàm số x
 0 và y  y 0  2. C§   C§
 Chọn đáp án D.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0 x  1   y  1  Ta có: 3 2
y  4x  4x  0  x  0  y  2 ; y  12x  4 
x  1 y  1  Ta có: y   1  8; y  
1  8  0; y 0  4   0.
Vậy hàm số đạt cực đại tại x  0 và y
 y 0  2; hàm số đạt cực tiểu tại x  1  ; x  1 C§   và y  y 1   y 1  1. CT    
Câu 7. Tìm cực tiểu của hàm số 4 2
y  x  2x  2.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................4
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB A. 1. B. 1.  C. 0. D. 2.
Lời giải: TXĐ: D  .  x  1   y  1  Ta có: 3
y  4x  4x  0  x  0  y  2 . 
x  1 y  1 
Cách 1: (Dấu hiện I) Lập bảng biến thiên. x  1  0 1  f x  0  0  0   2  f x 1 1
Dựa vào bảng biến thiên, điểm cực đại của hàm số x  1  ; x  1 và CT CT y  y 1   y 1  1. CT    
 Chọn đáp án A.
Cách 2: (Dấu hiện II) Xét dấu f  x với x là nghiệm phương trình f x  0. 0  0 x  1   y  1  Ta có: 3 2
y  4x  4x  0  x  0  y  2 ; y  12x  4 
x  1 y  1  Ta có: y   1  8; y  
1  8  0; y 0  4   0.
Vậy hàm số đạt cực đại tại x  0 và y
 y 0  2; hàm số đạt cực tiểu tại x  1  ; x  1 C§   và y  y 1   y 1  1. CT    
Câu 8. Tìm điểm cực đại của đồ thị hàm số 3
y  x  3x  2. A. 4;   1 . B.  1  ; 4. C. 1; 0. D. 0;  1 .
Lời giải: TXĐ: D  .  x  1   y  4 Ta có: 2
y  3x  3  0   .
x  1  y   0 Bảng biến thiên. x  1  1  f x  0  0  4  f x  0
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................5
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Dựa vào bảng biến thiên, điểm cực đại của đồ thị hàm số là  1  ; 4.
 Chọn đáp án B.
Câu 9. Tìm điểm cực tiểu của đồ thị hàm số 3 2
y  x  3x  2. A. 0; 2. B. 2; 0. C. 2; 2  . D. 4; 2  .
Lời giải: TXĐ: D  . 
x  0  y  2 Ta có: 2
y  3x  6x  0   .
x  2  y  2   Bảng biến thiên. x  0 2  f x  0  0  2  f x  2 
Dựa vào bảng biến thiên, điểm cực tiểu của đồ thị hàm số là 2; 4  .
 Chọn đáp án C. 2 x  4
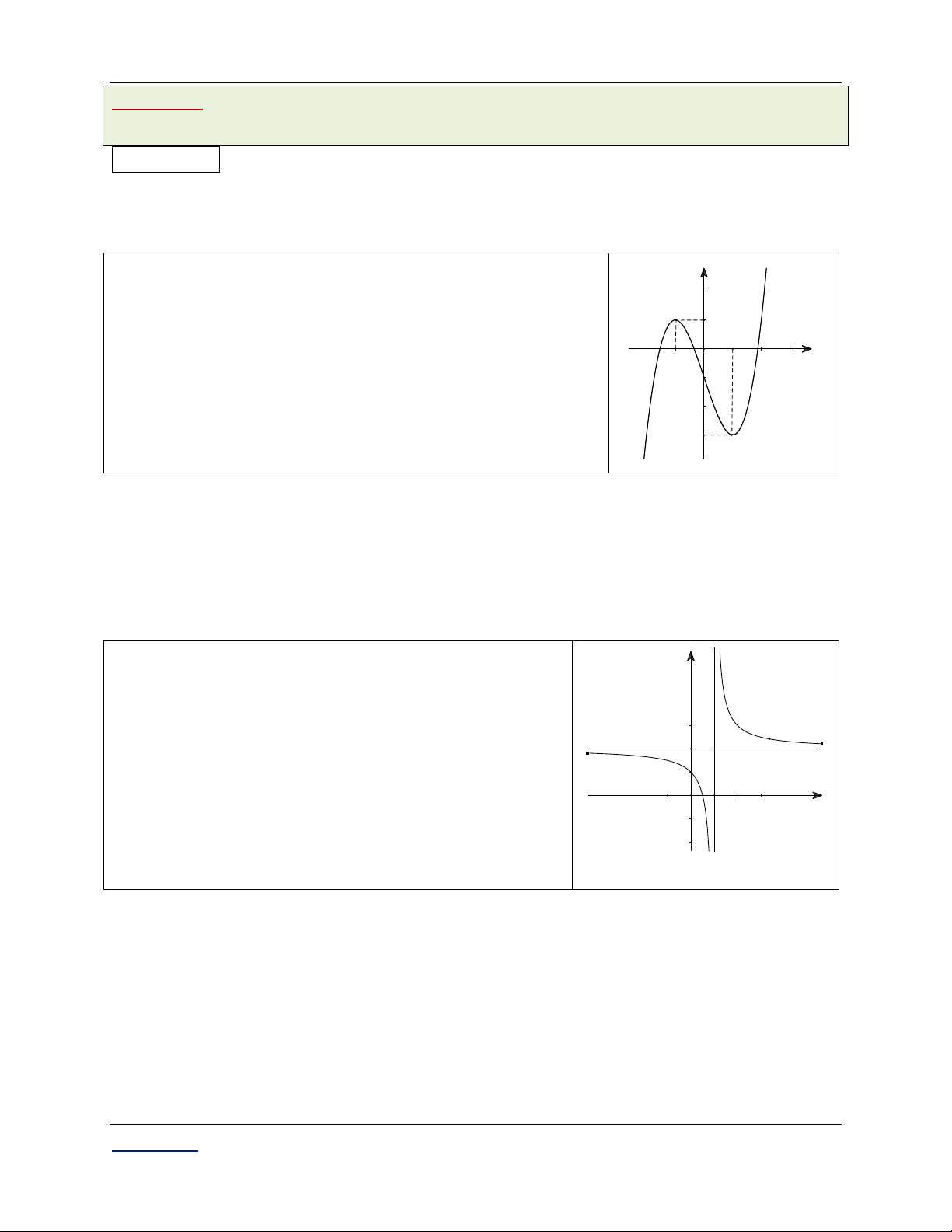
Câu 10. Tìm điểm cực đại của hàm số y  . x A. 2. B. 2.  C. 4.  D. 4.
Lời giải: TXĐ: D    \  0 . 2 x  4 x  2   y  4  Ta có: y   0   . 2 x
x  2  y   4 Bảng biến thiên: x  2  0 2  f 'x  0   0    4  f x 4  
Dựa vào bảng biến thiên, điểm cực đại của hàm số là x  2.  C§
 Chọn đáp án B. 2 x  4
Câu 11. Tìm cực tiểu của hàm số y  . x A. 2. B. 2.  C. 4.  D. 4.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................6
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Lời giải: TXĐ: D    \  0 . 2 x  4 x  2   y  4  Ta có: y   0   . 2 x
x  2  y   4 Bảng biến thiên: x  2  0 2  f 'x  0   0    4  f x 4  
Dựa vào bảng biến thiên, cực tiểu của hàm số là y  4. CT
 Chọn đáp án D.
Câu 12. Gọi x , x lần lượt là điểm cực đại và điểm cực tiểu của hàm số C§ CT 3
y  x  3x  2. Tính S  x  2x . C§ CT A. S  1. B. S  0. C. S  4. D. S  1. 
Lời giải: TXĐ: D  .  x  1   y  4 Ta có: 2
y  3x  3  0   .
x  1  y   0 Bảng biến thiên. x  1  1  f x  0  0  4  f x  0
Dựa vào bảng biến thiên, ta suy ra x  1
 , x  1 S  x  2x  1. C§ CT C§ CT
 Chọn đáp án A.
Câu 13. Gọi x , x lần lượt là điểm cực đại và điểm cực tiểu của hàm số 3 y  x  3 . x C§ CT Tính 4 4 S  x  x . C§ CT A. S  32. B. S  0. C. S  4. D. S  2.
Lời giải: TXĐ: D  .  x  1   y  2 Ta có: 2
y  3x  3  0   .
x  1  y  2   Bảng biến thiên.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................7
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB x  1  1  f x  0  0  2  f x  2 
Dựa vào bảng biến thiên, ta suy ra x   4 4 1, x
 1 S  x  x  2. C§ CT C§ CT
 Chọn đáp án D.
Câu 14. Gọi y , y lần lượt là cực đại và điểm cực tiểu của hàm số 3 y  x  3 . x Tính C§ CT S  2y  3y 1. C§ CT A. S  1.  B. S  0. C. S  4. D. S  2.
Lời giải: TXĐ: D  .  x  1   y  2 Ta có: 2
y  3x  3  0   .
x  1  y  2   Bảng biến thiên. x  1  1  f x  0  0  2  f x  2 
Dựa vào bảng biến thiên, ta suy ra y  2, y  2
  S  2y  3y 1  1  . C§ CT C§ CT
 Chọn đáp án A.
Câu 15. Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số 3 y  x  3 .
x Tính độ dài đoạn thẳng . AB A. AB  2 3. B. AB  4. C. AB  5. D. AB  2 5.
Lời giải: TXĐ: D  .  x  1   y  2 Ta có: 2
y  3x  3  0   .
x  1  y  2   Bảng biến thiên. x  1  1  f x  0  0  2  f x  2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................8
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB 
Dựa vào bảng biến thiên, ta suy ra A 1  ;2,B1; 2
   AB  2; 4
   AB  2 5.
 Chọn đáp án D.
Câu 16. Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số 3 2
y  x  3x  2. Trung điểm I của đoạn thẳng AB có tọa độ nào dưới đây? A. 1;  1 . B. 2; 0. C. 1; 0. D. 1; 2  .
Lời giải: TXĐ: D  . 
x  0  y  2 Ta có: 2
y  3x  6x  0   .
x  2  y  2   Bảng biến thiên. x  0 2  f x  0  0  2  f x  2 
Dựa vào bảng biến thiên, ta suy ra A0; 2 ,B2; 2
   I  1;0.
 Chọn đáp án C.
Câu 17. Gọi A, B, C là ba điểm cực trị của đồ thị hàm số 4 2
y  x  2x  3. Tìm tọa độ
trọng tâm của tam giác AB . C  7   7   5   5  A. 0; . B. 1; . C. 1   ; . D. 1; .  3   3   3   3 
Lời giải: TXĐ: D  .  x  1   y  2  Ta có: 3
y  4x  4x  0  x  0  y  3 . 
x  1 y  2  Bảng biến thiên. x  1  0 1  f x  0  0  0   3  f x 2 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................9
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Dựa vào bảng biến thiên, suy ra các điểm cực trị của đồ thị hàm số là  7  A 1
 ; 2, B0;3, C1;2 . Vậy tọa độ trọng tâm của tam giác ABC là 0; .  3 
 Chọn đáp án A.
Câu 18. Gọi y , y lần lượt là cực đại và cực tiểu của hàm số 4 2
y  x  2x  2. Tính C§ CT
giá trị biểu thức M  y .y  y  y . C§ CT C§ CT A. M  3.  B. M  3. C. M  1. D. M  1. 
Lời giải: TXĐ: D  .  x  1   y  3   Ta có: 3
y  4x  4x  0  x  0  y  2  . 
x  1 y  3   Bảng biến thiên. x  1  0 1  f x  0  0  0   2   f x 3  3 
Dựa vào bảng biến thiên, suy ra y  2  , y  3
 .Vậy M  y .y  y  y  1. C§ CT C§ CT C§ CT
 Chọn đáp án C. 2 x  1
Câu 19. Gọi x , x lần lượt là điểm cực đại và điểm cực tiểu của hàm số y  . C§ CT x Tính S  2x  3x . C§ CT A. S  4. B. S  2. C. S  1.  D. S  1.
Lời giải: TXĐ: D    \  0 . 2 x  1 x  1   y  2  Ta có: y   0   . 2 x
x  1  y   2 Bảng biến thiên: x  1  0 1  f 'x  0   0    2  f x 2  
Dựa vào bảng biến thiên, suy ra x  1
 , x  1 S  2x  3x  1. C§ CT C§ CT
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................10
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
 Chọn đáp án D. 2 x  1
Câu 20. Gọi y , y lần lượt là cực đại và điểm cực tiểu của hàm số y  . Tính C§ CT x S  2y  3y . C§ CT A. S  4. B. S  2. C. S  1.  D. S  1.
Lời giải: TXĐ: D    \  0 . 2 x  1 x  1   y  2  Ta có: y   0   . 2 x
x  1  y   2 Bảng biến thiên: x  1  0 1  f 'x  0   0    2  f x 2  
Dựa vào bảng biến thiên, suy ra y  2
 , y  2  S  2x  3x  2. C§ CT C§ CT
 Chọn đáp án B.
Câu 21. Gọi P, Q lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số 2 x  2x  2 y 
. Tính độ dài đoạn thẳng . PQ x  1 A. PQ  3 2. B. PQ  2 5. C. PQ  5. D. PQ  4.
Lời giải: TXĐ: D    \  1 . 2 x  2x
x  0  y  2  Ta có: y      x  0 . 2
x  2  y    2 1 Bảng biến thiên: x  0 1 2  f 'x  0   0    2  f x 2   
Dựa vào bảng biến thiên, suy ra P0; 2
 , Q2;2  PQ  2;4  PQ  2 5.
 Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................11
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
SỬ DỤNG DẤU HIỆU 2 ĐỂ TÌM CỰC TRỊ CỦA HÀM SỐ
(Trong loạt bài tập này, tác giả quy ước k, m ).
Câu 22. Điểm nào sau đây là điểm cực đại của hàm số y  2sin x  1?   A.  . B. . C. 3. D. 1.  2 2
Lời giải: TXĐ: D  .        
Ta có: y  2 cos x  0  x 
 k. Kiểm tra được: y  y       0. 2  2   2     
Ta có: y x  2  sin x, y  2   0  x   
là điểm cực đại của hàm số và y  3;  2  2 C§     y 
 2  0  x    
là điểm cực tiểu của hàm số và y  1.   2  2 CT
 Chọn đáp án B.
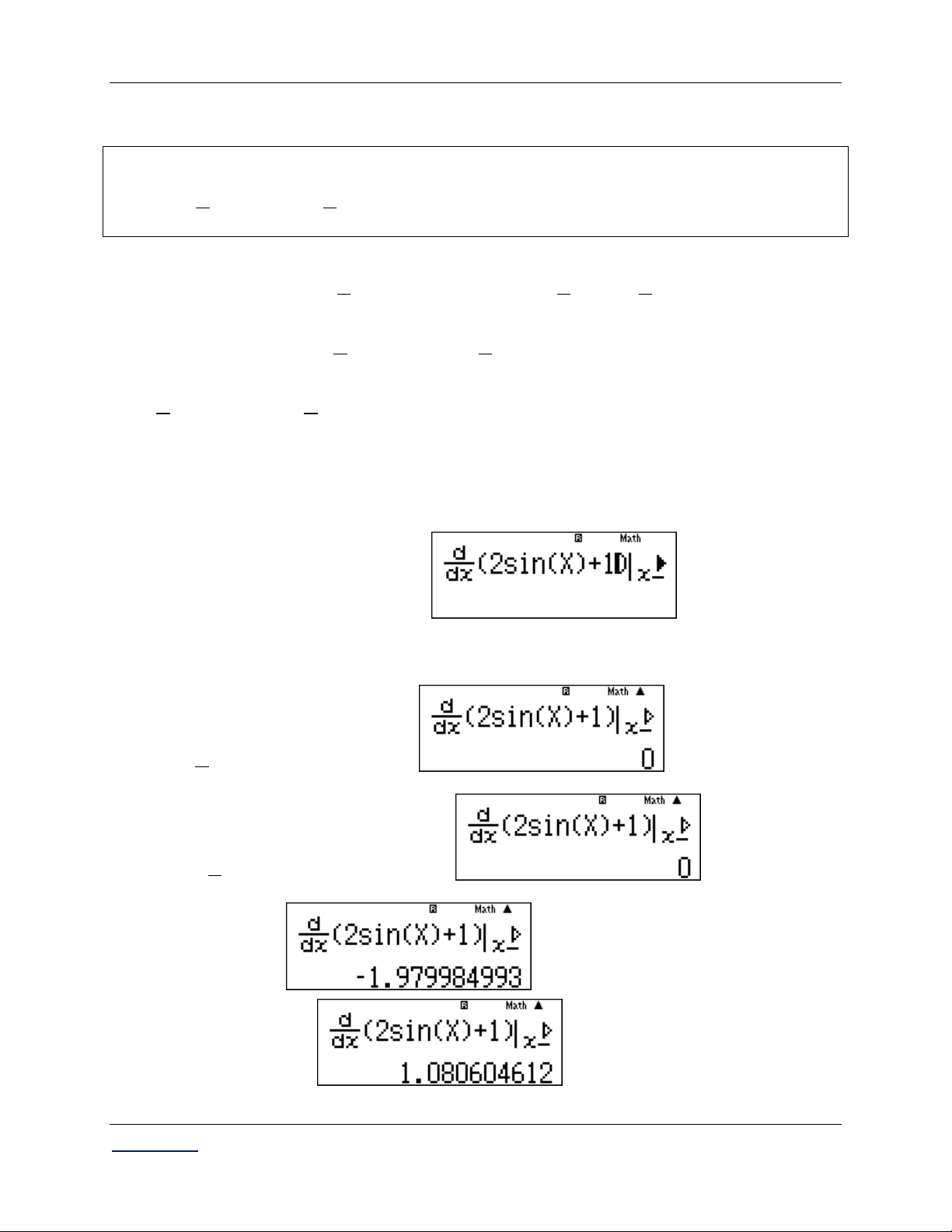
Kỹ thuật sử dụng MTCT:
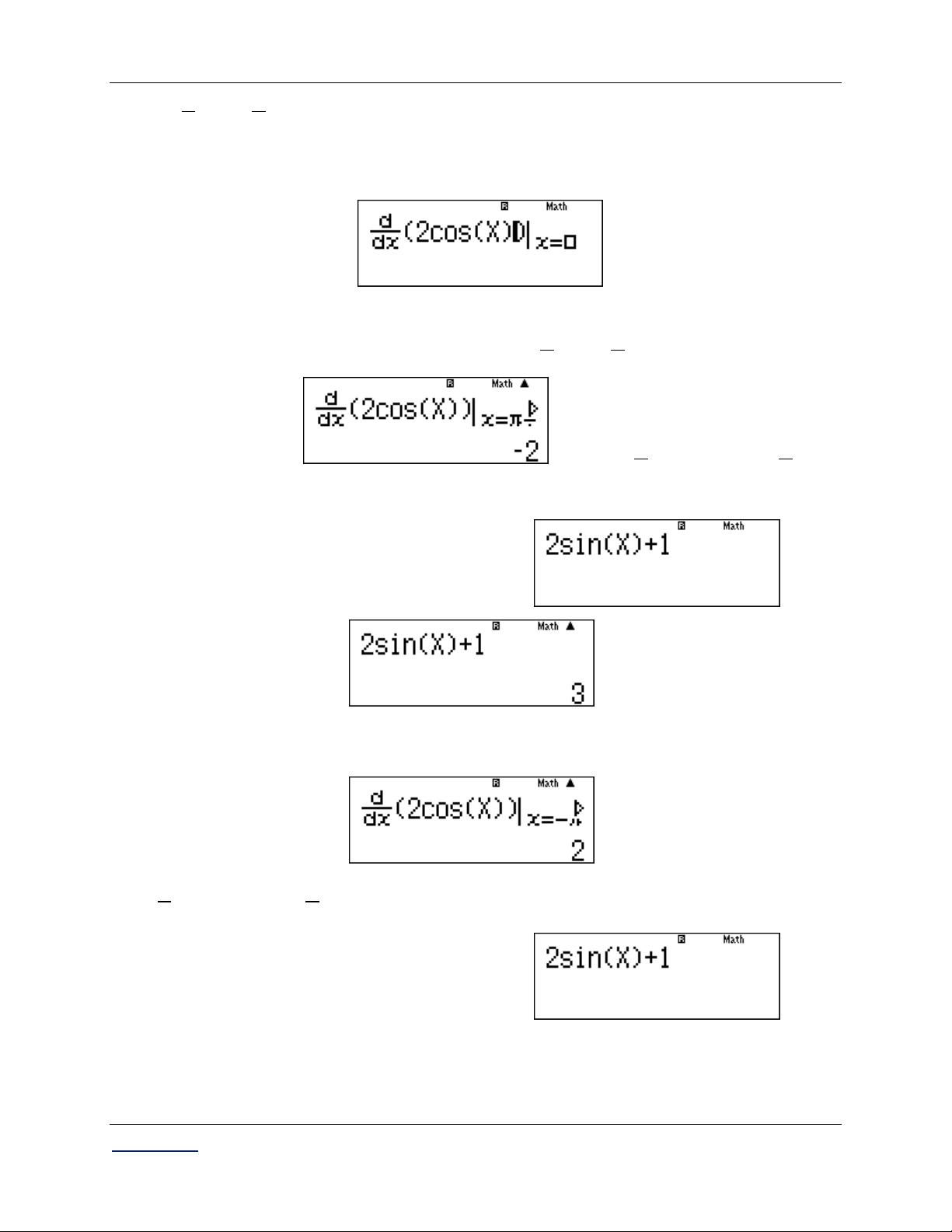
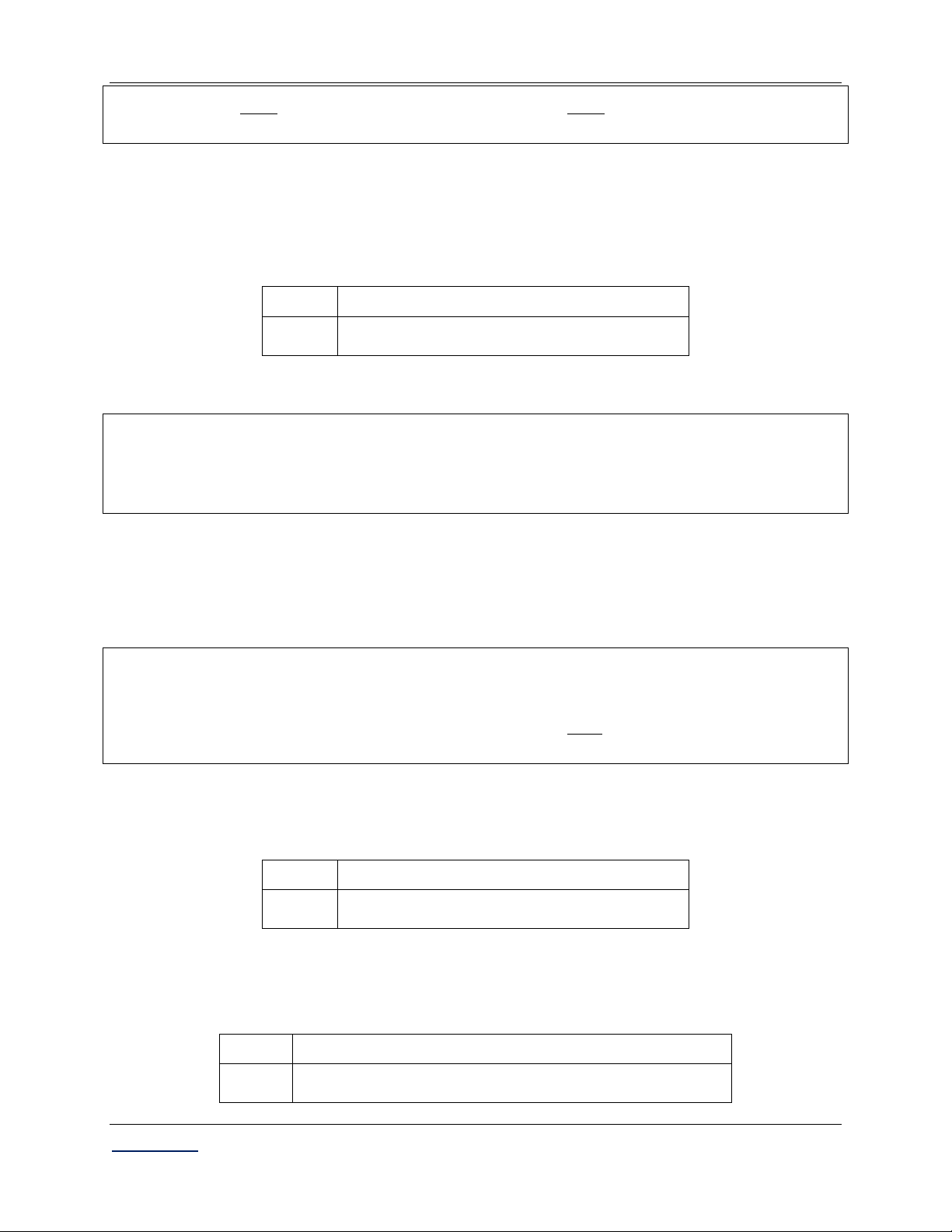
Bước 1: Nhập biểu thức đạo hàm của hàm số vào máy tính: qy2jQ))+1
Bước 2: Kiểm tra giá trị nào là nghiệm của đạo hàm:  Nhập x  : qKP2= 2  Nhập x   : pqKP2= 2
Nhập x  3 : 3=
Nhập x  1 : p1=
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................12
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB   Vậy x  ; x  
là các nghiệm của f x. 2 2
Bước 3: Nhập biểu thức đạo hàm cấp hai của hàm số vào máy tính:
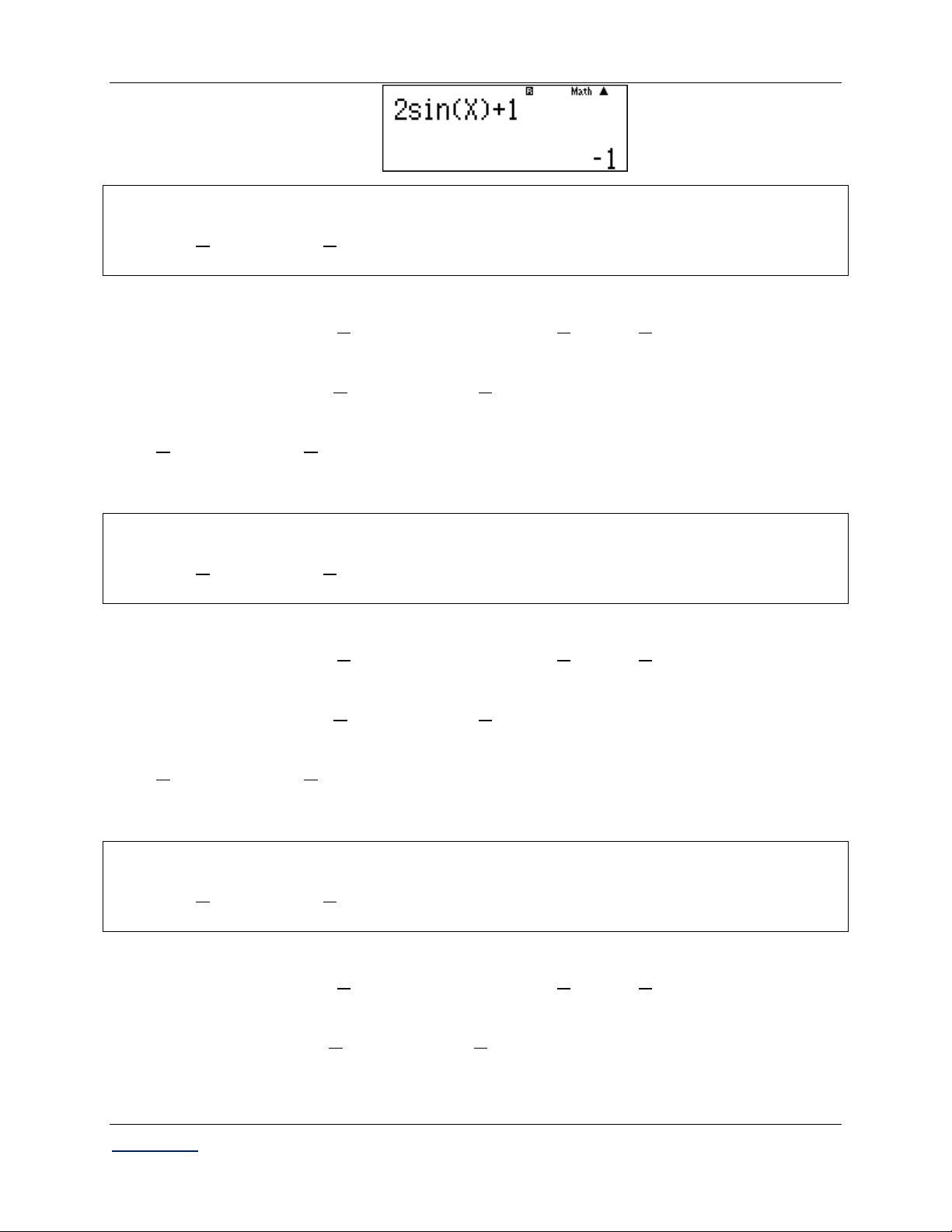
Nhập y  2 cos x ô chứa đạo hàm trong phím đạo hàm. qy2kQ))  
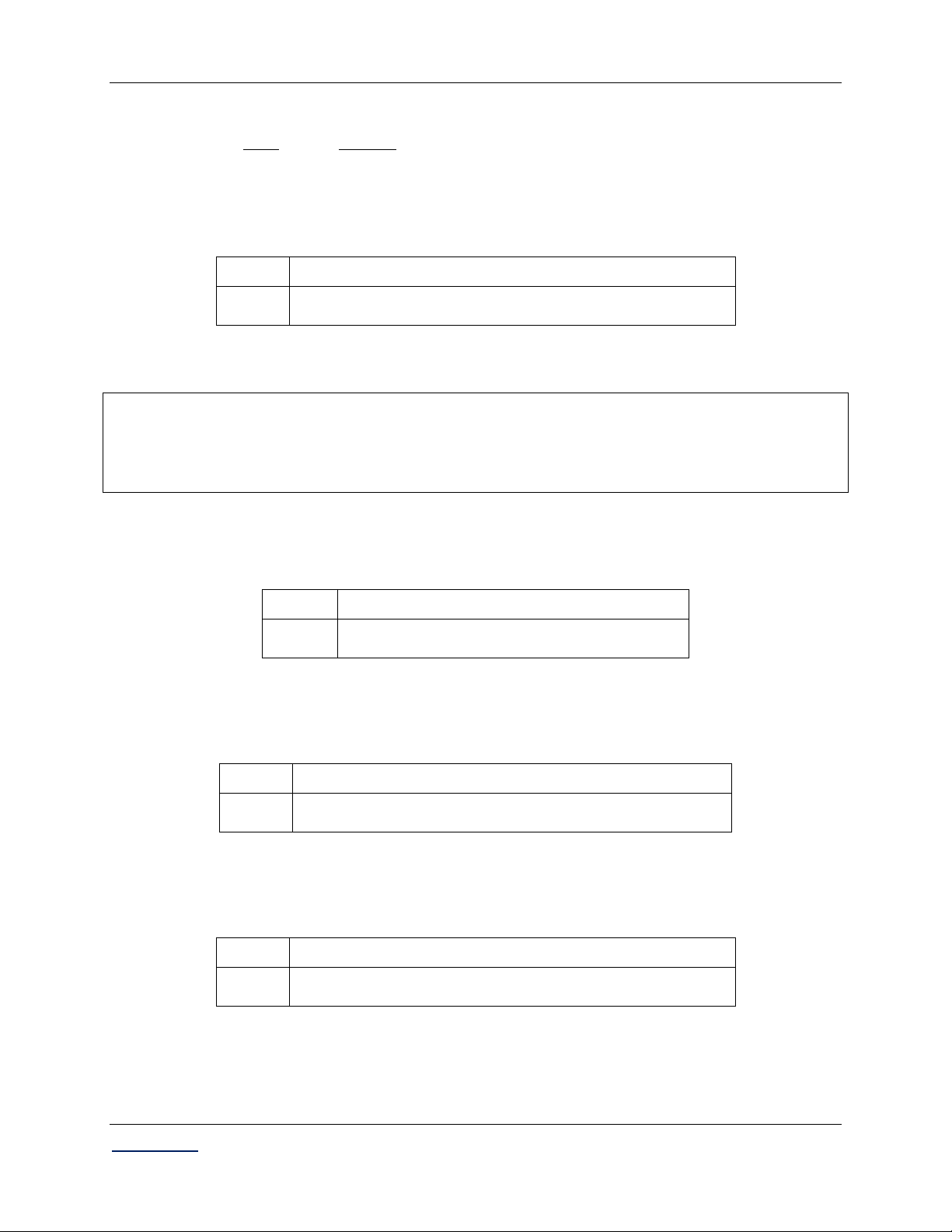
Kiểm tra dấu của đạo hàm cấp hai tại các giá trị x  ; x   . 2 2     +) qKP2= Vậy f   2   0  x    là  2  2
điểm cực đại của hàm số.
*) Tính y . Nhập 2jQ))+1 C§ rqKP2= Vậy y  3. C§ +) pqKP2= Vậy     f  
 2  0  x    
là điểm cực tiểu của hàm số.  2  2
*) Tính y . Nhập 2jQ))+1 CT
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................13
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB rqpKP2= Vậy y  1.  CT
Câu 23. Điểm nào sau đây là điểm cực tiểu của hàm số y  2sin x  1?   A.  . B. . C. 3. D. 1.  2 2
Lời giải: TXĐ: D  .        
Ta có: y  2 cos x  0  x 
 k. Kiểm tra được: y  y       0. 2  2   2     
Ta có: y x  2  sin x, y  2   0  x   
là điểm cực đại của hàm số và y  3;  2  2 C§     y 
 2  0  x    
là điểm cực tiểu của hàm số và y  1.   2  2 CT
 Chọn đáp án A.
Câu 24. Giá trị nào sau đây là cực đại của hàm số y  2sin x  1?   A.  . B. . C. 3. D. 1.  2 2
Lời giải: TXĐ: D  .        
Ta có: y  2 cos x  0  x 
 k. Kiểm tra được: y  y       0. 2  2   2     
Ta có: y x  2  sin x, y  2   0  x   
là điểm cực đại của hàm số và y  3;  2  2 C§     y 
 2  0  x    
là điểm cực tiểu của hàm số và y  1.   2  2 CT
 Chọn đáp án C.
Câu 25. Giá trị nào sau đây là cực tiểu của hàm số y  2sin x  1?   A.  . B. . C. 3. D. 1.  2 2
Lời giải: TXĐ: D  .        
Ta có: y  2 cos x  0  x 
 k. Kiểm tra được: y  y       0. 2  2   2     
Ta có: y x  2  sin x, y  2   0  x   
là điểm cực đại của hàm số và y  3;  2  2 C§
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................14
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB     y 
 2  0  x    
là điểm cực tiểu của hàm số và y  1.   2  2 CT
 Chọn đáp án D.
Câu 26. Điểm nào sau đây là điểm cực đại của hàm số y  cos 2x  1?   A. 0. B. . C. . D. 2. 2 4
Lời giải: TXĐ: D  .      Ta có: y  2
 sin 2x  0  x  k . Kiểm tra được: y  y0    0. 2  2     
Ta có: y x  4  cos2x, y  4  0  x   
là điểm cực tiểu của hàm số và y  0;  2  2 CT y 0  4
  0  x  0 là điểm cực đại của hàm số và y  2. C§
 Chọn đáp án A.
Câu 27. Điểm nào sau đây là điểm cực tiểu của hàm số y  cos 2x  1?  A. 0. B. . C.  . D. 2. 2
Lời giải: TXĐ: D  .      Ta có: y  2
 sin 2x  0  x  k . Kiểm tra được: y  y0    0. 2  2     
Ta có: y x  4  cos2x, y  4  0  x   
là điểm cực tiểu của hàm số và y  0;  2  2 CT y 0  4
  0  x  0 là điểm cực đại của hàm số và y  2. C§
 Chọn đáp án B.
Câu 28. Giá trị nào sau đây là cực tiểu của hàm số y  cos 2x  1?  A. 0. B. . C.  . D. 2. 2
Lời giải: TXĐ: D  .      Ta có: y  2
 sin 2x  0  x  k . Kiểm tra được: y  y0    0. 2  2     
Ta có: y x  4  cos2x, y  4  0  x   
là điểm cực tiểu của hàm số và y  0;  2  2 CT y 0  4
  0  x  0 là điểm cực đại của hàm số và y  2. C§
 Chọn đáp án A.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................15
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 29. Giá trị nào sau đây là cực đại của hàm số y  cos 2x  1?  A. 0. B. . C.  . D. 2. 2
Lời giải: TXĐ: D  .      Ta có: y  2
 sin 2x  0  x  k . Kiểm tra được: y  y0    0. 2  2     
Ta có: y x  4  cos2x, y  4  0  x   
là điểm cực tiểu của hàm số và y  0;  2  2 CT y 0  4
  0  x  0 là điểm cực đại của hàm số và y  2. C§
 Chọn đáp án D.
Câu 30. Tìm tất cả các điểm cực đại của hàm số y  2sin 2x  1.   A.   k. B.  k. C. 3. D. 1.  4 4
Lời giải: TXĐ: D  .      2x   k2 x   k   Ta có: 2 4
y  4 cos 2x  0     .     2x    k2 x    k  2  4    
Ta có: y x  8  sin 2x, y  k  8   0  x    
k là các điểm cực đại của hàm số  4  4        và y  y  k  
 3; y   k  8  0  x     
k là điểm cực tiểu của hàm số C§  4   4  4    và y
 y   k  1.    CT  4 
 Chọn đáp án B.
Câu 31. Tìm tất cả các điểm cực tiểu của hàm số y  2sin 2x  1.   A.   k. B.  k. C. 3. D. 1.  4 4
Lời giải: TXĐ: D  .      2x   k2 x   k   Ta có: 2 4
y  4 cos 2x  0     .     2x    k2 x    k  2  4    
Ta có: y x  8  sin 2x, y  k  8   0  x    
k là các điểm cực đại của hàm số  4  4
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................16
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB        và y  y  k  
 3; y   k  8  0  x     
k là điểm cực tiểu của hàm số C§  4   4  4    và y
 y   k  1.    CT  4 
 Chọn đáp án A.
Câu 32. Tìm cực đại của hàm số y  2sin 2x  1.   A.   k. B.  k. C. 3. D. 5. 4 4
Lời giải: TXĐ: D  .      2x   k2 x   k   Ta có: 2 4
y  4 cos 2x  0     .     2x    k2 x    k  2  4    
Ta có: y x  8  sin 2x, y  k  8   0  x    
k là các điểm cực đại của hàm số  4  4        và y  y  k  
 3; y   k  8  0  x     
k là điểm cực tiểu của hàm số C§  4   4  4    và y
 y   k  1.    CT  4 
 Chọn đáp án C.
Câu 33. Tìm cực tiểu của hàm số y  2sin 2x  1.   A.   k. B.  k. C. 3.  D. 1.  4 4
Lời giải: TXĐ: D  .      2x   k2 x   k   Ta có: 2 4
y  4 cos 2x  0     .     2x    k2 x    k  2  4    
Ta có: y x  8  sin 2x, y  k  8   0  x    
k là các điểm cực đại của hàm số  4  4        và y  y  k  
 3; y   k  8  0  x     
k là điểm cực tiểu của hàm số C§  4   4  4    và y
 y   k  1.    CT  4 
 Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................17
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 34. Tìm tất cả các điểm cực đại của hàm số y  2cos 2x  3.  A. k . B. x   k. C. 5. D. 1. 2
Lời giải: TXĐ: D  .  x  k 2x  k2 Ta có: y 4 sin 2x 0          .
2x    k2
x   k  2
Ta có: y x  8
 cos2x, y k   8
  0  x  k là các điểm cực đại của hàm số và     y
 y k  5; y
 k  8  0  x    
k là điểm cực tiểu của hàm số và C§    2  2    y  y  k    1. CT  2 
 Chọn đáp án A.
Câu 35. Tìm tất cả các điểm cực tiểu của hàm số y  2cos 2x  3.  A. k . B. x   k. C. 5. D. 1. 2
Lời giải: TXĐ: D  .  x  k 2x  k2 Ta có: y 4 sin 2x 0          .
2x    k2
x   k  2
Ta có: y x  8
 cos2x, y k   8
  0  x  k là các điểm cực đại của hàm số và     y
 y k  5; y
 k  8  0  x    
k là điểm cực tiểu của hàm số và C§    2  2    y  y  k    1. CT  2 
 Chọn đáp án B.
Câu 36. Tìm cực đại của hàm số y  2 cos 2x  3.  A. k . B. x   k. C. 5. D. 8. 2
Lời giải: TXĐ: D  .  x  k 2x  k2 Ta có: y 4 sin 2x 0          .
2x    k2
x   k  2
Ta có: y x  8
 cos2x, y k   8
  0  x  k là các điểm cực đại của hàm số và
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................18
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB     y
 y k  5; y
 k  8  0  x    
k là điểm cực tiểu của hàm số và C§    2  2    y  y  k    1. CT  2 
 Chọn đáp án C.
Câu 37. Tìm cực tiểu của hàm số y  2cos 2x  3.  A. k . B. x   k. C. 3.  D. 1. 2
Lời giải: TXĐ: D  .  x  k 2x  k2 Ta có: y 4 sin 2x 0          .
2x    k2
x   k  2
Ta có: y x  8
 cos2x, y k   8
  0  x  k là các điểm cực đại của hàm số và     y
 y k  5; y
 k  8  0  x    
k là điểm cực tiểu của hàm số và C§    2  2    y  y  k    1. CT  2 
 Chọn đáp án D.
Câu 38. Tìm tất cả các điểm cực đại của hàm số y  sin x  cos x  2. 5  A.  k2. B. x   k2. C. 2  2. D. 2  2. 4 4
Lời giải: TXĐ: D  .    x   k2   Ta có: 4
y  cos x  sin x  0  sin x  cos x  tan x  1  x   k   . 4  5 x   k2  4    
Ta có: y x  cos x  sin ; x y
 k2   2  0  x    
k2 là các điểm cực đại  4  4     5  5 của hàm số và y  y  k2  2    2; y
 k2  2  0  x     k2 là C§  4   4  4  5 
điểm cực tiểu của hàm số và y  y  k2  2    2. CT  4 
 Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................19
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 39. Tìm tất cả các điểm cực tiểu của hàm số y  sin x  cos x  2. 5  A.  k2. B. x   k2. C. 2  2. D. 2  2. 4 4
Lời giải: TXĐ: D  .    x   k2   Ta có: 4
y  cos x  sin x  0  sin x  cos x  tan x  1  x   k   . 4  5 x   k2  4    
Ta có: y x  cos x  sin ; x y
 k2   2  0  x    
k2 là các điểm cực đại  4  4     5  5 của hàm số và y  y  k2  2    2; y
 k2  2  0  x     k2 là C§  4   4  4  5 
điểm cực tiểu của hàm số và y  y  k2  2    2. CT  4 
 Chọn đáp án A.
Câu 40. Tìm cực đại của hàm số y  sin x  cos x  2. 5  A.  k2. B. x   k2. C. 2  2. D. 2  2 2. 4 4
Lời giải: TXĐ: D  .    x   k2   Ta có: 4
y  cos x  sin x  0  sin x  cos x  tan x  1  x   k   . 4  5 x   k2  4    
Ta có: y x  cos x  sin ; x y
 k2   2  0  x    
k2 là các điểm cực đại  4  4     5  5 của hàm số và y  y  k2  2    2; y
 k2  2  0  x     k2 là C§  4   4  4  5 
điểm cực tiểu của hàm số và y  y  k2  2    2. CT  4 
 Chọn đáp án C.
Câu 41. Tìm cực tiểu của hàm số y  sin x  cos x  2. 5  A.  k2. B. x   k2. C. 2  4 2. D. 2  2. 4 4
Lời giải: TXĐ: D  . 
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................20
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB   x   k2   Ta có: 4
y  cos x  sin x  0  sin x  cos x  tan x  1  x   k   . 4  5 x   k2  4    
Ta có: y x  cos x  sin ; x y
 k2   2  0  x    
k2 là các điểm cực đại  4  4     5  5 của hàm số và y  y  k2  2    2; y
 k2  2  0  x     k2 là C§  4   4  4  5 
điểm cực tiểu của hàm số và y  y  k2  2    2. CT  4 
 Chọn đáp án D.
Câu 42. Giá trị nào sau đây là điểm cực đại của hàm số y  sin 2x  2sin x?   3 3 3 3 A.  k2. B. x    k2. C. . D.  . 3 3 2 2
Lời giải: TXĐ: D  .  Ta có: y  x  x    2 x   2 2 cos 2 2 cos 0 2 2 cos
1  2 cos x  0  4 cos x  2 cos x  2  0 
x    k2 cos x  1     
 x   k2 . 1  cos x   3  2  
x    k2  3    
Ta có: y x  4  sin 2x  2sin ; x y  k2  3
 3  0  x    
k2 là các điểm cực  3  3    3 3    
đại của hàm số và y  y  k2    ; y 
 k2  3 3  0 x      k 2 là C§  3  2  3  3    3 3
điểm cực tiểu của hàm số và y
 y   k2     . CT  3  2
 Chọn đáp án A.
Câu 43. Giá trị nào sau đây là điểm cực tiểu của hàm số y  sin 2x  2sin x?   3 3 3 3 A.  k2. B. x    k2. C. . D.  . 3 3 2 2
Lời giải: TXĐ: D  .  Ta có: y  x  x    2 x   2 2 cos 2 2 cos 0 2 2 cos
1  2 cos x  0  4 cos x  2 cos x  2  0
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................21
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB 
x    k2 cos x  1     
 x   k2 . 1  cos x   3  2  
x    k2  3    
Ta có: y x  4  sin2x  2sin ; x y  k2  3
 3  0  x    
k2 là các điểm cực  3  3    3 3    
đại của hàm số và y  y  k2    ; y 
 k2  3 3  0 x      k 2 là C§  3  2  3  3    3 3
điểm cực tiểu của hàm số và y
 y   k2     . CT  3  2
 Chọn đáp án B.
Câu 44. Giá trị nào sau đây là cực đại của hàm số y  sin 2x  2sin x?   3 3 9 3 A.  k2. B. x    k2. C. . D. . 3 3 2 2
Lời giải: TXĐ: D  .  Ta có: y  x  x    2 x   2 2 cos 2 2 cos 0 2 2 cos
1  2 cos x  0  4 cos x  2 cos x  2  0 
x    k2 cos x  1     
 x   k2 . 1  cos x   3  2  
x    k2  3    
Ta có: y x  4  sin 2x  2sin ; x y  k2  3
 3  0  x    
k2 là các điểm cực  3  3    3 3    
đại của hàm số và y  y  k2    ; y 
 k2  3 3  0 x      k 2 là C§  3  2  3  3    3 3
điểm cực tiểu của hàm số và y
 y   k2     . CT  3  2
 Chọn đáp án C.
Câu 45. Giá trị nào sau đây là cực tiểu của hàm số y  sin 2x  2sin x?   3 3 9 3 A.  k2. B. x    k2. C.  . D.  . 3 3 2 2
Lời giải: TXĐ: D  . 
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................22
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB Ta có: y  x  x    2 x   2 2 cos 2 2 cos 0 2 2 cos
1  2 cos x  0  4 cos x  2 cos x  2  0 
x    k2 cos x  1     
 x   k2 . 1  cos x   3  2  
x    k2  3    
Ta có: y x  4  sin 2x  2sin ; x y  k2  3
 3  0  x    
k2 là các điểm cực  3  3    3 3    
đại của hàm số và y  y  k2    ; y 
 k2  3 3  0 x      k 2 là C§  3  2  3  3    3 3
điểm cực tiểu của hàm số và y
 y   k2     . CT  3  2
 Chọn đáp án C.
Câu 46. Giá trị nào sau đây là điểm cực đại của hàm số y  cos 2x  2sin x?    3 A.  k2. B. x    k2. C. x   k2. D. . 6 2 2 2
Lời giải: TXĐ: D  .  cos x  0 Ta có: y
2 sin 2x 2 cos x 0
2 cos x1 2 sin x 0           1  sin x   2   x   k2  2  
x    k2  2      .      
         
Ta có: y x 4 cos 2x 2 sin ; x y  k2  3 0 x k2 là   6  6 x   k2  6  5 x   k2  6    3
các điểm cực đại của hàm số và y  y  k2    . C§  6  2
 Chọn đáp án A.
Dạng toán 2: X¸c ®Þnh sè ®iÓm cùc trÞ, cùc trÞ cña hµm sè. Phương pháp:
Lập bảng xét dấu f x hoặc lập bảng biến thiên để đưa ra kết luận.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................23
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB x
Câu 47. Tìm số điểm cực trị của hàm số y  . x  1 A. 1. B. 1.  C. 0. D. 4.
Lời giải: TXĐ: D    \  1 . 1  Ta có: y     
Do y không có nghiệm và không đổi dấu trên D nên x   0, x . D 2 1
hàm số y không có cực trị.
 Chọn đáp án C. ax  b
Kết quả: Hàm số y   ; a ;
b c; d   không có cực trị. cx  d
Câu 48. Hàm số nào sau đây không có cực trị? x  A. f x 2  x . B. g x 3  x  3 . x C. h x 1  . D. k x 4  x . x  1 Lời giải: x  1 2
Xét hàm số hx   h   0, x
  D  h x không có cực trị. 2   x  1 x 1
Nhận xét: Dựa vào kết quả trên, trong một nốt nhạc, ta chọn đáp án C.
 Chọn đáp án C.
Câu 49. Hàm số nào sau đây có cực trị? x  x  A. f x 1  . B. g x 3  x  3 . x C. h x 1  . D. k x 4  x . x x  1 Lời giải:
Dễ thấy f x , hx không có cực trị. Xét g x 3 2
 x  3x  g  3x  3  0, x
   gx không có cực trị.
Cách khác: Xét k x 4 3
 x  k  4x  0  x  0. Bảng xét dấu: x  0  f x  0 
Dựa vào bảng xét dấu, suy ra hàm số đạt cực tiểu tại x  0.
 Chọn đáp án D.
Câu 50. Hàm số nào sau đây có số điểm cực trị khác với số điểm cực trị của các hàm số còn lại?
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................24
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB x  x  A. f x 1  . B. g x 3
 x  3x 1. C. hx 2  . D. k x 4  x . x  2 x  4
Lời giải: Dễ thấy f x , hx không có cực trị. Xét g x 3 2
 x  3x  g  3x  3  0, x
   gx không có cực trị.
Cách khác: Xét k x 4 3
 x  k  4x  0  x  0. Bảng xét dấu: x  0  f x  0 
Dựa vào bảng xét dấu, suy ra hàm số đạt cực tiểu tại x  0.
 Chọn đáp án D.
Câu 51. Hàm số nào sau đây có số điểm cực trị khác với số điểm cực trị của các hàm số còn lại? A. f x 2  x . B. g x 4  x . C. hx 3  x . D. k x 6  x . Lời giải:
Dễ thấy f x , gx , k x đều có một điểm cực trị (Các em lập bảng xét dấu). Xét hx 3 2
 x  h  3x  0  hx không có điểm cực trị.
 Chọn đáp án C.
Câu 52. Hàm số nào sau đây có số điểm cực trị nhiều nhất so với số điểm cực trị của các hàm số còn lại? x A. f x 2
 x 1. B. gx 4 2  x  2x . C. h x  . D. k x 3  x  3 . x x  1 Lời giải:
+) Ta có: f x 2
 x 1 f   2x  0  x  0 . Bảng xét dấu: x  0  f x  0 
Suy ra f x có một điểm cực trị.
+) Ta có: g x 4 2 3
 x  2x  g  4x  4x  0  x  0  x  1   x  1. Bảng xét dấu: x  1  0 1  gx  0  0  0 
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................25
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Suy ra g x có ba điểm cực trị. x 1 
+) Ta có: hx   h   0, x
  D  h x không có cực trị. 2   x  1 x 1
+) Ta có: k x 3 2
 x  3x  k  3x  3  0  x  1   x  1. Bảng xét dấu: x  1  1  kx  0  0 
Suy ra k x có hai điểm cực trị.
 Chọn đáp án B.
Câu 53. Hàm số nào sau đây có số điểm cực trị ít nhất so với số điểm cực trị của các hàm số còn lại? A. f x 4
 x  2. B. gx 4 2  x  2x . C. hx 2 3  3x  x . D. k x 3  x  3 . x Lời giải:
+) Ta có: f x 4 3
 x  2  f   4x  0  x  0 . Bảng xét dấu: x  0  f x  0 
Suy ra f x có một điểm cực trị.
+) Ta có: g x 4 2 3
 x  2x  g  4x  4x  0  x  0  x  1   x  1. Bảng xét dấu: x  1  0 1  gx  0  0  0 
Suy ra g x có ba điểm cực trị.
+) Ta có: hx 2 3 2
 3x  x  h  6x  3x  0  x  0  x  2. Bảng xét dấu: x  0 2  hx  0  0 
Suy ra h x có hai điểm cực trị.
+) Ta có: k x 3 2
 x  3x  k  3x  3  0  x  1   x  1. Bảng xét dấu:
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................26
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB x  1  1  kx  0  0 
Suy ra k x có hai điểm cực trị.
 Chọn đáp án A.
Câu 54. Cho hàm số y  f x có đạo hàm f x 2
 x x  
1 . Tìm số điểm cực trị của hàm số
y  f x. A. 0. B. 1. C. 2. D. 3. Lời giải: Bảng xét dấu: x  1  0  kx  0  0 
Suy ra f x có một điểm cực trị (cực tiểu).
 Chọn đáp án B.
Câu 55. Cho hàm số y  f x có đạo hàm f x 3
 x x  
1 . Tìm số điểm cực trị của hàm số
y  f x. A. 0. B. 1. C. 2. D. 3. Lời giải: Bảng xét dấu: x  1  0  kx  0  0 
Suy ra f x có hai điểm cực trị.
 Chọn đáp án C.
Câu 56. Cho hàm số y  f x có đạo hàm f x 2
 x x  
1 x  2 . Tìm số điểm cực trị của
hàm số y  f x. A. 0. B. 1. C. 2. D. 3. Lời giải: Bảng xét dấu: x  1  0 2  f x  0  0  0 
Suy ra f x có hai điểm cực trị.
 Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................27
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB 4 3
Câu 57. Cho hàm số y  f x có đạo hàm f x 4
 x x  
1 x  2 . Tìm số điểm cực trị của
hàm số y  f x. A. 0. B. 1. C. 2. D. 3. Lời giải: Bảng xét dấu: x  1  0 2  f x  0  0  0 
Suy ra f x có một điểm cực trị.
 Chọn đáp án B.
Dạng toán 2: T×m ®iÒu kiÖn cña tham sè ®Ó hµm sè cã cùc trÞ vµ
tháa m·n c¸c yªu cÇu kh¸c.
Phương pháp:Xét các hàm số f x có đạo hàm trên tập xác định của nó.
+) Kết quả 1: f x có  *
n n   điểm cực trị khi và chỉ khi f x  0 có n nghiệm và
f x đổi dấu khi qua tất cả n nghiệm đó.
+) Kết quả 2: Tính chất của các điểm cực trị của hàm số được xử lí thông qua tính chất
nghiệm của phương trình f x (khi đã thỏa mãn điều kiện có cực trị tương ứng).
+) Kết quả 3: f x đạt cực trị (CĐ hoặc CT) tại x thì f x  0. Đây là chiều suy ra, 0  0
nên khi thực hiện yêu cầu cụ thể là cực đại hay cực tiểu thì học sinh tiến hành kiểm tra lại các
trường hợp của tham số (bằng dấu hiệu 1 hay dấu hiệu 2) để đưa ra kết luận.
Câu 58. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 3 2
y  x  3x  mx đạt
cực đại tại x  1. A.   3 . B. .  C.   1 . D. 1,  3 .
Lời giải: TXĐ: D  .  Ta có: 2
y  3x  6x  .
m Hàm số đạt cực đại tại x  1  f   1  0  m  3. 2
+) Kiểm tra lại: Với m  f x 2 3 :
 3x 6x  3  3 x 1  0  f x không có cực trị.
 Chọn đáp án B.
Câu 59. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 3 x y    2 m  m 2 3
x  12x đạt cực đại tại x  2. 3 A.   2 . B. .  C.   1 . D. 1,  2 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................28
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Lời giải: TXĐ: D  .  Ta có: 2
y  x   2
2 m  3mx 12.
Hàm số đạt cực đại tại x   f   2 2 2  0  4
 m 12m 8  0  m  1 m 2. +) Với m  f x 2 1:
 x  4x 12  0  x  2 x  6
 ; f  x 2x 4  f  2  8  0 
Hàm số đạt cực tiểu tại x  2 (không thỏa mãn). +) Với m  f x 2 2 :
 x  4x 12  0  x  2 x  6; f  x 2x 4  f  2  8  0 
Hàm số đạt cực tiểu tại x  2 (không thỏa mãn).
 Chọn đáp án B.
Câu 60. Tìm tập hợp tất cả giá trị thực của tham số k để hàm số 3 x y    2 k  k 2 3
x  12x  1 đạt cực tiểu tại x  2. 3 A.   2 . B. .  C.   1 . D. 1,  2 .
Lời giải: TXĐ: D  .  Ta có: 2
y  x   2
2 k  3kx 12.
Hàm số đạt cực tiểu tại x   f   2 2 2  0  4
 k 12k  8  0  k  1 k  2. +) Với k  f x 2 1:
 x  4x 12  0  x  2 x  6; f  x  2x 4  f  2  8  0 
Hàm số đạt cực tiểu tại x  2 (thỏa mãn). +) Với k  f x 2 2 :
 x  4x 12  0  x  2 x  6
 ; f  x  2x  4  f  2  8  0 
Hàm số đạt cực tiểu tại x  2 (thỏa mãn).
 Chọn đáp án D.
Câu 61. Tìm tập hợp tất cả giá trị thực của tham số k để hàm số
 2k  k 2 3 5 x x y  
 5 2kx  2 đạt cực tiểu tại x  1. 3 2 A.   1 . B. .  C.   6 . D. 1,  6 .
Lời giải: TXĐ: D  .  Ta có: 2
y  x   2
k  5kx  5  2 . k
Hàm số đạt cực tiểu tại x   f   2 1
1  0  k  7k  6  0  k  1 k  6. +) Với k  f x 2 1:
 x  4x  3  0  x  1 x  3; f  x  2x 4  f  1 2   0  Hàm
số đạt cực đại tại x  1 (không thỏa mãn).
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................29
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB +) Với k  f x 2 6 :
 x  6x 7  0  x  1 x  7; f  x  2x 6  f  1 8  0  Hàm
số đạt cực tiểu tại x  1 (thỏa mãn).
 Chọn đáp án C.
Câu 62. Tìm tập hợp tất cả giá trị thực của tham số a để hàm số
 2a  a 2 3 5 x x y  
 5 2ax đạt cực đại tại x  1. 3 2 A.   1 . B. .  C.   6 . D. 1,  6 .
Lời giải: TXĐ: D  .  Ta có: 2
y  x   2
a  5a x  5  2 . a
Hàm số đạt cực tiểu tại x   f   2 1
1  0  a  7a  6  0  a  1 a  6. +) Với a  f x 2 1:
 x  4x  3  0  x  1 x  3; f  x 2x 4  f  1 2   0  Hàm
số đạt cực đại tại x  1 (thỏa mãn). +) Với a  f x 2 6 :
 x  6x 7  0  x  1 x  7; f  x  2x 6  f  1 8  0  Hàm
số đạt cực tiểu tại x  1 (không thỏa mãn).
 Chọn đáp án A. 1
Câu 63. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 3 2 y 
x  x  mx có 3 cực trị. A. 1  ;   . B. ;  1 . C. 1; . D. ;1. 
Lời giải: TXĐ: D  .  Ta có: 2
y  x  2x  .
m Để hàm số có cực trị (cụ thể là 2 cực trị) thì y  0 có hai nghiệm
phân biệt và y đổi dấu khi qua hai nghiệm đó.
Yêu cầu bài toán       0 m 1. y
 Chọn đáp án B.
Nhận xét: Đối với hàm số bậc ba thì yêu cầu có cực trị tương đương với yêu cầu có 2 cực trị. 1
Câu 64. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 3 2
y  mx  x  mx có 3 cực trị. A. 1  ;   . B.  1  ;  1  \  0 . C.  1  ;  1 . D. ;1. 
Lời giải: TXĐ: D  . 
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................30
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB Ta có: 2
y  mx  2x  .
m Để hàm số có cực trị (cụ thể là 2 cực trị) thì y  0 có hai nghiệm
phân biệt và y đổi dấu khi qua hai nghiệm đó.
+) TH 1: Xét m  0  y  2
 x  0  x  0. Bảng xét dấu: x  0  f x  0 
Trong trường hợp này, hàm số đạt CĐ tại x  0 (thỏa mãn). +) TH 2: Xét m  0. Yêu cầu bài toán 2            4 4m 0
1 m 1. Vậy m 1;  1 . y
 Chọn đáp án C. 1
Câu 65. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 3 2
y  mx  mx  x có 3 cực trị. A.  ;  01;. B.  1  ;  1  \  0 . C.  1  ;  1 . D. 0;1 .  
Lời giải: TXĐ: D  .  Ta có: 2
y  mx  2mx  1. Để hàm số có cực trị (cụ thể là 2 cực trị) thì y  0 có hai
nghiệm phân biệt và y đổi dấu khi qua hai nghiệm đó.
+) TH 1: Xét m  0  y  1  0
Trong trường hợp này, hàm số không có cực trị (không thỏa mãn). +) TH 2: Xét m  0. Yêu cầu bài toán 2               4m 4m 0 m  ; 0 1;
. Vậy m ;0 1; . y
 Chọn đáp án A.
Câu 66. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 4 2
y  x  mx  2 có ba điểm cực trị. A. 0;   . B. ; 0. C. 0; . D. ; 0. 
Lời giải: TXĐ: D  .  x  0 Ta có: 3
y  4x  4mx  4x  2
x  m  0   2 x   m (1)
Để hàm số có ba điểm cực trị thì y  0 có ba nghiệm phân biệt và y đổi dấu khi qua ba nghiệm đó.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................31
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB m  0 Yêu cầu bài toán    m  0. 2 0  m
 Chọn đáp án C.
Cách khác: Áp dụng công thức giải nhanh. Ta có a  1; b  m .
Yêu cầu bài toán  ab  0  1.m  0  m  0.
Lưu ý kết quả giải nhanh:
+) Đối với hàm số trùng phương 4 2
y  ax  bx  c a  0. Hàm số có ba cực trị ab  0.
Hàm số có duy nhất một cực trị. ab  0.
+) Đối với hàm số bậc ba 3 2
y  ax  bx  cx  d a  0.
Hàm số có cực trị (có 2 cực trị)   0 y
Hàm số không có cực trị.   0 y
Câu 67. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 4
y  mx  m   2 1 x có ba điểm cực trị. A. 1  ;   . B. 0;  1 . C.  ;
 01;. D. ;0. 
Lời giải: TXĐ: D  .  x  0 Ta có: 3
y  4mx  2m   1 x  2x 2
2mx  m   1  0   2
2mx  m  1   0 (1)
Để hàm số có ba điểm cực trị thì y  0 có ba nghiệm phân biệt và y đổi dấu khi qua ba nghiệm đó   
1 có hai nghiệm phân biệt khác 0. m  0 m  0 m  0   
Yêu cầu bài toán    0
 0  8m1 m  0  m;01;    m  1  0  m  1 m  1  m ;  01;.
 Chọn đáp án C.
Cách khác: Áp dụng công thức giải nhanh. Ta có a  ;
m b  1 m .
Yêu cầu bài toán  ab  0  .
m 1 m  0  m ;  01;.
Câu 68. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 4
y  mx   2 m   2
9 x  10 có ba điểm cực trị. A. 3;   . B. 0; 3. C.  ;  3
 3;. D.  ;  3  0;3.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................32
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Lời giải: TXĐ: D  .  Ta có: 3
y  mx   2
m   x  x 2 2 4 2 9 2
2mx  m  9. x  0
Ta có: y  0   . 2 2
2mx  m  9   0
Hàm số có 3 điểm cực trị  Phương trình y  0 có 3 nghiệm phân biệt (khi đó y đổi
dấu khi qua các nghiệm)  Phương trình 2 2
2mx  m  9  0 có 2 nghiệm phân biệt  0 m  0  2 m  9 m  3  Ta có: 2 2 2
2mx  m  9  0  
 . Yêu cầu bài toán   0   . 2 m 9 x   2m 0  m   3  2m
Vậy các giá trị m cần tìm là m ;  3  0;3..
 Chọn đáp án D.
Cách khác: Áp dụng công thức giải nhanh. Ta có a  m 2
; b  m  9.
Yêu cầu bài toán  ab   m  2 0
. m  9  0  m ;  3  0;3.
Câu 69. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 2 3 2 y  x  mx   2 m   2 2 3
1 x  có hai điểm cực trị x và x sao cho x x  2 x  x  1. 1 2  1 2 3 3 1 2  2  2  A. 0, . B.   0 . C.  . D. .   3  3 
Lời giải: TXĐ: D  .  Ta có: 2
y  x  mx   2 2 2 2 3m   1 .
Đồ thị hàm số có hai điểm cực trị khi và chỉ phương trình y  0 có hai nghiệm phân biệt 2 2 13 2 13
 13m  4  0  m    m 
* . Ta có: x  x  m và 2
x .x  1 3m . 13 13 1 2 1 2 m  0 Theo giả thiết: x x 2x x  2 1 1 3m 2m 1          1 2 1 2 2 m   3 2
Kiểm tra điều kiện * , ta có m  là yêu cầu bài toán. 3
 Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................33
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 70. (NC) Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số 3 2 2 3
y  x  3x  3(m 1)x  3m 1 có các điểm cực trị cách đều gốc toạ độ. 1   1  1 1  A.  , 1. B.  ,  1. C. 1,   1 . D.  ,  . 2   2  2 2 
Lời giải: TXĐ: D  .  Ta có: 2
y   x  x   2 m   2 2 3 6 3
1 , y  0  x  2x  m  1  0 (1)
Hàm số có cực trị  Phương trình (1) có 2 nghiệm phân biệt 2  
  m  0  m  0.
Gọi A, B là 2 điểm cực trị của đồ thị hàm số  A 3
 m   m  B 3 1 ; 2 2 , 1 ; m 2   2m   1 m  
Do O cách đều A và B 3 2
 OA  OB  8m  2m  
(thỏa mãn m  0 )  1 m    2 1 1
Vậy các giá trị m cần tìm là m  ; m   . 2 2
 Chọn đáp án D.
Câu 71. (NC) Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số 4
y  x  m   2 2
1 x  m có ba điểm cực trị A, B, C sao cho OA  BC; trong đó O là gốc
tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại. A. 2  2 2, 2. B. 2  2 2,  2. C.  2, 2.
D. 2  2 2, 2  2 2.
Lời giải: TXĐ: D  .  x  0 Ta có: 3
y  4x  4m   1 x  4x  2
x  m  1  0   2 x  m  1 (1)
Đồ thị hàm số có ba điểm cực trị, khi chỉ khi (1) có 2 nghiệm phân biệt khác 0  m  
1 (*) . Khi đó: A m B 2 0; ,
 m 1; m  m   1 và C  2
m  1; m  m   1 m  2  2 2 Suy ra: 2
OA  BC  m  4m   2
1  m  4m  4  0   (thỏa (*)). m  2   2 2
Vậy các giá trị m cần tìm là m  2  2 2; m  2  2 2.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................34
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
 Chọn đáp án D.
Câu 72. (NC) Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số 4
y  x  m   2 2 2
1 x  m có ba điểm cực trị tạo thành một tam giác vuông. A. 0,   1 . B.   0 . C.   1 . D. . 
Lời giải: TXĐ: D  .  Ta có: 3
y  x  m   x  x 2 4 4 1 4 x  m   1 .
Đồ thị có 3 điểm cực trị khi và chỉ khi m  1  0  m   1 (*).
Các điểm cực trị của đồ thị là: A 2
0; m  , B m1; 2  m  
1 và C  m 1; 2  m   1   2 2
Suy ra: AB   m1;m 
1  và AC   m1;m  1  . Ta có: AB  AC nên tam giác ABC vuông khi và chi khi  
AB AC   m  4 . 0 1  m   1  0.
Kết hợp điều kiện (*), ta được m  0 .
 Chọn đáp án B.
Câu 73. (NC) Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số 3 2 3
y  x  3mx  3m có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng
48 (với O là gốc tọa độ). 1   1  1 1  A.  , 2. B.  ,  2. C. 2,   2 . D.  ,  . 2   2  2 2 
Lời giải: TXĐ: D  .  x  0 Ta có: 2
y  3x  6mx  0   x   2m
Đồ thị hàm số có 2 điểm cực trị khi và chỉ khi m  0 (*).
Các điểm cực trị của đồ thị là A 3
0; 3m  và B 3 2 ; m m  . 3
Suy ra: OA  3 m , dB,OA  2 m . 1 m  2 Theo giả thiết: S
 48  d B OA OA   m    (thỏa mãn). O  AB  ,  4 . 48 3 48 2 m  2  
 Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................35
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 74. (NC) Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số 3
y  x  m   2 2 3
1 x  6mx có hai điểm cực trị A và B sao cho đường thẳng AB vuông
góc với đường thẳng y  x  2.  1  A. 0,  2 . B. 0,   2 . C. 2,   2 . D. 2,  .  2 
Lời giải: TXĐ: D  .  x  1 Ta có: 2
y  6x  6m  
1 x  6m ; y  0   . x   m
Điều kiện để hàm số có cực trị  m  1 . Lúc đó: A m   B 3 2 1; 3 1 , ;
m m  3m . Hệ số góc của đường thẳng AB là k  m  2 1 .
Đường thẳng AB vuông góc với đường thẳng y  x  2  k  1.       m  2 m 0 1  1    . m   2
Vậy giá trị m cần tìm là m  0 ; m  2 .
 Chọn đáp án A.
Câu 75. (NC) Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số 3
y  x  3mx  1 có hai điểm cực trị B và C sao cho tam giác ABC cân tại A , với A2;3.  1  1  1  1  A. 0, . B.  . C.  . D. 0,  .  2  2   2   2 
Lời giải: TXĐ: D  .  Ta có 2
y  3x  3 .
m Để hàm số có hai điểm cực trị  Phương trình y  0 có hai
nghiệm phân biệt  m  0. (*) 
Tọa độ các điểm cực trị là B 3  m m   C 3 m 
m    BC   3 ; 2 1 , ; 2 1 2 m; 4  m .  
Gọi I là trung điểm BC, suy ra I 0;1 . Ta có tam giác ABC cân tại A  AI.BC  0 m  0 3 4 m 8 m 0       1  . m   2
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................36
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB 1
Đối chiếu điều kiện (*), ta có m  là yêu cầu bài toán. 2
 Chọn đáp án B. Kỹ năng 1:
§äc b¶ng biÕn thiªn (b¶ng xÐt dÊu). Phương pháp:
Câu 76. Cho hàm số y  f x xác định, liên tục trên  và có bảng biến thiên sau: x  0 1  f x  0  0  2  f x  3 
Khẳng định nào sau đây sai?
A. f x đồng biến trên ; 0.
B. f x đồng biến trên 2; 3.
C. f x nghịch biến trên 0;  1 .
D. f x đạt cực đại bằng 0. Lời giải:
Dựa vào bảng biến thiên ta có f x  0, x   ;
 01;  f x đồng biến trên các
khoảng ; 0 và 1; .
f x  0, x  0; 
1  f x nghịch biến trên khoảng 0;  1 .
Hàm số đạt cực đại tại x
 0 và y  2; hàm số đạt cực tiểu tại x  1 và y  3.  C§ C§ CT CT
 Chọn đáp án D.
Câu 77. Cho hàm số y  f x xác định, liên tục trên  và có bảng biến thiên sau: x  0 1  f x  0  0  2  f x  3 
Khẳng định nào sau đây đúng?
A. Cực tiểu của f x là 1.
B. Điểm cực tiểu của f x là 1.
C. f x đạt cực đại tại 2.
D. f x đạt cực đại bằng 0. Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................37
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Hàm số đạt cực đại tại x
 0 và y  2; hàm số đạt cực tiểu tại x  1 và y  3.  C§ C§ CT CT
 Chọn đáp án B.
Câu 78. Cho hàm số y  f x xác định, liên tục trên  và có bảng biến thiên sau: x  1  0 1  f x  0  0  0   3  f x 2  2 
Khẳng định nào sau đây đúng?
A. f x đồng biến trên  2  ; 3.
B. f x đồng biến trên  1  ;01;.
C. Cực đại của f x bằng 3.
D. f x đạt cực tiểu tại 2.  Lời giải:
Dựa vào bảng biến thiên ta có f x  0, x   1
 ;01;  f x đồng biến trên các khoảng  1  ;0 và 1;.
f x  0, x   ;    1 0; 
1  f x nghịch biến trên các khoảng ;   1 và 0;  1 .
Hàm số đạt cực đại tại x
 0 và y  3; hàm số đạt cực tiểu tại x  1; x  1  và C§ C§ CT CT y  2.  CT
 Chọn đáp án C.
Câu 79. Cho hàm số y  f x xác định, liên tục trên   \ 1
 và có bảng biến thiên sau: x  1  1  y   0   4 y 0  
Khẳng định nào sau đây đúng?
A. f x đồng biến trên ;  1 .
B. f x đồng biến trên  ;   1  \   1 .
C. Cực đại của hàm số bằng 1.
D. Điểm 1; 4 là điểm cực đại của đồ thị hàm số. Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................38
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Dựa vào bảng biến thiên ta có f x  0, x   ;    1  1  ; 
1  f x đồng biến trên các khoảng ;   1 và  1  ;  1 .
f x  0, x
 1;  f x nghịch biến trên khoảng 1;.
Hàm số đạt cực đại tại x  1 và y  4. C§ C§
 Chọn đáp án D.
Câu 80. Cho hàm số y  f x có bảng xét dấu đạo hàm như sau: x  2  0 2  f x  0   0 
Khẳng định nào sau đây đúng?
A. f x đồng biến trên  2  ;0.
B. f x đồng biến trên ; 0.
C. f x đạt cực đại tại x  2. 
D. f x đạt cực đại tại x  2. Lời giải:
Dựa vào bảng xét dấu đạo hàm ta có f x  0, x   ;  2
 2;  f x đồng biến
trên các khoảng ; 2   và 2;.
f x  0, x   2
 ;00;2  f x nghịch biến trên các khoảng  2  ;0 và 0;2.
Hàm số đạt cực đại tại x  2
 và hàm số đạt cực tiểu tại x  2. C§ CT
 Chọn đáp án C.
Câu 81. Cho hàm số y  f x có bảng xét dấu đạo hàm như sau: x  1  0 1  f x  0   0 
Khẳng định nào sau đây sai?
A. f x đồng biến trên  1  ;0.
B. f x nghịch biến trên ; 3  .
C. f x có hai điểm cực trị.
D. f x có ba điểm cực trị. Lời giải:
Dựa vào bảng xét dấu đạo hàm ta có f x  0, x   1  ;00; 
1  f x đồng biến trên các khoảng  1  ;0 và 0;  1 .
f x  0, x   ;   
1 1;   f x nghịch biến trên các khoảng ;   1 và
1;. Qua các giá trị 1
 ; 1 thì f x đổi dấu nên f x có hai điểm cực trị.
 Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................39
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB Kỹ năng 2:
§äc ®å thÞ hµm sè vµ sö dông c¸c phÐp biÕn ®æi ®å thÞ ®¬n gi¶n. Phương pháp:
Dựa vào đồ thị, trên khoảng nào mà đồ thị f x là đường đi lên (đi xuống) từ trái sang
phải thì khoảng đó hàm số f x đồng biến (nghịch biến).
Câu 82. Cho hàm số y  f x xác định, liên tục trên  và y
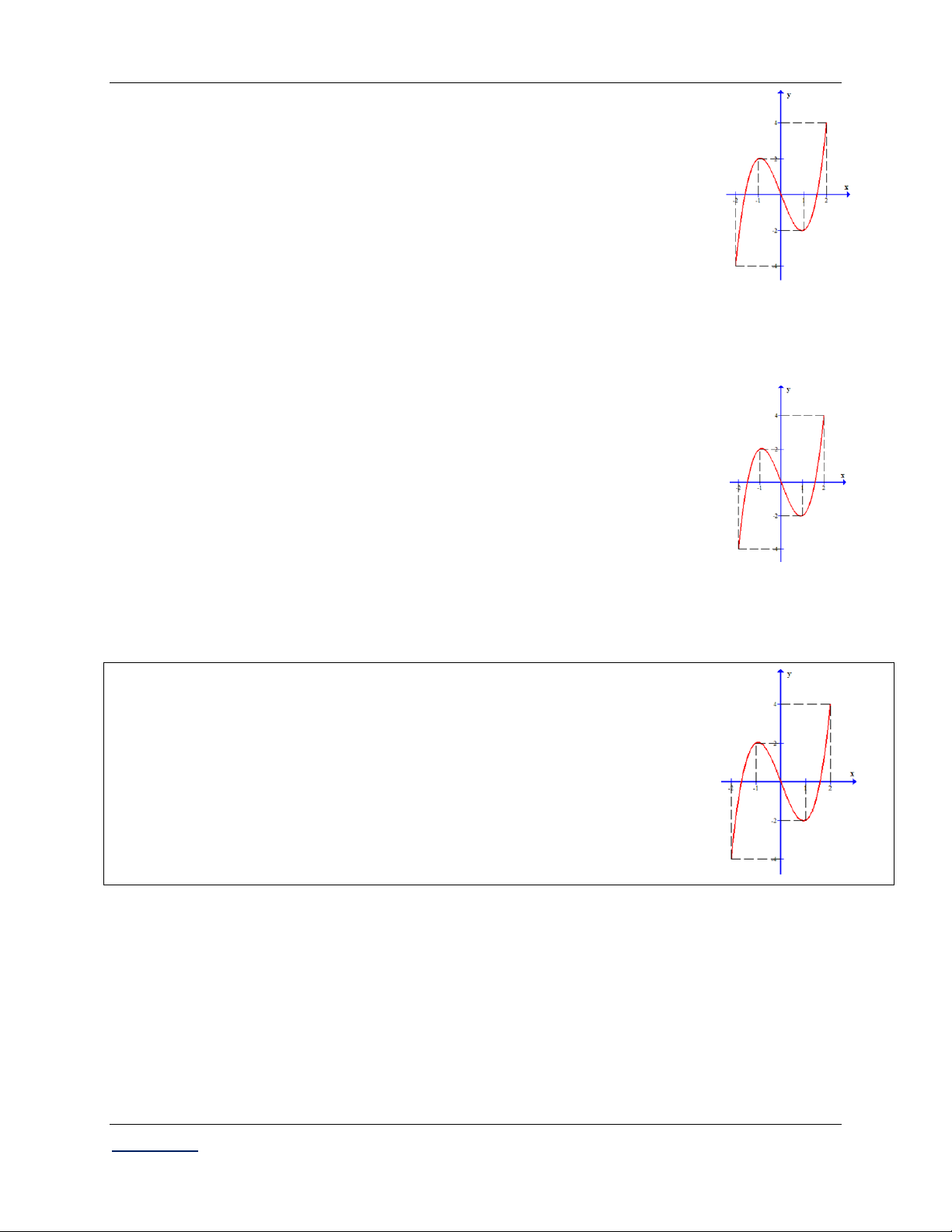
có đồ thị như hình bên. Khẳng định nào sau đây đúng? 1
A. f x đồng biến trên ; 0. O 1 -1 x
B. f x nghịch biến trên  1  ; 2.
C. f x đạt cực đại bằng 1. -3
D. f x đạt cực tiểu tại x  3.  Lời giải:
Dựa vào đồ thị ta có f x đồng biến trên các khoảng ;  
1 và 1;  và f x
nghịch biến trên khoảng  1  ;  1 .
Hàm số đạt cực đại tại x  1
 và y  1; hàm số đạt cực tiểu tại x  1 và y  3.  C§ C§ CT CT
 Chọn đáp án C.
Câu 83. Cho hàm số y  f x xác định, liên tục trên y
 và có đồ thị như hình bên. Khẳng định nào sau đây đúng? 2
A. f x đồng biến trên ; 0. 1
B. f x nghịch biến trên   \  1 . O 1 x
C. f x nghịch biến trên 0; 2.
D. f x không có cực trị. Lời giải:
Dựa vào đồ thị ta có f x nghịch biến trên các khoảng  
;1 và 1; . Vậy f x không có cực trị.
 Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................40
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
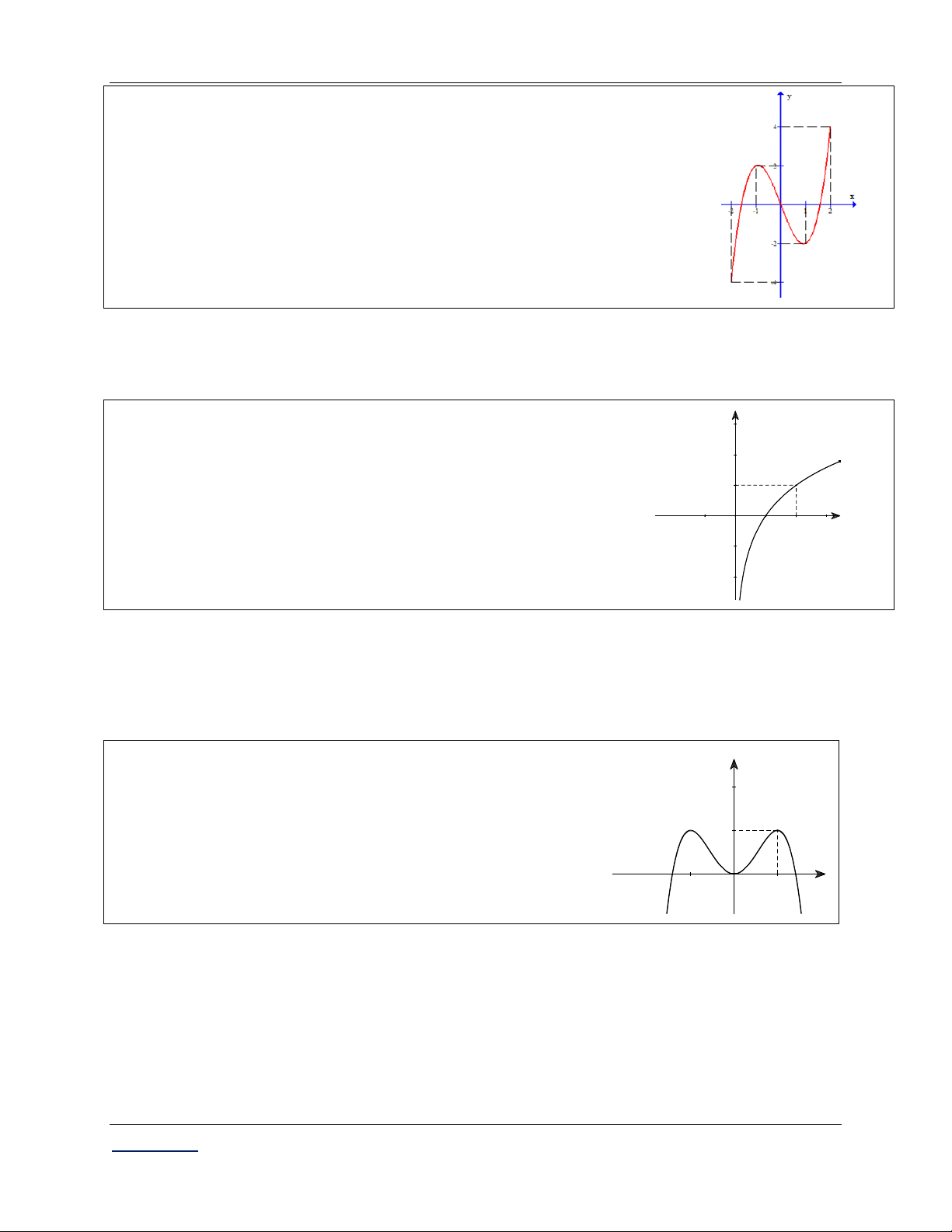
Câu 84. (Đề minh họa 2 2017) Cho hàm số y  f x xác định, liên tục trên đoạn  2  ;2 
 và có đồ thị là đường cong trong hình vẽ bên. Hàm
số f x đạt cực đại tại điểm nào dưới đây? A. x  2  . B. x  1  .
C. x  1. D. x  2 . Lời giải:
Hàm số đạt cực đại tại x  1
 và y  2; hàm số đạt cực tiểu tại x  1 và y  2.  C§ C§ CT CT
 Chọn đáp án B.
Câu 85. Cho hàm số y  f x xác định, liên tục trên đoạn  2  ;2   và
có đồ thị là đường cong trong hình vẽ bên. Hàm số f x đạt cực tiểu
tại điểm nào dưới đây? A. x  2  . B. x  1  .
C. x  1. D. x  2 . Lời giải:
Hàm số đạt cực đại tại x  1
 và y  2; hàm số đạt cực tiểu tại x  1 và y  2.  C§ C§ CT CT
 Chọn đáp án C.
Câu 86. Cho hàm số y  f x xác định, liên tục trên đoạn  2  ;2   và
có đồ thị là đường cong trong hình vẽ bên. Cực đại của hàm số f x
là giá trị nào nào dưới đây? A. 2  . B. 1  . C. 1. D. 2 . Lời giải:
Hàm số đạt cực đại tại x  1
 và y  2; hàm số đạt cực tiểu tại x  1 và y  2.  C§ C§ CT CT
 Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................41
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 87. Cho hàm số y  f x xác định, liên tục trên đoạn  2  ;2   và
có đồ thị là đường cong trong hình vẽ bên. Cực tiểu của hàm số f x
là giá trị nào nào dưới đây? A. 2  . B. 1  . C. 1. D. 2 . Lời giải:
Hàm số đạt cực đại tại x  1
 và y  2; hàm số đạt cực tiểu tại x  1 và y  2.  C§ C§ CT CT
 Chọn đáp án A.
Câu 88. (NC) Cho hàm số y  f x xác định, liên tục trên  y
và hàm số đạo hàm f x của f x có đồ thị như hình bên.
Tìm số điểm cực trị của hàm số y  f x. 1 A. 0. B. 2. O 1 2 x C. 3. D. 1. Lời giải:
Hàm số có f x  0, x
  1; f x  0, x
  1 và f  
1  0. Vậy hàm số có duy nhất một
điểm cực trị và x  1 là điểm cực tiểu của hàm số y  f x.
 Chọn đáp án D.
Câu 89. (NC) Cho hàm số y  f x xác định, liên tục y
trên  và hàm số đạo hàm f x của f x có đồ thị như
hình bên. Tìm số điểm cực trị của hàm số y  f x. 1 A. 0. B. 2. C. 3. D. 1. O 1 x Lời giải:
Hàm số có f x có ba giao điểm với trục hoành (tức là phương trình f x có ba
nghiệm) và f x đổi dấu hai lần khi qua ba nghiệm đó. Vậy hàm số có hai điểm cực trị
(cụ thể là một điểm cực đại và một điểm cực tiểu).
 Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................42
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
Câu 90. (NC) Cho hàm số y  f x xác định, liên tục trên y
 và hàm số đạo hàm f x của f x có đồ thị như hình
bên. Tìm số điểm cực trị của hàm số
y  f x. O x A. 1. B. 2. C. 3. D. 0. Lời giải:
Hàm số có f x có ba giao điểm với trục hoành (tức là phương trình f x có ba
nghiệm) và f x không đổi dấu khi qua ba nghiệm đó. Vậy hàm số không có cực trị
 Chọn đáp án D.
Câu 91. (NC) Cho hàm số y  f x xác định, liên tục trên y
 và có đồ thị như hình bên. Tìm số điểm cực trị của hàm
số y  f x . x O A. 4. B. 2. C. 3. D. 5. Lời giải:
Thực hiện phép biến đổi đồ thị:
+) Giữ phần đồ thị hàm số f x phía trên trục y
Ox, bỏ phần đồ thị f x phía dưới trục . Ox
+) Lấy đối xứng phần đồ thị f x phía dưới O 1 x trục Ox qua . Ox
Dựa vào đồ thị y  f x suy ra hàm số y  f x có 5 điểm cực trị.
 Chọn đáp án D.
Câu 92. (NC) Cho hàm số y  f x xác định, liên tục y
trên  và có đồ thị như hình bên. Tìm số điểm cực trị
của hàm số y  f  x . x A. 4. B. 2. O C. 3. D. 5.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................43
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB Lời giải:
Thực hiện phép biến đổi đồ thị:
+) Giữ phần đồ thị hàm số f x phía bên phải y
trục Oy, bỏ phần đồ thị f x phía bên trái trục . Oy
+) Lấy đối xứng phần đồ thị f x phía bên phải trục Oy qua . Oy x O 1
Dựa vào đồ thị y  f  x  suy ra hàm số y  f  x  có 3 điểm cực trị.
 Chọn đáp án C.
Câu 93. (NC) Cho hàm số y  f x xác định, liên y
tục trên  và có đồ thị như hình bên. Tìm số điểm
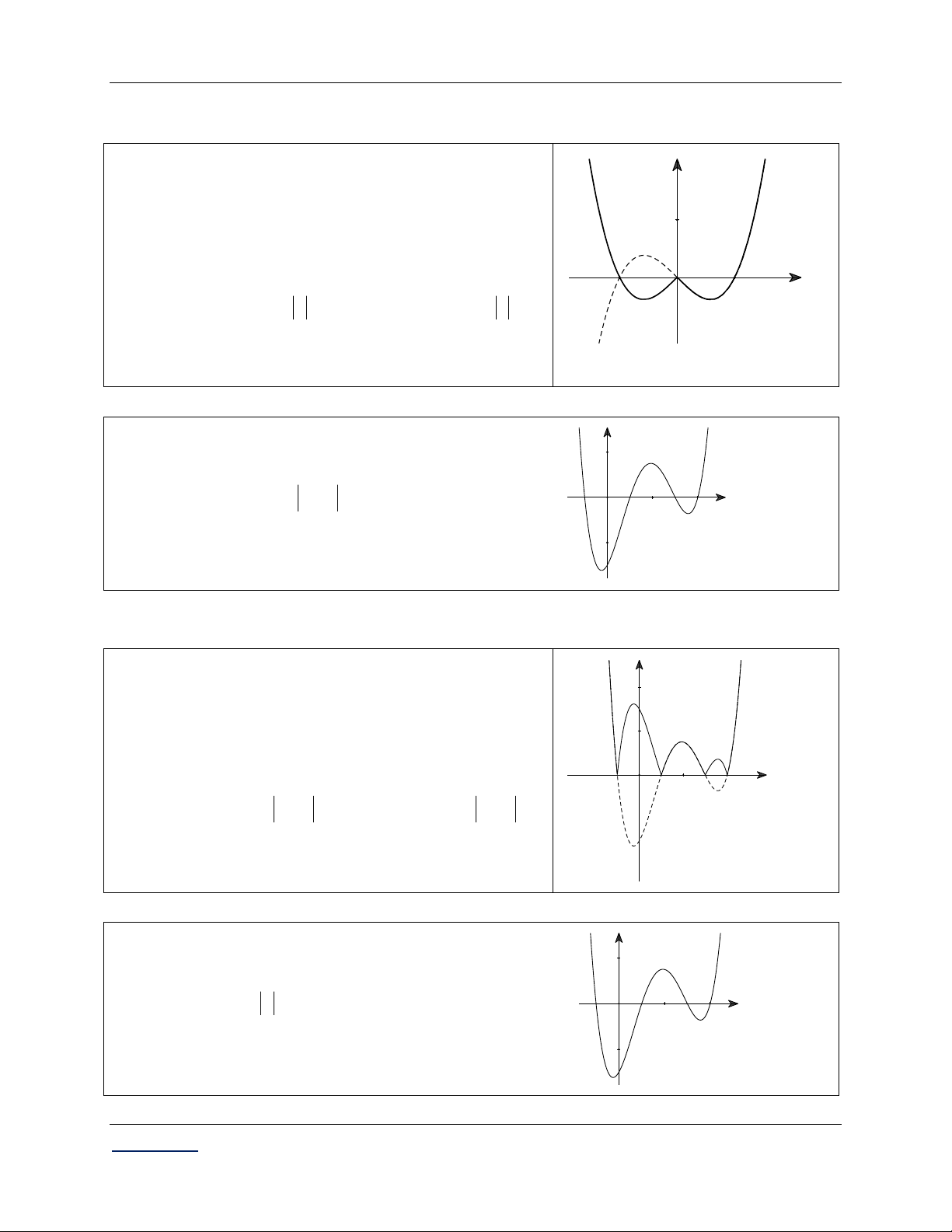
cực trị của hàm số y  f x . O x A. 4. B. 6. C. 5. D. 7. Lời giải:
Thực hiện phép biến đổi đồ thị:
+) Giữ phần đồ thị hàm số f x phía trên trục y
Ox, bỏ phần đồ thị f x phía dưới trục . Ox
+) Lấy đối xứng phần đồ thị f x phía dưới trục Ox qua . Ox O x
Dựa vào đồ thị y  f x suy ra hàm số y  f x có 7 điểm cực trị.
 Chọn đáp án D.
Câu 94. (NC) Cho hàm số y  f x xác định, liên tục y
trên  và có đồ thị như hình bên. Tìm số điểm cực trị
của hàm số y  f  x . O x A. 4. B. 6. C. 5. D. 7.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................44
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB Lời giải:
Thực hiện phép biến đổi đồ thị:
+) Giữ phần đồ thị hàm số f x phía bên phải y
trục Oy, bỏ phần đồ thị f x phía bên trái trục . Oy
+) Lấy đối xứng phần đồ thị f x phía bên O phải trục Oy qua . Oy x
Dựa vào đồ thị y  f  x  suy ra hàm số y  f  x  có 3 điểm cực trị.
 Chọn đáp án C.
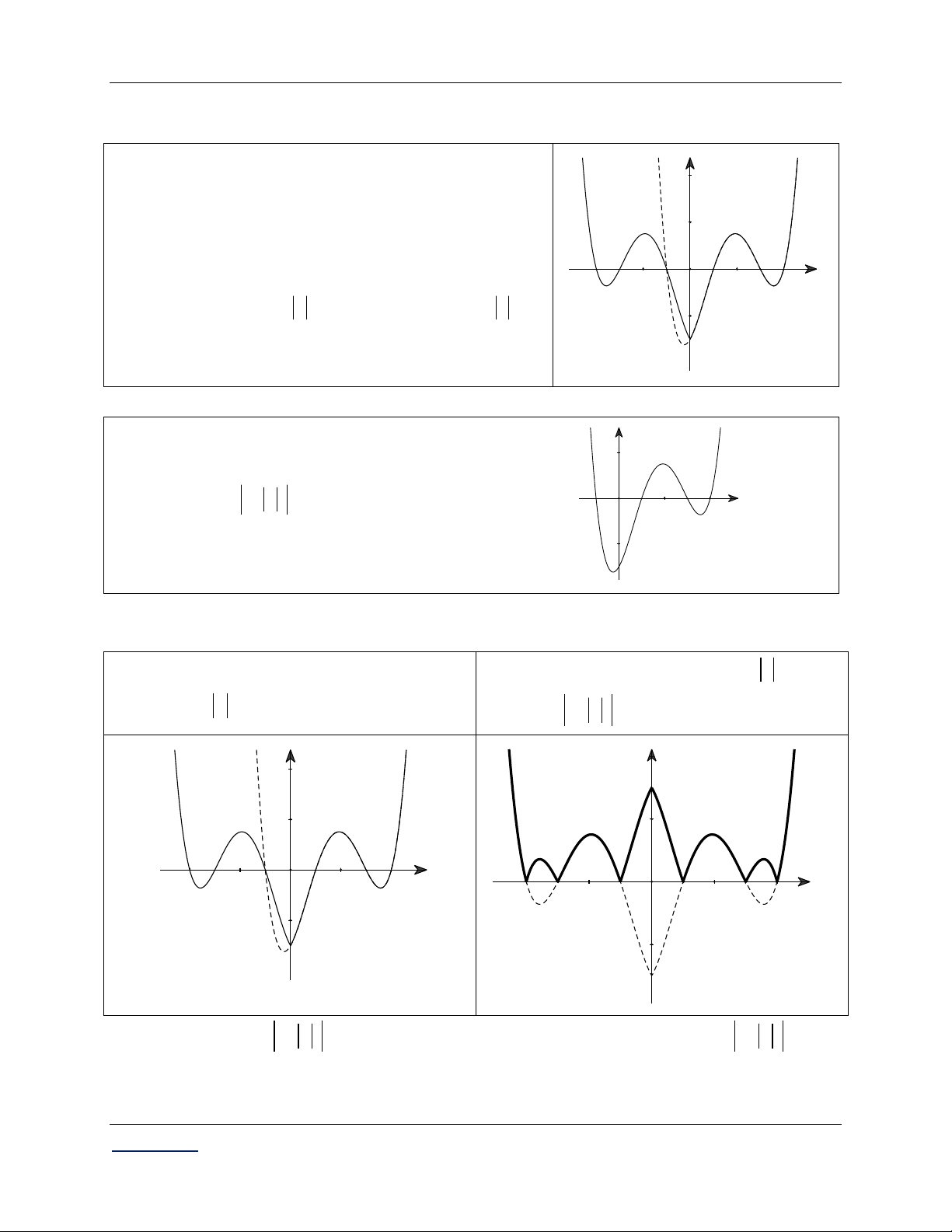
Câu 95. (NC) Cho hàm số y  f x xác định, liên tục y
trên  và có đồ thị như hình bên. Tìm số điểm cực trị
của hàm số y  f  x  . O x A. 4. B. 11. C. 7. D. 10. Lời giải:
Thực hiện hai phép biến đổi đồ thị:
Phép biến đổi 1: Từ đồ thị y  f x suy ra Phép biến đổi 2: Từ đồ thị y  f  x  suy ra
đồ thị y  f  x . (Kỹ năng câu 94).
đồ thị y  f  x  .(Kỹ năng câu 93). y y O x O x
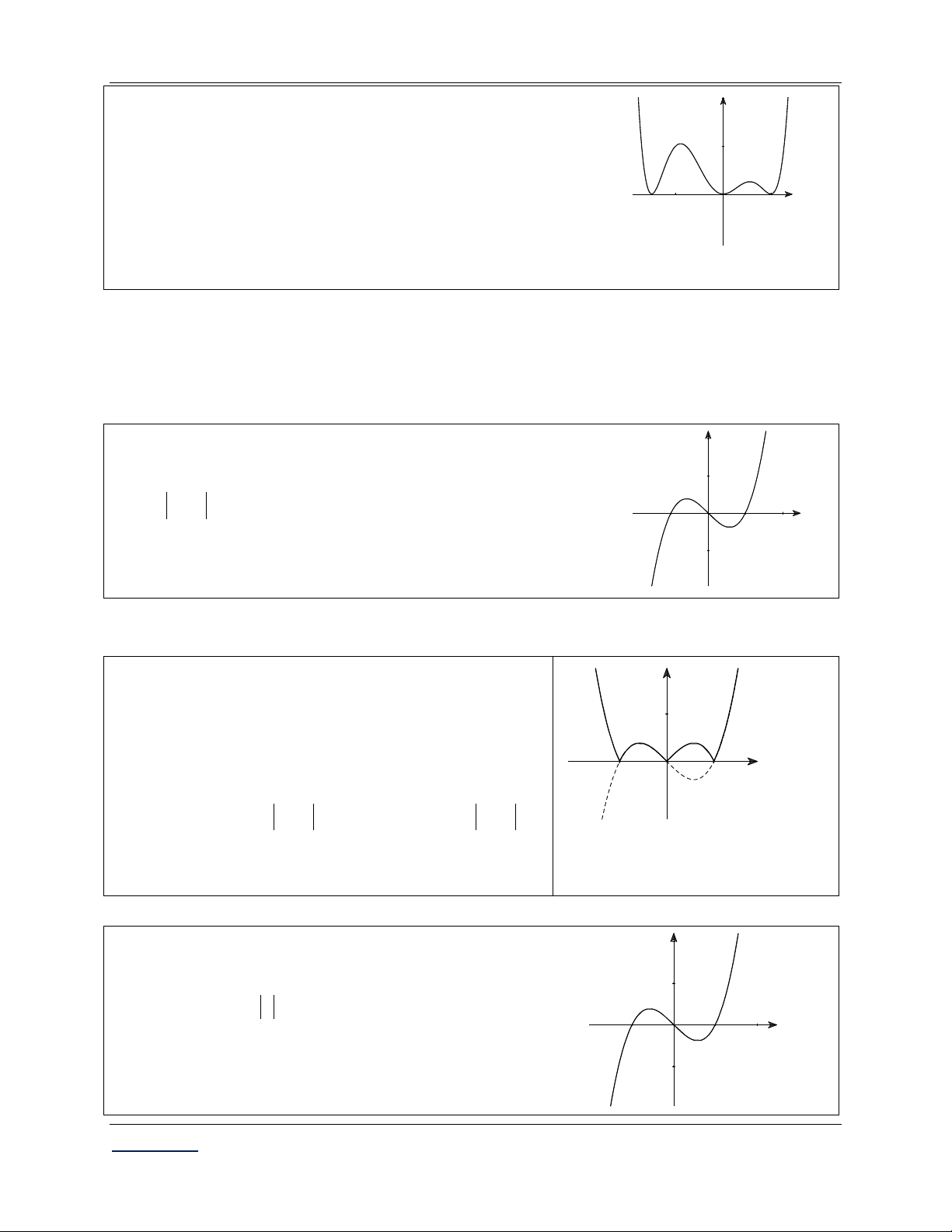
Dựa vào đồ thị y  f  x  sau phép biến đổi đồ thị số 2, suy ra hàm số y  f  x  có 11 điểm cực trị.
 Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................45
[...Các chuyên đề Trắc nghiệm Toán THPT...] Giải tích 12 CB
SẼ CÒN UPDATE TIẾP......
Các em cùng thầy cô cố gắng nhé?! Thầy tin mọi việc rồi sẽ tốt đẹp thôi! À
quên, nếu có nhầm gì thì các em phản hồi giúp thầy nhé?! Hẹn gặp lại các em ở
những chủ đề sau!
Huế, ngày 29 tháng 8 năm 2017!
P/S: Trong quá trình biên soạn chắc chắn không tránh khỏi sai sót, rất mong nhận được
sự góp ý của quý thầy cô giáo và các em học sinh thân yêu để các bài viết tiếp theo được hoàn
thiên hơn. Xin chân thành cảm ơn!
CLB GIÁO VIÊN TRẺ TP HUẾ
Phụ trách chung: Giáo viên LÊ BÁ BẢO.
Đơn vị công tác: Trường THPT Đặng Huy Trứ, Thừa Thiên Huế.
Email: lebabaodanghuytru2016@gmail.com Facebook: Lê Bá Bảo
Số điện thoại: 0935.785.115
Giáo viên: LÊ BÁ BẢO...0935.785.115... CLB Giáo viên trẻ TP Huế ...................46

Bài tập trắc nghiệm cực trị của hàm số có lời giải chi tiết – Lê Bá Bảo Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số