Bài tập trắc nghiệm cực trị của hàm số – Ngọc Đàn Toán 12

Bài tập trắc nghiệm cực trị của hàm số – Ngọc Đàn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

100 50 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

65 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 1
VẤN ĐỀ 1. TÌM CỰC TRỊ CỦA HÀM SỐ
Phương pháp
Quy tắc 1.
Bước 1. Tìm t󰉝󰉬nh.
Bước 2. Tính
fx
.T󰉨m
i
x
mà t󰉗
0fx
ho󰉢󰉬nh.
Bước 3. L󰉝p b󰉘ng bi󰉦n thiên.
Bước 4. K󰉦t lu󰉝n v󰉧 󰉨m c󰊁c tr󰉬.
Quy tắc 2.
Bước 1. Tìm t󰉝󰉬nh.
Bước 2. Tính
fx
.T󰉨m
i
x
mà t󰉗
0fx
.
Bước 3. Tính
fx

và
i
fx

Bước 4. D󰊁a vào d󰉙u c󰉻a
i
fx

󰉨 k󰉦t lu󰉝n v󰉧 󰉨m c󰊁c tr󰉬
i
x
.
A. VẬN DỤNG
Ví dụ 1. T󰉨m c󰊁c tr󰉬 c󰉻a các hàm s󰉯 sau
1)
2)
42
2 4 4y x x
3)
43
85y x x
4)
42
8 10y x x
5)
53
2
53
xx
y
Ví dụ 2. Tìm 󰉨m c󰊁c tr󰉬 c󰉻a các hàm s󰉯 sau
1)
2
1x
y
x
2)
2
23
1
xx
y
x

3)
2
24
2
xx
y
x

DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 2
Ví dụ 3. 󰉨m c󰊁c tr󰉬 c󰉻a các hàm s󰉯 sau
1)
2
16y x x
Đs:
: 2 2; : 2 2CD x CT x
2)
2
8yx
Đs:
:0CD x
3)
1
x
y
x
Đs:
:1CD x
4)
2
21y x x
Đs:
2
:
2
CT x 
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Tìm c󰊁c tr󰉬 c󰉻a các hàm s󰉯 sau
1)
32
3 9 5y x x x
2)
23
32y x x
3)
42
1
3
2
y x x
4)
42
13
22
y x x
5)
42
6 8 1y x x x
6)
4 3 2
3 4 24 48 5y x x x x
7)
32
2 2 1y x x x
8)
32
1
4 15
3
y x x x
9)
4
2
5
2
x
yx
10)
42
45y x x
11)
3
13y x x
12)
34
21y x x
Bài tập 2. Tìm c󰊁c tr󰉬 c󰉻a các hàm s󰉯 sau
1)
4
1
2
yx
x
2)
2
2
45
x
y
xx

3)
3
2
1
x
y
x
4)
2
36
2
xx
y
x
5)
2
3 4 5
1
xx
y
x

6)
2
2 15
3
xx
y
x

7)
2
2
4 2 1
23
xx
y
xx


8)
2
2
3 4 4
1
xx
y
xx


9)
2
1
1
x
y
x
10)
2
16
yx
x

11)
2
2
4 2 1
23
xx
y
xx


Bài tập 3. Tìm c󰊁c tr󰉬 c󰉻a các hàm s󰉯 sau
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 3
1)
2
4y x x
2)
2
25y x x
3)
2
2y x x x
4)
2
9y x x
5)
3
2
9
x
y
x
6)
32
3y x x
7)
2
2 1 2 8y x x
8)
2
21y x x
Đs:
2
: 0; : 2,
2
CD x CT x x
9)
2
2 12 3y x x
Đs:
:1CT x 
10)
3y x x
Đs:
:2CD x
C. BÀI TẬP TRẮC NGHIỆM
ĐỀ 1.
Câu 1. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
42
23f x x x
là:
A. 0 B. 1 C. 2 D. 3
Câu 2. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
42
33y x x
là
A. 1 B. 3 C. 2 D. 0
Câu 3. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
42
18 1y x x
là
A.
0; 1
B.
0;1
C.
1;0
D.
3;80
và
3;80
Câu 4. Trong các m󰉪󰉧 sau hãy tìm m󰉪󰉧 sai. Ch󰉭n 1 câu sai
A. Hàm s󰉯
32
31y x x
có c󰊁󰉗i và c󰊁c ti󰉨u.
B. Hàm s󰉯
32
32y x x
có c󰊁c tr󰉬
C. Hàm s󰉯
1
21
2
yx
x
không có c󰊁c tr󰉬
D. Hàm s󰉯
1
1
1
yx
x
có hai c󰊁c tr󰉬
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 4
Câu 5. Hàm s󰉯
32
2 9 12 5y x x x
có m󰉙󰉨m c󰊁c tr󰉬 ?
A. 1 B. 2 C. 3 D. 4
Câu 6. Cho hàm s󰉯
42
23y x x
.M󰉪󰉧 
A. Hàm s󰉯 có m󰉳󰉨m c󰊁c tr󰉬 B. Hàm s󰉯 không có c󰊁c tr󰉬
C. Hàm s󰉯 󰉨m c󰊁c tr󰉬 D. Hàm s󰉯 󰉰ng bi󰉦n trên
Câu 7. Cho hàm s󰉯
32
32y x x
, kh󰉠󰉬 đúng?
A. 󰉨m c󰊁c tr󰉬 B 󰉨m c󰊁c tr󰉬
C. Có ch󰉫 m󰉳󰉨m c󰊁c tr󰉬 D. Có hai c󰊁c tr󰉬 cùng d󰉙u.
Câu 8. Hàm s󰉯
32
34y x x
󰉗t c󰊁󰉗i t󰉗󰉨m:
A.
2x 
B.
2x
C.
0x
D.
1x
Câu 9. Hàm s󰉯
32
4
23
3
y x x x
có s󰉯 󰉨m c󰊁c tr󰉬 là:
A. 0 B. 1 C. 2 D. 3
Câu 10. Hàm s󰉯
42
21y x x
󰉗t c󰊁󰉗i t󰉗i x b󰉟ng
A.
0
B.
2
C.
1
D.
2
Câu 11. 󰉰 th󰉬 hàm s󰉯
4
2
3
2
x
yx
󰉨m c󰊁c ti󰉨u là:
A.
2
1;
5



B.
5
1;
2



C.
5
;1
2



D.
2
;1
5



Câu 12. Hàm s󰉯
4
2
4
3
23
x
yx
có s󰉯 󰉨m c󰊁c tr󰉬 là:
A. 3 B. 0 C. 2 D. 1
Câu 13. Hàm s󰉯
3
34y x x
󰉗t c󰊁c ti󰉨u t󰉗i x b󰉟ng
A.
–3
B.
1
C.
–1
D.
3
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 5
Câu 14. Hàm s󰉯
42
1
23
2
y x x
󰉗t c󰊁c ti󰉨u t󰉗i x b󰉟ng
A.
2
B.
2
C. 0 D.
–2
Câu 15. 󰉰 th󰉬 hàm s󰉯
42
1
26
4
y x x
󰉨m c󰊁c ti󰉨u?
A. 3 B. 1 C. 2 D. 0
Câu 16. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
42
65y x x
là:
A.
3;0M
B.
3; 4N 
C.
3;4P
D.
0;2Q
Câu 17. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
43
41y x x
là:
A.
2; 15M
B.
1;2N
C.
3; 26P
D.
4; 6Q
Câu 18. Hàm s󰉯
1
yx
x

󰉗t c󰊁󰉗i t󰉗󰉨󰉳 là
A. 2 B. 1 C.
1
D. 0
Câu 19. Trong các m󰉪󰉧 sau, hãy tìm m󰉪󰉧 sai:
A. Hàm s󰉯
3
31y x x
có c󰊁c tr󰉬 B. Hàm s󰉯
1
1
1
yx
x
có hai c󰊁c tr󰉬
C. Hàm s󰉯
1
2
y
x
không có c󰊁c tr󰉬 D. Hàm s󰉯
32
33y x x
có c󰊁󰉗i và c󰊁c ti󰉨u
Câu 20. Hàm s󰉯
2
2
1
1
xx
y
x

󰉨m c󰊁c tr󰉬:
A. 0 B. 1 C. 2 D. 3
Câu 21. Kh󰉠󰉬󰉧 hàm s󰉯
42
42y x x
?
A. 󰉗t c󰊁c ti󰉨u t󰉗i
0x
B. Có c󰊁󰉗i và không có c󰊁c ti󰉨u
C. Có c󰊁󰉗i và c󰊁c ti󰉨u D. Không có c󰊁c tr󰉬.
Câu 22. 󰉰 th󰉬 c󰉻a các hàm s󰉯 󰉨󰉨m c󰊁c tr󰉬 :
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 6
A.
42
24y x x
B.
42
21y x x
C.
42
2 4 1y x x
D.
42
21y x x
Câu 23. Hàm s󰉯
42
21y x x
󰉨m c󰊁c tr󰉬:
A. 1 B. 2 C. 3 D. 0
Câu 24. 󰉰 th󰉬 hàm s󰉯
42
1
21
4
y x x
có
A. M󰉳t c󰊁󰉗i và hai c󰊁c ti󰉨u. B. M󰉳t c󰊁c ti󰉨u và hai c󰊁󰉗i.
C. M󰉳t c󰊁󰉗i và không có c󰊁c ti󰉨u . D. M󰉳t c󰊁c ti󰉨u và m󰉳t c󰊁󰉗i.
Câu 25. S󰉯 c󰊁c tr󰉬 c󰉻a hàm s󰉯
42
33y x x
là:
A. 1 B. 2 C. 3 D. 4
Câu 26. Hàm s󰉯
y f x
󰉗o hàm
2
3
1
fx
x
. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯 là:
A. 0 B. 1 C. 2 D. 3
Câu 27. Kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
3
4 3 1y x x
là
A.
1
B.
0
C.
26
2
D.
2
Câu 28. Cho hàm s󰉯
y f x
󰉬nh liên t󰉺c và liên t󰉺c trên và có b󰉘ng bi󰉦n
󰉼
x
- 2 0
,
y
+ 0 - 0 +
y
0
4
Kh󰉠󰉬󰉠󰉬nh đúng?
A. Hàm s󰉯 có hai c󰊁c tr󰉬. B. Hàm s󰉯 có giá tr󰉬 c󰊁c ti󰉨u b󰉟ng 0.
C. Hàm s󰉯 có giá tr󰉬 c󰊁󰉗i b󰉟ng -4. D. Hàm s󰉯 có giá tr󰉬 c󰊁󰉗i t󰉗i x = 0.
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 7
Câu 29. Hàm s󰉯 󰉨m c󰊁c tr󰉬 :
A.
42
21y x x
B.
42
21y x x
C.
42
2 4 1y x x
D.
42
21y x x
Câu 30. Trong các hàm s󰉯 󰉯 nào không có c󰊁c tr󰉬
A.
32
33y x x
B.
42
1y x x
C.
3
2yx
D.
4
3yx
Câu 31. Cho hàm s󰉯 󰉰 th󰉬 󰉼󰉥.
󰉯󰉨󰊁󰉬
A. 0
B. 1
C. 2
D. 3
Câu 32. Trong các hàm s󰉯 sau, hàm s󰉯 󰉳󰉨m c󰊁c tr󰉬
A.
22yx
B.
42
32y x x
C.
3
32y x x
D.
42
32y x x
Câu 33. 󰉰 th󰉬 c󰉻a hàm s󰉯 không 󰉨m c󰊁c tr󰉬:
A.
3
21y x x
B.
42
21y x x
C.
42
31y x x
D.
42
21y x x
Câu 34. Cho hàm s󰉯
y f x
󰉬nh, liên t󰉺c trên và có b󰉘ng bi󰉦n thiên:
x
0
3
5
1
,
y
+ 0 + 0 - 0 +
y
108
3125
0
0
Kh󰉠󰉬󰉠󰉬nh đúng ?
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 8
A.
0x
không ph󰉘󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯. B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
0x
C. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
1x
. D. Hàm s󰉯 có giá tr󰉬 l󰉵n nh󰉙t b󰉟ng
108
3125
.
Câu 35. 󰉰 th󰉬 󰉼󰉥. S󰉯 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯 
A. 3
B. 0
C. 2
D. 1
ĐỀ 02.
Câu 1. Hàm s󰉯 b󰉝c ba có th󰉨 có bao nhiêu c󰊁c tr󰉬 ?
A. 1 ho󰉢c 2 ho󰉢c 3 B. 0 ho󰉢c 2 C. 0 ho󰉢c 1 ho󰉢c 2 D. 2
Câu 2. Hàm s󰉯
42
1
21
4
y x x
có:
A. M󰉳t c󰊁󰉗i và hai c󰊁c ti󰉨u C. M󰉳t c󰊁󰉗i và không có c󰊁c ti󰉨u
B. M󰉳t c󰊁c ti󰉨u và hai c󰊁󰉗i D. M󰉳t c󰊁c ti󰉨u và m󰉳t c󰊁󰉗i
Câu 3. Hàm s󰉯
32
34y x x
có giá tr󰉬 c󰊁󰉗i b󰉟ng
A.
4
B.
1
C.
0
D.
24
Câu 4. 󰉰 th󰉬 hàm s󰉯
42
23y x x
có:
A. M󰉳t c󰊁󰉗i và hai c󰊁c ti󰉨u. B. M󰉳t c󰊁c ti󰉨u và hai c󰊁󰉗i.
C. M󰉳t c󰊁c ti󰉨u và không c󰊁󰉗i. D. Không có c󰊁󰉗i và c󰊁c ti󰉨u.
Câu 5. Hàm s󰉯
43
82y x x
󰉨m c󰊁c tr󰉬
A. 3 B. 2 C. 1 D. 0
Câu 6. Hàm s󰉯
23
32y x x
󰉗t c󰊁c tr󰉬 t󰉗i:
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 9
A.
D
1; 0
C CT
xx
B.
D
1; 0
C CT
xx
C.
D
0; 1
C CT
xx
D.
D
0; 1
C CT
xx
Câu 7. Hàm s󰉯 󰊁c tr󰉬:
A.
3
3y x x
B.
2
21
x
y
x
C.
1
yx
x

D.
42
2y x x
Câu 8. Hàm s󰉯 󰊁󰉗i và c󰊁c ti󰉨u ?
A.
42
2y x x
B.
3
2y x x
C.
3
yx
D.
2
21y x x
Câu 9. Cho hàm s󰉯
3
32y x x
. Kh󰉠󰉬sai ?
A. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
1x 
B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
1x
C. Hàm s󰉯 không có c󰊁c tr󰉬. D. Hàm s󰉯 󰉨m c󰊁c tr󰉬.
Câu 10. Trong các m󰉪󰉧 sau, hãy tìm m󰉪󰉧 sai ?
A. Hàm s󰉯
1
2
y
x
không có c󰊁c tr󰉬.
B. Hàm s󰉯
32
31y x x
có c󰊁󰉗i và c󰊁c ti󰉨u.
C. Hàm s󰉯
1
1
yx
x

có hai c󰊁c tr󰉬.
D. Hàm s󰉯
3
2y x x
có c󰊁c tr󰉬.
Câu 11. 󰉰 th󰉬 hàm s󰉯
42
12y x x
có m󰉙󰉨m c󰊁c tr󰉬:
A. 4 B. 3 C. 2 D. 1
Câu 12. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
3
7
3
x
yx
là:
A. 0 B. 1 C. 2 D. 3
Câu 13. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
42
21y x x
là:
A. 0 B. 1 C. 2 D. 3
Câu 14. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
43
8 12y x x
là:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 10
A. 0 B. 1 C. 2 D. 3
Câu 15. Hàm s󰉯
6
2 4 7y x x
có s󰉯 󰉨m c󰊁c tr󰉬 là:
A. 0 B. 1 C. 2 D. 3
Câu 16. Hàm s󰉯
32
3 9 2y x x x
󰉨m c󰊁c ti󰉨u t󰉗i:
A.
1x 
B.
3x
C.
1x
D.
3x 
Câu 17. Tìm giá tr󰉬 c󰊁c 󰉗i
3
32y x x
c󰉻󰉰 th󰉬 hàm s󰉯
A.
4
CD
y
B.
1
CD
y
C.
0
CD
y
D.
1
CD
y 
Câu 18. Giá tr󰉬 c󰊁󰉗i c󰉻a hàm s󰉯 là:
A.
2
B.
1
C.
6
D.
1
Câu 19. Hàm s󰉯
1
yx
x

có giá tr󰉬 c󰊁󰉗i là:
A.
2
B.
2
C.
1
D.
1
Câu 20. Hàm s󰉯
3
3y x x
có giá tr󰉬 c󰊁c ti󰉨u là:
A.
2
B.
2
C.
1
D.
1
Câu 21. Giá tr󰉬 c󰊁󰉗i c󰉻a hàm s󰉯
32
3 3 2y x x x
b󰉟ng:
A.
3 4 2
B.
3 4 2
C.
3 4 2
D.
3 4 2
Câu 22. Hàm s󰉯
4
2
21
4
x
yx
󰉗t c󰊁󰉗i t󰉗i:
A.
2x
B.
2x 
C.
0x
D.
2x 
Câu 23. Hàm s󰉯
3
2
2 3 5
3
x
y x x
󰉗t c󰊁c ti󰉨u t󰉗i:
A.
1x
B.
3x
C.
1x 
D.
3x 
Câu 24. Hàm s󰉯
2
33
2
xx
y
x

󰉗t c󰊁󰉗i t󰉗i:
A.
1x
B.
2x
C.
3x
D.
0x
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 11
Câu 25. Hàm s󰉯
42
1
23
2
y x x
󰉗t c󰊁󰉗i t󰉗i x b󰉟ng:
A. 0. B.
2
C.
2
D.
2
Câu 26. M󰉳t hàm s󰉯
fx
󰉗o hàm là
2 3 5
1 2 3f x x x x x
. H󰉮i hàm s󰉯
này có bao nhiêu c󰊁c tr󰉬 ?
A. 4 B. 3 C. 2 D. 1
Câu 27. H󰉪 th󰉽c liên h󰉪 gi󰊀a giá tr󰉬 c󰊁󰉗i
CD
y
và giá tr󰉬 c󰊁c ti󰉨u
CT
y
c󰉻󰉰 th󰉬 hàm
s󰉯
3
2y x x
là:
A.
2
CT CD
yy
B.
23
CT CD
yy
C.
CT CD
yy
D.
0
CT CD
yy
Câu 28. Hàm s󰉯
2
2
3
2y x x
󰉗t c󰊁c tr󰉬 t󰉗󰉨󰉳 là:
A.
1x
B.
0; 1xx
C.
0; 1; 2x x x
D. Hàm s󰉯 󰉨m c󰊁c tr󰉬.
Câu 29. Cho hàm s󰉯
32
1
3
2
y x x x
. Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
12
,xx

t󰉱ng
22
12
S x x
có giá tr󰉬 là:
A.
11
3
B.
13
3
C.
1
2
D.
3
2
Câu 30. Hàm s󰉯
42
25y x x
󰉨m c󰊁c tr󰉬 l󰉚󰉼󰉹t là
1 2 3
,,x x x
thì tích
1 2 3
..x x x
là:
A.
2
B.
1
C.
0
D.
1
Câu 31. Hàm s󰉯
3
1yx
x
có t󰉱󰉨m c󰊁󰉗i và c󰊁c ti󰉨u b󰉟ng:
A.
2
B.
1
C.
0
D.
2
Câu 32. Hàm s󰉯
2
41
1
xx
y
x

󰉨m c󰊁󰉗i và c󰊁c ti󰉨u b󰉟ng:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 12
A.
2
B.
5
C.
1
D.
4
Câu 33. Cho hàm s󰉯
2
21
1
xx
y
x

. Kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 là:
A.
45
B.
4
C.
8
D.
52
Câu 34. Cho hàm s󰉯
32
1
4 5 17
3
y x x x
󰉨m c󰊁c tr󰉬 là
12
,xx

12
.xx
b󰉟ng:
A.
5
B.
5
C.
8
D.
2 11
Câu 35. Cho hàm s󰉯
2
2
1
xx
y
x

. Hàm s󰉯 󰉨m c󰊁c tr󰉬
12
,xx
.Tích
12
.xx
b󰉟ng
A.
3
B.
2
C.
2
D.
3
ĐỀ 03.
Câu 1. Hàm s󰉯 󰊁c tr󰉬
A.
2
35y x x
B.
3
31y x x
C.
42
21y x x
D.
1
1
x
y
x
Câu 2. Hàm s󰉯
3
34y x x
󰉗t c󰊁c ti󰉨u t󰉗i x b󰉟ng:
A.
1
B. 1 C.
3
D. 3
Câu 3. Hàm s󰉯
2
3
1y x x
󰉗t c󰊁󰉗i t󰉗i:
A.
1x
B.
1x 
C.
3
5
x
D. 
Câu 4. 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯
32
2 3 2y x x
là:
A.
0; 2M
B.
2;2N
C.
1; 3P
D.
1; 7Q 
Câu 5. T󰉭󰉳 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
42
2y x x
là:
A.
0;0M
B.
1;1N
C.
1;1P
D.
1;0Q
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 13
Câu 6. T󰉭󰉳 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯
32
12
23
33
y x x x
là:
A.
1;3M
B.
1;0N
C.
1;2P
D.
3;1Q
Câu 7. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
32
33y x x
là:
A.
1;1M
B.
2;1N
C.
0; 3P
D.
1; 6Q
Câu 8. 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯
42
6 8 1y x x x
là:
A.
2;24M
B.
2;25N
C.
7;3P
D.
1; 6Q
Câu 9. Hàm s󰉯
42
23y x x
󰉗t c󰊁c tr󰉬 t󰉗󰉨m :
A.
0x
B.
1x
C.
1x 
D.
2x
Câu 10. Cho hàm s󰉯
y f x
liên t󰉺󰉗o hàm liên t󰉺󰉦n c󰉙p 2 trên t󰉝p
0
xK
. Kh󰉠󰉬
A. 󰉨m
0
x
󰉨m c󰊁󰉗i c󰉻a hàm s󰉯 n󰉦u
0
0fx
và
0
0fx

B. 󰉨m
0
x
󰉨m c󰊁󰉗i c󰉻a hàm s󰉯 n󰉦u
0
0fx

C. 󰉨m
0
x
󰉨m c󰊁c ti󰉨u c󰉻a hàm s󰉯 n󰉦u
0
0fx
và
0
0fx

D. 󰉨m
0
x
󰉨m c󰊁c ti󰉨u c󰉻a hàm s󰉯 n󰉦u
0
0fx

Câu 11. G󰉭i
12
,yy
l󰉚󰉼󰉹t là giá tr󰉬 c󰊁󰉗i và giá tr󰉬 c󰊁c ti󰉨u c󰉻a hàm s󰉯
42
10 9y x x

12
yy
b󰉟ng:
A.
7
B.
8
C.
9
D.
25
Câu 12. 󰉰 th󰉬 hàm s󰉯
3
3y x x
󰉨m c󰊁󰉗i là :
A.
1;2
B.
1;0
C.
1; 2
D.
1;0
Câu 13. Hàm s󰉯
3
31y x x
󰉗t c󰊁󰉗i t󰉗󰉨󰉳:
A.
1x
B.
0x
C.
1x 
D.
2x
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 14
Câu 14. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
42
18 1y x x
là
A.
0; 1
B.
0;1
C.
1;0
D.
3;80 ; 3;80
Câu 15. Kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
3
4 3 1y x x
là
A.
1
B.
0
C.
26
2
D.
2
Câu 16. Cho hàm s󰉯
32
31y x x
.Tích các giá tr󰉬 c󰊁󰉗i và c󰊁c ti󰉨u c󰉻a hàm s󰉯 b󰉟ng
A.
3
B.
6
C.
0
D.
3
Câu 17. S󰉯 c󰊁c tr󰉬
32
3 3 1y x x x
c󰉻a hàm s󰉯 là:
A. 0 B. 1 C. 2 D. 3
Câu 18. Cho hàm s󰉯
42
34y x x
. Kh󰉠󰉬
A. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i g󰉯c t󰉭󰉳.
B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i g󰉯c t󰉭󰉳.
C. Hàm s󰉯 không có c󰊁c tr󰉬.
D. 󰉨m
1; 1M
󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
Câu 19. 󰉰 th󰉬 hàm s󰉯
42
1y x x
󰉨m c󰊁c tr󰉬 󰉳 󰉼󰉴
A. 3 B. 1 C. 2 D. 0
Câu 20. Hàm s󰉯
42
22y x x
A. Có m󰉳󰉨m c󰊁c tr󰉬. B. 󰉨m c󰊁c tr󰉬 t󰉗o thành tam giác vuông.
C. 󰉨m c󰊁c tr󰉬 D. 󰉨m c󰊁c tr󰉬 t󰉗󰉧u.
Câu 21. Cho hàm s󰉯
32
31y x x
. Tích giá tr󰉬 c󰊁󰉗i và giá tr󰉬 c󰊁c ti󰉨u c󰉻a hàm s󰉯
b󰉟ng:
A.
6
B.
0
C.
3
D.
3
Câu 22. Trong các kh󰉠󰉬nh sau v󰉧 hàm s󰉯
4
2
1
3
42
x
yx
, kh󰉠󰉬
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 15
A. Hàm s󰉯 󰉨m c󰊁c ti󰉨u là
0x
B. Hàm s󰉯 󰉨m c󰊁󰉗i là
1, 1xx
C. Hàm s󰉯 có 3 c󰊁c tr󰉬 D. Hàm s󰉯 󰉨m c󰊁󰉗i là
0x
Câu 23. Tìm giá tr󰉬 c󰊁c ti󰉨u c󰉻a hàm s󰉯
32
34y x x
.
A.
4
CT
y 
B.
1
CT
y
C.
2
CT
y 
D.
0
CT
y
Câu 24. Cho hàm s󰉯
4
2
3
22
x
yx
. Kh󰉠󰉬󰉠󰉬nh sai ?
A. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
3
2
x
. B. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
0x
.
C. Giá tr󰉬 c󰊁󰉗i c󰉻a hàm s󰉯 là
D
3
2
C
y
. D. 󰉰 th󰉬 hàm s󰉯 󰉳󰉨m c󰊁c tr󰉬.
Câu 25. Hàm s󰉯
2
41
1
xx
y
x

󰉨m c󰊁c tr󰉬 là
12
,xx

12
.xx
b󰉟ng:
A.
5
B.
5
C.
2
D.
2
Câu 26. Cho hàm s󰉯
32
31y x x
. Bi󰉨u th󰉽c liên h󰉪 gi󰊀a giá tr󰉬 c󰊁󰉗i
DC
y
và giá
tr󰉬 c󰊁c ti󰉨u
CT
y
là:
A.
3
CD CT
yy
B.
3
CD CT
yy
C.
3
CT CD
yy
D.
CD CT
yy
Câu 27. Cho hàm s󰉯
y f x
󰉗o hàm t󰉗i
0
x
. Tìm m󰉪󰉧 
A. Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗i
0
x
thì
0
0fx
B. N󰉦u
0
0fx
thì hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗i
0
x
C. Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗i
0
x
thì
fx
󰉱i d󰉙u khi qua
0
x
D. N󰉦u hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗i
0
x
thì
0
0fx
Câu 28. Gi󰉘 s󰉿 hàm s󰉯
y f x
󰉗o hàm c󰉙p hai. Ch󰉭n phát bi󰉨
A. N󰉦u
0
0fx
và
0
0fx

thì hàm s󰉯
y f x
󰉗t c󰊁󰉗i t󰉗i
0
x
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 16
B. N󰉦u
0
0fx
và
0
0fx

thì hàm s󰉯
y f x
󰉗t c󰊁c ti󰉨u t󰉗i
0
x
C. N󰉦u
0
0fx
và
0
0fx

thì hàm s󰉯
y f x
󰉗t c󰊁󰉗i t󰉗i
0
x
D. N󰉦u
0
0fx

thì hàm s󰉯
y f x
󰉗t c󰊁󰉗i t󰉗i
0
x
Câu 29. Giá tr󰉬 c󰊁󰉗i c󰉻a hàm s󰉯
2
21y x x
là:
A.
2
2
B.
2
2
C.
2
4
D. Không có
CD
y
Câu 30. Giá tr󰉬 c󰊁󰉗i c󰉻a hàm s󰉯
2cosy x x
trên kho󰉘ng
0;
là:
A.
3
6
B.
5
3
6
C.
5
3
6
D.
3
6
Câu 31. Hàm s󰉯
cosyx
󰉗t c󰊁c ti󰉨u t󰉗i:
A.
,
2
x k k
B.
2,x k k

C.
2,x k k

D.
,x k k

Câu 32. Hàm s󰉯
2sin2 3yx
󰉗t c󰊁c ti󰉨u t󰉗i:
A.
,
42
k
xk

B.
,
4
x k k
C.
,
2
x k k
D.
,
4
x k k
Câu 33. Hàm s󰉯
3 cos cos2y x x
󰉗t c󰊁c ti󰉨u t󰉗i:
A.
2,x k k

B.
,x k k

C.
2,
2
x k k
D.
,
2
x k k
Câu 34. Hàm s󰉯
sin cosyxx
có c󰊁c tr󰉬 là
A.
, ; 2
4
3
2 , ; 2
4
CT CT
CD CD
x k k y
x k k y
B.
3
2 , ; 2
4
, ; 2
4
CT CT
CD CD
x k k y
x k k y
C.
3
, ; 2
4
CT CT
x k k y
D.
, ; 2
4
CD CD
x k k y
Câu 35. G󰉭󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
3
31y x x
󰉗n
th󰉠ng AB b󰉟ng :
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 17
A.
25
B.
35
C.
22
D.
32
ĐỀ 04.
Câu 1. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
42
33y x x
là
A. 1 B. 2 C. 3 D. 0
Câu 2. 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯
3
32y x x
là:
A.
0; 2
B.
2;0
C.
1;4
D.
1;0
Câu 3. Cho hàm s󰉯
32
3 9 1y x x x
. T󰉱ng các giá tr󰉬 c󰊁󰉗i và c󰊁c ti󰉨u c󰉻󰉰 th󰉬
hàm s󰉯 là:
A.
20
B.
26
C.
6
D.
20
Câu 4. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
4
2
3
2
x
yx
là:
A.
5
1;
2



B.
2
1;
4



C.
5
;1
2



D.
5
;1
2



Câu 5. Hàm s󰉯
42
41y x x
󰉗t c󰊁c ti󰉨u t󰉗󰉨󰉳:
A.
2x 
B.
1x 
C.
1x
D.
2x 
Câu 6. 󰉰 th󰉬 hàm s󰉯
3
3y x x
󰉨m c󰊁󰉗i là :
A.
1;2
B.
1;0
C.
1; 2
D.
1;0
Câu 7. Hàm s󰉯 󰊁c tr󰉬
A.
35yx
B.
32
25y x x
C.
3
1yx
D.
3
1y x x
Câu 8. 󰉰 thi hàm s󰉯
3
31y x x
󰉨m c󰊁󰉗i là:
A.
1; 1
B.
1;3
C.
1; 1
D.
1;3
Câu 9. Cho hàm s󰉯
32
31y x x
. Giá tr󰉬 c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯 là
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 18
A.
1
B.
3
C.
0
D.
3
Câu 10. S󰉯 c󰊁c tr󰉬 c󰉻a hàm s󰉯
42
23y x x
là:
A. 1 B. 2 C. 3 D. 4
Câu 11. Cho hàm s󰉯
42
84y x x
. Ch󰉭n phát bi󰉨󰉨u sau:
A. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
0x
B. Hàm s󰉯 có c󰊁󰉗󰉼󰊁c ti󰉨u
C. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
0x
D. Hàm s󰉯 có c󰊁c ti󰉨󰉼󰊁󰉗i
Câu 12. Cho hàm s󰉯
2
41
1
xx
y
x

.Hàm s󰉯 󰉨m c󰊁c tr󰉬
12
,xx
.Tích
12
.xx
b󰉟ng
A.
5
B.
4
C.
1
D.
2
Câu 13. Kh󰉠󰉬󰉯
42
1
21
4
y x x
có
A. m󰉳t c󰊁󰉗i và không có c󰊁c ti󰉨u B. m󰉳t c󰊁c ti󰉨u và hai c󰊁󰉗i
C. m󰉳t c󰊁󰉗i và hai c󰊁c ti󰉨u D. m󰉳t c󰊁󰉗i và m󰉳t c󰊁c ti󰉨u
Câu 14. Cho hàm s󰉯
3
2
2
23
33
x
y x x
. T󰉭󰉳 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯 là:
A.
2
3;
3



B.
1;2
C.
1;2
D.
1; 2
Câu 15. Cho hàm s󰉯
3
2
2
23
33
x
y x x
. To󰉗 󰉳 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯 là :
A.
1;2
B.
1;3
C.
2
3;
3



D.
1; 2
Câu 16. Kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
3 9 5y x x x
là:
A.
4 65
B.
37 2
C.
2 65
D.
2 37
Câu 17. Cho hàm s󰉯
32
12
23
33
y x x x
. To󰉗 󰉳 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯 là
A.
1;2
B.
1; 2
C.
1; 2
D.
1;2
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 19
Câu 18. Cho hàm s󰉯
32
3 9 4y x x x
. N󰉦u hàm s󰉯 󰉗t c󰊁󰉗i
1
x
và c󰊁c ti󰉨u
2
x
thì
tích
12
.y x y x
b󰉟ng:
A.
207
B.
302
C.
82
D.
25
Câu 19. 󰉨m c󰊁󰉗i và c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
3
32y x x
có t󰉭󰉳 l󰉚󰉼󰉹t
là:
A.
1;4
và
1;0
B.
1;2
và
1;0
C.
1;0
và
1;4
D.
1;0
và
1;4
Câu 20. S󰉯 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
53
21y x x
là:
A. 1 B. 3 C. 5 D. 7
Câu 21. Cho hàm s󰉯
32
3 21 1y x x x
. Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
12
,xx

t󰉱ng
22
12
S x x
có giá tr󰉬 là:
A.
18
B.
24
C.
36
D.
48
Câu 22. Cho hàm s󰉯
32
31y x x
. Tích giá tr󰉬 c󰊁󰉗i và c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
là:
A.
6
B.
3
C.
0
D.
3
Câu 23. G󰉭i
12
,yy
l󰉚󰉼󰉹t là giá tr󰉬 c󰊁󰉗i và giá tr󰉬 c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
42
10 9y x x
󰉬 c󰉻a bi󰉨u th󰉽c
12
T y y
b󰉟ng:
A.
7
B.
9
C.
25
D.
25
Câu 24. Cho hàm s󰉯
32
2 3 5y x x
T󰉱ng các giá tr󰉬 c󰊁c tr󰉬 c󰉻a hàm s󰉯 là:
A.
9
B.
1
C.
1
D.
5
Câu 25. 󰉰 th󰉬 hàm s󰉯
2
2
1
yx
x

?
CD CT
yy
A.
3 2 2
B.
3 2 2
C.
2
D.
6
Câu 26. 󰉰 th󰉬 hàm s󰉯
2
9yx
có m󰉙󰉨m c󰊁c tr󰉬 ?
A. 0 B. 1 C. 2 D. 3
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 20
Câu 27. Hàm s󰉯
2sin 2y x x
󰉗t c󰊁c ti󰉨u t󰉗i:
A.
,
3
x k k
B.
,
3
x k k
C.
2,
3
x k k
D.
2
,
3
x k k
Câu 28. Cho hàm s󰉯
cos2 1, ;0y x x
thì kh󰉠󰉬
A. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
7
12
x

B. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
11
12
x

C. T󰉗i
2
x

hàm s󰉯 󰉗t c󰊁󰉗i. D. : Hàm S󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
2
x

Câu 29. 󰉨m c󰊁󰉗i c󰉻a hàm s󰉯
sin2y x x
là .
A.
2
3
xk
B.
6
xk
C.
6
xk

D.
6
xk
Câu 30. Kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
3
34y x x
là:
A.
4
B.
5
C.
5
D.
25
Câu 31. Cho hàm s󰉯
y f x
󰉬nh, liên t󰉺c trên và có b󰉘ng bi󰉦n thiên.
x
0 1
,
y
+ || - 0 -
y
0
1
Kh󰉠󰉬󰉠󰉬
A. Hàm s󰉯 󰉳t c󰊁c tr󰉬.
B. Hàm s󰉯 có giá tr󰉬 c󰊁c ti󰉨u b󰉟ng 1
C. Hàm s󰉯 có giá tr󰉬 l󰉵n nh󰉙t b󰉟ng 0 và giá tr󰉬 nh󰉮 nh󰉙t b󰉟ng -1
D. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉗t c󰊁c ti󰉨u t󰉗i x=1
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 21
Câu 32. 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
42
41y x x
t󰉗o thành m󰉳t tam giác cân có
di󰉪n tích S b󰉟ng
A.
22S
B.
82S
C.
32S
D.
42S
Câu 33. 󰉰 th󰉬 hàm s󰉯
sinyx
có m󰉙󰉨m c󰊁c tr󰉬 ?
A. 3 B. 2 C. 1 D. Vô s󰉯.
Câu 34. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
2
1
2
xx
y
x

là
A.
1; 1 ; 3; 5
B.
3; 5
C.
1; 1
D.
1; 3
Câu 35. Kho󰉘ng cách gi󰊀a hai c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
là:
A.
5
B.
25
C.
35
D.
85
ĐỀ 05
Câu 1. Hàm s󰉯
2
33
1
xx
y
x

có tích các giá tr󰉬 c󰊁󰉗i và c󰊁c ti󰉨u b󰉟ng:
A.
3
B.
1
C.
1
D.
2
Câu 2. Kh󰉠󰉬󰉧 󰉰 th󰉬 hàm s󰉯
2
25
1
xx
y
x
:
A.
0
CD CT
yy
B.
4
CT
y 
C.
1
CD
x 
D.
3
CD CT
xx
Câu 3. Cho hàm s󰉯
32
3
2
x
y x x
Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
12
,xx
󰉱ng
22
12
S x x
có giá tr󰉬 là:
A.
12
B.
12
C.
18
D.
20
Câu 4. Cho hàm s󰉯
4
3
41
4
x
y x x
. G󰉭i
12
,xx
là 2 nghi󰉪m c󰉻󰉼󰉴
0y
.
󰉱ng
12
xx
b󰉟ng:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 22
A.
1
B.
2
C.
0
D.
1
Câu 5. Hàm s󰉯
32
32y x x
có m󰉙󰉨m c󰊁c tr󰉬?
A. 0 B. 1 C. 2 D. 3
Câu 6. Cho hàm s󰉯
32
3 3 1y x x x
, m󰉪󰉧 
A. Hàm s󰉯 luôn luôn ngh󰉬ch bi󰉦n trên
; 
. B. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
1x
C. Hàm s󰉯 󰉰ng bi󰉦n
; 
D. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
1x
Câu 7. 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯
32
5 7 3y x x x
là:
A.
1;0
B.
0; 3
C.
7 32
;
3 27



D.
7 32
;
3 27



Câu 8. Cho hàm s󰉯
2
41
1
xx
y
x

, hàm s󰉯 󰉨m c󰊁c tr󰉬
12
,xx
. Tích
12
.xx
b󰉟ng
A.
5
B.
4
C.
1
D.
2
Câu 9. Hàm s󰉯
32
3 4 14y x x x
󰉗t c󰊁c tr󰉬 t󰉗󰉨m
12
,xx
󰉯
12
.xx
là:
A.
1
9
B.
1
7
C.
1
D.
3
Câu 10. Cho hàm s󰉯
32
3 4 14y x x x
. Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
12
,xx

t󰉱ng
12
xx
có giá tr󰉬 là:
A.
1
9
B.
1
7
C.
8
9
D.
1
Câu 11. Cho hàm s󰉯
32
5 6 2y x x x
. Hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
12
,xx

t󰉱ng
12
xx
có giá tr󰉬 là:
A.
10
3
B.
10
3
C.
1
D. 
Câu 12. Cho hàm s󰉯
32
2 3 2y x x

DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 23
A. Hàm s󰉯 󰉗t c󰊁c ti󰉨u trên
11
;
22



B. Hàm s󰉯 󰉗t c󰊁󰉗i trên
1
;2
2



C. Hàm s󰉯 có 2 c󰊁c tr󰉬 trên
1
;2
2



D. Hàm s󰉯 có 2 c󰊁c tr󰉬 trên
1
;3
3



Câu 13. Hàm s󰉯 󰉫 có c󰊁󰉗i mà không có c󰊁c ti󰉨u ?
A.
32
32y x x
B.
1
2
x
y
x
C.
4
2
1
2
x
yx
D.
2
1
x
y
x
Câu 14. Cho hàm s󰉯
432
1 4 7
21
4 3 2
y x x x x
.Kh󰉠󰉬
A. Hàm s󰉯 không có c󰊁c tr󰉬. B. Hàm s󰉯 có c󰊁c ti󰉨u, không có c󰊁󰉗i.
C. Hàm s󰉯 có 1 c󰊁󰉗i và 2 c󰊁c ti󰉨u D. Hàm s󰉯 có 1 c󰊁c ti󰉨u và 2 c󰊁󰉗i.
Câu 15. Xét tính c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
2
25
1
xx
y
x

ta có:
A.
3; 4M 
󰉨m c󰊁c ti󰉨u. B.
1; 4N
󰉨m c󰊁󰉗i.
C.
3; 4P 
󰉨m c󰊁󰉗i. D. Hàm s󰉯 không có c󰊁c tr󰉬.
Câu 16. Cho hàm s󰉯
43
34y x x
. Kh󰉠󰉬
A. Hàm s󰉯 không có c󰊁c tr󰉬. B. 󰉨m
1; 1A
󰉨m c󰊁c ti󰉨u.
C. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i g󰉯c t󰉭󰉳. D. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i g󰉯c t󰉭󰉳.
Câu 17. Cho hàm s󰉯
2
41
1
xx
y
x

󰉨m c󰊁c tr󰉬
12
,xx
. Tích
12
xx
b󰉟ng
A.
2
B.
5
C.
1
D.
4
Câu 18. M󰉳t hàm s󰉯
fx
󰉗o hàm là
32
2f x x x x
. S󰉯 c󰊁c tr󰉬 c󰉻a hàm s󰉯 là:
A. 0 B. 1 C. 2 D. 3
Câu 19. 󰉰 th󰉬 hàm s󰉯 󰉫 󰉨m c󰊁c tr󰉬 ?
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 24
A.
42
2 4 2y x x
B.
2
2 4 2
4 9 1y m x x
C.
42
21y x x
D.
4 2 2
11y x m x
Câu 20. G󰉭i A, B l󰉚󰉼󰉹󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
34y x x

di󰉪n tích tam giác OBC (v󰉵i O là g󰉯c t󰉭󰉳) có giá tr󰉬 b󰉟ng bao nhiêu ?
A.
2
B.
4
C.
25
D.
8
Câu 21. G󰉭i A, B l󰉚󰉼󰉹󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
32y x x

di󰉪n tích tam giác ABC v󰉵i
1;1C
có giá tr󰉬 b󰉟ng bao nhiêu ?
A. 1 B. 2 C. 3 D. 4
Câu 22. G󰉭i A, B l󰉚n 󰉼󰉹󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
2 3 36 10y x x x
󰉪n tích c󰉻a tam giác ABC v󰉵i
2;3C
có giá tr󰉬 b󰉟ng bao nhiêu ?
A. 78 B.
87
3
C.
287
3
D.
285
2
Câu 23. G󰉭i A, B l󰉚󰉼󰉹󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
2
12y x x

di󰉪n tích c󰉻a tam giác ABC v󰉵i
1; 3C
có giá tr󰉬 b󰉟ng bao nhiêu ?
A.
3
5
B.
8
3
C.
7
D. 
Câu 24. Ti󰉦p tuy󰉦n t󰉗󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
3
2
2 3 5
3
x
y x x
A. Song song v󰉵󰉼󰉶ng th󰉠ng
1x
B. Song song v󰉵i tr󰉺c hoành.
C. Có h󰉪 s󰉯 󰉼󰉴 D. Có h󰉪 s󰉯 góc b󰉟ng -1
Câu 25. P󰉼󰉴󰉦p tuy󰉦n c󰉻󰉰 th󰉬 hàm s󰉯
42
21y x x
t󰉗󰉨m c󰊁c ti󰉨u
là:
A.
10y 
B.
0y
C.
10xy
D.
yx
Câu 26. Kho󰉘ng cách t󰉾 󰉨m c󰊁󰉗i c󰉻󰉰 th󰉬 hàm s󰉯
3
31y x x
󰉦󰉼󰉶ng
phân giác góc ph󰉚󰉼󰉽 hai trong h󰉪 tr󰉺c Oxy là:
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 25
A.
1
B.
2
C.
2
D.
3
Câu 27. Ti󰉦p tuy󰉦n t󰉗󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
42
0y ax bx c a
󰉢c
bi󰉪t
A. Song song v󰉵i tr󰉺c tung. B. Có h󰉪 s󰉯 󰉼󰉴
C. Song song ho󰉢c ho󰉢c trùng v󰉵i tr󰉺c hoành. D. 󰉯c t󰉭󰉳.
Câu 28. V󰉵i giá tr󰉬 nào c󰉻a tham s󰉯 󰉼󰉶ng th󰉠ng
:d y x m

󰉨m c󰉻󰉗n th󰉠ng n󰉯󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
69y x x x
A.
0m
B.
1m
C.
2m
D.
3m
Câu 29. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
3
2
x
?
A.
1
2
x
y
x
B.
2
32y x x
C.
2
4 12 8y x x
D.
4 3 2
1
3
2
y x x x x
Câu 30. Cho hàm s󰉯
2
32y x x
󰉨󰉨m nào có t󰉭󰉳 
󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯 
A.
1;2M
B.
3;0N
C.
1;0P
D.
2; 3Q
Câu 31. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
2
4y x x
là:
A.
2;2M
B.
2;1N
C.
2; 2P 
D.
2;2Q
Câu 32. Cho hàm s󰉯
2 1 4 1y x x
. Tìm m󰉪󰉧 󰉪󰉧 sau ?
A. Giá tr󰉬 c󰊁󰉗i b󰉟ng
1
2
B. 󰉨m c󰊁c ti󰉨u có t󰉭󰉳 là
1
;1
2
M



C. 󰉨m c󰊁c ti󰉨u là
11
;
42
N



D. Hàm s󰉯 không có c󰊁c tr󰉬.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 26
Câu 33. G󰉭i A, B, C 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
42
2 4 1y x x
H󰉮i di󰉪n tích
tam giác ABC là bao nhiêu ?
A. 4 B. 2 C. 1 D.
3
2
Câu 34. Kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
2
1
x mx m
y
x

b󰉟ng:
A.
5
B.
25
C.
45
D.
55
Câu 35. (SGD Bắc Ninh, 2017) Hàm s󰉯
32
31y x x
󰉨m c󰊁c ti󰉨u b󰉟ng
A.
2
. B.
0
. C.
3
. D. 1
ĐỀ 06
Câu 1. (SGD Bắc Ninh, 2017) Hàm s󰉯
42
21y x x
có m󰉙󰉨m c󰊁c tr󰉬?
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 2. (SGD Hải Phòng, 2017) Cho hàm s󰉯
42
y x 2x 2
. Hãy ch󰉭n m󰉪󰉧 
A. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m x = 1. B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m x = 0.
C. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m x = -1 D. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m x = -1.
Câu 3. (SGD Long An, 2017) Cho hàm s󰉯
y f x
󰉬nh trên và có b󰉘ng bi󰉦n thiên
󰉼󰉥:
Ch󰉭n kh󰉠󰉬
A. Hàm s󰉯 󰉨m c󰊁c tr󰉬. B. Hàm s󰉯 󰉨m c󰊁c tr󰉬.
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 27
C. Hàm s󰉯 󰉨m c󰊁c tr󰉬. D. Hàm s󰉯 󰉨m c󰊁c tr󰉬.
Câu 4. (SGD Bình Phước, Lần 1, 2017) Cho hàm s󰉯
42
42y x x
.Kh󰉠󰉬nh nào sau
 ?
A. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
2x 
và
2x
.
B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
0x
.
C. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
2y 
.
D. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
2; 2
và
2; 2
.
Câu 5. (SGD Bình Phước, Lần 1, 2017) Hàm s󰉯
y f x
có b󰉘ng bi󰉦
Hàm s󰉯
fx
󰉗t c󰊁c ti󰉨u t󰉗󰉨m
A.
0x
. B.
1y 
. C.
0y
. D.
1x 
.
Câu 6. (SGD Hà Nội, Lần 1, 2017) Cho hàm s󰉯
y f x
liên t󰉺c trên 󰉗o hàm
23
1 1 .f x x x x
Hàm s󰉯 󰉨m c󰊁c tr󰉬?
A. 󰉨m c󰊁c tr󰉬. B. Không có c󰊁c tr󰉬.
C. 󰉨m c󰊁c tr󰉬. D. Ch󰉫 󰉨m c󰊁c tr󰉬.
Câu 7. (SGD Hà Nội, Lần 1, 2017) 󰉨m c󰊁c ti󰉨u
CT
x
c󰉻a hàm s󰉯
32
3 9 .y x x x
A.
1
CT
x 
. B.
3
CT
x 
. C.
1
CT
x
. D.
0
CT
x
.
Câu 8. (SGD HCM cụm 2, 2017) H󰉮i trong b󰉯n hàm s󰉯 󰉼󰉹c li󰉪󰉼󰉵󰉯 nào
không có c󰊁c tr󰉬?
0
0
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 28
A.
32
5.y x x x
B.
3
.yx
C.
42
1.y x x
D.
4
1.yx
Câu 9. (SGD HCM cụm 2, 2017) Tìm giá tr󰉬 c󰊁c ti󰉨u
CT
y
c󰉻a hàm s󰉯
3
3y x x
.
A.
4
CT
y 
. B.
2
CT
y
. C.
2
CT
y 
. D.
1
CT
y 
.
Câu 10. (SGD HCM cụm 4, 2017) 󰉰 th󰉬 hàm s󰉯
3
3y x x
󰉨m c󰊁󰉗i là
A.
1; 2 .
B.
1;0 .
C.
1;2 .
D.
1;0 .
Câu 11. (THPT QG 2017) Cho hàm s󰉯
y f x
có b󰉘ng bi󰉦󰉼
Tìm giá tr󰉬 c󰊁󰉗i
CĐ
y
và giá tr󰉬 c󰊁c ti󰉨u
CT
y
c󰉻a hàm s󰉯 
A.
3
CĐ
y
và
0
CT
y
. B.
3
CĐ
y
và
2
CT
y 
.
C.
2
CĐ
y 
và
2
CT
y
. D.
2
CĐ
y
và
0
CT
y
.
Câu 12. (THPT QG 2017) Cho hàm s󰉯
y f x
có b󰉘ng bi󰉦󰉼
x
0 2
,
y
+ 0 - 0 +
y
4
2
2
5
M󰉪󰉧 󰉼󰉵
A. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
5x 
. B. Hàm s󰉯 có b󰉯󰉨m c󰊁c tr󰉬.
C. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
2x
. D. Hàm s󰉯 không có c󰊁c 󰉗i.
Câu 13. (THPT QG 2017)󰈚󰈨󰈖󰈘
32
35y x x
󰈜󰉼󰈨 󰈨
A

B
󰈨
S
󰈖
OAB
󰉴 
O
󰈘󰈨󰈨
A.
9S
. B.
10
3
S
. C.
10S
. D.
5S
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 29
Câu 14. (THPT QG 2017) Cho hàm s󰉯
y f x
có b󰉘ng bi󰉦󰉼
M󰉪󰉧 󰉼󰉵
A. Hàm s󰉯 có b󰉯󰉨m c󰊁c tr󰉬. B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
2x
.
C. Hàm s󰉯 không có c󰊁󰉗i. D. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
5x 
.
Câu 15. (THPT QG 2017) Hàm s󰉯
23
1
x
y
x
󰉨m c󰊁c tr󰉬 ?
A.
3.
B.
0.
C.
2
. D.
1
.
Câu 16. (THPT AMSTERDAM 2017) Hàm s󰉯
32
34y x x
󰉗t c󰊁c ti󰉨u t󰉗󰉨m:
A.
0x
B.
2x
C.
4x
D.
0x
và
2x
Câu 17. (THPT AMSTERDAM 2017) S󰉯 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
1
2
x
y
x
là:
A.
0
B.
1
C.
2
D.
3
Câu 18. (THPT Nguyễn Đình Chiểu Bình Định 2017) Hàm s󰉯
32
32y x x
có giá
tr󰉬 c󰊁c ti󰉨u
CT
y
là
A.
2
CT
y
. B.
2
CT
y 
. C.
4
CT
y 
. D.
6
CT
y
.
Câu 19. (Nguyễn Thái Học, Vĩnh Phúc, Lần 1, 2017) Cho hàm s󰉯
42
21 y x x
.
Kh󰉠󰉬
A. 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c ti󰉨u. B. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
1x
.
C. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
1x
. D. Giá tr󰉬 c󰊁c ti󰉨u b󰉟ng 0.
Câu 20. (Nguyễn Thái Học, Vĩnh Phúc, Lần 1, 2017) Cho hàm s󰉯
32
31 y x x
.
Kh󰉠󰉬
A. 󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯 là
(2; 5)
. B. Giá tr󰉬 c󰊁c ti󰉨u b󰉟ng
0
.
C. Giá tr󰉬 c󰊁󰉗i c󰉻a hàm s󰉯 là
d
2
c
y
. D. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
2x
.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 30
Câu 21. (SGD HCM cụm 5, 2017) Tìm c󰊁c ti󰉨u c󰉻a hàm s󰉯
32
6 15 10y x x x
.
A.
5.
B.
110.
C.
2.
D.
1.
Câu 22. (SGD HCM cụm 6, 2017) Cho hàm s󰉯
fx
󰉗o hàm là
24
12f x x x x x
. S󰉯 󰉨m c󰊁c ti󰉨u c󰉻a hàm s󰉯
fx
là
A.
2
. B. 0. C.
1
. D.
3
.
Câu 23. (SGD HCM cụm 7, 2017) Cho hàm s󰉯
3
y x 3x 3.
Kh󰉠󰉬nh nào sau

A. Hàm s󰉯 󰉨m c󰊁c tr󰉬. B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
x 1.
C. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
x 1.
D. Hám s󰉯 󰉨m c󰊁󰉗i.
Câu 24. (SGD Huế, 2017) Cho hàm s󰉯
()y f x
liên t󰉺c trên kho󰉘ng
( ; )ab
và
0
x
là m󰉳t
󰉨m thu󰉳c kho󰉘󰉠󰉬
A. N󰉦u
0
''( ) 0fx
thì
0
x
󰉨m c󰊁󰉗i c󰉻a hàm s󰉯.
B. N󰉦u
0
''( ) 0fx
thì
0
x
󰉨m c󰊁c ti󰉨u c󰉻a hàm s󰉯.
C. N󰉦u
0
'( ) 0fx
và
0
''( ) 0fx
thì
0
x
󰉨m c󰊁c ti󰉨u c󰉻a hàm s󰉯..
D. N󰉦u
0
'( ) 0fx
và
0
''( ) 0fx
thì
0
x
󰉨m c󰊁󰉗i c󰉻a hàm s󰉯.
Câu 25. (SGD Nam Định, Lần 1, 2017) Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
0x
.
A.
yx
. B.
4
1yx
. C.
2
2x
y
x
. D.
3
yx
.
Câu 26. (SGD Quảng Ninh, 2017) Hàm s󰉯 nào trong b󰉯n hàm s󰉯 󰉼󰉹c li󰉪t kê 󰉷 b󰉯n
󰉼󰉵󰉼󰉵󰊁c tr󰉬?
A.
32
3 4 1y x x x
. B.
42
43y x x
.
C.
3
35y x x
. D.
4
1
x
y
x
.
Câu 27. (SGD Quảng Ninh, 2017) 󰉨m c󰊁󰉗i
CĐ
x
(n󰉦u có) c󰉻a hàm s󰉯
36y x x
.
A.
3
CĐ
x
. B.
6
CĐ
x
. C.
6
CĐ
x
. D. Hàm s󰉯 không có 󰉨m c󰊁󰉗i.
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 31
Câu 28. (SGD Thanh Hóa, 2017) Cho hàm
s󰉯
()y f x
liên t󰉺c trên 󰉰 th󰉬 là
󰉼󰉶󰉼󰉥 󰉨m c󰊁c
ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯
()y f x
.
A.
2.y 
B.
0.x
C.
(0; 2).M
D.
(2;2).N
Câu 29. (SGD Thanh Hóa, 2017) G󰉭i
12
,xx
󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
2
4
1
xx
y
x
.
Tính giá tr󰉬 c󰉻a bi󰉨u th󰉽c
12
.P x x
.
A.
5.P 
B.
2.P 
C.
1.P 
D.
4.P 
VẤN ĐỀ 2. Tìm tham số m để hàm số đạt cực trị tại
0
x
cho trước
Phương pháp 1
Bước 1. Hàm s󰉯
fx
󰉗t c󰊁c tr󰉬 t󰉗i
0
x
thì suy ra:
0
0fx
ho󰉢c
'fx
󰉬nh t󰉗i
󰉨m
0
x
󰉼󰉹c tham s󰉯 m.
Bước 2. Thay tham s󰉯 m v󰉾󰉼󰉹c và l󰉝p b󰉘ng bi󰉦󰉨 K󰉦t lu󰉝n
Phương pháp 2
Sử dụng dấu hiệu 2. Tính
,f x f x
.
+) N󰉦u
0
0fx
thì hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
0
x
.
+) N󰉦u
0
0fx
thì hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗󰉨m
0
x
.
Chú ý: N󰉦u
0
0
'0
"0
fx
fx
thì không th󰉨 k󰉦t lu󰉝n gì v󰉧 󰉨m
0
x
(Ph󰉘i s󰉿 d󰉺󰉼󰉴
A. ÁP DỤNG
x
y
O
2
1
2
-1
-2
-2
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 32
Ví dụ 1. 󰉨 hàm s󰉯
3 2 2
1
11
3
y x mx m m x
󰉗t c󰊁c ti󰉨u t󰉗i
0
1x
Ví dụ 2. 󰉨 hàm s󰉯
3 2 2
1
11
3
y x mx m m x
󰉗t c󰊁󰉗i t󰉗i
0
1x
Ví dụ 3. 󰉨 hàm s󰉯
3
y x mx
󰉗t c󰊁c tr󰉬 t󰉗i
0
0x
. Đs: không t󰉰n t󰉗i m
Ví dụ 4. 󰉨 hàm s󰉯
4
y x mx
󰉗t c󰊁c tr󰉬 t󰉗i
0
0x
. Đs:
0m
Ví dụ 5. Cho hàm s󰉯
3 2 2 2
1
2 3 1 5
3
y x m m x m x m
󰉨 hàm s󰉯 󰉗t
c󰊁c ti󰉨u t󰉗i
0
2x 
? Đs:
3m
Ví dụ 6. Cho hàm s󰉯
2
1x mx
y
xm

󰉨 hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
2x
?
Đs:
3m 
Ví dụ 7. Cho hàm s󰉯
2
3 3 4x m x m
y
xm
󰉨 hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
2x
?
Đs:
4m
Ví dụ 8. Cho hàm s󰉯
2
ax bx ab
y
ax b

. Tìm a, b sao cho hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
0x
và
4x
? Đs:
2; 4ab
Ví dụ 9. Cho hàm s󰉯
2
2ax bx
y
xa

. Tìm a, b sao cho hàm s󰉯 󰉗t c󰊁c tr󰉬 t󰉗󰉨m
0x
và
4x
? Đs:
2; 1ab
Ví dụ 10. Cho hàm s󰉯
4
2
2
x
y ax b
󰉨 hàm s󰉯 󰉗t c󰊁c tr󰉬 b󰉟ng -2 t󰉗󰉨m
0
1x
? Đs:
3
1;
2
ab
B. BÀI TẬP VẬN DỤNG
Bài tập 1. 󰉨 hàm s󰉯
32
35y x m x mx m
󰉗t c󰊁c ti󰉨u t󰉗󰉨m
0
2x
?
Đs:
0m
Bài tập 2. 󰉨 hàm s󰉯
2 3 2
5 6 6 6y m m x mx x
󰉗t c󰊁󰉗i t󰉗󰉨m
0
1x
?
Đs:
1m
Bài tập 3. 󰉨 hàm s󰉯
3 2 2
1
42
3
y x mx m x
󰉗t c󰊁󰉗i t󰉗󰉨m
0
1x
?
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 33
Đs:
3m 
Bài tập 4. Cho hàm s󰉯
1
sin sin3
3
y m x x
󰉨 hàm s󰉯 󰉗t c󰊁󰉗i t󰉗󰉨m
3
x
?
Đs:
2m
Bài tập 5. 󰉨 hàm s󰉯
2
11
1
x m x
y
xm

󰉗t c󰊁󰉗i t󰉗󰉨m
0
2x
?
Đs:
2m 
Bài tập 6. 󰉨 hàm s󰉯
2
1x mx
y
xm

󰉗t c󰊁󰉗i t󰉗󰉨m
0
2x
?
Đs:
3m 
Bài tập 7. Cho hàm s󰉯
42
1
4
y x ax b
󰉨 hàm s󰉯 có c󰊁c tr󰉬 b󰉟ng -2 t󰉗i
1x
?
Đs:
17
;
24
ab
Bài tập 8. Cho hàm s󰉯
32
y x ax bx c
󰉨 hàm s󰉯 có giá tr󰉬 b󰉟ng 1 t󰉗󰉨m
0x
󰉗t c󰊁c tr󰉬 t󰉗󰉨m
2x
và giá tr󰉬 c󰊁c tr󰉬 là -3? Đs:
3; 0; 1a b c
C. BÀI TẬP TRẮC NGHIỆM
ĐỀ 01
Câu 1. 󰉰 th󰉬 hàm s󰉯
2
3
2
x x m
y
x
nh󰉝󰉨m
0;3A
làm c󰊁c tr󰉬 󰉼󰉴
trình c󰉻a hàm s󰉯 có d󰉗ng là:
A.
2
36
2
xx
y
x
B.
2
31
2
xx
y
x
C.
2
36
2
xx
y
x
D.
2
3
2
xx
y
x

Câu 2. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 󰉨 hàm s󰉯
32
3y x x mx
󰉗t c󰊁c
ti󰉨u t󰉗i
2x
A.
0m
B.
0m
C.
0m
D.
0m
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 34
Câu 3. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 󰉨 hàm s󰉯
32
1 2 1y x m x m
󰉗t c󰊁󰉗i t󰉗i
2x
A.
2m
B.
1m
C.
5m
D.
3m
Câu 4. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 󰉨 hàm s󰉯
32
2
7
3
y x mx m x



có c󰊁c tr󰉬 t󰉗i
1x
A.
7
9
m 
B.
3m 
C.
7m
D.
7m 
Câu 5. Hàm s󰉯
3 2 2 2
1
2 3 1 1
3
y x m m x m
󰉗t c󰊁c ti󰉨u t󰉗i
2x 
khi và ch󰉫
khi.
A.
1
3
m
m
B.
1
3
m
m


C.
1m
D.
3m
Câu 6. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 m sao cho hàm s󰉯
3 2 2
3 3 1y x mx m
󰉗t c󰊁󰉗i t󰉗i
1x
. K󰉦t qu󰉘 
A. Không có m B.
2m
C.
1m 
D.
2m 
Câu 7. Hàm s󰉯
32
3y x x mx
󰉗t c󰊁c ti󰉨u t󰉗i
2x
khi giá tr󰉬 c󰉻a tham s󰉯 m th󰉮a
mãn:
A.
0m
B.
0m
C.
0m
D.
0m
Câu 8. V󰉵i giá tr󰉬 nào c󰉻a m thì hàm s󰉯
3
21y x mx
󰉗t c󰊁c ti󰉨u t󰉗i
1x
:
A.
2
3
m
B.
3
2
m 
C.
2
3
m
D.
2
3
m 
Câu 9. Hàm s󰉯
3
1
5
3
y x mx m
󰉗t c󰊁c ti󰉨u t󰉗i
2x
khi tham s󰉯 m l󰉙y giá tr󰉬
b󰉟ng bao nhiêu?
A.
4m
B.
1m
C.
3m 
D.
1m 
Câu 10. 󰉨 hàm s󰉯
32
32y x mx x
󰉗t c󰊁c ti󰉨u t󰉗i
2x
?
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 35
A.
15
4
m 
B.
4
15
m
C.
4
15
m 
D.
15
4
m
Câu 11. Tìm m 󰉨 hàm s󰉯
32
3 12 2y mx x x
󰉗t c󰊁󰉗i t󰉗i
2x
?
A.
2m 
B.
3m 
C.
0m
D.
1m 
Câu 12. Hàm s󰉯
32
3y x x mx
󰉗t c󰊁c ti󰉨u t󰉗i
2x
khi:
A.
0m
B.
0m
C.
0m
D.
0m
Câu 13. Hàm s󰉯
3 2 2
1
11
3
y x mx m m x
󰉗t c󰊁󰉗i t󰉗󰉨m
1x
khi:
A.
12mm
B.
1m
C.
2m
D.
m
Câu 14. Hàm s󰉯
3
11y x m x
󰉗t c󰊁c ti󰉨u t󰉗󰉨m
2x
khi:
A.
13m
B.
13m
C.
1m
D.
m
Câu 15. Hàm s󰉯
3 2 2
6 4 1 2y x mx m x
󰉗t c󰊁󰉗i t󰉗󰉨m
2x
khi:
A.
0m
B.
11
2
m
C.
4m
D.
4m 
ĐỀ 02
Câu 1. Hàm s󰉯
32
21y x x mx
󰉗t c󰊁c ti󰉨u t󰉗i
1x
khi:
A.
1m
B.
1m 
C.
2m
D. Không có m
Câu 2. Hàm s󰉯
3 2 2
1
2 3 3
3
y x mx m x m
󰉗t c󰊁c ti󰉨u t󰉗i
1x 
khi:
A.
1m 
B.
1m
C.
1
3
m
D.
1
3
m 
Câu 3. Hàm s󰉯
32
12y x m x m
󰉗t c󰊁󰉗i t󰉗󰉨m
2x
khi:
A.
0m
B.
11
2
m
C.
4m
D.
4m 
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 36
Câu 4. Hàm s󰉯
3 2 2
22y x mx m x
󰉗t c󰊁c ti󰉨u t󰉗󰉨m
1x
khi:
A.
1m 
B.
1m
C.
2m
D.
2m 
Câu 5. Hàm s󰉯
32
1
1
32
m
y x x m x
󰉗t c󰊁󰉗i t󰉗i
1x
khi:
A.
2m
B.
2m
C.
2m
D.
m
Câu 6. Hàm s󰉯
32
32y x m x mx m
󰉗t c󰊁c ti󰉨u t󰉗󰉨m
2x
khi:
A.
0m
B.
11
2
m
C.
4m
D.
4m 
Câu 7. Hàm s󰉯
3 2 2
1
1 3 2 5
3
y x m x m m x
󰉗t c󰊁c tr󰉬 t󰉗i
0x
khi:
A.
1m
B.
2m
C. 󰉧 D. 󰉧u sai.
Câu 8. Hàm s󰉯
3 2 2
1
1
3
y x mx m m x
󰉗t c󰊁c tr󰉬 t󰉗i
1x
khi:
A.
0m
B.
1m
C.
2m
D.
3m
Câu 9. Hàm s󰉯
4 2 2
25y x m x
󰉗t c󰊁c ti󰉨u t󰉗i
1x 
khi:
A.
1m
B.
1m 
C. 󰉧 D. 󰉧u sai.
Câu 10. Hàm s󰉯
42
2 2 3y x m x m
󰉗t c󰊁󰉗i t󰉗󰉨m
1x
khi:
A.
3m
B.
5m
C.
3m
D.
5m
Câu 11. Hàm s󰉯
42
31y x mx
󰉗t c󰊁c ti󰉨u t󰉗󰉨m
2x 
khi:
A.
8
3
m 
B.
8
3
m
C.
3m
D.
8m
Câu 12. . Hàm s󰉯
42
1
4
y x ax b
có c󰊁c tr󰉬 t󰉗i
1x
và giá tr󰉬 c󰊁c tr󰉬 󰉼󰉴󰉽ng b󰉟ng
2
thì giá tr󰉬 c󰉻a l󰉚󰉼󰉹t là:
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 37
A.
1
2
9
4
a
b
B.
1
2
9
4
a
b

C.
1
2
9
4
a
b

D.
1
2
9
4
a
b


Câu 13. 󰉰 th󰉬 hàm s󰉯
42
y ax bx c
󰉗t c󰊁󰉗i t󰉗i
0; 3A
󰉗t c󰊁c ti󰉨u t󰉗i
1; 5B 
thì s󰉥 có giá tr󰉬 c󰉻a
,,abc
l󰉚󰉼󰉹t là:
A.
2;4; 3
B.
3; 1; 5
C.
2;4; 3
D.
2; 4; 3
Câu 14. Hàm s󰉯
32
5y ax x x b
󰉗t c󰊁c ti󰉨u t󰉗i
1x
và giá tr󰉬 c󰊁c ti󰉨u b󰉟ng
2
khi:
A.
1
5
a
b

B.
1
5
a
b
C.
1
5
a
b

D.
1
1
a
b

Câu 15. Hàm s󰉯
32
2 4 2016y x ax bx
󰉗t c󰊁󰉗i t󰉗i
1x
󰉱ng
ab
là:
A.
4
3
B.
4
3
C.
3
4
D.
3
4
ĐỀ 03
Câu 1. Hàm s󰉯
1
.sin sin3
3
y m x x
󰉗t c󰊁c tr󰉬 t󰉗󰉨m
3
x
khi:
A.
2m 
B.
0m
C.
2m
D.
3m
Câu 2. Hàm s󰉯
2
1x mx
y
xm

󰉗t c󰊁c ti󰉨u t󰉗i
1x
khi:
A.
2m 
B.
20mm
C.
0m
D. Không có th󰉮a yêu c󰉚u bài toán.
Câu 3. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 󰉨 hàm s󰉯
3 2 2
2 1 4 1y x m x m x m
󰉗t c󰊁c ti󰉨u t󰉗i
0x
A.
2m
B.
2m 
C.
3m 
D.
3m
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 38
Câu 4. Cho hàm s󰉯
3
21y x mx
. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯 󰉗t c󰊁c ti󰉨u
t󰉗i
1x
A.
3
2
m
B.
3
2
m 
C.
2
3
m
D.
2
3
m 
Câu 5. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 󰉨 hàm s󰉯
42
31y x mx m
󰉗t
c󰊁c ti󰉨u t󰉗i
0x
A.
0m
B. Không có giá tr󰉬 th󰊁c nào c󰉻a m th󰉮a mãn yêu c󰉚󰉧 bài.
C.
0m
D.
0m
Câu 6. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
3
21y x mx
󰉗t c󰊁c ti󰉨u t󰉗i
1x
là:
A.
2
3
m 
B.
2
3
m
C.
3
2
m 
D.
3
2
m
Câu 7. Hàm s󰉯
3 2 2
3 3 1y x mx m x
󰉗t c󰊁c ti󰉨u t󰉗i
0
1x
khi :
A.
2m
B.
0m
C.
0
2
m
m
D.
0
2
m
m
Câu 8. Hàm s󰉯
3 2 2
1
45
3
y x mx m x
󰉗t c󰊁c ti󰉨u t󰉗i
1x 
khi:
A.
3m 
B.
1m 
C.
0m
D.
1m
Câu 9. 󰉰 th󰉬 hàm s󰉯
32
y ax bx cx d
󰉨m c󰊁c tr󰉬
0;0 , 1;1AB
thì các h󰉪
s󰉯
, , ,a b c d
có giá tr󰉬 l󰉚󰉼󰉹t là:
A.
2; 0; 0; 3a b c d
B.
0; 0; 2; 3a b c d
C.
2; 0; 3; 0a b c d
D.
2; 3; 0; 0a b c d
Câu 10. Hàm s󰉯
3 2 2
22y x mx m x
󰉗t c󰊁c ti󰉨u t󰉗i
1x
khi m b󰉟ng:
A.
1m 
B.
1m
C.
2m
D.
2m 
Câu 11. Bi󰉦󰉰 th󰉬 hàm s󰉯
42
2y x px q
có m󰉳󰉨m c󰊁c tr󰉬 là
1;2M
,th󰉦 thì
kho󰉘ng cách gi󰊀󰉨m c󰊁c ti󰉨󰉨m c󰊁󰉗i là:
A.
26
B.
5
C.
2
D.
2
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 39
Câu 12. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
3 2 2
1
11
3
y x mx m m x
󰉗t c󰊁󰉗i t󰉗󰉨m
1x
A.
1m
B.
2m
C.
1; 2mm
D. Không có m
Câu 13. V󰉵i giá tr󰉬 nào c󰉻a m thì hàm s󰉯
3 2 2
3 3 1y x mx m
󰉗t c󰊁󰉗i t󰉗i
1x
A. Không có giá tr󰉬 m B.
2m
C.
1m 
D.
2m 
Câu 14. Hàm s󰉯
32
1
2 1 3
3
y x m x m
󰉗t c󰊁󰉗i t󰉗i
0x
khi và ch󰉫 khi:
A.
1
2
m
B.
1
2
m
C.
1
2
m
D.
1
2
m
Câu 15. 󰉨 hàm s󰉯
32
3 12 2y mx x x
󰉗t c󰊁󰉗i t󰉗i
0
2x
A.
2m 
B.
3m 
C.
0m
D.
1m 
ĐỀ 04
Câu 1. Hàm s󰉯
42
1
4
y x ax b
có c󰊁c tr󰉬 t󰉗i
1x
và giá tr󰉬 󰉼󰉴󰉽ng b󰉟ng 2 thì giá
tr󰉬 c󰉻a a, b l󰉚󰉼󰉹t là
A.
1
2
9
4
a
b
B.
1
2
9
4
a
b

C.
1
2
9
4
a
b

D.
1
2
9
4
a
b


Câu 2. 󰉨 hàm s󰉯
42
2 2 1 3 2y mx m x m
󰉗t c󰊁c ti󰉨u t󰉗i
1x
A.
2m 
B.
1m 
C.
2m
D.
1m
Câu 3. 󰉨 hàm s󰉯
2
14x m x m
y
xm
󰉗t c󰊁󰉗i t󰉗i
1x
A.
3m 
B.
3m
C.
3; 1mm
D.
3; 1mm
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 40
Câu 4. Hàm s󰉯
2
x mx m
y
xm

󰉗t c󰊁c 󰉗i t󰉗i
2x
thì m b󰉟ng
A.
1m 
B.
3m 
C.
1m
D. Không t󰉰n t󰉗i m
Câu 5. 󰉨 hàm s󰉯
53
2
1 2 2
53
xx
y m m x
󰉗t c󰊁c tr󰉬 t󰉗i
1x
A.
1m
B.
2m 
C.
1; 2mm
D. Không t󰉰n t󰉗i m
Câu 6. Hàm s󰉯
32
3y x x mx
󰉗t c󰊁c ti󰉨u t󰉗i
2x
thì giá tr󰉬 c󰉻a m là
A.
0m
B.
0m
C.
0m
D.
0m
Câu 7. 󰉨 hàm s󰉯
3 2 2
1
1 3 2 5
3
y x m x m x x
󰉗t c󰊁c ti󰉨u t󰉗i
0x
A.
6m
B.
2m
C.
1m
D.
1; 2mm
Câu 8. Hàm s󰉯
4 2 2
11y x m x m m x
󰉗t c󰊁󰉗i t󰉗i
0x
khi
A.
1m
B.
0m
C.
0; 1mm
D. Không t󰉰n t󰉗i m
Câu 9. Hàm s󰉯
4 2 2
5y x m x
󰉗t c󰊁󰉗i t󰉗i
2x 
khi
A.
2m 
B.
2m
C.
2m 
D. Không t󰉰n t󰉗i m
Câu 10. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 m sao cho hàm s󰉯
42
1y x m x m
󰉗t c󰊁c ti󰉨u t󰉗i
0x
A.
1m
B.
1m
C.
1m
D.
1m
Câu 11. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
32
2y x x mx
󰉗t c󰊁c ti󰉨u t󰉗i
1x 
là
A.
1m
B.
1m 
C.
1m
D.
1m 
Câu 12. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
4 2 2
12y mx m x m
󰉗t c󰊁c ti󰉨u
t󰉗i
1x
là
A.
1m 
B.
1
3
m
C.
1m
D.
1
3
m 
Câu 13. 󰉨 hàm s󰉯
2
23
2
x mx
y
x

󰉗t c󰊁c ti󰉨u t󰉗i
1x
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 41
A.
1m 
B.
2m 
C.
1m
D.
3m 
Câu 14. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
2
1x mx
y
xm

󰉗t c󰊁c tr󰉬 t󰉗i
2x
A.
3; 1mm
B.
1m 
C.
3m 
D.
4m
Câu 15. Hàm s󰉯
2
22x mx
y
xm

󰉗t c󰊁c ti󰉨u t󰉗i
2x
khi
A.
1m 
B.
1m
C.
1m 
D. không t󰉰n t󰉗i m
Câu 30. (SGD HCM cụm 4, 2017) Tìm
a
,
b
,
c
󰉰 th󰉬 hàm s󰉯
42
y ax bx c
qua
O
và có m󰉳󰉨m c󰊁c ti󰉨u
3; 9 .A
A.
1; 6; 0.a b c
B.
1; 6; 0.a b c
C.
1; 0; 0.a b c
D.
1; 6; 0.a b c
Câu 16. (SGD HCM cụm 7, 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 󰉨 hàm s󰉯
3 2 2
y x 2mx m x 2
󰉗t c󰊁c ti󰉨u t󰉗i
x 1.
A.
m 1.
B.
m 3.
C.
m 1 m 3.
D.
m 1.
Câu 17. (SGD HCM cụm 7, 2017) Bi󰉦t r󰉟󰉰 th󰉬 hàm s󰉯
42
y f x ax bx c
có
󰉨m c󰊁c tr󰉬 là
A 0;2 ,B 2; 14 .
Tính
f 1 .
A.
f 1 5.
B.
f 1 0.
C.
f 1 6.
D.
f 1 7.
Câu 18. (SGD Đà Nẵng, 2017) Cho hàm s󰉯
32
2 3 1y x mx m
v󰉵i
m
là tham s󰉯. Tìm
t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯
m
󰉨 hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
2.x
A.
2.m
B.
1.m 
C.
1.m
D.
0.m
Câu 19. (THPT Nguyễn Đình Chiểu Bình Định 2017) Hàm s󰉯
3
22
x 1 x 1
3
x
y m m
󰉗t c󰊁󰉗i t󰉗i
1x
khi giá tr󰉬
m
là
A. 1. B. 0. C. 2. D.
2
.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 42
VẤN ĐỀ 3. TÌM THAM SỐ M ĐỂ HÀM SỐ CÓ HOẶC KHÔNG CÓ CỰC TRỊ
Phương pháp
Bi󰉪n lu󰉝n s󰉯 nghi󰉪m c󰉻󰉼󰉴
y
A. ÁP DỤNG
Ví dụ 1. Cho hàm s󰉯
32
1
2 5 8 1
3
y x mx m x
. 󰉨 hàm s󰉯 có m󰉳t c󰊁󰉗i và
m󰉳t c󰊁c ti󰉨u? Đs:
2; 8mm
Ví dụ 2. Cho hàm s󰉯
2
2
1
x m x m
y
x
. 󰉨 hàm s󰉯 có m󰉳t c󰊁󰉗i và m󰉳t c󰊁c
ti󰉨u? Đs:
1
2
m 
Ví dụ 3. Cho hàm s󰉯
42
13
22
y x mx
󰉨 hàm s󰉯 có c󰊁c ti󰉨u mà không có c󰊁c
󰉗i? Đs:
0m
Ví dụ 4. Cho hàm s󰉯
32
1
2 4 1 4
3
y x m x m x m
󰉨 hàm s󰉯 󰉨m c󰊁c
󰉗i và c󰊁c ti󰉨󰉨m c󰊁c ti󰉨u n󰉟󰉼󰉶ng th󰉠ng
: 3 8 0d x y
Đs:
1m
Ví dụ 5. Cho hàm s󰉯
32
3
2 3 1 1
2
y x m x m x
󰉨 hàm s󰉯 có c󰊁󰉗i và
c󰊁c ti󰉨󰉰ng th󰉶󰉳 󰉨m c󰊁c ti󰉨u nh󰉮 󰉴 Đs:
3, 0mm
Ví dụ 6. Cho hàm s󰉯
32
3 1 3 2 1y x m x m m x
󰉨 hàm s󰉯 có c󰊁󰉗i và
c󰊁c ti󰉨󰉰ng th󰉶i giá tr󰉬 c󰊁󰉗i l󰉵󰉴 Đs:
3, 0mm
B. BÀI TẬP VẬN DỤNG
Bài tập 1. 󰉨 hàm s󰉯 sau có c󰊁󰉗i và c󰊁c ti󰉨u
1)
2 3 2
1
1 1 3 5
3
y m x m x x
Đs:
1 2; 1mm
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 43
2)
32
35y x mx mx
Đs:
0; 9mm
3)
32
23y m x x mx m
Đs:
3 1; 2mm
Bài tập 2. 󰉨 hàm s󰉯 sau có c󰊁󰉗i và c󰊁c ti󰉨u
1)
2
2x mx m
y
xm

Đs:
10m
2)
2
11
2
mx m x
y
mx
Đs:
2; 0mm
Bài tập 3. 󰉨 hàm s󰉯 󰉨m c󰊁c tr󰉬
1)
4 2 2
9 10y mx m x
Đs:
3;0 3mm
2)
42
23y x mx
Đs:
0m
Bài tập 4. 󰉨 hàm s󰉯 󰉨m c󰊁c tr󰉬
1)
42
1 1 2y mx m x m
Đs:
0; 1mm
2)
42
1 2 1y m x mx m
Đs:
0; 1mm
Bài tập 5. 󰉨 hàm s󰉯 không có c󰊁c tr󰉬
1)
32
3 4 3y mx x m x
Đs:
13m
2)
32
3 2 3y m x mx
Đs:
0m
Bài tập 6. 󰉨 hàm s󰉯 sau không có c󰊁c tr󰉬
1)
2
31
2
mx mx
y
x

Đs:
0; 1mm
2)
2
31
2
mx mx
y
x

Đs:
0; 1mm
Bài tập 7. 󰉨 hàm s󰉯
42
13
22
y x mx
có c󰊁c ti󰉨u mà không có c󰊁󰉗i.
Bài tập 8. Cho hàm s󰉯
2
11
1
x m x m
y
x
. Ch󰉽ng minh v󰉵i m󰉭󰉰 th󰉬 hàm s󰉯
󰉨m c󰊁󰉗i, c󰊁c ti󰉨u và kho󰉘ng cách gi󰊀󰉨
20
.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 44
Bài tập 9. Cho hàm s󰉯
2
1
x mx m
y
x

. Ch󰉽ng minh v󰉵i m󰉭󰉰 th󰉬 hàm s󰉯 luôn có
󰉨m c󰊁󰉗i, c󰊁c ti󰉨u và kho󰉘ng cách gi󰊀󰉨󰉱i.
Bài tập 10. Ch󰉽ng minh hàm s󰉯
2
2
2
2
x x m
y
x

luôn có m󰉳t c󰊁󰉗i và m󰉳t c󰊁c ti󰉨u
Bài tập 11. 󰉨 hàm s󰉯
2 2 2
2 5 3x m x m m
y
x
có c󰊁c ti󰉨u trong kho󰉘ng
0;2m
Đs:
13
1;
22
mm
Bài tập 12. Cho hàm s󰉯
32
2 3 2 1 6 1 1y x m x m m x
󰉨 hàm s󰉯 có c󰊁󰉗i
và c󰊁c ti󰉨u và giá tr󰉬 c󰊁󰉗i l󰉵󰉴 Đs:
3
0
2
m
C. BÀI TẬPTRẮC NGHIỆM
ĐỀ 01.
Câu 1. Cho hàm s󰉯
32
1
4 3 1
3
y x mx m x
󰉬nh các giá tr󰉬 c󰉻󰉨 hàm s󰉯
󰉗t c󰊁󰉗i và c󰊁c ti󰉨u?
A.
13m
B.
1m
C.
3m
D.
13mm
Câu 2. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
42
2y x mx
󰉳󰉨m c󰊁c tr󰉬 :
A.
0m
B.
0m
C.
1m 
D.
0m
Câu 3. 󰉨 hàm s󰉯
3 2 2
1
12
3
y x m x m m x
có c󰊁󰉗i và c󰊁c ti󰉨u
A.
2m
B.
1
3
m 
C.
2
3
m 
D.
1m 
Câu 4. Hàm s󰉯
3 2 2
1
21
3
y x mx m m x
󰉨m c󰊁c tr󰉬 khi và ch󰉫 khi:
A.
0m
B.
0m
C.
0m
D.
0m
Câu 5. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
42
21y mx x
󰉨m c󰊁c tr󰉬.
A.
0m
B.
0m
C.
0m
D.
0m
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 45
Câu 6. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 m sao cho hàm s󰉯
32
5y x x mx
có hai
c󰊁c tr󰉬. Ch󰉭n k󰉦t qu󰉘 
A.
1
3
m
B.
1
3
m
C.
1
3
m
D.
1
3
m
Câu 7. Hàm s󰉯
32
17
3
m
y x m x mx
có hai c󰊁c tr󰉬 khi và ch󰉫 khi:
A.
1
2
0
m
m

B.
3m
C.
0m
D.
5m
Câu 8. Cho hàm s󰉯
32
3 3 1 2y x x m x
. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
có c󰊁c tr󰉬.
A.
0m
B.
2m
C.
2m
D.
0m
Câu 9. T󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
32
1
2 5 8 1
3
y x mx m x
󰉗t c󰊁󰉗i và
c󰊁c ti󰉨u.
A.
28mm
B.
28m
C.
28m
D.
28mm
Câu 10. Tìm t󰉙t c󰉘 giá tr󰉬 󰉨 hàm s󰉯
42
3 2 1y mx m x m
ch󰉫 󰉗t c󰊁󰉗i mà
không có c󰊁c ti󰉨u
A.
3m 
B.
0m
C.
3
0
m
m
D.
3m
ĐỀ 02
Câu 1. Tìm t󰉙t c󰉘 giá tr󰉬 󰉨 hàm s󰉯
4 2 2 2
12y m x m m x m
󰉨m c󰊁c
tr󰉬
A.
01
2
m
m

B.
12
0
m
m

C.
11
2
m
m
D.
12
1
m
m


Câu 2. Hàm s󰉯
3
23y x mx
󰉨m c󰊁c tr󰉬 khi :
A.
0m
B.
0m
C.
0m
D.
0m
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 46
Câu 3. 󰉰 th󰉬 hàm s󰉯
42
0y ax bx c a
󰉨m c󰊁c tr󰉬 khi và ch󰉫 khi:
A.
0b
B.
0ab
C.
0ab
D.
0ab
Câu 4. 󰉰 th󰉬 hàm s󰉯
42
0y ax bx c a
có m󰉳󰉨m c󰊁c tr󰉬 khi và ch󰉫 khi:
A.
0b
B.
0ab
C.
0ab
D.
0b
Câu 5. 󰉰 th󰉬 hàm s󰉯
42
0y ax bx c a
󰉨m c󰊁󰉗󰉨m c󰊁c ti󰉨u
khi và ch󰉫 khi:
A.
0
0
a
b
B.
0
0
a
b
C.
0
0
a
b
D.
0
0
a
b
Câu 6. 󰉰 th󰉬 hàm s󰉯
42
0y ax bx c a
 󰉨m c󰊁c ti󰉨󰉨m c󰊁󰉗i
khi và ch󰉫 khi:
A.
0
0
a
b
B.
0
0
a
b
C.
0
0
a
b
D.
0
0
a
b
Câu 7. 󰉰 th󰉬 hàm s󰉯
32
,0y ax bx cx d a
󰉨m c󰊁c tr󰉬 khi và ch󰉫 khi:
A.
2
4 12 0b ac
B.
2
4 12 0b bc
C.
2
4 12 0b ac
D.
2
4 12 0b ac
Câu 8. 󰉰 th󰉬 hàm s󰉯
32
,0y ax bx cx d a
 󰉨m c󰊁c tr󰉬 khi và ch󰉫 khi:
A.
2
4 12 0b ac
B.
2
4 12 0b bc
C.
2
4 12 0b ac
D.
2
4 12 0b ac
Câu 9. 󰉧u ki󰉪n c󰉻a tham s󰉯 󰉨 hàm s󰉯
32
3 3 2y x x mx m
có c󰊁c tr󰉬 là:
A.
1m
B.
1m
C.
1m
D.
1m
Câu 10. Hàm s󰉯
3
1y x mx
có 2 c󰊁c tr󰉬 khi:
A.
0m
B.
0m
C.
0m
D.
0m
ĐỀ 03
Câu 1. V󰉵i giá tr󰉬 nào c󰉻a m thì hàm s󰉯
32
3 2 1y x mx x m
có c󰊁󰉗i, c󰊁c ti󰉨u ?
A.
3;3m
B.
; 3 3;mm  
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 47
C.
3;3m
D.
; 3 3;m 
Câu 2. Hàm s󰉯
3 2 2 2
3 3 2 1y x mx m m x m
󰉨m c󰊁c tr󰉬 khi:
A.
0m
B.
0m
C.
1m
D.
m
tùy ý.
Câu 3. Hàm s󰉯
32
1
21
3
y x m x mx
có c󰊁󰉗i, c󰊁c ti󰉨u khi:
A.
0m
B.
m
C.
m
D.
1m
Câu 4. Giá tr󰉬 c󰉻a tham s󰉯 󰉨 hàm s󰉯
3
23y m x mx
không có c󰊁c tr󰉬 là:
A.
0
2
m
m
B.
2m
C.
0
2
m
m
D.
02m
Câu 5. 󰉰 th󰉬 hàm s󰉯
33
3
y x a x b x
có c󰊁󰉗i, c󰊁c ti󰉨u khi:
A.
.0ab
B.
.0ab
C.
.0ab
D.
.0ab
Câu 6. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
2 2 1y x mx m
󰉨m c󰊁c tr󰉬 ?
A.
0m
B.
1m 
C.
0m
D.
1m
Câu 7. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
21y x m x m
󰉨m c󰊁c tr󰉬 ?
A. Không có m B.
1m
C.
1m
D.
1m
Câu 8. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
4 2 2
2 2 5 5y x m x m m
 󰉨m
c󰊁c tr󰉬 ?
A.
2m
B.
3m
C.
1m
D.
1m
Câu 9. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
2 1 1y x m x m
󰊁c tr󰉬 ?
A.
1m 
B.
1m 
C. 󰉧 D. 󰉧u sai.
Câu 10. 󰉰 th󰉬 hàm s󰉯
42
11
4
m
y x m x m
 󰉨m c󰊁c tr󰉬 khi:
A.
01m
B.
1m
C.
0m
D.
;0 1;mm
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 48
ĐỀ 04
Câu 1. 󰉰 th󰉬 hàm s󰉯
42
2 1 2y x m x
có c󰊁c ti󰉨u mà không có c󰊁󰉗i khi:
A.
1m
B.
1m
C.
1m
D.
1m
Câu 2. 󰉰 th󰉬 hàm s󰉯
42
2 5 2y x m x
có c󰊁󰉗i mà không có c󰊁c ti󰉨u khi:
A.
5m
B.
5m
C.
5m
D.
5m
Câu 3. Hàm s󰉯
2
2 2 1
21
x mx m
y
x
󰉨m c󰊁c tr󰉬 khi:
A.
1m 
B.
1m 
C.
1m 
D.
m
Câu 4.
Có t󰉙t c󰉘 bao nhiêu s󰉯 nguyên m th󰉮󰉧u ki󰉪n hàm s󰉯
3 2 2
1
2 25 10
3
y x mx m x
có hai c󰊁c tr󰉬
A.
13
B.
10
C.
9
D.
7
Câu 5. Tìm t󰉙t c󰉘 các giá tr󰉬 󰉨 hàm s󰉯
3 2 2
1
2 4 1
3
y x mx m x m
A.
2
2
m
m

B.
22m
C.
1
1
m
m

D.
2m
Câu 6. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
3y x mx
 󰉨m c󰊁c tr󰉬 ?
A.
0m
B.
0m
C.
0m
D. Không có m
Câu 7. 󰉰 th󰉬 hàm s󰉯
42
24y x m x m
có 2 c󰊁󰉗i, 1 c󰊁c ti󰉨u khi:
A.
2m
B.
2m
C.
2m
D.
2m
Câu 8. Tìm tham s󰉯 󰉨 hàm s󰉯
3 2 2
33y x mx m
󰉨m c󰊁c tr󰉬 ?
A.
0m
B.
0m
C.
0m
D.
0m
Câu 9. 󰉰 th󰉬 hàm s󰉯
32
3 3 3 4y x mx mx m
không có c󰊁c tr󰉬 khi:
A.
0m
B.
1m
C.
01m
D.
01m
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 49
Câu 10. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
1 2 1y m x mx m
󰊁c tr󰉬 ?
A.
m
B.
0m
C.
01m
D.
\ 0;1
ĐỀ 05
Câu 1. Tính t󰉱ng t󰉙t c󰉘 các tham s󰉯 m th󰉮󰉧u ki󰉪n hàm s󰉯
3 2 2
11
1
32
y x m x mx
󰉗t c󰊁c ti󰉨u t󰉗i
1x
A.
2
B.
1
C.
1
D.
0
Câu 2. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
32
3 12 10y x mx x
có hai c󰊁c tr󰉬
A.
2
2
m
m

B.
22m
C.
1
1
m
m

D.
2m
Câu 3. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨
32
1
3
m
y x m x mx
có c󰊁c tr󰉬
A.
2
0
m
m

B.
1
0
m
m

C.
1
2
m 
D.
0m
Câu 4. Có t󰉙t c󰉘 bao nhiêu s󰉯 nguyên m th󰉮󰉧u ki󰉪n hàm s󰉯
3 2 2
3 3 2 16 2017y x mx m x m
có hai c󰊁c tr󰉬
A.
13
B.
10
C.
9
D.
7
Câu 5. Có t󰉙t c󰉘 bao nhiêu s󰉯 nguyên m th󰉮󰉧u ki󰉪n hàm s󰉯
2 3 2
2 16 3 2y m x x x m
có 󰉳t c󰊁c tr󰉬
A.
3
B.
2
C.
0
D. Vô s󰉯
Câu 6. Hàm s󰉯
32
1
1 2 3 2 1
3
y m x mx m x
có c󰊁󰉗i, c󰊁c ti󰉨u khi và ch󰉫 khi.
A.
5 33 5 33
; ; \ 1
22
m

 
B.
5 33 5 33
; ; \ 1
22
m

 


DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 50
C.
5 33 5 33
;
22
m




D.
5 33 5 33
;;
22
m

 


Câu 7. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 m sao cho hàm s󰉯
42
13
22
y x mx
có m󰉳t
c󰊁c tr󰉬
A.
0m
B.
0m
C.
0m
D.
0m
Câu 8. Cho hàm s󰉯
32
2 3 3 11 3y x m x m
󰉬󰉨 hàm s󰉯 có c󰊁󰉗i và c󰊁c
ti󰉨u
A.
3m
B.
3m
C.
3m
D.
m
Câu 9. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻󰉨 hàm s󰉯
3
1y x mx
có 2 c󰊁c tr󰉬.
A.
0m
B.
0m
C.
0m
D.
0m
Câu 10. Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻󰉨 hàm s󰉯
4 2 2
21y x mx m
󰉨m
c󰊁c tr󰉬.
A.
0m
B.
0m
C.
0m
D.
0m
ĐỀ 06
Câu 1. Cho hàm s󰉯
32
1
2 1 1
3
y x mx m x
M󰉪󰉧 
A.
1m
thì hàm s󰉯 󰉨m c󰊁c tr󰉬
B. Hàm s󰉯 luôn luôn có c󰊁󰉗i và c󰊁c ti󰉨u
C.
1m
thì hàm s󰉯 có c󰊁󰉗i và c󰊁c ti󰉨u
D.
1m
thì hàm s󰉯 có c󰊁c tr󰉬
Câu 2. Tìm t󰉙t c󰉘 giá tr󰉬 󰉨 hàm s󰉯
32
36y x mx mx m
󰉨m c󰊁c tr󰉬
A.
0
2
m
m
B.
08m
C.
0
8
m
m
D.
0
2
m
m
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 51
Câu 3. Cho hàm s󰉯
42
2 2 1y x mx m
. V󰉵i giá tr󰉬 nào c󰉻a m thì hàm s󰉯 󰉨m
c󰊁c tr󰉬:
A.
0m
B.
0m
C.
0m
D.
0m
Câu 4. V󰉵i giá tr󰉬 nào c󰉻a tham s󰉯 󰉨 hàm s󰉯
32
11
21
32
y x mx x
có c󰊁c tr󰉬 là:
A. 0 B. 3 C. 4 D. C󰉘 A, B, C.
Câu 5. 󰉧u ki󰉪n c󰉻󰉨 hàm s󰉯
32
32y x x mx m
 󰉨m c󰊁c tr󰉬 là:
A.
3m
B.
3m
C.
m
D.
m
Câu 6. Hàm s󰉯
32
12y x m x x
có c󰊁󰉗i, c󰊁c ti󰉨u khi:
A.
1 3 1 3m
B.
1 3 1 3m
C.
13
13
m
m


D.
13
13
m
m


Câu 7. Hàm s󰉯
3 2 2
1
1 3 4 1
3
y x m x m m x m
có c󰊁󰉗i, c󰊁c ti󰉨u khi:
A.
01m
B.
01m
C.
0m
D.
1m
Câu 8. Hàm s󰉯
32
3 2 2y x m x mx
có c󰊁󰉗i và c󰊁c ti󰉨u khi:
A.
3m
B.
6 3 3 6 3 3m
C.
6 3 3
6 3 3
m
m


D.
6 3 3
6 3 3
m
m


Câu 9. 󰉰 th󰉬 hàm s󰉯
32
2 2 6 3 1y x m x m x m
không có c󰊁c tr󰉬 khi:
A.
16m 
B.
2m
C.
16 2m
D.
2 16m
Câu 10. 󰉰 th󰉬 hàm s󰉯
32
3 1 1y mx mx m x
không có c󰊁c tr󰉬 khi:
A.
1
0
4
m
B.
1
0
4
m
C.
0m
D.
1
4
m
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 52
ĐỀ 07
Câu 1. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
4 2 2
3y x m x
󰉨m c󰊁c tr󰉬 ?
A.
0m
B.
0m
C.
0m
D.
m
Câu 2. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
2 1 3y x m x
󰉨m c󰊁c tr󰉬 ?
A.
0m
B.
1m 
C.
1m
D.
0m
Câu 3. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
42
1 2 1y x m x m
󰉨m c󰊁c tr󰉬 ?
A.
1m 
B.
1m 
C.
1m 
D.
1m 
Câu 4. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
4 2 4
22y x mx m m
󰉨m c󰊁c tr󰉬 ?
A.
2m 
B.
1m 
C.
0m
D.
2m
Câu 5. 󰉰 th󰉬 hàm s󰉯
42
2 2 1 3y x m x
󰉳󰉨m c󰊁c tr󰉬 khi:
A.
1
2
m
B.
1
2
m
C.
1
2
m
D.
1
2
m
Câu 6. 󰉰 th󰉬 hàm s󰉯
42
2 3 2y x m x
󰉨m c󰊁c tr󰉬 khi:
A.
3m
B.
3m
C.
3m
D.
3m
Câu 7. 󰉰 th󰉬 hàm s󰉯
42
: 2 2 1 3C y x m x
󰉨m c󰊁c tr󰉬 khi
A.
1
2
m
B.
1
2
m
C.
1
2
m
D.
1
2
m
Câu 8. 󰉰 th󰉬 hàm s󰉯
42
15
22
m
y x mx
có c󰊁󰉗i mà không có c󰊁c ti󰉨u khi:
A.
1;0m
B.
1;0m
C.
1;0m
D.
1;0m
Câu 9. Hàm s󰉯
2
1x mx
y
xm

luôn có c󰊁c tr󰉬 khi:
A.
0m
B.
1m
C.
m
D.
m
Câu 10. Tìm tham s󰉯 󰉨 󰉰 th󰉬 hàm s󰉯
2
4 2 2
23y x m x m
󰉨m c󰊁c tr󰉬 ?
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 53
A.
3m
B.
0m
C.
0m
D.
0m
Câu 11. (SGD HCM cụm 7, 2017) 󰉨 hàm s󰉯
42
y mx 2 m 1 x 2
có hai
c󰊁c ti󰉨u và m󰉳t c󰊁󰉗i.
A.
m 0.
B.
0 m 1.
C.
m 2.
D.
1 m 2.
Câu 12. (SGD HCM cụm 1, 2017) 󰉰 th󰉬 hàm s󰉯
42
1 4y x m x
󰉨m c󰊁c
tr󰉬 khi và ch󰉫 khi:
A.
1m 
. B.
1m 
. C.
1m 
. D.
1m 
.
Câu 13. (Nguyễn Thái Học, Vĩnh Phúc, Lần 1, 2017) Hàm s󰉯
32
3 1 3 1 y mx m x m x m
có c󰊁c tr󰉬 khi và ch󰉫 khi
A.
1
; \ 0
3




m
. B.
1
;
3




m
. C.
1
3
m
. D.
1m
.
VẤN ĐỀ 4. PHƯƠNG TRÌNH ĐƯỜNG THẲNG ĐI QUA CÁC ĐIỂM CỰC TRỊ
Phương pháp
1) Cho hàm số
32
(C)y ax bx cx d
+) N󰉦󰉨m c󰊁c tr󰉬 󰉼󰉹c:
.y y mx n x

󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 là:
yx


2) Cho hàm số
2
ax bx c
y
Ax B

+) N󰉦󰉨m c󰊁c tr󰉬
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 54
󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 là:
2
ax bx c
y
Ax B

Ví dụ 1. Cho hàm s󰉯:
3
3y x mx m C
.
1) Tìm m 󰉨 󰉨m c󰊁c tr󰉬?
2) Vi󰉦󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻a (C)
Đs:
0; 2m y mx m
Ví dụ 2. Cho hàm s󰉯:
3 2 2 3 2
3 3 1y x mx m x m m C
.
 󰉨 󰉨m c󰊁c tr󰉬?
2) Vi󰉦󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻a (C)
Đs:
2
;2m y x m m
Ví dụ 3. Cho hàm s󰉯
2
11x m x m
y
xm
 󰉨 󰉨m c󰊁c tr󰉬?
2) Vi󰉦󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻a (C)
Đs:
; 2 1m y x m
Ví dụ 4. Cho hàm s󰉯
2
22
1
x x m
y
xm

 󰉨 󰉨m c󰊁c tr󰉬?
2) Vi󰉦󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻a (C)
Đs:
; 2 2m y x
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Cho hàm s󰉯:
3 2 2
3 1 2 3 2 1y x m x m m x m m C
.
 󰉨 󰉨m c󰊁c tr󰉬?
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 55
2) Vi󰉦󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻a (C)
Đs:
22
3 5 3 5 2 2
; ; 3 1 3 1 1
2 2 3 3
m m y m m x m m m

Bài tập 2. Cho hàm s󰉯
3
2
1
3
mx
y mx x
󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u và tung
󰉳 󰉨m c󰊁󰉗i, c󰊁c ti󰉨u .
1) Cùng d󰉙u Đs:
1m
2) Trái d󰉙u Đs:
0m
Bài tập 3. Cho hàm s󰉯
32
6 3 2 6y x x m x m
󰉨 hàm s󰉯 có c󰊁󰉗i và c󰊁c
ti󰉨󰉰ng th󰉶i hai giá tr󰉬 c󰊁c tr󰉬 cùng d󰉙u ? Đs:
17
2
4
m
Bài tập 4. Cho hàm s󰉯
32
3 1 3 1 1y x m x m x
󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c
ti󰉨󰉰ng th󰉶󰉼󰉶ng th󰉠ng n󰉯󰉨m c󰊁c tr󰉬 󰉨m
0; 3M
?
Đs:
1; 3mm
Bài tập 5. Cho hàm s󰉯
32
2 3 1 6 2 1y x m x m x
󰉨 󰉰 th󰉬 hàm s󰉯 có c󰊁c
󰉗i, c󰊁c ti󰉨󰉰ng th󰉶󰉼󰉶ng th󰉠ng n󰉯󰉨m c󰊁c tr󰉬 󰉵󰉼󰉶ng th󰉠ng
43yx
? Đs:
1; 5mm
Bài tập 6. Cho hàm s󰉯
32
3 3 1 3 1y x x m x m C
󰉨 󰉰 th󰉬 hàm s󰉯 có
c󰊁󰉗i, c󰊁c ti󰉨󰉰󰉨m c󰊁c tr󰉬 󰉵i g󰉯c t󰉭a 󰉳 O t󰉗o thành m󰉳t tam giác
di󰉪n tích là 4 ? Đs:
1m
Bài tập 7. Cho hàm s󰉯
32
1
3
y x x mx m
󰉨 󰉰 th󰉬 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u
󰉰ng kho󰉘ng cách gi󰊀󰉨m c󰊁c tr󰉬 󰉟ng
2 15
? Đs:
1m
Bài tập 8. Cho hàm s󰉯
32
11
1
32
y x m x mx
󰉨 󰉰 th󰉬 hàm s󰉯 có c󰊁󰉗i, c󰊁c
ti󰉨󰉰ng th󰉶󰉨m c󰊁c tr󰉬 󰉯i x󰉽󰉼󰉶ng th󰉠ng
24 4 33 0xy
Đs:
1m
Bài tập 9. Cho hàm s󰉯
32
2 3 1 6y x m x mx
󰉨 󰉰 th󰉬 hàm s󰉯 có hai c󰊁c tr󰉬 A
󰉼󰉶ng th󰉠ng AB vuông góc v󰉵󰉼󰉶ng th󰉠ng
2yx
?
Đs:
0; 2mm
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 56
Bài tập 10. Cho hàm s󰉯
32
73y x mx x
󰉨 󰉰 th󰉬 hàm s󰉯 có hai c󰊁c tr󰉬 󰉰ng
th󰉶󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 󰉵󰉼󰉶ng
35yx
?
Đs:
3 10
2
m 
Bài tập 11. Cho hàm s󰉯
32
3
3 1 1
2
y x mx m x
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m
c󰊁c tr󰉬 󰉰ng th󰉶󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 󰉵󰉼󰉶ng th󰉠ng
1yx
? Đs:
33
3
m
Bài tập 12. Cho hàm s󰉯
3 2 3
34y x ax a
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬 󰉯i
x󰉽󰉼󰉶ng
yx
? Đs:
2
2
m 
Bài tập 13. Cho hàm s󰉯
32
2 3 2 1 6 1 1y x m x m m x
󰉨 󰉰 th󰉬 hàm s󰉯 có
󰉨m c󰊁c tr󰉬 󰉯i x󰉽󰉼󰉶ng
2yx
? Đs:
1 17
1;
4
mm

Bài tập 14. Cho hàm s󰉯
32
32y x x mx m
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬
󰉯i x󰉽󰉼󰉶ng
3
4
yx
? Đs:
3
4
m
Bài tập 15. Cho hàm s󰉯
32
2 3 3 6 1y x mx m x
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m
c󰊁c tr󰉬 󰉰ng th󰉶󰉨m A, B và
3;5C
th󰉠ng hàng? Đs:
4m
Bài tập 16. Cho hàm s󰉯
3 2 3
33y x mx m
󰉨 󰉰 th󰉬 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u
󰉰󰉨m c󰊁c tr󰉬 v󰉵i g󰉯c t󰉭󰉳 O t󰉗o thành m󰉳t tam giác di󰉪n tích là 48 ?
Đs:
2m 
Bài tập 17. Cho hàm s󰉯
32
31y x x m
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬 A,
B cùng v󰉵i
2;4C
t󰉗o thành m󰉳t tam giác di󰉪n tích là 7 ? Đs:
2;3m
Bài tập 18. Cho hàm s󰉯
3
32y x mx
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬 A, B
cùng v󰉵i
1;1C
t󰉗o thành m󰉳t tam giác di󰉪n tích là
32
? Đs:
2m
Bài tập 19. Cho hàm s󰉯
2
21
1
x mx m
y
x
󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u và tung
󰉳 󰉨m c󰊁󰉗i, c󰊁c ti󰉨u .
1) Cùng d󰉙u Đs:
1 5 1 5
;2
22
mm

2) Trái d󰉙u Đs:
1 5 1 5
22
m


DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 57
Bài tập 20. Cho hàm s󰉯
2
8x mx
y
xm

 󰉨 󰉨m c󰊁c tr󰉬?
2) Vi󰉦t 󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻a (C)
Bài tập 21. Cho hàm s󰉯
2
1 3 2
1
x m x m
y
x
󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u và
󰉰ng th󰉶i giá tr󰉬 c󰊁󰉗i, c󰊁c ti󰉨u cùng d󰉙u? Đs:
1 5 4 2; 5 4 2mm
Bài tập 22. Cho hàm s󰉯
2
1 3 2
1
x m x m
y
x
󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u và
󰉰ng th󰉶i giá tr󰉬 c󰊁󰉗i, c󰊁c ti󰉨u cùng d󰉙u? Đs:
2 2 6; 2 2 6 5mm
Bài tập 23. Cho hàm s󰉯
2
2 3 2
1
x m x m
y
x
󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u.
Khi 󰉙y ch󰉽ng minh
22
1
2
CD CT
yy
? Đs:
1
2
m 
Bài tập 24. Cho hàm s󰉯
2
23x x m
y
xm

󰉨 hàm s󰉯 có c󰊁󰉗i, c󰊁c ti󰉨u th󰉮a
8
CD CT
yy
Đs:
1
2
m 
B. BÀI TẬP TRẮC NGHIỆM
ĐỀ 01
Câu 1. 󰉰 th󰉬 hàm s󰉯
2
22
1
xx
y
x

󰉨m c󰊁c tr󰉬 n󰉟󰉼󰉶ng th󰉠ng
y ax b
thì giá tr󰉬 c󰉻a t󰉱ng
ab
b󰉟ng bao nhiêu ?
A.
4
B.
4
C.
2
D.
2
Câu 2. 󰉰 th󰉬 hàm s󰉯
1
1
1
yx
x
󰉨m c󰊁c tr󰉬 n󰉟󰉼󰉶ng th󰉠ng
y ax b
thì tích
.ab
b󰉟ng:
A.
0
B.
2
C.
4
D.
2
Câu 3. Hàm s󰉯
32
6 9 1y x x x
󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c
tr󰉬 là:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 58
A.
27yx
B.
27yx
C.
27yx
D.
27yx
Câu 4. Cho hàm s󰉯
3
3y x x
󰉰 th󰉬 󰉼󰉴󰉼󰉶ng th󰉠󰉨m
c󰊁c tr󰉬 c󰉻a (C) là:
A.
yx
B.
yx
C.
2yx
D.
2yx
Câu 5. Cho hàm s󰉯
3 2 2 3 2
3 3 1y x mx m x m m
󰉨m c󰊁c tr󰉬 A, B. Tìm m
󰉨 󰉼󰉶ng th󰉠󰉨m
0; 2M
A.
02mm
B.
12mm
C.
02mm
D.
12mm
Câu 6. 󰉼󰉴󰉼󰉶ng th󰉠󰉼󰉴󰉼󰉶ng th󰉠
󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
69y x x x
A.
26yx
B.
26yx
C.
62yx
D.
3yx
Câu 7. Tìm t󰉙t c󰉘 giá tr󰉬 󰉨m
1;0I
thu󰉳󰉼󰉶ng th󰉠󰉨m c󰊁c
tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
32
32y x mx
A.
1m 
B.
2m 
C.
0m
D.
m
Câu 8. Cho hàm s󰉯
32
31y x x
. Vi󰉦󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁c
󰉗󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬 hàm s󰉯 
A.
21yx
B.
21yx
C.
21yx
D.
21yx
Câu 9. 󰉰 th󰉬 hàm s󰉯
32
32y x mx m
󰉨m c󰊁c tr󰉬 󰉯i x󰉽󰉼󰉶ng
th󰉠ng
2 1 0xy
khi và ch󰉫 khi :
A.
1;0;1m
B.
1m 
C.
1m 
D.
m
Câu 10. 󰉼󰉴󰉼󰉶ng th󰉠󰉼󰉴󰉼󰉶ng th󰉠
󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
A.
2yx
B.
2yx
C.
22yx
D.
22yx
ĐỀ 02
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 59
Câu 1. 󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
3
35y x x
có h󰉪 s󰉯
góc là
A.
2
B.
1
C.
2
D.
5
Câu 2. Cho hàm s󰉯
3 2 2 3
3 3 1y x mx m x m m
󰉼󰉴󰉼󰉶ng th󰉠ng n󰉯i
󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯 có d󰉗ng:
A.
20xy
B.
30mx y
C.
2
2y x m
D.
y x m
Câu 3. 󰉼󰉴󰉼󰉶ng th󰉠󰉨m c󰊁󰉗󰉨m c󰊁c ti󰉨u c󰉻󰉰 th󰉬
hàm s󰉯
32
2 5 1y x x x
có d󰉗ng:
A.
3 9 2 0xy
B.
45yx
C.
38 9 19 0xy
D.
17 11yx
Câu 4. 󰉰 th󰉬 hàm s󰉯
32
3y x x mx m
󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬
song song v󰉵󰉼󰉶ng th󰉠ng
: 2 1d y x
khi:
A.
1
2
m
B.
2
3
m
C.
6m
D.
3
2
m
Câu 5. 󰉰 th󰉬 hàm s󰉯
32
32y x x mx
󰉼󰉶ng th󰉠󰉨m c󰊁c tr󰉬 song
song v󰉵󰉼󰉶ng th󰉠ng
:4 3 0d x y
khi:
A.
1m
B.
2m
C.
3m
D.
4m
Câu 6. 󰉰 th󰉬 hàm s󰉯
32
3 1 6 2 1y x m x m x
󰉼󰉶ng th󰉠
󰉨m c󰊁c tr󰉬 song song v󰉵󰉼󰉶ng th󰉠ng
: 1 4d y x
khi:
A.
1m
B.
3m
C.
13mm
D.
13mm
Câu 7. 󰉰 th󰉬 hàm s󰉯
32
2 3 1 6y x m x mx
󰉨m c󰊁c tr󰉬 A, B. V󰉵i giá tr󰉬
nào c󰉻a tham s󰉯 󰉼󰉶ng th󰉠ng
:2d y x
vuông góc v󰉵󰉼󰉶ng th󰉠ng AB
A.
0m
B.
2m
C.
02mm
D.
02mm
Câu 8. 󰉰 th󰉬 hàm s󰉯
2
55
22
xx
y
x

󰉨m c󰊁c tr󰉬 A, B n󰉟󰉼󰉶ng th󰉠ng d
. H󰉪 s󰉯 góc c󰉻󰉼󰉶ng th󰉠ng d là:
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 60
A.
1
B.
1
C.
3
D.
5
Câu 9. 󰉰 th󰉬 hàm s󰉯
2
35
2
xx
y
x

󰉨m c󰊁c tr󰉬 A, B n󰉟󰉼󰉶ng th󰉠ng d
󰉼󰉴
y ax b
thì giá tr󰉬 c󰉻a
T a b
là:
A.
1
B.
1
C.
3
D.
5
Câu 10. 󰉰 th󰉬 hàm s󰉯
2
24
2
xx
y
x

󰉨m c󰊁c tr󰉬 A, B n󰉟󰉼󰉶ng th󰉠ng d
󰉼󰉴
y ax b
thì giá tr󰉬 c󰉻a
T a b
là:
A.
1
B.
0
C.
1
D.
2
Bài tập 1. Cho hàm s󰉯
3 2 2
4 3 7 10 5y x m x m m x m
󰉨 󰉰 th󰉬 hàm s󰉯
󰉨m c󰊁󰉗i và c󰊁c ti󰉨u n󰉟m v󰉧 hai phía c󰉻a tr󰉺c tung? Đs:
52m
Bài tập 2. Cho hàm s󰉯
3 2 2
3 2 3 4y x mx m m x
󰉨 󰉰 th󰉬 hàm s󰉯 có hai
󰉨m c󰊁󰉗i và c󰊁c ti󰉨u n󰉟m v󰉧 hai phía c󰉻a tr󰉺c tung? Đs:
31m
Bài tập 3. Cho hàm s󰉯
3 2 2 2
3 3 1 3 1y x x m x m
󰉨 󰉰 th󰉬 hàm s󰉯 có hai
󰉨m c󰊁󰉗i, c󰊁c ti󰉨󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯 󰉧u g󰉯c t󰉭󰉳 O ?
Đs:
1
2
m 
Bài tập 4. Cho hàm s󰉯
32
2 12 13y x mx x
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁󰉗i ,
c󰊁c ti󰉨󰉨󰉧u tr󰉺c tung. Đs:
0m
Bài tập 5. Cho hàm s󰉯
3 2 2
2
1 4 3 1
3
y x m x m m x
󰉨 󰉰 th󰉬 hàm s󰉯 có
󰉨m c󰊁󰉗i và c󰊁c ti󰉨u t󰉗󰉨󰉳 󰉼󰉴 Đs:
53m
Bài tập 6. Cho hàm s󰉯
32
3 1 3 2 1.y x m x m m x
󰉨 hàm s󰉯 có c󰊁󰉗i,
c󰊁c ti󰉨u t󰉗󰉨󰉳 󰉼󰉴 Đs:
0m
VẤN ĐỀ 5. TÌM THAM SỐ M ĐỂ HÀM SỐ CÓ CỰC TRỊ
THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
A. BÀI TẬP ÁP DỤNG
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 61
Bài tập 7. Cho hàm s󰉯
32
11
1 3 2
33
y mx m x m x
󰉨 hàm s󰉯 có c󰊁󰉗i ,
c󰊁c ti󰉨󰉨m c󰊁c tr󰉬 này th󰉮a mãn
12
21xx
? Đs:
2
2;
3
m



Bài tập 8. Cho hàm s󰉯
3 2 2
2 9 12 1y x mx m x
󰉨 hàm s󰉯 có c󰊁󰉗i
1
x
󰉨m
c󰊁c ti󰉨u
2
x
sao cho
2
12
xx
Đs:
2m 
Bài tập 9. Cho hàm s󰉯
32
1 1 50
2 1 1
3 2 9
y x m x x
󰉨 hàm s󰉯 có c󰊁󰉗i
1
x
và
󰉨m c󰊁c ti󰉨u
2
x
sao cho
12
2xx
? Đs:
2m 
Bài tập 10. Cho hàm s󰉯
3 2 2
22
2 3 1
33
y x mx m x
󰉨 hàm s󰉯 có c󰊁󰉗i
1
x
và
󰉨m c󰊁c ti󰉨u
2
x
sao cho
1 2 1 2
21x x x x
? Đs:
2
3
m
Bài tập 11. Cho hàm s󰉯
3 2 2 2
2 1 4 1 2 1y x m x m m x m
󰉨 hàm s󰉯 có
c󰊁󰉗i
1
x
󰉨m c󰊁c ti󰉨u
2
x
sao cho
12
12
1 1 1
2
xx
xx
? Đs:
1;5m
Bài tập 12. Cho hàm s󰉯
32
1
32
3
y x mx mx
󰉨 hàm s󰉯 󰉨m c󰊁c tr󰉬
12
,xx
th󰉮a mãn
12
4xx
? Đs:
4; 1mm
Bài tập 13. Cho hàm s󰉯
4 2 4
22y x mx m m
󰉨 󰉰 th󰉬 hàm s󰉯 có ba c󰊁c tr󰉬 A, B,
󰉰ng th󰉶󰉨m A, B, C t󰉗o thành tam giác th󰉮󰉧u ki󰉪n
Đs:
1m
Đs:
3
3m
Đs:
4m
Đs:
3
1
3
m
 󰉼󰉶ng tròn ngo󰉗i ti󰉦p b󰉟ng 1. Đs:
15
1;
2
mm


Bài tập 14. Cho hàm s󰉯
4 2 2
2y x mx m m
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬
t󰉗o thành tam giác có tr󰉭ng tâm là O. Đs:
3m 
1) Tam giác ABC vuông ?
 󰉧u?
3) Tam giác ABC có di󰉪n tích 32
4) Tam giác ABC có góc 120
0
?
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 62
Bài tập 15. Cho hàm s󰉯
42
1
3 1 2 1
4
y x m x m
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m
c󰊁c tr󰉬 t󰉗o thành tam giác có tr󰉭ng tâm là O. Đs:
1
3
m
Bài tập 16. Cho hàm s󰉯
32
3 1 12 3 4y x m x mx m
󰉨 󰉰 th󰉬 hàm s󰉯 có các
󰉨m c󰊁c tr󰉬 󰉨m này cùng v󰉵󰉨m
9
1;
2
C




t󰉗o thành tam giác có
tr󰉭ng tâm là O. Đs:
1
2
m 
Bài tập 17. Cho hàm s󰉯
42
3 1 3 2y x m x m
󰉨 hàm s󰉯 󰉨m c󰊁c tr󰉬 t󰉗o
thành tam giác có tr󰊁c tâm là
35
0;
4
H



Đs:
5
3
m
Bài tập 18. Cho hàm s󰉯
42
22y x mx m
󰉨 hàm s󰉯 󰉨m c󰊁c tr󰉬 t󰉗o thành
tam giác có tr󰉭ng tâm là
31
0;
4
H



. Đs:
4m
Bài tập 19. Cho hàm s󰉯
4 2 2
21y x m x m
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬
t󰉗󰉫nh c󰉻a m󰉳t tam giác vuông? Đs:
0m
Bài tập 20. Cho hàm s󰉯
4 2 2
21y x m x
󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬 t󰉗o
󰉫nh c󰉻a m󰉳󰉧u? Đs:
6
3m 
Bài tập 21. Cho hàm s󰉯
42
23y x m m x m
󰉨 hàm s󰉯 có ba c󰊁c tr󰉬 󰉰ng th󰉶i
󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯 t󰉗o thành m󰉳󰉼󰉶ng tròn
ngo󰉗i ti󰉦p b󰉟ng
5
4
R
.
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
32
31y x x mx
󰉨m c󰊁c tr󰉬
12
,xx
th󰉮a mãn
22
12
3xx
là:
A.
1m
B.
2m 
C.
3
2
m
D.
1
2
m
Câu 2. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
3 2 2 2
3 3 1 3 1y x x m x m
có c󰊁󰉗i và c󰊁c ti󰉨u
󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯 󰉧u g󰉯c to󰉗 󰉳 O là:
A.
1
2
m 
B.
3m
C.
1
0;
2
mm
D.
0; 2mm
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 63
Câu 3. Giá tr󰉬 󰉨 󰉰 th󰉬 hàm
42
21y x mx
󰉨m c󰊁c tr󰉬 t󰉗o thành m󰉳t tam
󰉧u.
A.
1m
B.
3
3m
C.
3
3m 
D.
1m 
Câu 4. Giá tr󰉬 󰉨 󰉰 th󰉬 hàm
42
21y x mx
󰉨m c󰊁c tr󰉬 t󰉗o thành m󰉳t tam
giác có di󰉪n tích b󰉟ng
42
A.
2m
B.
3m 
C.
2m 
D.
1m
Câu 5. Giá tr󰉬 c󰉻󰉨 hàm s󰉯
32
3y x x m
có c󰊁󰉗i, c󰊁c ti󰉨u sao cho
DC
y
và
CT
y
trái d󰉙u?
A.
4m
B.
04m
C.
0m
D.
04mm
Câu 6. Cho hàm s󰉯
32
1
2 1 2
3
y x mx m x m
có c󰊁󰉗i, c󰊁c ti󰉨󰉳
󰉨m c󰊁c tr󰉬 󰉼󰉴󰉝p giá tr󰉬 c󰉻a m b󰉟ng
A.
1
;
2




B.
\1
C.
1
; \ 1
2




D.
;0
Câu 7. (SGD Gia Lai, 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯
m
󰉰 th󰉬 hàm
s󰉯
4 2 4
22y x mx m m
󰉨m c󰊁c tr󰉬 󰉫nh c󰉻a m󰉳t tam giác có di󰉪n tích
b󰉟ng
42
.
A.
2m
. B.
0m
. C.
32m
. D.
2m 
.
Câu 8. (SGD Bà Rịa Vũng Tàu, 2017) Cho hàm s󰉯
32
1– 2 2 – 2y x m x m x m
(1) Tìm t󰉝p h󰉹p t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻󰉨 󰉰
th󰉬 hàm s󰉯 󰉨m c󰊁󰉗󰉨m c󰊁c ti󰉨󰉰ng th󰉶󰉳 c󰉻󰉨m c󰊁c ti󰉨u
nh󰉮 󰉴
A.
.
5
5
;
4
7
m



B.
5
;
7
4
; 1 .
5
m




C.
7
;.
5
m




D.
2; .m 
Câu 9. (SGD Thanh Hóa, 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯 m 󰉨 󰉰 th󰉬
hàm s󰉯
42
4( 1) 2 1y x m x m
󰉨m c󰊁c tr󰉬 󰉫nh c󰉻a m󰉳t tam giác có s󰉯 
m󰉳t góc b󰉟ng
0
120
.
DẠY KÈM - LUYỆN THI MÔN TOÁN 0987 668 965 0935 875 953
Việc tuy nhỏ, không làm không nên. DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 64
A.
3
1
1.
24
m 
B.
3
1
1.
16
m 
C.
3
1
1.
48
m 
D.
3
1
1.
2
m 
Câu 10. (SGD Quảng Ninh, 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯
m
󰉨 󰉰 th󰉬
hàm s󰉯
3 2 2
4 1 1y x x m x
󰉨m c󰊁c tr󰉬 n󰉟m v󰉧 󰉯i v󰉵i
tr󰉺c tung?
A.
11
33
m
. B.
1
1
m
m

. C.
11m
. D.
11m
.
Câu 11. (SGD HCM cụm 1, 2017) Bi󰉦t r󰉟󰈘
32
4 – 6 1y x x
󰈨󰉼

Phát bi󰉨phát bi󰉨
A. 󰉰 th󰉬 hàm s󰉯
32
4 – 6 1xy x
có 2 c󰊁c tr󰉬.
B. 󰉰 th󰉬 hàm s󰉯
32
4 – 6 1xy x
có 5 c󰊁c tr󰉬.
C. 󰉰 th󰉬 hàm s󰉯
32
4 – 6 1xy x
có 3 c󰊁c tr󰉬.
D. 󰉰 th󰉬 hàm s󰉯
32
4 – 6 1xy x
có 1 c󰊁c tr󰉬.
Câu 12. (THPT QG 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯
m
󰉨 󰉰 th󰉬 c󰉻a
hàm s󰉯
42
2y x mx
󰉨m c󰊁c tr󰉬 t󰉗o thành m󰉳t tam giác có di󰉪n tích nh󰉮 󰉴
1
.
A.
3
04m
. B.
1m
. C.
01m
. D.
0m
.
Câu 13. (THPT QG 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 th󰊁c c󰉻a tham s󰉯
m
󰉨 󰉰 th󰉬 c󰉻a hàm
s󰉯
42
2y x mx
󰉨m c󰊁c tr󰉬 t󰉗o thành m󰉳t tam giác có di󰉪n tích nh󰉮 󰉴
A.
0.m
B.
1.m
C.
3
0 4.m
D.
0 1.m
Câu 14. (THPT QG 2017)󰈘󰈖󰈨󰉼󰈨 󰈖 󰈘
m
󰈜󰈚󰈨󰈖
󰈘
3 2 3
34y x mx m
󰈜󰉼󰈨
A

B

OAB

󰈢
4
󰉴 
O
󰈘󰈨󰈨
A.
4
1
2
m 
;
4
1
2
m
. B.
1m 
;
1m
.
DẠY KÈM - LUYỆN THI MÔN TOÁN
Giải Tích 12
NGỌC ĐÀN – 0987 668 965 Đường tuy ngắn, không đi không đến. 65
C.
1m
. D.
0m
.
Câu 15. (SGD Đà Nẵng, 2017) Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 m 󰉨 󰉰 th󰉬 hàm s󰉯
42
21y x m x m
󰉨m c󰊁c tr󰉬 t󰉗󰉫nh c󰉻a m󰉳t tam giác vuông.
A.
0.m
B.
1.m
C.
3.m
D.
2m
Câu 16. Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 󰉨 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
4 2
6 4 x( )1y x m m
󰉫nh c󰉻a m󰉳t tam giác vuông.
A.
2
3
m
. B.
1
3
m
. C.
1m 
. D.
3
3m
.
Câu 17. (SGD Bà Rịa Vũng Tàu, 2017) Cho hàm s󰉯
32
= 3 3 – 1y x mx m
. Tìm t󰉝p
h󰉹p t󰉙t c󰉘 giá tr󰉬 th󰊁c c󰉻󰉨 󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁󰉗󰉨m c󰊁c ti󰉨󰉯i
x󰉽ng v󰉵󰉼󰉶ng th󰉠ng
: 8 +8 0.d x y
A.
0m
. B.
2,0 .m
C.
23
;0 .
4
m






D.
23
0; ;2 .
4
m





| 1/65
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
VẤN ĐỀ 1. TÌM CỰC TRỊ CỦA HÀM SỐ Phương pháp Quy tắc 1.
Bước 1. Tìm tập xác định.
Bước 2. Tính f x .Tìm các điểm x mà tại đó f x  0 hoặc không xác định. i
Bước 3. Lập bảng biến thiên.
Bước 4. Kết luận về các điểm cực trị. Quy tắc 2.
Bước 1. Tìm tập xác định.
Bước 2. Tính f x .Tìm các điểm x mà tại đó f x  0. i
Bước 3. Tính f  x và f x i
Bước 4. Dựa vào dấu của f x để kết luận về điểm cực trị x . i i A. VẬN DỤNG Ví dụ 1.
Tìm các điểm cực trị của các hàm số sau 1) 3 2
y x  3x  2 2) 4 2
y  2x  4x  4 3) 4 3
y x  8x  5 5 3 4) x x 4 2
y x  8x 10 5) y    2 5 3 Ví dụ 2.
Tìm các điểm cực trị của các hàm số sau 2  2   2   1) x 1 x 2x 3 x 2x 4 y  2) y  3) y x x 1 x  2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 1
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Ví dụ 3.
Tìm các điểm cực trị của các hàm số sau 1) 2
y x 16  x
Đs: CD : x  2 2;CT : x  2  2 2) 2 y  8  x
Đs: CD: x  0 3) x y
Đs:CD : x 1 x 1 4) 2
y x  2x 1 Đs: 2 CT : x   2
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Tìm cực trị của các hàm số sau 1) 3 2 1
y x  3x  9x  5 2) 2 3
y  3x  2x 3) 4 2 y x x  3 2 4) 1 3 4 2 y   x x  5) 4 2
y x  6x  8x 1 6) 4 3 2
y  3x  4x  24x  48x  5 2 2 4 7) x 3 2 1
y x  2x  2x 1 8) 3 2
y   x  4x 15x 9) 2 y   x  5 3 2 10) 4 2 3 3 4
y x  4x  5
11) y  x   1 3  x
12) y  x  2 x   1
Bài tập 2. Tìm cực trị của các hàm số sau 2 3 1) 4 x x y x 1 2) y  3) y x  2 2 x  4x  5 2 x 1 2    2   2   4) x 3x 6 3x 4x 5 x 2x 15 y  5) y  6) y x  2 x 1 x  3 2   2   7) 4x 2x 1 3x 4x 4 x 1 y  8) y  9) y  2 2x x  3 2 x x 1 2 x 1 2   10) 16 4x 2x 1 2 y x  11) y x 2 2x x  3
Bài tập 3. Tìm cực trị của các hàm số sau
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 2
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 1) 2 y x x  4 2) 2 y x  2x  5 3) 2
y x  2x x 3 4) x 2
y x 9  x 5) y  6) 3 2
y  x  3x 2 x  9 7) 2
y  2x 1 2x  8 8) 2
y x  2x 1 Đs: 2
CD : x  0;CT : x  2, x   2 9) 2
y x  2  12  3x
Đs: CT : x  1 
10) y x 3 x
Đs: CD : x  2
C. BÀI TẬP TRẮC NGHIỆM ĐỀ 1. Câu 1.
Số điểm cực trị của hàm số f x 4 2
 x  2x  3 là: A. 0 B. 1 C. 2 D. 3 Câu 2.
Số điểm cực trị của hàm số 4 2
y x  3x  3 là A. 1 B. 3 C. 2 D. 0 Câu 3.
Điểm cực tiểu của đồ thị hàm số 4 2
y  x 18x 1 là A. 0;  1 B. 0;  1 C. 1;0 D.  3  ;80 và 3;80 Câu 4.
Trong các mệnh đề sau hãy tìm mệnh đề sai. Chọn 1 câu sai A. Hàm số 3 2
y  x  3x 1 có cực đại và cực tiểu. B. Hàm số 3 2
y  x  3x  2 có cực trị C. Hàm số 1 y  2  x 1 không có cực trị x  2 D. Hàm số 1 y x 1 có hai cực trị x 1
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 3
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 5. Hàm số 3 2
y  2x  9x 12x  5 có mấy điểm cực trị ? A. 1 B. 2 C. 3 D. 4 Câu 6. Cho hàm số 4 2
y  x  2x  3 .Mệnh đề nào sau đây đúng?
A. Hàm số có một điểm cực trị
B. Hàm số không có cực trị
C. Hàm số có ba điểm cực trị
D. Hàm số đồng biến trên Câu 7. Cho hàm số 3 2
y x  3x  2 , khẳng định nào sau đây đúng?
A. Có đúng hai điểm cực trị
B. Không có điểm cực trị
C. Có chỉ một điểm cực trị
D. Có hai cực trị cùng dấu. Câu 8. Hàm số 3 2
y x  3x  4 đạt cực đại tại điểm: A. x  2  B. x  2 C. x  0 D. x 1 Câu 9. 4 Hàm số 3 2 y  
x  2x x  3 có số điểm cực trị là: 3 A. 0 B. 1 C. 2 D. 3 Câu 10. Hàm số 4 2
y x  2x 1 đạt cực đại tại x bằng A. 0 B. 2 C. 1  D. 2 4 Câu 11. x Đồ thị hàm số 2 y
x  3 có điểm cực tiểu là: 2 A.  2         1;   B. 5 1;   C. 5 ; 1    D. 2 ; 1     5   2   2   5  4 Câu 12. x 4 Hàm số 2 y  3x
có số điểm cực trị là: 2 3 A. 3 B. 0 C. 2 D. 1 Câu 13. Hàm số 3
y  x  3x  4 đạt cực tiểu tại x bằng A. –3 B. 1 C. –1 D. 3
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 4
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 14. 1 Hàm số 4 2 y
x  2x  3 đạt cực tiểu tại x bằng 2 A. 2 B.  2 C. 0 D. –2 Câu 15. 1 Đồ thị hàm số 4 2 y
x  2x  6 có bao nhiêu điểm cực tiểu? 4 A. 3 B. 1 C. 2 D. 0 Câu 16.
Điểm cực tiểu của đồ thị hàm số 4 2
y x  6x  5 là:
A. M  3;0 B. N  3; 4  
C. P 3;4 D. Q0;2 Câu 17.
Điểm cực tiểu của đồ thị hàm số 4 3
y x  4x 1 là: A. M 2; 15   B. N 1;2 C. P3; 2  6 D. Q4;6 Câu 18. Hàm số 1 y x
đạt cực đại tại điểm có hoành độ là x A. 2 B. 1 C. 1  D. 0 Câu 19.
Trong các mệnh đề sau, hãy tìm mệnh đề sai: A. Hàm số 3
y x  3x 1 có cực trị B. Hàm số 1 y x 1 có hai cực trị x 1 C. Hàm số 1 y
không có cực trị D. Hàm số 3 2
y  x  3x  3 có cực đại và cực tiểu x  2 2 Câu 20. x x 1 Hàm số y
có bao nhiêu điểm cực trị: 2 x 1 A. 0 B. 1 C. 2 D. 3 Câu 21.
Khẳng định nào sau đây là đúng về hàm số 4 2
y x  4x  2 ?
A. Đạt cực tiểu tại x  0
B. Có cực đại và không có cực tiểu
C. Có cực đại và cực tiểu
D. Không có cực trị. Câu 22.
Đồ thị của các hàm số nào sau đây có 3 điểm điểm cực trị :
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 5
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 4 2
y x  2x  4 B. 4 2
y x  2x 1 C. 4 2
y  2x  4x 1 D. 4 2
y  x  2x 1 Câu 23. Hàm số 4 2
y x  2x 1 có bao nhiêu điểm cực trị: A. 1 B. 2 C. 3 D. 0 Câu 24. 1 Đồ thị hàm số 4 2 y
x  2x 1 có 4
A. Một cực đại và hai cực tiểu.
B. Một cực tiểu và hai cực đại.
C. Một cực đại và không có cực tiểu .
D. Một cực tiểu và một cực đại. Câu 25.
Số cực trị của hàm số 4 2
y x  3x  3 là: A. 1 B. 2 C. 3 D. 4 Câu 26. 3
Hàm số y f x có đạo hàm f x 
. Số điểm cực trị của hàm số là: x  2 1 A. 0 B. 1 C. 2 D. 3 Câu 27.
Khoảng cách giữa 2 điểm cực trị của hàm số 3
y  4x  3x 1 là A. 1 B. 0 C. 26 D. 2 2 Câu 28.
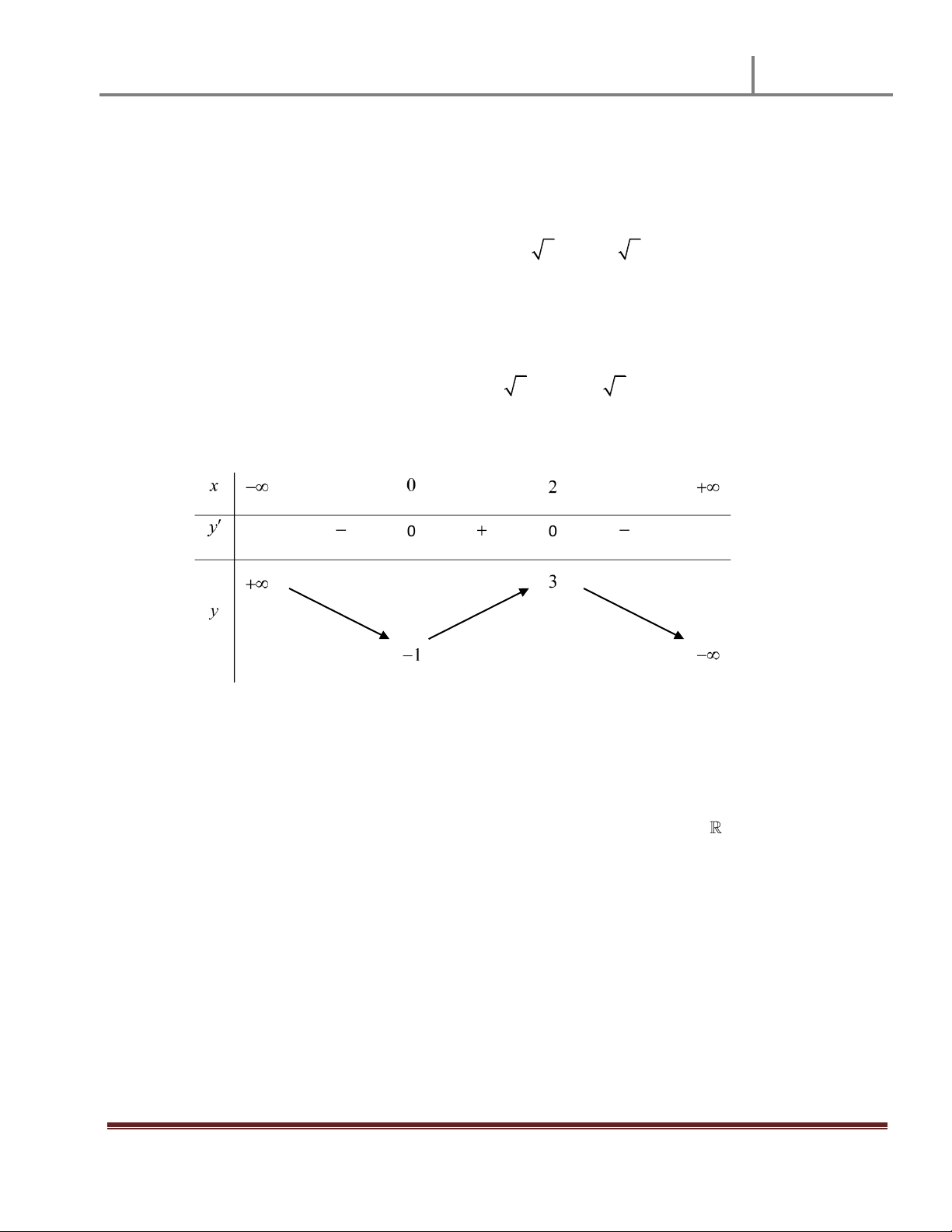
Cho hàm số y f x xác định liên tục và liên tục trên và có bảng biến thiên như sau: x   - 2 0   , y + 0 - 0 + 0   y   4
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có hai cực trị.
B. Hàm số có giá trị cực tiểu bằng 0.
C. Hàm số có giá trị cực đại bằng -4.
D. Hàm số có giá trị cực đại tại x = 0.
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 6
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 29.
Hàm số nào sau đây có 3 điểm cực trị : A. 4 2
y x  2x 1 B. 4 2
y x  2x 1 C. 4 2
y  2x  4x 1 D. 4 2
y  x  2x 1 Câu 30.
Trong các hàm số sau đây, hàm số nào không có cực trị A. 3 2
y x  3x  3 B. 4 2
y x x 1 C. 3 y x  2 D. 4 y  x  3 Câu 31.
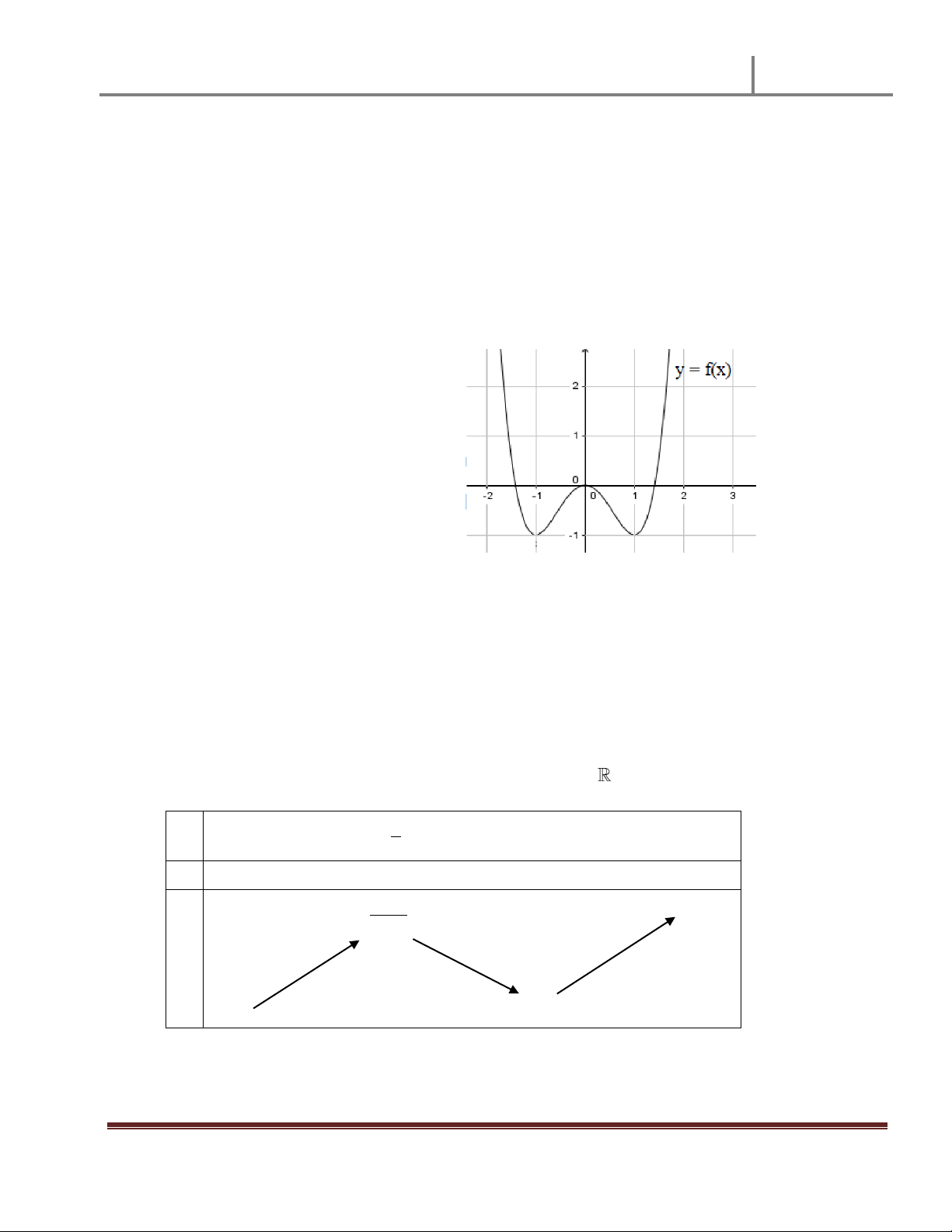
Cho hàm số có đồ thị như hình vẽ. Số điểm cực trị là: A. 0 B. 1 C. 2 D. 3 Câu 32.
Trong các hàm số sau, hàm số nào có đúng một điểm cực trị
A. y  2x  2 B. 4 2
y  x  3x  2 C. 3
y x  3x  2 D. 4 2
y x  3x  2 Câu 33.
Đồ thị của hàm số nào sau đây không có điểm cực trị: A. 3
y x  2x 1 B. 4 2
y  2x x 1 C. 4 2
y x  3x 1 D. 4 2
y x  2x 1 Câu 34.
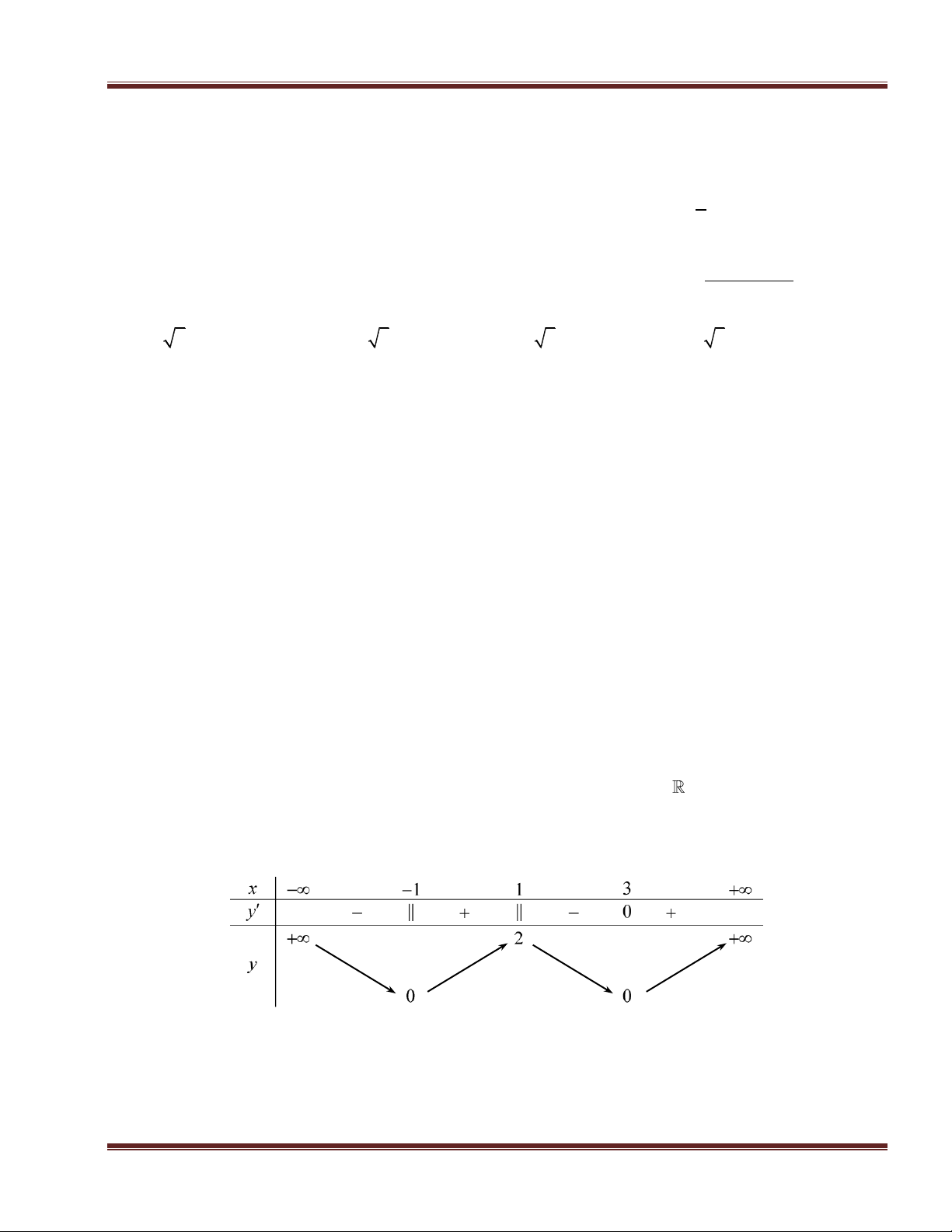
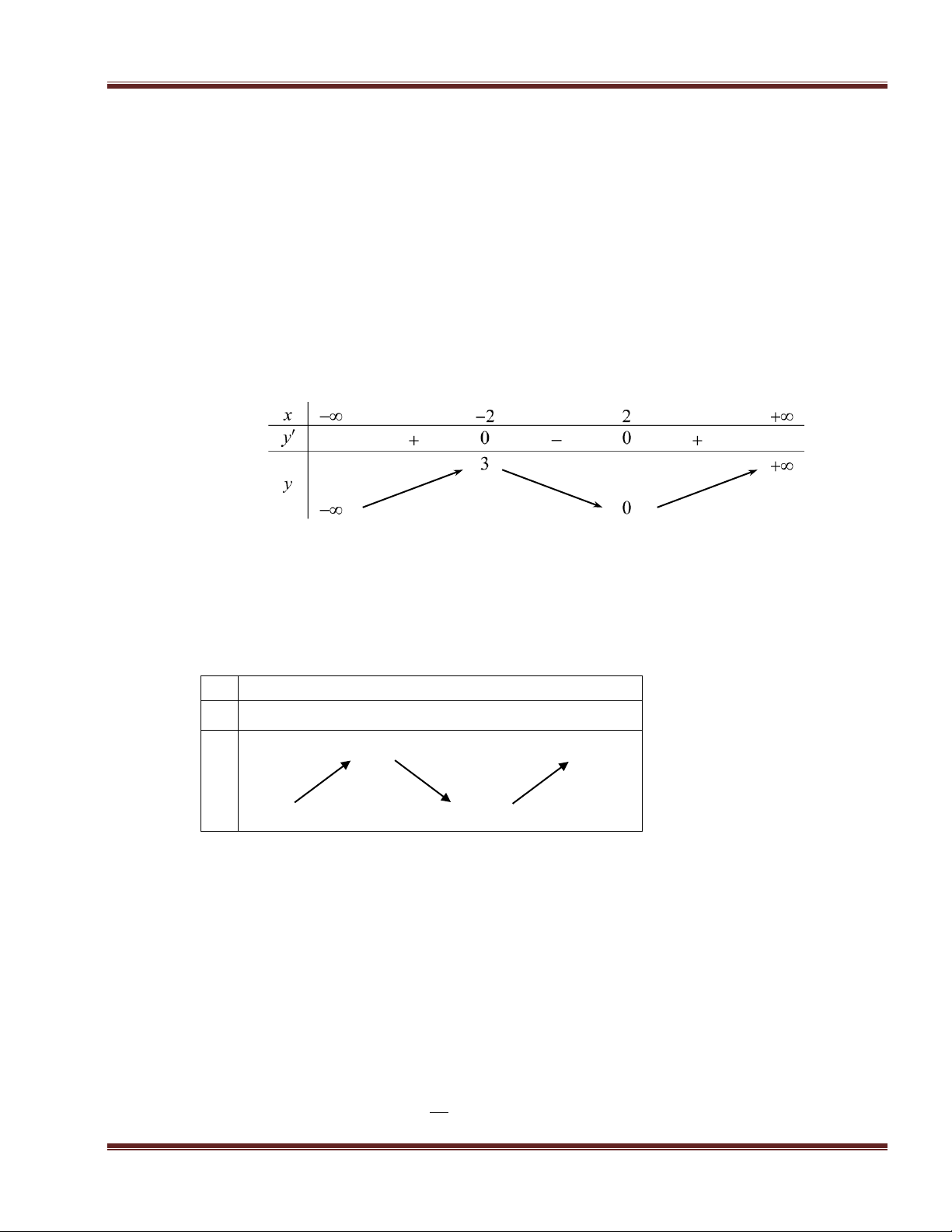
Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên: x   3 0 1   5 , y + 0 + 0 - 0 + 108   3125 y 0 0  
Khẳng định nào sau đây là khẳng định đúng ?
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 7
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
A. x  0 không phải là điểm cực trị của hàm số. B. Hàm số đạt cực tiểu tại điểm x  0
C. Hàm số đạt cực đại tại điểm x 1 . D. Hàm số có giá trị lớn nhất bằng 108 . 3125 Câu 35.
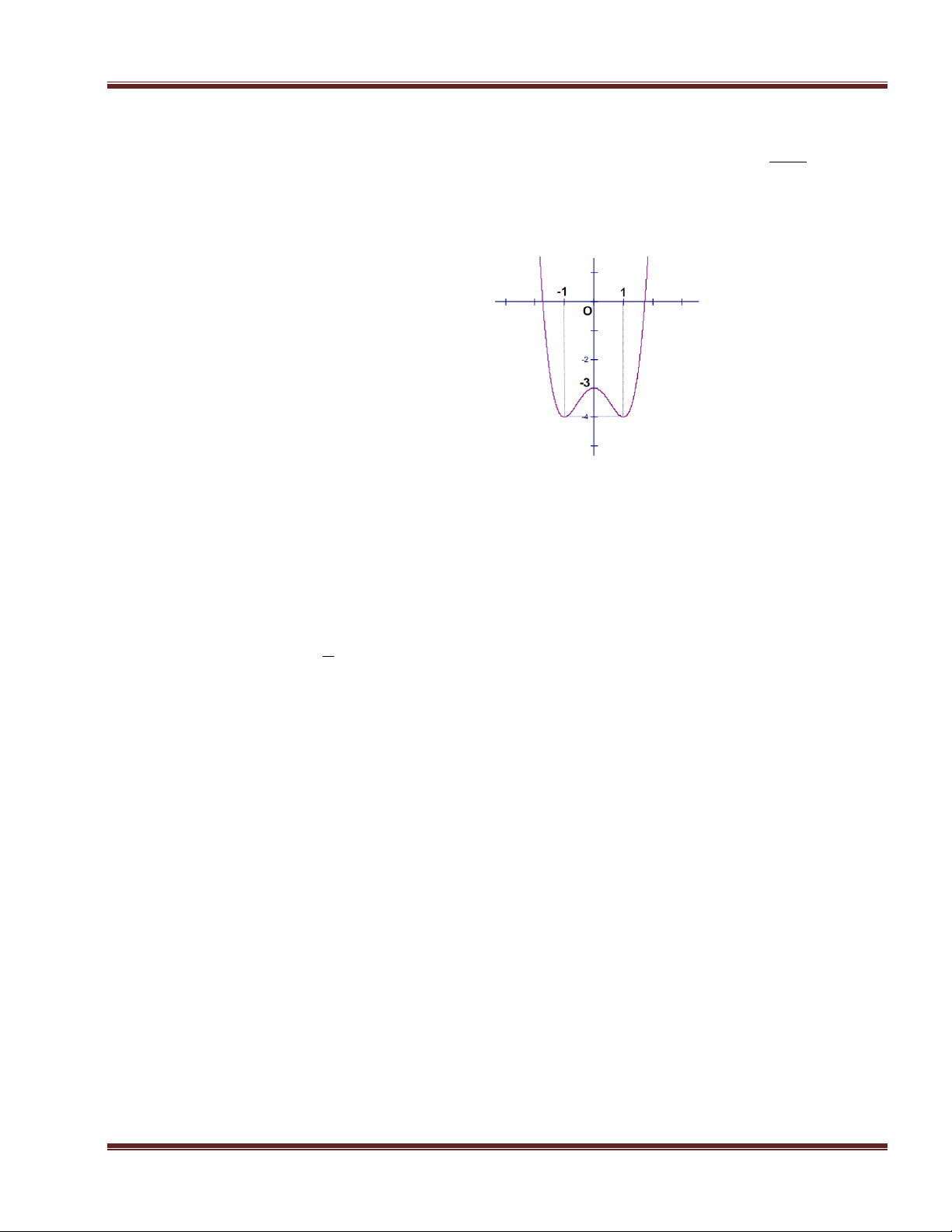
Cho đồ thị như hình vẽ. Số điểm cực đại của đồ thị hàm số đã cho là: A. 3 B. 0 C. 2 D. 1 ĐỀ 02. Câu 1.
Hàm số bậc ba có thể có bao nhiêu cực trị ? A. 1 hoặc 2 hoặc 3 B. 0 hoặc 2 C. 0 hoặc 1 hoặc 2 D. 2 Câu 2. 1 Hàm số 4 2 y
x  2x 1 có: 4
A. Một cực đại và hai cực tiểu
C. Một cực đại và không có cực tiểu
B. Một cực tiểu và hai cực đại
D. Một cực tiểu và một cực đại Câu 3. Hàm số 3 2
y x  3x  4 có giá trị cực đại bằng A. 4 B. 1 C. 0 D. 24  Câu 4. Đồ thị hàm số 4 2
y x  2x  3 có:
A. Một cực đại và hai cực tiểu.
B. Một cực tiểu và hai cực đại.
C. Một cực tiểu và không cực đại.
D. Không có cực đại và cực tiểu. Câu 5. Hàm số 4 3
y x  8x  2 có bao nhiêu điểm cực trị A. 3 B. 2 C. 1 D. 0 Câu 6. Hàm số 2 3
y  3x  2x đạt cực trị tại:
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 8
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
A. x 1; x  0 B. x  1
 ; x  0 C. x  0; x  1 
D. x  0; x 1 D C CT D C CT D C CT D C CT Câu 7.
Hàm số nào sau đây không có cực trị: A.  3 x
y x  3x B. 2 y C. 1 y x D. 4 2
y x  2x 2x 1 x Câu 8.
Hàm số nào sau đây không có cực đại và cực tiểu ? A. 4 2
y x  2x B. 3
y x  2x C. 3 y x D. 2
y x  2x 1 Câu 9. Cho hàm số 3
y x  3x  2 . Khẳng định nào sau đây sai ?
A. Hàm số đạt cực đại tại x  1 
B. Hàm số đạt cực tiểu tại x 1
C. Hàm số không có cực trị.
D. Hàm số có 2 điểm cực trị. Câu 10.
Trong các mệnh đề sau, hãy tìm mệnh đề sai ? A. Hàm số 1 y  không có cực trị. x  2 B. Hàm số 3 2
y  x  3x 1 có cực đại và cực tiểu. C. Hàm số 1 y x  có hai cực trị. x 1 D. Hàm số 3
y x x  2 có cực trị. Câu 11. Đồ thị hàm số 4 2
y x x 12 có mấy điểm cực trị: A. 4 B. 3 C. 2 D. 1 3 Câu 12. x
Số điểm cực trị của đồ thị hàm số y    x  7 là: 3 A. 0 B. 1 C. 2 D. 3 Câu 13.
Số điểm cực trị của đồ thị hàm số 4 2
y x  2x 1 là: A. 0 B. 1 C. 2 D. 3 Câu 14.
Số điểm cực trị của đồ thị hàm số 4 3
y x  8x 12 là:
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 9
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 0 B. 1 C. 2 D. 3 Câu 15. Hàm số 6
y  2x  4x  7 có số điểm cực trị là: A. 0 B. 1 C. 2 D. 3 Câu 16. Hàm số 3 2
y x  3x  9x  2 có điểm cực tiểu tại: A. x  1  B. x  3 C. x 1 D. x  3  Câu 17. Tìm giá trị cực đại 3
y x  3x  2 của đồ thị hàm số A. y  4 B. y 1 yD. y  1  CD CD C. 0 CD CD Câu 18.
Giá trị cực đại của hàm số là: A. 2 B. 1 C. 6 D. 1  Câu 19. Hàm số 1 y x
có giá trị cực đại là: x A. 2 B. 2 C. 1 D. 1  Câu 20. Hàm số 3
y x  3x có giá trị cực tiểu là: A. 2 B. 2 C. 1 D. 1  Câu 21.
Giá trị cực đại của hàm số 3 2
y x  3x  3x  2 bằng: A. 3   4 2 B. 3 4 2 C. 3 4 2 D. 3   4 2 4 Câu 22. x Hàm số 2 y  
 2x 1 đạt cực đại tại: 4 A. x  2 B. x  2  C. x  0 D. x  2  3 Câu 23. x Hàm số 2 y
 2x  3x 5 đạt cực tiểu tại: 3 A. x 1 B. x  3 C. x  1  D. x  3  2 Câu 24. x  3x  3 Hàm số y  đạt cực đại tại: x  2 A. x 1 B. x  2 C. x  3 D. x  0
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 10
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 25. 1 Hàm số 4 2 y
x  2x  3 đạt cực đại tại x bằng: 2 A. 0. B.  2 C.  2 D. 2 Câu 26. Một hàm số 2 3 5
f x có đạo hàm là f  x  x x  
1  x  2  x  3 . Hỏi hàm số
này có bao nhiêu cực trị ? A. 4 B. 3 C. 2 D. 1 Câu 27.
Hệ thức liên hệ giữa giá trị cực đại y và giá trị cực tiểu y của đồ thị hàm CD CT số 3
y x  2x là:
A. y  2y
B. 2y  3y
C. y y yy CT CD CT CD CT CD D. 0 CT CD Câu 28.
Hàm số y  x x2 2 3 2
đạt cực trị tại điểm có hoành độ là: A. x 1
B. x  0; x 1
C. x  0; x 1; x  2
D. Hàm số không có điểm cực trị. Câu 29. 1 Cho hàm số 3 2
y  x  3x
x . Hàm số đạt cực trị tại 2 điểm x , x . Khi đó 2 1 2 tổng 2 2
S x x có giá trị là: 1 2 A. 11 B. 13 C. 1 D. 3 3 3 2 2 Câu 30. Hàm số 4 2
y x  2x  5 có các điểm cực trị lần lượt là x , x , x thì tích x .x .x 1 2 3 1 2 3 là: A. 2 B. 1  C. 0 D. 1 Câu 31. Hàm số 3 y x 1
có tổng các điểm cực đại và cực tiểu bằng: x A. 2 B. 1  C. 0 D. 2 2 Câu 32. x  4x 1 Hàm số y
có tích các điểm cực đại và cực tiểu bằng: x 1
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 11
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 2 B. 5  C. 1  D. 4 2 Câu 33. x  2x 1 Cho hàm số y
. Khoảng cách giữa hai điểm cực trị là: x 1 A. 4 5 B. 4 C. 8 D. 5 2 Câu 34. 1 Cho hàm số 3 2
y   x  4x  5x 17 có hai điểm cực trị là x , x . Khi đó tích 1 2 3 x .x bằng: 1 2 A. 5 B. 5  C. 8 D. 2  11 2 Câu 35. x x  2 Cho hàm số y
. Hàm số có hai điểm cực trị x , x .Tích x .x bằng x 1 1 2 1 2 A. 3  B. 2 C. 2 D. 3 ĐỀ 03. Câu 1.
Hàm số nào sau đây có ba cực trị  A. x 2
y x  3x  5 B. 3
y x  3x 1 C. 4 2
y x  2x 1 D. 1 y x1 Câu 2. Hàm số 3
y  x  3x  4 đạt cực tiểu tại x bằng: A. 1  B. 1 C. 3  D. 3 Câu 3.
Hàm số y x   x2 3 1 đạt cực đại tại: A. x 1 B. x  1  C. 3 x D. Đáp án khác. 5 Câu 4.
Điểm cực đại của đồ thị hàm số 3 2
y  2x  3x  2 là: A. M 0; 2   B. N 2;2 C. P1; 3   D. Q 1  ; 7   Câu 5.
Tọa độ điểm cực tiểu của đồ thị hàm số 4 2
y  x  2x là: A. M 0;0 B. N 1;  1 C. P 1   ;1 D. Q 1  ;0
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 12
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 6. 1 2
Tọa độ điểm cực đại của đồ thị hàm số 3 2 y
x  2x  3x  là: 3 3 A. M 1;3 B. N 1;0 C. P 1;2 D. Q3;  1 Câu 7.
Điểm cực tiểu của đồ thị hàm số 3 2
y x  3x  3 là: A. M 1  ;1 B. N  2   ;1 C. P0; 3  
D. Q 1;6 Câu 8.
Điểm cực đại của đồ thị hàm số 4 2
y  x  6x  8x 1 là: A. M  2  ;24
B. N 2;25 C. P7;3
D. Q 1;6 Câu 9. Hàm số 4 2
y x  2x  3 đạt cực trị tại điểm : A. x  0 B. x 1 C. x  1  D. x  2 Câu 10.
Cho hàm số y f x liên tục và có đạo hàm liên tục đến cấp 2 trên tập x K 0
. Khẳng định nào sau đây đúng?
A. Điểm x là điểm cực đại của hàm số nếu f x  0 và f  x  0 0  0  0
B. Điểm x là điểm cực đại của hàm số nếu f  x  0 0  0
C. Điểm x là điểm cực tiểu của hàm số nếu f x  0 và f  x  0 0  0  0
D. Điểm x là điểm cực tiểu của hàm số nếu f x  0 0  0 Câu 11.
Gọi y , y lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số 1 2 4 2
y  x 10x  9 . Khi đó, y y bằng: 1 2 A. 7 B. 8 C. 9 D. 2 5 Câu 12. Đồ thị hàm số 3
y x  3x có điểm cực đại là : A.  1  ;2 B.  1  ;0 C. 1; 2   D. 1;0 Câu 13. Hàm số 3
y  x  3x 1 đạt cực đại tại điểm có hoành độ: A. x 1 B. x  0 C. x  1  D. x  2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 13
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 14.
Điểm cực tiểu của đồ thị hàm số 4 2
y  x 18x 1 là A. 0;  1 B. 0;  1 C. 1;0 D.  3  ;80;3;80 Câu 15.
Khoảng cách giữa 2 điểm cực trị của hàm số 3
y  4x  3x 1 là A. 1 B. 0 C. 26 D. 2 2 Câu 16. Cho hàm số 3 2
y x  3x 1.Tích các giá trị cực đại và cực tiểu của hàm số bằng A. 3  B. 6  C. 0 D. 3 Câu 17. Số cực trị 3 2
y  x  3x  3x 1 của hàm số là: A. 0 B. 1 C. 2 D. 3 Câu 18. Cho hàm số 4 2
y  3x  4x . Khẳng định nào sau đây đúng.
A. Hàm số đạt cực đại tại gốc tọa độ.
B. Hàm số đạt cực tiểu tại gốc tọa độ.
C. Hàm số không có cực trị.
D. Điểm M 1; 
1 là điểm cực tiểu của đồ thị hàm số Câu 19. Đồ thị hàm số 4 2
y x x 1 có bao nhiêu điểm cực trị có tung độ dương? A. 3 B. 1 C. 2 D. 0 Câu 20. Hàm số 4 2
y  x  2x  2
A. Có một điểm cực trị.
B. Có 3 điểm cực trị tạo thành tam giác vuông.
C. Có hai điểm cực trị
D. Có 3 điểm cực trị tạo thành tam giác đều. Câu 21. Cho hàm số 3 2
y x  3x 1 . Tích giá trị cực đại và giá trị cực tiểu của hàm số bằng: A. 6  B. 0 C. 3  D. 3 4 Câu 22. x 1
Trong các khẳng định sau về hàm số 2 y
x 3 , khẳng định nào đúng? 4 2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 14
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
A. Hàm số có điểm cực tiểu là x  0
B. Hàm số có 2 điểm cực đại là x 1, x  1 
C. Hàm số có 3 cực trị
D. Hàm số có điểm cực đại là x  0 Câu 23.
Tìm giá trị cực tiểu của hàm số 3 2
y x  3x  4 . A. y  4  B. y 1 C. y  2  D. y  0 CT CT CT CT 4 Câu 24. x 3 Cho hàm số 2 y  
x  . Khẳng định nào sau đây là khẳng định sai ? 2 2
A. Hàm số đạt cực đại tại điểm 3 x  .
B. Hàm số đạt cực đại tại điểm x  0 . 2
C. Giá trị cực đại của hàm số là 3 y
 . D. Đồ thị hàm số có đúng một điểm cực trị. D C 2 2 Câu 25. x  4x 1 Hàm số y
có hai điểm cực trị là x , x , khi đó tích x .x bằng: x 1 1 2 1 2 A. 5  B. 5 C. 2 D. 2 Câu 26. Cho hàm số 3 2
y x  3x 1. Biểu thức liên hệ giữa giá trị cực đại  y và giá CD 
trị cực tiểu  y là: CT A. y  3  y
B. y  3y C. y  3  y y  y CD CT CD CT CT CD D. CD CT Câu 27.
Cho hàm số y f x có đạo hàm tại x . Tìm mệnh đề đúng ? 0
A. Hàm số đạt cực trị tại x thì f x  0 0  0
B. Nếu f x  0 thì hàm số đạt cực trị tại x 0  0
C. Hàm số đạt cực trị tại x thì f x đổi dấu khi qua x 0 0
D. Nếu hàm số đạt cực trị tại x thì f x  0 0  0 Câu 28.
Giả sử hàm số y f x có đạo hàm cấp hai. Chọn phát biểu đúng ?
A. Nếu f x  0 và f x  0 thì hàm số y f x đạt cực đại tại x 0  0  0
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 15
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
B. Nếu f x  0 và f  x  0 thì hàm số y f x đạt cực tiểu tại x 0  0  0
C. Nếu f x  0 và f  x  0 thì hàm số y f x đạt cực đại tại x 0  0  0
D. Nếu f  x  0 thì hàm số y f x đạt cực đại tại x 0  0 Câu 29.
Giá trị cực đại của hàm số 2
y x  2x 1 là: A. 2 B. 2  C. 2 D. Không có y 2 2 4 CD Câu 30.
Giá trị cực đại của hàm số y x  2cos x trên khoảng 0;  là:     A.  3 B. 5  3 C. 5  3 D.  3 6 6 6 6 Câu 31.
Hàm số y  cos x đạt cực tiểu tại: 
A. x   k,k
B. x    k2,k
C. x k2,k
D. x k,k  2 Câu 32.
Hàm số y  2sin 2x 3 đạt cực tiểu tại:      A. k x   , k
B. x    k,k
C. x   k,k
D. x   k,k  4 2 4 2 4 Câu 33.
Hàm số y  3 cos x  cos 2x đạt cực tiểu tại:  
A. x k2,k
B. x k,k
C. x   k2,k
D. x   k,k  2 2 Câu 34.
Hàm số y  sin x  cos x có cực trị là  3 x
   k ,k  ; y   2 x
k2 ,k  ; y  2 CT CT CT CT A. 4 B. 4 3  x
k2 , k  ; y  2 x
   k , k  ; y   2 CD 4 CD CD 4 CD   C. 3 x
k,k  ; y  2
D. x    k,k  ; y   2 CT 4 CT CD 4 CD Câu 35.
Gọi A, B là hai điểm cực trị của đồ thị hàm số 3
y x  3x 1 . Khi đó đoạn thẳng AB bằng :
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 16
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. 2 5 B. 3 5 C. 2 2 D. 3 2 ĐỀ 04. Câu 1.
Số điểm cực trị của hàm số 4 2
y x  3x  3 là A. 1 B. 2 C. 3 D. 0 Câu 2.
Điểm cực đại của đồ thị hàm số 3
y  x  3x  2 là: A. 0; 2   B.  2  ;0 C. 1;4 D. 1;0 Câu 3. Cho hàm số 3 2
y x  3x  9x 1 . Tổng các giá trị cực đại và cực tiểu của đồ thị hàm số là: A. 20  B. 26  C. 6  D. 20 4 Câu 4. x
Điểm cực tiểu của đồ thị hàm số 2 y   x  3 là: 2 A.  5         1;   B. 2 1;   C. 5 ; 1    D. 5 ;1    2   4   2   2  Câu 5. Hàm số 4 2
y x  4x 1 đạt cực tiểu tại điểm có hoành độ: A. x   2 B. x  1 
C. x 1 D. x  2  Câu 6. Đồ thị hàm số 3
y x  3x có điểm cực đại là : A. 1;2 B. 1;0 C. 1;2 D. 1;0 Câu 7.
Hàm số nào sau đây có cực trị
A. y  3x  5 B. 3 2
y x  2x  5 C. 3
y x 1 D. 3
y x x 1 Câu 8. Đồ thi hàm số 3
y x  3x 1 có điểm cực đại là: A.  1  ;  1 B.  1  ;3 C. 1;  1  D. 1;3 Câu 9. Cho hàm số 3 2
y x  3x 1 . Giá trị cực đại của đồ thị hàm số là
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 17
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 1 B. 3  C. 0 D. 3 Câu 10.
Số cực trị của hàm số 4 2
y  x  2x  3 là: A. 1 B. 2 C. 3 D. 4 Câu 11. Cho hàm số 4 2
y  x  8x  4 . Chọn phát biểu đúng trong các phát biểu sau:
A. Hàm số đạt cực tiểu tại x  0
B. Hàm số có cực đại nhưng không có cực tiểu
C. Hàm số đạt cực đại tại x  0
D. Hàm số có cực tiểu nhưng không có cực đại 2 Câu 12. x  4x 1 Cho hàm số y
.Hàm số có hai điểm cực trị x , x .Tích x .x bằng x 1 1 2 1 2 A. 5  B. 4 C. 1  D. 2 Câu 13. 1
Khẳng định nào sau đây là đúng. Hàm số 4 2 y
x  2x 1có 4
A. một cực đại và không có cực tiểu
B. một cực tiểu và hai cực đại
C. một cực đại và hai cực tiểu
D. một cực đại và một cực tiểu 3 Câu 14. x 2 Cho hàm số 2 y
 2x  3x  . Tọa độ điểm cực đại của đồ thị hàm số là: 3 3 A.  2  3;   B. 1;2 C. 1;2 D. 1;2  3  3 Câu 15. x 2 Cho hàm số 2 y
 2x  3x  . Toạ độ điểm cực đại của đồ thị hàm số là : 3 3 A.    1; 2 B.  1  ;3 C. 2 3;   D. 1;2  3  Câu 16.
Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số 3 2
y x  3x  9x  5 là: A. 4 65 B. 37 2 C. 2 65 D. 2 37 Câu 17. 1 2 Cho hàm số 3 2 y
x  2x  3x
. Toạ độ điểm cực đại của đồ thị hàm số là 3 3 A. 1;2 B. 1;2 C.  1  ;2 D. 1;2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 18
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 18. Cho hàm số 3 2
y x  3x  9x  4 . Nếu hàm số đạt cực đại x và cực tiểu x thì 1 2
tích y x .y x bằng: 1   2  A. 207  B. 302  C. 82  D. 25 Câu 19.
Điểm cực đại và cực tiểu của đồ thị hàm số 3
y x  3x  2 có tọa độ lần lượt là:
A. 1;4 và 1;0
B. 1;2 và 1;0 C. 1;0 và 1;4 D. 1;0 và 1;4 Câu 20.
Số các điểm cực trị của hàm số y    x5 x  3 2 1 là: A. 1 B. 3 C. 5 D. 7 Câu 21. Cho hàm số 3 2
y x  3x  21x 1. Hàm số đạt cực trị tại 2 điểm x , x . Khi đó 1 2 tổng 2 2
S x x có giá trị là: 1 2 A. 18 B. 24 C. 36 D. 48 Câu 22. Cho hàm số 3 2
y x  3x 1. Tích giá trị cực đại và cực tiểu của đồ thị hàm số là: A. 6  B. 3  C. 0 D. 3 Câu 23.
Gọi y , y lần lượt là giá trị cực đại và giá trị cực tiểu của đồ thị hàm số 1 2 4 2
y  x 10x  9 . Khi đó giá trị của biểu thức T y y bằng: 1 2 A. 7 B. 9 C. 25 D. 2 5 Câu 24. Cho hàm số 3 2 y  2
x  3x  5 Tổng các giá trị cực trị của hàm số là: A. 9  B. 1 C. 1  D. 5  Câu 25. Cho đồ thị hàm số 2
y  2  x
. Khi đó y y  ? x 1 CD CT A. 3 2 2 B. 3 2 2 C. 2 D. 6 Câu 26. Đồ thị hàm số 2 y  9  x
có mấy điểm cực trị ? A. 0 B. 1 C. 2 D. 3
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 19
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 27.
Hàm số y x  2sin x  2 đạt cực tiểu tại:  
A. x    k,k
B. x   k,k  3 3  
C. x    k2,k D. 2 x    k,k  3 3 Câu 28.
Cho hàm số y  cos 2x 1, x  
 ;0 thì khẳng định nào sau đây sai ?  
A. Hàm số đạt cực tiểu tại điểm 7 x  
B. Hàm số đạt cực đại tại điểm 11 x   12 12  
C. Tại x  
hàm số không đạt cực đại. D. : Hàm Số đạt cực tiểu tại điểm x   2 2 Câu 29.
Điểm cực đại của hàm số y x sin 2x là .    
A. x    k2
B. x    k
C. x   k
D. x    k 3 6 6 6 Câu 30.
Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số 3
y x  3x  4 là: A. 4 B. 5 C. 5 D. 2 5 Câu 31.
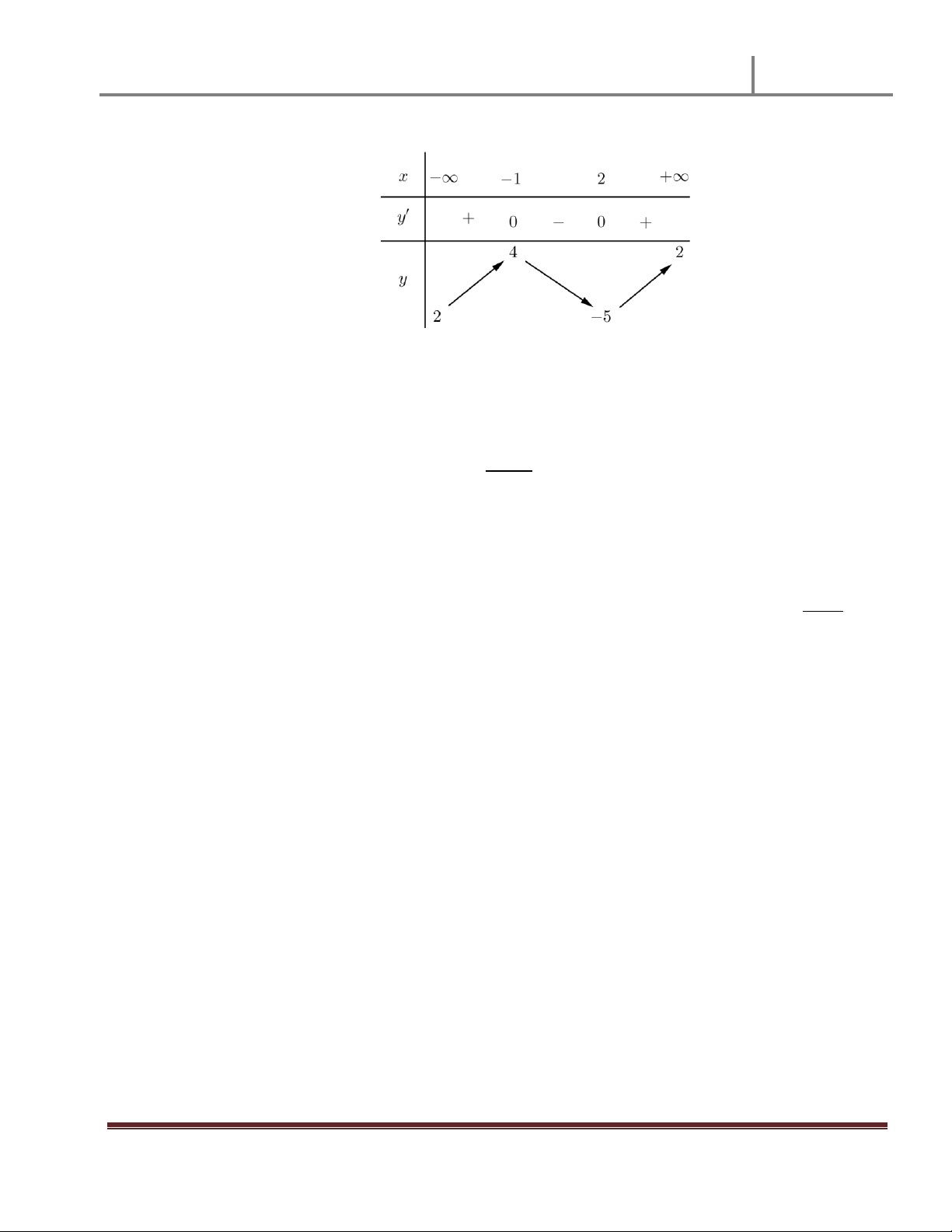
Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên. x   0 1   , y + || - 0 - 0   y   1 
Khẳng định nào sao đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1
D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 20
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 32.
Ba điểm cực trị của hàm số 4 2
y x  4x 1 tạo thành một tam giác cân có diện tích S bằng A. S  2 2 B. S  8 2 C. S  3 2 D. S  4 2 Câu 33.
Đồ thị hàm số y  sin x có mấy điểm cực trị ? A. 3 B. 2 C. 1 D. Vô số. 2 Câu 34. x x 1
Điểm cực tiểu của đồ thị hàm số y  là x  2 A.  1  ;  1 ; 3  ; 5   B.  3  ; 5   C.  1  ;  1 D.  1  ;3 Câu 35.
Khoảng cách giữa hai cực trị của đồ thị hàm số 3 2
y x  3x  3 là: A. 5 B. 2 5 C. 3 5 D. 8 5 ĐỀ 05 2 Câu 1. x  3x  3 Hàm số y
có tích các giá trị cực đại và cực tiểu bằng: x 1 A. 3  B. 1  C. 1 D. 2 2 Câu 2.
x  2x  5
Khẳng định nào sau đây là đúng về đồ thị hàm số y  : x 1
A. y y  0 B. y  4  C. x  1 
D. x x  3 CD CT CT CD CD CT Câu 3. x Cho hàm số 3 2
y  x  3x
Hàm số đạt cực trị tại 2 điểm x , x Khi đó tổng 2 1 2 2 2
S x x có giá trị là: 1 2 A. 12  B. 12 C. 18 D. 20 4 Câu 4. x Cho hàm số 3 y
x  4x 1. Gọi x , x là 2 nghiệm của phương trình y  0 . 4 1 2
Khi đó tổng x x bằng: 1 2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 21
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 1  B. 2 C. 0 D. 1 Câu 5. Hàm số 3 2
y x  3x  2 có mấy điểm cực trị? A. 0 B. 1 C. 2 D. 3 Câu 6. Cho hàm số 3 2
y  x  3x  3x 1 , mệnh đề nào sau đây là đúng?
A. Hàm số luôn luôn nghịch biến trên  ;   .
B. Hàm số đạt cực đại tại x 1
C. Hàm số luôn luôn đồng biến  ;  
D. Hàm số đạt cực tiểu tại x 1 Câu 7.
Điểm cực đại của đồ thị hàm số 3 2
y x  5x  7x  3 là: A.      1; 0 B. 0;3 C. 7 32 ;    D. 7 32 ;    3 27   3 27  2 Câu 8. x  4x 1 Cho hàm số y
, hàm số có 2 điểm cực trị x , x . Tích x .x bằng x 1 1 2 1 2 A. 5  B. 4 C. 1  D. 2 Câu 9. Hàm số 3 2
y  3x  4x x 14 đạt cực trị tại hai điểm x , x . Khi đó tích số x .x 1 2 1 2 là: A. 1  B. 1 C. 1 D. 3 9 7 Câu 10. Cho hàm số 3 2
y  3x  4x x 14 . Hàm số đạt cực trị tại 2 điểm x , x Khi đó 1 2
tổng x x có giá trị là: 1 2 A. 1  B. 1 C. 8 D. 1  9 7 9 Câu 11. Cho hàm số 3 2
y x  5x  6x  2 . Hàm số đạt cực trị tại 2 điểm x , x . Khi đó 1 2
tổng x x có giá trị là: 1 2 A. 10 B. 10  C. 1 D. Đáp án khác 3 3 Câu 12. Cho hàm số 3 2 y  2
x  3x  2 . Câu nào sau đây sai ?
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 22
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
A. Hàm số đạt cực tiểu trên  1 1     ;  
B. Hàm số đạt cực đại trên 1 ;2    2 2   2 
C. Hàm số có 2 cực trị trên  1     ; 2  
D. Hàm số có 2 cực trị trên 1 ;3    2   3  Câu 13.
Hàm số nào sau đây chỉ có cực đại mà không có cực tiểu ?  4  A. x x x 3 2
y  x  3x  2 B. 1 y C. 2 y    x 1 D. 2 y  2  x 2 x 1 Câu 14. 1 4 7 Cho hàm số 4 3 2 y x x
x  2x 1 .Khẳng định nào sau đây đúng ? 4 3 2
A. Hàm số không có cực trị.
B. Hàm số có cực tiểu, không có cực đại.
C. Hàm số có 1 cực đại và 2 cực tiểu
D. Hàm số có 1 cực tiểu và 2 cực đại. 2 Câu 15. x  2x  5
Xét tính cực trị của đồ thị hàm số y  ta có: x 1 A. M  3  ; 4
  là điểm cực tiểu. B. N 1; 4
  là điểm cực đại. C. P 3  ; 4
  là điểm cực đại.
D. Hàm số không có cực trị. Câu 16. Cho hàm số 4 3
y  3x  4x . Khẳng định nào sau đây đúng ?
A. Hàm số không có cực trị.
B. Điểm A1;  1 là điểm cực tiểu.
C. Hàm số đạt cực đại tại gốc tọa độ.
D. Hàm số đạt cực tiểu tại gốc tọa độ. 2 Câu 17. x  4x 1 Cho hàm số y
có hai điểm cực trị x , x . Tích x x bằng x 1 1 2 1 2 A. 2 B. 5  C. 1  D. 4 Câu 18.
Một hàm số f x có đạo hàm là f x 3 2
x  2x x . Số cực trị của hàm số là: A. 0 B. 1 C. 2 D. 3 Câu 19.
Đồ thị hàm số nào sau đây chỉ có 1 điểm cực trị ?
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 23
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 4 2
y  2x  4x  2
B. y  m  2 2 4 2 4 x  9x 1 C. 4 2
y  x  2x 1 D. 4
y  x   2 m   2 1 x 1 Câu 20.
Gọi A, B lần lượt là 2 điểm cực trị của đồ thị hàm số 3 2
y x  3x  4 . Khi đó
diện tích tam giác OBC (với O là gốc tọa độ) có giá trị bằng bao nhiêu ? A. 2 B. 4 C. 2 5 D. 8 Câu 21.
Gọi A, B lần lượt là 2 điểm cực trị của đồ thị hàm số 3 2
y x  3x  2 Khi đó
diện tích tam giác ABC với C 1; 
1 có giá trị bằng bao nhiêu ? A. 1 B. 2 C. 3 D. 4 Câu 22.
Gọi A, B lần lượt là 2 điểm cực trị của đồ thị hàm số 3 2
y  2x  3x  36x 10
Khi đó diện tích của tam giác ABC với C 2;3 có giá trị bằng bao nhiêu ? A. 78 B. 87 C. 287 D. 285 3 3 2 Câu 23.
Gọi A, B lần lượt là 2 điểm cực trị của đồ thị hàm số y  x  2
1 2  x Khi đó
diện tích của tam giác ABC với C 1; 3
  có giá trị bằng bao nhiêu ? A. 3 B. 8 C. 7 D. Đáp án khác. 5 3 3 Câu 24. x
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 2 y
 2x  3x 5 3
A. Song song với đường thẳng x 1
B. Song song với trục hoành.
C. Có hệ số góc dương.
D. Có hệ số góc bằng -1 Câu 25.
Phương trình tiếp tuyến của đồ thị hàm số 4 2
y x  2x 1 tại điểm cực tiểu là: A. y 1  0 B. y  0
C. x y 1 0
D. y  x Câu 26.
Khoảng cách từ điểm cực đại của đồ thị hàm số 3
y x  3x 1 đến đường
phân giác góc phần tư thứ hai trong hệ trục Oxy là:
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 24
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. 1 B. 2 C. 2 D. 3 Câu 27.
Tiếp tuyến tại điểm cực trị của đồ thị hàm số 4 2
y ax bx c a  0 có gì đặc biệt
A. Song song với trục tung.
B. Có hệ số góc dương.
C. Song song hoặc hoặc trùng với trục hoành.
D. Luôn đi qua gốc tọa độ. Câu 28.
Với giá trị nào của tham số m thì đường thẳng d : y x m đi qua trung
điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số 3 2
y x  6x  9x A. m  0 B. m 1 C. m  2 D. m  3 Câu 29.
Hàm số nào sau đây đạt cực tiểu tại 3 x  ? 2  A. x 1 y B. 2
y  x  3x  2 x  2 C. 1 2
y  4x 12x  8 D. 4 3 2 y
x x x  3x 2 Câu 30. Cho hàm số 2
y  3  2x x . Trong các điểm sau, điểm nào có tọa độ sau đây
là điểm cực trị của hàm số đã cho: A. M  1  ;2 B. N  3  ;0 C. P1;0 D. Q 2  ; 3 Câu 31.
Điểm cực tiểu của đồ thị hàm số 2
y x 4  x là:
A. M  2;2
B. N  2;  1 C. P 2; 2   D. Q 2;2 Câu 32.
Cho hàm số y  2x 1 4x 1 . Tìm mệnh đề đúng trong các mệnh đề sau ?
A. Giá trị cực đại bằng 1 
B. Điểm cực tiểu có tọa độ là  1  M ; 1    2  2 
C. Điểm cực tiểu là  1 1  N ;   
D. Hàm số không có cực trị.  4 2 
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 25
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 33.
Gọi A, B, C là ba điểm cực trị của đồ thị hàm số 4 2
y  2x  4x 1 Hỏi diện tích
tam giác ABC là bao nhiêu ? A. 4 B. 2 C. 1 D. 32 2 Câu 34.
x mx m
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y  bằng: x 1 A. 5 B. 2 5 C. 4 5 D. 5 5 Câu 35.
(SGD Bắc Ninh, 2017) Hàm số 3 2
y  x  3x 1 có điểm cực tiểu bằng A. 2 . B. 0 . C. 3 . D. 1 ĐỀ 06
Câu 1. (SGD Bắc Ninh, 2017) Hàm số 4 2
y  x  2x 1 có mấy điểm cực trị? A. 0 . B. 3 . C. 2 . D. 1.
Câu 2. (SGD Hải Phòng, 2017) Cho hàm số 4 2
y  x  2x  2 . Hãy chọn mệnh đề đúng
A. Hàm số đạt cực đại tại điểm x = 1.
B. Hàm số đạt cực tiểu tại điểm x = 0.
C. Hàm số đạt cực đại tại điểm x = -1
D. Hàm số đạt cực tiểu tại điểm x = -1.
Câu 3. (SGD Long An, 2017) Cho hàm số y f x xác định trên và có bảng biến thiên như hình vẽ:
Chọn khẳng định đúng?
A. Hàm số có 2 điểm cực trị.
B. Hàm số có 1 điểm cực trị.
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 26
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
C. Hàm số có 3 điểm cực trị.
D. Hàm số không có điểm cực trị.
Câu 4. (SGD Bình Phước, Lần 1, 2017) Cho hàm số 4 2
y x  4x  2 .Khẳng định nào sau đây là đúng ?
A. Hàm số đạt cực tiểu tại hai điểm x   2 và x  2 .
B. Hàm số đạt cực tiểu tại điểm x  0 .
C. Hàm số đạt cực tiểu tại điểm y  2  .
D. Hàm số đạt cực đại tại hai điểm  2; 2   và  2; 2   .
Câu 5. (SGD Bình Phước, Lần 1, 2017) Hàm số y f x có bảng biến thiên sau đây: 0 0
Hàm số f x đạt cực tiểu tại điểm A. x  0 . B. y  1  . C. y  0. D. x  1  .
Câu 6. (SGD Hà Nội, Lần 1, 2017) Cho hàm số y f x liên tục trên , có đạo hàm
f x  xx  2 x  3 1
1 . Hàm số đã cho có bao nhiêu điểm cực trị?
A. Có 3 điểm cực trị.
B. Không có cực trị.
C. Có 2 điểm cực trị.
D. Chỉ có 1 điểm cực trị.
Câu 7. (SGD Hà Nội, Lần 1, 2017) Tìm điểm cực tiểu x của hàm số 3 2
y x  3x  9 . x CT A. x  1  . B. x  3  . C. x 1. D. x  0 . CT CT CT CT
Câu 8. (SGD HCM cụm 2, 2017) Hỏi trong bốn hàm số được liệt kê dưới đây, hàm số nào
không có cực trị?
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 27
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 3 2
y x x  5 . x B. 3 y x . C. 4 2
y x x 1. D. 4 y  x 1.
Câu 9. (SGD HCM cụm 2, 2017) Tìm giá trị cực tiểu y của hàm số 3
y x  3x . CT A. y  4  . B. y  2 . C. y  2  . D. y  1  . CT CT CT CT Câu 10.
(SGD HCM cụm 4, 2017) Đồ thị hàm số 3
y x  3x có điểm cực đại là A. 1;2. B.  1  ;0. C.  1  ;2. D. 1;0. Câu 11.
(THPT QG 2017) Cho hàm số y f x có bảng biến thiên như sau
Tìm giá trị cực đại y và giá trị cực tiểu y của hàm số đã cho. CĐ CT
A. y  3 và y  0 .
B. y  3 và y  2  . CĐ CT CĐ CT C. y  2  và y  2 .
D. y  2 và y  0 . CĐ CT CĐ CT Câu 12.
(THPT QG 2017) Cho hàm số y f x có bảng biến thiên như sau x   0 2   , y + 0 - 0 + 4 2 y 2 5 
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x  5 .
B. Hàm số có bốn điểm cực trị.
C. Hàm số đạt cực tiểu tại x  2.
D. Hàm số không có cực đại. Câu 13.
(THPT QG 2017) Đo thi cu a ha m so 3 2
y  x  3x  5 co hai đie m cư c tri A
va B . T nh die n t ch S cu a tam gia c OAB vơ i O la go c to a đo . A. S  9 . B. 10 S  . C. S  10 . D. S  5 3
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 28
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 14.
(THPT QG 2017) Cho hàm số y f x có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng ?
A. Hàm số có bốn điểm cực trị.
B. Hàm số đạt cực tiểu tại x  2 .
C. Hàm số không có cực đại.
D. Hàm số đạt cực tiểu tại x  5  . Câu 15. x
(THPT QG 2017) Hàm số 2 3 y
có bao nhiêu điểm cực trị ? x 1 A. 3. B. 0. C. 2 . D.1. Câu 16.
(THPT AMSTERDAM 2017) Hàm số 3 2
y x  3x  4 đạt cực tiểu tại điểm: A. x  0 B. x  2 C. x  4
D. x  0 và x  2  Câu 17. x
(THPT AMSTERDAM 2017) Số điểm cực trị của đồ thị hàm số 1 y  là: 2  x A. 0 B. 1 C. 2 D. 3 Câu 18.
(THPT Nguyễn Đình Chiểu Bình Định 2017) Hàm số 3 2
y  x  3x  2 có giá
trị cực tiểu y là CT A. y  2 . B. y  2  . C. y  4  . D. y  6 . CT CT CT CT Câu 19.
(Nguyễn Thái Học, Vĩnh Phúc, Lần 1, 2017) Cho hàm số 4 2
y  x  2x 1 .
Khẳng định nào sau đây đúng:
A. Đồ thị hàm số có hai điểm cực tiểu.
B. Hàm số đạt cực đại tại x 1.
C. Hàm số đạt cực tiểu tại x  1  .
D. Giá trị cực tiểu bằng 0. Câu 20.
(Nguyễn Thái Học, Vĩnh Phúc, Lần 1, 2017) Cho hàm số 3 2
y x  3x 1.
Khẳng định nào sau đây đúng:
A. Điểm cực tiểu của đồ thị hàm số là (2; 5  ) .
B. Giá trị cực tiểu bằng 0 .
C. Giá trị cực đại của hàm số là y  2  .
D. Hàm số đạt cực đại tại x  2 . d c
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 29
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 21.
(SGD HCM cụm 5, 2017) Tìm cực tiểu của hàm số 3 2
y  x  6x 15x 10 . A. 5. B. 110. C. 2. D. 1.  Câu 22.
(SGD HCM cụm 6, 2017) Cho hàm số f x có đạo hàm là
f  x  x x  2  x  4 1 2 x
  . Số điểm cực tiểu của hàm số f x là A. 2 . B. 0. C. 1. D. 3 . Câu 23.
(SGD HCM cụm 7, 2017) Cho hàm số 3
y  x  3x  3. Khẳng định nào sau đây sai?
A. Hàm số có 2 điểm cực trị.
B. Hàm số đạt cực tiểu tại x  1  .
C. Hàm số đạt cực đại tại x 1.
D. Hám số có 2 điểm cực đại. Câu 24.
(SGD Huế, 2017) Cho hàm số y f (x)liên tục trên khoảng ( ;
a b) và x là một 0
điểm thuộc khoảng đó. Khẳng định nào sau đây đúng?
A. Nếu f ' (x )  0 thì x là điểm cực đại của hàm số. 0 0
B. Nếu f ' (x )  0 thì x là điểm cực tiểu của hàm số. 0 0
C. Nếu f '(x )  0 và f ' (x )  0 thì x là điểm cực tiểu của hàm số.. 0 0 0
D. Nếu f '(x )  0 và f ' (x )  0 thì x là điểm cực đại của hàm số. 0 0 0 Câu 25.
(SGD Nam Định, Lần 1, 2017) Hàm số nào sau đây đạt cực đại tại điểm x  0 . 2 A. x  2 y x . B. 4 y x 1. C. y  . D. 3 y x . x Câu 26.
(SGD Quảng Ninh, 2017) Hàm số nào trong bốn hàm số được liệt kê ở bốn
phướng án A, B, C, D dưới đây, không có cực trị? A.  3 2 x
y x  3x  4x 1. B. 4 2
y  x  4x  3 . C. 3
y x  3x  5 . D. 4 y  . x 1 Câu 27.
(SGD Quảng Ninh, 2017) Tìm điểm cực đại x (nếu có) của hàm số CĐ y
x  3  6  x . A. x  3 .
B. x  6 . C. x  6 .
D. Hàm số không có điểm cực đại. CĐ CĐ CĐ
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 30
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 28.
(SGD Thanh Hóa, 2017) Cho hàm y
số y f (x) liên tục trên  và có đồ thị là 2
đường cong như hình vẽ bên. Tìm điểm cực x
tiểu của đồ thị hàm số y f (x) . -2 -1 O 1 2 A. y  2.  B. x  0. -2 C. M (0; 2  ). D. N(2;2). 2 Câu 29. x  4x
(SGD Thanh Hóa, 2017) Gọi x , x là hai điểm cực trị của hàm số y  . 1 2 x 1
Tính giá trị của biểu thức P x .x . 1 2 A. P  5.  B. P  2.  C. P  1.  D. P  4. 
VẤN ĐỀ 2. Tìm tham số m để hàm số đạt cực trị tại x cho trước 0 Phương pháp 1
Bước 1. Hàm số f x đạt cực trị tại x thì suy ra: f x  0 hoặc f ' x không xác định tại 0  0
điểm x  ta tìm được tham số m. 0
Bước 2. Thay tham số m vừa tìm được và lập bảng biến thiên để Kết luận Phương pháp 2
Sử dụng dấu hiệu 2. Tính f x, f  x .
+) Nếu f x  0 thì hàm số đạt cực đại tại điểm x . 0  0
+) Nếu f x  0 thì hàm số đạt cực tiểu tại điểm x . 0  0  f '   x  0 0  Chú ý: Nếu 
thì không thể kết luận gì về điểm x (Phải sử dụng Phương pháp 1)  0 f "  x  0 0  A. ÁP DỤNG
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 31
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Ví dụ 1. 1 Tìm m để hàm số 3 2 y
x mx   2 m m  
1 x 1 đạt cực tiểu tại x  1 0 3 Ví dụ 2. 1 Tìm m để hàm số 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại x  1 0 3 Ví dụ 3. Tìm m để hàm số 3
y x mx đạt cực trị tại x  0 .
Đs: không tồn tại m 0 Ví dụ 4. Tìm m để hàm số 4
y x mx đạt cực trị tại x  0 . Đs: m  0 0 Ví dụ 5. 1 Cho hàm số 3 y x   2
m m  2 2 x   2 3m  
1 x m  5 . Tìm m để hàm số đạt 3
cực tiểu tại x  2  ? Đs: m  3 0 2 Ví dụ 6. x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? x m Đs: m  3  2
x  m  3 Ví dụ 7. x  3m  4
Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? x m
Đs: m  4 2 Ví dụ 8.
ax bx ab Cho hàm số y
. Tìm a, b sao cho hàm số đạt cực trị tại điểm ax b
x  0 và x  4 ? Đs: a  2  ;b  4 2 Ví dụ 9. ax bx  2 Cho hàm số y
. Tìm a, b sao cho hàm số đạt cực trị tại điểm x  0 x a và x  4 ? Đs: a  2  ;b 1 4 Ví dụ 10. x Cho hàm số 2 y
ax b . Tìm m để hàm số đạt cực trị bằng -2 tại điểm 2 x  1 ? Đs: 3
a  1;b   0 2
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Tìm m để hàm số 3
y x  m   2
3 x mx m  5 đạt cực tiểu tại điểm x  2 ? 0
Đs: m  0
Bài tập 2. Tìm m để hàm số y   2 m m 3 2 5
x  6mx  6x  6 đạt cực đại tại điểm x  1? 0
Đs: m 1 Bài tập 3. 1
Tìm m để hàm số 3 2 y
x mx   2
m  4 x  2 đạt cực đại tại điểm x  1? 0 3
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 32
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Đs: m  3  Bài tập 4. Cho hàm số 1
y msin x  sin 3x . Tìm m để hàm số đạt cực đại tại điểm x  ? 3 3 Đs: m  2 2
x  m   Bài tập 5. 1 x 1
Tìm m để hàm số y
đạt cực đại tại điểm x  2 ? x m 1 0 Đs: m  2  2 Bài tập 6. x mx 1
Tìm m để hàm số y
đạt cực đại tại điểm x  2 ? x m 0 Đs: m  3  Bài tập 7. 1 Cho hàm số 4 2 y
x ax b . Tìm a, b để hàm số có cực trị bằng -2 tại x 1 ? 4 Đs: 1 7 a  ;b   2 4
Bài tập 8. Cho hàm số 3 2
y x ax bx c . Tìm a, b, c để hàm số có giá trị bằng 1 tại điểm
x  0 và đạt cực trị tại điểm x  2 và giá trị cực trị là -3? Đs: a  3
 ;b  0;c 1
C. BÀI TẬP TRẮC NGHIỆM ĐỀ 01 2 Câu 1.
x  3x m
Đồ thị hàm số y
nhận điểm A0;3 làm cực trị thì phương x  2
trình của hàm số có dạng là: 2    2    2    2   A. x 3x 6 x 3x 1 x 3x 6 x 3x y B. y C. y D. y x  2 x  2 x  2 x  2 Câu 2.
Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x  3x mx đạt cực tiểu tại x  2 A. m  0 B. m  0 C. m  0 D. m  0
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 33
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 3.
Tìm tất cả các giá trị thực của tham số m để hàm số 3
y  x  m   2 1 x  2m 1
đạt cực đại tại x  2 A. m  2 B. m 1 C. m  5 D. m  3 Câu 4.  
Tìm tất cả các giá trị thực của tham số m để hàm số 2 3 2
y x mx m x  7    3 
có cực trị tại x 1 A. 7 m   B. m  3  C. m  7 D. m  7  9 Câu 5. 1 Hàm số 3 y x   2
m m  2 2 x   2 3m  
1 1 đạt cực tiểu tại x  2  khi và chỉ 3 khi.      A. m 1 mB. 1  C. m 1 D. m  3 m  3 m  3  Câu 6.
Tìm tất cả các giá trị của tham số m sao cho hàm số 3 2
y x mx   2 3 3 m   1
đạt cực đại tại x 1. Kết quả nào đúng? A. Không có m B. m  2 C. m  1  D. m  2  Câu 7. Hàm số 3 2
y x  3x mx đạt cực tiểu tại x  2 khi giá trị của tham số m thỏa mãn: A. m  0 B. m  0 C. m  0 D. m  0 Câu 8.
Với giá trị nào của m thì hàm số 3
y x  2mx 1 đạt cực tiểu tại x 1 : A. 2 m B. 3 m   C. 2 m D. 2 m   3 2 3 3 Câu 9. 1 Hàm số 3 y
x mx m  5 đạt cực tiểu tại x  2 khi tham số m lấy giá trị 3 bằng bao nhiêu? A. m  4 B. m 1 C. m  3  D. m  1  Câu 10. Tìm m để hàm số 3 2
y x mx  3x  2 đạt cực tiểu tại x  2 ?
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 34
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. 15 m   B. 4 m C. 4 m   D. 15 m  4 15 15 4 Câu 11. Tìm m để hàm số 3 2
y mx  3x 12x  2 đạt cực đại tại x  2 ? A. m  2  B. m  3  C. m  0 D. m  1  Câu 12. Hàm số 3 2
y x  3x mx đạt cực tiểu tại x  2 khi: A. m  0 B. m  0 C. m  0 D. m  0 Câu 13. 1 Hàm số 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại điểm x 1 khi: 3
A. m 1 m  2 B. m 1 C. m  2 D. mCâu 14. Hàm số 3
y x  m  
1 x 1 đạt cực tiểu tại điểm x  2 khi: A. m 13 B. m 13 C. m 1 D. m Câu 15. Hàm số 3 2
y x mx   2 6 4m  
1 x  2 đạt cực đại tại điểm x  2 khi: A. m  0 B. 11 m C. m  4 D. m  4  2 ĐỀ 02 Câu 1. Hàm số 3 2
y x  2x mx 1đạt cực tiểu tại x 1 khi: A. m 1 B. m  1  C. m  2 D. Không có m Câu 2. 1 Hàm số 3 2 2 y
x  2mx  3m x  3m đạt cực tiểu tại x  1  khi: 3 A. m  1  B. m 1 C. 1 m D. 1 m   3 3 Câu 3. Hàm số 3
y  x  m   2
1 x m  2 đạt cực đại tại điểm x  2 khi: A. m  0 B. 11 m C. m  4 D. m  4  2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 35
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 4. Hàm số 3 2 2
y x  2mx m x  2 đạt cực tiểu tại điểm x 1 khi: A. m  1  B. m 1 C. m  2 D. m  2  Câu 5. 1 m Hàm số 3 2 y x
x  m  
1 x đạt cực đại tại x 1 khi: 3 2 A. m  2 B. m  2 C. m  2 D. m   Câu 6. Hàm số 3
y x  m   2
3 x mx m  2 đạt cực tiểu tại điểm x  2 khi: A. m  0 B. 11 m C. m  4 D. m  4  2 Câu 7. 1 Hàm số 3 y
x  m   2 1 x   2
m  3m  2 x  5 đạt cực trị tại x  0 khi: 3 A. m 1 B. m  2
C. A, B đều đúng. D. A, B đều sai. Câu 8. 1 Hàm số 3 2 y
x mx   2 m m  
1 x đạt cực trị tại x 1 khi: 3 A. m  0 B. m 1 C. m  2 D. m  3 Câu 9. Hàm số 4 2 2
y x  2m x  5 đạt cực tiểu tại x  1  khi: A. m 1 B. m  1 
C. A, B đều đúng. D. A, B đều sai. Câu 10. Hàm số 4
y  x  m   2 2
2 x m  3 đạt cực đại tại điểm x 1 khi: A. m  3 B. m  5 C. m  3 D. m  5 Câu 11. Hàm số 4 2
y x  3mx 1 đạt cực tiểu tại điểm x  2  khi: A. 8 m   B. 8 m C. m  3 D. m  8 3 3 Câu 12. 1 . Hàm số 4 2 y
x ax b có cực trị tại x 1 và giá trị cực trị tương ứng bằng 4
2 thì giá trị của lần lượt là:
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 36
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12  1  1  1  1 a   a    a   a    A.  2     B. 2  C. 2  D. 2  9 9 9 9 b            b b b  4  4  4  4 Câu 13. Đồ thị hàm số 4 2
y ax bx c đạt cực đại tại A0; 3
  đạt cực tiểu tại B  1  ; 5
  thì sẽ có giá trị của a, , b c lần lượt là: A. 2;4; 3  B. 3  ; 1  ; 5  C. 2  ;4; 3  D. 2; 4  ; 3  Câu 14. Hàm số 3 2
y ax x  5x b đạt cực tiểu tại x 1 và giá trị cực tiểu bằng 2 khi:          A. a 1 a a aB. 1  C. 1  D. 1  b   5 b   5 b   5  b  1 Câu 15. Hàm số 3 2
y x  2ax  4bx  2016 đạt cực đại tại x 1 . Khi đó tổng a b là: A. 4  B. 4 C. 3  D. 3 3 3 4 4 ĐỀ 03 Câu 1. Hàm số 1 y  .
m sin x  sin 3x đạt cực trị tại điểm x  khi: 3 3 A. m  2  B. m  0 C. m  2 D. m  3 2 Câu 2. x mx 1 Hàm số y
đạt cực tiểu tại x 1khi: x m A. m  2  B. m  2   m  0 C. m  0
D. Không có thỏa yêu cầu bài toán. Câu 3.
Tìm tất cả các giá trị thực của tham số m để hàm số 3
y x  m   2 x   2 2 1
m  4 x m 1 đạt cực tiểu tại x  0 A. m  2 B. m  2  C. m  3  D. m  3
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 37
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 4. Cho hàm số 3
y x  2mx 1. Tìm tất cả các giá trị của m để hàm số đạt cực tiểu tại x 1 A. 3 m B. 3 m   C. 2 m D. 2 m   2 2 3 3 Câu 5.
Tìm tất cả các giá trị thực của tham số m để hàm số 4 2
y x  3mx m 1 đạt
cực tiểu tại x  0 A. m  0
B. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. C. m  0 D. m  0 Câu 6.
Giá trị của m để hàm số 3
y x  2mx 1 đạt cực tiểu tại x 1 là: A. 2 m   B. 2 m C. 3 m   D. 3 m  3 3 2 2 Câu 7. Hàm số 3 2
y x mx   2 3 3 m  
1 x đạt cực tiểu tại x  1 khi : 0     A. m m m  2 B. m  0 C. 0  D. 0  m  2 m  2 Câu 8. 1 Hàm số 3 2 y
x mx   2
m  4 x  5 đạt cực tiểu tại x  1  khi: 3 A. m  3  B. m  1 
C. m  0
D. m 1 Câu 9. Đồ thị hàm số 3 2
y ax bx cx d có hai điểm cực trị A0;0, B 1  ;1 thì các hệ số , a , b ,
c d có giá trị lần lượt là: A. a  2
 ;b  0;c  0;d  3
B. a  0;b  0;c  2  ;d  3 C. a  2
 ;b  0;c  3;d  0 D. a  2
 ;b  3;c  0;d  0 Câu 10. Hàm số 3 2 2
y x  2mx m x  2 đạt cực tiểu tại x 1 khi m bằng: A. m  1  B. m 1 C. m  2 D. m  2  Câu 11. Biết đồ thị hàm số 4 2
y x  2 px q có một điểm cực trị là M 1; 2 ,thế thì
khoảng cách giữa điểm cực tiểu và điểm cực đại là: A. 26 B. 5 C. 2 D. 2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 38
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 12. 1
Giá trị của m để hàm số 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại điểm 3 x 1 A. m 1 B. m  2
C. m 1;m  2 D. Không có m Câu 13.
Với giá trị nào của m thì hàm số 3 2
y x mx   2 3 3 m  
1 đạt cực đại tại x 1
A. Không có giá trị m B. m  2 C. m  1  D. m  2  Câu 14. 1 Hàm số 3 y
x  2m   2
1 x m  3 đạt cực đại tại x  0 khi và chỉ khi: 3 A. 1 m B. 1 m C. 1 m D. 1 m  2 2 2 2 Câu 15. Tìm m để hàm số 3 2
y mx  3x 12x  2 đạt cực đại tại x  2 0 A. m  2  B. m  3  C. m  0 D. m  1  ĐỀ 04 Câu 1. 1 Hàm số 4 2 y
x ax b có cực trị tại x 1 và giá trị tương ứng bằng 2 thì giá 4
trị của a, b lần lượt là  1  1  1  1 a   a    a   a    A.  2     B. 2  C. 2  D. 2  9 9 9 9 b            b b b  4  4  4  4 Câu 2. Tìm m để hàm số 4
y mx   m   2 2 2
1 x  3  2m đạt cực tiểu tại x 1 A. m  2  B. m  1  C. m  2 D. m 1 2
x  m   Câu 3. 1 x  4  m
Tìm m để hàm số y
đạt cực đại tại x 1 x m A. m  3  B. m  3 C. m  3  ;m 1
D. m  3;m  1 
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 39
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 2 Câu 4.   Hàm số x mx m y
đạt cực đại tại x  2 thì m bằng x m A. m  1  B. m  3  C. m 1 D. Không tồn tại m 5 3 Câu 5. Tìm m để hàm số x      x y m   2 1
m  2 x  2 đạt cực trị tại x 1 5 3 A. m 1 B. m  2 
C. m 1;m  2  D. Không tồn tại m Câu 6. Hàm số 3 2
y x  3x mx đạt cực tiểu tại x  2 thì giá trị của m là A. m  0 B. m  0 C. m  0 D. m  0 Câu 7. 1 Tìm m để hàm số 3 y
x  m   2 1 x   2
m  3x  2 x  5 đạt cực tiểu tại x  0 3 A. m  6 B. m  2 C. m 1
D. m 1;m  2 Câu 8. Hàm số 4
y x  m   2 x   2 1
m mx 1 đạt cực đại tại x  0 khi A. m 1 B. m  0
C. m  0;m 1 D. Không tồn tại m Câu 9. Hàm số 4 2 2
y x m x  5 đạt cực đại tại x  2  khi A. m  2  B. m  2 C. m  2  D. Không tồn tại m Câu 10.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4
y x  m   2 1 x m
đạt cực tiểu tại x  0 A. m 1 B. m 1 C. m 1 D. m 1 Câu 11.
Giá trị của m để hàm số 3 2
y  x  2x mx đạt cực tiểu tại x  1  là A. m 1 B. m  1  C. m 1 D. m  1  Câu 12.
Tìm tất cả các giá trị của m để hàm số 4
y mx  m   2 2
1 x m  2 đạt cực tiểu tại x 1là A. m  1  B. 1 m C. m 1 D. 1 m   3 3 2 Câu 13. x  2mx  3
Tìm m để hàm số y
đạt cực tiểu tại x 1 x  2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 40
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. m  1  B. m  2  C. m 1 D. m  3  2 Câu 14.  
Tìm tất cả các giá trị của m để hàm số x mx 1 y
đạt cực trị tại x  2 x m A. m  3  ;m  1  B. m  1  C. m  3  D. m  4 2 Câu 15.   Hàm số x 2mx 2 y
đạt cực tiểu tại x  2 khi x m A. m  1  B. m 1 C. m  1  D. không tồn tại m Câu 30.
(SGD HCM cụm 4, 2017) Tìm a , b , c sao cho đồ thị hàm số 4 2
y ax bx c qua O và có một điểm cực tiểu A 3; 9  . A. a  1
 ;b  6;c  0.
B. a 1;b  6;c  0. C. a  1
 ;b  0;c  0. D. a 1;b  6  ;c  0. Câu 16.
(SGD HCM cụm 7, 2017) Tìm tất cả các giá trị của tham số m để hàm số 3 2 2
y  x  2mx  m x  2 đạt cực tiểu tại x  1. A. m 1. B. m  3. C. m 1  m  3. D. m  1  . Câu 17.
(SGD HCM cụm 7, 2017) Biết rằng đồ thị hàm số    4 2 y f x  ax  bx  c có
hai điểm cực trị là A0;2,B2; 14  . Tính f   1 . A. f   1  5  . B. f   1  0. C. f   1  6  . D. f   1  7. Câu 18.
(SGD Đà Nẵng, 2017) Cho hàm số 3 2 y  2
x  3mx m 1 với m là tham số. Tìm
tất cả các giá trị của tham số m để hàm số đạt cực đại tại x  2. A. m  2. B. m  1. C. m 1. D. m  0. Câu 19.
(THPT Nguyễn Đình Chiểu Bình Định 2017) Hàm số 3 x 2 y   m   2 x m  
1 x 1 đạt cực đại tại x 1 khi giá trị m là 3 A. 1. B. 0. C. 2. D. 2 .
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 41
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
VẤN ĐỀ 3. TÌM THAM SỐ M ĐỂ HÀM SỐ CÓ HOẶC KHÔNG CÓ CỰC TRỊ Phương pháp
Biện luận số nghiệm của phương trình yA. ÁP DỤNG Ví dụ 1. 1 Cho hàm số 3 2 y
x mx  25m 8 x 1. Tìm m để hàm số có một cực đại và 3 một cực tiểu?
Đs: m  2;m  8 2
x  m  2 Ví dụ 2. x m Cho hàm số y
. Tìm m để hàm số có một cực đại và một cực x 1 tiểu? Đs: 1 m   2 Ví dụ 3. 1 3 Cho hàm số 4 2 y x mx
. Tìm m để hàm số có cực tiểu mà không có cực 2 2 đại? Đs: m  0 Ví dụ 4. 1 Cho hàm số 3 y
x  m  2 2
x  4m  
1 x  4m . Tìm m để hàm số có điểm cực 3
đại và cực tiểu và điểm cực tiểu nằm trên đường thẳng d : x  3y 8  0 Đs: m 1 Ví dụ 5. 3 Cho hàm số 3
y x  m  2 2
x  3m  
1 x 1 . Tìm m để hàm số có cực đại và 2
cực tiểu đồng thời hoành độ điểm cực tiểu nhỏ hơn 2. Đs: m  3,m  0 Ví dụ 6. Cho hàm số 3
y x  m   2 3
1 x  3m m  2 x 1 . Tìm m để hàm số có cực đại và
cực tiểu đồng thời giá trị cực đại lớn hơn 1. Đs: m  3  ,m  0
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Tìm m để hàm số sau có cực đại và cực tiểu 1) 1 y   2 m   3
1 x  m   2 1 x  3x  5 Đs: 1
  m  2;m 1 3
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 42
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 2) 3 2
y x mx  3mx  5
Đs: m  0;m  9
3) y  m   3 2
2 x  3x mx m Đs: 3
  m 1;m  2 
Bài tập 2. Tìm m để hàm số sau có cực đại và cực tiểu 2   1) x 2mx m y Đs: 1   m  0 x m 2
mx  m    2) 1 x 1 y
Đs: m  2;m  0 mx  2
Bài tập 3. Tìm m để hàm số có 3 điểm cực trị 1) 4
y mx   2 m   2 9 x 10 Đs: m  3  ;0  m  3 2) 4 2
y  x  2mx  3 Đs: m  0
Bài tập 4. Tìm m để hàm số có 1 điểm cực trị 1) 4
y mx  m   2 1 x 1 2m
Đs: m  0;m 1
2) y    m 4 2 1
x mx  2m 1
Đs: m  0;m 1
Bài tập 5. Tìm m để hàm số không có cực trị 1) 3 2
y mx  3x  m  4 x  3
Đs: 1 m  3
2) y  m   3 2
3 x  2mx  3 Đs: m  0
Bài tập 6. Tìm m để hàm số sau không có cực trị 2   2   1) mx 3mx 1 mx 3mx 1 y
Đs: m  0;m 1 2) y
Đs: m  0;m 1 x  2 x  2 Bài tập 7. 1 3
Tìm m để hàm số 4 2 y x mx
có cực tiểu mà không có cực đại. 2 2 2
x  m   Bài tập 8. 1 x m 1
Cho hàm số y
. Chứng minh với mọi m thì đồ thị hàm số x 1
luôn có điểm cực đại, cực tiểu và khoảng cách giữa hai điểm đó là 20 .
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 43
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 2 Bài tập 9.
x mx m
Cho hàm số y
. Chứng minh với mọi m thì đồ thị hàm số luôn có x 1
điểm cực đại, cực tiểu và khoảng cách giữa hai điểm đó là không đổi. 2 Bài tập 10.
x  2x m
Chứng minh hàm số y
luôn có một cực đại và một cực tiểu 2 x  2 2 2 2 Bài tập 11.
x m x  2m  5m  3
Tìm m>0 để hàm số y
có cực tiểu trong khoảng x 0;2mĐs: 1 3  m 1;m  2 2
Bài tập 12. Cho hàm số 3
y x   m   2 2 3 2
1 x  6m m  
1 x 1 . Tìm m để hàm số có cực đại
và cực tiểu và giá trị cực đại lớn hơn 1. Đs: 3   m  0 2
C. BÀI TẬPTRẮC NGHIỆM ĐỀ 01. Câu 1. 1 Cho hàm số 3 2 y
x mx  4m  3 x 1 . Xác định các giá trị của m để hàm số 3
đạt cực đại và cực tiểu? A. 1 m  3 B. m 1 C. m  3
D. m 1 m  3 Câu 2.
Giá trị của m để hàm số 4 2
y x mx  2 có đúng một điểm cực trị : A. m  0 B. m  0 C. m  1  D. m  0 Câu 3. 1 Tìm m để hàm số 3 y
x  m   2 1 x   2
m mx  2 có cực đại và cực tiểu 3 A. m  2 B. 1 m   C. 2 m   D. m  1  3 3 Câu 4. 1 Hàm số 3 2 y
x mx   2
m  2mx 1 có hai điểm cực trị khi và chỉ khi: 3 A. m  0 B. m  0 C. m  0 D. m  0 Câu 5.
Tìm tất cả các giá trị của m để hàm số 4 2
y mx  2x 1 có ba điểm cực trị. A. m  0 B. m  0 C. m  0 D. m  0
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 44
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 6.
Tìm tất cả các giá trị của tham số m sao cho hàm số 3 2
y x x mx  5 có hai
cực trị. Chọn kết quả đúng: A. 1 m B. 1 m C. 1 m D. 1 m  3 3 3 3 Câu 7. m Hàm số 3 y
x  m   2
1 x mx  7 có hai cực trị khi và chỉ khi: 3  1    A. m  2 B. m  3 C. m  0 D. m  5 m  0 Câu 8. Cho hàm số 3 2
y x  3x  3m  
1 x  2 . Tìm tất cả các giá trị của m để hàm số có cực trị. A. m  0 B. m  2 C. m  2 D. m  0 Câu 9. 1
Tất cả các giá trị của m để hàm số 3 2 y
x mx  25m 8 x 1 đạt cực đại và 3 cực tiểu.
A. m  2 m  8 B. 2  m  8 C. 2  m  8
D. m  2 m  8 Câu 10.
Tìm tất cả giá trị m để hàm số 4
y mx  m   2
3 x  2m 1 chỉ đạt cực đại mà không có cực tiểu   A. m m  3  B. m  0 C. 3  D. m  3 m  0 ĐỀ 02 Câu 1.
Tìm tất cả giá trị m để hàm số y  m   4 x   2 m m 2 2 1 2 x m có ba điểm cực trị             A. 0 m 1 m m mB. 1 2  C. 1 1  D. 1 2  m  2 m  0 m  2 m  1 Câu 2. Hàm số 3
y  x  2mx  3 có 2 điểm cực trị khi : A. m  0 B. m  0 C. m  0 D. m  0
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 45
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Câu 3. Đồ thị hàm số 4 2
y ax bx c
a  0 có ba điểm cực trị khi và chỉ khi: A. b  0 B. ab  0 C. ab  0 D. ab  0 Câu 4. Đồ thị hàm số 4 2
y ax bx c
a  0 có một điểm cực trị khi và chỉ khi: A. b  0 B. ab  0 C. ab  0 D. b  0 Câu 5. Đồ thị hàm số 4 2
y ax bx c
a  0 có 1 điểm cực đại và 2 điểm cực tiểu khi và chỉ khi:         A. a 0 a a aB. 0  C. 0  D. 0  b   0 b   0 b   0 b   0 Câu 6. Đồ thị hàm số 4 2
y ax bx c
a  0 có 1 điểm cực tiểu và 2 điểm cực đại khi và chỉ khi:         A. a 0 a a aB. 0  C. 0  D. 0  b   0 b   0 b   0 b   0 Câu 7. Đồ thị hàm số 3 2
y ax bx cx d , a  0 có hai điểm cực trị khi và chỉ khi: A. 2 4b 12ac  0 B. 2
4b 12bc  0 C. 2
4b 12ac  0 D. 2 4b 12ac  0 Câu 8. Đồ thị hàm số 3 2
y ax bx cx d , a  0 không có điểm cực trị khi và chỉ khi: A. 2 4b 12ac  0 B. 2
4b 12bc  0 C. 2
4b 12ac  0 D. 2 4b 12ac  0 Câu 9.
Điều kiện của tham số m để hàm số 3 2
y x  3x  3mx m  2 có cực trị là: A. m 1 B. m 1 C. m 1 D. m 1 Câu 10. Hàm số 3
y x mx 1 có 2 cực trị khi: A. m  0 B. m  0 C. m  0 D. m  0 ĐỀ 03 Câu 1.
Với giá trị nào của m thì hàm số 3 2
y x mx  3x  2m 1 có cực đại, cực tiểu ? A. m 3  ;3 B. m ;  3
  m3;
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 46
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
C. m 3;  3 D. m ;    3 3; Câu 2. Hàm số 3 2
y x mx   2 m m 2 3 3
x  2m 1 có 2 điểm cực trị khi: A. m  0 B. m  0 C. m 1 D. m  tùy ý. Câu 3. 1 Hàm số 3 y
x  m  2 2
x mx 1 có cực đại, cực tiểu khi: 3 A. m  0 B. m C. m   D. m 1 Câu 4.
Giá trị của tham số m để hàm số y  m   3
2 x mx  3 không có cực trị là:     A. m 0 mB. m  2 C. 0  D. 0  m  2 m  2 m  2 Câu 5.
Đồ thị hàm số    3    3 3 y x a x b
x có cực đại, cực tiểu khi: A. . a b  0 B. . a b  0 C. . a b  0 D. . a b  0 Câu 6.
Tìm tham số m để đồ thị hàm số 4 2
y  x  2mx  2m 1 có 3 điểm cực trị ? A. m  0 B. m  1  C. m  0 D. m 1 Câu 7.
Tìm tham số m để đồ thị hàm số 4
y x  m   2 2
1 x m có 3 điểm cực trị ? A. Không có m B. m 1 C. m 1 D. m 1 Câu 8.
Tìm tham số m để đồ thị hàm số 4
y x  m   2 2 2
2 x m  5m  5 có 3 điểm cực trị ? A. m  2 B. m  3 C. m 1 D. m 1 Câu 9.
Tìm tham số m để đồ thị hàm số 4
y x  m   2 2
1 x m 1 có đúng 1 cực trị ? A. m  1  B. m  1 
C. A, B đều đúng. D. A, B đều sai. Câu 10. m Đồ thị hàm số 4 y
x  m   2
1 x m 1 có đúng 1 điểm cực trị khi: 4 A. 0  m 1 B. m 1 C. m  0 D. m ; m 0 1; 
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 47
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 ĐỀ 04 Câu 1. Đồ thị hàm số 4
y x    m 2 2 1
x  2 có cực tiểu mà không có cực đại khi: A. m 1 B. m 1
C. m 1
D. m 1 Câu 2. Đồ thị hàm số 4
y  x    m 2 2 5
x  2 có cực đại mà không có cực tiểu khi: A. m  5 B. m  5 C. m  5 D. m  5 2 Câu 3.
2x mx  2m 1 Hàm số y
có hai điểm cực trị khi: 2x 1 A. m  1  B. m  1  C. m  1  D. m   Câu 4.
Có tất cả bao nhiêu số nguyên m thỏa mãn điều kiện hàm số 1 3 2 y x mx   2
2m  25 x 10 có hai cực trị 3 A. 13 B. 10 C. 9 D. 7 Câu 5. 1
Tìm tất cả các giá trị m để hàm số 3 2 y x mx   2
2m  4 x m 1 3       A. m 2 mB. 2   m  2 C. 1  D. m  2 m  2 m  1 Câu 6.
Tìm tham số m để đồ thị hàm số 4 2
y x mx  3 có 3 điểm cực trị ? A. m  0 B. m  0
C. m  0 D. Không có m Câu 7. Đồ thị hàm số 4
y  x   m   2 2
4 x m có 2 cực đại, 1 cực tiểu khi: A. m  2 B. m  2 C. m  2 D. m  2 Câu 8.
Tìm tham số m để hàm số 3 2 2
y x  3mx  3m có 2 điểm cực trị ? A. m  0 B. m  0
C. m  0 D. m  0 Câu 9. Đồ thị hàm số 3 2
y x  3mx  3mx  3m  4 không có cực trị khi: A. m  0 B. m 1 C. 0  m 1 D. 0  m 1
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 48
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 10.
Tìm tham số m để đồ thị hàm số y    m 4 2 1
x mx  2m 1 có đúng 1 cực trị ? A. m B. m  0 C. 0  m 1 D. \ 0  ;1 ĐỀ 05 Câu 1.
Tính tổng tất cả các tham số m thỏa mãn điều kiện hàm số 1 1 3 y x   2 m   2
1 x mx đạt cực tiểu tại x 1 3 2 A. 2 B. 1  C. 1 D. 0 Câu 2.
Tìm tất cả các giá trị của m để hàm số 3 2
y x  3mx 12x 10 có hai cực trị       A. m 2 mB. 2   m  2 C. 1  D. m  2 m  2 m  1 Câu 3. m
Tìm tất cả các giá trị của m để 3 y
x  m   2
1 x mx có cực trị 3       A. m 2 mB. 1  C. 1 m   D. m  0 m  0 m  0 2 Câu 4.
Có tất cả bao nhiêu số nguyên m thỏa mãn điều kiện hàm số 3 2
y x mx   2 3
3 2m 16 x m  2017 có hai cực trị A. 13 B. 10 C. 9 D. 7 Câu 5.
Có tất cả bao nhiêu số nguyên m thỏa mãn điều kiện hàm số y   2 m   3 2 2
16 x x  3x m  2 có đúng một cực trị A. 3 B. 2 C. 0 D. Vô số Câu 6. 1
Hàm số y  m  3 2
1 x  2mx  3m  2 x 1 có cực đại, cực tiểu khi và chỉ khi. 3             A. 5 33 5 33 5 33 5 33 m   ;    ;   \   1     B. m ;    ;   \   1   2 2     2 2    
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 49
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953           C. 5 33 5 33 m   ;  D. 5 33 5 33 m   ;    ;     2 2   2 2     Câu 7. 1 3
Tìm tất cả các giá trị của tham số m sao cho hàm số 4 2 y x mx  có một 2 2 cực trị A. m  0 B. m  0 C. m  0 D. m  0 Câu 8. Cho hàm số 3
y x  m   2 2 3
3 x 11 3m . Định m để hàm số có cực đại và cực tiểu A. m  3 B. m  3 C. m  3 D. mCâu 9.
Tìm tất cả các giá trị của m để hàm số 3
y x mx 1 có 2 cực trị. A. m  0 B. m  0 C. m  0 D. m  0 Câu 10.
Tìm tất cả các giá trị thực của m để hàm số 4 2 2
y x  2mx m 1 có 3 điểm cực trị. A. m  0 B. m  0 C. m  0 D. m  0 ĐỀ 06 Câu 1. 1 Cho hàm số 3 2 y
x mx  2m  
1 x 1 Mệnh đề nào sau đây là sai? 3 A. m
 1 thì hàm số có hai điểm cực trị
B. Hàm số luôn luôn có cực đại và cực tiểu C. m
 1 thì hàm số có cực đại và cực tiểu D. m
 1 thì hàm số có cực trị Câu 2.
Tìm tất cả giá trị m để hàm số 3 2
y x  3mx  6mx m có hai điểm cực trị       A. m 0 m mB. 0  m  8 C. 0  D. 0  m  2 m  8 m  2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 50
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 3. Cho hàm số 4 2
y  x  2mx  2m 1. Với giá trị nào của m thì hàm số có 3 điểm cực trị: A. m  0 B. m  0 C. m  0 D. m  0 Câu 4. 1 1
Với giá trị nào của tham số m để hàm số 3 2 y x
mx  2x 1 có cực trị là: 3 2 A. 0 B. 3 C. 4 D. Cả A, B, C. Câu 5.
Điều kiện của m để hàm số 3 2
y x  3x mx m  2 có 2 điểm cực trị là: A. m  3 B. m  3 C. mD. m Câu 6. Hàm số 3
y x  m   2
1 x x  2 có cực đại, cực tiểu khi:
A. 1 3  m 1 3
B. 1 3  m 1 3       C. m 1 3 mD. 1 3  m 1 3 m 1 3 Câu 7. 1 Hàm số 3 y
x  m   2 1 x   2
3m  4m  
1 x m có cực đại, cực tiểu khi: 3 A. 0  m 1 B. 0  m 1 C. m  0 D. m 1 Câu 8. Hàm số 3
y  x    m 2 3
x  2mx  2 có cực đại và cực tiểu khi:       A. m m m  3
B. 6 3 3  m  6 3 3 C. 6 3 3  D. 6 3 3  m  6  3 3 m  6  3 3 Câu 9. Đồ thị hàm số 3
y x  m   2 2
2 x  6  3mx m 1 không có cực trị khi: A. m  16  B. m  2 C. 1
 6  m  2 D. 2   m 16 Câu 10. Đồ thị hàm số 3 2
y mx  3mx  m  
1 x 1 không có cực trị khi: A. 1 0  m B. 1 0  m C. m  0 D. 1 m  4 4 4
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 51
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 ĐỀ 07 Câu 1.
Tìm tham số m để đồ thị hàm số 4 2 2
y x m x  3 có 3 điểm cực trị ? A. m  0 B. m  0 C. m  0 D. mCâu 2.
Tìm tham số m để đồ thị hàm số 4
y x  m   2 2
1 x  3 có 3 điểm cực trị ? A. m  0 B. m  1  C. m 1 D. m  0 Câu 3.
Tìm tham số m để đồ thị hàm số 4
y x  m   2
1 x  2m 1 có 3 điểm cực trị ? A. m  1  B. m  1  C. m  1  D. m  1  Câu 4.
Tìm tham số m để đồ thị hàm số 4 2 4
y x  2mx  2m m có 3 điểm cực trị ? A. m  2  B. m  1 
C. m  0 D. m  2 Câu 5. Đồ thị hàm số 4
y  x   m   2 2 2
1 x  3 có đúng một điểm cực trị khi: A. 1 m B. 1 m C. 1 m D. 1 m  2 2 2 2 Câu 6. Đồ thị hàm số 4
y x    m 2 2 3
x  2 có đúng 1 điểm cực trị khi: A. m  3 B. m  3
C. m  3
D. m  3 Câu 7.
Đồ thị hàm số C 4
y  x   m   2 : 2 2
1 x  3 có đúng 1 điểm cực trị khi A. 1 m B. 1 m C. 1 m D. 1 m  2 2 2 2 Câu 8. m 1 5 Đồ thị hàm số 4 2 y x mx
có cực đại mà không có cực tiểu khi: 2 2 A. m 1  ;  0 B. m 1  ;0
C. m 1;0 D. m 1  ;0 2 Câu 9. x mx 1 Hàm số y  luôn có cực trị khi: x m A. m  0 B. m 1 C. m   D. m Câu 10.
Tìm tham số m để đồ thị hàm số y x  m  2 4 2 2 2 3
x m có 3 điểm cực trị ?
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 52
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 A. m  3 B. m  0 C. m  0 D. m  0 Câu 11.
(SGD HCM cụm 7, 2017) Tìm m để hàm số 4      2 y mx 2 m 1 x  2 có hai
cực tiểu và một cực đại. A. m  0. B. 0  m 1. C. m  2. D. 1 m  2. Câu 12.
(SGD HCM cụm 1, 2017) Đồ thị hàm số 4
y x  m   2
1 x  4 có ba điểm cực
trị khi và chỉ khi: A. m  1  . B. m  1  . C. m  1  . D. m  1  . Câu 13.
(Nguyễn Thái Học, Vĩnh Phúc, Lần 1, 2017) Hàm số 3
y mx  m   2 3
1 x  3m  
1 x m có cực trị khi và chỉ khi A.  1    m   ;  \     0 . B. 1 m   ;    . C. 1 m  . D. m 1.  3   3  3
VẤN ĐỀ 4. PHƯƠNG TRÌNH ĐƯỜNG THẲNG ĐI QUA CÁC ĐIỂM CỰC TRỊ Phương pháp 1) Cho hàm số 3 2
y ax bx cx d (C)
+) Nếu (C) có hai điểm cực trị và chia y cho y’ ta được: y y .mx n  x  
+) Thì phương trình đường thẳng đi qua hai điểm cực trị là: y   x   2   2) Cho hàm số ax bx c y Ax B
+) Nếu (C) có hai điểm cực trị
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 53
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953   2
ax bx c
+) Thì phương trình đường thẳng đi qua hai điểm cực trị là: y    Ax BVí dụ 1. Cho hàm số: 3
y x  3mx mC.
1) Tìm m để (C) có hai điểm cực trị?
2) Viết phương trình đường thẳng đi qua hai điểm cực trị của (C)
Đs: m  0; y  2  mx m Ví dụ 2. Cho hàm số: 3 2
y  x mx   2  m  3 2 3 3 1
x m mC  .
1) Tìm m để (C) có hai điểm cực trị?
2) Viết phương trình đường thẳng đi qua hai điểm cực trị của (C) Đs: 2  ;
m y  2x m m 2
x  m   Ví dụ 3. 1 x m 1 Cho hàm số y x m
1) Tìm m để (C) có hai điểm cực trị?
2) Viết phương trình đường thẳng đi qua hai điểm cực trị của (C) Đs:  ;
m y  2x m 1 2 Ví dụ 4.
x  2x m  2 Cho hàm số y x m 1
1) Tìm m để (C) có hai điểm cực trị?
2) Viết phương trình đường thẳng đi qua hai điểm cực trị của (C) Đs:  ;
m y  2x  2
B. BÀI TẬP VẬN DỤNG
Bài tập 1. Cho hàm số: 3
y x  m   2 x   2 3 1
2m  3m  2 x m m   1 C  .
1) Tìm m để (C) có hai điểm cực trị?
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 54
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12
2) Viết phương trình đường thẳng đi qua hai điểm cực trị của (C) Đs: 3  5 3  5 2 m  ; m  ; y    2 2 m  3m   1 x   2 m  3m   1 m   1 2 2 3 3 3 Bài tập 2. mx Cho hàm số 2 y
mx x 1 . Tìm m để hàm số có cực đại, cực tiểu và tung 3
độ các điểm cực đại, cực tiểu . 1) Cùng dấu
Đs: m 1 2) Trái dấu
Đs: m  0
Bài tập 3. Cho hàm số 3 2
y x  6x  3m  2 x m  6 . Tìm m để hàm số có cực đại và cực
tiểu đồng thời hai giá trị cực trị cùng dấu ? Đs: 17   m  2 4
Bài tập 4. Cho hàm số 3
y x  m   2 3
1 x  3m  
1 x 1 . Tìm m để hàm số có cực đại, cực
tiểu đồng thời đường thẳng nối hai điểm cực trị đó đi qua điểm M 0; 3   ? Đs: m  1  ;m  3
Bài tập 5. Cho hàm số 3
y x  m   2 2 3
1 x  6 m  2 x 1 . Tìm m để đồ thị hàm số có cực
đại, cực tiểu đồng thời đường thẳng nối hai điểm cực trị đó song song với đường thẳng y  4  x  3 ?
Đs: m 1;m  5
Bài tập 6. Cho hàm số 3 2
y x  3x  31 mx  3m 1 C  . Tìm m để đồ thị hàm số có
cực đại, cực tiểu đồng các điểm cực trị đó cùng với gốc tọa độ O tạo thành một tam giác diện tích là 4 ? Đs: m 1 Bài tập 7. 1 Cho hàm số 3 2 y
x x mx m . Tìm m để đồ thị hàm số có cực đại, cực tiểu 3
đồng khoảng cách giữa hai điểm cực trị đó bằng 2 15 ? Đs: m 1 Bài tập 8. 1 1 Cho hàm số 3 y
x  m   2
1 x mx . Tìm m để đồ thị hàm số có cực đại, cực 3 2
tiểu đồng thời các điểm cực trị đó đối xứng nhau qua đường thẳng 24x  4y 33  0 Đs: m 1
Bài tập 9. Cho hàm số 3
y x  m   2 2 3
1 x  6mx . Tìm m để đồ thị hàm số có hai cực trị A
và B sao cho đường thẳng AB vuông góc với đường thẳng y x  2 ?
Đs: m  0;m  2
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 55
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
Bài tập 10. Cho hàm số 3 2
y x mx  7x  3 . Tìm m để đồ thị hàm số có hai cực trị đồng
thời đường thẳng đi qua điểm cực trị đó vuông góc với đường y  3x  5 ? Đs: 3 10 m   2 Bài tập 11. 3 Cho hàm số 3 2 y x
mx  3m  
1 x 1 . Tìm m để đồ thị hàm số có hai điểm 2
cực trị đồng thời đường thẳng đi qua điểm cực trị đó song song với đường thẳng 
y  x 1 ? Đs: 3 3 m  3
Bài tập 12. Cho hàm số 3 2 3
y x  3ax  4a . Tìm m để đồ thị hàm số có hai điểm cực trị đối
xứng nhau qua đường y x ? Đs: 2 m   2
Bài tập 13. Cho hàm số 3
y x   m   2 2 3 2
1 x  6m m  
1 x 1 . Tìm m để đồ thị hàm số có
hai điểm cực trị đối xứng nhau qua đường   y x  2 ? Đs: 1 17 m  1  ;m  4
Bài tập 14. Cho hàm số 3 2
y x  3x  2mx m . Tìm m để đồ thị hàm số có hai điểm cực trị
đối xứng nhau qua đường 3 y x  ? Đs: 3 m  4 4
Bài tập 15. Cho hàm số 3 2
y  2x  3mx  3m  6 x 1. Tìm m để đồ thị hàm số có hai điểm
cực trị A, B đồng thời các điểm A, B và C 3;5 thẳng hàng? Đs: m  4
Bài tập 16. Cho hàm số 3 2 3
y x  3mx  3m . Tìm m để đồ thị hàm số có cực đại, cực tiểu
đồng các điểm cực trị đó cùng với gốc tọa độ O tạo thành một tam giác diện tích là 48 ? Đs: m  2 
Bài tập 17. Cho hàm số 3 2
y x  3x m 1 . Tìm m để đồ thị hàm số có hai điểm cực trị A,
B cùng với C 2;4 tạo thành một tam giác diện tích là 7 ? Đs: m 2  ;  3
Bài tập 18. Cho hàm số 3
y x  3mx  2 . Tìm m để đồ thị hàm số có hai điểm cực trị A, B cùng với C 1; 
1 tạo thành một tam giác diện tích là 3 2 ? Đs: m  2 2 Bài tập 19.
x  2mx m 1
Cho hàm số y
. Tìm m để hàm số có cực đại, cực tiểu và tung x 1
độ các điểm cực đại, cực tiểu . 1) Cùng dấu Đs: 1 5 1 5 m  ;  m  2 2 2 2) Trái dấu Đs:1 5 1 5  m  2 2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 56
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 2 Bài tập 20. x mx  8
Cho hàm số y x m
1) Tìm m để (C) có hai điểm cực trị?
2) Viết phương trình đường thẳng đi qua hai điểm cực trị của (C) 2
x  m   Bài tập 21. 1 x  3m  2
Cho hàm số y
. Tìm m để hàm số có cực đại, cực tiểu và x 1
đồng thời giá trị cực đại, cực tiểu cùng dấu? Đs: 1
  m  5 4 2;m  5 4 2 2
x  m   Bài tập 22. 1 x  3m  2
Cho hàm số y
. Tìm m để hàm số có cực đại, cực tiểu và x 1
đồng thời giá trị cực đại, cực tiểu cùng dấu? Đs: m  2   2 6; 2
  2 6  m  5 2
x  m  2 Bài tập 23. x  3m  2
Cho hàm số y
. Tim m để hàm số có cực đại, cực tiểu. x 1 Khi ấy chứng minh 1 2 2 yy  ? Đs: 1 m   CD CT 2 2 2 Bài tập 24.
2x  3x m
Cho hàm số y
. Tìm m để hàm số có cực đại, cực tiểu thỏa x m yy  8 Đs: 1 m   CD CT 2
B. BÀI TẬP TRẮC NGHIỆM ĐỀ 01 2 Câu 1. x  2x  2
Đồ thị hàm số y
có điểm cực trị nằm trên đường thẳng 1 x
y ax b thì giá trị của tổng a b bằng bao nhiêu ? A. 4 B. 4 C. 2 D. 2 Câu 2. Đồ thị hàm số 1 y x 1
có hai điểm cực trị nằm trên đường thẳng x 1
y ax b thì tích . a b bằng: A. 0 B. 2 C. 4 D. 2 Câu 3. Hàm số 3 2
y x  6x  9x 1 có phương trình đường thẳng đi qua hai điểm cực trị là:
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 57
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953
A. y  2x  7
B. y  2x  7 C. y  2  x  7 D. y  2  x  7 Câu 4. Cho hàm số 3
y x  3x có đồ thị (C). Phương trình đường thẳng qua 2 điểm cực trị của (C) là:
A. y x
B. y  x
C. y  2x D. y  2  x Câu 5. Cho hàm số 3 2
y  x mx   2  m  3 2 3 3 1
x m m
có hai điểm cực trị A, B. Tìm m
để đường thẳng AB đi qua điểm M 0; 2  
A. m  0 m  2 B. m  1   m  2
C. m  0 m  2  D. m  1   m  2  Câu 6.
Phương trình đường thẳng nào sau đây là phương trình đường thẳng đi qua
hai điểm cực trị của đồ thị hàm số 3 2
y x  6x  9x
A. y  2x  6
B. y  2x  6
C. y  6  2x
D. y  3x Câu 7.
Tìm tất cả giá trị m sao cho điểm I 1;0 thuộc đường thẳng qua 2 điểm cực
trị của đồ thị hàm số 3 2
y x  3mx  2 A. m  1  B. m  2  C. m  0 D. mCâu 8. Cho hàm số 3 2
y x  3x 1 . Viết phương trình đường thẳng đi qua điểm cực
đại và điểm cực tiểu của đồ thị hàm số đã cho. A. y  2  x 1
B. y  2x 1 C. y  2  x 1
D. y  2x 1 Câu 9. Đồ thị hàm số 3 2
y x  3mx  2m có hai điểm cực trị đối xứng nhau qua đường
thẳng x  2y 1 0 khi và chỉ khi : A. m 1  ;0  ;1 B. m  1  C. m  1  D. mCâu 10.
Phương trình đường thẳng nào sau đây là phương trình đường thẳng đi qua
hai điểm cực trị của đồ thị hàm số 3 2
y x  3x  2
A. y x  2
B. y  2  x
C. y  2  2x
D. y  2x  2 ĐỀ 02
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 58
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 1.
Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3
y x  3x  5 có hệ số góc là A. 2 B. 1 C. 2 D. 5 Câu 2. Cho hàm số 3 2
y x mx   2 m   3 3 3
1 x m m Phương trình đường thẳng nối
hai điểm cực trị của đồ thị hàm số có dạng:
A. 2x y  0
B. 3mx y  0 C. 2
y  2x m
D. y x m Câu 3.
Phương trình đường thẳng d đi qua điểm cực đại và điểm cực tiểu của đồ thị hàm số 3 2
y x  2x  5x 1 có dạng:
A. 3x 9y  2  0
B. y  4x 5
C. 38x  9y 19  0 D. y 17x 11 Câu 4. Đồ thị hàm số 3 2
y x  3x mx m có đường thẳng đi qua hai điểm cực trị
song song với đường thẳng d : y  2x 1 khi: A. 1 m B. 2 m C. m  6 D. 3 m  2 3 2 Câu 5. Đồ thị hàm số 3 2
y x  3x mx  2 có đường thẳng đi qua hai điểm cực trị song
song với đường thẳng d : 4x y 3  0 khi: A. m 1 B. m  2 C. m  3 D. m  4 Câu 6. Đồ thị hàm số 3
y x  m   2 3
1 x  6 m  2 x 1 có đường thẳng đi qua hai
điểm cực trị song song với đường thẳng d : y 1 4x khi: A. m 1 B. m  3
C. m 1 m  3
D. m 1 m  3  Câu 7. Đồ thị hàm số 3
y x  m   2 2 3
1 x  6mx có hai điểm cực trị A, B. Với giá trị
nào của tham số m thì đường thẳng d : y  2  x vuông góc với đường thẳng AB A. m  0 B. m  2
C. m  0 m  2
D. m  0 m  2  2 Câu 8. 5x x  5
Đồ thị hàm số y
có hai điểm cực trị A, B nằm trên đường thẳng d 2x  2
. Hệ số góc của đường thẳng d là:
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 59
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 1  B. 1 C. 3 D. 5 2 Câu 9. 3x x  5
Đồ thị hàm số y
có hai điểm cực trị A, B nằm trên đường thẳng d x  2
có phương trình y ax b thì giá trị của T a b là: A. 1  B. 1 C. 3 D. 5 2 Câu 10. x  2x  4
Đồ thị hàm số y
có hai điểm cực trị A, B nằm trên đường thẳng d x  2
có phương trình y ax b thì giá trị của T a b là: A. 1  B. 0 C. 1 D. 2
VẤN ĐỀ 5. TÌM THAM SỐ M ĐỂ HÀM SỐ CÓ CỰC TRỊ
THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
A. BÀI TẬP ÁP DỤNG
Bài tập 1. Cho hàm số 3
y x   m   2 x   2 4 3
m  7m 10 x m  5 . Tìm m để đồ thị hàm số
có hai điểm cực đại và cực tiểu nằm về hai phía của trục tung? Đs: 5   m  2 
Bài tập 2. Cho hàm số 3 2
y x mx   2 3
m  2m  3 x  4 . Tìm m để đồ thị hàm số có hai
điểm cực đại và cực tiểu nằm về hai phía của trục tung? Đs: 3   m 1
Bài tập 3. Cho hàm số 3 2
y  x x   2 m   2 3 3
1 x  3m 1. Tìm m để đồ thị hàm số có hai
điểm cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O ? Đs: 1 m   2
Bài tập 4. Cho hàm số 3 2
y  2x mx 12x 13 . Tìm m để đồ thị hàm số có điểm cực đại ,
cực tiểu và các điểm này cách đều trục tung.
Đs: m  0 Bài tập 5. 2 Cho hàm số 3 y
x  m   2 1 x   2
m  4m  3 x 1. Tìm m để đồ thị hàm số có 3
hai điểm cực đại và cực tiểu tại các điểm có hoành độ dương? Đs: 5   m  3 
Bài tập 6. Cho hàm số 3
y x  m   2 3
1 x  3m m  2 x 1. Tìm m để hàm số có cực đại,
cực tiểu tại các điểm có hoành độ dương?
Đs: m  0
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 60
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Bài tập 7. 1 1 Cho hàm số 3 y
mx  m   2
1 x  3m  2 x  . Tìm m để hàm số có cực đại , 3 3
cực tiểu và các điểm cực trị này thỏa mãn   x  2x  1? Đs: 2 m  2;  1 2  3
Bài tập 8. Cho hàm số 3 2 2
y  2x  9mx 12m x 1 . Tìm m để hàm số có cực đại x và điểm 1
cực tiểu x sao cho 2 x x Đs: m  2  2 1 2 Bài tập 9. 1 1 50 Cho hàm số 3 y
x  2m   2 1 x
x 1. Tìm m để hàm số có cực đại x và 1 3 2 9
điểm cực tiểu x sao cho x  2x ? Đs: m  2  2 1 2 Bài tập 10. 2 2 Cho hàm số 3 2 y
x mx  2 2 3m   1 x
. Tìm m để hàm số có cực đại x và 1 3 3
điểm cực tiểu x sao cho x x  2 x x 1 ? Đs: 2 m  1 2  1 2  2 3
Bài tập 11. Cho hàm số 3
y x  m   2 x   2
m m   x   2 2 1 4 1 2 m  
1 . Tìm m để hàm số có cực đại 1 1 1
x và điểm cực tiểu x sao cho   x x ?
Đs: m1;  5 1 2  1 2 x x 2 1 2 Bài tập 12. 1 Cho hàm số 3 2 y
x mx  3mx  2 . Tìm m để hàm số có hai điểm cực trị x , x 1 2 3
thỏa mãn x x  4 ?
Đs: m  4;m  1  1 2
Bài tập 13. Cho hàm số 4 2 4
y x  2mx  2m m . Tìm m để đồ thị hàm số có ba cực trị A, B,
C đồng thời các điểm A, B, C tạo thành tam giác thỏa mãn điều kiện 1) Tam giác ABC vuông ? Đs: m 1 2) Tam giác ABC đều? Đs: 3 m  3
3) Tam giác ABC có diện tích 32 Đs: m  4
4) Tam giác ABC có góc 1200? Đs: 1 m  3 3
5) Tam giác ABC có bán kính đường tròn ngoại tiếp bằng 1. Đs: 1   5 m  1; m  2
Bài tập 14. Cho hàm số 4 2 2
y x  2mx m m . Tìm m để đồ thị hàm số có ba điểm cực trị
tạo thành tam giác có trọng tâm là O. Đs: m  3 
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 61
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 Bài tập 15. 1 Cho hàm số 4 y
x  3m   2
1 x  2m  
1 . Tìm m để đồ thị hàm số có ba điểm 4
cực trị tạo thành tam giác có trọng tâm là O. Đs: 1 m  3
Bài tập 16. Cho hàm số 3
y x   m   2 3
1 x 12mx  3m  4 . Tìm m để đồ thị hàm số có các
điểm cực trị A, B sao cho hai điểm này cùng với điểm  9  C 1  ; 
 tạo thành tam giác có  2  trọng tâm là O. Đs: 1 m   2
Bài tập 17. Cho hàm số 4
y x  m   2 3
1 x  3m  2 . Tìm m để hàm số có ba điểm cực trị tạo
thành tam giác có trực tâm là  35  H 0;    Đs: 5 m   4  3
Bài tập 18. Cho hàm số 4 2
y x  2mx  2m . Tìm m để hàm số có ba điểm cực trị tạo thành
tam giác có trọng tâm là  31  H 0;    . Đs: m  4  4 
Bài tập 19. Cho hàm số 4
y x  m   2 2 2
1 x m . Tìm m để đồ thị hàm số có ba điểm cực trị
tạo thành ba đỉnh của một tam giác vuông?
Đs: m  0
Bài tập 20. Cho hàm số 4 2 2
y x  2m x 1 . Tìm m để đồ thị hàm số có các điểm cực trị tạo
thành ba đỉnh của một tam giác đều? Đs: 6 m   3
Bài tập 21. Cho hàm số 4
y x m m   2 2
3 x m . Tìm m để hàm số có ba cực trị đồng thời
các điểm cực trị của đồ thị hàm số tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 5 R  . 4
B. BÀI TẬP TRẮC NGHIỆM Câu 1.
Giá trị của m để hàm số 3 2
y x  3x mx 1 có hai điểm cực trị
x , x thỏa mãn 2 2 x x  3 là: 1 2 1 2 A. m 1 B. m  2  C. 3 m D. 1 m  2 2 Câu 2.
Giá trị của m để hàm số 3 2
y  x x   2 m   2 3 3
1 x  3m 1 có cực đại và cực tiểu
và các điểm cực trị của đồ thị hàm số cách đều gốc toạ độ O là: A. 1 m   B. m  3 C. 1
m  0; m  
D. m  0;m  2 2 2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 62
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 Câu 3.
Giá trị m để đồ thị hàm 4 2
y x  2mx 1 có ba điểm cực trị tạo thành một tam giác đều. A. m 1 B. 3 m  3 C. 3 m   3 D. m  1  Câu 4.
Giá trị m để đồ thị hàm 4 2
y x  2mx 1 có ba điểm cực trị tạo thành một tam
giác có diện tích bằng 4 2 A. m  2 B. m  3  C. m  2  D. m 1 Câu 5.
Giá trị của m để hàm số 3 2
y x  3x m có cực đại, cực tiểu sao cho y và y CD CT trái dấu? A. m  4 B. 0  m  4 C. m  0
D. 0  mm  4 Câu 6. 1 Cho hàm số 3 2 y
x mx  2m  
1 x m  2 có cực đại, cực tiểu và hoành độ 3
các điểm cực trị dương thì tập giá trị của m bằng A.  1   1  ;    B. \   1 C. ;  \     1 D.  ;  0  2   2  Câu 7.
(SGD Gia Lai, 2017) Tìm tất cả các giá trị thực của tham số m đồ thị hàm số 4 2 4
y x  2mx  2m m có ba điểm cực trị là ba đỉnh của một tam giác có diện tích bằng 4 2 . A. m  2 . B. m  0. C. m  32 . D. m  2  . Câu 8.
(SGD Bà Rịa Vũng Tàu, 2017) Cho hàm số 3 y x   m 2 1– 2
x  2 – mx m  2 (1) Tìm tập hợp tất cả các giá trị thực của m để đồ
thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành độ của điểm cực tiểu nhỏ hơn 1 A.  5 7   7    m  ; .   B. m ;    5 1  ; .   C. 7 m  ;  .  
D. m2;.  4 5   4 5   5  Câu 9.
(SGD Thanh Hóa, 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2
y x  4(m 1)x  2m 1 có ba điểm cực trị là ba đỉnh của một tam giác có số đo một góc bằng 0 120 .
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 63
DẠY KÈM - LUYỆN THI MÔN TOÁN
0987 668 965 0935 875 953 A. 1 1 1 1 m  1 . B. m 1 . C. m 1 . D. m 1 . 3 24 3 16 3 48 3 2 Câu 10.
(SGD Quảng Ninh, 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 3 2
y x x   2 4
1 m x 1 có hai điểm cực trị nằm về hai phía khác nhau đối với trục tung?   A. 1 1   m m  . B. 1  . C. 1   m 1. D. 1   m 1. 3 3 m  1 Câu 11.
(SGD HCM cụm 1, 2017) Biết rằng ha m so 3 2
y  4x – 6x  1 co đo thi như h nh ve be n.
Phát biểu nào sau đây là phát biểu đúng?
A. Đồ thị hàm số 3 2
y  4x – 6x  1 có 2 cực trị.
B. Đồ thị hàm số 3 2
y  4x – 6x  1 có 5 cực trị.
C. Đồ thị hàm số 3 2
y  4x – 6x  1 có 3 cực trị.
D. Đồ thị hàm số 3 2
y  4x – 6x  1 có 1 cực trị. Câu 12.
(THPT QG 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y x  2mx có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1 . A. 3 0  m  4 . B. m  1.
C. 0  m  1. D. m  0. Câu 13.
(THPT QG 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y x  2mx có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. m  0. B. m 1. C. 3 0  m  4. D. 0  m 1. Câu 14.
(THPT QG 2017) T m ta t ca ca c gia tri thư c cu a tham so m đe đo thi cu a ha m so 3 2 3
y x  3mx  4m co hai đie m cưc tri A va B sao cho tam gia c OAB co dien t ch
ba ng 4 vơ i O la go c to a đo . A. 1 1 m   ; m  . B. m  1  ; m 1. 4 2 4 2
Việc tuy nhỏ, không làm không nên.
DẠY KÈM LUYỆN THI MÔN TOÁN - BMT 64
DẠY KÈM - LUYỆN THI MÔN TOÁN Giải Tích 12 C. m 1. D. m  0 . Câu 15.
(SGD Đà Nẵng, 2017) Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4
y x  m   2 2
1 x m có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác vuông. A. m  0. B. m 1. C. m  3. D. m  2 Câu 16.
Tìm tất cả các giá trị của tham số m để ba điểm cực trị của đồ thị hàm số 4 2
y x  (6m  4) x 1 m là ba đỉnh của một tam giác vuông. A. 2 m  . B. 1 m  . C. m  1  . D. 3 m  3 . 3 3 Câu 17.
(SGD Bà Rịa Vũng Tàu, 2017) Cho hàm số 3 2
y =  x  3mx  3m – 1. Tìm tập
hợp tất cả giá trị thực của m để thì đồ thị hàm số có điểm cực đại, điểm cực tiểu đối
xứng với nhau qua đường thẳng d : x 8y +8  0.     A.   m   0 . B. m 2  ,  0 . C. 23 m   ; 0. D. 23 m  0  ; ; 2.  4    4  
NGỌC ĐÀN – 0987 668 965
Đường tuy ngắn, không đi không đến. 65