Bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng – Nguyễn Phú Khánh, Huỳnh Đức Khánh Toán 12

Bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng – Nguyễn Phú Khánh, Huỳnh Đức Khánh Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

97 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
3.
Baøi 01
NGUYEÂN HAØM
 
Cho hàm số
(
)
f x
xác định trên khoảng
K
. Hàm số
(
)
F x
được gọi là nguyên hàm
của hàm số
(
)
f x
nếu
(
)
(
)
'
F x f x
với mọi
x K
∈
.
Nhận xét.Nếu
(
)
F x
là một nguyên hàm của
(
)
f x
thì
(
)
(
)
, F x C C
+ ∈
ℝ
cũng là
nguyên hàm của
(
)
f x
.
Ký hiệu:
( ) ( )
d
f x x F x C
= +
∫
.
 
( )
(
)
( )
/
d
f x x f x
=
∫
.
(
)
(
)
(
)
. d . d , 0
a f x x a f x x a a= ∈ ≠
∫ ∫
ℝ
.
(
)
(
)
(
)
(
)
d d d
f x g x x f x x g x x
± = ±
∫ ∫ ∫
.
 

d
k x kx C
= +
∫
,
k
là hằng số
( )
1
d 1
1
x
x x C
α
α
α
+
= + ≠ −
∫
( )
(
)
1
1
d .
1
ax b
ax b x C
a
α
α
+
+
+ = +
∫
1
d ln
x x C
x
= +
∫
1 1
d ln
x ax b C
ax b a
= + +
∫
d
x x
e x e C
= +
∫
1
d
ax b ax b
e x e C
a
+ +
= +
∫
d
ln
x
x
a
a x C
a
= +
∫
d
.ln
mx n
mx n
a
a x C
m a
+
+
= +
∫
cos d sin
x x x C
= +
∫
( ) ( )
1
cos d sin
ax b x ax b C
a
+ = + +
∫
sin d cos
x x x C
= − +
∫
( ) ( )
1
sin d cos
ax b x ax b C
a
+ = − + +
∫
2
1
d tan
cos
x x C
x
= +
∫
(
)
( )
2
1 1
d tan
cos
x ax b C
aax b
= + +
+
∫
2
1
d cot
sin
x x C
x
= − +
∫
(
)
( )
2
1 1
d cot
sin
x ax b C
aax b
= − + +
+
∫
VAØ ÖÙNG DUÏNG
CHUÛ ÑEÀ NGUYEÂN HAØM -–TÍCH PHAÂN
!"#$%&'(&)*+,!-.$&/0
-.#12-*$34$5-$– $#6-$7!4$5-$
89:;<=;>?@A&BCDE+F
B?@G?$#6-$7!4$5-$–HIJKHLI
 MNNOOOPQ=RR9RNS9HHK
4?TU P?VQOR;SWX;?Y
P?VQOR;SWG G;?Z?@R[?@S\
!] Hàm số
(
)
f x
có nguyên hàm trên
K
nếu:
^.
(
)
f x
xác định trên
K
. .
(
)
f x
có giá trị lớn nhất trên
K
.
!.
(
)
f x
có giá trị nhỏ nhất trên
K
. F.
(
)
f x
liên tục trên
K
.
B??? Nếu hàm số
(
)
f x
liên tục trên
K
thì nó có nguyên hàm trên
K
.
!<F
!] Mệnh đề nào sau đây là sai?
^. Nếu
(
)
F x
là một nguyên hàm bất kỳ của
(
)
f x
trên
(
)
;
a b
thì
(
)
(
)
d
f x x F x C
= +
∫
với
C
là hằng số.
. Mọi hàm số liên tục trên khoảng
(
)
;
a b
đều có nguyên hàm trên khoảng
(
)
;
a b
.
!.
(
)
F x
là một nguyên hàm của
(
)
f x
trên
(
)
(
)
(
)
(
)
/
; , ;
a b f x F x x a b
⇔ = ∀ ∈
.
F.
( )
(
)
( )
/
d
f x x f x
=
∫
.
B??? !<! Sửa lại cho đúng là:
''
(
)
F x
là một nguyên hàm của
(
)
f x
trên
(
)
;
a b
(
)
(
)
(
)
/
, ; ''.
F x f x x a b
⇔ = ∀ ∈
!] Xét hai khẳng định sau:
_ Mọi hàm số
(
)
f x
liên tục trên đoạn
[
]
;
a b
đều có đạo hàm trên đoạn đó.
_ Mọi hàm số
(
)
f x
liên tục trên đoạn
[
]
;
a b
đều có nguyên hàm trên đoạn đó.
Trong hai khẳng định trên:
^. Chỉ có _ đúng. `. Chỉ có _ đúng. !. Cả hai đều đúng. F. Cả hai đều sai.
B??? Hàm số có đạo hàm tại
0
x
thì liên tục tại
0
x
. Ngược lại hàm số liên tục tại
0
x
thì chưa chắc đã có đạo hàm tại
0
x
. Chẳng hạn xét hàm số
(
)
f x x
tại điểm
0
x
=
. !<
!]` Trong các khẳng định sau nói về nguyên hàm của một hàm số
(
)
f x
xác định
trên khoảng
D
, khẳng định nào là sai?
_
(
)
F x
là nguyên hàm của
(
)
f x
trên
D
nếu và chỉ nếu
(
)
(
)
' , D.
F x f x x
= ∀ ∈
_ Nếu
(
)
f x
liên tục trên
D
thì
(
)
f x
có nguyên hàm trên
D
.
_ Hai nguyên hàm trên
D
của cùng một hàm số thì sai khác nhau một hằng số.
^. Khẳng định _ sai. . Khẳng định _ sai.
!. Khẳng định _ sai. F. Không có khẳng định nào sai.
B??? !<F
!]KGiả sử
(
)
F x
là một nguyên hàm của hàm số
(
)
f x
trên khoảng
(
)
;
a b
. Giả sử
(
)
G x
cũng là một nguyên hàm của
(
)
f x
trên khoảng
(
)
;
a b
. Mệnh đề nào sau đây là
đúng?
^.
(
)
(
)
F x G x
trên khoảng
(
)
;
a b
.
.
(
)
(
)
G x F x C
= −
trên khoảng
(
)
;
a b
, với
C
là hằng số.
!.
(
)
(
)
F x G x C
= +
với mọi
x
thuộc giao của hai miền xác định
(
)
F x
và
(
)
G x
,
C
là hằng số.
F. Cả ba câu trên đều sai.
B??? Vì hai nguyên hàm trên
D
của cùng một hàm số thì sai khác nhau một
hằng số. Do đó B đúng. !<
!]a Xét hai khẳng định sau:
_
(
)
(
)
(
)
(
)
(
)
(
)
d d d
f x g x x f x x g x x F x G x C
+ = + = + +
∫ ∫ ∫
, trong đó
(
)
F x
và
(
)
G x
tương ứng là nguyên hàm của
(
)
(
)
,
f x g x
.
_ Mỗi nguyên hàm
(
)
(
)
. 0
a f x a
là tích của
a
với một nguyên hàm của
(
)
f x
.
Trong hai khẳng định trên:
^. Chỉ có _ đúng. . Chỉ có _ đúng.
!. Cả hai đều đúng. F. Cả hai đều sai.
B??? !<!
!]J Khẳng định nào sau đây là sai?
^. Nếu
(
)
(
)
d
f x x F x C
= +
∫
thì
(
)
(
)
d
f u u F u C
= +
∫
.
.
(
)
(
)
d d
kf x x k f x x
=
∫ ∫
(
k
là hằng số và
0
k
≠
).
!. Nếu
(
)
F x
và
(
)
G x
đều là nguyên hàm của hàm số
(
)
f x
thì
(
)
(
)
.
F x G x
F.
(
)
(
)
(
)
(
)
1 2 1 2
d d d
f x f x x f x x f x x
+ = +
∫ ∫ ∫
.
B??? Các nguyên hàm sai khác nhau hằng số nên C là đáp án sai. !<!
!]LTrong các khẳng định sau, khẳng định nào sai?
^. 0d
x C
=
∫
(
C
là hằng số). .
1
d ln
x x C
x
= +
∫
(
C
là hằng số).
!.
1
d
1
x
x x C
α
α
+
= +
∫
(
C
là hằng số). F.
d
x x C
= +
∫
(
C
là hằng số).
B??? !<! Vì kết quả này không đúng với trường hợp
1
= −
.
!]I Hàm số
( )
1
cos
f x
x
= có nguyên hàm trên khoảng nào với các khoảng đã cho
sau đây?
^.
(
)
0;
π
. .
;
2 2
π π
−
. !.
(
)
;2
π π
. F.
;
2 2
π π
−
.
B??? Hàm số
( )
1
cos
f x
x
= xác định và liên tục trên
;
2 2
π π
−
nên có nguyên hàm
trên khoảng này. !<
!]HKí hiệu
(
)
F y
là một nguyên hàm của hàm số
(
)
f y
, biết
(
)
2
F y x xy C
= + +
.
Hỏi hàm số
(
)
f y
là hàm số nào trong các hàm số sau?
^
(
)
f y x
=
. 
(
)
3
f y x y
= +
. !
(
)
f y y
=
. F
(
)
2
f y x y
= +
.
B??? Để tìm
(
)
f y
ta đi lấy đạo hàm của
(
)
F y
theo biến
y
(tức là bây giờ
x
đóng vai trò là tham số).
Ta có
(
)
'
F y x
=
. !<^ 
!]Kí hiệu
(
)
F x
là một nguyên hàm của hàm số
(
)
f x
và
(
)
2
sin
F x
xác định thì
(
)
2
sin
F x
là một nguyên hàm của hàm số nào trong các hàm số sau?
^
(
)
2
sin .
f x

(
)
2
cos .
f x
!
(
)
2
2 sin sin .
xf x
F
(
)
2
sin 2 sin .
xf x
B??? Theo định nghĩa, ta có
(
)
(
)
(
)
(
)
d .
f x x F x C F x f x
′
= + ←→ =
∫
Áp dụng:
(
)
(
)
(
)
(
)
/
2 2 / 2 2
sin sin sin sin 2 . sin
F x x F x x f x
′
= =
. !<F
!]Xác định
( )
d
f x x
∫
biết
(
)
2 1.
f x x
= +
^
(
)
2 1 d 2.
x x
+ =
∫
 
(
)
2 1 d .
x x C
+ =
∫
!
(
)
2
2 1 d .
x x x x
+ = +
∫
F
(
)
2
2 1 d .
x x x x C
+ = + +
∫
B??? !<F
!] Hàm số nào sau đây không phải là nguyên hàm của hàm số
(
)
(
)
4
3
f x x= − ?
^.
( )
(
)
5
3
5
x
F x x
−
= +
. .
( )
(
)
5
3
5
x
F x
−
=
.
!.
( )
(
)
5
3
2017
5
x
F x
−
= +
. F.
( )
(
)
5
3
1
5
x
F x
−
= −
.
B??? Xét đáp án A, ta có
(
)
(
)
(
)
4
' 3 1
F x x f x
= − + ≠
. !<^
!G;>?@Ta thấy hàm số
(
)
F x
ở các đáp án B, C, D sai khác nhau hằng
số nên dung phương pháp loại suy, ta chọn được được đáp án A.
!]` Kí hiệu
(
)
F x
là một nguyên hàm của hàm số
( )
(
)
2
2
1
f x x= + và
( )
28
1
15
F
= ⋅
Khẳng định nào sau đây là đúng?
^.
( )
5 3
2
.
5 3
x x
F x x
= + +
.
( )
5 3
2
.
5 3
x x
F x x C
= + + +
!.
(
)
(
)
2
4 1 .
F x x x
= +
F.
( )
5 3
2
1.
5 3
x x
F x x
= + + +
B??? Ta có
( ) ( )
5 3
2
2 4 2
2
1 d 2 1 d .
5 3
x x
x x x x x x C
+ = + + = + + +
∫ ∫
Theo giả thiết
( )
28 1 2 28
1 1 0
15 5 3 15
F C C
= → + + + = → =
. !<^
!]K Tìm hàm số
(
)
F x
biết
(
)
2
' 3 2 1
F x x x
= + +
và đồ thị hàm số
(
)
y F x
cắt
trục tung tại điểm có tung độ bằng
e
.
^
(
)
2
.
F x x x e
= + +

(
)
cos 2 1.
F x x e
= + −
!
(
)
3 2
1.
F x x x x
= + + +
D
(
)
3 2
.
F x x x x e
= + + +
B??? Ta có
(
)
(
)
2 3 2
3 2 1 d .
F x x x x x x x C
= + + = + + +
∫
Đồ thị
(
)
y F x
cắt trục tung tại điểm có tung độ bằng
e
nên ta có
(
)
0 .
F e C e
= ⇔ =
Vậy
(
)
3 2
.
F x x x x e
= + + +
!<F
!]a Kí hiệu
(
)
F x
là một nguyên hàm của hàm số
(
)
4 1
f x x
= −
. Đồ thị hàm số
(
)
y F x
và đồ thị hàm số
(
)
y f x
cắt nhau tại một điểm thuộc trục tung. Tọa độ
các điểm chung của hai đồ thị hàm số trên là:
^.
(
)
0; 1
−
. .
5
;9
2
. !.
(
)
0; 1
−
và
5
;9
2
. F.
(
)
0; 1
−
và
5
;8
2
.
B??? Ta có
(
)
(
)
2
4 1 d 2
F x x x x x C
= − = − +
∫
.
Giả sử
(
)
0;
M m Oy
là giao điểm của đồ thị hai hàm số
(
)
F x
và
(
)
f x
.
Ta có hệ phương trình
(
)
( )
( )
2
2
4.0 1
1
2 1
1
2.0 0
M f x
m
m
F x x x
C
C m
M F x
− =
= −
⇔ ⇔ ⇒ = − −
= −
− + =
∈
.
Hoành độ giao điểm của đồ thị hai hàm số
(
)
F x
và
(
)
f x
là nghiệm của phương trình:
( )
2
0 1
2 1 4 1 2 5 0 .
5
9
2
x y
x x x x x
x y
= ⇒ = −
− − = − ⇔ − = ⇔
= ⇒ =
Vậy tọa độ các điểm cần tìm là
(
)
0; 1
−
và
5
;9
2
. !<!
!] J Biết rằng
(
)
(
)
(
)
3 2
2 1
F x ax a b x a b c x
= + + + − + +
là một nguyên hàm của
(
)
2
3 6 2.
f x x x
= + +
Tính tổng
.
S a b c
= + +
^
5.
S
=

4.
S
=
!
3.
S
=
F
2.
S
=
B??? Ta có
(
)
2 3 2
3 6 2 d 3 2
x x x x x x C
+ + = + + +
∫
.
Suy ra
(
)
3 2
3 2 1
F x x x x
= + + +
.
Đồng nhất ta được
1 1
3 2 5
2 2 2
a a
a b b a b c
a b c c
= =
+ = ⇔ = → + + =
− + = =
. !<^
!]Lbc$d-.$&/0Ha–HJ_ Biết
(
)
F x
là một nguyên hàm của hàm
số
( )
1
1
f x
x
=
−
và
(
)
2 1.
F
=
Tính
(
)
3 .
F
^
(
)
3 ln 2 1.
F
= −

(
)
3 ln 2 1.
F
= +
!
( )
1
3
2
F
= ⋅
F
( )
7
3
4
F
= ⋅
B??? Ta có
d
ln 1 .
1
x
x C
x
= − +
∫
Theo giả thiết
(
)
2 1 ln 2 1 1 1.
F C C
= → − + = ⇔ =
Suy ra
(
)
(
)
ln 1 1 3 ln 2 1.
F x x F
= − + → = +
!<
!]I Cho hàm số
(
)
y f x
=
có đạo hàm
( )
1
'
2 1
f x
x
=
−
và
(
)
1 1
f
=
. Tính
(
)
5
f
.
^.
(
)
5 ln 2.
f
.
(
)
5 ln 3.
f
!.
(
)
5 ln 2 1.
f
= +
F.
(
)
5 ln 3 1.
f
= +
B??? Ta có
( ) ( )
d 1
' d ln 2 1 .
2 1 2
x
f x f x x x C
x
= = = − +
∫ ∫
Theo giả thiết
( )
1
1 1 ln 2.1 1 1 1
f C C
= → − + = ⇔ =
.
Suy ra
( ) ( )
1 1 1
ln 2 1 1 5 ln 2.5 1 1 ln 9 1 ln 3 1.
2 2 2
f x x f
= − + → = − + = + = +
!<F
!]HTìm hàm số
(
)
f x
thỏa mãn đồng thời
( )
2 3
1
x
f x
x
+
′
=
+
và
(
)
0 1.
f
=
^
(
)
2
ln 1 .
f x x x
= + +

(
)
2 ln 2 1 1.
x xf x
= + + −
!
(
)
2 ln 1 1.
x xf x
= + + +
F
(
)
ln 1 1.
x xf x
= + + +
B??? Ta có
2 3 1
d 2 d 2 ln 1 .
1 1
x
x x x x C
x x
= + = + + +
+ +
∫ ∫
Theo giả thiết
(
)
0 1 2.0 ln 0 1 1 1.
f C C
= → + + + = ⇔ =
Suy ra
(
)
2 ln 1 1.
f x x x
= + + +
!<!
!]  Gọi
(
)
F x
là một nguyên hàm của hàm số
( )
(
)
2
1
2
x
f x
x
+
=
và thỏa mãn
( )
1
1
2
F
− = ⋅
Tính
(
)
2 .
F
^
(
)
2 2 ln 2.
F
= +

(
)
(
)
2 2 1 ln 2 .
F
= −
!
(
)
(
)
2 2 1 ln 2 .
F
= +
F
(
)
2 4.
F
=
B??? Ta có
(
)
(
)
2
2
1 2 1
2 1 1
2 2 2 2
x x x
x x
x
x x x x
+ + +
+ +
= = = +
+ + + +
(
)
2
2
1
1
d d ln 2 C.
2 2 2
x
x
x x x x
x x
+
→ = + = + + +
+ +
∫ ∫
Theo giả thiết
( )
(
)
2
1
1 1
1 ln 1 2 0.
2 2 2
F C C
− = → + − + + = ⇔ =
Suy ra
( ) ( ) ( )
2
ln 2 2 2 ln 4 2 1 ln 2 .
x
F x x F= + + → = + = + !<!
!] Hàm số nào sau đây là nguyên một hàm của hàm số
( )
(
)
3
2
1
2
x
f x
x
−
=
?
^.
( )
2
3 3 1
ln
4 2 2 2
x x
F x x
x
= − + + . .
( )
(
)
4
3
3 1
4
x
F x
x
−
= .
!.
( )
2
2 3
3 1 1
4 2
2
x x
F x
x x
= − − −
. F.
( )
(
)
2
3 1
4
x
F x
x
−
=
.
B??? Ta có
(
)
3
3 2
2 2
1
3 3 1
d d
2 2
x
x x x
x x
x x
−
− + −
=
∫ ∫
2
2
3 3 1 3 3 1
d ln .
2 2 2 4 2 2 22
x x x
x x C
x xx
= − + − = − + + +
∫
Chọn
( )
2
3 3 1
0 ln .
4 2 2 2
x x
C F x x
x
= → = − + +
!<^
!]  Biết
(
)
F x
là nguyên hàm của hàm số
( )
3
2
1
4 3
f x x x
x
= − +
và thỏa mãn
(
)
(
)
5 1 2 43
F F
+ =
. Tính
(
)
2 .
F
^
( )
151
2 .
4
F = 
(
)
2 23.
F
!
( )
45
2 .
2
F = F
( )
86
2 .
7
F =
B??? Ta có
( )
3 4 2
2
1 1 3
4 3 d .
2
F x x x x x x C
xx
= − + = + + +
∫
Theo giả thiết
( ) ( )
7 45 1
5 1 2 43 5 43 .
2 2 2
F F C C C
+ = → + + + = ⇔ =
Suy ra
( ) ( )
4 2 4 2
1 3 1 1 3 1
2 2 .2 23.
2 2 2 2 2
F x x x F
x
= + + + → = + + + =
!<
!]`Hàm số nào sau đây là một nguyên hàm của hàm số
( )
2
1
f x
x x
= ⋅
^
(
)
ln ln 1 .
F x x x
= − − −

(
)
ln ln 1 .
F x x x
= − −
!
(
)
ln ln 1 .
F x x x
= − + −
F
(
)
ln ln 1 .
F x x x
= + −
B??? Ta có
(
)
2
1 1 1 1
1 1
x x x xx x
= = − +
− −
−
2
1 1 1
d d ln ln 1 .
1
x x x x C
x xx x
→ = − + = − + − +
∫ ∫
!<!
!]KGọi
(
)
F x
là một nguyên hàm của hàm số
( )
2
1
3 2
f x
x x
=
− +
và thỏa mãn
3
0.
2
F
=
Tính
(
)
3 .
F
^
(
)
3 ln 2.
F

(
)
3 2 ln 2.
F
!
(
)
3 2 ln 2.
F
= −
F
(
)
3 ln 2.
F
= −
B??? Ta có
(
)
(
)
2
1 1 1 1
1 2 1 2
3 2 x x x xx x
= = − +
− − − −
− +
2
1 1 1
d d ln 1 ln 2 .
1 23 2
x x x x C
x xx x
→ = − + = − − + − +
− −
− +
∫ ∫
Theo giả thiết
3 3 3
0 ln 1 ln 2 0 0.
2 2 2
F C C
= →− − + − + = ⇔ =
Suy ra
(
)
(
)
ln 1 ln 2 3 ln 2.
F x x x F
= − − + − → = −
!<F
!]aXác định
(
)
d
f x x
∫
biết
( )
2
3
3 2
x
f x
x x
= ⋅
+ +
^
(
)
d 2 ln 2 ln 1 .
f x x x x C
= + − + +
∫

(
)
d 2 ln 1 ln 2 .
f x x x x C
= + − + +
∫
!
(
)
d 2 ln 1 ln 2 .
f x x x x C
= + + + +
∫
F
(
)
d ln 1 2 ln 2 .
f x x x x C
= + + + +
∫
B??? Ta có
(
)
(
)
2
3 3 2 1
1 2 1 2
3 2
x x
x x x xx x
+ +
= = −
+ + + +
+ +
2
3 2 1
d d 2 ln 1 ln 2 .
1 23 2
x
x x x x C
x xx x
→ = − = + − + +
+ +
+ +
∫ ∫
!<
!]J Cho hàm số
(
)
f x
có đạo hàm
( )
(
)
(
)
2 2
2 1
2 1 1
f x
x x
′
= −
− −
và thỏa
( )
1
2
3
f
= − ⋅
Biết phương trình
(
)
1
f x
= −
có nghiệm duy nhất
0
.
x x
Tính
0
2017 .
x
T
^
2017.
T

1.
T
=
!
2017.
T
F
3
2017 .
T
B??? Ta có
( )
( ) ( )
2 2
2 1 1 1
' d d .
1 2 1
2 1 1
f x x x C
x x
x x
= − = − +
− −
− −
∫ ∫
Theo giả thiết
( )
1 1 1 1
2 1.
3 1 3 3
f C C
= − → − + = − ⇔ = −
Suy ra
( )
(
)
(
)
1
1 2 1
x
f x
x x
= −
− −
.
Suy ra
( )
(
)
(
)
0
0
1 1 1 0 2017 1.
1 2 1
x
f x x x T
x x
= − ⇔ − = − ⇔ = = → = =
− −
!<
!]LTìm một nguyên hàm
(
)
F x
của hàm số
(
)
(
)
.
f x g x
, biết
(
)
d
f x x x C
= +
∫
,
( )
2
d
x
g x x C
= +
∫
và
(
)
2 5
F
=
.
^
( )
2
4.
x
F x
= +

( )
2
5.
x
F x
= +
!
( )
3
5.
x
F x
= +
F
( )
3
3.
x
F x
= +
B??? Ta có
(
)
(
)
d 1
f x x x C f x
= + → =
∫
và
( ) ( )
2
1
d .
4 2
x
g x x C g x x
= + → =
∫
Khi đó
( ) ( )
2
1 1
. d d .
2 4
f x g x x x x x C
= = +
∫ ∫
Theo giả thiết
( )
2
1
2 5 .2 5 4.
F C C
= → + = ⇔ =
Suy ra
( )
2
4.
x
F x
= +
!<^
!]I Cho
ln 2
2 d
x
I x
x
=
∫
. Mệnh đề nào sau đây là sai?
^.
2
x
I C
= +
. .
1
2
x
I C
+
= +
. !.
(
)
2 2 1
x
I C
= + +
. F.
(
)
2 2 1
x
I C
= − +
.
B??? Ta có
(
)
(
)
(
)
/ /
/
1 ln 2
2 2 .2 ln 2 .2 ln 2 2 .
2
x x x x x
C x
x x
+ = = = ≠ !<^
!G;>?@Ta thấy các đáp án B, C, D sai khác nhau nên hằng số nên dễ
dàng nhận ra đáp án A là không thỏa mãn.
!]H Tìm giá trị của các tham số
, ,
a b c
để hàm số
(
)
(
)
2
2 3
F x ax bx c x
= + + −
với
3
2
x
>
là một nguyên hàm của hàm số
( )
2
20 30 7
.
2 3
x x
f x
x
− +
=
^.
4, 2, 1
a b c
= = =
. .
4, 2, 1
a b c
= = − = −
.
!.
4, 2, 1
a b c
= = − =
. F.
4, 2, 1
a b c
= = = −
.
B??? Theo bài ra ta có
(
)
(
)
'
F x f x
.
(
)
*
Ta có
( ) ( )
(
)
(
)
2
2
5 3 6 3
' 2 2 3 .
2 3 2 3
ax bx c
ax b a x b c
F x ax b x
x x
+ +
+ − − +
= + − + =
− −
Để
(
)
*
xảy ra
5 20 4
3 6 30 2
3 7 1
a a
b a b
c b c
= =
⇔ − = − ⇔ = −
− = =
. !<!
!] Nếu
( )
1
d ln
f x x x C
x
= + +
∫
thì
(
)
f x
là hàm số nào trong các hàm số sau?
^.
(
)
ln
f x x x C
= + +
. .
( )
1
f x x C
x
= − + +
.
!.
( )
2
1
ln
f x x C
x
= − + +
. F.
( )
2
1
x
f x
x
−
=
.
B??? Theo định nghĩa
(
)
(
)
(
)
(
)
/
d .
f x x F x F x f x
= → =
∫
Do đó hàm số cần tìm
( )
/
2 2
1 1 1 1
ln
x
f x x C
x x x x
−
= + + = − + =
. !<F
!] Cho
(
)
F x
là một nguyên hàm của hàm số
(
)
3
x
f x e
và thỏa mãn
(
)
0 1.
F
=
Mệnh đề nào sau đây là đúng?
^
( )
3
1
1.
3
x
F x e
= +

( )
3
1
.
3
x
F x e
=
!
( )
3
1 2
3 3
x
F x e
= + ⋅
F
( )
3
1 4
3 3
x
F x e
= − + ⋅
B??? Ta có
3 3
1
d
3
x x
e x e C
= +
∫
.
Theo giả thiết
( )
1 2
0 1 1 .
3 3
F C C= → + = ⇔ =
Suy ra
( )
3
1 2
3 3
x
F x e
= + ⋅
!<!
!] Biết
(
)
F x
là một nguyên hàm của hàm số
(
)
3 1
x
f x e
+
và thỏa
( )
0
3
e
F
= ⋅
Tính
(
)
3
ln 3 1 .
F
^
(
)
3
ln 3 1 64.
F

(
)
3
ln 3 1 8.
F
= −
!
(
)
3
ln 3 1 81.
F
F
(
)
3
ln 3 1 27.
F
B??? Ta có
3 1 3 1
1
d .
3
x x
e x e C
+ +
= +
∫
.
Theo giả thiết
( )
0 0.
3 3 3
e e e
F C C
= → + = ⇔ =
Suy ra
( ) ( )
3 3 3 41
1
ln 3 1
1
3
ln 3. 64.
3
x
F eF x e
+
= =
= → !<^
!]` Tìm nguyên hàm của hàm số
(
)
1
. .
x x
f x e e
+
^.
1 1
. d .
x x x x
e e x e e C
+ +
= +
∫
. .
1 2 1
1
. d
x x x
e e x e C
+ +
= +
∫
.
!.
1 2 1
. d 2
x x x
e e x e C
+ +
= +
∫
. F.
1 1
. d .
x x x x
e e x e e C
+ +
= + +
∫
B??? Ta có
1 2 1 2 1
1
.
x x x x
e e dx e dx e C
+ + +
= = +
∫ ∫
. !<
!]K Tìm nguyên hàm
(
)
F x
của hàm
(
)
2
2
.
x
f x
^
( )
1
.
4 . ln 4
x
F
C
x
= +

( )
4
.
ln 4
x
C
F x
= +
!
(
)
4 .ln 4 .
x
F x
C
= +
F
(
)
4 .
x
F x
C
= +
B??? Ta có
2
4
d 4 d2
.
ln 4
x
x
x
x x C
= = +
∫ ∫
!<
!]a Hàm số
(
)
3
2018
x
F x e= + là một nguyên hàm của hàm số nào trong các hàm
số sau đây?
^.
(
)
3
x
f x e
= . .
(
)
3
2
3 .
x
f x x e
= . !.
( )
3
2
3
x
e
f x
x
= . F.
(
)
3
3 1
.
x
f x x e
−
= .
B??? Hàm số
(
)
F x
là một nguyên hàm của hàm số
(
)
(
)
(
)
'
f x F x f x
←→ =
.
Suy ra hàm số cần tìm
( )
(
)
(
)
(
)
3 3 3 3
/ /
/
3 2
2018 . 3 . .
x x x x
f x e e x e x e
= + = = = !<
!]J Hàm số
( )
3
3
x
x
F x e
= +
là một nguyên hàm của hàm số nào trong các hàm số
sau đây?
^.
( )
4
.
3
x
x
f x e
= +
.
(
)
2
3
x
f x x e
= +
. !.
( )
4
12
x
x
f x e
= +
. F.
(
)
2
x
f x x e
= +
.
B??? Hàm số
(
)
F x
là một nguyên hàm của hàm số
(
)
(
)
(
)
'
f x F x f x
←→ =
.
Suy ra hàm số cần tìm
( )
/
3
2
.
3
x x
x
f x e x e
= + = +
!<F
!]L Biết
(
)
F x
là một nguyên hàm của hàm số
( )
(
)
2
3
2
x
f x e= + thỏa
( )
3
0
2
F
= ⋅
Tính
1
3
F
⋅
^
2
1 8 8
3 6
e e
F
+ +
= ⋅

2
1 6 6
3 8
e e
F
+ +
= ⋅
!
2
1 6 6
3 8
e e
F
− +
= ⋅
F
2
1 8 8
3 6
e e
F
− +
= ⋅
B??? Ta có
( ) ( )
2
3 3 6 6 3
1 4
2 d 4 4 d 4 .
6 3
x x x x x
e x e e x e e x C
+ = + + = + + +
∫ ∫
.
Theo giả thiết
( )
3 1 4 3
0 0.
2 6 3 2
F C C
= → + + = ⇔ =
Suy ra
( )
2
6 3 2
1 4 1 1 4 4 8 8
4 .
6 3 3 6 3 3 6
x x
e e
F x e e x F e e
+ +
= + + → = + + =
!<^
!]I Tìm một nguyên hàm
(
)
F x
của hàm số
(
)
(
)
2 1
x x
f x e e
−
= +
, biết
(
)
0 1.
F
=
^
(
)
2 .
x
F x x e
−
= +

(
)
2 2.
x
F x x e
−
= − +
!
(
)
2 .
x
F x e
−
= +
 F
(
)
2 1.
x
F x x e
−
= − +
B??? Ta có
(
)
(
)
2 1 d 2 2 .
x x x x
e e x e dx x e C
− − −
+ = + = − +
∫ ∫
Theo giả thiết
(
)
0 1 1 1 2.
F C C
= →− + = ⇔ =
Suy ra
(
)
2 2.
x
F x x e
−
= − +
!<
!]`H Giả sử
(
)
(
)
2
x
F x ax bx c e
= + +
là một nguyên hàm của hàm số
(
)
2
x
f x x e
.
Tính tích
.
P abc
^.
1
P
=
. .
4
P
= −
. !.
5
P
= −
. F.
3
P
= −
.
B???
Ta có
( )
(
)
(
)
(
)
( )
/ /
/ 2 2 2
. . 2 .
x x x
F x ax bx c e ax bx c e ax a b x b c e
= + + + + + = + + + +
Vì
(
)
F x
là một nguyên hàm của
(
)
f x
nên ta có
(
)
(
)
/
,
F x f x x
= ∀
.
Do đó
(
)
(
)
2 2 2 2
2 . . 2
x x
ax a b x b c e x e ax a b x b c x
+ + + + = ⇔ + + + + =
.
Đồng nhất hệ số hai vế, ta được
1 1
2 0 2 4
0 2
a a
a b b P abc
b c c
= =
+ = ⇔ = − → = = −
+ = =
. !<
!] ` Giả sử hàm số
(
)
(
)
2
.
x
f x ax bx c e
−
= + +
là một nguyên hàm của hàm số
(
)
(
)
1
x
g x x x e
−
= −
. Tính tổng
S a b c
= + +
.
^.
2
S
= −
. .
4
S
=
. !.
1
S
=
. F.
3
S
=
.
B??? Ta có
(
)
(
)
(
)
(
)
(
)
/ 2 2
2 2 .
x x x
f x ax b e ax bx c e ax a b x b c e
− − −
= + − + + = − + − + −
Vì
(
)
f x
là một nguyên hàm của
(
)
g x
nên ta có
(
)
(
)
/
,
f x g x x
= ∀
.
Do đó
(
)
(
)
(
)
(
)
(
)
2 2 2
2 1 2 .
x x
ax a b x b c e x x e ax a b x b c x x
− −
− + − + − = − ⇔ − + − + − = − +
Đồng nhất hệ số hai vế, ta được
1
2 1 1 3.
0
a
a b a b c S a b c
b c
− = −
− = ⇔ = = = → = + + =
− =
!<F
!]` bc$d-.$&/0Ha–HJ_
Tìm nguyên hàm của hàm số
(
)
cos 2 .
f x x
^
( )
1
d sin 2 .
f x x x C
= +
∫

( )
1
d sin 2 .
f x x x C
= − +
∫
!
(
)
d 2 sin 2 .
f x x x C
= +
∫
F
(
)
d 2 sin 2 .
f x x x C
= − +
∫
B??? Ta có
( )
1
d cos 2 d sin 2 .
f x x x x x C
= = +
∫ ∫
!<^
!]` Biết rằng
(
)
F x
là một nguyên hàm của hàm số
(
)
(
)
sin 1 2
f x x
= −
và thỏa
mãn
1
1.
2
F
=
Mệnh đề nào sau đây là đúng?
^
(
)
(
)
cos 1 2 1.
F x x
= − +

(
)
(
)
cos 1 2 .
F x x
= −
!
( ) ( )
1 3
cos 1 2
2 2
F x x
= − − + ⋅
F
( ) ( )
1 1
cos 1 2
2 2
F x x
= − + ⋅
B??? Ta có
( ) ( )
1
sin 1 2 d cos 1 2 .
x x x C
− = − +
∫
Theo giả thiết
1 1 1
1 cos0 1 .
2 2 2
F C C
= → + = ⇔ =
Suy ra
( ) ( )
1 1
cos 1 2 .
2 2
F x x= − + !<F
!]`` Cho hàm số
(
)
f x
thỏa các điều kiện
(
)
2 cos 2
f x x
= +
và
2 .
2
f
π
=
Mệnh
đề nào sau đây là sai?
^
(
)
0 .
f
π

( )
sin 2
2 .
x
f x x
π
= + +
!
( )
sin 2
2 .
x
f x x
π
= − +
F
0.
2
f
− =
B??? Ta có
( ) ( )
1
d 2 cos 2 d 2 sin 2 .
f x x x x x x C
′
= + = + +
∫ ∫
Theo giả thiết
2 2 .
2
f C C
π π π π
= → + = ⇔ =
Suy ra
( )
1
2 sin 2 .
f x x x
π
= + +
!<
!]`K Một nguyên hàm
(
)
F x
của hàm số
(
)
2
sin
f x x
là kết quả nào sau đây, biết
nguyên hàm này bằng
8
π
khi
4
x
π
=
?
^.
( )
3
sin
.
3
x
F x =
.
( )
sin 2
.
2 4
x x
F x = −
!.
( )
sin 2 1
.
2 4 4
x x
F x = − + F.
( )
3
sin 2
.
3 12
x
F x = −
B??? Ta có
( )
2
1 cos 2
d sin d d
x
f x x x x x
= =
∫ ∫ ∫
( )
1 1 1
1 cos 2 d sin 2 .
2 2 2
x x x x C
= − = − +
∫
Theo giả thiết
1 1 1
. sin .
4 8 2 4 4 2 8 4
F C C
π π π π π
= → − + = ⇔ =
Suy ra
( )
sin 2 1
.
2 4 4
x x
F x = − +
!<!
!]`a Tìm nguyên hàm của hàm số
(
)
2
tan .
f x x
^
2
tan d tan .
x x x x C
= − +
∫

2
tan d tan .
x x x x
= −
∫
!
3
2
tan
tan d
x
x x
x
= ⋅
∫
F
3
2
tan
tan d .
x
x x C
x
= +
∫
B??? Dùng kỹ thuật thêm bớt, ta được
(
)
2 2
tan d 1 tan 1 d
x x x x
= + −
∫ ∫
( )
2
2
1
1 tan d d d d tan .
cos
x x x x x x x C
x
= + − = − = − +
∫ ∫ ∫ ∫
''
Nếu đề bài yêu cầu tìm họ nguyên hàm thì ta chọn A, còn yêu cầu tìm một nguyên
hàm thì ta chọn B
''
.
Ở đây yêu cầu tìm nguyên hàm, tức là phải tìm họ nguyên hàm. !<^
!]`J Cho nguyên hàm
(
)
d sin 2 cos
f x x x x C
= +
∫
. Mệnh đề nào sau đây là đúng?
^.
( ) ( )
1
3cos 3 cos
f x x x
= + . .
( ) ( )
1
cos 3 cos
f x x x
= + .
!.
( ) ( )
1
3cos 3 cos
f x x x
= − . F.
( ) ( )
1
cos 3 cos
f x x x
= − .
B??? Ta có
( ) ( )
1
d sin 2 cos sin 3 sin .
f x x x x x x
= = +
∫
Suy ra
( ) ( ) ( )
/
1 1
sin 3 sin 3cos 3 cos .
2 2
f x x x x x
= + = + !<^
!]`L Tìm giá trị thực của các tham số
,
a b
để hàm số
(
)
(
)
cos sin
x
F x a x b x e
= +
là
một nguyên hàm của hàm số
(
)
cos .
x
f x e x
^.
1, 0
a b
= =
. .
0, 1
a b
= =
. !.
1
a b
= =
. F.
1
2
a b
= =
.
B???
Ta có
(
)
(
)
(
)
(
)
(
)
/
sin cos cos sin cos sin .
x x x
F x a x b x e a x b x e b a x b a x e
= − + + + = + + −
Vì
(
)
F x
là một nguyên hàm của
(
)
f x
nên ta có
(
)
(
)
/
,
F x f x x
= ∀
.
Do đó
(
)
(
)
(
)
(
)
cos sin cos cos sin cos .
x x
b a x b a x e e x b a x b a x x
+ + − = ⇔ + + − =
Đồng nhất hệ số hai vế, ta được
1
1
.
0
2
b a
a b
b a
+ =
⇔ = =
− =
!<F
!]`I Biết
(
)
F x
là một nguyên hàm của hàm số
( )
2
4
sin
m
f x x
= + và thỏa mãn
(
)
0 1
F
=
,
4 8
F
π π
=
. Tìm
m
.
^.
4
3
m
= −
. .
3
4
m
=
. !.
3
4
m
= −
. F.
4
3
m
=
.
B??? Ta có
( )
2 2
4 4
d sin d d sin d
m m
f x x x x x x x
π π
= + = +
∫ ∫ ∫ ∫
( )
4 1 4 1 1
d 1 cos 2 d sin 2 .
2 2 2
m m
x x x x x x C
π π
= + − = + − +
∫ ∫
Theo giả thiết
(
)
0 1
1
1
.
1 1
3
2 4 2 8
4
4 8
F
C
C
m C
m
F
π π
π π
=
=
=
→ ⇔
+ − + =
= −
=
!<!
!]KHBiết
(
)
F x
là một nguyên hàm của hàm số
( )
2
1
sin
f x
x
=
và đồ thị hàm số
(
)
y F x
đi qua điểm
;0
6
M
. Tính
3
F
π
.
^
0
3
F
=
. 
2 3
.
3 3
F
π
=
!
3 1
.
3
3
F
π
−
=
F
2
.
3 3
F
=
B??? Ta có
2
1
d cot
sin
x x C
x
= − +
∫
.
Đồ thị
(
)
y F x
đi qua điểm
;0
6
M
nên
0 cot 0 3.
6 6
F C C
π π
= →− + = ⇔ =
Suy ra
( )
2 3
cot 3 .
3 3
F x x F
π
= − + → =
!<
Baøi 02
MOÄT SOÁ PHÖÔNG PHAÙP TÌM NGUYEÂN HAØM
1. Phương pháp đổi biến số
Nếu
(
)
(
)
d
f x x F x C
= +
∫
thì
(
)
(
)
(
)
. ' d
f u x u x x F u x C
= +
∫
.
Giả sử ta cần tìm họ nguyên hàm
(
)
d
I f x x
=
∫
, trong đó ta có thể phân tích
(
)
(
)
(
)
'
f x g u x u x
thì ta thực hiện phép đổi biến số
(
)
t u x
, suy ra
(
)
d ' d
t u x x
.
Khi đó ta được nguyên hàm:
(
)
(
)
(
)
d .
g t t G t C G u x C
= + = +
∫
Chú ý: Sau khi tìm được họ nguyên hàm theo
t
thì ta phải thay
(
)
t u x
.
2. Phương pháp lấy nguyên hàm từng phần
Cho hai hàm số
u
và
v
liên tục trên đoạn
[
]
;
a b
và có đạo hàm liên tục trên đoạn
[
]
;
a b
. Khi đó:
d d .
u v uv v u
= −
∫ ∫
(
)
*
Để tính nguyên hàm
(
)
d
f x x
∫
bằng từng phần ta làm như sau:
Bước 1. Chọn
,
u v
sao cho
(
)
d d
f x x u v
(chú ý
(
)
d ' d
v v x x
).
Sau đó tính
d
v v
=
∫
và
d '.d
u u x
.
Bước 2. Thay vào công thức
(
)
*
và tính
d
v u
∫
.
Chú ý. Cần phải lựa chọn
u
và
d
v
hợp lí sao cho ta dễ dàng tìm được
v
và tích
phân
d
v u
∫
dễ tính hơn
d
u v
∫
. Ta thường gặp các dạng sau
● Dạng 1.
( )
sin
d
cos
x
I P x x
x
=
∫
, trong đó
(
)
P x
là đa thức.
Với dạng này, ta đặt
(
)
sin
d d
cos
u P x
x
v x
x
=
.
● Dạng 2.
(
)
d
ax b
I P x e x
+
=
∫
, trong đó
(
)
P x
là đa thức.
Với dạng này, ta đặt
(
)
d d
ax b
u P x
v e x
+
=
.
● Dạng 3.
(
)
(
)
ln d
I P x mx n x
= +
∫
, trong đó
(
)
P x
là đa thức.
Với dạng này, ta đặt
(
)
( )
ln
d d
u mx n
v P x x
= +
=
.
● Dạng 4.
sin
d
cos
x
x
I e x
x
=
∫
.
Với dạng này, ta đặt
sin
cos
d d
x
x
u
x
v e x
=
=
hoặc có thể đặt ngược lại
.
sin
d d
cos
x
u e
x
v x
x
=
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1. PHƯƠNG PHÁP ĐỔI BIẾN SỐ
Câu 1. Biết
(
)
(
)
d .
f u u F u C
= +
∫
Mệnh đề nào dưới đây đúng ?
A.
(
)
(
)
2 1 d 2 2 1 .
f x x F x C
− = − +
∫
B.
(
)
(
)
2 1 d 2 1 .
f x x F x C
− = − +
∫
C.
(
)
(
)
2 1 d 2 1 .
f x x F x C
− = − +
∫
D.
( ) ( )
1
2 1 d 2 1 .
f x x F x C
− = − +
∫
Lời giải. Đặt
2 1 2
u x du dx
= − → =
Khi đó
( ) ( ) ( ) ( ) ( )
d 1 1 1
2 1 d d 2 1 .
2 2 2 2
u
f x x f u f u u F u C F x C
− = = = + = − +
∫ ∫ ∫
Chọn D.
Câu 2. Tìm hàm số
(
)
F x
thỏa mãn
(
)
(
)
2017
2 1F x x
′
= + và
1
2018.
2
F
− =
A.
( )
(
)
2018
2 1
2018.
2018
x
F x
+
= +
B.
( )
(
)
2018
2 1
2018.
4036
x
F x
+
= +
C.
(
)
(
)
2016
2017 2 1 2018.
F x x= + + D.
(
)
(
)
2016
4034 2 1 2018.
F x x= + +
Lời giải. Ta có
(
)
2017
2 1 d .
x x
+
∫
Đặt
2 1 2
u x du dx
= + → =
Khi đó
( )
(
)
2018
2018
2017
2017
2 1
1 1
2 1 d d . .
2 2 2018 4036
x
u
x x u u C C
+
+ = = + = +
∫ ∫
Theo giả thiết
1
2018 2018.
2
F C
− = → =
Vậy
( )
(
)
2018
2 1
2018
4036
x
F x
+
= + . Chọn B.
Câu 3. Tìm nguyên hàm của hàm số
( )
(
)
9
2
1 .
f x x x= +
A.
( )
( )
10
2
1
d 1 .
20
f x x x C
= − + +
∫
B.
( )
( )
10
2
1
d 1 .
20
f x x x C
= + +
∫
C.
( )
(
)
10
2
d 2 1 .
f x x x C
= + +
∫
D.
( )
(
)
10
2
d 1 .
f x x x C
= + +
∫
Lời giải. Ta có
( )
(
)
9
2
d 1 d .
f x x x x x
= +
∫ ∫
Đặt
2
1 d 2 d
t x t x x
= + → =
.
Khi đó
( ) ( )
10
9 10
2 9 2
1 1 1
1 d d . 1 .
2 2 10 20
t
x x x t t C x C
+ = = + = + +
∫ ∫
Vậy
( )
( )
10
2
1
d 1 .
20
f x x x C
= + +
∫
Chọn B.
Câu 4. (ĐỀ MINH HỌA NĂM 2016 – 2017)
Tìm nguyên hàm của hàm số
(
)
2 1.
f x x
= −
A.
( ) ( )
2
d 2 1 2 1 .
3
f x x x x C
= − − +
∫
B.
( ) ( )
1
d 2 1 2 1 .
3
f x x x x C
= − − +
∫
C.
( )
1
d 2 1 .
3
f x x x C
= − − +
∫
D.
( )
1
d 2 1 .
f x x x C
= − +
∫
Lời giải. Ta có
(
)
d 2 1d .
f x x x x
= −
∫ ∫
Đặt
2
2 1 2 1 d d .
t x t x t t x
= − → = − → =
Khi đó
( )
3
2
1
2 1d . d d 2 1 2 1 .
3 3
t
x x t t t t t C x x C
− = = = + = − − +
∫ ∫ ∫
Chọn B.
Câu 5. Biết
(
)
F x
là một nguyên hàm của hàm số
( )
2
ln
ln 1
x
f x x
x
= ⋅ +
và
( )
1
1
3
F
= ⋅
Tính
( )
2
.
F e
A.
( )
2
8
3
F e
= ⋅
B.
( )
2
8
9
F e
= ⋅
C.
( )
2
1
3
F e
= ⋅
D.
( )
2
1
9
F e
= ⋅
Lời giải. Ta có
2
ln
ln 1d
x
x x
x
⋅ +
∫
.
Đặt
( )
2 2 2
ln
ln 1 ln 1 d d .
x
t x t x t t x
x
= + ⇒ = + → =
Khi đó
(
)
3
2
3
2 2
ln 1
ln
ln 1d d .
3 3
x
x t
x x t t C C
x
+
⋅ + = = + = +
∫ ∫
Theo giả thiết
( )
1 1 1
1 0.
3 3 3
F C C
= → + = ⇔ =
Suy ra
( )
(
)
( )
3
2
2
ln 1
8
3 9
x
F x F e
+
= → = ⋅
Chọn B.
Câu 6. Biết
(
)
F x
là một nguyên hàm của hàm số
( )
ln
x
f x
x
=
và
(
)
2
4
F e
=
. Mệnh đề
nào sau đây là đúng?
A.
( )
2
ln
x
F x C
= +
. B.
( )
2
ln
2
x
F x
= +
.
C.
( )
2
ln
2
x
F x
= −
. D.
( )
2
ln
x
F x x C
= + +
.
Lời giải. Ta có
( )
ln
d d
x
f x x x
x
=
∫ ∫
. Đặt
d
ln d .
x
t x t
x
= → =
Khi đó
2 2
ln ln
d d .
2 2
x t x
x t t C C
x
= = + = +
∫ ∫
Theo giả thiết
( )
(
)
2 2
2
ln
4 4 2.
e
F e C C
= → + = ⇔ =
Suy ra
( )
2
ln
2.
x
F x
= +
Chọn B.
Chú ý: Đáp án A được gọi là họ nguyên hàm của hàm số
(
)
f x
.
Câu 7. Biết
(
)
F x
là một nguyên hàm của hàm số
( )
1
1
x
f x
e
=
+
và thỏa
(
)
0 ln 2
F
= −
.
Tìm tập nghiệm
S
của phương trình
(
)
(
)
ln 1 3.
x
F x e
+ + =
A.
{
}
3 .
S
= ±
B.
{
}
3 .
S
C.
.
S
= ∅
D.
{
}
3 .
S
= −
Lời giải. Ta có
1 1
d d d d d .
1 1 1 1
x x x x
x x x x
e e e e
x x x x x x
e e e e
+ −
= = − = −
+ + + +
∫ ∫ ∫ ∫ ∫
Đặt
1 d d
x x
t e t e x
= + → =
. Khi đó
( )
d
d ln ln 1 ln 1 .
1
x
x x
x
e t
x t C e C e C
te
= = + = + + = + +
∫ ∫
Do đó
( )
1
d ln 1 .
1
x
x
x x e C
e
= − + +
∫
Theo giả thiết
(
)
0 ln 2 0 ln 2 ln 2 0.
F C C
= − → − + = − ⇔ =
Suy ra
(
)
(
)
ln 1 .
x
F x x e
= − +
Xét phương trình
(
)
(
)
(
)
(
)
ln 1 3 ln 1 ln 1 3 3.
x x x
F x e x e e x
+ + = ⇔ − + + + = ⇔ =
Chọn B.
Câu 8. Hàm
(
)
F x
nào dưới đây không phải là một nguyên hàm của hàm số
(
)
2
x
f x xe
=
?
A.
( )
2
1
2
x
F x e
= +
. B.
( )
(
)
2
1
5
x
F x e
= +
.
C.
( )
2
1
x
F x e C
= − +
. D.
( )
(
)
2
1
2
x
F x e
= − −
.
Lời giải. Ta có
(
)
2
d d .
x
f x x xe x
=
∫ ∫
Đặt
2
1
d 2 d d d .
t x t x x x x t
= → = → =
Khi đó
( )
2
1 1 1
d d
2 2 2
t t x
f x x e t e C e C
= = + = +
∫ ∫
.
Vì
(
)
F x
là một nguyên hàm của
(
)
f x
nên đáp án A đúng với
2
C
=
, đáp án B đúng
với
5
2
C
=
, đáp án D đúng với
1
C
= −
. Vậy chỉ có đáp án C là sai. Chọn C.
Cách trắc nghiệm. Ta thấy các đáp án A, B, D sai khác nhau hằng số nên chắc chắn
rằng nó là một nguyên hàm của
(
)
f x
.
Câu 9. Cho
ln
d
x
e
I x
x
=
∫
và
ln .
t x
=
Mệnh đề nào sau đây là đúng?
A.
d .
t
I te t
=
∫
B.
d .
t
I e t
=
∫
C.
d .
t
e
I t
t
=
∫
D.
d .
I t t
=
∫
Lời giải. Đặt
1
ln d d
t x t x
x
= → = . Khi đó
d
t
I e t
=
∫
. Chọn B.
Câu 10. Kí hiệu
(
)
F x
là họ các nguyên hàm của hàm số
(
)
4
sin cos
f x x x
. Mệnh đề
nào sau đây là đúng?
A.
( )
5
cos
5
x
F x C
= +
. B.
( )
4
cos
x
F x C
= +
.
C.
( )
4
sin
x
F x C
= +
. D.
( )
5
sin
5
x
F x C
= +
.
Lời giải. Ta có
(
)
4
d sin cos d
f x x x x x
=
∫ ∫
. Đặt
sin d cos d
t x t x x
= → =
.
Khi đó
( )
5 5
4
sin
d d .
5 5
t x
f x x t t C C
= = + = +
∫ ∫
Chọn D.
Câu 11. Biết
(
)
F x
là một nguyên hàm của hàm số
( )
sin
1 3cos
x
f x
x
=
và
2.
2
F
=
Tính
(
)
0 .
F
A.
( )
1
0 ln 2 2.
3
F
= − +
B.
( )
2
0 ln 2 2.
3
F
= − +
C.
( )
2
0 ln 2 2.
3
F
= − −
D.
( )
1
0 ln 2 2.
3
F
= − −
Lời giải. Ta có
sin
d
1 3cos
x
x
x
∫
.
Đặt
1
1 3cos d 3sin d sin d d .
3
t x t x x x x t
= + → = − → = −
Khi đó
sin 1 d 1 1
d ln ln 1 3cos .
1 3cos 3 3 3
x t
x t C x C
x t
= − = − + = − + +
∫ ∫
Theo giả thiết
2 2.
2
F C
= → =
Suy ra
( ) ( )
2
1 1 2
ln 1 3 cos 2 0 2 ln 2 2 ln 2.
3 3 3
F x x F= − + + → = − = − Chọn B.
Câu 12. Cho
(
)
F x
là một nguyên hàm của hàm số
(
)
cot
f x x
trên
2
0;
3
π
thỏa
0.
4
F
=
Tính
2
F
π
⋅
A.
ln 2.
2
F
= −
B.
1
ln 2.
2 2
F
=
C.
ln 2.
2
F
= −
D.
2 ln 2.
2
F
= −
Lời giải. Ta có
cos
cot d d .
sin
x
x x x
x
=
∫ ∫
Đặt
sin d cos d
t x t x x
= → =
.
Khi đó
cos d
cot d d ln ln sin .
sin
x t
x x x t C x C
x t
= = = + = +
∫ ∫ ∫
Theo giả thiết
( )
1
0 ln 0 ln 2 .
4
2
F C C
= → + = ⇔ =
Suy ra
( )
( )
(
)
(
)
1
ln sin ln 2 ln 2 ln 2.
2 2
F x x F
= + → = =
Chọn B.
Câu 13. Gọi
(
)
F x
là một nguyên hàm của hàm số
(
)
tan 2
f x x
thỏa mãn
(
)
0 0.
F
=
Tính
6 2
2 .
F F
T e e
π π
= −
A.
1.
T
=
B.
2.
T
C.
2.
T
= −
D.
0.
T
=
Lời giải. Ta có
sin 2
tan 2 d d .
cos 2
x
x x x
x
=
∫ ∫
Đặt
1
cos 2 d 2 sin 2 d sin 2 d d .
t x t x x x x t
= → = − → = −
Khi đó
sin 2 1 d 1 1
tan 2 d d .ln ln cos 2 .
cos 2 2 2 2
x t
x x x t C x C
x t
= = − = − + = − +
∫ ∫ ∫
Theo giả thiết
(
)
0 0 0.
F C
= → =
Suy ra
( )
1
ln cos 2 0
2 2
F x x F
= − → =
và
(
)
1 1
ln ln 2
6 2 2
F
= − =
.
Vậy
ln 2 0
2. 2 1 1.
T e e
= − = − =
Chọn A.
Câu 14. Biết
(
)
F x
là một nguyên hàm của hàm số
(
)
sin
cos
x
f x e x
và
(
)
5
F
=
.
Khẳng định nào sau đây là đúng?
A.
(
)
sin
4
x
F x e
= +
. B.
(
)
sin x
F x e C
= +
.
C.
(
)
cos
4
x
F x e
= +
. D.
(
)
cosx
F x e C
= +
.
Lời giải. Ta có
(
)
sin
d cos d .
x
f x x e x x
=
∫ ∫
Đặt
sin d cos d .
t x t x x
= → =
Khi đó
(
)
sin sin
d cos d d
x t t x
f x x e x x e t e C e C
= = = + = +
∫ ∫ ∫
.
Theo giả thiết
(
)
sin
5 5 1 5 4.
F e C C C
π
= → + = ⇔ + = ⇔ =
Suy ra
(
)
sin
4.
x
F x e
= +
Chọn A.
Câu 15. Biết
(
)
F x
là một nguyên hàm của hàm số
( )
tan
2
cos
x
e
f x
x
=
và
(
)
0 2017
F
.
Khẳng định nào sau đây là đúng?
A.
(
)
tan
.
x
F x e
B.
(
)
tan
.
x
F x e
−
C.
(
)
tan
2016.
x
F x e
= +
D.
(
)
tan
2018.
x
F x e
= +
Lời giải. Ta có
( )
tan
2
d d .
cos
x
e
f x x x
x
=
∫ ∫
Đặt
2
1
tan d d .
cos
t x t x
x
= → =
Khi đó
( )
tan
tan
2
d d d .
cos
x
t t x
e
f x x x e t e C e C
x
= = = + = +
∫ ∫ ∫
Theo giả thiết
(
)
tan 0
0 2017 2017 2016.
F e C C
= → + = ⇔ =
Suy ra
(
)
tan
2016.
x
F x e
= +
Chọn C.
Vấn đề 2. PHƯƠNG PHÁP LẤY NGUYÊN HQM TỪNG PHẦN
Câu 16. Gọi
(
)
F x
là một nguyên hàm của hàm số
(
)
ln
f x x
và thỏa mãn
(
)
1 3.
F
=
Tính
(
)
2
.
F e
A.
(
)
2
4.
F e
=
B.
(
)
2 2
3 4.
F e e
= +
C.
(
)
2 2
4.
F e e
= − +
D.
(
)
2 2
4.
F e e
= +
Lời giải. Ta có
ln d
x x
∫
. Đặt
d
ln
d
.
d d
x
u x
u
x
v x
v x
=
=
⇒
=
=
Khi đó
ln d ln d ln .
x x x x x x x x C
= − = − +
∫ ∫
Theo giả thiết
(
)
1 3 1 3 4.
F C C
= →− + = ⇔ =
Suy ra
(
)
(
)
2 2
.ln 4 4.
F x x x x F e e
= − + → = +
Chọn D.
Câu 17. (ĐỀ CHÍNH THỨC 2016 – 2017) Cho
( )
3
1
3
F x
x
= −
là một nguyên hàm của
hàm số
(
)
f x
x
. Tìm nguyên hàm của hàm số
(
)
' ln
f x x
.
A.
( )
3 5
ln 1
' ln d .
5
x
f x x x C
x x
= + +
∫
B.
3 5
ln 1
'( ) ln d .
5
x
f x x x C
x x
= − +
∫
C.
( )
3 3
ln 1
' ln d .
3
x
f x x x C
x x
= + +
∫
D.
( )
3 3
ln 1
' ln d .
3
x
f x x x C
x x
= − + +
∫
Lời giải. Ta có
( )
(
)
( )
2
6 4 3
1 3 1 1
' . .
3
f x
x
F x f x
x
x x x
= = = → =
Xét
(
)
' ln d .
f x x x
∫
Đặt
( )
( )
1
ln
d d
.
' d
u x
u x
x
dv f x x
v f x
=
=
⇔
=
=
Khi đó
( ) ( )
(
)
3 3
ln 1
' ln d ln . d .
3
f x
x
f x x x x f x x C
x
x x
= − = + +
∫ ∫
Chọn C.
Câu 18. Tìm nguyên hàm của hàm số
( )
(
)
ln ln
.
x
f x
x
=
A.
(
)
( )
ln ln
d ln .ln ln .
x
x x x C
x
= +
∫
B.
(
)
( )
ln ln
d ln .ln ln ln .
x
x x x x C
x
= + +
∫
C.
(
)
( )
ln ln
d ln .ln ln ln .
x
x x x x C
x
= − +
∫
D.
(
)
( )
ln ln
d ln ln ln .
x
x x x C
x
= + +
∫
Lời giải. Đặt
d
ln d
x
t x t
x
= ⇒ =
. Suy ra
(
)
ln ln
d ln d
x
x t t
x
=
∫ ∫
.
Đặt
d
ln
d
d d
t
u t
u
t
v t
v t
=
=
⇒
=
=
.
Khi đó
(
)
ln d ln d ln ln .ln ln ln .
t t t t t t t t C x x x C
= − = − + = − +
∫ ∫
Chọn C.
Câu 19. Tìm nguyên hàm của hàm số
(
)
.
x
f x xe
A.
d .
x x x
xe x e xe C
= + +
∫
B.
2
d .
x x
x
xe x e C
= +
∫
C.
d .
x x x
xe x xe e C
= − +
∫
D.
2
d .
x x x
x
xe x e e C
= + +
∫
Lời giải. Ta có
d .
x
xe x
∫
Đặt
d d
.
d d
x x
u x u x
v e x v e
= =
⇒
= =
Khi đó
d d .
x x x x x
xe x xe e x xe e C
= − = − +
∫ ∫
Chọn C.
Câu 20. Biết
(
)
F x
là một nguyên hàm của hàm số
(
)
(
)
1
x
f x x e
= −
và thỏa mãn
(
)
0 1.
F
=
Tìm
(
)
F x
.
A.
(
)
(
)
1
x
F x x e
= −
. B.
(
)
(
)
2
x
F x x e
= −
.
C.
(
)
(
)
1 1
x
F x x e
= + +
. D.
(
)
(
)
2 3
x
F x x e
= − +
.
Lời giải. Ta có
(
)
1 d
x
x e x
−
∫
. Đặt
1 d d
.
d d
x x
u x u x
v e x v e
= − =
⇒
= =
Khi đó
(
)
(
)
(
)
(
)
1 d 1 d 1 2 .
x x x x x x
x e x x e e x x e e C x e C
− = − − = − − + = − +
∫ ∫
Theo giả thiết
(
)
(
)
0
0 1 0 2 1 3.
F e C C
= → − + = ⇔ =
Vậy
(
)
(
)
2 3
x
F x x e
= − +
. Chọn D.
Câu 21. Cho
(
)
F x
là một nguyên hàm của hàm số
(
)
.
x
f x x e
−
thỏa mãn điều kiện
(
)
0 1.
F
= −
Tính tổng
S
các nghiệm của phương trình
(
)
1 0.
F x x
+ + =
A.
3.
S
= −
B.
0.
S
=
C.
2.
S
=
D.
1.
S
= −
Lời giải. Ta có
. d
x
x e x
−
∫
. Đặt
d d
.
d
x x
u x u x
dv e x v e
− −
= =
⇒
= = −
Khi đó
d d .
x xx x x
x
x xe e x xe e C
e
− − − − −
= − + =− − +
∫ ∫
Theo giả thiết
(
)
0 1
1 1 0.
CF C
→− + = − ⇔ =
= −
Suy ra
(
)
(
)
1
x x x
F x xe e e x
− −
= − − = − +
.
Xét phương trình
(
)
(
)
1 0 1 1 0
x
F x x e x x
+ + = ⇔ − + + + =
( )
( )
1
1 1 0 1 0 1.
0
x
x
x e S
x
= −
⇔ + − + = ⇔ → = − + = −
=
Chọn D.
Câu 22. Biết
(
)
F x
là một nguyên hàm của hàm số
(
)
sin
f x x x
và thỏa mãn
(
)
2 .
F
π π
Tính giá trị của biểu thức
(
)
(
)
2 0 8 2 .
T F F
π
= −
A.
6 .
T
π
B.
4 .
T
π
C.
8 .
T
π
D.
T
π
Lời giải. Ta có
d
sin
x x
x
∫
. Đặt
d d
.
d sin d cos
u x u x
v x x v x
= =
⇒
= = −
Khi đó
sin d cos cos d cos sin .
x x x x x x x x x x C
= − + = − + +
∫ ∫
Theo giả thiết
(
)
22
.
C CF
π π π
π π
→ + = ⇔ =
Suy ra
( )
(
)
( )
( )
0
cos si
2 0
2
8. 1n
.
T
F
F x x x x
F
π π π
π
π π
= − + + → →
=
= − − =
−
Chọn D.
Câu 23. Biết
(
)
F x
là một nguyên hàm của hàm số
( )
2
cos
2
x
f x x= và thỏa
( )
1
0
2
F
= ⋅
Tính
(
)
.
F
π
A.
( )
2
1
2 2
F
π
= + ⋅
B.
( )
2
1
4 2
F
π
= − ⋅
C.
( )
2
1
4 2
F
π
= + ⋅
D.
( )
2
1.
F
π
= +
Lời giải. Ta có
2
1 cos 1 1
cos d d d cos d .
2 2 2 2
x x
x x x x x x x x x
= = +
∫ ∫ ∫ ∫
2 2
1 1
1 1
d . .
2 2 2 4
x x
x x C C
= + = +
∫
(
)
1
1
cos d .
x x x
∫
Đặt
d d
.
d cos d sin
u x u x
v x x v x
= =
⇒
= =
Suy ra
(
)
( )
2
1 1 1
cos d sin sin d sin cos .
2 2 2
x x x x x x x x x x C
= − = + +
∫ ∫
(
)
2
Từ
(
)
1
và
(
)
2
, suy ra
( )
2
2
1 2
1
cos d sin cos
2 4 2
x x
x x C x x x C
= + + + +
∫
.
Theo giả thiết
( )
1 2 1 2
1 1 1 1 1
0 0.
2 2 2 2 2
F C C C C
= → + + = ⇔ + =
Suy ra
( ) ( ) ( )
2 2
1 1
sin cos .
4 2 4 2
x
F x x x x F
π= + + → = − Chọn B.
Câu 24. Tìm nguyên hàm của hàm số
(
)
2
cos .
f x x x
A.
2 2
cos d sin 2 cos 2 sin 2 .
x x x x x x x x C
= − + +
∫
B.
2 2
cos d sin 2 cos 2 sin .
x x x x x x x x
= + −
∫
C.
2 2
cos d sin 2 cos 2 sin 2 .
x x x x x x x x C
= + − −
∫
D.
2 2
cos d sin cos sin .
x x x x x x x x C
= + − −
∫
Lời giải. Đặt
2
d 2 d
.
sin
d cos d
u x x
u x
v x
v x x
=
⇒
=
=
Khi đó
2 2
cos d sin 2 sin d
x x x x x x x x
= −
∫ ∫
.
(
)
1
Tính
sin d
x x x
∫
. Đặt
d d
.
d sin d cos
u x u x
v x x v x
= =
⇒
= = −
Ta được
sin d cos cos d cos sin .
x x x x x x x x x x C
= − + = − + +
∫ ∫
(
)
2
Từ
(
)
1
và
(
)
2
, suy ra
(
)
2 2
cos d sin 2 cos sin
x x x x x x x x C
= − − + +
∫
2
sin 2 cos 2 sin 2 .
x x x x x C
= + − −
Chọn C.
Câu 25. Tìm nguyên hàm của hàm số
(
)
sin .
x
f x e x
A.
sin d sin .
x x
e x x e x C
= +
∫
B.
( )
1
sin d sin cos .
x x x
e x x e x e x C
= + +
∫
C.
sin d cos .
x x
e x x e x C
= +
∫
D.
( )
1
sin d sin cos
x x x
e x x e x e x C
= − +
∫
.
Lời giải. Đặt
sin d cos d
d d
x x
u x u x x
v e x v e
= =
⇒
= =
.
Khi đó
sin d sin cos d sin
x x x x
xe x e x xe x e x K
= − = −
∫ ∫
.
(
)
1
Tính
cos d
x
K xe x
=
∫
. Đặt
cos d sin d
.
d d
x x
u x u x x
v e x v e
= = −
⇒
= =
Suy ra
cos sin d .
x x
K e x xe x
= +
∫
(
)
2
Từ
(
)
1
và
(
)
2
, suy ra
(
)
sin d sin cos sin d
x x x x
xe x e x e x xe x
= − +
∫ ∫
( )
1
2 sin d sin cos sin d sin cos .
x x x x x x
xe x e x e x xe x e x e x
⇔ = − ⇔ = −
∫ ∫
Vì các nguyên hàm sai khác nhau hằng số
C
nên ta Chọn D.
Baøi 03
TÍCH PHAÂN
1. Định nghĩa
Cho
(
)
f x
là hàm số liên tục trên
K
và
,
a b
là hai số bất kì thuộc
K
. Giả sử
(
)
F x
là một nguyên hàm của
(
)
f x
trên
K
thì hiệu số
(
)
(
)
F b F a
−
được gọi là tích phân của
(
)
f x
từ
a
đến
b
và kí hiệu là
( ) ( ) ( ) ( )
d
b
b
a
a
f x x F x F b F a
= = −
∫
.
2. Tính chất
Tích phân tại một giá trị xác định của biến số thì bằng
0
, tức là
( )
d 0
a
a
f x x
=
∫
.
Đổi cận thì đổi dấu, tức là
( ) ( )
d d
b a
a b
f x x f x x
= −
∫ ∫
.
Hằng số trong tích phân có thể đưa ra ngoài dấu tích phân, tức là
( ) ( )
d d
b b
a a
kf x x k f x x
=
∫ ∫
(
k
là hằng số).
Tích phân một tổng bằng tổng các tích phân, tức là
( ) ( ) ( ) ( )
d d d
b b b
a a a
f x g x x f x x g x x
± = ±
∫ ∫ ∫
.
Tách đôi tích phân, tức là
( ) ( ) ( )
d d d
b c b
a a c
f x x f x x f x x
= +
∫ ∫ ∫
.
Chú ý: Tích phân
( )
d
b
a
f x x
∫
chỉ phụ thuộc vào hàm
f
và các cận
,
a b
mà không
phụ thuộc vào biến số
x
, tức là
( ) ( )
d d
b b
a a
f x x f t t
=
∫ ∫
.
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. TÍNH CHẤT TÍCH PHÂN
Câu 1. Giả sử hàm số
(
)
f x
liên tục trên
ℝ
và các số thực
.
a b c
< <
Mệnh đề nào sau
đây sai?
A.
( ) ( ) ( )
d d d .
c b c
a a b
f x x f x x f x x
= +
∫ ∫ ∫
B.
( ) ( ) ( )
d d d .
b c c
a a b
f x x f x x f x x
= −
∫ ∫ ∫
C.
( ) ( ) ( )
d d d .
b a c
a b a
f x x f x x f x x
= +
∫ ∫ ∫
D.
( ) ( )
. d d .
b b
a a
c f x x c f x x
=
∫ ∫
Lời giải. Chọn C.
Câu 2. Cho
(
)
(
)
,
f x g x
là hai hàm số liên tục trên
ℝ
và các số thực
, ,
a b c
. Mệnh đề
nào sau đây sai?
A.
( ) ( )
d d .
b b
a a
f x x f y y
=
∫ ∫
B.
( ) ( ) ( ) ( )
d d d .
b b b
a a a
f x g x x f x x g x x
+ = +
∫ ∫ ∫
C.
( )
d 0.
a
a
f x x
=
∫
D.
( ) ( ) ( ) ( )
. d d . d .
b b b
a a a
f x g x x f x x g x x
=
∫ ∫ ∫
Lời giải. Chọn D.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A.
1
1
d 1
x
−
=
∫
.
B.
( ) ( ) ( ) ( )
1 2 1 2
. d d . d
b b b
a a a
f x f x x f x x f x x
=
∫ ∫ ∫
.
C. Nếu
(
)
f x
liên tục và không âm trên đoạn
[
]
;
a b
thì
( )
d 0
b
a
f x x
≥
∫
.
D.
( )
.d ,
b
a
k x k a b k
= − ∀ ∈
∫
ℝ
.
Lời giải. Ta có
1
1
1
1
d 2.
x x
−
−
= =
∫
Do đó A sai.
Theo tính chất tích phân thì B sai (vì không có tính chất này).
Xét đáp án C. Giả sử
(
)
F x
là một nguyên hàm của hàm số
(
)
f x
trên đoạn
[
]
;
a b
.
Suy ra
(
)
(
)
[
]
/
0, ;
F x f x x a b
= ≥ ∀ ∈
.
●
(
)
[
]
/
0, ;
F x x a b
= ∀ ∈
, suy ra
(
)
F x
là hàm hằng nên
( ) ( )
d 0.
b
b
a
a
f x x F x
= =
∫
●
(
)
[
]
/
0, ;
F x x a b
> ∀ ∈
, suy ra
(
)
F x
đồng biến trên đoạn
[
]
;
a b
nên
(
)
(
)
F b F a
.
Do đó
( ) ( ) ( ) ( )
d 0
b
b
a
a
f x x F x F b F a
= = − >
∫
. Do đó C đúng. Chọn C.
Ta có
( )
.d . d .
b b
b
a
a a
k x k x k x k b a
= = = − →
∫ ∫
D sai.
Câu 4. Cho hàm số
(
)
f x
thỏa mãn
( )
5
2
d 10
f x x =
∫
. Tính
( )
2
5
2 4 d .
I f x x
= −
∫
A.
32.
I
B.
34.
I
C.
36.
I
D.
40.
I
Lời giải. Ta có
( ) ( )
2 2 2
5 5 5
2 4 d 2 d 4 d
I f x x x f x x
= − = −
∫ ∫ ∫
( ) ( )
5
2
5
2
2 4 d 2. 2 5 4.10 34
x f x x= + = − + =
∫
. Chọn B.
Câu 5. Cho hàm số
(
)
f x
thỏa mãn
( )
3
1
d 2016
f x x =
∫
và
( )
3
4
d 2017.
f x x =
∫
Tính tích phân
( )
4
1
d .
I f x x
=
∫
A.
4023.
I
B.
1.
I
=
C.
1.
I
= −
D.
0.
I
=
Lời giải. Ta có
( ) ( ) ( )
4 3 4
1 1 3
d d d
I f x x f x x f x x
= = +
∫ ∫ ∫
( ) ( )
3 3
1 4
d d 2016 2017 1
f x x f x x
= − = − = −
∫ ∫
. Chọn C.
Câu 6. Cho hàm số
(
)
f x
thỏa mãn
( )
2
1
d 1
f x x
=
∫
và
( )
4
1
d 3
f t t
= −
∫
.
Tính tích phân
( )
4
2
d .
I f u u
=
∫
A.
2
= −
. B.
4
= −
. C.
4.
I
=
D.
2.
I
Lời giải. Ta có
( ) ( )
2 2
1 1
d d 1
f u u f x x
= =
∫ ∫
và
( ) ( )
4 4
1 1
d d 3
f u u f t t
= = −
∫ ∫
.
Suy ra
( ) ( ) ( ) ( ) ( )
4 1 4 2 4
2 2 1 1 1
d d d d d 1 3 4.
I f u u f u u f u u f u u f u u
= = + = − + = − − = −
∫ ∫ ∫ ∫ ∫
Chọn B.
Câu 7. Cho hàm số
(
)
f x
thỏa mãn
( )
6
0
d 4
f x x
=
∫
và
( )
6
2
d 3
f x t
= −
∫
.
Tính tích phân
( )
2
0
3 d .
I f v v
= −
∫
A.
1.
I
=
B.
2.
I
C.
4.
I
D.
3.
I
=
Lời giải. Ta có
( ) ( ) ( )
2 2 2
2
0
0 0 0
3 d d 3 d 6.
I f v v f v v v f v v
= − = − = −
∫ ∫ ∫
Mà
( ) ( ) ( ) ( ) ( ) ( )
2 2 6 6 6 6
0 0 2 2 0 2
d d d d d d
f v v f v v f v v f v v f v v f v v
= + − = −
∫ ∫ ∫ ∫ ∫ ∫
( ) ( ) ( )
6 6
0 2
d d 4 3 7.
f x x f x x
= − = − − =
∫ ∫
Vậy
7 6 1
I
= − =
. Chọn A.
Câu 8. Cho hàm số
(
)
f x
thỏa mãn
( )
10
0
d 7
f x x
=
∫
và
( )
6
2
d 3.
f x x
=
∫
Tính tích phân
( ) ( )
2 10
0 6
d d .
I f x x f x x
= +
∫ ∫
A.
10.
I
B.
4.
I
C.
7.
I
=
D.
4.
I
= −
Lời giải. Ta có
( ) ( ) ( ) ( ) ( ) ( )
2 10 2 6 10 6
0 6 0 2 6 2
d d d d d d
I f x x f x x f x x f x x f x x f x x
= + = + + −
∫ ∫ ∫ ∫ ∫ ∫
( ) ( )
10 6
0 2
d d 7 3 4.
f x x f x x
= − = − =
∫ ∫
Chọn B.
Câu 9. Cho hàm số
(
)
f x
thỏa mãn
( ) ( )
d 10, d 8
d d
a b
f x x f x x
= =
∫ ∫
và
( )
d 7
c
a
f x x
=
∫
.
Tính tích phân
( )
d .
c
b
I f x x
=
∫
A.
5
I
= −
. B.
7.
I
=
C.
5.
I
=
D.
7
I
= −
.
Lời giải. Ta có
( ) ( ) ( ) ( )
d d d d
c d a c
b b d a
I f x x f x x f x x f x x
= = + +
∫ ∫ ∫ ∫
( ) ( ) ( )
d d d 8 10 7 5.
d d c
b a a
f x x f x x f x x
= − + = − + =
∫ ∫ ∫
Chọn C.
Câu 10. Cho hàm số
(
)
f x
thỏa mãn
( ) ( )
3 4
1 1
d 2, d 3
f x x f x x
= − =
∫ ∫
và
( )
4
1
d 7
g x x
=
∫
.
Khẳng định nào sau đây là sai?
A.
( ) ( )
4
1
d 10.
f x g x x
+ =
∫
B.
( )
4
3
d 1.
f x x
=
∫
C.
( )
3
4
d 5.
f x x
= −
∫
D.
( ) ( )
4
1
4 2 d 2.
f x g x x
− = −
∫
Lời giải. Ta có
( ) ( ) ( ) ( )
4 4 4
1 1 1
d d d 3 7 10
f x g x x f x x g x x
+ = + = + =
∫ ∫ ∫
. Do đó A đúng.
Ta có
( ) ( ) ( )
4 1 4
3 3 1
d d d
f x x f x x f x x
= +
∫ ∫ ∫
( ) ( ) ( )
3 4
1 1
d d 2 3 5
f x x f x x
= − + = − − + =
∫ ∫
. Do đó B sai, C đúng. Chọn B.
Ta có
( ) ( ) ( ) ( )
4 4 4
1 1 1
4 2 d 4 d 2 d 4.3 2.7 2
f x g x x f x x g x x
− = − = − = −
∫ ∫ ∫
. Do đó D đúng.
Câu 11. Cho hàm số
(
)
f x
thỏa
( ) ( )
2
1
3 2 d 1
f x g x x
+ =
∫
và
( ) ( )
2
1
2 d 3
f x g x x
− = −
∫
.
Tính tích phân
( )
2
1
d .
I f x x
=
∫
A.
1.
I
=
B.
2.
I
=
C.
5
.
7
I
= −
D.
1
.
2
I =
Lời giải. Ta có
( ) ( ) ( ) ( )
2 2 2
1 1 1
3 2 d 1 3 d 2 d 1.
f x g x x f x x g x x
+ = ←→ + =
∫ ∫ ∫
( ) ( ) ( ) ( )
2 2 2
1 1 1
2 d 3 2 d d 3.
f x g x x f x x g x x
− = − ←→ − = −
∫ ∫ ∫
Đặt
( )
2
1
d
f x x u
=
∫
và
( )
2
1
d
g x x v
=
∫
, ta có hệ phương trình
5
3 2 1
7
.
2 3 11
7
u
u v
u v
v
= −
+ =
⇔
− = −
=
Vậy
( )
2
1
5
d
7
I f x x u
= = = −
∫
. Chọn C.
Câu 12. (ĐỀ THỬ NGHIỆM 2016 – 2017) Cho hàm số
(
)
f x
có đạo hàm liên tục
trên đoạn
[
]
1;2
và thỏa mãn
(
)
(
)
1 1, 2 2.
f f
= =
Tính
( )
2
1
d .
I f x x
′
=
∫
A.
1.
I
=
B.
1.
I
= −
C.
3.
I
=
D.
7
2
I
= ⋅
Lời giải. Ta có
( ) ( ) ( ) ( )
2
2
1
1
d 2 1 1.
I f x x f x f f
′
= = = − =
∫
Chọn A.
Câu 13. Cho hàm số
(
)
f x
có đạo hàm liên tục trên
ℝ
và thỏa mãn
(
)
0 1.
f
=
Kí hiệu
( )
0
' d .
x
I f t t
=
∫
Mệnh đề nào sau đây là đúng?
A.
(
)
1.
I f x
= +
B.
(
)
.
I f x
C.
(
)
1 .
I f x
= +
D.
(
)
1.
I f x
= −
Lời giải. Ta có
( ) ( ) ( ) ( ) ( )
0
0
' d 0 1.
x
x
I f t t f t f x f f x
= = = − = −
∫
Chọn D.
Câu 14. Cho hàm số
( )
2
ln 1 .
f x x x
= + +
Tính tích phân
( )
1
0
d .
f x x
′
∫
A.
( )
1
0
d ln 2.
f x x
′
=
∫
B.
( )
( )
1
0
d ln 1 2 .
f x x
′
= +
∫
C.
( )
1
0
d 1 ln 2.
f x x
′
= +
∫
D.
( )
1
0
d 2 ln 2.
f x x
′
=
∫
Lời giải. Ta có
( ) ( )
1
1
0
0
d
f x x f x
′
=
∫
( )
1
2 2 2
0
ln 1 ln 1 1 1 ln 0 0 1 ln 1 2 .
x x= + + = + + − + + = + Chọn B.
Câu 15. Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[1;4]
và thỏa mãn
(
)
1 12
f
,
( )
4
1
' d 17.
f x x =
∫
Tính giá trị của
(
)
4 .
f
A.
(
)
4 29.
f
B.
(
)
4 5.
f
=
C.
(
)
4 9.
f
=
D.
(
)
4 19.
f
Lời giải. Ta có
( ) ( ) ( ) ( )
4
4
1
1
' d 4 1 .
f x x f x f f= = −
∫
Theo giả thiết
( ) ( ) ( ) ( ) ( )
4
1
' d 17 4 1 17 4 17 1 17 12 29.
f x x f f f f= ⇔ − = → = + = + =
∫
Chọn A.
Câu 16. Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[
]
1;ln 3
và thỏa mãn
(
)
2
1
f e
=
,
( )
ln 3
2
1
' d 9 .
f x x e
= −
∫
Tính giá trị của
(
)
ln 3 .
f
A.
(
)
2
ln 3 9 2 .
f e
= −
B.
(
)
ln 3 9.
f
=
C.
(
)
ln 3 9.
f
= −
D.
(
)
2
ln 3 2 9.
f e
= −
Lời giải. Ta có
( ) ( ) ( ) ( )
ln 3
ln 3
1
1
' d ln 3 1 .
f x x f x f f= = −
∫
Theo giả thiết
( ) ( ) ( )
ln 3
2 2
1
' d 9 ln 3 1 9
f x x e f f e
= − ⇔ − = −
∫
(
)
(
)
2 2 2
ln 3 9 1 9 9.
f e f e e
→ = − + = − + =
Chọn B.
Câu 17. Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[
]
1;3
và thỏa mãn
(
)
1 1
f
=
,
(
)
3 .
f m
Tìm tham số thực
m
để
( )
3
1
d 5.
f x x
′
=
∫
A.
6.
m
=
B.
5.
m
=
C.
4.
m
=
D.
4.
m
= −
Lời giải. Ta có
( ) ( ) ( ) ( )
3
3
1
1
d 3 1 .
f x x f x f f
′
= = −
∫
Theo giả thiết
( ) ( ) ( )
3
1
d 5 3 1 5 1 5 6.
f x x f f m m
′
= ⇔ − = ⇔ − = ⇔ =
∫
Chọn A.
Câu 18. Cho hàm số
( ) ( )
0
cos d .
x
g x t x t t
= −
∫
Tính
'
2
g
π
.
A.
' 1.
2
g
= −
B.
' 1.
2
g
=
C.
' 0.
2
g
=
D.
' 2.
2
g
=
Lời giải. Đặt
( ) ( )
d d
.
d cos d sin
u t u t
v x t t v x t
= =
→
= − = − −
Khi đó
( ) ( ) ( ) ( ) ( )
0 0 0
0
sin sin d sin cos 1 cos .
x
x x x
g x t x t x t t t x t x t x
= − − + − = − − + − = −
∫
Suy ra
( )
' sin ' sin 1.
2 2
g x x g
π π
= → = =
Chọn B.
Câu 19. Tính đạo hàm của hàm số
( )
2
0
cos d
x
F x t t
=
∫
với
0.
x
>
A.
(
)
2
' cos .
F x x x
B.
(
)
' 2 cos .
F x x x
C.
(
)
' cos .
F x x
D.
(
)
' cos 1.
F x x
= −
Lời giải. Đặt
2
2 d d .
y t y t y y t
= ⇒ = → =
Đổi cận:
2
0 0
.
t y
t x y x
= → =
= → =
Khi đó
( )
0
cos .2 d
x
F x y y y
=
∫
. Đặt
2 d 2d
d cos d sin
u y u y
v y y v y
= =
→
= =
.
Suy ra
( )
0 0 0
0
2 sin 2 sin d 2 sin 2cos 2 sin 2 cos 2
x
x x x
F x y y y y y y y x x x
= − = + = + −
∫
(
)
' 2 sin 2 cos 2 sin 2 cos .
F x x x x x x x
→ = + − =
Chọn B.
Câu 20. Tìm giá trị nhỏ nhất
m
của hàm số
( )
( )
2
1
d
x
F x t t t
= +
∫
trên đoạn
[
]
1;1
−
.
A.
1
.
6
m =
B.
2.
m
=
C.
5
.
6
m
= −
D.
5
.
6
m =
Lời giải. Ta có
( )
( )
3 2 3 2
2
1
1
5
d .
3 2 3 2 6
x
x
t t x x
F x t t t
= + = + = + −
∫
Xét hàm số
( )
3 2
5
3 2 6
x x
F x
= + −
trên đoạn
[
]
1;1
−
.
Đạo hàm
( ) ( )
[
]
[ ]
2
0 1;1
' ' 0 .
1 1;1
x
F x x x F x
x
= ∈ −
= + → = ⇔
= − ∈ −
Ta có
( )
( )
( )
[ ]
( ) ( )
1;1
2
1
3
5 5
0 min 0 .
6 6
1 0
F
F F x F
F
−
− = −
= − → = = −
=
Chọn C.
Câu 21. Tính đạo hàm của hàm số
( )
2
1
1 d
x
F x t t
= +
∫
.
A.
( )
/
2
1
x
F x
x
=
. B.
(
)
/ 2
1
F x x
= +
.
C.
( )
/
2
1
1
F x
x
=
. D.
( )
(
)
/ 2 2
1 1 .
F x x x
= + +
Lời giải. Gọi
(
)
H t
là một nguyên hàm của
2
1
t
, suy ra
(
)
2
' 1 .
H t t
= +
Khi đó
( ) ( ) ( ) ( )
2
1
1
1 d 1
x
x
F x t t H t H x H= + = = −
∫
( ) ( ) ( ) ( )
/
2
' 1 ' 1 .
F x H x H H x x
→ = − = = +
Chọn B.
Câu 22. Tính đạo hàm của hàm số
( )
2
1
sin d
x
F x t t
=
∫
với
0
x
>
.
A.
(
)
' sin .
F x x
B.
( )
sin
'
2
x
F x
x
= . C.
( )
2 sin
'
x
F x
x
= . D.
(
)
' sin
F x x
= .
Lời giải. Gọi
(
)
H t
là một nguyên hàm của
2
sin
t
, suy ra
(
)
2
' sin .
H t t
Khi đó
( ) ( )
( )
( )
2
1
1
sin d 1
x
x
F x t t H t H x H= = = −
∫
( )
( )
( )
( )
(
)
/
/ /
sin
' 1 .
2 2
H x
x
F x H x H H x
x x
→ = − = = =
Chọn B.
Chú ý:
(
)
(
)
/
/
.
H x H x
≠
Câu 23. Tính đạo hàm của hàm số
(
)
f x
, biết
(
)
f x
thỏa mãn
( ) ( )
0
d
x
f t f x
te t e
=
∫
.
A.
(
)
' .
f x x
=
B.
(
)
2
' 1.
f x x
= +
C.
( )
1
' .
f x
x
=
D.
(
)
' 1.
f x
=
Lời giải. Gọi
(
)
F t
là một nguyên hàm của
(
)
f t
te
, suy ra
(
)
(
)
'
f t
F t te
= .
Khi đó
( )
( ) ( ) ( )
( )
( ) ( )
0
0
d 0 0
x
x
f t f x
te t F t F x F e F x F= = − ←→ = −
∫
.
Đạo hàm hai vế, ta được
(
)
(
)
(
)
(
)
(
)
(
)
(
)
' . ' ' . ' .
f x f x f x
f x e F x f x e xe f x x
= ←→ = → =
Chọn A.
Câu 24. Cho hàm số
(
)
f x
thỏa mãn
(
)
( )
2
0
d cos .
f x
t t x x
π=
∫
Tính
(
)
4 .
f
A.
(
)
4 2 3.
f = B.
(
)
4 1.
f
= −
C.
( )
1
4 .
2
f = D.
(
)
3
4 12.
f =
Lời giải. Ta có
(
)
( )
( ) ( )
3
3
2
0
0
1
d cos .
3 3
f x
f x
t
t t f x x x
π
= = =
∫
Cho
4
x
=
, ta được
( ) ( )
3
3
1
4 4 cos 4 4 12.
3
f fπ
= → =
Chọn D.
Câu 25. Cho hàm số
(
)
y f x
có
(
)
1 ' 4
f x
≤ ≤
với mọi
[
]
2;5
x
. Hỏi khẳng định nào
dưới đây là khẳng định đúng?
A.
(
)
(
)
3 5 2 12.
f f
≤ − ≤
B.
(
)
(
)
12 5 2 3.
f f
− ≤ − ≤
C.
(
)
(
)
1 5 2 4.
f f
≤ − ≤
D.
(
)
(
)
4 5 2 1.
f f
− ≤ − ≤−
Lời giải. Đầu tiên ta phải nhận dạng được
( ) ( ) ( )
5
2
5 2 ' d
f f f x x
− =
∫
.
Do
( ) [ ] ( )
5 5 5
2 2 2
3 12
1 ' 4, 2;5 1d ' d 4d .
f x x x f x x x
≤ ≤ ∀ ∈ → ≤ ≤
∫ ∫ ∫
Vậy
(
)
(
)
3 5 2 12.
f f
≤ − ≤
Chọn A.
Vấn đề 2. TÍCH PHÂN CƠ BẢN
Câu 26. Tìm số thực
1
a
>
để tích phân
1
1
d
a
x
x
x
+
∫
có giá trị bằng
.
e
A.
1
a
e
=
. B.
a e
=
. C.
2
e
a
=
. D.
2
a e
=
.
Lời giải. Ta có
( )
1
1 1
1 1
d 1 ln ln 1 .
a a
a
x
x dx x x a a e
x x
+
= + = + = + − =
∫ ∫
Thử các đáp án đã cho, có
a e
=
thỏa mãn. Thật vậy ln 1
e e e
+ − =
. Chọn B.
Cách CASIO. Thiết lập hiệu
1
1
d
a
x
x e
x
+
−
∫
.
Thử từng đáp án, ví dụ với đáp án A ta nhập vào máy
1
1
1
d
e
x
x e
x
+
−
∫
và nhấn dấu =.
Màn hình xuất hiện số khác 0 nên không thỏa mãn. Tương tự thử với đáp án B.
Câu 27. Tính tích phân
5
1
d
.
2 1
x
I
x
=
−
∫
A.
ln 3.
I
B.
ln 2.
I
C.
ln 9.
I
D.
ln 6.
I
Lời giải. Ta có
( )
5
5
1
1
d 1 1 1
ln 2 1 ln 9 ln1 ln 9 ln 3.
2 1 2 2 2
x
x
x
= − = − = =
−
∫
Chọn A.
Câu 28. Nếu kết quả của
2
1
d
3
x
x
+
∫
được viết ở dạng
ln
a
b
với
,
a b
là các số nguyên
dương và ước chung lớn nhất của
,
a b
bằng
1
. Mệnh đề nào sau đây là sai?
A.
3 12
a b
− <
. B.
2 13
a b
+ =
. C.
2
a b
− >
. D.
2 2
41
a b
+ =
.
Lời giải. Ta có
2
2
1
1
d 5
ln 3 ln 5 ln 4 ln .
3 4
x
x
x
= + = − =
+
∫
Suy ra
5
1 2.
4
a
a b
b
→ − = <
=
Do đó C sai. Chọn C.
Câu 29. Tính tích phân
2016
0
7 d .
x
I x
=
∫
A.
2016
7 1
ln7
I
−
= ⋅
B.
2016
7 ln 7.
I
= −
C.
2017
7
7.
2017
I
= −
D.
2015
2016.7 .
I
Lời giải. Ta có
2016
2016
2016
0
0
7 7 1
7 d .
ln7 ln7 ln 7
x
x
I x= = = −
∫
Chọn A.
Câu 30. Kết quả của tích phân
2
3
cos d
I x x
π
π
=
∫
được viết ở dạng
3
I a b
= +
, với
a
và
b
là các số hữu tỉ. Tính
4 .
P a b
= −
A.
9
4
2
P a b
= − = ⋅
B.
4 3.
P a b
= − =
C.
1
4
2
P a b
= − = − ⋅
D.
1
4
2
P a b
= − = ⋅
Lời giải. Ta có
2
2
3
3
3 1
cos d sin 1 1 . 3
2 2
I x x x
π
π
π
π
= = = − = + −
∫
1
4 3.
1
2
a
P a b
b
→ → = − =
= −
Chọn B.
Câu 31. Cho hàm số
(
)
(
)
sin
f x A x B
= +
(
,
A B
thuộc
ℝ
) thỏa mãn
( )
2
0
d 4
f x x
=
∫
và
(
)
' 1 2
f
=
. Tính giá trị biểu thức
.
P A B
= +
A.
4.
P
=
B.
0.
P
=
C.
2.
P
= −
D.
4.
P
= −
Lời giải. Ta có
( ) ( ) ( )
2
2 2
0
0 0
d sin d cos 2
A
f x x A x B x x Bx B
π π
π
= + = − + =
∫ ∫
.
Suy ra
2 4 2
B B
= ⇔ =
.
Lại có
( ) ( ) ( )
2
' cos ' 1 2 cos 2 .
f x A x f A Aπ π π π
π
= → = ⇔ = ⇔ = −
Vậy
2
; 2 0.
A B P A Bπ
= − = → = + =
Chọn B.
Câu 32. Biết rằng tích phân
0
cos 2 d 0
m
x x
=
∫
với
m
là tham số. Khẳng định nào sau
đây là đúng?
A.
(
)
2 .
m k k
= ∈
ℤ
B.
(
)
.
m k k
= ∈
ℤ
C.
( )
.
m k k
= ∈
ℤ
D.
(
)
(
)
2 1 .
m k k
= + ∈
ℤ
Lời giải. Ta có
0
0
1 1
0 cos 2 d sin 2 sin 2
2 2
m
m
x x x m
= = =
∫
( )
sin 2 0 2 .
k
m m k m k
π→ = ⇔ = ⇔ = ∈
ℤ
Chọn C.
Câu 33. Biết rằng tích phân
2
0
1
sin d 0
2
x
t t
− =
∫
với
x
là tham số. Khẳng định nào
sau đây là đúng?
A.
(
)
2 .
x k k
= ∈
ℤ
B.
(
)
.
x k k
= ∈
ℤ
C.
( )
.
x k k
= ∈
ℤ
D.
(
)
(
)
2 1 .
x k k
= + ∈
ℤ
Lời giải. Ta có
2
0 0 0
1 1 cos 2 1 1
sin d d cos 2 d
2 2 2 2
x x x
t
t t t t t
−
− = − = −
∫ ∫ ∫
0
1 1
sin 2 sin 2 .
4 4
x
t x
= − = −
Theo giả thiết
( )
2
0
1
sin d 0 sin 2 0 2 .
2 2
x
t t x x k x k k
π
π
− = ⇔ = ⇔ = ⇔ = ∈
∫
ℤ
Chọn C.
Câu 34. Tính tích phân
( )
1
1
d
I f x x
−
=
∫
, biết rằng
( )
2017
2017
2 khi 0
.
2 khi 0
x
x
x
f x
x
−
≥
=
<
A.
2018
2
2 2
log .
2017
I e
= B.
2018
2
2 1
log .
2017
I e
=
C.
2018
2 1
ln 2.
2017
I
=
D.
2017
2 1
.
2017 ln 2
I
=
Lời giải. Ta có
( ) ( ) ( )
1 0 1
1 1 0
d d d
I f x x f x x f x x
− −
= = +
∫ ∫ ∫
0 1
10
2017 2017 2018
2017 2017
2
0
11 0
2 2 2 2
2 d 2 d log .
2017 ln 2 2017 ln 2 2017
x x
x x
x x e
−
−
−−
−
= + = − + =
∫ ∫
Chọn A.
Câu 35. Tính tích phân
( )
2
2
0
min 1, d .
I x x
=
∫
A.
3
4
I
=
. B.
4
=
. C.
4
3
I
=
. D.
3
4
I
= −
.
Lời giải. Ta có
[
]
(
)
[ ]
(
)
2 2
2
0;1 min 1,
.
1;2 min 1, 1
x x x
x x
∈ → =
∈ → =
Do đó
( ) ( )
1 2 1 2
1 2
3
2 2 2
0
10 1 0 1
1 4
min 1, d min 1, d d 1.d 1 .
3 3 3
x
I x x x x x x x x= + = + = + = + =
∫ ∫ ∫ ∫
Chọn C.
Vấn đề 3. ỨNG DỤNG THỰC TIỄN
Giả sử
(
)
v t
là vận tốc của vật
M
tại thời điểm
t
và
(
)
s t
là quãng đường vật đi được
sau khoảng thời gian
t
tính từ lúc bắt đầu chuyển động. Ta có mối liên hệ giữa
(
)
s t
và
(
)
v t
như sau:
● Đạo hàm của quãng đường là vận tốc:
(
)
(
)
.
s t v t
● Nguyên hàm của vận tốc là quãng đường
(
)
(
)
d .
s t v t t
=
∫
→
từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian
[
]
;
t a b
là
( ) ( ) ( )
d .
b
a
v t t s b s a
= −
∫
Nếu gọi
(
)
a t
là gia tốc của vật
M
thì ta có mối liên hệ giữa
(
)
v t
và
(
)
a t
như sau:
● Đạo hàm của vận tốc là gia tốc:
(
)
(
)
v t a t
.
● Nguyên hàm của gia tốc là vận tốc:
(
)
(
)
d .
v t a t t
=
∫
Câu 36. (ĐỀ MINH HỌA 2016 – 2017) Một ô tô đang chạy với vận tốc 10m/s thì
người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc
(
)
(
)
5 10 m/s
v t t
= − +
, trong đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A. 0,2m. B. 2m. C. 10m. D. 20m.
Lời giải. Lúc dừng hẳn thì
(
)
0 5 10 0 2.
v t t t
= →− + = ⇔ =
Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô đi được quãng đường là
( )
2
2
2
0
0
5
5 10 d 10 10m.
2
s t t t t
= − + = − + =
∫
Chọn C.
Câu 37. Một ô tô đang đi với vận tốc lớn hơn
72km/h,
phía trước là đoạn đường chỉ
cho phép chạy với tốc độ tối đa là
72km/h,
vì thế người lái xe đạp phanh để ô tô
chuyển động chậm dần đều với vận tốc
(
)
(
)
30 2 m/s ,
v t t
= −
trong đó
t
là khoảng thời
gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến
lúc đạt tốc độ
72km/h,
ô tô đã di chuyển quãng đường là bao nhiêu mét?
A.
100m.
B.
125m.
C.
150m.
D.
175m.
Lời giải. Ta có
72km/h 20m/s
.
Từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ
72km/h,
ta có phương trình
30 2 20 5.
t t
− = ⇔ =
Vậy từ lúc đạp phanh đến khi ô tô đạt tốc độ
72km/h
, ô tô đi được quãng đường là
( )
5
0
30 2 d 125m.
s t t= − =
∫
Chọn B.
Câu 38. Một vật đang chuyển động với vận tốc
6m/s
thì tăng tốc với gia tốc
( )
2
3
m/s
1
a t
t
=
, trong đó
t
là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng
tốc. Hỏi vận tốc của vật sau 10 giây gần nhất với kết quả nào sau đây?
A.
14 m/s
. B.
13m/s
. C.
11m/s
. D.
12 m/s
.
Lời giải. Ta có
( )
3
d 3 ln 1 .
1
v t t t C
t
= = + +
∫
Tại thời điểm lúc bắt đầu tăng tốc
0
t
=
thì
6m/s
v
nên ta có
3 ln1 6 6.
C C
+ = ⇔ =
Suy ra
(
)
(
)
3 ln 1 6 m/s .
v t t
= + +
Tại thời điểm
(
)
10 10 3ln11 6 13m/s.
t s v
= → = + ≈
Chọn B.
Câu 39. Một vật đang chuyển động với vận tốc
10m/s
thì tăng tốc với gia tốc
(
)
(
)
2 2
3 m/s
a t t t
= +
, trong đó
t
là khoảng thời gian tính bằng giây kể từ lúc bắt đầu
tăng tốc. Hỏi quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt
đầu tăng tốc bằng bao nhiêu mét?
A.
4000
m
3
. B.
4300
m
3
. C.
1900
m
3
. D.
2200
m
3
.
Lời giải. Ta có
( )
( )
2 3
2
3
3 d .
2 3
t t
v t t t t C
= + = + +
∫
Tại thời điểm lúc bắt đầu tăng tốc
0
t
=
thì
10m/s
v
nên suy ra
10.
C
Suy ra
( ) ( )
2 3
3
10 m/s .
2 3
t t
v t = + +
Vậy quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng
tốc bằng
10
2 3 3 4
10
0
0
3 4300
10 10 m
2 3 2 12 3
t t t t
s dt t
= + + = + + =
∫
. Chọn B.
Câu 40. Một ô tô đang chuyển động với vận tốc
30m/s
thì người lái đạp phanh; từ thời điểm
đó, ô tô chuyển động chậm dần đều với gia tốc
( )
(
)
2
2
20
m/s
1 2
a t
t
= −
+
, trong đó
t
là
khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi quãng đường ô tô đi
được trong khoảng thời gian 2 giây kể từ lúc bắt đầu đạp phanh là bao nhiêu mét?
A.
46
m.
B.
47
m.
C.
48
m.
D.
49
m.
Lời giải. Ta có
( )
(
)
2
20 10
.
1 2
1 2
v t dt C
t
t
= = +
+
+
∫
Tại thời điểm lúc bắt đầu đạp phanh
0
t
=
thì
30m/s
v
nên suy ra
20.
C
Suy ra
( ) ( )
10
20 m/s .
1 2
v t
t
= +
Vậy quãng đường ô tô đi được trong khoảng thời gian 2 giây kể từ lúc bắt đầu đạp
phanh bằng
( ) ( )
( )
2 2
2
0
0 0
10
d 20 d 5 ln 1 2 20 48m.
1 2
s v t t t t t
t
= = + = + + ≈
+
∫ ∫
Chọn C.
Câu 41. Một ô tô đang chạy thẳng đều với vận tốc
(
)
0
m/s
v
thì người đạp phanh, từ
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc
(
)
(
)
0
5 m/s ,
v t t v
= − +
trong
đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp
phanh đến lúc dừng hẳn ô tô di chuyển được
40m
thì vận tốc ban đầu
0
v
bằng bao
nhiêu?
A.
0
40m/s.
v
B.
0
80m/s.
v
C.
0
20m/s.
v
D.
0
25m/s.
v
Lời giải. Lúc dừng hẳn thì
( )
0
0
0 5 0 .
5
v
v t t v t= →− + = ⇔ =
Theo giả thiết, ta có
( )
0
0
5
2 2 2
2
0 0 0
5
0 0
0
0
5
40m= 5 d
2 10 5 10
v
v
v v v
t v t t v t
− + = − + = − + =
∫
2
0
0
40m 20m/s
10
v
v→ = → =
. Chọn C.
Câu 42. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao
162
m so
với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng,
khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật
(
)
(
)
2
10 m/s
v t t t
= −
, trong đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
chuyển động. Hỏi lúc vừa tiếp đất, vận tốc
v
của khí cầu bằng bao nhiêu?
A.
5m/s.
v
B.
7m/s.
v
C.
9m/s.
v
D.
3m/s.
v
Lời giải. Do
(
)
2
10 0 10.
v t t t t
= − → < <
Giả sử chiếc khí cầu chạm đất kể từ lúc bắt đầu chuyển động là
1
t
giây
(
)
1
0 10
t
< <
.
Theo đề bài ta có phương trình
( )
1
1
3
3
2 2 2
1
1
0
0
162 10 d 5 5
3 3
t
t
t
t
t t t t t
= − = − = −
∫
( )
1
3
0 10
2
1
1 1
5 162 0 9 9 9m/s.
3
t
t
t t v
< <
⇔ − + − = → = → =
Chọn C.
Câu 43. Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường
s
(mét) đi được của đoàn tàu là một hàm số của thời gian
t
(giây) có phương trình là
2 3
6 .
s t t
= −
Thời điểm mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất là:
A.
6 .
t s
B.
4 .
t s
C.
2 .
t s
D.
1 .
t s
=
Lời giải. Vận tốc
(
)
(
)
2
' 12 3
v t s t t t
= = −
.
Bậy giờ ta đi tìm giá trị lớn nhất của hàm số
(
)
2
12 3
v t t t
= −
.
Ta có
[ ]
2
2
3
0
1
6
0
2 3 0 4 0;4 .
0
v t t t t
t
s t t
= − ≥ ≤ ≤
= −
⇔
⇒ ∈
≥
Đạo hàm và lập bảng biến thiên ta tìm được
[ ]
(
)
0;4
max
v t
đạt tại
2s.
t
Chọn C.
Câu 44. (ĐỀ THI CHÍNH THỨC 2016 – 2017) Một vật chuyển động theo quy luật
3 2
1
6
s t t
= − + với
t
(giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động
và
s
(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian
6
giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt
được bằng bao nhiêu?
A.
24m/s.
B.
108m/s.
C.
18m/s.
D.
64m/s.
Lời giải. Vận tốc
( ) ( )
2
3
' 12
v t s t t t
= = − + .
Ycbt là đi tìm GTLN của hàm số
( )
2
3
12
v t t t
= − + với
0 8.
t
≤ ≤
Đạo hàm và lập bảng biến thiên ta tìm được
[ ]
(
)
(
)
0;8
max 4 24m/s.
v t v
= =
Chọn A.
Câu 45. Một tàu lửa đang chạy với vận tốc
200 m/s
thì người lái tàu đạp phanh. Từ
thời điểm đó, tàu chuyển động chậm dần đều với vận tốc
(
)
(
)
t 200 m/s
v at
= +
, trong
đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh và
(
)
2
m/s
a
là
gia tốc. Biết rằng khi đi được 1500m thì tàu dừng, hỏi gia tốc của tàu bằng bao nhiêu?
A.
( )
2
40
m/s .
3
a =
B.
2
200
m/s .
13
a = −
C.
2
40
m/s .
3
a = −
D.
2
100
m/s .
13
a = −
Lời giải. Khi tàu dừng hẳn thì
( )
200
0 200 0 m/s .
v at t
a
= ⇔ + = → = −
Theo đề bài ta có phương trình
( )
200
200
2
0
0
40000 40000
1500 200 d 200
2 2
a
a
at
at t t
a a
−
−
= + = + = − +
∫
.
Suy ra
( )
2
40
m/s .
3
a = − Chọn C.
Câu 46. Một người chạy trong thời gian 1 giờ, vận tốc
v
(km/h) phụ
thuộc vào thời gian
t
(h) có đồ thị là một phần parabol với đỉnh
1
; 8
2
I
và trục đối xứng song song với trục tung như hình bên. Tính
quảng đường
s
người đó chạy được trong khoảng thời gian 45 phút,
kể từ khi chạy.
A.
4
s
=
km. B.
2,3
s
km.
C.
4,5
s
km. D.
5,3
s
km.
Lời giải. Hàm vận tốc
(
)
2
v t at bt c
= + +
có dạng là đường parabol đi qua các điểm
(
)
0; 0
O ,
(
)
1; 0
A và
1
; 8
2
I
nên suy ra
0 32
0 32
0
8
4 2
c a
a b c b
a b c
c
= = −
+ + = ⇔ =
=
+ + =
(
)
(
)
2
32 32 m/s .
v t t t
→ = − +
Vậy quảng đường người đó đi được trong khoảng thời gian 45 phút là:
( )
3
4
2
0
32 32 d 4,5km.
s t t t= − + =
∫
Chọn C.
Câu 47. Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu tăng
tốc với vận tốc tăng liên tục được biểu thị bằng đồ thị là
đường cong parabol có hình bên. Biết rằng sau 10s thì xe đạt
đến vận tốc cao nhất 50 m/s và bắt đầu giảm tốc. Hỏi từ lúc
bắt đầu tăng tốc đến lúc đạt vận tốc cao nhất thì xe đã đi
được quãng đường bao nhiêu mét?
A.
1000
m
3
. B.
1100
m
3
.
C.
1400
m
3
. D.
300m
.
t
50
v(t)
10
O
Lời giải. Hàm vận tốc
(
)
2
v t at bt c
= + +
có dạng là đường parabol có đỉnh
(
)
10;50
I ,
đồng thời đi qua gốc tọa độ
(
)
0;0
O
nên suy ra
2
0 0
1
10
2 2
10
.10 .10 50
c c
b
a
a
b
a b c
= =
− = ⇔ = −
=
+ + =
( ) ( )
2
1
10 m/s .
v t t t→ = − +
Theo đồ thị thì xe bắt đầu tăng tốc lúc
0
t
=
và đạt vận tốc cao nhất lúc
10
t
=
s nên
quãng đường đi được của xe từ lúc bắt đầu tăng tốc đến lúc đạt vận tốc cao nhất là:
( )
10 10
10
2 3 2
0
0 0
1 1 1000
d 10 d 5 m.
2 6 3
s v t t t t t t t
= = − + = − + =
∫ ∫
Chọn A.
Câu 48. Một vật chuyển động trong
3
giờ với vận tốc
(
)
km/h
v phụ
thuộc thời gian
(
)
h
t
có đồ thị là một phần của đường parabol có đỉnh
(
)
2;9
I và trục đối xứng song song với trục tung như hình bên. Tính
quãng đường
s
mà vật di chuyển được trong
3
giờ đó.
A.
26,75km.
s
B.
25,25km.
s
C.
24,25km.
s
D.
24,75km.
s
Lời giải. Hàm vận tốc
(
)
2
v t at bt c
= + +
có dạng là đường parabol đi qua có đỉnh
(
)
2;9
I và đi qua điểm
(
)
0;6
A nên suy ra
2
6 6
3
2
2 4
3
.2 .2 9
c c
b
a
a
b
a b c
= =
− = ⇔ = −
=
+ + =
( ) ( )
2
3
3 6 m/s
v t t t→ = − + + .
Vậy quảng đường người đó đi được trong khoảng thời gian 3 giờ là:
3
2
0
3
3 6 d 24,75km.
4
s t t t
= − + + =
∫
Chọn D.
Câu 49. Một vật chuyển động trong 4 giờ với vận tốc
(
)
km/h
v
phụ thuộc thời gian
(
)
h
t
có đồ thị của vận tốc như hình bên.
Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ
thị đó là một phần của đường parabol có đỉnh
(
)
2;9
I với trục đối
xứng song song với trục tung, khoảng thời gian còn lại đồ thị là
một đoạn thẳng song song với trục hoành. Tính quãng đuờng
s
mà vật chuyển động trong 4 giờ đó.
A.
26,5km.
s
B.
28,5km.
s
C.
27km.
s
D.
24km.
s
Lời giải. Hàm vận tốc
(
)
2
v t at bt c
= + +
có dạng là đường parabol đi qua có đỉnh
(
)
2;9
I và đi qua điểm
(
)
0;0
O nên suy ra
2
0 0
9
2
2 4
9
.2 .2 9
c c
b
a
a
b
a b c
= =
− = ⇔ = −
=
+ + =
( ) ( )
2
9
9 m/s .
v t t t→ = − + Suy ra
( ) ( )
27
3 m/s .
v =
Vậy quảng đường người đó đi được trong khoảng thời gian 4 giờ là:
3 4
2
0 3
9 27
9 d d 27km.
4 4
s t t t t
= − + + =
∫ ∫
Chọn C.
Câu 50. Cho đồ thị biểu diễn vận tốc của hai xe
A
và
B
khởi hành cùng một lúc, bên cạnh nhau và trên cùng một
con đường. Biết đồ thị biểu diễn vận tốc của xe
A
là một
đường parabol, đồ thị biểu diễn vận tốc của xe
B
là một
đường thẳng ở hình bên. Hỏi sau khi đi được 3 giây
khoảng cách giữa hai xe là bao nhiêu mét.
A.
90 m.
B.
60 m.
C.
0 m.
D.
270 m.
t
60
v
3
O
4
A
v
B
v
Lời giải. Hàm vận tốc
(
)
2
A
v t at bt c
= + +
có dạng là đường parabol đi qua các điểm
(
)
0;0
O ,
(
)
3;60
A và
(
)
4;0
B nên suy ra
(
)
(
)
2
20 80 m/s .
A
v t t t
= − +
Hàm vận tốc
(
)
B
v t at b
= +
có dạng là đường thẳng đi qua gốc tọa độ
(
)
0;0
O và điểm
(
)
3;60
A nên suy ra
(
)
(
)
20 m/s .
B
v t t
Quãng đường đi được sau 3 giây của xe A là
( )
3
2
0
20 80 d 180m.
A
s t t t= − + =
∫
Quãng đường đi được sau 3 giây của xe B là
3
0
20 d 90m.
B
s t t= =
∫
Vậy khoảng cách giữa hai xe sau 3 giây sẽ bằng:
90 m.
A B
s s
− =
Chọn A.
Câu 51. Tốc độ thay đổi số dân của một thị trấn kể từ năm 1970 được mô tả bằng
công thức
( )
(
)
2
120
5
f t
t
′
=
+
, với
t
là thời gian tính bằng năm (thời điểm
0
t
=
ứng với
năm 1970). Biết rằng số dân của thị trấn vào năm 1970 là 2000 người. Hỏi số dân của
thị trấn đó vào năm 2018 gần nhất với số nào sau đây?
A. 22 nghìn người. B. 23 nghìn người.
C. 24 nghìn người. D. 25 nghìn người.
Lời giải. Tốc độ thay đổi số dân của thị trấn vào năm thứ
t
là
( )
(
)
2
120
5
f t
t
′
=
+
. Suy ra
nguyên hàm của
(
)
f t
′
là hàm số
(
)
f t
mô tả số dân của thị trấn vào năm thứ
t
.
Ta có
( ) ( )
(
)
2
120 120
5
5
f t f t dt dt C
t
t
′
= = = +
+
+
∫ ∫
.
Số dân của thị trấn vào năm 1970 (ứng với
0
t
=
) là
( ) ( )
120 120
0 2 2 26 26.
0 5 5
f C C f t
t
− −
= ⇔ + = ⇔ = → = +
+ +
Vậy số dân của thị trấn vào năm 2018 (ứng với
48
t
) là
( )
120
48 26 23,73
48 5
f
= + =
nghìn người. Chọn C.
Câu 52. Biết tốc độ phát triển của vi khuẩn HP (Helicobacter pylori) gây đau dạ dày
tại ngày thứ
t
là
( )
1000
'
2 1
F t
t
=
+
và ban đầu bệnh nhân có 2000 con vi khuẩn. Sau 15
ngày bệnh nhân phát hiện ra bị bệnh. Hỏi khi đó có bao nhiêu con vi khuẩn trong dạ
dày ?
A. 5434 con. B. 1500 con. C. 283 con. D. 3717 con.
Lời giải. Tốc độ phát triển của vi khuẩn tại ngày thứ
t
là
( )
1000
2 1
F t
t
′
=
+
. Suy ra số
lượng vi khuẩn vào ngày thứ
t
được tính theo công thức
( ) ( )
1000
500 ln 2 1
2 1
F t F t dt dt t C
t
′
= = = + +
∫ ∫
.
Lúc ban đầu bệnh nhân có 2000 con vi khuẩn nên
(
)
(
)
0 2000 500 ln 2.0 1 2000 2000 500 ln 2 1 2000.
F C C F t t
= ⇔ + + = ⇔ = → = + +
Số vi khuẩn sau 15 ngày là:
(
)
15 500 ln 2.15 1 2000 3716,99
F
= + + =
. Chọn D.
Câu 53. Một đám vi trùng ngày thứ
t
có số lượng là
(
)
N t
. Biết rằng
( )
4000
'
1 0,5
N t
t
=
và lúc đầu đám vi trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ
hàng đơn vị):
A. 264.334 con. B. 257.167 con. C. 258.959 con. D. 253.584 con.
Lời giải. Ta có
( ) ( ) ( )
4000
' 8000.ln 1 0,5
1 0,5
N t N t dt dt t C
t
= = = + +
∫ ∫
.
Tại thời điểm ban đầu
(
)
0
t
thì
(
)
(
)
(
)
0 8000.ln1 250000 250000 8000.ln 1 0,5 250000
N C C N t t
= + = ⇔ = → = + +
.
Sau 10 ngày
(
)
10
t
thì
(
)
(
)
10 8000.ln 1 0,5.10 250000 264.334
N
= + + =
con. Chọn A.
Câu 54. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức
(
)
' 100 .
t
S t r e
(con/giờ) với
r
là tỷ lệ tăng trưởng đặc trưng của vi khuẩn. Ban đầu có
100 con vi khuẩn. Hỏi sau bao lâu số lượng vi khuẩn ban đầu sẽ tăng gấp đôi. Biết
rằng số lượng vi khuẩn sau 5 giờ là 300 con.
A. 4 giờ35 phút. B. 3 giờ 9 phút. C. 4 giờ 30 phút. D. 4 giờ 2 phút.
Lời giải. Sự tăng trưởng của vi khuẩn tại giờ thứ
t
là
(
)
' 100 .
t
S t r e
. Suy ra số lượng
vi khuẩn vào giờ thứ
t
được tính theo công thức
(
)
(
)
' 100 .
t
S t S t dt r e dt
= =
∫ ∫
.
Số lượng vi khuẩn sau 5 giờ là 300 con nên ta có:
5
5
0
300 100 . 100 . 100 300 0,020351.
t
r e r e r r= ←→ − = → =
∫
Suy ra thời gian để số vi khuẩn tăng lên 200 con là:
0
200 100.0,020351.
t
t
e
=
∫
(
)
100.0,020351 1 200 4,597
t
e t→ − = ←→ ≃ giờ (4 giờ 35 phút). Chọn A.
Câu 55. Người ta thay nước mới cho một bể bơi có dạng hình hộp chữ nhật có độ sâu
là
280cm.
Giả sử
(
)
h t
là chiều cao (tính bằng cm) của mực nước bơm được tại thời
điểm
t
giây, biết rằng tốc độ tăng của chiều cao mực nước tại giây thứ
t
là
( )
3
1
' 3
500
h t t
= +
và lúc đầu hồ bơi không có nước. Hỏi sau bao lâu thì nước bơm được
3
4
độ sâu của hồ bơi?
A. 3 giờ 34 giây. B. 2 giờ 34 giây. C. 3 giờ 38 giây. D. 2 giờ 38 giây.
Lời giải. Ta có
( ) ( ) ( )
4
3
3
1 3
' 3 3 .
500 2000
h t h t dt t dt t C
= = + = + +
∫ ∫
Lúc ban đầu (tại
0
t
=
) hồ bơi không chứa nước, nghĩa là
( ) ( )
7
4
3
3
3 3
0 0 0 3 0 .
2000 2000
h C C= ←→ + + = ←→ = −
Suy ra mực nước bơm được tại thời điểm
t
giây là
( ) ( )
7
4
3
3
3 3
3
2000 2000
h t t= + − .
Theo giả thiết, lượng nước bơm được bằng
3
4
độ sâu của hồ bơi nên ta có:
( ) ( ) ( )
7
4 4
3
3 3
3 3 3
.280 3 210 3 140004,33 7234s
4 2000 2000
h t t t t= ←→ + − = ←→ + = ←→ =
.
Vậy sau khoảng thời gian 2 giờ 34 giây thì bơm được
3
4
độ sâu của hồ bơi. Chọn B.
Baøi 04
MOÄT SOÁ PHÖÔNG PHAÙP TÍNH TÍCH PHAÂN


Giả sử cần tính tích phân
( )
d
b
a
I f x x
=
∫
ta thực hiện các bước sau:
 Đặt
(
)
x u t
(với
(
)
u t
là hàm có đạo hàm liên tục trên
[
]
;
α β
,
(
)
f u t
xác
định trên
[
]
;
α β
và
(
)
(
)
,
u a u b
α β
= =
) và xác định
,
α β
.
 Thay vào, ta có
( ) ( ) ( ) ( ) ( ) ( )
. ' d dI f u t u t t g t t G t G G
β β
β
α
α α
β α
= = = = −
∫ ∫
.
 !
Dấu hiệu Cách chọn
2 2
a x
[ ]
sin ;
2 2
cos 0;
x a t t
x a t t
π π
π
= ∈ −
= ∈
2 2
x a
{ }
[ ]
; \ 0
sin 2 2
0; \
cos 2
a
x t
t
a
x t
t
π π
π
π
= ∈ −
= ∈
2 2
x a
+
tan ;
2 2
x a t t
π π
= ∈ −

Tương tự như nguyên hàm, ta có thể tính tích phân bằng phương pháp đổi biến số
(ta gọi là loại 2) như sau:
Để tính tích phân
( )
d
b
a
I f x x
=
∫
nếu
(
)
(
)
(
)
. '
f x g u x u x
, ta có thể thực hiện phép
đổi biến như sau:
 Đặt
(
)
(
)
d ' d
t u x t u x x
= ⇒ =
.
Đổi cận
(
)
( )
.
x a t u a
x b t u b
= ⇒ =
= ⇒ =
 Thay vào ta có
( ) ( )
( )
( )
( )
( )
d .
u b
u b
u a
u a
I g t t G t= =
∫
"#$%
Cho hai hàm số
u
và
v
liên tục trên
[
]
;
a b
và có đạo hàm liên tục trên
[
]
;
a b
.
Khi đó:
d d .
b b
b
a
a a
u v uv v u
= −
∫ ∫
Một số tích phân các hàm số dễ phát hiện
u
và
d
v
&
( ) ( )
ln d
f x g x x
β
α
∫
Đăt
(
)
( )
ln
d d
u g x
v f x x
=
=
&
( )
sin
cos d
ax
ax
f x ax x
e
β
α
∫
Đặt
(
)
sin
d cos d
ax
u f x
ax
v ax x
e
=
&'
sin
d
cos
ax
ax
e x
ax
β
α
∫
Đặt
sin
cos
d d
ax
ax
u
ax
v e x
=
=
Ưu tiên đặt
u
theo quy tắc
''
nhất log, nhì đa, tam lượng, tứ mũ
''
. Tức là trong
hàm số dưới dấu tích phân hợp bởi
2
trong
4
hàm số trên thì ta đặt
u
theo thứ tự ưu
tiên như trên, còn lại thì đặt là
d
v
.
CAÂU HOÛI TRAÉC NGHIEÄM
()*+,-./+012334.567893
:#; Cho tích phân
8
2
0
16 d
I x x
= −
∫
và
4 sin
x t
. Mệnh đề nào sau đây đúng?
<.
4
2
0
16 cos d .
I t t
π
= −
∫
.
( )
4
0
8 1 cos 2 d
I t t
π
= +
∫
.
:.
4
2
0
16 sin d .
I t t
π
=
∫
&.
( )
4
0
8 1 cos 2 d
I t t
π
= −
∫
.
7 = Với
4 sin
x t
, suy ra
2 2 2
d 4 cos d
.
16 16 16 sin 16 cos 4 cos
x t t
x t t t
− = − = =
Đổi cận:
0 0
.
8
4
x t
x t
π
= → =
= → =
Khi đó
( )
4 4 4
2
0 0 0
16 cos cos d 16 cos d 8 1 cos 2 d .
I t t t t t t t
π π π
= = = +
∫ ∫ ∫
:>
:#; Cho tích phân
1
2
0
d
4
x
I
x
=
∫
và
2 sin
x t
. Mệnh đề nào sau đây đúng?
<.
6
0
d
I t
π
=
∫
. .
6
0
d
I t t
π
=
∫
. :.
6
0
d
t
I
t
π
=
∫
. &.
3
0
d
I t
π
=
∫
.
7 = Với
2 sin
x t
, suy ra
2 2 2
d 2 cos d
.
4 4 4 sin 2 cos 2 cos
x t t
x t t t
− = − = =
Đổi cận:
0 0
.
1
6
x t
x t
π
= → =
= → =
Vậy
6 6 6
0 0 0
2 cos 2 cos
d d d .
2 cos 2 cos
t t
I t t t
t t
π π π
= = =
∫ ∫ ∫
:><
:#; ' Biến đổi tích phân
2
2
1
5 4 d
I x x x
−
= + −
∫
thành tích phân
( )
2
0
d
I f t t
π
=
∫
với
cách đặt
2 3 sin
x t
= −
. Khẳng định nào sau đây là đúng?
<
(
)
2
9 sin .
f t t
(
)
2
9 cos .
f t t
= −
:
( ) ( )
9
1 cos 2 .
f t t
= +
&
( ) ( )
9
1 cos 2 .
f t t
= −
7 = Tích phân viết lại
( )
2 2
2
2 2
1 1
5 4 d 3 2 d .
I x x x x x
− −
= + − = − −
∫ ∫
Với
2 3sin
2 3 sin
d 3cos d
x t
x t
x t t
− =
= − →
= −
. Đổi cận:
1
.
2
2 0
x t
x t
π
= − → =
= → =
Khi đó
0
2 2
2 2
0 0
2
3 9 9 sin .cos d 3 9 cos .cos d 9 cos .cos d .
I t t t t t t t t t
π π
π
= − − = =
∫ ∫ ∫
( )
2 2
2
0 0
9
9 cos d 1 cos 2 d
2
t t t t
π π
= = +
∫ ∫
. :>:
:#;? Cho tích phân
3
2
3
1
d
3
I x
x
=
+
∫
và
3 tan
x t
. Mệnh đề nào sau đây đúng?
<.
3
4
3 d .
I t
π
π
=
∫
.
3
4
3 d
.
3
t
I
t
π
π
=
∫
:.
3
4
3
d .
3
I t t
π
π
=
∫
&.
3
4
3
d .
3
I t
π
π
=
∫
7 = Với
3 tan
x t
, suy ra
(
)
2
d 3 1 tan d .
x t t
= +
Đổi cận:
3
4
.
3
3
x t
x t
π
π
= → =
= → =
Khi đó
( )
2
3 3
2
4 4
3 1 tan d
3
d .
33 tan 3
t t
I t
t
π π
π π
+
= =
+
∫ ∫
:>&
:#;@ Cho tích phân
2
2
3
1
1
d
x
I x
x
−
=
∫
và
1
sin
x
t
= . Mệnh đề nào sau đây đúng?
<.
2
2
4
sin d .
I t t
π
π
=
∫
.
2
2
4
cos d .
I t t
π
π
=
∫
:.
( )
2
4
1 cos 2 d .
I t t
π
π
= +
∫
&.
( )
2
4
1 cos 2 d .
I t t
π
π
= −
∫
7 = Với
1
sin
x
t
= , suy ra
2
2
2
2 2
cos
d d
sin
.
cos
1 cos
1 1
sin
sin sin
t
x t
t
t
t
x
t
t t
= −
− = − = =
Đổi cận:
1
2
.
2
4
x t
x t
π
= → =
= → =
Khi đó
4 2
2 2
3 3
2 4
cos cos
sin sin
cos cos
. d . d
1 1
sin sin
sin sin
t t
t t
t t
I t t
t t
t t
π π
π π
= − =
∫ ∫
( )
2 2
2
4 4
1
cos d 1 cos 2 d .
2
t t t t
π π
π π
= = +
∫ ∫
:>
()*+,-./+012334.567893
:#;A Cho hàm số
(
)
f x
có nguyên hàm trên
ℝ
. Mệnh đề nào sau đây đúng?
<.
( ) ( )
1 1
0 0
d 1 d .
f x x f x x
= −
∫ ∫
.
( ) ( )
0
d 2 d .
a a
a
f x x f x x
−
=
∫ ∫
:.
( ) ( )
0 0
sin d cos d .
f x x f x x
π π
= −
∫ ∫
&.
( ) ( )
1 2
0 0
1
d d .
2
f x x f x x
=
∫ ∫
7 = :><. Đặt
1 d d
x t x t
= − ⇒ = −
. Đổi cận
1 0
.
0 1
x t
x t
= ⇒ =
= ⇒ =
Suy ra
( ) ( ) ( ) ( )
1 0 1 1
0 1 0 0
d 1 d 1 d 1 d .
f x x f t t f t t f x x
= − − = − = −
∫ ∫ ∫ ∫
B, C, D sai. Ta có thể chọn hàm
(
)
f x x
=
để kiểm tra.
:#;B Hàm số
(
)
f x
có nguyên hàm trên
(
)
;
a b
đồng thời thỏa mãn
(
)
(
)
.
f a f b
Mệnh đề nào sau đây đúng?
<.
( )
( )
' d 0
b
f x
a
f x e x
=
∫
. .
( )
( )
' d 1
b
f x
a
f x e x
=
∫
.
:.
( )
( )
' d 1
b
f x
a
f x e x
= −
∫
. &.
( )
( )
' d 2
b
f x
a
f x e x
=
∫
.
7 = Đặt
(
)
t f x
, suy ra
(
)
d ' d
t f x x
. Đổi cận
(
)
( )
.
x a t f a
x b t f b
= → =
= → =
Khi đó
( )
( )
( )
(
)
( ) ( )
' d d 0
f b
b
f x f b f a
t
a f a
f x e x e t e e
= = − =
∫ ∫
(do
(
)
(
)
f a f b
). :><
:#;CCho hàm số
(
)
f x
có nguyên hàm trên
ℝ
. Xét các mệnh đề sau:
1)
( ) ( )
1
2
0 0
sin 2 . sin d 2 . d .
x f x x x f x x
π
=
∫ ∫
2)
(
)
(
)
1
2
0 1
d d
x
e
x
f e
f x
x x
e x
=
∫ ∫
.
3)
( )
( )
2
3 2
0 0
1
d d
2
a a
x f x x xf x x
=
∫ ∫
.
Có bao nhiêu mệnh đề đúng?
<. 1. . 2. :. 3. &. 0.
7 = Xét 1) Ta có
( ) ( )
2 2
0 0
sin 2 . sin d 2 sin . sin .cos d
x f x x x f x x x
π π
=
∫ ∫
.
Đặt
sin
t x
, suy ra
d cos d
t x x
. Đổi cận
0 0
.
1
2
x t
x t
π
= → =
= → =
Khi đó
( ) ( ) ( )
1 1
2
0 0 0
2 sin . sin .cos d 2 . d 2 . d .
x f x x x t f t t x f x x
π
= =
∫ ∫ ∫
Do đó 1) đúng.
Xét 2) Đặt
x
t e
=
và kết luận được 2) đúng.
Xét 3) Đặt
2
t x
=
và kết luận được 3) đúng.
Vậy cả 3 mệnh đề đều đúng. :>:
:#;D Cho tích phân
( )
d
a
a
I f x x
−
=
∫
. Mệnh đề nào sau đây đúng?
<
( ) ( )
0
d .
a
I f x f x x
= − −
∫
( ) ( )
0
d .
a
I f x a f a x x
= − − −
∫
:
( ) ( )
0
d .
a
I f x f a x x
= − −
∫
&
( ) ( )
0
d .
a
I f x a f x x
= − +
∫
7 = Ta có
( ) ( ) ( )
0
0
d d d .
a a
a a
I f x x f x x f x x
− −
= = +
∫ ∫ ∫
Xét
( )
0
d .
a
J f x x
−
=
∫
Đặt
d d .
x t a x t
= − → =
Đổi cận
0
.
0
x a t
x t a
= − → =
= → =
Khi đó
( ) ( ) ( )
0
0 0
d d d .
a a
a
J f x x f t a t f x a x
−
= = − = −
∫ ∫ ∫
Vậy
( ) ( ) ( ) ( ) ( )
0 0 0 0
d d d d .
a a a a
I J f x x f x a x f x x f x a f x x
= + = − + = − +
∫ ∫ ∫ ∫
:>&
:#;E Cho hàm số
(
)
f x
liên tục trên
[
]
;
a b
và thỏa
(
)
(
)
[
]
; .
f a b x f x x a b
+ − = ∀ ∈
Mệnh đề nào sau đây đúng?
<
( ) ( )
d d .
2
b b
a a
b a
xf x x f x x
−
=
∫ ∫

( ) ( )
d d .
2
b b
a a
b a
xf x x f x x
+
=
∫ ∫
:
( ) ( ) ( )
d d .
b b
a a
xf x x b a f x x
= −
∫ ∫
&
( ) ( ) ( )
d d .
b b
a a
xf x x b a f x x
= +
∫ ∫
7 = Đặt
x a b t
= + −
, suy ra
d d
x t
= −
. Đổi cận
x a t b
x b t a
= → =
= → =
.
Khi đó
( ) ( ) ( ) ( ) ( )
d d d
b a b
a b a
xf x x a b t f a b t t a b t f a b t t
= − + − + − = + − + −
∫ ∫ ∫
( ) ( )
( ) ( )
( ) ( ) ( )
d d d .
b b b
f a b x f x
a a a
a b x f a b x x a b f x x xf x x
+ − =
= + − + − = + −
∫ ∫ ∫
Suy ra
( ) ( ) ( ) ( ) ( )
2 d d d d .
2
b b b b
a a a a
a b
xf x x a b f x x xf x x f x x
+
= + → =
∫ ∫ ∫ ∫
:>
:#; Cho
(
)
f x
là hàm số lẻ và liên tục trên
[
]
;
a a
. Mệnh đề nào sau đây đúng?
<.
( ) ( )
0
d 2 d
a a
a
f x x f x x
−
=
∫ ∫
. B.
( )
d 0
a
a
f x x
−
=
∫
.
:.
( ) ( )
0
d 2 d
a
a a
f x x f x x
− −
=
∫ ∫
. &.
( ) ( )
0
d 2 d
a a
a
f x x f x x
−
= −
∫ ∫
.
7 = Ta có
( ) ( ) ( )
0
0
d d d
a a
a a
f x x f x x f x x
− −
= +
∫ ∫ ∫
.
Xét tích phân
( )
0
d
a
f x x
−
∫
. Đặt
d d
x t x t
= − ⇒ = −
. Đổi cận
0 0
x a t a
x t
= − ⇒ =
= ⇒ =
.
Do
(
)
f x
là hàm số lẻ và liên tục trên
[
]
;
a a
nên
(
)
(
)
(
)
(
)
f x f x f t f t
− = − ⇒ − = −
.
Khi đó
( ) ( ) ( ) ( ) ( ) ( )
0 0 0 0
0 0
d d d d d d .
a a
a a a a
f x x f t t f t t f t t f t t f x x
−
= − − = − − = = − = −
∫ ∫ ∫ ∫ ∫ ∫
Vậy
( ) ( ) ( )
0 0
d d d 0
a a a
a
f x x f x x f x x
−
= − + =
∫ ∫ ∫
. :>
:#;Cho
(
)
f x
là hàm số lẻ và
( )
0
2
d 2
f x x
−
=
∫
. Tính tích phân
( )
2
0
d .
I f x x
=
∫
<
2.
I
=

2.
I
= −
:
1.
I
=
&
1.
I
= −
7 = Áp dụng kết quả câu trên, ta có
''
Nếu
(
)
f x
là hàm số lẻ và liên tục trên
đoạn
[
]
;
a a
thì
( )
d 0 ''.
a
a
f x x
−
=
∫
Thay
2
a
=
ta được
( ) ( ) ( )
2 0 2
2 2 0
0 d d d
f x x f x x f x x
− −
= = +
∫ ∫ ∫
( ) ( )
2 0
0 2
d 2.
f x x f x dx
−
→ = − = −
∫ ∫
:>
:#;'Tính tích phân
1
2017 2
1
2017d .
I x x x
−
= +
∫
<
0.
I

2.
I
:
2.
I
= −
&
1
3
I
= ⋅
7 = Xét hàm số
(
)
2017 2
2017
f x x x= + là hàm số lẻ, liên tục trên đoạn
[
]
1;1 .
Vậy
1
2017 2
1
2017d 0.
I x x x
−
= + =
∫
:><
:#;? Cho
(
)
f x
là hàm số chẵn và liên tục trên
[
]
;
a a
. Mệnh đề nào sau đây sai?
<.
( ) ( )
0
d 2 d
a a
a
f x x f x x
−
=
∫ ∫
. 
( ) ( )
0
d 2 d .
a
a a
f x x f x x
− −
=
∫ ∫
:.
( ) ( )
0
0
d d
a
a
f x x f x x
−
=
∫ ∫
. &.
( )
d 0.
a
a
f x x
−
=
∫
7 = Ta có
( ) ( ) ( )
0
0
d d d .
a a
a a
f x x f x x f x x A B
− −
= + = +
∫ ∫ ∫
Xét
( )
0
d
a
A f x x
−
=
∫
. Đặt
x t
= −
, suy ra
d d
x t
= −
. Đổi cận
.
0 0
x a t a
x t
= − → =
= → =
Khi đó
( ) ( ) ( )
( )
( )
0
chan
0 0 0
d d d d .
a a a
f x
a
A f t t f t t f x x f x x B
= − − = − = − = =
∫ ∫ ∫ ∫
Vậy A, B, C đúng; D sai. :>&
:#;@ Cho
(
)
f x
là hàm số chẵn và thỏa mãn
( )
0
1
d 3
f x x
−
=
∫
. Tính
( )
1
1
d .
I f x x
−
=
∫
<
3.
I
=

2.
I
:
6.
I
&
3
I
= − ⋅
7 = Áp dụng kết quả câu trên, ta có
( ) ( )
1 0
1 1
d 2 d 2.3 6.
f x x f x x
− −
= = =
∫ ∫
:>:
:#;A Biết rằng
1
2
0
d ln
1
x
I x a
x
= =
+
∫
với
a
là số thực dương. Tìm
.
a
<.
2.
a
=
.
1
2
a
=
. :.
2
a
. &.
4
a
=
.
7 = Đặt
2
1
t x
= +
, suy ra
d
d 2 d d
2
t
t x x x x= → = . Đổi cận:
0 1
.
1 2
x t
x t
= → =
= → =
Khi đó
2
2
1
1
1 d 1 1
ln ln 2 ln 2 2.
2 2 2
t
I t a
t
= = = = → =
∫
:>:
:#;B Cho tích phân
(
)
1
3
2
4
0
4
d
2
x
I x
x
=
+
∫
và
4
2.
t x
= +
Mệnh đề nào sau đây đúng?
<
3
2
2
d
4 .
t
I
t
=
∫
 
1
2
0
d
4 .
t
I
t
=
∫
:
3
2
2
d
.
t
I
t
=
∫
&
1
2
0
d
.
t
I
t
=
∫
7 = Với
4
2
t x
= +
, suy ra
3
d 4 d
t x x
. Đổi cận
0 2
.
1 3
x t
x t
= → =
= ⇒ =
Khi đó
3
2
2
d
.
t
I
t
=
∫
:>:
:#;C Tính tích phân
(
)
2017
2
2019
1
2
d .
x
I x
x
+
=
∫
<
2018 2018
3 2
.
2018
I
=

2018 2018
3 2
.
4036
I
=
:
2017 2018
3 2
.
4034 2017
I = − &
2021 2021
3 2
.
4040
I
=
7 = Ta có
2017
2
2
1
2 1
. d .
x
I x
x x
+
=
∫
Đặt
2 2
1
x
t
x x
= = +
, suy ra
2 2
2 d 1
d d d
2
x
t x t
x x
= − → = − . Đổi cận
1 3
.
2 2
x t
x t
= → =
= → =
Khi đó
2 3
2018 2018 2018
3
2017 2017
2
3 2
1 1 3 2
d d .
2 2 4036 4036
t
I t t t t
−
= − = = =
∫ ∫
:>
:#;D Tính tích phân
2
2016
2
d
1
x
x
I x
e
−
=
+
∫
.
<
0.
I
=

2018
2
.
2017
I =
:
2017
2
.
2017
I =
&
2018
2
.
2018
I =
7 = Ta có
2 0 2
2016 2016 2016
2 2 0
d d d .
1 1 1
x x x
x x x
I x x x A B
e e e
− −
= = + = +
+ + +
∫ ∫ ∫
Tính
0
2016
2
d
1
x
x
A x
e
−
=
+
∫
. Đặt
x t
= −
, suy ra
d d .
x t
= −
Đổi cận
2 2
.
0 0
x t
x t
= − → =
= → =
Khi đó
(
)
2016
0 2 2
2016 2016
2 0 0
. .
d d d .
1 1 1
t x
t t x
t
t e x e
A t t x
e e e
−
−
= − = =
+ + +
∫ ∫ ∫
Vậy
(
)
2016
2 2 2 2
2016 2016
2016
0 0 0 0
. 1
.
d d d d
1 1 1
x
x
x x x
x e
x e x
I A B x x x x x
e e e
+
= + = + = =
+ + +
∫ ∫ ∫ ∫
2017 2017
2
0
2
.
2017 2017
x
= = :>:
:#;E Tính tích phân
( )
1
2
0
1 d
n
I x x x
= −
∫
với
n
nguyên dương.
<
1
2 2
I
n
= ⋅

1
2 1
I
n
= ⋅
+
:
1
2
I
n
= ⋅
&
1
2 1
I
n
= ⋅
−
7 = Đặt
2
1
t x
= −
, suy ra
1
d 2 d d d .
2
t x x x x t
= − → = − Đổi cận
0 1
.
1 0
x t
x t
= → =
= → =
Khi đó
(
)
0 1
1
1
0
1 0
1 1 1 1
d d . .
2 2 2 1 2 1
n
n n
t
I t t t t
n n
+
= − = = =
+ +
∫ ∫
:><
:#; Kết quả tích phân
1
2
0
1 d
I x x x
= +
∫
được viết ở dạng
1
a a
I
b
−
=
với
,
a b
là
các số nguyên dương. Tính giá trị của biểu thức
2 .
T a b
= +
<
1.
T
=

7.
T
=
:
5.
T
=
&
8.
T
=
7 = Đặt
2 2 2
1 1
t x t x
= + ⇒ = +
, suy ra
d d .
t t x x
Đổi cận
0 1
.
1 2
x t
x t
= → =
= → =
Khi đó
2
3
2
2
1
1
2
2 2 1
d 2 8.
3
3 3
a
I
t
t t T a b
b
=
−
= = → → = + =
=
=
∫
:>&
:#; Cho tích phân
2
2
1
2 1d
I x x x
= −
∫
và
2
1.
u x
= −
Mệnh đề nào sau đây sai?
<.
3
0
d
I u u
=
∫
. .
2
1
d
I u u
=
∫
. :.
3
3
2
0
2
3
I u
=
. &.
I
.
7 = Với
2
1
u x
= −
, suy ra
d 2 d
u x x
. Đổi cận
1 0
.
2 3
x u
x u
= → =
= → =
Suy ra
2 3
2
1 0
2 1d d
I x x x u u
= − =
∫ ∫
. Do đó B sai. :>
:#;' Tính tích phân
3
2
0
d .
1
a
x x
I x
x
+
=
∫
<
(
)
2 2
1 1 1.
I a a
= + + −

(
)
2 2
1 1 1.
I a a
= + + +
:
( )
2 2
1
1 1 1 .
3
I a a
= + + +
&
( )
2 2
1
1 1 1 .
3
I a a
= + + −
7 = Đặt
2 2 2
1 1
t x t x
= + ⇒ = +
, suy ra
d d
t t x x
. Đổi cận
2
0 1
.
1
x t
x a at
= → =
= → = +
Khi đó
(
)
( )
2
2
1
2
3
2 2
2 2
0 0
3
1
2
1
1
1
1
d d 1 1 1 .
3
1 1
d
3
a
a
a a
x
x x
I x x x a a
x x
t
t t
+
+
+
+
= = = + + −
= =
∫∫ ∫
:>&
:#;?Tính tích phân
2
2 3
0
1d
I x x x
= +
∫
.
<.
16
.
9
I =
.
16
.
9
I = −
:.
52
.
9
I =
&.
52
.
9
I = −
7 = Đặt
3 2 3
1 1
t x t x
= + ⇒ = +
, suy ra
2 2
2
2 d 3 d d d .
3
t t x x t t x x
= → =
Đổi cận:
0 1
.
2 3
x t
x t
= → =
= → =
Vậy
3
3
3
2
1
1
2 2 52
d .
3 9 9
t
I t t= = =
∫
:>:
:#;@ Biến đổi tích phân
3
0
d
1 1
x
x
x+ +
∫
thành tích phân
( )
2
1
d
f t t
∫
với
1
t x
= +
.
Khi đó
(
)
f t
là hàm số nào trong các hàm số sau?
<.
(
)
2
2 2
f t t t
= −
. .
(
)
2
f t t t
= +
. :.
(
)
2
f t t t
= −
. &.
(
)
2
2 2
f t t t
= +
.
7 = Với
2
1 1
t x t x
= + ⇒ = +
, suy ra
2 d d
t t x
. Đổi cận
0 1
.
3 2
x t
x t
= → =
= → =
Khi đó
( )
3 2 2
2
2
0 1 1
1
d .2 d 2 2 d .
1
1 1
x t
x t t t t t
t
x
−
= = −
+
+ +
∫ ∫ ∫
Vậy
(
)
2
2 2
f t t t
= −
. :><
:#;A Kết quả tích phân
5
1
1
d
1 3 1
I x
x
=
+ +
∫
được viết ở dạng
ln 3 ln 5
I a b c
= + +
với
, ,
a b c
là các số hữu tỷ. Tính tổng
.
S a b c
= + +
<
4
3
S
= ⋅

5
3
S
= ⋅
:
7
3
S
= ⋅
&
8
3
S
= ⋅
7 = Đặt
2
3 1 3 1
t x t x
= + ⇒ = +
, suy ra
2
2 d 3d d d
3
t t x x t t
= → =
.
Đổi cận
1 2
.
5 4
x t
x t
= → =
= → =
Khi đó
( )
4 4
4
2
2 2
2 2 1 2 4 2 2
d 1 d ln 1 ln 3 ln 5
3 1 3 1 3 3 3 3
t
I t t t t
t t
= = − = − + = + −
+ +
∫ ∫
4 2 2 4
, , .
3 3 3 3
a b c S→ = = = − → = :><
:#;B Kết quả tích phân
2 2
2 2
3
d
1 1
x
I x
x x
=
− + +
∫
được viết ở dạng
ln 5 ln 2
I a b
= +
với
,
a b
là các số hữu tỷ. Tính tổng
.
S a b
= +
<
2
.
3
S
= −

1
.
3
S
= −
:
1
.
3
S =
&
2
.
3
S =
7 = Đặt
2 2 2
1 1
t x t x
= + ⇒ = +
, suy ra
2 2 2 2
2 d 2 d d d
.
1 1
t t x x t t x x
x t x t
= =
→
= − = −
Đổi cận:
3 2
.
2 2 3
x t
x t
= → =
= → =
Khi đó
(
)
(
)
3 3 3
2
2 2 2
1 1 2
d d d
1 2 3 1 22
t t
I t t t
t t t tt t
= = = +
− + − +− +
∫ ∫ ∫
( )
3
2
2
1 2 1
ln 1 2 ln 2 ln 5 ln 2 .
3
3 3 3
1
a
t t S
b
=
= − + + = − → → =−
= −
:>
:#;C Cho tích phân
3
2
2
1
1
d
x
I x
x
+
=
∫
và
2
1
x
t
x
+
= . Mệnh đề nào sau đây đúng?
<.
2
3
2
2
2
d
1
t t
I
t
= −
−
∫
. .
3
2
2
2
d
1
t t
I
t
=
+
∫
. :.
2
3
2
2
2
d
1
t t
I
t
=
−
∫
. &.
3
2
2
d
1
I
t
=
+
∫
.
7 = Ta có
( )
3 3
2
2
2
2 2
1 1
1 d
d 1 . .
1
x x
I x x
x
x x
+
= = +
∫ ∫
Với
2
2 2
2 2
2 2 2
2 2 2 2
1
d d
1
1
.
1 1 1
1 1
1 1
t x
x
x x
t
x
x t
t x x
x x t t
= −
+
+
= ⇒
+
= = + ⇒ = ⇒ + =
− −
Đổi cận:
1 2
2
3
3
x t
x t
= ⇒ =
= ⇒ =
. Suy ra
2
3
2
2
2
d
1
t
I t
t
= −
−
∫
. :><
:#;D Biết rằng
( )
2
3
1
d
ln 2 ln 2 1
1
x
I a b c
x x
= = + − +
∫
với
, ,
a b c
là các số hữu tỷ.
Mệnh đề nào sau đây đúng?
<.
1
.
3
a
= −
.
2
.
3
b = :.
2
.
3
c = − &.
0.
a b c
+ + =
7 = Viết lại
2 2
2
3 3 3
1 1
d d
.
1 1
x x x
I
x x x x
= =
+ +
∫ ∫
Đặt
3 2
2 3
3
2
2
1
1
1 .
2
d d
2 d 3 d
3
x t
t x
t x
x x t t
t t x x
= −
= +
= + ⇒ ⇒
=
=
Đổi cận:
1 2
.
2 3
x t
x t
= → =
= → =
Suy ra
(
)
3
3 3
2
2
2 2
2 d 1 1 1 1 1 1 1 2 1
d ln ln ln
3 3 1 1 3 1 3 2
1
2 1
t t t
I t
t t t
t t
− −
= = − = = −
− + +
−
+
∫ ∫
(
)
(
)
(
)
2
1 1 1 1 1 2
ln 2 ln 3 2 2 ln 2 ln 2 1 ln 2 ln 2 1 .
3 3 3 3 3 3
= − − − = − − − = − − −
Suy ra
1 2
; ; 0
3 3
a b c
= − = − =
. :><
:#;'E Biết rằng
5
1
d
ln 3 ln 5
3 1
x
I a b
x x
= = +
+
∫
với
, .
a b
∈
ℤ
Tính tổng
.
S a b
= +
<
2.
S
=

3.
S
=
:
1.
S
−
&
1.
S
=
7 = Đặt
2
3 1 3 1
t x t x
= + ⇒ = +
, suy ra
2
1
3
.
2
d d
3
t
x
x t t
−
=
=
Đổi cận
1 2
.
5 4
x t
x t
= → =
= → =
Khi đó
4 4 4
2 2
2 2 2
2 1 d 1 1
d 2 d
3 1 11 1
t
I t t
t tt t
= = = −
− +− −
∫ ∫ ∫
( )
4
2
2
ln 1 ln 1 2 ln 3 ln 5 1.
1
a
t t S
b
= − − + = − → → =
= −
:>&
:#;'Tính tích phân
2
1
ln
d
x
I x
x
=
∫
.
<.
2.
I
=
.
2
ln 2
.
2
I = :.
ln 2.
I
:.
2
ln 2
.
2
I = −
7 =Đặt
ln
t x
, suy ra
d
d
x
t
x
=
. Đổi cận:
1 0
.
2 ln 2
x t
x t
= → =
= → =
Khi đó
ln 2
2 2
ln 2
0
0
ln 2
d .
2 2
t
I t t= = =
∫
:>
:#;' Cho tích phân
2
1
1 ln
d
e
x
I x
x
−
=
∫
và
ln
u x
. Mệnh đề nào sau đây đúng?
<.
( )
0
1
1 d .
u
I u e u
= −
∫
.
( )
1
0
1 d .
u
I u e u
−
= −
∫
:.
( )
0
2
1
1 d .
u
I u e u
−
= −
∫
&.
( )
0
2
1
1 d .
u
I u e u
= −
∫
7 = Với
u x
suy ra
1
d d
d d d
.
u
u
u
u x
x x u e u
x
x e
x e
=
= =
→
=
=
Đổi cận
1 0
.
1
x u
x e u
= → =
= → =
Khi đó
( )
1 1
0 0
1
d 1 d .
u
u
u
I u u e u
e
−
−
= = −
∫ ∫
:>
:#;'' Cho
1
1 3 ln
d
e
x
I x
x
+
=
∫
và
1 3 ln .
t x
= +
Mệnh đề nào sau đây là sai?
<.
2
1
2
d .
3
I t t
=
∫
.
2
2
1
2
d .
3
I t t
=
∫
:.
2
3
1
2
9
I t
= . &.
14
.
9
I =
7 = Với
2
1 3 ln 1 3 ln
t x t x
= + ⇒ = +
, suy ra
3 d 2
2 d d d .
3
x
t t x t t
x x
= → =
Đổi cận:
1 1
.
2
x t
x e t
= → =
= → =
Khi đó
2
2
2 3
1
1
2 2 14
d .
3 9 9
I t t t= = =
∫
Do đó A sai. :><
:#;'? Biến đổi tích phân
(
)
2
1
ln
d
ln 2
e
x
x
x x +
∫
thành
( )
3
2
d
f t t
∫
với
ln 2
t x
= +
. Khi đó
(
)
f t
là hàm nào trong các hàm số sau?
<.
( )
2
2 1
f t
t
t
= −
. .
( )
2
1 2
f t
t
t
= − +
. :.
( )
2
2 1
f t
t
t
= +
. &.
( )
2
2 1
f t
t
t
= − +
.
7 = Với
ln 2
t x
= +
, suy ra
d
d
.
ln 2
x
t
x
x t
=
= −
Đổi cận:
1 2
.
3
x t
x e t
= → =
= → =
Khi đó
(
)
3 3
2 2 2
1 2 2
ln 2 1 2
d d d .
ln 2
e
x t
x t t
t
t t
x x
−
= = −
+
∫ ∫ ∫
:>&
:#;'@ Kết quả của tích phân
(
)
2
1
ln
d
ln 1
e
x
I x
x x
=
+
∫
được viết ở dạng ln 2
I a b
= +
với
,
a b
là những số hữu tỷ. Khẳng định nào sau đây là đúng?
<.
2 1.
a b
+ =
.
2 2
4
a b
+ =
. :.
1.
a b
− =
&.
2
ab
=
.
7 = Đặt
2
ln 1
t x
= +
, suy ra
2 ln ln d
d d d .
2
x x t
t x x
x x
= → =
Đổi cận:
1 1
.
2
x t
x e t
= → =
= → =
Khi đó
2
2
1
1
1 d 1 1 1
ln ln 2 , 0.
2 2 2 2
t
I t a b
t
= = = → = =
∫
:><
:#;'ATính tích phân
2
1
0
d .
x
I xe x
=
∫
<.
.
2
e
I = .
1
.
2
e
I
+
= :.
1
.
2
e
I
−
= &.
.
I e
=
7 = Đặt
2
,
t x
suy ra
1
d 2 d d d .
t x x x x t
= → =
Đổi cận:
0 0
.
1 1
x t
x t
= → =
= → =
Khi đó
1
1
0
0
1 1 1
d . .
2 2 2
t t
e
I e t e
−
= = =
∫
:>:
:#;'B Cho tích phân
ln 2
0
1d
x x
I e e x
= −
∫
và
1.
x
t e
= −
Mệnh đề nào sau đây sai?
<.
1
2
0
2 d
I t t
=
∫
. .
1
2
0
d
I t t
=
∫
. :.
3
1
0
2
3
t
I = . &.
2
3
I
=
.
7 = Với
2
1 1
x x
t e t e
= − ⇒ = −
, suy ra
2 d d .
x
t t e x
Đổi cận:
0 0
.
ln 2 1
x t
x t
= → =
= → =
Khi đó
1
3
1
2
0
0
2 2
2 d .
3 3
t
I t t= = =
∫
Do đó B sai. :>
:#;'C Tìm
,
a
biết
2
3
1
d
ln
2
x
x
e x ae e
I
ae b
e
−
+
= =
+
+
∫
với
,
a b
là các số nguyên dương.
<.
1
3
a
=
. .
1
3
a
= −
. :.
2
a
=
. &.
2
a
= −
.
7 = Đặt
x
t e
=
, suy ra
d d .
x
t e x
Đổi cận:
2
1
1
.
2
x t
e
x t e
= − → =
= → =
Suy ra
( )
2
2
2 3
2
1
1
d 1 2 2
ln 2 ln 2 ln 2 ln ln .
1
2 2 1
2
e
e
e
e
t e e e
I t e
t e e
+ +
= = + = + − + = =
+ +
+
∫
2; 1.
a b
→ = =
:>:
:#;'D Cho tích phân
2
2
sin 3
0
sin cos d
x
I e x x x
π
=
∫
và
2
sin .
t x
Chọn khẳng định đúng?
<.
( )
1
0
1
1 d
2
t
I e t t
= −
∫
. .
1 1
0 0
2 d d
t t
I e t te t
= +
∫ ∫
.
:.
( )
1
0
2 1 d
t
I e t t
= −
∫
. &.
1 1
0 0
1
d d
2
t t
I e t te t
= +
∫ ∫
.
7 = Viết lại
2 2
2 2
sin 3 sin 2
0 0
sin cos d .cos .sin cos d .
x x
I e x x x e x x x x
π π
= =
∫ ∫
Với
2
sin ,
t x
suy ra
1
d 2 sin cos d sin cos d d .
t x x x x x x t
= → =
Đổi cận
0 0
.
1
2
x t
x t
π
= → =
= → =
Khi đó
( )
1
0
1
1 d
2
t
I e t t
= −
∫
. :><
:#;?E Biến đổi tích phân
2
2
sin
4
sin 2 d
x
e x x
π
π
∫
thành
( )
1
1
2
d
f t t
∫
với
2
sin
t x
. Khi đó
(
)
f t
là hàm nào trong các hàm số sau?
<.
(
)
sin 2
t
f t e t
. .
(
)
t
f t e
=
. :.
(
)
sin
t
f t e t
. &.
( )
1
2
t
f t e
=
.
7 = Với
2
sin ,
t x
suy ra
d 2 sin cos d sin 2 d .
t x x x x x
= =
Đổi cận:
1
4 2
.
1
2
x t
x t
π
= → =
= → =
Khi đó
1
1
2
d .
t
I e t
=
∫
:>
:#;?F1G3.++H<EA–EBTính tích phân
3
0
cos sin d .
I x x x
π
=
∫
<.
4
1
.
I
π
= − .
4
.
I
π
= −
:.
0
I
=
. &.
1
.
4
I = −
7 =Đặt
cos ,
t x
suy ra
d sin d .
t x x
= −
Đổi cận:
0 1
.
1
x t
x tπ
= → =
= → = −
Khi đó
1 1
4
1
3 3
1
1 1
d d 0.
4
t
I t t t t
−
−
−
= − = = =
∫ ∫
:>:
:#;?Thực hiện phép đổi biến
sin
u x
thì tích phân
2
4
0
sin cos d
x x x
π
∫
sẽ trở thành
tích phân nào trong các tích phân sau đây?

2
4
0
d .
u u
π
∫
 <
1
4 2
0
1 d .
u u u
−
∫
:
1
4
0
d .
u u
∫
&
2
3 2
0
1 d .
u u u
π
−
∫
7 =Với
sin ,
u x
suy ra
d cos d .
u x x
Đổi cận
0 0
.
1
2
x u
x u
π
= → =
= → =
Khi đó
1
4
0
d .
uI
u
=
∫
:>:
:#;?' Biết rằng
6
0
1
sin cos d
64
n
I x x x
π
= =
∫
. Tìm
n
.
<.
3.
n
=
.
4
n
=
. :.
6.
n
=
&.
5.
n
=
7 =Đặt
sin ,
t x
suy ra
d cos d .
t x x
Đổi cận
0 0
.
1
6 2
x t
x t
π
= → =
= → =
Khi đó
(
)
1
1
1
2
1
2
1
0
0
1
1 1
2
d 3.
1 1 641 2
n
n
n
n
t
I t t n
n n n
+
+
+
= = = = = ⇔ =
+ + +
∫
:><
Cách trắc nghiệm. Thay lần lượt từng đáp án và bấm máy tính.
:#;?? Tính tích phân
( )
2
0
1 cos sin d
n
I x x x
π
= −
∫
.
<.
1
.
1
I
n
=
+
.
1
.
1
I
n
=
−
:.
1
.
2
I
n
=
&.
1
.
I
n
=
7 =Đặt
1 cos ,
t x
= −
suy ra
d sin d .
t x x
Đổi cận:
0 0
.
1
2
x t
x t
π
= → =
= → =
Khi đó
1
1
1
0
0
1
d .
1 1
n
n
t
I t t
n n
+
= = =
+ +
∫
:><
:#;?@Tính tích phân
( )
2
3
2
0
sin 2 1 sin d
I x x x
π
= +
∫
.
<.
4
64
I
π
=
. .
15
4
I =
. :.
31
4
I =
. &.
7
4
I
=
.
7 =Đặt
2
1 sin ,
t x
= +
sauy ra
d 2 sin cos d sin 2 d .
t x x x x x
= =
Đổi cận:
0 1
.
2
2
x t
x t
π
= → =
= → =
Khi đó
2
2
4
3
1
1
15
d .
4 4
t
I t t= = =
∫
:>
:#;?ACho tích phân
2
0
sin 2
d
1 cos
x
I x
x
π
=
+
∫
và
1 cos .
t x
= +
Chọn khẳng định đúng?
<
1
3
2
4
d
.
4
t t
I t
t
−
=
∫

1
3
2
4 4
d
.
t t
I t
t
−
=
∫
:
( )
2
2
1
4 1
.
d
I t t
= −
∫
&
( )
2
2
1
4 1 d
.
I t t
= − −
∫
7 =Tích phân viết lại
2 2
0 0
sin 2 cos .sin
d 2 d .
1 cos 1 cos
x x x
I x x
x x
π π
= =
+ +
∫ ∫
Với
2
1 cos 1 cos
t x t x
= + ⇒ = +
, suy ra
2 2
cos 1 cos 1
.
2 d sin d sin d 2 d
x t x t
t t x x x x t t
= − = −
→
= − = −
Đổi cận:
0 2
.
1
2
x t
x t
π
= → =
= → =
K hi đó
( )
( )
1 2
2
2
1
2
.
1
2 2 d 4 1 d
t
I t t t t
t
−
= − − =− −
∫ ∫
:>&
:#;?B Cho
4
2
0
6 tan
d
cos 3 tan 1
x
I x
x x
π
=
+
∫
và
3 tan 1.
u x
= +
Mệnh đề nào sau đây đúng?
<.
( )
2
2
1
4
2 1 d
3
I u u
= +
∫
. .
( )
2
2
1
4
1 d
3
I u u
= +
∫
.
:.
( )
2
2
1
4
1 d
3
I u u
= −
∫
. &.
( )
2
2
1
4
2 1 d
3
I u u
= −
∫
.
7 =Với
2
3 tan 1 3 tan 1,
u x u x
= + ⇒ = +
suy ra
2
2
6 tan 2 2
.
d 2
d
3cos
x u
x
u u
x
= −
=
Đổi cận
0 1
.
2
4
x u
x u
π
= → =
= → =
Vậy
( )
2 2
2
2
1 1
2 2 2 4
d 1 d
3 3
u
I u u u u
u
−
= = −
∫ ∫
. :>:
:#;?CCho số nguyên dương
a
thỏa mãn
4
0
cos 2
d ln 3.
1 2 sin 2
a
x
x
x
π
=
+
∫
Mệnh đề nào sau
đây đúng?
<
1
;3 .
2
a
∈

7
3; .
2
a
∈
:
7 9
; .
2 2
a
∈
&
9 11
; .
2 2
a
∈
7 =. Đặt
sin 2 ,
t x
suy ra
1
d 2 cos 2 d cos 2 d d .
t x x x x t
= → =
Đổi cận
0 0
.
2
sin
x t
x t m
a a
π π
= → =
= → = =
Khi đó
0
0
1 d 1 1
ln 2 1 ln 2 1 .
2 2 1 4 4
m
m
t
I t m
t
= = + = +
+
∫
Theo giả thiết ta có
4
1
1 1 1
ln 2 1 ln 3 ln 2 1 ln 3 2 1 3 .
2
4 4 4
m
m m m
m
+ = ⇔ + = ⇔ + = ⇔
= −
Với
( )
2
2 sin 2 .
m
a
= − → = −
loaïi
Với
0
2 2 4
1 sin 1 2 .
4
2 1 4
a
k
k
m k a
a
a a k
π π π
π
+
∈
∈
= → = ⇔ = + ⇔ = →
=
+
ℤ
ℤ
:>:
:#;?DCho số nguyên dương
n
thỏa mãn
( )
5
2
0
1 tan
1
d
6
cos
n
x
x
x
π
−
= ⋅
∫
Mệnh đề nào sau đây
đúng?
<
[
]
1;2 .
n

[
]
3; 4 .
n
:
[
]
5;6 .
n
&
[
]
7;8 .
n
7 =Đặt
tan ,
t x
suy ra
2
d
d .
cos
x
t
x
=
Đổi cận
0 0
.
tan
x t
x t m
n n
π π
= → =
= → = =
Khi đó
( )
(
)
(
)
6 6
5
0
0
1 1 1
1 d .
6 6
m
m
t m
I t t
− − −
= − = − =
∫
Theo giả thiết ta có
(
)
6
1 1
1
1.
6 6
m
m
− −
= ⇔ =
Với
0
4
1 tan 1 .
4
4 1 4
n
k
k
m k n
n
n n k
π π π
π
+
∈
∈
= → = ⇔ = + ⇔ = →
=
+
ℤ
ℤ
:>
:#;@ECó bao nhiêu số thực
a
thuộc khoảng
(
)
0;20
π
sao cho
5
0
2
sin sin 2 d
7
a
x x x
= ⋅
∫
<
20.

19.
:
9.
&
10.
7 =Ta có
5 6
0 0
sin sin 2 d 2 sin .cos d .
a a
I x x x x x x
= =
∫ ∫
Đặt
sin ,
t x
=
suy ra
d cos d .
t x x
Đổi cận:
0 0
.
sin
x t
x a t a m
= → =
= → = =
Khi đó
7
6 7
0
0
2 2
2 d .
7 7
m
m
m
I t t t= = =
∫
Theo giả thiết ta có
7
2 2
1.
7 7
m
m
= ⇔ =
Với
1 sin 1 2 .
m a a k
π
= → = ⇔ = +
Vì
(
)
0;20
a
π
nên
{ }
1
0 2 20 10 0;1;2;3;...;9
2 2
k
k k k
π π
∈
< + < ⇔ − < < → ∈
ℤ
→
có
10
giá trị của
k
→
có
10
giá trị của
.
a
:>&
:#;@ Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[
]
2;4
và thỏa mãn
(
)
2 2
f
=
,
(
)
4 2018.
f
Tính
( )
2
1
2 d .
I f x x
′
=
∫
<
1008.
I
= −

2018.
I
:
1008.
I
&
2018.
I
= −
7 = Đặt
2 ,
t x
suy ra
1
d 2d d d .
t x x t
= → = Đổi cận:
1 2
.
2 4
x t
x t
= → =
= → =
Khi đó
( ) ( ) ( ) ( ) ( ) ( )
2 4
4
2
1 2
1 1 1 1
2 d d . . 4 2 2018 2 1008.
2 2 2 2
I f x x f t t f t f f
′ ′
= = = = − = − =
∫ ∫
:>:
:#;@ F1G:+I.+J+K:EA–EB Cho
( )
6
0
d 12
f x x =
∫
. Tính
( )
2
0
3 d .
I f x x
=
∫
<
2.
I
=

4.
I
=
:
6.
I
=
&
36.
I
7 = Đặt
3 ,
t x
suy ra
1
d 3d d d .
3
t x x t
= → = Đổi cận:
0 0
.
2 6
x t
x t
= → =
= → =
Khi đó
( )
6
0
1 1
d .12 4.
3 3
I f t t
= = =
∫
:>
Tổng quát: Nếu
( )
d
b
a
f x x k
=
∫
thì
( )
d .
b
m
a
m
k
f mx x
m
=
∫
:#;@' Cho hàm số
(
)
f x
thỏa mãn
( )
2017
0
d 1.
f x x
=
∫
Tính
( )
1
0
2017 d .
I f x x
=
∫
<
2017.
I

0.
I
=
:
1.
I
=
&
1
2017
I
= ⋅
7 = Đặt
2017 ,
t x
suy ra
d
d 2017d d .
2017
t
t x x= → =
Đổi cận
0 0
.
1 2017
x t
x t
= → =
= → =
Khi đó
( ) ( )
2017 2017
0 0
1 1 1 1
. d d .1 .
2017 2017 2017 2017
I f t t f x x= = = =
∫ ∫
:>&
:#;@? Cho hàm số
(
)
f x
liên tục trên
ℝ
và
( ) ( )
1 9
0 1
d 1, d 2.
f x x f x x= =
∫ ∫
Tính giá
trị của biểu thức
( )
3
0
3 d .
3
x
I f f x x
= +
∫
<
4.
I
=

4.
I
= −
:
9
I
=
. &
9.
I
= −
7 = Từ giả thiết ta có
( ) ( ) ( )
1 9 9
0 1 0
d d d 1 2 3.
f x x f x x f x x
+ = = + =
∫ ∫ ∫
Ta có
( ) ( )
3 3 3
0 0 0
3 d d 3 d .
3 3
x x
I f f x x f x f x x
= + = +
∫ ∫ ∫
Xét
3
0
d
3
x
f x
∫
. Đặt
,
3
x
t =
suy ra
1
d d d 3d .
3
t x x t
= → =
Đổi cận
0 0
.
3 1
x t
x t
= → =
= → =
Khi đó
( ) ( )
3 1 1
0 0 0
d 3 d 3 d 3.1 3.
3
x
f x f t t f x x
= = = =
∫ ∫ ∫
Xét
( )
3
0
3 d .
f x x
∫
Đặt
3 ,
u x
suy ra
1
d 3d d d .
3
u x x u
= → =
Đổi cận
0 0
.
3 9
x u
x u
= → =
= → =
Khi đó
( ) ( ) ( )
3 9 9
0 0 0
1 1 1
3 d d d .3 1.
3 3 3
f x x f u u f x x
= = = =
∫ ∫ ∫
Vậy
3 1 4.
I
= + =
:><
:#;@@ Cho hàm số
(
)
f x
liên tục trên
ℝ
và thỏa mãn
( )
2
0
d 4.
f x x
π
=
∫
Tính tích
phân
( )
4
0
2 sin d .
I f x x x
π
= −
∫
<
2
2
2
I
= + ⋅

2
3
2
I
= − ⋅
:
2
1
2
I
= + ⋅
&
2
2
2
I
= − ⋅
7 = Ta có
( ) ( )
4 4 4
0 0 0
2 sin d 2 d sin d .
I f x x x f x x x x
π π π
= − = −
∫ ∫ ∫
Tính
( )
4
0
2 d
J f x x
π
=
∫
. Đặt
2 ,
t x
suy ra
d
d 2d d .
2
t
t x x= → =
Đổi cận
0 0
.
4 2
x t
x t
π π
= → =
= → =
Khi đó
( ) ( )
2 2
0 0
1 1 1
d .4 2.
2 2 2
J f t t f x dx
π π
= = = =
∫ ∫
Tính
( )
4
4
0
0
2
sin d cos 1 .
2
K x x x
π
π
= = − = = −
∫
Vậy
2
1 .
2
I J K= − = + :>:
:#;@A Cho hàm số
(
)
f x
liên tục trên
ℝ
và thỏa mãn
( )
4
2
d 2.
f x x
−
=
∫
Mệnh đề nào
sau đây sai?
<
( )
2
1
2 d 1.
f x x
−
=
∫

( )
3
3
1 d 2.
f x x
−
+ =
∫
:
( )
2
1
2 d 2.
f x x
−
=
∫
&
( )
6
0
2 d 2.
f x x
− =
∫
7 = Xét tích phân
( )
2
1
2 d .
f x x
−
∫
Đặt
2 ,
t x
suy ra
1
d 2d d d .
t x x t
= → =
Đổi cận
1 2
.
2 4
x t
x t
= − → = −
= → =
Khi đó
( ) ( ) ( )
2 4 4
1 2 2
1 1 1
2 d d d .2 1.
2 2 2
f x x f t t f x x
− − −
= = = =
∫ ∫ ∫
Suy ra A đúng, C sai.:>:
B đúng vì
( ) ( )
3 4
1
3 2
1 d d 2.
t x
f x x f t t
= +
− −
+ → =
∫ ∫
D đúng vì
( ) ( )
6 4
2
0 2
2 d d 2.
t x
f x x f t t
= −
−
− → =
∫ ∫
:#;@BCho
( )
2017
1
d 2.
f x x
=
∫
Tính tích phân
( )
2017
1
2018 d
I f x x
= −
∫
.
<
1.
I
=
2.
I
=
:
3.
I
=
&
5.
I
=
7 =Đặt
2018 ,
t x
= −
suy ra
d d .
x t
= −
Đổi cận
1 2017
.
2017 1
x t
x t
= → =
= → =
Khi đó
( ) ( ) ( )
1 2017 2017
2017 1 1
d d d 2.
I f t t f t t f x x= − = = =
∫ ∫ ∫
:>
:#;@C Cho
( )
3
1
3 1 d 20.
f x x− =
∫
Tính tích phân
( )
5
2
d .
I f x x
=
∫
<
20.
I

40.
I
:
10.
I
&
60.
I
7 = Đặt
3 1,
x t
= −
suy ra
d 3d .
x t
Đổi cận
2 1
.
5 2
x t
x t
= → =
= → =
Khi đó
( ) ( ) ( )
5 2 2
2 1 1
d 3 3 1 d 3 3 1 d 3.20 60.
I f x x f t t f x x= = − = − = =
∫ ∫ ∫
:>&
:#; @D Cho hàm số
(
)
f x
liên tục trên đoạn
[
]
0;1
và thỏa mãn
( )
1
3
0
d 1
f x x
=
∫
,
( )
1
2
1
6
2 d 13
f x x =
∫
. Tính tích phân
( )
1
2 3
0
d .
I x f x x
=
∫
<
6.
I
=

7.
I
=
:
8.
I
=
&
9.
I
7 = Xét
( )
1
2
1
6
2 d 13.
f x x =
∫
Đặt
2 ,
t x
suy ra
2d d d .
dt x x t
= → =
Đổi cận
1 1
6 3
.
1
1
2
x t
x t
= → =
= → =
Khi đó
( ) ( ) ( )
1
1 1
2
1 1 1
6 3 3
1
2 d 13 d 13 d 26.
2
f x x f t t f t t= ⇔ = ⇔ =
∫ ∫ ∫
Xét tích phân cần tính
( )
1
2 3
0
d .
I x f x x
=
∫
Đặt
3
,
u x
suy ra
2 2
1
d 3 d d d .
3
t x x x x t
= → =
Đổi cận
0 0
.
1 1
x u
x u
= → =
= → =
Khi đó
( ) ( ) ( ) ( ) ( )
1
1 1 1
3
1
0 0 0
3
1 1 1 1
d d d d 1 26 9.
3 3 3 3
I f t t f x x f x x f x x
= = = + = + =
∫ ∫ ∫ ∫
:>&
:#;AE Cho hàm số
(
)
f x
liên tục trên đoạn
[
]
0;9
và thỏa mãn
( )
9
0
d 729,
f x x =
∫
( )
3
0
6 d 513.
f x x+ =
∫
Tính tích phân
( )
2
0
3 d .
I f x x
=
∫
<
414.
I

72.
I
:
342
I
. &
I
7 = Xét
( )
3
0
6 d 513.
f x x+ =
∫
Đặt
6,
t x
= +
suy ra
d d .
x t
Đổi cận
0 6
.
3 9
x t
x t
= → =
= → =
Khi đó
( ) ( )
3 9
0 6
6 d 513 d 513.
f x x f t t+ = ⇔ =
∫ ∫
Xét tích phân cần tính
( )
2
0
3 d .
I f x x
=
∫
Đặt
3 ,
u x
suy ra
1
d 3d d d .
3
u x x u
= → =
Đổi cận
0 0
.
2 6
x u
x u
= → =
= → =
Khi đó
( ) ( ) ( ) ( )
6 6 9 6
0 0 0 9
1 1 1
. d . d d d
3 3 3
I f u u f x x f x x f x x
= = = +
∫ ∫ ∫ ∫
( ) ( ) ( )
9 9
0 6
1 1
d d 729 513 72.
3 3
f x x f x x
= − = − =
∫ ∫
:>
:#;A Cho
( )
2
1
d .
f x x a
=
∫
Tính tích phân
( )
1
2
0
1 d .
I xf x x
= +
∫
<
2 .
I a

4 .
I a
:
2
a
I
= ⋅
&
4
a
I
= ⋅
7 = Đặt
2
1,
t x
= +
suy ra
1
d 2 d d d .
t x x x x t
= → =
Đổi cận
0 1
.
1 2
x t
x t
= → =
= → =
Khi đó
( ) ( )
2 2
1 1
1 1 1
. d . d . .
2 2 2 2
a
I f t t f x x a= = = =
∫ ∫
:>:
:#;A Cho
( )
2
1
d 2016.
f x x =
∫
Tính tích phân
( )
1
0
1
. 3 1 d .
3 1
I f x x
x
= +
+
∫
<
2016.
I
1008.
I
:
1344.
I
&
3024.
I
7 = Đặt
2
3 1 3 1,
t x t x
= + ⇒ = +
suy ra
2
2 d 3d d d .
3
t t x x t t
= → =
Đổi cận
0 1
.
1 2
x t
x t
= → =
= → =
Khi đó
( ) ( )
2 2
1 1
2 2 2
. d . d .2016 1344.
3 3 3
I f t t f x x= = = =
∫ ∫
:>:
:#;A'Cho
( )
2017
0
d 2
f x x
=
∫
. Tính tích phân
( )
2017
1
2
2
0
. ln 1 d .
1
e
x
I f x x
x
−
= +
+
∫
<
1.
I
=

2.
I
=
:
4.
I
=
&
5.
I
=
7 = Đặt
(
)
2
ln 1 ,
t x
= +
suy ra
2 2
2 d d d
d .
2
1 1
x x x x t
t
x x
= → =
+ +
Đổi cận:
2017
0 0
.
1 2017
x t
x e t
= → =
= − → =
Khi đó
( ) ( )
2017 2017
0 0
1 1 1
d d .2 1.
2 2 2
I f t t f x x
= = = =
∫ ∫
:><
:#;A? Cho hàm số
(
)
f x
liên tục trên
ℝ
và thỏa mãn
(
)
1
ln
d .
e
f x
x e
x
=
∫
Mệnh đề
nào sau đây đúng?
<
( )
1
0
d 1.
x x
=
∫

( )
1
0
d .
x x e
=
∫
:
( )
0
d 1.
e
x x
=
∫
&
( )
0
d .
e
x x e
=
∫
7 = Đặt
ln ,
t x
suy ra
d
d .
x
t
x
=
Đổi cận:
1 0
.
1
x t
x e t
= → =
= → =
Khi đó
(
)
( ) ( )
1 1
1 0 0
ln
d d d .
e
f x
e x f t t f x x
x
= = =
∫ ∫ ∫
:>
:#;A@Cho
( )
1
0
d 2017.
f x x =
∫
Tính tích phân
( )
4
0
sin 2 cos 2 d .
I f x x x
π
=
∫
<
2
2017
I
= ⋅

2017
2
I
= ⋅
:
2017.
I
&
2017
2
I
= − ⋅
7 = Đặt
sin 2 ,
t x
suy ra
1
d 2 cos 2 d cos 2 d d .
t x x x x t
= → =
Đổi cận
0 0
.
1
4
x t
x t
π
= → =
= → =
Khi đó
( ) ( )
1 1
0 0
d 1 1 2017
d .2017 .
2 2 2 2
t
I f t f x x= = = =
∫ ∫
:>
:#;AA Cho
( )
2
0
cos . sin d 2017
I x f x x
π
= =
∫
. Tính tích phân
( )
2
0
sin . cos d .
J x f x x
π
=
∫
<
2017
.
2
J = 
2017.
J
= −
:
2017
J
. &
2017
.
2
J = −
7 = Đặt
cos ,
t x
suy ra
d sin d sin d d .
t x x x x t
= − → = −
Đổi cận
0 1
0
2
x t
x t
π
= → =
= → =
. Khi đó
( ) ( )
0 1
1 0
d d .
J f t t f t t
= − =
∫ ∫
Tiếp tục ta đặt
sin ,
t u
suy ra
d cos d .
t u u
Đổi cận
0 0
.
1
2
t u
t u
π
= → =
= → =
Khi đó
( ) ( )
2 2
0 0
sin cos d cos . sin d 2017.
I f u u u x f x x
π π
= = =
∫ ∫
:>:
:#;ABCho
( )
1
0
d 2017.
f x x =
∫
Tính tích phân
( )
8
0
tan 2
d .
1 cos 4
f x
I x
x
π
=
+
∫
<
2017.
I
2017
.
2
I = :
2017
.
4
I = &
2017
.
8
I =
7 = Viết lại
( ) ( )
8 8
2
0 0
tan 2 tan 2
d d
1 cos 4 2 cos 2
f x f x
I x x
x x
π π
= =
+
∫ ∫
.
Đặt
tan 2 ,
t x
suy ra
2 2
2 d 1
d d d .
4cos 2 2 cos 2
x
t x t
x x
= → = =
Đổi cận
0 0
.
1
8
x t
x t
π
= → =
= → =
Khi đó
( ) ( )
1 1
0 0
1 1 2017
. d . d .
4 4 4
I f t t f x x= = =
∫ ∫
:>:
:#;AC Cho hàm số
(
)
f x
liên tục trên
ℝ
và
( ) ( )
1 1
2 2
1
0
4
d 3, 2 d 10.
f x x f x x= =
∫ ∫
Tính
tích phân
( )
2
0
cos . sin d .
I x f x x
π
=
∫
<
23.
I
10.
I
:
8.
I
=
&
7.
I
=
7 = Xét tích phân
( )
1
2
1
4
2 d 10.
f x x =
∫
Đặt
2 ,
t x
suy ra
1
d 2d d d .
t x x t
= → = Đổi cận:
1 1
4 2
.
1
1
2
x t
x t
= → =
= → =
Khi đó
( ) ( )
1
1
2
1 1
4 2
1
10 2 d d
2
f x x f t t
= =
∫ ∫
( )
1
1
2
d 20
f t t→ =
∫
hay
( )
1
1
2
d 20.
f x x =
∫
Xét tích phân
( )
2
0
cos . sin d .
I x f x x
π
=
∫
Đặt
sin ,
u x
suy ra
d cos d .
u x x
Đổi cận:
0 0
.
1
2
x u
x u
π
= → =
= → =
Khi đó
( ) ( ) ( ) ( )
1
1 1 1
2
1
0 0 0
2
d d d d 3 20 23.
I f u u f x x f x x f x x= = = + = + =
∫ ∫ ∫ ∫
:><
:#; AD Cho hàm số
(
)
f x
liên tục trên
ℝ
và
( )
( )
1
2
4
2
0 0
tan d 4, d 2.
1
x f x
f x x x
x
π
= =
+
∫ ∫
Tính tích phân
( )
1
0
d .
I f x x
=
∫
<
6.
I
=

2.
I
=
:
3.
I
=
&
1.
I
=
7 = Xét
( )
4
0
tan d 4.
f x x
π
=
∫
Đặt
tan ,
t x
suy ra
( )
2
2 2
1 d
d d tan 1 d d .
cos 1
t
t x x x x
x t
= = + → =
Đổi cận:
0 0
.
1
4
x t
x t
π
= → =
= → =
Khi đó
( )
( ) ( )
1 1
4
2 2
0 0 0
4 tan d d d .
1 1
f t f x
f x x t x
t x
π
= = =
+ +
∫ ∫ ∫
Từ đó suy ra
( )
(
)
(
)
1 1 1
2
2 2
0 0 0
d d d 4 2 6.
1 1
f x x f x
I f x x x x
x x
= = + = + =
+ +
∫ ∫ ∫
:><
:#; BE Cho hàm số
(
)
f x
liên tục trên
ℝ
và thỏa mãn
( )
4
2
0
tan . cos d 1,
x f x x
π
=
∫
(
)
2
2
ln
d 1.
ln
e
e
f x
x
x x
=
∫
Tính tích phân
(
)
2
1
4
2
d .
f x
I x
x
=
∫
<
1.
I
=

2.
I
=
:
3.
I
=
&
4.
I
7 =● Xét
( )
4
2
0
tan . cos d 1
A x f x x
π
= =
∫
.Đặt
2
cos .
t x
Suy ra
2
d
d 2 sin cos d 2 cos tan d 2 .tan d tan d .
2
t
t x x x x x x t x x x x
t
= − = − = − → = −
Đổi cận:
0 1
.
1
4 2
x t
x t
π
= → =
= → =
Khi đó
( ) ( ) ( ) ( )
1
1 1 1
2
1 1 1
1
2 2 2
1 1 1
1 d d d d 2.
2 2 2
f t f t f x f x
A t t x x
t t x x
= = − = = → =
∫ ∫ ∫ ∫
● Xét
(
)
2
2
ln
d 1.
ln
e
e
f x
B x
x x
= =
∫
Đặt
2
ln .
u x
Suy ra
2
2 ln 2 ln 2 d du
d d d d .
ln ln ln 2
x x u x
u x x x
x x x x x x x u
= = = → =
Đổi cận:
2
1
.
4
x e u
x e u
= → =
= → =
Khi đó
(
)
(
)
(
)
4 4 4
1 1 1
1 1
1 d d d 2.
2 2
f u f x f x
B u x x
u x x
= = = → =
∫ ∫ ∫
● Xét tích phân cần tính
(
)
2
1
2
2
d .
f x
I x
x
=
∫
Đặt
2 ,
v x
suy ra
1
d d
2
.
2
x v
v
x
=
=
Đổi cận:
1 1
.
4 2
2 4
x v
x v
= → =
= → =
Khi đó
(
)
(
)
(
)
(
)
4 4 1 4
1 1 1
1
2 2 2
d d d d 2 2 4.
f v f x f x f x
I v x x x
v x x x
= = = + = + =
∫ ∫ ∫ ∫
:>&
:#;B Cho hàm số
(
)
f x
liên tục trên
ℝ
và
(
)
( )
9
2
1 0
d 4, sin cos d 2.
f x
x f x x x
x
π
= =
∫ ∫
Tính tích phân
( )
3
0
d .
I f x x
=
∫
<
2.
I
=

6.
I
=
:
4.
I
=
&
10.
I
7 = Xét
(
)
9
1
d 4.
f x
x
x
=
∫
Đặt
2
,
t x t x
= ⇒ =
suy ra
2 d d .
t t x
Đổi cận
1 1
.
9 3
x t
x t
= → =
= → =
Suy ra
(
)
( ) ( )
9 3 3
1 1 1
4 d 2 2d d 2.
f x
x f t t f t t
x
= = → =
∫ ∫ ∫
Xét
( )
2
0
sin cos d 2.
f x x x
π
=
∫
Đặt
sin ,
u x
suy ra
d cos d .
u x x
Đổi cận
0 0
.
1
2
x u
x u
π
= → =
= → =
Suy ra
( ) ( )
1
2
0 0
2 sin cos d d .
f x x x f t t
π
= =
∫ ∫
Vậy
( ) ( ) ( )
3 1 3
0 0 1
d d d 4.
I f x x f x x f x x
= = + =
∫ ∫ ∫
:>:
:#; B Ký hiệu
(
)
F x
là một nguyên hàm của hàm số
( )
x
e
f x
x
= trên khoảng
(
)
0;
+∞
. Tính tích phân
2
3
1
d .
x
e
I x
x
=
∫
<
(
)
(
)
3 2 1 .
I F F
= −

(
)
(
)
6 3 .
I F F
= −
:
(
)
(
)
6 3
.
3
F F
I
=
&
(
)
(
)
3 6 3 .
I F F
= −
7 = Đặt
3 ,
t x
suy ra
1
d 3d
d d
3
.
3
3
t x
x t
t
t
x
x
=
=
→
=
=
Đổi cận
1 3
.
2 6
x t
x t
= ↔ =
= → =
Khi đó
( ) ( ) ( )
6 6 6
6
3
3 3 3
dt
. d d 6 3 .
3
3
t t x
e e e
I t x F x F F
t
t x
= = = = = −
∫ ∫ ∫
:>
:#;B' Ký hiệu
(
)
F x
là một nguyên hàm của hàm số
( )
cos
2
x
f x
x
=
trên khoảng
(
)
0;
+∞
. Tính tích phân
4
1
cos 2
d
x
I x
x
=
∫
.
<
(
)
(
)
2. 8 2 .
I F F
= −

(
)
(
)
2. 8 2 .
I F F
= +
:
(
)
(
)
2. 8 2. 2 .
I F F
= −
&
(
)
(
)
2. 8 2. 2 .
I F F
= +
7 = Đặt
2 ,
t x
suy ra
1
d 2d
d d
2
.
2
2
t x
x t
t
t
x
x
=
=
→
=
=
Đổi cận
1 2
.
4 8
x t
x t
= → =
= → =
Khi đó
( ) ( ) ( )
8 8 8 8
8
2
2 2 2 2
cos d cos cos cos
d d 2. d 2. 2 8 2 2 .
2 2
2
t t t x x
I t x x F x F F
t
t x x
= = = = = = −
∫ ∫ ∫ ∫
:>:
:#;B? Cho hàm số
(
)
f x
có đạo hàm liên tục trên
ℝ
và
(
)
(
)
2016 , 2017
f a f b
= =
(
)
, .
a b
ℝ
Tính tích phân
( ) ( )
2016
2014
2017
2015 . d .
I f x f x x
′
=
∫
<
2017 2017
.
I b a
= −

2016 2016
.
I a b
= −
:
2015 2015
.
I a b
= −
&
2015 2015
.
I b a
= −
7 = Đặt
(
)
,
t f x
suy ra
(
)
(
)
d d .
t f x x
Đổi cận
(
)
( )
2016 2016
.
2017 2017
x t f a
x t f b
= → = =
= → = =
Khi đó
2014 2015 2015 2015
2015. d .
a
a
b
b
I t t t a b= = = −
∫
:>:
:#;B@ Cho hàm số
(
)
f x
liên tục trên
ℝ
và
( )
2
0
d 3.
f x x
=
∫
Tính
( )
1
1
2 d .
I f x x
−
=
∫
<
0.
I
=

3
.
2
I =
:
3.
I
=
&
6.
I
7 = Ta có
( ) ( ) ( )
1 0 1
1 1 0
2 d 2 d 2 d .
I f x x f x x f x x
− −
= = +
∫ ∫ ∫
Xét
( )
0
1
2 d .
f x x
−
∫
Đặt
,
x t
= −
suy ra
d d
x t
= −
. Đổi cận
1 1
.
0 0
x t
x t
= − → =
= → =
Khi đó
( ) ( ) ( ) ( )
0 0 1 1
1 1 0 0
2 d 2 d 2 d 2 d .
f x x f t t f t t f t t
−
= − − = − =
∫ ∫ ∫ ∫
Do đó
( )
( )
1 1
0 0
2 2 d 2 2 d
I f x x f x x
= =
∫ ∫
(vì
[
]
2 0, 0;1
x x
≥ ∀ ∈
).
Bây giờ ta cần tính
( )
1
0
2 2 d .
I f x x
=
∫
Đặt
2 d 2d .
u x u x
= → =
Đổi cận:
0 0
.
1 2
x u
x u
= → =
= → =
Khi đó
( ) ( )
2 2
0 0
d d 3.
I f u u f x x
= = =
∫ ∫
:>:
()*+,-./+0JI:++L.JM./+N.
:#;BATính tích phân
2
1
ln d .
I x x
=
∫
<.
2 ln 2 1.
I
= +
.
(
)
ln 4 .
I e
= −
:.
ln 4 log10
I
= −
. &.
ln 4 .
I e
7 =Đặt
d
ln
d
d d
x
u x
u
x
v x
v x
=
=
⇒
=
=
.
Khi đó
2
2 2 2
1 1 1
1
ln d ln 2 ln 2 1 ln 4 log10.
I x x x x x x= − = − = − = −
∫
:>:
: :<538 Có 2 cách bấm, cụ thể như sau:
Bấm trực tiếp tích phân
2
1
ln d
x x
∫
và so sánh với các kết quả ở các đáp án.
Thiết lập hiệu, ví dụ với đáp án A ta bấm
2
1
ln d 2 ln 2 1
x x
− −
∫
. Nếu màn hình hiện
số 0 thì đáp án đó đúng.
:#;BB Kết quả của tích phân
( )
2
1
ln 1 d
I x x
= +
∫
được viết ở dạng ln 3 ln 2
I a b c
= + +
với
, ,
a b c
là các số nguyên. Tính
.
P a b c
= + +
<
0.
P
=

1.
P
=
:
2.
P
=
&
3.
P
=
7 =Đặt
( )
d
ln 1
d
.
1
d d
1
x
u x
u
x
v x
v x
= +
=
⇒
+
=
= +
Khi đó
( ) ( ) ( ) ( )
2
2 2 2
1 1 1
1
1 .ln 1 d 1 ln 1
I x x x x x x
= + + − = + + −
∫
3
3ln 3 2 ln 2 1 2 0.
1
a
b P
c
= − − → = − → =
= −
:><
::<538Tính tích phân
( )
2
1
ln 1 d
I x x
= +
∫
rồi lưu vào biến
A.
Khi đó
( )
ln 3 ln 2 A ln 3 .2 . ln 3 .2 . 3 .2 .
A
a b c A a b c A a b
c
e
a b c e e e e
e
+ + = ←→ = ←→ = ↔ =
Để tính được
3 .2
a b
ta sử dụng chức năng MODE 7 với hàm
( )
.
A
X
e
f X
e
=
Với thiết lập
Start 9, End 10, Step 1
(do
, ,
a b c
là các số nguyên).
Dễ thấy với
1
X c
= = −
thì
3 2
27
3 .2 6.75 3 .2 3; 2.
a b
a b
−
= = = → = = −
:#;BCF1G3.++H<EA–EB Tính tích phân
1
ln d .
e
I x x x
=
∫
<
1
.
2
I = 
2
2
.
e
I
= :
2
1
.
e
I
+
= &
2
1
.
4
e
I
−
=
7 =Đặt
2
d
d
ln
d d
2
x
u
u x
x
v x x
x
v
=
=
⇒
=
=
.
Khi đó
2 2 2 2
1 1
1
ln 1 1
d
2 2 2 4 4
e
e e
x x e x e
I x x
+
= − = − =
∫
. :>:
:#;BDKết quả của tích phân
( )
1
2
0
ln 2 d
I x x x
= +
∫
được viết ở dạng ln 3 ln 2
I a b c
= + +
với
, ,
a b c
là các số hữu tỉ. Tính tổng
.
S a b c
= + +
<.
0.
S
=
.
1.
S
=
:.
3
.
2
S = &.
2.
S
=
7 =Đặt
( )
2
2
2 2
2
d d
ln 2
2
.
2
d d
1
2 2
x
u x
u x
x
x x
v x x
v
=
= +
+
⇒
+
=
= + =
Khi đó
( )
1
2 2
1 1
2
0 0
0
2 3 3 1
ln 2 d ln 3 ln 2 ln 3 ln 2
2 2 2 2 2
x x
I x x x
+
= + − = − − = − −
∫
.
Suy ra
3 1
, 1, 0.
2 2
a b c S a b c
= = − = − → = + + =
:><
.O PQChắc có bạn đọc không hiểu tại sao chỗ
2
d d 1
x
v x x v
= → = +
. Vì ta
thường làm
2
d d
2
x
v x x v= → = . Sao lại cộng thêm
1
ở đây? Ta biết rằng các nguyên
hàm sai khác nhau hằng số nên ta cộng thêm hằng số là bao nhiêu cũng được. Vậy
vấn đề là sao không cộng số khác mà là số
1
. Ở đây số
1
được thêm vào để tạo ra
lượng mà rút gọn được, cụ thể đó là lượng
2
2 .
x
:#;CE Cho hai số nguyên dương
,
a b
thỏa mãn
( ) ( )
5
4
19
1 ln 3 d 5 ln
a
x x x a
b
+ − = − ⋅
∫
Tính
.
S a b
= +
<
4.
S
=

6.
S
=
:
8.
S
=
&
0.
S
=
7 =Tính
( ) ( )
5
4
1 ln 3 d .
I x x x
= + −
∫
Đặt
( )
( )
2 2
1
d d
ln 3
3
.
2
d 1 d
2 2
u x
u x
x
x x x
v x x
v x
=
= −
−
⇒
+
= +
= + =
Khi đó
( )
(
)
5 5
2 2 2
5
4
4 4
2 35 ln 2 1 2
.ln 3 d d .
2 2 3 2 2 3
x x x x x
I x x x x
x x
+ +
= + − − = −
− −
∫ ∫
Tính
5 5
2 2
5
4
4 4
2 15 19
d 5 d 5 15 ln 3 15 ln 2.
3 3 2 2
x x x
J x x x x x
x x
+
= = + + = + + − = +
− −
∫ ∫
Vậy
2
35 ln 2 1 35 ln 2 1 19 19 19
15 ln 2 10 ln 2 5ln 2 .
2 2 2 2 2 4 4
I J
= − = − + = − = −
Suy ra
2; 4 6.
a b S a b
= = → = + =
:>
:#;CKết quả của tích phân
( )
1
2017
0
ln 2 1 d
I x x x
= +
∫
được viết ở dạng
ln 3
a
I
b
= với
phân số
a
b
tối giản. Tính tổng
.
a b
+
<
6057.
a b
+ =

6059.
a b
+ =
:
6058.
a b
+ =
&
6056.
a b
+ =
7 =Ta có
( ) ( )
1 1
2017
0 0
ln 2 1 d 2017 ln 2 1 d
I x x x x x x
= + = +
∫ ∫
.
Tính
( )
1
0
ln 2 1 d .
J x x x
= +
∫
Đặt
( )
2
2
d d
ln 2 1
2 1
.
d d
2
u x
u x
x
v x x
x
v
=
= +
+
⇒
=
=
Khi đó
( )
1 1
2 2
1
0
0 0
1 1 1 1 1
.ln 2 1 d ln 3 . d
2 2 1 2 2 4 4 2 1
x x
J x x x x
x x
= + − = − − +
+ +
∫ ∫
1
2
0
1 1 1 1 1 1 3
ln 3 .ln 2 1 ln 3 ln 3 ln 3.
2 4 4 8 2 8 8
x x x
= − − + + = − =
Suy ra
6051
6051
2017. ln 3 6059.
8
8
a
I J a b
b
= = → → + =
=
:>
:#;C Cho
, ,
a b c
là các số nguyên dương thỏa mãn
2
2
1
ln .d ln 2
9
a c
x x x
b
= −
∫
với
a
b
là phân số tối giản. Tính giá trị biểu thức
(
)
2 2 2
2 .
T a b c ab bc ca
= + + − + −
<
252.
T

T
:
16.
T
= −
&
T
= −
7 =Đặt
2 3
1
d d
ln
.
d d
3
u x
u x
x
v x x x
v
=
=
⇒
=
=
Khi đó
2 2
3
2 2
2 2 3
1 1
1 1
1 8 1 8 7
ln .d .ln d ln 2 . ln 2 .
3 3 3 9 3 9
x
x x x x x x x
= − = − = −
∫ ∫
8; 3; 7 144.
a b c T
→ = = = → =
:>
:#;C' Giả sử
3
1
3 1
ln d
e
a
e
I x x x
b
+
= =
∫
với
,
a b
là các số nguyên dương. Trong các
khẳng định sau, khẳng định nào đúng?
<.
64
ab
. .
46
ab
. :.
12
a b
− =
. &.
4
a b
− =
.
7 =Đặt
3
4
1
d d
ln
d d
4
u x
u x
x
v x x
x
v
=
=
⇒
=
=
.
Khi đó
4 4 4 4 4 4
3
1 1
1
ln 1 1 3 1
d .
4 4 4 16 4 16 16
e
e e
x x e x e e e
I x x
− +
= − = − = − =
∫
Suy ra
4; 16
a b
= =
. :><
:#;C? Biết
2
1
ln 1 1
d ln 2
2 2
a
x
I x
x
= = −
∫
. Giá trị của
a
bằng:
<.
2
a
=
. .
ln 2
a
. :.
4
a
=
. &.
8
a
=
.
7 =Đặt
2
d
ln
d
d
1
d
x
u x
u
x
x
v
v
x
x
=
=
⇒
=
= −
.
Khi đó
2
1
1
1
ln d ln 1 ln 1
1.
a
a
a
x x a a
I
x a x a ax
= − + = − − = − − +
∫
Theo giả thiết
1 1 ln 1 1 1
ln 2 1 ln 2 2.
2 2 2 2
a
I a
a a
= − ⇔ − − + = − + → =
:><
::<538Thiết lập hiệu
2
1
ln 1 1
d ln 2
2 2
a
x
x
x
− +
∫
và bài toán cần tìm
a
để hiệu
bằng 0. Thử với
2
a
=
, ta nhập hiệu
2
2
1
ln 1 1
d ln 2
2 2
x
x
x
− +
∫
vào máy tính CASIO và
nhấn dấu =. Thật may mắn màn hình xuất hiện số 0, ta chọn A. Nếu màn hình
không xuất hiện số 0 thì ta thử tới đáp án B.
:#;C@ Xét
1
ln d
e
k
k
I x
x
=
∫
với
k
là số nguyên dương. Nếu
2
k
I e
< −
thì tổng các giá
trị của
k
bằng:
<.
3.
.
5.
:.
7.
&.
9.
7 =Ta có
( )
1 1 1 1
ln d ln ln d ln d ln d .
e e e e
k
k
I x k x x k x x x
x
= = − = −
∫ ∫ ∫ ∫
●
( )
1
1
ln d ln . 1 ln
e
e
A k x k x e k
= = = −
∫
.
●
1
ln d
e
B x x
=
∫
. Đặt
1 1 1
1
d
ln
d
ln d ln 1.
d d
e
e e e
x
u x
u
B x x x x x x
x
v x
v x
=
=
⇒ → = − = − =
=
=
∫
Do đó
(
)
1 ln 1
k
I A B e k
= − = − −
.
Theo giả thiết, ta có
(
)
2 1 ln 1 2
k
I e e k e
< − ⇔ − − < −
(
)
{
}
1 ln 1 ln 1 1;2
k
e k e k k e k
+
∈
⇔ − < − ⇔ < ⇔ < → =
ℤ
. :><
:#;CATính tích phân
1
0
2 d
x
I x x
=
∫
.
<.
2
2 ln 2 1
.
ln 2
I
−
= .
2 ln 2 1
.
ln 2
I
−
= :.
2
2 ln 2 1
.
ln 2
I
+
= &.
2 ln 2 1
.
ln 2
I
+
=
7 =Đặt
d d
.
2
d 2 d
ln 2
x
x
u x
u x
v x
v
=
⇒
=
=
Khi đó
1
1 1 1
2 2
0 0 0
0
2 1 2 2 2 ln 2 1
2 .
ln 2 ln 2 ln 2
ln 2 ln 2
x x x
x
x x
I dx
−
= − = − =
∫
:><
:#;CB Kết quả tích phân
( )
1
0
2 3 d
x
I x e x
= +
∫
được viết dưới dạng
I ae b
= +
với
,
a b
là
các số hữu tỷ. Khẳng định nào sau đây là đúng?
<.
2
a b
− =
. .
3 3
28
a b
+ =
. :.
3.
ab
=
&.
2 1
a b
+ =
.
7 =Đặt
2 3 d 2d
.
d d
x x
u x u x
v e x v e
= + =
⇒
= =
Khi đó
( ) ( )
1
1 1 1
0 0 0
0
2 3 2 d 2 3 2 3 1.
x x x x
I x e e x x e e e
= + − = + − = −
∫
Suy ra
3, 1
a b
= = −
. :>&
:#;CC Cho
, ,
a b c
là các số nguyên dương và
1
c
≠
thỏa
ln 2
2
0
1 ln 2
d
4
x
b
xe x
a c
−
= − ⋅
∫
Tính giá trị biểu thức
(
)
.
T abc ab bc ca
= − + +
<
24.
T

6.
T
=
:
2.
T
= −
&
9.
T
=
7 =Đặt
2
2
d d
.
1
d d
2
x
x
u x
u x
v e
v e x
−
−
=
⇒
= −
=
Khi đó
ln 2 ln 2
ln 2 ln 2
2 2 2 2
0 0
0 0
1 1 ln 2 1 3 ln 2
d d
2 2 8 4 16 8
x x x x
xe x xe e x e
− − − −
= − + = − − = −
∫ ∫
1 3 ln 2
4; 3; 2 2.
4 4 2
a b c T
= − → = = = → = −
:>:
:#;CD Cho
, ,
a b c
là các số nguyên thỏa mãn
1
1 3 2
0
3 d .
5 3
x
a b
e x e e c
+
= + +
∫
Tính giá
trị của biểu thức
2 3
b c
T a
= + + ⋅
<
6.
T
=

9.
T
=
:
10.
T
&
5.
T
=
7 =Đặt
2
1 3 1 3 2 d 3d .
t x t x t t x
= + ⇒ = + ⇒ =
Đổi cận
0 1
.
1 2
x t
x t
= ⇒ =
= ⇒ =
Khi đó
2
1
2 d
t
I te t
=
∫
. Đặt
2 d 2d
.
d d
t t
u t u t
v e t v e
= =
⇒
= =
Suy ra
2
2 2 2
2
1 1 1
1
10
2 2 2 2 2 0 10.
0
t t t t
a
I te e dt te e e b T
c
= − = − = → = → =
=
∫
:>:
:#;DE Cho tham số
0
a
>
thỏa mãn
( )
2
2
0
3
1 d .
4
a
x
e
x e x
−
− =
∫
Tính
2
2017.
P a
= +
<.
2021.
P
.
2026.
P
:.
2033.
P
&.
2018.
P
7 =Đặt
2
2
d d
1
.
1
d d
2
x
x
u x
u x
v e
v e x
= −
⇒
=
=
Khi đó
( ) ( )
2 2 2 2
0
0 0 0
1 1 1 1
1 d 1
2 2 2 4
a
a a a
x x x x
I x e e x x e e= − − = − −
∫
2
2 2
1 1 1 3 2 3
.
2 2 4 4 4
a
a a
a e a
e e
− − −
= + − = +
Suy ra
1.
a
=
:>&
::<538Thiết lập hiệu
( )
2
2
0
3
1 d
4
a
x
e
x e x
−
− −
∫
và bài toán cần tìm
a
để hiệu
bằng 0. Với đáp án A, suy ra
2
a
=
, ta nhập hiệu
( )
2
2
2
0
3
1 d
4
x
e
x e x
−
− −
∫
vào máy tính
CASIO và nhấn dấu =. Màn hình không xuất hiện số 0 nên ta tiếp tục thử đến đáp
án B, C và D.
:#;DTính tích phân
4
0
sin 2 d
I x x x
π
=
∫
.
<.
1
I
=
. .
2
I
π
. :.
1
4
I
=
. &.
3
4
I
=
.
7 =Đặt
d d
.
cos 2
d sin 2 d
2
u x
u x
x
v x x
v
=
⇒
=
= −
Khi đó
4
4 4 4
0 0 0
0
cos 2 1 cos 2 sin 2 1
cos 2 d .
2 2 2 4 4
x x x x x
I x x
π
π π π
= − + = − + =
∫
:>:
:#;D Kết quả tích phân
2
0
cos d
I x x x
π
=
∫
được viết ở dạng
1.
I
m
= −
Tính
2
9 6
m
−
.
<.
2
9 6 3
m
− =
. .
2
9 6 30
m
− =
. :.
2
9 6 3
m
− = −
. &.
2
9 6 30
m
− = −
.
7 =Đặt
d d
.
d cos d sin
u x u x
v x x v x
= =
⇒
= =
Khi đó
2
2 2 2
0 0 0
0
sin sin sin cos 1.
2
I x x xdx x x x
π
π π π
π
= − = + = −
∫
Suy ra
2
2 9 6 30.
m m
= → − =
:>
:#;D' Cho tham số
m
thỏa mãn
( )
2
2
0
sin 2 d 1I x x m x
π
π
= + = +
∫
. Mệnh đề nào sau
đây là đúng?
<.
1 0.
m
− < <
.
0 2.
m
≤ ≤
:.
3 5.
m
< <
&.
5.
m
≥
7 =Tính
2
0
sin d
A x x x
π
=
∫
. Đặt
d d
.
d sin d cos
u x u x
v x x v x
= =
⇒
= = −
Suy ra
( )
2
2 2
0
0 0
cos cos d sin 1.
A x x x x x
π
π π
= − + = =
∫
Do đó
2
2
2
2
0
0
2 d 1 1 .
4
m
I A m x x mx
π
π
π
= + = + = +
∫
Theo giả thiết
( )
2 2
2 2
1 1 4 3;5 .
4 4
m m
m
π π
π π+ = + ⇔ = ⇔ = ∈ :>:
:#; D? Kết quả của tích phân
( )
2
0
2 1 sin d
x x x
π
− −
∫
được viết ở dạng
1
1
a b
π
− −
.
Khẳng định nào sau đây là sai?
<.
2 8
a b
+ =
. .
5
a b
+ =
. :.
2 3 2
a b
− =
. &.
2
a b
− =
.
7 =Ta có
( )
( )
2
2
2
2
0
0
1
2 1 sin d cos 1 1.
4 2 4 2
x x x x x x
π
π
π π π
π
− − = − + = − − = − −
∫
Suy ra
4
2
a
b
=
=
. :>
:#;D@ Cho
2 2
0 0
cos d , sin d
x x
I e x x J e x x
π π
= =
∫ ∫
và
0
cos 2 d
x
K e x x
π
=
∫
. Khẳng định nào
sau đây là đúng?
F3
I J e
π
+ =
. F33
I J K
− =
. F333
1
5
e
K
π
−
=
.
<. Chỉ (I). . Chỉ (II). :. Chỉ (III). &. Cả (II) và (III).
7 = Xét (I). Ta có
2 2
0 0
cos d sin d
x x
I J e x x e x x
π π
+ = +
∫ ∫
.
( )
2 2
0
0 0
sin cos d d 1.
x x x
e x x x e x e e
π π
π
π
= + = = = −
∫ ∫
Vậy (I) sai.
Xét (II). Ta có
2 2
0 0
cos d sin d
x x
I J e x x e x x
π π
− = −
∫ ∫
( )
2 2
0 0
cos sin d cos 2 d .
x x
e x x x e x x K
π π
= − = =
∫ ∫
Vậy (II) đúng.
Xét (III). Đặt
cos 2 d 2 sin 2 d
.
d d
x x
u x u x x
v e x v e
= = −
⇒
= =
Suy ra
( )
0
0
cos 2 2 sin 2 d 1 2 .
x x
K e x e x x e M
π
π
π
= + = − +
∫
Tính
0
sin 2 d
x
M e x x
π
=
∫
. Ta đặt
1 1
1 1
sin 2 d 2 cos 2 d
.
d d
x x
u x u x x
v e x v e
= =
⇒
= =
Suy ra
( )
0
0
sin 2 2 cos 2 d 2
x x
M e x e x x K
π
π
= − = −
∫
.
Khi đó
( )
1
1 2 2 5 1
5
e
K e K K e K
π
π π
−
= − + − ⇔ = − ⇔ =
. Vậy (III) đúng. :>&
:#; DA Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[
]
1;2
và thỏa mãn
(
)
(
)
1 0, 2 2,
f f
= =
( )
2
1
d 1.
f x x
=
∫
Tính
( )
2
1
. d .
I x f x x
′
=
∫
<
2.
I
=

1.
I
=
:
3.
I
=
&
8.
I
=
7 =Đặt
( ) ( )
d d
.
d d
u x u x
v f x x v f x
= =
⇒
′
= =
Khi đó
( ) ( ) ( ) ( ) ( )
2 2
2
1
1 1
. d 2 2 1 d 2.2 0 1 3.
I x f x f x x f f f x x
= − = − − = − − =
∫ ∫
:>:
:#; DB Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[
]
0;2
và thỏa mãn
( ) ( )
2
0
2 16, d 4.
f f x x
= =
∫
Tính tích phân
( )
1
0
. 2 d .
I x f x x
′
=
∫
<
13.
I

2
.
1
I
:
0
.
2
I
&
7
.
I
=
7 =Đặt
( )
( )
d d
.
1
d 2 d
2
2
u x
u x
v f x x
v f x
=
⇒
′
=
=
Khi đó
( ) ( ) ( ) ( ) ( )
1 1 1
1
0
0 0 0
1 1 1 1 1
2 2 d 2 2 d 8 2 d .
2 2 2 2 2
I xf x f x x f f x x f x x
= − = − = −
∫ ∫ ∫
Tính
( )
1
0
2 d .
f x x
∫
Đặt
2 d 2d
t x t x
= → =
. Đổi cận:
0 0
.
1 2
x t
x t
= → =
= → =
Suy ra
( ) ( )
1 2
0 0
1 1
2 d d .4 2.
2 2
f x x f t t
= = =
∫ ∫
Vậy
1
8 .2 8 1 7.
I
= − = − =
:>&
:#;DCCho hàm số
(
)
y f x
có đạo hàm
(
)
'
f x
liên tục trên đoạn
[
]
1;2
và thỏa mãn
(
)
(
)
1 4 2 ,
f f
( )
2
1
d 1
xf x x
=
∫
. Tính tích phân
( )
2
2
1
' d .
I x f x x
=
∫
<
2.
I
=

2.
I
= −
:
1.
I
=
&
1.
I
= −
7 =Đặt
( )
( )
2
d 2 d
.
d ' d
u x x
u x
v f x
v f x x
=
⇒
=
=
Khi đó
( ) ( ) ( ) ( ) ( )
2 2
2
2
1
1 1
2 d 4 2 1 2 d .
I x f x xf x x f f xf x x
= − = − −
∫ ∫
( )
2
1
2 d 2.1 2
xf x x
= − =− = −
∫
. :>
:#;DDCho hai hàm số
(
)
y f x
và
(
)
y g x
=
có đạo hàm liên tục trên đoạn
[
]
1;2
.
Biết
(
)
(
)
(
)
(
)
1 . 1 1, 2 . 2 2
f g f g
= =
và
( ) ( )
2
1
. d 3
g x f x x
′
=
∫
. Tính
( ) ( )
2
1
. d .
I f x g x x
′
=
∫
<
4.
I
= −

4.
I
:
2.
I
= −
&
2.
I
=
7 =Đặt
(
)
( )
(
)
( )
d ' d
.
d ' d
u f x u f x x
v g x x v g x
= =
⇒
= =
Khi đó
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2 2
2
1
1 1
. . ' d 2 . 2 1 . 1 . ' d
I f x g x g x f x x f g f g g x f x x
= − = − −
∫ ∫
2 1 3 2.
= − − = −
:>:
:#;EECho hàm số
(
)
y f x
có đạo hàm
(
)
'
f x
liên tục trên đoạn
[
]
0;1
và thỏa
mãn
(
)
1 1
f
=
,
( )
1
0
d 2
f x x
=
∫
. Tính tích phân
( )
1
0
' d .
I f x x
=
∫
<
1.
I
= −

1.
I
=
:
2.
I
=
&
2.
I
= −
7 =Đặt
2
2 d d .
t x t x t t x
= → = → =
Đổi cận
0 0
1 1
x t
x t
= → =
= → =
.
Khi đó
( )
1
0
2 ' d 2
I tf t t A
= =
∫
.
Tính
( )
1
0
' d
A tf t t
=
∫
. Đặt
( ) ( )
d d
.
d ' d
u t u t
v f t t v f t
= =
→
= =
Suy ra
( ) ( ) ( ) ( )
1 1
1
0
0 0
d 1 d 1 2 1 2 2.
A tf t f t t f f t t I A
= − = − = − = − → = = −
∫ ∫
:>&
()*'JI:++L.R.+S56
:#;E Cho
(
)
f x
là hàm số chẵn trên đoạn
[
]
1;1
−
và thỏa mãn
( )
1
1
d 4
f x x
−
=
∫
.
Tính tích phân
(
)
1
1
d
2 1
x
f x
I x
−
=
+
∫
.
<
2
=
. 
4.
I
:
8.
I
=
&
16.
I
7 = Đặc trưng của dạng
(
)
d
1
a
x
a
f x
x
β
−
+
∫
là đổi biến
d d .
t x x t
= − → = −
Đổi cận
1 1
.
1 1
x t
x t
= − → =
= → = −
Khi đó
(
)
1
1
d
2 1
t
f t
I t
−
−
= −
+
∫
(
)
(
)
( )
(
)
(
)
1 1 1 1
chan
1 1 1 1
2 . 2 . 2 .
d d d d .
2 1 1 2 2 1 2 1
t t x
f x
t t t x
f t f t f t f x
t t t x
−
− − − −
− −
= = = =
+ + + +
∫ ∫ ∫ ∫
Suy ra
(
)
(
)
( )
1 1 1
1 1 1
2 .
2 d d d 4 2.
2 1 2 1
x
x x
f x f x
I I I x x f x x I
− − −
= + = + = = → =
+ +
∫ ∫ ∫
:><
:TUVWX Chọn
(
)
2
h x x
thỏa mãn giả thiết là hàm chẵn.
Ta có
1
2
1
2
d
3
x x
−
= →
∫
chọn
( ) ( )
2
4
6 .
2
3
f x h x x
= =
Khi đó
(
)
1 1
2
1 1
6
d d .
2 1 2 1
x x
f x
x
I x x
− −
= =
+ +
∫ ∫
Dùng CASIO tính được kết quả bằng
2.
TUVWX
 Chọn một hàm số bất kỳ thỏa mãn bài toán. Nếu bài toán không nói gì thì
thường chọn
(
)
1
h x
=
, nếu là hàm số lẻ thì chọn
(
)
h x x
=
, hàm số chẵn thì chọn
(
)
2
.
h x x
 Tính
( ) ( ) ( )
d d d .
b b b
a a a
N N N
h x x M h x x h x x M N
M M M
= → = = =
∫ ∫ ∫
.
Do đó ta sẽ chọn
( ) ( )
.
N
f x h x
=
' Tính
( ) ( )
d d
b b
a a
A
I f u x h u x
B
= =
∫ ∫
bằng máy tính là xong.
("Y Cho hàm số
(
)
f x
thỏa mãn
( )
2017
1
d 2
f x x
=
∫
. Tính tích phân
( )
2017
1
2018 d
f x x
−
∫
.
Hướng dẫn. Ta chọn
( ) ( )
2017
1
2 1
1 1d 2016 .
2016 1008
h x x f x= → = → = =
∫
Khi đó
( )
2017 2017
1 1
1
2018 d d 2.
1008
f x x x
− = =
∫ ∫
:#;E Cho hàm số
(
)
f x
liên tục trên
ℝ
và thỏa
(
)
(
)
2 2 cos 2
f x f x x
+ − = + với
mọi x
∈
ℝ
. Tính
( )
3
2
3
2
d
I f x x
π
π
−
=
∫
.
<
6
I
= −
. 
0
I
=
. :
2
= −
. &
6
I
=
.
7 = Đặt
d d .
t x x t
= − → = −
Đổi cận:
3 3
2 2
.
3 3
2 2
x t
x t
π π
π π
= − → =
= → = −
Khi đó
( ) ( ) ( )
3 3 3
2 2 2
3 3 3
2 2 2
d d d .
I f t t f t t f x x
π π π
π π π
−
− −
= − − = − = −
∫ ∫ ∫
Suy ra
( ) ( )
3 3 3
2 2 2
CASIO
3 3 3
2 2 2
2 d 2 2 cos 2 d 2 cos d 12 6.
I f t f t t t t t t I
π π π
π π π
− − −
= + − = + = = → =
∫ ∫ ∫
:>&
:TUVW Chọn
( )
CASIO
1
2 2 cos 2 6.
f x x I
= + → =
Chú ý: Khi gặp bài toán
''
Cho hàm số
(
)
y f x
liên tục trên
ℝ
và thỏa mãn
(
)
(
)
(
)
mf x nf x g x
+ − =
với
(
)
g x
là hàm số chẵn và
0.
m n
+ ≠
Tính tích phân
( )
d
a
a
I f x x
−
=
∫
''
thì ta chọn
( ) ( )
1
.
f x g x
m n
=
+
("Y Cho hàm số
(
)
y f x
liên tục trên
ℝ
và thỏa mãn
( ) ( )
2
1
2 3
4
f x f x
x
+ − =
.
Tính tích phân
( )
2
2
d
I f x x
−
=
∫
. +Z: Chọn
( )
2
1 1
.
5 4
f x
x
=
:#;E'Cho hàm số
(
)
y f x
liên tục trên
(
)
0;
+∞
và thỏa
( ) ( )
2
0
d cos
x
f t t x x
π
=
∫
.
Tính
(
)
4
f
.
<
( )
1
4
2
f
=
. 
(
)
4 1
f
=
. :
(
)
4 2
f
=
. &
( )
1
4
4
f
=
.
7 = Giả sử
(
)
F x
là một nguyên hàm của
(
)
f x
, suy ra
(
)
(
)
( ) ( )
/
2 2
'
.
2 '
F x f x
F x xf x
=
Khi đó
( ) ( )
( )
( )
( )
( )
2
2
2 2
0
0
d 0 cos 0
x
x
f t t F t F x F x x F x Fπ= = − ←→ = −
∫
.
Lấy đạo hàm hai vế, ta được:
(
)
2
cos sin 2 0
x x x xf x
π π π
− = −
.
Cho
2
x
=
, ta được
( ) ( )
1
1 4 4 4
4
f f
= ←→ =
. :>&
:#;E?Cho
0
a
>
và
(
)
f x
là hàm số liên tục trên
[
)
;a
+∞
. Tìm giá trị của
a
biết
rằng
(
)
2
d 6 2
t
a
f x
x t
x
+ =
∫
với mọi
.
t a
>
<
5.
a
=
9.
a
=
:
19.
a
&
3.
a
=
7 = Gọi
(
)
F x
là một nguyên hàm của hàm số
(
)
2
f x
x
trên đoạn
[
]
;
a t
.
Khi đó ta có
( )
(
)
( ) ( ) ( )
( )
( ) ( )
2
2
'
.
d 2 6 2 6
t
t
a
a
f x
F x
x
f x
F t F a F x x t F t t F a
x
=
− = = = − → = + −
∫
Suy ra
( )
(
)
( )
2
1
'
f t
F t f t t t
t
t
= = → = hay
(
)
f x x x
=
(
)
2
1
d d 2 2 2 .
t t
t
a
a a
f x
x x x t a
x
x
→ = = = −
∫ ∫
Theo giả thiết
2 2 2 6 9.
t a t a
− = − → =
:>
:  Từ đẳng thức
(
)
2
d 6 2
t
a
f x
x t
x
+ =
∫
, lấy đạo hàm hai vế theo
t
, ta được
(
)
2
1
f t
t
t
= . Suy ra
(
)
f t t t
= hay
(
)
f x x x
= .
:#; E@ Cho hàm số
(
)
f x
có đạo hàm liên tục trên đoạn
[
]
1;2
và thỏa mãn
(
)
[
]
0, 1;2 .
f x x
> ∀ ∈
Biết rằng
( )
2
1
d 10
f x x
′
=
∫
và
(
)
(
)
2
1
d ln 2.
f x
x
f x
=
∫
Tính
(
)
2 .
f
<
(
)
2 10.
f
= −

(
)
2 20.
f
:
(
)
2 10.
f
&
(
)
2 20.
f
= −
7 = Ta có
( ) ( ) ( ) ( )
2
2
1
1
d 10 10 2 1 10.
f x x f x f f
′
= ⇔ = ⇔ − =
∫
(
)
1
Lại có
(
)
(
)
( ) ( )
2
2 2
1 1
1
d ln 2 ln ln 2 ln ln 2
f x
x f x f x
f x
= ⇔ = ⇔ =
∫
(do
(
)
[
]
0, 1;2
f x x
> ∀ ∈
)
( ) ( )
(
)
(
)
(
)
(
)
2 2
ln 2 ln 1 ln 2 ln ln 2 2.
1 1
f f
f f
f f
⇔ − = ⇔ = ⇔ =
(
)
2
Từ
(
)
1
và
(
)
2
, suy ra
(
)
2 20.
f
:>
:#; EA Cho hàm số
(
)
y f x
có đạo hàm liên tục trên đoạn
[
]
1;1
, thỏa mãn
(
)
0, f x x
> ∀ ∈
ℝ
và
(
)
(
)
' 2 0
f x f x
+ =
. Tính
(
)
1
f
−
, biết rằng
(
)
1 1
f
=
.
<
(
)
2
1 .
f e
−
− =
(
)
3
1 .
f e
− =
:
(
)
4
1 .
f e
− =
&
(
)
1 3.
f
− =
7 = Ta có
( ) ( ) ( ) ( )
(
)
(
)
'
' 2 0 ' 2 2
f x
f x f x f x f x
f x
+ = ⇔ = − ⇔ = −
(do
(
)
0
f x
>
).
Lấy tích phân cận từ
1
−
đến
1
hai vế, ta được
(
)
(
)
( )
1 1
1 1
'
d 2 d
f x
x x
f x
− −
= −
∫ ∫
( ) ( )
1 1 1 1
1 1 1 1
ln 2 ln 2
f x x f x x
− − − −
⇔ = − ⇔ = −
(do
(
)
0,f x x
> ∀ ∈
ℝ
)
(
)
(
)
(
)
ln 1 ln 1 4 ln1 ln 1 4
f f f
⇔ − − = − ⇔ − − = −
(
)
(
)
4
ln 1 4 1 .
f f e
⇔ − = → − =
:>:
:#;EBGiả sử hàm số
(
)
f x
có đạo hàm liên tục trên
ℝ
, nhận giá trị dương trên
khoảng
(
)
0;
+∞
và thỏa mãn
(
)
1 1,
f
=
(
)
(
)
3 1
f x f x x
= +
với mọi
0.
x
>
Mệnh đề
nào sau đây là đúng?
<
(
)
1 5 2.
f
< <

(
)
4 5 5.
f
< <
:
(
)
2 5 3.
f
< <
&
(
)
3 5 4.
f
< <
7 = Ta có
( ) ( )
(
)
(
)
'
1
' . 3 1
3 1
f x
f x f x x
f x
x
= + ⇔ =
+
.
Lấy tích phân cận từ
1
đến
5
hai vế, ta được
(
)
(
)
5 5
1 1
'
d
d
3 1
f x
x
x
f x
x
=
+
∫ ∫
( ) ( )
5 5 5 5
1 1 1 1
2 2
ln 3 1 ln 3 1
3 3
f x x f x x
⇔ = + ⇔ = +
(do
(
)
0, 0
f x x
> ∀ >
)
( ) ( ) ( ) ( ) ( )
4
3
4 4 4
ln 5 ln 1 ln 5 ln1 ln 5 5 3,793.
3 3 3
f f f f f e
⇔ − = ⇔ − = ⇔ = ⇔ =
≃
:>&
:#; EC Cho hàm số
(
)
f x
có đạo hàm liên tục trên
ℝ
và thỏa mãn
(
)
0,f x x
> ∀ ∈
ℝ
. Biết
(
)
0 1
f
=
và
(
)
(
)
'
2 2
f x
x
f x
= −
, tìm tất cả các giá trị thực của tham
số
m
để phương trình
(
)
f x m
có hai nghiệm thực phân biệt.
<
m e
>
. 
0 1
m
< ≤
. :0
m e
< <
. &1
m e
< <
.
7 = Lấy nguyên hàm hai vế
(
)
(
)
'
2 2
f x
x
f x
= −
, ta được
(
)
(
)
( )
d 2 2 d
f x
x x x
f x
= −
∫ ∫
(
)
(
)
2 2
ln 2 ln 2
f x x x C f x x x C
⇔ = − + ⇔ = − +
(do
(
)
0,f x x
> ∀ ∈
ℝ
)
(
)
2
2
x x C
f x e
− +
⇔ = .
Theo giả thiết
(
)
0 1 1 0
C
f e C
= → = ⇔ =
. Suy ra
(
)
2
2
.
x x
f x e
−
=
Xét phương trình
( )
2
2 2
2
2 ln 2 ln 0
.
0 0
x x
x x m x x m
f x m e m
m m
−
− + = − + − =
= ⇔ = ⇔ ⇔
> >
Phương trình
(
)
f x m
có hai nghiệm thực phân biệt
1 ln 0
0
0
m
m e
m
∆ = − >
⇔ ⇔ < <
>
.
:>:
:#;EDCho hàm số
(
)
f x
liên tục trên
ℝ
và
0
a
>
. Giả sử rằng với mọi
[
]
0;
x a
, ta
có
(
)
0
f x
>
và
(
)
(
)
1
f x f a x
− =
. Tính
(
)
0
d
1
a
x
I
f x
=
+
∫
.
<
2
a
I
=
.
2 .
I a
:
.
3
a
I = &
(
)
ln 1 .
I a a
= +
7 = Từ giả thiết, suy ra
( )
(
)
1
f a x
f x
− = .
Đặt
d d
t a x t x
= − → = −
. Đổi cận:
0
0
x t a
x a t
= → =
= → =
.
Khi đó
( )
(
)
(
)
( )
(
)
( )
0
0 0 0
d d
d d .
1
1 1 1
1
a a a
a
f t f x
t t
I t x
f a t f t f x
f t
= − = = =
+ − + +
+
∫ ∫ ∫ ∫
Suy ra
(
)
(
)
(
)
0 0 0
d
2 d d .
1 1 2
a a a
f x
x a
I I I x x a I
f x f x
= + = + = = → =
+ +
∫ ∫ ∫
:><
:TUVWChọn
(
)
(
)
1 0 1
f x f a x
= > → − =
thỏa
(
)
(
)
1.
f x f a x
− =
Khi đó
0
0
d 1
.
1 1 2 2
a
a
x a
I x= = =
+
∫
:#;ECho số thực
0
a
≠
, đặt
(
)
1
d
2
a
x
a
b x
a x e
−
=
+
∫
. Tính
2
0
d
3
a
x
e
x
a x−
∫
theo
a
và
b
.
<
2
0
d .
3
a
x
a
e b
x
a x
e
=
−
∫

2
0
d .
3
a
x
a
e b
x
a x
e
=
−
∫
:
2
0
d . .
3
a
x
a
e
x b e
a x
=
−
∫
&
2
0
d .
3
a
x
b
e a
x
a x
e
=
−
∫
7 = Ta đổi biến để đưa tích phân cần tính về tích phân đã cho bằng cách đặt
d d
3 2 .
x t
a x a t
x a t
= −
− = + →
= −
Đổi cận:
0
.
2
x t a
x a t a
= → =
= → = −
Khi đó
( )
(
)
( )
(
)
1 1
d . d . d . .
2 2 2
a a a
a t
a a a
t t
a a a
e
t e t e t e b
a t a t e a t e
− −
−
−
− = − = =
+ + +
∫ ∫ ∫
:>:
O
y
x
b
a
(
)
y f x
=
(
)
y g x
=
y
O
a
b
(
)
y f x
=
x
Baøi 05
ÖÙNG DUÏNG TÍCH PHAÂN
1. Tính diện tích hình phẳng
Định lí
Cho hàm số
(
)
y f x
liên tục, không âm trên đoạn
[
]
;
a b
. Khi đó diện tích
S
của
hình thang cong giới hạn bởi đồ thị hàm số
(
)
y f x
, trục hoành và hai đường thẳng
,
x a x b
= =
là
( )
b
a
S f x x
=
∫
Bài toán 1. Cho hàm số
(
)
y f x
liên tục trên đoạn
[
]
;
a b
. Khi đó diện tích
S
của
hình phẳng
(
)
D
giới hạn bởi đồ thị hàm số
(
)
y f x
; trục hoành
Ox
(
0
y
=
) và hai
đường thẳng ;
x a x b
= =
là
( )
d
b
a
S f x x
=
∫
.
Bài toán 2. Diện tích hình phẳng giới hạn
bởi hai đồ thị
(
)
y f x
;
(
)
y g x
và hai
đường đường thẳng ;
x a x b
= =
là
( ) ( )
d .
b
a
S f x g x x
= −
∫
Chú ý:
1) Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau:
- Giải phương trình
(
)
(
)
f x g x
tìm nghiệm
(
)
1 2
, ,..., ;
n
x x x a b
(
)
1 2
...
n
x x x
< < <
.
- Tính
( ) ( ) ( ) ( )
1 2
1
d d
x x
a x
S f x g x x f x g x x
= − + − +
∫ ∫
( ) ( )
... d
n
b
x
f x g x x
+ −
∫
( ) ( )
( )
( ) ( )
( )
1
d ... d
n
x b
a x
f x g x x f x g x x
= − + + −
∫ ∫
.
Ngoài cách trên, ta có thể dựa vào đồ thị để bỏ dấu giá trị tuyệt đối.
2) Trong nhiều trường hợp, bài toán yêu cầu tính diện tích hình phẳng giới hạn bởi
hai đồ thị
(
)
y f x
;
(
)
y g x
.
Khi đó, ta có công thức tính như sau
( ) ( )
1
d
n
x
x
S f x g x x
= −
∫
.
Trong đó
1
x
và
n
x
tương ứng là nghiệm nhỏ nhất, lớn nhất của
(
)
(
)
f x g x
.
(
)
y f x
=
a
b
y
x
O
2. Tính thể tích khối tròn xoay
a) Tính thể tích của vật thể
Định lí
Cắt một vật thể
C
bởi hai mặt phẳng
(
)
P
và
(
)
Q
vuông góc với trục
Ox
lần lượt
tại
(
)
,
x a x b a b
= = <
. Một mặt phẳng bất kì vuông góc với
Ox
tại điểm
(
)
x a x b
≤ ≤
cắt
C
theo một thiết diện có diện tích
(
)
S x
. Giả sử
(
)
S x
là hàm liên tục trên đoạn
[
]
;
a b
. Khi đó thể tích của vật thể
C
giới hạn bởi hai mặt phẳng
(
)
P
và
(
)
Q
được tính
theo công thức
( )
b
a
V S x x
=
∫
b) Tính thể tích vậy tròn xoay
Bài toán 1. Tính thể tích vật thể tròn xoay
khi quay miền
D
được giới hạn bởi các
đường
(
)
; 0
y f x y
= =
;
;
x a
=
x b
=
quanh
trục
Ox
được tính theo công thức
( )
2
d
b
a
V f x x
π=
∫
.
Chú ý: Nếu hình phẳng
D
được giới hạn bởi các đường
(
)
;
y f x
(
)
y g x
và hai
đường
;
x a x b
= =
(với
(
)
(
)
[
]
. 0, ;
f x g x x a b
≥ ∀ ∈
) thì thể tích khối tròn xoay sinh bởi
khi quay
D
quanh trục
Ox
được tính bởi công thức
( ) ( )
2 2
d
b
a
V f x g x x
π= −
∫
.
Bài toán 2. Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng
D
giới hạn
bởi các đường
(
)
x g y
, trục tung và hai đường
,
y a y b
= =
quanh trục
Oy
được
tính theo công thức
( )
2
d
b
a
V g y y
π=
∫
.
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1. TÍNH DIỆN TÍCH HÌNH PHẲNG
Câu 1. Cho hàm số
(
)
y f x
liên tục trên
[
]
; .
Diện tích hình phẳng
S
giới hạn bởi
đường cong
(
)
,
y f x
trục hoành và các đường thẳng
(
)
,
x a x b a b
= = <
được xác
định bởi công thức nào sau đây?
A.
( )
d .
b
a
S f x x
=
∫
B.
( )
d .
a
b
S f x x
=
∫
C.
( )
d .
a
b
S f x x
=
∫
D.
( )
d .
b
a
S f x x
=
∫
Lời giải. Chọn D.
Câu 2. Cho đồ thị hàm số
(
)
y f x
như hình vẽ
bên. Diện tích
S
của hình phẳng phần tô đậm
trong hình được tính theo công thức nào sau đây?
A.
( )
3
2
d
S f x x
−
=
∫
.
B.
( ) ( )
0 3
2 0
d d
S f x x f x x
−
= +
∫ ∫
.
C.
( ) ( )
2 3
0 0
d d
S f x x f x x
−
= +
∫ ∫
.
D.
( ) ( )
0 0
2 3
d d
S f x x f x x
−
= +
∫ ∫
.
y=f(x)
y
x
O
3
-2
Lời giải. Theo hình vẽ, ta có
( ) ( ) ( )
3 0 3
2 2 0
d d d
S f x x f x x f x x
− −
= = − +
∫ ∫ ∫
( ) ( )
2 3
0 0
d d
f x x f x x
−
= +
∫ ∫
. Chọn C.
Câu 3. Cho hai hàm số
(
)
(
)
1 2
,
y f x y f x
= =
liên tục trên
[
]
; .
Diện tích hình phẳng
S
giới hạn các bởi đường cong
(
)
(
)
1 2
,
y f x y f x
= =
và các đường thẳng
,
x a
=
(
)
x b a b
= <
được xác định bởi công thức nào sau đây?
A.
( ) ( )
1 2
d .
b
a
S f x f x x
= −
∫
B.
( ) ( )
2 1
d .
b
a
S f x f x x
= −
∫
C.
( ) ( )
1 2
d .
b
a
S f x f x x
= −
∫
D.
( ) ( )
1 2
d .
b
a
S f x f x x
= +
∫
Lời giải. Chọn A.
Câu 4. Diện tích hình phẳng
S
giới hạn bởi
các đồ thị hàm số
2 , 4
y x y x
= = −
và trục
hoành
Ox
(như hình vẽ) được tính bởi công
thức nào dưới đây?
A.
( )
4 4
0 0
2 d 4 d .
S x x x x
= + −
∫ ∫
B.
( )
2 4
0 2
2 d 4 d .
S x x x x
= + −
∫ ∫
C.
( )
4
0
2 4 d .
S x x x
= − +
∫
D.
( )
2
0
4 2 d .
S x x x
= − −
∫
Lời giải. Xét các phương trình hoành độ giao điểm:
2
4
2 4 2;
10 16 0
4 0 4;
2 0 0.
x
x x x
x x
x x
x x
• = − ⇔ ⇔ =
− + =
• − = ⇔ =
• = ⇔ =
Dựa vào hình vẽ, ta có
( )
2 4
0 2
2 d 4 d .
S x x x x
= + −
∫ ∫
Chọn B.
Câu 5. Diện tích hình phẳng
S
giới hạn bởi các đồ
thị hàm số
3
, 2
y x y x
= = −
và trục hoành
Ox
(như
hình vẽ) được tính bởi công thức nào dưới đây?
A.
( )
1 2
3
0 1
d 2 d .
S x x x x
= + −
∫ ∫
B.
( )
2
3
0
2 d .
S x x x
= + −
∫
C.
1
3
0
1
d .
2
S x x
= +
∫
D.
( )
1
3
0
2 d .
S x x x
= − −
∫
Lời giải. Xét các phương trình hoành độ giao điểm:
3 3
3
2 2 0 1;
0 0;
2 0 2.
x x x x x
x x
x x
• = − ⇔ + − = ⇔ =
• = ⇔ =
• − = ⇔ =
Dựa vào hình vẽ, ta có
( )
1 2 1
3 3
0 1 0
1
d 2 d d .
2
S x x x x x x
= + − = +
∫ ∫ ∫
Chọn C.
Câu 6. Diện tích hình phẳng
S
giới hạn bởi các đồ thị hàm số
3
, 2
y x x y x
= − =
và
các đường
1, 1
x x
= − =
được xác định bởi công thức nào sau đây?
A.
( )
1
3
1
3 d .
S x x x
−
= −
∫
B.
( )
1
3
1
3 d .
S x x x
−
= −
∫
C.
( ) ( )
0 1
3 3
1 0
3 d 3 d .
S x x x x x x
−
= − + −
∫ ∫
D.
( ) ( )
0 1
3 3
1 0
3 d 3 d .
S x x x x x x
−
= − + −
∫ ∫
Lời giải. Xét phương trình hoành độ giao điểm:
[
]
[ ]
3 3
0 1;1
2 3 0 .
3 1;1
x
x x x x x
x
= ∈ −
− = ⇔ − = ⇔
= ± ∉ −
Diện tích hình phẳng cần tính:
0 1
3 3
1 0
2 d 2 d
S x x x x x x x x
−
= − − + − −
∫ ∫
( ) ( )
0 1
xet dau
3 3
1 0
3 d 3 d .
x x x x x x
−
= − + −
∫ ∫
Chọn C.
Câu 7. Sơ đồ ở bên phải phác thảo của một khung cửa sổ.
Diện tích
S
của cửa sổ được tính bởi công thức nào sau
đây?
A.
1
2
2
1
2
5
4 d
2
S x x
−
= −
∫
. B.
1
2
2
1
2
5
2 d
2
S x x
−
= −
∫
.
C.
1
2
2
1
2
2 d
S x x
−
=
∫
. D.
( )
1
2
2
1
2
1 4 d
S x x
−
= −
∫
.
x
y
1
2
1
2
−
O
2
5
2
2
y x
= −
2
2
y x
=
Lời giải. Dựa vào đồ thị ta thấy trên đoạn
1 1
;
2 2
−
thì đồ thị hàm số
2
1
5
2
y x
= −
nằm phía trên đồ thị hàm số
2
2
2
y x
.
Do đó
( )
1 1 1
2 2 2
2 2 2
1 2
1 1 1
2 2 2
5 5
d 2 2 d 4 d .
2 2
S y y x x x x x x
− − −
= − = − − = −
∫ ∫ ∫
Chọn A.
Câu 8. Cho hai hàm số
(
)
f x
và
(
)
g x
liên tục trên đoạn
[
]
;
a b
với
.
a b
<
Kí hiệu
1
S
là
diện tích hình phẳng giới hạn bởi các đường
(
)
(
)
2 , 2 ,
y f x y g x x a
= = =
và
;
x b
=
2
S
là diện tích hình phẳng giới hạn bởi các đường
(
)
(
)
2, 2,
y f x y g x x a
= − = − =
và
x b
=
. Mệnh đề nào sau đây là đúng?
A.
1 2
.
S S
B.
1 2
2 .
S S
C.
1 2
2 2.
S S
= −
D.
1 2
2 2.
S S
= +
Lời giải. Ta có
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
1
1 2
2
2 2 d 2 d
2 .
2 2 d d
b b
a a
b b
a a
S f x g x x f x g x x
S S
S f x g x x f x g x x
= − = −
→ =
= − − − = −
∫ ∫
∫ ∫
Chọn B.
Câu 9. Cho hàm số
(
)
f x
xác định và đồng biến trên đoạn
[
]
0;1
và
1
1
2
f
=
. Diện
tích hình phẳng
S
giới hạn bởi đồ thị của các hàm số
(
)
1
y f x
,
( )
2
2
y f x
=
và các
đường
0
x
=
,
1
x
=
được xác định bởi công thức nào sau đây?
A.
( ) ( ) ( ) ( )
1 1
2 2
0 1
1 d 1 d .
S f x f x x f x f x x
= − + −
∫ ∫
B.
( ) ( )
( )
1
2
0
d .
S f x f x x
= −
∫
C.
( ) ( ) ( ) ( )
1
1
2
1
0
2
1 d 1 d .
S f x f x x f x f x x
= − + −
∫ ∫
D.
( )
( )
( )
1
2
0
d .
S f x f x x
= −
∫
Lời giải. Gọi
S
là diện tích hình phẳng cần tính. Ta có
( ) ( )
1
2
0
d
S f x f x x
= −
∫
( ) ( ) ( ) ( ) ( ) ( )
1
1 1
2
1
0 0
2
. 1 d . 1 d 1 d .
f x f x x f x f x x f x f x x
= − = − + −
∫ ∫ ∫
Do hàm số
(
)
f x
đồng biến trên
[ ]
( )
( )
1 1
1, ;1
2 2
0;1
1 1
1, 0;
2 2
f x f x
f x f x
≥ = ∀ ∈
→
≤ = ∀ ∈
( ) ( )
( ) ( )
1
1 1, ;1
2
.
1
1 1 , 0;
2
f x f x x
f x f x x
− = − ∀ ∈
→
− = − ∀ ∈
Vậy
( ) ( ) ( ) ( )
1
1
2
1
0
2
1 d 1 d
S f x f x x f x f x x
= − + −
∫ ∫
. Chọn C.
Câu 10. Cho hàm số
(
)
f x
có đồ thị trên
đoạn
[
]
1;4
−
như hình vẽ bên. Tính tích
phân
( )
4
1
d .
I f x x
−
=
∫
A.
5
.
2
I =
B.
11
.
2
I =
C.
5.
I
=
D.
3.
I
=
Lời giải. Gọi
(
)
(
)
(
)
(
)
(
)
(
)
1;0 , 0;2 , 1;2 , 2;0 , 3; 1 , 4; 1
A B C D E F
− − −
và
(
)
(
)
(
)
1;0 , 3;0 , 4;0
H K L .
Khi đó
( ) ( ) ( ) ( ) ( ) ( )
4 0 1 2 3 4
1 1 0 1 2 3
d d d d d d
I f x x f x x f x x f x x f x x f x x
− −
= = + + + +
∫ ∫ ∫ ∫ ∫ ∫
( ) ( ) ( ) ( ) ( )
0 1 2 3 4
1 0 1 2 3
d d d d d
f x x f x x f x x f x x f x x
−
= + + − −
∫ ∫ ∫ ∫ ∫
(do
(
)
[
]
0, 1;2
f x x
≥ ∀ ∈ −
và
(
)
[
]
0, 2;4
f x x
≤ ∀ ∈
)
1 1 1 5
.2.1 2.1 .2.1 .1.1 1.1
2 2 2 2
ABO OBCH HCD DKE EFLK
S S S S S
= + + − − = + + − − =
. Chọn A.
Câu 11. Kí hiệu
1 2
,
S S
lần lượt là diện tích hình vuông cạnh bằng
1
và diện tích
hình phẳng giới hạn bởi các đường
2
1, 0, 1, 2.
y x y x x
= + = = − =
Trong các khẳng
định sau, khẳng định nào là đúng?
A.
1 2
S S
. B.
1 2
S S
>
. C.
1 2
1
2
S S
=
. D.
2
1
6
S
S
=
.
Lời giải. Ta có
1
1
S
=
và
( )
2 2
3
2
2 2
2
1
1 1
1 d 1 d 6
3
x
S x x x x x
−
− −
= + = + = + =
∫ ∫
2
1
6
S
S
→ =
. Chọn D.
Câu 12. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị của hai hàm số
2
2
y x
= +
và
3
y x
.
A.
2
S
=
. B.
3
S
=
. C.
1
2
S
=
. D.
1
6
S
=
.
Lời giải. Phương trình hoành độ giao điểm:
2
1
2 3 .
2
x
x x
x
=
+ = ⇔
=
Diện tích hình phẳng cần tính:
2
CASIO
2
1
1
2 3 d .
6
S x x x= + − =
∫
O
-
1
4
3
2
1
2
-
1
y
x
Chọn D.
Câu 13. (ĐỀ MINH HỌA 2016 – 2017) Tính diện tích hình phẳng
S
giới hạn bởi đồ
thị hàm số
3
y x x
= −
và đồ thị hàm số
2
.
y x x
= −
A.
37
.
12
S = B.
9
.
4
S = C.
81
.
12
S = D.
13.
S
Lời giải. Phương trình hoành độ giao điểm:
3 2
0
1 .
2
x
x x x x x
x
− = − ⇔ =
= −
Diện tích hình phẳng cần tính:
1
CASIO
3 2
2
37
2 d 3,083 .
12
S x x x x
−
= + − =
∫
≃
Chọn A.
Cách kiểm tra máy tính. Dùng CASIO tính tích phân
1
3 2
2
2 d
x x x x
−
+ −
∫
rồi lưu vào
biến A. Bây giờ ta thử với đáp án A có đúng không nhé? Ta xét hiệu
37
A
12
− và nhấn
dấu
. Nếu màn hình xuất hiện số 0 thì đáp án đó đúng.
Câu 14. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
2
3
y x x
= −
và hai
đường thẳng
15, 15.
x x
= − =
A.
2250.
S
B.
2259.
S
C.
1593.
S
D.
2925.
S
Lời giải. Diện tích hình phẳng cần tính:
15
2
15
3 d
S x x x
−
= −
∫
.
Bảng xét dấu của biểu thức
(
)
2
3
f x x x
= −
trên đoạn
[
]
15;15 .
Suy ra
( ) ( ) ( )
0 3 15
2 2 2
15 0 3
3 d 3 d 3 d
S x x x x x x x x x
−
= − − − + −
∫ ∫ ∫
3 2 3 2 3 2
0 3 15
15 0 3
3 3 3
2259.
3 2 3 2 3 2
x x x x x x
−
= − − − + − =
Chọn B.
Cách 2. Dùng máy tính cầm tay.
Đối với VINACAL. Ta tính
15
2
15
3 d 2259.
x x x
−
− =
∫
Đúng với kết quả tính tay.
Đối với CASIO. Ta tính
15
2
15
3 d 2250.
x x x
−
− =
∫
Không đúng với kết quả tính tay.
Lý do nào hai loại máy tính này cho ta hai kết quả khác nhau? Giải thích: Máy
CASIO
''
thường không đúng
''
cho tích phân trị tuyệt đối với hai cận chứa 3 đoạn đổi
dấu trở lên.
Câu 15. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
2
1
y x x
= +
, trục
hoành và đường thẳng
1
x
=
.
A.
1
.
3
S =
B.
2 2 1
.
3
S
−
= C.
2 2 1
.
3
S
+
= D.
(
)
2 2 1 .
S = −
Lời giải. Phương trình hoành độ giao điểm:
2
1 0 0.
x x x
+ = ⇔ =
Diện tích hình phẳng:
1 1
CASIO
2 2
0 0
2 2 1
1 d 1 d .
3
S x x x x x x
−
= + = + =
∫ ∫
Chọn B.
(
)
f x
0
15
3
0
15
−
x
0
+
−
+
Câu 16. Kí hiệu
1 2 3
, ,
S S S
lần lượt là diện tích hình vuông đơn vị (có cạnh bằng đơn
vị), hình tròn đơn vị (có bán kính bằng đơn vị), hình phẳng giới hạn bởi hai đường
2
2 1 ,
y x
= −
(
)
2 1
y x
= −
. Tính tỉ số
1 3
2
.
S S
S
A.
1 3
2
1
.
3
S S
S
= B.
1 3
2
1
.
4
S S
S
= C.
1 3
2
1
.
2
S S
S
= D.
1 3
2
1
.
5
S S
S
=
Lời giải. Ta tính được
2
1
1 1
S
= =
và
2
2
1 . .
S
π π
= =
Tính
3
.
S
Phương trình hoành độ giao điểm:
( )
2 CASIO
0
2 1 2 1 .
1
x
x x
x
=
− = − →
=
Khi đó
( )
1
2
3
0
2 1 2 1 d
S x x x
= − − −
∫
. Dùng CASIO tính tích phân và lưu vào biến A.
Tiếp theo bấm
1 A
π
và nhấn dấu . Màn hình hiện kết quả
1
2
. Chọn C.
Câu 17. Diện tích hình phẳng giới hạn bởi các đường
y x
=
và
2 0
x y
− =
bằng với
diện tích hình nào sau đây?
A. Diện tích hình vuông có cạnh bằng
2
.
B. Diện tích hình chữ nhật có chiều dài, chiều rộng lần lượt
5
và
3
.
C. Diện tích hình tròn có bán kính bằng
3
.
D. Diện tích toàn phần khối tứ diện đều có cạnh bằng
4
2 3
3
.
Lời giải. Phương trình hoành độ giao điểm:
2
0
0
.
4
2
4
x
x
x
x
x
x x
= ⇔ ⇔
=
=
Diện tích hình phẳng cần tính:
4
CASIO
0
4
d 1,3 .
2 3
x
S x x= − =
∫
≃
A. Diện tích hình vuông có cạnh bằng
2 4.
A
S
→ =
B. Diện tích hình chữ nhật có chiều dài, chiều rộng lần lượt
5
và
3
15.
B
S
→ =
C. Diện tích hình tròn có bán kính bằng
3
9 .
C
S
π
→ =
D. Diện tích toàn phần khối tứ diện đều có cạnh bằng
4
2 3
3
( )
2
4
canh . 3 .
3
D
S→ = =
Chọn D.
Câu 18. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
(
)
2
2
1
y
x
=
+
, trục
hoành và hai đường thẳng
0
x
=
,
4
x
=
.
A.
8
.
5
S
= −
B.
8
.
5
S =
C.
2
.
25
S =
D.
4
.
25
S =
Lời giải. Diện tích hình phẳng cần tính:
( )
4
CASIO
2
0
2 8
d .
5
1
S x
x
= =
+
∫
Chọn B.
Câu 19. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
ln
y x x
=
, trục
hoành và đường thẳng
x e
=
.
A.
2
1
4
e
S
+
= . B.
2
1
6
e
S
+
= . C.
2
1
8
e
S
+
= . D.
2
1
2
e
S
+
= .
Lời giải. Phương trình hoành độ giao điểm:
0
ln 0 1.
0
ln 0
x
x x x
x
x
= ⇔ ⇔ =
=
=
Diện tích hình phẳng cần tính:
CASIO
1
ln d 2,09726
e
S x x x=
∫
≃ .
Đối chiếu kết quả với bốn đáp án đã cho. Chọn A.
Câu 20. Biết rằng diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
ln
y x
,
trục hoành và hai đường thẳng
1
,
x x e
e
= =
được dưới dạng
1
1 .
S a
e
= −
Mệnh đề
nào sau đây là sai?
A.
2
3 2 0.
a a
− + =
B.
2
2 0.
a a
− − =
C.
2
3 4 0.
a a
+ − =
D.
2
2 3 2 0.
a a
− − =
Lời giải. Diện tích hình phẳng cần tính:
1
xet dau
1 1
1
ln d ln d ln d
e e
e e
S x x x x x x
= = − +
∫ ∫ ∫
( ) ( )
1
tung phan
1
1
1
ln ln 2 1 2.
e
e
x x x x x x a
e
= − − + − = − → =
Chọn C.
Câu 21. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
x
y e x
= +
, trục
hoành, trục tung và đường thẳng
1
x
=
.
A.
1
.
2
S e= + B.
1
.
2
S e= − C.
1.
S e
= +
D.
1.
S e
= −
Lời giải. Diện tích hình phẳng cần tính:
1
CASIO
0
d 2,21828
x
S e x x= +
∫
≃
.
Đối chiếu kết quả với bốn đáp án đã cho. Chọn B.
Câu 22. Tính diện tích hình phẳng
S
giới hạn bởi các đường
x
y e x
= +
,
1 0
x y
− + =
và
ln 5
x
.
A.
5 ln 4
S
= +
. B.
5 ln 4
S
= −
. C.
4 ln 5
S
= +
. D.
4 ln 5
S
= −
.
Lời giải. Ta có
1 0 1.
x y y x
− + = → = +
Phương trình hoành độ giao điểm:
1 1 0
x x
e x x e x
+ = + ⇔ = ⇔ =
.
Diện tích hình phẳng cần tính:
( )
( )
ln 5 ln 5
CASIO
0 0
1 d 1 d 2,39056.
x x
S e x x x e x= + − + = −
∫ ∫
≃
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 23. Tính diện tích hình phẳng
S
giới hạn bởi các đường
(
)
1
y e x
= +
và
(
)
1 .
x
y e x
= +
A.
2
2
e
S
+
= . B.
2
e
S
=
. C.
2
2
e
S
−
= . D.
2
4
e
S
−
= .
Lời giải. Phương trình hoành độ giao điểm:
( )
( )
( )
0
1 1 0 .
1
x x
x
e x e x x e e
x
+ = + ⇔ − = ⇔
=
Diện tích cần tính:
( )
( )
( )
1 1
CASIO
0 0
1 1 d d 0,35914.
x x
S e x e x x x e e x= + − + = −
∫ ∫
≃
Đối chiếu kết quả với bốn đáp án đã cho. Chọn C.
Câu 24. Tính diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
1
x
y e
= +
, trục
hoành và hai đường thẳng
ln 3
x
,
ln 8
x
.
A.
2
2 ln
3
S = + . B.
3
2 ln
2
S = + . C.
3
3 ln
2
S = + . D.
3
2 ln
2
S = − .
Lời giải. Diện tích hình phẳng cần tính:
ln 8 ln 8
CASIO
ln 3 ln 3
1 d 1d 2,40546.
x x
S e x e x= + = + =
∫ ∫
Đối chiếu kết quả với bốn đáp án đã cho. Chọn B.
Câu 25. (ĐỀ THỬ NGHIỆM 2016 – 2017) Cho
hình thang cong
(
)
H
giới hạn bởi các đường
, 0, 0, ln 4.
x
y e y x x
= = = =
Đường thẳng
x k
=
(
)
0 ln 4
k
< <
chia
(
)
H
thành hai phần có diện tích
là
1
S
và
2
S
như hình vẽ bên. Tìm
k
để
1 2
2
S S
.
A.
2
ln 4.
3
k =
B.
ln 2.
k
C.
8
ln .
3
k =
D.
ln 3.
k
Lời giải. Ta có
1
0
0
d 1
k
k
x x k
S e x e e
= = = −
∫
và
ln 4
ln 4
2
d 4 .
x x k
k
k
S e x e e
= = = −
∫
Theo giả thiết
(
)
1 2
2 1 2 4 ln 3
k k
S S e e k
= ⇔ − = − ⇔ =
. Chọn D.
Câu 26. Kí hiệu
(
)
H
là hình phẳng giới hạn bởi các
đường
x
y e
,
0
y
=
,
0
x
=
và
1
x
=
. Đường thẳng
(
)
0 1
x k k
= < <
chia
(
)
H
thành hai phần có diện
tích tương ứng
1 2
,
S S
như hình vẽ bên, biết
1 2
S S
>
.
Mệnh đề nào sau đây là đúng?
A.
3
.
2
k
e
e
+
> B.
2
.
2
k
e
e
>
C.
1
.
2
k
e
e
+
> D.
1
.
2
k
e
e
−
>
Lời giải. Ta có
1
0
0
d 1
k
k
x x k
S e x e e
= = = −
∫
và
1
1
2
d
x x k
k
k
S e x e e e
= = = −
∫
.
Theo giả thiết
1 2
1
1 .
2
k k k
e
S S e e e e
+
> ⇔ − > − ⇔ >
Chọn C.
Câu 27. Cho hình phẳng
(
)
H
giới hạn bởi các
đường
2
, 0, 0, 4.
y x y x x
= = = =
Đường thẳng
(
)
0 16
y k k
= < <
chia hình
(
)
H
thành hai
phần có diện tích
1 2
,
S S
(hình vẽ). Tìm
k
để
1 2
S S
.
A.
3
k
=
. B.
4
k
=
.
C.
5.
k
=
D.
8
k
=
.
Lời giải. Phương trình hoành độ giao điểm:
2
x k x k
= → =
. Ta có:
●
4
4
3
2
1 2
0
0
64
d .
3 3
x
S S x x+ = = =
∫
●
( )
4
4
3
2
1
2 64
d 4 .
3 3 3
k
k
x k k
S x k x kx k
= − = − = − + +
∫
Theo giả thiết
( )
1 2 1 1 2
1 2 64 32
4
2 3 3 3
k k
S S S S S k= → = + ⇔ − + + =
(
)
0 4
3 2
2 12 32 0 2 12 32 0 2 4.
t k t
k k k t t t k
= < <
⇔ − + = → − + = → = → =
Chọn B.
O
x
y
1
S
2
S
k
ln 4
Câu 28. Xét hình phẳng
(
)
H
giới hạn bởi đồ thị
hàm số
(
)
2
3
y x= +
, trục hoành và đường thẳng
0.
x
=
Gọi
(
)
0;9
A
,
(
)
;0
B b
(
)
3 0
b
− < <
. Tính giá trị
của tham số
b
để đoạn thẳng
AB
chia
(
)
H
thành
hai phần có diện tích bằng nhau.
A.
2
b
= −
. B.
1
2
b
= −
.
C.
1.
b
= −
D.
3
2
b
= −
.
Lời giải. Phương trình hoành độ giao điểm:
(
)
2
3 0 3.
x x
+ = ⇔ = −
Do đó
( )
( )
0
CASIO
2
3
3 d 9.
H
S x x
−
= + =
∫
Diện tích tam giác
OAB
bằng:
1 9
.
2 2
OAB
S OA OB b
= = .
Ycbt
( )
( )
3 0
1 9 9
1.
2 2 2
b
OAB
H
S S b b
− < <
←→ = ⇔ = → = −
Chọn C.
Câu 29. Cho hàm số
(
)
y f x
liên tục trên
ℝ
và hàm
số
(
)
(
)
2
.
y g x x f x
= =
có đồ thị trên đoạn
[
]
1;2
như
hình vẽ bên. Biết phần diện tích miền được tô màu là
5
2
S
=
, tính giá trị của tích phân
( )
4
1
d .
I f x x
=
∫
A.
5
.
2
I = B.
5
.
4
I =
C.
10.
I
D.
5.
I
=
Lời giải. Diện tích phần tô màu là
( )
2
1
d .
S g x x
=
∫
Theo giả thiết
( )
2
2
1
5 5
. d .
2 2
S x f x x= ⇔ =
∫
Đặt
2
d 2 d
t x t x x
= → =
. Đổi cận:
1 1
.
2 4
x t
x t
= → =
= → =
Khi đó
( )
( ) ( )
2 4 4
2
1 1 1
5 1
. d d d 5
2 2
x f x x f t t f t t
= = → =
∫ ∫ ∫
hay
( )
4
1
d 5.
f x x
=
∫
Chọn D.
Câu 30. Một khung cửa có hình dạng như hình vẽ,
phần phía trên là một parabol. Biết
2,5m
a
,
0,5m
b
,
2m
c
. Biết số tiền một mét vuông cửa là 1
triệu đồng. Số tiền cần để mua cửa là:
A.
14
3
triệu đồng. B.
13
7
triệu đồng.
C.
3
17
triệu đồng. D.
17
3
triệu đồng.
Lời giải. Diện tích khung cửa bằng: diện tích hình vuông + diện tích parabol.
Diện tích hình vuông
2
1
2.2 4 m
S
= =
.
Diện tích parabol
2
2
2 2
.2.0,5 m
3 3
S = = (Công thức giải nhanh
2
3
S Bh
= với
B
là chiều
dài của đáy,
h
là chiều cao).
Suy ra diện tích khung cửa
2
1 2
14
m
3
S S S= + = .
Khi đó số tiền cần phải trả:
14
1
3
T
= ×
triệu
14
3
= triệu đồng. Chọn A.
Câu 31. Biết rằng đường parabol
(
)
2
: 2
P y x
chia
đường tròn
(
)
2 2
: 8
C x y
+ =
thành hai phần lần lượt
có diện tích là
1 2
,
S S
(hình vẽ bên). Khi đó
2 1
b
S S a
c
π
− = −
với
, ,
a b c
nguyên dương và
b
c
là
phân số tối giản. Tính
.
S a b c
= + +
A.
13.
S
B.
14.
S
C.
15.
S
D.
16.
S
Lời giải. Đường tròn
(
)
C
có tâm
(
)
0;0
O
, bán kính
2 2R
= →
diện tích
8 .
S
π
Phương trình hoành độ giao điểm của
(
)
P
và
(
)
C
là:
2
2
2 2
0
2
2.
2 8
8
x
y x
x
x x
x y
≥
=
→ ↔ =
+ =
+ =
Suy ra
2 2 2
2
1 2 1
0 2
4 4
2 2 d 2 8 d 2 6
3 3
S x x x x S S Sπ π
= + − = + → = − = −
∫ ∫
.
2 1
4
8
4 8
3
3
a
S S b
c
π
=
→ − = − → =
=
. Chọn C.
Câu 32. Một bồn hình trụ chứa dầu được đặt nằm
ngang, có chiều dài 5m, bán kính đáy 1m, với nắp bồn
đặt trên mặt nằm ngang của mặt trụ. Người ta rút
dầu trong bồn tương ứng với 0,5m của đường kính
đáy. Tính thể tích gần đúng nhất của khối dầu còn lại
trong bồn.
A. 11,781
3
m .
B. 12,637
3
m .
C. 1
3
14,923 m .
D.
3
8,307 m .
Lời giải. Thể tích của bồn (hình trụ) đựng dầu là:
2 2 3
1
.1 .5 5 m .
V r h
π π π
= = =
Bây giờ ta tính phần dầu bị rút ra bằng 2 cách:
Cách 1. (Dùng tích phân)
Chọn hệ tục tọa độ như hình vẽ, gốc tọa độ gắn
với tâm của mặt đáy.
Đường tròn đáy có bán kính bằng 1 nên có
phương trình
2 2
1
x y
+ =
.
Suy ra
2
1
y x
= ± −
.
Diện tích phần hình tròn đáy bị mất:
1
2 2
1
2
2 1 d 0,61m .
S x x= − ≈
∫
Thể tích phần dầu bị rút ra ngoài:
1
2 3
2
1
2
2 1 d 5 3,07m
V S h x x= × = − × ≈
∫
.
Vậy thể tích của khối dầu còn lại trong bồn:
3
1 2
12,637m .
V V V
= − ≈
Chọn B.
Cách 2. (Áp dụng diện tích cung tròn khi biết góc ở tâm trừ đi
diện tích tam giác tạo bởi tâm và 2 đầu mút dây cung)
( )
2 2
1 1 1
. . .sin sin
2 2 2
viên phân
S R R R R
α α α α
= − = −
với
α
tính theo đơn vị radian.
Tính góc ở tâm:
1 2
cos .
2 2 2 3 3
OH OH
OA R
α α π π
α= = = → = ⇒ =
Diện tích phần hình tròn đáy bị mất (phần bôi đen)
( )
2 2 2
1 1 2 2
sin .1 . sin 0,61m .
2 2 3 3
viên phân
S R
π π
α α
= − = − ≈
H
B
A
O
Câu 33. Cho một viên gạch men có dạng hình
vuông
OABC
như hình vẽ. Sau khi tọa độ hóa,
ta có
(
)
(
)
(
)
(
)
0;0 , 0;1 , 1;1 , 1;0
O A B C
và hai đường
cong trong hình lần lượt là đồ thị hàm số
3
y x
và
3
.
y x
Tính tỷ số diện tích của phần tô đậm
so với diện tích phần còn lại của hình vuông.
A.
1
.
2
B.
5
.
4
C.
4
.
3
D.
1.
Lời giải. Diện tích hình vuông có cạnh bằng
1
là
2 2
1
1 1 m
S
= =
.
Diện tích phần tô đậm :
1
CASIO
3 2
3
2
0
1
d m .
2
S x x x= − = =
∫
Do đó diện tích phần còn lại :
2
2
1 2
1 1
1 m 1.
2 2
S
S S S
S
∆ = − = − = → =
Chọn D.
Câu 34. (ĐỀ THỬ NGHIỆM 2016 – 2017) Ông An có
một mảnh vườn hình Elip có độ dài trục lớn bằng
16
m
và độ dài trục bé bằng
10
m. Ông muốn trồng hoa trên
một dải đất rộng
8
m và nhận trục bé của elip làm
trục đối xứng (như hình vẽ).
Biết kinh phí để trồng hoa là
100.000
đồng
2
/m
. Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn)
A.
7.862.000
đồng. B.
7.653.000
đồng.
C.
7.128.000
đồng. D.
7.826.000
đồng.
Lời giải. Chọn hệ trục tọa độ
Oxy
như hình vẽ.
Giả sử elip có phương trình
2 2
2 2
1
x y
a b
+ =
.
Từ giả thiết, ta có
2 16 8
a a
= → =
và
2 10 5.
b b
= → =
Vậy phương trình của elip là
( )
( )
2
2 2
1
2
2
5
64
8
1
5
64 25
64
.
8
y x E
x y
y x E
= −
+ =
→
− −
=
Khi đó diện tích dải vườn được giới hạn bởi các đường
(
)
(
)
1 2
, , 4
E E x
= −
và
4
x
=
.
Do đó
4 4
2 2 2
4 0
5 5 3
2 64 d 64 d 80 m
8 2 6 4
S x x x x
π
−
= − = − = +
∫ ∫
.
Vậy số tiền mà ông An cần là
3
80 .100000 7652891,82 7.653.000
6 4
T
π
= + =
≃ .
Chọn B.
Vấn đề 2. TÍNH THỂ TÍCH KHỐI TRÒN XOAY
Câu 36. Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình
thang cong giới hạn bởi đồ thị hàm số
(
)
,
y f x
trục
Ox
và hai đường thẳng
(
)
, ,
x a x b a b
= = <
xung quanh trục
.
Ox
A.
( )
2
d .
b
a
V f x x
π=
∫
B.
( )
2
d .
b
a
V f x x
=
∫
C.
( )
d .
b
a
V f x x
π=
∫
D.
( )
d .
b
a
V f x x
π=
∫
Lời giải. Chọn A.
Câu 37. Cho hình phẳng trong hình bên (phần tô
đậm) quay quanh trục hoành. Thể tích khối tròn
xoay tạo thành được tính theo công thức nào trong
các công thức sau đây?
A.
( ) ( )
2 2
d
b
a
V g x f x x
π
= −
∫
.
B.
( ) ( )
2 2
d
b
a
V f x g x x
π
= −
∫
.
C.
( ) ( )
2
d
b
a
V f x g x x
π
= −
∫
. D.
( ) ( )
d
b
a
V f x g x x
π
= −
∫
.
Lời giải. Chọn B.
Câu 38. Viết công thức tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
vuông góc với trục
Ox
tại các điểm
(
)
, ,
x a x b a b
= = <
có thiết diện bị cắt bởi mặt
phẳng vuông góc với trục
Ox
tại điểm có hoành độ
(
)
x a x b
≤ ≤
là
(
)
S x
.
A.
( )
d .
b
a
V S x x
π=
∫
B.
( )
d .
b
a
V S x x
π=
∫
C.
( )
d .
b
a
V S x x
=
∫
D.
( )
2
d .
b
a
V S x x
π=
∫
Lời giải. Chọn C.
Câu 39. (ĐỀ THAM KHẢO 2016 – 2017) Tính thể tích
V
của phần vật thể giới hạn
bởi hai mặt phẳng
1
x
=
và
3
x
=
, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý
vuông góc với trục
Ox
tại điểm có hoành độ
x
(
)
1 3
x
≤ ≤
thì được thiết diện là một
hình chữ nhật có hai cạnh là
3
x
và
2
3 2
x
−
.
A.
124
3
V
π
= . B.
32 2 15.
V
= +
C.
124
3
V = . D.
(
)
32 2 15
V
π
= + .
Lời giải. Diện tích thiết diện (hình chữ nhật) là
(
)
2
3 3 2
S x x x
= −
.
Suy ra thể tích cần tính
( )
3 3
CASIO
2
1 1
124
d 3 3 2d .
3
V S x x x x x= = − =
∫ ∫
Chọn C.
Câu 40. Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
0
x
=
và
2
x
=
, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
Ox
tại điểm
có hoành độ
x
(
)
0 2
x
≤ ≤
thì được thiết diện là một phần tư hình tròn bán kính
2
2 .
x
A.
32 .
V
π
B.
64 .
V
π
=
C.
16
.
5
V
π
=
D.
8 .
V
π
Lời giải. Diện tích thiết diện (
1
4
hình tròn) là
( )
(
)
2
2 4
1 1
2 .
4 2
S x x x
π π= =
Suy ra thể tích cần tính
2
2
5
4
0
0
1 1 16
d . .
2 2 5 5
x
V x x
π
π π
= = =
∫
Chọn C.
Câu 41. Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
0
x
=
và
x
π
=
, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
Ox
tại điểm
có hoành độ
x
(
)
0 x
π
≤ ≤
thì được thiết diện là một tam giác đều cạnh là
2 sin .
x
A.
2 3 .
V
π
B.
8.
V
=
C.
2 3.
V
D.
8 .
V
π
Lời giải. Diện tích tam giác đều là
( )
4 sin . 3
3 sin .
x
S x x
= =
Suy ra thể tích cần tính
0
0
3 sin d 3 cos 2 3.
V x x x
π
π
= = − =
∫
Chọn C.
Câu 42. Cho hình phẳng
D
giới hạn bởi đường cong
2
2
y x x
= −
và trục hoành. Tính
thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục hoành.
A.
16
.
15
V
π
=
B.
11
.
15
V
π
=
C.
12
.
15
V
π
=
D.
4
.
15
V
π
=
Lời giải. Phương trình hoành đô giao điêm:
2
0
2 0 .
2
x
x x
x
=
− = ⇔
=
Thể tích cần tính
( )
2
CASIO
2
2
0
16
2 d .
15
V x x x
π
π= − =
∫
Chọn A.
Câu 43. (ĐỀ CHÍNH THỨC 2016 – 2107) Cho hình phẳng
D
giới hạn bởi đường
cong
2
1
y x
= +
, trục hoành và các đường thẳng
0, 1.
x x
= =
Tính thể tích
V
của
khối tròn xoay tạo thành khi quay
D
quanh trục hoành.
A.
4
.
3
V
π
= B.
2 .
V
π
C.
4
.
3
V = D.
2.
V
=
Lời giải. Thể tích cần tính
(
)
( )
1 1
2
CASIO
2 2
0 0
4
1 d 1 d .
3
V x x x x
π
π π= + = + =
∫ ∫
Chọn A.
Câu 44. Cho hình phẳng
D
giới hạn bởi đường cong
ln
y x
, trục hoành và đường
thẳng
.
x e
=
Tính thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục
hoành.
A.
(
)
1 .
V e
= +
B.
(
)
1 .
V e
= −
C.
.
V e
π
D.
(
)
2 .
V e
= −
Lời giải. Phương trình hoành độ giao điểm:
ln 0 1
x x
= ⇔ =
.
Thể tích cần tính
CASIO
2
1
ln d 2,25654.
e
V x xπ=
∫
≃
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 45. Kí hiệu
1 2
,
V V
lần lượt là thể tích của khối cầu bán kính đơn vị và thể tích
khối tròn xoay sinh ra khi quay quanh trục
Ox
hình phẳng giới hạn bởi đường thẳng
2 2
y x
= − +
và đường cong
2
2 1 .
y x
= −
Mệnh đề nào sau đây là đúng?
A.
1 2
V V
. B.
1 2
V V
. C.
1 2
V V
. D.
1 2
2
V V
.
Lời giải. Ta có
3 1
1 1
4 4
3 3
R
V R V
π π
=
= → =
(đvtt).
Phương trình hoành độ giao điểm:
( )
2 CASIO
0
2 1 2 1 .
1
x
x x
x
=
− = − →
=
Thể tích
(
)
( )
1 1
2
CASIO
2
2 2
2
0 0
4
2 1 2 1 d 8 8 d .
3
V x x x x x x
π
π π
= − − − = − + =
∫ ∫
Vậy
1 2
V V
. Chọn B.
Câu 46. Một Bác thợ gốm làm một cái lọ có dạng
khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường
1
y x
= +
(đồ thị
như hình vẽ) và trục
Ox
quay quanh trục
.
Ox
Biết đáy lọ và miệng lọ có đường kính lần lượt là
2dm
và
4dm.
Tính thể tích
V
của lọ.
A.
3
8 dm .
V
B.
3
15
dm .
V
= C.
3
7 dm .
V
D.
3
17 dm .
V
Lời giải. Từ giả thiết, suy ra bán kính hai đáy lần lượt là
1dm
và
2 dm
.
Suy ra
1 1 0
x x
+ = → =
và
1 2 3
x x
+ = → =
.
Thể tích của lọ
( )
( )
3 3
CASIO
2
3
0 0
15
1 d 1 d dm .
2
V x x x x
π
π π= + = + =
∫ ∫
Chọn B.
Câu 47. (ĐỀ CHÍNH THỨC 2016 – 2017) Cho hình phẳng
D
giới hạn bởi đường
cong
x
y e
, trục hoành và các đường thẳng
0, 1.
x x
= =
Tính thể tích
V
của khối
tròn xoay tạo thành khi quay
D
quanh trục hoành.
A.
2
2
e
V
π
= . B.
(
)
2
1
e
V
π
+
= . C.
2
1
2
e
V
−
= . D.
(
)
2
1
e
V
π
−
= .
Lời giải. Thể tích cần tính
( )
(
)
2
1 1
1
2
2 2
0
0 0
1
1
d d .
2 2
x x x
e
V e x e x e
π
π π π
−
= = = =
∫ ∫
Chọn D.
Câu 48. (ĐỀ MINH HỌA 2016 – 2017) Kí hiệu
(
)
H
là hình phẳng giới hạn bởi đồ
thị hàm số
(
)
2 1 ,
x
y x e
= −
trục tung và trục hoành. Tính thể tích
V
của khối tròn
xoay thu được khi quay hình
(
)
H
xung quanh trục
.
Ox
A.
4 2 .
V e
= −
B.
(
)
4 2 .
V e
π
= −
C.
2
5.
V e
= −
D.
(
)
2
5 .
V e
π
= −
Lời giải. Phương trình hoành độ giao điêm:
(
)
2 1 0 1 0 1.
x
x e x x
− = ⇔ − = ⇔ =
Thể tích cần tính
( ) ( )
1 1
CASIO
2
2
2
0 0
2 1 d 4 1 d 7,50544.
x x
V x e x x e xπ π
= − = − =
∫ ∫
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 49. (ĐỀ CHÍNH THỨC 2016 – 2017) Cho hình phẳng
D
giới hạn bởi đường
cong
2 cos
y x
= +
, trục hoành và các đường thẳng
0,
2
x x
π
= =
. Tính thể tích
V
của
khối tròn xoay tạo thành khi quay
D
quanh trục hoành.
A.
1.
V
= −
B.
(
)
1 .
V
π π
= −
C.
(
)
1 .
V
π π
= +
D.
1.
V
= +
Lời giải. Thể tích cần tính
( )
( )
2 2
CASIO
2
0 0
2 cos d 2 cos d 13,01119.
V x x x x
π π
π π= + = + =
∫ ∫
Đối chiếu kết quả với bốn đáp án đã cho. Chọn C.
Câu 50. (ĐỀ CHÍNH THỨC 2016 – 2017) Cho hình phẳng
D
giới hạn bởi đường
cong
2 sin
y x
= +
, trục hoành và các đường thẳng
0,x x
π
= =
. Khối tròn xoay tạo
thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
(
)
2 1 .
V
= +
B.
(
)
2 1 .
V
π π
= +
C.
2
2 .
V
π
D.
2 .
V
π
Lời giải. Thể tích cần tính
( )
( )
CASIO
2
0 0
2 sin d 2 sin d 26,02239.
V x x x x
π π
π π= + = + =
∫ ∫
Đối chiếu kết quả với bốn đáp án đã cho. Chọn B.
Câu 51. Ký hiệu
(
)
H
là hình phẳng giới hạn bởi các đường
sin cos
y x x m
= − +
,
0
y
=
,
0
x
=
và
2
x
π
=
với
m
là tham số thực lớn hơn
2
. Tìm
m
sao cho thể tích
V
của khối tròn xoay thu được khi quay hình
(
)
H
xung quanh trục hoành bằng
2
3
.
2
π
A.
6.
m
=
B.
4.
m
=
C.
3.
m
=
D.
9.
m
=
Lời giải. Thể tích cần tính
( )
( )
2 2
2
0 0
sin cos d sin cos d
V x x m x x x m x
π π
π π= − + = − +
∫ ∫
( ) ( )
2
2
0
cos sin 1 1 .
2 2
m m
x x mx
π
π π
π π π
= − − + = − + − − =
Theo giả thiết
2 2 2
3 3
3
2 2 2
m
V m
π π π
= ⇔ = ⇔ =
(thỏa mãn
2
m
>
). Chọn C.
Cách CASIO. Thể tích cần tính
( )
2
0
sin cos d
V x x m x
π
π= − +
∫
. Đến đây thử từng giá
trị
m
ở các đáp án vào, đáp án nào cho kết quả
2
3
2
π
thì nhận.
Câu 52. Cho hình phẳng
D
giới hạn bởi các đồ thị hàm số
2
.
4
x
y = và
y x
=
. Tính
thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục hoành.
A.
124
.
15
V
π
=
B.
126
.
15
V
π
=
C.
128
.
15
V
π
=
D.
131
.
15
V
π
=
Lời giải. Phương trình hoành độ giao điểm
2
0
.
4
4
x
x
x
x
= ⇔
=
Thể tích cần tính
2
4
2
CASIO
2
0
128
d .
4 15
x
V x x
π
π
= − =
∫
Chọn C.
Câu 53. Hình phẳng
(
)
H
giới hạn bởi các đường
2
1
y x
= +
, trục tung và tiếp tuyến
của đồ thị hàm số
2
1
y x
= +
tại điểm
(
)
1;2
. Khi quay hình
(
)
H
quanh trục
Ox
tạo
thành khối tròn xoay có thể tích
V
bằng:
A.
4
.
5
V
π
= B.
28
.
15
V
π
= C.
8
.
15
V
π
= D.
.
V
π
Lời giải. Tiếp tuyến của đồ thị
2
1
y x
= +
tại
điểm
(
)
1;2
có phương trình
2
y x
.
Thể tích cần tính
( )
( )
1
2
2
2
0
1 2 d
V x x x
π= + −
∫
( )
1 1
xet dau
4 2 4 2
0 0
8
2 1 d 2 1 d
15
x x x x x x
π
π π= − + = − + =
∫ ∫
.
Chọn C.
Câu 54. Cho hình phẳng
D
giới hạn bởi các đồ thị hàm số
2
4
y x
= −
và
2
2
y x
= +
.
Tính thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục hoành.
A.
10 .
V
π
B.
12 .
V
π
C.
14 .
V
π
D.
16 .
V
π
Lời giải. Phương trình hoành độ giao điểm:
2 2
4 2 1
x x x
− = + ⇔ = ±
.
Thể tích cần tính
( ) ( )
1 1
CASIO
2 2
2 2 2
1 1
4 2 d 12 12 d 16 .
V x x x x x
π π π
− −
= − − + = − =
∫ ∫
Chọn D.
Câu 55. Thể tích
V
của khối tròn xoay khi
cho hình phẳng giới hạn bởi các đường
2
1
y x
= −
và
2
1
y x
= −
quay quanh trục
Ox
được xác định bởi công thức nào sau
đây?
A.
( ) ( )
1
2 2
2 2
1
1 1 d .
V x x x
π
−
= − − −
∫
B.
( ) ( )
1
2 2
1
1 1 d .
V x x x
π
−
= − − −
∫
C.
( )
1
2
2
1
1 d .
V x x
π
−
= −
∫
D.
( ) ( )
1
2 2
2 2
1
1 1 d .
V x x x
−
= − − −
∫
Lời giải. Phương trình hoành độ giao điểm:
2 2
1 1 1.
x x x
− = − ⇔ = ±
Vì đồ thị hàm số
2
1
y x
= −
đối xứng với đồ thị hàm số
2
1
y x
= −
qua trục hoành nên
thể tích khối tròn xoay cần tính bằng thể tích khối tròn xoay khi cho hình phẳng giới
hạn bởi các đường
2
1 , 0, 1, 1
y x y x x
= − = = − =
quay quanh trục
Ox
.
Vậy công thức tính thể tích là
( )
1
2
2
1
1 d
V x x
π
−
= −
∫
. Chọn C.
Câu 56. Cho hình phẳng
(
)
H
giới hạn bởi các đường
2
y x
và
.
y x
Khối tròn
xoay tạo ra khi
(
)
H
quay quanh
Ox
có thể tích
V
được xác định bằng công thức nào
sau đây ?
A.
(
)
1
4
0
d
.
V x x x
π= −
∫
B.
(
)
1
2
0
d .
V x x x
π= −
∫
C.
( )
1
2
0
d .
V x x x
π= −
∫
D.
( )
1
4
0
d .
V x x x
π= −
∫
Lời giải. Phương trình hoành độ giao điểm:
2
0
.
1
x
x
x
x
=
= ⇔
=
Thể tích cần tính
( )
1 1
xet dau
0
4 4
0
d d .
V x x
x x x x
ππ − −= =
∫ ∫
Chọn D.
Câu 57. Cho hình phẳng
(
)
H
giới hạn bởi đồ thị
hàm số
,
y x
= −
đường thẳng
2
y x
= − +
và trục
hoành. Khối tròn xoay tạo ra khi
(
)
H
quay quanh
Ox
có thể tích
V
được xác định bằng công thức nào
sau đây ?
A.
( )
2 4
2
0 2
d 2 d .
V x x x x
π
= + −
∫ ∫
B.
( )
2 4
2
0 2
d 2 d .
V x x x x
π
= − −
∫ ∫
C.
( )
2 4
2
0 2
d 2 d .
V x x x x
π
= + −
∫ ∫
D.
( )
4 4
2
0 2
d 2 d .
V x x x x
π
= − −
∫ ∫
Lời giải. Gọi
1
V
là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị
hàm số
y x
= −
, trục hoành, đường thẳng
0, 4
x x
= =
xung quanh trục
Ox
( )
4 4
2
1
0 0
. d . d .
V x x x x
π π→ = − =
∫ ∫
Gọi
2
V
là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
y x
= − +
, trục hoành, đường thẳng
2, 4
x x
= =
xung quanh trục
Ox
( )
4
2
2
2
. 2 d .
V x x
π→ = −
∫
Suy ra thể tích cần tính
( )
4 4
2
1 2
0 2
. d . 2 d .
V V V x x x x
π π= − = − −
∫ ∫
Chọn D.
Câu 58*. Cho hình phẳng
(
)
H
giới hạn bởi
1
4
đường tròn có bán kính
2,
R
=
đường
cong
4
y x
= −
và trục hoành (miên tô đậm như hình vẽ). Tính thể tích
V
của khối
tạo thành khi cho hình
(
)
H
quay quanh trục
.
Ox
A.
77
6
V
π
= ⋅
B.
53
6
V
π
= ⋅
C.
67
6
V
π
= ⋅
D.
40
3
V
π
= ⋅
Lời giải. Phương trình hoành độ giao điểm:
4 0 4.
x x
− = ⇔ =
Gọi
1
V
là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi
1
4
đường tròn
có bán kính
2
R
=
(như hình vẽ), trục hoành và đường thẳng
0
x
=
xung quanh trục
Ox
→
thể tích tạo thành là nửa khối cầu bán kính
2.
R
=
3 3
1
1 4 2 16
. .2 .
2 3 3 3
V R
π
π π→ = = =
Gọi
2
V
là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
4 , 0, 0, 4
y x y x x
= − = = =
xung quanh trục
Ox
( )
4
2
0
4 d 8 .
V x x
π π
→ = − =
∫
Vậy thể tích cần tính
1 2
40
.
3
V V V
π
= + = Chọn D.
Câu 59*. Cho hình phẳng
(
)
H
giới hạn bởi các đường
2, 2, 1.
y x y x x
= − + = + =
Tính thể tích
V
của vật thể tròn xoay khi quay hình phẳng
(
)
H
quanh trục hoành.
A.
29
6
V
π
= . B.
9
2
V
π
= . C.
9
V
π
D.
55
6
V
π
= .
Lời giải. Đây thuộc bài toán khó, ta phải vẽ hình phát họa mới kiểm soát được.
Lấy đối xứng phần đồ thị hàm số
2
y x
= − +
qua trục hoành ta được đồ thị hàm số
2.
y x
= +
Khi đó thể tích
V
cần tính được tạo thành khi cho hình phẳng
(
)
'
H
giới
hạn bởi các đường
2, 2,
y x y x
= + = +
trục
Ox
và đường thẳng
1
x
=
quay quanh
trục hoành.
Xét các phương trình hoành độ giao điểm:
2
2 2
1
x
x x
x
= −
+ = + ⇔
= −
và
2 0 2
x x
+ = ⇔ = −
.
● Gọi
1
V
là thể tích khối tròn xoay khi quay hình phẳng là tam giác
ABC
được giới
hạn bởi các đường
2,
y x
= +
trục hoành và đường thẳng
1
x
=
quanh trục hoành
( )
1
2
1
2
2 d 9 .
V x x
π π
−
→ = + =
∫
● Gọi
2
V
là thể tích khối tròn xoay khi quay hình phẳng (phần tô màu) được giới hạn
bởi các đường
2
y x
= +
,
2
y x
= +
quanh trục hoành
( )
( )
1
2
2
2
2
2 2 d .
6
V x x x
π
π
−
−
→ = + − + =
∫
Vậy thể tích cần tính
1 2
55
9 .
6 6
V V V
π π
π= + = + = Chọn D.
Nhận xét. Bài này học sinh làm sai khá nhiều, lí do là không vẽ hình mà làm theo
công thức
( )
( )
1
2
2
2
9
2 2 d .
2
V x x x
π
π
−
= + − − + =
∫
Câu 60. Cho hình phẳng
(
)
H
giới hạn bởi các
đường
x
y e
,
0
y
=
,
0
x
=
và
x k
=
(
)
0
k
>
. Gọi
k
V
là thể tích khối tròn xoay khi quay hình
(
)
H
quanh trục
Ox
. Biết rằng
4
k
V
=
. Khẳng định nào
sau đây là khẳng định đúng:
A.
3
1 .
2
k< < B.
3
2.
k
< <
C.
1
1.
k
< <
D.
1
0 .
2
k< <
Lời giải. Thể tích
( ) ( )
2
2 2 2
0
0 0
d d 1 .
2 2
k k
k
x x x k
k
V e x e x e e
π π
π π= = = = −
∫ ∫
Theo giả thiết
( )
2 2
8
4 1 4
k k
k
V e e
π π
π
+
= ⇔ − = ⇔ =
1 8 1
ln ;1 .
2 2
k
→ = ∈
Chọn C.
Câu 61. Gọi
V
là thể tích khối tròn xoay
tạo thành khi quay hình phẳng giới hạn bởi
các đường
y x
,
0
y
=
và
4
x
=
quanh
trục
Ox
. Đường thẳng
(
)
0 4
x a a
= < <
cắt
đồ thị hàm số
y x
=
tại
M
(hình vẽ bên).
Gọi
1
V
là thể tích khối tròn xoay tạo thành
khi quay tam giác
OMH
quanh trục
Ox
.
Biết rằng
1
2
V V
. Khi đó:
A.
2
a
=
. B.
2 2
a
. C.
5
2
a
=
. D.
3
a
=
.
Lời giải. Phương trình hoành độ giao điểm:
0 0.
x x
= ⇔ =
Thể tích
4
0
d 8 .
V x x
π π
= =
∫
Ta có
(
)
;
M a a
. Khi quay tam giác
OMH
quanh trục
Ox
tạo thành hai hình nón có
chung đáy:
Hình nón
(
)
1
N
có đỉnh là
O
, chiều cao
OK a
=
, bán kính đáy
R MK a
= =
nên có
thể tích bằng
( )
2
2
2
1 1
. . .
3 3 3
a
R OK a a
π π= =
Hình nón
(
)
2
N
có đỉnh là
H
, chiều cao
4
HK a
= −
, bán kính đáy
R MK a
= =
nên có thể tích bằng
( )
( )
2
2
2
1 1 4
. 4 .
3 3 3
a a
R HK a a
π π
π π
= − =
Suy ra
2 2
1
4 4
.
3 3 3
a a a a
V
π π π π
= + =
Theo giả thiết
1
4
2 8 2. 3.
3
V V a aπ π
= ⇔ = → =
Chọn D.
Câu 62. Tính thể tích
V
của khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi đường tròn
(
)
(
)
2
2
: 3 1
C x y
+ − =
quanh trục hoành.
A.
6 .
V
π
B.
3
6 .
V
π
C.
2
3 .
V
π
D.
2
6 .
V
π
Lời giải. Ta có
(
)
2
2
3 1
x y
+ − =
[ ]
2
2
3 1
, 1;1 .
3 1
y x
x
y x
= + −
→ ∈ −
= − −
Thể tích cần tính
(
)
(
)
1
2 2
2 2
1
3 1 3 1 d
V x x x
π
−
= + − − − −
∫
1
CASIO
2
1
12 1 d 59,21762.
x xπ
−
= − =
∫
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 63. Cho hình vuông có độ dài cạnh bằng
8cm
và
một hình tròn có bán kính
5cm
được xếp chồng lên nhau
sao cho tâm của hình tròn trùng với tâm của hình vuông
như hình vẽ bên. Tính thể tích
V
của vật thể tròn xoay
tạo thành khi quay mô hình trên quanh trục
.
XY
A.
3
260
cm .
3
V
= B.
3
290
cm .
3
V
=
C.
3
520
cm .
3
V
= D.
3
580
cm .
3
V
=
Lời giải. Chọn hệ trục tọa độ như hình vẽ.
● Thể tích khối cầu
3 3
1
4 4 500
5 .
3 3 3
V R
π
π π= = =
● Gọi
2
V
là thể tích khối tròn xoay khi quay hình phẳng
(
)
H
(phần tô màu) được giới
hạn bởi đường thẳng
4
y
=
, đường tròn
2 2
25
y x
= −
và
4
x
=
quanh trục hoành
( )
4
2 2
2
3
10
4 25 d .
3
V x x
π
π→ = − − =
∫
-4
4
-4
-5
5
-5
54
3
y
x
O
Vậy thể tích cần tính
3
1 2
520
2 cm .
3
V V V
= + =
Câu 64. Bên trong hình vuông cạnh
a
, dựng
hình sao bốn cánh đều như hình vẽ bên (các
kích thước cần thiết cho như ở trong hình).
Tính thể tích
V
của khối tròn xoay sinh ra khi
quay hình sao đó quanh trục
Ox
.
A.
3
5
.
48
V a
=
B.
3
5
.
16
V a
=
C.
3
.
6
V a
=
D.
3
.
8
V a
=
Lời giải. Do hình sao có tính đối xứng nên ta quay theo trục thẳng đứng hay nằm
ngang đều cho thể tích như nhau.
Chọn hệ trục tọa độ như hình vẽ.
Gọi
V
là thể tích khối tròn xoay cần tính.
Gọi
1
V
là thể tích khối tròn xoay khi quay hình
phẳng được tô màu trong hình bên quanh trục
hoành. Khi đó
1
2 .
V V
Ta có
2 2
2 2
3
1
0
4
5
d 2 d .
2 4 2 96
a a
a
x a a a
V x x x
π
π π
= + − − =
∫ ∫
Suy ra thể tích cần tính
3
1
5
2 .
48
a
V V
= = Chọn A.
Câu 65. Cho hai tam giác cân có chung đường
cao
40cm
XY
và cạnh đáy lần lượt là
40cm
và
60cm
, được xếp chồng lên nhau sao cho đỉnh
của tam giác này là trung điểm cạnh đáy của
tam giác kia như hình vẽ bên. Tính thể tích
V
của vật thể tròn xoay được tạo thành khi quay
mô hình trên quanh trục
XY
.
A.
3
40480
cm .
3
V
=
B.
3
52000
cm .
3
V
=
C.
3
46240
cm .
3
V
=
D.
3
1920 cm .
V
Lời giải. Chọn hệ trục tọa độ như hình vẽ:
(
)
(
)
(
)
(
)
0;0 , 40;0 , 0;20 , 40;30
Y O X A M
.
Phương trình đường
3
: 3 4 0 .
4
x
YM x y y− = → =
Phương trình
40
: 2 40 0 .
x
AX x y y
+ − = → =
Phương trình hoành độ giao điểm của hai đường
YM
và
AX
là:
3 40
16.
4 2
x x
x
= ↔ =
Thể tích vật thể cần tính
2 2
16 40
3
0 16
40 3 46240
d d cm .
2 4 3
x x
V x x
π
π π
−
= + =
∫ ∫
Chọn C.
Y
X
40
16
20
30
B
A
N
M
y
x
| 1/97
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUÛ ÑEÀ NGUYEÂN HAØM -–TÍCH PHAÂN 3. VAØ ÖÙNG DUÏNG Baøi 01 NGUYEÂN HAØM 1. Định nghĩa
Cho hàm số f (x) xác định trên khoảng K . Hàm số F (x) được gọi là nguyên hàm
của hàm số f (x) nếu F '(x)= f (x) với mọi x ∈ K .
Nhận xét. Nếu F (x) là một nguyên hàm của f (x) thì F (x)+C, (C ∈ ℝ) cũng là
nguyên hàm của f (x) . Ký hiệu:
f (x )dx = F (x )+C ∫ . 2. Tính chất ( f (x) x ∫ )/ d = f (x) . .
a f (x)dx = . a
f (x )dx (a ∈ , a ≠ 0) ∫ ∫ ℝ .
f (x)± g(x)dx = f (x)dx ± g(x)dx ∫   ∫ ∫ .
3. Bảng nguyên hàm của một số hàm số thường gặp Bảng nguyên hàm
kdx = kx +C ∫ , k là hằng số + α 1 + α α 1 (ax + b) 1 α x x dx =
+C (α ≠ − ) 1 ∫
(ax +b) dx = . +C ∫ α +1 a α +1
1 dx = ln x +C ∫ 1 1 dx =
ln ax + b +C ∫ x ax + b a x d x e x = e +C ∫ 1 ax +b d ax +b e x = e +C ∫ a x a mx +n + a x a dx = +C ∫ mx n a dx = +C ∫ ln a . m ln a
cos xdx = sin x +C ∫ (ax +b) 1 cos dx =
sin(ax + b)+C ∫ a
sin xdx = −cos x +C ∫ (ax +b) 1 sin
dx = − cos(ax + b)+C ∫ a 1 1 1
dx = tan x +C ∫ dx =
tan ax + b +C ∫ 2 ( ) 2 cos x cos (ax + b) a 1 1 1
dx = −cot x +C ∫
dx = − cot ax + b +C ∫ 2 ( ) 2 sin x sin (ax + b) a
CÂU HỎI & B(I TẬP TRẮC NGHIỆM 12
NGUYỄN PHÚ KHÁNH HUỲNH ĐỨC KHÁNH –
Đăng ký mua trọn bộ trắc nghiệm 12 FILE WORD
Liên hệ tác giả HUỲNH ĐỨC KHÁNH 0975 120 189 –
https://www.facebook.com/duckhanh0205
Khi mua có sẵn file word đề riêng;
file word đáp án riêng thuận tiện cho việc dạy
Câu 1. Hàm số f (x) có nguyên hàm trên K nếu:
A. f (x) xác định trên K .
B. f (x) có giá trị lớn nhất trên K .
C. f (x) có giá trị nhỏ nhất trên K . D. f (x) liên tục trên K .
Lời giải. Nếu hàm số f (x) liên tục trên K thì nó có nguyên hàm trên K . Chọn D.
Câu 2. Mệnh đề nào sau đây là sai?
A. Nếu F (x) là một nguyên hàm bất kỳ của f (x) trên (a;b) thì
f (x)dx = F (x)+C ∫
với C là hằng số.
B. Mọi hàm số liên tục trên khoảng (a;b) đều có nguyên hàm trên khoảng (a;b) .
C. F (x) là một nguyên hàm của f (x) trên (a b) / ;
⇔ f (x)= F (x), ∀x ∈(a;b) . /
D. ( f (x)dx ∫ ) = f (x).
Lời giải. Chọn C. Sửa lại cho đúng là:
'' F (x) là một nguyên hàm của f (x ) trên (a;b) /
⇔ F (x)= f (x), ∀x ∈(a;b)' .
Câu 3. Xét hai khẳng định sau:
1) Mọi hàm số f (x) liên tục trên đoạn [a;b] đều có đạo hàm trên đoạn đó.
2) Mọi hàm số f (x) liên tục trên đoạn [a;b] đều có nguyên hàm trên đoạn đó.
Trong hai khẳng định trên:
A. Chỉ có 1) đúng. `B. Chỉ có 2) đúng. C. Cả hai đều đúng. D. Cả hai đều sai.
Lời giải. Hàm số có đạo hàm tại x thì liên tục tại x . Ngược lại hàm số liên tục tại 0 0
x thì chưa chắc đã có đạo hàm tại x . Chẳng hạn xét hàm số f (x) = x tại điểm 0 0
x = 0 . Chọn B.
Câu 4. Trong các khẳng định sau nói về nguyên hàm của một hàm số f (x) xác định
trên khoảng D , khẳng định nào là sai?
1) F (x) là nguyên hàm của f (x) trên D nếu và chỉ nếu F '(x)= f (x),∀x ∈ D.
2) Nếu f (x) liên tục trên D thì f (x) có nguyên hàm trên D .
3) Hai nguyên hàm trên D của cùng một hàm số thì sai khác nhau một hằng số.
A. Khẳng định 1) sai.
B. Khẳng định 2) sai.
C. Khẳng định 3) sai.
D. Không có khẳng định nào sai.
Lời giải. Chọn D.
Câu 5. Giả sử F (x) là một nguyên hàm của hàm số f (x) trên khoảng (a;b) . Giả sử
G (x) cũng là một nguyên hàm của f (x ) trên khoảng (a;b) . Mệnh đề nào sau đây là đúng?
A. F (x)= G(x) trên khoảng (a;b) .
B. G(x)= F (x)−C trên khoảng (a;b) , với C là hằng số.
C. F (x)= G(x)+C với mọi x thuộc giao của hai miền xác định F (x) và G(x), C là hằng số.
D. Cả ba câu trên đều sai.
Lời giải. Vì hai nguyên hàm trên D của cùng một hàm số thì sai khác nhau một
hằng số. Do đó B đúng. Chọn B.
Câu 6. Xét hai khẳng định sau: 1)
f (x)+ g(x) dx = f (x)dx + g(x)dx = F (x)+G(x)+C ∫   ∫ ∫
, trong đó F (x) và
G (x) tương ứng là nguyên hàm của f (x ), g (x ) . 2) Mỗi nguyên hàm .
a f (x ) (a ≠ 0) là tích của a với một nguyên hàm của f (x ) .
Trong hai khẳng định trên:
A. Chỉ có 1) đúng.
B. Chỉ có 2) đúng.
C. Cả hai đều đúng.
D. Cả hai đều sai.
Lời giải. Chọn C.
Câu 7. Khẳng định nào sau đây là sai? A. Nếu
f (x)dx = F (x)+C ∫ thì
f (u)du = F (u)+C ∫ .
B. kf (x)dx = k f (x)dx ∫ ∫
( k là hằng số và k ≠ 0 ).
C. Nếu F (x) và G(x) đều là nguyên hàm của hàm số f (x) thì F (x)= G(x).
D.  f x + f x  dx = f x dx + f x dx ∫ ∫ ∫ . 1 ( ) 2 ( ) 1 ( ) 2 ( )  
Lời giải. Các nguyên hàm sai khác nhau hằng số nên C là đáp án sai. Chọn C.
Câu 8. Trong các khẳng định sau, khẳng định nào sai?
A. 0dx = C ∫ (C là hằng số). B.
1 dx = ln x +C ∫ (C là hằng số). x α 1 + C. α x x dx = +C ∫
(C là hằng số). D. dx = x +C ∫ (C là hằng số). α +1
Lời giải. Chọn C. Vì kết quả này không đúng với trường hợp α = −1 .
Câu 9. Hàm số f (x) 1 =
có nguyên hàm trên khoảng nào với các khoảng đã cho cos x sau đây?     A. ( π π π π 0;   π) . B. − ;    .
C. (π;2π). D. − ;  .  2 2   2 2     
Lời giải. Hàm số π π f (x ) 1 =
xác định và liên tục trên − ;    nên có nguyên hàm cos x  2 2
trên khoảng này. Chọn B.
Câu 10. Kí hiệu F (y) là một nguyên hàm của hàm số f (y) , biết ( ) 2
F y = x + xy +C .
Hỏi hàm số f (y) là hàm số nào trong các hàm số sau?
A. f (y)= x .
B. f (y)= 3x + y . C. f (y)= y .
D. f (y)= 2x + y .
Lời giải. Để tìm f (y) ta đi lấy đạo hàm của F (y) theo biến y (tức là bây giờ x
đóng vai trò là tham số).
Ta có F '(y)= x . Chọn A.
Câu 11. Kí hiệu F (x) là một nguyên hàm của hàm số f (x) và F ( 2
sin x ) xác định thì F ( 2
sin x ) là một nguyên hàm của hàm số nào trong các hàm số sau? A. f ( 2 sin x ). B. f ( 2 cos x ). C. xf ( 2 2 sin sin x ). D. xf ( 2 sin 2 sin x ).
Lời giải. Theo định nghĩa, ta có f (x)dx F
= (x)+C ←→ F ′(x)= f (x). ∫ Áp dụng:  ′ F  ( x ) = . Chọn D.   ( x )/ 2 2 / F ( 2 x )= x f ( 2 sin sin sin sin 2 . sin x )  Câu 12. Xác định f (x )dx ∫
biết f (x)= 2x +1. A. (2x + ) 1 dx = 2. ∫ B. (2x + ) 1 dx = C. ∫ C. ( x + ) 2 2
1 dx = x + x. ∫ D. ( x + ) 2 2
1 dx = x + x +C. ∫
Lời giải. Chọn D.
Câu 13. Hàm số nào sau đây không phải là nguyên hàm của hàm số f (x)= (x − )4 3 ? (x − )5 (x − )5 A. 3 F (x) 3 = + x . B. F (x)= . 5 5 (x − )5 (x −3)5 C. F (x) 3 = + 2017 . D. F (x)= −1 . 5 5
Lời giải. Xét đáp án A, ta có F (x)= (x − )4 ' 3
+1 ≠ f (x) . Chọn A.
Cách trắc nghiệm. Ta thấy hàm số F (x) ở các đáp án B, C, D sai khác nhau hằng
số nên dung phương pháp loại suy, ta chọn được được đáp án A.
Câu 14. Kí hiệu F (x) là một nguyên hàm của hàm số f (x)= (x + )2 2 1 và F ( ) 28 1 = ⋅ 15
Khẳng định nào sau đây là đúng? 5 3 5 3 A. ( ) x 2x x 2x F x = + + x. B. F (x)= + + x +C. 5 3 5 3 5 3 C. x 2x
F (x) = x ( 2 4 x + ) 1 . D. F (x)= + + x +1. 5 3
Lời giải. Ta có ∫ ( + ) x x x
1 dx = ∫ (x +2x + ) 5 3 2 2 2 4 2 1 dx = + + x +C. 5 3
Theo giả thiết F ( ) 28 1 2 28 1 =  → + +1+C = 
→C = 0 . Chọn A. 15 5 3 15
Câu 15. Tìm hàm số F (x) biết F (x) 2 '
= 3x + 2x +1 và đồ thị hàm số y = F (x) cắt
trục tung tại điểm có tung độ bằng e . A. F (x) 2
= x + x + e.
B. F (x)= cos2x + e −1. C. F (x) 3 2
= x + x + x +1. D. F (x) 3 2
= x + x + x + e.
Lời giải. Ta có F (x)= ∫ ( 2x + x + ) 3 2 3 2
1 dx = x + x + x +C.
Đồ thị y = F (x) cắt trục tung tại điểm có tung độ bằng e nên ta có F (0)= e ⇔ C = e. Vậy F (x) 3 2
= x + x + x + e. Chọn D.
Câu 16. Kí hiệu F (x) là một nguyên hàm của hàm số f (x)= 4x −1. Đồ thị hàm số
y = F (x ) và đồ thị hàm số y = f (x) cắt nhau tại một điểm thuộc trục tung. Tọa độ
các điểm chung của hai đồ thị hàm số trên là:       A. (0;− ) 1 . B. 5  ;9        . C. (0;− ) 1 và 5 ;9   . D. (0;− ) 1 và 5 ;8   . 2  2  2 
Lời giải. Ta có F (x)= ( x − ) 2 4
1 dx = 2x − x +C ∫ .
Giả sử M (0;m)∈Oy là giao điểm của đồ thị hai hàm số F (x) và f (x) .
M ∈ f (x) 4.0−1= m  = − Ta có hệ phương trình m 1     ⇔  ⇔  ⇒ F (x) 2
= 2x − x −1. M ∈ F  (x) 2 2
 .0 −0 +C = m C  = −1   
Hoành độ giao điểm của đồ thị hai hàm số F (x) và f (x) là nghiệm của phương trình:
x = 0 ⇒ y = −1  2
2x − x −1 = 4x −1 ⇔ x (2x − ) 5 = 0 ⇔  5 . x = ⇒ y = 9  2  
Vậy tọa độ các điểm cần tìm là (0;− ) 1 và 5  ;9    . Chọn C. 2 
Câu 17. Biết rằng F (x) 3
= ax +(a +b) 2
x +(2a −b + c )x +1 là một nguyên hàm của f (x ) 2
= 3x + 6x + 2. Tính tổng S = a + b + c.
A. S = 5.
B. S = 4.
C. S = 3. D. S = 2.
Lời giải. Ta có ∫ ( 2x + x + ) 3 2 3 6
2 dx = x + 3x + 2x +C . Suy ra F (x) 3 2
= x +3x + 2x +1 . a  = 1 a =1   Đồng nhất ta được   a  +b = 3 ⇔ b  = 2 
→a + b + c = 5 . Chọn A.     2
a −b + c = 2 c  = 2  
Câu 18. (ĐỀ THỬ NGHIỆM 2016 2017) Biết F (x) là một nguyên hàm của hàm – số f (x) 1 =
và F (2) =1. Tính F (3). x −1
A. F (3)= ln 2−1. B. F (3)= ln 2 +1. C. F ( ) 1 3 = ⋅ D. F ( ) 7 3 = ⋅ 2 4 Lời giải. Ta có
dx = ln x −1 +C. ∫ x −1
Theo giả thiết F (2) =1 
→ ln 2−1 +C = 1 ⇔ C = 1.
Suy ra F (x) = ln x −1 +1  → F ( ) 3 = ln 2 +1. Chọn B.
Câu 19. Cho hàm số y = f (x) có đạo hàm f (x) 1 ' = và f ( ) 1 = 1 . Tính f ( ) 5 . 2x −1 A. f (5)= ln 2. B. f (5)= ln 3.
C. f (5)= ln 2 +1.
D. f (5)= ln 3+1.
Lời giải. Ta có f (x)= f (x ) dx 1 ' dx = = ln 2x −1 +C. ∫ ∫ 2x −1 2
Theo giả thiết f ( ) 1 1 = 1 
→ ln 2.1−1 +C = 1 ⇔ C = 1 . 2 Suy ra f (x) 1 = x − +  → f ( ) 1 1 ln 2 1 1 5 = ln 2.5 −1 +1 =
ln 9 +1 = ln 3 +1. Chọn D. 2 2 2
Câu 20. Tìm hàm số x +
f (x) thỏa mãn đồng thời f ′(x) 2 3 = và f (0)= 1. x +1 A. f (x) 2
= x + ln x +1 .
B. f (x)= 2x + ln 2x +1 −1.
C. f (x)= 2x + ln x +1 +1.
D. f (x)= x + ln x +1 +1. +  
Lời giải. Ta có 2x 3 1 dx = 2  ∫ ∫  +
dx = 2x + ln x +1 +C. x +1  x +1
Theo giả thiết f (0)=1 
→2.0 + ln 0 +1 +C = 1 ⇔ C = 1.
Suy ra f (x) = 2x + ln x +1 +1. Chọn C. (x + )2 Câu 21. Gọi 1
F (x ) là một nguyên hàm của hàm số f (x ) = và thỏa mãn x + 2 F (− ) 1 1 =
⋅ Tính F (2). 2
A. F (2)= 2 + ln 2.
B. F (2)= 2(1−ln 2).
C. F (2)= 2(1+ ln 2). D. F (2)= 4. (x + )2 2 1 x + 2x +1 x (x + 2)+ Lời giải. Ta có 1 1 = = = x + x + 2 x + 2 x + 2 x + 2 (x + )2 2 1  1  x  → dx = x  ∫ ∫  + dx = + ln x + 2 +C. x + 2  x + 2 2 1 ( )2 1
Theo giả thiết F (− ) 1 1 =  →
+ ln −1+ 2 +C = ⇔ C = 0. 2 2 2 2 Suy ra ( ) x F x = + ln x + 2 
→ F (2)= 2 + ln 4 = 2(1+ ln 2). Chọn C. 2 (x − )3
Câu 22. Hàm số nào sau đây là nguyên một hàm của hàm số f (x) 1 = ? 2 2x 2 3(x − )4 A. 1 F (x) x 3x 3 1 = − + ln x + . B. F (x)= . 4 2 2 2x 3 4 x 2 3(x − )2 C. 1 F (x) x 3x 1 1 = − − − . D. F (x)= . 2 3 4 2 x 2x 4 x (x − )3 3 2 Lời giải. Ta có 1
x −3x + 3x −1 dx = dx ∫ ∫ 2 2 2x 2x 2  x 3 3 1  x 3x 3 1 =   ∫  − + − dx = − + ln x + +C. 2
2 2 2x 2x  4 2 2 2x 2 Chọn C = 
→ F (x) x 3x 3 1 0 = − + ln x + . Chọn A. 4 2 2 2x Câu 23. Biết 1
F (x ) là nguyên hàm của hàm số f (x ) 3 = 4x − +3x và thỏa mãn 2 x 5F ( )
1 + F (2) = 43 . Tính F (2). A. F ( ) 151 2 = . B. F (2)= 23. C. F ( ) 45 2 = . D. F ( ) 86 2 = . 4 2 7  
Lời giải. Ta có F (x) 1 1 3 3 4 2 = 4x
∫  − +3xdx = x + + x +C. 2  x  x 2  
Theo giả thiết F ( )+ F ( ) 7 45 1 5 1 2 = 43  →5 +C+
+C = 43 ⇔ C = .   2  2 2 Suy ra F (x) 1 3 1 1 3 1 4 2
= x + + x +  → F (2) 4 2
= 2 + + .2 + = 23. Chọn B. x 2 2 2 2 2
Câu 24. Hàm số nào sau đây là một nguyên hàm của hàm số ( ) 1 f x = ⋅ 2 x − x
A. F (x)= −ln x −ln x −1 .
B. F (x)= ln x −ln x −1 .
C. F (x)= −ln x + ln x −1 .
D. F (x)= ln x + ln x −1 . Lời giải. Ta có 1 1 1 1 = = − + 2 x − x x (x − ) 1 x x −1  1   1 1   →  d  ∫   x = −   ∫  + d
 x = −ln x + ln x −1 +C. Chọn C. 2  x − x   x x −1 Câu 25. Gọi 1
F (x) là một nguyên hàm của hàm số f (x) = và thỏa mãn 2 x −3x + 2 3 F     = 0.   Tính F (3). 2
A. F (3)= ln 2. B. F (3)= 2 ln 2.
C. F (3)= −2 ln 2.
D. F (3)= −ln 2. Lời giải. Ta có 1 1 1 1 = = − + 2 x −3x + 2 (x − ) 1 (x − 2) x −1 x − 2  1   1 1   →  d  ∫   x = −   ∫  + d
 x = −ln x −1 +ln x −2 +C. 2  − +    x 3x 2
x −1 x −2   Theo giả thiết 3 3 3 F     = 0 
→−ln −1 + ln −2 +C = 0 ⇔ C = 0.  2 2 2
Suy ra F (x) = −ln x −1 + ln x −2  → F ( ) 3 = −ln 2. Chọn D. Câu 26. Xác định x + 3 f (x )dx ∫
biết f (x)= ⋅ 2 x + 3x + 2 A.
f (x)dx = 2 ln x + 2 − ln x +1 +C. ∫ B.
f (x)dx = 2 ln x +1 − ln x + 2 +C. ∫ C.
f (x)dx = 2 ln x +1 + ln x + 2 +C. ∫ D.
f (x)dx = ln x +1 + 2 ln x + 2 +C. ∫ Lời giải. Ta có x + 3 x + 3 2 1 = = − 2 x + 3x + 2 (x + ) 1 (x + 2) x +1 x + 2 x + 3  2 1   → dx =  ∫ ∫  − d
 x = 2 ln x +1 −ln x +2 +C. Chọn B. 2   x + 3x + 2
x +1 x + 2 Câu 27. Cho hàm số 2 1
f (x) có đạo hàm f ′(x) = − và thỏa f ( ) 1 2 = − ⋅ (2x − )2 1 (x − )2 1 3
Biết phương trình f (x)= −1 có nghiệm duy nhất x = x . Tính x0 T = 2017 . 0 A. T = 2017. B. T = 1. C. T = 2017. D. 3 T = 2017 .   Lời giải. Ta có   f (x) 2 1 1 1 ' dx = − dx = − +C. ∫ ∫  (  2x − )2 1 (x − )2 1 x  −1 2x −1  
Theo giả thiết f ( ) 1 1 1 1 2 = − 
→ − +C = − ⇔ C = −1. 3 1 3 3 Suy ra ( ) x f x = − .
(x − )( x − ) 1 1 2 1 Suy ra f (x) x 0 = −1 ⇔ − = − ⇔ = =  → = = Chọn B. ( − ) x x T x 1 (2x − ) 1 1 0 2017 1. 0 1
Câu 28. Tìm một nguyên hàm F (x) của hàm số f (x).g(x), biết
f (x)dx = x +C ∫ , 2 ( ) x g x dx = +C ∫ và F (2) = 5 . 4 2 2 3 3 A. ( ) x x x x F x =
+ 4. B. F (x) = +5. C. F (x)= +5. D. F (x)= +3. 4 4 4 4 2 Lời giải. Ta có x 1
f (x)dx = x +C  → f (x) = 1 ∫ và g (x)dx = +C 
→ g (x) = x. ∫ 4 2 Khi đó
f (x).g (x) 1 1 2 dx = xdx = x +C. ∫ ∫ 2 4
Theo giả thiết F (2) 1 2 = 5 
→ .2 +C = 5 ⇔ C = 4. 4 2 Suy ra ( ) x F x = + 4. Chọn A. 4 Câu 29. Cho ln 2 = 2 x I dx ∫
. Mệnh đề nào sau đây là sai? x A. = 2 x I +C . B. 1 2 x I + = +C . C. = 2(2 x I + )
1 +C . D. = 2(2 x I − ) 1 +C .
Lời giải. Ta có ( x + )/ =( x )/ =( )/ 1 ln 2 2 2 .2 x ln 2 =
.2 x ln 2 ≠ 2 x C x . Chọn A. 2 x x
Cách trắc nghiệm. Ta thấy các đáp án B, C, D sai khác nhau nên hằng số nên dễ
dàng nhận ra đáp án A là không thỏa mãn.
Câu 30. Tìm giá trị của các tham số a, b, c để hàm số F (x)= ( 2
ax + bx + c ) 2x −3 với 3 2 20x −30x + 7 x >
là một nguyên hàm của hàm số f (x) = . 2 2x −3
A. a = 4, b = 2, c = 1 .
B. a = 4, b = −2, c = −1 .
C. a = 4, b = −2, c = 1 .
D. a = 4, b = 2, c = −1 .
Lời giải. Theo bài ra ta có F '(x)= f (x). (*) ( 2
ax + bx + c ) 2
5ax +(3b −6a) − + Ta có
(x)= ( ax +b) x 3b c F ' 2 2x −3 + = . 2x −3 2x −3 5  a = 20 a  = 4   Để (   *) xảy ra ⇔ 3
b −6a = −30 ⇔ b  = −2 . Chọn C.     c  −3b = 7 c  = 1   Câu 31. Nếu f (x) 1 dx = + ln x +C ∫
thì f (x) là hàm số nào trong các hàm số sau? x
A. f (x)= x + ln x +C . B. ( ) 1 f x = − x + +C . x C. x −1 f (x) 1 = − + ln x +C . D. f (x)= . 2 x 2 x
Lời giải. Theo định nghĩa
f (x) x = F (x ) / d 
→ F (x)= f (x). ∫ /   Do đó hàm số cần tìm − f (x ) 1 1 1 x 1
=  + ln x +C = − + = . Chọn D. 2 2 x  x x x
Câu 32. Cho F (x) là một nguyên hàm của hàm số ( ) 3x f x = e
và thỏa mãn F (0) =1.
Mệnh đề nào sau đây là đúng? A. ( ) 1 1 3x F x = e +1. B. ( ) 3x F x = e . 3 3 C. ( ) 1 2 1 4 3x F x = e + ⋅ D. ( ) 3x F x = − e + ⋅ 3 3 3 3 Lời giải. Ta có 1 3x 3 d x e x = e +C ∫ . 3
Theo giả thiết F ( ) 1 2 0 = 1 
→ +C = 1 ⇔ C = . 3 3 Suy ra ( ) 1 2 3x F x = e + ⋅ Chọn C. 3 3 Câu 33. Biết e
F (x ) là một nguyên hàm của hàm số f (x) 3x 1 e + =
và thỏa F (0) = ⋅ 3 Tính 3 ln 3F ( ) 1  .   A. 3 ln 3F ( ) 1  = 64. 3   B. ln 3F ( ) 1  = −8.   C. 3 ln 3F ( ) 1  = 81. 3   D. ln 3F ( ) 1  = 27.   Lời giải. Ta có 1 3x 1 + 3x 1 e dx e + = +C. ∫ . 3 Theo giả thiết ( e e e F 0) = 
→ +C = ⇔ C = 0. 3 3 3   Suy ra F (x) 1 1 3x 1 3 = e +  → ln 3F ( ) 3 4
1  = ln 3. e  = 64.   Chọn A. 3  3   
Câu 34. Tìm nguyên hàm của hàm số f (x) x x 1 e .e + = . A. 1 x x 1 + x x 1 e .e dx e .e + = +C ∫ . B. x x 1 + 2 x 1 e .e dx e + = +C ∫ . 2 C. x x 1 + 2 x 1 e .e dx 2e + = +C ∫ . D. x x 1 + x 1 . d + x e e x = e + e +C. ∫ Lời giải. Ta có 1 x x 1 + 2 x 1 + 2 x 1 e .e dx e dx e + = = +C ∫ ∫ . Chọn B. 2
Câu 35. Tìm nguyên hàm F (x) của hàm ( ) 2 2 x f x = . x A. F (x) 1 = +C. B. F (x) 4 = +C. 4x. ln 4 ln 4 C. ( )= 4x F x . ln 4 +C. D. ( )= 4x F x +C. x Lời giải. Ta có 4 2 2 x d = 4x x dx = +C. ∫ ∫ Chọn B. ln 4 Câu 36. Hàm số ( ) 3 x F x = e
+ 2018 là một nguyên hàm của hàm số nào trong các hàm số sau đây? 3 x A. ( ) 3 e x f x = e . B. ( ) 3 2 = 3 . x f x x e . C. f (x)= . D. ( ) 3 3 1 . x f x x e − = . 2 3x
Lời giải. Hàm số F (x) là một nguyên hàm của hàm số f (x)←→ F '(x)= f (x) .
Suy ra hàm số cần tìm ( )= ( / / 3 x + ) =( 3x ) =( 3)/ 3 3 x 2 2018 . = 3 . x f x e e x e
x e . Chọn B. 3
Câu 37. Hàm số F (x) x x =
+ e là một nguyên hàm của hàm số nào trong các hàm số 3 sau đây? 4 4 A. x f (x) x x = + e . B. ( ) 2 = 3 x f x
x + e . C. f (x) x = + e . D. ( ) 2 x
f x = x + e . 3 12
Lời giải. Hàm số F (x) là một nguyên hàm của hàm số f (x)←→ F '(x)= f (x) . / 3   Suy ra hàm số cần tìm   f (x) x x 2 x = 
+ e  = x + e .   Chọn D.  3 
Câu 38. Biết F (x) là một nguyên hàm của hàm số ( )= ( + )2 3 2 x f x e thỏa F ( ) 3 0 = ⋅ 2   Tính 1 F    ⋅   3 2   2   A. 1 e + 8e + 8 1 e + 6e + 6 F     = ⋅    B. F  = ⋅ 3 6 3 8 2   2   C. 1 e − 6e + 6 1 e −8e + 8 F     = ⋅    D. F  = ⋅ 3 8 3 6
Lời giải. Ta có ∫ (2 x + )2 1 4 3 d = ∫ ( 3x 6 4 + 4 x + ) 6 x 3 d x e x e e x = e
+ e + 4x +C. . 6 3
Theo giả thiết F ( ) 3 1 4 3 0 = 
→ + +C = ⇔ C = 0. 2 6 3 2 2   Suy ra + + F (x) 1 4 1 1 4 4 e 8e 8 6 x 3x 2
= e + e + 4x  → F  
  = e + e + = . Chọn A. 6 3 3 6 3 3 6
Câu 39. Tìm một nguyên hàm F (x) của hàm số ( ) −x = (2 x f x e e + )
1 , biết F (0) = 1. A. ( ) 2 x F x x e− = + . B. ( ) 2 x F x x e− = − + 2. C. ( ) 2 x F x e− = + . D. ( ) 2 x F x x e− = − +1. Lời giải. Ta có −x
∫ (2 x + )1d = ∫ (2 −x + ) = 2 −x e e x e dx x − e +C.
Theo giả thiết F (0) =1 
→−1+C = 1 ⇔ C = 2. Suy ra ( ) 2 x F x x e− = − + 2. Chọn B.
Câu 40. Giả sử ( )= ( 2 + + ) x F x ax bx
c e là một nguyên hàm của hàm số ( ) 2 x f x = x e .
Tính tích P = abc. A. P =1. B. P = −4 . C. P = −5 . D. P = −3 . Lời giải. Ta có ( )= ( + + )/ x +( + + ) ( x )/ / 2 2 2 . . =  +  (2 + ) x F x ax bx c e ax bx c e ax a
b x + b + c e .  
Vì F (x) là một nguyên hàm của f (x) nên ta có /
F (x ) = f (x), ∀x . Do đó 2 ax +  ( a +b) x 2 x 2
x + b + c e = x e ⇔ ax +   ( a +b) 2 2 . . 2
x + b + c = x  . a  =1 a  =1  
Đồng nhất hệ số hai vế, ta được   2
a +b = 0 ⇔ b  = −2 
→ P = abc = −4 . Chọn B.     b  + c = 0 c  = 2  
Câu 41. Giả sử hàm số ( ) ( 2 ). x f x ax bx c e− = + +
là một nguyên hàm của hàm số ( ) (1 ) x g x x x e− = −
. Tính tổng S = a + b + c . A. S = −2 . B. S = 4 . C. S =1 . D. S = 3 .
Lời giải. Ta có / ( )= (
+ ) −x −( 2 + + ) −x 2 2 = − +(2 − ) +( −  ) −x f x ax b e ax bx c e ax a b x b c e .  
Vì f (x) là một nguyên hàm của g(x) nên ta có /
f (x ) = g (x), ∀x . Do đó 2  a − x + 
( a −b)x +(b −c) −xe = x   ( − x) −x 2 e ⇔ a
− x +( a −b)x +(b −c) 2 2 1 2 = −x + x.   a − = −1 
Đồng nhất hệ số hai vế, ta được 2
a −b = 1 ⇔ a = b = c = 1 → S = a + b + c = 3. Chọn D.
b−c = 0 
Câu 42. (ĐỀ THỬ NGHIỆM 2016 2017) –
Tìm nguyên hàm của hàm số f (x) = cos2x. A. f (x) 1 dx = sin 2x +C. ∫ B. f (x ) 1
dx = − sin 2x +C. ∫ 2 2 C.
f (x)dx = 2 sin 2x +C. ∫ D.
f (x)dx = −2 sin 2x +C. ∫ Lời giải. Ta có f (x) 1 dx = cos 2x dx = sin 2x +C. ∫ ∫ Chọn A. 2
Câu 43. Biết rằng F (x) là một nguyên hàm của hàm số f (x)= sin(1−2x) và thỏa   mãn 1 F     = 1. 
Mệnh đề nào sau đây là đúng? 2
A. F (x)= cos(1−2x)+1.
B. F (x)= cos(1−2x). C. 1 1 F (x) 1 = − ( − x) 3 cos 1 2 + ⋅
D. F (x)= cos(1−2x)+ ⋅ 2 2 2 2 Lời giải. Ta có ( − x) 1 sin 1 2 dx = cos(1−2x)+C. ∫ 2     Theo giả thiết 1 1 1 F     = 1  → cos 0   
+C = 1 ⇔ C = .     2 2  2 Suy ra F (x) 1 = ( − x) 1 cos 1 2 + . Chọn D. 2 2   Câu 44. Cho hàm số π
f (x) thỏa các điều kiện f ′(x) = 2 + cos 2x và f     = 2 . π   Mệnh  2 
đề nào sau đây là sai? A. x f (0) = . π B. f (x) sin 2 = 2x + + . π 2   C. ( ) sin 2x π f x = 2x − + .   π D. f −   = 0. 2    2  Lời giải. Ta có
f ′(x) x = ( + x ) 1 d 2 cos 2
dx = 2x + sin 2x +C. ∫ ∫ 2   Theo giả thiết π f     = 2π 
→π +C = 2π ⇔ C = . π    2  Suy ra f (x) 1
= 2x + sin 2x + . π Chọn B. 2
Câu 45. Một nguyên hàm F (x) của hàm số f (x) 2
= sin x là kết quả nào sau đây, biết
nguyên hàm này bằng π khi π x = ? 8 4 3 A. ( ) sin x x x F x = . B. F (x) sin 2 = − . 3 2 4 3 C. sin x 2 F (x) x sin 2x 1 = − + . D. F (x)= − . 2 4 4 3 12 Lời giải. Ta có − f (x) 1 cos 2x 2 dx = sin x dx = dx ∫ ∫ ∫ 2 1 = (   − x ) 1 1 1 cos 2 dx =  ∫
x − sin 2x+C.   2 2  2    Theo giả thiết π π 1 π 1 π π 1 F     = 
→ . − sin +C = ⇔ C = .   4  8 2 4 4 2 8 4
Suy ra F (x) x sin 2x 1 = − + . Chọn C. 2 4 4
Câu 46. Tìm nguyên hàm của hàm số f (x) 2 = tan x. A. 2
tan x dx = tan x − x +C. ∫ B. 2
tan x dx = tan x − x. ∫ 3 3 C. tan x tan x 2 tan x dx = ⋅ ∫ D. 2 tan x dx = +C. ∫ x x
Lời giải. Dùng kỹ thuật thêm bớt, ta được 2 x x ∫ ∫ ( 2 tan d  1 tan x  ) 1 = + − dx   = ∫ ( 1 2 1+ tan x )dx − dx = dx −
dx = tan x − x +C. ∫ ∫ ∫ 2 cos x
' Nếu đề bài yêu cầu tìm họ nguyên hàm thì ta chọn A, còn yêu cầu tìm một nguyên hàm thì ta chọn B ' .
Ở đây yêu cầu tìm nguyên hàm, tức là phải tìm họ nguyên hàm. Chọn A. Câu 47. Cho nguyên hàm
f (x)dx = sin 2x cos x +C ∫
. Mệnh đề nào sau đây là đúng? A. 1 f (x) 1
= (3cos3x +cos x) .
B. f (x)= (cos3x +cos x) . 2 2 C. 1 f (x ) 1
= (3cos3x −cos x) .
D. f (x)= (cos3x −cos x). 2 2 Lời giải. Ta có f (x) 1
dx = sin 2x cos x = (sin 3x + sin x). ∫ 2 Suy ra f (x) 1 = ( x + x )/ 1 sin 3 sin
= (3cos3x +cos x). Chọn A. 2 2
Câu 48. Tìm giá trị thực của các tham số a, b để hàm số ( )= ( cos + sin ) x F x a x b x e là
một nguyên hàm của hàm số ( ) x
f x = e cos x.
A. a = 1, b = 0 . B. a = 0, b = 1 .
C. a = b = 1 . D. 1 a = b = . 2 Lời giải.
Ta có / ( )= (− sin + cos ) x +( cos + sin ) x = ( + )cos +( − )sin x F x a x b x e a x b x e b a x b a x e .  
Vì F (x) là một nguyên hàm của f (x) nên ta có /
F (x ) = f (x), ∀x .
Do đó ( + )cos +( − )sin x x b a x b a
x e = e cos x ⇔ (b + a)cos x +(b − a)sin x = cos x.    + =
Đồng nhất hệ số hai vế, ta được b a 1 1 
⇔ a = b = . Chọn D. b  −a = 0 2  Câu 49. Biết 4m
F (x) là một nguyên hàm của hàm số f (x) 2 =
+ sin x và thỏa mãn πππ
F (0) = 1 , F     =  . Tìm m .  4  8 A. 4 m = − . B. 3 m = . C. 3 m = − . D. 4 m = . 3 4 4 3   Lời giải. Ta có f (x) 4m 4m 2 2 dx =  ∫
∫  +sin xdx = dx + sin d x x    ∫ ∫ ππ 4m 1   = x + ( − x ) 4m 1 1 d 1 cos 2 dx = x +  ∫ ∫
x − sin 2x+C.   π 2 π 2  2  F (0)=1 C  =1 C    = 1    Theo giả thiết        → 1   ⇔ Chọn C. π 1 π π π  3 .       =  +   F m      − +C = m  = −       4 8 2  4 2  8     4 Câu 50. Biết 1
F (x) là một nguyên hàm của hàm số f (x ) = và đồ thị hàm số 2 sin xπ  π
y = F (x ) đi qua điểm M  ;0     
. Tính F   .  6  3         A. π π π − π F     = 0         . B. 2 3 F   = . C. 3 1 F   = . D. 2 F   = .    3  3 3 3 3  3  3 Lời giải. Ta có 1
dx = −cot x +C ∫ . 2 sin x     Đồ thị π π π
y = F (x ) đi qua điểm M  ;0     
nên F   = 0 
→−cot +C = 0 ⇔ C = 3.  6  6 6   Suy ra π F (x) 2 3 = −cot x + 3  → F     = .  Chọn B.  3 3 Baøi 02
MOÄT SOÁ PHÖÔNG PHAÙP TÌM NGUYEÂN HAØM
1. Phương pháp đổi biến số Nếu
f (x)dx = F (x)+C ∫ thì
f u(x).u '(x)dx = F u(x) +C ∫     .
Giả sử ta cần tìm họ nguyên hàm I = f (x)dx ∫
, trong đó ta có thể phân tích
f (x ) = g u(x ) u '(x)  
thì ta thực hiện phép đổi biến số t = u(x), suy ra dt = u'(x)dx .
Khi đó ta được nguyên hàm:
g (t)dt = G (t)+C = G u(x) +C. ∫  
Chú ý: Sau khi tìm được họ nguyên hàm theo t thì ta phải thay t = u(x).
2. Phương pháp lấy nguyên hàm từng phần
Cho hai hàm số u và v liên tục trên đoạn [a;b] và có đạo hàm liên tục trên đoạn
[a;b]. Khi đó: d u v = uv − vd . u ∫ ∫ (*) Để tính nguyên hàm f (x )dx ∫
bằng từng phần ta làm như sau: Bước 1. Chọn ,
u v sao cho f (x)dx = udv (chú ý dv = v '(x)dx ).
Sau đó tính v = dv
∫ và du = u'.dx .
Bước 2. Thay vào công thức (*) và tính vdu ∫ .
Chú ý. Cần phải lựa chọn u và dv hợp lí sao cho ta dễ dàng tìm được v và tích phân vdu ∫
dễ tính hơn udv ∫
. Ta thường gặp các dạng sau  x
● Dạng 1. I = P (x) sin   dx ∫ , trong đó là đa thức.  P (x) cos x    u  = P (x) 
Với dạng này, ta đặt  sin x  . d  v  =   dx  cos x    ax +b
● Dạng 2. I = P (x )e dx ∫
, trong đó P (x) là đa thức. u  = P (x)
Với dạng này, ta đặt  . d ax +b
 v = e dx
● Dạng 3. I =
P (x)ln(mx + n)dx ∫
, trong đó P (x) là đa thức. u
 = ln(mx +n)
Với dạng này, ta đặt  . d  v  = P (x)dx   x x ● Dạng 4. sin I =   e dx ∫ . cos x    sin x x u  = e u  =   
Với dạng này, ta đặt  cos x   
 hoặc có thể đặt ngược lại     sin x .  d  v =   dx  d x
v = e dx   cos x   
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1. PHƯƠNG PHÁP ĐỔI BIẾN SỐ Câu 1. Biết
f (u)du = F (u)+C. ∫
Mệnh đề nào dưới đây đúng ? A. f (2x − )
1 dx = 2F (2x − ) 1 +C. ∫ B. f (2x − )
1 dx = 2F (x)−1+C. ∫ C. 1 f (2x − )
1 dx = F (2x − ) 1 +C. ∫ D. f (2x − ) 1 dx = F (2x − ) 1 +C. ∫ 2
Lời giải. Đặt u = 2x −1  →du = 2dx Khi đó
f ( x − ) x = f (u) du 1 = f (u) 1 u = F (u) 1 2 1 d d
+C = F (2x − ) 1 +C. ∫ ∫ ∫ 2 2 2 2 Chọn D.  
Câu 2. Tìm hàm số F (x) thỏa mãn F ′(x)= ( x + )2017 2 1 và 1 F   −   = 2018.   2 (2x + )2018 (2x + )2018 A. 1 F (x) 1 = + 2018. B. F (x)= + 2018. 2018 4036 C. F (x)= ( x + )2016 2017 2 1 + 2018. D. F (x)= ( x + )2016 4034 2 1 + 2018.
Lời giải. Ta có ( x + )2017 2 1 dx. ∫
Đặt u = 2x +1 
→du = 2dx + 2017 1 1 u 2x 1 2017 ( )2018 2018 Khi đó (2x + ) 1 dx = u du = . +C = +C. ∫ ∫ 2 2 2018 4036   Theo giả thiết 1 F   −   = 2018  →C = 2018.    2 (2x + )2018 Vậy F (x) 1 = + 2018 . Chọn B. 4036
Câu 3. Tìm nguyên hàm của hàm số f (x)= x (x + )9 2 1 . A. 1 f (x) 1 dx = − ∫ (x + )10 2 1 +C. B. f (x)dx = ∫ (x + )10 2 1 +C. 20 20 C. f (x) x = ∫ (x + )10 2 d 2 1 +C. D. f (x) x = ∫ (x + )10 2 d 1 +C. Lời giải. Ta có f (x) x = x (x + ∫ ∫ )9 2 d 1 dx. Đặt 2 t = x +1 
→dt = 2xdx . 10 Khi đó x ∫ (x + )9 1 1 t 1 1 dx = t dt = . +C = ∫ (x + )10 2 9 2 1 +C. 2 2 10 20 Vậy f (x) 1 dx = ∫ (x + )10 2 1 +C. Chọn B. 20
Câu 4. (ĐỀ MINH HỌA NĂM 2016 – 2017)
Tìm nguyên hàm của hàm số f (x) = 2x −1. A. 1 f (x) 2 dx = (2x − ) 1 2x −1 +C. ∫ B.
f (x)dx = (2x − ) 1 2x −1 +C. ∫ 3 3 C. f (x) 1 dx = − 2x −1 +C. ∫ D. f (x) 1 dx = 2x −1 +C. ∫ 3 2 Lời giải. Ta có f (x)dx = 2x −1dx. ∫ ∫ Đặt 2
t = 2x −1 → t = 2x −1  → d t t = dx. 3 Khi đó t 1 2 2x −1dx = t. d t t = t dt = +C = (2x − ) 1 2x −1 +C. ∫ ∫ ∫ Chọn B. 3 3 Câu 5. Biết ln x
F (x ) là một nguyên hàm của hàm số f (x) 2 =
⋅ ln x +1 và F ( ) 1 1 = ⋅ x 3
Tính F (e) 2 .  
A. F (e) 2 8  = ⋅  
B. F (e) 2 8  = ⋅  
C. F (e) 2 1  = ⋅  
D. F (e) 2 1  = ⋅   3 9 3 9
Lời giải. Ta có ln x 2 ⋅ ln x +1dx ∫ . x Đặt ln x 2 2
t = ln x +1 ⇒ t = ( 2 ln x + ) 1  → d t t = dx. x ln x +1 ln x t 2 2 ( )3 2 3 Khi đó ⋅ ln x +1dx = t dt = +C = +C. ∫ ∫ x 3 3
Theo giả thiết F ( ) 1 1 1 1 = 
→ +C = ⇔ C = 0. 3 3 3 ( ln x +1)3 2 Suy ra F (x) =  → F (e) 2 8  = ⋅   Chọn B. 3 9
Câu 6. Biết F (x) là một nguyên hàm của hàm số ( ) ln x f x = và F ( 2 e ) = 4 . Mệnh đề x nào sau đây là đúng? 2 2 A. ( ) ln x ln x F x = +C . B. F (x)= + 2 . 2 2 2 2 C. ( ) ln x ln x F x = −2 . D. F (x)= + x +C . 2 2 Lời giải. Ta có ( ) ln x x f x dx = dx ∫ ∫ . Đặt d t = ln x  →dt = . x x 2 2 Khi đó ln x t ln x dx = d t t = +C = +C. ∫ ∫ x 2 2 2 ln ( 2 e 2 )
Theo giả thiết F (e )= 4  →
+C = 4 ⇔ C = 2. 2 2 Suy ra ( ) ln x F x = + 2. Chọn B. 2
Chú ý: Đáp án A được gọi là họ nguyên hàm của hàm số f (x) .
Câu 7. Biết F (x) là một nguyên hàm của hàm số f (x) 1 =
và thỏa F (0)= −ln 2 . x e +1
Tìm tập nghiệm S của phương trình ( )+ ln( x F x e + ) 1 = 3. A. S = {± } 3 . B. S = { } 3 . C. S = . ∅ D. S = {− } 3 . x x x x Lời giải. Ta có 1 e +1− e e e dx = dx = dx − dx = x − dx. ∫ ∫ ∫ ∫ ∫ x e +1 x e +1 x e +1 x e +1 Đặt x = +1  →d x t e
t = e dx . Khi đó x e dt dx =
= ln t +C = ln x e +1 +C = ln ∫ ∫ ( xe + +C x )1 . e +1 t Do đó 1 dx = x − ln ∫ ( xe + +C x )1 . e +1
Theo giả thiết F (0)= −ln 2 
→0−ln 2 +C = −ln 2 ⇔ C = 0. Suy ra ( ) = −ln( x F x x e + ) 1 .
Xét phương trình ( )+ ln( x + ) 1 = 3 ⇔ − ln( x + ) 1 + ln( x F x e x e e + )
1 = 3 ⇔ x = 3. Chọn B.
Câu 8. Hàm F (x) nào dưới đây không phải là một nguyên hàm của hàm số ( ) 2 x f x = xe ? A. ( ) 2 1 x 2 1 F x = e + 2 . B. ( )= ( x F x e + ) 5 . 2 2 C. ( ) 2 1 x 2 1 F x = − e +C . D. ( )= − (2 x F x −e ). 2 2 Lời giải. Ta có ( ) 2 1 d x f x x = xe dx. ∫ ∫ Đặt 2 t = x 
→dt = 2xdx → d x x = dt. 2 Khi đó ( ) 2 1 t 1 t 1 d = d x f x x e t = e +C = e +C ∫ ∫ . 2 2 2
Vì F (x) là một nguyên hàm của f (x) nên đáp án A đúng với C = 2 , đáp án B đúng với 5 C =
, đáp án D đúng với C = −1. Vậy chỉ có đáp án C là sai. Chọn C. 2
Cách trắc nghiệm. Ta thấy các đáp án A, B, D sai khác nhau hằng số nên chắc chắn
rằng nó là một nguyên hàm của f (x) . ln x Câu 9. Cho e I = dx ∫
và t = ln x. Mệnh đề nào sau đây là đúng? x t A. e t I = te dt. ∫ B. t I = e dt. ∫ C. I = dt. ∫
D. I = tdt. ∫ t Lời giải. Đặt 1 t = ln x 
→dt = dx . Khi đó t I = e dt ∫ . Chọn B. x
Câu 10. Kí hiệu F (x) là họ các nguyên hàm của hàm số f (x) 4
= sin x cos x . Mệnh đề nào sau đây là đúng? 5 4 A. ( ) cos x cos x F x = +C . B. F (x)= +C . 5 4 4 5 C. ( ) sin x sin x F x = +C . D. F (x)= +C . 4 5 Lời giải. Ta có f (x ) 4 dx =
sin x cos xdx ∫ ∫
. Đặt t = sin x 
→ dt = cos xdx . 5 5 Khi đó f (x) t sin x 4 dx = t dt = +C = +C. ∫ ∫ Chọn D. 5 5   Câu 11. Biết x π
F (x ) là một nguyên hàm của hàm số f (x) sin = và F     = 2.   1+ 3 cos x  2  Tính F (0). A. F ( ) 1 0 = − ln 2 + 2. B. F ( ) 2 0 = − ln 2 + 2. 3 3 C. F ( ) 2 0 = − ln 2 − 2. D. F ( ) 1 0 = − ln 2 − 2. 3 3 Lời giải. Ta có sin x dx ∫ . 1+ 3 cos x Đặt 1
t = 1+ 3 cos x  →dt = −3sin d x x → sin d x x = − dt. 3 Khi đó sin x 1 dt 1 1 dx = −
= − ln t +C = − ln 1+3cos x + C. ∫ ∫ 1+ 3 cos x 3 t 3 3   Theo giả thiết π F     = 2  →C = 2.   2  Suy ra F (x) 1
= − ln 1+3cos x + 2  → F (0) 1 2 2
= 2− ln 2 = 2− ln 2. Chọn B. 3 3 3   Câu 12. Cho π
F (x ) là một nguyên hàm của hàm số f (x ) = cot x trên 2 0;    thỏa  3      π π F     = 0.   
Tính F  ⋅  4  2     A. π π F     = −ln 2.     B. 1
F   = ln 2.    2   2  2     C. π π F     = −ln 2.    D. F  = 2 − ln 2.  2  2 Lời giải. Ta có cos x cot x dx = dx. ∫ ∫
Đặt t = sin x 
→dt = cos xdx . sin x Khi đó cos x dt cot x dx = dx =
= ln t +C =ln sin x +C. ∫ ∫ ∫ sin x t     Theo giả thiết π 1 F     = 0  → ln  
+C = 0 ⇔ C = ln       ( 2). 4  2    Suy ra π F (x) =
( x )+ ( )→F     =   ( ) 1 ln sin ln 2 ln 2 = ln 2. Chọn B.  2  2
Câu 13. Gọi F (x) là một nguyên hàm của hàm số f (x)= tan 2x thỏa mãn F (0)= 0.     π π F     F       Tính      6  2 T 2e e  = − .
A. T = 1.
B. T = 2.
C. T = − 2.
D. T = 0. Lời giải. Ta có sin 2x tan 2x dx = dx. ∫ ∫ cos 2x Đặt 1
t = cos 2x 
→dt = −2 sin 2xdx → sin 2xdx = − dt. 2 Khi đó sin 2x 1 dt 1 1 tan 2x dx = dx = −
= − .ln t +C = − ln cos 2x +C. ∫ ∫ ∫ cos 2x 2 t 2 2
Theo giả thiết F (0) = 0  →C = 0.       Suy ra π π 1 1 F (x) 1 = − ln cos 2x  → F  
  = 0 và F     = − ln      = ln .     ( 2) 2 2 6 2 2 Vậy ln 2 0 T = 2.e
−e = 2−1 = 1. Chọn A.
Câu 14. Biết F (x) là một nguyên hàm của hàm số ( ) sin x f x = e
cos x và F (π) = 5 .
Khẳng định nào sau đây là đúng? A. ( ) sin x F x = e + 4 . B. ( ) sin x F x = e +C . C. ( ) cos x F x = e + 4 . D. ( ) cosx F x = e +C . Lời giải. Ta có ( ) sin d x f x x = e cos xdx. ∫ ∫
Đặt t = sin x 
→dt = cos xdx. Khi đó ( ) sin x t t sin d = cos d = d x f x x e x x
e t = e +C = e +C ∫ ∫ ∫ .
Theo giả thiết F ( ) sin 5 e π π =  →
+C = 5 ⇔ 1+C = 5 ⇔ C = 4. Suy ra ( ) sin x F x = e + 4. Chọn A. tan x Câu 15. Biết e
F (x) là một nguyên hàm của hàm số f (x) = và F (0)= 2017 . 2 cos x
Khẳng định nào sau đây là đúng? A. ( ) tan x F x = e . B. ( ) tan x F x e− = . C. ( ) tan x F x = e + 2016. D. ( ) tan x F x = e + 2018. tan x Lời giải. Ta có ( ) e 1 f x dx = dx. ∫ ∫
Đặt t = tan x  →dt = dx. 2 cos x 2 cos x tan x Khi đó f (x) e t t tan dx = dx = e d x
t = e +C = e +C. ∫ ∫ ∫ 2 cos x
Theo giả thiết F ( ) tan 0 0 = 2017  →e
+C = 2017 ⇔ C = 2016. Suy ra ( ) tan x F x = e + 2016. Chọn C.
Vấn đề 2. PHƯƠNG PHÁP LẤY NGUYÊN HQM TỪNG PHẦN
Câu 16. Gọi F (x) là một nguyên hàm của hàm số f (x)= ln x và thỏa mãn F ( ) 1 = 3. Tính F ( 2 e ).
A. F ( 2e )= 4.
B. F ( 2e ) 2
= 3e + 4. C. F ( 2 e ) 2 = e
− + 4. D. F ( 2 e ) 2 = e + 4.  dx  =  = Lời giải. Ta có u ln x du   ln xdx ∫ . Đặt  ⇒  x . d  v = dx   v  = x
Khi đó ln xdx = x ln x − dx x
= ln x − x +C. ∫ ∫
Theo giả thiết F ( ) 1 = 3 
→−1+C = 3 ⇔ C = 4.
Suy ra F (x) = x x − x +  → F ( 2 e ) 2 .ln 4
= e + 4. Chọn D.
Câu 17. (ĐỀ CHÍNH THỨC 2016 2017) Cho F (x) 1 = − là một nguyên hàm của – 3 3x f (x) hàm số
. Tìm nguyên hàm của hàm số f '(x)ln x . x A. ln x 1 f (x) ln x 1 ' ln xdx = + +C. ∫ B.
f '(x ) ln xdx = − +C. ∫ 3 5 x 5x 3 5 x 5x C. ln x 1 f (x) ln x 1 ' ln xdx = + +C. ∫ D.
f '(x)ln xdx = − + +C. ∫ 3 3 x 3x 3 3 x 3x 2 1 3x 1 f (x)
Lời giải. Ta có F (x)= = =  → f (x) 1 ' . = . 6 4 3 3 x x x x  1 u  = ln x d  u = dx Xét  
f '(x)ln xdx. ∫ Đặt  ⇔  dv = f  (x) x . ' dx   v  = f (x)  f (x) Khi đó f (x) x x = x f (x) ln x 1 ' ln d ln . − dx = + +C. ∫ ∫ Chọn C. 3 3 x x 3x ln(ln x)
Câu 18. Tìm nguyên hàm của hàm số f (x)= . x ln(ln x) ln(ln x ) A.
dx = ln x.ln(ln x)+C. ∫ B.
dx = ln x.ln(ln x)+ ln x +C. ∫ x x ln(ln x) ln(ln x ) C.
dx = ln x.ln(ln x)− ln x +C. ∫ D.
dx = ln(ln x)+ ln x +C. ∫ x x ln (ln x ) Lời giải. Đặt dx
t = ln x ⇒ dt = . Suy ra dx = ln t dt ∫ ∫ . x x  dt  =  = Đặt u ln t du    ⇒  t . d  v = dt   v  = t
Khi đó ln t dt = t ln t − dt = t ln t −t +C = ln x.ln(ln x)−ln x +C. ∫ ∫ Chọn C.
Câu 19. Tìm nguyên hàm của hàm số ( ) x f x = xe . 2 A. x x d x x xe
x = e + xe +C. ∫ B. x xe d x x = e +C. ∫ 2 2 C. x x d x x xe
x = xe − e +C. ∫ D. x xe d x x x = e + e +C. ∫ 2  =  = Lời giải. u x du dx Ta có x   xe dx. ∫ Đặt  ⇒  . d xv = e d x x v  = e   Khi đó x d x x = − d x x xe x xe e
x = xe − e +C. ∫ ∫ Chọn C.
Câu 20. Biết F (x) là một nguyên hàm của hàm số ( )= ( − ) 1 x f x x e và thỏa mãn
F (0) = 1. Tìm F (x). A. ( )= ( − ) 1 x F x x e .
B. ( )= ( −2) x F x x e . C. ( )= ( + ) 1 x F x x e +1 .
D. ( )= ( −2) x F x x e + 3 .  = −  = Lời giải. u x 1 du dx Ta có ( − )   1 x x e dx ∫ . Đặt  ⇒  . d xv = e d x x v  = e   Khi đó ( − ) 1 x d = ( − ) 1 x x − d = ( − ) 1 x x − + = ( −2) x x e x x e e x x e e C x e +C. ∫ ∫
Theo giả thiết F ( ) =  →( − ) 0 0 1 0
2 e +C = 1 ⇔ C = 3. Vậy ( ) = ( −2) x F x x
e + 3 . Chọn D.
Câu 21. Cho F (x) là một nguyên hàm của hàm số ( ) . x f x x e− = thỏa mãn điều kiện
F (0) = −1. Tính tổng S các nghiệm của phương trình F (x)+ x +1 = 0.
A. S = −3.
B. S = 0.
C. S = 2.
D. S = −1.  =  = Lời giải. u x du dx Ta có   . −x x e dx ∫ . Đặt  ⇒  . −x dv = e d −x x v  = e −   Khi đó x e− d −x −x = − + d −x −x x x xe e x =− xe −e +C. ∫ ∫
Theo giả thiết F (0)= −1 
→−1+C = −1 ⇔ C = 0. Suy ra ( ) −x −x x F x = −xe −e = e − (x + ) 1 .
Xét phương trình ( )+ +1 = 0 x F x x ⇔ e − (x + ) 1 + x +1 = 0  = − ⇔ (x + )( x x e − + ) 1 1 1 = 0 ⇔  
→S = −1+ 0 = −1. Chọn D.x = 0 
Câu 22. Biết F (x) là một nguyên hàm của hàm số f (x)= x sin x và thỏa mãn F (π) = 2 . π
Tính giá trị của biểu thức T = 2F (0)−8F (2π). A. T = 6 . π B. T = 4 . π C. T = 8 . π D. T = 10 . π  =  = Lời giải. Ta có u x u x   x sin xdx ∫ . Đặt d d  ⇒  . d
v = sin xdx v  = −cos x   Khi đó
x sin xdx = −x cos x +
cos xdx = −x cos x + sin x +C. ∫ ∫
Theo giả thiết F (π)= 2π 
→π +C = 2π ⇔ C = . π F (0)= π Suy ra 
F (x) = −x cos x + sin x + π  →  T
→ = 2π −8.( π − ) = 10 . π F  (2π) = π −  Chọn D. Câu 23. Biết x
F (x) là một nguyên hàm của hàm số f (x) 2 = x cos và thỏa F ( ) 1 0 = ⋅ 2 2
Tính F (π). 2 2 2 2 A. π π 1 π 1 π F (π) 1 =
+ ⋅ B. F (π)=
− ⋅ C. F (π)= + ⋅
D. F (π)= +1. 2 2 4 2 4 2 4  +  Lời giải. Ta có x 1 cos x 1 1 2 x cos dx = x   ∫ ∫  dx = xdx +
x cos xdx. ∫ ∫ 2  2  2 2 2 2 1 1 x x xdx = . +C = +C . ∫ ( ) 1 1 1 2 2 2 4  =  = 1 u x u x  
x cos xdx. ∫ Đặt d d  ⇒  . 2 d
v = cos xdx v  = sin x   Suy ra 1 1 x x x = ∫ (x x− x x ∫ ) 1 cos d sin sin d
= (x sin x + cos x +C . (2) 2 ) 2 2 2 2 Từ ( ) x x 1 1 và (2) , suy ra 2 x cos dx = +C +
x sin x + cos x +C ∫ . 1 ( 2 ) 2 4 2
Theo giả thiết F ( ) 1 1 1 1 1 0 = 
→C + + C = ⇔ C + C = 0. 1 2 1 2 2 2 2 2 2 2 2 Suy ra π F (x) x 1 = + (x x + x )  → F (π) 1 sin cos = − . Chọn B. 4 2 4 2
Câu 24. Tìm nguyên hàm của hàm số f (x) 2 = x cos x. A. 2 2
x cos xdx = x sin x − 2x cos x + 2 sin x + 2C. ∫ B. 2 2
x cos xdx = x sin x + 2x cos x − 2 sin x. ∫ C. 2 2
x cos xdx = x sin x + 2x cos x − 2 sin x − 2C. ∫ D. 2 2
x cos xdx = x sin x + x cos x − sin x −C. ∫ 2  =  =
Lời giải. Đặt u x du 2xdx    ⇒  . d
v = cos xdx v  = sin x   Khi đó 2 2
x cos xdx = x sin x − 2 x sin xdx ∫ ∫ . ( ) 1  =  = Tính u x u x   x sin xdx ∫ . Đặt d d  ⇒  . d
v = sin xdx v  = −cos x   Ta được
x sin xdx = −x cos x +
cos xdx = −x cos x + sin x +C. ∫ ∫ (2) Từ ( ) 1 và (2) , suy ra 2 2
x cos xdx = x sin x − 2(−x cos x + sin x +C ) ∫ 2
= x sin x + 2x cos x −2 sin x −2C. Chọn C.
Câu 25. Tìm nguyên hàm của hàm số ( ) x
f x = e sin x. A. x 1 x sin d x e
x x = e sin x +C. ∫ B. sin d = ∫ ( x sin x e x x e
x + e cos x )+C. 2 C. x 1 x sin d x e
x x = e cos x +C. ∫ D. sin d = ∫ ( x sin x e x x e
x − e cos x )+C . 2  =  = Lời giải. u sin x du cos xdx Đặt    ⇒  . d xv = e d x x v  = e   Khi đó sin xd x = sin − cos x d x xe x e x xe
x = e sin x − K ∫ ∫ . ( ) 1 u  = cos x d
 u = −sin xdx Tính =   cos x K xe dx ∫ . Đặt  ⇒  . d xv = e d x x v  = e   Suy ra x = cos + sin x K e x xe dx. ∫ (2) Từ ( ) 1 và (2) , suy ra sin x d x = sin − ∫ ( x cos + sin x xe x e x e x xe dx ∫ ) x x x x 1 ⇔ 2 sin d = sin − cos ⇔ sin d = ∫ ∫ ( x sin x xe x e x e x xe x e
x − e cos x ). 2
Vì các nguyên hàm sai khác nhau hằng số C nên ta Chọn D. Baøi 03 TÍCH PHAÂN 1. Định nghĩa
Cho f (x) là hàm số liên tục trên K và a, b là hai số bất kì thuộc K . Giả sử
F (x ) là một nguyên hàm của f (x) trên K thì hiệu số
F (b)− F (a)
được gọi là tích phân của f (x) từ a đến b và kí hiệu là b f (x ) b
dx = F (x ) = F (b)− F (a) ∫ . a a 2. Tính chất a
Tích phân tại một giá trị xác định của biến số thì bằng 0 , tức là
f (x)dx = 0 ∫ . a b a
Đổi cận thì đổi dấu, tức là
f (x)dx = − f (x)dx ∫ ∫ . a b
Hằng số trong tích phân có thể đưa ra ngoài dấu tích phân, tức là b b
kf (x)dx = k f (x )dx ∫ ∫
( k là hằng số). a a
Tích phân một tổng bằng tổng các tích phân, tức là b b b
f (x)± g(x) dx = f (x)dx ± g(x)dx ∫   ∫ ∫ . a a a b c b
Tách đôi tích phân, tức là f (x)dx =
f (x )dx + f (x)dx ∫ ∫ ∫ . a a c b Chú ý: Tích phân f (x)dx ∫
chỉ phụ thuộc vào hàm f và các cận a, b mà không a b b
phụ thuộc vào biến số x , tức là f (x)dx = f (t)dt ∫ ∫ . a a
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. TÍNH CHẤT TÍCH PHÂN
Câu 1. Giả sử hàm số f (x) liên tục trên ℝ và các số thực a < b < c. Mệnh đề nào sau đây sai? c b c b c c A. f (x)dx =
f (x )dx + f (x )dx. ∫ ∫ ∫ B. f (x)dx =
f (x )dx − f (x )dx. ∫ ∫ ∫ a a b a a b b a c b b C. f (x)dx =
f (x )dx + f (x )dx. ∫ ∫ ∫
D. c. f (x)dx = c f (x)dx. ∫ ∫ a b a a a
Lời giải. Chọn C.
Câu 2. Cho f (x), g(x) là hai hàm số liên tục trên ℝ và các số thực a, b, c . Mệnh đề nào sau đây sai? b b A. f (x)dx = f ( y)dy. ∫ ∫ a a b b b
B. f (x)+ g(x) dx = f (x)dx + g (x )dx. ∫   ∫ ∫ a a a a C.
f (x)dx = 0. ∫ a b b b
D. f (x).g(x) dx = f (x )dx. g (x )dx. ∫   ∫ ∫ a a a
Lời giải. Chọn D.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng? 1 A. dx = 1 ∫ . −1 b b b B. f x . f x dx = f x dx. f x dx ∫ ∫ ∫ . 1 ( ) 2 ( ) 1 ( ) 2 ( ) a a a b
C. Nếu f (x) liên tục và không âm trên đoạn [a;b] thì f (x)dx ≥ 0 ∫ . a b
D. k.dx = k(a −b), ∀k ∈ ∫ ℝ . a 1 1
Lời giải. Ta có dx = x = 2. ∫ Do đó A sai. 1 − −1
Theo tính chất tích phân thì B sai (vì không có tính chất này).
Xét đáp án C. Giả sử F (x) là một nguyên hàm của hàm số f (x) trên đoạn [a;b] . Suy ra /
F (x ) = f (x) ≥ 0, ∀x ∈[a;b]. b / b
● F (x ) = 0, ∀x ∈ [a;b], suy ra F (x ) là hàm hằng nên
f (x)dx = F (x) = 0. ∫ a a /
● F (x ) > 0, ∀x ∈ [a;b] , suy ra F (x ) đồng biến trên đoạn [a;b] nên F (b) > F (a) . b Do đó f (x) b
dx = F (x ) = F (b)− F (a)> 0 ∫
. Do đó C đúng. Chọn C. a a b b b
Ta có k.dx = k. dx = k.x = k(b −a)  → ∫ ∫ D sai. a a a 5 2
Câu 4. Cho hàm số f (x) thỏa mãn
f (x)dx = 10 ∫ . Tính I =
2−4 f (x) dx. ∫   2 5 A. I = 32.
B. I = 34. C. I = 36. D. I = 40. 2 2 2
Lời giải. Ta có I = 2−4 f (x) dx = 2 dx −4 f (x)dx ∫   ∫ ∫ 5 5 5 5 2 = 2x + 4
f (x)dx = 2.(2 − ) 5 + 4.10 = 34 ∫ . Chọn B. 5 2 3 3
Câu 5. Cho hàm số f (x) thỏa mãn
f (x)dx = 2016 ∫ và
f (x)dx = 2017. ∫ 1 4 4 Tính tích phân I = f (x)dx. ∫ 1
A. I = 4023.
B. I = 1.
C. I = −1. D. I = 0. 4 3 4
Lời giải. Ta có I =
f (x )dx = f (x)dx + f (x)dx ∫ ∫ ∫ 1 1 3 3 3 =
f (x)dx −
f (x)dx = 2016 −2017 = −1 ∫ ∫ . Chọn C. 1 4 2 4
Câu 6. Cho hàm số f (x) thỏa mãn
f (x )dx = 1 ∫ và
f (t)dt = −3 ∫ . 1 1 4 Tính tích phân I = f (u)d . u ∫ 2 A. I = −2 . B. I = −4 . C. I = 4. D. I = 2. 2 2 4 4 Lời giải. Ta có f (u)du =
f (x)dx = 1 ∫ ∫ và f (u)du =
f (t)dt = −3 ∫ ∫ . 1 1 1 1 4 1 4 2 4 Suy ra I = f (u)du = f (u)du +
f (u)du = − f (u)du +
f (u)du = −1−3 = −4. ∫ ∫ ∫ ∫ ∫ 2 2 1 1 1 Chọn B. 6 6
Câu 7. Cho hàm số f (x) thỏa mãn
f (x)dx = 4 ∫ và
f (x)dt = −3 ∫ . 0 2 2
Tính tích phân I =  f (v)−3 dv. ∫   0
A. I = 1.
B. I = 2.
C. I = 4. D. I = 3. 2 2 2 2
Lời giải. Ta có I =  f (v)−3 dv =
f (v)dv −3v =
f (v)dv −6. ∫   ∫ ∫ 0 0 0 0 2 2 6 6 6 6 Mà f (v)dv = f (v)dv +
f (v)dv − f (v)dv =
f (v)dv − f (v)dv ∫ ∫ ∫ ∫ ∫ ∫ 0 0 2 2 0 2 6 6 =
f (x)dx −
f (x)dx = 4 −(−3) = 7. ∫ ∫ 0 2
Vậy I = 7−6 = 1 . Chọn A. 10 6
Câu 8. Cho hàm số f (x) thỏa mãn
f (x)dx = 7 ∫ và
f (x)dx = 3. ∫ 0 2 2 10 Tính tích phân I = f (x)dx + f (x)dx. ∫ ∫ 0 6
A. I = 10.
B. I = 4.
C. I = 7. D. I = −4. Lời giải. Ta có 2 10 2 6 10 6 I =
f (x )dx + f (x)dx = f (x)dx +
f (x )dx +
f (x )dx − f (x )dx ∫ ∫ ∫ ∫ ∫ ∫ 0 6 0 2 6 2 10 6 =
f (x)dx −
f (x)dx = 7 −3 = 4. ∫ ∫ Chọn B. 0 2 d d c
Câu 9. Cho hàm số f (x) thỏa mãn f (x)dx =10,
f (x)dx = 8 ∫ ∫ và
f (x)dx = 7 ∫ . a b a c Tính tích phân I = f (x)dx. ∫ b A. I = −5 . B. I = 7. C. I = 5. D. I = −7 . c d a c
Lời giải. Ta có I = f (x)dx =
f (x )dx + f (x)dx + f (x)dx ∫ ∫ ∫ ∫ b b d a d d c =
f (x)dx − f (x)dx +
f (x)dx = 8−10 +7 = 5. ∫ ∫ ∫ Chọn C. b a a 3 4 4
Câu 10. Cho hàm số f (x) thỏa mãn
f (x)dx = −2,
f (x)dx = 3 ∫ ∫ và
g (x)dx = 7 ∫ . 1 1 1
Khẳng định nào sau đây là sai? 4 4
A.  f (x)+ g(x) dx = 10. ∫   B.
f (x)dx = 1. ∫ 1 3 3 4 C.
f (x)dx = −5. ∫
D. 4 f (x)−2g(x) dx = −2. ∫   4 1 4 4 4
Lời giải. Ta có  f (x)+ g(x) dx = f (x)dx +
g (x)dx = 3 +7 = 10 ∫   ∫ ∫ . Do đó A đúng. 1 1 1 4 1 4 Ta có f (x)dx =
f (x )dx + f (x)dx ∫ ∫ ∫ 3 3 1 3 4
= − f (x)dx +
f (x)dx = −(−2)+ 3 = 5 ∫ ∫
. Do đó B sai, C đúng. Chọn B. 1 1 4 4 4 Ta có
4 f (x)−2g(x) dx = 4 f (x)dx −2 g(x)dx = 4.3−2.7 = −2 ∫   ∫ ∫ . Do đó D đúng. 1 1 1 2 2
Câu 11. Cho hàm số f (x) thỏa 3 f (x)+ 2g(x) dx =1 ∫  −    và
2 f (x) g (x) dx = −3 ∫   . 1 1 2 Tính tích phân I = f (x)dx. ∫ 1 A. I = 1. B. I = 2. C. 5 I = − . D. 1 I = . 7 2 Lời giải. Ta có 2 2 2
3 f (x)+2g(x) dx =1←→3 f (x)dx +2 g(x)dx =1. ∫   ∫ ∫ 1 1 1 2 2 2
2 f (x)− g(x) dx = −3←→2 f (x)dx − g(x)dx = −3. ∫   ∫ ∫ 1 1 1  5  = − 2 2 u    + = Đặt 3u 2v 1    7
f (x)dx = u ∫ và
g (x)dx = v ∫
, ta có hệ phương trình  ⇔  . 2
u −v = −3  11   1 1 v  =  7 2 Vậy I = f (x) 5 dx = u = − ∫ . Chọn C. 7 1
Câu 12. (ĐỀ THỬ NGHIỆM 2016 2017) Cho hàm số f (x) có đạo hàm liên tục – 2
trên đoạn [1;2] và thỏa mãn f ( )
1 = 1, f (2) = 2. Tính I =
f ′(x )dx. ∫ 1 A. I = 1. B. I = −1. C. I = 3. D. 7 I = ⋅ 2 2 2
Lời giải. Ta có I =
f ′(x)dx = f (x) = f (2)− f ( ) 1 = 1. ∫ Chọn A. 1 1
Câu 13. Cho hàm số f (x) có đạo hàm liên tục trên ℝ và thỏa mãn f (0)= 1. Kí hiệu x I = f '(t)dt. ∫
Mệnh đề nào sau đây là đúng? 0
A. I = f (x)+1. B. I = f (x).
C. I = f (x + ) 1 .
D. I = f (x)−1. x x
Lời giải. Ta có I =
f '(t)dt = f (t) = f (x)− f (0) = f (x)−1. ∫ Chọn D. 0 0 1
Câu 14. Cho hàm số f (x) 2
= ln x + x +1 . Tính tích phân
f ′(x )dx. ∫ 0 1 1 A.
f ′(x )dx = ln 2. ∫ B.
f ′(x)dx = ln ∫ (1+ 2). 0 0 1 1 C.
f ′(x )dx = 1+ ln 2. ∫ D.
f ′(x )dx = 2 ln 2. ∫ 0 0 1 1 Lời giải. Ta có
f ′(x)dx = f (x ) ∫ 0 0 1 2 2 2 = ln x + x +1
= ln 1+ 1 +1 − ln 0 + 0 +1 = ln(1+ 2). Chọn B. 0
Câu 15. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;4] và thỏa mãn 4 f ( ) 1 = 12 ,
f '(x)dx = 17. ∫
Tính giá trị của f (4). 1 A. f (4)= 29. B. f (4)= 5. C. f (4)= 9. D. f (4)=19. 4 4 Lời giải. Ta có
f '(x )dx = f (x) = f (4)− f ( ) 1 . ∫ 1 1 4 Theo giả thiết
f '(x)dx = 17 ⇔ f (4)− f ( ) 1 = 17 
→ f (4)= 17 + f ( ) 1 = 17 +12 = 29. ∫ 1 Chọn A.
Câu 16. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;ln3] và thỏa mãn ln 3 f ( ) 2 1 = e , f '(x) 2 dx = 9 − e . ∫
Tính giá trị của f (ln ) 3 . 1 A. f ( ) 2 ln 3 = 9 − 2e . B. f (ln ) 3 = 9. C. f (ln ) 3 = −9. D. f ( ) 2 ln 3 = 2e − 9. ln 3 ln 3 Lời giải. Ta có
f '(x)dx = f (x) = f (ln ) 3 − f ( ) 1 . ∫ 1 1 ln 3 Theo giả thiết f '(x) 2
dx = 9 − e ⇔ f (ln ) 3 − f ( ) 2 1 = 9 − e ∫ 1  → f ( ) 2 = −e + f ( ) 2 2 ln 3 9
1 = 9 − e + e = 9. Chọn B.
Câu 17. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;3] và thỏa mãn f ( ) 1 = 1 , 3 f ( ) 3 = .
m Tìm tham số thực m để
f ′(x)dx = 5. ∫ 1 A. m = 6. B. m = 5. C. m = 4.
D. m = −4. 3 3 Lời giải. Ta có
f ′(x )dx = f (x) = f ( ) 3 − f ( ) 1 . ∫ 1 1 3 Theo giả thiết
f ′(x )dx = 5 ⇔ f ( ) 3 − f ( )
1 = 5 ⇔ m −1 = 5 ⇔ m = 6. ∫ Chọn A. 1 x   Câu 18. Cho hàm số π g (x) =
t cos(x − t)dt. ∫ Tính g '     .  2  0         A. π π π π g '    = 1 − .        
B. g '  =1.
C. g ' = 0.
D. g ' = 2.        2   2   2   2  u  = t d  u = dt
Lời giải. Đặt     →  v = 
(x −t) t v  = −   (x −t). d cos d sin  x x x x
Khi đó g(x)= t
− sin(x −t) + sin(x −t)dt = t
− sin(x −t) + cos(x −t) =1−cos x. ∫ 0 0 0 0     Suy ra π π
g '(x ) = sin x  → g '    = sin      = 1. Chọn B.  2  2 2 x
Câu 19. Tính đạo hàm của hàm số F (x)= cos tdt ∫ với x > 0. 0 A. F (x) 2 ' = x cos x.
B. F '(x)= 2x cos x.
C. F '(x)= cos x.
D. F '(x)= cos x −1.  = → = Lời giải. t 0 y 0 Đặt 2 
y = t ⇒ y = t 
→2ydy = dt. Đổi cận:  . 2 t
 = x → y = x  x  =  = Khi đó u y u y   F (x ) = cos . y 2 ydy ∫ . Đặt 2 d 2d   → . d  v = cos d y y v  = sin y   0 x x x x
Suy ra F (x) = 2y sin y −2 sin ydy = 2y sin y + 2cos y = 2x sin x + 2cos x −2 ∫ 0 0 0 0 
→ F '(x) = 2 sin x + 2x cos x −2 sin x = 2x cos x. Chọn B. x
Câu 20. Tìm giá trị nhỏ nhất m của hàm số F (x)= ∫ ( 2t +t)dt trên đoạn [−1; ]1. 1 A. 1 m = . B. m = 2. C. 5 m = − . D. 5 m = . 6 6 6 x x   Lời giải. Ta có  
F (x) = ∫ (t +t) 3 2 3 2 t t x x 5 2 dt =  +  = + − .    3 2  3 2 6 1 1 3 2
Xét hàm số F (x) x x 5 = + − trên đoạn [−1; ] 1 . 3 2 6 x = 0 ∈[−1; ] 1
Đạo hàm F '(x) 2 x x F '(x) 0  = +  → = ⇔ .  x  = −1∈[−1; ] 1  F (− ) 2 1 = −  3  Ta có F ( ) 5 = −  →
F (x) = F ( ) 5 0 min 0 = − . Chọn C.  [ 1 − ; ] 1 6 6 F( )1=0  x
Câu 21. Tính đạo hàm của hàm số F (x) 2 = 1+ t dt ∫ . 1 A. x / F (x ) = . B. / F (x ) 2 = 1+ x . 2 1+ x C. 1 / F (x ) = . D. / F (x ) = ( 2 x + ) 2 1 1+ x . 2 1+ x
Lời giải. Gọi H (t) là một nguyên hàm của 2
1+ t , suy ra H (t) 2 ' = 1+ t . x x Khi đó F (x) 2 =
1+ t dt = H (t) = H (x)− H ( ) 1 ∫ 1 1 
→ F (x) = H (x)−H ( ) / = H (x) 2 ' 1 ' = 1+ x .   Chọn B. x
Câu 22. Tính đạo hàm của hàm số F (x) 2 = sin t dt ∫ với x > 0 . 1 A. x x
F '(x ) = sin x. B. F (x ) sin ' = .
C. F (x) 2sin ' = .
D. F '(x)= sin x . 2 x x
Lời giải. Gọi H (t) là một nguyên hàm của 2
sin t , suy ra H (t) 2 ' = sin t . x x Khi đó F (x) 2 =
sin t dt = H (t) = H ∫ ( x)−H ( )1 1 1 / H x (      → x ) = H
 ( x )− H ( ) / = H   ( x ) / ( ) sin x F ' 1 = = .  Chọn B.     2 x 2 x / Chú ý:   H  ( x ) / ≠ H  ( x).   x
Câu 23. Tính đạo hàm của hàm số f (x) , biết f (x) thỏa mãn f (t) f (x ) te dt = e ∫ . 0
A. f '(x)= x. B. f (x) 2 ' = x +1.
C. f (x) 1 ' = .
D. f '(x)=1. x
Lời giải. Gọi F (t) là một nguyên hàm của f (t) te , suy ra ( ) ( ) ' f t F t = te . x x Khi đó f (t) te
dt = F (t) = F (x)− F (0) f (x) ←→e
= F (x)− F (0) ∫ . 0 0
Đạo hàm hai vế, ta được f '(x) f (x) .e
= F '(x)←→ f '(x) f (x) f (x) .e = xe 
→ f '(x) = x. Chọn A. f (x)
Câu 24. Cho hàm số f (x) thỏa mãn 2
t dt = x cos(πx ). ∫ Tính f (4). 0
A. f (4)= 2 3. B. f (4)= −1. C. f ( ) 1 4 = . D. f ( ) 3 4 = 12. 2 f (x ) 3 f (x) Lời giải. Ta có t 1 t dt = =  f (x) 3 2
 = x cos(πx). ∫ 3 3   0 0 Cho 1 3 x = 4 , ta được
f (4) = 4 cos4π  → f (4) 3 = 12.   Chọn D. 3
Câu 25. Cho hàm số y = f (x) có 1≤ f '(x)≤ 4 với mọi x ∈[2;5] . Hỏi khẳng định nào
dưới đây là khẳng định đúng? A. 3 ≤ f ( ) 5 − f (2) ≤12.
B. −12 ≤ f (5)− f (2)≤ 3.
C. 1≤ f (5)− f (2)≤ 4.
D. −4 ≤ f (5)− f (2)≤−1. 5
Lời giải. Đầu tiên ta phải nhận dạng được f (5)− f (2)= f '(x )dx ∫ . 2 5 5 5
Do 1≤ f '(x)≤ 4, ∀x ∈[2;5] → 1dx ≤
f '(x)dx ≤ 4dx . ∫ ∫ ∫ 2 2 2 3 12 Vậy 3 ≤ f ( )
5 − f (2) ≤12. Chọn A.
Vấn đề 2. TÍCH PHÂN CƠ BẢN a
Câu 26. Tìm số thực x +1
a > 1 để tích phân dx ∫
có giá trị bằng e. x 1 A. 1 e a = .
B. a = e . C. a = . D. 2 a = e . e 2 a a a +   Lời giải. Ta có x 1 1 dx = 1   ∫
∫  + dx =(x +ln x ) = a +lna−1= e. x  x  1 1 1
Thử các đáp án đã cho, có a = e thỏa mãn. Thật vậy e + ln e −1 = e . Chọn B. a
Cách CASIO. Thiết lập hiệu
x +1 dx −e ∫ . x 1 1 e
Thử từng đáp án, ví dụ với đáp án A ta nhập vào máy
x +1 dx −e ∫ và nhấn dấu =. x 1
Màn hình xuất hiện số khác 0 nên không thỏa mãn. Tương tự thử với đáp án B. 5
Câu 27. Tính tích phân dx I = . ∫ 2x −1 1 A. I = ln 3. B. I = ln 2. C. I = ln 9. D. I = ln 6. 5
Lời giải. Ta có 5 dx 1 1 = x − = ( − ) 1 ln 2 1 ln 9 ln1 = ln 9 = ln 3. ∫ Chọn A. 1 2x −1 2 1 2 2 2
Câu 28. Nếu kết quả của dx ∫ được viết ở dạng a ln
với a, b là các số nguyên x + 3 b 1
dương và ước chung lớn nhất của a, b bằng 1. Mệnh đề nào sau đây là sai?
A. 3a −b <12 .
B. a +2b =13 .
C. a −b > 2 . D. 2 2 a + b = 41 . 2 2 Lời giải. Ta có dx 5
= ln x + 3 = ln 5−ln 4 = ln . ∫ x + 3 1 4 1  = Suy ra a 5  
→a −b = 1< 2. Do đó C sai. Chọn C. b  = 4  2016
Câu 29. Tính tích phân = 7x I dx. ∫ 0 2016 2017 A. 7 −1 7 I = ⋅ B. 2016 I = 7 − ln7. C. I = −7. D. 2015 I = 2016.7 . ln 7 2017 2016 2016 x 2016 Lời giải. Ta có x 7 7 1 I = 7 dx = = − . ∫ Chọn A. ln 7 ln 7 ln 7 0 0 π 2
Câu 30. Kết quả của tích phân I = cos d x x ∫
được viết ở dạng I = a +b 3 , với a và π 3
b là các số hữu tỉ. Tính P = a − 4b. A. 9
P = a − 4b = ⋅
B. P = a −4b = 3. 2 C. 1
P = a − 4b = − ⋅ D. 1
P = a − 4b = ⋅ 2 2 π 2 π   Lời giải. Ta có 3 1 2 I = cos d x x = sin x = 1− = 1+  − ∫  . 3 π 2  2 π 3 3 a =1   → 1 
→ P = a −4b = 3. Chọn B. b  = −  2 2
Câu 31. Cho hàm số f (x)= A sin(πx)+ B ( ,
A B thuộc ℝ ) thỏa mãn
f (x)dx = 4 ∫ 0 và f '( )
1 = 2 . Tính giá trị biểu thức P = πA + B. A. P = 4. B. P = 0. C. P = −2. D. P = −4. 2 2 2   Lời giải. Ta có ( ) A f x dx = A sin( +  π x ) B dx = −
cos(πx)+ Bx = 2B ∫ ∫   .   π   0 0 0
Suy ra 2B = 4 ⇔ B = 2 .
Lại có f (x)= Aπ (πx)  → f ( ) 2 ' cos
' 1 = 2 ⇔ Aπ cos π = 2 ⇔ A = − . π Vậy 2
A = − ; B = 2 
→ P = πA + B = 0. Chọn B. π m
Câu 32. Biết rằng tích phân cos2xdx = 0 ∫
với m là tham số. Khẳng định nào sau 0 đây là đúng?
A. m = k2π (k ∈ ℤ).
B. m = kπ (k ∈ ℤ). C. π m = k (k ∈ ℤ).
D. m = (2k + )
1 π (k ∈ ℤ). 2 m m
Lời giải. Ta có 1 1 0 = cos 2xdx = sin 2x = sin 2m ∫ 2 0 2 0 kπ 
→sin 2m = 0 ⇔ 2m = kπ ⇔ m =
(k ∈ ℤ). Chọn C. 2 x  
Câu 33. Biết rằng tích phân 1 2 
∫ sin t − dt = 0 
với x là tham số. Khẳng định nào  2 0 sau đây là đúng?
A. x = k2π (k ∈ ℤ).
B. x = kπ (k ∈ ℤ). C. π x = k (k ∈ ℤ).
D. x = (2k + )
1 π (k ∈ ℤ). 2 x x x    −  Lời giải. Ta có 1 1 cos 2t 1 1 2 sin t ∫  − d  t =    ∫  − d  t =− cos 2tdt  ∫ 2  2 2 2 0 0 0 x 1 1
= − sin 2t = − sin 2x. 4 4 0 x   Theo giả thiết 1 2 π
∫ sin t − dt = 0 ⇔ sin2x = 0 ⇔ 2x = kπ ⇔ x = k (k ∈ ℤ).  Chọn C.  2 2 0 1 2017 x  ≥
Câu 34. Tính tích phân 2 khi x 0  I = f (x)dx ∫
, biết rằng f (x)=  . 2 − 017 x  < − 2 khi x 0 1  2018 2018 A. 2 −2 2 −1 I = log e. B. I = log e. 2 2017 2 2017 2018 2017 C. 2 −1 2 −1 I = ln 2. D. I = . 2017 2017 ln 2 1 0 1
Lời giải. Ta có I =
f (x )dx = f (x)dx + f (x)dx ∫ ∫ ∫ 1 − 1 − 0 0 1 − 0 1 2017 x 2017 x 2018 − − x x 2 2 2 2 2017 2017 = 2 dx + 2 dx = − + = log e. ∫ ∫ Chọn A. 2 2017 ln 2 2017 ln 2 2017 −1 0 1 − 0 2
Câu 35. Tính tích phân I = min ∫ ( 2 1, x )dx. 0 A. 3 I = . B. I = 4 . C. 4 I = . D. 3 I = − . 4 3 4 x ∈  [0; ] 1  →min( 2 1, x ) 2 = x
Lời giải. Ta có  .
x ∈[1;2]→min( 2 1, x ) = 1  1 2 1 2 1 2 3 Do đó x I = min ∫ ( 1 4 2 1, x )dx + min ∫ ( 2 1, x ) 2 dx = x dx + 1.dx = + x = +1 = . ∫ ∫ 3 3 3 0 1 0 1 0 1 Chọn C.
Vấn đề 3. ỨNG DỤNG THỰC TIỄN
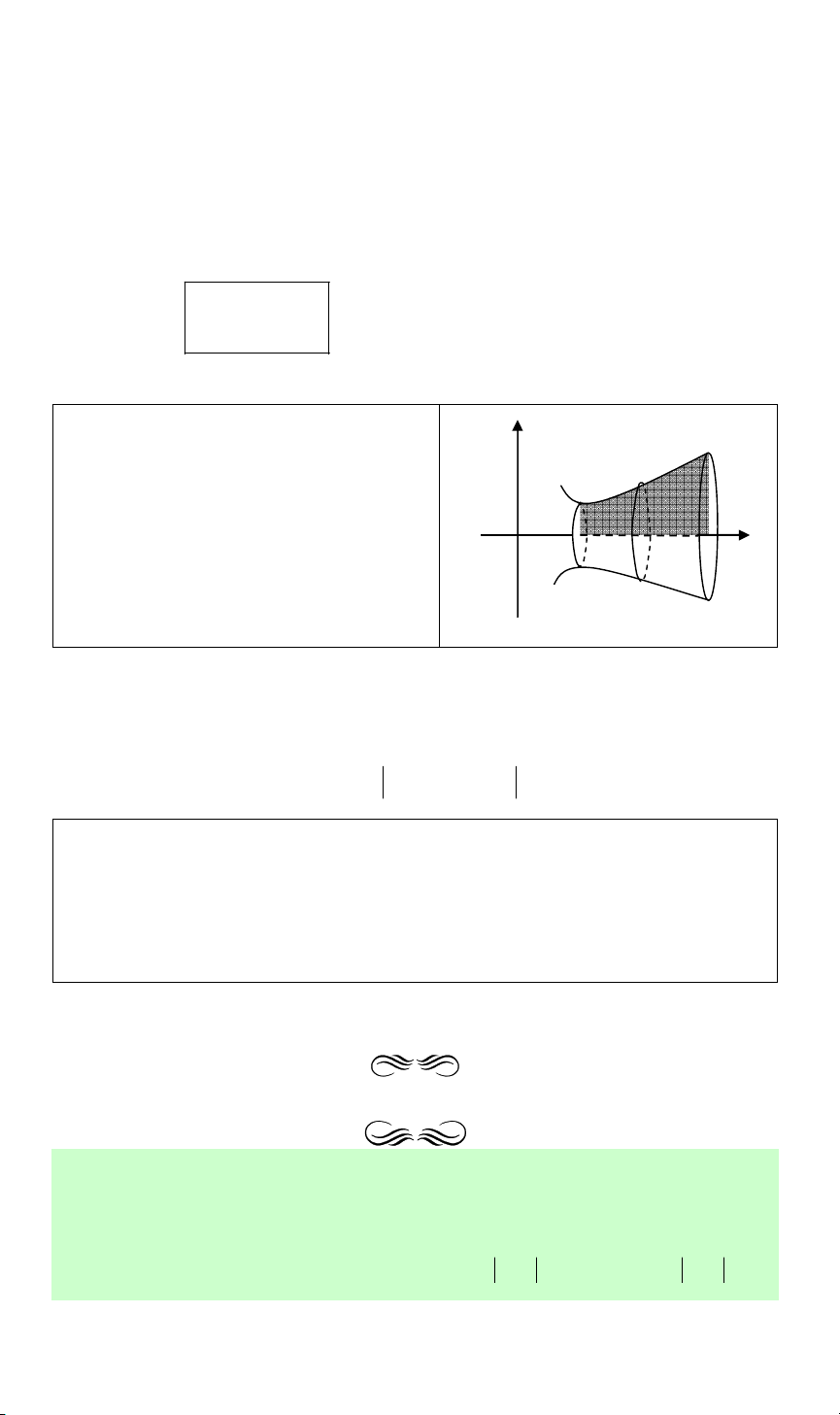
Giả sử v(t) là vận tốc của vật M tại thời điểm t và s(t) là quãng đường vật đi được
sau khoảng thời gian t tính từ lúc bắt đầu chuyển động. Ta có mối liên hệ giữa s(t)
và v(t) như sau:
● Đạo hàm của quãng đường là vận tốc: s′(t) = v (t).
● Nguyên hàm của vận tốc là quãng đường s (t) = v (t)dt. ∫ 
→ từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian t ∈[a;b] là b
v (t)dt = s (b)− s (a). ∫ a
Nếu gọi a(t) là gia tốc của vật M thì ta có mối liên hệ giữa v(t) và a(t) như sau:
● Đạo hàm của vận tốc là gia tốc: v′(t) = a(t).
● Nguyên hàm của gia tốc là vận tốc: v (t) = a (t)dt. ∫
Câu 36. (ĐỀ MINH HỌA 2016 2017) Một ô tô đang chạy với vận tốc 10m/s thì –
người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc
v (t) = −5t +10(m/s) , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m. B. 2m. C. 10m. D. 20m.
Lời giải. Lúc dừng hẳn thì v(t)= 0 
→−5t +10 = 0 ⇔ t = 2.
Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô đi được quãng đường là 2 2   s = (−5t +10) 5 2 dt = − t ∫  +10t = 10m.  Chọn C.  2  0 0
Câu 37. Một ô tô đang đi với vận tốc lớn hơn 72km/h, phía trước là đoạn đường chỉ
cho phép chạy với tốc độ tối đa là 72km/h, vì thế người lái xe đạp phanh để ô tô
chuyển động chậm dần đều với vận tốc v(t)= 30−2t ( m/s), trong đó t là khoảng thời
gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến
lúc đạt tốc độ 72km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét? A. 100m. B. 125m. C. 150m. D. 175m.
Lời giải. Ta có 72km/h = 20m/s .
Từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72km/h, ta có phương trình
30 − 2t = 20 ⇔ t = 5.
Vậy từ lúc đạp phanh đến khi ô tô đạt tốc độ 72km/h , ô tô đi được quãng đường là 5 s =
(30−2t)dt =125m. ∫ Chọn B. 0
Câu 38. Một vật đang chuyển động với vận tốc 6m/s thì tăng tốc với gia tốc a (t) 3 2 =
m/s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng t +1
tốc. Hỏi vận tốc của vật sau 10 giây gần nhất với kết quả nào sau đây? A. 14 m/s . B. 13m/s . C. 11m/s . D. 12 m/s .
Lời giải. Ta có v(t) 3 =
dt = 3 ln t +1 +C. ∫ t +1
Tại thời điểm lúc bắt đầu tăng tốc t = 0 thì v = 6m/s nên ta có 3ln1+C = 6 ⇔ C = 6.
Suy ra v(t)= 3ln t +1 + 6(m/s).
Tại thời điểm t = 10 s 
→v (10) = 3ln11+ 6 ≈ 13m/s. Chọn B.
Câu 39. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a (t) 2 = t + t ( 2 3
m/s ) , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu
tăng tốc. Hỏi quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt
đầu tăng tốc bằng bao nhiêu mét? A. 4000 m . B. 4300 m . C. 1900 m . D. 2200 m . 3 3 3 3
Lời giải. Ta có ( )= ∫ ( t t v t 3t + t ) 2 3 3 2 dt = + +C. 2 3
Tại thời điểm lúc bắt đầu tăng tốc t = 0 thì v = 10m/s nên suy ra C = 10. 2 3 Suy ra ( ) 3t t v t = + +10(m/s). 2 3
Vậy quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng 10 2 3 3 4 10     tốc bằng 3t t t t 4300     s =  + +10dt = ∫    + +10t = m . Chọn B.      2 3   2 12  0 3 0
Câu 40. Một ô tô đang chuyển động với vận tốc 30m/s thì người lái đạp phanh; từ thời điểm
đó, ô tô chuyển động chậm dần đều với gia tốc a(t) 20 2 = −
m/s , trong đó t là (1+2t)2
khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi quãng đường ô tô đi
được trong khoảng thời gian 2 giây kể từ lúc bắt đầu đạp phanh là bao nhiêu mét? A. 46m. B. 47m. C. 48m. D. 49m. Lời giải. Ta có − v (t) 20 10 = dt = +C. ∫ (1+2t)2 1+ 2t
Tại thời điểm lúc bắt đầu đạp phanh t = 0 thì v = 30m/s nên suy ra C = 20. Suy ra v(t) 10 = + 20(m/s). 1+ 2t
Vậy quãng đường ô tô đi được trong khoảng thời gian 2 giây kể từ lúc bắt đầu đạp 2 2 2  
phanh bằng s = v(t) 10 dt =  ∫ ∫ 
+ 20dt = (5ln(1+2t)+20t) ≈ 48m.  Chọn C. 1+ 2t  0 0 0
Câu 41. Một ô tô đang chạy thẳng đều với vận tốc v m/s thì người đạp phanh, từ 0 ( )
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t)= −5t +v m/s , trong 0 ( )
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp
phanh đến lúc dừng hẳn ô tô di chuyển được 40m thì vận tốc ban đầu v bằng bao 0 nhiêu?
A. v = 40m/s. B. v = 80m/s. C. v = 20m/s. D. v = 25m/s. 0 0 0 0
Lời giải. Lúc dừng hẳn thì v(t) v0 = 0 
→−5t +v = 0 ⇔ t = . 0 5 v0 5 v0 2 2 2   Theo giả thiết, ta có ( 5 v v v 40m=
−5t + v dt = − t ∫  +v t = − + = 0 ) 2 5 0 0 0 0  2  0 10 5 10 0 2 v0  → 40m = 
→v = 20m/s . Chọn C. 0 10
Câu 42. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 m so
với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng,
khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật v (t) 2
= 10t −t (m/s) , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
chuyển động. Hỏi lúc vừa tiếp đất, vận tốc v của khí cầu bằng bao nhiêu? A. v = 5m/s. B. v = 7m/s. C. v = 9m/s. D. v = 3m/s.
Lời giải. Do v(t) 2
= 10t −t  →0 < t <10.
Giả sử chiếc khí cầu chạm đất kể từ lúc bắt đầu chuyển động là t giây (0 < t <10 . 1 ) 1 1 t 3 t 3  
Theo đề bài ta có phương trình t t   162 = ∫ ( 2 10t − t ) 1 2 2 1 dt = 5
t −  = 5t −   1  3  0 3 0 3 t1 2 0< < 1 t 10
⇔ − +5t −162 = 0  →t = 9 
→v 9 = 9m/s. Chọn C. 1 1 ( ) 3
Câu 43. Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường s
(mét) đi được của đoàn tàu là một hàm số của thời gian t (giây) có phương trình là 2 3
s = 6t − t . Thời điểm mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất là:
A. t = 6s.
B. t = 4 .s
C. t = 2s.
D. t =1s.
Lời giải. Vận tốc v(t)= s (t) 2 ' = 12t −3t .
Bậy giờ ta đi tìm giá trị lớn nhất của hàm số v(t) 2 = 12t −3t . 2 3
s = 6t −t ≥ 0  Ta có  2 v
 = 12t −3t ≥ 0 ⇔ 0 ≤ t ≤ 4 ⇒ t ∈[0;4]. t ≥0 
Đạo hàm và lập bảng biến thiên ta tìm được max v(t) đạt tại t = 2s. Chọn C. [0;4]
Câu 44. (ĐỀ THI CHÍNH THỨC 2016 2017) Một vật chuyển động theo quy luật – 1 3 2
s = − t + 6t với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động 2
và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian 6 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. 24m/s. B. 108m/s. C. 18m/s. D. 64m/s.
Lời giải. Vận tốc v(t)= s '(t) 3 2 = − t +12t . 2
Ycbt là đi tìm GTLN của hàm số v(t) 3 2
= − t +12t với 0 ≤ t ≤ 8. 2
Đạo hàm và lập bảng biến thiên ta tìm được max v(t) = v(4) = 24m/s. Chọn A. [0;8]
Câu 45. Một tàu lửa đang chạy với vận tốc 20
0 m/s thì người lái tàu đạp phanh. Từ
thời điểm đó, tàu chuyển động chậm dần đều với vận tốc v(t)= 200 + at ( m/s), trong
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh và a( 2 m/s ) là
gia tốc. Biết rằng khi đi được 1500m thì tàu dừng, hỏi gia tốc của tàu bằng bao nhiêu? A. 40 200 40 100 a = ( 2
m/s ). B. a = − 2 m/s . C. a = − 2 m/s . D. a = − 2 m/s . 3 13 3 13
Lời giải. Khi tàu dừng hẳn thì v = ⇔ + at 200 0 200 = 0  →t = − (m/s). a
Theo đề bài ta có phương trình 200 − a 2 200   = ( −   + at) at 40000 40000 1500 200 dt = 200 a t +  = − + ∫   .  2  0 a 2a 0 Suy ra 40 a = − ( 2 m/s ). Chọn C. 3
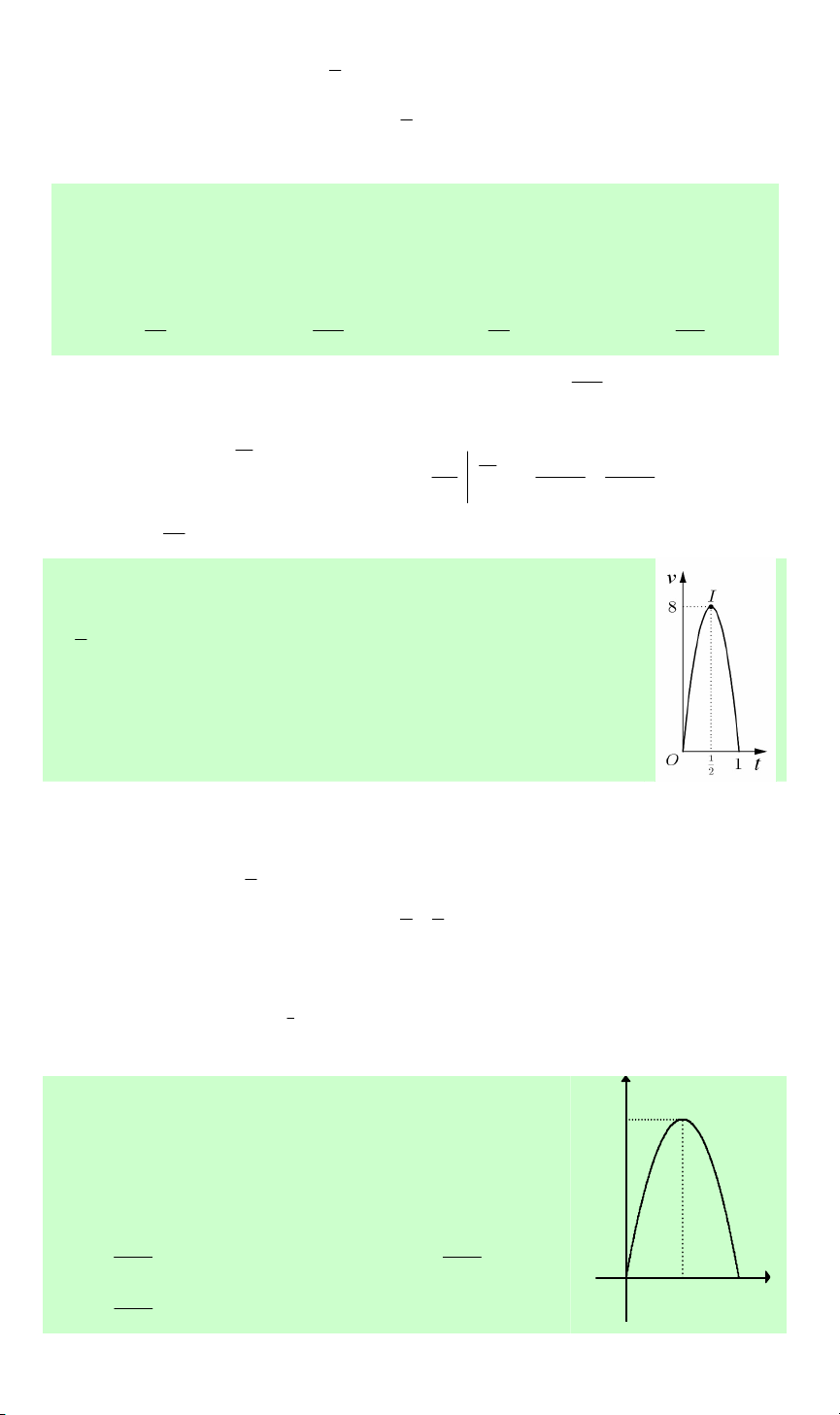
Câu 46. Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ
thuộc vào thời gian t (h) có đồ thị là một phần parabol với đỉnh 1  I  ; 8 
 và trục đối xứng song song với trục tung như hình bên. Tính 2 
quảng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi chạy. A. s = 4 km. B. s = 2,3 km. C. s = 4,5 km. D. s = 5,3 km.
Lời giải. Hàm vận tốc ( ) 2
v t = at + bt + c có dạng là đường parabol đi qua các điểm c =0 a  = −32      
O (0; 0) , A(1; 0) và 1 I  ; 8    nên suy ra a
 +b + c = 0 ⇔ b  = 32 2      a b c  = 0  + +c = 8  4 2  →v(t) 2
= −32t +32t (m/s).
Vậy quảng đường người đó đi được trong khoảng thời gian 45 phút là: 3 4 s = ∫ ( 2
−32t +32t)dt =4,5km. Chọn C. 0
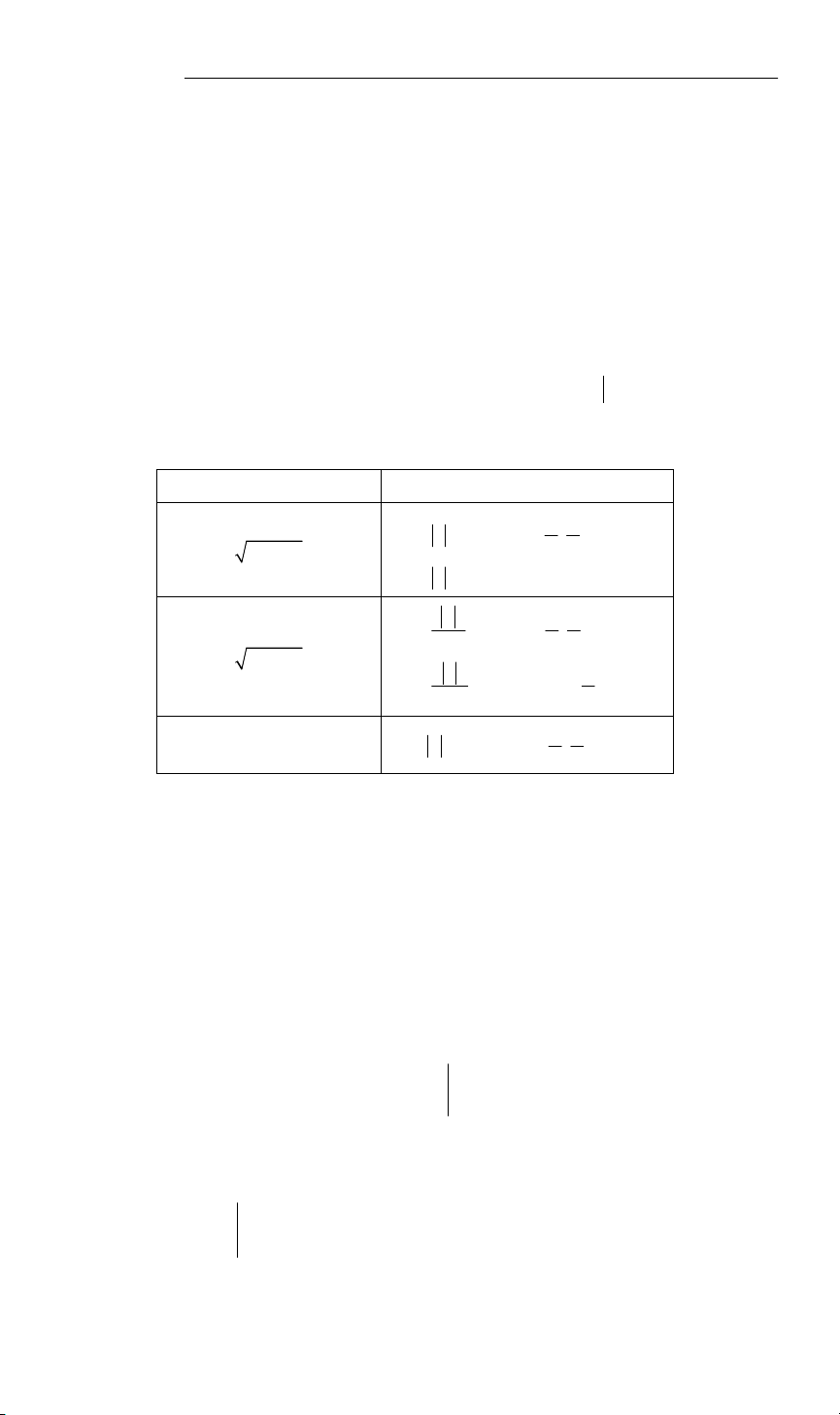
Câu 47. Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu tăng v(t)
tốc với vận tốc tăng liên tục được biểu thị bằng đồ thị là 50
đường cong parabol có hình bên. Biết rằng sau 10s thì xe đạt
đến vận tốc cao nhất 50 m/s và bắt đầu giảm tốc. Hỏi từ lúc
bắt đầu tăng tốc đến lúc đạt vận tốc cao nhất thì xe đã đi
được quãng đường bao nhiêu mét? A. 1000 m . B. 1100 m . t 3 3 O C. 1400 10 m . D. 300m . 3
Lời giải. Hàm vận tốc ( ) 2
v t = at + bt + c có dạng là đường parabol có đỉnh I (10;50) , c  = 0 c  = 0      
đồng thời đi qua gốc tọa độ b 1   O (0;0) nên suy ra −  = 10 ⇔ a  = −  2a  2     2
 .a10 + .b10+c = 50 b  = 10    →v(t) 1 2
= − t +10t (m/s). 2
Theo đồ thị thì xe bắt đầu tăng tốc lúc t = 0 và đạt vận tốc cao nhất lúc t = 10 s nên
quãng đường đi được của xe từ lúc bắt đầu tăng tốc đến lúc đạt vận tốc cao nhất là: 10 10 10     s = v (t) 1 1 1000 2 3 2 dt = − ∫
∫  t +10tdt =−    t + 5t  = m. Chọn A.  2   6  0 3 0 0
Câu 48. Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ
thuộc thời gian t (h)có đồ thị là một phần của đường parabol có đỉnh
I (2;9) và trục đối xứng song song với trục tung như hình bên. Tính
quãng đường s mà vật di chuyển được trong 3 giờ đó. A. s = 26,75km. B. s = 25,25km. C. s = 24,25km. D. s = 24,75km.
Lời giải. Hàm vận tốc ( ) 2
v t = at + bt + c có dạng là đường parabol đi qua có đỉnh c  = 6 c  = 6      b  3  
I (2;9) và đi qua điểm A(0;6) nên suy ra −  = 2 ⇔ a  = −  2a  4     2
 .a2 + .b2+c = 9 b  = 3    →v(t) 3 2
= − t +3t + 6(m/s) . 4
Vậy quảng đường người đó đi được trong khoảng thời gian 3 giờ là: 3  3  2 s = − t ∫ 
+3t + 6dt 2 = 4,75km.  Chọn D.  4  0
Câu 49. Một vật chuyển động trong 4 giờ với vận tốc v(km/h)
phụ thuộc thời gian t (h) có đồ thị của vận tốc như hình bên.
Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ
thị đó là một phần của đường parabol có đỉnh I (2;9) với trục đối
xứng song song với trục tung, khoảng thời gian còn lại đồ thị là
một đoạn thẳng song song với trục hoành. Tính quãng đuờng s
mà vật chuyển động trong 4 giờ đó. A. s = 26,5km. B. s = 28,5km. C. s = 27km.
D. s = 24km.
Lời giải. Hàm vận tốc ( ) 2
v t = at + bt + c có dạng là đường parabol đi qua có đỉnh c  = 0 c  = 0      b  9  
I (2;9) và đi qua điểm O (0;0) nên suy ra −  = 2 ⇔ a  = −  2a  4     2
 .a2 + .b2+c = 9 b  = 9    → 27 v (t) 9 2
= − t + 9t (m/s). Suy ra v(3) = (m/s). 4 4
Vậy quảng đường người đó đi được trong khoảng thời gian 4 giờ là: 3 4  9  27 2 s = − t ∫  + 9tdt + dt 2 = 7km.  ∫ Chọn C. 4  4 0 3
Câu 50. Cho đồ thị biểu diễn vận tốc của hai xe A và B v v v B A
khởi hành cùng một lúc, bên cạnh nhau và trên cùng một
con đường. Biết đồ thị biểu diễn vận tốc của xe A là một 60
đường parabol, đồ thị biểu diễn vận tốc của xe B là một
đường thẳng ở hình bên. Hỏi sau khi đi được 3 giây
khoảng cách giữa hai xe là bao nhiêu mét. t A. 90 m. B. 60 m. O 3 4 C. 0 m. D. 270 m.
Lời giải. Hàm vận tốc v (t) 2
= at +bt + c có dạng là đường parabol đi qua các điểm A
O (0;0), A(3;60) và B (4;0) nên suy ra v (t) 2
= −20t +80t (m/s). A
Hàm vận tốc v t = at +b có dạng là đường thẳng đi qua gốc tọa độ O (0;0) và điểm B ( )
A(3;60) nên suy ra v (t) = 20t (m/s). B 3
Quãng đường đi được sau 3 giây của xe A là s = ∫ ( 2
−20t +80t)dt =180m. A 0 3
Quãng đường đi được sau 3 giây của xe B là s = 20t dt = 90m. ∫ B 0
Vậy khoảng cách giữa hai xe sau 3 giây sẽ bằng: s − s = 90 m. Chọn A. A B
Câu 51. Tốc độ thay đổi số dân của một thị trấn kể từ năm 1970 được mô tả bằng
công thức f ′(t) 120 =
, với t là thời gian tính bằng năm (thời điểm t = 0 ứng với (t + )2 5
năm 1970). Biết rằng số dân của thị trấn vào năm 1970 là 2000 người. Hỏi số dân của
thị trấn đó vào năm 2018 gần nhất với số nào sau đây? A. 22 nghìn người. B. 23 nghìn người. C. 24 nghìn người. D. 25 nghìn người.
Lời giải. Tốc độ thay đổi số dân của thị trấn vào năm thứ 120
t là f ′(t) = . Suy ra (t + )2 5
nguyên hàm của f ′(t) là hàm số f (t) mô tả số dân của thị trấn vào năm thứ t . Ta có − f (t) = f ′(t) 120 120 dt = dt = +C ∫ ∫ . (t +5)2 t + 5
Số dân của thị trấn vào năm 1970 (ứng với t = 0 ) là − − f ( ) 120 = ⇔ +C = ⇔ C =  → f (t) 120 0 2 2 26 = + 26. 0 + 5 t + 5
Vậy số dân của thị trấn vào năm 2018 (ứng với t = 48 ) là − f ( ) 120 48 =
+ 26 = 23,73 nghìn người. Chọn C. 48 + 5
Câu 52. Biết tốc độ phát triển của vi khuẩn HP (Helicobacter pylori) gây đau dạ dày
tại ngày thứ t là F (t) 1000 ' =
và ban đầu bệnh nhân có 2000 con vi khuẩn. Sau 15 2t +1
ngày bệnh nhân phát hiện ra bị bệnh. Hỏi khi đó có bao nhiêu con vi khuẩn trong dạ dày ? A. 5434 con. B. 1500 con. C. 283 con. D. 3717 con.
Lời giải. Tốc độ phát triển của vi khuẩn tại ngày thứ t là F ′(t) 1000 = . Suy ra số 2t +1
lượng vi khuẩn vào ngày thứ t được tính theo công thức F (t) = F ′(t) 1000 dt =
dt = 500 ln 2t +1 +C ∫ ∫ . 2t +1
Lúc ban đầu bệnh nhân có 2000 con vi khuẩn nên
F (0) = 2000 ⇔ 500 ln 2.0 +1 +C = 2000 ⇔ C = 2000 
→ F (t) = 500 ln 2t +1 + 2000.
Số vi khuẩn sau 15 ngày là: F (1 )
5 = 500 ln 2.15 +1 + 2000 = 3716, 99 . Chọn D.
Câu 53. Một đám vi trùng ngày thứ t có số lượng là N (t). Biết rằng N (t) 4000 ' = 1+ 0,5t
và lúc đầu đám vi trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ hàng đơn vị):
A. 264.334 con. B. 257.167 con. C. 258.959 con. D. 253.584 con.
Lời giải. Ta có N (t)= N (t) 4000 ' dt =
dt = 8000.ln(1+ 0,5t)+C ∫ ∫ . 1+ 0,5t
Tại thời điểm ban đầu (t = 0) thì
N (0) = 8000.ln1+C = 250000 ⇔ C = 250000 
→ N (t)= 8000.ln(1+0,5t)+250000 .
Sau 10 ngày (t =10) thì N (10) = 8000.ln(1+0,5.10)+250000 = 264.334 con. Chọn A.
Câu 54. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức '( ) = 100 . t S t
r e (con/giờ) với r là tỷ lệ tăng trưởng đặc trưng của vi khuẩn. Ban đầu có
100 con vi khuẩn. Hỏi sau bao lâu số lượng vi khuẩn ban đầu sẽ tăng gấp đôi. Biết
rằng số lượng vi khuẩn sau 5 giờ là 300 con.
A. 4 giờ35 phút. B. 3 giờ 9 phút.
C. 4 giờ 30 phút. D. 4 giờ 2 phút.
Lời giải. Sự tăng trưởng của vi khuẩn tại giờ thứ t là '( )=100 . t S t
r e . Suy ra số lượng
vi khuẩn vào giờ thứ t được tính theo công thức ( )= '( ) = 100 . t S t S t dt r e dt ∫ ∫ .
Số lượng vi khuẩn sau 5 giờ là 300 con nên ta có: 5 t 5 300 = 100r.e ←
→100r.e −100r = 300  →r = 0,020351. ∫ 0 t
Suy ra thời gian để số vi khuẩn tăng lên 200 con là: 200 = 100.0,020351. te ∫ 0  →100.0,02035 ( 1 t e − ) 1 = 200 ←
→t ≃ 4,597 giờ (4 giờ 35 phút). Chọn A.
Câu 55. Người ta thay nước mới cho một bể bơi có dạng hình hộp chữ nhật có độ sâu
là 280cm. Giả sử h(t) là chiều cao (tính bằng cm) của mực nước bơm được tại thời
điểm t giây, biết rằng tốc độ tăng của chiều cao mực nước tại giây thứ t là h '(t) 1 3 =
t + 3 và lúc đầu hồ bơi không có nước. Hỏi sau bao lâu thì nước bơm được 500
3 độ sâu của hồ bơi? 4
A. 3 giờ 34 giây. B. 2 giờ 34 giây. C. 3 giờ 38 giây. D. 2 giờ 38 giây. 4
Lời giải. Ta có h(t)= h'(t) 1 3 3 dt = t + 3dt = (t +3)3 +C. ∫ ∫ 500 2000
Lúc ban đầu (tại t = 0 ) hồ bơi không chứa nước, nghĩa là 7 4 3 h(0) 3 = 0←→ (0 +3) 3 3 +C = 0 ← →C = − . 2000 2000 7 4 3
Suy ra mực nước bơm được tại thời điểm 3 3
t giây là h(t) = (t +3)3 − . 2000 2000
Theo giả thiết, lượng nước bơm được bằng 3 độ sâu của hồ bơi nên ta có: 4 7 4 3 4 h(t) 3 3 = .280←→ (t +3) 3 3 −
= 210←→(t +3)3 = 140004,33←→t = 7234s . 4 2000 2000
Vậy sau khoảng thời gian 2 giờ 34 giây thì bơm được 3 độ sâu của hồ bơi. Chọn B. 4 Baøi 04
MOÄT SOÁ PHÖÔNG PHAÙP TÍNH TÍCH PHAÂN
1. Phương pháp đổi biến số
a) Phương pháp đổi biến số loại 1 b
Giả sử cần tính tích phân I = f (x)dx ∫
ta thực hiện các bước sau: a
Bước 1. Đặt x = u(t) (với u(t) là hàm có đạo hàm liên tục trên [α;β] , f u(t)   xác định trên [ ;
α β ] và u(α) = a, u(β) = b ) và xác định , α β . β β
Bước 2. Thay vào, ta có I =
f u(t).u '(t)dt =
g (t)dt = G (t) β = G β − α ∫ ∫ . α ( ) G( )   α α
Một số dạng thường dùng phương pháp đổi biến số loại 1 Dấu hiệu Cách chọn   π π
x = a sin t t ∈ − ;   2 2   a − x  2 2  
x = a cost t ∈  [0;π]   aπ π x =
t ∈ − ;  \{0}  sin t  2 2     2 2 x − a a   π   x  =
t ∈ [0;π]\   cos t   2  π π 2 2 = ∈   x + a x
a tan t t −  ;     2 2 
b) Phương pháp đổi biến số loại 2
Tương tự như nguyên hàm, ta có thể tính tích phân bằng phương pháp đổi biến số
(ta gọi là loại 2) như sau: b
Để tính tích phân I = f (x)dx ∫
nếu f (x)= g u(x).u'(x)  
, ta có thể thực hiện phép a đổi biến như sau:
Bước 1. Đặt t = u(x)⇒ dt = u'(x)dx .
x = a ⇒ t = u(a) Đổi cận  .
x = b ⇒ t = u  (b)  u(b ) u(b)
Bước 2. Thay vào ta có I =
g (t)dt = G (t) . ∫ u(a) u(a )
2. Phương pháp tích phân từng phần
Cho hai hàm số u và v liên tục trên [a;b] và có đạo hàm liên tục trên [a;b]. b b b
Khi đó: udv = uv − vd . u ∫ ∫ a a a
Một số tích phân các hàm số dễ phát hiện u và dv β u
 = ln g(x)  Dạng 1  
f (x)ln  g (x) d  x ∫   Đặt  d
 v = f (x)dx α  u  = f (x)    sin ax   sin ax Dạng 2 β   Đặt    
f (x)cos ax d  x ∫     
dv = cos ax dx    α   ax     e   ax  e     sin ax u  =   Dạng 3 β     sin ax  Đặt  cos ax   ax e  d  x ∫    cos ax    d ax
v = e dxα
Ưu tiên đặt u theo quy tắc ' nhất log, nhì đa, tam lượng, tứ mũ ' . Tức là trong
hàm số dưới dấu tích phân hợp bởi 2 trong 4 hàm số trên thì ta đặt u theo thứ tự ưu
tiên như trên, còn lại thì đặt là dv .
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1.1. PHƯƠNG PHÁP ĐỔI BIẾN SỐ LOẠI 1 8
Câu 1. Cho tích phân 2 I = 16 − x dx ∫
và x = 4 sin t . Mệnh đề nào sau đây đúng? 0 π π 4 4 A. 2 I = −16 cos tdt. ∫
B. I = 8 (1+ cos2t)dt ∫ . 0 0 π π 4 4 C. 2 I = 16 sin d t t. ∫
D. I = 8 (1−cos2t)dt ∫ . 0 0 d
 x = 4 cos tdt Lời giải. Với 
x = 4 sin t , suy ra  . 2 2 2
 16−x = 16−16sin t = 16cos t = 4 cost 
x = 0 → t = 0  Đổi cận:  π . x = 8 → t =  4 π π π 4 4 4 Khi đó 2 I =
16 cos t cos tdt =
16 cos tdt = 8 (1+ cos 2t)dt. ∫ ∫ ∫ Chọn B. 0 0 0 1
Câu 2. Cho tích phân dx I = ∫
và x = 2 sin t . Mệnh đề nào sau đây đúng? 2 − 0 4 x π π π π 6 6 6 3 A. dt I = dt ∫ .
B. I = tdt ∫ . C. I = ∫ . D. I = dt ∫ . t 0 0 0 0 d
 x = 2cos tdt Lời giải. Với 
x = 2 sin t , suy ra  . 2 2 2
 4−x = 4−4sin t = 2 cos t = 2 cost   π π π x = 0 → t = 0  6 6 6 Đổi cận:  2 cos t 2 cos tπ . Vậy = = =  I dt dt dt. ∫ ∫ ∫ Chọn A. x = 1 → t =  2 cos t 2 cos t  6 0 0 0 π 2 2
Câu 3. Biến đổi tích phân 2 I =
5 + 4x − x dx ∫ thành tích phân I = f (t)dt ∫ với −1 0
cách đặt x = 2 −3sin t . Khẳng định nào sau đây là đúng? A. f (t) 2 = 9 sin t. B. f (t) 2 = −9 cos t. C. 9 f (t) 9 = (1+cos 2t).
D. f (t)= (1−cos2t). 2 2 2 2
Lời giải. Tích phân viết lại I =
5 + 4x − x dx = 3 −(2 − x)2 2 2 dx. ∫ ∫ −1 1 −    − =  π  = − → = Với 2 x 3 sin tx t
x = 2 −3 sin t  → . Đổi cận: 1  2 . d
x = −3costdt 
x = 2 → t = 0  π π 0 2 2 Khi đó 2 2 I = −3
9 − 9 sin t .cos tdt = 3
9 cos t .cos tdt = 9
cos t .cos tdt. ∫ ∫ ∫ π 0 0 2 π π 2 2 9 2 = 9 cos tdt = (1+cos2t)dt ∫ ∫ . Chọn C. 2 0 0 3
Câu 4. Cho tích phân 1 I = dx ∫
và x = 3 tan t . Mệnh đề nào sau đây đúng? 2 x + 3 3 π π π π 3 3 3 3 A. 3 dt 3 3 I = 3 dt.
∫ B. I = . ∫ C. I = d t t. ∫ D. I = dt. ∫ 3 t 3 3 π π π π 4 4 4 4
Lời giải. Với x = 3 tan t , suy ra x = ( 2 d 3 1+ tan t )dt.  ππ π x = 3 → t =  3 ( 2 3 1+ tan t ) 3 dt Đổi cận:  4 3  . Khi đó = =  I dt. ∫ ∫ Chọn D. π  2 3 tan t + 3 3 x = 3 → t = π π  3 4 4 2 2
Câu 5. Cho tích phân x −1 I = dx ∫ và 1 x =
. Mệnh đề nào sau đây đúng? 3 x sin t 1 π π 2 2 A. 2 I = sin tdt. ∫ B. 2 I = cos tdt. ∫ π π 4 4 π π 2 2
C. I = (1+cos2t)dt. ∫
D. I = (1−cos2t)dt. ∫ π π 4 4  cos t d  x = − dt  2  sin t Lời giải. Với 1  x = , suy ra  . sin t 2  1 cos t cos t 2  x −1 = −1 = = 2 2  sin t sin t sin t   π cos t cos tπ π x = 1 → t =  4 2 Đổi cận:  2 sin t cos t sin t cos t  . Khi đó = − =  I . dt . dt ∫ ∫ π  2 2 1 sin t 1 sin tx = 2 → t = π π  3 3 4 2 4 sin t sin t π π 2 2 1 2 = cos tdt = (1+cos2t)dt. ∫ ∫ Chọn B. 2 π π 4 4
Vấn đề 1.2. PHƯƠNG PHÁP ĐỔI BIẾN SỐ LOẠI 2
Câu 6. Cho hàm số f (x) có nguyên hàm trên ℝ . Mệnh đề nào sau đây đúng? 1 1 a a A. f (x)dx =
f (1− x )dx. ∫ ∫ B.
f (x)dx = 2 f (x )dx. ∫ ∫ 0 0 −a 0 π π 1 2 C. 1
f (sin x)dx = −
f (cos x)dx. ∫ ∫ D. f (x)dx = f (x)dx. ∫ ∫ 2 0 0 0 0  = ⇒ =
Lời giải. Chọn A. Đặt x t
x = 1− t ⇒ dx = d − t . Đổi cận 1 0  .
x = 0 ⇒ t = 1  1 0 1 1 Suy ra
f (x)dx = −
f (1− t)dt =
f (1−t)dt =
f (1− x)dx. ∫ ∫ ∫ ∫ 0 1 0 0
B, C, D sai. Ta có thể chọn hàm f (x)= x để kiểm tra.
Câu 7. Hàm số f (x) có nguyên hàm trên (a;b) đồng thời thỏa mãn f (a)= f (b).
Mệnh đề nào sau đây đúng? b b A.
f (x) f (x) ' e dx = 0 ∫ . B.
f (x) f (x) ' e dx = 1 ∫ . a a b b C.
f (x) f (x) ' e dx = −1 ∫ . D.
f (x) f (x) ' e dx = 2 ∫ . a a
x = a → t = f (a) Lời giải. Đặt 
t = f (x) , suy ra dt = f '(x)dx . Đổi cận  . x
 = b → t = f (b)  f (b b ) Khi đó
f (x) f (x) t f (b) f (a) ' e dx = e dt = e −e = 0 ∫ ∫
(do f (a)= f (b) ). Chọn A. a f (a)
Câu 8. Cho hàm số f (x) có nguyên hàm trên ℝ . Xét các mệnh đề sau: π 2 1
1) sin 2x. f (sin x)dx = 2 x. f (x)dx. ∫ ∫ 0 0 1 f ( x e ) e f (x ) 2) dx = dx ∫ ∫ . x 2 e x 0 1 2 a a 3) 1 3 x f ∫ ( 2 x )dx = xf (x)dx ∫ . 2 0 0
Có bao nhiêu mệnh đề đúng? A. 1. B. 2. C. 3. D. 0. π π 2 2
Lời giải. Xét 1) Ta có sin 2x. f (sin x)dx = 2 sin x. f (sin x).cos xdx ∫ ∫ . 0 0
x = 0 → t = 0  Đặt 
t = sin x , suy ra dt = cos xdx . Đổi cận  π . x = → t =1  2 π 2 1 1
Khi đó 2 sin x. f (sin x).cos xdx = 2 t. f (t)dt = 2 x. f (x)dx. ∫ ∫ ∫ Do đó 1) đúng. 0 0 0 Xét 2) Đặt x
t = e và kết luận được 2) đúng. Xét 3) Đặt 2
t = x và kết luận được 3) đúng.
Vậy cả 3 mệnh đề đều đúng. Chọn C. a
Câu 9. Cho tích phân I = f (x )dx ∫
. Mệnh đề nào sau đây đúng? −a a a
A. I =  f (x)− f (−x)dx. ∫  
B. I =  f (x −a)− f (a − x)dx. ∫   0 0 a a
C. I =  f (x)− f (a − x)dx. ∫  
D. I =  f (x −a)+ f (x)dx. ∫   0 0 a 0 a
Lời giải. Ta có I =
f (x )dx = f (x)dx + f (x)dx. ∫ ∫ ∫ −a −a 0 0  = − → = Xét x a tJ = f (x)dx. ∫
Đặt x = t −a 
→ dx = dt. Đổi cận 0  .
x = 0 → t = a −  a 0 a a Khi đó J =
f (x )dx =
f (t −a)dt =
f (x −a)dx. ∫ ∫ ∫ −a 0 0 a a a a Vậy I = J + f (x)dx =
f (x −a)dx + f (x)dx =
f (x −a)+ f (x)dx. ∫ ∫ ∫ ∫   Chọn D. 0 0 0 0
Câu 10. Cho hàm số f (x) liên tục trên [a;b] và thỏa f (a +b − x)= f (x) ∀x ∈[a;b].
Mệnh đề nào sau đây đúng? b b b b A. ( ) b − a b + a xf x dx = f (x )dx. ∫ ∫
B. xf (x)dx = f (x )dx. ∫ ∫ 2 2 a a a a b b b b
C. xf (x)dx = (b −a) f (x)dx. ∫ ∫
D. xf (x)dx = (b + a) f (x)dx. ∫ ∫ a a a a  = → = Lời giải. Đặt 
x = a + b − t , suy ra dx = d
− t . Đổi cận x a t b  .
x = b → t = a  b a b
Khi đó xf (x)dx = − (a +b −t) f (a +b −t)dt = (a +b −t) f (a +b −t)dt ∫ ∫ ∫ a b a b ( + − )= ( ) b b f a b x f x
= (a +b − x) f (a + b − x)dx =
(a +b) f (x)dx − xf (x)dx. ∫ ∫ ∫ a a a b b b b Suy ra a + b 2
xf (x)dx = (a + b)
f (x )dx 
→ xf (x)dx = f (x )dx. ∫ ∫ ∫ ∫ Chọn B. 2 a a a a
Câu 11. Cho f (x) là hàm số lẻ và liên tục trên [ a
− ;a] . Mệnh đề nào sau đây đúng? a a a A.
f (x)dx = 2 f (x)dx ∫ ∫ . B.
f (x)dx = 0 ∫ . −a 0 −a a 0 a a C.
f (x)dx = 2 f (x)dx ∫ ∫ . D.
f (x)dx = −2 f (x)dx ∫ ∫ . −a −a −a 0 a 0 a Lời giải. Ta có
f (x )dx = f (x)dx + f (x)dx ∫ ∫ ∫ . −a −a 0 0  = − ⇒ = Xét tích phân x a t af (x)dx ∫ . Đặt x = t − ⇒ dx = d
− t . Đổi cận  .
x = 0 ⇒ t = 0 −  a
Do f (x) là hàm số lẻ và liên tục trên [ a
− ;a] nên f (−x) = − f (x) ⇒ f ( t
− ) = − f (t) . 0 0 0 0 a a Khi đó
f (x)dx = − f ( t
− )dt = − − f (t) dt =
f (t)dt = −
f (t)dt = − f (x )dx. ∫ ∫ ∫   ∫ ∫ ∫ −a a a a 0 0 a a a Vậy
f (x)dx = − f (x)dx +
f (x)dx = 0 ∫ ∫ ∫ . Chọn B. −a 0 0 0 2
Câu 12. Cho f (x) là hàm số lẻ và f (x)dx = 2 ∫ . Tính tích phân I = f (x)dx. ∫ 2 − 0 A. I = 2. B. I = −2. C. I = 1. D. I = −1.
Lời giải. Áp dụng kết quả câu trên, ta có ' Nếu f (x) là hàm số lẻ và liên tục trên a đoạn [ a − ;a] thì
f (x)dx = 0 ' . ∫ −a 2 0 2
Thay a = 2 ta được 0 = f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ 2 − 2 − 0 2 0  →
f (x)dx = −
f (x)dx = −2. ∫ ∫ Chọn B. 0 2 − 1
Câu 13. Tính tích phân 2017 2 I = x x + 2017dx. ∫ −1
A. I = 0.
B. I = 2.
C. I = −2. D. 1 I = ⋅ 3
Lời giải. Xét hàm số f (x) 2017 2 = x
x + 2017 là hàm số lẻ, liên tục trên đoạn [−1; ] 1 . 1 Vậy 2017 2 I = x x + 2017dx = 0. ∫ Chọn A. −1
Câu 14. Cho f (x) là hàm số chẵn và liên tục trên [ a
− ;a] . Mệnh đề nào sau đây sai? a a a 0 A.
f (x)dx = 2 f (x)dx ∫ ∫ . B.
f (x)dx = 2 f (x )dx. ∫ ∫ −a 0 −a −a 0 a a C. f (x)dx = f (x )dx ∫ ∫ . D.
f (x)dx = 0. ∫ −a 0 −a a 0 a Lời giải. Ta có f (x)dx = f (x)dx +
f (x)dx = A + B. ∫ ∫ ∫ −a −a 0 0  = − → = Xét x a t aA = f (x)dx ∫ . Đặt x = t − , suy ra dx = d
− t . Đổi cận  .
x = 0 → t = 0 −  a 0 a a ( ) chan a f x
Khi đó A = − f ( t − )dt = f ( t − )dt =
f (−x)dx =
f (x)dx = B. ∫ ∫ ∫ ∫ a 0 0 0
Vậy A, B, C đúng; D sai. Chọn D. 0 1
Câu 15. Cho f (x) là hàm số chẵn và thỏa mãn
f (x )dx = 3 ∫ . Tính I = f (x)dx. ∫ −1 −1
A. I = 3.
B. I = 2.
C. I = 6. D. I = −3⋅ 1 0
Lời giải. Áp dụng kết quả câu trên, ta có
f (x)dx = 2
f (x)dx = 2.3 = 6. ∫ ∫ Chọn C. −1 1 − 1 Câu 16. Biết rằng x I = dx = ln a ∫
với a là số thực dương. Tìm . a 2 x +1 0 A. a = 2. B. 1 a = . C. a = 2 . D. a = 4 . 2  = → = Lời giải. Đặt t x t 2 
t = x +1 , suy ra d
dt = 2xdx  → xdx = . Đổi cận: 0 1  . 2
x = 1 → t = 2  2 2 Khi đó 1 dt 1 1 I =
= ln t = ln 2 = ln 2  →a = 2. ∫ Chọn C. 2 t 2 2 1 1 1 3
Câu 17. Cho tích phân 4x I = dx ∫ và 4
t = x + 2. Mệnh đề nào sau đây đúng? (x +2)2 4 0 3 1 3 1 A. dt dt dt dt I = 4 . ∫ B. I = 4 . ∫ C. I = . ∫ D. I = . ∫ 2 t 2 t 2 t 2 t 2 0 2 0  = → = Lời giải. Với x t 4 
t = x + 2 , suy ra 3
dt = 4x dx . Đổi cận 0 2  .
x = 1 ⇒ t = 3  3 Khi đó dt I = . ∫ Chọn C. 2 t 2 (x + 2)2017 2
Câu 18. Tính tích phân I = dx. ∫ 2019 x 1 2018 2018 2018 2018 A. 3 −2 3 −2 I = . B. I = . 2018 4036 2017 2018 2021 2021 C. 3 2 3 −2 I = − . D. I = . 4034 2017 4040 2 2017  +  Lời giải. Ta có x 2 1 I =   ∫   . dx.   2  x x 1  = → = Đặt x + 2 2 2 dx 1 x tt = = 1+ , suy ra dt = − dx  →
= − dt . Đổi cận 1 3  . x x 2 2 x x 2
x = 2 → t = 2  2 3 2018 3 2018 2018 Khi đó 1 1 t 3 −2 2017 2017 I = − t dt = t dt = = . ∫ ∫ Chọn B. 2 2 4036 2 4036 3 2 2 2016
Câu 19. Tính tích phân x I = dx ∫ . x e +1 2 − 2018 2017 2018 A. 2 2 2 I = 0. B. I = . C. I = . D. I = . 2017 2017 2018 2 0 2 2016 2016 2016 Lời giải. Ta có x x x I = dx = dx +
dx = A + B. ∫ ∫ ∫ x e +1 x e +1 x e +1 2 − 2 − 0 0 2016  = − → = Tính x x tA = dx ∫ . Đặt x = t − , suy ra dx = d − t. Đổi cận 2 2  . x e +1
x = 0 → t = 0  2 − ( t − )2016 0 2 2 2016 t 2016 x Khi đó t .e x .e A = − dt = dt = dx. ∫ − ∫ ∫ t e +1 t e +1 x e +1 2 0 0 2 2 2 2016 x x . x . (e x e x + ) 2 2016 2016 1 Vậy 2016
I = A + B = dx + dx = dx = x dx ∫ ∫ ∫ ∫ x e +1 x e +1 x e +1 0 0 0 0 2017 2 2017 x 2 = = . Chọn C. 2017 0 2017 1
Câu 20. Tính tích phân I = ∫ ( n 2
1− x ) xdx với n nguyên dương. 0 A. 1 I = ⋅ B. 1 I = ⋅ C. 1 I = ⋅ D. 1 I = ⋅ 2n + 2 2n +1 2n 2n −1  = → = Lời giải. Đặt x t 2 
t = 1− x , suy ra 1
dt = −2xdx 
→ xdx = − dt. Đổi cận 0 1  . 2
x = 1 → t = 0  0 1 n 1 + 1 Khi đó 1 t n 1 n 1 1 I = − t dt = t dt = . = . ∫ ∫ Chọn A. 2 2 2 n +1 0 2(n + ) 1 1 0 1
Câu 21. Kết quả tích phân a a − 2 I = x 1+ x dx ∫ được viết ở dạng 1 I =
với a, b là b 0
các số nguyên dương. Tính giá trị của biểu thức T = a + 2 . b
A. T = 1.
B. T = 7.
C. T = 5.
D. T = 8.
x = 0 → t =1 Lời giải. Đặt 2 2 2 
t = 1+ x ⇒ t = 1+ x , suy ra tdt = xdx. Đổi cận  . x  = 1 → t = 2  2 3 2 −  = Khi đó t 2 2 1 a 2 2  I = t dt = =  → ∫   T
→ = a + 2b = 8. Chọn D. 3  = 1 3 b 3  1 2
Câu 22. Cho tích phân 2 I = 2x x −1dx ∫ và 2
u = x −1. Mệnh đề nào sau đây sai? 1 3 2 3 3 A. 2 I = udu ∫ . B. I = udu ∫ . C. 2 I = u . D. I = 2 3 . 3 0 1 0  = → = Lời giải. Với x u 2 
u = x −1 , suy ra du = 2xdx . Đổi cận 1 0  .
x = 2 → u = 3  2 3 Suy ra 2 I = 2x x −1dx = udu ∫ ∫
. Do đó B sai. Chọn B. 1 0 a 3
Câu 23. Tính tích phân x + x I = dx. ∫ 2 + 0 x 1 A. I = ( 2 a + ) 2 1 a +1 −1. B. I = ( 2 a + ) 2 1 a +1 +1. C. 1   1   I = ( 2a +  ) 2 1 a +1 +1 .  D. I = ( 2 a +  ) 2 1 a +1 −1 .  3   3  
x = 0 → t = 1 Lời giải. Đặt 2 2 2 
t = x +1 ⇒ t = x +1 , suy ra tdt = xdx . Đổi cận  . 2
x = a → t = a +1  a a + ( 2 3 x + x x ) 2 a 1 2 3 a 1 1 + + Khi đó t 1 2   I = dx = xdx = t dt = = ∫ ∫ ∫ ( 2a +  ) 2 1 a +1 −1 .  2 2 3   1 3 + + 0 x 1 0 x 1 1 Chọn D. 2
Câu 24. Tính tích phân 2 3 I = x x +1dx ∫ . 0 A. 16 I = . B. 16 I = − . C. 52 I = . D. 52 I = − . 9 9 9 9 Lời giải. Đặt 2 3 2 3
t = x +1 ⇒ t = x +1 , suy ra 2 2
2tdt = 3x dx 
→ tdt = x dx. 3  = → = 3 3 3 Đổi cận: x 0 t 1  2 2t 52  . Vậy 2 = = =  I t dt . ∫ Chọn C. x = 2 → t = 3  3 9 1 9 1 3 2
Câu 25. Biến đổi tích phân x dx ∫ thành tích phân f (t)dt ∫
với t = 1+ x . 1+ 1+ x 0 1
Khi đó f (t) là hàm số nào trong các hàm số sau? A. f (t) 2
= 2t −2t . B. ( ) 2
f t = t + t . C. ( ) 2
f t = t − t . D. f (t) 2 = 2t + 2t .  = → = Lời giải. Với x t 2 
t = 1+ x ⇒ t = 1+ x , suy ra 2tdt = dx . Đổi cận 0 1  .
x = 3 → t = 2  3 2 2 2 Khi đó x t −1 dx = .2tdt = ∫ ∫ ∫ ( 2
2t − 2t)dt. Vậy f (t) 2
= 2t −2t . Chọn A. 1+ 1+ x 1+ t 0 1 1 5
Câu 26. Kết quả tích phân 1 I = dx ∫
được viết ở dạng I = a +b ln 3+ c ln5 1+ 3x +1 1
với a, b, c là các số hữu tỷ. Tính tổng S = a +b + c. A. 4 S = ⋅ B. 5 S = ⋅ C. 7 S = ⋅ D. 8 S = ⋅ 3 3 3 3 Lời giải. Đặt 2
t = 3x +1 ⇒ t = 3x +1 , suy ra 2
2tdt = 3dx 
→dx = tdt . 3  = → = Đổi cận x 1 t 2  .
x = 5 → t = 4  4 4 4   Khi đó 2 t 2 1 2 I = t =   ∫ ∫  −  t = (t − + t ) 4 2 2 d 1 d ln 1 = + ln 3− ln 5 3 1+ t 3  1+t  3 2 3 3 3 2 2 4 2 2 4 
→a = , b = , c = − 
→S = . Chọn A. 3 3 3 3 2 2
Câu 27. Kết quả tích phân x I = dx ∫
được viết ở dạng I = a ln 5+b ln 2 2 2 x −1+ x +1 3
với a, b là các số hữu tỷ. Tính tổng S = a + . b A. 2 S = − . B. 1 S = − . C. 1 S = . D. 2 S = . 3 3 3 3  =  = Lời giải. 2tdt 2xdx tdt xdx Đặt 2 2 2  
t = x +1 ⇒ t = x +1 , suy ra   → . 2 2 2 2 x = t −1 x = t −1    = → = Đổi cận: x 3 t 2  .
x = 2 2 → t = 3  3 3 3   Khi đó t t 1 1 2 I = dt = dt =  +  dt ∫ ∫ ∫ 2 t − 2 + t (t − ) 1 (t + 2) 3
t −1 t +2 2 2 2  2 1  ( =  = t − + t + ) 3 2 a 1 ln 1 2 ln 2 = ln 5−ln 2  → 3 
→S = − . Chọn B. 3  2 3 3 b  =−1  3 2 2
Câu 28. Cho tích phân 1+ x x +1 I = dx ∫ và t =
. Mệnh đề nào sau đây đúng? 2 x x 1 2 2 3 2 3 2 3 2 3 A. t dt t dt t dt tdt I = −∫ . B. I = ∫ . C. I = ∫ . D. I = ∫ . 2 t −1 2 t +1 2 t −1 2 t +1 2 2 2 2 3 3 2 Lời giải. Ta có 1+ x x I = dx = ∫ ∫ ( d 2 x +1 . . 2 ) 2 2 x + 1 1 x 1 x  1 d  t = − dx  2 2 2 +  Với x 1  x x +1 t = ⇒  .  2 2 xx +1 1 1 t 2 2 2 t  = = 1+ ⇒ x = ⇒ x +1 =  2 2 2 2  x x t −1 t −1  2 x = 1 ⇒ t = 2  3 2 Đổi cận:  t  2 . Suy ra = −  I dt ∫ . Chọn A. x = 3 ⇒ t =  2 t −1  3 2 2 Câu 29. Biết rằng dx I = = a ln 2 +b ln ∫
( 2− )1+c với a, b, c là các số hữu tỷ. 3 + 1 x 1 x
Mệnh đề nào sau đây đúng? A. 1 a = − . B. 2 b = . C. 2 c = − .
D. a +b + c = 0. 3 3 3 2 2 2
Lời giải. Viết lại dx x dx I = = . ∫ ∫ 3 3 3 + + 1 x 1 x 1 x 1 x 3 2  = − 2 3 x t 1  = +   Đặt t 1 x x = → t = 3    t = 1+ x ⇒  ⇒  . 2 Đổi cận: 1 2  . 2 2 2
 tdt = 3x dx x dx   = tdt  = → =  x 2 t 3   3 3 3 3     Suy ra 2 tdt 1 1 1 1 t −1 1 1 2 = =    −1 I ∫ ∫  −  t = =  −      3 ( d ln ln ln 2 t − ) 1 t 3
t −1 t +1 3 t +1 3  2 2 +1 2 2 2 = − − ( − )=− − ( − )2 1 1 1 1 1 2 ln 2 ln 3 2 2 ln 2 ln 2 1 = − ln 2 − ln( 2 − ) 1 . 3 3 3 3 3 3 Suy ra 1 2
a = − ; b = − ; c = 0 . Chọn A. 3 3 5 Câu 30. Biết rằng dx I = = a ln 3 +b ln 5 ∫
với a, b ∈ .
ℤ Tính tổng S = a + b. x 3x +1 1
A. S = 2.
B. S = 3.
C. S = −1.
D. S = 1. 2  t −1 x =  = → = Lời giải. Đặt  x t 2  
t = 3x +1 ⇒ t = 3x +1 , suy ra 3  . Đổi cận 1 2   . 2 
x = 5 → t = 4  d
x = tdt  3 4 4 4   Khi đó 2 1 dt 1 1 I = dt = 2 =   ∫ ∫ ∫  − dt 2 2 3 t −1 t −1
t −1 t +1 2 2 2 3 (  =  = t − − t + ) 4 a 2 ln 1 ln 1 = 2 ln 3−ln 5  → 
→S = 1. Chọn D.  = − 2 b 1  2
Câu 31. Tính tích phân ln x I = dx ∫ . x 1 2 2 A. ln 2 ln 2 I = 2. B. I = . C. I = ln 2. C. I = − . 2 2  = → = Lời giải. Đặt x x t
t = ln x , suy ra d dt = . Đổi cận: 1 0  . x
x = 2 → t = ln 2  ln 2 2 ln 2 2 Khi đó t ln 2 I = tdt = = . ∫ Chọn B. 2 0 2 0 e
Câu 32. Cho tích phân 1− ln x I = dx ∫
và u = ln x . Mệnh đề nào sau đây đúng? 2 x 1 0 1 A. = (1− ) u I u e d . u ∫ B. (1 ) u I u e− = − d . u ∫ 1 0 0 0 C. = (1− ) 2 − u I u e d . u ∫ D. = (1− ) 2u I u e d . u ∫ 1 1  1 u  =  = = Lời giải. du dx Với dx d x u e du  
u = ln x, suy ra  x  → . u     = u x ex = e    = → = 1 1 Đổi cận x 1 u 0  1−u  . Khi đó I = du = (1−u) u −  e d . u ∫ ∫ Chọn B.
x = e → u = 1  u e 0 0 e Câu 33. Cho 1+ 3 ln x I = dx ∫
và t = 1+3ln x. Mệnh đề nào sau đây là sai? x 1 2 2 2 A. 2 2 2 I = tdt. ∫ B. 2 I = t dt. ∫ C. 3 I = t . D. 14 I = . 3 3 9 9 1 1 1 Lời giải. Với x 2
t = 1+ 3 ln x ⇒ t = 1+ 3 ln x , suy ra 3 d 2 2 d t t = dx  → = d t t. x x 3  = → = 2 2 Đổi cận: x 1 t 1  2 2 14  . Khi đó 2 3 = = =  I t dt t . ∫
Do đó A sai. Chọn A.
x = e → t = 2  3 9 9 1 1 e 3
Câu 34. Biến đổi tích phân ln x dx ∫ thành f (t)dt ∫
với t = ln x + 2 . Khi đó x (ln x + 2)2 1 2
f (t) là hàm nào trong các hàm số sau? A. ( ) 2 1 1 2 2 1 2 1 f t =
− . B. f (t) = − + . C. f (t) = + .
D. f (t)= − + . 2 t t 2 t t 2 t t 2 t t  dx  =  = → = Lời giải. Với dtx t
t = ln x + 2 , suy ra  x . Đổi cận: 1 2   . 
x = e → t = 3 ln x = t −2   e 3 3 −   Khi đó ln x t 2 1 2 dx = dt =   ∫ ∫ ∫  − dt.   Chọn D. x (ln x + 2)2 2 2 tt t  1 2 2 e
Câu 35. Kết quả của tích phân ln x I = ∫
được viết ở dạng I = a ln 2 +b với x ( dx 2 ln x +1 1 )
a, b là những số hữu tỷ. Khẳng định nào sau đây là đúng?
A. 2a +b = 1. B. 2 2 a + b = 4 .
C. a −b = 1. D. ab = 2 . Lời giải. Đặt x x t 2
t = ln x +1 , suy ra 2 ln ln d dt = dx  → dx = . x x 2  = → = Đổi cận: x 1 t 1  .
x = e → t = 2  2 2 Khi đó 1 dt 1 1 1 I = = ln t = ln 2  →a = , b = 0. ∫ Chọn A. 2 t 2 1 2 2 1 1
Câu 36. Tính tích phân 2 x I = xe dx. ∫ 0 A. e e + e − I = . B. 1 I = . C. 1 I = .
D. I = e. 2 2 2 Lời giải. Đặt 2 t = x , suy ra 1 dt = 2 d x x  → d x x = dt. 2  = → = 1 1 Đổi cận: x 0 t 0  1 e − t 1 t 1  . Khi đó = = =  I e dt .e . ∫ Chọn C. x = 1 → t = 1  2 2 0 2 0 ln 2
Câu 37. Cho tích phân x x I = e e −1dx ∫ và x
t = e −1. Mệnh đề nào sau đây sai? 0 1 1 3 1 A. 2t 2 I = 2 t dt ∫ . B. 2 I = t dt ∫ . C. I = . D. 2 I = . 3 0 3 0 0 Lời giải. Với x 2 = −1 x t e
⇒ t = e −1, suy ra 2 d x
t t = e dx.  = → = 1 3 1 Đổi cận: x 0 t 0  2t 2  . Khi đó 2 = = =  I 2 t dt . ∫
Do đó B sai. Chọn B.
x = ln 2 → t = 1  3 0 3 0 2 x 3 Câu 38. Tìm e dx ae + e , a biết I = = ln ∫
với a, b là các số nguyên dương. 2 x + e ae + b 1 − A. 1 a = . B. 1 a = − . C. a = 2 . D. a = −2 . 3 3  1  = − → = Lời giải. Đặt x 1 t xt = e , suy ra d x
t = e dx. Đổi cận:  e .  2
x = 2 → t = e  2 e 2 e 2 3   Suy ra dt + e e + e I = = ln 2 + t = ln ∫ ( 1 2 2 2 2 + e − ln2  +  = ln = ln . 1 ) 2 + t  e  1 2e +1 1 e 2 + e e 
→a = 2; b = 1. Chọn C. π 2
Câu 39. Cho tích phân 2 sin x 3 I = e
sin x cos xdx ∫ và 2
t = sin x. Chọn khẳng định đúng? 0 1 1 1   A. 1 t I =
e (1−t)dt ∫ . B. 2 t  d t I e t te dt  = + ∫ ∫  . 2   0 0 0  1 1 1   C. = 1 2 t I
e (1−t)dt ∫ . D. t  d t I e t te dt  = + ∫ ∫  . 2   0 0 0  π π 2 2
Lời giải. Viết lại 2 2 sin x 3 sin x 2 I = e sin x cos d x x = e
.cos x.sin x cos xdx. ∫ ∫ 0 0 Với 2
t = sin x, suy ra 1
dt = 2 sin x cos xdx 
→sin x cos xdx = dt. 2
x = 0 → t = 0  1 Đổi cận  1  t π . Khi đó I = e (1−t)  dt ∫ . Chọn A. x = → t = 1  2  2 0 π 2 1
Câu 40. Biến đổi tích phân 2 sin x e sin 2x dx ∫ thành f (t)dt ∫ với 2
t = sin x . Khi đó π 1 4 2
f (t) là hàm nào trong các hàm số sau? A. ( ) t
f t = e sin 2t . B. ( ) t f t = e . C. ( ) t
f t = e sin t . D. ( ) 1 t f t = e . 2 Lời giải. Với 2
t = sin x, suy ra dt = 2 sin x cos xdx = sin 2 d x x.  π 1 x = → t =  1 Đổi cận:  4 2  . Khi đó t =  I e dt. ∫ Chọn B. π
x = → t =1 1  2 2 π
Câu 41. (ĐỀ MINH HỌA 2016 – 2017) Tính tích phân 3 I = cos x sin d x x. ∫ 0 A. 1 4 I = − π . B. 4 I = π − . C. I = 0 . D. 1 I = − . 4 4  = → = Lời giải. Đặt x t
t = cos x, suy ra dt = −sin xdx. Đổi cận: 0 1  .
x = π → t = −1  −1 1 4 1 Khi đó t 3 3
I = − t dt = t dt = = 0. ∫ ∫ Chọn C. 4 1 − 1 −1 π 2
Câu 42. Thực hiện phép đổi biến u = sin x thì tích phân 4 sin x cos d x x ∫ sẽ trở thành 0
tích phân nào trong các tích phân sau đây? π π 2 1 1 2 B. 4 u d . u ∫ A. 4 2 u 1−u d . u ∫ C. 4 u d . u ∫ D. 3 2 u 1−u d . u ∫ 0 0 0 0
x = 0 → u = 0  Lời giải. Với 
u = sin x, suy ra du = cos xdx. Đổi cận  π . x = → u =1  2 1 Khi đó 4 I = u du . ∫ Chọn C. 0 π 6 Câu 43. Biết rằng n 1 I =
sin x cos xdx = ∫ . Tìm n . 64 0 A. n = 3. B. n = 4 . C. n = 6. D. n = 5.
x = 0 → t = 0  Lời giải. Đặt 
t = sin x, suy ra dt = cos xdx. Đổi cận  π 1 . x = → t =  6 2 n 1 +   1 1 1     2 n 1 + 2   Khi đó t   n 2 1 1 I = t dt = = = = ⇔ n = ∫ Chọn A. n +1 n +1 (n + ) 3. n 1 1 2 + 64 0 0
Cách trắc nghiệm. Thay lần lượt từng đáp án và bấm máy tính. π 2
Câu 44. Tính tích phân = ( n I
1− cos x ) sin xdx ∫ . 0 A. 1 I = . B. 1 I = . C. 1 I = . D. 1 I = . n +1 n −1 2n n
x = 0 → t = 0  Lời giải. Đặt 
t = 1− cos x, suy ra dt = sin xdx. Đổi cận:  π . x = → t =1  2 1 n 1 + 1 Khi đó t n 1 I = t dt = = . ∫ Chọn A. n +1 0 n +1 0 π 2
Câu 45. Tính tích phân I = sin 2x ∫ (1+sin x)3 2 dx . 0 4 A. π I = . B. 15 I = . C. 31 I = . D. 7 I = . 64 4 4 4 Lời giải. Đặt 2
t = 1+ sin x, sauy ra dt = 2 sin x cos xdx = sin 2xdx.
x = 0 → t =1  2 2 4 Đổi cận:  t 15  3 π . Khi đó = = =  I t dt . ∫ Chọn B. x = → t = 2  4 4  2 1 1 π 2
Câu 46. Cho tích phân sin 2x I = dx ∫
và t = 1+ cos x. Chọn khẳng định đúng? 1+ cos x 0 1 3 1 3 A. 4t − 4t 4t − 4t I = dt. ∫ B. I = dt. ∫ t t 2 2 2 2
C. I = 4 ( 2t − ∫ )1dt.
D. I = −4 ( 2t − ∫ )1dt. 1 1 π π 2 2
Lời giải. Tích phân viết lại sin 2x cos x.sin x I = dx = 2 dx. ∫ ∫ 1+ cos x 1+ cos x 0 0 2 2  = −  Với cos x t 1 cos x = t −1 2  
t = 1+ cos x ⇒ t = 1+ cos x , suy ra   → . 2  d t t = −sin d x x s
 in xdx = −2 d t t  
x = 0 → t = 2  1 2 2 Đổi cận:  t −1  . 2 π K hi đó I = −2 (−2 d
t t ) = −4 (t − ∫ ∫ ) Chọn D.  1 dt. x = → t = 1 t  2 2 1 π 4 Câu 47. Cho 6 tan x I = dx ∫
và u = 3tan x +1. Mệnh đề nào sau đây đúng? 2 cos x 3 tan x +1 0 2 2 A. 4 4 I = ( 2 2u + ∫ )1du . B. I = ( 2u + ∫ )1du . 3 3 1 1 2 2 C. 4 4 I = ( 2u − ∫ )1du . D. I = ( 2 2u − ∫ )1du . 3 3 1 1 2 6
 tan x = 2u −2  Lời giải. Với 2 
u = 3 tan x +1 ⇒ u = 3 tan x +1, suy ra  . dx 2  = udu 2 cos x 3
x = 0 → u =1  2 2 2 Đổi cận  2 2u − 2 4  2 π . Vậy I = udu = (u − ∫ ∫ ) . Chọn C.  1 du x = → u = 2  3 u 3  4 1 1 π a
Câu 48. Cho số nguyên dương cos 2x a thỏa mãn 4 dx = ln 3. ∫ Mệnh đề nào sau 1+ 2 sin 2x 0 đây đúng?         A. 1 a ∈  ;3 .  ∈   ∈   ∈    B. 7 a 3  ; . C. 7 9 a  ; . D. 9 11 a  ; .  2   2 2 2 2 2 
Lời giải. Đặt t = sin 2x, suy ra 1
dt = 2 cos 2x dx 
→cos 2x dx = dt. 2
x = 0 → t = 0  m m Đổi cận  1 dt 1 1  π 2π . Khi đó = = + = +  I ln 2t 1 ln 2m 1 . ∫ x = → t = sin = m  2 2t +1 4 4  0  a a 0  = Theo giả thiết ta có 1 1 1 m 1 4 ln 2m +1 = ln 3 ⇔ ln 2m +1 =
ln 3 ⇔ 2m +1 = 3 ⇔  . 4 4 4 m = −2  Với 2π m = −2  →sin = −2 (loaïi). a  = Với 2π 2π π 4 + k 0 ℤ  m = 1  →sin = 1 ⇔ = + k2 a π ⇔ a ∈ =  → . Chọn C. a a 2 1+ 4 k k ∈ℤ a = 4  π n (1−tan x)5
Câu 49. Cho số nguyên dương 1 n thỏa mãn dx = ⋅ ∫ Mệnh đề nào sau đây 2 cos x 6 0 đúng? A. n ∈[1;2]. B. n ∈[3;4]. C. n ∈[5;6]. D. n ∈[7;8].
x = 0 → t = 0  Lời giải. Đặt dx
t = tan x, suy ra dt = . Đổi cận  π π . 2 cos x
x = → t = tan = m  n n m m − − − 5 (1 t)6 1 (1 m)6
Khi đó I = (1−t) dt = − = . ∫ 6 0 6 0 1−(1− m)6 Theo giả thiết ta có 1 = ⇔ m = 1. 6 6  = Với π π π 4 + k 0 ℤ  m = 1  → tan = 1 n
⇔ = + kπ ⇔ n ∈ =  → . Chọn B. n n 4 1+ 4 k k ∈ℤ n  = 4  a
Câu 50. Có bao nhiêu số thực 2
a thuộc khoảng (0;20π) sao cho 5
sin x sin 2xdx = ⋅ ∫ 7 0 A. 20. B. 19. C. 9. D. 10. a a Lời giải. Ta có 5 6 I = sin x sin 2 d x x = 2 sin x.cos d x x. ∫ ∫ 0 0  = → = Đặt x t
t = sin x, suy ra dt = cos d x x. Đổi cận: 0 0  .
x = a → t = sin a = m  m m 7 Khi đó 2 2m 6 7 I = 2t dt = t = . ∫ 7 0 7 0 7
Theo giả thiết ta có 2m 2 = ⇔ m = 1. 7 7 Với π m = 1 
→sin a = 1 ⇔ a = + k2 . π 2 Vì π 1
a ∈ (0;20π) nên 0 2π 20π 10 k k k ∈ < + < ⇔ − < < 
ℤ→ k ∈ {0;1;2;3;...;9} 2 2 
→ có 10 giá trị của k  → có 10 giá trị của . a Chọn D.
Câu 51. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [2;4] và thỏa mãn f (2)= 2 , 2
f (4) = 2018. Tính I =
f ′(2x)dx. ∫ 1
A. I = −1008.
B. I = 2018.
C. I = 1008.
D. I = −2018.  = → = Lời giải. Đặt x tt = 2x, suy ra 1 dt = 2dx 
→dx = dt. Đổi cận: 1 2  . 2
x = 2 → t = 4  2 4 4 Khi đó I = f ′( x ) 1 x = f ′(t) 1 t = f (t) 1 =
f ( )− f ( ) 1 2 d d . . 4 2  = (2018−2) = 1008. ∫ ∫ 2 2   2 2 2 1 2 Chọn C. 6 2
Câu 52. (ĐỀ CHÍNH THỨC 2016 2017) Cho f (x) = – dx = 12 ∫ . Tính I f (3x)dx. ∫ 0 0 A. I = 2. B. I = 4. C. I = 6. D. I = 36.  = → = Lời giải. Đặt x tt = 3x, suy ra 1 dt = 3dx 
→dx = dt. Đổi cận: 0 0  . 3
x = 2 → t = 6  6 Khi đó 1 I = f (t) 1 dt = .12 = 4. ∫ Chọn B. 3 3 0 b b m Tổng quát: Nếu k
f (x)dx = k ∫ thì
f (mx )dx = . ∫ m a a m 2017 1
Câu 53. Cho hàm số f (x) thỏa mãn
f (x )dx = 1. ∫ Tính I =
f (2017x )dx. ∫ 0 0
A. I = 2017.
B. I = 0.
C. I =1. D. 1 I = ⋅ 2017 Lời giải. Đặt t
t = 2017x, suy ra d
dt = 2017dx  →dx = . 2017  = → = Đổi cận x 0 t 0  .
x = 1 → t = 2017  2017 2017 Khi đó 1 I = f (t) 1 t = f (x) 1 1 . d dx = .1 = . ∫ ∫ Chọn D. 2017 2017 2017 2017 0 0 1 9
Câu 54. Cho hàm số f (x) liên tục trên ℝ và
f (x)dx = 1,
f (x)dx = 2. ∫ ∫ Tính giá 0 1 3     trị của biểu thức x I =  f  
∫  + f (3x)dx.  3    0 A. I = 4. B. I = −4. C. I = 9 . D. I = −9. 1 9 9
Lời giải. Từ giả thiết ta có f (x)dx + f (x)dx =
f (x )dx = 1+ 2 = 3. ∫ ∫ ∫ 0 1 0 3 3 3       Ta có x =    ∫  + ( x I f
f 3x ) dx = f     
∫  dx + f (3x)dx.  ∫ 3   3   0 0 0 3   Xét x x f   ∫  dx  . Đặt t = , suy ra 1 dt = dx  →dx = 3dt.  3 3 3 0  = → = 3 1 1   Đổi cận x 0 t 0  x  . Khi đó f  
∫  dx = 3 f (t)dt = 3 f (x) = =  dx 3.1 3. ∫ ∫ x = 3 → t = 1     3 0 0 0 3 Xét f (3x)dx. ∫
Đặt u = 3x, suy ra 1 du = 3dx  →dx = d . u 3 0  = → = 3 9 9 Đổi cận x 0 u 0  1 1 1  . Khi đó
f (3x)dx = f (u)du = f (x) = =  dx .3 1. ∫ ∫ ∫ x = 3 → u = 9  3 3 3 0 0 0
Vậy I = 3 +1 = 4. Chọn A. π 2
Câu 55. Cho hàm số f (x) liên tục trên ℝ và thỏa mãn
f (x)dx = 4. ∫ Tính tích 0 π 4
phân I =  f (2x)−sin x dx. ∫   0 A. 2 I = 2 + ⋅ B. 2 I = 3− ⋅ C. 2 I = 1+ ⋅ D. 2 I = 2 − ⋅ 2 2 2 2 π π π 4 4 4
Lời giải. Ta có I =  f (2x)−sin x dx = f (2x)dx − sin xdx. ∫   ∫ ∫ 0 0 0 π 4 Tính t J = f (2x)dx ∫
. Đặt t = 2x, suy ra d dt = 2dx  →dx = . 2 0  π π x = 0 → t = 0  2 2 Đổi cận  1 1 1  π
π . Khi đó J = f (t)dt = f (x ) = =  dx .4 2. ∫ ∫ x = → t =  2 2 2  4 2 0 0 π 4 π
Tính K = sin xdx = −(cos x) 2 4 = = 1− . ∫ 0 2 0 Vậy 2
I = J − K = 1+ . Chọn C. 2 4
Câu 56. Cho hàm số f (x) liên tục trên ℝ và thỏa mãn
f (x)dx = 2. ∫ Mệnh đề nào 2 − sau đây sai? 2 3 A.
f (2x)dx = 1. ∫ B. f (x + ) 1 dx = 2. ∫ −1 −3 2 6 C.
f (2x)dx = 2. ∫ D.
f (x −2)dx = 2. ∫ −1 0 2
Lời giải. Xét tích phân f (2x)dx. ∫
Đặt t = 2x, suy ra 1 dt = 2dx  →dx = dt. 2 −1  = − → = − 2 4 4 Đổi cận x 1 t 2  1 1 1  . Khi đó
f (2x)dx = f (t)dt = f (x ) = =  dx .2 1. ∫ ∫ ∫ x = 2 → t = 4  2 2 2 −1 2 − 2 −
Suy ra A đúng, C sai. Chọn C. 3 4 B đúng vì f (x + ) t =x 1 1 dx + →
f (t)dt = 2. ∫ ∫ −3 2 − 6 4 D đúng vì f (x −2) t =x −2 dx →
f (t)dt = 2. ∫ ∫ 0 −2 2017 2017 Câu 57. Cho
f (x)dx = 2. ∫ Tính tích phân I =
f (2018− x)dx ∫ . 1 1 A. I = 1. B. I = 2. C. I = 3. D. I = 5.  = → = Lời giải. Đặt x t
t = 2018 − x, suy ra dx = d − t. Đổi cận 1 2017  .
x = 2017 → t = 1  1 2017 2017 Khi đó I = − f (t)dt = f (t)dt =
f (x)dx = 2. ∫ ∫ ∫ Chọn B. 2017 1 1 3 5 Câu 58. Cho f (3x − ) 1 dx = 20. ∫ Tính tích phân I = f (x)dx. ∫ 1 2
A. I = 20.
B. I = 40.
C. I =10. D. I = 60.  = → = Lời giải. Đặt x t
x = 3t −1, suy ra dx = 3dt. Đổi cận 2 1  .
x = 5 → t = 2  5 2 2 Khi đó I =
f (x)dx = 3 f (3t − ) 1 dt = 3 f (3x − ) 1 dx = 3.20 = 60. ∫ ∫ ∫ Chọn D. 2 1 1 1 3
Câu 59. Cho hàm số f (x) liên tục trên đoạn [0; ] 1 và thỏa mãn
f (x )dx = 1 ∫ , 0 1 2 1
f (2x)dx = 13 ∫ . Tính tích phân 2 I = x f ∫ ( 3x)dx. 1 0 6 A. I = 6. B. I = 7. C. I = 8. D. I = 9. 1 2 Lời giải. Xét
f (2x )dx = 13. ∫
Đặt t = 2x, suy ra dt = 2dx  →dx = dt. 1 6  1 1  1 x = → t =  2 1 1 Đổi cận  6 3 1  . Khi đó
f (2x)dx = 13 ⇔
f (t)dt = 13 ⇔ f (t) =  dt 26. ∫ ∫ ∫ 1  2 x = → t = 1 1 1 1  2 6 3 3 1 Xét tích phân cần tính 2 I = x f ∫ ( 3x)dx. 0  = → = Đặt 1 x u 3  u = x , suy ra 2 2
dt = 3x dx 
→ x dx = dt. Đổi cận 0 0  . 3 x = 1→ u =1  1   1 1 3 1   Khi đó 1 I f (t) 1 t f (x ) 1 xf (x) x f (x) 1 d d d dx  = = = + = (1+26)= 9. ∫ ∫ ∫ ∫  Chọn D. 3 3 3 3   0 0 0 1    3  9
Câu 60. Cho hàm số f (x) liên tục trên đoạn [0;9] và thỏa mãn
f (x)dx = 729, ∫ 0 3 2
f (x + 6)dx = 513. ∫ Tính tích phân I = f (3x)dx. ∫ 0 0 A. I = 414. B. I = 72. C. I = 342 . D. I = 216. 3 Lời giải. Xét
f (x + 6)dx = 513. ∫
Đặt t = x + 6, suy ra dx = dt. 0  = → = 3 9 Đổi cận x 0 t 6  . Khi đó
f (x + 6)dx = 513 ⇔ f (t) =  dt 513. ∫ ∫ x = 3 → t = 9  0 6 2
Xét tích phân cần tính I = f (3x)dx. ∫ 0  = → = Đặt x uu = 3x, suy ra 1 du = 3dx  →dx = d . u Đổi cận 0 0  . 3
x = 2 → u = 6  6 6 9 6   Khi đó 1 I f (u) 1 u f (x) 1 . d . dxf (x )dx
f (x )dx = = = + ∫ ∫ ∫ ∫  3 3 3   0 0 0 9  9 9 1    f (x ) x f (x) 1 d dx  = − = (729−51 ) 3 = 72. ∫ ∫  Chọn B. 3 3   0 6  2 1 Câu 61. Cho
f (x)dx = . a ∫
Tính tích phân I = xf ( 2 x + ∫ )1dx. 1 0 A. a a I = 2 . a B. I = 4 . a
C. I = ⋅ D. I = ⋅ 2 4 Lời giải. Đặt 2
t = x +1, suy ra 1 dt = 2 d x x  → d x x = dt. 2  = → = 2 2 Đổi cận x 0 t 1  1 1 1 a  . Khi đó I = .
f (t)dt = . f (x) = =  dx .a . ∫ ∫ Chọn C. x = 1 → t = 2  2 2 2 2 1 1 2 1 Câu 62. Cho 1
f (x)dx = 2016. ∫ Tính tích phân I = . f ∫ ( 3x +1)dx. 3x +1 1 0 A. I = 2016. B. I = 1008. C. I = 1344. D. I = 3024. Lời giải. Đặt 2
t = 3x +1 ⇒ t = 3x +1, suy ra 2 2 d t t = 3dx  →dx = d t t. 3  = → = 2 2 Đổi cận x 0 t 1  2 2 2  . Khi đó I = .
f (t)dt = . f (x) = =  dx .2016 1344. ∫ ∫ Chọn C. x = 1 → t = 2  3 3 3 1 1 2017 2017 e 1 − Câu 63. Cho x
f (x)dx = 2 ∫ . Tính tích phân I . f ln ∫  ( 2 x 1  = + dx. 2 )   x 1  + 0 0 A. I =1. B. I = 2. C. I = 4. D. I = 5. Lời giải. Đặt 2 d x x xdx dt t = ( 2 ln x + ) 1 , suy ra dt =  → = . 2 2 x +1 x +1 2
x = 0 → t = 0 Đổi cận:  . 2017
x = e −1 → t = 2017  2017 2017 Khi đó 1 I = f (t) 1 t = f (x) 1 d dx = .2 = 1. ∫ ∫ Chọn A. 2 2 2 0 0 e f (ln x)
Câu 64. Cho hàm số f (x) liên tục trên ℝ và thỏa mãn dx = e. ∫ Mệnh đề x 1 nào sau đây đúng? 1 1 e e
A. (x)dx =1. ∫
B. (x)dx = e. ∫
C. (x)dx =1. ∫
D. (x)dx = e. ∫ 0 0 0 0  = → = Lời giải. Đặt x x t
t = ln x, suy ra d dt = . Đổi cận: 1 0  . x
x = e → t = 1  e f (ln x) 1 1 Khi đó e = dx = f (t)dt = f (x )dx. ∫ ∫ ∫ Chọn B. x 1 0 0 π 1 4 Câu 65. Cho
f (x)dx = 2017. ∫ Tính tích phân I =
f (sin 2x )cos 2 d x x. ∫ 0 0 A. 2 I = ⋅ B. 2017 I = ⋅
C. I = 2017. D. 2017 I = − ⋅ 2017 2 2
Lời giải. Đặt t = sin 2x, suy ra 1 dt = 2 cos 2 d x x  →cos 2 d x x = dt. 2
x = 0 → t = 0  1 1 Đổi cận  dt 1 1 2017  π . Khi đó I = f (t) = f (x) = =  dx .2017 . ∫ ∫ Chọn B. x = → t = 1  2 2 2 2  4 0 0 π π 2 2
Câu 66. Cho I = cos x. f (sin x)dx = 2017 ∫
. Tính tích phân J = sin x. f (cos x)dx. ∫ 0 0 A. 2017 J = . B. J = −2017. C. J = 2017 . D. 2017 J = − . 2 2
Lời giải. Đặt t = cos x, suy ra dt = −sin x dx  →sin x dx = d − t.
x = 0 → t =1  0 1 Đổi cận  π
. Khi đó J = − f (t)dt = f (t)  dt. ∫ ∫ x = → t = 0  2 1 0 t  = 0 → u = 0  Tiếp tục ta đặt  t = sin ,
u suy ra dt = cos u d . u Đổi cận  π . t  = 1→ u =  2 π π 2 2 Khi đó I =
f (sin u)cos udu =
cos x. f (sin x)dx = 2017. ∫ ∫ Chọn C. 0 0 π 1 8 f (tan 2x) Câu 67. Cho
f (x)dx = 2017. ∫ Tính tích phân I = dx. ∫ 1+ cos 4x 0 0 A. I = 2017. B. 2017 I = . C. 2017 I = . D. 2017 I = . 2 4 8 π π 8 f (tan 2x) 8 f (tan 2x )
Lời giải. Viết lại I = dx = dx ∫ ∫ . 2 1+ cos 4x 2 cos 2x 0 0 Đặt 2 dx 1
t = tan 2x, suy ra dt = dx  → = = dt. 2 2 cos 2x 2 cos 2x 4
x = 0 → t = 0  1 1 Đổi cận  1 1 2017  π . Khi đó I = .
f (t)dt = . f (x) =  dx . ∫ ∫ Chọn C. x = → t = 1  4 4 4  8 0 0 1 1 2 2
Câu 68. Cho hàm số f (x) liên tục trên ℝ và
f (x)dx = 3,
f (2x)dx = 10. ∫ ∫ Tính 0 1 4 π 2
tích phân I = cos x. f (sin x)dx. ∫ 0 A. I = 23. B. I =10. C. I = 8. D. I = 7. 1 2
Lời giải. Xét tích phân
f (2x )dx = 10. ∫ 1 4  1 1 x = → t =  Đặt  4 2 t = 2x, suy ra 1 dt = 2dx 
→dx = dt. Đổi cận:  . 2  1
x = → t =1  2 1 2 1 1 1 Khi đó = f ( x ) 1 10 2 dx = f (t)dt ∫ ∫  →
f (t)dt = 20 ∫ hay
f (x)dx = 20. ∫ 2 1 1 1 1 4 2 2 2 π 2
Xét tích phân I = cos x. f (sin x)dx. ∫ 0
x = 0 → u = 0  Đặt 
u = sin x, suy ra du = cos xdx. Đổi cận:  π . x = → u =1  2 1 1 1 2 1 Khi đó I = f (u)du =
f (x )dx = f (x)dx +
f (x)dx = 3 + 20 = 23. ∫ ∫ ∫ ∫ Chọn A. 0 0 0 1 2 π 4 1 2 x f (x)
Câu 69. Cho hàm số f (x) liên tục trên ℝ và
f (tan x )dx = 4, dx = 2. ∫ ∫ 2 x +1 0 0 1 Tính tích phân I = f (x)dx. ∫ 0 A. I = 6. B. I = 2. C. I = 3.
D. I =1. π 4 Lời giải. Xét
f (tan x )dx = 4. ∫ 0 Đặt 1 dt
t = tan x, suy ra dt = dx = ( 2
tan x +1 dx  →dx = . 2 ) 2 cos x 1+ t  π x = 0 → t = 0  4 1 f (t) 1 f (x) Đổi cận:  π . Khi đó 4 = f (tan x) = =  dx dt dx. ∫ ∫ ∫ x = → t = 1  2 2 t +1 x +1  4 0 0 0 1 1 f (x) 1 2 x f (x) Từ đó suy ra I =
f (x )dx = dx + dx = 4 + 2 = 6. ∫ ∫ ∫ Chọn A. 2 2 x +1 x +1 0 0 0 π 4
Câu 70. Cho hàm số f (x) liên tục trên ℝ và thỏa mãn tan x. f ∫ ( 2 cos x )dx = 1, 0 2 e f ( 2 ln x ) 2 f (2x ) dx = 1. ∫ Tính tích phân I = dx. ∫ x ln x x e 1 4 A. I = 1. B. I = 2. C. I = 3. D. I = 4. π 4
Lời giải. ● Xét A = tan x. f ∫ ( 2
cos x )dx = 1 . Đặt 2 t = cos x. 0 Suy ra dt 2
dt = −2 sin x cos xdx = −2 cos x tan d
x x = −2t.tan xdx 
→ tan xdx = − . 2t x = 0  →t = 1  Đổi cận:  . π 1 x  =  →t =  4 2 1 2 1 f (t) 1 1 f (t) 1 1 f (x ) 1 f (x) Khi đó 1 = A = − dt = dt = dx  → dx = 2. ∫ ∫ ∫ ∫ 2 t 2 t 2 x x 1 1 1 1 2 2 2 2 e f ( 2 ln x ) ● Xét B = dx = 1. ∫ Đặt 2 u = ln x. x ln x e 2 Suy ra 2 ln x 2 ln x 2u dx du du = dx = dx = dx  → = . x x ln x x ln x x ln x 2u  =  → = Đổi cận: x e u 1  . 2
x = e →u = 4  4 1 f (u) 4 1 f (x) 4 f (x) Khi đó 1 = B = du = dx  → dx = 2. ∫ ∫ ∫ 2 u 2 x x 1 1 1 2 f (2x )
● Xét tích phân cần tính I = dx. ∫ x 1 2  1 d  x = dv   1 1  =  → = Đặt  2 x v
v = 2x, suy ra  . Đổi cận:   4 2 . v   x =   x = 2  →v = 4   2 4 f (v) 4 f (x ) 1 f (x) 4 f (x) Khi đó I = dv = dx = dx + dx = 2 + 2 = 4. ∫ ∫ ∫ ∫ Chọn D. v x x x 1 1 1 1 2 2 2 π 9 f ( x ) 2
Câu 71. Cho hàm số f (x) liên tục trên ℝ và dx = 4, f (sin x)cos d x x = 2. ∫ ∫ x 1 0 3 Tính tích phân I = f (x)dx. ∫ 0 A. I = 2. B. I = 6. C. I = 4.
D. I = 10. 9 f ( x ) Lời giải. Xét dx = 4. ∫ Đặt 2
t = x ⇒ t = x, suy ra 2tdt = dx. x 1  = → = 9 f ( x ) 3 3 Đổi cận x 1 t 1  . Suy ra 4 = dx = 2
f (t)2dt  → f (t) =  dt 2. ∫ ∫ ∫ x = 9 → t = 3  x 1 1 1 π 2 Xét f (sin x)cos d x x = 2. ∫
Đặt u = sin x, suy ra du = cos d x x. 0  π x = 0 → u = 0  2 1 Đổi cận  π . Suy ra 2 =
f (sin x )cos xdx = f (t)  dt. ∫ ∫ x = → u = 1  2 0 0 3 1 3 Vậy I = f (x)dx = f (x)dx +
f (x )dx = 4. ∫ ∫ ∫ Chọn C. 0 0 1 x Câu 72. Ký hiệu e
F (x ) là một nguyên hàm của hàm số f (x) = trên khoảng x 2 3x ( e
0;+∞) . Tính tích phân I = dx. ∫ x 1
A. I = 3 F (2)− F ( ) 1  .  
B. I = F (6)− F ( ) 3 . F (6)− F (3) C. I = .
D. I = 3F (6)− F (3).   3  1 d  t = 3dx d  x = dt    = ↔ = Lời giải. Đặt   3 x t
t = 3x, suy ra  t  → . Đổi cận 1 3   . x =  t  
x = 2 → t = 6     3 x =  3 6 6 6 t t x 6 Khi đó e dt e e I = . = dt =
dx = F (x) = F (6)− F (3). ∫ ∫ ∫ Chọn B. t 3 t x 3 3 3 3 3 Câu 73. Ký hiệu x
F (x ) là một nguyên hàm của hàm số f (x) cos = trên khoảng 2x 4 ( cos 2x
0;+∞) . Tính tích phân I = dx ∫ . x 1
A. I = 2.F (8)− F (2).
B. I = 2.F (8)+ F (2).
C. I = 2.F (8)−2.F (2).
D. I = 2.F (8)+ 2.F (2).  1 d  t = 2dx d  x = dt    = → = Lời giải. Đặt   2 x t
t = 2x, suy ra  t  → . Đổi cận 1 2   . x =  t  
x = 4 → t = 8     2 x =  2 8 8 8 8 8 Khi đó cos t dt cos t cos x cos x I = = dt = dx = 2. dx 2
= .F (x) = 2F (8)−2F (2). ∫ ∫ ∫ ∫ t 2 t x 2x 2 2 2 2 2 2 Chọn C.
Câu 74. Cho hàm số f (x) có đạo hàm liên tục trên ℝ và f (2016)= ,
a f (2017) = b 2016
(a, b ∈ ℝ). Tính tích phân I = 2015 f ′(x) 2014 . f (x)dx. ∫ 2017 A. 2017 2017 I = b −a . B. 2016 2016 I = a −b . C. 2015 2015 I = a −b . D. 2015 2015 I = b −a .
x = 2016 → t = f (2016)= a Lời giải. Đặt 
t = f (x), suy ra dt = f ′(x )d(x). Đổi cận  . x
 = 2017 → t = f (2017) = ba a Khi đó 2014 2015 2015 2015 I = 2015. t dt = t = a −b . ∫ Chọn C. b b 2 1
Câu 75. Cho hàm số f (x) liên tục trên ℝ và f (x)dx = 3. ∫ Tính I = f ∫ ( 2x )dx. 0 −1
A. I = 0. B. 3 I = . C. I = 3. D. I = 6. 2 1 0 1
Lời giải. Ta có I = f
∫ ( 2x )dx = f
∫ ( 2x )dx + f ∫ ( 2x )dx. 1 − 1 − 0 0  = − → = Xét x tf
∫ ( 2x )dx. Đặt x = t − , suy ra dx = d − t . Đổi cận 1 1  .
x = 0 → t = 0 −  1 0 0 1 1 Khi đó f
∫ ( 2x )dx =− f
∫ (−2t )dt = f
∫ (−2t )dt = f ∫ ( 2t )dt. −1 1 0 0 1 1 Do đó I = 2 f
∫ ( 2x )dx = 2 f (2x)dx ∫
(vì 2x ≥ 0, ∀x ∈[0; ] 1 ). 0 0 1
Bây giờ ta cần tính I = 2 f (2x)dx. ∫
Đặt u = 2x → du = 2dx. 0  = → = 2 2 Đổi cận: x 0 u 0  . Khi đó I = f (u)du = f (x) =  dx 3. ∫ ∫ Chọn C. x = 1 → u = 2  0 0
Vấn đề 2. PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN 2
Câu 76. Tính tích phân I = ln d x x. ∫ 1
A. I = 2 ln 2 +1. B. I = ln(4 −e).
C. I = ln 4 − log10 . D. I = ln 4e.  dx  =  =
Lời giải. Đặt u ln x du    ⇒  x . d  v = dx   v  = x  2 2 2 2
Khi đó I = x ln x − dx = x ln x − x = 2 ln 2 −1 = ln 4 − log10. ∫ Chọn C. 1 1 1 1
Cách 2. CASIO Có 2 cách bấm, cụ thể như sau: 2
Bấm trực tiếp tích phân ln d x x ∫
và so sánh với các kết quả ở các đáp án. 1 2
Thiết lập hiệu, ví dụ với đáp án A ta bấm ln d x x − 2 ln 2 −1 ∫ . Nếu màn hình hiện 1
số 0 thì đáp án đó đúng. 2
Câu 77. Kết quả của tích phân I = ln(x + ) 1 dx ∫
được viết ở dạng I = a ln 3+ b ln 2 + c 1
với a, b, c là các số nguyên. Tính P = a + b + c. A. P = 0. B. P = 1. C. P = 2. D. P = 3.  x u  = ln(x + ) d  = Lời giải. Đặt 1 du    ⇒  x +1. d  v  = dx   v  = x +1  2 2 2 2
Khi đó I = (x + ) 1 . ln (x + ) 1 − dx = (x + ) 1 ln(x + ) 1 − x ∫ 1 1 1 1 a  = 3  = 3ln 3−2 ln 2−1  → b  = −2 
→ P = 0. Chọn A. c =−1  2
Cách 2. CASIO Tính tích phân I = ln(x + ) 1 dx ∫ rồi lưu vào biến A. 1 A Khi đó e
a ln 3 + b ln 2 + c = A ←
→ ln(3a.2b. ce )= ln A e ←
→3a.2b. c A
e = e ↔ 3a.2b = . c e A Để tính được e
3a.2b ta sử dụng chức năng MODE 7 với hàm f (X ) = . X e
Với thiết lập Start −9, End 10, Step 1 (do a, b, c là các số nguyên). Dễ thấy với a b 27
X = c = −1 thì 3 2 3 .2 6.75 3 .2− = = = 
→a = 3;b = −2. 4 e
Câu 78. (ĐỀ MINH HỌA 2016 2017) Tính tích phân = – I x ln xdx. ∫ 1 2 2 2 A. 1 e − 2 e +1 e −1 I = . B. I = . C. I = . D. I = . 2 2 4 4  dx d  u =   =
Lời giải. Đặt u ln x    x  ⇒  . 2 d  v = d x xx  v  =  2 2 e e 2 2 e 2 Khi đó x ln x 1 e x e +1 I = − xdx = − = ∫ . Chọn C. 2 2 2 4 4 1 1 1 1
Câu 79. Kết quả của tích phân I = x ln ∫ ( 2
2 + x )dx được viết ở dạng I = a ln 3 + b ln 2 + c 0
với a, b, c là các số hữu tỉ. Tính tổng S = a +b + c. A. S = 0. B. S =1. C. 3 S = . D. S = 2. 2  2xu = x u  = ln  ( d d 2 2 + x )  2  Lời giải. Đặt 2  + x  ⇒  . 2 2 d  v = d x xx 2   + x v  = +1 =  2 2 1 2 1 2 1 Khi đó 2 + x x I = ln ( 3 3 1 2
2 + x ) − xdx = ln 3−ln 2 − = ln 3−ln 2 − ∫ . 2 0 2 2 0 2 2 0 Suy ra 3 1
a = , b = −1, c = − 
→S = a + b + c = 0. Chọn A. 2 2 2
Nhận xét. Chắc có bạn đọc không hiểu tại sao chỗ x
dv = xdx  →v = +1 . Vì ta 2 2 thường làm x
dv = xdx  →v =
. Sao lại cộng thêm 1 ở đây? Ta biết rằng các nguyên 2
hàm sai khác nhau hằng số nên ta cộng thêm hằng số là bao nhiêu cũng được. Vậy
vấn đề là sao không cộng số khác mà là số 1. Ở đây số 1 được thêm vào để tạo ra
lượng mà rút gọn được, cụ thể đó là lượng 2 2 + x . 5
Câu 80. Cho hai số nguyên dương 19
a, b thỏa mãn ( + ) 1 ln( −3)d = 5 ln a x x x a − ⋅ ∫ b 4
Tính S = a +b.
A. S = 4.
B. S = 6.
C. S = 8.
D. S = 0.  1  = 5  = (x − ) du dx u ln 3  Lời giải. Tính   x −3 I = (x + ) 1 ln(x −3)dx. ∫ Đặt  ⇒  . d  v  = (x + ) 2 2 1 dxx x + 2x   4 v  = + x =  2 2 5 5 2    5 2 2 Khi đó x  =    +    ( + + x − ) x 2x 35 ln 2 1 x 2x I x .ln 3  − dx = − dx.  ∫ ∫  2     4 2   (x −3) 2 2 x −3  4 4 5 5 2 2 5 +     Tính x 2x 15 x 19 = =     J dx ∫ ∫ x +5+ dx = 
+5x +15ln x −3  = +15ln 2.     x −3  x −3  2  4 2 4 4   Vậy 35 ln 2 1 35 ln 2 1 19 19 19 2 I = − J =
−  +15ln 2 =10 ln 2− = 5ln 2 − .   2 2 2 2  2  4 4
Suy ra a = 2;b = 4 
→S = a + b = 6. Chọn B. 1
Câu 81. Kết quả của tích phân a I = x ln(2x + )2017 1 dx ∫
được viết ở dạng I = ln 3 với b 0
phân số a tối giản. Tính tổng a +b. b
A. a +b = 6057. B. a +b = 6059.
C. a +b = 6058.
D. a +b = 6056. 1 1
Lời giải. Ta có I = x ln(2x + )2017 1 dx = 2017 x ln(2x + ) 1 dx ∫ ∫ . 0 0  2 d  u = dx 1   u  = ln(2x + )  Tính 1 2x   +1 J = x ln(2x + ) 1 dx. ∫ Đặt  ⇒  . 2 d  v  = xdxx   0 v  =  2 1 1 2 1 2   Khi đó x J = ( x + ) x 1 1 1 1 1 .ln 2 1 − dx = ln 3−  x ∫ ∫  − + . dx 2   +  +  0 2x 1 2 2 4 4 2x 1 0 0 1 1 1 1 1  1 1 3 2
= ln 3− x − x + .ln 2x +1 = ln 3− ln 3 = ln 3. 2 4 4 8  0 2 8 8  = Suy ra 6051 a 6051  I = 2017.J = ln 3  →
→ a + b = 6059. Chọn B. 8 b  = 8  2 Câu 82. Cho a c
a, b, c là các số nguyên dương thỏa mãn 2
x ln x.dx = ln 2 − ∫ với a b 9 b 1
là phân số tối giản. Tính giá trị biểu thức 2 2 2
T = a + b + c − 2(ab + bc −ca).
A. T = 252.
B. T = 144.
C. T = −16.
D. T = −252.  1 d  u = dx    = Lời giải. u ln x  Đặt x    ⇒  . 2 3 d
v = x dxx  v  =  3 2 2 3 2 2   Khi đó x 1 8 1 8 7 2   2 3
x ln x.dx =  .ln x − x dx = ln 2 − .x = ln 2− . ∫    ∫  3  1 3 3 9 1 3 9 1 1 
→a = 8;b = 3;c = 7 
→T = 144. Chọn B. e a Câu 83. Giả sử 3e +1 3 I =
x ln xdx = ∫
với a, b là các số nguyên dương. Trong các b 1
khẳng định sau, khẳng định nào đúng? A. ab = 64 . B. ab = 46 .
C. a −b = 12 .
D. a −b = 4 .  1 d  u = dx    = Lời giải. u ln x Đặt    x  ⇒  . 3 4 d
v = x dxx  v  =  4 4 e e 4 4 e 4 4 4  −  Khi đó x ln x 1 e x e e 1 3e   +1 3 I = − x dx = − = −  = . ∫   4   1 4 4 16 1 4  16  16 1
Suy ra a = 4; b = 16 . Chọn A. a Câu 84. Biết ln x 1 1 I = dx = − ln 2 ∫
. Giá trị của a bằng: 2 x 2 2 1 A. a = 2 . B. a = ln 2 . C. a = 4 . D. a = 8 .  dx u  = ln x d  u =  
Lời giải. Đặt   x  dx ⇒  . d  v =  1   2  vx  = −  x a a a   Khi đó ln x dx ln a 1 ln a 1 I =   −   + = − − = − − +1.   2  x  ∫ x a x a a 1 1 1 Theo giả thiết 1 1 ln a 1 1 1 I = − ln 2 ⇔ − − +1 = − ln 2 + 
→a = 2. Chọn A. 2 2 a a 2 2 a
Cách 2. CASIO Thiết lập hiệu ln x 1 1 dx − + ln 2 ∫
và bài toán cần tìm a để hiệu 2 x 2 2 1 2 bằng 0. Thử với ln x 1 1
a = 2 , ta nhập hiệu dx − + ln 2 ∫ vào máy tính CASIO và 2 x 2 2 1
nhấn dấu =. Thật may mắn màn hình xuất hiện số 0, ta chọn A. Nếu màn hình
không xuất hiện số 0 thì ta thử tới đáp án B. e Câu 85. Xét k I = ln dx ∫
với k là số nguyên dương. Nếu I < e −2 thì tổng các giá k x k 1 trị của k bằng: A. 3. B. 5. C. 7. D. 9. e e e e Lời giải. Ta có k I = ln dx = k − x x = k x − x x ∫ ∫ ∫ ∫ k (ln ln )d ln d ln d . x 1 1 1 1 e e ● A = ln k
dx = ln k.x = (e − ) 1 ln k ∫ . 1 1  e  dx u  = ln x d e e e eu =   ● B = ln xdx ∫ . Đặt  ⇒  x 
→ B = x ln x − dx = x ln x − x = 1. ∫ d  v = dx  1 1 1   1 1 v  = x
Do đó I = A− B = (e − ) 1 ln k −1 . k
Theo giả thiết, ta có I < e −2 ⇔ (e − )
1 ln k −1 < e − 2 k ( ) + 1 ln 1 ln 1 k e k e k k e ∈ ⇔ − < − ⇔ < ⇔ < ℤ
→ k = {1;2}. Chọn A. 1
Câu 86. Tính tích phân = 2x I x dx ∫ . 0 A. 2 ln 2 −1 − 2 ln 2 +1 + I = . B. 2 ln 2 1 I = . C. I = . D. 2 ln 2 1 I = . 2 ln 2 ln 2 2 ln 2 ln 2 d  u = dx  =  Lời giải. u x Đặt   x  ⇒  . x 2 d  v = 2 dx v    =  ln 2 1 x 1 x 1 x 1 Khi đó x 2 1 x − x 2 2 2 ln 2 1 I = − 2 dx = − = . ∫ Chọn A. 2 2 ln 2 0 ln 2 ln 2 0 ln 2 0 ln 2 0 1
Câu 87. Kết quả tích phân = (2 + ) 3 x I x e dx ∫
được viết dưới dạng I = ae +b với a, b là 0
các số hữu tỷ. Khẳng định nào sau đây là đúng?
A. a −b = 2 . B. 3 3 a + b = 28 . C. ab = 3.
D. a + 2b = 1 .  = +  = Lời giải. u 2x 3 du 2dx Đặt    ⇒  . d xv = e d x x v  = e   1 1 1 1
Khi đó = (2 +3) x − 2 xd = (2 +3) x −2 x I x e e x x e e = 3e −1. ∫ 0 0 0 0
Suy ra a = 3, b = −1. Chọn D. ln 2   Câu 88. Cho − b x 1 ln 2
a, b, c là các số nguyên dương và c ≠ 1 thỏa 2 xe dx =   ∫  − ⋅ a  4 c  0
Tính giá trị biểu thức T = abc −(ab +bc +ca).
A. T = 24.
B. T = 6.
C. T = −2.
D. T = 9. d  u = dx  =  Lời giải. u x Đặt    ⇒  − 1 . 2 x 2 d  v = e d − x x v  = − e   2 ln 2 ln 2 ln 2 ln 2 Khi đó − x 1 − x 1 − x ln 2 1 − x 3 ln 2 2 2 2 2 xe dx = − xe + e dx = − − e = − ∫ ∫ 2 0 2 8 4 0 16 8 0 0 1  3 ln 2 =    −  
→a = 4;b = 3;c = 2  T → = −2.   Chọn C. 4  4 2  1 Câu 89. Cho + a b
a, b, c là các số nguyên thỏa mãn 1 3x 2 3e dx =
e + e + c. ∫ Tính giá 5 3 0 trị của biểu thức b c T = a + + ⋅ 2 3
A. T = 6.
B. T = 9.
C. T = 10.
D. T = 5.  = ⇒ = Lời giải. Đặt x t 2 
t = 1+ 3x ⇒ t = 1+ 3x ⇒ 2tdt = 3dx. Đổi cận 0 1  .
x = 1 ⇒ t = 2  2 u  = 2t d  u = 2dt Khi đó =   2 t I te dt ∫ . Đặt  ⇒  . d tv = e d t t v  = e   1  a  =10 2 2 2 2  Suy ra  t t t t 2 I = 2te −2 e dt = 2te −2e = 2e  → b ∫  = 0  T → = 10. Chọn C.  1  1 1 1 c  = 0  a 2 Câu 90. Cho tham số −e x 3 a > 0 thỏa mãn (x − ) 2 1 e dx = . ∫ Tính 2 P = a + 2017. 4 0 A. P = 2021. B. P = 2026. C. P = 2033. D. P = 2018. d  u = dx  = −  Lời giải. u x 1 Đặt    ⇒  1 . 2 x 2 d  v = e d x x v  = e   2 a a a a Khi đó 1 = ( − ) x 1 x 1 x 1 2 2 1 − d = ( − ) 2 2 1 x I x e e x x e − e ∫ 2 2 2 4 0 0 0 0    2 a 1 1 a   e    a  − −  − a 1 3 2 3 2  2 a =  e +   − 
Suy ra a = 1. Chọn D.     = + e .        2 2  4  4  4  a 2
Cách 2. CASIO Thiết lập hiệu ( − x − ) e x 3 2 1 e dx − ∫
và bài toán cần tìm a để hiệu 4 0 2 2
bằng 0. Với đáp án A, suy ra −e x 3
a = 2 , ta nhập hiệu (x − ) 2 1 e dx − ∫ vào máy tính 4 0
CASIO và nhấn dấu =. Màn hình không xuất hiện số 0 nên ta tiếp tục thử đến đáp án B, C và D. π 4
Câu 91. Tính tích phân I = x sin 2xdx ∫ . 0 A. π I = 1 . B. I = . C. 1 I = . D. 3 I = . 2 4 4 d  u = dx  = 
Lời giải. Đặt u x    ⇒  cos 2x . d
v = sin 2xdx v  = −   2 π π 4 π π Khi đó x cos 2x 1 x cos 2x sin 2x 1 4 4 4 I = − + cos 2xdx = − + = . ∫ Chọn C. 2 0 2 2 0 4 0 4 0 π 2
Câu 92. Kết quả tích phân π I = x cos xdx ∫
được viết ở dạng I = −1. Tính 2 9m − 6 . m 0 A. 2
9m − 6 = 3 . B. 2 9m − 6 = 30 . C. 2 9m − 6 = −3 . D. 2 9m − 6 = −30 .  =  =
Lời giải. Đặt u x du dx    ⇒  . d
v = cos xdx v  = sin x   π π 2 π π Khi đó π 2 2 2
I = x sin x
− sin xdx = x sin x + cos x = −1. ∫ 0 0 0 2 0 Suy ra 2 m = 2 
→9m −6 = 30. Chọn B. π 2
Câu 93. Cho tham số m thỏa mãn I = x (sin x +2m) 2 dx = 1+ π ∫ . Mệnh đề nào sau 0 đây là đúng?
A. −1< m < 0.
B. 0 ≤ m ≤ 2.
C. 3 < m < 5. D. m ≥ 5. π 2  =  = Lời giải. Tính u x u x   A = x sin xdx ∫ . Đặt d d  ⇒  . d
v = sin xdx v  = −cos x   0 π π π 2
Suy ra A = (−x cos x) 2 2
+ cos xdx = sin x = 1. ∫ 0 0 0 π π 2 2 Do đó 2 mπ 2
I = A + 2m
xdx = 1+ mx = 1+ . ∫ 4 0 0 2 2 Theo giả thiết mπ mπ 2 2 1+ = 1+ π ⇔
= π ⇔ m = 4 ∈(3;5). Chọn C. 4 4 π 2  
Câu 94. Kết quả của tích phân ( π
2x −1− sin x )dx ∫ được viết ở dạng 1 π    − −1   .  a b 0
Khẳng định nào sau đây là sai?
A. a + 2b = 8 .
B. a + b = 5 .
C. 2a −3b = 2 .
D. a −b = 2 . π π 2 2     Lời giải. Ta có ( π π π  
2x −1− sin x )dx = ∫
(x −x +cos x) 2 1 2 =  − −1 = π     − −1.  4 2     4 2 0 0  = Suy ra a 4  . Chọn B. b  = 2  π π π Câu 95. Cho x 2 x 2 I =
e cos xdx, J = e sin xdx ∫ ∫ và x K =
e cos 2xdx ∫ . Khẳng định nào 0 0 0 sau đây là đúng? π (I). e − I J e π + = .
(II). I −J = K . (III). 1 K = . 5 A. Chỉ (I). B. Chỉ (II). C. Chỉ (III).
D. Cả (II) và (III). π π
Lời giải. Xét (I). Ta có x 2 x 2 I + J =
e cos xdx + e sin xdx ∫ ∫ . 0 0 π π π x ∫ ( 2 2 sin cos )d x d x e x x x e x e eπ = + = = = −1. ∫ Vậy (I) sai. 0 0 0 π π Xét (II). Ta có x 2 x 2 I − J =
e cos xdx − e sin xdx ∫ ∫ 0 0 π π x = ∫ ( 2 2 cos −sin )d x e x x x =
e cos 2xdx = K . ∫ Vậy (II) đúng. 0 0 u  = cos 2x d
 u = −2 sin 2xdx Xét (III). Đặt    ⇒  . d xv = e d x x v  = e   π π Suy ra ( x cos2 ) 2 x K e x
e sin 2xdx eπ = + = −1+ 2M . ∫ 0 0 π u  = sin 2x d
 u = 2cos 2xdx Tính x   M =
e sin 2xdx ∫ . Ta đặt 1 1  ⇒  . d xv = e d x x v  = e   0 1  1 π π Suy ra = ( x sin 2 ) −2 x M e x
e cos 2xdx = −2K ∫ . 0 0 π Khi đó −
K = eπ − + (− K ) π e 1 1 2 2
⇔ 5K = e −1 ⇔ K =
. Vậy (III) đúng. Chọn D. 5
Câu 96. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;2] và thỏa mãn 2 2 f ( ) 1 = 0, f (2) = 2,
f (x)dx = 1. ∫
Tính I = x. f ′(x)dx. ∫ 1 1 A. I = 2. B. I = 1. C. I = 3.
D. I = 8. u  = x d  u = dx
Lời giải. Đặt    ⇒   v = f ′  (x) x v  = f   (x). d d  2 2 2
Khi đó I = x. f (x) − f (x)dx = 2 f (2)− f ( ) 1 −
f (x)dx = 2.2 − 0 −1 = 3.   ∫ ∫ Chọn C. 1 1 1
Câu 97. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0;2] và thỏa mãn 2 1 f (2) = 16,
f (x)dx = 4. ∫ Tính tích phân I =
x. f ′(2x )dx. ∫ 0 0 A. I = 13. B. I = 12. C. I = 20.
D. I = 7. du = dx u  = x
Lời giải. Đặt    ⇒   v = f ′  ( x) 1 d 2 dx v  = f   (2x).  2 1 1 1 1 Khi đó 1 I = xf ( x) 1 − f ( x ) 1 x = f ( ) 1 − f ( x) 1 2 2 d 2 2 dx = 8 −
f (2x )dx. ∫ ∫ ∫ 2 0 2 2 2 2 0 0 0 1  = → = Tính x tf (2x)dx. ∫
Đặt t = 2x 
→dt = 2dx . Đổi cận: 0 0  .
x = 1→ t = 2  0 1 2 Suy ra f ( x) 1 x = f (t) 1 2 d dt = .4 = 2. ∫ ∫ 2 2 0 0 Vậy 1
I = 8 − .2 = 8 −1 = 7. Chọn D. 2
Câu 98. Cho hàm số y = f (x) có đạo hàm f '(x) liên tục trên đoạn [1;2] và thỏa mãn 2 2 f ( ) 1 = 4 f (2),
xf (x )dx = 1 ∫ . Tính tích phân 2 I =
x f '(x)dx. ∫ 1 1 A. I = 2. B. I = −2. C. I = 1. D. I = −1. 2 u  = x d
 u = 2xdx
Lời giải. Đặt    ⇒   v = f  (x) x v  = f   (x) . d ' d  2 2 2 Khi đó 2
I = x f (x ) −2
xf (x)dx = 4 f (2)− f ( ) 1 − 2
xf (x )dx. ∫ ∫ 1 1 1 2
= −2 xf (x)dx = −2.1 = −2 ∫ . Chọn B. 1
Câu 99. Cho hai hàm số y = f (x) và y = g(x) có đạo hàm liên tục trên đoạn [1;2] . 2 2 Biết f ( ) 1 .g ( )
1 = 1, f (2).g (2) = 2 và
g (x). f ′(x)dx = 3 ∫ . Tính I =
f (x ).g ′(x)dx. ∫ 1 1 A. I = −4. B. I = 4. C. I = −2. D. I = 2. u  = f (x) d
 u = f '(x)dx
Lời giải. Đặt    ⇒  . d  v
= g '(x)dx v    = g (x)  2 2 2
Khi đó I = f (x).g(x) − g(x). f '(x)dx = f (2).g(2)− f ( ) 1 .g ( ) 1 −
g (x ). f '(x)dx ∫ ∫ 1 1 1
= 2 −1−3 = −2. Chọn C.
Câu 100. Cho hàm số y = f (x) có đạo hàm f '(x) liên tục trên đoạn [0; ] 1 và thỏa 1 1 mãn f ( ) 1 = 1 ,
f (x)dx = 2 ∫ . Tính tích phân I = f ' ∫ ( x)dx. 0 0 A. I = −1. B. I = 1. C. I = 2. D. I = −2.  = → = Lời giải. Đặt x t 2  t = x  →t = x 
→2tdt = dx. Đổi cận 0 0  .
x = 1 → t = 1  1
Khi đó I = 2 tf '(t)dt = 2A ∫ . 0 1 u  = t d  u = dt Tính   A = tf '(t)dt ∫ . Đặt   →  v = f  (t) t v  = f   (t). d ' d 0  1 1 1
Suy ra A = tf (t) − f (t)dt = f ( ) 1 −
f (t)dt = 1−2 = −1 
→ I = 2A = −2. ∫ ∫ Chọn D. 0 0 0
Vấn đề 3. TÍCH PHÂN ẨN HSM SỐ 1
Câu 101. Cho f (x) là hàm số chẵn trên đoạn [−1; ] 1 và thỏa mãn
f (x)dx = 4 ∫ . −1 1 f (x) Tính tích phân I = dx ∫ . 2x +1 −1 A. I = 2 . B. I = 4. C. I = 8. D. I = 16. a f (x)
Lời giải. Đặc trưng của dạng dx ∫
là đổi biến t = −x  →dx = d − t. x β +1 −a  = − → = −1 f ( t − ) Đổi cận x 1 t 1  . Khi đó = −  I dt ∫
x = 1 → t = −1  2−t +1 1 1 f ( t − )
1 2t. f ( t − ) ( )
1 2t. f (t) 1 chan 2x f x . f (x ) = dt = dt = dt = dx. ∫ ∫ ∫ ∫ 2−t +1 1+ 2t 2t +1 2x +1 −1 1 − −1 −1 1 f (x)
1 2x. f (x) 1
Suy ra 2I = I + I = dx + dx =
f (x )dx = 4  → I = 2. ∫ ∫ ∫ Chọn A. 2x +1 2x +1 1 − 1 − 1 −
Cách trắc nghiệm: Chọn ( ) 2
h x = x thỏa mãn giả thiết là hàm chẵn. 1 Ta có 2 4 2 x dx =  → ∫
chọn f (x)= h(x) 2 = 6x . 3 2 −1 3 1 f (x ) 1 2 Khi đó 6x I = dx = dx. ∫ ∫
Dùng CASIO tính được kết quả bằng 2. 2x +1 2x +1 −1 1 −
Phương pháp trắc nghiệm:
Bước 1. Chọn một hàm số bất kỳ thỏa mãn bài toán. Nếu bài toán không nói gì thì
thường chọn h(x)= 1, nếu là hàm số lẻ thì chọn h(x) = x , hàm số chẵn thì chọn h(x) 2 = x . b b b Bước 2. Tính ( ) N N N
h x dx = M  → h(x)dx = h(x)dx = .M = N ∫ ∫ ∫ . M M M a a a
Do đó ta sẽ chọn ( ) N f x = h(x ). M b b Bước 3. Tính = ( ) A I f u dx = h(u)dx ∫ ∫ bằng máy tính là xong. B a a 2017 2017
Ví dụ. Cho hàm số f (x) thỏa mãn
f (x )dx = 2 ∫ . Tính tích phân
f (2018 − x )dx ∫ . 1 1 2017
Hướng dẫn. Ta chọn h(x)=  → x =  → f (x) 2 1 1 1d 2016 = = . ∫ 2016 1008 1 2017 2017 Khi đó f ( − x) 1 2018 dx = dx = 2. ∫ ∫ 1008 1 1
Câu 102. Cho hàm số f (x) liên tục trên ℝ và thỏa f (x)+ f (−x)= 2 +2cos2x với 3π 2
mọi x ∈ ℝ . Tính I = f (x )d x ∫ . 3π − 2 A. I = −6 . B. I = 0 . C. I = −2 . D. I = 6 .  3π 3πx = − → t =  Lời giải. Đặt  2 2 t = −x  →dx = d
− t. Đổi cận:  .  3π 3π x = → t = −  2 2 3π 3π 3π − 2 2 2 Khi đó I = − f ( t − )dt = f ( t − )dt =
f (−x )dx. ∫ ∫ ∫ 3π 3π 3π − − 2 2 2 3π 3π 3π 2 2 2 CASIO Suy ra 2I =
f (t)+ f ( t − ) dt = 2 + 2 cos 2tdt =
2 cos t dt = 12  → I = 6. ∫   ∫ ∫ 3π 3π 3π − − − 2 2 2 Chọn D.
Cách trắc nghiệm. Chọn f (x) 1 CASIO =
2 + 2 cos 2x → I = 6. 2
Chú ý: Khi gặp bài toán ' Cho hàm số y = f (x) liên tục trên ℝ và thỏa mãn
mf (x )+ nf (−x ) = g (x) với g (x) là hàm số chẵn và m + n ≠ 0. Tính tích phân a I = f (x)dx ∫ ' thì ta chọn −a f (x ) 1 = g (x ). m + n
Ví dụ. Cho hàm số 1
y = f (x) liên tục trên ℝ và thỏa mãn 2 f (x)+ 3 f (−x) = . 2 4 + x 2 Tính tích phân 1 1 I = f (x)dx ∫
. Hướng dẫn: Chọn f (x) = . 2 5 4 + x 2 − 2 x
Câu 103. Cho hàm số y = f (x) liên tục trên (0;+∞) và thỏa
f (t)dt = x cos(πx ) ∫ . 0 Tính f (4). A. f ( ) 1 4 = . B. f (4) =1. C. f (4)= 2 . D. f ( ) 1 4 = . 2 4
F '(x)= f (x) 
Lời giải. Giả sử 
F (x) là một nguyên hàm của f (x ) , suy ra    F  (x ) / . 2  = 2xf '   ( 2x)  2 x 2 x Khi đó
f (t)dt = F (t) = F ∫
( 2x)−F (0)←→x cosπx = F ( 2x)−F (0). 0 0
Lấy đạo hàm hai vế, ta được: πx − πx πx = xf ( 2 cos sin 2 x )−0 .
Cho x = 2 , ta được = f ( )←→ f ( ) 1 1 4 4 4 = . Chọn D. 4
Câu 104. Cho a > 0 và f (x) là hàm số liên tục trên [a;+∞). Tìm giá trị của a biết t f (x ) rằng dx + 6 = 2 t ∫ với mọi t > . a 2 x a A. a = 5. B. a = 9. C. a = 19. D. a = 3. f (x)
Lời giải. Gọi F (x) là một nguyên hàm của hàm số
trên đoạn [a;t]. 2 x  f (x ) F '(x)= 2  Khi đó ta có x  t tf (x ) .
F (t)−F (a)= F (x) =
dx = 2 t − 6 
→ F (t) = 2 t + F (a)−6 ∫ 2  a x  a 1 f (t) Suy ra F '(t) = = 
→ f (t) = t t hay f (x)= x x 2 t t t f (x) t 1 t  → dx = dx = 2 x = 2 t −2 a. ∫ ∫ 2 x x a a a
Theo giả thiết 2 t −2 a = 2 t −6 
→a = 9. Chọn B. t f (x)
Cách 2. Từ đẳng thức dx + 6 = 2 t ∫
, lấy đạo hàm hai vế theo t , ta được 2 x a f (t) 1 =
. Suy ra f (t) = t t hay f (x)= x x . 2 t t
Câu 105. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;2] và thỏa mãn 2 2 f ′(x)
f (x) > 0, ∀x ∈[1;2]. Biết rằng
f ′(x )dx = 10 ∫ và = ∫ Tính f (2). f (x) dx ln 2. 1 1
A. f (2)= −10. B. f (2)= 20. C. f (2)= 10.
D. f (2)= −20. 2 2 Lời giải. Ta có
f ′(x)dx = 10 ⇔ f (x ) = 10 ⇔ f (2)− f ( ) 1 = 10. ∫ ( ) 1 1 1 2 f ′(x) 2 2 Lại có
dx = ln 2 ⇔ ln f (x)
= ln 2 ⇔ ln  f (x) = ∫
(do f (x)> 0,∀x ∈[1;2]) f (x) ln 2   1 1 1 f (2) f (2)
⇔ ln f (2)− ln f ( ) 1 = ln 2 ⇔ ln = ⇔ = (2) f ( ) ln 2 f ( ) 2. 1 1 Từ ( )
1 và (2) , suy ra f (2) = 20. Chọn B.
Câu 106. Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [−1; ] 1 , thỏa mãn
f (x )> 0, ∀x ∈ ℝ và f '(x)+ 2 f (x ) = 0 . Tính f (− ) 1 , biết rằng f ( ) 1 = 1 . A. f ( ) 2 1 e− − = . B. f (− ) 3 1 = e . C. f (− ) 4 1 = e . D. f (− ) 1 = 3. f '(x)
Lời giải. Ta có f '(x)+ 2 f (x)= 0 ⇔ f '(x)= −2 f (x) ⇔
= − (do f (x)> 0 ). f (x) 2 1 f '(x) 1
Lấy tích phân cận từ −1 đến 1 hai vế, ta được dx = (−2) ∫ ( ) dx ∫ f x −1 1 − 1 1 1 1 ⇔ ln f (x) = −2x
⇔ ln  f (x) = −2x  
(do f (x)> 0,∀x ∈ ℝ ) −1 1 − 1 − −1 ⇔ ln  f ( )
1  − ln  f (− )
1  = −4 ⇔ ln1− ln  f (− ) 1  = −4       ⇔
f (− ) =  → f (− ) 4 ln 1 4 1 = e .   Chọn C.
Câu 107. Giả sử hàm số f (x) có đạo hàm liên tục trên ℝ , nhận giá trị dương trên
khoảng (0;+∞) và thỏa mãn f ( )
1 = 1, f (x) = f ′(x) 3x +1 với mọi x > 0. Mệnh đề nào sau đây là đúng?
A. 1< f (5)< 2. B. 4 < f (5)< 5.
C. 2 < f (5)< 3.
D. 3 < f (5)< 4. f '(x )
Lời giải. Ta có f (x)= f (x) 1 ' . 3x +1 ⇔ = . f (x ) 3x +1 5 f '(x) 5 Lấy tích phân cận từ dx
1 đến 5 hai vế, ta được = ∫ ( ) dx ∫ f x 3x +1 1 1 5 5 5 5 ⇔ f (x) 2 = x + ⇔  f (x) 2 ln 3 1 ln  = 3x +1  
(do f (x)> 0,∀x > 0 ) 1 3 1 1 3 1 4 ⇔
f ( ) −  f ( ) 4  = ⇔  f ( ) 4  − = ⇔  f ( ) 4 ln 5 ln 1 ln 5 ln1 ln 5  = ⇔ f ( ) 3 5 = e 3,793.     3   3   ≃ 3 Chọn D.
Câu 108. Cho hàm số f (x) có đạo hàm liên tục trên ℝ và thỏa mãn f '(x)
f (x )> 0, ∀x ∈ ℝ . Biết f (0) = 1 và = −
, tìm tất cả các giá trị thực của tham ( ) 2 2x f x
số m để phương trình f (x)= m có hai nghiệm thực phân biệt.
A. m > e .
B. 0 < m ≤1.
C. 0 < m < e .
D. 1< m < e . f '(x ) f ′(x)
Lời giải. Lấy nguyên hàm hai vế = − , ta được dx = (2−2x) ( ) 2 2x dx ∫ ∫ f x f (x) ⇔ f (x) 2
= x − x +C ⇔  f (x) 2 ln 2 ln
 = 2x − x +C  
(do f (x)> 0,∀x ∈ ℝ ) ( ) 2 2 x x C f x e − + ⇔ = . Theo giả thiết (0)=1 C f 
→e = 1 ⇔ C = 0 . Suy ra ( ) 2 2 x x f x e − = . 2 2 − + =  Xét phương trình − + − =   f (x ) 2 x 2x ln m x 2x ln m 0 2 x −x = m ⇔ e = m ⇔  ⇔  . m  > 0 m  > 0   ∆  ′ = − > Phương trình m
f (x) = m có hai nghiệm thực phân biệt 1 ln 0 ⇔ 
⇔ 0 < m < e . m  > 0  Chọn C.
Câu 109. Cho hàm số f (x) liên tục trên ℝ và a > 0 . Giả sử rằng với mọi x ∈[0;a], ta a có dx
f (x )> 0 và f (x) f (a − x) = 1. Tính I = ∫ . 1+ f (x) 0 A. a a I = . B. I = 2 . a C. I = .
D. I = a ln(a + ) 1 . 2 3
Lời giải. Từ giả thiết, suy ra ( − ) 1 f a x = . f (x)  =  → = Đặt x t a
t = a − x  →dt = d − x . Đổi cận: 0  .
x = a →t = 0  0 a a a dt dt f (t) f (x) Khi đó I = − = = t = x ∫ ∫ ∫ ∫
1+ f (a −t) f (t) d +1 f (x) d . 1 +1 a 0 1 + f (t) 0 0 a a a dx f (x) Suy ra a
2I = I + I = + = =  → = ∫ ∫ ∫ Chọn A. + f (x) f (x) dx dx a I . 1 +1 2 0 0 0
Cách trắc nghiệm. Chọn f (x)=1> 0 
→ f (a − x) =1 thỏa f (x) f (a − x) =1. a a Khi đó dx 1 a I = = x = . ∫ 1+1 2 2 0 0 a 2a x
Câu 110. Cho số thực 1 e
a ≠ 0 , đặt b = ∫ . Tính ( dx ∫
theo a và b . a + x ) dx 2 x e 3a − x −a 0 2a x 2a x A. e b e b dx = . ∫ B. dx = . ∫ 3 a a − x e 3 a a − x 0 0 e 2a x 2a x C. e e a dx = . a b e . ∫ D. dx = . ∫ 3a − x 3 b a − x 0 0 e
Lời giải. Ta đổi biến để đưa tích phân cần tính về tích phân đã cho bằng cách đặt d  x = −dt
x = → t = a
3a − x = 2a + t  → . Đổi cận: 0   .
x = a − t 
x = 2a → t = a −  −a −a a a−t Khi đó e (− t) a 1 = e ( d − t) a 1 d . a = = ∫ ∫ ∫ Chọn C. a + t ( a +t) e . t e b t e ( a +t) d . . 2 2 2 t e a a −a Baøi 05
ÖÙNG DUÏNG TÍCH PHAÂN
1. Tính diện tích hình phẳng Định lí
Cho hàm số y = f (x) liên tục, không âm trên đoạn [a;b]. Khi đó diện tích S của
hình thang cong giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai đường thẳng
x = a, x = b là y b S = f (x )dx. ∫
y = f (x ) a x O a b
Bài toán 1. Cho hàm số y = f (x) liên tục trên đoạn [a;b]. Khi đó diện tích S của
hình phẳng (D) giới hạn bởi đồ thị hàm số y = f (x) ; trục hoành Ox ( y = 0 ) và hai b
đường thẳng x = a; x = b là S = f (x ) dx ∫ . a
Bài toán 2. Diện tích hình phẳng giới hạn y
bởi hai đồ thị y = f (x) ; y = g(x) và hai
y = f (x )
đường đường thẳng x = a; x = b là y = g b (x) S =
f (x)− g (x )dx. ∫ a x O a b Chú ý:
1) Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau:
- Giải phương trình f (x)= g(x) tìm nghiệm x , x ,..., x ∈ a;b (x < x <... < x . 1 2 n ) 1 2 n ( ) - Tính 1 x b S =
f (x )− g (x) x2 dx +
f (x )− g (x) dx + ∫ ∫ ...+
f (x)− g (x) dx ∫ a 1 x xn 1 x
= ∫ ( f (x)− g(x)) b
dx +... + ∫ ( f (x)− g(x))dx . a xn
Ngoài cách trên, ta có thể dựa vào đồ thị để bỏ dấu giá trị tuyệt đối.
2) Trong nhiều trường hợp, bài toán yêu cầu tính diện tích hình phẳng giới hạn bởi
hai đồ thị y = f (x) ; y = g(x). xn
Khi đó, ta có công thức tính như sau S =
f (x)− g (x) dx ∫ . 1 x
Trong đó x và x tương ứng là nghiệm nhỏ nhất, lớn nhất của f (x)= g(x). 1 n
2. Tính thể tích khối tròn xoay
a) Tính thể tích của vật thể Định lí
Cắt một vật thể C bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt
tại x = a, x = b (a < b). Một mặt phẳng bất kì vuông góc với Ox tại điểm x (a ≤ x ≤ b)
cắt C theo một thiết diện có diện tích S (x) . Giả sử S (x) là hàm liên tục trên đoạn
[a;b]. Khi đó thể tích của vật thể C giới hạn bởi hai mặt phẳng (P) và (Q) được tính b theo công thức V = S (x )dx. ∫ a
b) Tính thể tích vậy tròn xoay y
Bài toán 1. Tính thể tích vật thể tròn xoay
khi quay miền D được giới hạn bởi các
y = f (x )
đường y = f (x); y = 0 ; x = a; x = b quanh
trục Ox được tính theo công thức x b a b 2 O V = π f (x )dx ∫ . a
Chú ý: Nếu hình phẳng D được giới hạn bởi các đường y = f (x); y = g(x) và hai
đường x = a; x = b (với f (x).g(x)≥ 0,∀x ∈[a;b] ) thì thể tích khối tròn xoay sinh bởi
khi quay D quanh trục Ox được tính bởi công thức b 2 V = π f (x ) 2
− g (x) dx ∫ . a
Bài toán 2. Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng D giới hạn
bởi các đường x = g(y), trục tung và hai đường y = a, y = b quanh trục Oy được tính theo công thức b 2 V = π g (y)dy ∫ . a
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1. TÍNH DIỆN TÍCH HÌNH PHẲNG
Câu 1. Cho hàm số y = f (x) liên tục trên [a;b]. Diện tích hình phẳng S giới hạn bởi
đường cong y = f (x), trục hoành và các đường thẳng x = a, x = b (a < b) được xác
định bởi công thức nào sau đây? b a a b A. S = f (x)dx. ∫ B. S = f (x)dx. ∫ C. S = f (x) dx. ∫ D. S = f (x) dx. ∫ a b b a
Lời giải. Chọn D.
Câu 2. Cho đồ thị hàm số y = f (x) như hình vẽ y
bên. Diện tích S của hình phẳng phần tô đậm
trong hình được tính theo công thức nào sau đây? 3 A. S = f (x)dx ∫ . y=f(x) 2 − x O 0 3 B. -2 3 S = f (x)dx + f (x)dx ∫ ∫ . 2 − 0 2 − 3 C. S = f (x)dx + f (x)dx ∫ ∫ . 0 0 0 0 D. S = f (x)dx + f (x)dx ∫ ∫ . 2 − 3 3 0 3
Lời giải. Theo hình vẽ, ta có S =
f (x) dx = −
f (x )dx + f (x )dx ∫ ∫ ∫ 2 − 2 − 0 2 − 3 = f (x)dx + f (x)dx ∫ ∫ . Chọn C. 0 0
Câu 3. Cho hai hàm số y = f x , y = f x liên tục trên [a;b]. Diện tích hình phẳng 1 ( ) 2 ( )
S giới hạn các bởi đường cong y = f x , y = f
x và các đường thẳng x = , a 1 ( ) 2 ( )
x = b (a < b) được xác định bởi công thức nào sau đây? b b A. S = f x − f x dx. ∫
B. S =  f x − f x  dx. ∫ 2 ( ) 1 ( ) 1 ( ) 2 ( )   a a b b C. S =
f x − f x  dx . ∫ D. S = f x + f x dx. ∫ 1 ( ) 2 ( ) 1 ( ) 2 ( )   a a
Lời giải. Chọn A.
Câu 4. Diện tích hình phẳng S giới hạn bởi
các đồ thị hàm số y = 2x , y = 4 − x và trục
hoành Ox (như hình vẽ) được tính bởi công
thức nào dưới đây? 4 4 A. S = 2x dx + (4− x)dx. ∫ ∫ 0 0 2 4 B. S = 2x dx + (4− x)dx. ∫ ∫ 0 2 4 C.
S = ∫ ( 2x −4 + x)dx. 0 2
D. S = ∫ (4−x − 2x)dx. 0
Lời giải. Xét các phương trình hoành độ giao điểm: x ≤ 4 
• 2x = 4 − x ⇔  ⇔ x = 2; 2
x −10x +16 = 0 
• 4 − x = 0 ⇔ x = 4;
• 2x = 0 ⇔ x = 0. 2 4
Dựa vào hình vẽ, ta có S = 2x dx + (4− x)dx. ∫ ∫ Chọn B. 0 2
Câu 5. Diện tích hình phẳng S giới hạn bởi các đồ thị hàm số 3
y = x , y = 2 − x và trục hoành Ox (như
hình vẽ) được tính bởi công thức nào dưới đây? 1 2 A. 3 S = x dx + (x −2)dx. ∫ ∫ 0 1 2
B. S = ∫ ( 3x + x −2)dx . 0 1 C. 1 3 S = + x dx. ∫ 2 0 1 D. 3 S =
x −(2 − x) dx. ∫ 0
Lời giải. Xét các phương trình hoành độ giao điểm: 3 3
• x = 2 − x ⇔ x + x −2 = 0 ⇔ x = 1; 3
• x = 0 ⇔ x = 0;
• 2 − x = 0 ⇔ x = 2. 1 2 1 Dựa vào hình vẽ, ta có 1 3 S = x dx + (2− x) 3 dx = + x dx. ∫ ∫ ∫ Chọn C. 2 0 1 0
Câu 6. Diện tích hình phẳng S giới hạn bởi các đồ thị hàm số 3
y = x − x, y = 2x và
các đường x = −1, x = 1 được xác định bởi công thức nào sau đây? 1 1 A. S = ∫ ( 3
3x − x )dx . B. S = ∫ ( 3
3x − x )dx. 1 − 1 − 0 1 0 1
C. S = ∫ ( 3x −3x)dx +∫ ( 3
3x − x )dx. D. S = ∫ ( 3
3x − x )dx + ∫ ( 3
x −3x )dx. −1 0 −1 0
Lời giải. Xét phương trình hoành độ giao điểm: x = 0 ∈[−1; ] 1 3 3 
x − x = 2x ⇔ x −3x = 0 ⇔ . 
x = ± 3 ∉ [−1; ] 1  0 1
Diện tích hình phẳng cần tính: 3 3 S =
x − x − 2x dx +
x − x − 2x dx ∫ ∫ −1 0 0 1 xet dau = ∫ ( 3
x −3x )dx + ∫ ( 3
3x − x )dx. Chọn C. −1 0
Câu 7. Sơ đồ ở bên phải phác thảo của một khung cửa sổ. y 5 Diện tích 2
S của cửa sổ được tính bởi công thức nào sau y = −2x 2 đây? 1 1 2   2 A. 5 5 2 S = 
∫  −4x dx 2  . B. S = −2x dx  ∫ . 2  2 1 − 1 − 2 2 2 x = 1 1 y 2x 2 2 C. 1 2 1 S = 2x dx ∫ . D. S = ∫ ( 2
1− 4x )dx . − O 2 2 1 − 1 − 2 2  
Lời giải. Dựa vào đồ thị ta thấy trên đoạn 1 1 − 5
;  thì đồ thị hàm số 2 = −  y 2x 2 2    1 2
nằm phía trên đồ thị hàm số 2 y = 2x . 2 1 1 1 2 2 2    
Do đó S = (y − y ) 5 5 2 2 2 dx =  ∫
∫  −2x −2x dx =   
∫  −4x dx. Chọn A. 1 2 2  2  1 1 1 − − − 2 2 2
Câu 8. Cho hai hàm số f (x) và g(x) liên tục trên đoạn [a;b] với a < b. Kí hiệu S là 1
diện tích hình phẳng giới hạn bởi các đường y = 2 f (x), y = 2g(x), x = a và x = b; S 2
là diện tích hình phẳng giới hạn bởi các đường y = f (x)−2, y = g(x)−2, x = a và
x = b . Mệnh đề nào sau đây là đúng?
A. S = S .
B. S = 2S .
C. S = 2S −2.
D. S = 2S + 2. 1 2 1 2 1 2 1 2 b b
S = 2 f x −2g x dx =2 f x −g x dx ∫ ∫ 1 ( ) ( ) ( ) ( )  Lời giải. Ta có a a   →S = 2S . 1 2 b b
S =  f x −2−g x −2 dx = f x −g x dx  ∫ ∫ 2 ( ) ( ) ( ) ( )      a a Chọn B.  
Câu 9. Cho hàm số f (x) xác định và đồng biến trên đoạn [0; ] 1 và 1 f     = 1  . Diện 2
tích hình phẳng S giới hạn bởi đồ thị của các hàm số y = f x , y =  f x  2 ( ) 2 1 ( )   và các
đường x = 0 , x = 1 được xác định bởi công thức nào sau đây? 1 1 2 2 A. S = f (x) 1
 − f (x) dx + f (x) f (x)−1 dx. ∫   ∫   0 1 1 B.   S = f (x)− ∫ 
( f (x))2 dx.    0 1 2 1 C. S = f (x) 1
 − f (x) dx + f (x) f (x)−1 dx. ∫   ∫   0 1 2 1 D.   S = ∫ ( f
 (x))2 − f (x) dx.    0 1 Lời giải. Gọi 2
S là diện tích hình phẳng cần tính. Ta có S =
f (x)−  f (x ) dx ∫   0 1 1 2 1 =
f (x) . 1− f (x) dx =
f (x) . 1− f (x ) dx +
f (x) 1− f (x) dx. ∫ ∫ ∫ 0 0 1 2       f (x) 1 1 ≥ f  
  = 1, ∀x ∈  ;1        Do hàm số 2  2 
f (x) đồng biến trên [0; ] 1  →       f (x) 1 1 ≤ f  
  = 1, ∀x ∈ 0;     2  2        f
 (x)− = f (x) 1 1
−1, ∀x ∈  ;1  2      → .   
 f (x)− = − f (x) 1 1 1 , ∀x ∈ 0;    2    1 2 1 Vậy S = f (x) 1
 − f (x) dx + f (x) f (x)−1 dx ∫   ∫   . Chọn C. 0 1 2
Câu 10. Cho hàm số f (x) có đồ thị trên y
đoạn [−1;4] như hình vẽ bên. Tính tích 4 phân I = f (x)dx. ∫ 2 −1 A. 5 I = . 2 3 4 x B. 11 I = . -1 O 1 2 2 -1 C. I = 5. D. I = 3.
Lời giải. Gọi A(−1;0), B(0;2), C (1;2), D(2;0), E (3;− ) 1 , F (4;− ) 1
và H (1;0), K (3;0), L(4;0) . 4 0 1 2 3 4 Khi đó I = f (x)dx =
f (x )dx + f (x)dx + f (x)dx + f (x)dx + f (x )dx ∫ ∫ ∫ ∫ ∫ ∫ −1 1 − 0 1 2 3 0 1 2 3 4 =
f (x) dx +
f (x) dx +
f (x) dx −
f (x) dx − f (x) dx ∫ ∫ ∫ ∫ ∫ −1 0 1 2 3
(do f (x)≥ 0, ∀x ∈[−1;2] và f (x)≤ 0, ∀x ∈[2;4] ) 1 1 1 5 = S +S +S −S −S
= .2.1+ 2.1+ .2.1− .1.1−1.1 = . Chọn A. ABO OBCH HCD DKE EFLK 2 2 2 2
Câu 11. Kí hiệu S , S lần lượt là diện tích hình vuông cạnh bằng 1 và diện tích 1 2
hình phẳng giới hạn bởi các đường 2
y = x +1, y = 0, x = −1, x = 2. Trong các khẳng
định sau, khẳng định nào là đúng? A. 1 S S = S .
B. S > S .
C. S = S . D. 2 = 6 . 1 2 1 2 1 2 2 S1 2 2 3 2   Lời giải. Ta có x   S = 1 và 2 S = x +1 dx = ∫
∫ ( 2x +1 dx = +x = 6 2 ) 1    3  1 − 1 − 1 − S2  → = 6 . Chọn D. S1
Câu 12. Tính diện tích hình phẳng S giới hạn bởi đồ thị của hai hàm số 2 y = x + 2 và y = 3x . A. S = 2 . B. S = 3 . C. 1 S = . D. 1 S = . 2 6  =
Lời giải. Phương trình hoành độ giao điểm: x 1 2
x + 2 = 3x ⇔  . x = 2  2 CASIO
Diện tích hình phẳng cần tính: 1 2 S =
x + 2 −3x dx = . ∫ 6 1 Chọn D.
Câu 13. (ĐỀ MINH HỌA 2016 2017) Tính diện tích hình phẳng –
S giới hạn bởi đồ thị hàm số 3
y = x − x và đồ thị hàm số 2
y = x − x . A. 37 S = . B. 9 S = . C. 81 S = . D. S =13. 12 4 12 x = 0 
Lời giải. Phương trình hoành độ giao điểm: 3 2
x − x = x − x ⇔ x = 1 .  x = −2  1 CASIO
Diện tích hình phẳng cần tính: 37 3 2 S =
x + x − 2x dx 3,083 = . ∫ ≃ Chọn A. 12 2 − 1
Cách kiểm tra máy tính. Dùng CASIO tính tích phân 3 2
x + x − 2x dx ∫ rồi lưu vào 2 −
biến A. Bây giờ ta thử với đáp án A có đúng không nhé? Ta xét hiệu 37 A − và nhấn 12 dấu
. Nếu màn hình xuất hiện số 0 thì đáp án đó đúng.
Câu 14. Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số 2
y = x −3x và hai
đường thẳng x = −15, x = 15. A. S = 2250. B. S = 2259. C. S = 1593. D. S = 2925. 15
Lời giải. Diện tích hình phẳng cần tính: 2 S =
x −3x dx ∫ . −15
Bảng xét dấu của biểu thức f (x) 2
= x −3x trên đoạn [−15;15]. x −15 0 3 15 f (x ) + 0 − 0 + 0 3 15
Suy ra S = ∫ ( 2x −3x)dx −∫ ( 2
x −3x )dx + ∫ ( 2
x −3x )dx 1 − 5 0 3 3 2 0 3 2 3 3 2 15  x 3x   x 3x   x 3x        =  −  −    −  + Chọn B.      −  = 2259.      3 2    1 − 5 3 2 0 3 2  3
Cách 2. Dùng máy tính cầm tay. 15
Đối với VINACAL. Ta tính 2
x −3x dx = 2259. ∫
Đúng với kết quả tính tay. −15 15
Đối với CASIO. Ta tính 2
x −3x dx = 2250. ∫
Không đúng với kết quả tính tay. 1 − 5
Lý do nào hai loại máy tính này cho ta hai kết quả khác nhau? Giải thích: Máy
CASIO ' thường không đúng ' cho tích phân trị tuyệt đối với hai cận chứa 3 đoạn đổi dấu trở lên.
Câu 15. Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số 2
y = x 1+ x , trục
hoành và đường thẳng x = 1 . A. 1 − + S = . B. 2 2 1 S = . C. 2 2 1 S = .
D. S = 2( 2 − ) 1 . 3 3 3
Lời giải. Phương trình hoành độ giao điểm: 2
x 1+ x = 0 ⇔ x = 0. 1 1 CASIO Diện tích hình phẳng: 2 2 −1 2 2 S =
x 1+ x dx =
x 1+ x dx = . ∫ ∫ Chọn B. 3 0 0
Câu 16. Kí hiệu S , S , S lần lượt là diện tích hình vuông đơn vị (có cạnh bằng đơn 1 2 3
vị), hình tròn đơn vị (có bán kính bằng đơn vị), hình phẳng giới hạn bởi hai đường S + S 2
y = 2 1− x , y = 2(1− x) . Tính tỉ số 1 3 . S2 + + + + A. S S 1 S S 1 S S 1 S S 1 1 3 = . B. 1 3 = . C. 1 3 = . D. 1 3 = . S 3 S 4 S 2 S 5 2 2 2 2
Lời giải. Ta tính được 2 S = 1 = 1 và 2 S = 1 .π = . π 1 2  = Tính x 0
S . Phương trình hoành độ giao điểm: 2
2 1− x = 2(1− x) CASIO →  . 3 x = 1  1 Khi đó 2 S =
2 1− x − 2 1− x dx ∫
. Dùng CASIO tính tích phân và lưu vào biến A. 3 ( ) 0
Tiếp theo bấm 1+ A và nhấn dấu
. Màn hình hiện kết quả 1 . Chọn C. π 2
Câu 17. Diện tích hình phẳng giới hạn bởi các đường y = x và x − 2 y = 0 bằng với
diện tích hình nào sau đây?
A. Diện tích hình vuông có cạnh bằng 2 .
B. Diện tích hình chữ nhật có chiều dài, chiều rộng lần lượt 5 và 3 .
C. Diện tích hình tròn có bán kính bằng 3 . 4
D. Diện tích toàn phần khối tứ diện đều có cạnh bằng 2 3 . 3 x x ≥ 0  = Lời giải. x 0
Phương trình hoành độ giao điểm:  x = ⇔  ⇔  . 2 2 4x = xx = 4   4 CASIO
Diện tích hình phẳng cần tính: x 4 S = x − dx 1,3 = . ∫ ≃ 2 3 0
A. Diện tích hình vuông có cạnh bằng 2  →S = 4. A
B. Diện tích hình chữ nhật có chiều dài, chiều rộng lần lượt 5 và 3  →S = 15. B
C. Diện tích hình tròn có bán kính bằng 3  →S = 9 . π C 4
D. Diện tích toàn phần khối tứ diện đều có cạnh bằng 2 3  →S = = D ( )2 4 canh . 3 . 3 3 Chọn D.
Câu 18. Tính diện tích hình phẳng 2
S giới hạn bởi đồ thị hàm số y = , trục (x + )2 1
hoành và hai đường thẳng x = 0 , x = 4 . A. 8 S = − . B. 8 S = . C. 2 S = . D. 4 S = . 5 5 25 25 4 CASIO
Lời giải. Diện tích hình phẳng cần tính: 2 8 S = dx = . ∫ Chọn B. (x + )2 1 5 0
Câu 19. Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số y = x ln x , trục
hoành và đường thẳng x = e . 2 2 2 2 A. e +1 e +1 e +1 e +1 S = . B. S = . C. S = . D. S = . 4 6 8 2 x > 0  Lời giải.
Phương trình hoành độ giao điểm: 
x ln x = 0 ⇔ x = 0 ⇔ x = 1.  ln x = 0  e CASIO
Diện tích hình phẳng cần tính: S =
x ln x dx 2,09726 ∫ ≃ . 1
Đối chiếu kết quả với bốn đáp án đã cho. Chọn A.
Câu 20. Biết rằng diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = ln x ,  
trục hoành và hai đường thẳng 1
x = , x = e được dưới dạng 1 S = a 1    − .   Mệnh đề ee  nào sau đây là sai? A. 2
a − 3a + 2 = 0. B. 2
a − a − 2 = 0. C. 2
a + 3a − 4 = 0. D. 2
2a −3a − 2 = 0. e 1 e xet dau
Lời giải. Diện tích hình phẳng cần tính: S = ln x dx =
−ln xdx + ln xdx ∫ ∫ ∫ 1 1 1 e e tung phan 1 e = −(   x x − x ) 1 ln
+ x ln x − x = 2 1    −  
→a = 2. Chọn C. 1 ( )     1 e e
Câu 21. Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số x
y = e + x , trục
hoành, trục tung và đường thẳng x = 1 . A. 1 S = e + . B. 1 S = e − .
C. S = e +1.
D. S = e −1. 2 2 1 Lời giải. CASIO
Diện tích hình phẳng cần tính: x S =
e + x dx 2,21828 ∫ ≃ . 0
Đối chiếu kết quả với bốn đáp án đã cho. Chọn B.
Câu 22. Tính diện tích hình phẳng S giới hạn bởi các đường x
y = e + x , x − y +1 = 0 và x = ln 5 .
A. S = 5+ ln 4 .
B. S = 5−ln 4 .
C. S = 4 + ln 5 .
D. S = 4 −ln 5 .
Lời giải. Ta có x − y +1 = 0  → y = x +1.
Phương trình hoành độ giao điểm: x + = +1 x e x x
⇔ e = 1 ⇔ x = 0 . ln 5 ln 5 CASIO
Diện tích hình phẳng cần tính: = ∫ ( x + )−( + )1 d x S e x x x = e −1 dx 2,39056. ∫ ≃ 0 0
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 23. Tính diện tích hình phẳng S giới hạn bởi các đường y = (e + ) 1 x và = (1 x y + e )x. A + − − . e 2 e e e S = . B. S = . C. 2 S = . D. 2 S = . 2 2 2 4
Lời giải. Phương trình hoành độ giao điểm: ( x = x
+ e )x = (e + )x ⇔ x ( x e − e) 0 1 1 = 0 ⇔  . x =1  1 1 CASIO
Diện tích cần tính: = ∫ (1 x + ) −( + ) 1 d = ∫ ( x S e x e x x
x e − e) dx ≃ 0,35914. 0 0
Đối chiếu kết quả với bốn đáp án đã cho. Chọn C.
Câu 24. Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số x
y = e +1 , trục
hoành và hai đường thẳng x = ln 3 , x = ln 8 . A. 2 S = 2 + ln . B. 3 S = 2 + ln . C. 3 S = 3 + ln . D. 3 S = 2 − ln . 3 2 2 2 ln 8 ln 8 CASIO
Lời giải. Diện tích hình phẳng cần tính: x = +1 d x S e x =
e +1dx = 2,40546. ∫ ∫ ln 3 ln 3
Đối chiếu kết quả với bốn đáp án đã cho. Chọn B.
Câu 25. (ĐỀ THỬ NGHIỆM 2016 2017) Cho y –
hình thang cong (H ) giới hạn bởi các đường x
y = e , y = 0, x = 0, x = ln 4. Đường thẳng x = k
(0 < k < ln 4) chia (H ) thành hai phần có diện tích
là S và S như hình vẽ bên. Tìm k để S = 2S . 1 2 1 2 A. 2 k = ln 4. B. k = ln 2. 3 S2 C. 8 S k = ln . D. k = ln 3. 1 3 x O k ln 4 k k ln 4 ln 4 Lời giải. Ta có x = d x k S e x = e = e −1 ∫ và x S = e d x x = e = 4 k −e . ∫ 1 2 0 k 0 k Theo giả thiết = 2 k ⇔ −1 = 2(4 k S S e
−e ) ⇔ k = ln 3 . Chọn D. 1 2
Câu 26. Kí hiệu (H ) là hình phẳng giới hạn bởi các đường x
y = e , y = 0 , x = 0 và x = 1 . Đường thẳng
x = k (0 < k < )
1 chia (H ) thành hai phần có diện
tích tương ứng S , S như hình vẽ bên, biết S > S . 1 2 1 2
Mệnh đề nào sau đây là đúng? A. e + e + k 3 e > . B. k 2 e > . 2 2 + − C. e e k 1 e > . D. k 1 e > . 2 2 k k 1 1 Lời giải. Ta có x = d x k S e x = e = e −1 ∫ và x S = e d x k x = e = e −e ∫ . 1 2 0 k 0 k Theo giả thiết e + k k k 1
S > S ⇔ e −1 > e − e ⇔ e > . Chọn C. 1 2 2
Câu 27. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x , y = 0, x = 0, x = 4. Đường thẳng
y = k (0 < k <16) chia hình (H ) thành hai
phần có diện tích S , S (hình vẽ). Tìm k để 1 2 S = S . 1 2 A. k = 3 . B. k = 4 . C. k = 5. D. k = 8 .
Lời giải. Phương trình hoành độ giao điểm: 2 x = k 
→ x = k . Ta có: 4 4 3 x 64 ● 2 S + S = x dx = = . ∫ 1 2 3 3 0 0 4 4 3  x  2k k 64   ● S = ∫ ( 2
x − k dx =  −kx = −4k + + . 1 )    3  3 3 k k Theo giả thiết 1 2k k 64 32 S = S  →S = S + S ⇔ −4k + + = 1 2 1 ( 1 2 ) 2 3 3 3
t = k (0 t < <4) 3 2
⇔ 2k k −12k + 32 = 0 →2t −12t +32 = 0 → t = 2 
→ k = 4. Chọn B.
Câu 28. Xét hình phẳng (H ) giới hạn bởi đồ thị
hàm số y = (x + )2
3 , trục hoành và đường thẳng
x = 0. Gọi A(0;9) , B (b;0) (−3 < b < 0) . Tính giá trị
của tham số b để đoạn thẳng AB chia (H ) thành
hai phần có diện tích bằng nhau.
A. b = −2 . B. 1 b = − . 2 C. b = −1. D. 3 b = − . 2
Lời giải. Phương trình hoành độ giao điểm: (x + )2 3 = 0 ⇔ x = −3. 0 CASIO Do đó S = (x +3)2 = ( ) dx 9. ∫ H 3 −
Diện tích tam giác OAB bằng: 1 9 S = O . A OB = b . OAB 2 2 Ycbt 1 9 9 ( 3 − b < <0) ←→S = S ⇔ b = 
→b = − Chọn C. OAB (H ) 1. 2 2 2
Câu 29. Cho hàm số y = f (x) liên tục trên ℝ và hàm
số y = g (x) = x f ( 2 .
x ) có đồ thị trên đoạn [1;2] như
hình vẽ bên. Biết phần diện tích miền được tô màu là 4 5 S =
, tính giá trị của tích phân I = f (x)dx. ∫ 2 1 A. 5 I = . B. 5 I = . 2 4 C. I = 10. D. I = 5. 2
Lời giải. Diện tích phần tô màu là S = g (x)dx. ∫ 1 2 Theo giả thiết 5 S = ⇔ x. f ∫ ( 5 2 x )dx = . 2 2 1  = → = Đặt x t 2  t = x 
→dt = 2xdx . Đổi cận: 1 1  .
x = 2 → t = 4  2 4 4 4 Khi đó 5 = x. f ∫ ( 1 2 x )dx =
f (t)dt  →
f (t)dt = 5 ∫ ∫ hay
f (x)dx = 5. ∫ Chọn D. 2 2 1 1 1 1
Câu 30. Một khung cửa có hình dạng như hình vẽ,
phần phía trên là một parabol. Biết a = 2,5m ,
b = 0,5m , c = 2m . Biết số tiền một mét vuông cửa là 1
triệu đồng. Số tiền cần để mua cửa là:
A. 14 triệu đồng. B. 13 triệu đồng. 3 7
C. 3 triệu đồng. D. 17 triệu đồng. 17 3
Lời giải. Diện tích khung cửa bằng: diện tích hình vuông + diện tích parabol. Diện tích hình vuông 2 S = 2.2 = 4 m . 1 Diện tích parabol 2 2 2 S = .2.0,5 = m (Công thức giải nhanh 2 S =
Bh với B là chiều 2 3 3 3
dài của đáy, h là chiều cao).
Suy ra diện tích khung cửa 14 2
S = S + S = m . 1 2 3
Khi đó số tiền cần phải trả: 14 T = 1 × triệu 14 =
triệu đồng. Chọn A. 3 3
Câu 31. Biết rằng đường parabol (P) 2 : y = 2x chia đường tròn (C) 2 2
: x + y = 8 thành hai phần lần lượt
có diện tích là S , S (hình vẽ bên). Khi đó 1 2 b
S −S = aπ − với a, b, c nguyên dương và b là 2 1 c c
phân số tối giản. Tính S = a + b + c. A. S = 13. B. S = 14. C. S = 15.
D. S = 16.
Lời giải. Đường tròn (C) có tâm O(0;0), bán kính R = 2 2 
→ diện tích S = 8 . π
Phương trình hoành độ giao điểm của (P) và (C) là: 2 y = 2x x ≥ 0    →  ↔ x = 2. 2 2 2
x + y = 8 x +2x = 8   2 2 2 Suy ra 4 4 2 S = 2 2xdx 2 + 8 − x dx = + 2π 
→S = S −S = 6π − ∫ ∫ . 1 2 1 3 3 0 2 a  = 4  8  
→S −S = 4π −  → b  = 8 . Chọn C. 2 1 3 c =3 
Câu 32. Một bồn hình trụ chứa dầu được đặt nằm
ngang, có chiều dài 5m, bán kính đáy 1m, với nắp bồn
đặt trên mặt nằm ngang của mặt trụ. Người ta rút
dầu trong bồn tương ứng với 0,5m của đường kính
đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn. A. 11,781 3 m . B. 12,637 3 m . C. 1 3 14,923 m . D. 3 8,307 m .
Lời giải. Thể tích của bồn (hình trụ) đựng dầu là: 2 2 3 V = πr h = .
π 1 .5 = 5πm . 1
Bây giờ ta tính phần dầu bị rút ra bằng 2 cách:
Cách 1. (Dùng tích phân)
Chọn hệ tục tọa độ như hình vẽ, gốc tọa độ gắn với tâm của mặt đáy.
Đường tròn đáy có bán kính bằng 1 nên có phương trình 2 2 x + y = 1 . Suy ra 2 y = ± 1− x .
Diện tích phần hình tròn đáy bị mất: 1 2 2 S = 2
1− x dx ≈ 0,61m . ∫ 1 2 1
Thể tích phần dầu bị rút ra ngoài: 2 3
V = S ×h = 2
1− x dx ×5 ≈ 3,07m ∫ . 2 1 2
Vậy thể tích của khối dầu còn lại trong bồn: 3 V =V V −
≈ 12,637m . Chọn B. 1 2
Cách 2. (Áp dụng diện tích cung tròn khi biết góc ở tâm trừ đi A
diện tích tam giác tạo bởi tâm và 2 đầu mút dây cung) 1 1 1 2 2 S = R α − . . R . R sin α =
R α − sin α viên phân ( ) 2 2 2 O
với α tính theo đơn vị radian. H Tính góc ở tâm: α OH OH 1 α π 2π cos = = =  → = ⇒ α = . 2 OA R 2 2 3 3
Diện tích phần hình tròn đáy bị mất (phần bôi đen) B   1 1 2π 2 2 π S = R − =   α α  −  ≈ viên phân ( sin ) 2 2 .1 . sin 0, 61m .   2 2  3 3 
Câu 33. Cho một viên gạch men có dạng hình
vuông OABC như hình vẽ. Sau khi tọa độ hóa,
ta có O (0;0), A(0; ) 1 , B (1; )
1 , C (1;0) và hai đường
cong trong hình lần lượt là đồ thị hàm số 3 y = x và 3
y = x . Tính tỷ số diện tích của phần tô đậm
so với diện tích phần còn lại của hình vuông. A. 1 . B. 5 . 2 4 C. 4 . D. 1. 3
Lời giải. Diện tích hình vuông có cạnh bằng 1 là 2 2 S = 1 = 1 m . 1 1 CASIO
Diện tích phần tô đậm : 1 3 3 2 S =
x − x dx = = m . ∫ 2 2 0
Do đó diện tích phần còn lại : 1 1 S 2 2 S
∆ = S −S = 1− = m  → = 1. Chọn D. 1 2 2 2 S ∆
Câu 34. (ĐỀ THỬ NGHIỆM 2016 2017) Ông An có –
một mảnh vườn hình Elip có độ dài trục lớn bằng 16 m
và độ dài trục bé bằng 10 m. Ông muốn trồng hoa trên
một dải đất rộng 8 m và nhận trục bé của elip làm
trục đối xứng (như hình vẽ).
Biết kinh phí để trồng hoa là 100.000 đồng 2
/m . Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn) A. 7.862.000 đồng. B. 7.653.000 đồng. C. 7.128.000 đồng.
D. 7.826.000 đồng.
Lời giải. Chọn hệ trục tọa độ Oxy như hình vẽ. 2 2
Giả sử elip có phương trình x y + = 1 . 2 2 a b
Từ giả thiết, ta có 2a = 16 
→a = 8 và 2b = 10  →b = 5.  5 2  y = 64 − x E 2 2 ( 1)
Vậy phương trình của elip là x y  8 + = 1  →  . 64 25  5 2  y = − 64 − x (E2 )  8
Khi đó diện tích dải vườn được giới hạn bởi các đường (E , E , x = −4 và x = 4 . 1 ) ( 2 ) 4 4   Do đó 5 5 π 3 2 2   2 S = 2 64 − x dx =
64 − x dx = 80 + m ∫ ∫   . 8 2  6 4  4 − 0  
Vậy số tiền mà ông An cần là π 3   T = 80 + .  100000   = 7652891,82 7.653.000   6 4  ≃ . Chọn B.
Vấn đề 2. TÍNH THỂ TÍCH KHỐI TRÒN XOAY
Câu 36. Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình
thang cong giới hạn bởi đồ thị hàm số y = f (x), trục Ox và hai đường thẳng
x = a, x = b (a < b), xung quanh trục Ox. b b A. 2 V = 2 π f (x)dx. ∫ B. V = f (x )dx. ∫ a a b b
C. V = π f (x)dx. ∫ D. V = π f (x) dx. ∫ a a
Lời giải. Chọn A.
Câu 37. Cho hình phẳng trong hình bên (phần tô
đậm) quay quanh trục hoành. Thể tích khối tròn
xoay tạo thành được tính theo công thức nào trong các công thức sau đây? b A. 2 V =  −  π g
∫  (x) 2f (x) dx   . a b B. 2 V =  −  π f
∫  (x) 2g (x) dx   . a b b C. V =  −  =  −  π
f (x) g (x) 2 dx ∫   . D. V π
f (x ) g (x) dx ∫   . a a
Lời giải. Chọn B.
Câu 38. Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng
vuông góc với trục Ox tại các điểm x = a, x = b (a < b), có thiết diện bị cắt bởi mặt
phẳng vuông góc với trục Ox tại điểm có hoành độ x (a ≤ x ≤ b) là S (x) . b b b b A. V = 2 π S (x )dx. ∫
B. V = π S (x) dx. ∫
C. V = S (x)dx. ∫ D. V = π S (x)dx. ∫ a a a a
Lời giải. Chọn C.
Câu 39. (ĐỀ THAM KHẢO 2016 2017) Tính thể tích –
V của phần vật thể giới hạn
bởi hai mặt phẳng x = 1 và x = 3 , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý
vuông góc với trục Ox tại điểm có hoành độ x (1≤ x ≤ 3) thì được thiết diện là một
hình chữ nhật có hai cạnh là 3x và 2 3x − 2 . A. 124π V = .
B. V = 32 + 2 15. C. 124 V = .
D. V = (32+2 15)π . 3 3
Lời giải. Diện tích thiết diện (hình chữ nhật) là S (x) 2 = 3x 3x −2 . 3 3 CASIO
Suy ra thể tích cần tính V = S (x) 124 2 dx =
3x 3x − 2dx = . ∫ ∫ Chọn C. 3 1 1
Câu 40. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và
x = 2 , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm
có hoành độ x (0 ≤ x ≤ 2) thì được thiết diện là một phần tư hình tròn bán kính 2 2x . A. V = 32 . π B. V = 64 . π C. 16 V = . π D. V = 8 . π 5
Lời giải. Diện tích thiết diện ( 1 hình tròn) là S (x) 1 = π( 2x )2 1 2 4 = πx . 4 4 2 2 2 5  
Suy ra thể tích cần tính 1 1 x 16 4 π   V = π x dx =  . π  = . ∫   Chọn C. 2 2 5  5 0 0
Câu 41. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và
x = π , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm
có hoành độ x (0 ≤ x ≤ π) thì được thiết diện là một tam giác đều cạnh là 2 sin x. A. V = 2 3 . π
B. V = 8.
C. V = 2 3. D. V = 8 . π
Lời giải. Diện tích tam giác đều là S (x) 4 sin x. 3 = = 3 sin x. 4 π π
Suy ra thể tích cần tính V =
3 sin xdx = − 3 cos x = 2 3. ∫ Chọn C. 0 0
Câu 42. Cho hình phẳng D giới hạn bởi đường cong 2
y = 2x − x và trục hoành. Tính
thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành. A. 16π π π π V = . B. 11 V = . C. 12 V = . D. 4 V = . 15 15 15 15  =
Lời giải. Phương trình hoành đô x 0 ̣ giao điểm: 2
2x − x = 0 ⇔  . x = 2  2 CASIO Thể tích cần tính π
V = π∫ (2x − x )2 16 2 dx = . Chọn A. 15 0
Câu 43. (ĐỀ CHÍNH THỨC 2016 2107) Cho hình phẳng –
D giới hạn bởi đường cong 2
y = x +1 , trục hoành và các đường thẳng x = 0, x = 1. Tính thể tích V của
khối tròn xoay tạo thành khi quay D quanh trục hoành. A. 4π V = . B. V = 2 . π C. 4 V = . D. V = 2. 3 3 1 1 2 CASIO
Lời giải. Thể tích cần tính π V = π∫ ( 4 2
x +1) dx = π∫ ( 2 x + ) 1 dx = . Chọn A. 3 0 0
Câu 44. Cho hình phẳng D giới hạn bởi đường cong y = ln x , trục hoành và đường
thẳng x = e. Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành.
A. V = π(e + )
1 . B. V = π(e − ) 1 .
C. V = πe.
D. V = π(e −2).
Lời giải. Phương trình hoành độ giao điểm: ln x = 0 ⇔ x =1 . e CASIO Thể tích cần tính 2 V = π ln d x x 2,25654. ∫ ≃ 1
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 45. Kí hiệu V , V lần lượt là thể tích của khối cầu bán kính đơn vị và thể tích 1 2
khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi đường thẳng
y = −2x + 2 và đường cong 2
y = 2 1− x . Mệnh đề nào sau đây là đúng?
A. V < V .
B. V = V .
C. V > V .
D. V = 2 V . 1 2 1 2 1 2 1 2 Lời giải. Ta có 4 R= 4 3 1 V = π R  V → = π (đvtt). 1 1 3 3  =
Phương trình hoành độ giao điểm: x 0 2
2 1− x = 2(1− x) CASIO →  . x = 1  1 1 2 CASIO Thể tích π V = − −  −  π ∫ (2 1 x ) 2(1 x) 2 4 2 2 dx = π
−8x +8x dx = . ∫ 2   3 0 0
Vậy V = V . Chọn B. 1 2
Câu 46. Một Bác thợ gốm làm một cái lọ có dạng
khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y = x +1 (đồ thị
như hình vẽ) và trục Ox quay quanh trục Ox.
Biết đáy lọ và miệng lọ có đường kính lần lượt là
2dm và 4dm. Tính thể tích V của lọ. A. 15 3 π
V = 8πdm . B. 3 V = dm . C. 3
V = 7πdm . D. 3
V = 17πdm . 2
Lời giải. Từ giả thiết, suy ra bán kính hai đáy lần lượt là 1dm và 2 dm .
Suy ra x +1 = 1 → x = 0 và x +1 = 2 → x = 3 . 3 3 2 CASIO Thể tích của lọ π
V = π∫ ( x +1) dx = π (x + ) 15 3 1 dx = dm . ∫ Chọn B. 2 0 0
Câu 47. (ĐỀ CHÍNH THỨC 2016 2017) Cho hình phẳng –
D giới hạn bởi đường cong x
y = e , trục hoành và các đường thẳng x = 0, x = 1. Tính thể tích V của khối
tròn xoay tạo thành khi quay D quanh trục hoành. 2 2 π ( 2 e + ) 1 2 π (e − ) 1 A. πe e −1 V = . B. V = . C. V = . D. V = . 2 2 2 2 1 1 1 − 2 π e 1 x x 1 2 2 x ( 2 )
Lời giải. Thể tích cần tính V = π∫ (e ) dx = π e dx = πe = . ∫ Chọn D. 2 0 2 0 0
Câu 48. (ĐỀ MINH HỌA 2016 2017) Kí hiệu (H ) là hình phẳng giới hạn bởi đồ – thị hàm số = 2( − ) 1 x y x
e , trục tung và trục hoành. Tính thể tích V của khối tròn
xoay thu được khi quay hình (H ) xung quanh trục Ox.
A. V = 4 −2e.
B. V = (4 −2e) . 2 π C. 2 V = e − 5.
D. V = (e −5) . π
Lời giải. Phương trình hoành độ giao điểm: 2( − ) 1 x x
e = 0 ⇔ x −1 = 0 ⇔ x = 1. 1 1 CASIO Thể tích cần tính =  −  π 2 ∫  ( ) 2 1 x d = 4π   ( − )2 2 1 x V x e x x e dx = 7,50544.  ∫ 0 0
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 49. (ĐỀ CHÍNH THỨC 2016 2017) Cho hình phẳng –
D giới hạn bởi đường cong π
y = 2 + cos x , trục hoành và các đường thẳng x = 0, x =
. Tính thể tích V của 2
khối tròn xoay tạo thành khi quay D quanh trục hoành.
A. V = π −1.
B. V = (π − ) 1 . π
C. V = (π + ) 1 . π
D. V = π +1. π π 2 2 2 CASIO
Lời giải. Thể tích cần tính V = π∫ ( 2+cosx) dx = π (2+cosx)dx = 13,01119. ∫ 0 0
Đối chiếu kết quả với bốn đáp án đã cho. Chọn C.
Câu 50. (ĐỀ CHÍNH THỨC 2016 2017) Cho hình phẳng –
D giới hạn bởi đường
cong y = 2 + sin x , trục hoành và các đường thẳng x = 0, x = π . Khối tròn xoay tạo
thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
A. V = 2(π + )
1 . B. V = 2π(π + ) 1 . C. 2 V = 2π . D. V = 2 . π π π
Lời giải. Thể tích cần tính V = π∫ ( 2+sin x)2 dx = π (2+sin x) CASIO dx = 26,02239. ∫ 0 0
Đối chiếu kết quả với bốn đáp án đã cho. Chọn B.
Câu 51. Ký hiệu (H ) là hình phẳng giới hạn bởi các đường y = sin x −cos x + m , π
y = 0 , x = 0 và x =
với m là tham số thực lớn hơn 2 . Tìm m sao cho thể tích V 2 2
của khối tròn xoay thu được khi quay hình ( 3π
H ) xung quanh trục hoành bằng . 2 A. m = 6. B. m = 4. C. m = 3. D. m = 9. π π 2 2
Lời giải. Thể tích cần tính V = π∫ ( sin x −cos x +m)2 dx = π (sin x −cosx +m)dx ∫ 0 0 π 2 = (  mπ mπ − − + =   π cos x sin x mx ) 2 π −  1+ −π(− ) 1 = .     0 2 2 2 2 2 Theo giả thiết 3π mπ 3π V = ⇔ =
⇔ m = 3 (thỏa mãn m > 2 ). Chọn C. 2 2 2 π 2
Cách CASIO. Thể tích cần tính V = π (sin x −cos x +m)dx ∫
. Đến đây thử từng giá 0 2 trị 3π
m ở các đáp án vào, đáp án nào cho kết quả thì nhận. 2 2
Câu 52. Cho hình phẳng x
D giới hạn bởi các đồ thị hàm số y =
. và y = x . Tính 4
thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành. A. 124π π π π V = . B. 126 V = . C. 128 V = . D. 131 V = . 15 15 15 15 2  =
Lời giải. Phương trình hoành độ giao điểm x x 0 = x ⇔  . 4 x = 4  2 4 2   CASIO Thể tích cần tính x 128   2 π V = π
  − x dx = . ∫   Chọn C.  4  15 0
Câu 53. Hình phẳng (H ) giới hạn bởi các đường 2
y = x +1 , trục tung và tiếp tuyến của đồ thị hàm số 2
y = x +1 tại điểm (1;2) . Khi quay hình (H ) quanh trục Ox tạo
thành khối tròn xoay có thể tích V bằng: A. 4 V = . π B. 28 V = . π C. 8 V = . π D. V = . π 5 15 15
Lời giải. Tiếp tuyến của đồ thị 2 y = x +1 tại
điểm (1;2) có phương trình y = 2x . 1
Thể tích cần tính V = π∫ (x + )2 1 −(2x)2 2 dx 0 1 1 xet dau 8 4 2 π = π
x − 2x +1 dx = π ( 4 2 x − 2x + ) 1 dx = ∫ ∫ 15 0 0 . Chọn C.
Câu 54. Cho hình phẳng D giới hạn bởi các đồ thị hàm số 2
y = 4 − x và 2 y = 2 + x .
Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành. A. V = 10 . π B. V = 12 . π C. V = 14 . π D. V = 16 . π
Lời giải. Phương trình hoành độ giao điểm: 2 2
4 − x = 2 + x ⇔ x = ±1 . 1 1 CASIO
Thể tích cần tính V = π∫ (4−x )2 −(2+ x )2 2 2 2 dx = π
12 −12x dx = 16 . π ∫ Chọn D. 1 − 1 −
Câu 55. Thể tích V của khối tròn xoay khi
cho hình phẳng giới hạn bởi các đường 2 y = 1− x và 2
y = x −1 quay quanh trục
Ox được xác định bởi công thức nào sau đây? 1 1 A. V = 2 2 π
(1−x )2 −(x − ∫ )2 2 2 1 dx.
B. V = π (1−x )−(x − ∫ )1 dx. 1 − 1 − 1 1 C. 2 2   V = 2 2
π ∫ (1− x )2 2 dx.
D. V = ∫ (x  − )
1 −(1− x )  dx.   1 − 1 −
Lời giải. Phương trình hoành độ giao điểm: 2 2
1− x = x −1 ⇔ x = ±1. Vì đồ thị hàm số 2
y = 1− x đối xứng với đồ thị hàm số 2
y = x −1 qua trục hoành nên
thể tích khối tròn xoay cần tính bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đường 2
y = 1− x , y = 0, x = 1
− , x = 1 quay quanh trục Ox . 1
Vậy công thức tính thể tích là V = π∫ (1−x )2 2 dx . Chọn C. 1 −
Câu 56. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x và y = x . Khối tròn
xoay tạo ra khi (H ) quay quanh Ox có thể tích V được xác định bằng công thức nào sau đây ? A. 1 1 V = 2 π ∫ ( 4
x − x )dx.
B. V = π∫ (x − x)dx. 0 0 1 1 C. V = 4 π ∫ ( 2
x − x )dx.
D. V = π∫ (x −x )dx. 0 0  =
Lời giải. Phương trình hoành độ giao điểm: x 0 2 x = x ⇔  . x =1  1 1 xet dau Thể tích cần tính 4 V = π
x − x dx = π ∫ ∫ ( 4
x − x )dx. Chọn D. 0 0
Câu 57. Cho hình phẳng (H ) giới hạn bởi đồ thị
hàm số y = − x , đường thẳng y = −x + 2 và trục
hoành. Khối tròn xoay tạo ra khi (H ) quay quanh
Ox có thể tích V được xác định bằng công thức nào sau đây ? 2 4   2 4   A. 2 V   =   π x dx + (2− x)2 dx . ∫ ∫  B. V = π x dx − (2− x) dx . ∫ ∫      0 2  0 2  2 4   4 4   C. 2 V   =   π x dx + (x −2)2 dx . ∫ ∫
D. V = π x dx − (2− x) dx . ∫ ∫      0 2  0 2 
Lời giải. Gọi V là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị 1
hàm số y = − x , trục hoành, đường thẳng x = 0, x = 4 xung quanh trục Ox 4  V → = . π ∫ (− x ) 4 2 dx = . π x dx. ∫ 1 0 0
Gọi V là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y = − x + 2 , trục hoành, đường thẳng x = 2, x = 4 xung quanh trục Ox 4  V → = . π (2− x)2 dx. ∫ 2 2 4 4
Suy ra thể tích cần tính V =V V − = . π x dx − . π (2− x)2 dx. ∫ ∫ Chọn D. 1 2 0 2
Câu 58*. Cho hình phẳng (H ) giới hạn bởi 1 đường tròn có bán kính R = 2, đường 4
cong y = 4 − x và trục hoành (miền tô đậm như hình vẽ). Tính thể tích V của khối
tạo thành khi cho hình (H ) quay quanh trục Ox. A. 77π π π π V = ⋅ B. 53 V = ⋅ C. 67 V = ⋅ D. 40 V = ⋅ 6 6 6 3
Lời giải. Phương trình hoành độ giao điểm: 4 − x = 0 ⇔ x = 4.
Gọi V là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi 1 đường tròn 1 4
có bán kính R = 2 (như hình vẽ), trục hoành và đường thẳng x = 0 xung quanh trục Ox 
→ thể tích tạo thành là nửa khối cầu bán kính R = 2. 1 4 2 16 3 3 π  V → = . πR = . π 2 = . 1 2 3 3 3
Gọi V là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y = 4 − x , y = 0, x = 0, x = 4 xung quanh trục Ox 4  V → = π 4 − x dx = 8 . π ∫ 2 ( ) 0 Vậy thể tích cần tính 40π V =V +V = . Chọn D. 1 2 3
Câu 59*. Cho hình phẳng (H ) giới hạn bởi các đường y = − x +2, y = x +2, x = 1.
Tính thể tích V của vật thể tròn xoay khi quay hình phẳng (H ) quanh trục hoành. A. 29π π π V = . B. 9 V =
. C. V = 9π D. 55 V = . 6 2 6
Lời giải. Đây thuộc bài toán khó, ta phải vẽ hình phát họa mới kiểm soát được.
Lấy đối xứng phần đồ thị hàm số y = − x + 2 qua trục hoành ta được đồ thị hàm số
y = x + 2. Khi đó thể tích V cần tính được tạo thành khi cho hình phẳng (H ') giới
hạn bởi các đường y = x + 2, y = x + 2, trục Ox và đường thẳng x = 1 quay quanh trục hoành.
Xét các phương trình hoành độ giao điểm: x = −2
x + 2 = x + 2 ⇔  và . 
x + 2 = 0 ⇔ x = −2 x = −1 
● Gọi V là thể tích khối tròn xoay khi quay hình phẳng là tam giác ABC được giới 1
hạn bởi các đường y = x + 2, trục hoành và đường thẳng x = 1 quanh trục hoành 1  V
→ = π (x + 2)2 dx = 9 . π ∫ 1 2 −
● Gọi V là thể tích khối tròn xoay khi quay hình phẳng (phần tô màu) được giới hạn 2
bởi các đường y = x + 2 , y = x + 2 quanh trục hoành 1 − π  V →
= π∫ ( x +2)2 −(x +2)2 dx = . 2 6 −2 Vậy thể tích cần tính π 55π
V =V +V = 9π + = . Chọn D. 1 2 6 6
Nhận xét. Bài này học sinh làm sai khá nhiều, lí do là không vẽ hình mà làm theo 1 công thức π  
V = π∫  (x + ) −(− x + )2 2 9 2 2  dx = .   2 −2
Câu 60. Cho hình phẳng (H ) giới hạn bởi các đường x
y = e , y = 0 , x = 0 và x = k (k > 0). Gọi
V là thể tích khối tròn xoay khi quay hình (H ) k
quanh trục Ox . Biết rằng V = 4 . Khẳng định nào k
sau đây là khẳng định đúng: A. 3 1 < k < .
B. 3 < k < 2. 2 2
C. 1 < k <1. D. 1 0 < k < . 2 2 k k k
Lời giải. Thể tích π π V = π ( xe )2 2 x 2 dx = π e d x x = e = ( 2k e − ∫ ∫ k )1. 2 0 2 0 0 + Theo giả thiết π π V = 4 ⇔ e − = ⇔ e = k ( k k 8 2 ) 2 1 4 2 π 1 8 + π 1   → k = ln    ∈ 
  ;1. Chọn C. 2     π 2 
Câu 61. Gọi V là thể tích khối tròn xoay
tạo thành khi quay hình phẳng giới hạn bởi
các đường y = x , y = 0 và x = 4 quanh
trục Ox . Đường thẳng x = a (0 < a < 4) cắt
đồ thị hàm số y = x tại M (hình vẽ bên).
Gọi V là thể tích khối tròn xoay tạo thành 1 khi quay tam giác
OMH quanh trục Ox .
Biết rằng V = 2V . Khi đó: 1 A. a = 2 . B. a = 2 2 . C. 5 a = . D. a = 3 . 2
Lời giải. Phương trình hoành độ giao điểm: x = 0 ⇔ x = 0. 4
Thể tích V = π xdx = 8 . π ∫ 0
Ta có M (a; a) . Khi quay tam giác OMH quanh trục Ox tạo thành hai hình nón có chung đáy:
Hình nón (N có đỉnh là O , chiều cao OK = a , bán kính đáy R = MK = a nên có 1 ) thể tích bằng 1 1 πa π R .OK = π ( a ) 2 2 2 .a = . 3 3 3
Hình nón (N có đỉnh là H , chiều cao HK = 4−a , bán kính đáy R = MK = a 2 ) 2 nên có thể tích bằng 1 1 π −π π R HK = π ( a )2 4 a a 2 .(4 −a) = . 3 3 3 2 2 Suy ra πa 4πa − πa 4πa V = + = . 1 3 3 3 Theo giả thiết 4
V = 2V ⇔ 8π = 2. πa 
→a = 3. Chọn D. 1 3
Câu 62. Tính thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi đường tròn (C) x +(y − )2 2 : 3 = 1 quanh trục hoành. A. V = 6 . π B. 3 V = 6π . C. 2 V = 3π . D. 2 V = 6π .
Lời giải. Ta có x +(y − )2 2 3 = 1  2 y = 3 + 1− x   → , x  ∈[−1; ] 1 . 2
y = 3− 1− x  Thể tích cần tính 1  
V = π∫ (3+ 1− x )2 −(3− 1− x )2 2 2 d  x     1 − 1 CASIO 2 = 12π
1− x dx = 59,21762. ∫ 1 −
Đối chiếu kết quả với bốn đáp án đã cho. Chọn D.
Câu 63. Cho hình vuông có độ dài cạnh bằng 8cm và
một hình tròn có bán kính 5cm được xếp chồng lên nhau
sao cho tâm của hình tròn trùng với tâm của hình vuông
như hình vẽ bên. Tính thể tích V của vật thể tròn xoay
tạo thành khi quay mô hình trên quanh trục XY . A. 260π 290 3 π V = cm . B. 3 V = cm . 3 3 C. 520π 580 3 π V = cm . D. 3 V = cm . 3 3
Lời giải. Chọn hệ trục tọa độ như hình vẽ. 4 4 500π ● Thể tích khối cầu 3 3 V = π R = π5 = . 1 3 3 3
● Gọi V là thể tích khối tròn xoay khi quay hình phẳng (H ) (phần tô màu) được giới 2
hạn bởi đường thẳng y = 4 , đường tròn 2 2
y = 25− x và x = 4 quanh trục hoành 4 10 2 π  V → = π 4 − ∫ ( 2 25− x dx = . 2 ) 3 3 y 5 4 x -5 -4 3 4 5 O -4 -5 Vậy thể tích cần tính 520π 3
V =V + 2V = cm . 1 2 3
Câu 64. Bên trong hình vuông cạnh a , dựng
hình sao bốn cánh đều như hình vẽ bên (các
kích thước cần thiết cho như ở trong hình).
Tính thể tích V của khối tròn xoay sinh ra khi
quay hình sao đó quanh trục Ox . A. 5π 5 3 π V = a . B. 3 V = a . 48 16 C. π 3 π V = a . D. 3 V = a . 6 8
Lời giải. Do hình sao có tính đối xứng nên ta quay theo trục thẳng đứng hay nằm
ngang đều cho thể tích như nhau.
Chọn hệ trục tọa độ như hình vẽ.
Gọi V là thể tích khối tròn xoay cần tính.
Gọi V là thể tích khối tròn xoay khi quay hình 1
phẳng được tô màu trong hình bên quanh trục
hoành. Khi đó V = 2V . 1 a a 2 2 2 2 3     Ta có x a a 5πa V =   ∫  +  −   π dx π  
∫ 2x −  dx = . 1 2 4   2 96 0 a 4 3
Suy ra thể tích cần tính 5πa V = 2V = . Chọn A. 1 48
Câu 65. Cho hai tam giác cân có chung đường
cao XY = 40cm và cạnh đáy lần lượt là 40cm
và 60cm , được xếp chồng lên nhau sao cho đỉnh
của tam giác này là trung điểm cạnh đáy của
tam giác kia như hình vẽ bên. Tính thể tích V
của vật thể tròn xoay được tạo thành khi quay
mô hình trên quanh trục XY . A. 40480π 52000 3 π V = cm . B. 3 V = cm . 3 3 C. 46240π 3 V = cm . D. 3 V = 1920πcm . 3
Lời giải. Chọn hệ trục tọa độ như hình vẽ: y
Y ≡ O (0;0), X (40;0), A(0;20), M (40;30) . M 30 Phương trình đường 3x
YM : 3x − 4 y = 0 → y = . A 4 20 Phương trình 40 − x
AX : x + 2 y − 40 = 0 → y = . 2
Phương trình hoành độ giao điểm của hai đường Y X x x − x 16 40
YM và AX là: 3 40 = ↔ x = 16. 4 2
Thể tích vật thể cần tính 16 2 40 2 40− x  3x  46240π B 3 V =   ∫   +   π dx π   ∫   dx = cm .  2   4  3 0 16 N Chọn C.