-
Thông tin
-
Quiz
Bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng – Phùng Hoàng Em Toán 12
Bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng – Phùng Hoàng Em Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu
Toán 12 3.8 K tài liệu
Bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng – Phùng Hoàng Em Toán 12
Bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng – Phùng Hoàng Em Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu
Môn: Toán 12 3.8 K tài liệu
Thông tin:
Tác giả:
Preview text:
MỤC LỤC CHƯƠNG 3
NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG 1 1.
NGUYÊN HÀM VÀ PHƯƠNG PHÁP TÍNH NGUYÊN HÀM . . . . . . . . . . . . . . . . . . . . . . 1 A
SỬ DỤNG ĐỊNH NGHĨA, BẢNG CÔNG THỨC . . . . . . . . . . . . . . . . . . . . . . . . . 1
Dạng 1. Áp dụng bảng công thức nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Dạng 2. Tách hàm dạng tích thành tổng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Dạng 3. Tách hàm dạng phân thức thành tổng . . . . . . . . . . . . . . . . . . . . . . . . . 3 B
SỬ DỤNG PHƯƠNG PHÁP ĐỔI BIẾN SỐ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 4. Đổi biến dạng hàm lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 5. Đổi biến dạng hàm phân thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 6. Đổi biến dạng hàm vô tỉ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 7. Đổi biến dạng hàm lượng giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Dạng 8. Đổi biến dạng hàm mũ, hàm lô-ga-rit . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Dạng 9. Đổi biến dạng "hàm ẩn" . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 C
SỬ DỤNG PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN . . . . . . . . . . . . . 7
Dạng 10. Nguyên hàm từng phần với ”u = đa thức” . . . . . . . . . . . . . . . . . . . . 7
Dạng 11. Nguyên hàm từng phần với ”u = lôgarit” . . . . . . . . . . . . . . . . . . . . . . 7
Dạng 12. Nguyên hàm kết hợp đổi biến số và từng phần . . . . . . . . . . . . . . . 8
Dạng 13. Nguyên hàm từng phần dạng "lặp" . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Dạng 14. Nguyên hàm từng phần dạng "hàm ẩn". . . . . . . . . . . . . . . . . . . . . . . 8 2.
TÍCH PHÂN VÀ PHƯƠNG PHÁP TÍNH TÍCH PHÂN . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 A
TÍCH PHÂN DÙNG ĐỊNH NGHĨA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Dạng 1. Sử dụng định nghĩa, tính chất tích phân . . . . . . . . . . . . . . . . . . . . . . . 10
Dạng 2. Tách hàm dạng tích thành tổng các hàm cơ bản . . . . . . . . . . . . . . . 11
Dạng 3. Tách hàm dạng phân thức thành tổng các hàm cơ bản . . . . . . . . . 12 B
TÍCH PHÂN ĐỔI BIẾN SỐ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Dạng 4. Đổi biến loại t = u(x) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Dạng 5. Đổi biến loại x = ϕ(t) (Lượng giác hóa). . . . . . . . . . . . . . . . . . . . . . . . 14
Dạng 6. Đổi biến số dạng hàm ẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 C
TÍCH PHÂN TỪNG PHẦN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Dạng 7. Tích phân từng phần với "u = đa thức" . . . . . . . . . . . . . . . . . . . . . . . 16
Dạng 8. Tích phân từng phần với "u = logarit" . . . . . . . . . . . . . . . . . . . . . . . . 17
Dạng 9. Tích phân hàm ẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 3.
ỨNG DỤNG TÍCH PHÂN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 A
TÍNH DIỆN TÍCH HÌNH PHẲNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Dạng 1. Hình phẳng giới hạn bởi hai đồ thị y = f(x) và y = g(x) . . . . . . . . 19
Dạng 2. Hình phẳng giới hạn bởi nhiều hơn hai đồ thị hàm số . . . . . . . . . . . 22
Dạng 3. Toạ độ hoá một số "mô hình" hình phẳng thực tế . . . . . . . . . . . . . . 22 B
TÍNH THỂ TÍCH VẬT THỂ, KHỐI TRÒN XOAY . . . . . . . . . . . . . . . . . . . . . . 23
Dạng 4. Tính thể tích vật thể khi biết diện tích mặt cắt vuông góc với Ox 23
GV: Phùng V. Hoàng Em Trang i
Dạng 5. Tính thể tích của khối tròn xoay khi cho hình phẳng quay quanh
trục Ox . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Dạng 6. Bài tập tổng hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 C
MỘT SỐ BÀI TOÁN CHUYỂN ĐỘNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
GV: Phùng V. Hoàng Em Trang ii CHƯƠNG
3 NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
§ 1. NGUYÊN HÀM VÀ PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
A SỬ DỤNG ĐỊNH NGHĨA, BẢNG CÔNG THỨC
{ DẠNG 1. Áp dụng bảng công thức nguyên hàm Phương pháp giải. Z
Câu 1. Tính nguyên hàm x2 dx. 1 A. 3x2 +C. B. 2x +C. C. x3 +C. D. x3 + C. 3
Câu 2. Họ các nguyên hàm của hàm số f (x) = 5x4 − 6x2 + 1 là A. 20x3 − 12x +C. B. x5 − 2x3 + x +C. x4
C. 20x5 − 12x3 + x +C. D. + 2x2 − 2x +C. 4 Z Å 2 √ ã
Câu 3. Tính nguyên hàm I = x2 + − 3 x dx với x > 0. x x3 √ x3 √ A. I = − 2 ln |x| + 2 x3 +C. B. I = + 2 ln |x| + 2 x3 +C. 3 3 x3 √ x3 √ C. I = − 2 ln x − 2 x3 +C . D. I = + 2 ln |x| − 2 x3 +C . 3 3 Z
Câu 4. Cho F(x) là một nguyên hàm của hàm f (x). Tính I = [3 f (x) + 2x]dx A. I = 3F(x) + 2 +C. B. I = 3F(x) + x2 +C. C. I = 3F(x) + 2x +C. D. I = 3F(x) + x +C. Z Z x2 Câu 5. Cho f (x)dx = x2 +C1 và g(x)dx =
+C2. Tìm nguyên hàm của hàm số h(x) = f (x) − 3 g(x). Z x2 Z 2x2 A. h(x)dx = +C. B. h(x)dx = +C. 3 3 Z x2 Z 2x2 C. h(x)dx = − +C. D. h(x)dx = − +C. 3 3 1
Câu 6. Họ nguyên hàm của hàm số f (x) = 3x2 + là cos2 x A. x3 + cot x +C. B. x3 + tan x +C. C. 6x − cot x +C. D. 6x + tan x +C. Z 1
Câu 7. Nguyên hàm I = bằng 2x + 1 1 1
A. − ln |2x + 1| +C. B. − ln |2x + 1| +C. C. ln |2x + 1| +C. D. ln |2x + 1| +C. 2 2 1
Câu 8. Biết F(x) là một nguyên hàm của f (x) = và F(2) = 1. Tính F(3). x − 1 1 7 A. F(3) = ln 2 − 1. B. F(3) = ln 2 + 1. C. F(3) = . D. F(3) = . 2 4
GV: Phùng V. Hoàng Em Trang 1
Câu 9. Họ nguyên hàm của hàm số y = (2x + 1)2019 là (2x + 1)2018 (2x + 1)2020 (2x + 1)2020 (2x + 1)2018 A. +C. B. +C. C. +C. D. +C. 2018 4040 2020 4036 √
Câu 10. Tìm nguyên hàm F(x) của hàm số f (x) = 3 4x − 2 3 √ 2 √ A. F(x) = (4x − 2) 3 4x − 2 +C. B. F(x) = (4x − 2) 3 4x − 2 +C. 4 3 3 √ 1 C. F(x) = (4x − 2) 3 4x − 2 +C. D. F(x) = (4x − 2)− 23 +C. 16 3
Câu 11. Nguyên hàm của hàm số f (x) = sin 3x là 1 1 A. cos 3x +C. B. cos 3x +C. C. − cos 3x +C. D. − cos 3x +C. 3 3
Câu 12. Họ nguyên hàm của hàm số f (x) = e2x + x2 là e2x x3 A. F(x) = e2x + x3 +C. B. F(x) = + +C. 2 3 x3 C. F(x) = 2e2x + 2x +C. D. F(x) = e2x + +C. 3
Câu 13. Tìm nguyên hàm của hàm số f (x) = 32x+1. 32x+1 32x+1 A. (2x + 1)32x +C. B. +C. C. 32x+1 ln 3 +C. D. +C. ln 3 ln 9 Z Z Câu 14. Biết
f (x) dx = −x2 + 2x +C. Tính f (−x) dx. A. x2 + 2x +C0. B. −x2 + 2x +C0. C. −x2 − 2x +C0. D. x2 − 2x +C0.
Câu 15. Cho hàm số y = f (x) có đạo hàm f 0(x) = 3x2 − ex + 1 − m. Biết f (0) = 2, f (2) = 1 − e2.
Giá trị của m thuộc khoảng nào dưới đây? A. (4; 6). B. (5; +∞). C. (−2; 4). D. (3; 5).
Câu 16. Cho hàm số f (x) thỏa mãn f 00 (x) = 12x2 + 6x − 4 và f (0) = 1, f (1) = 3. Tính f (−1) . A. f (−1) = −5. B. f (−1) = 3. C. f (−1) = −3. D. f (−1) = −1.
Câu 17. Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây.
Cho h0(t) = 6at2 + 2bt và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là 90
m3, sau 6 giây thì thể tích nước trong bể là 504 m3. Tính thể tích nước trong bể sau khi bơm được 9 giây. A. 1458 m3. B. 1488 m3. C. 1450 m3. D. 1468 m3.
{ DẠNG 2. Tách hàm dạng tích thành tổng Phương pháp giải.
Câu 18. Họ nguyên hàm của hàm số f (x) = 2x(1 + 3x3) là Å Ç å 3 ã 6x3 A. 2x x + x4 +C. B. x2 1 + +C. 4 5 Å 3 ã Å 3 ã C. x2 1 + x2 +C. D. x2 x + x3 +C. 2 4
Câu 19. Họ nguyên hàm của hàm số f (x) = (x + 1)(x + 2) là x3 3 A. F(x) = + x2 + 2x +C. B. F(x) = 2x + 3 +C. 3 2 x3 2 x3 2 C. F(x) = + x2 + 2x +C. D. F(x) = − x2 + 2x +C. 3 3 3 3
Câu 20. Tìm nguyên hàm của hàm số f (x) = ex(1 + e−x). Z Z A. f (x) dx = ex + 1 +C. B. f (x) dx = ex + x +C.
GV: Phùng V. Hoàng Em Trang 2 Z Z C. f (x) dx = −ex + x +C. D. f (x) dx = ex +C.
Câu 21. Một nguyên hàm của hàm số y = cos 5x cos x là 1 Å 1 1 ã 1 Å sin 6x sin 4x ã A. F(x) = sin 6x + sin 4x . B. F(x) = − + . 2 6 4 2 6 4 1 Å 1 1 ã 1 C. F(x) = cos 6x + cos 4x . D. F(x) = sin 5x sin x. 2 6 4 5
Câu 22. Họ nguyên hàm của hàm số f (x) = 4x + sin2 x là 4x 1 sin3 x A. − sin 2x +C. B. 4x ln x + +C. ln 4 4 3 sin3 x 4x x 1 C. 4x ln x − +C. D. + − sin 2x +C. 3 ln 4 2 4
{ DẠNG 3. Tách hàm dạng phân thức thành tổng Phương pháp giải. 1 + 2x2
Câu 23. Biết F(x) là một nguyên hàm của hàm số f (x) =
thỏa mãn F(−1) = 3. Khẳng định x nào sau đây đúng?
A. F(x) = ln |x| + x + 2.
B. F(x) = ln |x| + x2 − 2.
C. F(x) = ln |x| + 2x2 + 1.
D. F(x) = ln |x| + x2 + 2. (x + 1)3
Câu 24. Tìm họ nguyên hàm F(x) của hàm số f (x) = , (x 6= 0). x3 3 1 3 1
A. F(x) = x − 3 ln |x| − + +C.
B. F(x) = x − 3 ln |x| + + +C. x 2x2 x 2x2 3 1 3 1
C. F(x) = x + 3 ln |x| − − +C.
D. F(x) = x − 3 ln |x| + − +C. x 2x2 x 2x2 1
Câu 25. Họ nguyên hàm của hàm số f (x) = là 2x2 − 3x + 1 Z 1 x − 1 Z 1 x + 2 A. f (x) dx = ln + C. B. f (x) dx = ln + C. 2 2x − 1 3 x − 1 Z x − 1 Z x − 1 C. f (x) dx = ln + C. D. f (x) dx = ln + C. x − 0, 5 2x − 1 2x − 5
Câu 26. Cho hàm số f (x) xác định trên R \ {1; 4} có f 0(x) =
thỏa mãn f (3) = 1 − ln 2. x2 − 5x + 4 Giá trị f (2) bằng A. 1 − ln 2. B. 2. C. 1 + 3 ln 2. D. −1 + 3 ln 2. 2x + 1
Câu 27. Cho F(x) là một nguyên hàm của f (x) =
trên khoảng (0; +∞) thỏa mãn x4 + 2x3 + x2 1 F(1) =
. Giá trị của biểu thức S = F(1) + F(2) + F(3) + · · · + F(2019) là 2 2019 2019.2021 1 2019 A. . B. . C. 2018 . D. − . 2020 2020 2020 2020 Z 2x + 2 1 Câu 28. Biết dx =
+ p ln |2x + 1| +C với m, n, p là các số hữu tỉ. Tổng m + n + p (2x + 1)2 mx + n bằng 11 11 13 13 A. − . B. . C. . D. − . 2 2 2 2 √ 1 − sin3 x π 2
Câu 29. Biết F(x) là một nguyên hàm của f (x) = và F = . Có bao nhiêu số thực sin2 x 4 2
x ∈ (0; 2018π) để F(x) = 1.
GV: Phùng V. Hoàng Em Trang 3 A. 2018. B. 1009. C. 2017. D. 2016. 1 π
Câu 30. Biết F(x) là một nguyên hàm của f (x) = và F = 1. Phương trình F(x) − sin2 x · cos2 x 4
1 = 0 có bao nhiêu nghiệm thuộc (0; 2020)? A. 2086. B. 643. C. 2019. D. 2020.
B SỬ DỤNG PHƯƠNG PHÁP ĐỔI BIẾN SỐ
{ DẠNG 4. Đổi biến dạng hàm lũy thừa Phương pháp giải. Z Câu 31. Tính
x(x2 + 7)15dx, ta được kết quả là 1 1 A. x2 + 716 +C. B. x2 + 716 +C. 2 32 1 1 C. − x2 + 716 +C. D. x2 + 716 +C. 32 16 Z Ä Câu 32. Cho I =
x 1 − x2ä10 dx. Đặt u = 1 − x2, khi đó viết I theo u và du ta được 1 Z Z Z 1 Z A. I = − u10 du. B. I = −2 u10 du. C. I = 2u10 du. D. I = u10 du. 2 2
Câu 33. Tìm nguyên hàm của hàm số f (x) = x(x + 1)2016. (x + 1)2018 (x + 1)2017
A. 2018(x + 1)2018 − 2017(x + 1)2017 +C. B. − +C. 2018 2017 (x + 1)2018 (x + 1)2017
C. 2018(x + 1)2018 + 2017(x + 1)2017 +C. D. + +C. 2018 2017 Z a
Câu 34. Cho hàm số f (x) = 2x · (x4 + 2x2 + 1)3. Biết f (x)dx =
(x2 + c)d + C, với a, b, c, d ∈ Z b a và
là phân số tối giản. Tính a + b + c + d. b A. 0. B. 15. C. 16. D. 22.
{ DẠNG 5. Đổi biến dạng hàm phân thức Phương pháp giải. x − 1
Câu 35. Tìm nguyên hàm của hàm số f (x) = . x2 − 2x − 3
A. ln |x2 − 2x − 3| +C.
B. (x − 1) ln |x2 − 2x − 3| +C. 1 1 1 C. ln |x2 − 2x − 3| +C. D. + +C. 2 x + 1 x − 3 Z x
Câu 36. Đổi biến t = x − 1 thì dx trở thành (x − 1)4 Z t − 1 Z (t + 1)4 Z t + 1 Z t + 1 A. dt. B. dt. C. dt. D. dt. t4 t t4 t Z (2x + 3) dx 1 Câu 37. Giả sử = −
+C (C là hằng số). Tính tổng của các nghiệm x(x + 1)(x + 2)(x + 3) + 1 g(x)
của phương trình g(x) = 0. A. −1. B. 1. C. 3. D. −3.
{ DẠNG 6. Đổi biến dạng hàm vô tỉ Phương pháp giải.
GV: Phùng V. Hoàng Em Trang 4 x2
Câu 38. Họ nguyên hàm của hàm số f (x) = √ là x3 + 1 1 2 √ 2 1 √ A. √ +C. B. x3 + 1 +C. C. √ +C. D. x3 + 1 +C. 3 x3 + 1 3 3 x3 + 1 3 Z √ √
Câu 39. Xét nguyên hàm I = x x + 2 dx. Nếu đặt t = x + 2 thì ta được Z Z Ä Ä A. I = t4 − 2t2ä dt. B. I = 4t4 − 2t2ä dt. Z Z Ä Ä C. I = 2t4 − 4t2ä dt. D. I = 2t4 − t2ä dt. Z 1
Câu 40. Tính nguyên hàm I = √ √ dx. 2x + x x + x 2 2 A. I = − √ +C. B. I = − √ +C. x + x x + 1 2 1 C. I = − √ +C. D. I = − √ +C. x + x + 1 2 x + x
{ DẠNG 7. Đổi biến dạng hàm lượng giác Phương pháp giải. √ √ Z 1 + tan x Câu 41. Đặt t = 1 + tan x thì
dx trở thành nguyên hàm nào? cos2 x Z Z Z Z A. 2t dt. B. t2 dt. C. dt. D. 2t2 dt. Z
Câu 42. Tìm nguyên hàm I = sin4 x cos x dx. sin5 x cos5 x sin5 x cos5 x A. +C. B. +C. C. − +C. D. − +C. 5 5 5 5 cos x
Câu 43. Tìm các hàm số f (x) biết f 0(x) = . (2 + sin x)2 sin x 1 A. f (x) = +C. B. f (x) = +C. (2 + sin x)2 2 + cos x 1 sin x C. f (x) = − +C. D. f (x) = +C. 2 + sin x 2 + sin x π
Câu 44. Cho F(x) là một nguyên hàm của hàm số f (x) = cos3 x. Biết F(0) = 0. Khi đó F = √ 4 a 2 a vơi
là phân số tối giản. Tính a + b. b b A. 17. B. 2. C. 16. D. 3. Z 1
Câu 45. Tìm nguyên hàm dx. cos4 x 1 A. +C. B. tan x + tan3 x +C. 3 cos3 x1 1 C. tan x + tan3 x +C. D. cos3 x +C. 3 3 2 cos x − 1
Câu 46. Cho hàm số F(x) là một nguyên hàm của hàm số f (x) = trên khoảng (0; π). √ sin2x
Biết rằng giá trị lớn nhất của F(x) trên khoảng (0; π) là
3. Chọn mệnh đề đúng trong các mệnh đề sau. √ Å ã π √ 2π 3 A. F = 3 3 − 4. B. F = . 6 3 2 Å ã π √ 5π √ C. F = − 3. D. F = 3 − 3. 3 6
GV: Phùng V. Hoàng Em Trang 5
{ DẠNG 8. Đổi biến dạng hàm mũ, hàm lô-ga-rit Phương pháp giải.
Câu 47. Cho F(x) là một nguyên hàm của hàm số f (x) = xex2. Hàm số nào sau đây không phải là
một nguyên hàm của hàm số f (x)? 1 1 A. F(x) = − ex2 +C.
B. F(x) = − (2 − ex2). 2 2 1 1 C. F(x) = (ex2 + 2). D. F(x) = (ex2 + 5). 2 2 e2x
Câu 48. Nguyên hàm của hàm số y = f (x) = là ex + 1 A. I = x − ln |x| +C.
B. I = ex + 1 − ln (ex + 1) +C. C. I = x + ln |x| +C.
D. I = ex + ln (ex + 1) +C. Z 1
Câu 49. Tìm nguyên hàm √ dx. x ln x + 1 2 √ A. p(lnx + 1)3 +C. B. ln x + 1 +C. 3 1 √ C. p(lnx + 1)2 +C. D. 2 ln x + 1 +C. 2 1
Câu 50. Cho F(x) là nguyên hàm của hàm số f (x) =
và F(0) = − ln 2e. Tập nghiệm S của ex + 1
phương trình F(x) + ln (ex + 1) = 2 là A. S = {3}. B. S = {2; 3}. C. S = {−2; 3}. D. S = {−3; 3}.
{ DẠNG 9. Đổi biến dạng "hàm ẩn" Phương pháp giải. Z Z p Ä Câu 51. Cho f (x) dx = x x2 + 1. Tìm I = x · f x2ä dx. √ x4 √ A. I = x2 x4 + 1 +C. B. I = x4 + 1 +C. 2 x2 √ √ C. I = x4 + 1 +C. D. I = x3 x4 + 1 +C. 2 Z Z Câu 52. Biết
f (2x) dx = sin2 x + ln x +C, tìm nguyên hàm f (x) dx. Z Z A.
f (x) dx = 2 sin2 x + 2 ln x +C. B.
f (x) dx = 2 sin2 x + 2 ln x − ln 2 +C. 2 Z Z C.
f (x) dx = 2 sin2 2x + 2 ln x − ln 2 +C. D. f (x) dx = sin2 x + ln x +C. 2 2
Câu 53 (THPT QUỐC GIA 2018). Cho hàm số f (x) thỏa mãn f (2) = − và f 0(x) = 2x[ f (x)]2 với 9
mọi x ∈ R. Giá trị của f (1) bằng 35 2 19 2 A. − . B. − . C. − . D. − . 36 3 36 15
Câu 54. Cho hàm số y = f (x) nhận giá trị dương, có đạo hàm liên tục trên (0; +∞) thỏa mãn f (2) =
1 và f0(x)+(2x+4)f2(x) = 0, ∀x ∈ (0;+∞). Tính f(1)+ f(2)+ f(3). 15 11 7 11 7 A. . B. . C. . D. . 30 15 15 30
Câu 55. Cho hàm số f (x) thỏa mãn [ f 0(x)]2 + f (x) · f 00(x) = 2x2 − x + 1, ∀x ∈ R và f (0) = f 0(0) = 3.
Giá trị của [ f (1)]2 bằng
GV: Phùng V. Hoàng Em Trang 6 19 A. 28. B. 22. C. . D. 10. 2
C SỬ DỤNG PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
{ DẠNG 10. Nguyên hàm từng phần với ”u = đa thức” Phương pháp giải. Z
Câu 56. Kết quả của I = xex dx là x2 x2 A. I = xex − ex +C. B. I = xex + ex +C. C. I = ex +C. D. I = ex + ex +C. 2 2
Câu 57. Tìm họ nguyên hàm f (x) = x cos 2x dx. x sin 2x cos 2x cos 2x A. − +C. B. x sin 2x − +C. 2 4 2 cos 2x x sin 2x cos 2x C. x sin 2x + +C. D. + +C. 2 2 4 Z Câu 58. Cho I =
x2. cos x dx và đặt u = x2, dv = cos x dx. Khẳng định nào sau đây là đúng? Z Z A. I = x2 sin x − x sin x dx. B. I = x2 sin x + x sin x dx. Z Z C. I = x2 sin x − 2 x sin x dx. D. I = x2 sin x + 2 x sin x dx.
Câu 59. Họ nguyên hàm của hàm số f (x) = x(ex − sin x) là
A. (x − 1)ex + x cos x − sin x +C.
B. (x + 1)ex + x cos x − sin x +C.
C. (x − 1)ex + x cos x + sin x +C.
D. (x − 1)ex − x cos x − sin x +C. Z x Câu 60. Cho
dx = Ax tan x + B ln |cos x| +C. Khi đó, giá trị của biểu thức T = A3 + B có 1 + cos 2x giá trị bằng bao nhiêu? 1 3 5 7 A. . B. . C. . D. . 8 8 8 8
{ DẠNG 11. Nguyên hàm từng phần với ”u = lôgarit” Phương pháp giải. Z
Câu 61. Tìm nguyên hàm I = ln x dx 1 1 A. +C. B. x ln x − x +C. C. x ln x + x +C. D. +C. x x2 1 + ln x
Câu 62. Họ nguyên hàm của hàm số f (x) = là x2 ln x 2 ln x 2 ln x 2 ln x 2 A. − + +C. B. − − +C. C. + +C. D. − +C. x x x x x x x x
Câu 63. Họ nguyên hàm của hàm số f (x) = (2x + 1) ln x là x2 A. (x2 + x) ln x − − x +C.
B. (x2 + x) ln x − x2 − x +C. 2 x2 C. (x2 + x) ln x − + x +C.
D. (x2 + x) ln x − x2 + x +C. 2 Z
Câu 64. Nguyên hàm I =
2x ln (1 + x) dx có kết quả là 1 1 A. x2 − 1 ln (x + 1) − x2 − 2x +C. B. x2 + 1 ln (x + 1) − x2 − 2x +C. 2 2
GV: Phùng V. Hoàng Em Trang 7 C.
x2 − 1 ln (x + 1) − x2 − x +C. D.
x2 − 1 ln (x + 1) − 2 x2 − 2x +C.
{ DẠNG 12. Nguyên hàm kết hợp đổi biến số và từng phần Phương pháp giải. Z Câu 65. Biết rằng
x3ex2 dx = P(x)ex2 + C (C ∈ R), trong đó P(x) là một hàm số đa thức. Hãy tính
giá trị của biểu thức T = P(5). 125 124 A. T = . B. T = 8. C. T = 12. D. T = . 2 3
Câu 66. Tìm họ nguyên hàm của hàm số f (x) = ecosx sin 2x. Z Z A.
f (x) dx = −2ecosx cos x + 2ecosx +C. B.
f (x) dx = 2ecosx cos x − 2ecosx +C. Z Z 1 C. f (x) dx = −2ecosx +C. D.
f (x) dx = − esinx cos 2x +C. 2 1 √
Câu 67. Cho hàm số y = f (x) với f 0(x) =
√ . Tìm f (x), biết f (0) = 2. cos2 x √ √ √ √ √ √ √ √ A. f (x) = 2 x tan x + ln |cos x| + 2. B. f (x) = x tan x + 2 ln |cos x| + 2. √ √ √ √ √ √ √ √ C. f (x) = 2 x tan x + 2 ln |cos x| − 2. D. f (x) = 2 x tan x + 2 ln |cos x| + 2.
Câu 68. Tìm một nguyên hàm y = F(x) của hàm số f (x) = x3 + 3x ex2 biết tiếp tuyến của đồ thị
hàm số y = F(x) tại điểm có hoành độ bằng 0 đi qua điểm M(−1; 2). 1 1 A. F(x) = x2ex2 + ex2 + 1. B. F(x) = x2ex2 + ex2 − 1. 2 2 1 C. F(x) = x2ex2 + 2ex2.
D. F(x) = x2ex2 + ex2 + 1. 2
{ DẠNG 13. Nguyên hàm từng phần dạng "lặp" Phương pháp giải. Z Câu 69. Cho F(x) =
ex. cos x dx = ex (A. cos x + B. sin x) + C với A, B ∈ Q và C ∈ R. Tính giá trị của biểu thức P = A + B. A. P = −2. B. P = −1. C. P = 2. D. P = 1. 1 1
Câu 70. Nguyên hàm của hàm số y = − có kết quả là ln x ln2x 1 x2 x x A. I = +C. B. I = +C. C. I = − +C. D. I = +C. x ln x ln x ln x ln x 1 Z Å ln x − 1 ã a (bx + m) Câu 71. Biết F(x) =
là một nguyên hàm của hàm số f (x) và f (x) + dx = + ln x ln2x ln x
C, với a, b, m ∈ Z. Tính tổng T = 2a + b + 3m. A. T = 4. B. T = 2. C. T = 5. D. T = 6. Z Å 1 ã 1 ax2−b Câu 72. Biết x +
+ 1 ex− x dx = x · e mx +C, với a, b, m ∈ Z. Tính a + b + m. x A. a + b + m = 0. B. a + b + m = 3. C. a + b + m = 1. D. a + b + m = −2.
{ DẠNG 14. Nguyên hàm từng phần dạng "hàm ẩn" Phương pháp giải.
GV: Phùng V. Hoàng Em Trang 8 Z Z Câu 73. Cho biết
f (x) ln x dx = ln x + 2x +C. Tính I = (2x + 1) f 0(x) dx. 1 1 A. I = − 2 ln x + 4x +C. B. I = − 2 ln x +C. x x 1 1 C. I = − ln x +C. D. I = + ln x + 4x +C. x x 1 f (x) Z
Câu 74. Biết F(x) = −
là một nguyên hàm của hàm số y = . Tính f 0(x) ln x dx. x2 x Z 2 ln x 1 Z 2 ln x 1 A. f 0(x) ln x dx = − + +C. B. f 0(x) ln x dx = + +C. x2 x2 x2 x2 Z 2 ln x 1 Z 2 ln x 1 C. f 0(x) ln x dx = − +C. D. f 0(x) ln x dx = − − +C. x2 x2 x2 x2
Câu 75. Cho F(x) = (x − 1)ex là một nguyên hàm của hàm số f (x)e2x. Tìm nguyên hàm của hàm số f 0(x)e2x. Z Z 2 − x A.
f 0(x)e2x dx = (4 − 2x)ex +C. B. f 0(x)e2x dx = ex +C. 2 Z Z C. f 0(x)e2x dx = (2 − x)ex +C. D. f 0(x)e2x dx = (x − 2)ex +C. —HẾT—
GV: Phùng V. Hoàng Em Trang 9
§ 2. TÍCH PHÂN VÀ PHƯƠNG PHÁP TÍNH TÍCH PHÂN
A TÍCH PHÂN DÙNG ĐỊNH NGHĨA
{ DẠNG 1. Sử dụng định nghĩa, tính chất tích phân Phương pháp giải. 9 Z
Câu 1. Cho hàm số f (x) liên tục trên R và F(x) là một nguyên hàm của f (x), biết f (x) dx = 9 và 0 F(0) = 3. Tính F(9). A. −6. B. 6. C. 12. D. −12. 2 5 5 Z Z Z Câu 2. Nếu f (x) dx = 3, f (x) dx = −1 thì f (x) dx bằng 1 2 1 A. −2. B. 2. C. 3. D. 4. 10 6 Z Z
Câu 3. Cho hàm số f (x) liên tục trên [0; 10] thỏa mãn f (x) dx = 7,
f (x) dx = 3. Tính giá trị của 0 2 2 10 Z Z P = f (x) dx + f (x) dx. 0 6 A. P = 3. B. P = 1. C. P = 4. D. P = 2. 3 Z
Câu 4. Cho f (x) và g(x) là hai hàm số liên tục trên đoạn [1; 3], thỏa mãn [ f (x) + 3g(x)] dx = 10 1 3 3 Z Z và
[2 f (x) − g(x)] dx = 6. Tính I = [ f (x) + g(x)] dx. 1 1 A. I = 6. B. I = 7. C. I = 9. D. I = 8. 0 Z
Câu 5. Cho y = f (x) xác định và liên tục trên tập R. Biết f (x) là hàm số lẻ thỏa f (x) dx = 4 và −3 5 5 Z Z f (x) dx = 7. Tính f (x) dx 3 −3 A. 15. B. 7. C. 4. D. −1.
Câu 6. Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [0; 1] và f (1) − f (0) = 2. Tích phân 1 Z I = f 0(x) − ex dx bằng 0 A. 1 − e. B. 1 + e. C. 3 − e. D. 3 + e. π 4 Z
Câu 7. Giá trị của sin 3x dx bằng 0 √ √ √ √ 2 + 2 −2 + 2 −2 − 2 2 − 2 A. . B. . C. . D. . 6 6 6 6
GV: Phùng V. Hoàng Em Trang 10 2018 Z Câu 8. Tích phân 2x dx bằng 0 22018 − 1 22018 A. 22018 − 1. B. . C. . D. 22018. ln 2 ln 2 1 ®1 − 2x nếu x > 0 Z
Câu 9. Cho hàm số f (x) =
. Tính giá trị biểu thức I = f (x) dx. cos x nếu x ≤ 0 − π2 1 A. I = −2. B. I = . C. I = 1. D. I = 0. 2
Câu 10. Cho hàm số y = f (x) liên tục trên [−2; 3] và có đồ thị như y 3 2 Z hình vẽ. Tính f (x) dx. −2 11 5 A. 2. B. 4 . C. . D. . O 2 3 2 2 x −2 −1 1
Câu 11. Cho F(x) là một nguyên hàm của hàm số f (x) =
trên (−∞; 2). Biết F(1) = 2, giá trị x − 2 của F(0) bằng A. 2 + ln 2. B. ln 2. C. 2 + ln(−2). D. ln(−2). 1
Câu 12. Cho hàm số f (x) xác định trên R \ {1} thỏa mãn f 0(x) = , f (0) = 2018, f (2) = 2019. x − 1 Tính S = f (3) − f (−1). A. S = ln 4035. B. S = 4. C. S = ln 2. D. S = 1. π 2 Z sin x Câu 13. Tính I = dx. 1 + x2 −π 2 π 1 A. I = . B. I = . C. I = 0. D. I = 1. 4 2
{ DẠNG 2. Tách hàm dạng tích thành tổng các hàm cơ bản Phương pháp giải.
Câu 14. Cho hàm số f (x) xác định trên R thỏa mãn f 0(x) = (x + 1)2, ∀x ∈ R và f (0) = 1. Giá trị của
biểu thức f (−1) + f (1) bằng 10 A. 4. B. . C. 2. D. 20. 3 π 8 Z π b b Câu 15. Biết sin2 x dx =
− √ , với a, b, c ∈ Z và tối giản. Tính a + b + c. a c 2 c 0 A. 40. B. 21. C. 12. D. 8. √ ln 2 Z √ Câu 16. Biết
(ex + 1)3 dx = a 2 + b ln 2 + c, với a, b, c ∈ Q. Tính a + b + c. 0 7 17 A. 6. B. 32. C. . D. . 3 6
GV: Phùng V. Hoàng Em Trang 11
{ DẠNG 3. Tách hàm dạng phân thức thành tổng các hàm cơ bản Phương pháp giải. 1 Z Å 1 1 ã 1 a a Câu 17. Biết − dx = ln
trong đó a, b nguyên dương và là phân số tối giản. 2x + 1 3x + 1 6 b b 0
Khẳng định nào sau đây là khẳng định sai? √ √ a b A. 3 a + b = 7. B. + = 7. C. a − b = 11. D. a + b < 22. 9 4 1 Z 2x + 3 Câu 18. Biết I =
dx = a ln 2 + b, (a, b ∈ Q). Khi đó a + 2b bằng 2 − x 0 A. 0. B. 2. C. 3. D. 7. 2 Z x2 Câu 19. Biết
dx = a + ln b (a, b ∈ Z). Gọi S = 2a + b, giá trị của S thuộc khoảng nào sau x + 1 0 đây? A. (4; 6). B. (8; 10). C. (2; 4). D. (6; 8). 2 Z x dx Câu 20. Cho I =
= a ln 2 + b ln 3 + c ln 5, với a, b, c ∈ Q. Tính S = a + b + c. (x + 1)(2x + 1) 1 A. S = 1. B. S = 0. C. S = −1. D. S = 2. 2 Z 1 Câu 21. Cho
dx = a ln 2 + b ln 3 + c ln 5, với a, b, c là các số nguyên. Mệnh đề nào dưới x2 + 5x + 6 1 đây đúng? A. a + b + c = 4. B. a + b + c = −3. C. a + b + c = 2. D. a + b + c = 6. 1 Z x2 + 2x a c a a Câu 22. Biết dx =
− ln , với a, b, c, d là các số nguyên dương và , là các phân x2 + 6x + 9 b d b b 0 a c
số tối giản. Giá trị của biểu thức T = + bằng b d 79 1429 1039 A. . B. 41. C. . D. . 12 324 12 Z 2 x2 + 5x + 2 Câu 23. Biết
dx = a + b ln 3 + c ln 5, (a, b, c ∈ Q). Giá trị của abc bằng 0 x2 + 4x + 3 A. −8. B. −10. C. −12. D. 16. 1 √ Z x a + b 3
Câu 24. Biết tích phân √ √ dx =
với a, b là các số nguyên. Tính tổng 3x + 1 + 2x + 1 c 0 T = a + b + c A. T = −10. B. T = 8. C. T = 25. D. T = 17. 2 √ √ Z dx a − b − c Câu 25. Biết I = √ √ =
với a, b, c là các số nguyên dương. Tính (2x + 2) x + 2x x + 1 2 1 P = a − b + c. A. P = 24. B. P = 12. C. P = 18. D. P = 22.
GV: Phùng V. Hoàng Em Trang 12
B TÍCH PHÂN ĐỔI BIẾN SỐ
{ DẠNG 4. Đổi biến loại t = u(x) Phương pháp giải. n Z Nhận dạng I =
f [u(x)] · u0(x) dx (có u(x) và đạo hàm của nó kèm theo là u0(x)). m Các bước giải:
¬ Đặt t = u(x) ⇒ dt = u0(x) dx Đổi cận • x = m ⇒ t = u(m) • x = n ⇒ t = u(n) u(n) Z ® Chuyển I =
f (t) · dt. Sau đó tính kết quả. u(m) π 2 Z Câu 26. Cho I =
sin2 x · cos x dx và u = sin x. Mệnh đề nào dưới đây đúng? 0 0 1 1 1 Z Z Z Z A. I = − u2 du. B. I = u2 du. C. I = − u2 du. D. I = 2 u du. −1 0 0 0 Z 4 √ p
Câu 27. Cho tích phân I = x x2 + 9 dx. Khi đặt t =
x2 + 9 thì tích phân đã cho trở thành 0 Z 5 Z 4 Z 4 Z 5 A. I = t dt. B. I = t dt. C. I = t2 dt. D. I = t2 dt. 3 0 0 3 1 Z x − 1 Câu 28. Tính dx. x2 − 2x + 2 0 √ √ A. ln 2. B. − ln 2. C. ln 2. D. − ln 2. 1 Z x dx Câu 29. Cho
= a + b ln 2 + c ln 3 với a, b, c là các số hữu tỉ. Giá trị của a + b + c bằng (2x + 1)2 0 1 5 1 1 A. . B. . C. − . D. . 12 12 3 4 e Z ln x 3 Câu 30. Biết dx = a ln
+ b, (a, b ∈ Q). Mệnh đề nào sau đây đúng? x(ln x + 2) 2 1 A. a − b = 1. B. 2a + b = 1. C. a2 + b2 = 4. D. a + 2b = 0. a Z x3 + x Câu 31. Tính I = √ dx. x2 + 1 0√ 1 √ î ó A. I = a2 + 1 a2 + 1 − 1. B. I = a2 + 1 a2 + 1 − 1 . 3 1 √ √ î ó C. I = a2 + 1 a2 + 1 + 1 . D. I = a2 + 1 a2 + 1 + 1. 3
GV: Phùng V. Hoàng Em Trang 13 3 Z x a Câu 32. Cho I = √ dx =
+ b ln 2 + c ln 3 với a, b, c là các số nguyên. Giá trị a + b + c 4 + 2 x + 1 3 0 bằng A. 9. B. 2. C. 1. D. 7. 1 Z 1 1 + e Câu 33. Cho dx = a + b ln
, với a, b là các số hữu tỉ. Tính S = a3 + b3. ex + 1 2 0 A. S = −2. B. S = 0. C. S = 1. D. S = 2. π 2 Z x sin x + cos x + 2x 2 π b b Câu 34. Biết dx = + ln
với a, b, c là các số nguyên dương và là phân số sin x + 2 a c c 0
tối giản. Tính P = a · b · c. A. P = 24. B. P = 13. C. P = 48. D. P = 96. 2 Z dx Câu 35. Cho
= a ln 5 + b ln 2 + c, với a, b, c là các số hữu tỉ. Giá trị của a + 2b + 4c bằng x5 + x3 1 5 A. 0. B. −1. C. − . D. 1. 8 1 Z (x2 + x)ex Câu 36. Cho
dx = ae + b ln(e + c) với a, b, c ∈ Z. Tính giá trị của P = a + 2b − c. x + e−x 0 A. P = −1. B. P = 1. C. P = −2. D. P = 0. π 2 Z sin x − cos x a a Câu 37. Nếu √ dx =
ln c, (với a, b, c ∈ Z, a > 0,
là phân số tối giản) thì a + 2b + 3c 1 + sin 2x b b π 4 là A. 13. B. 14. C. 9. D. 11. π Z 4 sin2x
Câu 38. Tính tích phân I =
dx bằng cách đặt u = tan x, mệnh đề nào dưới đây đúng? 0 cos4x π Z 4 Z 1 1 Z 1 Z 1 A. I = u2 du. B. I = du. C. I = − u2 du. D. I = u2 du. 0 0 u2 0 0 e2 Z x2 + 1 ln x + 1 ae4 + be2
Câu 39. Cho tích phân I = dx =
+ c + d ln 2. Chọn phát biểu đúng. x ln x 2 e √ 1 √ 1 √ 1 A. a = b = c = d. B. a = b2 = c = . C. a = b2 = d = . D. b = a2 = d = . d c c 1 Z 2x3 + 3x b b
Câu 40. Cho tích phân I = √ dx = a − ln 2, với a, b, c ∈ Z và là phân số tối giản. x x2 + 3 − 4 c c 0 Tính a2 + b + c. A. a2 + b + c = 0. B. a2 + b + c = 1. C. a2 + b + c = −1 . D. a2 + b + c = 9 .
{ DẠNG 5. Đổi biến loại x = ϕ(t) (Lượng giác hóa) Phương pháp giải. 1 Z dx
Câu 41. Đổi biến x = 2 sint thì tích phân √ trở thành 4 − x2 0
GV: Phùng V. Hoàng Em Trang 14 π π π π 6 3 6 6 Z Z Z Z dt A. tdt. B. tdt. C. dt. D. . t 0 0 0 0 √ 2 2 Z p
Câu 42. Cho tích phân I =
16 − x2 dx và x = 4 sint. Mệnh đề nào sau đây đúng? 0 π π 4 4 Z Z A. I = 8 (1 + cos 2t) dt. B. I = 16 sin2t dt. 0 0 π π 4 4 Z Z C. I = 8 (1 − cos 2t) dt. D. I = −16 cos2t dt. 0 0 2 Z p π b b
Câu 43. Cho tích phân I = 1 + 2x − x2 dx =
+ , với a, b, c là số nguyên dương và tối giản. a c c 1 Tính a2 + b2 + c2. A. 21. B. 18. C. 9. D. 16. √2 Z 1 … a a
Câu 44. Tính tích phân dx = π , với tối giản. Tính a + b. 2 + x2 b b 0 A. a + b = 30. B. a + b = 37. C. a + b = 35. D. a + b = 33. √3+2 Z 1
Câu 45. Tính tích phân dx. x2 − 4x + 5 2 π π π π A. . B. . C. . D. . 3 4 6 2
{ DẠNG 6. Đổi biến số dạng hàm ẩn Phương pháp giải. 4 1 Z Z Câu 46. Cho
f (x)dx = −1. Tính giá trị của I = f (4x)dx. 0 0 1 1 1 A. I = . B. I = −2. C. I = − . D. I = − . 4 4 2 0 2 Z Z
Câu 47. Cho hàm số y = f (x) là hàm lẻ, liên tục trên [−4; 4]. Biết f (−x) dx = 2 và f (−2x) dx = −2 1 4 Z 4. Tính I = f (x) dx. 0 A. I = −10. B. I = −6. C. I = 6. D. I = 10. 2 5 Z Z Câu 48. Cho f (x2 + 1)xdx = 2, khi đó f (x)dx bằng 1 2 A. 2. B. 1. C. −1. D. 4.
GV: Phùng V. Hoàng Em Trang 15 π 1 4 Z Z Câu 49. Cho f (x) dx = 2018. Tích phân f (cos 2x) sin 2x dx bằng 0 0 A. 2018. B. 1009. C. −1009. D. −2018. 5 Z
Câu 50. Cho f (x) là hàm số liên tục trên R và thỏa f (x3 + 3x + 1) = x + 2. Tính f (x) dx. 1 37 527 41 464 A. . B. . C. . D. . 6 3 4 3 3 5 1 Z Z Z
Câu 51. Cho hàm số f (x) liên tục trên R và có f (x) dx = 8 và f (x) dx = 4. Tính f (|4x − 0 0 −1 1|) dx. 9 11 A. 6. B. . C. 3. D. . 4 4 π 4 1 Z Z x2 f (x)
Câu 52. Cho hàm số f (x) liên tục trên R và các tích phân f (tan x) dx = 4, dx = 2. Tính x2 + 1 0 0 1 Z tích phân I = f (x) dx. 0 A. 2. B. 6. C. 3. D. 1.
Câu 53. Cho hàm số y = f (x) có đạo hàm đến cấp hai liên tục trên R. Biết tiếp tuyến của hàm số
y = f (x) tại các điểm có hoành độ x = 0 và x = 1 có phần đồ thị ở nửa trên trục hoành tạo với chiều 1 Z 2 f 0(x) · f 00(x)
dương trục Ox lần lượt các góc là 45◦ và 60◦. Tính I = dx. [ f 0(x)]2 + 1 0 A. I = ln 2. B. I = 0. C. I = ln 3. D. I = ln 5.
C TÍCH PHÂN TỪNG PHẦN
{ DẠNG 7. Tích phân từng phần với "u = đa thức" Phương pháp giải. π 4 Z
Câu 54. Giá trị của tích phân x sin x dx bằng 0 4 + π 2 − π 4 − π 2 + π A. √ . B. √ . C. √ . D. √ . 4 2 2 2 4 2 2 2 Z 1 Câu 55. Cho I =
xe2x dx = a · e2 + b với a, b ∈ Q. Tính tổng a + b. 0 1 1 A. . B. . C. 0. D. 1. 2 4 1 Z 1 Câu 56. Biết rằng x cos 2x dx =
(a sin 2 + b cos 2 + c), với a, b, c ∈ Z. Khẳng định nào sau đây 4 0 đúng? A. a + b + c = 1. B. a − b + c = 0. C. 2a + b + c = −1. D. a + 2b + c = 1.
GV: Phùng V. Hoàng Em Trang 16 π √ 3 Z x 3 Câu 57. Biết I = dx =
π − ln b, với a, b là các số nguyên dương. Tính giá trị của biểu cos2 x a 0 thức T = a2 + b. A. T = 9. B. T = 13. C. T = 7. D. T = 11. π 2 Z ea + 1 Câu 58. Biết I = ex · sin x dx =
với a ∈ R, b ∈ N. Khi đó sin a + cos 2a + b bằng b 0 A. 2 . B. 4 . C. 1 . D. 0 . 3 √ 2 2 Z 1 b Câu 59. Biết x3ex2 dx =
e c + d, với a, b, c, d ∈ Z. Tính a + b + c + d. a 0 67 65 A. 0. B. . C. . D. 35. 2 2
{ DẠNG 8. Tích phân từng phần với "u = logarit" Phương pháp giải. 3 Z Câu 60. Biết rằng
x ln x dx = m ln 3 + n ln 2 + p, trong đó m, n, p ∈ Q. Khi đó số m là 2 9 27 A. . B. 18. C. 9. D. . 2 4 3 Z
Câu 61. Bằng cách đặt u = ln x, dv = x2 dx thì tích phân
x2 ln x dx biến đổi thành kết quả nào sau 1 đây? 3 3 3 3 x3 ln x 1 Z x2 ln x 1 Z A. − x2 dx. B. − x2 dx. 3 3 2 3 1 1 1 1 3 3 3 3 x3 ln x 1 Z x3 ln x 1 Z C. + x2 dx. D. − − x2 dx. 3 3 3 3 1 1 1 1 4 Z a a Câu 62. Biết I = x ln(2x + 1) dx =
ln 3 − c, trong đó a, b, c là các số nguyên dương và là phân b b 0
số tối giản. Tính S = a + b + c. A. S = 60. B. S = 70. C. S = 72. D. S = 68. 2 Z ln x b
Câu 63. Cho tích phân dx =
+ a ln 2 với a là số thực và b, c là các số nguyên dương, đồng x2 c 1 b thời
là phân số tối giản. Tính giá trị của biểu thức P = 2a + 3b + c. c A. P = 6. B. P = −6. C. P = 5. D. P = 4. 2 Z x + ln x a 1 a Câu 64. Cho I = dx =
ln 2 − , với a, b, c là các số nguyên dương và là phân số tối (x + 1)2 b c b 1 a + b
giản. Tính giá trị của biểu thức S = . c
GV: Phùng V. Hoàng Em Trang 17 2 5 1 1 A. S = . B. S = . C. S = . D. S = . 3 6 2 3 1 Z a a
Câu 65. Biết tích phân (2x − 1) ln(x3 + 1) dx =
− c ln 2 trong đó a, b, c ∈ Z+; là phân số tối b b 0 giản. Tính a + b + c. A. 7. B. 12. C. −17. D. 12. 1 Z b b
Câu 66. Giả sử tích phân x · ln(2x + 1)2017 dx = a + ln 3. Với phân số tối giản. Lúc đó c c 0 A. b + c = 6057. B. b + c = 6059. C. b + c = 6058. D. b + c = 6056.
{ DẠNG 9. Tích phân hàm ẩn Phương pháp giải.
Câu 67. Cho các hàm số f (x) và g(x) liên tục, có đạo hàm trên R thỏa mãn f 0(0) · f 0(2) 6= 0 và 2 Z
g(x) · f 0(x) = x(x − 2)ex. Tính I = f (x) · g0(x) dx. 0 A. I = −4. B. I = e − 2. C. I = 4. D. I = 2 − e. 2 1 Z Z
Câu 68. Cho hàm số f (x) liên tục trên R và f (2) = 16, f (x) dx = 4. Tính I = x f 0 (2x) dx. 0 0 A. 12. B. 13. C. 20. D. 7. 1 Z 1
Câu 69. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0; 1] thỏa mãn f (1) = 0, x2 f (x) dx = . 3 0 1 Z Tính I = x3 f 0(x) dx. 0 A. −1. B. 1. C. 3. D. −3. 1 1 Z Z
Câu 70. Cho hàm số f (x) thỏa mãn
(x + 1) f 0(x)dx = 10 và 2 f (1) − f (0) = 2. Tính f (x)dx. 0 0 A. I = −12. B. I = 8. C. I = 1. D. I = −8.
Câu 71. Giả sử hàm số f (x) có đạo hàm liên tục trên đoạn [0; 1], thỏa mãn điều kiện f (0) = 6 và 1 1 Z Z
(2x − 2) f 0(x) dx = 6. Khi đó f (x) dx bằng 0 0 A. −3. B. −9. C. 3. D. 6.
Câu 72. Biết F(x) là một nguyên hàm của hàm số f (x) trên đoạn [1; 3] , F(1) = 1, F(3) = 3 và 3 3 Z F(x) Z dx = 4. Tính I = ln(3x − 1) f (x) dx. 3x − 1 1 1 A. I = 8 ln 2 + 12. B. I = 8 ln 2 − 4. C. I = 8 ln 2 − 12. D. I = −81. —HẾT—
GV: Phùng V. Hoàng Em Trang 18
§ 3. ỨNG DỤNG TÍCH PHÂN
A TÍNH DIỆN TÍCH HÌNH PHẲNG
{ DẠNG 1. Hình phẳng giới hạn bởi hai đồ thị y = f(x) và y = g(x) Phương pháp giải.
¬ Xác định 2 cận x = a và x = b, với a < b; b Z
Diện tích được tính theo công thức | f (x) − g(x)| dx a
Câu 1. Cho đồ thị hàm số y = f (x) như hình vẽ. Diện tích hình phẳng y
(phần gạch chéo) được tính bởi công thức nào sau đây? 2 −2 2 Z Z Z −2 A. f (x) dx. B. f (x) dx + f (x) dx. O 2 x −2 0 0 0 0 1 2 Z Z Z Z C. f (x) dx + f (x) dx. D. f (x) dx + f (x) dx. 2 −2 −2 1
Câu 2. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x2, trục hoành Ox, các đường thẳng x = 1, x = 2 là 7 8 A. S = . B. S = . C. S = 7. D. 8. 3 3
Câu 3. Diện tích hình phẳng giới hạn bởi các đường y = x2, y = 4, x = −1, x = 2 là 32 17 A. 4. B. . C. 9. D. . 3 4
Câu 4. Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = 3x2, y = 2x + 5, x = −1 và x = 2. 256 269 A. S = . B. S = . C. S = 9. D. S = 27. 27 27
Câu 5. Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x = π, đồ thị hàm số y = cos x và trục Ox là π π π π Z Z Z Z A. S = cos x dx. B. S = cos2 x dx. C. S = | cos x| dx. D. S = π | cos x| dx. 0 0 0 0
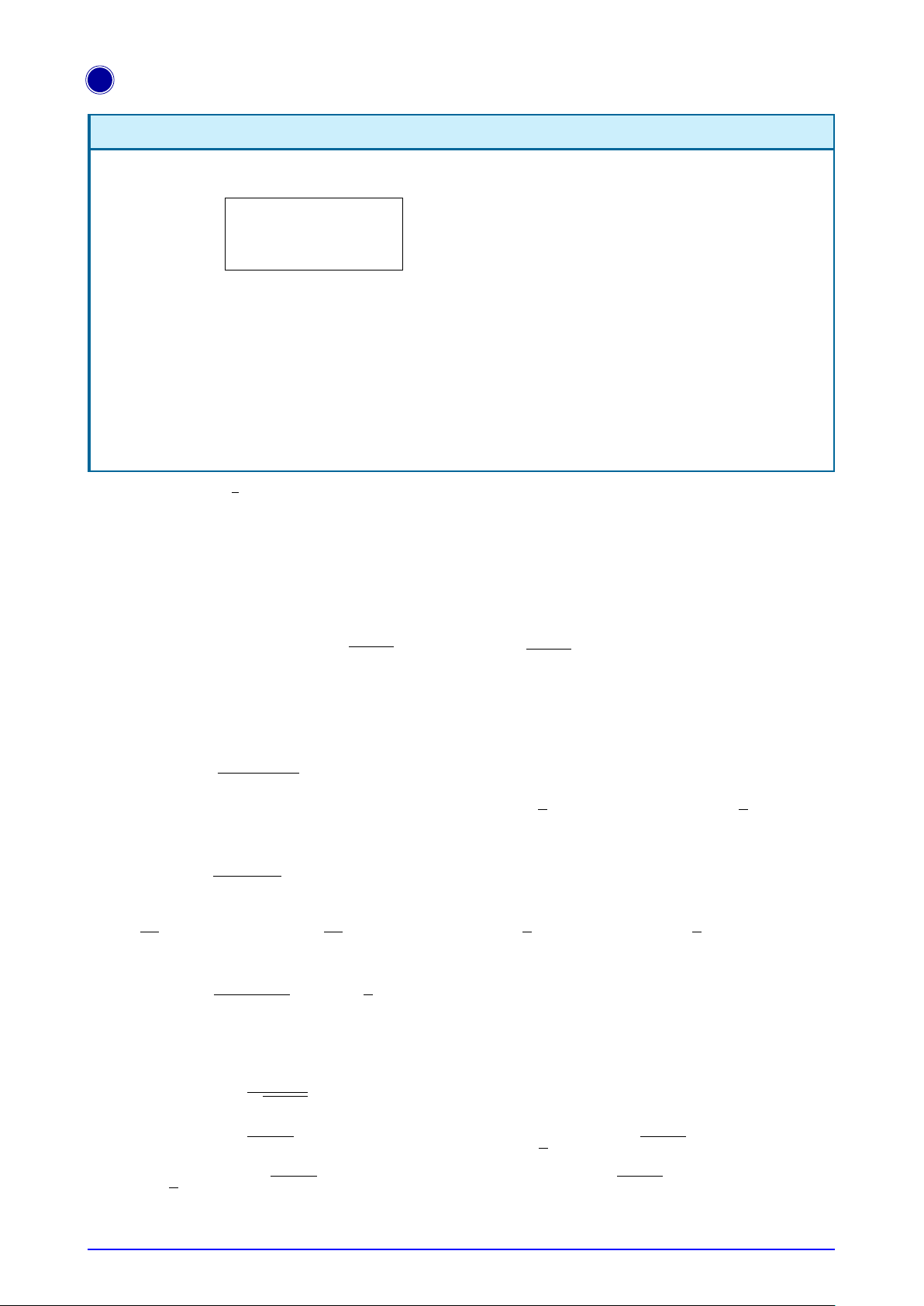
Câu 6. Biết diện tích hình phẳng giới hạn bởi các đường y = sin x, y = cos x, x = 0, x = a, với a ∈ h π π i 1 √ √ Ä ä ; là −3 + 4 2 −
3 . Hỏi số a thuộc khoảng nào sau đây? 4 2 2 Å 7 ã Å 51 11 ã Å 11 3 ã Å 51 ã A. ; 1 . B. ; . C. ; . D. 1; . 10 50 10 10 2 50 √
Câu 7. Tính diện tích hình phẳng giới hạn bởi các đường y = x x2 + 1; x = 1 và trục Ox. √ √ √ √ 3 2 − 1 5 − 2 2 2 − 1 5 − 2 2 − 1 A. . B. . C. . D. . 5 6 3 3
Câu 8. Tính diện tích của hình phẳng giới hạn bởi hai đường y = x2 − 2x, y = −x2 + x. 9π 27 9 27π A. . B. . C. . D. . 8 8 8 8
GV: Phùng V. Hoàng Em Trang 19
Câu 9. Tính diện tích hình phẳng được giới hạn bởi hai đồ thị (C1) : y = x2 + 2x và (C2) : y = x3. 83 15 37 9 A. S = . B. S = . C. S = . D. S = . 12 4 12 12 x2 − 2x − 15
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y =
và hai trục toạ độ bằng x − 3 3 256 A. 12 ln 2 − . B. . C. 17 + 12 ln 3. D. 16 + 12 ln 3. 2 3
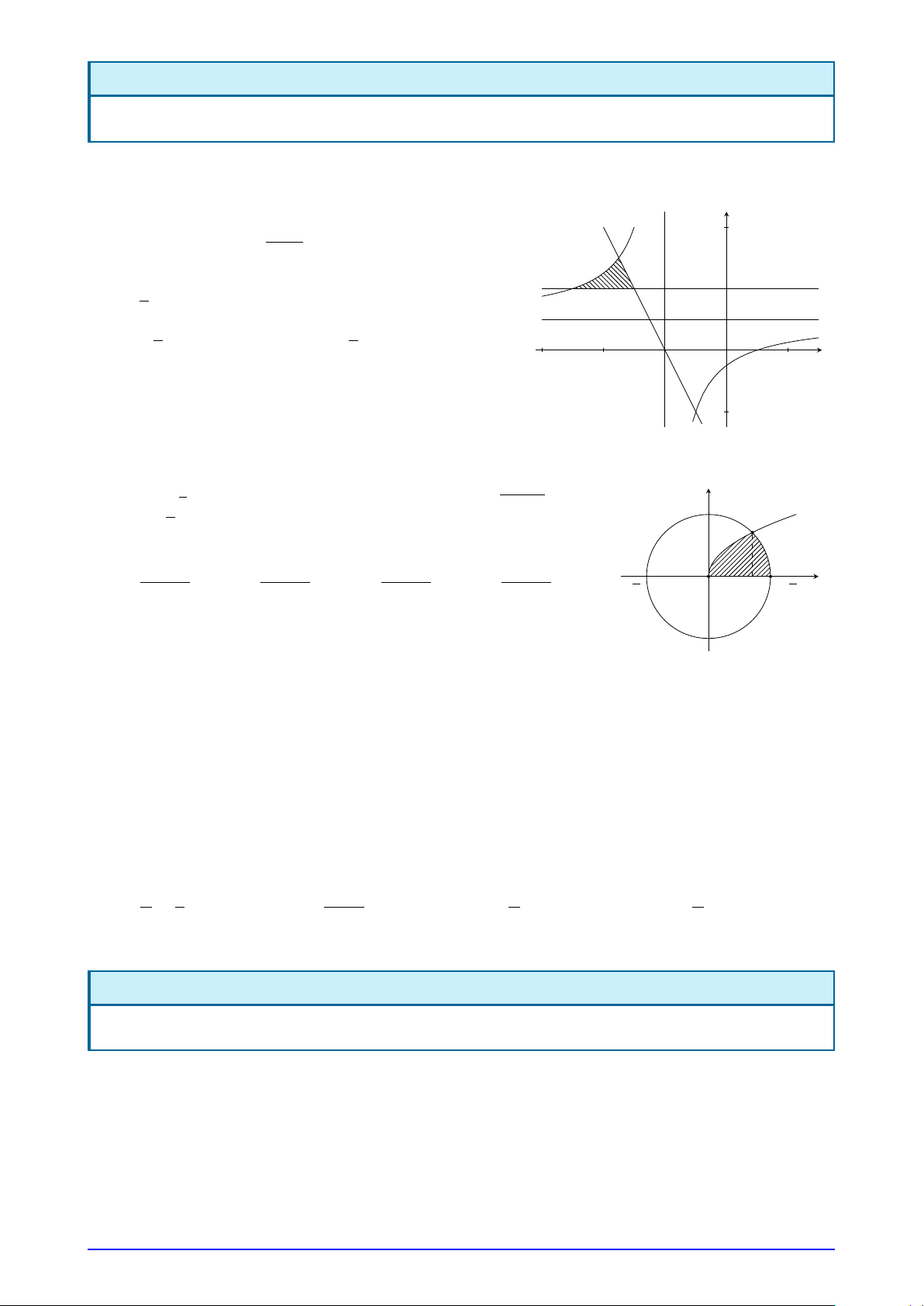
Câu 11. Cho hình phẳng (H) như hình vẽ (phần gạch sọc). Diện tích y y = x. ln x hình phẳng (H) là 9 3 A. ln 3 − . B. 1. 2 2 9 9 C. ln 3 − 4. D. ln 3 − 2. 2 2 O x 1 3
Câu 12. Cho parabol (P) có đồ thị như hình vẽ. Tính diện tích hình phẳng y
giới hạn bởi (P) và trục hoành. A. 1. B. 2. 5 4 C. . D. . 3 3 O 2 x 1 3 −1
Câu 13. Cho hình thang cong (H) giới hạn bởi các đường y = ex, y = 0, x = 0 và x = ln 8. Đường
thẳng x = k (0 < k < ln 8) chia hình (H) thành hai phần có diện tích là S1 và S2. Tìm k để S1 = S2. 9 2 A. k = ln . B. k = ln 4. C. k = ln 4. D. k = ln 5. 2 3
Câu 14. Xét hình phẳng (H ) giới hạn bởi đồ thị hàm số y = (x + y
3)2, trục hoành và đường thẳng x = 0. Gọi A(0; 9), B(b; 0) (−3 < 9 A
b < 0). Tính giá trị của tham số b để đoạn thẳng AB chia (H ) thành
hai phần có diện tích bằng nhau. 1 A. b = − . B. b = −2. 2 3 C. b = − . D. b = −1. O 2 − x 3 B x2 − 2x
Câu 15. Đặt S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = , đường thẳng x − 1
y = x − 1 và các đường thẳng x = m, x = 2m (m > 1). Giá trị của m sao cho S = ln 3 là A. m = 5. B. m = 4. C. m = 2. D. m = 3.
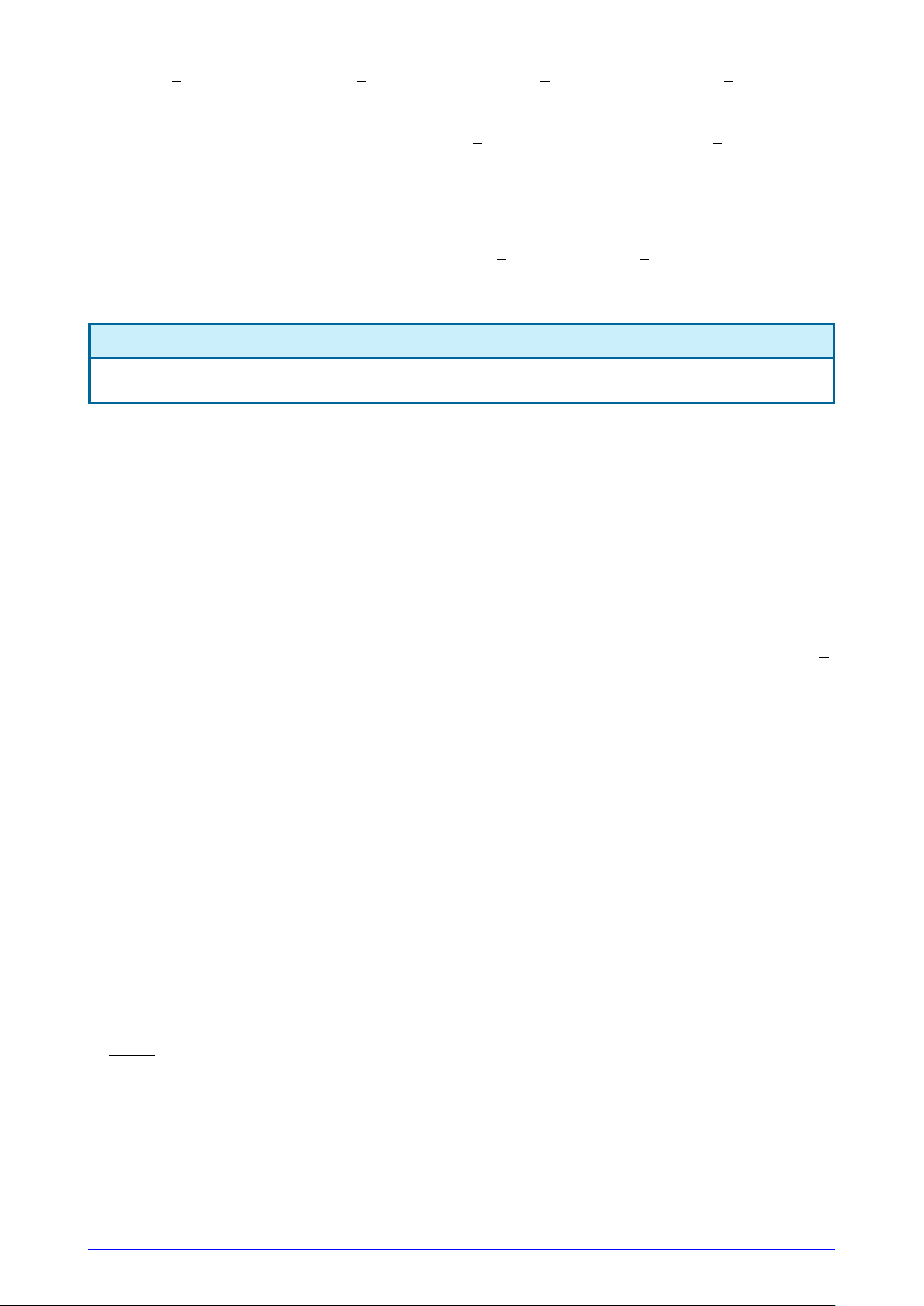
Câu 16. Cho hình phẳng giới hạn bởi các đường y
y = sin x, y = cos x và S1, S2 là diện tích của các
phần được gạch chéo như hình vẽ bên. Tính S2 + 1 S1 S2 S2. 2 √ O x
A. S2 + S2 = 10 − 2 2. 1 2 √ B. S2 + S2 = 10 + 2 2. 1 2 √
C. S2 + S2 = 11 − 2 2. 1 2 √ D. S2 + S2 = 11 + 2 2. 1 2
GV: Phùng V. Hoàng Em Trang 20
Câu 17. Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô y
đậm như hình bên được giới hạn bởi một đồ thị hàm số đa thức bậc 2
ba và một đường thẳng. Diện tích S của phần tô đậm đó bằng bao nhiêu? A. S = 8 (đvdt). B. S = 6 (đvdt). −2 O 1 C. S = 2 (đvdt). D. S = 4 (đvdt). x −1 2 −2
Câu 18. Cho hàm số y = f (x) liên tục trên R và có đồ thị như hình y 0 37 Z 3
vẽ bên. Biết rằng diện tích miền tô đậm bằng và f (x) dx = 12 −2 e 14 Z f (ln x) . Tính I = dx. 3 x O 2 1 x −2 −1 1 12 25 8 3 A. . B. . C. . D. . 25 12 3 8 −2
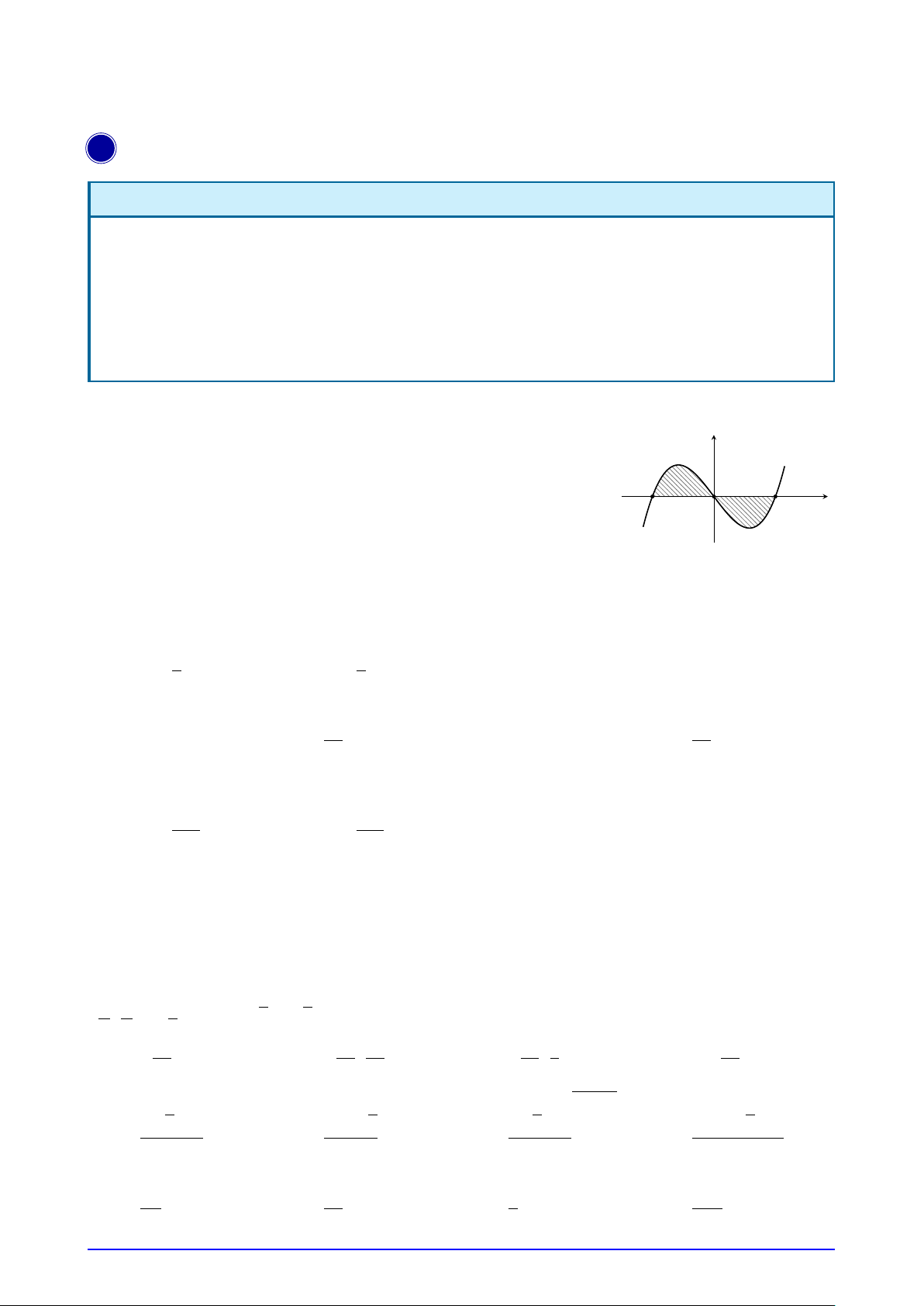
Câu 19. Cho hàm số y = f (x) có đồ thị y = f 0(x) cắt trục Ox y
tại ba điểm có hoành độ a < b < c như hình vẽ. Mệnh đề nào dưới đây là đúng?
A. f (c) > f (b) > f (a).
B. f (b) > f (a) > f (c).
C. f (a) > f (c) > f (b).
D. f (c) > f (a) > f (b). O a x b c 1
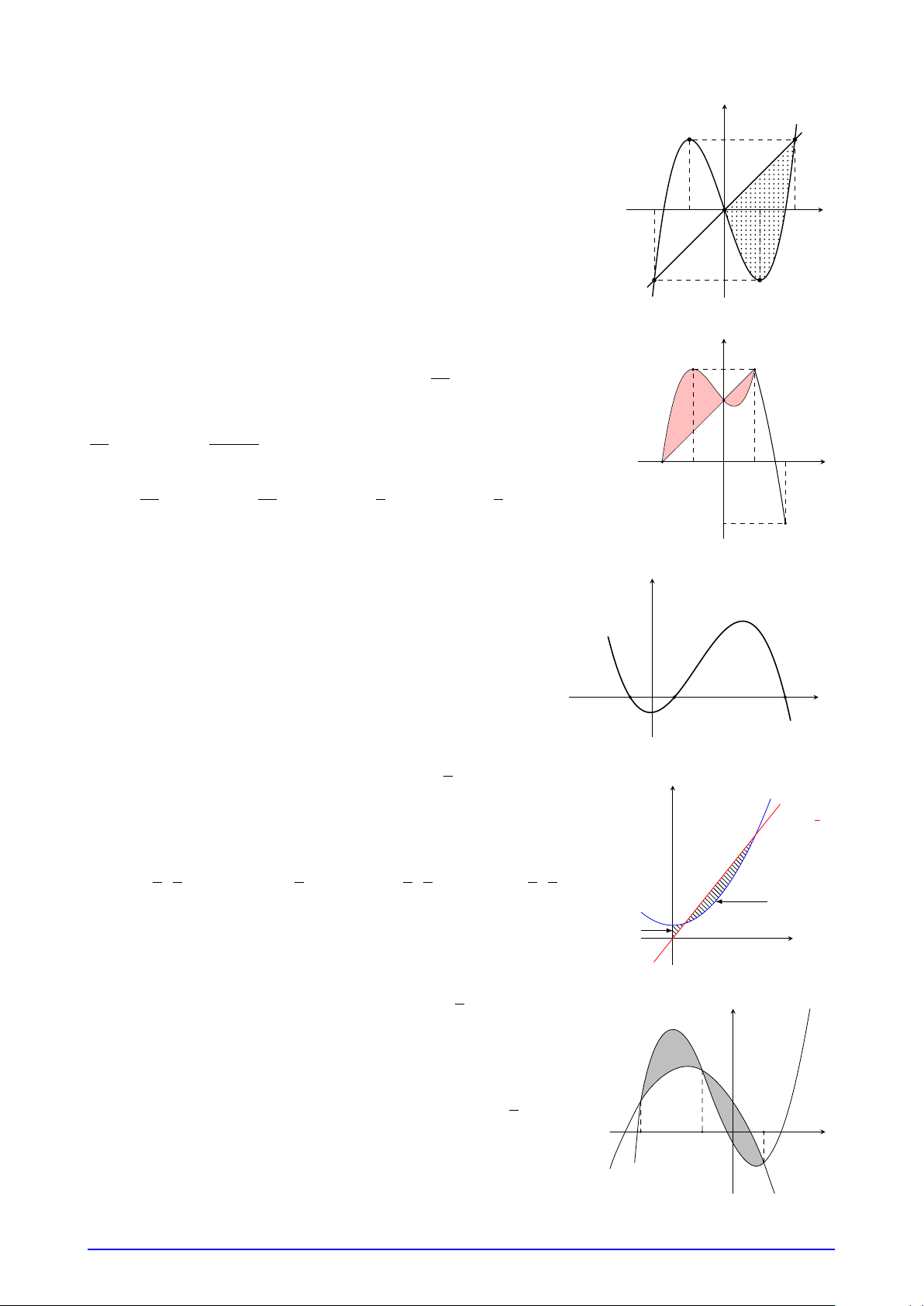
Câu 20. Cho đường thẳng y = x và parabol y = x2 + a (a là tham số 2 y = x2 + a y
thực dương). Gọi S1 và S2 lần lượt là diện tích của hai hình phẳng được y = 3 x
gạch chéo trong hình vẽ dưới đây. Khi S 2
1 = S2 thì a thuộc khoảng nào dưới đây? Å 3 1 ã Å 1 ã Å 1 2 ã Å 2 3 ã A. ; . B. 0; . C. ; . D. ; . 7 2 3 3 5 5 7 S2 x S1 O 1
Câu 21. Cho ha hàm số f (x) = ax3 + bx2 + cx − và g(x) = dx2 + y 2
ex + 1. Biết rằng đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại 3
điểm có hoành độ lần lượt là −3; −1; 1. Hình phẳng giới hạn bởi hai đồ thị đã cho bằng 9 A. 4. B. 5. C. 8. D. . 2 1 x −3 −1
GV: Phùng V. Hoàng Em Trang 21
{ DẠNG 2. Hình phẳng giới hạn bởi nhiều hơn hai đồ thị hàm số Phương pháp giải.
Câu 22. Tính diện tích của hình phẳng được giới hạn y x − 1 4
bởi đồ thị hàm số y =
và các đường thẳng y = 2, x + 2
y = −2x − 4 (như hình vẽ bên). 2 1 A. . B. 3 ln 3 − 2. 4 5 1 C. − + 3 ln 2. D. + 3 ln 2. 4 4 x −6 −4 −2 O 2 −2
Câu 23. Cho (H) là hình phẳng giới hạn bởi đường cong có phương √ √ y trình y =
x, nửa đường tròn có phương trình y = 2 − x2 (với √ 0 ≤ x ≤
2) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng 3π + 2 4π + 2 3π + 1 4π + 1 A. . B. . C. . D. . √ √ 12 12 12 6 O x 1 − 2 2
Câu 24. Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = x và y = ex, trục tung và đường
thẳng x = 1 được tính theo công thức nào dưới đây? 1 1 1 1 Z Z Z Z A. S = |ex − 1| dx. B. S = (ex − x) dx. C. S = (x − ex) dx. D. S = |ex − x| dx. 0 0 0 −1
Câu 25. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = |x − 1| và nửa trên của đường tròn x2 + y2 = 1 bằng π 1 π − 1 π π A. − . B. . C. − 1. D. − 1. 4 2 2 2 4
{ DẠNG 3. Toạ độ hoá một số "mô hình" hình phẳng thực tế Phương pháp giải.
Câu 26. Một mảnh vườn hình elip có trục lớn bằng 100 m, trục nhỏ bằng 80 m được chia thành 2
phần bởi một đoạn thẳng nối hai đỉnh liên tiếp của elip. Phần nhỏ hơn trồng cây con và phần lớn hơn
trồng rau. Biết lợi nhuận thu được là 2000 mỗi m2 trồng cây con và 4000 mỗi m2 trồng rau. Hỏi thu
nhập từ cả mảnh vườn là bao nhiêu? (Kết quả làm tròn đến hàng nghìn). A. 31904000. B. 23991000. C. 10566000. D. 17635000.
GV: Phùng V. Hoàng Em Trang 22
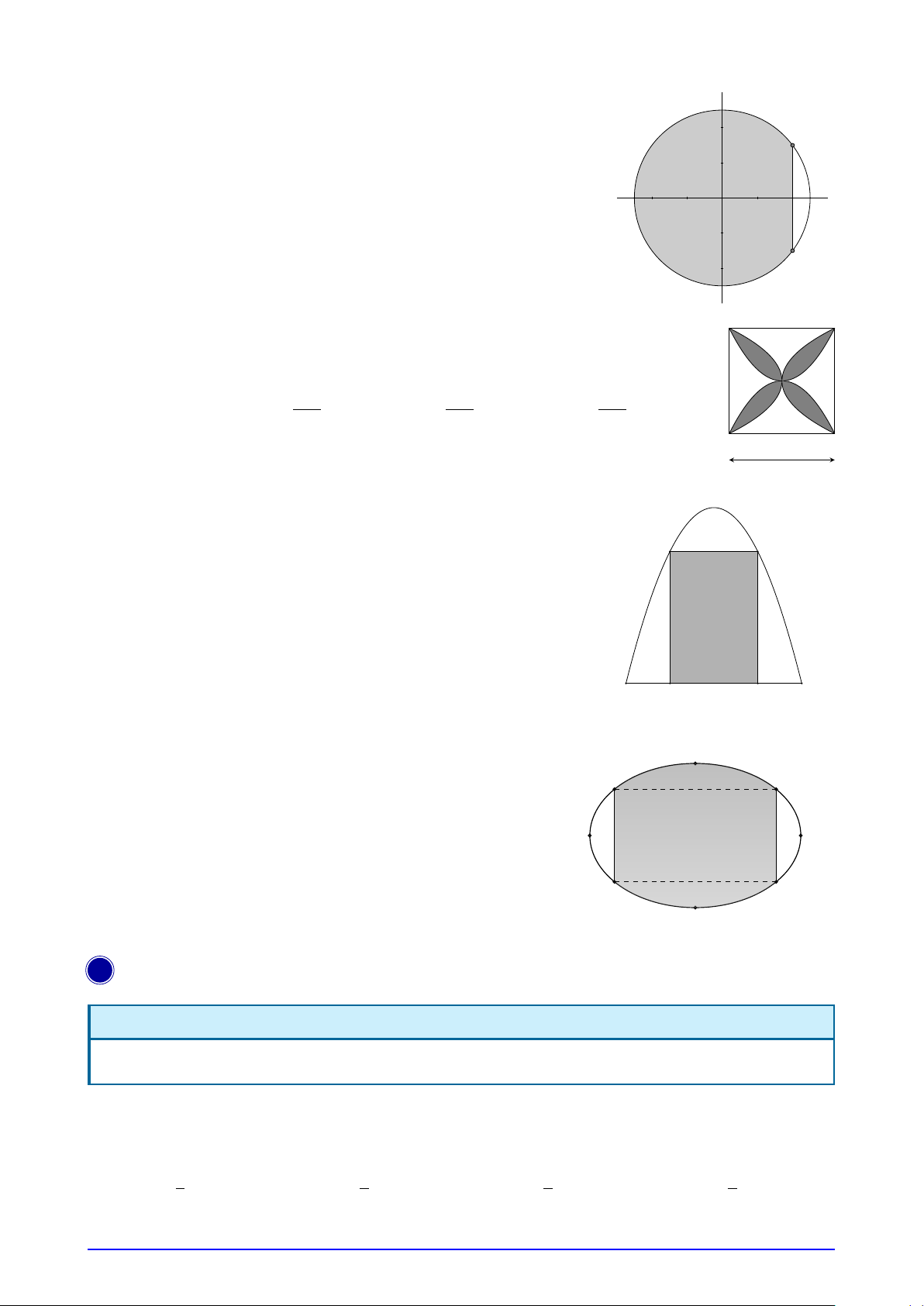
Câu 27. Một người có mảnh đất hình tròn có bán kính 5 m. Người
này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu 4 A
hoạch được 100 nghìn. Tuy nhiên, cần có khoảng trống để dựng chòi
và đồ dùng nên người này căng sợi dây 6 m vào hai đầu mút dây nằm 2
trên đường tròn xung quanh mảnh đất. Hỏi người này thu hoạch được
bao nhiêu tiền? (Tính theo đơn vị nghìn đồng và bỏ số thập phân). −4 −2 2 4 A. 3722. B. 7445. −2 C. 7446. D. 3723. −4 B
Câu 28. Một viên gạch hoa hình vuông cạnh 40 cm. Người ta đã dùng bốn đường
parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (phần tô đậm
như hình vẽ). Diện tích của mỗi cánh hoa đó bằng 800 400 200 A. 200 cm2. B. cm2. C. cm2. D. cm2. 3 3 3 40 cm
Câu 29. Một chiếc cổng có hình dạng là một Parabol có khoảng
cách giữa hai chân cổng là AB = 8 m. Người ta treo một tấm phông
hình chữ nhật có hai đỉnh M, N nằm trên Parabol và hai đỉnh P, Q M N
nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần
không tô đen) người ta mua hoa để trang trí với chi phí 1 m2 cần số
tiền mua hoa là 200.000 đồng, biết MN = 4 m, MQ = 6 m. Hỏi số
tiền mua hoa trang trí chiếc cổng gần với số tiền nào sau đây? A. 3.373.400 đồng. B. 3.434.300 đồng. C. 3.437.300 đồng. D. 3.733.300 đồng. A B Q P
Câu 30. Một biển quảng cáo có dạng hình elip với bốn đỉnh B2
A1, A2, B1, B2 như hình vẽ bên. Biết chi phí sơn phần tô đậm
là 200.000 đồng/m2 và phần còn lại là 100.000 đồng/m2. Hỏi M N
số tiền để sơn theo cách trên gần nhất với số tiền nào dưới
đây, biết A1A2 = 8 m, B2 = 6 m và tứ giác MNPQ là hình chữ A1 A2 nhật có MQ = 3 m. A. 7.322.000 đồng. B. 7.213.000 đồng. C. 5.526.000 đồng. D. 5.782.000 đồng. Q P B1
B TÍNH THỂ TÍCH VẬT THỂ, KHỐI TRÒN XOAY
{ DẠNG 4. Tính thể tích vật thể khi biết diện tích mặt cắt vuông góc với Ox Phương pháp giải.
Câu 31. Vật thể B giới hạn bởi mặt phẳng có phương trình x = 0 và x = 2. Cắt vật thể B với mặt
phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x, (0 ≤ x ≤ 2) ta được thiết diện có diện tích
bằng x2(2 − x). Thể tích của vật thể B là 2 2 4 4 A. V = π . B. V = . C. V = . D. V = π . 3 3 3 3
GV: Phùng V. Hoàng Em Trang 23
Câu 32. Tính thể tích V của vật thể nằm giữa 2 mặt phẳng x = 0, x = 3, biết thiết diện của vật thể bị
cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x (0 ≤ x ≤ 3) là một hình chữ nhật √
có hai kích thước là x và 2 9 − x2. A. V = 16. B. V = 17. C. V = 18. D. V = 19.
Câu 33. Xét vật thể (T ) nằm giữa hai mặt phẳng x = −1 và x = 1. Biết rằng thiết diện của vật thể
cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−1 ≤ x ≤ 1) là một hình vuông có √
cạnh 2 1 − x2. Thể tích vật thể (T ) bằng 16π 16 8 A. . B. . C. π. D. . 3 3 3
Câu 34. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3, biết rằng thiết
diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 3) là một √
hình tròn có đường kính bằng 36 − 3x2. 81π 81 A. V = . B. V = . C. V = 81π. D. V = 81. 4 4
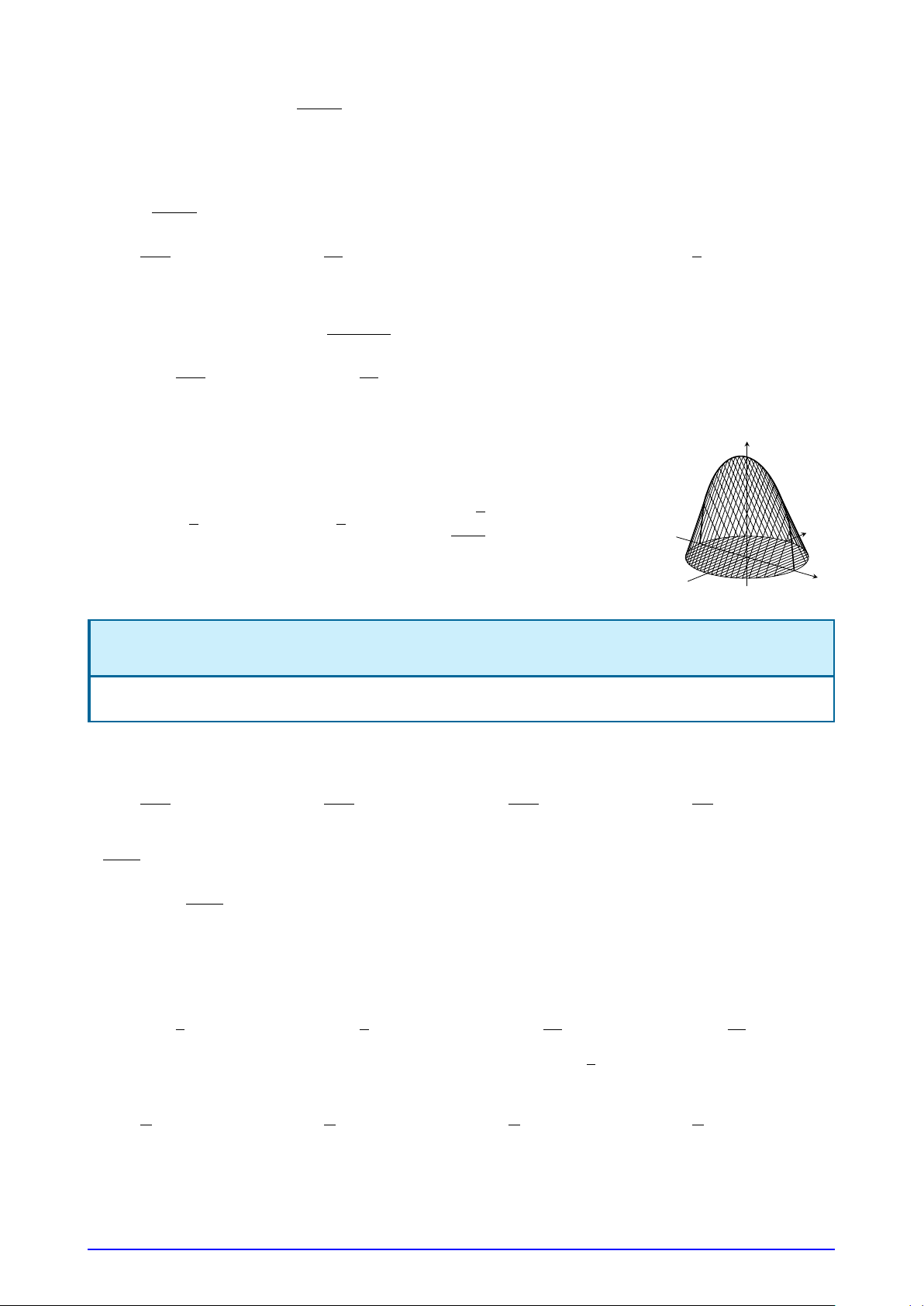
Câu 35. Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). z
Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
(−1 ≤ x ≤ 1) thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó. √ √ √ 4 3 A. V = 3. B. V = 3 3. C. V = . D. V = y π . 3 x
{ DẠNG 5. Tính thể tích của khối tròn xoay khi cho hình phẳng quay quanh trục Ox Phương pháp giải.
Câu 36. Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số y =
x2 − 2x, y = 0, x = −1, x = 2 quanh trục Ox bằng 16π 17π 18π 5π A. . B. . C. . D. . 5 5 5 18
Câu 37. Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường y =
√x−1, trục hoành, x = 2, x = 5 quanh trục Ox bằng 5 5 5 5 Z √ Z Z Z Ä ä2 A. π x − 1 dx. B. π (x − 1) dx. C. π y2 + 1 dx. D. (x − 1) dx . 2 2 2 2
Câu 38. Cho hình phẳng (H) giới hạn bởi đồ thị y = 2x − x2 và trục hoành. Tính thể tích V vật thể
tròn xoay sinh ra khi cho (H) quay quanh Ox. 4 4 16 16 A. V = . B. V = π . C. V = π . D. V = . 3 3 15 15 √
Câu 39. Thể tích vật thể tròn xoay giới hạn bởi các đường y =
x · ex, trục hoành và đường thẳng x = 1 khi quay quanh Ox là π π π π A. e2 + 1. B. e2 − 1. C. e2 − 1. D. e2 + 1. 4 4 2 2
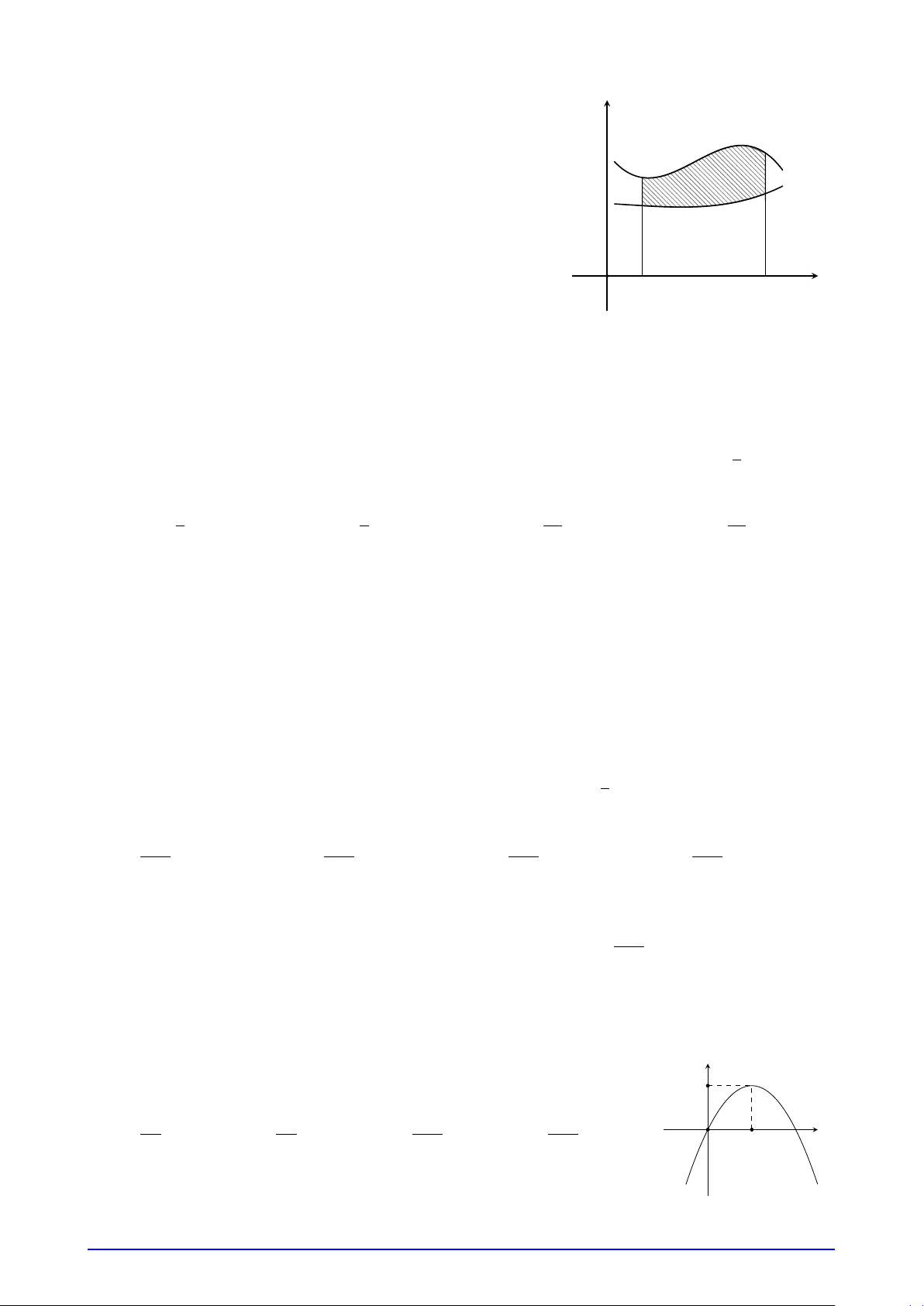
Câu 40. Cho hàm số y = f (x), y = g(x) xác định và liên tục trên đoạn [a; b] (có đồ thị như hình vẽ).
Gọi H là hình phẳng được tô đậm trong hình, khi quay H quanh trục Ox ta thu được khối tròn xoay có
thể tích V . Tìm mệnh đề đúng trong các mệnh đề sau đây
GV: Phùng V. Hoàng Em Trang 24 b Z A. V = [ f (x) − g(x)]2 dx. y a b y = f (x) Z B. V = π [ f (x) − g(x)]2 dx. a b Z C. V = y = g(x) π [ f (x) − g(x)] dx. a b Z î ó x D. V = O a π f 2(x) − g2(x) dx. b a
Câu 41. Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ
thị y = x2 − 4x + 6, y = −x2 − 2x + 6. A. 3π. B. π − 1. C. π. D. 2π. √
Câu 42. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường x = y, y = −x + 2,
x = 0 quay quanh trục Ox có giá trị là kết quả nào sau đây? 1 3 32 11 A. V = π . B. V = π . C. V = π . D. V = π . 3 2 15 6
Câu 43. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P) : y = x2 và đường
thẳng d : y = x xoay quanh trục Ox bằng 1 1 1 1 Z Z Z Z A. π x2 dx − π x4 dx. B. π x2 dx + π x4 dx. 0 0 0 0 1 1 Z Z Ä ä2 C. π x2 − x dx. D. π x2 − x dx. 0 0 √
Câu 44. Cho hình phẳng (S) giới hạn bởi đồ thị các hàm số y =
x, y = −x và x = 4. Quay hình
phẳng (S) quanh trục Ox ta được khối tròn xoay có thể tích bằng 43π 38π 40π 41π A. . B. . C. . D. . 2 3 3 3
Câu 45. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị y = x2 − ax với trục hoành (a 6= 0). Quay hình 16π
(H) xung quanh trục hoành ta thu được khối tròn xoay có thể tích V = . Tìm a. 15 A. a = −3. B. a = −2. C. a = 2. D. a = ±2.
Câu 46. Cho hàm bậc hai y = f (x) có đồ thị như hình vẽ bên. Tính thể tích y
khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số 1
y = f (x) và Ox quanh trục Ox. 4π 4π 16π 16π A. . B. . C. . D. . 3 5 15 5 x O 1
GV: Phùng V. Hoàng Em Trang 25 √3
Câu 47. Cho hình (H) giới hạn bởi đồ thị hàm số y = x3, cung y √ √ 9 3 y = x3 tròn có phương trình y =
4 − x2 (với 0 ≤ x ≤ 2) và trục hoành 2 9
(phần tô đậm trong hình vẽ). Biết thể tích của khối tròn xoay tạo a √ c
thành khi quay (H) quanh trục hoành là V = − 3 + π , b d a c trong đó a, b, c, d ∈ ∗ N và ,
là các phân số tối giản. Tính P = x b d O 2 a + b + c + d. A. P = 52. B. P = 40. C. P = 46. D. P = 34.
Câu 48. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = √ √ √ √ y
x, cung tròn có phương trình y = 6 − x2 (− 6 ≤ x ≤ 6) √
và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích y = x
V của vật thể tròn xoay sinh bởi khi quay hình phẳng D quanh trục Ox √ 22π √ A. V = 4 √ √ π 6 + . B. V = 8π 6 − 2π. x O 3 − 6 6 √ 22π √ 22π C. V = 8π 6 − . D. V = 8π 6 + . 3 3
Câu 49. Hình phẳng giới hạn bởi hai đồ thị hàm số y = |x| và y = x2 quay quanh trục tung tạo nên
một vật thể tròn xoay có thể tích bằng π π 2π 4π A. . B. . C. . D. . 6 3 15 15
{ DẠNG 6. Bài tập tổng hợp Phương pháp giải. 1
Câu 50. Cho hình phẳng (H) giới hạn bởi đường tròn có bán y √ 4
kính bằng 2, đường cong y =
4 − x và trục hoành (miền gạch sọc √ y = 4 − x
như hình vẽ). Tính thể tích V của khối tròn xoay khi cho hình (H) quay quanh trục Ox. 77π 53π 67π 40π − x A. V = . B. V = . C. V = . D. V = . 2 O 4 6 6 6 3
Câu 51. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : (x − 3)2 + (y − 4)2 = y
1. Tính thể tích của khối tròn xoay thu được khi quay hình phẳng giới hạn bởi 5
đường tròn (C) quanh trục hoành. I 4 B C A. 5 2 2 π . B. 9π . 3 C. 8 2 2 π . D. 6π . 2 1 A D x O 1 2 3 4
Câu 52. Du khách ghé thăm Bình Định không thể bỏ qua địa danh Tháp Bánh Ít nổi tiếng. Tháp có
hai cửa, mỗi cửa có hình dáng là một cung Parabol nằm cùng một trục (hướng Đông - Tây). Hai cửa
cách nhau 8 mét, có chiều cao 4 mét, lối đi rộng 1 mét thông hai cửa với nhau. Hãy tính thể tích phần
không gian lối đi giới hạn giữa hai cửa. 8 128π 64 8π A. V = . B. V = . C. V = . D. V = . 3 15 3 3
GV: Phùng V. Hoàng Em Trang 26
Câu 53. Bên trong hình vuông cạnh a, dựng hình sao bốn cánh đều như a y
hình vẽ (các kích thước cần thiết cho như ở trong hình). Tính thể tích V 2
của khối tròn xoay sinh ra khi quay hình sao đó quanh trục Ox. 5πa3 5πa3 5πa3 7πa3 A. V = . B. V = . C. V = . D. V = . x 24 48 96 24 − a O a 2 2 − a2 √
Câu 54. Cho đồ thị (C) : y = f (x) = x. Gọi (H) là hình y
phẳng giới hạn bởi (C), đường thẳng x = 9, Ox. Cho điểm
M thuộc (C), A(9; 0). Gọi V1 là thể tích khối tròn xoay M
khi quay (H) quanh Ox, V2 là thể tích khối tròn xoay khi
cho tam giác AOM quay quanh Ox. Biết V1 = 2V2. Tính O A
diện tích S phần hình phẳng giới hạn bởi (C), OM (hình x
vẽ không thể hiện chính xác điểm M). √ √ 27 3 3 3 4 A. S = 3. B. S = . C. S = . D. S = . 16 2 3
Câu 55. Một cốc rượu có hình dạng tròn xoay với chiều cao (của phần đựng 8 cm
rượu) bằng 10 cm và đường kính miệng cốc bằng 8 cm (tham khảo hình mô
phỏng ở bên). Biết thiết diện dọc (bổ dọc cốc thành hai phần bằng nhau) là một
parabol. Tính dung tích V của chiếc cốc (làm tròn đến hai chữ số thập phân, cm
coi thể tích thành cốc là không đáng kể). 10 A. V ≈ 320 cm3. B. V ≈ 1005,31 cm3. C. V ≈ 251,33 cm3. D. V ≈ 502,65 cm3.
Câu 56. Một vật thể có hai đáy trong đó có đáy lớn là một elip có độ dài trục lớn bằng 8, trục bé là
4 và đáy bé có độ dài trục lớn là 4 và trục bé là 2. Thiết diện vuông góc với đường thẳng nối hai tâm
của hai đáy luôn là một elip, biết chiều cao của vật thể là 4. Tính thể tích của vật thể này. 55π 56π 57π 58π A. . B. . C. . D. . 3 3 3 3
Câu 57. Cho hình vuông có độ dài cạnh bằng 8cm và một hình tròn có
bán kính 5cm được xếp chồng lên nhau sao cho tâm của hình tròn trùng
với tâm của hình vuông như hình vẽ bên. Tính thể tích V của vật thể
tròn xoay tạo thành khi quay mô hình trên quanh trục XY . X Y 260π 290π A. V = cm3. B. V = cm3. 3 3 520π 580π C. V = cm3. D. V = cm3. 3 3
C MỘT SỐ BÀI TOÁN CHUYỂN ĐỘNG
Câu 58. Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v(t) = −5t + 10 m/s. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 20 m. B. 2 m. C. 0,2 m. D. 10 m.
Câu 59. Một vật chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc được tính theo thời gian là
a(t) = t2 + 3t. Tính quãng đường vật đi được trong khoảng thời gian 3 giây kể từ khi vật bắt đầu tăng
GV: Phùng V. Hoàng Em Trang 27 tốc. 45 201 81 65 A. m. B. m. C. m. D. m. 2 4 4 2
Câu 60. Một chuyến máy bay chuyển động trên đường băng với vận tốc v(t) = t2 + 10t m/s với t là
thời gian được tính bằng giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc
200 m/s thì nó rời đường băng. Tính quãng đường máy bay đã di chuyển trên đường băng. 2500 4000 A. m. B. 2000 m. C. 500 m. D. m. 3 3
Câu 61. Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi 1 11 quy luật v(t) = t2 +
t m/s, trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển 180 18
động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A
nhưng chậm hơn 5 giây so với A và có gia tốc bằng a m/s2 ( a là hằng số). Sau khi B xuất phát được
10 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng A. 22 m/s. B. 15 m/s. C. 10 m/s. D. 7 m/s.
Câu 62. Một ôtô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t) = 2t (m/s). Đi được 12 giây,
người lái xe phát hiện chướng ngại vật và phanh gấp, ôtô tiếp tục chuyển động chậm dần đều với gia
tốc a = −12 (m/s2). Tính quãng đường s (m) đi được của ôtô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. A. s = 168 (m). B. s = 144 (m). C. s = 166 (m). D. s = 152 (m).
Câu 63. Một ô tô đang chạy đều với vận tốc a m/s thì người lái đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm đần đều với vận tốc v(t) = −5t + a trong đó thời gian tính bằng giây kể từ lúc đạp
phanh. Hỏi vận tốc ban đầu a của ô tô bằng bao nhiêu, biết từ lúc đạp phanh đến khi xe dừng hẳn ô tô đi được 40 m. A. a = 40. B. a = 20. C. a = 25. D. a = 10.
Câu 64. Trên đoạn thẳng AB dài 200 m có hai chất điểm X , Y . Chất điểm X xuất phát từ A, chuyển 1 1
động thẳng hướng đến B với vận tốc biến thiên theo thời gian bởi quy luật v(t) = t2 + t m/s, trong 80 3
đó t giây là khoảng thời gian tính từ lúc X bắt đầu chuyển động. Từ trạng thái nghỉ, chất điểm Y xuất
phát từ B và xuất phát chậm hơn 10 giây so với X ; Y chuyển động thẳng theo chiều ngược lại với X
và có gia tốc bằng a m/s2 (a là hằng số). Biết rằng hai chất điểm X , Y gặp nhau tại đúng trung điểm
đoạn thẳng AB. Gia tốc của chất điểm Y bằng A. 2 m/s2. B. 1,5 m/s2. C. 2,5 m/s2. D. 1 m/s2.
Câu 65. Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ thuộc thời gian v I Å 1 ã 8
t (h) có đồ thị làm một phần của đường parabol với đỉnh I ; 8 và trục đối xứng 2
song song với trục tung như hình vẽ. Tính quãng đường S người đó chạy được trong
khoảng thời gian 45 phút, kể từ khi bắt đầu chạy. A. S = 5,3 km. B. S = 4,5 km. C. S = 4 km. D. S = 2,3 km. O 1 1 t 2
Câu 66. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc thời v
gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ 9
khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh
I(2; 9) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ
thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật
di chuyển được trong 4 giờ đó. A. 28, 5 (km). B. 27 (km). C. 26, 5 (km). D. 24 (km). O 2 3 4 t
GV: Phùng V. Hoàng Em Trang 28
Câu 67. Hai người A và B ở cách nhau 180 (m) trên một đoạn đường thẳng và cùng chuyển động
thẳng theo một hướng với vận tốc biến thiên theo thời gian, A chuyển động với vận tốc v1(t) = 6t + 5
(m/s), B chuyển động với vận tốc v2(t) = 2at − 3 (m/s) (a là hằng số), trong đó t (giây) là khoảng thời
gian tính từ lúc A, B bắt đầu chuyển động. Biết rằng lúc đầu A đuổi theo B và sau 10 giây thì đuổi kịp.
Hỏi sau 20 (giây), A cách B bao nhiêu mét? A. 720 m. B. 360 m. C. 320 m. D. 380 m. —HẾT—
GV: Phùng V. Hoàng Em Trang 29
Document Outline
- NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
- NGUYÊN HÀM VÀ PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
- SỬ DỤNG ĐỊNH NGHĨA, BẢNG CÔNG THỨC
- blackDạng 1. Áp dụng bảng công thức nguyên hàm
- blackDạng 2. Tách hàm dạng tích thành tổng
- blackDạng 3. Tách hàm dạng phân thức thành tổng
- SỬ DỤNG PHƯƠNG PHÁP ĐỔI BIẾN SỐ
- blackDạng 4. Đổi biến dạng hàm lũy thừa
- blackDạng 5. Đổi biến dạng hàm phân thức
- blackDạng 6. Đổi biến dạng hàm vô tỉ
- blackDạng 7. Đổi biến dạng hàm lượng giác
- blackDạng 8. Đổi biến dạng hàm mũ, hàm lô-ga-rit
- blackDạng 9. Đổi biến dạng "hàm ẩn"
- SỬ DỤNG PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
- blackDạng 10. Nguyên hàm từng phần với ''u = đa thức''
- blackDạng 11. Nguyên hàm từng phần với ''u = lôgarit''
- blackDạng 12. Nguyên hàm kết hợp đổi biến số và từng phần
- blackDạng 13. Nguyên hàm từng phần dạng "lặp"
- blackDạng 14. Nguyên hàm từng phần dạng "hàm ẩn"
- TÍCH PHÂN VÀ PHƯƠNG PHÁP TÍNH TÍCH PHÂN
- TÍCH PHÂN DÙNG ĐỊNH NGHĨA
- blackDạng 1. Sử dụng định nghĩa, tính chất tích phân
- blackDạng 2. Tách hàm dạng tích thành tổng các hàm cơ bản
- blackDạng 3. Tách hàm dạng phân thức thành tổng các hàm cơ bản
- TÍCH PHÂN ĐỔI BIẾN SỐ
- blackDạng 4. Đổi biến loại t=u(x)
- blackDạng 5. Đổi biến loại x=(t) (Lượng giác hóa)
- blackDạng 6. Đổi biến số dạng hàm ẩn
- TÍCH PHÂN TỪNG PHẦN
- blackDạng 7. Tích phân từng phần với "u = đa thức"
- blackDạng 8. Tích phân từng phần với "u = logarit"
- blackDạng 9. Tích phân hàm ẩn
- ỨNG DỤNG TÍCH PHÂN
- TÍNH DIỆN TÍCH HÌNH PHẲNG
- blackDạng 1. Hình phẳng giới hạn bởi hai đồ thị y=f(x) và y=g(x)
- blackDạng 2. Hình phẳng giới hạn bởi nhiều hơn hai đồ thị hàm số
- blackDạng 3. Toạ độ hoá một số "mô hình" hình phẳng thực tế
- TÍNH THỂ TÍCH VẬT THỂ, KHỐI TRÒN XOAY
- blackDạng 4. Tính thể tích vật thể khi biết diện tích mặt cắt vuông góc với Ox
- blackDạng 5. Tính thể tích của khối tròn xoay khi cho hình phẳng quay quanh trục Ox
- blackDạng 6. Bài tập tổng hợp
- MỘT SỐ BÀI TOÁN CHUYỂN ĐỘNG
- NGUYÊN HÀM VÀ PHƯƠNG PHÁP TÍNH NGUYÊN HÀM